Machine learning opportunities for nucleosynthesis studies

Nuclear astrophysics is an interdisciplinary field focused on exploring the impact of nuclear physics on the evolution and explosions of stars and the cosmic creation of the elements. While researchers in astrophysics and in nuclear physics are separately using machine learning approaches to advance studies in their fields, there is currently little use of machine learning in nuclear astrophysics. We briefly describe the most common types of machine learning algorithms, and then detail their numerous possible uses to advance nuclear astrophysics, with a focus on simulation-based nucleosynthesis studies. We show that machine learning offers novel, complementary, creative approaches to address many important nucleosynthesis puzzles, with the potential to initiate a new frontier in nuclear astrophysics research.

1 Introduction

Machine learning (ML) is now broadly used in the field of astrophysics to study a wide variety of phenomena. A selection of recent examples includes projects in observational cosmology (Moriwaki et al., 2023), galactic evolution (Fraser et al., 2023), cosmic ray measurement interpretation (Arimura, 2023), star formation with dark matter (Hernández et al., 2023), galaxy spectral energy distributions (González-Morán et al., 2023), blazer observations (Ding et al., 2023), Ba star abundances (den Hartogh et al., 2023), and metallicity-dependent abundances (Sun, 2024). While not as widely used in nuclear physics, ML utilization there is growing, as reviewed in Boehnlein et al. (2022). Some more recent examples in nuclear physics include the use of ML for studies at low- and medium-energies (He et al., 2023), for neutron-induced reaction cross section evaluations (Xu et al., 2023), for heavy-ion fusion cross sections (Li Z. et al., 2024), for nuclear mass predictions (Le et al., 2023; Wu X. H. et al., 2024; Zhang et al., 2024; Li M. et al., 2024; Yüksel et al., 2024), for active-target time projection chamber data analysis (Wu H. et al., 2023), for analysis of time-of-flight data (Sanchez-Caballero et al., 2023), and for reaction cross section predictions (Gargouri et al., 2023).

From these examples, it would seem likely that ML would also be widely utilized in the interdisciplinary research that spans these two fields–that is, in nuclear astrophysics–but this is not the case. Researchers in nuclear astrophysics (Schatz et al., 2022; Arcones and Thielemann, 2023) explore the critical leverage that physics at the femtometer scale has on stellar systems that are ${10}^{24}$ times larger, as well as on the origin and evolution of the Universe. At the core of many of these studies are simulations that combine the results nuclear measurements, nuclear theory, and astrophysical observations to expand our understanding of the cosmic creation of the elements, and to decipher why systems like our sun, red giants, white dwarfs, variable stars, and others evolve peacefully while other stars end their lives in nova, supernova, hypernova, or even more exotic explosions. In this era of multi-messenger astronomy (Neronov, 2021), improved predictions of such simulations are needed more than ever to connect measurements at new and planned accelerator facilities (Wei et al., 2019; Motobayashi and Sakurai, 2012; Scheidenberge, 2017; Hong, 2023) and advances in nuclear theory driven by exascale supercomputers (NUCLEI, 2022) with observations from the latest generation of ground- and space-based telescopes (National Academies of Sciences et al., 2021).

While astrophysics and nuclear physics have separately used ML approaches to advance their frontiers, there is very little use of ML approaches in nuclear astrophysics. This is evident from recent journal articles, from presentations at the largest recent international symposia [e.g., NICXVII (2023); OMEG (2022)], and from the latest strategic planning documents for nuclear physics (Aidala et al., 2023); there are two exceptions (at the time of writing this article), Fan et al. (2022) and Grichener et al. (2024), which will be discussed below in Section 3. To address this paucity of ML studies, this article explores opportunities for ML approaches to advance the field of nuclear astrophysics, with a focus on simulation-based studies of the cosmic synthesis of the elements (Hix and Thielemann, 1999; Arnett, 1996). We show that ML offers novel, complementary, creative approaches to address many important nucleosynthesis puzzles. Since traditional approaches in this work have not changed in decades, ML has the potential to initiate a new frontier in nuclear astrophysics research.

To begin, we first give a brief description of a variety of widely-utilized ML algorithm types in Section 2. Some important nucleosynthesis puzzles are then described in Section 3, along with suggestions of methods to employ ML algorithms that may advance our knowledge. We then briefly discuss some of the challenges of ML approaches in Section 4, and then give a summary in Section 5.

2 Widely-utilized machine learning approaches

ML approaches have been shown to be very effective in addressing data-centric problems in a wide variety of fields. Common uses for ML algorithms are to classify data, make decisions, predict values, identify outliers or anomalies, find patterns, interpret large datasets, quantify uncertainties, efficiently map inputs to outputs, reduce dimensionalities, and find hidden functional relationships. Below we give a brief description of widely utilized ML algorithm types that are routinely used for these (and other) tasks. For convenience, we have grouped these algorithm types into six categories based roughly on functionality, but we note that many are routinely used for multiple purposes. The different ML algorithms will be discussed in Section 3 as possible approaches to address important challenges in nucleosynthesis research. Our algorithm summary may also inspire the use of ML approaches in other research fields, such as geophysics, biophysics, material science, and chemistry.

2.1 Regression

Linear Regression (LinR) (Kumar and Bhatnagar, 2022) – fitting a data set to a (single- or multivariate) linear function by least squares minimization is well understood and widely utilized for data sets with a linear input-output mapping. ML use emphasizes accurate predictions; usage in statistics emphasizes the correctness of the linear model.

Kernel Ridge Regression (KRR) (Hastie et al., 2009) – produces fits (predictions) over multiple variables that have high correlations (multicollinearities) that can cause problems in standard regressions; KRRs map the original data into a more complex kernel-defined feature space, but do not generate prediction uncertainties.

Logistic Regression (LogR) (Bisong and Bisong, 2019) – this widely used classification algorithm maps continuous quantities to (usually two) discrete quantities (e.g., “Yes/No”, “On/Off”) by fitting a sigmoid (logit) function to the data. This approach is easily understood (explainable) and works with non-linear data sets.

Gaussian Processes (GP) (Rasmussen and Williams, 2005) – use a collection of normally-distributed random variables to specify distributions over complex functions without knowing the exact form. GPs are useful for accurate predictions (regression) with uncertainties, as well as for classifications.

2.2 Classification

Classification Tree (CT) (Breiman, 2017) – these employ a set of cascading rule-based tests with a tree-like structure to sort (classify) labelled data into categories. A variation – Classification and Regression Trees (CARTs) – can be used for regression by partitioning data into groups with similar values of a dependent variable.

Decision Tree (DT) (Quinlan, 1986) – structurally similar to CTs, these trees make decisions (i.e., give answers) based on rule-based tests (i.e., questions). DTs can function as “expert systems” that drill down to a recommendation based on multivariate input.

Random Forest (RF) (Cutler et al., 2012) – instead of using rule-based data tests, RFs randomly generate many DTs that each “vote” on a classification, in order to overcome limitations of single DTs and add features like weighting and error estimation. RFs can also be used for regression when testing on a continuous variable.

Gradient Boost (GB) (Friedman, 2001) – in contrast to RFs which combine results of different DTs as a final step, a GB combines DT results in series to make successively stronger (better predictive) models. GBs have great flexibility for tuning and loss functions, and can give highly accurate predictions.

Isolation Forest (IF) (Liu et al., 2008) – since anomalies (outliers) in data tend to be “few and different” from other data, a tree structure can be used to separate them after only a few tests (i.e., near the “root” of the tree). IFs are characterized by fast execution and high performance for a wide range of anomalies.

Support Vector Machine (SVM) (Steinwart and Christmann, 2008) – for data with $n$ features, an $n$-dimensional vector is drawn with values on each coordinate corresponding to its feature value; classifications are made via relative data point distances in the $n$-space. SVM algorithms are robust against outliers and computationally efficient.

K Means Clustering (KM) (Xu et al., 2019) – unlabeled data points are grouped via distances in feature space to $k$ randomly-assigned centroids; data is classified by iteratively reassigning centroids until obtaining optimally separated clusters. Care is needed with this approach to avoid local minima.

K Nearest Neighbor (KNN) (Zhang, 2016) – used to classify (group) data points based on commonalities with the majority of its $k$ nearest neighbors in feature space. KNNs can also be used for regression where commonalities are treated as numerical distances.

2.3 Neural Networks

Neural Network (NN) (Suk et al., 2017) – layers of interconnected nodes (neurons), each with its own weighting, bias, and activation function, serve to process inputs to outputs; backpropagation is used to iteratively adjust weights by comparing outputs to training data, after which predictions can be made from new inputs. Widely used to model complex functions, deep NNs (DNNs) with many hidden layers are the basis of “deep learning” (DL).

Convolutional Neural Net (CNN) (Ankile et al., 2020) – these DNNs extract features by “sliding” (i.e., convolving) a set of filters (kernels) over data that has a grid-like structure. Filter outputs are subsequently collected and combined by fully connected NN layers for classification. CNNs are widely used for image analyses.

Bayesian Neural Net (BNN) (Jospin et al., 2022) – these NNs have stochastic weights to simulate, using a Bayesian inference framework, the predictions of multiple possible models and the probability distribution associated with each. In this way, BNNs are used to quantify the prediction uncertainties of NN-based models.

Recurrent Neural Net (RNN) (Lipton et al., 2015) – by structuring a DNN with repeating layers (loops) that link in forward and reverse (recurrent) directions, information can be stored (a “memory”) as inputs of arbitrary length are sequentially processed. RNNs are widely used to analyze time series data, speech, music, and text.

Graph Neural Net (GNN) (Wu et al., 2021) – graph-like data (e.g., entities plus their relationships, which can be images, texts, molecular structures, and more) are analyzed by an optimizable transformation of all graph attributes to find missing elements or relationships, identify/characterize subcomponents, or other prediction tasks.

Radial Basis Function Neural Net (RBFNN) (Lee et al., 1999) – useful for regression of non-linear functions or associated classification problems, these 3-layer NNs have a unique hidden layer with neuron weights determined by the (kernel-calculated) distance from a central point; they train quickly but can be difficult to set up.

Emulators (Kasim et al., 2021) – fast-executing ML models trained to approximately reproduce the results of (i.e., produce the same input - output mapping as) complex simulations. They facilitate exploring uncertainties, sensitivities, parameter spaces, and more. NNs, DNNs, CNNs, GPs, and RFs are often used as emulators.

2.4 Generative models

Generative Models (GEN) (Harshvardhan et al., 2020) – these models generate (create) new data (including images, text, sound, and more) that resembles training data. Some GENs learn patterns and structure to enable a mapping from a latent (feature) space to a data space, while others directly sample from a probability distribution.

Generative Adversarial Network (GAN) (Gonog and Zhou, 2019) – in training, these set a generative model against a competing discriminative algorithm to produce better outputs. GANs are widely used to generate images from text, reword text, create training data, and much more.

Diffusion Models (DIFF) (Yang et al., 2023) – these generative models add random noise to a clean input (e.g., image, video, signals, molecular structure) and then reverse the process to create a new (but different) output. They can well capture patterns in complex images and data distributions and generate similar but diverse outputs.

2.5 Deep learning language models

Large Language Model (LLM) (Zhao et al., 2023) – trained on up to $\sim {10}^{12}$ tokens using $\sim {10}^{12}$ parameters, these models include recurrent, generative, and other NN layers to recognize, predict, and generate text. LLMs use statistical approaches in contrast to traditional rule-based approaches of natural language processing.

Transformers (Vaswani et al., 2017) – a widely used, highly scalable DNN architecture that revolutionized LLMs by using the concept of attention to comprehend contextual relationships within text and sequential data. It excels at summarizing and translating text, answering questions, analyzing sequential data, and much more.

Generative Pre-trained Transformer (GPT) (OpenAI, 2022) – adding generative capabilities to a Transformer foundation trained on internet-scale textual data, this is a popular foundation for LLMs. Fine-tuned GPTs, some with chat interfaces for queries (prompts) (e.g., ChatGPT), work primarily with text but can have capabilities with images, music, video, and more.

Foundation Model (FM) (Bommasani et al., 2021) – trained on internet-scale unlabeled multi-modal datasets (text, time-series data, images, code, graphs, video, and more), these very large general purpose DL models can be fine-tuned for specific applications and may exhibit emergent capabilities.

2.6 Other algorithm types

Principal Component Analysis (PCA) (Kherif et al., 2020) – reduces the dimensionality of large multivariate data sets by finding fewer (sometimes new) parameters to “represent” the data collection with minimal information loss. PCA works well with highly correlated data sets that have many parameters.

Naïve Bayes (NB) (Webb et al., 2010) – uses information in the data to estimate Bayesian posterior probabilities with the (naïve) assumption that attributes are conditionally independent. Classifications and decisions are made by setting thresholds on probabilities.

Variational Autoencoder (VAE) (Kingma et al., 2019) – uses a neural net to compress/encode data as parameters of a distribution over random variables in a continuous lower-dimensional latent space, then generatively reconstruct/decode the data. This reduces noise, adds probabilities, and focuses on critical data features.

Symbolic Regression (SR) (Cava et al., 2021) – used to optimally specify a mathematical formula to input-to-output data mapping, by altering both the structure and parameters of an analytical model. This produces a model that can be more easily explained (i.e., interpreted).

3 Machine learning for nucleosynthesis studies

In any given astrophysical system, the complex mechanisms responsible for the cosmic synthesis of nuclei involve over ${10}^{50}$ nuclei spread over $\sim {10}^3$ nuclear species (isotopes) together with sequences of up to $\sim {10}^4$ interconnecting thermonuclear reactions that transmute nuclides of one species to another. To simulate nucleosynthesis in such a system, the specified initial abundances are numerically evolved, in short time steps, into their final abundances over an appropriate set of hydrodynamic conditions (Hix and Thielemann, 1999; Hix and Meyer, 2006). The compositional changes predicted by simulations are often given as one-dimensional (1D) plots of abundance histories [Figure 1 (Smith, 2024; Nesaraja et al., 2005; Smith et al., 2006; Hix, 2024)]. Because there are too many histories to show at once on these plots, 2D visualizations (Figure 2) are often used which display abundance values (mapped to colors) of each isotope at its location set by neutron number $N$ and proton number $Z$; such an $N$-$Z$ plane is referred to as the “nuclide chart”. At any time step in the simulation, such an image shows the cumulative effect of all reactions that have both created and destroyed (“burned”) each isotope up to that point in the simulation. A complementary 2D nuclide chart visualization (Figure 3) represents the amount of material changing from one isotope to another via individual reactions (the reaction “flux” (van Wormer et al., 1994)) as the width/pattern/color of arrows connecting the isotopes. Such “flow diagrams” are especially appropriate given that nucleosynthesis is often conceptualized as the flow of stellar material (abundances) from lighter- to heavier-mass nuclides.

Figure 1

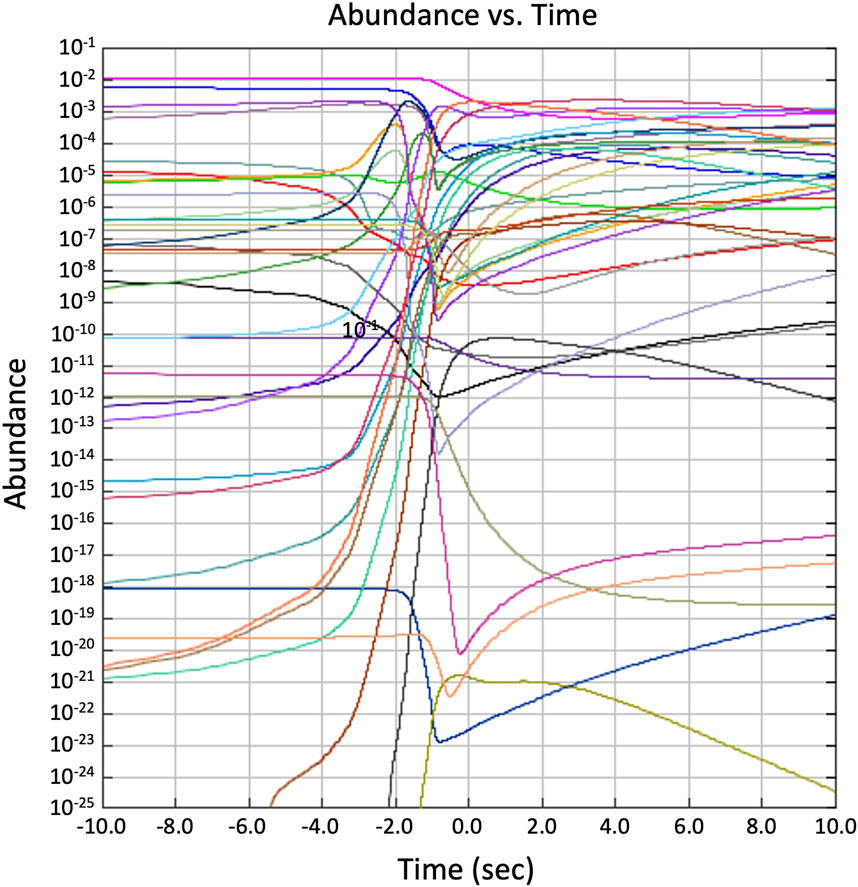
Figure 1. Nucleosynthesis simulation predictions shown as 1D plots of abundances versus time for numerous different isotopes. The zero time is set at the peak temperature of the event. The calculation was made with the Computational Infrastructure for Nuclear Astrophysics (CINA) (Smith, 2024; Nesaraja et al., 2005; Smith et al., 2006) running the XNET post-processing simulation code (Hix, 2024).

Figure 2

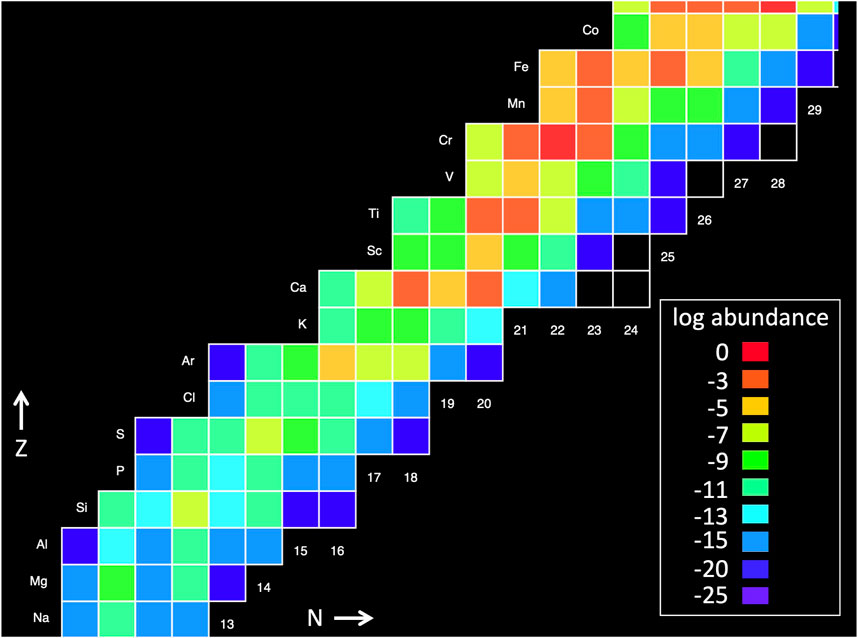
Figure 2. Nucleosynthesis abundance diagram where color indicates abundances for each isotope on the chart of the nuclides ($N$-$Z$ plane). The simulation was made with CINA (Smith, 2024).

Figure 3

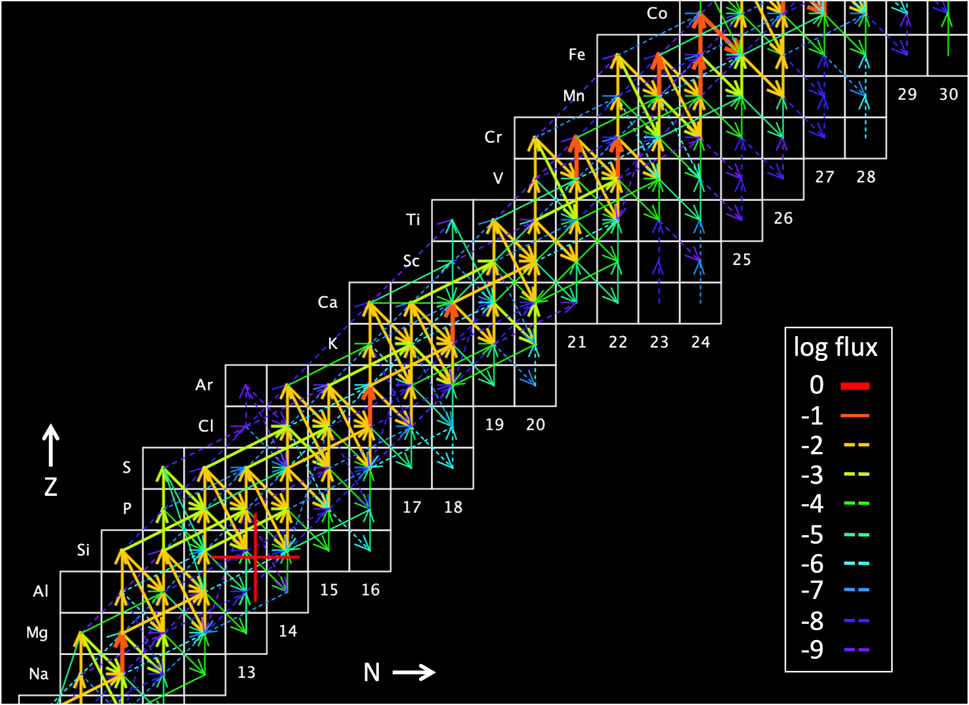
Figure 3. Nucleosynthesis flow diagram where arrows indicate reaction flux from one isotope to the next through individual thermonuclear reactions on the chart of the nuclides. The simulation was made with CINA (Smith, 2024).

While the overall approach of most simulation-based nucleosynthesis studies are similar, there are differences depending on the investigation goals, available computational power, and acceptable approximations. For studies exploring the importance of thermonuclear reactions on simulation predictions, a full treatment of thermonuclear burning is often used wherein the abundances of all relevant isotopes are solved numerically considering all interconnecting reactions. To speed execution, many studies employ a “post-processing” simulation approach where the full thermonuclear burning problem is computed over predetermined temperature and density vs time trajectories [e.g., Hix (2024), NUGRID Collaboration (2024)]. Additional execution speed is obtained by assuming spherical symmetry in the hydrodynamic trajectories, so calculations are made in one dimension (1D) along the system radius.

Some studies more realistically couple a full thermonuclear burn treatment to a 1D hydrodynamics code [e.g., Paxton et al. (2011); Weaver et al. (1978)]. This coupling, missing in post-processing studies, is critical because it produces self-consistent solutions. Further model enhancements require more complex hydrodynamics. For example, mixing length theory (Joyce and Tayar, 2023) is often used to approximate the complex effects of convection in 1D studies, but more realistic convection treatments require 2D or 3D hydrodynamics codes (Fryxell et al., 2000; Almgren et al., 2010). For certain effects like standing accretion shock instabilities (SASI) (Dunham et al., 2023) and stellar rotation, 3D hydrodynamic approaches are required. Because of the extreme computational demands of the 2D and 3D codes (Papatheodore and Messer, 2017), however, these simulations often employ a very truncated (approximate) treatment of thermonuclear burning that includes only the reactions and isotopes that most influence the hydrodynamics. To more accurately time-evolve the full isotopic inventory in such approaches, hydrodynamic trajectories are then extracted from the simulation for use in separate post-processing nucleosynthesis studies. This extraction is often done with a “tracer particle” approach, discussed further below in Section 3.1. There are, however, known issues with the use of truncated thermonuclear burning treatments, including problems with energy generation, neutrino heating, and nucleosynthesis in core-collapse supernovae (Navó et al., 2023). A major goal in nucleosynthesis studies is therefore to develop simulations that couple full thermonuclear burning with multi-dimensional hydrodynamics.

This goal has not yet been practically realized, however, due to the daunting computational requirements. For this reason, and because every relevant thermonuclear reaction and every set of hydrodynamic conditions cannot be investigated, it is critical to carry out studies that guide researchers on where to focus their efforts to make the most progress in understanding nucleosynthesis. Some such efforts, for example, strive to understand details of nucleosynthesis flows – a challenge as these flows reflect the interplay of the hydrodynamic conditions and the underlying relevant nuclear physics. Other efforts focus on devising approximations to nucleosynthesis flows – desirable to reveal underlying structures or symmetries, as well as to speed simulation execution and thereby accelerate scientific discoveries. There are also studies focusing on quantifying the uncertainties of model predictions to enable robust comparisons of predictions to observations. Sensitivity Analyses are another important approach, where changes in model predictions (outputs) caused by systematic variations of inputs are examined; this flags inputs that significantly impact critical simulation outputs for further investigation. And finally, there are efforts to improve models, such as by identifying and correcting anomalous inputs.

The following subsections give some details on possible studies in each of these areas mentioned above – nucleosynthesis flows, complexity reduction, uncertainty quantification, sensitivity analyses, and improving models – using ML algorithm types mentioned in Section 2. Some of these are novel and creative approaches that hold the promise of enabling significant progress for simulation-based nucleosynthesis studies, where the overall solution scheme has not changed in decades. A brief discussion of the utility of ML (especially LLMs) for speeding scientific workflows is also given. Furthermore, additional advances in the field may also be achieved by combining the approaches discussed below in innovative ways. We note that while the ML algorithms mentioned below have not been used for nucleosynthesis studies, many of them have been successfully used, for very different purposes, in nuclear physics [e.g., Boehnlein et al. (2022)] and in astrophysics [e.g., Bufano et al. (2022)].

3.1 Nucleosynthesis flows

3.1.1 Flow Patterns

Identifying and analyzing patterns in complex nucleosynthesis flows may provide insights, decouple overlapping (e.g., thermonuclear and hydrodynamic) effects, and pinpoint critical nuclides and reactions for future study. For example, many experimental efforts have been driven (Smith and Rehm, 2001) by the identification of (nearly) identical flow patterns over different portions of the nuclide chart (e.g., the Hot CNO, NeNa, MgAl, and SiP cycles (Figure 4)) in simulations of nucleosynthesis in nova explosions and X-ray bursts; see, for example, van Wormer et al. (1994), Rembges et al. (1997), Smith and Rehm (2001). Repetitive flow patterns may also arise from the use of thermonuclear rates derived from statistical reaction models, since these models generate very similar reaction cross sections for target nuclides separated by an alpha particle (i.e., two units in each of $N$ and $Z$) on the nuclide chart. Other interesting flow patterns include: interruptions in the flow from lower to higher masses at particular nuclides (“waiting point nuclei”) (Smith, 2011); a many-to-one reduction in the number of possible flow paths to higher masses (“bottleneck reactions”) (Smith, 2011); a rapid cessation of flow to higher masses, indicating expansive cooling of the system or exhaustion of the thermonuclear “fuel” of an exploding star (Roberts et al., 2006); and a balancing of flows through particle captures and their inverse photodisintegrations, indicating the condition of Nuclear Statistical Equilibrium (NSE) (Lippuner and Roberts, 2017).

Figure 4

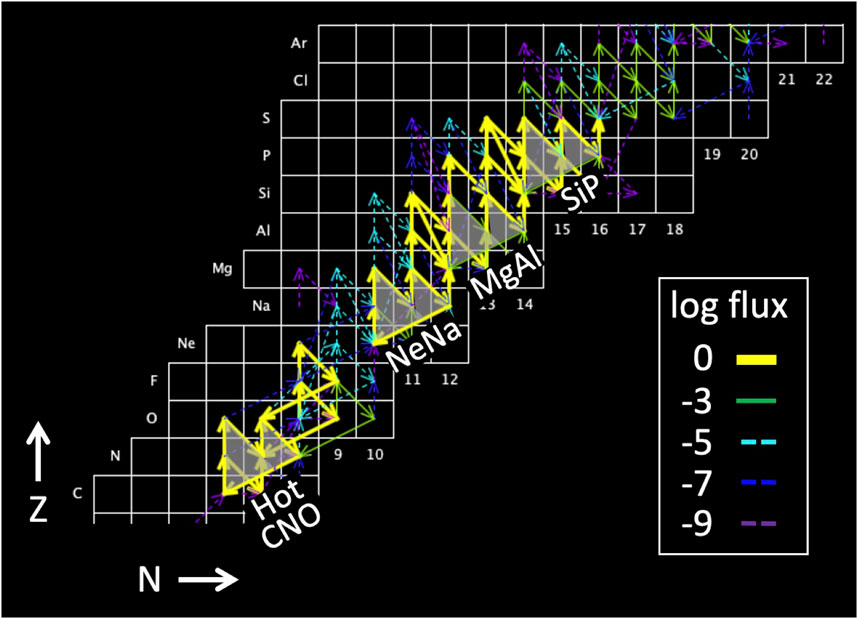
Figure 4. Repetitive reaction flow patterns–the Hot CNO, NeNa, MgAl, and SiP cycles–in a nucleosynthesis simulation of an energetic nova explosion. The simulation was made with CINA (Smith, 2024).

The complexity of simulation predictions has, however, limited systematic studies of the flow patterns mentioned above, and has hampered searches for novel flow patterns that could provide other important signatures of aspects of thermonuclear burning or the onset of certain hydrodynamic conditions. This is where ML approaches could be very useful. For example, by treating each isotope as a graph node, and each reaction flux arrow as a directed graph edge, a GNN could be employed to identify and analyze patterns in flow diagrams like Figure 3. For such a “flow graph”, there are a limited number of edges directed into, and directed out of, each node, representing the possible nuclear reactions (Figure 5). Because of these limited possible edges, and because these edges are localized to reach nearest (or near) neighbors, these graphs are much less complex than many routinely analyzed by GNNs. For a GNN-based nucleosynthesis study, the edges should be weighted by the reaction flux, and the nodes should be indexed by their $(\mathit{N},\mathit{Z})$ values and (if necessary) weighted by their abundance values.

Figure 5

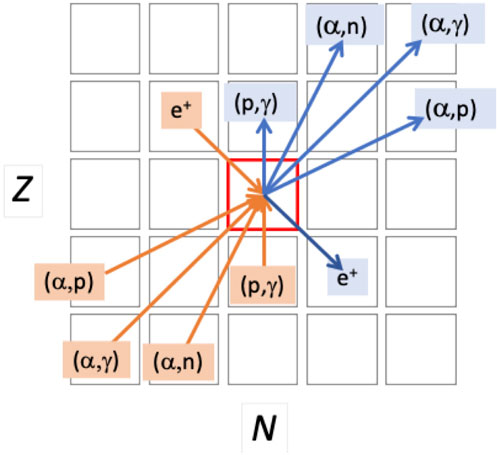
Figure 5. The prominent thermonuclear reactions that create (destroy) a given proton-rich nuclide are shown as orange (blue) arrows connecting isotopes on the $N$-$Z$ plane. Inverse reactions and some other reactions are not shown for clarity. For stable and for neutron-rich nuclides, the prominent reactions are different.

A GNN could take a flow graph as input, generate a representation in a lower-dimensional latent (feature) space, and then identify clusters of nodes, objects and their connections, and region classifications. These could facilitate studies of the numerous flow effects mentioned above, and perhaps identify some new effects as well. GNNs can also generate new graph visualizations which could reveal structures and anomalies not readily apparent in the original flow diagram. By weighting nodes with, for example, accelerator beam intensities, a GNN could be used to rank identified features (e.g., nucleosynthesis waiting points, bottlenecks, repetitive patterns) to prioritize experiments that match facility capabilities. By weighting graph edges with reaction energy release ($Q$-values), a GNN could identify a truncated selection of isotopes and reactions that generate nearly the same thermonuclear energy as the original simulation; this could subsequently be used for accelerated nucleosynthesis simulations coupling hydrodynamics and approximate (truncated) thermonuclear burning.

In a complementary manner, ML approaches may also help identify flow patterns in abundance diagrams like Figure 2; this can be especially useful because not all simulation codes generate flow diagrams like Figure 3. Noting that abundance diagrams are coarsely “pixelated” over the nuclide chart, CNNs are a natural approach to search for patterns using filters that “slide” over the image. Since the pixel values (abundances) change in time, ML video analysis approaches can be used on a series of sequential pixelated abundance images, like those shown in Figure 6. For example, a CNN could be used to extract high-level features from individual frames that are then fed to an RNN that keeps a memory of the frame-to-frame temporal correlations (Xu et al., 2016). Such a scheme could be used as a novel nucleosynthesis simulation emulator, as described below in Section 3.2.

Figure 6

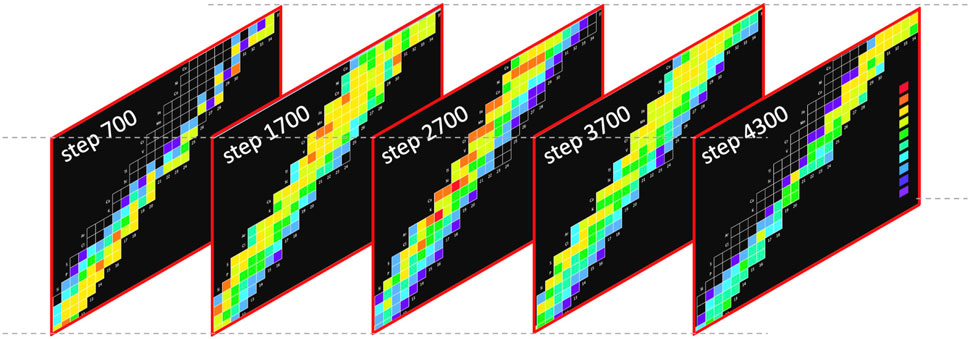
Figure 6. Snapshots of the evolution of isotopic abundances at different time steps of a simulation of a Type I X-ray burst. The simulation was made with CINA (Smith, 2024).

Adjusting the color palette could also aid in analyzing these images. First, in the image creation stage, abundances are usually continuously mapped to colors, but using a coarser discrete color binning (Smith, 2011) as in Figure 2 could accelerate CNN image analyses by reducing the dimension of the color space. Additionally, such binning could facilitate the use of KNN or KM clustering algorithms to find abundance patterns via groupings of isotopes in a combined color- and ($Z$, $N$)-space. After image generation, colors can be “quantized” using a variety of techniques (CNNs, RNNs, GANs, and more) that preserve visual structures over a smaller color palette for faster subsequent analyses (Hou et al., 2020). Alternatively, KNN and KM clustering algorithms could process (pre-image) numerical abundance values to determine optimal non-uniform color maps for improved CNN image analysis, or be used to reveal otherwise hidden patterns by bypassing image generation altogether.

Finally, since flows can be numerically approximated by the change of the abundances in Figure 2 in time (e.g., between sequential images), abundance time derivative images could be analyzed using CNNs, CNNs in combination with RNNs, or clustering algorithms to generate new insights, especially when flow diagrams are not available. Figure 7 shows an example of the evolution of abundance time derivatives for an energetic nova explosion. As the temperature rises to the peak, the abundances at nuclides with higher (lower) $Z$ values are increasing (decreasing) in time, with corresponding positive (negative) values for their abundance time derivatives; this is consistent with reaction flow towards higher $Z$ (i.e., upwards) on the $N$-$Z$ plane. After a transition near the peak temperature, these abundance time derivatives flip in sign, consistent with the reaction flow dominated by positron decays which flow diagonally downward and to the right on the nuclide chart. New thermonuclear burning insights may be derived by examining effects including: correlations between abundance time derivative sign changes and changes in hydrodynamic conditions; rapid fluctuations in abundance time derivative signs; patterns and groupings of isotopes with similar abundance time derivative signs and sign changes; and more.

Figure 7

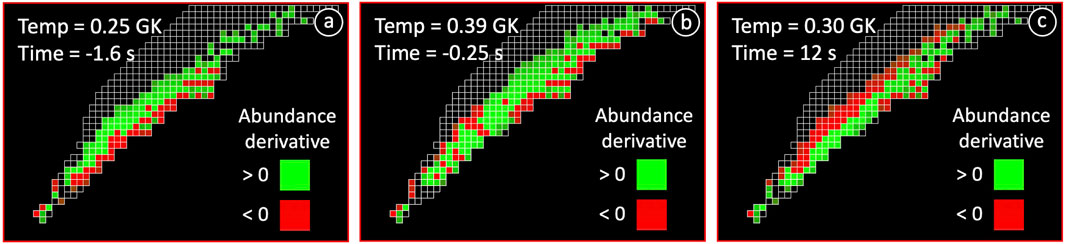
Figure 7. Evolution of the sign of the time derivative of abundances on the nuclide chart ($N$-$Z$ plane) for an energetic nova explosion at times before the peak temperature (A), nearly at peak (B), and after peak (C). The simulation was made with CINA (Smith, 2024).

3.1.2 Flow correlations

Instances where two or more isotopes have nearly identical predicted abundance vs time histories (Zhang et al., 2013) (Figure 8) may reveal underlying nucleosynthesis structures, especially for isotopes that have significant mass differences (i.e., are well separated from one another on the nuclide chart). In such cases, the flow correlations could be connecting groups of isotopes in a localized NSE, a condition called nuclear quasi-statistical equilibrium (QSE) (Meyer et al., 1998). Alternatively, correlations could be due to flows through a sequence of intervening reactions that connect these distant isotopes. However, because simulations track the abundances of so many isotopes, and because there are numerous general abundance time evolution trends (e.g., abundances increasing during rapid temperature rises), such flow correlations could merely be random. It is therefore important not only to search for such correlations, but also to determine if a causal relationship is present.

Figure 8

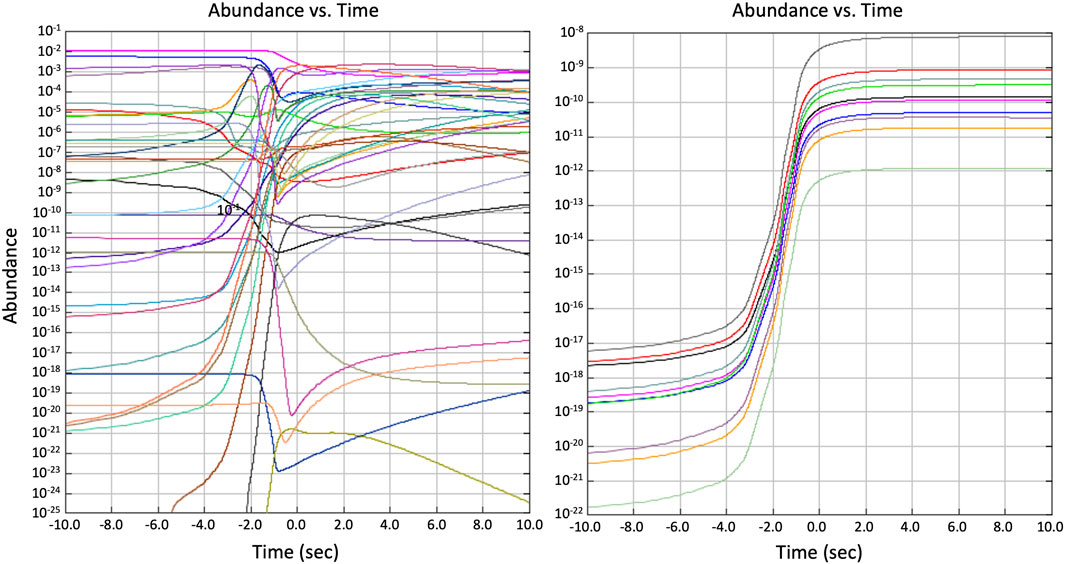
Figure 8. (Left) Abundance vs. time histories for many isotopes tracked in a nucleosythesis simulation (Right) subset of these isotopes exhibiting similar abundance vs. time behavior (Zhang et al., 2013). The zero time is set at the peak temperature of the event. The simulation was made with CINA (Smith, 2024).

There are numerous ML approaches that could be used to search for such causal flow correlations. For example, abundance histories could be pre-processed (in this case, labeled) by selecting their values (and/or time derivatives) over a coarse time grid and then using a KM or SVM clustering algorithm or a NN to group similar histories together. NNs could also be used to facilitate Dynamic Time Warping algorithms (Seshan, 2022) for picking out similar curves. A wider range of variations of abundance histories can likely be handled by “encoding” abundances histories with an RNN (or a 1D CNN) and then using another DNN for feature extraction and subsequent clustering and classification.

To show causality, analyses of 2D flow diagrams (like Figure 3) with a GNN could be used to identify cases where sequences of strong flows “connect” distant isotopes with correlated abundance histories, or more generally to identify new possible causal connections. This would involve weighting graph edges by reaction flux and graph nodes by abundance values and comparing nearby edges and nodes to find sequences of strong flows. For cases of QSE, analyses of the pixelated 2D abundance plots (like Figure 2) are appropriate, because it was noted in Meyer et al. (1998) that the shape of these groups in the $N$-$Z$ plane can critically impact final abundance predictions. CNNs would be useful for such analyses, as well as KNN and SVM clustering algorithms.

3.1.3 Tracer particles

In a hydrodynamics simulation, tracer particles (TPs) are passive Lagrangian mass elements that move along with the fluid; in spite of the name, they are not actually individual “particles” like a proton. By tracing (recording) the time-dependence of TP properties – position, velocities, angular momentum, temperature, density, composition – a characterization of complex fluid flows can be obtained. TPs are widely utilized in nucleosynthesis research to extract hydrodynamic profiles from simulations coupling multi-dimensional hydrodynamics with a truncated treatment of thermonuclear burning; by later following a full thermonuclear burn simulation over each TP profile and combining the results, a fuller treatment of thermonuclear burning can be obtained. Examples of this TP approach include studies of core collapse supernovae (Sieverding et al., 2023; Harris et al., 2017), binary neutron star mergers (Bovard and Rezzolla, 2017), and Type Ia supernovae (Seitenzahl et al., 2010; Seitenzahl et al., 2020). A few thousand TPs are typically used, in some cases evenly distributed across the entire spatial grid (Harris et al., 2017) and in other cases strategically located to track critical spatial regions.

There are a number of issues, however, that arise from the use of TPs. These include (Sieverding et al., 2023): the impact of initial tracer positions and velocities; the precise times when tracer particles are initiated and terminated in the simulation; the number of tracer particles to deploy; the challenges of obtaining convergence of post-processed abundances; problems with methods to add more tracer particles after the simulation is completed (which can aid in convergence); and that TP approaches do not generate uncertainties. There are other issues including possible discontinuities in velocity assignments (Tiede et al., 2022) as well as inadequate spatial resolution and inconsistent thermodynamic evolution. For core-collapse supernovae simulations, questions can arise as to which tracers are ejected from the explosion, and the very divergent nucleosynthesis results in asymmetrical explosions (Harris et al., 2017).

ML approaches can address some of issues arising from TP use. For example, outlier trajectories that may prevent convergence of post-processing nucleosynthesis abundances could be identified and removed using IF, SVM, and NNs, or clustering algorithms like KNN or KM. GPs could be used to smooth tracer particle trajectories to make them more generic or “representative” of the astrophysical environment, removing complex structure that may be tied to a specific model; this could help deal with velocity discontinuities or convergence issues. Going further, it could be advantageous to determine a smaller set of trajectories that could each represent many (tens to hundreds) individual TPs; these could be denoted as “pseudo-tracers”. These could be centroids of a cluster of TPs identified by KNN or KM, especially in combination with a GP that assigned uncertainties to TP trajectories. Runs with pseudo-tracers could then enable analyses with significantly improved 2D spatial resolution compared to the same number of TPs with the same computational power; this could help with abundance convergence and spatial resolution problems. Alternatively, an ensemble of pseudo-tracer runs with initial variations in parameters such as positions/velocities, start/stop times, or others could be used to address these and other issues in a more computationally efficient manner. Pseudo-tracers could also help reveal hidden flow structures or mark transitions between different flow regions (e.g., strong outflows vs convective regions).

For uncertainties, GPs could be utilized to add uncertainties to tracer particle trajectories, which could then be propagated through post-processing simulations with a Monte Carlo uncertainty quantification (UQ) approach as discussed below in Section 3.3. Finally, regarding nucleosynthesis in asymmetrical systems, clustering algorithms may be useful to divide TP trajectories into groups that, when appropriately mass weighted, could be used to determine final abundances in the system weighted over respective contributions from (for example) polar vs equatorial trajectories. Combined with GPs, this could also determine uncertainties in these weighted abundances.

3.2 Complexity reduction

3.2.1 Emulators

Nucleosynthesis simulations can be considered functions that map inputs (initial abundances, thermonuclear reaction rates, hydrodynamic conditions) to outputs (final abundances, nuclear energy generation). As discussed in Section 3.1, simulations with the most realistic hydrodynamics and a full treatment of thermonuclear burning are not yet computationally viable. By replacing such simulations with fast-executing approximations (i.e., emulators), the complexity of the problem is reduced, and more realistic simulations become viable. In this way, emulators may accelerate the pace of scientific discovery, and also enable the multiple runs of more realistic simulations as required for determining their uncertainties (see Section 3.3) as well as the sensitivities of their outputs to inputs (see Section 3.4).

NNs are a popular foundation for emulators as they are known to be universal function approximators. Specifically, a NN with fixed depth and arbitrary width can, to any specified accuracy, approximate any continuous function when the activation functions are continuous and nonpolynomial (Cybenko, 1989; Park et al., 2020). Numerous studies of different NN depths, widths, and activations have since been studied in this regard; for a review, see DeVore et al. (2021). By training a DNN on a set of nucleosynthesis simulation inputs and outputs, for example, that simulation would be effectively reverse engineered: loading a new set of inputs (within range of the training data) into a trained emulator would produce a new and consistent set of outputs. As with all ML approaches, running emulators with inputs outside of the training data range (i.e., making extrapolations) can produce problematic outputs; retraining the emulator is usually required for extrapolations. Besides DNNs, other ML algorithms have been used as emulators, including GPs, SVMs, and RFs. The choice of algorithm depends on the complexity of the problem, the size of the training data set, the available computational resources, the desired accuracy of the approximation, and the goals of the study.

For nucleosynthesis codes that couple hydrodynamics and thermonuclear burning, a natural first goal could be to replace either the hydrodynamics or thermonuclear burn with an emulator. To replace the hydrodynamics, an approach similar to that used in Stachenfeld et al. (2021) could be used, wherein a CNN-based architecture trained on only 16 simulations was found to calculate turbulent fluid dynamics more accurately than classical numerical solvers on a comparably low resolution spatial grid. Their modest system was also able to capture the behavior generated by the athena++ solver (Stone et al., 2020), a state-of-the-art magneto-hydrodynamics code used for high-performance computing astrophysics simulations.

An alternative approach is to emulate the thermonuclear burn (rather than hydrodynamics) calculations in a fully coupled nucleosynthesis code: at each time step, the emulator would give approximate results for the change in abundances of all the tracked species. This approach can offer improved performance if the emulator runs faster than the traditional linearized thermonuclear burn solution. As discussed below, the execution time of traditional simulations scales as the square of the number of tracked isotopes, so emulators will give more performance gains for simulations tracking many hundreds to thousands of isotopes. This approach was first attempted for supernova nucleosynthesis in Fan et al. (2022) with a DNN emulating a (very approximate) three-isotope system, and careful attention was given in that study to integrating the hydrodynamics with the emulator.

There are alternatives to using emulators that precisely mimic the approach used by standard nucleosynthesis codes, wherein all isotopic abundances are evolved through short time steps from initial to final values. Examples include: studies that predict only final abundances for all tracked isotopes in a system; studies to determine final abundances of a few particular isotopes to compare to observations [e.g., nova contributions to the galactic ⁷Li abundance (Starrfield et al., 2024)]; studies that track only isotopes with abundance values above a certain threshold; or studies to predict an observable light curve (e.g., an X-ray burst (Galloway et al., 2020)), especially valuable when there is little if any ejected material to observe. An example of the first can be found in a recent preprint (Grichener et al., 2024), where an 80-isotope simulation of nucleosynthesis in a massive star was emulated with a NN with two hidden layers of 256 nodes each. They trained their emulator on a set of final abundances of $6\times {10}^4$ simulations (with variable initial temperature and density conditions) and obtained – in some cases – qualitative agreement between the emulator and the traditional simulation. They plan to enlarge the training data set and utilize alternate NN architectures to explore the possibilities of quantitative agreement with the stellar simulations.

Additionally, DNNs can in some cases universally approximate a nonlinear continuous operator, such as the solution operator of a system of differential equations (Lu et al., 2021). This is relevant for nucleosynthesis studies because the traditional approach to solving the time-evolution of abundances, and the accompanying thermonuclear energy generation, in a given astrophysical environment involves numerically solving a first-order set of coupled differential equations. Usually this is done by linearizing the problem over small time steps and employing an implicit differencing approach for numerical stability [see, e.g., (Arnett, 1996)]. By using a deep operator network (DeepONet) (Lu et al., 2021), it may be possible to approximate the solution operator of a thermonuclear burn simulation and time evolve the abundances.

Moving even farther away from traditional approaches, emulators could be constructed to approximate a series of images of isotopic abundances on a nuclide chart, which essentially form the frames of a simulation animation as sketched in Figure 6. As briefly mentioned above in Section 3.1, such an emulator may be constructed with a CNN for image analysis combined with an RNN for frame-to-frame memory. Similarly, a GNN could be combined with an RNN to emulate a nucleosynthesis flow diagram animation. With these approaches, the time dependence of abundances or flows could be extracted from the emulated animation frames, thereby providing a novel nucleosynthesis solver.

An important approach for emulators is to incorporate physics equations into the loss function of a NN. Such “physics-driven” ML approaches have demonstrated improved performance over traditional NN systems, and typically require far less data for training. This approach was successfully used in Ma et al. (2022) to predict fluid flows (using the Navier-Stokes equations), in Zhang et al. (2020) to predict seismic responses (using equations of motion), and in Jin et al. (2020) to solve a nonlinear inverse problem in geological drilling (using a parameterized Earth model). A strong motivation for the growing popularity of these “hybrid” approaches that combine traditional physics modeling with ML is to realize their combined discovery potential (Rai and Sahu, 2020).

Given these successes and the promise for future emulator developments, it is likely that the first ML emulation of a realistic nucleosynthesis simulation will be created in the near future.

3.2.2 Reduce simulation dimensionality

The execution time for thermonuclear burn simulations roughly scales with the square of the number of nuclear species (isotopes) $N$ whose abundances are followed. This is because at each simulation time step, an $N$ by $N$ matrix–constructed to detail how each species transmutes into others – must be inverted to determine a linearized solution of the abundance changes (Arnett, 1996; Hix and Thielemann, 1999; Hix and Meyer, 2006). As discussed previously, realistic nucleosynthesis simulations with multi-dimensional hydrodynamics necessarily truncate their thermonuclear burning treatment–by following fewer nuclei–to be computationally viable. “Alpha nuclei” (e.g., ¹²C, ¹⁶O, ²⁰Ne … ⁵⁶Fe) are typically chosen for this as their interlinking alpha-capture reactions [e.g., ¹²C($\alpha ,\gamma$)¹⁶O … ] generate most of the thermonuclear energy in the system; a full treatment of the evolution of the complete isotopic inventory then requires an extraction of hydrodynamic profiles and a subsequent post-processing simulation.

For some astrophysical scenarios, it may be possible to use a similar approach of following fewer isotopes – specifically, those that can represent much of the isotopic inventory evolution (as well as the energy generation, if desired). Specifically, it may be possible to use a PCA or other dimension-reducing ML algorithm (Fodor, 2002; Espadoto et al., 2019) to help determine a small set of isotopes (hereafter denoted pseudo-isotopes) each of which represents multiple nuclide species, and track only the changes in their respective abundances (pseudo-abundances). The smaller number of tracked species will result in a significant reduction in complexity of the system and in the execution time of a standard nucleosynthesis simulation. The choice of pseudo-isotopes could be verified by running an ensemble of traditional simulations and identifying (a) the most abundant isotopes in a traditional simulation and (b) other “nearby” isotopes whose abundances ratios to them are similar throughout the ensemble. Such an analysis could be done with KNN, KM, or other clustering algorithms. The concept of pseudo-isotopes bears a resemblance to the clusters of nuclear species described in studies of Quasi Statistical Equilibrium (QSE) (Meyer et al., 1998) and the collection of nuclei involved in repetitive reaction flow patterns (Rembges et al., 1997); this latter is discussed below in approaches to approximating flows.

A more ML-centric approach would be to use a VAE as a simulation emulator, where the smaller set of pseudo-abundances (determined by the algorithm) form the lower dimensional space. The simplest approach would be to train the algorithm on final abundances only. In cases where it may be desirable to more closely mimic a traditional nucleosynthesis simulation, training could be done on the abundances at each time step (e.g., Figure 6). For analyses of such time-series data, VAEs (which use NNs) have some advantages in dimension reduction (Todo et al., 2022) over more traditional approaches such as wavelet decomposition or PCAs. A complementary approach would be to use an RNN to analyze the time-series data.

Overall, the advantages of using pseudo-isotopes is that their presence and identity could reveal hidden structures in the nucleosynthesis process that are not evident in traditional simulations. The pseudo-isotopes determined for one simulation could be reused for computationally-efficient parameter space explorations, or potentially reused in simulations of other astrophysical environments. Furthermore, a comparison of such pseudo-isotopes across simulations of different astrophysical environments could give a new perspective that aids in deconvolving nuclear and hydrodynamic effects that work together to create the elements of the Universe.

3.2.3 Approximating flows

In the above discussion of “alpha nuclei” like ¹²C and ¹⁶O, the interlinking alpha-capture reactions like ¹²C($\alpha ,\gamma$)¹⁶O were mentioned as being critical to track energy generation in this particular approximation to thermonuclear burning. This approach can be generalized to consider pseudo-reactions which link together pseudo-isotopes (or perhaps regions of the nuclide chart) for nucleosynthesis studies needing to approximate reaction flow and/or energy generation. ML techniques like those described above – PCAs, VAEs – could be used to identify the most critical reactions during particular time windows of a simulation, then the time evolution could be studied with VAEs or RNNs. Because the focus here is on reaction flow, it is natural to use a GNN (as described in Section 3.1) in combination with a VAE to reduce the dimensionality of the problem. Furthermore, by combining treatments of both pseudo-isotopes and interlinking pseudo-reactions, both reaction flows and isotopic abundances could be approximated simultaneously.

Some nucleosynthesis studies focus on reaction flow patterns that repeat over different portions of the nuclide chart. As mentioned in Section 3.1 above, Figure 4 gives an example of repetitive thermonuclear burning cycles that occur in a nucleosynthesis simulation of a nova explosion: the NeNa, MgAl, and SiP cycles, named for the isotopes involved. When such cycles occur in an explosive astrophysical environment, they are considered a “trap” or “sink” for material that otherwise would be processed by thermonuclear burning up to higher mass isotopes. These traps can be characterized by their “leakage rate” of material that escapes the trap and resumes a flow to higher masses. By representing all the isotopes in each cycle as a single pseudo-isotope, and interlinking cycles with pseudo-reactions that characterize the leakage from one to the next, the complexity of the reaction flow can be greatly reduced. A similar technique was used in a traditional nucleosynthesis simulation of an X-ray burst (Rembges et al., 1997), primarily to speed up the simulation execution. However, this novel work was never replicated, perhaps in part because advances in computing hardware made this approximation less necessary for post-processing nucleosynthesis studies. It could, however, prove fruitful to explore possible insights that may arise from this approach when applied to more realistic nucleosynthesis simulations.

3.2.4 Functional representations

As mentioned earlier, current approaches to solving the time-evolution of abundances and thermonuclear energy generation requires a numerical solution to a first-order set of coupled differential equations (Arnett, 1996). For 1D post-processing approaches that solve thermonuclear burn, these simulations can be completed rather quickly with very modest computing requirements. In the distant past, however, computational power was much more limited, and significant efforts were spent devising analytical approximations to estimate abundance changes and energy generation. In some cases, valuable scaling laws were devised [see, e.g., (Caughlan and Fowler, 1962; Parker et al., 1964; Clayton, 1983)] to approximate how predictions of these quantities changed with temperature or other variables, thereby significantly reducing the complexity of the model and allowing further detailed investigations.

While the field has largely moved away from these approaches, scaling laws may offer valuable insights – perhaps into the complex interplay of hydrodynamics and thermonuclear burning, or perhaps for “back-of-the-envelope” approximations – not readily apparent from numerical solutions. They may also facilitate large-scale explorations of parameter spaces because these approximations are so fast to calculate.

ML approaches could revitalize such scaling studies, by first creating an emulator to approximate the input-output mapping (as described above), then using a symbolic regression (SR) algorithm with a set of temperature-dependent functions. Such an approach could generate, for example, approximations for the values of abundance ratios, or the total nuclear energy generation, as a function of peak temperature in an astrophysical system. It is possible that such ML techniques could yield nucleosynthesis scaling laws as valuable as those used to explain the revival of a stalled shock wave in a core collapse supernova by neutrino heating (Bethe and Wilson, 1985) – a work that revolutionized studies of the core collapse mechanism. There are, in fact, recent suggestions that using NNs in combination with SRs are not just a way to approximate the behavior of a physical system, but also a way to uncover previously hidden physical laws (Cranmer et al., 2020).

3.3 Uncertainty quantification

The quantitative comparison of nucleosynthesis simulation predictions to observations is critical for advancing studies of many astrophysical environments. One example comes from the Big Bang, where comparisons of the primordial ⁷Li abundance to model predictions (Smith et al., 1993), the “cosmic lithium problem”, has driven studies of diverse effects including lithium depletion in stars, dark matter, exotic particles, thermonuclear reaction rates, and observational techniques (Fields et al., 2023). The material ejected from Type Ia supernovae provide another example: observations of isotopic nickel abundances from these explosions are compared to nucleosynthesis predictions to discriminate between different explosion mechanisms (Seitenzahl et al., 2020). Measurements of isotopic abundance ratios in grains of meteorites provide a third example, where comparisons to nucleosynthesis predictions are used to attribute the origin of some meteorites to Asymptotic Giant Branch stars and Carbon stars (Liu et al., 2021), and others to novae, supernovae, or elsewhere in the cosmos (Nittler, 2003; Zinner, 2003).

Uncertainties in simulation predictions are needed to make robust comparisons to observations. While lacking in many nucleosynthesis research efforts, uncertainty quantification (UQ) treatments are now becoming routine for many simulation-based physics studies (Ghanem et al., 2017). A widely-utilized UQ treatment involves propagating input uncertainties through a simulation (Kroese et al., 2013) using Monte Carlo input sampling. Specifically, a large (1,000–10,000) ensemble of simulations are executed, each of which has small independent random variations of the input parameters over their respective probability distribution functions; the ensemble outputs are then analyzed to determine the prediction uncertainties. This approach has previously been used for nucleosynthesis studies of the big bang (Smith et al., 1993), novae (Hix et al., 2003), X-ray bursts (Roberts et al., 2006), and red giant stars and other scenarios (Rauscher et al., 2018). However, it has not been used for more realistic multi-dimensional nucleosynthesis simulations due to the long execution time required for each run of the ensemble.

This could change by utilizing any of the ML complexity-reduction approaches mentioned above in Section 3.2. Specifically, the fast execution times of simulation emulators, pseudo-abundances, flow approximations, or functional representations could make viable Monte Carlo UQ approaches with multi-dimensional simulations that couple hydrodynamics with thermonuclear burning. This approach could also facilitate 1D coupled and post-processing simulations that employ the larger thermonuclear reaction networks needed for more complex problems, especially in cases where larger ensemble sizes needed for more precise uncertainty determinations.

Another ML-based UQ approach is based on BNNs. Gaining use in theoretical nuclear physics (Boehnlein et al., 2022), BNNs employ stochastic weights for NNs used in a Bayesian framework. By constructing a simulation emulator with a BNN, uncertainties of the NN predictions are naturally generated. A related approach is based on deep ensembles (Lakshminarayanan et al., 2017) wherein numerous DNNs, here used as emulators, are trained with random initializations of their model parameters. This approach was recently used to extract resonance parameters with uncertainties from nuclear scattering data (Kim et al., 2024). Deep ensembles can be viewed as a Bayesian approach using delta-function posteriors, but have the added flexibility to capture different posterior modes if needed (Gustafsson et al., 2020).

Deep ensembles are just one of many approaches to UQ that can be used for deep learning (i.e., DNN-based) studies (Abdar et al., 2021); others include Monte Carlo dropout, Bootstrapping, and Gaussian Mixture Models (Hubschneider et al., 2019). There are also specialized UQ approaches developed for DNNs that model time-series data (Song et al., 2020); an application of this for nucleosynthesis would be to use an RNN to predict a set of abundance vs. time values with uncertainties. Most of the approaches mentioned above can be configured to incorporate uncertainties arising from training data as well as those from the DNN architecture itself; in this manner, a more complete uncertainty characterization can be obtained.

Finally, diffusion-based uncertainty quantification (DBUQ) (Lu et al., 2024) is a novel new method that develops a parameterized generative model which is then approximated with a NN via supervised learning to enable rapid generation of UQ parameter posterior samples. This general-purpose approach was shown to require 30 times less computing time and be less memory intensive (Lu et al., 2024) than traditional Markov Chain Monte Carlo uncertainty approaches (Lu et al., 2012). This technique builds on work that shows generative diffusion models have increased stability in image processing over GANs (Ho et al., 2022) and generalizes it for scientific inverse problems.

3.4 Sensitivity analyses

Sensitivity Analyses (SA) are examinations of changes in one or more target outputs of a simulation resulting from variation of an individual input, while keeping all other inputs and model parameters fixed. SA are widely utilized to understand the relationships of inputs to outputs in complex systems, and especially to identify those inputs which have the strongest impact on outputs. SA have been widely used in nuclear astrophysics, for example, to identify which thermonuclear reaction inputs or hydrodynamic conditions – when varied – have a significant impact on predicted isotopic abundances or nuclear energy generation [see, e.g., Beun et al. (2008), Mumpower et al. (2016); Smith (2023)].

SA typically involve less than 100 simulation runs, far fewer than those of the Monte Carlo-based UQ study described above in Section 3.3. In spite of this, SA are often computationally prohibitive for nucleosynthesis models with multi-dimensional hydrodynamics and full thermonuclear burning. Similar to aiding UQ studies, the ML complexity-reducing strategies discussed in Section 3.2, such as NN-based emulators, can be used to facilitate SA of more realistic nucleosynthesis models. In this way, better guidance can be given for setting priorities for future studies of simulation inputs.

Since the variation of inputs are much larger in SA (orders of magnitude) compared to that in UQ studies (usually a few standard deviations), the corresponding ML algorithm training parameter space is much larger for SA than for UQ determinations. A recent example from reactor physics illustrated how a DNN constructed to emulate a high-fidelity reactor simulation was used for both UQ and SA (Radaideh and Kozlowski, 2020). This study utilized a Group Method of Data Handling approach (Ivakhnenko, 1971) with a DNN for parametric optimization in high-dimensional spaces in a manner that may be useful for emulating nucleosynthesis simulations.

There are other ways in which ML algorithms can help with SA. One approach is to include a “feature importance” score as an added domain knowledge in DTs (Al Iqbal et al., 2012) (or with other categorization algorithms like RFs). By identifying important features, this is complementary to traditional SA approaches. Another technique is to use GPs or BNNs to identify which simulation predictions have the largest uncertainties, and set these as target outputs for a traditional SA. A third approach is active learning (Settles, 2009), where an iterative procedure (either manual or automated) is used to determine which new data (or features) would reduce prediction uncertainties (for example, from a GP or BNN) when added to the training data set. While active learning is primarily used to boost efficiency via the use of smaller training data sets, it can also help identify critical data that change predictions and/or reduce prediction uncertainties.

These examples show that there are a number of ways that traditional SA can be advanced, or complemented, by ML approaches, and this can be very useful for identifying the most critical nucleosynthesis simulation inputs. There are also a number of deeper connections between SA and ML, which are discussed in Scholbeck et al. (2023). These include how SA can be used for ML interpretability, and how some ML approaches are redevelopments of earlier work in SA [e.g., using Gaussian processes as emulators to speed up SA (Le Gratiet et al., 2017)].

3.5 Improved models

Some of the ML techniques mentioned above have focused on working with existing model outputs to find patterns or correlations in nucleosynthesis flows that can improve our understanding, while others focused on speeding up model execution (with emulators, approximations, or dimension reductions) to aid UQ and SA that can guide future studies. This subsection describes how ML approaches can be used to improve models, independently or in combination with those efforts mentioned above, specifically by examining model inputs and outputs.

Thermonuclear reaction rates are critical simulation inputs, with some astrophysical environments requiring thousands of input rates to fully describe the relevant nucleosynthesis. These rates are temperature dependent and are collected in large libraries; see Smith (2023) for a detailed discussion. Rates are determined by convoluting an energy-dependent nuclear reaction cross section with the temperature-dependent Maxwell-Boltzmann distribution of relative energies of nuclei in an astrophysical environment (Rolfs and Rodney, 1988; Arnett, 1996). For the widely utilized REACLIB library (Cyburt et al., 2010) containing 55,000 rates, this convolution is performed numerically for each rate and then fit to a 7-parameter analytical temperature-dependent function, and the fit parameters for each reaction are then stored in the library and subsequently input into a simulation. It is very challenging, however, to obtain precise parameter fits because the rates vary by up to 30 orders of magnitude over temperatures relevant for nucleosynthesis; precision is needed because fit deviations of a few percent can significantly alter nucleosynthesis predictions. ML approaches for regression including LinR, KRR, GP, GB, SVM, and NNs could be very useful to better determine these reaction rate fit parameters.

Rate improvements can also be realized by examining the underlying reaction cross sections. While some cross sections are determined from experimental measurements, the majority (nearly 90%) are determined from theoretical reaction models (Smith, 2023). A single flawed rate can distort model predictions, but it is challenging to individually check thousands of rates for anomalies. Theoretically based rates, however, usually exhibit smooth variations across the $N$-$Z$ plane, making some ML approaches well suited to look for outliers based on comparisons of the shapes of cross section vs energy (or rate vs temperature) curves for reactions spanning the nuclide chart. Specifically, IF, SVM, and NNs may help with this, as well as clustering algorithms like KNN and KM.

In addition to finding outliers of theoretical rates, ML approaches can aid in improving cross sections determined from measurements. A recent example is the use of KNN and DT algorithms to improve evaluations of the ²³³U + $n$ and ³⁵Cl$(n,p)$ reactions (Vicente-Valdez et al., 2021) that are important for nuclear security and nuclear energy applications. Another is the deep ensemble approach mentioned above to analyze nuclear scattering data (Kim et al., 2024), as an alternative to phenomenological R-matrix analyses. Approaches similar to these could be useful for reactions needed for nuclear astrophysics. There is also a long-term effort to revamp the workflow for producing evaluated cross section libraries using nuclear data elements (datasets, evaluated cross sections, validation benchmarks) wrapped in software containers, linked in a Bayesian network, and updated via GPs; first results are reported in Schnabel et al. (2021). Additional examples of ML utilizations for improving nuclear data and nuclear physics can be found in Boehnlein et al. (2022).

ML approaches can also be utilized to improve the hydrodynamic inputs for nucleosynthesis simulations. As discussed in Section 3.1, tracer particle input for nucleosynthesis simulations can contain outliers that could be identified and removed with IF, SVM, and NNs or with KNN, KM, or other clustering algorithms. Also, GPs could be used to smooth tracer particle trajectories to make them more “representative” of the astrophysical environment rather than tied to the specific hydrodynamics model that generated them.

The same GP-based smoothing approach could also be utilized for modifying hydrodynamic profiles extracted from multiple spatial zones. Figure 9 shows such (unsmoothed) temperature profiles of zones extracted from a nova simulation (Politano et al., 1995); GP smoothing could be done in a manner that removes significant zone-to-zone discontinuities that may skew post-processing nucleosynthesis predictions. ML outlier approaches (as mentioned above) could also be helpful to search for anomalous profiles extracted from “full” (coupled hydrodynamics + thermonuclear burning) models, whereas clustering (KNN and KM) and other ML techniques could improve the consistency of profile extractions from the full coupled model output.

Figure 9

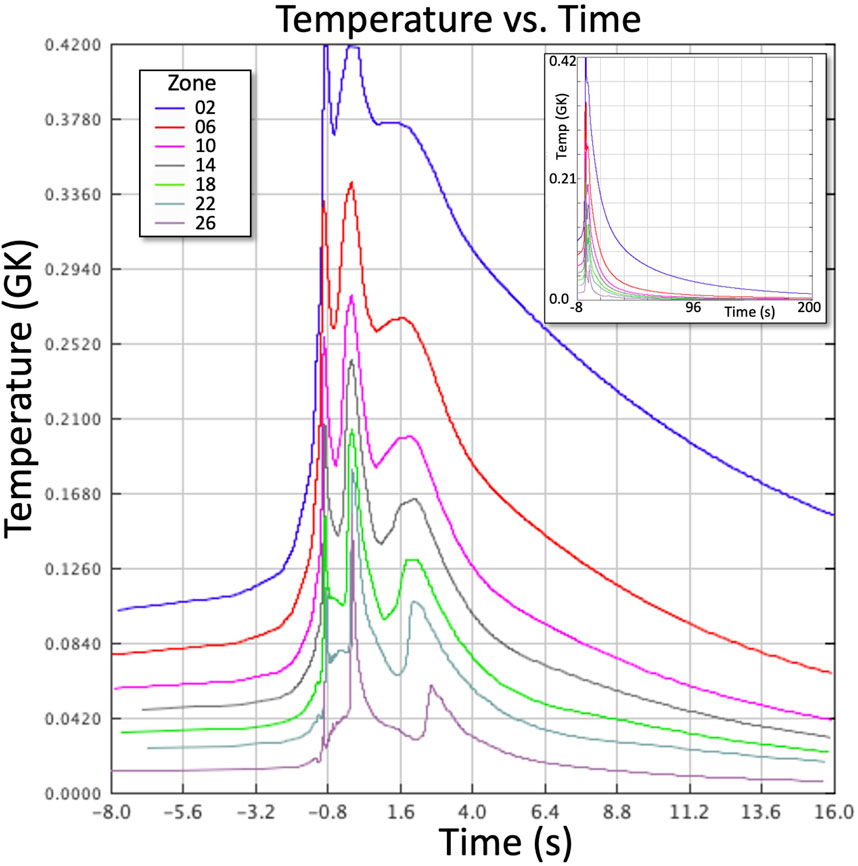
Figure 9. Temperature profiles for some of the hydrodynamic zones of an energetic nova explosion (Politano et al., 1995). The innermost (outermost) zones have the highest (lowest) peak temperatures. Some zones are not plotted for clarity. The zero time is set at the peak temperature of the event. Inset: The same profiles shown over a longer time scale.

While there are other numerical techniques that could be used for the above input manipulations, the ML approaches mentioned could produce excellent results that are complementary to traditional techniques used for regression, smoothing, and outlier detection.

Another approach to improving models is to identify outliers in model predictions or outputs. For example, when running a Monte Carlo ensemble of simulations for UQ as described above in Section 3.3, ML outlier approaches could be used to flag any anomalous outputs; the inputs for that particular simulation run could then be examined for anomalies and appropriately corrected. This “back-tracing” of outlying outputs to find anomalous inputs with ML could also be invaluable for parameter space explorations which are so widely used in many fields including nucleosynthesis [e.g., Nakamura et al. (1999)]; more discussions of parameter space explorations are given in the next subsection.

3.6 Scientific workflows

3.6.1 Exploring parameter space

The above subsections have detailed some of the discovery potential of ML to improve our understanding and approximations of nucleosynthesis flows, to perform SA, to determine prediction uncertainties, and to improve inputs for nucleosynthesis simulations. Many of these ML-based investigations likely begin by developing an appropriate model, obtaining or generating an extensive training dataset, and training and adjusting the model. For some projects, it is then necessary to execute the model hundreds or thousands of times to explore some particular input parameter space, followed by the critical steps of processing, analyzing, visualizing, and comparing results of each run before choosing the next set of inputs. The immense parameter space of some problems – which for nuclear astrophysics could be initial abundances, hydrodynamic histories over a multi-dimensional spatial grid, and thermonuclear reaction rate values – along with the complexity of operations at each execution makes many such projects computationally intractable without extensive parameter space truncations and/or model approximations. As an example, the parameter study of core-collapse supernova models in Nakamura et al. (1999). used approximations for generating an explosion (artificially depositing energy in the core) as well as for exploring nucleosynthesis (tracking only 13 nuclides, followed by post-processing calculations that tracked 211 species).

In some fields, ML approaches are now removing the need for such approximations when exploring large parameter spaces. An example is the high-profile 3D protein folding problem, where new protein discoveries can tremendously impact drug development, medical research, environmental remediation, and many other fields. AlphaFold (Jumper et al., 2021), a DNN protein folding model designed for these searches, was able to predict over 350,000 stable 3D protein folding structures in 2021; this number grew to $2\times {10}^7$ one year later. In comparison, traditional techniques had yielded only 70,000 structures in 60 years of work, a pace requiring $\sim {10}^9$ years to match the performance of AlphaFold. Similarly, the GNoME Project (Merchant et al., 2023) used GNNs to explore the vast parameter space of crystalline structures for materials science research. It predicted 2.2 million new structures, of which about one-quarter are thought to be especially stable; this work thereby expanded the number of such materials known to man by an order of magnitude.

A promising approach to explore the expansive nucleosynthesis parameter spaces described above may be to have algorithms that interact with the space in order to most efficiently direct (“steer”) searches. This suggests a reinforcement learning approach, wherein an “agent” interacts with an environment and learns in stages to make decisions that maximize a reward function (Arulkumaran et al., 2017). For nucleosynthesis studies, the reward function could be the production of certain ratios of abundances or certain radiation fluxes to match observations. LLMs are now being used to generate rewards that outperform those engineered by human experts (Ma et al., 2024), without the need to train on task-specific examples. Since reinforcement learning approaches are growing more popular in physics research (Martín-Guerrero and Lamata, 2021), it is quite possible that (LLM-powered) reinforcement learning could soon be utilized to advance our understanding of nucleosynthesis.

Such examples give a glimpse into the rapidly-expanding capabilities of ML for exploring large parameter spaces – a proficiency that could be extremely useful for nucleosynthesis research.

3.6.2 Transforming workflows

The workflow of most research projects includes many important, but rote, tasks such as literature searches/summaries and generating reports and presentations. For many, these and related efforts are serious productivity bottlenecks that can limit time spent generating new insights and discoveries. Fortunately, LLMs can be used to reduce some of these burdens, as well as streamline and accelerate many other critical aspects of scientific workflows.

Triggered by the development of the Transformers architecture (Vaswani et al., 2017) and the use of (up to) $\sim {10}^{11}$ DNN model parameters trained on enormous textual datasets of $\sim {10}^{12}$ tokens (words), LLMs have rapidly (since 2022) gained wide acceptance through their ability to adeptly answer text queries (denoted as “prompts”) via a familiar chat interface (e.g., ChatGPT (OpenAI, 2022)). LLMs can quickly provide detailed background information, summarize and synthesize literature results, refine text passages, outline and draft reports and papers, generate computer codes, process and visualize data, recommend and prioritize research problems, and perform many other important research tasks. In essence, LLMs can function as research assistants.

There is currently a race to develop larger and ever-more capable LLMs and LLM-based tools, especially those fine-tuned to have multi-modal (text, audio/video, data analysis, coding, and more) capabilities. Foundation models FMs (Bommasani et al., 2021) are pre-trained on unlabeled multi-model data as general purpose tools, allowing even further fine-tuning that may make them particularly well suited to serve as research assistants with extensive data analysis capabilities.

As with any new approach, LLMs and FMs have limitations and problems, both technical (Nejjar et al., 2023) and conceptual (Birhane et al., 2023); some of these are discussed in Section 4 below along with recent approaches to their solution. In spite of their issues, the use of LLMs in research, and their acceptance as an invaluable tool, is rapidly growing. It would be advantageous for nucleosynthesis researchers to capitalize on the rapidly-developing capabilities of LLMs and FMs for their work.

4 Challenges

Given the widespread utilization of ML in many fields, much attention has been given to enumerating and addressing the challenges and limitations of these approaches. We briefly discuss some critical issues (and their possible solutions) below; for more details, see the review on ML for physics in Carleo et al. (2019).

4.1 Training datasets

The success of any ML model depends in large part to the availability of large, high-quality, low-noise, bias-free data sets for training. For many research problems, these are not easy to obtain or generate. The first step is to determine the training data contents needed for a particular study. For simulation-based studies of nucleosynthesis, the contents may likely consist of collections of ($input$, $output$) pairs, where the $input$ would describe the astrophysical environment type (e.g., core-collapse supernova) and properties (e.g., mass distribution, entropy, and electron fraction in the core), initial abundances, a thermonuclear reaction rate library, and thermodynamics information such as initial conditions for hydrodynamics calculations or temperature and density histories for post-processing simulations. The $output$ depends on the nature of the problem being addressed. For the studies discussed in Section 3, these include: the final abundances for all relevant isotopes; a collection of abundances at various time steps during the simulation; those time-dependent abundances with added hydrodynamic and/or position information; images of final abundances (e.g., Figure 2) or reaction fluxes (e.g., Figure 3) on the nuclide chart; time-dependent nuclide chart images of abundances (e.g., Figure 6), reaction fluxes, or abundance derivatives (e.g., Figure 7) along with hydrodynamics information; one-dimensional plots of abundance vs time (e.g., Figure 1); abundances and hydrodynamics information from tracer particles (see Section 3.1); or combinations of the above information.

Once the data contents for a new study are determined, a dataset can be established by processing or augmenting datasets from previous studies or external sources, or can be generated through many new executions of the relevant simulation(s). For simulation-based studies of nucleosynthesis, this latter option – running many simulations with a variety of inputs to generate “synthetic” data – is ideal, if the researcher has the appropriate astrophysical codes. One critical factor here is to ensure that the distribution of input values are representative of the actual distribution so as to avoid biased results. There is an extensive general-purpose literature on this topic and methods to reduce biases; for details, see Jeong et al. (2018) and Mehrabi et al. (2021). Another key point is to include a sufficiently wide variation of inputs for these simulation runs so that they span the range needed for future use of the trained ML model. That is, the ML model should be used to generate interpolations rather than (less reliable) extrapolations whenever possible. Other well-studied, important training techniques include methods to avoid over-fitting (Ying, 2019), and partitioning datasets for training/testing/validation (Xu and Goodacre, 2018).

Since some nucleosynthesis researchers do not have access to simulation codes, and few researchers have access to codes for all astrophysical environments, a set of curated archives of nucleosynthesis simulation results would be invaluable to enable many more in the community to launch ML-based studies.

4.2 Model choice, execution, and performance

For a given problem, selecting an appropriate ML algorithm to use among the many choices can be a challenge in this quickly-evolving field. For example, some algorithms adapt to larger or changing data sets better than others, and some are flexible enough to be used for multiple projects with minimal changes. There is also a steep learning curve for some ML algorithms, which constrains the number of researchers adopting these approaches – and which suggests the utility of collaborating with ML experts. Additionally, the lack of “interpretability” of many ML models – especially NNs – limit their acceptance by many researchers (including peer reviewers). The complex nature of the algorithms often makes it nearly impossible to determine which features of the data are responsible for the predictions (Barbierato and Gatti, 2024). However, some models are more interpretable than others, suggesting that careful model choice may help with collaborative research projects as well as with publication peer review. The topic of ML model interpretability is reviewed in Rudin et al. (2022) and is discussed in terms of sensitivity analyses in Scholbeck et al. (2023).

Regarding execution, most ML approaches are computationally intensive, so the availability of adequate compute resources (particularly those with graphical processing units or tensor processing units) is essential. Large storage systems with fast I/O are needed for handling the large data sets needed for model training. Knowledge of the python coding language is essential for some projects, as is access to python libraries such as pyTorch, TensorFlow, Matplotlib, NumPy, Scikit-learn, and others (Raschka, 2015; Saabith et al., 2020).

Regarding model performance, extrapolating models to parameter regions beyond those in the training data can provide significant limitations on the potential for scientific insights from ML techniques. This can be partially addressed by interpretable models (Muckley et al., 2023) and by physics-driven models (Brahma et al., 2021), but is best handled by generating predictions within the bounds of the training data. Another issue is over-fitting (Ying, 2019) and under-fitting, both of which can lead to poor model performance. Because this is a widely known issue, there are many established mechanisms to monitor and avoid such effects (Salman and Liu, 2019).

4.3 Large Language Model Challenges

The extremely rapid development of LLMs makes it likely that any list of challenges with their use will be quickly outdated, because many current issues will be solved while new problems will arise as capabilities increase. For this reason, Kaddour et al. (2023) systematically formulated 16 major categories of open problems for LLMs and then comprehensively discussed, for each, the latest examples and solution approaches. Below, we will describe some of the issues with LLMs that are the most relevant for scientific research: flawed output, lack of reasoning, and data handling.

For the first issue, there are many different examples of incorrect or nonsensical LLM output, including: when models have incomplete, biased, or no training on data in a particular scientific domain; when the training data is outdated by recent research; when their (statistically-generated) responses differ from the “ground truth”; and when responses are nonsensical or are fabricated lies that are presented in an authoritative manner (“hallucinations” (Yao J. Y. et al., 2023)). Given these numerous flaws, users must be cautious when using LLM output for research purposes. There are many approaches being pursued to rectify these issues. The first is better training, both in general and especially domain-specific, which could be done by some users with smaller LLMs on their own data. Another is requiring the LLM to utilize “ground truth” information – via manually-uploaded curated data sets (Perplexity, 2024), accessing a database via knowledge trees (Dietterich, 2023; Sarthi et al., 2024) or (especially) knowledge graphs (Diffbot, 2024), attaching a web browser to the LLM (Google, 2024), or using a retrieval-augmented generation (RAG) framework (Lewis et al., 2020). In this latter approach, relevant “expert” content is first retrieved from a source (e.g., a database or the internet) and then fed to an LLM along with the query to generate a response along with the expert reference. Additionally, improved prompting (shorter, multi-step queries) has been shown to improve response quality, as have “mixture of experts”/“mixture of models” approaches wherein multiple models are given the same prompt and answers are polled and combined.

The second major issue – a lack of scientific reasoning – arises because LLMs are trained on internet-scale amounts of textual data to generate the most probable response to a query, rather than understanding the underlying scientific principles (e.g., cause and effect). As a result, LLMs often cannot generate a step-by-step reasoning process for a response, have difficulty in verifying or reproducing results, have limited capabilities to review scientific papers, and generally perform more poorly than humans on reasoning benchmarks (Yu et al., 2022). The overwhelming need to use and display reasoning in LLM responses has led to much research activity in this topic. One approach that has improved reasoning abilities is to use “chain-of-thought” prompting (Wei et al., 2022) wherein exemplars of intermediate reasoning steps are provided as LLM input. Another approach is LangChain (Topsakal and Akinci, 2023), a modular approach to building LLM-driven applications where subroutines and external programs can be called in a user-defined sequence to perform, for example, calculations or searches that supplement and enhance the LLM output. This is effectively hard-wiring a workflow that includes an LLM. A third approach is “visualization of thought” (Wu W. et al., 2024) wherein reasoning steps are spatially visualized and followed; this approach could be useful for interpreting causality in reaction flow diagrams.

A fourth approach to incorporating scientific reasoning is the ReAct framework (Yao S. et al., 2023) that combines tasks devoted to reasoning with those for action, in an effort to mimic human learning. Specifically, an LLM is prompted to generate a “chain-of-thought” reasoning response, and then to generate an appropriate action, get feedback from the environment (an observation), and repeat the process. As a hypothetical example for nucleosynthesis, if the task is to answer the question “Has the approach to uncertainty quantification used in this nucleosynthesis journal article been used for studies of other astrophysical scenarios?”, then the first reasoning result could be “I need to search this journal article and find which uncertainty quantification method was used”. The first action could then be to carry out the search, and if the observation (the search result) is null (e.g., no mention of “uncertainty quantification method” in the article), then the next round of reasoning could be “I need to determine other terminologies for ‘uncertainty quantification’ ” leading to a next round of action (a second search) and observation (that terms like “error analysis” or “probability distribution function determination” are possible alternatives). The iterative nature of reasoning/action/observation is a significant improvement over the return of a single response typical of most LLMs.

The third major issue – data handling – arises because LLMs are primarily trained on textual data rather than on tabular, time series, graphical, or other numerical data formats. While it may seem more appropriate to use other ML tools for data handling and analyses, LLMs are now becoming integrated into many scientific workflows, driving efforts to enhance their capabilities by fine-tuning on non-textual data. One approach is to greatly expand LLM fine-tuning training datasets to include labeled audio, video, and numerical data files. An example is provided in the recent release of ChatGPT 4o (OpenAI, 2024), which (among other advances) exhibits true multi-modal capabilities and can interpret user-provided tabular and graphical data. Another technique for numerical data handling is to use an “agent”-centered approach (Wu Q. et al., 2023) wherein a larger problem is broken up into subtasks, each of which is handled by a different ML model (some of which may be LLMs) playing a different role and collaborating in the overall solution. Even when all the agents are from a single LLM, this approach gives superior performance due to more targeted prompts. Including numerical-based models like those described in Section 2 as agents can boost performance with data handling, analysis, and interpretation tasks. This was demonstrated in Data-Copilot (Zhang et al., 2023) where a custom workflow with multiple data-centered tools combined with an LLM is autonomously created in response to complex problems provided by users. For problems that require writing computer code, researchers could consider integrating a software developer agent like Devin (Cognition Labs, 2024) into their workflow. Finally, the issue of data handling is naturally incorporated into the pre-training phase of FM development. This approach has the significant benefit of using unlabeled training data, and generates models that can handle a wide range of data sets and analysis goals (Jakubik et al., 2023).

Some researchers recommend that LLMs should play only a subsidiary role in research (Birhane et al., 2023), and some are concerned about possible emergent capabilities with FMs and their societal impact (Bommasani et al., 2021); there are others, however, who are strident advocates of the use of these tools [e.g., Chen et al. (2024) and Jakubik et al. (2023)]. Given the current rate of development of LLM and FM capabilities, it is likely that they will become an integral portion of the workflows of the next (and perhaps even the current) generation of researchers.

Overall, it is important to acknowledge that ML techniques are not a simple panacea for all research roadblocks. However, used with the appropriate caution, the examples given above illustrate the promise and possibilities of capitalizing on ML approaches to advance the methodology of simulation-based studies of nucleosynthesis and to improve our understanding of the cosmic creation of the elements.

5 Summary

Machine learning approaches have proven extremely useful in many fields including astrophysics and nuclear physics but have an untapped potential in nuclear astrophysics. Some very promising utilizations of ML are for studies to advance our understanding of the complex processes that synthesize nuclides in astrophysical environments. We briefly summarize the characteristics of 30 widely-utilized ML algorithm types, and then describe how they can be used for simulation-based nucleosynthesis studies. Specifically, we describe unexplored possibilities for ML to better understand and approximate nucleosynthetic flows, to quantify uncertainties, to perform sensitivity analyses, and to identify anomalous inputs. We also discuss how ML tools can speed up scientific workflows and improve research productivity. The use of ML to advance the decades-old methodology of simulation-based studies of nucleosynthesis has the potential to significantly improve our understanding of the cosmic creation of the elements and thereby open a new frontier in nuclear astrophysics research. This is especially the case given the rapid development of the capabilities of ML tools. Collaborations between nuclear astrophysicists and ML experts would be an excellent way to realize the promise of ML for nucleosynthesis studies.

Author contributions

MS: Writing–original draft, Writing–review and editing. DL: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the U.S. Department of Energy Office of Science, Office of Nuclear Physics, under Contract Number DE-AC05-00OR22725 with UT-Battelle, LLC, at ORNL.

Acknowledgments

The authors wish to thank John Sparger and Austin Harris for useful discussions and comments on the manuscript. The publisher acknowledges the US government license to provide public access under the DOE Public Access Plan (http://energy.gov/downloads/doe-public-access-plan).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdar, M., Pourpanah, F., Hussain, S., Rezazadegan, D., Liu, L., Ghavamzadeh, M., et al. (2021). A review of uncertainty quantification in deep learning: techniques, applications and challenges. Inf. Fusion 76, 243–297. doi:10.1016/j.inffus.2021.05.008

CrossRef Full Text | Google Scholar

Aidala, C., Aprahamian, A., Bedaque, P., Bernstein, L., Carlson, J., Carpenter, M., et al. (2023). A new era of discovery: the 2023 long-range plan for nuclear science. Livermore, CA (United States): Tech. rep., Lawrence Livermore National Laboratory LLNL.

Google Scholar

Al Iqbal, M. R., Rahman, S., Nabil, S. I., and Chowdhury, I. U. A. (2012). “Knowledge based decision tree construction with feature importance domain knowledge,” in 2012 7th international conference on electrical and computer engineering, Dhaka, Bangladesh, 20-22 December 2012 (IEEE), 659–662.

CrossRef Full Text | Google Scholar

Almgren, A. S., Beckner, V. E., Bell, J. B., Day, M. S., Howell, L. H., Joggerst, C. C., et al. (2010). CASTRO: a new compressible astrophysical solver. I. Hydrodynamics and self-gravity. Astrophys. J. 715, 1221–1238. doi:10.1088/0004-637X/715/2/1221

CrossRef Full Text | Google Scholar

Ankile, L. L., Heggland, M. F., and Krange, K. (2020). Deep convolutional neural networks: a survey of the foundations, selected improvements, and some current applications. arXiv preprint arXiv:2011. 12960.

Google Scholar

Arcones, A., and Thielemann, F. K. (2023). Origin of the elements. Astron. Astrophys. Rev. 31, 1. doi:10.1007/s00159-022-00146-x

CrossRef Full Text | Google Scholar

Arimura, R. (2023). A machine learning approach for mass composition analysis with TALE-SD data. Eur. Phys. J. Web Conf. 283, 02011. doi:10.1051/epjconf/2023283020111051/epjconf/202328302011

CrossRef Full Text | Google Scholar

Arnett, D. (1996). Supernovae and nucleosynthesis: an investigation of the history of matter, from the big bang to the present, 7. Princeton University Press. doi:10.1515/9780691221663

CrossRef Full Text | Google Scholar

Arulkumaran, K., Deisenroth, M. P., Brundage, M., and Bharath, A. A. (2017). Deep reinforcement learning: a brief survey. IEEE Signal Process. Mag. 34, 26–38. doi:10.1109/msp.2017.2743240

CrossRef Full Text | Google Scholar

Barbierato, E., and Gatti, A. (2024). The challenges of machine learning: a critical review. Electronics 13, 416. doi:10.3390/electronics13020416

CrossRef Full Text | Google Scholar

Bethe, H. A., and Wilson, J. R. (1985). Revival of a stalled supernova shock by neutrino heating. Astrophys. J. 295, 14–23. doi:10.1086/163343

CrossRef Full Text | Google Scholar

Beun, J., Blackmon, J. C., Hix, W. R., Mclaughlin, G. C., Smith, M. S., and Surman, R. (2008). Neutron capture on ¹³⁰Sn during r-process freeze-out. J. Phys. G. Nucl. Part. Phys. 36, 025201. doi:10.1088/0954-3899/36/2/025201

CrossRef Full Text | Google Scholar

Birhane, A., Kasirzadeh, A., Leslie, D., and Wachter, S. (2023). Science in the age of large language models. Nat. Rev. Phys. 5, 277–280. doi:10.1038/s42254-023-00581-4

CrossRef Full Text | Google Scholar

Bisong, E., and Bisong, E. (2019). Logistic regression. Build. Mach. Learn. Deep Learn. Models Google Cloud Platf. A Compr. Guide Beginners, 243–250. doi:10.1007/978-1-4842-4470-8_20

CrossRef Full Text | Google Scholar

Boehnlein, A., Diefenthaler, M., Sato, N., Schram, M., Ziegler, V., Fanelli, C., et al. (2022). Colloquium: machine learning in nuclear physics. Rev. Mod. Phys. 94, 031003. doi:10.1103/RevModPhys.94.031003

CrossRef Full Text | Google Scholar

Bommasani, R., Hudson, D. A., Adeli, E., Altman, R., Arora, S., von Arx, S., et al. (2021). On the opportunities and risks of foundation models. arXiv Prepr. arXiv:2108.07258. doi:10.48550/arXiv.2108.07258

CrossRef Full Text | Google Scholar

Bovard, L., and Rezzolla, L. (2017). On the use of tracer particles in simulations of binary neutron stars. Class. Quantum Gravity 34, 215005. doi:10.1088/1361-6382/aa8d98

CrossRef Full Text | Google Scholar

Brahma, I., Jennings, R., and Freid, B. (2021). Using physics to extend the range of machine learning models for an aerodynamic, hydraulic and combusting system: the toy model concept. Energy AI 6, 100113. doi:10.1016/j.egyai.2021.100113

CrossRef Full Text | Google Scholar

Breiman, L. (2017). Classification and regression trees. Routledge.

Google Scholar

Bufano, F., Riggi, S., Sciacca, E., and Schilliro, F. (2022). Machine learning for astrophysics in International conference 30 may (Springer), 1.

Google Scholar

Carleo, G., Cirac, I., Cranmer, K., Daudet, L., Schuld, M., Tishby, N., et al. (2019). Machine learning and the physical sciences. Rev. Mod. Phys. 91, 045002. doi:10.1103/revmodphys.91.045002

CrossRef Full Text | Google Scholar

Caughlan, G. R., and Fowler, W. A. (1962). The mean lifetimes of carbon, nitrogen, and oxygen nuclei in the cno bicycle. Astrophys. J. 136, 453. doi:10.1086/147399

CrossRef Full Text | Google Scholar

Cava, W. L., Orzechowski, P., Burlacu, B., de Franca, F. O., Virgolin, M., Jin, Y., et al. (2021). Contemporary symbolic regression methods and their relative performance. Thirty-fifth Conf. Neural Inf. Process. Syst. Datasets Benchmarks Track (Round 1) 1.

Google Scholar

Chen, L., Ahmed, N. K., Dutta, A., Bhattacharjee, A., Yu, S., Mahmud, Q. I., et al. (2024). Position paper: the landscape and challenges of HPC research and LLMs. arXiv Prepr. arXiv:2402.02018. doi:10.48550/arXiv.2402.02018

CrossRef Full Text | Google Scholar

Clayton, D. D. (1983). Principles of stellar evolution and nucleosynthesis. University of Chicago Press.

Google Scholar

Cognition Labs (2024). Introducing Devin, the first AI software engineer. Available at: https://www.cognition-labs.com/introducing-devin.

Google Scholar

Cranmer, M., Sanchez Gonzalez, A., Battaglia, P., Xu, R., Cranmer, K., Spergel, D., et al. (2020). Discovering symbolic models from deep learning with inductive biases. Adv. Neural Info. Proc. Sys. 33, 17429–17442.

Google Scholar

Cutler, A., Cutler, D. R., and Stevens, J. R. (2012). Random forests. New York, NY: Springer New York, 157–175. chap. 5. doi:10.1007/978-1-4419-9326-7_5

CrossRef Full Text | Google Scholar

Cybenko, G. (1989). Approximation by superpositions of a sigmoidal function. Math. control, signals Syst. 2, 303–314. doi:10.1007/bf02551274

CrossRef Full Text | Google Scholar

Cyburt, R. H., Amthor, A. M., Ferguson, R., Meisel, Z., Smith, K., Warren, S., et al. (2010). The JINA REACLIB database: its recent updates and impact on type-I X-ray bursts. Astrophys. J. Suppl. Ser. 189, 240–252. doi:10.1088/0067-0049/189/1/240

CrossRef Full Text | Google Scholar

den Hartogh, J. W., Yagüe López, A., Cseh, B., Pignatari, M., Világos, B., Roriz, M. P., et al. (2023). Barium stars as tracers of s-process nucleosynthesis in AGB stars. II. Using machine learning techniques on 169 stars. Astron. Astrophys. 672, A143. doi:10.1051/0004-6361/202244189

CrossRef Full Text | Google Scholar

DeVore, R., Hanin, B., and Petrova, G. (2021). Neural network approximation. Acta Numer. 30, 327–444. doi:10.1017/s0962492921000052

CrossRef Full Text | Google Scholar

Dietterich, T. G. (2023). What’s wrong with large language models and what we should be building instead. Available at: https://web.engr.oregonstate.edu/∼tgd/talks/dietterich-fixing-llms-cods-comad-2024.pdf.

Google Scholar

Diffbot (2024). Diffbot. Available at: https://www.diffbot.com/.

Google Scholar

Ding, J., Huang, Y., Li, X. D., Wang, X., Wang, Y., and Yang, L. (2023). Hybrid deep learning for blazar classification and correlation search with neutrinos. Mon. Not. Roy. Astron. Soc. 523, 4120–4135. doi:10.1093/mnras/stad1683

CrossRef Full Text | Google Scholar

Dunham, S. J., Endeve, E., Mezzacappa, A., Blondin, J. M., Buffaloe, J., and Holley-Bockelmann, K. (2023). A parametric study of the SASI comparing general relativistic and non-relativistic treatments. arXiv preprint arXiv:2307.10904.

Google Scholar

Espadoto, M., Martins, R. M., Kerren, A., Hirata, N. S., and Telea, A. C. (2019). Toward a quantitative survey of dimension reduction techniques. IEEE Trans. Vis. Comput. Graph. 27, 2153–2173. doi:10.1109/tvcg.2019.2944182

PubMed Abstract | CrossRef Full Text | Google Scholar

Fan, D., Willcox, D. E., DeGrendele, C., Zingale, M., and Nonaka, A. (2022). Neural networks for nuclear reactions in MAESTROeX. Astrophys. J. 940, 134. doi:10.3847/1538-4357/ac9a4b

CrossRef Full Text | Google Scholar

Fields, B. (2023). “Big bang nucleosynthesis: nuclear physics in the early Universe,” in Handbook of nuclear physics. Editors I. Tanihata, H. Toki, and T. Kajino (Singapore: Springer Nature Singapore), 111. doi:10.1007/978-981-15-8818-1_111-1

CrossRef Full Text | Google Scholar

Fodor, I. K. (2002). A survey of dimension reduction techniques. Tech. rep. Livermore, CA (United States): Lawrence Livermore National Lab. LLNL.

Google Scholar

Fraser, T. S., Tojeiro, R., and Chittenden, H. G. (2023). Applying unsupervised learning to resolve evolutionary histories and explore the galaxy-halo connection in IllustrisTNG. Mon. Not. Roy. Astron. Soc. 522, 5758–5774. doi:10.1093/mnras/stad015

CrossRef Full Text | Google Scholar

Friedman, J. H. (2001). Greedy function approximation: a gradient boosting machine. Ann. Statistics 29, 1189–1232. doi:10.1214/aos/1013203451

CrossRef Full Text | Google Scholar

Fryxell, B., Olson, K., Ricker, P., Timmes, F. X., Zingale, M., Lamb, D. Q., et al. (2000). FLASH: an adaptive mesh hydrodynamics code for modeling astrophysical thermonuclear flashes. Astrophys. J. Suppl. Ser. 131, 273–334. doi:10.1086/317361

CrossRef Full Text | Google Scholar

Galloway, D. K., Chenevez, J., Wörpel, H., Keek, L., Ootes, L., Watts, A. L., et al. (2020). The multi-instrument burst archive (MINBAR). Astrophys. J. Suppl. Ser. 249, 32. doi:10.3847/1538-4365/ab9f2e

CrossRef Full Text | Google Scholar

Gargouri, R., Akkoyun, S., Maalej, R., and Damak, K. (2023). Performance of machine learning algorithms on neutron activations for Germanium isotopes. Rad. Phys. Chem. 208, 110860. doi:10.1016/j.radphyschem.2023.110860

CrossRef Full Text | Google Scholar

Ghanem, R., Higdon, D., Owhadi, H., et al. (2017). Handbook of uncertainty quantification, 6. New York: Springer.

Google Scholar

Gonog, L., and Zhou, Y. (2019). A review: generative adversarial networks. 2019 14th IEEE Conf. Industrial Electron. Appl. (ICIEA), 505–510. doi:10.1109/ICIEA.2019.8833686

CrossRef Full Text | Google Scholar

González-Morán, A. L., Arrabal Haro, P., Muñoz-Tuñón, C., Rodríguez-Espinosa, J. M., Sánchez-Almeida, J., Calhau, J., et al. (2023). The PAU survey: classifying low-z SEDs using Machine Learning clustering. Mon. Not. Roy. Astron. Soc. 524, 3569–3581. doi:10.1093/mnras/stad2123

CrossRef Full Text | Google Scholar

Google (2024). Google gemini. Available at: https://gemini.google.com.

Google Scholar

Grichener, A., Renzo, M., Kerzendorf, W., Bellinger, E., Justham, S., Farmer, R., et al. (2024). Nuclear neural networks-implementing machine-learning methods for stellar nucleosynthesis. Available at: https://kspa.soe.ucsc.edu/sites/default/files/Aldana_Grichener___KSPA_final_report.pdf.

Google Scholar

Gustafsson, F. K., Danelljan, M., and Schon, T. B. (2020). Evaluating scaleable Bayesian deep learning methods for robust computer vision. Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit. Work., 318–319.

Google Scholar

Harshvardhan, G. M., Gourisaria, M. K., Pandey, M., and Rautaray, S. S. (2020). A comprehensive survey and analysis of generative models in machine learning. Comput. Sci. Rev. 38, 100285. doi:10.1016/j.cosrev.2020.100285

CrossRef Full Text | Google Scholar

Harris, J. A., Hix, W. R., Chertkow, M. A., Lee, C., Lentz, E. J., and Messer, O. B. (2017). Implications for post-processing nucleosynthesis of core-collapse supernova models with Lagrangian particles. Astrophys. J. 843, 2. doi:10.3847/1538-4357/aa76de

CrossRef Full Text | Google Scholar

Hastie, T., Tibshirani, R., Friedman, J., Hastie, T., Tibshirani, R., and Friedman, J. (2009). Kernel smoothing methods. Elem. Stat. Learn. Data Min. Inference, Predict., 191–218. doi:10.1007/978-0-387-84858-7_6

CrossRef Full Text | Google Scholar

He, W., Li, Q., Ma, Y., Niu, Z., Pei, J., and Zhang, Y. (2023). Machine learning in nuclear physics at low and intermediate energies. Sci. China Phys. Mech. and Astronomy 66, 282001. doi:10.1007/s11433-023-2116-0

CrossRef Full Text | Google Scholar

Hernández, C. A., González, R. E., and Padilla, N. D. (2023). Not hydro: using neural networks to estimate galaxy properties on a dark-matter-only simulation. Mon. Not. Roy. Astron. Soc. 524, 4653–4669. doi:10.1093/mnras/stad2112

CrossRef Full Text | Google Scholar

Hix, W. R. (2024). XNET. Available at: https://eagle.phys.utk.edu/xnet/trac/.

Google Scholar

Hix, W. R., and Meyer, B. S. (2006). Thermonuclear kinetics in astrophysics. Nuc. Phys. A 777, 188–207. doi:10.1016/j.nuclphysa.2004.10.009

CrossRef Full Text | Google Scholar

Hix, W. R., Smith, M. S., Starrfield, S., Mezzacappa, A., and Smith, D. L. (2003). Impact of nuclear reaction rate uncertainties on nova models. Nucl. Phys. A 718, 620–622. doi:10.1016/s0375-9474(03)00904-7

CrossRef Full Text | Google Scholar

Hix, W. R., and Thielemann, F. K. (1999). Computational methods for nucleosynthesis and nuclear energy generation. J. Comp. Appl. Math. 109, 321–351. doi:10.1016/s0377-0427(99)00163-6

CrossRef Full Text | Google Scholar

Ho, J., Saharia, C., Chan, W., Fleet, D. J., Norouzi, M., and Salimans, T. (2022). Cascaded diffusion models for high fidelity image generation. J. Mach. Learn. Res. 23, 1–33.

Google Scholar

Hong, B. (2023). Status of the RAON project in Korea. Assoc. Asia Pac. Phys. Soc. Bull. 33, 3. doi:10.1007/s43673-022-00074-z

CrossRef Full Text | Google Scholar

Hou, Y., Zheng, L., and Gould, S. (2020). Learning to structure an image with few colors. Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit. (CVPR), 10116. doi:10.1109/ICME.2016.7552971

CrossRef Full Text | Google Scholar

Hubschneider, C., Hutmacher, R., and Zöllner, J. M. (2019). Calibrating uncertainty models for steering angle estimation. 2019 IEEE Intell. Transp. Syst. Conf. (ITSC) (IEEE), 1511–1518. doi:10.1109/itsc.2019.8917207

CrossRef Full Text | Google Scholar

Ivakhnenko, A. G. (1971). Polynomial theory of complex systems. IEEE Trans. Syst., Man, Cybern., 364–378. doi:10.1109/tsmc.1971.4308320

CrossRef Full Text | Google Scholar

Jakubik, J., Roy, S., Phillips, C. E., Fraccaro, P., Godwin, D., Zadrozny, B., et al. (2023). Foundation models for generalist geospatial artificial intelligence. arXiv e-prints arXiv:2310.18660

Google Scholar

Jeong, W., Lee, K., Yoo, D., Lee, D., and Han, S. (2018). Toward reliable and transferable machine learning potentials: uniform training by overcoming sampling bias. J. Phys. Chem. C 122, 22790–22795. doi:10.1021/acs.jpcc.8b08063

CrossRef Full Text | Google Scholar

Jin, Y., Shen, Q., Wu, X., Chen, J., and Huang, Y. (2020). A physics-driven deep-learning network for solving nonlinear inverse problems. Petrophysics 61, 86–98. doi:10.30632/pjv61n1-2020a3

CrossRef Full Text | Google Scholar

Jospin, L. V., Laga, H., Boussaid, F., Buntine, W., and Bennamoun, M. (2022). Hands-on Bayesian neural networks—a tutorial for deep learning users. IEEE Comput. Intell. Mag. 17, 29–48. doi:10.1109/MCI.2022.3155327

CrossRef Full Text | Google Scholar

Joyce, M., and Tayar, J. (2023). A review of the mixing length theory of convection in 1D stellar modeling. Galaxies 11, 75. doi:10.3390/galaxies11030075

CrossRef Full Text | Google Scholar

Jumper, J., Evans, R., Pritzel, A., Green, T., Figurnov, M., Ronneberger, O., et al. (2021). Highly accurate protein structure prediction with AlphaFold. Nature 596, 583–589. doi:10.1038/s41586-021-03819-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Kaddour, J., Harris, J., Mozes, M., Bradley, H., Raileanu, R., and McHardy, R. (2023). Challenges and applications of large language models. arXiv preprint arXiv:2307.10169.

Google Scholar

Kasim, M. F., Watson-Parris, D., Deaconu, L., Oliver, S., Hatfield, P., Froula, D. H., et al. (2021). Building high accuracy emulators for scientific simulations with deep neural architecture search. Mach. Learn. Sci. Technol. 3, 015013. doi:10.1088/2632-2153/ac3ffa

CrossRef Full Text | Google Scholar

Kherif, F., and Latypova, A. (2020). “Chapter 12 - principal component analysis,” in Machine learning. Editors A. Mechelli, and S. Vieira (Academic Press), 209–225. doi:10.1016/B978-0-12-815739-8.00012-2

CrossRef Full Text | Google Scholar

Kim, C. H., Chae, K. Y., Smith, M. S., Bardayan, D. W., Brune, C. R., deBoer, R. J., et al. (2024). Probabilistic neural networks for improved analyses with phenomenological models. Phys. Rev. C 110. (in press).

CrossRef Full Text | Google Scholar

Kingma, D. P., Welling, M., et al. (2019). An introduction to variational autoencoders. Found. Trends Mach. Learn. 12, 307–392. doi:10.1561/2200000056

CrossRef Full Text | Google Scholar

Kroese, D. P., Taimre, T., and Botev, Z. I. (2013). Handbook of Monte Carlo methods. John Wiley and Sons.

Google Scholar

Kumar, S., and Bhatnagar, V. (2022). Review of regression models in machine learning. J. Intelligent Sys. Comput. 3, 40–47.

Google Scholar

Lakshminarayanan, B., Pritzel, A., and Blundell, C. (2017). Simple and scalable predictive uncertainty estimation using deep ensembles. Adv. neural Inf. Process. Syst. 30.

Google Scholar

Le, X. K., Wang, N., and Jiang, X. (2023). Nuclear mass predictions with multi-hidden-layer feedforward neural network. Nucl. Phys. 1038, 122707. doi:10.1016/j.nuclphysa.2023.122707

CrossRef Full Text | Google Scholar

Lee, C. C., Chung, P. C., Tsai, J. R., and Chang, C. I. (1999). Robust radial basis function neural networks. IEEE Trans. Syst. Man, Cybern. Part B Cybern. 29, 674–685. doi:10.1109/3477.809023

PubMed Abstract | CrossRef Full Text | Google Scholar

Le Gratiet, L., Marelli, S., and Sudret, B. (2017). Metamodel-based sensitivity analysis: polynomial chaos expansions and Gaussian processes. Springer International Publishing, 1289–1325. chap. 38. doi:10.1007/978-3-319-12385-1_38

CrossRef Full Text | Google Scholar

Lewis, P., Perez, E., Piktus, A., Petroni, F., Karpukhin, V., Goyal, N., et al. (2020). “Retrieval-augmented generation for knowledge-intensive NLP tasks,” in Adv. Neural info. Proc. Syst. Editors H. Larochelle, M. Ranzato, R. Hadsell, M. Balcan, and H. Lin (Curran Associates, Inc.), 33, 9459–9474.

Google Scholar

Li, M., Sprouse, T. M., Meyer, B. S., and Mumpower, M. R. (2024). Atomic masses with machine learning for the astrophysical r process. Phys. Lett. B 848, 138385. doi:10.1016/j.physletb.2023.138385

CrossRef Full Text | Google Scholar

Li Z., Z., Gao, Z., Liu, L., Wang, Y., Zhu, L., and Li, Q. (2024). Importance of physical information on the prediction of heavy-ion fusion cross sections with machine learning. Phys. Rev. C 109, 024604. doi:10.1103/physrevc.109.024604

CrossRef Full Text | Google Scholar

Lippuner, J., and Roberts, L. F. (2017). SkyNet: a modular nuclear reaction network library. Astrophys. J. Suppl. Ser. 233, 18. doi:10.3847/1538-4365/aa94cb

CrossRef Full Text | Google Scholar

Lipton, Z. C., Berkowitz, J., and Elkan, C. (2015). A critical review of recurrent neural networks for sequence learning. arXiv Prepr. arXiv:1506.00019. doi:10.48550/arXiv.1506.00019

CrossRef Full Text | Google Scholar

Liu, F. T., Ting, K. M., and Zhou, Z. H. (2008). Isolation Forest. Eighth IEEE Int. Conf. Data Mining, 413–422. doi:10.1109/ICDM.2008.17

CrossRef Full Text | Google Scholar

Liu, N., Barosch, J., Nittler, L. R., O’D Alexander, C. M., Wang, J., Cristallo, S., et al. (2021). New multielement isotopic compositions of presolar SiC grains: implications for their stellar origins. Ap. J. Lett. 920, L26. doi:10.3847/2041-8213/ac260b

CrossRef Full Text | Google Scholar

Lu, D., Liu, Y., Zhang, Z., Bao, F., and Zhang, G. (2024). A diffusion-based uncertainty quantification method to advance E3SM land model calibration. J. Geophys. Res. Mach. Learn. Comput. 1. In press. doi:10.1029/2024jh000234

CrossRef Full Text | Google Scholar

Lu, D., Ye, M., and Hill, M. C. (2012). Analysis of regression confidence intervals and Bayesian credible intervals for uncertainty quantification. Water Resour. Res. 48. doi:10.1029/2011wr011289

CrossRef Full Text | Google Scholar

Lu, L., Jin, P., Pang, G., Zhang, Z., and Karniadakis, G. E. (2021). Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators. Nat. Mach. Intell. 3, 218–229. doi:10.1038/s42256-021-00302-5

CrossRef Full Text | Google Scholar

Ma, H., Zhang, Y., Thuerey, N., Hu, X., and Haidn, O. J. (2022). Physics-driven learning of the steady Navier-Stokes equations using deep convolutional neural networks. Comm. Comp. Phys. 32, 715–736. doi:10.4208/cicp.OA-2021-0146

CrossRef Full Text | Google Scholar

Ma, Y. J., Liang, W., Wang, G., Huang, D. A., Bastani, O., Jayaraman, D., et al. (2024). Eureka: human-level reward design via coding large language models. arXiv preprint arXiv:2310.12931

Google Scholar

Martín-Guerrero, J. D., and Lamata, L. (2021). Reinforcement learning and physics. Appl. Sci. 11, 8589. doi:10.3390/app11188589

CrossRef Full Text | Google Scholar

Mehrabi, N., Morstatter, F., Saxena, N., Lerman, K., and Galstyan, A. (2021). A survey on bias and fairness in machine learning. ACM Comput. Surv. (CSUR) 54, 1–35. doi:10.1145/3457607

CrossRef Full Text | Google Scholar

Merchant, A., Batzner, S., Schoenholz, S. S., Aykol, M., Cheon, G., and Cubuk, E. D. (2023). Scaling deep learning for materials discovery. Nature 624, 80–85. doi:10.1038/s41586-023-06735-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Meyer, B. S., Krishnan, T. D., and Clayton, D. D. (1998). Theory of quasi-equilibrium nucleosynthesis and applications to matter expanding from high temperature and density. Astrophys. J. 498, 808–830. doi:10.1086/305562

CrossRef Full Text | Google Scholar

Moriwaki, K., Nishimichi, T., and Yoshida, N. (2023). Machine learning for observational cosmology. Rep. Prog. Phys. 86, 076901. doi:10.1088/1361-6633/acd2ea

CrossRef Full Text | Google Scholar

Motobayashi, T., and Sakurai, H. (2012). Research with fast radioactive isotope beams at RIKEN. Prog. Theor. Expt. Phys. 2012, 03C001. doi:10.1093/ptep/pts059

CrossRef Full Text | Google Scholar

Muckley, E. S., Saal, J. E., Meredig, B., Roper, C. S., and Martin, J. H. (2023). Interpretable models for extrapolation in scientific machine learning. Digit. Discov. 2, 1425–1435. doi:10.1039/d3dd00082f

CrossRef Full Text | Google Scholar

Mumpower, M. R., Surman, R., McLaughlin, G., and Aprahamian, A. (2016). The impact of individual nuclear properties on r-process nucleosynthesis. Prog. Part. Nucl. Phys. 86, 86–126. doi:10.1016/j.ppnp.2015.09.001

CrossRef Full Text | Google Scholar

Nakamura, T., Umeda, H., Nomoto, K., Thielemann, F. K., and Burrows, A. (1999). Nucleosynthesis in type II supernovae and the abundances in metal-poor stars. Astrophys. J. 517, 193–208. doi:10.1086/307167

CrossRef Full Text | Google Scholar

National Academies of Sciences, Engineering, and Medicine (2021). Pathways to discovery in astronomy and astrophysics for the 2020s. Washington, DC: The National Academies Press. doi:10.17226/26141

CrossRef Full Text | Google Scholar

Navó, G., Reichert, M., Obergaulinger, M., and Arcones, A. (2023). Core-collapse supernova simulations with reduced nucleosynthesis networks. Astrophys. J. 951, 112. doi:10.3847/1538-4357/acd640

CrossRef Full Text | Google Scholar

Nejjar, M., Zacharias, L., Stiehle, F., and Weber, I. (2023). LLMs for science: usage for code generation and data analysis. Journal of Software: Evolution and Process. doi:10.1002/smr.2723

CrossRef Full Text | Google Scholar

Neronov, A. (2021). Multi-messenger astronomy. J. Phys. Conf. Ser. 2156, 012006. doi:10.1088/1742-6596/2156/1/012006

CrossRef Full Text | Google Scholar

Nesaraja, C., Lingerfelt, E., Scott, J., Smith, M., Hix, W., Bardayan, D., et al. (2005). A new Computational Infrastructure for Nuclear Astrophysics. Nucl. Phys. A 758, 174C–177C. doi:10.1016/j.nuclphysa.2005.05.173

CrossRef Full Text | Google Scholar

NICXVII (2023). 17th international symposium on nuclei in the cosmos. Available at: https://indico.ibs.re.kr/event/548/timetable/#all.

Google Scholar

Nittler, L. R. (2003). Presolar stardust in meteorites: recent advances and scientific frontiers. Earth Plan. Sci. Lett. 209, 259–273. doi:10.1016/S0012-821X(02)01153-6

CrossRef Full Text | Google Scholar

NUCLEI (2022). Nuclear Computational Low Energy Initiative. Available at: https://nuclei.mps.ohio-state.edu/nuclei_home.php.

Google Scholar

NUGRID Collaboration (2024). NUGRID. Available at: https://nugrid.github.io/content/codes_collab.html.

Google Scholar

OMEG (2022). Origins of matter and evolution of galaxies. Available at: https://indico.maygiatoc.com/event/1/timetable/#all.detailed.

Google Scholar

OpenAI (2024). Hello GPT-4o. Available at: https://openai.com/index/hello-gpt-4o/.

Google Scholar

OpenAI (2022). ChatGPT. Available at: https://chatgpt.com.

Google Scholar

Papatheodore, T., and Messer, O. B. (2017). Exposing hierarchical parallelism in the flash code for supernova simulation on Summit and other architectures. Exascale Sci. Appl. Scalability Perform. Portability, 95–118. doi:10.1201/b21930-4

CrossRef Full Text | Google Scholar

Park, S., Yun, C., Lee, J., and Shin, J. (2020). Minimum width for universal approximation. arXiv preprint arXiv:2006.08859.

Google Scholar

Parker, P. D., Bahcall, J. N., and Fowler, W. A. (1964). Termination of the proton-proton chain in stellar interiors. Astrophys. J. 139, 602. doi:10.1086/147789

CrossRef Full Text | Google Scholar

Paxton, B., Bildsten, L., Dotter, A., Herwig, F., Lesaffre, P., and Timmes, F. (2011). Modules for Experiments in Stellar Astrophysics (MESA). Astrophys. J. Suppl. Ser. 192, 3. doi:10.1088/0067-0049/192/1/3

CrossRef Full Text | Google Scholar

Perplexity, A. I. (2024). Perplexity AI. Available at: https://www.perplexity.ai/.

Google Scholar

Politano, M., Starrfield, S., Truran, J., Weiss, A., and Sparks, W. (1995). Hydrodynamic studies of accretion onto massive white dwarfs: ONeMg-enriched nova outbursts. I. Dependence on white dwarf mass. Astrophys. J. 448, 807. doi:10.1086/176009

CrossRef Full Text | Google Scholar

Quinlan, J. R. (1986). Induction of decision trees. Mach. Learn. 1, 81–106. doi:10.1007/bf00116251

CrossRef Full Text | Google Scholar

Radaideh, M. I., and Kozlowski, T. (2020). Analyzing nuclear reactor simulation data and uncertainty with the group method of data handling. Nucl. Eng. Technol. 52, 287–295. doi:10.1016/j.net.2019.07.023

CrossRef Full Text | Google Scholar

Rai, R., and Sahu, C. K. (2020). Driven by data or derived through physics? A review of hybrid physics guided machine learning techniques with cyber-physical system (cps) focus. IEEe Access 8, 71050–71073. doi:10.1109/access.2020.2987324

CrossRef Full Text | Google Scholar

Raschka, S. (2015). Python machine learning. Packt publishing ltd.

Google Scholar

Rasmussen, C. E., and Williams, C. K. I. (2005). Gaussian processes for machine learning. The MIT Press. doi:10.7551/mitpress/3206.001.0001

CrossRef Full Text | Google Scholar

Rauscher, T., Nishimura, N., Cescutti, G., Hirschi, R., and Murphy, A. S. J. (2018). Abundance uncertainties obtained with the PIZBUIN framework for Monte Carlo reaction rate variations. AIP Conf. Proc. AIP Publ. 1947, 020015. doi:10.1063/1.5030819

CrossRef Full Text | Google Scholar

Rembges, F., Freiburghaus, C., Rauscher, T., Thielemann, F. K., Schatz, H., and Wiescher, M. (1997). An Approximation for the rp-Process. Astrophys. J. 484, 412–423. doi:10.1086/304300

CrossRef Full Text | Google Scholar

Roberts, L. F., Hix, W. R., Smith, M. S., and Fisker, J. L. (2006). Monte Carlo simulations of Type I X-ray burst nucleosyntheis. Proc. Sci., 202. doi:10.22323/1.028.0202

CrossRef Full Text | Google Scholar

Rolfs, C. E., and Rodney, W. S. (1988). Cauldrons in the cosmos: nuclear astrophysics. University of Chicago press.

Google Scholar

Rudin, C., Chen, C., Chen, Z., Huang, H., Semenova, L., and Zhong, C. (2022). Interpretable machine learning: fundamental principles and 10 grand challenges. Stat. Surv. 16, 1–85. doi:10.1214/21-ss133

CrossRef Full Text | Google Scholar

Saabith, A. S., Vinothraj, T., and Fareez, M. (2020). Popular python libraries and their application domains. Int. J. Adv. Eng. Res. Dev. 7.

Google Scholar

Salman, S., and Liu, X. (2019). Overfitting mechanism and avoidance in deep neural networks. arXiv Prepr. arXiv:1901.06566. doi:10.48550/arXiv.1901.06566

CrossRef Full Text | Google Scholar

Sanchez-Caballero, A., Alcayne, V., Cano-Ott, D., Mendoza, E., and de Rada, A. P. (2023). A case study on deep learning applied to capture cross section data analysis. Eur. Phys. J. Web Conf. EDP Sci. 284, 16001. doi:10.1051/epjconf/202328416001

CrossRef Full Text | Google Scholar

Sarthi, P., Abdullah, S., Tuli, A., Khanna, S., Goldie, A., and Manning, C. D. (2024). RAPTOR: recursive abstractive processing for tree-organized retrieval. arXiv Prepr. arXiv:2401.18059. doi:10.48550/arXiv.2401.18059

CrossRef Full Text | Google Scholar

Schatz, H., Becerril Reyes, A. D., Best, A., Brown, E. F., Chatziioannou, K., Chipps, K. A., et al. (2022). Horizons: nuclear astrophysics in the 2020s and beyond. J. Phys. G. 49, 110502. doi:10.1088/1361-6471/ac8890

CrossRef Full Text | Google Scholar

Scheidenberge, C. (2017). NUSTAR experiments on the way from GSI to FAIR. Eurasian J. Phys. Funct. Matl. 1, 19. doi:10.29317/ejpfm.2017010103

CrossRef Full Text | Google Scholar

Schnabel, G., Capote, R., Koning, A., and Brown, D. (2021). Nuclear data evaluation with Bayesian networks. arXiv preprint arXiv:2110.10322.

Google Scholar

Scholbeck, C. A., Moosbauer, J., Casalicchio, G., Gupta, H., Bischl, B., and Heumann, C. (2023). Position paper: bridging the gap between machine learning and sensitivity analysis. arXiv Prepr. arXiv:2312.13234. doi:10.48550/arXiv.2312.13234

CrossRef Full Text | Google Scholar

Seitenzahl, I. R., and Pakmor, R. (2020). “Nucleosynthesis and tracer methods in type Ia supernovae,” in Handbook of nuclear physics. Editors I. Tanihata, H. Toki, and T. Kajino (Singapore: Springer Nature Singapore), 1–34. doi:10.1007/978-981-15-8818-1_87-1

CrossRef Full Text | Google Scholar

Seitenzahl, I. R., Röpke, F. K., Fink, M., and Pakmor, R. (2010). Nucleosynthesis in thermonuclear supernovae with tracers: convergence and variable mass particles. Mon. Not. Roy. Astron. Soc. 407, 2297–2304. doi:10.1111/j.1365-2966.2010.17106.x

CrossRef Full Text | Google Scholar

Seshan, A. (2022). Using machine learning to augment dynamic time warping based signal classification. arXiv Prepr. arXiv:2206.07200. doi:10.48550/arXiv.2206.07200

CrossRef Full Text | Google Scholar

Settles, B. (2009). Active learning literature survey. Available at: https://minds.wisconsin.edu/bitstream/handle/1793/60660/TR1648.pdf.

Google Scholar

Sieverding, A., Waldrop, P. G., Harris, J. A., Hix, W. R., Lentz, E. J., Bruenn, S. W., et al. (2023). Tracer particles for core-collapse supernova nucleosynthesis: the advantages of moving backward. Astrophys. J. 950, 34. doi:10.3847/1538-4357/acc8d1

CrossRef Full Text | Google Scholar

Smith, M. S. (2011). Nuclear data for astrophysics research: a new online paradigm. J. Korean Phys. Soc. 59, 761–766. doi:10.3938/jkps.59.761

CrossRef Full Text | Google Scholar

Smith, M. S. (2023). Nuclear data resources and initiatives for nuclear astrophysics. Front. Astron. Space Sci. 10, 1243615. doi:10.3389/fspas.2023.1243615

CrossRef Full Text | Google Scholar

Smith, M. S. (2024). Computational Infrastructure for Nuclear Astrophysics (CINA). Available at: https://nucastrodata.org/infrastructure/.

Google Scholar

Smith, M. S., Kawano, L. H., and Malaney, R. A. (1993). Experimental, computational, and observational analysis of primordial nucleosynthesis. Astrophys. J. Suppl. Ser. 85, 219–247. doi:10.1086/191763

CrossRef Full Text | Google Scholar

Smith, M. S., Lingerfelt, E. J., Scott, J. P., Nesaraja, C. D., Hix, W. R., Chae, K., et al. (2006). Computational Infrastructure for Nuclear Astrophysics. Proc. Origin of Matter and Evolution of galaxies. AIP Conf. Proc. 847, 470.

CrossRef Full Text | Google Scholar

Smith, M. S., and Rehm, K. E. (2001). Nuclear astrophysics measurements with radioactive beams. Ann. Rev. Nucl. Part. Sci. 51, 91–130. doi:10.1146/annurev.nucl.51.101701.132430

CrossRef Full Text | Google Scholar

Song, T., Ding, W., Liu, H., Wu, J., Zhou, H., and Chu, J. (2020). Uncertainty quantification in machine learning modeling for multi-step time series forecasting: example of recurrent neural networks in discharge simulations. Water 12, 912. doi:10.3390/w12030912

CrossRef Full Text | Google Scholar

Stachenfeld, K., Fielding, D. B., Kochkov, D., Cranmer, M., Pfaff, T., Godwin, J., et al. (2021). Learned coarse models for efficient turbulence simulation. arXiv preprint arXiv:2112.15275

Google Scholar

Starrfield, S., Bose, M., Iliadis, C., Hix, W. R., Woodward, C. E., and Wagner, R. M. (2024). Hydrodynamic simulations of oxygen–neon classical novae as galactic ⁷Li producers and potential accretion-induced collapse progenitors. Astrophys. J. 962, 191. doi:10.3847/1538-4357/ad1836

CrossRef Full Text | Google Scholar

Steinwart, I., and Christmann, A. (2008). Support vector machines. Springer Science and Business Media.

Google Scholar

Stone, J. M., Tomida, K., White, C. J., and Felker, K. G. (2020). The athena++ adaptive mesh refinement framework: design and magnetohydrodynamic solvers. Astrophys. J. Suppl. Ser. 249, 4. doi:10.3847/1538-4365/ab929b

CrossRef Full Text | Google Scholar

Suk, H. I. (2017). “Chapter 1 - an introduction to neural networks and deep learning,” in Deep learning for medical image analysis. Editors S. K. Zhou, H. Greenspan, and D. Shen (Academic Press), 3–24. doi:10.1016/B978-0-12-810408-8.00002-X

CrossRef Full Text | Google Scholar

Sun, H. (2024). Machine learning refinements to metallicity-dependent isotopic abundances. arXiv Prepr. arXiv:2403.02678. doi:10.48550/arXiv.2403.02678

CrossRef Full Text | Google Scholar

Tiede, C., Zrake, J., MacFadyen, A., and Haiman, Z. (2022). How binaries accrete: hydrodynamic simulations with passive tracer particles. Astrophys. J. 932, 24. doi:10.3847/1538-4357/ac6c2b

CrossRef Full Text | Google Scholar

Todo, W., Laurent, B., Loubes, J. M., and Selmani, M. (2022). Dimension reduction for time series with Variational AutoEncoders. arXiv preprint arXiv:2204.11060.

Google Scholar

Topsakal, O., and Akinci, T. C. (2023). Creating large language model applications utilizing langchain: a primer on developing LLM apps fast. Int. Conf. Appl. Eng. Nat. Sci. 1, 1050–1056. doi:10.59287/icaens.1127

CrossRef Full Text | Google Scholar

van Wormer, L., Görres, J., Iliadis, C., Wiescher, M., and Thielemann, F. K. (1994). Reaction rates and reaction sequences in the rp-process. Astrophys. J. 432, 326. doi:10.1086/174572

CrossRef Full Text | Google Scholar

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., et al. (2017). Attention is all you need. Adv. Neural Info. Proc. Sys. 30.

Google Scholar

Vicente-Valdez, P., Bernstein, L., and Fratoni, M. (2021). Nuclear data evaluation augmented by machine learning. Ann. Nucl. Energy 163, 108596. doi:10.1016/j.anucene.2021.108596

CrossRef Full Text | Google Scholar

Weaver, T. A., Zimmerman, G. B., and Woosley, S. E. (1978). Presupernova evolution of massive stars. Astrophys. J. 225, 1021–1029. doi:10.1086/156569

CrossRef Full Text | Google Scholar

Webb, G. I., Keogh, E., and Miikkulainen, R. (2010). Naïve Bayes. Encycl. Mach. Learn. 15, 713–714. doi:10.1007/978-0-387-30164-8_576

CrossRef Full Text | Google Scholar

Wei, J., Ao, H., Beher, S., Bultman, N., Casagrande, F., Cogan, S., et al. (2019). Advances of the FRIB project. Int. J. Mod. Phys. E 28, 1930003. doi:10.1142/s0218301319300030

CrossRef Full Text | Google Scholar

Wei, J., Wang, X., Schuurmans, D., Bosma, M., and Xia, F. (2022). “Chain-of-Thought prompting elicits reasoning in large language models,” in Advances in neural information processing systems. Editors S. Koyejo, S. Mohamed, A. Agarwal, D. Belgrave, K. Cho, and A. Oh (Curran Associates, Inc.), 35, 24824–24837.

Google Scholar

Wu, H., Wang, Y., Wang, Y., Deng, X., Cao, X., Fang, D., et al. (2023). Machine learning method for ¹²C event classification and reconstruction in the active target time-projection chamber. Nucl. Inst. Meth. A 1055, 168528. doi:10.1016/j.nima.2023.168528

CrossRef Full Text | Google Scholar

Wu, Q., Bansal, G., Zhang, J., Wu, Y., Zhang, S., Zhu, E., et al. (2023). Autogen: enabling next-gen LLM applications via multi-agent conversation framework. arXiv Prepr. arXiv:2308.08155. doi:10.48550/arXiv.2308.08155

CrossRef Full Text | Google Scholar

Wu, W., Mao, S., Zhang, Y., Xia, Y., Dong, L., Cui, L., et al. (2024). Visualization-of-Thought elicits spatial reasoning in large language models. arXiv Prepr. arXiv:2404.03622. doi:10.48550/arXiv.2404.03622

CrossRef Full Text | Google Scholar

Wu, X. H., Pan, C., Zhang, K. Y., and Hu, J. (2024). Nuclear mass predictions of the relativistic continuum Hartree-Bogoliubov theory with the kernel ridge regression. Phys. Rev. C 109, 024310. doi:10.1103/PhysRevC.109.024310

CrossRef Full Text | Google Scholar

Wu, Z., Pan, S., Chen, F., Long, G., Zhang, C., and Yu, P. S. (2021). A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Sys 32, 4–24. doi:10.1109/TNNLS.2020.2978386

CrossRef Full Text | Google Scholar

Xu, J., and Lange, K. (2019). “Power k-means clustering,” in Proc. 36th int. Conf. Machine learning. Editors K. Chaudhuri, and R. Salakhutdinov (PMLR), 97, 6921–6931.

Google Scholar

Xu, R., Ge, Z., Tian, Y., Tao, X., Jin, Y., Zhang, Y., et al. (2023). Covariance evaluation of neutron cross sections in CENDL. Eur. Phys. J. Web Conf. EDP Sci. 281, 00029. doi:10.1051/epjconf/202328100029

CrossRef Full Text | Google Scholar

Xu, Y., and Goodacre, R. (2018). On splitting training and validation set: a comparative study of cross-validation, bootstrap and systematic sampling for estimating the generalization performance of supervised learning. J. Analysis Test. 2, 249–262. doi:10.1007/s41664-018-0068-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, Z., Hu, J., and Deng, W. (2016). Recurrent convolutional neural network for video classification. 2016 IEEE Int. Conf. Multimedia Expo (ICME), 1–6. doi:10.1109/ICME.2016.7552971

CrossRef Full Text | Google Scholar

Yang, L., Zhang, Z., Song, Y., Hong, S., Xu, R., Zhao, Y., et al. (2023). Diffusion models: a comprehensive survey of methods and applications. ACM Comput. Surv. 56, 1–39. doi:10.1145/3626235

CrossRef Full Text | Google Scholar

Yao, J. Y., Ning, K. P., Liu, Z. H., Ning, M. N., and Yuan, L. (2023). LLM lies: hallucinations are not bugs, but features as adversarial examples. arXiv preprint arXiv:2310.01469. doi:10.48550/arXiv.2310.01469

CrossRef Full Text | Google Scholar

Yao, S., Zhao, J., Yu, D., Du, N., Shafran, I., Narasimhan, K., et al. (2023). ReAct: synergizing reasoning and acting in language models. arXiv Prepr. arXiv:2210.03629. doi:10.48550/arXiv.2210.03629

CrossRef Full Text | Google Scholar

Ying, X. (2019). An overview of overfitting and its solutions. J. Phys. Conf. Ser. IOP Publ. 1168, 022022. doi:10.1088/1742-6596/1168/2/022022

CrossRef Full Text | Google Scholar

Yu, P., Wang, T., Golovneva, O., AlKhamissi, B., Verma, S., Jin, Z., et al. (2022). ALERT: adapting language models to reasoning tasks. arXiv Prepr. arXiv:2212.08286. doi:10.48550/arXiv.2212.08286

CrossRef Full Text | Google Scholar

Yüksel, E., Soydaner, D., and Bahtiyar, H. (2024). Nuclear mass predictions using machine learning models. arXiv Prepr. arXiv:2401.02824 109, 064322. doi:10.1103/physrevc.109.064322

CrossRef Full Text | Google Scholar

Zhang, L., Smith, M. S., Hix, W. R., and Lingerfelt, E. J. (2013). Abundance correlations in explosive nucleosynthesis simulations. AIP Conf. Proc. 1594, 437.

Google Scholar

Zhang, R., Liu, Y., and Sun, H. (2020). Physics-guided convolutional neural network (PhyCNN) for data-driven seismic response modeling. Eng. Struct. 215, 110704. doi:10.1016/j.engstruct.2020.110704

CrossRef Full Text | Google Scholar

Zhang, W., Shen, Y., Lu, W., and Zhuang, Y. (2023). Data-copilot: bridging billions of data and humans with autonomous workflow. arXiv Prepr. arXiv:2306.07209. doi:10.48550/arXiv.2306.07209

CrossRef Full Text | Google Scholar

Zhang, X., Li, W., Fang, J., and Niu, Z. (2024). Nuclear mass predictions with the naïve Bayesian model averaging method. Nucl. Phys. A 1043, 122820. doi:10.1016/j.nuclphysa.2024.122820

CrossRef Full Text | Google Scholar

Zhang, Z. (2016). Introduction to machine learning: k-nearest neighbors. Ann. Transl. Med. 4, 218. doi:10.21037/atm.2016.03.37

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, W. X., Zhou, K., Li, J., Tang, T., Wang, X., Hou, Y., et al. (2023). A survey of large language models. arXiv preprint arXiv:2303.18223

Google Scholar

Zinner, E. K. (2003). Presolar grains. Treatise Geochem. 1, 711–733. doi:10.1016/B0-08-043751-6/01144-0

CrossRef Full Text | Google Scholar