Unsteady Dungey cycle from the point of view of Stokes’ theorem

The Dungey cycle is considered from the formation of a magnetic barrier and necessary for dayside reconnection conditions till the electric field generation around the Birkeland current loop and magnetic flux circulation balance. Data-based modeling of the magnetosheath magnetic field makes it possible to quantitatively assess the main factors that control formation and destruction of the magnetospheric magnetic barrier, such as the field line draping and the field intensity increase from the bow shock to the magnetopause, as well as their dependence on the orientation of the interplanetary magnetic field (IMF). The Dungey cycle has been revised to take into account the essentially time-dependent effects of magnetic reconnection. It is shown by means of the Stokes’ theorem that a powerful electric field with an effective potential difference of several tens of kV is generated around the developing substorm current system. The emerging Birkeland current loop is an important particle acceleration element in the magnetosphere, contributing to the energization of ring current protons and electrons. The electric field that arises in the dipolarization zone magnifies the already existing ring current, and the closure of its amplified part through the ionosphere generates the Region 2 field-aligned currents. The motion of the expanding partial ring current around the magnetosphere, combined with the particle drift, transfers the magnetic flux from the night side of the magnetosphere to the dayside. At the dayside magnetopause, the reconnection is also responsible for the creation of the Birkeland loop, but now the electric field in the loop area decelerates the ring current particles, and regions of weakened ring current are formed. Closure of these weakened loop currents results in a transfer of the magnetic flux from the dayside to the night side, thus ensuring its overall balance and completing the Dungey cycle.

1 Introduction

As time passes, it becomes clearer and clearer that the Dungey model (Dungey, 1961) of the open magnetosphere is not even so much a model, but rather a whole program of studies of the interaction of the solar wind with the Earth’s magnetosphere for many years ahead. It generated such a wide spectrum of problems (Cowley and Lockwood, 1992; Coroniti and Kennel, 1973; Lui, 1996; Pudovkin and Semenov, 1985; Trattner et al., 2021; Samsonov et al., 2024; Dai et al., 2024; Zhu et al., 2024) that it is virtually impossible to mention them all. In the present work, unlike in an encyclopaedic paper by Borovsky and Valdivia, 2018, we focus on only two, but, in our opinion, key problems that are missing in their list.

This is, first of all, the magnetic barrier or Plasma Depletion Layer (PDL) where, as we believe, the conditions necessary for the dayside reconnection are developed. Earlier, the research on the magnetic barrier/PDL gained much attention (Spreiter et al., 1966; Zwan and Wolf, 1976; Pudovkin and Semenov, 1977; Pudovkin and Semenov, 1985; Erkaev, 1986; Song and Russell, 2002). However, after Phan et al., 1994 showed by the superimposed epoch analysis that the PDL is clearly visible for the low shear magnetopause, but completely absent for the high shear magnetopause, the prevailing view became that the flow of the solar wind near the magnetopause is fully controlled by the reconnection at the magnetopause (Borovsky, 2008). Nevertheless, as recent studies (Michotte de Welle et al., 2022; Michotte de Welle et al., 2024; Tsyganenko et al., 2023; Tsyganenko et al., 2024; Han et al., 2024; Dimmock and Nykyri, 2013) have shown, the features of the magnetic barrier, namely, draping, the increase of the magnetic field and the plasma depletion from the bow shock to the magnetopause are observed for all directions of the IMF. These new results prompted us to revisit the somewhat forgotten idea that the formation of a magnetic barrier is an important factor in creating the conditions necessary for reconnection at the dayside magnetopause.

The second issue is the mechanism of magnetic flux transfer, which nowadays is understood completely as a result of magnetospheric plasma convection (Cowley and Lockwood, 1992; Trattner et al., 2021; Samsonov et al., 2024; Dai et al., 2024). Thus, the other purpose of this article is to show that there is another mechanism of the magnetic flux transfer. We show that the generation of the Birkeland substorm current loop gives rise to a strong vortex electric field induced by magnetic field variation. The Birkeland current loop is therefore an important accelerating factor in the magnetosphere, which calls for a significant modification of the Dungey scheme. In particular, one needs to consider regions of amplification or weakening of the ring current, which play an important role in the magnetic flux transfer via the Dungey cycle.

As a tool for analyzing the dynamical phenomena in the magnetosphere, we use Stokes’ theorem and apply it to a specific magnetic contour, a technique first used to assess the electric field at the reconnection line in the magnetospheric tail, based on the observed speed of the near-pole auroral arc (Semenov and Sergeev, 1981).

The paper is organized as follows. Section 2 contains the necessary information about the Stokes’ theorem and equations describing the magnetic contour method. The Section 3 addresses the magnetic barrier and discusses the conditions for reconnection. In Section 4, the main points of the method are discussed on the example of applying the magnetic contour method to the simplest case of reconnection in a planar current layer. Section 5 studies in detail the modeling of the Substorm Current Wedge (SCW) (Sergeev et al., 2014; Nikolaev et al., 2015) and shows that a vortex electric field appears in the dipolarization area. In Section 6, it is shown that the resulting vortex electric field results in amplification of the ring current and formation of a partial ring current associated with Region 2 field-aligned currents. Section 7 considers the dayside reconnection and in Section 8 we show that the night side inner magnetosphere can operate as a charged particle accelerator. The final section 9 summarizes the main conclusions of the paper.

2 Stokes’ theorem

Stokes’ theorem for a contour moving with velocity u relates the circulation of the electric field E′ along the contour l to the change in the magnetic flux permeating the surface stretched on this contour

$\begin{array}{cc}\hfill \oint E_l^{\prime }dl& =-\frac{1}{c}\frac{d}{dt}{\int }_{\mathrm{\Sigma }}{B}_{n}dS\hfill \\ \hfill {\overrightarrow{E}}^{\prime }& =\overrightarrow{E}+\frac{1}{c}\overrightarrow{u}\times \overrightarrow{B}\hfill \end{array}(1)$

Here $\overrightarrow{E}$ is the electric field in the stationary (laboratory) frame of reference, ${\overrightarrow{E}}^{\prime }$ is the electric field in the contour frame of reference, B_n is the magnetic field component normal to the surface. The derivation (see Landau and Lifshitz, 1984; Bittencourt, 2004) takes into account that the contour may suffer deformation with time. A well-known theorem of MagnetoHydroDynamics (MHD) states that in an ideal medium the magnetic flux does not change through a contour moving with plasma velocity v (u = v), see left panel in Figure 1 (Baumjohann and Treumann, 1996). This is a direct consequence of Stokes’ theorem (Equation 1), since in an ideal plasma the electric field E′ in the plasma associated frame of reference vanishes (Landau and Lifshitz, 1984; Bittencourt, 2004), then the circulation in Equation 1 is identically zero and the magnetic flux is conserved.

Figure 1

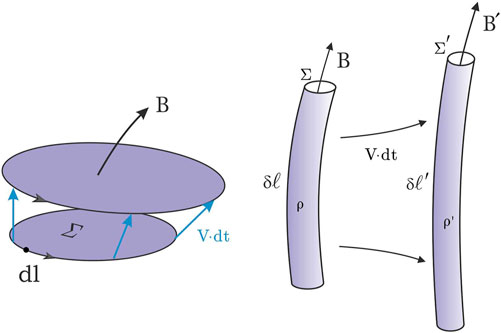
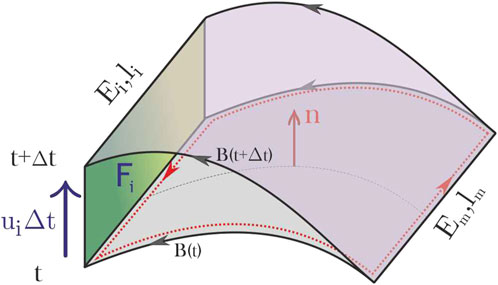
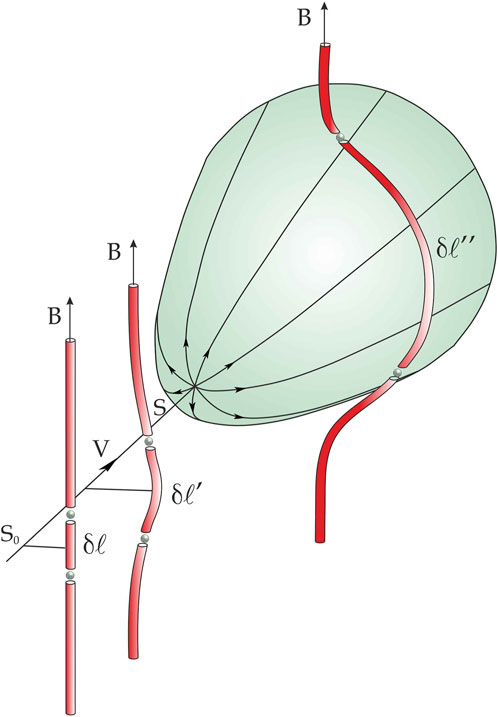
Figure 1. On the left: Magnetic flux conservation through a surface, confined by the contour moving with plasma velocity. On the right: Stretching of moving magnetic flux tubes.

Using this result it is useful to derive the equation of motion of the magnetic flux tube. Let us consider a small segment of the magnetic flux tube of length δl (Figure 1, right panel). As a consequence of conservation of magnetic flux, we have

$B·\mathrm{\Sigma }={\mathrm{B}}^{\prime }·{\mathrm{\Sigma }}^{\prime }(2)$

Plasma mass is also conserved under frozen-in conditions:

$\rho ·\delta l·\mathrm{\Sigma }={\rho }^{\prime }·\delta l^{\prime }·{\mathrm{\Sigma }}^{\prime }(3)$

It follows from Equations 2, 3 that the ratio of magnetic field strength to plasma density is proportional to the stretching of the magnetic flux tube (Landau and Lifshitz, 1984):

$\frac{B^{\prime }}{{\rho }^{\prime }}=\frac{B}{\rho }·\frac{\delta l^{\prime }}{\delta l}(4)$

In the future, we will need a special kind of contour, the so-called magnetic contour. Let us choose a segment perpendicular to the magnetic field lines in the equatorial plane of the magnetosphere and from each of its points let out a field line to the intersection with the ionosphere first at time t and then at time (t + dt). Stokes’ theorem (Equation 1) is applied to the moving contour thus constructed (Figure 2).

Figure 2

Figure 2. Scheme of magnetic contour.

Since the surface stretched on the magnetic contour is woven of magnetic lines of force, the magnetic flux through such a surface is identically zero, hence the circulation of the electric field in the reference frame of the contour is also zero and we obtain, neglecting the field-aligned electric fields:

$\left(\overrightarrow{E_i}+\frac{1}{c}\overrightarrow{u_i}\times \overrightarrow{B_i}\right)·\overrightarrow{l_i}=\overrightarrow{E_m}·\overrightarrow{l_m}(5)$

Here $\overrightarrow{E_i}$ and $\overrightarrow{B_i}$ are the electric and magnetic fields in the ionosphere, $\overrightarrow{u_i}$ is the velocity of the segment projection in the ionosphere, $\overrightarrow{l_i}$ is the length of the segment projection in the ionosphere, $\overrightarrow{E_m}$ is the electric field in the magnetosphere, and $\overrightarrow{l_m}$ is the length of the original segment. The same expression can be rewritten in the following form:

$∆\stackrel{\sim }{{\phi }_i}+\frac{1}{c}\frac{\partial F_i}{\partial t}=∆\stackrel{\sim }{{\phi }_m}(6)$

Where $∆\stackrel{\sim }{{\phi }_i}$ is the electromotive force along the projection of the segment in the ionosphere, F_i is the magnetic flux in the ionosphere drawn by the moving projection of the segment, $∆\stackrel{\sim }{{\phi }_m}$ electromotive force along the projection of the segment in the magnetosphere. That is, the electromotive force (EMF) in the magnetosphere differs from EMF in the ionosphere by the magnitude of the magnetic flux drawn by the moving projection of the segment in the ionosphere.

In the stationary case, the shape of the field lines does not change with time, the contour becomes stationary, the velocity u = 0, and the EMF coincides with the electric field potential difference, which, as it follows from Equation 6, can be carried along the magnetic field lines. Therefore, the change in the magnetic flux drawn by the moving projection of the segment in the ionosphere can be considered as a measure of the emerging vortex electric field (induced by magnetic field variation), which can significantly change the coupling of the magnetospheric and ionospheric electric fields. We will refer the velocity of the segment projection motion in the ionosphere u (associated with magnetic flux change) as the projection velocity. If the projection velocity is less (better much less) than the velocity of electro-drift (u << V_E), the magnetic field configuration may be considered as quasi-stationary and the magnetic fields lines may be considered equipotential. In the opposite case, u >> V_E, the arising vortex electric fields must be taken into account when projecting the electric field along magnetic field lines.

It is interesting to note that the two kinds of contours considered above (the one moving with the ideal plasma and the magnetic contour) are peculiar antipodes: in the first case in Stokes’ theorem (Equation 1) the circulation is identically zero since E’ = 0, and then the magnetic flux is conserved. In the second case the magnetic flux is identically zero by construction, then the circulation is also zero and we arrive at Equations 5, 6. Knowing the behavior of the magnetospheric segment projection in the ionosphere, which often appears as a moving arc of the aurora borealis, we can obtain the distribution of the electric field in the magnetosphere. The magnetic contour was first used in Semenov and Sergeev (1981) to estimate the electric field at the reconnection line in the tail of the magnetosphere from the velocity of the near-pole auroral arc.

3 Solar wind flow around the magnetosphere

When building a model of the interaction between the solar wind and the Earth’s magnetosphere, the following difficulty immediately arises (Pudovkin and Semenov, 1985; Pulkkinen et al., 2007). The main energy comes to the magnetosphere in the form of solar wind kinetic energy, while the magnetospheric disturbance is controlled by the southern B_z component of the IMF (Paschmann, 2008; Borovsky and Valdivia, 2018). In the solar wind, the typical value of the Mach-Alfvén numbers M_A = V_SW/V_A lies within 8–10, i.e., the magnetic energy density of the IMF is 1.5-2 orders of magnitude less than the kinetic energy density. It turns out that the low-energy factor (B_z component of the IMF), carrying only 1%–2% of the solar wind energy, is the key interaction factor. At first sight, this fact seems counterintuitive; to clarify it, it is necessary to trace the sequence of transformations of different types of energy in the magnetosheath and find out, what physical phenomenon is responsible for creating conditions necessary for starting reconnection in the vicinity of the magnetopause.

Since the solar wind is both supersonic and super-Alfvénic, a bow shock appears in front of the magnetosphere, on which the first and perhaps the main redistribution of energy takes place. According to the MHD model of the subsolar magnetosheath (Spreiter et al., 1966; Erkaev et al., 1999), at the bow shock the solar wind speed decreases inversely proportional to density, while the density and magnetic field intensity increase approximately in 3 times for typically large solar wind sonic and Alfvén Mach numbers. However just after the shock, the sum of the thermal and kinetic plasma energy still prevails the magnetic energy.

A further redistribution of energies occurs in the magnetosheath, as the solar wind flows around the magnetosphere. The stationary flow implies that at the magnetopause the solar wind velocity remains everywhere tangential to the surface, with a stagnation point at the nose, from which the streamlines envelop the entire boundary (Figure 3). At the stagnation point, the flow velocity v(s) is zero, such that expanding v(s) into a Taylor series over a distance s from the stagnation point and keeping only the first term, one obtains v(s)= − k s. Then the time T required for a magnetic flux tube to travel from some initial point s₀ to the stagnation point is equal to:

$T=-\underset{s\to 0}{\lim }{\int }_{s_0}^s\frac{ds}{k·s}=\frac{1}{k}\mathit{ln}\left(\frac{s_0}{s}\right)\to \infty (7)$

Figure 3

Figure 3. Stretching of magnetic flux tubes in a process of solar wind flow around magnetosphere.

That is, the entire magnetopause turns out to be unreachable for the thin flux tubes (Pudovkin and Semenov, 1977; Pudovkin and Semenov, 1985). When flowing by the magnetosphere (and, in general, any blunt body), a part of the magnetic flux tube lying in the neighborhood of the stagnation point is strongly braked, while the rest of it continues to move with the solar wind. As a result, the tube is strongly stretched and, as a consequence of Equation 4, the ratio of magnetic field to plasma density B/ρ increases, and, considering Equation 7, B/ρ tends to infinity at the magnetopause. Since the field B is limited due to a finite limit on the magnetic pressure, the plasma density drops to zero over the entire surface enveloped by streamlines, and the magnetic field value peaks at the braking point. It should be kept in mind, however, that the B/ρ singularity due to the density convergence to zero has a weak logarithmic character (Erkaev, 1986), so it usually disappears in numerical calculations due to the numerical dissipation.

The above noted singularity is a mere consequence of the frozen-in magnetic field and the presence of a stagnation point. One may wonder whether it is possible to organize the flow in such a way that there is no stagnation point at all. The answer to this question is negative, as the famous algebraic topology theorem about the “hairy ball” states that there is no velocity field without singularities on sphere-like surfaces (Renteln, 2014).

Therefore, the only possibility to eliminate the difficulty and thus consistently resolve the problem of interaction of the solar wind with the magnetosphere is to abandon the ideal plasma model and to introduce some dissipation into the model, which would break the frozen-in condition of the magnetic field at least locally.

According to modern concepts, such a mechanism is the magnetic reconnection, in which the frozen-in condition is broken in small diffusion regions near the X lines or separatrices. The magnetic reconnection requires to create special conditions, first of all, a formation of a thin current sheet and accumulation of magnetic energy. As shown below, the solar wind flow with a magnetic field having a transverse component to the streamlines not only creates conditions necessary for the reconnection, but also makes it inevitable.

Since the stagnation point is nevertheless unavoidable, the magnetic flux tubes are strongly stretched when the magnetosphere is flown around by the solar wind. As a consequence, a layer is formed near the magnetopause with reduced plasma density and increased magnetic field intensity. Zwan and Wolf (1976) were among the first to discover that effect and, based on the fact of density decrease, called this layer a “Plasma Depletion Layer” (PDL). Erkaev (1986), on his part, singled out the increase of the magnetic field intensity as the main feature and, based on that, called that layer the “magnetic barrier”. Both these terms are now used interchangeably in the modern literature. Using the Lagrangian formalism, the so-called “frozen-in coordinate system” was introduced by Pudovkin and Semenov (1977), Pudovkin and Semenov (1985), in which the magnetic flux tubes played the main role. On that basis, a method was developed to solve the magnetic barrier problem in the ideal MHD approximation (Erkaev et al., 1994; Erkaev et al., 1998; Erkaev et al., 1999; Erkaev et al., 2003). The main features of the magnetic barrier were also investigated analytically by Nabert et al. (2013) and numerically by Wang et al. (2004). These features are:

1. Draping of the magnetic field lines. Due to their braking in the front part of the magnetosphere, the magnetic field lines envelop the streamlined surface, creating a peculiar cocoon around the magnetopause. This effect is clearly visible both in theoretical calculations (Erkaev et al., 1999) and in experimental data (Michotte de Welle et al., 2022; Michotte de Welle et al., 2024; Tsyganenko et al., 2023; Tsyganenko et al., 2024; Dai et al., 2023; Dimmock and Nykyri, 2013; Han et al., 2024). The magnetic field draping in the magnetosheath for different IMF orientations, derived in data-based modeling from in-situ spacecraft observations (Tsyganenko et al., 2023), is shown in Figure 4.

As demonstrated in the next Figure 5 the magnetic field steadily increases earthward. Due to the stretching of the magnetic flux tubes, the magnetic field increases, while the plasma density and pressure decrease. To preserve the force balance, these changes occur consistently: the gas pressure decrease is compensated by an increase in the magnetic pressure, such that the total pressure remains nearly constant across the magnetosheath, $p+\raisebox{1ex}{$B^2$}\!\left/ \!\raisebox{-1ex}{$8\pi $}\right.=const$ (Erkaev et al., 2003; Nabert et al., 2013; Phan et al., 1994).

2. Stagnation line. Due to the stretching of the magnetic flux tubes and their draping around the magnetopause, the Ampere’s force accelerates the plasma across the magnetic field lines, while the weakened gas pressure pushes the plasma along the magnetic field with less and less efficiency. This results in a change of the flow topology: instead of an axisymmetric flow away from the stagnation point (as in Figure 3), a stagnation line begins to form, extending along the magnetic field, as shown in Figure 6, Erkaev et al. (1998).

3. Anisotropy of the gas pressure. The stretching of the magnetic flux tubes during the flow around the magnetosphere results in a progressive increase of the transverse plasma pressure, such that it gradually becomes dominant over the parallel pressure on approaching the magnetopause. This can provoke the onset of instabilities: first of the mirror type and then followed by the ion-cyclotron instability. The mirror instability occurs in an anisotropic magnetized plasma when the difference between perpendicular and parallel plasma pressures exceeds a threshold value that depends on the perpendicular plasma beta. This leads to enhanced plasma fluctuations, which in turn results in a relaxation of difference between parallel and perpendicular temperatures (see experimental data in Soucek et al., 2008). Mirror perturbations do not propagate and are carried by the plasma flow along the streamlines. Using an anisotropic stationary MHD flow model allows to calculate the growth of mirror fluctuations from the bow shock to the magnetopause along the Sun-Earth stream line. As shown by Erkaev et al. (1999), the ion-cyclotron instability begins to dominate in the immediate vicinity of the magnetic barrier, where the plasma β parameter is less than unity.

4. Scaling. A natural question that arises is how wide is the layer by the magnetopause, in which the magnetic barrier effects are important? If one defines the outer boundary of the magnetic barrier as a surface on which the gas pressure becomes equal to the magnetic pressure (i.e., β = 1), it appears (Erkaev et al., 1998) that the thickness of the magnetic barrier is δ = L/M_A², where L is the radius of curvature of the streamlined body. Assuming the IMF strength of 5 nT, this corresponds to M_A = 8, which gives a magnetic barrier thickness of about 2000 km. It turns out that the layer in which the magnetic barrier effects are important is rather thin, such that the greater part of the magnetosheath remains mostly unaffected. Nevertheless, it is just the magnetic barrier area, where the conditions necessary for the reconnection are created.

Figure 4

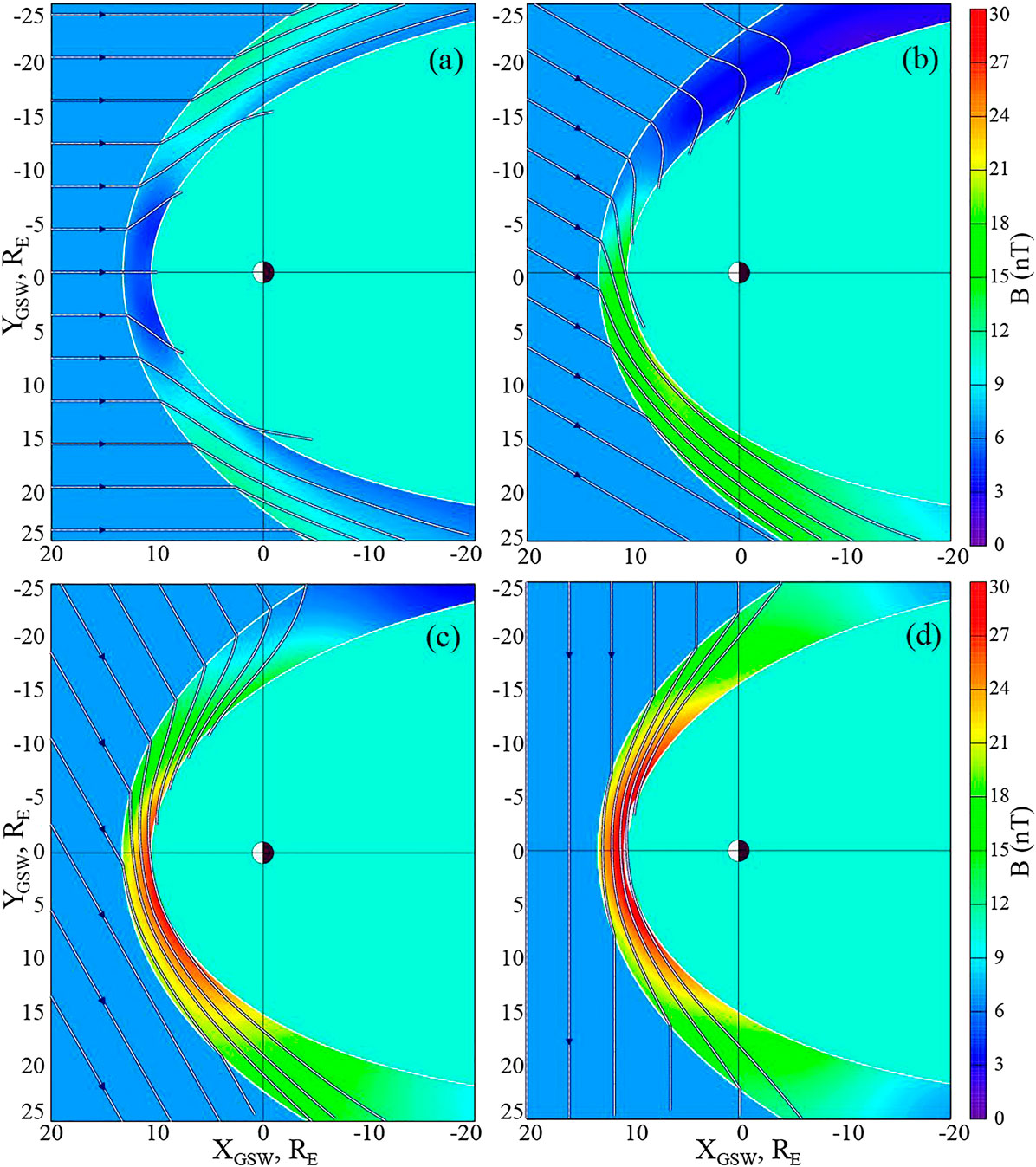
Figure 4. Draping of the magnetic field in the magnetosheath (equatorial plane) as obtained in the empirical model of Tsyganenko et al., 2023 with B = 7 nT for four values of the IMF cone angle: θ = 0° (A), θ = 30^◦ (B), θ = 60^◦ (C), and θ = 90^◦ (D).

Figure 5

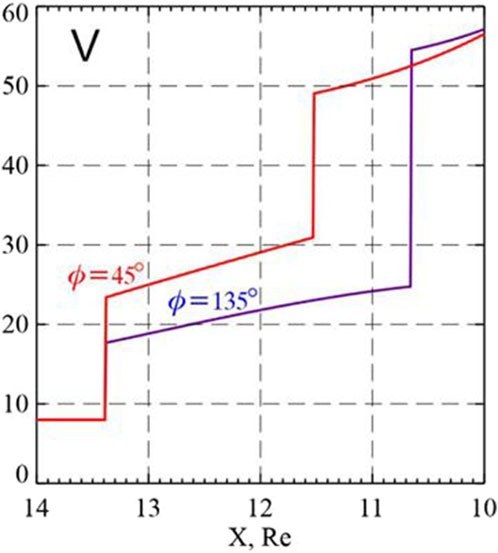
Figure 5. Increase of the total magnetic field B along the Sun-Earth line for a typical spiral-type IMF orientation, with IMF Bz = + 5.0 (red) and Bz = − 5.0 nT (blue). In both cases, the total IMF magnitude is 8 nT and its cone angle equals 120° (after Tsyganenko et al., 2024)

Figure 6

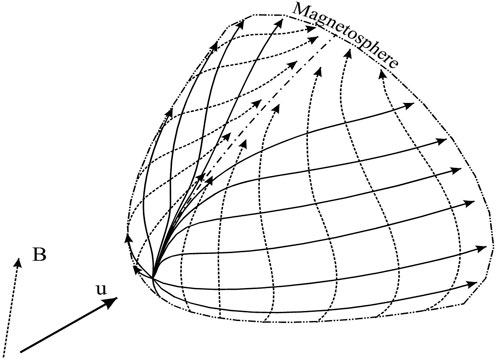
Figure 6. The structure of the magnetic field (dotted lines) and solar wind plasma flow (solid lines) around the magnetosphere according to numerical simulation (Erkaev et al., 1998).

To address this issue from the data-based modeling viewpoint, let us consider the electric current density at the magnetopause:

$\overrightarrow{J}=ne\left(\overrightarrow{v_p}-\overrightarrow{v_e}\right)(8)$

The current density j is determined mainly by the magnetic field jump across the magnetopause (Michotte de Welle et al., 2024; Tsyganenko et al., 2024; Han et al., 2024) (Figure 7). For the southern IMF at the dayside magnetopause, it increases about twice, the plasma density decreases, such that the current velocity $\left(\overrightarrow{v_p}-\overrightarrow{v_e}\right)$ in Equation 8 should increase significantly along with the strengthening of the magnetic barrier. Thus, the conditions necessary for the magnetic reconnection, namely, the formation of a thin current sheet and accumulation of magnetic energy in its vicinity, are created.

Figure 7

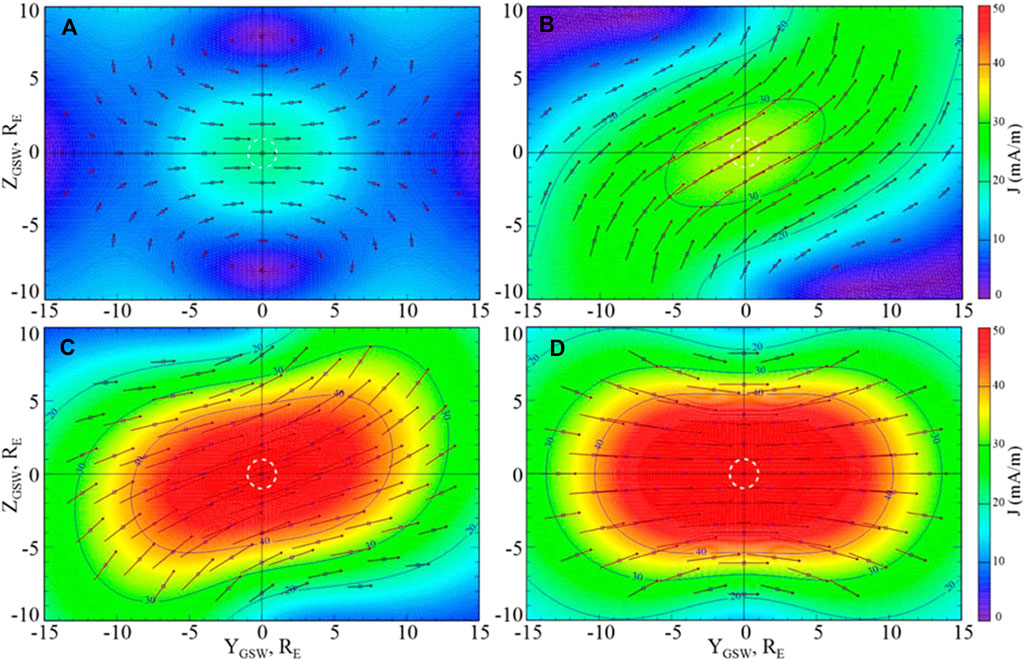
Figure 7. Color-coded electric current surface density (in mA/m) at the dayside magnetopause as viewed from the Sun, for four values of the IMF clock angle: ϕ = 0° (A), 60° (B), 120° (C), and 180° (D). The J vector projections on Y–Z plane are also shown with arrows (after the empirical model of Tsyganenko et al., 2024).

An important parameter that determines the characteristic values of plasma density and magnetic field at the current sheet boundary is the dissipative length d_dif, at which the frozen-in condition is violated. In plasma, there is a whole hierarchy of scales at which this can happen. At the smallest scale, the inertial length of the electrons d_e, the electrons are unfrozen. As the PIC-simulation shows, it is the electron inertial length d_e that determines the thickness of the electron diffusion region (Vasyliunas, 1975; Hesse et al., 2016). At the scale of the proton inertial length d_i, the proton component is unfrozen, the protons cease to be magnetized and their connection with the magnetic flux tubes is lost (Hesse et al., 2016). In the magnetosheath, another scale associated with turbulence is distinguished, the so-called magnetic correlation length, of the order of ∼10 d_i, characteristic for reconnection in thin electron current sheets (Stawarz et al., 2022). All these scales differ from each other by 1-2 orders of magnitude, and which one should be used is not completely clear. Fortunately, both in the Petschek type reconnection model and in the magnetic barrier theory, the main parameters that determine the reconnection rate (Petschek, 1964; Erkaev et al., 2000), plasma density, and magnetic field near the magnetopause (Pudovkin and Semenov, 1985, Erkaev, 1986) only weakly (logarithmically) depend on the dissipative length, so its actual value is not much important. What is really important is that taking into account the dissipative length removes the singularity, such that the density does not fall to zero, but remains at a finite level (Song and Russell, 2002; Dimmock and Nykyri, 2013; Han et al., 2024).

Thus, in the absence of reconnection, the magnetic barrier is formed in the same way for all IMF directions (as the magnetopause approaches, the magnetic field increases, the density and gas pressure decrease, and a plasma flow with a field-aligned stagnation line emerges). At the same time, due to the stretching of the flux tubes, for each specific IMF direction, a specific region appears on the magnetopause in which the currents on the magnetopause (and, as a consequence, the probability of reconnection) are maximal (see Figure 7). For B_z < 0, the vicinity of the subsolar point acts as such a region (Figure 7D), for B_z > 0, the region behind the cusps (Figure 7A). After the reconnection has begun, the flow pattern changes dramatically, since the reconnection line (which now plays the role of a stagnation line for the flow) must be located across the magnetic field.

The formation of a magnetic barrier is a necessary element that guarantees the onset of magnetic reconnection on the dayside, as the beginning of the Dungey cycle.

4 Magnetic contour and reconnection

Though the Dungey cycle is initiated by the dayside reconnection, we find it more convenient for understanding to start the analysis from the night side. Also for the sake of simplicity, we begin with reconnection of antiparallel fields in a planar two-dimensional current sheet (Figure 8), in which the magnetospheric and ionospheric scales in Equation 5 are the same: l_m = l_i. In such a setting, the model ionosphere is a planar surface perpendicular to the current sheet. As shown in Figure 8, the reconnection line (X-line) projection along the separatrix maps the reconnected magnetic flux F_rec and, hence, the associated model auroral bulge onto this plane, such that the bulge velocity u is proportional to the electric field E along the reconnection line. These two quantities, electric field at X-line and reconnected magnetic flux, are the most important characteristics of the non-stationary reconnection process (Semenov et al., 1983; Biernat et al., 1987; Semenov et al., 1992).

Figure 8

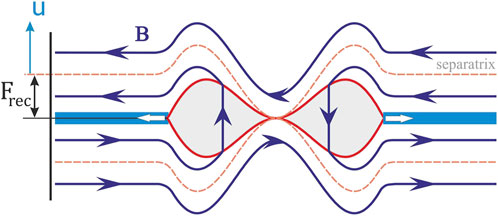
Figure 8. 2D time-dependent reconnection in a planar current sheet model. The projection of the X-line along the separatrix maps the reconnected magnetic flux F_rec on the plane, perpendicular to the current sheet.

It is interesting to discuss in detail the formation of the reconnection region projection. The problem lies in that the causality principle limits the speed of any signal propagation by the speed of light. At the same time, during the reconnection the X-line projection (hence, the model bulge) is formed instantaneously, i.e., with infinite speed. However, it is clear that before the arrival of the first physical agent (kinetic Alfvén wave, ordinary Alfvén wave, energetic particles, see Sergeev, et al., 2021; Duan et al., 2016; Dai, et al., 2017) to the ionosphere, there should be no physical perturbations. This means that, during this entire time period, the following relation must be strictly satisfied:

$\frac{1}{c}\frac{\partial F_i}{\partial t}=∆\stackrel{\sim }{{\phi }_m}(9)$

or, for maximal values:

$\frac{1}{c}{u}_{\mathit{max}}·B_i·l_i=\max \left(E_m\right)·l_m(10)$

which sets the maximum projection velocity that guarantees complete absence of perturbations in the ionosphere. In other words, the auroral bulge comes into existence as soon as the reconnection starts in the current sheet, but it remains undisturbed (hence, invisible) until the physical agents (waves, particles, field-aligned currents) arrive. These agents can often be associated with various auroral forms (arcs, rays, brightening spots, filaments). If an auroral arc [e.g., at the near-pole edge of the auroral bulge (Akasofu, 1964)] is traveling at a velocity close to u_max (see Equation 10), one will not see anything in the ionosphere, since the above relation disconnects the ionosphere from the reconnection region. The magnetospheric EMF is compensated by the projection term in Stokes’ theorem (9) and does not appear in the ionosphere in any way. This is the direct consequence of the causality principle.

5 Stokes’ theorem and Substorm Current Wedge (SCW)

Figure 9 shows a scheme of a three-dimensional reconnection with finite X-line length in a planar current sheet following an electric field pulse on the X-line (Semenov et al., 1992; Semenov et al., 2004; Pudovkin and Semenov, 1985). Figure 9 shows the situation when the reconnection at the X line has already ended, the auroral bulge has formed and no longer changes.

Figure 9

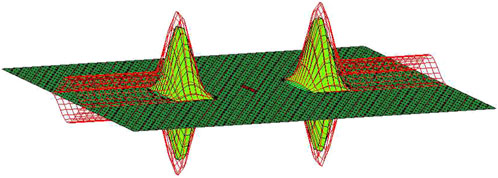
Figure 9. Modeling of BBF accelerated plasma flows propagating in both directions from the X-line (red segment in the center). At this time moment, the reconnection is already complete and the electric field at the X-line has disappeared. In this case, the accelerated plasma flows, bounded by slow shock waves (light green), detach from the X-line and propagate as solitary waves. The last reconnected magnetic field lines form a separatrix (red).

If we place the magnetospheric segment on the path of the moving Bursty Bulk Flow (BBF), it is easy to see that its projection to the ionosphere first appears at the equatorial bulge edge and then spreads to the entire bulge, and reaches its pole edge at the moment of the time when the magnetospheric segment exits from the BBF. Moving the magnetospheric segment closer and closer to Earth, this pattern will be repeated: the projection starts at the equator edge and runs to the pole. The main question here is: what will be observed in the ionosphere when the physical agents actually get there.

Before answering it, let us consider the current system arising from a reconnection pulse with finite X-line length in a planar current sheet (Figure 10). In the diffusion region with reduced effective conductivity, the electric current is weakened, which triggers an Alfvén wave propagating on both sides of the X-line. The resulting field-aligned currents are responsible for generating the magnetic field component normal to the current sheet. Over time, the Alfvén wave reaches the ionosphere, forming a SCW, which is the most important element in the whole concept of a magnetospheric substorm. It is important to note that during the reconnection process, not only the magnetic flux, mass, and energy are transferred along the current sheet, but also the electric current (Semenov et al., 1998).

Figure 10

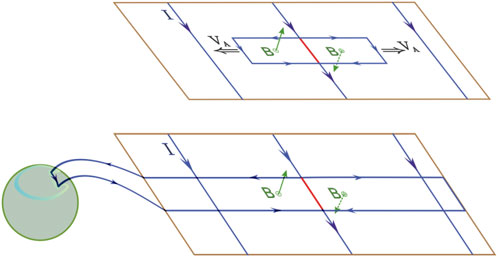
Figure 10. The current system of time dependent reconnection of antiparallel fields with finite X-line (red). Drop of plasma conductivity in diffusion region launched Alfvénic wave, propagating in both directions from X-line and carrying field-aligned currents. Upper panel–initial stage, low panel–final stage, which shows appearance of SWC.

It can be assumed that such a current system is a fundamental feature of the magnetic reconnection not only in a planar current sheet, where analytical results can be obtained, but also in the real current sheets.

The current wedge of a substorm was proposed by Boström (1964), McPherron et al. (1973) based on the analysis and generalization of ground-based and satellite magnetic variation data. Subsequently, this current wedge was comprehensively studied and developed in numerous papers (Vasilyev et al., 1986; Sergeev et al., 2014; Nikolaev et al., 2015; Birn and Hesse, 2013; Birn and Hesse, 2014; Palin et al., 2016), which constituted the basic element of the magnetospheric substorm concept.

A natural bridge between the Stokes’ theorem and the substorm current systems is the modeling of the SCW, calculating the projections and comparing the results obtained with experimental data. In the modeling by Nikolaev et al. (2015), the current loop consisted of two parts (see Figure 11): the high-latitude R1 field-aligned currents flowing into the ionosphere at dawn and out at dusk, with the total current of 1 MA, and the oppositely directed R2 currents located closer to the Earth with a lower intensity of 0.5 MA. A strong increase of the equatorial B_z component inside the loop is clearly seen, indicating the field dipolarization, such that virtually all magnetic perturbations are confined within the SCW sector. The following Figure 12 shows how the field-aligned projections of the equatorial circular segments are deformed at ionospheric altitudes. Analyzing these projections makes it possible to distinguish three characteristic deformation regions, as follows.

Figure 11

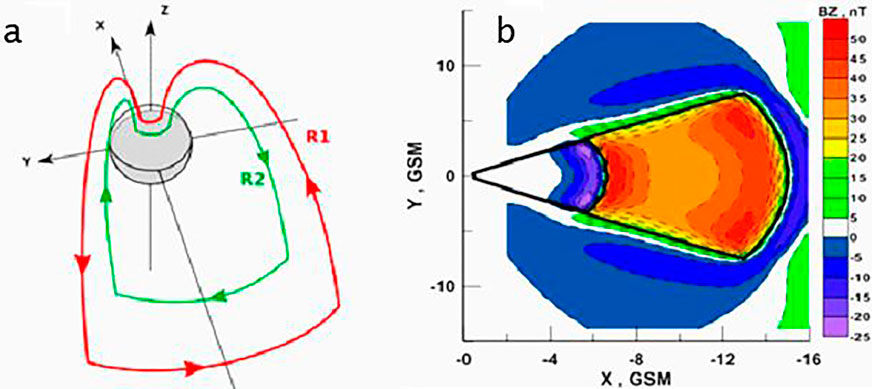
Figure 11. Modeling the SWC. (A) - a schematic picture of R1 and R2 currents of magnetospheric substorm; (B) - Bz component of magnetic field distribution in equatorial plane after a substorm associated dipolarization occurred (after Nikolaev et al., 2015).

Figure 12

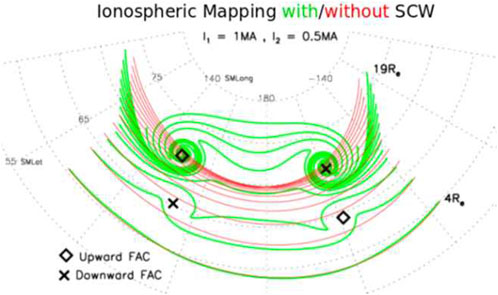
Figure 12. Ionospheric mapping of equatorial geocentric circle arcs. The red lines show neutral sheet mapping using the T89+IGRF model; the green lines show mapping of the same points using the influence of SCW. Ionospheric locations of upward (downward) FACs are indicated by diamond (cross) symbols (after Nikolaev et al., 2015).

The first one is the dipolarization region in the equatorial plane between the R1 and R2 currents. Here the B_z component significantly increases after the onset of the current wedge, such that all ionospheric projections shift poleward by as much as 8 degrees of latitude.

The second region corresponds to the twisting of the force lines around the field-aligned segment of the R1 current, manifested by the spiral-shaped contours in Figure 12. The combination of the type 1 and type 2 deformations creates a large-scale structure resembling the auroral bulge expanding poleward.

The third deformation region is due to the R2 current in the equatorial plane, placed here at a distance of 6Re. Ionospheric projections corresponding to equatorial distances closer than 6Re are shifted equatorward, owing to the field line twisting around the R2 currents. The resulting ionospheric pattern protrudes equatorward and also has a bulge-like shape, but it is smaller in size than the auroral bulge.

The above described modeling of the current wedge shows that the natural boundary separating the essentially different types of deformations is the projection into the ionosphere of the equatorial current R2. North of it is the auroral bulge, in which the projections of circular segments are shifted to the pole. From the Stokes’ theorem it then follows that a westward electric field is set in the dipolarization region in the magnetosphere. South of the projection of the equatorial current R2 there is an equatorial bulge in which the projections of circular segments shift to the equator. It then follows from Stokes’ theorem that an eastward-directed electric field must appear in the corresponding region of the magnetosphere. It is still difficult to say anything about the magnitude of the electric field because the Stokes’ theorem does not include the displacements of the projections themselves, but their velocities, and then the disturbance level depends on how quickly the current wedge appears.

Sergeev et al. (2019), found an event on 28 July 2017, in which it was possible to control the electric field reconnection near the X line in the tail of the magnetosphere on the MMS satellites and the corresponding development of the auroral bulge in the ionosphere. It turned out that the reconnection rate E = 3.3 mV/m (in terms of the effective potential difference of 42 kV/R_e) led to the formation of an auroral bulge propagating toward the pole with a velocity of 2 km/s, which apparently corresponds to a near-maximum value. Typical velocities are usually half as fast (1 km/s), giving 21 kV/R_e. Nevertheless, the conclusion turns out to be rather important: strong electric fields with an effective potential difference of several tens of kV should appear in the zone of the current loop of a substorm. Such fields have not been taken into account properly in the development of the magnetospheric substorm concept so far, and their consideration should lead to its substantial modernization.

6 Substorm Current Wedge and particle acceleration

As already mentioned, a Bursty Bulk Flow (BBF), i.e., a reconnected magnetic flux tube with an increased B_z component and a decreased plasma density relative to the background, is triggered by a reconnection pulse in the tail of the magnetosphere usually at a distance of 20 Re (Baumjohann et al., 1990). Propagating along magnetic field lines, the BBF carries magnetic flux, energy, mass, and electric current to the Earth (Semenov et al., 1998). The most important question here is how deep the BBF can penetrate into the inner magnetosphere, where its effective interaction with the ring current is possible. According to modern understanding, confirmed by both theory and MHD calculations (Birn et al., 2009; Kepko et al., 2015), as well as by comparison with satellite data (Dubyagin et al., 2010), the BBF moves Earthward until its entropy is equal to the entropy of the surrounding plasma. This usually occurs near the transition between stretched and dipole field lines near the inner edge of the tail current sheet, but can vary depending on geomagnetic activity (Kepko et al., 2015).

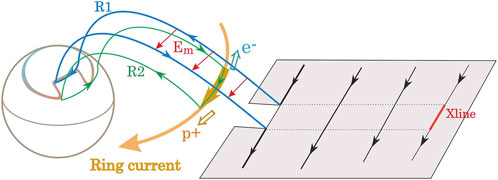
Thus, a dipolarization zone in the inner magnetosphere appears, which is blown by the ring current, with protons drifting to the west and electrons to the east (Figure 13). As was shown in the previous section, an electric field with an effective potential difference of the order of several tens of kV (as on the X line) should be generated in this region, which accelerates charged particles as they drift around the Earth. Since protons and electrons are magnetized in the inner magnetosphere, the energy gain occurs due to betatron acceleration: the particles are pushed by the electric field to the inner L shells with a stronger magnetic field, and while the magnetic moment W_┴/B = const, the energy of the particle W increases. The energy gain depends on how long the charged particle is in the acceleration zone. As the theory shows (Baumjohann and Treumann, 1996) the average drift period (that is, the time required to perform a complete circuit around the Earth) in hours is simply:

${〈{\tau }_d〉}_p={〈{\tau }_d〉}_e\cong \frac{1.05}{W\left(MeV\right)·L}{\left(1+0.43\sin {\alpha }_{eq}\right)}^{-1}\left(hours\right)$

Here W is particle energy in MeV, L-is the L-shell number, ${\alpha }_{eq}$ is the equatorial pitch-angle. To estimate the time when any particle is inside the accelerating region this value must be multiplied by the coefficient (dt_MLT/24) where dt_MLT is the width of the Birkeland loop in hours. Let us take for estimation dt_MLT = 2 h and L = 6, then for a 100 keV particle we get 9 min, and for a 1 keV particle this time increases to 15 h. A powerful electric field arises in the SCW zone for relatively short periods of time of 5–10 min, therefore ring current particles with an energy of 100 keV and higher are able to effectively gain energy, and current sheet particles with keV energy must undergo many acceleration events, before they gain noticeable energy.

Figure 13

Figure 13. Generation of electric field Em in the region of dipolarization inside SCW.

In the early phase of SCW formation, the polar arc of the auroral bulge moves with a maximum speed of the order of km/s (Akasofu, 1964), which, according to Stokes’ theorem, creates a maximum electric field in the dipolarization region. This field accelerates protons and electrons (mainly of the ring current), increases their azimuthal speed and as a result creates a pulse of enhanced ring current, or rather even two pulses - separately protons to the west and electrons to the east. Subsequently, these accelerated particles drift around the Earth and transfer the magnetic flux from the night side to the dayside in the regions of enhanced ring current. This, in fact, is the main our idea about the role of the ring current in the Dungey cycle.

Closing through the ionosphere, the pulse of the enhanced ring current gives rise to field-aligned currents of the R2 (Figure 13), which is a partial ring current expanding to the west with protons and to the east with electrons with a drift speed.

In the ionosphere at the initial phase, as already mentioned, there should be no noticeable disturbances - the magnetospheric source is compensated by the projection term in the Stokes’ theorem (see Equation 9). This seems strange, since the Alfvén wave with a field-aligned current has already reached the ionosphere, so there is a current, but there are no disturbances. The fact is that in the reference frame of the running polar edge of the auroras, the electric field of the wave is equal to zero, which is the condition for its complete reflection. In turn, the reflected Alfvén wave gives rise to a train of Pi2 pulsations, which is an important diagnostic signature of the onset of a substorm. In a certain sense, recalling the reasons for the connection between the magnetospheric electric field and the change in magnetic flux through the auroral bulge (see Equation 9), it turns out that the launch of Pi2 pulsations is associated with the principle of causality.

As time passes, the current system R2 begins to increase, the projection velocity u decreases, and to fulfill Stokes’ theorem the electric field in the ionosphere E_i must increase. This means that the ionosphere is connected to the magnetospheric source, the substorm begins.

Briefly, the chain of events leading to the development of a substorm appears as follows. The initiator of a substorm is a magnetic reconnection in the tail of the magnetosphere, it triggers a BBF moving towards the Earth. The BBF carries energy, magnetic flux, electric field and electric current in the form of an Alfvén wave, which penetrating into the inner magnetosphere creates an R1 current system, a dipolarization region and an electric field in this region. Energetic particles of the ring current are accelerated by this electric field and create an electric current pulse propagating with drifting protons to the west and with electrons to the east, which transfers the magnetic flux from the night side to the day side. This current pulse is an expanding partial ring current that closes into the ionosphere creating the R2 current system. The increasing current in this system decreases the projected velocity and connects the ionosphere to the magnetospheric source, the substorm begins.

7 Dayside reconnection

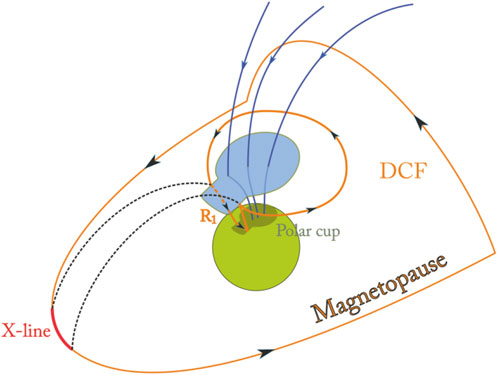
The reconnection at the magnetopause at the subsolar X-line is similar to the night side reconnection, but has a number of important differences. In contrast to the tail of the magnetosphere, the current sheet at the magnetopause is curvilinear, strongly asymmetric (cold dense moving plasma on the solar wind side and hot rarefied plasma with a strong magnetic field on the magnetosphere side), and the role of the edge of the current sheet is played by the cusp region, more precisely by the boundary of the polar cap.

For IMF B_z < 0, the most probable place of reconnection is the X line in the subsolar region. We again consider a time-limited reconnection pulse that triggers an accelerated plasma flow moving along the magnetopause with reconnected open magnetic flux tubes. This plasma flow carries magnetic flux, electric field, and electric current like any other reconnection-related jet. In the cusp area, it partially branches off to the ionosphere to form the dayside auroral bulge (Cowley and Lockwood, 1992) and the Birkeland current system of the R1 (Figure 14).

Figure 14

Figure 14. Scheme of magnetic reconnection on the day side magnetopause.

The important question is how the zone of interaction between the reconnected flux tube and the ring current looks like. At a first glance it is absent, since the reconnected tube is aligned along the magnetopause and then descends to the boundary of the polar cap, whereas the ring current is mainly concentrated near the equatorial plane. The point is that a strong electric field is present not only inside the reconnected tubes, but also in the inflow region, where it is delivered by a fast magnetosonic wave. For night side events this is not so important, since the X-line is far away (∼20 Re according to Baumjohann et al., 1990) and has little effect on the inner magnetosphere, but for dayside reconnection this is of decisive importance. The ring current is directly adjacent to the subsolar part of the magnetosphere, appearing in the region of the influence of the electric field of the reconnection (Figure 14).

The electric field of the reconnection on the dayside (as well as on the night side) is directed to the west, but now it acts against the ring current, slows down the drifting protons and electrons and pushes them to the outer L-shells with a weaker magnetic field. As a result, two pulses (protons and electrons) of the weakened ring current are formed, propagating at the drift velocity from the dayside to the night side and carrying the magnetic flux. Closing in the ionosphere, this pulse is an expanding partial ring current of the R2 zone.

In the balance, the transfer of magnetic flux from the dayside to the night side and back is compared and we arrive at the classical Dungey cycle with a constant electric field and stationary convection of magnetospheric plasma.

8 Inner magnetosphere as an accelerator of energetic particles

In the stationary case in a constant electric field the ring current particles drifting around the Earth, of course, cannot gain energy, the gain of energy on the night side is fully compensated by its loss on the dayside. However, in reality, the reconnection current pulses at the magnetopause and in the tail of the magnetosphere, which are separated by huge distances, can hardly be the same, so some imbalance in activity is quite probable, and the question of energy gain needs more careful consideration.

On the dayside, the region of interaction between the ring current and the reconnection electric field is adjacent to the magnetopause and is located at about distances L = 7–10. Protons and electrons are braked in this area and pushed to higher drift shells. On the night side, the interaction zone is determined by the entropy criterion; it appears to be located somewhat closer at L = 5–9. Charged particles suffer electric drift in the current wedge region towards the Earth and may well appear at L = 3-5, where in the absence of strong electric fields they are able to persist for a long time. Taking into account these considerations, one can conclude that the inner magnetosphere, more precisely its night side, is an accelerator of charged particles.

It is important to note that the energy gain by particles in the SCW zone is even more effective than on the X-line in the tail, although, it would seem, they pass the same potential difference (E_ml_m). In the tail in the diffusion region the particles gain energy under the action of electric field of reconnection moving along X-line, where B = 0. This motion is unstable, as soon as the particle slightly deflects from the X-line, the magnetic field immediately appears, and then the Lorentz force throws the particle out of the region of acceleration. Therefore, the characteristic velocity that the particles gain in the reconnection process is the Alfvén velocity and the corresponding energy is of the order of first keV.

In the SCW region, the hot (>100 keV) particles undergo a gradient and centrifugal drifts around the Earth and pierce the acceleration zone, gaining additional energy (E_ml_m). This means that they add a few tens of keV more to the existing 100 keV. In the course of a magnetic storm, several hundred reconnection events can occur, and then some ring current particles can gain energy up to a few MeV. For this purpose, they need to get into randomly appearing small current wedges of substorms, and then energization will require a considerable time - days or even weeks.

In the paper by Hua et al. (2022) the relativistic electron fluxes in the Earth’s outer radiation belts were analyzed using 5-year measurements on Van Allen probes. The fluxes were found to reach a maximum around L ∼ 4.7 near the center of the outer belt, showing much greater variability at higher energy values (>1 MeV) than at the energies of hundreds of keV. Their stronger correlation with the time-integrated substorm indices (AL, AE) confirms the significant cumulative effect of substorms on the electron dynamics. Judging from the maximum correlation coefficient, electrons with energies of 0.3 MeV appear immediately, electrons with energies of 1 MeV after 4–5 days, and electrons with energies of 2.2 MeV after 8–12 days after the onset of the storm. In other words, it takes quite a long time, 1–2 weeks, to accelerate electrons to relativistic energies.

Since the time-integrated AL index serves as some measure of the magnetic flux released by the magnetosphere, the result by Hua et al. (2022) suggests that the more magnetic flux enters the Earth’s magnetosphere, the higher the energies to which the acceleration of charged particles is possible, with the acceleration time being proportional to the reconnected magnetic flux. This is quite consistent with the proposed scenario of the Dungey cycle.

In Tverskaya (1986) an important correlation between the position L_max of the maximum of the relativistic electron fluxes after the magnetic storm (i.e., a few days after its onset) and the minimum value of the Dst variation during the storm (i.e., a few hours after its onset) was obtained.

$\left|Dst\right|=\frac{2.75·{10}^4}{L_{\mathit{max}}^4}$

Here Dst is measured in nT. At the initial phase of the storm, the main contribution to the minimum value of the Dst variation is determined by the tail currents (Maltsev et al., 1996) and, therefore, this value serves as a measure of the current density in the tail and, as a consequence, is proportional to the magnetic flux accumulated in the tail lobes. In this connection, the Tverskaya (1986) relation can be interpreted in such a way that the larger the reconnected magnetic flux, the deeper the energetic particles are pushed inside the inner magnetosphere by the electric field. This also corresponds to the proposed scheme of the Dungey cycle.

9 Results

An analysis of the entire set of experimental data from the Geotail, Cluster, Themis, and MMS missions shows that the solar wind with a frozen-in magnetic field flows around the magnetosphere. Then, as follows from the well-known theorem of algebraic topology, at least one stagnation point in which the wind velocity is zero should form on the streamlined surface (magnetopause). As shown above, those parts of magnetic flux tubes that pass through the vicinity of the stagnation point experience particularly strong braking, while the rest of their parts continue to move with the solar wind. As a result, the flux tubes experience strong stretching, while the magnetic field strength increases and the density decreases as they approach the magnetopause. That fact became clear from the very beginning when Spreiter et al. (1966) made a gas-dynamic calculation of the flow around the magnetosphere and then tried to find the magnetic field according to the frozen-in approximation (Song and Russell, 2002; Pudovkin and Semenov, 1985). We draw attention to the fact that the flux tube passing through the stagnant point must experience not just strong, but infinite stretching and, therefore, must break and, hence, reconnect with the magnetospheric magnetic field. In other words, the flow around the magnetosphere with the IMF not parallel to the solar wind inevitably leads to the reconnection at the dayside magnetopause. Therefore, the observed signatures of stretching of magnetic flux tubes (draping, the magnetic field increase and the plasma density decrease) create conditions necessary for reconnection at the magnetopause.

Reconnection at the dayside magnetopause triggers a Dungey cycle, one of the main features of which is the transfer of the magnetic flux first from the dayside to the nightside, and then back. Dungey himself (1961) and all later researchers (Cowley and Lockwood, 1992; Trattner et al., 2021; Samsonov et al., 2024; Dai et al., 2024; Zhu et al., 2024) associated the magnetic flux transfer with the convection of magnetospheric plasma. Recently, many important and interesting results have been obtained in numerical 3D MHD modeling of magnetospheric convection (Samsonov et al., 2024; Dai et al., 2024). However, it should be realized that the MHD approximation ignores particle effects, such as their gradient/centrifugal drifts and, therefore, does not directly describe the ring current.

As shown above, a powerful electric field arises around the SCW, capable to accelerate ring current particles, create pulses of amplified current, and carry the magnetic flux. This mechanism of the magnetic flux transfer operates in combination with the convective one, such that the areas of amplification and weakening of the ring current play here a key role. To consistently take into account both mechanisms, methods and approaches developed at Rice University as a RCM model to embed particle effects into the MHD codes (Toffoletto et al., 2003; Cramer et al., 2017) are very useful.

The main results in regard to the ring current mechanism can be summarized as:

1. The Birkeland current loop associated with SCW results in a buildup of powerful electric field, with EMF equal to the potential difference along the X-line in the magnetospheric tail.

2. On the night side in the loop zone, the ring current intensifies, its effective magnetic moment increases, and the magnetic flux is transferred to the dayside.

3. On the dayside in the loop zone, the ring current weakens, the effective magnetic moment decreases, and the magnetic flux is transferred to the night side.

4. SCW related field-aligned currents having the polarity of R1 currents arise as a result of magnetic reconnection in the magnetotail and the transfer of tail currents by the Alfvén wave. Region 2 of field-aligned currents arises as a result of the generation of a partial ring current due to its amplification in the dipolarization region.

5. The inner magnetosphere operates as an accelerator with the SCW as an accelerating element.

6. Acceleration occurs in two stages: to the Alfvén velocity (energy of several keV) during the reconnection process in the magnetospheric tail and then to an energy of several tens of keV due to passing the potential difference along the X-line inside the inner magnetosphere in dipolarisation region.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

VS: Conceptualization, Formal Analysis, Investigation, Methodology, Project administration, Supervision, Validation, Writing–original draft, Writing–review and editing. IK: Conceptualization, Investigation, Supervision, Visualization, Writing–review and editing. NT: Conceptualization, Methodology, Writing–review and editing. NE: Conceptualization, Methodology, Writing–review and editing. MK: Supervision, Visualization, Writing–review and editing. XW: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work is supported by the Russian Science Foundation Grant #23–47-00084 “Magnetic Reconnection in Space and Laboratory Plasmas: Computer Simulations and Empirical Modeling.” XW. was supported by National Science Foundation of China (NSFC) Grant #42011530086 and #42261134533.

Acknowledgments

We thank Professor Victor Sergeev for fruitful discussions and valuable comments.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akasofu, S.-I. (1964). The development of the auroral substorm. Planet. Space Sci. 12, 273–282. doi:10.1016/0032-0633(64)90151-5

CrossRef Full Text | Google Scholar

Baumjohann, W., Paschmann, G., and Lühr, H. (1990). Characteristics of high-speed ion flows in the plasma sheet. J. Geophys. Res. 95, 3801–3809. doi:10.1029/JA095iA04p03801

CrossRef Full Text | Google Scholar

Baumjohann, W., and Treumann, R. A. (1996). Basic space plasma physics. London: Imperial College Press. doi:10.1142/p015

CrossRef Full Text | Google Scholar

Biernat, H. K., Heyn, M. F., and Semenov, V. S. (1987). Unsteady Petschek reconnection. J. Geophys. Res. 92 (A4), 3392–3396. doi:10.1029/JA092iA04p03392

CrossRef Full Text | Google Scholar

Birn, J., and Hesse, M. (2013). The substorm current wedge in MHD simulations. J. Geophys. Res. 118, 3364–3376. doi:10.1002/jgra.50187

CrossRef Full Text | Google Scholar

Birn, J., and Hesse, M. (2014). The substorm current wedge: further insights from MHD simulations. J. Geophys. Res. 119, 3503–3513. doi:10.1002/2014JA019863

CrossRef Full Text | Google Scholar

Birn, J., Hesse, M., Schindler, K., and Zaharia, S. (2009). Role of entropy in magnetotail dynamics. J. Geophys. Res. 114. doi:10.1029/2008JA014015

CrossRef Full Text | Google Scholar

Bittencourt, J. A. (2004). Fundamentals of plasma physics. Springer.

Google Scholar

Borovsky, J. E. (2008). The rudiments of a theory of solar wind/magnetosphere coupling derived from first principles. J. Geophys. Res. 113, A08228. doi:10.1029/2007JA012646

CrossRef Full Text | Google Scholar

Borovsky, J. E., and Valdivia, J. A. (2018). The earth’s magnetosphere: a systems science overview and assessment. Surv. Geophys 39, 817–859. doi:10.1007/s10712-018-9487-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Boström, R. (1964). A model of the auroral electrojets. J. Geophys. Res. 69 (23), 4983–4999. doi:10.1029/JZ069i023p04983

CrossRef Full Text | Google Scholar

Coroniti, F. V., and Kennel, C. F. (1973). Can the ionosphere regulate magnetospheric convection? J. Geophys. Res. 78 (16), 2837–2851. doi:10.1029/JA078i016p02837

CrossRef Full Text | Google Scholar

Cowley, S. W. H., and Lockwood, M. (1992). Excitation and decay of solar driven flows in the magnetosphere-ionosphere system. Ann. Geophys. 10, 103–115.

Google Scholar

Cramer, W. D., Raeder, J., Toffoletto, F. R., Gilson, M., and Hu, B. (2017). Plasma sheet injections into the inner magnetosphere: two-way coupled OpenGGCM-RCM model results. J. Geophys. Res. Space Phys. 122 (5), 5077–5091. doi:10.1002/2017JA024104

PubMed Abstract | CrossRef Full Text | Google Scholar

Dai, L., Han, Y., Wang, Ch., Yao, Sh., Gonzalez, W., Duan, S., et al. (2023). Geoeffectiveness of interplanetary Alfven waves: I. Magnetopause magnetic reconnection and directly-driven substorms. Astrophysical J. 945 (1), 47. doi:10.3847/1538-4357/acb267

CrossRef Full Text | Google Scholar

Dai, L., Wang, C., Zhang, Y., Lavraud, B., Burch, J., Pollock, C., et al. (2017). Kinetic Alfvén wave explanation of the Hall fields in magnetic reconnection. Geophys. Res. Lett. 44, 634–640. doi:10.1002/2016GL071044

CrossRef Full Text | Google Scholar

Dai, L., Zhu, M., Ren, Y., Gonzalez, W., Wang, C., Sibeck, D., et al. (2024). Global-scale magnetosphere convection driven by dayside magnetic reconnection. Nat. Commun. 15 (1), 639. doi:10.1038/s41467-024-44992-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Dimmock, A. P., and Nykyri, K. (2013). The statistical mapping of magnetosheath plasma properties based on THEMIS measurements in the magnetosheath interplanetary medium reference frame. J. Geophys. Res. 118 (8), 4963–4976. doi:10.1002/jgra.50465

CrossRef Full Text | Google Scholar

Duan, S. P., Dai, L., Wang, C., Liang, J., Lui, A. T. Y., Chen, L. J., et al. (2016). Evidence of kinetic Alfvén eigenmode in the near-Earth magnetotail during substorm expansion phase. J. Geophys. Res. Space Phys. 121, 4316–4330. doi:10.1002/2016JA022431

CrossRef Full Text | Google Scholar

Dubyagin, S., Sergeev, V., Apatenkov, S., Angelopoulos, V., Nakamura, R., McFadden, J., et al. (2010). Pressure and entropy changes in the flow-braking region during magnetic field dipolarization. J. Geophys. Res. 115, A10225. doi:10.1029/2010JA015625

CrossRef Full Text | Google Scholar

Dungey, J. W. (1961). Interplanetary magnetic field and the auroral zones. Phys. Rev. Lett. 6, 47–48. doi:10.1103/physrevlett.6.47

CrossRef Full Text | Google Scholar

Erkaev, N. V. (1986). Peculiarities of MHD flow around the magnetosphere in the vicinity of the deceleration point. Geomagnetism aeronomy 26, 705–709.

Google Scholar

Erkaev, N. V., Farrugia, C. J., and Biernat, H. K. (1998). “Comparison of gasdynamics and MHD predictions for magnetosheath flow,” in Polar cap boundary phenomena. NATO ASI series. Editors J. Moen, A. Egeland, and M. Lockwood (Dordrecht: Springer), 509, 27–40. doi:10.1007/978-94-011-5214-3_3

CrossRef Full Text | Google Scholar

Erkaev, N. V., Farrugia, C. J., and Biernat, H. K. (1999). Three-dimensional, one-fluid, ideal MHD model of magnetosheath flow with anisotropic pressure. J. Geophys. Res. 104 (A4), 6877–6887. doi:10.1029/1998JA900134

CrossRef Full Text | Google Scholar

Erkaev, N. V., Farrugia, C. J., and Biernat, H. K. (2003). The role of the magnetic barrier in the Solar wind-magnetosphere interaction. Planet. Space Sci. 51 (12), 745–755. doi:10.1016/S0032-0633(03)00111-9

CrossRef Full Text | Google Scholar

Erkaev, N. V., Mezentsev, A. V., Biernat, H. K., Besser, B. P., Bachmaier, G. A., Semenov, V. S., et al. (1994). The solar wind flow along the subsolar line in the magnetic barrier and reconnection at the magnetopause. Adv. Space Res. 14 (7), 81–86. doi:10.1016/0273-1177(94)90051-5

CrossRef Full Text | Google Scholar

Erkaev, N. V., Semenov, V. S., and Jamitzky, F. (2000). Reconnection rate for the inhomogeneous resistivity Petschek model. Phys. Rev. Lett. 84, 1455–1458. doi:10.1103/PhysRevLett.84.1455

PubMed Abstract | CrossRef Full Text | Google Scholar

Han, Y., Dai, L., Ren, Y., Wang, C., Gonzalez, W., and Zhu, M. (2024). Correlations of plasma properties between the upstream magnetosheath and the downstream outflow region of magnetopause reconnection. J. Geophys. Res. Space Phys. 129, e2024JA032817. doi:10.1029/2024JA032817

CrossRef Full Text | Google Scholar

Hesse, M., Aunai, N., Birn, J., Cassak, P., Denton, R. E., Drake, J. F., et al. (2016). Theory and modeling for the magnetospheric multiscale mission. Space Sci. Rev. 199, 577–630. doi:10.1007/s11214-014-0078-y

CrossRef Full Text | Google Scholar

Hua, M., Bortnik, J., Chu, X., Aryan, H., and Ma, Q. (2022). Unraveling the critical geomagnetic conditions controlling the upper limit of electron fluxes in the Earth's outer radiation belt. Geophys. Res. Lett. 49, e2022GL101096. doi:10.1029/2022GL101096

CrossRef Full Text | Google Scholar

Kepko, L., McPherron, R. L., Amm, O., Apatenkov, S., Baumjohann, W., Birn, J., et al. (2015). Substorm current wedge revisited. Space Sci. Rev. 190, 1–46. doi:10.1007/s11214-014-0124-9

CrossRef Full Text | Google Scholar

Landau, L. D., and Lifshitz, E. M. (1984). Electrodynamics of continuous media. Pergamon: Elsevier Ltd.

Google Scholar

Lui, A. T. Y. (1996). Current disruption in the Earth’s magnetosphere: observations and models. J. Geophys. Res. 101, 13067–13088. doi:10.1029/96ja00079

CrossRef Full Text | Google Scholar

Maltsev, Y. P., Arykov, A. A., Belova, E. G., Gvozdevsky, B. B., and Safargaleev, V. V. (1996). Magnetic flux redistribution in the storm time magnetosphere. J. Geophys. Res. 101, 7697–7704. doi:10.1029/95ja03709

CrossRef Full Text | Google Scholar

McPherron, R. L., Russell, C. T., and Aubry, M. A. (1973). Satellite studies of magnetospheric substorms on August 15, 1968: 9. Phenomenological model for substorms. J. Geophys. Res. 78, 3131–3149. doi:10.1029/JA078i016p03131

CrossRef Full Text | Google Scholar

Michotte de Welle, B., Aunai, N., Lavraud, B., Genot, V., Nguyen, G., Ghisalberti, A., et al. (2024). Global environmental constraints on magnetic reconnection at the magnetopause from in situ measurements. J. Geophys. Res. Space Phys. 129, e2023JA032098. doi:10.1029/2023JA032098

CrossRef Full Text | Google Scholar

Michotte de Welle, B., Aunai, N., Nguyen, G., Lavraud, B., Génot, V., Jeandet, A., et al. (2022). Global three-dimensional draping of magnetic field lines in Earth’s magnetosheath from in-situ spacecraft measurements. J. Geophys. Res. Space Phys. 127 (12), e2022JA030996. doi:10.1029/2022JA030996

CrossRef Full Text | Google Scholar

Nabert, C., Glassmeier, K.-H., and Plaschke, F. (2013). A new method for solving the MHD equations in the magnetosheath. Ann. Geophys. 31, 419–437. doi:10.5194/angeo-31-419-2013

CrossRef Full Text | Google Scholar

Nikolaev, A. V., Sergeev, V. A., Tsyganenko, N. A., Kubyshkina, M. V., Opgenoorth, H., Singer, H., et al. (2015). A quantitative study of magnetospheric magnetic field line deformation by a two-loop substorm current wedge. Ann. Geophys. 33, 505–517. doi:10.5194/angeo-33-505-2015

CrossRef Full Text | Google Scholar

Palin, L., Opgenoorth, H. J., Ågren, K., Zivkovic, T., Sergeev, V. A., Kubyshkina, M. V., et al. (2016). Modulation of the substorm current wedge by bursty bulk flows: 8 September 2002—revisited. J. Geophys. Res. Space Phys. 121, 4466–4482. doi:10.1002/2015JA022262

CrossRef Full Text | Google Scholar

Paschmann, G. (2008). Recent in-situ observations of magnetic reconnection in near-Earth space. Geophys. Res. Lett. 35, L19109. doi:10.1029/2008GL035297

CrossRef Full Text | Google Scholar

Petschek, H. E. (1964). “Magnetic field annihilation,” in AAS/NASA symposium on the physics of solar flares. Editor W. N. Hess (Washington, D. C), 425. NASA SP-50.

Google Scholar

Phan, T. D., Paschmann, G., Baumjohann, W., Sckopke, N., and Luhr, H. (1994). The magnetosheath region adjacent to the dayside magnetopause: AMPTE/IRM observations. J. Geophys. Res. 99, 121–141. doi:10.1029/93ja02444

CrossRef Full Text | Google Scholar

Pudovkin, M. I., and Semenov, V. S. (1977). Stationary frozen-in co-ordinate system. Ann. Geophys. 33, 429–433.

Google Scholar

Pudovkin, M. I., and Semenov, V. S. (1985). Magnetic field reconnection theory and the solar wind-Magnetosphere interaction: a review. Space Sci. Rev. 41 (1–2), 1–89. doi:10.1007/bf00241346

CrossRef Full Text | Google Scholar

Pulkkinen, T. I., Palmroth, M., Tanskanen, E. I., Ganushkina, N.Yu., Shukhtina, M. A., and Dmitrieva, N. P. (2007). Solar wind—magnetosphere coupling: a review of recent results. J. Atmos. Solar-Terrestrial Phys. 69 (Issue 3), 256–264. doi:10.1016/j.jastp.2006.05.029

CrossRef Full Text | Google Scholar

Renteln, P. (2014). Manifolds, tensors, and forms: an introduction for mathematicians and physicists. Cambridge, United Kingdom: Cambridge Univ. Press.

Google Scholar

Samsonov, A., Milan, S., Buzulukova, N., Sibeck, D., Forsyth, C., Branduardi- Raymont, G., et al. (2024). Time sequence of magnetospheric responses to a southward IMF turning. J. Geophys. Res. Space Phys. 129, e2023JA032378. doi:10.1029/2023JA032378

CrossRef Full Text | Google Scholar

Semenov, V. S., Heyn, M. F., and Ivanov, I. B. (2004). Magnetic reconnection with space and time varying reconnection rates in a compressible plasma. Phys. Plasmas 11 (1), 62–70. doi:10.1063/1.1630055

CrossRef Full Text | Google Scholar

Semenov, V. S., Heyn, M. F., and Kubyshkin, I. V. (1983). Reconnection of magnetic field lines in a nonstationary case. Sov. Astron. 27, 660–665.

Google Scholar

Semenov, V. S., Kubyshkin, I. V., Lebedeva, V. V., Rijnbeek, R. P., Heyn, M. F., Biernat, H. K., et al. (1992). A comparison and review of steady-state and time-varying reconnection. Planet. Space Sci. 40 (1), 63–87. doi:10.1016/0032-0633(92)90150-M

CrossRef Full Text | Google Scholar

Semenov, V. S., and Sergeev, V. A. (1981). A simple semi-empirical model for the magnetospheric substorm. Planet. Space Sci. 29, 271–281. doi:10.1016/0032-0633(81)90014-3

CrossRef Full Text | Google Scholar

Semenov, V. S., Volkonskaya, N. N., and Biernat, H. K. (1998). Effect of a snow plow in bursty magnetic reconnection. Phys. Plasmas 5 (9), 3242–3248. doi:10.1063/1.872991

CrossRef Full Text | Google Scholar

Sergeev, V. A., Apatenkov, S. V., Nakamura, R., Baumjohann, W., Khotyaintsev, Y. V., Kauristie, K., et al. (2019). Substorm-related near-Earth reconnection surge: combining telescopic and microscopic views. Geophys. Res. Lett. 46, 6239–6247. doi:10.1029/2019GL083057

CrossRef Full Text | Google Scholar

Sergeev, V. A., Apatenkov, S. V., Nakamura, R., Plaschke, F., Baumjohann, W., Panov, E. V., et al. (2021). MMS observations of reconnection separatrix region in the magnetotail at different distances from the active neutral X-line. J. Geophys. Res. Space Phys. 126, e2020JA028694. doi:10.1029/2020JA028694

CrossRef Full Text | Google Scholar

Sergeev, V. A., Nikolaev, A. V., Tsyganenko, N. A., Angelopoulos, V., Runov, A. V., Singer, H. J., et al. (2014). Testing a two-loop pattern of the substorm current wedge (SCW2L). J. Geophys. Res. 119, 947–963. doi:10.1002/2013JA019629

CrossRef Full Text | Google Scholar

Song, P., and Russell, C. T. (2002). Flow in the magnetosheath: the legacy of john spreiter. Planet. Space Sci. 50 (5–6), 447–460. doi:10.1016/S0032-0633(02)00025-9

CrossRef Full Text | Google Scholar

Soucek, J., Lucek, E., and Dandouras, I. (2008). Properties of magnetosheath mirror modes observed by Cluster and their response to changes in plasma parameters. J. Geophys. Res. 113, A04203. doi:10.1029/2007JA012649

CrossRef Full Text | Google Scholar

Spreiter, J. R., Summers, A. L., and Alksne, A. Y. (1966). Hydromagnetic flow around the magnetosphere. Planet. Space Sci. 14 (3), 223–253. doi:10.1016/0032-0633(66)90124-3

CrossRef Full Text | Google Scholar

Stawarz, J. E., Eastwood, J. P., Phan, T. D., Gingell, I. L., Pyakurel, P. S., Shay, M. A., et al. (2022). Turbulence-driven magnetic reconnection and the magnetic correlation length: observations from Magnetospheric Multiscale in Earth's magnetosheath. Phys. Plasmas. 29 (1), 012302. doi:10.1063/5.0071106

CrossRef Full Text | Google Scholar

Toffoletto, F., Sazykin, S., Spiro, R., and Wolf, R. (2003). Inner magnetospheric modeling with the Rice convection model. Space Sci. Rev. 107 (1/2), 175–196. doi:10.1023/A:1025532008047

CrossRef Full Text | Google Scholar

Trattner, K. J., Petrinec, S. M., and Fuselier, S. A. (2021). The location of magnetic reconnection at Earth’s magnetopause. Space Sci. Rev. 217 (3), 41. doi:10.1007/s11214-021-00817-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsyganenko, N. A., Semenov, V. S., and Erkaev, N. V. (2023). Data-based modeling of the magnetosheath magnetic field. J. Geophys. Res. Space Phys. 128, e2023JA031665. doi:10.1029/2023JA031665

CrossRef Full Text | Google Scholar

Tsyganenko, N. A., Semenov, V. S., Erkaev, N. V., and Gubaidulin, N. T. (2024). Magnetic fields and electric currents around the dayside magnetopause as inferred from data-constrained modeling. Front. Astron. Space Sci. 11, 1425165. doi:10.3389/fspas.2024.1425165

CrossRef Full Text | Google Scholar

Tverskaya, L. V. (1986). The boundary of electron injection into the earth magnetosphere. Geomagn. Aeron. 26, 864–865.

Google Scholar

Vasilyev, E. P., Sergeev, V. A., and Malkov, M. V. (1986). Three-dimensional effects of the Birkeland current loop. Geomagn. Aeron. 26, 114–118.

Google Scholar

Vasyliunas, V. M. (1975). Theoretical models of magnetic field line merging. Rev. Geophys. 13 (1), 303–336. doi:10.1029/RG013i001p00303

CrossRef Full Text | Google Scholar

Wang, Y. L., Raeder, J., and Russell, C. T. (2004). Plasma depletion layer: magnetosheath flow structure and forces. Ann. Geophys. 22, 1001–1017. doi:10.5194/angeo-22-1001-2004

CrossRef Full Text | Google Scholar

Zhu, M., Dai, L., Wang, C., Gonzalez, W., Samsonov, A., Guo, X., et al. (2024). The influence of ionospheric conductance on magnetospheric convection during the southward IMF. J. Geophys. Res. Space Phys. 129, e2024JA032607. doi:10.1029/2024JA032607

CrossRef Full Text | Google Scholar

Zwan, B. J., and Wolf, R. A. (1976). Depletion of solar wind plasma near a planetary boundary. J. Geophys. Res. 81, 1636–1648. doi:10.1029/JA081i010p01636

CrossRef Full Text | Google Scholar