Energy transport through Earth’s plasma sheet in 3-D

A statistical analysis of energy transport through Earth’s plasma sheet is performed using 6 years of Magnetospheric Multi-Scale (MMS) mission observations. The analysis entails a complete decomposition of the contributions to transport including the ion heat flux and enthalpy flux derived from the full ion pressure tensor to provide a three-dimensional (3-D) picture of plasma sheet energy transport. It is shown that the Poynting flux and enthalpy flux compete to dominate the total energy transport, while the heretofore ignored heat flux generally contributes a larger fraction of the total energy flux than the bulk kinetic energy flux. The spatial distribution of these fluxes are consistent with magnetic reconnection driven transport from an X-line statistically located at $X\sim -20R_E$. Kinetic fluxes stream Earthward from this point peaking mid-tail along the neutral sheet, while Poynting fluxes peak at higher latitudes and along the inner edge of the plasma sheet.

1 Introduction

Energy transport through Earth’s magnetotail occurs primarily in fast flows. It is believed that more than $50\%$ of the energy in the magnetotail is transported in this manner (Liu et al., 2014). Enhanced flows sustained over 10 min or more and during which the flow velocity exhibits a large amplitude peak have been described as bursty bulk flows (BBFs) (Angelopoulos et al., 1992). Studies show that in the inner plasma sheet (IPS), BBFs carry around $60-100\%$ of the total Earthward mass, energy, and magnetic flux transport (Angelopoulos et al., 1994). As this earthward-transported plasma slows down, the associated flux “pile-up” in the near-Earth region leads to dipolarization (Hesse and Birn, 1991). Subsequent studies established that this process is driven by magnetic flux carried by dipolarizing flux bundles, which are generated by magnetic reconnection occurring in the mid-tail region (Liu et al., 2013; Lui, 2024). Shiokawa et al. (1997) identified this flow-braking region as the inner edge of the neutral sheet demarking the boundary between the dipolar field of the inner magnetosphere and the tail-like field of the plasma sheet, where these high-speed flows are diverted (Juusola et al., 2011b; Kissinger et al., 2012). Dipolarization in the magnetotail is usually associated with an increase in wave power (Smith et al., 2023). The energy from the DFs is transported to the ionosphere through the field-aligned Poynting flux of the low-frequency waves (Qin et al., 2020) and field-aligned currents. In a recent study, it is observed that BBFs can penetrate into the outer edge of the radiation belt to provide a source population for the outer radiation belt (Ergun et al., 2022). While the energy transport is carried by the fast flows, convection in the plasma sheet is dominated by slow speed flows (Juusola et al., 2011a).

The primary role of magnetic reconnection in driving magnetotail transport has been demonstrated in a number of studies that characterize the energy and momentum flux in high speed flows emanating from reconnection sites (Birn and Hesse, 2005; McPherron et al., 2020). For example, local energy release from reconnection X-lines has been shown to be primarily in the form of the enthalpy flux of outward streaming ion jets (Eastwood et al., 2013). On the other hand, at dipolarization fronts (DFs), the primary form of energy transport is the enthalpy flux of heated electrons (Liu et al., 2021). Below the ion cyclotron frequency, a broad spectrum Alfvén waves extending from MHD to kinetic scales plays an important role in energy transport (Perraut et al., 2000; Contel et al., 2001). Angelopoulos et al. (2002) found large Poynting fluxes carried by kinetic Alfvén waves (KAWs) in the frequency range $\sim 0.05-1$ Hz embedded within fast magnetotail plasma flows. These waves have been shown to provide as much as $50\%$ of the outward energy transport from the magnetotail reconnection sites (Chaston et al., 2009),and to comprise a significant fraction of the total energy transport in fast plasma sheet flows under certain conditions (Chaston et al., 2012).

The relationship between the different forms of energy transport is intrinsic to understanding energy release through the magnetotail and its manifestation in space weather events. Kinetic energy and Poynting flux carried by flows and field variations, for example, transport mass and energy Earthward to power the aurorae (Wygant et al., 2000; Keiling et al., 2003), pump up the ring current (Sandhu et al., 2018), and modulate the radiation belts (Baker, 2000). These manifestations are consequences of different forms of transport and the distribution of the corresponding fluxes through the magnetotail. Statistical studies exploring these distributions have for instance, demonstrated that the kinetic energy flux (the sum of enthalpy and bulk kinetic energy flux) exceeded the Poynting flux in the inner plasma sheet (IPS) (Angelopoulos et al., 1994), while the statistical analysis by Miyashita et al. (2012) suggested that in the plasma sheet (PS), the bulk kinetic energy flux is much smaller than the Poynting flux and enthalpy flux. Conversely, during substorm periods in the tail-lobe region, the Poynting flux was found to surpass the enthalpy flux (Ohtani, 2019). The statistical study by Kaufmann and Paterson (2008) predicted heat flux near the neutral sheet $\left(|z|<0.3R_E\right)$ to be the second largest after enthalpy flux.

Here we extend these studies by decomposing the energy flux observed through Earth’s plasma sheet into its elemental ion kinetic and electromagnetic contributions. This is performed using the full vector fields and ion pressure tensor measured from the Magnetospheric Multi-Scale Spacecraft (MMS) over 6 years of operation. This decomposition provides a 3-D picture of the distribution of the various modes of energy transport through the plasma sheet not previously realised.

2 Data and methodology

2.1 Event selection

We use measurements recorded along traversals through Earth’s magnetotail by the MMS spacecraft over the years 2017–2022. These traversals are identified based on the information provided by the new mission phases and science region of interest of MMS (https://lasp.colorado.edu/galaxy/display/MFDPG/1.3+Mission+Phases+and+Science+Regions+of+Interest) and by visual inspection when no such information is available. In what follows field and particle measurements from MMS1 alone are shown noting that the results returned from the other spacecraft are for our purposes identical. Survey mode magnetic field data from the Flux-gate Magnetometer (FGM) (Russell et al., 2014) and fast-mode electric field data (Ergun et al., 2014; Lindqvist et al., 2014) from the Electric Double Probe (EDP) instrument (Torbert et al., 2014) are employed to evaluate the Poynting flux in GSM coordinates. Measurements from the Fast Plasma Investigation (FPI) instrument (Pollock et al., 2016) in the form of velocity moments evaluated over the energy range above the spacecraft potential and below the 30 keV upper limit of the instrument are employed to derive the kinetic terms. These data are returned every of 4.5 s. This cadence defines the “base” time resolution of the measurements we report. The evaluation of these moments incorporates corrections due to spacecraft charging to eliminate spurious contributions from secondaries and photo-electrons.

From these measurements a database is created by averaging over consecutive intervals defined by advection in the flow corresponding to a distance of $2\pi {\rho }_i$, with ${\rho }_i=\left(\frac{m{v}_{th}}{qB}\right)$ being the ion gyro radius and $m,q$ and $v_{th}$ are respectively the mass, charge, and thermal speed of the protons. This approach eliminates sub-gyro radius variations in the contributions to the moments and in the Poynting fluxes derived, while still quantifying the transport into the outer kinetic range. Notably, variations on electron scales are eliminated by this approach. Those intervals where the peak in the differential ion energy flux spectrum exceeds the 30 keV energy per charge, maximum of the FPI instrument are flagged and estimates recorded at these times are not included in the results shown here. It is worth mentioning that fast flows and hence large bulk kinetic energy fluxes, large enthalpy fluxes, and large heat fluxes that exceed the instrumental limit are not included in the present analysis, so the average values may be somewhat underestimated. While there is no criterion on flow speed, measurements nominally restricted to the plasma sheet by setting the ion number density to $N_i\ge 1c{m}^{-3}$, following the approach of Hasegawa (2012). With these criteria a total of 582,414 data points are collected throughout the PS from MMS1, with each of these points composed of an average of measurements over $2\pi$ times an advected thermal ion gyro-radius. Measurements from MMS2, MMS3, and MMS4 produce equivalent results.

2.2 Analysis

The energy flux is decomposed into the electromagnetic energy, or Poynting flux, kinetic fluxes including the enthalpy flux and heat flux, and the bulk kinetic energy flux. The temporal evolution of total energy density $\left(W\right)$ is (e.g., Birn and Hesse, 2005; Liu et al., 2021)

$\frac{dW}{dt}=-\mathbf{\nabla }.\left[\frac{\rho v^2}{2}\mathbf{v}+\left(\frac{\mathbf{v}Tr\left(\stackrel{⃡}{P}\right)}{2}+\mathbf{v}\cdot \stackrel{⃡}{P}\right)+{\mathbf{Q}}_H+\frac{1}{{\mu }_0}\left(\mathbf{E}\times \mathbf{B}\right)\right](1)$

Here, we evaluate each term on the RHS, where the first term represents the bulk kinetic energy flux, where $\rho =n_i{m}_i$ denotes the ion mass density and $\mathbf{v}$ is the ion flow speed. The second term within the parenthesis provides the expression for the enthalpy flux computed from the full pressure tensor, $\stackrel{⃡}{P}$ and includes the contribution of the internal energy. The Dual Ion Spectrometer (DIS), part of the FPI suite aboard MMS, provides 3D angular coverage and measures the 3D distribution function of ions in space (Pollock et al., 2016). The zeroth-order moment of which provides the number density, the first-order moment yields the bulk velocity, and the second-order moment determines the pressure tensor, which have been used for flux calculations in this study. Additionally, the third-order moment calculates the heat flux, which contributes to the third term on RHS. To compute the Poynting flux, as denoted by the last term on the RHS, we utilized survey mode magnetic field $\left(\mathbf{B}\right)$ data from the FGM and the fast survey mode electric field $\left(\mathbf{E}\right)$ data from the EDP instruments. We have used averages over $2\pi$ advected gyro-radii in $\mathbf{E}$ and $\mathbf{B}$ and report the total Poynting flux as we seek to evaluate the total electromagnetic energy transport. This is consistent with studies by Angelopoulos et al. (2002), Chaston et al. (2012). The FGM and EDP data undergo filtering and down-sampling to coincide with the FPI measurements. Notably, in the plasma sheet Equation 1, the electron bulk kinetic energy flux can be ignored due to the significantly larger ion mass, electron enthalpy flux can also be neglected owing to the ion-to-electron temperature ratio of $\sim 5$ or greater in the plasma sheet (Kaufmann et al., 2005). Additionally, all of the contributions to the energy flux are evaluated over an advected spatial scale of $2\pi {\rho }_i$, so that peak variations in the electron heat flux do not feature prominently in the statistics and on this scale and larger are generally equal to or less than the ion heat flux, while representing a minority fraction of the total transport. A comparison of the ion to electron contributions on this scale are provided in the next section to demonstrate this point.

3 Results

3.1 Energy transport topology

A representative interval measured from MMS1 on 1 August 2018 is presented in Figure 1 showing time-series fields and plasma parameters and the corresponding derived energy flux components on which the database is based. As shown, the spacecraft journeys from $-15R_E$ to the more distant magnetotail around $-24R_E$. The three components of the ion bulk flow and their absolute value in geocentric solar magnetospheric (GSM) coordinates are presented in Figures 1B, C, respectively. Predominantly, the ion flow is directed earthward, as evidenced by the positive x-component of the ion bulk flow. Four distinct regions of enhanced transport, delineated by colored dashed lines, can be identified as follows: region-1 (magenta; 00:45:00–01:40:00 UT), region-2 (blue; 14:07:00–14:54:00), region-3 (red; 17:53:00–19:25:00), and region-4 (black; 22:47:00–23:59:00). Each comprise intervals when the absolute value of the ion bulk flow exceeds 50 km/s for an extended period and correspond to a rise in differential ion energy flux as illustrated in Figure 1A. In region-1, MMS1 transitions into the plasma sheet, as indicated by a sudden rise in ion temperature (Figure 1E) and an increase in ion density (Figure 1D). Additionally, ion plasma beta (Figure 1F) approached approximately $\sim 1.0$. During this interval, a slow dipolarization in the background magnetic field is observed, while the wave electric field exhibits intensified oscillations as depicted in Figures 1G, H, respectively. The resultant Poynting flux shown in Figure 1I is mostly Earthward (+x-direction), albeit with significant dawn-ward and dusk-ward components (+/− y-direction). The ion enthalpy flux, bulk kinetic energy flux, and heat flux are also predominantly directed earthward as depicted in Panels (j) (k), and (l), respectively with the enthalpy flux dominant. A similar pattern is captured in Regions 2, 3, and 4 for the enthalpy, bulk kinetic and heat flux, while the Poynting flux is predominantly in the y-direction, which is an often repeated pattern of enhanced electromagnetic and kinetic transport in association with fast flows. While this is a well-known feature of magnetotail energy transport (Angelopoulos et al., 1994), there are appreciable variations in the relative contributions of each component that are dependent on location, the field geometry and plasma beta. Indeed, persistent morphological structuring emerges in the examination of the statistical distribution of these energy fluxes as we now describe.

Figure 1

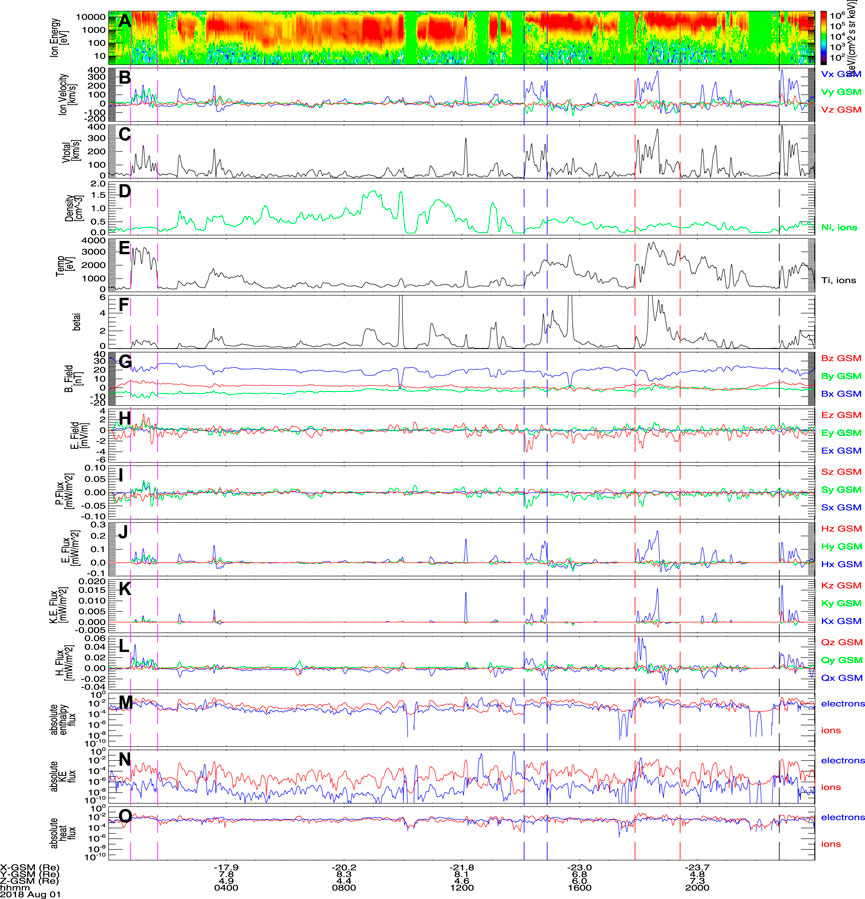
Figure 1. Shows (A) differential energy flux of ions, (B) three components of ion flow speed in geocentric solar magnetospheric (GSM) coordinate, (C) absolute value of ion flow speed, (D) ion density, (E) ion temperature, (F) ion plasma beta, (G) magnetic field, (H) electric field, and three components of the (I) Poynting flux, ion (J) enthalpy flux (K) bulk kinetic energy flux, and (L) heat flux in GSM coordinates, respectively. Absolute values of (M) enthalpy flux (N) bulk kinetic energy flux, and (O) heat flux of electrons and ions are shown in blue and red curves, respectively for comparison. Regions identified by dashed vertical lines indicate absolute ion bulk flow speed exceeding 50 km/s for extended period of time.

Figures 1M–O presents a comparison of absolute values of enthalpy flux, bulk kinetic energy flux and heat flux for electrons (blue curve) and ions (red curve), respectively. As discussed in Section 2.2, the contributions of ion enthalpy and bulk kinetic energy fluxes are generally higher than those of the electrons, and the electron and ion heat flux contributions are nearly equal over this interval.

Using the procedures outlined in Section 2.1, statistics describing the decomposed energy transport contributions in GSM coordinates were compiled over the spatial range covered by the MMS spacecraft within Earth’s magnetotail. For the purpose of presenting summary distributions in this report, each GSM plane in the magnetotail (i.e., XY, XZ, and YZ planes) is partitioned into bins with a window size of $1R_E\times 1R_E$. Each bin considered in compiling the statistics contains at least 10 gyro-averaged measurements of the absolute value of each transport quantity. The distribution of events per bin is shown in the Supplementary Figures 1–3. Inspection of the distributions within each bin shows a form symmetric about the mean values we report here. In Figures 2, 3, the color bar indicates the corresponding in situ absolute value of the energy flux (as specified in the figures), measured in $mW/m^2$, at a location corresponding to the (abscissa, ordinate) pair depicted in figures. A separation into Earthward and tailward transport is considered in the context of pressure balance and field geometry in Section 3.2 while we reserve a description of the full vector quantities for subsequent work. In this study, the magnetotail region characterized by $X_{\mathit{GSM}}<-15R_E$ is designated as the distant magnetotail, while the area where $-15R_E\le X_{\mathit{GSM}}\le -5R_E$ is identified as the near-Earth magnetotail region. Moreover, the region with $-12R_E\le Y_{\mathit{GSM}}\le +12R_E$ is demarcated as the central region, and that with $|Y_{\mathit{GSM}}|>+12R_E$ is considered the edge of the distribution plane.

Figure 2

Figure 2. Shows the distribution of the absolute value of (A) Poynting flux, (B) enthalpy flux, (C) bulk kinetic energy flux, and (D) heat flux in XY-plane. The color-blind friendly version of Figures 2–4 can be found in the Supplementary Figures S5-S7.

Figure 3

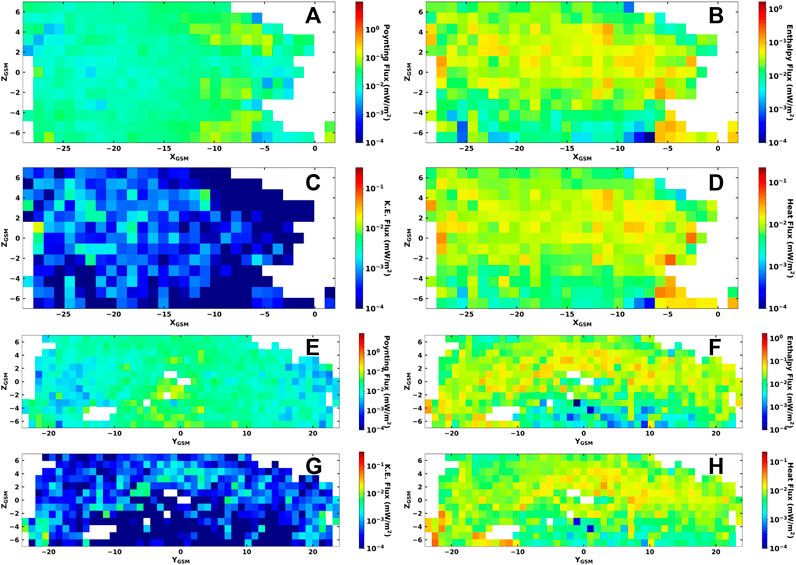
Figure 3. Shows the distribution of the absolute value of (A) Poynting flux, (B) enthalpy flux, (C) bulk kinetic energy flux, and (D) heat flux in XZ-plane. Furthermore, in YZ-plane, the distribution of the absolute value of (E) Poynting flux, (F) enthalpy flux, (G) bulk kinetic energy flux, and (H) heat flux.

Figure 2A illustrates the distribution of Poynting flux in the equatorial plane (XY-plane). The Poynting flux exhibits a gradual increase from the distant tail region to the near-Earth region, attaining its maximum value in the near-Earth region. Further, Poynting flux decreases from the central region towards the edges of the XY-plane. The corresponding distribution of enthalpy flux shown in Figure 2B is more irregular or patchy with comparatively larger values than the Poynting flux in the distant magnetotail. Moreover, in contrast to the Poynting flux distribution, the enthalpy flux is somewhat enhanced on the flanks of the near-Earth region, and most prominently in the dusk-ward sector. Additionally, unlike the Poynting flux, where the flux is maximum close to the origin in $Y_{\mathit{GSM}}$-axis, there are multiple enthalpy flux maxima distributed throughout the X-Y plane. The distribution of bulk kinetic energy flux shown in Figure 2C has relatively larger value in the distant magnetotail central plane and decreases towards the near-Earth region. Its minimum occurs around X $\sim (-10\text{to}-5R_E)$. The significant depression at X $\sim -15R_E$ in the dawn-ward sector provides an asymmetric distribution with larger values observed on the dusk-side. Further, the flux value in the central region of the XY-plane is comparatively larger than the edge of the XY-plane in the distant magnetotail region, while it is larger at the edge of the XY-plane than the central portion in the near-Earth region. The heat flux distribution replicates that of the enthalpy flux (Figure 2D).

The distribution of the energy fluxes in the GSM XZ-plane, is depicted in Figures 3A–D. The Poynting flux increases gradually from the distant magnetotail to the near-Earth region, as previously identified (cf. Figure 2A). There is a general depletion at low values of $Z_{\mathit{GSM}}$ with average minima residing at generally small positive $Z_{\mathit{GSM}}$ values. Conversely (Figure 3B), reveals that, unlike the Poynting flux, the peak of the distribution in enthalpy flux is located near the equatorial plane in the GSM system with a progressive shift toward more positive $Z_{\mathit{GSM}}$ values with distance downtail. Significantly, the maximum of the average distribution occupies the region of depletion in the Poynting flux. The bulk kinetic energy and heat flux distributions shown in Figures 2C, D share a similar morphology, albeit the bulk kinetic energy flux is greatly reduced within $X_{\mathit{GSM}}>-10R_E$.

The distributions in the YZ-plane are presented in Figures 3E–H. In Figure 3E, the distribution shows that most of the Poynting flux is concentrated within the range $-12R_E\le Y_{\mathit{GSM}}\le +12R_E$, while occupying the entire range of $Z_{\mathit{GSM}}$. Furthermore, within this region, the fluxes are accentuated in the south reflecting of the distribution at the inner edge of the plasma sheet shown in Figure 3A. In contrast, the distribution of the enthalpy flux in the YZ-plane (Figure 3F) shows that for $abs(Y_{\mathit{GSM}})>10R_E$, the enthalpy flux is enhanced in the south, while at smaller $Y_{\mathit{GSM}}$ values, the flux is predominantly enhanced in the north. The latter reflects the distribution in the XZ-plane shown in Figure 3B. A similar morphology is found in the distribution of heat flux (Figure 3H) and bulk kinetic energy flux (Figure 3G), albeit with reduced flux.

3.2 Energy transport in pressure balance coordinates

To provide physical insight into the distribution of these energy fluxes, we resample the statistics into a 2-D coordinate system defined by pressure balance (Baumjohann et al., 1990; Xing et al., 2010) and the magnitude and orientation of the magnetic field in the X-Z plane. Following the formulation outlined by Watanabe et al. (2019) the magnetic field in the lobes is defined as

$\frac{B_{\mathit{lobe}}^2}{2{\mu }_0}=n_i{k}_B\left(T_i+T_e\right)+\frac{B^2}{2{\mu }_0},(2)$

where, $B^2=\left(B_x^2+B_y^2+B_z^2\right)$. The observations are organized according to the normalized fields, $sign(B_x)\sqrt{B_x^2+B_y^2}/B_{\mathit{lobe}}\text{and}{B}_z/B_{\mathit{lobe}}$, where $sign\left(B_x\right)=B_x/|B_x|$. The ratio $sign(B_x)\sqrt{B_x^2+B_y^2}/B_{\mathit{lobe}}$ varies between $-1$ and $+1$, indicating the southern and northern lobes respectively with the neutral sheet located at $sign(B_x)\sqrt{B_x^2+B_y^2}/B_{\mathit{lobe}}=0$. Positive and negative values of $B_z/B_{\mathit{lobe}}$ signify regions Earthward and tail-ward of a nominal X-line as depicted in Figure 4B. Different regions in the physical XZ-plane and their corresponding counterparts in the transformed system are denoted by A, B, C, D, and E, which are useful in identifying Earthward (B and D), tail-ward (A and C) region, and the reconnection (E) line in the plane. Within this system the statistics are distributed into bins of size $0.1sign(B_x)\sqrt{B_x^2+B_y^2}/B_{\mathit{lobe}}\times 0.1B_z/B_{\mathit{lobe}}$, and the average values of various energy fluxes and plasma parameters evaluated within each. The x-component of the ion flow and energy fluxes in this system are illustrated in Figure 4H, and Figures 4C–F, respectively. Consistent with this formulation the direction of the flow and energy flux contributions reverse at $B_z/B_{\mathit{lobe}}=0$, while $\left|sign(B_x)\sqrt{B_x^2+B_y^2}/B_{\mathit{lobe}}\right|\to 0$ along this reversal identifies the x-line where very high plasma beta necessarily occurs (Figure 4G). The distribution of $X_{\mathit{GSM}}$ values over this plane, depicted in Figure 4I, indicates that the statistical location of the x-line is approximately at $X=-20R_E$. It is also apparent from Figures 4I, J that with increasing distance down-tail the neutral sheet resides at increasingly positive Z-GSM values thereby accounting for the shift in the flux distributions toward positive $Z_{\mathit{GSM}}$ identified in the X-Z plane in Figure 3.

Figure 4

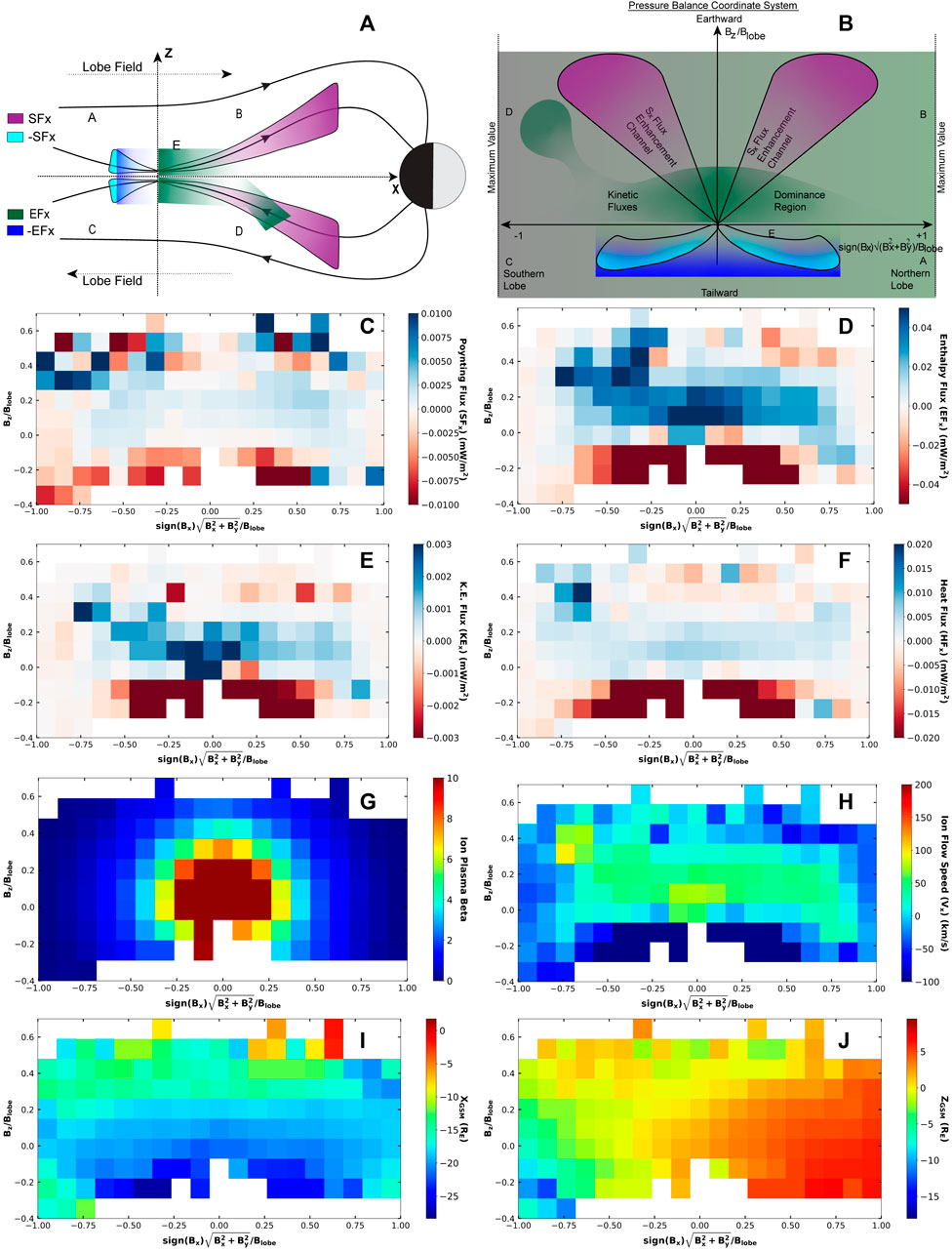
Figure 4. Shows (A) Physical Coordinate plane XZ of magnetotail, (B) Overview of pressure balance coordinate system. In the $sign(B_x)\sqrt{B_x^2+B_y^2}/B_{\mathit{lobe}},B_z/B_{\mathit{lobe}}$ plane the distribution of (C) Poynting Flux, (D) enthalpy flux, (E) bulk kinetic energy flux, (F) heat flux, (G) ion plasma beta, (H) x-component of ion flow speed $(V_{ix})$, (I) $X_{\mathit{GSM}}$, and (J) $Z_{\mathit{GSM}}$. In (B) $S_x$ denotes the x-component of the Poynting flux. Furthermore, the color code in the schematic (A) and (B) indicates the respective positive and negative fluxes.

Several salient features of the energy transport distributions emerge in this coordinate system (Equation 2). Firstly, near the x-line, the fluxes in the tail-ward direction (i.e., negative $B_z$) without exception are larger than those in the Earthward (positive $B_z$) direction. This disparity may stem from the formation of a near-Earth neutral line during active times, resulting in more frequent occurrences of tailward flows when fluxes are larger. Secondly, the x-component of Poynting flux, illustrated in Figure 4C, is observed to be smallest near the reconnection point and gradually increases in the Earthward direction in two channels displaced from, and roughly symmetric about the neutral sheet with localized peaks at the inner edge plasma sheet. Based on the $X_{\mathit{GSM}}$ distribution, the location of maximum Poynting flux is estimated to be around $X_{\mathit{GSM}}\ge -10R_E$, falling within the range of the flow braking region (Shiokawa et al., 1997). While our interest here is primarily in the dominant X-directed fluxes, we present in Supplementary Figure 4 accompanying this article the z-component of the Poynting flux. As found in previous studies (Miyashita et al., 2012) this component is convergent on the neutral sheet with values approaching the X-directed fluxes near the lobes. Thirdly, in contrast to the Poynting flux, the x-component of kinetic fluxes (i.e., enthalpy, heat and bulk kinetic energy fluxes) peak mid-tail in the neutral sheet albeit somewhat broadly dispersed in $sign(B_x)\sqrt{B_x^2+B_y^2}/B_{\mathit{lobe}}$. Finally, there is a region of enhanced flow at negative $sign(B_x)\sqrt{B_x^2+B_y^2}/B_{\mathit{lobe}}$ corresponding to the southern inner plasma sheet that provides a secondary peak in the kinetic fluxes. The origin of this enhancement is not clear at the time of writing. These features in the electromagnetic and kinetic fluxes complete a picture whereby the kinetic contributions provide the bulk of the energy transport through the central plasma sheet with the Poynting flux providing a comparable fraction of the transport through the high-latitude flanks and dominating at the inner edge of the plasma sheet. The overall pattern is represented schematically in Figures 4A, B representing energy flows divergent from the statistically identified X-line and requiring energy conversion at that location as described by Equation (1).

4 Conclusion

We used 6 years (2017–2022) of measurements from the MMS mission to statistically map the distribution of energy transport through Earth’s magnetotail. The use of the full pressure tensor and 3-D electromagnetic fields provide a more complete account of energy transport through this region than previously possible. It is found that the ion heat flux, previously overlooked in earlier studies, makes a substantial contribution to the total ion energy flux within Earth’s magnetotail and is found to have larger contribution than the bulk kinetic energy flux most of the time. While earlier studies of ion heat flux were limited to the neutral sheet represented as a 2-D projection in the equatorial plane (Kaufmann and Paterson, 2008), our study resolves the distribution of ion heat flux throughout the plasma sheet and reports results in 3-D. In the XY-GSM plane, the Poynting flux exhibits a smooth variation, increasing gradually from the distant magnetotail to the near-Earth region. Meanwhile, both the ion enthalpy and heat fluxes in the same plane display a slight enhancement on the dusk side near the inner edge of the plasma sheet but are otherwise nearly uniform, albeit patchy or intermittent in their distribution over the spatial range considered. On the other hand, the ion bulk kinetic energy flux in the XY-plane generally decreases with proximity to Earth with an abrupt fall off inside $X=-10R_E$ and a depleted region on the dawn side. While asymmetric distributions are observed in the X-Z GSM plane this we believe is largely due to the displacement of the neutral sheet to increasingly positive values of Z-GSM with distance down-tail.

In closing, we note that a persistent feature throughout the statistics reported here is the anti-correlation between the Poynting and ion kinetic fluxes. When organized in a coordinate system relative to an empirically inferred X-line a pattern emerges suggestive of results returned via large scale MHD simulations of the magnetotail (Birn and Hesse, 2005). In this coordinate system the kinetic contributions transport energy Earthward through the central plasma sheet mostly within channels of X-directed Poynting flux displaced in Z that peak at the inner edge of the plasma sheet and extend to high latitudes. An examination of the physical relationship between the ion kinetic and electromagnetic fluxes suggested by this picture goes beyond what can be considered here. However, a consideration of the vector fluxes and corresponding spatial gradients inherent to conversion between these modes of transport may be pursued in a later study.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://figshare.com/s/2abfa217a8e75dc5bdd5.

Author contributions

KB: Conceptualization, Investigation, Methodology, Visualization, Writing–original draft, Writing–review and editing. CC: Conceptualization, Funding acquisition, Supervision, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was supported by NASA Grant 80NSSC21K0580.

Acknowledgments

The data provided through NASA Magnetospheric Multi-Scale mission MODA.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2024.1481448/full#supplementary-material

References

Angelopoulos, V., Baumjohann, W., Kennel, C. F., Coroniti, F. V., Kivelson, M. G., Pellat, R., et al. (1992). Bursty bulk flows in the inner central plasma sheet. J. Geophys. Res. Space Phys. 97, 4027–4039. doi:10.1029/91JA02701

CrossRef Full Text | Google Scholar

Angelopoulos, V., Chapman, J. A., Mozer, F. S., Scudder, J. D., Russell, C. T., Tsuruda, K., et al. (2002). Plasma sheet electromagnetic power generation and its dissipation along auroral field lines. J. Geophys. Res. Space Phys. 107, 14–20. doi:10.1029/2001JA900136

CrossRef Full Text | Google Scholar

Angelopoulos, V., Kennel, C. F., Coroniti, F. V., Pellat, R., Kivelson, M. G., Walker, R. J., et al. (1994). Statistical characteristics of bursty bulk flow events. J. Geophys. Res. Space Phys. 99, 21257–21280. doi:10.1029/94JA01263

CrossRef Full Text | Google Scholar

Baker, D. (2000). The role of magnetospheric substorms in high-energy particle production within the 1. earth’s Magnetos. 443, 419.

Google Scholar

Baumjohann, W., Paschmann, G., and Lühr, H. (1990). Pressure balance between lobe and plasma sheet. Geophys. Res. Lett. 17, 45–48. doi:10.1029/GL017i001p00045

CrossRef Full Text | Google Scholar

Birn, J., and Hesse, M. (2005). Energy release and conversion by reconnection in the magnetotail. Ann. Geophys. 23, 3365–3373. doi:10.5194/angeo-23-3365-2005

CrossRef Full Text | Google Scholar

Chaston, C. C., Bonnell, J. W., Clausen, L., and Angelopoulos, V. (2012). Energy transport by kinetic-scale electromagnetic waves in fast plasma sheet flows. J. Geophys. Res. Space Phys. 117. doi:10.1029/2012JA017863

CrossRef Full Text | Google Scholar

Chaston, C. C., Johnson, J. R., Wilber, M., Acuna, M., Goldstein, M. L., and Reme, H. (2009). Kinetic alfvén wave turbulence and transport through a reconnection diffusion region. Phys. Rev. Lett. 102, 015001. doi:10.1103/PhysRevLett.102.015001

PubMed Abstract | CrossRef Full Text | Google Scholar

Contel, O. L., Roux, A., Perraut, S., Pellat, R., Holter, Ø., Pedersen, A., et al. (2001). Possible control of plasma transport in the near-Earth plasma sheet via current-driven Alfvén waves (ƒ ∼ = ƒ_H+). J. Geophys. Res. Space Phys. 106, 10817–10827. doi:10.1029/2001JA900013

CrossRef Full Text | Google Scholar

Eastwood, J. P., Phan, T. D., Drake, J. F., Shay, M. A., Borg, A. L., Lavraud, B., et al. (2013). Energy partition in magnetic reconnection in earth’s magnetotail. Phys. Rev. Lett. 110, 225001. doi:10.1103/PhysRevLett.110.225001

PubMed Abstract | CrossRef Full Text | Google Scholar

Ergun, R. E., Tucker, S., Westfall, J., Goodrich, K. A., Malaspina, D. M., Summers, D., et al. (2014). The axial double probe and fields signal processing for the MMS mission. Space Sci. Rev. 199, 167–188. doi:10.1007/s11214-014-0115-x

CrossRef Full Text | Google Scholar

Ergun, R. E., Usanova, M. E., Turner, D. L., and Stawarz, J. E. (2022). Bursty bulk flow turbulence as a source of energetic particles to the outer radiation belt. Geophys. Res. Lett. 49. doi:10.1029/2022GL098113

CrossRef Full Text | Google Scholar

Hasegawa, H. (2012). Structure and dynamics of the magnetopause and its boundary layers. Monogr. Environ. Earth Planets 1, 71–119. doi:10.5047/meep.2012.00102.0071

CrossRef Full Text | Google Scholar

Hesse, M., and Birn, J. (1991). On dipolarization and its relation to the substorm current wedge. J. Geophys. Res. Space Phys. 96, 19417–19426. doi:10.1029/91JA01953

CrossRef Full Text | Google Scholar

Juusola, L., Østgaard, N., and Tanskanen, E. (2011a). Statistics of plasma sheet convection: ps statistics. J. Geophys. Res. Space Phys. 116, n/a. doi:10.1029/2011JA016479

CrossRef Full Text | Google Scholar

Juusola, L., Østgaard, N., Tanskanen, E., Partamies, N., and Snekvik, K. (2011b). Earthward plasma sheet flows during substorm phases: ps flows during substorms. J. Geophys. Res. Space Phys. 116. doi:10.1029/2011JA016852

CrossRef Full Text | Google Scholar

Kaufmann, R. L., and Paterson, W. R. (2008). Ion heat flux and energy transport near the magnetotail neutral sheet. J. Geophys. Res. Space Phys. 113. doi:10.1029/2007JA012929

CrossRef Full Text | Google Scholar

Kaufmann, R. L., Paterson, W. R., and Frank, L. A. (2005). Relationships between the ion flow speed, magnetic flux transport rate, and other plasma sheet parameters. J. Geophys. Res. Space Phys. 110. doi:10.1029/2005JA011068

CrossRef Full Text | Google Scholar

Keiling, A., Wygant, J. R., Cattell, C. A., Mozer, F. S., and Russell, C. T. (2003). The global morphology of wave Poynting flux: powering the aurora. Science 299, 383–386. doi:10.1126/science.1080073

PubMed Abstract | CrossRef Full Text | Google Scholar

Kissinger, J., McPherron, R. L., Hsu, T., and Angelopoulos, V. (2012). Diversion of plasma due to high pressure in the inner magnetosphere during steady magnetospheric convection. J. Geophys. Res. Space Phys. 117. doi:10.1029/2012JA017579

CrossRef Full Text | Google Scholar

Lindqvist, P.-A., Olsson, G., Torbert, R. B., King, B., Granoff, M., Rau, D., et al. (2014). The spin-plane double probe electric field instrument for MMS. Space Sci. Rev. 199, 137–165. doi:10.1007/s11214-014-0116-9

CrossRef Full Text | Google Scholar

Liu, C. M., Fu, H. S., Yu, Y. Q., Lu, H. Y., Liu, W. L., Xu, Y., et al. (2021). Energy flux densities at dipolarization fronts. Geophys. Res. Lett. 48. doi:10.1029/2021GL094932

CrossRef Full Text | Google Scholar

Liu, J., Angelopoulos, V., Zhou, X., Runov, A., and Yao, Z. (2013). On the role of pressure and flow perturbations around dipolarizing flux bundles. J. Geophys. Res. Space Phys. 118, 7104–7118. doi:10.1002/2013JA019256

CrossRef Full Text | Google Scholar

Liu, J., Angelopoulos, V., Zhou, X.-Z., and Runov, A. (2014). Magnetic flux transport by dipolarizing flux bundles. J. Geophys. Res. Space Phys. 119, 909–926. doi:10.1002/2013JA019395

CrossRef Full Text | Google Scholar

Lui, A. T. Y. (2024). Dipolarizing flux bundles and magnetic flux transport. J. Geophys. Res. Space Phys. 129, e2024JA032632. doi:10.1029/2024ja032632

CrossRef Full Text | Google Scholar

McPherron, R. L., El-Alaoui, M., Walker, R. J., and Richard, R. (2020). Characteristics of reconnection sites and fast flow channels in an mhd simulation. J. Geophys. Res. Space Phys. 125, e2019JA027701. doi:10.1029/2019ja027701

CrossRef Full Text | Google Scholar

Miyashita, Y., Machida, S., Nosé, M., Liou, K., Saito, Y., and Paterson, W. R. (2012). A statistical study of energy release and transport midway between the magnetic reconnection and initial dipolarization regions in the near-earth magnetotail associated with substorm expansion onsets. J. Geophys. Res. Space Phys. 117. doi:10.1029/2012JA017925

CrossRef Full Text | Google Scholar

Ohtani, S. (2019). Substorm energy transport from the magnetotail to the nightside ionosphere. J. Geophys. Res. Space Phys. 124, 8669–8684. doi:10.1029/2019JA026964

CrossRef Full Text | Google Scholar

Perraut, S., Contel, O. L., Roux, A., Pellat, R., Korth, A., Holter, Ø., et al. (2000). Disruption of parallel current at substorm breakup. Geophys. Res. Lett. 27, 4041–4044. doi:10.1029/2000GL000054

CrossRef Full Text | Google Scholar

Pollock, C., Moore, T., Jacques, A., Burch, J., Gliese, U., Saito, Y., et al. (2016). Fast plasma investigation for magnetospheric multiscale. Space Sci. Rev. 199, 331–406. doi:10.1007/s11214-016-0245-4

CrossRef Full Text | Google Scholar

Qin, P., Ge, Y., Du, A., Huang, C., Zhang, Y., Luo, H., et al. (2020). Coupling between the magnetospheric dipolarization front and the earth’s ionosphere by ultralow-frequency waves. Astrophysical J. 895, L13. doi:10.3847/2041-8213/ab8e48

CrossRef Full Text | Google Scholar

Russell, C. T., Anderson, B. J., Baumjohann, W., Bromund, K. R., Dearborn, D., Fischer, D., et al. (2014). The magnetospheric multiscale magnetometers. Space Sci. Rev. 199, 189–256. doi:10.1007/s11214-014-0057-3

CrossRef Full Text | Google Scholar

Sandhu, J. K., Rae, I. J., Freeman, M. P., Forsyth, C., Gkioulidou, M., Reeves, G. D., et al. (2018). Energization of the ring current by substorms. J. Geophys. Res. Space Phys. 123, 8131–8148. doi:10.1029/2018JA025766

PubMed Abstract | CrossRef Full Text | Google Scholar

Shiokawa, K., Baumjohann, W., and Haerendel, G. (1997). Braking of high-speed flows in the near-earth tail. Geophys. Res. Lett. 24, 1179–1182. doi:10.1029/97gl01062

CrossRef Full Text | Google Scholar

Smith, A. W., Rae, I. J., Forsyth, C., Watt, C. E. J., and Murphy, K. R. (2023). Statistical characterization of the dynamic near-earth plasma sheet relative to ultra-low frequency (ulf) wave growth at substorm onset. J. Geophys. Res. Space Phys. 128. doi:10.1029/2022JA030491

CrossRef Full Text | Google Scholar

Torbert, R. B., Russell, C. T., Magnes, W., Ergun, R. E., Lindqvist, P.-A., LeContel, O., et al. (2014). The FIELDS instrument suite on MMS: scientific objectives, measurements, and data products. Space Sci. Rev. 199, 105–135. doi:10.1007/s11214-014-0109-8

CrossRef Full Text | Google Scholar

Watanabe, K., Keika, K., Hoshino, M., Kitamura, N., Saito, Y., Giles, B. L., et al. (2019). Statistical study on electron and ion temperatures in the near-earth reconnection and magnetic pileup regions. Geophys. Res. Lett. 46, 14223–14229. doi:10.1029/2019GL084837

CrossRef Full Text | Google Scholar

Wygant, J. R., Keiling, A., Cattell, C. A., Johnson, M., Lysak, R. L., Temerin, M., et al. (2000). Polar spacecraft based comparisons of intense electric fields and Poynting flux near and within the plasma sheet-tail lobe boundary to uvi images: an energy source for the aurora. J. Geophys. Res. Space Phys. 105, 18675–18692. doi:10.1029/1999JA900500

CrossRef Full Text | Google Scholar

Xing, X., Lyons, L. R., Angelopoulos, V., Larson, D., Carlson, C., Runov, A., et al. (2010). Plasma sheet pressure evolution related to substorms. J. Geophys. Res. Space Phys. 115. doi:10.1029/2009JA014315

CrossRef Full Text | Google Scholar