Relativistic reflection modeling in AGN and related variability from PCA: a brief review

X-ray observations of active galactic nuclei (AGNs) reveal relativistic reflections from the innermost regions of accretion disks, which contain general-relativistic footprints caused by spinning supermassive black holes (SMBH). We anticipate the spin of a SMBH to be stable over the human timeframe, so brightness changes in the high-energy corona above the SMBH should slightly alter relativistic reflection. In this brief review, we discuss the latest developments in modeling relativistic reflection, as well as the rapid small variation in relativistic emission disclosed by the principal component analysis (PCA) of X-ray variability in AGN. PCA studies of X-ray spectra from AGNs have shown that relativistically blurred reflection has negligible fluctuations over the course of observations, which could originate from rapid (intrahour) intrinsic variations in near-horizon accretion flows and photon rings. The PCA technique is an effective way to disclose relativistic reflection from X-ray observations of AGNs, simplifying the complexity of largely variable X-ray data for automated spectral analysis with machine learning algorithms.

1 Introduction

The center of of the Milky Way is characterized by a supermassive black hole (SMBH), which is supported by indirect but compelling observational evidence such as stellar orbits in the vicinity of Sagittarius A^* (Sgr A^*; Ghez et al., 1998; Ghez et al., 2005) and the near-infrared luminosity of Sgr A^* being consistent with the presence of an event horizon (Broderick and Narayan, 2006; Broderick et al., 2009). Similarly, we expect that active galactic nuclei (AGNs) in other galaxies host SMBHs at their centers (Kormendy, 1988; Kormendy and Richstone, 1992; Kormendy et al., 1997; Cretton and van den Bosch, 1999), which are essential to explaining the X-ray features of quasars and AGNs (see review by Mushotzky et al., 1993). Several techniques, such as the reverberation mapping (Blandford and McKee, 1982), spectral energy distribution (SED) fitting (Shields, 1978; Malkan, 1983), and broad-line region size–luminosity correlation (Vestergaard, 2002), have been developed to validate the presence of SMBHs and estimate their masses (e.g., Kormendy and Richstone, 1995; Miyoshi et al., 1995; Wandel et al., 1999; Peterson et al., 2004; Calderone et al., 2013; Capellupo et al., 2015; Bentz and Katz, 2015; Mejía-Restrepo et al., 2016). Our constraints on SMBH masses have allowed us to establish the connections between SMBHs and the evolution of their host galaxies (e.g., Magorrian et al., 1998; Ferrarese and Merritt, 2000; Häring and Rix, 2004; Heckman and Best, 2014).

Some solutions of standard general relativity simply characterize black holes using two parameters, mass and spin (Kerr, 1963), which can fully describe the properties of SMBHs. In this regard, spins of SMBHs, along with masses, could produce some of the fundamental mechanisms for powering relativistic jets (e.g., Garofalo et al., 2010; Tchekhovskoy and McKinney, 2012), as well as describing the discrepancy between radio-loud and radio-quiet AGNs (Wilson and Colbert, 1995; Moderski et al., 1998), galaxy evolution (Di Matteo et al., 2005; Volonteri et al., 2013; Sesana et al., 2014), and galaxy mergers (Hughes and Blandford, 2003; Volonteri et al., 2005; Berti and Volonteri, 2008). In particular, ultra-fast outflows (UFOs) have been detected in X-ray observations of several radio-quiet AGNs (e.g., Tombesi et al., 2010; 2011; 2012; Danehkar et al., 2018; Boissay-Malaquin et al., 2019), while extended relativistic jets have been seen in radio observations of radio-loud AGNs (see review by Blandford et al., 2019). The spins of SMBHs could have a potential role in the formation of UFOs and jets seen in AGNs and quasars (MacDonald et al., 1986; Thorne et al., 1986). These phenomena can be explained by spinning SMBHs according to the Blandford–Znajek (Blandford and Znajek, 1977) and Penrose mechanism (Penrose, 1969; 2002; Penrose and Floyd, 1971), as well as frame-dragging vortexes (e.g., Owen et al., 2011; Nichols et al., 2011; Danehkar, 2020). Alternatively, they could originate magnetically from the innermost accretion disk in the vicinity of a spinning SMBH according to the Blandford–Payne mechanism (Blandford and Payne, 1982).

In the Boyer–Lindquist coordinates, the Kerr metric (Kerr, 1963) of a spinning black hole is expressed using the set of oblate spheroidal coordinates ($r$, $\theta$, $\varphi$) as follows (Boyer and Lindquist, 1967):

$\begin{array}{ll}\hfill d{s}^2& =-\left(1-\frac{r_{\text{s}}r}{\mathrm{\Sigma }}\right)c^{2}d{t}^2-\frac{2\bar{a}{r}_{\text{s}}r{\sin }^2\theta }{\mathrm{\Sigma }}cdtd\varphi +\frac{\mathrm{\Sigma }}{\mathrm{\Delta }}d{r}^2\hfill \\ \hfill & +\mathrm{\Sigma }d{\theta }^2+\left(r^2+{\bar{a}}^2+\frac{{\bar{a}}^2{r}_{\text{s}}r{\sin }^2\theta }{\mathrm{\Sigma }}\right){\sin }^2\theta d{\varphi }^2,\hfill \end{array}(1)$

where $\mathrm{\Sigma }=r^2+{\bar{a}}^2{\cos }^2\theta$, $\mathrm{\Delta }=r^2-r_{\text{s}}r+{\bar{a}}^2$, $r_{\text{s}}=2GM/c^2$ is the Schwarzschild radius, $\bar{a}=J/Mc$ is called the Kerr spin parameter describing angular momentum per unit mass having the length dimension, $J$ the black hole angular momentum, $M$ the black hole mass, $G$ the Newtonian constant of gravitation, and $c$ the speed of light. The dimensionless spin parameter, which is frequently used in the astrophysical community, is defined as $a\equiv 2\bar{a}/r_{\text{s}}=Jc/(G{M}^2)$, while $-1\le a\le 1$; negative values describe retrograde rotation, in which the black hole rotates in the opposite direction of the accretion disk, whereas positive values are associated with prograde rotation, and zero implies non-rotating black holes. The outer and inner event horizons are determined by the roots of $\mathrm{\Delta }=0$, which are $r_{\pm }=r_{\text{s}}(1\pm \sqrt{1-a^2})/2$. In the case of $a=0$, Equation 1 reduces to the Schwarzschild metric (Schwarzschild, 1916) with the event horizon at $r=r_{\text{s}}$. Unlike the Schwarzschild metric, which has a singularity at $r=0$, the Kerr metric has one at $\mathrm{\Sigma }=0$. The innermost stable circular orbit (ISCO) of the accretion disk is located at a radius of marginal stability, $r_{\text{ms}}$, which is given by (Bardeen et al., 1972):

$r_{\text{ms}}\left(a\right)=\frac{GM}{c^2}\left(3+Z_2-\mathrm{s}\mathrm{g}\mathrm{n}\left(a\right)\sqrt{\left(3-Z_1\right)\left(3+Z_1+2Z_2\right)}\right),(2)$

where $\mathrm{s}\mathrm{g}\mathrm{n}(a)$ is the signum function having the value $-1$, 1 or 0 according to the sign of $a$, while $Z_1$ and $Z_2$ are defined as,

$Z_1=1+{\left(1-a^2\right)}^{1/3}\left[{\left(1+a\right)}^{1/3}+{\left(1-a\right)}^{1/3}\right],$

$Z_2=\sqrt{3a^2+Z_1^2}.$

This implies that the accretion disk has a limited extent at the marginal stability radius $(r_{\text{ms}})$, also called the ISCO radius. The value of this radius depends upon the dimensionless spin parameter, e.g.,

$r_{\text{ms}}=\left\{\begin{array}{cc}0.5r_{\text{s}}\hfill & \text{for}a=1\hfill \\ 3r_{\text{s}}\hfill & \text{for}a=0\hfill \\ 4.5r_{\text{s}}\hfill & \text{for}a=-1\hfill \end{array}\right..$

In prograde rotation, the ISCO radius shrinks to nearly half of the Schwarzschild radius as it approaches a near-maximal spin $(a\approx 1)$, while it expands in retrograde rotation $(-1<a<0)$. For a non-spinning black hole, the ISCO radius is precisely three times the Schwarzschild radius.

There are different methods available to measure the spin of a single SMBH (see review by Brenneman, 2013). All of them are based on general relativity solutions of the Kerr spacetime in the vicinity of the black hole. They use the aforementioned fact that the ISCO radius $(r_{\text{ms}})$ of the accretion disk depends on the spin, as seen in Equation 2, and assume a geometrically thin disk that is capable of irradiating the corona radiation with light-bending in the innermost regions (see Figure 1 bottom-left). Below are the techniques that have been used to constrain the spins of SMBHs:

Figure 1

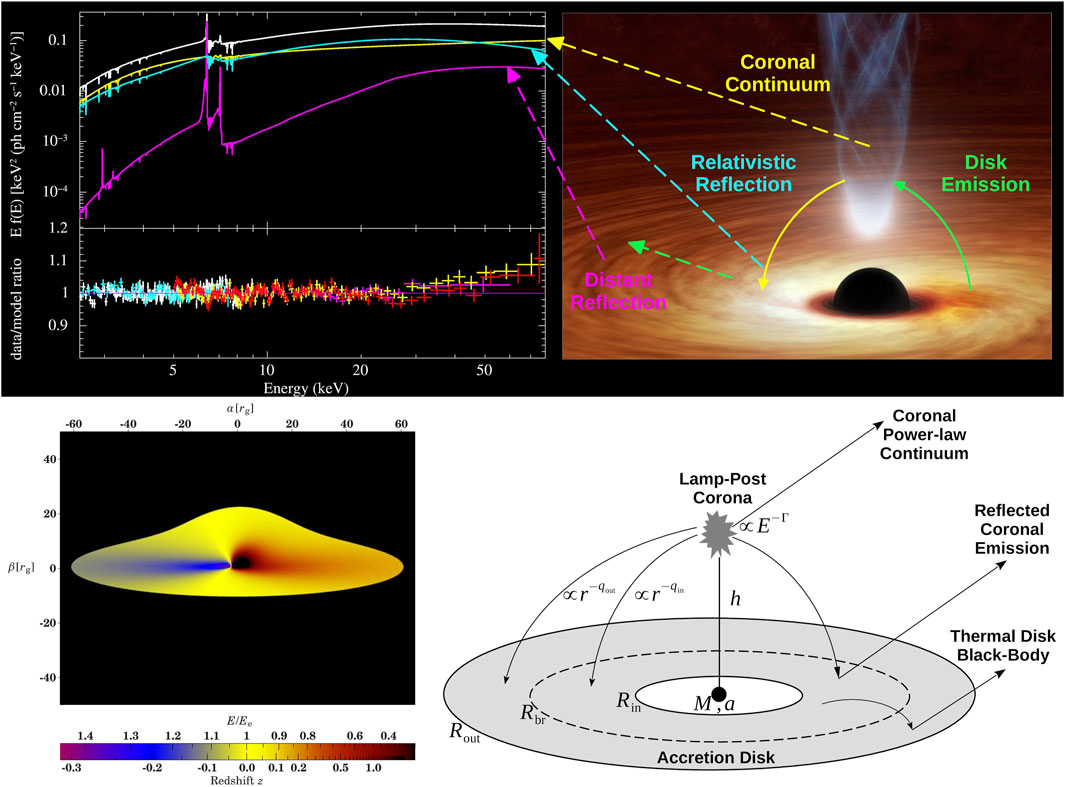
Figure 1. Top: A schematic view of X-ray relativistic reflection. Spectral model (left panel) of the Seyfert 1.5 galaxy NGC 4151, consisting of a coronal continuum (highecut$\times$zpowerlw; yellow), relativistic reflection (relconv$\times$xillver; light blue), and distant reflection (xillver; purple), fitted to NuSTAR and Suzaku observations, from Keck et al. (2015). An artist’s illustration (right) of the radiation reflection from the accretion disk around a black hole (courtesy of NASA/JPL-Caltech/R. Hurt at IPAC/R. Connors at Caltech). Bottom: A simulated image (left panel) of an accretion disk, inclined with $i=80°$ (relative to the line of sight), gravitationally distorted by general-relativistic light-bending effects of a black hole at the center, from García et al. (2014). A diagram (right) illustrating the lamp-post corona with a power-law-shaped continuum $(\propto E^{-\mathrm{\Gamma }})$ situated at a height $(h)$ above a black hole simply described by its mass $(M)$ and spin $(a)$, and the innermost accretion disk characterized by the boundary radii ($R_{\text{in}}$ and $R_{\text{out}}$) and the break radius $(R_{\text{br}})$ to describe the coronal emissivity laws $\propto r^{-q_{\text{in}}}$ $(R_{\text{in}}<r<R_{\text{br}})$ and $\propto r^{-q_{\text{out}}}$ $(R_{\text{br}}<r<R_{\text{out}})$, as well as corresponding thermal disk black-body and reflected coronal emission, adopted from Dauser (2014) and Hoormann et al. (2016).

1.1 X-ray reflection spectroscopy

High-energy radiation from a corona or the base of a jet illuminates the accretion disk, reflecting scattered photons, which forms the basis of this method. Multiple Compton scatterings (Comptonization) of soft thermal photons lead to the cooling of the hot electrons in the corona (Haardt and Maraschi, 1991; 1993). A portion of the comptonized radiation undergoes scattering outside of the ionizing source, resulting in the formation of a power-law-shaped continuum that is typically observed in X-rays from AGN (Haardt and Maraschi, 1991). However, a fraction of the scattered photons will undergo reflection on the surface of the disk (Haardt and Maraschi, 1993), as seen in Figure 1 (top). If the disk is not fully ionized, the continuum includes the emission of various fluorescent emission lines at energies below 7 keV, in addition to the Compton hump with a peak at around 20–30 keV caused by downscattering, as seen in Figure 1 (top panel). The most notable line is Fe K$\alpha$, with a rest-frame energy of 6.4 keV, which is produced due to the significant iron abundance and fluorescence process. This line is the most important tool for describing the relativistic reflection from the innermost disk, as it becomes broadened and skewed due to Doppler and general-relativistic effects (see reviews by Reynolds and Nowak, 2003; Miller, 2007; Reynolds, 2013; 2014; 2019; Bambi -et al., 2021). The truncation of its low-energy tail directly corresponds to the ISCO radius, i.e., the spin. This feature, independent of mass or distance from the black hole, enables the measurement of black hole spins. One of the drawbacks of this method for AGN is the complex absorption from line-of-sight material, typically found at lower energies in the red tail. Moreover, exceptionally high counts are required to properly constrain the spin; $2\times 10^5$ (Guainazzi et al., 2006) or $1.5\times 10^5$ counts (de La Calle Pérez et al., 2010) in the energy range of 2–10 keV. Furthermore, this approach is actually model-dependent, as demonstrated by a list of reflection models in Table 1. However, the advancements in X-ray spectroscopy above 10 keV with the Nuclear Spectroscopic Telescope Array (NuSTAR; Harrison et al., 2013), which has no pile-up effects, have significantly improved the reliability of this approach by including the Compton hump reflection at high energies ($>10$ keV, peaking within 20–30 keV; see, e.g., Parker et al., 2014c; Keck et al., 2015; Victoria-Ceballos et al., 2023). Most of the spectral models developed for X-ray relativistic reflection are briefly reviewed in Section 2.

Table 1

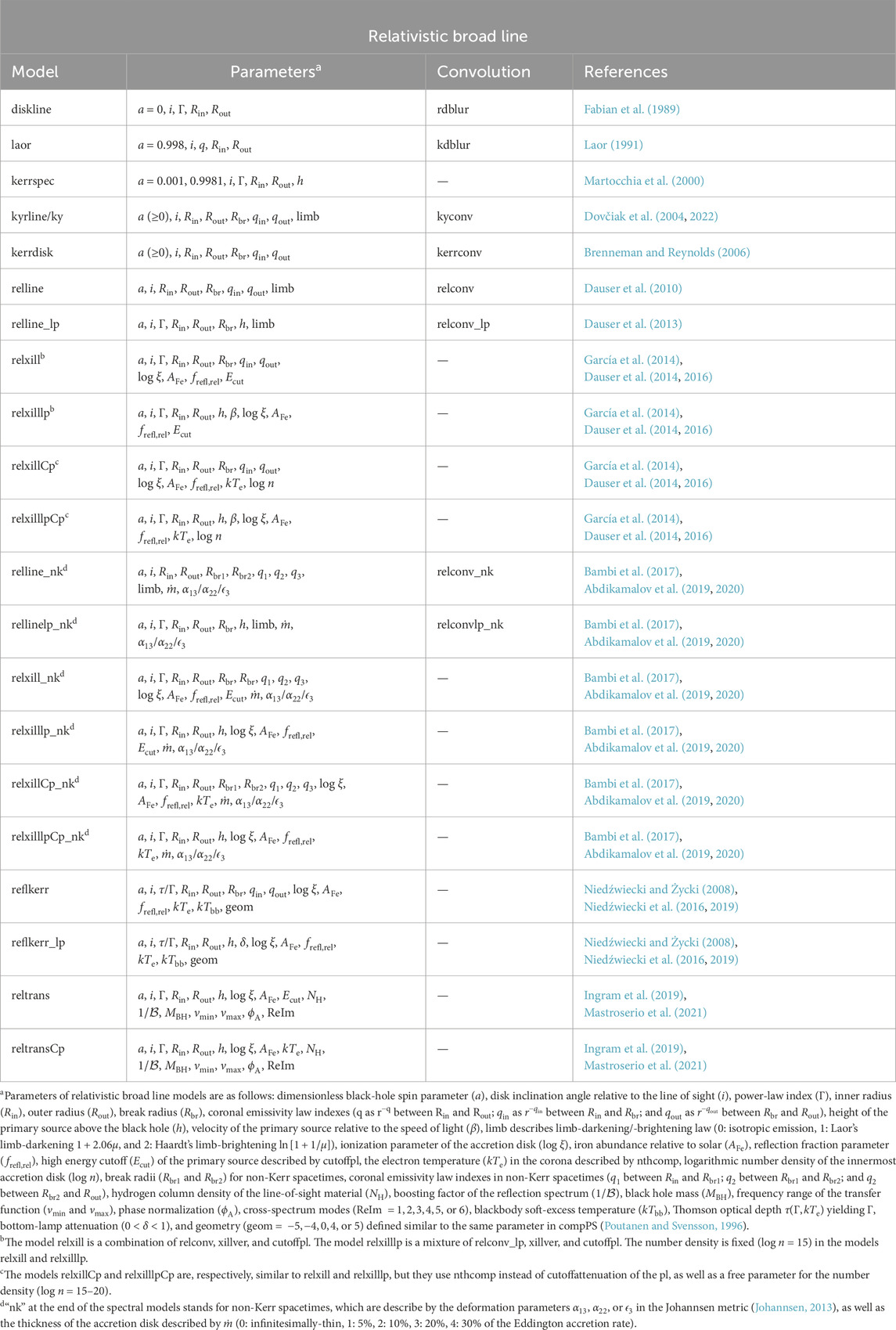
Table 1. A list of spectral models developed for relativistically broadened emission of the accretion disk.

1.2 Broad-band SED fitting

This method was initially began to be deployed for X-ray binaries by Zhang et al. (1997) and Gierliński et al. (2001). This approach depends on the distance, mass, and disk inclination angle of the accretion disk (see review by Remillard and McClintock, 2006), so it has mostly been used for the spin measurement of stellar-mass black holes (e.g., Shafee et al., 2006; McClintock et al., 2006). This method was first exploited by Done et al. (2013) to put constraints on the spins of SMBHs with the optxconv model (based on optxagnf; Done et al., 2012), which contains the SED spectrum made by a (color-temperature-corrected) blackbody, an optically thick warm Comptonisation (soft excess; $<2$ keV) component, and an optically thin, hot Comptonisation (power-law; $>2$ keV) component. Later, the same technique was employed to measure the spins of AGNs at $z\sim 1.5$ that evolved just after cosmic noon (Capellupo et al., 2015; Capellupo et al., 2016), and was benchmarked against X-ray reflection measurements for NGC 3783, an AGN known for its relativistically broadened Fe K$\alpha$ line (Capellupo et al., 2017). This method was employed to constrain the masses and spins of SMBSH in four blazars at high redshifts (Campitiello et al., 2018), which was implemented using the kerrbb model (Li et al., 2005) of multi-temperature blackbody spectrum of a thin accretion disk around a spinning black hole. The optxconv SED model (Done et al., 2012; Done et al., 2013) was also used by Porquet et al. (2019) to derive a well-measured spin rate of the SMBH in Ark 120, a well-known bare AGN with no intrinsic absorption along the line-of-sight. Subsequently, new SED models of the broad-band continuum of AGN, called agnsed and qsosed (Kubota and Done, 2018; Petrucci et al., 2018), have been developed, followed by a super-Eddington accretion model of the slim disk (agnslim; Kubota and Done, 2019), which provide better constraints on the masses and spins of SMBHs. More recently, Hagen and Done (2023) made a fully general-relativistic implementation of agnsed, referred to as the relagn model that includes general-relativistic ray tracing and the relativistic Novikov–Thorne disk model (Novikov and Thorne, 1973), leading to a complex disk spectrum in the soft excess instead of a simple blackbody, and was utilized to determine the SMBH spin in Fairall 9 from the broad-band spectrum, extending from Optical/UV to the X-ray.

1.3 Radio event horizon imaging

This method employs sub-mm data collected by several very long baseline interferometry (VLBI) stations over different locations (e.g., JCMT, SMT, SPT, IRAM, APEX, and ALMA) to achieve micro-arcsecond spatial resolution images of an SMBH event horizon (Event Horizon Telescope Collaboration et al., 2019a; Event Horizon Telescope Collaboration et al., 2022a). This has enabled the first-ever images of the accretion flow in the vicinity of nearby SMBHs to be produced, namely M87 and Sgr A^* (Event Horizon Telescope Collaboration et al., 2019b; Event Horizon Telescope Collaboration et al., 2022b). We can determine the SMBH spin by accurately modeling the appearance of accretion flows in VLBI images, accounting for general-relativistic light bending (see Figure 1 bottom-left) based on various characteristics such as the ISCO radius $(r_{\text{ms}})$. The VLBI imaging techniques have recently been used to deduce the spin values according to high-spatial-resolution images in Sgr A^* and M87 (Event Horizon Telescope Collaboration et al., 2019c; Event Horizon Telescope Collaboration et al., 2021b; Event Horizon Telescope Collaboration et al., 2022c; Event Horizon Telescope Collaboration et al., 2022d). This method has the disadvantage of only being suitable for nearby SMBHs.

2 Relativistic reflection modeling

Various spectral models have been constructed to reproduce the general-relativistic effects of the Kerr metric on the iron K$\alpha$ line profile. Table 1 summarizes most of the well-known spectral models made for X-ray data analysis of relativistically blurred emission, along with their key parameters. The basic parameters in these models are the dimensionless spin parameter $(a=Jc/G{M}^2)$, the line-of-sight inclination angle $(i)$ of the accretion disk, the spectral photon index $(\mathrm{\Gamma })$ of the primary source – the corona or the base of a jet above the black hole –, as well as the boundary radii ($R_{\text{in}}$ and $R_{\text{out}}$) of the innermost accretion disk. Most of these models can be loaded into tools for X-ray spectral analysis, particularly the X-ray spectral fitting package xspec¹ (Arnaud, 1996; Arnaud et al., 1999) of HEASoft’s data analysis package for X-ray astronomy xanadu (NASA HEASARC, 2014), MIT’s Interactive Spectral Interpretation System² (isis; Houck and Denicola, 2000), CXC³’s Modeling and Fitting Package Sherpa⁴ (Freeman et al., 2001; Doe et al., 2007) of the Chandra Interactive Analysis of Observation (ciao; Fruscione et al., 2006), and SRON⁵’s X-ray high-resolution spectral modeling and fitting package spex⁶ (Kaastra et al., 1996; de Plaa et al., 2020). These models are often applied to integrated spectra of AGNs without accounting for the variability of the X-ray sources.

The early models, developed to analyze relativistic reflection, featured fiducial values for the spin parameter. Black hole spin measurement began with the diskline (Fabian et al., 1989) and laor (Laor, 1991) fixed-spin models, which were run with fiducial spin values of $a=0$ and 0.998, respectively. The diskline model was based on analytic, time-consuming calculations, whereas the laor model relied on extensive pre-calculated tabulated Flexible Image Transport System (FITS) data created for different combinations of the model parameters: inclination angle, spectral photon index $(\mathrm{\Gamma })$, inner radius $(R_{\text{in}})$, and outer radius $(R_{\text{out}})$. The laor model recreates the relativistic line shape by interpolating data from the extensive FITS table. Later, Martocchia and Matt (1996) examined how the “lamp post” geometry affected the broad iron K$\alpha$ lines, in which the ionizing source is located on the polar axis at a height $(h)$ above the black hole, as illustrated in Figure 1 (bottom-right). This investigation was followed by a comprehensive analysis for $a=0.001$ and 0.9981 leading to the kerrspec model (Martocchia et al., 2000; Martocchia et al., 2002). We should note that the reflection continuum was not included in these models and needed to be handled by a separate model such as reflionx (Ross et al., 1999; Ross and Fabian, 2005; Ross and Fabian, 2007), which should be convolved with the corresponding convolution models to make a smoothed spectrum of relativistic smearing in an accretion disk. The convolution models rdblur and kdblur were prepared using diskline and laor, respectively, which can be used with a reflection model (e.g., reflionx). Nandra et al. (2007) used a modified version of the kdblur model to characterize the broad iron K$\alpha$ line in XMM-Newton observations of a sample of Seyfert galaxies. However, the spectral models with fixed spin rates obviously prevented us from straightforwardly measuring the black hole spin.

The next-generation of relativistic reflection models has a free parameter for the positive spin rates, which allows for the determination of the black hole spin in prograde rotation $(0⩽a<1)$. The kyrline (or ky) model (Dovčiak, 2004; Dovčiak et al., 2004; Dovčiak et al., 2022) was developed to incorporate extensive tables calculated for transfer functions. This model rapidly computes the shape of relativistically broadened line emission using transfer function tables without relying heavily on interpolation, yielding a significantly greater level of spectral resolution compared to the laor model. Furthermore, the black hole spin was a free parameter, ranging from $a=0$ to 1. The model can therefore reproduce the relativistic blurred emission more accurately than the laor model for all positive spin rates and inclination degrees. In addition, the kyrline model features coronal emissivity law indexes ($q_{\text{in}}$ as $r^{-q_{\text{in}}}$ between $R_{\text{in}}$ and $R_{\text{br}}$; and $q_{\text{out}}$ as $r^{-q_{\text{out}}}$ between $R_{\text{br}}$ and $R_{\text{out}}$) for precisely creating the emitted radiation (see Figure 1 bottom-right), describing the emissivity characteristics on both sides of the break radius $(R_{\text{br}})$, as well as including the limb prescriptions for limb-darkening/-brightening laws (Chandrasekhar, 1960), namely isotropic emission $(I\propto 1)$, Laor’s limb-darkening ($I\propto 1+2.06\mu$; Laor, 1991), and Haardt’s limb-brightening ($I\propto \ln (1+1/\mu )$; Haardt, 1993), where $\mu =\cos ({\theta }_{\text{e}})$ and ${\theta }_{\text{e}}$ is the inclination angle of the emitted radiation with respect to the disk. These features were accomplished by computing them for inclusion in the comprehensive FITS table. In order to address the problems with the excessive table size and lack of smoothness in the kyrline model, Brenneman and Reynolds (2006) created an alternative model for relativistic reflection known as kerrdisk (Brenneman, 2007). Their model has a relatively smaller FITS table and a robust interpolation approach. Using a high level of smoothness in the transfer function allows for effective interpolation in kerrdisk. Furthermore, this model employs a distinct methodology, approximating the narrow line of the distant reflection from the accretion disk using a $\delta$-function instead of a Gaussian function. Their model computes a larger portion of the integration using analytic approaches, thereby excluding the emissivity law from the calculated table. However, fitting methods can handle the modeling of the emissivity law. This model effectively reduces the table size to a fraction of the kyrline FITS table. Nevertheless, the relativistic emission produced by kerrdisk appears less smooth than those made by kyrline, with some noticeable spikes in the red wing of the relativistic line. However, data accumulated with the spectral resolutions of detectors aboard the XMM-Newton and Suzaku telescopes could not distinguish these spikes. The kyrline model has been used to conduct an XMM-Newton survey on a sample of radio-quiet Type 1 AGNs (de La Calle Pérez et al., 2010). Unlike the fixed-spin models (laor and diskline), kyrline and kerrdisk, which can relativistically be convolved with a reflection model (e.g., reflionx) using the kyconv and kerrconv models, respectively, are more accurate in producing the shape of relativistic emission for any positive spin rates. However, a black hole spinning in retrograde relative to the accretion disk $(-1<a<0)$ could not have its spin constrained by the kyrline and kerrdisk models.

Since 2010, several spectral models have been developed for relativistic blurred emission (see Table 1) that incorporate both positive and negative spin values, enabling the measurement of the black hole’s spin in both the prograde and retrograde directions with respect to the accretion disk. To accommodate the full spin range $(-0.998⩽a⩽+0.998)$, Dauser et al. (2010) has created the relline model, together with relline_lp, featuring the “lamp post” geometry (for detail see Dauser, 2010), using FITS tables for Cunningham’s photon transfer function (Cunningham, 1975) pre-calculated with a customized version of the F77 program photon_transferfct⁷ (also called spx; Speith, 1993; Speith et al., 1995) (a gravitationally-distorted appearance of an accretion disk made with a modified version of this program is shown in the bottom-left panel of Figure 1). The relline model employs Green’s functions to calculate the radiated radiation for arbitrary angular and radial variations, as well as robust interpolation techniques that lead to a decrease in pre-calculated tabulated data. Moreover, relativistic line profiles calculated for a hard X-ray source located on the rotational axis at a height $(h)$ above the black hole, i.e., the “lamp post” geometry, are provided in the relline_lp model (Dauser et al., 2013). Both the models includes prescriptions for the limb-darkening/-brightening laws. Their corresponding convolution models, relconv and relconv_lp, are able to convolve the reflection continuum created by a reflection model such as reflionx (Ross et al., 1999; Ross and Fabian, 2005; Ross and Fabian, 2007) and xillver (García, 2010; García and Kallman, 2010; García et al., 2011; García et al., 2013). As this simple combination of the relativistic convolution model (relconv) and the reflection model (xillver) can lead to inconsistent results, García et al. (2014) made a self-consistent implementation of the spectrum reflected from the disk irradiated by an ionizing source and relativistically blurred emission in a new model called relxill, as well as an additional new model called relxill_lp for a lamp-post geometry.⁸ These models incorporated angle-dependent reflection tables of xillver⁹ into the relativistic blurring calculations, which exhibits like behavior to a convolution of xillver and relconv (or relconv_lp), albeit with self-consistently calculated X-ray reflection (Dauser, 2014). Subsequently, Dauser et al. (2014) and Dauser et al. (2016), further extended them to include the reflection fraction parameter $(f_{\text{refl,rel}})$, a flux ratio between the direct and reflected radiation that depends on the geometry and location of the radiation source. In the updated model relxillCp (Dauser et al., 2016), the primary source is made by a thermally Comptonized continuum model (nthcomp; Zdziarski et al., 1996; Życki et al., 1999) and offers a free parameter for the disk density ranging from $10^{15}$ to $10^{20}$ ${\mathrm{c}\mathrm{m}}^{-3}$, whereas the previous model relxill uses a power law with a high-energy exponential cutoff (zcutoffpl) and assumes a disk density of $10^{15}$ ${\mathrm{c}\mathrm{m}}^{-3}$. Recently, the inclusion of returning radiation is implemented in the latest model of relxilllpCp by Dauser et al. (2022), featuring the “lamp post” geometry with a thermally comptonized continuum as the primary source and an unrestricted density parameter ($10^{15}$–$10^{20}$ ${\mathrm{c}\mathrm{m}}^{-3}$). Additionally, García et al. (2022) also present the model relxillNS featuring a black body spectrum, specifically tailored to accommodate the reflection from the disk around an accreting neutron star. The relativistic X-ray reflection models provided by the relxill package were also extended to describe the reflection spectrum in the Johannsen metric (Johannsen, 2013), referred to as relline_nk (Bambi et al., 2017; Abdikamalov et al., 2019; Abdikamalov et al., 2020; Abdikamalov et al., 2021b; Abdikamalov et al., 2021a),^{10, 11} whose model names contain “nk” at the end (e.g., relxill_nk and relxillCp_nk stand for non-Kerr spacetimes) to distinguish them from those in the Kerr metric (see Table 1). These models allow to validate the Kerr metric through the deformation parameters ${\alpha }_{13}$, ${\alpha }_{22}$, or ${ϵ}_3$ in the Johannsen metric, where ${\alpha }_{13}={\alpha }_{22}={ϵ}_3=0$ restores the Kerr metric (for non-Kerr metrics, see review by Bambi, 2017).

X-ray time-resolved observations of AGNs have shown variability in the relativistically blurred reflection (e.g., MCG–6-30-15; Fabian and Vaughan, 2003; Vaughan and Fabian, 2004; Larsson et al., 2007; Miller et al., 2008) that could be caused by general relativistic effects, particularly light bending near the black hole event horizon. Niedźwiecki and Życki (2008) and Niedźwiecki and Miyakawa (2010) investigated variability patterns of the red wing in X-ray reflection of the AGN in the Seyfert 1 galaxy MCG–6-30-15 using a detailed light-bending model (Miniutti and Fabian, 2004), which led to the development of the spectral model reflkerr and its corresponding lamp-post model reflkerr_lp (Niedźwiecki et al., 2016; Niedźwiecki et al., 2019).¹² In particular, Niedźwiecki et al. (2016) identified some inconsistencies between reflkerr and relxilllp owing to the neglect of the general-relativistic redshift of the direct coronal radiation in relxilllp, though they found that the relxilllp model still produces acceptable results in weak-gravity in the energies below 80 keV. Moreover, the lamp-post model reflkerr_lp developed by Niedźwiecki et al. (2019) demonstrated a departure from relxilllp in the energies above 30 keV. Another model-family for spectral and timing variability in accreting black holes has been developed (Ingram et al., 2019; Mastroserio et al., 2021; 2022), named reltrans and reltransCp,¹³ which calculated the emergent reflection spectrum using xillver (or xillverCp in the case of reltransCp). The reltrans model considers all the general-relativistic effects to calculate the time delays and energy changes that occur when X-ray photons from the corona reflect from the accretion disk and scatter towards the observer. The calculations of reltrans incorporate both continuum lags and reverberation lags in a self-consistent manner to produce most of the practical X-ray variability time scales.

3 Variability in relativistic reflection from PCA

Principal component analysis (PCA; Hotelling, 1933),¹⁴ also referred to as the “Hotelling transform,” is a well-known method in multivariate statistics relying on eigenvalues and eigenvectors (see review by Jolliffe and Cadima, 2016) that has been extensively discussed in detail in the literature (e.g., Mardia et al., 1979; Jolliffe, 2002; Izenman, 2008; Rencher and Christensen, 2012). It bears a close relation to the “Kosambi–Karhunen–Loève transform” (Kosambi, 1943; Karhunen, 1947; Loève, 1948) in probability theory, and is among three classical techniques in multivariate analysis to determine the principal dimensions of large data, along with independent component analysis (ICA; Hérault and Ans, 1984; Hérault et al., 1985; Hérault and Jutten, 1986) and non-negative matrix factorization (NMF; Lee and Seung, 1999; Lee and Seung, 2000). PCA can be employed to separate various characteristics that are mostly responsible for complex variations in large data in astronomy (e.g., Wall and Jenkins, 2012; Ivezić et al., 2020) as well as to simplify complex data for machine learning approaches (e.g., Bishop, 2006; Müller and Guido, 2016; Witten et al., 2017; Géron, 2019). This is implemented by reducing the number of available data into a group of independent PCA components, which then provide information about the different levels of their contributions to the complexity of the entire data. Astronomers have extensively employed it as a practical multivariate method. The early application of this technique in astronomy (see review by Francis and Wills, 1999) can be traced back to some studies on spectral analyses of stars (Deeming, 1964; Whitney, 1983), galaxies (Faber, 1973; Bujarrabal et al., 1981; Efstathiou and Fall, 1984), and quasars (Mittaz et al., 1990; Francis et al., 1992; Boroson and Green, 1992). This approach was also employed for imaging analysis of the interstellar medium (Heyer and Schloerb, 1997; Brunt et al., 2009). It was later used for X-ray binaries (e.g., Malzac et al., 2006; Koljonen et al., 2013; Koljonen, 2015) and blazars (Gallant et al., 2018), and more recently for X-ray variability in symbiotic stars (Danehkar et al., 2024a) and starburst regions (Danehkar et al., 2024b). Especially, it has extensively been leveraged for X-ray data analysis of AGNs in Seyfert 1 galaxies (e.g., Vaughan and Fabian, 2004; Miller et al., 2008; Parker et al., 2014b; Gallo et al., 2015).

PCA can decompose time-resolved spectroscopic data into groups of PCA components and eigenvectors, yielding eigenvalues in the process. Normalized eigenvalues can yield the contribution of each eigenvector to the temporal evolution of the whole data over time. Each decomposed PCA component and eigenvector can be referred to as a principal spectrum with its corresponding light curve. The process of conducting PCA requires performing the decomposition of a matrix into its eigenvectors and eigenvalues. To analyze variability of a source in astronomy, this data matrix for PCA contains a set of spectroscopic data collected at $n$ time intervals, each binned into $m$ spectral channels. Let consider a rectangular $(m\times n)$ matrix $\mathbf{X}$ consisting of $n$ rows by $m$ columns, one can determine the principal components of $\mathbf{X}$ through the following three methods:

3.1 Singular value decomposition

The most common approach to obtaining the PCA components is the singular value decomposition (SVD; Beltrami, 1873; Jordan, 1874a; Jordan, 1874b; Sylvester, 1889a; Sylvester, 1889b; Sylvester, 1889c). The SVD of $\mathbf{X}$ is performed as follows:

$\mathbf{X}=\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^{⊺},(3)$

where $\mathbf{U}$ is a square matrix of order $m$ containing principal components (spectra in time-resolved spectroscopic data), $\mathbf{\Sigma }$ is a rectangular diagonal matrix $(m\times n)$ containing square roots of eigenvalues in its diagonal, i.e., $\mathbf{\Lambda }={\mathbf{\Sigma }}^{⊺}\mathbf{\Sigma }=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}({\lambda }_1,\dots ,{\lambda }_n)$ (contribution fractions in spectral variability), $\mathbf{V}$ is a square matrix of order $n$ containing eigenvectors (light curves in astronomical data).

3.2 Eigendecomposition

A classical way to determine the PCA components is through the eigenvalue decomposition (EVD; Cauchy, 1829a; Cauchy, 1829b)¹⁵ of the covariance matrix expressed as ${\mathbf{C}}_{\text{XX}}={\mathbf{X}}^{⊺}\mathbf{X}$, which is a square matrix of order $m$. The eigendecomposition of ${\mathbf{C}}_{\text{XX}}$ is as follows:

${\mathbf{C}}_{\text{XX}}=\mathbf{V}\mathbf{\Lambda }{\mathbf{V}}^{⊺},$

which yields eigenvectors $(\mathbf{V})$ and eigenvalues $(\mathbf{\Lambda })$. The principal components $(\mathbf{U})$ are obtained from the decomposed eigenvectors and eigenvalues by considering Equation 6, which leads to the following solution:¹⁶

$\mathbf{X}\mathbf{V}=\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^{⊺}\mathbf{V}=\mathbf{U}\mathbf{\Sigma }.$

Constructing the diagonal matrix $\mathbf{\Sigma }={\mathbf{\Lambda }}^{\frac{1}{2}}$ from the eigenvalues $(\mathbf{\Lambda })$ and obtaining the least-squares solution to $\mathbf{X}\mathbf{V}=\mathbf{U}\mathbf{\Sigma }$ lead to the principal components $(\mathbf{U})$ of $\mathbf{X}$.

3.3 QR decomposition

Another faster method suitable for high-performance computing, which was proposed by Sharma et al. (2013) to conduct PCA, is performed using QR decomposition (Golub, 1965), also known as QR factorization (Golub and van Loan, 1996; Trefethen and Bau, 1997). In this approach, $\mathbf{X}$ is first factorized into an orthogonal matrix $\mathbf{R}$ of $n\times m$ dimensions and an upper triangular square matrix $\mathbf{R}$ of order $m$:

$\mathbf{X}=\mathbf{Q}\mathbf{R}.$

Then, the SVD of ${\mathbf{R}}^{⊺}$ is obtained:

${\mathbf{R}}^{⊺}=\bar{\mathbf{U}}\bar{\mathbf{\Sigma }}{\bar{\mathbf{V}}}^{⊺}.$

As demonstrated by Sharma et al. (2013), this leads to the same diagonal matrix and eigenvectors of Equation 3, $\mathbf{\Sigma }=\bar{\mathbf{\Sigma }}$ and $\mathbf{V}=\bar{\mathbf{U}}$, while the equivalent principal components are obtained via $\mathbf{U}=\mathbf{Q}\bar{\mathbf{V}}$.

For a set of timing spectroscopic data stored in a data matrix, the PCA components $(\mathbf{U})$, the eigenvectors $(\mathbf{V})$, and the eigenvalues $(\mathbf{\Lambda }={\mathbf{\Sigma }}^2)$ decomposed from the data matrix via either SVD, EVD, or QR are the principal spectra, the corresponding light curves, and their contribution fractions, respectively. As shown in Supplementary Material, these PCA methods can simply implemented with the linear algebra functions of NumPy in Python, albeit with neither CPU parallelization nor GPU acceleration. Currently, there are two publicly available packages made for PCA in the astronomical community: (1) the SVD-based Python package pca¹⁷ (Parker et al., 2015) based on the SVD function (Press et al., 1997) from NumPy (Harris et al., 2020), and (2) the QR-based library qrpca in Python¹⁸ and R¹⁹ (de Souza et al., 2022a; de Souza et al., 2022b) implemented with pyTorch (Paszke et al., 2019) and Scikit-learn (Pedregosa et al., 2011) in Python, and with torch (Falbel and Luraschi, 2022) and the built-in prcomp function in R, allowing for seamless GPU acceleration. In particular, the package pca distributed by Parker et al. (2015) is capable of conducting PCA on X-ray XMM-Newton EPIC-pn observations. To perform PCA with this package, it is necessary to generate a set of X-ray spectra sliced at fixed time intervals (e.g., 10 ks) from event data via custom reduction methods (for details, see Danehkar et al., 2024a).

Vaughan and Fabian (2004) made initial attempts to conduct PCA on X-ray variability in AGN using low-spectral resolution data, suggesting that the X-ray variations in MCG–6-30-15 reported by Fabian and Vaughan (2003) are primarily due to a variable power-law component, with a small partial fraction likely originating from a reflection-dominated component. Later, Miller et al. (2007) employed SVD for PCA, resulting in the generation of exhaustive principal spectra of Mrk 766, which Turner et al. (2007) confirmed these spectral variations through time-resolved spectroscopy. Moreover, Miller et al. (2008) investigated the X-ray variability of MCG–6-30-15 using PCA, resulting in similar spectral components (absorbed, varying power-law) in MCG–6-30-15 and Mrk 766, with a less variable, heavily absorbed component characterizing the relativistically broadened red wing. PCA conducted by Parker et al. (2014a) and Parker et al. (2014b) demonstrated that SVD can successfully separate different spectral components responsible for the X-ray variability in AGNs by exploiting large archival data. In particular, Parker et al. (2014a) discovered that the X-ray variations in MCG–6-30-15 are mostly caused by only three spectral components (see Figure 2): the normalization factor of the power-law continuum (variability fraction of $\sim 96$%), the power-law spectral index ($\sim 2.1$%), and the normalization factor of a relativistically broadened reflection emission ($\sim 0.5$%). Similarly, PCA by Parker et al. (2015) provided evidence for the slight variability ($\lesssim 0.5$%) of relativistic reflection in other AGNs hosted by other Seyfert 1 galaxies (NGC 4051, NGC 3516, Mrk 766, and 1H 0707-495), as seen in Figure 2. Various spectral analysis approaches, including PCA, performed by Gallo et al. (2015) also indicated that the variability in the narrow-line Seyfert 1 galaxy, Mrk 335, is mostly caused by changes in the power-law flux and photon index, although small variations in the ionization state of the reflection were found to be necessary. The PCA study of the extreme narrow-line Seyfert 1 galaxy IRAS 13224–3,809 by Parker et al. (2017a) also showed three principal spectra: a varying power-law continuum, a slightly variable soft excess, and a less variable broad soft excess being linked to strong reflection (see Figure 2 bottom). In addition, the PCA component associated with a variable power-law continuum contain absorption footprints caused by the relativistic UFO detected by Parker et al. (2017b).

Figure 2

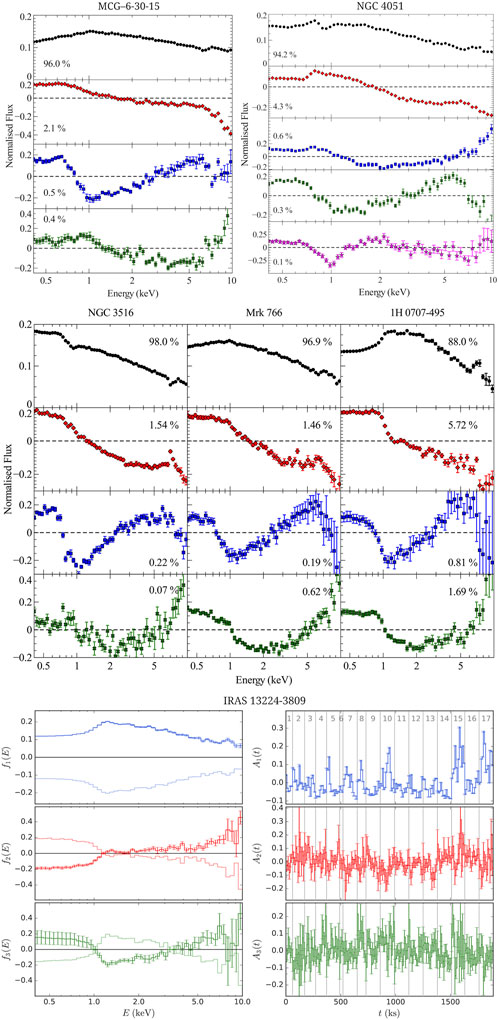
Figure 2. PCA spectra found in different AGNs hosted by nearby Seyfert 1 galaxies: MCG –6-30–15 (Parker et al., 2014a), NGC 4051, NGC 3516, Mrk 766, and 1H 0707-495 (Parker et al., 2015), with percentages of variability fractions, as well as PCA spectra $f_{\mathrm{1}-\mathrm{3}}(E)$ and related light curves $A_{\mathrm{1}-\mathrm{3}}(t)$ found in IRAS 13224-3,809 (Parker et al., 2017a). The PCA components from the first to the third or/and fourth order, respectively, correspond to variations in the power-law normalization, the power-law spectral index, and the relativistic reflection.

As seen in Figure 2, the third or/and fourth PCA components obtained by Parker et al. from X-ray observations of five AGNs (MCG –6-30–15, NGC 4051, NGC 3516, Mrk 766, and 1H 0707-495) resemble the relativistically broadened iron emission features shown in Figure 1 (top). Their normalized eigenvalues of $\lesssim 0.5$% imply that they have negligible variations compared to the X-ray variability in the power-low source continuum. This insignificant variability in the relativistic emission is consistent with the fact that the SMBH spin remains constant over the course of the human timescale. Magnetohydrodynamic (MHD) simulations of an black hole accretion disk by Schnittman et al. (2006) revealed that the light curves indeed contain very low levels of variability (see animations by Schnittman, 2019). Further MHD simulations by Schnittman et al. (2013) suggested that the noticeable X-ray variability mostly originates from the corona and not the disk. This is in agreement with the results found by Parker et al., which show $\gtrsim 90$% of X-ray variations are due to changes in the power-law continuum, i.e., the corona. General-relativistic magnetohydrodynamic (GRMHD) simulations by Shiokawa et al. (2017) also indicated the presence of some flux fluctuations in the emission from the innermost accretion disk due to the fast-moving turbulent formations, as well as some variations in the photon ring with spin-dependent frequencies (see animations by Shiokawa, 2017). Interestingly, the polarimetric light-curve observations of Sgr A^* have also shown intraday variability in circular polarization (Bower et al., 2002) and linear polarization (Marrone et al., 2006), as well as Faraday rotation variability on timescales from hours to months (Marrone et al., 2007; Bower et al., 2018). Similarly, the near-infrared GRAVITY-Very Large Telescope Interferometer (VLTI) observations exhibited that the polarization loop in Sgr A^* is regularly changing clockwise over $\sim 30$ min, indicating a closed, loop motion with the speed of $0.3c$ (GRAVITY Collaboration et al., 2018). The observed polarization variations in Sgr A^* were in line with predictions from general-relativistic ray-tracing models of slightly tilted accretion flows in the presence of powerful magnetic fields (GRAVITY Collaboration et al., 2020). More recently, the polarimetric Event Horizon Telescope (EHT) imaging observations of the SMBHs in M87 and SgrA^* confirmed rapid (intrahour) intrinsic variations in near-horizon accretion flows and polarized rings, which were attributed to spiraling polarization structures based on the results from GRMHD simulations (Event Horizon Telescope Collaboration et al., 2021a; Event Horizon Telescope Collaboration et al., 2021b; Event Horizon Telescope Collaboration et al., 2023; Event Horizon Telescope Collaboration et al., 2024a; Event Horizon Telescope Collaboration et al., 2024b). Therefore, the recent polarization GRAVITY-VLTI and EHT imaging observations of two nearby SMBHs (Sgr A* and M87), together with numerical simulations, imply that small variations in the relativistically broadened iron emission revealed by PCA could be associated with intrahour intrinsic variations and varying spiraling polarization features in near-horizon accretion flows and photon rings.

4 Future perspective: machine learning

SVD and PCA decomposition closely relate to the optimal solution for neural networks in auto-association mode (Bourlard and Kamp, 1988; Baldi and Hornik, 1989). As discussed by Hertz et al. (1991) in the context of unsupervised Hebbian learning, PCA can be used for dimensionality reduction of large data before proceeding with machine learning algorithms, such as artificial neural networks (ANNs). PCA can indeed alleviate the “curse of dimensionality” (coined by Bellman, 1957; Bellman, 1961), also known as the “Hughes phenomenon” (Hughes, 1968) or “peaking phenomenon” (Trunk, 1979), which often arises when searching for patterns in unknown large data. It has been extensively demonstrated in the literature that PCA can be utilized as a pre-processing step to simplify complex data prior to machine learning (e.g., Bishop, 2006), data mining (Witten et al., 2017), and deep learning (Goodfellow et al., 2017). Recently, Ivezić et al. (2020) also discussed in detail the applications of PCA, ICA, and NMF in dimensionality reduction for data mining and machine learning in astronomy.

Using PCA for the pre-processing of astronomical data enables a significant reduction in dimensionality and complexity of data, leading to an improvement in machine learning performance. The use of PCA to reduce the dimensionality of the data for training ANNs can be traced back to earlier efforts on the classification of galaxy spectra (Folkes et al., 1996; Lahav et al., 1996) and stellar spectra (Bailer-Jones et al., 1998; Singh et al., 1998). Later, Zhang and Zhao (2003) applied PCA to the multiwavelength data of AGNs, stars, and normal galaxies in order to reduce the dimensionality of the parameter space for support vector machines (SVM) and learning vector quantization (LVQ), two supervised classification algorithms in machine learning, resulting in the classification of stars, AGNs, and normal galaxies. PCA also reduced the complexity of image data for the morphological classification of galaxies with an ANN (de la Calleja and Fuentes, 2004). Moreover, Bu and Pan (2015) deployed PCA to pre-assemble stellar atmospheric parameters from spectra for Gaussian process regression (GPR) and then compared the results of GPR with those from ANNs, kernel regression (KR), and support-vector regression (SVR). Kuntzer et al. (2016) also conducted stellar classification from single-band images using pre-processed data from PCA to train ANNs to determine the spectral type. More recently, we see the application of PCA to construct input data for ANNs in stellar population synthesis modeling (Alsing et al., 2020), finding thermal components in X-ray spectra of the Perseus cluster (Rhea et al., 2020), and finally X-ray spectral analysis of AGN (Parker et al., 2022).

The avenue of automated spectral analysis with machine learning algorithms has not yet been fully explored for constraining the relativistically broadened iron emission in AGN, mostly because of the complicated variability seen in the X-rays over the course of observations. X-ray observations of AGNs have shown some X-ray changes in power-law continua, which were ascribed to so-called transient obscuration events caused by eclipsing material near the primary source, such as NGC 3783 (Mehdipour et al., 2017), NGC 3227 (Turner et al., 2018), and Mrk 335 (Longinotti et al., 2019; Parker et al., 2019), or flaring variations in the corona in the innermost central regions, e.g., PDS 456 (Matzeu et al., 2017; Reeves et al., 2021) and NGC 3516 (Mehdipour et al., 2022). This kind of change in X-rays over time, along with a relatively large number of parameters in relativistic reflection models (see Table 1), makes it much more complicated for machine learning algorithms to automatically determine the spins of SMBHs from the archival X-ray data. Nevertheless, as seen in Figure 2, the dimensionality reduction offered by PCA can avoid the curse of dimensionality in the X-ray data of AGNs. In the future, we will be able to use machine learning to automatically conduct the spin analysis of SMBHs in AGNs thanks to the principal spectra of relativistic reflection disentangled by PCA from X-ray observations.

Author contributions

AD: Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The author acknowledges financial support from the National Aeronautics and Space Administration (NASA) for an Astrophysics Data Analysis Program grant under no. 80NSSC22K0626.

Acknowledgments

The author would like to express his gratitude for the invitation to speak at the ‘Frontiers in Astronomy and Space Sciences: A Decade of Discovery and Advancement, 10th Anniversary Conference,’ as well as to the editor who requested a concise review of that presentation. The author thanks Michael Parker for permission to use figures from his publications and useful discussions; Javier García, Thomas Dauser, and Laura Brenneman for permission to use figures from their publications; and the reviewer for careful reading of the manuscript and constructive comments.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2024.1479301/full#supplementary-material

Footnotes

¹https://heasarc.gsfc.nasa.gov/xanadu/xspec/

²https://space.mit.edu/cxc/isis/

³The Chandra X-Ray Center (CXC) is operated for NASA by the Smithsonian Astrophysical Observatory (SAO).

⁴https://cxc.cfa.harvard.edu/sherpa/

⁵Netherlands Institute for Space Research (Stichting Ruimteonderzoek Nederland; SRON) is a Dutch institute for astrophysical research.

⁶https://www.sron.nl/astrophysics-spex/

⁷https://pisrv1.am14.uni-tuebingen.de/∼speith/misc.html

⁸https://www.sternwarte.uni-erlangen.de/∼dauser/research/relxill/

⁹https://sites.srl.caltech.edu/∼javier/xillver/

¹⁰https://www.tat.physik.uni-tuebingen.de/∼nampalliwar/relxill_nk/

¹¹https://github.com/ABHModels/relxill_nk, doi:10.5281/zenodo.13906295

¹²https://users.camk.edu.pl/mitsza/reflkerr/

¹³https://adingram.bitbucket.io/reltrans.html

¹⁴It was first innovated by Pearson (1901) in the context of principal axes of ellipsoids in geometry, but it was independently developed and called the method of principal components by Hotelling (1933) for statistical analysis.

¹⁵For a historical review, see Hawkins (1975).

¹⁶Based on the fast that ${\mathbf{V}}^{⊺}\mathbf{V}=\mathbf{I}$, where $\mathbf{I}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}(1,\dots ,1)$ is the identity matrix of order $n$, so $\mathbf{\Sigma }\mathbf{I}=\mathbf{\Sigma }$ and $\mathbf{\Lambda }\mathbf{I}=\mathbf{\Sigma }$.

¹⁷https://www.michaelparker.space/pca-code

¹⁸https://github.com/xuquanfeng/qrpca

¹⁹https://github.com/RafaelSdeSouza/qrpca

References

Abdikamalov, A. B., Ayzenberg, D., Bambi, C., Dauser, T., García, J. A., and Nampalliwar, S. (2019). Public release of relxill_NK: a relativistic reflection model for testing einstein’s gravity. Astrophys. J. 878, 91. doi:10.3847/1538-4357/ab1f89

CrossRef Full Text | Google Scholar

Abdikamalov, A. B., Ayzenberg, D., Bambi, C., Dauser, T., García, J. A., Nampalliwar, S., et al. (2020). Testing the Kerr black hole hypothesis using X-ray reflection spectroscopy and a thin disk model with finite thickness. Astrophys. J. 899, 80. doi:10.3847/1538-4357/aba625

CrossRef Full Text | Google Scholar

Abdikamalov, A. B., Ayzenberg, D., Bambi, C., Liu, H., and Tripathi, A. (2021a). A reflection model with a radial disk density profile. Astrophys. J. 923, 175. doi:10.3847/1538-4357/ac3237

CrossRef Full Text | Google Scholar

Abdikamalov, A. B., Ayzenberg, D., Bambi, C., Liu, H., and Zhang, Y. (2021b). Implementation of a radial disk ionization profile in the relxill_nk model. Phys. Rev. D. 103, 103023. doi:10.1103/PhysRevD.103.103023

CrossRef Full Text | Google Scholar

Alsing, J., Peiris, H., Leja, J., Hahn, C., Tojeiro, R., Mortlock, D., et al. (2020). SPECULATOR: emulating stellar population synthesis for fast and accurate galaxy spectra and photometry. Astrophys. J. Suppl. 249, 5. doi:10.3847/1538-4365/ab917f

CrossRef Full Text | Google Scholar

Arnaud, K., Dorman, B., and Gordon, C. (1999). XSPEC: an X-ray spectral fitting package. Astrophys. Source Code Libr. Rec. ascl:9910.005.

Google Scholar

Arnaud, K. A. (1996). “XSPEC: the first ten years. In astronomical data analysis Software and systems V,”. ASP, vol. 101 of astronomical Society of the pacific conf. Ser. Editors G. H. Jacoby, and J. Barnes (San Francisco, CA), 17.

Google Scholar

Bailer-Jones, C. A. L., Irwin, M., and von Hippel, T. (1998). Automated classification of stellar spectra - II. Two-dimensional classification with neural networks and principal components analysis. Mon. Not. R. Astron. Soc. 298, 361–377. doi:10.1046/j.1365-8711.1998.01596.x

CrossRef Full Text | Google Scholar

Baldi, P., and Hornik, K. (1989). Neural networks and principal component analysis: learning from examples without local minima. Neural Netw. 2, 53–58. doi:10.1016/0893-6080(89)90014-2

CrossRef Full Text | Google Scholar

Bambi, C. (2017). Testing black hole candidates with electromagnetic radiation. Rev. Mod. Phys. 89, 025001. doi:10.1103/RevModPhys.89.025001

CrossRef Full Text | Google Scholar

Bambi, C., Brenneman, L. W., Dauser, T., García, J. A., Grinberg, V., Ingram, A., et al. (2021). Towards precision measurements of accreting black holes using X-ray reflection spectroscopy. Space Sci. Rev. 217, 65. doi:10.1007/s11214-021-00841-8

CrossRef Full Text | Google Scholar

Bambi, C., Cárdenas-Avendaño, A., Dauser, T., García, J. A., and Nampalliwar, S. (2017). Testing the Kerr black hole hypothesis using X-ray reflection spectroscopy. Astrophys. J. 842, 76. doi:10.3847/1538-4357/aa74c0

CrossRef Full Text | Google Scholar

Bardeen, J. M., Press, W. H., and Teukolsky, S. A. (1972). Rotating black holes: locally nonrotating frames, energy extraction, and scalar synchrotron radiation. Astrophys. J. 178, 347–370. doi:10.1086/151796

CrossRef Full Text | Google Scholar

Bellman, R. E. (1957). Dynamic programming. Princeton: Princeton Univ. Press.

Google Scholar

Bellman, R. E. (1961). Adaptive control processes: a guided tour. Princeton: Princeton Univ. Press.

Google Scholar

Beltrami, E. (1873). Sulle funzioni bilineari (English: on bilinear functions). G. Mat. XI, 98–106.

Google Scholar

Bentz, M. C., and Katz, S. (2015). The AGN black hole mass database. Publ. Astron. Soc. Pac. 127, 67–73. doi:10.1086/679601

CrossRef Full Text | Google Scholar

Berti, E., and Volonteri, M. (2008). Cosmological black hole spin evolution by mergers and accretion. Astrophys. J. 684, 822–828. doi:10.1086/590379

CrossRef Full Text | Google Scholar

Bishop, C. M. (2006). Pattern recognition and machine learning. New York: Springer.

Google Scholar

Blandford, R., Meier, D., and Readhead, A. (2019). Relativistic jets from active galactic nuclei. Ann. Rev. Astron. Astrophys. 57, 467–509. doi:10.1146/annurev-astro-081817-051948

CrossRef Full Text | Google Scholar

Blandford, R. D., and McKee, C. F. (1982). Reverberation mapping of the emission line regions of Seyfert galaxies and quasars. Astrophys. J. 255, 419–439. doi:10.1086/159843

CrossRef Full Text | Google Scholar

Blandford, R. D., and Payne, D. G. (1982). Hydromagnetic flows from accretion discs and the production of radio jets. Mon. Not. R. Astron. Soc. 199, 883–903. doi:10.1093/mnras/199.4.883

CrossRef Full Text | Google Scholar

Blandford, R. D., and Znajek, R. L. (1977). Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 179, 433–456. doi:10.1093/mnras/179.3.433

CrossRef Full Text | Google Scholar

Boissay-Malaquin, R., Danehkar, A., Marshall, H. L., and Nowak, M. A. (2019). Relativistic components of the ultra-fast outflow in the quasar PDS 456 from Chandra/HETGS, NuSTAR, and XMM-Newton observations. Astrophys. J. 873, 29. doi:10.3847/1538-4357/ab0082

CrossRef Full Text | Google Scholar

Boroson, T. A., and Green, R. F. (1992). The emission-line properties of low-redshift quasi-stellar objects. Astrophys. J. Suppl. 80, 109. doi:10.1086/191661

CrossRef Full Text | Google Scholar

Bourlard, H., and Kamp, Y. (1988). Auto-association by multilayer perceptrons and singular value decomposition. Biol. Cybern. 59, 291–294. doi:10.1007/BF00332918

PubMed Abstract | CrossRef Full Text | Google Scholar

Bower, G. C., Broderick, A., Dexter, J., Doeleman, S., Falcke, H., Fish, V., et al. (2018). ALMA polarimetry of Sgr A*: probing the accretion flow from the event horizon to the bondi radius. Astrophys. J. 868, 101. doi:10.3847/1538-4357/aae983

CrossRef Full Text | Google Scholar

Bower, G. C., Falcke, H., Sault, R. J., and Backer, D. C. (2002). The spectrum and variability of circular polarization in Sagittarius A* from 1.4 to 15 GHz. Astrophys. J. 571, 843–855. doi:10.1086/340064

CrossRef Full Text | Google Scholar

Boyer, R. H., and Lindquist, R. W. (1967). Maximal analytic extension of the Kerr metric. J. Math. Phys. 8, 265–281. doi:10.1063/1.1705193

CrossRef Full Text | Google Scholar

Brenneman, L. (2013). Measuring the angular momentum of supermassive black holes. New York: Springer. doi:10.1007/978-1-4614-7771-6

CrossRef Full Text | Google Scholar

Brenneman, L. W. (2007). A spectral survey of black hole spin in active galactic nuclei. College Park: University of Maryland Ph.D. thesis.

Google Scholar

Brenneman, L. W., and Reynolds, C. S. (2006). Constraining black hole spin via X-ray spectroscopy. Astrophys. J. 652, 1028–1043. doi:10.1086/508146

CrossRef Full Text | Google Scholar

Broderick, A. E., Loeb, A., and Narayan, R. (2009). The event horizon of Sagittarius A. Astrophys. J. 701, 1357–1366. doi:10.1088/0004-637X/701/2/1357

CrossRef Full Text | Google Scholar

Broderick, A. E., and Narayan, R. (2006). On the nature of the compact dark mass at the galactic center. Astrophys. J. Lett. 638, L21–L24. doi:10.1086/500930

CrossRef Full Text | Google Scholar

Brunt, C. M., Heyer, M. H., and Mac Low, M. M. (2009). Turbulent driving scales in molecular clouds. Astron. Astrophys. 504, 883–890. doi:10.1051/0004-6361/200911797

CrossRef Full Text | Google Scholar

Bu, Y., and Pan, J. (2015). Stellar atmospheric parameter estimation using Gaussian process regression. Mon. Not. R. Astron. Soc. 447, 256–265. doi:10.1093/mnras/stu2063

CrossRef Full Text | Google Scholar

Bujarrabal, V., Guibert, J., and Balkowski, C. (1981). Multidimensional statistical analysis of normal galaxies. Astron. Astrophys. 104, 1–9.

Google Scholar

Calderone, G., Ghisellini, G., Colpi, M., and Dotti, M. (2013). Black hole mass estimate for a sample of radio-loud narrow-line Seyfert 1 galaxies. Mon. Not. R. Astron. Soc. 431, 210–239. doi:10.1093/mnras/stt157

CrossRef Full Text | Google Scholar

Campitiello, S., Ghisellini, G., Sbarrato, T., and Calderone, G. (2018). How to constrain mass and spin of supermassive black holes through their disk emission. Astron. Astrophys. 612, A59. doi:10.1051/0004-6361/201731897

CrossRef Full Text | Google Scholar

Capellupo, D. M., Netzer, H., Lira, P., Trakhtenbrot, B., and Mejía-Restrepo, J. (2015). Active galactic nuclei at z 1.5 - I. Spectral energy distribution and accretion discs. Mon. Not. R. Astron. Soc. 446, 3427–3446. doi:10.1093/mnras/stu2266

CrossRef Full Text | Google Scholar

Capellupo, D. M., Netzer, H., Lira, P., Trakhtenbrot, B., and Mejía-Restrepo, J. (2016). Active galactic nuclei at z 1.5 - III. Accretion discs and black hole spin. Mon. Not. R. Astron. Soc. 460, 212–226. doi:10.1093/mnras/stw937

CrossRef Full Text | Google Scholar

Capellupo, D. M., Wafflard-Fernandez, G., and Haggard, D. (2017). A comparison of two methods for estimating black hole spin in active galactic nuclei. Astrophys. J. Lett. 836, L8. doi:10.3847/2041-8213/aa5cac

CrossRef Full Text | Google Scholar

Cauchy, A.-L. (1829a). Sur l’équation à l’aide de laquelle on détermine les inégalités séculaires des mouvements des planètes. Exer. math. 4, 174–195.

Google Scholar

Cauchy, A.-L. (1829b). Sur l’équation à l’aide de laquelle on détermine les inégalités séculaires des mouvements des planètes. Oeuvres Complètes (IIème Série) 9, 174–195. doi:10.1017/CBO9780511702686.009

CrossRef Full Text | Google Scholar

Chandrasekhar, S. (1960). Radiative transfer. New York: Dover.

Google Scholar

Cretton, N., and van den Bosch, F. C. (1999). Evidence for a massive black hole in the S0 galaxy NGC 4342. Astrophys. J. 514, 704–724. doi:10.1086/306971

CrossRef Full Text | Google Scholar

Cunningham, C. T. (1975). The effects of redshifts and focusing on the spectrum of an accretion disk around a Kerr black hole. Astrophys. J. 202, 788–802. doi:10.1086/154033

CrossRef Full Text | Google Scholar

Danehkar, A. (2020). Gravitational fields of the magnetic-type. Int. J. Mod. Phys. D. 29, 2043001. doi:10.1142/S0218271820430014

CrossRef Full Text | Google Scholar

Danehkar, A., Drake, J. J., and Luna, G. J. M. (2024a). X-ray variability in the symbiotic binary RT Cru: principal component analysis. Astrophys. J. 972, 109. doi:10.3847/1538-4357/ad5cf6

CrossRef Full Text | Google Scholar

Danehkar, A., Nowak, M. A., Lee, J. C., Kriss, G. A., Young, A. J., Hardcastle, M. J., et al. (2018). The ultra-fast outflow of the quasar PG 1211+143 as viewed by time-averaged Chandra grating spectroscopy. Astrophys. J. 853, 165. doi:10.3847/1538-4357/aaa427

CrossRef Full Text | Google Scholar

Danehkar, A., Silich, S., Herenz, E. C., and Östlin, G. (2024b). Disentangling the X-ray variability in the Lyman continuum emitter Haro 11. Astron. Astrophys. 689, A333. doi:10.1051/0004-6361/202449388

CrossRef Full Text | Google Scholar

Dauser, T. (2010). Theoretical modeling of broad emission lines. Germany: Friedrich Alexander University of Erlangen-Nuremberg. Master’s thesis.

Google Scholar

Dauser, T. (2014). Relativistic reflection around black holes: theory and observation. Germany: Friedrich Alexander University of Erlangen-Nuremberg. Ph.D. thesis.

Google Scholar

Dauser, T., Garcia, J., Parker, M. L., Fabian, A. C., and Wilms, J. (2014). The role of the reflection fraction in constraining black hole spin. Mon. Not. R. Astron. Soc. 444, L100–L104. doi:10.1093/mnrasl/slu125

CrossRef Full Text | Google Scholar

Dauser, T., García, J., Walton, D. J., Eikmann, W., Kallman, T., McClintock, J., et al. (2016). Normalizing a relativistic model of X-ray reflection. Definition of the reflection fraction and its implementation in relxill. Astron. Astrophys. 590, A76. doi:10.1051/0004-6361/201628135

CrossRef Full Text | Google Scholar

Dauser, T., Garcia, J., Wilms, J., Böck, M., Brenneman, L. W., Falanga, M., et al. (2013). Irradiation of an accretion disc by a jet: general properties and implications for spin measurements of black holes. Mon. Not. R. Astron. Soc. 430, 1694–1708. doi:10.1093/mnras/sts710

CrossRef Full Text | Google Scholar

Dauser, T., García, J. A., Joyce, A., Licklederer, S., Connors, R. M. T., Ingram, A., et al. (2022). The effect of returning radiation on relativistic reflection. Mon. Not. R. Astron. Soc. 514, 3965–3983. doi:10.1093/mnras/stac1593

CrossRef Full Text | Google Scholar

Dauser, T., Wilms, J., Reynolds, C. S., and Brenneman, L. W. (2010). Broad emission lines for a negatively spinning black hole. Mon. Not. R. Astron. Soc. 409, 1534–1540. doi:10.1111/j.1365-2966.2010.17393.x

CrossRef Full Text | Google Scholar

Deeming, T. J. (1964). Stellar spectral classification. I. Application of component analysis. Mon. Not. R. Astron. Soc. 127, 493–516. doi:10.1093/mnras/127.6.493

CrossRef Full Text | Google Scholar

de la Calleja, J., and Fuentes, O. (2004). Machine learning and image analysis for morphological galaxy classification. Mon. Not. R. Astron. Soc. 349, 87–93. doi:10.1111/j.1365-2966.2004.07442.x

CrossRef Full Text | Google Scholar

de La Calle Pérez, I., Longinotti, A. L., Guainazzi, M., Bianchi, S., Dovčiak, M., Cappi, M., et al. (2010). FERO: finding extreme relativistic objects: I. Statistics of relativistic Fe K_αlines in radio-quiet Type 1 AGN⋆. Astron. Astrophys. 524, A50. doi:10.1051/0004-6361/200913798

CrossRef Full Text | Google Scholar

de Plaa, J., Kaastra, J. S., Gu, L., Mao, J., and Raassen, T. (2020). SPEX: high-resolution spectral modeling and fitting for X-ray astronomy. In astronomical data analysis software and systems XXIX, 527. Editors R. Pizzo, E. R. Deul, J. D. Mol, J. de Plaa, and H. Verkouter (San Francisco, CA: ASP), Astronomical Society of the Pacific Conf. Ser. 725. doi:10.48550/arXiv.1912.07897

CrossRef Full Text | Google Scholar

de Souza, R. S., Quanfeng, X., Shen, S., Peng, C., and Mu, Z. (2022a). qrpca: a package for fast principal component analysis with GPU acceleration. Astron. Comput. 41, 100633. doi:10.1016/j.ascom.2022.100633

CrossRef Full Text | Google Scholar

de Souza, R. S., Quanfeng, X., Shen, S., Peng, C., and Mu, Z.(2022b). qrpca: QR-based Principal Components Analysis. Astrophys. Source Code Libr. Rec. ascl:2208.002.

Google Scholar

Di Matteo, T., Springel, V., and Hernquist, L. (2005). Energy input from quasars regulates the growth and activity of black holes and their host galaxies. Nature 433, 604–607. doi:10.1038/nature03335

PubMed Abstract | CrossRef Full Text | Google Scholar

Doe, S., Nguyen, D., Stawarz, C., Refsdal, B., Siemiginowska, A., Burke, D., et al. (2007). Developing Sherpa with Python. In astronomical data analysis software and systems XVI. Editors R. A. Shaw, F. Hill, and D. J. Bell (San Francisco, CA: ASP), 376. Astronomical Society of the Pacific Conf. Ser., 543.

Google Scholar

Done, C., Davis, S. W., Jin, C., Blaes, O., and Ward, M. (2012). Intrinsic disc emission and the soft X-ray excess in active galactic nuclei. Mon. Not. R. Astron. Soc. 420, 1848–1860. doi:10.1111/j.1365-2966.2011.19779.x

CrossRef Full Text | Google Scholar

Done, C., Jin, C., Middleton, M., and Ward, M. (2013). A new way to measure supermassive black hole spin in accretion disc-dominated active galaxies. Mon. Not. R. Astron. Soc. 434, 1955–1963. doi:10.1093/mnras/stt1138

CrossRef Full Text | Google Scholar

Dovčiak, M. (2004). Radiation of accretion discs in strong gravity. Prague: Charles University. Ph.D. thesis.

Google Scholar

Dovčiak, M., Karas, V., and Yaqoob, T. (2004). An extended scheme for fitting X-ray data with accretion disk spectra in the strong gravity regime. Astrophys. J. Suppl. 153, 205–221. doi:10.1086/421115

CrossRef Full Text | Google Scholar

Dovčiak, M., Papadakis, I. E., Kammoun, E. S., and Zhang, W. (2022). Physical model for the broadband energy spectrum of X-ray illuminated accretion discs: fitting the spectral energy distribution of NGC 5548. Astron. Astrophys. 661, A135. doi:10.1051/0004-6361/202142358

CrossRef Full Text | Google Scholar

Efstathiou, G., and Fall, S. M. (1984). Multivariate analysis of elliptical galaxies. Mon. Not. R. Astron. Soc. 206, 453–464. doi:10.1093/mnras/206.3.453

CrossRef Full Text | Google Scholar

Event Horizon Telescope CollaborationAkiyama, K., Alberdi, A., Alef, W., Asada, K., Azulay, R., et al. (2019a). First M87 event horizon telescope results. I. The shadow of the supermassive black hole. Astrophys. J. Lett. 875, L1. doi:10.3847/2041-8213/ab0ec7

CrossRef Full Text | Google Scholar

Event Horizon Telescope Collaboration Akiyama, K., Alberdi, A., Alef, W., Asada, K., Azulay, R., et al. (2019b). First M87 event horizon telescope results. IV. Imaging the central supermassive black hole. Astrophys. J. Lett. 875, L4. doi:10.3847/2041-8213/ab0e85

CrossRef Full Text | Google Scholar

Event Horizon Telescope Collaboration Akiyama, K., Alberdi, A., Alef, W., Asada, K., Azulay, R., et al. (2019c). First M87 event horizon telescope results. V. Physical origin of the asymmetric ring. Astrophys. J. Lett. 875, L5. doi:10.3847/2041-8213/ab0f43

CrossRef Full Text | Google Scholar

Event Horizon Telescope Collaboration Akiyama, K., Algaba, J. C., Alberdi, A., Alef, W., Anantua, R., et al. (2021a). First M87 event horizon telescope results. VII. Polarization of the ring. Astrophys. J. Lett. 910, L12. doi:10.3847/2041-8213/abe71d

CrossRef Full Text | Google Scholar

Event Horizon Telescope Collaboration Akiyama, K., Algaba, J. C., Alberdi, A., Alef, W., Anantua, R., et al. (2021b). First M87 event horizon telescope results. VIII. Magnetic field structure near the event horizon. Astrophys. J. Lett. 910, L13. doi:10.3847/2041-8213/abe4de

CrossRef Full Text | Google Scholar

Event Horizon Telescope Collaboration Akiyama, K., Alberdi, A., Alef, W., Algaba, J. C., Anantua, R., et al. (2022a). First Sagittarius A* event horizon telescope results. I. The shadow of the supermassive black hole in the center of the Milky way. Astrophys. J. Lett. 930, L12. doi:10.3847/2041-8213/ac6674

CrossRef Full Text | Google Scholar

Event Horizon Telescope Collaboration Akiyama, K., Alberdi, A., Alef, W., Algaba, J. C., Anantua, R., et al. (2022b). First Sagittarius A* event horizon telescope results. III. Imaging of the galactic center supermassive black hole. Astrophys. J. Lett. 930, L14. doi:10.3847/2041-8213/ac6429

CrossRef Full Text | Google Scholar

Event Horizon Telescope Collaboration Akiyama, K., Alberdi, A., Alef, W., Algaba, J. C., Anantua, R., et al. (2022c). First Sagittarius A* event horizon telescope results. V. Testing astrophysical models of the galactic center black hole. Astrophys. J. Lett. 930, L16. doi:10.3847/2041-8213/ac6672

CrossRef Full Text | Google Scholar

Event Horizon Telescope Collaboration Akiyama, K., Alberdi, A., Alef, W., Algaba, J. C., Anantua, R., et al. (2022d). First Sagittarius A* event horizon telescope results. VI. Testing the black hole metric. Astrophys. J. Lett. 930, L17. doi:10.3847/2041-8213/ac6756

CrossRef Full Text | Google Scholar

Event Horizon Telescope Collaboration Akiyama, K., Alberdi, A., Alef, W., Algaba, J. C., Anantua, R., et al. (2023). First M87 event horizon telescope results. IX. Detection of near-horizon circular polarization. Astrophys. J. Lett. 957, L20. doi:10.3847/2041-8213/acff70

CrossRef Full Text | Google Scholar

Event Horizon Telescope Collaboration Akiyama, K., Alberdi, A., Alef, W., Algaba, J. C., Anantua, R., et al. (2024a). First Sagittarius A* event horizon telescope results. VII. Polarization of the ring. Astrophys. J. Lett. 964, L25. doi:10.3847/2041-8213/ad2df0

CrossRef Full Text | Google Scholar

Event Horizon Telescope Collaboration Akiyama, K., Alberdi, A., Alef, W., Algaba, J. C., Anantua, R., et al. (2024b). First Sagittarius A* event horizon telescope results. VIII. Physical interpretation of the polarized ring. Astrophys. J. Lett. 964, L26. doi:10.3847/2041-8213/ad2df1

CrossRef Full Text | Google Scholar

Faber, S. M. (1973). Variations in spectral-energy distributions and absorption-line strengths among elliptical galaxies. Astrophys. J. 179, 731–754. doi:10.1086/151912

CrossRef Full Text | Google Scholar

Fabian, A. C., Rees, M. J., Stella, L., and White, N. E. (1989). X-ray fluorescence from the inner disc in Cygnus X-1. Mon. Not. R. Astron. Soc. 238, 729–736. doi:10.1093/mnras/238.3.729

CrossRef Full Text | Google Scholar

Fabian, A. C., and Vaughan, S. (2003). The iron line in MCG-6-30-15 from XMM-Newton: evidence for gravitational light bending? Mon. Not. R. Astron. Soc. 340, L28–L32. doi:10.1046/j.1365-8711.2003.06465.x

CrossRef Full Text | Google Scholar

Falbel, D., and Luraschi, J. (2022). Torch: tensors and neural networks with ’GPU’ acceleration. Available at: https://torch.mlverse.org/docshttps://github.com/mlverse/torch

Google Scholar

Ferrarese, L., and Merritt, D. (2000). A fundamental relation between supermassive black holes and their host galaxies. Astrophys. J. Lett. 539, L9–L12. doi:10.1086/312838

CrossRef Full Text | Google Scholar

Folkes, S. R., Lahav, O., and Maddox, S. J. (1996). An artificial neural network approach to the classification of galaxy spectra. Mon. Not. R. Astron. Soc. 283, 651–665. doi:10.1093/mnras/283.2.651

CrossRef Full Text | Google Scholar

Francis, P. J., Hewett, P. C., Foltz, C. B., and Chaffee, F. H. (1992). An objective classification scheme for QSO spectra. Astrophys. J. 398, 476. doi:10.1086/171870

CrossRef Full Text | Google Scholar

Francis, P. J., and Wills, B. J. (1999). “Introduction to principal components analysis,” in Quasars and cosmology. Editors G. Ferland, and J. Baldwin, 363. doi:10.48550/arXiv.astro-ph/9905079

CrossRef Full Text | Google Scholar

Freeman, P., Doe, S., and Siemiginowska, A. (2001). “Sherpa: a mission-independent data analysis application,” in Astronomical Data Analysis (Bellingham: SPIE), 4477 proc. SPIE conf. Ser. Editors J.-L. Starck, and F. D. Murtagh, 76–87. doi:10.1117/12.447161

CrossRef Full Text | Google Scholar

Fruscione, A., McDowell, J. C., Allen, G. E., Brickhouse, N. S., Burke, D. J., Davis, J. E., et al. (2006). . “CIAO: Chandra’s data analysis system,” in Observatory Operations: Strategies, Processes, and Systems, Editors D. R. Silva, and R. E. Doxsey (Bellingham: SPIE), vol. 6270 of Proc. SPIE Conf. Ser., 62701V. doi:10.1117/12.671760

CrossRef Full Text | Google Scholar

Gallant, D., Gallo, L. C., and Parker, M. L. (2018). X-ray spectral variability of blazars using principal component analysis. Mon. Not. R. Astron. Soc. 480, 1999–2010. doi:10.1093/mnras/sty1987

CrossRef Full Text | Google Scholar

Gallo, L. C., Wilkins, D. R., Bonson, K., Chiang, C. Y., Grupe, D., Parker, M. L., et al. (2015). Suzaku observations of Mrk 335: confronting partial covering and relativistic reflection. Mon. Not. R. Astron. Soc. 446, 633–650. doi:10.1093/mnras/stu2108

CrossRef Full Text | Google Scholar

García, J., Dauser, T., Lohfink, A., Kallman, T. R., Steiner, J. F., McClintock, J. E., et al. (2014). Improved reflection models of black hole accretion disks: treating the angular distribution of X-rays. Astrophys. J. 782, 76. doi:10.1088/0004-637X/782/2/76

CrossRef Full Text | Google Scholar

García, J., Dauser, T., Reynolds, C. S., Kallman, T. R., McClintock, J. E., Wilms, J., et al. (2013). X-ray reflected spectra from accretion disk models. III. A complete grid of ionized reflection calculations. Astrophys. J. 768, 146. doi:10.1088/0004-637X/768/2/146

CrossRef Full Text | Google Scholar

García, J., and Kallman, T. R. (2010). X-Ray reflected spectra from accretion disk models. I. Constant density atmospheres. Astrophys. J. 718, 695–706. doi:10.1088/0004-637X/718/2/695

CrossRef Full Text | Google Scholar

García, J., Kallman, T. R., and Mushotzky, R. F. (2011). X-Ray reflected spectra from accretion disk models. II. Diagnostic tools for X-ray observations. Astrophys. J. 731, 131. doi:10.1088/0004-637X/731/2/131

CrossRef Full Text | Google Scholar

García, J. A. (2010). Modeling high-resolution spectra from x-ray illuminated accretion disks. Washington DC: Catholic University. Ph.D. thesis.

Google Scholar

García, J. A., Dauser, T., Ludlam, R., Parker, M., Fabian, A., Harrison, F. A., et al. (2022). Relativistic X-ray reflection models for accreting neutron stars. Astrophys. J. 926, 13. doi:10.3847/1538-4357/ac3cb7

CrossRef Full Text | Google Scholar

Garofalo, D., Evans, D. A., and Sambruna, R. M. (2010). The evolution of radio-loud active galactic nuclei as a function of black hole spin. Mon. Not. R. Astron. Soc. 406, 975–986. doi:10.1111/j.1365-2966.2010.16797.x

CrossRef Full Text | Google Scholar

Géron, A. (2019). Hands-on machine learning with scikit-learn, keras, and TensorFlow: concepts, tools, and techniques to build intelligent systems. (Sebastopol, CA: O’Reilly).

Google Scholar

Ghez, A. M., Klein, B. L., Morris, M., and Becklin, E. E. (1998). High proper-motion stars in the vicinity of Sagittarius A*: evidence for a supermassive black hole at the center of our galaxy. Astrophys. J. 509, 678–686. doi:10.1086/306528

CrossRef Full Text | Google Scholar

Ghez, A. M., Salim, S., Hornstein, S. D., Tanner, A., Lu, J. R., Morris, M., et al. (2005). Stellar orbits around the galactic center black hole. Astrophys. J. 620, 744–757. doi:10.1086/427175

CrossRef Full Text | Google Scholar

Gierliński, M., Maciołek-Niedźwiecki, A., and Ebisawa, K. (2001). Application of a relativistic accretion disc model to X-ray spectra of LMC X-1 and GRO J1655-40. Mon. Not. R. Astron. Soc. 325, 1253–1265. doi:10.1046/j.1365-8711.2001.04540.x

CrossRef Full Text | Google Scholar

Golub, G. (1965). Numerical methods for solving linear least squares problems. Numer. Math. 7, 206–216. doi:10.1007/BF01436075

CrossRef Full Text | Google Scholar

Golub, G. H., and van Loan, C. F. (1996). Matrix computations. 3rd edn. Baltimore: Johns Hopkins Univ. Press.

Google Scholar

Goodfellow, I., Bengio, Y., and Courville, A. (2017). Deep learning. Cambridge, MA: MIT Press.

Google Scholar

GRAVITY Collaboration Abuter, R., Amorim, A., Bauböck, M., Berger, J. P., Bonnet, H., et al. (2018). Detection of orbital motions near the last stable circular orbit of the massive black hole SgrA. Astron. Astrophys. 618, L10. doi:10.1051/0004-6361/201834294

CrossRef Full Text | Google Scholar

GRAVITY Collaboration Jiménez-Rosales, A., Dexter, J., Widmann, F., Bauböck, M., Abuter, R., et al. (2020). Dynamically important magnetic fields near the event horizon of Sgr A. Astron. Astrophys. 643, A56. doi:10.1051/0004-6361/202038283

CrossRef Full Text | Google Scholar

Guainazzi, M., Bianchi, S., and Dovčiak, M. (2006). Statistics of relativistically broadened Fe Kα lines in AGN. Astron. Nachr. 327, 1032–1038. doi:10.1002/asna.200610687

CrossRef Full Text | Google Scholar

Haardt, F. (1993). Anisotropic comptonization in thermal plasmas: spectral distribution in plane-parallel geometry. Astrophys. J. 413, 680. doi:10.1086/173036

CrossRef Full Text | Google Scholar

Haardt, F., and Maraschi, L. (1991). A two-phase model for the X-ray emission from Seyfert galaxies. Astrophys. J. Lett. 380, L51. doi:10.1086/186171

CrossRef Full Text | Google Scholar

Haardt, F., and Maraschi, L. (1993). X-ray spectra from two-phase accretion disks. Astrophys. J. 413, 507. doi:10.1086/173020

CrossRef Full Text | Google Scholar

Hagen, S., and Done, C. (2023). Estimating black hole spin from AGN SED fitting: the impact of general-relativistic ray tracing. Mon. Not. R. Astron. Soc. 525, 3455–3467. doi:10.1093/mnras/stad2499

CrossRef Full Text | Google Scholar

Häring, N., and Rix, H.-W. (2004). On the black hole mass-bulge mass relation. Astrophys. J. Lett. 604, L89–L92. doi:10.1086/383567

CrossRef Full Text | Google Scholar

Harris, C. R., Millman, K. J., van der Walt, S. J., Gommers, R., Virtanen, P., Cournapeau, D., et al. (2020). Array programming with NumPy. Nature 585, 357–362. doi:10.1038/s41586-020-2649-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Harrison, F. A., Craig, W. W., Christensen, F. E., Hailey, C. J., Zhang, W. W., Boggs, S. E., et al. (2013). The nuclear spectroscopic telescope Array (NuSTAR) high-energy X-ray mission. Astrophys. J. 770, 103. doi:10.1088/0004-637X/770/2/103

CrossRef Full Text | Google Scholar

Hawkins, T. (1975). Cauchy and the spectral theory of matrices. Hist. Math. 2, 1–29. doi:10.1016/0315-0860(75)90032-4

CrossRef Full Text | Google Scholar

Heckman, T. M., and Best, P. N. (2014). The coevolution of galaxies and supermassive black holes: insights from surveys of the contemporary universe. Ann. Rev. Astron. Astrophys. 52, 589–660. doi:10.1146/annurev-astro-081913-035722

CrossRef Full Text | Google Scholar

Hérault, J., and Ans, B. (1984). Neuronal network with modifiable synapses: decoding of composite sensory messages under unsupervised and permanent learning. C.R. Acad. Sci. Paris 299, 525–528.

Google Scholar

Hérault, J., and Jutten, C. (1986). Space or time adaptive signal processing by neural network models. AIP Conf. Proc. 151, 206–211. doi:10.1063/1.36258

CrossRef Full Text | Google Scholar

Hérault, J., Jutten, C., and Ans, B. (1985). Détection de grandeurs primitives dans un message composite par une architecture de calcul neuromimétique en apprentissage non supervisé. Actes Du. Xème Colloq. (Nice, France: GRETSI) 2, 1017–1020.

Google Scholar

Hertz, J., Krogh, A., and Palmer, R. G. (1991). Introduction to the theory of neural computation. Redwood City, CA: Addison-Wesley.

Google Scholar

Heyer, M. H., and Schloerb, F. P. (1997). Application of principal component analysis to large-scale spectral line imaging studies of the interstellar medium. Astrophys. J. 475, 173–187. doi:10.1086/303514

CrossRef Full Text | Google Scholar

Hoormann, J. K., Beheshtipour, B., and Krawczynski, H. (2016). Testing general relativity’s no-hair theorem with x-ray observations of black holes. Phys. Rev. D. 93, 044020. doi:10.1103/PhysRevD.93.044020

CrossRef Full Text | Google Scholar

Hotelling, H. (1933). Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 24, 417–441. doi:10.1037/h0071325

CrossRef Full Text | Google Scholar

Houck, J. C., and Denicola, L. A. (2000). “ISIS: an interactive spectral interpretation System for high resolution X-ray spectroscopy,” In Astronomical Data Analysis Software and Systems IX (San Francisco, CA: ASP) vol. 216 of astronomical Society of the pacific conf. Ser. Editors N. Manset, C. Veillet, and D. Crabtree, 591.

Google Scholar

Hughes, G. (1968). On the mean accuracy of statistical pattern recognizers. IEEE Trans. Inf. Theory 14, 55–63. doi:10.1109/TIT.1968.1054102

CrossRef Full Text | Google Scholar

Hughes, S. A., and Blandford, R. D. (2003). Black hole mass and spin coevolution by mergers. Astrophys. J. Lett. 585, L101–L104. doi:10.1086/375495

CrossRef Full Text | Google Scholar

Ingram, A., Mastroserio, G., Dauser, T., Hovenkamp, P., van der Klis, M., and García, J. A. (2019). A public relativistic transfer function model for X-ray reverberation mapping of accreting black holes. Mon. Not. R. Astron. Soc. 488, 324–347. doi:10.1093/mnras/stz1720

CrossRef Full Text | Google Scholar

Ivezić, Ž., Connolly, A. J., VanderPlas, J. T., and Gray, A. (2020). Statistics, data mining, and machine learning in astronomy: a practical Python guide for the analysis of survey data. Princeton: Princeton Univ. Press. doi:10.1515/9780691197050

CrossRef Full Text | Google Scholar

Izenman, A. J. (2008). Modern multivariate statistical techniques: regression, classification, and manifold learning. Berlin: Springer. doi:10.1007/978-0-387-78189-1

CrossRef Full Text | Google Scholar

Johannsen, T. (2013). Regular black hole metric with three constants of motion. Phys. Rev. D. 88, 044002. doi:10.1103/PhysRevD.88.044002

CrossRef Full Text | Google Scholar

Jolliffe, I. T. (2002). Principal component analysis. Berlin: Springer. doi:10.1007/b98835

CrossRef Full Text | Google Scholar

Jolliffe, I. T., and Cadima, J. (2016). Principal component analysis: a review and recent developments. Philos. Trans. R. Soc. A 374, 20150202. doi:10.1098/rsta.2015.0202

PubMed Abstract | CrossRef Full Text | Google Scholar

Jordan, C. (1874a). Mémoire sur les formes bilinéaires (English: Memory on bilinear forms). J. Math. Pures Appl. Paris 19, 35–54.

Google Scholar

Jordan, C. (1874b). Sur la réduction des formes bilinéaires (English: On the reduction of bilinear forms). C. R. Acad. Sci. Paris 78, 614–617.

Google Scholar

Kaastra, J. S., Mewe, R., and Nieuwenhuijzen, H. (1996). “SPEX: a new code for spectral analysis of X and UV spectra,” in UV and X-ray spectroscopy of astrophysical and laboratory plasmas, 411–414.

Google Scholar

Karhunen, K. (1947). “Über lineare methoden in der wahrscheinlich-keitsrechnung. Ann. Acad. Sci. Fennicea, Ser. A1 37. Trans. by I. Selin (1960)“ “On Linear Methods in Probability Theory” T-131. Santa Monica, CA: RAND Corp.

Google Scholar

Keck, M. L., Brenneman, L. W., Ballantyne, D. R., Bauer, F., Boggs, S. E., Christensen, F. E., et al. (2015). NuSTAR and Suzaku X-ray spectroscopy of NGC 4151: evidence for reflection from the inner accretion disk. Astrophys. J. 806, 149. doi:10.1088/0004-637X/806/2/149

CrossRef Full Text | Google Scholar

Kerr, R. P. (1963). Gravitational field of a spinning mass as an example of algebraically special metrics. Phys. Rev. Lett. 11, 237–238. doi:10.1103/PhysRevLett.11.237

CrossRef Full Text | Google Scholar

Koljonen, K. I. I. (2015). Unsupervised spectral decomposition of X-ray binaries with application to GX 339-4. Mon. Not. R. Astron. Soc. 447, 2981–2991. doi:10.1093/mnras/stu2663

CrossRef Full Text | Google Scholar

Koljonen, K. I. I., McCollough, M. L., Hannikainen, D. C., and Droulans, R. (2013). 2006 May-July major radio flare episodes in Cygnus X-3: spectrotiming analysis of the X-ray data. Mon. Not. R. Astron. Soc. 429, 1173–1188. doi:10.1093/mnras/sts404

CrossRef Full Text | Google Scholar

Kormendy, J. (1988). Evidence for a supermassive black hole in the nucleus of M31. Astrophys. J. 325, 128–141. doi:10.1086/165988

CrossRef Full Text | Google Scholar

Kormendy, J., Bender, R., Magorrian, J., Tremaine, S., Gebhardt, K., Richstone, D., et al. (1997). Spectroscopic evidence for a supermassive black hole in NGC 4486B. Astrophys. J. Lett. 482, L139–L142. doi:10.1086/310720

CrossRef Full Text | Google Scholar

Kormendy, J., and Richstone, D. (1992). Evidence for a supermassive black hole in NGC 3115. Astrophys. J. 393, 559–578. doi:10.1086/171528

CrossRef Full Text | Google Scholar

Kormendy, J., and Richstone, D. (1995). Inward bound—the search for supermassive black holes in galactic nuclei. Ann. Rev. Astron. Astrophys. 33, 581–624. doi:10.1146/annurev.aa.33.090195.003053

CrossRef Full Text | Google Scholar

Kosambi, D. D. (1943). Statistics in function space. J. Indian Math. Soc. 7, 115–123. doi:10.1007/978-81-322-3676-4_15

CrossRef Full Text | Google Scholar

Kubota, A., and Done, C. (2018). A physical model of the broad-band continuum of AGN and its implications for the UV/X relation and optical variability. Mon. Not. R. Astron. Soc. 480, 1247–1262. doi:10.1093/mnras/sty1890

CrossRef Full Text | Google Scholar

Kubota, A., and Done, C. (2019). Modelling the spectral energy distribution of super-Eddington quasars. Mon. Not. R. Astron. Soc. 489, 524–533. doi:10.1093/mnras/stz2140

CrossRef Full Text | Google Scholar

Kuntzer, T., Tewes, M., and Courbin, F. (2016). Stellar classification from single-band imaging using machine learning. Astron. Astrophys. 591, A54. doi:10.1051/0004-6361/201628660

CrossRef Full Text | Google Scholar

Lahav, O., Naim, A., Sodré, J. L., and Storrie-Lombardi, M. C. (1996). Neural computation as a tool for galaxy classification: methods and examples. Mon. Not. R. Astron. Soc. 283, 207–221. doi:10.1093/mnras/283.1.207

CrossRef Full Text | Google Scholar

Laor, A. (1991). Line profiles from a disk around a rotating black hole. Astrophys. J. 376, 90. doi:10.1086/170257

CrossRef Full Text | Google Scholar

Larsson, J., Fabian, A. C., Miniutti, G., and Ross, R. R. (2007). Exploring the X-ray spectral variability of MCG-6-30-15 with XMM-Newton. Mon. Not. R. Astron. Soc. 376, 348–352. doi:10.1111/j.1365-2966.2007.11436.x

CrossRef Full Text | Google Scholar

Lee, D. D., and Seung, H. S. (1999). Learning the parts of objects by non-negative matrix factorization. Nature 401, 788–791. doi:10.1038/44565

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, D. D., and Seung, H. S. (2000). “Algorithms for non-negative matrix factorization,”. Advances in neural information processing systems. Editors T. Leen, T. Dietterich, and V. Tresp (Cambridge, MA: MIT Press), 13, 556–562.

Google Scholar

Li, L.-X., Zimmerman, E. R., Narayan, R., and McClintock, J. E. (2005). Multitemperature blackbody spectrum of a thin accretion disk around a Kerr black hole: model computations and comparison with observations. Astrophys. J. Suppl. 157, 335–370. doi:10.1086/428089

CrossRef Full Text | Google Scholar

Loève, M. (1948). “Fonctions Aléatoires de second order,” in Processus Stochastiques et Movement Brownien. Editor P. Lévy (Paris, France: Gauthier-Villars).

Google Scholar

Longinotti, A. L., Kriss, G., Krongold, Y., Arellano-Cordova, K. Z., Komossa, S., Gallo, L., et al. (2019). The XMM-Newton/HST view of the obscuring outflow in the Seyfert galaxy Mrk 335 observed at extremely low X-ray flux. Astrophys. J. 875, 150. doi:10.3847/1538-4357/ab125a

CrossRef Full Text | Google Scholar

MacDonald, D. A., Thorne, K. S., Price, R. H., and Zhang, X. H. (1986). “Astrophysical applications of black-hole electrodynamics,” in Black holes: the membrane paradigm. Editors K. S. Thorne, R. H. Price, and D. A. MacDonald (New Haven, CT: Yale Univ. Press), 121–145.

Google Scholar

Magorrian, J., Tremaine, S., Richstone, D., Bender, R., Bower, G., Dressler, A., et al. (1998). The demography of massive dark objects in galaxy centers. Astron. J. 115, 2285–2305. doi:10.1086/300353

CrossRef Full Text | Google Scholar

Malkan, M. A. (1983). The ultraviolet excess of luminous quasars. II. Evidence for massive accretion disks. Astrophys. J. 268, 582–590. doi:10.1086/160981

CrossRef Full Text | Google Scholar

Malzac, J., Petrucci, P. O., Jourdain, E., Cadolle Bel, M., Sizun, P., Pooley, G., et al. (2006). Bimodal spectral variability of Cygnus X-1 in an intermediate state. Astron. Astrophys. 448, 1125–1137. doi:10.1051/0004-6361:20053614

CrossRef Full Text | Google Scholar

Mardia, K. V., Kent, J. T., and Bibby, J. M. (1979). Multivariate analysis. London: Academic Press.

Google Scholar

Marrone, D. P., Moran, J. M., Zhao, J.-H., and Rao, R. (2006). Interferometric measurements of variable 340 GHz linear polarization in Sagittarius A*. Astrophys. J. 640, 308–318. doi:10.1086/500106

CrossRef Full Text | Google Scholar

Marrone, D. P., Moran, J. M., Zhao, J.-H., and Rao, R. (2007). An unambiguous detection of Faraday rotation in Sagittarius A*. Astrophys. J. Lett. 654, L57–L60. doi:10.1086/510850

CrossRef Full Text | Google Scholar

Martocchia, A., Karas, V., and Matt, G. (2000). Effects of Kerr space-time on spectral features from X-ray illuminated accretion discs. Mon. Not. R. Astron. Soc. 312, 817–826. doi:10.1046/j.1365-8711.2000.03205.x

CrossRef Full Text | Google Scholar

Martocchia, A., and Matt, G. (1996). Iron Kα line intensity from accretion discs around rotating black holes. Mon. Not. R. Astron. Soc. 282, L53–L57. doi:10.1093/mnras/282.4.L53

CrossRef Full Text | Google Scholar

Martocchia, A., Matt, G., Karas, V., Belloni, T., and Feroci, M. (2002). Evidence for a relativistic iron line in GRS 1915+105. Astron. Astrophys. 387, 215–221. doi:10.1051/0004-6361:20020359

CrossRef Full Text | Google Scholar

Mastroserio, G., Ingram, A., Wang, J., García, J. A., van der Klis, M., Cavecchi, Y., et al. (2021). Modelling correlated variability in accreting black holes: the effect of high density and variable ionization on reverberation lags. Mon. Not. R. Astron. Soc. 507, 55–73. doi:10.1093/mnras/stab2056

CrossRef Full Text | Google Scholar

Mastroserio, G., Ingram, A., Wang, J., Lucchini, M., Nathan, E., and Garcia, J. (2022). RELTRANS: a public spectral-timing model to fit X-ray reverberation in accreting black holes. 44th COSPAR Sci. Assem. 44, 2345. Held 16-24 July.

Google Scholar

Matzeu, G. A., Reeves, J. N., Nardini, E., Braito, V., Turner, T. J., and Costa, M. T. (2017). X-ray flaring in PDS 456 observed in a high-flux state. Mon. Not. R. Astron. Soc. 465, 2804–2819. doi:10.1093/mnras/stw2673

CrossRef Full Text | Google Scholar

McClintock, J. E., Shafee, R., Narayan, R., Remillard, R. A., Davis, S. W., and Li, L.-X. (2006). The spin of the near-extreme Kerr black hole GRS 1915+105. Astrophys. J. 652, 518–539. doi:10.1086/508457

CrossRef Full Text | Google Scholar

Mehdipour, M., Kaastra, J. S., Kriss, G. A., Arav, N., Behar, E., Bianchi, S., et al. (2017). Chasing obscuration in type-I AGN: discovery of an eclipsing clumpy wind at the outer broad-line region of NGC 3783. Astron. Astrophys. 607, A28. doi:10.1051/0004-6361/201731175

CrossRef Full Text | Google Scholar

Mehdipour, M., Kriss, G. A., Brenneman, L. W., Costantini, E., Kaastra, J. S., Branduardi-Raymont, G., et al. (2022). Changing-look event in NGC 3516: continuum or obscuration variability? Astrophys. J. 925, 84. doi:10.3847/1538-4357/ac42ca

CrossRef Full Text | Google Scholar

Mejía-Restrepo, J. E., Trakhtenbrot, B., Lira, P., Netzer, H., and Capellupo, D. M. (2016). Active galactic nuclei at z ∼ 1.5 - II. Black hole mass estimation by means of broad emission lines. Mon. Not. R. Astron. Soc. 460, 187–211. doi:10.1093/mnras/stw568

CrossRef Full Text | Google Scholar

Miller, J. M. (2007). Relativistic X-ray lines from the inner accretion disks around black holes. Ann. Rev. Astron. Astrophys. 45, 441–479. doi:10.1146/annurev.astro.45.051806.110555

CrossRef Full Text | Google Scholar

Miller, L., Turner, T. J., and Reeves, J. N. (2008). An absorption origin for the X-ray spectral variability of MCG-6-30-15. Astron. Astrophys. 483, 437–452. doi:10.1051/0004-6361:200809590

CrossRef Full Text | Google Scholar

Miller, L., Turner, T. J., Reeves, J. N., George, I. M., Kraemer, S. B., and Wingert, B. (2007). The variable X-ray spectrum of Markarian 766. I. Principal components analysis. Astron. Astrophys. 463, 131–143. doi:10.1051/0004-6361:20066548

CrossRef Full Text | Google Scholar

Miniutti, G., and Fabian, A. C. (2004). A light bending model for the X-ray temporal and spectral properties of accreting black holes. Mon. Not. R. Astron. Soc. 349, 1435–1448. doi:10.1111/j.1365-2966.2004.07611.x

CrossRef Full Text | Google Scholar

Mittaz, J. P. D., Penston, M. V., and Snijders, M. A. J. (1990). Ultraviolet variability of NGC 4151: a study using principal component analysis. Mon. Not. R. Astron. Soc. 242, 370–378. doi:10.1093/mnras/242.3.370

CrossRef Full Text | Google Scholar

Miyoshi, M., Moran, J., Herrnstein, J., Greenhill, L., Nakai, N., Diamond, P., et al. (1995). Evidence for a black hole from high rotation velocities in a sub-parsec region of NGC4258. Nature 373, 127–129. doi:10.1038/373127a0

CrossRef Full Text | Google Scholar

Moderski, R., Sikora, M., and Lasota, J. P. (1998). On the spin paradigm and the radio dichotomy of quasars. Mon. Not. R. Astron. Soc. 301, 142–148. doi:10.1046/j.1365-8711.1998.02009.x

CrossRef Full Text | Google Scholar

Müller, A. C., and Guido, S. (2016). Introduction to machine learning with Python (Sebastopol, CA: O’Reilly)

Google Scholar

Mushotzky, R. F., Done, C., and Pounds, K. A. (1993). X-ray spectra and time variability of active galactic nuclei. Ann. Rev. Astron. Astrophys. 31, 717–761. doi:10.1146/annurev.aa.31.090193.003441

CrossRef Full Text | Google Scholar

Nandra, K., O’Neill, P. M., George, I. M., and Reeves, J. N. (2007). An XMM-Newton survey of broad iron lines in Seyfert galaxies. Mon. Not. R. Astron. Soc. 382, 194–228. doi:10.1111/j.1365-2966.2007.12331.x

CrossRef Full Text | Google Scholar

NASA HEASARC(2014). HEAsoft: unified release of FTOOLS and XANADU. Astrophys. Source Code Libr. Rec. ascl:1408.004.

Google Scholar

Nichols, D. A., Owen, R., Zhang, F., Zimmerman, A., Brink, J., Chen, Y., et al. (2011). Visualizing spacetime curvature via frame-drag vortexes and tidal tendexes: general theory and weak-gravity applications. Phys. Rev. D. 84, 124014. doi:10.1103/PhysRevD.84.124014

CrossRef Full Text | Google Scholar

Niedźwiecki, A., and Miyakawa, T. (2010). General relativistic models of the X-ray spectral variability of MCG-6-30-15. Astron. Astrophys. 509, A22. doi:10.1051/0004-6361/200911919

CrossRef Full Text | Google Scholar

Niedźwiecki, A., Szanecki, M., and Zdziarski, A. A. (2019). Improved spectral models for relativistic reflection. Mon. Not. R. Astron. Soc. 485, 2942–2955. doi:10.1093/mnras/stz487

CrossRef Full Text | Google Scholar

Niedźwiecki, A., Zdziarski, A. A., and Szanecki, M. (2016). On the lamppost model of accreting black holes. Astrophys. J. Lett. 821, L1. doi:10.3847/2041-8205/821/1/L1

CrossRef Full Text | Google Scholar

Niedźwiecki, A., and Życki, P. T. (2008). On the variability and spectral distortion of fluorescent iron lines from black hole accretion discs. Mon. Not. R. Astron. Soc. 386, 759–780. doi:10.1111/j.1365-2966.2008.12735.x

CrossRef Full Text | Google Scholar

Novikov, I. D., and Thorne, K. S. (1973). “Astrophysics of black holes,” in Black holes (les astres occlus). Editors C. Dewitt, and B. S. Dewitt (New York: Gordon & Breach), 343–450.

Google Scholar

Owen, R., Brink, J., Chen, Y., Kaplan, J. D., Lovelace, G., Matthews, K. D., et al. (2011). Frame-dragging vortexes and tidal tendexes attached to colliding black holes: visualizing the curvature of spacetime. Phys. Rev. Lett. 106, 151101. doi:10.1103/PhysRevLett.106.151101

PubMed Abstract | CrossRef Full Text | Google Scholar

Parker, M. L., Alston, W. N., Buisson, D. J. K., Fabian, A. C., Jiang, J., Kara, E., et al. (2017a). Revealing the ultrafast outflow in IRAS 13224-3809 through spectral variability. Mon. Not. R. Astron. Soc. 469, 1553–1558. doi:10.1093/mnras/stx945

CrossRef Full Text | Google Scholar

Parker, M. L., Fabian, A. C., Matt, G., Koljonen, K. I. I., Kara, E., Alston, W., et al. (2015). Revealing the X-ray variability of AGN with principal component analysis. Mon. Not. R. Astron. Soc. 447, 72–96. doi:10.1093/mnras/stu2424

CrossRef Full Text | Google Scholar

Parker, M. L., Lieu, M., and Matzeu, G. A. (2022). AGN X-ray spectroscopy with neural networks. Mon. Not. R. Astron. Soc. 514, 4061–4068. doi:10.1093/mnras/stac1639

CrossRef Full Text | Google Scholar

Parker, M. L., Longinotti, A. L., Schartel, N., Grupe, D., Komossa, S., Kriss, G., et al. (2019). The nuclear environment of the NLS1 Mrk 335: obscuration of the X-ray line emission by a variable outflow. Mon. Not. R. Astron. Soc. 490, 683–697. doi:10.1093/mnras/stz2566

CrossRef Full Text | Google Scholar

Parker, M. L., Marinucci, A., Brenneman, L., Fabian, A. C., Kara, E., Matt, G., et al. (2014a). Principal component analysis of MCG-06-30-15 with XMM-Newton. Mon. Not. R. Astron. Soc. 437, 721–729. doi:10.1093/mnras/stt1925

CrossRef Full Text | Google Scholar

Parker, M. L., Pinto, C., Fabian, A. C., Lohfink, A., Buisson, D. J. K., Alston, W. N., et al. (2017b). The response of relativistic outflowing gas to the inner accretion disk of a black hole. Nature 543, 83–86. doi:10.1038/nature21385

PubMed Abstract | CrossRef Full Text | Google Scholar

Parker, M. L., Walton, D. J., Fabian, A. C., and Risaliti, G. (2014b). PCA of PCA: principal component analysis of partial covering absorption in NGC 1365. Mon. Not. R. Astron. Soc. 441, 1817–1824. doi:10.1093/mnras/stu712

CrossRef Full Text | Google Scholar

Parker, M. L., Wilkins, D. R., Fabian, A. C., Grupe, D., Dauser, T., Matt, G., et al. (2014c). The NuSTAR spectrum of Mrk 335: extreme relativistic effects within two gravitational radii of the event horizon? Mon. Not. R. Astron. Soc. 443, 1723–1732. doi:10.1093/mnras/stu1246

CrossRef Full Text | Google Scholar

Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., et al. (2019). PyTorch: an imperative style, high-performance deep learning library. In Advances in neural information processing systems, Editors H. Wallach, H. Larochelle, A. Beygelzimer, F. d'Alché-Buc, E. Fox, and R. Garnett (Vancouver, Canada: Curran Associates, Inc.), vol. 32

Google Scholar

Pearson, K. (1901). LIII. On lines and planes of closest fit to systems of points in space. Philos. Mag. 2, 559–572. doi:10.1080/14786440109462720

CrossRef Full Text | Google Scholar

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., et al. (2011). Scikit-learn: machine learning in Python. J. Mach. Learn. Res. 12, 2825–2830. doi:10.48550/arXiv.1201.0490

CrossRef Full Text | Google Scholar

Penrose, R. (1969). Gravitational collapse: the role of general relativity. Nuovo Cimento Riv. Ser. 1, 252.

Google Scholar

Penrose, R. (2002). “Golden oldie”: gravitational collapse: the role of general relativity. Gen. Relativ. Gravit. 7, 1141–1165. doi:10.1023/A:1016578408204

CrossRef Full Text | Google Scholar

Penrose, R., and Floyd, R. M. (1971). Extraction of rotational energy from a black hole. Nat. Phys. Sci. 229, 177–179. doi:10.1038/physci229177a0

CrossRef Full Text | Google Scholar

Peterson, B. M., Ferrarese, L., Gilbert, K. M., Kaspi, S., Malkan, M. A., Maoz, D., et al. (2004). Central masses and broad-line region sizes of active galactic nuclei. II. A homogeneous analysis of a large reverberation-mapping database. Astrophys. J. 613, 682–699. doi:10.1086/423269

CrossRef Full Text | Google Scholar

Petrucci, P. O., Ursini, F., De Rosa, A., Bianchi, S., Cappi, M., Matt, G., et al. (2018). Testing warm Comptonization models for the origin of the soft X-ray excess in AGNs. Astron. Astrophys. 611, A59. doi:10.1051/0004-6361/201731580

CrossRef Full Text | Google Scholar

Porquet, D., Done, C., Reeves, J. N., Grosso, N., Marinucci, A., Matt, G., et al. (2019). A deep X-ray view of the bare AGN Ark 120. V. Spin determination from disc-Comptonisation efficiency method. Astron. Astrophys. 623, A11. doi:10.1051/0004-6361/201834448

CrossRef Full Text | Google Scholar

Poutanen, J., and Svensson, R. (1996). The two-phase pair corona model for active galactic nuclei and X-ray binaries: how to obtain exact solutions. Astrophys. J. 470, 249. doi:10.1086/177865

CrossRef Full Text | Google Scholar

Press, W. H., Teukolsky, S. A., Vetterling, W. T., and Flannery, B. P. (1997). Numerical recipes in fortran 77. The art of scientific computing vol. 1. 2nd Edn. Cambridge, UK: Cambridge University Press.

Google Scholar

Reeves, J. N., Braito, V., Porquet, D., Lobban, A. P., Matzeu, G. A., and Nardini, E. (2021). The flaring X-ray corona in the quasar PDS 456. Mon. Not. R. Astron. Soc. 500, 1974–1991. doi:10.1093/mnras/staa3377

CrossRef Full Text | Google Scholar

Remillard, R. A., and McClintock, J. E. (2006). X-ray properties of black-hole binaries. Ann. Rev. Astron. Astrophys. 44, 49–92. doi:10.1146/annurev.astro.44.051905.092532

CrossRef Full Text | Google Scholar

Rencher, A. C., and Christensen, W. F. (2012). Methods of multivariate analysis. 3rd edn. Hoboken: Wiley. doi:10.1002/9781118391686

CrossRef Full Text | Google Scholar

Reynolds, C. S. (2013). The spin of supermassive black holes. Class. Quantum Gravity 30, 244004. doi:10.1088/0264-9381/30/24/244004

CrossRef Full Text | Google Scholar

Reynolds, C. S. (2014). Measuring black hole spin using X-ray reflection spectroscopy. Space Sci. Rev. 183, 277–294. doi:10.1007/s11214-013-0006-6

CrossRef Full Text | Google Scholar

Reynolds, C. S. (2019). Observing black holes spin. Nat. Astron. 3, 41–47. doi:10.1038/s41550-018-0665-z

CrossRef Full Text | Google Scholar

Reynolds, C. S., and Nowak, M. A. (2003). Fluorescent iron lines as a probe of astrophysical black hole systems. Phys. Rep. 377, 389–466. doi:10.1016/S0370-1573(02)00584-7

CrossRef Full Text | Google Scholar

Rhea, C., Hlavacek-Larrondo, J., Perreault-Levasseur, L., Gendron-Marsolais, M.-L., and Kraft, R. (2020). A novel machine learning approach to disentangle multitemperature regions in galaxy clusters. Astron. J. 160, 202. doi:10.3847/1538-3881/abb468

CrossRef Full Text | Google Scholar

Ross, R. R., and Fabian, A. C. (2005). A comprehensive range of X-ray ionized-reflection models. Mon. Not. R. Astron. Soc. 358, 211–216. doi:10.1111/j.1365-2966.2005.08797.x

CrossRef Full Text | Google Scholar

Ross, R. R., and Fabian, A. C. (2007). X-ray reflection in accreting stellar-mass black hole systems. Mon. Not. R. Astron. Soc. 381, 1697–1701. doi:10.1111/j.1365-2966.2007.12339.x

CrossRef Full Text | Google Scholar

Ross, R. R., Fabian, A. C., and Young, A. J. (1999). X-ray reflection spectra from ionized slabs. Mon. Not. R. Astron. Soc. 306, 461–466. doi:10.1046/j.1365-8711.1999.02528.x

CrossRef Full Text | Google Scholar

Schnittman, J. D. (2019). Black hole accretion disk visualization. NASA scientific visualization studio. Goddard Space Flight Center. (Greenbelt, MD: NASA). Available at: https://svs.gsfc.nasa.gov/13326.

Google Scholar

Schnittman, J. D., Krolik, J. H., and Hawley, J. F. (2006). Light curves from an MHD simulation of a black hole accretion disk. Astrophys. J. 651, 1031–1048. doi:10.1086/507421

CrossRef Full Text | Google Scholar

Schnittman, J. D., Krolik, J. H., and Noble, S. C. (2013). X-ray spectra from magnetohydrodynamic simulations of accreting black holes. Astrophys. J. 769, 156. doi:10.1088/0004-637X/769/2/156

CrossRef Full Text | Google Scholar

Schwarzschild, K. (1916). On the gravitational field of a mass point according to einstein’s theory. Sitzber. Dtsch. Akad. Wiss. Berl. Kl. Math. Phys., 189–196.

Google Scholar

Sesana, A., Barausse, E., Dotti, M., and Rossi, E. M. (2014). Linking the spin evolution of massive black holes to galaxy kinematics. Astrophys. J. 794, 104. doi:10.1088/0004-637X/794/2/104

CrossRef Full Text | Google Scholar

Shafee, R., McClintock, J. E., Narayan, R., Davis, S. W., Li, L.-X., and Remillard, R. A. (2006). Estimating the spin of stellar-mass black holes by spectral fitting of the X-ray continuum. Astrophys. J. Lett. 636, L113–L116. doi:10.1086/498938

CrossRef Full Text | Google Scholar

Sharma, A., Paliwal, K. K., Imoto, S., and Miyano, S. (2013). Principal component analysis using QR decomposition. Int. J. Mach. Learn. and Cyber. 4, 679–683. doi:10.1007/s13042-012-0131-7

CrossRef Full Text | Google Scholar

Shields, G. A. (1978). Thermal continuum from accretion disks in quasars. Nature 272, 706–708. doi:10.1038/272706a0

CrossRef Full Text | Google Scholar

Shiokawa, H. (2017). Simulations of accretion disk. Event horizon telescope collaboration. Available at: https://eventhorizontelescope.org/simulations-gallery.

Google Scholar

Shiokawa, H., Gammie, C. F., and Doeleman, S. S. (2017). Time domain filtering of resolved images of Sgr A^∗. Astrophys. J. 846, 29. doi:10.3847/1538-4357/aa82b7

CrossRef Full Text | Google Scholar

Singh, H. P., Gulati, R. K., and Gupta, R. (1998). Stellar spectral classification using principal component analysis and artificial neural networks. Mon. Not. R. Astron. Soc. 295, 312–318. doi:10.1046/j.1365-8711.1998.01255.x

CrossRef Full Text | Google Scholar

Speith, R. (1993). Rotverschiebung längs Photonenbahnen in der Nähe Aktiver Galaktischer Kerne English: Redshift along Photon Trajectories near Active Galactic Nuclei. Germany: Eberhard Karls University of Tubingen. Master’s thesis.

Google Scholar

Speith, R., Riffert, H., and Ruder, H. (1995). The photon transfer function for accretion disks around a Kerr black hole. Comput. Phys. Commun. 88, 109–120. doi:10.1016/0010-4655(95)00067-P

CrossRef Full Text | Google Scholar

Sylvester, J. J. (1889a). A new proof that a general quadric may be reduced to its canonical form (that is, a linear function of squares) by means of a real orthogonal substitution. Messenger Math. 19, 1–5.

Google Scholar

Sylvester, J. J. (1889b). On the reduction of a bilinear quantic of the nth order to the form of a sum of n products by a double orthogonal substitution. Messenger Math. 19, 42–46.

Google Scholar

Sylvester, J. J. (1889c). Sur la réduction biorthogonale d’une forme linéo-linéaire à sa forme canonique. C. R. Acad. Sci. Paris 108, 651–653.

Google Scholar

Tchekhovskoy, A., and McKinney, J. C. (2012). Prograde and retrograde black holes: whose jet is more powerful? Mon. Not. R. Astron. Soc. 423, L55–L59. doi:10.1111/j.1745-3933.2012.01256.x

CrossRef Full Text | Google Scholar

Thorne, K. S., Price, R. H., and MacDonald, D. A. (1986). Black holes: the membrane paradigm. New Haven, CT: Yale Univ. Press.

Google Scholar

Tombesi, F., Cappi, M., Reeves, J. N., and Braito, V. (2012). Evidence for ultrafast outflows in radio-quiet AGNs - III. Location and energetics. Mon. Not. R. Astron. Soc. 422, 1–5. doi:10.1111/j.1745-3933.2012.01221.x

CrossRef Full Text | Google Scholar

Tombesi, F., Cappi, M., Reeves, J. N., Palumbo, G. G. C., Braito, V., and Dadina, M. (2011). Evidence for ultra-fast outflows in radio-quiet active galactic nuclei. II. Detailed photoionization modeling of Fe K-shell absorption lines. Astrophys. J. 742, 44. doi:10.1088/0004-637X/742/1/44

CrossRef Full Text | Google Scholar

Tombesi, F., Cappi, M., Reeves, J. N., Palumbo, G. G. C., Yaqoob, T., Braito, V., et al. (2010). Evidence for ultra-fast outflows in radio-quiet AGNs: I. Detection and statistical incidence of Fe K-shell absorption lines. Astron. Astrophys. 521, A57. doi:10.1051/0004-6361/200913440

CrossRef Full Text | Google Scholar

Trefethen, L. N., and Bau, D. I. (1997). Numerical linear algebra. Philadelphia, PA: Society for Industrial and Applied Mathematics.

Google Scholar

Trunk, G. V. (1979). A problem of dimensionality: a simple example. IEEE Trans. Pattern Anal. Mach. Intell. PAMI-1, 306–307. doi:10.1109/TPAMI.1979.4766926

PubMed Abstract | CrossRef Full Text | Google Scholar

Turner, T. J., Miller, L., Reeves, J. N., and Kraemer, S. B. (2007). The variable X-ray spectrum of Markarian 766. II. Time-resolved spectroscopy. Astron. Astrophys. 475, 121–131. doi:10.1051/0004-6361:20077947

CrossRef Full Text | Google Scholar

Turner, T. J., Reeves, J. N., Braito, V., Lobban, A., Kraemer, S., and Miller, L. (2018). A rapid occultation event in NGC 3227. Mon. Not. R. Astron. Soc. 481, 2470–2478. doi:10.1093/mnras/sty2447

CrossRef Full Text | Google Scholar

Vaughan, S., and Fabian, A. C. (2004). A long hard look at MCG-6-30-15 with XMM-Newton- II. Detailed EPIC analysis and modelling. Mon. Not. R. Astron. Soc. 348, 1415–1438. doi:10.1111/j.1365-2966.2004.07456.x

CrossRef Full Text | Google Scholar

Vestergaard, M. (2002). Determining central black hole masses in distant active galaxies. Astrophys. J. 571, 733–752. doi:10.1086/340045

CrossRef Full Text | Google Scholar

Victoria-Ceballos, C. I., González-Martín, O., Masegosa, J., Longinotti, A. L., Esparza-Arredondo, D., and Osorio-Clavijo, N. (2023). Testing physical scenarios for the reflection features of type-1 AGNs using XMM-Newton and NuSTAR simultaneous observations. Astrophys. J. 954, 96. doi:10.3847/1538-4357/ace785

CrossRef Full Text | Google Scholar

Volonteri, M., Madau, P., Quataert, E., and Rees, M. J. (2005). The distribution and cosmic evolution of massive black hole spins. Astrophys. J. 620, 69–77. doi:10.1086/426858

CrossRef Full Text | Google Scholar

Volonteri, M., Sikora, M., Lasota, J.-P., and Merloni, A. (2013). The evolution of active galactic nuclei and their spins. Astrophys. J. 775, 94. doi:10.1088/0004-637X/775/2/94

CrossRef Full Text | Google Scholar

Wall, J. V., and Jenkins, C. R. (2012). Practical statistics for astronomers. 2nd edn. Cambridge, UK: Cambridge Univ. Press.

Google Scholar

Wandel, A., Peterson, B. M., and Malkan, M. A. (1999). Central masses and broad-line region sizes of active galactic nuclei. I. Comparing the photoionization and reverberation techniques. Astrophys. J. 526, 579–591. doi:10.1086/308017

CrossRef Full Text | Google Scholar

Whitney, C. A. (1983). Principal components analysis of spectral data. I. Methodology for spectral classification. Astron. Astrophys. Suppl. Ser. 51, 443–461.

Google Scholar

Wilson, A. S., and Colbert, E. J. M. (1995). The difference between radio-loud and radio-quiet active galaxies. Astrophys. J. 438, 62. doi:10.1086/175054

CrossRef Full Text | Google Scholar

Witten, I. H., Frank, E., Hall, M. A., and Pal, C. J. (2017). Data mining: practical machine learning tools and techniques. Cambridge, MA: Elsevier. doi:10.1016/C2009-0-19715-5

CrossRef Full Text | Google Scholar

Zdziarski, A. A., Johnson, W. N., and Magdziarz, P. (1996). Broad-band -ray and X-ray spectra of NGC 4151 and their implications for physical processes and geometry. Mon. Not. R. Astron. Soc. 283, 193–206. doi:10.1093/mnras/283.1.193

CrossRef Full Text | Google Scholar

Zhang, S. N., Cui, W., and Chen, W. (1997). Black hole spin in X-ray binaries: observational consequences. Astrophys. J. Lett. 482, L155–L158. doi:10.1086/310705

CrossRef Full Text | Google Scholar

Zhang, Y., and Zhao, Y. (2003). Classification in multidimensional parameter space: methods and examples. Publ. Astron. Soc. Pac. 115, 1006–1018. doi:10.1086/376847

CrossRef Full Text | Google Scholar

Życki, P. T., Done, C., and Smith, D. A. (1999). The 1989 May outburst of the soft X-ray transient GS 2023+338 (V404 Cyg). Mon. Not. R. Astron. Soc. 309, 561–575. doi:10.1046/j.1365-8711.1999.02885.x

CrossRef Full Text | Google Scholar