Ultra-relativistic electron flux enhancement under persistent high speed solar wind stream

The physical mechanisms usually applied to explain the relativistic electron enhancement have been delved into to elucidate non-adiabatic electron acceleration resulting in the ultra-relativistic electron population observed in the outer radiation belt. We considered multisatellite observations of the solar wind parameters, magnetospheric waves, and particle flux to report an unusual local acceleration of ultra-relativistic electrons under a prolonged high-speed solar wind stream (HSS). A corotating interaction region reaches the Earth’s bowshock on August 3, 2016, causing a minor geomagnetic storm. Following this, the magnetosphere was driven for 72 h by a long-term HSS propagating at 600 km/s. During this period, the magnetosphere sustained both ultra-low frequency (ULF) and very-low frequency (VLF) waves in the outer radiation belt region. Besides the waves, the relativistic and ultra-relativistic electron fluxes were enhanced with different time lags regarding the magnetic storm main phase. The efficiency of wave-particle interaction in enhancing ultrarelativistic electrons is evaluated by the diffusion coefficient rates, considering both ULF and VLF waves together with phase space density analyses. Results show that local acceleration by whistler mode chorus waves can occur in a time scale of 2–4 h, whereas ULF waves take around 10’s of hours and magnetosonic waves take a time scale of days. This result is confirmed by the phase space density analysis. Accordingly, it shows that peaks of local acceleration of 1 MeV electrons are consistent with the observation of the highest chorus wave amplitude at the same L-shell and MLT. Thus, we argue that whistler mode chorus waves interacting with relativistic electrons are the main physical mechanisms leading to ultra-relativistic electron enhancement, while ULF and fast magnetosonic waves are found as secondary physical processes. Lastly, our analysis contributes to understanding how whistler and ULF waves can contribute to ultra-relativistic electrons showing up in the inner magnetosphere under the HSS driver.

1 Introduction

In the interplanetary medium, high-speed solar wind streams (HSS) propagate at a speed greater than the ambient solar wind because they follow solar magnetic field lines opening to the heliosphere due to the magnetic topology found at coronal holes (Cranmer, 2009). Thus, the slow (ambient) solar wind and the HSS can interact and generate corotating interaction regions (CIR). Often, HSS can rotate with the sun over a period of 27 days and recurrently interact with the inner and outer magnetosphere, triggering several physical processes that impact the ionosphere, and thermosphere, causing disturbances in the geomagnetic field (Crowley et al., 2008). The enhanced solar wind velocity has been shown to be related to the enhancement of the relativistic (Paulikas and Blake, 1979; Baker et al., 1997; Baker et al., 2001) and ultra-relativistic particle populations in the outer radiation belt (Reeves et al., 2011; Baker et al., 2019), and it can be related to wave activity (for whistler mode chorus waves, see e.g., Aryan et al. (2016), and for ultra-low frequency waves, see e.g., Mathie and Mann (2001), especially in the outer radiation belts region.

The acceleration processes responsible for the electron’s energy increase in the outer radiation belt, specifically in the range of 1–3 MeV, can be attributed to physical mechanisms organized into two main classes: adiabatic and non-adiabatic processes. The adiabatic and non-adiabatic inward ULF waves drift resonance, play a significant role in transporting low-energy particles (around tens of keV) through the inner magnetosphere. Additionally, local acceleration occurs due to the presence of whistler-mode waves, with a notable contribution from chorus waves. Studies by Gabrielse et al. (2014), Jaynes et al. (2015), Ozeke et al. (2019), da Silva et al. (2019), Da Silva et al. (2023a), Summers et al. (1998), Thorne (2010), Thorne et al. (2013), and Turner et al. (2010) all support these findings. However, for the enhancements in the population of ultra-relativistic electrons, these typical methods provide a partial explanation, which requires further investigation.

Baker et al. (2013), Reeves et al. (2013), Baker et al. (2016), Li et al. (2016), Moya et al. (2017), Zhao et al. (2017), Zhao et al. (2018), and Agapitov et al. (2018) have established a connection between the increase of ultra-relativistic electrons and geomagnetic storms based on Van Allen Probes measurements. In these works, the authors discussed whether the electromagnetic whistler-mode wave-particle interaction is the main physical mechanism responsible for acceleration. Thorne et al. (2013) showed that chorus waves could explain the increase of relativistic and ultra-relativistic electron flux and the alteration of pitch angle distribution. Zhao et al. (2019a) observed local acceleration leading electrons to 3–5 MeV, and then, ULF-driven inward diffusion further accelerating these electrons to 7 MeV. Later, Allison and Shprits (2020) showed that first the electrons are accelerated to relativistic energy and then to ultra-relativistic energy. Furthermore, magnetospheric plasma density number was found as a controlling parameter (Allison et al., 2021; Agapitov et al., 2019) in the relativistic electron acceleration due to wave-particle interaction with the low plasma density number being favorable for relativistic electron acceleration (Horne et al., 2003; Horne et al., 2005; Thorne et al., 2013; Allison et al., 2021). Nasi et al. (2022) analyzed extreme relativistic and ultra-relativistic electron enhancement and concluded that different physical mechanisms contribute to the enhancement of different electron energy populations.

The whistler-mode chorus waves happen outside the plasmasphere as localized energetic emissions. The electron gyrofrequency (Ω_ce) and electron plasma density (n_e) are what determine its frequency range (Tsurutani and Smith, 1977; Tsurutani and Smith, 1974). Chorus waves can interact with seed electron populations, causing acceleration (Summers et al., 1998; Jaynes et al., 2015; da Silva et al., 2022; Da Silva et al., 2023a) and replenishing the outer radiation core electrons at relativistic energy (0.7–2 MeV) (see, e.g., Horne et al. (2005), Shprits et al. (2008), Reeves et al. (2013), Thorne et al. (2013)). The wave-particle interaction occurs since the resonance condition is fulfilled for a given harmonic number n (Summers et al., 2012; Shprits et al., 2022; Alves et al., 2023).

The whistler-mode hiss waves occur inside the plasmasphere in all magnetic local time (MLT) (Thorne et al., 1973), below more than 10 kHz of the electron gyrofrequency, and present quasi-coherent ascendent and descendent tons similarly to chorus waves (Summers et al., 2014). Their amplitudes are high on the dayside (Meredith et al., 2004), and the propagation is predominantly parallel to the magnetic field in low magnetic latitudes, becoming oblique in high magnetic latitudes. These waves can interact with the electrons through the pitch angle scattering mechanism, which can cause electron precipitation into the atmosphere (Abel and Thorne, 1998; Da Silva et al., 2022; Da Silva et al., 2023b).

The whistler-mode fast magnetosonic (MS) waves are generated in the equatorial region (Chen and Bortnik, 2020; Gary et al., 2010; Russell et al., 1969) as a result of the release of free energy provided by proton/ion ring distribution instabilities (Ma et al., 2016, and references therein; Boardsen et al., 2016). They propagate in a frequency range that spans from the proton gyrofrequency to the lower hybrid frequency (from around several Hz to hundreds of kHz) confined in the equatorial latitude (Santolík et al., 2004). MS waves are observed outside and inside the plasmasphere (Horne et al., 2000; Ma et al., 2013). It can propagate (from discrete emission to a continuous shape (Sun et al., 2016)) in a nearly perpendicular direction to the ambient magnetic field (WNA ≥75), with a polarization almost linear, and typically has a low ellipticity (≤0.2). They can cause loss of particles or a change in pitch angle distribution (Bortnik and Thorne, 2010; Bortnik et al., 2015; Ma et al., 2016; Li et al., 2017; Maldonado and Chen, 2018). Furthermore, they can cause local acceleration of a few MeV electrons near the plasmapause (Horne et al., 2007; Baker et al., 2016; Baker, 2021).

In this case study, we investigate an important ultra-relativistic electron acceleration that happens in the outside plasmasphere when the high-speed solar wind stream (HSS) lasts for a long time. The persistent HSS causes several disturbances in the Earth’s magnetosphere, which in turn generate waves that participate in the acceleration physical processes. Multi-satellite observations from the solar wind and Earth’s radiation belt are analyzed. We investigate the role of ULF and whistler waves, which include fast magnetosonic, chorus, and hiss waves observed during a case event. Insitu parameters measured by instruments onboard Van Allen Probes differentiate the whistler waves in the magnetospheric trough. The bouncing average diffusion coefficients are calculated using analytical equations provided by Mourenas et al. (2013) and Artemyev et al. (2013) for the waves participating in the ultra-relativistic electron’s enhancement. We differentiate the electron populations in the radiation belt into relativistic core electrons (0.7–3.0 MeV) and ultra-relativistic electrons (>3.0 MeV), according to Shprits et al. (2022). The contribution of the waves to the electron’s acceleration and the efficiency of the physical process associated with each wave are discussed regarding the electron’s pitch angle distribution, besides the agreement of the resonance condition. We use phase space density analyses to identify the local acceleration signatures associated with wave-particle acceleration.

2 Data selection and methodology

The insitu measurements of the interplanetary magnetic field components (IMF) Bx, By, and Bz are obtained from the magnetic field detector (MAG) and the particle detector Solar Wind Electron, Proton, and Alpha Monitor (SWEPAN) onboard the Advanced Composition Explorer (ACE) satellite located at Lagrangian point L1. The solar wind (SW) speed, density, and interplanetary magnetic field components Bx, By, and Bz are in the geocentric solar magnetospheric (GSM) coordinate system, with a five-minute time resolution. The parameters measured by the ACE satellite were shifted to the bow shock. From the solar wind parameters, we calculate the magnetopause stand-off distance (Rmp) by using the model described by Shue et al. (1998). Besides, NASA OMINIWeb data base provides the geomagnetic symmetric index (Sym-H), auroral electrojet index (AE), and Kp index.

Figure 1 depicts satellites that traveled through the inner magnetosphere during the event. The Magnetospheric Multiscale (MMS) (Burch et al., 2016) traveled from the nightside magnetospheric sector toward the dayside. MMS-1 crossed the radiation belt at the nightside sector around 11–14 UT on 04 August, then the probe traveled toward perigee, progressed to the dayside sector, and reached the radiation belt region at around 15 UT. The magnetic field, electric field, and wave power spectral density data were collected using flux gate magnetometers (FGM) (Russell et al., 2016), electric field double probes (EDP) (Ergun et al., 2016), and digital signal processors (DSP) in the FIELDS (Torbert et al., 2016) instrumentation suite, respectively. The Fly’s Eye energetic particle spectrometer (FEEPS) sensors (Blake et al., 2016) detected energy and pitch angle-resolved electron differential fluxes from 25 keV to 650 keV (not shown). NASA’s CdaWeb database provided DSP data, including magnetic (BPSD) and electric (EPSD) field power spectral densities covering frequency ranges of 0.2–6,000 Hz and 1–8,000 Hz, respectively.

Figure 1

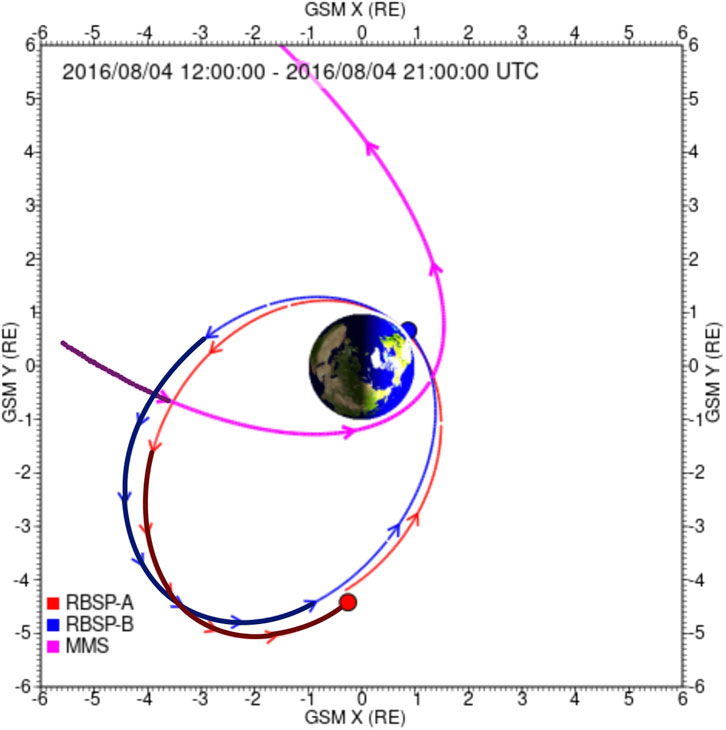
Figure 1. Satellites orbits during the period of the ultra-relativistic enhancement. Van Allen Probes A and B (red and blue) and MMS-1 (green). Probes A follows probe B, travelling around 2 h in advance from the midnight to dawn, with the apogee at 3 MLT and 2.5 MLT, respectively. MMS-1 travels from the midnight sector to dawn, it passes through the outer radiation belt for short periods, from 11:30 UT to 13:30 UT, and then around 15 UT.

Van Allen Probe B orbit preceded Probe A, traveling from the night sector toward dusk (Figure 1). Instruments onboard Van Allen Probes A and B measure the plasma wave parameters and the outer radiation belt electron flux (Mauk et al., 2013). On 4 August 2016, the Van Allen Probe A (B) orbit traveled in the dawnside sector of the magnetosphere; the satellite apogee was at around 3.0 (2.6) MLT. We measured the relativistic electron flux in the 1.8–3.4 MeV energy channels and the 5.2 MeV ultra-relativistic energy channel using the Relativistic Electron Proton Telescope (REPT) (Baker et al., 2013). We obtained both spin-averaged and pitch-angle resolved differential flux. The electron flux is shown as a function of time, magnetic local time (MLT), L*, and magnetic latitude (MLat).

The electron phase space density analyses are provided by https://rbspgway.jhuapl.edu/psd. This quantity is a function of the electron’s motion adiabatic invariants μ, K, and L*. Since the outer radiation belt electron flux is pitch angle resolved, we can choose a set of K values varying from equatorial to polar values, i.e., in the range 0.01 G^1/2R_E < K < 0.22 G^1/2R_E. Regarding the energy range of interest, the set of μ values was 2,500 MeVG^-1 < μ < 12,000 MeVG^-1, corresponding to the energy range (at L* ∼5) from 3.4 MeV to 6.3 MeV.

The Electric and Magnetic Field Instrument Suite and Integrated Science (EMFISIS) (Kletzing et al., 2013) provides the magnetospheric density (dataset level-4) and the whistler wave ellipticity, planarity, wave normal angle, and Poynting vector. The dataset level-3 provides us one-second time resolution, a high-frequency range, and burst mode (10–12.000 Hz) magnetic field measurements.

The magnitude of chorus and MS waves is derived from spectrograms of the magnetic field in relation to frequency and observation time, acquired by the EMFISIS instrument aboard Van Allen Probes A and B. The whistler wave amplitude is integrated following the analyses by Ni et al. (2020) and Han and Kim (2023), which identify the waves and band emission by considering parameters such as normal angles, ellipticity, and planarity.

The 32 samples/s electric field was obtained by the Electric Field and Waves (EFW) (Wygant et al., 2013) and used to calculate the power spectral density of ultra-low frequency (ULF) waves. The electric field was decimated by a factor of 32 to have the same time resolution of the magnetic field component to calculate power spectral density, respectively $P_m^E$ and $P_m^B$ at the resonant drift frequency of and wave number m (for more detail on the power spectral density calculation see Marchezi et al., 2022). These terms were computed using the integrated power spectrum density in the frequency band of ULF waves (0.1–10 mHz).

3 Case study 04 August 2016

The Earth’s magnetosphere was under the influence of the HSS from August 3 to 8 August 2016. The arrival of the preceding corotating interaction region (CIR) around 05:15 UT on August 2 initiated a geomagnetic storm (not shown). Then, at 15:00 UT on August 3, a HSS arrived. The SW plasma parameters depicted in Figures 2, 3 show that the HSS arrival gave rise to the geomagnetic storm main phase, as indicated in Figures 2F–H, respectively, from 00:00 UT to 12:00, the Sym-H index reached −60 nT at 06:00 UT, and the AE index oscillated around 1,000 nT, also, the Kp index ranged from 5o to 4+. The SW speed (panel e) suddenly increased from 400 km/s to 600 km/s at 12 UT on 03 August, and it remained elevated for the next 50 h. Figure 3 panel d shows that the solar wind density ranged from 18 a.u. cm^-3 at 00:00 UT to ∼5 a.u. cm^-3 at noon, the IMF Bz component (Figure 3 panel f) rotates around ±20 nT, characteristic of an interplanetary magnetic cloud structure. The convective electric field Ey (not shown) varies abruptly from +8 mV/m to −8 mV/m, indicating a significant amount of energy delivered in the magnetosphere due to magnetic reconnection for a short period of time. In Figure 3 panel e, both Bx and By components oscillated around −5 nT and +20 nT. Accordingly, Figure 3 panel a, shows the outer radiation belt electron flux observed by Probes A at L-shell 4.5 shows a minor decrease in the 1.8–3.2 MeV (panel b) energy range, while the 5.2 MeV electron flux is very low, as seen in panel a.

Figure 2

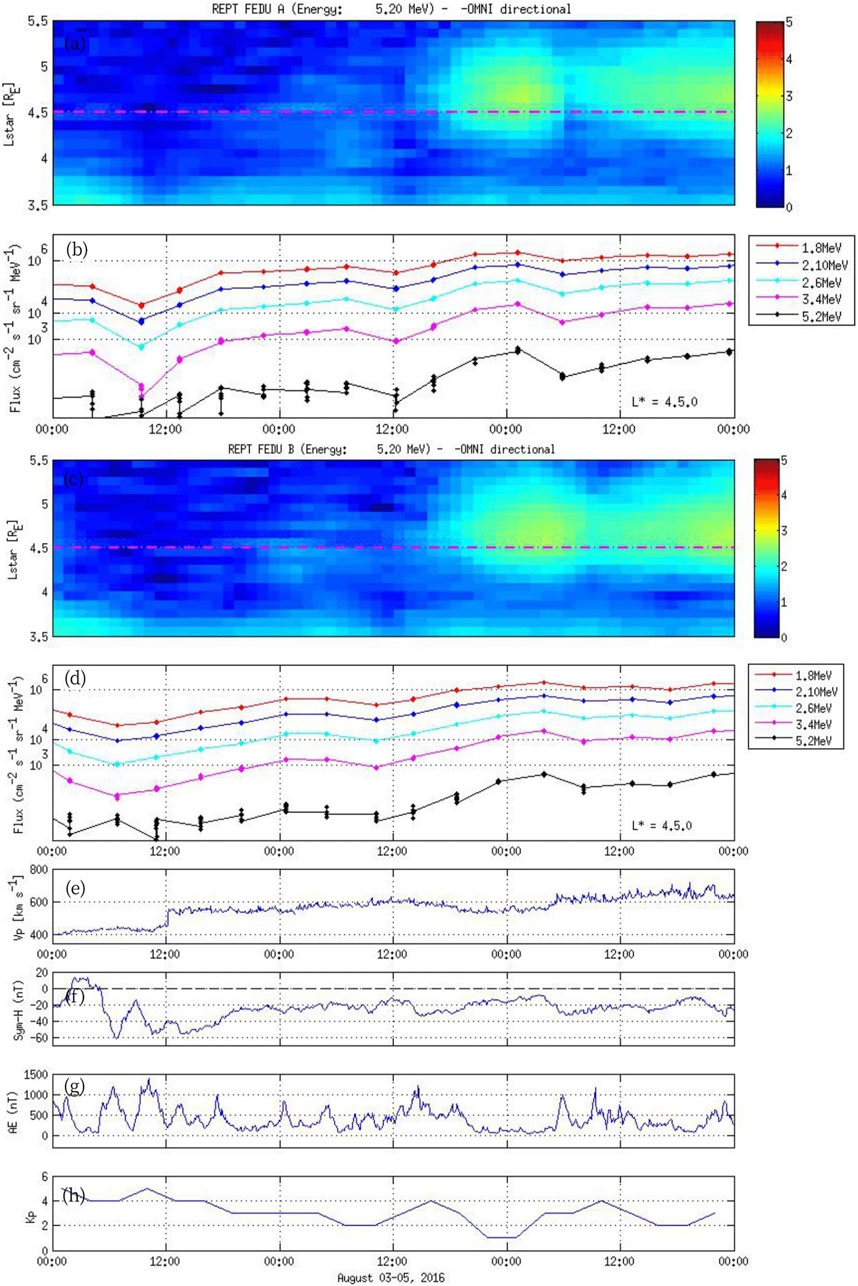
Figure 2. (A) The interpolated outer radiation belt ultra-relativistic electron for 5.2 MeV as a function of L* for the Van Allen Probe A. (B) Electron flux measured at L* ∼5, for 1.8–3.4 MeV and the ultra-relativistic 5.2 MeV for the Van Allen Probe A. (C, D) are the same as (A, B), respectively, for the Van Allen Probe B. (E) Solar wind speed (F–H) Geomagnetic index Sym-H, AE, and Kp, respectively. Measurements are shown for August 3–5, 2016. A geomagnetic storm is observed from 00:00 to 20:00 UT on August 03.

Figure 3

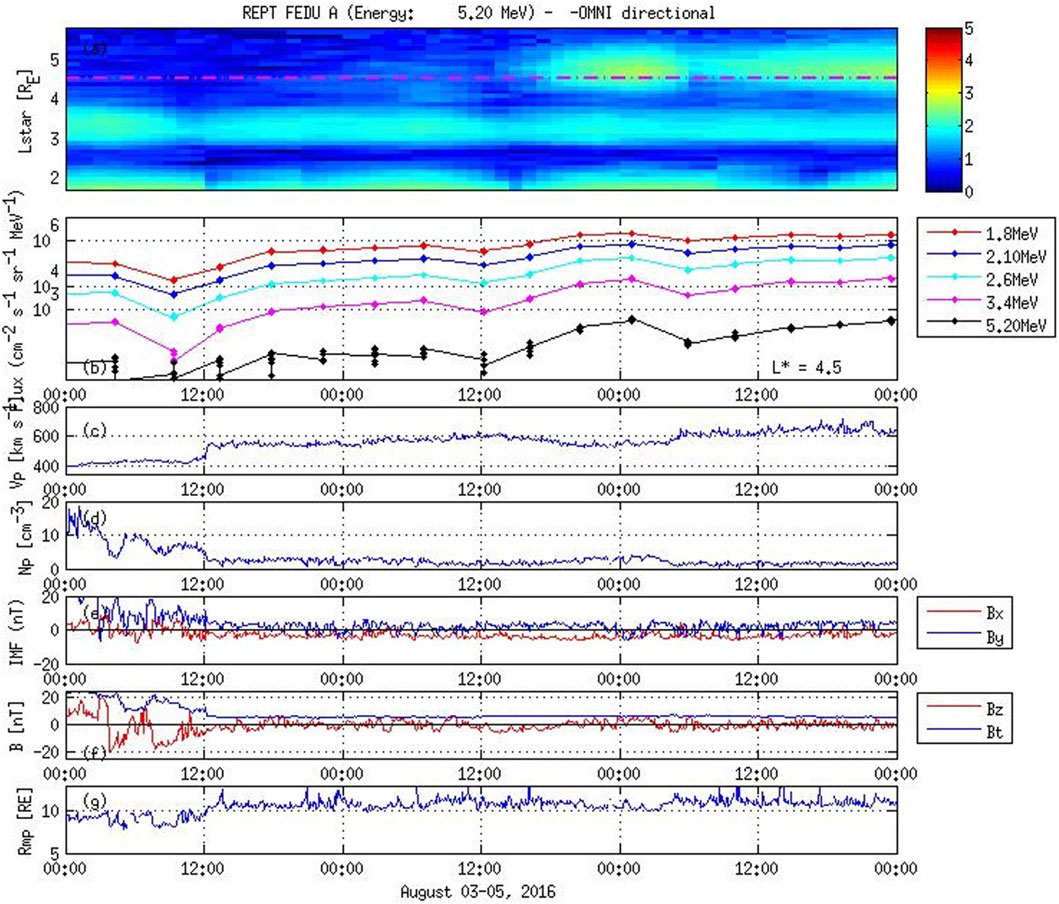
Figure 3. (A) The interpolated outer radiation belt ultra-relativistic electron for 5.2 MeV as a function of L* for the Van Allen Probe A. (B) Electron flux measured at L* ∼5, for 1.8–3.4 MeV and the ultra-relativistic 5.2 MeV for the Van Allen Probe A. (C) Solar wind speed in GSM coordinate system. (D) Solar wind plasma density. (E, F) respectively, the interplanetary magnetic fields components Bx, By, and Bz and Btotal measured by ACE satellite in the Lagrangian point L1 corrected to the bow shock. (G) Magnetopause stand-off distance at the subsolar point calculated by Shue model (Shue et al., 1998).

Later, a second period characterized by a prolonged HSS at a speed of ∼600 km/s (Figure 2 panel e), driving a long-standing magnetospheric disturbance is observed for at least 72 h. The Alfvénic-type fluctuations in the components of the magnetic field and velocity are transported through Earth’s magnetosphere. Since these fluctuations have a south Bz component, it can continuously and persistently interact with the geomagnetic field in the magnetopause region. As a result, the HSS inputs mass, momentum, and energy into the magnetosphere through the physical process of magnetic reconnection (Dungey, 1961). This process may not be continuous as the solar wind Bz component rotates from the south to the north (related to intermittent and continuous magnetic reconnection at the magnetopause and magnetotail; see, e.g., Jauer et al. (2022)). Under these circumstances, the relativistic electron flux is continuously increased (from 12 UT in August 03), and it reached their maximum flux late evening of August 04 (Figure 2 panels b and d). The ultra-relativistic 5.2 MeV electron flux (Figure 2 panels a and c) increased by one order of magnitude as the 1.8 MeV electrons reach their maximum flux. The enhancement of the ultra-relativistic electron takes a time lag of 1.5 days following the storm main phase peak.

The Alfvénic fluctuation transported by a fast solar wind stream is often related to ultra-low frequency (ULF) waves in the magnetosphere (see, e.g., Jauer et al. (2019), Jauer et al. (2022)), especially in the outer radiation belt (e.g., Da Silva et al., 2019; Da Silva et al., 2021). To evaluate the contribution of the ULF waves to the relativistic and ultra-relativistic electron acceleration we plotted the diffusion coefficient (D_LL) as a function of time and L*. Results presented in Figure 9 indicate that D_LL was lower than 0.8 days^-1 through the period of interest, which is low, however the contribution of ULF waves is not ruled out, since we will compare with the diffusion coefficients calculated for the other waves.

According to Figure 1, the MMS1 satellite crosses the outer radiation belt region in the night side sector at the same time of Van Allen Probes A and B. The MMS1 observed whistler mode chorus waves only at this time, from 12 to 13 UT in L-shell 5.5 until 4.0, as shown in Figure 4. After that, the satellite moves toward dayside sector and crosses the radiation belt L-shells at the second time, however chorus waves are not observed in this sector. Figures 5, 6 show Van Allen Probes B and A, respectively, and are organized similarly, from top to bottom the panel show whistler mode chorus waves power spectral density; 1.8 MeV electron distributed in pitch angles; 4.2 MeV electrons distributed in pitch angles and the plasmaspheric electron density. We observe that plasmasphere was compressed with plasmapause below L = 3.2 Re, as shown in Figures 5, 6 bottom panel. The whistler mode-chorus waves are observed first by the Van Allen Probe B, from around 13:30 UT (coincident with MMS1 observation) to 19:30 UT (top panel) with wave frequency (ω) ranging in several frequencies from 0.1 < ω < 0.9 Ω_ce, marked by the white and yellow lines, respectively. The emission in the MS wave spectral band, which is below the lower hybrid frequency (f_LH pink line in painel i-a), is observed for 45 min at a 100 Hz signal, close to the plasmasphere.

Figure 4

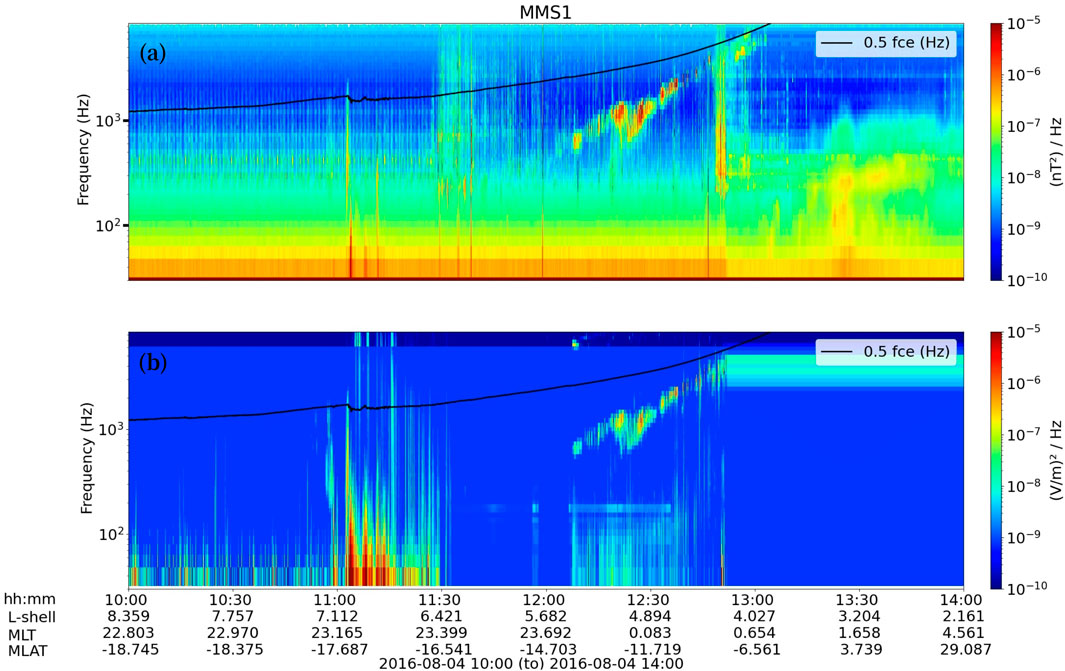
Figure 4. Whistler-mode chorus waves measured by MMS1 from 12:15–13 UT in the L-shell 5.5 to 4.0. Magnetic (A) and Electric (B) power spectral density of whistler-mode chorus waves, low band frequency emissions <0.5 electron gyrofrequency (f_ce).

Figure 5

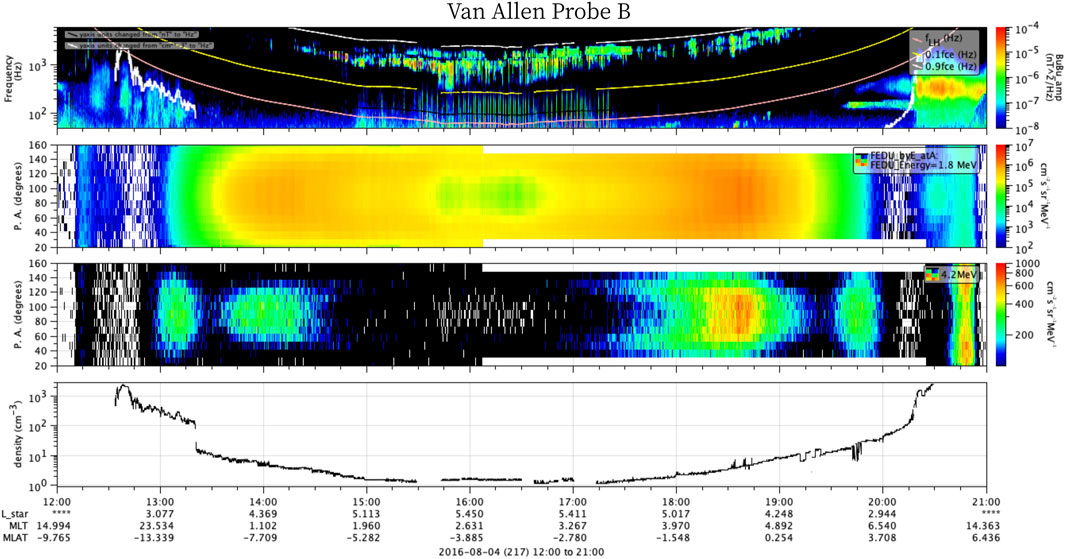
Figure 5. Van Allen Probe B measurements organized in panels from topo to bottom power spectral density [nT²/Hz] of whistler-mode chorus waves, frequency emissions >0.1 electron gyrofrequency (f_ce), and MS wave frequency below lower hybrid frequency (f_LH), the white and yellow lines mark 0.1 f_ce and 0.9 f_ce, respectively; 1.8 MeV; 4.2 MeV electron flux [cm^-2s^-1sr⁻¹MeV^-1] pitch angle distribution, measured by REPT; and magnetospheric plasma density [cm^-3] indicating the transition from magnetospheric trough to plasmasphere. Additional axis shows L*, MLT and MLat from REPT.

Figure 6

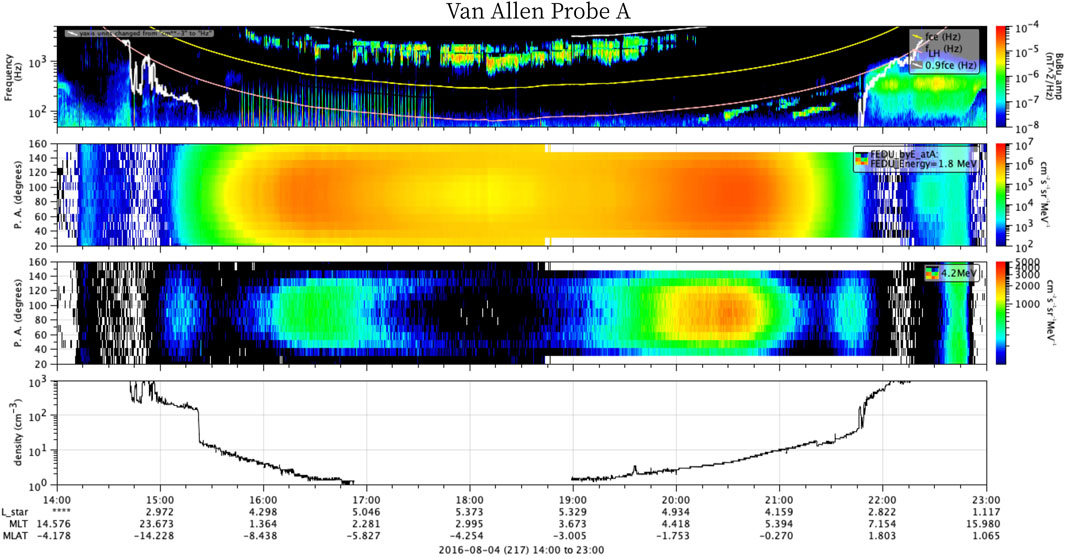
Figure 6. Same as Figure 5 for van allen probes A.

On 4 August, 14 UT, the 1.8 MeV relativistic electron flux (Figure 5, second panel) was around than 10⁶ cm^-2 s^-1 sr⁻¹ MeV^-1, organized in a flat top pitch angle distribution. Due to several physical processes, the 90° relativistic electron flux shows a significant loss at around 16 UT. After that, the flux is yet enhanced (due to seed population acceleration and other processes; see, e.g., Jaynes et al. (2015)) to an excess of 10⁷ cm^-2 s^-1 sr⁻¹ MeV^-1, flat top distributed, as seen at 18:30 UT (Figure 5 second panel). At 14 UT, the 4.2 MeV ultra-relativistic electrons (Figure 5 third panel) are concentrated at L* ∼4.4, in the equatorial region MLat ∼ -7° and in the night side sector (MLT ∼1.0). Pitch angle distribution is flat-top. As the satellite moves from apogee to perigee, i.e. from L* ∼5.4 until 5.0 (at 17 UT), it observes an enhancement in the ultrarelativistic electron flux and a change in pitch angle distribution from flat-top into butterfly. Then, as the probe B reaches inner magnetosphere, i.e. from L* ∼5.0 to 4.2, the PAD shape evolves to a flat top distribution in L* ∼4.5 (at 18:30 UT, MLT ∼4 and MLat ∼0) reaching the maximum flux enhancement. After that, a 90-peaked distribution in L* ∼4 (at 19:15 UT, MLT ∼5, MLat ∼0.5) is observed as the satellite approaches perigee.

Probe A measurements are shown in Figure 6. The whistler mode-chorus waves were observed from 16 UT to 20 UT (panel ii-a), with the emission concentrated at around 0.5Ω_ce. After that, from 20 to 22 UT, thus we observe MS waves in a frequency (ω_m) range of 100–200 Hz, below the lower-hybrid frequency (indicated by the pink line) corresponding to 0.012–0.024 Ωce, as the satellite moves to the perigee. Probe A observe the MS waves emission for 3-hours. Figure 6 second panel shows that the relativistic electrons observed by Probe A follows a dynamic variation similar to that described previously, for Probe B. The 4.2 MeV electron flux is further enhanced in the interval from 19–21 UT. The pitch angle distribution in the outer boundary, i.e. at L* ∼5.1 (at 17:30 UT) and 5.3 (at 19:00) is observed in a butterfly configuration. Then, as Probe A approaches L* ∼5 (MLT ∼4.4 and MLat ∼ −1.7), the ultra-relativistic electron flux was further increased and distributed at all pitch angles.

4 Discussion

4.1 Role of whistler waves: relativistic and ultra-relativistic electron resonance condition for whistler wave

The Doppler-shifted cyclotron resonance condition for both magnetosonic and chorus whistler-mode waves (with a given wave vector (k) and frequency (ω)) interacting with electrons (propagating at velocity v_e) outside the plasmasphere is described as

$\omega -k_{//}{v}_{e//}=sn\frac{{\mathrm{\Omega }}_{e,i}}{\gamma }(1)$

Where ${\mathrm{k}}_{//}$ = k cosθ and ${\mathrm{v}}_{\mathrm{e}//}$ = v_e cosα, s = ± 1 is the sign of the particle, Ω_e,i is the absolute value of the nonrelativistic electron (proton) gyrofrequency (Albert, 2005), n is the harmonic number, with Landau resonance (n = 0) and the Doppler shifted harmonic resonances n = 1, 2, 3,…. The scalar product considers only the parallel component of the electron velocity vector. To solve Equation 1, we use the dispersion relation (η) provided by the general Appleton-Hartree equation, for whistler mode waves propagating at any wave normal angle, in a low-density plasma (following Summers et al., 2012 and Alves et al., 2023). Thus, we get the resonant electron speed (v_e) as a function of the η(ω), the wave normal angle (θ) and particle pitch angle (α)

$\frac{v_e}{c}=\frac{\eta \mathit{cos}\theta \mathit{cos}\alpha +\left(n{\mathrm{\Omega }}_e/\omega \right){\left[{\eta }^2{\mathit{cos}}^2\theta {\mathit{cos}}^2\alpha +\left({\mathrm{\Omega }}_e^2/{\omega }^2-1\right)\right]}^{1/2}}{{\eta }^2{\mathit{cos}}^2\theta {\mathit{cos}}^2\alpha +\left(n^2{\mathrm{\Omega }}_e^2/{\omega }^2\right)}(2)$

We considered that high energy electrons undergo Landau resonant wave-particle interaction at a specific pitch angle with oblique MS waves can reach ultra-relativistic energies. In addition, cyclotron resonance at n = −1 can be reached by chorus waves parallel propagating in a low plasma density condition interacting with 1 MeV electrons. The resonant kinetic energy was calculated from Equation 2 considering the wave frequency measured by the in-situ satellites. The resonant kinetic energy calculations for both whistler waves use the ambient plasma parameters (such as density shown in Figures 5, 6, bottom panels and ambient magnetic field, not shown) and the magnetic waves frequency (Figures 5, 6, top panels) measured by Van Allen Probes A. The resonant kinetic energy is applied in the diffusion coefficient calculation discussed in the following. In Figures 5, 6 and Supplementary Figure S1 MS waves are differentiated from chorus and exohiss (hiss waves outside plasmapause) (Zhu et al., 2019) according to the following characteristics: MS waves occurs right outside the plasmapause (Lpp ∼3.2 Re) (Figure 6, top panel), with electron plasma density increasing from ∼2 cm^-3 to 20 cm^-3 as the satellite crosses the plasma trough towards the perigee (Figures 5, 6, top panels). The ratio of plasma frequency over electron gyrofrequency (ω_pe/Ω_ce) is constant around 3 (figure not shown), with low ellipticity (e < 0.2) and high planarity ∼1 (panels ii-d and ii-e in Supplementary Figure S1), propagating highly obliquely to the ambient magnetic field, i.e., WNA >75° (Supplementary Figure S1, ii-c).

Thus, we estimate the efficiency of the wave-particle interaction related to chorus and magnetosonic waves by means of the bouncing averaged pitch angle $〈D_{\alpha \alpha }^{ch}〉,〈D_{\alpha \alpha }^{MS}〉$ and energy $〈D_{ee}^{ch}〉,〈D_{ee}^{MS}〉$ diffusion coefficient rates for both chorus and MS waves. The resonant kinetic energy considered in the diffusion coefficient calculation are 7 ω_ci and 0.6Ω_ce for the wave particle interaction by MS and chorus waves, respectively.

In the present case study, the electrons drifting at L-shell ∼4 (ambient magnetic field ∼150 nT), highly confined at 80° of pitch angle, interact via Landau resonance with MS waves propagating at 80° in the plasma trough (plasma number density <2 cm^-3). The pitch angle and energy diffusion coefficient rates for MS waves were calculated using Equations (17), (18) from Mourenas et al. (2013) and Equation (29) from Glauert and Horne (2005), and are shown in Figure 7 panels a and b, respectively. In Figure 7, the magnetic wave amplitude was 25 pT, which is the averaged root-mean square MS amplitude around L = 4.5 calculated from THEMIS (Angelopoulos et al., 2008) data (Shprits et al., 2013). The horizontal dotted line in panels (a) and (b) corresponds to 10 days as an estimate of the electron lifetime, according to $\tau \sim 1/〈D_{\alpha \alpha }〉$. Horne et al. (2007) proposed MS wave as a potential mechanism for the 1 MeV electron acceleration at the plasma through ratio of Ω_pe/Ω_ce ∼ 3, with acceleration timescale of a day. In addition, Mourenas et al. (2013) suggested that the MS wave impact on 1 MeV electron lifetime can be more significant than that caused on the low energy population when considering L-shell = 4.5 and high density. Later, Shprits et al. (2013) compared the 1 and 3 MeV electron accelerations in the plasmasphere and plasma trough due to MS waves. The authors showed that the time scales are comparable in both regions and, in general, are higher than 30 days. In this case study, Van Allen Probes A observed an averaged wave amplitude of about 100 pT for the highly oblique (WNA = 82°) MS waves at L-shell ∼4.5, which give an electron lifetime of about a day, i.e. around 10⁵ s, however according to the diffusion coefficient rates, pitch angle diffusion is more efficient than the energy diffusion by less than one order of magnitude for electrons bouncing at 60° of pitch angle.

Figure 7

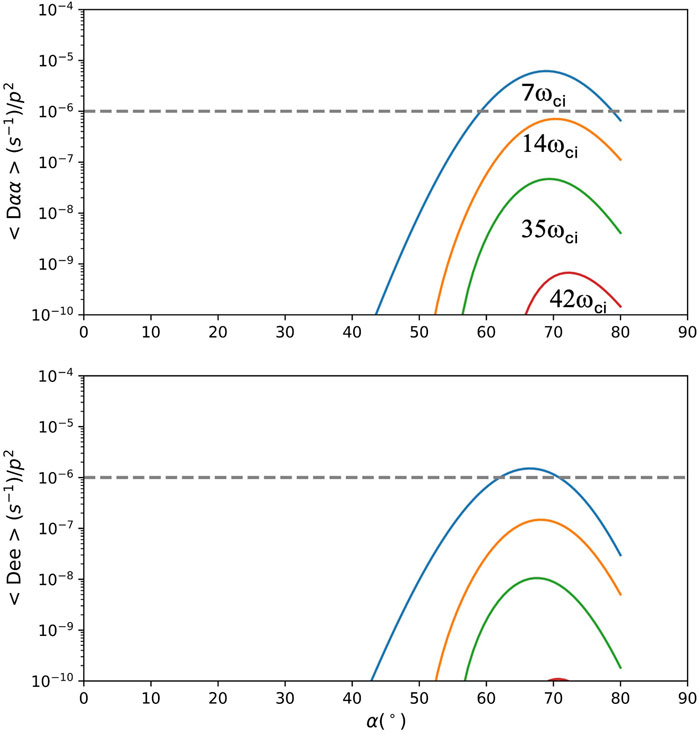
Figure 7. Bouncing-averaged (top panel) pitch angle and (bottom) energy diffusion coefficient for MS waves outside plasmasphere calculated for four wave frequencies multiples of the ion’s gyrofrequency ω_ci. The dotted horizontal line indicates 10 days.

Chorus emissions was observed in a frequency range of 0.3–0.6 Ωce during approximately 5.25 h (B) and 4.0 h (A), which corresponds to 4.2 < L* <5.0. The averaged chorus waves amplitude changed as the satellite travelled toward apogee, reaching the maximum value of about 100 pT, at both lower and upper bands. To estimate the wave-particle interaction efficiency related to the local acceleration produced by chorus waves, we calculated the energy diffusion coefficient rates considering the approach proposed by Artemyev et al. (2013) in Equations 4, 8, which are valid for quasi-parallel whistler mode chorus waves (small θ) interacting with electrons bouncing at low equatorial pitch (lower than 45°) and large equatorial pitch angle, respectively (According to the authors, the analytical solution of Equation 4 shows a significant difference from that obtained by numerical models for α > 40°). The bouncing averaged pitch angle $〈D_{\alpha \alpha }〉$ and energy diffusion $〈D_{ee}〉$ coefficients calculated for 1 MeV electrons bouncing at low pitch angles are shown in Figure 8 panels a and b, respectively. It was considered that the interaction occurs at the resonance condition for harmonic number n = −1, ambient magnetic field corresponding to L-shell = 4.5, and low plasma density conditions, i.e., Ω_pe/Ω_ce ∼ 2.5. The average magnetic amplitude at dayside magnetosphere under disturbed conditions (Kp = 3) is around 100 pT (Shprits et al., 2007), however in this case study the upper band magnetic wave amplitude was 150 pT.

Figure 8

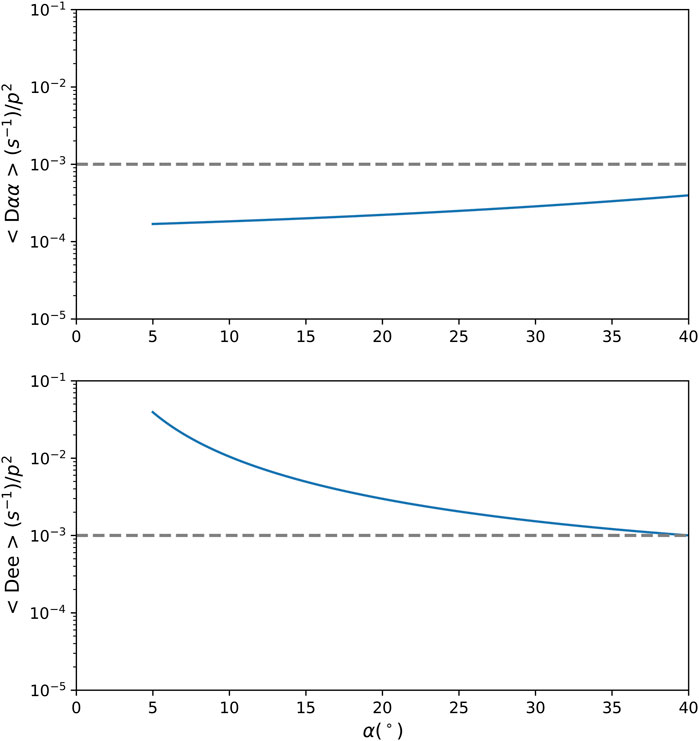
Figure 8. Bouncing-averaged (top panel) pitch angle and (bottom) energy diffusion coefficient for Chorus waves outside plasmasphere, calculated for parallel propagating waves resonantly interacting with 1 MeV electrons bouncing at lower pitch angles (θ < 40°). The dotted horizontal line indicates time scale of 1 h.

The results presented in Figure 8 and also for large pitch angles (figure not shown) show that the energy diffusion $〈D_{ee}^{ch}〉$ via chorus wave interaction in this case study is more efficient than the diffusion via pitch angle $〈D_{\alpha \alpha }^{ch}〉$, leading to the successful local acceleration of 1 MeV electrons bouncing with pitch angles in the range 10° < α < 55°. The time scale related to the electron energization occurs in a time scale of hours, as indicated by the horizontal line in the panels (a) and (b), which is correspondent to the observations shown in the PSD section.

Finally, the plasmaspheric hiss waves are whistler-mode emission in the 20 Hz - few kHz range, with the highest occurrence rates on the dayside (Meredith et al., 2004; Cao et al., 2005). Hiss waves were observed approximately at 22:00 UT on 4 August 2016 (Figures 5, 6), with ellipticity ≥0.5 and planarity ≥0.2 (e.g., Li et al. (2015), Da Silva et al. (2022)). Therefore, hiss waves can interact resonantly with the relativistic electrons through the pitch angle scattering mechanism, causing ultra-relativistic electron flux to decrease within the plasmasphere (Lyons et al., 1972; Abel and Thorne, 1998; Da Silva et al., 2023b; Da Silva et al., 2022) and, thus it is not related to the enhancement of ultra-relativistic electrons.

4.2 Role of ULF waves

Radial diffusion occurs when fluctuating magnetic and electric fields influence the radial location of an electron, initiating a random walk and diffusive movement similar to the way particles spread out due to Brownian motion in a gas. The equation governing radial diffusion is:

$\frac{\partial f}{\partial t}=L^2\frac{\partial }{\partial L}\left[\frac{D_{LL}}{L^2}\frac{\partial f}{\partial t}\right]-\frac{PSD}{\tau }(3)$

Equation 3 accounts for how the phase space density (f) evolves over time for a specific L* and places limits on the gradients caused by external sources of acceleration. The rate at which diffusion happens is determined by the coefficient D_LL, which depends on L* and the levels of magnetic and electric field fluctuations and can manifest in different ways.

Various forms of quantifying the diffusion coefficients due to ULF waves power have been proposed. Here we are considering the model proposed by Fei et al. (2006). He assumed that the coefficients can be separated into magnetic and electric components, as shown is Equations 4, 5, with the total diffusion being the sum of it. Fei et al. (2006) compute the electric (D^E_LL), and magnetic (D^B_LL) coefficients in the form:

$D_{LL}^E=\frac{1}{8{B_E^{2}R}_E^2}{L}^6{\displaystyle \sum _m}{P}_m^E\left(L,m{\omega }_d\right)(4)$

$D_{LL}^B=\frac{{\mu }^2}{8q^2{\gamma }^2{B}_E^2{R}_E^2}L{\displaystyle \sum _m}{m}^2{P}_m^B\left(L,m{\omega }_d\right)(5)$

Where, L is the McIlwian parameter, $\mathrm{\mu }=\frac{p_{\perp }^2{L}^3}{2m_e{B}_E}$ represents the first adiabatic invariant and $\mathrm{\gamma }={\left(1-{v_e}^2/c^2\right)}^{-1/2}$ the Lorentz factor. B_E are the equatorial magnetic field strength at the surface of the Earth and R_E the Earth’s radius; q is the electron charge. The total electron speed is represented by v_e and the speed of light by c. The $P_m^E,P_m^B$ are the power spectrum density of the electric and magnetic field disturbances integrated in the frequency band of ULF waves (0.1–10 mHz) which is the resonant drift frequency, and wave number m. We assume that ULF wave power is concentrated in the lowest mode (m = 1), this assumption is widely regarded as reasonable and is supported by several studies. These studies suggest that, especially during the storm recovery phase, the m = 1 mode predominantly contains the magnetic wave power. This perspective is backed by research from Elkington et al (2013), Olifer et al., (2019), and Tu et al (2012), indicating a significant concentration of wave power in this mode.

Figure 9 shows the ULF diffusion coefficients for azimuthal component of the electric field (top panel) and the compressional mode of the magnetic field (bottom panel). We can observe from Figure 9 that D_LL was lower than 0.8 days^-1 for the period of interest in the D^E_LL for higher L* values. The D_LL is a measure of the diffusion rate, in other words, how much diffusion occurs per day. The inward ULF-resonant diffusion time scale was estimated as τ_d ∼ 1 day for the 4 < L* <6. This indicates a relatively rapid diffusion process, that would occur in a time scale of day.

Figure 9

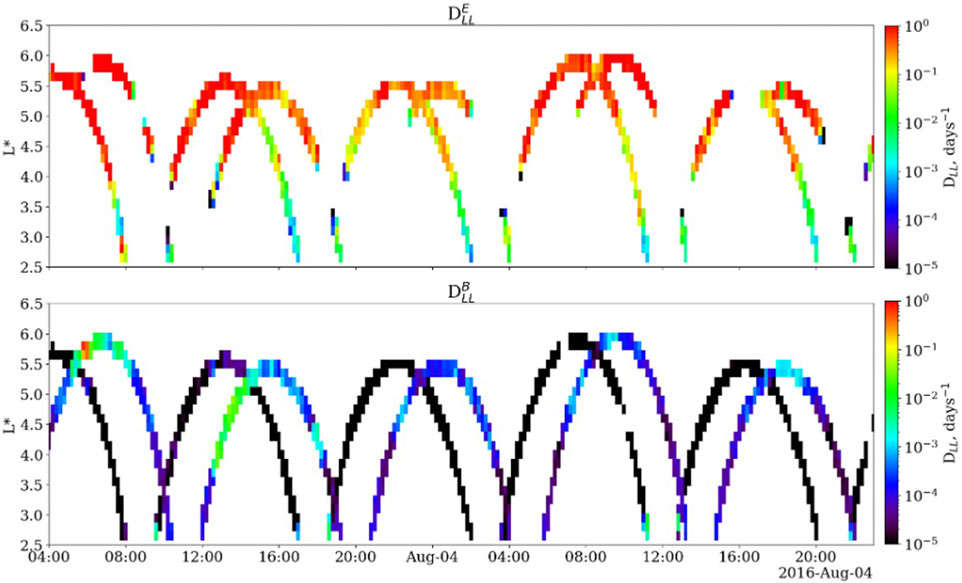
Figure 9. Top panel: the diffusion coefficient of the electric field (D_LL^E), and bottom panel: the diffusion coefficient of the magnetic field (D_LL^B). The coefficients were computed using the electric and magnetic fields recorded by the instruments EFW and EMFISIS onboard Van Allen Probes A and B.

4.3 Electron phase space density (PSD) analyses

We analyze the contribution of radial diffusion and local acceleration signatures in the relativistic and ultra-relativistic electron PSD to describe the role of ULF, chorus, and MS waves in the resonant wave-particle interaction that results in the ultra-relativistic electron enhancement. Figure 10 shows in panel (a) the power spectral density of whistler mode chorus and MS waves as measured by Van Allen Probe A, the lower-band chorus emission is between 0.1 fce and 0.5 fce, and the higher-band is between 0.5 fce and 0.9 fce, as indicated in the plot. According to the observations panel (b), the lower-band magnetic wave time-averaged amplitude increases from ∼50 pT at 16 UT (L ∼ 4.0) to ∼150 pT at 18–19 UT (L ∼ 5.7) as the satellite moves toward the apogee. The higher-band chorus waves follow the same increase as the lower-band, although the upper-band chorus wave time-averaged magnetic amplitude starts with a lower amplitude and a late emission ∼17 UT (L ∼ 5.3) when compared with the lower-band. The maximum time-average amplitude is 150 pT at 18:00 UT–18:30 UT (L ∼ 5.7) for both lower and upper bands. The calculated PSDs for two consecutive passages of Probe A (see red and blue lines in panels c–f) show that the ultra-relativistic energy electrons (panels c–e) increased by one order of magnitude in the L-shells 4.7–5.3, and the maximum increase of the PSD was observed in the L-shell >5. The magnetic latitude where chorus waves are observed in this case is consistent with the equatorial latitude. According to panel (b), as the satellite moves from L-shell 4.5 to 5, only the lower-band chorus wave has a significant amplitude (∼50 pT), thus it is likely that the lower-band chorus wave interacted with 1 MeV electrons inner radiation belt, resulting in the ultra-relativistic electron enhancement. Using Ωpe/Ωce = 2.45 and Bw = 50 pT, we found that the acceleration time scale 1/Dee was about 4 h, which matches the increase seen in the satellite’s speed during two consecutive passes. This was longer than the pitch angle scattering time scale 1/Daa, which was tens of hours, as shown in Figure 8.

Figure 10

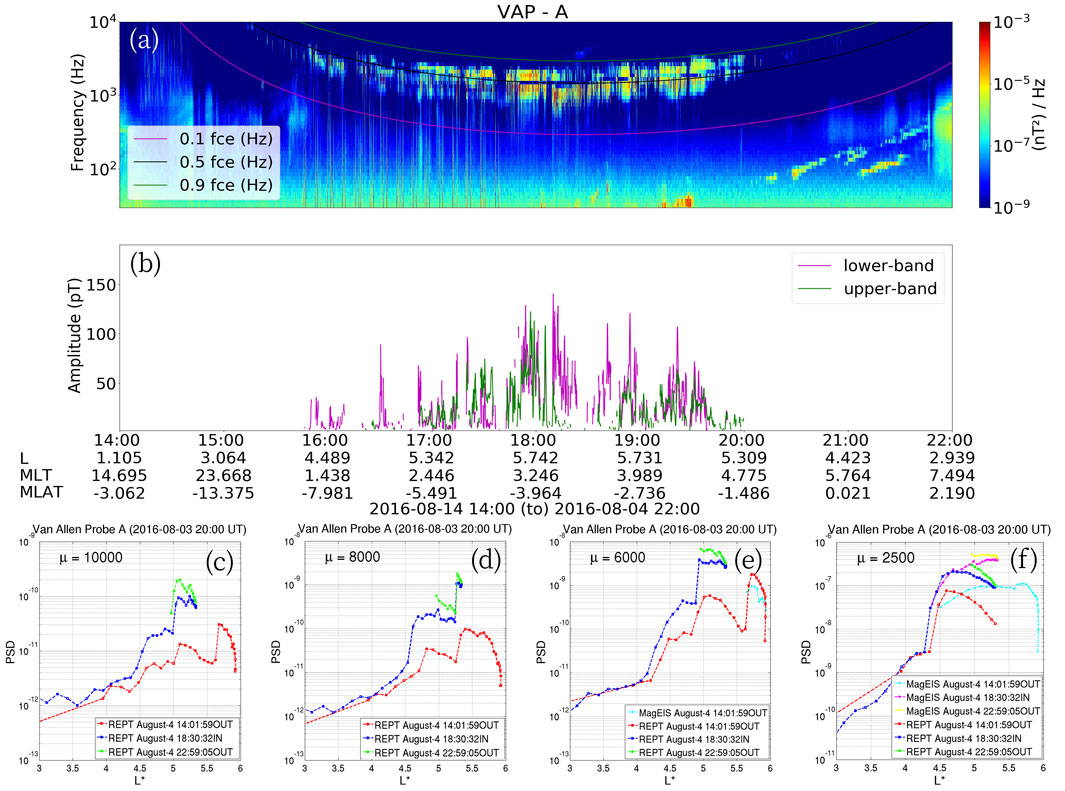
Figure 10. Van Allen Probe A (A) power spectral density [nT²/Hz] of whistler-mode chorus waves, frequency emissions. The red, blue and green lines mark 0.1 f_ce, 0.5 f_ce, and 0.9 f_ce, respectively. (B) Time-averaged magnetic wave amplitude Bw [pT]. (C–F) Inbound and outbound time-evolution of PSD [(cm Mev)³sr⁻¹] radial profiles at first adiabatic invariant (A–D) μ = 10,000, 8,000 and 6,000 MeVG^-1, and (F) μ = 2,500 MeVG^-1, second adiabatic invariant K = 0.1 G^1/2R_E. The additional parameters indicated at x-axis in panel b are provided by REPT dataset.

Furthermore, through the 18–19 UT time interval in panel (b), both lower and upper band chorus waves reach their maximum amplitude of ∼150 pT. The consecutive PSD plots show the highest enhancement, reaching more than 1 order of magnitude in several energy levels at L-shells >5.3. Regarding the efficiency of electron acceleration, we calculate the strength of the acceleration process by $S=〈D_{ee}〉/〈D_{\alpha \alpha }〉$ (according to Agapitov et al. (2019), Mourenas, et al. (2014)), which is higher than 1 for pitch angles up to 55° which indicates the acceleration process is dominant in this event. Finally, the whistler mode chorus wave amplitude resumes to be lower than 100 pT, and a minor increase in L-shell >5 is measured by the consecutive (red to green) PSD plots.

Following previous results from Horne et al. (2005), Thorne et al. (2013), Allison et al. (2021), we found that the enhancement occurs under low plasma density conditions and a huge flux of 1 MeV relativistic electron that surpasses 10⁶ cm^-2 s^-1 sr⁻¹ MeV^-1 spread out over several pitch angles, including those particles mirroring at the equatorial plane. According to Horne et al. (2005), the 1 MeV electron flux takes around 24 h to be enhanced by one order of magnitude due to whistler mode chorus wave-particle interaction. Finally, comparing the time lag between the magnetic storm onset on August 3 and the one order of magnitude increase in the ultrarelativistic flux, we observed that the enhancement of 5.2 MeV electrons occurred around 12 h after the 1.8 MeV electron enhancement (and 36 h after the onset of the storm). Accordingly, Shprits et al. (2022) observed a local acceleration of multi-MeV electrons 3 days after the storm’s onset, while Nasi et al. (2022) noted an increase of 4.2 MeV electrons approximately 18 h after the 1.8 MeV electrons. Thorne et al. (2013) observed that the enhancement of ultra-relativistic electrons happened around 10 h after the enhancement of 2.3 MeV electrons (and around 30 h after the sudden storm commencement).

5 Conclusion

In this case study, we describe an unusual increase of ultra-relativistic electrons (>3 MeV) in the heart of the outer radiation belt (4.5 < L* <5.5) during a prolonged high-speed stream (V = 600 km/s persistent for 72 h). The persistent HSS drives the generation of multiple waves in ultra-low and very low frequency ranges. Furthermore, it leads the magnetospheric trough density lower than 10 cm^-3. The combination of ULF and VLF waves propagating in a low-density magnetospheric trough promote the relativistic electron flux to surpass 10⁶ cm^-2 s^-1 sr⁻¹ MeV^-1. Under these conditions, both relativistic and ultra-relativistic electron populations reach their maximum at L* ∼5.5. The lower-density plasma trough together with the high level of the relativistic flux are suggested as important parameters for the enhancement of the ultra-relativistic electrons, in accordance with previous authors (see e.g., Shprits et al. (2022), Allison et al. (2021), Agapitov et al. (2019), Horne et al. (2003), Horne et al. (2005), Thorne et al. (2013)).

HSS is known to drive ULF waves in the magnetosphere; it is also related to the increase of lower-energy electrons, which in turn can be locally accelerated by whistler modes. Although ULF waves are observed in this event, the local acceleration is the dominant physical process, as shown by the energy diffusion coefficients calculation whose time scale is consistent with the phase space density plot analyses. This result agreed with previous studies e.g., Zhao et al., 2019b; Allison and Shprits (2020), Shprits et al. (2022); Guo et al., 2023. We measured the efficiency of local acceleration related to ultra-relativistic electron enhancement calculating the strength factor S between energy and pitch angle diffusion coefficients, for chorus waves observed at MLT ∼4.0–5.0 and L*∼ 4.5, after a geomagnetic storm. The results show that whistler-mode chorus wave energy diffusion is more efficient than pitch angle diffusion for electrons bouncing at equatorial pitch angles or even low pitch angles. Our results agree with the statistical survey in Agapitov et al., 2019. The time scale of energy diffusion is around 4 h for the lowest magnetic amplitude case. In addition, we obtained the ULF wave energy diffusion coefficient (in units of s^-1) and the MS wave diffusion coefficient from analytical models. The time scales for the ULF and MS waves are around a day, indicating that these latter processes participate in this case study, but they are not the main process in the acceleration of ultra-relativistic. Since the observed enhancement occurs outside the plasmasphere, hiss waves do not participate in this process.

Regarding, the calculated PSD for two consecutive passages of Probe A confirms that local acceleration due to whistler mode chorus waves play critical role in the acceleration, while MS waves and ULF waves play less significant roles. The PSDs for electrons with energy higher than 3 MeV are increased by one order of magnitude in the L-shells 4.7–5.3, and the maximum increase in the PSD was observed in the L-shell >5. As the satellite moves from L-shell 4.5 to 5, only the lower-band chorus wave has a significant amplitude (∼50 pT) to likely interact with the relativistic electrons. Considering the ambient plasma conditions, the acceleration time scale was comparable to the time elapsed between two consecutive passages of the satellite, while the other acceleration process (ULF inward-driven and MS local acceleration) may take several satellite passages to be observed. After that, in the 18–19 UT time interval, both lower and upper band chorus waves reach their maximum amplitude. We observe a concurrent highest enhancement, reaching more than 1 order of magnitude in several energy levels during this time. However, the efficiency of local electron acceleration is evaluated by the strength parameter of acceleration, which was higher than 1 for pitch angles up to 55°, indicating the local acceleration process as dominant in this event.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

LA: Conceptualization, Formal Analysis, Methodology, Project administration, Writing–original draft, Writing–review and editing. LdS: Conceptualization, Data curation, Investigation, Methodology, Writing–review and editing. VD: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Writing–review and editing. JM: Conceptualization, Data curation, Investigation, Methodology, Writing–review and editing. PJ: Data curation, Investigation, Methodology, Writing–review and editing. GS: Data curation, Writing–review and editing. DS: Data curation, Investigation, Methodology, Resources, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

We thank the Brazilian Ministry of Science, Technology, and Innovation and the Brazilian Space Agency. LA thanks the financial support provided by CNPq through PQ-grant 309026/2021–0. LS and PJ thank the financial support provided by the China-Brazil Joint Laboratory for Space Weather (CBJLSW), the National Space Science Center (NSSC), and the Chinese Academy of Science (CAS). LA thanks the Autoplot platform. We acknowledge the NASA Van Allen Probes, Harlan E. Spence (PI ECT; University of New Hampshire), and John R. Wygant (PI EFW; University of Minnesota) for the use of data.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2024.1478489/full#supplementary-material

SUPPLEMENTARY FIGURE S1Van Allen Probe B dataset are indicated by (i) and A dataset by (ii): (A) power spectral density [nT²/Hz] and (B) amplitude [pT] of whistler-mode magnetosonic and chorus waves; (C) WNA [degree], (D) ellipticity, and (C) planarity. Whistler-mode magnetosonic waves show the following characteristics: low ellipticity (e < 0.2), high planarity ∼ 1, propagating highly obliquely to the ambient magnetic field, i.e., WNA > 75o.

References

Abel, B., and Thorne, R. M. (1998). Electron scattering loss in Earth’s inner magnetosphere: 1. Dominant physical processes. J. Geophys. Res. Space Phys. 103 (A2), 2385–2396. doi:10.1029/97JA02919

CrossRef Full Text | Google Scholar

Agapitov, O., Mourenas, D., Artemyev, A., Hospodarsky, G., and Bonnell, J. W. (2019). Time scales for electronquasi-linear diffusion by lower-band chorus waves: the effects of ωpe/Ωce dependence on geomagnetic activity. Geophys. Res. Lett. 46, 6178–6187. doi:10.1029/2019GL083446

CrossRef Full Text | Google Scholar

Agapitov, O. V., Mourenas, D., Artemyev, A. V., Mozer, F. S., Hospodarsky, G., Bonnell, J., et al. (2018). Synthetic empirical chorus wave model from combined Van Allen Probes and Cluster statistics. J. Geophys. Res. Space Phys. 123, 297–314. doi:10.1002/2017JA024843

CrossRef Full Text | Google Scholar

Albert, J. M. (2005). Evaluation of quasi-linear diffusion coefficients for whistler mode waves in a plasma with arbitrary density ratio. J. Geophys. Res. 110, A03218. doi:10.1029/2004JA010844

CrossRef Full Text | Google Scholar

Allison, H. J., and Shprits, Y. Y. (2020). Local heating of radiation belt electrons to ultra-relativistic energies. Nat. Commun. 11, 4533. doi:10.1038/s41467-020-18053-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Allison, H. J., Shprits, Y. Y., Zhelavskaya, I. S., Wang, D., and Smirnov, A. G. (2021). Gyroresonant wave-particle interactions with chorus waves during extreme depletions of plasma density in the Van Allen radiation belts. Sci. Adv. 7 (5), eabc0380. doi:10.1126/sciadv.abc0380

PubMed Abstract | CrossRef Full Text | Google Scholar

Alves, L. R., Alves, M. E. S., da Silva, L. A., Deggeroni, V., Jauer, P. R, and Sibeck, D. G: (2023). Relativistic kinematic effects in the interaction time of whistler-mode chorus waves and electrons in the outer radiation belt, Ann. Geophys., 41, 429–447. doi:10.5194/angeo-41-429-2023

CrossRef Full Text | Google Scholar

Angelopoulos, V. (2008). The THEMIS mission. Space Sci. Rev. 141 (1–4), 5–34. doi:10.1007/s11214-008-9336-1

CrossRef Full Text | Google Scholar

Artemyev, A. V., Mourenas, D., Agapitov, O. V., and Krasnoselskikh, V. V. (2013). Parametric validations of analytical lifetime estimates for radiation belt electron diffusion by whistler waves. Ann. Geophys. 31, 599–624. doi:10.5194/angeo-31-599-2013

CrossRef Full Text | Google Scholar

Aryan, H., Sibeck, D., Balikhin, M., Agapitov, O., and Kletzing, C. (2016). Observation of chorus waves by the Van Allen Probes: dependence on solar wind parameters and scale size. J. Geophys. Res. Space Phys. 121, 7608–7621. doi:10.1002/2016JA022775

CrossRef Full Text | Google Scholar

Baker, D. N. (2021). Wave–particle interaction effects in the Van Allen belts. Earth Planets Space 73, 189. doi:10.1186/s40623-021-01508-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Baker, D. N., Hoxie, V., Zhao, H., Jaynes, A. N., Kanekal, S., Li, X., et al. (2019). Multi-year measurements of radiation belt electrons: acceleration, transport, and loss. J. Geophys. Res. Space Phys. 124, 2588–2602. doi:10.1029/2018JA026259

PubMed Abstract | CrossRef Full Text | Google Scholar

Baker, D. N., Jaynes, A. N., Kanekal, S. G., Foster, J. C., Erickson, P. J., Fennell, J. F., et al. (2016). Highly relativistic radiation belt electron acceleration, transport, and loss: large solar storm events of March and June 2015. J. Geophys. Res. Space Phys. 121, 6647–6660. doi:10.1002/2016JA022502

PubMed Abstract | CrossRef Full Text | Google Scholar

Baker, D. N., Kanekal, S. G., Blake, J. B., and Pulkkinen, T. I. (2001). The global efficiency of relativistic electron production in the Earth's magnetosphere. J. Geophys. Res. 106 (A9), 19169–19178. doi:10.1029/2000JA003023

CrossRef Full Text | Google Scholar

Baker, D. N., Kanekal, S. G., Hoxie, V.C., et al. (2013). The Relativistic Electron-Proton Telescope (REPT) Instrument on Board the Radiation Belt Storm Probes (RBSP) Spacecraft: Characterization of Earth's Radiation Belt High-Energy Particle Populations. Space Sci Rev 179, 337–381. doi:10.1007/s11214-012-9950-9

CrossRef Full Text | Google Scholar

Baker, D. N., Li, X., Turner, N., Allen, J. H., Bargatze, L. F., Blake, J. B., et al. (1997). Recurrent geomagnetic storms and relativistic electron enhancements in the outer magnetosphere: ISTP coordinated measurements. J. Geophys. Res. 102 (A7), 14,141–14,148. doi:10.1029/97JA00565

CrossRef Full Text | Google Scholar

Blake, J. B., Mauk, B. H., Baker, D. N., Carranza, P., Clemmons, J. H., Craft, J., et al. (2016). The fly’s Eye energetic particle spectrometer (FEEPS) sensors for the magnetospheric Multiscale (MMS) mission. Space Sci. Rev. 199, 309–329. doi:10.1007/s11214-015-0163-x

CrossRef Full Text | Google Scholar

Bortnik, J., and Thorne, R. M. (2010). Transit time scattering of energetic electrons due to equatorially confined magnetosonic waves. J. Geophys. Res. 115, A07213. doi:10.1029/2010JA015283

CrossRef Full Text | Google Scholar

Bortnik, J., Thorne, R. M., Ni, B., and Li, J. (2015). Analytical approximationof transit time scattering due tomagnetosonic waves. Geophys.Res. Lett. 42, 1318–1325. doi:10.1002/2014GL062710

CrossRef Full Text | Google Scholar

Burch, J. L., Torbert, R. B., Phan, T. D., Chen, L. J., Moore, T. E., Ergun, R. E., et al. (2016). Electron-scale measurements of magnetic reconnection in space. Science 352 (6290), aaf2939. doi:10.1126/science.aaf2939

PubMed Abstract | CrossRef Full Text | Google Scholar

Cao, J. B., Liu, Z. X., Yang, J. Y., Yian, C. X., Wang, Z. G., Zhang, X. H., et al. (2005). First results of low frequency electromagnetic wave detector of TC-2/Double Star program. Ann. Geophys. 23 (8), 2803–2811. doi:10.5194/angeo-23-2803-2005

CrossRef Full Text | Google Scholar

Chen, L., and Bortnik, J. (2020). “Wave-particle interactions with coherent magnetosonic waves,” in The dynamic loss of Earth’s radiation belts. Editors A. N. Jaynes, and M. E. Usanova (Elsevier), 99–120. doi:10.1016/b978-0-12-813371-2.00004-4

CrossRef Full Text | Google Scholar

Cranmer, S. R. (2009). Coronal holes. Living Rev. Sol. Phys. 6, 3. doi:10.12942/lrsp-2009-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Crowley, G., Reynolds, A., Thayer, J. P., Lei, J., Paxton, L. J., Christensen, A. B., et al. (2008). Periodic modulations in thermospheric composition by solar wind high speed streams. Geophys. Res. Lett. 35, L21106. doi:10.1029/2008GL035745

CrossRef Full Text | Google Scholar

Da Silva, L. A., Shi, J., Alves, L. R., Sibeck, D., Marchezi, J. P., Medeiros, C., et al. (2021). High-energy electron flux enhancement pattern in the outer radiation belt in response to the Alfvénic fluctuations within High-Speed solar wind stream: a statistical analysis. J. Geophys. Res. Space Phys. 126, e2021JA029363. doi:10.1029/2021JA029363

CrossRef Full Text | Google Scholar

Da Silva, L. A., Shi, J., Marchezi, J. P., Agapitov, O. V., Sibeck, D., Alves, L. R., et al. (2023a). High-energy electron flux enhancement pattern in the outer radiation belt in response to the interplanetary coronal mass ejections. J. Geophys. Res. Space Phys. 128, e2023JA031360. doi:10.1029/2023JA031360

CrossRef Full Text | Google Scholar

Da Silva, L. A., Shi, J., Resende, L. C. A., Agapitov, O. V., Alves, L. R., Batista, I. S., et al. (2022). The role of the inner radiation belt dynamic in the generation of auroral-type sporadic E-layers over south American magnetic anomaly. Front. Astronomy Space Sci. 9, 1–23. doi:10.3389/fspas.2022.970308

CrossRef Full Text | Google Scholar

Da Silva, L. A., Shi, J., Vieira, L. E., Agapitov, O. V., Resende, L. C. A., Alves, L. R., et al. (2023b). Why can the auroral-type sporadic E layer be detected over the South America Magnetic Anomaly (SAMA) region? An investigation of a case study under the influence of the high-speed solar wind stream. Front. Astronomy Space Sci. 10, 1. doi:10.3389/fspas.2023.1197430

CrossRef Full Text | Google Scholar

Da Silva, L. A., Sibeck, D., Alves, L. R., Souza, V. M., Jauer, P. R., Claudepierre, S. G., et al. (2019). Contribution of ULF wave activity to the global recovery of the outer radiation belt during the passage of a high-speed solar wind stream observed in September 2014. J. Geophys. Res. Space Phys. 124, 1660–1678. doi:10.1029/2018JA026184

CrossRef Full Text | Google Scholar

Dungey, J. W. (1961). Interplanetary magnetic field and the auroral zones. Phys. Rev. Lett. 6, 47–48. doi:10.1103/PhysRevLett.6.47

CrossRef Full Text | Google Scholar

Ergun, R. E., Tucker, S., Westfall, J., Goodrich, K. A., Malaspina, D. M., Summers, D., et al. (2016). The axial double probe and fields signal processing for the MMS mission. Space Sci. Rev. 199, 167–188. doi:10.1007/s11214-014-0115-x

CrossRef Full Text | Google Scholar

Fei, Y., Chan, A. A., Elkington, S. R., and Wiltberger, M. J. (2006). Radial diffusion and mhd particle simulations of relativistic electron transport by ulfwaves in the september 1998 storm. J. Geophys. Res. Space Phys. 111, A12. doi:10.1029/2005JA011211

CrossRef Full Text | Google Scholar

Gabrielse, C., Angelopoulos, V., Runov, A., and Turner, D. L. (2014). Statistical characteristics of particle injections throughout the equatorial magnetotail. J. Geophys. Res. Space Phys. 119, 2512–2535. doi:10.1002/2013JA019638

CrossRef Full Text | Google Scholar

Gary, S. P., Liu, K., Winske, D., and Denton, R. E. (2010). Ion Bernstein instability in the terrestrial magnetosphere: linear dispersion theory. J. Geophys. Res. Space Phys. 115 (A12). doi:10.1029/2010ja015965

CrossRef Full Text | Google Scholar

Guo, D., Xiang, Z., Ni, B., Jin, T., Zhou, R., Yi, J., et al. (2023). Three-dimensional simulations of ultra-relativistic electron acceleration during the 21 April 2017 storm. J. Geophys. Res. Space Phys. 128, e2023JA031407. doi:10.1029/2023JA031407

CrossRef Full Text | Google Scholar

Han, Y.-G., and Kim, K.-C. (2023). Characteristics and occurrence of magnetosonic waves in plasmaspheric plumes. J. Geophys. Res. Space Phys. 128, e2023JA031854. doi:10.1029/2023JA031854

CrossRef Full Text | Google Scholar

Horne, R. B., Glauert, S. A., and Thorne, R. M. (2003). Resonant diffusion of radiation belt electrons by whistler-mode chorus. Geophys. Res. Lett. 30, 1493. doi:10.1029/2003GL016963

CrossRef Full Text | Google Scholar

Horne, R. B., Thorne, R. M., Glauert, S. A., Albert, J. M., Meredith, N. P., and Anderson, R. R. (2005). Timescale for radiation belt electron acceleration by whistler mode chorus waves. J. Geophys. Res. 110, A03225. doi:10.1029/2004JA010811

CrossRef Full Text | Google Scholar

Horne, R. B., Thorne, R. M., Glauert, S. A., Meredith, N. P., Pokhotelov, D., and Santolík, O. (2007). Electron acceleration in the Van Allen radiation belts by fast magnetosonic waves. Geophys. Res. Lett. 34, L17107. doi:10.1029/2007GL030267

CrossRef Full Text | Google Scholar

Horne, R. B., Wheeler, G. V., and Alleyne, H.St.C. K. (2000). Proton and electron heating by radially propagating fast magnetosonic waves. J. Geophys. Res. 105 (27), 27597–27610. doi:10.1029/2000ja000018

CrossRef Full Text | Google Scholar

Jauer, P. R., Wang, C., Echer, E., Souza, V. M., Da Silva, L. A., Marchezi, J. P., et al. (2022). Global modeling of the inner magnetosphere under the influence of a magnetic cloud associated with an interplanetary coronal mass ejection: energy conversion and ultra-low frequency wave activity. J. Geophys. Res. Space Phys. 127, e2022JA030615. doi:10.1029/2022JA030615

CrossRef Full Text | Google Scholar

Jauer, P. R., Wang, C., Souza, V. M., Alves, M. V., Alves, L. R., Pádua, M. B., et al. (2019). A global magnetohydrodynamic simulation study of ultra-low-frequency wave activity in the inner magnetosphere: corotating interaction region + alfvénic fluctuations. ApJ 886, 59. doi:10.3847/1538-4357/ab4db5

CrossRef Full Text | Google Scholar

Jaynes, A. N., Baker, D. N., Singer, H. J., Rodriguez, J. V., Loto’aniu, T. M., Ali, A. F., et al. (2015). Source and seed populations for relativistic electrons: their roles in radiation belt changes. J. Geophys. Res. Space Phys. 120, 7240–7254. doi:10.1002/2015JA021234

CrossRef Full Text | Google Scholar

Li, J., Bortnik, J., Thorne, R. M., Li, W., Ma, Q., Baker, D. N., et al. (2016). Ultrarelativistic electron butterfly distributions created by parallel acceleration due to magnetosonic waves. J. Geophys. Res. Space Phys. 121, 3212–3222. doi:10.1002/2016JA022370

CrossRef Full Text | Google Scholar

Li, L. Y., Yu, J., Cao, J. B., Yang, J. Y., Li, X., Baker, D. N., et al. (2017). Roles of whistler mode waves and magnetosonic waves in changing the outer radiation belt and the slot region. J. Geophys. Res. Space Phys. 122, 5431–5448. doi:10.1002/2016JA023634

CrossRef Full Text | Google Scholar

Li, W., Ma, Q., Thorne, R. M., Bortnik, J., Kletzing, C. A., Kurth, W. S., et al. (2015). Statistical properties of plasmaspheric hiss derived from Van Allen Probes data and their effects on radiation belt electron dynamics. J. Geophys. Res. Space Phys. 120 (5), 3393–3405. doi:10.1002/2015JA021048

CrossRef Full Text | Google Scholar

Lyons, L. R., Thorne, R. M., and Kennel, C. F. (1972). Pitch-angle diffusion of radiation belt electrons within the plasmasphere. J. Geophys. Res. 77 (19), 3455–3474. doi:10.1029/ja077i019p03455

CrossRef Full Text | Google Scholar

Ma, Q., Li, W., Thorne, R. M., and Angelopoulos, V. (2013). Global distribution of equatorial magnetosonic waves observed by THEMIS. Geophys. Res. Lett. 40, 1895–1901. doi:10.1002/grl.50434

CrossRef Full Text | Google Scholar

Ma, Q., Li, W., Thorne, R. M., Bortnik, J., Kletzing, C. A., Kurth, W. S., et al. (2016). Electron scattering by magnetosonic waves in the inner magnetosphere. J. Geophys. Res. Space Phys. 121, 274–285. doi:10.1002/2015JA021992

CrossRef Full Text | Google Scholar

Maldonado, A. A., and Chen, L. (2018). On the diffusion rates of electron bounce resonant scattering by magnetosonic waves. Geophys. Res. Lett. 45, 3328–3337. doi:10.1002/2017GL076560

CrossRef Full Text | Google Scholar

Marchezi, J. P., Dai, L., Alves, L. R., Da Silva, L. A., Sibeck, D. G., Lago, A. D., et al. (2022). Electron flux variability and ultra-low frequency wave activity in the outer radiation belt under the influence of interplanetary coronal mass ejections and High-Speed solar wind streams: a statistical analysis from the Van Allen Probes era. J. Geophys. Res. Space Phys. 127, e2021JA029887. doi:10.1029/2021JA029887

CrossRef Full Text | Google Scholar

Mathie, R. A., and Mann, I. R. (2001). On the solar wind control of Pc5 ULF pulsation power at mid-latitudes: implications for MeV electron acceleration in the outer radiation belt. J. Geophys. Res. 106 (A12), 29,783–29,796. doi:10.1029/2001JA000002

CrossRef Full Text | Google Scholar

Mauk, B., Fox, N. J., Kanekal, S., Kessel, R., Sibeck, D., and Ukhorskiy, A. (2013). Science objectives and rationale for the radiation belt storm probes mission. Space Sci. Rev. 179, 3–27. doi:10.1007/978-1-4899-7433-4_2

CrossRef Full Text | Google Scholar

Meredith, N. P., Horne, R. B., Thorne, R. M., Summers, D., and Anderson, R. R. (2004). Substorm dependence of plasmaspheric hiss. J. Geophys. Res. Space Phys. 109 (A6), 6209. doi:10.1029/2004JA010387

CrossRef Full Text | Google Scholar

Mourenas, D., Artemyev, A. V., Agapitov, O. V., and Krasnoselskikh, V. (2013). Analytical estimates of electron quasi-linear diffusion by fast magnetosonic waves. J. Geophys. Res. Space Phys. 118, 3096–3112. doi:10.1002/jgra.50349

CrossRef Full Text | Google Scholar

Mourenas, D., Artemyev, A. V., Agapitov, O. V., and Krasnoselskikh, V. (2014). Consequences of geomagnetic activity on energization and loss of radiation belt electrons by oblique chorus waves. J. Geophys. Res. Space Phys. 119, 2775–2796. doi:10.1002/2013JA019674

CrossRef Full Text | Google Scholar

Moya, P. S., Pinto, V. A., Sibeck, D. G., Kanekal, S. G., and Baker, D. N. (2017). On the effect of geomagnetic storms on relativistic electrons in the outer radiation belt: Van Allen Probes observations. J. Geophys. Res. Space Phys. 122. doi:10.1002/2017JA024735

CrossRef Full Text | Google Scholar

Nasi, A., Katsavrias, C., Daglis, I. A., Sandberg, I., Aminalragia-Giamini, S., Li, W., et al. (2022). An event of extreme relativistic and ultra-relativistic electron enhancements following the arrival of consecutive corotating interaction regions: coordinated observations by Van Allen Probes, Arase, THEMIS and Galileo satellites. Front. Astron. Space Sci. 9, 949788. doi:10.3389/fspas.2022.949788

CrossRef Full Text | Google Scholar

Ni, B., Yan, L., Fu, S., Gu, X., Cao, X., Xiang, Z., et al. (2020). Distinct formation and evolution characteristics of outer radiation belt electron butterfly pitch angle distributions observed by Van Allen Probes. Geophys. Res. Lett. 47, e2019GL086487. doi:10.1029/2019GL086487

CrossRef Full Text | Google Scholar

Olifer, L., Mann, I. R., Ozeke, L. G., Rae, I. J., and Morley, S. K. (2019). On the relative strength of electric and magnetic ULF wave radial diffusion during the March 2015 geomagnetic storm. J. Geophys. Res. Space Phys. 124, 2569–2587. doi:10.1029/2018JA026348

CrossRef Full Text | Google Scholar

Ozeke, L. G., Mann, I. R., Claudepierre, S. G., Henderson, M., Morley, S. K., Murphy, K. R., et al. (2019). The March 2015 superstorm revisited: phase space density profiles and fast ULF wave diffusive transport. J. Geophys. Res. Space Phys. 124, 1143–1156. doi:10.1029/2018JA026326

CrossRef Full Text | Google Scholar

Paulikas, G. A., and Blake, J. B. (1979). “Effects of the solar wind on magnetospheric dynamics: energetic electrons at the synchronous orbit,” in Quantitative modeling of magnetospheric processes. Editor W. P. Olson (Wiley). doi:10.1029/GM021p0180

CrossRef Full Text | Google Scholar

Reeves, G. D., Morley, S. K., Friedel, R. H. W., Henderson, M. G., Cayton, T. E., Cunningham, G., et al. (2011). On the relationship between relativistic electron flux and solar wind velocity: paulikas and Blake revisited. J. Geophys. Res. 116, A02213. doi:10.1029/2010JA015735

CrossRef Full Text | Google Scholar

Reeves, G. D., Spence, H. E., Henderson, M. G., Morley, S. K., Friedel, R. H. W., Funsten, H. O., et al. (2013). Electron acceleration in the heart of the Van Allen radiation belts. Science 341 (6149), 991–994. doi:10.1126/science.1237743

PubMed Abstract | CrossRef Full Text | Google Scholar

Russell, C. T., Anderson, B. J., Baumjohann, W., Bromund, K. R., Dearborn, D., Fischer, D., et al. (2016). The magnetospheric Multiscale magnetometers. Space Sci. Rev. 199, 189–256. doi:10.1007/s11214-014-0057-3

CrossRef Full Text | Google Scholar

Russell, C. T., Holzer, R. E., and Smith, E. J. (1969). OGO 3 observations of ELF noise in the magnetosphere: 1. Spatial extent and frequency of occurrence. J. Geophys. Res. 74 (3), 755–777. doi:10.1029/ja074i003p00755

CrossRef Full Text | Google Scholar

Santolík, O., Němec, F., Gereová, K., Macúšová, E., de Conchy, Y., and Cornilleau-Wehrlin, N. (2004). Systematic analysis of equatorial noise below the lower hybrid frequency. Ann. Geophys. 22, 2587–2595. doi:10.5194/angeo-22-2587-2004

CrossRef Full Text | Google Scholar

Shprits, Y. Y., Allison, H. J., Wang, D., Drozdov, A., Szabo-Roberts, M., Zhelavskaya, I., et al. (2022). A new population of ultra-relativistic electrons in the outer radiation zone. J. Geophys. Res. Space Phys. 127, e2021JA030214. doi:10.1029/2021JA030214

CrossRef Full Text | Google Scholar

Shprits, Y. Y., Meredith, N. P., and Thorne, R. M. (2007). Parameterization of radiation belt electron loss timescales due to interactions with chorus waves. Geophys. Res. Lett. 34, L11110. doi:10.1029/2006GL029050

CrossRef Full Text | Google Scholar

Shprits, Y. Y., Runov, A., and Ni, B. (2013). Gyro-resonant scattering of radiation belt electrons during the solar minimum by fast magnetosonic waves. J. Geophys. Res. Space Phys. 118, 648–652. doi:10.1002/jgra.50108

CrossRef Full Text | Google Scholar

Shprits, Y. Y., Subbotin, D. A., Meredith, N. P., and Elkington, S. R. (2008). Review of modeling of losses and sources of relativistic electrons in the outer radiation belt II: local acceleration and loss. J. Atmos. Solar-Terrestrial Phys. 70 (14), 1694–1713. doi:10.1016/j.jastp.2008.06.014

CrossRef Full Text | Google Scholar

Shue, J. H., Song, P., Russell, C. T., Steinberg, J. T., Chao, J. K., Zastenker, G. A. L., et al. (1998). Magnetopause location under extreme solar wind. J. Geophys. Res. 103 (A8), 17,691–17. doi:10.1029/98JA01103

CrossRef Full Text | Google Scholar

Summers, D., Omura, Y., Miyashita, Y., and Lee, D.-H. (2012). Nonlinear spatiotemporal evolution of whistler mode chorus waves in Earth’s inner magnetosphere. J. Geophys. Res. 117, A09206. doi:10.1029/2012JA017842

CrossRef Full Text | Google Scholar

Summers, D., Omura, Y., Nakamura, S., and Kletzing, C. A. (2014). Finestructure of plasmaspheric hiss. J. Geophys. Res. SpacePhysics 119, 9134–9149. doi:10.1002/2014JA020437

CrossRef Full Text | Google Scholar

Summers, D., Thorne, R. M., and Xiao, F. (1998). Relativistic theory of wave-particle resonant diffusion with application to electron acceleration in the magnetosphere. J. Geophys. Res. 103 (A9), 20,487–20,500. doi:10.1029/98ja01740

CrossRef Full Text | Google Scholar

Sun, J., Gao, X., Chen, L., Lu, Q., Tao, X., and Wang, S. (2016). A parametric study for the generation of ion Bernstein modes from a discrete spectrum to a continuous one in the inner magnetosphere. I. Linear theory. Phys. Plasmas 23 (2), 022901. doi:10.1063/1.4941283

CrossRef Full Text | Google Scholar

Thorne, R., Li, W., Ni, B., Ma, Q., Bortnik, J., Chen, L., et al. (2013). Rapid local acceleration of relativistic radiation-belt electrons by magnetospheric chorus. Nature 504, 411–414. doi:10.1038/nature12889

PubMed Abstract | CrossRef Full Text | Google Scholar

Thorne, R. M. (2010). Radiation belt dynamics: the importance of wave-particle interactions. Geophys. Res. Lett. 37, L22107. doi:10.1029/2010GL044990

CrossRef Full Text | Google Scholar

Thorne, R. M., Smith, E. J., Burton, R. K., and Holzer, R. E. (1973). Plasmaspheric hiss. J. Geophys. Res. 78 (10), 1581–1596. doi:10.1029/ja078i010p01581

CrossRef Full Text | Google Scholar

Torbert, R. B., Russell, C. T., Magnes, W., Ergun, R. E., Lindqvist, P. A., LeContel, O., et al. (2016). The FIELDS instrument suite on MMS: scientific objectives, measurements, and data products. Space Sci. Rev. 199, 105–135. doi:10.1007/s11214-014-0109-8

CrossRef Full Text | Google Scholar

Tsurutani, B. T., and Smith, E. J. (1974). Postmidnight chorus: a substorm phenomenon. J. Geophys. Res. 79 (1), 118–127. doi:10.1029/JA079i001p00118

CrossRef Full Text | Google Scholar

Tsurutani, B. T., and Smith, E. J. (1977). Two types of magnetospheric ELF chorus and their substorm dependences. J. Geophys. Res. (1896-1977) 82 (32), 5112–5128. doi:10.1029/JA082i032p05112

CrossRef Full Text | Google Scholar

Turner, D. L., Li, X., Reeves, G. D., and Singer, H. J. (2010). On phase space density radial gradients of Earth's outer-belt electrons prior to sudden solar wind pressure enhancements: results from distinctive events and a superposed epoch analysis. J. Geophys. Res. 115, A01205. doi:10.1029/2009JA014423

CrossRef Full Text | Google Scholar

Wygant, J., Bonnell, J., Goetz, K., Ergun, R., Mozer, F., Bale, S., et al. (2013). The electric field and waves instruments on the radiation belt storm probes mission. Space Sci. Rev. 179, 183–220. doi:10.1007/978-1-4899-7433-4_6

CrossRef Full Text | Google Scholar

Zhao, H., Baker, D. N., Jaynes, A. N., Li, X., Elkington, S. R., Kanekal, S. G., et al. (2017). On the relation between radiation belt electrons and solar * wind parameters/geomagnetic indices: dependence on the first adiabatic invariant and L. J. Geophys. Res. Space Phys. 122, 1624–1642. doi:10.1002/2016JA023658

CrossRef Full Text | Google Scholar

Zhao, H., Baker, D. N., Li, X., Jaynes, A. N., and Kanekal, S. G. (2018). The acceleration of ultrarelativistic electrons during a small to moderate storm of 21 April 2017. Geophys. Res. Lett. 45, 5818–5825. doi:10.1029/2018GL078582

CrossRef Full Text | Google Scholar

Zhao, H., Baker, D. N., Li, X., Jaynes, A. N., and Kanekal, S. G. (2019b). The effects of geomagnetic storms and solar wind conditions on the ultrarelativistic electron flux enhancements. J. Geophys. Res. Space Phys. 124, 1948–1965. doi:10.1029/2018JA026257

CrossRef Full Text | Google Scholar

Zhao, H., Baker, D. N., Li, X., Malaspina, D. M., Jaynes, A. N., and Kanekal, S. G. (2019a). On the acceleration mechanism of ultrarelativistic electrons in the center of the outer radiation belt: a statistical study. J. Geophys. Res. Space Phys. 124, 8590–8599. doi:10.1029/2019JA027111

CrossRef Full Text | Google Scholar

Zhu, H., Gu, W., and Chen, L. (2019). Statistical analysis on plasmatrough exohiss waves from the Van Allen Probes. J. Geophys. Res. Space Phys. 124, 4356–4364. doi:10.1029/2018JA026359

CrossRef Full Text | Google Scholar