Statistical survey of pitch angle anisotropy of relativistic electrons in the outer radiation belt and its variation with solar wind/geomagnetic activity

Introduction: In this study, we use 7 years (2012–2019) of pitch angle resolved electron flux measurements from Van Allen Probe-B spacecraft to study the variation of near-equatorial pitch angle distributions (PADs) of outer radiation belt (L $\ge$ 3) relativistic electrons (E $\ge$ 0.5 MeV) with different levels of geomagnetic activity.

Methods: We calculate a pitch angle anisotropy index (PAI) to categorize the PADs into three types: pancake, PAI $\ge$ 1.05; butterfly, PAI $\le$ 0.95; and flattop, 0.95 $<$ PAI $<$ 1.05.

Results and Discussion: Our statistical results show that L shells $\ge$ 5 are dominated by pancake PADs on the dayside (9 $<$ MLT $<$ 15), butterfly PADs on the nightside (21 $<$ MLT $<$ 3), and flattop PADs in the dawn (3 $<$ MLT $<$ 9) and dusk (15 $<$ MLT $<$ 21) sectors, across almost all relativistic energies. In the inner L shells, the pancake and flattop PADs exhibit dependence on both L-shell and energy, with the occurrence rate increasing with decreasing L and increasing energy. For the butterfly PADs, we discovered a second population of low-L butterflies that are present at almost all local times. When the variation of electron PAI is compared with solar wind dynamic pressure ${\text{P}}_{\mathit{dyn}}$ and geomagnetic indices SYM-H and AL, ${\text{P}}_{\mathit{dyn}}$ is found to be the dominant parameter in driving the outer radiation belt pitch angle anisotropy. During periods of enhanced ${\text{P}}_{\mathit{dyn}}$, pancake PADs on the dayside become more $90°$-peaked, butterfly PADs on the nightside exhibit enhanced flux dips around $90°$ pitch angle along with an enhanced azimuthal and radial extent, and flattop PADs turn into either pancake or butterfly PADs.

1 Introduction

Earth’s radiation belt is a torus shaped region filled with energetic electrons and ions trapped by the geomagnetic field. The radiation belts occupy the space between $\sim$1–9 ${\text{R}}_E$, where ${\text{R}}_E$ is the Earth radius (Bloch et al., 2021), and is comprised of an inner belt ($\sim$1–2 ${\text{R}}_E$), an outer belt ($>$ 3 ${\text{R}}_E$), and a slot region in between. The shape and structure of the radiation belt depend largely on external drivers and particle energy (e.g., Ripoll et al. (2016); Mei et al. (2021)). The complex dynamics of this region is maintained by a competing balance between different acceleration, transport and loss processes (Reeves et al., 2003; Baker et al., 2004; Summers et al., 2004; Hudson et al., 2008; Li et al., 2019; Ripoll et al., 2020; Lejosne et al., 2022). The acceleration processes include local acceleration by whistler-mode chorus waves (Horne and Thorne, 1998; Summers et al., 1998; Horne et al., 2005; Thorne et al., 2010; Millan and Baker, 2012; Ukhorskiy and Sitnov, 2013; Artemyev et al., 2016; Allanson et al., 2021; Gao et al., 2022a; Gao et al., 2022b; Chakraborty et al., 2022b) and radial diffusion by ultra low frequency waves (Fälthammar, 1965; Elkington et al., 1999; Hudson et al., 2000; Elkington et al., 2003; Ozeke et al., 2012; Mann et al., 2013; Ozeke et al., 2014a; Ozeke et al., 2014b; Jaynes et al., 2018; Zhao et al., 2018; Ozeke et al., 2020). The loss of electrons from the radiation belts happens either through drift shell splitting and magnetopause shadowing (e.g., Tu et al. (2014), Turner et al. (2012)), or through wave-particle interactions with various plasma waves, such as the plasmaspheric hiss (e.g., Zhao et al. (2019)), chorus (e.g., Shprits et al. (2016), Chakraborty et al. (2022b), Drozdov et al. (2022)), electromagnetic ion cyclotron (EMIC) waves (e.g., Ross et al. (2021)), and very low frequency (VLF) transmitter waves (e.g., Hua et al. (2020)). During periods of strong geomagnetic activity, the trapped electron fluxes can increase by several orders of magnitude over a brief period that can damage instruments on board spacecraft orbiting in this region of space, and in some extreme cases, can even lead to complete failure. As our modern society has become increasingly reliant on space-based technologies, understanding the complex dynamics of the radiation belt is of utmost importance to mitigate space weather hazards.

One effective way to indirectly determine what physical processes are occurring in the radiation belts is to examine the pitch angle distributions (PADs) of the trapped electrons and ions. This is because different physical processes in the radiation belt can generate different types of PADs. Apart from radiation belts, electron PADs have also been studied in the outer magnetosphere to provide useful information about the underlying physical processes (e.g., Li et al. (2020); Liu et al. (2020). In the outer radiation belt, the three most prevalent types of electron PADs are pancake, butterfly, and flattop. Pancake distributions have a peak flux at $90°$ pitch angle with smooth decrease towards lower pitch angles (field aligned directions). Inward radial diffusion (causing betatron acceleration) and wave-particle interactions (causing loss of electrons at lower pitch angles) are thought to generate this type of PAD (e.g., Schulz and Lanzerotti (1974), Summers et al. (1998), Xiao et al. (2009a), Xiao et al. (2009b), Xiao et al. (2012); Xiao et al. (2014); Thorne et al. (2013b)). Pancake distributions are generated by drift resonance with ultra-low frequency (ULF) waves. Due to radial diffusion, the electrons transport radially inwards, generating pancake distributions through a process similar to betatron acceleration (e.g., Xiao et al. (2009b); Xiao et al. (2009a), Xiao et al. (2012); Xiao et al. (2014); Thorne et al. (2013a)). Cyclotron resonance with whistler mode chorus waves can also generate pancake distributions. Pitch angle scattering and consequent loss of electrons through the filling of the loss cone can result in narrow pancake distributions (e.g., Thorne et al. (2010), Chakraborty et al. (2022b)). Butterfly distributions have a flux minimum at $90°$ pitch angle with peak flux located at lower pitch angles, preferably around $45°$ or $65°$. Drift shell splitting combined with magnetopause shadowing or wave-particle interactions heating off-equatorial electrons are believed to generate butterfly distributions (e.g., Sibeck et al. (1987), Selesnick and Blake (2002), Horne et al. (2005), Li et al. (2016), Ozeke et al. (2022)). Butterfly distributions are generated through wave-particle interactions with chorus waves, magnetosonic waves, and/or electromagnetic ion cyclotron (EMIC) waves (e.g., Xiao et al. (2014), Yu et al. (2016)). Resonance of electrons at lower pitch angles with these wave modes results in electron heating along field-aligned directions, thereby forming butterfly distributions. Flattop distributions have relatively similar flux values over a wide range of pitch angles around $90°$. They are considered as an intermediate stage between the pancake and butterfly distributions, and wave-particle interactions are thought to be the primary driver (e.g., Horne and Thorne (2003), Zhao et al. (2017), Chakraborty et al. (2022a), Killey et al. (2023); Killey et al. (2024)). Flattop distributions are generated by pitch angle diffusion with chorus waves. Pitch angle diffusion results in flattening of the distributions, thereby, forming flattop PADs from initial pancake distributions (e.g., Horne and Thorne (2003), Zhao et al. (2017)).

Previous studies have tried to approximate observed PADs using several fitting functions. One of the most commonly used function is a sinusoidal function of the form $si{n}^n(\alpha )$, where $\alpha$ is the electron pitch angle and n is a steepness parameter that provides an estimate of the pitch angle anisotropy (e.g., Vampola (1997), Gannon et al. (2007), Ni et al. (2015); Pandya et al. (2020), Greeley et al. (2021)). However, one major drawback of using a sinusoidal function is that it can not fit butterfly distributions. To overcome such limitations, some studies used a combination of two sinusoidal functions (e.g., Allison et al. (2018)). A more effective and widely applied method is using Legendre polynomials, where a combination of different orders of the Legendre coefficients are used to fit the observed PADs (e.g., Chen et al. (2014), Zhao et al. (2018), Zhao et al. (2020); Chakraborty et al. (2022a)). Recently, Smirnov et al. (2022a), Smirnov et al. (2022b) used a Fourier sine series expansion to fit the observed equatorial PADs, which was found to be effective in fitting all the different types of PADs prevalent in the outer radiation belt. Apart from these fitting methods, recent studies have also used machine learning techniques to identify different PADs in the outer radiation belt and study their storm time evolution (e.g. Killey et al. (2023), Killey et al. (2024)), to rectify some of the issues as mentioned above.

Previous studies have shown that electron PADs in the outer radiation belt are dependent on electron energy, L-shell, and MLT. For example, at tens of keV energies, the PADs are pancake at all L-shells and MLTs, while at higher energies, such as at hundreds of keV or several MeV, pancake PADs are observed on the dayside while butterfly PADs are observed on the nightside at larger L-shells (e.g., West et al. (1973), Gannon et al. (2007), Ni et al. (2015), Pandya et al. (2020), Chakraborty et al. (2022a), Killey et al. (2023); Killey et al. (2024)). The electron PADs also exhibit strong dependence on geomagnetic activity, with the anisotropy of the distributions increasing with enhanced activity level. Some studies have also reported the dependence of the evolution of electron PADs with different storm drivers (e.g., Pandya et al. (2020), Greeley et al. (2021), Chakraborty et al. (2022a)).

Although PADs in the Earth’s radiation belts have been extensively studied in the past, as mentioned before, most of them used fitting functions to examine the morphology of the electron PADs. One drawback of using fitting functions is that it requires examining the variation of a combination of multiple parameters. For example, while using Legendre polynomials, pancake PADs are categorized by large negative c2 (second order Legendre coefficient) and near-zero c4 (fourth order Legendre coefficient), butterfly PADs are categorized by large negative c4 and nearly negligible c2, and flattops are categorized by both negative c2 nd c4 (e.g., Zhao et al. (2018); Zhao et al. (2020); Zhao et al. (2021)). Similar is the case when using Fourier sine series expansion as used by Smirnov et al. (2022a), Smirnov et al. (2022b). This makes the interpretation of the results slightly complicated. To avoid such complications, in this study, instead of using the fitting methods described, the primary motivation was to use a simplified formula (Equation 1) to estimate an electron pitch angle anisotropy index purely from pitch angle resolved electron flux measurements, and then use that index to categorize the different electron PADs in the outer radiation belt to study their variation with geomagnetic activity. Towards that goal, we used pitch angle resolved electron flux measurements from Van Allen Probe-B spacecraft over its entire lifespan (2012–2019) to provide an extensive statistical survey of near-equatorial PADs of relativistic electrons, having energy $\ge$0.5 MeV, in the outer radiation belt (L $\ge$ 3).

2 Data and methodology

In this study, we used $\sim$11 s resolution of pitch angle resolved (Level 3) electron flux measurements from both the Magnetic Electron Ion Spectrometer (MagEIS) and Relativistic Electron Proton Telescope (REPT) instruments, which are parts of the Energetic Particle, Composition and Thermal Plasma (ECT) Suite (Baker et al., 2013; Blake et al., 2013; Spence et al., 2013) onboard the Van Allen Probe-B spacecraft, during the entire period of operation (September 2012 - July 2019). First, we calculated 5-min average of the measured electron fluxes for each energy channel, specifically, 0.5 MeV, 0.6 MeV, 0.7 MeV, 0.9 MeV, 1.1 MeV and 1.5 MeV from MagEIS, and 1.8 MeV, 2.1 MeV, 2.6 MeV, 3.4 MeV and 4.2 MeV from REPT, as a function of pitch angle and time. Next, we used a selection criterion of considering measurements only when MLAT was less than $\pm 10°$ to limit our observations close to the geomagnetic equator, and used a lower threshold to remove bad data points: for MagEIS measurements, the lower threshold was set at ${10}^2$/${\mathrm{c}\mathrm{m}}^2$/s/sr/MeV (Ni et al., 2020), and for REPT measurements, the lower threshold was set at ${10}^{-2}$/${\mathrm{c}\mathrm{m}}^2$/s/sr/MeV (Baker et al., 2013). Finally, we normalized the fluxes by the maximum flux value within the entire pitch angle range so that for each measurement (corresponding to the spatial location: L-shell, MLT and MLAT, and time), the flux values vary between 0 and 1.

We used the near-equatorial normalized electron fluxes to calculate the pitch angle anisotropy index. For the rest of this article, we will refer to the pitch angle anisotropy index as PAI. Considering a symmetric pitch angle distribution around $90°$ pitch angle (PA), PAI is calculated using the formula:

$PAI=\frac{flu{x}_{90°}}{avg\left(flux\left[P{A}_a:P{A}_b,180°-P{A}_b:180°-P{A}_a\right]\right)}(1)$

where ${\text{flux}}_{90°}$ is the normalized flux at $90°$ PA, and avg (${\text{flux}[\text{PA}}_a$:${\mathrm{P}\mathrm{A}}_b$]) is the average of normalized fluxes within the PA range $40.91°$ (${\text{PA}}_a$) to $73.64°$ (${\text{PA}}_b$) for MagEIS, and $47.65°$ (${\text{PA}}_a$) to $79.41°$ (${\text{PA}}_b$) for REPT.

We used this PAI to categorize the different PADs of relativistic electrons (E $\ge$ 0.5 MeV) in the outer radiation belt (L $\ge$ 3). In this study, we choose L $\ge$ 3 as a fixed inner boundary to make sure that the electron flux measurements throughout the study are within the outer radiation belt, instead of being in the slot region or contaminated by inner radiation belt protons. Pancake distributions are categorized by PAI values $\ge$ 1.05, butterfly distributions are categorized by PAI values $\le$ 0.95, and flat top distributions are categorized by PAI values within the range of 0.95–1.05. Here we choose an upper limit of PAI for butterfly distributions at 0.95 in agreement with Ni et al. (2016) who used a different methodology but the same threshold to distinguish between butterfly and non-butterfly distributions. The choice of a narrow range of PAI values for flattop distributions agrees with Yu et al. (2016), who also used a different methodology but assigned a similar narrow range of pitch angle indices for flattop PADs.

Figure 1 shows the average shape of the three PADs and the temporal evolution of PAD and PAI of 1.8 MeV electrons from 0320 UT to 0620 UT on 17 March 2015. Here we have used 1.8 MeV as a representative energy, as the average shapes of the three PADs at other energies are identical. In Figure 1 panels a, b, and c, the local pitch angle (in degrees) is along the x-axis and the normalized flux is along the y-axis. The filled circles are the median flux values, and the error bars denote the interquartile ranges (IQRs) at the measured pitch angles. In panel 1d, time in UT is along the x-axis, pitch angle in degrees is along the y-axis, and the colorbar at the right denotes the electron flux. The black dashed horizontal line shows $90°$ pitch angle. In panel 1e, time in UT is along the x-axis, and the PAI is along the y-axis. The two dotted horizontal lines denote the thresholds used to identify the different PAD types. Several important features can be noted from Figure 1: (1) for pancake PAD (panel 1a), the flux at $90°$ is always maximum, as evident from the disappearing IQR. (2) For butterfly PAD (panel 1b), the flux is less at $90°$ and peaks at $\sim 45°$/$135°$. However, the large IQRs at these PA values indicate that the flux is not always maximum at $\sim 45°$/$135°$. This supports the presence of the two types of butterfly PADs peaking at two different PAs as reported by Ozeke et al. (2022) and Killey et al. (2024). (3) For flattop PAD (panel 1c), the flux values remain almost similar over a broad range of PAs ($\sim 60°$ - $120°$) as evident from the small IQRs within this PA range. Panels 1d and 1e depict the temporal evolution of the electron PADs and how the PAI is used to classify the electron PADs into three different types. From 0320 UT to 0400 UT, PAI values are greater than 1.05, thereby the electron PADs being classified as pancake distributions. Between 0400 UT and 0410 UT, PAI values are within the range of 0.95 and 1.05, leading to the electron PADs being classified as flattop distributions. After 0410 UT, PAI values are less than 0.95, the electron PADs are therefore classified as butterfly distributions.

Figure 1

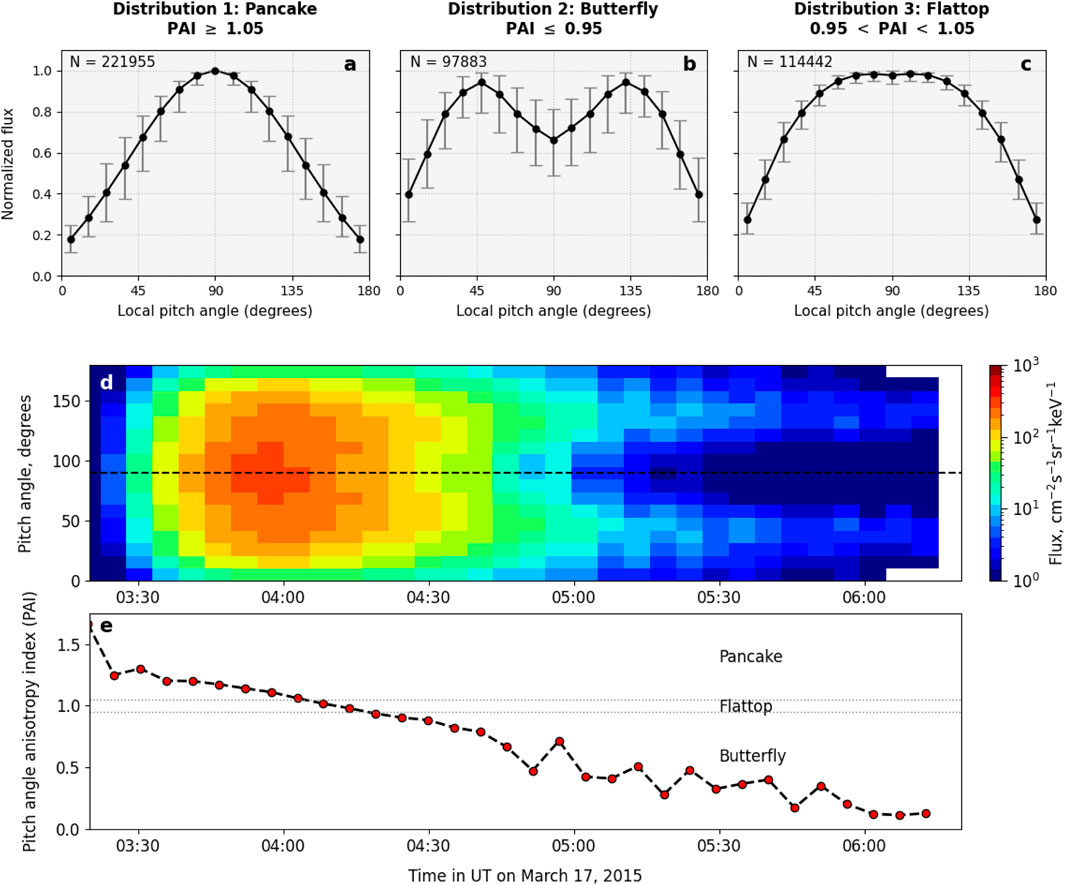
Figure 1. Average shape of (A) Pancake, (B) Butterfly, and (C) Flattop pitch angle distribution (PAD) of 1.8 MeV electrons in the outer radiation belt (L $\ge$ 3) across all MLTs. Along the x-axis is the local pitch angle (in degrees) and along the y-axis is the normalized flux. The filled circles are the median normalized fluxes, and the error bars are the interquartile ranges (IQRs) at each measured pitch angle value. The fluxes are normalized by the maximum flux values in the entire pitch angle range. Pancake PADs have an anisotropy index $\ge$1.05, butterfly PADs have an anisotropy index $\le$0.95, and flattop PADs have an anisotropy index in the range of 0.95–1.05. The number of observations (N) of each PAD is highlighted in the panels. Panels (D) and (E) show the temporal evolution of pitch angle distribution and pitch angle anisotropy index of 1.8 MeV electrons from 0320 UT to 0620 UT on 17 March 2015. In panel (D), time in UT is along the x-axis, pitch angle in degrees is along the y-axis, and the colorbar at the right denote the electron fluxes. The black dashed horizontal line denote $90°$ pitch angle. In panel (E), time in UT is along the x-axis, and the pitch angle anisotropy index is along the y-axis. The two dotted horizontal lines denote the thresholds used to identify the different PAD types.

The large IQRs in all three PADs indicate high variability in the electron flux, as well as in the PAI. This motivated us to study any existing correlation between the PAI, and solar wind drivers and geomagnetic indices. We used the 5-min resolution OMNI data of the z-component of the interplanetary magnetic field, solar wind dynamic pressure, SYM-H, and AL indices for this purpose (Papitashvili and King, 2020). Further, to study the variation of electron PAI with the solar wind parameters and geomagnetic indices, the OMNI data is interpolated to match the timestamp of the Van Allen Probe electron flux measurements. This processed combined dataset of the electron PAI, solar wind parameters, and geomagnetic indices is then used to examine the variation of electron PAI with geomagnetic activity.

3 Statistical results

In this Section, we present statistical results of the spatial (L, MLT), energy, and geomagnetic activity dependence of the different electron PADs, and their associated PAI values.

3.1 Spatial (L, MLT) distribution of electron PADs

In Figure 2, we present the L-MLT distribution of the three types of electron PADs in the outer radiation belt for four specific energies: 0.5 MeV (panels a–c), 0.9 MeV (panels d–f), 1.8 MeV (panels g–i) and 3.4 MeV (panels j–l). The polar plots show the normalized occurrence of each type of PAD, where the occurrences are normalized by the maximum occurrences in a particular L-MLT bin. The distributions are plotted in bins of size 1 h in MLT $\times$ 0.5 in L. The Sun is at the top of each panel. In the supplementary document, Supplementary Figure S1 shows the relative occurrence of the three types of electron PADs normalized by the number of observations in each L-MLT bin.

Figure 2

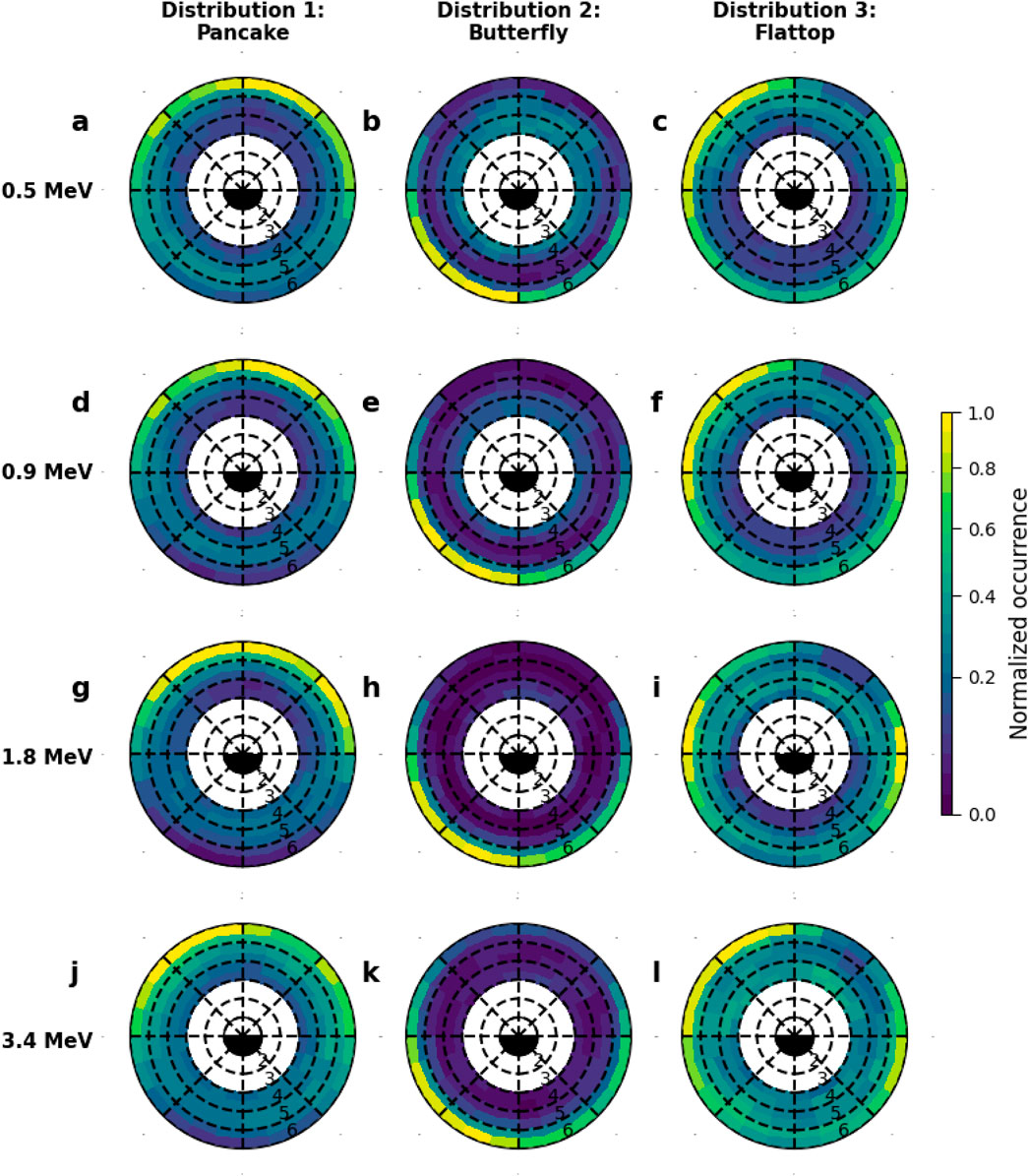
Figure 2. L-MLT distribution of the normalized occurrence (normalized by the maximum occurrence in a particular L-MLT bin) of pancake (column 1), butterfly (column 2), and flattop (column 3) pitch angle distributions (PADs) of (A–C) 0.5 MeV, (D–F) 0.9 MeV, (G–I) 1.8 MeV, and (J–L) 3.4 MeV electrons, denoted by the colorbar at the right. The distributions are plotted in bins of size 1 h in MLT $\times$ 0.5 in L. For each panel, the Sun is at the top.

The important points to note from Figure 2 are: (1) pancake PADs (column 1) are observed across almost all MLTs, with the highest occurrence within the MLT range of $\sim$6–18 and L $>$ 5. Although pancake PADs are observed for L values greater than 5 on the dayside, on the nightside, they are restricted to L values less than 5. (2) Butterfly PADs (column 2) are observed on the nightside with the maximum occurrence within the MLT range of $\sim$20–5 outside L = 5. At lower energies, e.g., 0.5 MeV (panel b) and 0.9 MeV (panel e), we can see a second population of butterfly PADs at low L-shells (L = 3–4) and across all MLTs with a low occurrence rate ($\sim$0.4). (3) Flattop PADs (column 3) are observed across almost all MLTs, with the highest occurrences around the dawn (MLT $\approx$ 4–8) and the dusk (MLT $\approx$13–19) sectors outside L = 5. The spatial distribution of the electron PADs obtained by using PAI (Equation 1) is consistent with the previous studies, both using fitting methods (e.g., Chen et al. (2014), Zhao et al. (2018), Pandya et al. (2020), Greeley et al. (2021), Zhao et al. (2021), Chakraborty et al. (2022a), Smirnov et al. (2022a), Smirnov et al. (2022b)) and machine learning techniques (e.g., Killey et al. (2023); Killey et al. (2024)).

3.2 Energy dependence of electron PADs

Although the overall features of the spatial distribution of the three types of electron PADs are similar across the different energies, there are some noticeable differences between them. For example, butterfly PADs have a smaller spatial extent at the lowest energy, i.e., 0.5 MeV (Figure 2 panel b) compared to the highest energy, i.e., 3.4 MeV (Figure 2 panel k). This motivated us to extensively study the energy dependence of the spatial distribution of the electron PADs. Now the electron PADs are a function of three variables: L-shell, MLT, and energy, but on a 2d plot, we can accommodate only two variables. Therefore, to make the plots readable, we looked at the MLT-averaged distribution of the electron PADs as a function of L-shell and energy.

Figure 3 shows the MLT-averaged normalized occurrence of the three electron PADs as a function of L-shell and energy. The entire range of MLT is divided into four sectors, namely, dusk: 15–21 MLT (panels a–c), midnight: 21–3 MLT (panels d–f), dawn: 3 - 9 MLT (panels g–i), and noon: 9–15 MLT (panels j–l). In each panel, L is along the x-axis, and electron energy (in MeV) is along the y-axis. The colorbar at the right denotes the normalized occurrence such that the occurrences of the three types of electron PADs corresponding to a particular energy bin and L-shell range add up to unity.

Figure 3

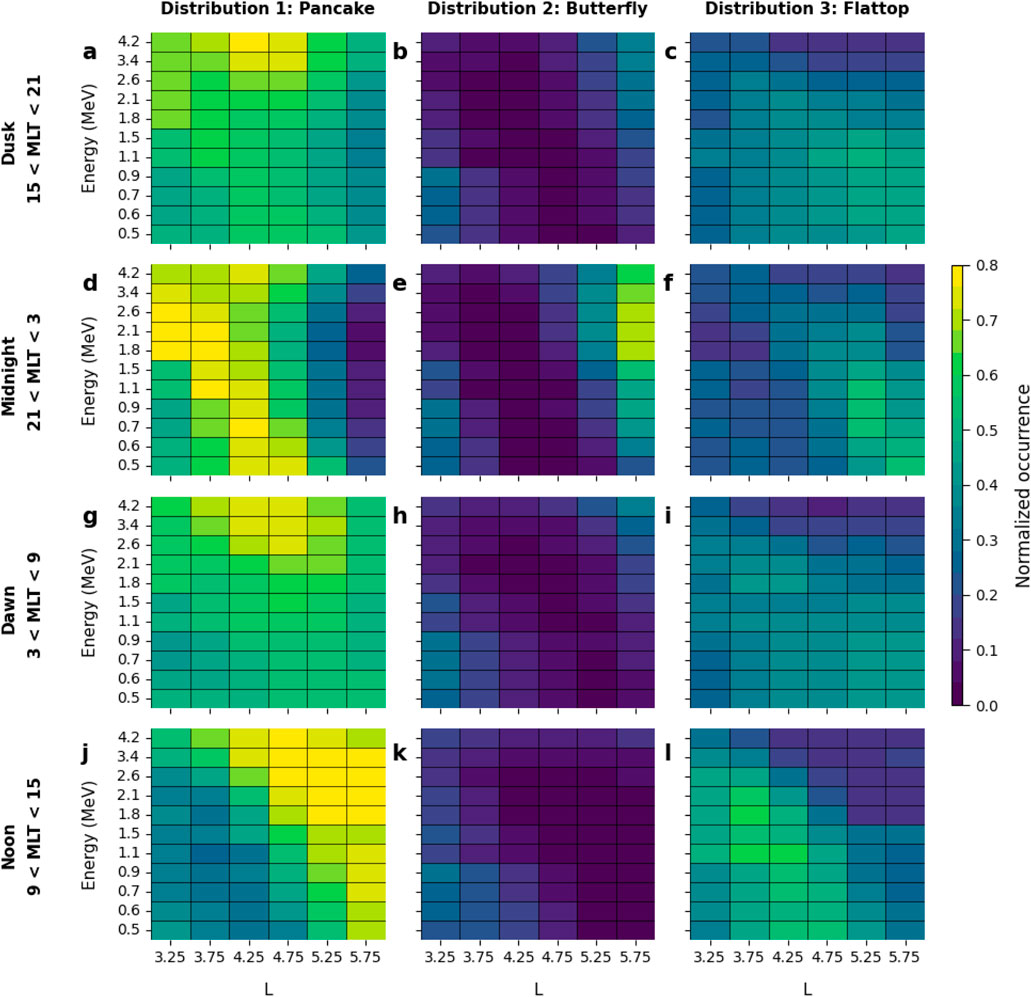
Figure 3. Normalized occurrence of pancake (column 1), butterfly (column 2), and flattop (column 3) pitch angle distribution (PAD) as a function of electron energy and L averaged over four MLT sectors: (A–C) dusk, 15–21 MLT; (D–F) midnight, 21–3 MLT; (G–I) dawn, 3 – 9 MLT; and (J–L) noon, 9–15 MLT. Along the x-axis is L, and along the y-axis is the electron energy (in MeV). The colorbar at the right denotes the normalized occurrence such that the occurrence of the three PADs for a particular energy bin and L range adds up to unity.

3.2.1 Pancake distributions

Pancake distributions are the most prevalent types of distribution in the noon sector (Figure 3 panel j), mostly observed at higher L-shell ranges. In the midnight sector (Figure 3 panel d), pancake distributions are observed mostly in L-shells less than 5, while in the dusk (Figure 3 panel a) and dawn (Figure 3 panel g) sectors, they are observed in almost all L-shell and energy bins.

Pancake distributions exhibit weak dependence on L-shell and energy in the dawn and dusk sectors, while they exhibit a strong dependence on both of them in the noon and midnight sectors, with the normalized occurrence at noon increasing with increasing L at a specific energy channel.

3.2.2 Butterfly distributions

Butterfly distributions across all MLTs are observed in two L-shell ranges: one outside L = 4.5, and another within L = 3–4. For radial distances outside L = 4.5, butterfly PADs are the most prevalent types of distribution in the midnight sector (Figure 3 panel e). In the dawn (Figure 3 panel h) and dusk sectors (Figure 3 panel b), the outer-L butterfly PADs are present with low occurrence rates, while in the noon sector (Figure 3 panel k), they are almost absent. The low-L butterfly PADs are observed in all MLTs with almost similar occurrence rates.

The outer-L butterfly PADs exhibit strong dependence on L-shell and energy, with the occurrence rate increasing with increasing energy. The outer-L butterfly PADs also exhibit an extension of the inward boundary in the midnight sector compared to the dusk/dawn sectors. The low-L butterfly PADs however do not exhibit any strong energy dependence. This is consistent with the findings of Killey et al. (2024) and may be related to other generation mechanisms, the investigation of which we leave for future studies.

3.2.3 Flattop distributions

Flattop distributions in the dusk (Figure 3 panel c) and dawn (Figure 3 panel i) sectors are observed mostly at lower energies in outer L-shell ranges and higher energies in inner L-shell ranges. Flattop distributions in the midnight sector (Figure 3 panel f) are observed mostly in the mid-L-shell ranges, while in the noon sector (Figure 3 panel l), they are observed mostly in the inner L-shell ranges. The normalized occurrence of flattop distributions in all the MLT sectors increases with decreasing L and increasing energy.

3.3 Variation of electron PAI with geomagnetic activity

The statistical results presented in the previous subsections are for the entire lifespan of the Van Allen Probes, which includes times of both low and high geomagnetic activity. Therefore, from Figures 2, 3, it is not possible to extract any direct correlation between the outer radiation belt electron pitch angle anisotropy and the level of geomagnetic activity. To comprehensively examine the same, in this subsection, we provide results after splitting the full duration of our study into different activity levels.

For this purpose, we used solar wind dynamic pressure (hereafter ${\text{P}}_{\mathit{dyn}}$), SYM-H (to estimate storm intensity), and AL (to estimate substorm intensity) indices. Further, when we split the parameters into times during which the z-component of the interplanetary magnetic field (hereafter IMF Bz) is positive (northward) and times during which IMF Bz is negative (southward), we didn’t find any notable difference between the two parameter distributions (see Supplementary Figure S2 in the supporting document). Hence, we examine the variation of pitch angle anisotropy with geomagnetic activity for all values of IMF Bz (both positive and negative). First, we present statistical results of the variation of PAI of pancake and butterfly distributions with the different drivers in preferred spatial location and a particular energy bin, and then extend our analyses to present MLT-averaged variation of PAI as a function of L-shell and electron energy during different levels of geomagnetic activity.

3.3.1 Variation of PAI of pancake and butterfly PADs with geomagnetic activity within specific L-MLT ranges

Figure 4 shows two-dimensional (2d) histogram (left column) and probability distribution function (PDF, right column) between PAI of pancake PADs and ${\text{P}}_{\mathit{dyn}}$ (panels a and b), SYM-H (panels c and d), and AL index (panels e and f) in the MLT sector 9–15 and L $>$ 5 for 1.8 MeV electrons. We selected this specific spatial range as from Figure 3, we can see that pancake PADs are the most dominant distribution in this particular L-MLT range. In the other L-MLT ranges, other distributions are also prevalent, and therefore including them in the statistical analyses might lead to a reduced correlation, and the overall effect might become difficult to identify. For each panel, the range of PAI and the parameters are divided into $18\times 18$ bins. To calculate the PDFs, we normalized the distributions such that the probability of finding observations in each vertical column adds up to unity. Also, the range of each parameter is chosen in such a way that it includes $\sim$95% of the entire dataset (see Supplementary Figure S1 for reference).

Figure 4

Figure 4. 2d histogram (left column) and probability distribution function (PDF, right column) between pitch angle anisotropy index for pancake distribution of 1.8 MeV electrons on the dayside sector (MLT range 9–15, and L $>$ 5) and (A, B) solar wind dynamic pressure, (C, D) SYMH index, and (E, F) AL index. For each panel, the parameter is along the x-axis and the anisotropy index is along the y-axis. The entire set of observations within the plotted range of both the anisotropy index and the solar wind parameter/geomagnetic indices are split into $18\times 18$ bins. The 2d histograms are plotted on a log scale, as indicated by the bottom left colorbar. For the PDF, the data is normalized such that the probability of finding observations in each vertical column adds up to unity, as indicated by the bottom right colorbar.

To study the variation of the PAI of pancake PADs (PAI $\ge$ 1.05) with ${\text{P}}_{\mathit{dyn}}$, we choose ${\text{P}}_{\mathit{dyn}}$ to vary in the range of 0–6 nPa. The 2d histogram (Figure 4 panel a) shows that most of the observations are limited to low ${\text{P}}_{\mathit{dyn}}$ and PAI values (refer to the bottom left colorbar). This suggests a highly imbalanced dataset with more quiet times than disturbed times, thus, the system being less anisotropic at most times. However, it also shows a weak correlation between the PAI and ${\text{P}}_{\mathit{dyn}}$, which becomes more clearly evident once we calculate the PDF (Figure 4 panel b). In Figure 4 panel b, we can see that the PAI increases with increasing ${\text{P}}_{\mathit{dyn}}$, implying that the pancake distributions become more anisotropic, i.e., narrow peak around $90°$ PA, as ${\text{P}}_{\mathit{dyn}}$ increases.

To study the variation of PAI of pancake PADs with the SYM-H index, we choose SYM-H to vary between −60 nT and 20 nT. Similar to ${\text{P}}_{\mathit{dyn}}$, Figure 4 panel c shows that most of the observations are limited to low SYM-H ($\sim$0 to −20 nT) and PAI values (refer to colorbar at the bottom left). The 2d distribution (Figure 4 panel c) does not exhibit any clear correlation between PAI and SYM-H, although a very weak trend of increasing PAI with decreasing SYM-H can be seen. As SYM-H is a measure of storm intensity, it suggests that the pancake PADs become more anisotropic as the storm intensity increases. This is consistent with the recent findings of Killey et al. (2024) where they identified a narrow pancake distribution during the main and early recovery phases of geomagnetic storms (using SYM-H to define the different storm phases) dominant on the dayside magnetosphere at higher L-shells. This feature becomes more evident when we plot the PDF in Figure 4 panel d. In addition, now we see an interesting feature in the variation of PAI with the SYM-H index. There are two distinct ranges of the SYM-H index where the anisotropy is higher: one when the SYM-H index is positive and the other when it is negative, with the minimum anisotropy being around SYM-H $\approx$ 0 nT. To understand this physically, we know that when a pressure impulse hits the Earth’s magnetosphere, it leads to a sharp increase in the SYM-H index. Thus, the subset of positive SYM-H values corresponds to this pressure impulse impact which can lead to an enhanced anisotropy through a mechanism similar to betatron acceleration. Negative SYM-H corresponds to enhanced storm intensity which can again lead to an enhanced anisotropy. SYM-H values close to 0 nT correspond to non-storm times during which the anisotropy is low, the combined effect thus producing the “V”-shaped variation of PAI with SYM-H.

To study the variation of electron PAI with the AL index, we choose the AL index to vary between 0 and -400 nT. The 2d distribution (Figure 4 panel e) does not exhibit any clear correlation between the PAI and the AL index. The PDF (Figure 4 panel f), however, shows a weak correlation between the two parameters, with the PAI increasing with decreasing AL. As the AL index is a measure of the substorm intensity, this means that with more severe substorms, the anisotropy increases. However, the correlation of PAI with the AL index is not as strong as the other two parameters.

Figure 5 shows the 2d distribution (left column) and the PDF (right column) of butterfly PADs of 1.8 MeV electrons in the MLT sector 21–3 and L $>$ 5, in the same manner as in Figure 4. Similar to pancake distributions, the reason behind choosing this specific spatial range for butterfly distributions is that butterfly PADs are the most dominant distributions within this particular L-MLT sector (see Figure 3). One important point to note is that for butterfly PADs, a lower value of electron PAI indicates an enhanced anisotropy. Thus, the variation of PAI for butterfly PADs with each parameter is in the opposite sense to that for pancake PADs. With that in mind, from Figure 5, we can see that the overall variations of the butterfly electron PAI with the different parameters are quite similar to that for pancake PADs, such as: (i) from the 2d distributions (Figure 5 panels a, c, and e), we can see that most of the observations are limited to low values of the parameters and corresponding low PAI values, suggesting more quiet time data than disturbed time data, hence, the butterfly PADs being less anisotropic for most of the times. (ii) The anisotropy of butterfly PADs increases with increasing ${\text{P}}_{\mathit{dyn}}$ as evident from the PDF in Figure 5 panel b. (iii) For the SYM-H index, there are two ranges where the anisotropy of butterfly PADs is higher (Figure 5 panel d). One where the SYM-H index is positive and the other when the SYM-H index is negative, with a reduced anisotropy around SYM-H $\approx$ 0 nT. (iv) The anisotropy of butterfly PADs increases with decreasing AL index, i.e., with increasing substorm intensity (Figure 5 panel f). However, for butterfly distributions, the correlation between PAI and the drivers is strongest for ${\text{P}}_{\mathit{dyn}}$.

Figure 5

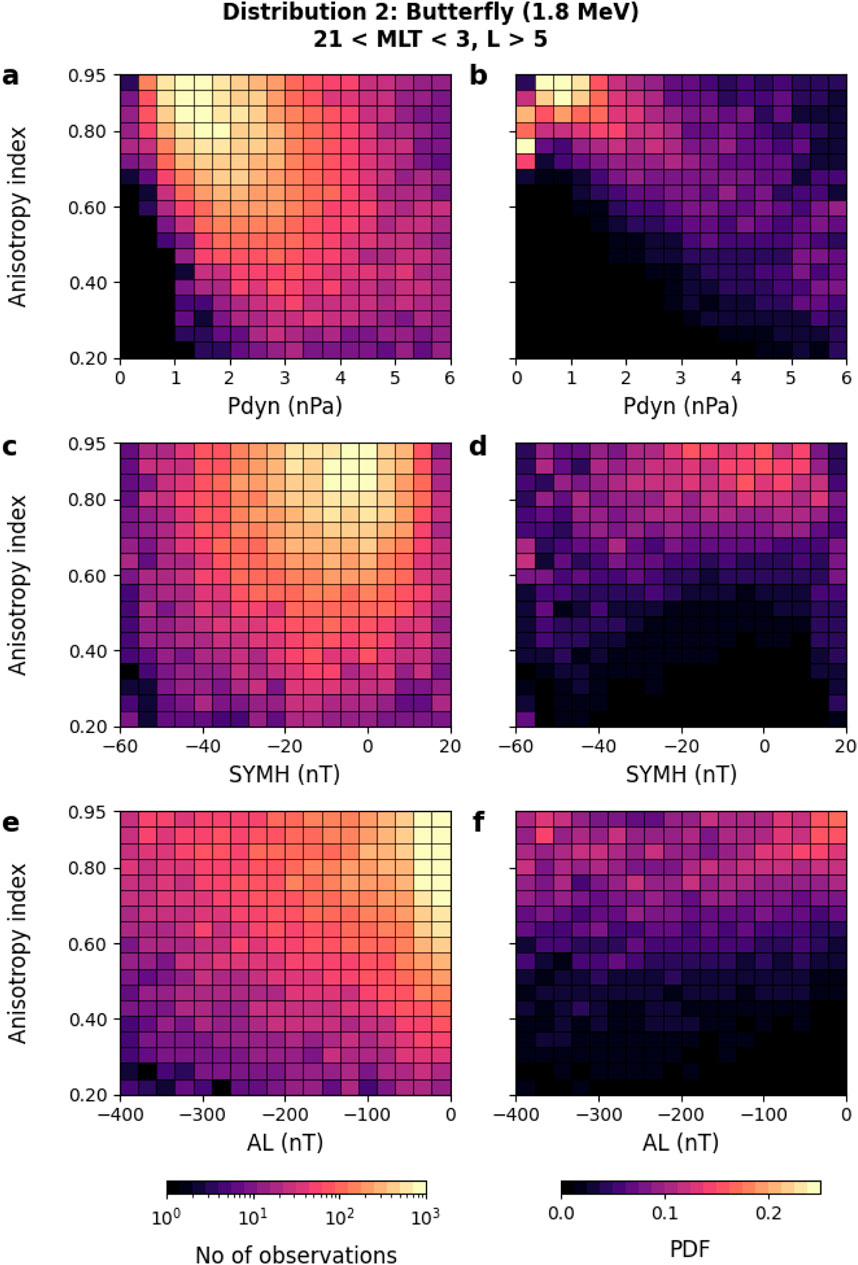
Figure 5. Same as in Figure 4 but for butterfly distribution of 1.8 MeV electrons on the nightside sector (MLT range 21–3, and L $>$ 5).

3.3.2 MLT-averaged variation of electron PAI with geomagnetic activity as a function of L and energy

In the previous subsection, Figures 4, 5 showed the overall variation of the anisotropy of 1.8 MeV electrons in two specific spatial ranges. To obtain a more general picture, in this subsection, we extend our analyses to present an MLT-averaged variation of the electron PAI as a function of L, energy, and the level of geomagnetic activity. To do so, we define a low geomagnetic activity level by ${\text{P}}_{\mathit{dyn}}$ and AL index having values less than their 25th percentile, while a high geomagnetic activity level is defined by ${\text{P}}_{\mathit{dyn}}$ and AL index having values greater than their 75th percentile. For the SYM-H index, we use a slightly different criterion, as from Figures 4, 5, we found that the electron PAI exhibits a “V”-shaped variation with the SYM-H index. Therefore, if we use the same criterion as for ${\text{P}}_{\mathit{dyn}}$ and AL index to split the SYM-H index, the low and high activity levels would correspond to almost similar PAI values, thereby resulting in no notable differences. For this reason, we used a SYM-H range of 0 to −25 nT to define the low activity level and SYM-H values less than −25 nT to define the high activity level. In addition, to be consistent with the findings from Figures 4, 5 that the electron PAI of both pancake and butterfly PADs (i.e., effectively the overall anisotropy) of 1.8 MeV electrons is best correlated with ${\text{P}}_{\mathit{dyn}}$, in the main article, we provide the MLT-averaged variation of electron PAI with ${\text{P}}_{\mathit{dyn}}$ only. The variation of electron PAI with the other drivers is provided in the supplementary document (Supplementary Figures S3, S4). The interquartile range (IQR) during low (left column) and high (right column) levels of geomagnetic activity for P_dyn, SYMH, and AL are shown in Supplementary Figures S5, S6, S7, respectively.

Figure 6 shows the MLT-averaged variation of electron PAI as a function of L and energy during different levels of geomagnetic activity. The left column corresponds to low activity levels defined by ${\text{P}}_{\mathit{dyn}}$ values less than the 25th percentile, here 1.2 nPa. The middle column corresponds to high activity levels defined by ${\text{P}}_{\mathit{dyn}}$ values greater than the 75th percentile, here 2.5 nPa. The right column shows the difference in electron PAI between the two activity levels. For each panel, L is plotted along the x-axis in the range of 3–6, split into 6 bins with bin width 0.5. Energy is plotted along the y-axis in the range of 0.5–4.2 MeV, split into 11 energy bins. In each bin, the median of the electron PAI is plotted along with the actual values highlighted, and indicated by the colorbar at the top right. The colorbar at the bottom right denotes the percentage differences in the electron PAI. Red color indicates an increase in the values of PAI, white indicates no/small changes, and blue indicates a decrease in the values of PAI.

Figure 6

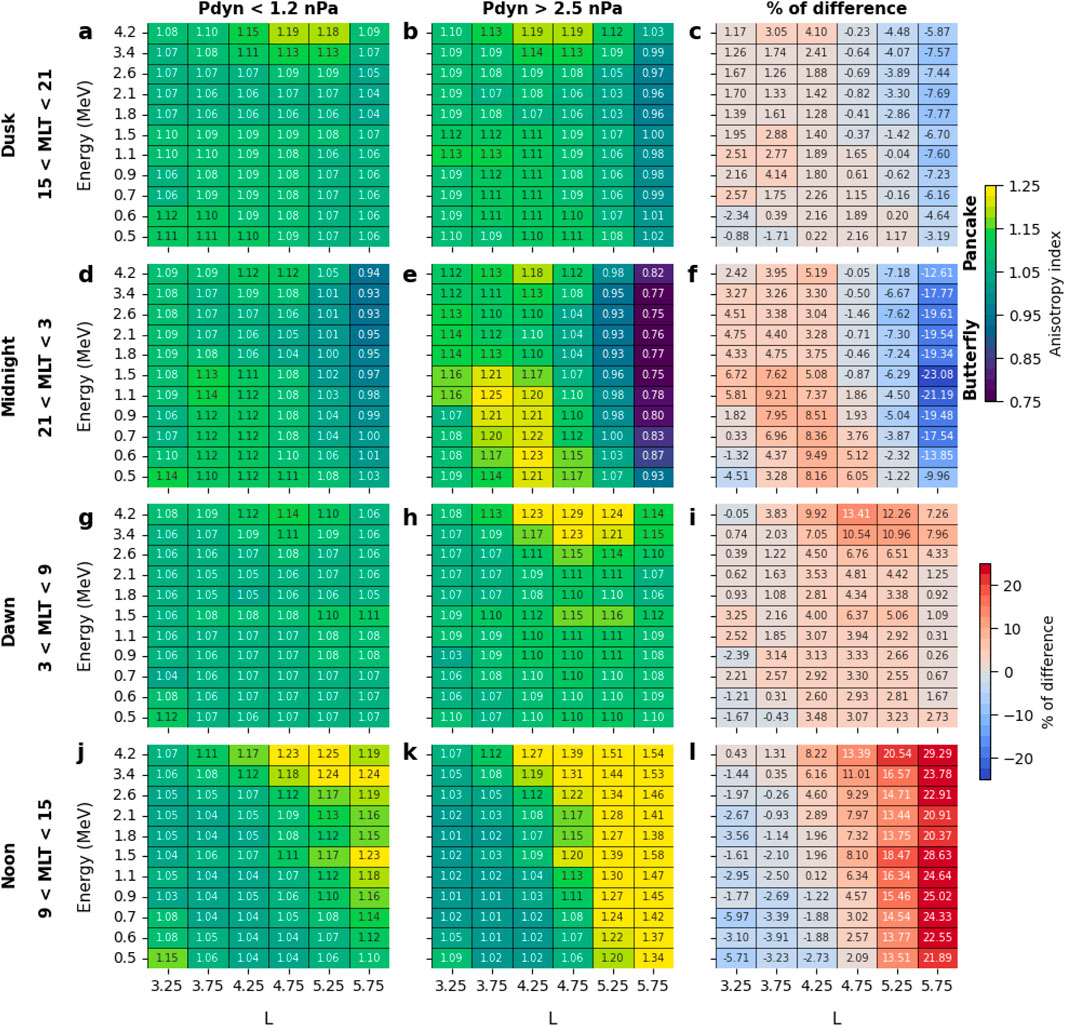
Figure 6. Median pitch angle anisotropy index as a function of electron energy and L averaged over four MLT sectors: (A–C) dusk (MLT = 15–21), (D–F) midnight (MLT = 21–3), (G–I) dawn (MLT = 3–9), and (J–L) noon (MLT = 9–15) for low geomagnetic activity (first column) and high geomagnetic activity (second column), and the percentage of difference in the median anisotropy index between the two activity levels (third column). For each panel, L is along the x-axis, and electron energy (in MeV) is along the y-axis. A low level of geomagnetic activity corresponds to values less than the 25th percentile of solar wind dynamic pressure (Pdyn) and a high level of geomagnetic activity corresponds to values greater than the 75th percentile of Pdyn, as indicated on the top of the panels (A) and (B) respectively.

From Figure 6, we can see that in the dusk sector (MLT = 15–21), during low activity levels (panel a), pancake PADs (PAI $\ge$ 1.05) dominate in all L-shell and energy bins. During high activity levels (panel b), pancake distributions in the L-shell range of 5.5 - 6 become flattops (0.95 $<$ PAI $<$ 1.05), while in other L-shell ranges, the distributions remain pancake types. Only looking at the median PAI values does not provide a clear idea of the dominant PAD type in a particular L-MLT-energy bin. However, the IQRs combined with the median PAI values give a better idea of the dominant PAD type. The IQRs in Supplementary Figure S5b suggest that although the median PAI values are within the range used to identify flattop distributions, some of the distributions become butterflies during periods of high geomagnetic activity. From Figure 6 panel c, we can see an energy and L-shell dependent change in the median anisotropy index values. In the L-shell range of 5.5–6, the anisotropy index decreases across all energy bins, in the L-shell range of 5–5.5, anisotropy index decreases for electron energies greater than 0.7 MeV, and in the L-shell range of 4.5–5, the anisotropy index decreases for electron energies greater than 1.5 MeV. In all other energy and L-shell bins, the anisotropy index exhibits an increase, except in a few low energy and L-shell bins. As discussed earlier, the reduction in the median PAI values in the L-shell range of 5.5 - 6 might result from an increase in the occurrence of butterfly PADs, thereby reducing the median of the overall distribution. This is equally true for other L-MLT-energy bins and geomagnetic indices, which suggests that although the median PAI values during a certain level of geomagnetic activity might often fall within a range used to define a particular PAD type, the entire distribution might encompass PADs from other types as well.

In the midnight sector (MLT = 21–3), during levels of low geomagnetic activity (Figure 6 panel d), in the L-shell range of 5.5–6, the distributions are butterfly (PAI $\le$ 0.95) at energies greater than 1.8 MeV and flattop at lower energies. In the L-shell range of 5–5.5, the distributions are flattop at energies greater than 0.7 MeV and pancake at lower energies. In all other L-shell ranges ($<$ 5), the distributions are pancake across all energies. During levels of high geomagnetic activity (Figure 6 panel e), the distributions in the L-shell range of 5.5 - 6 become butterfly at all energies with significant increases in anisotropy (see Figure 6 panel f, with an average increase of anisotropy by $\sim$10%–23%). In the L-shell range of 5–5.5, the flattop distributions turn butterflies at higher energies ($\ge$ 1.8 MeV), thereby exhibiting an enhanced anisotropy and inward intrusion of the butterfly PADs during geomagnetically disturbed times. In the lower L-shell range ($<$ 5), the pancake PADs become more anisotropic with an average increase of anisotropy by $\sim$2%–8%.

In the dawn sector (MLT = 3–9), during levels of low geomagnetic activity (Figure 6 panel g), the distributions are mostly pancake in all L-shell bins and at all energies. During levels of high geomagnetic activity (Figure 6 panel h), the pancake distributions become more anisotropic with an increase in anisotropy by $\sim$1%–13% (Figure 6 panel i).

In the noon sector (MLT = 9–15), during levels of low geomagnetic activity (Figure 6 panel j), the distributions in the outer L-shell range ($\ge$ 4.5) are pancake at all energies, while in the inner L-shell range ($<$ 4.5), the distributions are pancake at higher energies and flattop at lower energies. During levels of high geomagnetic activity (Figure 6 panel k), the pancake distributions in the outer L-shell range become highly anisotropic with an average increase of anisotropy by $\sim$2%–30% (Figure 6 panel l). In the inner L-shell range, the pancake distributions at higher energies become more anisotropic, while the flattop distributions remain flattop, but with slight decreases in anisotropy.

4 Discussion and conclusion

In this study, we used 7 years (2012–2019) of Van Allen Probe-B pitch angle resolved electron flux measurements to examine the spatial distribution and energy dependence of different types of relativistic ($\ge$0.5 MeV) near-equatorial (MLAT $\le \pm 10°$) electron PADs in the outer radiation belt (L $\ge$ 3), and to investigate the variation of electron pitch angle ansiotropy with different levels of geomagnetic activity.

As the first step, we applied Equation 1 to calculate a pitch angle anisotropy index (PAI) which we used to categorize the electron PADs into three types, namely, pancake: PAI $\ge$ 1.05, butterfly: PAI $\le$ 0.95, and flattop: 0.95 $<$ PAI $<$ 1.05. To obtain the spatial distribution of the electron PADs, we calculated MLT-averaged normalized occurrence of the PADs in 6 L-shell bins (3–6) and 11 energy bins (0.5–4.2 MeV). To investigate the variation of pitch angle anisotropy with different levels of geomagnetic activity, we used the 5 min OMNI database of solar wind parameters and geomagnetic indices to monitor ${\text{P}}_{\mathit{dyn}}$, SYM-H, and AL, and split them into periods of low and high activity.

The major findings from this study can be summarized as follows:

1. In the dawn and dusk sectors, the L range of 5 - 6 is dominated by butterfly and pancake PADs at higher energies ($\ge$1.5 MeV in the dusk sector, and $\ge$2.6 MeV in the dawn sector), and flattop and pancake PADs at the corresponding lower energies. The L range of 4–5 is dominated by pancake PADs at higher energies ($\ge$1.5 MeV), and flattop PADs at lower energies. The L range of 3 - 4 is dominated by mostly pancake PADs.

2. In the midnight sector, the L range of 5.5–6 is dominated by butterfly PADs across almost all energies. The L range of 4.5–5.5 is dominated by butterfly PADs at higher energies ($\ge$1.8 MeV), and flattop PADs at lower energies. The L range of 3–4.5 is mostly dominated by pancake PADs.

3. In the noon sector, the L range of 4.5–6 is dominated by pancake PADs across all energies. In the L range of 4–4.5, pancake PADs are dominant at higher energies ($\ge$1.5 MeV), and flattop PADs are dominant at lower energies. In the L range of 3–4, flattop PAD is the most dominant distribution.

4. In the L range of 3–4, we found a second population of butterfly distributions at low energies, mostly at energies less than 1 MeV at almost all MLTs.

5. The anisotropy of the entire outer radiation belt increases during periods of high geomagnetic activity. In the outer L-shell range, butterfly and pancake PADs which were already present in the midnight and noon sector during low activity times, respectively, become highly anisotropic and extend to lower L-shell and wider MLT ranges at all the relativistic energies. In the inner L-shell range, the anisotropy increases too, with either flattops turning into pancakes or pancakes becoming more anisotropic (narrowly peaked at $90°$ PA) in all the MLT sectors.

6. The correlation between outer radiation belt pitch angle anisotropy and the solar wind drivers is found to be strongest for ${\text{P}}_{\mathit{dyn}}$.

The statistical results related to the spatial distribution of the different electron PADs (findings 1, 2, and 3) are consistent with previous findings, both using fitting methods or machine learning techniques (e.g., Chen et al. (2014), Zhao et al. (2018), Pandya et al. (2020), Greeley et al. (2021), Zhao et al. (2021), Chakraborty et al. (2022a); Killey et al. (2023); Killey et al. (2024), etc.). However, in most of the past studies, butterfly PADs are usually reported to be present on the nightside in outer L-shell ranges, $\ge$ 5 (e.g., Ni et al. (2016); Ozeke et al. (2022), etc.). Here, in addition, we found a second population of low-L (3 $<$ L $<$ 4) butterfly PADs across all MLTs and low energies ($<$ 1 MeV), with a lower occurrence rate compared to the outer-L butterflies (finding 4). This is consistent with the very recent findings of Killey et al. (2024). One possible mechanism might be wave-particle interactions heating off-equatorial electrons (e.g., Horne and Thorne (2003)), as magnetopause shadowing is unlikely to create butterfly PADs at such low L-shells. A detailed analysis is required to understand the generation mechanism of these low-L butterflies, which we plan to do in a future study.

The results related to the variation of outer radiation belt pitch angle anisotropy with solar wind forcing (finding 5) are consistent with Killey et al. (2024) who showed the storm time evolution of the relativistic electron PADs in the outer radiation belt using machine learning techniques (Figure 3 of Killey et al. (2024)). However, in Killey et al. (2024), the storm phases are defined based on the SYM-H index. In our study, we found that ${\text{P}}_{\mathit{dyn}}$ is the dominant factor in driving the radiation belt pitch angle anisotropy, compared to SYM-H and AL indices (finding 6). This agrees with Smirnov et al. (2022a) who studied the storm-time evolution of electron PADs during 129 geomagnetic storms in the Van Allen Probe era and found ${\text{P}}_{\mathit{dyn}}$ to be more effective than SYM-H and solar wind electric field in driving the observed enhancement in electron pitch angle anisotropy. Based on these results, in a companion paper, Smirnov et al. (2022b) developed an empirical model of the equatorial electron pitch angle distribution driven by ${\text{P}}_{\mathit{dyn}}$. In another earlier paper, Yu et al. (2016) used 3 years of Van Allen Probe measurements (2012–2015) to study the effect of ${\text{P}}_{\mathit{dyn}}$ and IMF Bz on the outer radiation belt electrons. They found that during periods of enhanced ${\text{P}}_{\mathit{dyn}}$, pancake PADs on the dayside become more $90°$ peaked, while the nightside butterfly PADs extend azimuthally and also radially inwards. Our results thus confirm such findings by providing evidence of the correlation between the calculated electron pitch angle anisotropy and the driving solar wind parameters or geomagnetic indices.

Physically, this implies that when a pressure impulse hits the Earth’s magnetosphere, it globally compresses the entire system. As a result of this global compression, some of the electrons are lost through magnetopause shadowing, while others get pushed radially inwards. As the electrons transport radially inwards, they move from a region of weaker to a stronger magnetic field. In the course of this motion, to preserve the first and second adiabatic invariants, they gain energy in the perpendicular direction more than that in the parallel direction through a process similar to betatron acceleration, leading to an enhanced anisotropy. This causes the pancake distributions to become more narrow. On the other hand, the $90°$ electrons that are lost through drift shell splitting and magnetopause shadowing into the interplanetary space lead to more deepening of the butterfly distributions. In addition, wave-particle interactions also play a significant role in the evolution of radiation belt electron pitch angle distributions. Magnetospheric plasma waves are generated either from particle injection leading to the enhancement of temperature anisotropy that provides free energy for the generation of waves, or from the global reconfiguration of the magnetosphere generating large-scale MHD waves. Resonant interaction with these waves violates the conservation of either one of the three adiabatic invariants of the resonating electrons, thereby leading to either loss or non-adiabatic heating, and thus generating different PAD types. This is depicted schematically in Figure 7.

Figure 7

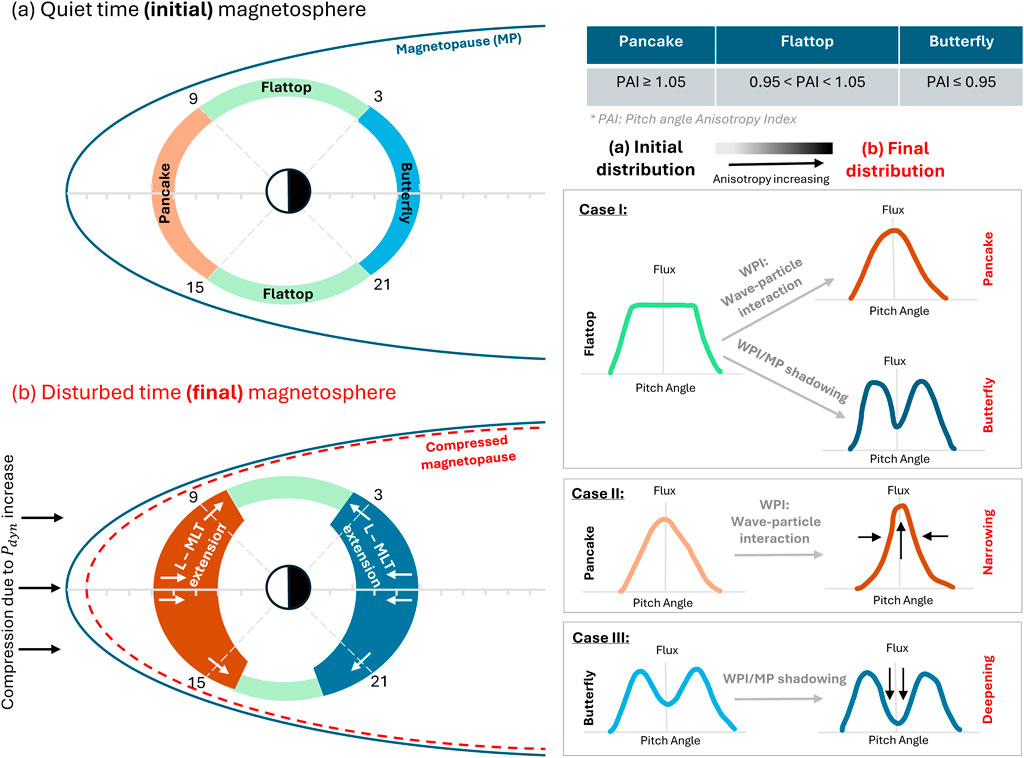
Figure 7. A schematic to show the outer radiation belt electron pitch angle distributions (PADs) during (A) quiet time and (B) disturbed time magnetospheric conditions. The table at the top right shows the ranges of pitch angle anisotropy index (PAI) for the three PAD types. Three possible changes in the PADs can be observed in the outer radiation belt during enhanced geomagnetic activity, such as, Case I: flattop PADs turning into pancake/butterfly distributions, Case II: pancake PADs turning into narrow pancakes, and Case III: butterfly PADs turning into deep butterflies.

To summarize, our results show that a simplified formula (Equation 1) could capture the overall spatial and energy dependence of the outer radiation belt relativistic electron PADs. The results also confirm that ${\text{P}}_{\mathit{dyn}}$ is the dominant parameter in governing the outer radiation belt pitch angle anisotropy, and thus can be used as a driver in radiation belt models, as used by Smirnov et al. (2022b). In future, we plan to extend our study to resolve the two butterfly distributions peaking at two different pitch angles, as reported by Ozeke et al. (2022) and Killey et al. (2024), and also to understand the generation mechanism of the low-L butterfly PADs.

Data availability statement

All Van Allen Probe ECT data used for this study are publicly available at the website https://rbsp-ect.newmexicoconsortium.org/rbsp_ect.php. The solar wind parameters and geomagnetic indices data used in this study are publicly available at the website https://omniweb.gsfc.nasa.gov/form/omni_min.html, and also in Papitashvili and King (2020).

Author contributions

SC: Conceptualization, Data curation, Methodology, Data analysis, Investigation, Visualization, Validation, Writing - original draft. IR: Conceptualization, Supervision, Investigation, Visualization, Validation, Writing - Review and Editing. SK: Data curation, Visualization, Validation, Writing - Review and Editing. BO: Visualization, Writing - Review and Editing. CW: Writing - Review and Editing. CP: Formal analysis, Writing - review and editing. EI: Formal analysis, Writing - review and editing. GE: Formal analysis, Writing - review and editing. KJ: Formal analysis, Writing - review and editing. NM: Formal analysis, Writing - review and editing. TG: Formal analysis, Writing - review and editing. TS: Formal analysis, Writing - review and editing. XL: Formal analysis, Writing - review and editing. YC: Formal analysis, Writing - review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. SC, IJR and CEJW are all supported in part by STFC Grants ST/V006320/1, ST/X001008/1 and ST/W000369/1, and NERC Grants NE/V002554/2, NE/P017185/2 and NE/V0002759/2. SK is funded by Northumbria University and STFC Grant 2597922 for PhD support. BO is supported by STFC Grant ST/W000369/1.

Acknowledgments

We thank the MagEIS and REPT teams for the Van Allen Probe data. We also acknowledge use of NASA/GSFC’s Space Physics Data Facility’s OMNIWeb service, and OMNI data. Some of the preliminary analyses for this study were conducted as part of an outreach program named ORBYTS at the Royal Grammar School, Newcastle upon Tyne, United Kingdom. We thank the school to allow us to conduct the project.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2024.1474503/full#supplementary-material

References

Allanson, O., Watt, C. E. J., Allison, H. J., and Ratcliffe, H. (2021). Electron diffusion and advection during nonlinear interactions with whistler-mode waves. J. Geophys. Res. Space Phys. 126. doi:10.1029/2020JA028793

CrossRef Full Text | Google Scholar

Allison, H. J., Horne, R. B., Glauert, S. A., and Del Zanna, G. (2018). Determination of the equatorial electron differential flux from observations at low earth orbit. J. Geophys. Res. Space Phys. 123, 9574–9596. doi:10.1029/2018JA025786

CrossRef Full Text | Google Scholar

Artemyev, A., Agapitov, O., Mourenas, D., Krasnoselskikh, V., Shastun, V., and Mozer, F. (2016). Oblique whistler-mode waves in the Earth’s inner magnetosphere: energy distribution, origins, and role in radiation belt dynamics. Space Sci. Rev. 200, 261–355. doi:10.1007/s11214-016-0252-5

CrossRef Full Text | Google Scholar

Baker, D. N., Kanekal, S. G., and Blake, J. B. (2004). Characterizing the Earth’s outer Van Allen zone using a radiation belt content index. Space Weather. 2. doi:10.1029/2003SW000026

CrossRef Full Text | Google Scholar

Baker, D. N., Kanekal, S. G., Hoxie, V. C., Batiste, S., Bolton, M., Li, X., et al. (2013). The relativistic electron-proton telescope (REPT) instrument on board the radiation belt storm Probes (RBSP) spacecraft: characterization of Earth’s radiation belt high-energy particle populations. Space Sci. Rev. 179, 337–381. doi:10.1007/s11214-012-9950-9

CrossRef Full Text | Google Scholar

Blake, J. B., Carranza, P. A., Claudepierre, S. G., Clemmons, J. H., Crain, W. R., Dotan, Y., et al. (2013). The magnetic electron ion spectrometer (MagEIS) instruments aboard the radiation belt storm Probes (RBSP) spacecraft. Space Sci. Rev. 179, 383–421. doi:10.1007/s11214-013-9991-8

CrossRef Full Text | Google Scholar

Bloch, T., Watt, C. E. J., Owens, M. J., Thompson, R. L., and Agiwal, O. (2021). Constraining the location of the outer boundary of Earth’s outer radiation belt. Earth Space Sci. 8, e2020EA001610. doi:10.1029/2020EA001610

CrossRef Full Text | Google Scholar

Chakraborty, S., Chakrabarty, D., Reeves, G. D., Baker, D. N., and Rae, I. J. (2022a). Statistical investigation on equatorial pitch angle distribution of energetic electrons in Earth‘s outer radiation belt during CME- and CIR-driven storms. Front. Astronomy Space Sci. 9. doi:10.3389/fspas.2022.986061

CrossRef Full Text | Google Scholar

Chakraborty, S., Mann, I. R., Watt, C. E. J., Rae, I. J., Olifer, L., Ozeke, L. G., et al. (2022b). Intense chorus waves are the cause of flux-limiting in the heart of the outer radiation belt. Sci. Rep. 12, 21717. doi:10.1038/s41598-022-26189-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Y., Friedel, R. H. W., Henderson, M. G., Claudepierre, S. G., Morley, S. K., and Spence, H. E. (2014). REPAD: an empirical model of pitch angle distributions for energetic electrons in the Earth’s outer radiation belt. J. Geophys. Res. Space Phys. 119, 1693–1708. doi:10.1002/2013JA019431

CrossRef Full Text | Google Scholar

Drozdov, A. Y., Allison, H. J., Shprits, Y. Y., Usanova, M., Saikin, A., and Wang, D. (2022). Depletions of multi-MeV electrons and their association to minima in phase space density. Geophys. Res. Lett. 49, e2021GL097620. doi:10.1029/2021GL097620

PubMed Abstract | CrossRef Full Text | Google Scholar

Elkington, S. R., Hudson, M. K., and Chan, A. A. (1999). Acceleration of relativistic electrons via drift-resonant interaction with toroidal-mode Pc-5 ULF oscillations. Geophys. Res. Lett. 26, 3273–3276. doi:10.1029/1999GL003659

CrossRef Full Text | Google Scholar

Elkington, S. R., Hudson, M. K., and Chan, A. A. (2003). Resonant acceleration and diffusion of outer zone electrons in an asymmetric geomagnetic field. J. Geophys. Res. Space Phys. 108. doi:10.1029/2001JA009202

CrossRef Full Text | Google Scholar

Fälthammar, C.-G. (1965). Effects of time-dependent electric fields on geomagnetically trapped radiation. J. Geophys. Res. 70, 2503–2516. doi:10.1029/JZ070i011p02503

CrossRef Full Text | Google Scholar

Gannon, J. L., Li, X., and Heynderickx, D. (2007). Pitch angle distribution analysis of radiation belt electrons based on Combined Release and Radiation Effects Satellite Medium Electrons A data. J. Geophys. Res. Space Phys. 112. doi:10.1029/2005JA011565

CrossRef Full Text | Google Scholar

Gao, X., Chen, R., Lu, Q., Chen, L., Chen, H., and Wang, X. (2022a). Observational evidence for the origin of repetitive chorus emissions. Geophys. Res. Lett. 49, e2022GL099000. doi:10.1029/2022GL099000

CrossRef Full Text | Google Scholar

Gao, X., Lu, Q., Kang, N., Ke, Y., Ma, J., Tsurutani, B., et al. (2022b). Study on source region and generation mechanism of oblique whistler-mode waves in the Earth’s magnetosphere. J. Geophys. Res. Space Phys. 127, e2022JA030804. doi:10.1029/2022JA030804

CrossRef Full Text | Google Scholar

Greeley, A. D., Kanekal, S. G., Sibeck, D. G., Schiller, Q., and Baker, D. N. (2021). Evolution of pitch angle distributions of relativistic electrons during geomagnetic storms: van allen Probes observations. J. Geophys. Res. Space Phys. 126. doi:10.1029/2020JA028335

CrossRef Full Text | Google Scholar

Horne, R. B., and Thorne, R. M. (1998). Potential waves for relativistic electron scattering and stochastic acceleration during magnetic storms. Geophys. Res. Lett. 25, 3011–3014. doi:10.1029/98GL01002

CrossRef Full Text | Google Scholar

Horne, R. B., and Thorne, R. M. (2003). Relativistic electron acceleration and precipitation during resonant interactions with whistler-mode chorus. Geophys. Res. Lett. 30. doi:10.1029/2003GL016973

CrossRef Full Text | Google Scholar

Horne, R. B., Thorne, R. M., Shprits, Y. Y., Meredith, N. P., Glauert, S. A., Smith, A. J., et al. (2005). Wave acceleration of electrons in the Van Allen radiation belts. Nature 437, 227–230. doi:10.1038/nature03939

PubMed Abstract | CrossRef Full Text | Google Scholar

Hua, M., Li, W., Ni, B., Ma, Q., Green, A., Shen, X., et al. (2020). Very-Low-Frequency transmitters bifurcate energetic electron belt in near-earth space. Nat. Commun. 11, 4847. doi:10.1038/s41467-020-18545-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Hudson, M., Elkington, S., Lyon, J., and Goodrich, C. (2000). Increase in relativistic electron flux in the inner magnetosphere: ULF wave mode structure. Adv. Space Res. 25, 2327–2337. doi:10.1016/S0273-1177(99)00518-9

CrossRef Full Text | Google Scholar

Hudson, M. K., Kress, B. T., Mueller, H.-R., Zastrow, J. A., and Bernard Blake, J. (2008). Relationship of the Van Allen radiation belts to solar wind drivers. J. Atmos. Solar-Terrestrial Phys. 70, 708–729. doi:10.1016/j.jastp.2007.11.003

CrossRef Full Text | Google Scholar

Jaynes, A. N., Ali, A. F., Elkington, S. R., Malaspina, D. M., Baker, D. N., Li, X., et al. (2018). Fast diffusion of ultrarelativistic electrons in the outer radiation belt: 17 March 2015 storm event. Geophys. Res. Lett. 45 (10), 10874–10882. doi:10.1029/2018GL079786

PubMed Abstract | CrossRef Full Text | Google Scholar

Killey, S., Rae, I. J., Chakraborty, S., Smith, A. W., Bentley, S. N., Bakrania, M. R., et al. (2023). Using machine learning to diagnose relativistic electron distributions in the Van Allen radiation belts. RAS Tech. Instrum. 2, 548–561. doi:10.1093/rasti/rzad035

CrossRef Full Text | Google Scholar

Killey, S., Rae, I. J., Smith, A. W., Bentley, S. N., Watt, C. E. J., Chakraborty, S., et al. (2024). Identifying typical relativistic electron pitch angle distributions: evolution during geomagnetic storms. doi:10.22541/essoar.171838456.69176315/v1

CrossRef Full Text | Google Scholar

Lejosne, S., Allison, H. J., Blum, L. W., Drozdov, A. Y., Hartinger, M. D., Hudson, M. K., et al. (2022). Differentiating between the leading processes for electron radiation belt acceleration. Front. Astronomy Space Sci. 9. doi:10.3389/fspas.2022.896245

CrossRef Full Text | Google Scholar

Li, H., Peng, Q., Tang, R., Zhang, H., Zhong, Z., Deng, X., et al. (2020). Statistical characteristics of electron pitch angle distributions inside the magnetopasue based on MMS observations. J. Geophys. Res. Space Phys. 125. doi:10.1029/2020JA028291

CrossRef Full Text | Google Scholar

Li, J., Bortnik, J., An, X., Li, W., Angelopoulos, V., Thorne, R. M., et al. (2019). Origin of two-band chorus in the radiation belt of Earth. Nat. Commun. 10, 4672. doi:10.1038/s41467-019-12561-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J., Bortnik, J., Thorne, R. M., Li, W., Ma, Q., Baker, D. N., et al. (2016). Ultrarelativistic electron butterfly distributions created by parallel acceleration due to magnetosonic waves. J. Geophys. Res. Space Phys. 121, 3212–3222. doi:10.1002/2016JA022370

CrossRef Full Text | Google Scholar

Liu, C. M., Fu, H. S., Liu, Y. Y., Wang, Z., Chen, G., Xu, Y., et al. (2020). Electron pitch-angle distribution in Earth’s magnetotail: pancake, cigar, isotropy, butterfly, and rolling-pin. J. Geophys. Res. Space Phys. 125, e2020JA027777. doi:10.1029/2020JA027777

CrossRef Full Text | Google Scholar

Mann, I. R., Lee, E. A., Claudepierre, S. G., Fennell, J. F., Degeling, A., Rae, I. J., et al. (2013). Discovery of the action of a geophysical synchrotron in the Earth’s Van Allen radiation belts. Nat. Commun. 4, 2795. doi:10.1038/ncomms3795

CrossRef Full Text | Google Scholar

Mei, Y., Ge, Y., Du, A., Gu, X., Summers, D., Li, X., et al. (2021). Energy-dependent boundaries of Earth’s radiation belt electron slot region. Astrophysical J. 922, 246. doi:10.3847/1538-4357/ac25ec

CrossRef Full Text | Google Scholar

Millan, R. M., and Baker, D. N. (2012). Acceleration of particles to high energies in Earth‘s radiation belts. Space Sci. Rev. 173, 103–131. doi:10.1007/s11214-012-9941-x

CrossRef Full Text | Google Scholar

Ni, B., Yan, L., Fu, S., Gu, X., Cao, X., Xiang, Z., et al. (2020). Distinct Formation and evolution characteristics of outer radiation belt electron butterfly pitch angle distributions observed by van allen Probes. Geophys. Res. Lett. 47, e2019GL086487. doi:10.1029/2019GL086487

CrossRef Full Text | Google Scholar

Ni, B., Zou, Z., Gu, X., Zhou, C., Thorne, R. M., Bortnik, J., et al. (2015). Variability of the pitch angle distribution of radiation belt ultrarelativistic electrons during and following intense geomagnetic storms: Van Allen Probes observations. J. Geophys. Res. Space Phys. 120, 4863–4876. doi:10.1002/2015JA021065

CrossRef Full Text | Google Scholar

Ni, B., Zou, Z., Li, X., Bortnik, J., Xie, L., and Gu, X. (2016). Occurrence characteristics of outer zone relativistic electron butterfly distribution: a survey of Van Allen Probes REPT measurements. Geophys. Res. Lett. 43, 5644–5652. doi:10.1002/2016GL069350

CrossRef Full Text | Google Scholar

Ozeke, L. G., Mann, I. R., Murphy, K. R., Jonathan Rae, I., and Milling, D. K. (2014a). Analytic expressions for ULF wave radiation belt radial diffusion coefficients. J. Geophys. Res. Space Phys. 119, 1587–1605. doi:10.1002/2013JA019204

PubMed Abstract | CrossRef Full Text | Google Scholar

Ozeke, L. G., Mann, I. R., Murphy, K. R., Rae, I. J., Milling, D. K., Elkington, S. R., et al. (2012). ULF wave derived radiation belt radial diffusion coefficients. J. Geophys. Res. Space Phys. 117. doi:10.1029/2011JA017463

CrossRef Full Text | Google Scholar

Ozeke, L. G., Mann, I. R., Olifer, L., Claudepierre, S. G., Spence, H. E., and Baker, D. N. (2022). Statistical characteristics of energetic electron pitch angle distributions in the van allen Probe era: 1. Butterfly distributions with flux peaks at preferred pitch angles. J. Geophys. Res. Space Phys. 127, e2021JA029907. doi:10.1029/2021JA029907

CrossRef Full Text | Google Scholar

Ozeke, L. G., Mann, I. R., Olifer, L., Dufresne, K. Y., Morley, S. K., Claudepierre, S. G., et al. (2020). Rapid outer radiation belt flux dropouts and fast acceleration during the March 2015 and 2013 storms: the role of ultra-low frequency wave transport from a dynamic outer boundary. J. Geophys. Res. Space Phys. 125. doi:10.1029/2019JA027179

CrossRef Full Text | Google Scholar

Ozeke, L. G., Mann, I. R., Turner, D. L., Murphy, K. R., Degeling, A. W., Rae, I. J., et al. (2014b). Modeling cross L shell impacts of magnetopause shadowing and ULF wave radial diffusion in the Van Allen belts. Geophys. Res. Lett. 41, 6556–6562. doi:10.1002/2014GL060787

CrossRef Full Text | Google Scholar

Pandya, M., Bhaskara, V., Ebihara, Y., Kanekal, S. G., and Baker, D. N. (2020). Evolution of pitch angle-distributed megaelectron volt electrons during each phase of the geomagnetic storm. J. Geophys. Res. Space Phys. 125. doi:10.1029/2019JA027086

CrossRef Full Text | Google Scholar

Papitashvili, N. E., and King, J. H. (2020). OMNI 5-min data set. NASA Space Phys. Data Facil. doi:10.48322/gbpg-5r77

CrossRef Full Text | Google Scholar

Reeves, G. D., McAdams, K. L., Friedel, R. H. W., and O’Brien, T. P. (2003). Acceleration and loss of relativistic electrons during geomagnetic storms. Geophys. Res. Lett. 30. doi:10.1029/2002GL016513

CrossRef Full Text | Google Scholar

Ripoll, J.-F., Claudepierre, S. G., Ukhorskiy, A. Y., Colpitts, C., Li, X., Fennell, J. F., et al. (2020). Particle dynamics in the Earth’s radiation belts: review of current research and open questions. J. Geophys. Res. Space Phys. 125, e2019JA026735. doi:10.1029/2019JA026735

CrossRef Full Text | Google Scholar

Ripoll, J.-F., Reeves, G. D., Cunningham, G. S., Loridan, V., Denton, M., Santolik, O., et al. (2016). Reproducing the observed energy-dependent structure of Earth’s electron radiation belts during storm recovery with an event-specific diffusion model. Geophys. Res. Lett. 43, 5616–5625. doi:10.1002/2016GL068869

CrossRef Full Text | Google Scholar

Ross, J. P. J., Glauert, S. A., Horne, R. B., Watt, C. E. J., and Meredith, N. P. (2021). On the variability of EMIC waves and the consequences for the relativistic electron radiation belt population. J. Geophys. Res. Space Phys. 126, e2021JA029754. doi:10.1029/2021JA029754

CrossRef Full Text | Google Scholar

Schulz, M., and Lanzerotti, L. (1974). Particle diffusion in the radiation belts. New York: Springer. doi:10.1007/978-3-642-65675-0

CrossRef Full Text | Google Scholar

Selesnick, R. S., and Blake, J. B. (2002). Relativistic electron drift shell splitting. J. Geophys. Res. Space Phys. 107. doi:10.1029/2001JA009179

CrossRef Full Text | Google Scholar

Shprits, Y. Y., Drozdov, A. Y., Spasojevic, M., Kellerman, A. C., Usanova, M. E., Engebretson, M. J., et al. (2016). Wave-induced loss of ultra-relativistic electrons in the Van Allen radiation belts. Nat. Commun. 7, 12883. doi:10.1038/ncomms12883

PubMed Abstract | CrossRef Full Text | Google Scholar

Sibeck, D. G., McEntire, R. W., Lui, A. T. Y., Lopez, R. E., and Krimigis, S. M. (1987). Magnetic field drift shell splitting: cause of unusual dayside particle pitch angle distributions during storms and substorms. J. Geophys. Res. Space Phys. 92, 13485–13497. doi:10.1029/JA092iA12p13485

CrossRef Full Text | Google Scholar

Smirnov, A., Shprits, Y., Allison, H., Aseev, N., Drozdov, A., Kollmann, P., et al. (2022a). Storm-time evolution of the equatorial electron pitch angle distributions in Earth‘s outer radiation belt. Front. Astronomy Space Sci. 9. doi:10.3389/fspas.2022.836811

CrossRef Full Text | Google Scholar

Smirnov, A., Shprits, Y. Y., Allison, H., Aseev, N., Drozdov, A., Kollmann, P., et al. (2022b). An empirical model of the equatorial electron pitch angle distributions in Earth’s outer radiation belt. Space Weather. 20, e2022SW003053. doi:10.1029/2022SW003053

CrossRef Full Text | Google Scholar

Spence, H. E., Reeves, G. D., Baker, D. N., Blake, J. B., Bolton, M., Bourdarie, S., et al. (2013). Science goals and overview of the radiation belt storm Probes (RBSP) energetic particle, composition, and thermal plasma (ECT) suite on NASA’s van allen Probes mission. Space Sci. Rev. 179, 311–336. doi:10.1007/s11214-013-0007-5

CrossRef Full Text | Google Scholar

Summers, D., Ma, C., and Mukai, T. (2004). Competition between acceleration and loss mechanisms of relativistic electrons during geomagnetic storms. J. Geophys. Res. Space Phys. 109. doi:10.1029/2004JA010437

CrossRef Full Text | Google Scholar

Summers, D., Thorne, R. M., and Xiao, F. (1998). Relativistic theory of wave-particle resonant diffusion with application to electron acceleration in the magnetosphere. J. Geophys. Res. Space Phys. 103, 20487–20500. doi:10.1029/98JA01740

CrossRef Full Text | Google Scholar

Thorne, R. M., Li, W., Ni, B., Ma, Q., Bortnik, J., Baker, D. N., et al. (2013a). Evolution and slow decay of an unusual narrow ring of relativistic electrons near L ∼ 3.2 following the September 2012 magnetic storm. Geophys. Res. Lett. 40, 3507–3511. doi:10.1002/grl.50627

CrossRef Full Text | Google Scholar

Thorne, R. M., Li, W., Ni, B., Ma, Q., Bortnik, J., Chen, L., et al. (2013b). Rapid local acceleration of relativistic radiation-belt electrons by magnetospheric chorus. Nature 504, 411–414. doi:10.1038/nature12889

PubMed Abstract | CrossRef Full Text | Google Scholar

Thorne, R. M., Ni, B., Tao, X., Horne, R. B., and Meredith, N. P. (2010). Scattering by chorus waves as the dominant cause of diffuse auroral precipitation. Nature 467, 943–946. doi:10.1038/nature09467

PubMed Abstract | CrossRef Full Text | Google Scholar

Tu, W., Cunningham, G. S., Chen, Y., Morley, S. K., Reeves, G. D., Blake, J. B., et al. (2014). Event-specific chorus wave and electron seed population models in DREAM3D using the Van Allen Probes. Geophys. Res. Lett. 41, 1359–1366. doi:10.1002/2013GL058819

CrossRef Full Text | Google Scholar

Turner, D. L., Shprits, Y., Hartinger, M., and Angelopoulos, V. (2012). Explaining sudden losses of outer radiation belt electrons during geomagnetic storms. Nat. Phys. 8, 208–212. doi:10.1038/nphys2185

CrossRef Full Text | Google Scholar

Ukhorskiy, A. Y., and Sitnov, M. I. (2013). Dynamics of radiation belt particles. Space Sci. Rev. 179, 545–578. doi:10.1007/s11214-012-9938-5

CrossRef Full Text | Google Scholar

Vampola, A. (1997). “Outer zone energetic electron environment update,” in Conference on the High Energy Radiation Background in Space. Workshop Record, Snowmass, CO, USA, 22-23 July 1997, 128–136doi. doi:10.1109/CHERBS.1997.660263

CrossRef Full Text | Google Scholar

West, H. I., Buck, R. M., and Walton, J. R. (1973). Electron pitch angle distributions throughout the magnetosphere as observed on Ogo 5. J. Geophys. Res. 78, 1064–1081. doi:10.1029/JA078i007p01064

CrossRef Full Text | Google Scholar

Xiao, F., Su, Z., Zheng, H., and Wang, S. (2009a). Modeling of outer radiation belt electrons by multidimensional diffusion process. J. Geophys. Res. Space Phys. 114. doi:10.1029/2008JA013580

CrossRef Full Text | Google Scholar

Xiao, F., Yang, C., He, Z., Su, Z., Zhou, Q., He, Y., et al. (2014). Chorus acceleration of radiation belt relativistic electrons during March 2013 geomagnetic storm. J. Geophys. Res. Space Phys. 119, 3325–3332. doi:10.1002/2014JA019822

CrossRef Full Text | Google Scholar

Xiao, F., Zhang, S., Su, Z., He, Z., and Tang, L. (2012). Rapid acceleration of radiation belt energetic electrons by Z-mode waves. Geophys. Res. Lett. 39. doi:10.1029/2011GL050625

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiao, F., Zong, Q.-G., and Chen, L. (2009b). Pitch-angle distribution evolution of energetic electrons in the inner radiation belt and slot region during the 2003 Halloween storm. J. Geophys. Res. Space Phys. 114. doi:10.1029/2008JA013068

CrossRef Full Text | Google Scholar

Yu, J., Li, L., Cao, J. B., Reeves, G. D., Baker, D. N., and Spence, H. (2016). The influences of solar wind pressure and interplanetary magnetic field on global magnetic field and outer radiation belt electrons. Geophys. Res. Lett. 43, 7319–7327. doi:10.1002/2016GL069029

CrossRef Full Text | Google Scholar

Zhao, H., Baker, D. N., Califf, S., Li, X., Jaynes, A. N., Leonard, T., et al. (2017). Van allen Probes measurements of energetic particle deep penetration into the low L region (L < 4) during the storm on 8 april 2016. J. Geophys. Res. Space Phys. 122, 12,140–12,152. doi:10.1002/2017JA024558

CrossRef Full Text | Google Scholar

Zhao, H., Baker, D. N., Li, X., Jaynes, A. N., and Kanekal, S. G. (2018). The acceleration of ultrarelativistic electrons during a small to moderate storm of 21 april 2017. Geophys. Res. Lett. 45, 5818–5825. doi:10.1029/2018GL078582

CrossRef Full Text | Google Scholar

Zhao, H., Friedel, R. H. W., Chen, Y., Baker, D. N., Li, X., Malaspina, D. M., et al. (2020). Equatorial pitch angle distributions of 1–50 keV electrons in Earth’s inner magnetosphere: an empirical model based on the van allen Probes observations. J. Geophys. Res. Space Phys. 126. doi:10.1029/2020JA028322

CrossRef Full Text | Google Scholar

Zhao, H., Friedel, R. H. W., Chen, Y., Baker, D. N., Li, X., Malaspina, D. M., et al. (2021). Equatorial pitch angle distributions of 1â€;50 keV electrons in Earth’s inner magnetosphere: an empirical model based on the van allen Probes observations. J. Geophys. Res. Space Phys. 126. doi:10.1029/2020JA028322

CrossRef Full Text | Google Scholar

Zhao, H., Ni, B., Li, X., Baker, D. N., Johnston, W. R., Zhang, W., et al. (2019). Plasmaspheric hiss waves generate a reversed energy spectrum of radiation belt electrons. Nat. Phys. 15, 367–372. doi:10.1038/s41567-018-0391-6

CrossRef Full Text | Google Scholar