Day-to-day and longitudinal variability of the equatorial electrojet as viewed from the Sun-synchronous CSES satellite

Yamazaki, Yosuke; Stolle, Claudia; Xiong, Chao; Alken, Patrick; Yang, Yanyan; Zhima, Zeren; Harding, Brian; Yan, Rui

doi:10.3389/fspas.2024.1460312

ORIGINAL RESEARCH article

Front. Astron. Space Sci., 22 November 2024

Sec. Space Physics

Volume 11 - 2024 | https://doi.org/10.3389/fspas.2024.1460312

This article is part of the Research Topic Frontier Research in Equatorial Aeronomy and Space Physics View all 9 articles

Day-to-day and longitudinal variability of the equatorial electrojet as viewed from the Sun-synchronous CSES satellite

Yosuke Yamazaki¹*

Claudia Stolle¹

Chao Xiong²

Patrick Alken³

Yanyan Yang^4,5

Zeren Zhima^4,5

Brian Harding⁶

Rui Yan^4,7

¹Leibniz Institute of Atmospheric Physics at the University of Rostock, Kühlungsborn, Germany
²Department of Space Physics, College of Electronic Information, Wuhan University, Wuhan, China
³Cooperative Institute for Research in Environmental Sciences, University of Colorado Boulder, Boulder, CO, United States
⁴National Institute of Natural Hazards, Ministry of Emergency Management of China, Beijing, China
⁵Center for Satellite Application in Earthquake Science, China Earthquake Administration, Beijing, China
⁶Space Sciences Laboratory, University of California, Berkeley, Berkeley, CA, United States
⁷School of Information Engineering, Institute of Disaster Prevention, Langfang, China

The intensity of the equatorial electrojet (EEJ) derived from the magnetic field measurements by the China Seismo-Electromagnetic Satellite (CSES) is analyzed for the low solar activity period of July 2018–April 2022. The CSES spacecraft flies in a Sun-synchronous orbit, providing the first continuous satellite observations of the afternoon EEJ at a fixed local time at 2 p.m. The EEJ intensities from CSES and concurrent observations from the Swarm satellite mission show a good correlation, supporting the reliability of the CSES EEJ data. Spectral analysis of the CSES data reveals the presence of three distinct oscillatory components in the day-to-day variation of the afternoon EEJ: (1) an eastward-propagating 2–3-day oscillation with zonal wavenumber 1, (2) a westward-propagating 5–6-day oscillation with zonal wavenumber 1, and (3) a zonally-symmetric 14–15-day oscillation. These oscillations result from upward-propagating waves in the atmosphere. That is, the first two can be attributed to the ultra-fast Kelvin wave and quasi-6-day wave, respectively, while the latter is likely due to the atmospheric lunar tide. The CSES EEJ data are also compared with lower thermospheric wind measurements by the Michelson Interferometer for Global High-Resolution Thermospheric Imaging (MIGHTI) onboard the Ionospheric Connection Explorer (ICON). The results suggest that the EEJ intensity correlates negatively with the equatorial eastward wind at 100–115 km, consistent with earlier studies. Contributions of different tidal wind components to longitudinal structures of the EEJ are evaluated. A four-peak structure during July–September can be largely explained by the eastward-propagating diurnal tide with zonal wavenumber 3 (DE3), while a two- or three-peak structure during December–January is mainly due to the combined effect of DE3 and the eastward-propagating diurnal tide with zonal wavenumber 2 (DE2). Furthermore, the CSES EEJ data are compared with the electron density measurements from the Langmuir probe onboard CSES. There is a positive correlation between the EEJ intensity and in-situ electron densities at $\sim$ 510 km from the same orbit, reflecting the plasma fountain effect. The correlation tends to be higher in the summer hemisphere, which may be due to the meridional wind in the thermosphere.

1 Introduction

When geomagnetic storms are absent, daily variations of the geomagnetic field on the ground at middle and low latitudes are primarily due to electric currents in the E-region ionosphere (e.g., Campbell, 2003; Yamazaki and Maute, 2017). These ionospheric currents are generated through the process called ionospheric wind dynamo (e.g., Richmond, 1995; Maute, 2021), where the kinetic energy possessed by the neutral atmosphere is partially converted into electromagnetic energy through collisional interactions between neutral and plasma particles. The E-region dynamo currents are mostly confined to the dayside ionosphere, as the electrical conductivity of the E-region ionosphere is much lower on the night side due to low plasma density (e.g., Richmond, 2011). On the dayside, there are usually two large-scale vortices of the dynamo current: one counter-clockwise vortex in the Northern Hemisphere and one clockwise vortex in the Southern Hemisphere, which can be deduced from magnetic field measurements at the ground (e.g., Matsushita and Maeda, 1965; Campbell et al., 1993; Takeda, 2002a; Owolabi et al., 2022; Chen et al., 2024) and in space (e.g., Pedatella et al., 2011; Chulliat et al., 2016; Alken et al., 2017; Yamazaki, 2022). The intensity of the zonal current is enhanced along the magnetic equator, where the geomagnetic field is perfectly horizontal (e.g., Hirono, 1950; Chapman, 1951). The unique configuration of the geomagnetic field at the magnetic equator allows the establishment of a vertical electric field, which drives a Hall current in the zonal direction (e.g., Sugiura and Poros, 1969; Richmond, 1973; Raghavarao and Anandarao, 1987; Du and Stening, 1999). This additional Hall current is commonly referred to as the equatorial electrojet (EEJ) (e.g., Forbes, 1981; Rastogi, 1989; Lühr et al., 2021a). The EEJ is confined near the magnetic equator, within approximately $\pm 3 °$ latitude from the magnetic equator, where the vertical electric field can be maintained (e.g., Doumouya et al., 1998; Rigoti et al., 1999; Rabiu et al., 2013). The EEJ is usually directed eastward but occasionally turns westward, which is sometimes referred to as counter electrojet (e.g., Mayaud, 1977; Zhou et al., 2018; Soares et al., 2019; Zhang et al., 2024).

The intensity of the EEJ is determined by various factors. For instance, the EEJ intensity varies with local time, season, longitude and solar activity (e.g., Doumouya et al., 2003; Alken and Maus, 2007; Abdul Hamid et al., 2015). The local time and solar activity dependence can be ascribed to the effect of solar extreme ultraviolet radiation on the electrical conductivity of the E-region ionosphere (e.g., Takeda, 2002b). The seasonal dependence of the EEJ is primarily controlled by neutral wind forcing (Yamazaki et al., 2014b). The change in the solar zenith angle (and hence solar radiation ionization) plays only a secondary role for the seasonal variation of the EEJ (Chapman and Rao, 1965). The longitude dependence of the EEJ is partly due to the background geomagnetic field (e.g., Rastogi, 1962; Doumbia and Grodji, 2016; Pandey et al., 2021), which affects the E-region conductivity (Takeda and Araki, 1985), and partly due to neutral wind forcing by atmospheric tides (e.g., England et al., 2006; Lühr et al., 2008; Soares et al., 2018). Moreover, the EEJ intensity depends on the phase of the Moon (e.g., Rastogi and Trivedi, 1970; Lühr et al., 2012; Yamazaki et al., 2017), which can be understood as the effect of neutral wind forcing associated with the atmospheric lunar tide (e.g., Vial and Forbes, 1994; Pedatella et al., 2012b; Zhang and Forbes, 2013). The EEJ intensity is also subject to the influence of geomagnetic activity (e.g., Rastogi, 1977; Yamazaki and Kosch, 2015; Xiong et al., 2016a). This is generally attributed to the prompt penetration of the polar electric field into equatorial latitudes (e.g., Nishida, 1968; Kikuchi et al., 2008; Manoj et al., 2008; Yizengaw et al., 2016) and to the dynamo electric field generated by storm-time winds (e.g., Blanc and Richmond, 1980; Le Huy and Amory-Mazaudier, 2005; Pandey et al., 2018). Even in the apparent absence of variability in solar and geomagnetic activity, the EEJ intensity can exhibit large day-to-day variability (e.g., Marriott et al., 1979; Reddy, 1989), as neutral winds are constantly changing.

The E-region vertical electric field that drives the EEJ is closely associated with the vertical current and zonal electric field (e.g., Hysell et al., 2002; Alken and Maus, 2010). The zonal electric field at low latitudes is mapped along equipotential magnetic field lines to the equatorial F-region ( $>$ 150 km), where both ions and electrons tend to move with the E $\times$ B drift (e.g., Heelis, 2004). Observations have found a good correlation between the EEJ intensity with the equatorial E $\times$ B vertical plasma drift velocity (e.g., Anderson et al., 2002; Alken et al., 2013a; Kumar et al., 2016). Since the E $\times$ B drift is a primary transport mechanism for F-region plasmas and thus is an important factor determining the F-region plasma density, there is also a correlation between the EEJ intensity and F-region plasma density (e.g., Rush and Richmond, 1973; Rastogi and Klobuchar, 1990; Chen et al., 2008; Stolle et al., 2008; Venkatesh et al., 2015). Therefore, understanding the behavior of the EEJ is important not only for the E-region electrodynamics but also for the F-region dynamics and its broader impact on space weather phenomena (e.g., Stening, 2003).

The equatorial zonal wind at altitudes of the E-region ionosphere (90–150 km) plays an important role for determining the EEJ intensity (e.g., Yamazaki et al., 2014a; 2021; Harding et al., 2022). Neutral winds at these altitudes are predominantly due to atmospheric solar tides (e.g., McLandress et al., 1996; Wu et al., 2008a; b; Yamazaki et al., 2023). They consist of two parts: locally-generated tides and upward-propagating tides from below. The two parts exert a comparable influence on the EEJ (Yamazaki et al., 2014b). Locally-generated tides are produced through in situ absorption of solar radiation by thermospheric constituents such as O, $O_{2}$ and $N_{2}$ . They are primarily vertically trapped mode of the diurnal tide (e.g., Forbes, 1982; Hagan et al., 2001). On the other hand, upward-propagating tides are generated mainly in the troposphere and stratosphere (e.g., Hagan and Forbes, 2002; 2003). They propagate vertically upward and reach the lower thermosphere before being dissipated (e.g., Oberheide et al., 2011; Truskowski et al., 2014). Upward-propagating tides at E-region altitudes are highly variable, as their production and vertical propagation are dependent on the meteorological state of the lower and middle atmosphere (e.g., Miyoshi and Fujiwara, 2003; Liu, 2014; Dhadly et al., 2018; Zhou X. et al., 2022; Oberheide et al., 2024). Thus, upward-propagating tides, along with other upward-propagating waves, can be an important source of the day-to-day and longitudinal variability of the EEJ (e.g., Kawano-Sasaki and Miyahara, 2008; Yamazaki et al., 2014a).

A mathematical expression for a tidal wave in an atmospheric variable such as temperature, density and wind velocities is given as follows:

A_{n s} \cos [2 π (n \frac{t}{24} - s \frac{λ}{360}) - P_{n s}], (1)

where $A_{n s}$ and $P_{n s}$ are the amplitude and phase of the tide, $t$ is the universal time in hours, and $λ$ is the longitude in degrees. $n$ is a positive integer, with $n$ = 1, 2, 3, 4 corresponding to the 24-h (diurnal), 12-h (semidiurnal), 8-h (terdiurnal) and 6-h tides, respectively. $| s |$ is the zonal wavenumber (i.e., the number of wave cycles that can fit along the latitude circle at a given latitude). $s >$ 0 and $s <$ 0 correspond to eastward and westward propagating waves, respectively, and $s =$ 0 represents the oscillation that is independent of longitude, which is often referred to as zonally-symmetric oscillation (e.g., Pancheva et al., 2007; Forbes et al., 2018). We use the conventional tidal nomenclature such as DE3, SW2 and T0 (e.g., Forbes et al., 2003; Jones Jr et al., 2013), where the first letter indicates the period (i.e., “D” for diurnal, “S” for semidiurnal, and “T” for terdiurnal), the second letter represents the propagation direction (i.e., “E” for eastward and “W” for westward), and the last number is the zonal wavenumber (i.e., $| s |$ ). Different components of tides can be evaluated by fitting Equation 1 to atmospheric measurements obtained at any given height and latitude (e.g., Forbes et al., 2008). Lühr and Manoj (2013) applied this method to EEJ data and examined the tidal composition of the EEJ based on 10 years of satellite magnetic field measurements. Soares et al. (2022), combining EEJ data from multiple satellites and ground stations, determined the tidal composition of the EEJ for individual years. Both studies found that migrating tides ( $n$ + $s$ = 0) such as DW1 and SW2 are dominant tidal components of the EEJ. Some non-migrating tides ( $n$ + $s \neq$ 0) such as DE3 and DE2 are also found to be significant tidal components of the EEJ. The tidal composition of the EEJ is, however, not necessarily the same as the tidal composition of neutral winds that drive the EEJ. This is because the tidal composition of the EEJ is determined not only by tidal winds but also by the E-region conductivity, which is strongly local-time dependent. Thus, tidal wind components contributing to the EEJ have yet to be identified.

Apart from atmospheric tides, the EEJ is also influenced by some global-scale atmospheric waves with a period longer than a day. For instance, the westward-propagating quasi-6-day wave (Q6DW) with zonal wavenumber 1 is often observed in the lower thermosphere (e.g., Lieberman et al., 2003; Gan et al., 2018; Qin et al., 2021), and studies have reported the occurrence of $\sim$ 6-day oscillation in the EEJ intensity during Q6DW events (e.g., Yamazaki et al., 2018; 2020a). Similarly, the eastward-propagating ultra-fast Kelvin wave (UFKW) with a period of 2–3 days and zonal wavenumber 1 is frequently detected in the equatorial lower thermosphere (e.g., Forbes et al., 2009; Davis et al., 2012; Gu et al., 2014), and corresponding 2–3-day oscillations have been observed in the EEJ (e.g., Yamazaki et al., 2020b; Lühr et al., 2021b; Sun et al., 2024). Other planetary waves, such as the westward-propagating quasi-2-day wave (Q2DW) with zonal wavenumber 3 (e.g., Yue et al., 2012; Gu et al., 2013; He et al., 2021) and quasi-16-day wave (16DW) with zonal wavenumber 1 (e.g., Forbes et al., 1995; Day and Mitchell, 2010; Fan et al., 2022), also seem to have some influence on the ionospheric electrodynamics (e.g., Yamada, 2009; Elhawary and Forbes, 2016; Jadhav et al., 2023; 2024), but their capability of modulating the EEJ intensity is still to be established.

Characterization of the EEJ variability due to tides and other global-scale waves mentioned above can greatly benefit from global observations by low-Earth-orbit (LEO) satellites. When a LEO satellite flies over the magnetic equator, the magnetic effect of the EEJ is observed as a latitudinally localized depression in the field strength (e.g., Cain and Sweeney, 1972; Jadhav et al., 2002; Lühr et al., 2004; Alken et al., 2015; Stolle et al., 2021). The intensity of the EEJ can be estimated from the magnitude of the magnetic field depression. Since LEO satellites have orbital periods of 90–120 min, they complete 12–16 orbits per day. In other words, 12–16 measurements of the dayside EEJ intensity can be made in each day at different longitudes.

The EEJ data from the CHAMP (Reigber et al., 2002) and Swarm (Friis-Christensen et al., 2006; 2008) missions have been extensively analyzed in previous studies (e.g., Lühr et al., 2004; Alken et al., 2015). In both missions, the spacecraft have been deployed in a near-circular near-polar orbit that slowly precesses in local time at a rate of about 5 minutes per day. Thus, for instance, the local time of the EEJ measurement changes by more than 2 hours in a month. This change in the local time sometimes made it difficult to accurately interpret the day-to-day variation of the EEJ observed by CHAMP and Swarm, because the EEJ variation associated with the local time change and other changes (e.g., changes in geomagnetic activity or neutral wind forcing) cannot be distinguished. The day-to-day variation of the EEJ may be more easily captured by ground-based magnetometer measurements. However, it is difficult to obtain good longitudinal coverage with ground-based observations. A solution to this problem is to use EEJ data from a Sun-synchronous orbit, where the local time is always the same. The SAC-C satellite mission (Colomb et al., 2004) operated in a Sun-synchronous orbit at an altitude of $\sim$ 700 km and provided the EEJ data at a fixed local time of 10:25 a.m. during the solar maximum period of 2001–2003 (Alken and Maus, 2007). In this study, we employ the EEJ data from the China Seismo-Electromagnetic Satellite (CSES) (Shen et al., 2018), which flies in a Sun-synchronous orbit at approximately 2 a.m.–2 p.m. The CSES data provide the first continuous satellite observations of the afternoon EEJ at 2 p.m. local time.

Zhou Y. et al. (2022) presented a preliminary analysis of the CSES magnetic field measurements for detecting the EEJ. This study extends the analysis of the EEJ magnetic signatures derived from CSES, and advances the characterization of its spatial and temporal variability on day-to-day and seasonal time scales. In Section 3.1, we will conduct a statistical comparison between CSES and Swarm EEJ to validate the reliability of the CSES EEJ data. In Section 3.2, we will perform a spectral analysis of the CSES EEJ to provide insight into the source of the day-to-day EEJ variability. In Section 3.3, we will compare the CSES EEJ data with neutral wind measurements by the Ionospheric Connection Explorer (ICON) satellite mission (Immel et al., 2018) to evaluate the effect of neutral winds on the EEJ. In Section 3.4, we will show how the seasonal and longitudinal variations of the EEJ are related to those in neutral winds. We will also examine the tidal components that are important for the longitudinal structure of the EEJ. In Section 3.5, we will compare the CSES EEJ data (evaluated at 110 km altitude) with CSES in-situ measurements of the electron density ( $\sim$ 510 km altitude), providing insight into electrodynamic coupling between the ionospheric E and F regions.

2 Data

The intensity of the EEJ was derived using the 1 Hz scalar magnetic field measurements by CSES (Yang et al., 2021). The data are available from the mission website (https://www.leos.ac.cn/). The method for retrieving the EEJ intensity is the same as that developed for the Swarm Level 2 (L2) Product of the EEJ (Alken et al., 2013b; 2015). Briefly, the method involves the following three steps. In the first step, the core field, lithospheric field, and magnetospheric field are evaluated and removed from the observed magnetic field. In the second step, the residual field is further separated into the “Sq field,” which is large-scale, and the “EEJ field,” which is localized near the magnetic equator. In the final step, the EEJ intensity is estimated according to the Biot-Savart law using an inversion model of the EEJ that assumes line currents at an altitude of 110 km following zonally along the magnetic equator. More detailed description of each step can be found in the article by Alken (2020).

As mentioned, the CSES spacecraft flies in a Sun-synchronous orbit, and the local time of the equatorial crossing is 2 a.m. and 2 p.m. We use the measurements made at 2 p.m. during the period July 2018–April 2022. Figure 1A shows the number of observations in each month. In addition to the total number of observations, the numbers of eastward and westward EEJ events are also indicated. The occurrence rate of the westward EEJ is approximately 20%, which is consistent with previous studies based on ground-based observations and other satellites (e.g., Soares et al., 2019). The absence of data during January–May 2020 and during June 2021–January 2022 is not due to a lack of magnetic field measurements; instead, it is because the EEJ data were still to be processed at the time of writing this paper.

Figure 1

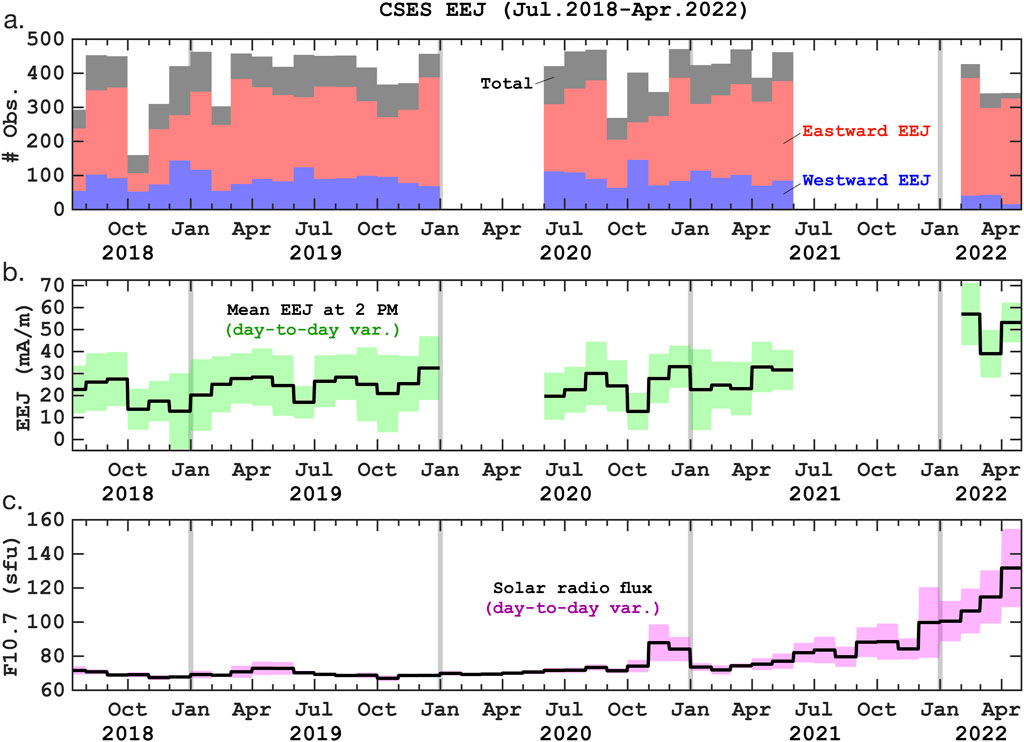
Figure 1. (A) Number of CSES equatorial electrojet (EEJ) measurements at 2 p.m. local time in each month during July 2018–April 2022. Besides the total number of measurements, the numbers of eastward and westward EEJ events are also indicated. (B) Monthly mean values of the daily mean EEJ intensity. Shading indicates the magnitude of the day-to-day variability $(\pm 1 σ)$ of the daily mean EEJ intensity. (C) Monthly mean values of the daily solar radio flux index $F_{10.7}$ . Shading indicates the magnitude of the day-to-day variability $(\pm 1 σ)$ of the $F_{10.7}$ index.

Figure 1B shows monthly values of the daily mean EEJ intensity. Green shading indicates the magnitude of the day-to-day variability. On each day, the CSES spacecraft completes $\sim$ 15 orbits. The longitude of the equatorial crossing changes by $23.7 °$ from one orbit to the next. Thus, the CSES satellite effectively covers all longitudes in 1 day ( $15 \times 23.7$ $°$ = $355.5 °$ ). For this reason, the daily mean is a good representation of the longitudinally averaged EEJ at 2 p.m. local time. In Figure 1B, the mean EEJ intensity during the last 3 month (February–April 2022) is appreciably higher than that over the preceding period. This is due to an increase in solar activity. Figure 1C shows monthly mean values of the $F_{10.7}$ index (Tapping, 2013), representing solar radiation activity, which controls E-region ionization and hence the E-region conductivity. The EEJ intensity is known to increase with increasing $F_{10.7}$ (e.g., Yamazaki et al., 2010; Matzka et al., 2017). Solar activity affects not only the mean EEJ intensity but also the occurrence rate of the westward EEJ. It is known that an increase in solar activity results in a decrease in the occurrence of the westward EEJ in the afternoon (e.g., Marriott et al., 1979; Soares et al., 2018), which can be confirmed in Figure 1A.

We perform a validation of the CSES EEJ data through comparisons with EEJ intensities derived from the magnetic field measurements by Swarm. The Swarm constellation, operational since November 2013, consists of three identical satellites, namely, Swarm A, Swarm B and Swarm C. Swarm A and C fly side by side at an altitude of approximately 460 km, while Swarm B flies separately at a higher altitude of $\sim$ 510 km. As one of the L2 products of Swarm, EEJ data from each satellite are available at the ESA Swarm website (https://swarm-diss.eo.esa.int/). For the present study, we use the EEJ intensities from Swarm A and B.

We use neutral wind observations by the ICON mission. Measurement of the horizontal wind velocity is made by the Michelson Interferometer for Global High-Resolution Thermospheric Imaging (MIGHTI) instrument onboard ICON (e.g., Englert et al., 2017; Harding et al., 2017). Version 5 of the MIGHTI wind product based on the oxygen green-line emission at 557.7 nm wavelength is used for the evaluation of the local wind effect on the EEJ. We use only the measurements with the “wind quality factor” being one, corresponding to the best quality data. Detailed description and validation of version 5 ICON/MIGHTI data can be found in the article by Englert et al. (2023). The Level 2.2 MIGHTI Cardinal Winds can be downloaded from the ICON mission website (https://icon.ssl.berkeley.edu/Data/Data-Product-Matrix) as well as from DOI in Harding et al. (2023).

We also use the empirical wind model of Yamazaki et al. (2023), which is based on the ICON/MIGHTI green-line wind measurements during April 2020–March 2022. It uses a formula similar to Equation 1 in the introduction section with $n$ being from 0 to 4 and $s$ being from $- 4$ to 4, where the [ $n$ = 0, $s$ = 0] term corresponds to the zonal-mean wind (ZMW), the [ $n$ = 0, $s >$ 0] terms correspond to stationary planetary waves (SPWs), and the rest of the ( $n$ , $s$ ) terms are tides. Besides, the model takes into account the dependence of each ( $n$ , $s$ ) component on month of year. The model outputs are zonal and meridional wind velocities for the latitude range of $12 °$ S to $40 °$ N and for the altitude range of 91–112 km.

The Langmuir probe (LAP) onboard CSES (Yan et al., 2018) provides electron density $(N_{e})$ data at the satellite location ( $\sim$ 510 km altitude). We make a comparison between the CSES EEJ intensity and $N_{e}$ from the same orbital path to assess the relationship of the two quantities. The CSES LAP data can be obtained from the same website as the CSES magnetic field data (https://www.leos.ac.cn/). The validation of CSES $N_{e}$ data is presented by Yan et al. (2020) through comparisons with other satellite and ground-based observations. Yan et al. (2022) described artificial signals found in the CSES $N_{e}$ data. We have eliminated those artificial signals before the comparison with the EEJ data is performed.

3 Results and discussion

3.1 Comparison with swarm EEJ

Figure 2 presents comparisons of the EEJ intensities derived from CSES and Swarm magnetic field measurements. Only the data during concurrent measurements by CSES and Swarm are used. Our criteria for a CSES-Swarm conjunction are as follows: (1) the time difference between the two measurements is less than 15 min, and (2) the longitudinal separation of the two measurements is less than $15 °$ . 497 concurrent measurements are found for the CSES-Swarm A pair (Figure 2A), while 265 concurrent measurements are found for the CSES-Swarm B pair (Figure 2B). In both cases, there is a good correlation between the EEJ intensities from CSES and Swarm, with the correlation coefficient of $R \sim$ 0.9. The results support the reliability of the CSES EEJ data. However, the slope of the regression line is less than 1.0 in both cases: 0.85 [0.82–0.89] for the CSES-Swarm A pair and 0.86 [0.79–0.91] for the CSES-Swarm B pair, where the range in the square brackets indicates the 95% confidence interval estimated by the bootstrap method. The results seem to imply a systematic underestimation of the CSES EEJ compared to the Swarm EEJ. The cause of this discrepancy is unclear. We do not attempt to calibrate the CSES EEJ with Swarm EEJ; however, possible underestimation of the CSES EEJ intensity by $\sim$ 15% should be kept in mind while interpreting the results presented in this paper. The intersect of the regression line is small in both cases (1–2 mA/m), and thus the direction of the CSES EEJ (i.e., eastward or westward) is considered to be accurate.

Figure 2

Figure 2. Comparison of the equatorial electrojet (EEJ) intensity derived from the magnetic field measurements by CSES with those from concurrent magnetic field measurements by (A) Swarm A and (B) Swarm B.

3.2 Spectral analysis of day-to-day variability

Characteristics of the day-to-day variability of the afternoon EEJ are examined. Figure 3A displays the CSES EEJ intensity during the selected period of 2 April–30 May 2021, as a function of time (day of year; DoY) and longitude, highlighting the day-to-day variability of the EEJ at 2 p.m. local time. A close inspection of the data reveals a wave-like pattern that appears to propagate westward, as indicated by the white dashed lines. Figure 3B depicts the amplitude spectrum obtained by the Fourier-wavelet analysis described by Yamazaki (2023). The horizontal axis shows the zonal wavenumber and the vertical axis shows the period of oscillation. The Fourier-wavelet technique involves the Fourier transform in longitude and the wavelet transform in time, and is applicable to 2-D longitude-time data for evaluating global-scale waves (e.g., tides and planetary waves) with different zonal wavenumbers. The spectrum shows an amplitude peak at a period of $\sim$ 6 days and zonal wavenumber $-$ 1, indicating the involvement of a westward-propagating Q6DW. Previously, Yamazaki et al. (2018) reported several events where EEJ intensities from CHAMP and Swarm satellites show Q6DW signatures.

Figure 3

Figure 3. (A) An example of the CSES equatorial electrojet (EEJ) data at 2 p.m. local time, plotted as a function of time (day of year) and longitude for the time period 2 April 2021–30 May 2021, and (B) the corresponding zonal wavenumber-period spectrum as derived using the Fourier-wavelet technique (Yamazaki, 2023). Positive and negative zonal wavenumbers correspond to eastward- and westward-propagating waves, respectively. (C, D) Same as (A, B) but for the time period 2 January–18 February 2019.

Figure 3C depicts the CSES EEJ intensity during another selected period of 2 January 2019–18 February 2019. A temporal oscillation is seen in the EEJ intensity, as indicated by the white dashed line. Unlike the previous example presented in Figure 3A, the phase of the oscillation is constant with respect to longitude. The Fourier-wavelet spectrum shown in Figure 3D reveals an amplitude peak at a period of 14–15 days and zonal wavenumber 0. This semimonthly oscillation can be attributed to the effect of the atmospheric lunar tide, which appears as a 14.8 days oscillation in the EEJ at a fixed local time (e.g., Rastogi and Trivedi, 1970; Yamazaki et al., 2012). The dominant mode of the atmospheric lunar tide is the semidiurnal $M_{2}$ oscillation with a period of 12.42 h (e.g., Lindzen and Chapman, 1969). The 14.8-day oscillation is basically an alias caused by the sampling of the $M_{2}$ oscillation at a rate of 24.0 h. During January–February 2019, the new Moon occurred on 6 January (DoY = 6) and 4 February (DoY = 35), and the full Moon occurred on 21 January (DoY = 21) and 19 February (DoY = 50). The CSES EEJ at 2 p.m. local time is seen to be relatively weak on the days of the new Moon and full Moon, which is consistent with previously reported lunar tidal effect on the EEJ (e.g., Yamazaki et al., 2012). Moreover, previous studies reported that the amplitude of the semimonthly EEJ oscillation can be amplified during sudden stratospheric warming events (e.g., Park et al., 2012; Yamazaki, 2013; Siddiqui et al., 2015; 2018). In January 2019, there was an Arctic sudden stratospheric warming event (e.g., Siddiqui et al., 2021), which might have contributed to the semimonthly oscillation in the EEJ during this month.

As demonstrated in Figure 3, the Fourier-wavelet spectrum of the CSES EEJ can be obtained for any given period of time. The average spectrum for the entire period of July 2018–May 2021 is derived to provide a climatological picture of the CSES EEJ spectrum under solar minimum conditions (see Figure 1C for solar activity). Figure 4A shows the result, revealing three distinct components: (1) an eastward-propagating oscillation with a period of 2–3 days and zonal wavenumber 1, (2) a westward-propagating oscillation with a period of 5–6 days and zonal wavenumber 1, and (3) a zonally-symmetric oscillation with a period of 14–15 days. They correspond to different modes of atmospheric waves, namely, the UFKW, Q6DW and atmospheric lunar tide, respectively. It is noted that previous studies based on CHAMP and Swarm magnetic field measurements were not able to provide the climatological spectrum of the EEJ at a fixed local time similar to Figure 4A because the local time of the EEJ measurement by these satellites changes over time.

Figure 4

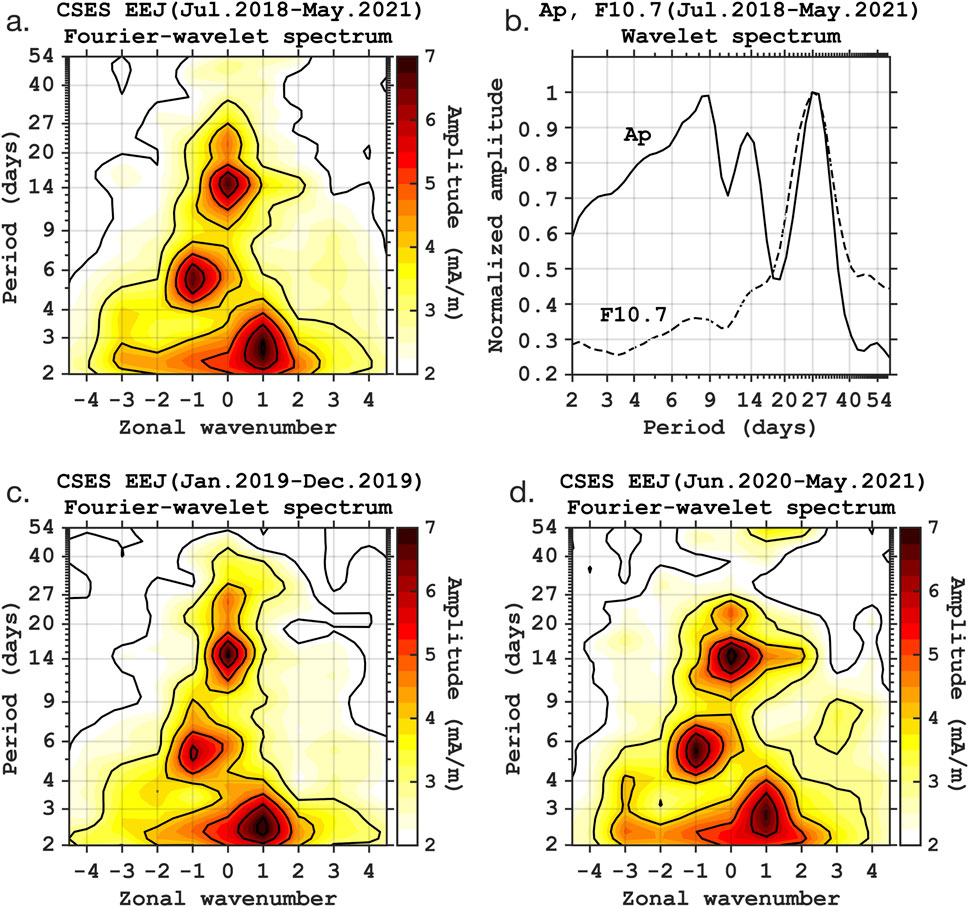
Figure 4. (A) Zonal wavenumber-period spectrum of the CSES equatorial electrojet (EEJ) intensity at 2 p.m. local time, averaged over the time period July 2018–May 2021. Positive and negative zonal wavenumbers correspond to eastward- and westward-propagating waves, respectively. (B) Wavelet amplitude spectra of the geomagnetic activity index $A p$ and solar activity index $F_{10.7}$ during July 2018–May 2021. The amplitudes are normalized by the corresponding maximum values. (C) Same as (A) but over the 1-year period January–December 2019. (D) Same as (A) but over the 1-year period July 2020–May 2021.

The day-to-day variation of the EEJ could contain signatures of varying solar and geomagnetic activity. The wavelet spectra presented in Figure 4B reveal the presence of 27-, 13.5- and 9-day oscillations in the daily geomagnetic activity index $A p$ (Matzka et al., 2021) and a 27-day oscillation in the solar activity index $F_{10.7}$ during July 2018–May 2021. The 27-day oscillation represents the effect of solar rotation, and 13.5- and 9-day oscillations are its harmonics. These oscillations do not seem to have a significant impact on the EEJ in our dataset. One may suspect the influence of the $A p$ oscillation at 13.5 days on the EEJ oscillation at 14–15 days. However, if the 13.5-day oscillation in $A p$ is effective in modulating the EEJ, the 27- and 9-day oscillations should also be visible in the EEJ spectrum (Figure 4A), which is not the case. Besides, there is no correlation between the occurrence of the 14–15-day EEJ oscillation and the 13.5-day $A p$ oscillation. For example, during 2 January–18 February 2019, when the EEJ exhibited a large semimonthly oscillation (Figures 3C,D), the 13.5-day oscillation was absent in $A p$ (not shown here). Figures 4C,D are the same as Figure 4A but for different periods of time (i.e., January–December 2019 for Figure 4B and July 2020–May 2021 for Figure 4C). The results obtained for these two separate 1-year periods are remarkably similar, indicating that the influences of the UFKW, Q6DW and atmospheric lunar tide on the EEJ are robust.

It is important to note that UFKW and Q6DW signatures in the EEJ spectrum (Figure 4) do not necessarily mean the direct effects of these waves on the EEJ. It is known that when measurements from a Sun-synchronous satellite are analyzed, a spectral peak corresponding to a planetary wave cannot be distinguished from those associated with the secondary waves arising from the nonlinear interaction between the same planetary wave and any migrating (i.e., Sun-synchronous) tide (e.g., Forbes and Zhang, 2015). In the present context, secondary waves from the nonlinear interaction between the UFKW and a migrating tide can alias into the UFKW signature. Similarly, secondary waves from the nonlinear interaction between the Q6DW and a migrating tide can alias into the Q6DW signature. Miyoshi and Yamazaki (2020) examined the strong Q6DW signature in the noon-time EEJ during September 2019 using a numerical model, and demonstrated that the spectral peak corresponding to the Q6DW in the noon-time EEJ was largely due to neutral wind forcing by the secondary waves resulting from the nonlinear interaction between the Q6DW and migrating semidiurnal tide, rather than forcing by the Q6DW itself. At this time, it is not clear whether the EEJ spectral peaks corresponding to UFKW and Q6DW in Figure 4 are directly caused by these waves, or by the secondary waves from their nonlinear interactions with migrating tides which produce identical spectral peaks. For the lunar tide, on the other hand, its direct effect on the E-region dynamo currents is well established through previous research (e.g., Tarpley, 1970; Eccles et al., 2011).

3.3 Comparison with ICON/MIGHTI winds

The influence of the neutral wind on the EEJ is examined using concurrent measurements of the EEJ by CSES and wind profiles by ICON/MIGHTI. The criteria for a ICON/MIGHTI-CSES conjunction are as follows: 1) the wind measurement is obtained within $\pm$ 15 min from the time of the EEJ observation at the magnetic equator; 2) the wind measurement is obtained within $\pm 5 °$ from the magnetic equator; 3) the wind measurement is obtained within $\pm 10 °$ from the longitude of the EEJ measurement. These criteria are the same as those used by Yamazaki et al. (2021) for a comparison of ICON/MIGHTI winds and Swarm EEJ. Also following Yamazaki et al. (2021), only the data obtained under the quiet geomagnetic activity condition Hp30 $<$ 3 are used, where Hp30 (Yamazaki et al., 2022) is a geomagnetic activity index similar to the three-hourly Kp index (Matzka et al., 2021) but with a higher temporal resolution of 30 min. When there are more than one wind profiles that satisfy all the criteria for the same EEJ measurement, we use only one wind profile that has the smallest time difference from the EEJ measurement.

The results obtained from the analysis of the concurrent measurements of the CSES EEJ and ICON/MIGHTI winds are presented in Figure 5. Figure 5A compares the average magnetic eastward wind profiles during times of the eastward and westward EEJ. During times of the eastward EEJ, the average wind tends to be westward at all heights with relatively small height variation, while during times of the westward EEJ, the average wind is eastward at 100–120 km and westward above. Such a systematic difference is not seen in the average magnetic northward wind profiles for the eastward and westward EEJ, as depicted in Figure 5B. Earlier, Yamazaki et al. (2021) also reported the difference in the magnetic eastward wind profiles during times of the eastward and westward EEJ based on the Swarm EEJ and ICON/MIGHTI winds, but they were not able to completely separate the wind effect on the EEJ from the local time variation of the EEJ, as the local time of the Swarm EEJ measurement constantly changes. The results presented in Figures 5A,B are in alignment with those by Yamazaki et al. (2021) but at a fixed local time of 2 p.m., eliminating the ambiguity due to the local time change.

Figure 5

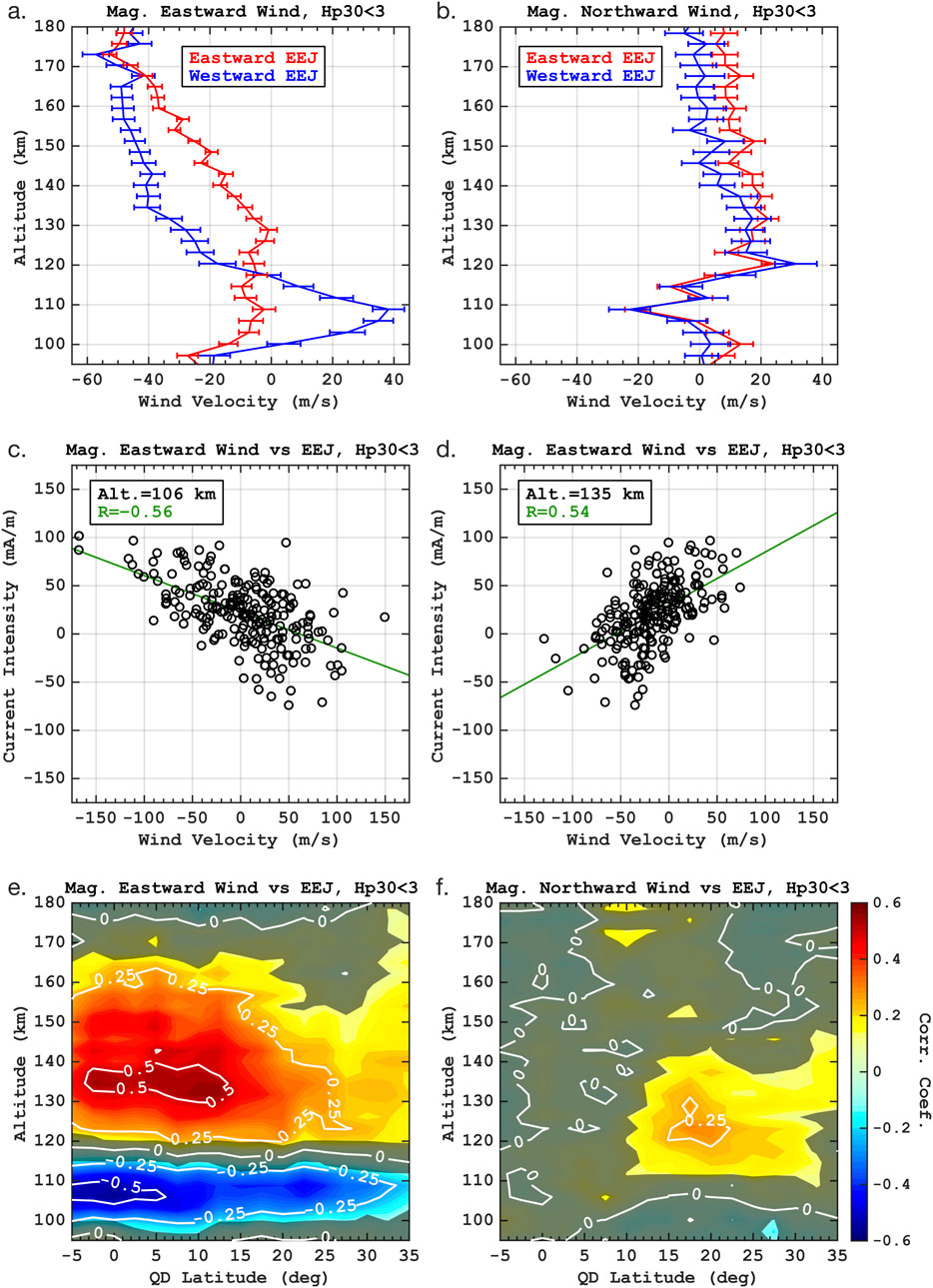
Figure 5. (A) Average vertical profiles of the ICON/MIGHTI magnetic eastward wind during concurrent measurements with the CSES equatorial electrojet (EEJ) at 2 p.m. local time for times of the eastward and westward EEJ. (B) Same as (A) but for the magnetic meridional wind. (C) Scatter plot for the ICON/MIGHTI magnetic eastward wind velocity at 106 km and the CSES EEJ intensity at 2 p.m. local time from their concurrent measurements. Note that the EEJ intensity is evaluated at an altitude of 110 km. The green line shows the linear regression. (D) Same as (C) but for the ICON/MIGHTI magnetic eastward wind velocity at 135 km. (E) Correlation coefficient between the CSES EEJ intensity at 2 p.m. local time at 110 km altitude at the magnetic equator and the ICON/MIGHTI magnetic eastward wind observed at the same time, plotted as a function of quasi-dipole (QD) latitude and altitude. The shading indicates the lack of statistical significance at the 95% confidence level. (F) Same as (E) but for the ICON/MIGHTI magnetic northward wind.

Figures 5C,D provide examples showing the relationship between the magnetic eastward wind and EEJ. At 106 km, there is a negative correlation ( $R$ = $-$ 0.56) between the two parameters, while at 135 km, the correlation is positive ( $R$ = 0.54). The results are consistent with previous observations based on the Swarm EEJ and ICON/MIGHTI winds (Yamazaki et al., 2021). The results are also consistent with those in the simulation study by Yamazaki et al. (2014a), which predicted that the EEJ intensity correlates negatively and positively with the equatorial eastward wind in the Hall region (100–120 km) and Pedersen region (120–180 km), respectively. We further extend the correlation analysis including other latitudes. Figure 5E presents the distribution of the correlation coefficient between the ICON/MIGHTI magnetic eastward wind and CSES EEJ as a function of magnetic latitude and altitude. The magnetic latitude is based on quasi-dipole (QD) coordinates (e.g., Laundal and Richmond, 2017). Significant correlation ( $p <$ 0.05) is found mostly between 100 and 115 km and between 120 and 160 km in altitude. The region of relatively high negative correlation ( $R < -$ 0.5) is limited near the magnetic equator between 105 and 110 km, while the region of relatively high positive correlation ( $R >$ 0.5) is limited between 130 and 140 km. They do not extend deep into middle latitudes, being mostly confined below $15 °$ magnetic latitude. Figure 5F is similar to Figure 5E but shows the correlation coefficient between the magnetic northward wind and EEJ. In this case, significant correlation is found around 10– $30 °$ magnetic latitude and between 110 and 140 km in altitude. However, the correlation is weak everywhere ( $| R | <$ 0.5), indicating that the meridional wind is not as effective as the equatorial zonal wind in modulating the EEJ. The spatial patterns of the correlation coefficient depicted in Figures 5E,F are in qualitative agreement with those predicted by Yamazaki et al. (2014a). It is noted that Figures 5E,F mainly focuses on the Northern Hemisphere, because ICON/MIGHTI measurements are limited between $\sim 10 °$ S and $\sim 40 °$ N latitude.

3.4 Seasonal and longitudinal variability

Figure 6 depicts the seasonal and longitudinal variations of the EEJ (Figures 6A,C,D) and eastward wind (Figure 6B), which are all evaluated at a fixed local time of 2 p.m. Figure 6A is derived from the CSES EEJ data during 2019 under the geomagnetically quiet condition of Hp30 $<$ 3. Figures 6C,D are based on the principal component analysis of the EEJ data (Kp $\leq$ 3) from Swarm A and B satellites and several ground-based magnetometers during 2018 and 2017 as described by Soares et al. (2022). The seasonal and longitudinal variations of the CSES EEJ for 2019 (Figure 6A) are in fair agreement with those derived from independent data for 2018 and 2017 (Figures 6C,D) with correlation coefficients $R$ = 0.70 for the 2018 case and $R$ = 0.72 for the 2017 case. Differences are expected from the year-to-year variation of the EEJ. Figure 6B shows the eastward wind at $2.5 °$ N latitude and at 109 km altitude as derived from the empirical model of Yamazaki et al. (2023), which is based on the ICON/MIGHTI wind measurements (Hp30 $<$ 3) during April 2020–March 2022. The selected latitude ( $2.5 °$ N) corresponds to the model grid closest to the zonal mean of the geographic latitude of the magnetic equator. As expected from the results in the previous section, there are some similarities between the seasonal-longitudinal patterns in the eastward wind and the EEJ. The correlation coefficients between the patterns in the eastward wind and the EEJ are $R = -$ 0.33, $R = -$ 0.37 and $R = -$ 0.39 for the 2019, 2018 and 2017 cases, respectively. It is noted that these comparisons are not based on simultaneous measurements of the EEJ and wind like those presented in the previous section. Also, the empirical model of Yamazaki et al. (2023) outputs the geographic eastward wind, not the magnetic eastward wind that was used in the previous section. Nevertheless, the correlations are reasonably good and close to those presented in the previous section (Figures 5C,E).

Figure 6

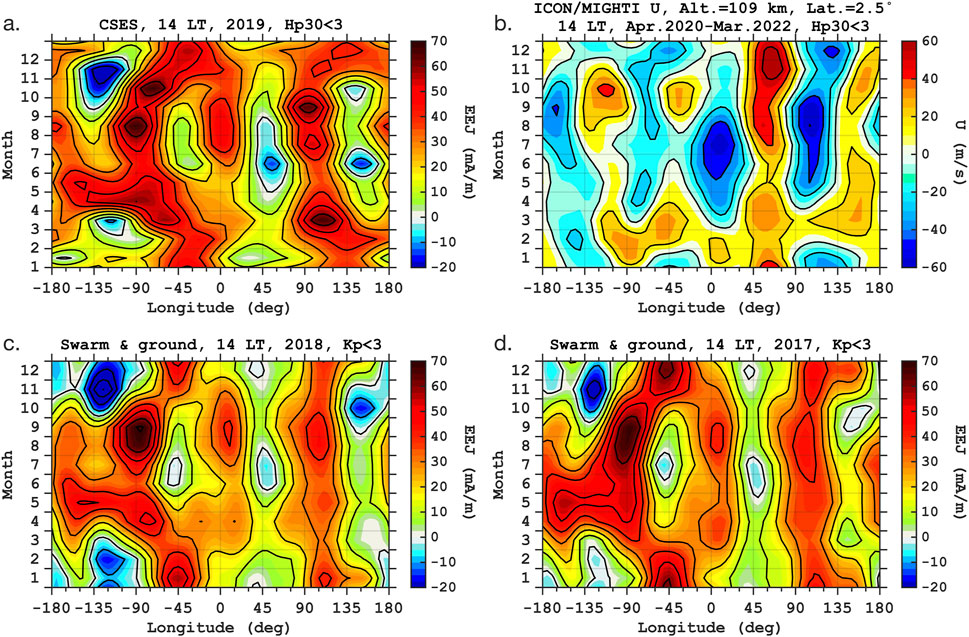
Figure 6. (A) CSES equatorial electrojet (EEJ) intensity at 2 p.m. local time at 110 km altitude for the year 2019, plotted as a function of longitude and month. (B) Eastward wind velocity at 2 p.m. local time at a latitude of $2.5 °$ N and an altitude of 109 km, as derived from the empirical wind model of Yamazaki et al. (2023). (C) EEJ intensity at 2 p.m. local time at 110 km altitude for the year 2018, as derived from the analysis of Soares et al. (2022). (D) Same to (C) but for the year 2017.

It is known that the longitudinal variation of the EEJ is dominated by a four-peak pattern during July–September (e.g., Lühr et al., 2008; Lühr and Manoj, 2013), which can also be seen in Figures 6A,C,D. A similar four-peak pattern exists in the eastward wind during these months (Figure 6B). Figure 7A compares the four-peak structures in the EEJ and eastward wind. It shows that the EEJ tends to be weak where the eastward wind at 109 km is strong, and vice versa. Since the wind velocities in the Yamazaki et al. (2023) model are described as a superposition of contributions by the zonal-mean wind, tides and stationary planetary waves, which are assigned with different combinations of $n$ and $s$ , it is possible to assess the relative importance of different ( $n$ , $s$ ) components for the four-peak structure in the zonal wind presented in Figure 7A. The table in Figure 7B lists the five largest ( $n$ , $s$ ) components of the eastward wind at longitudes of local maxima and minima. The components that have the magnitude larger than 5 m/s are highlighted in red, in consideration that the estimated 1- $σ$ uncertainty of individual components is typically in the range of 1.0–4.5 m/s (Yamazaki et al., 2023). The results suggest that DE3 is largely responsible for the four-peak structure in the eastward wind during July–September. Previous theoretical studies also concluded that DE3 is the major contributor to the four-peak structure of the equatorial zonal electric field and current (e.g., Ren et al., 2010; Jin et al., 2008; Wan et al., 2012; Pedatella et al., 2012a). The production mechanism and seasonal variation of DE3 are discussed in detail by Zhang et al. (2010). Apart from DE3, migrating tides (DW1 and SW2) and other non-migrating tides (DE2 and DE1) are relatively large, but their individual contributions are less than half of that by DE3. It is noted that although migrating tides do not have any longitudinal structure at a fixed local time, they can contribute to individual longitudinal peaks of the EEJ.

Figure 7

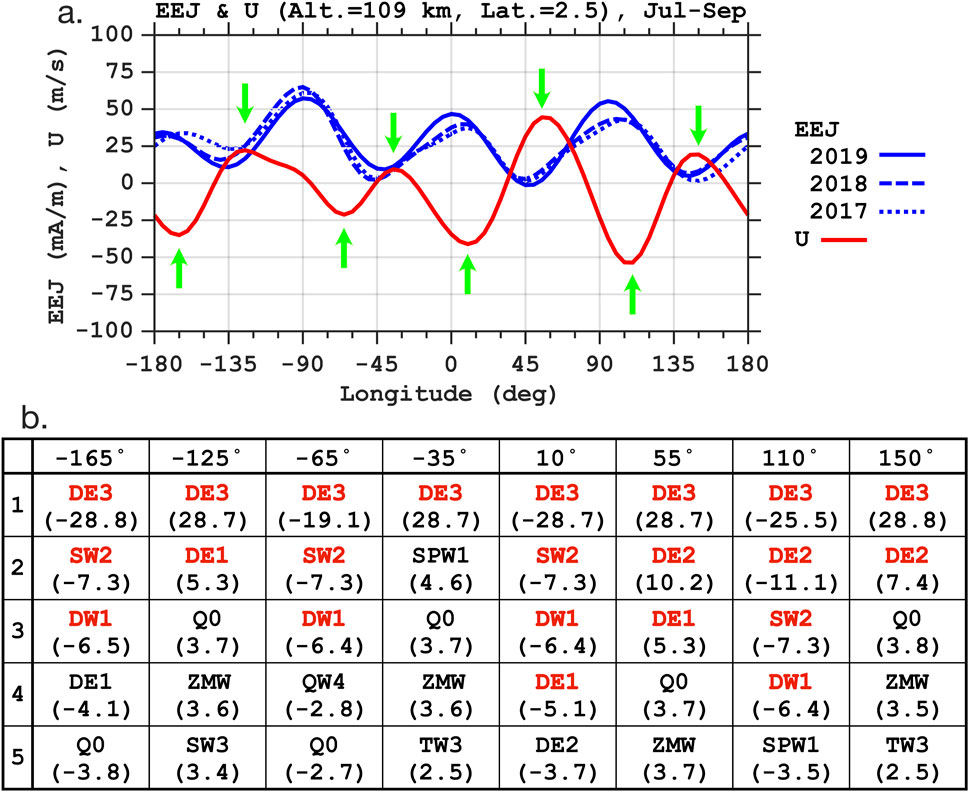
Figure 7. (A) Eastward wind velocity at 2 p.m. local time at a latitude of $2.5 °$ N and an altitude of 109 km during July–September, as derived from the empirical wind model of Yamazaki et al. (2023), along with the equatorial electrojet (EEJ) intensity at 2 p.m. local time at 110 km altitude at the magnetic equator for the years 2017, 2018 and 2019. The EEJ data for 2019 are obtained from the CSES magnetic field measurements, while those for 2017 and 2018 are based on the analysis presented by Soares et al. (2022). (B) Tidal composition of the eastward wind at longitudes of local maxima and minima. The components with the magnitude larger than 5 m/s are highlighted in red.

It is also known that during December–January, the four-peak pattern is largely absent from the longitudinal variation of the EEJ, and a two- or three-peak pattern is more evident (e.g., Lühr et al., 2008; Lühr and Manoj, 2013). Figure 8 is similar to Figure 7 but for December–January. In Figure 8A, the EEJ has two prominent local maxima around $45 °$ W and $125 °$ E longitudes. They coincide with the local minima of the eastward wind, underscoring the importance of the local wind effect on the EEJ. The table in Figure 8B suggests that there is no single dominant component that determines the longitudinal structure of the zonal wind during December–January, unlike the July–September case where DE3 is much larger than other components (see the table in Figure 7B). Nevertheless, eastward-propagating diurnal tides DE2 and DE3 are the most significant components. Westward-propagating semidiurnal tides SW2, SW3 and SW4 are also relatively large. It is interesting to note that DE3 is still important during December–January, while the amplitude of DE3 reaches its seasonal minimum around the December solstice (e.g., Forbes et al., 2003; Oberheide et al., 2006).

Figure 8

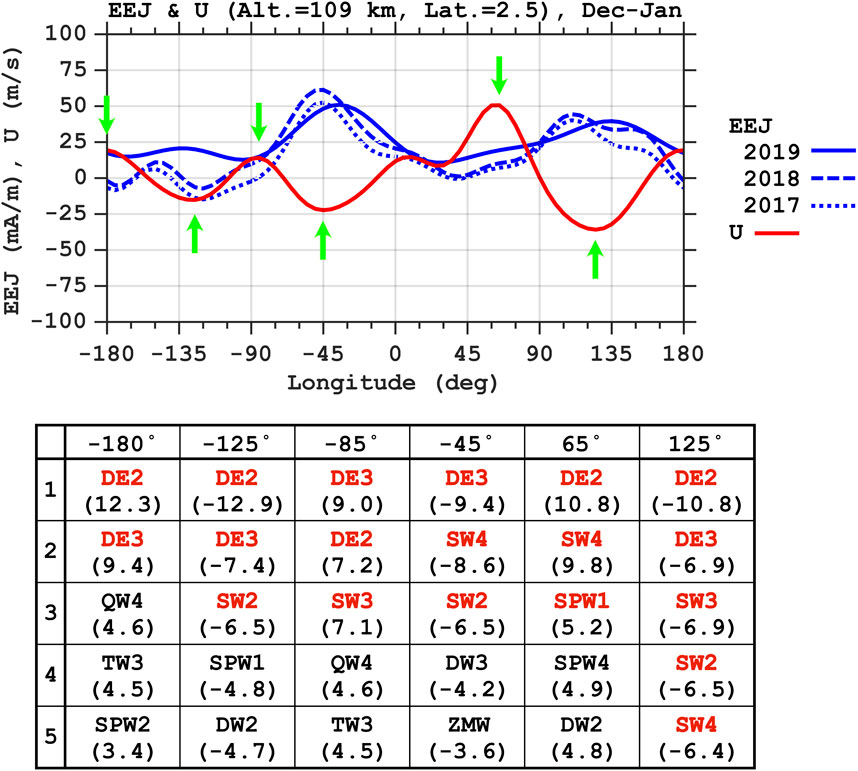
Figure 8. Same as Figure 7 but for December–January.

3.5 Comparison with in-situ electron density measurements

The in-situ measurements of $N_{e}$ from the LAP instrument onboard CSES ( $\sim$ 510 km altitude) are analyzed along with the CSES EEJ data. The $N_{e}$ data are used only when the EEJ data are available from the same orbit; see Figure 1A for the EEJ data availability. Also, only the measurements made under the geomagnetically quiet condition of Hp30 $<$ 3 are used. Figure 9A depicts the QD-latitude dependence of CSES/LAP $N_{e}$ at 2 p.m. local time during August 2018–May 2021. The meridional structure of $N_{e}$ for a given month exhibits a single peak near the magnetic equator within approximately $\pm 10 °$ QD latitude. This is somewhat unexpected, as previous studies based on in-situ measurements of $N_{e}$ at 2∼p.m. local time by other LEO satellites have shown a double-peak meridional structure known as the equatorial ionization anomaly (EIA), characterized by a density trough at the magnetic equator and density crests at approximately $\pm 15 °$ QD latitudes (e.g., Xiong et al., 2013; 2016b). The discrepancy may be attributable to two factors. The first is the altitude of the CSES satellite, which is higher than those of the satellites used in Xiong et al. (2013, 2016b). The double-peak EIA structure of $N_{e}$ is most evident at the altitude of the peak plasma density (300–400 km) (e.g., Lin et al., 2007; Tulasi Ram et al., 2009), and thus may not be visible at the altitude of the CSES satellite ( $\sim$ 510 km). The second is solar activity, which was very low during the period of interest (August 2018–May 2021; see Figure 1C for $F_{10.7}$ ). The altitude of the daytime peak plasma density over low latitudes tends to be lower during low solar activity periods (e.g., Yue et al., 2015; Zhao et al., 2017), which would make it difficult for the CSES satellite at $\sim$ 510 km to observe the double-peak EIA structure of $N_{e}$ . It is noted that the meridional profile of CSES/LAP $N_{e}$ from an individual orbit sometimes shows the double-peak structure, although it is not visible in the average meridional profiles depicted in Figure 9A.

Figure 9

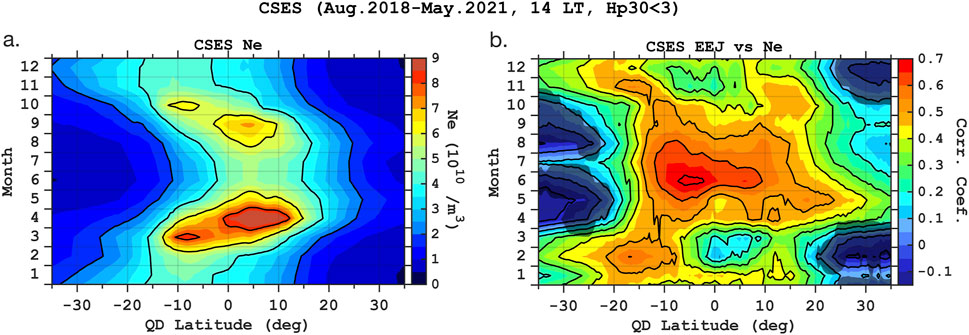
Figure 9. (A) Electron density $(N_{e})$ at 2 p.m. local time at an altitude of $\sim$ 510 km observed by the Langmuir probe onboard CSES, plotted as a function of quasi-dipole (QD) latitude and month. (B) Correlation coefficient between the CSES equatorial electrojet (EEJ) intensity at 2 p.m. local time at 110 km altitude and CSES $N_{e}$ from the same orbit. The shading indicates the lack of statistical significance at the 95% confidence level.

Figure 9A also presents the seasonal variation in CSES/LAP $N_{e}$ at 2 p.m. local time. $N_{e}$ shows a semiannual variation with equinoctial maxima around the magnetic equator between approximately $\pm 10 °$ QD latitude. An annual variation with a local-summer maximum becomes more prominent with increasing latitude. The results are in agreement with the earlier study by Zhu et al. (2023), which examined the annual and semiannual variations in CSES/LAP $N_{e}$ . The seasonal dependence of $N_{e}$ involves various mechanisms. One important factor is the seasonal variation in the solar zenith angle. The main constituent of the F-region plasma is atomic oxygen ion $O^{+}$ , which is produced through the photoionization of atomic oxygen O. The ionization by solar radiation depends on the solar zenith angle (Chapman, 1931), which varies semiannually at low latitudes and annually at higher latitudes due to Earth’s geometry relative to the Sun. Another important factor is the seasonal variation in neutral composition. The $O^{+}$ density is controlled not only by the production of $O^{+}$ through the photoionization of O, but also by the loss of $O^{+}$ by recombination through ion-exchange reactions that involve $N_{2}$ . Thus, the $O^{+}$ density (and hence $N_{e}$ ) varies with the density ratio [O]/( $N_{2}$ ) (e.g., Rishbeth, 1998). The neutral composition of the thermosphere, [O]/( $N_{2}$ ), varies with the season due to the large-scale circulation of the thermosphere (Fuller-Rowell, 1998) as well as wave forcing from the middle atmosphere (Jones Jr et al., 2017; 2018).

Figure 9B displays the correlation coefficient between the CSES EEJ and $N_{e}$ as a function of magnetic latitude and month of year. The correlation was calculated between the EEJ at the magnetic equator and $N_{e}$ binned at every $0.5 °$ QD latitude from the same orbit. At low latitudes below $\pm 20 °$ QD latitude, the correlation is positive and significant ( $p <$ 0.01) throughout the year but $R$ varies considerably, in the range of 0.10–0.73, depending on the latitude and month. The positive correlation at low latitudes is anticipated as the effect of the equatorial plasma fountain (e.g., Balan et al., 2018). That is, in the presence of the eastward electric field, which is associated with the EEJ, low-latitude plasmas move upward to F-region altitudes by the E $\times$ B drift. Stolle et al. (2008) reported a positive correlation between the EEJ intensity and F-region plasma density. However, they did their analysis exclusively at the South American sector, and did not reveal seasonal dependence. In this respect, our analysis is an extension of previous work. Stolle et al. (2008) found that the maximum response of the F-region plasma density to a change in the EEJ intensity occurs a few hours after the EEJ variation. In the present study, we are not able to assess the delay in the $N_{e}$ response to the EEJ because CSES $N_{e}$ and EEJ measurements are made at the same local time.

At higher latitudes (above $\pm 20 °$ ), the correlation is significant only in the summer hemisphere. The hemispheric difference in the $N_{e}$ response to the EEJ might be due to the effect of the meridional wind. The neutral wind at F-region altitudes blows from the summer hemisphere to the winter hemisphere (e.g., Dickinson et al., 1977; Drob et al., 2015). The meridional wind pushes the plasmas upward along the magnetic field line in the summer hemisphere and downward in the winter hemisphere. Thus, the meridional wind acts to help and hinder the vertical transport of the plasmas to higher altitudes in the summer and winter hemispheres, respectively, which might affect the detectability of the $N_{e}$ response to the EEJ at the CSES altitude ( $\sim$ 510 km).

Figure 10 compares the latitudinal structures of $N_{e}$ during times of the eastward and westward EEJ. $N_{e}$ is greater during times of the eastward EEJ regardless of the month. The difference in $N_{e}$ is more prominent in the Southern Hemisphere during October–March and in the Northern Hemisphere during April–September, which could be due to the meridional wind effect discussed above. Whether the EEJ is eastward or westward, the double-peak EIA structure is hardly visible in the average meridional profiles of CSES/LAP $N_{e}$ at $\sim$ 510 km under these low solar activity conditions.

Figure 10

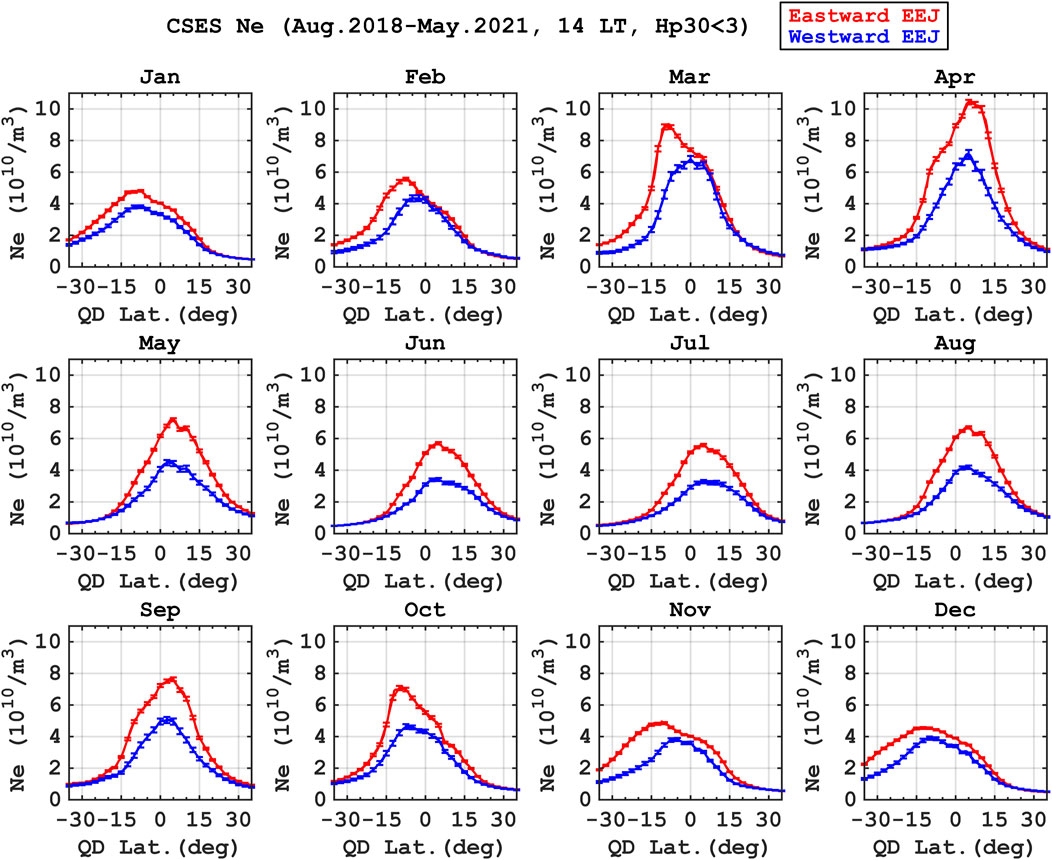
Figure 10. Electron density $(N_{e})$ at 2 p.m. local time at an altitude of $\sim$ 510 km observed by the Langmuir probe onboard CSES during times of the eastward and westward equatorial electrojet (EEJ) at 110 km altitude.

4 Summary and conclusion

The magnetic field measurements by the CSES mission provide the first continuous satellite observations of the afternoon equatorial electrojet (EEJ) at a fixed local time of 2 p.m. during the low solar activity period of July 2018–April 2022. The method used for the retrieval of the EEJ is the same as that developed for the Swarm EEJ product (Alken et al., 2013b; 2015). The comparison between the CSES and Swarm EEJ intensities during satellite conjunctions reveals a good correlation between the two (Figure 2), supporting the reliability of the CSES data in capturing the EEJ variability. The CSES data, however, seem to underestimate the EEJ intensity by $\sim$ 15%, the reason for which is still to be investigated.

Using the CSES data, it is possible to derive the zonal wavenumber-period spectrum of day-to-day EEJ variation for any given time period (e.g., Figure 3). The climatological mean spectrum of the EEJ at 2 p.m. local time is presented for the first time (Figure 4), which reveals three distinct oscillatory components with comparable amplitudes: (1) an eastward-propagating 2–3-day oscillation with zonal wavenumber 1, (2) a westward-propagating 5–6-day oscillation with zonal wavenumber 1, and (3) a zonally-symmetric 14–15-day oscillation. They all can be associated with atmospheric waves that propagate from the lower atmosphere. That is, (1), (2) and (3) can be attributed to the ultra-fast Kelvin wave, quasi-6-day wave, and atmospheric lunar tide, respectively. However, uncertainty remains as to whether (1) and (2) are caused by the direct effect of those waves or by the secondary waves resulting from their nonlinear interactions with migrating tides.

The comparison of the CSES EEJ with the concurrent measurements of neutral winds by ICON/MIGHTI shows that the EEJ intensity at 2 p.m. local time at 110 km altitude is positively and negatively correlated with the magnetic eastward wind in the Hall region (100–115 km) and Pedersen region (120–160 km) over the magnetic equator, respectively (Figure 5). This is consistent with Swarm-ICON/MIGHTI observations including different local times (Yamazaki et al., 2021). The present results exclude the possibility that the correlation between the EEJ and magnetic eastward wind is due to similarity in their local time variations. Also, the dependence of the correlation on QD latitude (Figures 5E,F) is addressed. The results are in agreement with the previous model predictions at the local noon (Yamazaki et al., 2014a).

The longitudinal and seasonal variations of the EEJ are compared with those in the equatorial zonal wind at 109 km as derived from the empirical model of Yamazaki et al. (2023) (Figure 6), which expresses wind velocities as a superposition of contributions by the zonal-mean wind, tides and stationary planetary waves. The longitudinal variation of the EEJ at 2 p.m. local time is dominated by a four-peak pattern during July–September, which can be largely explained by the non-migrating diurnal tide DE3 (Figure 7). During December–January, a two- or three-peak pattern is more evident, which is mainly due to the combined effect of the non-migrating diurnal tides DE3 and DE2 (Figure 8).

The CSES EEJ data are also compared with the in-situ electron density $(N_{e})$ measurements by the LAP instrument onboard CSES from the same orbit. There is a positive correlation between the EEJ intensity and $N_{e}$ at low latitudes (below $\pm 20 °$ magnetic latitude) regardless of the season (Figures 9, 10), which can be explained as the effect of the equatorial plasma fountain. The magnitude of the correlation is seasonally dependent. For example, the correlation coefficient $R$ is larger for April–September (0.4–0.7) than for October–March (0.1–0.4) near the magnetic equator. The positive correlation extends to higher latitudes but only in the summer hemisphere. The reduced correlation in the winter hemisphere might be due to the meridional wind, which pushes the plasmas down along the magnetic field line, possibly preventing the plasmas to reach the altitude of the CSES spacecraft ( $\sim$ 510 km).

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: CSES scalar magnetic field measurements and electron density measurements are available on the website at https://www.leos.ac.cn. Swarm EEJ data are available on the website at https://swarm-diss.eo.esa.int. ICON/MIGHTI neutral wind data are available on the website at https://icon.ssl.berkeley.edu/Data/Data-Product-Matrix. The EEJ data for 2017 and 2018 presented in Figures 6–8 are available on the website https://doi.org/10.5880/GFZ.2.3.2022.003.

Author contributions

YoY: Writing–original draft, Writing–review and editing. CS: Writing–review and editing. CX: Funding acquisition, Writing–review and editing. PA: Data curation, Funding acquisition, Methodology, Writing–review and editing. YaY: Data curation, Writing–review and editing. ZZ: Data curation, Funding acquisition, Writing–review and editing. BH: Data curation, Funding acquisition, Validation, Writing–review and editing. RY: Data curation, Methodology, Validation, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work is supported by the Dragon six cooperation 2024–2028 (Project No. 95437), the National Key Research and Development Program of China 2023YFE0117300, and the National Natural Science Foundation of China Grant No. 42274214. This work is also supported by Swarm DISC activities funded by ESA under contract No. 4000109587/13/I-NB.

Acknowledgments

The authors thank the engineering and science teams of the CSES, Swarm and ICON missions. CSES is supported by China National Space Administration (CNSA) and China Earthquake Administration (CEA). The Swarm mission is supported by the European Space Agency (ESA). The ICON mission is supported by National Aeronautics and Space Administration (NASA) Explorers Program (NNG12FA45C and NNG12FA42I).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor declared a past collaboration with the author CS at the time of review.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdul Hamid, N. S., Liu, H., Uozumi, T., and Yoshikawa, A. (2015). Empirical model of equatorial electrojet based on ground-based magnetometer data during solar minimum in fall. Earth, planets space 67, 205–208. doi:10.1186/s40623-015-0373-1