Constraining the minimally extended varying speed of light model using time dilations

Lee, Seokcheon

doi:10.3389/fspas.2024.1453806

MINI REVIEW article

Front. Astron. Space Sci., 02 August 2024

Sec. Cosmology

Volume 11 - 2024 | https://doi.org/10.3389/fspas.2024.1453806

This article is part of the Research Topic Frontiers in Astronomy and Space Sciences: A Decade of Discovery and Advancement - 10th Anniversary Conference View all 5 articles

Constraining the minimally extended varying speed of light model using time dilations

Seokcheon Lee*

Department of Physics, Institute of Basic Science, Sungkyunkwan University, Suwon, Republic of Korea

The Robertson–Walker (RW) metric, derived from the cosmological principle and Weyl’s postulate, characterizes the $Λ$ CDM cosmological model. Traditionally, in this framework, the assumption of a constant speed of light leads to specific cosmological time dilation (TD). However, because the Robertson–Walker metric lacks a way to define time dilation, the speed of light, like wavelength and temperature, may vary with cosmic time. The minimally extended varying speed of light (meVSL) model fits standard cosmological observations while considering the evolution of physical constants. One model-independent test for the meVSL model is cosmological time dilation. However, current data cannot distinguish between the meVSL model and the standard model.

1 Introduction

The contemporary $Λ$ CDM model, based on the Robertson–Walker (RW) metric, assumes large-scale spatial homogeneity and isotropy, supported by the uniformity of the cosmic microwave background (CMB) (Hinshaw et al., 2013; Aghanim et al., 2020) and large-scale structures (Guzzo et al.; Cawthon et al., 2022). This model describes an expanding universe, evidenced by the redshift of light from distant galaxies, where the redshift indicates the stretching of photon wavelengths due to space expansion (Weinberg, 2008).

The traditional RW metric can derive a specific relationship regarding cosmological time dilation (TD) based on the postulate of a constant speed of light. However, it is not directly derived from the metric’s fundamental principles. Various projects using supernova light curves (Leibundgut et al., 1996; Riess et al., 1997; Foley et al., 2005; Blondin and Tonry, 2007; Blondin et al., 2008; White et al.), gamma-ray bursts (Band, 1994; Norris et al., 1994; Wijers and Paczynski, 1994; Meszaros and Meszaros, 1996; Lee and Petrosian, 1997; Chang, 2001; Crawford; Zhang et al., 2013; Singh and Desai, 2022), and quasars (Hawkins, 2001; Dai et al., 2012; Lewis and Brewer, 2023) have attempted to measure cosmological TD, but conflicting results have prevented convincing detection. The speed of light in the RW metric might change with cosmic time without clear rules determining TD, just like other physical parameters like temperature and mass density. This variation supports the hypothesis of a varying speed of light (VSL) (Lee, 2021; Lee, 2023a; Lee, 2023b; Lee, 2024). In the RW universe, a hypersurface of specific time defines uniform physical quantities such as temperature or density, and these quantities are cosmologically redshifted due to the universe’s expansion.

One can rewrite the RW metric with the possibility of the VSL as follows:

\begin{array}{l} d s^{2} = - c {)t(}^{2} d t^{2} + a {)t(}^{2}]\frac{d r^{2}}{1 - K r^{2}} + r^{2})d θ^{2} + \sin^{2} θ d ϕ^{2}([ \\ \equiv - c {)t(}^{2} d t^{2} + a {)t(}^{2} d l_{3 D}^{2} . \end{array} (1)

Physical quantities like the scale factor $a (t)$ , density $ρ (t)$ , pressure $P (t)$ , temperature $T (t)$ , and $c (t)$ evolve over cosmic time, governed by solutions from Einstein’s field equations and Bianchi’s identity, accounting for fluid equations of state. Redshift calculation involves using the geodesic equation in co-moving coordinates, ensuring the consistency of radial light signals $d l_{3 D}$ :

\begin{array}{l} d l_{3 D} = \frac{c (t_{i}) d t_{i}}{a (t_{i})} : \frac{c_{1} d t_{1}}{a_{1}} \\ = \frac{c_{2} d t_{2}}{a_{2}} \Rightarrow \{\begin{cases} c_{1} = c_{2} = c & i f \frac{d t_{1}}{a_{1}} = \frac{d t_{2}}{a_{2}} S M C \\ c_{1} = {)\frac{a_{1}}{a_{2}}(}^{\frac{b}{4}} c_{2} & i f \frac{d t_{1}}{a_{1}^{1 - \frac{b}{4}}} = \frac{d t_{2}}{a_{2}^{1 - \frac{b}{4}}} m e V S L \end{cases}), \end{array} (2)

where SMC stands for the standard model cosmology and $d t_{i} = 1 / ν (t_{i})$ represents the time interval between successive crests of light at $t_{i}$ (i.e., the inverse of the frequency $ν_{i}$ at $t_{i}$ ). This expresses the TD in the meVSL model as $T_{0} = {(1 + z)}^{1 - b / 4} T$ (i.e., the present time is dilated by a factor ${(1 + z)}^{1 - b / 4}$ ).

2 Methods

In an expanding universe described by the RW metric, galaxies uniformly recede from each other, and TD affects clocks differently depending on the distance. Whether the speed of light is constant or not influences local clock rates, thus playing a crucial role in understanding TD. Therefore, it is important to obtain the precise relationship of TD by comparing observational data such as distant Type Ia supernovae (SNeIa) light curves and spectral evolution.

Supernova light curves (LCs) track brightness changes over time, crucial for understanding their evolution and properties, especially for SNeIa used as cosmological standard candles. Comparing LCs across different distances reveals TD effects due to cosmic expansion, indicating the stretching of distant LCs compared to nearby LCs. The spectral evolution of SNeIa provides a reliable method to measure aging and confirm TD, offering insights into the Universe’s expansion rate and dark energy dynamics.

We present aging rate measurements of 13 high-redshift SNeIa data provided in Blondin et al. (2008), as shown in Table 1. These data are derived from a sample of 35 spectra of 13 SNeIa in the redshift range $0.28 \leq z \leq 0.62$ , comparing the differences between observer- and rest-frame ages.

Table 1

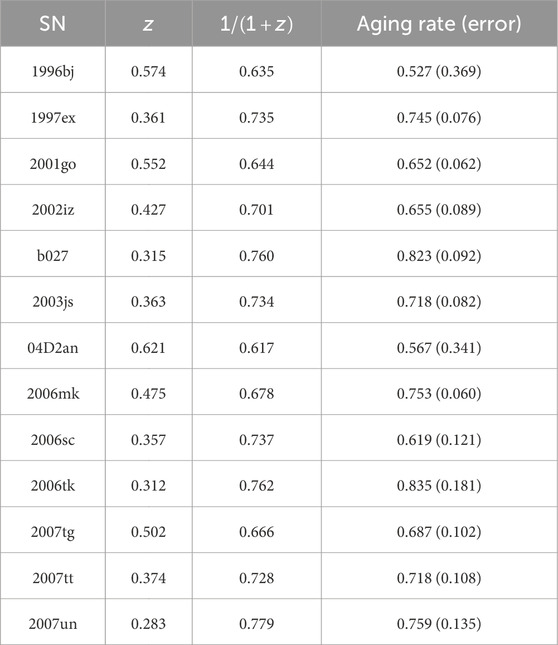
Table 1. Aging rate measurements from SNeIa observation (Blondin et al., 2008).

We perform a least-square fit to the data using the SMC and meVSL model predictions. The fitting is given by

χ^{2} = \sum_{i = 1}^{13} \frac{{({(1 + z_{i})}_{obs}^{- 1} - {(1 + z_{i})}^{- 1 + b / 4})}^{2}}{σ_{i}^{2}}, (3)

where ${(1 + z_{i})}_{obs}^{- 1}$ corresponds to the 13 data points and $σ_{i}$ represents their errors, as listed in Table 1.

3 Results

The aging rate analysis based on the SMC, using $1 / (1 + z)$ , achieves a good fit to the data with $χ^{2} = 3.6$ for 13 degrees of freedom (d.o.f), indicating a high goodness-of-fit (GoF) of 99.5%. Conversely, applying the meVSL model yields a best-fit parameter value of $b = 0.198$ with a 1- $σ$ error interval of $\pm 0.415$ . The minimum $χ^{2}$ value obtained is 3.4, with 12 d.o.f, corresponding to a GoF of 99.3%. Detailed results are summarized in Table 2 and illustrated in Figure 1, where vertical lines represent the 13 data points along with their measurement errors. The dashed line illustrates the SMC prediction of the aging rate $1 / (1 + z)$ , while the solid line with shaded regions depicts the meVSL model within its 1- $σ$ confidence interval. These findings suggest that the current observational data do not conclusively distinguish between the predictions of the meVSL model and those of the SMC.

Table 2

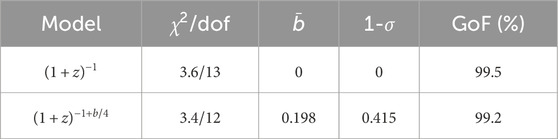
Table 2. A simple $χ^{2}$ analysis for both the SM and meVSL model using TD data (Blondin et al., 2008). The best-fit value for the $b$ exponent is $b = 0.198$ with 0.415 for the 1- $σ$ confidence interval.

Figure 1

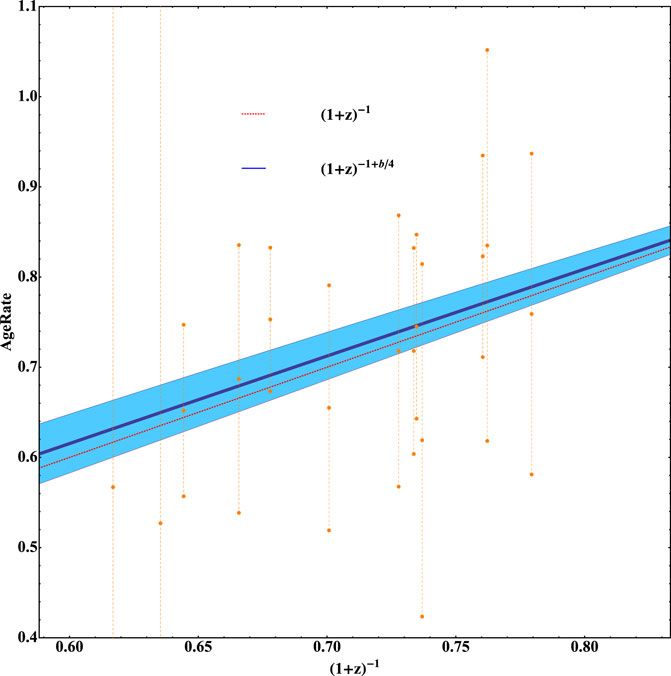
Figure 1. Time dilation for two models with data points. The dashed line depicts the SC prediction of TD. The thick solid line represents the best-fit value predicted TD of the meVSL model. The shaded region represents the 1- $σ$ confidence interval region.

4 Discussion

We derived the time dilation formula in the minimally extended varying speed of light model as $T (z) = T_{0} {(1 + z)}^{1 - b / 4}$ . Analyzing data from 13 high-redshift SNeIa, we found $b = 0.198 \pm 0.415$ at the 1- $σ$ confidence level, less precise than cosmological chronometers (Lee, 2023c). Using $(H_{0}, Ω_{m 0})$ values from Planck18 (Aghanim et al., 2020) and Pantheon22 (Brout et al., 2022), we obtained optimal $b$ fits of $- 0.105 \pm 0.178$ and $0.584 \pm 0.184$ , respectively. These results align with the standard model cosmology and the meVSL model, reflecting data from SNe where distinguishing between models remains inconclusive. Recent Dark Energy Survey results also support the standard model of cosmology (White et al.). Time dilation data from gamma-ray bursts are sparse (Singh and Desai, 2022), but a study of 190 quasars confirmed cosmic time dilation (Lewis and Brewer, 2023), detecting redshift-dependent effects with $n \equiv (1 - b / 4) = 1.2 8_{- 0.29}^{+ 0.28}$ . Challenges in previous quasar studies highlight the need for larger, diverse samples to detect time dilation effects across various redshifts. Future observations may clarify model distinctions as data accrues. A study exploring an Einstein–de Sitter cosmological model that generalizes the redshift-time dilation relation demonstrates that this model can fit the data from 1,048 supernovae comparably to the standard model (Benedetto et al., 2024). The authors propose this intriguing formalism as an alternative to the standard cosmological model without the need for dark energy. This study appears to be another interesting research using time dilation.

Author contributions

SL: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, validation, visualization, writing–original draft, and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was funded by the National Research Foundation of Korea (NRF), funded both by the Ministry of Science, ICT, and Future Planning (grant no. NRF-2019R1A6A1A10073079) and the Ministry of Education (grant no. NRF-RS202300243411).

Acknowledgments

The author is grateful for the invitation to present at the ‘Frontiers in Astronomy and Space Sciences: A Decade of Discovery and Advancement, 10th Anniversary Conference’. Additionally, the author would like to express his gratitude to the editor, who requested a mini-review related to this presentation.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aghanim, N., Akrami, Y., Arroja, F., Ashdown, M., Aumont, J., Baccigalupi, C., et al. (2020). Planck2018 results: I. Overview and the cosmological legacy ofPlanck. Astron. Astrophys. 641, A1. arXiv:1807.06205 [astro-ph.CO]]. doi:10.1051/0004-6361/201833880