Resistivity effect in the vicinity of a coronal magnetic null point

Introduction: We aim to examine how magnetic resistivity impacts the movement of magnetoacoustic waves near a magnetic null-point in the solar corona.

Method: The resistive, nonlinear MHD simulations are solved by the PLUTO code in 2.5D for different amount of the resistivity.

Results and Discussion: Propagation of magnetoacoustic waves in the vicinity of a magnetic null point has the potential to create current sheets with high current density excitation and plasmoid generation. During the entire duration of the simulation, it is discovered that plasma density became significant due to the plasmoid and also current density is high for high resistivity. It is depicted that high resistivity also leads to bigger plasmoids or magnetic islands in comparison to small resistivity.

1 Introduction

Due to the strong magnetic field gradients around magnetic null points, MHD waves endure substantial consequences nearby these null points. Because magnetic null points are rather common in the solar atmosphere, it becomes crucial to study properties of the MHD waves and their interaction with the surrounding plasma McLaughlin et al. (2011); Sabri et al. (2018); Sabri et al. (2019); Sabri et al. (2020a); Sabri et al. (2020b); Karampelas et al. (2022a); Sabri et al. (2021); Sabri and Ebadi (2021); Sabri et al. (2023); Sabri et al. (2022). Longcope and Priest (2007) found that fast magnetoacoustic waves propagate at the Alfvén speed independent of the resistivity, at least in the linear regime. Furthermore, it has been suggested that turbulent activities take place within the current sheet in the nonlinear regime, potentially resulting in an impact comparable to resistivity.

The impact of turbulence on small scales was investigated by Jacobson and Moses (1984) through the manipulation of ohmic resistivity. This would have a negligible impact on the Sweet-Parker rate. In a similar manner, the two-dimensional simulations conducted by Matthaeus and Lamkin (1985); Matthaeus and Lamkin (1986) were not able to give a comprehensive understanding of the actual three-dimensional processes involved in magnetic reconnection. The Alfvenic mode is responsible for the movement of the magnetic field. This particular characteristic is not present in 2D simulations. It is crucial to note that we employed the 2.5D method, which successfully solved the problem.

Researchers have explored a methodology for numerically simulating the complete nonlinear progression of the field and flow’s shapes in reaction to a disturbance in a closed system. This system allows for a finite amount of energy supplied to participate Craig and McClymont (1993); Hassam (1992); Craig and Watson (1992); McClymont and Craig (1996); Priest and Forbes (2000); Kowal et al. (2020). Such simulations have indicated that the collapse is eventually restricted by either resistive diffusion or the build up of an opposing pressure by the associated converging flow. This can occur through plasma compression or the compression of a guide field component perpendicular to the plane. Null collapse is still of interest as it can create current sheets in different scenarios, even though it may not lead to energy release right away due to the plasma parameters. In addition, there has been minimal analytical or computational research conducted on the behavior that occurs following the implosion. Afterwards, we made the decision to thoroughly examine this procedure, specifically focusing on its correlation with resistivity, and explore the developments of flows and current density following an implosion.

Similar to null collapse, there are analytical solutions available for cold, ideal plasmas that forecast singularity in finite time (Forbes, 1982). Although analytical forecasts expect singularity in a finite amount of time, in reality, the implosions are also constrained by their eventual transition to small diffusive scales. The limitations of 1D similarity solution were discussed by Forbes (1982). The study conducted numerical simulations of the process without taking into account resistivity and found that the numerical and analytical solutions matched well during the initial collapse phase under specific assumptions. Recently, Takeshige et al. (2015) revisited the problem under adiabatic limitations, considering ideal MHD and the presence of finite ambient gas pressure. The researchers confirmed the presence of a shock and the existence of a thin current sheet that remains in a static state of force balance. This balance occurs between the magnetic pressure directed inwardly and the gas pressure gradient directed outwardly. They discovered that when dissipation is not present, the total amount of current remains constant, along with the magnitudes of related factors like current density and the force that causes the flow, known as the Lorentz force. In other words, the collapse of a magnetic X-point into an O-point is a type of MHD implosion where the null point acts as the center for the converging magnetic flux. The compression and refraction of plasma occur as a result of the converging and diverging flows caused by the Lorentz force. The collapsing process continues until certain events, such as the plasma pressure increasing, occur and are able to halt this concentration.

The collapses of X-points are explained by a model that considers the reconnection process to be dependent on time. The central concept is that disturbances should be more likely to concentrate around the null points due to the refraction effect (Thurgood and McLaughlin, 2012). The phenomenon of refraction could cause the accumulation of high current density on a small scale, leading to effective dissipation (Dungey, 1953). The production of thin layers of strong electric current, referred to as current sheets, is essential for quick reconnection (Thurgood et al., 2018b). Thurgood et al. (2018b) introduced initial background magnetic field perturbations or different initial current density in 1D and 2D. They examined the characteristics of a nonlinear oscillation in the vicinity of the null point and investigated how resistivity and perturbation energy influenced the oscillation’s duration. They discovered that for linear disturbances, the period of oscillation is determined by the inverse Lundquist number.

In the past few years, several research studies have examined the mechanism of oscillatory reconnection to gain a better understanding of how it is influenced by different parameter modifications (Talbot et al., 2024; Karampelas et al., 2022a; Karampelas et al., 2022b). The researchers investigated the process of oscillatory reconnection by conducting a study on a cold plasma with a homogeneous density. The study included adjusting the resistivity parameter over a wide range of eight orders of magnitude Talbot et al. (2024). They investigated the evolution of the oscillating current density at the null point and its associated periodicity. They performed calculations of the resistive nonlinear magnetohydrodynamic (MHD) equations in 2.5 dimensions, considering different degrees of resistivity. It was found that there was no connection between the level of background resistivity and the frequency of the oscillatory reconnection mechanism. However, they showed that the resistivity is essential in determining both the maximum level of electric current and the rate at which it diminishes. Additionally, Karampelas et al. (2022a); Karampelas et al. (2022b); Karampelas et al. (2023) aimed to examine the influence of various environmental factors, including temperature, density, and the strength of the background magnetic field, on the duration of the oscillatory reconnection mechanism. These studies result in the derivation of an empirical formula for the period of the oscillatory reconnection in the electric current density.

In this study, we build upon the findings of the research conducted by Sabri et al. (2020a) to explore the effects of resistivity on the properties of magnetoacoustic waves. Furthermore, we also examine the impact of plasma parameters and plasma flows. Due to not utilizing the cold plasma approximation, there exists a slow magnetoacoustic wave in addition to the fast mode. This introduces complexity as their coupling and interactions are also present. In this statement, varying levels of resistivity have been added to the experimental configurations while keeping all other factors the same.

2 Numerical setup

The focus of this study is is based on the MHD theory. It emphasizes the overall movement of MHD waves near a magnetic null-point. This study does not take into account the impacts of solar gravity and plasma viscosity. This is because their importance in the solar corona is lower compared to the lower solar atmosphere. This declaration is backed up by the extremely low plasma density in the solar corona (Aschwanden, 2005). Therefore, the sole factor that is taken into account as a dissipative term in the MHD equations is the magnetic diffusivity. It is important to mention that the topological dissipation discussed by Parker (1979) is a way of explaining the heating of the corona. This occurs because magnetic fields in ideal plasmas naturally form tangential discontinuities, which are seen as electric current singularities. Even though the magnetic diffusivity might be low in the solar corona, the presence of strong current sheets plays a significant role in the dissipation of energy. This led to a desire to study the impacts associated with the magnetic diffusivity and the magnetic topological dissipation in current sheets.

Here, the resistive MHD set of equations is considered by taking in to account a constant scalar magnetic diffusivity $(\eta )$ as

$\rho \left[\frac{\partial \mathbf{V}}{\partial t}+\left(\mathbf{V}\cdot \nabla \right)\mathbf{V}\right]=\left(\frac{1}{\mu }\nabla \times \mathbf{B}\right)\times \mathbf{B}-\nabla P,(1)$

$\frac{\partial \mathbf{B}}{\partial t}=\nabla \times \left(\mathbf{V}\times \mathbf{B}\right)+\eta {\nabla }^2\mathbf{B},(2)$

$\frac{\partial \rho }{\partial t}+\nabla \cdot \left(\rho \mathbf{V}\right)=0,(3)$

$\frac{\partial P}{\partial t}+\left(\mathbf{V}\cdot \nabla \right)P=-\gamma P\nabla \cdot \mathbf{V}+\left(\gamma -1\right)\eta /\left(\mu \right){\left(\nabla \times \mathbf{B}\right)}^2,(4)$

$\nabla \cdot \mathbf{B}=0,(5)$

where $\mathit{\rho }$, $\mathbf{V}$, $\mathbf{B}$, and $P$ represent the plasma density, plasma velocity, magnetic field, and thermal plasma pressure, respectively. The constants $\mu$, $\eta$, and $\gamma =5/3$ denote the magnetic permeability, the magnetic diffusivity, and the ratio of specific heats at constant pressure and volume, respectively. We consider the permeability of vacuum, i.e., $\mu =4\pi \times 10^{-7}$ ${\mathrm{H}\mathrm{m}}^{-1}$. Note that the magnetic diffusivity is considered constant in the whole domain. Besides, initial plasma temperature and plasma beta have the value $T_0=6\times 10^5$ K and $\beta =0.01$, respectively.

For the initial configuration, we consider a static $({\mathbf{V}}_{\mathbf{0}}=0)$ background plasma in Cartesian coordinates with a magnetic field given by the Equation 6.

$\mathbf{B}=\frac{B_0}{L}x{\vec{1}}_x-\frac{B_0}{L}y{\vec{1}}_y,(6)$

The symbol $B_0=10^{-3}$ T represents a specific magnetic field strength, while the variable $L=10^8$ cm represents the scale at which magnetic field changes occur. The magnetic equilibrium considered in the present study is curl-free and includes a single null-point located at the origin. It is important to mention that this magnetic configuration is invalid at relatively far distances from the null point because the magnetic field strength becomes infinite as it moves away from the null point. The vector potential can also be used to represent the magnetic field (in according to the Equation 7).

$\mathbf{A}=\frac{B_0}{L}xy{\vec{1}}_z.(7)$

In the present study, the PLUTO code is used which is perfect for simulating nonlinear time-dependent dynamics of waves in magnetized plasmas (Mignone et al., 2007). The resistive MHD set of Equations 1–5 are solved with the Godunov method (approximate Riemann solver). The key dimensionless parameters used in the simulations are represented by ${\rho }_0=10^{-15}$ g ${\mathrm{c}\mathrm{m}}^{-3}$, $L_0=10^8$ cm, and $V_0=c_A=10^8$ ${\mathrm{c}\mathrm{m}\mathrm{s}}^{-1}$. These values correspond to the characteristic density, length, and velocity, respectively. Given the expression for the magnetic Reynolds number $R_m\simeq \frac{L_0{V}_0}{\eta }$, the range of this number can be calculated by considering the upper and lower limits of resistivity. With considering magnetic diffusivity values $\eta =10^{-6}$ and 10 ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$, the range of magnetic Reynolds number is estimated to be between $10^{15}$ and $10^{22}$. The Cartesian coordinate system is used with components denoted as $x_1,x_2,x_3\equiv x,y,z$.

Our initial assumption takes into account the parameters in both the x and y directions. However, when the fast magnetoacoustic wave propagates near the null point, it causes changes in the magnetic field in the z direction and also disrupts Alfven waves. Put simply, when there are variations in the pulse shape compared to the background magnetic field, it leads to the formation of longitudinal and transverse daughter disturbances (Thurgood and McLaughlin, 2013).

In this line, a steady magnetic null point is targeted by an incident circular fast magnetoacoustic wave. As the center of the magnetoacoustic pulse is located at the magnetic null-point its presence is formulated as the Equation 8 (Gruszecki et al., 2011; Sabri et al., 2019; Sabri et al., 2020a)

$V_{\text{f}}=2{\mathrm{A}}_{\mathrm{0}}\sin \left[\pi \left(\sqrt{x^2+y^2}-r_1\right)\right],(8)$

with $5\le r=\sqrt{x^2+y^2}\le 6$ and $r_1=5$ with initial amplitude $(A_0)$ equal to unity which accompanies with the nonlinear dynamic (McLaughlin et al., 2009).

The magnetic field $\mathbf{B}$ is defined on the cell faces in a way that throughout the simulations the equation $\nabla \cdot \mathbf{B}=0$ is complied with. The simulation domain has been considered as $(-\mathrm{10,10})\times (-\mathrm{10,10})\times (-\mathrm{5,5})$ ${\mathrm{M}\mathrm{m}}^3$ with open boundaries and with $1600\times 1600\times 1000$ grid points. Open or outflow boundaries mean that all of the quantities have zero gradient at the boundaries of the computational domain. This prevents reflection from the boundaries that is in contrast to the case where the presence of reflective boundary conditions is considered. Nonetheless, the boundaries are placed at a far distance from the null point. As for the simulations carried out by Sabri et al. (2020a) a stretched grid has been implemented to see the majority of the grid points near the magnetic null-point. Therefore, we set $1200\times 1200$ grid points in the numerical domain $(-\mathrm{6,6})\times (-\mathrm{6,6})$ Mm with an effective resolution of $\delta x\approx \delta y\approx 1/100$ Mm. It must be noted that the stretched grid is applied near the null point which results in high resolution around there. Because in the present study, the aim is to focus on the fast and slow magnetoacoustic waves as they approach a magnetic null-point together with their effects on the physical parameters and quantities that constitute and characterize the magnetic null-point neighborhood.

3 Numerical results and discussion

3.1 Fast magnetoacoustic wave

The perpendicular velocity of the simulations represents the fast magnetoacoustic wave profile which is $v_{\perp }=[(\mathbf{V}\times {\mathbf{B}}_{\mathbf{0}})\cdot z]/\sqrt{b_x^2+b_y^2}=(v_x{b}_y-v_y{b}_x)/\sqrt{b_x^2+b_y^2}$. The initial fast magnetoacoustic pulse is circular, with the center at the origin, and completely surrounds the null as illustrated in Figure 1 corresponds to the initial pulse of (Sabri et al., 2020a). Magnetic null point is located at the origin and separatrices, which separate four areas with different magnetic conductivity, are paced along x and y axis. In the present study, the aim is to highlight the effects connected with the magnetic diffusivity in the context of magnetoacoustic wave interaction with the magnetic null point. The first row of the Figure 2 includes snapshots of a fast magnetoacoustic wave around a magnetic null-point at three time scales respectively equal to 2, 17.6, and $t=20.4$ s where the magnetic diffusivity is very low equal to ${10}^{-6}$ ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$. The second row of Figure 2 corresponds to a domain with a higher magnetic diffusivity equal to 10 ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$.

Figure 1

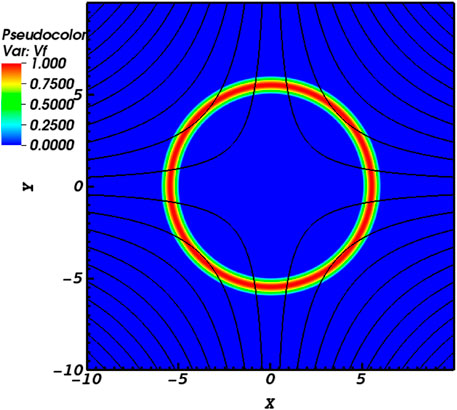
Figure 1. Indicative lines of the equilibrium magnetic field structure and contours of the initial fast pulse at $t=0$. Separatrices are located along x and y axis and magnetic X-point is placed at the origin.

Figure 2

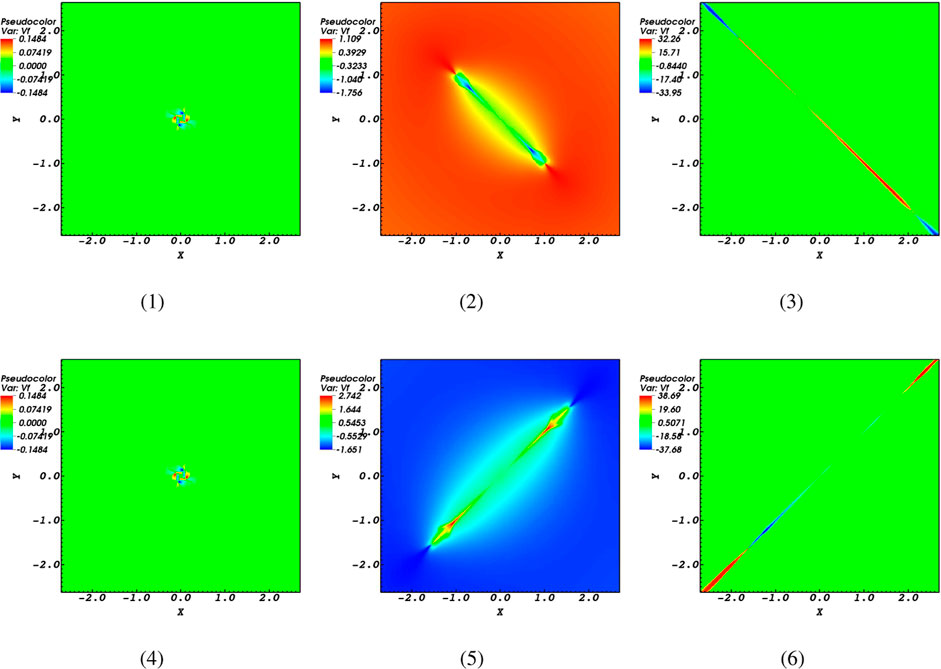
Figure 2. Numerical simulations of the perpendicular speed $v_{\perp }=v_f$ (normalized by ${\mathbf{v}}_{\mathbf{0}}=\mathbf{1}{\mathbf{0}}^{\mathbf{8}}$ cm ${\mathrm{s}}^{-1}$) which corresponds to the dynamics of the fast magnetoacoustic wave at three time scales of $t=2$ s, $t=17.6$ s, and $t=20.4$ ${\mathrm{s}}^{-1}$, for the second row $(\eta )$ has been considered equal to 10 ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$. X and Y coordinates are between [−10, 10] Mm, but to see the exact behavior of the waves, they were zoomed in [−2, 2] Mm.

Compare the snapshots of Figure 2 at the same timescales to observe how the magnetic diffusivity affects the behavior of the magnetoacoustic fast wave during its interaction with the null-point. Panels (a) and (d) of Figure 2 depict the characteristics of the fast magnetoacoustic wave when it reaches the null point. It is evident that their behavior is identical. Thence, in both scenarios where resistivity is high or low, the fast magnetoacoustic wave wraps around the null point and focuses at the null, which is referred to as the refraction effect. Hence, it is demonstrated that the refraction phenomenon is observed even in high resistivity conditions and causes the fast wave to concentrate around the null point. Because of the refraction phenomenon that concentrates the magnetoacoustic waves in a limited region, we infer that it might result in intriguing outcomes like the buildup of high current density and subsequent consequences.

In addition, since the null point has a sound speed greater than zero, fast waves can pass through it. The fact that higher magnetic diffusivities result in larger spreading domains is intriguing, as shown by panels (b) and (e). In simpler terms, when comparing panel (b) and panel (e), it can be seen that panel (e), which represents the highest resistivity ($\eta =10$ ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$), has a greater spreading.

When the fast magnetoacoustic wave passes through the null point, it also exhibits a comparable shape but in a distinct orientation. Alternatively, for small resistivity, the fast magnetoacoustic wave moves away from the null point at a perpendicular direction compared to situations with high resistivity. It could be associated to the oscillatory reconnection phenomena see also Thurgood et al. (2018). Additionally, it was illustrated by Tarr et al. (2017) that a magnetic null point collapses to shape a current sheet originally directed at 45° to the seperatrices. They found that the current sheet which forms at the null oscillates between $\pm \sim 45$°, indicating evidence of oscillatory reconnection. As a result, this orientation could be associated to the variation of the plasma resistivity. It must be noted that there is no distinction in the behavior of the fast magnetoacoustic wave for high and low resistivity until it reaches the null point.

3.2 Slow magnetoacoustic wave

The slow magnetoacoustic wave, which is a longitudinal wave, is a wave that aligns with and travels parallel to the magnetic field described as $v_{\Vert }=(\mathbf{V}\cdot {\mathbf{B}}_{\mathbf{0}})/\sqrt{b_x^2+b_y^2}=(v_x{b}_x+v_y{b}_y)/\sqrt{b_x^2+b_y^2}$. The panels of Figure 3 depict the behaviour of the parallel component of the velocity corresponding to the slow magnetoacoustic wave for two values of magnetic diffusivity respectively equal to ${10}^{-6}$ ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$ (at the first row) and 10 ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$ (at the second row) at time scales $t=2$, 17.6, and 20.4 s. By comparing the panels corresponding to the same time scales of Figures 2, 3 it could be deduced that the fast magnetoacoustic wave arrives at the null point earlier than the slow magnetoacoustic wave. In according to the same time scales of the panels in Figure 3, like the fast mode, the slow magnetoacoustic wave possesses a similar shape regardless of the magnetic diffusivity value. Additionally, similar to the fast wave, with considering panels ((b) and (e)), slow magnetoacoustic wave extends over a larger region on the middle panel, which is related to a higher resistivity value $(\eta =10)$.

Figure 3

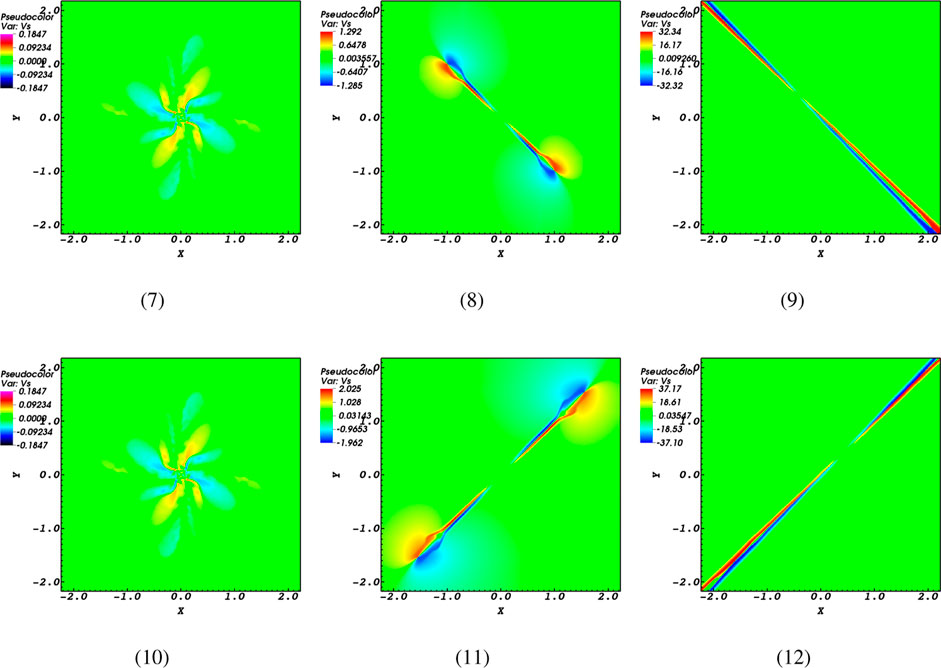
Figure 3. Numerical simulations of the parallel speed $v_{\Vert }=v_s$ (normalized by ${\mathbf{v}}_{\mathbf{0}}=\mathbf{1}{\mathbf{0}}^{\mathbf{8}}$ cm ${\mathrm{s}}^{-1}$) which corresponds to the dynamics of the slow magnetoacoustic wave at three time scales of $t=2$, $t=17.6$ and $t=20.4$ s for two different resistivity as mentioned in previous figure. X and Y coordinates are between [−10, 10] Mm, but to see the exact behavior of the waves, they were zoomed in [−2, 2] Mm.

Actually, magnetic field is zero at the magnetic null point. Due to the magnetic diffusivity being the primary factor in compensating for the lack of a magnetic field at the magnetic-null point, it is expected to play a promising role against the significant gradient of the magnetic field. Therefore, the study includes examining the changes in different physical parameters at different resistivity levels near the null point. As seen in Figures 2, 3, in contrast to the fast magnetoacoustic wave, the slow magnetoacoustic wave velocity behaves differently from the fast magnetoacoustic wave, exhibiting both positive and negative values. It must be noted that anti-phase property means that the slow magnetoacoustic wave has both positive and negative velocities. This characteristic is visible in every panel of Figure 3.

In addition, the impact of magnetic diffusivity on the amplitude of the slow magnetoacoustic wave is not significant. The question that arises in this stage is that why does the amplitude of the waves increase after going through the magnetic null point? The answer lies in the induction of a strong current density together with the creation of magnetic islands or plasmoids (in accordance to the Figure 8) which is dealt with in the proceeding section. The exact cause of this wave formation during the reconnection is still unknown. It has been noted that due to amplification of the slow magnetoacoustic modes, the damping of the slow modes could be important. Interestingly, the excitation of mass-transporting slow modes that happens due to the magnetic reconnection may explain the reason of propagating intensity disturbances observed in the open-field corona (DeForest and Gurman, 1998; Banerjee et al., 2011). As a matter of fact, slow magnetoacoustic mode becomes dominate and moves away from the current sheet.

3.3 The properties of the current sheet

According to the classical standard model of solar flares, the conversion of magnetic energy into thermal and kinetic energies of plasmas occurs quickly as a result of magnetic reconnection (Shibata and Magara, 2011). Rapid reconnection necessitates a significantly narrower current sheet width compared to its length (Yamada et al., 2010). Recent studies have shown that the non-adiabatic effects of thermal conduction, radiative cooling, background heat also play role in the instability growth rate for explosive reconnection events in a current layer (Ledentsov, 2021; Sen and Keppens, 2022). Therefore, a key concern in comprehending the cause of explosive events is to determine the mechanism behind the creation of narrow current layers. There is ample evidence from observations that supports the activation and development of a current sheet between a flaring loop with a cusp shape and a flux rope that is erupting (Liu et al., 2010).

Maron and Goldreich (2001) utilized a pseudospectral code to model turbulence in incompressible Magnetohydrodynamics (MHD). They showed that there is typically a strong level of turbulence in MHD (magnetohydrodynamic) systems, indicating that the waves within it undergo considerable distortions of the same scale as their durations within a similar time frame. They further mentioned that wave packets undergo alterations in their form while moving along magnetic field lines that have been disrupted by waves moving in opposing directions. Moreover, they discovered that the decay of MHD turbulence becomes more unstable when there is a greater imbalance between the fluxes of waves that are moving in opposite directions along the magnetic field. In addition, the dynamic variables’ gradients are concentrated in sheets that are parallel to the magnetic field. These layers have a thickness that is comparable to the dissipation scale.

McClymont and Craig (1996) examined how the resistivity affects the physical properties and reconnection rate in MHD simulations. They discovered that the influence of gas pressure does not greatly alter the relationship between current sheet thickness and resistivity. Takeshige et al. (2015) suggested conducting 2D MHD simulations to study the merging of plasmoids and examining the current sheet formation between these plasmoids in detail, similar to what we have done in 2.5D.

In this line, we further examine how resistivity affects magnetoacoustic waves by analyzing the current density patterns shown in Figure 4. The nature of the current sheet in the current research is influenced by both the kind of wave that generates it (as seen in Figures 2–4) and the magnitude of magnetic diffusivity.

Figure 4

Figure 4. Numerical simulations of the current density at $t=18.0$ s. The first and second panels respectively correspond to magnetic diffusivity values equal to ${10}^{-6}$ ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$ and 10 ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$.

In other words, when the magnetic diffusivity is relatively low (such as $10^{-6}$ ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$), the current density is oriented at a 90° angle in the x-y planes compared to when the magnetic diffusivity is relatively high (like 10 ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$). However, the magnetic diffusivity causes a reversal in the direction of the current density. This reversal can be seen by comparing the two panels in Figure 4, which demonstrates the oscillatory behavior of the magnetic null-point as a result of its interaction with magnetoacoustic waves, see also Thurgood et al. (2018). To find the approximate range of the numerical resistivity, we applied different resistivities and investigate their effect on the plasma parameters. It was found that $\eta =1$ is the critical value of the resistivity. In addition, Tarr et al. (2017) demonstrated that a magnetic null point undergoes a collapse to form a current sheet that initially points at an angle of approximately 45° relative to the separatrix lines. They discovered that the current layer generated at the null point undergoes oscillations of approximately 45°, providing evidence of reconnection that occurs in an oscillatory manner.

Reversal of current-sheet polarity was associated with the oscillatory reconnection happens near the X-point in 2.5D and 3D structures (Thurgood et al., 2017; Forbes, 1986). It was stated that local force imbalance resulted in the establishment of standing oscillations of the field. They also concluded that increasing resistivity leads to comparatively weak decrease in the main reversal period (relative to the linear case), and an increasingly smooth time-variation. Besides, Thurgood et al. (2017) explained that nonlinear fast wave collapses in a quasi-1D fashion, altering the magnetic field in the vicinity of the null point. They also associated the reversals with the back-pressure-driven overshoots and this reverses the sign of current at the null, and thus reverses the sense of the reconnection. They concluded that the oscillatory reconnection mechanisms may play a role in explaining periodicity in astrophysical phenomena associated with magnetic reconnection, such as the observed quasi-periodicity of solar and stellar flare emission.

It can be said that the build-up of current density occurs in bigger regions with greater intensities in the relatively high resistivity ($\eta =10$ ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$). In simpler terms, when the magnetic diffusivities are lower, the amplitude of the current density is smaller compared to when the magnetic diffusivities are higher. This is because the concept of non potential flux arises, where free energy is stimulated in the form of current sheets. The reason for this is that when there is a uniform resistivity, a current layer similar to the “Sweet-Parker” phenomenon is formed. This current layer grows continuously due to the enduring force acting on it.

Regarding Figure 4, it can be observed that there are differences not only in the direction of the current density accumulation, but also in its magnitude around the null point. The current density value is positive at the null point when using high resistivity setups, but it is negative with small resistivity values. This indicates that the direction of current density is opposite for high and low resistivities. These excitations of current sheets with opposite polarity may explain why the null point collapse occurs in the opposite direction. It is important to mention that this could also be linked to the number of reconnections observed. The oscillatory reconnection occurs due to the competition between the forces. To provide additional information, soon after the initial collapse is halted, powerful plasma pressure differences emerge at the ends of the jet, which leads to a force opposing the outflow.

In McClymont and Craig (1996), it was stated that in the linear theory, taking into account zero plasma beta, the speed at which energy is released at an X-type null point only shows a logarithmic dependence on the plasma resistivity. They investigated how the X-point reacts to disturbances of a certain size under conditions that are closer to reality. The complexity of the evolution dynamics means that it is still uncertain what specific conditions are needed for fast reconnection to occur. The density variations were disregarded in order to establish an approximate connection between current density and plasma resistivity. Moreover, they investigated the issue in both the linear and nonlinear states. However, they discovered that the linear analysis produced an asymptotic outcome that is only valid for $\eta =10^{-4}$ ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$. However, they determined that when there is a plasma of reasonable gas pressure, such as in the solar corona, the initial collapse onto the X-point does not lead to rapid reconnection. The plasma that is pushed into the current sheet stops the collapse from occurring and prevents any significant dissipation from happening. However, when the disruption is considerable, the magnetic pressure of the collapsing wave forces the confined gas to be expelled from the edges of the existing current sheet at the speed of sound in that area. As a result, the sheet becomes thinner and reconnection happens more quickly. The intricacies of wave interactions are captivating and intricate, and are still not completely comprehended. In this study, it was decided to continue with the pursuit of the topic.

To provide additional information, we graphed the changes in current density and plasma density over two separate time series. These time series include the entire simulation time, as well as a specific period around the initial time when the plasma density remains relatively constant (Figures 5, 6). According to Forbes (1982), the discussion on the connection between current density and resistivity involved an analysis of the relationship. The researchers relied on the assumption of low plasma density, indicating that their findings are applicable when considering small plasma density. During the entire duration of the simulation, it was discovered that as plasma density increases, the current density also becomes high when the resistivity is high, specifically at a value of $\eta =10$ ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$. It must be noted when the current density falls down, it means that magnetic reconnection happens and decreasing the plasma density is because of the reconnection that results in acceleration of the plasma or plasma flows. And the second increasing of the current density in the second row of Figure 6 is because of the next reconnection and it can be considered as oscillatory magnetic reconnection that is a kind of plasmoid mediated magnetic reconnection (in according to Figure 8). Propagation of fast magnetoacoustic wave around the null point results in plasmoids or magnetic islands generation. Then plasma trapped through the plasmoids and turbulence would be important. High resistivity could result in an increase in microinstabilities, which may be accompanied by higher plasma density, current density, and temperature. During the early stages of the simulation, plasma density remains relatively low, however, the accumulation of current density is significant when the resistivity is low, specifically at a value of $\eta ={10}^{-6}$ ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$. Therefore, it can be inferred that the correlation between current density and resistivity holds for situations with low plasma density, as explained in Forbes (1982).

Figure 5

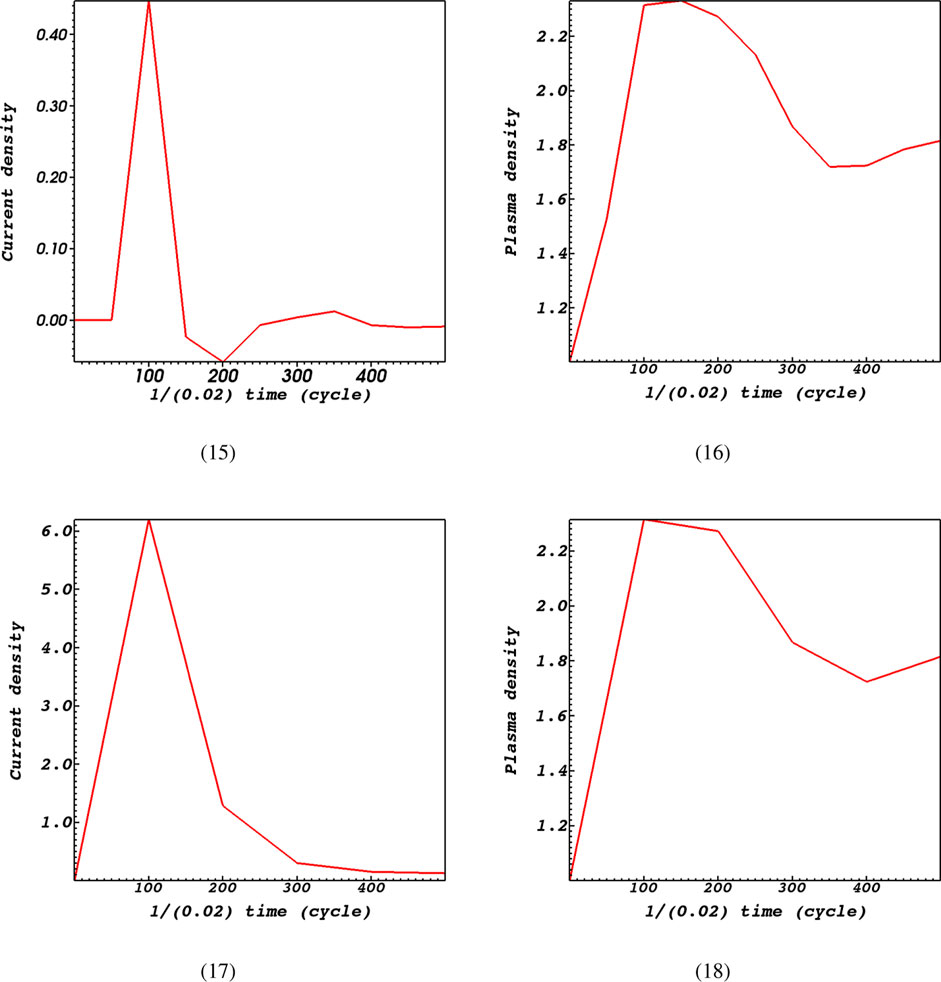
Figure 5. Time evolution of current density and plasma density around the initial time for $\eta =10^{-6}$ ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$ at first row and $\eta =10$ ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$ for the second row.

Figure 6

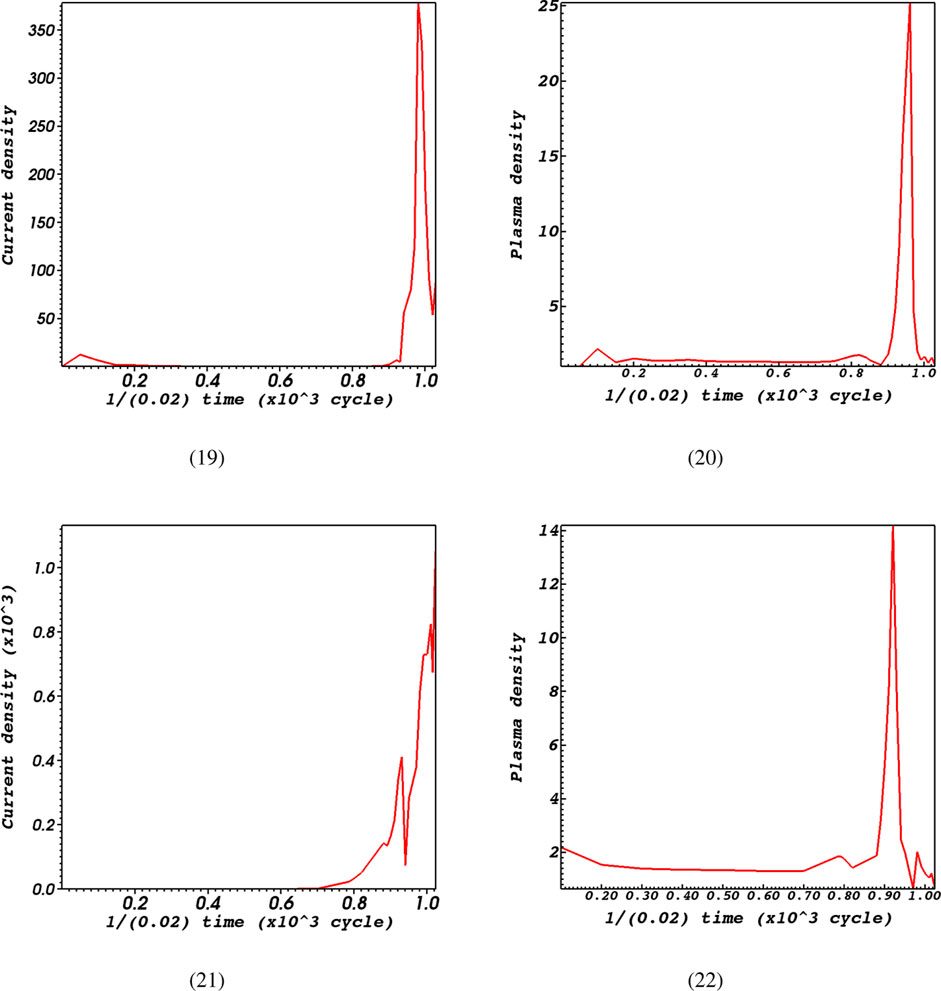
Figure 6. Time evolution of current density and plasma density at the whole simulation time for $\eta =10^{-6}$ ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$ at first row and $\eta =10$ ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$ for the second row.

Furthermore, when examining the characteristics of fast and slow magnetoacoustic waves in relation to the profiles of current density, it becomes evident that there is a similarity between the current density profile and the fast magnetoacoustic wave. Therefore, it could be stated that fast magnetoacoustic waves align better with the variations in current density. However, it should be observed that the fluctuations of the fast magnetoacoustic wave and current density exhibit opposite behaviors. This statement is made because the regions where the fast magnetoacoustic wave shows significant strength align with the regions where the current density is minimal. So, the fast magnetoacoustic wave and the strength of electric current would follow a comparable trend, however, in an opposite way. It is noteworthy to see the references mentioned in Nickeler et al. (2013); Zhou et al. (2015); Zhou et al. (2016).

3.4 Temperature distribution

In course of interaction between MHD waves and magnetic null-points, a significant amount of magnetic energy is converted into heating due to various physical mechanisms which contributes towards coronal heating (Van Doorsselaere et al., 2020). In fact, the presence of heating occurs at magnetic reconnection sites. Certainly, the heating of the plasma is caused by the resistivity of the plasma itself, which is due to the strong gradients in the magnetic field structure near the magnetic null point (Thurgood et al., 2018). Now, what effects does the magnetic diffusivity have on the heating process when magnetoacoustic waves interact with null points? To address this, changes in temperature for various magnetic diffusivity values are depicted and examined thoroughly in the snapshots presented in Figure 7. At first look, it is interesting that the temperature distribution evolves in a different manner with respect to the current density. This means that the temperature distribution initially has a pattern similar to that of a butterfly, with many areas of localized heating. Figure 7 provides evidence for the existence of specific heating points in the sun’s corona. It should be pointed out that the heating process in this butterfly structure occurs prior to the excitement of plasmoids. The presence of plasmoids and high-current density excitations that occur during microinstabilities leads to elevated plasma temperature within a confined region, similar to the shape of the current density distribution.

Figure 7

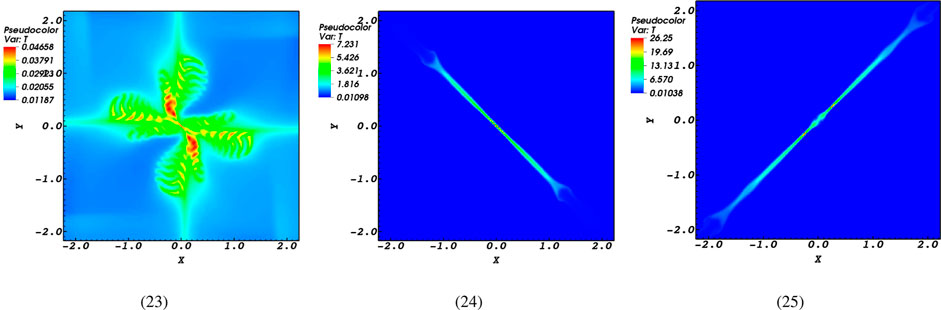
Figure 7. Contours of the temperature for $t=16.0$ s and $t=18.0$ s with $\eta =10^{-6}$ ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$ (first and second panels), and at $t=18.0$ s for $\eta =10$ ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$ (last panel).

It can be inferred from the snapshots shown in Figure 7 that when the magnetic diffusivity is relatively high ($\eta =10$ ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$), the heating is an order of magnitude greater. Additionally, given that the amplitudes of the waves are roughly equal for various resistivity values, it can be concluded that the observed heating arises from the transfer of momentum directly from the MHD waves to the plasma via the Lorentz force. It is important to remember that the buildup of high current density occurs at relatively high levels of magnetic diffusivity. This can be observed in Figure 4.

One could infer that apart from the current density and resulted ohmic heating, there exist other factors that play a role in coronal heating. This is because the solar corona has a complex structure that allows for many different heating processes to occur. As mentioned earlier, the presence of magnetic islands or O-points leads to the creation of turbulence. Magnetohydrodynamic turbulence plays a role in the rapid release of energy and the creation of intricate thermal structures. Additionally, the accumulation of current density observed in this study is also a result of the turbulence. In addition, according to Lazarian and Vishniac (1999), turbulent motions can lead to swirling and mixing of the field.

In this line, it is instructive to study the magnetic field structure for two cases: one with $\eta =10$ ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$ and another with $10^{-6}$ ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$, as shown in Figure 8, in relation to the stimulation of plasmoids. Prior to the present study, the propagation of magnetoacoustic waves in the vicinity of a magnetic null-point has been studied that resulted in magnetic reconnection and magnetic islands or plasmoids provoking turbulence in the plasma (Sabri et al., 2020a). Nevertheless, in our current investigation, we examine the identical experimental arrangement in order to explore the impact of magnetic diffusivity on the nature of magnetoacoustic waves near the magnetic null point. It is clear that the propagation of the fast wave around the null point results in the O-point magnetic field structure generation. The last panel of Figure 8 illustrates that when the magnetic diffusivity value is relatively high ($\eta =10$ ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$), plasmoids or magnetic islands are bigger compared to situations with low magnetic diffusivity.

Figure 8

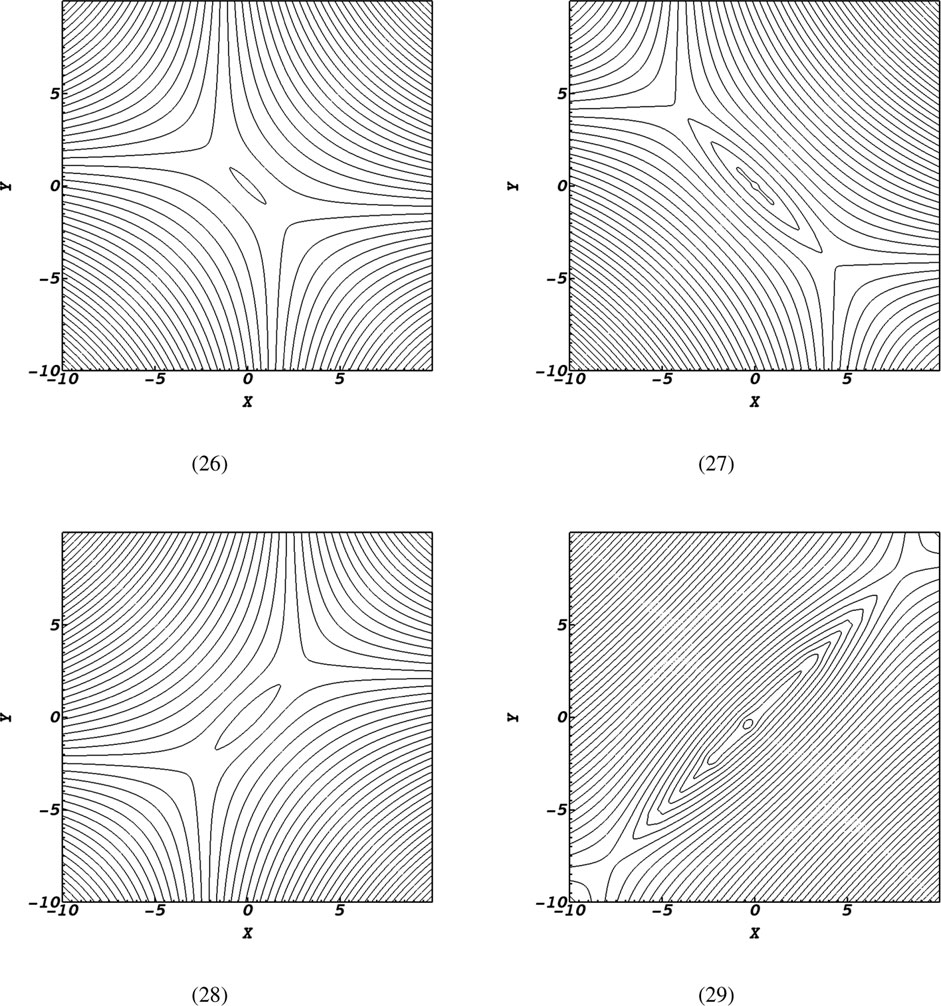
Figure 8. Contours of the magnetic field structure for timescales $t=18.0$ s and $t=19.0$ s for $\eta =10^{-6}$ ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$ (top row) and for $\eta =10$ ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$ (bottom row).

3.5 Plasma flows

As mentioned earlier, magnetic reconnection leads to the acceleration of particles and the movement of plasma. In this section, Figures 9, 10 present the progress of the plasma flow’s x and y components. The snapshots in Figures 9, 10 clearly demonstrate that the extent to which the induced flow spreads is greatly influenced by the magnetic diffusivity, as seen in the comparison of two last panels. This statement has various aspects. First of all, we can observe both incoming (represented by red profiles) and outgoing (represented by blue profiles) flows in the context of high magnetic diffusivity cases with $\eta =10$ ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$ (shown in the last panel). It is noteworthy that in comparison to the first two panels that depict low magnetic diffusivity cases with $\eta =10^{-4}$, direction of the flows is reversed.

Figure 9

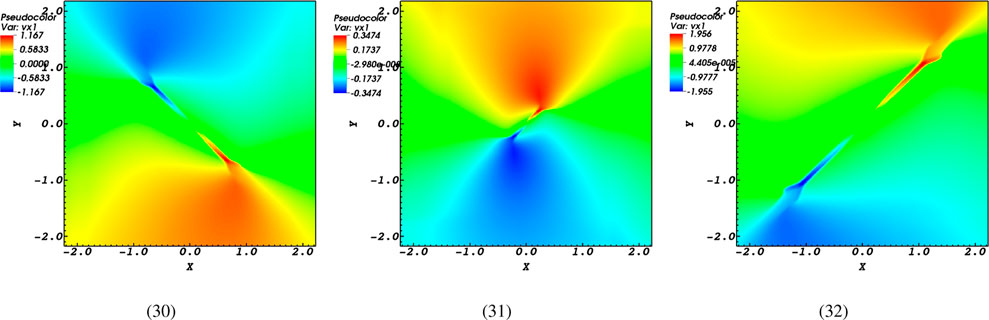
Figure 9. Snapshots of the $x$ component of the flow for $t=17.6$ s at the null point for $\eta =10^{-4}$ ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$ (left panels), for $\eta =1$ ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$ (middle panels), and for $\eta =10$ ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$ (right panels).

Figure 10

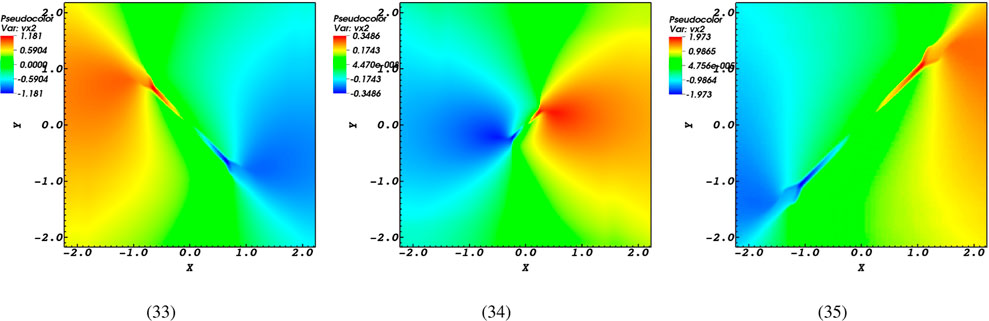
Figure 10. Snapshots of the $y$ component of the flow for $t=17.6$ s at the null point for $\eta =10^{-4}$ ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$ (left panels), for $\eta =1$ ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$ (middle panels), and for $\eta =10$ ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$ (right panels).

Additionally, the changes in flow speeds induced in the $y$ direction exhibit a similar pattern and magnitude as those in the $x$ direction, but in a direction perpendicular to it. To put it differently, the plasma flow’s $x$ component corresponds to the fast magnetoacoustic wave. This shows that the fast magnetoacoustic wave creates boundaries for the path that the stimulated flows have to follow. This points out that the magnitude of the excited plasma flows near the magnetic null point, caused by the propagation of magnetoacoustic waves, is similar to the amplitude of the magnetoacoustic waves themselves. This is the reason why, in certain instances, it is difficult to differentiate waves from flows.

Due to the similarity between profiles of the current density and plasma flows, it can be inferred that magnetic reconnection is highly likely to be responsible for the formation of jets and plasma flows. Please be aware that the current sheet excitation and the resulting flows occur at very similar time intervals. Therefore, the production of the present density may occur as a result of the eruptions, just like the notion proposed by Dungey (1953); Dungey (1958) when discussing the mechanisms responsible for acceleration in astrophysical systems. Furthermore, Forbes (1982) mentioned that as the density increases, the X-type magnetic field undergoes a collapse and transforms into a sheet-like structure. This is accompanied by the observation of plasma flows in one dimension, which aligns with the findings of our current study.

In addition to impacting the extent to which the plasma flow is transmitted, magnetic diffusivity also plays a role in determining the intensity of the flow. Moreover, in addition to the perpendicular characteristic of the flows at low and high levels of magnetic diffusivity, when there is an outward flow in the high diffusivity scenario, there are inward flows in the low diffusivity scenario. As a result, both the collapse of magnetic field lines and the reverse direction of flows occur due to the high magnetic diffusivity value.

4 Conclusion

We have investigated the characteristics of magnetoacoustic waves around a 2.5D magnetic null point using the resistive MHD set of equations. The focus has been on studying the influence of low moderate and high magnetic diffusivity conditions appropriate for solar coronal conditions. The study of magnetic diffusivity was motivated by the presence of turbulent processes occurring around current sheets in nonlinear regimes. Thus, in this study the effect of magnetic diffusivity regarding magnetoacoustic wave interaction with a magnetic null point taken under consideration in the nonlinear regime. By taking advantage of a parallel code, we have introduced different small and large values for the magnetic diffusivity to highlight its effect on the behaviour of MHD waves and the plasma parameters.

Cemeljic et al. (2014) investigated the differences between outflow in a highly resistive accretion disc corona $\eta =\mathrm{10,100}$ and the results with smaller or vanishing resistivity $\eta =10^{-4},10^{-6}$. Since we have been trying to find the behavior of the MHD waves around the magnetic null point, numerical resistivity is inevitable. To find the approximate range of the numerical resistivity, we applied different resistivities and investigate their effect on the plasma parameters. It was found that $\eta =1$ is the critical value of the resistivity. In the case of diffusion term that is typically very small $\eta \simeq 10^{-14}$ for solar coronal condition, but it always dominates in the presence of the magnetic null points Craig and McClymont (1991). Moreover, Thurgood et al. (2019) considered ${\rho }_0=10^{-10}$ kg ${\mathrm{m}}^{-3}$ and $\eta =1$ ${\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$ as reasonably representative of solar coronal plasma. They found that in nonlinear regime perturbation energy are only weakly-dependent on the resistivity. Since we applied cgs units, then $\eta =10^4$ ${\mathrm{c}\mathrm{m}}^2$ ${\mathrm{s}}^{-1}$ would be also correct for the solar coronal plasma.

In this line, an initial fast magnetoacoustic wave has been introduced at a specific distance from a 2.5D magnetic null point. Due to the non-zero plasma-$\beta$ conditions, both fast and slow magnetoacoustic waves have featured themselves. One important characteristic of magnetoacoustic waves is their tendency to collapse toward the magnetic null point, due the spatially varying Alfvén speed around the magnetic null. This results in high current density accumulation at small scales around the magnetic null points that themselves host events such as magnetic reconnection, collapsing of the X-magnetic null point to an O-point or plasmoids and turbulence (Sabri et al., 2020a). However, the coalescence of plasmoids enables shock formation that accelerates particles which is a feature that motivates further study especially regarding the induction of plasma flows during plasmoids Takeshige et al. (2015). The key results of this paper may be summarized as follows

1. The impact of magnetic diffusivity on the amplitude of the magnetoacoustic waves was determined to be insignificant.

2. It is demonstrated that the refraction phenomenon is observed even in high resistivity conditions and causes the waves to concentrate around the null point.

3. It was depicted that fast magnetoacoustic waves are more consistent with the current density fluctuations in comparison to the slow magnetoacoustic wave.

4. It was observed that increased magnetic diffusivity causes magnetic fields to collapse and results in a reversal of induced flows. This confirms the occurrence of oscillatory behavior in the magnetic null-point as a result of its interaction with magnetoacoustic waves.

5. It was illustrated that high magnetic diffusivity value leads to larger plasmoids or magnetic islands in comparison to small magnetic diffusivity conditions.

6. The amplitude of the current density is smaller for small values of the magnetic diffusivities compared to higher values roots in the concept of non potential flux where free energy is excited in the form of current sheets. This lies in the fact that when uniform resistivity is present, a “Sweet-Parker” type current layer is generated, and it undergoes a continuous growth due to the continues force.

7. During the entire duration of the simulation, it was discovered that plasma density gets significant due to the plasmoid and current density is high for high resistivity.

8. It was revealed that the temperature distribution initially appears in a pattern resembling a butterfly, with several local heating points that verify the presence of localized heating in the solar corona. This butterfly heating structure occurs prior to the excitement of plasmoids.

9. Finally, it was depicted that fast magnetoacoustic wave plays main role in the behaviour of plasma flows. Furthermore, the amplitude of the plasma flows that are generated by the magnetoacoustic wave propagation near the magnetic null point is comparable with the magnetoacoustic waves amplitude. This is why in some cases the distinction between waves and flows is non-trivial.

This research has provided insights into how resistivity affects the flow of magnetoacoustic waves and subsequently impacts the surrounding plasma in the solar atmosphere, as explained by solar atmospheric seismology. It was illustrated that the waves behave similarly before reaching the null point regardless of resistivity. However, after passing through the null point, the direction of wave accumulation varies depending on the resistivity, whether it is low or high.

The variation of current density accumulation direction was reported by different reference that investigated the behavior of the MHD waves around the null point Thurgood et al. (2017); Forbes (1986). The main reason of this variation was considered to be the magnetic reconnection and collapsing of the magnetic structure that considered as oscillation. Collapsing of the null is a class of MHD implosions with the null being the center of converting magnetic flux and of plasma compression and rarefaction because of the converging and diverging flow driven by the Lorentz force Thurgood et al. (2018). They reported that the implosions continues until some confined process such as resistive dissipation and heating, a growth of plasma back-pressure inside the current concentration due to the adiabatic heating can develop sufficiently to oppose this focusing. Thurgood et al. (2017) considered the reversals with the back-pressure-driven overshoots and their reverses the sign of the current at the null, and then reverses the sense of the reconnection. They concluded the current density accumulation was instead directed along the dominant direction of the Lorentz force. Besides, Thurgood et al. (2018) found that the halting of implosions happens rapidly after reaching the diffusion scale by sudden Ohmic heating of the dense plasma within the current sheet, which provides a pressure gradient sufficient to oppose further collapse and decelerate the converging flow. They suggested that ohmic heating after reaching the diffusion scale plays a main role in the full halting process.

Moreover, it was discovered that the occurrence of plasmoid generations, along with their magnitude and subsequent turbulence, significantly influence the behavior of plasma. Since profiles of the current density and plasma flows coincide with each other, it could be concluded that magnetic reconnection is one of the most probable creators of jets and plasma flows. This scenario itself contributes to a sustainable acceleration process for fueling the solar wind, as well as the sustainable process of heating it. The interaction of magnetoacoustic waves with magnetic null-points could play a main role in the widespread events occurring in the solar corona, including eruptions, plasma heating, flares, and particle acceleration.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

SS: Conceptualization, Formal Analysis, Visualization, Writing–original draft, Writing–review and editing. SP: Investigation, Validation, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. SP acknowledges support from the projects C14/19/089 (C1 project Internal Funds KU Leuven), G0B5823N and G002523N (WEAVE) (FWO-Vlaanderen), 4000134474 (SIDC Data Exploitation, ESA Prodex-12), and Belspo project B2/191/P1/SWiM.

Acknowledgments

For the computations we used the infrastructure of the VSC$-$Flemish Supercomputer Center, funded by the Hercules foundation and the Flemish Government$-$department EWI.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2024.1450975/full#supplementary-material

References

Aschwanden, M. J. (2005). Physics of the solar corona: an introduction with problems and solutions. 2nd edition. Berlin, Heidelberg: Springer.

Google Scholar

Banerjee, D., Gupta, G. R., and Teriaca, L. (2011). Propagating MHD waves in coronal holes. SSRv 158, 267–288. doi:10.1007/s11214-010-9698-z

CrossRef Full Text | Google Scholar

Cemeljic, M., Vlahakis, N., and Tsinganos, K. (2014). Large resistivity in numerical simulations of radially self-similar outflows. MNRAS 442, 1133–1141. doi:10.1093/mnras/stu952

CrossRef Full Text | Google Scholar

Craig, I. J. D., and McClymont, A. N. (1991). Dynamic magnetic reconnection at an X-type neutral point. Astrophysical J. Lett. 371, L41. doi:10.1086/185997

CrossRef Full Text | Google Scholar

Craig, I. J. D., and McClymont, A. N. (1993). Linear theory of fast reconnection at an X-type neutral point. Astrophysical J. 405, 207. doi:10.1086/172354

CrossRef Full Text | Google Scholar

Craig, I. J. D., and Watson, P. G. (1992). Fast dynamic reconnection at X-type neutral points. Astrophysical J. 393, 385. doi:10.1086/171512

CrossRef Full Text | Google Scholar

DeForest, C. E., and Gurman, J. B. (1998). Observation of quasi-periodic compressive waves in solar polar plumes. Astrophysical J. Lett. 501, L217–L220. doi:10.1086/311460

CrossRef Full Text | Google Scholar

Dungey, J. W. (1953). LXXVI. Conditions for the occurrence of electrical discharges in astrophysical systems. Lond. Edinb. Dublin Philosophical Mag. J. Sci. 44, 725–738. doi:10.1080/14786440708521050

CrossRef Full Text | Google Scholar

Dungey, J. W. (1958). Cosmical electrodynamics. Cambridge, England: Cambridge University Press.

Google Scholar

Forbes, T. G. (1982). Implosion of a uniform current sheet in a low-beta plasma. Plasma Phys. 27, 491–505. doi:10.1017/s002237780001103x

CrossRef Full Text | Google Scholar

Forbes, T. G. (1986). Fast-shock formation in line-tied magnetic reconnection models of solar flares. Astrophysical J. 305, 553. doi:10.1086/164268

CrossRef Full Text | Google Scholar

Gruszecki, M., Vasheghani Farahani, S., Nakariakov, V. M., and Arber, T. D. (2011). Magnetoacoustic shock formation near a magnetic null point. Astronomy Astrophysics 531, A63. doi:10.1051/0004-6361/201116753

CrossRef Full Text | Google Scholar

Hassam, A. B. (1992). Reconnection of stressed magnetic fields. Astrophysical J. 399, 159. doi:10.1086/171911

CrossRef Full Text | Google Scholar

Jacobson, A. R., and Moses, R. W. (1984). Nonlocal dc electrical conductivity of a Lorentz plasma in a stochastic magnetic field. Phys. Rev. A 29, 3335–3342. doi:10.1103/physreva.29.3335

CrossRef Full Text | Google Scholar

Karampelas, K., McLaughlin, J. A., Botha, G. J. J., and Regnier, S. (2022a). Oscillatory reconnection of a 2D X-point in a hot coronal plasma. Astrophysical J. 925, 195. doi:10.3847/1538-4357/ac3b53

CrossRef Full Text | Google Scholar

Karampelas, K., McLaughlin, J. A., Botha, G. J. J., and Regnier, S. (2022b). The independence of oscillatory reconnection periodicity from the initial pulse. Astrophysical J. 933, 142. doi:10.3847/1538-4357/ac746a

CrossRef Full Text | Google Scholar

Karampelas, K., McLaughlin, J. A., Botha, G. J. J., and Regnier, S. (2023). Oscillatory reconnection as a plasma diagnostic in the solar corona. Astrophysical J. 943, 131. doi:10.3847/1538-4357/acac90

CrossRef Full Text | Google Scholar

Kowal, G., Falceta-Goncalves, D. A., Lazarian, A., and Vishniac, E. T. (2020). Astrophysical J. 892, 50. doi:10.3847/1538-4357/ab7a13

CrossRef Full Text

Lazarian, A., and Vishniac, E. T. (1999). Reconnection in a weakly stochastic field. Astrophysical J. 517, 700–718. doi:10.1086/307233

CrossRef Full Text | Google Scholar

Ledentsov, L. (2021). Thermal trigger for solar flares I: fragmentation of the preflare current layer. Sol. Phys. 296, 74. doi:10.1007/s11207-021-01817-1

CrossRef Full Text | Google Scholar

Liu, R., Lee, J., Wang, T., Stenborg, G., Liu, C., and Wang, H. (2010). Astrophysical J. Lett. 723, L28–L33. doi:10.1088/2041-8205/723/1/l28

CrossRef Full Text

Longcope, D. W., and Priest, E. (2007). Fast magnetosonic waves launched by transient, current sheet reconnection. Phys. Plasmas 14, 122905. doi:10.1063/1.2823023

CrossRef Full Text | Google Scholar

Maron, J., and Goldreich, P. (2001). Simulations of incompressible magnetohydrodynamic turbulence. Astrophysical J. 554, 1175–1196. doi:10.1086/321413

CrossRef Full Text | Google Scholar

Matthaeus, W. H., and Lamkin, S. L. (1985). Rapid magnetic reconnection caused by finite amplitude fluctuations. Phys. Fluids. 28, 303–307. doi:10.1063/1.865147

CrossRef Full Text | Google Scholar

Matthaeus, W. H., and Lamkin, S. L. (1986). Turbulent magnetic reconnection. Phys. Fluids. 29, 2513–2534. doi:10.1063/1.866004

CrossRef Full Text | Google Scholar

McClymont, A. N., and Craig, I. J. D. (1996). Dynamical finite-amplitude magnetic reconnection at an X-type neutral point. Astrophysical J. 466, 487. doi:10.1086/177526

CrossRef Full Text | Google Scholar

McLaughlin, J. A., De Moortel, I., Hood, A. W., and Brady, C. S. (2009). Nonlinear fast magnetoacoustic wave propagation in the neighbourhood of a 2D magnetic X-point: oscillatory reconnection. Astronomy Astrophysics 493, 227–240. doi:10.1051/0004-6361:200810465

CrossRef Full Text | Google Scholar

McLaughlin, J. A., Hood, A. W., and De Moortel, I. (2011). Review article: MHD wave propagation near coronal null points of magnetic fields. Space Sci. Rev. 158, 205–236. doi:10.1007/s11214-010-9654-y

CrossRef Full Text | Google Scholar

Mignone, A., Bodo, G., Massaglia, S., Matsakos, T., Tesileanu, O., Zanni, C., et al. (2007). PLUTO: a numerical code for computational astrophysics. Astrophys. J. Suppl. 170, 228–242. doi:10.1086/513316

CrossRef Full Text | Google Scholar

Nickeler, D. H., Karlický, M., Wiegelmann, T., and Kraus, M. (2013). Fragmentation of electric currents in the solar corona by plasma flows. Astronomy Astrophysics 556, A61. doi:10.1051/0004-6361/201321847

CrossRef Full Text | Google Scholar

Parker, E. N. (1979). Cosmical magnetic fields. Oxford, United Kingdom: Oxford University Press.

Google Scholar

Priest, E. R., and Forbes, T. (2000). Magnetic reconnection: MHD theory and application. Cambridge, England: Cambridge University Press.

Google Scholar

Sabri, S., and Ebadi, H. (2021). Iran. J. Astronomy Astrophysics 8 (2), 63. doi:10.22128/ijaa.2021.516.1115

CrossRef Full Text

Sabri, S., Ebadi, H., and Poedts, S. (2020a). Plasmoids and resulting blobs due to the interaction of magnetoacoustic waves with a 2.5D magnetic null point. Astrophysical J. 902, 11. doi:10.3847/1538-4357/abb081

CrossRef Full Text | Google Scholar

Sabri, S., Ebadi, H., and Poedts, S. (2021). Propagation of the Alfvén wave and induced perturbations in the vicinity of a 3D proper magnetic null point. Astrophysical J. 924, 126. doi:10.3847/1538-4357/ac3b5f

CrossRef Full Text | Google Scholar

Sabri, S., Ebadi, H., and Poedts, S. (2022). Propagation of the Alfvén wave and induced perturbations in the vicinity of a 3D proper magnetic null point. Astrophysical J. 924, 126. doi:10.3847/1538-4357/ac3b5f

CrossRef Full Text | Google Scholar

Sabri, S., Ebadi, H., and Poedts, S. (2023). How nonlinearity changes different parameters in the solar corona. Astrophysical J. 944, 72. doi:10.3847/1538-4357/acb04e

CrossRef Full Text | Google Scholar

Sabri, S., Poedts, S., and Ebadi, H. (2019). Plasma heating by magnetoacoustic wave propagation in the vicinity of a 2.5D magnetic null-point. Astronomy Astrophysics 623, A81. doi:10.1051/0004-6361/201834286

CrossRef Full Text | Google Scholar

Sabri, S., Vasheghani Farahani, S., Ebadi, H., Hosseinpour, M., and Fazel, Z. (2018). Alfvén wave dynamics at the neighbourhood of a 2.5D magnetic null-point. Mon. Notices R. Astronomical Soc. 479 (4), 4991–4997. doi:10.1093/mnras/sty1407

CrossRef Full Text | Google Scholar

Sabri, S., Vasheghani Farahani, S., Ebadi, H., and Poedts, S. (2020b). How Alfvén waves induce compressive flows in the neighborhood of a 2.5D magnetic null-point. Sci. Rep. 10, 15603. doi:10.1038/s41598-020-70995-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Sen, S., and Keppens, R. (2022). Thermally enhanced tearing in solar current sheets: explosive reconnection with plasmoid-trapped condensations. Astronomy Astrophysics 666, A28. doi:10.1051/0004-6361/202244152

CrossRef Full Text | Google Scholar

Shibata, K., and Magara, T. (2011). Solar flares: magnetohydrodynamic processes. Living Rev. Sol. Phys. 8, 6. doi:10.12942/lrsp-2011-6

CrossRef Full Text | Google Scholar

Takeshige, S., Takasao, S., and Shibata, K. (2015). A Theoretical Model Of A Thinning Current Sheet In The Low-Βplasmas. Astrophysical J. 807, 159. doi:10.1088/0004-637x/807/2/159

CrossRef Full Text | Google Scholar

Talbot, J., McLaughlin, J. A., Botha, G. J. J., and Hancock, M. (2024). The effect of resistivity on the periodicity of oscillatory reconnection. Astrophysical J. 965, 133. doi:10.3847/1538-4357/ad2a5d

CrossRef Full Text | Google Scholar

Tarr, L. A., Linton, M., and Leake, J. (2017). Magnetoacoustic waves in a stratified atmosphere with a magnetic null point. Astrophysical J. 837, 94. doi:10.3847/1538-4357/aa5e4e

CrossRef Full Text | Google Scholar

Thurgood, J. O., and McLaughlin, J. A. (2012). Linear and nonlinear MHD mode coupling of the fast magnetoacoustic wave about a 3D magnetic null point. Astronomy Astrophysics 545, A9. doi:10.1051/0004-6361/201219850

CrossRef Full Text | Google Scholar

Thurgood, J. O., and McLaughlin, J. A. (2013). On ponderomotive effects induced by Alfvén waves in inhomogeneous 2.5D MHD plasmas. Sol. Phys. 288, 205–222. doi:10.1007/s11207-013-0298-4

CrossRef Full Text | Google Scholar

Thurgood, J. O., Pontin, D. I., and McLaughlin, J. A. (2017). Three-dimensional oscillatory magnetic reconnection. Astrophysical J. 844, 2. doi:10.3847/1538-4357/aa79fa

CrossRef Full Text | Google Scholar

Thurgood, J. O., Pontin, D. I., and McLaughlin, J. A. (2018a). Implosive collapse about magnetic null points: a quantitative comparison between 2D and 3D nulls. Astrophysical J. 855, 50. doi:10.3847/1538-4357/aab0a0

CrossRef Full Text | Google Scholar

Thurgood, J. O., Pontin, D. I., and McLaughlin, J. A. (2018b). Resistively-limited current sheet implosions in planar anti-parallel (1D) and null-point containing (2D) magnetic field geometries. Phys. Plasmas 25, 072105. doi:10.1063/1.5035489

CrossRef Full Text | Google Scholar

Thurgood, J. O., Pontin, D. I., and McLaughlin, J. A. (2019). On the periodicity of linear and nonlinear oscillatory reconnection. Astronomy Astrophysics 621, A106. doi:10.1051/0004-6361/201834369

CrossRef Full Text | Google Scholar

Van Doorsselaere, T., Srivastava, A. K., Antolin, P., Magyar, N., Vasheghani Farahani, S., Tian, H., et al. (2020). Coronal heating by MHD waves. Space Sci. Rev. 216, 140. doi:10.1007/s11214-020-00770-y

CrossRef Full Text | Google Scholar

Yamada, M., Kulsrud, R., and Ji, H. (2010). Magnetic reconnection. Rev. Mod. Phys. 82, 603–664. doi:10.1103/revmodphys.82.603

CrossRef Full Text | Google Scholar

Zhou, X., Büchner, J., Bárta, M., Gan, W., and Liu, S. (2015). Astrophysical J. 815 (6), 6. doi:10.1088/0004-637x/815/1/6

CrossRef Full Text

Zhou, X., Büchner, J., Bárta, M., Gan, W., and Liu, S. (2016). Astrophysical J. 827, 94. doi:10.3847/0004-637x/827/2/94

CrossRef Full Text