Overlapping cusp ion dispersions formed by flux ropes on the day-side magnetopause

Introduction: Cusp ion dispersion signatures reflect properties of remote magnetic reconnection. Since the cusp is easier to observe in situ compared to the reconnection x-line, ion dispersions provide key insight on whether reconnection is variable in space and time. This study is motivated by a specific dispersion signature having two ion populations separated in energy but not space. These are known as overlapping dispersions because when observed by low-Earth orbiting satellites traversing the cusp, they appear as two dispersed ion populations overlapping in magnetic latitudes. Overlapping dispersion signatures have been observed for all interplanetary magnetic field (IMF) orientations and have been associated with multiple reconnection processes, but the three-dimensional magnetic reconnection topology and particle trajectories have not been examined.

Methods: Forward particle tracing using the GAMERA-CHIMP global magnetohydrodynamic (MHD) with test particle framework is carried out to construct ion dispersion signatures throughout the cusp. Under idealized solar wind driving with steady purely southward IMF, both standard and overlapping dispersions are found.

Results: Analysis of the test particle trajectories shows that the higher energy population of the overlapping dispersion travels along the axis of a flux rope before heading into the cusp, whereas the lower energy population goes directly into the cusp. Furthermore, the overlapping dispersions observed by the synthetic satellites compare well to Defense Meteorological Satellite Program (DMSP) F16 observations during strongly southward IMF.

Discussion: It is thus concluded that during strongly southward IMF, cusp-entering particles interacting with a magnetopause flux rope (generated by secondary reconnection) is one way to produce an overlapping dispersion. This study lays the groundwork for the forthcoming NASA Tandem Reconnection and Cusp Electrodynamics Reconnaissance Satellites (TRACERS) mission, which will connect the cusp to the magnetosphere—discovering how spatial or temporal variations in magnetic reconnection drive cusp dynamics. The expected launch of TRACERS is in 2025.

1 Introduction

Day-side magnetic reconnection at Earth’s magnetopause drives global convection of magnetic field lines. The convection pattern is largely controlled by the reconnection topology, which depends on the upstream interplanetary magnetic field (IMF). When the day-side reconnection x-line is active, particles spanning a range of energies are injected onto magnetic field lines newly connected to the Earth. Due to the time-of-flight effect associated with field line convection, spacecraft flying through the geomagnetic cusp in low Earth orbits (LEOs) observe energy dispersion of the ions (Lockwood and Smith, 1989; Basinska et al., 1992; Lavraud and Trattner, 2021). A recent review of results from the Cluster mission described the cusp as a highly dynamic environment [see Pitout and Bogdanova (2021) and references therein], with some large scale cusp structures being stable spatial phenomenon, and others related to the sporadic nature of reconnection. Thus properties of observed dispersion signatures have the potential to shed light on the variability of reconnection in both time and space, a central question of space physics.

During steady strongly southward IMF, at the day-side magnetopause reconnected magnetic field lines are convecting away from the reconnection site [see, e.g., Burkholder et al. (2023) Figure 3], which corresponds roughly to motion towards the magnetic poles when mapped into the cusp at LEO. Thus, LEO spacecraft in the northern hemisphere observe dispersed particle energies with the highest energy particles at lowest magnetic latitude (Mlat), and lowest energy particles at highest Mlat [in this study, we follow the convention that the Mlat range is (−90,90) degrees with −90° being the south magnetic pole and 90° the north magnetic pole]. Correspondingly, the highest energy particles are observed at the lowest absolute Mlats in the southern hemisphere. This dispersion can be understood because the highest energy particles arrive before the lowest energies, while field lines convect from low to high absolute Mlat [see Pitout et al. (2009) for a description of mid-altitude cusp morphologies and resulting dispersion signatures]. This example is known as the “standard” cusp dispersion for southward IMF (e.g., da Silva et al., 2022), but other types of dispersion are known. Connor et al. (2015) constructed dispersion signatures for different IMF clock angles using the global MHD with test particle approximation. The standard cusp dispersions for southward and northward IMF were found, in addition to a double reverse dispersion with ${\mathrm{B}}_y$ (GSE coordinates) dominant IMF. Recently, “V” type dispersions during northward IMF were explained in terms of intermittent lobe reconnection (Xiong et al., 2024). Of interest to this study, da Silva et al. (2024) showed that a special type of dispersion, which has two populations of different energy that overlap in Mlat, has been observed during nearly all IMF orientations.

Overlapping dispersions are hypothesized to be formed by a multiple reconnection process (Lockwood, 1995; Trattner et al., 1998; Trattner et al., 2012). Observationally, this is supported by in situ measurements, which have linked multiple reconnections to flux transfer events (FTEs) and the subsequent detection of overlapping dispersion in the cusp (Fuselier et al., 2018; Fuselier et al., 2022). Pitout et al. (2012) interpreted overlapping ion structures in the mid-altitude cusp as a signature of dual lobe reconnection during northward IMF. Global hybrid simulation results show features that are qualitatively similar to an overlapping dispersion and these were found to be associated with multiple x-line reconnection (Tan et al., 2012). Overlapping dispersions have also been demonstrated with a global hybrid-Vlasov simulation with purely southward IMF (Grandin et al., 2020). Despite these advances it has not been shown exactly how the different populations evolve to produce an overlapping dispersion, which is the motivation for this study.

2 Global MHD + test particle simulation

A Grid Agnostic MHD for Extended Research Applications (GAMERA) simulation (Zhang et al., 2019; Sorathia et al., 2020) of Earth’s magnetosphere was performed to calculate time-dependent magnetic and electric fields under idealized solar driving conditions, the same as Simulation 2 from Burkholder et al. (2023). The simulation uses Solar Magnetospheric (SM) coordinates, which have the z-axis parallel to Earth’s dipole axis and y-axis perpendicular to the Earth-Sun line. There is no dipole tilt so the IMF is always directed purely southward [(${\mathrm{B}}_x$,${\mathrm{B}}_y$,${\mathrm{B}}_z$) = (0,0,−5) nT]. The solar wind velocity ($v_{sw}=400$ km/s) and density ($\rho =5$ ${\mathrm{c}\mathrm{m}}^{-3}$) are held constant at typical values. This idealized scenario leads to persistent production of day-side magnetopause flux ropes via secondary reconnection. There is no explicit resistivity in the ideal MHD equations; numerical resistivity is localized where current sheets collapse to the grid scale. The simulation inner boundary is coupled to the RE-developed Magnetosphere-Ionosphere Coupler/Solver (REMIX, Merkin and Lyon, 2010). Forward proton test particle tracing is performed within the GAMERA fields using the Conservative Hamiltonian Integrator for Magnetospheric Particles (CHIMP, Sorathia et al., 2018). CHIMP removes the magnetic field parallel electric field to avoid anomalous particle heating. GAMERA-REMIX-CHIMP is part of the Multiscale Atmosphere-Geospace Environment (MAGE) model developed by the NASA DRIVE Science Center for Geospace Storms.

The energy of each particle is initialized as 1 keV with pitch angles uniformly distributed in the range [80,100] degrees. Initially field-aligned particles are excluded because they are easily lost to the outer boundary before reaching the magnetopause. Clearly, all of the particles having the same energy is not representative of the magnetosheath plasma. However, the newly initialized particles quickly evolve a distribution of energies (and pitch angles) once they interact with the magnetopause, so the unrealistic initial population is not expected to have an effect on the conclusions of this study. Tests were performed to assure that the initial energy and pitch angle distributions would not effect the conclusions of this study.

Figure 1A shows ${\mathrm{v}}_z$ at $y=0$, with the MHD inner boundary covered by a black circle and the test particle inner boundary in red. The black field lines are traced using the in-plane magnetic field. The location of the x-point in this plane corresponds to the accelerated flow reversal at $z\sim -1$ ${\mathrm{R}}_E$ and $x\sim 10$ ${\mathrm{R}}_E$. The trajectory along a field line from the x-point to the inner boundary is indicated by a thick black curve. A 1 keV proton with pitch angle 100$°$ travels $\sim 1$ ${\mathrm{R}}_E$/min along a field line, and the estimated travel distance based on the thick black curve is $\sim$10 ${\mathrm{R}}_E$. Therefore, it would take $\sim$10 min for this particle to go from the x-line to the inner boundary (if it did not undergo any acceleration). Since most particles are accelerated when they cross the magnetopause, a typical travel time is faster than 10 min. Thus, protons are streamed into the simulation for a period of 15 min and integration of the particle trajectories continues for 5 min after the end of streaming. This allows $\ge$1 keV particles with a range of pitch angles, which are on a trajectory to hit the inner boundary, to complete the journey within the simulation run-time. Furthermore, synthetic satellite observations are generated during the interval from 8 to 15 min so that there are no artificial dispersion signatures caused by the start and end of particle streaming.

Figure 1

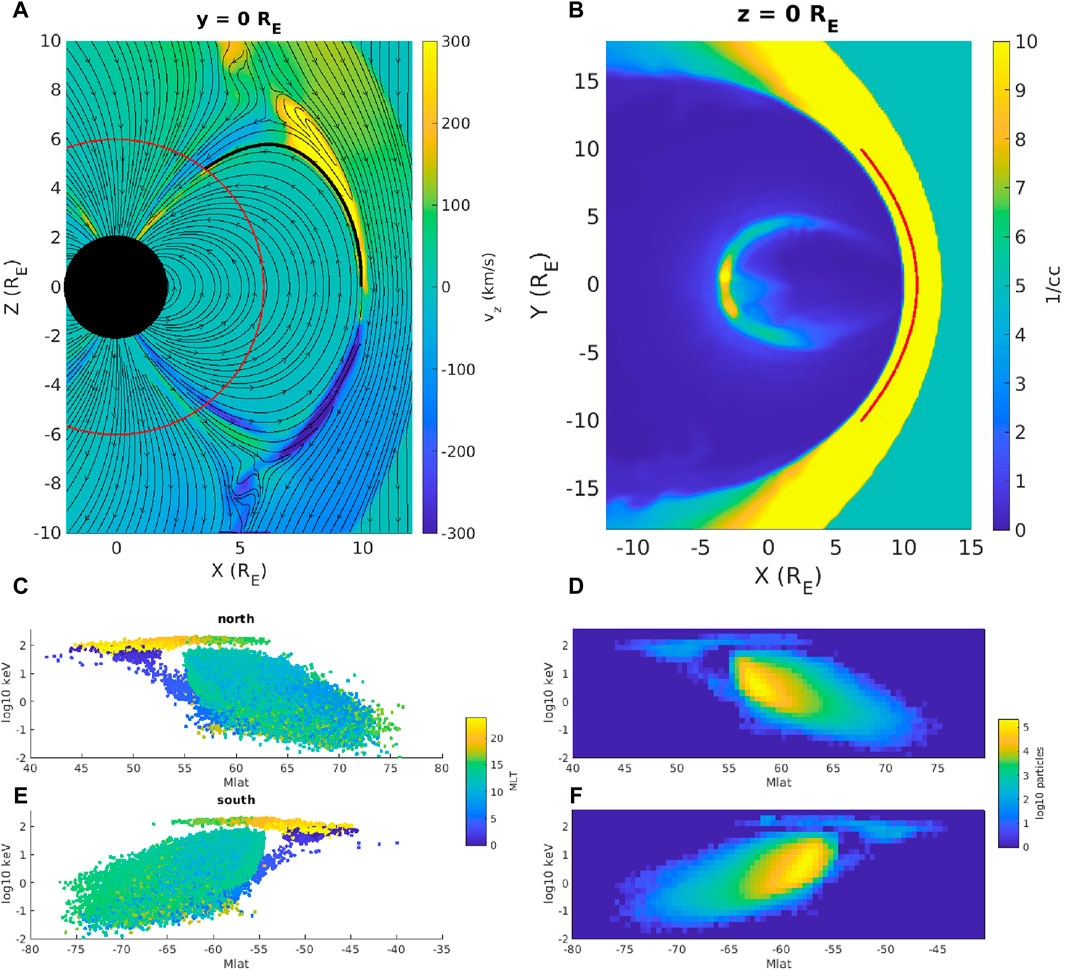
Figure 1. (A) In-plane magnetic field streamlines and ${\mathrm{V}}_z$ colormap. Solid black circle is the inner boundary of the MHD simulation, red circle is the inner boundary of the test particle simulation. The solid black curve is an estimate of the distance a particle travels from the x-line to the inner boundary: $\sim 10$ ${\mathrm{R}}_E$. (B) The colormap shows density and the red parabola shows where particles are streamed in. (C) Scatter representation of precipitated particle energy and Mlat in the northern hemisphere, colored by MLT. (D) Distribution of particle energies and Mlat of precipitation in the northern hemisphere. (E) Scatter representation of precipitated particle energy and Mlat in the southern hemisphere, colored by MLT. (F) Distribution of particle energies and Mlat of precipitation in the southern hemisphere.

The total number of particles initialized was 300 million with $\sim$7.5 million reaching the inner boundary over the course of the 20 min simulation. All particles have initial $x-y$ coordinates lying on the red parabola depicted in Figure 1B. These locations approximate the shape of the equatorial magnetopause, which can be roughly considered as the strong density gradient (Figure 1B colormap). Notice, the test particle initialization curve is always on the sunward side of the equatorial magnetopause. The initial $z$ range is [−5,5] ${\mathrm{R}}_E$. This places each particle on a magnetosheath field line (curved field lines connecting from top to bottom of Figure 1A). This initialization procedure is optimized to investigate dispersion signatures in a large volume of the day-side cusp.

Given that relatively few particles $(\sim 2.5\%)$ were collected at the inner boundary, it is worth noting why forward test particle tracing was used for this study, as opposed to backwards tracing. In the case of backwards tracing to the footpoint of a moving satellite, while providing the desirable level of particle statistics, it devotes every particle to a single spacecraft trajectory. Forward tracing has the advantage that one simulation can be used to investigate synthetic spacecraft observations throughout the entire cusp, which is a necessary task for this study because it is not trivial to determine which synthetic satellite trajectories will produce overlapping dispersions. Backwards particle tracing can also be performed over some finite area, rather than along a single spacecraft trajectory, but this would be at the expense of the number of particles that are collected by each satellite. In short, to investigate the cusp imprint of transient magnetopause dynamics via test particle simulation, there is no way to avoid using a large number of particles.

One way to collect more particles is to move the inner boundary of the test particle simulation to higher altitude. This allows particles with a greater range of pitch angles at any given energy to hit the inner boundary. Furthermore, the higher the altitude, the less magnetic focusing of the cusp field lines, making it easier to identify overlapping populations that are connected to transient magnetopause dynamics. In this study, the inner boundary radius is 6 ${\mathrm{R}}_E$ because this is slightly below the altitude at which the dipole field no longer dominates (see red circle, Figure 1A). This altitude is far above Earth compared to the orbit of Defense Meteorological Satellite Program (DMSP) F16 at $\sim$ 850 km (and the future Tandem Reconnection and Cusp Electrodynamics Reconnaissance Satellites—TRACERS at $\sim$500–625 km), with which the synthetic observations will be compared. However, the inner boundary of the MHD simulation is at 2 ${\mathrm{R}}_E$, so it is not possible to approach the altitudes observed by DMSP with this simulation anyway. Moving the test particle inner boundary to 6 ${\mathrm{R}}_E$ implies the assumption that particle energies entering the cusp do not change significantly once they enter the region dominated by the dipole. Tests were performed to assure that the same dispersion signatures are observed at altitudes lower than 6 ${\mathrm{R}}_E$, which confirms the validity of the assumption within the limits of the model. Note that wave particle interactions are not included in the MHD with test particle approximation. In addition, ring current and plasmasphere effects are not included in the model, which may be important at lower altitudes.

3 Overlapping dispersion

The overall dispersion pattern of particles collected at the simulation inner boundary is shown in Figures 1C–F. The scatter plots (Figures 1C, E, northern and southern hemispheres, respectively) show each particle that hit the inner boundary plotted in Mlat-energy space, with the energy axis in logarithmic units and color corresponding to magnetic local time (MLT). In this study, 12 MLT points to the nose of the magnetosphere (the noon meridian) and 0 MLT is in the central magnetotail (the midnight meridian), with 6 MLT and 18 MLT pointing to the top and bottom of Figure 1B, respectively, and corresponding to the dawn and dusk terminators. Figures 1C, E show 2 distinct populations separated by day-side (6–18 MLT, blue-green colors) and night-side (18–24 and 0–6 MLT, yellow and dark blue colors) MLT sectors. The spectrograms in Figures 1D, F show the corresponding particle counts in the same Mlat-energy bins. Particles hitting the inner boundary on the day-side have a standard dispersion signature, with the highest energy particles at lower absolute Mlats. All particles that hit the inner boundary over the course of the simulation are collected for these spectrograms. Therefore, they represent a time-averaged dispersion that smooths out structures associated with dynamics of the day-side x-line, which occur on a time scale of a few minutes in this simulation (Burkholder et al., 2023). The day-side flux ropes, for instance, move from the equator into the cusp on a time scale of $\sim$5–10 min. Figures 1D, F show particles collected on the night-side are relatively few compared to the day-side. How these particles access the night-side and what the resulting dispersion signatures can tell us about magnetotail reconnection is a promising direction for future exploration. However, the particle initialization was not designed to produce many particles with these trajectories, so this population is not the focus of this study.

To construct synthetic dispersion signatures that can be compared to Earth orbiting satellites, synthetic spacecraft are launched with constant values of MLT at an altitude of 6 ${\mathrm{R}}_E$, corresponding to a circular orbit along the test particle inner boundary. The synthetic spacecraft collect particles which are binned by time. Examples of synthetic spacecraft trajectories in the northern and southern hemispheres are depicted in Figures 2A, B (red lines). A surface is plotted at 6 ${\mathrm{R}}_E$ altitude with color corresponding to the average energy of particles which hit the inner boundary over the course of the simulation. Where the plot is white, no particles hit the inner boundary at that location. The red lines are the trajectories and the motion is from low to high absolute Mlat, in the direction of the red arrow in Figure 2A. The absolute Mlat covered by each trajectory is 57–60°, with step lengths of 0.04°. The width of bins is 0.1° Mlat by 0.1° longitude (results of this study were found to be insensitive to smaller bin size), and each step advances the test particle simulation 5 s. In other words, the satellite collects each particle that precipitated in a $0.1\times 0.1$ degree bin over a 5 s interval, then steps 0.04° in Mlat and bins again for the next 5 s interval, and so on, for a total 380 s. This motion at 0.008°/s is similar to the DMSP satellite moving at 0.015°/s through the cusp region (see DMSP observations in Figure 7).

Figure 2

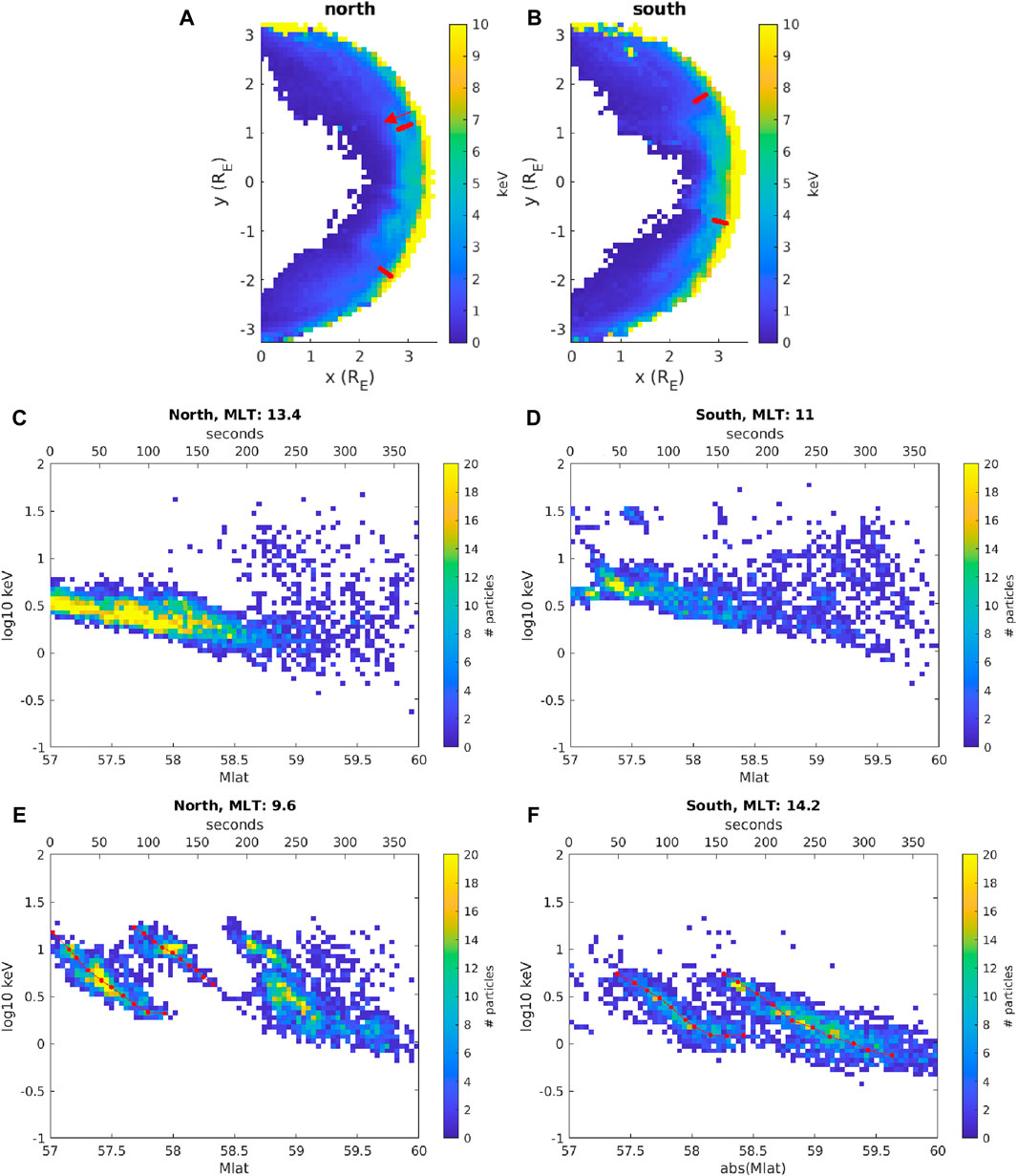
Figure 2. Colormaps show the (A) Northern and (B) Southern hemisphere average energy of precipitated particles at the inner boundary (6 ${\mathrm{R}}_E$ altitude). The red lines show trajectories used to produce the synthetic observations in (C–F). The trajectories move from lower to higher absolute Mlat, as indicated by the red arrow in (A). (C,D) Standard dispersion signatures constructed in the northern and southern hemispheres, respectively. (E,F) Overlapping dispersions constructed in the northern and southern hemispheres, respectively. The MLTs for (C–F) are indicated in the titles. Red dots in (E,F) are used to calculate the local slope in Figure 8.

Synthetic observations at the example MLTs are shown in Figures 2C–F. Figures 2C, D show between absolute Mlats of 57 and 58.5°, the energy of ions decreases steadily. These are examples of standard dispersion during southward IMF. These correspond to the trajectories taken at MLT 13.4 in the northern hemisphere (Figure 2C) and MLT 11 in the southern hemisphere (Figure 2D). Figures 2E, F show examples of overlapping dispersions in the northern (MLT 9.8) and southern hemispheres (MLT 14.2), respectively. The red dots, which will be discussed alongside Figure 8, are plotted through the central portion of nonzero fluxes, which is not necessarily the highest flux at each Mlat but it is generally close. The dispersions are standard in the sense that the energy of both populations decreases with increasing absolute Mlat. The defining feature is the region of overlap with a near absence of particles at energies between the two populations. The distance of the overlap is $\le$0.5° for both cases. The example dispersions in Figures 2C–F were chosen among the infinity of possible spacecraft trajectories to demonstrate that there can be different types of dispersion during steady southward IMF. Overlapping dispersions are found at all MLTs with sufficient precipitated test particle statistics to construct synthetic dispersions. It is possible that overlapping dispersions can be preferentially observed at some locations in the cusp but this is left for future work. The focus of this study is their formation mechanism.

Figure 3 examines the two populations of particles that produced the overlapping dispersion in Figure 2E. Figure 3A shows the individual particles that were collected from 57 to 58.3° Mlat. The color indicates whether the particle belongs to the lower (blue) or higher (green) energy population of the overlapping dispersion, which were separated based on the red line. These terms “lower” and “higher” will be used hereafter to refer to the dispersion containing the lower or higher energy particles in the region of overlap. Following the same color scheme, Figure 3B plots each particle where it hit the inner boundary of the test particle simulation. It is clear that there is a region where the two populations are co-located, which serves to demonstrate that the two populations in Figure 2E are overlapping rather than only appearing so due to the finite size binning. A blue particle and a green particle have been singled out with magenta star markers. Figure 3A shows that these two particles hit the inner boundary at the same Mlat in the overlapping region of the dispersion. In Figure 3B the same particles can be identified by magenta stars with colored points representing the blue or green population. Figure 3B shows that the spatial separation of the starred particles at the inner boundary is $<0.06$ ${\mathrm{R}}_E$, which equates to $\sim 0.01$ ${\mathrm{R}}_E$ when mapped along the magnetic field to the simulation inner boundary: an order of magnitude smaller than the closest grid separation. The trajectories for these particles will be further investigated in Figures 4, 5. Notice it is possible to find a green and blue particle in Figure 3B which hit the inner boundary at nearly the same location, but it would be extremely unlikely for any 2 particles to hit at exactly the same location. Therefore despite the small separations, conceptually none of the precipitated particles inhabit the exact same magnetic field line as any other (this conceptual point applies to spacecraft observations too, because of finite integration times). Due to the close separations and finite numerical precision the overlapping populations can be considered as traveling along the same magnetic flux tube, where a flux tube means a bundle of magnetic field lines that have the same plasma and are being convected in the same way.

Figure 3

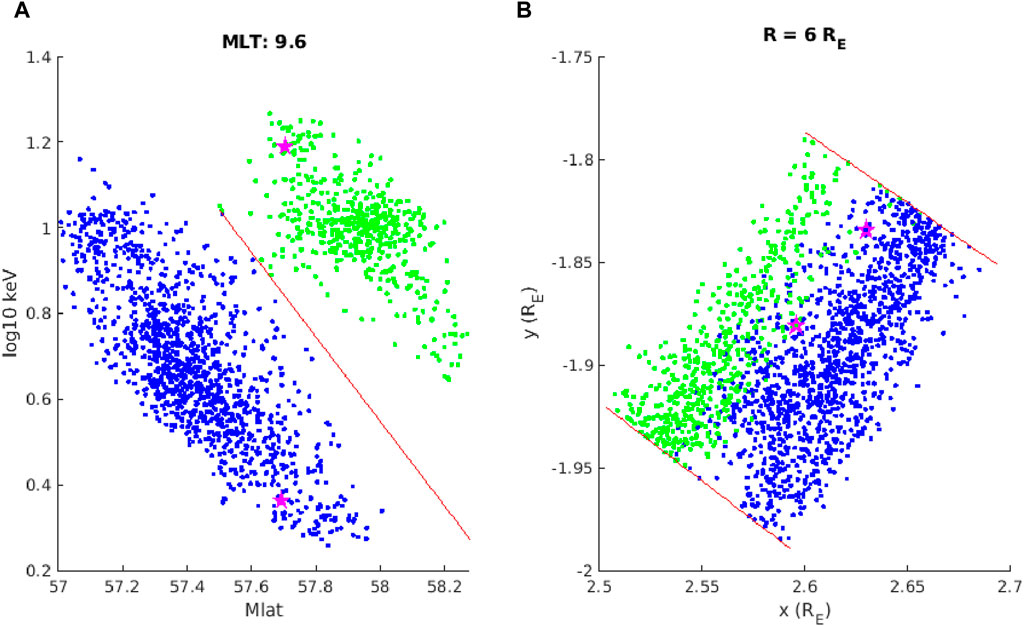
Figure 3. (A) Individual particles, plotted on Mlat-energy axes, that were collected by the synthetic satellite in Figure 2E from 57 to 58.3° Mlat (energy axis is in logarithmic units). The red line separates the two overlapping populations with the higher energy population colored green and the lower energy population colored blue. (B) Plots all the same particles at their location of precipitation at the inner boundary (in SM coordinates). The red lines show the size of the MLT bins. This demonstrates that the overlapping populations are co-located in coordinate space, not just appearing so in Mlat-energy space because of finite sized binning. Particles with a star marker are examined in Figures 4, 5.

Figure 4

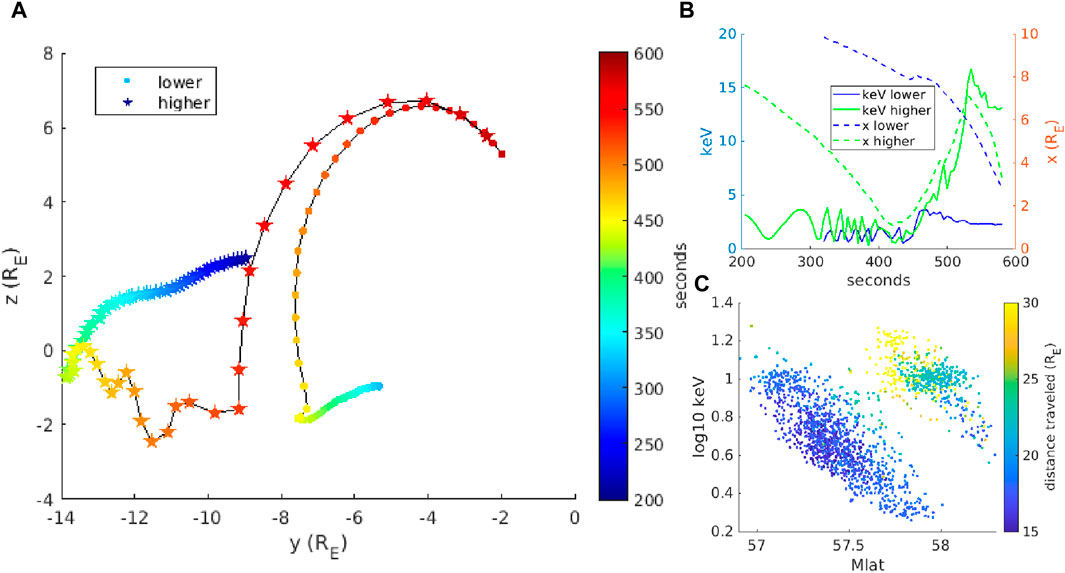
Figure 4. (A) Trajectories viewed in the $y-z$ plane for the starred particles from Figure 3. The stars show the path of the higher energy particle from the green population and the circles are for the lower energy particle in the blue population. Color represents time since the beginning of the test particle simulation. (B) Energy (solid lines, left axis) and x-coordinate (dashed lines, right axis) of the higher and lower energy particles, with the same green and blue colors. The time axis represents time since the beginning of the test particle simulation. (C) Total distance traveled for particles in the Figure 2E overlapping dispersion, showing the higher energy portion of the overlap travels 10–15 ${\mathrm{R}}_E$ further.

Figure 5

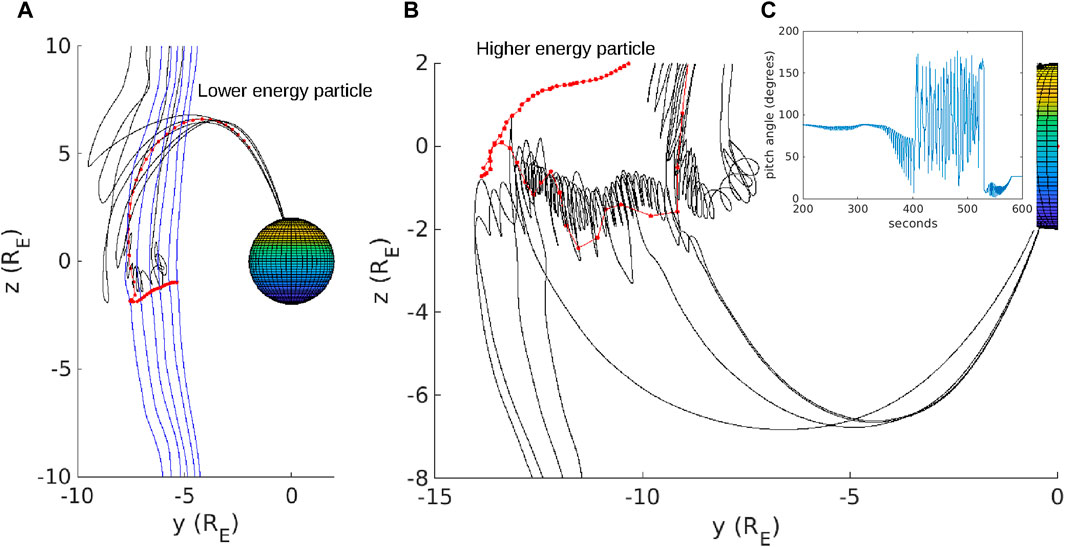
Figure 5. (A) Three-dimensional magnetic field lines traced from the lower energy particle location as it moved from its initial location to the inner boundary. Blue represents magnetosheath magnetic field with no connection to the simulation inner boundary, and black represents open magnetic field with only 1 end connected to the inner boundary. (B) Three-dimensional magnetic field lines at the higher energy particle location. Field lines are only drawn while the particle traverses along the axis of a flux rope and as they enter the cusp. (C) Pitch angle of the higher energy particle, which oscillates between field-aligned and anti-field aligned during the period $\sim$400–520 s, when the particle is trapped inside the flux rope.

Figure 4A shows trajectories projected onto the $y-z$ plane for a single particle from the blue population (circles) and the green population (stars) as identified by stars in Figure 3. The position is plotted every 5 s. The color of the particle indicates time. The circle marker trajectory shows that the particle from the lower energy population initially moved in the negative $y-$direction. It then abruptly changed course in the $z-$direction and followed a curved trajectory to the inner boundary. As the particle approached the inner boundary (from yellow to red colors), it moved along the magnetosphere side of a recently reconnected field line into the cusp. These recently reconnected field lines (see Figure 5A for a 3D representation) are moving poleward with the large scale convection pattern, so the energy of the particle determines where it will hit the inner boundary: the origin of the average dispersions shown in Figure 1 (higher energy particles hit the inner boundary first, when the field line has only convected away from the x-line a little, and lower energy particles hit the inner boundary later, when the field line has convected further). The particle from the higher energy population (Figure 4A, stars) moved much farther towards the dawn flank, then moved in the positive $y-$direction for $\sim 1$ min, and finally made an abrupt change of direction before going into the cusp. Ion motion opposite the magnetosheath flow has been identified in test particle simulations before (Sorathia et al., 2017), and its origin will be discussed below. Similar to the lower energy particle, the higher energy particle accesses the cusp by traversing the magnetosphere side of a recently reconnected field line. These field lines are retreating from the x-line with the large-scale convection pattern such that the location where the particle will hit the inner boundary is energy dependent. Thus, the origin of the dispersion for the higher and lower energy populations of the overlapping dispersion is the same. It will be shown that the difference in energy is due to a different acceleration history before particles access the magnetosphere side of a recently reconnected field line.

Figure 4B shows energy of the two particles as a function of time (solid lines, left axis), along with their x-coordinates (dashed lines, right axis). The colors blue and green correspond to the circles and stars from Figure 4A, respectively (and the colors in Figure 3). The blue particle undergoes an acceleration at t$\sim$450 s, corresponding to the abrupt change of trajectory from moving towards the flank (x-coordinate of particle slowly decreasing), to going into the cusp (sudden change of x-coordinate and subsequent faster decrease). The energy of the green particle increases about 5 times more compared to the blue particle, and the acceleration occurs from ∼400 to 520 s. This is during the time when the x-coordinate of the particle is increasing, which corresponds to motion of the particle back towards 12 MLT, as shown in Figure 4A (yellow-orange portion of the stars trajectory). Figure 4C shows the scatter representation of the overlapping dispersion from Figure 2E, with color corresponding to the total distance traveled by the particle before reaching the inner boundary. In the region of overlap, all particles in the higher energy population traversed 10–15 ${\mathrm{R}}_E$ more than the lower energy portion of the overlap. This serves to demonstrate that the single star trajectory from Figure 4A is a representative path for particles in the higher energy population of the overlap.

Figure 5 shows magnetic field lines traced at the location of the two particles along their respective journeys to the inner boundary. The lower energy particle trajectory is shown by the red dots in Figure 5A at 5 s resolution. A field line was traced every 25 s and the color of the field line corresponds to magnetosheath (blue) or connected to the inner boundary at 1 end only (black). As the particle moved initially in the $y$-direction towards the dawn flank, it was on a magnetosheath field line. The abrupt change of direction of the particle into the positive $z$-direction is associated with a change of magnetic connectivity to a black open field line mapping to the inner boundary in the northern cusp (in this study we refer to magnetic field lines with only 1 end connected to the inner boundary as open field lines). The first open field line that the particle encountered traces out a small flux rope with scale size $<2$ ${\mathrm{R}}_E$ along the axis, but the trajectory of the particle is directly into the cusp rather than along the flux rope axis. Notice, the sequence of black field lines shows that as the particle approached the cusp, the open field line it was gyrating about was convecting poleward, away from the x-line. In a classical 2D reconnection picture the newly reconnected field line would retreat directly poleward away from the x-line. However, the magnetosheath flow also drags those field lines tail-ward so in addition to the poleward convection there is some motion in the y-direction.

The higher energy particle trajectory is shown by the red dots in Figure 5B. As the particle initially moved from y$\sim -10$ ${\mathrm{R}}_E$ to y$\sim -14$ ${\mathrm{R}}_E$ (negative $y$-direction), it was on consecutive magnetosheath field lines (not shown). Eventually, the particle changed direction and moved in the positive $y$-direction while it was being accelerated (see Figure 4B). The particle’s pitch angle (shown at 0.05 s resolution in Figure 5C) was oscillating between field-aligned and anti-field aligned during the acceleration interval ($\sim$400–520 s). The frequency of this oscillation is the same as the local ion gyrofrequency ($\sim 0.2$ Hz). This corresponds to a particle whose gyro-center is very close to the magnetopause and whose gyroradius is such that it accesses southward ${\mathrm{B}}_z$ in the magnetosheath during half a gyro-period and northward ${\mathrm{B}}_z$ in the magnetosphere during the other half. This type of motion would likely not be possible if the IMF were not strongly southward. Analytical solutions demonstrate that an ion periodically crossing a current sheet in this way will be accelerated (Speiser, 1965; Speiser, 1967). Furthermore, the three-dimensional magnetic field line traces show that during this motion the ion is funneled along the axis of a magnetic flux rope (black helical field lines extending from $y\sim -13$ ${\mathrm{R}}_E$ to $y\sim -9$ ${\mathrm{R}}_E$). The flux rope field lines were identified using the particle location as the seed point for field line integrations, so there is no mistaking that the particle is trapped in the flux rope. The particle escaped the large dawn flank flux rope at $y\sim -9$ ${\mathrm{R}}_E$, immediately after which it was on a field line comprising the same small flux rope as the particle encountered in Figure 5A. At this point the higher energy particle’s motion is the same as the lower energy particle, but it is moving faster, so in order to hit the inner boundary at the same time as the lower energy particle, the higher energy particle was injected onto the magnetosphere side of the open flux tube slightly later in time. It is thus concluded that the overlapping higher energy population takes an indirect route into the cusp, by moving along the axis of a flux rope before precipitating. The higher energy is obtained due to acceleration inside the flux rope.

Notice, magnetic field lines comprising the flux rope in Figure 5B have one end connected to the southern hemisphere inner boundary and the other end open to the magnetosheath. It is not trivial to see how particles trapped in this flux rope can end up in the northern cusp. The key aspect of the magnetic flux rope is that all types of magnetic topology exist within the flux rope (Pu et al., 2013; Zhong et al., 2013, see also Burkholder et al., 2023 Figure 6). Reconnection can occur between open field lines (one end connected to the inner boundary) and closed field lines (connected to both northern and southern hemispheres) which are twisted around the flux rope. This type of reconnection allows particles which are initially trapped in the flux rope to precipitate in the northern hemisphere cusp. Particles accelerated in the flux rope are thus able to access the same flux tube where an earlier population of less energetic particles, like Figure 5A, precipitated on.

Figure 6

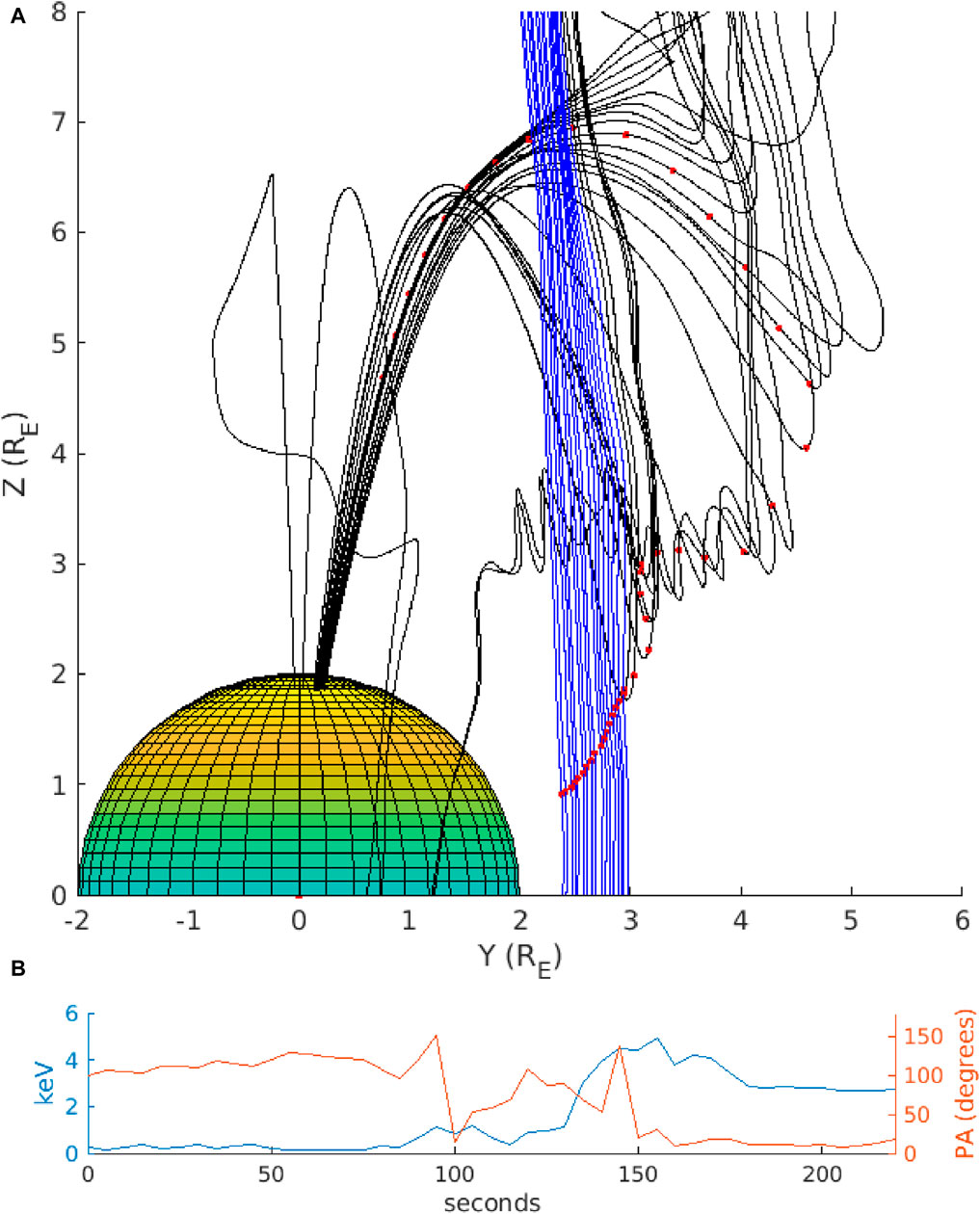
Figure 6. (A) Three-dimensional magnetic field lines traced from a particle location (red dot) having initial energy 0.1 keV and initial pitch angle 100°. Blue and black magnetic field lines represent the same magnetic connections as Figure 5. (B) Energy (blue, left axis) and pitch angle (orange, right axis) evolution of the particle. The energy increase occurs while the pitch angle oscillates between field-aligned and anti-field-aligned, the same motion as the particle in Figure 5B executes while traversing the flux rope.

Figure 6 shows another example of an ion test particle traversing the axis of a flux rope. This particle was not part of the simulation described in Section 2, but was from a testing run performed to confirm the robustness of this paper’s conclusions against different particle initializations. Essentially every aspect of this simulation was the same as described in Section 2 except there were only 10 million total particles and the initial energy was 0.1 keV. This specific particle was chosen because it precipitated into the northern cusp with a population of particles that form the higher energy portion of an overlapping dispersion. Figure 6A shows the ion was initially on a magnetosheath field line (blue), and eventually accessed an open field line (black) with 1 end connected to the inner boundary. The first open field line that the particle accessed was not part of a magnetic flux rope, but after about 20 s the particle trajectory became confined to a magnetic flux rope. The particle eventually escaped the flux rope and traveled into the northern cusp on a poleward convecting open field line. Figure 6B shows the energy (left-side blue axis) and pitch angle (right-side orange axis) for this particle. During the acceleration interval from $\sim 100-150$ s, the pitch angle is oscillating between field-aligned and anti-field aligned (the frequency of the oscillation is much smaller than Figure 5C because the pitch angle is only plotted every 5 s), indicating the particle is oscillating from the magnetosheath to magnetosphere side of the current sheet as it traversed the flux rope axis. The particle was trapped in the flux rope for less than half the amount of time compared to Figure 5B and thus only gained $\sim 5$ keV because it crossed the current sheet fewer times. In this case the flux rope has a scale size along its axis of $\sim 2$ ${\mathrm{R}}_E$ (less than half of Figure 5B), and is magnetically connected mostly to the northern hemisphere. Notice the handedness of ion gyromotion means that the particle traverses the axis of the flux rope in the same direction as the magnetosheath flow in the dusk sector, as opposed to Figure 5B in the dawn sector.

4 Comparison of simulation and DMSP

Figures 7A, C show observations from Special Sensor J (SSJ) on the DMSP F16 satellite (Redmon et al., 2017). The instrument gives ion differential energy flux in the range 30 eV to 30 keV, at a nominal altitude of 850 km. These events were taken from the database of overlapping dispersions identified by da Silva et al. (2024). They were chosen specifically because the IMF is strongly southward in both instances (see Figures 7B, D titles), as drawn from the OMNIWeb data product. They were also both observed in the day-side cusp region (near 14 MLT for event 1 and 12 MLT for event 2), similar to the synthetic observations in Figure 2. The blue and green lines in Figures 7A, C, corresponding to the two overlapping populations, were drawn to trace the lower and upper dispersions, respectively. The region of overlap lies between the vertical dashed lines. In Figure 7A the overlap is $\sim$0.7° Mlat, and in Figure 7C it is $\sim$0.2°. The synthetic overlapping dispersions in Figures 2E, F overlap for 0.4° and 0.3°, respectively.

Figure 7

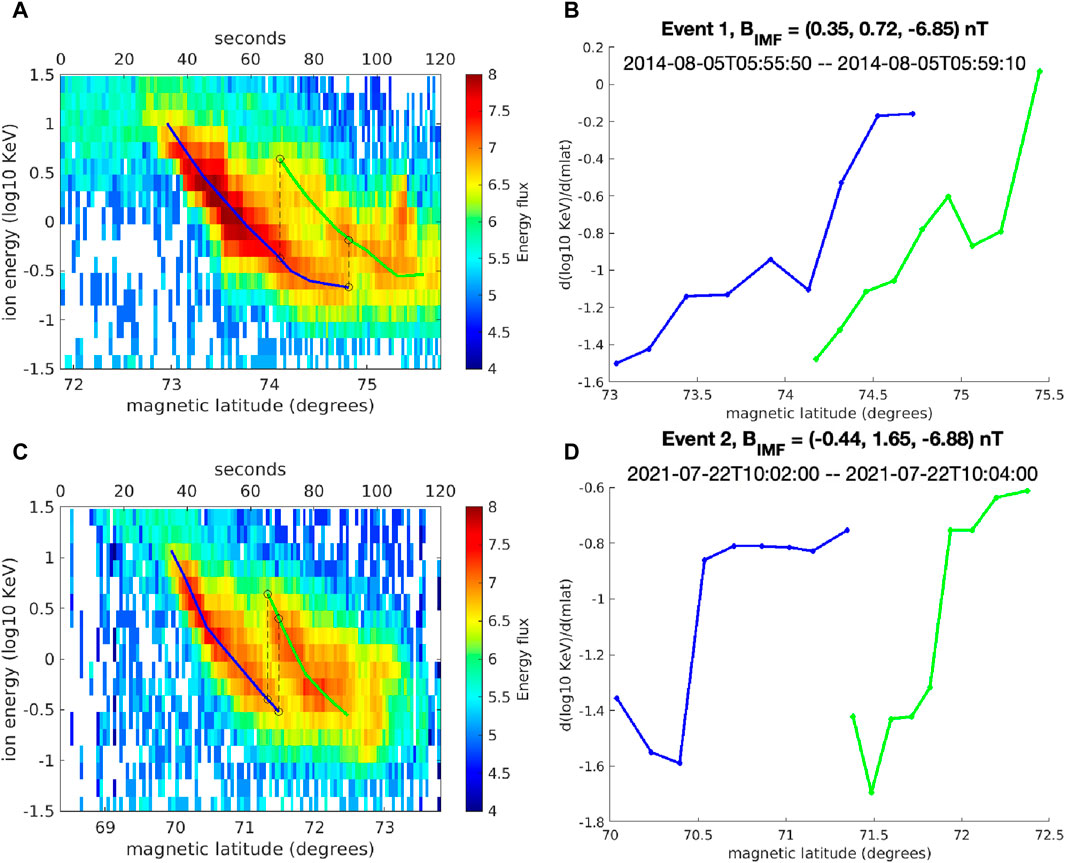
Figure 7. (A,C) Two examples of overlapping dispersions observed by DMSP during strongly southward IMF. The blue (green) line was drawn through the region of highest flux at each Mlat for the lower (higher) energy population of the overlapping dispersion. The vertical dashed lines show the region of overlap. (B,D) The corresponding local slopes of the green and blue lines drawn in (A,C).

The slope of the overlapping dispersions in Mlat-energy space can also be compared from the simulation and observation. Lockwood and Smith (1992) showed that the slope of the dispersion could be related to the upstream reconnection rate at the magnetopause. Figures 7B, D show the slope as a function of Mlat for the DMSP observations, with blue and green lines giving the slope corresponding to the blue and green lines in Figures 7A, C. Locally, the slopes are somewhat variable but the general trend is that the slope gets shallower with increasing Mlat. In both instances the lower portion (blue) of the overlapping dispersions have an average slope of about 1 order of magnitude keV per degree Mlat and for the higher portion (green) it is only slightly shallower.

The slopes of the synthetic overlapping dispersions were also calculated (see red dots in Figures 2E, F, similar to the blue and green lines in Figures 7A, C) and the comparison with DMSP observations is shown in Figure 8. The slopes are given as a function of energy (on a logarithmic scale). The slopes for the lower portions of the overlapping dispersions are plotted in Figure 8A and the slopes of the upper portions are plotted in Figure 8B. The blue and black lines in Figure 8A show the local slopes for the lower portions of the simulation dispersions. These have a trend of steeper slope at higher energy, the same as DMSP (red and green). The upper portion of the simulation dispersions (Figure 8B) shows steeper slopes at higher energy for black (corresponding to Figure 2F), comparing well with red and green. The blue slopes (corresponding to Figure 2E) are fairly constant (about 1 order of magnitude keV per degree Mlat) through their entire energy range. This is probably because there were few particles collected for this dispersion with $<$10 keV.

Figure 8

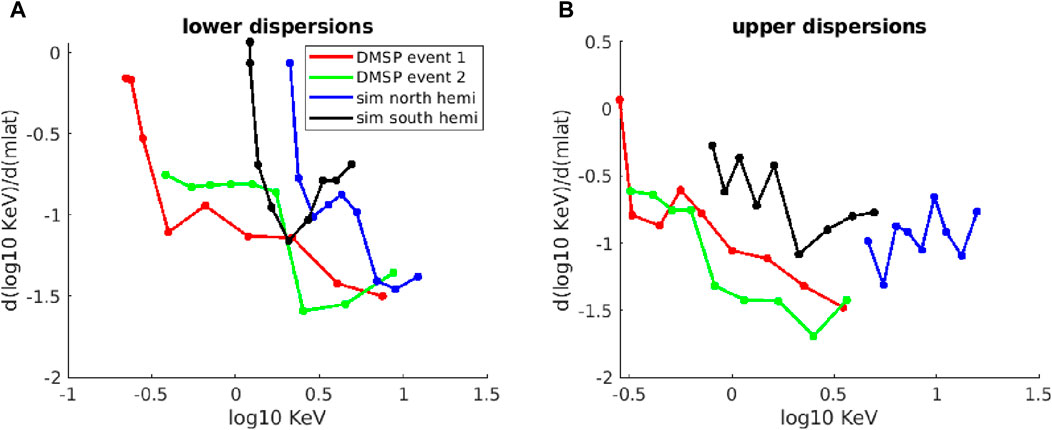
Figure 8. (A) Slope as a function of energy for lower portions of the simulated and observed overlapping dispersion signatures. Black and blue are calculated from the simulated overlapping dispersions in Figures 2E, F, respectively. Green and red are calculated from the observed overlapping dispersions in Figures 7A, C, respectively. (B) Slope as a function of energy for upper portions of the simulated and observed overlapping dispersion signatures, with same colors as (A). Energy axes are in logarithmic units.

Another quantity to compare is the energy separation of the overlapping populations. It is about 15 keV for Figure 2E and 4 keV for Figure 2F, compared to $\sim$3 keV for both Figures 7A, C. The reason the energy separation may be a meaningful quantity is that Figure 4B indicates the particle from the higher energy population undergoes a roughly constant increase of energy. Thus, for the population that was accelerated inside a flux rope, this leads to the possibility of calculating the amount of distance the particle traversed inside the flux rope, if the initial energy can be estimated, and therefore approximate the flux rope length. However, a better description of the acceleration than the MHD with test particle approach is needed to approximate the rate of energy gain [like global hybrid modeling (Tan et al., 2012)], and aspects of the flux rope would also need to be known, like the typical radius and winding number. These possibilities are left for future work.

5 Summary and discussion of conclusion

The global MHD with test particle approximation was employed to understand the origin of overlapping cusp ion dispersion signatures during steady strongly southward IMF. It was found that different satellite paths through the cusp give different dispersion signatures, with some having overlapping populations and others having the standard dispersion (for southward IMF). By examining the trajectory of a particle in each population of an overlapping dispersion, it was determined that the higher energy population is formed by particles traversing the axis of a flux rope before going into the cusp. Particles from the lower energy population travel more directly from a magnetosheath field line into the cusp without being trapped. Trapped particles are energized as they gyrate across the magnetopause current sheet, accessing both magnetosphere and magnetosheath fields which have a magnetic shear angle of $\sim 180°$ (Speiser, 1965; Speiser, 1967). These trapped particles escape onto the same open magnetic flux tube that was earlier allowing into the magnetosphere particles which received a comparatively smaller acceleration (by crossing the magnetopause without becoming trapped in a flux rope).

Different acceleration histories for energy-separated populations which end up on the same open magnetic flux tube is a fundamentally new physical mechanism to account for overlapping dispersions. The existing interpretation of overlapping dispersions has different energy populations which underwent a similar acceleration history. That mechanism invokes the existence of multiple reconnection sites on the same open magnetic flux tube, leading to multiple injection events (Lockwood, 1995). The initial reconnection existed longer, and thus injects a lower energy population. A secondary reconnection of the same flux tube field lines, more recently been initiated, injects a higher energy population. Despite this difference, the formation of magnetic flux ropes and the magnetic topology changes that allow particles to escape flux ropes are also secondary reconnection processes, so it is the case that both the new and existing mechanisms rely on multiple reconnection of the same flux tube field lines. Missions targeting the day-side magnetopause, like NASA’s Magnetospheric Multiscale (MMS), may be able to determine the properties of particles traversing flux ropes and confirm whether the new mechanism is occurring. Otherwise, it is possible that flux ropes in global MHD simulation are not sufficiently realistic or the particles escape them via some kinetic processes not resolved in the test particle approximation.

Even these two mechanisms (traditional multiple reconnection of the same flux tube field lines, described above, and flux rope traversal, the subject of this paper) are unlikely to account for all observed overlapping dispersions, especially given the range of solar wind and IMF conditions that can impact Earth. There are different ways that multiple reconnection can occur, such as local flux tube interchange (Ma et al., 2019) associated with the Kelvin-Helmholtz instability (most likely near the flank regions) and interlinked flux tube reconnection (Cardoso et al., 2013; Øieroset et al., 2019). The observation and simulation comparisons in this study show remarkable similarity, but future work is needed to determine observational differences in overlapping dispersions caused by different multiple reconnection processes. Furthermore there is also the possibility that particles sourced elsewhere than the magnetosheath and solar wind play a role in the formation of overlapping dispersion signatures. For instance, particles trapped in the cusp diamagnetic cavity can escape due to magnetic topology changes (Nykyri et al., 2011; Nykyri et al., 2012; Burkholder et al., 2021) and if they end up deeper in the cusp they may be overlapping with a solar wind population when they precipitate, depending on how much energy was gained in the diamagnetic cavity.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/supplementary material.

Author contributions

BB: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. YG: Formal Analysis, Investigation, Writing–review and editing. AP: Data curation, Formal Analysis, Investigation, Visualization, Writing–review and editing. L-JC: Conceptualization, Writing–review and editing. JD: Writing–review and editing. XM: Writing–review and editing. DD: Writing–review and editing. HC: Writing–review and editing. SP: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work is provided by NASA Magnetospheric Multiscale (MMS) Early Career Grant 80NSSC22K0949.

Acknowledgments

We acknowledge use of NASA/GSFC’s Space Physics Data Facility’s OMNIWeb, and also the Texas Advanced Computing Center (TACC) at The University of Texas at Austin for providing HPC resources that have contributed to the research results reported within this paper http://www.tacc.utexas.edu. We thank the team of the Center for Geospace Storms for providing the MAGE model.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Basinska, E. M., Burke, W. J., Maynard, N. C., Hughes, W. J., Winningham, J. D., and Hanson, W. B. (1992). Small-scale electrodynamics of the cusp with northward interplanetary magnetic field. J. Geophys. Res. Space Phys. 97, 6369–6379. doi:10.1029/91JA03023

CrossRef Full Text | Google Scholar

Burkholder, B. L., Chen, L.-J., Sorathia, K., Sciola, A., Merkin, S., Trattner, K. J., et al. (2023). The complexity of the day-side x-line during southward interplanetary magnetic field. Front. Astronomy Space Sci. 10. doi:10.3389/fspas.2023.1175697

CrossRef Full Text | Google Scholar

Burkholder, B. L., Nykyri, K., Ma, X., Sorathia, K., Michael, A., Otto, A., et al. (2021). The structure of the cusp diamagnetic cavity and test particle energization in the gamera global mhd simulation. J. Geophys. Res. Space Phys. 126, e2021JA029738. doi:10.1029/2021JA029738

CrossRef Full Text | Google Scholar

Cardoso, F. R., Gonzalez, W. D., Sibeck, D. G., Kuznetsova, M., and Koga, D. (2013). Magnetopause reconnection and interlinked flux tubes. Ann. Geophys. 31, 1853–1866. doi:10.5194/angeo-31-1853-2013

CrossRef Full Text | Google Scholar

Connor, H. K., Raeder, J., Sibeck, D. G., and Trattner, K. J. (2015). Relation between cusp ion structures and dayside reconnection for four imf clock angles: openggcm-ltpt results. J. Geophys. Res. Space Phys. 120, 4890–4906. doi:10.1002/2015JA021156

CrossRef Full Text | Google Scholar

da Silva, D., Chen, L. J., Fuselier, S., Wang, S., Elkington, S., Dorelli, J., et al. (2022). Automatic identification and new observations of ion energy dispersion events in the cusp ionosphere. J. Geophys. Res. Space Phys. 127, e2021JA029637. doi:10.1029/2021JA029637

CrossRef Full Text | Google Scholar

da Silva, D. E., Chen, L. J., Fuselier, S. A., Petrinec, S. M., Trattner, K. J., Cucho-Padin, G., et al. (2024). Statistical analysis of overlapping double ion energy dispersion events in the northern cusp. Front. Astronomy Space Sci. 10. doi:10.3389/fspas.2023.1228475

CrossRef Full Text | Google Scholar

Fuselier, S. A., Kletzing, C. A., Petrinec, S. M., Trattner, K. J., George, D., Bounds, S. R., et al. (2022). Multiple reconnection x-lines at the magnetopause and overlapping cusp ion injections. J. Geophys. Res. Space Phys. 127, e2022JA030354. doi:10.1029/2022JA030354

CrossRef Full Text | Google Scholar

Fuselier, S. A., Petrinec, S. M., Trattner, K. J., Broll, J. M., Burch, J. L., Giles, B. L., et al. (2018). Observational evidence of large-scale multiple reconnection at the earth’s dayside magnetopause. J. Geophys. Res. Space Phys. 123, 8407–8421. doi:10.1029/2018JA025681

CrossRef Full Text | Google Scholar

Grandin, M., Turc, L., Battarbee, M., Ganse, U., Johlander, A., Pfau-Kempf, Y., et al. (2020). Hybrid-Vlasov simulation of auroral proton precipitation in the cusps: comparison of northward and southward interplanetary magnetic field driving. J. Space Weather Space Clim. 10, 51. doi:10.1051/swsc/2020053

CrossRef Full Text | Google Scholar

Lavraud, B., and Trattner, K. J. (2021). The polar cusps of the earth’s magnetosphere. American Geophysical Union AGU 11, 163–176. doi:10.1002/9781119815624.ch11

CrossRef Full Text | Google Scholar

Lockwood, M. (1995). Overlapping cusp ion injections: an explanation invoking magnetopause reconnection. Geophys. Res. Lett. 22, 1141–1144. doi:10.1029/95GL00811

CrossRef Full Text | Google Scholar

Lockwood, M., and Smith, M. F. (1989). Low-altitude signatures of the cusp and flux transfer events. Geophys. Res. Lett. 16, 879–882. doi:10.1029/GL016i008p00879

CrossRef Full Text | Google Scholar

Lockwood, M., and Smith, M. F. (1992). The variation of reconnection rate at the dayside magnetopause and cusp ion precipitation. J. Geophys. Res. Space Phys. 97, 14841–14847. doi:10.1029/92JA01261

CrossRef Full Text | Google Scholar

Ma, X., Delamere, P. A., Thomsen, M. F., Otto, A., Neupane, B., Burkholder, B., et al. (2019). Flux tube entropy and specific entropy in saturn’s magnetosphere. J. Geophys. Res. Space Phys. 124, 1593–1611. doi:10.1029/2018JA026150

CrossRef Full Text | Google Scholar

Merkin, V. G., and Lyon, J. G. (2010). Effects of the low-latitude ionospheric boundary condition on the global magnetosphere. J. Geophys. Res. Space Phys. 115. doi:10.1029/2010JA015461

CrossRef Full Text | Google Scholar

Nykyri, K., Otto, A., Adamson, E., Dougal, E., and Mumme, J. (2011). Cluster observations of a cusp diamagnetic cavity: structure, size, and dynamics. J. Geophys. Res. (Space Phys.) 116, A03228. doi:10.1029/2010JA015897

CrossRef Full Text | Google Scholar

Nykyri, K., Otto, A., Adamson, E., Kronberg, E., and Daly, P. (2012). On the origin of high-energy particles in the cusp diamagnetic cavity. J. Atmos. Solar-Terrestrial Phys. 87-88, 70–81. doi:10.1016/j.jastp.2011.08.012

CrossRef Full Text | Google Scholar

Øieroset, M., Phan, T. D., Drake, J. F., Eastwood, J. P., Fuselier, S. A., Strangeway, R. J., et al. (2019). Reconnection with magnetic flux pileup at the interface of converging jets at the magnetopause. Geophys. Res. Lett. 46, 1937–1946. doi:10.1029/2018GL080994

CrossRef Full Text | Google Scholar

Pitout, F., and Bogdanova, Y. V. (2021). The polar cusp seen by cluster. J. Geophys. Res. Space Phys. 126, e2021JA029582. doi:10.1029/2021JA029582

CrossRef Full Text | Google Scholar

Pitout, F., Escoubet, C. P., Klecker, B., and Dandouras, I. (2009). Cluster survey of the mid-altitude cusp - part 2: large-scale morphology. Ann. Geophys. 27, 1875–1886. doi:10.5194/angeo-27-1875-2009

CrossRef Full Text | Google Scholar

Pitout, F., Escoubet, C. P., Taylor, M. G. G. T., Berchem, J., and Walsh, A. P. (2012). Overlapping ion structures in the mid-altitude cusp under northward imf: signature of dual lobe reconnection? Ann. Geophys. 30, 489–501. doi:10.5194/angeo-30-489-2012

CrossRef Full Text | Google Scholar

Pu, Z. Y., Raeder, J., Zhong, J., Bogdanova, Y. V., Dunlop, M., Xiao, C. J., et al. (2013). Magnetic topologies of an in vivo fte observed by double star/tc-1 at earth’s magnetopause. Geophys. Res. Lett. 40, 3502–3506. doi:10.1002/grl.50714

CrossRef Full Text | Google Scholar

Redmon, R. J., Denig, W. F., Kilcommons, L. M., and Knipp, D. J. (2017). New dmsp database of precipitating auroral electrons and ions. J. Geophys. Res. Space Phys. 122, 9056–9067. doi:10.1002/2016ja023339

PubMed Abstract | CrossRef Full Text | Google Scholar

Sorathia, K. A., Merkin, V. G., Panov, E. V., Zhang, B., Lyon, J. G., Garretson, J., et al. (2020). Ballooning-interchange instability in the near-earth plasma sheet and auroral beads: global magnetospheric modeling at the limit of the mhd approximation. Geophys. Res. Lett. 47, e2020GL088227. doi:10.1029/2020GL088227

PubMed Abstract | CrossRef Full Text | Google Scholar

Sorathia, K. A., Merkin, V. G., Ukhorskiy, A. Y., Mauk, B. H., and Sibeck, D. G. (2017). Energetic particle loss through the magnetopause: a combined global mhd and test-particle study. J. Geophys. Res. Space Phys. 122, 9329–9343. doi:10.1002/2017JA024268

CrossRef Full Text | Google Scholar

Sorathia, K. A., Ukhorskiy, A. Y., Merkin, V. G., Fennell, J. F., and Claudepierre, S. G. (2018). Modeling the depletion and recovery of the outer radiation belt during a geomagnetic storm: combined mhd and test particle simulations. J. Geophys. Res. Space Phys. 123, 5590–5609. doi:10.1029/2018JA025506

CrossRef Full Text | Google Scholar

Speiser, T. W. (1965). Particle trajectories in model current sheets: 1. analytical solutions. J. Geophys. Res. (1896-1977) 70, 4219–4226. doi:10.1029/JZ070i017p04219

CrossRef Full Text | Google Scholar

Speiser, T. W. (1967). Particle trajectories in model current sheets: 2. applications to auroras using a geomagnetic tail model. J. Geophys. Res. (1896-1977) 72, 3919–3932. doi:10.1029/JZ072i015p03919

CrossRef Full Text | Google Scholar

Tan, B., Lin, Y., Perez, J. D., and Wang, X. Y. (2012). Global-scale hybrid simulation of cusp precipitating ions associated with magnetopause reconnection under southward imf. J. Geophys. Res. Space Phys. 117. doi:10.1029/2011JA016871

CrossRef Full Text | Google Scholar

Trattner, K. J., Coates, A. J., Fazakerley, A. N., Johnstone, A. D., Balsiger, H., Burch, J. L., et al. (1998). Overlapping ion populations in the cusp: polar/timas results. Geophys. Res. Lett. 25, 1621–1624. doi:10.1029/98GL01060

CrossRef Full Text | Google Scholar

Trattner, K. J., Petrinec, S. M., Fuselier, S. A., Omidi, N., and Sibeck, D. G. (2012). Evidence of multiple reconnection lines at the magnetopause from cusp observations. J. Geophys. Res. Space Phys. 117. doi:10.1029/2011JA017080

CrossRef Full Text | Google Scholar

Xiong, Y.-T., Han, D.-S., Wang, Z.-w., Shi, R., and Feng, H.-T. (2024). Intermittent lobe reconnection under prolonged northward interplanetary magnetic field condition: insights from cusp spot event observations. Geophys. Res. Lett. 51, e2023GL106387. doi:10.1029/2023GL106387

CrossRef Full Text | Google Scholar

Zhang, B., Sorathia, K. A., Lyon, J. G., Merkin, V. G., Garretson, J. S., and Wiltberger, M. (2019). GAMERA: a three-dimensional finite-volume MHD solver for non-orthogonal curvilinear geometries. Astrophysical J. Suppl. Ser. 244, 20. doi:10.3847/1538-4365/ab3a4c

CrossRef Full Text | Google Scholar

Zhong, J., Pu, Z. Y., Dunlop, M. W., Bogdanova, Y. V., Wang, X. G., Xiao, C. J., et al. (2013). Three-dimensional magnetic flux rope structure formed by multiple sequential x-line reconnection at the magnetopause. J. Geophys. Res. Space Phys. 118, 1904–1911. doi:10.1002/jgra.50281

CrossRef Full Text | Google Scholar