A machian model as potential alternative to dark matter halo thesis in galactic rotational velocity prediction

A novel axially symmetric metric is proposed to solve the Einstein field equations. This provides an analytical solution within the matter in the equatorial plane for any galaxy density profile. The solution predicts the observed increase in rotational velocity up to the edge of the galaxy’s bulge. However, beyond the bulge, the rotational velocity remains constant, which contradicts the observed peak curves. The existence of the Universe is then considered by approximating the gravitational fields within the galaxy as the sum of those generated by the galaxy and the Universe. The resulting solution explicitly includes a Universe frame-dragging term, aligning with the sixth version of Mach’s principle proposed by Bondi and Samuel: “inertial mass is affected by the global distribution of matter”. Neglecting the presence of the Universe, stars only have a relative rotation to the bulge, and their rotational velocities monotonically increase with the radial distance r to balance the increasing mass contained in distances < r. At larger distances, the bulge’s attraction and its frame-dragging effect decrease, resulting in a constant rotational velocity. When the Universe is considered, stars also have a relative rotation to the non-rotating Universe and experience an additional centrifugal force at any distance from the bulge. This component induces a decrease in rotational velocity as the gravitational influence of the bulge diminishes with r. This model predicts the observed rotational velocity curves for the galaxies M31, M101, and M81 without requiring any dark matter halo or adjustable parameters. This success substantiates Mach’s idea as an alternative to the dark matter halo theory.

1 Introduction

Most galaxies are dominated by a central mass according to their observed luminous material. However, the observed rotational velocity in these galaxies increases up to a radial distance significantly greater than what Newtonian dynamics predicts. Solving this discrepancy has been the subject of numerous studies.

Slight modifications to the law of gravitation, such as modified Newtonian dynamics (MOND), were proposed to address this issue (Milgrom, 2002). However, the most accepted theory is the presence of a dark matter halo, with several proposed profiles (Navarro, 1996; Merritt et al., 2005; Merritt et al., 2006).

Numerous axially symmetric solutions to the Einstein field equations have been derived and studied (Bronnikov et al., 2020). Recently, it has been demonstrated that the full resolution of the Einstein field equations using the Weyl–Lewis–Papapetrou coordinates could explain the flatness of the rotational velocity curve (Cooperstock and Tieu, 2007, Beordo et al., 2024). A simplified Mach’s principle added to Newtonian dynamics has also been proposed as an explanation for the flatness of the velocity curve (Darabi, 2013).

In a lecture on the origin of the general theory of relativity, Albert Einstein mentioned that he was already familiar with the intriguing idea of Ernst Mach that the inertia of anybody is the result of the interaction of that body with the rest of the bodies in the Universe (though this formulation by Einstein is not found in Ernst Mach’s work (Mach 1901)). Einstein further said: “This idea fascinated me; but it did not provide a basis for a new theory” (Einstein 1933). Although general relativity is not directly based on this idea, Einstein was enthusiastic about the existence of the Lense–Thirring effect, widely considered as a Machian manifestation of the general relativity (Lense and Thirring, 1918; Bondi and Samuel, 1997). However, some exact solutions, such as the Gödel rotating Universe (Gödel, 1949) and the completely empty hyperboloid Universe found by De Sitter in 1917 which was of particular concern to Einstein (Janssen, 2016), are in complete contradiction to Mach’s principle.

The relationship between Mach’s principle and general relativity has been a controversial topic, intensely discussed throughout the 20th century (Sciama, 1953; Rindler, 1994; Bondi and Samuel, 1997; Narlikar, 2003). At the Tübingen conference on Mach’s principle in 1995, an exit poll showed that three participants believed general relativity was Machian, while 21 did not; 14 participants believed general relativity using appropriate boundary conditions was Machian, while seven did not (Barbour et al., 1995). Several attempts have been made to integrate Mach’s principle with general relativity (Brans, 1962; Licata et al., 2016), Einstein himself attempted to reformulate it to fully agree with this principle.

In recent decades, researchers have focused more on searching for a perturbing body, i.e., dark matter, rather than on improving or developing theories. A winning strategy to explain the anomaly of Uranus’ orbit, but which failed to explain the perihelion anomaly of Mercury via the hypothetical planet Vulcan (Baum and Sheehan 2013).

This study proposes an axially symmetric metric that enables an analytical solution to the Einstein field equations and investigates whether a solution explaining the observed galactic rotational velocity profiles can emerge by adding Machian properties.

2 Method

2.1 General solution derivation

We consider the following stationary axially symmetric diagonal metric in the coordinate system [t, r, ϕ, z]:

$d{s}^2={\displaystyle {\sum }_{i=0}^3}{g}_{ii}d{x}^i=c^2{e}^{2\lambda }d{t}^2-e^{-2\beta }\left(d{r}^2+e^{2\gamma }d{z}^2\right)-{e^{-2\lambda }r}^{2}d{\phi }^2(1)$

where λ, β, and γ depend only on r and z.

All the differentials and tensors were computed using wxMaxima 22.04.0 (https://wxMaxima-developers.github.io/wxmaxima/) and analytical integrations with https://www.integral-calculator.com/.

The non-null components of the mixed Einstein tensor for this metric are as follows (see the cyl_metrics.wxmx file, which in this paper ranges from zero to three rather than from one to four in Maxima):

${ein}_0^0=\frac{e^{2\beta }\left(r{e}^{-2\gamma }\left({\lambda }_{zz}-{\left({\lambda }_z\right)}^2-{\gamma }_z{\lambda }_z-{\beta }_z{\gamma }_z+{\beta }_{zz}\right)+r{\lambda }_{rr}-r{\left({\lambda }_r\right)}^2+r{\gamma }_r{\lambda }_r+2{\lambda }_r-r{\gamma }_{rr}-r{\left({\gamma }_r\right)}^2+r{\beta }_r{\gamma }_r-{\gamma }_r+r{\beta }_{rr}\right)}{r}(2)$

${ein}_1^1=-\frac{e^{2\beta }\left({re}^{-2\gamma }{\left({\lambda }_z\right)}^2-r{\left({\lambda }_r\right)}^2+{\lambda }_r+{\gamma }_r-{\beta }_r\right)}{r}(3)$

$\begin{array}{l}{ein}_2^2=-e^{2\beta }\left(e^{-2\gamma }\left({\lambda }_{zz}+{\left({\lambda }_z\right)}^2-{\gamma }_z{\lambda }_z+{\beta }_z{\gamma }_z-{\beta }_{zz}\right)\right.\\ \left.+{\lambda }_{rr}+{\left({\lambda }_r\right)}^2+{\gamma }_r{\lambda }_r+{\gamma }_{rr}+{\left({\gamma }_r\right)}^2-{\beta }_r{\gamma }_r-{\beta }_{rr}\right)\end{array}(4)$

${ein}_3^3=\frac{e^{2\beta }\left(r{e}^{-2\gamma }{\left({\lambda }_z\right)}^2-r{\left({\lambda }_r\right)}^2+{\lambda }_r-{\beta }_r\right)}{r}(5)$

${ein}_3^1=e^{2\lambda }{ein}_1^3=\frac{e^{2\beta }\left(2r{\lambda }_r{\lambda }_z-{\lambda }_z+{\beta }_z\right)}{r}(6)$

With regard to the length of the equations, we maintained the compact Maxima notation in Eqs 2–6, i.e., the coordinates in the subscript refer to the differential against these coordinates.

The r-collapse is prevented by imposing:

${ein}_1^1=\kappa \rho \left(r,z\right)u_1{u}^1=0\to r{e}^{-2\gamma }{\left({\lambda }_z\right)}^2-r{\left({\lambda }_r\right)}^2+{\lambda }_r+{\gamma }_r-{\beta }_r=0(7)$

${ein}_3^1=\kappa \rho \left(r,z\right)u_3{u}^1=0\to 2r\left({\lambda }_r\right)\left({\lambda }_z\right)-{\lambda }_z+{\beta }_z=0(8)$

where $\kappa$ is the Einstein gravitational constant, $\rho \left(r,z\right)$ is the fluid density, and u is the four-velocity of the fluid modeling the galaxy. The condition ${ein}_3^3=0$ was not implemented. Indeed, in these axially symmetric metrics, orbital obliquity, which could balance the gravitational attraction in the z-direction, is not feasible. Evidently, ${ein}_2^2=0$ is also not imposed because the purpose is to study the rotating velocity within the matter.

Notably, by using the metric in Eq. 1, we neglected the handling of the components ${ein}_0^2$ and ${ein}_2^0$, which should be non-null to fit the terms $\kappa \rho u^2{u}_0$ and $\kappa \rho u^0{u}_2$ of the stress-energy tensor. We will come back to this issue in section 2.2.

The introduction of an integrating factor is a well-known method that involves multiplying nonlinear differential equations by a factor to facilitate their solution (Hermann et al., 2016). To facilitate the solutions of Eqs. 7, 8, we use a similar strategy, except for the introduction here of an additive integrating factor $\mu \left(r,z\right)$ defined by:

$\beta =\lambda +\gamma +\mu (9)$

To overcome the nonlinearity of Eq. 4, we focus on systems modeled by:

$\lambda =\chi \left(r\right)\zeta \left(z\right)(10)$

As explained at the end of this section, in the solution, $\chi \left(r\right)$ and $\zeta \left(z\right)$ determine the radial and transverse galaxy density profiles, respectively. Combining Eq. 9 with Eq. 10 results in:

${\mu }_z+{\gamma }_z={-r\chi \chi }_r{\left({\zeta }^2\right)}_z(11)$

Eq. 11 can be directly integrated into:

$\mu +\gamma =A-\frac{1}{2}r\left({\chi }_r^2\right){\zeta }^2(12)$

where A is an arbitrary function of r. By introducing Eqs. 10, 12 into Eq. 9, we derive:

$\beta =A+\chi \zeta -\frac{1}{2}r\left({\chi }_r^2\right){\zeta }^2(13)$

By inserting Eqs. 9, 10, 13 into Eq. 7 and multiplying by ${2e}^{2\gamma }$, we obtain:

${\left(e^{2\gamma }\right)}_r-\left(2r{\left({\chi }_r\zeta \right)}^2+2A_r-{\left(r{{\chi }^2}_r\right)}_r{\zeta }^2\right)e^{2\gamma }+2r{\chi }^2{\left({\zeta }_z\right)}^2=0(14)$

The general solution is as follows:

$e^{2\gamma }=2{\left({\zeta }_z\right)}^2{e}^{-h\left(r,z\right)}{\int }_r^{r_0}{r}^{\prime }{\left(\chi \left(r^{\prime }\right)\right)}^2{e}^{h\left(r^{\prime },z\right)}d{r}^{\prime }(15)$

where $r_0$ is an arbitrary integration constant and:

$h\left(r,z\right)=-2{\int }_0^r{r}^{\prime }{\left({\chi }_{r^{\prime }}\zeta \right)}^{2}d{r}^{\prime }-2A+r{\chi }_r^2{\zeta }^2(16)$

After substituting Eqs. 15, 16 into eq. 14, a straightforward calculation proved that these equations are the solutions.

As mentioned earlier, the resolution is based on the introduction of an additive integrating factor $\mu \left(r,z\right)$, which is finally not explicitly present in the metric solution.

Eqs. 15, 16 can be analytically computed only for some simple power functions of r, such as:

$\lambda =r\zeta \left(z\right),(17)$

Using Eq. 17 results in the following galaxy density and rotation velocity equations (see cyl_metric_1_r_z.wxmx):

$\rho \left(r,z\right)=\frac{2}{\kappa c^2}\frac{\zeta \left(z\right)}{r}(18)$

$2\pi \frac{d\phi }{dt}=2\pi \sqrt{\zeta \left(z\right)r}c(19)$

Eq. 19 shows that the rotational velocity monotonically increases with r, which contradicts the observed profiles.

2.2 Rotational velocity on the equatorial plane

Eq. 18 shows that the transverse density profile is directly given by $\zeta \left(z\right)$, while the radial density profile is given by $\frac{{\left(r{\chi }_r\right)}_r}{r}$ which will be proved at the end of this section.

We consider a galaxy for which the transverse $\zeta \left(z\right)$ density profile is modeled by a pseudo-Gaussian, i.e.,:

$\lambda \left(r,z\right)=\chi \left(r\right)e^{-\frac{z^{2+\epsilon }}{T^2}}(20)$

where ε is any strictly positive dimensionless small constant. For simplicity, and owing to the dimensionless nature of coefficients λ, β, and γ, we did not choose the normalized distribution form. Notably, even if the transverse density profile $\zeta \left(z\right)$ is independent of the radial coordinate r, the transverse full width at half maximum of the whole galaxy decreases with the radial coordinate r due to the presence of the term $\frac{{\left(r{\chi }_r\right)}_r}{r}$.

With this distribution, the first- and second-order differentials of the metric components versus z vanish in the z = 0 plane, facilitating to an analytical solution to the Einstein field equations on the equatorial plane of the galaxy.

To handle the components $\kappa \rho u^2{u}_0$ and $\kappa \rho u^0{u}_2$ of the stress-energy tensor, we consider the following metric:

$\begin{array}{l}d{s}^2=c^2{e}^{2\chi }d{t}^2-e^{-2\chi -2A}\left(d{r}^2+d{z}^2\right)\\ +\left(N^2{e}^{2\chi }-r^2{e}^{-2\chi }\right)d{\phi }^2+2Nc{e}^{2\chi }dtd\phi \end{array}(21)$

where N denotes a function of r. We could have kept the term $e^{2\gamma }$ present in Eq. 1, but at the end $\gamma$ must be set to zero in the equatorial plane to ensure ${ein}_1^1=0$. This is because, Eq. 8 is automatically satisfied in the equatorial plane using the distribution in Eq. 20.

All the following equations in this study are formulated for the equatorial plane, with only the lowest order in each equation explicitly maintained (see ax_gal_z0. wxmx for the derivation of the following equations). On this plane, the cancellation of ${ein}_1^1$ and ${ein}_3^3$ is obtained using the following choice:

$A_r=\frac{{\left(N_r\right)}^2{e}^{4\chi }-4r^2{\left({\chi }_r\right)}^2}{4r}(22)$

We now begin with a domino cascade. Using Eq. 22, the resulting density equation at the lowest order is:

$\kappa \rho c^2={ein}_0^0+{ein}_2^2\approx \frac{2{\left(r{\chi }_r\right)}_r+O\left(N^2\right)}{r}(23)$

Eq. 23 shows that $\chi =O\left(\rho \right)$ and $N$ is at least in the order of ${\rho }^{\frac{1}{2}}$. The time equation is:

${ein}_0^0=\kappa \rho u^0{u}_0=\kappa \rho u^0{c^{2}u}^0+\kappa \rho u^{0}N{u}^2\approx \frac{4r^2{\left(r{\chi }_r\right)}_r+O\left(N^2\right)}{2r^3}(24)$

The right-hand side of Eq. 24 shows that ${ein}_0^0=O\left(\rho \right)$, and thus, the third member, $\kappa \rho u^0{c^{2}u}^0$ shows that $u^0=O\left({\rho }^0\right)$.

The rotational velocity equation is:

$\begin{array}{l}{ein}_2^2=\kappa \rho u^2{u}_2\approx \kappa \rho \left(N-r^2\right)u^2{u}^2+\kappa \rho {Nu}^2{u}^0\\ \approx -\frac{4r^3\left({\chi }_r\right){\left(r{\chi }_r\right)}_r+O\left(\chi N^2\right)+O\left(N^2\right)}{2r^3}\end{array}(25)$

As the classical centrifugal force is $\rho {\left(u^2\right)}^2$ and balances the gravitation force $O\left({\rho }^2\right)$, we have $u^2=O\left({\rho }^{\frac{1}{2}}\right)$, which involves ${ein}_2^2=O\left({\rho }^2\right)$ and Eq. 25 involves that $N$ is at least in the order $\rho$.

The cross terms equation ${ein}_0^2$ at the lowest order is:

${ein}_0^2=\kappa \rho u^2{u}_0\approx \kappa \rho {N{u}^{2}u}^2+\kappa \rho {c^2{u}^{2}u}^0\approx -\frac{c\left(\left(N_{rr}\right)r-N_r\right)}{2r^3}(26)$

The right-hand side member shows that in reality $N=O\left({\rho }^{\frac{3}{2}}\right)$. Thus, rewriting the equations at the lowest order gives:

$\kappa \rho c^2={ein}_0^0+{ein}_2^2\approx \frac{2{\left(r{\chi }_r\right)}_r}{r}(27)$

${ein}_2^2=\kappa \rho u^2{u}_2\approx \kappa \rho \left(-r^2\right)u^2{u}^2\approx -2\left({\chi }_r\right){\left(r{\chi }_r\right)}_r(28)$

${ein}_2^0=\kappa \rho u^0{u}_2\approx \kappa \rho \left(-r^2\right)u^0{u}^2\approx \frac{\left(N_{rr}\right)r-\left(N_r\right)}{2\text{rc}}(29)$

Eqs. 26, 29 are identical and define the function N, the explicit knowledge of which is not required to predict the rotational velocity.

For typical galaxy density $\rho$, the metric matrix $g_{ij}$ is close to $diag\left(c^2,-1,-r^2,-1\right)$ within the galaxy, giving marginal length and time contraction. Thus, Eq. 28 accurately yields the rotational velocity as a function of the observed radial distance.

Using Eqs. 20, 21 and directly integrating Eq. 27 to derive ${\chi }_r$, we obtain the rotation velocity:

$2\pi r\frac{d\phi }{dt}\approx 2\pi \sqrt{\frac{\kappa c^2}{2}{\int }_0^{r}r\rho dr}c(30)$

Eq. 30 shows that the rotation velocity monotonically increases for any density distribution $\rho$, which contradicts the observed peak curves. This discrepancy results from the fact that Eqs. 27, 28 model a lone galaxy in empty space. Undeniably, when $\chi \to 0$, the metric expressed by Eq. 21 reduces to the Minkoswki metric, for which the Einstein tensor vanishes, and thus, corresponds to an empty space according to the field equations.

Consequently, the universe-frame-dragging was missing. Indeed, a uniformly dense Universe is modeled using $\chi =\kappa \frac{\overline{\rho }}{8}{r^{2}c}^2$ in Eq. 27. However, in this case, Eq. 28 shows that the Universe has a non-null rotation velocity around the z-axis, which increases with the radial distance r, similar to the non-Machian Gödel solution (Gödel, 1949). Furthermore, this rotation does not make sense for the modeling of a Universe because the position and direction of the z-axis are arbitrary.

2.3 Machian solution to the rotating Universe problem

The Einstein formulation of Mach’s principle presented in Section 1 implies that the complete treatment of a specific body cannot be performed without considering the impact of all the other bodies. Unfortunately, computing the metric of a rotating disk surrounded by uniformly dense matter at rest from the Einstein field equations is unfeasible. An easy way to address this issue in the study of finite-size bodies (stars, galaxies, and galaxy clusters) is to consider the following modified equation:

${ein}_i^j+{\overline{ein}}_i^j=\kappa \rho u_i{u}^j(31)$

where ${\overline{ein}}_i^j$ is the Einstein tensor corresponding to the Universe metric. Eq. 31 signifies that the gravitational fields within a galaxy are approximated by the sum of those generated by the galaxy and by the Universe. This makes sense from the perspective of the low density of galaxies and Universe. For a homogeneous Universe, Eq. 31 can be rewritten as follows:

${ein}_i^j+\kappa \overline{\rho }{\overline{u}}_i{\overline{u}}^j=\kappa \rho u_i{u}^j(32)$

where $\overline{\rho }$ and $\overline{u}$ are the uniform density and speed of the Universe, respectively. Now, Eq. 32 satisfies the requirement of treating all the bodies together. Indeed, the galaxy of interest is modeled by the right-hand side term, whereas the impact of all other bodies is modeled by the middle term. Notably, Eqs. 31, 32 preserve the tensorial nature of the Einstein field equations.

With Eq. 32, the null-Einstein tensor, Minkowski metric now corresponds to a uniformly dense Universe as it involves $\rho =\overline{\rho }$.

Choosing a reference frame co-moving with the Universe, we have ${\overline{u}}_i={\overline{u}}^i=0$ for $i\ne 0$. Thus, only Eq. 27 is modified, which becomes:

$\kappa \rho c^2\approx 2\frac{1}{r}{\left(r{\chi }_r\right)}_r+\kappa \overline{\rho }{c}^2(33)$

Finally, Eqs. 28, 33 provide the rotational velocity of the galaxy:

$2\pi r\frac{d\phi }{dt}\approx 2\pi \sqrt{\frac{\kappa c^2}{2}{\int }_0^{r}r\left(\rho -\overline{\rho }\right)dr}\sqrt{1-\frac{\overline{\rho }}{\rho }}c(34)$

The first square root of Eq. 34 represents the gravitational force, which is a monotonically increasing term. Interestingly, this term contains a virtual negative density $-\overline{\rho }$ within the galaxy, which is an effect of the whole Universe mass on the metric within the galaxy. The last square root represents the inverse of the frame-dragging of the Universe. This term reduces the rotation velocity to zero when the galactic density $\rho$ becomes equal to the mean Universe density $\overline{\rho }$.

Figure 1 illustrates the prediction results of rotational velocity for the three galaxies M31, M81, and M101 (see M81_M101_M31_velocity.xlsx file) using Eq. 34 and the following density profile:

$\rho =a{e}^{-b{r}^k}+p{e}^{-m{r}^q}+\overline{\rho }(35)$

Figure 1

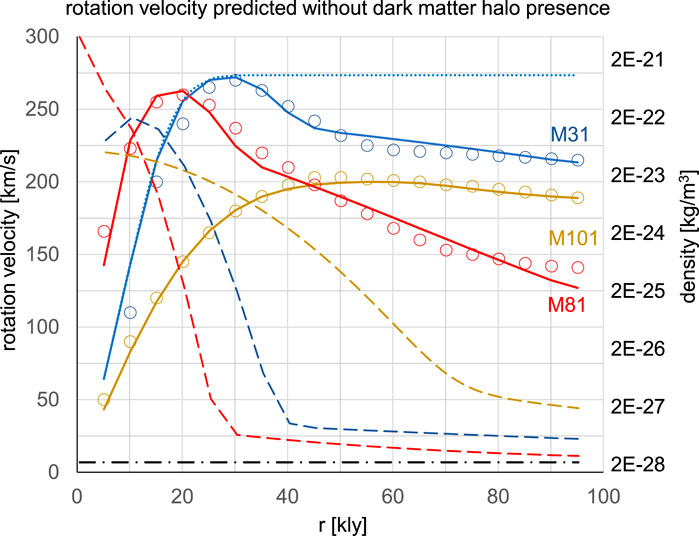
Figure 1. Left vertical axis: circles are the rotational velocities observed by Roberts and Rots in 1973; solid lines are velocities predicted by Eq. 34 in the absence of dark matter halo; blue dotted line is predicted velocity of M31 without universe matter, i.e., $\overline{\rho }=0$ (Eq. 26). Right vertical axis: dashed lines are the radial densities of the galaxy, and the dotted-dashed black line represents the mean universe density.

The rotational velocities of the three galaxies were predicted using the same value of the current estimate of the mean Universe density present in Eq. 35, i.e., $\overline{\rho }=2.2\times {10}^{-28}kg/m^3$. For the three galaxies, the exponent k modeling the bulge was close to two and the exponent q modeling the disk tail close to 1. The prediction of the M81 bulge density and size was in line with the observations, i.e., $5\times {10}^{-21}kg/m3\approx {10}^{10}{M}_{ʘ}within10kly$ (Feng et al., 2014).

The measurement of the rotational velocity in 1973 of these three galaxies by Roberts and Rots (Roberts and Rots, 1973) initiated the dark matte halo genesis.

3 Discussion

The proposed solutions (Eqs 28, 33) accurately predicted the rotational velocity shapes of the galaxies. After reaching a peak, the velocity declined and finally vanished when the galaxy density $\rho$ reached the mean Universe density $\overline{\rho }$. Without considering the Universe, i.e., $\overline{\rho }=0$ in Eq. 34 or using Eq. 30, the rotation velocity monotonically increases for any density profile. This indicates the importance of the frame-dragging effects on galaxy rotation, which cannot be derived from Newtonian dynamics.

Although the model provides the gravitational field and motion equations (Eqs 27, 28), it does not provide any information regarding the actual metrics within the galaxy. The metrics in Eq. 1 or 21 correspond to the metrics for a lone galaxy in empty space. Therefore, no physical implications could be derived directly from these metrics.

As galaxies have low densities and stars move at low velocities, galactic rotation is widely considered as a non-relativistic problem, for which the Einstein field equations should not provide results very different from the Newtonian limit. However, special relativity tells us that making such a shortcut can be hazardous: the low-speed limit of kinetic energy in special relativity does not vanish as it does in the Newtonian mechanics, rather, it becomes $m{c}^2$. Particle creation and annihilation prove this value as the real energy at rest and not only as a pure offset in theory.

Mach and Einstein were concerned that, similar to constant motion, acceleration should make sense only relative to the other mass bodies. A later study showed that, according to the Einstein field equations, a body at rest but surrounded by masses in rotation undergoes inertial forces induced by the rotating masses (Pfister, 2007). Therefore, even if the stars are moving at low velocities, the centrifugal force experienced by a star can strongly depend on its relative rotation with the bulge of the galaxy and with the other celestial bodies too.

The proposed solution based on Eq. 34 clearly integrates this process. If the galaxy alone was modeled, i.e., $\overline{\rho }=0$, the stars rotate relatively to the bulge only, and their rotational velocities monotonically increase with r to balance the increasing mass contained in the region < r. At larger distances, the bulge attraction and its frame-dragging effect decrease, resulting in a constant rotational velocity.

When the Universe density $\overline{\rho }$ is modeled, stars also rotate relatively to the matter in the Universe, and thus, undergo an additional centrifugal force at any distance from the bulge. This last component decreases the rotational velocity as gravitation due to the bulge decreases with the radial distance r. Rewritten in the classical form, i.e., $m_{i}r{\omega }^2=\frac{G}{r^2}{m}_g{M}_g\left(r\right)$, where m_i and m_g are the inertial and gravitational masses of a star, respectively, and $M_g\left(r\right)$ is the total gravitational mass within r, Eq. 34 becomes:

$\frac{1}{2}\frac{\rho }{\rho -\overline{\rho }}\rho dvr{\left(\frac{d\phi }{dt}\right)}^2\approx \frac{G}{r^2}\rho dv2\pi r{\int }_0^{r}r\left(\rho -\overline{\rho }\right)dr(36)$

Eq. 36 differs from the Newtonian theory in three aspects:

- The term $\frac{1}{2}$ rescales the observed classical inertial mass $\rho dv$ to what could be observed if our galaxy was isolated in an empty space. The scaling factor is low because all the stars in the galaxy rotate in the same direction, which reduces their relative rotation.

This partial Machian property of the metric resulted from the fact that in the domino cascade Eqs. 23–26, the priority has been made to consider that χ should determine the galaxy density. This choice at the end results in a marginal impact of the term N in the final solution. In other axial metrics (Cooperstock and Tieu, 2007; Bronnikov et al., 2020), the cross term directly represented galactic rotation, which resulted in different solutions. Both solutions are mathematically valid but have different physical implications. Based on these considerations, Eq. 31 does not work with the other axially symmetric metrics.

- At the center of the galaxy, the inertial mass is primarily generated by the galaxy itself. When r increases, the inertial mass is gradually more impacted by the Universe and becomes equal to the classical value when:

$\rho =\frac{1}{1-\frac{1}{2}}\overline{\rho }\approx 2\overline{\rho }(37)$

The divergence of this term when $\rho$ decreases to $\overline{\rho }$ results from the simplicity of the model, which assumes a uniformly dense fluid at rest filling the whole space. This implies that this model cannot be applied to small scale systems such as the empty space surrounding dense rotating stars.

- The fact that it is not the whole galaxy mass included in the sphere radius r which appears in the gravitational force ($r{\int }_0^{r}r\dots$ in place of $\left.{\int }_0^r{r}^2\dots \right)$ is a consequence of the axial symmetry and of the fact that the fluid motion is governed by the metric that the rotating fluid itself produces. The fact that one power of r is shifted in front the integral is a consequence of having consider that χ should determine the galaxy density (see first property description).

The two first properties showed that the present model satisfies the sixth version of Mach’s principle proposed in (Bondi and Samuel, 1997), i.e., “inertial mass is affected by the global distribution of matter,” with the scaling factor being

$\frac{1}{2}\frac{\rho }{\rho -\overline{\rho }}(38)$

Definitely, Eqs 37, 38 shows that the inertial mass is affected by both, the galactic distribution of matter $\rho$ and by the Universe distribution matter $\overline{\rho }$ as well.

Mach’s principle was intuitively proposed to explain the curve flatness with Newtonian dynamics (Darabi, 2013), where $m_i=C$ within the bulge and decreases as $m_i=\frac{C}{r}$ beyond the bulge, where C is a tunable parameter. However, the intuitive explanation of this dependence arising from inertial dilution because of the expansion of the Universe appears erroneous. This was deduced from the Newtonian mechanics, which suffered from underestimation of the rotation velocity beyond the bulge. This decrease in inertia beyond the bulge contradicts Mach’s principles. Indeed, the impact of the bulge decreases with distance. Thus, inertia is increasingly governed by the non-rotating Universe. The relative rotation of galactic matter with the Universe is greater than that with the bulge, which rotates in the same direction as the disk of the galaxy. Eq. 38 shows that, if the inertia is constant within the bulge, where $\rho \gg \overline{\rho }$, it increases beyond the bulge due to the decrease of $\rho$.

An analytical solution of the first G order for a free-pressure rotating fluid has already been obtained to explain the flatness of the rotation velocity curve (Cooperstock and Tieu, 2007). An explanation for the rotation curve of the Milky Way as a consequence of the frame-dragging effect was recently proposed (Beordo et al., 2024). Both studies used a non-diagonal metric solution based on the Weyl–Lewis–Papapetrou coordinates.

The proposed metric expressed by Eq. 21 on the equatorial plane was obtained through an intuitive deduction process. First, a diagonal axial metric (Eq. 1) enabled the resolution of the Einstein field equations within a free-pressure stationary rotating fluid, i.e., without radial collapse. In this resolution, the cross-time-angular components of the stress tensor were neglected. Subsequently, the metric was slightly modified by adding a cross-time angular term. By keeping the fact that the galaxy density is determined by χ, the resolution of the field equations reveals that this cross-time term does not appear in the equatorial rotation velocity in the first density order (Eqs. 30, 34). We do not see any physical reason why this cross term could become significant when moving away from the equatorial plane. However, we could not prove this mathematically.

By transposing the density term of the Universe to the right-hand side of Eq. 32, it could be considered as an undetectable virtual negative density matter filling the entire space. However, it has some benefits compared to the dark matter halo thesis: it does not contain any adjustable parameter, while the observer is free to choose the dark matter halo distribution to explain their observations; it has a straightforward physical interpretation as the impact of the gravitational field of the Universe, which results in the implementation of Mach’s principle.

Eq. 34 includes the frame-dragging, which reduces the rotational velocity and cancels it when the galaxy density $\rho$ decreases to the mean Universe density $\overline{\rho }$. Finally, this solution predicted the rotational velocity profiles for all the three galaxy types, M31, M81, and M101.

Our success in predicting the rotational velocity profiles substantiates Mach’s ideas about the nature of inertial forces as an alternative to the dark matter halo thesis. Further investigations should be performed to determine whether the obtained solution does not violate any physical constraints. Finally, the impact of Eq. 32 in galaxy genesis and formation should be evaluated to support or discard the model. In this evaluation, statistical fluctuations could be added to $\overline{\rho }$ to consider the heterogeneities of the Universe.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://data.mendeley.com/datasets/x32hn4kxsh/1.

Author contributions

SW: Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The author thanks the reviewers for their valuable comments which helped in improving the paper.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2024.1429235/full#supplementary-material

References

Barbour, J. B., Pfister, H., Beordo, W., Crosta, M., Lattanzi, M. G., Re Fiorentin, P., et al. (1995). Geometry-driven and dark-matter-sustained Milky way rotation curves with gaia DR3. Mon. Notices R. Astronomical Soc. 529, 4681–4698. stae855. doi:10.1093/mnras/stae855

CrossRef Full Text | Google Scholar

Baum, R. P., and Sheehan, W. (2013). In search of planet Vulcan: the ghost in Newton’s clockwork universeSpringer.

Beordo, W., Crosta, M., Lattanzi, M. G., Re Fiorentin, P., and Spagna, A. (2014). Geometry-driven and dark-matter-sustained Milky Way rotation curves with Gaia DR3Monthly Notices of the Royal Astronomical Society529 (4), 4681–4698.

Beordo, W, Crosta, M, Lattanzi, MG, Re Fiorentin, P, and Spagna, A. Geometry-driven and dark-matter-sustained Milky Way rotation curves with Gaia DR3. Monthly Notices of the Royal Astronomical Society. 529(4), 4681–98.

Google Scholar

Bondi, H., and Samuel, J. (1997). The Lense-Thirring effect and Mach's principle. Phys. Lett. A 228, 121–126. doi:10.1016/s0375-9601(97)00117-5

CrossRef Full Text | Google Scholar

Brans, C. H. (1962). Mach's principle and the locally measured gravitational constant in general relativity. Phys. Rev. 125, 388–396. doi:10.1103/physrev.125.388

CrossRef Full Text | Google Scholar

Bronnikov, K. A., Santos, N., and Wang, A. (2020). Classical and quantum gravity, 37.113002

CrossRef Full Text | Google Scholar

Cooperstock, F. I., and Tieu, S. (2007). Int. J. Mod. Phys. A 22, 2293–2325. doi:10.1142/s0217751x0703666x

CrossRef Full Text

Darabi, F. (2013). Mon. Notices R. Astronomical Soc. 433, 1729–1735. doi:10.1093/mnras/stt847

CrossRef Full Text

Einstein, A., Feng, C.-C., Lin, L.-H., Wang, H.-H., and Taam, R. E. (1933). Glasgow: jackson wylie and Co. Astrophysical J. 785, 103. doi:10.1088/0004-637x/785/2/103

CrossRef Full Text | Google Scholar

Feng, C. C., Lin, L. H., Wang, H. H., and Taam, R. E. (2014). Spiral density waves in M81. I. Stellar spiral density wavesThe Astrophysical Journal785 (2), 103.

CrossRef Full Text | Google Scholar

Gödel, K. (1949). An example of a new type of cosmological solutions of einstein's field equations of gravitation. Rev. Mod. Phys. 21, 447–450. doi:10.1103/revmodphys.21.447

CrossRef Full Text | Google Scholar

Hermann, M., Saravi, M., Hermann, M., and Saravi, M. (2016). Nonlinear ordinary differential equations: analytical approximation and numerical methods, 1.

Google Scholar

Janssen, M. (2016). HSci/Phys, 4121.

Google Scholar

Lense, J., and Thirring, H. (1918). Physikalische zeitschrift, 19, 156.

Google Scholar

Licata, I., Corda, C., and Benedetto, E. (2016) Gravitation and cosmology, 22, 48.

Google Scholar

Mach, E., Brockhaus, M. D., Graham, A. W., Moore, B., Diemand, J., and Terzić, B. (1901). Empirical models for dark matter halos. I. Nonparametric construction of density profiles and comparison with parametric models. Astronomical J. 132, 2685–2700. doi:10.1086/508988

CrossRef Full Text | Google Scholar

Merritt, D., Navarro, J. F., Ludlow, A., and Jenkins, A. (2005). Astrophysical J. 624, L85–L88. doi:10.1086/430636

CrossRef Full Text

Milgrom, M. (2002). MOND—theoretical aspects. New Astron. Rev. 46, 741–753. doi:10.1016/s1387-6473(02)00243-9

CrossRef Full Text | Google Scholar

Narlikar, J. (2003). Action at a distance and cosmology: a historical perspective. Annu. Rev. Astronomy Astrophysics 41, 169–189. doi:10.1146/annurev.astro.41.112202.151716

CrossRef Full Text | Google Scholar

Navarro, J. F. (1996). The structure of cold dark matter halos. Symposium-international Astron. union. Camb. Univ. Press 171, 255–258. doi:10.1017/s0074180900232452

CrossRef Full Text | Google Scholar

Pfister, H. (2007). General relativity and gravitation, 39, 1735.

CrossRef Full Text | Google Scholar

Rindler, W. (1994). Phys. Lett., 187–236. doi:10.1016/0375-9601(94)90900-8

CrossRef Full Text

Roberts, M., and Rots, A. (1973). Astronomy Astrophysics 26, 483–485.

Sciama, D. W. (1953). Mon. Notices R. Astronomical Soc. 34, 113. doi:10.1093/mnras/113.1.34

CrossRef Full Text