Hadron-quark phase transition in the neutron star with vector MIT bag model and Korea-IBS-Daegu-SKKU functional

Employing the Korea-IBS-Daegu-SKKU (KIDS) density functional for the hadron phase and the MIT bag model with vector (vBag) model for the quark phase, we obtain hadron-quark phase transition in neutron stars considering Maxwell construction. The structural properties of the resultant hybrid stars are computed for three different values of bag constant $(B)$ in the range $B^{1/4}=\left(145-\right.$160 MeV). We study the effects of symmetry energy $(J)$ on the hybrid star properties with the different KIDS model and found that $J$ has important influence not only on the transition properties like the transition mass, transition radius and jump in density due to phase transition, but also on the stability of the hybrid stars. The vector repulsion of the quark phase via the parameter $G_V$ has profound influence in obtaining reasonable hybrid star configurations, consistent with the recent astrophysical constraints on the structural properties of compact stars. Within the aforesaid range of $B$, the value of $G_V$ is constrained to be 0.3 $\lesssim G_V\lesssim$ 0.4 in order to obtain reasonable hybrid star configurations.

1 Introduction

Mass-radius $(M-R)$ diagram of the neutron star is unprecedentedly crowded with modern astronomical data that covers the neutron star mass from about $0.5M_{\odot }$ to more than $2.0M_{\odot }$. They consist of GW170817 by the LIGO/Vigro Collaboration (Abbott et al., 2018), PSR J0030 + 0451 by NICER (Miller et al., 2019; Riley et al., 2019) and PSR J0740 + 6620 (Fonseca et al., 2021; Miller et al., 2021; Riley et al., 2021) and HESS J1731-347 (Doroshenko et al., 2022). Simultaneous measurement of the mass and radius for a single object helps greatly deepen our understanding of the state of matter at densities above the nuclear saturation.

A naive but quite certain scenario is the phase transition from hadronic matter to quark matter. Initially the matter is composed of nucleons at low densities, where they are far apart. Since the nucleon has a finite size, they start to overlap to each other at a density higher than the saturation. As the density evolves furthermore, confinement of quarks in the initial nucleon becomes uncertain, and finally quarks are completely released from the nucleons and form a deconfined quark matter. The key points to the hadron-quark phase transition are the physical properties of the nucleon and quarks, and their interactions at finite densities. The main concern of the present work is to examine the effect of the uncertainties in the interactions of quarks and nucleons to the equation of state (EoS) and the phase transition in the core of neutron stars, forming hybrid stars. For the calculation of the EoS, we use the MIT bag model with vector repulsion (vBag) (Kumar et al., 2022; Lopes et al., 2022; Kumar et al., 2023; Laskos-Patkos et al., 2023) for the quark matter, and the Korea-IBS-Daegu-SKKU (KIDS) density functional (Gil et al., 2021; Gil and Hyun, 2021; Gil et al., 2022) for the hadron phase. Phase transition is achieved with the help of Maxwell construction assuming that the surface tension of the interface is high enough ($>$70 MeV ${\mathrm{f}\mathrm{m}}^{-2}$) to ensure that the transition occurs at a sharp interface (Maruyama et al., 2008). However, the value of the surface tension at the hadron-quark interface is still not well defined. Therefore, when it is $<$70 MeV ${\mathrm{f}\mathrm{m}}^{-2}$ the formation of mixed phase is also possible following Gibbs construction. Other mechanisms like hadron-quark crossover (Constantinou et al., 2021; Huang et al., 2022; Qin et al., 2023; Sotani and Kojo, 2023) and constant speed of sound parameterization (Laskos-Patkos and Moustakidis, 2023; Sun and Wen, 2023) etc. are also adopted in literature to obtain the properties of hybrid stars.

In the vBag model, stiffness of the quark matter is controlled by the bag constant and the vector repulsion (Kumar et al., 2022; Lopes et al., 2022; Kumar et al., 2023; Laskos-Patkos et al., 2023). The two quantities have different physical origins and implications. Bag constant is introduced in the original bag model. In the simplest description of the baryon bags, quarks are treated as free particles within a bag. In order to confine the quarks within the baryon, inward pressure is assumed to be exerted on the quarks. The inward pressure is described in terms of the bag constant, so it is a natural way to determine the bag constant from the baryon masses in free space. In this work, as a lower limit of the bag constant, we adopt $B^{1/4}=145$ MeV as an upper limit of the bag from Ref. (Johnson, 1975). As far as the baryon spectrum in free space is concerned, there is no upper limit to the bag constant. However, if one adopts the Bodmer-Witten conjecture which states that the quark matter composed of $u$, $d$ and $s$ quarks is the most stable state of matter in the quark stars, an upper limit value can be determined. In case of hybrid stars, it is not mandatory to satisfy the Bodmer-Witten conjecture and in this case the only possible way to constrain $B$ is to test the structural properties of hybrid stars in the light of the various astrophysical constraints (Nandi and Char, 2018; Rather et al., 2020). We use $B^{1/4}=160$ MeV as upper limit, following Ref. (Rather et al., 2020). In this work, uncertainty arising from the bag constant is accounted by considering three values, the lower limit 145 MeV, a middle value 155 MeV and the upper limit 160 MeV.

While the bag constant is inherent in the bag model, there is no repulsive force in the original bag model. The reason might be that it is sufficient to produce the baryon spectrum accurately with the kinetic energy of quarks and the bag constant. With these two ingredients, however, it is hard to satisfy the observation of large mass stars, $M\ge 2M_{\odot }$ because the EoS is too soft to sustain the strong gravity of super dense matter (Lopes et al., 2022). Request for more stiff EoS demands a repulsive interaction in terms of the vector field. Nowadays, it is common to include vector repulsion in the widely used quark models such as Nambu-Jona-Lasino model as well as the bag model. An issue related to the vector force is how strong the repulsion is. Thanks to the improvement in the precision and diversity of the neutron star observational data, it becomes feasible to constrain the strength of vector repulsion more precisely. Combined with the uncertainties of the bag constant and the symmetry energy, we can propose values of the vector coupling constant that are compatible with the observed neutron star properties.

In the description of neutron-rich hadronic matter, the largest uncertainty comes from the symmetry energy. Its value at the saturation density is relatively accurately determined, most conservatively in the range 30$-$34 MeV, but its density dependence is much more uncertain. The average density of a neutron star whose mass is larger than the canonical mass is well above the saturation density, so the neutron star provides a dependable way to determine the density dependence of the symmetry energy. In recent works, symmetry energy has been constrained by using the neutron star data (Gil et al., 2021; Gil and Hyun, 2021; Gil et al., 2022), and the uncertainty could be reduced substantially. Nevertheless, the density dependence still has sizable ambiguity, and it can have critical impact to the transition to deconfined quark matter. In order to investigate the influence of the symmetry energy, we adopt the KIDS-A, B, C, D models (Gil and Hyun, 2021), which are determined to satisfy the nuclear properties, neutron star data and gravitational wave measurements simultaneously, and have evidently different stiffness of the symmetry energy.

In the calculation of the EoS, we treat the bag constant as a free parameter, and determine the range of vector coupling constants to satisfy the data of GW170817, NICER and HESS simultaneously for the given models of the symmetry energy. In the result, we find that the critical density at which the phase transition occurs is sensitive the bag constant, vector coupling constant and the symmetry energy. However, maximum mass depends on the bag constant and the symmetry energy weakly, so we can obtain appreciably model-independent range of the vector coupling constant.

We organize the work in the following order. In Section 2, models for the quark and hadronic matters are described. Section 3 shows the results and we present the discussions on them. The work is summarized in Section 4.

2 Model

2.1 MIT bag with vector repulsion

We consider quark matter with $u$, $d$ and $s$ quarks and the electrons as a lepton. The Lagrangian for the bag model with vector repulsion is given by

$\begin{array}{cc}\hfill \mathcal{L}& ={\displaystyle \sum _{f=u,d,s}}\left[{\bar{\psi }}_f\left\{{\gamma }^{\mu }\left(i{\partial }_{\mu }-g_{\mathit{qqV}}{V}_{\mu }\right)-m_f\right\}{\psi }_f-B\right]\mathrm{\Theta }\left({\bar{\psi }}_f{\psi }_f\right)\hfill \\ \hfill & +\frac{1}{2}{m}_V^2{V}_{\mu }{V}^{\mu }-\frac{1}{4}{V}_{\mu \nu }{V}^{\mu \nu }+{\bar{\psi }}_e\left(i{\gamma }_{\mu }{\partial }^{\mu }-m_e\right){\psi }_e,\hfill \end{array}(1)$

where $V_{\mu }$ denotes the vector field, $g_{\mathit{qqV}}$ is the quark-vector meson coupling constant, $B$ is the bag constant, $V_{\mu \nu }={\partial }_{\mu }{V}_{\nu }-{\partial }_{\nu }{V}_{\mu }$ and the Heaviside function $\mathrm{\Theta }$ = 1 inside the bag in Eq. 1. For the vector coupling constant, we assume $g_{\mathit{uuV}}=g_{\mathit{ddV}}$ and $X_{\mathit{V}}=g_{\mathit{ssV}}/g_{\mathit{uuV}}$ = 0.4. It is shown that the variation on the ratio $g_{\mathit{ssV}}/g_{\mathit{uuV}}$ does not affect the EoS as much as the bag constant or the vector coupling constant (Pal et al., 2023). Since the vector meson is an isoscalar particle, it corresponds to the $\omega$ meson, so we use the $\omega$ meson mass 783 MeV for $m_V$. In the quark matter EoS, vector coupling constant contributes in the form ${(g_{\mathit{qqV}}/m_V)}^2$, so we use $G_V={(g_{\mathit{uuV}}/m_V)}^2$ as a parameter to be constrained from the neutron star data. The bag constant is considered in the range $B^{1/4}=$ 145–160 MeV, so three values 145, 155 and 160 MeV are used in the calculation.

2.2 KIDS functional

In the KIDS density functional framework, energy of a nucleon in nuclear matter is expanded in powers of ${\rho }^{1/3}$ where $\rho$ is the matter density as

$\mathcal{E}=\mathcal{T}+{\displaystyle \sum _{i=0}}{\rho }^{1+i/3}\left({\alpha }_i+{\beta }_i{\delta }^2\right).(2)$

In Eq. 2, $\mathcal{T}$ is the kinetic energy, and $\delta =({\rho }_n-{\rho }_p)/\rho$ where ${\rho }_n$ and ${\rho }_p$ are the neutron and the proton density, respectively. Coefficients ${\alpha }_i$ are determined from the properties of symmetric nuclear matter, and ${\beta }_i$ are constrained by the neutron star data in the KIDS-A, B, C, D models. Incompressibility of the symmetric matter $K_0$ and the symmetry energy parameters are summarized in Table 1.

Table 1

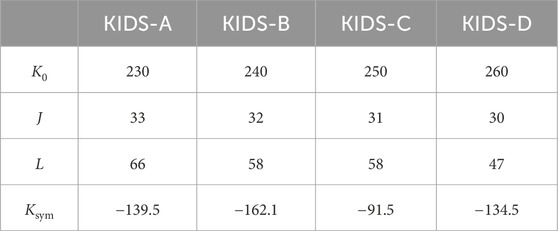
Table 1. Incompressibility $K_0$ of the symmetric nuclear matter and the symmetry energy parameters $J$, $L$ and $K_{\text{sym}}$ in units of MeV for the KIDS-A, B, C, D models.

2.3 Phase transition

In the present work, phase transition is achieved via Maxwell construction assuming that the surface tension at the hadron-quark interface is sufficiently large (Maruyama et al., 2008). Maxwell construction is based on the local charge neutrality condition which implies that both the hadronic (H) and quark (Q) phases must be individually charge neutral,

$q_H=0;q_Q=0.(3)$

Following Maxwell criteria, phase transition occurs when the pressure $(P)$ and baryon chemical potential $({\mu }_B)$ of each phase become equal,

${\mu }_B^H={\mu }_B^Q;P_H=P_Q.(4)$

In case of Maxwell construction, based on Eqs 3, 4, ${\mu }_B$ is continuous while there is jump in electron chemical potential ${\mu }_e$ at the interface between the two phases. Therefore, the transition is thus characterized by jump in density from hadronic to quark phase, pressure being constant within the interval (Contrera et al., 2017). The transition point $({\mu }_t,P_t)$ of the hadronic and quark phases in the $({\mu }_B-P)$ plane corresponds to two specific transition densities—one in the hadronic phase $({\rho }_t^H)$ and another in the quark phase $({\rho }_t^Q)$. ${\rho }_t^H$ marks the end of pure hadronic phase while ${\rho }_t^Q$ denotes the starting of pure quark phase in terms of density. The jump in density is given by the difference between ${\rho }_t^Q$ and ${\rho }_t^H$.

The resultant hybrid EoS is employed to obtain the mass $M$ and the radius $R$ of hybrid stars using the Tolman-Oppenheimer-Volkoff (TOV) equations (Oppenheimer and Volkoff, 1939; Tolman, 1939) while dimensionless tidal deformability $\mathrm{\Lambda }$ is then calculated following (Hinderer, 2008; Hinderer et al., 2010). The jump in density at the hadron-quark interface is taken care of by implementing the correction in calculation of $\mathrm{\Lambda }$ as suggested by Ref. (Takatsy and Kovacs, 2020). For the outer crust region, we adopt the Baym-Pethick-Sutherland EoS (Baym et al., 1971) and for the inner crust, we have considered the EoS including the pasta phases (Grill et al., 2014). The crust-core transition density in the present work is around 0.0055${\rho }_0$.

3 Result

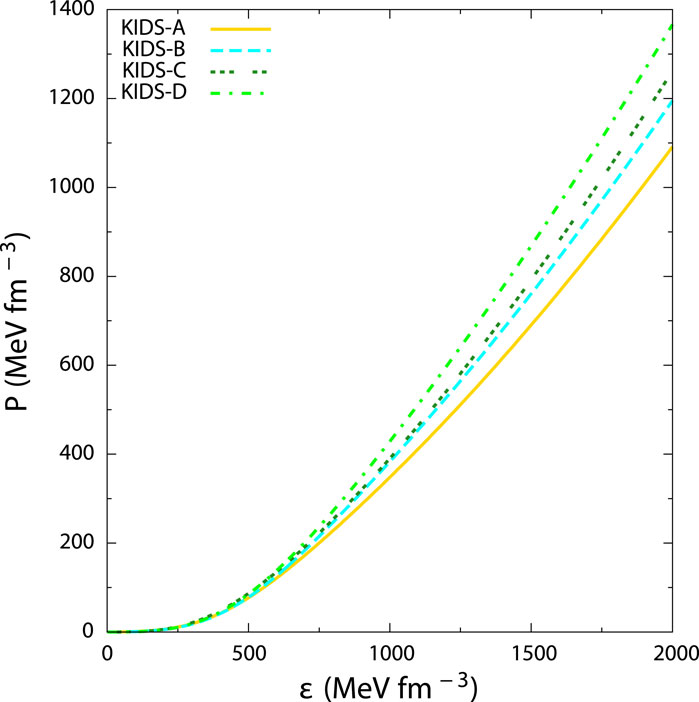
We first examine the dependence of symmetry energy on the properties of hadronic stars with the four different KIDS models with different symmetry energy as tabulated in Table 1. For the hadronic model, as the symmetry energy $(J)$ and its slope $(L)$ decrease and compression modulus $K_0$ increases from KIDS-A to KIDS-D in Table 1, the EoS stiffens (as seen from Figure 1) and hence the maximum mass increases. For example, the maximum mass for KIDS-A model ($J$ = 33 MeV, $L$ = 66 MeV and $K_0$ = 230 MeV) is $2.10M_{\odot }$ while it is $2.26M_{\odot }$ for the KIDS-D model ($J$ = 30 MeV, $L$ = 47 MeV and $K_0$ = 260 MeV). Consistent with the results of (Li et al., 2020) we find that the radius of canonical neutron star $(R_{1.4})$ also increases with the increase of $L$ e.g., $R_{1.4}$ = 12.28 km for KIDS-A model and $R_{1.4}$ = 12.10 km for KIDS-D model. From Figure 2 it can be seen that the hadronic star configurations with all the four KIDS model satisfy the present day astrophysical constraints on the mass-radius relation of compact stars viz., the maximum mass constraint from PSR J0740 + 6620 (Fonseca et al., 2021) with corresponding radius constraint (Miller et al., 2021; Riley et al., 2021), the constraints from GW170817 (Abbott et al., 2018), NICER experiment for PSR J0030 + 0451 (Miller et al., 2019; Riley et al., 2019) and HESS J1731-347 (Doroshenko et al., 2022).

Figure 1

Figure 1. Equation of state of hadronic matter in neutron star with the four KIDS functionals.

Figure 2

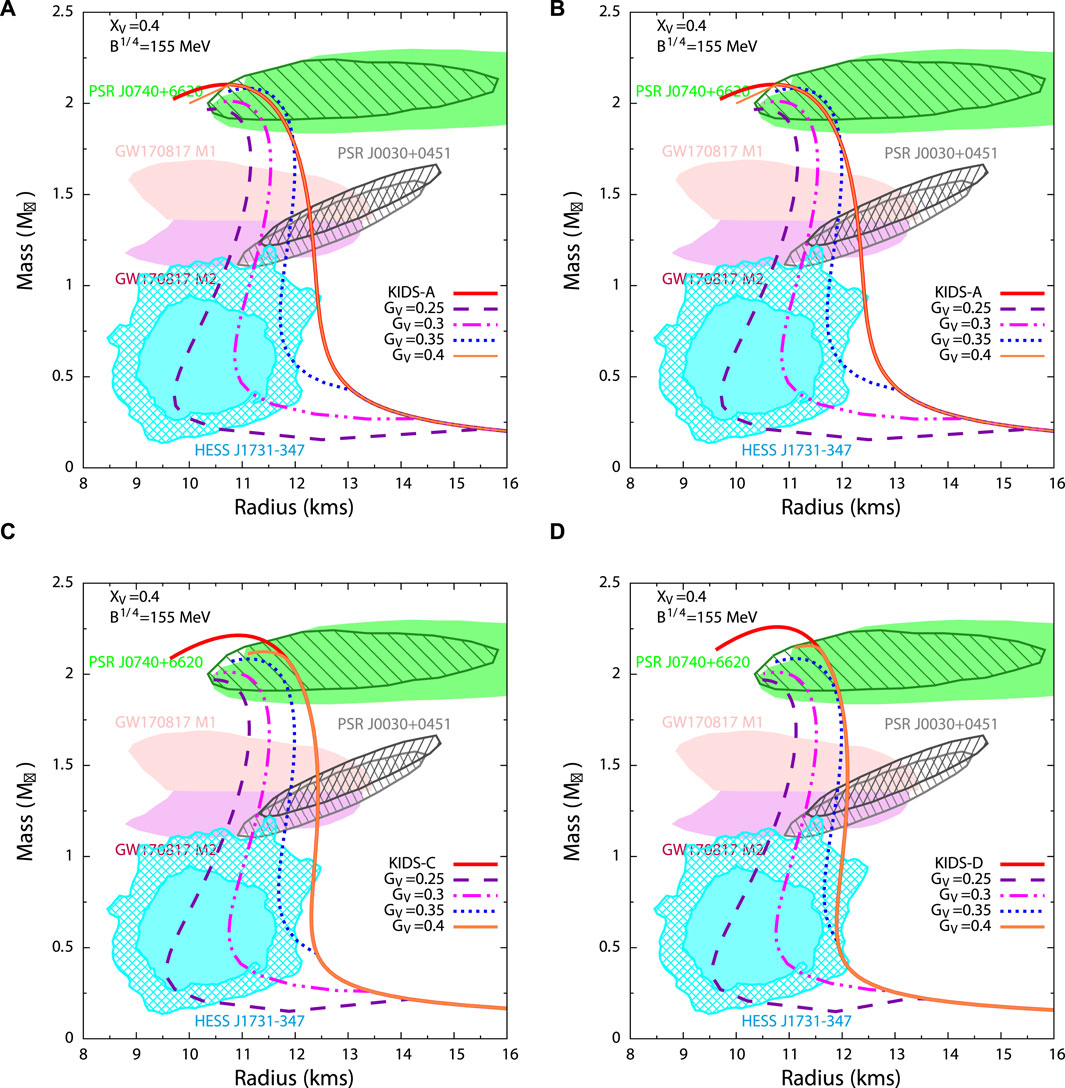
Figure 2. Variation of mass with radius of hadronic star (solid lines) and hybrid stars (dashed lines) with hadronic models (A) KIDS-A, (B) KIDS-B, (C) KIDS-C and (D) KIDS-D for different values of $G_V$ and $B^{1/4}=$155 MeV. Observational limits imposed from the most massive pulsar PSR J0740 + 6620 on maximum mass (Fonseca et al., 2021) and corresponding radius (Miller et al., 2021; Riley et al., 2021) are also indicated. The constraints on $M-R$ plane prescribed from GW170817 (Abbott et al., 2018), NICER experiment for PSR J0030 + 0451 (Miller et al., 2019; Riley et al., 2019) and HESS J1731-347 (Doroshenko et al., 2022) are also compared.

In order to study the influence of symmetry energy on the phase transition and the hybrid star structure, we consider the vBag model with $B^{1/4}$ = 155 MeV. In Figure 3 we illustrate the variation of pressure as a function of baryon chemical potential of the hadronic and quark phase, for example, with the KIDS-A model. The transition points $({\mu }_t,P_t)$ are also marked. The corresponding ${\rho }_t^H$ and ${\rho }_t^Q$ are tabulated in Table 2. We find that phase transition is quite early for low values of $G_V$ but the transition point shifts abruptly to high chemical potential and pressure (density) at $G_V$ = 0.4. This is consistent with the result obtained by Lopes et al. (2022).

Figure 3

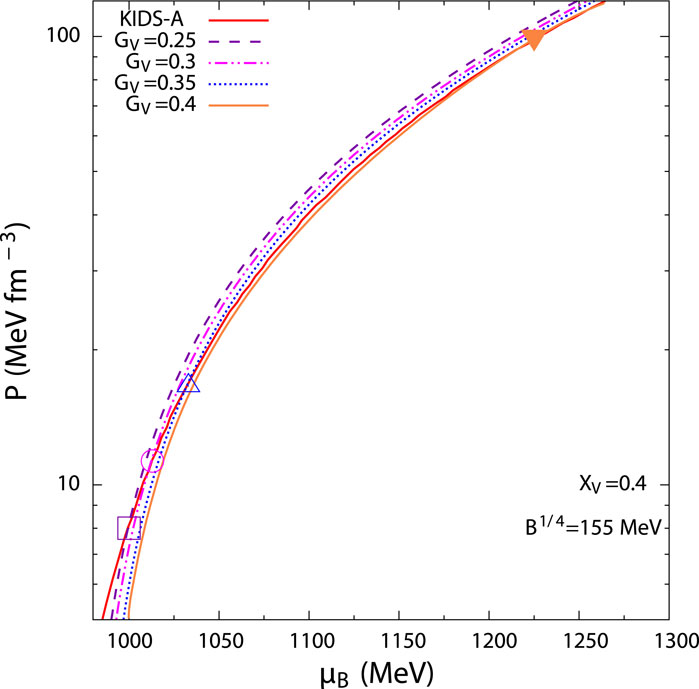
Figure 3. Variation of pressure as a function of baryon chemical potential for hadronic matter with KIDS-A model and quark matter for different values of $G_V$ with $X_V=$0.4 and $B^{1/4}=$155 MeV. The transition points are also marked with points.

Table 2

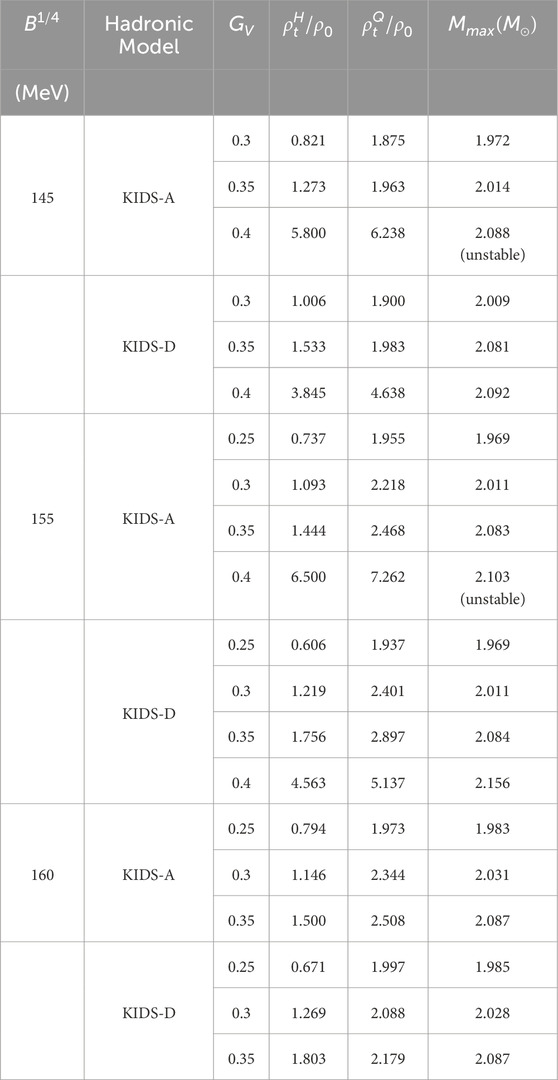
Table 2. Comparison of hadron-quark transition densities, and maximum mass for different $G_V$ with different values of $B$.

As a result we observe in Figures 2A–D that for any particular hadronic model, the maximum mass and corresponding radius of the hybrid stars increase with increasing repulsion via $G_V$. The value of $R_{1.4}$ and the radius of low mass hybrid stars are greatly affected by $G_V$. Figure 2 also confirms that all the present day astrophysical constraints are satisfied by the hybrid star configurations with all the four KIDS model with the chosen values of $G_V$ except for 0.25, for which the NICER data for PSR J0030 + 0451 are not satisfied. Also for any particular hadronic model, the recently obtained HESS J1731-347 data for different values of $G_V$ with $X_V$ = 0.4 and $B^{1/4}$ = 155 MeV is better satisfied with lower repulsion, i.e., lower values of $G_V$. The transition mass $(M_t)$ increases while the transition radius $(R_t)$ decreases with increasing values of $G_V$, and for $G_V$ = 0.4 there is an abrupt jump in the value of $M_t$ for all the hadronic models as a consequence of the delayed transition. Such delayed transition leads to unstable hybrid star configurations obtained with both KIDS-A and KIDS-B hadronic models as seen from Figures 2A, B.

We show the dependence of transition properties like $M_t$, $R_t$ and the energy difference $(\mathrm{\Delta }\epsilon ={\epsilon }_t^Q-{\epsilon }_t^H)$ or the jump in density from hadronic to quark phase as functions of symmetry energy $J$ in Figures 4, 5. We do not show the case for $G_V$ = 0.4 since it leads to unstable hybrid star configurations for high values of $J$. For any particular value of $G_V$, the relationships (fitted) between $M_t$ and $R_t$ with $J$ show that symmetry energy has a considerable influence on the transition properties of hybrid stars. From Figure 4 we find that for increasing (decreasing) values of $J$ $(K_0)$ the transition mass decreases considerably (Figure 4A) while the transition radius follows the reverse trend (Figure 4B). The relation between $\mathrm{\Delta }\epsilon$ and $J$ in Figure 5 shows that $\mathrm{\Delta }\epsilon$ also increases with increasing $J$ or decreasing $K_0$ for any particular value of $G_V$. The dependence of $\mathrm{\Delta }\epsilon$ on $J$ is almost linear and the slope is almost independent of the value of $G_V$.

Figure 4

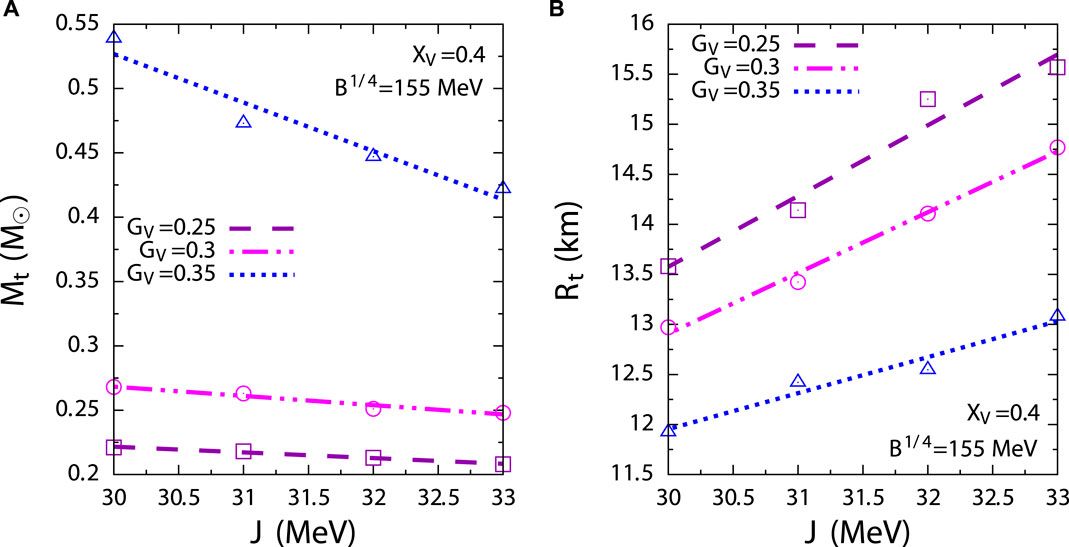
Figure 4. Variation of (A) transition mass and (B) transition radius of hybrid stars with respect to symmetry energy for different values of $G_V$ with $X_V=$0.4 and $B^{1/4}=$155 MeV.

Figure 5

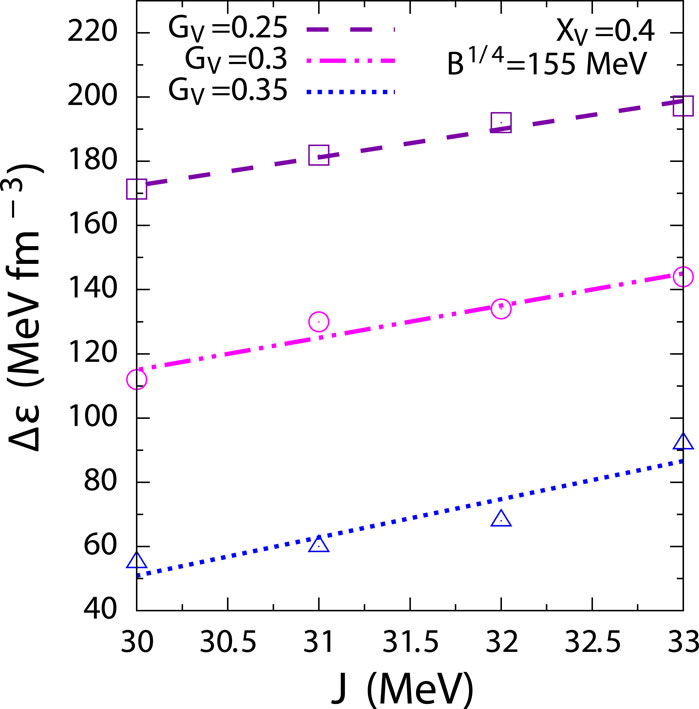
Figure 5. Variation of jump in energy density of hybrid stars with respect to symmetry energy for different values of $G_V$ with $X_V=$0.4 and $B^{1/4}=$155 MeV.

We also study the variation of the dimensionless tidal deformability with the canonical mass of hadronic and hybrid stars in Figure 6, where it is seen that the values of ${\mathrm{\Lambda }}_{1.4}$ for all the hadronic and hybrid star configurations are in good agreement with the constraint from GW170817 (Abbott et al., 2018). However, dependence on the $G_V$ value is evident, so ${\mathrm{\Lambda }}_{1.4}\simeq 260$ with $G_V$ = 0.25 but ${\mathrm{\Lambda }}_{1.4}\simeq$ 380 with $G_V$ = 0.35. Accurate measurement of the tidal deformability will certainly help determine $G_V$ value less ambiguously.

Figure 6

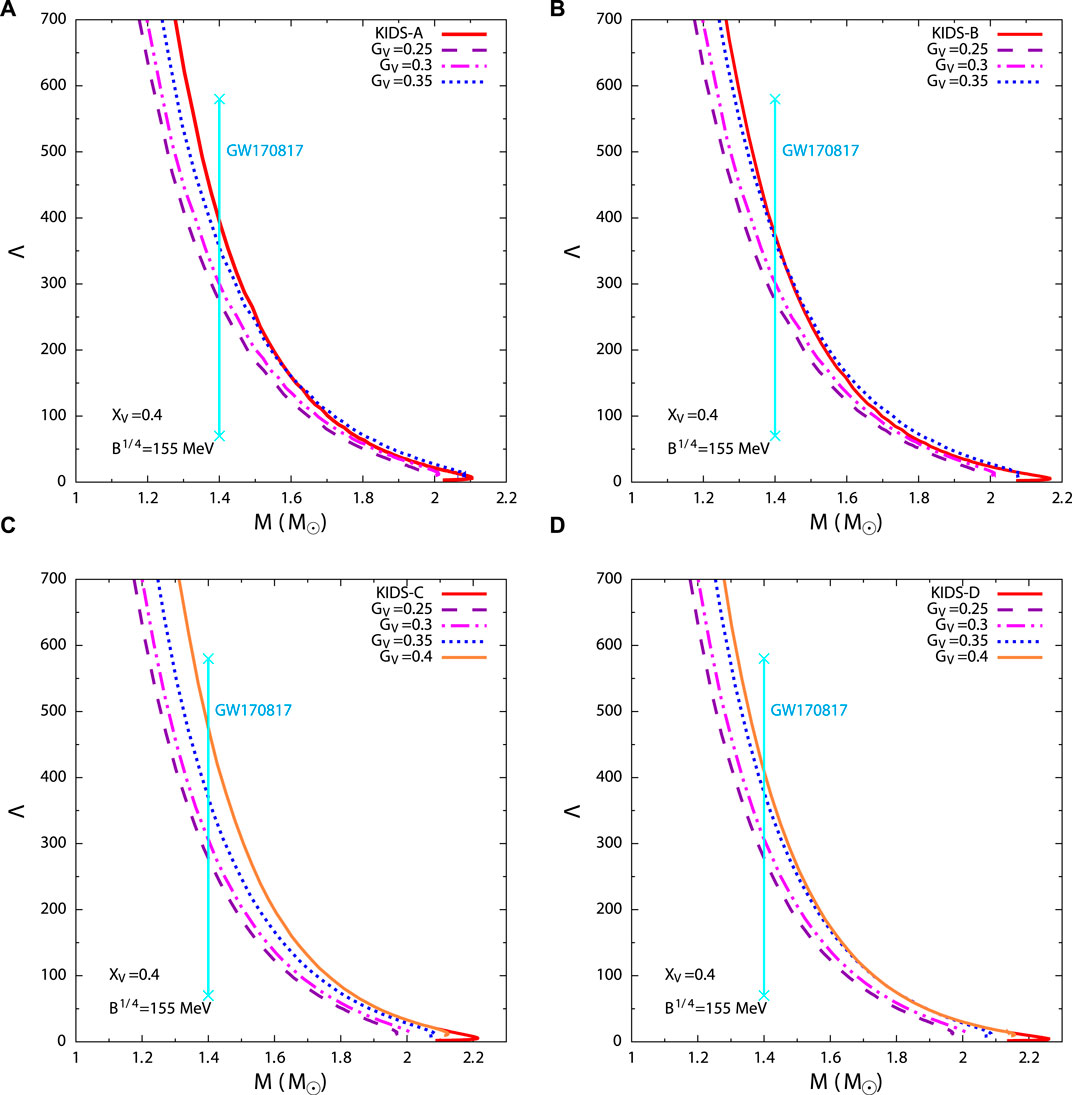
Figure 6. Variation of tidal deformability with mass of hadronic star (solid lines) and hybrid stars (dashed lines) with hadronic models (A) KIDS-A, (B) KIDS-B, (C) KIDS-C and (D) KIDS-D for different values of $G_V$ and $B^{1/4}=$155 MeV.

We next consider a lower value of $B$ as $B^{1/4}=$145 MeV. We have already seen from Figure 2 that for $B^{1/4}=$155 MeV, none of the hybrid star configurations obtained with $G_V$ = 0.25 and the four KIDS model could satisfy the NICER data for PSR J0030 + 0451 due to early transition. Therefore, it can be expected that further low value of $B$ will lead to further early or no transition at all. For $B^{1/4}=$145 MeV we do not consider $G_V$ = 0.25. We, however, consider $G_V$ = 0.4 to check if early transition for lower value of $B$ can give rise to stable hybrid stars. For the purpose we consider the softest (KIDS-A) and the stiffest (KIDS-D) among the four KIDS models. As expected, phase transition is early in the case of $B^{1/4}$ = 145 MeV. This is also reflected in Figures 7A, B where it can be seen that the transition mass is lower than that in case of $B^{1/4}=$155 MeV for a particular value of $G_V$. For example, considering the KIDS-A model ($J$ = 33 MeV) and $G_V$ = 0.35, $M_t$ = 0.422 $M_{\odot }$ when $B^{1/4}$ = 155 MeV as seen from Figures 4A, 2A while $M_t$ = 0.389 $M_{\odot }$ when $B^{1/4}=$145 MeV as seen from Figure 7A. Considering KIDS-D model ($J$ = 30 MeV) and $G_V$ = 0.35, $M_t$ = 0.539 $M_{\odot }$ as seen from Figures 4A, 2D for $B^{1/4}$ = 155 MeV while $M_t$ = 0.397 $M_{\odot }$ in case of $B^{1/4}=$145 MeV as seen from Figure 7B. Simultaneously, the transition radius is also affected by $B$. For example, in case of KIDS-A and $G_V$ = 0.35, $R_t$ = 13.081 km for $B^{1/4}$ = 155 MeV as seen from Figures 4B, 2A while $R_t$ = 13.255 km in case of $B^{1/4}$ = 145 MeV as seen from Figure 7A. Considering the KIDS-D model and $G_V$ = 0.35, $R_t$ = 11.924 km as seen from Figures 4B, 2D for $B^{1/4}$ = 155 MeV while $R_t$ = 12.171 km in case of $B^{1/4}$ = 145 MeV as seen from Figure 7B. Therefore transition mass is lowered while transition radius is increased for lower value of $B$. Similar to the case of higher value of $B^{1/4}$ = 155 MeV, the hybrid star configurations obtained for $G_V$ = 0.4 with $B^{1/4}$ = 145 MeV is unstable for the KIDS-A model as seen from Figures 2A, 7A. It is, however, stable with both the values of $B$ and $G_V$ = 0.4 in case of KIDS-D model having value of slope of symmetry energy $L$ much lower than that of the KIDS-A model as reflected in Table 1. So, it can be said that slope of symmetry energy $L$ also affects the stability of hybrid stars and EoS with lower value of the symmetry energy is more suitable for obtaining stable hybrid star configurations with large quark repulsion $G_V>$ 0.35. We also find that for $B^{1/4}$ = 145 MeV, all the present day astrophysical constraints are satisfied with $G_V$ = 0.3, 0.35 and 0.4 in terms of mass, radius (Figures 7A, B) and tidal deformability (Figures 7C, D). Another notable result is, similar to the result of $B^{1/4}=155$ MeV, there is a huge gap in the transition mass and transition density between $G_V=0.35$ and $G_V$ = 0.4. The transition mass is close to the maximum mass for $G_V$ = 0.4, which means that this delayed transition do not let the maximum mass of the hybrid star increase substantially above the transition mass.

Figure 7

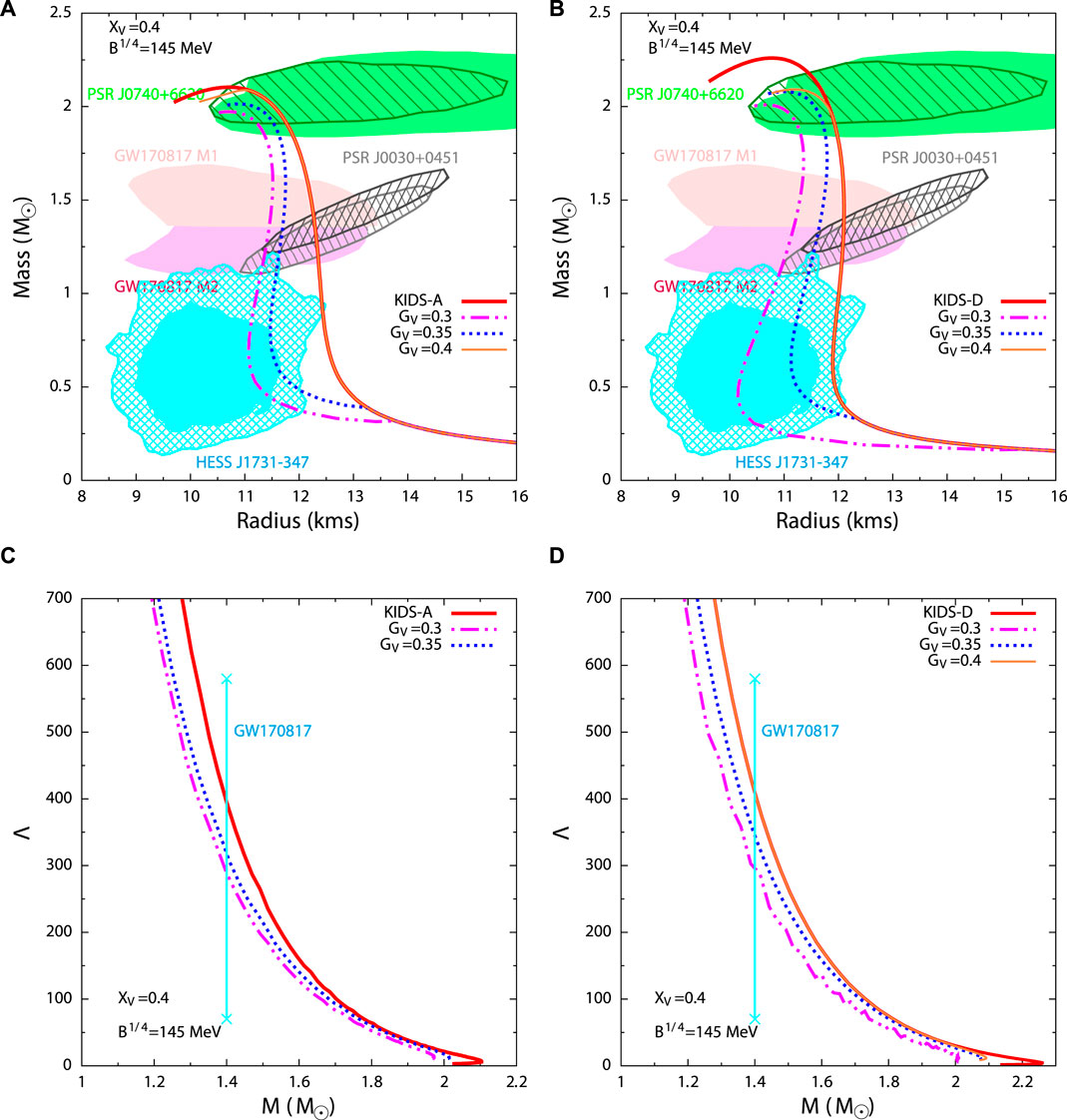
Figure 7. Variation of mass with radius (A,B) and tidal deformability with mass (C,D) of hadronic star (solid lines) and hybrid stars (dashed lines) with hadronic models KIDS-A and KIDS-D for different values of $G_V$ and $B^{1/4}=$145 MeV.

We finally consider a higher value of $B$ as $B^{1/4}$ = 160 MeV which we consider as the upper limit of $B$ to obtain hybrid star configurations with the KIDS-A and KIDS-D hadronic models. With this choice of $B$, it is expected that for $G_V$ = 0.4, transition will be further delayed and since we already obtained unstable hybrid star configurations with lower values of $B$, we do not consider $G_V$ = 0.4 in case of the maximum value of $B$. However, with low values of $G_V$ in case of $B^{1/4}$ = 160 MeV, transition density may be suitable to achieve reasonable hybrid star configurations. Therefore we also consider $G_V$ = 0.25 along with 0.3 and 0.35 in this case. The results are displayed in Figures 8A–D. We find from Figures 8A, B that even low quark repulsion ($G_V$ = 0.25) can satisfactorily satisfy all the astrophysical and observational constraints including the NICER data for PSR J0030 + 0451 which was not satisfied with the lower values of bag constant. Considering $G_V$ = 0.35 and $B^{1/4}$ = 160 MeV, $M_t$ = 0.798$M_{\odot }$ and 0.963$M_{\odot }$ while $R_t$ = 12.479 km and 11.905 km for the KIDS-A and KIDS-D models, respectively. It can thus be concluded that for a particular value of $G_V$ and $J$, $M_t$ increases with $B$ while $R_t$ follows the reverse trend. Also, for a particular value of $G_V$ and $B$, $M_t$($R_t$) decreases (increases) with a larger $J$. However, the variation of $J$ is quite small compared to that of $L$ in the case of the four KIDS model considered in the present work. So it can be said that the transition and hybrid star properties are more sensitive to the value of $L$. Summarizing the results up to now, depending on the value of the bag constant and the symmetry energy, the hybrid star configurations for $G_V$ values in the range $0.25\lesssim G_V\lesssim 0.4$ are consistent with the observational data.

Figure 8

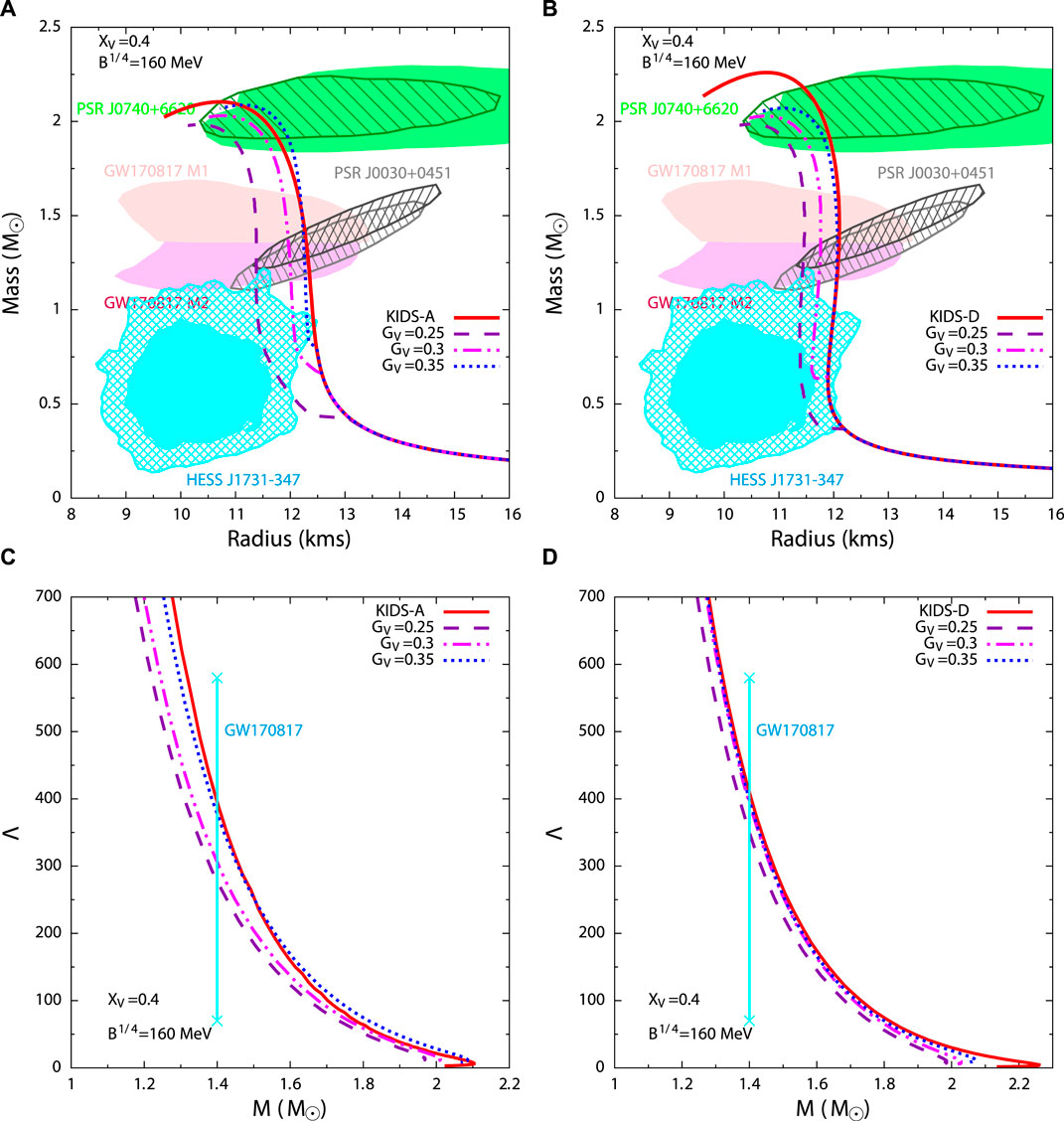
Figure 8. Variation of mass with radius (A,B) and tidal deformability with mass (C,D) of hadronic star (solid lines) and hybrid stars (dashed lines) with hadronic models KIDS-A and KIDS-D for different values of $G_V$ and $B^{1/4}=$160 MeV.

In Table 2 we display the transition densities and the maximum mass of the various hybrid star configurations. At the saturation density ${\rho }_0$ = 0.16 ${\mathrm{f}\mathrm{m}}^{-3}$, the volume occupied by a nucleon is $V$ = 1/${\rho }_0$ = 6.25 ${\mathrm{f}\mathrm{m}}^3$. Assuming that the nucleon is a sphere located at the center of a cube whose volume is 6.25 ${\mathrm{f}\mathrm{m}}^3$, the distance between the center of two nucleons is 1.84 fm. The radius of a nucleon is about 0.8 fm, so there is no overlapping between the nucleons at the saturation density. When the distance between the center of two nucleons is 1.6 fm, the surface of a nucleon touches the surface of other nucleons. The volume of a cube with the length of one side 1.6 fm is 4.10 ${\mathrm{f}\mathrm{m}}^3$, and it gives a density $\rho$ = 0.244 ${\mathrm{f}\mathrm{m}}^{-3}$ = 1.53${\rho }_0$. Taking into account the swelling of nucleons in nuclear medium, onset of the overlapping could happen at densities smaller than $1.5{\rho }_0$, but it must be larger than the saturation density. Considering this mechanical condition for the phase transition, $G_V$ = 0.25 is ruled out in any combinations of $B$ and the symmetry energy. Even $G_V$ = 0.3 is not acceptable for some cases. Therefore, combining the consistency with the astronomical data and the mechanical condition for the phase transition, acceptable range of $G_V$ is $0.3\lesssim G_V\lesssim 0.4$. Since for high values of $J$, $G_V$ = 0.4 yields unstable hybrid star configurations and for high values of $B$ there is no transition at all, $G_V$ = 0.4 could be regarded as an upper limit of $G_V$ value if one assumes the phase transition in the neutron star.

4 Summary

The present work is dedicated to study hadron-quark phase transition and the structural properties of hybrid stars. They depend on the properties of both the hadronic and quark phases like the symmetry energy of the former and the bag constant and the strength of quark repulsion of the latter. In order to investigate the effects of symmetry energy on the hybrid star properties we consider four KIDS models with different symmetry energy while the vBag model is adopted for the quark phase to study the influence of quark repulsion via the different values of vector coupling $G_V$ at three individual values of bag constant $B$.

We found that for any particular value of $G_V$ and $J$, higher bag constant leads to delayed transition in terms of both density and mass. Therefore, the maximum mass $M_{\mathit{max}}$ of hybrid stars also increases with increasing value of $B$. Moreover, the transition mass $M_t$ increases with $B$ while $R_t$ follows the reverse trend.

For any particular value of $B$ and $J$, $M_{\mathit{max}}$ increases with increasing value of $G_V$. The value of $R_{1.4}$ is also greatly affected by $G_V$. The radius of low mass hybrid stars are seen to increase with increasing values of $G_V$. $M_t$ increases while $R_t$ decreases with the increase of $G_V$.

For fixed values of $G_V$ and $B$, $M_{\mathit{max}}$ increases with decreasing value of $J$. $M_t$($R_t$) decreases (increases) with increasing $J$. The jump in energy density $\mathrm{\Delta }\epsilon$ from hadronic to quark phase also increases with increasing value of $J$ for any particular value of $G_V$. The dependence (fitted) of $\mathrm{\Delta }\epsilon$ on $J$ is linear and the slope is almost independent of the value of $G_V$. Considering a reasonable and moderately wide range of $B^{1/4}$=(145$-$160) MeV and symmetry energy $J$=(30$-$33) MeV, we find that the most suitable value of $G_V$ is approximately 0.3 $\lesssim G_V\lesssim$ 0.4 for the hybrid stars to satisfy all the present day astrophysical constraints on the structural properties of compact stars. $G_V\le$ 0.25 is allowed only when the bag constant is as high as $B^{1/4}>$ 155 MeV in the light of the NICER data for PSR J0030 + 0451. The stability of hybrid stars configurations with large quark repulsion $G_V>$ 0.35 is also affected by symmetry energy. We find that lower values of symmetry energy ($J<$ 32 MeV) are more suitable for obtaining stable hybrid star configurations with large quark repulsion $G_V>$ 0.35. Accurate measurement of the tidal deformability can make a significant contribution to reducing the uncertainty of $G_V$ in a narrower range.

In recent literature, it is shown that the consideration of extensive microscopic methods for the hadronic and quark matter suggests that the crossover transition is more likely to happen than the strong first-order transition in the core of neutron stars (Constantinou et al., 2021; Huang et al., 2022; Qin et al., 2023; Sotani and Kojo, 2023). Therefore, it will be interesting to study the possibilities of such crossover transition in neutron stars in our near future projects.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

DS: Conceptualization, Writing–original draft, Writing–review and editing, Formal Analysis, Visualization. HG: Formal Analysis, Writing–review and editing, Data curation, Investigation. CH: Writing–review and editing, Conceptualization, Methodology, Writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Research Foundation of Korea (Grant Nos 2018R1A5A1025563 and 2023R1A2C1003177).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbott, B. P., Abbott, R., Abbott, T., Acernese, F., Ackley, K., Adams, C., et al. (2018). GW170817: measurements of neutron star radii and equation of state. Phys. Rev. Lett. 121, 161101. arXiv:1805.11581 [gr-qc]. doi:10.1103/physrevlett.121.161101

PubMed Abstract | CrossRef Full Text | Google Scholar

Baym, G., Pethick, C., and Sutherland, P. (1971). The ground state of matter at high densities: equation of state and stellar models. Astrophys. J. 170, 299. doi:10.1086/151216

CrossRef Full Text | Google Scholar

Constantinou, C., Han, S., Jaikumar, P., and Prakash, M. (2021). g modes of neutron stars with hadron-to-quark crossover transitions. Phys. Rev. D. 104 (12), 123032. doi:10.1103/physrevd.104.123032

CrossRef Full Text | Google Scholar

Contrera, G. A., Ranea-Sandoval, I. F., and Weber, F. (2017). Hybrid stars in the framework of NJL models. Int. J. Mod. Phys. Conf. Ser. 45, 1760026. arXiv:1612.09485 [nucl-th]. doi:10.1142/s2010194517600266

CrossRef Full Text | Google Scholar

Doroshenko, V., Suleimanov, V., Puhlhofer, G., and Santangelo, A. (2022). A strangely light neutron star within a supernova remnant. Nat. Astron. 6, 1444–1451. doi:10.1038/s41550-022-01800-1

CrossRef Full Text | Google Scholar

Fonseca, E., Cromartie, H. T., Pennucci, T. T., Ray, P. S., Kirichenko, A. Y., Ransom, S. M., et al. (2021). Refined mass and geometric measurements of the high-mass PSR J0740+ 6620. Astrophys. J. Lett. 915, L12. arXiv:2104.00880 [astro-ph.HE]. doi:10.3847/2041-8213/ac03b8

CrossRef Full Text | Google Scholar

Gil, H., and Hyun, C. H. (2021). Compression modulus and symmetry energy of nuclear matter with KIDS density functional. New Phys. Sae Mulli 71, 242–248. arXiv:2012.00930 [nucl-th]. doi:10.3938/npsm.71.242

CrossRef Full Text | Google Scholar

Gil, H., Kim, Y.-M., Papakonstantinou, P., and Hyun, C. H. (2021). Constraining the density dependence of the symmetry energy with nuclear data and astronomical observations in the Korea-IBS-Daegu-SKKU framework. Phys. Rev. C 103, 034330. arXiv:2010.13354 [nucl-th]. doi:10.1103/physrevc.103.034330

CrossRef Full Text | Google Scholar

Gil, H., Papakonstantinou, P., and Hyun, C. H. (2022). Constraints on the curvature of nuclear symmetry energy from recent astronomical data within the KIDS framework. Int. J. Mod. Phys. E 31, 2250013. arXiv:2110.09802 [nucl-th]. doi:10.1142/s0218301322500136

CrossRef Full Text | Google Scholar

Grill, F., Pais, H., Providência, C., Vidaña, I., and Avancini, S. S. (2014). Equation of state and thickness of the inner crust of neutron stars. Phys. Rev. C 90, 045803. arXiv:1404.2753 [nucl-th]. doi:10.1103/physrevc.90.045803

CrossRef Full Text | Google Scholar

Hinderer, T. (2008). Tidal love numbers of neutron stars. Astrophys. J. 677, 1216–1220. arXiv:0711.2420 [astro-ph]. doi:10.1086/533487

CrossRef Full Text | Google Scholar

Hinderer, T., Lackey, B. D., Lang, R. N., and Read, J. S. (2010). Tidal deformability of neutron stars with realistic equations of state and their gravitational wave signatures in binary inspiral. Phys. Rev. D. 81, 123016. arXiv:0911.3535 [astro-ph.HE]. doi:10.1103/physrevd.81.123016

CrossRef Full Text | Google Scholar

Huang, Y.-J., Baiotti, L., Kojo, T., Takami, K., Sotani, H., Togashi, H., et al. (2022). Merger and postmerger of binary neutron stars with a quark-hadron crossover equation of state. Phys. Rev. Lett. 129 (18), 181101. doi:10.1103/physrevlett.129.181101

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnson, K. (1975). The MIT bag model. Acta Phys. Pol. B 6, 865.

Google Scholar

Kumar, A., Thapa, V. B., and Sinha, M. (2022). Compact star merger events with stars composed of interacting strange quark matter. Mon. Not. Roy. Astron. Soc. 513, 3788–3797. arXiv:2204.11034 [astro-ph.HE]. doi:10.1093/mnras/stac1150

CrossRef Full Text | Google Scholar

Kumar, A., Thapa, V. B., and Sinha, M. (2023). Hybrid stars are compatible with recent astrophysical observations. Phys. Rev. D. 107, 063024. arXiv:2303.06387 [astro-ph.HE]. doi:10.1103/physrevd.107.063024

CrossRef Full Text | Google Scholar

Laskos-Patkos, P., Koliogiannis, P. S., and Moustakidis, C. C. (2023). Hybrid stars in light of the HESS J1731-347 remnant and the PREX-II experiment. arXiv:2312.07113 [astro-ph.HE].

Google Scholar

Laskos-Patkos, P., and Moustakidis, C. C. (2023). Signatures of quark deconfinement through the r-modes of twin stars. Phys. Rev. D. 107 (12), 123023. doi:10.1103/physrevd.107.123023

CrossRef Full Text | Google Scholar

Li, J. J., Sedrakian, A., and Weber, F. (2020). Rapidly rotating Δ-resonance-admixed hypernuclear compact stars. Phys. Lett. B 810, 135812. doi:10.1016/j.physletb.2020.135812

CrossRef Full Text | Google Scholar

Lopes, L. L., Biesdorf, C., and Menezes, D. P. (2022). Hypermassive quark cores. Mon. Not. Roy. Astron. Soc. 512, 5110–5121. arXiv:2111.13732 [hep-ph]. doi:10.1093/mnras/stac793

CrossRef Full Text | Google Scholar

Maruyama, T., Chiba, S., Schulze, H. J., and Tatsumi, T. (2008). Quark deconfinement transition in hyperonic matter. Phys. Lett. B 659, 192–196. doi:10.1016/j.physletb.2007.10.056

CrossRef Full Text | Google Scholar

Miller, M. C., Lamb, F. K., Dittmann, A. J., Bogdanov, S., Arzoumanian, Z., Gendreau, K. C., et al. (2019). PSR J0030+ 0451 mass and radius from NICER data and implications for the properties of neutron star matter. Astrophys. J. Lett. 887, L24. arXiv:1912.05705 [astro-ph.HE]. doi:10.3847/2041-8213/ab50c5

CrossRef Full Text | Google Scholar

Miller, M. C., Lamb, F. K., Dittmann, A. J., Bogdanov, S., Arzoumanian, Z., Gendreau, K. C., et al. (2021). The radius of PSR J0740+ 6620 from NICER and XMM-Newton data. Astrophys. J. Lett. 918, L28. arXiv:2105.06979 [astro-ph.HE]. doi:10.3847/2041-8213/ac089b

CrossRef Full Text | Google Scholar

Nandi, R., and Char, P. (2018). Hybrid stars in the light of GW170817. Astrophys. J. 857 (1), 12. doi:10.3847/1538-4357/aab78c

CrossRef Full Text | Google Scholar

Oppenheimer, J. R., and Volkoff, G. M. (1939). On massive neutron cores. Phys. Rev. 55, 374–381. doi:10.1103/physrev.55.374

CrossRef Full Text | Google Scholar

Pal, S., Podder, S., Sen, D., and Chaudhuri, G. (2023). Speed of sound in hybrid stars and the role of bag pressure in the emergence of special points on the M−R variation of hybrid stars. Phys. Rev. D. 107, 063019. arXiv:2303.04653 [nucl-th]. doi:10.1103/physrevd.107.063019

CrossRef Full Text | Google Scholar

Qin, P., Bai, Z., Wang, S., Wang, C., and Qin, S. X. (2023). Hadron-quark phase transition in neutron star by combining the relativistic Brueckner-Hartree-Fock theory and Dyson-Schwinger equation approach. Phys. Rev. D. 107, 103009. doi:10.1103/PhysRevD.107.103009

CrossRef Full Text | Google Scholar

Rather, I. A., Das, H. C., Imran, M., Usmani, A. A., and Patra, S. K. (2020). Constraining bag constant for hybrid neutron stars. Int.J.Mod Phys.E 29 (07), 2050044. doi:10.1142/s0218301320500445

CrossRef Full Text | Google Scholar

Riley, T. E., Watts, A. L., Bogdanov, S., Ray, P. S., Ludlam, R. M., Guillot, S., et al. (2019). A NICER view of PSR J0030+ 0451: millisecond pulsar parameter estimation. Astrophys. J. Lett. 887, L21. arXiv:1912.05702 [astro-ph.HE]. doi:10.3847/2041-8213/ab481c

CrossRef Full Text | Google Scholar

Riley, T. E., Watts, A. L., Ray, P. S., Bogdanov, S., Guillot, S., Morsink, S. M., et al. (2021). A NICER view of the massive pulsar PSR J0740+ 6620 informed by radio timing and XMM-Newton spectroscopy. Astrophys. J. Lett. 918, L27. arXiv:2105.06980 [astro-ph.HE]. doi:10.3847/2041-8213/ac0a81

CrossRef Full Text | Google Scholar

Sotani, H., and Kojo, T. (2023). Universality in quasinormal modes of neutron stars with quark-hadron crossover. Phys. Rev. D. 108 (6), 063004. doi:10.1103/physrevd.108.063004

CrossRef Full Text | Google Scholar

Sun, H., and Wen, D. (2023). Implications of supermassive neutron stars for the form of the equation of state of hybrid stars. Phys. Rev. C 108 (2), 025801. doi:10.1103/physrevc.108.025801

CrossRef Full Text | Google Scholar

Takatsy, J., and Kovacs, P. (2020). Comment on “Tidal Love numbers of neutron and self-bound quark stars”. Phys. Rev. D. 102, 028501. doi:10.1103/physrevd.102.028501

CrossRef Full Text | Google Scholar

Tolman, R. C. (1939). Static solutions of einstein's field equations for spheres of fluid. Phys. Rev. 55, 364–373. doi:10.1103/physrev.55.364

CrossRef Full Text | Google Scholar