Electron cyclotron maser instability by evolving fast electron beams in the flare loops

The electron cyclotron maser instability (ECMI) stands as a pivotal coherent radio emission mechanism widely implicated in various astrophysical phenomena. In the context of solar activity, ECMI is primarily instigated by energetic electrons generated during solar eruptions, notably flares. These electrons, upon leaving the acceleration region, traverse the solar atmosphere, forming fast electron beams (FEBs) along magnetic field lines. It is widely accepted that as these FEBs interact with the ambient plasma and magnetic fields, they give rise to radio and hard X-ray emission. Throughout their journey in the plasma, FEBs undergo modifications in their energy spectrum and velocity spatial distribution due to diverse energy loss mechanisms and changes in ambient plasma parameters. In this study, we delve into the impact of the evolving energy spectrum and velocity anisotropic distribution of FEBs on ECMI during their propagation in flare loops. Our findings indicate that if we solely consider the progressively flattened lower energy cutoff behavior as FEBs descend along flare loops, the growth rates of ECMI decrease accordingly. However, when accounting for the evolution of ambient magnetic plasma parameters, the growth rates of ECMI increase as FEBs delve into denser atmosphere. This underscores the significant influence of the energy spectrum and velocity anisotropy distribution evolution of FEBs on ECMI. Our study sheds light on a more comprehensive understanding of the dynamic spectra of solar radio emissions.

1 Introduction

The Sun is a highly active star, and flares represent some of the most powerful eruptions it experiences. During a flare event, an excess of 10³² erg of stored magnetic energy can be rapidly released (Fletcher et al., 2011). This released energy is transferred into the thermal energy of local plasma, the enhanced emission of the entire electromagnetic spectrum, plasma motions such as jets and coronal mass ejections (CME), and the acceleration of particles. While the mechanism by which flares convert magnetic energy into energetic particles remains an unanswered question, magnetic reconnection is generally accepted as a triggering mechanism (Masuda et al., 1994; Yokoyama et al., 2001; Imada et al., 2013). For instance, energetic particles can be accelerated by the electric fields within large-scale reconnecting current sheets during a large two-ribbon flare (Benka and Holman, 1994; Zharkova and Gordovskyy, 2004; Sharykin et al., 2014). As these flare-accelerated faste and interact with the ambient plasma, they produce radio and hard X-ray radiation. Consequently, FEBs can be inferred indirectly from solar radio bursts and hard X-ray bursts (Dulk et al., 1992; Holman et al., 2011), or directly detected by particle detectors as they travel into near-Earth interplanetary space (Lin, 2011). The most direct radio observational evidence of FEBs is type III solar radio bursts, which are generally accepted to be produced by FEBs during flare events.

Type III solar radio bursts are one of the most extensively studied during the past few decades. The key issue is how the FEBs generate electromagnetic waves near the local plasma frequency. A so-called plasma emission theory was put forth by (Ginzburg and Zhelezniakov, 1958) to explain the observed characteristics of type III bursts, in which the beam-generated Langmuir waves play a key role. This plasma theory was developed by many authors (Cairns, 1987a; Cairns, 1987b; Cairns, 1987c; Wu et al., 1994; Yoon, 1995; Yoon, 1997; Yoon, 1998) and they all assume that the ambient magnetic field in the source region of type III radio bursts is very weak. For the most solar radio bursts, including type III bursts, they usually produced near an active region in the low corona, so the weak magnetic field approximation is not appropriate because the plasma in the source region is strongly magnetized.

Another important coherent radiation process, the electron cyclotron maser instability (ECMI), which emits radiation near the electron cyclotron frequency and its harmonics via wave-particle interaction was first suggested by Twiss (1958) and Schneider (1959). This early maser instability theory has also been applied to various radio emissions, such as solar radio type I bursts (Twiss and Roberts, 1958; Mangeney and Veltri, 1976), and Jovian decametric radiation (Hirshfield, 1963; Goldstein and Eviatar, 1972; Melrose, 1976). The ECMI theory achieved a major breakthrough when Wu and Lee (1979) accounted for weak relativistic effects and applied this theory to auroral kilometer radiation (AKR). Since then, the ECMI theory has been extensively studied and discussed, being applied to radio emissions from magnetized planets (Hewitt et al., 1981; Zarka, 1998; Hess et al., 2007), various solar radio bursts (Melrose and Dulk, 1982; Aschwanden and Benz, 1988; Aschwanden, 1990; Vlasov et al., 2002; Wu et al., 2002; Yoon et al., 2002; Wang, 2004; Treumann et al., 2011; Zhao et al., 2013), and radio emissions from various stellar environments (Stepanov et al., 2001; Begelman et al., 2005; Hallinan et al., 2008; Callingham et al., 2021). Most earlier theories suggest that ECMI is excited by various velocity anisotropic distributions of energetic electrons, which exhibit an inverted perpendicular population as ∂f_b/∂v_⊥ > 0, providing free energy for ECMI. Hard X-ray observations demonstrate that flare-accelerated FEBs usually have an approximate power-law energy spectrum (Lin, 1974; Hudson and Ryan, 1995; Aschwanden, 2002). These power-law FEBs traveling in the solar atmosphere are the main source of solar radio bursts (Aschwanden, 2002; Fleishman, 2004; Wu et al., 2007). A series of recent works (Wu and Tang, 2008; Tang and Wu, 2009; Tang et al., 2011; Tang et al., 2012) have shown that the low-energy cutoff behavior of power-law electrons is another effective driving source of ECMI.

As mentioned above, it is the FEBs traveling in the solar atmosphere and interacting with the ambient plasma that produce radio and hard X-ray radiation. The strong correlation between SRBs and HXRs in some statistical works (Kosugi et al., 1988; White et al., 2011) also implies that they have the same source, i.e., the FEBs (Raoult et al., 1990; Aschwanden, 2002; White et al., 2011). High-resolution imaging observations of HXRs show that the HXR source of a flare often consists of a coronal looptop source and two or more footpoint sources (Hudson, 1978; Hoyng et al., 1981). The standard flare HXR emission model, which involves thin- and thick-target bremsstrahlung emission at looptop and footpoints, respectively, indicates a spectral index difference between the looptop source and footpoint sources, Δγ = 2. However, the majority of HXR observations show that the spectral index difference Δγ ≠ 2, implying that the energy spectra of FEBs change during their propagation in the flare loops from the top to foots. The collisional energy loss and deceleration by induced electric fields of energetic electrons are the main reasons for the change of the energy spectra of FEBs. Considering the collisional and noncollisional energy losses of electrons, Tang et al. (2020) investigated the parametric evolution of power-law spectra of flare-accelerated FEBs when propagating in the flare loops. The variations of the energy spectral parameters of power-law FEBs, such as the spectral index α, the steepness index δ, and lower cutoff energy E_c, all have important effects on the maser instability. Tang et al. (2016) investigated the ECMI driven by evolving FEBs in the coronal loop preliminarily. In their model, the magnetic field configuration of the source region is a giant expansion arch structure, and the CME-driven shock front is the acceleration site for FEBs. Since the specific models of density and magnetic field for the coronal loop are not considered, the energy loss of energetic electrons described by the loss factor Q and the magnetic mirror ratio parameter σ are empirically determined. Therefore, further research is needed to fully understand the ECMI theory excited by evolving FEBs and other related issues.

In this paper, we focus on the influence of the evolution of FEBs when propagating in the flare loop on ECMI. We propose that the flare-accelerated FEBs initially exhibit a power-law energy distribution and travel along the flare loop from the acceleration region to the footpoints. Utilizing the coronal magnetic field and density models of active region by Zhao (1995), the semiempirical homogeneous plane-parallel flare atmospheric model by Machado et al. (1980), and the evolution of energy spectral parameters of FEBs by Tang et al. (2020), we investigate the characteristics of ECMI excited by evolving FEBs propagating along the flare loops. The structure of this paper is organized as follows: Section 2 introduces the density and magnetic field models of the flare loop. In Section 3, we present the calculating results of maser instability. Finally, Section 4 provides the discussion and conclusions.

2 The physical model

2.1 Density and magnetic field models of flare loops

It is generally believed that the acceleration of charged particles by magnetic reconnection in the impulsive phase may be the most prominent feature of a solar flare. In this paper, we assume that the flare-accelerated FEBs have an initial power-law distribution with a lower energy cutoff, denoted as E_c, when they leave the acceleration region. Following the results of Tang et al. (2020), we analyze the influence of the evolving FEBs on ECMI when traveling in the flare loops. The height of the electron acceleration site, approximately corresponding to the height of the flare loops, is about 20–50 Mm (Aschwanden et al., 1998; Reid et al., 2011). Therefore, Tang et al. (2020) utilized the semiempirical homogeneous plane-parallel flare atmospheric model (F2 model) (Machado et al., 1980) and extended the loop to a height of h = 40 Mm. Observations and studies show that flares tend to occur strongly in magnetic active regions. Hence, we approximately model the magnetic field of the flare loop and extend the density distribution from the transition region to the looptop using the solar active regions model proposed by Zhao (1995):

$B\left(r,h\right)=\frac{{\left[r^2+4{\left(h+d\right)}^2\right]}^{1/2}}{2{\left[r^2+{\left(h+d\right)}^2\right]}^2}{d}^3{B}_0,(1)$

and

$N\left(r,h\right)=7.272\times 10^{17}\mu \left(r\right)h^{-0.9978}.(2)$

In Eqs 1, 2, r represents the distance to the central axis of the active region, h denotes the height above the photosphere, and d indicates the depth of a vertical dipole sunspot below the photosphere. B₀ represents the magnetic field strength at the point on the axis of the sunspot and at the photospheric level, i.e., (r = 0, h = 0).

Figure 1A illustrates the radial distribution of plasma density and magnetic field along the flare loops. The density curve n_e is plotted based on the flare atmospheric model (Machado et al., 1980) and coronal density model of active regions (Eq. (2)). Here, we set μ(r) = 4, r = 0, d = 2 × 10⁴ km, and magnetic field B₀ = 2000 G, respectively. In Figure 1B, the radial distribution of the ratio of the electron plasma frequency (ω_p) to the cyclotron frequency (ω_ce) is presented. It is evident from Figure 1B that the plasma frequency ω_p is smaller than the electron cyclotron frequency ω_ce in the height range from the upper part of the transition region to near the top of the flare loop. This suggests that ECM is a viable emission mechanism in almost the entire flare loops. Morosan et al. (2016) and Régnier (2015) similarly reported that the condition for ECMI (ω_p/ω_ce < 1) is possible at heights $<1.1R_{\odot }$ and $<1.2R_{\odot }$ within the active region. Figure 2 displays the radial distribution of the magnetic mirror ratio parameter σ with the height of flare loops.

Figure 1

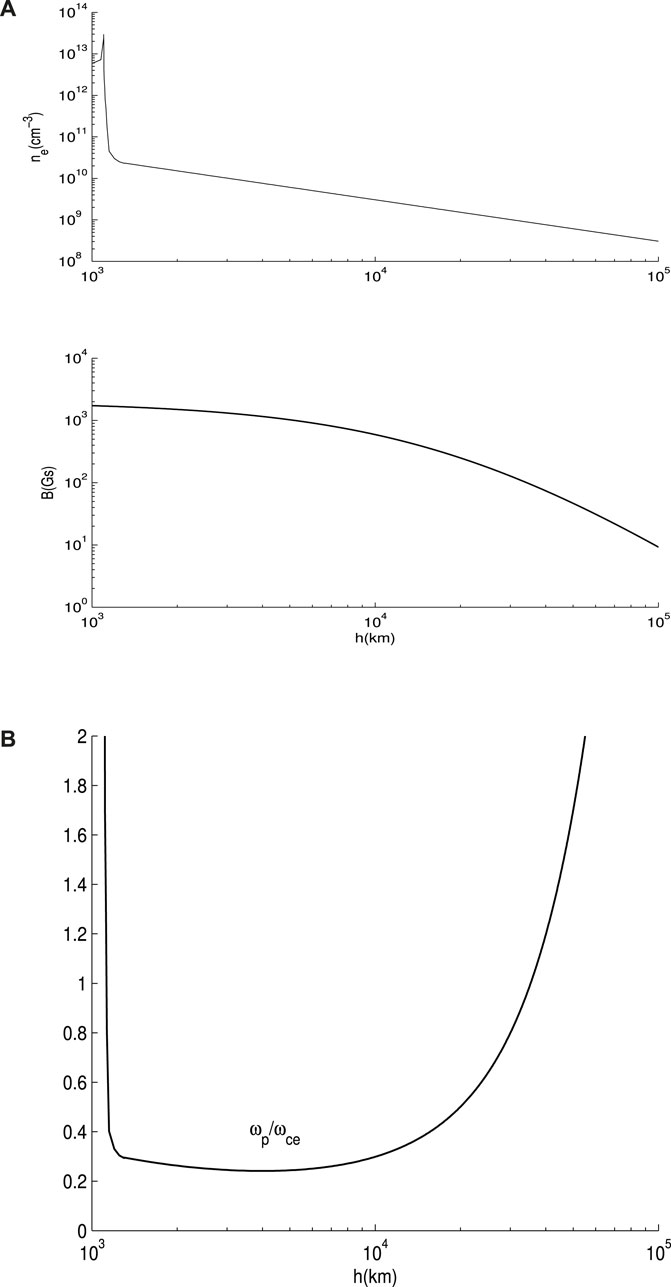
Figure 1. (A): Density and magnetic field strength in the flare loop vs. height. (B): Radial distribution of the ratio of plasma frequency ω_p to electron cyclotron frequency ω_ce along the flare loop.

Figure 2

Figure 2. The magnetic mirror ratio σ vs. height of flare loop.

2.2 The evolving FEBs

As we know, FEBs propagating along the magnetic field in the solar atmosphere are believed to be the sources of solar radio bursts and HXR bursts. However, due to various reasons such as energy loss, diffusion caused by wave-particle interactions, etc., the distribution of FEBs is highly unstable. Due to energy loss during their long journey, the properties of FEBs, such as the energy spectral parameters, can be significantly modified (Tang et al., 2020). Melrose and Wheatland (2016) and Ning et al. (2021) proposed that a horseshoe distribution can be formed when beam electrons traveling inside flare loops. It is generally believed that when a parallel electric field exists, the acceleration effect of the parallel electric field causes electrons to escape, forming a horseshoe distribution. The corresponding relaxation includes the time for establishing the parallel electric field, electron acceleration, and then escape. In the case of AKR, it is indeed observed that there are parallel electric fields and horseshoe distributions in the auroral electron acceleration region. Here, we have not considered the issue of parallel electric fields at the moment, so we have also not considered horseshoe distributions. For loss cone distribution, since it directly forms from electron leakage at small injection angles without undergoing diffusion, acceleration, or other kinetic processes, there is no relaxation time. If we must define a relaxation time, it would be the escape time of quasi-parallel (small injection angle) electrons, which should be extremely short and can be considered instantaneous. Considering the initial beam-like velocity distribution of accelerated electron beams (Wang, 2004) and the power-law energy distribution, we employ the distribution function of FEBs when they leave the acceleration site as follows:

$\begin{array}{ll}\hfill F_0\left(u,\mu \right)& =A_0\tanh {\left(\frac{u}{u_c}\right)}^{2\delta }{\left(\frac{u}{u_c}\right)}^{-2\alpha }\hfill \\ \hfill & \times \exp \left[-\frac{{\left(u\mu -u_s\right)}^2}{{\beta }^2}-\frac{u^2\left(1-{\mu }^2\right)}{{\beta }^2}\right].\hfill \end{array}(3)$

Here, $u^2=u_{\perp }^2+u_{\Vert }^2$, where u denotes the momentum per unit mass, u_‖ and u_⊥ represent the components of u parallel and perpendicular to the ambient magnetic field, respectively. μ = u_‖/u is the pitch angle cosine. A₀ is the normalization coefficient. The hyperbolic tangent function $\tanh {(u/u_c)}^{2\delta }$ describes the general cutoff behavior, with parameters δ and α representing the steepness index and spectrum index of FEBs, respectively. $E_c=\frac{1}{2}m{u}_c^2$ denotes the cutoff energy. u_s represents the beam velocity, and β is the momentum dispersion in parallel and perpendicular directions.

The results of Tang et al. (2020) show that as the FEBs precipitate in the flare loops, the steepness cutoff behavior will be flatten, the lower cutoff energy E_c decreases, and the initial single power-law spectrum can evolve into a broken power-law spectrum. Taking into account the magnetic mirror effect caused by the convergence of magnetic fields in the lower atmosphere and disregarding the influence of the double power-law spectrum on the ECM, we can approximate the distribution function of FEBs at a certain height as follows:

$\begin{array}{ll}\hfill F\left(u,\mu \right)& =A_0\tanh {\left(\frac{u}{u_{ch}}\right)}^{2{\delta }_h}{\left(\frac{u}{u_{ch}}\right)}^{-2{\alpha }_h}\hfill \\ \hfill & \times \left[1-\exp \left[\left(1-{\sigma }_h\right)\frac{1-{\mu }^2}{{\mu }^2}\right]\right]\hfill \\ \hfill & \times \exp \left[-\frac{{\left(u\mu -u_s\right)}^2}{{\beta }^2}-\frac{u^2\left(1-{\mu }^2\right)}{{\beta }^2}\right],\hfill \end{array}(4)$

here, $E_{ch}=\frac{1}{2}m{u}_{ch}^2$, δ_h, α_h, and σ_h represent the cutoff energy, the steepness index, the spectrum index, and the magnetic mirror ratio parameter of FEBs at a certain height h.

3 Numerical results

3.1 General formulation of ECMI

ECMI is a coherent mechanism that directly amplifies electromagnetic radiation near the electron cyclotron frequency and its harmonic frequencies. Due to its high efficiency, ECMI has been extensively investigated and applied to various high-power radio bursts in magnetized plasma. Electromagnetic waves can be amplified when the resonance condition between energetic electrons and waves is met:

$\gamma -s\mathrm{\Omega }/{\omega }_q-N_q\mu \cos \theta u/c=0.(5)$

Here, γ and s denote the Lorentz factor and harmonic number, respectively. Parameters Ω represent the electron cyclotron frequency, and ω_q is the frequency of the excited wave, with all frequencies normalized by the plasma frequency ω_p. N_q denotes the refractive index of the excited wave propagating with a phase angle θ to the magnetic field. The subscript q = ± indicates the wave modes for the ordinary mode (O mode, q = +) and the extraordinary mode (X mode, q = −), respectively.

We consider the density of FEBs to be much lower than that of the background plasma. Therefore, when discussing the dispersion relation of waves, the FEBs can be neglected. However, when discussing the growth rate, the effect of the FEBs predominates. So, the dispersion relation of the excited wave can be approximately by the cold-plasma theory (Chen et al., 2002; Wu et al., 2002):

$N_q^2=1-\frac{1}{{\omega }_q\left({\omega }_q+{\tau }_q\mathrm{\Omega }\right)},(6)$

and

$\begin{array}{ll}\hfill {\tau }_q& =-s_q+q\sqrt{s_q^2+{\cos }^2\theta }\hfill \\ \hfill s_q& ={\omega }_q\mathrm{\Omega }{\sin }^2\theta /2\left({\omega }_q^2-1\right).\hfill \end{array}(7)$

When the frequency of the excited wave ω ≃ sΩ, the temporal growth rate can be given by the following (Wu et al., 2002):

$\begin{array}{ll}\hfill \frac{{\omega }_{qi}}{{\omega }_{ce}}& =\frac{\pi }{2}\frac{n_b}{n_0}\int \int \int d^3\mathbf{u}\frac{\gamma \left(1-{\mu }^2\right)}{\mathrm{\Omega }{\omega }_q\left(1+T_q^2\right)R_q}\delta \left(\gamma -\frac{s\mathrm{\Omega }}{{\omega }_q}-\frac{N_q\mu u}{c}\cos \theta \right)\hfill \\ \hfill & \times \left\{\frac{{\omega }_q}{\mathrm{\Omega }}\left[\gamma K_q\sin \theta +T_q\left(\gamma \cos \theta -\frac{N_q\mu u}{c}\right)\right]\right.\times {\left.\frac{J_s\left(b_q\right)}{b_q}+J_s^{\prime }\left(b_q\right)\right\}}^2\hfill \\ \hfill & \times \left[u\frac{\partial }{\partial u}+\left(\frac{N_{q}u\cos \theta }{c\gamma }-\mu \right)\frac{\partial }{\partial \mu }\right]F_b\left(u,\mu \right),\hfill \end{array}(8)$

and

$\begin{array}{ll}\hfill b_q& =N_q\frac{{\omega }_q}{\mathrm{\Omega }}\frac{u}{c}\sqrt{1-{\mu }^2}\sin \theta ,\hfill \\ \hfill R_q& =1-\frac{\mathrm{\Omega }{\tau }_q}{2{\omega }_q{\left({\omega }_q+{\tau }_q\mathrm{\Omega }\right)}^2}\left(1-\frac{q{s}_q}{\sqrt{s_q^2+{\cos }^2\theta }}\frac{{\omega }_q^2+1}{{\omega }_q^2-1}\right),\hfill \\ \hfill K_q& =\frac{\mathrm{\Omega }\sin \theta }{\left({\omega }_q^2-1\right)\left({\omega }_q+{\tau }_q\mathrm{\Omega }\right)},\hfill \\ \hfill T_q& =-\frac{\cos \theta }{{\tau }_q}.\hfill \end{array}(9)$

Here, n_b and n₀ denote the number densities of energetic electrons and ambient thermal electrons, respectively. J_s (b_q) represents the first kind of Bessel function.

3.2 ECMI by the evolving FEBs

As mentioned above, the energy spectra of FEBs can significantly vary due to their interaction with the ambient plasma as they travel down along the flare loop (Tang et al., 2020). With the evolving distribution function F (u, μ) given by Eq. 4, the growth rates of ECMI by FEBs when they reach a certain height can be calculated based on Eq. 8. For the given initial parameters (α, δ, u_c, u_s, β) of FEBs, the evolving energy spectral parameters, such as the cutoff energy E_ch (u_ch), the power-law spectral index α_h, and the steepness index δ_h at a certain height are based on the calculation results of Tang et al. (2020). The frequency ratio Ω and the magnetic mirror ratio σ are deduced from the density and magnetic field models of the flare loops. Figures 3–5 illustrate the effect of the parametric evolution of FEBs energy spectrum on ECMI when propagating from the loop top to a certain height. The growth rate depends on the frequency and propagation angle of the excited wave, i.e., on parameters ω_q and θ. The peak growth rates ω_i are normalized by ω_cen_b/n₀. The parameter n_b/n₀ represents the density ratio between energetic electrons and background electrons, and it actually varies as the FEBs move through the solar atmosphere. Different density ratios have an impact on both the dispersion relation and the growth rate of the excited wave (Winglee and Dulk, 1986; Yasnov and Karlický, 2004; Li et al., 2019; Ning et al., 2023). Here, the density ratio n_b/n₀ ≪ 1. Therefore, the state of the background plasma does not directly affect the growth rate, but only indirectly affects it through the dispersion relation. Of course, for relatively large ratios of beam/background electron densities, the state of background electrons may indeed have a direct impact on the calculation of the growth rate.

Figure 3

Figure 3. Peak growth rates of the fundamental waves for O mode and harmonic waves (s = 2) for X mode excited by the FEBs traveling down along the flare loop. The initial parameters of FEBs, such as spectrum index α = 7, steepness index δ = 12, E_c = 50 keV, and u_s = 0.3c, and β = 0.2c have been used.

Figure 4

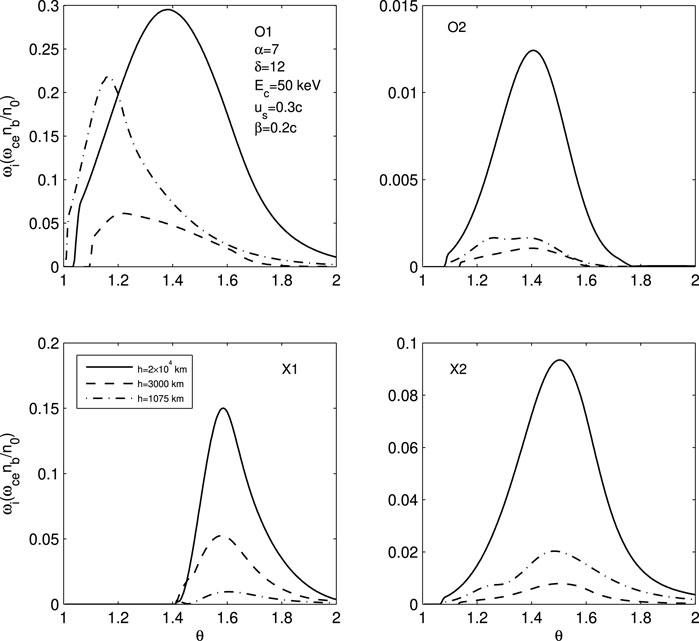
Figure 4. Peak growth rates of the fundamental waves and harmonic waves (s = 2) for O and X modes excited by the FEBs when traveling down along flare loop. Here, the frequency ratio Ω and the magnetic mirror ratio σ vary with the magnetic field and density models of the flare loop, other parameters are same as in Figure 3.

Figure 5

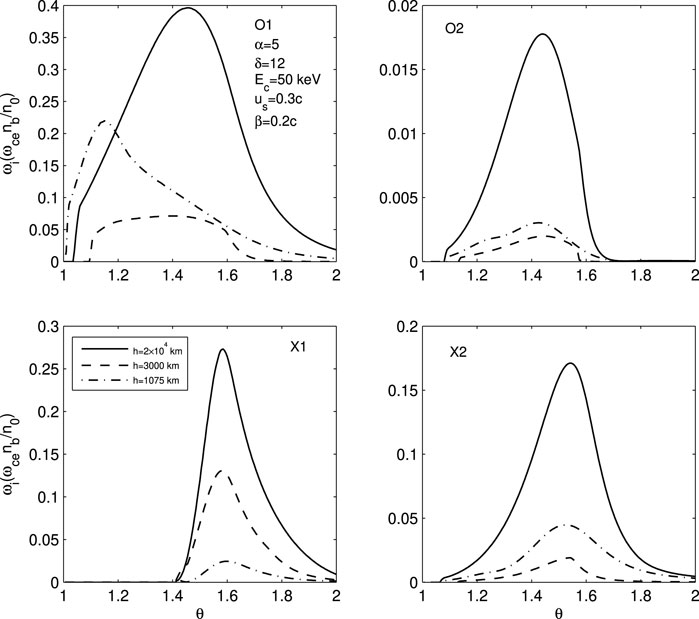
Figure 5. Peak growth rates of the fundamental waves and harmonic waves (s = 2) for O and X modes excited by the FEBs when traveling down along flare loop. Here, the frequency ratio Ω and the magnetic mirror ratio σ vary with the magnetic field and density models of the flare loop, the initial spectrum index α = 5, other parameters are same as in Figure 3.

Figure 3 depict the peak growth rates calculated by varying the frequency ω_q for a given wave phase angle θ, where O1 and X2 are the fundamental waves (s = 1) for the O mode and the harmonic waves (s = 2) for the X mode, respectively. In this figure, the frequency ratio Ω and the magnetic mirror ratio parameter σ are fixed, and we only consider the influence of the energy spectrum parameters on ECMI. The initial parameters of FEBs when they leave the acceleration site, such as the spectrum index α = 7, steepness index δ = 12, E_c = 50 keV, u_s = 0.3c, and β = 0.2c have been used. The energetic electrons of FEBs are accelerated at the top of a flare loop with the height h = 4 × 10⁴ km. Here, the solid lines, dashed lines, and dot-dashed lines denote the peak growth rates of ECMI excited by the evolving FEBs when they reach a height of h = 2 × 10⁴ km, h = 3000 km, and h = 1075 km, respectively. According to the calculation results of Tang et al. (2020), we have the steepness index δ_h = 10.9, spectral index α_h = 6.6, cutoff energy E_ch = 47.5 keV for height h = 3000 km, and δ_h = 7.3, α_h = 4.8, E_ch = 33 keV for height h = 1075 km. Since the energy loss of energetic electrons is extremely small in the upper corona, we take the spectral parameters at h = 2 × 10⁴ km as the initial valves approximately. As seen from Figure 3, the peak growth rates of ECMI decrease rapidly as FEBs precipitate down along the flare loops. This indicates that the variations of the energy spectral parameters of FEBs do have a significant effect on the ECMI.

Figure 4 illustrates the peak growth rates of the fundamental waves and harmonic waves (s = 2) for the O and X modes by the evolving FEBs. In this Figure, except for the frequency ratio Ω and magnetic mirror ratio σ, the initial parameters of FEBs (α, δ, E_c, u_s and β) and the evolving energy spectral parameters (α_h, δ_h and E_ch) are the same as in Figure 3. Based on the magnetic field and density models of the flare loop as shown in Figure 1A, we can determine the frequency radio Ω = ω_ce/ω_p and magnetic mirror ratio σ at a certain height. The solid lines, dashed lines, and dot-dashed lines also represent the ECMI growth rates by the evolving FEBs at height h = 2 × 10⁴ km, h = 3000 km, and h = 1075 km, respectively.

The results from Figure 4 show that O1, O2, and X2 modes exhibit similar variations in growth rates. The peak growth rates of these three modes at height h = 2 × 10⁴ km are nearly an order of magnitude greater than those at h = 3000 km. However, the growth rates increase as FEBs precipitate downward into deeper height (such as h = 1075 km), especially for the O1 mode. This suggests that the energy spectral parameters of FEBs have a significant effect on ECMI. Moreover, compared with Figure 3, the growth rate increases at lower altitudes, indicating that the velocity anisotropy of FEBs, such as loss-cone distribution due to the convergence of magnetic fields, mainly affects the ECMI in the transition region. For mode X1, as the FEBs descend from the loop top to a height of h = 1075 km, the peak growth rate decreases monotonically. The peak growth rate at h = 2 × 10⁴ km is approximately three times higher than that at h = 3000 km. From Figure 4, it can be seen that the O1 mode has the highest growth rate, while the growth rate of the O2 mode is more than one order of magnitude lower than that of the O1 mode.

In Figures 5, 6, we also present the peak growth rates of the fundamental waves and harmonic waves (s = 2) for O and X modes. For Figure 5, we have used the initial spectrum index α = 5 and steepness index δ = 12, while for Figure 6, we have used α = 7 and δ = 15. Other initial parameters of FEBs, such as E_c = 50 keV, u_s = 0.3c, and β = 0.2c, as well as the frequency ratio Ω and mirror ratio σ, remain the same as in Figure 4. The different curves, solid lines, dashed lines, and dot-dashed lines, also represent the peak growth rates of ECMI when FEBs reach heights of h = 2 × 10⁴ km, h = 3000 km, and h = 1075 km, respectively. The evolving energy spectral parameters α_h = 4.8, δ_h = 11, E_ch = 47.5 keV and α_h = 3.6, δ_h = 7.1, E_ch = 33 keV for height h = 3000 km and h = 1075 km in Figure 5, and α_h = 6.6, δ_h = 13.5, E_ch = 47.5 keV and α_h = 4.8, δ_h = 8.9, E_ch = 33 keV for h = 3000 km and h = 1075 km in Figure 6 have been used, respectively. Figures 5, 6 show that, as the FEBs descend, the characteristics of the peak growth rates change are similar to those in Figure 4, except for the specific numerical values of the growth rates. For the O1, O2, and X2 modes, the peak growth rates decrease initially in corona and then increase as FEBs travel down into denser atmosphere. And for the X1 mode, the peak growth rates decreases monotonically as FEBs precipitate along the loop. Similarly, the O1 mode consistently exhibits the highest growth rates, while the growth rates of O2 mode is more than one order of magnitude lower.

Figure 6

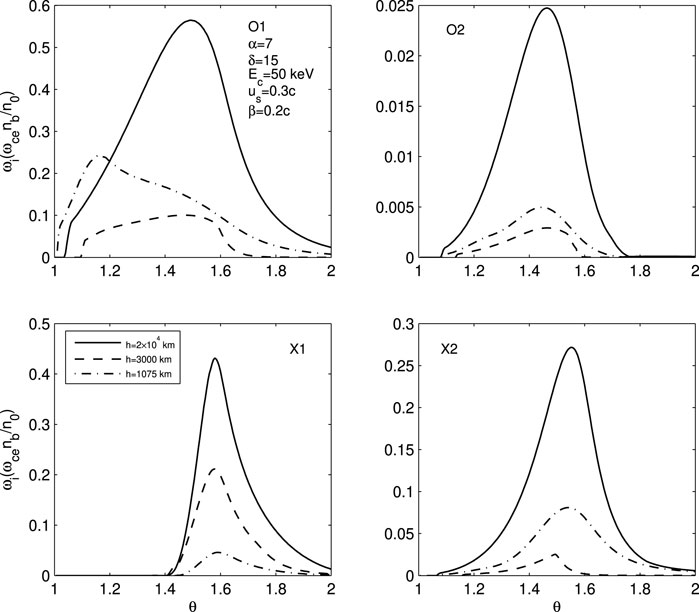
Figure 6. Peak growth rates of the fundamental waves and harmonic waves (s = 2) for O and X modes excited by the FEBs when traveling down along flare loop. Here, the frequency ratio Ω and the magnetic mirror ratio σ vary with the magnetic field and density models of the flare loop, the initial steepness index δ = 15, other parameters are same as in Figure 3.

The calculations presented in Figures 3–6 demonstrate that the loss-cone velocity anisotropy of FEBs, resulting from the convergence of magnetic fields, has a more significant effect on the O1 mode than other three modes.

4 Summary and conclusion

Particle acceleration stands as one of the most crucial and widespread processes observed in various burst activities within space and cosmic plasma environments. Concerning the Sun, it is widely accepted that the energetic electrons are generated through the magnetic reconnection process during solar flare (Masuda et al., 1994; Yokoyama et al., 2001; Imada et al., 2013), or via shock acceleration near the corona shock wave (Drury, 1983; Blandford and Eichler, 1987; Park et al., 2012; Guo and Giacalone, 2015). These accelerated electrons propagate along magnetic fields as FEBs, which in turn produce solar radio bursts and HXR bursts in the solar atmosphere. One of the most direct pieces of evidence for FEBs is provided by solar radio type III bursts, which are excited as FEBs propagate upward along open magnetic field structures. As FEBs propagate downward along magnetic loop, both radio and hard X-ray emissions can be generated. The pivotal question lies in understanding how FEBs contribute to the generation of radio radiation.

ECMI represent a coherent radio radiation mechanism that directly amplify electromagnetic waves near the electron gyrofrequency and its harmonics within magnetized plasma. ECMI has been extensively studied and applied to various radio phenomena, including AKR from Earth and other magnetized planets (Wu and Lee, 1979; Zarka, 1998), various solar radio bursts (Melrose and Dulk, 1982; Wu et al., 2002; Yoon et al., 2002; Treumann et al., 2011), and radio emission from flare stars (Stepanov et al., 2001), M dwarf stars (Callingham et al., 2021), and Blazar jets (Begelman et al., 2005).

Various energy loss processes, including collisions with ambient plasma and deceleration by induced electric fields, can lead to significant changes in the energy spectrum distribution of FEBs. Additionally, the spatial velocity anisotropic distributions of FEBs can arise due to variations of ambient magnetic field as they travel through the solar atmosphere. The lower energy cutoff behavior of power-law electrons and various velocity anisotropic distributions, such as loss-cone and temperature anisotropy, serve as effective driving sources for ECMI. Therefore, it is crucial to investigate ECMI produced by evolving FEBs.

In this paper, the beam electrons are accelerated near the looptop by the magnetic reconnection process during flares. The parametric evolution of power-law spectra of FEBs is based on the calculations of Tang et al. (2020). Taking into account the density and magnetic field models of active regions (Zhao, 1995) and the semiempirical homogeneous plane-parallel flare atmospheric model (Machado et al., 1980), we investigate the characteristics of ECMI by beam electrons traveling downward along a flare loop. Our results demonstrate that the evolution of the energy spectrum and velocity anisotropic distributions significantly influence ECMI as FEBs propagate in the flare loop.

When the ambient magnetic plasma parameters, frequency ratio Ω, and the magnetic mirror ratio σ are fixed, it is evident from Figure 3 that the growth rates of ECMI decrease as FEBs precipitate from the top of the flare loop to the footpoint. This decrease in growth rates is caused by the evolution of the lower energy cutoff behavior, which becomes increasingly flat as FEBs precipitate down along flare loops. Considering the magnetic field and density models of flare loops, the results of Figures 4–6 show that the growth rates of O1, O2, and X2 modes decrease initially as FEBs propagate in the corona and then increase as FEBs precipitate into the denser transition region. This suggests that the velocity anisotropy distribution of FEBs, caused by the convergence of magnetic fields, is an important driving source of ECMI in the denser transition region, and this new driver is more efficient for the O1 mode. For the X mode, it is strongly excited at the fundamental as Melrose and Dulk (1982) and (Treumann, 2006) pointed out. And the growth rate of X1 mode decreases continuously as the FEBs descend. It is absolutely clear that the O mode can easily leave the plasma as there is no restriction on its propagation. However, the X1 mode cannot escape directly. It may undergo resonance mode conversion or nonlinear wave-wave coupling to become an escapable radiation wave. Baumjohann and Treumann (2023) investigated the excitation of X mode, involving nonlinear wave-wave interaction and favored for its large expected growth rates. However, the issue of how the X1 mode can escape from the plasma is quite a different subject which deserves a completely separate investigation, and this is beyond the scope of the current article’s main focus. It could be a subject for further separate discussion in the future. This evolutionary trend of the growth rates is similar to the results presented in Figures 2, 3 of Tang et al. (2016). Emission excited by such evolving FEBs in flare loops will form three separate radio sources. Additionally, our results indicate that the anisotropic driving source also affects the phase angles θ of the maximum growth rates of O1 mode, causing them to deviate more from the vertical direction. These findings contribute to a more comprehensive understanding of the dynamic spectra of solar radio bursts.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

JT: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft. DW: Writing–review and editing. LC: Writing–review and editing. CT: Writing–review and editing. JW: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work acknowledges the support from the National Natural Science Foundation of China (NSFC) under grants 12173076 and 42174195, from the Lishui University Initial Funding under grant QD2182, from the National Key R&D Program of China under grant 2021YFA1600503, as well as from the Strategic Priority Research Program of the Chinese Academy of Sciences under grant XDB0560000.

Acknowledgments

We also acknowledge the Project Supported by the Specialized Research Fund for State Key Laboratories.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aschwanden, M. J. (1990). The saturation of the electron-cyclotron maser instability and the interpretation of solar millisecond spikes. Astronomy Astrophysics 237, 512.

Google Scholar

Aschwanden, M. J. (2002). Particle acceleration and kinematics in solar flares – a synthesis of recent observations and theoretical concepts (invited review). Space Sci. Rev. 101, 1–227. doi:10.1023/A:1019712124366

CrossRef Full Text | Google Scholar

Aschwanden, M. J., and Benz, A. O. (1988). On the electron-cyclotron maser instability. II. Pulsations in the quasi-stationary state. ApJ 332, 466. doi:10.1086/166670

CrossRef Full Text | Google Scholar

Aschwanden, M. J., Schwartz, R. A., and Dennis, B. R. (1998). Deconvolution of directly precipitating and trap-precipitating electrons in solar flare hard X-rays. II.Compton gamma ray ObservatoryData Analysis. ApJ 502, 468–480. doi:10.1086/305891

CrossRef Full Text | Google Scholar

Baumjohann, W., and Treumann, R. A. (2023). ECMI resonance in AKR revisited: hyperbolic resonance, harmonics, and wave–wave interaction. Front. Phys. 11, 1174557. doi:10.3389/fphy.2023.1174557

CrossRef Full Text | Google Scholar

Begelman, M. C., Ergun, R. E., and Rees, M. J. (2005). ApJ 625, 51–59. doi:10.1086/429550

CrossRef Full Text

Benka, S. G., and Holman, G. D. (1994). A thermal/nonthermal model for solar hard X-ray bursts. ApJ 435, 469. doi:10.1086/174829

CrossRef Full Text | Google Scholar

Blandford, R., and Eichler, D. (1987). Particle acceleration at astrophysical shocks: a theory of cosmic ray origin. Phys. Rep. 154, 1–75. doi:10.1016/0370-1573(87)90134-7

CrossRef Full Text | Google Scholar

Cairns, I. H. (1987a). Fundamental plasma emission involving ion sound waves. J. Plasma Phys. 38, 169–178. doi:10.1017/S0022377800012496

CrossRef Full Text | Google Scholar

Cairns, I. H. (1987b). Second harmonic plasma emission involving ion sound waves. J. Plasma Phys. 38, 179–198. doi:10.1017/S0022377800012502

CrossRef Full Text | Google Scholar

Cairns, I. H. (1987c). Third and higher harmonic plasma emission due to Raman scattering. J. Plasma Phys. 38, 199–208. doi:10.1017/S0022377800012514

CrossRef Full Text | Google Scholar

Callingham, J. R., Pope, B. J. S., Feinstein, A. D., Vedantham, H. K., Shimwell, T. W., Zarka, P., et al. (2021). Low-frequency monitoring of flare star binary CR Draconis: long-term electron-cyclotron maser emission. A&A 648, A13. doi:10.1051/0004-6361/202039144

CrossRef Full Text | Google Scholar

Chen, Y. P., Zhou, G. C., Yoon, P. H., and Wu, C. S. (2002). A beam-maser instability: direct amplification of radiation. Phys. Plasmas 9, 2816–2821. doi:10.1063/1.1481748

CrossRef Full Text | Google Scholar

Drury, L. O. (1983). An introduction to the theory of diffusive shock acceleration of energetic particles in tenuous plasmas. Rep. Prog. Phys. 46, 973–1027. doi:10.1088/0034-4885/46/8/002

CrossRef Full Text | Google Scholar

Dulk, G. A., Kiplinger, A. L., and Winglee, R. M. (1992). Characteristics of hard X-ray spectra of impulsive solar flares. ApJ 389, 756. doi:10.1086/171248

CrossRef Full Text | Google Scholar

Fleishman, G. D. (2004). Natural spectral bandwidth of electron cyclotron maser emission. Astron. Lett. 30, 603–614. doi:10.1134/1.1795949

CrossRef Full Text | Google Scholar

Fletcher, L., Dennis, B. R., Hudson, H. S., Krucker, S., Phillips, K., Veronig, A., et al. (2011). An observational overview of solar flares. SSRv 159, 19–106. doi:10.1007/s11214-010-9701-8

CrossRef Full Text | Google Scholar

Ginzburg, V. L., and Zhelezniakov, V. V. (1958). On the possible mechanisms of sporadic solar radio emission (radiation in an isotropic plasma). Sov. Ast. 2, 653.

Google Scholar

Goldstein, M. L., and Eviatar, A. (1972). The plasma Physics of the jovian decameter radiation. ApJ 175, 275. doi:10.1086/151555

CrossRef Full Text | Google Scholar

Guo, F., and Giacalone, J. (2015). The acceleration of electrons at collisionless shocks moving through A turbulent magnetic field. ApJ 802, 97. doi:10.1088/0004-637X/802/2/97

CrossRef Full Text | Google Scholar

Hallinan, G., Antonova, A., Doyle, J. G., Bourke, S., Lane, C., and Golden, A. (2008). Confirmation of the electron cyclotron maser instability as the dominant source of radio emission from very low mass stars and Brown dwarfs. ApJ 684, 644–653. doi:10.1086/590360

CrossRef Full Text | Google Scholar

Hess, S., Mottez, F., and Zarka, P. (2007). Jovian S burst generation by Alfvén waves. J. Geophys. Res. (Space Phys.) 112, A11212. doi:10.1029/2006JA012191

CrossRef Full Text | Google Scholar

Hewitt, R. G., Melrose, D. B., and Ruennmark, K. G. (1981). A cyclotron theory for the beaming pattern of jupiter’s decametric radio emission. PASA 4, 221–226. doi:10.1017/S132335800001643X

CrossRef Full Text | Google Scholar

Hirshfield, J. L., and Bekefi, G. (1963). Decameter radiation from jupiter. Nature 198, 20–22. doi:10.1038/198020a0

CrossRef Full Text | Google Scholar

Holman, G. D., Aschwanden, M. J., Aurass, H., Battaglia, M., Grigis, P. C., Kontar, E. P., et al. (2011). Implications of X-ray observations for electron acceleration and propagation in solar flares. SSRv 159, 107–166. doi:10.1007/s11214-010-9680-9

CrossRef Full Text | Google Scholar

Hoyng, P., Duijveman, A., Machado, M. E., Rust, D. M., Svestka, Z., Boelee, A., et al. (1981). Origin and location of the hard X-ray emission in a two-ribbon flare. ApJL 246, L155. doi:10.1086/183574

CrossRef Full Text | Google Scholar

Hudson, H., and Ryan, J. (1995). High-energy particles in solar flares. ARA&A 33, 239–282. doi:10.1146/annurev.aa.33.090195.001323

CrossRef Full Text | Google Scholar

Hudson, H. S. (1978). A purely coronal hard X-ray event. ApJ 224, 235. doi:10.1086/156370

CrossRef Full Text | Google Scholar

Imada, S., Aoki, K., Hara, H., Watanabe, T., Harra, L. K., and Shimizu, T. (2013). ApJL 776, L11. doi:10.1088/2041-8205/776/1/L11

CrossRef Full Text

Kosugi, T., Dennis, B. R., and Kai, K. (1988). Energetic electrons in impulsive and extended solar flares as deduced from flux correlations between hard X-rays and microwaves. ApJ 324, 1118. doi:10.1086/165967

CrossRef Full Text | Google Scholar

Li, C., Chen, Y., Kong, X., Hosseinpour, M., and Wang, B. (2019). Effect of the temperature of background plasma and the energy of energetic electrons on Z-mode excitation. ApJ 880, 31. doi:10.3847/1538-4357/ab270f

CrossRef Full Text | Google Scholar

Lin, R. P. (1974). Non-relativistic solar electrons. SSRv 16, 189. doi:10.1007/BF00240886

CrossRef Full Text | Google Scholar

Lin, R. P. (2011). Energy release and particle acceleration in flares: summary and future prospects. SSRv 159, 421–445. doi:10.1007/s11214-011-9801-0

CrossRef Full Text | Google Scholar

Machado, M. E., Avrett, E. H., Vernazza, J. E., and Noyes, R. W. (1980). Semiempirical models of chromospheric flare regions. ApJ 242, 336. doi:10.1086/158467

CrossRef Full Text | Google Scholar

Mangeney, A., and Veltri, P. (1976). On the theory of type I solar radio bursts. I - beam plasma instabilities in a turbulent magnetized plasma. II - a model for the source. A&A 47, 165.

Google Scholar

Masuda, S., Kosugi, T., Hara, H., Tsuneta, S., and Ogawara, Y. (1994). A loop-top hard X-ray source in a compact solar flare as evidence for magnetic reconnection. Nature 371, 495–497. doi:10.1038/371495a0

CrossRef Full Text | Google Scholar

Melrose, D. B. (1976). An interpretation of Jupiter's decametric radiation and the terrestrial kilometric radiation as direct amplified gyroemission. ApJ 207, 651. doi:10.1086/154532

CrossRef Full Text | Google Scholar

Melrose, D. B., and Dulk, G. A. (1982). Electron-cyclotron masers as the source of certain solar and stellar radio bursts. ApJ 259, 844. doi:10.1086/160219

CrossRef Full Text | Google Scholar

Melrose, D. B., and Wheatland, M. S. (2016). SoPh 291, 3637–3658. doi:10.1007/s11207-016-1006-y

CrossRef Full Text

Morosan, D. E., Zucca, P., Bloomfield, D. S., and Gallagher, P. T. (2016). Conditions for electron-cyclotron maser emission in the solar corona. A&A 589, L8. doi:10.1051/0004-6361/201628392

CrossRef Full Text | Google Scholar

Ning, H., Chen, Y., Li, C., Ye, S., Kuznetsov, A., and Wu, S. (2023). Excitation of extraordinary modes inside the source of Saturn’s kilometric radiation. A&A 678, A94. doi:10.1051/0004-6361/202347149

CrossRef Full Text | Google Scholar

Ning, H., Chen, Y., Ni, S., Li, C., Zhang, Z., Kong, X., et al. (2021). Harmonic electron-cyclotron maser emissions driven by energetic electrons of the horseshoe distribution with application to solar radio spikes. A&A 651, A118. doi:10.1051/0004-6361/202140427

CrossRef Full Text | Google Scholar

Park, J., Workman, J. C., Blackman, E. G., Ren, C., and Siller, R. (2012). Particle-in-cell simulations of particle energization from low Mach number fast mode shocks. Phys. Plasmas 19, 062904. doi:10.1063/1.4729913

CrossRef Full Text | Google Scholar

Raoult, A., Mangeney, A., and Vlahos, L. (1990). A&A 233, 229.

Régnier, S. (2015). A new approach to the maser emission in the solar corona. A&A 581, A9. doi:10.1051/0004-6361/201425346

CrossRef Full Text | Google Scholar

Reid, H. A. S., Vilmer, N., and Kontar, E. P. (2011). Characteristics of the flare acceleration region derived from simultaneous hard X-ray and radio observations. A&A 529, A66. doi:10.1051/0004-6361/201016181

CrossRef Full Text | Google Scholar

Schneider, J. (1959). Stimulated emission of radiation by relativistic electrons in a magnetic field. PhRvL 2, 504–505. doi:10.1103/PhysRevLett.2.504

CrossRef Full Text | Google Scholar

Sharykin, I., Liu, S., and Fletcher, L. (2014). Onset of electron acceleration in A flare loop. ApJ 793, 25. doi:10.1088/0004-637X/793/1/25

CrossRef Full Text | Google Scholar

Stepanov, A. V., Kliem, B., Zaitsev, V. V., Fürst, E., Jessner, A., Krüger, A., et al. (2001). Microwave plasma emission of a flare on AD Leo. A&A 374, 1072–1084. doi:10.1051/0004-6361:20010518

CrossRef Full Text | Google Scholar

Tang, J., Wu, D., and Yan, Y. (2012). Effects of power-law spectrum behaviors of nonthermal electrons on a ring-beam maser instability. Mech. Astronomy 55, 744–750. doi:10.1007/s11433-012-4683-z

CrossRef Full Text | Google Scholar

Tang, J. F., and Wu, D. J. (2009). Electron-cyclotron maser emission by power-law electrons in coronal loops. A&A 493, 623–628. doi:10.1051/0004-6361:200810792

CrossRef Full Text | Google Scholar

Tang, J. F., Wu, D. J., Chen, L., Xu, L., and Tan, B. L. (2020). Parametric evolution of power-law energy spectra of flare accelerated electrons in the solar atmosphere. ApJ 904, 1. doi:10.3847/1538-4357/abc2ca

CrossRef Full Text | Google Scholar

Tang, J. F., Wu, D. J., Chen, L., Zhao, G. Q., and Tan, C. M. (2016). Electron cyclotron maser emissions from evolving fast electron beams. ApJ 823, 8. doi:10.3847/0004-637X/823/1/8

CrossRef Full Text | Google Scholar

Tang, J. F., Wu, D. J., and Yan, Y. H. (2011). Effects of the temperature anisotropy on the maser instability excited by lower energy cutoff behavior. ApJ 727, 70. doi:10.1088/0004-637X/727/2/70

CrossRef Full Text | Google Scholar

Treumann, R. A. (2006). The electron–cyclotron maser for astrophysical application. A&A Rv 13, 229–315. doi:10.1007/s00159-006-0001-y

CrossRef Full Text | Google Scholar

Treumann, R. A., Nakamura, R., and Baumjohann, W. (2011). A model of so-called &quot;Zebra&amp;quot; emissions in solar flare radio burst continua. Ann. Geophys. 29, 1673–1682. doi:10.5194/angeo-29-1673-2011

CrossRef Full Text | Google Scholar

Twiss, R. Q. (1958). Radiation transfer and the possibility of negative absorption in radio Astronomy. Aust. J. Phys. 11, 564. doi:10.1071/PH580564

CrossRef Full Text | Google Scholar

Twiss, R. Q., and Roberts, J. A. (1958). Electromagnetic radiation from electrons rotating in an ionized medium under the action of a uniform magnetic field. Aust. J. Phys. 11, 424. doi:10.1071/PH580424

CrossRef Full Text | Google Scholar

Vlasov, V. G., Kuznetsov, A. A., and Altyntsev, A. T. (2002). The maser mechanism for solar millisecond spikegeneration in inhomogeneous plasma. A&A 382, 1061–1069. doi:10.1051/0004-6361:20011601

CrossRef Full Text | Google Scholar

Wang, D.-y. (2004). A model for the coherent emission of solar radio moving type IV bursts. Chin. Astronomy Astrophysics 28, 404–411. doi:10.1016/j.chinastron.2004.09.004

CrossRef Full Text | Google Scholar

White, S. M., Benz, A. O., Christe, S., Fárník, F., Kundu, M. R., Mann, G., et al. (2011). The relationship between solar radio and hard X-ray emission. Space Sci. Rev. 159, 225–261. doi:10.1007/s11214-010-9708-1

CrossRef Full Text | Google Scholar

Winglee, R. M., and Dulk, G. A. (1986). The electron-cyclotron maser instability as a source of plasma radiation. Astrophysical J. 307, 808. doi:10.1086/164467

CrossRef Full Text | Google Scholar

Wu, C. S., and Lee, L. C. (1979). A theory of the terrestrial kilometric radiation. ApJ 230, 621. doi:10.1086/157120

CrossRef Full Text | Google Scholar

Wu, C. S., Wang, C. B., Yoon, P. H., Zheng, H. N., and Wang, S. (2002). Generation of type III solar radio bursts in the low corona by direct amplification. ApJ 575, 1094–1103. doi:10.1086/341468

CrossRef Full Text | Google Scholar

Wu, C. S., Yoon, P. H., and Zhou, G. C. (1994). Generation of radiation in solar corona and interplanetary space by energetic electrons. ApJ 429, 406. doi:10.1086/174331

CrossRef Full Text | Google Scholar

Wu, D. J., Huang, J., Tang, J. F., and Yan, Y. H. (2007). Solar microwave drifting spikes and solitary kinetic alfvén waves. ApJL 665, L171–L174. doi:10.1086/521360

CrossRef Full Text | Google Scholar

Wu, D. J., and Tang, J. F. (2008). Effects of the lower energy cutoff behavior of power-law electrons on the electron-cyclotron maser instability. ApJL 677, L125–L128. doi:10.1086/588025

CrossRef Full Text | Google Scholar

Yasnov, L. V., and Karlický, M. (2004). The Growth rate of upper-hybrid waves and dynamics of microwave zebra structures. SoPh 219, 289–299. doi:10.1023/B:SOLA.0000022942.17621.88

CrossRef Full Text | Google Scholar

Yokoyama, T., Akita, K., Morimoto, T., Inoue, K., and Newmark, J. (2001). Clear evidence of reconnection inflow of a solar flare. ApJL 546, L69–L72. doi:10.1086/318053

CrossRef Full Text | Google Scholar

Yoon, P. H. (1995). Plasma emission by a nonlinear beam instability. Phys. Plasmas 2, 537–548. doi:10.1063/1.870979

CrossRef Full Text | Google Scholar

Yoon, P. H. (1997). Plasma emission by a nonlinear beam instability in a weakly magnetized plasma. Phys. Plasmas 4, 3863–3881. doi:10.1063/1.872508

CrossRef Full Text | Google Scholar

Yoon, P. H. (1998). On the higher-order nonlinear corrections to the theory of plasma emission by a nonlinear beam instability. Phys. Plasmas 5, 2590–2595. doi:10.1063/1.872945

CrossRef Full Text | Google Scholar

Yoon, P. H., Wu, C. S., and Wang, C. B. (2002). Generation of type III solar radio bursts in the low corona by direct amplification. II. Further numerical study. ApJ 576, 552–560. doi:10.1086/341634

CrossRef Full Text | Google Scholar

Zarka, P. (1998). Auroral radio emissions at the outer planets: observations and theories. J. Geophys. Res. 103, 20159–20194. doi:10.1029/98JE01323

CrossRef Full Text | Google Scholar

Zhao, G. Q., Chen, L., and Wu, D. J. (2013). Solar type iii radio bursts modulated by homochromous alfvén waves. ApJ 779, 31. doi:10.1088/0004-637X/779/1/31

CrossRef Full Text | Google Scholar

Zhao, R.-Y. (1995). A model of solar (Radio) active regions. Ap&SS 234, 125–137. doi:10.1007/BF00627287

CrossRef Full Text | Google Scholar

Zharkova, V. V., and Gordovskyy, M. (2004). Particle acceleration asymmetry in a reconnecting nonneutral current sheet. ApJ 604, 884–891. doi:10.1086/381966

CrossRef Full Text | Google Scholar