Magnetohydrodynamical modeling of star-disk formation: from isolated spherical collapse towards incorporation of external dynamics

The formation of protostars and their disks has been understood as the result of the gravitational collapse phase of an accumulation of dense gas that determines the mass reservoir of the star-disk system. Against this background, the broadly applied scenario of considering the formation of disks has been to model the collapse of a dense core assuming spherical symmetry. Our understanding of the formation of star-disk systems is currently undergoing a reformation though. The picture evolves from interpreting disks as the sole outcome of the collapse of an isolated prestellar core to a more dynamic picture where disks are affected by the molecular cloud environment in which they form. In this review, we provide a status report of the state-of-the-art of spherical collapse models that are highly advanced in terms of the incorporated physics together with constraints from models that account for the possibility of infall onto star-disk systems in simplified test setups, as well as in multi-scale simulations that cover a dynamical range from the Giant Molecular Cloud environment down to the disk. Considering the observational constraints that favor a more dynamical picture of star formation, we finally discuss the challenges and prospects in linking the efforts of tackle the problem of star-disk formation in combined multi-scale, multi-physics simulations.

1 Introduction

The by-now classical approach of modeling the formation of a star dates back to more than half a century to the pioneering work of (Larson, 1969), who started from the assumption of an isolated spherical core that collapses due to its own gravity. This assumption has become the standard approach in modeling the formation of individual stars and their disks that form as a result of conservation of angular momentum during the collapse phase. However, in recent years it has become more and more clear that the morphology of the precursors of stars, namely, prestellar cores, often deviates significantly from spherical symmetry in turbulent filamentary Giant Molecular Clouds (André et al., 2014). In addition, asymmetric features (‘streamers’) (see review by Pineda et al., 2023), as well as strong indications for late infall (e.g., SU Ginski et al., 2021) challenge our traditional view on disk formation. This review is an attempt to concisely summarize the developments made in developing state-of-the-art multi-physics models of spherical collapse, and put those in context to multi-scale models that account for the larger scale dynamics of the molecular cloud environment. We emphasize that the scope of the review is the formation process of disks. These disks evolve over time and disperse. An overview of important effects regarding disk dispersal through binary interactions (e.g., Kuruwita and Federrath, 2019; Offner et al., 2023), stellar flybys (e.g., Cuello et al., 2023; Smallwood et al., 2023) or external photoevaporation (e.g., Winter and Haworth, 2022) can be found in the respective references. Note that developments that later marked important advancements for modeling disk formation were initially included in studies that focused on binary/multiple formation. Examples are the use of adaptive mesh refinement (AMR) (Truelove et al., 1998; Kratter et al., 2010) or nested grids (Burkert and Bodenheimer, 1993; Matsumoto and Hanawa, 2003) in spherical collapse simulations. The focus on multiplicity rather than disk properties is not surprising considering that disks easily form in hydrodynamical simulations.

This review focuses on results obtained through modeling of (proto-)star formation. The presented results are derived using various codes that adopt different methodology. Traditionally, star formation has either been modeled following a Lagrangian approach, i.e., smoothed particle hydrodynamics (SPH), or an Eulerian approach, i.e., a mesh/grid codes. In SPH codes, the gas distribution is represented through particles and the properties of the gas is computed through averaging over the nearest neighbors of interacting particles. SPH codes that are used for modeling disk formation are dragon (Goodwin et al., 2004), phantom (Price et al., 2018), optimized versions of sphNG (Benz et al., 1990), as well as Godunov SPH methods (Iwasaki and Inutsuka, 2011). In Eulerian codes, the gas is discretized in form of a mesh or grid consisting of cells, and the evolution of the gas is simulated by calculating the flux through the cell boundaries to update the cell quantities. The grid is typically assumed to be cartesian or spherical in star formation models. Examples of grid codes used for disk modeling are athena (Stone et al., 2008), athena++ (Stone et al., 2020), dispatch (Nordlund et al., 2018), enzo (Bryan et al., 2014), flash (Fryxell et al., 2000), Pluto (Mignone et al., 2012), Orion (Klein, 1999), ramses (Teyssier, 2002; Fromang et al., 2006), sfumato (Matsumoto, 2007) and zeus (Stone and Norman, 1992). While SPH codes intrinsically adapt to resolve the higher densities during the star formation process, many grid codes offer the possibility to resolve the process by the use of a grid with flexible cell sizes. The resolution of the grid can either be fixed at the beginning of the simulation in form of static or flexible through AMR. Static grids are often used for spherical or nested grids, where the forming star is located at the center such that by construction the gas close to the star is resolved with higher resolution than the gas at larger radial distances. Nowadays, the traditional distinction between SPH and grid codes has become increasingly softened by the development of methods that contain properties of both approaches such as moving mesh codes (arepo Springel, 2010a; Weinberger et al., 2020) and codes allowing for the use of meshless methods (gizmo Hopkins, 2015). Each method has its benefits and disadvantages. On the one hand for instance, it is by construction straight-forward to handle advection of flows with SPH algorithms, while more care is required in grid codes. On the other hand, the use of constrained transport in grid codes (Evans and Hawley, 1988; Balsara and Spicer, 1999; Londrillo and del Zanna, 2004) guarantees the absence of unphysical magnetic monopoles $(\nabla \cdot \mathbf{B}=0)$, whereas a careful implementation of divergence-cleaning is required to achieve this condition in SPH (see for instance Tricco and Price, 2012; Tricco et al., 2016).

For more details on the methods that are commonly used in star formation modeling, we refer the reader to dedicated reviews. For the technicalities of SPH, see for instance (Tricco, 2023, in this volume) or previous reviews (Rosswog, 2009; Springel, 2010b; Price, 2012). For an overview of the numerical methods in grid-based codes, we refer to Teyssier (2015); Teyssier and Commerçon (2019) as well as to the respective papers corresponding to the individual codes. Alternatives to the more traditional methods are presented and discussed in Hopkins (2015).

Section 2 of this review provides an overview of disk formation in spherical collapse with a focus on how to solve the magnetic braking problem. Section 3 focuses on the dynamics beyond the prestellar core and how modeling can be used to account for the effect of infall onto the disk formation process. Section 4 summarizes the results and provides an outlook on how multi-scale, multi-physics models can help to understand the small-scale subtleties of disk formation that is important for planet formation in the context of the larger-scale dynamics.

2 Formation of disks in models of isolated spherical collapse

In general, the assumption of spherical collapse is the obvious first choice for modeling gravitational collapse. The assumption of spherical symmetry simplifies the three-dimensional spatial problem to a one-dimensional problem. Moreover, it allows to study the effect of various parameters in a well-defined setup. Over the years, more and more parameters were added to the setup to test their effect on the collapse phase. An important additional parameter of the setup was to initialize the sphere with a net rotation rate. Theory predicts that during the collapse, the vertical velocity components cancel out each other, but the net rotational component remains such that the collapse leads to the formation of a rotationally supported disk as a consequence of angular momentum conservation. Purely hydrodynamical models (i.e., models without magnetic fields) demonstrated the formation of disks with smaller/larger disk sizes for initially weak/strong rotation of the sphere using smoothed particle hydrodynamics (SPH) (Bate, 1998; 2010; Walch et al., 2009; 2010), adaptive mesh refinement (AMR) (Truelove et al., 1998; Banerjee et al., 2004) or nested grid codes (Yorke et al., 1993; Saigo et al., 2008; Machida et al., 2010).

To prevent very low time steps during the collapse, it is common practice in many models to introduce a sink particle that is created at the center once a critical density is exceeded and possible additional criteria are fulfilled. During the further evolution, the sink accretes mass from the surrounding gas according to a prescribed recipe (for a detailed overview on numerical methods including sink particles, please refer to the review by Teyssier and Commerçon, 2019).

As the next step, models started to account for the presence of magnetic fields in molecular clouds (Crutcher, 2012) by carrying out magnetohydrodnamical simulations. To account for magnetic fields in the setup, the sphere is typically initialized with a magnetization defined by the ratio of enclosed mass $M$ and magnetic flux threading the sphere $\mathrm{\Phi }=\pi R^{2}B$, where $B=|\mathbf{B}|$ is the magnitude of the magnetic field strength. It is common practice to state the magnetization relative to the magnetized mass

$M_{\mathrm{\Phi }}=c_{\mathrm{\Phi }}\frac{\mathrm{\Phi }}{\sqrt{G}},(1)$

with a numerical constant $c_{\mathrm{\Phi }}$ and gravitational constant $G$ in terms of the normalized mass-to-flux ratio

${\mu }_{\mathrm{\Phi }}=\frac{M}{M_{\mathrm{\Phi }}}.(2)$

According to theory, cores are magnetically supported against collapse for ${\mu }_{\mathrm{\Phi }}<1$, whereas the core undergoes collapse for ${\mu }_{\mathrm{\Phi }}>1$. $c_{\mathrm{\Phi }}$ depends on the exact configuration of the field. In the case of a sphere threaded by a uniform parallel magnetic field, $c_{\mathrm{\Phi }}$ is 0.126 (Mouschovias and Spitzer, 1976), and for the case of a field with a constant-mass-to-flux ratio, $c_{\mathrm{\Phi }}=0.17$ (Tomisaka et al., 1988), which is similar to $c_{\mathrm{\Phi }}=1/(2\pi )$ for a uniformly magnetized sheet (Nakano and Nakamura, 1978). In the latter case, the mass-to-flux ratio becomes, using these values for Equation 2 the mass-to-flux ratio (Equation 1) becomes

${\mu }_{\mathrm{\Phi }}=2\pi \sqrt{G}\frac{M}{\mathrm{\Phi }},(3)$

but in this section we focus on spherical collapse and therefore refer to a scenario for which Equation 3 is not applicable. The first generations of these collapse simulations considered the ideal MHD case of sufficiently ionized gas such that the magnetic field is well coupled to the bulk neutral gas. The induction equation corresponding to ideal MHD is

$\frac{\partial \mathbf{B}}{\partial t}=\mathrm{\nabla }\times \left(\mathbf{v}\times \mathbf{B}\right)(4)$

with bulk velocity of the gas velocity $\mathbf{v}$. As the magnetic field lines are perfectly coupled to the gas motion, they are dragged towards the center of mass during the collapse, which yields a characteristic hour-glass shape. While the gas collapse, magnetic pinching induces the formation of a flattened structure around the forming protostar. In contrast to the Keplerian disk that is forming around the star in the hydrodynamical cases, the flattened structure is not rotationally supported and therefore referred to as ‘pseudodisk’ in the analytical (Galli and Shu, 1993a) and numerical works by Galli and Shu (1993b). The pseudodisk is larger in size than the rotationally supported disk, and in the classical picture, it marks a transition zone between the protostellar environment and the rotationally supported disk (e.g., Väisälä et al., 2023, for a recent study exploring the properties of pseudodisks). In this review, we focus on the formation of rotationally supported disks, and for simplicity only refer to them as disks. When the magnetic field lines get wrapped up in azimuthal direction, they exert a torque opposing the rotation of the disk (Lüst and Schlüter, 1955). In other words, magnetic fields provide a form of angular momentum transport to slow down rotation, and it is hence referred to as ‘magnetic braking’ (Mestel, 1968). If the magnetic torque is sufficiently high, it quenches the formation of the disk. This scenario is referred to as ‘magnetic braking catastrophe’. Analytical work by Joos et al. (2012) showed that this is the case for ${\mu }_{\mathrm{\Phi }}\lesssim 10$ in good agreement with models adopting a 2D grid (Allen et al., 2003; Mellon and Li, 2008), 3D grid (Machida et al., 2005; Galli et al., 2006; Hennebelle and Fromang, 2008; Duffin and Pudritz, 2009; Seifried et al., 2011; Santos-Lima et al., 2012) and 3D SPH (Price and Bate, 2007). While these earlier MHD simulations did not account for radiation of the forming protostar, quenching of disk formation has proven to be a robust result independently of incorporating radiative transfer schemes for ${\mu }_{\mathrm{\Phi }}\lesssim 10$ in grid (Boss, 1997; 1999; 2002; Commerçon et al., 2010; Tomida et al., 2010; 2013; 2015; Tomida, 2014; Vaytet et al., 2018) or SPH codes (Bate et al., 2014; Tsukamoto et al., 2015b). Exemplarily, the second column in Figure 1 illustrates the magnetic braking catastrophe.

Figure 1

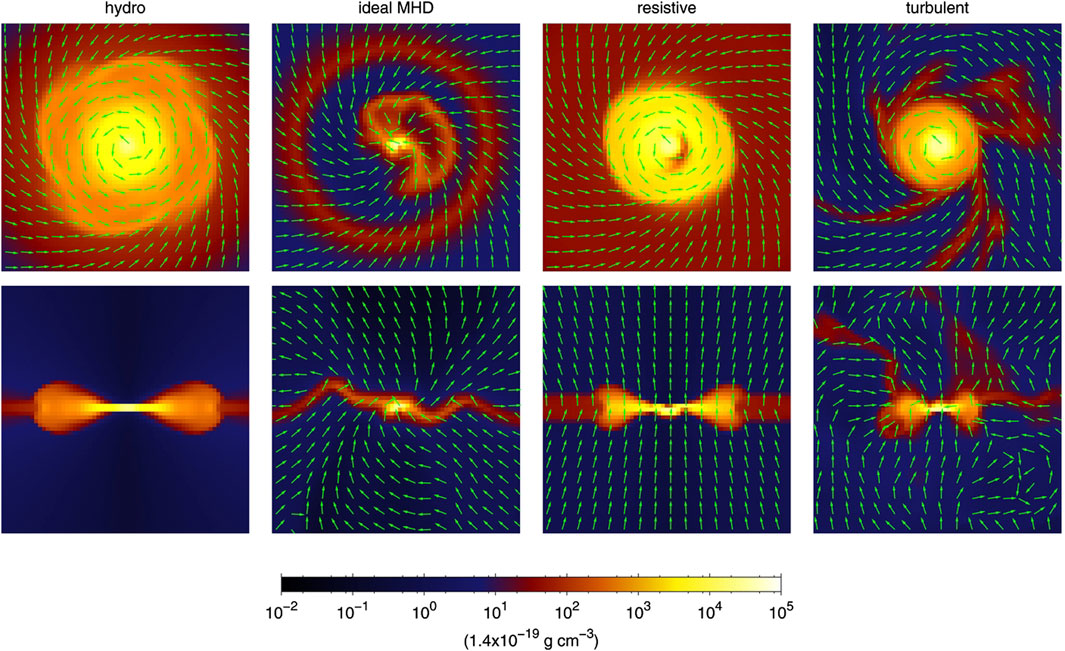
Figure 1. Illustration of the effect of initial conditions on the collapse phase shown face-on (top panels) and edge-on (bottom panels). From left to right: hydrodynamical case (no $B$-field), ideal MHD with $B$-field, non-ideal MHD (ambipolar diffusion and ohmic dissipation), and ideal MHD with turbulence. The figure is adopted from (Santos-Lima et al., 2012).

Until the late 2000s, including magnetic fields into the setup was therefore considered catastrophic for disk formation, which was at tension with the growing evidence of Keplerian disks in observations (Brinch et al., 2007; Lommen et al., 2008; Jørgensen et al., 2009; Lee, 2011; Murillo et al., 2013; Codella et al., 2014; Harsono et al., 2014). At the same time, magnetic fields are the most promising candidate for producing these fast jets and low-velocity disk winds (Donati et al., 2010; Bjerkeli et al., 2016; Lee et al., 2018; Moscadelli et al., 2022) though winds especially at later stages of disk evolution might also be launched by photoevaporation (Alexander et al., 2014). While part of the material in the disk subsequently accretes onto the protostar, a substantial amount of the mass is ejected vertically from the system in narrow protostellar jets (Guszejnov et al., 2021; 2022), or in disk winds that have wider opening angles (Watson et al., 2016). Constraining the role of magnetic fields is challenging because they are difficult to observe. To get an idea of the magnetic field structure in star forming regions, one can measure the linear polarization of non-spherical dust grains as they tend to align with the underlying magnetic field due to radiative torques (Sadavoy et al., 2019; Le Gouellec et al., 2020). However, dust polarization in disks seems to be dominated by effects of self-scattering within about 100 AU from the star (Kataoka et al., 2016), (though dichroic extinction may be responsible for parts of the polarization signal in disks, too) (Lee et al., 2021). That means dust polarization is a good tracer of the structure (though not on the strength) of magnetic fields on scales of the protostellar environment beyond the disk, which allows us to at least obtain loose constraints on the role of magnetic fields in the star formation process (Pattle et al., 2023). As these observations inform us about the presence of magnetic fields in the star-forming regions (Le Gouellec et al., 2020), there is consensus that they are the important ingredient of magnetically driven disks (Lesur et al., 2023).

The challenging question for modelers was therefore: ‘how to avoid this catastrophe during spherical collapse?’ As of today, there is consensus that magnetic braking can be sufficiently reduced to allow disk formation even for spherical collapse setups with high magnetization of ${\mu }_{\mathrm{\Phi }}\lesssim 10$ if at least one of the following ingredient is considered in the models.

• non-ideal MHD, or

• misalignment between magnetic field orientation and rotational axis, or

• turbulence.

We emphasize that there are already reviews (e.g., Wurster and Li, 2018; Zhao et al., 2020b; Tsukamoto et al., 2023b) in the literature available that summarize the progress made in overcoming the magnetic braking catastrophe during the last $\approx$20 years. We refer the reader to those reviews as well as to reviews in this issue (e.g., Young, 2023) for a more in-depth coverage of the progress made in accounting for additional physics in spherical collapse models, especially related to non-ideal MHD. The following sections provide a more comprehensive review on those efforts and the progress made.

2.1 Non-ideal MHD

One way of overcoming the magnetic braking catastrophe is by accounting for resistive effects (commonly referred to as ‘non-ideal MHD’) such that the magnetic field lines are no longer tightly coupled to the bulk motion of the gas. In fact, dense cores in molecular clouds are weakly ionized (Bergin and Tafalla, 2007) and according to models the ionization rates can reach values of $n_{\text{e}}/n_{{\text{H}}_2}\sim 10^{-14}$ (Nakano and Umebayashi, 1986; Umebayashi and Nakano, 1990; Nishi et al., 1991; Nakano et al., 2002). One distinguishes between three non-ideal MHD resistivities $\eta$, ohmic dissipation ${\eta }_{\text{O}}$, ambipolar diffusion ${\eta }_{\text{AD}}$ and the Hall effect ${\eta }_{\text{H}}$. Ohmic resistivity corresponds to the regime, where all charged species (electrons, ions and charged grains) are entirely decoupled from the magnetic field. Hall resistivity describes the regime in which the electrons are coupled to the magnetic field, but the ions and charged grains are not. In other words, Hall resistivity represents the effect of ion-electron drift. Ambipolar diffusion is active in the regime, where all three charged components are tightly coupled to the magnetic field, and hence experience a drift force induced by the neutrals that are decoupled from the magnetic fields. Note that most generally, resistivities are tensor quantities as each resistivity can have a directional component that differs for each dimension. In practice, it is a fair approximation to consider the resistivities as scalar values as the directional variations are relatively small with respect to other uncertainties in dense cores. Furthermore, it is common practice to study protostellar collapse in models adopting the following additional assumptions. As the mass density is typically dominated by the mass of the neutral gas, and as collisions between charged and neutral particles dominate the momentum equation, it is safe to ignore pressure and momentum from the charged species. Considering, in addition, long evolutionary timescales of the magnetic field and the flow of neutrals compared to those of the charged ones, one can approximate the continuity equation to be dominated by the total mass, and hence only solve this equation as the continuum equation of the gas. (For more details, see for instance Wardle and Koenigl, 1993; Ciolek and Mouschovias, 1994; Mac Low et al., 1995; Wardle and Ng, 1999). Under these assumptions, the major change is in the induction equation (Equation 4), which can be written in its modified form for non-ideal MHD

$\begin{array}{ll}\frac{\partial \mathbf{B}}{\partial t}\hfill & =\mathrm{\nabla }\times \left(\mathbf{v}\times \mathbf{B}\right)-\mathrm{\nabla }\times \left[{\eta }_{\text{O}}\left(\mathrm{\nabla }\times \mathbf{B}\right)\right]\hfill \\ \hfill & -\mathrm{\nabla }\left\{{\eta }_{\text{H}}\left[\left(\mathrm{\nabla }\times \mathbf{B}\right)\times \frac{\mathbf{B}}{|\mathbf{B}|}\right]\right\}-\mathrm{\nabla }\left\{{\eta }_{\text{AD}}\frac{\mathbf{B}}{|\mathbf{B}|}\times \left[\left(\mathrm{\nabla }\times \mathbf{B}\right)\times \frac{\mathbf{B}}{|\mathbf{B}|}\right]\right\}.\hfill \end{array}(5)$

Moreover, the energy equation for the time evolution of internal energy $u$ becomes

$\begin{array}{ll}\hfill \frac{\partial u}{\partial t}& =-\frac{P}{\rho }\mathrm{\nabla }\cdot \mathbf{v}+{\eta }_{\text{O}}\frac{|\mathrm{\nabla }\times \mathbf{B}{|}^2}{\rho }\hfill \\ \hfill & +{\eta }_{\text{AD}}\frac{1}{\rho }\left\{|\mathrm{\nabla }\times \mathbf{B}{|}^2-{\left[\left(\mathrm{\nabla }\times \mathbf{B}\right)\cdot \frac{\mathbf{B}}{|\mathbf{B}|}\right]}^2\right\}.\hfill \end{array}(6)$

If expressed in terms of total energy $E_{\text{tot}}=\rho ϵ+\frac{1}{2}\rho v^2+\frac{1}{2}|\mathbf{B}{|}^2$ with specific internal energy $ϵ$ and using total pressure $P_{\text{tot}}=(\gamma -1)\rho ϵ+\frac{1}{2}|\mathbf{B}{|}^2$ with adiabatic index $\gamma$, the energy equation becomes

$\begin{array}{ll}\hfill \frac{\partial E_{\text{tot}}}{\partial t}& =-\mathrm{\nabla }\cdot \left\{\left(E_{\text{tot}}+P_{\text{tot}}\right)\mathbf{v}-\left(\mathbf{v}\cdot \mathbf{B}\right)\mathbf{B}\right.\hfill \\ \hfill & -{\eta }_{\text{AD}}\frac{\left[\left(\mathrm{\nabla }\times \mathbf{B}\right)\times \mathbf{B}\right]\times \mathbf{B}}{|\mathbf{B}{|}^2}\times \mathbf{B}-{\eta }_{\text{H}}\frac{\left(\mathrm{\nabla }\times \mathbf{B}\right)\times \mathbf{B}}{|\mathbf{B}|}\times \mathbf{B}\hfill \\ \hfill & -\left.{\eta }_{\text{O}}\left(\mathrm{\nabla }\times \mathbf{B}\right)\times \mathbf{B}\right\}.\hfill \end{array}(7)$

Note that the Hall resistivity does not affect the internal energy equation because in contrast to ohmic dissipation and ambipolar diffusion, it is a dispersive, non-dissipative process. Using the modified induction equation (Equation 5), and a modified equation for internal (Equation 6) or total energy (Equation 7), one can carry out single-fluid non-ideal MHD simulations.

2.1.1 Ohmic resistivity

Reflecting the complexity in accounting for the effects numerically, the first non-ideal effect included in models was ohmic dissipation, followed by ambipolar diffusion and at last the Hall effect. In the early approaches, ohmic resistivity was set to constant values (Shu et al., 2006; Krasnopolsky et al., 2010) with the goal to test which values of ${\eta }_{\text{O}}$ would be required to allow disk formation despite the presence of strong magnetic fields. Inutsuka et al. (2010), Machida and Matsumoto (2011) and Machida et al. (2011) found the formation of large disks with ohmic resistivity only at late stages of the collapse phase when most of the envelope material had accreted onto the protostar already. The physical explanation for this was first laid out by Mellon and Li (2008). Angular momentum transport became less efficient in these models at later stages because there was almost zero gas available at larger scales to transport the material to, making magnetic braking less efficient. The results are also qualitatively consistent with semi-analytic results (Dapp and Basu, 2010; Dapp et al., 2012) and 3D models (Wurster et al., 2016). The smaller disk sizes of $\sim 10$ au derived by the latter groups instead of $\sim 100$ au (Inutsuka et al., 2010; Machida et al., 2011) are explained by the assumption of lower resistivities and a larger sink particle by Wurster et al. (2016). While it was found that disks can form with high ${\eta }_{\text{O}}$, those values can typically only be reached very close to the center of the first hydrostatic core (see papers by (Marchand et al., 2016) and Wurster et al. (2016). However, the values at lower densities and temperatures prevalent during protostellar disk formation are expected to be significantly smaller.

2.1.2 Ambipolar resistivity

The low probability of obtaining the right conditions for circumventing strong magnetic braking solely through ohmic resistivity gave rise to a revival of seriously accounting for ambipolar diffusion as it is the dominant process at lower densities present in prestellar cores. The idea of considering ambipolar diffusion as an important process of individual star formation dates back to the 1970s (Mouschovias, 1976; 1977; 1979), when it was studied in the context of redistributing the magnetic field to avoid the pile-up of magnetic pressure at the center due to magnetic-flux freezing that would prevent protostellar collapse (see Das and Basu, 2021, for a more recent linear instability analysis of magnetized sheets with ambipolar diffusion). Against this background, Hennebelle et al. (2016) estimated that disks form with typical disk sizes around 18 au based on analytical calculations that account for ambipolar diffusion.

Early 2D models by Mellon and Li (2009) did not find evidence for disk formation induced by including ambipolar diffusion, but their setup disallowed disk formation on radii less than $\sim 10$ au because of the sink accretion recipe. Later studies that did not introduce a sink particle found the formation of disks enabled by ambipolar diffusion. 3D models by Tsukamoto et al. (2015b) demonstrated the increase in angular momentum for the model case with ambipolar diffusion compared to the model case without it, which resulted in the early formation of a small $\sim 1$ au disk, which is in good agreement with results obtained by Tomida et al. (2015); Machida and Basu (2019). Similarly, conducting very detailed collapse simulations of the early collapse stage, Vaytet et al. (2018) discovered the formation of an even smaller Keplerian disk of less than 0.1 au in radius briefly after the first collapse phase. It is important to point out that these disks form at a very early stage of star formation associated with the first collapse, and that this evolutionary stage is very short-lived ($\sim 10^3$ kyr). The review by Young (2023) presents the state-of-the art of this phase in detail.

As anticipated in previous models (Tomida et al., 2013), a follow-up study by Tomida et al. (2017) that introduced a sink particle, demonstrated the formation of significantly larger disks $\sim 100$ au in size due to dissipation of both the envelope and the magnetic field. This result is in agreement with 3D models by Masson et al. (2016), who found the formation of relatively large disks of about 80 au for collapse simulations initialized with 50 times higher gravitational to rotational energy and a mass-to-flux ratio of $\mu =5$. Other studies that evolve the collapse to later times find a similar trend of larger disks at later phases (Marchand et al., 2020; Lee Y.-N. et al., 2021; Tu et al., 2024) for initial core masses $\sim 1$ to $\sim 10$ ${\mathrm{M}}_{\odot }$, as well as studies that consider the collapse of a more massive spherical core with a mass of $\sim 100$ ${\mathrm{M}}_{\odot }$ (Rosen et al., 2019; Mignon-Risse et al., 2021; Commerçon et al., 2022; Oliva and Kuiper, 2023). Comparing the results of ideal MHD with results obtained accounting for ambipolar diffusion, Masson et al. (2016) find a sharp upper limit of B-field strength of 0.1 G even at high densities of $\rho >10^{-12}$ g ${\mathrm{c}\mathrm{m}}^{-3}$ in the $\rho$-$B$ phase space induced by ambipolar diffusion, whereas in the ideal MHD case the field strength exceeds 1 G at these higher densities. Such a plateau value is consistent with the theoretical analysis by Hennebelle et al. (2016) of a collapsing singular isothermal sphere (Shu, 1977)for the assumption of a commonly assumed cosmic-ray ionization rate of $\sim 10^{-17}$ ${\mathrm{s}}^{-1}$, and similar plateau values around 0.1 G were also found in other studies by (Tsukamoto et al., 2017; Hennebelle et al., 2020; Xu and Kunz, 2021; Zier et al., 2024b).

2.1.3 Hall effect

The Hall effect is the most difficult resistivity to implement and therefore the one that has been less studied although its possible influence on protostellar collapse was previously pointed out and studied (semi-)analytically (Wardle and Ng, 1999; Wardle, 2004; Braiding and Wardle, 2012). Today there is a decent number of papers presenting the results of spherical collapse simulations that incorporate the Hall effect in 2D grid simulations using zeus (Krasnopolsky et al., 2011; Li et al., 2011; Zhao et al., 2020a; Zhao et al., 2021), 3D SPH simulations using a Godunov SPH code (Tsukamoto et al., 2015a; 2017) as well as (Wurster et al., 2016; Wurster et al., 2018a; Wurster et al., 2018b; Wurster et al., 2019; Wurster et al., 2022), 3D AMR simulations with ramses (Marchand et al., 2018; 2019), and 3D moving mesh simulations using arepo (Zier et al., 2024a) that incorporate Hall resistivity. In theory, the Hall resistivity can adopt positive or negative values, but in practice it is typically negative during the protostellar collapse as shown in SPH (Tsukamoto et al., 2015a; Wurster et al., 2016) as well as in cartesian grid simulations (Marchand et al., 2016). In contrast to ohmic dissipation and ambipolar diffusion, the Hall effect depends on the direction of the magnetic field. In the case of anti-parallel alignment of magnetic field and angular momentum, it can cause spin up of the gas and lead to the formation of a larger disk. Contrary, in the case of parallel alignment of $\mathbf{B}$-field and initial rotation, the disk is small. For high values of ${\eta }_{\text{H}}$ the outer envelope can even become counter-rotating with respect to the rotation of the inner disk (Krasnopolsky et al., 2011; Li et al., 2011; Zhao et al., 2020a; 2021). One would therefore expect a bimodal distribution of disk sizes under conditions were the Hall-effect is dominant (Tsukamoto et al., 2015a; Wurster et al., 2016), if only the two extreme scenarios of parallel or anti-parallel alignment were possible. Reflecting the key constraints obtained from non-ideal MHD models, Lee et al. (2021) expanded the analytical model of disk formation by Hennebelle et al. (2016) to additionally cover the effects of ohmic dissipation and the Hall effect in addition to ambipolar diffusion.

2.1.4 Misalignment between magnetic field and rotational axis

The relative orientation of initial rotational axis and $\mathbf{B}$-field direction affects the collapse phase also in other ways than the Hall effect. Early studies by Matsumoto and Tomisaka (2004) investigated misalignment of initial magnetic field orientation with respect to the angular momentum vector of the core in ideal MHD simulations. They find that, during core collapse, the orientation of the angular momentum vector, the magnetic field, and the pseudodisk converge to align in the central region of the cloud core due to angular momentum transport through magnetic braking. Moreover, misalignment between initial rotational axis and $\mathbf{B}$-field direction can reduce the efficiency of magnetic braking as first pointed out by Hennebelle and Ciardi (2009). In fact, models showed that misalignment can enable disk formation in ideal MHD models, where disk formation is quenched when the axes are initially aligned (Joos et al., 2012; Krumholz et al., 2013; Li et al., 2013; Gray et al., 2018). Tsukamoto et al. (2018) investigated the effects of misalignment between rotational and magnetic field axis considering the cases of perpendicular and parallel orientation. They find three possible mechanisms in which the misalignment can affect disk formation, namely, selective accretion of material with high angular momentum in the perpendicular case and vice verse, magnetic braking during the isothermal collapse phase and magnetic braking of the disk. The authors point out that magnetic braking during the collapse phase would yield to the opposite effect on disk formation as reported by the aforementioned groups. Therefore, the consensus is that this effect is negligible for disk formation. In the recent review chapter, Tsukamoto et al. (2023b) emphasize that the differences in disk braking is primarily responsible for enhanced disk formation in the misalignment scenario because the magnetic field acts on longer time scales to transport angular momentum in a disk that is supported by centrifugal forces compared to the much shorter free fall time corresponding to the collapse phase. Analyzing results obtained in the models by Li et al. (2013), Väisälä et al. (2019) and Wang et al. (2022) emphasized the formation of time-variable features extending from the disk such as spiral features in the pseudodisk. In summary, the combination of models allowed to increasingly cover the parameter space of spherical collapse. The recently updated analytical model by Lee et al. (2024) incorporates these constraints on misalignment between $B$-field and rotational axis, in addition to non-ideal MHD effects.

2.1.5 Turbulence

While it is consensus that magnetic braking quenches disk formation in ideal MHD models of spherical collapse with alignment between rotational and $\mathbf{B}$-field axis, it is also clear that these are highly idealized initial conditions. A mechanism of circumventing catastrophic braking in ideal MHD models of spherical collapse is by introducing turbulence. Several studies of spherical collapse demonstrated that disks can form when initializing the spherical core with a turbulent velocity field (Santos-Lima et al., 2012; Seifried et al., 2012; Seifried et al., 2013; Joos et al., 2013). While in theory, there is no diffusivity in the ideal MHD limit, it is in practice a common feature that occurs at the resolution limit when solving the ideal MHD equations numerically. Santos-Lima et al. (2012) therefore proposed that the random motions intrinsic to turbulence induce an effective magnetic diffusivity on the smallest scales via so-called turbulent reconnection. Adopting a resolution of about one au, this artificial resistivity therefore quenches the pile-up of magnetic fields during the collapse at values below $\sim 1$ G, which leads to a similar effect as reported for ambipolar diffusion. In agreement with the occurrence at the resolution limit, it is also clear that it is less efficient in simulations with higher resolution of less than one au (Joos et al., 2013) because higher magnetic field strengths are reached during the collapse, which implies more efficient magnetic braking. This means there is no numerical convergence in spherical collapse ideal MHD models down to sub-au resolution, while there is in models with ambipolar diffusion, where the $\mathbf{B}$-field strength reaches a characteristic plateau value that depends on the assumed ionization rate. Collapse models with turbulence find that the effect of turbulence is reduced when non-ideal MHD effects are incorporated as well (see results found by (Lam et al., 2019; Wurster and Lewis, 2020), which is interpreted as turbulent diffusion being a secondary effect for disk formation (Tsukamoto et al., 2023b).

However, it has also been pointed out by Seifried et al. (2012), who considered a larger ($\approx 50000$ au) and more massive core (50 ${\mathrm{M}}_{\odot }$) with the adaptive mesh refinement code code flash that turbulence leads to the formation of filaments and intrinsically induces misalignment between $\mathbf{B}$-field axis and rotational axis. Considering the fundamental role of turbulence in the star formation process in the Giant Molecular Cloud, Seifried et al. (2012) therefore emphasize that turbulence is the cause for deviations from symmetry such as the relative orientation between rotational and $\mathbf{B}$-field axis, which reduces the braking efficiency and helps to circumvent the magnetic braking catastrophe. Results obtained from SPH simulations by Wurster et al. (2019), who carried out a parameter study of a turbulent collapsing core with 50 ${\mathrm{M}}_{\odot }$ in mass, varying mass-to-flux ratios of 3, 5, 10 and 20 and even all three non-ideal MHD effects included are in good agreement with that. In Wurster et al. (2019), the core was initialized with a random velocity distribution such that the initial mean sonic Mach number was $\mathsf{M}=6.4$. The major conclusion of this work is that there is no magnetic braking catastrophe and disks form frequently. In agreement with Seifried et al. (2012), this even holds true for the case of ideal MHD without any non-ideal MHD resistivities included. Taking into account for turbulence within the core and ohmic dissipation at high densities, AMR simulations with the SFUMATO code (Matsumoto, 2007) also showed the formation of warped disks on timescales of $\sim 1000$ yr as a result of misalinged infall induced by the underlying turbulence Matsumoto et al. (2017).

2.1.6 The role of the ionization rate

Today, it is consensus that non-ideal MHD effects can resolve the magnetic braking problem of disk formation in spherical collapse simulations. The bigger question today is how much they affect the collapse and disk formation phase. Especially, early models assumed resistivities relatively crudely only roughly accounting for the dependency on density. The individual resistivities depend on the underlying physical conditions and current state-of-the-art models account for this dependency by using pre-computed values that are assigned to the local density, magnetic field strength and temperature. The computation of the table of resistivities is done by using chemical equilibrium models. For instance, Marchand et al. (2016) illustrated the differences compared to the values assumed in previous studies by Duffin and Pudritz (2009) and Machida et al. (2007). Apart from that there are some differences depending on the chemical model that was used to compute the tables. In the table by Zhao et al. (2016) the Hall resistivity is lower than the ambipolar resistivity for a cosmic-ray ionization rate of $10^{-17}{\mathrm{s}}^{-1}$ at any density, whereas the Hall resistivity exceeds ambipolar resistivity and ohmic dissipation in the range of number densities of $n=10^6{\mathrm{c}\mathrm{m}}^{-3}$ to $n=10^{10}{\mathrm{c}\mathrm{m}}^{-3}$ in the table by Marchand et al. (2016).

While these differences between the tables are generally more subtle, another physical effect is more crucial. It is common practice to assume non-ideal MHD coefficients that were computed for a fixed cosmic-ray ionization rate $\zeta$. Typical values that are assumed for non-ideal MHD models are in the range of $\zeta \sim 10^{-18}{\mathrm{s}}^{-1}$ to $\zeta \sim 10^{-17}$ ${\mathrm{s}}^{-1}$. The latter value is often referred to as the canonical value dating back to estimates by Spitzer and Tomasko (1968). While early measurements of the cosmic-ray ionization rate in dense cores (Caselli et al., 1998; Padovani et al., 2009) are in broad agreement with these values, there has been an increasing number of observations that report significantly higher values in cores at higher densities (Ceccarelli et al., 2014; Podio et al., 2014; Fontani et al., 2017; Favre et al., 2018; Cabedo et al., 2023) together with observations of significant scatter of ionization rates between different cores (Indriolo and McCall, 2012). Such an increase towards higher densities was initially hard to explain as cosmic-rays were expected to be shielded and mirrored at the relatively densities in dense cores (e.g., Padovani and Galli, 2013). It is, however, consistent with more recent modeling results that predict an enhancement of cosmic-ray ionization rates through protostellar accretion shocks (Padovani et al., 2016; Gaches and Offner, 2018). In fact, first maps of the cosmic-ray ionization rate of a low-mass star-forming region (NGC1333 Pineda et al., 2024) and of two massive clumps (AG351 and AG354 Sabatini et al., 2023) confirm the variation and show enhanced cosmic-ray ionization values toward some of the denser gas. It has therefore become more and more clear that cosmic-ray ionization rates can vary by orders of magnitude depending on the protostellar stage as well as on the environment in which the star is forming.

Wurster et al. (2018c) carried out a parameter study of the very early protostellar collapse phase with all three non-ideal MHD effects using resistivities corresponding to cosmic-ray ionization rate in the range of $\zeta \sim 10^{-30}$ ${\mathrm{s}}^{-1}$ to $\zeta \sim 10^{-10}$ ${\mathrm{s}}^{-1}$. For $\zeta \gtrsim 10^{-14}$ ${\mathrm{s}}^{-1}$, the models evolve similar to the ideal MHD models, while the outcome becomes diminishingly different from pure hydrodynamical models for $\zeta \lesssim 10^{-24}$ ${\mathrm{s}}^{-1}$. Similarly, Kuffmeier et al. (2020) demonstrated that the assumption of a higher (smaller) cosmic ray ionization rate leads to stronger (weaker) magnetic braking, and thereby to smaller (larger) disks. Considering the various environments in which star-formation occurs, the effect of non-ideal MHD is expected to differ significantly between the regions (see also discussion and speculation about starburst galxies or the Galactic Center by Wurster and Li, 2018).

2.2 Dust

2.2.1 The role of dust on the resistivities

The resistivities are also affected by the assumed dust distribution (Zhao et al., 2018; Koga et al., 2019; Marchand et al., 2020). For a distribution with a large number of small grains ($\lesssim 10\mu$m), the resistivities become smaller as the grains adsorb charged particles. Early studies by (Mellon and Li, 2009; Li et al., 2011) assumed a distribution in which such small grains were present. However, grains are expected to grow efficiently beyond $10\mu$m in dense cores, which implies that higher resistivities are expected. Considering dust growth during the collapse, Lebreuilly et al. (2023) showed how the resistivities can drastically change. Models by Tsukamoto et al. (2023a) also show the effect of dust growth on the resistivities, but they also find a convergence towards a more steady distribution once the grains have grown beyond 1 mm in size, such that the resistivities for ambipolar diffusion can be described by density-dependent power-laws of ${\eta }_{\text{AD}}\propto n^{-0.5}$ for densities $\rho \lesssim 10^{-13}$ g ${\mathrm{c}\mathrm{m}}^{-3}$. Studying the relative importance on the resistivities of the size distribution with the cosmic-ray ionization rate, Kobayashi et al. (2023) find that the size distribution is a less significant factor compared to the cosmic-ray ionization rate.

2.2.2 Incorporation of dust dynamics and growth in collapse models

In the context of planet formation, essential ingredients to incorporate in the models are dust dynamics and dust growth. This is particularly important considering the growing evidence for an early onset of planet formation. Some (magneto-)hydrodynamical models started to include the dynamics of dust in young forming disks in spherical collapse simulations. Vorobyov et al. (2019) and Bate (2022), independently carried out hydrodynamical simulations of disk formation in which they included the dynamics of dust particles during disk formation. Consistent with analytical predictions, they find size-dependent radial drift of dust particles. Lebreuilly et al. (2020) demonstrated that dust drifts toward the inner part of the disks with larger grains accumulating in the inner parts of the disk, where they cause an enhanced dust-to-gas ratio. More recently (Vorobyov et al., 2024), followed up on their earlier work that already included dust growth and drift, by also accounting for the back-reaction of the dust on the gas (Stoyanovskaya et al., 2018). They concluded that the dust-to-gas ratio becomes high enough for the onset of planetesimal formation after only $\sim 20$ kyr. Considering the different properties of dust particles depending on their size and the underlying gas density in this context, Stoyanovskaya et al. (2020) highlighted the importance of the underlying Mach number on the assumption of the drag coefficients.

Tsukamoto et al. (2021) also modeled the drift of dust particles during the collapse, but also considered grain growth. In contrast to Lebreuilly et al. (2020), they find that a fraction of the dust particles can be elevated by an outflow in the inner part of the disk, become entrained in the envelope, and eventually fall back onto the outer part of the disk. This idea is conceptually similar to earlier scenarios suggested to explain the transport of the oldest solids in the Solar System, namely, CAIs and chondrules (Shu et al., 1996; 1997). Tsukamoto et al. (2021) envision a scenario of multiple cycles that contribute to grain growth. The dust grains drift through the disk, grow during the drift phase, are ejected through an outflow in the inner disk and fall back onto the outer disk as a larger grain. Considering multiple cycles of this mechanism, this could lead to a grain size distribution in the disk that is shifted towards larger grains and which should be imprinted in the dust opacity spectral index of the envelope around the forming star-disk system. Considering the meteoritic record, the transport mechanism could potentially explain the imprints of reprocessing reported for some chondrules. Recently, Cacciapuoti et al. (2024) followed up on this transport scenario by measuring the dust opacity spectral index in a few cores with outflows. Their results do not reveal an unambiguous correlation of dust growth with outflow strength though and future observations are required to further test the scenario.

3 Beyond isolated spherical collapse

While variations in disk sizes between different models with non-ideal MHD are often solely explained as a sign of the underlying non-ideal MHD resistivities, another aspect tends to be overlooked, namely, the role of the initial and boundary conditions. It is a challenge to draw conclusions about the importance of individual effects from results that were obtained using different model setups codes. Some groups start from initial conditions assuming a density profile according to a Bonnor-Ebert (BE) sphere, whereas others start with a uniform density distribution. Considering this general issue, the parameter study by Machida et al. (2014) stands out in terms of constraining the role of various effects. They adopted several model setups that were previously used by groups (Hennebelle and Ciardi, 2009; Li et al., 2011; Machida et al., 2011; Joos et al., 2012; Krasnopolsky et al., 2012; Seifried et al., 2012) and recomputed those models with their own code. Activating the same non-ideal MHD effects and starting from similar initial mass-to-flux ratios, they found significant differences in disk formation depending on the assumption of the initial density profile. Models starting with a uniform density distribution led to disk sizes of the order of 10 au, while models starting with a density distribution of a Bonnor-Ebert sphere yield larger disk sizes of about 100 au. They also emphasized the role of the accretion recipe onto a sink. Under identical initial conditions, allowing the sink to accrete from a smaller region in its vicinity favors the formation of larger disks compared to a sink that is allowed to accrete from a larger region.

These results point to a more fundamental issue of modeling individual star formation as the outcome of the collapse of an isolated sphere. In fact, Larson (1969) stated already that they assumed ‘the simplest assumptions’ on the boundary condition and they ‘again adopted the simplest assumptions’ for the initial conditions in the spherical collapse scenario. While the assumption of spherical collapse has proven to be very helpful in constraining the effect of various physical parameters during collapse, it is important to keep in mind that reality can differ significantly from this idealized approximation. It seems that the assumption of spherical symmetry is a fair assumption for the earliest phase of protostellar collapse corresponding to the formation of the first and second core, and model predictions about the properties of protostars during the first few thousands of years are likely to be very accurate - except for the uncertainty of the ionization rate at these early stages.

However, (almost) all of the observed disks are significantly older than $10^3$ yr–even those associated with protostars that are classified as Class 0 objects. Observations revealed that stars are embedded in filamentary molecular clouds, and that they, at most, rarely form in isolation. Their formation and evolution is influenced by the environment in which they form and evolve. Variations of the magnetic field strength, the level of turbulence or the cosmic-ray ionization are factors that determine disk formation. These effects can be incorporated in spherical collapse models by varying the initial conditions within the core, relying on the crucial assumption that once a core has formed with specific initial conditions it can be considered as being detached from the dynamics and processes in the molecular cloud.

We know, however, from observations that the morphology of prestellar cores is significantly affected by the underlying dynamics in filamentary Giant Molecular Clouds (André et al., 2014; Kainulainen et al., 2017; Hacar et al., 2023; Pineda et al., 2023). This implies to investigate the process of disk formation with a different approach than the spherical core setup has become timely. As of today, there are relatively few studies compared to the large number of classical collapse models that account for larger-scale dynamics, such as infall or binary interaction, in the context of disk formation. Both stellar encounters as well as infall have been modeled in computing-intense zoom-in simulations as well as in simplified model setups that allow to carry out cheaper models in terms of computing-time. In the following, we will summarize the efforts made in recent years distinguishing between the progress made in models that were configured to model specific scenarios through parameter studies and compute-intense models that aim for resolving the processes in multi-scale simulations.

3.1 The role of infall

Considering the presence of accretion streamers even around presumably evolved stars, it is becoming increasingly evident that disk formation models need to take into account for the possibility of infall that is often anisotropic (Kuffmeier et al., 2017; Kuznetsova et al., 2019; 2020). Currently most of the numerical constraints on infall are from models that model the cloud dynamics, but do not resolve the formation of disks. Padoan et al. (2014) demonstrated that infall through Bondi-Hoyle accretion can induce accretion bursts that are a prominent explanation for the luminosity problem. Moreover, in line with the interpretation of the inertial flow model proposed by Padoan et al. (2020), Pelkonen et al. (2021) showed that a significant amount of the material accreting onto the star was initially not gravitationally bound to the core, and the relative mass fraction of accreting material scales with the final mass of the star. This is also consistent with earlier results by Smith et al. (2011), who reported a prolonged accretion history of the more massive stars in their hydrodynamical simulations of a turbulent cloud. Following up on these results, Kuffmeier et al. (2023) also showed that a Class II young stellar object can return to Class I or even Class 0 phase in the event of massive infall. It remains to be self-consistently modeled how the disk reacts to such events. However, there are parameter studies that considered the effect of individual infall events on the properties of star-disk systems.

Starting from spherical collapse models, several groups considered the case of infall from the envelope onto an existing disk (Bae et al., 2015; Lesur et al., 2015; Vorobyov et al., 2015; Kuznetsova et al., 2022). They all find that the infall can trigger instabilities in the disk. Carrying out hydrodynamical simulations, Vorobyov et al. (2015) showed that infall can trigger gravitational instabilities that trigger accretion bursts of the star. Bae et al. (2015) and Kuznetsova et al. (2022) find that these infall events trigger Rossby-wave instabilities, which Kuznetsova et al. (2022) attribute as possible seeds for gap, ring and structure formation in disks. Considering the possibility of misaligned infall from the envelope, Thies et al. (2011) demonstrated in hydrodynamical simulations of a collapsing sphere with differences in the angular momentum orientation of the outer infalling radial layer that such infall can induce the formation of an outer disk that is misaligned with respect to the primordial inner disk. Considering the indications for late, post-collapse infall, Dullemond et al. (2019) developed a model of cloudlet capture, in which a low-mass gaseous cloudlet encounters a star modeled as a point mass with an impact parameter. As a result of the encounter the hydrodynamical simulations carried out with the Pluto code showed the formation of extended arm features similar to structures seen around Herbig stars such as for instance AB Aurigae. The formation of such an extended arm (streamer) was also reported in the cloudlet capture models by Hanawa et al. (2022, 2024). Kuffmeier et al. (2020) followed up on the cloudlet capture scenario by carrying out simulations with the arepo code, in which they showed that such encounters cannot only lead to the formation of extended arms, but also to the formation of a second-generation disk. In the presence of an already (or still) existing primordial disk, such an event can lead to the formation of a system consisting of misaligned inner and outer disk (Kuffmeier et al., 2021), which is observable as shadows in the outer disk in scattered light observations (Krieger et al., 2024). SU Aur is the most prominent candidate that might undergo such an event today (Ginski et al., 2021). The cloudlet capture scenario has also been adopted by Unno et al. (2022), who considered an encounter of a magnetized cloudlet. They showed that the event can lead to magnetic acceleration of the existing inner disk for a favorable orientation of the magnetic field of the cloudlet compared to the field orientation in the disk.

3.2 Clump to disk

Bate (2018) carried out 3D hydrodynamical simulations with $3.5\times 10^7$ particles to produce the first disk population synthesis study. As an initial condition of the simulation, they assumed a sphere with radius 0.404 pc. The mass of the cloud was set to 500 ${\mathrm{M}}_{\odot }$, which corresponds to a density of $1.2\times 10^{-19}$ g ${\mathrm{c}\mathrm{m}}^{-3}$. Simulating the extended range of scales came at the cost of reduced physics compared to state-of-the-art simulations of spherical collapse simulations. Radiative transfer was included, but magnetic fields were not taking into account such that magnetic braking is not accounted. The cloud was initialized with a supersonic velocity field to account for turbulence in the cloud by generating a divergence-free random Gaussian velocity field with a power spectrum scaling with wave number $k$ as $P(k)\propto k^{-4}$, which is the same recipe as used in previous works by Ostriker et al. (2001) and Bate et al. (2003). The resulting mean Mach number was $\mathsf{M}=13.7$. The simulation was run for 1.2 free-fall times, which corresponds to about 220 kyr. By the end of the simulations, it showed a diverse distribution of more than 100 disks. Interestingly, there sample shows a non-negligible distribution of more exotic configurations such as misaligned or even counter-rotating disks that are the result of infalling material after the initial formation phase or form via interaction with other stars through stellar encounters. Moreover, the cloud dynamics led to the formation of circumbinary and circummultiple disks. Using the same setup as Bate (2019), Elsender and Bate (2021) investigated the role of the metallicity on the disk distribution. They used metallicities of 0.01, 0.1, 1, and 3 times the solar metallicity, and they find that disk sizes decrease for decreasing metallicities in the clump. In a further follow-up study, Elsender et al. (2023) investigated the frequency of circumbinary disks and they find that $90\%$ of close binaries (separation less than one au) host disks. Their distribution of circumbinary disks is bimodal with a second enhanced fraction of about 50 $\%$ for binaries with a separation of about 50 au.

In the case of Bate (2018), simulating the extended range of scales came at the cost of reduced physics compared to state-of-the-art simulations of spherical collapse simulations. Radiative transfer was included, but magnetic fields were not taking into account such that magnetic braking is not accounted. Lebreuilly et al. (2021) followed a similar approach of modeling the formation of stars dynamics of a massive turbulent sphere with an initial mass of 1,000 ${\mathrm{M}}_{\odot }$ and radius of $R_0\sim 0.38$ pc, but with magnetic fields included. The cloud is initialized with a ratio of thermal-to-gravitational energy of $\alpha =\frac{5R_0{k}_{\text{B}}{T}_0}{2G{M}_0{\mu }_{\text{g}}{m}_{\text{H}}}$ with Boltzmann constant $k_{\text{B}}$, a defined temperature $T_0$, clump mass $M_0$, mean molecular weight ${\mu }_{\text{g}}$ and the mass of a hydrogen atom $m_{\text{H}}$. The simulations include magnetic fields and they account for ambipolar diffusion using the adaptive mesh-refinement MHD code ramses. The initial average Mach number is set seven and the mass-to-flux ratio is set to $\mu =10$. Overall, Lebreuilly et al. (2021) draw a similar conclusion to Wurster et al. (2019) that disk formation is a frequent outcome of star formation regardless of ideal MHD or non-ideal MHD. Interestingly, there is no significant difference in mean disk size between the ideal and non-ideal MHD run, the mean disk size for the ideal MHD runs are even slightly larger.

The authors caution nonetheless state that non-ideal MHD is important for disk formation. Based on the results of collapse simulations with higher resolution (Joos et al., 2013) they expect that magnetic braking will be more efficient and the disks therefore smaller if the resolution at the highest levels was higher than $\sim 1$ au. In a follow-up study, Lebreuilly et al. (2024a) extended the parameter space by carrying out five additional simulations with similar setups. In one simulation, they carried out the identical simulation, but increased the accretion luminosity efficiency of sink particles from 0.1 to 0.5. The result is an increase of radiative feedback, which leads to more thermal support and less fragmentation in the clump. The resulting number of sink particles in the run with increased accretion luminosity efficiency is very similar to the result obtained for the ideal MHD run, but accretion luminosity efficiency of 0.1. As expected, an increase of the initial mass-to-flux ratio from 10 to 50 results in an increase of the final number of stars by more than 50%. The star-formation efficiency increases by more than a factor 2 for runs with half the initial mass (500 ${\mathrm{M}}_{\odot }$ instead of 1,000 ${\mathrm{M}}_{\odot }$), and hence twice the initial thermal-to-gravitational energy ratio. Finally, the authors report an increase in star-formation by about 40%, when adopting a barotropic equation-of-state instead of treating the radiative transfer with the flux-limited-diffusion recipe (Commerçon et al., 2011; 2014). Regarding the disk population, the authors conclude that disk formation is ubiquitous for all setups. In addition, the disk population is practically the same regardless of account for outflows or not although outflows reduce the accretion rate, and hence the luminosity of the protostar (Lebreuilly et al., 2024b). Similarly to the hydrodynamical models by Bate (2018) the derived disk sizes are in approximate agreement with observations regardless of ideal or non-ideal MHD (e.g., Maury et al., 2019; Sheehan et al., 2022), while the disk masses are systematically higher in the models compared to disk masses derived from observations (Sheehan et al., 2022).

Comparing the ambipolar diffusion runs with mass-to-flux ratios of $\mu =10$ and $\mu =50$, the study shows that the disk sizes in the less magnetized run are significantly larger by about $30\%$ to $50\%$, which confirms the effect of magnetic fields on the disk size during their formation. Considering the difference between the models with ideal MHD and ambipolar diffusion, the authors point out, however, that the conditions in the disks are significantly different. In the ideal MHD case, the magnetic field strength in the disk is significantly higher implying plasma-beta values of $\beta <1$ in the disk, while the disks in the ambipolar diffusion case are generally dominated by thermal pressure with $1<\beta <100$.

3.3 Giant Molecular Cloud to disk

While the clump-models by Bate (2018); Elsender and Bate (2021) as well as Lebreuilly et al. (2021, 2024a) allowed to derive disk population synthesis, the models starting from an initial spherical clump of $<0.5$ pc cannot truly account for the Giant Molecular Cloud dynamics. While it is common practice to study star formation in molecular cloud simulations, almost all models do not have the resolution to resolve the scales necessary to form disks. The zoom-in simulations by Kuffmeier et al. (2017) mark an exception in this regard. They modeled the dynamics of a Giant Molecular Cloud including supernova feedback from massive stars that drives the turbulence in 3D simulations of a cubical box with 40 pc in length and assuming periodic boundary conditions. The simulations included magnetic fields and solved the equations of ideal MHD. Using the zoom-in technique, they then resolved the formation of six stars with highest resolution of two au, and of three additional stars with highest resolution of eight au. The temperature in the cloud is computed using tables for heating and cooling, though the gas at highest densities corresponding to the inner $\sim 100$ au is treated as quasi-isothermal with a temperature of 10 K. The study showed a diversity of the disk formation process and demonstrated that star formation is a heterogeneous process depending on the parental environment. In fact, the models predicted the frequent occurrence of filamentary accretion channels that feed the young disk with fresh material from the environment. On scales of 10 to $\sim 100$ au, this filamentary mode of accretion through streamers is consistent with results from previous protostellar collapse models with turbulence as first prominently reported by Seifried et al. (2013) and as also seen by other groups (Offner et al., 2010; Joos et al., 2013; Li et al., 2014; Heigl et al., 2024). On larger scales, the star-disk systems forming in more turbulent and massive environments are also fed with additional material through filamentary arms on core scales and beyond $\sim 1000$ au to 10,000 au. Independently, He and Ricotti (2023) carried out zoom-in simulation for massive cores of $\sim 10$ ${\mathrm{M}}_{\odot }$ to $\sim 100$ ${\mathrm{M}}_{\odot }$ in size starting from a Giant Molecular Cloud down to a disk forming around a massive star using radiative transfer MHD simulations. The dynamical range is similar in the high resolution case ($\approx 7$ au) and the study also reveals a connection of the forming disks to the molecular cloud environment through filamentary arms of $\sim 1000$ to $\sim 10000$ au in length. Considering bridge structures of $\sim 1000$ au in length similar to those observed for IRAS16293, Kuffmeier et al. (2019) showed and Lee et al. (2019) independently confirmed that such structures can occur as transient phenomena during protostellar multiple formation in a turbulent environment.

Kuffmeier et al. (2018) also carried out a zoom-in simulations for one of the stars with a resolution as high as 0.06 au for a time interval of 1,000 years at about 50 kyr after star formation. These simulations resolved the infall of a gas blob onto the disk that triggered a gravitational instability that was responsible for an accretion burst. While the dynamical range of the simulation allowed to take into account for the larger scale environment, important physical effects such as non-ideal MHD and/or a more realistic treatment of the thermodynamics was lacking in these models compared to state-of-the-art models of spherical collapse. The challenge for the upcoming decade will be to fill the gap between spherical collapse models with advanced multi-physics treatment, but highly idealized initial and boundary conditions, and multi-scale models that self-consistently account for the Giant Molecular Cloud dynamics, but lack advanced treatment of relevant physical processes. The improvements of infrastructure of more powerful supercomputers together with optimized numerical codes that enable more efficient computing (e.g., Hopkins, 2017; Nordlund et al., 2018; Price et al., 2018; Stone et al., 2020; Weinberger et al., 2020) allow us to accept this challenge. This also includes the possibility to account for stellar feedback mechanisms that can shape and affect disk formation. For instance, UV radiation feedback plays an important role for the overall cloud dispersal as shown in radiation hydrodynamics models (Kim et al., 2018; Fukushima et al., 2020). Together with implementations of protostellar outflows, e.g., Guszejnov et al. (2021) or Lebreuilly et al. (2024b), these are potentially important effects shaping the accretion process of stars and thereby their disks. More recently, as part of the STARFORGE initiative (Grudić et al., 2021), Guszejnov et al. (2022) already demonstrated the possibility to study supernova feedback, stellar radiation, protostellar jets and winds together in one simulation. Continuing these efforts while applying high enough resolution will allow us to test the frequency and properties of various outcomes of infall-induced features such as misaligned disks or disk instabilities that are possible outcomes of a heterogeneous star formation process happening in Giant Molecular Clouds (see illustration in Figure 2).

Figure 2

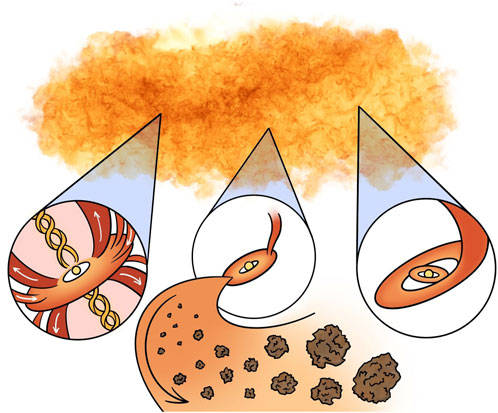
Figure 2. Illustration of heterogeneous star formation and possible outcomes of disk formation in a Giant Molecular Cloud. The upper panel shows the density fluctuations in a filamentary cloud based on data from (Kuffmeier et al., 2017). The remaining part sketches different stages of the disk. The left inset shows a young disk with a strong magnetically-induced outflow enclosing a jet, the middle inset shows infall through a streamer solely delivering material, while the right inset shows the scenario where infall leads to the formation of a misaligned outer disk during a late infall event. The cartoons were made by Martine Lützen, a former Master student at the Niels Bohr Institute.

4 Reflections and outlook

Since the first models of protostellar collapse of a spherical core (Larson, 1969), there have been a lot of successful efforts in improving our understanding of protostellar formation. It is possible to resolve the collapse with a resolution that even allows to model the dynamics within the inner one au of the forming protostar, while there also as has been systematical incorporation and testing of additional physical effects. Starting from the crucial assumption for disk formation of initial rotation, models have improved to a degree where it is possible to account for more subtle effects such as the role of the ionization rate or the dust size distribution on the resistivities, which modify the efficiency of magnetic braking of the forming disk.

Regarding initial and boundary conditions, the assumption of spherical collapse of an isolated prestellar core has proven to be successful as a the commonly used, fiducial assumption to test and compare the parameter space. In fact, the early ALMA images of dust continuum (Partnership et al., 2015; Andrews et al., 2018), despite their substructures and diversity, gave the impression as if the disks are indeed isolated entities that can be considered detached from the environment in which they are embedded in. However, today we know that there is a severe observational bias in observing dust emission at relatively large wavelength of about 1 mm. Gas observations of disks, reveal a different picture (Öberg et al., 2021) than dust continuum images obtained at $\sim 1$ mm wavelength. First, the gaseous parts of disks are significantly larger and less structured. The smaller size of the dusty parts of disks can be explained by radial drift of dust particles (Weidenschilling, 1977). Second, and of fundamental importance for our assumptions on the initial and boundary conditions of our models, there is clear evidence of filamentary arms, nowadays commonly referred to as streamers (Pineda et al., 2023). It is especially striking that HL Tau, the prime target of ALMA, hosts a prominent streamer (Yen et al., 2019) that impacts the disk (Garufi et al., 2022). By now, observations of various chemical tracers confirmed streamers on multiple scales ranging from small spiral-like features of a few 10 to 100 au in length around young disks with ongoing dust growth (Oph IRS63) (Segura-Cox et al., 2020; Flores et al., 2023; Segura-Cox, 2023) to arcs that are several 1,000 au in length associated with prestellar cores (Per-emb-2) (Pineda et al., 2020). There is also observational evidence for streamers associated with ongoing simultaneous star and planet formation in the cases of [BHB2007]-1 (Alves et al., 2020), and (Per-emb-50) (Valdivia-Mena et al., 2022). A systematic search of streamer candidates in NGC 1333 revealed a fraction of $\approx 40\%$ associated with young protostellar sources (Valdivia-Mena et al., 2024). The detection of large-scale streamers that are supposed to replenish the mass reservoir for star and disk formation is consistent with modeling results that predict infall of a substantial fraction of the accreting mass that was initially not bound to the prestellar core (Smith et al., 2011; Pelkonen et al., 2021; Kuffmeier et al., 2023). In addition, models of star formation in a Giant Molecular Cloud show that for many stars a significant amount of the final stellar mass accretes late (i.e., $>$100,000 years after stellar birth) and it is considered as a probable solution to the luminosity problem of protostars (Padoan et al., 2014). It is consistent with observations of streamers around more evolved Class II Young Stellar Objects such as AB Aur (Grady et al., 1999), SU Aur (Akiyama et al., 2019; Ginski et al., 2021), GM Aur, (Huang et al., 2021), Elias 2-27 (Paneque-Carreño et al., 2021), DR Tau (Mesa et al., 2022; Huang et al., 2023), RU Lup (Huang et al., 2020), DO Tau (Huang et al., 2022) as well as strong indications of late infall from statistics of reflection nebulae (Guptaet al., 2023).

As elaborated in Section 3.1, the late addition of gas with substantial angular momentum even offers an additional path to disk formation beyond the initial protostellar collapse phase. In agreement with earlier suggestions by Padoan et al. (2005), Kuffmeier et al. (2023) demonstrated that the larger contribution of late infall can explain the subtle trend of larger disk sizes for increasing mass of the corresponding host stars seen in CO observations (Long et al., 2022). Furthermore, the infall of material is typically misaligned with respect to the orientation of the star-disk system (Kuffmeier et al., 2024), especially at later stages (Pelkonen et al., 2024), leading to a more chaotic pathway of star-disk formation (Bate et al., 2010). Most recently, conceptual papers followed up on the possibility of post-collapse disk formation arguing that a significant amount of observed Class II disks are in fact the result of prolonged Bondi-Hoyle like accretion in the turbulent interstellar medium (Padoan et al., 2024; Winter et al., 2024). If this mode of second-generation disk formation proves to be significant, it also implies that interpreting surveys of stellar age-dependent disk fractions (Haisch et al., 2001; Mamajek, 2009; Richert et al., 2018) solely as an outcome of the evolution of either viscous or wind-driven disks (e.g., review by Manara et al., 2023, and references therein) is misleading. In the post-collapse infall picture, the lower fraction of disks around more evolved stars instead reflects the decreasing probability of experiencing mass replenishment through late gas encounters. Disks around older stars should instead be considered as either disks that experience prolonged mass replenishment or as second-generation disks that formed several million years after the initial protostellar collapse phase through post-collapse gas encounters.

Considering the compelling observational evidence, we have recently started to consider filamentary accretion via streamers as part of the disk formation process. The effect of infall on the processes in the disk and their impact on planet formation has only been poorly investigated yet, though infall through streamers may be of key importance (Bae et al., 2015; Lesur et al., 2015; Kuffmeier et al., 2018; Kuznetsova et al., 2022). In particular, infall likely plays an important role in.

• regulating the disk size,

• triggering instabilities in young disks and thereby initiating substructures,

• inducing misaligned disks visible as shadows in scattered light observations,

• seeding finite amplitude pressure traps,

• potentially modifying the chemical composition of planetary systems,

• resetting the disk entirely.

Also we commonly use the term ‘streamer’ regardless whether it describes filamentary infall on scales of $\sim$10 au onto a very young disk or a $\sim 10^3$ au elongated arm associated with an evolved YSO Class II object. All streamers, to some extent, reflect the turbulent nature of Giant Molecular Clouds, but there are indications from modeling that there are differences in their origin. While small-scale accretion streamers around young stars were already seen in spherical collapse models of individual protostars, larger scale arms around more evolved stars were best described by a star capturing material during an encounter with dense gas, for simplicity assumed as a cloudlet of gas in early models (Dullemond et al., 2019; Kuffmeier et al., 2020). This suggests that the small-scale streamers might be a direct outcome of gravitational collapse with perturbations induced by turbulence, whereas the latter is analogous to Bondi-Hoyle like accretion with an impact parameter. This interpretation would be consistent with the scenario that star formation is a two-stage process (Kuffmeier et al., 2023), or three-phase when including the process leading to core formation in the sequence (Padoan et al., 2020), consisting of an early collapse phase followed by an optional post-collapse phase of material that is initially not gravitationally bound to the collapsing core. Apart from that, the majority of stars is associated with stellar multiples (Duquennoy and Mayor, 1991; Connelley et al., 2008; Raghavan et al., 2010), and multiplicity is already common among young, deeply embedded protostars (Chen et al., 2013; Tobin et al., 2015). In this context, it will be important to consider the possible effects and perturbations through stellar interactions that may well affect the properties of disks, too (see for instance reviews by Offner et al., 2023; Cuello et al., 2023, and references therein).

What is lacking at the current stage is a model that allows us to distinguish between the relevance and occurrence of the different modes without an intrinsic bias in the model setup that favors or even excludes possibly important scenarios. A self-consistent model of the accretion process of star-disk systems with high resolution together with the molecular cloud dynamics for long enough times (i.e., beyond $\sim 1$ Myr) would fill this gap. Developing such models is particularly timely considering the progress in the field of planet formation. While it has been broad consensus that planets form in protoplanetary disks that themselves are a byproduct of the star formation process happening in Giant Molecular Clouds, the traditional understanding of considering disk formation isolated from the molecular cloud dynamics still is the leading paradigm when considering planet formation. This picture has been and is increasingly disrupted in recent years, such that we are moving to a more dynamic interconnected picture of star and planet formation. Since the advent of Herschel, it is clear that molecular clouds are filamentary in nature with cores generally forming associated with these filaments. This implies that the individual cores are less isolated than in the traditional illustration of a protostar that forms at the center of a symmetrical core. Moreover, observations of rings and gaps in dust continuum images of disks are commonly interpreted as signs of ongoing dust growth, which is a necessary precursor of planet formation. This led to a paradigm shift towards an onset of planet formation in embedded disks as it is reflected by a change in terminology from referring to circumstellar disks as ‘planet-forming’ rather than ‘protoplanetary’. Accepting the revised picture implies that planet formation already occurs at a time when the disk is still in its formation phase and prone to infall. Nowadays, star and planet formation are therefore considered as processes that are much more interlinked than we used to think for many decades.

From a technical point of view, the challenge for the upcoming years will be to connect state-of-the-art multi-physics models with multi-scale models that currently lack parts of the physics that is important for disk formation on smaller scales. Future models will allow us to fill the currently existing gap in understanding to what extent the properties of disks are governed by the protostellar environment and how frequent various outcomes such as infall-induced misaligned disks and instabilities are. The prospects in succeeding with this task are bright. Some models have already succeeded in resolving young disks with a resolution of less than 0.1 au in the context of a magnetized Giant Molecular Cloud that is $\sim 10$ au in scale. Others provided first synthetic disk populations based on disk formation in a star-forming clump with non-ideal MHD. The increasing necessity to account for the star formation process against the background of a presumably early onset of planet formation in embedded disks together with the tremendous development of computational resources and techniques for the exascale era of supercomputing, will presumably lead to rapid progress in our understanding of disk formation and evolution by the end of the decade.

Author contributions

MK: Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The research of MK is supported by a H2020 Marie Skłodowska-Curie Actions grant (897524) and a Carlsberg Reintegration Fellowship (CF22-1014).

Acknowledgments

MK thanks the two referees for constructive feedback and useful suggestions that helped to improve the quality of the manuscript. MK also thanks the organizers of the workshop Simulating Physics in Celestial Ecosystems (SPiCE) in Sendai, Japan, for an inspiring week full of exciting science and discussions.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akiyama, E., Vorobyov, E. I., Liu, H. B., Dong, R., de Leon, J., Liu, S.-Y., et al. (2019). A tail structure associated with a protoplanetary disk around SU aurigae. AJ 157, 165. doi:10.3847/1538-3881/ab0ae4

CrossRef Full Text | Google Scholar

Alexander, R., Pascucci, I., Andrews, S., Armitage, P., and Cieza, L. (2014). “The dispersal of protoplanetary disks,” in Protostars and planets VI. Editors H. Beuther, R. S. Klessen, C. P. Dullemond, and T. Henning, 475–496. doi:10.2458/azu_uapress_9780816531240-ch021

CrossRef Full Text | Google Scholar

Allen, A., Li, Z.-Y., and Shu, F. H. (2003). Collapse of magnetized singular isothermal toroids. II. Rotation and magnetic braking. ApJ 599, 363–379. doi:10.1086/379243

CrossRef Full Text | Google Scholar

Alves, F. O., Cleeves, L. I., Girart, J. M., Zhu, Z., Franco, G. A. P., Zurlo, A., et al. (2020). A case of simultaneous star and planet formation. ApJ 904, L6. doi:10.3847/2041-8213/abc550

CrossRef Full Text | Google Scholar

André, P., Di Francesco, J., Ward-Thompson, D., Inutsuka, S. I., Pudritz, R. E., and Pineda, J. E. (2014). “From filamentary networks to dense cores in molecular clouds: toward a new paradigm for Star Formation,” in Protostars and planets VI. Editors H. Beuther, R. S. Klessen, C. P. Dullemond, and T. Henning, 27–51. doi:10.2458/azu_uapress_9780816531240-ch002

CrossRef Full Text | Google Scholar

Andrews, S. M., Huang, J., Pérez, L. M., Isella, A., Dullemond, C. P., Kurtovic, N. T., et al. (2018). The disk substructures at high angular resolution project (DSHARP). I. Motivation, sample, calibration, and overview. ApJ 869, L41. doi:10.3847/2041-8213/aaf741

CrossRef Full Text | Google Scholar

Bae, J., Hartmann, L., and Zhu, Z. (2015). Are protoplanetary disks born with vortices? Rossby wave instability driven by protostellar infall. ApJ 805, 15. doi:10.1088/0004-637X/805/1/15

CrossRef Full Text | Google Scholar

Balsara, D. S., and Spicer, D. S. (1999). A staggered mesh algorithm using high order Godunov fluxes to ensure solenoidal magnetic fields in magnetohydrodynamic simulations. J. Comput. Phys. 149, 270–292. doi:10.1006/jcph.1998.6153

CrossRef Full Text | Google Scholar

Banerjee, R., Pudritz, R. E., and Holmes, L. (2004). The formation and evolution of protostellar discs; three-dimensional adaptive mesh refinement hydrosimulations of collapsing, rotating Bonnor-Ebert spheres. MNRAS 355, 248–272. doi:10.1111/j.1365-2966.2004.08316.x

CrossRef Full Text | Google Scholar

Bate, M. R. (1998). Collapse of a molecular cloud core to stellar densities: the first three-dimensional calculations. ApJ 508, L95–L98. doi:10.1086/311719

CrossRef Full Text | Google Scholar

Bate, M. R. (2010). Collapse of a molecular cloud core to stellar densities: the radiative impact of stellar core formation on the circumstellar disc. MNRAS 404, L79–L83. doi:10.1111/j.1745-3933.2010.00839.x

CrossRef Full Text | Google Scholar

Bate, M. R. (2018). On the diversity and statistical properties of protostellar discs. MNRAS 475, 5618–5658. doi:10.1093/mnras/sty169

CrossRef Full Text | Google Scholar

Bate, M. R. (2019). The statistical properties of stars and their dependence on metallicity. MNRAS 484, 2341–2361. doi:10.1093/mnras/stz103

CrossRef Full Text | Google Scholar

Bate, M. R. (2022). Dust coagulation during the early stages of star formation: molecular cloud collapse and first hydrostatic core evolution. MNRAS 514, 2145–2161. doi:10.1093/mnras/stac1391

CrossRef Full Text | Google Scholar

Bate, M. R., Bonnell, I. A., and Bromm, V. (2003). The formation of a star cluster: predicting the properties of stars and brown dwarfs. MNRAS 339, 577–599. doi:10.1046/j.1365-8711.2003.06210.x

CrossRef Full Text | Google Scholar

Bate, M. R., Lodato, G., and Pringle, J. E. (2010). Chaotic star formation and the alignment of stellar rotation with disc and planetary orbital axes. MNRAS 401, 1505–1513. doi:10.1111/j.1365-2966.2009.15773.x

CrossRef Full Text | Google Scholar

Bate, M. R., Tricco, T. S., and Price, D. J. (2014). Collapse of a molecular cloud core to stellar densities: stellar-core and outflow formation in radiation magnetohydrodynamic simulations. MNRAS 437, 77–95. doi:10.1093/mnras/stt1865

CrossRef Full Text | Google Scholar

Benz, W., Bowers, R. L., Cameron, A. G. W., and Press, W. H. (1990). Dynamic mass exchange in doubly degenerate binaries. I - 0.9 and 1.2 solar mass stars. ApJ 348, 647. doi:10.1086/168273

CrossRef Full Text | Google Scholar

Bergin, E. A., and Tafalla, M. (2007). Cold dark clouds: the initial conditions for Star Formation. ARA&A 45, 339–396. doi:10.1146/annurev.astro.45.071206.100404

CrossRef Full Text | Google Scholar

Bjerkeli, P., van der Wiel, M. H. D., Harsono, D., Ramsey, J. P., and Jørgensen, J. K. (2016). Resolved images of a protostellar outflow driven by an extended disk wind. Nature 540, 406–409. doi:10.1038/nature20600

PubMed Abstract | CrossRef Full Text | Google Scholar

Boss, A. P. (1997). Collapse and fragmentation of molecular cloud cores. V. Loss of magnetic field support. ApJ 483, 309–319. doi:10.1086/304213

CrossRef Full Text | Google Scholar

Boss, A. P. (1999). Collapse and fragmentation of molecular cloud cores. VI. Slowly rotating magnetic clouds. ApJ 520, 744–750. doi:10.1086/307479

CrossRef Full Text | Google Scholar

Boss, A. P. (2002). Collapse and fragmentation of molecular cloud cores. VII. Magnetic fields and multiple protostar formation. ApJ 568, 743–753. doi:10.1086/339040

CrossRef Full Text | Google Scholar

Braiding, C. R., and Wardle, M. (2012). The Hall effect in star formation. MNRAS 422, 261–281. doi:10.1111/j.1365-2966.2012.20601.x

CrossRef Full Text | Google Scholar

Brinch, C., Crapsi, A., Jørgensen, J. K., Hogerheijde, M. R., and Hill, T. (2007). A deeply embedded young protoplanetary disk around L1489 IRS observed by the Submillimeter Array. A&A 475, 915–923. doi:10.1051/0004-6361:20078249

CrossRef Full Text | Google Scholar

Bryan, G. L., Norman, M. L., O’Shea, B. W., Abel, T., Wise, J. H., Turk, M. J., et al. (2014). ENZO: an adaptive mesh refinement code for Astrophysics. ApJS 211, 19. doi:10.1088/0067-0049/211/2/19

CrossRef Full Text | Google Scholar

Burkert, A., and Bodenheimer, P. (1993). Multiple fragmentation in collapsing protostars. MNRAS 264, 798–806. doi:10.1093/mnras/264.4.798

CrossRef Full Text | Google Scholar

Cabedo, V., Maury, A., Girart, J. M., Padovani, M., Hennebelle, P., Houde, M., et al. (2023). Magnetically regulated collapse in the B335 protostar? II. Observational constraints on gas ionization and magnetic field coupling. A&A 669, A90. doi:10.1051/0004-6361/202243813

CrossRef Full Text | Google Scholar

Cacciapuoti, L., Testi, L., Podio, L., Codella, C., Maury, A. J., De Simone, M., et al. (2024). Protostellar chimney flues: are jets and outflows lifting submillimeter dust grains from disks into envelopes? ApJ 961, 90. doi:10.3847/1538-4357/ad0f17

CrossRef Full Text | Google Scholar

Caselli, P., Walmsley, C. M., Terzieva, R., and Herbst, E. (1998). The ionization fraction in dense cloud cores. ApJ 499, 234–249. doi:10.1086/305624

CrossRef Full Text | Google Scholar

Ceccarelli, C., Dominik, C., López-Sepulcre, A., Kama, M., Padovani, M., Caux, E., et al. (2014). Herschel finds evidence for stellar wind particles in a protostellar envelope: is this what happened to the young sun? ApJ 790, L1. doi:10.1088/2041-8205/790/1/L1

CrossRef Full Text | Google Scholar

Chen, X., Arce, H. G., Zhang, Q., Bourke, T. L., Launhardt, R., Jørgensen, J. K., et al. (2013). SMA observations of class 0 protostars: a high angular resolution survey of protostellar binary systems. ApJ 768, 110. doi:10.1088/0004-637X/768/2/110

CrossRef Full Text | Google Scholar

Ciolek, G. E., and Mouschovias, T. C. (1994). Ambipolar diffusion, interstellar dust, and the formation of cloud cores and protostars. 3: typical axisymmetric solutions. ApJ 425, 142. doi:10.1086/173971

CrossRef Full Text | Google Scholar

Codella, C., Cabrit, S., Gueth, F., Podio, L., Leurini, S., Bachiller, R., et al. (2014). The ALMA view of the protostellar system HH212. The wind, the cavity, and the disk. A&A 568, L5. doi:10.1051/0004-6361/201424103

CrossRef Full Text | Google Scholar

Commerçon, B., Debout, V., and Teyssier, R. (2014). A fast, robust, and simple implicit method for adaptive time-stepping on adaptive mesh-refinement grids. A&A 563, A11. doi:10.1051/0004-6361/201322858

CrossRef Full Text | Google Scholar

Commerçon, B., González, M., Mignon-Risse, R., Hennebelle, P., and Vaytet, N. (2022). Discs and outflows in the early phases of massive star formation: influence of magnetic fields and ambipolar diffusion. A&A 658, A52. doi:10.1051/0004-6361/202037479

CrossRef Full Text | Google Scholar

Commerçon, B., Hennebelle, P., Audit, E., Chabrier, G., and Teyssier, R. (2010). Protostellar collapse: radiative and magnetic feedbacks on small-scale fragmentation. A&A 510, L3. doi:10.1051/0004-6361/200913597

CrossRef Full Text | Google Scholar

Commerçon, B., Teyssier, R., Audit, E., Hennebelle, P., and Chabrier, G. (2011). Radiation hydrodynamics with adaptive mesh refinement and application to prestellar core collapse. I. Methods. A&A 529, A35. doi:10.1051/0004-6361/201015880

CrossRef Full Text | Google Scholar

Connelley, M. S., Reipurth, B., and Tokunaga, A. T. (2008). The evolution of the multiplicity of embedded protostars. II. Binary separation distribution and analysis. AJ 135, 2526–2536. doi:10.1088/0004-6256/135/6/2526

CrossRef Full Text | Google Scholar

Crutcher, R. M. (2012). Magnetic fields in molecular clouds. ARA&A 50, 29–63. doi:10.1146/annurev-astro-081811-125514

CrossRef Full Text | Google Scholar

Cuello, N., Ménard, F., and Price, D. J. (2023). Close encounters: how stellar flybys shape planet-forming discs. Eur. Phys. J. Plus 138, 11. doi:10.1140/epjp/s13360-022-03602-w

CrossRef Full Text | Google Scholar

Dapp, W. B., and Basu, S. (2010). Averting the magnetic braking catastrophe on small scales: disk formation due to Ohmic dissipation. A&A 521, L56. doi:10.1051/0004-6361/201015700

CrossRef Full Text | Google Scholar

Dapp, W. B., Basu, S., and Kunz, M. W. (2012). Bridging the gap: disk formation in the Class 0 phase with ambipolar diffusion and Ohmic dissipation. A&A 541, A35. doi:10.1051/0004-6361/201117876

CrossRef Full Text | Google Scholar

Das, I., and Basu, S. (2021). Linear stability analysis of a magnetic rotating disk with ohmic dissipation and ambipolar diffusion. ApJ 910, 163. doi:10.3847/1538-4357/abdb2c

CrossRef Full Text | Google Scholar

Donati, J. F., Skelly, M. B., Bouvier, J., Gregory, S. G., Grankin, K. N., Jardine, M. M., et al. (2010). Magnetospheric accretion and spin-down of the prototypical classical T Tauri star AA Tau. MNRAS 409, 1347–1361. doi:10.1111/j.1365-2966.2010.17409.x

CrossRef Full Text | Google Scholar

Duffin, D. F., and Pudritz, R. E. (2009). The early history of protostellar disks, outflows, and binary stars. ApJ 706, L46–L51. doi:10.1088/0004-637X/706/1/L46

CrossRef Full Text | Google Scholar

Dullemond, C. P., Küffmeier, M., Goicovic, F., Fukagawa, M., Oehl, V., and Kramer, M. (2019). Cloudlet capture by transitional disk and FU Orionis stars. A&A 628, A20. doi:10.1051/0004-6361/201832632

CrossRef Full Text | Google Scholar

Duquennoy, A., and Mayor, M. (1991). Multiplicity among solar type stars in the solar neighbourhood - Part Two - distribution of the orbital elements in an unbiased sample. A&A 248, 485.

Google Scholar

Elsender, D., and Bate, M. R. (2021). The statistical properties of protostellar discs and their dependence on metallicity. MNRAS 508, 5279–5295. doi:10.1093/mnras/stab2901

CrossRef Full Text | Google Scholar

Elsender, D., Bate, M. R., Lakeland, B. S., Jensen, E. L. N., and Lubow, S. H. (2023). On the frequencies of circumbinary discs in protostellar systems. MNRAS 523, 4353–4364. doi:10.1093/mnras/stad1695

CrossRef Full Text | Google Scholar

Evans, C. R., and Hawley, J. F. (1988). Simulation of magnetohydrodynamic flows: a constrained transport model. ApJ 332, 659. doi:10.1086/166684

CrossRef Full Text | Google Scholar

Favre, C., Ceccarelli, C., López-Sepulcre, A., Fontani, F., Neri, R., Manigand, S., et al. (2018). SOLIS IV. Hydrocarbons in the OMC-2 FIR4 region, a probe of energetic particle irradiation of the region. ApJ 859, 136. doi:10.3847/1538-4357/aabfd4

CrossRef Full Text | Google Scholar

Flores, C., Ohashi, N., Tobin, J. J., Jørgensen, J. K., Takakuwa, S., Li, Z.-Y., et al. (2023). Early planet formation in embedded disks (eDisk) XII: accretion streamers, protoplanetary disk, and outflow in the Class I source oph IRS63. arXiv e-prints, arXiv:2310.14617. doi:10.48550/arXiv.2310.14617

CrossRef Full Text | Google Scholar

Fontani, F., Ceccarelli, C., Favre, C., Caselli, P., Neri, R., Sims, I. R., et al. (2017). Seeds of life in space (SOLIS): I. Carbon-Chain growth in the solar-type protocluster OMC2-fir4⋆⋆⋆. A&A 605, A57. doi:10.1051/0004-6361/201730527

CrossRef Full Text | Google Scholar

Fromang, S., Hennebelle, P., and Teyssier, R. (2006). A high order Godunov scheme with constrained transport and adaptive mesh refinement for astrophysical magnetohydrodynamics. A&A 457, 371–384. doi:10.1051/0004-6361:20065371

CrossRef Full Text | Google Scholar

Fryxell, B., Olson, K., Ricker, P., Timmes, F. X., Zingale, M., Lamb, D. Q., et al. (2000). FLASH: an adaptive mesh hydrodynamics code for modeling astrophysical thermonuclear flashes. ApJS 131, 273–334. doi:10.1086/317361

CrossRef Full Text | Google Scholar

Fukushima, H., Yajima, H., Sugimura, K., Hosokawa, T., Omukai, K., and Matsumoto, T. (2020). Star cluster formation and cloud dispersal by radiative feedback: dependence on metallicity and compactness. MNRAS 497, 3830–3845. doi:10.1093/mnras/staa2062

CrossRef Full Text | Google Scholar

Gaches, B. A. L., and Offner, S. S. R. (2018). Exploration of cosmic-ray acceleration in protostellar accretion shocks and a model for ionization rates in embedded protoclusters. ApJ 861, 87. doi:10.3847/1538-4357/aac94d

CrossRef Full Text | Google Scholar

Galli, D., Lizano, S., Shu, F. H., and Allen, A. (2006). Gravitational collapse of magnetized clouds. I. Ideal magnetohydrodynamic accretion flow. ApJ 647, 374–381. doi:10.1086/505257

CrossRef Full Text | Google Scholar

Galli, D., and Shu, F. H. (1993a). Collapse of magnetized molecular cloud cores. I. Semianalytical solution. ApJ 417, 220. doi:10.1086/173305

CrossRef Full Text | Google Scholar

Galli, D., and Shu, F. H. (1993b). Collapse of magnetized molecular cloud cores. II. Numerical results. ApJ 417, 243. doi:10.1086/173306

CrossRef Full Text | Google Scholar

Garufi, A., Podio, L., Codella, C., Segura-Cox, D., Vander Donckt, M., Mercimek, S., et al. (2022). ALMA chemical survey of disk-outflow sources in Taurus (ALMA-DOT). VI. Accretion shocks in the disk of DG Tau and HL Tau. A&A 658, A104. doi:10.1051/0004-6361/202141264

CrossRef Full Text | Google Scholar

Ginski, C., Facchini, S., Huang, J., Benisty, M., Vaendel, D., Stapper, L., et al. (2021). Disk evolution study through imaging of nearby young stars (DESTINYS): late infall causing disk misalignment and dynamic structures in SU Aur. ApJ 908, L25. doi:10.3847/2041-8213/abdf57

CrossRef Full Text | Google Scholar

Goodwin, S. P., Whitworth, A. P., and Ward-Thompson, D. (2004). Simulating star formation in molecular cloud cores. I. The influence of low levels of turbulence on fragmentation and multiplicity. A&A 414, 633–650. doi:10.1051/0004-6361:20031594

CrossRef Full Text | Google Scholar

Grady, C. A., Woodgate, B., Bruhweiler, F. C., Boggess, A., Plait, P., Lindler, D. J., et al. (1999). [ITAL]Hubble space telescope[/ITAL] space telescope imaging spectrograph coronagraphic imaging of the Herbig ae star AB aurigae. ApJ 523, L151–L154. doi:10.1086/312270

CrossRef Full Text | Google Scholar

Gray, W. J., McKee, C. F., and Klein, R. I. (2018). Effect of angular momentum alignment and strong magnetic fields on the formation of protostellar discs. MNRAS 473, 2124–2143. doi:10.1093/mnras/stx2406

CrossRef Full Text | Google Scholar

Grudić, M. Y., Guszejnov, D., Hopkins, P. F., Offner, S. S. R., and Faucher-Giguère, C.-A. (2021). STARFORGE: towards a comprehensive numerical model of star cluster formation and feedback. MNRAS 506, 2199–2231. doi:10.1093/mnras/stab1347

CrossRef Full Text | Google Scholar

Gupta, A., Miotello, A., Manara, C. F., Williams, J. P., Facchini, S., Beccari, G., et al. (2023). Reflections on nebulae around young stars. A systematic search for late-stage infall of material onto Class II disks. A&A 670, L8. doi:10.1051/0004-6361/202245254

CrossRef Full Text | Google Scholar

Guszejnov, D., Grudić, M. Y., Hopkins, P. F., Offner, S. S. R., and Faucher-Giguère, C.-A. (2021). STARFORGE: the effects of protostellar outflows on the IMF. MNRAS 502, 3646–3663. doi:10.1093/mnras/stab278

CrossRef Full Text | Google Scholar

Guszejnov, D., Grudić, M. Y., Offner, S. S. R., Faucher-Giguère, C.-A., Hopkins, P. F., and Rosen, A. L. (2022). Effects of the environment and feedback physics on the initial mass function of stars in the STARFORGE simulations. MNRAS 515, 4929–4952. doi:10.1093/mnras/stac2060

CrossRef Full Text | Google Scholar

Hacar, A., Clark, S. E., Heitsch, F., Kainulainen, J., Panopoulou, G. V., Seifried, D., et al. (2023). “Initial conditions for Star Formation: a physical description of the filamentary ISM,” in Protostars and planets VII. Editors S. Inutsuka, Y. Aikawa, T. Muto, K. Tomida, and M. Tamura (San Francisco: Astronomical Society of the Pacific Conference Series), 534, 153. doi:10.48550/arXiv.2203.09562

CrossRef Full Text | Google Scholar

Haisch, J., Karl, E., Lada, E. A., and Lada, C. J. (2001). Disk frequencies and lifetimes in young clusters. ApJ 553, L153–L156. doi:10.1086/320685

CrossRef Full Text | Google Scholar

Hanawa, T., Garufi, A., Podio, L., Codella, C., and Segura-Cox, D. (2024). Cloudlet capture model for the accretion streamer onto the disc of DG Tau. MNRAS 528, 6581–6592. doi:10.1093/mnras/stae338

CrossRef Full Text | Google Scholar

Hanawa, T., Sakai, N., and Yamamoto, S. (2022). Cloudlet capture model for asymmetric molecular emission lines observed in TMC-1A with ALMA. ApJ 932, 122. doi:10.3847/1538-4357/ac6e6a

CrossRef Full Text | Google Scholar

Harsono, D., Jørgensen, J. K., van Dishoeck, E. F., Hogerheijde, M. R., Bruderer, S., Persson, M. V., et al. (2014). Rotationally-supported disks around Class I sources in Taurus: disk formation constraints. A&A 562, A77. doi:10.1051/0004-6361/201322646

CrossRef Full Text | Google Scholar

He, C.-C., and Ricotti, M. (2023). Massive pre-stellar cores in radiation-magneto-turbulent simulations of molecular clouds. MNRAS 522, 5374–5392. doi:10.1093/mnras/stad1289

CrossRef Full Text | Google Scholar

Heigl, S., Hoemann, E., and Burkert, A. (2024). Protostellar disk accretion in turbulent filaments. arXiv e-prints, arXiv:2401.03779. doi:10.48550/arXiv.2401.03779

CrossRef Full Text | Google Scholar

Hennebelle, P., and Ciardi, A. (2009). Disk formation during collapse of magnetized protostellar cores. A&A 506, L29–L32. doi:10.1051/0004-6361/200913008

CrossRef Full Text | Google Scholar

Hennebelle, P., Commerçon, B., Chabrier, G., and Marchand, P. (2016). Magnetically self-regulated formation of early protoplanetary disks. ApJ 830, L8. doi:10.3847/2041-8205/830/1/L8

CrossRef Full Text | Google Scholar

Hennebelle, P., Commerçon, B., Lee, Y.-N., and Charnoz, S. (2020). What determines the formation and characteristics of protoplanetary discs? A&A 635, A67. doi:10.1051/0004-6361/201936714

CrossRef Full Text | Google Scholar

Hennebelle, P., and Fromang, S. (2008). Magnetic processes in a collapsing dense core. I. Accretion and ejection. A&A 477, 9–24. doi:10.1051/0004-6361:20078309

CrossRef Full Text | Google Scholar

Hopkins, P. F. (2014). GIZMO: multi-method magneto-hydrodynamics + gravity code. Astrophys. Source Code Libr. Rec. ascl:1410.003.

Google Scholar

Hopkins, P. F. (2015). A new class of accurate, mesh-free hydrodynamic simulation methods. MNRAS 450, 53–110. doi:10.1093/mnras/stv195

CrossRef Full Text | Google Scholar

Hopkins, P. F. (2017). A new public release of the GIZMO code. arXiv e-prints, arXiv:1712.01294. doi:10.48550/arXiv.1712.01294

CrossRef Full Text | Google Scholar

Huang, J., Andrews, S. M., Öberg, K. I., Ansdell, M., Benisty, M., Carpenter, J. M., et al. (2020). Large-scale CO spiral arms and complex kinematics associated with the T tauri star RU Lup. ApJ 898, 140. doi:10.3847/1538-4357/aba1e1

CrossRef Full Text | Google Scholar

Huang, J., Bergin, E. A., Bae, J., Benisty, M., and Andrews, S. M. (2023). Molecular mapping of DR tau’s protoplanetary disk, envelope, outflow, and large-scale spiral arm. ApJ 943, 107. doi:10.3847/1538-4357/aca89c

CrossRef Full Text | Google Scholar

Huang, J., Bergin, E. A., Öberg, K. I., Andrews, S. M., Teague, R., Law, C. J., et al. (2021). Molecules with ALMA at planet-forming scales (MAPS). XIX. Spiral arms, a tail, and diffuse structures traced by CO around the GM Aur disk. ApJS 257, 19. doi:10.3847/1538-4365/ac143e

CrossRef Full Text | Google Scholar

Huang, J., Ginski, C., Benisty, M., Ren, B., Bohn, A. J., Choquet, É., et al. (2022). Disk evolution study through imaging of nearby young stars (destinys): a panchromatic view of do tau’s complex kilo-astronomical-unit environment. ApJ 930, 171. doi:10.3847/1538-4357/ac63ba

CrossRef Full Text | Google Scholar

Indriolo, N., and McCall, B. J. (2012). INVESTIGATING THE COSMIC-RAY IONIZATION RATE IN THE GALACTIC DIFFUSE INTERSTELLAR MEDIUM THROUGH OBSERVATIONS OF H⁺₃. ApJ 745, 91. doi:10.1088/0004-637X/745/1/91

CrossRef Full Text | Google Scholar

Inutsuka, S.-i., Machida, M. N., and Matsumoto, T. (2010). Emergence of protoplanetary disks and successive formation of gaseous planets by gravitational instability. ApJ 718, L58–L62. doi:10.1088/2041-8205/718/2/L58

CrossRef Full Text | Google Scholar

Iwasaki, K., and Inutsuka, S.-I. (2011). Smoothed particle magnetohydrodynamics with a Riemann solver and the method of characteristics. MNRAS 418, 1668–1688. doi:10.1111/j.1365-2966.2011.19588.x

CrossRef Full Text | Google Scholar

Joos, M., Hennebelle, P., and Ciardi, A. (2012). Protostellar disk formation and transport of angular momentum during magnetized core collapse. A&A 543, A128. doi:10.1051/0004-6361/201118730

CrossRef Full Text | Google Scholar

Joos, M., Hennebelle, P., Ciardi, A., and Fromang, S. (2013). The influence of turbulence during magnetized core collapse and its consequences on low-mass star formation. A&A 554, A17. doi:10.1051/0004-6361/201220649

CrossRef Full Text | Google Scholar

Jørgensen, J. K., van Dishoeck, E. F., Visser, R., Bourke, T. L., Wilner, D. J., Lommen, D., et al. (2009). PROSAC: a submillimeter array survey of low-mass protostars. II. The mass evolution of envelopes, disks, and stars from the Class 0 through I stages. A&A 507, 861–879. doi:10.1051/0004-6361/200912325

CrossRef Full Text | Google Scholar

Kainulainen, J., Stutz, A. M., Stanke, T., Abreu-Vicente, J., Beuther, H., Henning, T., et al. (2017). Resolving the fragmentation of high line-mass filaments with ALMA: the integral shaped filament in Orion A. A&A 600, A141. doi:10.1051/0004-6361/201628481

CrossRef Full Text | Google Scholar

Kataoka, A., Tsukagoshi, T., Momose, M., Nagai, H., Muto, T., Dullemond, C. P., et al. (2016). Submillimeter polarization observation of the protoplanetary disk around HD 142527. ApJ 831, L12. doi:10.3847/2041-8205/831/2/L12

CrossRef Full Text | Google Scholar

Kim, J.-G., Kim, W.-T., and Ostriker, E. C. (2018). Modeling UV radiation feedback from massive stars. II. Dispersal of star-forming giant molecular clouds by photoionization and radiation pressure. ApJ 859, 68. doi:10.3847/1538-4357/aabe27

CrossRef Full Text | Google Scholar

Klein, R. I. (1999). Star formation with 3-D adaptive mesh refinement: the collapse and fragmentation of molecular clouds. J. Comput. Appl. Math. 109, 123–152. doi:10.1016/s0377-0427(99)00156-9

CrossRef Full Text | Google Scholar

Kobayashi, Y., Takaishi, D., and Tsukamoto, Y. (2023). Cosmic ray ionization rate versus dust fraction: which plays a crucial role in the early evolution of the circumstellar disc? MNRAS 521, 2661–2669. doi:10.1093/mnras/stad711

CrossRef Full Text | Google Scholar

Koga, S., Tsukamoto, Y., Okuzumi, S., and Machida, M. N. (2019). Dependence of Hall coefficient on grain size and cosmic ray rate and implication for circumstellar disc formation. MNRAS 484, 2119–2136. doi:10.1093/mnras/sty3524

CrossRef Full Text | Google Scholar

Krasnopolsky, R., Li, Z.-Y., and Shang, H. (2010). Disk Formation enabled by enhanced resistivity. ApJ 716, 1541–1550. doi:10.1088/0004-637X/716/2/1541

CrossRef Full Text | Google Scholar

Krasnopolsky, R., Li, Z.-Y., and Shang, H. (2011). Disk Formation in magnetized clouds enabled by the Hall effect. ApJ 733, 54. doi:10.1088/0004-637X/733/1/54

CrossRef Full Text | Google Scholar

Krasnopolsky, R., Li, Z.-Y., Shang, H., and Zhao, B. (2012). Protostellar accretion flows destabilized by magnetic flux redistribution. ApJ 757, 77. doi:10.1088/0004-637X/757/1/77

CrossRef Full Text | Google Scholar

Kratter, K. M., Matzner, C. D., Krumholz, M. R., and Klein, R. I. (2010). On the role of disks in the formation of stellar systems: a numerical parameter study of rapid accretion. ApJ 708, 1585–1597. doi:10.1088/0004-637X/708/2/1585

CrossRef Full Text | Google Scholar

Krieger, A., Kuffmeier, M., Reissl, S., Dullemond, C. P., Ginski, C., and Wolf, S. (2024). Feasibility of detecting shadows in disks induced by infall. arXiv e-prints, arXiv:2403.08388. doi:10.48550/arXiv.2403.08388

CrossRef Full Text | Google Scholar

Krumholz, M. R., Crutcher, R. M., and Hull, C. L. H. (2013). Protostellar disk formation enabled by weak, misaligned magnetic fields. ApJl 767, L11. doi:10.1088/2041-8205/767/1/L11

CrossRef Full Text | Google Scholar

Kuffmeier, M., Calcutt, H., and Kristensen, L. E. (2019). The bridge: a transient phenomenon of forming stellar multiples. Sequential formation of stellar companions in filaments around young protostars. A&A 628, A112. doi:10.1051/0004-6361/201935504

CrossRef Full Text | Google Scholar

Kuffmeier, M., Dullemond, C. P., Reissl, S., and Goicovic, F. G. (2021). Misaligned disks induced by infall. A&A 656, A161. doi:10.1051/0004-6361/202039614

CrossRef Full Text | Google Scholar

Kuffmeier, M., Frimann, S., Jensen, S. S., and Haugbølle, T. (2018). Episodic accretion: the interplay of infall and disc instabilities. MNRAS 475, 2642–2658. doi:10.1093/mnras/sty024

CrossRef Full Text | Google Scholar

Kuffmeier, M., Goicovic, F. G., and Dullemond, C. P. (2020). Late encounter events as source of disks and spiral structures. Forming second generation disks. A&A 633, A3. doi:10.1051/0004-6361/201936820

CrossRef Full Text | Google Scholar

Kuffmeier, M., Haugbølle, T., and Nordlund, Å. (2017). Zoom-in simulations of protoplanetary disks starting from GMC scales. ApJ 846, 7. doi:10.3847/1538-4357/aa7c64

CrossRef Full Text | Google Scholar

Kuffmeier, M., Jensen, S. S., and Haugbølle, T. (2023). Rejuvenating infall: a crucial yet overlooked source of mass and angular momentum. Eur. Phys. J. Plus 138, 272. doi:10.1140/epjp/s13360-023-03880-y

CrossRef Full Text | Google Scholar

Kuffmeier, M., Pineda, J. E., Segura-Cox, D., and Haugbølle, T. (2024). Constraints on the (re-)orientation of star-disk systems through infall. arXiv e-prints, arXiv:2405.12670.

Google Scholar

Kuffmeier, M., Zhao, B., and Caselli, P. (2020). Ionization: a possible explanation for the difference of mean disk sizes in star-forming regions. A&A 639, A86. doi:10.1051/0004-6361/201937328

CrossRef Full Text | Google Scholar

Kuruwita, R. L., and Federrath, C. (2019). The role of turbulence during the formation of circumbinary discs. MNRAS 486, 3647–3663. doi:10.1093/mnras/stz1053

CrossRef Full Text | Google Scholar

Kuznetsova, A., Bae, J., Hartmann, L., and Mac Low, M.-M. (2022). Anisotropic infall and substructure formation in embedded disks. ApJ 928, 92. doi:10.3847/1538-4357/ac54a8

CrossRef Full Text | Google Scholar

Kuznetsova, A., Hartmann, L., and Heitsch, F. (2019). The origins of protostellar core angular momenta. ApJ 876, 33. doi:10.3847/1538-4357/ab12ce

CrossRef Full Text | Google Scholar

Kuznetsova, A., Hartmann, L., and Heitsch, F. (2020). Angular momenta, magnetization, and accretion of protostellar cores. ApJ 893, 73. doi:10.3847/1538-4357/ab7eac

CrossRef Full Text | Google Scholar

Lam, K. H., Li, Z.-Y., Chen, C.-Y., Tomida, K., and Zhao, B. (2019). Disc formation in magnetized dense cores with turbulence and ambipolar diffusion. MNRAS 489, 5326–5347. doi:10.1093/mnras/stz2436

CrossRef Full Text | Google Scholar

Larson, R. B. (1969). Numerical calculations of the dynamics of a collapsing proto-star*. MNRAS 145, 271–295. doi:10.1093/mnras/145.3.271

CrossRef Full Text | Google Scholar

Lebreuilly, U., Commerçon, B., and Laibe, G. (2020). Protostellar collapse: the conditions to form dust-rich protoplanetary disks. A&A 641, A112. doi:10.1051/0004-6361/202038174

CrossRef Full Text | Google Scholar

Lebreuilly, U., Hennebelle, P., Colman, T., Commerçon, B., Klessen, R., Maury, A., et al. (2021). Protoplanetary disk birth in massive star-forming clumps: the essential role of the magnetic field. ApJl 917, L10. doi:10.3847/2041-8213/ac158c

CrossRef Full Text | Google Scholar

Lebreuilly, U., Hennebelle, P., Colman, T., Maury, A., Tung, N. D., Testi, L., et al. (2024a). Synthetic populations of protoplanetary disks: impact of magnetic fields and radiative transfer. A&A 682, A30. doi:10.1051/0004-6361/202346558

CrossRef Full Text | Google Scholar

Lebreuilly, U., Hennebelle, P., Maury, A., González, M., Traficante, A., Klessen, R., et al. (2024b). Influence of protostellar outflows on star and protoplanetary disk formation in a massive star-forming clump. A&A 683, A13. doi:10.1051/0004-6361/202347913

CrossRef Full Text | Google Scholar

Lebreuilly, U., Vallucci-Goy, V., Guillet, V., Lombart, M., and Marchand, P. (2023). Protostellar collapse simulations in spherical geometry with dust coagulation and fragmentation. MNRAS 518, 3326–3343. doi:10.1093/mnras/stac3220

CrossRef Full Text | Google Scholar

Lee, A. T., Offner, S. S. R., Kratter, K. M., Smullen, R. A., and Li, P. S. (2019). The Formation and evolution of wide-orbit stellar multiples in magnetized clouds. ApJ 887, 232. doi:10.3847/1538-4357/ab584b

CrossRef Full Text | Google Scholar

Lee, C.-F. (2011). A rotating disk in the HH 111 protostellar system. ApJ 741, 62. doi:10.1088/0004-637X/741/1/62

CrossRef Full Text | Google Scholar

Lee, C.-F., Hwang, H.-C., Ching, T.-C., Hirano, N., Lai, S.-P., Rao, R., et al. (2018). Unveiling a magnetized jet from a low-mass protostar. Nat. Commun. 9, 4636. doi:10.1038/s41467-018-07143-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, C.-F., Li, Z.-Y., Yang, H., Daniel Lin, Z.-Y., Ching, T.-C., and Lai, S.-P. (2021a). What produces dust polarization in the HH 212 protostellar disk at 878 \mum: dust self-scattering or dichroic extinction? ApJ 910, 75. doi:10.3847/1538-4357/abe53a

CrossRef Full Text | Google Scholar

Lee, Y.-N., Charnoz, S., and Hennebelle, P. (2021b). Protoplanetary disk formation from the collapse of a prestellar core. A&A 648, A101. doi:10.1051/0004-6361/202038105

CrossRef Full Text | Google Scholar

Lee, Y.-N., Ray, B., Marchand, P., and Hennebelle, P. (2024). Protoplanetary disk size under non-ideal magnetohydrodynamics: a general formalism with inclined magnetic field. arXiv e-prints, 02845doi. arXiv:2401. doi:10.48550/arXiv.2401.02845

CrossRef Full Text | Google Scholar

Le Gouellec, V. J. M., Maury, A. J., Guillet, V., Hull, C. L. H., Girart, J. M., Verliat, A., et al. (2020). A statistical analysis of dust polarization properties in ALMA observations of Class 0 protostellar cores. A&A 644, A11. doi:10.1051/0004-6361/202038404

CrossRef Full Text | Google Scholar

Lesur, G., Flock, M., Ercolano, B., Lin, M., Yang, C., Barranco, J. A., et al. (2023). “Hydro-, magnetohydro-, and dust-gas dynamics of protoplanetary disks,” in Astronomical society of the pacific conference series. Editors S. Inutsuka, Y. Aikawa, T. Muto, K. Tomida, and M. Tamura (San Francisco: Astronomical Society of the Pacific Conference Series), 534, 465.

Google Scholar

Lesur, G., Hennebelle, P., and Fromang, S. (2015). Spiral-driven accretion in protoplanetary discs. I. 2D models. A&A 582, L9. doi:10.1051/0004-6361/201526734

CrossRef Full Text | Google Scholar

Li, Z.-Y., Krasnopolsky, R., and Shang, H. (2011). Non-ideal MHD effects and magnetic braking catastrophe in protostellar disk formation. ApJ 738, 180. doi:10.1088/0004-637X/738/2/180

CrossRef Full Text | Google Scholar

Li, Z.-Y., Krasnopolsky, R., and Shang, H. (2013). Does magnetic-field-rotation misalignment solve the magnetic braking catastrophe in protostellar disk formation? ApJ 774, 82. doi:10.1088/0004-637X/774/1/82

CrossRef Full Text | Google Scholar

Li, Z.-Y., Krasnopolsky, R., Shang, H., and Zhao, B. (2014). On the role of pseudodisk warping and reconnection in protostellar disk formation in turbulent magnetized cores. ApJ 793, 130. doi:10.1088/0004-637X/793/2/130

CrossRef Full Text | Google Scholar

Lommen, D., Jørgensen, J. K., van Dishoeck, E. F., and Crapsi, A. (2008). SMA observations of young disks: separating envelope, disk, and stellar masses in class I YSOs. A&A 481, 141–147. doi:10.1051/0004-6361:20077543

CrossRef Full Text | Google Scholar

Londrillo, P., and del Zanna, L. (2004). On the divergence-free condition in Godunov-type schemes for ideal magnetohydrodynamics: the upwind constrained transport method. J. Comput. Phys. 195, 17–48. doi:10.1016/j.jcp.2003.09.016

CrossRef Full Text | Google Scholar

Long, F., Andrews, S. M., Rosotti, G., Harsono, D., Pinilla, P., Wilner, D. J., et al. (2022). Gas disk sizes from CO line observations: a test of angular momentum evolution. ApJ 931, 6. doi:10.3847/1538-4357/ac634e

CrossRef Full Text | Google Scholar

Lüst, R., and Schlüter, A. (1955). Drehimpulstransport durch Magnetfelder und die Abbremsung rotierender Sterne. Mit 4 Textabbildungen. ZAp 38, 190.

Google Scholar

Machida, M. N., and Basu, S. (2019). The first two thousand years of Star Formation. ApJ 876, 149. doi:10.3847/1538-4357/ab18a7

CrossRef Full Text | Google Scholar

Machida, M. N., Inutsuka, S.-i., and Matsumoto, T. (2007). Magnetic fields and rotations of protostars. ApJ 670, 1198–1213. doi:10.1086/521779

CrossRef Full Text | Google Scholar

Machida, M. N., Inutsuka, S.-i., and Matsumoto, T. (2010). Formation process of the circumstellar disk: long-term simulations in the main accretion phase of star Formation. ApJ 724, 1006–1020. doi:10.1088/0004-637X/724/2/1006

CrossRef Full Text | Google Scholar

Machida, M. N., Inutsuka, S.-I., and Matsumoto, T. (2011). Effect of magnetic braking on circumstellar disk formation in a strongly magnetized cloud. PASJ 63, 555–573. doi:10.1093/pasj/63.3.555

CrossRef Full Text | Google Scholar

Machida, M. N., Inutsuka, S.-i., and Matsumoto, T. (2014). Conditions for circumstellar disc formation: effects of initial cloud configuration and sink treatment. MNRAS 438, 2278–2306. doi:10.1093/mnras/stt2343

CrossRef Full Text | Google Scholar

Machida, M. N., and Matsumoto, T. (2011). The origin and formation of the circumstellar disc. MNRAS 413, 2767–2784. doi:10.1111/j.1365-2966.2011.18349.x

CrossRef Full Text | Google Scholar

Machida, M. N., Matsumoto, T., Tomisaka, K., and Hanawa, T. (2005). Collapse and fragmentation of rotating magnetized clouds - I. Magnetic flux-spin relation. MNRAS 362, 369–381. doi:10.1111/j.1365-2966.2005.09297.x

CrossRef Full Text | Google Scholar

Mac Low, M.-M., Norman, M. L., Konigl, A., and Wardle, M. (1995). Incorporation of ambipolar diffusion into the ZEUS magetohydrodynamics code. ApJ 442, 726. doi:10.1086/175477

CrossRef Full Text | Google Scholar

Mamajek, E. E. (2009). “Initial conditions of planet formation: lifetimes of primordial disks,”. Exoplanets and disks: their formation and diversity. Editors T. Usuda, M. Tamura, and M. Ishii (American Institute of Physics Conference Series), 1158, 3–10. doi:10.1063/1.3215910

CrossRef Full Text | Google Scholar

Manara, C. F., Ansdell, M., Rosotti, G. P., Hughes, A. M., Armitage, P. J., Lodato, G., et al. (2023). “Demographics of young stars and their protoplanetary disks: lessons learned on disk evolution and its connection to planet formation,”. Protostars and planets VII. Editors S. Inutsuka, Y. Aikawa, T. Muto, K. Tomida, and M. Tamura (San Francisco: Astronomical Society of the Pacific Conference Series), 534, 539. doi:10.48550/arXiv.2203.09930

CrossRef Full Text | Google Scholar

Marchand, P., Commerçon, B., and Chabrier, G. (2018). Impact of the Hall effect in star formation and the issue of angular momentum conservation. A&A 619, A37. doi:10.1051/0004-6361/201832907

CrossRef Full Text | Google Scholar

Marchand, P., Masson, J., Chabrier, G., Hennebelle, P., Commerçon, B., and Vaytet, N. (2016). Chemical solver to compute molecule and grain abundances and non-ideal MHD resistivities in prestellar core-collapse calculations. A&A 592, A18. doi:10.1051/0004-6361/201526780

CrossRef Full Text | Google Scholar

Marchand, P., Tomida, K., Commerçon, B., and Chabrier, G. (2019). Impact of the Hall effect in star formation, improving the angular momentum conservation. A&A 631, A66. doi:10.1051/0004-6361/201936215

CrossRef Full Text | Google Scholar

Marchand, P., Tomida, K., Tanaka, K. E. I., Commerçon, B., and Chabrier, G. (2020). Protostellar collapse: regulation of the angular momentum and onset of an ionic precursor. ApJ 900, 180. doi:10.3847/1538-4357/abad99

CrossRef Full Text | Google Scholar

Masson, J., Chabrier, G., Hennebelle, P., Vaytet, N., and Commerçon, B. (2016). Ambipolar diffusion in low-mass star formation. I. General comparison with the ideal magnetohydrodynamic case. A&A 587, A32. doi:10.1051/0004-6361/201526371

CrossRef Full Text | Google Scholar

Matsumoto, T. (2007). Self-gravitational magnetohydrodynamics with adaptive mesh refinement for protostellar collapse. PASJ 59, 905–927. doi:10.1093/pasj/59.5.905

CrossRef Full Text | Google Scholar

Matsumoto, T., and Hanawa, T. (2003). Fragmentation of a molecular cloud core versus fragmentation of the massive protoplanetary disk in the main accretion phase. ApJ 595, 913–934. doi:10.1086/377367

CrossRef Full Text | Google Scholar

Matsumoto, T., Machida, M. N., and Inutsuka, S.-i. (2017). Circumstellar disks and outflows in turbulent molecular cloud cores: possible formation mechanism for misaligned systems. ApJ 839, 69. doi:10.3847/1538-4357/aa6a1c

CrossRef Full Text | Google Scholar

Matsumoto, T., and Tomisaka, K. (2004). Directions of outflows, disks, magnetic fields, and rotation of young stellar objects in collapsing molecular cloud cores. ApJ 616, 266–282. doi:10.1086/424897

CrossRef Full Text | Google Scholar

Maury, A. J., André, P., Testi, L., Maret, S., Belloche, A., Hennebelle, P., et al. (2019). Characterizing young protostellar disks with the CALYPSO IRAM-PdBI survey: large Class 0 disks are rare. A&A 621, A76. doi:10.1051/0004-6361/201833537

CrossRef Full Text | Google Scholar

Mellon, R. R., and Li, Z.-Y. (2008). Magnetic braking and protostellar disk formation: the ideal MHD limit. ApJ 681, 1356–1376. doi:10.1086/587542

CrossRef Full Text | Google Scholar

Mellon, R. R., and Li, Z.-Y. (2009). Magnetic braking and protostellar disk formation: ambipolar diffusion. ApJ 698, 922–927. doi:10.1088/0004-637X/698/1/922

CrossRef Full Text | Google Scholar

Mesa, D., Ginski, C., Gratton, R., Ertel, S., Wagner, K., Bonavita, M., et al. (2022). Signs of late infall and possible planet formation around DR Tau using VLT/SPHERE and LBTI/LMIRCam. A&A 658, A63. doi:10.1051/0004-6361/202142219

CrossRef Full Text | Google Scholar

Mestel, L. (1968). Magnetic braking by a stellar wind-I. MNRAS 138, 359–391. doi:10.1093/mnras/138.3.359

CrossRef Full Text | Google Scholar

Mignone, A., Zanni, C., Tzeferacos, P., van Straalen, B., Colella, P., and Bodo, G. (2012). The PLUTO code for adaptive mesh computations in astrophysical. Fluid Dyn. 198, 7. doi:10.1088/0067-0049/198/1/7

CrossRef Full Text | Google Scholar

Mignon-Risse, R., González, M., Commerçon, B., and Rosdahl, J. (2021). Collapse of turbulent massive cores with ambipolar diffusion and hybrid radiative transfer. I. Accretion and multiplicity. A&A 652, A69. doi:10.1051/0004-6361/202140617

CrossRef Full Text | Google Scholar

Moscadelli, L., Sanna, A., Beuther, H., Oliva, A., and Kuiper, R. (2022). Snapshot of a magnetohydrodynamic disk wind traced by water maser observations. Nat. Astron. 6, 1068–1076. doi:10.1038/s41550-022-01754-4

CrossRef Full Text | Google Scholar

Mouschovias, T. C. (1976). Nonhomologous contraction and equilibria of self-gravitating, magnetic interstellar clouds embedded in an intercloud medium: star formation. II. Results. ApJ 207, 141–158. doi:10.1086/154478

CrossRef Full Text | Google Scholar

Mouschovias, T. C. (1977). A connection between the rate of rotation of interstellar clouds, magnetic fields, ambipolar diffusion, and the periods of binary stars. ApJ 211, 147–151. doi:10.1086/154912

CrossRef Full Text | Google Scholar

Mouschovias, T. C. (1979). Ambipolar diffusion in interstellar clouds: a new solution. ApJ 228, 475–481. doi:10.1086/156868

CrossRef Full Text | Google Scholar

Mouschovias, T. C., and Spitzer, J. L. (1976). Note on the collapse of magnetic interstellar clouds. ApJ 210, 326. doi:10.1086/154835

CrossRef Full Text | Google Scholar

Murillo, N. M., Lai, S.-P., Bruderer, S., Harsono, D., and van Dishoeck, E. F. (2013). A Keplerian disk around a Class 0 source: ALMA observations of VLA1623A. A&A 560, A103. doi:10.1051/0004-6361/201322537

CrossRef Full Text | Google Scholar

Nakano, T., and Nakamura, T. (1978). Gravitational instability of magnetized gaseous disks 6. PASJ 30, 671–680.

Google Scholar

Nakano, T., Nishi, R., and Umebayashi, T. (2002). Mechanism of magnetic flux loss in molecular clouds. ApJ 573, 199–214. doi:10.1086/340587

CrossRef Full Text | Google Scholar

Nakano, T., and Umebayashi, T. (1986). Dissipation of magnetic fields in very dense interstellar clouds. I - formulation and conditions for efficient dissipation. MNRAS 218, 663–684. doi:10.1093/mnras/218.4.663

CrossRef Full Text | Google Scholar

Nishi, R., Nakano, T., and Umebayashi, T. (1991). Magnetic flux loss from interstellar clouds with various grain-size distributions. ApJ 368, 181. doi:10.1086/169682

CrossRef Full Text | Google Scholar

Nordlund, Å., Ramsey, J. P., Popovas, A., and Küffmeier, M. (2018). DISPATCH: a numerical simulation framework for the exa-scale era - I. Fundamentals. MNRAS 477, 624–638. doi:10.1093/mnras/sty599

CrossRef Full Text | Google Scholar

Öberg, K. I., Guzmán, V. V., Walsh, C., Aikawa, Y., Bergin, E. A., Law, C. J., et al. (2021). Molecules with ALMA at planet-forming scales (MAPS). I. Program overview and highlights. ApJs 257, 1. doi:10.3847/1538-4365/ac1432

CrossRef Full Text | Google Scholar

Offner, S. S. R., Kratter, K. M., Matzner, C. D., Krumholz, M. R., and Klein, R. I. (2010). The Formation of low-mass binary star systems via turbulent fragmentation. ApJ 725, 1485–1494. doi:10.1088/0004-637X/725/2/1485

CrossRef Full Text | Google Scholar

Offner, S. S. R., Moe, M., Kratter, K. M., Sadavoy, S. I., Jensen, E. L. N., and Tobin, J. J. (2023). “The origin and evolution of multiple star systems,” in Protostars and planets VII. Editors S. Inutsuka, Y. Aikawa, T. Muto, K. Tomida, and M. Tamura (San Francisco: Astronomical Society of the Pacific Conference Series), 534, 275. doi:10.48550/arXiv.2203.10066

CrossRef Full Text | Google Scholar

Oliva, A., and Kuiper, R. (2023). Modeling disks and magnetic outflows around a forming massive star. I. Investigating the two-layer structure of the accretion disk. A&A 669, A80. doi:10.1051/0004-6361/202243835

CrossRef Full Text | Google Scholar

Ostriker, E. C., Stone, J. M., and Gammie, C. F. (2001). Density, velocity, and magnetic field structure in turbulent molecular cloud models. ApJ 546, 980–1005. doi:10.1086/318290

CrossRef Full Text | Google Scholar

Padoan, P., Haugbølle, T., and Nordlund, Å. (2014). Infall-driven protostellar accretion and the solution to the luminosity problem. ApJ 797, 32. doi:10.1088/0004-637X/797/1/32

CrossRef Full Text | Google Scholar

Padoan, P., Kritsuk, A., Norman, M. L., and Nordlund, Å. (2005). A solution to the pre-main-sequence accretion problem. ApJl 622, L61–L64. doi:10.1086/429562

CrossRef Full Text | Google Scholar

Padoan, P., Pan, L., Juvela, M., Haugbølle, T., and Nordlund, Å. (2020). The origin of massive stars: the inertial-inflow model. ApJ 900, 82. doi:10.3847/1538-4357/abaa47

CrossRef Full Text | Google Scholar

Padoan, P., Pan, L., Pelkonen, V.-M., Haugboelle, T., and Nordlund, A. (2024). Protoplanetary disks from pre-main sequence bondi-hoyle accretion. arXiv e-prints, arXiv:2405.07334. doi:10.48550/arXiv.2405.07334

CrossRef Full Text | Google Scholar

Padovani, M., and Galli, D. (2013). “Cosmic-ray propagation in molecular clouds,” in Cosmic rays in star-forming environments. Editors D. F. Torres, and O. Reimer (San Francisco: Astrophysics and Space Science Proceedings), 34, 61–82. doi:10.1007/978-3-642-35410-6_6

CrossRef Full Text | Google Scholar

Padovani, M., Galli, D., and Glassgold, A. E. (2009). Cosmic-ray ionization of molecular clouds. A&A 501, 619–631. doi:10.1051/0004-6361/200911794

CrossRef Full Text | Google Scholar

Padovani, M., Marcowith, A., Hennebelle, P., and Ferrière, K. (2016). Protostars: forges of cosmic rays? A&A 590, A8. doi:10.1051/0004-6361/201628221

CrossRef Full Text | Google Scholar

Paneque-Carreño, T., Pérez, L. M., Benisty, M., Hall, C., Veronesi, B., Lodato, G., et al. (2021). Spiral arms and a massive dust disk with non-keplerian kinematics: possible evidence for gravitational instability in the disk of Elias 2-27. ApJ 914, 88. doi:10.3847/1538-4357/abf243

CrossRef Full Text | Google Scholar

Partnership, ALMA, Brogan, C. L., Pérez, L. M., Hunter, T. R., Dent, W. R. F., Hales, A. S., et al. (2015). The 2014 ALMA long baseline campaign: first results from high angular resolution observations toward the HL Tau region. ApJ 808, L3. doi:10.1088/2041-8205/808/1/L3

CrossRef Full Text | Google Scholar

Pattle, K., Fissel, L., Tahani, M., Liu, T., and Ntormousi, E. (2023). “Magnetic fields in Star Formation: from clouds to cores,”. Protostars and planets VII. Editors S. Inutsuka, Y. Aikawa, T. Muto, K. Tomida, and M. Tamura (San Francisco: Astronomical Society of the Pacific Conference Series), 534, 193. doi:10.48550/arXiv.2203.11179

CrossRef Full Text | Google Scholar

Pelkonen, V. M., Padoan, P., Haugbølle, T., and Nordlund, Å. (2021). From the CMF to the IMF: beyond the core-collapse model. MNRAS 504, 1219–1236. doi:10.1093/mnras/stab844

CrossRef Full Text | Google Scholar

Pelkonen, V.-M., Padoan, P., Juvela, M., Haugbølle, T., and Nordlund, Å. (2024). Origin and evolution of angular momentum of Class II disks. arXiv e-prints, arXiv:2405.06520. doi:10.48550/arXiv.2405.06520

CrossRef Full Text | Google Scholar

Pineda, J. E., Arzoumanian, D., Andre, P., Friesen, R. K., Zavagno, A., Clarke, S. D., et al. (2023). “From bubbles and filaments to cores and disks: gas gathering and growth of structure leading to the formation of stellar systems,” in Protostars and planets VII. Editors S. Inutsuka, Y. Aikawa, T. Muto, K. Tomida, and M. Tamura (San Francisco: Astronomical Society of the Pacific Conference Series), 534, 233. doi:10.48550/arXiv.2205.03935

CrossRef Full Text | Google Scholar

Pineda, J. E., Segura-Cox, D., Caselli, P., Cunningham, N., Zhao, B., Schmiedeke, A., et al. (2020). A protostellar system fed by a streamer of 10,500 au length. Nat. Astron. 4, 1158–1163. doi:10.1038/s41550-020-1150-z

CrossRef Full Text | Google Scholar

Pineda, J. E., Sipilä, O., Segura-Cox, D. M., Valdivia-Mena, M. T., Neri, R., Kuffmeier, M., et al. (2024). Probing the physics of star formation (ProPStar): I. First resolved maps of the electron fraction and cosmic-ray ionization rate in NGC 1333. arXiv e-prints, arXiv:2402.16202. doi:10.48550/arXiv.2402.16202

CrossRef Full Text | Google Scholar

Podio, L., Lefloch, B., Ceccarelli, C., Codella, C., and Bachiller, R. (2014). Molecular ions in the protostellar shock L1157-B1. A&A 565, A64. doi:10.1051/0004-6361/201322928

CrossRef Full Text | Google Scholar

Price, D. J. (2012). Smoothed particle hydrodynamics and magnetohydrodynamics. J. Comput. Phys. 231, 759–794. doi:10.1016/j.jcp.2010.12.011

CrossRef Full Text | Google Scholar

Price, D. J., and Bate, M. R. (2007). The impact of magnetic fields on single and binary star formation. MNRAS 377, 77–90. doi:10.1111/j.1365-2966.2007.11621.x

CrossRef Full Text | Google Scholar

Price, D. J., Wurster, J., Tricco, T. S., Nixon, C., Toupin, S., Pettitt, A., et al. (2018). Phantom: a smoothed particle hydrodynamics and magnetohydrodynamics code for Astrophysics. PASA 35, e031. doi:10.1017/pasa.2018.25

CrossRef Full Text | Google Scholar

Raghavan, D., McAlister, H. A., Henry, T. J., Latham, D. W., Marcy, G. W., Mason, B. D., et al. (2010). A survey of stellar families: multiplicity of solar-type stars. ApJs 190, 1–42. doi:10.1088/0067-0049/190/1/1

CrossRef Full Text | Google Scholar

Richert, A. J. W., Getman, K. V., Feigelson, E. D., Kuhn, M. A., Broos, P. S., Povich, M. S., et al. (2018). Circumstellar disc lifetimes in numerous galactic young stellar clusters. MNRAS 477, 5191–5206. doi:10.1093/mnras/sty949

CrossRef Full Text | Google Scholar

Rosen, A. L., Li, P. S., Zhang, Q., and Burkhart, B. (2019). Massive-star formation via the collapse of subvirial and virialized turbulent massive cores. ApJ 887, 108. doi:10.3847/1538-4357/ab54c6

CrossRef Full Text | Google Scholar

Rosswog, S. (2009). Astrophysical smooth particle hydrodynamics. New A Rev. 53, 78–104. doi:10.1016/j.newar.2009.08.007

CrossRef Full Text | Google Scholar

Sabatini, G., Bovino, S., and Redaelli, E. (2023). First ALMA maps of cosmic-ray ionization rate in high-mass star-forming regions. ApJl 947, L18. doi:10.3847/2041-8213/acc940

CrossRef Full Text | Google Scholar

Sadavoy, S. I., Stephens, I. W., Myers, P. C., Looney, L., Tobin, J., Kwon, W., et al. (2019). Dust polarization toward embedded protostars in ophiuchus with ALMA. III. Survey overview. ApJs 245, 2. doi:10.3847/1538-4365/ab4257

CrossRef Full Text | Google Scholar

Saigo, K., Tomisaka, K., and Matsumoto, T. (2008). Evolution of first cores and formation of stellar cores in rotating molecular cloud cores. ApJ 674, 997–1014. doi:10.1086/523888

CrossRef Full Text | Google Scholar

Santos-Lima, R., de Gouveia Dal Pino, E. M., and Lazarian, A. (2012). The role of turbulent magnetic reconnection in the formation of rotationally supported protostellar disks. ApJ 747, 21. doi:10.1088/0004-637X/747/1/21

CrossRef Full Text | Google Scholar

Segura-Cox, D. (2023). Streamers: how to keep planet-forming disks well-fed. Am. Astronomical Soc. Meet. Abstr. 55, 334.

Google Scholar

Segura-Cox, D. M., Schmiedeke, A., Pineda, J. E., Stephens, I. W., Fernández-López, M., Looney, L. W., et al. (2020). Four annular structures in a protostellar disk less than 500,000 years old. Nature 586, 228–231. doi:10.1038/s41586-020-2779-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Seifried, D., Banerjee, R., Klessen, R. S., Duffin, D., and Pudritz, R. E. (2011). Magnetic fields during the early stages of massive star formation - I. Accretion and disc evolution. MNRAS 417, 1054–1073. doi:10.1111/j.1365-2966.2011.19320.x

CrossRef Full Text | Google Scholar

Seifried, D., Banerjee, R., Pudritz, R. E., and Klessen, R. S. (2012). Disc formation in turbulent massive cores: circumventing the magnetic braking catastrophe. MNRAS 423, L40–L44. doi:10.1111/j.1745-3933.2012.01253.x

CrossRef Full Text | Google Scholar

Seifried, D., Banerjee, R., Pudritz, R. E., and Klessen, R. S. (2013). Turbulence-induced disc formation in strongly magnetized cloud cores. MNRAS 432, 3320–3331. doi:10.1093/mnras/stt682

CrossRef Full Text | Google Scholar

Sheehan, P. D., Tobin, J. J., Looney, L. W., and Megeath, S. T. (2022). The VLA/ALMA nascent disk and multiplicity (VANDAM) survey of orion protostars. VI. Insights from radiative transfer modeling. ApJ 929, 76. doi:10.3847/1538-4357/ac574d

CrossRef Full Text | Google Scholar

Shu, F. H. (1977). Self-similar collapse of isothermal spheres and star formation. ApJ 214, 488–497. doi:10.1086/155274

CrossRef Full Text | Google Scholar

Shu, F. H., Galli, D., Lizano, S., and Cai, M. (2006). Gravitational collapse of magnetized clouds. II. The role of ohmic dissipation. ApJ 647, 382–389. doi:10.1086/505258

CrossRef Full Text | Google Scholar

Shu, F. H., Shang, H., Glassgold, A. E., and Lee, T. (1997). X-rays and fluctuating X-winds from protostars. Science 277, 1475–1479. doi:10.1126/science.277.5331.1475

CrossRef Full Text | Google Scholar

Shu, F. H., Shang, H., and Lee, T. (1996). Toward an astrophysical theory of chondrites. Science 271, 1545–1552. doi:10.1126/science.271.5255.1545

CrossRef Full Text | Google Scholar

Smallwood, J. L., Yang, C.-C., Zhu, Z., Martin, R. G., Dong, R., Cuello, N., et al. (2023). Exciting spiral arms in protoplanetary discs from flybys. MNRAS 521, 3500–3516. doi:10.1093/mnras/stad742

CrossRef Full Text | Google Scholar

Smith, R. J., Glover, S. C. O., Bonnell, I. A., Clark, P. C., and Klessen, R. S. (2011). A quantification of the non-spherical geometry and accretion of collapsing cores. MNRAS 411, 1354–1366. doi:10.1111/j.1365-2966.2010.17775.x

CrossRef Full Text | Google Scholar

Spitzer, J., and Lyman and Tomasko, M. G. (1968). Heating of H i regions by energetic particles. ApJ 152, 971. doi:10.1086/149610

CrossRef Full Text | Google Scholar

Springel, V. (2010a). E pur si muove: Galilean-invariant cosmological hydrodynamical simulations on a moving mesh. MNRAS 401, 791–851. doi:10.1111/j.1365-2966.2009.15715.x

CrossRef Full Text | Google Scholar

Springel, V. (2010b). Smoothed particle hydrodynamics in Astrophysics. ARA&A 48, 391–430. doi:10.1146/annurev-astro-081309-130914

CrossRef Full Text | Google Scholar

Stone, J. M., Gardiner, T. A., Teuben, P., Hawley, J. F., and Simon, J. B. (2008). Athena: a new code for astrophysical MHD. ApJs 178, 137–177. doi:10.1086/588755

CrossRef Full Text | Google Scholar

Stone, J. M., and Norman, M. L. (1992). ZEUS-2D: a radiation magnetohydrodynamics code for astrophysical flows in two space dimensions. I - the hydrodynamic algorithms and tests. II - the magnetohydrodynamic algorithms and tests. ApJs 80, 753. doi:10.1086/191680

CrossRef Full Text | Google Scholar

Stone, J. M., Tomida, K., White, C. J., and Felker, K. G. (2020). The Athena++ adaptive mesh refinement framework: design and magnetohydrodynamic solvers. ApJs 249, 4. doi:10.3847/1538-4365/ab929b

CrossRef Full Text | Google Scholar

Stoyanovskaya, O. P., Glushko, T. A., Snytnikov, N. V., and Snytnikov, V. N. (2018). Two-fluid dusty gas in smoothed particle hydrodynamics: fast and implicit algorithm for stiff linear drag. Astronomy Comput. 25, 25–37. doi:10.1016/j.ascom.2018.08.004

CrossRef Full Text | Google Scholar

Stoyanovskaya, O. P., Okladnikov, F. A., Vorobyov, E. I., Pavlyuchenkov, Y. N., and Akimkin, V. V. (2020). Simulations of dynamical gas-dust circumstellar disks: going beyond the epstein regime. Astron. Rep. 64, 107–125. doi:10.1134/S1063772920010072

CrossRef Full Text | Google Scholar

Teyssier, R. (2002). Cosmological hydrodynamics with adaptive mesh refinement. A new high resolution code called RAMSES. A&A 385, 337–364. doi:10.1051/0004-6361:20011817

CrossRef Full Text | Google Scholar

Teyssier, R. (2015). Grid-based hydrodynamics in astrophysical fluid flows. ARA&A 53, 325–364. doi:10.1146/annurev-astro-082214-122309

CrossRef Full Text | Google Scholar

Teyssier, R., and Commerçon, B. (2019). Numerical methods for simulating Star Formation. Front. Astronomy Space Sci. 6, 51. doi:10.3389/fspas.2019.00051

CrossRef Full Text | Google Scholar

Thies, I., Kroupa, P., Goodwin, S. P., Stamatellos, D., and Whitworth, A. P. (2011). A natural formation scenario for misaligned and short-period eccentric extrasolar planets. MNRAS 417, 1817–1822. doi:10.1111/j.1365-2966.2011.19390.x

CrossRef Full Text | Google Scholar

Tobin, J. J., Looney, L. W., Wilner, D. J., Kwon, W., Chandler, C. J., Bourke, T. L., et al. (2015). A sub-arcsecond survey toward class 0 protostars in perseus: searching for signatures of protostellar disks. ApJ 805, 125. doi:10.1088/0004-637X/805/2/125

CrossRef Full Text | Google Scholar

Tomida, K. (2014). Radiation magnetohydrodynamic simulations of protostellar collapse: low-metallicity environments. ApJ 786, 98. doi:10.1088/0004-637X/786/2/98

CrossRef Full Text | Google Scholar

Tomida, K., Machida, M. N., Hosokawa, T., Sakurai, Y., and Lin, C. H. (2017). Grand-design spiral arms in a young forming circumstellar disk. ApJl 835, L11. doi:10.3847/2041-8213/835/1/L11

CrossRef Full Text | Google Scholar

Tomida, K., Okuzumi, S., and Machida, M. N. (2015). Radiation magnetohydrodynamic simulations of protostellar collapse: nonideal magnetohydrodynamic effects and early formation of circumstellar disks. ApJ 801, 117. doi:10.1088/0004-637X/801/2/117

CrossRef Full Text | Google Scholar

Tomida, K., Tomisaka, K., Matsumoto, T., Hori, Y., Okuzumi, S., Machida, M. N., et al. (2013). Radiation magnetohydrodynamic simulations of protostellar collapse: protostellar core formation. ApJ 763, 6. doi:10.1088/0004-637X/763/1/6

CrossRef Full Text | Google Scholar

Tomida, K., Tomisaka, K., Matsumoto, T., Ohsuga, K., Machida, M. N., and Saigo, K. (2010). Radiation magnetohydrodynamics simulation of proto-stellar collapse: two-component molecular outflow. ApJl 714, L58–L63. doi:10.1088/2041-8205/714/1/L58

CrossRef Full Text | Google Scholar

Tomisaka, K., Ikeuchi, S., and Nakamura, T. (1988). Equilibria and evolutions of magnetized, rotating, isothermal clouds. II. The extreme case: nonrotating clouds. ApJ 335, 239. doi:10.1086/166923

CrossRef Full Text | Google Scholar

Tricco, T. S. (2023). Smoothed particle magnetohydrodynamics. Front. Astronomy Space Sci. 10, 1288219. doi:10.3389/fspas.2023.1288219

CrossRef Full Text | Google Scholar

Tricco, T. S., and Price, D. J. (2012). Constrained hyperbolic divergence cleaning for smoothed particle magnetohydrodynamics. J. Comput. Phys. 231, 7214–7236. doi:10.1016/j.jcp.2012.06.039

CrossRef Full Text | Google Scholar

Tricco, T. S., Price, D. J., and Bate, M. R. (2016). Constrained hyperbolic divergence cleaning in smoothed particle magnetohydrodynamics with variable cleaning speeds. J. Comput. Phys. 322, 326–344. doi:10.1016/j.jcp.2016.06.053

CrossRef Full Text | Google Scholar

Truelove, J. K., Klein, R. I., McKee, C. F., Holliman, I., John, H., Howell, L. H., et al. (1998). Self-gravitational hydrodynamics with three-dimensional adaptive mesh refinement: methodology and applications to molecular cloud collapse and fragmentation. ApJ 495, 821–852. doi:10.1086/305329

CrossRef Full Text | Google Scholar

Tsukamoto, Y., Iwasaki, K., Okuzumi, S., Machida, M. N., and Inutsuka, S. (2015a). Bimodality of circumstellar disk evolution induced by the Hall current. ApJl 810, L26. doi:10.1088/2041-8205/810/2/L26

CrossRef Full Text | Google Scholar

Tsukamoto, Y., Iwasaki, K., Okuzumi, S., Machida, M. N., and Inutsuka, S. (2015b). Effects of Ohmic and ambipolar diffusion on formation and evolution of first cores, protostars, and circumstellar discs. MNRAS 452, 278–288. doi:10.1093/mnras/stv1290

CrossRef Full Text | Google Scholar

Tsukamoto, Y., Machida, M. N., and Inutsuka, S.-i. (2021). “Ashfall” induced by molecular outflow in protostar evolution. ApJl 920, L35. doi:10.3847/2041-8213/ac2b2f

CrossRef Full Text | Google Scholar

Tsukamoto, Y., Machida, M. N., and Inutsuka, S.-i. (2023a). Co-evolution of dust grains and protoplanetary disks. PASJ 75, 835–852. doi:10.1093/pasj/psad040

CrossRef Full Text | Google Scholar

Tsukamoto, Y., Maury, A., Commercon, B., Alves, F. O., Cox, E. G., Sakai, N., et al. (2023b). “The role of magnetic fields in the formation of protostars, disks, and outflows,” in Astronomical society of the pacific conference series. Editors S. Inutsuka, Y. Aikawa, T. Muto, K. Tomida, and M. Tamura, 534, 317.

Google Scholar

Tsukamoto, Y., Okuzumi, S., Iwasaki, K., Machida, M. N., and Inutsuka, S. (2018). Does misalignment between magnetic field and angular momentum enhance or suppress circumstellar disk formation? ApJ 868, 22. doi:10.3847/1538-4357/aae4dc

CrossRef Full Text | Google Scholar

Tsukamoto, Y., Okuzumi, S., Iwasaki, K., Machida, M. N., and Inutsuka, S.-i. (2017). The impact of the Hall effect during cloud core collapse: implications for circumstellar disk evolution. PASJ 69, 95. doi:10.1093/pasj/psx113

CrossRef Full Text | Google Scholar

Tu, Y., Li, Z.-Y., Lam, K. H., Tomida, K., and Hsu, C.-Y. (2024). Protostellar discs fed by dense collapsing gravomagneto sheetlets. MNRAS 527, 10131–10150. doi:10.1093/mnras/stad3843

CrossRef Full Text | Google Scholar

Umebayashi, T., and Nakano, T. (1990). Magnetic flux loss from interstellar clouds. MNRAS 243, 103–113. doi:10.1093/mnras/243.1.103

CrossRef Full Text | Google Scholar

Unno, M., Hanawa, T., and Takasao, S. (2022). Magnetohydrodynamic model of late accretion onto a protoplanetary disk: cloudlet encounter event. ApJ 941, 154. doi:10.3847/1538-4357/aca410

CrossRef Full Text | Google Scholar

Väisälä, M. S., Shang, H., Galli, D., Lizano, S., and Krasnopolsky, R. (2023). Exploring the formation of resistive pseudodisks with the GPU code astaroth. ApJ 959, 32. doi:10.3847/1538-4357/acfb00

CrossRef Full Text | Google Scholar

Väisälä, M. S., Shang, H., Krasnopolsky, R., Liu, S.-Y., Lam, K. H., and Li, Z.-Y. (2019). Time evolution of 3D disk formation with misaligned magnetic field and rotation axes. ApJ 873, 114. doi:10.3847/1538-4357/ab0307

CrossRef Full Text | Google Scholar

Valdivia-Mena, M. T., Pineda, J. E., Caselli, P., Segura-Cox, D. M., Schmiedeke, A., Spezzano, S., et al. (2024). Probing the Physics of Star-Formation (ProPStar): II. The first systematic search for streamers toward protostars. arXiv e-prints, arXiv:2404.02144. doi:10.48550/arXiv.2404.02144

CrossRef Full Text | Google Scholar

Valdivia-Mena, M. T., Pineda, J. E., Segura-Cox, D. M., Caselli, P., Neri, R., López-Sepulcre, A., et al. (2022). PRODIGE - envelope to disk with NOEMA. I. A 3000 au streamer feeding a Class I protostar. A&A 667, A12. doi:10.1051/0004-6361/202243310

CrossRef Full Text | Google Scholar

Vaytet, N., Commerçon, B., Masson, J., González, M., and Chabrier, G. (2018). Protostellar birth with ambipolar and ohmic diffusion. A&A 615, A5. doi:10.1051/0004-6361/201732075

CrossRef Full Text | Google Scholar

Vorobyov, E. I., Kulikov, I., Elbakyan, V. G., McKevitt, J., and Güdel, M. (2024). Dust growth and pebble formation in the initial stages of protoplanetary disk evolution. A&A 683, A202. doi:10.1051/0004-6361/202348023

CrossRef Full Text | Google Scholar

Vorobyov, E. I., Lin, D. N. C., and Guedel, M. (2015). The effect of external environment on the evolution of protostellar disks. A&A 573, A5. doi:10.1051/0004-6361/201424583

CrossRef Full Text | Google Scholar

Vorobyov, E. I., Skliarevskii, A. M., Elbakyan, V. G., Pavlyuchenkov, Y., Akimkin, V., and Guedel, M. (2019). Gravitoviscous protoplanetary disks with a dust component. I. The importance of the inner sub-au region. A&A 627, A154. doi:10.1051/0004-6361/201935438

CrossRef Full Text | Google Scholar

Walch, S., Burkert, A., Whitworth, A., Naab, T., and Gritschneder, M. (2009). Protostellar discs formed from rigidly rotating cores. MNRAS 400, 13–25. doi:10.1111/j.1365-2966.2009.15293.x

CrossRef Full Text | Google Scholar

Walch, S., Naab, T., Whitworth, A., Burkert, A., and Gritschneder, M. (2010). Protostellar discs formed from turbulent cores. MNRAS 402, 2253–2263. doi:10.1111/j.1365-2966.2009.16058.x

CrossRef Full Text | Google Scholar

Wang, W., Väisälä, M. S., Shang, H., Krasnopolsky, R., Li, Z.-Y., Lam, K. H., et al. (2022). Magnetic spirals in accretion flows originated from misaligned magnetic fields. ApJ 928, 85. doi:10.3847/1538-4357/ac4d2e

CrossRef Full Text | Google Scholar

Wardle, M. (2004). Star Formation and the Hall effect. Ap&SS 292, 317–323. doi:10.1023/B:ASTR.0000045033.80068.1f

CrossRef Full Text | Google Scholar

Wardle, M., and Koenigl, A. (1993). The structure of protostellar accretion disks and the origin of bipolar flows. ApJ 410, 218. doi:10.1086/172739

CrossRef Full Text | Google Scholar

Wardle, M., and Ng, C. (1999). The conductivity of dense molecular gas. MNRAS 303, 239–246. doi:10.1046/j.1365-8711.1999.02211.x

CrossRef Full Text | Google Scholar

Watson, D. M., Calvet, N. P., Fischer, W. J., Forrest, W. J., Manoj, P., Megeath, S. T., et al. (2016). Evolution of mass outflow in protostars. ApJ 828, 52. doi:10.3847/0004-637X/828/1/52

CrossRef Full Text | Google Scholar

Weidenschilling, S. J. (1977). Aerodynamics of solid bodies in the solar nebula. MNRAS 180, 57–70. doi:10.1093/mnras/180.2.57

CrossRef Full Text | Google Scholar

Weinberger, R., Springel, V., and Pakmor, R. (2020). The AREPO public code release. ApJs 248, 32. doi:10.3847/1538-4365/ab908c

CrossRef Full Text | Google Scholar

Winter, A. J., Benisty, M., and Andrews, S. M. (2024). Planet formation regulated by galactic-scale interstellar turbulence. doi:10.48550/arXiv.2405.08451

CrossRef Full Text | Google Scholar

Winter, A. J., and Haworth, T. J. (2022). The external photoevaporation of planet-forming discs. Eur. Phys. J. Plus 137, 1132. doi:10.1140/epjp/s13360-022-03314-1

CrossRef Full Text | Google Scholar

Wurster, J., Bate, M. R., Price, D. J., and Bonnell, I. A. (2022). On the origin of magnetic fields in stars - II. The effect of numerical resolution. MNRAS 511, 746–764. doi:10.1093/mnras/stac123

CrossRef Full Text | Google Scholar

Wurster, J., Bate, M. R., and Price, D. J. (2018a). Hall effect-driven formation of gravitationally unstable discs in magnetized molecular cloud cores. MNRAS 480, 4434–4442. doi:10.1093/mnras/sty2212

CrossRef Full Text | Google Scholar

Wurster, J., Bate, M. R., and Price, D. J. (2018b). The collapse of a molecular cloud core to stellar densities using radiation non-ideal magnetohydrodynamics. MNRAS 475, 1859–1880. doi:10.1093/mnras/stx3339

CrossRef Full Text | Google Scholar

Wurster, J., Bate, M. R., and Price, D. J. (2018c). The effect of extreme ionization rates during the initial collapse of a molecular cloud core. MNRAS 476, 2063–2074. doi:10.1093/mnras/sty392

CrossRef Full Text | Google Scholar

Wurster, J., Bate, M. R., and Price, D. J. (2019). There is no magnetic braking catastrophe: low-mass star cluster and protostellar disc formation with non-ideal magnetohydrodynamics. MNRAS 489, 1719–1741. doi:10.1093/mnras/stz2215

CrossRef Full Text | Google Scholar

Wurster, J., and Lewis, B. T. (2020). Non-ideal magnetohydrodynamics versus turbulence - I. Which is the dominant process in protostellar disc formation? MNRAS 495, 3795–3806. doi:10.1093/mnras/staa1339

CrossRef Full Text | Google Scholar

Wurster, J., and Li, Z.-Y. (2018). The role of magnetic fields in the formation of protostellar discs. Front. Astronomy Space Sci. 5, 39. doi:10.3389/fspas.2018.00039

CrossRef Full Text | Google Scholar

Wurster, J., Price, D. J., and Bate, M. R. (2016). Can non-ideal magnetohydrodynamics solve the magnetic braking catastrophe? MNRAS 457, 1037–1061. doi:10.1093/mnras/stw013

CrossRef Full Text | Google Scholar

Xu, W., and Kunz, M. W. (2021). Formation and evolution of protostellar accretion discs - I. Angular-momentum budget, gravitational self-regulation, and numerical convergence. MNRAS 502, 4911–4929. doi:10.1093/mnras/stab314

CrossRef Full Text | Google Scholar

Yen, H.-W., Gu, P.-G., Hirano, N., Koch, P. M., Lee, C.-F., Liu, H. B., et al. (2019). HL Tau disk in HCO⁺ (3–2) and (1–0) with ALMA: gas density, temperature, gap, and one-arm spiral. ApJ 880, 69. doi:10.3847/1538-4357/ab29f8

CrossRef Full Text | Google Scholar

Yorke, H. W., Bodenheimer, P., and Laughlin, G. (1993). The formation of protostellar disks. I - 1 M(solar). ApJ 411, 274. doi:10.1086/172827

CrossRef Full Text | Google Scholar

Young, A. K. (2023). Insights into the first and second hydrostatic core stages from numerical simulations. Front. Astronomy Space Sci. 10, 1288730. doi:10.3389/fspas.2023.1288730

CrossRef Full Text | Google Scholar

Zhao, B., Caselli, P., and Li, Z.-Y. (2018). Effect of grain size on differential desorption of volatile species and on non-ideal MHD diffusivity. MNRAS 478, 2723–2736. doi:10.1093/mnras/sty1165

CrossRef Full Text | Google Scholar

Zhao, B., Caselli, P., Li, Z.-Y., Krasnopolsky, R., Shang, H., and Lam, K. H. (2020a). Hall effect in protostellar disc formation and evolution. MNRAS 492, 3375–3395. doi:10.1093/mnras/staa041

CrossRef Full Text | Google Scholar

Zhao, B., Caselli, P., Li, Z.-Y., Krasnopolsky, R., Shang, H., and Lam, K. H. (2021). The interplay between ambipolar diffusion and Hall effect on magnetic field decoupling and protostellar disc formation. MNRAS 505, 5142–5163. doi:10.1093/mnras/stab1295

CrossRef Full Text | Google Scholar

Zhao, B., Caselli, P., Li, Z.-Y., Krasnopolsky, R., Shang, H., and Nakamura, F. (2016). Protostellar disc formation enabled by removal of small dust grains. MNRAS 460, 2050–2076. doi:10.1093/mnras/stw1124

CrossRef Full Text | Google Scholar

Zhao, B., Tomida, K., Hennebelle, P., Tobin, J. J., Maury, A., Hirota, T., et al. (2020b). Formation and evolution of disks around young stellar objects. aar 216, 43. doi:10.1007/s11214-020-00664-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Zier, O., Mayer, A. C., and Springel, V. (2024a). Non-ideal magnetohydrodynamics on a moving mesh II: Hall effect. MNRAS 527, 8355–8368. doi:10.1093/mnras/stad3769

CrossRef Full Text | Google Scholar

Zier, O., Springel, V., and Mayer, A. C. (2024b). Non-ideal magnetohydrodynamics on a moving mesh I: ohmic and ambipolar diffusion. MNRAS 527, 1563–1579. doi:10.1093/mnras/stad3200

CrossRef Full Text | Google Scholar