On the overall properties of young neutron stars: an application to the Crab pulsar

In this brief report, we present a model that complements the well-established canonical model for the spin evolution of rotation-powered pulsars, which is typically used to estimate ages, spin-down luminosity, and surface magnetic fields of middle-aged pulsars. We analytically explore the growth of the magnetic field during a pulsar’s early history, a period shortly after supernova explosion from which the neutron star forms, encompassing the hypercritical phase and subsequent reemergence of the magnetic field. We analyze the impact of such growth on the early dynamics of the pulsar. Investigations into a pulsar’s magnetic evolution are not new, and we expand the knowledge in this area by examining the evolutionary implications in a scenario governed by growth functions. The proposed growth functions, calibrated with data from the Crab pulsar, exhibit satisfactory physical behaviors.

1 Introduction

Neutron stars (NSs) are extremely dense remnants that result from the supernova explosion of massive stars that have undergone a core-collapse. Although NSs were proposed theoretically long ago by Baade and Zwicky (1934), their existence was only confirmed observationally in the form of pulsars by Hewish et al. (1968). These pulsars were interpreted as rapidly rotating magnetized NSs by Gold (1968). These NSs, in which rotation is responsible for the observed luminosity, are known as rotation-powered pulsars (RPPs).

As the NS spins, it loses rotational energy, which is converted into electromagnetic radiation emitted from the star. Therefore, the source of electromagnetic radiation in RPPs is not nuclear fusion or gravitational energy, but simply the rotational energy stored in the rapid rotation of the star (Ghosh, 2007). To account for the spin-down and the energy of RPPs, a dipolar oblique rotator model was proposed by Gold (1968) for the NS, allowing a simple yet effective description of the fundamental mechanisms that lead to the observed pulsations in RPPs. This consolidated, canonical model provides insights into the radiation energy, signal periodicity, and the evolving rotational dynamics of middle-aged NS. In addition, it yields a constant braking index when the NS is considered a rigid rotating sphere with a very strong magnetic field.

Although the canonical model is adequate to explain some characteristics of mature pulsars, it assumes a constant magnetic field since the birth of the pulsar. Observational, theoretical, and numerical evidence suggests that this is not always the case (Chevalier and Emmering, 1986; Muslimov and Page, 1995; Geppert et al., 1999; Bernal et al., 2010; Bernal et al., 2013; Bransgrove et al., 2018). A newborn NS is exposed to strong accretion shortly after the supernova explosion that resulted in its formation. In this scenario, the shock wave sweeps through the outer layers of the progenitor until it encounters a density discontinuity. This triggers a reverse shock wave, leading to a fallback episode that deposits large amounts of the material on the stellar surface in a short period of time. During this phase, the stellar magnetic field can be submerged beneath the newly formed crust of the NS.

This scenario was recently reconsidered by Ho (2011) and Viganò and Pons (2012) and was applied to the study of the field evolution of central compact objects (CCO) (Pavlov et al., 2004). In addition, Shabaltas and Lai (2012) explored the idea that a substantial sub-surface magnetic field exists in the crust of the young neutron star in Kes 79, which produces diffuse hot spots on the stellar surface due to anisotropic heat conduction, giving rise to the observed X-ray pulsations. Recently, Bernal et al. (2010), Bernal et al. (2013), Fraija et al. (2014), Fraija and Bernal (2015), Fraija et al. (2018), and Dehman et al. (2023) performed 2D–3D magnetohydrodynamic (MHD) simulations with detailed physical components, showing that the magnetic field is indeed submerged under the stellar surface of such objects, regardless of their initial configuration or its strength.

When the hypercritical accretion phase ends, the magnetic field may diffuse back to the surface, resulting in the delayed switch-on of a pulsar (Michel, 1994; Muslimov and Page, 1995). However, depending on the amount of the accreted matter, the submergence could be so deep that the NS may be born but remains unmagnetized for centuries (Geppert et al., 1999). In a more recent work, Igoshev et al. (2016) distinguished three evolutionary epochs in the reemergence process: the growth of the internal toroidal field, the advection of the buried poloidal field, and the slow ohmic diffusion. This indicates that these multipolar diffusion processes in such extreme systems would occur at different speeds.

In the present work, we explore the early dynamics of the young NS after conclusion of its hypercritical phase. As previously mentioned, such objects can exhibit a range of behaviors, including initial complex magnetic field configurations and high-energy phenomena, and may not strictly adhere to the rotating magnetic dipole model. Specifically, the submergence of the magnetic field under the crust of the newborn NS during the hypercritical phase and its subsequent reemergence through various mechanisms (such as magnetic reconnection, turbulent dynamos, or thermomagnetic instabilities) present a challenging problem that typically requires extensive numerical treatment. On the other hand, an analytical approach could yield an estimate of the effects of an early increasing magnetic field on the overall dynamic properties of the pulsar until it reaches the canonical behavior expected for a mature pulsar.

The understanding of the growth of the magnetic field through such an approach could allow us to analyze, for instance, how the periodicity of the pulsar would be altered, contrasting with the assumption of stable, unchanging periodicity existent in the canonical model. Furthermore, an analytical approach could help us understand whether the reemergence of magnetic fields has significant consequences for the energy content of pulsars and their spin evolution, as such a reemergence is expected to introduce an additional source of energy and torque that may influence the long-term behavior of these objects. This possibility requires a reevaluation of how pulsars produce and radiate energy.

The proposition of analytical functions for the growth of the magnetic field allows us to derive analytical formulas to examine the early behavior of physical quantities of interest in the dynamics of the pulsar, thus avoiding complex and time-consuming numerical treatments. As the focus of this work is the initial phase of the pulsar’s life, the subsequent decay of the magnetic field was not approached here; this decay has already been widely discussed in previous works and is outside the scope of the present research.

Section 2 revisits the canonical model for RPPs. Section 3 describes our proposed model for analyzing the early dynamics of pulsars, including analytical growth functions that describe the behavior of the magnetic field, along with other consequences. Finally, Section 4 presents and discussed our results.

2 The canonical model for rotation-powered pulsars

Assuming that the NS rotates with angular velocity Ω and has moment of inertia I, the rotational energy (E_rot) and the spin-down luminosity associated with the rotation $({\dot{E}}_{\mathit{rot}})$ in terms of the observable parameters are given by the following equations:

$E_{\mathit{rot}}=I{\mathrm{\Omega }}^2/2\simeq 2\times 10^{46}{I}_{45}{P}^{-2}\mathrm{e}\mathrm{r}\mathrm{g},(1)$

${\dot{E}}_{\mathit{rot}}\simeq I\mathrm{\Omega }\dot{\mathrm{\Omega }}\simeq -4\times 10^{32}{I}_{45}{P}^{-3}{\dot{P}}_{-14}\mathrm{e}\mathrm{r}\mathrm{g}{\mathrm{s}}^{-\mathrm{1}},(2)$

where I₄₅ is the moment of inertia in units of 10⁴⁵ g cm² (we assume a solid, rigid, spherical star), P = 2π/Ω is the rotational period in seconds, and ${\dot{P}}_{-14}$ is the period derivative in units of 10^–14ss⁻¹, which are typical parameters for NSs. Any changes in the moment of inertia will be considered negligible. In addition, the dipolar oblique rotator, which has a magnetic moment μ inclined at an angle α with respect to the axis of rotation, radiates magnetic energy according to the Larmor formula, which is as follows:

${\dot{E}}_{\mathit{mdr}}=\frac{2{\mu }^2{\mathrm{\Omega }}^4{\sin }^2\alpha }{3c^3}\simeq 10^{31}{B}_{12}^2{R}_6^6{\sin }^2\alpha P^{-4}\mathrm{e}\mathrm{r}\mathrm{g}{\mathrm{s}}^{-\mathrm{1}},(3)$

where c is the speed of light in vacuum, B₁₂ is the magnetic field in units of 10¹² G, and R₆ is the NS radius in units of 10⁶ cm, which are typical values for such objects. The superficial magnetic field scales with distance R as B_s = 2μ/R³ (Ghosh, 2007), where μ ≃ 10³⁰ G cm³ is the magnetic moment for rotating pulsars. If the whole rotational energy is assumed to radiate according to such a mechanism, then, using Equations 2 and 3, the superficial magnetic field results in the following:

$B_{12}\simeq 6\frac{{\left(I_{45}P{\dot{P}}_{-14}\right)}^{0.5}}{\left(R_6^3\sin \alpha \right)}\mathrm{G}.(4)$

On the other hand, the braking index n for pulsars, including RPPs, measures how the pulsar’s rotational frequency changes over time. It is a valuable parameter for understanding the rotational dynamics of the pulsar that can be obtained directly from timing observations through its definition: $n\equiv \mathrm{\Omega }\ddot{\mathrm{\Omega }}/{(\dot{\mathrm{\Omega }})}^2$.

In order to derive a theoretical relationship involving n and the observable parameters (P, $\dot{P}$, and $\ddot{P}$) from the canonical model, a balance must be established between the rotational luminosity and the energy lost through radiation: ${\dot{E}}_{\mathit{rot}}=I\dot{\mathrm{\Omega }}\mathrm{\Omega }\simeq -{\dot{E}}_{\mathit{mdr}}$, where $I\dot{\mathrm{\Omega }}$ is the magnetic torque acting on the pulsar. Consequently, the equation of motion of the pulsar is as follows:

$\dot{\mathrm{\Omega }}=-k{\mathrm{\Omega }}^n,k=\frac{2{\mu }^2{\sin }^2\alpha }{3I{c}^3},(5)$

where k is a constant including the structural factors of the pulsar and n is the theoretical braking index. The case n = 3 corresponds to purely dipolar radiation, which is the case for the canonical model. Different values of n would correspond to different processes of rotational energy loss, or braking, and the value of the constant k would be different for these processes.

Equation 5 can be integrated in a simple and direct way to yield the characteristic age of the pulsar, as in the following equation:

$\tau =\frac{P}{\left(n-1\right)\dot{P}}\left[1-{\left(\frac{P_0}{P}\right)}^{n-1}\right],(6)$

which is valid only when n ≠ 1. The parameter P₀ is the initial period. In the limit when P₀ ≪ P, the canonical characteristic age of the pulsar, assuming n = 3, is given by $\tau =P/(n-1)\dot{P}=P/2\dot{P}$. This expression is frequently taken as the definition of the characteristic age, despite the fact that n can be different from 3.

Likewise, the spin-down luminosity $\dot{E}(t)$ and the spin period P(t) evolve over time according to the following equation:

$\dot{E}={\dot{E}}_0{\left[1+\frac{t}{{\tau }_0}\right]}^{-\frac{\left(n+1\right)}{\left(n-1\right)}},P=P_0{\left[1+\frac{t}{{\tau }_0}\right]}^{\frac{1}{n-1}},(7)$

where ${\tau }_0=P_0/(n-1){\dot{P}}_0$ is the initial spin-down timescale of the pulsar and ${\dot{E}}_0$ is the initial spin-down luminosity. When t ≪ τ₀, this model implies a roughly constant energy output, $\dot{E}\propto {\dot{E}}_0$. At a later time t ≫ τ₀, the spin-down luminosity evolves as $\dot{E}\propto t^{-(n+1)/(n-1)}$. Similarly, P ∝ P₀ for t ≪ τ₀ and evolves at later times as P ∝ t^1/(n−1) (Gaensler and Slane, 2006).

Finally, the evolution of the time derivative of the period is given by the following equation:

$\dot{P}=\frac{P_0}{{\tau }_0\left(n-1\right)}{\left[1+\frac{t}{{\tau }_0}\right]}^{\frac{\left(2-n\right)}{n-1}}.(8)$

The effects of the alignment $\left(d\alpha /dt>0\right)$ or misalignment $\left(d\alpha /dt<0\right)$ on n were theoretically calculated by Ghosh (1984). For a dipolar field, n changes from 3 by an amount $2\tau \left(d(\ln {\sin }^2\alpha )/dt\right)$ due to the alignment or misalignment between the rotational and magnetic axes. Nevertheless, observations of alignment or misalignment are very complicated to carry out because large amounts of data are required to make a statistical estimate. Therefore, in both the canonical model and the model with magnetic field growth described below, we do not take this effect into account and interpret the magnetic field B as the component perpendicular to the stellar surface, hence assuming that sin α ≃ 1.

3 Low braking index and early magnetic field growth

To date, not many braking indices have been determined from observations, mostly for young pulsars, and in all cases, n_obs < 3 (Archibald et al., 2015; Araujo et al., 2023). These results suggest that the energy balance in a pulsar is more complex than that assumed in the canonical model. For example, more complicated plasma processes in the magnetosphere of the pulsar could be contributing to a decrease in n. The typical factors that may affect the braking index (see Muslimov and Page (1995) and references therein) are: (a) multipolar electromagnetic radiation, n ≥ 5; (b) quadrupole gravitational radiation, n = 5; (c) decay of the magnetic field, n > 3; (d) radial deformation of the magnetic field lines, 1 ≤ n ≤ 3; (e) relativistic winds, n < 3; and (f) transverse velocity of the pulsar, n < 3.

Other factors also investigated are as follows: (g) intense emission of neutrinos in the early evolution of the pulsar, n < 0 (Alpar and Oegelman, 1990); (h) crustal movement of the NS by tectonic plates can produce n > 3 or n < 3 (Ruderman, 1991); (i) growth of the magnetic field due to thermomagnetic instabilities in the crust of the NS, n < 3 (Blandford and Romani, 1988); (j) growth of an intense magnetic field submerged under the NS crust in the hypercritical accretion phase, which reemerges by ohmic diffusion, n < 3 (Muslimov and Page, 1995; Bernal et al., 2010; Bernal et al., 2013; Viganò and Pons, 2012); (k) changes in the moment of inertia of the NS, n < 3 (Weber and Papoyan, 1999; Glendenning, 2003); (l) tidal torques exerted on the pulsar by a fallback disk can result in a braking index less than 3 (Chen and Li, 2006); and (m) the braking torque caused by the interaction between the fallback disk and the strong magnetic field of the pulsar can produce a braking index of 0.9 ± 0.2 (Chen and Li, 2016). A more recent work also accounts for the connection between n and the characteristic age (Igoshev and Popov, 2020).

For the present study, it is noteworthy that the growth of an intense magnetic field submerged under the crust of an NS during the hypercritical accretion phase, which reemerges by ohmic diffusion (factor (j) above), is one of the most plausible mechanisms to reduce the braking index obtained in the canonical model, yielding values closer to the observational ones. In the core-collapsed supernova scenario, the generated reverse shock can induce hypercritical accretion ($\dot{M}>{\dot{M}}_{\mathit{Edd}}$, where ${\dot{M}}_{\mathit{Edd}}$ is the Eddington accretion rate onto the newborn NS on a timescale of hours. During this phase, photons are trapped within the flow, and the energy generated by the accretion is released through neutrino emission near the NS’s surface. When the reverse shock reaches the NS surface and rebounds, a third shock develops and begins moving outward against the in-falling matter. Once this accretion shock stabilizes, it will separate the in-falling matter from an extended envelope in quasi-hydrostatic equilibrium.

Chevalier (1989) argued in favor of such a scenario and developed an analytical model for the hypercritical regime. In such a model, neutrino cooling plays an important role in the formation of a quasi-hydrostatic envelope around the compact remnant. In addition, Muslimov and Page (1995) proposed the physical conditions present in the formation of an NS inside supernovae: convective envelope, hyperaccretion of the material, and submergence of the magnetic field under the stellar crust. With these suggestions, Geppert et al. (1999) presented simple, one-dimensional ideal MHD simulations to investigate the effect of hypercritical accretion on the magnetic field of the newborn NS, demonstrating that such submergence could occur. The result was a rapid submergence of the magnetic field beneath the NS crust. Recent high-dimensional MHD numerical results have confirmed that this is indeed the case (Bernal et al., 2010; Bernal et al., 2013; Ho, 2011).

In previous works by Muslimov and Page (1995) and Viganò and Pons (2012), it was found that when the hypercritical phase concludes, the magnetic field can reemerge through MHD instabilities and complex thermomagnetic processes present in the stellar crust. The diffusion time in such a case is τ_B ∼ 10^2–3yr. This is the timescale for growing a magnetic field from a low value B ∼ 10^8–9G to a high value B ∼ 10^12–13G, depending on the early thermomagnetic history of the pulsar, initial magnetic flux distribution, and electric resistivity in the crust. It was found that an accreted mass of 0.01M_⊙ would be enough to submerge the magnetic field (which corresponds to an accretion rate of $\sim 100{\mathrm{M}}_{\odot }\mathrm{y}{\mathrm{r}}^{-\mathrm{1}}$ in few hours). Although many observed pulsars show clear evidence for the presence of strong magnetic fields (from radio pulsars with 10^12–13G to magnetars with 10^14–15 G), lower magnetic fields are, however, found in millisecond pulsars (Phinney and Kulkarni, 1994) and in NSs in low-mass X-ray binaries (Psaltis, 2004), but in both cases, past or present, respectively, accretion is thought to be the cause of the magnetic field reduction. In addition, there is a small group of NSs, found in young supernova remnants, that exhibit little or no evidence of the presence of a magnetic field. Finally, Magalhaes et al. (2012) admitted that young pulsars are rotating magnetic dipoles with magnetic field growth, but they did not propose any intrinsic mechanism for such growth.

Following these ideas regarding the variability of a pulsar’s magnetic field, we developed a model for the growth of the magnetic field when it reemerges from the NS crust, and we analyzed its consequences and impacts on the overall dynamical properties of the pulsar. In our model, we assume that the magnetic field has an early time dependence B(t) (in contrast to the canonical model) and that after a diffusion time, the typical behavior of a rotating pulsar is reached (saturation regime). Such a temporal dependence is expected to relate to the intrinsic properties of the pulsar, impacting the structural constant k of the ansatz (5). Therefore, in general, this structural factor should also have a time dependence resulting from B(t), expressed as k(t) = kf(t), which is an analytical adjustment to the canonical model through the introduction of f(t) to account for the magnetic field early evolution, with k being the canonical constant of (5). The dynamic evolution is governed by selected mathematical functions f(t) > 0 that allow a rapid growth of the magnetic field within a characteristic diffusion time. Consequently, the new equation of motion for the pulsar’s spin-down is given as follows:

$\dot{\mathrm{\Omega }}=-k\left(t\right){\mathrm{\Omega }}^n,k\left(t\right)=kf\left(t\right).(9)$

This proposal is not novel (e.g., Blandford and Romani, 1988; Negreiros and Bernal, 2015; Rogers and Safi-Harb, 2016), but an analysis of its impacts on the dynamical properties of the pulsar through a set of well-behaved growth functions has not been fully performed. As in the case of the canonical model, we can calculate the expressions for the relevant properties of the very young pulsar, now assuming the growth of the magnetic field. This is the novelty brought about by this work.

The braking index now has a time dependence, which is modulated by the function f(t) and its time derivative $\dot{f}(t)$ as follows:

$n_{\mathit{obs}}=n+\frac{\dot{f}\left(t\right)}{f\left(t\right)}\frac{\mathrm{\Omega }}{\dot{\mathrm{\Omega }}}=n-\frac{\dot{f}\left(t\right)}{f\left(t\right)}\frac{P}{\dot{P}}.(10)$

It is worth noting that in order to obtain n_obs < 3, as expected from observations, and given that observationally $\dot{P}>0$, then $\dot{f}(t)>0$, which implies that the growth of the magnetic field is required to explain these braking indexes.

On the other hand, the characteristic age now depends on the format of the analytical growth function, which is as follows:

$\tau =\frac{1}{f\left(t\right)}\left[{\tau }_0+{\int }_0^{t}f\left(t^{\prime }\right)d{t}^{\prime }\right],(11)$

where the initial characteristic age has the same definition as in the canonical model. The spin-down luminosity and the spin period evolve over time in this growth phase, as

$\dot{E}={\dot{E}}_{0}f\left(t\right){\left[\frac{\tau }{{\tau }_0}f\left(t\right)\right]}^{-\frac{\left(n+1\right)}{\left(n-1\right)}},P=P_0{\left[\frac{\tau }{{\tau }_0}f\left(t\right)\right]}^{\frac{1}{n-1}},(12)$

where the initial spin-down luminosity and the initial period are defined as in the canonical model. Additionally, n remains the theoretical value. Finally, the spin-period derivative evolves as follows:

$\dot{P}=\frac{P_{0}f\left(t\right)}{{\tau }_0\left(n-1\right)}{\left[\frac{\tau }{{\tau }_0}f\left(t\right)\right]}^{\frac{\left(2-n\right)}{n-1}}.(13)$

Regardless of what the mathematical growth function f(t) proposed is, the main requirement is that f(t) allows the growth of the magnetic field rapidly within a diffusion timescale τ_B from a low value to a canonical value (B ∼ 10^12–13G for normal pulsars or B ∼ 10^14–15G for magnetars). Therefore, it must satisfy f(t = 0) → ϵ and f(t > τ_B) → 1, where the factor that measures the growth of the magnetic field is $ϵ={(B_0/B)}^2\ll 1$, and B₀ is the initial low magnetic field. Hence, when f(t) = 1, the canonical properties for the dipolar oblique rotator model must be recovered.

In Table 1, we present a few carefully selected, well-behaved functions that satisfy the aforementioned requirements in terms of the free parameters ϵ and τ_B.

Table 1

Table 1. Analytical growth functions proposed to describe the magnetic field behavior in the early history of the pulsar.

The growth functions proposed in Table 1 represent different mathematical models for the time evolution of the magnetic field in NSs, particularly in scenarios where the magnetic field is initially buried or submerged by the material from the supernova and then reemerges or grows over time. Each function describes a specific way in which the magnetic field might grow to its final, observable state:

(a) The exponential function: this model represents a rapid initial increase in magnetic field strength, followed by a leveling off as it approaches a maximum value. The exponential function is indicative of processes where the rate of change decreases as the field strength approaches its maximum. Physically, this could represent the magnetic field “unburying” itself from beneath the surface of the NS as the suppressive effects of the accreted material diminish, possibly through diffusive processes, turbulent dynamo, or heat-driven movement of the material.

(b) The hyperbolic function: this function suggests a smooth and steady increase toward a stable maximum value, much like a saturation curve. This could physically represent the gradual alignment of magnetic domains within the neutron star or the reconnection of magnetic field lines that were disrupted or misaligned during the star’s formation, reaching a stable configuration as the internal conditions of the star settle.

(c) The power-law 1 function: this function indicates a slower growth that accelerates over time but remains bound—a more gradual and conservative growth compared to the exponential one. This might physically correspond to scenarios where the magnetic field is influenced by ongoing but decaying external pressures or where the field’s growth is moderated by feedback mechanisms within the star, such as counteracting magnetic or thermal pressures.

(d) The power-law 2 function: this function models a very gradual increase that is linear at first but slowly approaches an asymptote, representing a scenario where the magnetic field’s growth is steady and limited by continuously acting constraints. Physically, this could be due to the persistent effects of accretion or continued interaction with the fallback material that gradually becomes less significant as the material is either assimilated or expelled.

Each of these growth functions provides a different lens to view the complex dynamics of magnetic field evolution in young pulsars, influenced by a variety of physical processes such as accretion, magnetic reconfiguration, and interactions with the environment immediately post-supernova.

4 Results and discussion

In this section, we present the time evolution of the dynamical parameters of very young NSs for the proposed growth functions and compare them to the canonical model. As a particular case, we adjust our free parameters ϵ and τ_B for the Crab Pulsar case using observational data from Bühler and Blandford (2014) and Araujo et al. (2023), which are given by: t_crab = 969 yr, τ_crab = 1240 yr, P_crab = 33.4 ms, P₀ = 15.6 ms, $\dot{P}=4.1874\times 10^{-13}$ ss⁻¹, ${\dot{E}}_{\mathit{crab}}=5\times 10^{38}$ ergs⁻¹, $\dot{E_0}=1\times 10^{40}$ ergs⁻¹, B_crab = 3.8 × 10¹² G, and n_crab = 2.5. We chose the Crab pulsar to test our models because it constitutes an exemplary case, given the extensive dataset available on this object. However, like many other astrophysical objects, the Crab pulsar presents several challenges and complexities in terms of observational data. Particularly, its initial conditions are not directly observable and must be inferred from its currently observed properties using pulsar evolution models. This is so despite the Crab pulsar being the only one with a well-established birth date. For example, the initial period is estimated based on the current spin period and the rate of spin-down, using models of pulsar evolution. These models often assume a constant braking index and use the pulsar’s characteristic age to estimate how much the pulsar has slowed down since its birth. Since the use of the characteristic age, rather than the true age, can lead to considerable errors, it is desirable to have an independent age measurement. The age of a supernova remnant (SNR) that originated as a pulsar in the same explosion can serve as such an estimator, but the only pulsar for which the age of an associated SNR is clearly known is the Crab pulsar (Huang and ji Wu, 2003). As well, the initial spin-down luminosity, representing the rate at which the pulsar’s rotational energy was lost at the time of its formation, is also calculated by extrapolating current measurements. For the Crab pulsar, this luminosity may have initially been very high if the pulsar started with a short rotation period, indicating that it was spinning faster and, therefore, had more rotational energy to lose (Torres et al., 2013). Over time, as the pulsar slows down, its rotational luminosity decreases.

In Figure 1 the three panels show the evolution of the magnetic field, of the braking index, and of the characteristic age for each of the proposed growth functions f(t). In all the cases, we choose τ_B = 500yr and ϵ = 10^–6, which are the best values that fit the braking index data for the Crab Pulsar.

Figure 1

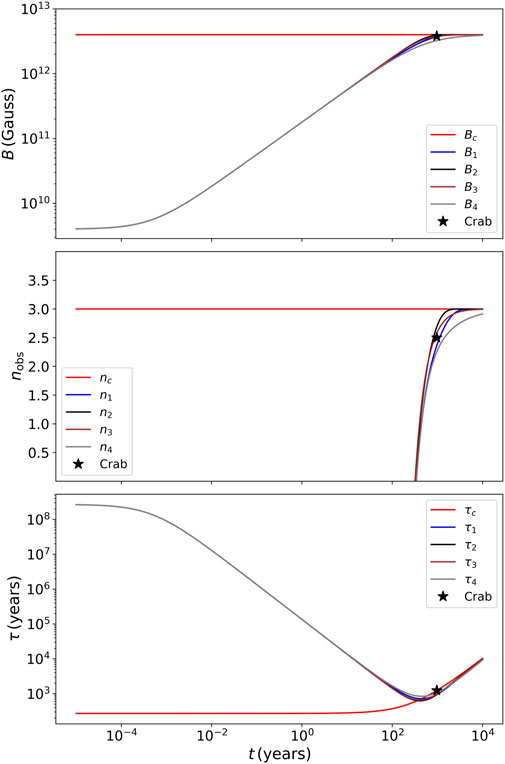
Figure 1. Time evolution of the magnetic field B, the braking index n,and characteristic age τ for the growth functions displayed in Table 1(respectively). The free parameters ϵ= 10^–6and τ_B= 500 yr were chosen to fit the observational parameters of the Crab pulsar. The red curve (“c” sub index) corresponds to the canonical model.

In the top panel, we note that the magnetic field growth is efficient in the sense that to grow a magnetic field by three orders of magnitude (from B₀ = 10¹⁰G to B = 10¹³G) required only a few centuries. The Crab Pulsar is presently in the saturation phase of B, well-fitted with all the proposed functions, but power-law 2 showed the worst fit among the four functions proposed.

In the middle panel, we show the braking index given by our model, which is dependent on τ_B and ϵ and also with a direct dependence on the period P and its derivative $\dot{P}$, since t → 0 implies $n\to 3-P{\dot{P}}^{-1}/ϵ{\tau }_B$. The plot shows that, after a diffusion timescale τ_B, our model evolves as the familiar canonical model. That is, the growth of the magnetic field allows the braking index to grow from a low value to the canonical value. Note that the exponential, hyperbolic, and power-law 1 functions best fit the observed value for the Crab pulsar, while power-law 2 shows the poorest fit. This may be so because the three first functions might represent scenarios where the interplay between the magnetic field growth and the neutron star’s rotational dynamics is relatively harmonized. The braking indices under these functions show similar patterns, suggesting a consistent model of interaction between the magnetic torque and rotational inertia. In the case of the last mentioned function, a much lower braking index indicates a possibly more complex or disrupted magnetic field development or a different interaction with the pulsar’s rotation. This could reflect (i) a delayed stabilization of the magnetic field, leading to a prolonged phase of irregular spin-down behavior or (ii) anomalies in the neutron star’s internal composition or external torque mechanisms, such as enhanced particle winds or irregular magnetic dipole alignment.

In the bottom panel, the characteristic age (τ) given by our model is shown. This parameter is initially different from the canonical value, but after a diffusion timescale τ_B, all functions overlap with the canonical model, as expected. The main reason responsible for this behavior is the parameter ϵ in the growth functions f(t) because when t → 0, τ → τ₀/ϵ, where τ₀ is the canonical initial spin-down timescale of the pulsar. Note that when the pulsar’s age is approximately t ∼ τ_B, the magnetic field is actively undergoing significant growth or adjustment, leading to (i) rapid changes in the magnetic field strength, (ii) alterations in the rate of spin-down due to increased or altered electromagnetic torque exerted by the evolving magnetic field, and (iii) a transitional phase where the pulsar adjusts from its initial spin-down behavior to a new regime governed by the grown magnetic field.

In Figure 2 we show three panels with the evolution of the spin-down luminosity, the spin period, and the period derivative. The top panel displays the spin-down luminosity given by our model. As in the plot of B in Figure 1, initially, $\dot{E}$ is smaller than the canonical value, but after a diffusion timescale τ_B, it evolves as expected from the canonical model. Again, the reason for this behavior is the parameter ϵ because when $t\to 0,\dot{E}\to ϵ{\dot{E}}_0$, where ${\dot{E}}_0$ is the canonical initial spin-down luminosity of the pulsar. This means that for an initial low magnetic field B₀, the corresponding initial spin-down luminosity is several orders of magnitude smaller than in the canonical case. For the Crab pulsar, the spin-down luminosity from our model would be entering the canonical regime after a period with maximum luminosity, possibly due to the progressive stabilization of the magnetic field with the consequent increase in the braking index.

Figure 2

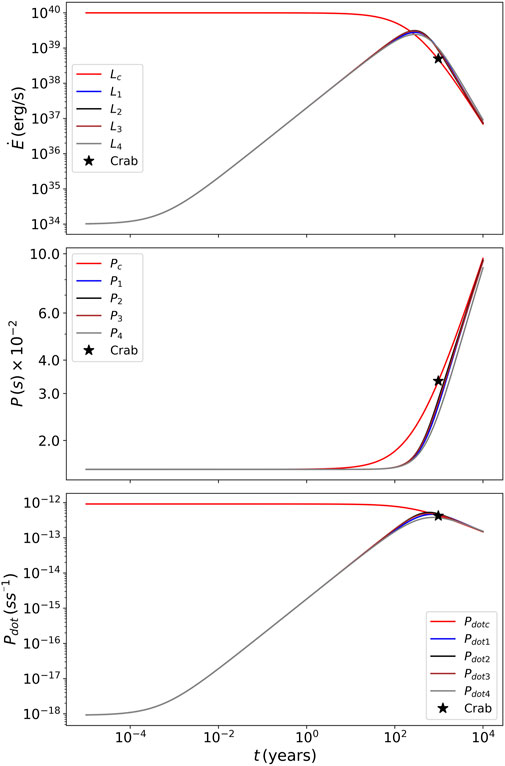
Figure 2. Evolution of the spin-down luminosity $(\dot{E})$, the spin period (P),and the period derivative $(\dot{P})$for the growth functions investigated. As in Figure 1, the free parameters ϵ and τ_Bwere chosen to fit the observational parameters for the Crab pulsar, and the red curve (“c” sub index) corresponds to the canonical model.

In the middle panel, we show the evolution of the rotational period over time. Here, when t → 0, P → P₀, no initial change in its value is expected. At later times, for different growth functions, small variations occur in the period as a result of the changes in the magnetic field.

Finally, in the bottom panel, we show the time derivative of the period. When t → 0, then $\dot{P}\to (ϵP_0)/(2{\tau }_0)$, indicating an initial variation of the period smaller than the canonical one. As time passes, the period variation increases, which is correlated to the growth of the magnetic field. For these last two parameters, Crab pulsar’s observational data lie in the saturation threshold in the growth of the magnetic field.

It is worth mentioning that the fact that the evolutionary curves for most physical parameters appear almost identical for t < τ_B and t > τ_B, except for the braking index, can be attributed to (a) t < τ_B: the pulsar’s properties are largely influenced by the initial conditions set forth at the time of the neutron star’s formation. During this phase, the magnetic field is still in a growth phase but has not yet reached its peak or stable state, so changes in pulsar properties follow a more predictable and less volatile pattern. (b) t > τ_B: the magnetic field has likely reached a stable configuration or a peak state, and changes in the pulsar properties proceed at a more uniform rate determined by the now stable magnetic field (canonical model).

In light of our model’s predictions, future observational efforts focusing on the Crab pulsar could be particularly revealing. An increase in the braking index and a concurrent decrease in $\dot{P}$, as suggested by our findings, would not only support the proposed mechanisms in our models but also offer deeper insights into the interplay between magnetic field dynamics and neutron star spin-down. We encourage the astrophysical research community to consider these aspects in upcoming observational studies, which could crucially validate or refine the theoretical frameworks discussed herein.

5 Conclusion

As was extensively discussed in this work, the dynamics of pulsars is very complex, and various factors, such as the effects of early hyperaccretion, can lead to deviations from the idealized canonical model for RPPs, which has long provided a framework for understanding the evolution of such objects. However, recent observations and computational simulations have unveiled a remarkable phenomenon—the early reemergence of magnetic fields in these nascent NSs. This discovery challenges the traditional pulsar model, reshaping our understanding of the behavior of these stars, and expands our understanding of the magnetic field generation, evolution, and its role in shaping the birth and early life of NSs.

In the present work, we used an analytical approach to tackle the problem of matching the canonical model to the early dynamics of a pulsar. In our growth models, we assumed a hypercritical accretion phase preceding the emergence of the magnetic field. This period of vigorous accretion has the effect of burying the dipole magnetic field component within the neutron star crust, reducing rotational energy loss and causing the neutron star to appear significantly older than its associated supernova remnant. In this alternative model for evolution of early neutron star, field growth is necessary to explain the initially small braking index and low surface magnetic fields. The results obtained with this method, using data from the Crab pulsar for calibration, are not only consistent with those obtained numerically by Viganò and Pons (2012) and Ho (2011), but they also allowed us to deduce analytical formulas for the overall relevant physical parameters for the pulsar dynamics.

In addition, we recognize that relying solely on the Crab pulsar to model and understand pulsar evolution may introduce biases or inaccuracies, as it could represent an outlier. The Crab pulsar is exceptionally young and energetic, and its unique characteristics may not generalize well to other pulsars. Nevertheless, one of our goals was to explain the low braking index value for this object, which was achieved by adjusting some plausible free parameters. In addition, we employed a fixed initial spin period across all models to standardize a key variable and isolate the effects of different magnetic field evolution mechanisms on pulsar spin-down behavior. We acknowledge that this approach primarily serves an illustrative purpose, highlighting theoretical possibilities rather than predicting exact current-day parameters of pulsars like the Crab pulsar. Recognizing the limitations of this method, we plan to recalibrate the initial spin period self-consistently for each model in future work. This adjustment will better align the initial conditions with the distinct dynamics of each model, enhancing the accuracy of our comparisons with empirical data and improving our understanding of pulsar evolution.

Finally, we aim to expand the dataset by incorporating more pulsars, which would enhance the reliability of our early-pulsar model, particularly those in supernova remnants with well-determined ages and environmental characteristics. We also plan to include, with similar analytical treatment, possible changes in the moment of inertia of the newborn pulsar (Oliveira et al., 2018) and a model for the alignment of the magnetic field with the axis of rotation. These additions will provide a better explanation for the values of the braking index observed in very young pulsars. Additionally, a numerical treatment for the reemergence of the magnetic field inside the hot plasma would allow the inclusion of other detailed physical properties present in these systems. Such an investigation is outside the scope of this research, and we anticipate it as a future work.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

CB: writing–review and editing, writing–original draft, validation, supervision, project administration, methodology, investigation, and conceptualization. CF: writing–review and editing, writing–original draft, visualization, supervision, and conceptualization. HH: writing–review and editing, writing–original draft, visualization, software, methodology, and investigation. BM: writing–review and editing, writing–original draft, visualization, software, methodology, and investigation. NM: writing–review and editing, writing–original draft, visualization, methodology, and investigation. LS: writing–review and editing, writing–original draft, visualization, software, methodology, and investigation.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The grant is CNPq No. 312454/2021-0.

Acknowledgments

Authors B. Minari, H. D. Hirsch, and L. B. Selbach are grateful to CAPES (Brazil) for support. Author C. Frajuca thanks FAPESP (Brazil) and CNPq (Brazil).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alpar, M. A., and Oegelman, H. (1990). Spin-up of young pulsars due to rapid cooling by neutrino emission. Astrophysical J. 349, L55–L58. doi:10.1086/185650

CrossRef Full Text | Google Scholar

Araujo, E., De Lorenci, V., Peter, P., and Ruiz, L. (2023). Modelling the braking “index” of isolated pulsars. Available at: https://arxiv.org/abs/2302.13322.

Google Scholar

Archibald, R., Kaspi, V., Beardmore, A., Gehrels, N., and Kennea, J. (2015). On the braking index of the unusual high-brotation-powered pulsar psr j1846–0258. Astrophysical J. 810, 67. doi:10.1088/0004-637x/810/1/67

CrossRef Full Text | Google Scholar

Baade, W., and Zwicky, F. (1934). Cosmic rays from super-novae. Proc. Natl. Acad. Sci. 20, 259–263. doi:10.1073/pnas.20.5.259

PubMed Abstract | CrossRef Full Text | Google Scholar

Bernal, C. G., Page, D., and Lee, W. H. (2013). Hypercritical accretion onto a newborn neutron star and magnetic field submergence. Astrophysical J. 770, 106. doi:10.1088/0004-637x/770/2/106

CrossRef Full Text | Google Scholar

Blandford, R. D., and Romani, R. W. (1988). On the interpretation of pulsar braking indices. Mon. Notices R. Astronomical Soc. 234, 57P–60P. doi:10.1093/mnras/234.1.57p

CrossRef Full Text | Google Scholar

Bransgrove, A., Levin, Y., and Beloborodov, A. (2018). Magnetic field evolution of neutron stars–I. Basic formalism, numerical techniques and first results. Mon. Notices R. Astronomical Soc. 473, 2771–2790. doi:10.1093/mnras/stx2508

CrossRef Full Text | Google Scholar

Bühler, R., and Blandford, R. (2014). The surprising crab pulsar and its nebula: a review. Rep. Prog. Phys. 77, 066901. doi:10.1088/0034-4885/77/6/066901

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, W.-C., and Li, X.-D. (2006). Why the braking indices of young pulsars are less than 3? Astronomy Astrophysics 450, L1–L4. doi:10.1051/0004-6361:200600019

CrossRef Full Text | Google Scholar

Chen, W.-C., and Li, X.-D. (2016). Low braking index of PSR J1734-3333: an interaction between fall-back disc and magnetic field? Mon. Notices R. Astronomical Soc. 455, L87–L90. doi:10.1093/mnrasl/slv152

CrossRef Full Text | Google Scholar

Chevalier, R. A. (1989). Neutron star accretion in a supernova. Astrophysical J. 346, 847–859. doi:10.1086/168066

CrossRef Full Text | Google Scholar

Chevalier, R. A., and Emmering, R. T. (1986). Are pulsars born as slow rotators? Astrophysical J. 304, 140–153. doi:10.1086/164150

CrossRef Full Text | Google Scholar

[Dataset] Bernal, C. G., Lee, W. H., and Page, D.(2010). Hypercritical accretion onto a magnetized neutron star surface: a numerical approach. Available at: https://arxiv.org/abs/1006.3003.

Google Scholar

[Dataset] Negreiros, R., and Bernal, C.(2015). Growth of the magnetic field in young neutron stars. Available at: https://inspirehep.net/literature/1369301.

Google Scholar

[Dataset] Psaltis, D.(2004). Accreting neutron stars and black holes: a decade of discoveries. Available at: https://ui.adsabs.harvard.edu/abs/2004astro.ph.10536P/abstract.

Google Scholar

Dehman, C., Viganò, D., Ascenzi, S., Pons, J. A., and Rea, N. (2023). 3d evolution of neutron star magnetic-fields from a realistic core-collapse turbulent topology. Mon. Notices R. Astronomical Soc. 523 (4), 5198–5206. doi:10.1093/mnras/stad1773

CrossRef Full Text | Google Scholar

Fraija, N., Bernal, C., Morales, G., and Negreiros, R. (2018). Hypercritical accretion scenario in central compact objects accompanied with an expected neutrino burst. Phys. Rev. D. 98, 083012. doi:10.1103/physrevd.98.083012

CrossRef Full Text | Google Scholar

Fraija, N., and Bernal, C. G. (2015). Hypercritical accretion phase and neutrino expectation in the evolution of cassiopeia a. Mon. Notices R. Astronomical Soc. 451, 455–466. doi:10.1093/mnras/stv1015

CrossRef Full Text | Google Scholar

Fraija, N., Bernal, C. G., and Hidalgo-Gamez, A. M. (2014). Signatures of neutrino cooling in the sn1987a scenario. Mon. Notices R. Astronomical Soc. 442, 239–250. doi:10.1093/mnras/stu872

CrossRef Full Text | Google Scholar

Gaensler, B. M., and Slane, P. O. (2006). The evolution and structure of pulsar wind nebulae. Annu. Rev. Astron. Astrophys. 44, 17–47. doi:10.1146/annurev.astro.44.051905.092528

CrossRef Full Text | Google Scholar

Geppert, U., Page, D., and Zannias, T. (1999). Submergence and re-diffusion of the neutron star magnetic field after the supernova. Astronomy Astrophysics 345, 847–854.

Google Scholar

Ghosh, P. (1984). Braking index diagnostics of pulsars. i. alignment, counteralignment and slowing-down noise. J. Astrophysics Astronomy 5, 307–316. doi:10.1007/bf02714546

CrossRef Full Text | Google Scholar

Ghosh, P. (2007) Rotation and accretion powered pulsars, vol. 7. World Scientific.

Google Scholar

Glendenning, N. K. (2003). “Dense matter,” in New worlds in astroparticle Physics (World Scientific), 3–19.

CrossRef Full Text | Google Scholar

Gold, T. (1968). Rotating neutron stars as the origin of the pulsating radio sources. Nature 218, 731–732. doi:10.1038/218731a0

CrossRef Full Text | Google Scholar

Hewish, A., Bell, S. J., Pilkington, J. D. H., Scott, P. F., and Collins, R. A. (1968). Observation of a rapidly pulsating radio source. Nature 217, 709–713. doi:10.1038/217709a0

CrossRef Full Text | Google Scholar

Ho, W. C. (2011). Evolution of a buried magnetic field in the central compact object neutron stars. Mon. Notices R. Astronomical Soc. 414, 2567–2575. doi:10.1111/j.1365-2966.2011.18576.x

CrossRef Full Text | Google Scholar

Huang, Z., and ji Wu, X. (2003). An estimation of the initial period of pulsars. Chin. J. Astronomy Astrophysics 3, 166–174. doi:10.1088/1009-9271/3/2/166

CrossRef Full Text | Google Scholar

Igoshev, A. P., Elfritz, J. G., and Popov, S. B. (2016). Post-fall-back evolution of multipolar magnetic fields and radio pulsar activation. Mon. Notices R. Astronomical Soc. 462, 3689–3702. doi:10.1093/mnras/stw1902

CrossRef Full Text | Google Scholar

Igoshev, A. P., and Popov, S. B. (2020). Braking indices of young radio pulsars: theoretical perspective. Mon. Notices R. Astronomical Soc. 499, 2826–2835. doi:10.1093/mnras/staa3070

CrossRef Full Text | Google Scholar

Magalhaes, N. S., Miranda, T. A., and Frajuca, C. (2012). Predicting ranges for pulsars’braking indices. Astrophysical J. 755, 54. doi:10.1088/0004-637x/755/1/54

CrossRef Full Text | Google Scholar

Michel, F. C. (1994). Magnetic structure of pulsar winds. Astrophysical J. 431 (1), 397–401. doi:10.1086/174493

CrossRef Full Text | Google Scholar

Muslimov, A., and Page, D. (1995). Magnetic and spin history of very young pulsars. Astrophysical J. 458, 347. doi:10.1086/176817

CrossRef Full Text | Google Scholar

Oliveira, H. O., Magalhaes, N. S., Marinho, R. M., Carvalho, G. A., and Frajuca, C. (2018). Relating braking indices of young pulsars to the dynamics of superfluid cores. JCAP 2018, 205. doi:10.1088/1475-7516/2018/11/025

CrossRef Full Text | Google Scholar

Pavlov, G. G., Sanwal, D., and Teter, M. A. (2004). “Central compact objects in supernova remnants,” in Symposium-International Astronomical Union (Cambridge: Cambridge University Press), 239–246.

CrossRef Full Text | Google Scholar

Phinney, E., and Kulkarni, S. (1994). Binary and millisecond pulsars. Annu. Rev. astronomy astrophysics 32, 591–639. doi:10.1146/annurev.astro.32.1.591

CrossRef Full Text | Google Scholar

Rogers, A., and Safi-Harb, S. (2016). On the diversity of compact objects within supernova remnants – i. a parametric model for magnetic field evolution. Mon. Notices R. Astronomical Soc. 457, 1180–1189. doi:10.1093/mnras/stw014

CrossRef Full Text | Google Scholar

Ruderman, M. (1991). Neutron star crustal plate tectonics. I - magnetic dipole evolution in millisecond pulsars and low-mass X-ray binaries. Astrophysical J. 366, 261–269. doi:10.1086/169558

CrossRef Full Text | Google Scholar

Shabaltas, N., and Lai, D. (2012). The hidden magnetic field of the young neutron star in kesteven 79. Astrophysical J. 748, 148. doi:10.1088/0004-637x/748/2/148

CrossRef Full Text | Google Scholar

Torres, D. F., Martín, J., Wilhelmi, E. O., and Cillis, A. (2013). The effects of magnetic field, age and intrinsic luminosity on crab-like pulsar wind nebulae. Mon. Notices R. Astronomical Soc. 436, 3112–3127. doi:10.1093/mnras/stt1793

CrossRef Full Text | Google Scholar

Viganò, D., and Pons, J. A. (2012). Central compact objects and the hidden magnetic field scenario. Mon. Notices R. Astronomical Soc. 425, 2487–2492. doi:10.1111/j.1365-2966.2012.21679.x

CrossRef Full Text | Google Scholar

Weber, F., and Papoyan, V. (1999). Elastodynamical properties of nuclear matter from the observed activity of neutron stars. Phys. Part. Nucl. 30, 436. doi:10.1134/1.953114

CrossRef Full Text | Google Scholar