Cosmic ray contributions from rapidly rotating stellar mass black holes: cosmic Ray GeV to EeV proton and anti-proton sources

In Radio Super Novae (RSNe) a magnetic field of $(B\times r)=10^{16.0\pm 0.12}\text{\hspace{0.17em}Gauss\hspace{0.17em}}\times \text{\hspace{0.17em}cm}$ is observed; these are the same numbers for Blue Super Giant (BSG) star explosions as for Red Super Giant (RSG) star explosions, despite their very different wind properties. The EHT data for M87 as well for low power radio galaxies all show consistency with just this value of the quantity $(B\times r)$, key for angular momentum and energy transport, and can be derived from the radio jet data. We interpret this as a property of the near surroundings of a black hole (BH) at near maximal rotation, independent of BH mass. In the commonly used green onion model, in which a $2\pi$ flow changes over to a jet flow we interpret this as a wind emanating from the BH/accretion disk system and its surroundings. Near the BH collisions in the wind can produce a large fraction of anti-protons. In this scenario the cosmic Ray (CR) population from the wind/jet is proposed to be visible as EeV protons and anti-protons in the CR data to EeV energy, with a $E^{-7/3}$ spectrum. This can be connected to a concept of inner and outer Penrose zones in the ergo-region. The observed numbers for the magnetic field imply the Planck time as the governing time scale: A BH rotating near maximum can accept a proton per log bin of energy in an extended spectrum with the associated pions every Planck time.

1 Introduction: energetic particles and black holes

Energetic particles, commonly called Cosmic Ray particles, or short just Cosmic Rays have been researched since their discovery in 1912 (with a recent review with many references in Biermann et al. (2018)); further important viewpoints and history are given by Colgate (1994), Yodh (1992), Yodh (2003), Yodh (2005), Yodh (2006). Cosmic Ray (short CRs) particles have been observed from below GeV, with stellar sources responsible up to a few EeV, as discussed here, and extragalactic sources up to a few hundred EeV. Many of them, both Galactic and extragalactic, can be traced to the activity of black holes.

The various possible sources of CRs were discussed in Biermann et al. (2018), Biermann et al. (2019), and earlier papers (Biermann, 1993; Biermann and Cassinelli, 1993; Biermann and Strom, 1993; Stanev et al., 1993; Rachen et al., 1993) with reviews in Biermann (1994), Biermann (1997). A main distinction, which we have made (Stanev et al., 1993), is to differentiate between SNe, that explode into their own wind, wind-SNe, and those that explode into the Interstellar Medium (ISM), ISM-SNe. It is also necessary to sub-divide those two groups: There are Red Super Giant (RSG) stars with slow dense winds, and Blue Super Giant (BSG) stars that explode into tenuous fast winds, heavily enriched in the chemical elements of higher nucleon $A$ and charge number $Z$. Furthermore, almost all massive stars are in binaries, or multiple systems (Chini et al., 2012; Chini et al., 2013a; Chini et al., 2013b), while the binary frequency is reduced for lower mass stars. This naturally explains the rapid change in the chemical composition of CRs all across the knee (Stanev et al., 1993), and a knee energy at about $10^{17.3\pm 0.2}eV$ for Fe (Stanev et al., 1993; Biermann et al., 2018); note that for the model worked out in 1993 the magnetic field in winds had not been known as well it is now, as today the magnetic fields are known to be stronger, and so all ensuing particle energies higher. Of those SNe that explode into the ISM, there are SN Ia that are exploding white dwarfs, and massive star SNe, that make neutron stars producing much lower particle energies. In the model of Gaisser et al. (2013) there is a Galactic component of near EeV protons, that matches the model in Stanev et al. (1993) using the better magnetic field numbers now known. A test has been made of this model in Thoudam et al. (2016). Allen et al. (2024) focusses on those SNe, that explode into fast winds: On this basis we discussed there the new highly accurate AMS data on CRs. The sum of the CRS arising from ISM-SNe and wind-SNe, and their secondaries, gives structure to the spectrum at low energies (Stanev et al., 1993; Biermann et al., 2019; Allen et al., 2024). The essential message (Allen et al., 2024) is that almost all CR elements contain spallation secondaries, and we identified a spallation sequence, from a small secondary component, like for CR O, to a dominant secondary component like CR ³He. There is a large secondary component in CR protons.

The area around a rotating black hole (BH) has been observed by the EHT-Coll (2019a), EHT-Coll (2019b), EHT-Coll (2021a), EHT-Coll (2021b) and is found to be highly variable; in such a zone one may expect a population of energetic particles driven by stochastic processes, such as the second order Fermi process (Fermi, 1949; Fermi, 1954), followed by reconnection and other mechanisms (e.g., Meli and Mastichiadis, 2008; Meli and Nishikawa, 2021; Meli et al., 2023). The particle energy may go up to the maximum which space allows for the Larmor motion. In Radio Super-Novae (RSNe) a wind of typically $10^{-5}{\text{M}}_{\odot }{\text{yr}}^{-1}$ (a summary in Biermann et al. (2018), a shock speed of about $0.1c$, and a magnetic field of $(B\times r)=10^{16.0\pm 0.12}\text{\hspace{0.17em}Gauss\hspace{0.17em}}\times \text{\hspace{0.17em}cm}$ are implied by the radio observations (Kronberg et al., 1985; Allen and Kronberg, 1998; Allen, 1999; Biermann et al., 2019); these are the same numbers for Blue Super Giant star explosions as for Red Super Giant star explosions, despite their very different wind properties (Kronberg et al., 1985; Allen and Kronberg, 1998; Allen, 1999; Kronberg et al., 2000; Biermann et al., 2018; Biermann et al., 2019), as mentioned above. It is important to note that this latter quantity is independent of radial distance $r$ (Parker, 1958; Weber and Davis, 1967). In fact, the EHT data for M87 (EHT-Coll, 2019b) as well the low power radio galaxies (Punsly and Zhang, 2011) all show consistency with just this value of the quantity $(B\times r)$. The quantity $(B\times r)$ is key for angular momentum and energy transport, and can be derived from the radio jet data. We note that just recently the super-massive black hole in M87 experienced a merger with another black hole, with a spin-flip visible in the data (Owen et al., 2000); it might be possible that most, if not all radio galaxies evolve via many mergers of their central black holes as well as their host galaxies (Rottmann, 2001; Gopal-Krishna et al., 2003; Gopal-Krishna et al., 2012; Jaroschewski et al., 2023). In the commonly used green onion model, in which a $2\pi$ flow changes over to a jet flow (on both sides) we interpret the observations of RSNe as a wind emanating from the black hole/accretion disk system and its near surroundings, after a stellar explosion which produced a rapidly rotating black hole (BH) (Chieffi and Limongi, 2013; Limongi and Chieffi, 2018; Limongi and Chieffi, 2020).

The goal of this paper (see Table 1 for the run of the argument) is to understand the origin and the consequences of the quantity $(B\times r)$ showing the same number for stellar mass BHs and super-massive BHs, when we have reason to assume that in these cases the BH is rotating near maximum. Can we learn something about BHs from CR observations, and the answer we propose is “yes”. We will propose an origin of the numerical value of $(B\times r)$ as rooted in a property of rotating BHs.

Table 1

Table 1. Run of arguments in this paper.

1.1 Black holes

A better understanding of the nature of black holes (BHs) has been sought ever since Schwarzschild’s discovery Schwarzschild, 1916) of a solution of Einstein’s equations (Einstein, 1915) with an essential singularity (black hole), and Kerr’s generalization of the solution to a rotating BH (Kerr, 1963; Rees et al., 1974; Rueda et al., 2022). The most significant flaw is the failure to merge gravitational physics with quantum physics, with some convincing first steps (Penrose and Floyd, 1971; Bekenstein, 1973; Bardeen et al., 1973; Hawking, 1974; Hawking, 1975; Rueda and Ruffini, 2020; Rueda and Ruffini 2021); some early and recent books are Misner et al. (1973), Misner et al. (2017), Rees et al. (1974), Joshi (1993), Joshi (2007), Joshi (2011), Joshi (2014), Joshi (2015). The best hope to explore BH physics is to consider more detailed observations e.g. Mirabel et al. (2011). The goal of this paper is to further the understanding of BHs by exploring the observations of Super-Nova Remnants (SNRs) which are produced in those SN explosions which lead to BHs. These sources are referred to as Radio Super-Novae (RSNe). Numerous observational data have been obtained for these stellar explosions, which make BHs, at various wavelengths.

There are a number of samples of Radio Super Novae (RSNe): First is the large set of RSNe in the discovery paper (Kronberg et al., 1985), 28 sources certain, and 43 possible. Then there are the independent observations by the team of Muxlow, (Muxlow et al., 1994; McDonald et al., 2002; Muxlow et al., 2005; Muxlow et al., 2010), of the same population of RSNe in M82 (30 classified as SNR). There is the newly observed list of the M82 RSNe collected and analyzed in Allen and Kronberg (1998). Then there are the lists assembled in Biermann et al. (2018) of Red Super Giant (RSG) and Blue Super Giant (BSG) RSNe, all from the literature. For the RSNe collected in Biermann et al. (2018) we know the moment of explosion, with all accompanying information; the radio interferometric observations (VLBI) have followed the expansion to a radial scale of order $10^{16}\mathrm{c}\mathrm{m}$. For the RSNe in M82 we have only estimates when the explosion occurred, but from ram pressure arguments (Biermann et al., 2019) one can show that these RSNe must have originated in most cases from the explosion of a Blue Super Giant (BSG) star; in these cases the expansion can be followed to a radial scale of order $10^{18.5}\mathrm{c}\mathrm{m}$. All these RSNe are consistent with just different stages of the same kind of explosions, from RSG as well as BSG stars, for the large radial scales mostly BSG star explosions. Considering the independent data shown in the papers by Muxlow and his group (e.g., Muxlow et al., 1994; McDonald et al., 2002; Muxlow et al., 2005; Muxlow et al., 2010), they give the same value of $(B\times r)$, just with a larger error bar, as the data obtained and analyzed by Allen and Kronberg (1998). The collection in Biermann et al. (2019) is based on the Allen and Kronberg (1998) analysis and data. Moreover, there is an independent discussion using another data set of very energetic explosions by Soderberg et al. (2010), leading to about the same value for $(B\times r)$, as shown in Biermann et al. (2018).

It has been argued that very massive star SN lead to a BH by direct collapse, without leaving a visible trace (e.g., Smartt, 2009; Smartt, 2015; Van, 2017; Humphreys et al., 2020). These arguments are based on visual and infrared data, and are influenced by obscuration and selection effects. However, gamma-ray line data and radio data (e.g.; Diehl et al., 2006; Diehl et al. 2010; Diehl et al. 2011; Prantzos et al., 2011; Diehl, 2013; Siegert et al., 2016b; Biermann et al., 2018) clearly give much more accurate SN statistics data, unaffected by obscuration. These data show for instance [summarized in Biermann et al. (2018)], that Blue Super Giant star explosions happen in our Galaxy about once every 600 years, and in other galaxies at corresponding frequencies, scaled with the star formation rate, derivable from both far-infrared and radio observations, as they scale with each other (e.g., Tabatabaei et al., 2017).

These RSN range from RSG star explosions to BSG star explosions, which cover vastly different environments in density. Among the BSG star explosions they probably cover the entire range of masses [summarized in Biermann et al. (2018) based on the work of Chieffi and Limongi (2013), Limongi and Chieffi (2018), Limongi and Chieffi (2020)], which can be derived from the now many lists in LIGO/VIRGO-Coll (2019), LIGO/VIRGO-Coll (2021a), LIGO/VIRGO-Coll (2021b), LIGO/VIRGO/KAGRA-Coll (2021c). Of course, the lists of observed mergers of stellar mass BHs encompasses second generation mergers, and that is why the BH mass can reach relatively high values, up to four times the highest single BH mass.

The only common feature of all these explosions is that they form a BH, and the explosions happen into a wind. SN-explosions that make a neutron star explode into the ISM. Here we consider explosions into a wind: and yet, the quantity $(B\times r)$ is consistent with having the same value for all explosions. We note that the EHT data for M87 are consistent with the same number; the radio galaxy M87 harbors a central black hole with a mass approaching $10^{10}{M}_{\odot }$, suspected to be near maximal rotation (Daly, 2019; EHT-Coll, 2019b). The minimum jet powers in Punsly and Zhang (2011) are also consistent with the same values. So, we explore the possibility that this quantity is actually related to the BH in the sense that this quantity refers to a near maximal rotation of the black hole, independent of the mass, but with energetically negligible accretion.

In the following we will assume that the physics around black holes scales such that fundamental principles carry over across all masses observed (Merloni et al., 2003; Merloni et al., 2006; Falcke and Markoff, 2004; Markoff et al., 2015; Gültekin et al., 2019); this is commonly referred to as the “Fundamental plane of black hole accretion”. Much of the accretion physics is mass-invariant. As a consequence we will assume the same physical concepts across all masses of black holes discussed in the following.

2 Radio super novae (RSNe) with freshly formed black holes (BHs)

Where do we witness the formation of black holes? In massive star Super Novae (SNe), from stars of an initial mass (Zero Age Main Sequence or ZAMS) above about $25M_{\odot }$ (at Solar abundances: (Woosley et al., 2002; Heger et al., 2003; Chieffi and Limongi, 2013; Limongi and Chieffi, 2018; Limongi and Chieffi, 2020), best observable as Radio Super Novae (RSNe). The radio data can be interpreted as follows: We observe a Parker wind, as $(B\times r)$ follows two rules i) $(B\times r)=const$ for a given RSN, over a range in radius, and also ii) that value is the same for different RSNe, in different galaxies and for very different radii $r$ (Parker, 1958; Weber and Davis, 1967; Biermann et al., 2018; Biermann et al., 2019); the best data are obtained from the starburst galaxy M82 (Kronberg et al., 1985; Allen and Kronberg, 1998; Allen, 1999); the M82 sample can be checked also independently using the observations of Muxlow et al. (2005), and in other galaxies (Biermann et al., 2018); the radial range over which $(B\times r)=const$ covers a factor of over 100. The quantity is $(B\times r)=10^{16\pm 0.12}\text{\hspace{0.17em}Gauss\hspace{0.17em}}\times \text{\hspace{0.17em}cm}$ (Allen and Kronberg, 1998; Allen, 1999; Biermann et al., 2019). Probably all the Radio-Super-Novae (RSNe) detected in M82 can be traced back to BSG stars, all of which make black holes. This argument is based on the wind ram pressure, which is very much larger for a BSG star than for a Red Super Giant (RSG) star (Biermann et al., 2019). A wind from a RSG star is not expected to reach such large radii as parsec scale in an environment at a pressure like in the starburst galaxy M82. An expansion as in ISM-Super Novae (Cox, 1972) (i.e., SN exploding into the Interstellar Medium (ISM), the most common SNe) would not allow the quantity $(B\times r)$ to be constant; various other proposed explosion scenarios have been worked through in Biermann et al. (2019); none of them allow to understand such a constant value for $(B\times r)$, independent of environment and of radius $r$. Furthermore, since the value of $(B\times r)$ is the same in all examples, in different locations in M82 as well as in different galaxies, also at a much earlier stage of RSN evolution, it is clear that the environment does not play a role in the expansion. The concept of a wind driven by a rotating compact object at its center (Parker, 1958; Weber and Davis, 1967) has been generalized (e.g., Chevalier, 1984), to neutron stars (Goldreich and Julian, 1969), to black holes (Blandford and Znajek, 1977) and to entire galaxies (e.g., Breitschwerdt et al., 1991). We note that the generic approach developed by Pacini and Salvati (1973) in their development phase 2 gives a relationship as shown by the observations here, $(B\times r)=const$., with the difference that the magnetic field is too high by an order of magnitude; however, the approach of Pacini and Salvati (1973) was proposed for neutron stars which would be expected to yield somewhat different numbers as compared to BHs. Weiler and Panagia (1980) applied this approach to the observations of supernova remnants driven by the slowing down of a central neutron star, which they called “plerions”. Latest simulations are, e.g., those of Davis and Gammie (2020), White et al. (2020), Wong et al. (2021), Marszewski et al. (2021), Lucchini et al. (2022), Cho et al. (2023). Much of this work focusses on the Magnetically Arrested Disk (MAD) models (Igumenshchev et al., 2003; Narayan et al., 2003), also postulating that the driver of activity is the spin-down of the central black hole. Here we focus on what the observations tell us about a wind driven by the central object in RSNe, a rotating black hole. The well established idea of a central spinning object driving activity by spin-down starting with Parker (1958) is used here as well. The key difference here is the observation that the magnetic field in terms of $(B\times r)$ appears to be the same value for the RSNe observed.

In support of arguing that these RSNe contain BHs rotating near maximum, we note, that in radio galaxies it has been shown that the central BHs do rotate near maximum (Daly, 2019, EHT-Coll, 2019b), with the same magnetic field directly measured or the magnetic field inferred in terms of the quantity $(B\times r)$ (Punsly and Zhang, 2011) from the jet power (Falcke and Biermann, 1995; Falcke et al., 2004).

We wish to emphasize here that all these RSNe clearly derive from a spectrum of BH masses, as the black hole merger data as well as the optical stellar observations of original stars show (LIGO/VIRGO-Coll, 2019; LIGO/VIRGO-Coll, 2021a; LIGO/VIRGO-Coll, 2021b; LIGO/VIRGO/KAGRA-Coll, 2021c; Chini et al., 2012; Chini et al., 2013a; Chini et al., 2013b). So the quantity $(B\times r)$ does not depend on the BH mass at its center. Massive stars producing black holes almost all start in a binary, triple or quadruple system, allowing the final BH initially near maximum spin from a tidal lock in the tight binaries (Chini et al., 2012; Chini et al., 2013a; Chini et al., 2013b; Limongi and Chieffi, 2018; Limongi and Chieffi, 2020). Simulations suggest (Limongi and Chieffi, 2018; Limongi and Chieffi, 2020) that the black holes formed may reach a high rotation rate, possibly even slightly exceeding maximal just before a black hole is actually formed (see Figure 1).

Figure 1

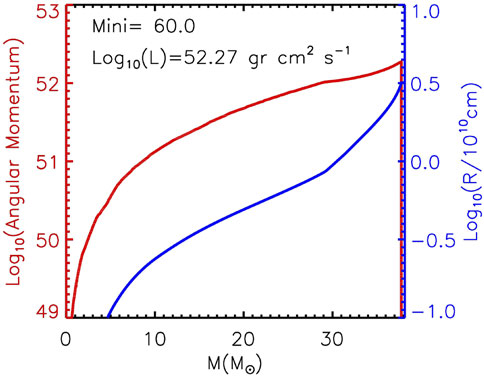
Figure 1. Internal structure of 60 $M_{\odot }$ star just before making a black hole of 38 $M_{\odot }$. Source: Chieffi 2019 priv.comm (Limongi and Chieffi 2018). Spin is $10^{52.27}\text{\hspace{0.17em}erg\hspace{0.17em}}s$, a factor of $\sim 10^{0.21}$ over limit at $38M_{\odot }$; relatively similar excess for other masses. Considering different radii each time the angular momentum is close to the maximum allowed for the mass contained in this radius; that means we have maximal differential rotation.

3 The EeV cosmic ray proton component

At solar chemical abundances, stars $\gtrsim 25M_{\odot }$ Zero Age Main Sequence (ZAMS) mass evolve to RSG stars, while those $\gtrsim 33M_{\odot }$ ZAMS mass become BSG stars. Both classes of stars produce BHs (Limongi and Chieffi, 2018; Limongi and Chieffi 2020). Stars between a ZAMS mass of about $\sim 10M_{\odot }$ and $\sim 25M_{\odot }$ produce neutron stars.

Magnetic fields (Kronberg, 1994; Kronberg, 2016) are observed in the winds of massive stars (e.g., Maheswaran and Cassinelli, 1992). Detailed further observation reveal, that massive stars are usually combined in binaries, triplets or quadruplets. This implies that these stars may lose orbital angular momentum efficiently, driving them progressively together - see the work in the group of Chini (Chini et al., 2012; Chini et al., 2013a; Chini et al., 2013b; Barr Domínguez et al., 2013; Pozo Nunez et al., 2019). Tidal locking then ensures that their rotation increases, resulting in the high rotation rates used in the simulations of Limongi and Chieffi (2018), Limongi and Chieffi (2020). These simulations show that massive stars can eventually lead to BHs which initially rotate near the maximum allowed (Chieffi and Limongi, 2013; Limongi and Chieffi, 2018; Limongi and Chieffi 2020).

We interpret the observed radio emissions as a wind, which is driven by a BH rotating near the maximum allowed via the Penrose/Blandford/Znajek mechanisms (Penrose and Floyd, 1971; Blandford and Znajek, 1977). This wind is thought of as keeping the energy and angular momentum transport processes functioning in the Radio Super-Novae (RSNe). The RSN data show that the slowest angular momentum transport time scale, derived from the afore-mentioned quantity $(B\times r)=10^{16.0\pm 0.12}\text{\hspace{0.17em}Gauss\hspace{0.17em}}\times \text{\hspace{0.17em}cm}$, is $\sim 10^{3.7}\mathrm{y}\mathrm{r}\mathrm{s}(M_{BH}/M_{\odot })$, following (Parker, 1958) and (Weber and Davis, 1967). Here we interpret the magnetic field observed, with $(B\times r)$ a constant without any indication of the magnetic field’s direction, as $B_{\varphi }$. The specific number for the angular momentum transport time-scale depends on three factors, which together amount to a term between unity and ten in the case of near maximal allowed rotation. As a compromise number here we adopt the value of 5, with a large uncertainty. From the connection of mass, irreducible mass, and spin, we can derive in the limit of near-maximal rotation that $(d{M}_{BH})/(M_{BH}dt)=(1/2)(d{J}_{BH})/(J_{BH}dt)$, where $J_{BH}$ is the angular momentum of the black hole. This gives a luminosity of $\sim 10^{42.8}\mathrm{e}\mathrm{r}\mathrm{g}/\mathrm{s}$, independent of BH mass in the mass range considered here. This corresponds to within a factor of unity to the Poynting flux energy flow (e.g., Nokhrina, 2020); such an interpretation suggests that the wind is split into a fast jet along the symmetry axis and a slower wind around it, i.e., over much of $4\pi$ (see the General Relativity Magneto-Hydrodynamic - GRMHD - simulations of Mościbrodzka et al. (2016), Davelaar et al. (2018), Porth et al. (2019)). The Super-Nova Remnant (SNR) data of Cas A in X-rays are compatible with this possibility (Hwang et al., 2004).

This is fully consistent with the voltage drop expected near a black hole (Lovelace, 1976; Kronberg et al., 2011). In Kronberg et al. (2011) the voltage near a black hole was worked out, and inserting the observed numbers corresponds to $10^{18.9}\mathrm{e}\mathrm{V}$ independent of black hole mass. This value is consistent with the observed magnetic field strength in terms of $(B\times r)$.

To summarize the concept used here: When a massive star explodes, it explodes into its magnetic wind, which has pushed out a substantial fraction of its Zero Age Main Sequence (ZAMS) mass already prior to the explosion. A magnetic wind emanating from a compact object, here thought to be a rotating black hole, enhances the energy and angular momentum transport processes and provides an outward pressure. Thus all the primary CRs are accelerated in the SN shock, but an additional weaker “special” CR component is proposed to come from the environment of the compact object, which we identify as $3^{*}$ of Gaisser et al. (2013); but also refer to Thoudam et al. (2016). We propose that this component is currently also visible in data near EeV (see Auger-Coll, 2020a). This is indeed a small proton component, if we think of pop $3^{*}$, in either Tables 2, 3 (Gaisser et al., 2013).

Noting that massive stars explode as SNe in our Galaxy on average about every 75 years (summarized in Biermann et al. (2018); the error on these numbers is $10^{\pm 0.11}$: see Diehl et al. (2006), Diehl et al. (2010)), and those leading to BHs every 400 years (i.e., both RSG and BSG stars); we can check the energy budget. Here we take the numbers of Gaisser et al. (2013), which indicate that one needs to account for $10^{41}\mathrm{e}\mathrm{r}\mathrm{g}/\mathrm{s}$ for CR production in our Galaxy. Following these authors, we adopt 10 percent of the kinetic energy as leading to CR production. This then suggests that every massive star which makes a neutron star produces $10^{50}$ erg in CRs, i.e., $\sim 5\cdot 10^{40}\mathrm{e}\mathrm{r}\mathrm{g}/\mathrm{s}$, requiring $10^{50.8}\mathrm{e}\mathrm{r}\mathrm{g}$ in CRs of those stars which make BHs to match the energy budget given by Gaisser et al. (2013). This is in accordance with numerous observations of massive star SN explosions (see, e.g., Păvălaş, 2001), in that they produce about an order of magnitude more energy than the more common SNe which lead to neutron stars (Biermann et al., 2018). The CR production of SN explosions of type Ia has been discussed in Biermann et al. (2019).

In this work, we will use the Gaisser et al. (2013) tabular fits (their Table 3). In Gaisser et al. (2013) there is a population of protons, referred to as either “Pop. 3”, with a cutoff energy of 1.3 EeV, a differential spectral index of 2.4, and a relative abundance of 0.002, or as “Pop. $3^{*}$” with 1.5 EeV, 2.4, and 0.0017, respectively. For reference, we note that assuming a slightly flatter spectral index of $7/3\simeq 2.33$ lowers these relative abundances by a factor of about 4, i.e., to $0.002/4=0.0005$ or $0.0017/4=0.000425$.

The RSNe expand to about 1–2 pc (Kronberg et al., 1985; Allen and Kronberg, 1998; Allen, 1999) with an observed shock speed of $c/10$ (Biermann et al., 2018), giving a time scale of $10^9$ to $10^{9.3}\mathrm{s}$, which in turn gives a total electromagnetic energy output of $10^{51.8}$ to $10^{52.1}\mathrm{e}\mathrm{r}\mathrm{g}$, consistent with the numbers inferred above. This energy supply is similar to the SN mechanism of Bisnovatyi-Kogan (1970), which is worked out in, (e.g., Bisnovatyi-Kogan and Moiseenko, 2008), and many further papers. This is consistent with observations of the explosions of similar stars (in the starburst galaxy M82 Blue Super Giant stars, (Biermann et al., 2018; Biermann et al., 2019), mentioned above (see [Păvălaş (2001)], for an earlier demonstration of such energetics); these stars have a ZAMS (Zero Age Main Sequence) mass of $\gtrsim 33M_{\odot }$ at Solar chemical abundances (Limongi and Chieffi, 2018; Limongi and Chieffi, 2020). The observed RSN wind allows an energy flow of an energetic particle population of $\sim 10^{39.8}\mathrm{e}\mathrm{r}\mathrm{g}/\mathrm{s}$ at most, so the energy flow is down by $\sim 10^{-3}$ from the total energy flow. This corresponds to the CR population, “3” as well as “$3^{*}$” in Gaisser et al. (2013). By fitting the Larmor motion diameter into the space available, we obtain a maximal energy of $(1/2)(e*B\times r)=10^{18.15\pm 0.12}\mathrm{e}\mathrm{V}$, which is the same quantity which rules angular momentum flow. This also matches the Gaisser fit to the maximum proton energy in the range of 1.3–1.5 EeV (Gaisser et al., 2013).

These ideas are in good agreement with Auger. The relevant statement (Auger-Coll, 2020b) is that at energies below 1 EeV, even though the amplitudes are not significant, their phases determined in most of the bins are not far from the R.A. of the Galactic center - $R{A}_{GC}=-94\mathrm{d}\mathrm{e}\mathrm{g}$. This suggests a predominantly Galactic origin for anisotropies at these energies. The reconstructed dipole phases in energy bins above 4 EeV point instead to R.A.’s that are almost opposite to the Galactic center R.A.: They suggest a possible extragalactic CR origin (cited nearly verbatim from Auger-Coll, 2020b). In the Gaisser et al. (2013) data analysis the components “3” or “3^*” referred to above have a cutoff at 1.3 to 1.5 EeV, and this is the component argued about here quite explicitly. Therefore this EeV CR proton component appears to be fully consistent with Auger data, and is in fact almost required by the data (see Figure 5 in Gaisser et al. (2013)). In a chemical composition analysis of the Auger data a proton component with such a cutoff is clearly detectable (see Figure 2 in Auger-Coll (2020a)). The mixed chemical composition around the knee and above was predicted in Stanev et al. (1993), is consistent with Gaisser et al. (2013), confirmed in Thoudam et al. (2016), and is visible in the new Auger data (Auger-Coll, 2020a).

4 Why this value of $(B\times r)$?

4.1 The magnetic field due to the convection

The magnetic field observed via non-thermal radio emission in the winds of massive stars (Abbott et al., 1984; Drake et al., 1987; Churchwell et al., 1992) can be attributed to the dynamo process working in the central convection zone of massive stars (Biermann and Cassinelli, 1993). The rotation and convection allows the magnetic field to be amplified right up to the stress limit. Then the magnetic field can meander in flux tubes through the radiative zone, and penetrate into the wind. The estimate gives the right order of magnitude, but does not allow to comprehend, that the resulting magnetic field observed in the post-shock region of the SN-explosion racing through the wind is the same number for very different stars, RSG and BSG stars, with extremely different wind properties.

4.1.1 The magnetic field due to the SN-shock

The magnetic field could be enhanced through the SN-shock itself, observed to be at a velocity of about 0.1 $c$ for both RSG and BSG star explosions (Biermann et al., 2018). The Bell-Lucek mechanism (Lucek and Bell, 2000; Bell and Lucek, 2001) can certainly produce strong magnetic fields, but to give the same strength of the magnetic field in two very different types of winds is highly implausible; the ram pressure of the SN-shock in these two types of wind is orders of magnitude different due to the much higher density in RSG star winds than in BSG star winds, as they show about the same shock speed, and the same mass loss in the prior wind.

4.1.2 The magnetic field due to the central object

The central object and its immediate environment could also determine the magnetic field strength of the wind visible, just as in the Pacini and Salvati (1973) approach. The observations show that all RSNe show the same magnetic field in terms of $(B\times r)$, a constant for $B_{\varphi }$ throughout a Parker wind (Parker, 1958), despite the fact that massive stars over a wide range of masses produce such SNe, including RSG stars with slow and dense winds (Biermann et al., 2018). Furthermore, the environment of the big black hole in the galaxy M87 also shows a magnetic field consistent with the same number in these terms (EHT-Coll, 2019b). This can speculatively attributed to the environment of a rapidly rotating black hole, rotating near maximum, and independent of the mass of the black hole. This magnetic field can be translated into a wind or jet power, and the magnetic field observed corresponds to the minimum jet power in radio galaxies (Punsly and Zhang, 2011). So it is plausible to interpret this number as due to a pure spin-down power, as done in EHT-Coll (2019b). This implies that radio galaxies relatively quickly revert to pure spin-down power after a merger of two central super-massive black holes, as demonstrated by the X-shape of the radio galaxy Cen A (Gergely and Biermann, 2009; Gopal-Krishna et al., 2003).

4.2 Some important questions

At this point there are some important questions:

$\mathbf{1}:$ What is the reason for the observed specific number $(B\times r)=10^{16.0\pm 0.12}\text{Gauss\hspace{0.17em}}\times \text{\hspace{0.17em}cm}$? It can be written as an energy flow with ${(B\times r)}^{2}c=\{\hslash c\}/e^2\{m_X{c}^2\}/{\tau }_{Pl}$ with $m_X$ close to the proton or neutron mass, and ${\tau }_{Pl}$ the Planck time (see, e.g., Rueda and Ruffini, 2021). Below, in the paragraph headed by “Frequency of the Penrose process” we will derive such a relationship based on angular momentum flow; this relationship supported by observations requires the Planck time, and so connects gravitation and quantum mechanics.

$\mathbf{2}:$ Is there a possible physical connection to a relationship between magnetic field and rotational frequency (here equivalent to radius at maximum spin) also well known for super-conducting spheres (Hirsch, 2014; Hirsch, 2019)?

$\mathbf{3}:$ Does this also explain that knee and ankle energy are independent of the mass of the star which explodes and makes a BH? This has in fact been proposed (e.g., Biermann, 1993; Biermann and Astroph, 1993; Biermann and Cassinelli, 1993; Biermann and Strom, 1993; Stanev et al., 1993; Biermann et al., 2018; Biermann et al., 2019). Finding the relationship between magnetic field and angular momentum transport, as explained here in this paper, provides this argument.

$\mathbf{4}:$ Do all BHs near maximal rotation have the same magnetic field in terms of $(B\times r)$ independent of mass? That does seem to be the case, comparing magnetic field strength numbers in RSNe and in M87 (EHT-Coll, 2019b) and the inferred energy flow in radio quasars (Punsly and Zhang, 2011). The relationship derived below supports this conclusion.

$\mathbf{5}:$ What is the magnetic field at lower spin? Here the Galactic Center SMBH will be a useful test. This will be derived in a subsequent paper. Some dependencies on spin are derived below.

$\mathbf{6}:$ What is the effect of electric drift currents (Northrop, 1963; Equation 1.79) allowed by an energetic population of $E^{-2}$ particles? Such electric drift currents can occur in electrically neutral plasmas and can be extremely fast. This was worked out in Gopal-Krishna and Biermann (2024), where it was shown that electric gradient drift currents, electric fields, and violent discharges are quite common in variable jets and winds.

All this provides motivation for deeper study.

5 Angular momentum transport

Since the quantity $(B\times r)$ is strongly connected to angular momentum transport, we consider this next.

5.1 A Parker limit approximation

At first we consider a Parker limit approximation to understand what is required at the inner boundary even in the simple Newtonian limit approximation. In this case we can include the $\varphi$-dependence, which we cannot do in the GR approximation. We posit

$r^2{B}_r=B_0{r}_H^{2}H\left(r-r_H\right)\left\{\cos \theta \right\}\left\{\cos \varphi \right\}(1)$

$r{B}_{\theta }=-B_0{r}_H^2\delta \left(r-r_H\right)\frac{\sin \theta }{2}\left\{\cos \varphi \right\}+B_1{r}_{H}H\left(r-r_H\right)\frac{\sin \theta }{2}\left\{\sin \varphi \right\}(2)$

$r{B}_{\varphi }=B_1{r}_{H}H\left(r-r_H\right)\left\{\sin \theta \right\}\left\{\cos \theta \right\}\left\{\cos \varphi \right\}(3)$

$r_H$ is the radius of the horizon, assumed at first to be independent of $\theta$. $H(r-r_H)$ is the Heaviside function, and its derivative is the $\delta$-function $\delta (r-r_H)$. This allows the angular momentum transport $B_{\varphi }{B}_r{r}^3$ to be of the same sign everywhere. This construction immediately allows the divergence equation to be satisfied, and avoids any requirement for a monopole. In this solution the magnetic field stops at $r_H$, and does not penetrate inside. It is obvious that the magnetic field could be expanded into a long series, just as in Parker (1958), but these are simple first terms. This results in

$\begin{array}{ll}\hfill & B_1{r}_{H}H(r-r_H)\left[2{\cos }^2\theta -{\sin }^2\theta \right]\{\cos \varphi \}-B_1{r}_{H}H(r-r_H)\frac{\{\cos \varphi \}}{2}\hfill \\ \hfill & -B_0{r}_H^2\delta (r-r_H)\frac{\{\sin \varphi \}}{2}=\frac{4\pi r^2}{c}{j}_r\hfill \end{array}$

This allows the surface integral of the radial current $j_r$ to be zero, separately in $\theta$ and $\varphi$. It also shows that the electric current runs in the same direction, both at $\theta =0$ and at $\theta =\pi$, both either outwards or inwards. The current scales with $+B_1$ near the two poles, and is negative with $-B_1$ at the equator, with negative values in a broad equatorial band.

$-B_1{r}_H\delta \left(r-r_H\right)\sin \theta \cos \theta \left\{\cos \varphi \right\}-B_0{r_H}^2\frac{H\left(r-r_H\right)}{r^2}\frac{\cos \theta }{\sin \theta }\left\{\sin \varphi \right\}=\frac{4\pi r}{c}{j}_{\theta }(4)$

and

$\left[B_0{r}_H^2\frac{\delta \left(r-r_H\right)}{r-r_H}\frac{1}{2}+B_0{r}_H^2\frac{H\left(r-r_H\right)}{r^2}\right]\sin \theta \left\{\cos \varphi \right\}+B_1{r}_H\delta \left(r-r_H\right)\frac{\sin \theta \left\{\sin \varphi \right\}}{2}=\frac{4\pi r}{c}{j}_{\varphi }(5)$

Considering the $\delta$-function as a narrow Gaussian this suggests a double-layer in the $\varphi$-current, plus an asymmetric term.

This clearly shows that already in this simple approximation we get a $\delta$-function term, and even the derivative of a $\delta$-function term for the electric current at the inner boundary. It also demonstrates that the density of the current carrying charged particles diverges at the boundary, which implies that collisions also diverge in this approximation. One part of the end-product of these collisions is accreted to the BH, and the other part is ejected in the wind with a known magnetic power flow independent of BH mass.

5.2 A General Relativity solution

Here we derive the angular momentum transport in the terms of General Relativity, so allowing to treat the behavior of the magnetic field close to the black hole, for any rotation. In this section we set the speed of light $c$ to unity for simplicity.

The metric tensor elements for the Kerr metric are given in Boyer - Lindquist coordinates by

$\begin{array}{ll}\hfill d{s}^2& =\frac{{d\varphi }^2{\sin }^2(\theta )\left({\left(a^2+r^2\right)}^2-a^2{\sin }^2(\theta )\mathrm{\Delta }(r)\right)}{\rho {(r,\theta )}^2}\hfill \\ \hfill & -\frac{(dtd\varphi +dtd\varphi )\left(2a{G}_N{M}_{BH}r{\sin }^2(\theta )\right)}{\rho {(r,\theta )}^2}\hfill \\ \hfill & +{d\theta }^2\rho {(r,\theta )}^2+\frac{{dr}^2\rho {(r,\theta )}^2}{\mathrm{\Delta }(r)}+{dt}^2\left(-\left(1-\frac{2G_N{M}_{BH}r}{\rho {(r,\theta )}^2}\right)\right).\hfill \end{array}(6)$

where $G_N$ is the universal gravitational constant, $M_{BH}$ is the mass of the black hole and

$\rho {(r,\theta )}^2=r^2+a^2{\cos }^2(\theta ),\mathrm{\Delta }(r)=r^2-2G_N{M}_{BH}r+a^2.(7)$

The electromagnetic tensor is

$F_{\mu \nu }=\left(\begin{array}{cccc}\hfill 0\hfill & \hfill 0\hfill & \hfill {\tilde{E}}_{\theta }(r,\theta )\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\tilde{B}}_{\varphi }(r,\theta )\hfill & \hfill -{\tilde{B}}_{\theta }(r,\theta )\hfill \\ \hfill -\tilde{E}(r,\theta )\hfill & \hfill -{\tilde{B}}_{\varphi }(r,\theta )\hfill & \hfill 0\hfill & \hfill {\tilde{B}}_r(r,\theta )\hfill \\ \hfill 0\hfill & \hfill {\tilde{B}}_{\theta }(r,\theta )\hfill & \hfill -{\tilde{B}}_r(r,\theta )\hfill & \hfill 0\hfill \end{array}\right),(8)$

and the components of $F_{\mu \nu }$ are determined from the vector potential components $A_{\mu }$

$F_{\mu \nu }={\partial }_{\mu }\left(\sqrt{g_{\nu \nu }}{A}_{\nu }(r,\theta )\right)-{\partial }_{\nu }\left(\sqrt{g_{\mu \mu }}{A}_{\mu }(r,\theta )\right).(9)$

The measured components of the electric and magnetic fields are related to the tilde components in $F_{\mu \nu }$ by the relations

$\begin{array}{ll}\hfill {\tilde{E}}_{\theta }(r,\theta )& =E_{\theta }(r,\theta )\hfill \\ \hfill {\tilde{B}}_r(r,\theta )& =\sqrt{g_{\theta \theta }{g}_{\varphi \varphi }}{B}^r(r,\theta )\hfill \\ \hfill {\tilde{B}}_{\theta }(r,\theta )& =-\sqrt{g_{rr}{g}_{\varphi \varphi }}{B}^{\theta }(r,\theta )\hfill \\ \hfill {\tilde{B}}_{\varphi }(r,\theta )& =\sqrt{g_{rr}{g}_{\theta \theta }}{B}^{\varphi }(r,\theta )\hfill \end{array}(10)$

These expressions are based on the definitions of the electric and magnetic fields given in Komissarov (2004). They have the asymptotic forms given in Weber and Davis (1967). We are assuming that the $r$- and $\varphi$-components of the electric field are zero. The $E_{\theta }(r,\theta )$ component of the electric field can be determined for the case of a static magnetic field, $\partial \vec{B}/\partial t=0$, from the relation

${\left(\nabla \times \vec{E}\right)}_{\varphi }=0.(11)$

This relation requires that

${\text{E}}_{\theta }(\text{r},\theta )=\frac{{\text{E}}_0}{\rho (\text{r},\theta )},(12)$

where ${\text{E}}_0$ is a constant. The $B^r(r,\theta )$ component of the magnetic field is obtained from the divergence relation

$\nabla \cdot \vec{B}(r,\theta )=0.(13)$

For $B^{\theta }(r,\theta )=0$ (Weber and Davis, 1967) this relation requires that

$B^r(r,\theta )=\frac{{\text{B}}_0}{\sqrt{g_{rr}{g}_{\theta \theta }{g}_{\varphi \varphi }}},(14)$

where ${\text{B}}_0$ is a constant. The remaining components of the magnetic field are undetermined. Based on observational radio data extensively discussed in Biermann et al. (2018), Biermann et al. (2019), we assume that

$\sqrt{g_{rr}{g}_{\theta \theta }}{B}^{\varphi }(r,\theta )=\text{\hspace{0.17em}constant\hspace{0.17em}}={\text{B}}_{p0}.(15)$

Here both $B^r$ and $B^{\varphi }\sim {\mathrm{\Delta }}^{1/2}$. The ratio between $B_{\varphi }$ and $B_r$ is given by the Parker model, and this indicates that $B_{p0}/B_0\sim \chi /M_{BH}$, where $\chi$ is the dimensionless spin (i.e., maximum unity), so $\chi =a/M_{BH}$. Furthermore we assume that the total radial magnetic field energy is proportional to the available rotational energy, which results in $B_0\sim \chi M_{BH}$, in the $\chi \ll 1$ approximation. From this it follows that $B_{p0}\sim {\chi }^2$. Using observations of radio loud quasars (Punsly and Zhang, 2011) we can check on the implications, since GR solutions and far-distant solutions have to be consistent in their dependence on $\chi$ and $M_{BH}$, namely, $L_{\mathit{jet}}\sim {\chi }^4$, independent of BH mass $M_{BH}$. Furthermore $E_0\sim {\chi }^2{M}_{BH}$ from the consistency requirement of the energy flow and angular momentum flow, worked out below.

The energy flux is obtained from the contraction of the covariant form of the Killing vector $k_t^{\mu }$ with the electromagnetic energy-momentum tensor

${\mathcal{E}}^{\mu }=T^{\mu \nu }{(k_t)}_{\nu },(16)$

and the angular momentum flux is obtained from the contraction of the covariant form of the Killing vector $k_{\varphi }^{\mu }$ with the electromagnetic energy-momentum tensor

${\mathcal{L}}^{\mu }=T^{\mu \nu }{(k_{\varphi })}_{\nu }.(17)$

The $r$- and $\theta$-spatial components of the energy flux and the angular momentum flux are given by

$\begin{array}{ll}\hfill {\mathcal{E}}^r& =\frac{{\text{B}}_{p0}{\text{E}}_0\mathrm{\Delta }(r)}{\rho {(r,\theta )}^5}\hfill \\ \hfill {\mathcal{E}}^{\theta }& =0\hfill \\ \hfill {\mathcal{L}}^r& =\frac{{\text{B}}_0{\text{B}}_{p0}\mathrm{\Delta }{(r)}^{3/2}}{\rho {(r,\theta )}^5}\hfill \\ \hfill {\mathcal{L}}^{\theta }& =0.\hfill \end{array}(18)$

The energy flux and the angular momentum flux are related via the expression

${\mathcal{E}}^r=\omega (r,\theta ){\mathcal{L}}^r,(19)$

where

$\begin{array}{ll}\hfill \omega & =\frac{\widetilde{E_{\theta }}}{\widetilde{B_r}}\hfill \\ \hfill & =\frac{{\text{E}}_0}{{\text{B}}_0\sqrt{\mathrm{\Delta }}}.\hfill \end{array}(20)$

This is the same relation as the one in Equation 4.4 of Blandford and Znajek (1977). Here $\omega \sim \chi /M_{BH}$.

The location of the horizon is determined by the condition $\mathrm{\Delta }(r)=0$, so the flux components ${\mathcal{E}}^r$ and ${\mathcal{L}}^r$ vanish on the horizon. On the equator of the black hole $(\theta =\pi /2)$ the radial component of the angular momentum flux reaches a maximum at a radius of slightly less than three horizon radii, Figure 2. These expressions are similar to the ones obtained by Blandford and Znajek (1977), but there are significant differences due to the differences between our model and theirs. In the BZ model both of the poloidal components of the energy flux are non-zero, while in our model both of the fluxes in the $\theta$-direction (polar direction) are zero. The vanishing of the $\theta$-component of the energy flux in our model is due to setting the $r$- and $\varphi$-components of the electric field equal to zero, and the vanishing of the $\theta$-component of the angular momentum flux is due to setting the $\theta$-component of the magnetic field equal to zero, following Weber and Davis (1967).

Figure 2

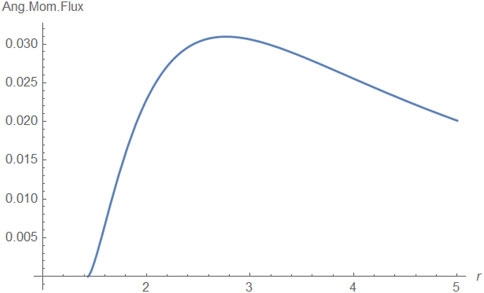
Figure 2. Radial component of the angular momentum flux vs the radius at the equator of the black hole $(\theta =\pi /2)$. In this specific plot as in the next two plots in the abscissa the unit is the Kerr radius, in contradiction to the text, where $r$ scales to the Kerr radius; so there $r$ has as a minimum the Kerr radius $\{G_N{M}_{BH}\}/c^2$, but with $c$ set to unity in this section. The ordinate is determined by the mathematical expression, setting all other constants to unity. The angular momentum per unit mass constant, $a$, is $a=0.9$.

5.3 Calculation of energy extraction and angular momentum extraction

As seen by an observer at infinity the rate of energy extraction is given by

${\dot{E}}_{\mathit{rad}}=\int {\mathcal{E}}^r\rho {(r,\theta )}^{2}d\mathrm{\Omega },(21)$

and the rate of angular momentum extraction is given by

${\dot{L}}_{\mathit{rad}}=\int {\mathcal{L}}^r\rho {(r,\theta )}^{2}d\mathrm{\Omega },(22)$

where $d\mathrm{\Omega }$ is the infinitesimal solid angle. The evaluation of these integrals gives (note that the radius $r$ refers to the BH mass, so that spin $a$, radius $r$, and $G_N{M}_{BH}$ have the same unit in this section)

$\begin{array}{ll}\hfill {\dot{E}}_{\mathit{rad}}& =\frac{4\pi {\text{B}}_{p0}{\text{E}}_0\left(a^2+r(r-2G_N{M}_{BH})\right)}{r^2\sqrt{a^2+r^2}}\hfill \\ \hfill {\dot{L}}_{\mathit{rad}}& =\frac{4\pi {\text{B}}_0{\text{B}}_{p0}{\left(a^2+r(r-2G_N{M}_{BH})\right)}^{3/2}}{r^2\sqrt{a^2+r^2}}.\hfill \end{array}(23)$

Here ${\dot{E}}_{\mathit{rad}}\sim {\chi }^4$, and ${\dot{L}}_{\mathit{rad}}\sim {\chi }^3{M}_{BH}$, consistent with a derivation following (Weber and Davis, 1967; Falcke and Biermann, 1995).

Here the power is proportional to ${\chi }^4$ and the angular momentum transport to ${\chi }^3{M}_{BH}$. Since the power put out via magnetic fields is also proportional to $B_0^2$ Falcke and Biermann, 1995 this is consistent. The angular momentum transport by magnetic fields (Weber and Davis, 1967; Equation 9, integrated over $4\pi r^2$) runs as $B_0\times B_{p0}\sim {\chi }^3{M}_{BH}$, so this is also consistent. In these graphs (Figures 2–4) the lower limit of $r$ is given by the condition $\mathrm{\Delta }(r)=0$, so for maximal spin, that radius is $r=\{G_N{M}_{BH}\}/c^2$, the Kerr radius.

Figure 3

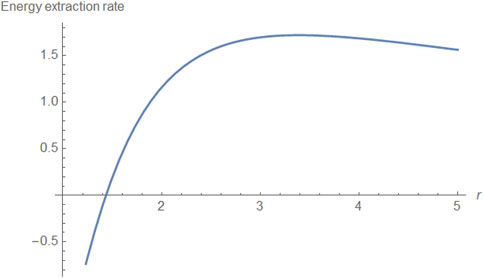
Figure 3. Radial component of the magnitude of the rate of energy extraction. The angular momentum per unit mass constant, $a$, is $a=0.9$. All other constants are set equal to 1. The extrapolation to negative values of this extraction rate is without consequence for an observer, as this part of the curve is inside the horizon.

Figure 4

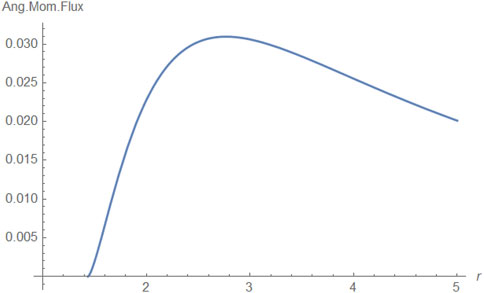
Figure 4. Radial component of the magnitude of the angular momentum extraction rate vs the radius. The angular momentum per unit mass constant, $a$, is $a=0.9$. All other constants are set equal to 1. Here the radial range considered is very large to show how this angular momentum transport approaches a constant despite the simplicity of the model.

5.4 Calculation of the current

The current can be calculated from the covariant divergence of the electromagnetic field tensor

${\nabla }_{\mu }{F}^{\mu \nu }=J^{\nu }(24)$

For the radial and theta components of the current this calculation gives

$\begin{array}{ll}\hfill J^r& =-\frac{4a^2{\text{B}}_{p0}\sin (\theta )\cos (\theta )\left(a^2+r(r-2G_N{M}_{BH})\right)}{{\left(a^2{\cos }^2(\theta )+r^2\right)}^3}\hfill \\ \hfill J^{\theta }& =-\frac{2{\text{B}}_{p0}\left(a^2{\cos }^2(\theta )(G_N{M}_{BH}-r)+r\left(2a^2+r(r-3G_N{M}_{BH})\right)\right)}{{\left(a^2{\cos }^2(\theta )+r^2\right)}^3}\hfill \end{array}(25)$

The $J^t$ and $J^{\varphi }$ components are non-zero, but their expressions are much longer. The latter two components decrease much more rapidly with $r$ than either $J^r$ or $J^{\theta }$.

5.5 Charge density

The expression for the charge density as obtained from the covariant divergence relation is given by

$\begin{array}{ll}\hfill J^0& =\frac{2\sqrt{(2)}{a}^2\sin (2\theta )\left(6a^4{\text{E}}_0\right){\cos }^2(\theta )-20a{\text{B}}_0{G}_N{M}_{BH}r\sqrt{a^2+r(r-2G_N{M}_{BH})}}{\left(a^2+r(r-2G_N{M}_{BH})\right){\left)a^2\cos (2\theta )+a^2+2r^2\right(}^{7/2}}\hfill \\ \hfill & +\frac{2{\text{E}}_0{r}^3\left(4G_N\left(M_{BH}+3r\right)\right)}{\left(a^2+r(r-2G_N{M}_{BH})\right){\left)a^2\cos (2\theta )+a^2+2r^2\right(}^{7/2}}\hfill \\ \hfill & +\frac{2\sqrt{(2)}{a}^2\sin (2\theta )(a^2{\text{E}}_{0}r)(14G_N{M}_{BH}+9r+3(-2G_N{M}_{BH}+r)\cos (2\theta ))}{\left(a^2+r(r-2G_N{M}_{BH})\right){\left)a^2\cos (2\theta )+a^2+2r^2\right(}^{7/2}}\hfill \end{array}(26)$

This shows that in terms of the local charge density we also get a divergence at the inner boundary, at the horizon. This is proportional to ${\chi }^4{M}_{BH}^{-2}$. In more detail the leading terms with $B_0$ as well as $E_0$ run as ${\chi }^4{M}_{BH}^{-2}$, while the terms with $E_0$ have two further terms running as ${\chi }^8{M}_{BH}^{-2}$ and ${\chi }^6{M}_{BH}^{-2}$. It follows that the density may get high enough for lots of energetic collisions.

Furthermore the term running with $B_0$ has the factor ${\mathrm{\Delta }}^{-1/2}$, while the terms running with $E_0$ all have the factor ${\mathrm{\Delta }}^{-1}$. When $\mathrm{\Delta }$ approaches a value small compared to radius $r$, and writing the spin parameter as $\chi =1-\delta \chi$ with $\delta \chi \ll 1$, then $\mathrm{\Delta }=(r-r_g(1+\sqrt{2\delta \chi }))\times (r-r_g(1-\sqrt{2\delta \chi }))$. Writing the first term in brackets as $\delta r$, then $\mathrm{\Delta }$ becomes $\delta r\times (\delta r+2\sqrt{2\delta \chi })$. If we could constrain the collision rate then it follows that we could also constrain $\delta \chi$ to be a possibly small number.

To work out the numbers we note that $B_{p0}$ is observed to be $10^{16.0\pm 0.12}\mathrm{G}\mathrm{a}\mathrm{u}\mathrm{s}\mathrm{s}\times cm$ (Biermann et al., 2018; Biermann et al., 2019); writing all other terms with their proper dimensions using the equatorial outer radius of the ergo-region of a $10M_{\odot }$ BH, so $10^{6.4}\mathrm{c}\mathrm{m}$, gives a charged particle density of about $10^{14.0}\mathrm{c}{\mathrm{m}}^{-\mathrm{3}}$, ignoring here the factors with some power of $\mathrm{\Delta }$, and adopting the limit $\chi \simeq 1$.

This suggests that collisions could an important process, and this is what we explore further.

5.6 Neutrinos from the ergo-region?

There is an inconsistency between what the mass transport is in the wind (assuming equipartition with the observed magnetic fields) and what accretion to the BH is needed to sustain the luminosity of $\sim 10^{43.}\mathrm{e}\mathrm{r}\mathrm{g}/\mathrm{s}$, if one were to power this emission simply by accretion, as equality would require 100% efficiency. This inconsistency can be resolved by considering the pure spin-down mode (Blandford and Znajek, 1977), which implies very little accretion. Here we note that in the pair production variant to the Penrose process, this could imply that the BH accretes predominantly particle/anti-particle pairs, most of which never get out. The creation of such pairs costs at least two proton masses in energy, but energetically pion production dominates by far (below we use a factor of about 30 based on the ratio of cross sections to make pions and to make proton-anti-proton pairs from p-p collisions). They are available from interaction with magnetic irregularities and non-linear waves, such as shock waves. In fact, from the mismatch in mass turnover, one might speculate that the energetic protons initiate a cascade process similar to the interaction of ultra high energy CR particles entering the atmosphere of the Earth. In such a cascade a very large number of secondary particles is produced. By analogy with the Penrose argument one may expect that half the cascade particles are directly on orbits falling into the BH; the other half are initially on orbits to escape. These particles interact with the magnetic field. At the outer boundary of the ergo-region, the particles may transfer a significant fraction of their energy and angular momentum to the magnetic fields and fall back down in accretion to the BH (see Penrose and Floyd, 1971). In processes such as $\bar{\mathrm{p}}$’s colliding with $\mathrm{p}$’s, pions and multiple neutrinos are produced. These neutrinos have a good chance to escape altogether. All this should be re-evaluated using proper frames (e.g., Bardeen et al., 1972; Shaymatov et al., 2015; Bambhaniya et al., 2021), although a collision-dominated gas with a magnetic field, in which some energetic particles have Larmor radii which are close to the scale of the system, is a challenge. What we present here is a detailed balancing of different particle species in the local frame.

Many different losses go into production of pions, which quickly decay into energetic electrons, positrons, photons and neutrinos. In the model proposed the photons are optically thick in their propagation. This is akin to the model published for blazars, and their neutrino emission in Kun et al. (2021). The electrons/positrons and neutrinos have a chance of escaping. Based on the ratio of cross-sections for p-p-collisions to make pions versus p-p-collisions to make proton-anti-proton pairs, about 30 times as much energy goes into an electron/positrons pair plasma from pion decay (ratio of cross sections and energy turnover), and neutrinos, as goes into proton-anti-proton pairs, in terms of what gets out. The neutrinos - in the model proposed - range from MeV to very much higher energy, and for those the IceCube data provide a serious upper limit, if the model is used at TeV energies and beyond. Other than an electron/positron plasma neutrinos could be a second main escape path. That is a main point of the model.

A check with data can be done: the proposal is consistent with IceCube-Coll et al. (2016), IceCube-Coll et al. (2021) and INTEGRAL data (Diehl et al., 2006; Diehl et al., 2010; Siegert et al., 2016a; Siegert et al., 2016b):

In the model proposed the cosmic ray flux of the component going to EeV energies is about $10^{-2.8}$ of the normal CR flux at GeV energies (numbers taken from Gaisser et al. (2013), Table 3, CR components 3 or $3^{*}$; pop three contains all elements (Table 2) and pop $3^{*}$ contains only protons); correcting for a slightly flatter spectrum assumed here, anchored at EeV, gives about $10^{-3.4}$. This implies $10^{37.6}\mathrm{e}\mathrm{r}\mathrm{g}/\mathrm{s}$, again using Gaisser’s et al. numbers for the entire Galaxy of $10^{41}\mathrm{e}\mathrm{r}\mathrm{g}/\mathrm{s}$. Falcke and Markoff (2013) give an estimate of the accretion rate measured close to the central BH in our Galaxy, and it corresponds to a power of about $10^{37.8}\mathrm{e}\mathrm{r}\mathrm{g}/\mathrm{s}$, consistent with the number above. INTEGRAL (Siegert et al., 2016b) gives a positronium production of $10^{43.5}{\mathrm{s}}^{-\mathrm{1}}$ in a very large region, with a scale height of several kpc and along the plane from a larger region than any other recognizable source class, corresponding to about $10^{37.5}\mathrm{e}\mathrm{r}\mathrm{g}/\mathrm{s}$, again consistent with the Gaisser et al. (2013) number. The papers by Diehl et al. support the point of view that there could be plenty more electrons and positrons that escape from the Galactic disk unseen. The production of a large number of electrons/positrons is demonstrated by observations of the BH V404 Cyg (Siegert et al., 2016a). The electron/positron pair plasma production in our Galaxy appears to be due to many sources, possibly the Galactic Center black hole (GC BH) and most probably many stellar/SN/BH sources, including microquasars and SN Ia supernovae (Martin et al., 2010; Prantzos et al., 2011; Prantzos, 2017; Mera Evans et al., 2022). Diehl et al. propose that all black holes produce an electron/positron pair plasma, often in outbursts. Based on gamma-ray line spectroscopy (Diehl et al., 2006; Diehl et al., 2010, Diehl, 2017) give a SN rate of those SNe making black holes in the Galaxy of about 1 SN per 400 years (again, with an uncertainty of $10^{\pm 0.11}$); this has been worked through in Biermann et al. (2018); this includes both Red Super Giant and Blue Super Giant star progenitors, both of which produce black holes, or short BH-SNe. The time scale of the activity is at least 30 years (1 parsec at $0.1c$), as observed numbers from Radio Super-Novae given in Biermann et al. (2019), based on the M82 data of Radio Super-Novae (RSNe) (Allen and Kronberg, 1998; Kronberg et al., 1985; Kronberg et al., 2000). It ensues that each BH-SN contributes - again using the numbers in Gaisser et al. (2013) - about $10^{50.8}\mathrm{e}\mathrm{r}\mathrm{g}$ in CRs, as shown above. For this specific low level HE CR component this translates to $10^{47.4}\mathrm{e}\mathrm{r}\mathrm{g}$, as well as $10^{48.9}\mathrm{e}\mathrm{r}\mathrm{g}$ in $e^{+}$ $e^{-}$ plasma and MeV neutrinos, by virtue of the 30 times larger cross section (p-p collisions making pions versus p-p collisions making $p$-$\bar{p}$ pairs). This translates into a maximal flux, using the shortest reasonable time scale - of $10^{39.9}\mathrm{e}\mathrm{r}\mathrm{g}/\mathrm{s}$ initially. The observed power of about $10^{37.5}\mathrm{e}\mathrm{r}\mathrm{g}/\mathrm{s}$ in the Galactic Center region (by INTEGRAL) in electron/positron plasma means, if produced by a SN, that the activity could be down now by $e^{-400/30}\simeq 10^{-5.8}$, for a possible initial power of $10^{43.3}\mathrm{e}\mathrm{r}\mathrm{g}/\mathrm{s}$ for all SN contributors summed together. This in fact approximately matches the spin-down power seen in both M87 (EHT-Coll, 2019a; EHT-Coll, 2019b), many other radio galaxies in their minimum jet power (e.g., Punsly and Zhang, 2011), and in Radio Super-Nova Remnants interpreting them as driven by a relativistic wind from a spinning compact object, presumably a BH.

Using the starburst galaxy M82 (Kronberg et al., 1985; Allen and Kronberg, 1998; Kronberg et al., 2000) itself as our IceCube limit for point sources (IceCube-Coll et al., 2016; IceCube-Coll et al., 2020; IceCube-Coll et al., 2021) gives about $10^{-12.0}$ TeV events $\mathrm{c}{\mathrm{m}}^{-\mathrm{2}}{\text{s}}^{-1}$, assuming a $E^{-2}$ spectrum, corresponding to a limit of about $10^{-11.0}\mathrm{e}\mathrm{r}\mathrm{g}\mathrm{c}{\mathrm{m}}^{-2}{\text{s}}^{-1}$ at GeV for a $E^{-7/3}$ spectrum assumed here for the relevant CR spectrum, where the Gaisser et al. (2013) numbers are anchored. This corresponds to a limiting luminosity at TeV of $10^{39.1}\mathrm{e}\mathrm{r}\mathrm{g}/\mathrm{s}$ at the distance of M82, and $10^{33.9}\mathrm{e}\mathrm{r}\mathrm{g}/\mathrm{s}$ at the distance of the Galactic Center. Since there is evidence from the Telescope Array et al. (2020) as well as Auger-Coll (2018), that both starburst galaxies M82 in the North and NGC253 in the South may have been detected in UHECRs, we assume that the detailed analysis of recent Radio Super-Novae (RSNe) in M82 applies also to NGC253 (Kronberg et al., 1985; Allen and Kronberg, 1998; Kronberg et al., 2000), where the specific IceCube limit mentioned above applies and so a limit for all sources is $<10^{39.1}\mathrm{e}\mathrm{r}\mathrm{g}/\mathrm{s}$. In M82 there are about 40 such sources (Kronberg et al., 1985), so the limit per source is $<10^{37.5}\mathrm{e}\mathrm{r}\mathrm{g}/\mathrm{s}$, if all sources contribute equally. However, again, for a possible decay time of 30 years, only one source may contribute, and this possibility would imply a luminosity of $<10^{39.1}\mathrm{e}\mathrm{r}\mathrm{g}/\mathrm{s}$ for that one source. To within the large errors of such an estimate this is still consistent with the data, which give an expectation for a single contributing source at $10^{39.9}\mathrm{e}\mathrm{r}\mathrm{g}/\mathrm{s}$. Allowing for a slightly steeper spectrum would loosen these constraints, as would an even faster change with time of any single source. The age of the youngest source 41.9 + 58 is sufficiently large so that it may have decayed already significantly. Of course, if the HE neutrinos were pointed in their emission, then their luminosity could be quite a bit higher without showing up in our observations.

To do a further test: Applying the same neutrino flux limit to possible sources in the Galactic Center (GC) region gives a limit of about $10^{5.1}$ times stronger, so $<10^{34.4}\mathrm{e}\mathrm{r}\mathrm{g}/\mathrm{s}$. As shown above this is fully consistent with the rate of BH-SNe occurring; the expected flux reduction is $10^{-5.8}$ for an initial luminosity limit of $<10^{40.3}\mathrm{e}\mathrm{r}\mathrm{g}/\mathrm{s}$, again consistent. One problem in such an argument is that the sources are known to be highly fluctuating (e.g., Siegert et al., 2016a). It is possible to repeat this exercise for the Cyg region, which is much closer than the Galactic Center. This gives a limiting luminosity of $10^{33.2}\mathrm{e}\mathrm{r}\mathrm{g}/\mathrm{s}$, and it is again consistent, since the BH-SN rate is very low near to us, 1 BH-SN per about $10^5$ years, so predicting a huge reduction from the expected initial luminosity of $10^{39.9}\mathrm{e}\mathrm{r}\mathrm{g}/\mathrm{s}$ worked out above; Cygnus might be close enough to provide an actual source of the Galactic EeV CRs identified by Gaisser et al. (2013).

5.7 Collisions

Analyses of particle collisions near to BHs and singularities have been carried out, (Patil et al., 2010; Patil and Joshi, 2011a; Patil and Joshi, 2011b; Patil and Joshi, 2012; Patil et al., 2012; Patil and Joshi, 2014; Patil et al., 2015; Patil et al., 2016; Liu et al., 2011; Banados et al., 2009; Banados et al., 2011). These papers did not have the benefit of insight provided by the RSN observations, the most detailed of which by Allen and Kronberg (1998), Allen (1999), Kronberg et al. (2000). The latter provide a newer solid foundation to develop the approach.

As an example, we calculate the particle density and flux for the ergo-region around a stellar mass BH of $10M_{\odot }$: The magnetic field, extrapolated to near the BH, at radius $R=10^{6.4}\mathrm{c}\mathrm{m}$, is about $10^{9.6}\mathrm{G}\mathrm{a}\mathrm{u}\mathrm{s}\mathrm{s}$. In equipartition, $(B^2)/(8\pi )\simeq n{k}_{B}T$, leading to a particle density of $n\simeq 10^{21.6}\mathrm{c}{\mathrm{m}}^{-\mathrm{3}}$ at a weakly relativistic temperature of $\sim 10^{12}\mathrm{K}$. This, in turn, allows a flow of particles of $4\pi R^{2}nc\simeq 10^{46}{\mathrm{s}}^{-\mathrm{1}}$. Interactions give a similar number, using a cross section of $10^{-27}\mathrm{c}{\mathrm{m}}^{\mathrm{2}}$ (valid for making proton-anti-proton pairs (Winkler, 2017; Reinert and Winkler, 2018); the inelastic cross-section is about 30 times higher well above threshold), as obtained from $4\pi R^3{n}^2\sigma c\simeq 10^{47}{\mathrm{s}}^{-\mathrm{1}}$, which is more than what is needed to explain the observations; as even a smaller cross-section could be accommodated. This latter quantity cannot be readily extrapolated to a higher BH mass, as we discuss below.

Using the general approach of EHT-Coll (2019b) we can show that this optical depth may reach order 10, independent of radius. This means that the interaction time to produce proton-anti-proton pairs is less than the residence time, possibly considerably less.

The observations show that $B=10^{16.0\pm 0.12}/r\mathrm{G}\mathrm{a}\mathrm{u}\mathrm{s}\mathrm{s}$, with $r$ in $\mathrm{c}\mathrm{m}$. This relationship has been observed over the range of radius from about $10^{18.5}\mathrm{c}\mathrm{m}$ down to order $10^{16}\mathrm{c}\mathrm{m}$, with the highest resolution observations done by radio interferometry (VLBI). Using the analogy with the Solar wind (Parker, 1958; Weber and Davis, 1967) we extrapolate it down for the case of fast rotation. The EHT observations of M87 suggest that such an extrapolation is reasonable (EHT-Coll, 2019b): There the product $(B\times r)$ has about the same value as in RSNe at about five gravitational radii; the M87 black hole has been suspected to be in substantial rotation, perhaps near maximal (Daly, 2019; EHT-Coll, 2019b and later). The jet power of M87 is consistent with what is derived for RSNe using the available energy content of a maximally rotating black hole, and the time-scale derived from angular momentum transport (Weber and Davis, 1967). This suggests that the jet power far outside the ergo-region is already visible at five gravitational radii.

Putting in numbers as observed (EHT-Coll, 2019b) extrapolated to a stellar mass BH suggests that the production time scale for making proton-anti-proton pairs is safely of order $<1$ of the resident time scale in the inner region around the ergo-region.

This argument works for stellar mass black holes, and we can speculate here that the model proposed would allow this to work also for more massive black holes.

5.8 Anti-protons

The concept is that the energetic particles are confined by the magnetic field and so stay in the ergo-region; the magnetic field is due to electric currents in the (weakly relativistic) thermal matter, which is held in the gravitational field. In momentum phase space there is a cone, inside of which all particles are on orbit to accrete to the BH. This is akin to arguments in Hills (1975), Bahcall and Wolf (1976), Frank and Rees (1976). In that approach, stars interact with molecular clouds to fill a cone in momentum phase space which allows accretion to a central BH. This is referred to as the loss cone mechanism. Here, charged particles interact with the magnetic fields (Strong et al., 2007; Moskalenko and Seo, 2019), and also with each other, to also finally accrete to the BH.

Given all the above arguments, what are the predictions in these scenarios? In these conditions, one can ask what the fraction of anti-protons $n_{\bar{\mathrm{p}}}/n_{\text{p}}$ might be. The observed fraction of anti-protons is about $10^{-3.7}$ (AMS Coll, 2016), with a spectral shape dependence of about $E^{-2.7}$ for both protons and anti-protons. We assume that this spectrum changes for both towards a flatter spectrum at higher energy since at lower energies, both components have other contributions (see, e.g., Biermann et al., 2018). Could this match the observed flux of anti-protons? Fitting above 200 GeV, the CR flux is about $10^{-3}$ relative to other CR-populations from the similar SN-explosions. Using a spectrum such as $E^{-7/3}$, this modifies the factor of $10^{-3}$ to $10^{-3.3}$ to $10^{-3.4}$. However, at EeV, the sum of protons and anti-protons is observed, while at lower energy, anti-protons are observed separately. Thus, correcting the prediction by another factor of order two gives $10^{-3.6}$ to $10^{-3.7}$, which allows the observed $10^{-3.7}$. Consequently, we propose a model to explain the flux, energy content, spectrum, maximal particle energy, and particle/anti-particle ratio of highly energetic protons. It follows then, that the spectrum of anti-protons continues all the way to ankle energies, with a spectral shape near $E^{-7/3}$. The energetic protons would approach the spectrum of the anti-protons at some energy slightly above PeV. AMS may well detect some of these anti-protons among its highest energy particles, around TeV.

One may well ask whether anti-protons survive their path to us: Their cross-section to interaction is the same as for protons, and since we see protons at EeV (Auger-Coll, 2020a) without being able to distinguish protons and anti-protons, the particles detected may well contain anti-protons, in this proposal here possibly half.

If there are in fact large numbers of cascades, then many of the secondaries, including electrons and positrons might also escape, creating a funnel in the Galactic disk which allows them to flow out (see Diehl et al., 2006; Diehl et al., 2011; Diehl, 2013; Siegert et al., 2016b). The total positron production in a large region around the Galactic Center corresponds to a power on the order of $10^{37.1}\mathrm{e}\mathrm{r}\mathrm{g}/\mathrm{s}$. This is $10^{-4.6}$ of the maximal energetic particle flow, of order $10^{51}\mathrm{e}\mathrm{r}\mathrm{g}$ in about $10^{9.3}\mathrm{s}$ (see above) even for a single massive star SN event, suggesting that much of the energy is vented out to the Galactic halo. Even allowing for a reduction by about a factor of 100, to account for the difference in CR electron fluxes from CR proton and Helium, would still leave a factor of $10^{-2.6}$. The contribution from the Galactic Center BH seems to be less than that which any possible surrounding sources could contribute.

In the balance between production of anti-protons from p - p collisions, as well as $\bar{\mathrm{p}}$ - $\bar{\mathrm{p}}$ collisions, the annihilation process p - $\bar{\mathrm{p}}$ dominates. Those interactions will limit not only the $\bar{\mathrm{p}}$ net production, but will also produce large numbers of neutrinos. On the other hand, the $\mathrm{p}$ vs $\bar{\mathrm{p}}$ interaction decreases with energy, while the $\mathrm{p}$ vs $\mathrm{p}$ interaction cross-section to produce $\mathrm{p}$ - $\bar{\mathrm{p}}$ pairs, rises with energy. These neutrinos will be crudely commensurate with the Poynting flux energy flow. They, however, could exceed the Poynting flux, if the production and immediate destruction of $\bar{\mathrm{p}}$ greatly exceed the rate of accretion of $\bar{\mathrm{p}}$, as this runs with the ratio of the cross sections. Consequently, this process could emit a significant fraction of the rotational energy of the BH via neutrinos.

We consider the following reactions: first for creating and annihilating anti-protons; here we include the primary protons. Note that these densities represent integrals over the momentum distribution, and the cross-sections include weighting due to the momentum phase-space distribution:

1)

$\mathrm{p}+\mathrm{p}\to \mathrm{p}+\mathrm{p}+\mathrm{p}+\bar{\mathrm{p}}(27)$

with cross section

${\sigma }_{pr,\mathrm{p}\bar{\mathrm{p}}};(28)$

protons have density $n_{\text{p}}$ and anti-protons density $n_{\bar{\mathrm{p}}}$;

2)

$\mathrm{p}+\bar{\text{p}}\to \mathrm{m}\mathrm{u}\mathrm{l}\mathrm{t}\mathrm{i}\mathrm{p}\mathrm{l}\mathrm{e}\pi (29)$

with cross-section

${\sigma }_{de,\mathrm{p}\bar{\mathrm{p}}}.(30)$

– The pions decay into neutrinos and other leptons.

3) The reaction

$\bar{\mathrm{p}}+\bar{\mathrm{p}}\to \bar{\mathrm{p}}+\bar{\mathrm{p}}+\mathrm{p}+\bar{\mathrm{p}}(31)$

has the same cross section as above for protons,

${\sigma }_{pr,\mathrm{p}\bar{\mathrm{p}}}.(32)$

4) The production of anti-neutrons

$\bar{\mathrm{p}}+\bar{\mathrm{p}}\to \bar{\mathrm{p}}+\bar{\mathrm{n}}+\bar{\mathrm{\pi }}(33)$

has the cross section

${\sigma }_{\bar{\mathrm{n}},\bar{\mathrm{p}}\bar{\mathrm{p}}}.(34)$

There are corresponding analogous processes for producing or destroying protons.

The detailed balance equations are (adopting $c$ as an approximate typical velocity for the particles):

$\begin{array}{ll}\hfill \frac{d{n}_{\bar{\mathrm{p}}}}{dt}& ={\sigma }_{pr,\mathrm{p}\bar{\mathrm{p}}}c{n}_{\mathrm{p}}^2-{\sigma }_{de,\mathrm{p}\bar{\mathrm{p}}}c{n}_{\bar{\mathrm{p}}}{n}_{\text{p}}+{\sigma }_{pr,\mathrm{p}\bar{\mathrm{p}}}c{n}_{\bar{\mathrm{p}}}^2\hfill \\ \hfill & -{\sigma }_{\bar{\mathrm{n}},\bar{\mathrm{p}}\bar{\mathrm{p}}}c{n}_{\bar{\mathrm{p}}}^2-\frac{n_{\bar{\mathrm{p}}}}{{\tau }_{BH}},\hfill \end{array}(35)$

and

$\begin{array}{ll}\hfill \frac{d{n}_{\text{p}}}{dt}& ={\sigma }_{pr,\mathrm{p}\bar{\mathrm{p}}}c{n}_{\text{p}}^2-{\sigma }_{de,\mathrm{p}\bar{\mathrm{p}}}c{n}_{\bar{\mathrm{p}}}{n}_{\text{p}}+{\sigma }_{pr,\mathrm{p}\bar{\mathrm{p}}}c{n}_{\bar{\mathrm{p}}}^2\hfill \\ \hfill & -{\sigma }_{\text{n},\mathrm{p}\mathrm{p}}c{n}_{\text{p}}^2-\frac{n_{\text{p}}}{{\tau }_{BH}}+\frac{n_{\text{p}}}{{\tau }_{\mathit{gal}}}.\hfill \end{array}(36)$

Here the last term in the previous equation, and the last two terms in this equation, represent accretion to the BH, and accretion from the outside, from an accretion disk for instance. Accretion from outside constitutes positive baryon number accretion. If many secondaries are created and accreted, their net baryon number is zero. Baryon number accretion derives from both populations.

Initially, we assume that the accretion terms are negligible. By virtue of particles and anti-particles behaving the same in corresponding cross-sections, we can now consider two situations:

First we consider the case, where $n_{\bar{\mathrm{p}}}\ll n_{\text{p}}$. In this case, the production of anti-protons via pair creation dominates, and for protons the reaction leading to neutron production dominates. So, in this case, the anti-protons grow in number, and the protons decrease in number. The situation is not stationary.

Next, the condition of exact stationarity can be required, and the two equations above can be subtracted from each other: By virtue of the symmetry of cross-sections between particles and anti-particles, the first three terms in the first equation are equal to the first three terms in the subsequent equation, leaving the fourth term. This gives

$n_{\bar{\mathrm{p}}}^2{\sigma }_{\bar{\mathrm{n}},\bar{\mathrm{p}}\bar{\mathrm{p}}}-{\sigma }_{\text{n},\mathrm{p}\mathrm{p}}{n}_{\text{p}}^2=0.(37)$

By virtue of the equivalence between particles and anti-particles, the two cross-sections are identical and can be cancelled out. The result of the above operation is

$n_{\bar{\mathrm{p}}}^2-n_{\text{p}}^2=0,(38)$

thus the density of protons and anti-protons is the same in stationarity, neglecting accretion both from outside and to the BH. This does not violate baryon number conservation since in this model, both protons and anti-protons are secondary; the baryon number is exactly zero.

It follows that the ratio of neutrino production via pion decay to $\mathrm{p}\bar{\mathrm{p}}$ pair-production runs with the ratio of the two cross-sections, which is large; however, the cross-sections have to be weighted with the momentum phase space distribution as noted above. It follows that the time scale for refilling the momentum phase space necessary to yield large interaction rates is key to the effective neutrino luminosity. Correspondingly, the ratio of neutron production to $\mathrm{p}\bar{\mathrm{p}}$ pair-production runs with the ratio of the two cross-sections, which is also large. The cross-section to make pions and ensuing neutrinos starts at small energy and is large, and so dominates over the neutron production. In this simplified picture creation and destruction balance, and so the momentum distribution adjusts itself to make the effective cross-sections match, moderated by the time scales of redistributing particles in momentum phase space.

Second, we allow for the accretion terms to be relevant. Then the difference of the two terms leads to

$\left(n_{\text{p}}-n_{\bar{\mathrm{p}}}\right)\left({\sigma }_{\text{n},\mathrm{p}\mathrm{p}}\left(n_{\text{p}}+n_{\bar{\mathrm{p}}}\right)+\frac{1}{{\tau }_{BH}}\right)=\frac{n_{\text{p}}}{{\tau }_{\mathit{disk}}}.(39)$

This means if the sum of the neutron production and the BH net accretion is much larger than the outside accretion (from, e.g., an accretion disk), then the relative difference

$\left(n_{\text{p}}-n_{\bar{\mathrm{p}}}\right)/n_{\text{p}}(40)$

is small. The anti-proton density approaches the proton density. Next consider the sum of the two equations: A solution is possible, in which the creation of secondaries is mostly balanced by destruction, with some accreting to the BH, and an even smaller number providing net loss of particles to the outside.

The pion decay leading to neutrino production can be approximated well by the approach of Penrose and Floyd (1971), leading to an accretion of neutrinos to the BH. It also leads to a corresponding luminosity of outgoing neutrinos.

In summary, the test is clearly to determine the anti-proton fraction at the EeV energy scale. If that fraction is half of the sum of protons and anti-protons, then the neutrino luminosity is predicted to be large, with most neutrinos near GeV energies. We observe TeV energies in neutrinos, and above.

5.9 The Penrose zones with magnetic fields

All these arguments depend on the Penrose process (Penrose and Floyd, 1971, Bardeen et al., 1972). However, the main difference to the collisional Penrose process (e.g., Bejger et al., 2012; Hod, 2016; Leiderschneider and Piran, 2016; Schnittman, 2018) is that in our approach, based on the magnetic field observations, particles are scattered by magnetic field irregularities frequently and throughout the ergo-region. We can write the spectrum of magnetic field irregularities $I(k)k$ as energy density with wavenumber $k$, so that the mean free path can be written as

$r_g\frac{B^2/\left\{8\pi \right\}}{I\left(k\right)k}(41)$

where $r_g$ is the Larmor radius of the motion of a charged particle. This mean free path is far smaller then the scale of the ergo-region except for the very highest particle energies, spanning more than nine orders of magnitude (from the values of $B\times r$) observed, as discussed above and in Biermann et al. (2018), Biermann et al. (2019).

Here we focus on the angular momentum transport and work out, how frequently the data show that the Penrose process happens; however, first we have to comment on orbits of particles versus the local 3D momentum phase space distribution.

5.9.1 Momentum phase space distribution

The near-BH region, the ergo-region (also referred to as the ergo-sphere, but is never actually anything near spherical, see Figure 5) and its immediate outer environment, is full of a strong magnetic field (near ${10}^{10}$ Gauss for a ten Solar mass BH, as observed Biermann et al., 2018), with a full spectrum of irregularities $I(k)$: Therefore the charged particle momentum phase space distribution is highly an-isotropic, and includes locally an extension to all possible orbits to EeV energies, the maximum allowed by the magnetic field. Magnetic field scattering remixes the orbits continuously in the locally non-rotating frame (Bardeen et al., 1972); the magnetic field and the particles at all energies refer to the rotation, and so carry angular momentum. Similar to stellar orbits in globular clusters (King, 1966), where the orbits are cut off by tidal forces, the phase space distribution cuts off where plunge orbits take all particles away. This is also akin to the loss-cone process (Hills, 1975) where stars are taken out of the distribution by going straight into a BH. So the angular momentum transport is governed on the outside of the ergo-region by a region with the thickness of scrambling the orbits by magnetic fields, which governs the ejection of particles carrying angular momentum, and anchoring the magnetic fields; so the thickness is strongly dependent on particle energy: we call this the outer Penrose zone: This consideration gives the angular momentum loss of the BH together with the ergo-region. The angular momentum transport on the inside of the ergo-region is governed by ubiquitous particle interaction, producing secondary protons and anti-protons with many more pions of either charge. The orbits are also scrambled in this zone by magnetic fields, but also by the new production of secondaries. Many of those particles going into the black hole carry less specific angular momentum than the BH itself (Bardeen et al., 1972), and so take angular momentum net from the BH. We dub this the inner Penrose zone. The balance between loss towards the outside in the outer Penrose zone and loss to the inside, the BH, on the inside in the inner Penrose zone gives the net angular momentum loss of the BH. At the highest particle energies the outer and inner Penrose zones might touch. Since the transport in this concept is given by secondary particles, the net transport to the outside is visible in the magnetic fields (Biermann et al., 2018) and also in electron-positron pairs (Siegert et al., 2016a), and, we posit, in pop $3^{*}$ of Gaisser et al. (2013), which in this concept should carry an about equal number of anti-protons and protons. We note that all jets carry an electric current, driven by a proton-anti-proton pair plasma with a spectrum of $E^{-2}$ (Gopal-Krishna and Biermann, 2024) to EeV energies, which we identify here with this CR population, steepened by an ISM Kolmogorov spectrum of magnetic irregularities in the Galactic disk, so 1/3. Variable jets drive an electric field, which upon discharge drives particle energies much higher (Gopal-Krishna and Biermann, 2024). Such discharges have been seen ubiquitously as synchrotron radio filaments (Gopal-Krishna and Biermann, 2024; Yusef-Zadeh et al., 2022). One prediction in our model is that pop $3^{*}$ of Gaisser et al. (2013) should be composed by an equal number of protons and anti-protons, and this may be detectable around and above TeV energies.

Figure 5

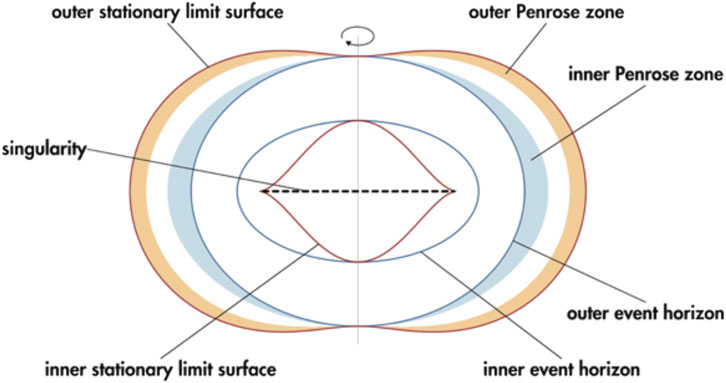
Figure 5. The key elements of the Kerr black hole with rotation parameter $a=0.95$ are represented in a planar section containing the axis of rotation. The infinite curvature ring singularity appears from lateral side view as a segment. This is hidden inside a structure of two horizons, the outer horizon being the boundary of the Kerr black hole. Two stationary limit surfaces (where $g_{tt}=0$) are positioned inside the inner horizon and outside the outer horizon, respectively. At the outer stationary limit surface the redshift is infinite and photons cannot counterrotate, while inside it they will always corotate, similarly to all the other particles, irrespective of their initial direction. The ergo-region, lying between the outer stationary limit surface and the outer event horizon, contains the outer and inner Penrose zones, attached to these limiting surfaces.

In Bardeen et al. (1972) their Figure 3 shows what fraction of velocity phase space - there simplified to equatorial orbits, so planar orbits - goes down into the BH. Because of the scrambling of charged particle orbits by the relatively strong magnetic fields there are in reality no orbits from or to infinity, within an interaction length of the horizon only orbits that either remain in the ergo-region or plunge down into the BH. Further inside the ergo-region all orbits are such that the particles remain in the ergo-region. So as soon as magnetic scattering or new particle creation by collisions puts an orbit into the plunge region of momentum phase space that particle is directly lost. Since this part of phase space is not generally a cone, instead of a “loss-cone” we refer to it as the “plunge region of momentum phase space”. That plunge region of momentum phase space exists only within an interaction length of the horizon, see the equation above, accounting both for magnetic scattering or particle collisions with creation of new particles. The magnetic scattering interaction length is rigidity dependent, depending on the Larmor radius scaling linearly with rigidity, and the spectrum of resonant irregularities $I(k)$. For a spectrum of $I(k)\sim k^{-\beta }$, this gives an interaction length scaling with the power of $2-\beta$. For a Kolmogorov spectrum this gives an interaction scaling with rigidity to a 1/3 power, lightning dominated turbulence gives a 5/3 power, while shock dominated turbulence gives an interaction length independent of rigidity (Allen et al., 2024). Collisions of particles to create new particles, such as lots of pions, or proton-anti-proton pairs, produces the most particles on such an orbit. As both $B^r$ and $B^{\varphi }$, the observed components, scale as ${\mathrm{\Delta }}^{1/2}$, the Larmor radius diverges near the horizon, and so the scattering by the magnetic field is weakened; on the other hand, the charged particle density also diverges near the horizon, both clear from the expressions above. For the collision rate between protons with other protons, including secondary protons, to be faster than pion decay implies extraordinary densities, of order $10^{24}\mathrm{c}{\mathrm{m}}^{-\mathrm{3}}$ or higher, easily possible with the expression above for the charged particle density. This means that near the horizon the injection of mostly new particles into the plunge orbit part of momentum phase space dominates over pure magnetic field scattering. This has been the main thrust here, that secondary particles go onto plunge orbits, and so determine the spin-down.

5.9.2 Frequency of the Penrose process

In pure spin-down angular momentum transport provides the main constraints:

The data show that the quantity $(B\times r)$ has the value $10^{16\pm 0.12}\mathrm{G}\mathrm{a}\mathrm{u}\mathrm{s}\mathrm{s}\times cm$ for both red supergiant and blue super-giant RSNe (Biermann et al., 2018; Biermann et al., 2019); this value is consistent with the numbers for super-massive black holes (EHT-Coll, 2019b). Using Equation 9 of Weber and Davis (1967) this corresponds, as seen from afar, to an angular momentum transport of $10^{38.4\pm 0.24}\{\mathrm{e}\mathrm{r}\mathrm{g}\mathrm{s}\}/\mathrm{s}$ for a 10 Solar mass BH, and using the assumption, that at the outer radius of the ergo-region (at $10^{6.4}\mathrm{c}\mathrm{m}$ on the equator) the radial magnetic field is equal to the tangential field. This is the angular momentum transport just via the magnetic field. This angular momentum transport is enhanced by thermal and non-thermal particles, and similar to the ISM we assume here that non-thermal particles give the same angular momentum transport as the pure magnetic field, and the thermal particles give the same as this sum, the magnetic field and non-thermal particles added together: This gives a factor of $f_{\mathit{ISM}}=4$ over the pure magnetic field case, for a final angular momentum transport of $10^{39.0\pm 0.24}\{\mathrm{e}\mathrm{r}\mathrm{g}\mathrm{s}\}/\mathrm{s}$. This number has to consistent with what particles transport.

How does this compare with what is carried by particles, also seen from afar? The argument starts with protons and anti-protons, so $10^{-23.8}\mathrm{g}$, at $10^{6.4}\mathrm{c}\mathrm{m}$ with close to the velocity of light $c$, so $10^{-6.9}\mathrm{g}\mathrm{c}{\mathrm{m}}^2{\mathrm{s}}^{-1}$ as a base unit of angular momentum. Extending the spectrum to EeV energies gives for an $E^{-2}$ spectrum (Gopal-Krishna and Biermann, 2024) a factor of the natural log of the range, so about $f_{CR}=10^{1.2}$. Considering that pions result energetically 30 times as often from p-p collisions as proton-anti-proton pairs adds another factor of $f_{{\pi }^{\prime }s}=10^{1.5}$ for a total angular momentum of $10^{-4.2}\mathrm{g}\mathrm{c}{\mathrm{m}}^{\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$. We will normalize these three factors to their nominal values, and the write $f_{\mathit{ISM}}=4f_{\mathit{ISM,0.6}}$, $f_{CR}=10^{1.2}{f}_{CR,1.2}$, and $f_{{\pi }^{\prime }s}=10^{1.5}{f}_{{\pi }^{\prime }s,1.5}$. So $10^{-4.2}\mathrm{g}\mathrm{c}{\mathrm{m}}^{\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$ gets a factor of $f_{CR,1.2}{f}_{{\pi }^{\prime }s,1.5}$. What time scale per such step is required to match the observed angular momentum transport? The implied time scale is the Planck time of ${\tau }_{Pl}=10^{-43.3}\mathrm{s}$ (Planck, 1900), which yields here $10^{39.1}\{\mathrm{e}\mathrm{r}\mathrm{g}\mathrm{s}\}/\mathrm{s}$, consistent with the number indicated by magnetic field observations, as derived above. This says, that the Penrose process happens most efficiently for an $E^{-2}$ spectrum (also required for the electric current, and the large Debye length Gopal-Krishna and Biermann, 2024), and equally for each log bin of particle energy in the particle spectrum. It also says, that the Penrose process happens for a BH of any mass at near maximal rotation about $10^{46}$ times per second in terms of protons/anti-protons, and an order magnitude more often in terms of pions. This relies solely on the production of secondaries via collisions, and no accretion from far outside.

On the basis of observations discussed above we derive therefore the relationship

${\left(B\times r\right)}^2=\frac{f_{CR}{f}_{{\pi }^{\prime }s}}{f_{\mathit{ISM}}}\frac{m_{p}c}{{\tau }_{Pl}}(42)$

for a BH of any mass in nearly maximal rotation, and in pure spin-down, so without any accretion.

The outer radius of the ergo-region drops out, and so this relationship becomes independent of proximity to the BH, as long as the scale is outside the ergo-region. The term with the factors $f_{CR}$, $f_{{\pi }^{\prime }s}$, and $f_{\mathit{ISM}}$, perhaps by coincidence, approximately equals $\{\hslash c\}/e^2$. The observations leading to this relationship range from a few $M_{\odot }$, to about $10^{10}{M}_{\odot }$.

We emphasize that in this interpretation radio observations of the magnetic field close to what we have proposed are near maximally rotating black holes, require the Planck time to match with protons/anti-protons and pions in angular momentum transport. This interpretation allows to understand the strength of the magnetic field; the magnetic field is determined by this process. This argument is valid for any black hole in near maximal rotation, and without any accretion.

This leads to the question, whether this can be thought of as spontaneous emission of a black hole in the sense of Einstein (1917) and Feynman et al. (1963): Feynman Lectures of Physics, vol. I, p. 42.9). And if so, what qualifies as stimulated emission (see Falcke and Biermann, 1995; Gopal-Krishna and Biermann, 2024)? The magnetic field in terms of $(B\times r)$ is larger by the square-root of the ratio of the power of the source to the minimum power implied here (also observed Punsly and Zhang, 2011; Biermann et al., 2018; Biermann et al., 2019; EHT-Coll, 2019b). Therefore also in that case the Planck time is used.

5.9.3 Circular orbits in the inner Penrose zone

The lowest energies correspond to locally circular orbits in the inner Penrose zone (Bardeen et al., 1972). This zone is governed predominantly by the numerous pions and their decay products; secondary protons and anti-protons feed the acceleration to the maximal energy allowed, but are way down in number. As pion production is energetically about 30 times proton-anti-proton pair production, and pions have about 1/10 the rest mass of protons/anti-protons, it entails that pions are about 300 times as numerous as protons/anti-protons if produced sufficiently fast. Neutrinos escape, but electron/positrons are trapped by the magnetic fields. They lose energy rather quickly, but can also be accelerated again in the bath of many waves. We can derive this temperature crudely as follows: Charged particles are easily thermalized in any post-shock region: if the equation of state is relativistic then the speed of sound is given by $c_{\mathit{rel}}^2=c^2/3$, so that the typical velocities are some fraction of the speed of light, post-shock easily $c/3$, which for pions corresponds to order 30 MeV. Basically pions dominate the thermodynamics despite their short life-time. This requires that all time scales, like for producing pions, must be faster, and the densities correspondingly high. The conditions that p-p collisions to make proton-anti-proton pairs are faster than pion decay requires densities above $10^{24.5}$ per cc, a charged particle density plausible close to the horizon by the expression above.

5.9.4 Observational tests

This argument, that requires the Planck time, is derived from radio observations and their interpretation.

A priori we do not know, how many of the secondary particles are released to the outside, but in the interpretation, that the pop $3^{*}$ of Gaisser et al. (2013) and the particles driving an electric current in jets (Gopal-Krishna and Biermann, 2024) corresponds to the ejection of secondary protons and anti-protons from the Penrose zones around young stellar mass BHs, the strongest prediction to test is that AMS may be capable of determining these anti-protons and protons near to and beyond TeV. Annihilation of protons and anti-protons may also be detectable.

The electron-positrons detected by Martin et al. (2010), Prantzos et al. (2011), Siegert et al. (2016a), Siegert et al. (2016b), Prantzos (2017), Mera Evans et al. (2022) may correspond to just the population derived from pion production and decay.

6 Conclusion

In the scenarios proposed here, we predict anti-protons to be seen above TeV energies AMS-Coll. (2016) with the EeV proton component detected in fits of the cosmic ray data in Gaisser et al. (2013), Thoudam et al. (2016), Auger-Coll (2020a). These concepts lead us to a number of predictions and inferences:

$•$ Massive stars, commonly found in multi-star systems, lose orbital angular momentum through magnetic winds.

$•$ This, in turn, allows a tightening of the binary system, and by tidal locking to an increase of rotation. Alternatively the core of the nascent star may rotate fast and remain in fast rotation during its rapid evolution.

$•$ Resulting BHs rotate initially near the maximum allowed value. This phase of high rotation is short-lived.

$•$ RSNe of former Red Super Giant stars and Blue Super Giant stars can be interpreted as winds emanating from the direct environment of the ergo-region of a BH, which rotates near the maximum allowed value.

$•$ The constancy of the value of the quantity $(B\times r)$, being independent of BH mass, in RSNe shows that protons can attain EeV energies.

$•$ The quantity $(B\times r)$ gives an angular momentum loss time scale of the BH of $\sim 10^{3.7}\mathrm{y}\mathrm{r}\mathrm{s}(M_{BH}/M_{\odot })$, so is proportional to the mass of the BH, here scaled to one Solar mass. For super-massive BHs we obtain the same value of the quantity $(B\times r)$, directly from M87 observations (EHT-Coll, 2019b), and indirectly from the minimum power observed (Punsly and Zhang, 2011). The time scale of angular momentum loss exceeds the age of the universe for any such BH of mass larger than $10^{6.5}{M}_{\odot }$, assuming it started at near maximal rotation. This value is remarkably close to the mass of our Galactic Center BH (EHT-Coll, 2019b). It follows that without spin-up intermediate mass BH are expected to rotate slowly (Fuller and Lu, 2022).

$•$ This quantity leads to a power outflow of $\sim 10^{42.8}\mathrm{e}\mathrm{r}\mathrm{g}/\mathrm{s}$, independent of BH mass. This is seen for low power radio galaxies Punsly and Zhang (2011). For stellar mass BHs this is far above the Eddington power.

$•$ This power outflow comes purely from spin-down (Blandford and Znajek, 1977), and is thus a minimum, matching observations of radio-quasars (Punsly and Zhang, 2011).

$•$ The wind emanating from the ergo-region injects a CR population with an observed spectrum of $E^{-7/3}$ (due to transport out of the Galaxy, pop $3^{*}$ in Gaisser et al. (2013); Table 3) and a maximum energy at EeV level. This population is predicted to show a fraction of anti-protons, half. At such a high charged particle density as required to make anti-protons, all higher mass nuclei will be destroyed by spallation; this component is only protons and anti-protons in our proposal. This directly matches the argument about electric currents in jets being driven by a proton-anti-proton plasma with a spectrum of $E^{-2}$ (Gopal-Krishna and Biermann, 2024). This is in addition to the stronger CR flux of all elements which is produced by SN-shocks (pop 1, 2 and 3 in Gaisser et al. (2013), Table 2). This destruction of heavier nuclei is actually a consistency check of our model, since the Gaisser et al. model (Gaisser et al., 2013) does not show such a heavy nuclei component, with this spectrum $E^{-7/3}$.

$•$ This model provides a floor to the anti-proton spectrum seen by AMS and limits determined by HAWC AMS-Coll. (2016), HAWC-Coll. (2018) in the range of GeV to TeV. A consequence is that this component of the anti-protons should show a straight spectrum from near TeV energies all the way to EeV energies, with a $E^{-7/3}$ power law throughout.

$•$ The model suggests that in the ergo-region there is a cascading, collisional production of energetic particles, producing an abundance of secondaries. An electron/positron plasma is a primary product from these collisions. These secondaries produce strong drift currents, and exchange energy and angular momentum with the magnetic field (Gopal-Krishna and Biermann, 2024).

$•$ The cascading might lead to a much higher production of anti-protons and protons than the number of protons actually accreted from far outside. Most of the anti-protons get annihilated in collisions with protons. In such a reaction, large numbers of neutrinos are produced, and those which escape can remove angular momentum. This could lead to an efficient reduction of rotational energy of the BH. This is possibly detectable as neutrinos with energies near GeV.

$•$ This scenario can be connected to a concept of inner and outer Penrose zones in the ergo-region. The observed numbers for the magnetic field imply the Planck time as the governing time scale: A BH rotating near maximum can accept a proton of low specific angular momentum per log bin of energy with the associated pions every Planck time.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

MA: Writing–review and editing. PB: Writing–original draft, Writing–review and editing. AC: Writing–review and editing. RC: Writing–review and editing. DF: Writing–review and editing. LG: Writing–review and editing. G-K: Writing–review and editing. BH: Writing–review and editing. IJ: Writing–review and editing. Gopal-Krishna: Writing-review and editing. PJ: Writing–review and editing. PK: Writing–review and editing. EK: Writing–review and editing. AM: Writing–original draft, Writing–review and editing. E-SS: Writing–review and editing. TS: Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

PB wishes to thank Nasser Barghouty, Susanne Blex, Julia Becker Tjus, Silke Britzen, Roland Diehl, Matthias Kaminski, Wolfgang Kundt, Norma Sanchez, and Gary Webb for stimulating discussions, as well as Carola Dobrigkeit, Roger Clay, Roland Diehl and several others for helpful comments on the manuscript. The two coauthors BH and PK passed away during the work for this manuscript, but were integral in the discussions leading up to it for decades. The comments by the referees were extremely helpful in sharpening the argument, and adding further references.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbott, D. C., Bieging, J. H., and Churchwell, E. (1984). ; the detection of variable, nonthermal radio emission from two O type stars. Astrophys. J. 280, 671–678. doi:10.1086/162040

CrossRef Full Text | Google Scholar

AMS Coll Aguilar, M., Ali Cavasonza, L., Alpat, B., Ambrosi, G., Arruda, L., et al. (2016). Antiproton flux, antiproton-to-proton flux ratio, and properties of elementary particle fluxes in primary cosmic rays measured with the alpha magnetic spectrometer on the international space station. Phys. Rev. Lett. 117, 091103. doi:10.1103/physrevlett.117.091103

PubMed Abstract | CrossRef Full Text | Google Scholar

Allen, M. L. (1999). Radio continuum studies of the evolved starburst in M82. PhD thesis U. Tor.

Google Scholar

Allen, M. L., Biermann, P. L., Chieffi, A., Frekers, D., Gergely, L. Á., Harms, B., et al. (2024). Loaded layer-cake model for cosmic ray interaction around exploding super-giant stars making black holes. Astropart. Phys. 161, 102976. doi:10.1016/j.astropartphys.2024.102976

CrossRef Full Text | Google Scholar

Allen, M. L., and Kronberg, P. P. (1998). Radio spectra of selected compact sources in the nucleus of M82. Astrophys. J. 502, 218–228. doi:10.1086/305894

CrossRef Full Text | Google Scholar

Auger-Coll Aab, A., Abreu, P., Aglietta, M., Albuquerque, I. F. M., Allekotte, I., Almela, A., et al. (2018). An indication of anisotropy in arrival directions of ultra-high-energy cosmic rays through comparison to the flux pattern of extragalactic gamma-ray sources. Astrophys. J. Lett. 853, L29. doi:10.3847/2041-8213/aaa66d

CrossRef Full Text | Google Scholar

Auger-Coll Aab, A., Abreu, P., Aglietta, M., Albuquerque, I. F. M., Albury, J. M., Allekotte, I., et al. (2020b). Cosmic-ray anisotropies in right ascension measured by the pierre auger observatory. Astrophys. J. 891, 142.

CrossRef Full Text | Google Scholar

Auger-Coll Aab, A., Abreu, P., Aglietta, M., Albury, J. M., Allekotte, I., Almela, A., et al. (2020a). Features of the energy spectrum of cosmic rays above 2.5×10¹⁸ eV using the pierre auger observatory. Phys. Rev. Lett. 125, 121106. doi:10.1103/PhysRevLett.125.121106

PubMed Abstract | CrossRef Full Text | Google Scholar

Bahcall, J. N., and Wolf, R. A. (1976). Star distribution around a massive black hole in a globular cluster. Astrophys. J. 209, 214–232. doi:10.1086/154711

CrossRef Full Text | Google Scholar

Bambhaniya, P., Solanki, D. N., Dey, D., Joshi, A. B., Joshi, P. S., and Patel, V. (2021). Precession of timelike bound orbits in Kerr spacetime. Eur. Phys. Journ. C 81, 205. doi:10.1140/epjc/s10052-021-08997-x

CrossRef Full Text | Google Scholar

Banados, M., Hassanain, B., Silk, J., and West, St.M. (2011). Emergent flux from particle collisions near a Kerr black hole. Phys. Rev. D. 83, 023004. doi:10.1103/physrevd.83.023004

CrossRef Full Text | Google Scholar

Banados, M., Silk, J., and West, S. M. (2009). Kerr black holes as particle accelerators to arbitrarily high energy. Phys. Rev. Lett. 103, 111102. doi:10.1103/physrevlett.103.111102

PubMed Abstract | CrossRef Full Text | Google Scholar

Bardeen, J. M., Carter, B., and Hawking, S. W. (1973). The four laws of black hole mechanics. Commun. Math. Phys. 31, 161–170. doi:10.1007/bf01645742

CrossRef Full Text | Google Scholar

Bardeen, J. M., Press, W. H., and Teukolsky, S. A. (1972). Rotating black holes: locally nonrotating frames, energy extraction, and scalar synchrotron radiation. Astrophys. J. 178, 347–370. doi:10.1086/151796

CrossRef Full Text | Google Scholar

Barr Domínguez, A., Chini, R., Pozo Nunez, F., Haas, M., Hackstein, M., Drass, H., et al. (2013). Eclipsing high-mass binaries: I. Light curves and system parameters for CPD − 51° 8946, PISMIS 24-1, and HD 319702⋆. Astron. and Astroph 557, A13. doi:10.1051/0004-6361/201321642

CrossRef Full Text | Google Scholar

Bejger, M., Piran, T., Abramowicz, M., and kanson, F. (2012). Collisional Penrose process near the horizon of extreme Kerr black holes. Phys. Rev. Lett. 109, 121101. doi:10.1103/physrevlett.109.121101

PubMed Abstract | CrossRef Full Text | Google Scholar

Bekenstein, J. D. (1973). Black holes and entropy. Phys. Rev. 7, 2333–2346. doi:10.1103/physrevd.7.2333

CrossRef Full Text | Google Scholar

Bell, A. R., and Lucek, S. G. (2001). Cosmic ray acceleration to very high energy through the non-linear amplification by cosmic rays of the seed magnetic field. Mon. Not. Roy. Astr. Soc. 321, 433–438. doi:10.1046/j.1365-8711.2001.04063.x

CrossRef Full Text | Google Scholar

Biermann, P. L. (1993). Cosmic rays I. The cosmic ray spectrum between 10⁴GeV and 310⁹GeV 271, 649. doi:10.48550/arXiv.astro-ph/9301008

CrossRef Full Text | Google Scholar

Biermann, P. L. (1994). “Invited plenary lecture at 23rd international conference on cosmic rays,” in Proc. “Invited, Rapporteur and Highlight papers. Cosmic rays: origin and acceleration - what can we learn from radio astronomy. Editor D. A. Leahy (Singapore: World Scientific), 45.

Google Scholar

Biermann, P. L. (1997). “Invited review chapter,” in Cosmic winds and the heliosphere. Editor J. R. Jokipii (Tucson, AZ: Univ. of Arizona press), 887–957. astro-ph/9501030.

Google Scholar

Biermann, P. L., and Astroph, A. (1993). The cosmic ray spectrum between 10⁴ GeV and 310⁹ GeV. Cosm. rays I 271, 649.

Google Scholar

Biermann, P. L., Becker Tjus, J., Boer, W. de, Caramete, L. I., Chieffi, A., Diehl, R., et al. (2018). Invited review: supernova explosions of massive stars and cosmic rays. Adv. Space Res. 62, 2773–2816. arXiv:1803.10752. doi:10.1016/j.asr.2018.03.028

CrossRef Full Text | Google Scholar

Biermann, P. L., and Cassinelli, J. P. (1993). Cosmic rays II. Evidence for a magnetic rotator Wolf-Rayet star origin. Astron. and Astroph 277, 691–706.

Google Scholar

Biermann, P. L., Kronberg, P. P., Allen, M. L., and Seo, E.-S. (2019). The origin of the most energetic galactic cosmic rays: supernova explosions into massive star plasma winds. Galaxies 7 (2), 48. doi:10.3390/galaxies7020048

CrossRef Full Text | Google Scholar

Biermann, P. L., and Strom, R. G. (1993). Cosmic Rays III. The cosmic ray spectrum between 1 GeV and 104 GeV and the radio emission from supernova remnants. Astron. and Astroph 275, 659.

Google Scholar

Bisnovatyi-Kogan, G. S. (1970). The explosion of a rotating star as a supernova mechanism. Astron. Zh. 47, 813. transl. Sov. Astron. 14, 652.

Google Scholar

Bisnovatyi-Kogan, G. S., and Moiseenko, S. G. (2008). Magnetorotational supernovae with jets. Chin. J. Astr. and Astroph. Suppl. 8, 330–340.

Google Scholar

Blandford, R. D., and Znajek, R. L. (1977). Electromagnetic extraction of energy from Kerr black holes. Mon. Not. Roy. Astr. Soc. 179, 433–456. doi:10.1093/mnras/179.3.433

CrossRef Full Text | Google Scholar

Breitschwerdt, D., McKenzie, J. F., and Voelk, H. J. (1991). Galactic winds. I. Cosmic ray and wave-driven winds from the galaxy. Astron. and Astroph. 245, 79–98.

Google Scholar

Chevalier, R. A. (1984). The interaction of Crab-like supernova remnants with their surroundings. Astrophys. J. 280, 797–801. doi:10.1086/162053

CrossRef Full Text | Google Scholar

Chieffi, A., and Limongi, M. (2013). Pre-supernova evolution of rotating solar metallicity stars in the mass range 13-120 M_⊙ and their explosive yields. Astrophys. J. 764, 21. doi:10.1088/0004-637x/764/1/21

CrossRef Full Text | Google Scholar

Chini, R., Barr, A., Buda, L. S., Dembsky, T., Drass, H., Nasseri, A., et al. (2013a). The multiplicity of high-mass stars. Centr. Eur. Astrophys. Bull. 37, 295–310.

Google Scholar

Chini, R., Hoffmeister, V. H., Nasseri, A., Stahl, O., and Zinnecker, H. (2012). A spectroscopic survey on the multiplicity of high-mass stars. Mon. Not. Roy. Astr. Soc. 424, 1925–1929. doi:10.1111/j.1365-2966.2012.21317.x

CrossRef Full Text | Google Scholar

Chini, R., Nasseri, A., Dembsky, T., Buda, L.-S., Fuhrmann, K., and Lehmann, H. (2013b). “Stellar multiplicity across the mass spectrum,”in Setting a new standard in the analysis of binary stars Editors K. Pavlovski, A. Tkachenko, and G. Torres (Paris, France: EAS Publ. Ser.) 64, 155–162. doi:10.1051/eas/1364022

CrossRef Full Text | Google Scholar

Cho, H., Prather, B. S., Narayan, R., Natarajan, P., Su, K.-Y., Ricarte, A., et al. (2023). Bridging scales in black hole accretion and feedback: magnetized bondi accretion in 3D GRMHD. Letters 959, 022.

Google Scholar

Churchwell, E., Bieging, J. H., van der Hucht, K. A., Williams, P. M., Spoelstra, T. A. Th., and Abbott, D. C. (1992). The wolf-rayet system wr 147: a binary radio source with thermal and nonthermal components. Astrophys. J. 393, 329–340. doi:10.1086/171508

CrossRef Full Text | Google Scholar

Colgate, S. A. (1994). Acceleration in astrophysics. Phys. Scr. T52, 96–105. doi:10.1088/0031-8949/1994/t52/017

CrossRef Full Text | Google Scholar

Cox, D. P. (1972). Cooling and evolution of a supernova remnant. Astrophys. J. 178, 159–168. doi:10.1086/151775

CrossRef Full Text | Google Scholar

Daly, R. A. (2019). Black hole spin and accretion disk magnetic field strength estimates for more than 750 active galactic nuclei and multiple galactic black holes. Astrophys. J. 886, 37. doi:10.3847/1538-4357/ab35e6

CrossRef Full Text | Google Scholar

Davelaar, J., Mościbrodzka, M., Bronzwaer, T., and Falcke, H. (2018). General relativistic magnetohydrodynamical κ-jet models for Sagittarius A∗. Astron. and Astroph. 612, A34. doi:10.1051/0004-6361/201732025

CrossRef Full Text | Google Scholar

Davis, S. W., and Gammie, C. F. (2020). Covariant radiative transfer for black hole spacetimes. Astrophys. J. 888, 94. doi:10.3847/1538-4357/ab5950

CrossRef Full Text | Google Scholar

Diehl, R. (2013). Nuclear astrophysics lessons from INTEGRAL. Rep. Pro.Phys. 76, 026301. doi:10.1088/0034-4885/76/2/026301

PubMed Abstract | CrossRef Full Text | Google Scholar

Diehl, R. (2017). “Gamma-ray line measurements from supernova explosions,” in Proc. IAU symposium 331 ”SN1987A 30 years after”, La reunion, feb. 2017 (Cambridge, United Kingdom: IAU Conf 331 Proc.), 157–163. (2017); eprint arXiv:1704.05937.

CrossRef Full Text | Google Scholar

Diehl, R., Halloin, H., Kretschmer, K., Lichti, G. G., Schönfelder, V., Strong, A. W., et al. (2006). Radioactive ²⁶Al from massive stars in the Galaxy. Nature 439, 45–47. doi:10.1038/nature04364

PubMed Abstract | CrossRef Full Text | Google Scholar

Diehl, R., Hartmann, D. H., and Prantzos, N. (2011). “Astronomy with radioactivities,” in Lecture notes in physics (Berlin: Springer), 812.

Google Scholar

Diehl, R., Lang, M. G., Martin, P., Ohlendorf, H., Preibisch, Th., Voss, R., et al. (2010). Radioactive 26Al from the scorpius-centaurus association. Astron. and Astroph. 522, A51. doi:10.1051/0004-6361/201014302

CrossRef Full Text | Google Scholar

Drake, St.A., Abbott, D. C., Bastian, T. S., Bieging, J. H., Churchwell, E., Dulk, G., et al. (1987). The discovery of nonthermal radio emission from magnetic bp - ap stars. Astrophys. J. 322, 902–908. doi:10.1086/165784

CrossRef Full Text | Google Scholar

EHT-Coll Akiyama, K., Alberdi, A., Alef, W., Asada, K., Azulay, R., Baczko, A.-K., et al. (2019a). First M87 event horizon telescope results. I. The shadow of the supermassive black hole. Astrophys. J. Lett. 875, L1. doi:10.3847/2041-8213/ab0ec7

CrossRef Full Text | Google Scholar

EHT-Coll Akiyama, K., Alberdi, A., Alef, W., Asada, K., Azulay, R., Baczko, A.-K., et al. (2019b). First M87 event horizon telescope results. V. Physical origin of the asymmetric ring. Astrophys. J. Lett. 875, L5. doi:10.3847/2041-8213/ab0f43

CrossRef Full Text | Google Scholar

EHT-Coll Akiyama, K., Algaba, J. C., Alberdi, A., Alef, W., Anantua, R., Asada, K., et al. (2021a). First M87 event horizon telescope results. VII. Polarization of the ring. Astrophys. J. Lett. 910, L12. doi:10.3847/2041-8213/abe71d

CrossRef Full Text | Google Scholar

EHT-Coll Akiyama, K., Algaba, J. C., Alberdi, A., Alef, W., Anantua, R., Asada, K., et al. (2021b). First M87 event horizon telescope results. VIII. Magnetic field structure near the event horizon. Astrophys. J. Lett. 910, L13. doi:10.3847/2041-8213/abe4de

CrossRef Full Text | Google Scholar

Einstein, A. (1915). Zur allgemeinen relativitätstheorie. Sitz. Ber. Preuß. Akad. Wiss., 778–786.

Google Scholar

Einstein, A. (1917). Zur Quantentheorie der Strahlung. (To a quantum theory of radiation). Phys. Zeitschr. 18, 121–128.

Google Scholar

Falcke, H., and Biermann, P. L. (1995). The jet-disk symbiosis. I. Radio X-ray Emiss. models quasars 293, 665–682.

Google Scholar

Falcke, H., Körding, E., and Markoff, S. (2004). A scheme to unify low-power accreting black holes. Jet-dominated accretion flows and the radio/X-ray correlation. Astron. and Astroph. 414, 895–903. doi:10.1051/0004-6361:20031683

CrossRef Full Text | Google Scholar

Falcke, H., and Markoff, S. (2013). Toward the event horizon - the supermassive black hole in the Galactic Center. Cl. Quantum Grav. 30, 244003. doi:10.1088/0264-9381/30/24/244003

CrossRef Full Text | Google Scholar

Fermi, E. (1949). On the origin of the cosmic radiation. Phys. Rev. 75, 1169–1174. doi:10.1103/physrev.75.1169

CrossRef Full Text | Google Scholar

Fermi, E. (1954). Galactic magnetic fields and the origin of cosmic radiation. Astrophys. J. 119, 1–6. doi:10.1086/145789

CrossRef Full Text | Google Scholar

Feynman, R. P., Leighton, R. B., and Sands, M. (1963). The feynman Lectures on physics (book), 42–49. here.

Google Scholar

Frank, J., and Rees, M. J. (1976). Effects of massive central black holes on dense stellar systems. Mon. Not. Roy. Astr. Soc. 176, 633–647. doi:10.1093/mnras/176.3.633

CrossRef Full Text | Google Scholar

Fuller, J., and Lu, W. (2022). The spins of compact objects born from helium stars in binary systems. Mon. Not. Roy. Astr. Soc. 511, 3951–3964. doi:10.1093/mnras/stac317

CrossRef Full Text | Google Scholar

Gaisser, T. K., Stanev, T., and Tilav, S. (2013). Cosmic ray energy spectrum from measurements of air showers. Front. Phys. 8, 748–758. doi:10.1007/s11467-013-0319-7

CrossRef Full Text | Google Scholar

Gergely, L. Á., and Biermann, P. L. (2009). Supermassive black hole mergers. Astrophys. J. 697, 1621–1633. arXiv:0704.1968. doi:10.1088/0004-637x/697/2/1621

CrossRef Full Text | Google Scholar

Goldreich, P., and Julian, W. H. (1969). Pulsar electrodynamics. Astrophys. J. 157, 869–880. doi:10.1086/150119

CrossRef Full Text | Google Scholar

Gopal-Krishna, L., Biermann, P. L., Gergely, L. Á., and Wiita, P. J. (2012). On the origin of X-shaped radio galaxies. Res. Astron. and Astroph. 12, 127–146. doi:10.1088/1674-4527/12/2/002

CrossRef Full Text | Google Scholar

Gopal-Krishna, P., and Biermann, P. L. (2024). Collimated synchrotron threads in wide-angle-tail radio galaxies: cosmic thunderbolts? Mon. Not. Roy. Astr. Soc. Lett. 529, L135–L139. doi:10.1093/mnrasl/slad191

CrossRef Full Text | Google Scholar

Gopal-Krishna, P., Biermann, P. L., Wiita, P. J., and Astrophys, J. (2003). The origin of X-shaped radio galaxies: clues from the Z-symmetric secondary lobes. Letters 594, L103–L106. doi:10.1086/378766

CrossRef Full Text | Google Scholar

Gültekin, K., King, A. L., Cackett, E. M., Nyland, K., Miller, J. M., Di Matteo, T., et al. (2019). The fundamental plane of black hole accretion and its use as a black hole-mass estimator. Astrophys. J. 871, 80. doi:10.3847/1538-4357/aaf6b9

CrossRef Full Text | Google Scholar

HAWC-Coll Abeysekara, A. U., Albert, A., Alfaro, R., Alvarez, C., Álvarez, J. D., Arceo, R., et al. (2018). Constraining the p¯/p ratio in TeV cosmic rays with observations of the Moon shadow by HAWC. Phys. Rev. D. 97, 102005.

Google Scholar

Hawking, S. W. (1974). Black hole explosions? Nature 248 (5443), 30–31. doi:10.1038/248030a0

CrossRef Full Text | Google Scholar

Hawking, S. W. (1975). Particle creation by black holes. Commun. Math. Phys. 43, 199–220. doi:10.1007/bf02345020

CrossRef Full Text | Google Scholar

Heger, A., Fryer, C. L., Woosley, S. E., Langer, N., and Hartmann, D. H. (2003). How massive single stars end their life. Astrophys. J. 591, 288–300. doi:10.1086/375341

CrossRef Full Text | Google Scholar

Hills, J. G. (1975). Possible power source of Seyfert galaxies and QSOs. Nature 254, 295–298. doi:10.1038/254295a0

CrossRef Full Text | Google Scholar

Hirsch, J. E. (2014). The London moment: what a rotating superconductor reveals about superconductivity. Phys. Scr. 89, 015806. arXiv/1310.3834. doi:10.1088/0031-8949/89/01/015806

CrossRef Full Text | Google Scholar

Hirsch, J. E. (2019). Defying inertia: how rotating superconductors generate magnetic fields. Ann. Phys. 531, 190212. arXiv/1812.06780. doi:10.1002/andp.201900212

CrossRef Full Text | Google Scholar

Hod, Sh. (2016). Upper bound on the center-of-mass energy of the collisional Penrose process. Phys. Lett.B 759, 593–595. doi:10.1016/j.physletb.2016.06.028

CrossRef Full Text | Google Scholar

Humphreys, R. M., Helmel, G., Jones, T. J., and Gordon, M. S. (2020). Exploring the mass-loss histories of the red supergiants. Astron. J. 160, 145. doi:10.3847/1538-3881/abab15

CrossRef Full Text | Google Scholar

Hwang, U., Laming, J. M., Badenes, C., Berendse, F., Blondin, J., Cioffi, D., et al. (2004). A million second Chandra view of Cassiopeia A. Astrophys. J. Lett. 615, L117–L120. doi:10.1086/426186

CrossRef Full Text | Google Scholar

IceCube-Coll Aartsen, M. G., Abraham, K., Ackermann, M., Adams, J., Aguilar, J. A., Ahlers, M., et al. (2016). Lowering IceCube’s energy threshold for point searches in the southern sky. Astrophys. J. Lett. 824, L28. doi:10.3847/2041-8205/824/2/l28

CrossRef Full Text | Google Scholar

IceCube-Coll Aartsen, M. G., Ackermann, M., Adams, J., Aguilar, J. A., Ahlers, M., Ahrens, M., et al. (2020). Time-integrated neutrino source searches with 10 Years of IceCube data. Phys. Rev. Lett. 124, 051103. doi:10.1103/physrevlett.124.051103

PubMed Abstract | CrossRef Full Text | Google Scholar

IceCube-Coll Abbasi, R., Ackermann, M., Adams, J., Aguilar, J. A., Ahlers, M., Ahrens, M., et al. (2021). Search for multi-flare neutrino emissions in 10 yr of IceCube data from a catalog of sources. Astrophys. J. Lett. 920, 45. doi:10.3847/2041-8213/ac2c7b

CrossRef Full Text | Google Scholar

Igumenshchev, I. V., Narayan, R., and Abramowicz, M. A. (2003). Three-dimensional magnetohydrodynamic simulations of radiatively inefficient accretion flows. Astrophys. J. 592, 1042–1059. doi:10.1086/375769

CrossRef Full Text | Google Scholar

Jaroschewski, I., Becker Tjus, J., and Biermann, P. L. (2023). Extragalactic neutrino emission induced by supermassive and stellar mass black hole mergers. Mon. Not. Roy. Astr. Soc. 518, 6158–6182. arXiv:2210.11337.

Google Scholar

Joshi, P. S. (1993). Global aspects in gravitation and cosmology. OUP Clarendon Press. Oxford (1993), International Series of Monographs in Physics.

Google Scholar

Joshi, P. S. (2007). Gravitational collapse and spacetime singularities. Cambridge, UK: Cambridge University Press. paperback edition 2012.

Google Scholar

Joshi, P. S. (2011). “Key problems in black hole physics today,” in Fluid flows to black holes: a tribute to S. Chandrasekhar on his birth centenary. Editors D. J. Saikia, and V. Trimble (World Scientific).

CrossRef Full Text | Google Scholar

Joshi, P. S. (2014). Spacetime singularities. Springer handbook of spacetime. Springer-Verlag Berlin Heidelberg.

Google Scholar

Joshi, P. S. (2015). The story of collapsing stars-black holes, naked singularities and the cosmic play of quantum gravity. Oxford: Oxford University Press.

CrossRef Full Text | Google Scholar

Kerr, R. P. (1963). Gravitational field of a spinning mass as an example of algebraically special metrics. Phys. Rev. Lett. 11, 237–238. doi:10.1103/physrevlett.11.237

CrossRef Full Text | Google Scholar

King, I. R. (1966). The structure of star clusters. III. Some simple dvriamical models. Astron. J. 71, 64–75. doi:10.1086/109857

CrossRef Full Text | Google Scholar

Komissarov, S. S. (2004). Electrodynamics of black hole magnetospheres. Mon. Not. Roy. Astr. Soc. 350, 427–448. doi:10.1111/j.1365-2966.2004.07598.x

CrossRef Full Text | Google Scholar

Kronberg, P. P. (1994). Extragalactic magnetic fields. Rep. Pro.Phys. 57, 325–382. doi:10.1088/0034-4885/57/4/001

CrossRef Full Text | Google Scholar

Kronberg, P. P. (2016). Cosmic magnetic fields. Cambridge, United Kingdom: Cambridge U. Press, 283.

Google Scholar

Kronberg, P. P., Biermann, P. L., and Schwab, F. R. (1985). The nucleus of M82 at radio and X-ray bands: discovery of a new radio population of supernova candidates. Astrophys. J. 291, 693–707. doi:10.1086/163108

CrossRef Full Text | Google Scholar

Kronberg, P. P., Lovelace, R. V. E., Lapenta, G., and Colgate, S. A. (2011). Measurement of the electric current in a kpc-scale jet. Astrophys. J. Lett. 741, L15. doi:10.1088/2041-8205/741/1/l15

CrossRef Full Text | Google Scholar

Kronberg, P. P., Sramek, R. A., Birk, G. T., Dufton, Q. W., Clarke, T. W., and Allen, M. L. (2000). A search for flux density variations in 24 compact radio sources in M82. Astrophys. J. 535, 706–711. doi:10.1086/308881

CrossRef Full Text | Google Scholar

Kun, E., Bartos, I., Becker Tjus, J., Biermann, P. L., Halzen, F., and Mezö, G. (2021). Cosmic neutrinos from temporarily gamma-suppressed blazars. ApJL 911, L18. doi:10.3847/2041-8213/abf1ec

CrossRef Full Text | Google Scholar

Leiderschneider, E., and Piran, T. (2016). Maximal efficiency of the collisional Penrose process. Phys. Rev. D. 93, 043015. doi:10.1103/physrevd.93.043015

CrossRef Full Text | Google Scholar

LIGO/VIRGO-Coll Abbott, B. P., Abbott, R., Abbott, T. D., Abraham, S., Acernese, F., Ackley, K., et al. (2019). GWTC-1: a gravitational-wave transient catalog of compact binary mergers observed by LIGO and virgo during the first and second observing runs. Phys. Rev. X 9, 031040. doi:10.1103/physrevx.9.031040

CrossRef Full Text | Google Scholar

LIGO/VIRGO-Coll Abbott, R., Abbott, T. D., Abraham, S., Acernese, F., Ackley, K., Adams, A., et al. (2021a). GWTC-2: compact binary coalescences observed by LIGO and virgo during the first half of the third observing run. Phys. Rev. X 11, 021053. doi:10.1103/physrevx.11.021053

CrossRef Full Text | Google Scholar

LIGO/VIRGO-Coll Abbott, R., Abbott, T. D., Acernese, F., Ackley, K., Adams, C., Adhikari, N., et al. (2021b). GWTC-2.1: deep extended catalog of compact binary coalescences observed by LIGO and virgo during the first half of the third observing run. Phys. Rev. D. 109, 022001. eprint arXiv:2108.01045. doi:10.1103/physrevd.109.022001

CrossRef Full Text | Google Scholar

LIGO/VIRGO/KAGRA-Coll Abbott, R., Abbott, T. D., Acernese, F., Ackley, K., Adams, C., Adhikari, N., et al. (2021c). GWTC-3: compact binary coalescences observed by LIGO and virgo during the second part of the third observing run; Phys. Rev. X 13, 041039. doi:10.1103/physrevx.13.041039

CrossRef Full Text | Google Scholar

Limongi, M., and Chieffi, A. (2018). Presupernova evolution and explosive nucleosynthesis of rotating massive stars in the metallicity range –3 ≤ [Fe/H] ≤0. Astrophys. J. Suppl. 237, 13. doi:10.3847/1538-4365/aacb24

CrossRef Full Text | Google Scholar

Limongi, M., and Chieffi, A. (2020). Hydrodynamical modeling of the light curves of core-collapse supernovae with HYPERION. IThe mass range 13-25 –3 ≤ [Fe/H] ≤0, and the case of SN 1999em. Astrophys. J. 902, 95. doi:10.3847/1538-4357/abb4e8

CrossRef Full Text | Google Scholar

Liu, Ch., Chen, S., Ding, Ch., and Jing, J. (2011). Particle acceleration on the background of the Kerr-Taub-NUT spacetime. Phys. Lett.B 701, 285–290. doi:10.1016/j.physletb.2011.05.070

CrossRef Full Text | Google Scholar

Lovelace, R. V. E. (1976). Dynamo model of double radio sources. Nature 262, 649–652. doi:10.1038/262649a0

CrossRef Full Text | Google Scholar

Lucchini, M., Ceccobello, C., Markoff, S., Kini, Y., Chhotray, A., Connors, R. M. T., et al. (2022). Bhjet: a public multizone, steady state jet + thermal corona spectral model. Mon. Not. Roy. Astr. Soc. 517, 5853–5881. doi:10.1093/mnras/stac2904

CrossRef Full Text | Google Scholar

Lucek, S. G., and Bell, A. R. (2000). Non-linear amplification of a magnetic field driven by cosmic ray streaming. Mon. Not. Roy. Astr. Soc. 314, 65–74. doi:10.1046/j.1365-8711.2000.03363.x

CrossRef Full Text | Google Scholar

Maheswaran, M., and Cassinelli, J. P. (1992). Constraints on the surface magnetic fields of hot stars with winds. Astrophys. J. 386, 695–702. doi:10.1086/171049

CrossRef Full Text | Google Scholar

Markoff, S., Nowak, M. A., Gallo, E., Hynes, R., Wilms, J., Plotkin, R. M., et al. (2015). As above, so below: exploiting mass scaling in black hole accretion to break degeneracies in spectral interpretation. Astrophys. J. Lett. 812, L25. doi:10.1088/2041-8205/812/2/l25

CrossRef Full Text | Google Scholar

Marszewski, A., Prather, B. S., Joshi, A. V., Pandya, A., and Gammie, Ch.F. (2021). Updated transfer coefficients for magnetized plasmas. Astrophys. J. 921, 17. doi:10.3847/1538-4357/ac1b28

CrossRef Full Text | Google Scholar

Martin, P., Vink, J., Jiraskova, S., Jean, P., and Diehl, R. (2010). Annihilation emission from young supernova remnants. Astron. and Astroph. 519, A100. doi:10.1051/0004-6361/201014171

CrossRef Full Text | Google Scholar

McDonald, A. R., Muxlow, T. W. B., Wills, K. A., Pedlar, A., and Beswick, R. J. (2002). A parsec-scale study of the 5/15-GHz spectral indices of the compact radio sources in M82. Mon. Not. Roy. Astr. Soc. 334, 912–924. doi:10.1046/j.1365-8711.2002.05580.x

CrossRef Full Text | Google Scholar

Meli, A., Becker, J., and Quenby, J. J. (2008). On the origin of ultra high energy cosmic rays: subluminal and superluminal relativistic shocks. Astron. & Astroph. 492, 323–336. doi:10.1051/0004-6361:20078681

CrossRef Full Text | Google Scholar

Meli, A., Nishikawa, K., Köhn, Ch., Duţan, I., Mizuno, Y., Kobzar, O., et al. (2023). 3D PIC Simulations for relativistic jets with a toroidal magnetic field. Mon. Not. Roy. Astr. Soc. 519, 5410–5426. doi:10.1093/mnras/stac3474

CrossRef Full Text | Google Scholar

Meli, A., and Nishikawa, K.-I. (2021). Particle-in-Cell simulations of astrophysical relativistic jets. Universe 7, 450. doi:10.3390/universe7110450

CrossRef Full Text | Google Scholar

Mera Evans, T. B., Hoeflich, P., and Diehl, R. (2022). Galactic positrons from thermonuclear supernovae. Astrophys. J. 930, 107. eprintarXiv:2202.0541. doi:10.3847/1538-4357/ac5253

CrossRef Full Text | Google Scholar

Merloni, A., Heinz, S., and di Matteo, T. (2003). A Fundamental Plane of black hole activity. Mon. Not. Roy. Astr. Soc. 345, 1057–1076. doi:10.1046/j.1365-2966.2003.07017.x

CrossRef Full Text | Google Scholar

Merloni, A., Körding, E., Heinz, S., Markoff, S., Di Matteo, T., and Falcke, H. (2006). Why the fundamental plane of black hole activity is not simply a distance driven artifact. New Astron 11, 567–576. doi:10.1016/j.newast.2006.03.002

CrossRef Full Text | Google Scholar

Mirabel, I. F., Dijkstra, M., Laurent, P., Loeb, A., and Pritchard, J. R. (2011). Stellar black holes at the dawn of the universe. Astron. and Astroph. 528, A149. doi:10.1051/0004-6361/201016357

CrossRef Full Text | Google Scholar

Misner, Ch.W., Thorne, K. S., and Wheeler, J. A. (1973). Gravitation. San Francisco: W. H. Freeman. latest edition 2017.

Google Scholar

Mościbrodzka, M., Falcke, H., and Noble, S. (2016). Scale-invariant radio jets and varying black hole spin. Astron. and Astroph. 596, A13. doi:10.1051/0004-6361/201629157

CrossRef Full Text | Google Scholar

Moskalenko, I. V., and Seo, E.-S. (2019). Advances in cosmic-ray astrophysics and related areas. Adv. Space Res 64, 2417. doi:10.1016/j.asr.2019.10.025

CrossRef Full Text | Google Scholar

Muxlow, T. W. B., Beswick, R. J., Garrington, S. T., Pedlar, A., Fenech, D. M., Argo, M. K., et al. (2010). Discovery of an unusual new radio source in the star-forming galaxy M82: faint supernova, supermassive black hole or an extragalactic microquasar? Mon. Not. Roy. Astr. Soc. Lett. 404, L109–L113. doi:10.1111/j.1745-3933.2010.00845.x

CrossRef Full Text | Google Scholar

Muxlow, T. W. B., Pedlar, A., Beswick, R. J., Argo, M. K., O’Brien, T. J., Fenech, D., et al. (2005). Is 41.95+575 in M82 actually an SNR? Mem. S.A. 76, 586–588.

Google Scholar

Muxlow, T. W. B., Pedlar, A., Wilkinson, P. N., Axon, D. J., Sanders, E. M., de Bruyn, A. G., et al. (1994). The structure of young supernova remnants in M82. Astr. Soc. 266, 455–467. doi:10.1093/mnras/266.2.455

CrossRef Full Text | Google Scholar

Narayan, R., Igumenshchev, I. V., and Abramowicz, M. A. (2003). Magnetically arrested disk: an energetically efficient accretion flow. Publ. Astron.Soc.Japan 55, L69–L72. doi:10.1093/pasj/55.6.l69

CrossRef Full Text | Google Scholar

Nokhrina, E. E. (2020). The correlation between the total jet power and the Poynting flux at the jet base. Perseus Sicily Black Hole Clust. Outskirts. Proc. IAU 342, 197–200. doi:10.1017/s1743921318006087

CrossRef Full Text | Google Scholar

Northrop, T. G. (1963). The adiabatic motion of charged particles. New York: Interscience Publ.

Google Scholar

Owen, F. N., Eilek, J. A., and Kassim, N. E. (2000). M87 at 90 centimeters: a different picture. Astrophys. J. 543, 611–619. doi:10.1086/317151

CrossRef Full Text | Google Scholar

Pacini, F., and Salvati, M. (1973). On the evolution of supernova remnants. Evolution of the magnetic field, particles, content, and luminosity. Astrophys. J. 186, 249–266. doi:10.1086/152495

CrossRef Full Text | Google Scholar

Parker, E. N. (1958). Dynamics of the interplanetary gas and magnetic fields. Astrophys. J. 128, 664–676. doi:10.1086/146579

CrossRef Full Text | Google Scholar

Patil, M., Harada, T., Nakao, K., Joshi, P. S., and Kimura, M. (2016). Infinite efficiency of the collisional Penrose process: can a overspinning Kerr geometry be the source of ultrahigh-energy cosmic rays and neutrinos? Phys. Rev. D. 93, 104015. doi:10.1103/physrevd.93.104015

CrossRef Full Text | Google Scholar

Patil, M., and Joshi, P. S. (2011a). Kerr naked singularities as particle accelerators. Cl. Quant. Grav. 28, 235012. doi:10.1088/0264-9381/28/23/235012

CrossRef Full Text | Google Scholar

Patil, M., and Joshi, P. S. (2011b). High energy particle collisions in superspinning Kerr geometry. Phys. Rev. 84, 104001. doi:10.1103/physrevd.84.104001

CrossRef Full Text | Google Scholar

Patil, M., and Joshi, P. S. (2012). Ultrahigh energy particle collisions in a regular spacetime without black holes or naked singularities. Phys. Rev. D. 86, 044040. doi:10.1103/physrevd.86.044040

CrossRef Full Text | Google Scholar

Patil, M., and Joshi, P. S. (2014). Particle acceleration by Majumdar-Papapetrou di-hole. General Relat. and Grav 46, 1801. doi:10.1007/s10714-014-1801-4

CrossRef Full Text | Google Scholar

Patil, M., Joshi, P. S., Kimura, M., and Nakao, K. i. (2012). Acceleration of particles and shells by Reissner-Nordström naked singularities. Phys. Rev. D. 86, 084023. doi:10.1103/physrevd.86.084023

CrossRef Full Text | Google Scholar

Patil, M., Joshi, P. S., and Malafarina, D. (2010). Naked singularities as particle accelerators. PRD 82, 104049. doi:10.1103/PhysRevD.82.104049

CrossRef Full Text | Google Scholar

Patil, M., Joshi, P. S., Nakao, K., Kimura, M., and Harada, T. (2015). Timescale for trans-Planckian collisions in Kerr spacetime. Europhys. Lett. 110, 30004. doi:10.1209/0295-5075/110/30004

CrossRef Full Text | Google Scholar

Păvălaş, G. (2001). The energetics of the cosmic ray contribution from massive stars. Bucharest, Romani: M.Sc. thesis Univ. Bucharest.

Google Scholar

Penrose, R., and Floyd, R. M. (1971). Extraction of rotational energy from a black hole. Nature 229, 177–179. doi:10.1038/physci229177a0

CrossRef Full Text | Google Scholar

Planck, M. (1900). Ueber irreversible strahlungsvorgänge. Annal- Phys. 306, 69–122. doi:10.1002/andp.19003060105

CrossRef Full Text | Google Scholar

Porth, O., Chatterjee, K., Narayan, R., Gammie, Ch.F., Mizuno, Y., Anninos, P., et al. (2019). The event horizon general relativistic magnetohydrodynamic code comparison project. Astrophys. J. Suppl. 243, 26. doi:10.3847/1538-4365/ab29fd

CrossRef Full Text | Google Scholar

Pozo Nunez, F., Chini, R., Barr Domínguez, A., Fein, Ch., Hackstein, M., Pietrzyński, G., et al. (2019). A survey for high-mass eclipsing binaries. Mon. Not. Roy. Astr. Soc. 490, 5147–5173. doi:10.1093/mnras/stz2953

CrossRef Full Text | Google Scholar

Prantzos, N. (2017). High-energy astrophysics: a rare Galactic antimatter source? Nat. Astron 1, 0149. doi:10.1038/s41550-017-0149

CrossRef Full Text | Google Scholar

Prantzos, N., Boehm, C., Bykov, A. M., Diehl, R., Ferrière, K., Guessoum, N., et al. (2011). The 511 keV emission from positron annihilation in the Galaxy. Rev. Mod. Phys. 83, 1001–1056. doi:10.1103/revmodphys.83.1001

CrossRef Full Text | Google Scholar

Punsly, B., and Zhang, S. (2011). The jet power and emission line correlations of radio loud optically selected quasars. Astrophys. J. Lett. 753, L3. doi:10.1088/2041-8205/735/1/l3

CrossRef Full Text | Google Scholar

Rachen, J. P., Stanev, T., Biermann, P. L., Astron, , and Astroph, (1993). astro-ph/9302005. Extragalactic ultra high energy cosmic rays II. Comp. Exp. data 273, 377. doi:10.48550/arXiv.astro-ph/9302005

CrossRef Full Text | Google Scholar

Rees, M., Ruffini, R., and Wheeler, J. A. (1974). “Black holes, gravitational waves, and cosmology: an introduction to current research,” in Topics in Astrophysics and space physics (New York: Gordon & Breach).

Google Scholar

Reinert, A., and Winkler, M. W. (2018). A precision search for WIMPS with charged cosmic rays. J. Cosmol. Astrop. Phys. 01, 055. doi:10.1088/1475-7516/2018/01/055

CrossRef Full Text | Google Scholar

Rottmann, H. (2001). Jet-reorientation in X-shaped radio galaxies. PhD thesis Univ. Bonn.

Google Scholar

Rueda, J. A., and Ruffini, R. (2020). The blackholic quantum. Eur. Phys. Journ. C 80, 300. doi:10.1140/epjc/s10052-020-7868-z

CrossRef Full Text | Google Scholar

Rueda, J. A., and Ruffini, R. (2021). The quantum emission of an alive black hole. Int. J. Mod. Phys. D 30, 2141003. doi:10.1142/s0218271821410030

CrossRef Full Text | Google Scholar

Rueda, J. A., Ruffini, R., and Kerr, R. P. (2022). Gravitomagnetic interaction of a Kerr black hole with a magnetic field as the source of the jetted GeV radiation of gamma-ray bursts. Astrophys. J. 929 (id.56), 56. 2022); eprint arXiv:2203.03471. doi:10.3847/1538-4357/ac5b6e

CrossRef Full Text | Google Scholar

Schnittman, J. D. (2018). The collisional Penrose process. Gen. Rel. Grav 50, 77. doi:10.1007/s10714-018-2373-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Schwarzschild, K. (1916). On the gravitational field of a mass point according to Einstein’s theory. Sitz. Ber. Preuß. Akad. Wiss., 189–196.

Google Scholar

Shaymatov, S., Patil, M., Ahmedov, B., and Ĵoshi, P. S. (2015). Destroying a near-extremal Kerr black hole with a charged particle: can a test magnetic field serve as a cosmic censor? Phys. Rev. D. 91, 064025. doi:10.1103/physrevd.91.064025

CrossRef Full Text | Google Scholar

Siegert, T., Diehl, R., Greiner, J., Krause, M. G. H., Beloborodov, A. M., Cadolle Be, M., et al. (2016a). Positron annihilation signatures associated with the outburst of the microquasar V404 Cygni. Nature 531, 341–343. doi:10.1038/nature16978

PubMed Abstract | CrossRef Full Text | Google Scholar

Siegert, T., Diehl, R., Khachatryan, G., Krause, M. G. H., Guglielmetti, F., Greiner, J., et al. (2016b). Gamma-ray spectroscopy of positron annihilation in the Milky Way. Astron. and Astroph. 386, A84. doi:10.1051/0004-6361/201527510

CrossRef Full Text | Google Scholar

Smartt, St.J. (2009). Progenitors of core-collapse supernovae. Annu. Rev. Astron. and Astrophys. 47, 63–106. doi:10.1146/annurev-astro-082708-101737

CrossRef Full Text | Google Scholar

Smartt, St.J. (2015). Observational constraints on the progenitors of core-collapse supernovae: the case for missing high-mass stars, Publ. Astron. Soc. Aust. 32, e016. doi:10.1017/pasa.2015.17

CrossRef Full Text | Google Scholar

Soderberg, A. M., Chakraborti, S., Pignata, G., Chevalier, R. A., Chandra, P., Ray, A., et al. (2010). A relativistic type Ibc supernova without a detected γ-ray burst. Nature 463, 513–515. doi:10.1038/nature08714

PubMed Abstract | CrossRef Full Text | Google Scholar

Stanev, T., Biermann, P. L., and Gaisser, T. K. (1993). Cosmic rays IV. The spectrum and chemical composition above 10⁴ GeV. Astron. and Astroph 274, 902. astro-ph/9303006.

Google Scholar

Strong, A. W., Moskalenko, I. V., and Ptuskin, V. S. (2007). Cosmic-ray propagation and interactions in the galaxy. Annu. Rev. Nucl. and Part. Sci. 57, 285–327. doi:10.1146/annurev.nucl.57.090506.123011

CrossRef Full Text | Google Scholar

Tabatabaei, F. S., Schinnerer, E., Krause, M., Dumas, G., Meidt, S., Damas-Segovia, A., et al. (2017). The radio spectral energy distribution and star-formation rate calibration in galaxies. Astrophys. J. 836, 185. doi:10.3847/1538-4357/836/2/185

CrossRef Full Text | Google Scholar

Telescope-Array, C., Abbasi, R. U., Abe, M., Abu-Zayyad, T., Allen, M., Azuma, R., et al. (2020). Evidence for a supergalactic structure of magnetic deflection multiplets of ultra-high- energy cosmic rays. Astrophys. J. 899, 86. doi:10.3847/1538-4357/aba26c

CrossRef Full Text | Google Scholar

Thoudam, S., Rachen, J. P., van Vliet, A., Achterberg, A., S. Buitink, S., Falcke, H., et al. (2016). Cosmic-ray energy spectrum and composition up to the ankle: the case for a second Galactic component. Astron. and Astroph. 595, A33. doi:10.1051/0004-6361/201628894

CrossRef Full Text | Google Scholar

Van, D., and Sch, D. (2017). The direct identification of core-collapse supernova progenitors. Phil. Trans. Roy. Soc. A 375, 20160277. doi:10.1098/rsta.2016.0277

CrossRef Full Text | Google Scholar

Weber, E. J., and Davis, L. (1967). The angular momentum of the solar wind. Astrophys. J. 148, 217–227. doi:10.1086/149138

CrossRef Full Text | Google Scholar

Weiler, K. W., and Panagia, N. (1980). Vela X and the evolution of plerions. Astron. and Astroph 90, 269–282.

Google Scholar

White, Ch.J., Quataert, E., and Gammie, Ch.F. (2020). The structure of radiatively inefficient black hole accretion flows. Astrophys. J. 891, 63. doi:10.3847/1538-4357/ab718e

CrossRef Full Text | Google Scholar

Winkler, M. W. (2017). Cosmic ray antiprotons at high energies. J. Cosmol. Astrop. Phys. 02, 048. doi:10.1088/1475-7516/2017/02/048

CrossRef Full Text | Google Scholar

Wong, G. N., Du, Y., Prather, B. S., and Gammie, C. F. (2021). The jet-disk boundary layer in black hole accretion. Astrophys. J. 914, 55. doi:10.3847/1538-4357/abf8b8

CrossRef Full Text | Google Scholar

Woosley, S. E., Heger, A., and Weaver, T. A. (2002). The evolution and explosion of massive stars. Rev. Mod. Phys. 74, 1015–1071. doi:10.1103/revmodphys.74.1015

CrossRef Full Text | Google Scholar

Yodh, G. B. (1992). Ultra-high-energy astronomy and cosmic rays^a. Ann. N. Y. Acad. Sci. 655, 160–184. doi:10.1111/j.1749-6632.1992.tb17070.x

CrossRef Full Text | Google Scholar

Yodh, G. B. (2003). Composition near the knee: results from the CACTI experiment. Nucl. Phys. B - Proc. Suppl. 122, 239–242. doi:10.1016/s0920-5632(03)80388-2

CrossRef Full Text | Google Scholar

Yodh, G. B. (2005). “Cosmic rays, particle physics and the high energy frontier. Proc. 29th Int. Cosmic Ray Conf. 10, 13–32.

Google Scholar

Yodh, G. B. (2006). The knee: theory and experiment. J. Phys. Conf. Ser. 47, 1–14. doi:10.1088/1742-6596/47/1/001

CrossRef Full Text | Google Scholar

Yusef-Zadeh, F., Arendt, R. G., Wardle, M., Heywood, I., Cotton, W., and F. Camilo, F. (2022). Statistical properties of the population of the galactic center filaments: the spectral index and equipartition magnetic field. ApJL 925, L18. doi:10.3847/2041-8213/ac4802

CrossRef Full Text | Google Scholar