Transport of energetic particles in turbulent space plasmas: pitch-angle scattering, telegraph, and diffusion equations

Introduction: In this article, we revisit the pitch-angle scattering equation describing the propagation of energetic particles through magnetized plasma. In this case, solar energetic particles and cosmic rays interact with magnetohydrodynamic turbulence and experience stochastic changes in the pitch-angle. Since this happens over an extended period of time, a pitch-angle isotropization process occurs, leading to parallel spatial diffusion. This process is described well by the pitch-angle scattering equation. However, the latter equation is difficult to solve analytically even when considering special cases for the scattering coefficient.

Methods: In the past, a so-called subspace approximation was proposed, which has important applications in the theory of perpendicular diffusion. Alternatively, an approach based on the telegraph equation (also known as telegrapher’s equation) has been developed. We show that two-dimensional subspace approximation and the description based on the telegraph equation are equivalent. However, it is also shown that the obtained distribution functions contain artifacts and inaccuracies that cannot be found in the numerical solution to the problem. Therefore, an N-dimensional subspace approximation is proposed corresponding to a semi-analytical/semi-numerical approach. This is a useful alternative compared to standard numerical solvers.

Results and Discussion: Depending on the application, the N-dimensional subspace approximation can be orders of magnitude faster. Furthermore, the method can easily be modified so that it can be used for any pitch-angle scattering equation.

1 Introduction

The motion of energetic particles such as cosmic rays through plasma is a complicated stochastic process. It is described via transport equations containing different diffusion parameters. The simplest form of a transport equation which is used in this field is the pitch-angle scattering equation ( Shalchi, 2009; Zank, 2014)

$\frac{\partial f}{\partial t}+v\mu \frac{\partial f}{\partial z}=\frac{\partial }{\partial \mu }\left[D_{\mu \mu }\left(\mu \right)\frac{\partial f}{\partial \mu }\right],(1)$

where we have used time t, particle position along the mean magnetic field z, pitch-angle cosine μ, particle speed v, and pitch-angle scattering coefficient D_μμ. The analytical form of the latter parameter is difficult to determine since it contains information about the interaction between magnetohydrodynamic turbulence and energetic and electrically charged particles. Very originally, a quasi-linear approach was developed to determine the coefficient D_μμ (Jokipii 1966). However, this approach is inaccurate, and it fails to describe correctly the scattering of particles at 90° corresponding to μ = 0 (Shalchi 2009). Therefore, the so-called second-order quasi-linear theory (SOQLT) was developed by Shalchi (2005), which provides non-vanishing scattering at μ = 0, resolving the 90°-problem. This theory was further explored analytically in Shalchi et al. (2009), and the so-called isotropic form

$D_{\mu \mu }=\left(1-{\mu }^2\right)D(2)$

was derived in the limit of a stronger turbulent magnetic field. In Eq. 2, the parameter D does not depend on μ, but it is a complicated function of turbulence and particle properties (Shalchi et al., 2009).

In addition to the question of what the correct analytical form of D_μμ is, one desires to find solutions to Eq. 1. However, so far, no exact solution to the pitch-angle scattering equation has been found, and one has to rely on either a numerical approach or approximations. However, one can show that in the late-time limit, the pitch-angle-averaged distribution function

$M\left(z,t\right)=\frac{1}{2}{\int }_{-1}^{+1}d\mu f\left(\mu ,z,t\right)(3)$

satisfies a diffusion or heat transfer equation of the form

$\frac{\partial M}{\partial t}={\kappa }_{\Vert }\frac{{\partial }^{2}M}{\partial t^2},(4)$

where the parallel spatial diffusion coefficient is related to the pitch-angle scattering coefficient via (Earl, 1974)

${\kappa }_{\Vert }=\frac{v^2}{8}{\int }_{-1}^{+1}d\mu \frac{{\left(1-{\mu }^2\right)}^2}{D_{\mu \mu }\left(\mu \right)}.(5)$

The heat transfer equation shown above can easily be solved. For sharp initial conditions, for instance, the solution is simply a normalized Gaussian distribution

$M\left(z,t\right)=\frac{1}{\sqrt{4\pi {\kappa }_{\Vert }t}}{e}^{-\frac{z^2}{4{\kappa }_{\Vert }t}}(6)$

centered at z = 0 and having the second moment ⟨z²⟩ = 2κ_‖t. One can also write down the more general solution

$M\left(z,t\right)=\frac{1}{\sqrt{4\pi {\kappa }_{\Vert }t}}{\int }_{-\infty }^{+\infty }d{z}^{\prime }M\left(z^{\prime },t=0\right)e^{-\frac{{\left(z-z^{\prime }\right)}^2}{4{\kappa }_{\Vert }t}}(7)$

which depends on the initial distribution M(z′, t = 0) and has a Gaussian integral kernel.

More recently (Tautz and Lerche, 2016 and references therein), it was argued that the diffusive solution does not always provide a good approximation, and one should instead use a telegraph equation of the form

$\tau \ddot{M}+\dot{M}={\kappa }_{\Vert }\frac{{\partial }^{2}M}{\partial z^2},(8)$

where we have used the telegraph time scale τ. It should be noted that using the telegraph equation instead of the diffusion equation was, in particular, suggested in the context of adiabatic focusing (Litvinenko and Schlickeiser, 2013; Effenberger and Litvinenko, 2014), but this effect is omitted in this paper.

Independently, a two-dimensional subspace approximation to the solution of Eq. 1 has been developed (see Shalchi et al. (2011) for the original description of this approach and Shalchi (2020) for a review). Although this approach provides only an approximation to the solution of Eq. 1 for the isotropic case, it provides a pitch-angle-dependent solution. The two-dimensional subspace approximation was successfully applied in the theory of perpendicular transport and contributed significantly to the development of advanced particle transport theories (Shalchi, 2020; Shalchi, 2021).

In this paper, we revisit pitch-angle scattering and parallel spatial diffusion as well as the corresponding transport equations. Through this study, we aim to perform the following tasks:

1. We review the two-dimensional subspace approximation and summarize the corresponding results.

2. We show the equivalence of the two-dimensional subspace approximation and the telegraph equation.

3. We derive an approximation for the Fourier-transformed distribution function corresponding to the correctly normalized solution of the telegraph equation.

4. We propose an N-dimensional subspace approximation to numerically solve the pitch-angle scattering equation. This approach can be several orders of magnitude faster than standard solvers.

5. All numerical and analytical approaches are compared with each other. This will help us understanding the respective advantages and disadvantages of the different techniques.

Those tasks will be performed in Sections. 2–4, and in Section 5, we provide the summary and and conclusions. This article has several appendices containing mathematical details.

2 The two-dimensional subspace approximation

The two-dimensional subspace approximation was originally developed by Shalchi et al. (2011) to solve pitch-angle scattering Equation 1. We summarize the corresponding results, rewrite previously found solutions, and discuss the relation to the telegraph equation as follows. The following three subsections were mostly taken from Shalchi (2020) but have been modified significantly.

2.1 The isotropic scattering coefficient

For the isotropic scattering coefficient, as given by Eq. 2, the parallel spatial diffusion coefficient is obtained via Eq. 5. Alternatively, we can compute the parallel mean free path that is defined via λ_‖ = 3κ_‖/v. For the isotropic case, those parameters are given by

${\kappa }_{\Vert }=\frac{v^2}{6D}\mathrm{a}\mathrm{n}\mathrm{d}{\lambda }_{\Vert }=\frac{v}{2D}.(9)$

Eq. 1 corresponds to a partial differential equation with the variables t, z, and μ. As a first step toward a solution, we use the Fourier transform

$f\left(z,\mu ,t\right)={\int }_{-\infty }^{+\infty }dk{F}_k\left(\mu ,t\right)e^{ikz}(10)$

so that the pitch-angle scattering equation becomes

$\frac{\partial F_k}{\partial t}+iv\mu k{F}_k=\frac{\partial }{\partial \mu }\left[D_{\mu \mu }\frac{\partial F_k}{\partial \mu }\right].(11)$

The inverse Fourier transform is then given by the following equation:

$F_k\left(\mu ,t\right)=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }dzf\left(z,\mu ,t\right)e^{-ikz}.(12)$

For the isotropic scattering coefficient, Eq. 11 is simplified to

$\frac{\partial F_k}{\partial t}+iv\mu k{F}_k=D\frac{\partial }{\partial \mu }\left[\left(1-{\mu }^2\right)\frac{\partial F_k}{\partial \mu }\right].(13)$

To continue, we expand the solution of Eq. 13 in a series of Legendre polynomials

$F_k\left(\mu ,t\right)={\displaystyle \sum _{n=0}^{\infty }}{C}_n\left(t\right)P_n\left(\mu \right),(14)$

where the coefficients C_n are functions of time, though they also depend on k. This dependence is not explicitly written down during the following investigations. Using Eq. 14 in the differential Equation 13 yields

$\begin{array}{cc}\hfill & {\displaystyle \sum _n}{\dot{C}}_n{P}_n+iv\mu k{\displaystyle \sum _n}{C}_n{P}_n\hfill \\ =\hfill & D{\displaystyle \sum _n}{C}_n\frac{\partial }{\partial \mu }\left[\left(1-{\mu }^2\right)\frac{\partial P_n}{\partial \mu }\right],\hfill \end{array}(15)$

where ${\dot{C}}_n$ denotes the time derivative of the coefficient C_n. In order to further valuate Eq. 15, we use the following two relations for Legendre polynomials (Abramowitz and Stegun, 1974)

$\frac{\partial }{\partial \mu }\left[\left(1-{\mu }^2\right)\frac{\partial P_n}{\partial \mu }\right]=-n\left(n+1\right)P_n(16)$

and

$\mu P_n=\frac{n+1}{2n+1}{P}_{n+1}+\frac{n}{2n+1}{P}_{n-1}.(17)$

With those two relations, Eq. 15 can be written as follows:

$\begin{array}{cc}\hfill & {\displaystyle \sum _n}{\dot{C}}_n{P}_n+ivk{\displaystyle \sum _n}{C}_n\left(\frac{n+1}{2n+1}{P}_{n+1}+\frac{n}{2n+1}{P}_{n-1}\right)\hfill \\ \hfill & =-D{\displaystyle \sum _n}{C}_{n}n\left(n+1\right)P_n.\hfill \end{array}(18)$

To continue, we multiply this equation by the Legendre polynomial P_m, integrate over μ, and use the orthogonality relation of Legendre polynomials (Abramowitz and Stegun, 1974)

${\int }_{-1}^{+1}d\mu P_n{P}_m=\frac{2}{2m+1}{\delta }_{nm}.(19)$

After performing those steps, we derive the recurrence relation

$\begin{array}{cc}{\dot{C}}_m\hfill & =-Dm\left(m+1\right)C_m-ivk\frac{m}{2m-1}{C}_{m-1}\hfill \\ \hfill & -ivk\frac{m+1}{2m+3}{C}_{m+1}.\hfill \end{array}(20)$

Alternatively, one can use the coefficient Q_m defined via

$C_m=\left(2m+1\right){\left(-i\right)}^m{Q}_m.(21)$

With this, the recurrence relation can be written as follows

$\begin{array}{cc}\left(2m+1\right){\dot{Q}}_m\hfill & =-Dm\left(m+1\right)\left(2m+1\right)Q_m\hfill \\ \hfill & +vkm{Q}_{m-1}-vk\left(m+1\right)Q_{m+1}.\hfill \end{array}(22)$

For the case of no scattering D = 0, we can compare this with the relation (see Equation of Abramowitz and Stegun (1974))

$\left(2n+1\right)j_n^{\prime }=n{j}_{n-1}-\left(n+1\right)j_{n+1},(23)$

where we have used spherical Bessel functions. Thus, we find Q_m = j_m(vkt) for the scatter-free case and

$C_m=\left(2m+1\right){\left(-i\right)}^m{j}_m\left(vkt\right).(24)$

Using this in Eq. 14 yields

$\begin{array}{cc}{F}_k\left(\mu ,t\right)\hfill & ={\displaystyle \sum _{n=0}^{\infty }}\left(2n+1\right){\left(-i\right)}^n{j}_n\left(vkt\right)P_n\left(\mu \right)\hfill \\ \hfill & =e^{-iv\mu kt},\hfill \end{array}(25)$

where we have used Equation 92 from Shalchi et al. (2011). This is also known as plane wave expansion widely used in quantum mechanics. It should be noted that Eq. 25 corresponds to the unperturbed or scatter-free solution. It can be easily obtained directly from Eq. 11 for the case D = 0.

We use Eq. 20 which corresponds to an infinite set of coupled ordinary differential equations. For m = 0, for instance, we find

${\dot{C}}_0=-\frac{1}{3}ivk{C}_1(26)$

and for m = 1, we obtain

${\dot{C}}_1=-2D{C}_1-ivk{C}_0-\frac{2}{5}ivk{C}_2.(27)$

It is problematic here that the coefficients C₀ and C₁ are coupled to C₂. Therefore, it is not possible to derive an exact solution for the coefficients C_n.

2.2 The two-dimensional approximation

Since an exact solution to Eq. 20 seems impossible to be found, one needs to rely on approximations. In the following, we discuss the two-dimensional (2D) subspace approximation originally developed by Shalchi et al. (2011), meaning we set

$C_m=0\mathrm{f}\mathrm{o}\mathrm{r}m\ge 2(28)$

so that only the coefficients C₀ and C₁ are used. In Lasuik and Shalchi (2019), one can find the solution obtained by using a three-dimensional subspace approximation. It is shown that the three-dimensional (3D) solution is too complicated for most applications.

Within the two-dimensional subspace approximation, the expansion (14) is reduced to

$F\left(\mu ,t\right)=C_0+\mu C_1.(29)$

In this case, Eqs 26, 27 can be combined to eliminate C₁. Since we set C₂ = 0, we found the second-order differential equation

${\ddot{C}}_0=-2D{\dot{C}}_0-\frac{1}{3}{v}^2{k}^2{C}_0.(30)$

Using the ansatz

$C_0=b{e}^{\omega t}(31)$

leads to the quadratic equation

${\omega }^2+2D\omega +\frac{1}{3}{v}^2{k}^2=0.(32)$

Alternatively, for C₂ = 0, Eqs 26, 27 can be written as the matrix equation

$\left(\begin{array}{c}\hfill {\dot{C}}_0\hfill \\ \hfill {\dot{C}}_1\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill 0\hfill & \hfill -ivk/3\hfill \\ \hfill -ivk\hfill & \hfill -2D\hfill \end{array}\right)\left(\begin{array}{c}\hfill C_0\hfill \\ \hfill C_1\hfill \end{array}\right).(33)$

After using Eq. 31 for both functions C₀(t) and C₁(t), the problem of finding the two ω is expressed as

$\det \left(\begin{array}{cc}\hfill \omega \hfill & \hfill ivk/3\hfill \\ \hfill ivk\hfill & \hfill \omega +2D\hfill \end{array}\right)=0,(34)$

leading to the same quadratic equation as given by Eq. 32. The latter equation can easily be solved by the following equation:

${\omega }_{\pm }=-D\pm \sqrt{D^2-\frac{1}{3}{v}^2{k}^2}.(35)$

We conclude that the eigenvalues can be complex depending on the wave number k. With this, the coefficient C₀ can be written as the linear combination

$C_0=b_{+}{e}^{{\omega }_{+}t}+b_{-}{e}^{{\omega }_{-}t}(36)$

with the two unknown coefficients b_±. It follows from Eq. 26 that

$C_1=-\frac{3}{ivk}\left(b_{+}{\omega }_{+}{e}^{{\omega }_{+}t}+b_{-}{\omega }_{-}{e}^{{\omega }_{-}t}\right).(37)$

The coefficients b_± will be determined below. Before we perform this task, we write down the solution for F_k(μ, t). We need to combine Eq. 29 with Eqs 36, 37 to derive

$\begin{array}{cc}{F}_k\left(\mu ,t\right)\hfill & =b_{+}{e}^{{\omega }_{+}t}+b_{-}{e}^{{\omega }_{-}t}\hfill \\ \hfill & -\frac{3\mu }{ivk}\left(b_{+}{\omega }_{+}{e}^{{\omega }_{+}t}+b_{-}{\omega }_{-}{e}^{{\omega }_{-}t}\right).\hfill \end{array}(38)$

In order to find the coefficients b_±, we can use the initial condition

$f\left(z,\mu ,t=0\right)=2\delta \left(z\right)\delta \left(\mu -{\mu }_0\right),(39)$

meaning that the particle has its initial position at z = 0 and the initial pitch-angle cosine μ₀. Using this in the inverse Fourier transform given by Eq. 12, yields after some straightforward algebra

$F_k\left(\mu ,t=0\right)=\frac{1}{\pi }\delta \left(\mu -{\mu }_0\right).(40)$

The latter initial condition used in expansion (Eq. 14) allows us to write

${\displaystyle \sum _n}{C}_n\left(t=0\right)P_n\left(\mu \right)=\frac{1}{\pi }\delta \left(\mu -{\mu }_0\right).(41)$

In order to determine the coefficients C_n(t = 0), we multiply this by P_m and integrate over μ to get

$C_m\left(t=0\right)=\frac{2m+1}{2\pi }{P}_m\left({\mu }_0\right).(42)$

To perform this task, we have used again the orthogonality relation (Eq. 19). For m = 0 and m = 1, this yields¹

$C_0\left(t=0\right)=\frac{1}{2\pi }(43)$

and

$C_1\left(t=0\right)=\frac{3{\mu }_0}{2\pi }.(44)$

To determine the coefficients b_±, we write down Eqs 36, 37 for t = 0 and use Eqs 43, 44 to deduce

$\begin{array}{cc}{b}_{+}+b_{-}\hfill & =\frac{1}{2\pi },\hfill \\ b_{+}{\omega }_{+}+b_{-}{\omega }_{-}\hfill & =-\frac{ivk{\mu }_0}{2\pi }.\hfill \end{array}(45)$

This system of two equations is solved by the following equation

$b_{\pm }=\mp \frac{ivk{\mu }_0+{\omega }_{\mp }}{2\pi \left({\omega }_{+}-{\omega }_{-}\right)}.(46)$

Using this result and Eq. 35 in Eq. 38 provides the two-dimensional subspace approximation to the solution F_k(μ, t). In Section 2.4, we provide a more detailed discussion of this solution.

Our solution is based on the expansion given by Eq. (29). One can easily demonstrate using Eq. 3 and

$J\left(z,t\right)=\frac{v}{2}{\int }_{-1}^{+1}d\mu \mu f\left(\mu ,z,t\right),(47)$

together with the orthogonality relation (Eq. 19), that the function C₀(t) corresponds to the Fourier transform of the pitch-angle-averaged distribution function M(z, t), and C₁(t) corresponds to the Fourier transform of the current density or diffusion flux J(z, t). Those two quantities are related to each other via the one-dimensional continuity equation

$\frac{\partial M}{\partial t}+\frac{\partial J}{\partial z}=0(48)$

which is obtained by averaging Eq. 1 over all μ and using Eqs 3, 47. The exact relations to the coefficients are

$M\left(z,t\right)={\int }_{-\infty }^{+\infty }dk{C}_0\left(t\right)e^{ikz}(49)$

and

$J\left(z,t\right)=\frac{v}{3}{\int }_{-\infty }^{+\infty }dk{C}_1\left(t\right)e^{ikz}.(50)$

It should be noted that the latter relation is obtained by combining Eq. 47 with Eq. 10 and the expansion given by Eq. 14. After combining these three relations and using the orthogonality relation (Eq. 19), one can obtain Eq. 50. As demonstrated, the coefficients C₀(t) and C₁(t) are directly linked to physical quantities. In particular, the coefficient C₀(t) is very important because it is simply the Fourier transform of the pitch-angle-averaged distribution function M(z, t).

2.3 Further physical quantities

An important quantity in particle transport theory is the characteristic function ⟨e^±ikz⟩. We define the ensemble average via

$⟨A⟩=\frac{1}{4}{\int }_{-1}^{+1}d\mu {\int }_{-1}^{+1}d{\mu }_0{\int }_{-\infty }^{+\infty }dzA\left(z,\mu ,t\right)f\left(z,\mu ,t\right).(51)$

It should be noted that in some cases, one could aim for a result that depends on μ₀. Then, the corresponding average is omitted.

To determine the characteristic function, we average over all quantities, and thus, we have

$\begin{array}{cc}⟨e^{-ikz}⟩\hfill & =\frac{1}{4}{\int }_{-1}^{+1}d{\mu }_0{\int }_{-1}^{+1}d\mu \hfill \\ \hfill & \times {\int }_{-\infty }^{+\infty }dz{e}^{-ikz}f\left(z,\mu ,t\right).\hfill \end{array}(52)$

Replacing f(z, μ, t) therein by using Eq. 12 leads to

$⟨e^{-ikz}⟩=\frac{\pi }{2}{\int }_{-1}^{+1}d{\mu }_0{\int }_{-1}^{+1}d\mu F_k\left(\mu ,t\right).(53)$

We now replace F_k(μ, t) by using Eq. 14 and use P₀(μ) = 1 to get

$⟨e^{-ikz}⟩=\frac{\pi }{2}{\int }_{-1}^{+1}d{\mu }_0{\int }_{-1}^{+1}d\mu {\displaystyle \sum _{n=0}^{\infty }}{C}_n{P}_n{P}_0.(54)$

Due to the orthogonality of Legendre polynomials (Eq. 19), this is reduced to

$⟨e^{-ikz}⟩=\pi {\int }_{-1}^{+1}d{\mu }_0{C}_0.(55)$

To solve the remaining integral, we use Eq. 36 to write

$⟨e^{-ikz}⟩=\pi {\int }_{-1}^{+1}d{\mu }_0\left(b_{+}{e}^{{\omega }_{+}t}+b_{-}{e}^{{\omega }_{-}t}\right).(56)$

In order to replace b_±, we use Eq. 46. The integrals over the terms containing μ₀ vanish, and we finally find

$⟨e^{\pm ikz}⟩=\frac{{\omega }_{+}{e}^{{\omega }_{-}t}-{\omega }_{-}{e}^{{\omega }_{+}t}}{{\omega }_{+}-{\omega }_{-}}.(57)$

It should be noted that the parameters ω_± are given by Eq. 35. For the case that the ω_± are real, the characteristic function given by Eq. 57 is real as well. For the case that the ω_± are complex, it follows from Eq. 35 that ${\omega }_{+}^{*}={\omega }_{-}$. Therefore, the characteristic function is always real, and we have ⟨e^+ikz⟩ = ⟨e^−ikz⟩.

Based on Eq. 35, it can be shown that Eq. 57 contains two asymptotic limits, namely, (see Shalchi (2020) for more details)

$⟨e^{\pm ikz}⟩\approx \left\{\begin{array}{cc}{e}^{-{\kappa }_{\Vert }{k}^{2}t}\hfill & \mathrm{f}\mathrm{o}\mathrm{r}{v}^2{k}^2\ll 3D^2\hfill \\ \cos \left(\frac{vkt}{\sqrt{3}}\right)e^{-Dt}\hfill & \mathrm{f}\mathrm{o}\mathrm{r}{v}^2{k}^2\gg 3D^2.\hfill \end{array}\right.(58)$

For small wave numbers, we find the characteristic function of diffusion Equation 4. The result obtained for large wave numbers can be understood as a damped unperturbed orbit.

By comparing Eq. 53 with Eq. 10 and using Eq. 3, we can relate the characteristic function to the μ- and μ₀-averaged functions M(z, t). This relation is given by the following equation:

$M\left(z,t\right)=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }dk⟨e^{\pm ikz}⟩e^{ikz}.(59)$

Furthermore, we can compare this with Eq. 49 to find

$⟨e^{\pm ikz}⟩=2\pi C_0\left(t\right).(60)$

As an example, we consider the limit D → ∞ so that we can use the first line of Eq. 58 in Eq. 59. We can easily derive

$\begin{array}{cc}M\left(z,t\right)\hfill & =\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }dk\cos \left(kz\right)e^{-{\kappa }_{\Vert }{k}^{2}t}\hfill \\ \hfill & =\frac{1}{\sqrt{4\pi {\kappa }_{\Vert }t}}{e}^{-\frac{z^2}{4{\kappa }_{\Vert }t}}\hfill \end{array}(61)$

corresponding to a Gaussian solution. The result obtained here is the diffusive solution that one would expect in this case (see Eq. 6 in this paper).

Other physical quantities can be derived by using the subspace approximation, alternative approximations, or even exact calculations (Shalchi, 2006; Shalchi, 2011).

2.4 Rewriting the solution

Eq. 29 corresponds to an integral representation of the solution of the Fourier-transformed pitch-angle scattering equation. This result is based on the 2D subspace approximation. Using therein Eqs 36 and 37, as well as (Eq. 46) yields

$\begin{array}{cc}{F}_k\left(\mu ,t\right)\hfill & =\frac{3{\mu }_0\mu {\omega }_{+}-{\omega }_{-}-ivk\left({\mu }_0+\mu \right)}{2\pi \left({\omega }_{+}-{\omega }_{-}\right)}{e}^{{\omega }_{+}t}\hfill \\ \hfill & -\frac{3{\mu }_0\mu {\omega }_{-}-{\omega }_{+}-ivk\left({\mu }_0+\mu \right)}{2\pi \left({\omega }_{+}-{\omega }_{-}\right)}{e}^{{\omega }_{-}t},\hfill \end{array}(62)$

where the functions ω_± are given by Eq. 35.

The μ- and μ₀-averaged solution is then

$\begin{array}{cc}{M}_k\left(t\right)\hfill & =\frac{1}{4}{\int }_{-1}^{+1}d{\mu }_0{\int }_{-1}^{+1}d\mu F_k\left(\mu ,t\right)\hfill \\ \hfill & =\frac{1}{2\pi \left({\omega }_{+}-{\omega }_{-}\right)}\left[{\omega }_{+}{e}^{{\omega }_{-}t}-{\omega }_{-}{e}^{{\omega }_{+}t}\right]\hfill \end{array}(63)$

in Fourier space. To find the solution in the configuration space, we use Eq. 10 to derive

$\begin{array}{cc}\hfill & M\left(z,t\right)=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }dk\left[\frac{{\omega }_{+}}{{\omega }_{+}-{\omega }_{-}}{e}^{{\omega }_{-}t}-\frac{{\omega }_{-}}{{\omega }_{+}-{\omega }_{-}}{e}^{{\omega }_{+}t}\right]e^{-ikz}.\hfill \end{array}(64)$

Alternatively, this result can also be obtained by combining Eqs 57, 59.

It is convenient to define the parameter

$\xi ≔\sqrt{D^2-\frac{1}{3}{v}^2{k}^2},(65)$

and it follows from Eq. 35 that

${\omega }_{\pm }=-D\pm \xi .(66)$

From this, we can easily deduce

${\omega }_{+}-{\omega }_{-}=2\xi .(67)$

Therewith, the solution in the configuration space is given as the following Fourier transform

$\begin{array}{cc}M\left(z,t\right)\hfill & =\frac{1}{2\pi }{e}^{-Dt}{\int }_0^{\infty }dk\left[\left(1+\frac{D}{\xi }\right)e^{\xi t}+\left(1-\frac{D}{\xi }\right)e^{-\xi t}\right]\hfill \\ \hfill & \times \cos \left(kz\right),\hfill \end{array}(68)$

where we have used the integrand, which is an even function of k. With the help of hyperbolic functions, this can be written in a more compact form

$M\left(z,t\right)=\frac{1}{\pi }{e}^{-Dt}{\int }_0^{\infty }dk\left[\cosh \left(\xi t\right)+\frac{D}{\xi }\sinh \left(\xi t\right)\right]\cos \left(zk\right).(69)$

It should be noted that the quantity ξ, given by Eq. 65, can either be real or imaginary depending on the value of k. Eq. 69 provides an integral representation of the μ- and μ₀-averaged distribution function based on the 2D subspace approximation. Alternative forms are presented in Supplementary Appendix S1 of this paper. In Supplementary Appendix S2, we provide an approximative solution of the remaining integral.

2.5 Relation to the Telegrapher’s equation

We have derived an ordinary differential equation for the function C₀(t) previously (Eq. 30), which can be written as follows

${\ddot{C}}_0+2D{\dot{C}}_0=-\frac{1}{3}{v}^2{k}^2{C}_0.(70)$

As shown via Eq. 49, C₀(t) is the Fourier transform of the distribution function M(z, t). Thus, working in the configuration space instead of the Fourier space allows us to write Eq. 70 as

$\ddot{M}+2D\dot{M}=\frac{1}{3}{v}^2\frac{{\partial }^{2}M}{\partial z^2}.(71)$

The latter equation has the same form as Eq. 8, and, thus, it corresponds to a telegraph equation. A quick alternative derivation of the latter equation can be found in Supplementary Appendix S3. It should be noted that the coefficient C₀(t) used here depends also on the initial pitch-angle cosine μ₀. If one averages over the latter quantity, the two-dimensional subspace approximation provides Eq. 69. In Supplementary Appendix S4, we demonstrate that the latter form indeed solves Eq. 71. Using therein Eq. 9 and the scattering time τ = 1/(2D) yields the telegraph equation, as given by Eq. 8. Therefore, we have shown the complete equivalence of the two-dimensional subspace approximation and the telegraph equation. The solution given by Eq. 69 is correctly normalized. In order to demonstrate this, we consider

$\begin{array}{cc}{\int }_{-\infty }^{+\infty }dzM\left(z,t\right)\hfill & =\frac{1}{\pi }{e}^{-Dt}{\int }_0^{\infty }dk\left[\cosh \left(\xi t\right)+\frac{D}{\xi }\sinh \left(\xi t\right)\right]\hfill \\ \hfill & \times {\int }_{-\infty }^{+\infty }dz\cos \left(zk\right).\hfill \end{array}(72)$

Therein, we use (Zwillinger, 2012)

${\int }_{-\infty }^{+\infty }dz{e}^{i\left(k^{\prime }-k\right)z}=2\pi \delta \left(k^{\prime }-k\right)(73)$

to write this as

$\begin{array}{cc}{\int }_{-\infty }^{+\infty }dzM\left(z,t\right)\hfill & =e^{-Dt}{\int }_{-\infty }^{+\infty }dk\left[\cosh \left(\xi t\right)+\frac{D}{\xi }\sinh \left(\xi t\right)\right]\delta \left(k\right)\hfill \\ \hfill & =e^{-Dt}{\left[\cosh \left(\xi t\right)+\frac{D}{\xi }\sinh \left(\xi t\right)\right]}_{k=0}.\hfill \end{array}(74)$

From Eq. 65, it follows that ξ_k=0 = D, and, thus, we find

$\begin{array}{cc}{\int }_{-\infty }^{+\infty }dzM\left(z,t\right)\hfill & =e^{-Dt}\left[\cosh \left(Dt\right)+\sinh \left(Dt\right)\right]\hfill \\ \hfill & =1.\hfill \end{array}(75)$

As already pointed out in Tautz and Lerche (2016), one can use the transformation

$M\left(z,t\right)=\mathrm{\Psi }\left(z,t\right)e^{-Dt},(76)$

and Eq. 8 becomes

$\tau \ddot{\mathrm{\Psi }}-{\kappa }_{\Vert }\frac{{\partial }^2\mathrm{\Psi }}{\partial z^2}=\frac{1}{4\tau }\mathrm{\Psi }.(77)$

This corresponds to the Klein–Gordon equation but with imaginary mass. After comparing Eqs 69, 76 with each other, we can easily read off the function $\mathrm{\Psi }\left(z,t\right)$.

We have focused on the function C₀(t) previously. We can also derive an ordinary differential equation for C₁(t). By combining Eqs 26, 27, we derive

${\ddot{C}}_1+2D{\dot{C}}_1=-\frac{1}{3}{v}^2{k}^2{C}_1,(78)$

where we have set C₂ = 0 corresponding to the 2D subspace approximation. Eq. 78 is the same equation as we have derived above for C₀. The function C₁(t) corresponds to the Fourier-transformed current density, as shown by Eq. 50. Therefore, the telegraph and Klein–Gordon equations can also be derived for the current density function. In order to obtain the current density, as a further solution to the telegraph equation, we can combine Eq. 69 with the continuity Equation 48. We can easily derive

$J\left(z,t\right)=\frac{v^2}{3\pi }{e}^{-Dt}{\int }_0^{\infty }dk\frac{k}{\xi }\sinh \left(\xi t\right)\sin \left(zk\right),(79)$

where ξ is given by Eq. 65. Of course, integrating the obtained $J\left(z,t\right)$ over all z yields 0, meaning that the found solution to the telegraph equation is not normalized to 1.

3 The N-dimensional subspace approximation

Previously, we have used the expansion in the Legendre polynomials (see Eq. 14 of this paper). The functions C_n(t) therein are given by the recurrence relation (Eq. 20). This relation is still exact and can be written as the following matrix equation

$\frac{d}{dt}\vec{C}=\mathbf{A}\vec{C}(80)$

with the tridiagonal matrix A having the components

$\begin{array}{cc}\hfill A_{n,n-1}& =-ivk\frac{n}{2n-1},\hfill \\ \hfill A_{n,n}& =-n\left(n+1\right)D,\hfill \\ \hfill A_{n,n+1}& =-ivk\frac{n+1}{2n+3}.\hfill \end{array}(81)$

The vector $\vec{C}$ in Eq. 80 contains the functions C_n(t) needed in the expansion given by Eq. 14. The formal solution of Eq. 80 can be written as follows:

$\vec{C}\left(t\right)=e^{\mathbf{A}t}\vec{C}\left(t=0\right),(82)$

where we have used the matrix exponential. The initial conditions C_n(t = 0) are given by Eq. 42. Eq. 82 can be easily evaluated with software such as MATLAB. However, it is required to work with a finite matrix A. This corresponds to the subspace approximation outlined above. Let us assume that we work with an N × N-matrix. This then corresponds to an N-dimensional subspace approximation. The method described here corresponds to a semi-numerical/semi-analytical approach that solves the pitch-angle scattering equation, but this method can be faster if one needs the solution only for a specific time t. Standard numerical solvers (see Supplementary Appendix S5 of this paper) require a high time resolution to be accurate. Therefore, one typically needs to work with roughly thousand time-steps so that the solution converges to the true solution of the differential equation. The N-dimensional subspace approximation can be applied to a single time value. As shown via Figures 2–9, an accurate solution is obtained for N = 10.

For certain applications, one could be interested in the μ- and μ₀-averaged solution only. Analytical solutions of diffusion and telegraph equations are incomplete and inaccurate depending on the considered application. For the case of pitch-angle-averaged solutions, the N-dimensional subspace approximation is particularly powerful, as outlined below. First, we define the matrix exponential used already above via

$\mathbf{E}≔e^{\mathbf{A}t}.(83)$

Then, Eq. 82 can be written as follows

$\vec{C}\left(t\right)=\mathbf{E}\vec{C}\left(t=0\right)(84)$

or in component notation,

$C_n\left(t\right)={\displaystyle \sum _{m=0}^{N-1}}{E}_{nm}{C}_m\left(t=0\right).(85)$

At the initial time, the components of the vector $\vec{C}\left(t=0\right)$ are given by Eq. 42. If those coefficients are averaged over μ₀, we can easily derive

$C_m\left(t=0\right)=\frac{1}{2\pi }{\delta }_{m0},(86)$

meaning that all coefficients are 0, except C₀(t = 0). Therefore, we can write the time-dependent coefficients as

$C_n\left(t\right)=E_{n0}{C}_0\left(t=0\right)\equiv \frac{1}{2\pi }{E}_{n0}.(87)$

Furthermore, the μ-dependent solution is given by Eq. 14. After μ-averaging of the latter expansion, we find

$M_k\left(t\right)=C_0\left(t\right)=\frac{1}{2\pi }{E}_{00},(88)$

where M_k(t) is the Fourier-transformed distribution function as observed by Eq. 49. It should be noted that the function C₀(t) discussed here is also μ₀-averaged. Furthermore, the characteristic function is easily obtained via

$⟨e^{\pm ikz}⟩=E_{00},(89)$

meaning that the 00-component is simply the characteristic function. Thus, it follows from Eq. 59 that

$M\left(z,t\right)=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }dk{E}_{00}\left(k,t\right)e^{ikz},(90)$

which is an integral and matrix exponential representation of the μ- and μ₀-averaged distribution function. Therefore, in order to obtain the distribution function M(z, t) for given z and t, we need to numerically solve the k-integral in Eq. 90. For each value of k, we set up the matrix A defined via Eq. 81, numerically compute the matrix exponential E, and use the component E₀₀ in the numerically evaluated k-integral. The distribution functions shown in Figures 6, 7, based on the 10D subspace approximation, for instance, can be computed with a regular computer within a few seconds. Figure 1 shows a comparison in speed between different numerical methods. This comparison includes the N-dimensional subspace approximation described above and the pure numerical approach described in Supplementary Appendix S5 of this paper, which corresponds to an implicit Euler method.

Figure 1

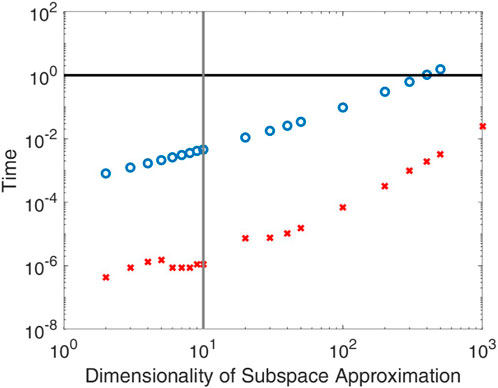
Figure 1. Shown are runtimes of codes used to solve the pitch-angle scattering equation based on different techniques. The black horizontal line represents the pure numerical solution, providing a result which depends on the pitch-angle cosine μ and the initial pitch-angle cosine μ₀. This pure numerical method is described in Supplementary Appendix S5 and corresponds to an implicit Euler method. The blue circles represent the N-dimensional subspace approximation described in Section 3 also providing a pitch-angle-dependent result. The red crosses represent the N-dimensional subspace approximation for the μ- and μ₀-averaged case. For a small dimensionality (small N), the runtimes are insignificant. It should also be noted that one obtains an accurate result for N = 10 (vertical gray line), meaning that the subspace approximation is several orders of magnitude faster than standard numerical solvers. It should be noted that all results are normalized with respect to the runtime of the pure numerical method and have been obtained by using MATLAB running on the same computer.

The μ- and μ₀-dependent Fourier-transformed solution is given by the following equation:

$F_k\left(\mu ,t\right)=\frac{1}{2\pi }{\displaystyle \sum _{n,m}}\left(2m+1\right)E_{nm}\left(k,t\right)P_n\left(\mu \right)P_m\left({\mu }_0\right),(91)$

where we have combined Eqs 14, 42, and 85. The Fourier transform can be performed using Eq. 10 and solving the k-integral numerically. Of course, obtaining and plotting the pitch-angle-dependent result is more time-consuming when compared to the pitch-angle-averaged solution.

In certain analytical theories developed for describing the perpendicular transport of energetic particles, one needs to know the function (Shalchi, 2010; Shalchi, 2017; Shalchi, 2020; Shalchi, 2021)

${\mathrm{\Gamma }}_k\left(t\right)≔⟨{\mu }_0\mu e^{-ikz}⟩(92)$

that is somewhat similar but not identical compared to the characteristic function discussed above. In order to express Γ_k(t) as before, we perform the same mathematical steps. The pitch-angle-dependent solution is given by Eq. 14. In order to obtain Γ_k(t), we need

$\begin{array}{cc}{\mathrm{\Gamma }}_k\left(t\right)\hfill & =\frac{1}{4}{\int }_{-1}^{+1}d\mu {\int }_{-1}^{+1}d{\mu }_0\mu {\mu }_0\hfill \\ \hfill & \times {\int }_{-\infty }^{+\infty }dzf\left(z,\mu ,t\right)e^{-ikz}.\hfill \end{array}(93)$

To evaluate this further, we use Eqs 12, 14. After using those two relations, we derive

$\begin{array}{cc}{\mathrm{\Gamma }}_k\left(t\right)\hfill & =\frac{\pi }{2}{\int }_{-1}^{+1}d\mu {\int }_{-1}^{+1}d{\mu }_0\mu {\mu }_0{F}_k\left(\mu ,t\right)\hfill \\ \hfill & =2\pi {\displaystyle \sum _{n=0}^{\infty }}\frac{1}{2}{\int }_{-1}^{+1}d{\mu }_0{\mu }_0{C}_n\left(t\right)\frac{1}{2}{\int }_{-1}^{+1}d\mu \mu P_n\left(\mu \right).\hfill \end{array}(94)$

For the μ-integral, we can use the orthogonality relation (Eq. 19) to find

$\frac{1}{2}{\int }_{-1}^{+1}d\mu \mu P_n\left(\mu \right)=\frac{1}{3}{\delta }_{n1}.(95)$

Using the above relation allows us to perform the following steps:

$\begin{array}{cc}{\mathrm{\Gamma }}_k\left(t\right)\hfill & =\frac{\pi }{3}{\int }_{-1}^{+1}d{\mu }_0{\mu }_0{C}_1\left(t\right)\hfill \\ \hfill & =\frac{\pi }{3}{\displaystyle \sum _{m=0}^{N-1}}{E}_{1m}{\int }_{-1}^{+1}d{\mu }_0{\mu }_0{C}_m\left(t=0\right)\hfill \\ \hfill & =\frac{1}{6}{\displaystyle \sum _{m=0}^{N-1}}\left(2m+1\right)E_{1m}{\int }_{-1}^{+1}d{\mu }_0{P}_1\left({\mu }_0\right)P_m\left({\mu }_0\right)\hfill \\ \hfill & =\frac{1}{3}{\displaystyle \sum _{m=0}^{N-1}}{E}_{1m}{\delta }_{m1}\hfill \\ \hfill & =\frac{1}{3}{E}_{11},\hfill \end{array}(96)$

where we have used Eqs 19, 42, and 85. Therefore, the derived function ${\mathrm{\Gamma }}_k\left(t\right)$ corresponds to the matrix element E₁₁ which can be computed quickly based on the N-dimensional subspace approximation. Figure 12 shows some example plots for the quantity ${\mathrm{\Gamma }}_k\left(t\right)$.

4 Comparison of results

We have solved the pitch-angle scattering equation numerically using an implicit Euler method (Supplementary Appendix S5) and the N-dimensional subspace approximation outlined in the previous section. We have considered two cases, namely, N = 2 (corresponding to the pure analytical case discussed above) and N = 10 (which provides an accurate result). In most cases, we have only considered the μ-averaged solution to reduce the number of plots. Some results are also averaged over the initial pitch-angle cosine μ₀.

Figures 2–5 show the characteristic function ⟨e^ikz⟩≡⟨e^−ikz⟩, which corresponds to the Fourier transform of the distribution function $M\left(z,t\right)$. In Figures 2, 3, the characteristic function is plotted versus the dimensionless wave number $\tilde{k}=vk/D$ for different values of the dimensionless time $\tilde{t}=Dt$. We have also shown the solution of the diffusion equation as given by the first line of Eq. 58. We can easily see that all solutions agree with each other at later times. This is not the case for early times where the 2D subspace approximation and the diffusive solution differ significantly from the numerical solution. The 10D subspace approximation agrees very well with the numerical solution in all considered cases.

Figures 4, 5 show the characteristic function versus time $\tilde{t}$ for different values of $\tilde{k}$. We can easily see agreement for smaller values of $\tilde{k}$ but disagreement for larger values. However, the 10D subspace approximation and the numerical solution agree very well with each other. It has to be emphasized that the 10D subspace approximation solution, which can be seen as a semi-analytical/semi-numerical technique, is several orders of magnitude faster than standard numerical solvers.

Figure 2

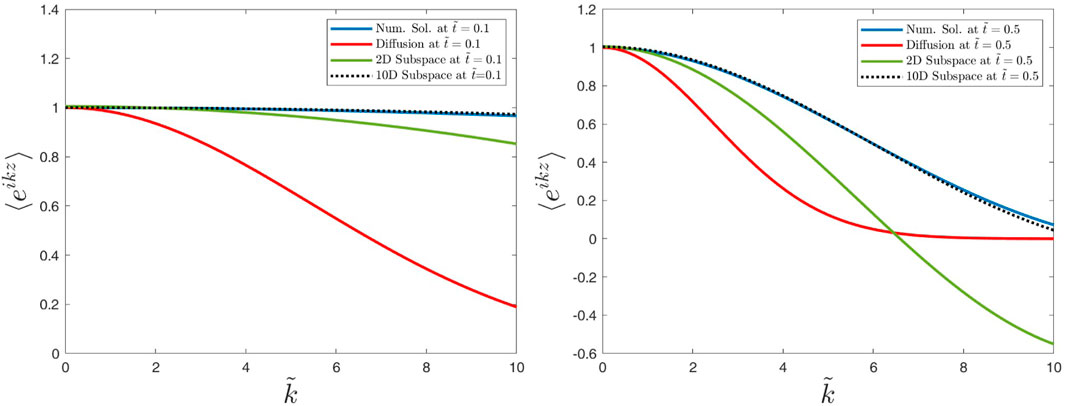
Figure 2. Numerical and analytical solutions obtained for the characteristic function ⟨e^ikz⟩ versus the dimensionless wave number $\tilde{k}=vk/D$. The numerical solution refers to the implicit Euler method described in Supplementary Appendix S5, and the N-dimensional subspace approximation, which is a semi-analytical/semi-numerical method, is described in Section 3. Shown are plots for $\tilde{t}=Dt=0.1$ (left panel) and $\tilde{t}=0.5$ (right panel). For the initial pitch-angle cosine, we have used μ₀ = 0. It should be noted that the characteristic function is μ-averaged.

Figure 3

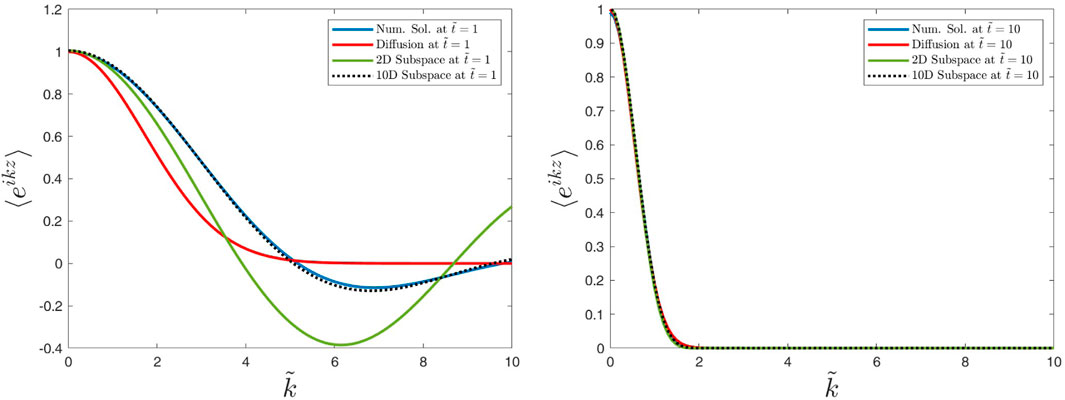
Figure 3. Caption is as in Figure 2, but we have considered the times $\tilde{t}=1$ (left panel) and $\tilde{t}=10$ (right panel). It should be noted that for the latter case, all four results are in coincidence.

Figure 4

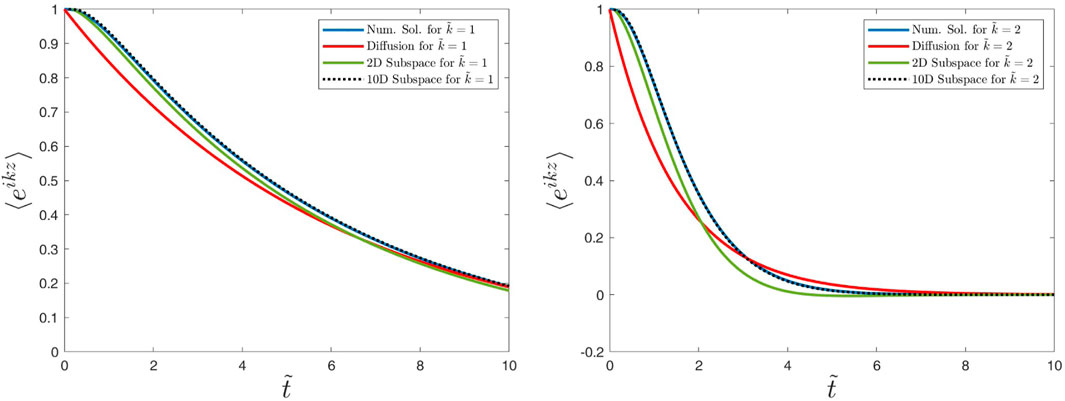
Figure 4. Numerical and analytical solutions obtained for the characteristic function ⟨e^ikz⟩ versus dimensionless time $\tilde{t}=Dt$. Shown are plots for $\tilde{k}=1$ (left panel) and $\tilde{k}=2$ (right panel). For the initial pitch-angle cosine, we have used μ₀ = 0. It should be noted that the characteristic function is μ-averaged.

Figure 5

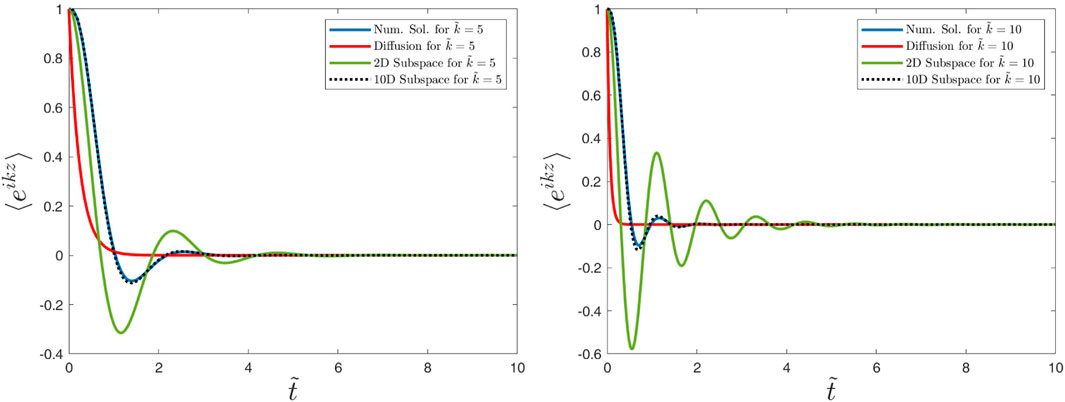
Figure 5. Caption is as in Figure 4, but we have considered the values $\tilde{k}=5$ (left panel) and $\tilde{k}=10$ (right panel).

Figures 6–9 show the distribution function $M\left(z,t\right)$. Figures 6, 7 show this function versus the dimensionless position $\tilde{z}=Dz/v$ for different times. For late times, all considered results agree with each other, as expected. The corresponding distributions are well-described by the Gaussian given by Eq. 6. For early times, however, diffusive and 2D subspace results do not agree well with the pure numerical solution. The 2D subspace solution contains spikes that are a consequence of the Dirac delta (Supplementary Appendix S2). The diffusive solution is non-zero everywhere in space. Numerical and 10D subspace solutions correctly describe that the distribution function is exactly 0 for $\left|z\right|>vt$ due to the finite propagation speed of the particles. The latter effect can be observed much better by plotting the distribution function versus time $\tilde{t}$ for different values of $\tilde{z}$. This is done via Figures 8, 9.

Figure 6

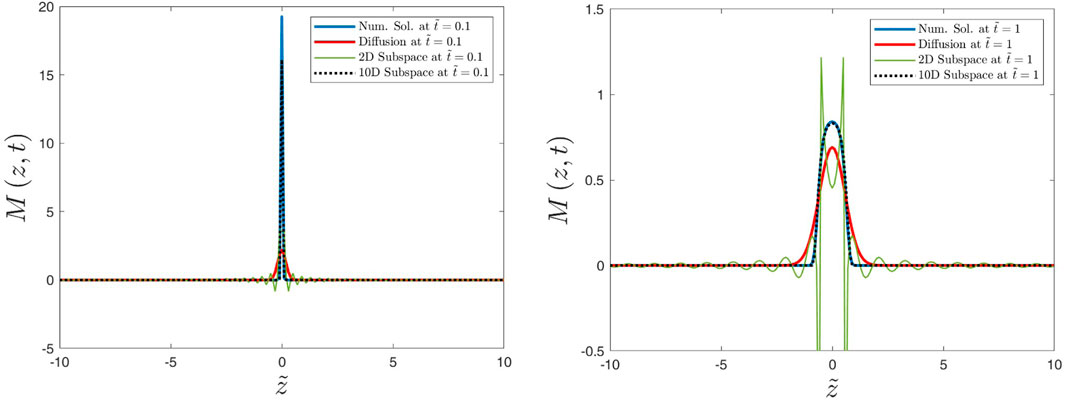
Figure 6. Numerical and analytical solutions for the μ-averaged distribution function M(z, t) versus the parallel position $\tilde{z}=Dz/v$. Shown are plots for $\tilde{t}=0.1$ (left panel) and $\tilde{t}=1$ (right panel). For the initial pitch-angle cosine, we have used μ₀ = 0.

Figure 7

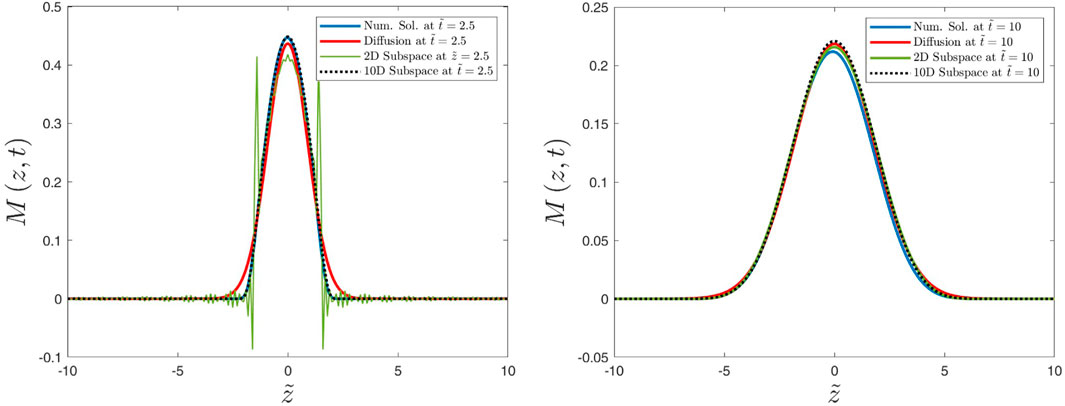
Figure 7. Caption is as in Figure 6, but we have considered the times $\tilde{t}=2.5$ (left panel) and $\tilde{t}=10$ (right panel).

Figure 8

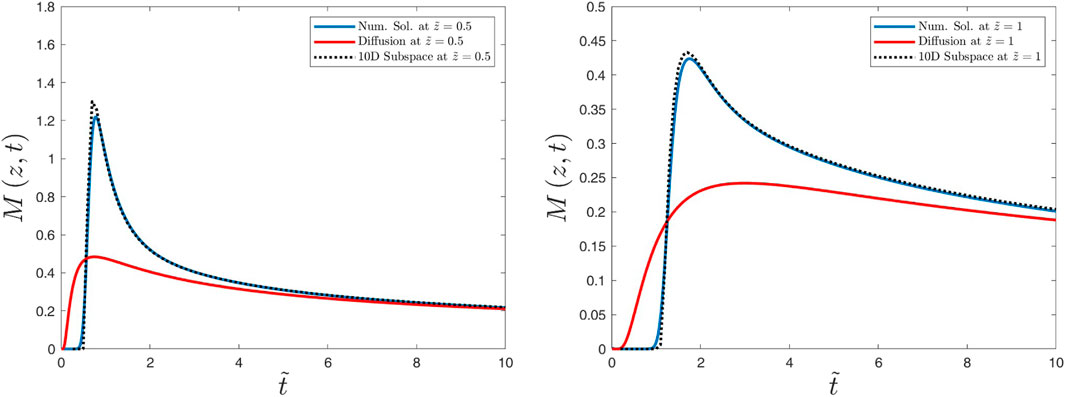
Figure 8. Numerical and analytical solutions for the μ-averaged distribution function M(z, t) versus time $\tilde{t}$. Shown are plots for $\tilde{z}=0.5$ (left panel) and $\tilde{z}=1$ (right panel). For the initial pitch-angle cosine, we have used μ₀ = 0.5.

Figure 9

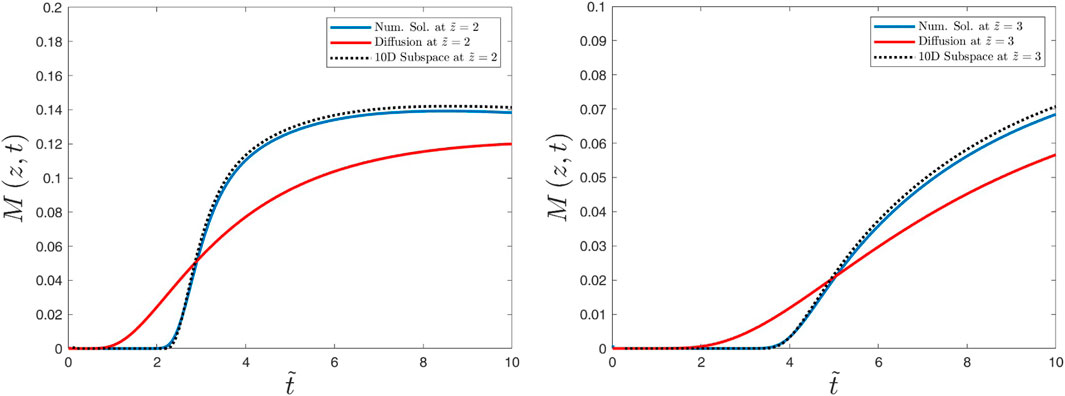
Figure 9. Caption is as in Figure 8, but we have considered $\tilde{z}=2$ (left panel) and $\tilde{z}=3$ (right panel).

Figure 10 shows the comparison of the time evolution of $M\left(z,t\right)$ based on diffusion equation and the 10D subspace approximation. We can clearly see the similarity for later times. For early times, on the other hand, we observe significant differences. In particular, the 10D solution provides $M\left(\left|z\right|>vt\right)=0$ as needed. Alternatively, we have plotted $M\left(z,t\right)$ versus time for different positions (Figure 11) where the aforementioned effect can be observed more clearly.

Figure 10

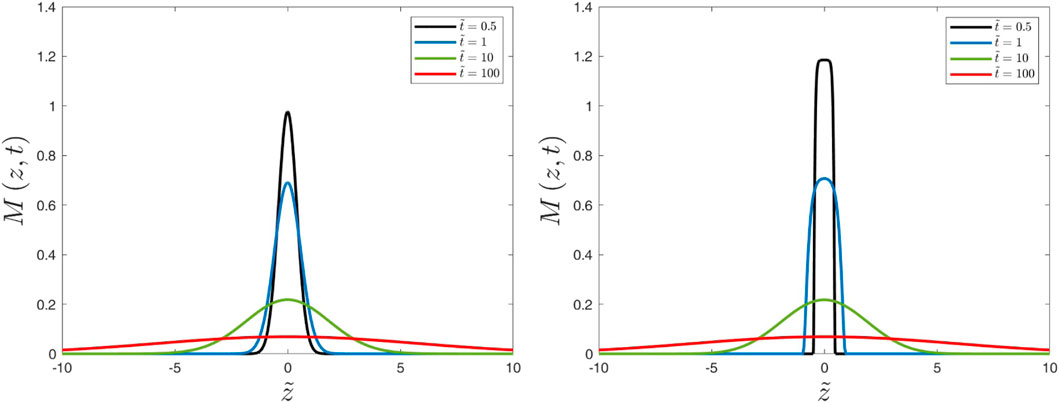
Figure 10. Time evolution of distribution functions. The left panel shows the solution of the diffusion equation as given by Eq. 6 for different times, and the right panel shows the μ₀-and μ-averaged solutions of the pitch-angle scattering equation based on the 10D dimensional subspace approximation.

Figure 11

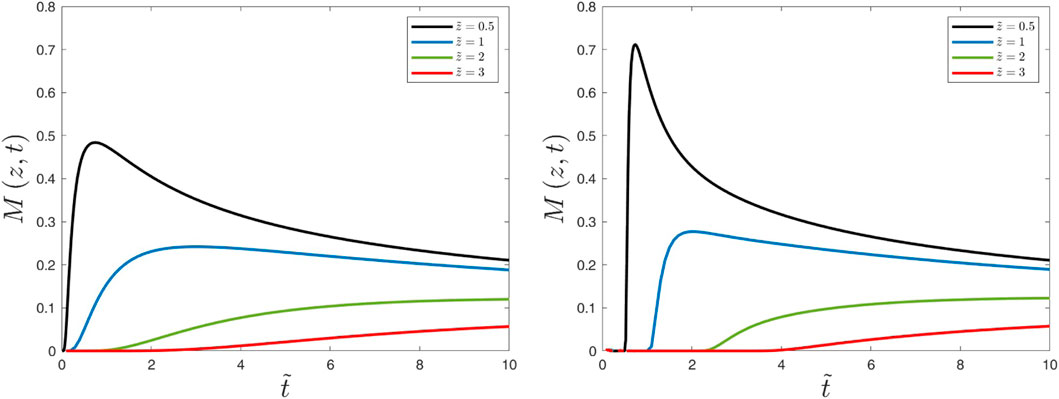
Figure 11. Distribution functions versus time $\tilde{t}$ at given positions $\tilde{z}$. The left panel shows the solution of the diffusion equation as given by Eq. 6 for different positions, and the right panel shows the μ₀-and μ-averaged solutions of the pitch-angle scattering equation based on the 10-dimensional subspace approximation.

Last but not the least, we have computed the function ${\mathrm{\Gamma }}_k\left(t\right)$ defined via Eq. 92. The latter function enters certain analytical theories for perpendicular diffusion. According to Figure 12, the 2D subspace approximation works overall well for computing this quantity. This explains why analytical theories for perpendicular diffusion, in which the 2D subspace approximation was used, agree well with performed test-particle simulations (Shalchi, 2020; Shalchi, 2021).

Figure 12

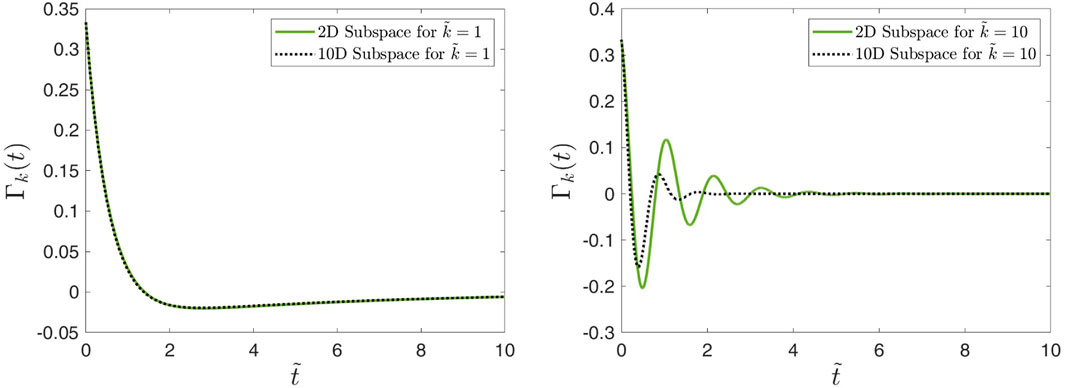
Figure 12. Numerical results for the function Γ_k(t) as defined via Eq. 92 based on 2D and 10D subspace approximations. The left panel shows results for $\tilde{k}=1$ and the right panel for $\tilde{k}=10$. It should be noted that it follows from the definition of this function that Γ_k(t = 0) = 1/3. The results for smaller values of $\tilde{k}$ are not shown here, but the agreement between 2D and 10D subspace approximations would be almost perfect in such cases.

5 Summary and conclusion

In this paper, we have focused on the most basic transport equation, namely, the pitch-angle scattering equation, as given by Eq. 1. Analytical and numerical investigations of pitch-angle-dependent transport equations have been the subject of several papers published during recent years. In addition to studies of the basic pitch-angle scattering equation (Shalchi et al., 2011; Tautz and Lerche, 2016; Lasuik and Shalchi, 2017; Lasuik and Shalchi, 2019), authors have explored the impact of so-called focusing, an effect which is related to a non-constant mean magnetic field (Danos et al., 2013; Litvinenko and Schlickeiser, 2013; Effenberger and Litvinenko, 2014; Lasuik et al., 2017; Wang and Qin, 2020; Wang and Qin, 2021; Wang and Qin, 2023). Even more complicated cases, including perpendicular particle transport, have been investigated by Wang and Qin (2024).

In this article, we have reviewed the two-dimensional subspace approximation originally developed by Shalchi et al. (2011) and discussed the provided solutions in configuration and Fourier spaces. We have also demonstrated that the two-dimensional subspace approximation is equivalent to using a telegraph equation. Normalized solutions in configuration and Fourier spaces are also discussed. However, we also argue that such solutions do not often provide appropriate results even if the pitch-angle average is considered. Although it was often argued that the telegraph equation is more complete than the usual diffusion approach (Tautz and Lerche, 2016), the solution discussed here contains artifacts that are not realistic. In particular, we observe spikes at z = ±vt (Figures 6, 7 as well as Supplementary Appendix S2).

Therefore, it is important to solve the pitch-angle scattering equation numerically. However, standard approaches such as implicit Euler or Crank–Nicolson solvers are time-consuming to use. In this paper, we have, thus, developed an N-dimensional subspace approach. This method can be seen as a semi-analytical/semi-numerical method. It has the advantage of being is several orders of magnitude faster than standard solvers (see Figure 1 of this paper). This is in particular the case if one is only interested in pitch-angle-averaged solutions at a given time. Standard solvers require a high time resolution in order to provide an accurate result. The N-dimensional subspace technique can be applied for a single time value if this is everything what is needed. It should also be emphasized that the N-dimensional subspace method can be easily parallelized since for a given k and t, one can compute the matrix exponentials independently of other values. This is also valid if one is looking for a μ- and μ₀-dependent result.

In this paper, we have computed several quantities such as distribution and characteristic functions as well as the function ${\mathrm{\Gamma }}_k\left(t\right)$ which is defined via Eq. 92 of this paper. We have compared numerical solutions obtained by using a standard solver with results obtained by using the N-dimensional subspace approximation for different values of N and the diffusive solution. The main difference is that pure numerical and 10D solutions provide $M\left(\left|z\right|>vt\right)=0$, meaning that the particles have a finite propagation speed. All results are visualized in Figures 2–12. One can clearly see that for N = 10, we obtain an accurate result that agrees well with the pure numerical solution of the pitch-angle scattering equation.

It has to be noted that the N-dimensional subspace method presented in this paper was specifically developed for the basic pitch-angle scattering equation and an isotropic scattering coefficient. However, this approach can be easily modified so that it can be used for more general transport equations including focused transport equations and other forms of the pitch-angle scattering coefficient.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

AS: writing–original draft and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The authors also acknowledge the support by the Natural Sciences and Engineering Research Council (NSERC) of Canada.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2024.1385820/full#supplementary-material

Footnotes

¹Note: there is a typo in Shalchi (2020) where one can find the incorrect formula C₀(t = 0) = 1/(3π).

References

Abramowitz, M., and Stegun, I. A. (1974). Handbook of mathematical functions. New York: Dover Publications.

Google Scholar

Crank, J., and Nicolson, P. (1947). A practical method for numerical evaluation of solutions of partial differential equations of the heat conduction type. Proc. Camb. Phil. Soc. 43, 50–67. doi:10.1017/s0305004100023197

CrossRef Full Text | Google Scholar

Danos, R. J., Fiege, J. D., and Shalchi, A. (2013). Numerical analysis of the fokker-planck equation with adiabatic focusing: isotropic pitch-angle scattering. Astrophysical J. 772, 35. doi:10.1088/0004-637x/772/1/35

CrossRef Full Text | Google Scholar

Earl, J. A. (1974). The diffusive idealization of charged-particle transport in random magnetic fields. Astrophys. J. 193, 231. doi:10.1086/153152

CrossRef Full Text | Google Scholar

Effenberger, F., and Litvinenko, Y. E. (2014). The diffusion approximation versus the telegraph equation for modeling solar energetic particle transport with adiabatic focusing, I. Isotropic pitch-angle scattering. Astrophysical J. 783, 15. doi:10.1088/0004-637x/783/1/15

CrossRef Full Text | Google Scholar

Gradshteyn, I. S., and Ryzhik, I. M. (2000). Table of integrals, series, and products. New York: Academic Press.

Google Scholar

Jokipii, J. R. (1966). Cosmic-Ray propagation. I. Charged particles in a random magnetic field. Astrophys. J. 146, 480. doi:10.1086/148912

CrossRef Full Text | Google Scholar

Lasuik, J., Fiege, J. D., and Shalchi, A. (2017). Numerical analysis of the Fokker-Planck equation with adiabatic focusing: realistic pitch-angle scattering. Adv. Space Res. 59, 722–735. doi:10.1016/j.asr.2016.10.027

CrossRef Full Text | Google Scholar

Lasuik, J., and Shalchi, A. (2017). Solutions of the cosmic ray velocity diffusion equation. Adv. Space Res. 60, 1532–1546. doi:10.1016/j.asr.2017.06.035

CrossRef Full Text | Google Scholar

Lasuik, J., and Shalchi, A. (2019). Subspace approximations to the cosmic ray Fokker-Planck equation. Mon. Notices R. Astronomical Soc. 485, 1635–1650. doi:10.1093/mnras/stz474

CrossRef Full Text | Google Scholar

Litvinenko, Y. E., and Schlickeiser, R. (2013). The telegraph equation for cosmic-ray transport with weak adiabatic focusing. A A 554, A59. doi:10.1051/0004-6361/201321327

CrossRef Full Text | Google Scholar

Press, W. H., Teukolsky, S. A., Vetterling, W. T., and Flannery, B. P. (2007). Numerical Recipes. Cambridge University Press.

Google Scholar

Shalchi, A. (2005). Second-order quasilinear theory of cosmic ray transport. Phys. Plasmas 12, 052905. doi:10.1063/1.1895805

CrossRef Full Text | Google Scholar

Shalchi, A. (2006). Analytical investigation of the two-dimensional cosmic ray Fokker-Planck equation. Astronomy Astrophysics 448, 809–816. doi:10.1051/0004-6361:20053664

CrossRef Full Text | Google Scholar

Shalchi, A. (2009). Nonlinear cosmic ray diffusion theories. Astrophysics Space Sci. Libr. 362. Springer, Berlin. doi:10.1007/978-3-642-00309-7

CrossRef Full Text | Google Scholar

Shalchi, A. (2010). A unified particle diffusion theory for cross-field scattering: subdiffusion, recovery of diffusion, and diffusion in 3D turbulence. Astrophys. J. 720, L127–L130. doi:10.1088/2041-8205/720/2/l127

CrossRef Full Text | Google Scholar

Shalchi, A. (2011). Velocity correlation functions of charged particles derived from the fokker-planck equation. Adv. Space Res. 47, 1147–1164. doi:10.1016/j.asr.2010.12.002

CrossRef Full Text | Google Scholar

Shalchi, A. (2017). Time-dependent perpendicular transport of energetic particles in magnetic turbulence with transverse complexity. Phys. Plasmas 24, 050702. doi:10.1063/1.4982805

CrossRef Full Text | Google Scholar

Shalchi, A. (2020). Perpendicular transport of energetic particles in magnetic turbulence. Space Sci. Rev. 216, 23. doi:10.1007/s11214-020-0644-4

CrossRef Full Text | Google Scholar

Shalchi, A. (2021). Perpendicular diffusion of energetic particles: a complete analytical theory. Astrophys. J. 923, 209. doi:10.3847/1538-4357/ac2363

CrossRef Full Text | Google Scholar

Shalchi, A., Škoda, T., Tautz, R. C., and Schlickeiser, R. (2009). Analytical description of nonlinear cosmic ray scattering: isotropic and quasilinear regimes of pitch-angle diffusion. Astron. Astrophys. 507, 589–597. doi:10.1051/0004-6361/200912755

CrossRef Full Text | Google Scholar

Shalchi, A., Tautz, R. C., and Rempel, T. J. (2011). Test-particle transport: higher-order correlations and time-dependent diffusion. Plasma Phys. control. Fusion 53, 105016. doi:10.1088/0741-3335/53/10/105016

CrossRef Full Text | Google Scholar

Tautz, R. C., and Lerche, I. (2016). Application of the three-dimensional telegraph equation to cosmic-ray transport. Res. Astronomy Astrophysics 16, 162. doi:10.1088/1674-4527/16/10/162

CrossRef Full Text | Google Scholar

Wang, J. F., and Qin, G. (2020). The invariance of the diffusion coefficient with iterative operations of the charged particle transport equation. Astrophysical J. 899, 39. doi:10.3847/1538-4357/aba3c8

CrossRef Full Text | Google Scholar

Wang, J. F., and Qin, G. (2021). Study of momentum diffusion with the effect of adiabatic focusing. Astrophysical J. Suppl. Ser. 257, 44. doi:10.3847/1538-4365/ac1bb3

CrossRef Full Text | Google Scholar

Wang, J. F., and Qin, G. (2023). Relationship of transport coefficients with statistical quantities of charged particles. Astrophysical J. 954, 213. doi:10.3847/1538-4357/ace9d3

CrossRef Full Text | Google Scholar

Wang, J. F., and Qin, G. (2024). The effect of solar wind on charged particles’ diffusion coefficients. Astrophysical J. 961, 6. doi:10.3847/1538-4357/ad09b7

CrossRef Full Text | Google Scholar

Watson, G. N. (2011). A treatise on the theory of Bessel functions. Cambridge: Cambridge Mathematical Library.

Google Scholar

Zank, G. P. (2014). Transport processes in space Physics and astrophysics. Lect. Notes Phys. 877. Springer, New York. doi:10.1007/978-1-4614-8480-6

CrossRef Full Text | Google Scholar

Zwillinger, D. (2012). Standard mathematical tables and formulae. Boca Raton: CRC Press.

Google Scholar