Modification of the turbulence properties at the bow shock: statistical results

Turbulent solar wind is known to be a main driver of the processes inside the magnetosphere, including geomagnetic storms and substorms. Experimental studies of the last decade demonstrate additional ways of interplanetary plasma transport to the magnetosphere, including small-scale processes in the magnetosphere boundary layers. This fact implies that properties of the solar wind turbulence can affect the geomagnetic activity. However, in front of the magnetosphere are a bow shock and a magnetosheath region which contribute to the changes in the properties of the solar wind turbulence and may result in destructions of the association between solar wind turbulence and the magnetosphere. The present study provides the statistics of two-point simultaneous measurements of the turbulence properties in the solar wind and the magnetosheath based on Wind and THEMIS spacecraft data. Changes in the turbulence properties are analyzed for different background conditions. Solar wind bulk speed and temperature are shown to be the main factors that influence the modification of turbulence at the quasi-perpendicular bow shock at frequencies higher than the break frequency (ion transition range). Inside the magnetosheath, significant steepening of spectra occurs with an increase in temperature anisotropy without a connection to the upstream spectrum scaling that underlines the crucial role of the instabilities in turbulence properties behind the bow shock.

1 Introduction

The turbulent nature of solar wind (SW) fluctuations has been known since the beginning of measurements in the interplanetary space (Coleman, 1968). Due to a large number of spacecraft data during the last three decades, to date, the turbulence properties of the SW plasma are generally described (Alexandrova et al., 2013; Bruno and Carbone, 2013; Alexandrova et al., 2021). The SW turbulence is characterized by the presence of several ranges of scales. At large scales (>10⁶ km), energy is injected into the system, and the fluctuation spectra follow the f⁻¹ power law. At intermediate scales (MHD scales or inertial range), the energy is transferred to smaller scales by the nonlinear interaction of eddies, and the spectra typically follow the f^−5/3 power law (Kolmogorov scaling). The scaling may be different for perpendicular and parallel mutual directions between the magnetic field and plasma velocity due to the turbulence anisotropy (Horbury et al., 2008; Chen et al., 2011). At ion scales (∼10³ km), kinetic effects become important, the spectrum breaks, and a transition to kinetic scales occurs; at these scales, the spectra usually follow the power law f^−a, where a ranges from −4 to −2 (Smith et at, 2006a,b; Sahraoui et al., 2013). During the last decade, comprehensive studies of turbulence up to electron scales provided more information on the nature of the turbulent cascade and an interplay between the turbulence and reconnection (Alexandrova et al., 2009; Sahraoui et al., 2009; Sahraoui et al., 2013). However, the electron-scale turbulence is much less studied to date.

The SW (and interplanetary disturbances, mainly) is known to be the main driver of magnetospheric activity (Russell et al., 1974; Burton et al., 1975). However, magnetospheric perturbations may occur during undisturbed SW conditions. Some of the experimental results suggested turbulence to be a cause of these disturbances (D'Amicis et al., 2007; Vörös et al., 2002; Jankovicova et al., 2008; Borovsky and Funsen, 2003). The current status of a possible role of the SW turbulence in the geomagnetic perturbations is described in D'Amicis et al. (2020).

When the supersonic and superalfvenic SW meets the magnetosphere, a detached bow shock (BS) is formed with a region behind it called the magnetosheath (MSH). Properties of the MSH plasma and magnetic field have been known to differ from the undisturbed SW since the early space era (see the review by Song and Russell, 1997). This region is dominated by wave activity (Lacombe and Belmont, 1995; Schwarz et al., 1996), coherent structures including magnetic jets (Plaschke et al., 2018; Dmitriev et al., 2021), magnetic islands (Huang et al., 2016), Alfvén vortices (Alexandrova et al., 2006), and current sheets (Yordanova et al., 2020). Unlike the SW, the turbulence in the MSH is significantly less studied (see reviews by Rakhmanova et al., 2021; Zimbardo et al., 2010; Sahraoui et al., 2020) despite the obvious importance of MSH processes for the solar wind–magnetosphere coupling (Vörös et al., 2023).

Statistical studies on the MSH turbulence have demonstrated that the properties of the cascade are significantly modified at the BS. Czaykowska et al. (2001) showed the magnetic field fluctuation spectra following f⁻¹ scaling at the MHD scales behind the BS. The observation of f⁻¹ scaling in the regions just downstream of the quasi-perpendicular BS may be attributed to the presence of uncorrelated Alfvén and mirror waves arising there (Schwartz et al., 1996; Alexandrova, 2008), which may be convected by the solar wind flow away from the BS. Further statistical analysis by Huang et al. (2017) demonstrated that such kind of spectra can be found throughout the MSH even at a significant distance from the subsolar region (X_GSE∼0 R_E) and from the BS. The authors suggested that the crossing of the BS destroyed the turbulence properties and the inertial range of the cascade, which further developed again when plasma moved away from the BS. This suggestion questions the connection between SW turbulence and magnetospheric disturbances as it implies that the properties of the turbulent cascade in front of the magnetopause are formed locally in the MSH.

Later, Rakhmanova et al. (2018b) demonstrated that the spectra with f⁻¹ scaling at frequencies below the break were typical for ion flux-value fluctuations in the vicinity of the quasi-perpendicular BS, while other regions of the MSH exhibited Kolmogorov scaling of the fluctuations. On the other hand, statistical results obtained by Li et al. (2020) demonstrated a steeper mean spectrum of magnetic field fluctuations with slope −1.47 in the vicinity of the BS of both kinds, although the spectra became steeper with the distance from the BS and from the Sun–Earth line. A case study of several BS crossings demonstrated that sometimes, the scaling of the SW spectra survived behind the BS (Rakhmanova L. S. et al., 2020). Further case study of simultaneous measurements at three points—in the SW, in the dayside MSH, and at the MSH flank—showed that for most of the cases, the spectra had f⁻¹ scaling at the MHD scales in the dayside MSH or were dominated by wave activity and then restored a −5/3 power exponent at the flanks, regardless of the properties of the turbulence in the SW. This result confirmed the suggestions of Huang et al. (2017). However, eventually, the spectra exhibited Kolmogorov scaling in the dayside MSH.

While the changes at the MHD scales were not doubtful for the great majority of the cases, no changes at the kinetic scales were found by Huang et al. (2017) and Li et al. (2020). The authors suggested that ion-scale fluctuations did not “notice” the presence of the BS, i.e., a very short time is needed for the scaling restoration behind the BS. On the other hand, Rakhmanova L. et al. (2018) demonstrated a slight steepening of the spectra behind the BS and their restoration closer to the magnetopause. Note that former studies considered the fluctuations in the magnetic field vector (i.e., both compressible and incompressible components), while the latter study concentrated on the fluctuations in the ion flux value (compressible component). Further study of the evolution of the compressive fluctuation spectra in the MSH (Rakhmanova et al., 2022) showed significant steepening of the spectra at the kinetic scales at the BS for disturbed SW periods. Such steepening may be associated with compressive wave modes in the MSH, i.e., mirror mode. Furthermore, the authors demonstrated different scenarios of spectrum development at the kinetic scales depending on the SW type while plasma moved toward the flanks.

At the Earth’s orbit, most of the studies demonstrated variations in the slope value from −4 to −2 in the frequency range above the ion break (Smith et al., 2006). Further improvements in the experimental techniques helped find a well-established f^−2.8 spectrum at higher frequencies (sub-ion scales) and attributed the variable slope at frequencies around the break to an ion transition range (Sahraoui et al., 2010; Alexandrova et al., 2013). Recently, the presence of the ion transition range and significant steepening of the spectrum in this range was demonstrated and studied at small heliocentric distances and attributed to strong dissipation or nonlinear effects (Bowen et al., 2020a; Duan et al., 2021). Bowen et al. (2020b) showed that at 0.17 au, this transition range is dominated by ion-scale electromagnetic waves associated most probably with local instabilities due to temperature anisotropy. Similar conditions occur typically behind the BS. However, the steepening in the MSH was demonstrated rarely.

Thus, to date, evidence shows that the BS can modify the properties of the SW turbulence both at the MHD and kinetic scales, but there is no clear answer on how often and in which cases the turbulence properties can survive across the BS. The present paper aims to address these questions by comparing the properties of the turbulence in the SW and in the MSH with the help of statistics of simultaneous measurements in the SW and downstream of the BS, taking into account plasma propagation time. Wind measurements are used in the SW, and THEMIS measurements are analyzed in the MSH. Note that the plasma properties differ substantially for the MSH behind the quasi-perpendicular and quasi-parallel BS (Shevyrev and Zastenker, 2005; Breuillard et al., 2018a; Yordanova et al., 2020), with the most modified spectra occurring behind the quasi-perpendicular BS (Breuillard et al., 2018b; Yordanova et al., 2020). Moreover, processes behind the quasi-parallel BS are affected by the foreshock (Gutynska et al., 2012), and the turbulence modification could be indistinguishable. Here, we focus on the MSH behind the quasi-perpendicular BS to trace the changes arising at the BS. Altogether, approximately 400 h of direct measurements were considered for various SW conditions. Comparison of the spectral features in the SW and the MSH for the MHD and kinetic scales is done. Changes in the spectral slopes as functions of a set of plasma and magnetic field parameters are considered to detect the factors that determine the turbulence modification at the BS.

2 Data

The present study uses THEMIS mission (Angelopoulos, 2008) measurements in the MSH and simultaneous Wind measurements in the SW. The analysis covers years 2008 and 2014, which correspond to minimum and maximum of the solar cycle, respectively. In 2008, the orbits of all five THEMIS spacecraft were elongated with different apogees and seasonally drifted from dawn to dusk MSH flanks, which provided good coverage of the measurements throughout the dayside MSH. In 2014, three of the five spacecraft were in the dayside MSH, while the other two were sent to the Moon orbit and crossed the MSH at the flanks at distances X_GSE ∼ -60 R_E. The data were obtained from https://cdaweb.gsfc.nasa.gov/.

All periods during which one of the THEMIS spacecraft was in the MSH for more than 1.5 h were chosen for the analysis. Plasma parameters (ion density, velocity, and temperature) measured by the ESA instrument (McFadden et al., 2008) were used with a time resolution of 3–4 s, and L2 on-board moments were chosen. Magnetic field measurements obtained using the FGM device (Auster et al., 2008) with a time resolution of 0.25 s were used. The THEMIS position inside the MSH was identified with visual inspection of the data quicklooks. Density, velocity, and temperature parameters were used together with the ESA spectrograms. Transition from the SW to the MSH is typically characterized with density and temperature increase and velocity decrease accompanied by a non-zero V_y component and broadening of the proton energy spectrum. At the flanks, these changes are less pronounced but clearly visible. Crossing of the magnetopause and entrance to the magnetosphere can be determined by a decrease in the ion density and velocity. Visual inspection ensures that the crossings of the BS or magnetopause are excluded from the intervals. For cases when simultaneous measurements of the spacecraft were available at closely located (with distances less than 1R_E) points, single-spacecraft data were chosen based on data quality. Altogether, data of 850 h of MSH measurement were collected.

For all periods of the THEMIS measurements in the MSH, the corresponding simultaneous Wind measurements in the SW were analyzed. SWE measurements (Ogilvie et al., 1995) with a time resolution of 92 s were used to obtain the ion density, velocity, and temperature. MFI instrument (Lepping et al., 1995) measurements of the magnetic field vector with a time resolution of 92 ms were used.

During the analyzed periods, the THEMIS data included measurements at X_GSE ∼ −60 R_E and X_GSE > −10 R_E. The latter region is further referred to as the dayside MSH and is focused on in this study. The same region was analyzed by previous statistical studies on the turbulence properties in the MSH (Huang et al., 2017; Li et al., 2020). This reduces the statistics to 550 h of measurements. Here, 70% of the dataset refers to the year 2008, and the remaining 30% refers to the year 2014.

The time shifts between data series in the SW and MSH were obtained using cross-correlation analysis. Since the time of the SW propagation from L1 to Earth is approximately 60 min for mean SW conditions, the correlation coefficient of THEMIS and Wind observations (interpolated to 92 s time resolution) was computed as a function of the time shift dt in the range −30 min < dt < 90 min for each of the 150 MSH crossings. The shift T₁, which corresponded to the maximum of the correlation, was chosen for further analysis. Then, all the time shifts were manually inspected. When good visual correspondence of density measurements at both spacecraft was observed, T₁ was approved for the analysis. Otherwise, the time shift was determined manually based on good visual correspondence of the time series. The method and its problems are described in more detail in Rakhmanova et al. (2022).

Figure 1 presents an example of the comparison of Wind measurements in the SW with THEMIS-D measurements in the MSH on 25 June 2008. Wind was located at (259; −40; 22) R_E, while THEMIS-D was located at (5.8; 9.5; −2.9) R_E. At 20:23, THEMIS-D crossed the magnetopause and stayed in the MSH till the second crossing of the magnetopause at 23:40. Panel a demonstrates density measurements on board Wind (red line) and THEMIS-D (black line); Wind measurements are shifted by T₁ = 3,451 s. The blue line shows the THEMIS-D density linearly interpolated to 92 s time resolution (to match the SWE sampling rate) for the cross-correlation analysis. The left ordinate axis corresponds to THEMIS-D measurements in the MSH, while the right ordinate axis corresponds to Wind measurements in the SW. Correlation coefficient R (T₁) for this interval is 0.56. Good correspondence between Wind and THEMIS-D plasma structures can be observed: although the absolute value of density differs by a factor of ∼2 in the MSH, most of the time, similar changes in the density profiles can be observed for both spacecraft. However, sometimes, differences in the time profiles occur at small scales (e.g., at 23:00–23:30), which is a typical property of the small-scale variations in the MSH and is supposed to be the manifestation of the turbulent nature of the MSH plasma (Rakhmanova et al., 2016).

Figure 1

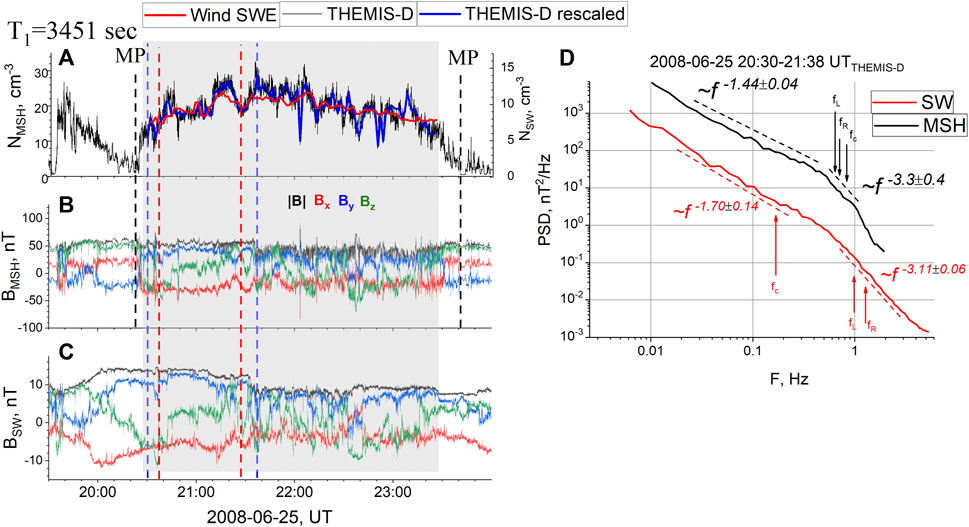
Figure 1. (A) Ion density measured on board the THEMIS-D (black line—full time resolution; blue line—time resolution reduced to match SWE time resolution) and WIND (red line), (B) magnetic field measurements obtained by THEMIS-D, (C) and magnetic field measurements obtained by Wind. Wind data are shifted by plasma propagation time; (D) spectra of magnetic field fluctuations in the MSH (black line, THEMIS-D) and in the SW (red line, Wind).

Panels b and c show the magnetic field vector registered in the MSH and the SW, respectively. The SW data are shifted in time by T₁. Time profiles of the magnetic field components on the two spacecraft also demonstrate good correspondence. Thus, we conclude that during the considered interval, both spacecraft have observed the same plasma. The gray shadow shows the interval chosen for further analysis.

3 Methods

The properties of the turbulence were estimated using Fourier transform of magnetic field vector fluctuations. Each of the collected time intervals in the MSH was cut into subintervals with a duration of 68 min, overlapped by 34 min. The duration of the intervals was chosen to guarantee enough number of data points for the reliable determination of the turbulence properties and quasi-stationary background parameters. For each MSH subinterval, the corresponding subinterval in the SW was determined. The Wind and THEMIS magnetometers have different time resolutions, which results in different durations of subintervals for the Fourier analysis—50 min in the SW versus 68 min in the MSH. The center of the SW subinterval corresponds to the center of the MSH subinterval.

When considering the properties of the turbulence using a single spacecraft, the Taylor hypothesis is usually adopted, which allows a simple conversion from spatial to frequency space when a wave speed of fluctuations is significantly lower than the speed of background plasma. This is typically valid for the SW plasma but may be invalid for the dayside MSH, where plasma is slowed down, heated, and compressed, and additional instabilities and, sometimes, whistler waves (Lacombe et al., 2006) occur. Klein et al. (2014) reported that the conversion from spatial to frequency space does not change the shape of a spectrum while the ratio T_a = V_a/V > 0.3, where V is the plasma speed and V_a is the local Alfvén speed. However, the presence of whistlers or other dispersive modes may result in the incorrect determination of the turbulence properties with the single-spacecraft measurements.

For each subinterval considered, the ratio T_a was checked. Among 705 subintervals considered, 662 satisfied the condition T_a > 0.3. However, the presence of dispersive wave modes has not been checked. We assumed that these modes were rare, and their possible presence would not affect the statistical results. Then, the Fourier transform was performed on each subinterval. The Hamming window was used in a frequency domain to decrease noise in spectra and to make them appropriate for approximation. Figure 1D presents an example of the resulting spectrum in the MSH (black line) and corresponding spectrum in the SW (red line) for the interval 20:30–21:38 in the MSH (20:39–21:29 in the SW), marked in panels (a–c) by vertical dashed lines (red lines refer to the SW subinterval, and blue lines refer to the MSH subinterval). For the analyzed spectra, the ion scales are R^sw = 52 km, L^sw = 73 km, and F_c^sw = 0.17 Hz in the SW and R^msh = 36 km, L^msh = 50 km, and F_c^msh = 0.8 Hz in the MSH, where R refers to the proton gyroradius, L refers to the proton inertial length, and F_c is the proton cyclotron frequency. Arrows at the spectra denote corresponding Doppler-shifted frequencies f_R = V/2πR and f_L = F/2πL, as well as F_c. The values of these frequencies are f_R = 1.4 Hz and f_L = 1 Hz in the SW and f_R = 0.71 Hz and f_L = 0.66 Hz in the MSH. As shown by the example, the break in each spectrum occurs at the frequencies close to one of the characteristic frequencies. The question on the exact position of the break is still debated (Chen et al., 2014; Šafránková et al., 2015; Woodham et al., 2018; Park et al., 2023) and is out of the scope of the present paper.

For the SW spectrum, two linear parts in a log–log space can be easily observed, namely, ∼ 0.02–0.2 Hz and 0.7–3 Hz. Within each of these two ranges, the spectrum can be approximated with the function log(PSD) = A + P^*log(F), where A and P are parameters of approximation. The approximation procedure is performed inside each range of frequencies independently. P_1,2 are the spectrum slopes that correspond to the power exponents. For the considered example in the SW, the approximation yields slope P₁ = −1.70, which is close to the Kolmogorov −5/3 scaling. The break in the spectrum occurs at frequency ∼0.55 Hz, and at the kinetic scales, the spectrum is characterized by slope −3.11. Note that this slope is somewhat lower than typically observed for the undisturbed SW as the observed period is attributed to the fast flow of the corotating interaction region (Bruno et al., 2014; Riazantseva et al., 2020). Furthermore, the turbulent cascade may be dominated by Alfvén vortices (Alexandrova et al., 2006; Perrone et al., 2017). Although lower than −2.9, observed typically in the SW at frequencies above the break, the slope value −3.11 lies within the values [-4, −2] specific for the ion transition range.

The shape of the spectrum in the MSH is more complex and includes three linear ranges of scales, namely, 0.02–0.4 Hz, 0.6–1 Hz, and 1–1.8 Hz. Approximation with the function used for the SW spectrum yields P₁ = −1.44 ± 0.04, P₂ = −3.3 ± 0.4, and P₃ = −5.3 ± 0.2. In the analyzed statistics, the last range of spectrum steepening sometimes occurs at a specific frequency of 1 Hz, and its nature is unknown. We suggest that the presence of this steepening is an artifact of data as it is not typical for magnetic field fluctuation spectra in the MSH. Another explanation of this steepening is the presence of high-frequency waves or a network of dipole vortices (Alexandrova, 2008). This steepening confines the considered range of frequencies above the break to 1 Hz when it is present. Figure 1 shows that, in the MSH, the properties of the turbulence differ slightly from those in the SW. The spectrum is flatter at the MHD scales and deviates from the Kolmogorov scaling. At the kinetic scales, slight steepening occurs.

All subintervals were processed in a similar way using a semi-manual routine. Typically, algorithms of automatic determination of spectral slopes and break frequencies of the spectra yield good results when the spectra exhibit a particular shape with two power laws divided by a break (Riazantseva et al., 2019; Park et al., 2023). However, in the dayside MSH, the spectra often exhibit peculiarities in the range of scales around a break (Rakhmanova et al., 2016; Alexandrova and Saur, 2008). These peculiarities have a form of bumps, spectral peaks, spectral knees, or flattening due to instabilities, ion-scale waves, or coherent structures and complicate a routine approximation of the spectra. In the present study, linear approximation in the log–log scales was performed independently in two ranges of frequencies—0.02–0.1 Hz and 0.8–1.5 Hz. Similar to the example above, the approximation was made with the function log(PSD) = A + P^*log(F), and parameters A and P were determined. The edges of the frequency ranges were varied by 1–5 points, and the approximation that had the minimum error was chosen. This variation of the edges helped account for the modification of a spectrum by ion-scale peculiarities or high-frequency flattening due to noise for most of the cases. For each spectrum, the number of points used for approximation was fixed, and spectral slopes obtained on a basis of less than 10 points were eliminated.

All of the spectra were visually inspected. The approximation procedure determined most of the spectral slopes in cases when the spectra exhibited two power laws with a break or a bump at frequencies 0.1–0.6 Hz. However, sometimes, the bump was shifted to lower frequencies, or the high-frequency range exhibited noises or artifacts of data processing. Such spectra were determined during visual inspection, and the corresponding slopes were eliminated from further analysis. Determination of the MHD-scale slope was impossible for 20% of cases in the dayside MSH. At the kinetic scales, 66% of spectra in the SW and for 75% of spectra in the MSH exhibited reasonable fit.

In the case of Wind MFI data, the spectra were often dominated by noise at frequencies higher than 0.7 Hz and for PSD<0.003 nT²/Hz. This point was carefully discussed in Woodham et al. (2018). The contribution of the noise may result in the flattening of the spectrum at the kinetic scales. However, visual inspection allows us to remove the frequency range affected by the noise from the approximation procedure. Spectra with the slope at the kinetic scales higher than the one at the MHD scales were not considered as they were likely to be the result of instrument noise (Smith et al., 2006). Furthermore, the criteria proposed by Woodham et al. (2018) were tested on the collected dataset and showed similar results for the approximation. Thus, we assume that there are no effects of instrument noise in our results.

For each spectrum, mean background parameters were determined both in the SW and the MSH. To analyze the influence of the BS and the magnetopause on the turbulence properties, a fractional distance D of the MSH spacecraft was calculated for each interval. The fractional distance was defined as D = (R-R_mp)/(R_BS-R_mp) (Verigin et al., 2006), where R was a radius vector of the spacecraft and R_mp and R_BS were distances of the magnetopause and the BS from Earth along R, determined by models (Shue et al., 1998; Verigin et al., 2001). D varies from 0 to 1, where 0 corresponds to the magnetopause crossing and 1 refers to the BS crossing. To determine the type of the BS for each spectrum, the θ_BN angle between the interplanetary magnetic field vector and a local BS normal was calculated in the point of the plasma entrance to the MSH (determined by the flow lines from the model proposed by Spreiter et al. (1966) and Wind input data). Altogether, ∼540 spectra in the MSH satisfied the criterion θ_BN > 45⁰ and were established for further analysis.

4 Results

4.1 Statistics

Figure 2 presents the values of the slope P₁ at the MHD scales in the MSH versus the same slopes in the SW. Panel a demonstrates a direct comparison for each pair of intervals; the histograms denote distributions of the P₁ values in the dayside MSH (panel b) and the SW (panel с) for the same periods. Note that the number of points in panel a corresponds to the number of pairs of intervals when both SW and MSH spectra have been approximated successfully. Numbers N specified at the histograms correspond to the number of spectra in the region, which can be successfully approximated regardless of the corresponding spectrum in another region. For this reason, the numbers of intervals involved in the distributions are slightly different.

Figure 2

Figure 2. (A) MHD-scale slope of the magnetic field fluctuations in the MSH versus SW; (B) distribution of slope P₁ in the dayside MSH; (C) distribution of the slope P₁ in the SW; and (D) distribution of the P₁ change at the BS.

The figure shows that at the MHD scales, 1) in the SW, the spectra typically follow Kolmogorov −5/3 scaling; 2) the spectra flatten in the dayside MSH and deviate from Kolmogorov −5/3 scaling; and 3) there is no relation between P₁ values in the L1 point and downstream of the quasi-perpendicular BS.

Figure 3 is organized in the same way as Figure 2 and demonstrates relations between kinetic-scale slopes P₂. At the kinetic scales, the spectrum slope in the MSH typically has a value close to −8/3, as predicted in some of the theoretical approaches (Boldyrev and Perez, 2012). However, the distribution is not symmetric, and there is a portion of steeper spectra, and the mean value of the slopes moves to −3.0 ± 0.4. In the SW, the distribution is not symmetric as well, with the maximum close to −7/3 and a mean value of −2.6 ± 0.4. No direct relations can be observed between the slopes measured in the SW and downstream from the BS.

Figure 3

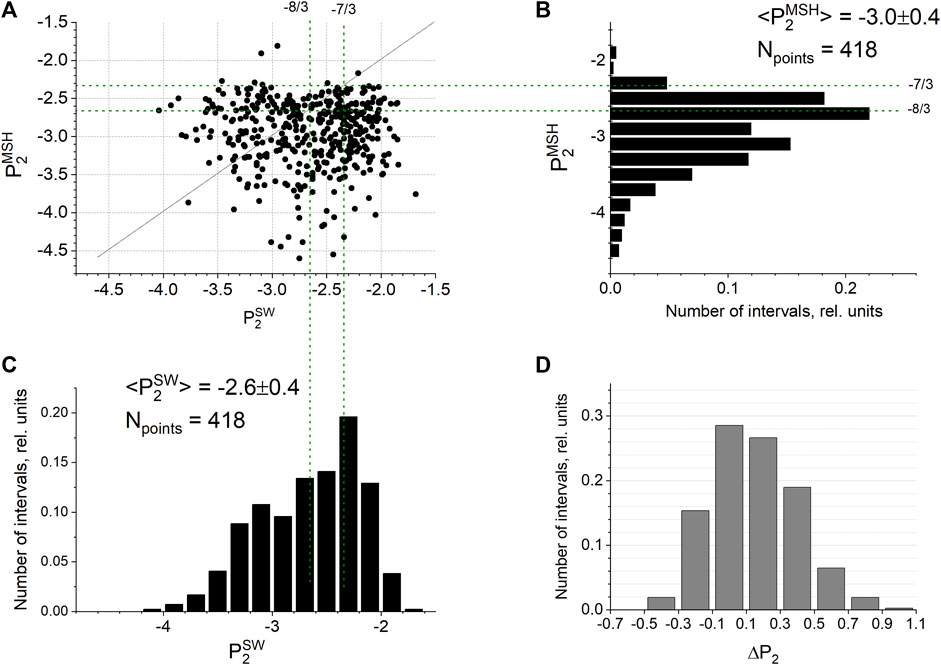
Figure 3. (A) Kinetic-scale slope of the magnetic field fluctuations in the MSH versus SW; (B) distribution of slope P2 in the dayside MSH; (C) distribution of the slope P2 in the SW; and (D) distribution of the P2 change at the BS.

To estimate the number of cases when plasma crossed the BS without changes in the turbulence properties at the MHD or kinetic scales, the distributions of the slope changes were considered. A change in the spectral slope at the BS was determined as ΔP_a=(P_a^MSH-P_a^SW)/P_a^SW, where a = 1 for the MHD-scale slope and a = 2 for the kinetic scales. The value ΔP_a >0 refers to the steepening of the spectrum at the BS, while ΔP_a <0 refers to the flattening of the spectrum. The distributions of ΔP are shown in Figure 2D for the MHD scales and in Figure 3D for the kinetic scales. For 14% of cases, |ΔP₁|<0.1; for these cases, the mean value of the P₁ slope was −1.6 ± 0.2. Note that for |ΔP₁|<0.1, the errors of ΔP₁ determination vary from 0.03 to 0.2 with the mean and most probable values of 0.1. Thus, for 14% of cases, the Kolmogorov scaling survived across the BS.

At the kinetic scales, the slope remains unchanged more frequently—at 28% of cases (the most probable error value of ΔP₂ determination for |ΔP₂|<0.1 is 0.06). For 50% of cases, steepening occurs, with the slope changing by 10% and more. The statistics includes 306 spectral pairs, which can be approximated at both ranges of scales. Among these pairs of spectra, 12% are characterized by the differences |ΔP₁|<0.1 and |ΔP₂|<0.1, i.e., the turbulence properties remain unchanged during the BS crossing or are re-established to those of the SW.

4.2 Effect of the background parameters

Previous studies demonstrated dependencies of the turbulence properties in the MSH on a number of background parameters, including the SW velocity (Gutynska et al., 2012), MSH and SW densities (Rakhmanova et al., 2022), and distance to the MSH boundaries (Rakhmanova L. et al., 2018; Li et al., 2020). Here, we address the parameters that affect not only the value of the slope in the MSH but also its change at the BS.

We have calculated correlation coefficients between the slopes P₁ and P₂ both in the SW and in the MSH, as well as their changes ΔP_1,2 for a set of background parameters, including fractional distance D, SW bulk speed, density and temperature, IMF magnitude and B_z component value, MSH magnetic field magnitude, ion density and temperature, plasma parameter β_p for protons in the SW and the MSH, temperature anisotropy, and the angle between the velocity and magnetic field vectors in the MSH. The number of points for calculation varies from 290 to 523 depending on the parameter and the slope type. Obviously, there is no sense to correlate the SW slope with the MSH parameters. For those relations that have a correlation of the MSH slopes with the MSH parameters, similar correlations are considered for the SW slope and the SW parameter and vice versa.

Table 1 gives the correlation coefficients between the chosen set of parameters and the spectral slopes in the SW (R_P_a^SW) and in the MSH (R_P_a^MSH), as well as its change (R_ΔP_a) at the BS for both ranges of scales (a = 1 and 2 for MHD and kinetic ranges, respectively). Correlation coefficients that exceed 0.5 are in bold.

Table 1

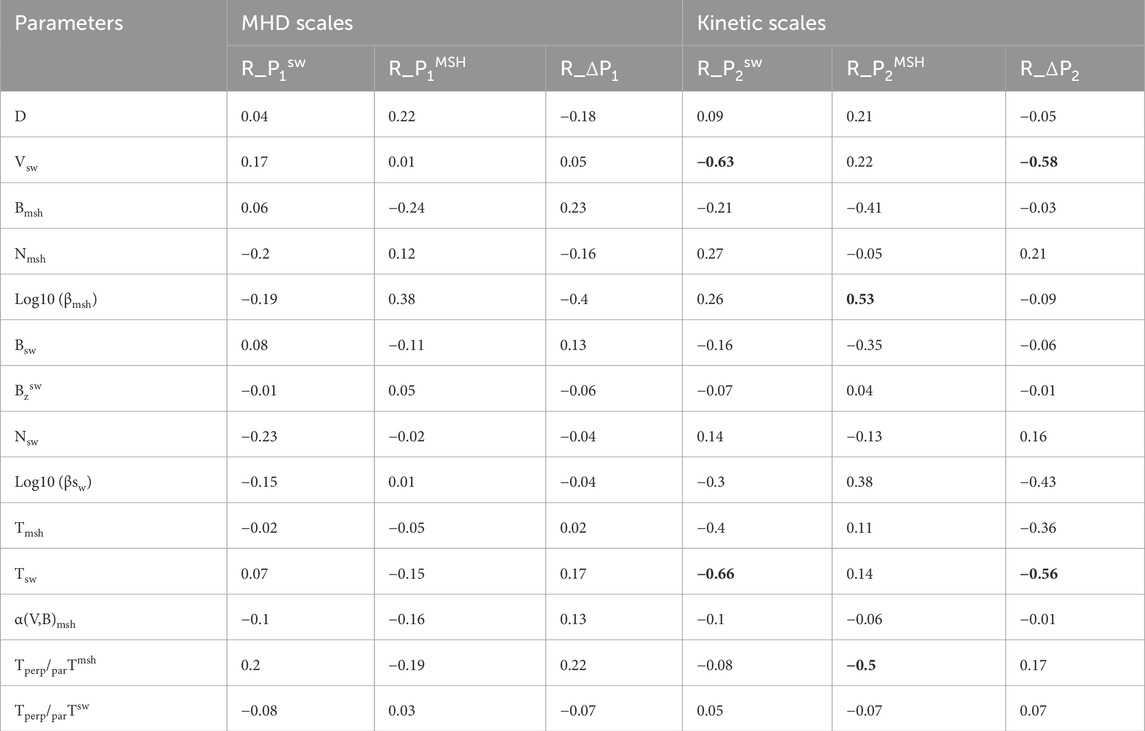
Table 1. Correlations between the turbulence properties and background parameters. Significant correlation values are bolded.

The MHD-scale slope and its changes at the BS are slightly affected by the plasma parameter β_p in the MSH: increasing β_p results in an increase of P₁ behind the BS and in more substantial flattening of the spectrum at the BS. Figures 4A–C show the dependence of P₁ on β_p in the SW, the MSH, and the change ΔP₁ on β_p in the MSH. Although the correlation is rather low (∼–0.4), one can observe a tendency to find spectra with Kolmogorov scaling in the MSH for low values of β_p in the MSH.

Figure 4

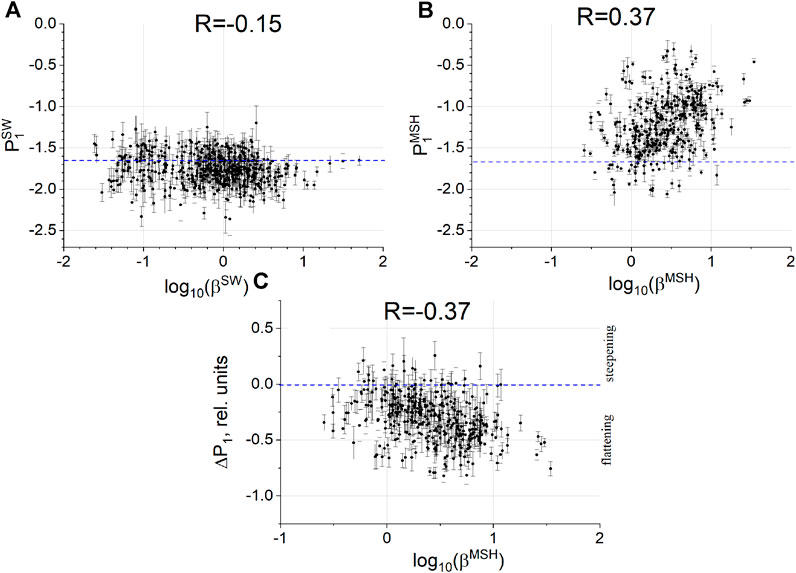
Figure 4. (A) MHD-scale slope in the SW versus SW plasma parameter, (B) MHD-scale slope in the MSH, and (C) change in the MHD-scale slope at the BS as functions of the MSH plasma parameter β_p.

Other plasma and magnetic field parameters are uncorrelated with slope P₁ in the MSH or its changes at the BS.

At the kinetic scales, several clear dependencies occur. Figures 5A–C show a dependence of P₂ in the SW, in the MSH, and the change ΔP₂ on the SW bulk speed. In the SW, the spectra become steeper with increasing speed. In the MSH, there is no clear dependence of the slope on SW bulk speed, but the steepest spectra can usually be found for the slow SW. The change in the slope at the BS is well-correlated with the SW speed. The red line in Figure 5C denotes the mean values of the slope for several equidistant ranges of the bulk speed values. Interestingly, for slow SW, the spectra tend to steepen behind the BS, while for the high-speed SW (V_SW>500 km/s), slight flattening of the spectra occurs behind the BS.

Figure 5

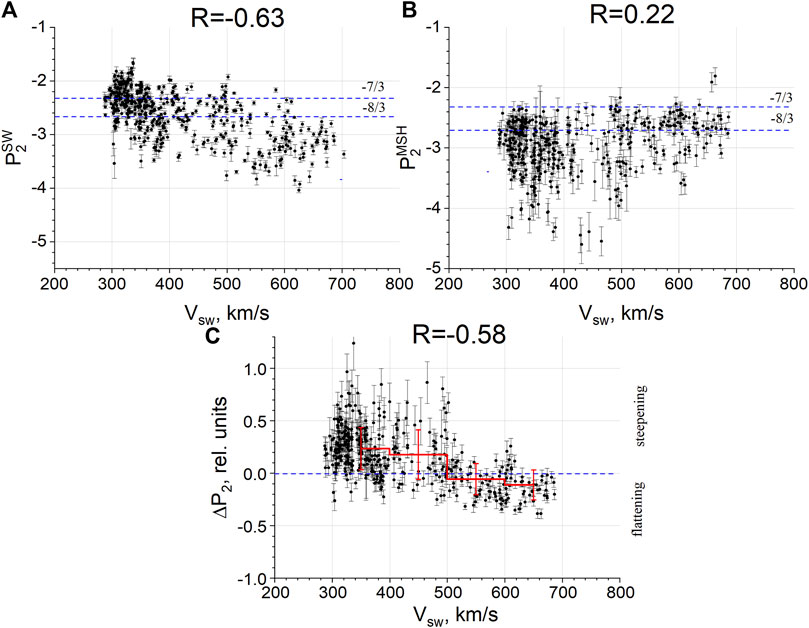
Figure 5. (A) Kinetic-scale slope in the SW, (B) kinetic-scale slope in the MSH, and (C) change in the kinetic-scale slope at the BS as functions of SW speed.

Figure 6A shows the dependence of the kinetic-scale slope in the SW on the SW plasma parameter β_p. Panels (b–c) of Figure 6 present dependencies of the kinetic-scale slope in the MSH and its change at the BS on the MSH plasma parameter β_p. There is no relation between the spectral properties and β_p in the SW, and there is no relation between the change in the slope at the BS and β_p; however, inside the MSH, the spectra are substantially steeper for low-beta plasma. Thus, this dependency can be attributed to processes of the turbulent cascade development inside the MSH, which do not have any relation to the SW or the BS.

Figure 6

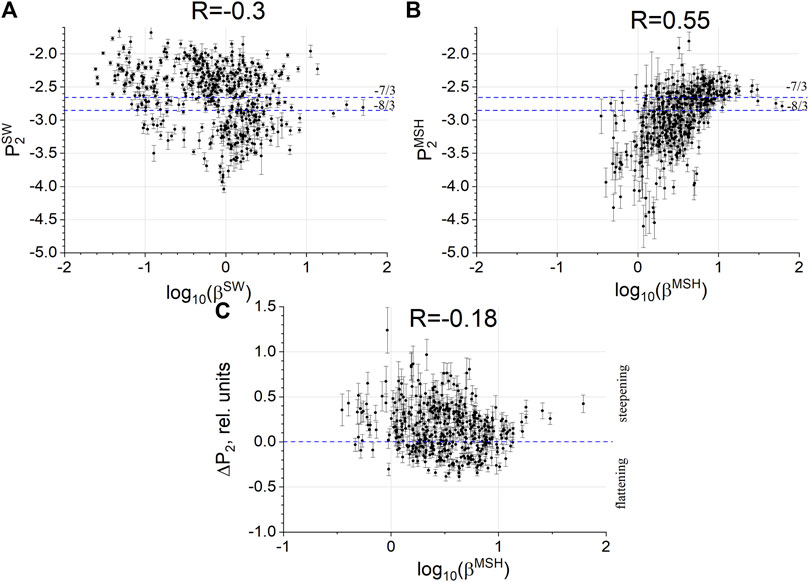
Figure 6. (A) Kinetic-scale slope in the SW versus the SW plasma parameter β_p; (B) kinetic-scale slope in the MSH; and (C) change in the kinetic-scale slope at the BS as functions of the MSH plasma parameter β_p.

Figure 7 and Table 1 show that there is no dependence of slope P₂ in the SW on the temperature anisotropy, and there is no dependence of the change in slope ΔP₂ on the temperature anisotropy, both in the SW and in the MSH. However, significant steepening of spectra occurs in the MSH with the increase in temperature anisotropy. The dependences on temperature anisotropy in the MSH exhibit very similar features to the dependence on β_p.

Figure 7

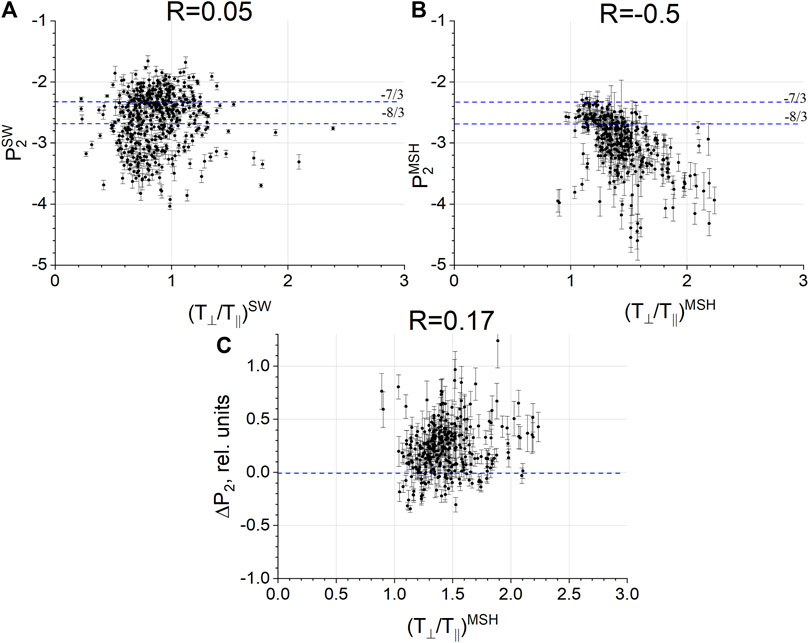
Figure 7. (A) Kinetic-scale slope in the SW versus the SW temperature anisotropy; (B) kinetic-scale slope in the MSH, and (C) change in the kinetic-scale slope at the BS as functions of the MSH temperature anisotropy.

Figure 8 demonstrates the dependence of the kinetic-scale slope on the SW ion temperature in the same manner as Figure 5 . In the SW, the spectra become steeper with the increase in temperature (Figure 8A). On the contrary, in the MSH, the spectra tend to become flatter with increasing SW temperature (Figure 8B). The resulting change in the spectral slopes at the BS is well-correlated to the SW ion temperature (Figure 8C). The most significant steepening of the spectra occurs for SW ion temperatures below 10 eV, while for higher temperatures, the spectra may remain unchanged or slightly flatten at the BS.

Figure 8

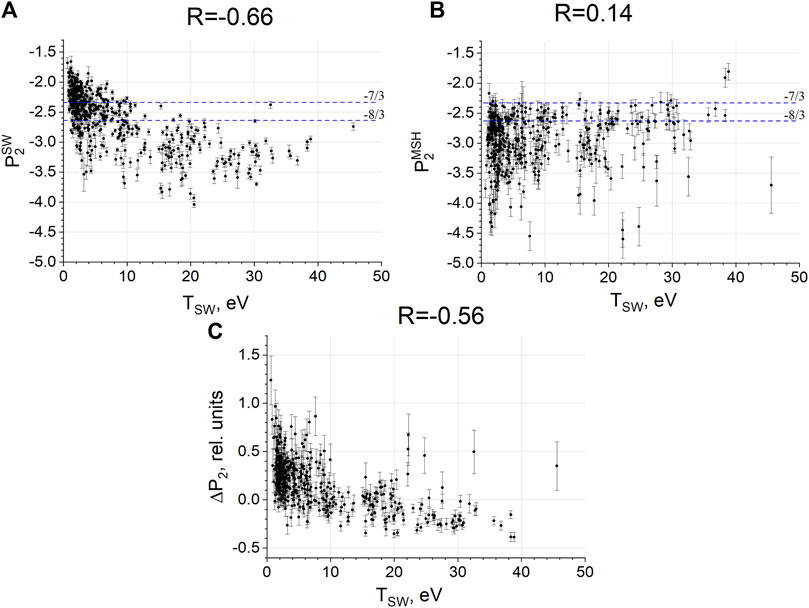
Figure 8. (A) Kinetic-scale slope in the SW; (B) kinetic-scale slope in the MSH; and (C) change in the kinetic-scale slope at the BS versus the SW ion temperature.

5 Discussion

The present study compares the turbulence properties in the SW and downstream of the quasi-perpendicular BS for the simultaneous measurements in these regions. The adopted method implies the consideration of the same plasma in the two regions. Values of the scaling exponents (slopes) P₁ and P₂ and their changes at the BS—ΔP_1,2—are considered at the MHD and kinetic scales, respectively. Note that the considered range of frequencies above the break for most of the cases is attributed to ion scales rather than to well-established sub-ion scales. In other words, the transition or dissipation range of the cascade is observed.

Mean properties of the turbulence both in the SW and in the MSH are consistent with previously published results. Šafránková et al. (2019) presented the mean spectral slopes of the perpendicular component to be −1.63 at the MHD scales and −2.68 at the kinetic scales. The present study considers the spectra of magnetic field vector fluctuations, which are dominated by the perpendicular component in the SW. Thus, the values < P₁^SW>=-1.7 ± 0.2 and <P₂^SW ≥ −2.6 ± 0.4 obtained here are consistent with results obtained by Šafránková et al. (2019). Smith C. W. et al. (2006) showed the statistics of the spectral slopes of Wind magnetic field fluctuation spectra for open magnetic field lines (separately from the magnetic clouds): at the MHD scales < P₁>=−1.63 ± 0.14 and at the kinetic scales < P₂>=-2.61 ± 0.96. The reported values are similar to those shown in the present study. For regions just upstream from the quasi-perpendicular BS, Czaykowska et al. (2001) showed a spectrum f^−1.3 without a break. In the downstream region, the authors showed flattening of the spectrum to f^−1.1 at the frequencies below the break and steepening to f^−2.6 at higher frequencies. Changes in spectral scaling obtained in the present study correspond to the results obtained by Czaykowska et al. (2001), although the scaling in the upstream region is different. This difference may be due to local processes in the SW in the vicinity of the BS, which are out of the scope of the present study. Statistics obtained by Huang et al. (2017) based on cluster data in the MSH showed that the P₁ value ranged from −2.2 to −0.3, with a peak at −1.2 at the MHD scales, which corresponds well to Figure 2B. Furthermore, the value < P₂^MSH>=-3.0 ± 0.4 obtained in the present study corresponds to the statistical results obtained by Huang et al. (2014, 2017) for Cluster data in the MSH. Thus, we conclude that the used approximation methods are suitable and yield reliable results.

A direct comparison of spectral slopes upstream and downstream of the BS shows that there are no direct relations between turbulence properties in these two regions. This may indicate that the cascade ruins at the BS and is then reformed locally. On the other hand, similarity of slopes upstream and downstream of the BS may result either from the conservation of scaling during the BS crossing or from the development of the same slope behind the BS. If the latter is the case, one expects that the MHD and kinetic-scale fluctuations need different times to re-establish the spectrum. The time needed for re-establishment can be estimated as nonlinear time τ_NL = u/dV_u, where u is a scale and dV_u is the velocity fluctuation at the scale u. If the Taylor hypothesis is adopted, then u = V/(2πf), where f is the frequency of the fluctuation. Velocity fluctuation dV_u may be roughly estimated from the power spectrum density (Fourier spectrum) of trace velocity fluctuations at specific frequency f. Typically, the time resolution of THEMIS measurements is not high enough to analyze kinetic scales; however, several examples can be found when the break occurs at frequencies lower than 0.16 Hz (the highest frequency resolved for a velocity fluctuation spectrum). Estimations were prepared for one of such examples. The velocity was V = 103 km/s, and frequency bands 0.01 ± 0.001 Hz and 0.1 ± 0.01 Hz were chosen to estimate τ_NL at MHD and kinetic scales, respectively. Calculations yielded τ_NL = 915 s for MHD scales and τ_NL = 85 s for kinetic scales. At the MHD scales, this time is of the order of 10 min, which is close to the time of plasma propagation from the BS nose to flanks, consistent with observations in Huang et al. (2017). For the kinetic scales, Plank and Gingell (2023) estimated the time that is needed to re-establish the spectrum behind the quasi-perpendicular BS as ∼10 s. Our rough estimations yield τ_NL, which is several times higher. However, for the case considered in the present study, the break frequency is ∼10 times lower than that in the corresponding case studied by Plank and Gingell, (2023), which may cause the difference.

Statistical distributions demonstrate the flattening of the spectra at the MHD scales (Figure 2D): for more than 85% of cases, slope P₁ changes by more than 10% when the plasma crosses the BS. For 14% of cases, the Kolmogorov scaling either survives across the BS or is re-established soon after the BS crossing. Scaling of the spectra in the SW does not depend on plasma parameter β_p at the MHD (as well as at the kinetic) scale, consistent with the basic idea of a cascade of turbulent eddies independent on injection and dissipation mechanisms (Frisch, 1995). The absence of any dependence of the MHD-scale slope on the local plasma parameters in the SW also indicates the universality of the cascade properties. There is a medium correlation (R ∼ −0.4) between changes in the MHD-scale slope and the plasma parameter β_p: for low-beta MSH plasma, P₁ tends to remain unchanged in the MSH, while the most significant flattening occurs during high β_p values in the MSH. The slope in the SW does not depend on β_p, and in the MSH, the spectra at the MHD scales flatten with the increase in β_p with a similar correlation R∼0.4. Thus, this tendency of the slope change across the BS is due to the local MSH processes. The well-known feature of the MSH behind the quasi-perpendicular BS is the temperature anisotropy, which arises at the BS and tends to be resolved by the instability excitation (Lacombe and Belmont, 1995; Schwartz et al., 1996). The type of the instability depends on the background conditions, i.e., plasma parameter β_p: for low β_p, the theory predicts the excitation of Alfvén ion cyclotron (AIC) waves, while for high β_p, the mirror mode waves dominate (see Alexandrova (2008) for a detailed discussion on the topic). The result presented here implies that properties of the alfvénic turbulence survive when plasma crosses the BS, while the observed deviations from the SW scaling are due to a compressive component arising at the BS most of the time. Anderson et al. (1994) also showed the increase in the amplitude of compressive fluctuations in the MSH with β_p. Enhancement of the power of compressive fluctuations in the MSH is a well-known fact (Huang et al., 2017). However, differences in the changes in the properties of compressive and incompressive fluctuations at the BS should be tested more carefully in the future.

At the kinetic scale, for more than 50% of cases, the spectrum steepens behind the BS with slope P₂ changing by more than 10%. In 28% of cases, the spectrum scaling does not change at the kinetic scales. On the other hand, the slope at ion scales needs negligible time (compared to the interval duration) after the BS crossing to restore its shape. The absence of a direct relation between upstream and downstream scaling, together with similar values of the slope in 28% of cases, refers to the quick restoration of turbulence properties behind the BS rather than to survived scaling across the BS. A case study by Rakhmanova et al. (2022) revealed the linear dependence of the kinetic-scale spectral slopes in the MSH and in the SW for a compressive component of fluctuations (i.e., for fluctuations in the magnetic field magnitude). Furthermore, an increase in the MSH density resulted in the clear steepening of the kinetic-scale part of the spectra. However, their result was obtained using limited statistics of disturbed SW. On the other hand, the observed differences between the present study of trace magnetic field fluctuations and a previous study of compressive fluctuations may refer to differences in the changes in turbulence properties at the BS for compressive and incompressive fluctuations. The presence of compressive waves in the MSH favors this conjecture.

Park et al. (2023) presented a statistical comparison of the magnetic field spectral scaling upstream and downstream of the interplanetary shocks of different kinds. The authors demonstrated a clear flattening of the kinetic-scale range of the spectra in the downstream region of the fast reverse shocks compared to those in the upstream region and concluded that this was a result of lower speed in the downstream region. Furthermore, the authors showed Kolmogorov scaling at both sides of the interplanetary shocks. In the case of the BS (which is also a fast reverse shock), the MSH corresponds to a downstream region, and the SW refers to an upstream region. The present study shows opposite effects of BS crossing on the kinetic-scale turbulence—either steepening or no change in the spectra is observed downstream of the BS. Thus, it is the MSH processes rather than the BS dynamics that determine the properties of both MHD and kinetic-scale turbulence in the MSH.

Scaling of the spectra at frequencies above the break in the MSH is highly affected by local plasma parameter β_p and temperature anisotropy: the steepest spectra behind the BS occur for low β_p and high-temperature anisotropy. Note that there are no dependencies of the spectral scaling on local density, temperature, or magnetic field magnitude, only on the combined parameter β_p. The lowest values of β_p are characterized by the spectral slopes P₂∼–4, which is close to the values of the spectral slope in the presence of Alfvén vortices (Alexandrova, 2008). Moreover, low-beta plasma behind the quasi-perpendicular BS is favorable for the Alfvén vortex observation (Alexandrova et al., 2006; Alexandrova and Saur, 2008). Thus, steepening of the spectra with decreasing β_p may be a result of the increasing contribution of the Alfvén vortices to the fluctuations. β_p is typically lower in the SW than in the MSH, and Alfvén vortices may contribute to spectral formation at ion scales all the time (Perrone et al., 2016; 2017). Bowen et al. (2020b) reported that the ion-scale transition range (which is considered in the present study) can be dominated by ion-scale electromagnetic waves associated most probably with local instabilities due to temperature anisotropy. The steeper transition range of the spectra can be attributed to the presence of coherent structures (Lion et al., 2016; Perrone et al., 2016; 2017; Bowen et al., 2020a). Domination of ion-scale electromagnetic waves and coherent structures is the most probable explanation of steepening of the spectra in the MSH in the present study.

Interestingly, the present study does not reveal dependencies of the spectral slopes on the distance from the BS and the magnetopause, while these dependencies have been previously observed (Rakhmanova et al., 2018a; b, Li et al., 2020). On the other hand, Huang et al. (2017) also reported no dependency of the spectral slopes on the distance from the BS. This may be the result of the different durations of intervals under study. Rakhmanova et al. (2018a,b) and Li et al. (2020) considered intervals with durations less than 20 min, and ambient conditions had time to change across the MSH. The results obtained by Huang et al. (2017) refer to 1-h intervals, which is comparable to the period of the subsolar MSH crossing by a spacecraft. In this case, the 1-h interval of dayside MSH measurements may be affected both by the processes at the BS and at the magnetopause. This would result in smoothing of the boundary effect on the turbulence properties. The present study uses nearly 1-h intervals as well; thus, the presence of the BS and the magnetopause may be smoothed in this case.

While scaling of the MSH fluctuations is likely to be influenced by ion-scale instabilities (identified by the slope dependence on the plasma parameter and temperature anisotropy), there is no correlation between these parameters and the change in the slope at the BS. On the other hand, according to Figures 5, 8, changes in the kinetic-scale slope at the BS are influenced by the SW velocity and temperature: small-scale processes embedded to the high-speed and high-temperature plasma are not affected by the BS or are re-established faster behind the BS. Furthermore, the increase in thermal pressure (i.e., increase in temperature) (Smith C. W. et al., 2006; Lacombe et al., 2014; von Panen et al., 2014) is accompanied by the increase in the turbulence level. Thus, for a higher turbulence level in the SW, downstream turbulence development is less affected by ion-scale instabilities.

In the SW plasma, the speed and temperature are physically related. For the analyzed statistics, the correlation coefficient between these two values is close to 0.7, which corresponds well to previous statistical results (Borovsky, 2012; Elliot et al., 2012). Thus, we cannot conclude whether it is the temperature or speed that controls the changes in turbulence properties at the BS or their reformation behind it. However, all of the SW parameters are believed to be intercorrelated and to repeat some patterns corresponding to the SW origin at the Sun (Borovsky, 2018). Moreover, the SW of a different origin is known to have a different effect on the magnetosphere (Yermolaev et al., 2015; Borovsky, 2018). Borovsky (2018) reported that streams characterized by mean proton speed ∼550 km/s and proton temperatures ∼20 eV originate mainly in the coronal holes. The present results show that when the SW streams with similar parameters (see Figure 5C; Figure 8C) face the BS, the properties of the turbulent cascade at the kinetic scales either do not change at the BS or are re-established faster behind it. Borovsky (2018) reported that the interaction of the SW of the coronal-hole origin with the magnetosphere is characterized by an increased dayside reconnection driver. Thus, during this type of the SW flow, the kinetic-scale turbulence of the SW plasma may contribute to the magnetospheric disturbances. Furthermore, Borovsky and Funsen (2003) reported that the enhanced SW turbulence level (which is the case for higher temperatures and velocities) may affect the magnetospheric disturbances. Thereby, it is likely that when the SW from the coronal holes faces the magnetosphere, the SW turbulence may have an enhanced influence on the inner magnetospheric processes.

Note that changes at the BS for low-temperature and low-speed plasma are results of steeper spectra in the MSH, together with flatter spectra in the SW for these cases. In the SW, similar results were reported (Bruno et al., 2014;; Riazantseva et al., 2020). On the contrary, Li et al. (2020) did not find any relations between the turbulence features and the upstream SW speed in the MSH.

6 Summary

Statistics of more than 300 spectral pairs, registered for the same plasma in the SW and in the dayside MSH behind the quasi-perpendicular BS, demonstrates the following trends.

1 There is no clear relation between the spectral slopes in the SW and downstream of the BS; typically, substantial flattening occurs in the MSH at the MHD scales, accompanied by slight steepening at the kinetic scales.

2 The scaling of the dayside MSH spectra matches the scaling in the SW for 12% of cases.

3 The least modified spectra in the dayside MSH occur during periods of high-speed (>500 km/s) and high-temperature (>10 eV) SW flows

4 Modification of the spectra at the MHD scales is more pronounced for high-beta plasma behind the BS; spectra with Kolmogorov scaling are likely to be present in low-beta MSH plasma.

5 Regardless of the scaling of the SW turbulence, in the MSH, substantial steepening of the spectra (the slope values up to −5) occurs when beta decreases and temperature anisotropy increases.

The results show that in 12% of cases, the SW turbulent cascade may survive (or be quickly re-established) during the quasi-perpendicular BS crossing. High-speed and high-temperature SW streams (which are likely to be associated with coronal holes and increased turbulence level) favor the conservation of turbulence properties or their quicker restoration behind the BS. Thus, during the periods of fast SW streams, the SW turbulence may directly affect the inner magnetosphere processes. The association of the periods of unchanged turbulence properties with the streams from coronal holes and their geoefficiency is a subject of future work.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

LR: conceptualization, formal analysis, investigation, methodology, visualization, and writing–original draft. AK: data curation, software, and writing–original draft. MR: supervision and writing–review and editing. YY: supervision and writing–review and editing. GZ: conceptualization, supervision, and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The work was supported by the Russian Science Foundation, grant 22-72-00105.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alexandrova, O. (2008). Solar wind vs magnetosheath turbulence and Alfvén vortices. Nonlinear Process. Geophys. Nonlinear process. geophys. 15, 95–108. doi:10.5194/npg-15-95-2008

CrossRef Full Text | Google Scholar

Alexandrova, O., Chen, C. H. K., Sorriso-Valvo, L., Horbury, T. S., and Bale, S. D. (2013). Solar wind turbulence and the role of ion instabilities. Space Sci. Rev. 178, 101–139. doi:10.1007/s11214-013-0004-8

CrossRef Full Text | Google Scholar

Alexandrova, O., Jagarlamudi, V. K., Hellinger, P., Maksimovic, M., Shprits, Y., and Mangeney, A. (2021). Spectrum of kinetic plasma turbulence at 0.3–0.9 astronomical units from the Sun. Phys. Rev. E. 103, 063202. doi:10.1103/PhysRevE.103.063202

PubMed Abstract | CrossRef Full Text | Google Scholar

Alexandrova, O., Mangeney, A., Maksimovic, M., Cornilleau-Wehrlin, N., Bosqued, J.-M., and André, M. (2006). Alfvén vortex filaments observed in magnetosheath downstream of a quasi-perpendicular bow shock. J. Geophys. Res. 111, A12208. doi:10.1029/2006ja011934

CrossRef Full Text | Google Scholar

Alexandrova, O., and Saur, J. (2008). Alfvén vortices in Saturn's magnetosheath: cassini observations. Geophys. Res. Lett. 35, L15102. doi:10.1029/2008GL034411

CrossRef Full Text | Google Scholar

Alexandrova, O., Saur, J., Lacombe, C., Mangeney, A., Mitchell, J., Schwartz, S. J., et al. (2009). Universality of solar-wind turbulent spectrum from MHD to electron scales. Phys. Rev. Lett. 103, 165003. doi:10.1103/physrevlett.103.165003

PubMed Abstract | CrossRef Full Text | Google Scholar

Anderson, B. J., Fuselier, S. A., Gary, S. P., and Denton, R. E. (1994). Magnetic spectral signatures in the Earth’s magnetosheath and plasma depletion layer. J. Geophys. Res. 99, 5877–5891. doi:10.1029/93JA02827

CrossRef Full Text | Google Scholar

Angelopoulos, V. (2008). The THEMIS mission. Space Sci. Rev. 141, 5–34. doi:10.1007/s11214-008-9336-1

CrossRef Full Text | Google Scholar

Auster, H. U., Glassmeier, K. H., Magnes, W., Aydogar, O., Baumjohann, W., Constantinescu, D., et al. (2008). The THEMIS fluxgate magnetometer. Space Sci. Rev. 141, 235–264. doi:10.1007/s11214-008-9365-9

CrossRef Full Text | Google Scholar

Boldyrev, S., and Perez, J. C. (2012). Spectrum of kinetic alfven turbulence. Astrophys. J. Lett. 758 (2), L44. doi:10.1088/2041-8205/758/2/L44

CrossRef Full Text | Google Scholar

Borovsky, J. E. (2012). The velocity and magnetic field fluctuations of the solar wind at 1 AU: statistical analysis of Fourier spectra and correlations with plasma properties. J. Geophys. Res. 117, A05104. doi:10.1029/2011JA017499

CrossRef Full Text | Google Scholar

Borovsky, J. E. (2018). On the origins of the intercorrelations between solar wind variables. J. Geophys. Res. Space Phys. 123, 20–29. doi:10.1002/2017JA024650

CrossRef Full Text | Google Scholar

Borovsky, J. E., and Funsten, H. O. (2003). Role of solar wind turbulence in the coupling of the solar wind to the Earth’s magnetosphere. J. Geophys. Res. 108, 1246. doi:10.1029/2002JA009601

CrossRef Full Text | Google Scholar

Bowen, T. A., Mallet, A., Bale, S. D., Bonnell, J. W., Case, A. W., Chandran, B. D. G., et al. (2020a). Constraining ion-scale heating and spectral energy transfer in observations of plasma turbulence. Phys. Rev. Lett. 125, 025102. doi:10.1103/PhysRevLett.125.025102

PubMed Abstract | CrossRef Full Text | Google Scholar

Bowen, T. A., Mallet, A., Huang, J., Klein, K. G., Malaspina, D. M., Stevens, M., et al. (2020b). Ion-scale electromagnetic waves in the inner heliosphere. Astrophys. J. Suppl. 246, 66. doi:10.3847/1538-4365/ab6c65

CrossRef Full Text | Google Scholar

Breuillard, H., Le Contel, O., Chust, T., Berthomier, M., Retino, A., Turner, D. L., et al. (2018a). The properties of lion roars and electron dynamics in mirror mode waves observed by the Magnetospheric MultiScale mission. J. Geophys. Res. Space Phys. 123, 93–103. doi:10.1002/2017JA024551

CrossRef Full Text | Google Scholar

Breuillard, H., Matteini, L., Argall, M. R., Sahraoui, F., Andriopoulou, M., Contel, O.Le, et al. (2018b). New insights into the nature of turbulence in the Earth’s magnetosheath using magnetospheric MultiScale mission data. Astrophys. J. 859, 127. doi:10.3847/1538-4357/aabae8

CrossRef Full Text | Google Scholar

Bruno, R., and Carbone, V. (2013). The solar wind as a turbulence laboratory. Living Rev. Sol. Phys. 10. doi:10.12942/lrsp-2013-2

CrossRef Full Text | Google Scholar

Bruno, R., Trenchi, L., and Telloni, D. (2014). Spectral slope variation at proton scales from fast to slow solar wind. Astrophys. J. Lett. 793 (5pp), L15. doi:10.1088/2041-8205/793/1/L15

CrossRef Full Text | Google Scholar

Burton, R. K., McPherron, R. L., and Russell, C. T. (1975). An empirical relationship between interplanetary conditions and Dst. J. Geophys. Res. 80, 4204–4214. doi:10.1029/ja080i031p04204

CrossRef Full Text | Google Scholar

Chen, C. H., Leung, L., Boldyrev, S., Maruca, B. A., and Bale, S. D. (2014). Ion-scale spectral break of solar wind turbulence at high and low beta. Geophys. Res. Lett. 41, 8081–8088. doi:10.1002/2014GL062009

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, C. H. K., Mallet, A., Yousef, T. A., Schekochihin, A. A., and Horbury, T. S. (2011). Anisotropy of Alfvénic turbulence in the solar wind and numerical simulations. Mon. Notices R. Astronomical Soc. 415 (4), 3219–3226. doi:10.1111/j.1365-2966.2011.18933.x

CrossRef Full Text | Google Scholar

Coleman, P. J. J. (1968). Turbulence, viscosity and dissipation in the solar wind plasma. Astrophys. J. 153, 371–388. doi:10.1086/149674

CrossRef Full Text | Google Scholar

Czaykowska, A., Bauer, T. M., Treumann, R. A., and Baumjohann, W. (2001). Magnetic field fluctuations across the Earth’s bow shock. Ann. Geophys. 19, 275–287. doi:10.5194/angeo-19-275-2001

CrossRef Full Text | Google Scholar

D’Amicis, R., Bruno, R., and Bavassano, B. (2007). Is geomagnetic activity driven by solar wind turbulence? Geophys Res. Lett. 34, L05108. doi:10.1029/2006GL028896

CrossRef Full Text | Google Scholar

D’Amicis, R., Telloni, D., and Bruno, R. (2020). The effect of solar-wind turbulence on magnetospheric activity. Front. Phys. 8, 604857. doi:10.3389/fphy.2020.604857

CrossRef Full Text | Google Scholar

Dmitriev, A. V., Lalchand, B., and Ghosh, S. (2021). Mechanisms and evolution of geoeffective large-scale plasma jets in the magnetosheath. Universe 7, 152. doi:10.3390/universe7050152

CrossRef Full Text | Google Scholar

Duan, D., He, J., Bowen, T. A., Woodham, L. D., Wang, T., Chen, C. H. K., et al. (2021). Anisotropy of solar wind turbulence in the inner heliosphere at kinetic scales: PSP observations. Astrophys. J. Lett. 915, L8. doi:10.3847/2041-8213/ac07ac

CrossRef Full Text | Google Scholar

Elliott, H. A., Henney, C. J., McComas, D. J., Smith, C. W., and Vasquez, B. J. (2012). Temporal and radial variation of the solar wind temperaturespeed relationship. J. Geophys. Res. 117, A09102. doi:10.1029/2011JA017125

CrossRef Full Text | Google Scholar

Frisch, U. (1995). Turbulence : the legacy of A.N. Kolmogorov. doi:10.1017/S0022112096210791

CrossRef Full Text | Google Scholar

Gutynska, O., Šimůnek, J., Šafránková, J., Němeček, Z., and Přech, L. (2012). Multipoint study of magnetosheath magnetic field fluctuations and their relation to the foreshock. J. Geophys. Res. 117, A04214. doi:10.1029/2011JA017240

CrossRef Full Text | Google Scholar

Horbury, T. S., Forman, M., and Oughton, S. (2008). Anisotropic scaling of magnetohydrodynamic turbulence. Phys. Rev. Lett. 101, 175005. doi:10.1103/PhysRevLett.101.175005

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, S. Y., Hadid, L. Z., Sahraoui, F., Yuan, Z. G., and Deng, X. H. (2017). On the existence of the Kolmogorov inertial range in the terrestrial magnetosheath turbulence. Astrophys. J. Lett. 836, L10. doi:10.3847/2041-8213/836/1/L10

CrossRef Full Text | Google Scholar

Huang, S. Y., Sahraoui, F., Deng, X. H., He, J. S., Yuan, Z. G., Zhou, M., et al. (2014). Kinetic turbulence in the terrestrial magnetosheath: Cluster observations. Astrophys. J. 789, L28. doi:10.1088/2041-8205/789/2/L28

CrossRef Full Text | Google Scholar

Huang, S. Y., Sahraoui, F., Retino, A., Le Contel, O., Yuan, Z. G., Chasapis, A., et al. (2016). MMS observations of ion-scale magnetic island in the magnetosheath turbulent plasma. Geophys. Res. Lett. 43, 7850–7858. doi:10.1002/2016GL070033

CrossRef Full Text | Google Scholar

Jankovicova, D., Voros, Z., and Simkanin, J. (2008). The influence of solar wind turbulence on geomagnetic activity. Nonlinear Process Geophys 15, 53–59. doi:10.5194/npg-15-53-2008

CrossRef Full Text | Google Scholar

Klein, K. G., Howes, G. G., and Tenbarge, J. M. (2014). The violation of the taylor hypothesis in measurements of solar wind turbulence. Astrophys. J. Lett. 790, 20. doi:10.1088/2041-8205/790/2/L20

CrossRef Full Text | Google Scholar

Lacombe, C., Alexandrova, O., Matteini, L., Santolík, O., Cornilleau-Wehrlin, N., Mangeney, A., et al. (2014). Whistler mode waves and the electron heat flux in the solar wind: Cluster observations. Astrophys. J. 796, 5. doi:10.1088/0004-637X/796/1/5

CrossRef Full Text | Google Scholar

Lacombe, C., and Belmont, G. (1995). Waves in the Earth’s magnetosheath: observations and interpretations. Adv. Space Res. 15, 329–340. doi:10.1016/0273-1177(94)00113-F

CrossRef Full Text | Google Scholar

Lacombe, C., Samsonov, A. A., Mangeney, A., Maksimovic, M., Cornilleau-Wehrlin, N., Harvey, C., et al. (2006). Cluster observations in the magnetosheath – Part 2: intensity of the turbulence at electron scales. Ann. Geophys. 24, 3523–3531. doi:10.5194/angeo-24-3523-2006

CrossRef Full Text | Google Scholar

Lepping, R. P., Acuña, M. H., Burlaga, L. F., Farrell, W. M., Slavin, J. A., Schtten, K. H., et al. (1995). The WIND magnetic field investigation. Space Sci. Rev. 71, 207–229. doi:10.1007/bf00751330

CrossRef Full Text | Google Scholar

Li, H., Jiang, W., Wang, C., Verscharen, D., Zeng, C., Russell, C. T., et al. (2020). Evolution of the Earth’s magnetosheath turbulence: a statistical study based on mms observations. Astrophys. J. 898, L43. doi:10.3847/2041-8213/aba531

CrossRef Full Text | Google Scholar

Lion, S., Alexandrova, O., and Zaslavsky, A. (2016). Coherent events and spectral shape at ion kinetic scales in the fast solar wind turbulence. Astrophys. J. 824, 47. doi:10.3847/0004-637X/824/1/47

CrossRef Full Text | Google Scholar

McFadden, J. P., Carlson, C. W., Larson, D., Ludlam, M., Abiad, R., Elliott, B., et al. (2008). The THEMIS ESA plasma instrument and in-flight calibration. Space Sci. Rev. 141, 277–302. doi:10.1007/s11214-008-9440-2

CrossRef Full Text | Google Scholar

Ogilvie, K. W., Chornay, D. J., Fritzenreiter, R. J., Hunsaker, F., Keller, J., Lobel, J., et al. (1995). SWE, a comprehensive plasma instrument for the WIND spacecraft. Space Sci. Rev. 71, 55–77. doi:10.1007/bf00751326

CrossRef Full Text | Google Scholar

Park, B., Pitňa, A., Šafránková, J., Němeček, Z., Krupařová, O., Krupař, V., et al. (2023). Change of spectral properties of magnetic field fluctuations across different types of interplanetary shocks. Astrophys. J. Lett. 954, L51. doi:10.3847/2041-8213/acf4ff

CrossRef Full Text | Google Scholar

Perrone, D., Alexandrova, O., Mangeney, A., Maksimovic, M., Lacombe, C., Rakoto, V., et al. (2016). Compressive coherent structures at ion scales in the slow solar wind. Astrophys. J. 826, 196. doi:10.3847/0004-637X/826/2/196

CrossRef Full Text | Google Scholar

Perrone, D., Alexandrova, O., Roberts, O. W., Lion, S., Lacombe, C., Walsh, A., et al. (2017). Coherent structures at ion scales in fast solar wind: cluster observations. Astrophys. J. 849 (1), 49. doi:10.3847/1538-4357/aa9022

CrossRef Full Text | Google Scholar

Plank, J., and Gingell, I. L. (2023). Intermittency at Earth's bow shock: measures of turbulence in quasi-parallel and quasi-perpendicular shocks. Phys. Plasmas 30, 082906. doi:10.1063/5.0160439

CrossRef Full Text | Google Scholar

Plaschke, F., Hietala, H., Blanco-Cano, X., Kajdič, P., Karlsson, T., Sibeck, D., et al. (2018). Jets downstream of collisionless shocks. Space Sci. Rev. 214 (5), 81. doi:10.1007/s11214-018-0516-3

CrossRef Full Text | Google Scholar

Rakhmanova, L., Riazantseva, M., and Zastenker, G. (2021). Plasma and magnetic field turbulence in the Earth’s magnetosheath at ion scales. Front. Astron. Space Sci. 7, 616635. doi:10.3389/fspas.2020.616635

CrossRef Full Text | Google Scholar

Rakhmanova, L., Riazantseva, M., Zastenker, G., and Verigin, M. (2018a). Kinetic scale ion flux fluctuations behind the quasi-parallel and quasi-perpendicular bow shock. J. Geophys. Res. Space Phys. 123, 5300–5314. doi:10.1029/2018JA025179

CrossRef Full Text | Google Scholar

Rakhmanova, L., Riazantseva, M., and Zastenker, G. (2016). Plasma fluctuations at the flanks of the Earth’s magnetosheath at ion kinetic scales. Ann. Geophys. 34, 1011–1018. doi:10.5194/angeo-34-1011-2016

CrossRef Full Text | Google Scholar

Rakhmanova, L., Riazantseva, M., Zastenker, G., and Yermolaev, Y. (2022). Large-scale solar wind phenomena affecting the turbulent cascade evolution behind the quasi-perpendicular bow shock. Universe 8 (12), 611. doi:10.3390/universe8120611

CrossRef Full Text | Google Scholar

Rakhmanova, L. S., Riazantseva, M. O., Zastenker, G. N., and Verigin, M. I. (2018b). Effect of the magnetopause and bow shock on characteristics of plasma turbulence in the Earth’s magnetosheath. Geomagn. Aeron. 58, 718–727. doi:10.1134/S0016793218060129

CrossRef Full Text | Google Scholar

Rakhmanova, L. S., Riazantseva, M. O., Zastenker, G. N., Yermolaev, Y. I., Lodkina, I. G., and Chesalin, L. S. (2020). Turbulent cascade in the magnetosheath affected by the solar wind’s plasma turbulence. Cosm. Res. 57, 443–450. doi:10.1134/S0010952519060066

CrossRef Full Text | Google Scholar

Riazantseva, M. O., Rakhmanova, L. S., Zastenker, G. N., Yermolaev, Yu. I., Lodkina, I. G., and Chesalin, L. S. (2019). Small-Scale Plasma Fluctuations in Fast and Slow Solar Wind Streams. Cosmic Res. 57, 434–442. doi:10.1134/S0010952519060078

CrossRef Full Text | Google Scholar

Russell, C. T., McPherron, R. L., and Burton, R. K. (1974). On the cause of geomagnetic storms. J. Geophys. Res. 79, 1105–1109. doi:10.1029/ja079i007p01105

CrossRef Full Text | Google Scholar

Šafránková, J., Němeček, Z., Němec, F., Přech, L., Pitňa, A., Chen, C. H. K., et al. (2015). Solar wind density spectra around the ion spectral break. Astrophys. J. 803, 107. doi:10.1088/0004-637X/803/2/107

CrossRef Full Text | Google Scholar

Šafránková, J., Němeček, Z., Němec, F., Verscharen, D., Chen, C. H. K., Ďurovcová, T., et al. (2019). Scale-dependent polarization of solar wind velocity fluctuations at the inertial and kinetic scales. Astrophys. J. 870, 40. doi:10.3847/1538-4357/aaf239

CrossRef Full Text | Google Scholar

Sahraoui, F., Goldstein, M. L., Belmont, G., Canu, P., and Rezeau, L. (2010). Three dimensional anisotropic k spectra of turbulence at subproton scales in the solar wind phys. Rev. Lett. 105, 131101. doi:10.1103/PhysRevLett.105.131101

PubMed Abstract | CrossRef Full Text | Google Scholar

Sahraoui, F., Goldstein, M. L., Robert, P., and Khotyaintsev, Yu. (2009). Evidence of a cascade and dissipation of solar-wind turbulence at the electron gyroscale. Phys. Rev. Lett. 102, 231102. doi:10.1103/physrevlett.102.231102

PubMed Abstract | CrossRef Full Text | Google Scholar

Sahraoui, F., Hadid, L., and Huang, S. (2020). Magnetohydrodynamic and kinetic scale turbulence in the near-Earth space plasmas: a (short) biased review. Rev. Mod. Phys. 4, 4. doi:10.1007/s41614-020-0040-2

CrossRef Full Text | Google Scholar

Sahraoui, F., Huang, S. Y., Belmont, G., Goldstein, M. L., Rétino, A., Robert, P., et al. (2013). Scaling of the electron dissipation range of solar wind turbulence. Astrophys. J. 777, 15. doi:10.1088/0004-637x/777/1/15

CrossRef Full Text | Google Scholar

Schwartz, S. J., Burgess, D., and Moses, J. J. (1996). Low-frequency waves in the Earth’s magnetosheath: present status. Ann. Geophys. 14, 1134–1150. doi:10.1007/s00585-996-1134-z

CrossRef Full Text | Google Scholar

Shevyrev, N. N., and Zastenker, G. N. (2005). Some features of the plasma flow in the magnetosheath behind quasi-parallel and quasi-perpendicular bow shocks. Planet. Space Sci. 53, 95–102. doi:10.1016/j.pss.2004.09.033

CrossRef Full Text | Google Scholar

Shue, J.-H., Chao, J. K., Fu, H. C., Khurana, K. K., Zastenker, G., et al. (1998). Magnetopause location under extreme solar wind conditions. J. Geophys. Res. V. 103 (№ A8), 17691–17700. doi:10.1029/98JA01103

CrossRef Full Text | Google Scholar

Smith, C., Hamilton, K., Vasquez, B., and Leamon, R. (2006). Dependence of the dissipation range spectrum of interplanetary magnetic fluctuations on the rate of energy cascade. Astrophys. J. 645, L85–L88. doi:10.1086/506151

CrossRef Full Text | Google Scholar

Smith, C. W., Vasquez, B. J., and Hamilton, K. (2006b). Interplanetary magnetic fluctuation anisotropy in the inertial range. J. Geophys. Res. Space Phys. 111, 9111. doi:10.1029/2006JA011651

CrossRef Full Text | Google Scholar

Song, P., and Russell, C. T. (1997). What do we really know about the magnetosheath? Adv. Space Res. 20 (4–5), 747–765. doi:10.1016/S0273-1177(97)00466-3

CrossRef Full Text | Google Scholar

Spreiter, J. R., Summers, A. L., and Alksne, A. Y. (1966). Hydromagnetic flow around the magnetosphere. Planet. Space Sci. 14, 223–253. doi:10.1016/0032-0633(66)90124-3

CrossRef Full Text | Google Scholar

Verigin, M. I., Kotova, G. A., Slavin, J., Szabo, A., Kessel, M., Safrankova, J., et al. (2001). Analysis of the 3-D shape of the terrestrial bow shock by Interball/Magion 4 observations. Adv. Space Res. 28, 857–862. doi:10.1016/S0273-1177(01)00502-6

CrossRef Full Text | Google Scholar

Verigin, M. I., Tátrallyay, M., Erdős, G., and Kotova, G. A. (2006). Magnetosheath interplanetary medium reference frame: application for a statistical study of mirror type waves in the terrestrial plasma environment. Adv. Space Res. 37, 515–521. doi:10.1016/j.asr.2005.03.042

CrossRef Full Text | Google Scholar

von Papen, M., Saur, J., and Alexandrova, O. (2014). Turbulent magnetic field fluctuations in Saturn’s magnetosphere. J. Geophys. Res. Space Phys. 119, 2797–2818. doi:10.1002/2013JA019542

CrossRef Full Text | Google Scholar

Vörös, Z., Jankovicova, D., and Kovacs, P. (2002). Scaling and singularity characteristics of solar wind and magnetospheric fluctuations. Nonlinear Process Geophys 9, 149–162. doi:10.5194/npg-9-149-2002

CrossRef Full Text | Google Scholar

Vörös, Z., Roberts, O. W., Yordanova, E., Sorriso-Valvo, L., Nakamura, R., Narita, Y., et al. (2023). How to improve our understanding of solar wind-magnetosphere interactions on the basis of the statistical evaluation of the energy budget in the magnetosheath? Front. Astron. Space Sci. 10, 1163139. doi:10.3389/fspas.2023.1163139

CrossRef Full Text | Google Scholar

Woodham, L. D., Wicks, R. T., Verscharen, D., and Owen, C. J. (2018). The role of proton cyclotron resonance as a dissipation mechanism in solar wind turbulence: a statistical study at ion-kinetic scales. Astrophys. J. 856, 49. doi:10.3847/1538-4357/aab03d

CrossRef Full Text | Google Scholar

Yermolaev, Y. I., Lodkina, I. G., Nikolaeva, N. S., and Yermolaev, M. Y. (2015). Dynamics of large-scale solar-wind streams obtained by the double superposed epoch analysis. J. Geophys. Res. Space Phys. 120, 7094–7106. doi:10.1002/2015JA021274

CrossRef Full Text | Google Scholar

Yordanova, E., Vörös, Z., Raptis, S., and Karlsson, T. (2020). Current sheet statistics in the magnetosheath. Front. Astron. Sp. Sci. 7, 2. doi:10.3389/fspas.2020.00002

CrossRef Full Text | Google Scholar

Zimbardo, G., Greco, A., Sorriso-Valvo, L., Perri, S., Vörös, Z., Aburjania, G., et al. (2010). Magnetic turbulence in the geospace environment. Space Sci. Rev. 156, 89–134. doi:10.1007/s11214-010-9692-5

CrossRef Full Text | Google Scholar