The unsolved problem of solar-wind turbulence

Smith, Charles W.; Vasquez, Bernard J.

doi:10.3389/fspas.2024.1371058

REVIEW article

Front. Astron. Space Sci., 17 May 2024

Sec. Space Physics

Volume 11 - 2024 | https://doi.org/10.3389/fspas.2024.1371058

This article is part of the Research Topic Editor’s Challenge in Space Physics: Solved and Unsolved Problems in Space Physics View all 18 articles

The unsolved problem of solar-wind turbulence

Charles W. Smith*

Bernard J. Vasquez

Physics Department and Space Science Center, University of New Hampshire, Durham, NH, United States

The solar wind forms the largest wind tunnel for plasma and magnetofluid turbulence that is accessible to Earth. It evolves from what is thought to be a turbulent source that continues to drive nonlinear turbulent dynamics as it expands outward via large-scale, energy-containing wind shear and shocks. In the outer heliosphere, once the gradients in the flow have coalesced and they no longer provide an adequate source for the turbulence, the excitation of wave energy by the injection of interstellar pickup ions becomes the dominant source of energy that continues to drive the turbulence. While there are established formalisms for the determination of the strength of the turbulence and the evolution of the turbulent spectra is well-established, the actual nonlinear dynamics that are responsible for its formation and evolution remain unresolved and the subject of considerable debate. We examine the evidence and attempt to illuminate the various theories while demonstrating what is needed to resolve the debates and bring the subject of plasma turbulence into a new level of understanding.

1 Introduction

Many of the ideas developed here are discussed in other reviews on the subject (Smith, 2009; Matthaeus and Velli, 2011; Bruno and Carbone, 2013; 2016; Smith and Vasquez, 2021). The wealth of interplanetary magnetic field (IMF) and thermal particle measurements from many missions within the solar wind (Maruka et al., 2023) have shown that the spectra of the fluctuations form repeatable, universal observations that extend from the acceleration region near the Sun (Bandyopadhyay et al., 2020; Réville et al., 2020; Chhiber et al., 2021; Magyer and van Doorsselaere, 2022; Davis et al., 2023) and into the outer heliosphere (Matthaeus and Goldstein, 1982; Roberts et al., 1987a; Roberts et al., 1987b; Pine et al., 2020b). There is even evidence that the dynamics responsible for these observations extend into interstellar space (Armstrong et al., 1981; Spangler, 2009) and represent universal laws of plasma turbulence. One would think that with a wealth of observations spanning almost 60 years of space exploration by robotic spacecraft that possess the types of instruments that are required to document turbulent behavior, these dynamics would be well understood. However, that expectation is incorrect for a very simple reason–the dynamics are fundamentally multidimensional in character meaning that the spatial dependence of measurements must be known in all three dimensions (3D) while virtually all measurements in the solar wind are inherently one dimensional (1D). As a result, it is impossible to uncover the underlying nonlinear dynamics using a single spacecraft. This limitation has resulted in numerous conflicting interpretations of the observations and their possible underlying dynamics without obtaining definitive, objective measurements that can resolve the debate.

There are numerous space physics problems that depend in a fundamental way on a better understanding of the turbulent dynamics. One well-resolved observation is that the solar wind thermal plasma expands nonadiabatically and is heated in situ by some process (Smith et al., 2001). The multiple theories of solar wind turbulence have been able to reproduce the observed heating rates to greater and lesser degrees, depending on the theory, and it now seems established that turbulent dynamics are responsible for heating the solar wind plasma.

A second example of turbulence playing a fundamental role in understanding heliospheric dynamics is in energetic charged particle (cosmic ray) propagation (Bieber et al., 1994; Bieber et al., 1996; Matthaeus et al., 2003). Perhaps the best-known publication on charged particle propagation is based on resonant scattering by Alfvénic fluctuations (transverse fluctuations with a strong correlation between the magnetic and velocity fluctuations and reduced density compressions) often characterized as parallel-propagating Alfvén waves (Jokipii, 1966). The assumption often made in cosmic-ray scattering theories is that an energetic particle streams along the magnetic field faster than the fluctuations evolve and is scattered by the magnetic fluctuations at scales comparable to the distance traveled by the particle in one gyration and smaller. However, when the pitch angle (the angle formed by the particle motion and the mean magnetic field directions) approaches 90°, that assumption is violated and the scattering stalls. It then becomes necessary to include wave propagation with Alfvén waves propagating both Sunward and anti-Sunward. When the existence of a steepened dissipation-range spectrum discussed below is recognized, scattering through 90° pitch angle is again defeated and it is only with some form of turbulent decorrelation that particles successfully scatter through 90°. Numerous authors have attempted to overcome that problem by higher order calculations, but this does not remove the misordering of the theory. It is now believed that much of the fluctuation energy resides in wave vectors that are approximately perpendicular to the mean magnetic field, that this arises naturally through the turbulent dynamics, and that scattering is accomplished through some form of turbulent field line evolution that is not yet well understood.

A different view of particle scattering and propagation focuses on the field-line wandering that occurs in a turbulent magnetofluid (Matthaeus et al., 2003). In this instance, field lines separate ergodically and carry the charged particles with them to produce a spatial distribution of particles that may not require complete scattering.

We present here an overview of solar wind turbulence as the field exists today. This is not an exhaustive review of the literature. Rather, it is an attempt to explain the status and fundamental questions of the field. We present a brief review of the early observations and conclusions that have given way to more recent reinterpretations and show why those reinterpretations are needed. We will show that some form of universal nonlinear dynamics is required to explain the observations, and we will explain why those dynamics are unresolved today. It is possible, even likely, that no single dynamical model can describe all observations and that the best view of solar wind turbulence may be that of competing nonlinear dynamics. In the process, we will explain how this subject dovetails with the related investigations of cosmic ray scattering and propagation, shock acceleration, and reconnection. This makes the required multidimensional measurements all the more compelling.

2 Early measurements

One of the early surprises of the space age was the existence of a planetary bow shock (Freeman et al., 1963; Ness et al., 1964) supported by a collisionless supersonic gas of electrically charged particles (Neugebauer and Snyder, 1962). Conventional theory at the time held that a collisionless gas could not provide the abrupt transition required for shock formation. Magnetohydrodynamics (MHD) had already been developed to describe the magnetic properties of an electrically conducting fluid, but at that point it was widely assumed to apply only to collisional fluids such as liquid metals. The paradigm shift of the early space age was the recognition that the solar magnetic field embedded within the solar wind acts to form fluid elements that limit penetration of the collisionless gas across field lines forming nonpenetrating plasma volumes that interact in a fluid-like manner and provides a form of collision between fluid elements. This opened the door to understanding a wide range of solar wind dynamics including shocks, stream interfaces, and rarefactions as well as the ubiquitous fluctuations that permeate space.

Early attempts to apply both MHD and collisionless plasma theory to the observed fluctuations in the magnetic field and thermal ion distributions relied heavily on the limited number of characteristics that could be resolved using single spacecraft observations such as anisotropy and cross-field correlations. It is not possible to objectively resolve time-dependent behavior such as wave propagation using single-spacecraft measurements, nor multi-dimensional structure. For this reason, interpretation of the observations of solar wind fluctuations, which are ubiquitous, were subject to fundamental assumptions and remain that way to this day.

Solar wind turbulence displays many interesting characteristics that fuel the investigations both from the viewpoint of basic physics as well as the linkage between turbulence and other questions of interest. It is a generally accepted paradigm within plasma turbulence studies that solar wind turbulence observations span a broad range of spatial and temporal scales. Figure 1 shows a typical day of IMF data recorded by the Advanced Composition Explorer (ACE) spacecraft. The data is shown in (R, T, N) coordinates where $\hat{R}$ is directed from the Sun to the point of observations, $\hat{T}$ is coplanar with the Sun’s rotational equator and directed in the sense of rotations, and $\hat{N} = \hat{R} \times \hat{T}$ . The dashed lines represent the nominal direction of the IMF spiral (Parker, 1963). The variation in the field magnitude B is much less than the variation in the vector components.

Figure 1

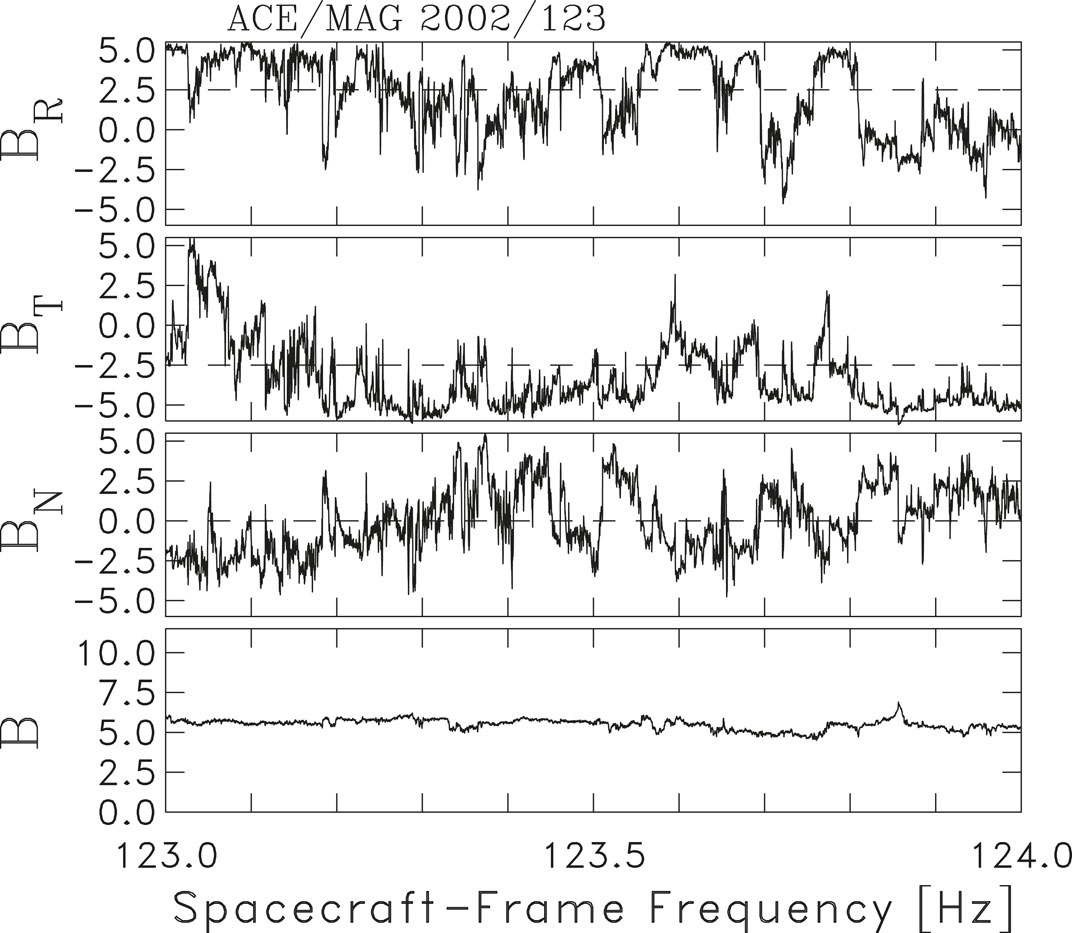
Figure 1. Plot of magnetic field data in heliocentric RTN coordinates obtained by the ACE/MAG instrument for DOY 123 of Year 2002. This is a fairly typical example of the IMF apart from ejecta and stream interfaces and we will return to it below. The nominal Parker spiral direction is given by dashed lines. Note that the field magnitude is far more constant than the individual components.

The majority of studies involve the collision-like fluid scales supported by ion dynamics in interaction with the ambient magnetic field. There is a growing focus on scales where the fluid approximation breaks down and dissipation sets in (Behannon, 1975; Denskat et al., 1983; Smith et al., 1990; Goldstein et al., 1994; Leamon et al., 1998a; Leamon et al., 1999; Leamon et al., 2000; Pine et al., 2020a). It is thought that dissipation occurs through a variety of resonant and nonresonant plasma dynamics that are describable by the Maxwell-Vlasov equations. Most recently, evidence has been presented of nonlinear dynamics at the smaller electron scales leading to reproducible observations that are thought to participate in the transport of energy to electron dissipation scales (Alexandrova et al., 2009).

3 Early theories

Due to a lack of the multi-dimensional measurements that are required to resolve the local dynamics, there continue to be debates on the relevant nonlinear processes that describe solar wind fluctuations. In early theories the fluctuations were viewed as noninteracting waves that propagate outward from the Sun. More recently, the view has evolved that the fluctuations are interacting to produce changes in their characteristics based on wind conditions and distance from the Sun. In one school of thought the fluctuations are treated as interacting waves that are themselves solutions to the Maxwell-Vlasov equations. In the other, the fluctuations are viewed as magnetofluid extensions of traditional hydrodynamics (HD).

Coleman (1966) observed that magnetic and velocity fluctuations are correlated in the solar wind and that they lie preferentially within the plane perpendicular to the mean magnetic field. From this he argued that the fluctuations are hydromagnetic Alfvén waves propagating away from the Sun (Belcher and Davis, 1971). This interpretation formed the basis for decades of study in solar wind fluctuation dynamics and influenced the more recent view that kinetic Alfvén waves form the basis for solar wind turbulence (Bale et al., 2005).

Coleman (1968) modified his earlier opinion on the basis of the form taken by the energy spectrum and other attributes to argue that the fluctuations must evolve in situ in a manner analogous to HD turbulence. Homogeneous, isotropic HD turbulence possesses what is called an “inertial range” where energy is transported from large to small scales via energy-conserving dynamics (Kolmogorov, 1941a). Both theory and observation show the inertial-range power spectrum displays a k^−5/3 form which is in good agreement with solar wind observations at MHD scales. Coleman writes, “From the spectral properties of the plasma fluctuations, it is tentatively concluded that the solar wind flow is often turbulent in the region near 1 AU. A heuristic model of the turbulent flow that is consistent with the observations is one in which the energy for the turbulence is derived from the differential motion of the streams in the solar wind plasma. Instabilities associated with the differential streaming produce long wavelength Alfvén waves. “The energy extracted from the differential motion cascades through a hierarchy of Alfvén waves until it reaches waves short enough for dissipation by proton cyclotron damping.” In so doing, he introduced the idea of solar wind turbulence built upon interacting plasma waves. This second interpretation by Coleman, with or without the underlying Alfvén wave assumption, has formed the basis for much of the solar wind turbulence studies since.

There is a problem with the turbulence view of Coleman in that a 1D system of noncompressive fluctuations does not possess any nonlinear interactions between the Alfvén waves. This becomes more significant with simulation. It is therefore necessary to relax any strict interpretation of wave propagation along the mean magnetic field, and subsequent analyses have more than relaxed this assumption.

There is another compelling reason to consider the presence of turbulent dynamics. Both MHD and kinetic plasma physics lack significant dissipation dynamics at scales larger than the particle gyroradius unless they are significantly compressive. In the solar wind, this means predominantly thermal protons. Compressible effects can produce dissipation at larger scales, but the density fluctuations in the solar wind are small, and the turbulence is generally regarded to be dominated by noncompressive dynamics. Since the bulk of the fluctuation energy exists at larger scales, while dissipation is a small-scale process associated with ion dynamics, the question must be asked, “Can a static fluctuation spectrum dissipate sufficient energy to produce the observed heating?” Schwartz et al. (1981) considered the rate of energy conversion for a static spectrum by using the sweeping of the dissipation scale to lower frequencies as the plasma is convected outward and concluded that it was insufficient to provide the necessary heating.

The cross-correlation between the magnetic and velocity fluctuations are consistent with a dominant outward propagation of waves (Belcher and Davis, 1971), but this dominance is reduced with increasing distance from the Sun until an equal admixture of Sunward and anti-Sunward propagation is inferred (Roberts et al., 1987a; Roberts et al., 1987b; Bavassano et al., 2001). Whether the fluctuations are described as waves or in a more general nonlinear sense (Elsässer, 1950), the nonlinear dynamics of incompressible MHD requires that the fluctuations are an admixture of positive and negative correlations between the magnetic and velocity fields and the evolution of this net correlation is generally accepted as an indication of turbulent dynamics of some type.

Perhaps the death nell for the noninteracting wave interpretation comes from the observation that the global heliospheric magnetic field wraps azimuthally around the Sun as it extends outward. Low-frequency plasma waves will not propagate along this rotating field (Völk and Alpers, 1973; Heinemann and Olbert, 1980). According to WKB theory, Alfvén waves refract toward the radial direction contrary to the observed transverse nature of the magnetic fluctuations which indicates that the magnetic fluctuations have wave vectors that oriented perpendicular to the mean magnetic field.

4 The governing equations

The equations that describe turbulence can be written down. They are understood. There is no fundamental physics that is missing although there is a debate on what set of physics is most important. The difficulty in understanding turbulent dynamics rests with two unavoidable traits: the solutions to the equations are ergodic requiring statistical techniques to gain insight, and the evaluation of the terms using data requires simultaneous measurements at many points.

We can demonstrate the second of these facts by examing the Navier-Stokes equation that describes incompressible hydrodynamic fluids such as water.

\frac{d V}{d t} + (V \cdot \nabla) V = - \nabla P + ν \nabla^{2} V (1)

\nabla \cdot V = 0 (2)

Where

\nabla \equiv \hat{x} \frac{\partial}{\partial x} + \hat{y} \frac{\partial}{\partial y} + \hat{z} \frac{\partial}{\partial z} (3)

defines the spatial gradient, V is the velocity field of the flow, t is time, ν is the viscosity that contributes to dissipation, and p is pressure.

Integration of Eqs. 1, 2 over a closed volume demonstrates that the total energy ∫V²dx is conserved when ν = 0 and that the term ν∇²V is the only term in Eq. 1 that dissipates energy (Batchelor, 1953; Frisch, 1995; Pope, 2000). Dissipation is therefore contained within the fluid approximation. This leaves (V⋅∇)V to transport energy through the spectrum and across the spacial scales, but the evaluation of Eq. 3 cannot be performed by a single-point measurement. The evaluation of the nonlinear term in Eq. 1 requires multi-point measurements separated by the scale of interest to obtain the differences that are needed to evaluate the multi-dimensional gradient. Moreover, there is no such thing as one-dimensional incompressible HD turbulence as there are no nonlinear dynamics under these conditions.

Simple scaling arguments can be constructed to guide theoretical treatments. One such argument derives from the general scaling of the nonlinear term in Eq. 1 as V²/L where V is the characteristic speed associated with the scale L. From this, the rate of energy transport (and the associated rate at which the energy of a turbulent eddy is consumed by the turbulence) scales as V³/L where energy is written simply as V². A formal derivation of the V³/L scaling is obtained from a third-order structure function analysis of the dynamical equations (Kolmogorov, 1941b). The third-moment formalism has been extended to incompressible magnetohydrodynamics (Politano and Pouquet, 1998a; Politano and Pouquet, 1998b). This provides a scaling for the lifetime of an eddy τ = L/V that argues the lifetime of an eddy is one turnover time. Third-moment theory provides a more exact expression for the V³/L scaling (Kolmogorov, 1941b).

There are two ways of approaching the solar wind fluctuations that we here describe as turbulence. One way is by adopting the Maxwell-Vlasov equations where the Vlasov equation is the collisionless Boltzman equation. The other way is through the MHD equations that can be derived for low-frequency dynamics at scales smaller than the ion inertial scale. The former is the foundation behind most descriptions of linear wave modes with the second-order expansion producing the coupling terms needed to maintain the nonlinear dynamics used in what is sometimes called “weak turbulence theory.” The second approach most often leads to analyses that are analogous to existing concepts in HD turbulence.

We will address the incompressible MHD equations since the density fluctuations are considered to be small in most applications of solar wind turbulence concepts. Neglecting compression and dissipation, the MHD equations can be combined and written as:

\frac{d Z^{\pm}}{d t} + (Z^{\mp} \cdot \nabla) Z^{\pm} = - \frac{1}{ρ} \nabla P \mp (⟨ B_{0} ⟩ \cdot \nabla) Z^{\pm} (4)

where the mean magnetic field is written in Alfvén units $B_{0} \to B_{0} / \sqrt{4 π ρ}$ and ⟨…⟩ represents an average on some relevant scale. The Elsässer variables are defined by $Z^{\pm} \equiv V \pm B / \sqrt{4 π ρ}$ (Elsässer, 1950). Writing the MHD equations in this way captures the basic property that turbulence is driven by the interaction of the Z⁺ and Z⁻ fields. When the equation is linearized, it yields the dispersion relation for the Alfvén waves with a wave vector component along (against) the mean magnetic field is associated with Z⁻ and Z⁺, respectively, but the dispersion relation is secondary to the observation that MHD turbulence requires the two interacting fields.

The similarity between Eqs. 2, 4 illustrates the strong similarity between the NS and MHD equations. The term Z^∓⋅∇Z^± in Eq. 4 demonstrates the coupling of the Z^± fluctuations that leads to the nonlinear dynamics supporting the turbulence. There are no nonlinear dynamics in Eq. 4 if the energy content of either Z⁺ or Z⁻ is zero. Both must be present to have turbulent dynamics. Also there are no nonlinear dynamics within Eq. 4 if the wave vector for all fluctuations are aligned with the mean magnetic field in the sense of parallel or anti-parallel alignment of the wave vector with the mean field. MHD turbulence requires that the distribution of energy be multi-dimensional and present in both Elassser energies ${(Z^{+})}^{2}$ and ${(Z^{-})}^{2}$ .

5 universal spectrum

Figure 2 shows a composite spectrum produced by analyzing 9 days of magnetic field measurements from the ACE spacecraft at 1 AU. It represents three out of five spectral subranges where different dynamics are thought to dominate. The names of these spectral subranges derive from traditional HD.

Figure 2

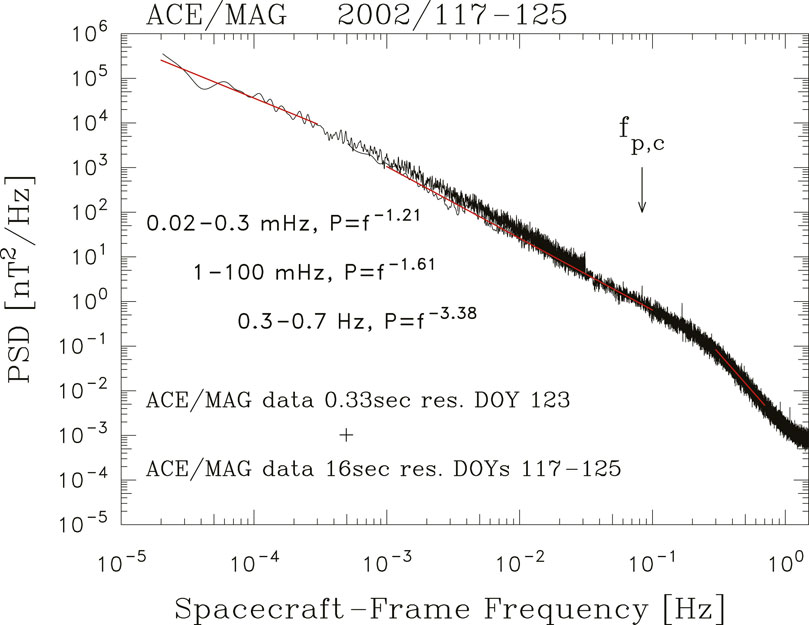
Figure 2. Composite spectrum taken from 9 days of magnetic field measurements by the ACE spacecraft. Reproduced from Smith and Vasquez (2021).

At f_sc < 0.4 mHz, the spectrum has the form $f_{s c}^{- 1.2}$ which is not universal, but it is typical of what is seen. This part of the spectrum is argued to be dominated by the unprocessed solar source (Matthaeus and Goldstein, 1986; Magyer and van Doorsselaere, 2022; Davis et al., 2023) due, at least in part, from the lifetime arguments in the previous section. Nonlinear dynamics erode the energy contained at these scales and that energy is then absorbed by the turbulence and used to drive the fluctuations at higher frequencies. This is called the energy-containing range because it acts as a reservoir to supply the energy that forms the spectrum at higher frequencies.

In the range 0.4 < f_sc < 200 mHz, it is widely argued that the nonlinear dynamics of the turbulence produces a net transfer of energy from large to small scales (low to high frequencies) in an energy-conserving manner (Matthaeus and Goldstein, 1982). This is the so-called inertial range and in the case shown in Figure 2 the spectrum varies as $f_{s c}^{- 1.6}$ . What makes this range of frequencies so interesting is that it possesses a similar spectral form to the inertial range of hydrodynamic fluctuations so that a parallel may be drawn between the HD and MHD dynamics as illustrated above having a spectral index from −5/3 [the prediction for MHD extensions of HD arguments (Matthaeus and Goldstein, 1982)] to −3/2 [predicted form for interacting Alfvénic fluctuations (Iroshnikov, 1964; Kraichnan, 1965)]. Solar wind magnetic spectra are seen to vary between these two predictions.

In HD, the −5/3 index for the inertial-range spectrum derives from the dimensional analysis based on the assumption that the rate of dissipation depends on amplitude of the power spectrum, the assumption that all nonlinearity is local in k-space, and the assumption that the wave vectors are isotropically distributed. Since it can be shown that the total energy (magnetic plus kinetic) is conserved by the nonlinear terms in Eq. 4, the same argument can be made for the inertial range of MHD turbulence. It also holds if the MHD spectrum is 2-D where the wave vectors are confined to the plane perpendicular to the mean magnetic field (Shebalin et al., 1983; Goldreich and Sridhar, 1995; Schekochihin, 2022). The added assumption of a dispersion relation alters the argument and breaks the similarity. The inertial-range index under the assumption that turbulence is comprised of interacting Alfvén fluctuations leads to the addition of the Alfvén speed in the scaling argument resulting in the flatter −3/2 prediction which again assumes an isotropic distribution of wave vectors.

At f_sc > 0.2 Hz, it is widely argued that collisionless kinetic processes become important and the energy that is transported through the inertial range is largely exchanged from fluctuation magnetic and bulk kinetic energy to ion thermal energy at scales associated with the proton Larmor radius, proton inertial scale, or cyclotron resonance (Leamon et al., 1998a; Markovskii et al., 2008; He et al., 2011; Šafránková et al., 2013; Bruno and Trenchi, 2014; Markovskii et al., 2015; Markovskii et al., 2016; Woodham et al., 2018; Woodham et al., 2021). This is called the dissipation range and in this instance it exhibits a spectral form $f_{s c}^{- 3.4}$ . The steepness of the dissipation range has been shown to vary with the rate of energy transport through the inertial range (Smith et al., 2006a; Bruno et al., 2014).

Although not shown, the magnetic spectrum continues to higher frequencies and spatial scales smaller than the ion inertial scale where it is argued that ion dynamics decouple from the magnetic field and a second inertial range is formed via electron dynamics until dissipation by the thermal electron population occurs (Alexandrova et al., 2009; Sahraoui et al., 2009; Sahraoui et al., 2010). It has also been argued that fluctuations at these smaller scales can be described in a general framework of out-of-equilibrium systems (Carbone et al., 2022; Chiappetta et al., 2023).

In frequency ranges where the power spectrum is largely reproducible and can be used to define the various ranges that contain different dynamics, the other properties of the spectrum vary to a greater degree. For instance, the polarization within the energy-containing and inertial ranges average to zero, but are generally seen to vary rapidly with frequency as shown in Figure 2 of Matthaeus and Goldstein (1982). However, the polarization within the dissipation range is often seen to be non-zero and has been taken to be an indication of the role played by kinetics.

Figure 3 illustrates several well-established characteristics of IMF turbulence. The frequencies shown represent the high-frequency end of the inertial range that terminates in the dissipation range. Figure 3 (top) shows the power spectra of the IMF components in mean-field coordinates. Top-to-bottom, they are the trace of the power spectral matrix (total power), the power in the two components perpendicular to the mean magnetic field, the power in the field-aligned component, and the power in the magnitude of the field. The inertial range can be fit to a spectral index $\sim 5 / 3$ that steepens at ion dissipation scales to an index $\sim 3$ . The spectrum of the parallel component is related to ion compressions and is a factor of $\sim 2$ smaller than the two perpendicular components. The spectrum of the magnitude is a factor of $\sim 1 0^{2}$ smaller than the trace. The resulting model for IMF turbulence is that the fluctuating field varies on a sphere of constant radius.

Figure 3

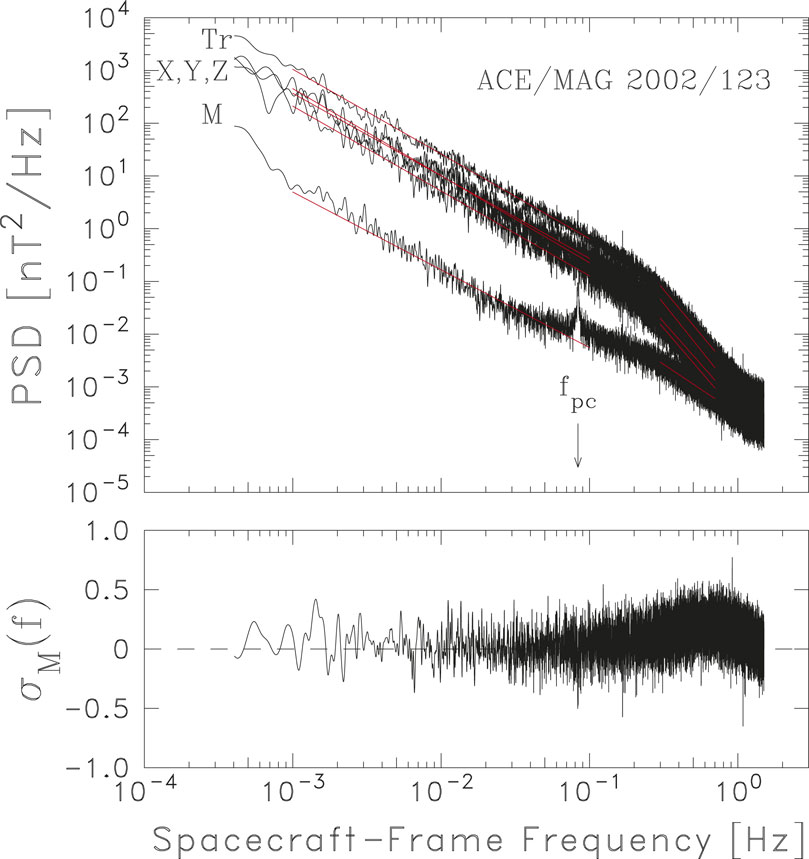
Figure 3. (top) Power spectra of magnetic fluctuations in mean-field coordinates. The two components perpendicular to the mean field have approximately equal power levels while the field-aligned component is a factor of $\sim 2$ lower. Note that the spectrum of the time series of the magnitude of the field is two orders-of-magnitude lower in intensity than the components indicating the established observation that the field magnitude is generally far more constant than the components. (bottom) Magnetic helicity normalized by the magnetic energy showing non-zero bias at the dissipation scales.

Figure 3 (top) shows the steepening of the power spectrum in all components at spacecraft-frame frequencies f_sc > 0.2 Hz, but a relatively shallow spectrum of the IMF magnitude. Figure 3 (bottom) shows the spectrum of the magnetic helicity normalized by the magnetic energy. Magnetic helicity is a spatial analog to polarization, which is defined as a temporal variation, and is a rugged invariant of incompressible MHD. The rugged invariants have been used to predict the turbulent spectra by establishing the ultimate equilibrium the system pursues, but do not yield insights into the nonlinear dynamics that form the cascade. The magnetic helicity, or polarization, at inertial-range frequencies fluctuates about zero. However, the onset of dissipation is often characterized by a bias away from zero of both helicity and polarization as shown. This has been shown to be consistent with cyclotron damping on protons playing a role in the dissipation process (Leamon et al., 1998a; Leamon et al., 1998b; Pine et al., 2020a) and also be explained as a compressional property of the fluctuations (Markovskii et al., 2016). As a demonstration of yet another unresolved question in turbulence studies, this same behavior is also a prediction of the helicity barrier theory (Meyrand et al., 2021) that are demonstrated in kinetic turbulence simulations (Squire et al., 2022).

The correlation between magnetic and velocity fluctuations in the inertial range that are indicative of anti-Sunward propagation degrade with increasing distance from the Sun and can be taken as an indication that the turbulence evolves into a balanced state between Elsässer energies (Roberts et al., 1987a; Roberts et al., 1987b). These things can be studied to better understand the source and evolution of the turbulence, but do not give the best diagnostics into the actual nonlinear dynamics.

6 Evolving theories

Two fundamental, repeatable aspects of solar wind turbulence are that the magnetic and velocity fluctuations are perpendicular to the mean magnetic field direction (resulting in a minimum variance direction aligned with the mean field direction) and the density fluctuations are small. This constitutes a classic signature of noncompressive low-frequency Alfvén waves propagating parallel to the background magnetic field, and for several decades this was the dominant interpretation of the solar wind fluctuations (Belcher and Davis, 1971). As views of interplanetary turbulence gained interest, some theories of solar wind turbulence were based on the second-order interaction of Alfvén waves (Iroshnikov, 1964; Kraichnan, 1965; Coleman, 1968).

When turbulence is included in MHD and kinetic simulations the turbulent energy cascade is found to be preferentially in the perpendicular direction with respect to the background magnetic field (Shebalin et al., 1983; Carbone and Veltri, 1990; Oughton et al., 1994; Goldstein et al., 1995; Matthaeus et al., 1996a; Matthaeus et al., 1998; Cho and Vishniac, 2000; Müller and Grappin, 2005; Horbury et al., 2008; Boldyrev et al., 2009; Parashar et al., 2009; Chen et al., 2010; Beresnyak, 2011; Forman et al., 2011; Markovskii and Vasquez, 2011; Servidio et al., 2012; 2014; 2015; Vasquez and Markovskii, 2012; Matthaeus et al., 2016; Valentini et al., 2016). This led to the view that fluctuations with quasi-perpendicular wave vectors prevail over those with quasi-parallel ones. This again results in a minimum variance direction along the mean field without density fluctuations as there is no preferred direction in the 2D plane and fluctuations can fill the plane randomly. Subsequent analyses employing one of the few single-spacecraft techniques for determining the statistical distribution of fluctuation energy associated with parallel and perpendicular wave vectors has revealed that the perpendicular wave vector component forms a dominant component of the multi-dimensional spectrum (Bieber et al., 1996; Leamon et al., 1998a; Hamilton et al., 2008; Pine et al., 2020c; Watson et al., 2022). There is growing observational evidence that this model is correct as will be described below. Simulations show that the principal nonlinearly that drives the energy cascade from large to small scales is derived from nonlinear generalized Reynolds stresses.

At the same time when there is a preferential transport to perpendicular wave vectors, individual realizations of the turbulence can be quite complex. This can be seen in numerical solutions of the MHD fluid equations as well as particle-in-cell simulations and in snapshots of the magnetic field or thermal ion moments. Figure 4 shows a point in time from a 3D particle-in-cell simulation providing one of many examples of the multi-dimensional nature of plasma turbulence (Vasquez et al., 2014).

Figure 4

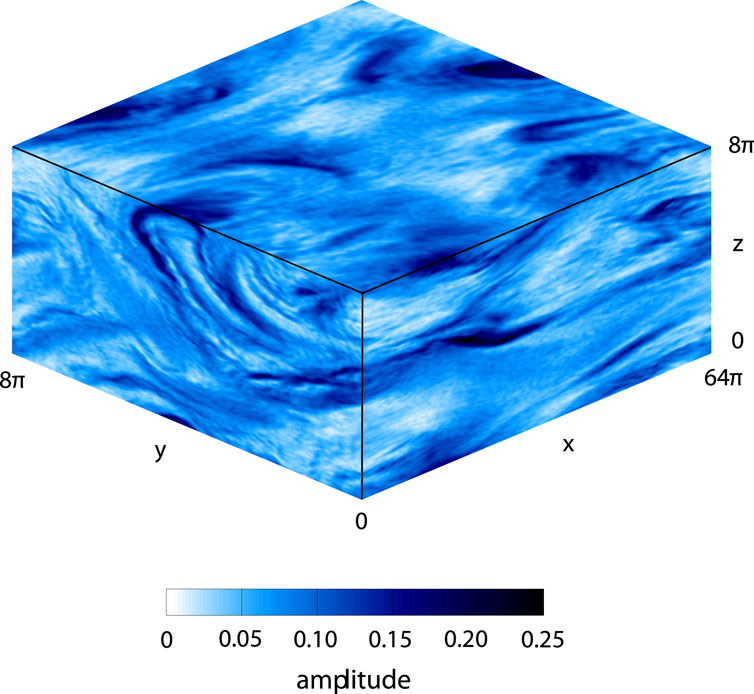
Figure 4. Fully developed turbulence in an kinetic proton and fluid electron plasma that is simulated with a hybrid numerical code. Plot of mean amplitude of fluctuating proton bulk velocity normalized to background Alfvén speed and magnetic field normalized to background magnetic field, which is in the x direction. Box sides are given in proton inertial lengths. Reproduced from Vasquez et al. (2014).

In a return to a variant of the earlier wave view, researchers have used other simulations to assert that the fluctuations are best described as interacting kinetic Alfvén waves with wave vectors nearly perpendicular to the mean magnetic field (Howes et al., 2008; Howes and Quataert, 2010; TenBarge et al., 2013; Hughes et al., 2017; Isenberg and Vasquez, 2019). This view is supported by the observed correlation between the magnetic and electric field fluctuations in the small-scale inertial and dissipation ranges (Bale et al., 2005). However, it has also been observed that this is a general property of Hall MHD and need not point to kinetic Alfvén waves (Matthaeus et al., 2008).

It is a fact of turbulence simulations that no simulation can contain all of the dynamics desired. Therefore, the researcher adopts some and discards others. This results in the dichotomy of views expressed above where different simulation methods yield different results and it is difficult for researchers to agree which of the assumptions are critical and which can be discarded. To a large degree, this has led to the disparate views of solar wind turbulence that are drawn from the same observations.

The rate of external heat addition to ions in the in situ solar wind has been assessed from the change of ion temperature with distance from the Sun as compared to that for adiabatic expansion (Marsch et al., 1982; Marsch et al., 1983; Verma et al., 1995; Vasquez et al., 2007; Hellinger et al., 2013) and one goal of the diverse turbulence theories is to reproduce these rates. Turbulent energy cascade rates based on power spectra correlate with proton heating rates in slow and fast winds (Verma et al., 1995; Vasquez et al., 2007). The Kolmogorov rate ϵ_Kol generalized to MHD and scaled with a larger Kolmogorov constant C_K than established in hydrodynamic experiments (C_K ≈ 1.6) approximately follows the inferred heating rate (Sorriso-Valvo et al., 2007; Vasquez et al., 2007; Carbone et al., 2009; Forman et al., 2010; Montagud-Camps et al., 2018). Kinetic simulations find that plasma heating rates scale in agreement with the Kolmogorov A³ scaling where A² = (δV ⋅ δV/2 + δB ⋅ δB/8πρ) has velocity squared units and ρ is the mass density (Wu et al., 2013; Vasquez et al., 2014; Vasquez, 2015). The rates determined from third-moment structure functions discussed below are also in accord with inferred heating rates for slow and fast winds.

The observation that quantities like fluctuation energy, cross-field correlation, and thermal particle heating vary with distance from the Sun, which implies there is temporal evolution to the turbulence, leads to modeling of the turbulence using principles of various turbulence theories. In these models, energy is injected into the energy containing scales at various distances from the Sun by velocity shears such as shocks and velocity stream interactions. When wave excitation by interstellar pickup ions is included, the models can be extended beyond the distance where wind shear energy is largely exhausted. The primary difference between some models is the assumed nonlinear dynamics that transport energy from the large scales to the dissipation scales and the rate at which that occurs. When the energy containing scales are dissipated at the von Karman rate, the heat addition to protons is obtained. Models based on MHD extensions of these traditional HD theories have successfully reproduced the observations once the added energy source of interstellar pickup ions is considered (Matthaeus and Zhou, 1989; Zhou and Matthaeus, 1990a; Zhou and Matthaeus, 1990b; Matthaeus et al., 1994; Matthaeus et al., 1996b; Zank et al., 1996; Smith et al., 2001; Isenberg et al., 2003; Breech et al., 2005; Smith et al., 2006b; Oughton et al., 2006; Breech et al., 2008; Breech et al., 2009; Isenberg et al., 2010; Oughton et al., 2011; Usmanov et al., 2012; Zank et al., 2012; Usmanov et al., 2014; Usmanov et al., 2016; Zank et al., 2017; Usmanov et al., 2018; Pine et al., 2020d; Watson et al., 2022).

Figure 5 shows an example where a version of the transport theory based on MHD extensions of HD leads to general agreement with the observed heating in the outer heliosphere. However, while the MHD models based on HD concepts contain parameters that are moderately well-constrained, treatments based on the theory of interacting waves have also achieved similar success (Cranmer, 2009; Ng et al., 2010).

Figure 5

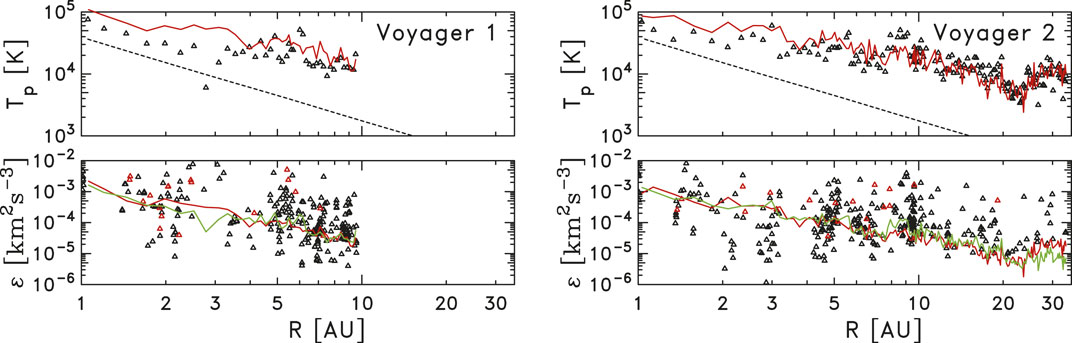
Figure 5. Application of turbulence transport theory to Voyager observations. (top) Average proton temperature computed over 27 days intervals plotted as a function of heliocentric distance. Dashed line represents the prediction of adiabatic expansion. Red curve marks the transport theory prediction as described in Pine et al. (2020d). (bottom) Rate of turbulent energy cascade computed from the spectra at 3 mHz (symbols) ϵ_K compared with the turbulent heating rate derived from transport theory ϵ_T (red curve) and the empirical analysis obtained by generalizing the Vasquez et al. (2007) analysis ϵ_V (green curve). Note the agreement in Voyager two results beyond 10 AU where wind shear is reduced and energy injection by interstellar pickup ion becomes significant. This figure is reproduced from Pine et al. (2020d).

Electrons, being so mobile, are dominated by non-local transport of energy. This has made it difficult to obtain a consistent and accurate measurement of the contribution of the turbulent energy cascade to electron heating (Pilipp et al., 1990; Scime et al., 2001; Cranmer et al., 2009; Štverák et al., 2015; Abraham et al., 2022). Where fluctuation A is large, protons tend to be 2–3 times hotter than electrons, suggesting that protons are heated much more than electrons by the turbulence. Simulations with both kinetic protons and electrons find that turbulence heats protons more than electrons when A is large, as it is in fast winds, and electrons more than protons when A is small, as occurs in some slow winds (Wu et al., 2013; Roy et al., 2022).

7 Single-spacecraft limitations

Spectra such as shown in Figure 2 are computed using the Taylor frozen-in-flux assumption (Taylor, 1938). The resulting expression for the measured frequency in the spacecraft frame is given by:

f_{s c} = {(2 π)}^{- 1} (k \cdot V + ω) (5)

where V is the plasma bulk velocity, k is the wave vector, and ω is the wave frequency in the plasma frame. There is no direct measurement of ω, the wave frequency in the plasma frame, that is obtained from the Taylor approximation. Most often it is assumed to be small compared to the convection term and ignored. Either way, Eq. 5 represents the projection of the wave vector onto the wind flow, and as such it yields the convection of a wave or other dynamic structure past the spacecraft. Similarly, the resulting spectrum can be thought of as an integration of the 3D spectrum across the two directions that are perpendicular to the solar wind velocity. Therefore, it yields no information about the dependence upon these two perpendicular directions and only produces information regarding the structure of an object along the plasma velocity (the Radial direction in the solar wind extending from the Sun to the point of interest) ignoring any time variability within the plasma frame. This means that the fully three-dimensional wave vector k as well as the wave frequency ω must be assumed based on properties of the observed fluctuation, but are unmeasured. In turn, the true nature of the fluctuations is equally undetermined. Over the range of scales examined here, the term ω was assumed to be Alfvénic and small (ω ≪k ⋅V), and therefore suppressed, in the production of Figure 2.

There are observational quantities that can be agreed upon with some variation in opinions that various theories of turbulence can attempt to reproduce. The spectra described above are examples of such observables. However, they are far from unambiguous measurements and can lead to multiple interpretations. Different inertial-range dynamics lead to different predictions for the energy dissipation rate and dynamics, and hence the thermal plasma heating rate, and this can be compared to the observed rate of heating as determined by statistical means using the observed temperature at different heliocentric distances (Vasquez et al., 2007; Lamarche et al., 2014; Pine et al., 2020d; Watson et al., 2022).

There are a few single-spacecraft analysis techniques that can produce insights into the nonlinear dynamics of the turbulence without making assumptions of the fundamental nature of the fluctuations. One technique is to compare the correlation function for whatever field of interest (magnetic, velocity, or density) as it varies with changing mean magnetic field direction. This leads to a direct comparison of the distribution of energy between the parallel and perpendicular wave vectors (Matthaeus et al., 1990; Milano et al., 2004; Dasso et al., 2005; Watson et al., 2022). The risk to this analyses is that the direction of the mean magnetic field can be correlated to other plasma characteristics and this may lead to an apples vs oranges situation (Dasso et al., 2005). Another technique is the comparison of the power spectra for the two components of the magnetic field perpendicular to the mean field. This leads to a statistical comparison of the energy distributed between parallel and perpendicular wave vectors (Bieber et al., 1996; Hamilton et al., 2008; Pine et al., 2020c; Watson et al., 2022). This technique generally shows a strong presence of wave vectors that are quasi-perpendicular to the mean magnetic field with a notable exception of the inertial range in fast-wind conditions (Dasso et al., 2005).

The third-moment technique is one method combining the magnetic field and bulk velocity measurements that can be used by single-spacecraft observations to accurately measure the rate of energy transport through the inertial range, but it requires an assumption of the underlying geometry, or distribution, of the wave vectors (Politano and Pouquet, 1998a; Politano and Pouquet, 1998b; MacBride et al., 2008; Smith et al., 2009; Stawarz et al., 2009; Stawarz et al., 2010; Stawarz et al., 2011; Coburn et al., 2012; Coburn et al., 2014; Coburn et al., 2015; Smith et al., 2018; Bandyopadhyay et al., 2020; MacBride et al., 2023). This method has shown that there can be back-transfer of energy to larger scales when the magnetic and velocity fields are strongly correlated and intermittent at any time and scale in data where the cross-field correlation is low (Smith et al., 2009; Coburn et al., 2015; Smith et al., 2018). When the technique is extended to multi-platform data, the assumption of an underlying geometry can be suspended (Pecora et al., 2023). This technique is remarkably general and derived from Eq. 4 without assuming any specific nonlinear dynamics, so as such it fails to illuminate the actual processes that form the turbulence.

None of these observations can answer the fundamental question, “What are the nonlinear dynamics that support the turbulence?” The observations are ubiquitous. Their variations are systematic. The turbulence of space has been studied in situ from the near-Sun observations of the Parker Solar Probe (Bandyopadhyay et al., 2020; Réville et al., 2020; Chhiber et al., 2021; Magyer and van Doorsselaere, 2022; Davis et al., 2023) to the interstellar plasma observations of the Voyager spacecraft (Armstrong et al., 1981), and still the fundamental question is, “What is turbulence?”

8 Cluster, MMS, and HelioSwarm

Both the Cluster and Magnetospheric MultiScale (MMS) missions operate as four spacecraft flying in formation in an attempt to resolve multi-dimensional dynamics (Escoubet et al., 2001; Burch et al., 2016). Both are primarily magnetospheric missions and conclusions from solar wind turbulence studies using these missions are mixed. Early studies concluded that the inertial- and dissipation-range dynamics were dominated by perpendicular propagating kinetic Alfvén waves (Sahraoui et al., 2010; Roberts et al., 2013) and possibly whistler waves at smaller scales (Narita et al., 2016a). However, later studies using a greater number of data intervals concluded that while some could be described in that manner, others are convected Alfvénic structures that are analogous to nonlinear dynamics of traditional HD (Roberts et al., 2015; Roberts and Li, 2015). The same techniques resolve mirror mode waves in the magnetosheath (Narita and Glassmeier, 2005; Narita et al., 2016b).

The problem with these missions from a solar wind perspective is that they never get very far upstream of the Earth’s bow shock. This means that much of the data are contaminated by foreshock dynamics involving wave excitation by suprathermal ions and electrons. These instabilities are stronger than the nonlinear dynamics that constitute the turbulence and can overwrite the results of turbulent evolution. Magnetosheath and magnetosphere observations can be similarly contaminated, but researchers attempt to work around such issues with careful data selection. This does not mean that such studies are without value in turbulence investigations. It only means that the results are often not pristine and cannot always be represented as uncontaminated examinations of solar wind turbulence dynamics.

NASA has selected a new mission to better resolve the nonlinear solar wind dynamics at scales where the onset of dissipation steepens the inertial-range spectrum to form the dissipation range (Klein et al., 2023). The mission is HelioSwarm and it consists of nine platforms flying in a loose formation with separations varying between 10s to 1,000s of km. Each platform will contain fluxgate and search coil magnetometers as well as a Faraday Cup to measure the solar wind velocity and density. The central Hub platform will also carry an electrostatic analyzer for both ions and electrons.

The nine platforms follow a highly elliptical, 2-week orbit. Due to orbital dynamics, the HS apogee will be in the solar wind $\sim 1 / 3$ of the time, the magnetosphere $\sim 1 / 3$ or the time, and in the foreshock region $\sim 1 / 3$ of the time. The estimated number of hours from the first year of the science phase are given in Table 2 of the HS overview paper (Klein et al., 2023). The intent is to allow the platform separation to vary slowly as they form and break polyhedral configurations at different separation scales and provide simultaneous measurements along and across the local magnetic field and solar wind velocity directions. This approach facilitates application of both the techniques of traditional HD analysis methods and the k-telescope analysis that is particularly designed for wave mode identification. The apoasis is about 60 R_E, significantly higher than either Cluster or MMS, whose apoapis are $\leq 25$ R_E, which enhances the opportunity for measurements outside the ion and electron foreshocks.

The European Space Agency is currently considering another mission called Plasma Observatory consisting of seven spacecraft forming an observatory similar in design to HelioSwarm that will have the capability of measuring energetic charged particles (Retino et al., 2022). This mission is now in a Phase A study. Part of the motivation behind this mission is to link an improved understanding of turbulence to the acceleration and propagation of energetic particles.

The goal, of course, is that by providing more detailed measurements of solar wind turbulence, the new insights will lead to better simulations and deeper theories. Simulations and theory have always been a source of new ideas for data analysis, so with a healthy simulation and theory program the goal of these missions is to evolve and refine both the questions and the techniques leading to new insights into the fundamental nature of magnetofluid turbulence.

9 Summary

HD turbulence is viewed as the interaction of circulating vortices where the application of the circulating flow of one vortex applied over the other causes distortion and smaller vortices to be spawned. One can therefore argue that HD turbulence possesses limited dynamics, and yet the resulting flow can be exceptionally complex. Understanding the nonlinear dynamics that support the turbulence enables the practical application of HD turbulence to engineering problems through the development of advanced computational methods often resulting in advanced modeling techniques. The theoretical techniques used to study HD turbulence at an analytical level focus in a fundamental way on the statistical properties of the fluctuations (correlation function, spectrum, structure functions, conserved quantities, etc.) and their dynamics.

MHD contains a greater and more diverse range of dynamics that can contribute to the turbulence. In part because of this, the study of MHD turbulence suffers from a cultural dichotomy that is deeply ingrained within the plasma community. Some researchers view MHD turbulence as an extension of HD turbulence concepts and bring to bear the same statistical techniques to study it. Other researchers view MHD turbulence in a manner analogous to what is called “weak turbulence theory” where the nonlinear equations are linearized to find normal modes of the system and then these normal modes are said to interact at second order. Some researchers try to adhere to the interacting wave viewpoint while admitting nonlinear waves and other complications, but in the end there are questions about the stability of single nonlinear waves in the presence of additional fluctuations and their ability to persist to form an description of evolving turbulent dynamics.

Single-spacecraft studies of space plasmas can never resolve the fundamental nature of the fluctuations that form the turbulence. Properties of the spectra can be pointed to and argued to be indicative or one dynamic or another, but in many cases there are multiple dynamics that possess similar observational qualities. There is no simpler or more immediate example of this ambiguity than to note that for decades the magnetic fluctuations in the solar wind were thought to be noninteracting, parallel-propagating Alfvén waves possessing a spectral remnant of the acceleration region simply because the fluctuations were generally transverse to the mean magnetic field, correlated with velocity fluctuations, and to a significant extent noncompressive (Belcher and Davis, 1971). From both data analysis and simulation the realization has developed that the wave vectors are quasi-perpendicular to the mean magnetic field which results in solutions that are equally adept at fitting the basic observations. This has resulted in the wave view proponents moving to a kinetic Alfvén waves interpretation, so the mode has changed, but the concept of turbulence via interacting waves remains. Despite this transformation, many of the early simulations that demonstrated energy transport to the perpendicular wave vectors can be shown to be lacking any linear mode waves which suggests that the fundamental nonlinear dynamics may be more broadly defined than that of interacting linear modes.

The CLUSTER and MMS missions have provided early multi-platform evaluations of space plasma turbulence. These missions have shown that some observations can be described as interacting kinetic Alfvén waves while others are not. A new mission, HelioSwarm, is now under development that will provide a greater number of platforms flying in lose formation with separation scales appropriate to the study of the small-scale inertial range extending into the dissipation range. It is the hope of this mission that the variation in spacecraft separation together with the greater time spent outside the Earth’s foreshock may better resolve the existing questions and point to the fundamental nonlinear dynamics that form turbulence in the solar wind.

Author contributions

CS: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. BV: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. CS is supported by NASA contract 80NSSC23K0540 for the Advanced Composition Explorer mission and by the MMS and HelioSwarm missions. BV is supported by NASA grant 80NSSC21K1674 and by the HelioSwarm mission.

Acknowledgments

The data used in this analysis are available from the NSSDC. The authors wish to thank J. E. Borovsky for the invitation to write this review and K. Klein for helpful suggestions. CS wishes to acknowledge the loss of two mentors in recent months: David C. Montgomery and Norman F. Ness. It is at times like these that one is reminded of unpaid and unpayable debts.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abraham, J. B., Verscharen, D., Wicks, R. T., Rueda, J. A., Owen, C. J., Nicolaou, G., et al. (2022). Thermal energy budget of electrons in the inner heliosphere: Parker Solar Probe observations. Astrophys. J. 941, 145. doi:10.3847/1538-4357/ac9fd8