
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Astron. Space Sci., 24 June 2024
Sec. Space Physics
Volume 11 - 2024 | https://doi.org/10.3389/fspas.2024.1369003
This article is part of the Research TopicSolar Radio Bursts and their Applications in Space Weather ForecastingView all 5 articles
 Valentin Melnik1*
Valentin Melnik1* Anatolii Brazhenko2
Anatolii Brazhenko2 Vladimir Dorovskyy1
Vladimir Dorovskyy1 Anatolii Frantsuzenko2
Anatolii Frantsuzenko2 Mykola Shevchuk1
Mykola Shevchuk1 Sergii Yerin1
Sergii Yerin1 Igor Bubnov1
Igor Bubnov1Spectral properties of a single type III burst in the wide frequency band from 10 to 70 MHz are studied in detail. It is shown that electrons corresponding to different levels of type III emission move with different velocities. Moreover, these electron velocities decrease from the maximum value, which corresponds to the 0.1 level of the maximum type III flux at its front, to the minimum value, corresponding to the 0.1 level of the maximum type III flux at its back. The velocity of electrons corresponding to the maximum type III flux was approximately 0.31 c. This value equals 0.6 of maximum velocity, and, namely, it was predicted by the gas dynamic theory of electron propagation through the coronal plasma. In addition, we adduce arguments that the type III radio emission is the harmonic emission. In supposition that type III electrons move through the Newkirk coronal plasma, we find electron velocities for every level of the type III burst. The duration dependence on frequency obtained from the observations is close to Elgaroy–Lingstad dependence. We discuss the contribution of electron velocity dispersion to the type III burst duration. In addition, we derived type III flux dependence on frequency in the frequency bands of 10–33 MHz and 33–62 MHz.
There are a number of papers (Wild, 1950; Malville, 1962; ; Aubier and Boischot, 1972; Alvarez and Haddock, 1973; Suzuki and Dulk, 1985; Mel'Nik et al., 2005; Saint-Hilaire et al., 2013; Reid and Ratcliffe, 2014; Melnik et al., 2015; Zhang et al., 2018; Raja et al., 2022) in which different properties of type III bursts in the frequency band from tens of kHz to hundreds of MHz are discussed. In particular, these are drift rates, durations and less often fluxes, polarizations, and spatial characteristics. Such a situation is connected with the capabilities of radio telescopes, such as time and frequency resolutions, sensitivities, and possibilities to measure the polarization of radio emission, sizes of sources, and locations at which radio emission was generated. The special place is given to the continuous frequency band, in which properties of type III bursts are measured. It is especially important for the decameter range because it corresponds to a wide range of heights, up to 1–2 solar radii, from which decameter radio emission comes out. Currently, there are some radio telescopes, such as LOFAR (Low-Frequency Array), MWA (Murchison Widefield Array), NenuFAR (New extension in Nançay upgrading LOFAR), and GURT (Giant Ukrainian Radio Telescope), which can observe solar radio emission in a wide frequency band with high frequency–time resolutions, high sensitivities, and a high dynamic range.
It allowed studying some properties of type III bursts in detail. For example, it is well-known that these bursts are generated by high-energy electrons with velocities of 0.2–0.6c (c is the speed of light) (Suzuki and Dulk, 1985). Reid and Kontar (2018a) were the first who showed that electrons with different velocities were responsible for radio emission of different parts of type III bursts—front, peak, and back. Faster and slower electrons are responsible for the front and the back of type III bursts correspondingly, and the peak of type III bursts is associated with electrons with middle velocities. They analyzed 31 type III bursts using the LOFAR radio telescope in the frequency band of 30–70 MHz. The result of Reid and Kontar was supported by Zhang et al. (2019), who considered a single-type III burst in the frequency band of 30–41 MHz. Frequency dependences of type III durations were also discussed in Reid and Kontar (2018a) and Zhang et al. (2019). Reid and Kontar (2018a) obtained average values of durations shorter than previously observed (Elgaroy and Lingstad, 1972; Melnik et al., 2011; Melnik et al., 2018) with large dispersion. They fairly connected it with the difference in properties of type III electron beams and background coronal plasmas because the analyzed type III bursts occurred in different days and months. In addition, they did not distinguish fundamentals and harmonics of type III bursts. A detailed analysis of single type III bursts in the decameter range (Melnik et al., 2021) reveals that these bursts (occurred at approximately one time) had different drift rates and duration dependences on frequency and all the more for the fundamental and harmonic components. Thus, it is very important to study the dynamics of different levels of a solitary and rather strong type III burst in a wide frequency band. This presents a significant challenge in spite of huge type III bursts observed for a long time (for example, the radio telescope URAN-2 (Ukrainian Radio interferometer of Academy Science) makes solar observations daily during 6–11 h all year round since 2011).
In this paper, we study one of such solitary type III bursts, which was observed not only by the URAN-2 radio telescope (the frequency band of 8–33 MHz) but also by the GURT radio telescope (the frequency band of 30–70 MHz). This allows us to find the dynamics of different levels of type III bursts in the wide frequency band of 10–70 MHz for the first time. We show that the obtained results agree with the electron propagation theory, gas dynamic theory, (Mel’Nik, 1995; Kontar et al., 1998), which is drawn to explain some properties of type III bursts. In addition, we find duration dependence on frequency for this type III burst and discuss the opportunity to explain it through the velocity dispersion of type III electrons (Zhang et al., 2019).
Observations of solar radio emission on 4 June 2020 were carried out using radio telescopes URAN-2 and GURT.
The radio telescope URAN-2 works in the continuous frequency band of 8–33 MHz (Brazhenko et al., 2005). Its effective area is 28,000
The radio telescope GURT works in the frequency band of 8–80 MHz (Konovalenko et al., 2016). Observations were made with a single section of GURT on 4 June 2020. Its effective area is
There were two active regions, namely, NOAA 2765 and NOAA 2764, at the visible solar disc on 4 June 2020. The active region NOAA 2765 located at the eastern limb was more active (its Hale index was
It was a single burst without a preceding type IIIb burst as it usually happens in the decameter range (Melnik et al., 2018), and this burst was convenient for detailed spectral analysis. This type III burst was powerful enough. Its fluxes were approximately
According to URAN-2 data, the polarization of this burst (<20%) and its duration (4–13 s) are close to those of the second harmonic of type III bursts in the decameter range (Melnik et al., 2018). So we suppose that the observed type III burst was generated at the second harmonic. It is interesting to notice that type III bursts can be superposition of both harmonics in the metric band (Rahman, Cairns, McCauley, 2020).
Note that broadband pulses in the dynamic spectrum (Figure 1A) were lightning’s, which occurred this day near the URAN-2 observatory (Poltava, Ukraine). GURT measured the parameters of this type III burst at frequencies below 70 MHz. The flux of the discussed type III burst according to GURT exceeded the background level by more than 10 times at frequencies >30 MHz (Figure 1B; see also Figure 3). Figure 2 shows flux dependence on frequency. The flux, as a rule, increases with the decreasing frequency for decameter type III bursts (Mel’Nik et al., 2005; Raja et al., 2022). For this burst, the flux dependence on frequency follows the equation
where frequency
where
It can be seen (Figures 3A,B) that the profiles of this burst are smooth without any frequency–time structures. So we can suppose that the electron beam responsible for this burst was homogeneous in contrast to the cases with internal frequency–time structures (see, for example, Mel’Nik et al., 2005). The flux maximum of the burst exceeds the background radio emission by 10 times its magnitude (as an example, see profiles at frequencies 14.37 and 44.56 MHz in Figures 3A,B). This gives an opportunity to study the spectral characteristics of this burst in more detail in the wide frequency band than in Reid and Kontar (2018a) and Zhang et al. (2019), from 10 to 70 MHz. So we analyze the frequency drifts of different levels of type III bursts as it was done by Reid and Kontar (2018a). In this paper, we consider drift rates at levels of 0.1, 0.37, 0.5, and 0.7 of the maxima, which are both the front and back of the burst, as well as the maximum itself. Figure 4A shows drifts of maxima and levels of 0.1 at the front and back of the burst. The rest of the levels drift in an analogous manner. The accuracy of the corresponding level locations in the dynamic spectra was defined by current time–frequency resolutions, which were 100 ms (about 10%) and 4 kHz (no worse than 1%) for URAN-2 and 100 ms and 38 kHz (less than 5%) for GURT. So uncertainties of electron velocities derived below are limited by 10%. Observed tracks were approximated by the following equation:
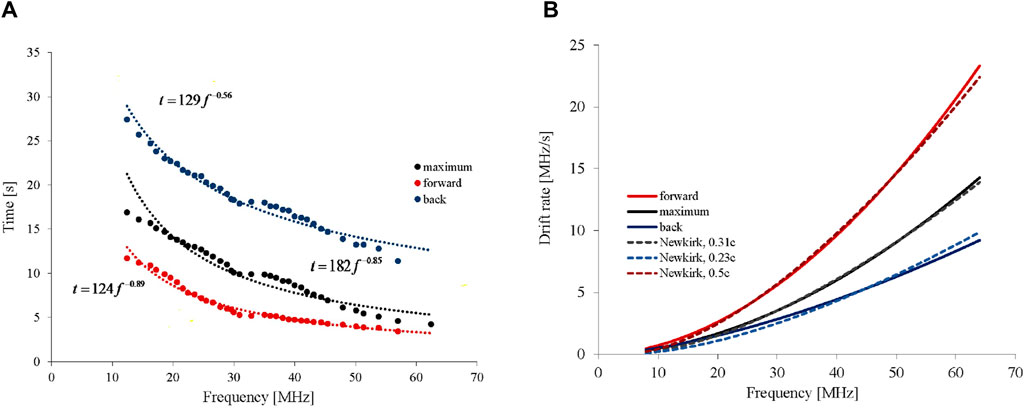
Figure 4. Tracks of maximum and 0.1 levels at the front and back of the type III burst (A). Drift rates of these levels as a dependence on frequency in the Newkirk model assuming the second harmonics of type III radio emission (B). Timing from the 12:26:39 UT.
Constants
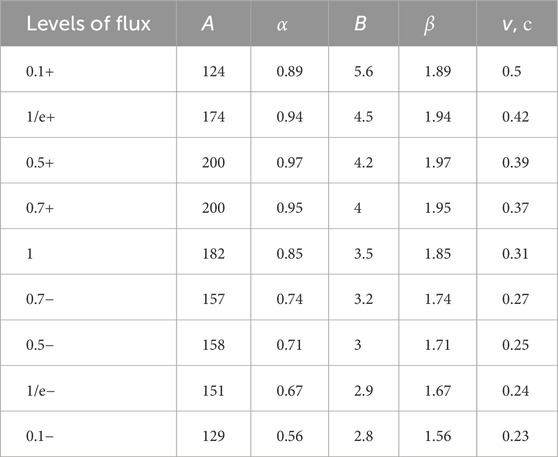
Table 1. Parameters of the type III burst track and electron velocities associated with different levels of the burst.
Taking the derivative of Eq. 1, we obtain the expression for the drift rate of the corresponding level of the type III burst:
They are approximated by the drift rates of sources with different velocities for the Newkirk solar corona (
The profile of type III bursts, as well as their dependence on electron velocity, is shown in Figure 5. We see that the electron velocity changes faster at the front than at the back. This can explain the faster increase in the type III profile in comparison with its decay (Figure 3). It is necessary to say that the ratio of the velocity of flux maximum to maximum velocity equals
Type III durations at different frequencies are shown in Figure 6. It was approximately 4 s at high frequencies and approximately 13 s at low frequencies. Such values are standard for the decameter range for the second harmonic (Melnik et al., 2018; Melnik et al., 2021). The approximation equation for the duration of this type III burst is
where
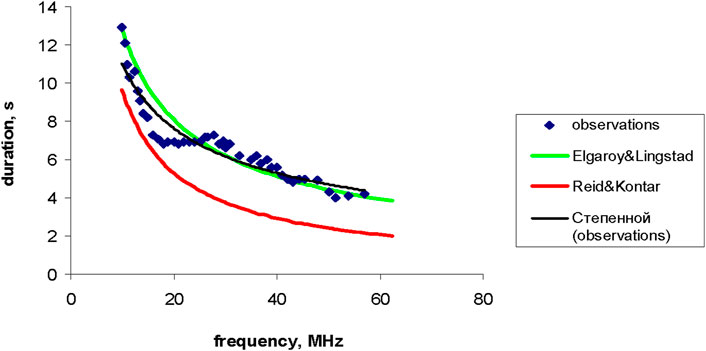
Figure 6. Duration dependence on the frequency for the discussed type III bursts according to URAN-2 (10–33 MHz) and GURT (33–62 MHz).
A physical cause of such dependence is unknown until now. Some authors speculated that the duration could be explained by particle collisions (Malville, 1962; Wild and Smerd, 1972; Smith and Davis, 1975; Suzuki and Dulk, 1985). At the same time, other authors connect it with scattering radio emission on the random density irregularities (Kontar et al., 2019; Krupar et al., 2020).
As we mentioned previously, Reid and Kontar (2018a) studied 31 type III bursts observed by LOFAR in the frequency band 30–70 MHz and obtained noticeably smaller durations (Figure 6). They connected it with the difference between type III electron velocities and background plasma properties. We demonstrated (Melnik et al., 2018) that the fundamentals and harmonics of these bursts had durations varying by a factor of 6–8. This circumstance could also have influenced the average duration of 31 bursts.
Our analysis of a single type III burst in the wide frequency band of 10–70 MHz shows that every level of the burst is associated with the electrons of different velocities. Fast electrons are responsible for the front of the burst, and slow electrons are responsible for its back. This confirms the results obtained earlier (Reid and Kontar, 2018a; Zhang et al., 2019). However, contrary to those, we built, for the first time, the velocity spectrum of type III bursts. This spectrum differs at the front and back of the burst (Figure 5). According to the gas dynamic theory of electron beam propagation through plasma (Mel’Nik, 1995; Mel'Nik et al., 1999), fastest electrons “evaporate” from the beam–plasma structure (Kontar et al., 1998). These electrons generate the beginning of the burst (Mel’Nik and Kontar, 2003). Their density
where
Such density of fast electrons allows considering their interaction with Langmuir waves in the frame of the theory of “weak turbulence” (Tsytovich, 1970) because the ratio of Langmuir energy to the density of thermal energy of plasma is small enough:
Note that in the opposite case
According to the theory of formation of beam–plasma structures (Mel’Nik, 1995), their velocities are defined by the equation
If the longitudinal size of the beam–plasma structure is larger than its transverse size, then the burst duration at some frequency is defined by the time of its passing across the given plasma level in the solar corona (Melnik et al., 2017):
where
This equation is correct for the case of radio emission at fundamental radio emission
Durations in Eqs 11, 12 are shown in Figure 7. We see that the dependence in Eq. 12 is closer to the observed duration. This again suggests that the discussed type III burst was generated at the second harmonic, not at the first. The difference with observational data can be connected by the fact that the transverse size of the beam–plasma structure, which initiates this burst, is comparable and even larger than its longitudinal size. Thus, it is necessary to take into account the path length difference from different regions of the source in transverse directions.
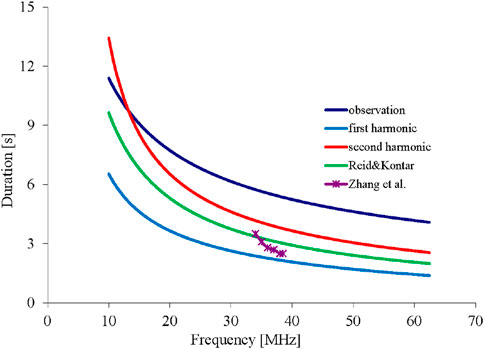
Figure 7. Durations of the burst at the first and the second harmonic in the Newkirk model for the solar corona if they are connected with electron velocity dispersion in the longitudinal direction according to Eqs 11, 12. In addition, the observational dependence is shown in Eq. 5.
Observations of an individual type III burst in the wide frequency band of 10–70 MHz and the data analysis allowed obtaining the following results:
- Each level of type III radio emission is associated with electrons with well-defined velocity. Moreover, electrons with larger velocities are responsible for earlier moments of the burst.
- An electron velocity spectrum of type III bursts was obtained for the first time.
- The electron velocity for the burst maximum equals to that predicted by the gas dynamic theory of electron propagation in plasma.
- Minimum electron velocity equal to the minimum value for the plateau at the electron distribution function gives the density of the fast electrons in the beam–plasma structure being a source of type III bursts
- It was demonstrated that fast electrons propagate through the Newkirk plasma, and radiation of type III bursts occurs at the second harmonic.
- The observational duration dependence on frequency is shown to be close to Elgaroy–Lingstad dependence.
- This dependence is also close to the calculated dependence under the supposition that radiation happened at the second harmonic in the Newkirk coronal plasma. Smaller values seem to be connected with the larger transverse sizes of the beam–plasma structure.
- The flux dependence on frequency for the type III bursts is power law with the exponent equal to 1.75 and 1.63 for 10–33 MHz and 30–70 MHz, respectively.
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
VM: conceptualization, formal analysis, investigation, methodology, project administration, supervision, validation, visualization, and writing–original draft. AB: conceptualization, data curation, formal analysis, investigation, methodology, project administration, resources, software, visualization, and writing–review and editing. VD: conceptualization, formal analysis, investigation, visualization, and writing–review and editing. AF: data curation, formal analysis, resources, software, visualization, and writing–review and editing. MS: data curation, formal analysis, investigation, visualization, and writing–review and editing. SY: data curation, formal analysis, software, visualization, writing–review and editing, and resources. IB: data curation, formal analysis, resources, visualization, and writing–review and editing.
The authors declare financial support was received for the research, authorship, and/or publication of this article. The work was financed within the framework of the projects “Complex researches of sporadic radio emission of the Sun during 25 cycle of solar activity” (Radius) (0122U000616) and “Study of the polarization characteristics of decameter radio emission from space sources using the URAN-2 radio telescope” (0118U009760) of the National Academy of Sciences of Ukraine.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Alvarez, H., and Haddock, F. T. (1973). Solar wind density model from km-wave type III bursts. Sol. Phys. 29, 197–209. SoPh, 29,197. doi:10.1007/BF00153449
Aubier, M., and Boischot, A. (1972). Exciter of type III bursts and coronal temperature. AAP 19, 343.
Brazhenko, A. I., Bulatsen, V. G., Vashchishin, R. V., Frantsuzenko, A. V., Konovalenko, A. A., Falkovich, I. S., et al. (2005). New decameter radiopolarimeter URAN-2. Kinemat. i Fiz. Nebesnykh Tel Suppl. 5, 43.
Elgaroy, O., and Lingstad, E. (1972). High-resolution observations of Type III solar radio bursts. AAP 16, 1.
Goldman, M. V. (1984). Strong turbulence of plasma waves. Rev. Mod. Phys. 56, 709–735. doi:10.1103/RevModPhys.56.709
Konovalenko, A., Sodin, L., Zakharenko, V., Zarka, P., Ulyanov, O., Sidorchuk, M., et al. (2016). The modern radio astronomy network in Ukraine: UTR-2, URAN and GURT. Exp. Astron 42, 11–48. doi:10.1007/s10686-016-9498-x
Kontar, E. P., Chen, X., Chrysaphi, N., Jeffrey, N. L. S., Emslie, A. G., Krupar, V., et al. (2019). Anisotropic radio-wave scattering and the interpretation of solar radio emission observations. ApJ 884, 122. doi:10.3847/1538-4357/ab40bb
Kontar, E. P., Lapshin, V. I., and Mel'nik, V. N. (1998). Numerical and analytical study of the propagation of a monoenergetic electron beam in a plasma. Plasma Phys. Rep. 24, 772.
Krupar, V., Szabo, A., Maksimovic, M., Kruparova, O., Kontar, E. P., Balmaceda, L. A., et al. (2020). Density fluctuations in the solar wind based on type III radio bursts observed by parker solar probe. ApJ 246, 57. doi:10.3847/1538-4365/ab65bd
Melnik, V., Shepelev, V., Brazhenko, A., Dorovskyy, V., Rucker, H., and Stefaan, S. (2017). Interferometer observations of solar type III bursts by the radio telescope UTR-2. Sun Geosph. 12, 105.
Mel'Nik, V. N. (1995). ``Gas-dynamic'' expansion of a fast-electron flux in a plasma. Plasma Phys. Rep. 21, 89. doi:10.48550/arXiv.1802.07806
Melnik, V. N., Brazhenko, A. I., Frantsuzenko, A. V., Dorovskyy, V. V., and Rucker, H. O. (2018). Properties of decameter IIIb-III pairs. Sol. Phys. 293, 26. doi:10.1007/s11207-017-1234-9
Melnik, V. N., Brazhenko, A. I., Konovalenko, A. A., Briand, C., Dorovskyy, V. V., Zarka, P., et al. (2015). Decameter type III bursts with changing frequency drift-rate signs. Sol. Phys. 290, 193–203. doi:10.1007/s11207-014-0577-8
Melnik, V. N., Brazhenko, A. I., Konovalenko, A. A., Frantsuzenko, A. V., Yerin, S. M., Dorovskyy, V. V., et al. (2021). Properties of type III and type IIIb bursts in the frequency band of 8 - 80 MHz during PSP perihelion at the beginning of april 2019. Sol. Phys. 296, 9. doi:10.1007/s11207-020-01754-5
Mel'Nik, V. N., Konovalenko, A. A., Abranin, E. P., Dorovskyy, V. V., Stanislavsky, A. A., Rucker, H. O., et al. (2005). Solar sporadic radio emission in the decametre waveband. Astronomical Astrophysical Trans. 24, 391–401. doi:10.1080/10556790600568854
Melnik, V. N., Konovalenko, A. A., Rucker, H. O., Boiko, A. I., Dorovskyy, V. V., Abranin, E. P., et al. (2011). Observations of powerful type III bursts in the frequency range 10 - 30 MHz. Sol. Phys. 269, 335–350. doi:10.1007/s11207-010-9703-4
Mel'Nik, V. N., and Kontar, E. P. (2003). Plasma radio emission of beam-plasma structures in the solar corona. Sol. Phys. 215, 335–341. doi:10.1023/A:1025689116449
Mel'Nik, V. N., Lapshin, V., and Kontar, E. (1999). Propagation of a monoenergetic electron beam in the solar corona. Sol. Phys. 184, 353–362. doi:10.1023/A:1005191910544
Newkirk, G. (1961). The solar corona in active regions and the thermal origin of the slowly varying component of solar radio radiation. ApJ 133, 983. doi:10.1086/147104
Rahman, M. M., Cairns, I. H., and McCauley, P. I. (2020). Spectropolarimetric imaging of metric type III solar radio bursts. Sol. Phys. 295, 51. doi:10.1007/s11207-020-01616-0
Raja, K. S., Maksimovic, M., Kontar, E. P., Bonnin, X., Zarka, P., Lamy, L., et al. (2022). Spectral analysis of solar radio type III bursts from 20 kHz to 410 MHz. ApJ 924, 58. doi:10.3847/1538-4357/ac34ed
Ratcliffe, H., Kontar, E. P., and Reid, H. A. S. (2014). Large-scale simulations of solar type III radio bursts: flux density, drift rate, duration, and bandwidth. AAP 572, A111–11. doi:10.1051/0004-6361/201423731
Reid, H., and Ratcliffe, H. (2014). A review of solar type III radio bursts. AAP 14, 773–804. doi:10.1088/1674-4527/14/7/003
Reid, H. A. S., and Kontar, E. P. (2018a). Solar type III radio burst time characteristics at LOFAR frequencies and the implications for electron beam transport. AAP 614, A69. doi:10.1051/0004-6361/201732298
Reid, H. A. S., and Kontar, E. P. (2018b). Spatial expansion and speeds of type III electron beam sources in the solar corona. ApJ 867, 158. doi:10.3847/1538-4357/aae5d4
Rudakov, L. I., and Tsytovich, V. N. (1978). Strong Langmuir turbulence. PhRe 40, 1–73. doi:10.1016/0370-1573(78)90114-X
Saint-Hilaire, P., Vilmer, N., and Kerdraon, A. A. (2013). A decade of solar type III radio bursts observed by the Nançay radioheliograph 1998-2008. ApJ 762, 60. doi:10.1088/0004-637X/762/1/60
Smith, D. F., and Davis, W. D. (1975). Type III radio bursts and their interpretation. Space Sci. Rev. 16, 91–144. doi:10.1007/bf00240884
Suzuki, S., and Dulk, G. A. (1985). “Bursts of type III and type V,” in Solar radiophysics: studies of emission from the Sun at metre wavelengths. Editors D. J. McLean, and N. R. Labrum (Cambridge: Cambridge Univ. Press), 289, 289.
Vedenov, A. A., and Ryutov, D. D. (1975). “Quasilinear effects in two-stream instabilities,” in Reviews of plasma Physics. Editor M. A. Leontovich (MD USA, New York: Published by Consultants Bureau), 6, 1.
Wild, J. P. (1950). Observations of the spectrum of high-intensity solar radiation at metre wavelengths. III. Isolated bursts. AuSRA 3, 541. doi:10.1071/CH9500541
Wild, J. P., and Smerd, S. F. (1972). Radio bursts from the solar corona. Annu. Rev. Astron. Astrophys. 10, 159–196. doi:10.1146/annurev.aa.10.090172.001111
Zhang, P., Yu, S., Kontar, E. P., and Wang, C. (2019). On the source position and duration of a solar type III radio burst observed by LOFAR. ApJ 885, 140. doi:10.3847/1538-4357/ab458f
Keywords: type III burst, decameter radio emission, frequency drift rates, duration, observations, plasma mechanism of radio emission
Citation: Melnik V, Brazhenko A, Dorovskyy V, Frantsuzenko A, Shevchuk M, Yerin S and Bubnov I (2024) Spectral features of a single type III burst in the frequency range of 10–70 MHz. Front. Astron. Space Sci. 11:1369003. doi: 10.3389/fspas.2024.1369003
Received: 11 January 2024; Accepted: 28 May 2024;
Published: 24 June 2024.
Edited by:
Peijin Zhang, University of Helsinki, FinlandReviewed by:
Anshu Kumari, NASA Goddard Space Flight Center, United StatesCopyright © 2024 Melnik, Brazhenko, Dorovskyy, Frantsuzenko, Shevchuk, Yerin and Bubnov. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Valentin Melnik, bWVsbmlrQHJpYW4ua2hhcmtvdi51YQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.