- Institute for Physical Science and Technology, University of Maryland, College Park, MD, United States
The acceleration and transport of solar energetic particles (SEPs) cause their abundance, measured at a constant velocity, to be enhanced or suppressed as a function of the magnetic rigidity of each ion, and hence, of its atomic mass-to-charge ratio of A/Q. Ion charges, in turn, depend upon the source electron temperature. In small “impulsive” SEP events, arising from solar jets, acceleration during magnetic reconnection causes steep power-law abundance enhancements. These impulsive SEP events can have 1,000-fold enhancements of heavy elements from sources at ∼2.5 MK and similar enhancements of 3He/4He and of streaming electrons that drive type-III radio bursts. Gamma-ray lines show that solar flares also accelerate 3He-rich ions, but their electrons and ions remain trapped in magnetic loops, so they dissipate their energy as X-rays, γ-rays, heat, and light. “Gradual” SEPs accelerated at shock waves, driven by fast coronal mass ejections (CMEs), can show power-law abundance enhancements or depressions, even with seed ions from the ambient solar corona. In addition, shocks can reaccelerate seed particles from residual impulsive SEPs with their pre-existing signature heavy-ion enhancements. Different patterns of abundance often show that heavy elements are dominated by a source different from that of H and He. Nevertheless, the SEP abundance, averaged over many large events, defines the abundance of the corona itself, which differs from the solar photosphere as a function of the first ionization potential (FIP) since ions, with FIP <10 eV, are driven upward by forces of electromagnetic waves, which neutral atoms, with FIP >10 eV, cannot feel. Thus, SEPs provide a measurement of element abundance in the solar corona, distinct from solar wind, and may even better define the photosphere for some elements.
1 Introduction
The relative abundance of chemical elements in any sample of material can be a clue to the identity and origin of that sample and to the nature of the physical processes it has undergone. Energetic particles are no exception. Abundances reveal the age of the galactic cosmic rays (GCRs) and the origin of unusual ions trapped in planetary magnetospheres. Solar energetic particles (SEPs) also display unique signature patterns of abundance that help us distinguish the physical processes that have formed them and the history they have traversed (Reames, 1988; Reames, 1999; Reames, 2013; Reames, 2021a; Reames, 2021b; Reames, 2021c).
A most unusual feature of SEP abundances is small 3He-rich events with 1,000-fold enhancements of 3He/4He, which were later found to have enhancements of heavy elements extending as powers of the element atomic mass-to-charge ratio A/Q from C and O to up to elements as heavy as Pb, also by a factor of ∼1,000 (e.g., Reames et al., 2014a). These SEP ions have been associated with magnetic reconnection in solar jets and flares (Kahler et al., 2001; Reames, 2013; Bučík, 2020; Reames, 2021a; Reames, 2021b; Reames, 2021c). In some larger SEP events, these “impulsive SEP” abundances often emerge as a signature of residual impulsive ions that have been reaccelerated by shock waves and exceed the average coronal abundances in some “gradual” SEP events (Reames, 1999; Desai and Giacalone, 2016; Reames, 2021a; Reames, 2021b). This not only divides element abundances of SEP events into haves and have-nots but also highlights variations in H and He, which can either participate or not participate in the heavy-element behavior (Reames, 2022b).
A most fundamental population that SEPs can measure is the abundance of elements in the corona itself, from which all SEPs are derived. Only in the corona are the densities low enough for ions to be accelerated without immediately losing their energy in Coulomb collisions. The corona not only provides a baseline for identifying other populations derived from it but also highlights the physical process that distinguishes it from the photosphere. We first discuss these reference coronal abundances and then the unique abundances of impulsive SEPs, followed by their presence or absence in the largest “gradual” SEP events. SEP abundances in this work are mainly derived from the Low-Energy Matrix Telescope (LEMT) on the Wind spacecraft (von Rosenvinge et al., 1995); ∼30 years of LEMT abundance data are available at https://omniweb.gsfc.nasa.gov/.
2 Reference abundances, solar corona, and the first ionization potential
The abundances of elements C, O, and the others mentioned above, in SEPs, were first measured using nuclear emulsion detectors on sounding rockets from Ft. Churchill, Manitoba by Fichtel and Guss (1961), and those measurements were later extended up through Fe using the same technique (Bertsch et al., 1969). As satellite measurements became available (e.g., Teegarden et al., 1973), comparisons of SEPs with other abundances became more common (e.g., Webber, 1975). Meyer (1985) summarized SEP abundance measurements in large SEP events as having a common baseline, derived from abundances in the solar corona where acceleration occurs, and a second component that varied from event to event as a power law in the particle charge-to-mass ratio Q/A (Breneman and Stone, 1985). A factor in this abundance variation was the pitch-angle scattering of the ions; thus, if Fe scatters less than O, Fe/O will be enhanced early in events but will be depleted later. Such variations might average out, so it was soon possible to average ∼50 or so large SEP events to remove the event-to-event variations and produce estimates of coronal abundances (Reames, 1995a; Reames, 2014); this could be compared with the solar photospheric abundances measured spectroscopically. A modern comparison of the SEPs/photospheric abundances vs. the first ionization potential (FIP) is shown in Figure 1. The photospheric abundances are a modification by Caffau et al. (2011) of the meteoritic abundances proposed by Lodders et al. (2009). A comparison using photospheric abundances proposed by Asplund et al. (2021) is shown, and the abundances are listed by Reames (2021b).
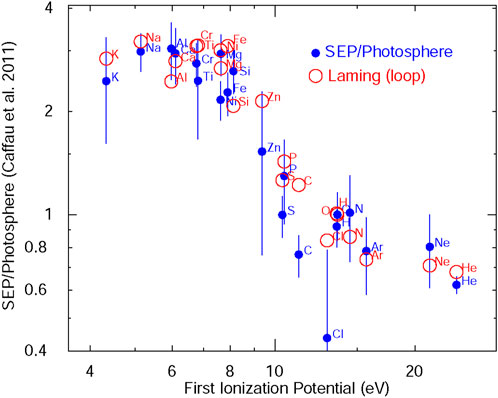
FIGURE 1. The ratio of solar energetic particles (SEPs) to photospheric abundances of elements is shown vs. the first ionization potential (solid blue circles) and is compared with the theory proposed by Laming et al. (2019) (open red circles) for element transport along closed loops in active regions.
In the theory proposed by Laming (2015) and Laming et al. (2019), shown in Figure 1, the ponderomotive force of Alfvén waves helps drive low-FIP ions up across the chromosphere into the corona, but it cannot affect un-ionized high-FIP neutral atoms. All elements become ionized in the hot ∼1 MK corona. SEPs have a different FIP pattern from that of solar wind or the solar wind accelerated by shock waves at co-rotating stream interfaces (Reames et al., 1991; Reames, 1995a; Mewaldt et al., 2002; Reames, 2018a; Reames, 2021a); thus, SEP abundances do not differ when measured in fast or slow wind (Kahler et al., 2009). SEPs are not accelerated solar wind. Differences between the FIP patterns of SEPs and solar wind may be caused by open vs. closed field lines, where Alfvén waves resonate with the loop length of closed loops (Reames, 2018a; Laming et al., 2019). A first-order examination of Figure 1 shows a reasonable agreement when comparing elements with a similar FIP but different A/Q, e.g., Mg or Si with Fe or Ni.
To what extent does this average of abundances, over many gradual SEP events, recapture coronal abundances? It is quite possible that the increasing and decreasing power laws of abundance vs. A/Q do not perfectly average out; however, a more outstanding disagreement seems to be the single element C. How can a single element, or actually a single ratio C/O, stand out? We will return to this question after discussing the patterns of known abundance variations and their probable causes.
3 Impulsive SEP events
The idea of two fundamental mechanisms of SEP acceleration began quite early (Wild et al., 1963) with solar radio observations that distinguished the sources of type-II and type-III radio bursts. The radio emission frequency depends upon the square root of the local electron density, which decreases with distance from the Sun. Type-III radio bursts exhibit a rapid frequency decrease corresponding to the speed of 10–100 keV electrons streaming out from the Sun, while type-II bursts show a much slower frequency decrease of ∼1,000 km s-1 shock waves driven out from the Sun. These streaming electrons propagate scatter-free because the resonant turbulence that would scatter them is absorbed by the plasma (Tan et al., 2011). Later, Lin (1970) observed beams of ∼40 keV electrons associated with the impulsive type-III bursts and thought that they might involve “pure” electron events, i.e., without ions. Relativistic electrons and energetic protons only accompanied the shock-associated type-II bursts.
Soon, the SEP world was surprised by the observations of 3He-rich events. While a typical solar or solar wind abundance is 3He/4He ≈ 5 × 10−4, an event was soon found with 3He/4He = 1.5 ± 0.1 (Serlemitsos and Balasubrahmanyan, 1975; Mason, 2007). Such a high ratio could not come from the fragmentation of 4He as that which occurred in GCRs since 3He was not accompanied by any 2H. The early idea of nuclear fragmentation was completely laid to rest by the later measurements of Be/O and B/O <2 × 10−4 (McGuire et al., 1979; Cook et al., 1984). Instead, this was a new mechanism involving resonant wave–particle interactions. The 3He gyrofrequency, dependent upon Q/A, lay isolated at Q/A = 2/3, between those of H at Q/A = 1 and 4He at Q/A = 1/2.
These two different features of impulsive SEPs, i.e., 1) “pure” electron beams producing type-III radio bursts and 2) 3He-rich events, were unified by Reames et al. (1985) as different properties of the same events, and Reames and Stone (1986) explored the kilometric radio properties of 3He-rich events, even tracking the flow of electrons out from the Sun. Early theories discussed selective heating by the resonant absorption of various types of plasma waves at the 3He gyrofrequency, followed by the acceleration of thermal tails by some unspecified mechanism (e.g., Fisk, 1978; see other references Reames, 2021c or Reames, 2023c), but Temerin and Roth (1992) proposed electromagnetic ion cyclotron (EMIC) waves generated by streaming electron beams and added their absorption by mirroring 3He for acceleration, in analogy with the production of ion conics observed in the Earth’s magnetosphere.
3.1 Element abundance
Enhancements of heavy elements up to Fe in impulsive events were first reported by Mogro-Comparo and Simpson (1972). These observations were improved in subsequent generations of experiments by Mason et al. (1986) and then by Reames et al. (1994). Groups of elements were eventually resolved up to Pb at 3–10 MeV amu−1 (Reames, 2000; Reames and Ng, 2004; Reames et al., 2014a) and below ∼1 MeV amu−1 (Mason et al., 2004). The average enhancement was found to be a power law in A/Q, with a power of 3.64 ± 0.15 above 1 MeV amu−1 and ∼3.26 below, using Q-values appropriate for ∼3 MK.
The early direct measurements of the ionization states of SEP elements up to Fe (Luhn et al., 1984; Luhn et al., 1987) found that QFe = 14.1 ± 0.2 in gradual SEP events, which would correspond to a typical source plasma temperature of ∼2 MK, but 3He-rich events had QFe = 20.5 ± 1.2, with elements up to Si being fully ionized, either suggesting a temperature >10 MK or the stripping of ions by passing through a small amount of material after acceleration. Reames et al. (1994) noted that impulsive ion enhancements, relative to the corona, formed three groups: 1) C, N, and O, like 4He, all seemed to be un-enhanced, 2) Ne, Mg, and Si were enhanced about a similar factor of ∼2.5, and 3) Fe was enhanced by a factor of ∼7. The first group was probably fully ionized with A/Q = 2, while the second group would have similar abundances in their states with 2 orbital electrons, which occur at approximately 3 MK. No enhancements could occur if Ne, Mg, and Si were fully ionized, as measured. The resolution of this dilemma is that the ions in impulsive SEP events are stripped after acceleration, and it was later found that the ionization states of Fe depended upon the ion velocity (DiFabio et al., 2008), as expected from stripping. This suggested that impulsive SEP events were accelerated at ∼1.5 RS. In contrast, gradual SEP events, found to be accelerated at shock waves driven out from the Sun by coronal mass ejections (CMEs), began at 2–3 RS (Tylka et al., 2003; Cliver et al., 2004; Reames, 2009a; Reames, 2009b).
3.2 Jets and flares
While gradual SEP events have a 96% correlation with fast, wide CMEs (Kahler et al., 1984), an early search found no meaningful association of 3He-rich events with CMEs observed using the Solwind coronagraph (Kahler et al., 1985). However, with improved coronagraph sensitivity of SOHO/LASCO, Kahler et al. (2001) found narrow CMEs that were associated with the larger 3He-rich events; the CME associated with the large impulsive SEP event of 1 May 2000 had a speed of 1,360 km s-1, easily fast enough to drive a shock that would reaccelerate particles. These observations led Kahler et al. (2001) to associate impulsive SEP events with solar jets (e.g., Shimojo and Shibata, 2000), an association that has been extended (Nitta et al., 2006; Wang et al., 2006; Bučík et al., 2018a; Bučík et al., 2018b) and reviewed by Bučík (2020). Jets are driven by energy from magnetic reconnection, as shown in Figure 2.
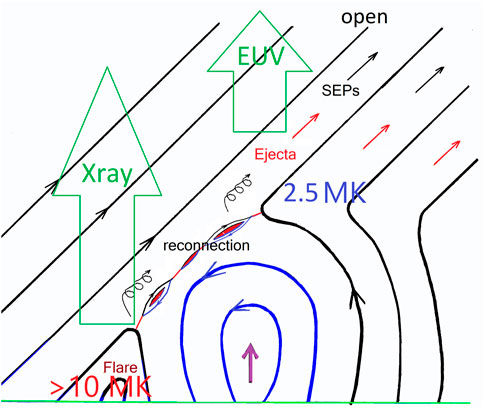
FIGURE 2. Sketches of the topology of a solar jet, where rising closed field lines of one magnetic polarity (blue) form islands of reconnection where they meet the oppositely directed open field lines (black). SEPs are accelerated in the reconnection region and escape along the open field lines, as does the CME plasma. Newly formed closed field lines at the lower left trap energetic electrons and ions that plunge into the deeper corona and form a flare. The hot flaring region (>10 MK) emits X-rays, while the open region is observed to be an EUV-emitting region at ∼2.5 MK (Reames, 2023c).
A particle-in-cell simulation of a reconnection region by Drake et al. (2009) found strong A/Q-dependent enhancements in the energetic heavy ions that could match those observed. The particles were Fermi-accelerated as they were reflected (mirrored) back and forth by the approaching ends of the collapsing islands of magnetic reconnection. However, the reconnection that opens some field lines always closes others, as shown in the lower left of Figure 2. These closing field lines trap newly accelerated particles that deposit their energy as heat or in the emission of X-rays or γ-rays—a solar flare. Thus, jets would always be expected to have accompanying flares that involve the same accelerated particles. Of course, there are more realistic models of jets (e.g., Archontis and Hood, 2013; Lee et al., 2015; Pariat et al., 2015) that better describe the CME emission, but jet models do not yet include SEP acceleration.
The relationship of jets vs. flares is a close one, with similar ion acceleration on open vs. closed field lines. Similar ion enhancements were first noted between impulsive SEPs and abundances from γ-ray line measurements in large flares by Murphy et al. (1991); then, Mandzhavidze et al. (1999) found that the energetic ions that were accelerated and trapped in all 20 available large solar flares were 3He-rich. The three γ-ray lines at 0.937, 1.04, and 1.08 MeV from the de-excitation of 19F* were unusually strong and were produced with an especially high cross-section in the reaction 16O (3He, p) 19F*. These were compared with other lines from excited 16O, 20Ne, and 56Fe to distinguish 3He from 4He in the “beam.” Some of the events had 3He/4He of ∼1, while all had 3He/4He >0.1. Murphy et al. (2016) later found 6 key ratios of γ-ray fluxes that were dependent upon 3He/4He in the beam, and all of them showed an average 3He/4He ratio of 0.05–3.0. These studies included ∼135 product de-excitation lines from ∼300 proton- and He ion-induced reactions (e.g., Kozlovsky et al., 2002). These γ-ray lines are from the largest flares, not small jet-associated impulsive flares, suggesting that impulsive SEP abundances are a general consequence of the physics of magnetic reconnection.
3.3 Power-law abundance from jets with or without shocks
We always compare element abundances at the same velocity, or MeV amu−1, but properties such as magnetic deflection and scattering depend upon magnetic rigidity, or the momentum per unit charge, also dependent upon A/Q, quite often depends upon a power of A/Q (e.g., Parker, 1965). Thus, it is not surprising that enhancements that depart from reference abundances vary as a power of A/Q. More specifically for impulsive SEPs, the theory proposed by Drake et al. (2009) related the power of A/Q to the power of the width distribution of reconnecting magnetic islands. However, the Q-values of the ions depend upon the source plasma temperature. Our strategy has simply been to try all temperatures in a reasonable range, determine the Q-values (using, e.g., Mazzotta et al., 1998 or Post et al., 1977), and choose the temperature and power law that yield the best least-squares fit of enhancement vs. A/Q (Reames et al., 2014b; Reames, 2018b; Reames, 2021a). Examples showing typical temperature dependence in enhancement vs. A/Q are shown in Figure 6 of the study by Reames (2022b), Figure 6 of the study by Reames (2018a), and Figure 2 of the study by Reames et al. (2014b).
Fitting 111 impulsive SEP events, Reames et al. (2014b) found 79 events at 2.5 MK and 29 at the neighboring 3.2 MK, i.e., very little variation in impulsive SEP events. Subsequently, these temperatures agree with the EUV temperatures in jets (Bučík et al., 2021). Figure 3 shows power-law fits to abundance enhancements in several impulsive SEP events. The time profiles of the events are shown in the lower panels, derived temperatures (and event durations) in the middle panels, and the best fits to the enhancements vs. A/Q in the upper panels. Event numbers marking each event onset in Figure 3 correspond to the impulsive SEP event list given by Reames et al. (2014a), along with all the events selected to have enhanced Fe/O abundances.
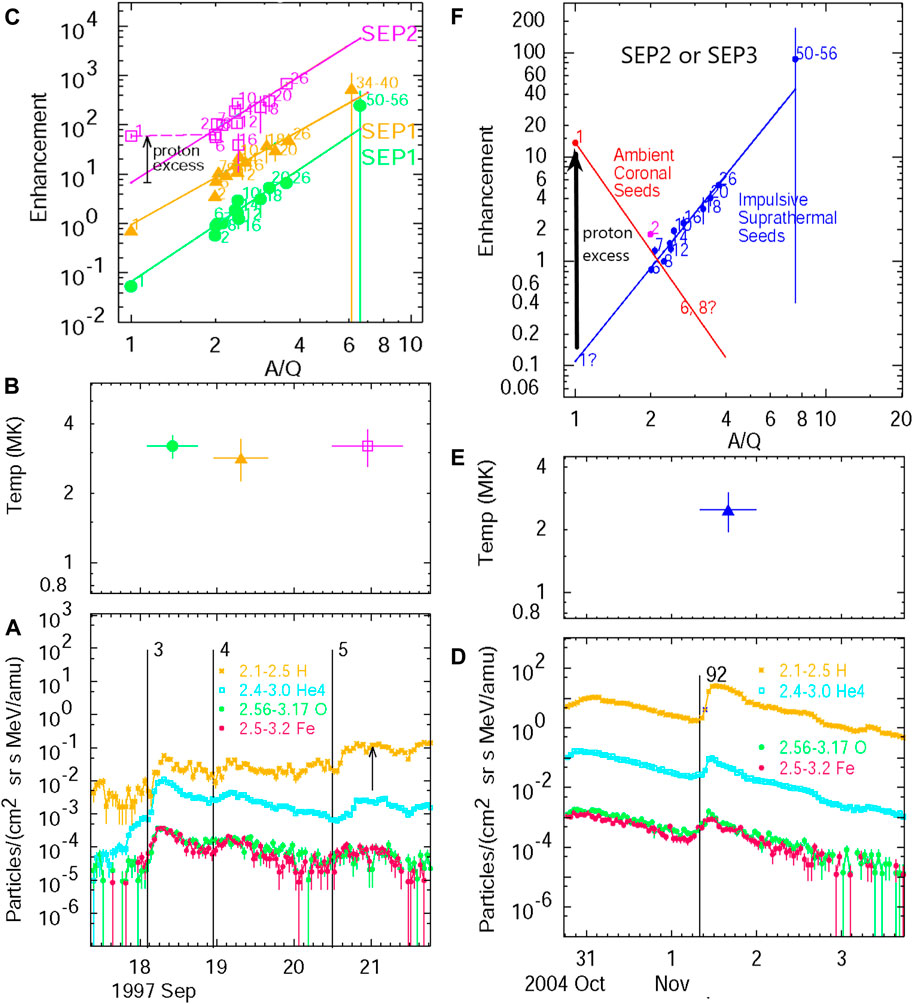
FIGURE 3. Panels (A and D) show intensities of H, 4He, O, and Fe at the listed energies in MeV amu−1 for (A), which is a sequence of three small impulsive SEP events, and (D), a larger event. Panels (B and E) show the derived best-fit temperatures (and durations) for each event below; panels (C and F) show the corresponding best-fit power-law abundance enhancements (normalized at O and shifted ×10 for each event), with the measurements for each element labeled by atomic numbers Z. Only elements with Z ≥6 are included in the fits. Panel (F) distinguished two possible seed populations, contributing to acceleration in the shock wave driven by the 925-km s-1-associated CME (see text).
For events 3 and 4 in Figure 3, the power-law fits, obtained for ions with Z ≥6, extend to include proton measurements at A/Q = 1. This is taken to mean that all of these ions come from the same population, i.e., the magnetic reconnection in the associated jet. Reames (2020a) defined these “pure” reconnection events as SEP1 events; they had either no visible CMEs or CME speeds <500 km s-1, i.e., no shock acceleration was likely. Event 5 is ambiguous; the excess protons do not fit the power law, but the theory proposed by Drake et al. (2009) allows for enhancements that start above Z = 2, and H and 4He could both be un-enhanced, i.e., at the same level, as in this event, which also shows no CMEs.
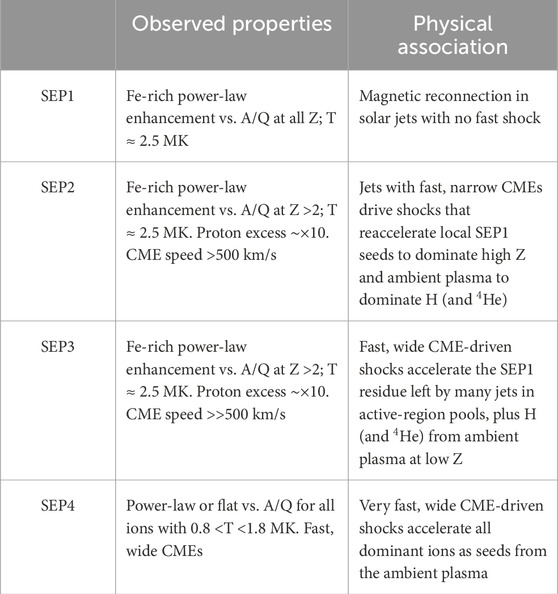
Earlier, there were thought to be only two types of SEP events, 3He-rich or “impulsive” SEP events with unique element abundances and shock-accelerated “gradual” SEP events that accelerated coronal ions. Abundances in the gradual events varied primarily because of the differences in element transport; since Fe scatters less than O, Fe/O will be enhanced early and depressed later, following a power law in A/Q. This was observed by Breneman and Stone (1985) and implied in the discussions by Meyer (1985). This simplicity ended when Mason et al. (1999) found the enhancement of 3He in a large gradual SEP event. Clearly, shocks could reaccelerate residual ions from small impulsive and ambient coronal ions, and these two seed populations became widely discussed (Tylka et al., 2001; Tylka et al., 2005; Desai et al., 2003; Tylka and Lee, 2006). Eventually, Reames (2020a) suggested organizing the combination of acceleration mechanisms and seed populations into four physical categories, as shown in Table 1.
However, event 92, as shown in Figure 3F, is an event with large proton excess and even an excess of 4He; it suggests power-law contributions that are shock-accelerated from two seed populations, ambient coronal ions for H and 4He and residual impulsive suprathermal ions for Z ≥6. The event would be classified as SEP2 if all the SEP1 ions came from a single impulsive jet event and as SEP3 if the pre-accelerated impulsive seed ions had been collected from many previous SEP1 or SEP2 events before shock acceleration. In fact, this seems to be a SEP3 event, despite its short duration, since its intensity is high, and an earlier event in the same location is similar in character. It should also be noted that the scatter of Z ≥6 points about the fit line, shown in Figure 3F, is quite small compared with those in Figure 3C, suggesting that the output of many small jets have been averaged to reduce abundance variations in SEP3 events (see Figure 8 in the study by Reames, (2020a)). We consider other SEP2 and SEP3 examples below.
The abundance of 4He in SEP events can vary because it can be dominated by either coronal or impulsive seed components. However, there are also other variations in 4He that have been summarized in greater detail by Reames (2022b).
4 Gradual SEP events
The first recognized SEP events (Forbush, 1946) were the immense ground-level enhancement (GLE) events, where GeV protons initiate nuclear cascades through the atmosphere that exceed those of GCRs. While these events were erroneously attributed to solar flares for many years (Gosling, 1993; Gosling, 1994), Kahler et al. (1984) had found that large SEP events had a 96% association with fast, wide shock waves, driven out from the Sun by CMEs, reaffirming the finding of shock acceleration in radio type-II bursts by Wild et al. (1963) two decades earlier. Mason et al. (1984) concluded that only “large-scale shock acceleration” could explain the extensive rigidity-independent spread of SEPs, and recent findings from missions like STEREO now show how shock waves and SEPs wrap around the Sun (e.g., Reames, 2023a; Reames, 2023b). Evidence for shock acceleration has grown (e.g., Reames, 1995b; Reames, 1999; Zank et al., 2000; Zank et al., 2007; Lee et al., 2012; Reames, 2013; Desai and Giacalone, 2016; Kouloumvakos et al., 2019; Reames, 2021b), especially for GLEs (Tylka and Dietrich, 2009; Gopalswamy et al., 2012; Mewaldt et al., 2012; Gopalswamy et al., 2013a; Raukunen et al., 2018).
One line of evidence has been the onset timing or solar particle release (SPR) time of the SEPs compared with X-ray or γ-ray onset times of associated flares. Ions with lower velocities have increasingly delayed onsets that extrapolate back to a single SPR time, with delay = distance along the observer’s field line divided by velocity. For impulsive events, the SPR times and X-ray onsets agree closely (Tylka et al., 2003), but for gradual events like GLEs, the SPR time can lag the X-ray and γ-ray onset by as much as half an hour (Tylka et al., 2003; Reames, 2009a; Reames, 2009b), sometimes even after the associated flare is completely over. The SPR time corresponds to the time the shock at the leading edge of the CME reaches 2–3 solar radii (Reames, 2009a; Reames, 2009b; Cliver et al., 2004), presumably when the shock emerges above closed magnetic loops and its speed exceeds the declining Alfvén speed. Type-II radio emission shows that shocks can begin at ∼1.5 AU (Gopalswamy et al., 2013b), but the SPR time depends upon the observer’s longitude, which often differs from that of the ewarliest source of radio emission (Reames, 2009b). Variations in these parameters or delays in the shock interception of the observer’s field line (Reames, 2023a; Reames, 2023b) cause variations in SPR delay.
Abundance enhancements or suppressions in gradual SEP events relative to the reference coronal abundances have been classed as SEP3 or SEP4 by Reames (2020a), depending upon whether the source of seed particles for shock acceleration is purely ambient coronal abundances (SEP4) or whether the residual impulsive suprathermal ions dominate the heavy elements (SEP3).
4.1 Moderate-sized SEP4 events
Figure 4 shows abundance data for two typical SEP4 events. These gradual events are intense enough to measure significant enhancements of most elements in several time intervals, e.g., every 8 h. The derived temperatures are less than those in impulsive events, and the abundance patterns vary little during the events, suggesting that there is too little variation in scattering to separate different elements in time. Most importantly, the power-law fits, obtained for elements C and above, can be extended to fit H and He reasonably well, suggesting that all the elements have originated from a single population. This, the declining enhancement, and the lower temperature suggest that the population is ambient coronal ions, un-enhanced by any impulsive pre-accelerated population. Similar plots can be observed in some events from three spacecraft (e.g., Wind and STEREO A and B) spaced at ∼120⁰ around the Sun (e.g., see Figure 7 in the study by Reames, (2022b)). The main reason for the systematic decline with A/Q may be that higher-rigidity elements leak away faster. The energy spectra of ions are correlated with variations in A/Q in these events (Reames, 2021d; Reames, 2022a) and are also relatively steep.
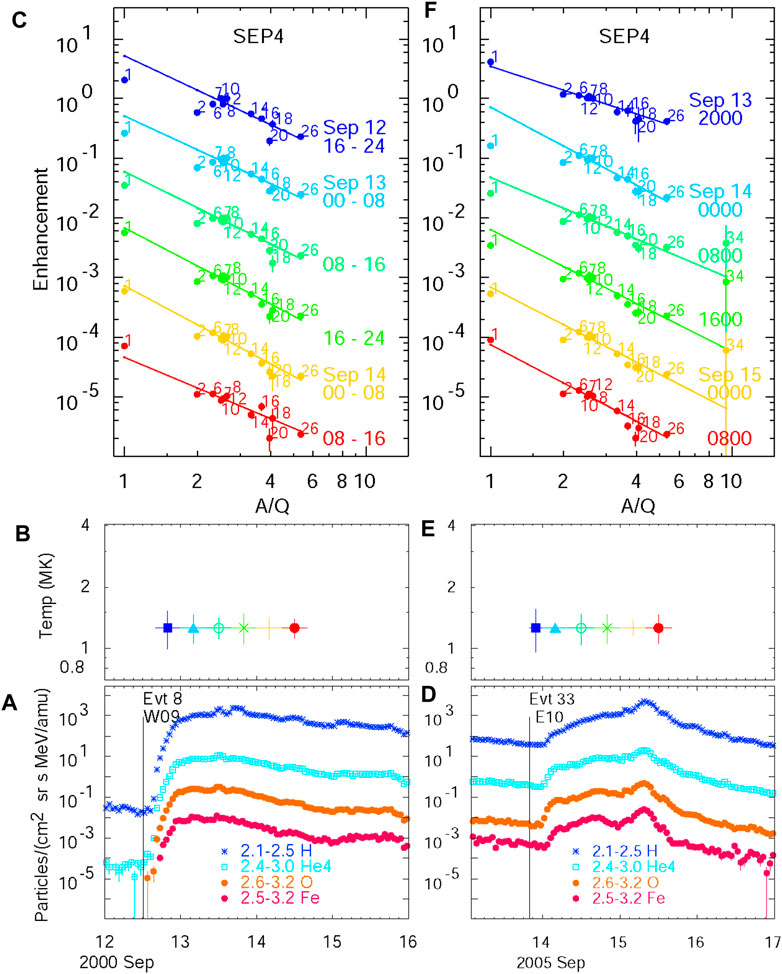
FIGURE 4. Typical small gradual SEP4 events. Panels (A and D) show the time evolution of the elements H, 4He, O, and Fe and the listed energies (in MeV amu−1) in two gradual SEP events numbered 8 and 33 (in reference to the list given by Reames, (2016)). Panels (B and E) show the derived source plasma temperatures in a series of intervals (colors) during each event. Panels (C and F) show abundance enhancements vs. A/Q for elements (normalized at O and shifted ×0.1 for each interval), with atomic numbers Z shown for each time interval (color) and the best fits of elements with Z ≥6 extended to A/Q = 1. All the elements, including H, tend to fit each power law.
Typically, enhancements decrease with A/Q in many gradual events, as shown in Figure 4, but there is also a class of events where A/Q dependence is flat, i.e., the abundances are nearly coronal. However, they cannot be used to determine a temperature well since the enhancements are independent of A/Q. Thus, these events are unremarkable and often overlooked. However, one is shown in Figure 5 as an example of an event where abundance enhancements (Figure 5C) begin as quite flat, i.e., independent of A/Q, but then steepen as the higher-rigidity ions preferentially leak away. Here, source temperatures are poorly determined when enhancements are flat but improve as they steepen.
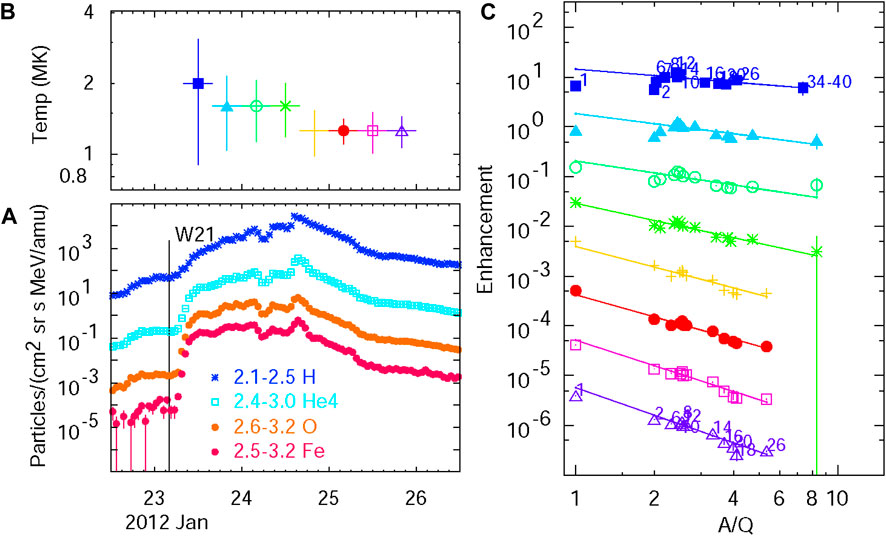
FIGURE 5. Typical gradual SEP4 event with initially flat (coronal) abundances. Panel (A) shows the time evolution of elements H, 4He, O, and Fe and the listed energies (in MeV amu−1) in the gradual SEPs. Panel (B) shows the derived source plasma temperatures in a series of intervals (colors and symbols) during the event. Panel (C) shows abundance enhancements vs. A/Q for elements in each time interval (color and symbols) ×0.1 and the best fits of elements with Z ≥6 extended to A/Q = 1. Element atomic numbers Z are listed for the first and last intervals.
4.2 GLEs that are SEP4 events
As intensities in gradual SEP events increase, the high-energy protons stream ahead to amplify Alfvén waves that scatter subsequent ions (Stix, 1992; Ng et al., 1999; Ng et al. 2003; Ng et al. 2012). Scattering varies as a power law in magnetic rigidity so that Fe can propagate away from the shock more easily than O; for example, Figure 6 shows abundance fits for two GLEs that are SEP4 events. The fitted temperatures are near ∼1 MK, and the fits for elements with Z ≥6 are in reasonable agreement with H and He for both positive and negative power-law slopes. Heavy elements tend to be enhanced ahead of the shock and, hence, depressed behind. These enhancements primarily originate from strengthened preferential scattering during transport in these events and not from impulsive seed particles, as indicated by the lower temperature, the inclusion of protons in a single seed population, and the return to heavy-element suppression behind the shock. Where abundances show an increase in A/Q, the energy spectra become quite flat in the plateau region (Reames and Ng, 2010; Ng et al., 2012; Reames and Ng, 2014; Reames, 2021a) because of the underlying correlation between abundances and spectra (Reames, 2021d; Reames, 2022a).
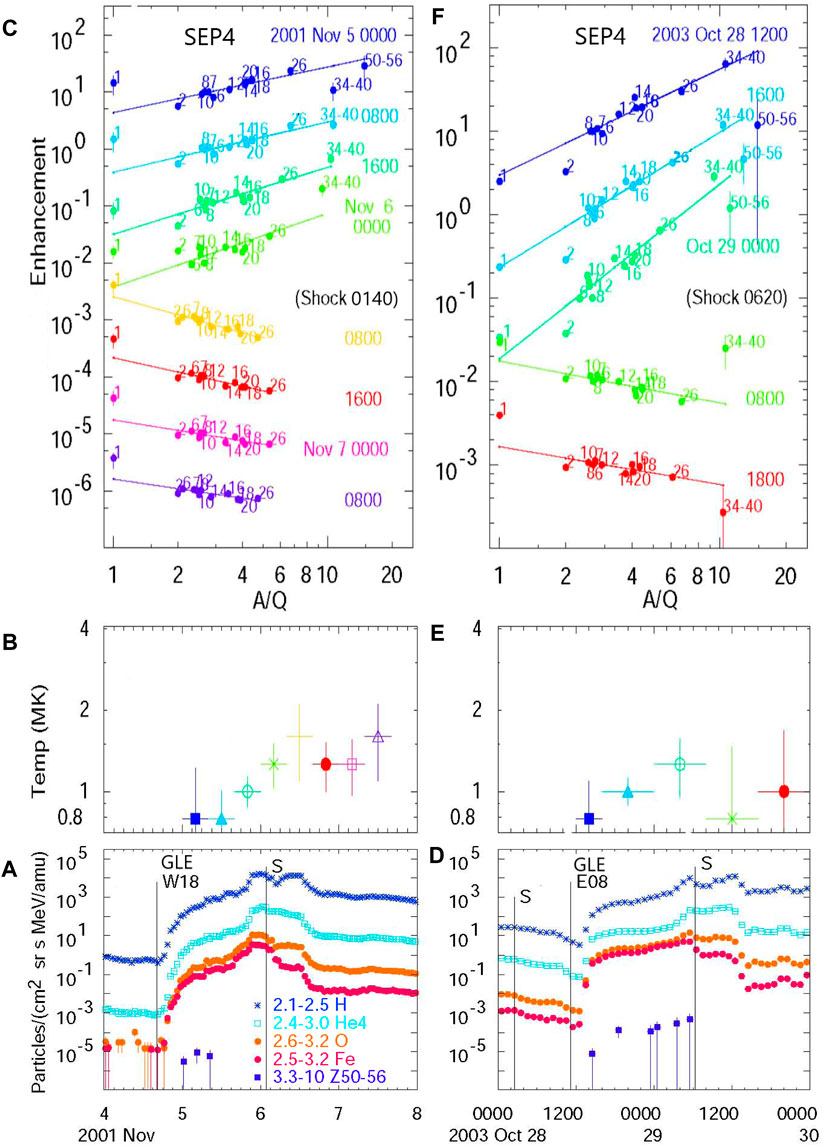
FIGURE 6. Large ground-level enhancements (GLEs) as gradual SEP4 events. Panels (A and D) show the time evolution of the elements H, 4He, O, and Fe, and elements with 50 ≤Z ≤56, along with the listed energies (in MeV amu−1) in 2 SEP4 events. Panels (B and E) show the derived source plasma temperatures in a series of intervals (colors) during each event. Panels (C and F) show abundance enhancements vs. A/Q for elements (normalized at O and shifted ×0.1 for each interval) with Z shown, for each time interval (color) and the best least-squares fits of elements with Z ≥6 extended to A/Q = 1. The high-Z enhancements go away after the shocks pass.
For these large events, transport out to 1 AU becomes much more important. The strong transport-induced abundance increases shown in Figure 6 are a consequence of the high SEP intensities. The high intensities of protons streaming away from the shock amplify resonant Alfvén waves (Melrose, 1980; Stix, 1992) that scatter subsequent ions. The wave number of resonant waves is k ≈ B/μP, where B is the magnetic field intensity, P is the particle rigidity or momentum per unit charge, and μ is the cosine of the particle pitch angle relative to B. The spectrum of waves not only traps particles near the shock but extends far out into space, bounding intensities at the “streaming limit” (Reames and Ng, 1998; Reames and Ng, 2010; Reames and Ng, 2014), thus driving more acceleration (Lee, 1983; Lee, 2005; Zank et al., 2000; Ng and Reames, 2008; Afanasiev et al., 2015; Afanasiev et al., 2023), and the transport strongly favors the escape of Fe vs. O (Parker, 1965; Ng et al., 1999; Tylka et al., 2001; Ng et al., 2003; Tylka et al., 2005; Tylka and Lee, 2006; Ng et al., 2012). In very large events, intensities of ions below ∼1 MeV amu−1 (and their abundances) remain in the pre-event background until the shock comes very near to the observer.
4.3 GLEs that are SEP3 events
However, large gradual SEP events, even GLEs, can pick up pre-accelerated residual impulsive seed particles from multi-jet collections, often observed to accumulate near active regions (Desai et al., 2003; Wiedenbeck et al., 2008; Bučík et al., 2014; Bučík et al., 2015; Chen et al., 2015; Reames, 2022a). Recently, Kouloumvakos et al. (2023) found an average connection time to 3He-rich active regions of 4.1 ± 1.8 days, suggesting a width of ∼52⁰ in longitude. These seed particles contribute with their characteristic enhancement pattern at high Z and its source temperature, but ambient coronal ions still dominate H and, possibly, He. Figure 7 shows three events sequentially, from a single region rotating across the Sun, which show the characteristic behavior of SEP2 and then SEP3 events: temperature >2 MK (like impulsive events) and the enhanced high-Z fit line that fails to include the proton intensities. Figures 7D, E show He being enhanced as well, and the high-Z enhancements flatten with time, probably from preferential leakage at high Z, making temperature measurement difficult. The source rotates from W71 to W84 to W120 at the rate of ∼13⁰ day-1. CME speeds for the three events are 830, 1,199, and 2,465 km s-1, and the last two events are both GLEs. These “double-dipping” SEP3 events are not uncommon (Reames, 2022a) and often include GLEs. Of course, the GLE is determined by the protons, not the high-Z ions, but the location or configuration of these events could be a factor.
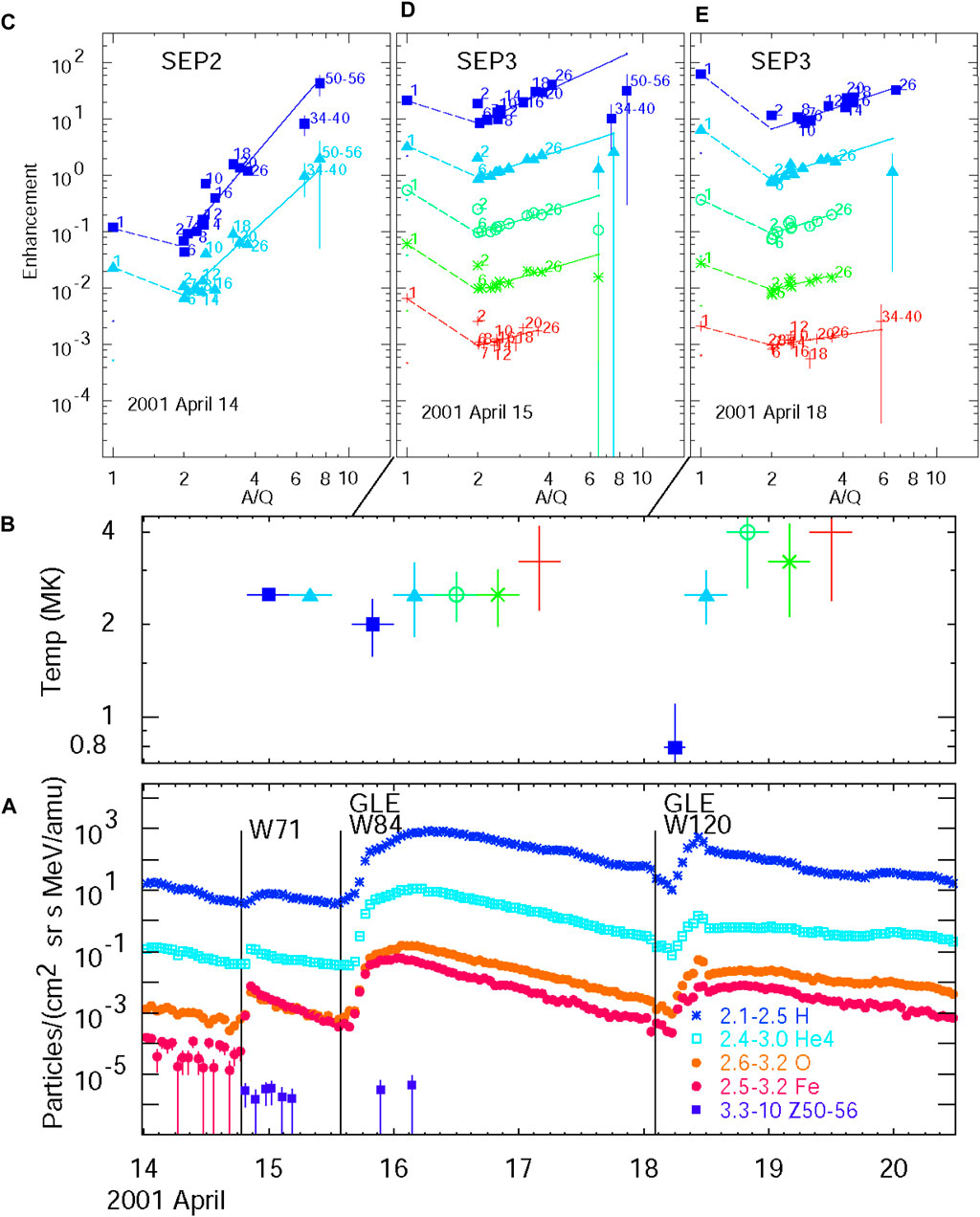
FIGURE 7. Large GLEs as gradual SEP3 events. Panel (A) shows the time evolution of elements H, 4He, O, and Fe, and elements with 50 ≤Z ≤56, along with the listed energies (in MeV amu−1) in 2 SEP3 events. Panel (B) shows the derived source plasma temperatures in a series of time intervals (colors) during the events. Panels (C, D, and E) show abundance enhancements vs. A/Q for elements (normalized at O and shifted ×0.1 for each interval), with representative atomic numbers Z shown, with the best least-squares fits of elements with Z ≥6, for each time interval (color) mapped to the events below. Two different seed populations dominate the high and low Z in SEP2 (C) and SEP3 (D and E) events.
While it is tempting to think that the single SEP2 event “feeds” the SEP3 events shown in Figure 7, details of the abundances differ. The SEP2 event has an unusually high Ne amount, as shown in Figure 7C, but the later SEP3 events shown in Figures 7D, E do not. Presumably, the seed population for the SEP3 events is fed by many subsequent smaller impulsive events on 15 April that do not contribute energetic ions at 1 AU. SEP3 abundances always show smaller variations than SEP2 events (e.g., Figure 8 in the study by Reames (2021b)). Otherwise, searches for abundance features, like the Ne enhancement here, sometimes implicate spectral fluctuations (Reames, 2019). However, below 1 MeV amu−1, Mason et al. (2016) found extreme spikes in S in 16 events in 16 years. S may be a second-harmonic resonance at A/Q = 3 related to the 3He resonance at A/Q = 1.5 since S and 3He have similar spectra. In contrast, S (Z = 16) is actually suppressed in Figure 3C.
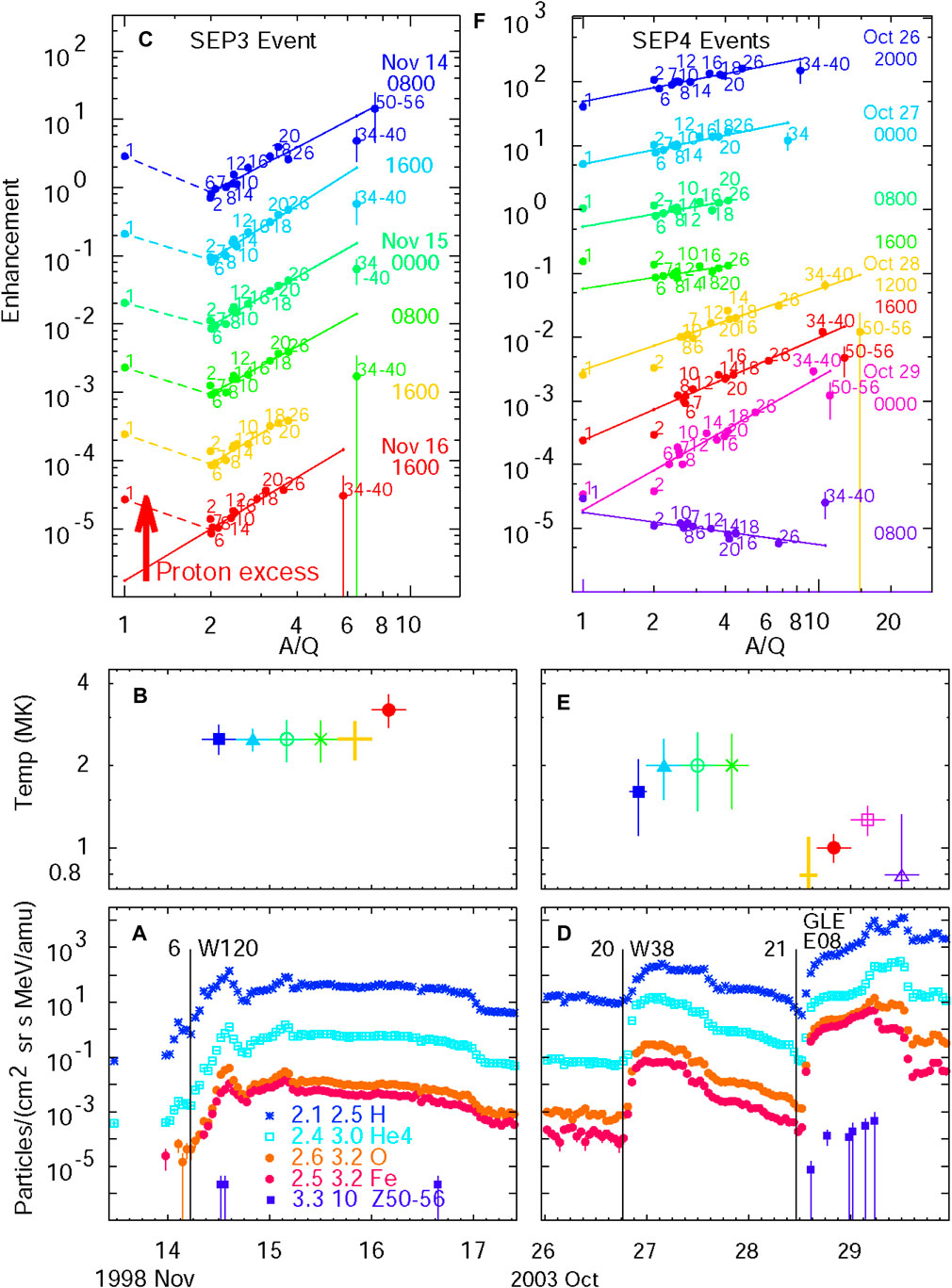
FIGURE 8. Compares a large SEP3 (left) event with a pair of large SEP4 events (right); one is a GLE. Panels (A and D) show the time evolution of the elements H, 4He, O, and Fe, and elements with 50 ≤Z ≤56, along with the listed energies (in MeV amu−1). Panels (B and E) show the derived source plasma temperatures in a series of intervals (colors) during each event. Panels (C and F) show abundance enhancements vs. A/Q for elements (normalized at O and shifted ×0.1 for each interval) with Z listed for each time interval (color), along with the best least-squares fits of elements with Z ≥6. Systematic proton excess suggests that the SEP3 event in (C) has two seed populations for the shock, while for SEP4 events in (F), all elements tend to fit a single power law.
It is common that the high-Z enhancement in SEP3 events is less than that in any preceding SEP2 events that may feed the impulsive pool, as shown in Figure 7. Shock acceleration probably reduces the enhancement from seed impulsive ions just as modest SEP4 events depress the abundances of the ambient coronal seed ions, as shown in Figure 4.
Figure 8 directly compares a SEP3 event with two SEP4 events. While the temperatures of the seed populations of the two event types differ, the most notable difference occurs in the proton enhancement. The protons fit the power-law extrapolation from high Z in Figure 8F, but they are clearly enhanced in Figure 8C, as they were in Figure 7. All three events shown in Figure 8 show enhancements of high-Z elements, at least initially, but it is the departure of the protons from the fit that suggests the presence of two seed populations in SEP3 (and SEP2) events.
It is important to realize that we cannot exclude the possibility of some impulsive suprathermal seeds in any gradual event, including SEP4 events. Mason et al. (1999) found a modest increase in 3He in a large gradual event. We cannot distinguish the presence of impulsive heavy elements unless they actually dominate the event so we see their characteristic A/Q pattern and higher temperature. If only ∼10% of Fe was from residual impulsive ions, we would never know it. It is also quite possible that very large events become SEP4 events because strong shocks sweep up enough ambient plasma to swamp any residual impulsive ions that are also available. It is also possible that SEP4 events occur because there are no residual SEP1 ions available for the shock to reaccelerate.
5 Conditions for SEP3 events
GLEs are determined by proton intensities, and protons are accelerated from the ambient plasma in both SEP3 and SEP4 events; so, GLE existence is independent of the dominant source of high-Z ions. In solar cycle 23, 6 of the 15 GLEs were SEP3 events and 9 were SEP4 events. Solar cycle 24 is much weaker with only 2 GLEs, both of which were SEP4 events. During solar cycle 24, STEREO plus Earth provided 3 approximately equally spaced locations around the Sun. Cohen et al. (2017) observed H, He, O, and Fe for gradual SEP events observed by two or three spacecraft. Of 41 events, 10 were measured on all three spacecraft. All of the 10 were SEP4 events, and only 1 of the 2-spacecraft events (4 August 2011) was a SEP3 event (see Figure 10 in the study by Reames (2020b)).
Why are there so few SEP3 events in cycle 24? These events require a stream of residual impulsive SEP1 or SEP2 ions flowing out from an active region. These streams or persistent 3He-rich regions are often observed during the solar maxima (Richardson et al., 1990; Desai et al., 2003; Wiedenbeck et al., 2008; Bučík et al., 2014; Bučík et al., 2015; Chen et al., 2015; Reames, 2022a). Then, that same region emits a fast, wide CME-driven shock that accelerates these residual impulsive ions, along with ambient ions that dominate the protons. In a weak solar cycle, 1) the number of sufficiently fast CMEs is reduced and 2) the probability of 3He-rich streams is reduced, so perhaps the number of SEP3 events is reduced by the product of the two factors. Perhaps a very strong cycle would mostly have SEP3 events.
What are the conditions for producing a SEP3 event? Gopalswamy et al. (2022) asked an important question: “Can type-III radio storms be a source of seed particles to shock acceleration?” These authors identify a large shock event that follows from the same active region as a storm of type-III bursts. Should we expect a SEP3 event? Figure 9 shows the time variation of SEP species during this period. He intensities show 3He/4He of ∼1 during the type-III storm, but the intensities are too small to show measurable Fe and O. Intensities of 3He are not reliable during the large event because of the background from 4He, but most likely, 3He/4He <0.1. However, Figure 9B and 9C quite clearly show that the large event is a SEP4 event and definitely not a SEP3 event. Source temperatures are quite low, the protons fit the same population as the high-Z ions, and the power-law fits actually tend to decrease with A/Q. Impulsive suprathermal seed ions do not dominate this event.
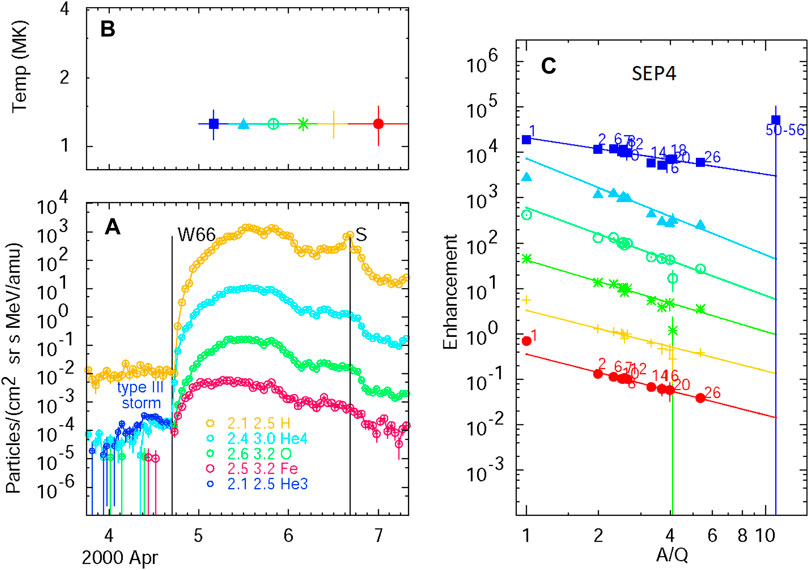
FIGURE 9. Panel (A) shows the intensities of the listed SEP ions that are shown during a type-III radio storm and the following large SEP4 event from the same active region studied by Gopalswamy et al. (2022). (B) shows the derived temperatures for the selected intervals. Panel (C) shows abundance enhancements vs. A/Q for elements with Z listed for each time interval (color and symbol), along with best least-squares fits of elements with Z ≥6 extended down to protons. Ions during the type-III storm are 3He-rich, but Fe/O is not measurable. 3He cannot be reliably measured during a large event because of the high-4He background. The large event is SEP4 and shows no evidence of impulsive seed ions from the type-III storm.
Unfortunately, the intensities shown in Figure 9 are insufficient for a firm conclusion since the type-III storm is too weak to show high-Z ions, but the large events are clearly not dominated by impulsive seeds, so it is unlikely that ions from the storm have contributed enough seed particles. There are other cases like this where large shock waves do not seem to reaccelerate the available impulsive suprathermal ions; many large SEP4 events are preceded by several type-III bursts. Are the intensities of impulsive seeds just too low? Yet, there are also many cases, like that shown in Figure 7, where consecutive large shocks dip into a single persistent impulsive population (Reames, 2022a). Worse, we have no cases where a single large event is SEP3 at one longitude and SEP4 at another; such cases might guide us to the location of the impulsive seeds, but there are too few of them in cycle 24. Perhaps, some shocks are driven in the direction of the impulsive seeds, while others are driven away from them, but we do not know for sure. The answer to the question posed by Gopalswamy et al. (2022) is not yet clear; impulsive seed ions are inadequate, or there may be other required conditions. However, the association of 3He with the type-III emission remains strong.
In fact, the measurements of 3He/4He during a type-III storm, as shown in Figure 9A, address another important question: are all the electron events that produce type-III bursts 3He-rich? A value of 3He/4He ≈ 1 persists during the entire type-III storm, suggesting that even these small events are 3He-rich. This may be the first reported measurement of 3He/4He associated with the small events in a type-III storm. At the other extreme, γ-ray lines show that some of the largest flares are 3He-rich (Mandzhavidze et al., 1999; Murphy et al., 2016). Are 3He-rich events a persistent consequence of magnetic reconnection?
6 C/O and the element abundance of the photosphere
After averaging over all the smooth power-law abundance variations, how could the variation of a single abundance C/O stand out so significantly in Figure 1? SEPs have C/O = 0.42 ± 0.01, while the recent photospheric values are 0.550 ± 0.76 (Caffau et al., 2011) and 0.589 ± 0.063 (Asplund et al., 2021). Earlier photospheric measurements by Anders and Grevesse (1989) of C/O = 0.489 were lower and in better agreement. Since the FIP of C is lower than that of O, it seems extremely unlikely that C/O could be suppressed in transit to the corona. The mixing of various seed populations, as described above, can surely cause doubt in the relative abundances of H and 4He, but the power-law behavior of both transport and acceleration most likely preserves the relationship of closely spaced C, N, and O. How could C/O in SEPs possibly be suppressed below that in the photosphere? We previously suggested that the problem might lie with the coronal abundance of C (Reames, 2021b).
It is well-known that the increasing photospheric abundances of “heavy elements,” like C, N, and O, have also caused problems for stellar models and helioseismology (e.g., Basu and Antica, 2008). These abundances determine the opacity of the stellar material, and the new (since 1990) lower abundances disagree with the helioseismic constraints.
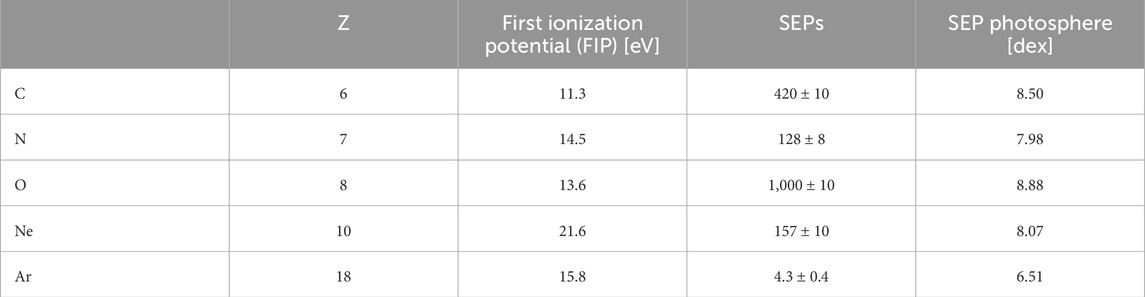
To correct the C/O problem shown in Figure 1, rather than decrease photospheric C, as previously considered, suppose we increase photospheric O instead. While this is less convenient, since O is our reference, reducing the photospheric C/O to 0.42 amounts to a reduction in SEPs of O by 31%, as shown in Figure 1. At this point, C, O, Ne, and Ar all line up. That is, their SEPs and photospheric abundances are the same. If we assume that the SEP-derived photosphere has the observed SEP abundance ratios of all high-FIP elements (other than H and He), normalized to the abundance of C observed by Caffau et al. (2011), we find the values in Table 2. The higher abundance of O returns to the values observed by Anders and Grevesse (1989).
7 Discussion
Our analysis of source temperatures has assumed Maxwellian electron velocity distributions controlling the relationship between plasma temperatures and Q-values of ions (e.g., Mazzotta et al., 1998). Recently, Lee et al. (2022) and Lee et al. (2024) tested this assumption using more realistic kappa distributions, which include high-energy tails of the electron distribution, to fit average impulsive event enhancements. These authors find that the derived source temperatures are not significantly affected and that A/Q values differ at most by 10%–20% in extreme cases. This is an important confirmation of the temperatures deduced from SEP abundances. These authors also note that the derived source temperatures agree with active-region temperatures, i.e., they are unaffected by electron heating. Thus, the SEPs must leave the acceleration region on a time scale shorter than their ionization time scales. However, at low densities, these ionization times could be quite long.
Laming and Kuroda (2023) suggested that heavy ions in impulsive SEP events are enhanced as part of the FIP process. Of course, the FIP process occurs in the dense chromosphere, while ion acceleration must occur at a much lower density in jets (Bučík, 2020), decoupling enhancement and acceleration; presumably, the enhancement could affect a region that would later release a jet. However, this would suggest that both SEPs and the CME from a jet would have strong A/Q-dependent enhancements, which have never been observed for CMEs. It is also true that the high-FIP elements He, C, N, O, Ne, S, and Ar fit the same pattern of enhancements as the low-FIP elements Mg, Si, Ca, and Fe (Figure 2 in the study by Reames, 2023c; Figure 8 in the study by Reames et al., 2014a). Independent of the impulsive abundance enhancements, we have separate evidence to show that acceleration occurs at magnetic reconnection sites in solar jets. Developing the power-law enhancement during this acceleration (Drake et al., 2009) seems to be most likely since only the SEPs would be affected.
However, concerning other mechanisms, we should again note that there is evidence that second-harmonic resonant processes related to the enhancement of 3He may contribute to low-energy abundance enhancements, especially of S in relatively rare, small impulsive events (Mason et al., 2016). These rare S-rich events have steep spectra that are only observed below ∼1 MeV amu−1 (Mason et al., 2016), probably where A/Q ≈ 3 for S, which occurs at ∼2 MK. These higher-order resonant enhancements are associated with the 3He resonance at A/Q ≈ 1.5. Resonant element enhancement at higher temperatures was studied by Roth and Temerin (1997). More recently, at even lower energies, i.e., <300 keV amu−1, Mason et al. (2023) found extreme enhancements in heavy elements, e.g., Fe/O, presumably because O has A/Q ≈ 2, and these resonant waves have been absorbed by 4He. This is reminiscent of the hot-plasma study of “the He valley” (Steinacker et al., 1997), where the wave absorption band of 4He can shape the abundances of other ions. Yet, all of the resonant modifications of Z >6 abundances seem to be confined to steep spectra below ∼1 MeV amu−1, while higher-energy abundances are dominated by power laws in A/Q.
There has been growing interest in the importance of streamers in SEP intensities and the production of GLEs. In streamers, higher densities and lower Alfvén speeds produce higher Alfvénic Mach numbers (Liu et al., 2023); regions of higher θBn (e.g., Kong et al., 2017; Kong et al., 2019) may also be a factor in shock acceleration. We have yet to explore any relationship between streamers and the streams of impulsive suprathermal ions above active regions that distinguish between SEP3 and SEP4 events.
8 Summary
SEP element abundances relative to O are compared at the same velocity (i.e., MeV amu−1), so that any dependence upon magnetic rigidity (often a power-law) appears as a dependence upon A/Q, assuming that a power law allows the best-fit determination of Q-values and, hence, the source temperature.
Impulsive events are accelerated in magnetic reconnection regions in solar jets and escape on open-field lines from sources at ∼2.5 MK. They produce 3He-rich events, heavy-ion enhancements, and electron beams that drive type-III radio bursts. The smaller SEP1 events have no fast shocks available for additional acceleration. Steep power-law abundance enhancements vs. A/Q (e.g., Figure 3C) include all elements, including H (events 3 and 4) or, in some cases, begin above 4He (event 5).
Gamma-ray line measurements show us that solar flares involve the same 3He-rich acceleration mechanisms as solar jets and show significant nuclear fragmentation, but the high (>10 MK) temperatures and nuclear fragments of bright, hot flares are not found in SEPs, indicating that the energetic ions in flares are efficiently trapped magnetically and are not observed to “leak out” into space. Thus, flares show no contribution to either impulsive or gradual SEPs.
In large gradual SEP4 events, fast, wide shock waves, driven by CMEs, are completely dominated by ions accelerated from ambient coronal seed material at 0.8–1.8 MK, beginning at 2–3 RS. All elements, including H and 4He, again tend to fit on a single power law vs. A/Q. Slopes of power-law abundance enhancements or depressions vs. A/Q mainly depend upon scattering during transport. 1) Intensities in smaller SEP4 events produce minimal amplification of Alfvén waves, allowing high-rigidity ions to leak away preferentially so abundances decrease vs. A/Q (Figures 4C, F). 2) Intensities in larger SEP4 events produce some amplification of Alfvén waves, producing balanced trapping and leakage over the A/Q range; so, abundances are initially quite flat vs. A/Q (Figure 5C). 3) Intensities of protons streaming out from very large SEP4 events (e.g., GLEs) produce significant amplification of Alfvén waves that scatter the subsequent ions during transport out from the shock but allow high-rigidity ions to preferentially reach the observer ahead the shock, so abundances increase vs. A/Q (Figures 6C, F); depleted high-rigidity ions are seen as a depression vs. A/Q downstream of the shock.
SEP events can include both shock-accelerated coronal seed ions and shock-reaccelerated impulsive residual seed ions. Impulsive SEP2 events are intended to involve both seeds and shock from a single jet, while gradual SEP3 events describe a large shock traversing an active region with a collection of impulsive ions from multiple previous jets. Both classes are dominated by H (and possibly 4He) from the coronal seeds and by Z ≥6 ions from the previously enhanced impulsive seeds. Figure 7C shows the enhancement pattern of an impulsive SEP2 event, Figures 7D, E and Figure 8C show clear SEP3 events, and Figure 3F shows an ambiguous single-jet event (SEP2) that occurs in a pre-existing impulsively seeded region (SEP3). SEP3 events tend to have smaller abundance fluctuations since they average over many individual jets.
SEP3 events are very rare in solar cycle 24, which is probably a combined effect of both fewer impulsive seeds and fewer large shocks to encounter them. Furthermore, while type-III storms clearly produce 3He-rich events, the subsequent strong shocks from that region do not necessarily find dominant high-Z impulsive seed particles.
The SEP value of C/O = 0.42 conflicts with much higher photospheric values of up to 0.59 and lacks explanation. Could the photospheric value of O actually be 30%–40% higher, as previously found, and as helioseismology independently suggests?
Author contributions
DR: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing.
Funding
The author declares that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Afanasiev, A., Battarbee, M., and Vainio, R. (2015). Self-consistent Monte Carlo simulations of proton acceleration in coronal shocks: effect of anisotropic pitch-angle scattering of particles. Astron. Astrophys. 584, 81. doi:10.1051/0004-6361/201526750
Afanasiev, A., Vainio, R., Trotta, D., Nyberg, S., Talebpour Sheshvan, N., Hietala, H., et al. (2023). Self-consistent modeling of the energetic storm particle event of November 10, 2012. Astron. Astrophys. 679 (2023), A111. doi:10.1051/0004-6361/202346220
Anders, E., and Grevesse, N. (1989). Abundances of the elements: meteoritic and solar. Geochim. Cosmochim. Acta 53, 197–214. doi:10.1016/0016-7037(89)90286-X
Archontis, V., and Hood, A. W. (2013). A numerical model of standard to blowout jets. Astrophys. J. Lett. 769, L21. doi:10.1088/2041-8205/769/2/l21
Asplund, M., Amarsi, A. M., and Grevesse, N. (2021). The chemical make-up of the Sun: a 2020 vision. Astron. Astrophys. 653, A141, 01661. arXiv:2105. doi:10.1051/0004-6361/202140445
Basu, S., and Antica, H. M. (2008). Helioseismology and solar abundances. Phys. Rep. 457, 217–283. doi:10.1016/j.physrep.2007.12.002
Bertsch, D. L., Fichtel, C. E., and Reames, D. V. (1969). Relative abundance of iron-group nuclei in solar cosmic rays. Astrophys. J. Lett. 157, L53. doi:10.1086/180383
Breneman, H. H., and Stone, E. C. (1985). Solar coronal and photospheric abundances from solar energetic particle measurements. Astrophys. J. Lett. 299, L57. doi:10.1086/184580
Bučík, R. (2020). 3He-rich solar energetic particles: solar sources. Space Sci. Rev. 216, 24. doi:10.1007/s11214-020-00650-5
Bučík, R., Innes, D. E., Chen, N. H., Mason, G. M., Gómez-Herrero, R., and Wiedenbeck, M. E. (2015). Long-lived energetic particle source regions on the Sun. J. Phys. Conf. Ser. 642, 012002. doi:10.1088/1742-6596/642/1/012002
Bučík, R., Innes, D. E., Mall, U., Korth, A., Mason, G. M., and Gómez-Herrero, R. (2014). Multi-spacecraft observations of recurrent 3He-rich solar energetic particles. Astrophys. J. 786, 71. doi:10.1088/0004-637X/786/1/71
Bučík, R., Innes, D. E., Mason, G. M., Wiedenbeck, M. E., Gómez-Herrero, R., and Nitta, N. V. (2018a). 3He-rich solar energetic particles in helical jets on the Sun. Astrophys. J. 852, 76. doi:10.3847/1538-4357/aa9d8f
Bučík, R., Mulay, S. M., Mason, G. M., Nitta, N. V., Desai, M. I., and Dayeh, M. A. (2021). Temperature in solar sources of 3He-rich solar energetic particles and relation to ion abundances. Astrophys. J. 908, 243. doi:10.3847/1538-4357/abd62d
Bučík, R., Wiedenbeck, M. E., Mason, G. M., Gómez-Herrero, R., Nitta, N. V., and Wang, L. (2018b). 3He-rich solar energetic particles from sunspot jets. Astrophys. J. Lett. 869, L21. doi:10.3847/2041-8213/aaf37f
Caffau, E., Ludwig, H.-G., Steffen, M., Freytag, B., and Bonofacio, P. (2011). Solar chemical abundances determined with a CO5BOLD 3D model atmosphere. Sol. Phys. 268, 255–269. doi:10.1007/s11207-010-9541-4
Chen, N. H., Bučík, R., Innes, D. E., and Mason, G. M. (2015). Case studies of multi-day 3He-rich solar energetic particle periods. Astron. Astrophys. 580, 16. doi:10.1051/0004-6361/201525618
Cliver, E. W., Kahler, S. W., and Reames, D. V. (2004). Coronal shocks and solar energetic proton events. Astrophys. J. 605, 902–910. doi:10.1086/382651
Cohen, C. M. S., Mason, G. M., and Mewaldt, R. A. (2017). Characteristics of solar energetic ions as a function of longitude. Astrophys. J. 843, 132. doi:10.3847/1538-4357/aa7513
Cook, W. R., Stone, E. C., and Vogt, R. E. (1984). Elemental composition of solar energetic particles. Astrophys. J. 279, 827. doi:10.1086/161953
Desai, M. I., and Giacalone, J. (2016). Large gradual solar energetic particle events. Living Rev. Sol. Phys. 13, 3. doi:10.1007/s41116-016-0002-5
Desai, M. I., Mason, G. M., Dwyer, J. R., Mazur, J. E., Gold, R. E., Krimigis, S. M., et al. (2003). Evidence for a suprathermal seed population of heavy ions accelerated by interplanetary shocks near 1 AU. Astrophys. J. 588, 1149–1162. doi:10.1086/374310
DiFabio, R., Guo, Z., Möbius, E., Klecker, B., Kucharek, H., Mason, G. M., et al. (2008). Energy-dependent charge states and their connection with ion abundances in impulsive solar energetic particle events. Astrophys. J. 687, 623–634. doi:10.1086/591833
Drake, J. F., Cassak, P. A., Shay, M. A., Swisdak, M., and Quataert, E. (2009). A magnetic reconnection mechanism for ion acceleration and abundance enhancements in impulsive flares. Astrophys. J. Lett. 700, L16–L20. doi:10.1088/0004-637X/700/1/L16
Fichtel, C. E., and Guss, D. E. (1961). Heavy nuclei in solar cosmic rays. Phys. Rev. Lett. 6, 495–497. doi:10.1103/PhysRevLett.6.495
Fisk, L. A. (1978). He-3-rich flares - a possible explanation. Astrophys. J. 224, 1048. doi:10.1086/156456
Forbush, S. E. (1946). Three unusual cosmic ray increases possibly due to charged particles from the Sun. Phys. Rev. 70, 771–772. doi:10.1103/physrev.70.771
Gopalswamy, N., Akiyama, S., Mäkelä, P., Yashiro, S., and Hong Xie, H. (2022). Can type III radio storms be a source of seed particles to shock acceleration? 3rd URSI AT-AP-RASC. Gran Canaria. arXiv:2205.15852.
Gopalswamy, N., Xie, H., Akiyama, S., Yashiro, S., Usoskin, I. G., and Davila, J. M. (2013a). The first ground level enhancement event of solar cycle 24: direct observation of shock formation and particle release heights. Astrophys. J. Lett. 765, L30. doi:10.1088/2041-8205/765/2/L30
Gopalswamy, N., Xie, H., Mäkelä, P., Yashiro, S., Akiyama, S., Uddin, W., et al. (2013b). Height of shock formation in the solar corona inferred from observations of type II radio bursts and coronal mass ejections. Adv. Space Res. 51, 1981–1989. doi:10.1016/j.asr.2013.01.006
Gopalswamy, N., Xie, H., Yashiro, S., Akiyama, S., Mäkelä, P., and Usoskin, I. G. (2012). Properties of Ground level enhancement events and the associated solar eruptions during solar cycle 23. Space Sci. Rev. 171, 23–60. doi:10.1007/s11214-012-9890-4
Gosling, J. T. (1993). The solar flare myth. J. Geophys. Res. 98, 18937–18949. doi:10.1029/93JA01896
Gosling, J. T. (1994). Corrections to “The solar flare myth.”. J. Geophys. Res. 99, 4259. doi:10.1029/94JA00015
Kahler, S. W., Reames, D. V., and Sheeley, N. R. (2001). Coronal mass ejections associated with impulsive solar energetic particle events. Astrophys. J. 562, 558–565. doi:10.1086/323847
Kahler, S. W., Reames, D. V., Sheeley, N. R., Howard, R. A., Kooman, M. J., and Michels, D. J. (1985). A comparison of solar 3He-rich events with type II bursts and coronal mass ejections. Astrophys. J. 290, 742. doi:10.1086/163032
Kahler, S. W., Sheeley, N. R., Howard, R. A., Koomen, M. J., Michels, D. J., McGuire, R. E., et al. (1984). Associations between coronal mass ejections and solar energetic proton events. J. Geophys. Res. 89, 9683–9693. doi:10.1029/JA089iA11p09683
Kahler, S. W., Tylka, A. J., and Reames, D. V. (2009). A comparison of elemental abundance ratios in SEP events in fast and slow solar wind regions. Astrophys. J. 701, 561–570. doi:10.1088/0004-637X/701/1/561
Kong, X., Guo, F., Chen, Y., and Giacalone, J. (2019). The acceleration of energetic particles at coronal shocks and emergence of a double power-law feature in particle energy spectra. Astrophys. J. 883, 49. doi:10.3847/1538-4357/ab3848
Kong, X., Guo, F., Giacalone, J., Li, H., and Chen, Y. (2017). The acceleration of high-energy protons at coronal shocks: the effect of large-scale streamer-like magnetic field structures. Astrophys. J. 851, 38. doi:10.3847/1538-4357/aa97d7
Kouloumvakos, A., Mason, G. M., Ho, G. C., Allen, R. C., Wimmer-Schweingruber, R. F., Rouillard, A. P., et al. (2023). Extended 3He-rich time periods observed by solar orbiter: magnetic connectivity and sources. Astrophys. J. 956, 123. doi:10.3847/1538-4357/acf44e
Kouloumvakos, A., Rouillard, A. P., Wu, Y., Vainio, R., Vourlidas, A., Plotnikov, I., et al. (2019). Connecting the properties of coronal shock waves with those of solar energetic particles. Astrophys. J. 876, 80. doi:10.3847/1538-4357/ab15d7
Kozlovsky, B., Murphy, R. J., and Ramaty, R. (2002). Nuclear deexcitation gamma-ray lines from accelerated particle interactions. Astrophys. J. Suppl. 141, 523–541. doi:10.1086/340545
Laming, J. M. (2015). The FIP and inverse FIP effects in solar and stellar coronae. Living Rev. Sol. Phys. 12, 2. doi:10.1007/lrsp-2015-2
Laming, J. M., and Kuroda, N. (2023). Element abundances in impulsive solar energetic particle events. Astrophys. J. 951, 86. doi:10.3847/1538-4357/acd69a
Laming, J. M., Vourlidas, A., Korendyke, C., Chua, D., Cranmer, S. R., Ko, Y. K., et al. (2019). Element abundances: a new diagnostic for the solar wind. Astrophys. J. 879, 124. doi:10.3847/1538-4357/ab23f1
Lee, E. J., Archontis, V., and Hood, A. W. (2015). Plasma jets and eruptions in solar coronal holes: a three-dimensional flux emergence experiment. Astrophys. J. Lett. 798, L10. doi:10.1088/2041-8205/798/1/L10
Lee, J. Y., Kahler, S., Ko, Y. K., and Raymond, J. C. (2022). “A study of mass-to-charge ratio with various kappa values in impulsive SEP events,” in AGU Fall Meeting, Chicago, IL, Bibcode. 2022AGUFMSH42A.04L.
Lee, J. Y., Kahler, S., Raymond, J. C., and Ko, Y. K. (2024). Solar energetic particle charge states and abundances with nonthermal electrons. Astrophys. J. in press, arXiv: 2024arXiv240101604L.
Lee, M. A. (1983). Coupled hydromagnetic wave excitation and ion acceleration at interplanetary traveling shocks. J. Geophys. Res. 88, 6109–6119. doi:10.1029/JA088iA08p06109
Lee, M. A. (2005). Coupled hydromagnetic wave excitation and ion acceleration at an evolving coronal/interplanetary shock. Astrophys. J. Suppl. 158, 38–67. doi:10.1086/428753
Lee, M. A., Mewaldt, R. A., and Giacalone, J. (2012). Shock acceleration of ions in the heliosphere. Space Sci. Rev. 173, 247–281. doi:10.1007/s11214-012-9932-y
Lin, R. P. (1970). The emission and propagation of 40 keV solar flare electrons. I: the relationship of 40 keV electron to energetic proton and relativistic electron emission by the sun. Sol. Phys. 12, 266. doi:10.1007/BF00227122
Liu, W., Kong, X., Guo, F., Zhao, L., Feng, S., Yu, F., et al. (2023). Effects of coronal magnetic field configuration on particle acceleration and release during the ground level enhancement events in solar cycle 24. Astrophys. J. 954, 203. doi:10.3847/1538-4357/ace9d2
Lodders, K., Palme, H., and Gail, H.-P. (2009). “Abundances of the elements in the solar system,” in Landolt-börnstein, new series VI/4B. Editor J. E. Trümper (Berlin: Springer), 560. Chap. 4.4. doi:10.1007/978-3-540-88055-4_34
Luhn, A., Klecker, B., Hovestadt, D., Gloeckler, G., Ipavich, F. M., Scholer, M., et al. (1984). Ionic charge states of N, Ne, Mg, Si and S in solar energetic particle events. Adv. Space Res. 4, 161. doi:10.1016/0273-1177(84)90307-7
Luhn, A., Klecker, B., Hovestadt, D., and Möbius, E. (1987). The mean ionic charge of silicon in He-3-rich solar flares. Astrophys. J. 317, 951. doi:10.1086/165343
Mandzhavidze, N., Ramaty, R., and Kozlovsky, B. (1999). Determination of the abundances of subcoronal 4He and of solar flare-accelerated 3He and 4He from gamma-ray spectroscopy. Astrophys. J. 518, 918–925. doi:10.1086/307321
Mason, G. M. (2007). 3He-rich solar energetic particle events. Space Sci. Rev. 130, 231–242. doi:10.1007/s11214-007-9156-8
Mason, G. M., Gloeckler, G., and Hovestadt, D. (1984). Temporal variations of nucleonic abundances in solar flare energetic particle events. II - evidence for large-scale shock acceleration. Astrophys. J. 280, 902. doi:10.1086/162066
Mason, G. M., Mazur, J. E., and Dwyer, J. R. (1999). [TSUP]3[/TSUP]H[CLC]e[/CLC] Enhancements in Large Solar Energetic Particle Events. Astrophys. J. Lett. 525, L133–L136. doi:10.1086/312349
Mason, G. M., Mazur, J. E., Dwyer, J. R., Jokippi, J. R., Gold, R. E., and Krimigis, S. M. (2004). Abundances of heavy and ultraheavy ions in 3He-rich solar flares. Astrophys. J. 606, 555–564. doi:10.1086/382864
Mason, G. M., Nitta, N. V., Wiedenbeck, M. E., and Innes, D. E. (2016). Evidence for a common acceleration mechanism for enrichments of 3He and heavy ions in impulsive SEP events. Astrophys. J. 823, 138. doi:10.3847/0004-637X/823/2/138
Mason, G. M., Reames, D. V., Klecker, B., Hovestadt, D., and von Rosenvinge, T. T. (1986). The heavy-ion compositional signature in He-3-rich solar particle events. Astrophys. J. 303, 849. doi:10.1086/164133
Mason, G. M., Roth, I., Nitta, N. V., Bučík, R., Lario, D., Ho, G. C., et al. (2023). Heavy-ion acceleration in 3He-rich solar energetic particle events: new insights from Solar Orbiter. Astrophys. J. 957, 112. doi:10.3847/1538-4357/acf31b
Mazzotta, P., Mazzitelli, G., Colafrancesco, S., and Vittorio, N. (1998). Ionization balance for optically thin plasmas: rate coefficients for all atoms and ions of the elements H to Ni. Astron. Astrophys. Suppl. 133, 403–409. doi:10.1051/aas:1998330
McGuire, R. E., von Rosenvinge, T. T., and McDonald, F. B. (1979). “A survey of solar cosmic ray composition,” in Proc. 16th Int. Cosmic Ray Conf., Tokyo, 61.
Mewaldt, R. A., Cohen, C. M. S., Leske, R. A., Christian, E. R., Cummings, A. C., Stone, E. C., et al. (2002). Fractionation of solar energetic particles and solar wind according to first ionization potential. Advan. Space Res. 30, 79–84. doi:10.1016/S0273-1177(02)00263-6
Mewaldt, R. A., Looper, M. D., Cohen, C. M. S., Haggerty, D. K., Labrador, A. W., Leske, R. A., et al. (2012). Energy spectra, composition, and other properties of ground-level events during solar cycle 23. Space Sci. Rev. 171, 97–120. doi:10.1007/s11214-012-9884-2
Meyer, J. P. (1985). The baseline composition of solar energetic particles. Astrophys. J. Suppl. 57, 151. doi:10.1086/191000
Mogro-Campero, A., and Simpson, J. A. (1972). Enrichment of very heavy nuclei in the composition of solar accelerated particles. Astrophys. J. Lett. 171, L5. doi:10.1086/180856
Murphy, R. J., Kozlovsky, B., and Share, G. H. (2016). Evidence for enhanced 3He in flare-accelerated particles based on new calculations of the gamma-ray line spectrum. Astrophys. J. 833, 196. doi:10.3847/1538-4357/833/2/196
Murphy, R. J., Ramaty, R., Kozlovsky, B., and Reames, D. V. (1991). Solar abundances from gamma-ray spectroscopy: comparisons with energetic particle, photospheric, and coronal abundances. Astrophys. J. 371, 793. doi:10.1086/169944
Ng, C. K., and Reames, D. V. (2008). Shock acceleration of solar energetic protons: the first 10 minutes. Astrophys. J. Lett. 686, L123–L126. doi:10.1086/592996
Ng, C. K., Reames, D. V., and Tylka, A. J. (1999). Effect of proton-amplified waves on the evolution of solar energetic particle composition in gradual events. Geophys. Res. Lett. 26, 2145–2148. doi:10.1029/1999GL900459
Ng, C. K., Reames, D. V., and Tylka, A. J. (2003). Modeling shock-accelerated solar energetic particles coupled to interplanetary Alfvén waves. Astrophys. J. 591, 461–485. doi:10.1086/375293
Ng, C. K., Reames, D. V., and Tylka, A. J. (2012). Solar energetic particles: shock acceleration and transport through self-amplified waves. AIP Conf. Proc. 1436, 212. doi:10.1063/1.4723610
Nitta, N. V., Reames, D. V., DeRosa, M. L., Yashiro, S., and Gopalswamy, N. (2006). Solar sources of impulsive solar energetic particle events and their magnetic field connection to the earth. Astrophys. J. 650, 438–450. doi:10.1086/507442
Pariat, E., Dalmasse, K., DeVore, C. R., Antiochos, S. K., and Karpen, J. T. (2015). Model for straight and helical solar jets. I. Parametric studies of the magnetic field geometry. Astron. Astrophys. 573, A130. doi:10.1051/0004-6361/201424209
Parker, E. N. (1965). The passage of energetic charged particles through interplanetary space. Planet. Space Sci. 13, 9–49. doi:10.1016/0032-0633(65)90131-5
Post, D. E., Jensen, R. V., Tarter, C. B., Grasberger, W. H., and Lokke, W. A. (1977). Steady-state radiative cooling rates for low-density, high temperature plasmas. At. Data Nucl. Data tables. 20, 397–439. doi:10.1016/0092-640X(77)90026-2
Raukunen, O., Vainio, R., Tylka, A. J., Dietrich, W. F., Jiggens, P., Heynderickx, D., et al. (2018). Two solar proton fluence models based on ground level enhancement observations. J. Spa. Wea. Spa. Clim. 8, A04. doi:10.1051/swsc/2017031
Reames, D. V. (1988). Bimodal abundances in the energetic particles of solar and interplanetary origin. J. Lett. 330, L71. doi:10.1086/185207
Reames, D. V. (1995a). Coronal Abundances determined from energetic particles. Adv. Space Res. 15 (7), 41–51. doi:10.1016/0273-1177(94)00018-v
Reames, D. V. (1995b). Solar energetic particles: a paradigm shift. Revs. Geophys. Suppl. 33, 585–589. doi:10.1029/95RG00188
Reames, D. V. (1999). Particle acceleration at the Sun and in the heliosphere. Space Sci. Rev. 90, 413–491. doi:10.1023/A:1005105831781
Reames, D. V. (2000). Abundances of trans-iron elements in solar energetic particle events. Astrophys. J. Lett. 540, L111–L114. doi:10.1086/312886
Reames, D. V. (2009a). Solar release times of energetic particles in ground-level events. Astrophys. J. 693, 812–821. doi:10.1088/0004-637X/693/1/812
Reames, D. V. (2009b). Solar energetic-particle release times in historic ground-level events. Astrophys. J. 706, 844–850. doi:10.1088/0004-637X/706/1/844
Reames, D. V. (2013). The two sources of solar energetic particles. Space Sci. Rev. 175, 53–92. doi:10.1007/s11214-013-9958-9
Reames, D. V. (2014). Element abundances in solar energetic particles and the solar corona. Sol. Phys. 289, 977–993. doi:10.1007/s11207-013-0350-4
Reames, D. V. (2016). Temperature of the source plasma in gradual solar energetic particle events. Sol. Phys. 291, 911–930. doi:10.1007/s11207-016-0854-9
Reames, D. V. (2018a). The "FIP effect" and the origins of solar energetic particles and of the solar wind. Sol. Phys. 293, 47. doi:10.1007/s11207-018-1267-8
Reames, D. V. (2018b). Abundances, ionization states, temperatures, and FIP in solar energetic particles. Space Sci. Rev. 214, 61. doi:10.1007/s11214-018-0495-4
Reames, D. V. (2019). Helium suppression in impulsive solar energetic-particle events. Sol. Phys. 294, 32. (arXiv: 1812.01635). doi:10.1007/s11207-019-1422-x
Reames, D. V. (2020a). Four distinct pathways to the element abundances in solar energetic particles. Space Sci. Rev. 216, 20. doi:10.1007/s11214-020-0643-5
Reames, D. V. (2020b). Distinguishing the rigidity dependences of acceleration and transport in solar energetic particles. Sol. Phys. 295, 113. arXiv 2006.11338. doi:10.1007/s11207-020-01680-6
Reames, D. V. (2021a). “Solar energetic particles,” in Lec. Notes phys. 978. Second Edition (Cham, Switzerland: Springer Nature). open access. doi:10.1007/978-3-030-66402-2
Reames, D. V. (2021b). Sixty years of element abundance measurements in solar energetic particles. Space Sci. Rev. 217, 72. doi:10.1007/s11214-021-00845-4
Reames, D. V. (2021c). Fifty years of 3He-rich events. Front. Astron. Space Sci. 8, 164. doi:10.3389/fspas.2021.760261
Reames, D. V. (2021d). On the correlation between energy spectra and element abundances in solar energetic particles. Sol. Phys. 296, 24. doi:10.1007/s11207-021-01762-z
Reames, D. V. (2022a). Energy spectra vs. element abundances in solar energetic particles and the roles of magnetic reconnection and shock acceleration. Sol. Phys. 297, 32. doi:10.1007/s11207-022-01961-2
Reames, D. V. (2022b). Solar energetic particles: spatial extent and implications of the H and He abundances. Space Sci. Rev. 218, 48. doi:10.1007/s11214-022-00917-z
Reames, D. V. (2023a). How do shock waves define the space-time structure of gradual solar energetic-particle events? Space Sci. Rev. 219, 14. doi:10.1007/s11214-023-00959-x
Reames, D. V. (2023b). Review and outlook of solar-energetic-particle measurements on multispacecraft missions. Front. Astron. Space Sci. 10. doi:10.3389/fspas.2023.1254266
Reames, D. V. (2023c). Element abundances in impulsive solar energetic-particle events. Universe 9, 466. doi:10.3390/universe9110466
Reames, D. V., Cliver, E. W., and Kahler, S. W. (2014a). Abundance enhancements in impulsive solar energetic-particle events with associated coronal mass ejections. Sol. Phys. 289, 3817–3841. doi:10.1007/s11207-014-0547-1
Reames, D. V., Cliver, E. W., and Kahler, S. W. (2014b). Variations in abundance enhancements in impulsive solar energetic-particle events and related CMEs and flares. Sol. Phys. 289, 4675–4689. doi:10.1007/s11207-014-0589-4
Reames, D. V., Meyer, J. P., and von Rosenvinge, T. T. (1994). Energetic-particle abundances in impulsive solar flare events. Astrophys. J. Suppl. 90, 649. doi:10.1086/191887
Reames, D. V., and Ng, C. K. (1998). Streaming-limited intensities of solar energetic particles. Astrophys. J. 504, 1002–1005. doi:10.1086/306124
Reames, D. V., and Ng, C. K. (2004). Heavy-element abundances in solar energetic particle events. Astrophys. J. 610, 510–522. doi:10.1086/421518
Reames, D. V., and Ng, C. K. (2010). Streaming-limited intensities of solar energetic particles on the intensity plateau. Astrophys. J. 723, 1286–1293. doi:10.1088/0004-637X/723/2/1286
Reames, D. V., and Ng, C. K. (2014). The streaming limit of solar energetic-particle intensities, living with a star workshop on extreme space weather events. Boulder, Co. June 9-11 (2014) arXiv 1412.2279.
Reames, D. V., Richardson, I. G., and Barbier, L. M. (1991). On the differences in element abundances of energetic ions from corotating events and from large solar events. Astrophys. J. Lett. 382, L43. doi:10.1086/186209
Reames, D. V., and Stone, R. G. (1986). The identification of solar 3He-rich events and the study of particle acceleration at the sun. Astrophys. J. 308, 902. doi:10.1086/164560
Reames, D. V., von Rosenvinge, T. T., and Lin, R. P. (1985). Solar 3He-rich events and nonrelativistic electron events - a new association. Astrophys. J. 292, 716. doi:10.1086/163203
Richardson, I. G., Reames, D. V., Wenzel, K. P., and Rodriguez-Pacheco, J. (1990). Quiet-time properties of low-energy (less than 10 MeV per nucleon) interplanetary ions during solar maximum and solar minimum. Astrophys. J. Lett. 363, L9. doi:10.1086/185853
Roth, I., and Temerin, M. (1997). Enrichment of 3He and heavy ions in impulsive solar flares. Astrophys. J. 477, 940–957. doi:10.1086/303731
Serlemitsos, A. T., and Balasubrahmanyan, V. K. (1975). Solar particle events with anomalously large relative abundance of 3He. Astrophys. J. 198, 195. doi:10.1086/153592
Shimojo, M., and Shibata, K. (2000). Physical parameters of solar X-ray jets. Astrophys. J. 542, 1100–1108. doi:10.1086/317024
Steinacker, J., Meyer, J.-P., Steinacker, A., and Reames, D. V. (1997). The helium valley: comparison of impulsive solar flare ion abundances and gyroresonant acceleration with oblique turbulence in a hot multi-ion plasma. Astrophys. J. 476, 403–427. doi:10.1086/303589
Tan, L. C., Reames, D. V., Ng, C. K., Shao, X., and Wang, L. (2011). What causes scatter-free transport of non-relativistic solar electrons? Astrophys. J. 728, 133. doi:10.1088/0004-637X/728/2/133
Teegarden, B. J., von Rosenvinge, T. T., and McDonald, F. B. (1973). Satellite measurements of the charge composition of solar cosmic rays in the 6 ≤ Z ≤ 26 interval. Astrophys. J. 180, 571. doi:10.1086/151985
Temerin, M., and Roth, I. (1992). The production of 3He and heavy ion enrichment in 3He-rich flares by electromagnetic hydrogen cyclotron waves. Astrophys. J. Lett. 391, L105. doi:10.1086/186408
Tylka, A. J., Cohen, C. M. S., Dietrich, W. F., Krucker, S., McGuire, R. E., Mewaldt, R. A., et al. (2003). in Proc. 28th Int. Cosmic Ray Conf., Tsukuba, 3305.
Tylka, A. J., Cohen, C. M. S., Dietrich, W. F., Lee, M. A., Maclennan, C. G., Mewaldt, R. A., et al. (2005). Shock geometry, seed populations, and the origin of variable elemental composition at high energies in large gradual solar particle events. Astrophys. J. 625, 474–495. doi:10.1086/429384
Tylka, A. J., Cohen, C. M. S., Dietrich, W. F., Maclennan, C. G., McGuire, R. E., Ng, C. K., et al. (2001). Evidence for remnant flare suprathermals in the source population of solar energetic particles in the 2000 bastille day event. Astrophys. J. Lett. 558, L59–L63. doi:10.1086/323344
Tylka, A. J., and Dietrich, W. F. (2009). “A new and comprehensive analysis of proton spectra in ground-level enhanced (GLE) solar particle events,” in Proceedings of 31st International Cosmic Ray Conference Lodz. http://icrc2009.uni.lodz.pl/proc/pdf/icrc0273.pdf.
Tylka, A. J., and Lee, M. A. (2006). A model for spectral and compositional variability at high energies in large, gradual solar particle events. Astrophys. J. 646, 1319–1334. doi:10.1086/505106
von Rosenvinge, T. T., Barbier, L. M., Karsch, J., Liberman, R., Madden, M. P., Nolan, T., et al. (1995). The energetic particles: acceleration, composition, and transport (EPACT) investigation on the wind spacecraft. Space Sci. Rev. 71, 155–206. doi:10.1007/BF00751329
Wang, Y.-M., Pick, M., and Mason, G. M. (2006). Coronal holes, jets, and the origin of 3He-rich particle events. Astrophys. J. 639, 495–509. doi:10.1086/499355
Webber, W. R. (1975). Solar and galactic cosmic ray abundances – a comparison and some comments. Proc. 14th Int. Cos, Ray Conf., Municxh. 5, 1597.
Wiedenbeck, M. E., Cohen, C. M. S., Cummings, A. C., de Nolfo, G. A., Leske, R. A., Mewaldt, R. A., et al. (2008). Persistent energetic 3He in the inner heliosphere. Proc. 30th Int. Cosm. Ray Conf. (Mérida) 1, 91.
Wild, J. P., Smerd, S. F., and Weiss, A. A. (1963). Solar bursts. Annu. Rev. Astron. Astrophys. 1, 291–366. doi:10.1146/annurev.aa.01.090163.001451
Zank, G. P., Li, G., and Verkhoglyadova, O. (2007). Particle acceleration at interplanetary shocks. Space Sci. Rev. 130, 255–272. doi:10.1007/s11214-007-9214-2
Keywords: solar energetic particles, solar system abundance, solar jets, solar flares, shock waves, coronal mass ejections, heliosphere
Citation: Reames DV (2024) Element abundance and the physics of solar energetic particles. Front. Astron. Space Sci. 11:1368043. doi: 10.3389/fspas.2024.1368043
Received: 09 January 2024; Accepted: 16 February 2024;
Published: 08 March 2024.
Edited by:
Gang Li, University of Alabama in Huntsville, United StatesReviewed by:
Subhamoy Chatterjee, Southwest Research Institute Boulder, United StatesAthanasios Papaioannou, National Observatory of Athens, Greece
Yang Wang, Harbin Institute of Technology, China
Copyright © 2024 Reames. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Donald V. Reames, ZHZyZWFtZXNAZ21haWwuY29t
†ORCID: Donald V. Reames, orcid.org/0000-0001-9048-822X
 Donald V. Reames
Donald V. Reames