Oblique instability of quasi-parallel whistler waves in the presence of cold and warm electron populations

Whistler waves propagating nearly parallel to the ambient magnetic field experience a nonlinear instability due to transverse currents when the background plasma has a population of sufficiently low energy electrons. Intriguingly, this nonlinear process may generate oblique electrostatic waves, including whistlers near the resonance cone with properties resembling oblique chorus waves in the Earth’s magnetosphere. Focusing on the generation of oblique whistlers, earlier analysis of the instability is extended here to the case where low-energy background plasma consists of both a “cold” population with energy of a few eV and a “warm” electron component with energy of the order of 100 eV. This is motivated by spacecraft observations in the Earth’s magnetosphere where oblique chorus waves were shown to interact resonantly with the warm electrons. The main new results are: 1) the instability producing oblique electrostatic waves is sensitive to the shape of the electron distribution at low energies. In the whistler range of frequencies, two distinct peaks in the growth rate are typically present for the model considered: a peak associated with the warm electron population at relatively low wavenumbers and a peak associated with the cold electron population at relatively high wavenumbers; 2) overall, the instability producing oblique whistler waves near the resonance cone persists (with a reduced growth rate) even in the cases where the temperature of the cold population is relatively high, including cases where cold population is absent and only the warm population is included; 3) particle-in-cell simulations show that the instability leads to heating of the background plasma and formation of characteristic plateau and beam features in the parallel electron distribution function in the range of energies resonant with the instability. The plateau/beam features have been previously detected in spacecraft observations of oblique chorus waves. However, they have been attributed to external sources and have been proposed to be the mechanism generating oblique chorus. In the present scenario, the causality link is reversed and the instability generating oblique whistler waves is shown to be a possible mechanism for formation of the plateau and beam features.

1 Introduction

Whistler waves play a critical role in the dynamics of the Earth’s magnetosphere since wave-particle interactions with whistlers play a dual role of both accelerating and scattering of energetic electrons. The corresponding diffusion coefficients depend on the global distribution of spectral power and polarization of the waves, making understanding of these properties essential for successful modeling of ring current or radiation belt dynamics (Thorne, 2010). As a consequence, there exists a significant interest in understanding of the basic physical processes affecting evolution of the magnetospheric waves in general and of whistler waves in particular.

Statistical studies show that whistler waves in the Earth’s magnetosphere appear either as “chorus”, i.e., discrete emissions appearing typically in two distinct frequency bands in a region outside the plasmasphere (Burtis and Helliwell, 1969; Tsurutani and Smith, 1974; Li et al., 2013), or “hiss”, i.e., broadband emissions found predominantly in the plasmasphere (Dunckel and Helliwell, 1969; Russell et al., 1969; Thorne et al., 1973; Hartley et al., 2018) and in plasmaspheric plumes (Chan and Holzer, 1976). The chorus waves are associated with local energization of energetic particles (Summers et al., 1998; Meredith et al., 2002; Meredith et al., 2003), as well as electron precipitation in the form of diffuse (Swift, 1981; Ni et al., 2014) and pulsating aurora (Nishimura et al., 2010; Kasahara et al., 2018), or microbursts (Oliven and Gurnett, 1968; Breneman et al., 2017). Chorus waves observed in the Earth’s magnetosphere can reach very large amplitudes, e.g., (Cattell et al., 2008; Wilson et al., 2011; Tyler et al., 2019b; Tyler et al., 2019a). For small magnetic latitudes, lower-band chorus waves are predominantly field-aligned (Hayakawa et al., 1984; Haque et al., 2010; Li et al., 2011; Agapitov et al., 2012; Li et al., 2013; Teng et al., 2019), which is consistent with their excitation via a cyclotron instability of anisotropic electrons with energies in the range of several to tens of keV (Kennel and Petschek, 1966; Gary and Wang, 1996; Gary et al., 2011; Fu et al., 2014). In addition to the field-aligned chorus waves, waves near the resonance cone angle are often present (Santolík et al., 2009; Agapitov et al., 2012; Li et al., 2013; Li et al., 2016; Teng et al., 2019). The oblique waves play an important role in scattering of energetic electrons (Mourenas et al., 2014; Artemyev et al., 2015). In general, the whistler waves become more oblique as they propagate to high latitudes. They may further experience significant radial propagation, which complicates identification of their sources (Chen et al., 2013). Nevertheless, it is likely that the oblique chorus at small magnetic latitudes is generated by a mechanism distinct from that producing field-aligned chorus (Artemyev et al., 2015). Analyses of specific events often find plateau/beam-like features in the parallel electron energy distribution with typical energy from $\sim 100$ eV (Li et al., 2016) to several keV (Agapitov et al., 2015). This led to suggestions that oblique modes are generated by a linear instability associated either with temperature anisotropy of ∼ keV electrons plus a plateau/beam distribution at lower energies or with a beam-plasma instability driven by low-energy (≲ 1 keV) beams (Mourenas et al., 2015; Artemyev et al., 2016; Li et al., 2016). An alternative mechanism was proposed by Fu et al. (2017), who suggested that oblique chorus waves are generated by wave-wave nonlinear coupling from the interaction of quasi-field-aligned chorus waves in the lower band and mildly oblique upper-band chorus waves.

Since chorus waves are typically observed in the regions adjacent to the plasmasphere, the density of cold plasma populations in these regions is often significant (here “cold” is loosely defined to mean energies below approximately 100 eV.) In fact, in cases where the total plasma density can be measured by spacecraft (e.g., from the frequency of the upper-hybrid line), it is often found that cold plasma populations dominate the total density. The focus of this paper is on a recently identified nonlinear instability experienced by whistler waves in the presence of cold plasma populations (Roytershteyn and Delzanno, 2021). Specifically, kinetic simulations and theory were used to show that in the presence of cold electron populations, quasi-field-aligned whistler waves of sufficiently large amplitude experience a parametric nonlinear instability. This process leads to damping of quasi-field-aligned waves, heating of the cold plasma, and generation of oblique electrostatic modes, including oblique whistlers waves near the resonance cone. The latter in particular are of significant interest since the instability in question may provide a new mechanism of generating oblique chorus that is complementary to the earlier proposed models. In this paper, we extend the analysis of the instability to the case of a multi-component distribution of low-energy electrons, focusing specifically on the generation of the oblique whistlers. Inclusion of such additional electron populations is motivated by the need to make a closer contact with observations that often show presence of “warm” electron populations with energies in the range of $\sim 100$ eV, which can also strongly interact with the oblique chorus waves (e.g., Agapitov et al., 2015; Li et al., 2016; Li et al., 2019). Using theoretical analysis and kinetic particle-in-cell (PIC) simulations, we show that the previously identified instability producing oblique whistler waves is robust in the sense that is remains operational in the presence of such warm electron populations. Further, it may produce observed features of the electron distributions, such as formation of a plateau or a weak beam in the resonant range of energies.

Properties of cold plasma populations, especially of the electrons, are hard to measure because their typical energies are comparable to the spacecraft potential and/or the energy of the photo-electrons emitted by the spacecraft (see, e.g., a review in Delzanno et al., 2021). Photo-electrons, in particular, strongly confound the measurements of ambient cold electrons for spacecraft in sunlight. As a result, the energy distribution of the cold populations remains poorly constrained by observations even if the total plasma density could sometimes be estimated from wave measurements. In the present work, we treat the temperature of the cold populations as an unknown and vary it parametrically.

In what follows, we use the following notations: the background magnetic field B₀ is along z in a local Cartesian (x, y, z) system. Perpendicular and parallel directions are defined with respect to B₀. The plasma frequency for species s is defined by ${\omega }_{p,s}^2=4\pi e^2{n}_s/m_s$, with n_s the density of species s, e is the absolute value of the electron charge, and m_s is the species mass. Index s = eC, eW, eH, i labels cold (eC), warm (eW) and hot (eH) electrons and ions (i). Here “hot” refers to an anisotropic population with energies in the range of several keV and above. The electron plasma frequency computed with the total electron density n₀ = n_0eC + n_0eW + n_0eH is denoted by ω_pe and the total electron inertial length is d_e = c/ω_pe with c the speed of light. The cyclotron frequency is Ω_c,s = eB₀/m_sc. The species thermal velocity is $v_{t,s}=\sqrt{T_s/m_s}$, where T_s is the temperature (which could be anisotropic). The inertial length is d_s = c/ω_p,s. We will interchangeably use the terms “parent,” “driver,” or “primary” wave to refer to quasi field-aligned (whistler) wave that is the source of energy for the nonlinear interactions considered.

2 Linear theory

The specific nonlinear mechanisms that are the focus of this investigation originate from relative drifts between cold electrons and ions transverse to the background magnetic field. In principle, it is well known that transverse drifts, when present, may produce instabilities that play an important role in many settings in laboratory and space plasmas (see, e.g., a review of instabilities in the shock foot by Muschietti and Lembège (2017)). In the cases discussed here, the drifts are induced by the oscillating electric field of the parent whistler wave. The key observations are: i) whistlers are often present in the region where density is dominated by cold plasma populations and ii) for large, but realistic amplitude of whistlers (i.e., comparable to the observed values), the drifts can be significant in relation to the thermal speed of the cold electron component.

The kinetic theory to study the instabilities of quasi-parallel whistler waves caused by relative transverse drift was presented by Roytershteyn and Delzanno (2021). The key features of the theory are: 1) the underlying equilibrium corresponds to a time-dependent circularly-polarized flow of cold plasma populations induced by the primary whistler wave; 2) The dispersion relation for a given wavevector k couples several frequencies, separated by harmonics of the driver frequency ω₀; 3) For typical parameters of magnetospheric plasmas, the dominant instabilities are either quasi-perpendicular, short-wavelength modes related to Electron Cyclotron Drift Instability (Forslund et al., 1970; Forslund et al., 1972), or oblique short-wavelength whistler modes near the resonance cone.

Specifically, the electrostatic dispersion relation, generalized here to account for multiple electron species, reads:

$\begin{array}{l}\left\{k^2+{\displaystyle \sum _{s=eC,eW}}\frac{{\omega }_{pe,s}^2}{v_{t,s}^2}{\displaystyle \sum _{n=-\infty }^{+\infty }}\left[1+\frac{\omega }{\sqrt{2}{𝜐}_{t,s}{k}_z}Z\left({\xi }_{s,n}\right)\right]{\mathrm{\Gamma }}_n\left({\lambda }_s\right)\right\}\tilde{\varphi }\left(\mathit{k},\omega \right)\hfill \\ =\frac{{\omega }_{pi}^2}{2v_{ti}^2}{\displaystyle \sum _{p,m=-\infty }^{+\infty }}{J}_p\left(a\right)J_m\left(a\right)Z^{\prime }\left(\frac{\omega +p{\omega }_0}{\sqrt{2}k{v}_{ti}}\right)\tilde{\varphi }\left(\mathit{k},\omega +\left(p-m\right){\omega }_0\right).\hfill \end{array}(1)$

Expression (1) is written in the electron co-moving (rotating) frame of reference. Here ω is the frequency, k = |k| is the magnitude of the wavevector k = {0, k_y, k_z}, a = k_yV₀/ω₀, ${\mathrm{\Gamma }}_n(\lambda )=e^{-\lambda }{I}_n\left(\lambda \right)$, ${\lambda }_s=k_y^2{v}_{t,s}^2/{\mathrm{\Omega }}_{ce}^2$, ${\xi }_{s,n}=(\omega -n{\mathrm{\Omega }}_{ce})/(\sqrt{2}{v}_{t,s}{k}_z)$, Z is the plasma dispersion function, J_m (I_n) is the (modified) Bessel function of first kind, and $\tilde{\varphi }(\mathit{k},\omega )$ is the Fourier component of the electrostatic potential in that frame, while V₀ and ω₀ are the amplitude and frequency of the equilibrium electron flow induced by a primary whistler wave. Eq. 1 is derived under assumption that the spatial variation of the driving quasi-parallel whistler mode can be neglected. This is rigorously justified under condition k_z ≫ k_z0, where k_z0 is characteristic wavenumber of the driving mode. We note that in deriving Eq. 1, we assumed that the cold and warm populations are isotropic. Accounting for anisotropy is straighforward: corresponding expressions describing electron response (in non-rotating frame) are given in many textbooks, e.g., Stix (1992).

As is emphasized above, expression (1) couples the response of the system at a given k and ω with that at the same k but at at different values of ω, Doppler-shifted by the frequency of the driver ω₀. Thus, relation (1) constitutes a system of equations for ω and sidebands ω ± pω₀, where p is integer. However, when |ω + pω₀|≫ kv_ti the ion contribution (terms on the right-hand side of Eq. 1) can be neglected. In this case, system (1) describes the usual electron waves in a hot plasma, expressed however in the rotating frame. Instabilities may appear near intersections of a specific hot-plasma electron wave with the Doppler-shifted ion response, i.e., when |ω + pω₀|≲ kv_ti. Finally, the transformation between Fourier components of any quantity A in the co-moving frame $\tilde{A}$ and those in the stationary (ion) frame $\widehat{A}$ is given by $\tilde{A}(\omega ,k)={\sum }_m{J}_m(a)\widehat{A}(\omega +m{\omega }_0,k)$ (Kaw and Lee, 1973). Since observations are made in the stationary frame, this implies that a mode with a single frequency ω in the co-moving frame may be observed as a series of sidebands.

A variety of useful approximations to Eq. 1 could be readily obtained. First, we ignore coupling to the side-bands and focus on perturbations in the vicinity of the resonance cone ω ≈ Ω_ce cos θ to obtain a simplified dispersion relation (c.f. Eq. 7 of Roytershteyn and Delzanno (2021)):

$\begin{array}{ll}\hfill & k^2+{\displaystyle \sum _{s=eC,eW}}\frac{{\omega }_{pe,s}^2}{v_{t,s}^2}{\displaystyle \sum _{n=-\infty }^{+\infty }}\left[1+\frac{\omega }{\sqrt{2}{𝜐}_{t,s}{k}_z}Z\left({\xi }_{e,n}\right)\right]{\mathrm{\Gamma }}_n\left(\lambda \right)\hfill \\ \hfill & =\frac{{\omega }_{pi}^2}{2{𝜐}_{ti}^2}|J_1\left(a\right){|}^2{Z}^{\prime }\left(\frac{\omega -{\omega }_0}{\sqrt{2}k{𝜐}_{ti}}\right)\hfill \end{array}(2)$

A justification of the assumptions leading to Eq. 2 was discussed by Roytershteyn and Delzanno (2021).

A further insight into the nature of the instability generating oblique whistler modes can be obtained by by considering a configuration where the warm population is absent and using cold plasma approximation for the left-hand side, |Ω_ce/(k_yv_te)|≫ 1 and |Ω_ce/(k_z𝜐_te)|≫ 1. The system (1) then reduces to

$k_y^2\left(1-\frac{{\omega }_{pe}^2}{{\omega }^2-{\mathrm{\Omega }}_{ce}^2}\right)+k_z^2\left(1-\frac{{\omega }_{pe}^2}{{\omega }^2}\right)-\frac{{\omega }_{pi}^2}{2{𝜐}_{ti}^2}{J}_{-1}^2\left(a\right)Z^{\prime }\left(\zeta \right)=0,$

with $\zeta =(\omega -{\omega }_0)/(\sqrt{2}{𝜐}_{ti})$, and a = k_y|V₀|/ω₀. Expanding the Z function in the small argument limit, $Z^{\prime }\sim -2i\sqrt{\pi }\zeta \exp (-{\zeta }^2)-2$, and assuming γ/ω_r ≪ 1, where γ = Im ω and ω_r = Reω, yields an analytic expression for the instability growth rate:

$\frac{\gamma }{{\omega }_r}=\frac{\sqrt{\pi }}{2}\frac{m_e}{m_i}\frac{J_{-1}^2\left(a\right)}{{𝜐}_{ti}^2}\frac{{\omega }_0-{\omega }_r}{\sqrt{2}k{𝜐}_{ti}}{\left[\frac{k_y^2{\omega }_r^2}{{\left({\omega }_r^2-{\mathrm{\Omega }}_{ce}^2\right)}^2}+\frac{k_z^2}{{\omega }_r^2}\right]}^{-1}$

where ω_r is the solution of

$k_y^2\left(1-\frac{{\omega }_{pe}^2}{{\omega }_r^2-{\mathrm{\Omega }}_{ce}^2}\right)+k_z^2\left(1-\frac{{\omega }_{pe}^2}{{\omega }_r^2}\right)+\frac{{\omega }_{pi}^2}{{𝜐}_{ti}^2}{J}_{-1}^2\left(a\right)=0.(3)$

The nature of the instability now becomes evident. When there is no flow, the terms involving J₋₁ are zero and there is no coupling between electrons and ions. In that case there is no instability and Eq. 3 describes whistler waves near the resonance cone angle, cos θ_R ≈ ω_r/Ω_ce. The presence of the flow leads to coupling with the ions and to a drift instability when ω_r < ω₀ which leads to the generation of the oblique whistler waves near the resonance cone.

In order to understand the influence of the low-energy part of the electron energy spectrum on the instability, we turn to the form of the dispersion relation given by Eq. 2, which retains the resonance terms. An example of its solution is presented in Figure 1. Here, we assumed parameters approximately corresponding to simulation case D discussed in Section 3 below: ω_pe/Ω_ce = 4, n_0eW/n₀ = 0.2, n_0eC/n₀ = 0.75, T_eC = T_i = 5eV, T_eW = 100eV, ω₀ = 0.3Ω_ce, V₀ ≈ 0.8v_teC, and m_i/m_e = 1836. We observe that in the presence of warm and cold populations, there are typically two distinct peaks in the growth rate, one at relatively low values of k and the other at relatively high values of k. The nature of these two peaks could be elucidated by varying the parameters of the background plasma. For example, increasing the temperature of the cold populations by a factor of two strongly affects the peak at higher values of k, but leaves the peak at low values of k virtually unchanged (see curve labeled T_eC × 2 in Figure 1). In contrast, increasing the temperature of the warm population affects both peaks, significantly reducing the growth rate at the low values of k (curve labeled T_eW × 2). Examination of the case where the warm population is absent (curve labeled n_eW = 0) suggests that the peaks are formed due to suppression of the growth rate in the range of wavenumbers where the warm population is resonant with the mode |ξ_eW,0| = 1.

Figure 1

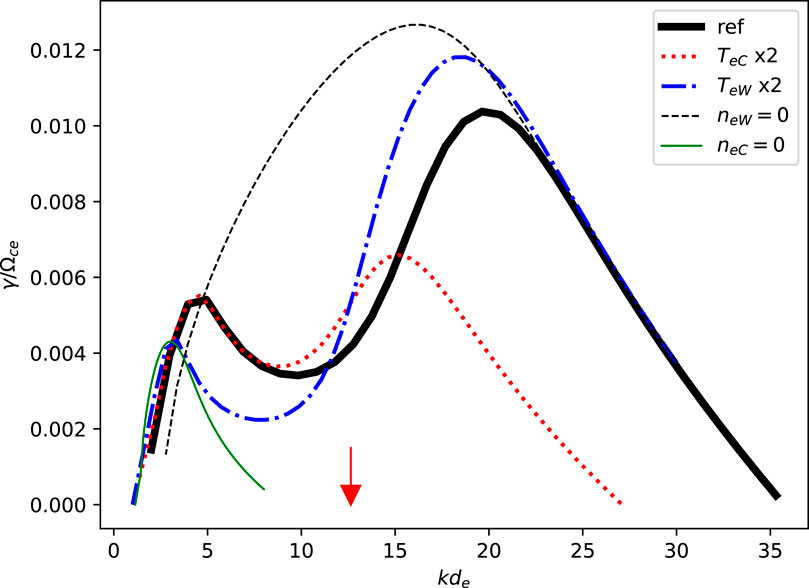
Figure 1. Linear theory: effect of the warm electron population. The figure shows dispersion relation γ(k) obtained by solving Eq. 2 for angle θ corresponding to the resonance cone cos θ = ω₀/Ω_ce, for reference case with the parameters indicated in the text, two cases with the temperatures of the cold and warm population increased by a factor of 2 compared to the reference case, and for the cases where the warm or cold populations are absent. The wavenumber corresponding to condition |ξ_eW,0| = 1 is indicated by the red arrow at kd_e ≈ 12.6.

Overall, the results of the linear analysis illustrate strong dependence of the instability properties on the energy spectrum of the electrons in the range below a few hundred eV. Further, it may be anticipated that development of the instability may influence distribution functions in this part of the energy spectrum, leading, for example, to formation of plateau and/or beam features in the distribution due to resonances. This point is illustrated further in the following section using PIC simulations.

We also note that the oblique instability near the whistler resonance cone persists (for a fixed driver amplitude) for relatively large values of electron temperature. For the parameters considered in the example above, that included cases where the cold population was absent and only the warm population with T_eW = 100eV was included, as shown in Figure 1. While the corresponding growth rate becomes lower with increasing temperature of the background populations, this behavior is in contrast to the strong temperature dependence of quasi-perpendicular ECDI-type modes. The latter generally appear when the magnitude of the transverse drift V₀ is comparable to the thermal speed of the low-energy populations 𝜐_te. The oblique instability of the whistler type clearly exist in the regime V₀ < 𝜐_te. This observation suggests that the oblique chorus generated by the mechanism presented here could often accompany large-amplitude quasi-field aligned chorus waves in the Earth’s magnetosphere.

3 Evolution of the oblique instabilities and energization of the background plasma: PIC simulations

3.1 Simulation model

In the simulation model presented here, the field-aligned whistler waves are excited by cyclotron (temperature anisotropy) instability of an electron population with the energy in the range of $\sim 10$ keV. The initial conditions correspond to plasma with protons and up to three species of electrons with different energies. All populations are initially characterized by (bi-) Maxweillian distributions with density n_0s, parallel (along the background magnetic field) temperature T_s‖ and perpendicular temperature T_s⊥. The hot (∼keV) electrons are characterized by the anisotropy A = T_eH⊥/T_eH‖ − 1. The cold (∼eV) and warm (∼100eV) electrons and the ions are isotropic and hence can be identified by a single temperature, T_eC, T_eW and T_i. Simulations are performed with the Particle-In-Cell (PIC) code VPIC (Bowers et al., 2008) using the parameters summarized in Table 1. The simulations are performed in a two-dimensional Cartesian domain (y, z) of dimension L_y × L_z, discretized by N_y × N_z cells and use a uniform time step Δt. In all cases ω_pe/Ω_ce = 4 and n_i/n₀ = 1.

Table 1

Table 1. Parameters of the PIC simulations. ω_pe/Ω_ce = 4 and n_i/n₀ = 1 in all cases.

We mainly vary the temperature of the cold electrons and ions relative to the 100 eV warm electrons to investigate the influence of cold plasma temperature on the growth of oblique whistlers and ECDI. The simulation domain size was selected to accommodate the growth of waves expected from the linear theory described in the previous section. Some additional runs were performed to investigate a fully 3D system, and special cases with no warm electrons present.

3.2 Simulation results

All of the simulations summarized here behave qualitatively in the same way. The initial configuration is unstable to a cyclotron instability due to the presence of an anisotropic hot electron population. This instability quickly creates the primary, predominantly field aligned, whistler waves. After the primary whistler waves reach saturation, electrostatic fluctuations with finite k_⊥ appear, which are driven by the nonlinear processes discussed in Section 2. For the parameters considered, the oblique fluctuations are related to electron Bernstein modes and oblique electrostatic whistler modes near the resonance cone. These fluctuations lead to damping of the primary whistler modes and heating of the cold and warm electrons. For most of the simulations considered in this study, the most intense transfer of energy from the primary whistler to the low-energy electron populations is associated with the oblique electrostatic whistlers. The final state of the system is characterized by the presence of the oblique whistler modes. An important observational property of these waves is that they have nearly the same frequency as the primary, field-aligned whistlers, but higher wavenumbers and wave-normal angles near the resonance cone.

In order to illustrate this typical behavior, we focus on simulation D (see Table 1). Figure 2 summarizes time-evolution of several relevant diagnostics. Panel a) shows evolution of the average magnitude of the magnetic field fluctuations. The energy density P_E of the electric field fluctuations with finite k_⊥ is shown in Panel b). To differentiate between electron Bernstein and oblique electrostatic whistler waves, P_E is computed in two narrow ranges of perpendicular wavenumbers $P_E(k_1,k_2)={\sum }_{k_{\perp }=k_1}^{k_2}|\mathit{E}(\mathit{k}){|}^2$, where |E(k)|² = |E_x(k)|² + |E_y(k)|² + |E_z(k)|². Panel c) shows parallel and perpendicular cold electron temperatures. The spectrogram of the electric field fluctuations is shown in panel d). This is computed by performing Fast Fourier Transform (FFT) in a sliding time window of width $100{\mathrm{\Omega }}_{ce}^{-1}$, averaged over y and z. Panel e) shows the wave normal angle computed using singular value decomposition (SVD) of the electromagnetic wave correlation matrix (Santolík et al., 2003) in the same sliding windows. The results are only shown in the areas where the spectrum density S_E (ω, t) in panel d) is larger than a chosen threshold. To complement this estimate, Figure 2F shows the wave normal angle for the peak of the wavenumber spectrum at a given time.

Figure 2

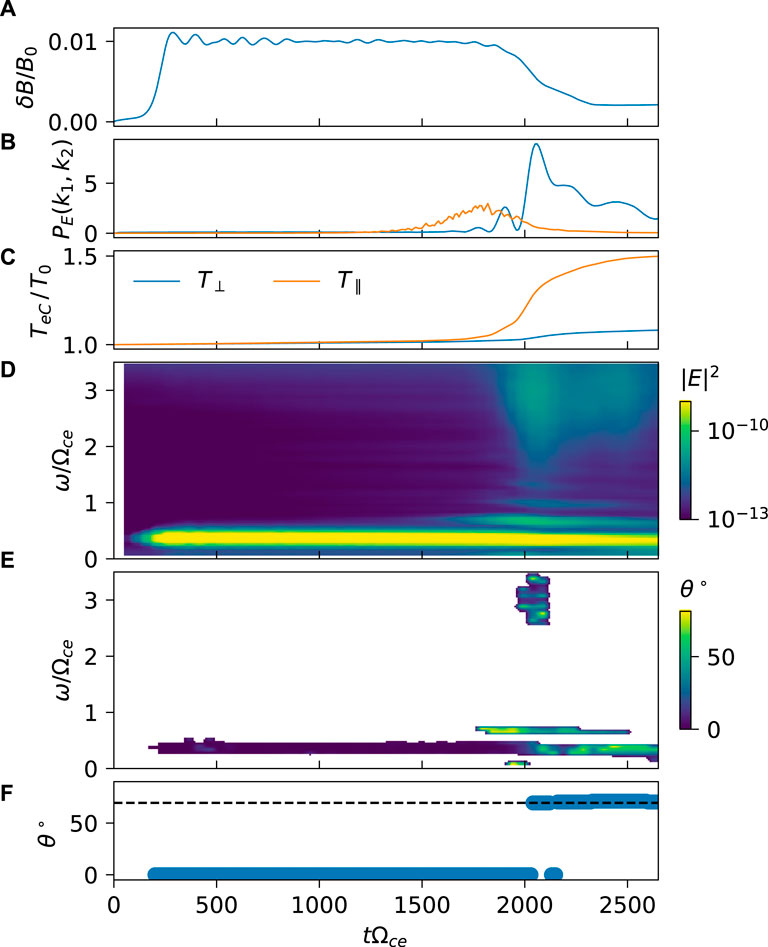
Figure 2. Time evolution in simulation D: (A) amplitude of the transverse magnetic field perturbation δB relative to the background magnetic field B₀; (B) energy density of electric field fluctuations |E|² in a narrow range of wavenumbers corresponding to the highly oblique whistler waves (blue) and the electron Bernstein waves (orange, multiplied by 10 for clarity); (C) temperature of cold electrons normalized to the initial cold temperature T₀ = 5eV; (D) spectrogram of electric field fluctuations |E|²; (E) wave normal angle spectrum obtained by the SVD method; (F) wave normal angle corresponding to the peak of the spectrum in panel (D). The dashed line corresponds to the resonance angle θ_R = 69.5°. See text for details.

As is seen in panel a) of Figure 2, the primary whistler waves in simulation D grow on a timescale of a few hundred ${\mathrm{\Omega }}_{ce}^{-1}$. The waves are characterized by frequency ω ≈ 0.35Ω_ce (see panel d) and are field-aligned (see panels e and f). Electrostatic fluctuations with finite k_⊥ appear in the electric field at tΩ_ce ∼ 1500. The orange line in panel b) of Figure 2 corresponds to quasi-perpendicular electron Bernstein-like waves (P_E is computed in the range 100 ≤ k_⊥d_e ≤ 120) and is multiplied by 10 for clarity, while the blue line corresponds to the highly oblique whistler waves near the resonance cone and is obtained by taking 2πd_e/L_⊥ ≤ k_⊥d_e ≤ 50 while computing P_E. Note that when the electrostatic fluctuations appear, the amplitude of the primary whistler waves begins to decrease (panel a). The most intense damping coincides with excitation of the highly oblique whistlers. The final amplitude of the magnetic field fluctuations associated with the primary whistler waves is 20% of the initial saturated amplitude. Moreover, as the primary whistler waves damp, cold electrons heat, as seen in Panel c) of Figure 2. After approximately tΩ_ce = 2000, the spectrum is dominated by the highly oblique waves at the same frequency of the initial parent wave (see panels e and f). Harmonics of the initial wave frequency ω₀ are clearly evident in panel (d), corresponding to both the highly oblique whistlers and the electron Bernstein waves. In particular, the transition at around tΩ_ce = 2000, when the amplitude of the secondary modes is the highest (see panel b), is characterized by a rich spectral signature.

The properties of the electric field fluctuations appearing at tΩ_ce > 1500 are consistent with the predictions of the kinetic linear theory introduced above. Figure 3 (left) shows the spectrum of fluctuations of the magnitude of the electric field |E(k)|² for simulation D, computed at Ω_cet ≈ 1520, once the electrostatic fluctuations are beginning to appear. On the right panel, the contour levels for γ/ω_pe = 0.001 (blue) and γ/ω_pe = 0.005 (red) are plotted, obtained from the full dispersion relation (1) with N = 3 sidebands and keeping ± 20 terms in the summation over n. The other necessary parameters are extracted from the saturated state of the primary whistler wave before the onset of the secondary instabilities and correspond to ω₀ = 0.35Ω_ce and V₀/c = 2 × 10⁻³One can see that the linear theory reproduces quite well the range of unstable secondary modes seen in the simulation. The highly oblique whistler waves are excited near the resonance cone indicated by the white dashed lines in Figure 3 (left), which corresponds to a wave normal angle of $\approx 70°$. Moreover, quasi-perpendicular electron Bernstein are also excited, characterized in Figure 3 (left) by large values of the perpendicular wave number, k_⊥d_e ∼ 100. Note that k_⊥d_e ∼ 100 corresponds to k_⊥ρ_eC ∼ 1.25, i.e., the Bernstein waves have wavelengths of the order of the cold electron gyroradius.

Figure 3

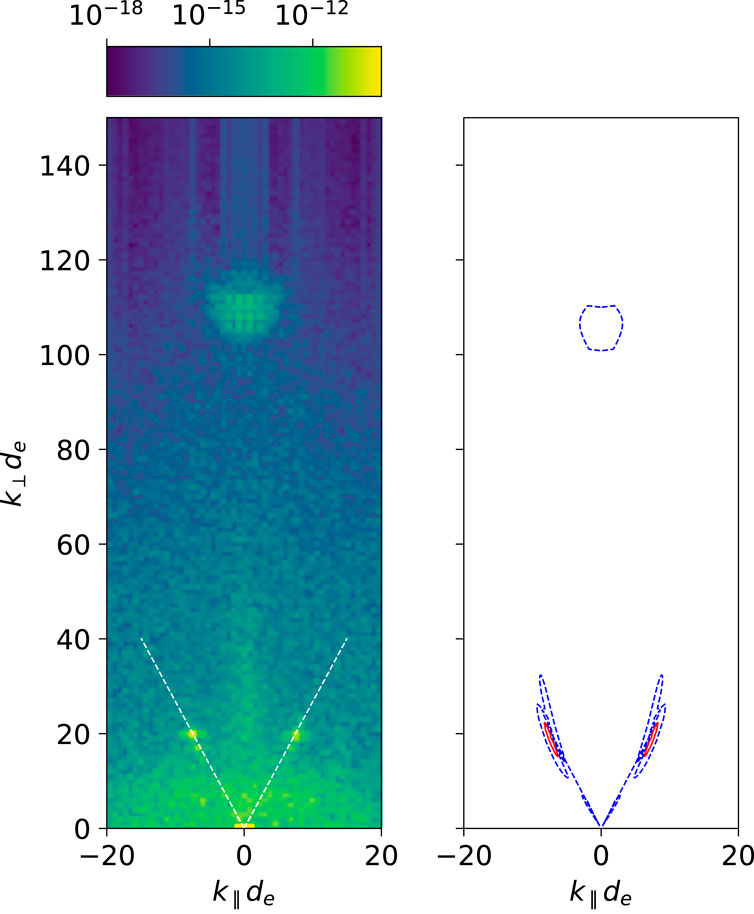
Figure 3. Comparison of the wavenumber spectrum of electric field fluctuations measured in the simulation D (left) with the prediction of the linear theory (right).

Resonant interaction of the oblique whistler modes with low-energy electrons leads to formation of the beam-like features in the electron distribution function. This is illustrated by Figure 4, which shows the electron distribution function in the (𝜐_⊥, 𝜐_‖) space (top panel) and the distribution function along the cut corresponding to pitch angles α = 10° (bottom panel). The latter roughly corresponds to the angular resolution of the Helium, Oxygen, Proton, and Electron (HOPE) mass spectrometer (Funsten et al., 2013) on the Van Allen Probes spacecraft. The energy resolution of the presented diagnostic is however much higher than that of HOPE, enabling unequivocal resolution of sub-100eV structures that may not be picked up by a survey using HOPE. Flattening of the distribution function at parallel energies around 50 eV is apparent. Using the value of k_‖ corresponding to the peak growth rate from the linear stability analysis, k_‖d_e ∼ 7, and the Landau resonance condition with the highly oblique whistler waves at ω/Ω_ce ≈ 0.35, V_‖ = ω/k_‖, leads to |V_‖|/c = 0.0125 and a resonant energy of $\sim 40$ eV. This is in good agreement with the position of the plateau. It is also interesting that the distribution function is slightly non-monotonic as a function of parallel energy, reminiscent of a shallow beam. The non-monotonicity is not an artifact of a particular choice of α and is present at all small angles, as well as in the integral of the distribution function over small pitch angles. As was discussed in the introduction, beams are often present concomitant with observations of highly oblique chorus waves. This led to the hypothesis that the oblique waves are in fact driven by the electron beams. In the present scenario, the plateau/beam-feature forms due to the secondary drift instabilities and is the consequence of the appearance of the highly oblique whistler waves.

Figure 4

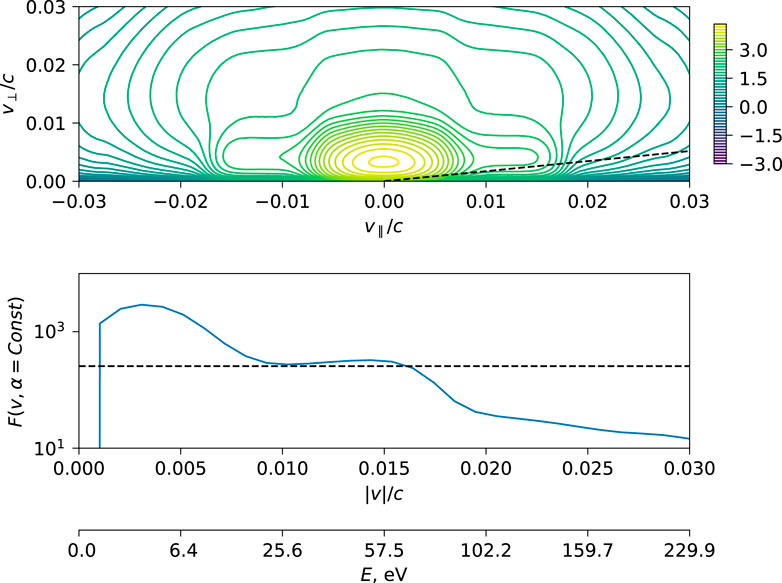
Figure 4. Iso-contours of the total electron distribution function log  F_e (v_‖, v_⊥) (top) and the cut of distribution at pitch-angle α = 10° (bottom). The second axis on the bottom panel indicates energy in eV corresponding to the given value of the electron velocity. The horizontal dashed line is included as a visual guide, to highlight existence of a velocity range with a weak positive gradient in the distribution.

The features observed in simulation D are common to all of the simulations in Table 2. In all cases the highly oblique whistler waves are formed with large wave normal angles near the resonance cone, as shown in Figure 5. The primary whistler waves damp significantly, losing at least 50% of the |δB|² acquired after the initial saturation, and in some cases damping almost completely $(\ge 95\%)$. This is reported in Table 2, showing ΔB² = 1 − max|δB|²/|δB (t_end)|², where max|δB|² is the maximum of |δB|² = |B − B₀|² and t_end is the final simulation time. Since quasi-linear resonant diffusion rates scale as |δB|², such a drastic reduction in wave amplitude also implies a drastic reduction in resonant pitch-angle scattering and energization rates.

Table 2

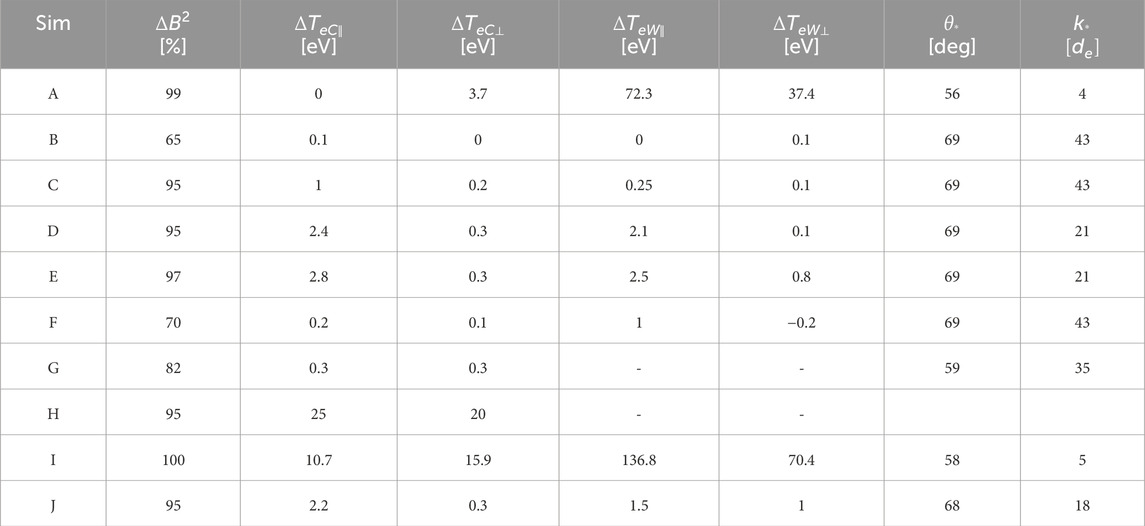
Table 2. Results of PIC simulations. Notes: 1) heating in cases B and F is strongly affected by numerical errors; 2) simulation H is 3D.

Figure 5

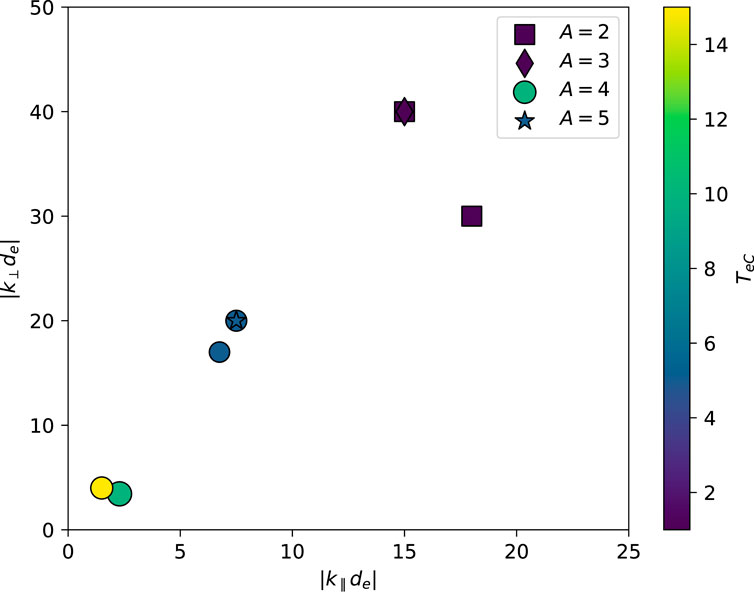
Figure 5. Wavenumbers of the spectral peaks corresponding to highly oblique whistler waves observed in the simulations (excluding cases H and I from Table 1). The color represents the initial temperature of the cold population T_eC, while symbols mark cases with the different initial anisotropy of the hot electrons A. For a given T_eC, the amplitude of the excited primary field-aligned waves generally increases with A.

Part of the primary wave energy is converted into heating of cold/warm electrons, as shown in Table 2 which reports the change in temperature ΔT in the perpendicular and parallel directions, respectively. This gives an indication of heating, although we remark that the electron temperature is not always fully saturated at the end of the simulations. An insight into the nature of the energization of background plasma could be obtained by comparing the ratio of cold-to-warm energy change ΔT_eC/ΔT_eW with the ratio of growth rates at the two peaks of the dispersion relation at small and large values of k discussed in Section 2. This is presented in Figure 6, where the scaling of ΔT_eC/ΔT_eW with the growth rate ratio is shown for both parallel and perpendicular direction. The growth rates for each case were obtained by numerically solving Eq. 2 with the parameters of the corresponding simulations and searching for a local maximum of the growth rate as a function of k and θ in two ranges of wavenumbers. We excluded cases B and F from the analysis since in each case the numerical heating appears to strongly influence the results. The remaining cases follow a linear scaling for both the parallel and perpendicular direction. There is more variability in the perpendicular energization, which may be related to the contribution from the heating by electron Bernstein modes.

Figure 6

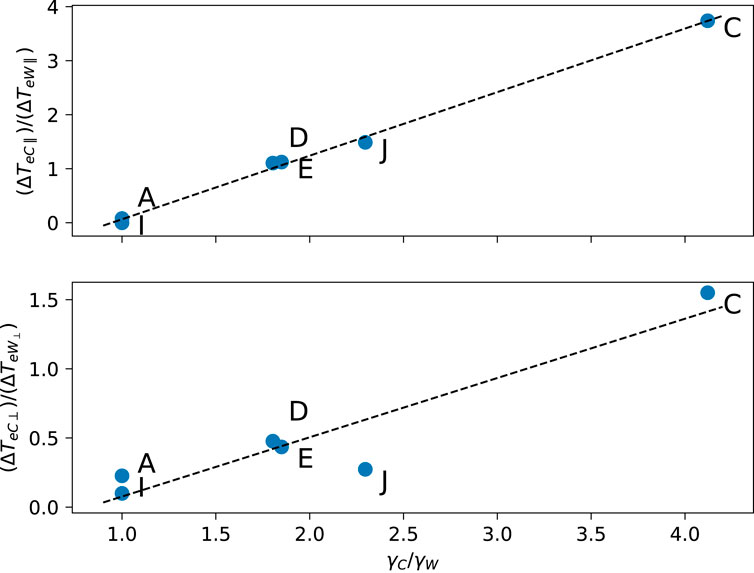
Figure 6. Scaling of electron heating with linear growth rate. The figure shows ratios of ΔT_eC/ΔT_eW for parallel (top) and perpendicular (bottom) direction as a function of the ratio between linear growth rate peaks at high and low wavenumbers (see Figure 1).

We remark that most of the simulations of Table 2 were performed in relatively short spatial domains (admitting only one wavelength of the most unstable modes). The saturation amplitude is generally higher in longer domains, as could be seen by comparing cases A and I. While this limitation may affect specific values of ΔB² and ΔT for given initial conditions, it does not affect the overall conclusions. In fact, one can simply interpret the reported values as being representative of situations where primary waves of a given amplitude have been generated, but the driving mechanism is no longer operational, either because the waves propagated out of the source region, or because the anisotropy of the hot population has reached marginal stability.

4 Summary and discussion

Quasi-field-aligned whistler waves experience a nonlinear instability due to transverse currents when they propagate through a background plasma of sufficiently low energy. One of the most interesting effects associated with the instability is the generation of oblique electrostatic waves, including highly oblique whistler waves near the resonance cone. These modes are of great interest due to their possible connection with oblique whistler-mode chorus waves in the Earth’s magnetosphere that are routinely observed by spacecraft and are known to play an important role in wave-particle interactions. The results presented in this paper extend earlier analysis of Roytershteyn and Delzanno (2021) to the case where low-energy background consists of both a cold electron population with characteristic energy in the range of a few eV and a warm component with characteristic energy in range of $\sim 100$ eV. This is motivated by spacecraft observations in the Earth’s magnetosphere where oblique chorus waves were shown to interact resonantly with the warm electrons.

In the presented analysis the low-energy electrons are modeled by including two (cold + warm) Maxwellian populations. The main conclusions are: 1) the instability producing oblique electrostatic waves is sensitive to the shape of the electron distribution at low energies. This is manifested by the sensitivity of both the wavenumbers corresponding to the maximum growth rate and the growth rate magnitude to the temperatures and the relative density of the two low-energy populations. Typically, two distinct peaks in the growth rate are present for the model considered: a peak at relatively low wavenumbers that is most sensitive to the properties of the warm population and a peak at relatively high wavenumbers that is most sensitive to the properties of the cold population. The sensitivity of these processes to the low-energy electron distribution function reinforces the need for the development of robust techniques for in-situ measurements in this energy range (Delzanno et al., 2021; Maldonado et al., 2023); 2) overall, the instability producing oblique whistler waves near the resonance cone persists even in the cases where the temperature of the cold populations is relatively high. For a reference case with (high) amplitude of the parent field-aligned whistler wave δB/B₀ ∼ 0.01, the maximum growth rate of the oblique whistler mode was γ/Ω_ce ≈ 4 × 10⁻³ when the background consisted only of the warm component with temperature equal to 100 eV. 3) PIC simulations show that the development of the instability leads to heating of the low-energy electrons and formation of characteristic plateau and beam features in the parallel electron distribution function in the range of energies resonant with the instability. The characteristic energy of the resonant particles changes from 50 eV to 1 keV for the cases considered depending on the parameters of the background plasma and the driver. The plateau/beam features have been previously detected in spacecraft observations of oblique chorus waves. However, they have been previously attributed to external sources and have been proposed to be one of the mechanisms producing the oblique chorus (Li et al., 2016). In the present scenario, the causality link is reversed and the oblique whistler waves generated by the instability of the parent quasi-field-aligned whistler are the reason for formation of the plateau and the beam. Finally, 4) the relative energization of the background populations in the simulations, quantified by the relative change in energy between the cold and the warm populations, have been shown to scale linearly with the ratio of the corresponding peak values of the linear growth rates. We note that formation of the plateau in the parallel electron distribution functions has been proposed by Li et al. (2019) as the mechanism responsible for two-banded structure of the chorus. In that scenario, plateau is formed due to interaction with a slightly oblique primary whistler waves (in our terminology) and is consequently located at higher energies compared to the case discussed here, where the plateau is formed by interaction with highly oblique secondary whistlers.

In the presented analysis, the effect of drift-type instabilities associated with the presence of cold plasma has been to a large degree isolated by imposing geometrical constraints on the simulations. For example, the simulations were mostly 2D, were performed in relatively small domains with periodic boundary conditions, and considered only uniform background magnetic field and plasma conditions. Relaxing these constraints and changing the configuration towards a more realistic one (e.g., a dipolar magnetic field with non-uniform density) will introduce other important nonlinear phenomena into the problem, such as frequency chirping and the formation of rising or falling chorus elements (Omura et al., 2012), nonlinear scattering of whistlers (Ganguli et al., 2010), parametric interaction of whistler waves with electrostatic modes (Boswell and Giles, 1977; Umeda et al., 2017), and several others, e.g., (Artemyev et al., 2016; Demekhov et al., 2017; Agapitov et al., 2018; Vasko et al., 2018). Understanding of the relative significance of the processes discussed in this paper in the presence of other phenomena is an important future direction of this work.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

VR: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Software, Visualization, Writing–original draft, Writing–review and editing. GD: Conceptualization, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Software, Writing–original draft, Writing–review and editing. JH: Investigation, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. GD was supported by the Laboratory Directed Research and Development (LDRD)—Directed Research Program and Exploratory Research Program of Los Alamos National Laboratory (LANL) under project number 20200073DR and 20220453ER. JH was supported by LANL through its Center for Space and Earth Science (CSES). CSES is funded by the LDRD program under project number 20210528CR. LANL is operated by Triad National Security, LLC, for the National Nuclear Security Administration of U.S. Department of Energy (Contract No. 89233218CNA000001). VR was partially supported by NSF award 2031024 and NASA grant 80NSSC22K1014.

Acknowledgments

The authors gratefully acknowledge discussions with George Hospodarsky. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility located at Lawrence Berkeley National Laboratory, operated under Contract No. DE-AC02-05CH11231, resources provided by the NASA High-End Computing (HEC) Program through the NASA Advanced Supercomputing (NAS) Division at Ames Research Center, and resources at the Texas Advanced Computing Center (TACC) at The University of Texas at Austin.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Agapitov, O., Drake, J. F., Vasko, I., Mozer, F. S., Artemyev, A., Krasnoselskikh, V., et al. (2018). Nonlinear electrostatic steepening of whistler waves: the guiding factors and dynamics in inhomogeneous systems. Geophys. Res. Lett. 45, 2168–2176. doi:10.1002/2017GL076957

CrossRef Full Text | Google Scholar

Agapitov, O., Krasnoselskikh, V., Khotyaintsev, Y. V., and Rolland, G. (2012). Correction to “A statistical study of the propagation characteristics of whistler waves observed by Cluster”. Geophys. Res. Lett. 39. doi:10.1029/2012GL054320

CrossRef Full Text | Google Scholar

Agapitov, O. V., Artemyev, A. V., Mourenas, D., Mozer, F. S., and Krasnoselskikh, V. (2015). Nonlinear local parallel acceleration of electrons through Landau trapping by oblique whistler mode waves in the outer radiation belt. Geophys. Res. Lett. 42 (10), 140–149. doi:10.1002/2015GL066887

CrossRef Full Text | Google Scholar

Artemyev, A., Agapitov, O., Mourenas, D., Krasnoselskikh, V., and Mozer, F. (2015). Wave energy budget analysis in the earth’s radiation belts uncovers a missing energy. Nat. Commun. 6, 7143. doi:10.1038/ncomms8143

PubMed Abstract | CrossRef Full Text | Google Scholar

Artemyev, A., Agapitov, O., Mourenas, D., Krasnoselskikh, V., Shastun, V., and Mozer, F. (2016). Oblique whistler-mode waves in the earth’s inner magnetosphere: energy distribution, origins, and role in radiation belt dynamics. Space Sci. Rev. 200, 261–355. doi:10.1007/s11214-016-0252-5

CrossRef Full Text | Google Scholar

Boswell, R. W., and Giles, M. (1977). Generation of whistler-mode radiation by parametric decay of Bernstein waves. Phys. Rev. Lett. 39, 277–280. doi:10.1103/PhysRevLett.39.277

CrossRef Full Text | Google Scholar

Bowers, K. J., Albright, B. J., Yin, L., Bergen, B., and Kwan, T. J. T. (2008). Ultrahigh performance three-dimensional electromagnetic relativistic kinetic plasma simulation. Phys. Plasmas 15, 055703. doi:10.1063/1.2840133

CrossRef Full Text | Google Scholar

Breneman, A. W., Crew, A., Sample, J., Klumpar, D., Johnson, A., Agapitov, O., et al. (2017). Observations directly linking relativistic electron microbursts to whistler mode chorus: van allen probes and FIREBIRD ii. Geophys. Res. Lett. 44 (11), 265–272. doi:10.1002/2017GL075001

CrossRef Full Text | Google Scholar

Burtis, W. J., and Helliwell, R. A. (1969). Banded chorus — a new type of VLF radiation observed in the magnetosphere by OGO 1 and OGO 3. J. Geophys. Res. (1896-1977) 74, 3002–3010. doi:10.1029/JA074i011p03002

CrossRef Full Text | Google Scholar

Cattell, C., Wygant, J. R., Goetz, K., Kersten, K., Kellogg, P. J., von Rosenvinge, T., et al. (2008). Discovery of very large amplitude whistler-mode waves in Earth’s radiation belts. Geophys. Res. Lett. 35, L01105. doi:10.1029/2007GL032009

CrossRef Full Text | Google Scholar

Chan, K.-W., and Holzer, R. E. (1976). ELF hiss associated with plasma density enhancements in the outer magnetosphere. J. Geophys. Res. 81, 2267–2274. doi:10.1029/JA081i013p02267

CrossRef Full Text | Google Scholar

Chen, L., Thorne, R. M., Li, W., and Bortnik, J. (2013). Modeling the wave normal distribution of chorus waves. J. Geophys. Res. Space Phys. 118, 1074–1088. doi:10.1029/2012JA018343

CrossRef Full Text | Google Scholar

Delzanno, G. L., Borovsky, J. E., Henderson, M. G., Resendiz Lira, P. A., Roytershteyn, V., and Welling, D. T. (2021). The impact of cold electrons and cold ions in magnetospheric physics. J. Atmos. Solar-Terrestrial Phys. 220, 105599. doi:10.1016/j.jastp.2021.105599

CrossRef Full Text | Google Scholar

Demekhov, A. G., Taubenschuss, U., and Santolík, O. (2017). Simulation of VLF chorus emissions in the magnetosphere and comparison with THEMIS spacecraft data. J. Geophys. Res. Space Phys. 122, 166–184. doi:10.1002/2016JA023057

CrossRef Full Text | Google Scholar

Dunckel, N., and Helliwell, R. A. (1969). Whistler-mode emissions on the OGO 1 satellite. J. Geophys. Res. (1896-1977) 74, 6371–6385. doi:10.1029/JA074i026p06371

CrossRef Full Text | Google Scholar

Forslund, D. W., Morse, R. L., and Nielson, C. W. (1970). Electron cyclotron drift instability. Phys. Rev. Lett. 25, 1266–1270. doi:10.1103/PhysRevLett.25.1266

CrossRef Full Text | Google Scholar

Forslund, D. W., Morse, R. L., Nielson, C. W., and Fu, J. (1972). Electron cyclotron drift instability and turbulence. Phys. Fluids 15, 1303–1318. doi:10.1063/1.1694082

CrossRef Full Text | Google Scholar

Fu, X., Cowee, M. M., Friedel, R. H., Funsten, H. O., Gary, S. P., Hospodarsky, G. B., et al. (2014). Whistler anisotropy instabilities as the source of banded chorus: Van Allen probes observations and particle-in-cell simulations. J. Geophys. Res. Space Phys. 119, 8288–8298. doi:10.1002/2014JA020364

PubMed Abstract | CrossRef Full Text | Google Scholar

Fu, X., Gary, S. P., Reeves, G. D., Winske, D., and Woodroffe, J. R. (2017). Generation of highly oblique lower band chorus via nonlinear three-wave resonance. Geophys. Res. Lett. 44, 9532–9538. doi:10.1002/2017GL074411

CrossRef Full Text | Google Scholar

Funsten, H. O., Skoug, R. M., Guthrie, A. A., MacDonald, E. A., Baldonado, J. R., Harper, R. W., et al. (2013). Helium, oxygen, proton, and electron (HOPE) mass spectrometer for the radiation belt storm probes mission. Space Sci. Rev. 179, 423–484. doi:10.1007/s11214-013-9968-7

CrossRef Full Text | Google Scholar

Ganguli, G., Rudakov, L., Scales, W., Wang, J., and Mithaiwala, M. (2010). Three dimensional character of whistler turbulence. Phys. Plasmas 17, 052310. doi:10.1063/1.3420245

CrossRef Full Text | Google Scholar

Gary, S. P., Liu, K., and Winske, D. (2011). Whistler anisotropy instability at low electron β: particle-in-cell simulations. Phys. Plasmas 18, 082902. doi:10.1063/1.3610378

CrossRef Full Text | Google Scholar

Gary, S. P., and Wang, J. (1996). Whistler instability: electron anisotropy upper bound. J. Geophys. Res. Space Phys. 101, 10749–10754. doi:10.1029/96JA00323

CrossRef Full Text | Google Scholar

Haque, N., Spasojevic, M., Santolík, O., and Inan, U. S. (2010). Wave normal angles of magnetospheric chorus emissions observed on the polar spacecraft. J. Geophys. Res. Space Phys. 115. doi:10.1029/2009JA014717

CrossRef Full Text | Google Scholar

Hartley, D. P., Kletzing, C. A., Santolík, O., Chen, L., and Horne, R. B. (2018). Statistical properties of plasmaspheric hiss from Van Allen probes observations. J. Geophys. Res. Space Phys. 123, 2605–2619. doi:10.1002/2017JA024593

CrossRef Full Text | Google Scholar

Hayakawa, M., Yamanaka, Y., Parrot, M., and Lefeuvre, F. (1984). The wave normals of magnetospheric chorus emissions observed on board geos 2. J. Geophys. Res. Space Phys. 89, 2811–2821. doi:10.1029/JA089iA05p02811

CrossRef Full Text | Google Scholar

Kasahara, S., Miyoshi, Y., Yokota, S., Mitani, T., Kasahara, Y., Matsuda, S., et al. (2018). Pulsating aurora from electron scattering by chorus waves. Nature 554, 337 EP–340. doi:10.1038/nature25505

PubMed Abstract | CrossRef Full Text | Google Scholar

Kaw, P. K., and Lee, Y. (1973). Parametric excitation of lower hybrid instabilities. Phys. Fluids 16, 155–157. doi:10.1063/1.1694164

CrossRef Full Text | Google Scholar

Kennel, C. F., and Petschek, H. E. (1966). Limit on stably trapped particle fluxes. J. Geophys. Res. (1896-1977) 71, 1–28. doi:10.1029/JZ071i001p00001

CrossRef Full Text | Google Scholar

Li, J., Bortnik, J., An, X., Li, W., Angelopoulos, V., Thorne, R. M., et al. (2019). Origin of two-band chorus in the radiation belt of Earth. Nat. Commun. 10, 4672. doi:10.1038/s41467-019-12561-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, W., Bortnik, J., Thorne, R. M., and Angelopoulos, V. (2011). Global distribution of wave amplitudes and wave normal angles of chorus waves using THEMIS wave observations. J. Geophys. Res. Space Phys. 116. doi:10.1029/2011JA017035

CrossRef Full Text | Google Scholar

Li, W., Bortnik, J., Thorne, R. M., Cully, C. M., Chen, L., Angelopoulos, V., et al. (2013). Characteristics of the poynting flux and wave normal vectors of whistler-mode waves observed on THEMIS. J. Geophys. Res. Space Phys. 118, 1461–1471. doi:10.1002/jgra.50176

CrossRef Full Text | Google Scholar

Li, W., Mourenas, D., Artemyev, A. V., Bortnik, J., Thorne, R. M., Kletzing, C. A., et al. (2016). Unraveling the excitation mechanisms of highly oblique lower band chorus waves. Geophys. Res. Lett. 43, 8867–8875. doi:10.1002/2016GL070386

CrossRef Full Text | Google Scholar

Maldonado, C. A., Resendiz Lira, P. A., Delzanno, G. L., Larsen, B. A., Reisenfeld, D. B., and Coffey, V. (2023). A review of instrument techniques to measure magnetospheric cold electrons and ions. Front. Astronomy Space Sci. 9. doi:10.3389/fspas.2022.1005845

CrossRef Full Text | Google Scholar

Meredith, N. P., Horne, R. B., Iles, R. H. A., Thorne, R. M., Heynderickx, D., and Anderson, R. R. (2002). Outer zone relativistic electron acceleration associated with substorm-enhanced whistler mode chorus. J. Geophys. Res. Space Phys. 107, 29–14. doi:10.1029/2001JA900146

CrossRef Full Text | Google Scholar

Meredith, N. P., Horne, R. B., Thorne, R. M., and Anderson, R. R. (2003). Favored regions for chorus-driven electron acceleration to relativistic energies in the Earth’s outer radiation belt. Geophys. Res. Lett. 30. doi:10.1029/2003GL017698

CrossRef Full Text | Google Scholar

Mourenas, D., Artemyev, A. V., Agapitov, O. V., and Krasnoselskikh, V. (2014). Consequences of geomagnetic activity on energization and loss of radiation belt electrons by oblique chorus waves. J. Geophys. Res. Space Phys. 119, 2775–2796. doi:10.1002/2013JA019674

CrossRef Full Text | Google Scholar

Mourenas, D., Artemyev, A. V., Agapitov, O. V., Krasnoselskikh, V., and Mozer, F. S. (2015). Very oblique whistler generation by low-energy electron streams. J. Geophys. Res. Space Phys. 120, 3665–3683. doi:10.1002/2015JA021135

CrossRef Full Text | Google Scholar

Muschietti, L., and Lembège, B. (2017). Two-stream instabilities from the lower-hybrid frequency to the electron cyclotron frequency: application to the front of quasi-perpendicular shocks. Ann. Geophys. 35, 1093–1112. doi:10.5194/angeo-35-1093-2017

CrossRef Full Text | Google Scholar

Ni, B., Bortnik, J., Nishimura, Y., Thorne, R. M., Li, W., Angelopoulos, V., et al. (2014). Chorus wave scattering responsible for the Earth’s dayside diffuse auroral precipitation: a detailed case study. J. Geophys. Res. Space Phys. 119, 897–908. doi:10.1002/2013JA019507

CrossRef Full Text | Google Scholar

Nishimura, Y., Bortnik, J., Li, W., Thorne, R. M., Lyons, L. R., Angelopoulos, V., et al. (2010). Identifying the driver of pulsating aurora. Science 330, 81–84. doi:10.1126/science.1193186

PubMed Abstract | CrossRef Full Text | Google Scholar

Oliven, M. N., and Gurnett, D. A. (1968). Microburst phenomena: 3. An association between microbursts and VLF chorus. J. Geophys. Res. (1896-1977) 73, 2355–2362. doi:10.1029/JA073i007p02355

CrossRef Full Text | Google Scholar

Omura, Y., Nunn, D., and Summers, D. (2012). Generation processes of whistler mode chorus emissions: current status of nonlinear wave growth theory (American Geophysical Union AGU), 243–254. doi:10.1029/2012GM001347

CrossRef Full Text | Google Scholar

Roytershteyn, V., and Delzanno, G. L. (2021). Nonlinear coupling of whistler waves to oblique electrostatic turbulence enabled by cold plasma. Phys. Plasmas 28, 042903. doi:10.1063/5.0041838

CrossRef Full Text | Google Scholar

Russell, C. T., Holzer, R. E., and Smith, E. J. (1969). OGO 3 observations of ELF noise in the magnetosphere: 1. spatial extent and frequency of occurrence. J. Geophys. Res. (1896-1977) 74, 755–777. doi:10.1029/JA074i003p00755

CrossRef Full Text | Google Scholar

Santolík, O., Gurnett, D. A., Pickett, J. S., Chum, J., and Cornilleau-Wehrlin, N. (2009). Oblique propagation of whistler mode waves in the chorus source region. J. Geophys. Res. Space Phys. 114. doi:10.1029/2009JA014586

CrossRef Full Text | Google Scholar

Santolík, O., Parrot, M., and Lefeuvre, F. (2003). Singular value decomposition methods for wave propagation analysis. Radio Sci. 38. doi:10.1029/2000RS002523

CrossRef Full Text | Google Scholar

Stix, T. H. (1992). Waves in plasmas (Springer Science & Business Media).

Google Scholar

Summers, D., Thorne, R. M., and Xiao, F. (1998). Relativistic theory of wave-particle resonant diffusion with application to electron acceleration in the magnetosphere. J. Geophys. Res. Space Phys. 103, 20487–20500. doi:10.1029/98JA01740

CrossRef Full Text | Google Scholar

Swift, D. W. (1981). Mechanisms for auroral precipitation: a review. Rev. Geophys. 19, 185–211. doi:10.1029/RG019i001p00185

CrossRef Full Text | Google Scholar

Teng, S., Tao, X., and Li, W. (2019). Typical characteristics of whistler mode waves categorized by their spectral properties using Van Allen probes observations. Geophys. Res. Lett. 46, 3607–3614. doi:10.1029/2019GL082161

CrossRef Full Text | Google Scholar

Thorne, R. M. (2010). Radiation belt dynamics: the importance of wave-particle interactions. Geophys. Res. Lett. 37, L22107. doi:10.1029/2010GL044990

CrossRef Full Text | Google Scholar

Thorne, R. M., Smith, E. J., Burton, R. K., and Holzer, R. E. (1973). Plasmaspheric hiss. J. Geophys. Res. (1896-1977) 78, 1581–1596. doi:10.1029/JA078i010p01581

CrossRef Full Text | Google Scholar

Tsurutani, B. T., and Smith, E. J. (1974). Postmidnight chorus: a substorm phenomenon. J. Geophys. Res. (1896-1977) 79, 118–127. doi:10.1029/JA079i001p00118

CrossRef Full Text | Google Scholar

Tyler, E., Breneman, A., Cattell, C., Wygant, J., Thaller, S., and Malaspina, D. (2019a). Statistical distribution of whistler mode waves in the radiation belts with large magnetic field amplitudes and comparison to large electric field amplitudes. J. Geophys. Res. Space Phys. 124, 6541–6552. doi:10.1029/2019JA026913

CrossRef Full Text | Google Scholar

Tyler, E., Breneman, A., Cattell, C., Wygant, J., Thaller, S., and Malaspina, D. (2019b). Statistical occurrence and distribution of high-amplitude whistler mode waves in the outer radiation belt. Geophys. Res. Lett. 46, 2328–2336. doi:10.1029/2019GL082292

CrossRef Full Text | Google Scholar

Umeda, T., Saito, S., and Nariyuki, Y. (2017). Rapid decay of nonlinear whistler waves in two dimensions: full particle simulation. Phys. Plasmas 24. doi:10.1063/1.4982609

CrossRef Full Text | Google Scholar

Vasko, I. Y., Agapitov, O. V., Mozer, F. S., Bonnell, J. W., Artemyev, A. V., Krasnoselskikh, V. V., et al. (2018). Electrostatic steepening of whistler waves. Phys. Rev. Lett. 120, 195101. doi:10.1103/PhysRevLett.120.195101

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilson, L. B., Cattell, C. A., Kellogg, P. J., Wygant, J. R., Goetz, K., Breneman, A., et al. (2011). The properties of large amplitude whistler mode waves in the magnetosphere: propagation and relationship with geomagnetic activity. Geophys. Res. Lett. 38. doi:10.1029/2011GL048671

CrossRef Full Text | Google Scholar