The radiative association of PO/PH+ and the photodissociation of PH+

The potential energy curves (PECs) and transition dipole moments (TDMs) of PH⁺ and PO are computed with the multireference configuration interaction method, and the cross-sections for the radiative association (RA) of PH⁺ and PO, which is the most efficient way to form the ground states, are presented via the quantum mechanical (QM) theory and computed using ab initio molecular data. The thermal rate coefficients are also expressed and fitted with the standard formula $k\left(T\right)=A{\left(\frac{T}{300}\right)}^{\alpha }{e}^{-\frac{\beta }{T}}$ in the range of 10 K–15,000 K. Meanwhile, the photodissociation, that is the inverse process of RA for PH⁺, is also studied, including eight photodissociation channels for the computation of state-resolved cross-sections. Careful comparisons with the Leiden Observatory database are made. Considering the cross-sections mentioned above, the local thermodynamic equilibrium cross-sections at the temperatures of 0, 500, 1,000, and 2,000 K are also shown. We expect the results to be helpful for studies of phosphorus chemistry in the interstellar medium and planetary atmospheres.

1 Introduction

Phosphorus (P) is one of the essential elements for the development of life and in forming large biomolecules. So far, astronomical observations have shown that the interstellar medium contains a variety of phosphorus-bearing molecular species such as PN (Turner and Bally, 1987), CP (Guelin et al., 1990), PO (Tenenbaum et al., 2007), PO⁺ (Rivilla et al., 2022), SiP (Koelemay et al., 2022), HCP (Agúndez et al., 2007), CCP (Halfen et al., 2008), and PH₃ (Agúndez et al., 2008). PH⁺ is one of the simplest phosphorus-containing molecules, and this molecule could be important for the formation of larger phosphohydrogens, such as PH₃ (Agúndez et al., 2008). Meanwhile, in our galaxy, the initial element mixture of all stars is oxygen-rich; in other words, the abundance of oxygen is more than that of carbon (Zhukovska et al., 2008). The trace of PO was first detected (Tenenbaum et al., 2007) in the envelope of the oxygen-rich supergiant star VY Canis Majoris (VY CMa) using the Submillimeter Telescope. Therefore, the knowledge of the PH⁺/PO formation rate coefficient which is essential for further modeling of the chemical network involving phosphorus is not well-documented.

Regarding how diatomic molecules are formed in interstellar medium, radiative association (RA) might be a possible molecular formation mechanism that was first floated (Swings, 1942). Due to experimental difficulties, most processes related to the interstellar medium must have their rate coefficients obtained by theoretical methods.

For the PO molecule, Andreazza et al. (2016), by using a semiclassical (SC) approach, have computed the rate coefficients of the P (3s²3s³)+O (2s²2p⁴)→PO(X¹Π) +hν radiative association corresponding to transition B²Σ⁺→X²Π for temperatures from 300 to 14,000 K hitherto. However, as was shown recently (Gustafsson et al., 2012), the conventional SC theory overestimates the high-energy cross-section; consequently, the high-temperature rate coefficient for RA is also overestimated. In our work, the radiative association cross-sections and rate coefficients of PO are calculated again using the fully QM approach. For the PH⁺ molecule, the rate coefficients of the P⁺+H→PH⁺+hν radiative association corresponding to transition 1²Σ⁻→X²Π have only been studied theoretically (Stancil et al., 2000). The radiative association rate coefficients are too small to be measured experimentally. However, its inverse process, known as photodissociation, may be studied in the laboratory. Recently, the experimental data of near-threshold dissociation of PH⁺ have been collected in the Leiden Observatory database (Heays et al., 2017). In this work, we study both the RA and photodissociation of PH⁺.

The two primary types of information in the QM approach are PECs and TDMs for calculating the photodissociation or RA cross-sections. Until now, some experimental and theoretical studies about electronic structures and transition properties needed by photodissociation or RA computations have been published. For PO, the PECs for different electronic states have been investigated using the Rydberg–Klein–Rees method (Rao et al., 1981). Using the internally contracted multireference configuration interaction (icMRCI) method with the augmented correlation-consistent basis set aug-cc-pV5z (aV5Z), the PECs and spectroscopic constants were determined (Izzaouihda et al., 2014).

The spectroscopic constants and first published transition moments as functions of the internuclear distance between the doublet states of PO are given in Andreazza et al. (2016). Liu et al. (2017) calculated the PECs of 27 Λ-S states and 73 Ω states and evaluated the spectroscopic parameters of some of their bound states. For PH⁺, the radiative lifetime and predissociation rates of the A²Δ state of PH⁺ were studied experimentally (Elander et al., 1985). Then, parts of the 0–1 band and the 1–2 band of the A²Δ-X²Π in a laser/ion beam experiment were recorded (Edwards et al., 1986). In theory, a few low-lying potential curves of the PH+ were performed in 1981, which shared spectroscopic constants for this system (Bruna et al., 1981). The first three PECs of the dissociation limits and some TDMs were computed (Li et al., 2015), considering spin–orbit coupling using the multireference configuration interaction plus Davidson correction (MRCI + Q) approach and the basis sets at the 5-ζ level. Tinacci et al. (2021) predicted the equilibrium structures and properties of PH⁺ at the M06-2X/cc-pVTZ level, and electric dipoles and total electronic energies were computed with CCSD(T)/aug-cc-pVTZ/M06-2X/cc-pVTZ single-point energy calculations.

However, the existing PECs and TDMs are still insufficient for us to study photodissociation or RA. As a result, this work computes the PECs for the first five dissociation limits of PH⁺ and the first dissociation limit of PO. In addition, the TDMs from the doublet excited state to the ground state are also calculated. Based on the calculated PECs and TDMs, we present cross-sections with the QM theory as a function of collision energy and provide rate coefficients over a range of temperatures, i.e., from 10 to 10,000 K for PH⁺ and from 150 to 15,000 K for PO. Additionally, for PH⁺, computations on the temperature-dependent photodissociation cross-sections are performed.

2 Methods and computation details

2.1 Molecular data

The ab initio computations related to PECs and TDMs needed in RA or photodissociation are carried out using the MOLPRO 2012 program package (Werner et al., 2012).

Since MOLPRO can use the Abelian point group symmetry only, the symmetry of C_2v is used to calculate the diatomic molecule (PO) and ion (PH⁺). There are four irreducible representations, namely, A₁, B₁, B₂, and A₂ in the C_2v group, the corresponding relations of which are Σ⁺ = A₁, Π = B₁+B₂, Δ = A₁+ A₂, and Σ⁻ = A₂, respectively. The aug-cc-pwCV5Z-DK (Wilson et al., 1999; de Jong et al., 2001; DeYonker et al., 2007) basis set is selected for P⁺/P, and the aug-cc-pV5Z-DK (Dunning, 1989) basis set is selected for H/O. For PH⁺ and PO, the computation of the PECs is carried out within the internuclear distances of 1.0–14.0 a₀ and 1.2–5.75 Å, respectively. For the former, the calculating step length is selected as 0.1 a₀ for R = 1.0–1.8 a₀, 0.05 a₀ for R = 1.8–2.5 a₀, 0.025 a₀ for 2.5–3.5 a₀, 0.1 a₀ for 3.5–5.5 a₀, 0.5 a₀ for 5.5–10.0 a₀, and 1.0 a₀ for 10.0–14.0 a₀. For the latter, the calculating step length is selected as 0.025 Å for R = 1.2–1.8 Å, 0.05 Å for R = 1.8–3.5 Å, 0.1 Å for R = 3.5–4.0 Å, and 0.25 Å for R = 4.0–5.75 Å.

The calculation’s details are as follows: first, a single configuration wave function of the ground state for PH⁺/PO is generated using the Hartree−Fock (HF) calculation. Second, the state-averaged complete active space self-consistent field (CASSCF) approach is used to optimize the wave function (Werner and Meyer, 1980; Werner and Knowles, 1985), and the multiconfiguration wave function was obtained. Finally, the energies of several lowest Λ−S doublet states are computed using the multireference configuration interaction approach (MRCI) (Werner and Knowles, 1988).

In the MRCI calculations, the 12 lowest Λ−S doublet states for PH⁺ and two lowest Λ−S doublet states for PO are determined. For PH⁺, the inner-shell 1s²2s² electrons of the P⁺ ion are added into the closed shell. The active space including seven molecular orbitals (MOs) are 3a₁, 2b₁, and 2b₂ symmetry molecular orbitals (3, 1, 1, and 0) correlating to the 3s3p of P⁺ and 1s of H valence orbitals. In order to balance the efficiency and accuracy of calculation, the 1s orbital of P⁺ is added into the core orbital. The inner-shell 1s²2s²2p⁶ electrons of P and the 1s²2s² electrons of O atom are added into the closed shell, and the valence MOs (3, 2, 2, and 0) are chosen as the active space. Meanwhile, the inner-shell 1s² electrons of P and O are placed in core orbitals. The electrons in the closed MOs are correlated in the MRCI procedure.

In addition, the second-order Douglas–Kroll Hamiltonian (DKH2) approximation is used for PO and PH⁺ to consider the scalar relativistic correction, and Davidson correction (+Q) was introduced to decrease the inaccuracy of size consistency (Langhoff and Davidson, 1974; Knowles and Werner, 1988; Werner and Knowles, 1988)

At the MRCI level, the TDMs have been evaluated. At the same time, based on the computed PECs of Λ−S states, the spectroscopic constants are determined by the LEVEL 8.0 (Le Roy, 2017) program by solving the radial Schrödinger equation.

2.2 Radiative association cross-sections and rate coefficients

The RA is one of several processes that contribute to production of molecules in the interstellar medium. A new molecule is created in this process when two particles collide, and the extra energy is dissipated through spontaneous emission of photons.

In quantum mechanics, the cross-sections for spontaneous radiative association of a heteronuclear diatomic molecule can be expressed as a sum over allowed transitions between a continuum state with a positive energy E and orbital angular momentum J to bound rovibrational states with vibrational quantum number v´ and orbital angular momentum J′. The expression of cross-sections is as follows (Zygelman and Dalgarno, 1990):

$\sigma \left(E\right)=\frac{1}{4\pi {ϵ}_0}\frac{64}{3}\frac{{\pi }^5}{c^3}\frac{p}{k^2}{\displaystyle \sum _{v^{\prime }{J}^{\prime }J}}{\upsilon }_{E,v^{\prime },J^{\prime }}^3{S}_{J{J}^{\prime }}{M}_{EJ,v^{\prime }{J}^{\prime }}^2(1)$

where ${ϵ}_0$ is the vacuum permittivity, c is the speed of light in vacuum, $k^2=2E\mu /{\hslash }^2$, $\mu$ is the reduced mass, ${\upsilon }_{E,v^{\prime },J^{\prime }}$ is the emitted photon frequency, and $p$ is the probability of the approach, namely, statistical weight in the initial electronic state, which can be given by

$p=\frac{\left(2S^{\prime }+1\right)\left(2-{\delta }_{0\mathrm{\Lambda }}\right)}{\left(2L_A+1\right)\left(2S_A+1\right)\left(2L_B+1\right)\left(2S_B+1\right)},(2)$

where L_A, S_A, L_B, and S_B represent the electronic orbital and spin angular momenta of the A and B atoms, respectively. $S^{\prime }$ is the spin quantum number of the electronic state $\mathrm{\Lambda }$. As usual, the Kronecker delta, ${\delta }_{0\mathrm{\Lambda }}$, equals 1 if $\mathrm{\Lambda }$ = 0 and equals 0 otherwise. Therefore, the value of $p$ for Σ of PH⁺ and PO is $\frac{1}{9}$ and $\frac{1}{18}$, respectively. Dipole moment transitions for Σ→Π, the Hönl–London factors (Huber and Herzberg, 1979a; Gianturco and Gori Giorgi, 1996), are $S_{J,J+1}=\frac{J+2}{4}$, $S_{J,J}=\frac{2J+1}{4}$, and $S_{J,J+1}=\frac{J-1}{4}$, respectively.

$M_{EJ,v^{\prime }{J}^{\prime }}={\int }_0^{\infty }{\varphi }_J\left(E,R\right)D\left(R\right){\psi }_{v^{\prime }{J}^{\prime }}\left(R\right)dR(3)$

is the matrix element of the transition dipole moment function $D\left(R\right)$ between the initial continuum radial wave function ${\varphi }_J\left(E,R\right)$ for the partial wave J and the final bound-state radial wave function ${\psi }_{v^{\prime }{J}^{\prime }}\left(R\right)$. The renormalized Numerov approach is used to derive both the continuum and bound wave functions (Johnson, 1977).

When the RA cross-sections are determined, the rate coefficient $K\left(T\right)$ (in units of cm³s^-1) with a Maxwellian velocity distribution for the formation of a molecule at temperature T is defined by

$K\left(T\right)={\left(\frac{8}{\mu \pi }\right)}^{\frac{1}{2}}{\left(\frac{1}{k_{B}T}\right)}^{\frac{3}{2}}{\int }_0^{\infty }E\sigma \left(E\right)e^{-\frac{E}{k_{B}T}}dE,(4)$

where $k_B$ = 1.381 $\times$ 10^–23 J.K⁻¹, that is the Boltzmann constant; $\mu$ is the reduced mass; and E is the relative motion of two atomic species.

2.3 Photodissociation cross-sections

The photodissociation cross-sections are computed with the aid of BCONT 2.2 (Roy and Kraemer, 2004). For a bound-free transition from an initial state to a final state, taking into account the degeneracies of the rotational states can give the following relationship (Le Roy et al., 1976; Lefebvre-Brion and Field, 1986; Van Dishoeck, 1988), in units [10⁻¹⁶cm²/molecule]:

$\begin{array}{ll}\hfill {\sigma }_s\left(v,J;\nu \right)& =\frac{8{\pi }^3\nu }{3hc}{\displaystyle \sum _{J^{\prime }}}\frac{S_J^{J^{\prime }}}{2J+1}{\left|<{\psi }_{E,J^{\prime }}\left(r\right)\left|M_s\left(r\right)\right|{\psi }_{v,J}\left(r\right)\right|}^2.\hfill \\ \hfill & =3.22696\times {10}^{-4}\overline{v}\sqrt{\frac{\mu }{K_S\left(E\right)}}{\displaystyle \sum _{J^{\prime }}}\frac{S_J^{J^{\prime }}}{2J+1}\hfill \\ \hfill & \times {\left({\int }_0^{\infty }{\psi }_{E,J^{\prime }}^{*}\left(r\right)M_s\left(r\right){\psi }_{v,J}\left(r\right)dr\right)}^2.\hfill \end{array}$

Here, $\overline{\mathrm{v}}=\frac{\mathrm{\nu }}{\mathrm{c}}$ is the transition energy, in cm⁻¹; $K_S\left(E\right)=\left[E-V_s\left(r=\infty \right)\right]$ is the asymptotic relative kinetic energy of the molecular fragments dissociating along the potential energy curve $V_s\left(r\right)$ of electronic states, in cm⁻¹; $S_{J{J}^{\prime }}$ is the usual Hönl–London rotational intensity factor³⁰, the unit of the reduced mass µ is u(atomic mass unit) and the transition moment function $M_s\left(r\right)$ is expressed in debye and incorporates the appropriate ratio of initial-to-final state electronic degeneracy factors.

The total thermal photodissociation cross-section may be written as

${\sigma }_{tot}\left(T;\nu \right)={\displaystyle \sum _s}{\sigma }_s\left(T;\nu \right)={\displaystyle \sum _v}{\displaystyle \sum _J}{F}_{v,J}\left(T\right){\sigma }_s\left(v,j,\nu \right).$

Here, $F_{v,J}\left(T\right)=\frac{\left(2J+1\right)}{Q\left(T\right)}{e}^{-\frac{E_{v,J}}{k_{B}T}}$ represents the fraction of the initial state population at the vibration rotation level $\left(v,J\right)$, and $Q\left(T\right)={\sum }_v{\sum }_J\left(2J+1\right)e^{-\frac{E_{v,J}}{k_{B}T}}$ is the molecular partition function for levels of the initial electronic state.

For designated vibrational and rotational quantum numbers, the total state-resolved cross-section is defined by

${\sigma }_{tot}\left(v,J;\nu \right)={\displaystyle \sum _s}{\sigma }_s\left(v,J,\nu \right).$

3 Results and discussion

3.1 The PECs and TDMs of the Λ–S electronic states

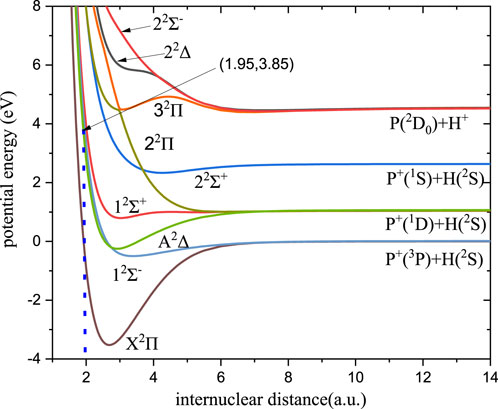
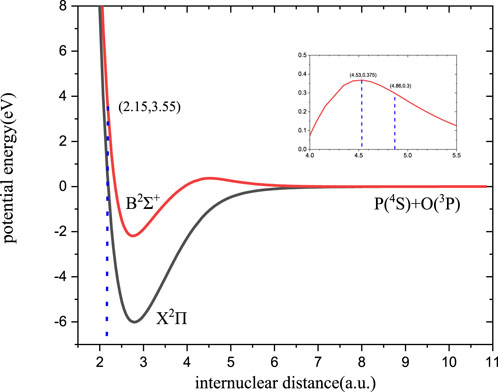
Based on the theoretical approaches described in Section 2.1, calculations are made for the lowest 12 Λ-S electronic states of PH⁺, which are correlated with the first 5 dissociation limits, and for the lowest six Λ-S electronic states of PO, which involve the first 1 atomic limit. However, only the doublet states are needed in this work. The potential curves of relevant states of the two molecules are shown in Figures 1, 2, respectively.

FIGURE 1

FIGURE 1. Potential energy curve of PH⁺.

FIGURE 2

FIGURE 2. Potential energy curve of PO.

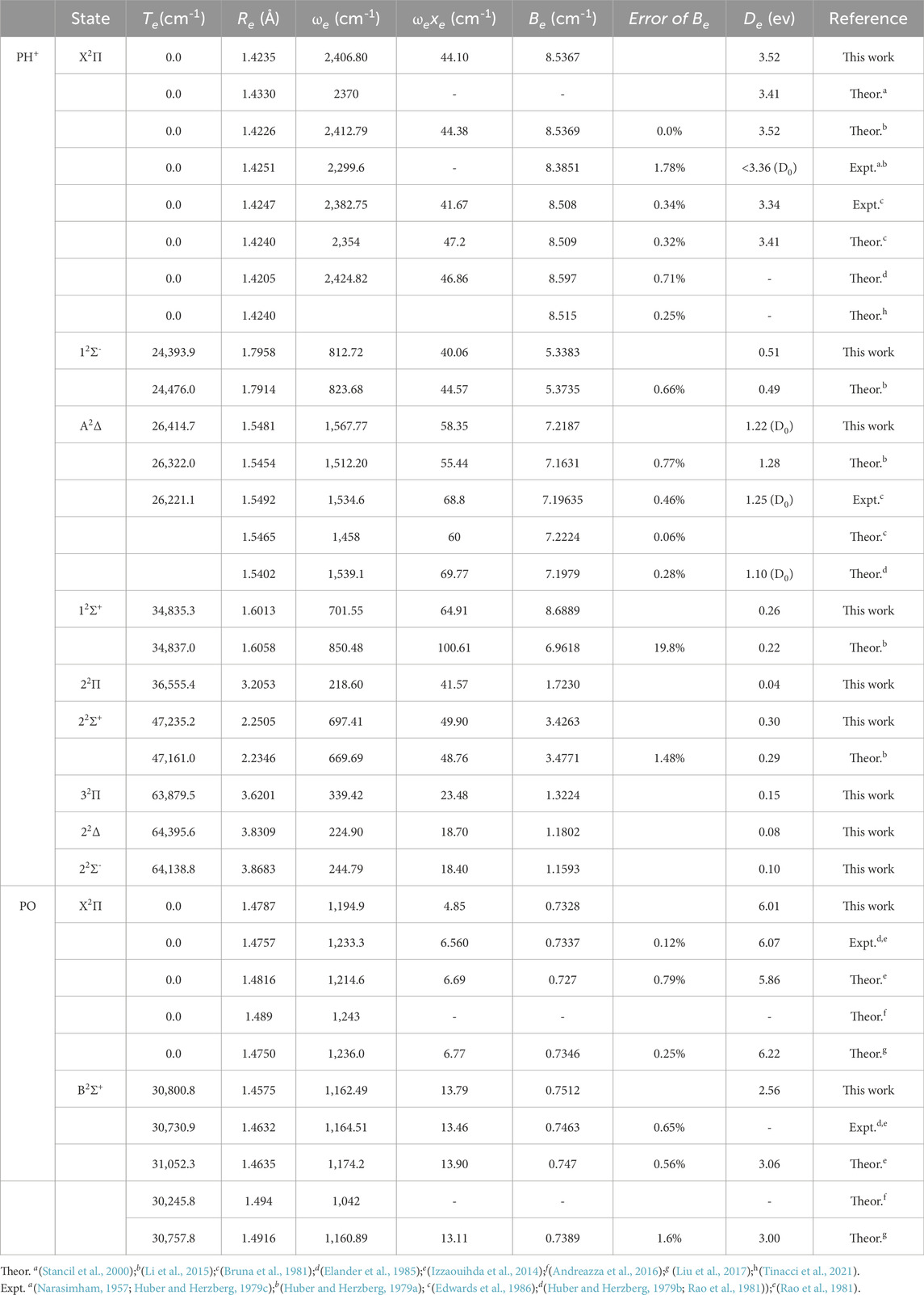
Table 1 lists the spectroscopic constants, T_e (equilibrium transition energy), R_e (equilibrium internuclear distance), B_e (equilibrium rotational constant), ω_e (harmonic frequency), ω_eχ_e (first-order anharmonic constant), and D_e (dissociation energies) of the computed low-lying bound double states for the two molecules along with the previous experimental and theoretical results.

TABLE 1

TABLE 1. Spectroscopic constants of the bound Λ–S states of PH⁺ and PO.

The value of B_e needs to be noticed, which guarantees the accuracy of quantum chemical approaches in structure determination (Puzzarini and Stanton, 2023). To have a better idea of the actual accuracy for B_e, the percentage error values of the literature theoretical data with respect to the calculated ones in the present paper are also listed in Table 1. From Table 1, it is found that the percentage error values of most B_e are within 1%.

For PH⁺, the value of B_e of X²Π is 8.5367 cm^-1, having a difference of approximately 0.0217 cm^-1 (0.25%) and 0.0287 (0.34%) with the latest theoretical data (Tinacci et al., 2021) and experimental value (Bruna et al., 1981), respectively. For PO, the value of B_e of X²Π is 0.7328 cm^-1, which is a difference of 0.0009 cm^-1 from the experimental value (Izzaouihda et al., 2014). In addition, the other fitted spectroscopic parameters of PH⁺ and PO are also in good agreement with the available theoretical data and experimental value, which ensures the accuracy of our computed PECs.

The estimated spectroscopic constants of X²Π and A²Δ of PH⁺ are also in consistence with those determined by experimentation (Edwards et al., 1986). In terms of PO, the spectroscopic constants of X²Π and B²Σ⁺ in this work are in better agreement with the experimental values (Huber and Herzberg, 1979b; Rao et al., 1981) than the previous report (Andreazza et al., 2016). Theoretically, the spectroscopic values also match with the existing theoretical data for other excited states for these two molecules.

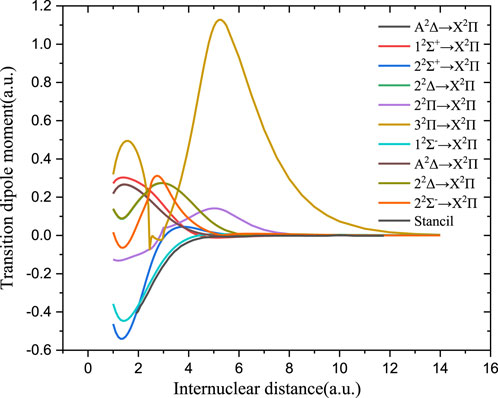
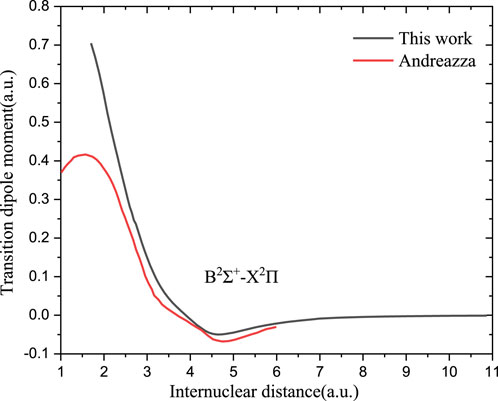
The TDMs using the ab initio method from the excited state to the ground state of PH⁺ and PO are shown in Figures 3, 4, respectively. The previously reported dipole moments of PO between 2.2 and 6.0 a₀ from ab initio calculations (Andreazza et al., 2016) and achieved by extrapolation in the short R region (R < 2.0 a₀) are also shown in Figure 4 for comparison.

FIGURE 3

FIGURE 3. Transition dipole moments of PH⁺.

FIGURE 4

FIGURE 4. Transition dipole moments of PO.

Figure 3 shows that the TDMs for the 1²Σ⁻→X²Π transition of PH⁺ agree well with the theoretical value (Stancil et al., 2000). The TDMs for other transitions that might contribute to the photodissociation are also given. As shown in Figure 4, the TDM value of B²Σ⁺→X²Π of PO is a bit larger than the previous computed value (Andreazza et al., 2016) in the Franck–Condon region. In the short internuclear region ($r<2.2a_0$), Andreazza et al. fit the TDMs using a cubic spline and joined smoothly with the forms $R_e\left(r\right)=a{r}^2+br$, and comparing with our computed values by the ab initio method, differences could be observed in this range.

In this work, for RA, when R is less than 1.0 a₀ for PH⁺ and 1.70 a₀ for PO, the potential curves are extrapolated by V (R) = A exp (−BR) + C, where A, B, and C are fitting parameters. When R is in the range of 14.0–400.0 a₀ for PH⁺ and 10.86–400.0 a₀ for PO, the following function (Watanabe et al., 2002) is used to fit the PECs:

$V\left(R\right)=-\frac{1}{2}\left(\frac{C_4}{R^4}+\frac{C_6}{R^6}+\frac{C_8}{R^8}\right),$

where $C_4$, $C_6$, and $C_8$ are related to the static dipole, quadrupole, and octupole polarizability, ${\alpha }_A$, ${\beta }_A$, and ${\gamma }_A$, of the atomic system, respectively (Marinescu et al., 1994; Côté and Dalgarno, 2000) by $C_4={\alpha }_A{Q_B}^2$, $C_6={\beta }_A{Q_B}^2$, and $C_8={\gamma }_A{Q_B}^2$,where $Q_B$ is the excess charges on the atomic systems (Dalgarno and Kingston, 1959). For the ion PH⁺ (P⁺+H), $Q_{{\mathrm{P}}^{+}}$ equals to 1, ${\alpha }_H$ equals to 4.5 (Shevelko and Vinogradov, 1979), and the $V_{{\text{PH}}^{+}}\left(R\right)=-\frac{1}{2}\frac{4.5}{R^4}$. When we take the value of $C_4$ into account, the calculated potential V_A(R) is smoothly connected to the dispersion potential V (R) at the value of R = 13 $a_0$, which means the values of $\beta$ and $\gamma$ have little effect on the long-range potentials. Therefore, the values of $\beta$ and $\gamma$ are both set to 0. Research reveals that the interaction potential of ions is much larger than that of molecules (Marinescu et al., 1994). In this work, we do not take the multipolar interaction potential in the range of larger than 10.86 a₀ for the PO molecule. For the photodissociation of PH⁺, similar extrapolation is used in the short-range and long-range potentials or TDMs.

3.2 The radiative association and photodissociation of PH⁺

3.2.1 The radiative association of PH ⁺

The large cross-sections of RA are produced when two species are close to each other along the PEC of an excited state and radiate via a strong dipole transition to the lower state (Thomas and David, 1999). In the region of the interstellar space with little dust, the number of excited states of atoms is negligible. Therefore, only molecular states that correspond to the ground-state asymptote need to be taken into account.

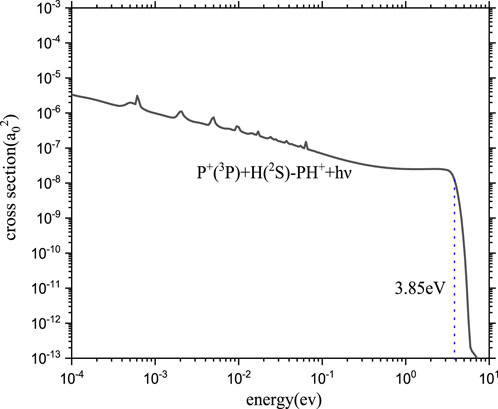
The RA of the P⁺ and H atoms can occur following an approach along the first dissociation asymptote P⁺ (³P) + H (²S) correlated with the electronic states 1²Σ⁻, X²Π, 1⁴Σ⁻, and 1⁴Π. Among these states, the PH⁺ molecule can be formed by the transition from 1²Σ⁻ to X²Π and from 1⁴Σ⁻ to 1⁴Π. However, there is little overlap between the bound vibrational wave functions in the 1⁴Σ⁻ state and continuum wave functions of repulsive states 1⁴Π, which is expected to contribute little to the RA in the collision of the first dissociation asymptotes. Therefore, radiative association through these states with high multiplicity will be negligible in our computations. The cross-sections and rate coefficients of RA for PH⁺ via 1²Σ⁻ - X²Π transition are computed and shown in Figures 5, 6, respectively.

FIGURE 5

FIGURE 5. Radiative association cross-section of PH⁺.

FIGURE 6

FIGURE 6. Radiative association rate coefficient of PH⁺.

There is the resonance structure with some complex resonances in Figure 5, which is a typical feature of the RA cross-section in quantum mechanics. There are two aspects for this. On the one hand, in the low-energy collision region (less than 10⁻²eV), the resonance phenomenon is caused by the long-range potential. On the other hand, in the relative high-energy collision region (more than 10⁻²eV), resonances arise from quasi-bound states supported by the effective potential $V_{eff}^A\left(R\right)=V_A\left(R\right)+\frac{J\left(J+1\right)}{2\mu R^2}$ of the initial electronic state. Because the value of our PEC ($V_A\left(R\right)$) is negative, the value of its effective potential ($V_{eff}^A\left(R\right)$) is also negative. With the increase of rotational quantum number J, the effective potential decreases gradually. When J reaches a certain value, the resonance structure disappears. Of course, the shallow well of 1²Σ⁻ with 10 vibrational levels and 212 rovibrational levels can lead to fewer resonances on the entire curve.

The overall tendency of the cross-section is also worthy of attention. In general, baselines display a monotonic decline. Especially, the cross-section decreases sharply when the energy is greater than 3.85 eV owing to non-Franck–Condon transitions.

Shortly after the first detection of polyatomic molecules in interstellar cold (10–20 K) molecular clouds in the late 1960s, the dominant role of positive ions in interstellar cold environments was recognized. Meanwhile, PH⁺ compounds (PH₃) have been found in the asymptotic giant branch star IRC+10216, in which the effective temperature is near 2,000–3,500 K (Groenewegen et al., 1998). Although PH⁺ is still being sought, based on the temperatures of the astrophysical counterparts mentioned above, the computed range of temperature for PH⁺ is from 10 K to 10,000 K.

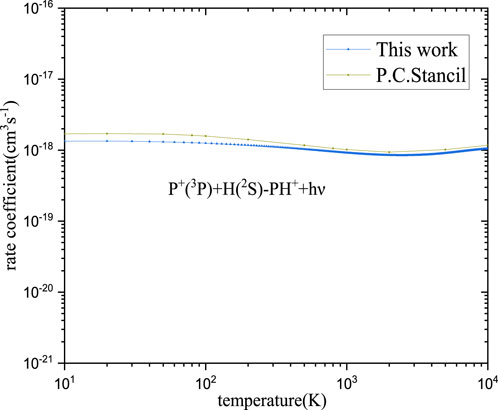
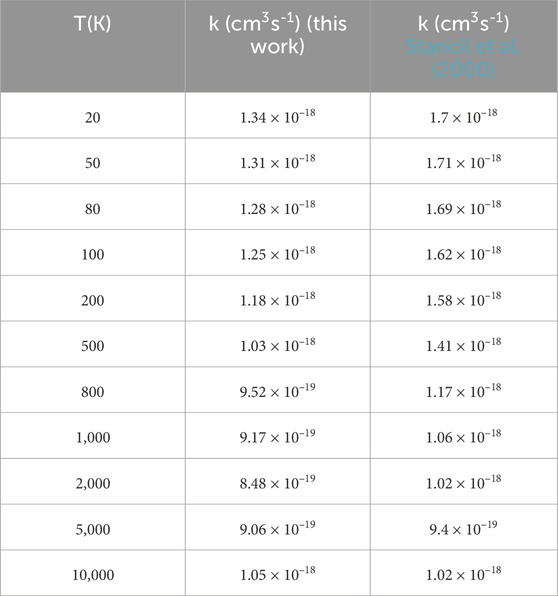
As seen in Figure 6, in general, the rate coefficients are in good agreement with the previous computed values (Stancil et al., 2000). The agreement at high temperatures is better than that at low temperatures. The specific rate coefficients of PH⁺ are shown in Table 2. As seen in Table 2, our calculated value is 1.34 $\times$ 10^–18 cm³s^-1 at the temperature of 20 K. The difference from the theoretical value (1.7 $\times$ 10^–18) (Stancil et al., 2000) is ∼20%, and when the temperature is 10,000 K, the value is 1.05 $\times$ 10^–18 cm³s^-1 and the error is ∼10%. The errors are within 20% over the temperature range of 10–10,000 K. The errors possibly come from different PECs and TDMs calculated by the ab initio method.

TABLE 2

TABLE 2. Radiative association rate coefficients of PH⁺.

The obtained rate coefficient for the formation of PH⁺ by RA is used to fit the three-parameter Arrhenius–Kooij function (Laidler, 1996) form:

$k\left(T\right)=A{\left(\frac{T}{300}\right)}^{\alpha }{e}^{-\frac{\beta }{T}},(5)$

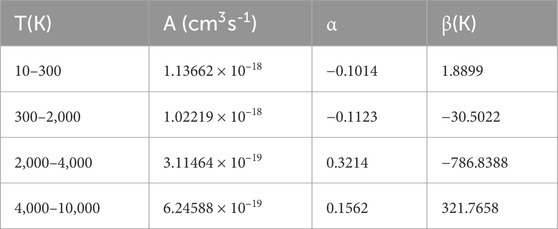
where A, α, and β are fitting parameters. The fitting parameters are listed in Table 3.

TABLE 3

TABLE 3. Fitting parameters of PH⁺.

3.2.2 The photodissociation of PH ⁺

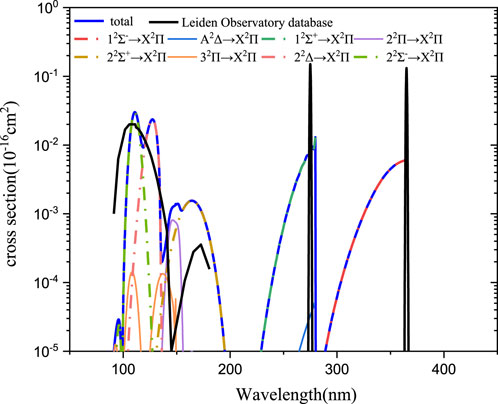
Based on the aforementioned theory, the state-resolved photodissociation cross-sections of PH⁺ have been calculated for eight transitions from X²Π to other excited states (1²Σ⁻, A²Δ, 1²Σ⁺, 2²Π, 2²Σ⁺, 3²Π, 2²Δ, and 2²Σ⁻). Cross-sections are computed as a function of wavelength that ranges from ∼50 to ∼400 nm. The state-resolved cross-section (here, the ground rovibrational level $\left(v,J\right)=\left(0,0\right)$) is exhibited in Figure 7 and compared with the Leiden Observatory database (Heays et al., 2017), which use a Gaussian profile with an assumed width of 1.0 nm FWHM.

FIGURE 7

FIGURE 7. Photodissociation cross-section at v = 0 and j = 0.

As shown in Figure 7, in the 90–200 nm range, two peaks in the curve of the photodissociation cross-section could be observed in the Leiden Observatory database (Heays et al., 2017). One is in the range of 90–150, and the other is in the range of 150–200 nm. Our computations indicate that the photodissociation cross-sections are mainly arising from the 2²Σ⁻←X²Π and 2²Δ←X²Π transitions in the range of 90–150 nm and from the 2²Σ⁺←X²Π transition in the range of 150–200 nm. The contributions of other transitions to these peaks are relatively small. For the former peak, the maximum cross-section is located at λ ≈ 110 nm. Our computed maximum value is in the same order of magnitude with the database (Heays et al., 2017) ( 0.02 $\times$ 10^–16 vs. 0.029 $\times$ 10^–16) and with a relative error of 45%. For the latter, the corresponding λ for the maximum cross-section is approximately equal to 170 nm. The difference between this work (0.00131 $\times$ 10^–16 cm²) and that in the database (0.000357 $\times$ 10^–16 cm²) is within one order of magnitude and approximately three times. Meanwhile, there are still two sharp peaks in the range of 230–285 nm and 285–380 nm, respectively, which are observed for the photodissociation cross-section in the database (Heays et al., 2017); these two peaks are attributed to the 1²Σ⁺←X²Π and 1²Σ⁻←X²Π transitions according to our work. The maximum cross-sections are located at the wavelengths of approximately 275 and 365 nm with 0.013 $\times$ 10⁻¹⁶ cm² and 0.006 $\times$ 10⁻¹⁶ cm², respectively; while our computed values are one order of magnitude smaller than 0.15 $\times$ 10^–16 cm² and 0.128 $\times$ 10^–16 cm² as in the Leiden Observatory database (Heays et al., 2017), respectively. The possible reason for such a large difference may be the influence of transitions involved in higher excited states, which are not included in this work. However, it is noted that the results of our computed cross sections are within the range allowed by the database—within a factor of 10 (Heays et al., 2017).

Based on state-resolved cross-sections, the total local thermodynamic equilibrium (LTE) cross-sections of eight transitions for PH⁺ at 0, 500, 1,000, and 2,000 K are presented in Figure 8. From the figure, two important features can be found. As the temperature increases, (i) the LTE cross-section values increase at longer wavelengths and (ii) the peak values of cross-sections decrease. The same behaviors are also found in the case of the SH⁺ system (McMillan et al., 2016).

FIGURE 8

FIGURE 8. Photodissociation cross-section at different temperatures.

3.3 The radiative association of PO

For the calculations on the radiative association cross-sections of PO, as the argument in Section 3.1.1, the B²Σ⁺→X²Π transition should be the dominant formation channel. The cross-sections and rate coefficient for the formation of PO have been calculated, and the results are shown in Figures 9, 10, respectively.

FIGURE 9

FIGURE 9. Radiative association cross-section of PO.

FIGURE 10

FIGURE 10. Radiative association rate coefficient of PO.

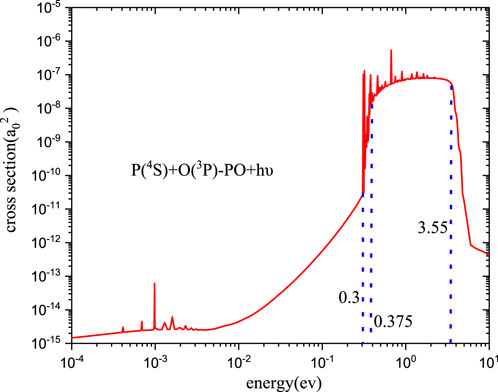
The discussions on cross-sections of PO given in Figure 9 are divided into two parts. First, the trend of the cross-sections is very important. At low energy levels (less than 10⁻²eV), the cross-sections are approximately equal to 10^–15 a₀² with little change. However, when the collision energy is between 10⁻²eV and 0.375 eV, the cross-section begins to exhibit sharp increases from 4.43 $\times$ 10^–15 to 5.18 $\times$ 10^–8 a₀². The reason is that the B²Σ⁺ state exhibits a 0.375 eV barrier located roughly R = 4.53 a₀, as shown in Figure 2. Because of the existence of the barrier, the PEC of B²Σ⁺ can be divided into two parts. If the value of R is larger than 4.53 a₀, the PEC of B²Σ⁺ is repulsive. In addition, if the value of R is less than 4.53 a₀, the PEC of B²Σ⁺ processes a deep well. For the repulsive part, there is little overlap between the continuum wave functions of the B²Σ⁺ state and the bound vibrational wave functions of the ground state (X²Π), which causes the cross-sections to decrease rapidly with decreasing collision energy. For the bound part, the cross-sections are larger than those in the repulsive part, as mentioned, due to more overlapped areas. When the collision energy is larger than 3.55 eV, the cross-sections monotonically decrease owing to the Franck–Condon principle.

Second, the peaks that come from the resonances are also fascinating. The trend of resonances for PO, which is analogous to PH⁺, will not be repeated here. Remarkably, no resonances are observed in the kinetic energy range of approximately 10⁻²-0.3 eV, and this is also correlated with the barrier of B²Σ⁺. When the energy is below 0.3 eV, the tunneling is too sluggish to produce any resonance. If the energy is between 0.3 and 0.375 eV, the resonance tunneling features emerge. At the same time, the number of resonances of PO is significantly more redundant than that of PH⁺ due to a relatively deep well of B²Σ⁺.

The observations indicate that the PO molecule exists in the circumstellar envelope of the star VY CMa (∼17 M_⊙) and AGB oxygen star IK Tau (1.0–8.0 M_⊙), and their effective temperature is near 3,450–3,700 K (Massey et al., 2006) and 2,000–3,500 K (Iben and Renzini, 1983; Herwig, 2005). Since VY CMa is thought to have evolved from a massive star of ∼ 25 M_⊙ (Wittkowski et al., 2012), the effective temperature may be more than 3,700 K. Meanwhile, based on the calculated temperature range by Andreazza et al., we focus on the temperature range of 150–15,000 K for PO.

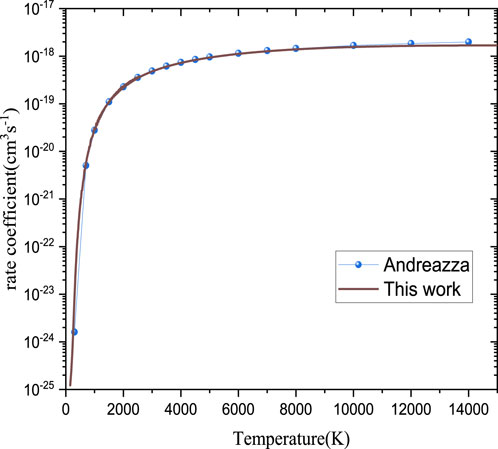
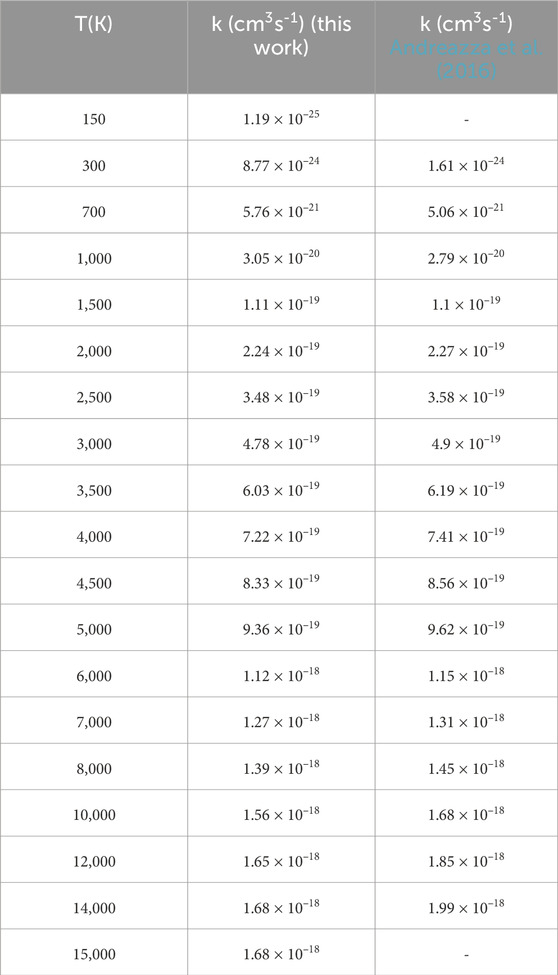
The RA rate coefficients for the formation of PO computed by the SC approach (Andreazza et al., 2016) and QM method (this work) are shown in Table 4 and Figure 10. On the whole, our results are in good agreement with the theoretical value (Andreazza et al., 2016). At 300 K, the rate coefficient estimated is 8.77 $\times$ 10^–24 cm³s^-1 and that mentioned in Andreazza et al. (2016) is 1.61 $\times$ 10^–24 cm³s^-1. The error between them is approximately 82% while within an order of magnitude. The reason for such a big difference is that the height of our B²Σ⁺ barrier is approximately 0.375 eV at R = 4.53 a₀, which is larger than the value of 0.300 eV at 4.8 a₀ reported (Andreazza et al., 2016). At low temperatures, the uncertainty in the rate coefficient is determined partly by the height of the potential barrier and partly due to tunneling resonance or shape resonances. When the temperature is in the range of 1,000 K–10,000 k, the rate coefficients are in good agreement between the SC approach and QM theory, and the errors are within 10%. This phenomenon can be found in other similar systems such as CN (Singh and Andreazza, 2000; Antipov et al., 2009). The maximum error is approximately 9.3% at the temperature of 1,000 K. The corresponding rate coefficient by the QM method is 3.05 $\times$ 10^–20 cm³s^-1, which is just a bit higher than the value of 2.79 $\times$ 10^–20 cm³s^-1 given by the SC method. When the temperature is larger than 10,000 K, the error increases over 7%. According to the available data, the maximum difference is approximately 15.6% at 14,000 K. The value of the corresponding rate coefficient is 1.68 $\times$ 10^–18 cm³s^-1, which is a bit lower than 1.99 $\times$ 10^–18 cm³s^-1 in reference Andreazza et al. (2016).

TABLE 4

TABLE 4. Radiative association rate coefficients of PO.

According to Eqs 1, 4, the rate coefficient depends on the square of the dipole moments. As shown in Figure 4, the dipole moment we calculated is overall higher than that in Andreazza et al. (2016). However, our computed rate coefficients are smaller than theoretical values at high temperatures (>2,000 K), which is reasonable as it is stated in the previous work that the conventional SC theory could overestimate the high-energy cross-section based on unrestricted transition probability (Gustafsson et al., 2012).

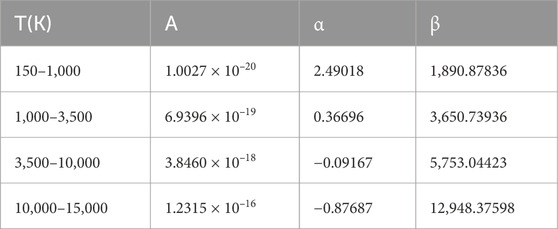
Over the temperature range of 150–15,000 K, we fit the rate coefficients with Eq. 5, and the fitting parameters are listed in Table 5 for further application.

TABLE 5

TABLE 5. Fitting parameters of PO.

4 Summary

In this study, we have computed the PECs and TDMs for PH⁺ and PO at the MRCI + Q/aug-cc-pwCV5Z-DK level of theory. Then, based on our computed molecular data, the RA cross-sections have been computed by the QM method. For PH⁺ and PO, the RA process is dominant through the 1²Σ⁻ and B²Σ⁺ excited states, respectively. The rate coefficients are obtained from their cross-sections with a Maxwellian velocity distribution; for PH⁺, the value of which varies from 1.34 $\times$ 10^–18 to 1.05 $\times$ 10⁻¹⁸ cm³s^-1 for temperatures ranging from 10 to 10,000 K, and the rate coefficients of PO range from 8.77 $\times$ 10^–24 to 1.68 $\times$ 10^–18 cm³s^-1 at temperatures between 150 and 15,000 K. Taking PH⁺ as an example, this work gives state-resolved photodissociation cross-sections at v = 0 and j = 0, and a comparison with the Leiden Observatory database is made. It is found that over the range of 100–150 nm, cross-sections are mainly generated from transitions 2²Σ⁻←X²Π and 2²Δ←X²Π, and in the range of 150–200, 200–300, and 300–400 nm, the maximum cross-section is contributed to the transitions of 2²Σ⁺←X²Π, 1²Σ⁺←X²Π, and 1²Σ⁻←X²Π, respectively. Based on state-resolved cross-sections, the total of LTE cross-sections for PH⁺ at 0, 500, 1,000, and 2,000 K are predicted. The presently computed results are expected to be helpful in studying the PH⁺ and PO chemical evolution in the interstellar medium and planetary atmospheres.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

YC: conceptualization, data curation, writing–original draft, and writing–review and editing. XL: methodology, software, and writing–review and editing. LX: investigation, visualization, and writing–review and editing. ZL: formal analysis, investigation, visualization, and writing–review and editing. SZ: supervision and writing–review and editing. YC: validation and writing–review and editing. YW: supervision, validation, and writing–review and editing. BY: supervision, validation, and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foundation of China (Grant Nos 12274178, 12203106, and 11874177), the High-Performance Computing Center (HPCC) of Jilin University, and the high-performance computing cluster tiger@ iamp.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Agúndez, M., Cernicharo, J., and Guélin, M. (2007). Discovery of phosphaethyne (HCP) in space: phosphorus chemistry in circumstellar envelopes. Astrophysical J. 662, L91–L94. doi:10.1086/519561

CrossRef Full Text | Google Scholar

Agúndez, M., Cernicharo, J., Pardo, J. R., Guélin, M., and Phillips, T. G. (2008). Tentative detection of phosphine in IRC +10216. Astronomy Astrophysics 485, L33–L36. doi:10.1051/0004-6361:200810193

CrossRef Full Text | Google Scholar

Andreazza, C. M., de Almeida, A. A., and Borin, A. C. (2016). The radiative association of P and O atoms. Mon. Not. R. Astron. Soc. 457, 3096–3100. doi:10.1093/mnras/stw116

CrossRef Full Text | Google Scholar

Antipov, S. V., Sjölander, T., Nyman, G., and Gustafsson, M. (2009). Rate coefficient of CN formation through radiative association: a theoretical study of quantum effects. J. Chem. Phys. 131, 074302. doi:10.1063/1.3196179

PubMed Abstract | CrossRef Full Text | Google Scholar

Bruna, P. J., Hirsch, G., Peyerimhoff, S. D., and Buenker, R. J. (1981). Non-empirical CI potential curves for the ground and excited states of PH and its positive ion. Mol. Phys. 42, 875–898. doi:10.1080/00268978100100681

CrossRef Full Text | Google Scholar

Côté, R., and Dalgarno, A. (2000). Ultracold atom-ion collisions. Phys. Rev. A 62, 012709. doi:10.1103/PhysRevA.62.012709

CrossRef Full Text | Google Scholar

Dalgarno, A., and Kingston, A. E. (1959). Van der Waals forces. Proc. Phys. Soc. 73, 455–464. doi:10.1088/0370-1328/73/3/312

CrossRef Full Text | Google Scholar

de Jong, W. A., Harrison, R. J., and Dixon, D. A. (2001). Parallel Douglas–Kroll energy and gradients in NWChem: estimating scalar relativistic effects using Douglas–Kroll contracted basis sets. J. Chem. Phys. 114, 48–53. doi:10.1063/1.1329891

CrossRef Full Text | Google Scholar

DeYonker, N. J., Peterson, K. A., and Wilson, A. K. (2007). Systematically convergent correlation consistent basis sets for molecular Core−Valence correlation effects: the third-row atoms gallium through krypton. J. Phys. Chem. A 111, 11383–11393. doi:10.1021/jp0747757

PubMed Abstract | CrossRef Full Text | Google Scholar

Dunning, T. H. (1989). Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 90, 1007–1023. doi:10.1063/1.456153

CrossRef Full Text | Google Scholar

Edwards, C. P., Jackson, P. A., Sarre, P. J., and Milton, D. J. (1986). Laser photofragment and emission spectroscopy of the A² Δ- X² Π system of PH ⁺. Mol. Phys. 57, 595–604. doi:10.1080/00268978600100431

CrossRef Full Text | Google Scholar

Elander, N., Erman, P., Gustafsson, O., Larsson, M., Rittby, M., and Rurarz, E. (1985). Experimental and theoretical studies of the radiative lifetime and predissociation rates of the A² Δ state of PH ⁺. Phys. Scr. 31, 37–44. doi:10.1088/0031-8949/31/1/007

CrossRef Full Text | Google Scholar

Gianturco, F. A., and Gori Giorgi, P. (1996). Radiative association of LiH(X 1 Σ +) from electronically excited lithium atoms. Phys. Rev. A 54, 4073–4077. doi:10.1103/PhysRevA.54.4073

PubMed Abstract | CrossRef Full Text | Google Scholar

Groenewegen, M. A. T., van der Veen, W. E. C. J., and Matthews, H. E. (1998). IRC +10 216 revisited II: the circumstellar CO shell.

Google Scholar

Guelin, M., Cernicharo, J., Paubert, G., and Turner, B. E. (1990). Free CP in IRC +10216. Astronomy Astrophysics 230, L9–L11. doi:10.1086/115421

CrossRef Full Text | Google Scholar

Gustafsson, M., Antipov, S. V., Franz, J., and Nyman, G. (2012). Refined theoretical study of radiative association: cross sections and rate constants for the formation of SiN. J. Chem. Phys. 137, 104301. doi:10.1063/1.4750029

PubMed Abstract | CrossRef Full Text | Google Scholar

Halfen, D. T., Clouthier, D. J., and Ziurys, L. M. (2008). Detection of the CCP radical (X² Π _<i>r</i>) in IRC +10216: a new interstellar phosphorus-containing species. Astrophysical J. 677, L101–L104. doi:10.1086/588024

CrossRef Full Text | Google Scholar

Heays, A. N., Bosman, A. D., and Van Dishoeck, E. F. (2017). Photodissociation and photoionisation of atoms and molecules of astrophysical interest. A&A 602, A105. doi:10.1051/0004-6361/201628742

CrossRef Full Text | Google Scholar

Herwig, F. (2005). Evolution of asymptotic giant branch stars. Annu. Rev. Astron. Astrophys. 43, 435–479. doi:10.1146/annurev.astro.43.072103.150600

CrossRef Full Text | Google Scholar

K.-P. Huber, and G. Herzberg (1979b). Molecular spectra and molecular structure. 4: constants of diatomic molecules (New York: van Nostrand Reinhold Comp).

Google Scholar

K.-P. Huber, and G. Herzberg (1979c). Molecular spectra and molecular structure. 4: constants of diatomic molecules (New York: van Nostrand Reinhold Comp).

Google Scholar

Huber, K. P., and Herzberg, G. (1979a). Molecular spectra and molecular structure. Boston, MA: Springer US. doi:10.1007/978-1-4757-0961-2

CrossRef Full Text | Google Scholar

Iben, I., and Renzini, A. (1983). Asymptotic giant branch evolution and beyond. Annu. Rev. Astron. Astrophys. 21, 271–342. doi:10.1146/annurev.aa.21.090183.001415

CrossRef Full Text | Google Scholar

Izzaouihda, S., Abou El Makarim, H., Komiha, N., Lahmar, S., and Ghalila, H. (2014). Ab-initio potential energy curves of valence and Rydberg electronic states of the PO radical. Comput. Theor. Chem. 1049, 102–108. doi:10.1016/j.comptc.2014.10.001

CrossRef Full Text | Google Scholar

Johnson, B. R. (1977). New numerical methods applied to solving the one-dimensional eigenvalue problem. J. Chem. Phys. 67, 4086–4093. doi:10.1063/1.435384

CrossRef Full Text | Google Scholar

Knowles, P. J., and Werner, H.-J. (1988). An efficient method for the evaluation of coupling coefficients in configuration interaction calculations. Chem. Phys. Lett. 145, 514–522. doi:10.1016/0009-2614(88)87412-8

CrossRef Full Text | Google Scholar

Koelemay, L. A., Burton, M. A., Singh, A. P., Sheridan, P. M., Bernal, J. J., and Ziurys, L. M. (2022). Laboratory and astronomical detection of the SiP radical (X2Π i): more circumstellar phosphorus. Astrophysical J. 940, L11. doi:10.3847/2041-8213/ac9d9b

CrossRef Full Text | Google Scholar

Laidler, K. J. (1996). A glossary of terms used in chemical kinetics, including reaction dynamics (IUPAC Recommendations 1996). Pure Appl. Chem. 68, 149–192. doi:10.1351/pac199668010149

CrossRef Full Text | Google Scholar

Langhoff, S. R., and Davidson, E. R. (1974). Configuration interaction calculations on the nitrogen molecule. Int. J. Quantum Chem. 8, 61–72. doi:10.1002/qua.560080106

CrossRef Full Text | Google Scholar

Lefebvre-Brion, H., and Field, R. W. (1986). “Introduction,” in Perturbations in the spectra of diatomic molecules (Elsevier), 1–27. doi:10.1016/B978-0-12-442690-0.50004-X

CrossRef Full Text | Google Scholar

Le Roy, R. J. (2017). LEVEL: a computer program for solving the radial Schrödinger equation for bound and quasibound levels. J. Quantitative Spectrosc. Radiat. Transf. 186, 167–178. doi:10.1016/j.jqsrt.2016.05.028

CrossRef Full Text | Google Scholar

Le Roy, R. J., Macdonald, R. G., and Burns, G. (1976). Diatom potential curves and transition moment functions from continuum absorption coefficients: Br ₂. J. Chem. Phys. 65, 1485–1500. doi:10.1063/1.433202

CrossRef Full Text | Google Scholar

Li, X., Zhang, X., and Yan, B. (2015). Ab initio study on the low-lying excited states of gas-phase PH+ cation including spin–orbit coupling. Spectrochimica Acta Part A Mol. Biomol. Spectrosc. 142, 1–7. doi:10.1016/j.saa.2015.01.070

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, H., Shi, D., Sun, J., and Zhu, Z. (2017). Accurate potential energy curves and spectroscopic properties of the 27 Λ-S states and 73 Ω states of the PO radical. Mol. Phys. 115, 714–730. doi:10.1080/00268976.2017.1280193

CrossRef Full Text | Google Scholar

Marinescu, M., Sadeghpour, H. R., and Dalgarno, A. (1994). Dispersion coefficients for alkali-metal dimers. Phys. Rev. A 49, 982–988. doi:10.1103/PhysRevA.49.982

PubMed Abstract | CrossRef Full Text | Google Scholar

Massey, P., Levesque, E. M., and Plez, B. (2006). Bringing VY Canis Majoris down to size: an improved determination of its effective temperature. ApJ 646, 1203–1208. doi:10.1086/505025

CrossRef Full Text | Google Scholar

McMillan, E. C., Shen, G., McCann, J. F., McLaughlin, B. M., and Stancil, P. C. (2016). Rovibrationally resolved photodissociation of SH ⁺. J. Phys. B At. Mol. Opt. Phys. 49, 084001. doi:10.1088/0953-4075/49/8/084001

CrossRef Full Text | Google Scholar

Narasimham, N. A. (1957). THE EMISSION SPECTRUM OF THE PH ⁺ MOLECULE. Can. J. Phys. 35, 901–911. doi:10.1139/p57-099

CrossRef Full Text | Google Scholar

Puzzarini, C., and Stanton, J. F. (2023). Connections between the accuracy of rotational constants and equilibrium molecular structures. Phys. Chem. Chem. Phys. 25, 1421–1429. doi:10.1039/D2CP04706C

PubMed Abstract | CrossRef Full Text | Google Scholar

Rao, T. V. R., Reddy, R. R., and Rao, P. S. (1981). Potential energy curves and dissociation energy of the PO molecule. Phys. B+C 106, 445–451. doi:10.1016/0378-4363(81)90073-5

CrossRef Full Text | Google Scholar

Rivilla, V. M., García De La Concepción, J., Jiménez-Serra, I., Martín-Pintado, J., Colzi, L., Tercero, B., et al. (2022). Ionize hard: interstellar PO+ detection. Front. Astronomy Space Sci. 9, 829288. doi:10.3389/fspas.2022.829288

CrossRef Full Text | Google Scholar

Roy, R. J. L., and Kraemer, G. T. (2004). BCONT 2.2 A computer program for calculating.

Google Scholar

Shevelko, V. P., and Vinogradov, A. V. (1979). Static dipole polarizability of atoms and ions in the thomas-fermi model. Phys. Scr. 19, 275–282. doi:10.1088/0031-8949/19/3/010

CrossRef Full Text | Google Scholar

Singh, P. D., and Andreazza, C. M. (2000). The Formation of CN and CN ⁺ by direct radiative association. ApJ 537, 261–263. doi:10.1086/309023

CrossRef Full Text | Google Scholar

Stancil, P. C., Kirby, K., Gu, J.-P., Hirsch, G., Buenker, R. J., and Sannigrahi, A. B. (2000). The formation of SiH ⁺, PH ⁺, and SH ⁺ byradiative association. Astron. Astrophys. Suppl. Ser. 142, 107–112. doi:10.1051/aas:2000141

CrossRef Full Text | Google Scholar

Swings, P. (1942). Considerations regarding cometary and interstellar molecules. ApJ 95, 270. doi:10.1086/144393

CrossRef Full Text | Google Scholar

Tenenbaum, E. D., Woolf, N. J., and Ziurys, L. M. (2007). Identification of phosphorus monoxide (X   ² Π_r) in VY Canis Majoris: detection of the first P–O bond in space. Astrophysical J. 666, L29–L32. doi:10.1086/521361

CrossRef Full Text | Google Scholar

Thomas, W. H., and David, A. W. (1999). The molecular astrophysics of stars and galaxies.

Google Scholar

Tinacci, L., Pantaleone, S., Maranzana, A., Balucani, N., Ceccarelli, C., and Ugliengo, P. (2021). Structures and properties of known and postulated interstellar cations. ApJS 256, 35. doi:10.3847/1538-4365/ac194c

CrossRef Full Text | Google Scholar

Turner, B. E., and Bally, J. (1987). Detection of interstellar PN - the first identified phosphorus compound in the interstellar medium. ApJ 321, L75. doi:10.1086/185009

CrossRef Full Text | Google Scholar

Van Dishoeck, E. F. (1988). “Photodissociation and photoionization processes,” in Rate Coefficients in Astrochemistry astrophysics and space science library. Editors T. J. Millar, and D. A. Williams (Dordrecht: Springer Netherlands), 49–72. doi:10.1007/978-94-009-3007-0_4

CrossRef Full Text | Google Scholar

Watanabe, A., Dutta, C. M., Nordlander, P., Kimura, M., and Dalgarno, A. (2002). Charge-transfer cross sections for radiative charge transfer in Na + H + and K + H + collisions at very low energies. Phys. Rev. A 66, 044701. doi:10.1103/PhysRevA.66.044701

CrossRef Full Text | Google Scholar

Werner, H., and Knowles, P. J. (1985). A second order multiconfiguration SCF procedure with optimum convergence. J. Chem. Phys. 82, 5053–5063. doi:10.1063/1.448627

CrossRef Full Text | Google Scholar

Werner, H., and Knowles, P. J. (1988). An efficient internally contracted multiconfiguration–reference configuration interaction method. J. Chem. Phys. 89, 5803–5814. doi:10.1063/1.455556

CrossRef Full Text | Google Scholar

Werner, H., and Meyer, W. (1980). A quadratically convergent multiconfiguration–self-consistent field method with simultaneous optimization of orbitals and CI coefficients. J. Chem. Phys. 73, 2342–2356. doi:10.1063/1.440384

CrossRef Full Text | Google Scholar

Werner, H.-J., Knowles, P. J., Knizia, G., Manby, F. R., and Schütz, M. (2012). Molpro: a general-purpose quantum chemistry program package. WIREs Comput. Mol. Sci. 2, 242–253. doi:10.1002/wcms.82

CrossRef Full Text | Google Scholar

Wilson, A. K., Woon, D. E., Peterson, K. A., and Dunning, T. H. (1999). Gaussian basis sets for use in correlated molecular calculations. IX. The atoms gallium through krypton. J. Chem. Phys. 110, 7667–7676. doi:10.1063/1.478678

CrossRef Full Text | Google Scholar

Wittkowski, M., Hauschildt, P. H., Arroyo-Torres, B., and Marcaide, J. M. (2012). Fundamental properties and atmospheric structure of the red supergiant VY Canis Majoris based on VLTI/AMBER spectro-interferometry. A&A 540, L12. doi:10.1051/0004-6361/201219126

CrossRef Full Text | Google Scholar

Zhukovska, S., Gail, H.-P., and Trieloff, M. (2008). Evolution of interstellar dust and stardust in the solar neighbourhood. A&A 479, 453–480. doi:10.1051/0004-6361:20077789

CrossRef Full Text | Google Scholar

Zygelman, B., and Dalgarno, A. (1990). The radiative association of He(+) and H. ApJ 365, 239. doi:10.1086/169475

CrossRef Full Text | Google Scholar