
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
METHODS article
Front. Astron. Space Sci., 06 March 2023
Sec. Extragalactic Astronomy
Volume 10 - 2023 | https://doi.org/10.3389/fspas.2023.989443
In today’s modern wide-field galaxy surveys, there is the necessity for parametric surface brightness decomposition codes characterised by accuracy, small degree of user intervention, and high degree of parallelisation. We try to address this necessity by introducing MORPHOFIT, a highly parallelisable python package for the estimate of galaxy structural parameters. The package makes use of wide-spread and reliable codes, namely, SEXTRACTOR and GALFIT. It has been optimised and tested in both low-density and crowded environments, where blending and diffuse light makes the structural parameters estimate particularly challenging. MORPHOFIT allows the user to fit multiple surface brightness components to each individual galaxy, among those currently implemented in the code. Using simulated images of single Sérsic and bulge plus disk galaxy light profiles with different bulge-to-total luminosity (B/T) ratios, we show that MORPHOFIT is able to recover the input structural parameters of the simulated galaxies with good accuracy. We also compare its estimates against existing literature studies, finding consistency within the errors. We use the package in a companion paper to measure the structural parameters of cluster galaxies in order to study the wavelength dependence of the Kormendy relation of early-type galaxies. The package is available on github1 and on the Pypi server2.
The accurate measurement of galaxy structural parameters (e.g., total magnitudes, sizes, Sérsic indices, position angles, ellipticities) provides extremely useful insights into galaxy formation and evolution studies. The photometric structural analysis of galaxies allows us to perform their morphological classification. This sheds light on the presence of common processes taking place during galaxy formation and evolution and provides qualitative information that supports galaxy classification schemes, which also helps to constrain the dynamical modelling of galaxies (e.g., Binney et al., 1990; van der Marel, 1991; Cappellari et al., 2013). Furthermore, magnitudes and sizes can be used to measure empirical scaling relations (e.g., the effective brightness—effective radius (or Kormendy) relation Kormendy 1977), while ellipticities and position angles can be used for shear and intrinsic alignment measurements (e.g., Lee et al., 2018; Kannawadi et al., 2019).
The measurement of galaxy structural parameters is usually conducted with 1D or 2D methods. The 1D methods, e.g., isophotal analysis, work well in low signal-to-noise conditions, since they azimuthally average the surface brightness along the elliptical isophotes. 2D methods are routinely performed by creating parametrised models for the 2D galaxy surface brightness. They have the advantage of allowing us to disentangle among different galaxy components, as well as taking into account the point-spread-function (PSF) of the observations through its convolution with the galaxy light profile (see Méndez-Abreu et al., 2008; Peng et al., 2010; Bonfini, 2014; Gao and Ho, 2017 and references therein for differences between 1D and 2D techniques). The most common parametrisation for the surface brightness distribution is the Sérsic model (Sérsic, 1963). It consists of a smooth surface brightness distribution with seven degrees of freedom, involving the profile centroid, the total magnitude, the effective radius, the Sérsic index, the axis ratio, and the position angle. The model owns his success not only to the fact that it is a good approximation of the surface brightness distribution of galaxies, but also to the fact that it can be used to disentangle between classical and pseudo-bulges (Fisher and Drory, 2008, but see Costantin et al., 2018 for a different approach), and, for n = 1, it approximates the exponential behaviour of galaxy disks. The Sérsic profile can also be used to discover hidden substructures. The latter may consist of spiral arms, rings, bars, that deviate from a smooth surface brightness distribution and, therefore, require additional modelling components with respect to the simple Sérsic profile (Sonnenfeld, 2022). The morphological description of galaxies can be conducted also with non-parametric techniques. However, their use is not advised in low signal-to-noise conditions: non-parametric techniques mostly rely on being able to measure a gradient in galaxies and that is possible only for high signal-to-noise conditions, especially in the case of shallow profile gradients. Additionally, the required background subtraction might cause a sky over-estimation when dealing with low signal-to-noise shallow gradients3.
Modern photometric and spectroscopic surveys have enabled the measurement of galaxy structural parameters for millions of galaxies. This allows astronomers to characterise galaxy properties and build relations among them with high statistical precision (e.g., La Barbera et al., 2010; Simard et al., 2011; Kelvin et al., 2012; Kawinwanichakij et al., 2021). This rapidly growing sample of galaxies with quality imaging has sparkled renovated interests in the development of codes for the measurement of galaxy structural parameters and galaxy morphological classification that are accurate, time efficient, and require very few input from the user. These codes involve the use of non-parametric fitting (cas Conselice, 2003, gini Lotz et al., 2004, morfometryka Ferrari et al., 2015), parametric fitting (gim2d Simard et al., 2002, budda de Souza et al., 2004, gasp2d Méndez-Abreu et al., 2008, pymorph Vikram et al., 2010, galapagos Häußler et al., 2011; Häußler et al., 2013, imfit Erwin, 2015, galight Ding et al., 2021, galapagos-2 Häußler et al., 2022) or machine learning methodologies (deeplegato Tuccillo et al., 2018, gamornet Ghosh et al., 2020, galnets Li et al., 2022).
In this work, we present a package called MORPHOFIT4. The package seeks to address the necessity of modern galaxy surveys for parametric surface brightness decomposition codes that are accurate, parallelisable, and automatic, meaning that they require a small degree of human inspection and intervention. The package is written in python and relies upon the well-tested and widespread codes GALFIT (Peng et al., 2010; Peng et al., 2011) and SEXTRACTOR (Bertin and Arnouts, 1996). MORPHOFIT allows the user to measure galaxy structural parameters in stamps around individual objects or by simultaneously fitting multiple galaxies in the image. It has been optimised and widely tested in low and high-density environments, the latter being characterised by the presence of blending and diffuse light effects. It contains routines to create PSF images from the knowledge of star positions in the images, as well as the ability to run SEXTRACTOR in forced photometry mode to use its parameters as either individual galaxy properties estimates or starting point for the GALFIT fit.
The package is written in a modular nature, such that each individual module can be run independently depending on the user necessities. The modules can be chained in a pipeline that constitutes a novel method to fit galaxies in a cluster environment. In particular, this method involves the surface brightness profile fit of galaxies in images of increasing sizes. This approach has already been adopted in Tortorelli et al., 2018b (hereafter, LT18) to measure the sample dependence of the Kormendy relation. In this work, we improve the methodology and we successfully apply it in Tortorelli et al. (2023) (hereafter, LT23) to measure the wavelength dependence of the Kormendy relation. It differs from the usual approach adopted in the literature, where the authors limit their surface brightness fit to stamps around individual galaxies. It has been shown (see Figure 5 of LT18) that this approach negatively impacts the estimated galaxy properties. By fitting the surface brightness profiles in stamps around galaxies, the minimisation algorithm converges to biased structural parameters since the local sky background is dominated, in the case of galaxy clusters, by the intracluster light and not by the actual image background. We refer the reader to Section 3.3 of LT18 for a more detailed analysis of this aspect. The cluster environment is particularly challenging for the fit in stamps because of the intracluster light and the high galaxy density. The latter requires a simultaneous fit of multiple sources to take into account light contamination among neighbouring objects. The former requires a careful modelling of its contribution, usually by adding an additional large Sérsic light profile to the brightest cluster galaxy (BCG) (Kluge et al., 2021), as well as a careful estimate of the image background. The methodology we propose addresses these two aspects. In order to deal with nearest neighbours, we use an iterative approach where we analyse images of increasing size. In order to deal with the intracluster light contamination in flux, instead, we average the structural parameters measured with different background estimation methods and we add a secondary Sérsic light profile (Kluge et al., 2021) to the BCG fit. This methodology is, therefore, especially useful in the case of galaxy clusters and compact groups.
In addition, since as mentioned earlier, sometimes galaxies are best fit by a multi-component surface brightness distribution, the package is designed such that each individual galaxy can be fit with multiple components among those currently implemented in the code (i.e., Sérsic, deVaucouleurs, exponential disk). However, the multi-component capabilities of MORPHOFIT have been tested up to two light profile components, therefore the user must use care when fitting a larger number of components for its own specific scientific case. Although galaxies may have a lot of structures (like rings, pseudorings, lenses, bars, envelops, and spiral arms), a parametric bulge-disk decomposition is one of the first possible quantitative steps to tag a galaxy as an early or late-type system.
This work is structured as follows. In Section 2, we present the main features of MORPHOFIT. In Section 3, we test the package against simulated data generated as both single Sérsic (Section 3.1) and bulge plus disk profiles with a variable B/T ratio (Section 3.2). Section 4 contains the comparison between the results obtained with this automated methodology and those from already published catalogues. We provide the main conclusions in Section 5.
MORPHOFIT has a modular nature. Each module can be run independently with respect to the others. For the sake of clarity, we describe the different modules that constitute MORPHOFIT following the pipeline for the morphological analysis of galaxies first introduced in LT18, improved in this work, and further used in LT23 (Figure 1). This pipeline has been designed to mitigate the challenging aspects of measuring the structural parameters in galaxy clusters, e.g., intracluster light and blending. It allows for the measurement of the structural parameters via an iterative approach by fitting images of increasing size (to deal with nearest neighbours), with different PSF image estimates, different sigma (noise) images and on multiple background estimations (to deal with the ICL contamination in flux). The various steps of the pipeline correspond to the different modules MORPHOFIT is built upon: SEXTRACTOR run in forced photometry mode to get an initial estimate of the galaxy structural parameters; creation of PSF images for the surface brightness profile convolution; GALFIT run on stamps using the SEXTRACTOR properties as input; GALFIT run on regions and full images, using the fit on stamps and regions, respectively, as initial guesses; creation of multi-wavelength catalogues of best-fitting structural parameters. We design the pipeline to be especially useful for fitting galaxy clusters and compact groups.
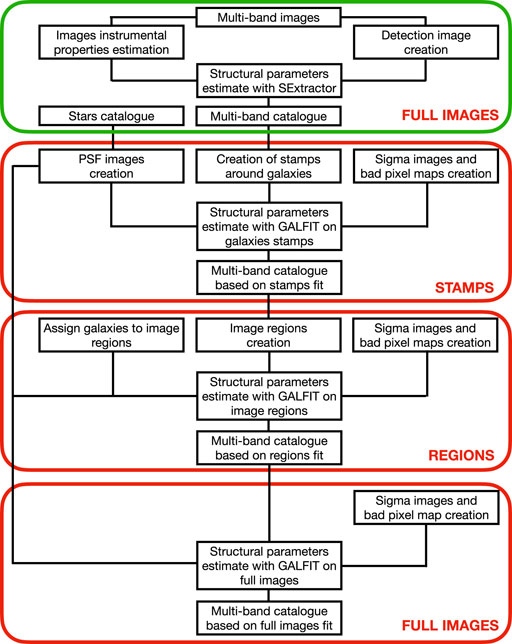
FIGURE 1. Flowchart describing the structural parameters measurement steps of the pipeline adopted in LT18 and LT23. The red boxes refer to estimates using GALFIT, while the green box using SEXTRACTOR.
Each MORPHOFIT module is constituted by two scripts. The first one creates an hdf5 table that stores file paths and variable values. The second script reads the hdf5 table and performs the measurement tasks. The scripts are run via esub-epipe5 (Zürcher et al., 2021, 2022), a python package that takes a single properly formatted python executable file and runs it as either single core job or multi-core job, on both local machines and computer clusters via job schedulers.
The initial estimate of the structural parameters is performed using SEXTRACTOR. MORPHOFIT first stores the science (sci), the root mean square (rms) and the exposure time (exp) images paths, the photometric parameters for SEXTRACTOR and the paths to SEXTRACTOR executable and required files into an hdf5 file. Then, in the main script, it derives the non-photometric parameters needed by SEXTRACTOR (GAIN, SATURATION, EXPOSURE_TIME, MAGNITUDE_ZEROPOINT), the image background value and the PSF full width at half maximum (FWHM). The non-photometric parameters are obtained by reading them from the image headers. If they are not present in the image header, they can be estimated via survey-specific functions the users might need to implement in MORPHOFIT (e.g., saturation by finding the highest value pixel in the image). The image background value is estimated by sigma clipping the image, where each source is masked according to a segmentation map. We obtain the latter by running SEXTRACTOR on the image in single image mode. The resulting background amplitude and rms are given by the median and the standard deviation of the sigma clipped masked image. The PSF FWHM of the image is estimated by fitting stars with a two-dimensional circular Moffat profile. The stars positions are provided by the user by means of an external catalogue (see Section 2.2). The different estimates of the FWHMs from the stars in the image are then median combined as described in Section 2.2.
In order to exploit the full potential of having multi-wavelength data, MORPHOFIT runs SEXTRACTOR in forced photometry mode. To do that, it needs a detection image. The latter is created by following the prescription in Coe et al., 2006 and references therein. This prescription involves stacking the sci images in the available wavelength bands by normalising them according to the rms of the background noise in each waveband. The detection image has the average PSF of all the stacked images. SEXTRACTOR estimates the isophotal apertures and sizes from this detection image. The inclusion of all the wavelengths allows MORPHOFIT to obtain a detection image where objects of different colours are present and detected by SEXTRACTOR. If provided, the rms images are used as weight images for SEXTRACTOR. MORPHOFIT creates the rms image for the detection image by doing the root sum squared of the rms images for each waveband normalised by the rms of the background noise in each waveband.
The final catalogue contains the measurement for all the detected objects in the available wavebands. MORPHOFIT then excludes stars by removing sources which have the
Accurate surface brightness fitting requires convolution of the galaxy light profile with the image PSF. MORPHOFIT contains a module that creates PSF images using four different methods (more methods can be easily added by the user). The PSF images can be created for each individual sci image (or parts of it) and wavelength. To create the PSF images, the package requires an input star catalogue for each waveband covering the same sky portion of the original image. The star catalogue can be either provided by a third-party source (e.g., GAIA catalogue, Gaia Collaboration et al., 2021) or generated by the user. In LT23, we generate the star catalogue by running SEXTRACTOR in single image mode on the sci image. Since the measurement of magnitudes and sizes are independent of the seeing estimate given to SEXTRACTOR, we set the
The PSF modelling is a critical aspect of the structural parameters derivation. A wrong choice of the PSF model could severely affect the measurements. Each image might have peculiarities that make the choice of the PSF used for fitting not universal. Since MORPHOFIT can be used on different types of images, either ground-based or space-based, in order to make it as generalisable as possible, we implement four different methods to create a PSF image. The different PSF creation routines are mutuated from methods that are widely used in the literature for different scientific applications.
Each method has as initial step the creation of M × N pixels wide stamps around observed stars from the target image. MORPHOFIT then subtracts the background value in each stamps to obtain a background subtracted observed star image. The background value estimate in each stamp is obtained by sigma-clipping the image and taking its median as background estimate. The star stamps are normalised to the maximum pixel value. The four PSF estimation methods implemented in MORPHOFIT are:
• “Moffat PSF”: The implementation of a “Moffat PSF” profile was motivated by a number of general properties it possesses. The “Moffat PSF” is numerically well-behaved when modelling narrow PSFs in Hubble Space Telescope (HST) images thanks to its polynomial structure (Trujillo et al., 2001). Additionally, it constitutes also an analytical approximation to the PSF predicted from atmospheric turbulence theory when b ∼ 4.765, allowing the modelling of the PSF wings present in real images obtained from ground-based telescopes. However, as detailed in Trujillo et al., 2001, it is not sufficient to consider a circular Moffat PSF profile to model the effects of seeing on the surface brightness distribution when the ratio of the effective radius to the FWHM is less than 2.5. Trujillo et al., 2001 provides a prescription to correct for this effect. To create a “Moffat PSF”, MORPHOFIT models the star light profile with a two-dimensional circular Moffat function:
where amplt is the model amplitude, (x0, y0) are the positions of the Moffat model maximum,
• “Observed PSF”: The “Observed PSF” is a fast method to approximate the PSF seen on the images that already includes the different seeing and detector effects. The final PSF image is given by the median of the normalised background subtracted star stamps.
• “PCA PSF”: The “PCA PSF” is a method that is commonly used in planetary science where the detailed star modelling is crucial (Amara and Quanz, 2012). We first compute a mean star stamp using all the background-subtracted normalised star stamps. We subtract the mean star stamp from the latter. MORPHOFIT flattens the mean subtracted star stamps and stores them into an array of size s = [number of stars, stamp size2]. It then performs a Principal Component analysis (PCA) on this array. The final PSF image is the linear combination of an user-defined number of Principal components resulting from the PCA. In principle, by having larger statistics, one can complexify the resulting PSF including the effects of skewness and asymmetries by adding higher order principal components (Herbel et al., 2018).
• “Effective PSF”: The “Effective PSF” is an empirical oversampled model of the HST PSF. The method relies on the Anderson empirical PSF library (Anderson and King, 2000; Anderson, 2016) that was obtained from observations of star associations with HST. MORPHOFIT builds the PSF image using the EPSFBuilder class of the photutils python package (Bradley et al., 2020). This package relies upon the method in Anderson and King 2000; Anderson 2016 to build the final PSF image. Its use is recommended only in the case of HST images.
In Figure 2, we show a comparison among the four PSF types from the LT23 analysis created using stars from the HST F814W images of the Abell S1063 cluster. The “Moffat PSF” appears smooth and regular given its analytical nature. The “Observed PSF” and the “PCA PSF” reproduce details from the actual stars in the HST images, including the wings of the PSF profile. The “Effective PSF” presents a smoother PSF with less pronounced wings. The difference among the last three methods is mostly due to the small sample of stars used to construct them, an effect that is less pronounced for the “Observed” and the “PCA” PSF. The latter is able to handle the small sample of stars by controlling the number of principal components used to construct it. The former provides a good result even with just one object by definition of observed star. In LT23, we do not use Tiny Tim (?) to model the HST PSF. Tiny Tim model PSFs are designed to be a good approximation of the single exposure ”.flt” images and not of the multidrizzled images6.
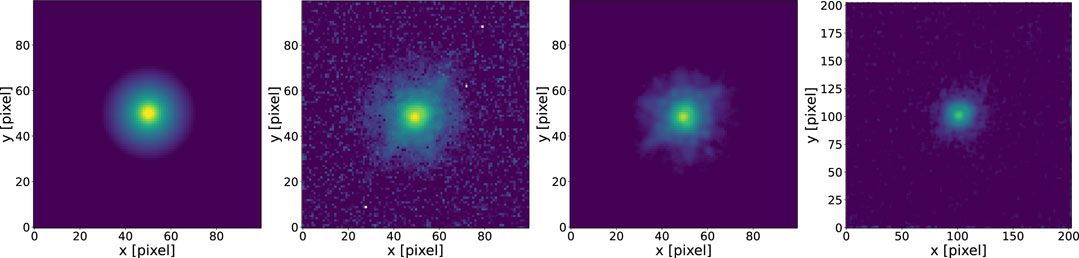
FIGURE 2. The panels show a comparison among the PSF images obtained with the methods described in Section 2.2. They refer to those of the Abell S1063 cluster in the F814W waveband from the LT23 analysis. From left to right, the panels show the “Moffat PSF”, the “Observed PSF”, the “PCA PSF” and the “Effective PSF”. The first three PSF images are 100 × 100 pixels wide, while the “Effective PSF” is 200 × 200 pixels since the minimum oversampling factor of the ‘Effective PSF’ relative to the input stars along each axis is 2 (see photutils manual for a detailed explanation).
In the flowchart shown in Figure 1, the parameter values estimated with SEXTRACTOR constitute the starting point for the GALFIT fit on stamps module. Since the run on stamps requires as input a catalogue, in principle any other external one can be used, provided that the appropriate properties are included.
For the fit on stamps, MORPHOFIT requires the user to provide a target and a source catalogue. The target catalogue contains the initial parameter values of the galaxies we are interested in. The source catalogue contains the properties of all the remaining sources in the image. This allows the user to simultaneously fit neighbouring objects falling in the stamps cut around the target galaxies.
Both the target and the source catalogues need to contain the properties that are required as initial values for the surface brightness fit with GALFIT. The surface brightness components implemented in MORPHOFIT are the Sérsic, the deVaucouleurs, and the exponential disk profiles. These require the galaxy centroids, the magnitudes, the effective radii, the Sérsic indices, the axis ratios, and the position angles. MORPHOFIT implements the possibility of fitting multiple components to the same galaxy (among the three previously mentioned), therefore the target and source catalogues additionally need information about which profile is being fit, the component number and whether to keep the values fixed or let them free to vary in the fit. The column names corresponding to the needed properties are provided by the user via command-line when running the code.
The first step of this module involves the creation of an hdf5 file that contains the sci, rms, exp and segmentation map (seg) images paths. Additionally, the table includes the target and source catalogues path, as well as a list of all the possible fit combinations for the different kind of PSF images, sigma images, background estimations, and wavebands for all the target galaxies.
In the main script, the first step is to create cutouts around each target galaxy. The cutouts are centred on the galaxy centroid. Following Vikram et al., 2010, the xsize and ysize pixel sizes of the stamps are given by.
where re is the effective radius of the target galaxy in pixels, γ is an user-defined enlarging factor, θ is the angle between the galaxy major axis and the image x-axis, and q is the galaxy axis ratio. Since the estimates might be different for different wavebands, the user can provide a reference band, whose values are used to create the cutout around the target galaxy. This ensures that the cutouts have the same pixel size for every waveband analysed. In LT23, these parameters are set to values of the SEXTRACTOR estimates in the HST F814W waveband7:
Rather than considering all the galaxies that fall inside the stamp, MORPHOFIT simultaneously fit only those neighbouring objects that have distance d in arcseconds from the target galaxy that is less than
where xsize and ysize are given by Eq. 3 with γ = 10 and pixel scale is the image pixel scale in arcsec/pixel.
GALFIT requires a “bad pixel image” to know which pixels of the image need to be fit. MORPHOFIT creates this ‘bad pixel image’ by assigning zeros to pixels belonging to the target and neighbouring galaxies, and greater than zero values to pixels belonging to sources not included in the fit. The latter might be galaxies having distances greater than d from the target galaxy or stars which are masked during the fitting procedure. In LT23, the “bad pixel image” is created using the SEXTRACTOR output segmentation map.
The sigma image used in GALFIT can be provided by the user, generated by MORPHOFIT or internally generated by GALFIT itself. We refer to them as “external sigma image”, “custom sigma image”, and “internal sigma image”, respectively. MORPHOFIT creates the last two, assuming the sci images are provided in units of electrons/s, according to the following prescriptions:
• “custom sigma image”: MORPHOFIT creates the sigma image σimg following GALFIT’s user manual8
where sci is the science image, bkg_amp is the amplitude of the science image background in the same units as the sci image, exp is either a fixed exposure time value or an exposure time image, and rms is the root mean square image. The negative values of the sci image are set to zero in creating the sigma image. The sigma image is further smoothed with a Gaussian kernel having a width value of w = 1.2 pixels and its pixel values are set to nan where the rms image pixel values exceeds 105. To avoid systematic errors and have a correct value of the reduced χ2, the units of the images and their header keywords need to be adjusted such that GAIN ×sci ×NCOMBINE = electrons, where NCOMBINE is the number of images used to create the sci image. In LT23, we work with HST images in units of electrons/s. Therefore, we set the following drizzled sci image keywords to:
where exptime is the drizzled image total exposure time in seconds, EXPTIME is the image header keywords detailing the sci image exposure time, GAIN details the detector instrumental gain, and NCOMBINE is the number of images combined to produce the sci image.
• “Internal sigma image”: in order to let GALFIT correctly create the sigma image, the sci image needs to be converted from electrons/s units to ADU. To do that, MORPHOFIT divides the sci image by the instrumental gain and multiplies it by the exp image or, if not provided, by the exposure time. A similar operation is performed on the background amplitude value. The package further sets the sci image header keyword BUNIT = ADU, the GAIN keyword to its instrumental value and the image zeropoint is updated such that zpt′ = zpt − 2.5 log10(GAIN).
GALFIT requires also an estimate of the sky background of an image. MORPHOFIT provides the possibility to either pass an user-defined value or to let GALFIT freely fit the background amplitude and gradient in the x and y directions. In LT23, the initial estimate of the sky background is obtained from the sigma clipped masked image (see Section 2.1). MORPHOFIT includes also the possibility to provide GALFIT with a parameter constraints file.
MORPHOFIT creates the input file for GALFIT, runs it on the individual stamps, reads and saves in a FITS table the best-fitting parameters from the GALFIT output files. It also creates diagnostic plots for each fitted galaxy. These diagnostic plots are:
• original, model, and residuals images from the GALFIT fit;
• pixel count histograms of original, model, and residuals images;
• Gaussian fit of the residuals image pixel count histogram;
• comparison between the best-fitting surface brightness profile and the azimutally averaged aperture fluxes.
Figure 3 shows an example of the diagnostic plots for the fit on a stamp around one of the simulated galaxies created in Section 3 in the F140W HST waveband. The galaxy is simulated as a bulge plus disk component. MORPHOFIT is able to correctly fit the double component as shown by the model and the residual images, and by the comparison between the best-fitting total light profile and the aperture photometry obtained with SEXTRACTOR.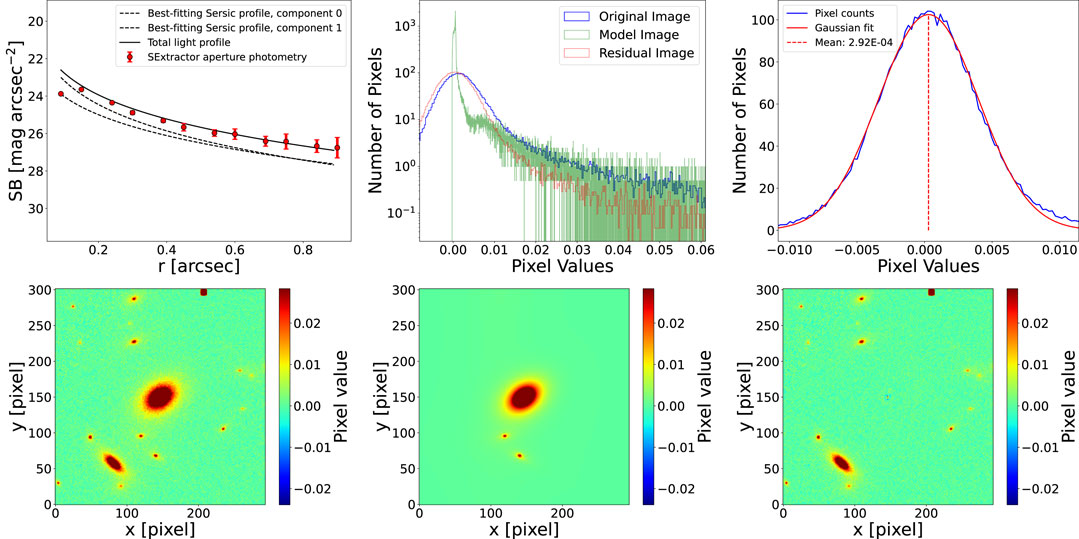
FIGURE 3. This figure shows the diagnostic plots automatically created by MORPHOFIT. Upper left panel shows the comparison between the two component surface brightness fit and the SEXTRACTOR aperture photometry for the target galaxy. The upper central panel shows the pixel value histograms of the original, model and residual images generated by GALFIT. The upper right plot shows a Gaussian fit to the pixel values distribution of the residuals image. The bottom panels show the original, model and residuals images after the fit with GALFIT.
The pipeline, as illustrated in Figure 1, involves the use of the results from the fit on stamps for estimating the galaxy properties on increased size images. These are obtained by creating image regions. MORPHOFIT contains a module that crops or divides into a number Nreg of equally sized regions the sci, rms, and exp images. After creating the hdf5 file containing the images paths and the Nreg value, the main script crops the image (if the appropriate keyword is set to “True”) and then divides it into Nreg regions. The crop routine is further sub-divided into two kinds: a size-based crop, where the user specifies the x and y pixel ranges, and a catalogue-based crop, where the initial image is restricted to the area containing sources inside an user-provided catalogue.
This module performs the surface brightness fitting of sources inside the regions created in Section 2.4. The hdf5 file contains the sci, rms, exp and seg images paths, the to-be-fitted galaxy catalogue path and the list of possible fit combinations for the different kind of PSF images, sigma images, backgroud estimations and wavebands. In the main script, MORPHOFIT performs similar operations as the ones described in Section 2.3. The only difference is that, in place of creating stamps, it finds the sources from the user-provided catalogue that fall into the specific region and use their parameter values as initial points of the surface brightness fit. In LT23, the fit on regions uses as initial values of the structural parameters those obtained from the GALFIT run on stamps, but any user-provided catalogue can be used as input, provided that the appropriate properties are included. The typical number of simultaneously fitted sources in LT23 is
The next step of the pipeline in Figure 1 is the fit of galaxies using the full image. This MORPHOFIT module performs the surface brightness fitting of user-specified sources inside the full image. This is the preferred choice if the user does not want to follow the procedure highlighted in LT18, LT23 and is not interested in cutting stamps around individual galaxies, but rather prefers to fit them simultaneously. The module works similarly to those in Sections 2.3, 2.5. The main difference is that it does not cut stamps around galaxies and it does not determine which sources fall into the image, but uses all the sources included in the user-provided catalogue. The main factor limiting the amount of components the user can simultaneously fit with GALFIT is the Random Access Memory (RAM). The amount of RAM we could allocate per core was our limiting factor as well. In this work, we use the high-performance computing facility “Euler”9 at ETH Zürich. The maximum amount of RAM we could request per core to avoid entering an unreasonable long queue waiting time was 32 gigabyte (Gb). This amount of RAM prevented us to simultaneously fit all the sources visible in Figure 4. For the application of this methodology in LT23, the amount of sources does not constitute a limitation since the aim is to fit only the spectroscopically confirmed cluster member galaxies

FIGURE 4. This figure shows the simulated HST Frontier Fields images (2000 × 2,300 pixels) for the clusters M1149 (upper panels) and AS1063 (lower panels). The M1149 simulations are shown in the F814W (upper left panel) and F160W wavebands (upper right panel). Galaxies in this cluster are rendered as single Sérsic profiles. The AS1063 simulations are shown in the F606W (bottom left panel) and F140W wavebands (bottom right panel). Galaxies in this cluster are rendered as bulge plus disk components with different B/T ratios. The simulated images have been created matching the background noise and the PSF FWHM of the real Frontier Fields observations. The matching noise features coming from the real rms images are visible for instance in the bottom and upper right corner of the lower right image. The images orientation and scale are the same, and are highlighted in the lower right figure.
At the end of the GALFIT on stamps, regions and full images modules, a number of surface brightness profile fits with different combinations of PSFs, sigma images, backgrounds, and wavebands are available for each target galaxy. In LT23, we use the seven wavebands of the HST Frontier Fields data (Lotz et al., 2017), all four PSF estimation methods described in Section 2.2, custom and internally generated sigma images, and both fixed and free to vary backgrounds. MORPHOFIT provides modules to combine these measurements into a single estimate of the structural parameters per individual galaxy via a weighted sum. This is crucial to penalise the combinations of PSFs, sigma images, and backgrounds that produce incorrect surface brightness fits, thereby providing a more robust estimate of the structural parameters with realistic errors. Indeed, it is known that the formal errors computed by GALFIT account only for statistical uncertainties in the flux (Peng et al., 2011).
The estimates Xest of the structural parameters for each individual galaxy per waveband are obtained via a weighted average of all the measurements Xi obtained with different combinations of PSFs, sigma images, and backgrounds:
where wi are the weights, Xi,err the errors quoted by GALFIT for each fit and “est”, “comb” stand for estimate and combinations, respectively.
The error on the estimates σest is computed as the square root of the unbiased weighted estimator sample variance:
where the terms have the same meaning as in Eq. 15.
In order to test MORPHOFIT and the performance of the pipeline, we create simulated HST images matching the characteristics of the data used in LT23. The images are simulated using the non-public code “Ultra Fast image generator”10 (ufig, Bergé et al., 2013; Bruderer et al., 2016; Herbel et al., 2017; Tortorelli et al., 2018a; Fagioli et al., 2020; Tortorelli et al., 2020, 2021). ufig is a fast software written in python wrapped around c++ code that simulates astronomical images in different optical filter bands. From internally generated or user-provided catalogues, ufig renders galaxies pixelated light profiles, including observational and instrumental effects, such as noise, PSF and pixel saturation. In the standard implementation, galaxy properties are drawn from a simple yet realistic galaxy population model that has been calibrated in Tortorelli et al., 2020, 2021. Galaxies are rendered on the image with random positions according to Sérsic light profiles.
We generate simulations matching the instrumental and observational effects of real HST Frontier Fields survey images for the clusters Abell S1063 (AS1063) and MACS J1149.5 + 2,223 (M1149). We use the Frontier Fields rms image to generate realistic background noise, we set the GAIN, SATURATION, PIXEL SCALE and MAGNITUDE ZEROPOINT of the simulated images to the same values as the real HST images. Furthermore, we set the FWHM of the image to the value measured on stars on the real image as described in Section 2.2.
We create two kinds of simulations with ufig: galaxies rendered as single Sérsic profiles following the Sérsic indices distribution used in Tortorelli et al., 2020, 2021 and galaxies rendered as bulge plus disk with B/T values in the range 0.1 ≤ B/T ≤ 0.9 and values of the Sérsic indices fixed to n = 4 and n = 1, respectively. Figure 4 shows an example of the quality of the simulated images we generate. The upper panels show single Sérsic profile simulations in the F814W and F160W wavebands with instrumental parameters matching those from the real M1149 Frontier Fields images. The bottom panels show the bulge plus disk simulations in the F606W and F140W wavebands with instrumental parameters matching those from the real AS1063 Frontier Fields images. The simulation of a realistic noise is particularly visible in the F140W and F160W wavebands, where noise features coming from the real rms images are visible. The differences with respect to the observed Frontier Fields images reside in the simplistic treatment of the stars that are rendered as circular Moffat profiles in the simulations, in the absence of galaxy clustering and in the more complicated morphology of real galaxies. However, these differences do not constitute a problem, since our aim is to test whether our methodology is able to recover the input magnitudes, sizes and Sérsic indices of the simulated objects, and whether the structural parameters estimated on real data are consistent with already existing literature values.
In the single Sérsic profile simulations, galaxy intrinsic properties are drawn from the empirical galaxy population model calibrated in Tortorelli et al., 2020, 2021. ufig uses these properties to render galaxies on a pixelated grid. To perform the surface brightness fitting of galaxies in the single Sérsic profile simulations, we follow the same pipeline adopted for the LT23 work. We run SEXTRACTOR on the simulated images and we use the resulting structural parameters as initial values for the surface brightness fitting with GALFIT on stamps. We select as target galaxies that have magnitude mF814W ≤ 22.5 (measured with SEXTRACTOR
Thanks to the high degree of parallelization of the package, these combinations can all be fit simultaneously, provided that the appropriate number of cores is available to the user. We use the high-performance computing facility ‘Euler’ at ETH Zürich for all the surface brightness fit carried out in this work and for the image simulations. The seven bands simulated images for both clusters are created using two cores and 8 Gb of RAM in roughly 10 min. The fit on stamps uses 6,944 cores, 4 Gb of RAM per core and a run-time that ranges from minutes to a couple of hours depending on how large the stamps are and, therefore, how many sources are simultaneously fit. The fit on regions uses 672 cores, 8 Gb of RAM per core and a run-time that ranges from less than an hour to almost 24 h depending on the number of sources per region. The fit on the full images requires more computational resources and is more time intensive. It uses less cores, 112, due to the smaller number of combinations, but 32 Gb of RAM per core and a run-time that ranges from 12 h to roughly 3–4 days. The latter is especially true for the bulge-disk component fit (see next section) that doubles the amount of simultaneous components to fit.
We use MORPHOFIT to fit the surface brightness distributions with single Sérsic profiles with the following seven free parameters:
• x, y centroid: we set the initial value of the centroid pixel coordinates by converting the SEXTRACTOR
• mag: we set the initial value of the total galaxy magnitude using the parameter
• re: we set the initial value of the effective radius in pixel using the SEXTRACTOR parameter
• n: we set the initial value of the Sérsic index to n = 2.5.
• q: we set the initial value of the axis ratio using the SEXTRACTOR parameters
• P.A.: we set the initial value of the position angle using the SEXTRACTOR parameter
We then create the catalogue containing the estimates of structural parameters for every single galaxy as described in Section 2.7. These are then used as initial values for the fit on regions and the results are, in turn, used for the fit on the full images. We use windowed positional parameters as initial values following the suggestions in the SEXTRACTOR manual11. The manual recommends the use of windowed parameters rather than its isophotal equivalents because, despite being more CPU intensive, they provide a less noisy estimate.
We show in Figure 5 the comparison between the structural parameters measured with MORPHOFIT and the input properties of the simulated images. We compare the magnitudes, the effective radii and the Sérsic indices of the target galaxies and their neighbours in the seven Frontier Fields wavebands. The magnitude comparison shows that bright galaxies (mF814W ≤ 22.5) at all wavebands are all consistent within the errors with the input values. The neighbouring objects that have magnitudes greater than mF814W > 22.5 lie close to the one-to-one relation as well, but they are consistent with the input values only at the 3σ level. The scatter of the effective radii and of the Sérsic indices is also remarkably small. Roughly 80% of the galaxies are consistent within the errors with the input values, while all of them become consistent with the input when we consider the 3σ level.
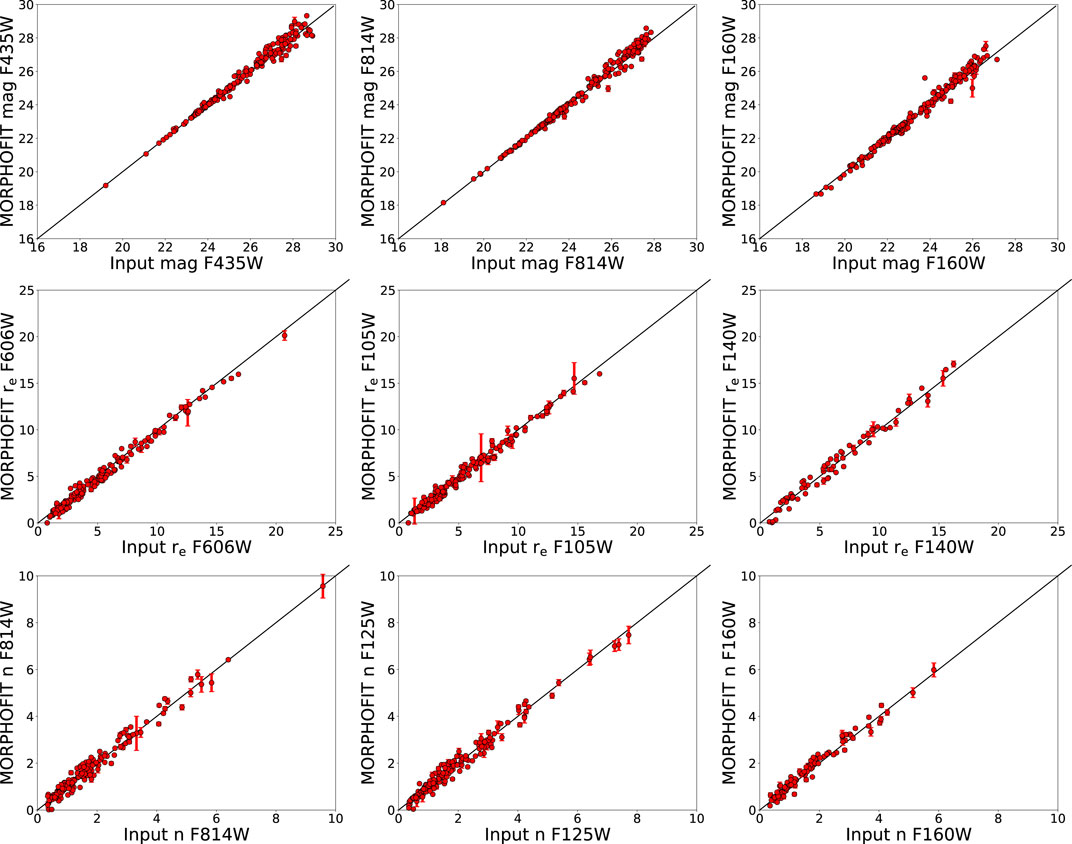
FIGURE 5. The top, middle and bottom panels show the comparison between the input simulated galaxy magnitudes, the galaxy effective radii, the galaxy Sérsic indices and the best-fitting magnitudes, effective radii, Sérsic indices from MORPHOFIT, respectively. Magnitudes are in the AB system, while the effective radii are expressed in units of pixels. mag, re and n refer to the total magnitude, the effective radius and the Sérsic index of the input and fitted Sérsic profile, respectively. For each row, we only select a sub-sample of the seven wavebands for plot clarity. Red points refer to the simulated target galaxies and their neighbouring objects. The black solid line represents the one-to-one relation between the input and the best-fitting quantities.
We draw new properties from the empirical galaxy population model for the bulge plus disk simulations. Galaxies have B/T ratios that are drawn from a uniform distribution in the range 0.1 ≤ B/T ≤ 0.9. The bulge and disk profiles of an individual galaxy have the same centers, while different Sérsic indices (n = 4 for bulge, n = 1 for disk) and different effective radii. The disk effective radius is re,disk = N × re,bulge, where N is drawn from a uniform distribution in the range [1, 4]. When fitting an exponential disk profile with GALFIT, the package requires as input the scale radius of the disk, Rs. Therefore, we input it by dividing the re,disk by 1.678 as explained in Peng et al., 2010.
The surface brightness fitting of these galaxies follows the pipeline in Figure 1 as well. We use the same selection of target galaxies and number of combinations for AS1063 and M1149 fit on stamps as in Section 3.1. We use MORPHOFIT to fit the surface brightness profile of each target galaxy using a Sérsic and exponential disk profiles for the bulge and the disk, respectively. The two profiles share the same initial values for the centroid (SEXTRACTOR
Figure 6 shows the comparison between the structural parameters estimated with MORPHOFIT and the input properties of simulated bulge plus disk galaxies. We report the results for the bulge and disk magnitudes and sizes, and for the bulge Sérsic indices, since the disk ones are kept fixed at the values used to generate the simulations. The results in this case show a larger scatter with respect to the single Sérsic profile. This is expected since we are trying to simultaneously minimise a larger number of parameters per galaxy, where the slightest change in light contribution of one of the components is immediately reflected on the parameters of the other one. Additionally, the disk component is more susceptible to the estimate of the image background, therefore caution must be applied when fitting the sky background value.
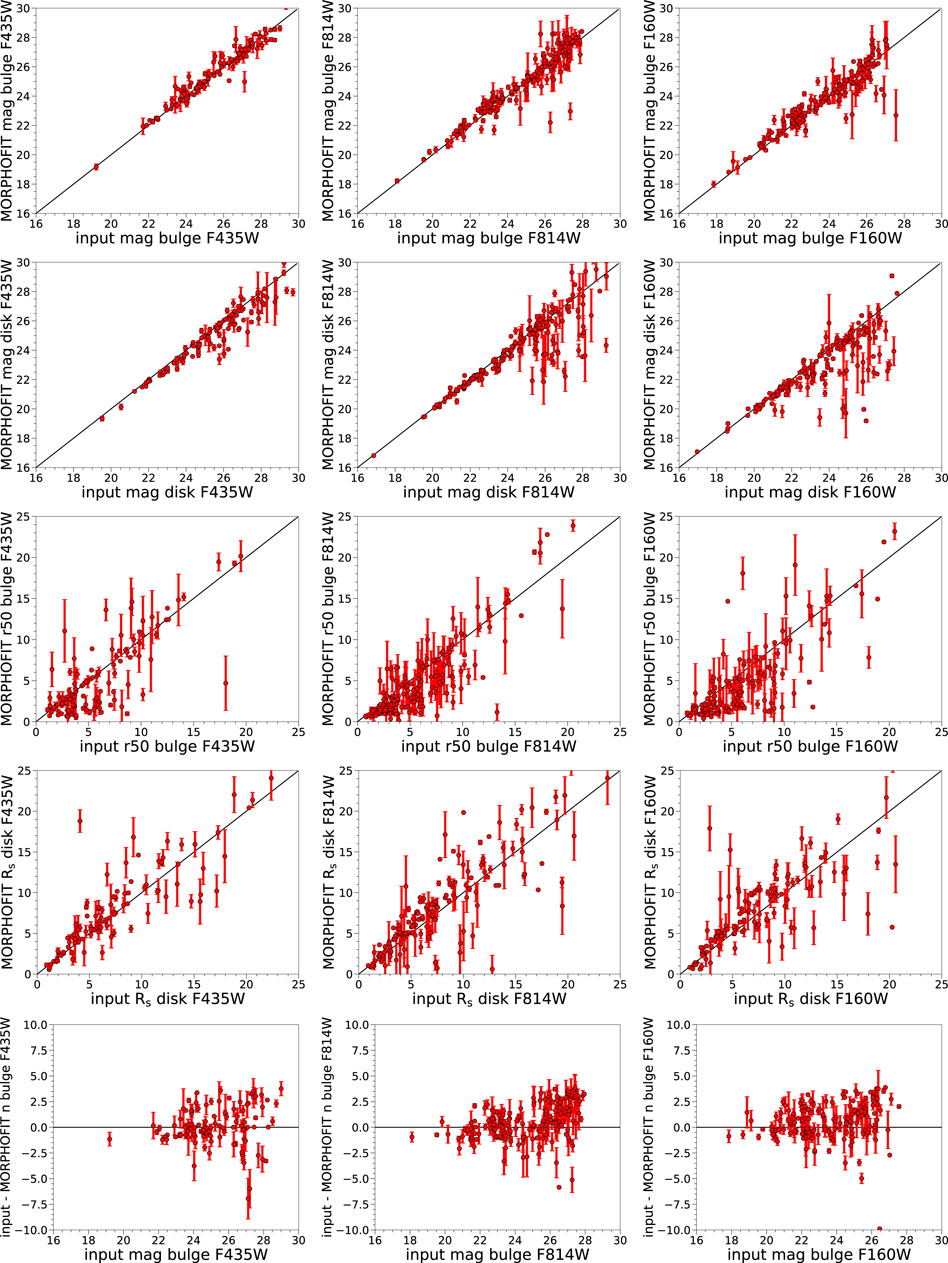
FIGURE 6. The first and second rows of panels show the comparison between the input simulated galaxy magnitudes of bulge (first row) and disk (second row), and the corresponding best-fitting magnitudes from MORPHOFIT. The third and fourth rows of panels show the comparison for the effective radii and the scale lengths. The fifth row shows the deviation of the recovered bulge Sérsic index with respect to the input one. For each row, we only select a sub-sample of the seven wavebands for plot clarity, comparing similar bands for the bulge and disk components. Red points refer to the simulated target galaxies and their neighbouring objects. The black solid line represents the one-to-one relation between the input and the best-fitting quantities.
Bright galaxy magnitudes keep being close to the one-to-one relation. The percentage of objects consistent with the input magnitudes is around 50% if we consider the 1σ level, while it is around 70% at the 3σ level. If we consider all galaxies, these percentages go to the 25% at the 1σ level and 55% at the 3σ level. The degeneracy arising in the simultaneous minimisation of two components is particularly evident in the larger errors and scatter of the effective radii and Sérsic indices. Bright galaxy bulges and disk effective radii have percentages of agreement with the input values within 1σ that are slightly lower than those obtained for the magnitudes
The simulations of single Sérsic profile galaxies show that MORPHOFIT is able to recover with good accuracy and within the errors the input parameters of the simulations. In the case of the bulge plus disk profile simulations, the simultaneous minimisation of two components per galaxy causes an increase in the scatter and in the uncertainties of the parameters. Despite that, MORPHOFIT provides good performances in the recovery of the input parameters for bright galaxies. It also provides a roughly 70% consistency within 3σ with the input values if we consider galaxies spanning the whole range of simulated magnitudes.
The tests on the simulated data demonstrate the good performances of MORPHOFIT in estimating the structural parameters, especially in the case of single Sérsic profiles. MORPHOFIT is used in LT23 to measure the structural parameters of intermediate redshift cluster galaxies in order to build the Kormendy relation as a function of wavelength.
In Figure 7, we compare the structural parameters estimated with MORPHOFIT in LT23 with already existing results in the literature for the same clusters. In particular, we fit galaxies with single Sérsic profiles and we compare the parameters of the F814W waveband with those measured in LT18 for AS1063 and M1149. We also reviewed papers with independent and publicly available catalogues. We compare the F160W waveband structural parameters with those measured in Annunziatella et al., 2017 (hereafter, MA17) for MACS J0416.1–2,403 (M0416). This allows us to check whether the MORPHOFIT structural parameters estimation and the methodology behind it perform similarly to already existing results in the literature. The studies of Merlin et al., 2016; Di Criscienzo et al., 2017; Shipley et al., 2018; Bradač et al., 2019; Pagul et al., 2021 have published photometric catalogues for AS1063, M1149, and M0416. However, either they do not use GALFIT at all, or they use galapagos (Barden et al., 2012) solely to account for the contamination of the intracluster light. The photometry that is released in these catalogues has been mainly obtained by running SEXTRACTOR (or a similar software), therefore it cannot be compared to our results and used to demonstrate that automatising the process yields similar results as those obtained from manual adjustments to the fit (see Appendix five for a comparison between the SEXTRACTOR structural parameters estimate and the MORPHOFIT one).
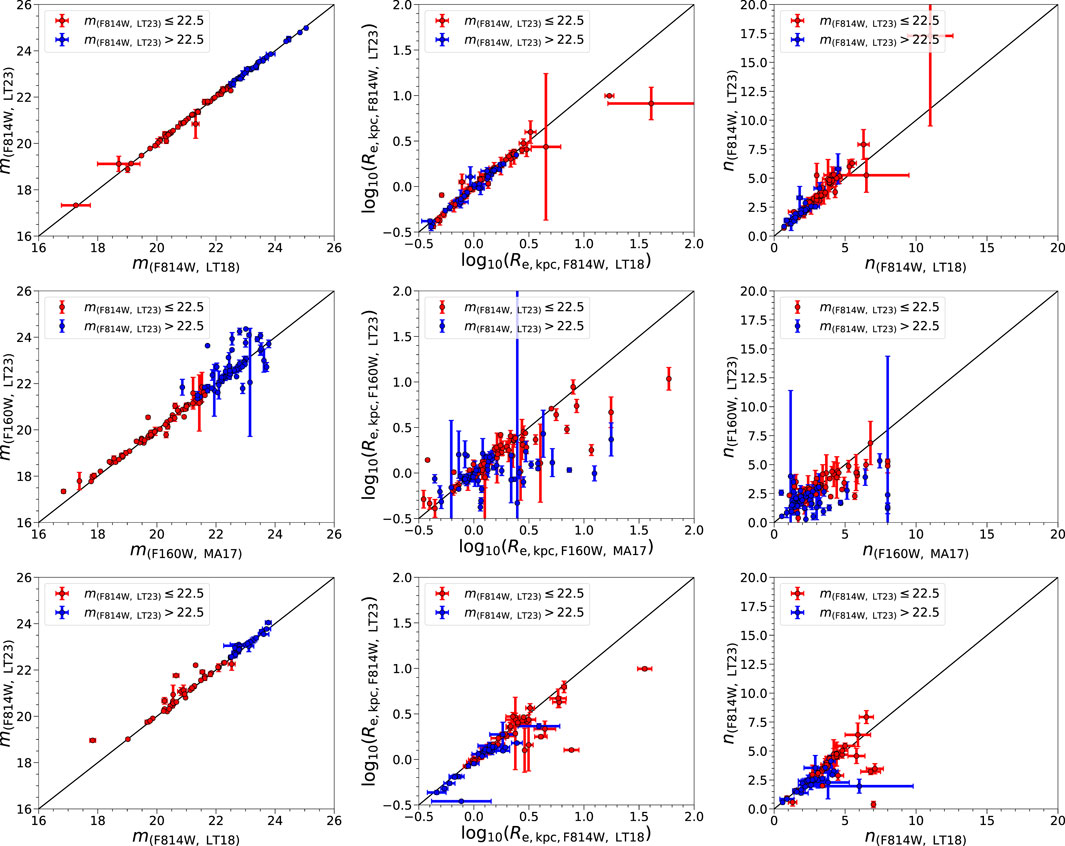
FIGURE 7. The panels show the comparison between the magnitudes, the log10Re, with Re in kpc, and the Sérsic indices in LT23 and those of LT18 (top and bottom panels) and MA17 (middle panels). LT18 structural parameters are measured for AS1063 and M1149, while MA17 for M0416. The comparisons with LT18 are in the F814W waveband, while the comparison with MA17 in the F160W waveband. In all panels, red points represent galaxies with magnitude m ≤ 22.5 in the F814W waveband, while blue points represent galaxies fainter than this limit in the same waveband. The black solid lines represent the one-to-one relations.
The magnitude comparison for AS1063 (upper left panel) shows that all galaxies are consistent within the errors with the one-to-one relation. For M0416 (central left panel), the consistency holds for bright galaxies. Faint galaxies show a large scatter, particularly those with mF160W > 22.5, and some of them are not consistent within the errors with the one-to-one relation. This is expected since fainter objects are increasingly harder to fit and different methodologies adopted in different works may lead to very different estimates. For M1149 (bottom left panel), the results are similar to those of AS1063, except for three objects (one of them being the BCG) that resides in the centre of the cluster where there is strong contamination from lensed objects.
The comparison of log10Re, with Re in kpc, for AS1063 (top central panel) shows that both faint and bright galaxies are consistent within the errors with the one-to-one relation at log10Re < 1.0. The two largest galaxies of the sample (one of them being the BCG) are not consistent. For such large galaxies, the different treatments of the background noise among different studies have a tremendous impact on the final value of the size. The trend for M0416 shows a more pronounced scatter with respect to the other two clusters. The majority of the bright objects at log10Re < 0.5 are consistent with the one-to-one relation, but with errors larger than the other two clusters. At log10Re > 0.5, MA17 sizes tend to be larger than the results from MORPHOFIT. For faint galaxies, only the smallest ones are consistent within the errors with the one-to-one relation, otherwise MA17 sizes are overestimated with respect to the MORPHOFIT estimates. M1149 shows a similar behaviour as AS1063, with the two largest galaxies (BCG included) not consistent with the one-to-one relation.
The AS1063 Sérsic indices (top right panel) estimated with MORPHOFIT are all consistent within the errors with the one-to-one relation. The larger the input Sérsic index, the larger is the error on the estimate. The M0416 Sérsic indices of bright galaxies below n < 5 are consistent within the errors with the one-to-one relation, while, above that threshold, MA17 Sérsic indices tend to be overestimated with respect to the MORPHOFIT estimates. For faint galaxies, only the ones with n < 2.5 are consistent with the one-to-one relation, while, at higher Sérsic indices, the MORPHOFIT estimate tends to be smaller than that from MA17. The M1149 Sérsic indices follow a similar trend as in AS1063, albeit with five sources at n > 5 that are not consistent with the one-to-one relation.
Overall, the comparison shows that there is a very good agreement of the MORPHOFIT properties with the literature ones, especially for AS1063 and M1149, while for M0416 the scatter is larger, but the consistency is still good. Faint galaxies in MA17 show a larger discrepancy with respect to the MORPHOFIT estimate. This is due to the larger impact that different treatments of PSF, sigma image and background estimation have on the morphological analysis of faint galaxies. The tests on simulations and literature data confirm the robustness of the parameters estimated with MORPHOFIT and, consequently, the analysis of the Kormendy relation carried out in LT23.
In this paper we introduce MORPHOFIT, a package for the estimate of galaxy structural parameters. The package is designed to answer to the necessity of modern wide-field surveys for surface brightness decomposition codes that are accurate, highly parallelisable and require a small degree of human intervention. The package is written in python and it is constituted by modules that can be run independently or in a pipeline. The latter allows the user to estimate the galaxy structural parameters in stamps around galaxies or using all the galaxies present in an image and it contains routines to create PSF images from imaged stars. MORPHOFIT allows the user to fit multiple components to each galaxy among those currently implemented in the code, namely, the Sérsic, the deVaucouleurs and the exponential disk profiles. It makes use of wide-spread and reliable codes, such as SEXTRACTOR and GALFIT. MORPHOFIT is also designed to take advantage of the pipeline first introduced in Tortorelli et al., 2018b, refined in this work and used in Tortorelli et al. (2023) to measure the Kormendy relation dependence on wavelength. Its parallelisation capabilities relies on the use of the python package esub-epipe.
We test the accuracy of the results by creating simulated images mimicking the observational and instrumental conditions of the HST Frontier Fields survey. We create two sets of simulations using ufig: one where galaxies are rendered as single Sérsic profiles and another one where galaxies are rendered as bulge plus disk components with a variable bulge-to-total luminosity ratio. This second set of simulations is of great importance because, although galaxies may have a lot of structures (like rings, pseudorings, lenses, bars, envelops, and spiral arms), a parametric bulge-disk decomposition is one of the first possible quantitative steps to tag a galaxy as an early or late-type system. We use MORPHOFIT and the pipeline described in Figure 1 to estimate the structural parameters of simulated galaxies and check whether we are able to recover the input parameters of the simulations within the errors. We find that the structural parameters measured by MORPHOFIT on the single Sérsic simulated galaxies are all consistent within the errors with the input ones. For the bulge plus disk components, the simultaneous minimisation of two components increases the degeneracies in the recovery of the parameters. This leads to roughly a 50% (70%) of bright objects that show recovered magnitudes consistent with the input ones at the 1σ (3σ) level, for both bulges and disks. A smaller degree of consistency is present for bright galaxies effective radii and Sérsic indices at the 1σ level (35%), while at the 3σ level the consistency is similar to the magnitude case.
We also compare the structural parameters estimated with MORPHOFIT on observed data with those from existing literature studies. We use the data of the clusters Abell S1063, MACS J1149.5 + 2,223 and MACS J0416.1–2,403 from the HST Frontier Fields survey. We compare the parameters of the F814W waveband for Abell S1063 and MACS J1149.5 + 2,223 with the results from Tortorelli et al., 2018b and of the F160W waveband for MACS J0416.1–2,403 with the results from Annunziatella et al., 2017. We find a very good consistency of the structural parameters for Abell S1063 and MACS J1149.5 + 2,223 with Tortorelli et al., 2018b. The consistency with Annunziatella et al., 2017 is also very good, especially for bright galaxies. Faint galaxies have a more sparse behaviour, but this is expected given the larger impact the different choice of PSF, sigma images and background estimations have on faint galaxies morphological properties.
Overall, MORPHOFIT is able to correctly recover the input simulated parameters, as well as being consistent with existing literature results. This shows that this package constitutes a promising tool that can be exploited with modern wide-field surveys to measure the structural parameters of a large number of galaxies in a parallel, accurate, and multi-component way, with a very small degree of human intervention. Future prospects include the addition of all the available GALFIT surface brightness profiles and the possibility to choose between the use of GALFIT and GALFITM (Häußler et al., 2013) for the simultaneous fit of all the wavebands.
The raw data supporting the conclusions of this article will be made available by the authors in the github page https://github.com/torluca/morphofit, without undue reservation.
LT wrote the Python package, generated the simulated data, tested the code and produced the plot. The idea of writing the package is shared between LT and AM. AM provided substantial contribution via scientific exchange of ideas, testing of the code and manuscript preparation.
The authors are grateful to Mario Nonino, Claudio Grillo and Giovanni Granata for helpful discussions and feedbacks on the package. LT acknowledges support by Swiss National Science Foundation (SNF) grant 200021_169130. The numerical simulations were performed on the Euler cluster operated by the High Performance Computing group at ETH Zürich. The CLASH Multi-Cycle Treasury Program is based on observations made with the NASA/ESA Hubble Space Telescope. The Space Telescope Science Institute is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-26555. Based on observations made with the European Southern Observatory Very Large Telescope (ESO/VLT) at Cerro Paranal, under programme IDs 60.A-9345(A), 095.A-0653(A), 294.A-5032(A) and 186.A-0798(A).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1https://github.com/torluca/morphofit.
2https://pypi.org/project/morphofit/.
3See https://users.obs.carnegiescience.edu/peng/work/galfit/TFAQ.html for a detailed discussion.
4https://github.com/torluca/morphofit.
5https://cosmo-gitlab.phys.ethz.ch/cosmo_public/esub-epipe.
6See https://www.stsci.edu/hst/instrumentation/focus-and-pointing/focus/tiny-tim-hst-psf-modeling for more details.
7See SEXTRACTOR’s user-manual for a detailed explanation of the keywords https://sextractor.readthedocs.io/en/latest/Param.html.
8users.obs.carnegiescience.edu/peng/work/galfit/README.pdf.
9https://scicomp.ethz.ch/wiki/Euler.
10https://cosmology.ethz.ch/research/software-lab/ufig.html.
11http://astroa.physics.metu.edu.tr/MANUALS/sextractor/sextractor.pdf.
Amara, A., and Quanz, S. P. (2012). Pynpoint: An image processing package for finding exoplanets. Mon. Notices R. Astronomical Soc. 427, 948–955. doi:10.1111/j.1365-2966.2012.21918.x
Anderson, J. (2016). Empirical models for the WFC3/IR PSF. Space Telescope WFC Instrument Science Report.
Anderson, J., and King, I. R. (2000). Toward high-precision astrometry with WFPC2. I. Deriving an accurate point-spread function. Publ. ASP 112, 1360–1382. doi:10.1086/316632
Annunziatella, M., Bonamigo, M., Grillo, C., Mercurio, A., Rosati, P., Caminha, G., et al. (2017). Mass profile decomposition of the frontier fields cluster MACS j0416-2403: Insights on the dark-matter inner profile. Astrophysical J. 851, 81. doi:10.3847/1538-4357/aa9845
Barden, M., Häußler, B., Peng, C. Y., McIntosh, D. H., and Guo, Y. (2012). Galapagos: From pixels to parameters. Mon. Notices R. Astronomical Soc. 422, 449–468. doi:10.1111/j.1365-2966.2012.20619.x
Bergé, J., Gamper, L., Réfrégier, A. r., and Amara, A. (2013). An ultra fast image generator (UFIG) for wide-field astronomy. Astronomy Comput. 1, 23–32. doi:10.1016/j.ascom.2013.01.001
Bertin, E., and Arnouts, S. (1996). SExtractor: Software for source extraction. Astronomy Astrophysicss 117, 393–404. doi:10.1051/aas:1996164
Binney, J. J., Davies, R. L., and Illingworth, G. D. (1990). Velocity mapping and models of the elliptical galaxies NGC 720, NGC 1052, and NGC 4697. Astrophysical J. 361, 78. doi:10.1086/169169
Bonfini, P. (2014). GALFIT-CORSAIR: Implementing the core-sérsic model into GALFIT. Publ. ASP 126, 935. doi:10.1086/678566
Bradač, M., Huang, K.-H., Fontana, A., Castellano, M., Merlin, E., Amorín, R., et al. (2019). Hubble frontier field photometric catalogues of Abell 370 and RXC j2248.7-4431: Multiwavelength photometry, photometric redshifts, and stellar properties. Mon. Notices R. Astronomical Soc. 489, 99–107. doi:10.1093/mnras/stz2119
Bradley, L., Sipőcz, B., Robitaille, T., Tollerud, E., Vinícius, Z., Deil, C., et al. (2020). astropy/photutils: 1.0.0. doi:10.5281/zenodo.4044744
Gaia Collaboration Brown, A. G. A., Vallenari, A., Prusti, T., de Bruijne, J. H. J., Babusiaux, C., et al. (2021). Gaia early data release 3. Summary of the contents and survey properties. Astronomy Astrophysics 649, A1. doi:10.1051/0004-6361/202039657
Bruderer, C., Chang, C., Refregier, A., Amara, A., Bergé, J., and Gamper, L. (2016). Calibrated ultra fast image simulations for the dark energy survey. Astrophysical J. 817, 25. doi:10.3847/0004-637X/817/1/25
Cappellari, M., Scott, N., Alatalo, K., Blitz, L., Bois, M., Bournaud, F., et al. (2013). The ATLAS3D project - XV. Benchmark for early-type galaxies scaling relations from 260 dynamical models: Mass-to-light ratio, dark matter, fundamental plane and mass plane. Mon. Notices R. Astronomical Soc. 432, 1709–1741. doi:10.1093/mnras/stt562
Coe, D., Benítez, N., Sánchez, S. F., Jee, M., Bouwens, R., and Ford, H. (2006). Galaxies in the Hubble ultra deep field. I. Detection, multiband photometry, photometric redshifts, and morphology. Astronomical J. 132, 926–959. doi:10.1086/505530
Conselice, C. J. (2003). The relationship between stellar light distributions of galaxies and their formation histories. Astrophysical J. Suppl. Ser. 147, 1–28. doi:10.1086/375001
Costantin, L., Corsini, E. M., Méndez-Abreu, J., Morelli, L., Dalla Bontà, E., and Pizzella, A. (2018). On the observational diagnostics to separate classical and disk-like bulges. Mon. Notices R. Astronomical Soc. 481, 3623–3642. doi:10.1093/mnras/sty1754
de Souza, R. E., Gadotti, D. A., and dos Anjos, S. (2004). Budda: A new two-dimensional bulge/disk decomposition code for detailed structural analysis of galaxies. Astrophysical J. Suppl. Ser. 153, 411–427. doi:10.1086/421554
Di Criscienzo, M., Merlin, E., Castellano, M., Santini, P., Fontana, A., Amorin, R., et al. (2017). The ASTRODEEP Frontier Fields catalogues. III. Multiwavelength photometry and rest-frame properties of MACS-J0717 and MACS-J1149. Astronomy Astrophysics 607, A30. doi:10.1051/0004-6361/201731172
Ding, X., Birrer, S., Treu, T., and Silverman, J. D. (2021). Galaxy shapes of light (GaLight): A 2D modeling of galaxy images. arXiv e-printsarXiv:2111.08721.
Erwin, P. (2015). Imfit: A fast, flexible new Program for astronomical image fitting. Astrophysical J. 799, 226. doi:10.1088/0004-637X/799/2/226
Fagioli, M., Tortorelli, L., Herbel, J., Zürcher, D., Refregier, A., and Amara, A. (2020). Spectro-imaging forward model of red and blue galaxies. J. Cosmol. Astropart. Phys. 2020, 050. doi:10.1088/1475-7516/2020/06/050
Ferrari, F., de Carvalho, R. R., and Trevisan, M. (2015). Morfometryka—a new way of establishing morphological classification of galaxies. Astrophysical J. 814, 55. doi:10.1088/0004-637X/814/1/55
Fisher, D. B., and Drory, N. (2008). The structure of classical bulges and pseudobulges: The link between pseudobulges and sérsic index. Astronomical J. 136, 773–839. doi:10.1088/0004-6256/136/2/773
Gao, H., and Ho, L. C. (2017). An optimal strategy for accurate bulge-to-disk decomposition of disk galaxies. Astrophysical J. 845, 114. doi:10.3847/1538-4357/aa7da4
Ghosh, A., Urry, C. M., Wang, Z., Schawinski, K., Turp, D., and Powell, M. C. (2020). Galaxy morphology network: A convolutional neural network used to study morphology and quenching in ∼100,000 sdss and ∼20,000 candels galaxies. Astrophysical J. 895, 112. doi:10.3847/1538-4357/ab8a47
Häußler, B., Bamford, S. P., Vika, M., Rojas, A. L., Barden, M., Kelvin, L. S., et al. (2013). MegaMorph - multiwavelength measurement of galaxy structure: Complete sérsic profile information from modern surveys. Mon. Notices R. Astronomical Soc. 430, 330–369. doi:10.1093/mnras/sts633
Häußler, B., Barden, M., Bamford, S. P., and Rojas, A. (2011). “Galapagos: A semi-automated tool for galaxy profile fitting,” in Astronomical data analysis software and systems XXof astronomical society of the pacific conference series. Editors I. N. Evans, A. Accomazzi, D. J. Mink, and A. H. Rots, 442, 155.
Häußler, B., Vika, M., Bamford, S. P., Johnston, E. J., Brough, S., Casura, S., et al. (2022). Galapagos-2/Galfitm/GAMA – multi-wavelength measurement of galaxy structure: Separating the properties of spheroid and disk components in modern surveys. arXiv e-prints , arXiv:2204.05907.
Herbel, J., Kacprzak, T., Amara, A., Refregier, A., Bruderer, C., and Nicola, A. (2017). The redshift distribution of cosmological samples: A forward modeling approach. J. Cosmol. Astropart. Phys. 035, 035. doi:10.1088/1475-7516/2017/08/035
Herbel, J., Kacprzak, T., Amara, A., Refregier, A., and Lucchi, A. (2018). Fast point spread function modeling with deep learning. J. Cosmol. Astropart. Phys. 054, 054. doi:10.1088/1475-7516/2018/07/054
Kannawadi, A., Hoekstra, H., Miller, L., Viola, M., Fenech Conti, I., Herbonnet, R., et al. (2019). Towards emulating cosmic shear data: Revisiting the calibration of the shear measurements for the kilo-degree survey. Astronomy Astrophysics 624, A92. doi:10.1051/0004-6361/201834819
Kawinwanichakij, L., Silverman, J. D., Ding, X., George, A., Damjanov, I., Sawicki, M., et al. (2021). Hyper suprime-cam subaru strategic Program: A mass-dependent slope of the galaxy size-mass relation at z < 1. Astrophysical J. 921, 38. doi:10.3847/1538-4357/ac1f21
Kelvin, L. S., Driver, S. P., Robotham, A. S. G., Hill, D. T., Alpaslan, M., Baldry, I. K., et al. (2012). Galaxy and mass assembly (GAMA): Structural investigation of galaxies via model analysis. Mon. Notices R. Astronomical Soc. 421, 1007–1039. doi:10.1111/j.1365-2966.2012.20355.x
Kluge, M., Bender, R., Riffeser, A., Goessl, C., Hopp, U., Schmidt, M., et al. (2021). Photometric dissection of intracluster light and its correlations with host cluster properties. Astrophysical J. Suppl. Ser. 252, 27. doi:10.3847/1538-4365/abcda6
Kormendy, J. (1977). Brightness distributions in compact and normal galaxies. II - structure parameters of the spheroidal component. Astrophysical J. 218, 333–346. doi:10.1086/155687
La Barbera, F., de Carvalho, R. R., de La Rosa, I. G., and Lopes, P. A. A. (2010). Spider - II. The Fundamental Plane of early-type galaxies in grizYJHK. Mon. Notices R. Astronomical Soc. 408, 1335–1360. doi:10.1111/j.1365-2966.2010.17091.x
Lee, B., Chary, R.-R., and Wright, E. L. (2018). Galaxy ellipticity measurements in the near-infrared for weak lensing. Astrophysical J. 866, 157. doi:10.3847/1538-4357/aadfd7
Li, R., Napolitano, N. R., Roy, N., Tortora, C., La Barbera, F., Sonnenfeld, A., et al. (2022). Galaxy light profile convolutional neural networks (GaLNets). I. Fast and accurate structural parameters for billion-galaxy samples. Astrophysical J. 929, 152. doi:10.3847/1538-4357/ac5ea0
Lotz, J. M., Koekemoer, A., Coe, D., Grogin, N., Capak, P., Mack, J., et al. (2017). The frontier fields: Survey design and initial results. Astrophysical J. 837, 97. doi:10.3847/1538-4357/837/1/97
Lotz, J. M., Primack, J., and Madau, P. (2004). A new nonparametric approach to galaxy morphological classification. Astronomical J. 128, 163–182. doi:10.1086/421849
Méndez-Abreu, J., Aguerri, J. A. L., Corsini, E. M., and Simonneau, E. (2008). Structural properties of disk galaxies. I. The intrinsic equatorial ellipticity of bulges. Astronomy Astrophysics 478, 353–369. doi:10.1051/0004-6361:20078089
Merlin, E., Amorín, R., Castellano, M., Fontana, A., Buitrago, F., Dunlop, J. S., et al. (2016). The ASTRODEEP frontier fields catalogues. Astronomy Astrophysics 590, A30. doi:10.1051/0004-6361/201527513
Pagul, A., Sánchez, F. J., Davidzon, I., and Mobasher, B. (2021). Hubble frontier field clusters and their parallel fields: Photometric and photometric redshift catalogs. Astrophysical J. Suppl. Ser. 256, 27. doi:10.3847/1538-4365/abea9d
Peng, C. Y., Ho, L. C., Impey, C. D., and Rix, H.-W. (2010). Detailed decomposition of galaxy images. II. Beyond axisymmetric models. Astronomical J. 139, 2097–2129. doi:10.1088/0004-6256/139/6/2097
Peng, C. Y., Ho, L. C., Impey, C. D., and Rix, H. W. (2011). Galfit: Detailed structural decomposition of galaxy images. Astrophysics Source Code Library.
Sérsic, J. L. (1963). Influence of the atmospheric and instrumental dispersion on the brightness distribution in a galaxy. Bol. Asoc. Argent. Astron. La Plata Argent. 6, 41–43.
Shipley, H. V., Lange-Vagle, D., Marchesini, D., Brammer, G. B., Ferrarese, L., Stefanon, M., et al. (2018). HFF-DeepSpace photometric catalogs of the 12 Hubble frontier fields, clusters, and parallels: Photometry, photometric redshifts, and stellar masses. Astrophysical J. Suppl. Ser. 235, 14. doi:10.3847/1538-4365/aaacce
Simard, L., Mendel, J. T., Patton, D. R., Ellison, S. L., and McConnachie, A. W. (2011). A catalog of Bulge+disk decompositions and updated photometry for 1.12 million galaxies in the sloan digital sky survey. Astrophysical J. Suppl. 196, 11. doi:10.1088/0067-0049/196/1/11
Simard, L., Willmer, C. N. A., Vogt, N. P., Sarajedini, V. L., Phillips, A. C., Weiner, B. J., et al. (2002). The DEEP groth strip survey. II. Hubble space telescope structural parameters of galaxies in the groth strip. Astrophysical J. Suppl. Ser. 142, 1–33. doi:10.1086/341399
Sonnenfeld, A. (2022). The effect of spiral arms on the Sérsic photometry of galaxies. Astronomy Astrophysics 659, A141. doi:10.1051/0004-6361/202142786
Tortorelli, L., Della Bruna, L., Herbel, J., Amara, A., Refregier, A., Alarcon, A., et al. (2018a2018). The PAU survey: A forward modeling approach for narrow-band imaging. J. Cosmol. Astropart. Phys. 035, 035. doi:10.1088/1475-7516/2018/11/035
Tortorelli, L., Fagioli, M., Herbel, J., Amara, A., Kacprzak, T., and Refregier, A. (2020). Measurement of the B-band galaxy luminosity function with approximate bayesian computation. J. Cosmol. Astropart. Phys. 2020, 048. doi:10.1088/1475-7516/2020/09/048
Tortorelli, L., Mercurio, A., Granata, G., Rosati, P., Grillo, C., Nonino, M., et al. (2023). The Kormendy relation of early-type galaxies as a function of wavelength in Abell S1063, MACS J0416.1-2403 and MACS J1149.5+2223. arXiv. doi:10.48550/arXiv.2302.07896
Tortorelli, L., Mercurio, A., Paolillo, M., Rosati, P., Gargiulo, A., Gobat, R., et al. (2018b). The Kormendy relation of galaxies in the frontier fields clusters: Abell S1063 and MACS J1149.5+2223. Mon. Notices R. Astronomical Soc. 477, 648–668. doi:10.1093/mnras/sty617
Tortorelli, L., Siudek, M., Moser, B., Kacprzak, T., Berner, P., Refregier, A., et al. (2021). The PAU survey: Measurement of narrow-band galaxy properties with approximate bayesian computation. J. Cosmol. Astropart. Phys. 2021, 013. doi:10.1088/1475-7516/2021/12/013
Trujillo, I., Aguerri, J. A. L., Cepa, J., and Gutiérrez, C. M. (2001). The effects of seeing on Sérsic profiles - II. The Moffat PSF. Mon. Notices R. Astronomical Soc. 328, 977–985. doi:10.1046/j.1365-8711.2001.04937.x
Tuccillo, D., Huertas-Company, M., Decencière, E., Velasco-Forero, S., Domínguez Sánchez, H., and Dimauro, P. (2018). Deep learning for galaxy surface brightness profile fitting. Mon. Notices R. Astronomical Soc. 475, 894–909. doi:10.1093/mnras/stx3186
van der Marel, R. P. (1991). The velocity dispersion anisotropy and mass-to-light ratio of elliptical galaxies. Mon. Notices R. Astronomical Soc. 253, 710–726. doi:10.1093/mnras/253.4.710
Vikram, V., Wadadekar, Y., Kembhavi, A. K., and Vijayagovindan, G. V. (2010). Pymorph: Automated galaxy structural parameter estimation using PYTHON. Mon. Notices R. Astronomical Soc. 409, 1379–1392. doi:10.1111/j.1365-2966.2010.17426.x
Zürcher, D., Fluri, J., Sgier, R., Kacprzak, T., Gatti, M., Doux, C., et al. (2022). Dark energy survey year 3 results: Cosmology with peaks using an emulator approach. Mon. Notices R. Astronomical Soc. 511, 2075–2104. doi:10.1093/mnras/stac078
SEXTRACTOR contains routines that allow the user to perform parametric surface brightness fitting. We compare the results of running MORPHOFIT on simulated single Sérsic profile galaxies (see Section 3.1) with the parametric fit performed by SEXTRACTOR on the same galaxies. Appendix Figure A1 shows that the magnitudes predicted by SEXTRACTOR lie close to the one-to-one relation with the input parameters, albeit with a larger scatter with respect to the MORPHOFIT estimates and larger errors at faint magnitudes. The figure also shows that SEXTRACTOR predicted Sérsic indices have larger errors with respect to the MORPHOFIT ones and are systematically under-estimated with respect to the input values for n > 2. Consequently, the effective radii are systematically over-estimated with respect to the input ones. We implement in MORPHOFIT the possibility for the user to access the SEXTRACTOR parametric fit feature and use those values as initial estimates for the fit with GALFIT.
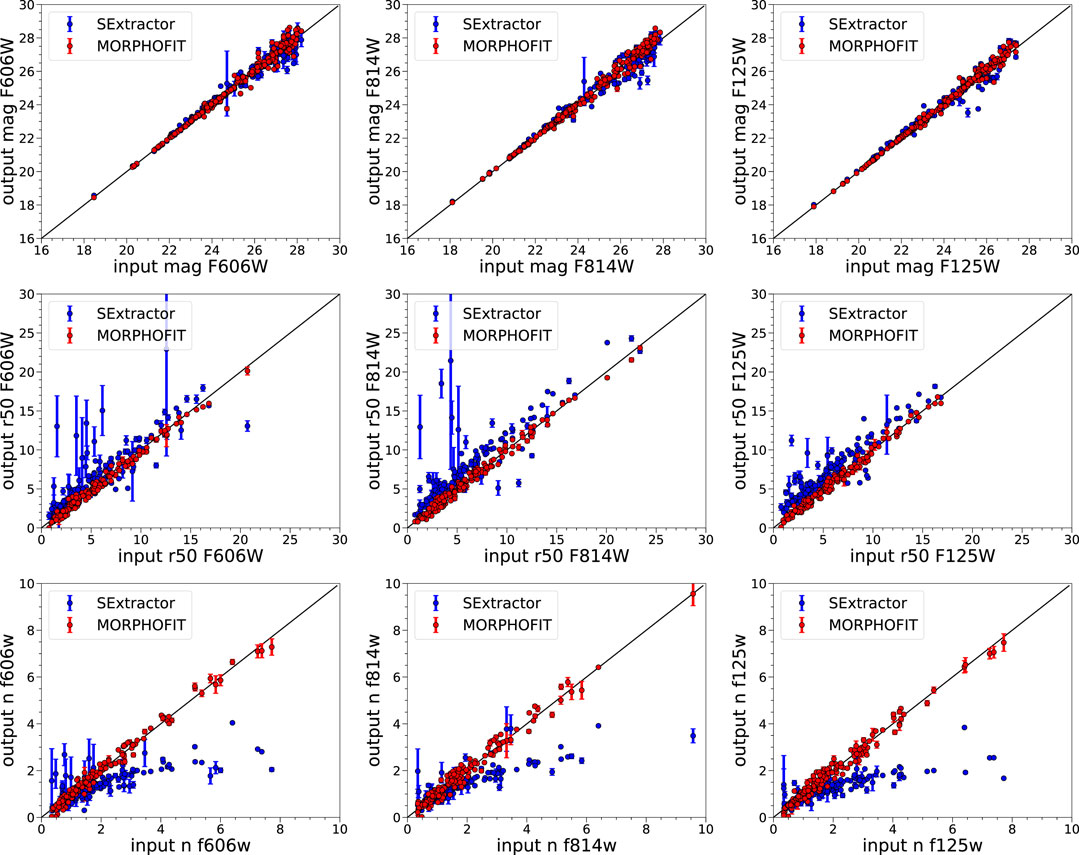
FIGURE A1. The top, middle and bottom panels show the comparison between the input simulated galaxy magnitudes, the input simulated galaxy effective radii, the input simulated galaxy Sérsic indices and the best-fitting magnitudes, effective radii, Sérsic indices from MORPHOFIT (in red) and SEXTRACTOR (in blue), respectively. Magnitudes are in the AB system, while the effective radii are expressed in units of pixels. mag, re and n refer to the total magnitude, the effective radius and the Sérsic index of the input and fitted Sérsic profile. For each row, we only select a sub-sample of the seven wavebands for plot clarity. The black solid line represents the one-to-one relation between the input and the best-fitting quantities.
Keywords: galaxies: morphology, methods: data analysis, techniques: photometric, galaxies: photometry, galaxies: fundamental parameters, galaxies: clusters: individual: Abell S1063, galaxies: clusters: individual: MACS J0416.1-2403, galaxies: clusters: individual: MACS J1149.5+2223
Citation: Tortorelli L and Mercurio A (2023) MORPHOFIT: An automated galaxy structural parameters fitting package. Front. Astron. Space Sci. 10:989443. doi: 10.3389/fspas.2023.989443
Received: 08 July 2022; Accepted: 14 February 2023;
Published: 06 March 2023.
Edited by:
Paola Marziani, Osservatorio Astronomico di Padova (INAF), ItalyReviewed by:
Lidia Makarova, Special Astrophysical Observatory (RAS), RussiaCopyright © 2023 Tortorelli and Mercurio. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Luca Tortorelli, THVjYS5Ub3J0b3JlbGxpQHBoeXNpay5sbXUuZGU=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.