Electron diffusion by chorus waves: effects of latitude-dependent wave power spectrum

In the present paper, we investigate the effects of latitude-dependent wave power spectrum on the interactions of chorus with electrons. Great errors in evaluating the electron diffusion coefficients and the resultant electron temporal evolutions are introduced by the widely adopted latitudinally constant model, compared with the latitudinally varying model. The latitudinally constant model tends to overestimate (underestimate) the diffusion coefficients for electrons below (above) 200 keV. The overestimation and underestimation are mainly confined in small to intermediate pitch angles, increase with decreasing pitch angles, and can reach up to several orders of magnitude. The large differences in diffusion coefficients significantly alter the net changes of electron phase space densities and the resultant shapes of electron pitch angle distributions. Our simulations demonstrate that the wave power spectrum distribution along the magnetic field line plays an important role in controlling the dynamics of radiation belt electrons.

1 Introduction

Whistler mode chorus waves are natural, coherent, and right-hand polarized electromagnetic emissions widely present in the Earth’s magnetosphere (Burtis and Helliwell, 1969; Meredith et al., 2001; Santolík et al., 2003; Cao et al., 2005; Cao et al., 2007; Fu et al., 2012; Li et al., 2013; Zhima et al., 2013; Yu et al., 2017; Su et al., 2018; Yu et al., 2020a; Liu et al., 2021; Yu et al., 2022). They are commonly believed to be excited near the magnetic equator through the cyclotron instability of anisotropic energetic electrons in the energy range of several keV to ∼100 keV injected from the plasma sheet during geomagnetic disturbed times (Kennel and Petschek, 1966; LeDocq et al., 1998; Su et al., 2014a; Yu et al., 2018; Liu and Chen, 2019). Chorus waves are typically separated into the lower-band (0.1–0.5f_ce) and upper-band (0.5–0.8f_ce) by the deep power gap at 0.5f_ce (f_ce is the equatorial electron gyrofrequency; Teng et al., 2019a) and are usually consist of discrete rising- or falling-tone elements with duration less than 1 s (Tsurutani and Smith, 1977; Santolík et al., 2003; Li et al., 2012; Teng et al., 2017; Yu et al., 2018; Teng et al., 2019b).

Chorus waves have caught increasing attention over the past few decades due to their fundamental dual role in precipitating trapped electrons into the upper atmosphere and accelerating seed electrons to relativistic energy in the outer radiation belt (Horne et al., 2005; Li et al., 2005; 2017; Ni et al., 2008; Su et al., 2010; Thorne et al., 2010; Ni et al., 2011a; Reeves et al., 2013; Thorne, 2013; Su et al., 2014b; Tu et al., 2014; Su et al., 2016; Yu et al., 2016; Yu et al., 2019a; Yu et al., 2020a). It is well known that the efficiency of resonant interaction between chorus waves and radiation belt electrons can be quantified by the quasi-linear diffusion coefficients (Lyons, 1974; Glauert and Horne, 2005), which are used as the inputs of the Fokker-Planck equation to model the temporal evolutions of electron distributions (Schulz and Lanzerotti, 1974; Li et al., 2016; Hua et al., 2018; Ma et al., 2018). However, in the computation of diffusion coefficients, most previous studies usually assume that the chorus wave power spectrum does not vary along the geomagnetic field line (e.g., Lyons, 1974; Albert, 2005; Glauert and Horne, 2005; Summers and Ni, 2008; Shprits and Ni, 2009; Xiao et al., 2009; Su et al., 2010; Subbotin et al., 2010; Thorne et al., 2010; He et al., 2011; Thorne, 2013; Su et al., 2014b; He et al., 2014; Tu et al., 2014; Xiao et al., 2015; Su et al., 2016; Li et al., 2017; Yu et al., 2019a; Yu et al., 2020a). In fact, recent statistics, based on the observations from Polar (Bunch et al., 2013), Cluster (Breuillard et al., 2015), and Van Allen Probes (Agapitov et al., 2018), have clearly shown that the power spectrum of lower-band chorus waves highly depends on the magnetic latitude which is probably caused by the wave amplification, damping and propagation (e.g., Bunch et al., 2013; Breuillard et al., 2015).

Some recent studies incorporated the effects of latitude-dependent chorus spectra in calculating the quasi-linear diffusion coefficients (e.g., Agapitov et al., 2018; Agapitov et al., 2019; Wang and Shprits, 2019; Aryan et al., 2020; Wang et al., 2020). In their works, the effects of some other parameters, including wave power, plasma density, wave normal angle, radial diffusion, etc., are also implied in the calculations and simulations by using statistical wave models. Their results are the comprehensive impacts of these all above parameters. Thus, the exact effects of the latitude-dependent wave power spectrum remain unclear since they are difficult to differentiate from the effects of other parameters. Bunch et al. (2013) evaluated the impact of latitude-dependent chorus spectra on the diffusion time scales only for 1 MeV electrons, indicating that it has a potentially significant impact. Nonetheless, their effects on electrons with other energies are still unknown. In addition, the dynamics of electrons with a certain energy relate to not only their own diffusion coefficients and distributions but also those electrons with other energies. Thus, the current research aims at addressing the effects of latitude-dependent wave power spectrum on both two-dimensional diffusion coefficients of radiation belt electrons and their temporal evolutions.

2 Model description

To compute the diffusion coefficients, the distributions of wave spectral intensity with frequency ($\omega$) and wave normal angle ($\theta$) are necessary to be predefined. Following previous studies, we assume that each of them is a Gaussian distribution expressed by (e.g., Glauret and Horne, 2005; Yu et al., 2019a)

$B^2\left(\omega \right)=\left\{\begin{array}{cc}{A}^2\exp \left(-{\left(\frac{\omega -{\omega }_m}{\delta \omega }\right)}^2\right)& {\omega }_{lc}\le \omega \le {\omega }_{uc}\hfill \\ 0& \text{otherwise},\hfill \end{array}\right.(1)$

with

$A^2=\frac{B_w^2}{\delta \omega }\frac{2}{\sqrt{\pi }}{\left[\mathrm{erf}\left(\frac{{\omega }_m-{\omega }_{lc}}{\delta \omega }\right)+\mathrm{erf}\left(\frac{{\omega }_{uc}-{\omega }_m}{\delta \omega }\right)\right]}^{-1},(2)$

$g\left(\theta \right)=\left\{\begin{array}{cc}\exp \left(-{\left(\frac{\tan \theta -\tan {\theta }_m}{\tan \delta \theta }\right)}^2\right)& {\theta }_{lc}\le \theta \le {\theta }_{uc}\hfill \\ 0& \text{otherwise},\hfill \end{array}\right.(3)$

where $B_w$ is the wave amplitude, ${\omega }_m$ (${\theta }_m$) is the frequency (normal angle) with peak wave power, $\delta \omega$ ($\delta \theta$) is the frequency (angular) width, ${\omega }_{lc}$ (${\theta }_{lc}$) is the lower cutoff frequency (normal angle), and ${\omega }_{uc}$ (${\theta }_{uc}$) is the upper cutoff frequency (normal angle).

To examine the effects of latitudinal dependence of wave power spectrum, two types of spectral models, namely, latitudinally varying and constant models, are adopted for the lower-band chorus waves in our calculations. The peak frequency varies linearly with magnetic latitude ($\lambda$) for the former (${\omega }_m/2\pi =\left(0.35-0.0125\lambda \right)f_{ce}$) taking from Agapitov et al. (2018), while it is independent on magnetic latitude for the latter (${\omega }_m/2\pi =0.35f_{ce}$) based on previous widely used models (e.g., Shprits and Ni, 2009). According to the statistical study of Agapitov et al. (2018), $\delta \omega /2\pi$, ${\omega }_{lc}/2\pi$, and ${\omega }_{uc}/2\pi$ are set to be $0.07f_{ce}$, $0.1f_{ce}$ and $0.5f_{ce}$, respectively. Along with previous works (e.g., Li et al., 2017; Yu et al., 2020a), we assume that the direction of wave propagation is essentially field-aligned with ${\theta }_m=0^{\circ }$, ${\theta }_w=30^{\circ }$, ${\theta }_{lc}=0^{\circ }$ and ${\theta }_{uc}={45}^{\circ }$. Additionally, the ratio of electron plasma frequency to equatorial electron gyrofrequency f_pe/f_ce is taken to be 2.5 at L = 5 (N_e = 3.74 cm⁻³; e.g., Shprits and Ni, 2009; Agapitov et al., 2019). Lastly, the amplitude of chorus is set to be 100 pT and the waves are assumed to be confined within $\left|\lambda \right|\le {20}^{\circ }$ to represent near equatorial nightside chorus (e.g., Agapitov et al., 2018; Yu et al., 2020a). Except for the peak frequency, all other parameters are the same for both models and are kept constant along the magnetic field line to eliminate their interferences.

Once the diffusion coefficients obtained, we can model the temporal evolutions of electron phase space density (F) distributions by numerically solving the two-dimensional bounce-averaged Fokker-Planck diffusion equation (Eq. 4) under reasonable initial distributions (Eq. 5) and boundary conditions (Eqs 6, 7), written as (Yu et al., 2019a)

$\begin{array}{ll}\hfill \frac{\partial F}{\partial t}& =\frac{1}{Gp}\frac{\partial }{\partial {\alpha }_{eq}}\left[G\left(〈D_{\alpha \alpha }〉\frac{1}{p}\frac{\partial F}{\partial {\alpha }_{eq}}+〈D_{\alpha p}〉\frac{\partial F}{\partial p}\right)\right]\hfill \\ \hfill & +\frac{1}{G}\frac{\partial }{\partial {\alpha }_{eq}}\left[G\left(〈D_{\alpha p}〉\frac{1}{p}\frac{\partial F}{\partial {\alpha }_{eq}}+〈D_{pp}〉\frac{\partial F}{\partial p}\right)\right],\hfill \end{array}(4)$

$F\left(t=0\right)=\exp \left[-E/0.1\right]\left(\sin {\alpha }_{eq}-\sin {\alpha }_{LC}\right)/p^2,(5)$

${\left.F\right|}_{{\alpha }_{eq}\le {\alpha }_{LC}}=0,{\left.\frac{\partial F}{\partial {\alpha }_{eq}}\right|}_{{\alpha }_{eq}=90°}=0,(6)$

${\left.F\right|}_{E=10\text{keV}}=\text{constant},{\left.F\right|}_{E=10\text{MeV}}=0,(7)$

where ${\alpha }_{LC}$ is the equatorial loss cone, $G=p^{2}T\left({\alpha }_{eq}\right)\sin {\alpha }_{eq}\cos {\alpha }_{eq}$ with $T\left({\alpha }_{eq}\right)\approx 1.30-0.56\sin {\alpha }_{eq}$, and $〈D_{\alpha \alpha }〉$, $〈D_{\alpha p}〉$ and $〈D_{pp}〉$ are respectively the bounce-averaged pitch angle, mixed and momentum diffusion coefficients computed by our previous developed code (e.g., Li et al., 2017; Yu et al., 2019a; Yu et al., 2020a) on the basis of aforementioned parameters.

3 Numerical results

Figure 1, from left to right, shows the resonant frequency, the resonant power for latitudinally varying and constant models of field-aligned chorus interacting with 0.5 (top) and 1.0 MeV (bottom) electrons as functions of equatorial pitch angles and magnetic latitudes. Consistent with previous studies, the resonant latitude increases with decreasing pitch angles. For electrons at a fixed pitch angle, they interact with higher frequency chorus waves at higher magnetic latitudes. Although the resonant latitude and resonant frequency remain unchanged (left column), the latitude-dependent wave model can significantly alter the resonant power of chorus waves interacting with electrons (middle column), especially for electrons at small pitch angles, compared with the latitude-independent wave model (right column). Thus, it is expected that these changes will strongly alter the chorus-induced electron diffusions which can be quantified by diffusion coefficients and simulated by Fokker-Planck equations.

FIGURE 1

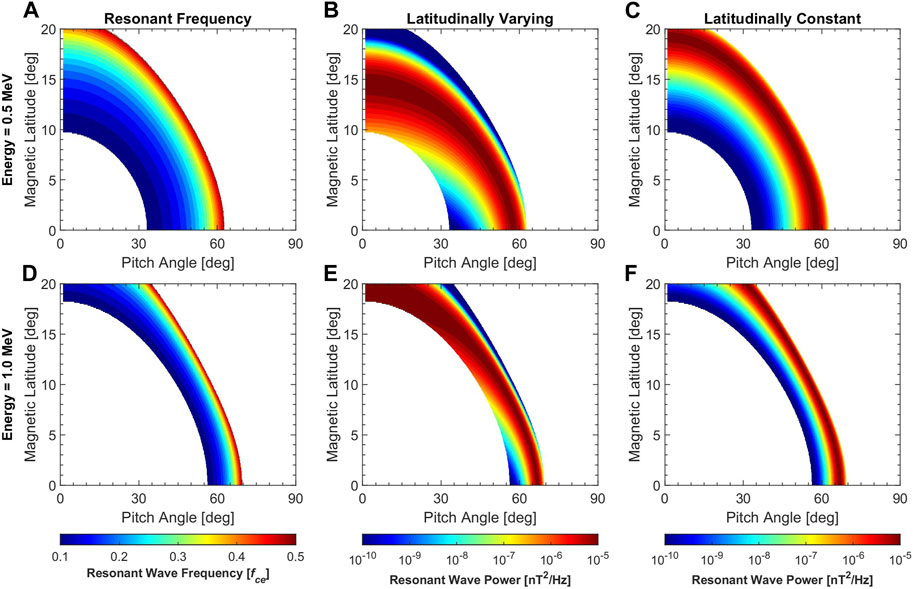
FIGURE 1. The wave frequency (A), wave power for latitudinally varying (B) and constant (C) models of field-aligned chorus resonant with 0.5 MeV electrons as functions of pitch angles and magnetic latitudes. (D–F) The same format as (A–C) except for 1.0 MeV electrons.

The two-dimensional bounce-averaged diffusion coefficients calculated separately by using the latitudinally varying and constant models are shown in the left and middle columns of Figure 2, and their normalized differences in the regions where $〈D_{\alpha \alpha }〉/p^2$ > 10⁻⁶ s⁻¹ are shown in the right column of Figure 2. The calculations of diffusion coefficients include the contributions from cyclotron harmonic resonances up to ±5 as well as Landau resonance. The normalized differences in diffusion coefficients between latitudinally varying (${〈D〉}_{\text{vary}}$) and constant (${〈D〉}_{\text{cont}}$) models are defined as $\frac{\left|{〈D〉}_{\text{vary}}\right|-\left|{〈D〉}_{\text{cont}}\right|}{\left|{〈D〉}_{\text{vary}}\right|+\left|{〈D〉}_{\text{cont}}\right|}$ with values close to 1 and -1 respectively representing that the former is substantially larger and ignorable smaller than the latter.

FIGURE 2

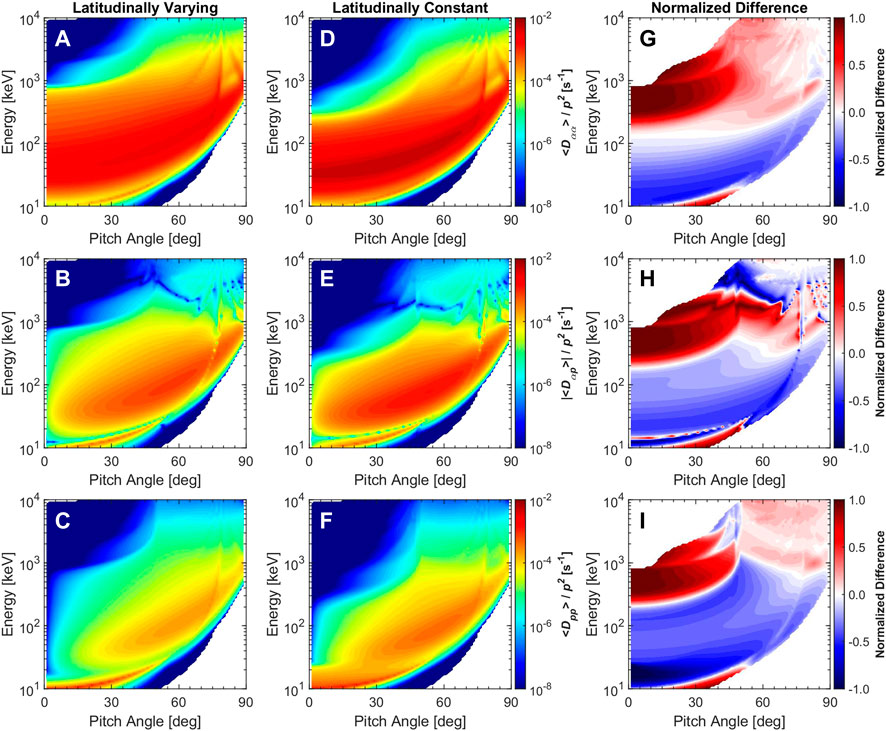
FIGURE 2. The 2-D bounce-averaged pitch angle (top panels: A, D, and G), mixed (middle panels: B, E, and H) and momentum (bottom panels: C, F, and I) diffusion coefficients for latitudinally varying (left panels: A–C) and constant (middle panels: D–F) models of chorus resonant with electrons. The corresponding normalized differences are shown in the right panels (G–I).

The trend of the diffusion coefficient variations for both models exhibits similar features, that is, the resonant range enlarges and the peak shifts to larger pitch angles with increasing electron energies (shown in Figures 2A–F), consistent with previous studies (e.g., He et al., 2014; Yu et al., 2020a). However, as shown in the right column of Figure 2, obvious differences between the two models are seen for electrons below 60° since only these electrons can interact with chorus waves at high latitudes where the wave power spectrum of these two models are significantly different (shown in Figure 1). The differences are more apparent (deeper colors) in the momentum diffusion coefficients for relatively low-energy electrons (<200 keV), while they are more apparent in the pitch angle diffusion coefficients for relatively high-energy electrons (>300 keV). As the pitch angle increases, the differences tend to reduce for all electron energies. Overall, the diffusion coefficients of electrons above 200 keV for the latitudinally varying model are substantially larger than those for the latitudinally constant model (positive normalized differences close to 1), while it is exactly opposite for those of electrons below 100 keV.

The differences in diffusion coefficients between the two models are shown more clearly by the lineplots in Figure 3. The diffusion coefficients at different electron energies using the latitudinally varying and constant models are represented by the solid and dashed color-coded curves, respectively. Obviously, the differences are more apparent in momentum diffusion coefficients for 0.02 and 0.1 MeV electrons which can exceed an order of magnitude for 0.02 MeV electrons near the loss cone (<20°). However, they are more apparent in pitch angle diffusion coefficients for 0.5, 1, and 2 MeV electrons which can reach approximately an order of magnitude at pitch angles below 40°. It is worth noting that the differences in both diffusion coefficients are extremely large for 0.5 MeV electrons. Compared with the results using the latitudinally constant model, the pitch angle diffusion coefficients of 0.5 MeV electrons using the latitudinally varying model are two to three orders of magnitude larger and exceed 10⁻⁴ s⁻¹ near the loss cone (<15°), indicating a much rapider pitch angle scattering loss.

FIGURE 3

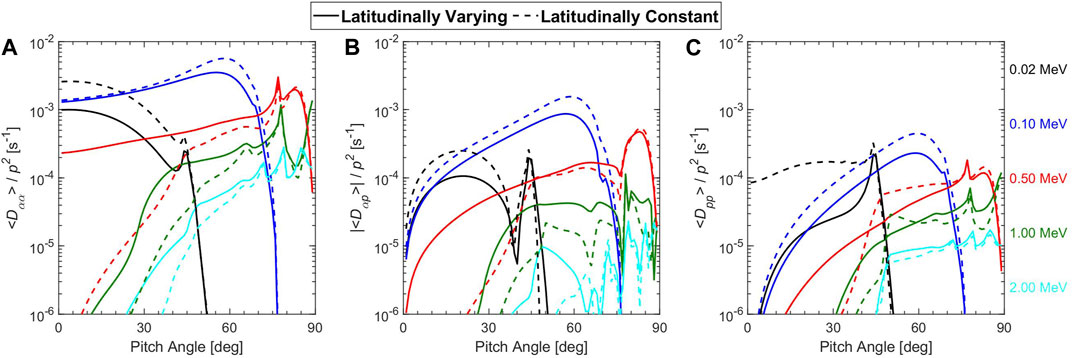
FIGURE 3. The bounce-averaged pitch angle (A), mixed (B) and momentum (C) diffusion coefficients for latitudinally varying (solid) and constant (dashed) models of chorus resonant with electrons at different indicated energies.

Figure 4 shows the temporal evolutions of electron distributions driven by chorus waves as functions of pitch angles and energies at different times (∆t = 1, 2 and 3 h). The initial distribution of electrons is shown in Figure 4A, while their temporal evolutions driven by latitudinally varying and constant chorus waves are shown in Figures 4B–G, respectively. Regardless of the wave power spectrum models, the temporal evolutions of electron distributions driven by chorus waves have similar tendency, namely, tens to hundreds of keV electrons are rapidly depleted while MeV electrons are efficiently enhanced. Obviously, the pitch angle coverage broadens for electron loss but narrows for electron acceleration as the electron energy increases. Generally, the depletion of tens of keV electrons is mainly confined in the small to intermediate pitch angles, whereas the depletion of hundreds of keV electrons occurs at almost all pitch angles. The enhancement of MeV electrons is mainly confined in the intermediate to large pitch angles. However, great differences are also found in the temporal evolutions of electron distributions under the impact of different models of chorus waves. The differences highly depend on the electron energy and tend to be more pronounced for lower and higher energy electrons. The involvement of latitudinal variations of wave power spectrum strongly weakens both the depletion of energetic electrons below ∼300 keV and the enhancement of relativistic electrons above ∼900 keV but deepens the depletion of electrons with energies between them.

FIGURE 4

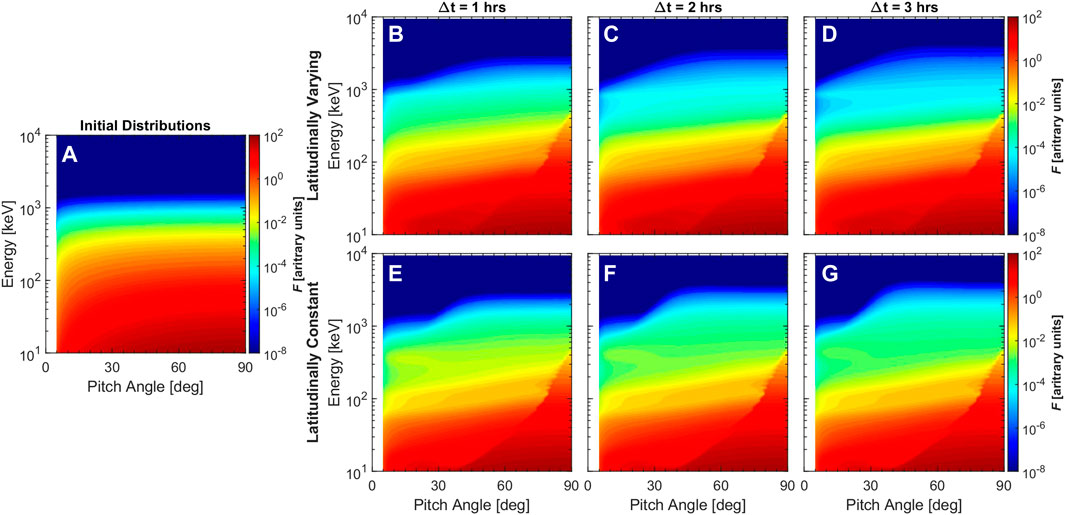
FIGURE 4. (A) The initial 2-D distributions of electron phase space density. The 2-D distribution evolutions of electron phase space density driven by the latitudinally varying (B–D) and constant (E–G) models of chorus waves.

Figure 5 illustrates the temporal evolutions of pitch angle distributions for five different indicated electron energies based on the latitudinally varying (top) and constant (bottom) models. The color-coded curves in each panel represent the electron pitch angle distributions from t = 0 (blue) to 3 (red) hours with 10 min time interval. Regardless of the wave power spectrum models, chorus waves lead to the formation of top-hat distributions for 0.02 and 0.10 MeV electrons through pitch angle scattering below ∼60° (first two columns) and flat-top distributions for 1.00 and 2.00 MeV electrons through acceleration above ∼30° (last two columns). In addition, the phase space densities of 0.5 and 1 MeV electrons firstly increase to their maximum values, and then start to decrease and remain at a stable level, showing a natural upper limit of electron acceleration as reported in the study of (Hua et al., 2022; Hua et al., 2023a). However, compared with latitudinally constant chorus waves, latitudinally varying chorus waves slow down both the depletion of 0.02 and 0.10 MeV electrons by several times and the enhancement of 1.00 and 2.00 MeV electrons by an order of magnitude but speed up the depletion of 0.50 MeV electrons. It is worth noting that the influence is stronger with decreasing pitch angles for 0.50 MeV electrons, whereas it is almost irrelative to pitch angles for the other four energy electrons. Consequently, the shape of pitch angle distributions changes from flat-top to pancake distributions for 0.50 MeV electrons, whereas it is kept almost unchanged for the electrons in other four energies. However, the top-hat distributions are weaker for 0.02 and 0.10 MeV electrons due to the weaker depletion, and the flat-top distributions are broader for 1.00 and 2.00 MeV electrons due to the wider pitch angle coverage of efficient acceleration.

FIGURE 5

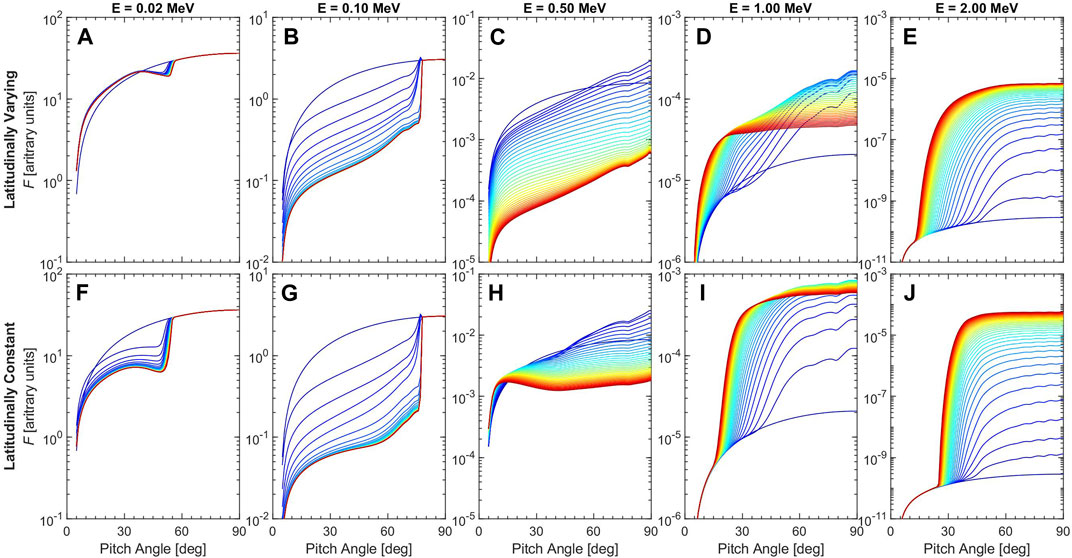
FIGURE 5. Temporal evolutions of pitch angle distributions for electrons with energies E = 0.02 MeV (A and F), 0.10 MeV (B and G), 0.50 MeV (C and H), 1.00 MeV (D and I) and 2.00 MeV (E and J) based on the latitudinally varying (A–E) and constant (F–J) models. The color-coded curves in each panel represent the electron pitch angle distributions from t = 0 (blue) to 3 (red) hours with 10 min time interval.

Figure 6 shows the temporal evolutions of energy spectra of electron phase space densities. The electron energy spectra have similar temporal evolutions regardless of the wave models. Low-energy (high-energy) electrons experience continuous losses (accelerations), and middle-energy electrons experience accelerations first followed by losses. When considering the variation of wave frequency spectrum along the latitude, the transition energy from loss to acceleration increases slightly from ∼700 keV to ∼900 keV. Around the transition energy, the accelerations of electrons with energies above it slow down, while the losses of electrons with energies below it speed up. For those electrons with energies far away from it, the impacts are limited.

FIGURE 6

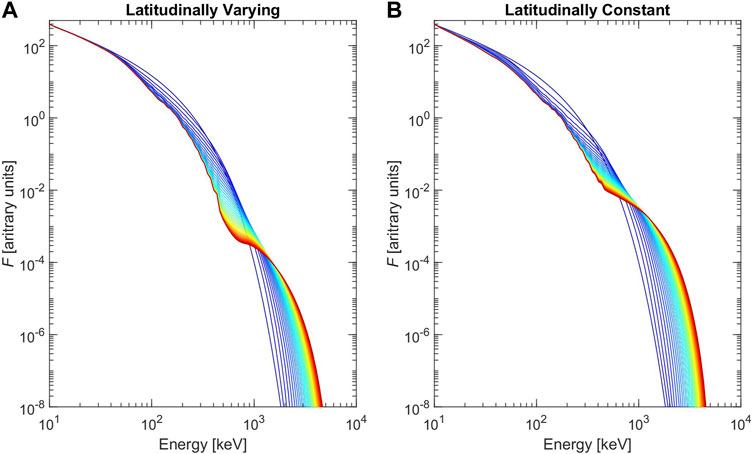
FIGURE 6. Temporal evolutions of energy spectra of omnidirectional electron phase space densities for the latitudinally varying (A) and constant (B) models. The color-coded curves in each panel represent the electron energy spectra from t = 0 (blue) to 3 (red) hours with 10 min time interval.

4 Conclusion and discussions

In the present paper, we investigate the effects of latitudinal dependence of wave power spectrum on the resonant interactions between chorus waves and radiation belt electrons. On the basis of quasi-linear theory, the bounce-averaged diffusion coefficients are firstly calculated, and the temporal evolutions of electron distributions are subsequently simulated using both the latitudinally varying and constant models. The computations show that the variations of chorus wave power spectrum with magnetic latitudes can significantly affect the electron diffusion coefficients and thus the electron temporal evolutions. Since the differences in wave power spectrum between the latitudinally varying and constant models increase with magnetic latitudes, their differences in diffusion coefficients, which can reach up to several orders of magnitudes, are mainly confined in small to intermediate pitch angles (<60°) and increase with decreasing pitch angles. Using the latitudinally constant model, the diffusion coefficients tend to be overestimated for electrons below 200 keV and underestimated for the energy above that. The overestimations are more apparent in momentum diffusion coefficients, while the underestimations are more apparent in pitch angle diffusion coefficients. Although the major differences in diffusion coefficients are confined below 60° pitch angles, their impacts on the temporal evolutions of electron distributions above 100 keV can expand to large pitch angles above that. The widely adopted assumption latitudinally constant model strongly overestimates both the depletion of energetic electrons below ∼300 keV and the enhancement of relativistic electrons above ∼900 keV but underestimates the depletion of electrons with energies between them. The errors can exceed an order of magnitude. Consequently, the inclusion of latitudinal variations of wave power spectrum tends to weaken the top-hat distributions of low-energy electrons, change the distribution shape of middle energy electrons, and broaden the flat-top distributions of high-energy electrons.

The study of Hua et al. (2023b) also investigated the influence of variations in chorus wave peak frequency on the simulated electron acceleration. In their work, the variations of the wave peak frequency and frequency spectrum are latitude-independent. Thus, electrons at all pitch angles will be affected during the bounce motion. Compared to their work, the influences of latitude-dependent wave frequency spectrum on electrons highly depend on the pitch angles. Since the peak wave frequency decreases linearly along the magnetic latitude, the variation of wave frequency spectrum is more pronounced with the increasing latitude. Thus, those electrons with lower pitch angles are affected more strongly due to their higher mirror latitudes whereas those nearly mirroring electrons are almost unaffected. As a result, their and our models have different impacts on diffusion coefficients. Such differences in diffusion coefficients will eventually result in the different processes of electron accelerations.

Previous numerical studies have shown that the magnetospheric wave-induced diffusions of radiation belt electrons are controlled by various parameters, such as the wave amplitude (e.g., Summers and Ni, 2008), wave normal angle (e.g., Shprit and Ni, 2009; Ni et al., 2011b), background magnetic field (e.g., Orlova and Shprits, 2010), plasma density (e.g., Summers and Ni, 2008; Agapitov et al., 2019) and hot plasmas (e.g., Chen et al., 2013; Yu et al., 2019b; Yu et al., 2020b). Their results show that the differences in wave-induced diffusion coefficients due to the variations of above parameters are mostly from several times up to orders of magnitude. Our calculations indicate that the differences due to the latitudinal dependence of wave power spectrum can be as large as orders of magnitude, which is comparable to or even over those other parameters. Thus, we strongly suggest that future statistical works are required to establish the realistic models of power spectrum of various magnetospheric waves (e.g., hiss and electromagnetic ion cyclotron waves) against magnetic latitude, which should be incorporated into future modeling to enrich our understanding of the radiation belt particle dynamics.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

JY: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Software, Writing–original draft. JW: Validation, Writing–review and editing. ZH: Software, Validation, Writing–review and editing. ZC: Validation, Writing–review and editing. LL: Validation, Writing–review and editing. JuC: Funding acquisition, Validation, Writing–review and editing. JiC: Validation, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work is supported by the National Natural Science Foundation of China (NSFC) through grants 42074193, 42174185, and 42261160643.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Agapitov, O., Mourenas, D., Artemyev, A., Hospodarsky, G., and Bonnell, J. W. (2019). Time scales for electron quasi-linear diffusion by lower-band chorus waves: the effects of ω_pe/Ω_ce dependence on geomagnetic activity. Geophys. Res. Lett. 46, 6178–6187. doi:10.1029/2019GL083446

CrossRef Full Text | Google Scholar

Agapitov, O. V., Mourenas, D., Artemyev, A. V., Mozer, F. S., Hospodarsky, G., Bonnell, J., et al. (2018). Synthetic empirical chorus wave model from combined Van Allen Probes and Cluster statistics. J. Geophys. Res. Space Phys. 123, 297–314. doi:10.1002/2017JA024843

CrossRef Full Text | Google Scholar

Albert, J. M. (2005). Evaluation of quasi-linear diffusion coefficients for whistler mode waves in a plasma with arbitrary density ratio. J. Geophys. Res. 110, A03218. doi:10.1029/2004JA010844

CrossRef Full Text | Google Scholar

Aryan, H., Agapitov, O. V., Artemyev, A., Mourenas, D., Balikhin, M. A., Boynton, R., et al. (2020). Outer radiation belt electron lifetime model based on combined Van Allen Probes and Cluster VLF measurements. J. Geophys. Res. Space Phys. 125, e2020JA028018. doi:10.1029/2020JA028018

CrossRef Full Text | Google Scholar

Breuillard, H., Agapitov, O., Artemyev, A., Kronberg, E. A., Haaland, S. E., Daly, P. W., et al. (2015). Field-aligned chorus wave spectral power in Earth’s outer radiation belt. Ann. Geophys. 33 (5), 583–597. doi:10.5194/angeo-33-583-2015

CrossRef Full Text | Google Scholar

Bunch, N. L., Spasojevic, M., Shprits, Y. Y., Gu, X., and Foust, F. (2013). The spectral extent of chorus in the off-equatorial magnetosphere. J. Geophys. Res. Space Phys. 118, 1700–1705. doi:10.1029/2012JA018182

CrossRef Full Text | Google Scholar

Burtis, W. J., and Helliwell, R. A. (1969). Banded chorus—a new type of VLF radiation observed in the magnetosphere by OGO 1 and OGO 3. J. Geophys. Res. 74 (11), 3002–3010. doi:10.1029/JA074i011p03002

CrossRef Full Text | Google Scholar

Cao, J., Yang, J., Yan, C., and Li, L. (2007). The observations of high energy electrons and associated waves by DSP satellites during substorm. Nucl. Phys. B - Proc. Suppl. 166, 56–61. doi:10.1016/j.nuclphysbps.2006.12.066

CrossRef Full Text | Google Scholar

Cao, J. B., Liu, Z. X., Yang, J. Y., Yian, C. X., Wang, Z. G., Zhang, X. H., et al. (2005). First results of low frequency electromagnetic wave detector of TC-2/Double Star program. Ann. Geophys. 23 (8), 2803–2811. doi:10.5194/angeo-23-2803-2005

CrossRef Full Text | Google Scholar

Chen, L., Thorne, R. M., Shprits, Y., and Ni, B. (2013). An improved dispersion relation for parallel propagating electromagnetic waves in warm plasmas: application to electron scattering. J. Geophys. Res. Space Phys. 118, 2185–2195. doi:10.1002/jgra.50260

CrossRef Full Text | Google Scholar

Fu, H. S., Cao, J. B., Mozer, F. S., Lu, H. Y., and Yang, B. (2012). Chorus intensification in response to interplanetary shock. J. Geophys. Res. 117 (A1), A01203. doi:10.1029/2011JA016913

CrossRef Full Text | Google Scholar

Glauert, S. A., and Horne, R. B. (2005). Calculation of pitch angle and energy diffusion coefficients with the PADIE code. J. Geophys. Res. 110, A04206. doi:10.1029/2004JA010851

CrossRef Full Text | Google Scholar

He, Z., Xiao, F., Zong, Q., Wang, Y., Chen, L., Yue, C., et al. (2011). Multi-satellite observations on the storm-time enhancements of energetic outer zone electron fluxes driven by chorus waves. Sci. CHINA Technol. Sci. 54 (8), 2209–2216. doi:10.1007/s11431-011-4445-6

CrossRef Full Text | Google Scholar

He, Z., Zhu, H., Liu, S., Zong, Q., Wang, Y., Lin, R., et al. (2014). Correlated observations and simulations on the buildup of radiation belt electron fluxes driven by substorm injections and chorus waves. Astrophysics Space Sci. 355 (2), 245–251. doi:10.1007/s10509-014-2180-8

CrossRef Full Text | Google Scholar

Horne, R. B., Thorne, R. M., Shprits, Y. Y., Meredith, N. P., Glauert, S. A., Smith, A. J., et al. (2005). Wave acceleration of electrons in the Van Allen radiation belts. Nature 437 (7056), 227–230. doi:10.1038/nature03939

PubMed Abstract | CrossRef Full Text | Google Scholar

Hua, M., Bortnik, J., Kellerman, A. C., Camporeale, E., and Ma, Q. (2023b). Ensemble modeling of radiation belt electron acceleration by chorus waves: dependence on key input parameters. Space weather. 21, e2022SW003234. doi:10.1029/2022SW003234

CrossRef Full Text | Google Scholar

Hua, M., Bortnik, J., and Ma, Q. (2022). Upper limit of outer radiation belt electron acceleration driven by whistler-mode chorus waves. Geophys. Res. Lett. 49, e2022GL099618. doi:10.1029/2022GL099618

CrossRef Full Text | Google Scholar

Hua, M., Bortnik, J., Spence, H. E., and Reeves, G. D. (2023a). Testing the key processes that accelerate outer radiation belt relativistic electrons during geomagnetic storms. Front. Astronomy Space Sci. 10, 1168636. doi:10.3389/fspas.2023.1168636

CrossRef Full Text | Google Scholar

Hua, M., Ni, B., Fu, S., Gu, X., Xiang, Z., Cao, X., et al. (2018). Combined scattering of outer radiation belt electrons by simultaneously occurring chorus, exohiss, and magnetosonic waves. Geophys. Res. Lett. 45. doi:10.1029/2018GL079533

CrossRef Full Text | Google Scholar

Kennel, C. F., and Petschek, H. E. (1966). Limit on stably trapped particle fluxes. J. Geophys. Res. 71 (1), 1–28. doi:10.1029/JZ071i001p00001

CrossRef Full Text | Google Scholar

LeDocq, M. J., Gurnett, D. A., and Hospodarsky, G. B. (1998). Chorus source locations from VLF Poynting flux measurements with the Polar spacecraft. Geophys. Res. Lett. 25 (21), 4063–4066. doi:10.1029/1998GL900071

CrossRef Full Text | Google Scholar

Li, L. Y., Cao, J., and Zhou, G. (2005). Combined acceleration of electrons by whistler-mode and compressional ULF turbulences near the geosynchronous orbit. J. Geophys. Res. 110 (A3), A03203. doi:10.1029/2004JA010628

CrossRef Full Text | Google Scholar

Li, L. Y., Yu, J., Cao, J. B., Yang, J. Y., Li, X., Baker, D. N., et al. (2017). Roles of whistler mode waves and magnetosonic waves in changing the outer radiation belt and the slot region. J. Geophys. Res. Space Phys. 122, 5431–5448. doi:10.1002/2016JA023634

CrossRef Full Text | Google Scholar

Li, L. Y., Yu, J., Cao, J. B., Zhang, D., Wei, X. H., Rong, Z. J., et al. (2013). Rapid loss of the plasma sheet energetic electrons associated with the growth of whistler mode waves inside the bursty bulk flows. J. Geophys. Res. Space Phys. 118, 7200–7210. doi:10.1002/2013JA019109

CrossRef Full Text | Google Scholar

Li, W., Ma, Q., Thorne, R. M., Bortnik, J., Zhang, X., Li, J., et al. (2016). Radiation belt electron acceleration during the 17 March 2015 geomagnetic storm: observations and simulations. J. Geophys. Res. Space Phys. 121, 5520–5536. doi:10.1002/2016JA022400

CrossRef Full Text | Google Scholar

Li, W., Thorne, R. M., Bortnik, J., Tao, X., and Angelopoulos, V. (2012). Characteristics of hiss-like and discrete whistler-mode emissions. Geophys. Res. Lett. 39, L18106. doi:10.1029/2012GL053206

CrossRef Full Text | Google Scholar

Liu, X., and Chen, L. (2019). Instability in a relativistic magnetized plasma. Phys. Plasmas 26 (4), 042902. doi:10.1063/1.5089749

CrossRef Full Text | Google Scholar

Liu, X., Gu, W., Xia, Z., Chen, L., and Horne, R. B. (2021). Frequency-dependent modulation of whistler-mode waves by density irregularities during the recovery phase of a geomagnetic storm. Geophys. Res. Lett. 48, e2021GL093095. doi:10.1029/2021GL093095

CrossRef Full Text | Google Scholar

Lyons, L. R. (1974). Pitch angle and energy diffusion coefficients from resonant interactions with ion-cyclotron and whistler waves. J. Plasma Phys. 12, 417–432. doi:10.1017/s002237780002537x

CrossRef Full Text | Google Scholar

Ma, Q., Li, W., Bortnik, J., Thorne, R. M., Chu, X., Ozeke, L. G., et al. (2018). Quantitative evaluation of radial diffusion and local acceleration processes during GEM challenge events. J. Geophys. Res. Space Phys. 123, 1938–1952. doi:10.1002/2017JA025114

CrossRef Full Text | Google Scholar

Meredith, N. P., Horne, R. B., and Anderson, R. R. (2001). Substorm dependence of chorus amplitudes: implications for the acceleration of electrons to relativistic energies. J. Geophys. Res. 106, 13165–13178. doi:10.1029/2000JA900156

CrossRef Full Text | Google Scholar

Ni, B., Thorne, R. M., Meredith, N. P., Horne, R. B., and Shprits, Y. Y. (2011a). Resonant scattering of plasma sheet electrons leading to diffuse auroral precipitation: 2. Evaluation for whistler mode chorus waves. J. Geophys. Res. 116, A04219. doi:10.1029/2010JA016233

CrossRef Full Text | Google Scholar

Ni, B., Thorne, R. M., Meredith, N. P., Shprits, Y. Y., and Horne, R. B. (2011b). Diffuse auroral scattering by whistler mode chorus waves: dependence on wave normal angle distribution. J. Geophys. Res. 116, A10207. doi:10.1029/2011JA016517

CrossRef Full Text | Google Scholar

Ni, B., Thorne, R. M., Shprits, Y. Y., and Bortnik, J. (2008). Resonant scattering of plasma sheet electrons by whistler-mode chorus: contribution to diffuse auroral precipitation. Geophys. Res. Lett. 35, L11106. doi:10.1029/2008GL034032

CrossRef Full Text | Google Scholar

Orlova, K. G., and Shprits, Y. Y. (2010). Dependence of pitch angle scattering rates and loss timescales on the magnetic field model. Geophys. Res. Lett. 37 (5). doi:10.1029/2009GL041639

CrossRef Full Text | Google Scholar

Reeves, G. D., Spence, H. E., Henderson, M. G., Morley, S. K., Friedel, R. H. W., Funsten, H. O., et al. (2013). Electron acceleration in the heart of the Van Allen radiation belts. Science 341 (6149), 991–994. doi:10.1126/science.1237743

PubMed Abstract | CrossRef Full Text | Google Scholar

Santolík, O., Gurnett, D. A., Pickett, J. S., Parrot, M., and Cornilleau-Wehrlin, N. (2003). Spatio-temporal structure of storm-time chorus. J. Geophys. Res. 108 (A7), 1278. doi:10.1029/2002JA009791

CrossRef Full Text | Google Scholar

Schulz, M., and Lanzerotti, L. J. (1974). “Particle diffusion in the radiation belts,” in Physics and chemistry in space (New York: Springer).

CrossRef Full Text | Google Scholar

Shprits, Y. Y., and Ni, B. (2009). Dependence of the quasi-linear scattering rates on the wave normal distribution of chorus waves. J. Geophys. Res. 114, A11205. doi:10.1029/2009JA014223

CrossRef Full Text | Google Scholar

Su, Z., Gao, Z., Zhu, H., Li, W., Zheng, H., Wang, Y., et al. (2016). Nonstorm time dropout of radiation belt electron fluxes on 24 September 2013. J. Geophys. Res. Space Phys. 121, 6400–6416. doi:10.1002/2016JA022546

CrossRef Full Text | Google Scholar

Su, Z., Liu, N., Zheng, H., Wang, Y., and Wang, S. (2018). Large-amplitude extremely low frequency hiss waves in plasmaspheric plumes. Geophys. Res. Lett. 45, 565–577. doi:10.1002/2017GL076754

CrossRef Full Text | Google Scholar

Su, Z., Xiao, F., Zheng, H., He, Z., Zhu, H., Zhang, M., et al. (2014b). Nonstorm time dynamics of electron radiation belts observed by the Van Allen Probes. Geophys. Res. Lett. 41, 229–235. doi:10.1002/2013GL058912

CrossRef Full Text | Google Scholar

Su, Z., Zheng, H., and Wang, S. (2010). A parametric study on the diffuse auroral precipitation by resonant interaction with whistler mode chorus. J. Geophys. Res. 115, A05219. doi:10.1029/2009JA014759

CrossRef Full Text | Google Scholar

Su, Z., Zhu, H., Xiao, F., Zheng, H., Wang, Y., He, Z., et al. (2014a). Intense duskside lower band chorus waves observed by Van Allen Probes: generation and potential acceleration effect on radiation belt electrons. J. Geophys. Res. Space Phys. 119, 4266–4273. doi:10.1002/2014JA019919

CrossRef Full Text | Google Scholar

Subbotin, D. A., Shprits, Y. Y., and Ni, B. (2010). Three-dimensional VERB radiation belt simulations including mixed diffusion. J. Geophys. Res. 115, A03205. doi:10.1029/2009JA015070

CrossRef Full Text | Google Scholar

Summers, D., and Ni, B. (2008). Effects of latitudinal distributions of particle density and wave power on cyclotron resonant diffusion rates of radiation belt electrons. Earth Planet Space 60, 763–771. doi:10.1186/BF03352825

CrossRef Full Text | Google Scholar

Teng, S., Li, W., Tao, X., Shen, X.-C., and Ma, Q. (2019b). Characteristics of rising tone whistler mode waves inside the Earth's plasmasphere, plasmaspheric plumes, and plasmatrough. Geophys. Res. Lett. 46, 7121–7130. doi:10.1029/2019gl083372

CrossRef Full Text | Google Scholar

Teng, S., Tao, X., and Li, W. (2019a). Typical characteristics of whistler mode waves categorized by their spectral properties using Van Allen Probes observations. Geophys. Res. Lett. 46, 3607–3614. doi:10.1029/2019GL082161

CrossRef Full Text | Google Scholar

Teng, S., Tao, X., Xie, Y., Zonca, F., Chen, L., Fang, W. B., et al. (2017). Analysis of the duration of rising tone chorus elements. Geophys. Res. Lett., 44, 12 74–12. doi:10.1002/2017GL075824

CrossRef Full Text | Google Scholar

Thorne, R. M., Li, W., Ni, B., Ma, Q., Bortnik, J., Chen, L., et al. (2013). Rapid local acceleration of relativistic radiation-belt electrons by magnetospheric chorus. Nature 504, 411–414. doi:10.1038/nature12889

PubMed Abstract | CrossRef Full Text | Google Scholar

Thorne, R. M., Ni, B., Tao, X., Horne, R. B., and Meredith, N. P. (2010). Scattering by chorus waves as the dominant cause of diffuse auroral precipitation. Nature 467, 943–946. doi:10.1038/nature09467

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsurutani, B. T., and Smith, E. J. (1977). Two types of magnetospheric ELF chorus and their substorm dependences. J. Geophys. Res. 82, 5112–5128. doi:10.1029/JA082i032p05112

CrossRef Full Text | Google Scholar

Tu, W., Cunningham, G. S., Chen, Y., Morley, S. K., Reeves, G. D., Blake, J. B., et al. (2014). Event-specific chorus wave and electron seed population models in DREAM3D using the Van Allen Probes. Geophys. Res. Lett. 41, 1359–1366. doi:10.1002/2013GL058819

CrossRef Full Text | Google Scholar

Wang, D., and Shprits, Y. Y. (2019). On how high-latitude chorus waves tip the balance between acceleration and loss of relativistic electrons. Geophys. Res. Lett. 46, 7945–7954. doi:10.1029/2019GL082681

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, D., Shprits, Y. Y., Zhelavskaya, I. S., Effenberger, F., Castillo, A., Drozdov, A. Y., et al. (2020). The effect of plasma boundaries on the dynamic evolution of relativistic radiation belt electrons. J. Geophys. Res. Space Phys. 125, e2019JA027422. doi:10.1029/2019JA027422

CrossRef Full Text | Google Scholar

Xiao, F., Su, Z., Zheng, H., and Wang, S. (2009). Modeling of outer radiation belt electrons by multidimensional diffusion process. J. Geophys. Res. 114, A03201. doi:10.1029/2008JA013580

CrossRef Full Text | Google Scholar

Xiao, F., Yang, C., Su, Z., Zhou, Q., He, Z., He, Y., et al. (2015). Wave-driven butterfly distribution of Van Allen belt relativistic electrons. Nat. Commun. 6, 8590. doi:10.1038/ncomms9590

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, J., Li, L. Y., Cao, J. B., Chen, L., Wang, J., and Yang, J. (2017). Propagation characteristics of plasmaspheric hiss: Van Allen Probe observations and global empirical models. J. Geophys. Res. Space Phys. 122, 4156–4167. doi:10.1002/2016JA023372

CrossRef Full Text | Google Scholar

Yu, J., Li, L. Y., Cui, J., Cao, J. B., and Wang, J. (2019a). Combined effects of equatorial chorus waves and high-latitude Z-mode waves on Saturn's radiation belt electrons. Geophys. Res. Lett. 46, 8624–8632. doi:10.1029/2019GL084004

CrossRef Full Text | Google Scholar

Yu, J., Li, L. Y., Cui, J., Cao, J. B., and Wang, J. (2019b). Effect of hot He⁺ ions on the electron pitch angle scattering driven by H⁺, He⁺, and O⁺ band EMIC waves. Geophys. Res. Lett. 46, 6306–6314. doi:10.1029/2019GL083456

CrossRef Full Text | Google Scholar

Yu, J., Li, L. Y., Cui, J., Cao, J. B., Wang, J., He, Z. G., et al. (2020b). Nonlinear interactions between relativistic electrons and EMIC waves in magnetospheric warm plasma environments. J. Geophys. Res. Space Phys. 125, e2020JA028089. doi:10.1029/2020JA028089

CrossRef Full Text | Google Scholar

Yu, J., Li, L. Y., Cui, J., and Wang, J. (2018). Ultrawideband rising-tone chorus waves observed inside the oscillating plasmapause. J. Geophys. Res. Space Phys. 123, 6670–6678. doi:10.1029/2018JA025875

CrossRef Full Text | Google Scholar

Yu, J., Wang, J., He, Z., Liu, N., Li, K., Ren, A., et al. (2022). Combined scattering of suprathermal electrons by whistler-mode chorus and electromagnetic ion cyclotron waves in the low-density plasmatrough. J. Geophys. Res. Space Phys. 127, e2022JA030640. doi:10.1029/2022JA030640

CrossRef Full Text | Google Scholar

Yu, J., Wang, J., Li, L. Y., Cui, J., Cao, J. B., and He, Z. G. (2020a). Electron diffusion by coexisting plasmaspheric hiss and chorus waves: multisatellite observations and simulations. Geophys. Res. Lett. 47, e2020GL088753. doi:10.1029/2020GL088753

CrossRef Full Text | Google Scholar

Yu, Y., Jordanova, V. K., Ridley, A. J., Albert, J. M., Horne, R. B., and Jeffery, C. A. (2016). A new ionospheric electron precipitation module coupled with RAM-SCB within the geospace general circulation model. J. Geophys. Res. Space Phys. 121, 8554–8575. doi:10.1002/2016JA022585

CrossRef Full Text | Google Scholar

Zhima, Z., Cao, J., Liu, W., Fu, H., Yang, J., Zhang, X., et al. (2013). DEMETER observations of high-latitude chorus waves penetrating the plasmasphere during a geomagnetic storm. Geophys. Res. Lett. 40, 5827–5832. doi:10.1002/2013GL058089

CrossRef Full Text | Google Scholar