- 1Center for Space Plasma and Aeronomic Research (CSPAR), University of Alabama in Huntsville, Huntsville, AL, United States
- 2Department of Space Science, University of Alabama in Huntsville, Huntsville, AL, United States
The distribution of turbulence in the heliosphere remains a mystery, due to the complexity in not only modeling the turbulence transport equations but also identifying the drivers of turbulence that vary with time and spatial location. Beyond the ionization cavity (a few astronomical units (AU) from the Sun), the turbulence is driven predominantly by freshly created pickup ions (PUIs), in contrast to the driving by stream shear and compression. Understanding the source characteristics is necessary to refine turbulence transport models and interpret measurements of turbulence and solar wind temperature in the outer heliosphere. Using a recent latitude-dependent solar wind speed model and the ionization rate of neutral interstellar hydrogen (H), we investigate the temporal and spatial variation in the strength of low-frequency turbulence driven by PUIs from 1998 to 2020. We find that the driving rate is stronger during periods of high solar activity and at lower latitudes in the outer heliosphere. The driving rates for parallel and anti-parallel propagating (relative to the background magnetic field) slab turbulence have different spatial and latitude dependences. The calculated generation rate of turbulence by PUIs is an essential ingredient to investigate the latitude dependence of turbulence in the outer heliosphere, which is important to understand the heating of the distant solar wind and the modulation of cosmic rays.
1 Introduction
Although turbulence plays a crucial role in multiple aspects of space physics and astrophysics, the distribution of turbulence in our solar system remains unclear, especially in the outer heliosphere, which has been explored by few spacecraft. Many models have been developed over the past few decades to describe the transport of turbulence in the heliosphere (Breech et al., 2008; Ng et al., 2010; Oughton et al., 2011; Usmanov et al., 2011; Zank et al., 2012; 2017; 2018; Nakanotani et al., 2020; Wang et al., 2022; Adhikari et al., 2023), and the source terms that describe the driving of turbulence are indispensable. Due to uncertainty in the model parameters, oversimplified source terms, and a lack of observations, a consensus has not been reached yet about the overall model, and consequently, different models coexist.
In this work, we investigated the temporal and latitudinal evolution of turbulence driven by pickup ions (PUIs). Beyond the ionization cavity for neutral hydrogen, turbulence is mainly driven by PUIs. The newborn PUIs initially form a ring-beam distribution, which is highly unstable and drives electromagnetic fluctuations. The energy transferred from PUIs to turbulence is free energy. The driving rate of turbulence by PUIs is the product of the free energy of a single PUI and the creation rate of PUIs. The latter is also closely related to solar activity and depends on latitude. To calculate the driving rate of turbulence by PUIs, we adopt the solar wind speed model derived from remote observations via interplanetary scintillations (IPSs). The heliospheric magnetic field measured by the ACE spacecraft in the ecliptic plane is used as the input for the Parker magnetic field model to obtain the magnetic field within the termination shock. The observation-based solar wind and extreme ultraviolet radiation data provide the ionization rates as a function of time and latitude. We investigate the evolution of the turbulence driving rate by PUIs (i.e., the source of turbulence due to PUIs) from 1998 to 2020.
2 Methods and results
In the outer heliosphere, beyond the ionization cavity, freshly created pickup ions are the main source of turbulence (Zank et al., 1996). The amplification of turbulence/waves due to newborn pickup ions is observed by multiple spacecraft (Smith et al., 2017; Sokół et al., 2022). The driving rate of the turbulence is given by Zank et al. (1996) as follows:
where nPUI(SW) is the pickup ion (solar wind) density, dnPUI/dt = naβ denotes the production rate of pickup ions, U is the solar wind speed, and vA is the Alfvén speed. na is the density of neutral H atoms, and β is the ionization rate. The factor vA/U represents the fraction of pickup ion kinetic energy available for the generation of turbulence (the so-called free energy) (Lee and Ip, 1987; Huddleston and Johnstone, 1992; Williams and Zank, 1994). Although this fraction gives the correct free energy for most of the heliospheric region where the solar wind velocity is perpendicular to the heliospheric magnetic field, the free energy for the slab turbulence that propagates parallel (E+) and anti-parallel (E−) relative to the large-scale magnetic field is generally different and depends on the angle between the solar wind velocity and large-scale magnetic field (θUB) (Williams and Zank, 1994)1.
where
where γ = rΩ sin(θ)/U and Ω is the angular frequency of the solar rotation. The three fast latitude scans of Ulysses measured the solar wind speed out of the ecliptic plane, covering nearly the entire range of solar latitudes in a relatively short time (07/94–08/95, 11/2000–10/2001, and 02/2007–02/2008) (McComas et al., 2002). During the first and third scans around the solar minimum, Ulysses observed a well-ordered solar wind structure, and the solar wind speed increased from
where Pi is the Legendre polynomial of ith order, Qi is the coefficient of ith polynomial, and N is the order. The coefficients are listed in Table 2. The deceleration of the solar wind speed in the outer heliosphere by PUIs is modeled as (Isenberg et al., 2010)
where U is measured in the units of km s−1 and r is measured in the units of AU.
For the heliospheric magnetic field, we use the Parker magnetic field model (Parker, 1958):
where B0 is a constant. The magnetic field in the elliptic plane is measured by the ACE spacecraft and can be obtained from the ACE Science Center2. With the solar wind speed and the heliospheric magnetic field, we can calculate their angle, θUB. As shown in Figure 1, in the inner heliosphere and at high latitudes, θUB is not as large as 90°, and thus, the more general Eqs 2, 3 are needed to accurately describe the free energies.
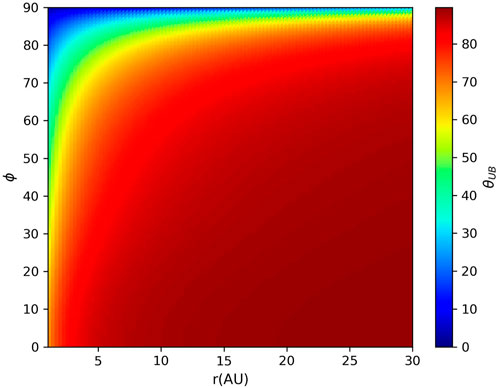
FIGURE 1. Angle between the solar wind velocity and heliospheric magnetic field (θUB) from 1 to 30 AU for the year 2009. The color bar chart indicates θUB from 0° to 90°.
To obtain the Alfvén speed for Eqs 2, 3, we further need the profile of the plasma density. The solar wind speed and density are linked through the solar wind energy flux, and the energy flux is independent of the latitude within a factor of 10% (Le Chat et al., 2012). The latitude-dependent density at 1 AU (ρ1(θ)) can be derived via (Le Chat et al., 2012)
where UE = U (r = 1AU, θ = π/2), ρE/mp is the measured solar wind proton density near Earth (mp is the proton mass), G is the gravitational constant, Ms is the mass of the Sun, and Rs is the radius of the Sun. We use the yearly averaged values to calculate ρ(θ). According to the mass continuity equation, the density in the outer heliosphere is
The driving rate is proportional to the creation rate of PUIs,
where
The ionization rate changes with latitude and solar activity cycle as a result of variation in the solar wind flow and the solar extreme ultraviolet (EUV) flux (Bzowski et al., 2013; Sokół et al., 2019; Sokół et al., 2020). The dominant ionization process for H atoms is the charge exchange with solar wind particles. The resulting ionization rate is equal to the product of solar wind (number) density, the relative speed between H atoms and solar wind speed, and the cross section as a function of relative speed. As the latitude dependence of the solar wind speed is derived from the fact that the energy flux of the solar wind is almost latitude-independent, the product of solar wind density and solar wind speed is approximately inversely proportional to the square of the solar wind speed, and the cross section decreases with an increase in solar wind speed (Barnett et al., 1990; Lindsay and Stebbings, 2005; Wang et al., 2023). Therefore, a higher solar wind speed leads to a smaller ionization rate and vice versa. Obviously, the ionization rate is closely related to latitude and the solar cycle. In this work, we use the data for the total ionization rate (sum of charge exchange, photoionization, and electron impact ionization) for H atoms from Sokół et al. (2020) based on the solar wind and solar EUV data.
The profiles of the driving rate (dE±/dt) of turbulence due to the creation of PUIs are shown in Figure 2 for 2000 and 2009, corresponding to the solar maximum and minimum of solar cycle 23. dE±/dt decreases with an increase in distance and strongly depends on latitude. At the solar minimum and within ∼ 5 AU from the Sun, dE−/dt is larger at intermediate and high latitudes than at low latitudes due to a higher solar wind speed (i.e., PUI kinetic energy), although the ionization rate is weaker. When the solar wind speed becomes nearly uniform at the solar maximum, the latitudinal dependence of the ionization rate becomes important, and thus, dE−/dt is larger at low latitudes. A small θUB value at high latitudes results in a large E− (and E+) value. This effect only plays a minor role in determining the latitudinal dependence of dE−/dt. However, E+ decreases quickly with an increase in θUB at high latitudes; therefore, dE+/dt is large at low latitudes. In the outer heliosphere, θUB approaches 90° for most of the region except near the poles, which leads to the difference between E− and E+ becoming smaller for different latitudes, correspondingly dE−/dt ≈ dE+/dt. Comparing the left and right panels, we can see that dE±/dt is larger at the solar maximum than at the solar minimum in the outer heliosphere. Yearly dE±/dt from 1998 to 2020 is illustrated in the Supplementary Material. As illustrated in Figure 3, the driving rates present a strong north–south asymmetry due to the asymmetric solar wind speed, especially near the solar maximum, and these differences change with latitude and radial distance.
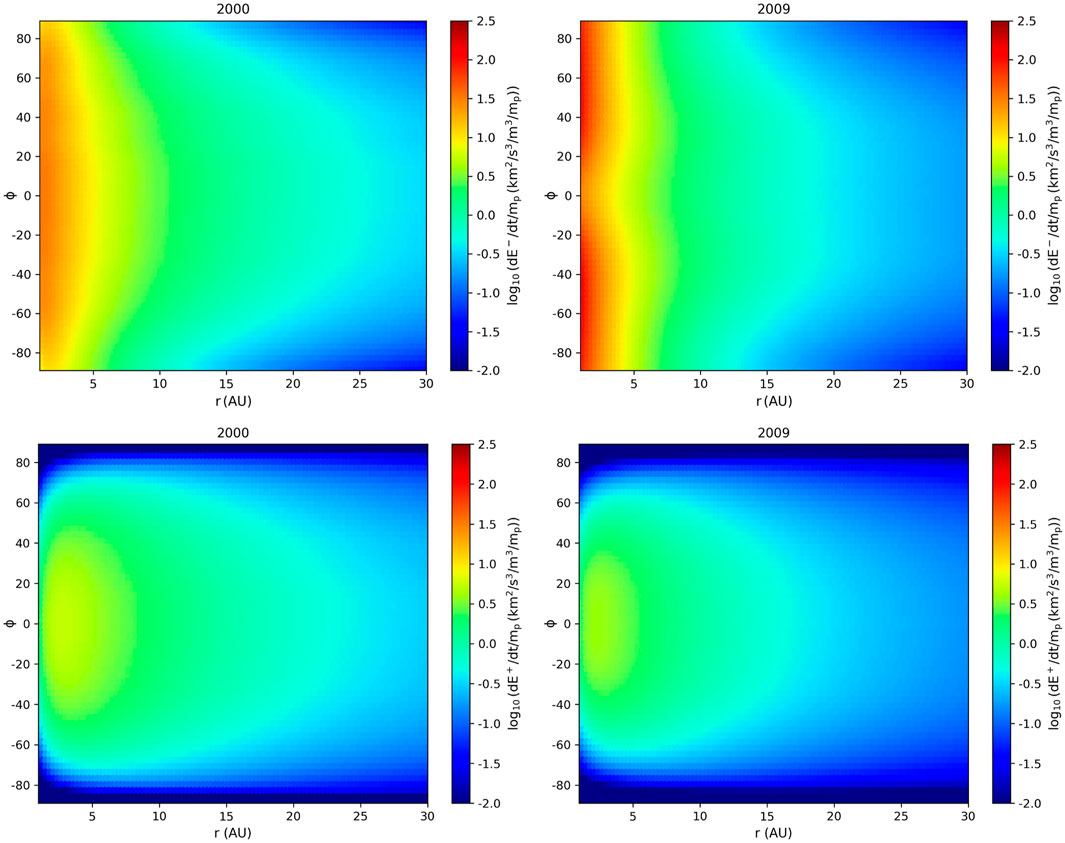
FIGURE 2. Profile for the driving rate of turbulence by PUIs during the solar maximum (2000) and minimum (2009) of solar cycle 23 as a function of heliocentric radius r and latitude θ. The upper (bottom) panels show the driving rate for slab turbulence mode propagating parallel (anti-parallel) to the heliospheric magnetic field dE−/dt (dE+/dt).
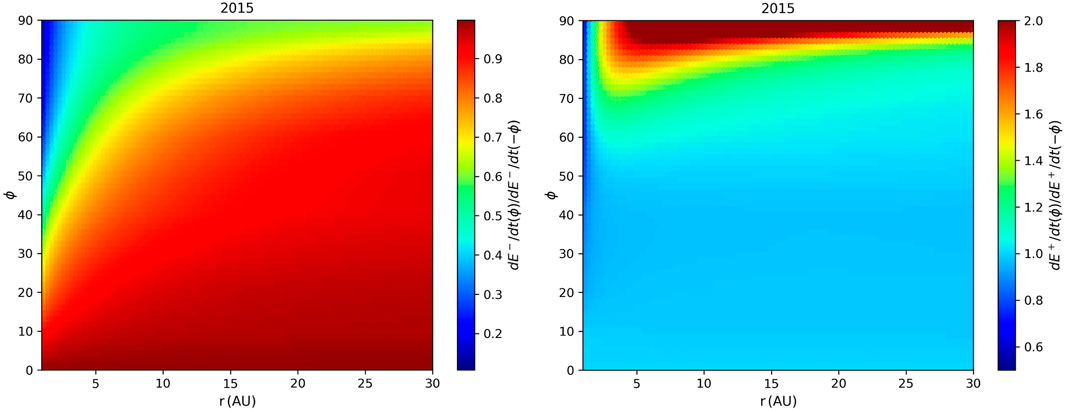
FIGURE 3. Ratios of the driving rate of turbulence by PUIs between the north and south heliospheres for 2015.
3 Conclusion
Turbulence in the outer heliosphere is predominantly driven by freshly created pickup ions. The resulting generation rate of turbulence energy depends on the solar wind speed, Alfvén speed, magnetic field-flow geometry, neutral density, and ionization rate. Using the latest latitudinal-dependent solar wind speed model inferred from the remote IPS observations, a comprehensive investigation of the ionization rate model, and the Parker magnetic field model inferred from the measurements by the ACE spacecraft, we calculated the yearly rate of turbulence energy generated by PUIs from 1998 to 2020. We found that the driving rate significantly changes with the solar cycle and latitude. In the outer heliosphere, the driving rate increases with the level of solar activity and decreases with an increase in the latitude. Our work shows that it is inappropriate to treat PUI-driven source terms in turbulence transport models as time-independent and latitude-independent (Adhikari et al., 2014). Improving the source term in turbulence transport models is important for understanding phenomena such as the heating of the solar wind (Matthaeus et al., 1999) and the scatting of cosmic rays (Zank et al., 1998; Zhao et al., 2018).
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
BW: writing–original draft. LZ: writing–review and editing. PA: writing–review and editing. GZ: writing–review and editing. LA: writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. BW, GZ, LZ, LA, and PA acknowledge the partial support of a NASA IBEX subaward under NASA contract 80NSSC20K0719, a NASA IMAP subaward under NASA contract 80GSFC19C0027, an NSF EPSCoR RII-Track-1 Cooperative Agreement OIA-2148653, and a NASA Heliospheric DRIVE Center award SHIELD 80NSSC22M0164.
Acknowledgments
BW would like to thank Dr. Justyna M. SokÓł for providing the ionization rate data and the ACE science team and the ACE Science Center (https://izw1.caltech.edu/ACE/ASC) for providing the magnetic field and plasma data.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2023.1298577/full#supplementary-material
Footnotes
1We note that there are typos in the equations for free energy given by Huddleston and Johnstone (1992), Eqs 27, 28. The correct expressions should be
2https://izw1.caltech.edu/ACE/ASC.
References
Adhikari, L., Zank, G. P., Hu, Q., and Dosch, A. (2014). Turbulence transport modeling of the temporal outer heliosphere. ApJ 793, 52. doi:10.1088/0004-637X/793/1/52
Adhikari, L., Zank, G. P., Wang, B., Zhao, L., Telloni, D., Pitna, A., et al. (2023). Theory and transport of nearly incompressible magnetohydrodynamic turbulence: high plasma beta regime. ApJ 953, 44. doi:10.3847/1538-4357/835/2/147
Barnett, C. F., Hunter, H. T., Fitzpatrick, M. I., Alvarez, I., Cisneros, C., and Phaneuf, R. A. (1990). “Atomic data for fusion,” in Volume 1: collisions of H, H2, He and Li atoms and ions with atoms and molecules.
Breech, B., Matthaeus, W. H., Minnie, J., Bieber, J. W., Oughton, S., Smith, C. W., et al. (2008). Turbulence transport throughout the heliosphere. J. Geophys. Res. (Space Phys. 113, A08105. doi:10.1029/2007JA012711
Bzowski, M., Sokół, J. M., Tokumaru, M., Fujiki, K., Quémerais, E., Lallement, R., et al. (2013). “Solar parameters for modeling the interplanetary background,” in Cross-calibration of far UV spectra of solar system objects and the heliosphere. Editors E. Quémerais, M. Snow, and R.-M. Bonnet (New York, NY: Springer), 67. doi:10.1007/978-1-4614-6384-9_3
Huddleston, D. E., and Johnstone, A. D. (1992). Relationship between wave energy and free energy from pickup ions in the Comet Halley Environment. J. Geophys. Res. 97, 12217–12230. doi:10.1029/92JA00726
Isenberg, P. A., Smith, C. W., Matthaeus, W. H., and Richardson, J. D. (2010). Turbulent heating of the distant solar wind by interstellar pickup protons in a decelerating flow. ApJ 719, 716–721. doi:10.1088/0004-637X/719/1/716
Le Chat, G., Issautier, K., and Meyer-Vernet, N. (2012). The solar wind energy flux. Sol. Phys. 279, 197–205. doi:10.1007/s11207-012-9967-y
Lee, M. A., and Ip, W. H. (1987). Hydromagnetic wave excitation by ionized interstellar hydrogen and helium in the solar wind. J. Geophys. Res. 92, 11041–11052. doi:10.1029/JA092iA10p11041
Lindsay, B. G., and Stebbings, R. F. (2005). Charge transfer cross sections for energetic neutral atom data analysis. J. Geophys. Res. (Space Phys. 110, A12213. doi:10.1029/2005JA011298
Matthaeus, W. H., Zank, G. P., Smith, C. W., and Oughton, S. (1999). Turbulence, spatial transport, and heating of the solar wind. Phys. Rev. Lett. 82, 3444–3447. doi:10.1103/PhysRevLett.82.3444
McComas, D. J., Barraclough, B. L., Funsten, H. O., Gosling, J. T., Santiago-Muñoz, E., Skoug, R. M., et al. (2000). Solar wind observations over Ulysses’ first full polar orbit. J. Geophys. Res. 105, 10419–10434. doi:10.1029/1999JA000383
McComas, D. J., Elliott, H. A., Gosling, J. T., Reisenfeld, D. B., Skoug, R. M., Goldstein, B. E., et al. (2002). Ulysses’ second fast-latitude scan: complexity near solar maximum and the reformation of polar coronal holes. Geophys. Res. Lett. 29, 1290. doi:10.1029/2001GL014164
Nakanotani, M., Zank, G. P., Adhikari, L., Zhao, L. L., Giacalone, J., Opher, M., et al. (2020). The downwind solar wind: model comparison with pioneer 10 observations. ApJ 901, L23. doi:10.3847/2041-8213/abb81e
Ng, C. S., Bhattacharjee, A., Munsi, D., Isenberg, P. A., and Smith, C. W. (2010). Kolmogorov versus Iroshnikov-Kraichnan spectra: consequences for ion heating in the solar wind. J. Geophys. Res. (Space Phys. 115, A02101. doi:10.1029/2009JA014377
Oughton, S., Matthaeus, W. H., Smith, C. W., Breech, B., and Isenberg, P. A. (2011). Transport of solar wind fluctuations: a two-component model. J. Geophys. Res. (Space Phys. 116, A08105. doi:10.1029/2010JA016365
Parker, E. N. (1958). Dynamics of the interplanetary gas and magnetic fields. ApJ 128, 664. doi:10.1086/146579
Pauls, H. L., and Zank, G. P. (1996). Interaction of a nonuniform solar wind with the local interstellar medium. J. Geophys. Res. 101, 17081–17092. doi:10.1029/96JA01298
Pauls, H. L., and Zank, G. P. (1997). Interaction of a nonuniform solar wind with the local interstellar medium 2. A two-fluid model. J. Geophys. Res. 102, 19779. doi:10.1029/97JA01716
Porowski, C., Bzowski, M., and Tokumaru, M. (2022). A New 3D solar wind speed and density model based on interplanetary scintillation. ApJS 259, 2. doi:10.3847/1538-4365/ac35d7
Smith, C. W., Aggarwal, P., Argall, M. R., Burlaga, L. F., Bzowski, M., Cannon, B. E., et al. (2017). Observations of low-frequency magnetic waves due to newborn interstellar pickup ions using ace, ulysses, and voyager data. J. Phys. Conf. Ser. 900, 012018. doi:10.1088/1742-6596/900/1/012018
Sokół, J. M., Bzowski, M., and Tokumaru, M. (2019). Interstellar neutral gas species and their pickup ions inside the heliospheric termination shock. Ionization rates for H, O, Ne, and He. ApJ 872, 57. doi:10.3847/1538-4357/aafdaf
Sokół, J. M., Kucharek, H., Baliukin, I. I., Fahr, H., Izmodenov, V. V., Kornbleuth, M., et al. (2022). Interstellar neutrals, pickup ions, and energetic neutral atoms throughout the heliosphere: present theory and modeling overview. Space Sci. Rev. 218, 18. doi:10.1007/s11214-022-00883-6
Sokół, J. M., McComas, D. J., Bzowski, M., and Tokumaru, M. (2020). Sun-heliosphere observation-based ionization rates model. ApJ 897, 179. doi:10.3847/1538-4357/ab99a4
Swaczyna, P., McComas, D. J., Zirnstein, E. J., Sokół, J. M., Elliott, H. A., Bzowski, M., et al. (2020). Density of neutral hydrogen in the sun’s interstellar neighborhood. ApJ 903, 48. doi:10.3847/1538-4357/abb80a
Thomas, G. E. (1978). The interstellar wind and its influence of the interplanetary environment. Annu. Rev. Earth Planet. Sci. 6, 173. doi:10.1146/annurev.ea.06.050178.001133
Usmanov, A. V., Matthaeus, W. H., Breech, B. A., and Goldstein, M. L. (2011). Solar wind modeling with turbulence transport and heating. ApJ 727, 84. doi:10.1088/0004-637X/727/2/84
Wang, B., Zank, G. P., Shrestha, B. L., Kornbleuth, M., and Opher, M. (2023). Relating energetic ion spectra to energetic neutral atoms. ApJ 944, 198. doi:10.3847/1538-4357/acb437
Wang, B. B., Zank, G. P., Adhikari, L., and Zhao, L. L. (2022). On the conservation of turbulence energy in turbulence transport models. ApJ 928, 176. doi:10.3847/1538-4357/ac596e
Williams, L. L., and Zank, G. P. (1994). Effect of magnetic field geometry on the wave signature of the pickup of interstellar neutrals. J. Geophys. Res. 99, 19229–19244. doi:10.1029/94JA01657
Zank, G., Matthaeus, W., Bieber, J., and Moraal, H. (1998). The radial and latitudinal dependence of the cosmic ray diffusion tensor in the heliosphere. J. Geophys. Res. Space Phys. 103, 2085–2097.
Zank, G., Matthaeus, W., and Smith, C. (1996). Evolution of turbulent magnetic fluctuation power with heliospheric distance. J. Geophys. Res. Space Phys. 101, 17093–17107.
Zank, G. P., Adhikari, L., Hunana, P., Shiota, D., Bruno, R., and Telloni, D. (2017). Theory and transport of nearly incompressible magnetohydrodynamic turbulence. ApJ 835, 147. doi:10.3847/1538-4357/835/2/147
Zank, G. P., Adhikari, L., Hunana, P., Tiwari, S. K., Moore, R., Shiota, D., et al. (2018). Theory and transport of nearly incompressible magnetohydrodynamic turbulence. IV. Solar coronal turbulence. ApJ 854, 32. doi:10.3847/1538-4357/aaa763
Zank, G. P., Dosch, A., Hunana, P., Florinski, V., Matthaeus, W. H., and Webb, G. M. (2012). The transport of low-frequency turbulence in astrophysical flows. I. Governing equations. ApJ 745, 35. doi:10.1088/0004-637X/745/1/35
Zank, G. P., Sterken, V., Giacalone, J., Möbius, E., von Steiger, R., Stone, E. S., et al. (2022). The early history of heliospheric science and the spacecraft that made it possible. Space Sci. Rev. 218, 34. doi:10.1007/s11214-022-00900-8
Keywords: magnetohydrodynamic turbulence, heliosphere, solar wind, waves and instabilities, pickup ions
Citation: Wang B, Zhao L, Abouhamzeh P, Zank GP and Adhikari L (2023) The temporal and latitudinal dependences of turbulence driven by pickup ions in the outer heliosphere. Front. Astron. Space Sci. 10:1298577. doi: 10.3389/fspas.2023.1298577
Received: 21 September 2023; Accepted: 14 November 2023;
Published: 01 December 2023.
Edited by:
Parisa Mostafavi, Johns Hopkins University, United StatesReviewed by:
Charles William Smith, University of New Hampshire, United StatesJeewoo Park, University of Maryland, United States
Copyright © 2023 Wang, Zhao, Abouhamzeh, Zank and Adhikari. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Bingbing Wang, YncwMTIxQHVhaC5lZHU=
 Bingbing Wang
Bingbing Wang Lingling Zhao
Lingling Zhao Paria Abouhamzeh
Paria Abouhamzeh Gary P. Zank
Gary P. Zank Laxman Adhikari
Laxman Adhikari