The high energy X-ray probe (HEX-P): a new window into neutron star accretion

Accreting neutron stars (NSs) represent a unique laboratory for probing the physics of accretion in the presence of strong magnetic fields (B ≳ 10⁸ G). Additionally, the matter inside the NS itself exists in an ultra-dense, cold state that cannot be reproduced in Earth-based laboratories. Hence, observational studies of these objects are a way to probe the most extreme physical regimes. Here we present an overview of the field and discuss the most important outstanding problems related to NS accretion. We show how these open questions regarding accreting NSs in both low-mass and high-mass X-ray binary systems can be addressed with the High-Energy X-ray Probe (HEX-P) via simulated data. In particular, with the broad X-ray passband and improved sensitivity afforded by a low X-ray background, HEX-P will be able to 1) distinguish between competing continuum emission models; 2) provide tighter upper limits on NS radii via reflection modeling techniques that are independent and complementary to other existing methods; 3) constrain magnetic field geometry, plasma parameters, and accretion column emission patterns by characterizing fundamental and harmonic cyclotron lines and exploring their behavior with pulse phase; 4) directly measure the surface magnetic field strength of highly magnetized NSs at the lowest accretion luminosities; as well as 5) detect cyclotron line features in extragalactic sources and probe their dependence on luminosity in the super-Eddington regime in order to distinguish between geometrical evolution and accretion-induced decay of the magnetic field. In these ways HEX-P will provide an essential new tool for exploring the physics of NSs, their magnetic fields, and the physics of extreme accretion.

1 Introduction

1.1 Accreting neutron stars

Accretion is a ubiquitous process in the Universe, from the formation of stars and planets to supermassive black holes at the center of galaxies. X-ray binary systems are composed of a compact object (CO), either a black hole (BH) or neutron star (NS), that accretes from a stellar companion. These systems can be further categorized based on the mass of the stellar companion: low-mass and high-mass (see Longair, 2011 for a more detailed review). Figure 1 shows a simple schematic for accretion onto NSs in several types of binary systems. Low-mass X-ray binaries (LMXBs) have a ≲ 1 M_⊙ companion that transfers matter via Roche-lobe overflow to form an accretion disk around the compact object. High-mass X-ray binaries (HMXBs) have a more massive (≳ 5 M_⊙), early-type stellar companion and accretion onto the CO can occur in various ways, including periodic Roche lobe overflow (such as when the CO passes through the decretion disk of a Be type star), or capture of material ejected through dense stellar winds. We note that there is a rare class of LMXBs that accrete from the slow winds of a late-type stellar companion and exhibit properties akin to HMXBs (see Bozzo et al. 2022 and references therein)¹.

FIGURE 1

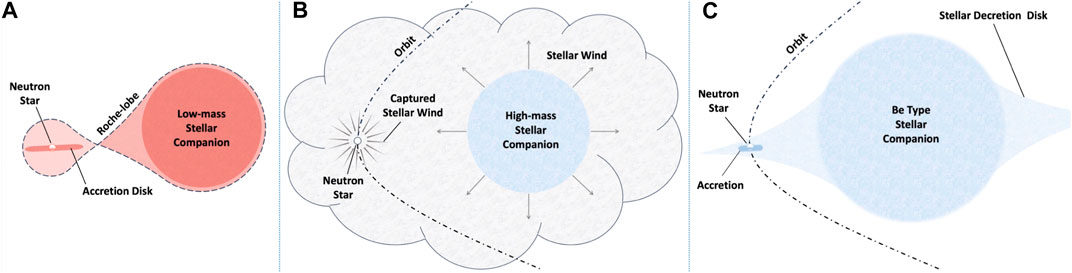
FIGURE 1. Simple schematic diagrams of several types of X-ray binary systems: (A) a LMXB system where the NS accretes from a stellar companion via Roche-lobe overflow, (B) a NS in a HMXB that accretes from material captured from stellar winds that are launched from the companion, and (C) a NS accreting from the decretion disk of a Be type stellar companion.

NSs are the densest known objects with a surface in the Universe. The matter inside a NS exists in an ultra-dense, cold state that cannot be replicated in terrestrial laboratories. The only way to discern how matter behaves under these conditions is by determining the equation of state (EoS). The EoS sets the mass and radius of the NS through the Tolman-Oppenheimer-Volkoff equations (Tolman, 1934; 1939; Oppenheimer and Volkoff, 1939) and astronomical measurements of NS masses and radii are therefore crucial for determining which theoretical EoS models are viable (see, e.g., Lattimer, 2011). In particular, accretion onto NSs probes the properties and behavior of matter in the presence of a strong magnetic field (B ∼ 10^8–9 G for LMXBs and B ∼ 10¹² G for HMXBs; see Caballero and Wilms, 2012).

In order to fully encapsulate the accretion emission from these systems, a broad X-ray passband is necessary (see Section 2 for LMXBs and Section 3 for HMXBs). Currently, NuSTAR (Harrison et al., 2013) is the only focusing hard X-ray telescope with a passband from 3 to 80 keV. Energies below 3 keV have to be supplemented with other X-ray telescopes, such as NICER (Gendreau et al., 2012), Swift (Gehrels et al., 2004), or XMM-Newton (Jansen et al., 2001), to construct a broad energy passband. While observations can be scheduled to occur during the same observing period, often the data are not strictly simultaneous due to the different orbits of the missions resulting in various degrees of overlap. Since NS binary systems are highly variable, sometimes on time-scales comparable to or shorter than the typical exposure itself, simultaneous observations over a broad X-ray passband are invaluable for studying these systems.

1.2 The high energy X-ray probe: HEX-P

The High Energy X-ray Probe (HEX-P; Madsen et al., 2023) is a probe-class mission concept that offers sensitive broad-band X-ray coverage (0.2–80 keV) with exceptional spectral, timing and angular capabilities. It features two high-energy telescopes (HETs) that focus hard X-rays and one low-energy telescope (LET) that focuses lower-energy X-rays.

The LET consists of a segmented mirror assembly coated with Ir on monocrystalline silicon that achieves an angular resolution of 3.5″, and a low-energy DEPFET detector, of the same type as the Wide Field Imager (WFI; Meidinger et al., 2020) onboard Athena (Nandra et al., 2013). It has 512 × 512 pixels that cover a field of view of 11.3′ × 11.3′. The LET has an effective passband of 0.2–25 keV, and a full frame readout time of 2 m, which can be operated in a 128 and 64 channel window mode for higher count-rates to mitigate pile-up and faster readout. Pile-up effects remain below an acceptable limit of ∼1% for fluxes up to ∼100 mCrab in the smallest window configuration. Excising the core of the PSF, a common practice in X-ray astronomy, will allow for observations of brighter sources, with a typical loss of up to ∼60% of the total photon counts.

The HET consists of two co-aligned telescopes and detector modules. The optics are made of Ni-electroformed full shell mirror substrates, leveraging the heritage of XMM-Newton, and coated with Pt/C and W/Si multilayers for an effective passband of 2–80 keV. The high-energy detectors are of the same type as flown on NuSTAR, and they consist of 16 CZT sensors per focal plane, tiled 4 × 4, for a total of 128 × 128 pixel spanning a field of view of 13.4′ × 13.4′.

This paper highlights interesting existing open questions about NSs and accretion in strong magnetic fields, and demonstrates HEX-P’s unique ability to address these with the current best estimate (CBE) mission capabilities. All simulations presented here were produced with a set of response files that represents the observatory performance based on CBEs as of Spring 2023 (see Madsen et al., 2023; in prep.). The effective area is derived from raytracing calculations for the mirror design including obscuration by all known structures. The detector responses are based on simulations performed by the respective hardware groups, with an optical blocking filter for the LET and a Be window and thermal insulation for the HET. The LET background was derived from a GEANT4 simulation (Eraerds et al., 2021) of the WFI instrument, and the HET background was derived from a GEANT4 simulation of the NuSTAR instrument. Both assume HEX-P is in an L1 orbit. The broad X-ray passband and superior sensitivity will provide a unique opportunity to study accretion onto NSs across a wide range of energies, luminosity, and dynamical regimes.

2 Low-mass X-ray binaries

2.1 Background

Persistently accreting NS LMXBs are divided into two types based upon characteristic shapes that are traced out in hardness-intensity diagrams and color-color diagrams (Hasinger and van der Klis, 1989): “Z” sources and “atoll” sources. Z sources trace out a Z-shaped pattern with three distinct branches: the horizontal, normal, and flaring branch (HB, NB, and FB, respectively), with the FB being the softest spectral state. They can be further divided into two subgroups, Sco-like and Cyg-like, based upon how much time they spend in the different branches. Sco-like sources spend little to no time in the HB and extended periods of time in the FB ($>12$ hours), whereas Cyg-like sources have a strong HB and spend little time in the FB (Kuulkers et al., 1997). Atoll sources are either observed in the soft “banana” state or hard “island” state. A difference in mass accretion rate is thought to be the primary driver between the behavioral differences between atoll and Z sources. Atoll sources probe a lower range in Eddington luminosity (∼0.01–0.5 L_Edd) in comparison to the near-Eddington Z sources (∼0.5–1.0 L_Edd: van der Klis, 2005). Further evidence that the average mass accretion rate is responsible for the observed difference between the two classes comes from observing transient NS LMXBs that have transitioned between the two classes during outburst (e.g., XTE J1701−462: Homan et al., 2010).

NS LMXBs occupy a number of spectral states which vary considerably in terms of the models and spectral parameters needed to describe the continuum emission (Barret, 2001). In the very hard state, the spectrum is dominated by Comptonization that can be modeled with an absorbed power-law component with a photon index Γ ∼ 1 (Ludlam et al., 2016; Parikh et al., 2017) or two thermal Comptonization components assuming two distinct populations of seed photons from different plasma temperatures (Fiocchi et al., 2019). In the hard state, the spectrum is dominated by a hard Comptonization component with Γ = 1.5–2.0 and a soft thermal component arising from a single temperature blackbody component or multi-color disk blackbody with a temperature ≲ 1 keV (Barret et al., 2000; Church and Balucińska-Church, 2001). In the soft state, the spectrum becomes thermally dominated with weakly Comptonized emission. Model choices for the thermal and Comptonization components in the soft state vary in the literature leading to two classical descriptions. The “Eastern” model, after Mitsuda et al. (1989), uses a multi-color disk blackbody in combination with a Comptonized blackbody component, while the “Western” model, after White et al. (1988), uses a single-temperature blackbody and a Comptonized disk component. Lin et al. (2007) devised a hybrid model for hard and soft state spectra based upon RXTE observations of two transient atoll systems that resulted in a coherent picture of the spectral evolution (e.g., the thermal components follow the expected L_x ∝ T⁴ relation). In this model, the soft state assumes two thermal components (i.e., a single-temperature blackbody and a disk blackbody) and weak Comptonization accounts for the power-law component. This hybrid double thermal model has been used in many NS LMXBs studies (e.g., Cackett et al., 2008; 2009; Lin et al., 2010), though not exclusively. For instance, a recent study using thermal Comptonization from a blackbody and a multi-color accretion disk blackbody (akin to the “Eastern” model) to model the X-ray spectra of the atoll 4U 1820-30 found good agreement with the observed jet variability in this system (Marino et al., 2023). In the absence of multi-wavelength data to support a choice of continuum model, it is difficult to ascertain which prescription of the spectra is appropriate. Due to the soft spectral shape in these states, the source spectrum typically becomes background dominated above 30 keV even when observed with NuSTAR. A broad X-ray passband with large effective collecting area and low X-ray background that can observe a large number of sources at various luminosity levels and spectral states is needed to further our understanding of these sources.

The accretion disks in these systems can be externally illuminated by hot electrons in the corona (Sunyaev et al., 1991) or from the thermal emission of the NS or boundary layer region (Popham and Sunyaev, 2001). We note that the exact geometry of the corona is unclear (see Degenaar et al. 2018 for some possible geometries), but X-ray polarization measurements with IXPE are beginning to shed light on coronal orientation and presence of boundary layer regions in some systems (e.g., Cocchi et al. 2023; Farinelli et al. 2023; Jayasurya et al. 2023; Ursini et al. 2023); building up our understanding of the accretion geometry when coupled with X-ray energy spectral studies. Regardless of the hard X-ray source, the disk reprocesses the hard X-ray emission and re-emits discrete emission lines superimposed upon a reprocessed continuum known as the ‘reflection’ spectrum (Ross and Fabian, 2005; García and Kallman, 2010). The spectrum is then relativistically blurred due to the extreme environment close to the NS, where accreting material reaches relativistic velocities as it falls into the NS’s deep gravitational well (Fabian et al., 1989; Dauser et al., 2013). Studying reflection in NS LMXBs allows for properties of NSs and the disk itself to be measured, such as the NS magnetic field strength (Cackett et al., 2009; Ibragimov and Poutanen, 2009; Ludlam et al., 2017b), extent of the boundary layer (Popham and Sunyaev, 2001; King et al., 2016; Ludlam et al., 2021), and NS radius (Cackett et al., 2008; Ludlam et al., 2017a; 2022). Of particular interest is both the inner disk radius, R_in, and dimensionless spin parameter, a = cJ/GM² (which is the mass normalized total angular momentum J of the CO); the latter is typically fixed in current studies due to limitations in data quality. The spin parameter has important consequences for both accreting NSs and BHs (see Connors et al., 2023, in prep., and Piotrowska et al., 2023, in prep., for HEX-P science with BH X-ray binaries and supermassive BHs, respectively). The spin sets the location of the innermost stable circular orbit (ISCO) where a higher spin corresponds to a smaller ISCO (Bardeen et al., 1972). Consequently, the position of the inner disk radius for higher spin values cannot be replicated by lower spin if the data is of sufficient quality to recover R_in accurately. The majority of NSs in LMXBs have spin a ≲ 0.3 (Galloway et al., 2008; Miller et al., 2011) and the difference in the location of the ISCO decreases from 6 gravitational radii (R_g = GM/c²) at a = 0 to 4.98 R_g at a = 0.3 (see Figure 2). Therefore, targeting an accreting NS with a higher spin, as indicated through a high measured spin frequency, can decrease the upper limit on NS radii obtained from reflection modeling by roughly 2–3 km.

FIGURE 2

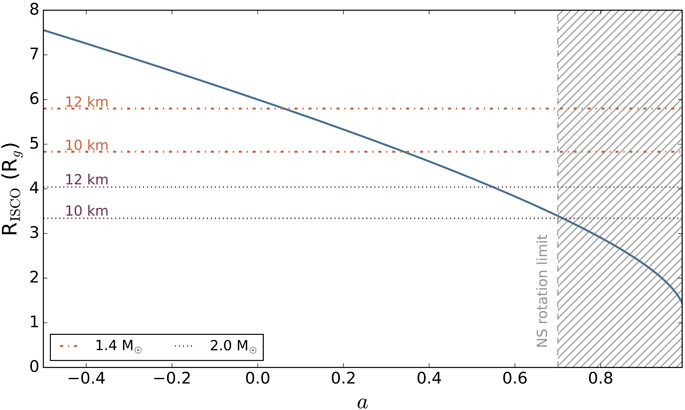
FIGURE 2. Position of the innermost stable circular orbit (ISCO) in units of gravitational radii versus the dimensionless spin parameter a of the CO. The hatched region indicates where the NS surpasses the rotational limit and would break apart. The horizontal dot-dashed lines indicate the corresponding values of 10 km and 12 km radius for a canonical NS mass of 1.4 M_⊙. The horizontal dotted lines indicate the same radius values for a more massive NS of 2.0 M_⊙.

In order to capture the entire reflection spectrum (i.e., the low-energy O VIII and iron (Fe) L emission lines near 1 keV (Madej et al., 2014; Ludlam et al., 2018; Ludlam et al., 2021), the Fe K emission lines at 6.4–6.97 keV, and the Compton backscattering hump above 15 keV), determine the appropriate continuum model, and measure the absorption column along the line of sight, a broad X-ray passband is necessary. Hence, the broad X-ray sensitivity provided by the LET and HETs on HEX-P is crucial for studying accreting NS LMXBs.

2.2 Simulated science cases for LMXBs

All simulations in this section were conducted in xspec (Arnaud, 1996) via the “fakeit” command, which draws photons from a randomized seed distribution, with V07 of the HEX-P response files selecting an 80% PSF correction, assuming the data would be extracted from a 15 arcsec region for the HET and 8 arcsec region for the LET, as well as the anticipated background for the telescope at L1. The simulated spectra were grouped via grppha to have a minimum of 25 counts per bin to allow for the use of χ² statistics. The flux for each of the following simulations can be found in Supplementary Table S1.

2.2.1 Distinguishing between continuum models

To demonstrate HEX-P’s ability to distinguish between different continuum models, we base our simulations on the models used to fit simultaneous NICER and NuSTAR observations of the accreting atoll 4U 1735–44 published in Ludlam et al. (2020). Model 1 is based on the hybrid double thermal continuum model of Lin et al. (2007) while Model 2 is based on the “Eastern” model of Mitsuda et al. (1989). Both models provide an adequate description of the data in the 0.3–30 keV energy band (the NuSTAR observations were background dominated above 30 keV) when neglecting the reflection spectrum, but data at higher energies would distinguish between these two continuum models. We take the continuum model and parameter values for Model 1 and Model 2 from Table 1 of Ludlam et al. (2020) as input for the HEX-P simulation; the exact values can be found in Supplementary Table S2. The overall models² are as follows: (a) Model 1: tbabs*(diskbb + bbody + pow) and (b) Model 2: tbabs*(diskbb + nthcomp). Note that we fix the absorption column index to a value between the ones used in Model 1 and Model 2, N_H = 4 × 10²¹ cm⁻², to focus on the difference in the spectral shape due to the model component choices rather than a difference in absorption column between the models. We chose an exposure time of 20 ks, roughly equivalent to the exposure time of the NuSTAR observation in the aforementioned study.

TABLE 1

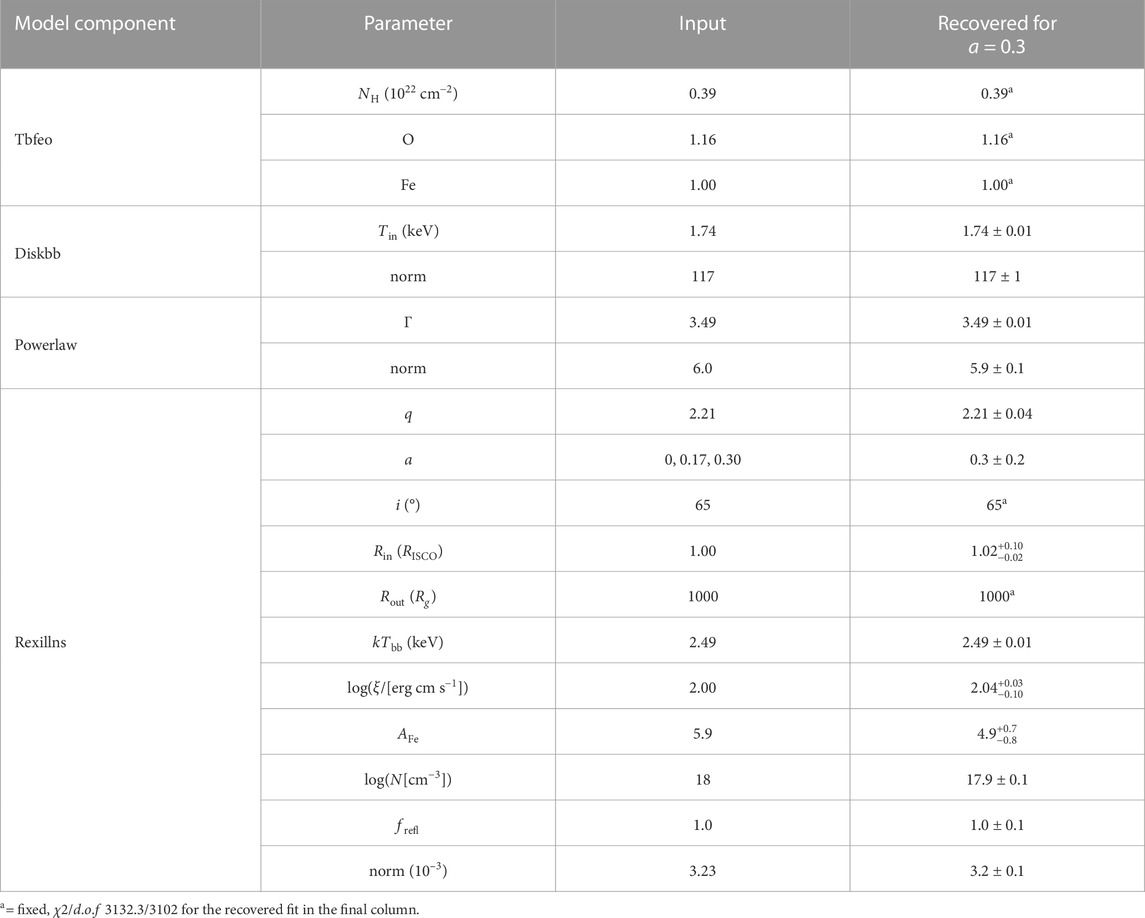
TABLE 1. Input model parameters for simulating reflection model data with HEX-P. Values are taken from Table 3: RNS1 of Ludlam et al. (2022) for Cygnus X-2 in the NB and updated using the public version of relxillNS (v2.2). Additionally, we show one case of the recovered model parameters from a simulated HEX-P spectrum after performing a Markov Chain Monte Carlo (MCMC) analysis with a burn-in of 10⁶ and chain length of 5 × 10⁵ to emulate a standard analysis of the data. Errors are reported at the 1σ confidence level, though the errors for R_in and a are drawn from the bivariate distribution between the two due to their correlated nature.

The simulated HEX-P spectra remain above the background in the HET bands up to 80 keV, though they dive into the LET background below 1 keV. This could be remedied by increasing the exposure time, though, notably, the spectrum above 30 keV is where the models diverge. The reduced χ² is $\le 1.03$ when fitting each simulation with its own input model. Attempting to fit each simulated spectrum with the opposing model description provides an inadequate fit with Δχ² > 1,000 for the same number of degrees of freedom (d.o.f.). Figure 3 shows the HEX-P spectrum for the Model 2 input of a thermal disk with a Comptonized blackbody from a boundary layer region. For direct comparison, we show a simulated spectrum using Model 1 (the double thermal continuum model with weak Comptonization) with parameter values from fitting the simulated spectrum of Model 2 below 30 keV, since these models perform equally well within this energy regime. This highlights that though these models are nearly identical below 30 keV, they diverge at higher energies inaccessible by current operating missions. The weakly Comptonized emission above 30 keV cannot be replicated by Model 2, and demonstrates the potential for a broadband X-ray mission like HEX-P to discern between competing continuum models that would otherwise equally describe the data below 30 keV.

FIGURE 3

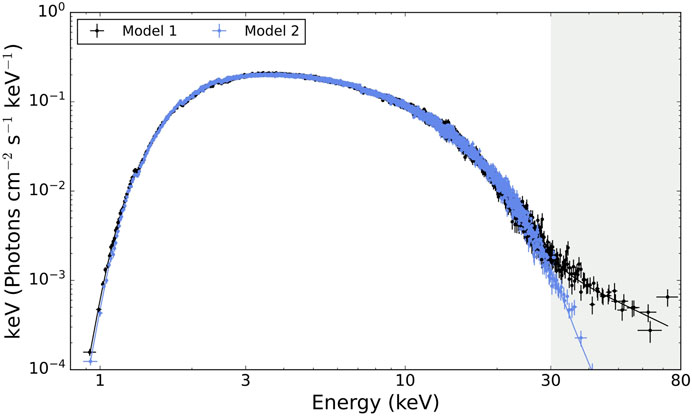
FIGURE 3. Comparison of simulated 20 ks HEX-P (LET+2 HETs) observation for two different continuum models typically used to describe NS LMXB soft state spectra: a double thermal continuum model with weak Comptonization (Model 1: black) and an accretion disk with blackbody Comptonization (Model 2: blue). The models diverge above 30 keV where currently available missions quickly become background dominated for the same exposure time. To emphasize this point, the same S/N near 30 keV could be achieved with NuSTAR in an exposure time of 96.6 ks. The broad X-ray passband and improved sensitivity of HEX-P will differentiate the models.

2.2.2 Neutron star radius constraints from relativistic reflection modeling

To demonstrate that HEX-P would improve the radius constraints obtained by reflection modeling of NSs, we base our simulations on the results of a recent investigation of Cygnus X-2 that utilized simultaneous data from NICER and NuSTAR (Ludlam et al., 2022). This source is of particular interest since it has a dynamical NS mass measurement of M_NS = 1.71 ± 0.21 M_⊙ (Casares et al., 2010). The source was analyzed in the NB, HB, and the vertex between those branches. Fixing the spin at a = 0, Ludlam et al. (2022) found that the inner disk radius remained close to R_ISCO. In the current literature it is customary to find studies in which the spin of the NS has been fixed while fitting models to the data given the highly degenerate nature of R_in and a. We set up our simulations using the Cygnus X-2 data in the NB modeled with the latest public release of the self-consistent reflection model tailored for thermal emission illuminating the accretion disk, relxillNS (v2.2: García et al., 2022). The input parameters for the simulation³ are provided in Table 1. We leave R_in at 1 R_ISCO for all simulations while varying the input spin since the disk remained consistent with this value while the source was in the various branches. We chose three spin values as test cases: non-rotating (a = 0), the highest value expected for a NS LMXB (a = 0.3), and a = 0.17 which is an approximation based on the spin frequency of the source (Mondal et al., 2018). We use an exposure time of 100 ks and investigate how well R_in and spin can be recovered independently.

Given the degenerate nature of the parameters of interest and that each spectrum simulated is created via a randomized photon generation, the results obtained can vary with each iteration. We therefore simulate 10⁴ spectra per spin value to determine the likelihood of constraining R_in and a. The LET data were modeled in the 0.3–15 keV energy band while the HET data were modeled in the 2–80 keV band. We impose an upper limit on the spin (a ≤ 0.7) when fitting the simulated spectra so as to not surpass the rotational break-up limit of a NS (Lattimer and Prakash, 2004). We fit each spectrum and then perform error scans to ensure that each iteration reached a minimum goodness of fit of χ²/d.o.f. ≤ 1.1 prior to obtaining values for inner disk radius and spin from each simulated spectrum, thus building up the posterior distribution shown in Figure 4.

FIGURE 4

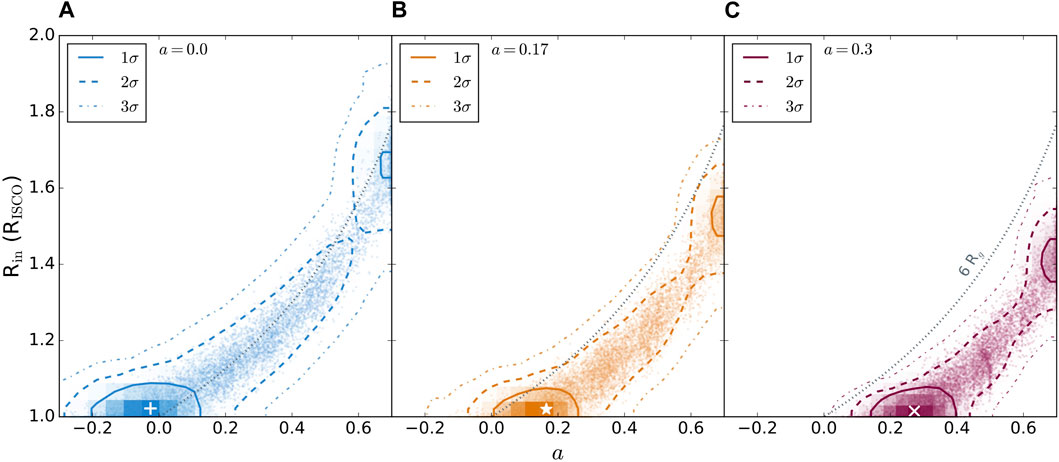
FIGURE 4. Posterior distribution of a and R_in for 10⁴ iterations of simulating HEX-P spectra for three spin values: (A) a = 0.0, (B) a = 0.17, and (C) a = 0.3. The 1σ, 2σ, and 3σ contours are shown. The white points indicate the highest probability value. The dotted grey line indicates a constant line of 6 R_g which corresponds to the ISCO for a = 0. The distribution tightens at high values of spin as relativistic effects become stronger. However, the distributions show that the data are able to trace out unique values of inner disk radii by trending towards lower values of R_g at higher a.

Errors are drawn from the bivariate posterior distribution due to their correlated nature and reported at the 1σ confidence level. We find that for an input of a = 0, we recover $a=-0.03_{-0.17}^{+0.15}$ and R_in $=1.02_{-0.02}^{+0.07}$ R_ISCO. For an input of a = 0.17, we recover $a=0.17_{-0.16}^{+0.09}$ and R_in $=1.02_{-0.02}^{+0.05}$ R_ISCO. Lastly, for an input of a = 0.30, we recover a = 0.27 ± 0.13 and R_in $=1.02_{-0.02}^{+0.05}$ R_ISCO. The ability to recover the input parameters improves at higher spin as the relativistic effects become stronger. Recall that the position of the inner disk radius for higher spin values cannot be replicated by lower spin, thus if the data is of sufficient quality to recover R_in accurately this will become apparent. For example, an input of R_in = 1 R_ISCO for a spin of a = 0 corresponds to 6 R_g. This value can be mimicked by a higher spin and R_in beyond 1 R_ISCO (e.g., 6 R_g is equal to 1.2 R_ISCO for a = 0.3). However, an input of R_in = 1 R_ISCO for a = 0.3 corresponds to 4.98 R_g and cannot be replicated by a lower spin so long as the upper limit recovered when fitting the data returns a value of R_in < 1.2 R_ISCO. We note that Cygnus X-2 is a bright LMXB (∼0.7 Crab) and would thus need to be observed in a configuration that would reduce pile-up effects in the LET. However, we obtain consistent results at the 1σ level when performing the same exercise with just the HETs, which do not suffer from pile-up, though the 3σ level can no longer rule out a non-rotating NS as is the case when the LET is included. Hence the combined observing power of the HETs and LET provide an improvement over the current capabilities of existing missions.

Figure 5 shows the improvement provided by HEX-P for reflection modeling of spinning NS LMXBs in comparison to simultaneous NICER and NuSTAR results with fixed spin. Additionally, the current best constraints from gravitational wave events of binary NS mergers and pulsar light curve modeling demonstrate how the various methods can work in concert to narrow down the allowable region for the EoS. Each method has its own underlying systematic uncertainties, so the firmest EoS constraints will require multiple measurement approaches. Utilizing the dynamical NS mass estimate of Cygnus X-2 (M_NS = 1.71 ± 0.21 M_⊙: Casares et al., 2010), Ludlam et al. (2022) reported an upper limit on the radius of R_NS = 19.5 km for M_NS = 1.92 M_⊙ and R_NS = 15.3 km for M_NS = 1.5 M_⊙. The lower limit on spin and upper limit on R_in return a conservative upper limit on the NS radius. From the HEX-P simulations we calculate an upper limit of R_NS = 16.7 km for M_NS = 1.92 M_⊙ and R_NS = 13.2 km for M_NS = 1.5 M_⊙ for an input of a = 0.3. This demonstrates the power of HEX-P to study rotating NSs with reflection studies. For comparison, we conducted the same simulation with NuSTAR response files. For the highest spin value of a = 0.3, NuSTAR recovers $a=0.67_{-0.54}^{+0.03}$ and R_in $=1.02_{-0.02}^{+0.16}$ R_ISCO. The conservative upper limit on the NS radius from the location of the inner disk radius is larger than 6 R_g and therefore does not provide an improvement over current reflection studies that assume the spin is fixed at a = 0. Performing this test with the combination of NICER and NuSTAR marginally improves the recovered spin value to $a=0.68_{-0.50}^{+0.02}$, but with a larger upper limit on R_in $=1.02_{-0.02}^{+0.18}$ R_ISCO, which is still $>1$ km larger than the constraints obtained from HEX-P (i.e., R_NS = 18.5 km for M_NS = 1.92 M_⊙ and R_NS = 14.4 km for M_NS = 1.5 M_⊙).

FIGURE 5

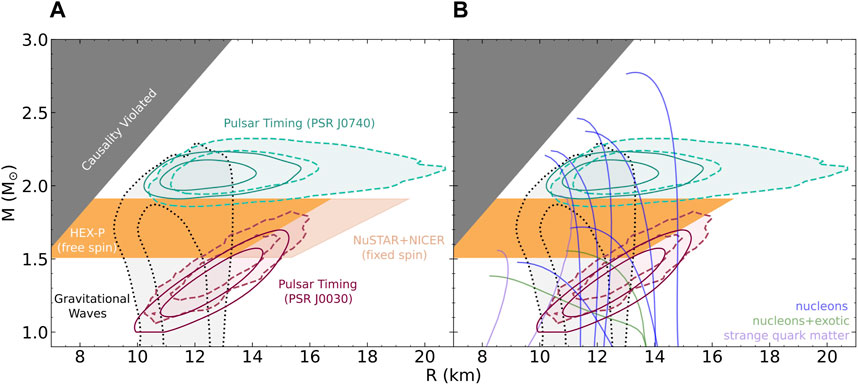
FIGURE 5. Mass and radius constraints from reflection modeling compared to NS gravitational wave events and NICER pulsar light curve modeling. The darker solid orange region indicates the improved radius constraints for reflection modeling of HEX-P data based on Cygnus X-2 for the case of high a. Note that both R_in and a are free parameters when fitting the HEX-P data, while the NuSTAR plus NICER analysis fixes a = 0 (lighter solid orange region in panel (A); Ludlam et al., 2022). The solid gray region indicates where causality is violated (i.e., the sound speed within the NS exceeds the speed of light). Pulsar light curve modeling of NICER data for PSR J0740 + 6620 is indicated in teal (dashed lines: Miller et al., 2021; solid lines; Riley et al., 2021). Maroon indicates the results for light curve modeling of PSR J0030 + 0452 (dashed lines: Miller et al., 2019; solid lines; Riley et al., 2019). The black dotted line denotes the mass-radius constraints from the combined GW170817 (Abbott et al., 2019) and GW190425 (The LIGO Scientific Collaboration et al., 2020) signatures using a piece-wise polytropic model as reported in Raaijmakers et al. (2021). Confidence contours correspond to the 68% and 95% credible regions. Panel (B) shows select EoS models from Lattimer and Prakash (2001) to demonstrate the behavior of different internal compositions on the mass-radius plane.

We demonstrate that these results do not depend on drawing from a posterior distribution of simulated spectra by conducting Markov Chain Monte Carlo (MCMC) analysis on one of the simulated HEX-P spectra with an input spin of a = 0.3. The results of this test are shown in Table 1 with the inclination fixed at the median value from optical and X-ray studies (Orosz and Kuulkers, 1999; Ludlam et al., 2022). The lower limit on spin of a = 0.1 and upper limit on R_in = 1.12 R_ISCO  still provides an improvement over current NICER and NuSTAR analyses, which fix a = 0. The MCMC analysis finds an upper limit of R_NS = 18 km for M_NS = 1.92 M_⊙ and R_NS = 14.1 km for M_NS = 1.5 M_⊙.

For completeness we note that the Kerr metric is used to describe the space-time close to the NS in the relativistic reflection model. As the angular momentum (i.e., spin) increases, the NS can become oblate, thus causing deviations in space-time from the Kerr metric due to an induced quadrupole moment. The exact induced deviation depends upon the EoS of the NS, but this has an effect $<10$% (Sibgatullin and Sunyaev, 1998) in the anticipated range of spin parameters for NS LMXBs (a ≲ 0.3). Given that our 1σ errors for R_in are larger than this deviation from the Kerr metric, the HEX-P spectra would not be sensitive enough to measure this effect. However, our conservative upper limits on NS radius are still at larger radii than the deviation in the R_ISCO and hence are not in conflict even if we are insensitive to an induced quadrupole moment. Therefore, reflection studies of accreting NS LMXBs with HEX-P would provide improved upper limits on NS radii in comparison to current studies.

3 High-mass X-ray binaries

3.1 Background

NSs in HMXBs are typically highly magnetized, with a dipolar magnetic field strength of ∼10¹²G. The pressure of the TeraGauss magnetic field disrupts the inflow of the accreting matter, channelling it onto the magnetic poles (Davies and Pringle, 1981). There, the kinetic energy of the matter is released as radiation in a highly anisotropic manner. Since the NS rotates, the sources are visible as X-ray pulsars. Studying this emission is crucial to understanding the physics of plasma accretion and the interaction of radiation with high magnetic fields that are orders of magnitude stronger than those achievable in laboratories on Earth. Due to their extreme surface magnetic field strength, quantum effects take place at the site of emission. In particular, the electron motion in the direction perpendicular to the magnetic field lines becomes quantized. This affects the electron scattering cross section, leading to a resonance at an energy that is proportional to the magnetic field strength (Meszaros, 1992). As a result, the spectra of X-ray pulsars (XRPs) can contain absorption line-like features called cyclotron resonant scattering features (CRSFs), or cyclotron lines, at an energy of

$E_{\mathit{cyc}}\approx \frac{n}{\left(1+z_g\right)}11.6B_{12}\mathrm{k}\mathrm{e}\mathrm{V},(1)$

where z_g is the gravitational redshift (typically 0.3 for standard NS mass and radius) and B₁₂ is the NS (polar) magnetic field strength in units of 10¹²G, while n is the number of Landau levels involved⁴. Cyclotron lines represent the most direct way to probe the NS magnetic field on or close to the NS surface. Up to now, cyclotron lines have been confirmed in the spectra of about 40 sources (Staubert et al., 2019). Figure 6 shows a schematic description of the formation of cyclotron harmonics.

FIGURE 6

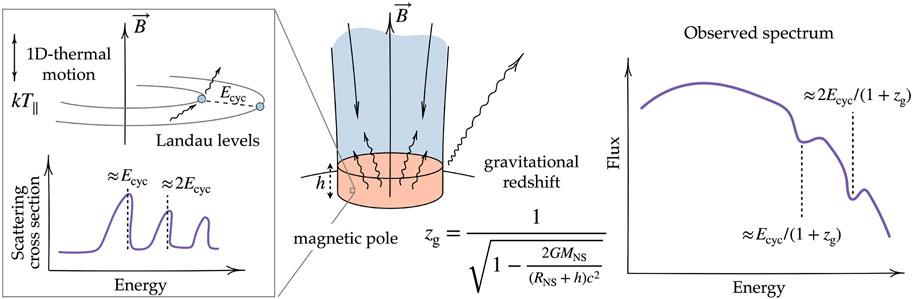
FIGURE 6. Simplified depiction of the formation of cyclotron lines in the spectra of accreting highly magnetized neutron stars due to photon scattering off electrons, whose motion perpendicular to the field lines is restricted by Landau quantization. The latter leads to strong cyclotron resonances in the Compton scattering cross section, broadened by the electron thermal motion parallel to the magnetic field. The centroid energies of the cyclotron lines in observed spectra approximately correspond to the redshited energies of the resonances (with some correction for the scattering redistribution effects during the lines’ formation). The gravitational redshift is dependent on the height of the line-forming region, h, above the surface of the neutron star.

When observed at typical outburst luminosity of ≳ 10³⁶ erg s⁻¹, the spectra of XRPs have been described with phenomenological models (a power-law with high-energy cutoff) modified by interstellar absorption, an Fe Kα emission line around 6.4 keV, low-temperature blackbody components and, at times, a component called the 10 keV feature (Mushtukov and Tsygankov, 2022, and references therein). However, at lower luminosity accretion regimes, the spectrum often exhibits a transition to a double-hump shape (Tsygankov et al., 2019a) which has recently been explained in terms of a low-energy thermal component peaking at ∼5 keV and a high-energy Comptonized component peaking at ∼35 keV representing the broadened red wing of the cyclotron line (Mushtukov et al., 2021; Sokolova-Lapa et al., 2021). A dip between the two components was sometimes interpreted as a cyclotron line (see, e.g., Doroshenko et al. (2012), for the case of X Per), but is likely a continuum feature, as was shown for sources with a known fundamental cyclotron line at higher energies after the transition to a low-luminosity state (see, e.g., Tsygankov et al. (2019a)).

These low luminosity states of accretion characterized by two-hump spectra are generally associated with braking of the accretion flow in the NS atmosphere [Mushtukov et al., 2021; Sokolova-Lapa et al., 2021, although a model assuming an extended collisionless shock instead was recently proposed by Becker and Wolff, (2022)]. Rapid deceleration of the plasma in the atmosphere proceeds mainly by Coulomb collisions and leads to the formation of an overheated outermost layer with electron temperatures of ∼30 keV. Such high temperatures significantly enhance Comptonization and together with resonant redistribution lead to the formation of the high-energy excess in the spectra around the cyclotron line. When the mass-accretion rate onto the poles is increased, the pressure of the emitted radiation starts affecting the dynamics of the accretion flow. The radiation becomes capable of decelerating the flow above the surface, reducing direct heating of the atmosphere and giving rise to a radiation-dominated shock (Basko and Sunyaev, 1976). The onset of this regime is typically associated with a critical luminosity (L_crit∼10³⁷ erg s⁻¹: Basko and Sunyaev, 1976; Becker et al., 2012; Mushtukov et al., 2015) and growth of the accretion column as an emitting structure. Modeling emission from accretion columns is a very challenging problem due to its dynamic nature, multi-dimensional geometry, and the necessity of including general relativistic effects. On the other hand, studying the low-luminosity regime with emission from the heated atmosphere of the polar cap allows easier access to fundamental parameters of accreting NSs (see Section 3.2.3 for more details).

Cyclotron lines exhibit variations with accretion luminosity, pulse phase, and over secular time scales. Variation of the cyclotron line centroid energy E_cyc with X-ray luminosity L_X can be exploited to gain insight into the accretion regime. For example, low-luminosity XRPs often show a positive correlation between E_cyc and L_X, while high-luminosity XRPs show a negative correlation [see, e.g., Klochkov et al. (2011)]. The two trends are assumed to be separated by the critical luminosity and thus are related to the transition between the different accretion regimes described above. On the other hand, studying the pulse-phase dependence of the E_cyc (as well as the line depth and width) can shed light upon the geometrical configuration of the NS (Nishimura, 2011). Moreover, some sources show evidence of a pulse phase-transient cyclotron line; i.e., a CRSF that only appears at certain pulse phases (Klochkov et al., 2008; Kong et al., 2022). Finally, secular variation of the cyclotron line has been attributed to a geometric reconfiguration of the polar field or to a magnetic field burial due to continued accretion (Bala et al., 2020; Staubert et al., 2020).

One of the biggest challenges for the detection and characterization of cyclotron lines is determining a robust broadband continuum model. The centroid energy of the line as well as its other parameters can show significantly different best-fit values when modelled with different continua. Due to this model-dependence, the very presence of a cyclotron line has been questioned at times (Di Salvo et al., 1998; Doroshenko et al., 2012; Doroshenko et al., 2020) as has its luminosity dependence (Müller et al., 2013). A similar argument also holds for the continuum best-fit values. The “true” continuum model can only be inferred if data cover a sufficiently wide energy passband to constrain absorption affecting the softer X-ray energies and the various spectral components at harder X-ray energies (Sokolova-Lapa et al., 2021; Malacaria et al., 2023a). Moreover, properly constraining the broadband continuum is necessary when multiple cyclotron line harmonics are present, as in the cases of 4U 0115 + 63 (Heindl et al., 2004) and V 0332 + 53 (Pottschmidt et al., 2005). In addition, observing the broadband continuum from accreting XRPs can help constraining physical parameters of the NSs thanks to the recent development of physically motivated spectral models (e.g., Farinelli et al. 2016; Becker and Wolff 2022, and references therein). This is especially important at low-luminosity, where the accretion flow free-falls on the NS surface and our understanding of the physical mechanisms is more uncertain concerning, e.g., how the flow transitions from radiation-dominated to gas-dominated, or the detailed production of seed photons from cyclotron, bremsstrahlung, and blackbody mechanisms at the site of impact. HEX-P will bring crucial contributions also in this field, as it will be able to probe broadband spectral emission from intrinsically dim sources whose required observing exposure with current facilities would be prohibitive.

Last but not least measuring phase-dependent spectral components with the highest sensitivity is required in order to develop consistent physical models for the emission process that include X-ray polarization properties. Recent IXPE observations of accreting pulsars like Cen X-3, Vela X-1, EXO 2030 + 375 and others provided new constraints as they showed low, energy-dependent polarization degrees of $<$10% (Tsygankov et al., 2022; Malacaria et al., 2023b; Forsblom et al., 2023). Radiative transfer models of highly magnetized plasmas predict considerably higher polarization degrees of 50%–80% (Meszaros et al., 1988; Caiazzo and Heyl, 2021; Sokolova-Lapa et al., 2023). Initial candidates for explaining the difference highlight the potential importance of the temperature structure of the plasma in the accretion column, of angle-dependent beaming, and of the propagation of X-rays in the magnetosphere for lowering the polarization degree. Furthermore it has been demonstrated that the X-ray continuum and cyclotron line profile can be expected to directly show subtle, complex imprints of polarization effects (Sokolova-Lapa et al., 2023). This is an intriguing possible reason for the occasionally observed and notoriously difficult to constrain “10 keV feature” mentioned above, as well as for the fact that some accreting pulsars do not show cyclotron lines.

Advancing our understanding of HMXBs in general and cyclotron line sources in particular therefore requires broadband spectra with high sensitivity throughout the relevant energy passband, with a limited background as provided by focusing X-ray facilities, and medium spectral energy resolution (Wolff et al., 2019). Thanks to its leap in observational capabilities, HEX-P will be capable of overcoming all above-mentioned challenges and push our understanding of accretion onto XRPs forward. In the next section, we simulate a few exemplary cases highlighting the gains enabled by HEX-P with respect to currently available X-ray facilities for which the investigated cyclotron lines centroid energy, accretion regime, or the necessary exposure time prevent a comprehensive study of the physical mechanisms at work.

3.2 Simulated science cases for HMXBs

The following simulations show HEX-P’s potential to tackle different cyclotron line science cases using several example sources. Each source has been chosen to represent a specific science case, either because it allows us to observe a certain accretion regime and luminosity range or due to its specific cyclotron line properties, such as the existence of n > 1 harmonics. We begin with the prototypical persistent cyclotron line sources Cen X-3 and Vela X-1, which show moderate to high fluxes and luminosities, and allow for exquisitely detailed and sensitive parameter constraints with HEX-P. Then we focus on transient accreting pulsars for which HEX-P will provide unprecedented access to low fluxes, allowing study of extreme luminosity regimes, e.g., for GX 304-1 in quiescence or for super-Eddington outbursts of extragalactic sources like SMC X-2. Similar to Section 2.2, all simulations were performed via the “fakeit” command in xspec (Arnaud, 1996) or ISIS (Houck and Denicola, 2000), employing version v07 of the HEX-P response files, selecting an 80% PSF correction, assuming a 15″ extraction region for the HETs and 8″ for the LET, as well as taking the expected background at L1 into account. The flux for each of the following simulations can be found in Supplementary Table S1.

3.2.1 Constraining magnetic field geometry from cyclotron line harmonics

As discussed earlier, cyclotron lines result from transitions between quantized Landau energy levels of electrons in the presence of a magnetic field (Meszaros, 1992). Measuring the energy, width, and strength of cyclotron lines in HMXBs is crucial for understanding the underlying physics of these systems. The energy of cyclotron lines provides insights into the line-forming region in the accretion column. The width of cyclotron lines provides valuable information about the geometry, temperature distribution, and plasma conditions within the accretion column [see e.g., Becker et al. (2012); Staubert et al. (2014) and references therein]. Broadening of cyclotron lines can be influenced by factors such as electron thermal motion, turbulence, and relativistic effects. In the last few decades, comprehensive analyses of HMXBs have directly unveiled many important properties of these systems [see, e.g., Staubert et al. (2019); Pradhan et al. (2021) and references therein]. In addition to the fundamental, higher harmonics of the cyclotron line are also sometimes present in the X-ray spectrum. They arise due to higher-order interactions between X-rays and the Landau levels. By detecting and analyzing fundamental cyclotron lines and their higher harmonics, one can determine the magnetic field strength in different regions of the accretion column. Furthermore, the strength or intensity of fundamental cyclotron lines and their higher harmonics relative to the fundamental line provide insight into the scattering efficiency and the fraction of scattered photons, improving our understanding of the emission processes and properties of the compact object [e.g., see Alexander and Meszaros, 1991; Schwarm et al., 2017 and references therein].

Given the limited passband and/or higher background of instruments like RXTE and Suzaku, there have been few studies to date of cyclotron lines higher harmonics in HMXBs (see Table 3 of Pradhan et al., 2021). More recent instruments like NuSTAR and Insight/HXMT provide a significant improvement, but as we look into the future, these studies will be revolutionized by a mission with a broad passband coupled with very low background like HEX-P. In order to test this, we simulated a 20 ks HEX-P spectrum of Cen X-3 in xspec. Due to its bright nature and that Cen X-3 is a strong hard X-ray emitter (see Supplementary Table S1), we concentrate on the HETs only which are devoid of pile-up although we have verified that the results below are consistent when including the LET. Cen X-3, an eclipsing HMXB, consists of an O star and a pulsar with a rotational period of ∼4.8 s (Chodil et al., 1967; Giacconi et al., 1971; Schreier et al., 1972). The X-ray spectrum of this source exhibits multiple emission lines (Fe, Si, Mg, Ne: Iaria et al., 2005; Tugay and Vasylenko, 2009; Naik and Paul, 2012; Aftab et al., 2019; Sanjurjo-Ferrín et al., 2021), and the X-ray emission has been detected beyond 70 keV. The fundamental cyclotron line occurs near 29 keV (Tomar et al., 2021) with a possible n₂ harmonic at ∼47 keV (Yang et al., 2023) as seen from recent HXMT results. With the passband of HEX-P extending up to 80 keV and significantly less background, we investigated the possibility of detecting an n₃ harmonic in the source.

The baseline model for our simulation is NPEX (Eq. 2; Mihara, 1995; Makishima et al., 1999) and the values of model parameters are taken from Table 1 (ObsID P010131101602) of Yang et al. (2023). The functional form of NPEX is given by

$\mathrm{N}\mathrm{P}\mathrm{E}\mathrm{X}\left(E\right)=\left(A{E}^{-{\mathrm{\Gamma }}_1}+B{E}^{+{\mathrm{\Gamma }}_2}\right){\mathrm{e}}^{-E/E_{\mathrm{f}\mathrm{o}\mathrm{l}\mathrm{d}}}(2)$

where Γ₁ and Γ₂ are the negative and positive power-law indices, respectively. Γ₂, which approximates a Wien hump, was fixed at 2.0, Γ₁ = 0.8, the folding energy E_fold = 6.9 keV, and the absorption column N_H = 2.06 × 10²² cm⁻².

The CRSFs are modeled with a multiplicative model of a line with a Gaussian optical depth profile with energy E_i, strength d_i, and width σ_i. The fundamental line, i = 1, is at ∼29 keV with d₁ ∼ 1.4 and σ₁ = 7.6 keV. The n₂ harmonic line, i = 2, is at ∼47 keV, with d₂ ∼ 2.3 and σ₂ = 9.7 keV. The 2–75 keV flux is ∼1 × 10⁻⁸ erg cm⁻² s⁻¹. In order to showcase the unparalleled accuracy of HEX-P in measuring magnetic fields correspondent to cyclotron line energies above 50 keV, we incorporated a representative example into our model: we include an n₃ harmonic line at 70 keV (i = 3), with the width (σ₃) and strength (d₃) set to match those of the n₂ harmonic line. By doing so, we investigate the ability of HEX-P to effectively detect these parameters in the n₃ harmonic line, from which we can constrain the magnetic field strength and details about the magnetic field structure.

A 20 ks observation HEX-P is able to constrain the energy of the n₃ harmonic well, to within 7% (see Figure 7). We also applied an F-test to calculate the probability of chance improvement, with and without the n₃ harmonic line, and found that the probability of chance improvement when adding the n₃ harmonic line is below 0.06%, confirming the robustness of the detection. We reiterate here that the clear improvement of HEX-P over its predecessors in terms of broadband coverage and sensitivity makes it possible to investigate higher harmonic features–which have clearly eluded NuSTAR [see e.g., Tomar et al. (2021)].

FIGURE 7

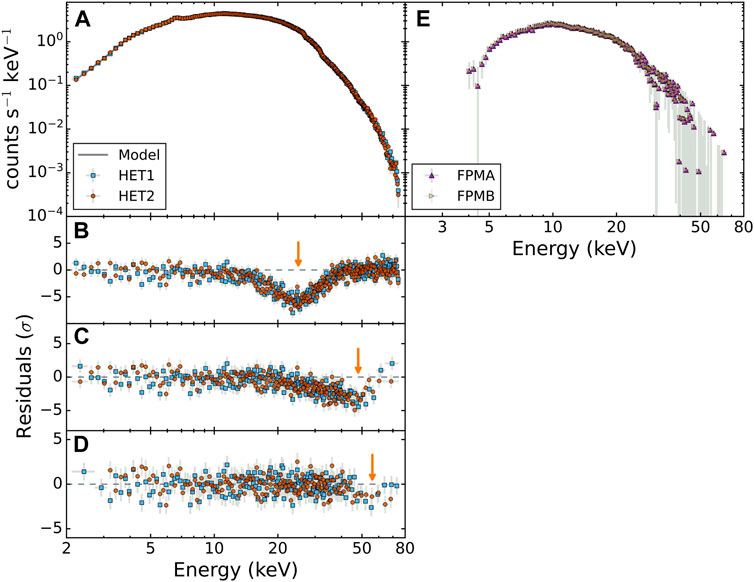
FIGURE 7. Simulated 20 ks HET spectra for Cen X-3, as well as the best-fit model are shown in panel (A). Panels (B–D) show the residuals obtained when we set the strength of fundamental, n₂ harmonic, and n₃ harmonic to zero, respectively. We re-binned the data visually and provide arrows for the cyclotron line components to aid with clarity. For comparison, we provide a simulated NuSTAR spectrum for using the same model and exposure time which is shown in panel (E). The NuSTAR data are strongly background dominated at these flux levels, which makes constraining the higher energy harmonics difficult even at much longer exposure times (see text for more details).

Since cyclotron lines result from the resonant scattering of photons by electrons whose energies are quantized into Landau levels by the strong magnetic field, and the quantized energy levels of the electrons are harmonically spaced, one would naively expect the energy of the n > 1 harmonics to be the integer multiples of the fundamental line. It has however been observed in various X-ray pulsars that this is generally not the case (see Yang et al., 2023; Orlandini et al., 2012 and discussions within). The discrepancy can be understood by assuming a difference in line formation mechanisms or in line-forming regions for the fundamental and higher harmonics. In the former case, the fundamental would primarily arise from resonant scattering, while the higher harmonics involve additional effects like multiple scattering and photon spawning [see e.g., Nishimura, (2003); Schönherr et al. (2007)]. This, however, can not be the only reason because some systems show an an-harmonic spacing larger than predicted by this effect. One way to explain this difference is to take into account that the optical depths of the fundamental and the higher harmonics can be different if they are formed at different heights above the NS. The higher harmonics could be closer to the NS surface and the fundamental line situated at a height with weaker magnetic field strength [see, e.g., Fürst et al. (2018)]. Another possibility is to consider a displacement of the magnetic dipole, which would also explain the energy difference of the two lines if the lines originate from the different poles of the NS (Rodes-Roca et al., 2009). Therefore, a significant phase dependence of the strength of the fundamental and higher harmonics is expected, which is not possible to probe with the current data sets. Here, too, HEX-P can provide revolutionary new capabilities though (see Section 3.2.2).

Finally, note that while the n₂ harmonic of Cen X-3 at 47 keV technically falls within the energy range covered by NuSTAR, meaningful constraints could not be derived with NuSTAR (see panel (e) of Figure 7) due to the dominant background in that energy range even when the exposure was set to 500 ks. However, with HEX-P, the parameters associated with the cyclotron line can be much better constrained, while also alleviating the degeneracies with the continuum. To emphasize the latter point, we present a contour plot in Figure 8 depicting the relationship between the fundamental cyclotron line energy and the cutoff energy for both HEX-P and NuSTAR data for the same model and exposure of 20 ks for Cen X-3. The plot clearly demonstrates that HEX-P provides significantly more stringent constraints compared to NuSTAR. Such accurate measurements in short exposure times will enable detailed pulse phase-resolved spectra to explore the accretion physics in the accretion column in unprecedented detail, as discussed in the following section.

FIGURE 8

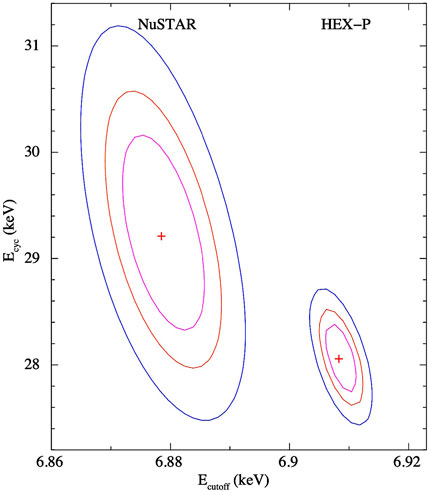
FIGURE 8. Contour plots (68%, 90%, and 99% confidence levels) for cutoff energy versus the fundamental cyclotron line energy for Cen X-3 using the same model and exposure for NuSTAR and HEX-P. As evident from the plot, HEX-P will provide better constraints on the continuum and cyclotron line parameters; thereby mitigating degeneracies between the two. Note that the cutoff energies are slightly shifted to aid visualization.

Note that Cen X-3 is highly variable, the X-ray flux varies by up-to two orders of magnitude even outside eclipses. Therefore, we also fit the actual NuSTAR data in bright flux state (ObsID 30101055002; exposure 21 ks), which has a flux an order of magnitude more than our simulations, and find the harmonics were not detected in the NuSTAR spectrum [see, Tomar et al. (2021)]. In order to make a comparison of HEX-P vs. NuSTAR for this bright state of Cen X-3, we simulated an HET spectrum using the NuSTAR model in bright state, while keeping the parameters of harmonics as above. We find that, even for this bright state of Cen X-3, NuSTAR will be able to obtain the same signal-to-noise as HEX-P only if the exposure is increased by 20 times (i.e., 420 ks).

3.2.2 Constraining accretion column emission geometry through pulse phase-resolved spectroscopy

Vela X-1 is an archetypical HMXB. It has been well studied with all current and past X-ray missions (see Kretschmar et al., 2021, for a recent review). While not being exceptionally luminous (∼10³⁶ erg s⁻¹), its close distance (d = 1.9 kpc) and X-ray eclipses make it an ideal system to study NS magnetic fields and their interaction with the stellar wind of the companion (i.e., the mass donor). The X-ray spectrum of Vela X-1 shows two CRSFs, the fundamental at around 25 keV and the n₂ harmonic around 55 keV (see Fürst et al., 2014, and references therein). These line energies are ideally covered by the HEX-P energy band. However, in Vela X-1, the fundamental line around 25 keV is much weaker and shallower than the n₂ harmonic line at 55 keV. In fact, the 25 keV line is so weak that there has been a long-standing discussion in the literature about its existence, which could only be settled once NuSTAR data were available (Kreykenbohm et al., 2002; Maitra and Paul, 2013; Fürst et al., 2014). The cyclotron lines in Vela X-1 therefore represent a good test case to explore HEX-P’s sensitivity to broad and shallow spectral features.

We performed simulations to study how well HEX-P can measure the energy, width, and depth of both CRSFs, in particular as a function of rotational phase of the NS. Variations of CRSF parameters as a function of phase constrain the magnetic field geometry and emission geometry of the accretion column [see, e.g., Iwakiri et al. (2019); Liu et al. (2020)].

We base our simulations on the spectral fits of NuSTAR data presented by Diez et al. (2022). In particular, the continuum is modeled by a powerlaw with an exponential cutoff at high energies (using the model “FDcut” in xspec, Eq. 3; Tanaka, 1986), modified by neutral absorption column at low energies:

$\mathrm{F}\mathrm{D}\mathrm{C}\mathrm{U}\mathrm{T}\left(E\right)=A{E}^{-\mathrm{\Gamma }}\frac{1}{1+{\mathrm{e}}^{\left(E-E_{\mathrm{c}\mathrm{u}\mathrm{t}}\right)/E_{\mathrm{f}\mathrm{o}\mathrm{l}\mathrm{d}}}}(3)$

where Γ is the power-law index, E_cut is the cutoff energy, and E_fold is the folding energy. In addition to the continuum model used by Diez et al. (2022) we also include soft X-ray emission lines at 6.4 keV (Fe Kα), 2.4 keV (S Kα), 1.8 keV (Si Kα), 1.4 keV (Mg Lα), and 0.9 keV (Ne IX), representing various atomic features in the spectrum (Diez et al., 2023). A simulated spectrum is shown in Figure 9.

FIGURE 9

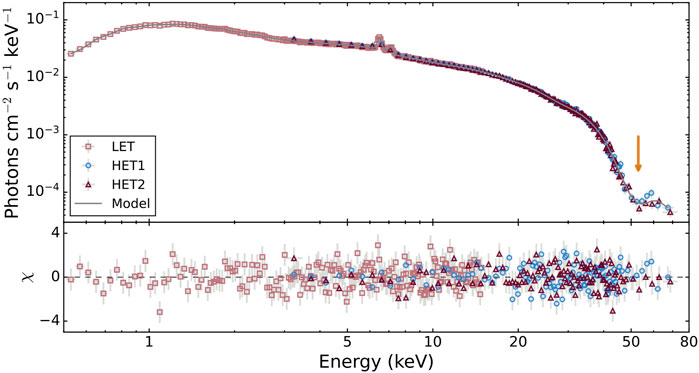
FIGURE 9. Simulated Vela X-1 spectrum for the bin covering phases 0–0.1 (see Figure 10 for the spectral values in that bin). The n₂ harmonic cyclotron line is clearly visible as a strong dip at the highest energies as indicated by the arrow.

As mentioned in Section 3.2.1, CRSFs are modeled using a multiplicative line model with a Gaussian optical depth profile described by its energy E_i, its strength d_i, and its width σ_i. Here the subscript i denotes either the fundamental line around 25 keV (i = 1) or the n₂ harmonic line around 55 keV (i = 2). The width σ₁ is set to 0.5 × σ₂ (Diez et al., 2022). Instead of relying on the [rather uncertain; see, e.g., Maitra et al. (2018)] current knowledge of the phase-resolved behavior of the CRSF parameters, we simulate that the four most relevant parameters (E₁, E₂, d₁, d₂) vary sinusoidally with random phase shifts to each other. This approach demonstrates the power of HEX-P to resolve small changes in any of the parameters, even for relatively weak lines. In particular, we assume that the fundamental line E₁ varies by about ±3.5 keV as a function of phase, while the n₂ harmonic line energy E₂ varies by ±5 keV. The strength d₁ and d₂ vary by ±0.3 keV and ±5.0 keV, respectively.

In addition, we also allow the absorption column of the partial absorber to vary, with ± 5 × 10²² cm⁻² around the average value of 32.1 × 10²² cm⁻². While we do not necessarily expect that the absorption column will vary significantly as function of pulse phase, this variability highlights the capabilities of the HEX-P/LET to measure small changes in absorbing columns on time-scales as short as 5 ks. These variations have been observed in time-resolved spectroscopy and allow us to study the physical properties, like density and clump sizes of the accreted medium (Diez et al., 2023). At the same time, the changes in N_H do not influence the high energy spectrum where the CRSFs are present.

For our simulations, we assume that LET will be operated in a fast readout mode to avoid pile-up and with negligible deadtime. We simulate spectra with 50 ks exposure time each, and split the data into 10 phase-bins so that each one has an exposure time of 5 ks We simulate 100 individual spectra for each phase-bin and calculate the standard deviation (SD) of that sample as uncertainties for each parameter. We additionally calculate the 90% and 10% percentile of the 90% uncertainties of each realization as a realistic estimate of the expected uncertainties in a real 50 ks observation. Using multiple realizations for each phase bin allows us to avoid issues with any one particular realization and shows that our uncertainties are properly sampled over the Poisson noise inherent to counting statistics. The results are shown in Figure 10.

FIGURE 10

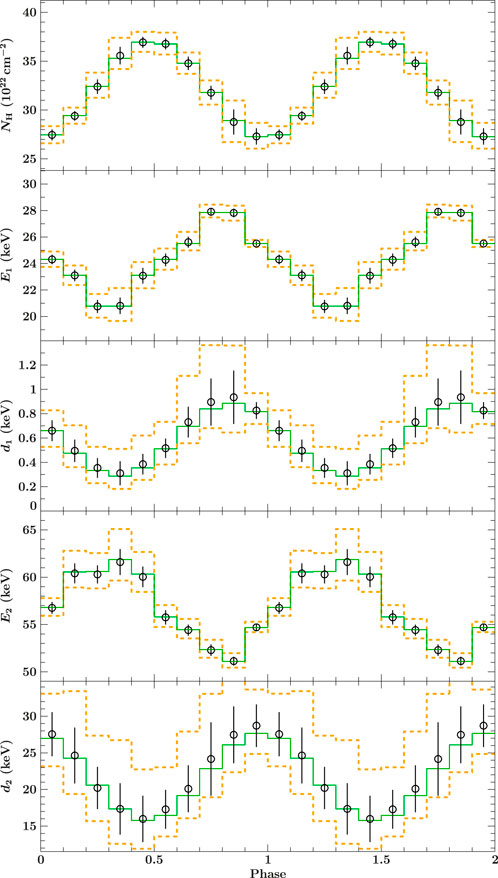
FIGURE 10. Absorption column and cyclotron line variability in Vela X-1, calculated from simulated phase-resolved HEX-P spectra using the results of Diez et al. (2022) with an average flux of 6.7 × 10⁻⁹ erg s⁻¹ cm⁻² in the 3–80 keV band. The parameters from top to bottom are: absorption column N_H, fundamental line energy (E₁), fundamental line strength (d₁), n₂ harmonic line energy (E₂), and n₂ harmonic line strength (d₂). Note that the fundamental line width is set to half of the n₂ harmonic width. The black uncertainties show the standard deviation for a sample of 100 simulations per phase bin. The orange dashed histogram indicates the expected 90% uncertainties on each individual realization. The green line indicates the input values for each phase bin. For details about the simulation set-up see Section 3.2.2; Supplementary Table S3.

All parameters can be very well reconstructed, with the fundamental energy having uncertainties $<0.5$ keV for phases where its strength is $>0.4$ keV (i.e., phases 0.5–1.0). Even for weaker lines (despite having larger uncertainties of about ± 1 keV), the line can be still significantly detected. This is a significant improvement over NuSTAR, for which Fürst et al. (2018) found that the energy was basically unconstrained for line strengths $<0.5$ keV.

The n₂ harmonic line energy can be very well constrained (with uncertainties $<$2 keV) for central energies of the line $<57$ keV. Due to the exposure time of only 5 ks per phase-bin and the low cutoff energy of ∼25 keV, the line appears at the very edge of the useful range of the spectrum. Therefore, higher energies become more difficult to constrain, as most of the line is outside the useful passband; however, we still find typical constraints of ±3–4 keV, even for a simulated line energy of 61 keV.

These results represent a significant improvement over previous phase-resolved studies of Vela X-1. For example, using RXTE, Kreykenbohm et al. (1999) found variations of the CRSF energies for both the fundamental and the n₂ harmonic line, but could only use 10 phase bins and still had average uncertainties of 2–3 keV for the fundamental line, and 5–10 keV for the n₂ harmonic. Recently, Liu et al. (2022) published results obtained on Vela X-1 with Insight/HXMT. Using 16 phase-bins for a ∼100 ks exposure, they found average uncertainties comparable to our HEX-P simulations for the n₂ harmonic line, but with significantly larger uncertainties (a few keV) for the fundamental line. We also note that Liu et al. (2022) found the n₂ harmonic line at energies between 40 and 50 keV, i.e., at much lower energies than simulated here and therefore in a part of the spectrum with a much higher signal-to-noise ratio.

HEX-P observations would therefore be a big step forward in being able to obtain phase-resolved spectroscopy of bright HMXBs, where we can constrain the CRSF parameters, in particular the energy, much better than with existing instruments in shorter exposure times. This reduction in exposure time means that we can either observe more sources in less time or slice the phase-resolved spectra finer to obtain a more detailed look at the emission and magnetic field geometry of the accretion column (Nishimura, 2003; Schönherr et al., 2007; Schwarm et al., 2017).

3.2.3 Constraining the surface magnetic field strength from quiescent observations of Be X-ray binaries

Details regarding the formation of cyclotron lines in the spectra of accreting NSs in HMXBs are highly debated in the literature. The observed positive and negative correlations of the cyclotron energy with luminosity are often interpreted as a change of the dynamics of the accretion process in different accretion regimes, distinguished by a critical luminosity where a radiation-dominated shock forms in the column above the NS surface. For high-luminosity regimes, when it is assumed that L_X > L_crit, several mechanisms for the formation of cyclotron lines have been suggested that explain the observed negative line energy versus luminosity correlation. These scenarios involve different locations for the line production: above the NS surface in an accretion column that is growing with increasing luminosity [see, e.g., Becker et al. (2012)] or in the illuminated atmosphere of the NS at lower magnetic latitudes, where the column radiation is reprocessed [as suggested by Poutanen et al. (2013); see, however; Kylafis et al. (2021)]. For lower luminosities, L_X ≲ L_crit, the formation of cyclotron lines is usually attributed to comparatively lower heights in the accretion column. In this case, a positive line energy versus luminosity correlation can be explained by the formation of a collisionless shock [see, e.g., Rothschild et al. (2017); Vybornov et al. (2017)] that is moving closer to the NS surface for higher luminosities or by the redshift due to bulk motion of the accretion flow (Nishimura, 2014; Mushtukov et al., 2015). However, to apply these models in a consistent way and to distinguish between their predictions, it is required to know the surface field at the magnetic pole of the NS. This can then serve as a reference to estimate, for example, the characteristic height of the line-forming region in the column or the velocity of the accretion flow near the surface.

Recent evidence of accretion in Be X-ray binaries in quiescence, i.e., with L_X ≪ L_crit, and the simple emission region geometry expected in this case (i.e., a hot spot on the NS surface) together represent a unique opportunity to observe cyclotron lines at the energy corresponding to the surface value of the magnetic field. From current observational examples it seems that for this accretion state to occur, the magnetic field of the source might have to be sufficiently high, B ≳ 5 × 10¹² G, and the spin period might have to be comparatively long, ≳ 100 s (as, e.g., for GX 304–1 and GRO J1008−57: Tsygankov et al., 2019b; Lutovinov et al., 2021). The low flux level, however, makes the detection of cyclotron lines at high energies very challenging. GX 304–1 is one of the first sources which unambiguously exhibited stable quiescent accretion (Rouco Escorial et al., 2018) with a cyclotron line known from outburst observations (Mihara et al., 2010; Malacaria et al., 2015). The corresponding flux level in the 2–10 keV energy band, ∼0.4 mCrab, is below the sensitivity of Insight/HXMT. With NuSTAR we can access the high-energy emission, but are typically unable to constrain the turnover of the second hump of the characteristic double-hump spectrum (see Section 3.1) and the cyclotron line (Tsygankov et al., 2019b, Zainab et al., in prep.).

The best way to probe the above mentioned science cases is to observe the source during the quiescent accretion regime, i.e., at a low-luminosity state that is typically below the detection threshold for X-ray all sky monitors and accessible only with pointed observations subsequent to an X-ray outburst. Such a regime is also of importance since the simplified physics of plasma stopping at the nearly-static NS atmosphere allows for more detailed modeling of emission processes. The tenuous flow of matter stops at the NS atmosphere by Coulomb collisions, resulting in a high temperature gradient from ∼30 keV at the top down to ∼2 keV in the lower layers, separated by only ∼10 m [see, e.g., Sokolova-Lapa et al. (2021)]. The intrinsic emission is mainly produced by magnetic bremsstrahlung (for sufficiently low magnetic fields, cyclotron photons are produced as well from collisional excitations of electrons moving in bulk; Mushtukov et al., 2021), which is then modified by Compton scattering. This regime of accretion allows, for the first time, to combine modeling of the temperature and density structure of the emission region with a joint simulation of the continuum and cyclotron line formation (Mushtukov et al., 2021; Sokolova-Lapa et al., 2021).

In this way, existing physically-motivated models principally provide access to information about the field strength at the poles of accreting highly magnetized NSs. However, the limitations of current high-energy missions do not permit us to constrain the corresponding cyclotron lines in the spectra. HEX-P will open a new avenue for the accreting NSs community by allowing us to detect such features with sufficiently long exposures.

In order to demonstrate HEX-P’s capabilities to measure the surface magnetic field strength of a NS in quiescence, we simulate observations of the quiescent state of the Be X-ray binary GX 304–1, the first system for which a transition to the two-component spectrum was observed by NuSTAR (Tsygankov et al., 2019b). We use the physical model polcap presented by Sokolova-Lapa et al. (2021), which describes emission for the low-luminosity accretion regime. Here, we adopt an updated parametrization of the model (using the same underlying pre-calculated spectra; E. Sokolova-Lapa, priv. comm.). The parameters are the mass flux, $\dot{M}/\pi r_0^2$, where $\dot{M}$ is the mass-accretion rate and r₀ is the polar cap radius; the cyclotron energy, E_cyc, corresponding to the polar magnetic field strength, B; and the normalization given in terms of $r_0^2/D^2$, where D is the distance to the source. We set the normalization and the mass flux based on the flux level and the shape of the spectrum as observed previously by NuSTAR. The magnetic field strength is set to B = ×5.35 10¹² G, derived from the centroid energy of the cyclotron line observed during the previous outburst [∼50 keV, Jaisawal et al. (2016)] and corrected by the gravitational redshift near the surface of the NS (z_g ≈ 0.24, assuming standard NS parameters). The corresponding spectrum calculated with the polcap model and the exact values of the parameters used for the simulations are shown in Figure 11. Due to internal averaging over the emission angles to obtain the total flux in the NS rest-frame [see details in Sokolova-Lapa et al. (2021)], the cyclotron line in the corresponding spectrum is located at ≈ 60 keV. Taking into account the gravitational redshift, the cyclotron line in the observed spectrum is therefore expected at ≈ 48 keV. We simulate a 60 ks observation for all three HEX-P instruments, combining the polcap model with tbabs (Wilms et al., 2000) to account for interstellar absorption (i.e., tbabs*polcap), fixing N_H to the Galactic value of 1.1 × 10²² cm⁻² in the direction of the source. The resulting luminosity in the 1–80 keV range is ∼8 × 10³³ erg s⁻¹.

FIGURE 11

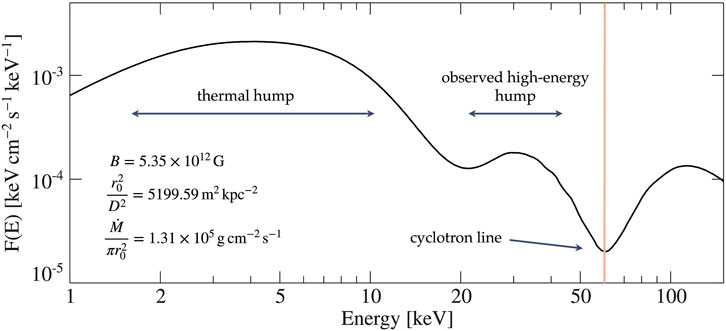
FIGURE 11. Model used to simulate the observation of the Be X-ray binary GX 304–1 in quiescence. The vertical orange line indicates the center of the cyclotron line. The cyclotron line and the continuum are calculated together using polarized radiative transfer simulations (Sokolova-Lapa et al., 2021). The low-energy “thermal” hump and the high-energy hump below the cyclotron line (the red wing of the cyclotron line) are typically observed as a “two-hump” spectrum from Be X-ray binaries in quiescence.

We compare the HEX-P spectra against a NuSTAR observation of the same exposure. We first fit both, the simulated HEX-P and existing NuSTAR observations, using a model that includes two independent Comptonized components (comptt; Titarchuk, 1994), tbabs*(comptt₁ + comptt₂). This model, with or without a multiplicative Gaussian-like cyclotron line (gabs), is commonly used to describe the two-component spectra of low-luminosity states [see, e.g., Tsygankov et al. (2019a); Lutovinov et al. (2021); Doroshenko et al. (2021)]. Similarly to earlier analyses (Tsygankov et al., 2019b), we obtain a good description of the NuSTAR data with this model, with ${\chi }_{\text{red}}^2=136.93/107=1.28$ for the best fit.

For the simulated HEX-P data, the same model consistent of two absorbed Comptonized components provides a formally satisfactory fit $({\chi }_{\text{red}}^2=322.64/275=1.17)$, however, the residuals are flat only at low and intermediate energies, but indicate a dip at around 40–60 keV, where the cyclotron line is expected from the underlying physical model (see Figure 11). The best fit for a model which includes an additional Gaussian absorption line at high energies to describe the cyclotron line, provides the line’s centroid energy of $46.5_{-2.7}^{+4.1}\mathrm{k}\mathrm{e}\mathrm{V}$, width $8.2_{-2.1}^{+3.1}\mathrm{k}\mathrm{e}\mathrm{V}$, and strength $54_{-21}^{+41}\mathrm{k}\mathrm{e}\mathrm{V}$, with the ${\chi }_{\text{red}}^2=261.23/276=0.95$. The centroid energy corresponds (within its uncertainties) to the redshifted cyclotron line from the physical model, which is expected to be at ≈ 60/(1 + z_g) keV ≈ 48 keV, assuming the standard NS parameters to estimate the redshift, z_g = 0.24. Figure 12 shows the resulting spectra and the corresponding best-fit models for the real NuSTAR and the simulated HEX-P observations.

FIGURE 12

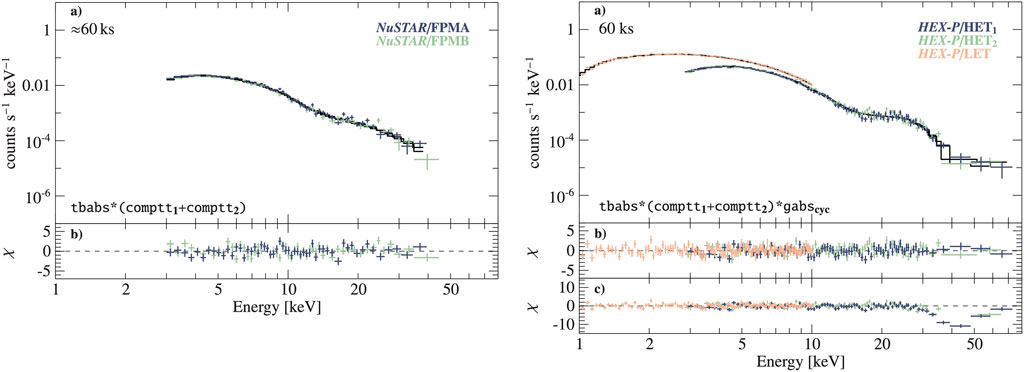
FIGURE 12. NuSTAR observation [left, (a)] and simulated HEX-P [right, (a)] spectra of a 60 ks observation of the Be X-ray GX 304–1 in quiescence and corresponding best-fit models. Both panels (b) show residuals for the best-fit models. For the simulated HEX-P spectra, we also show the residuals for the case when the cyclotron line strength is set to zero [left, (c)]. The high-energy cyclotron line can be constrained from the HEX-P data, with the centroid energy $46.5_{-2.7}^{+4.1}\mathrm{k}\mathrm{e}\mathrm{V}$.

This example shows that even at this exposure, which is relatively low for the quiescent state of Be X-ray binaries, we can constrain the cyclotron line energy and thus the surface magnetic field to within ∼20%. This capability is crucial for systems which have never been observed at high-luminosity states, that is, for which cyclotron lines have never been observed in the spectra. This class of Be X-ray binaries accreting in quiescence is actively growing, e.g., through NuSTAR follow-up of Be X-ray binary candidates found during the first eROSITA All Sky Survey [see, e.g., Doroshenko et al. (2022)]. More similar discoveries are expected as deeper X-ray survey data from eROSITA become available. The spectral shape of the latter sources, in particular, the location of the high-energy excess associated with the energies below the cyclotron resonance, suggests a similar magnetic field strength as in GX 304–1. The search for high-energy cyclotron lines, which makes it possible to unambiguously constrain the surface magnetic field of an accreting neutron star, requires superior sensitivity at hard X-rays, as will be provided by HEX-P.

For a discussion of NS science that can be done with HEX-P for B-fields in excess of ∼10¹⁴G (i.e., magnetars), we refer the reader to Alford et al. (2023), (in prep.).

3.2.4 Constraining super-critical accretion and the critical luminosity via cyclotron line evolution in extragalactic sources

A correlation between cyclotron line energy and X-ray luminosity has been reported for a handful of X-ray pulsars [see Staubert et al., 2019, and above]. The dependence of the line energy on luminosity can be attributed to changes in the height of the accretion column and can be positive or negative for low and high X-ray luminosity, respectively (Becker et al., 2012). However, in a couple of sources a secondary effect has been reported: for equal levels of luminosity, the energy of the cyclotron line can be different (up to 10% change) between the rise and the decay of an outburst or between different outbursts (e.g., V 0332 + 53, Cusumano et al. (2016) and SMC X-2; Jaisawal et al., 2023). Doroshenko et al. (2017) proposed that this effect is likely caused by a change of the emission region geometry (e.g., different combinations of height and width of the accretion column), while an alternative explanation is that it is due to accretion-induced decay of the NS’s magnetic field (Cusumano et al., 2016; Jaisawal et al., 2023).

Given this complex observational behavior, it is critical to detect CRSFs in more transient systems and to study their evolution over luminous outbursts. Although a significant population of HMXBs is found in the Milky Way, interpreting results from observing its members is often hampered by their uncertain distance and large foreground absorption. In that sense nearby galaxies like the star-forming Large and Small Magellanic Clouds (LMC and SMC) offer a unique laboratory to complement our studies of luminous Galactic HMXBs. Sources in these galaxies have well determined distances of ∼50 kpc (LMC) or ∼60 kpc (SMC) and low Galactic foreground absorption (∼10²⁰ cm⁻²) making them ideal targets for spectral and temporal studies during major outbursts. Based on past observations and recent statistics, an outburst that peaks above 2 × 10³⁸ erg s⁻¹ occurs in the Magellanic Clouds every few years [e.g., Vasilopoulos et al. (2014); Koliopanos and Vasilopoulos, (2018); Maitra et al. (2018); Vasilopoulos et al. (2020)]. Such outbursts are brighter than the Eddington luminosity for a typical NS, more precisely, they are brighter than the critical luminosity⁵, L_crit∼10³⁷ erg s⁻¹, for a typical accretion column (see Section 3.1). They are therefore called super-Eddington or super-critical outbursts.

SMC X-2 is a good example to demonstrate HEX-P’s capabilities to detect and follow the evolution of a CRSF during a bright outburst. This BeXRB pulsar has exhibited two outbursts which reached luminosities above the Eddington limit over the last decade, one in 2015 and another in 2022. Both outbursts were followed up with Swift/XRT, as well as with NuSTAR ToOs (three observations in 2015 and one in 2022), covering a broad range in luminosity of (2–6) × 10³⁸ erg s⁻¹ (see Figures 13A). When comparing the CRSF energy for the two outbursts at the same luminosity level, the line energy was about 2 keV higher during the 2022 outburst than observed previously in 2015 (see Figures 13B). This corresponds to a difference in magnetic field strength of B ∼ 2 × 10¹¹ G, akin to the difference reported by Cusumano et al. (2016) for V 0332 + 53.

FIGURE 13

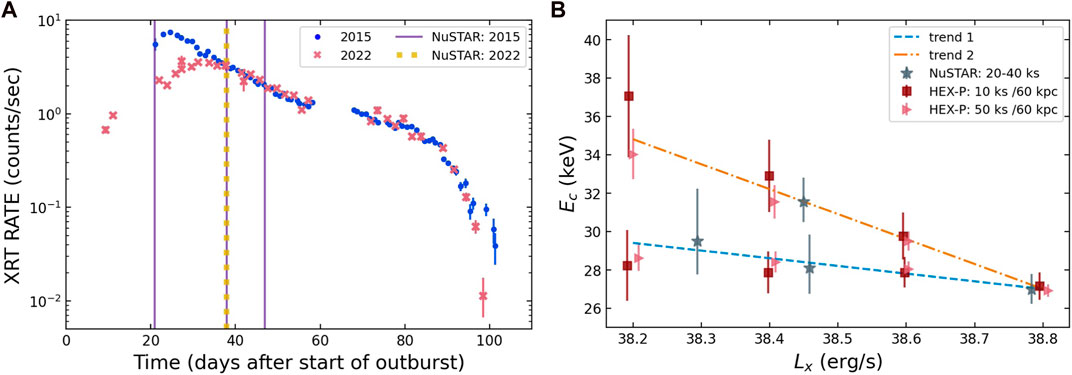
FIGURE 13. (A): The 2015 and 2022 super-critical outbursts of SMC X-2 observed by Swift/XRT. The vertical lines mark the epochs of four NuSTAR observations of the system. (B): The cyclotron line dependence on luminosity. The star symbols mark the measured CRSF values for SMC X-2 for the NuSTAR observations (Jaisawal et al., 2023). Note that the NuSTAR points on the trend 1 line are from the 2015 outburst, while the point on the trend 2 line was measured during the 2022 outburst; hence different cyclotron line energies can be measured even when the source is at nearly the same luminosity during outburst indicating an inherent difference between outbursts. We demonstrate HEX-P’s capabilities to discern between different possible trends in cyclotron line energy as a function of luminosity in these types of systems in as little at 10 ks, though greatly improved for 50 ks exposures.

In order to test HEX-P’s capabilities to detect CRSF features for extragalactic sources and determine if the data would be sufficient to distinguish trends with luminosity, we performed several simulations based on the spectral properties of SMC X-2 as measured by NuSTAR (Jaisawal et al., 2023). For all simulations we used both HET and LET detectors. For the continuum we used an absorbed (tbabs with N_H = 10²⁰ cm⁻²; Wilms et al., 2000) cut-off power-law model (i.e., cutoffpl) and a cyclotron absorption feature with the gabs model. We limited our simulations to the super-critical regime and a bolometric luminosity of 1.5–6 × 10³⁸ ergs s⁻¹ which yields an absorbed flux range of 2–8 × 10⁻¹⁰ ergs cm⁻² s⁻¹ (1–50 keV). We simulated spectra where the CRSF energy varied with luminosity assuming two arbitrary inverse linear energy dependencies (trend 1 and trend 2 in Figure 13). We then fit the spectra and derived the best-fit parameters for the line with corresponding uncertainties. The results are shown in Figures 13B. HEX-P can constrain the CRSF parameters (here the central line energy) at least two times better than NuSTAR and with an exposure time (10 ks) that is only between half and a fourth that of NuSTAR, as well as discern between different trend inputs. For a longer exposure time of 50 ks the line parameters can be measured with unparalleled accuracy at the distance of the SMC. Thus, HEX-P will be able to detect and follow cyclotron line evolution for super-critical outbursts in the Magellanic Clouds and thereby test competing physical models (i.e., similar to V 0332 + 53 Cusumano et al., 2016; Vybornov et al., 2018). Note that the flux regime for which these trends are simulated (see Supplementary Table S1) and the science cases of the previous subsections suggest that trends in CRSF energy can also be probed at sub-critical through super-critical luminosities in galactic sources. For science that can be executed with HEX-P regarding pulsations and cyclotron lines in extragalactic ultraluminous X-ray (ULX) sources which reach even higher luminosities of $>100\times$ their Eddington limit, we refer the reader to Bachetti et al. (in prep.).

In addition, it is expected that accreting XRPs crossing the critical luminosity should show a reversal of the cyclotron line energy versus luminosity correlation. To date only marginal evidence has been observed for such a trend reversal and in only a couple of sources (Doroshenko et al., 2017; Malacaria et al., 2022). As mentioned above, the Magellanic Clouds host comparatively many transient accreting pulsars displaying high-luminosity outbursts. HEX-P’s ability to constrain the cyclotron line energy with unprecedented accuracy across orders of magnitude in luminosity (and thus over distinct accretion regimes) will provide us with the opportunity to trace more and well defined trend reversals. This will allow us to constrain the critical luminosity for a given source which, in turn, places constraints on physical parameters of the observed system, such as the NS magnetic field strength or source distance (Becker et al., 2012).

4 Conclusion

We have presented open questions about NSs and accretion onto strongly magnetized sources, and demonstrated HEX-P’s unique ability to address these questions. The broad X-ray passband, improved sensitivity, and low X-ray background make HEX-P ideally suited to understand accretion in X-ray soft sources, down into low accretion rate regimes. In particular for LMXBs, we have shown that HEX-P observations will discriminate between competing continuum emission models that diverge above 30 keV; an energy band inaccessible to current focusing X-ray telescopes for these soft spectrum sources. Additionally, leveraging the improved sensitivity and broad X-ray passband, HEX-P will achieve tighter constraints on NS radius measurements through reflection modeling. These measurements are complementary and independent to other methodologies, and will narrow the allowed region on the NS mass-radius plane for viable EoS models for ultra-dense, cold matter, providing fundamental physics information in a regime inaccessible to terrestrial laboratories.

For the case of NSs in HMXBs, HEX-P will vastly improve our ability to: 1) detect multiple cyclotron line features in a single observation, aiding in our understanding of the magnetic field strength in different regions of the accretion column and the poorly known physical mechanisms behind the formation of higher harmonic features; 2) obtain detailed phase-resolved spectra to track the dependence of CRSFs on pulse phase in order to explore the geometric configuration of the accretion column emission in unprecedented details; 3) constrain the surface magnetic field strength of accreting NSs at the lowest accretion regime and characterize the continuum spectral formation to provide updated physically-motivated spectral models for future observations; and 4) identify CRSFs in extragalactic sources and follow the evolution of their line energy as a function of luminosity in order to distinguish between competing theories regarding changing emission region geometry or accretion-induced decay of the NS B-field.

HEX-P will provide a new avenue for testing magnetic field configuration, emission pattern, and accretion column physics close to the surface of NSs, as well as enhance our understanding of extreme accretion physics in both LMXBs and HMXBs.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

RL: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. CM: Conceptualization, Investigation, Methodology, Writing–original draft, Writing–review and editing. ES-L: Conceptualization, Formal Analysis, Investigation, Methodology, Writing–original draft, Writing–review and editing. FF: Conceptualization, Formal Analysis, Investigation, Methodology, Writing–original draft, Writing–review and editing. PP: Conceptualization, Formal Analysis, Investigation, Methodology, Writing–original draft, Writing–review and editing. AS: Conceptualization, Formal Analysis, Investigation, Methodology, Validation, Writing–original draft, Writing–review and editing. KP: Conceptualization, Supervision, Validation, Writing–original draft, Writing–review and editing. SP: Conceptualization, Writing–review and editing. GV: Conceptualization, Formal Analysis, Investigation, Methodology, Writing–original draft, Writing–review and editing. JW: Conceptualization, Validation, Writing–review and editing. JG: Writing–review and editing. KM: Writing–review and editing. DS: Writing–review and editing. CM: Writing–review and editing. MD: Writing–review and editing. DW: Writing–review and editing. MB: Writing–review and editing. JE: Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The material is based upon work supported by NASA under award number 80GSFC21M0002. GV acknowledges support by the Hellenic Foundation for Research and Innovation, (H.F.R.I.) through the project ASTRAPE (Project ID 7802). The work of DS was carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with NASA. ES-L and JW acknowledge partial funding under Deutsche Forschungsgemeinschaft grant WI 1860/11-2 and Deutsches Zentrum für Luft-und Raumfahrt grant 50 QR 2202.

Acknowledgments

RL and AS would like to thank Dr. Kazuhiko Shinki for providing consultation on statistical methods of Section 2.2.2. The authors thank the reviewers for their detailed comments that enhanced the science cases presented within the manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2023.1292500/full#supplementary-material

Footnotes

¹Although we do not discuss this special class of objects further, some of the science cases we explore (e.g., cyclotron line studies) are applicable to these sources as well.

²The definition of each model component and their parameters can be found in the xspec manual: https://heasarc.gsfc.nasa.gov/xanadu/xspec/manual/node128.html.

³Note that there was an update to the publicly available relxill model’s definition of the reflection fraction parameter for non-lamppost type models. As a result the values we use do not exactly match those of Ludlam et al. (2022), which used a proprietary developmental version of relxillNS. We have verified that the main results are consistent within errors when fitting the NuSTAR spectrum in the NB.

⁴In the following, the cyclotron line energy correspondent to n = 1 is labeled as fundamental, while for n > 1 lines are labeled as the n_i harmonic, with i = n.

⁵The critical luminosity is sometimes called the “local Eddington limit” which is descriptive but formally not well defined.

References

Abbott, B. P., Abbott, R., Abbott, T. D., Acernese, F., Ackley, K., Adams, C., et al. (2019). Properties of the binary neutron star merger GW170817. Phys. Rev. X 9, 011001. doi:10.1103/PhysRevX.9.011001

CrossRef Full Text | Google Scholar

Aftab, N., Paul, B., and Kretschmar, P. (2019). X-ray reprocessing: through the eclipse spectra of high-mass X-ray binaries with XMM-Newton. ApJ Suppl. 243, 29. doi:10.3847/1538-4365/ab2a77

CrossRef Full Text | Google Scholar

Alexander, S. G., and Meszaros, P. (1991). Cyclotron harmonics in accreting pulsars and gamma-ray bursters: effect of two-photon processes. ApJ 372, 565. doi:10.1086/170001

CrossRef Full Text | Google Scholar

Arnaud, K. A. (1996). “XSPEC: the first ten years,” in Astronomical data analysis software and systems V. San francisco: astron. Soc. Pacific). Editors G. H. Jacoby, and J. Barnes, 17. 101 of Astron. Soc. Pacific Conf. Ser.

Google Scholar

Bala, S., Bhattacharya, D., Staubert, R., and Maitra, C. (2020). Time evolution of cyclotron line of Her X-1: a detailed statistical analysis including new AstroSat data. MNRAS 497, 1029–1042. doi:10.1093/mnras/staa1988

CrossRef Full Text | Google Scholar

Bardeen, J. M., Press, W. H., and Teukolsky, S. A. (1972). Rotating black holes: locally nonrotating frames, energy extraction, and scalar synchrotron radiation. ApJ 178, 347–370. doi:10.1086/151796

CrossRef Full Text | Google Scholar

Barret, D. (2001). The broad band x-ray/hard x-ray spectra of accreting neutron stars. Adv. Space Res. 28, 307–321. doi:10.1016/S0273-1177(01)00414-8

CrossRef Full Text | Google Scholar

Barret, D., Olive, J. F., Boirin, L., Done, C., Skinner, G. K., and Grindlay, J. E. (2000). Hard X-ray emission from low-mass X-ray binaries. ApJ 533, 329–351. doi:10.1086/308651

CrossRef Full Text | Google Scholar

Basko, M. M., and Sunyaev, R. A. (1976). The limiting luminosity of accreting neutron stars with magnetic fields. MNRAS 175, 395–417. doi:10.1093/mnras/175.2.395

CrossRef Full Text | Google Scholar

Becker, P. A., Klochkov, D., Schönherr, G., Nishimura, O., Ferrigno, C., Caballero, I., et al. (2012). Spectral formation in accreting X-ray pulsars: bimodal variation of the cyclotron energy with luminosity. A&A 544, A123. doi:10.1051/0004-6361/201219065

CrossRef Full Text | Google Scholar

Becker, P. A., and Wolff, M. T. (2022). A generalized analytical model for thermal and bulk comptonization in accretion-powered X-ray pulsars. ApJ 939, 67. doi:10.3847/1538-4357/ac8d95

CrossRef Full Text | Google Scholar

Bozzo, E., Romano, P., Ferrigno, C., and Oskinova, L. (2022). The symbiotic X-ray binaries Sct X-1, 4U 1700+24, and IGR J17329-2731. MNRAS 513, 42–54. doi:10.1093/mnras/stac907

CrossRef Full Text | Google Scholar

Caballero, I., and Wilms, J. (2012). X-ray pulsars: a review. MemSAI 83, 230. doi:10.48550/arXiv.1206.3124

CrossRef Full Text | Google Scholar

Cackett, E. M., Altamirano, D., Patruno, A., Miller, J. M., Reynolds, M., Linares, M., et al. (2009). Broad relativistic iron emission line observed in SAX J1808.4−3658. ApJ 694, L21–L25. doi:10.1088/0004-637X/694/1/L21

CrossRef Full Text | Google Scholar

Cackett, E. M., Miller, J. M., Bhattacharyya, S., Grindlay, J. E., Homan, J., van der Klis, M., et al. (2008). Relativistic iron emission lines in neutron star low-mass X-ray binaries as probes of neutron star radii. ApJ 674, 415–420. doi:10.1086/524936

CrossRef Full Text | Google Scholar

Caiazzo, I., and Heyl, J. (2021). Polarization of accreting X-ray pulsars - II. Hercules X-1. MNRAS 501, 129–136. doi:10.1093/mnras/staa3429

CrossRef Full Text | Google Scholar

Casares, J., González Hernández, J. I., Israelian, G., and Rebolo, R. (2010). On the mass of the neutron star in Cyg X-2. MNRAS 401, 2517–2520. doi:10.1111/j.1365-2966.2009.15828.x

CrossRef Full Text | Google Scholar

Chodil, G., Mark, H., Rodrigues, R., Seward, F. D., and Swift, C. D. (1967). X-ray intensities and spectra from several cosmic sources. ApJ 150, 57. doi:10.1086/149312

CrossRef Full Text | Google Scholar

Church, M. J., and Balucińska-Church, M. (2001). Results of a LMXB survey: variation in the height of the neutron star blackbody emission region. A&A 369, 915–924. doi:10.1051/0004-6361:20010150

CrossRef Full Text | Google Scholar

Cocchi, M., Gnarini, A., Fabiani, S., Ursini, F., Poutanen, J., Capitanio, F., et al. (2023). Discovery of strongly variable X-ray polarization in the neutron star low-mass X-ray binary transient XTE J1701−462. A&A 674, L10. doi:10.1051/0004-6361/202346275

CrossRef Full Text | Google Scholar

Cusumano, G., La Parola, V., D’Aì, A., Segreto, A., Tagliaferri, G., Barthelmy, S. D., et al. (2016). An unexpected drop in the magnetic field of the X-ray pulsar V0332+53 after the bright outburst occurred in 2015. MNRAS 460, L99–L103. doi:10.1093/mnrasl/slw084

CrossRef Full Text | Google Scholar

Dauser, T., García, J., Wilms, J., Böck, M., Brenneman, L. W., Falanga, M., et al. (2013). Irradiation of an accretion disc by a jet: general properties and implications for spin measurements of black holes. MNRAS 430, 1694–1708. doi:10.1093/mnras/sts710

CrossRef Full Text | Google Scholar

Davies, R. E., and Pringle, J. E. (1981). Spindown of neutron stars in close binary systems - II. MNRAS 196, 209–224. doi:10.1093/mnras/196.2.209

CrossRef Full Text | Google Scholar

Degenaar, N., Ballantyne, D. R., Belloni, T., Chakraborty, M., Chen, Y.-P., Ji, L., et al. (2018). Accretion disks and coronae in the X-ray flashlight. Space Sci. Rev. 214, 15. doi:10.1007/s11214-017-0448-3

CrossRef Full Text | Google Scholar

Diez, C. M., Grinberg, V., Fürst, F., El Mellah, I., Zhou, M., Santangelo, A., et al. (2023). Observing the onset of the accretion wake in Vela X-1. A&A 674, A147. doi:10.1051/0004-6361/202245708

CrossRef Full Text | Google Scholar

Diez, C. M., Grinberg, V., Fürst, F., Sokolova-Lapa, E., Santangelo, A., Wilms, J., et al. (2022). Continuum, cyclotron line, and absorption variability in the high-mass X-ray binary Vela X-1. A&A 660, A19. doi:10.1051/0004-6361/202141751

CrossRef Full Text | Google Scholar

Di Salvo, T., Burderi, L., Robba, N. R., and Guainazzi, M. (1998). The two-component X-ray broadband spectrum of X persei observed by BeppoSAX. ApJ 509, 897–903. doi:10.1086/306525

CrossRef Full Text | Google Scholar

Doroshenko, R., Piraino, S., Doroshenko, V., and Santangelo, A. (2020). Revisiting BeppoSAX and NuSTAR observations of KS 1947+300 and the missing cyclotron line. MNRAS 493, 3442–3448. doi:10.1093/mnras/staa490

CrossRef Full Text | Google Scholar

Doroshenko, V., Santangelo, A., Kreykenbohm, I., and Doroshenko, R. (2012). The hard X-ray emission of X Persei. A&A 540, L1. doi:10.1051/0004-6361/201218878

CrossRef Full Text | Google Scholar

Doroshenko, V., Santangelo, A., Tsygankov, S. S., and Ji, L. (2021). SGR 0755−2933: a new high-mass X-ray binary with the wrong name. A&A 647, A165. doi:10.1051/0004-6361/202039785

CrossRef Full Text | Google Scholar

Doroshenko, V., Staubert, R., Maitra, C., Rau, A., Haberl, F., Santangelo, A., et al. (2022). SRGA J124404.1-632232/SRGA J124404.1–632232/SRGU J124403.8–632231: new X-ray pulsar discovered in the all-sky survey by the SRG. A&A 661, A21. doi:10.1051/0004-6361/202141147

CrossRef Full Text | Google Scholar

Doroshenko, V., Tsygankov, S. S., Mushtukov, A. A., Lutovinov, A. A., Santangelo, A., Suleimanov, V. F., et al. (2017). Luminosity dependence of the cyclotron line and evidence for the accretion regime transition in V 0332+53. MNRAS 466, 2143–2150. doi:10.1093/mnras/stw3236

CrossRef Full Text | Google Scholar

Eraerds, T., Antonelli, V., Davis, C., Hall, D., Hetherington, O., Holland, A., et al. (2021). Enhanced simulations on the athena/wide field imager instrumental background. J. Astronomical Telesc. Instrum. Syst. 7, 034001. doi:10.1117/1.JATIS.7.3.034001

CrossRef Full Text | Google Scholar

Fabian, A. C., Rees, M. J., Stella, L., and White, N. E. (1989). X-ray fluorescence from the inner disc in Cygnus X-1. MNRAS 238, 729–736. doi:10.1093/mnras/238.3.729

CrossRef Full Text | Google Scholar

Farinelli, R., Fabiani, S., Poutanen, J., Ursini, F., Ferrigno, C., Bianchi, S., et al. (2023). Accretion geometry of the neutron star low mass X-ray binary Cyg X-2 from X-ray polarization measurements. MNRAS 519, 3681–3690. doi:10.1093/mnras/stac3726

CrossRef Full Text | Google Scholar

Farinelli, R., Ferrigno, C., Bozzo, E., and Becker, P. A. (2016). A new model for the X-ray continuum of the magnetized accreting pulsars. A&A 591, A29. doi:10.1051/0004-6361/201527257

CrossRef Full Text | Google Scholar

Fiocchi, M., Bazzano, A., Bruni, G., Ludlam, R., Natalucci, L., Onori, F., et al. (2019). Quasi-simultaneous INTEGRAL, SWIFT, and NuSTAR observations of the new X-ray clocked burster 1RXS j180408.9-342058. ApJ 887, 30. doi:10.3847/1538-4357/ab4d59

CrossRef Full Text | Google Scholar

Forsblom, S. V., Poutanen, J., Tsygankov, S. S., Bachetti, M., Di Marco, A., Doroshenko, V., et al. (2023). IXPE observations of the quintessential wind-accreting X-ray pulsar Vela X-1. ApJ 947, L20. doi:10.3847/2041-8213/acc391

CrossRef Full Text | Google Scholar

Fürst, F., Falkner, S., Marcu-Cheatham, D., Grefenstette, B., Tomsick, J., Pottschmidt, K., et al. (2018). Multiple cyclotron line-forming regions in GX 301−2. A&A 620, A153. doi:10.1051/0004-6361/201732132

CrossRef Full Text | Google Scholar

Fürst, F., Pottschmidt, K., Wilms, J., Tomsick, J. A., Bachetti, M., Boggs, S. E., et al. (2014). NuSTAR discovery of a luminosity dependent cyclotron line energy in Vela X-1. ApJ 780, 133. doi:10.1088/0004-637X/780/2/133

CrossRef Full Text | Google Scholar

Galloway, D. K., Muno, M. P., Hartman, J. M., Psaltis, D., and Chakrabarty, D. (2008). Thermonuclear (type I) X-ray bursts observed by the rossi X-ray timing explorer. ApJ Suppl. 179, 360–422. doi:10.1086/592044

CrossRef Full Text | Google Scholar

García, J., and Kallman, T. R. (2010). X-Ray reflected spectra from accretion disk models. I. Constant density atmospheres. ApJ 718, 695–706. doi:10.1088/0004-637X/718/2/695

CrossRef Full Text | Google Scholar

García, J. A., Dauser, T., Ludlam, R., Parker, M., Fabian, A., Harrison, F. A., et al. (2022). Relativistic X-ray reflection models for accreting neutron stars. ApJ 926, 13. doi:10.3847/1538-4357/ac3cb7

CrossRef Full Text | Google Scholar

Gehrels, N., Chincarini, G., Giommi, P., Mason, K. O., Nousek, J. A., Wells, A. A., et al. (2004). TheSwiftGamma-ray burst mission. ApJ 611, 1005–1020. doi:10.1086/422091

CrossRef Full Text | Google Scholar

Gendreau, K. C., Arzoumanian, Z., and Okajima, T. (2012). “The Neutron star Interior Composition ExploreR (NICER): an Explorer mission of opportunity for soft x-ray timing spectroscopy,” in Space telescopes and instrumentation 2012: ultraviolet to gamma ray. SPIE). Editors T. Takahashi, S. S. Murray, J.-W. A. den Herder, and W. A. Bellingham, 8443. of Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series. doi:10.1117/12.926396844313

CrossRef Full Text | Google Scholar

Giacconi, R., Gursky, H., Kellogg, E., Schreier, E., and Tananbaum, H. (1971). Discovery of periodic X-ray pulsations in centaurus X-3 from UHURU. ApJ 167, L67. doi:10.1086/180762

CrossRef Full Text | Google Scholar

Harrison, F. A., Craig, W. W., Christensen, F. E., Hailey, C. J., Zhang, W. W., Boggs, S. E., et al. (2013). The nuclear spectroscopic telescope array (NuSTAR) high-energy X-ray mission. ApJ 770, 103. doi:10.1088/0004-637X/770/2/103

CrossRef Full Text | Google Scholar

Hasinger, G., and van der Klis, M. (1989). Two patterns of correlated X-ray timing and spectral behaviour in low-mass X-ray binaries. A&A 225, 79–96.

Google Scholar

Heindl, W. A., Rothschild, R. E., Coburn, W., Staubert, R., Wilms, J., Kreykenbohm, I., et al. (2004). “Timing and spectroscopy of accreting X-ray pulsars: the state of cyclotron line studies,” in X-Ray timing 2003: rossi and beyond. Editors P. Kaaret, F. K. Lamb, and J. H. Swank, 714, 323–330. of American Institute of Physics Conference Series. doi:10.1063/1.1781049

CrossRef Full Text | Google Scholar

Homan, J., van der Klis, M., Fridriksson, J. K., Remillard, R. A., Wijnands, R., Méndez, M., et al. (2010). XTE J1701−462 and its implications for the nature of subclasses in low-magnetic-field neutron star low-mass X-ray binaries. ApJ 719, 201–212. doi:10.1088/0004-637X/719/1/201

CrossRef Full Text | Google Scholar

Houck, J. C., and Denicola, L. A. (2000). “ISIS: an interactive spectral interpretation system for high resolution X-ray spectroscopy,” in Astronomical data analysis software and systems IX. San francisco: astron. Soc. Pacific. Editors N. Manset, C. Veillet, and D. Crabtree, 216, 591. of Astron. Soc. Pacific Conf. Ser.

Google Scholar

Iaria, R., Di Salvo, T., Robba, N. R., Burderi, L., Lavagetto, G., and Riggio, A. (2005). Resolving the Fe xxv triplet with chandra in centaurus X-3. ApJ 634, L161–L164. doi:10.1086/499040

CrossRef Full Text | Google Scholar

Ibragimov, A., and Poutanen, J. (2009). Accreting millisecond pulsar SAX J1808.4−3658 during its 2002 outburst: evidence for a receding disc. MNRAS 400, 492–508. doi:10.1111/j.1365-2966.2009.15477.x

CrossRef Full Text | Google Scholar

Iwakiri, W. B., Pottschmidt, K., Falkner, S., Hemphill, P. B., Fürst, F., Nishimura, O., et al. (2019). Spectral and timing analysis of the accretion-powered pulsar 4U 1626−67 observed with Suzaku and NuSTAR. ApJ 878, 121. doi:10.3847/1538-4357/ab1f87

CrossRef Full Text | Google Scholar

Jaisawal, G. K., Naik, S., and Epili, P. (2016). Suzaku view of the Be/X-ray binary pulsar GX 304−1 during Type I X-ray outbursts. MNRAS 457, 2749–2760. doi:10.1093/mnras/stw085

CrossRef Full Text | Google Scholar

Jaisawal, G. K., Vasilopoulos, G., Naik, S., Maitra, C., Malacaria, C., Chhotaray, B., et al. (2023). On the cyclotron absorption line and evidence of the spectral transition in SMC X-2 during 2022 giant outburst. MNRAS 521, 3951–3961. doi:10.1093/mnras/stad781

CrossRef Full Text | Google Scholar

Jansen, F., Lumb, D., Altieri, B., Clavel, J., Ehle, M., Erd, C., et al. (2001). XMM-Newton observatory. I. The spacecraft and operations. A&A 365, L1–L6. doi:10.1051/0004-6361:20000036

CrossRef Full Text | Google Scholar

Jayasurya, K. M., Agrawal, V. K., and Chatterjee, R. (2023). Detection of significant X-ray polarization from transient NS-LMXB XTE J1701-462 with IXPE and its implication on the coronal geometry. MNRAS 525, 4657–4662. doi:10.1093/mnras/stad2601

CrossRef Full Text | Google Scholar

King, A. L., Tomsick, J. A., Miller, J. M., Chenevez, J., Barret, D., Boggs, S. E., et al. (2016). Measuring a truncated disk in aquila X-1. ApJ 819, L29. doi:10.3847/2041-8205/819/2/L29

CrossRef Full Text | Google Scholar

Klochkov, D., Santangelo, A., Staubert, R., and Ferrigno, C. (2008). Giant outburst of EXO 2030+375: pulse-phase resolved analysis of INTEGRAL data. A&A 491, 833–840. doi:10.1051/0004-6361:200810673

CrossRef Full Text | Google Scholar

Klochkov, D., Staubert, R., Santangelo, A., Rothschild, R. E., and Ferrigno, C. (2011). Pulse-amplitude-resolved spectroscopy of bright accreting pulsars: indication of two accretion regimes. A&A 532, A126. doi:10.1051/0004-6361/201116800

CrossRef Full Text | Google Scholar

Koliopanos, F., and Vasilopoulos, G. (2018). Accreting, highly magnetized neutron stars at the Eddington limit: a study of the 2016 outburst of SMC X-3. A&A 614, A23. doi:10.1051/0004-6361/201731623

CrossRef Full Text | Google Scholar

Kong, L.-D., Zhang, S., Zhang, S.-N., Ji, L., Doroshenko, V., Santangelo, A., et al. (2022). Insight-HXMT discovery of the highest-energy CRSF from the first galactic ultraluminous X-ray pulsar Swift J0243.6+6124. ApJ 933, L3. doi:10.3847/2041-8213/ac7711

CrossRef Full Text | Google Scholar

Kretschmar, P., El Mellah, I., Martínez-Núñez, S., Fürst, F., Grinberg, V., Sander, A. A. C., et al. (2021). Revisiting the archetypical wind accretor Vela X-1 in depth. Case study of a well-known X-ray binary and the limits of our knowledge. A&A 652, A95. doi:10.1051/0004-6361/202040272

CrossRef Full Text | Google Scholar

Kreykenbohm, I., Coburn, W., Wilms, J., Kretschmar, P., Staubert, R., Heindl, W. A., et al. (2002). Confirmation of two cyclotron lines in Vela X-1. A&A 395, 129–140. doi:10.1051/0004-6361:20021181

CrossRef Full Text | Google Scholar

Kreykenbohm, I., Kretschmar, P., Wilms, J., Staubert, R., Kendziorra, E., Gruber, D. E., et al. (1999). VELA X-1 as seen by RXTE. A&A 341, 141–150. doi:10.48550/arXiv.astro-ph/9810282

CrossRef Full Text | Google Scholar

Kuulkers, E., van der Klis, M., Oosterbroek, T., van Paradijs, J., and Lewin, W. H. G. (1997). GX17+2: X-ray spectral and timing behaviour of a bursting Z source. MNRAS 287, 495–514. doi:10.1093/mnras/287.3.495

CrossRef Full Text | Google Scholar

Kylafis, N. D., Trümper, J. E., and Loudas, N. A. (2021). Cyclotron line formation by reflection on the surface of a magnetic neutron star. A&A 655, A39. doi:10.1051/0004-6361/202039361

CrossRef Full Text | Google Scholar

Lattimer, J. M. (2011). Neutron stars and the dense matter equation of state. Astrophys. Space Sci. 336, 67–74. doi:10.1007/s10509-010-0529-1

CrossRef Full Text | Google Scholar

Lattimer, J. M., and Prakash, M. (2001). Neutron star structure and the equation of state. ApJ 550, 426–442. doi:10.1086/319702

CrossRef Full Text | Google Scholar

Lattimer, J. M., and Prakash, M. (2004). The physics of neutron stars. Science 304, 536–542. doi:10.1126/science.1090720

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, D., Remillard, R. A., and Homan, J. (2007). Evaluating spectral models and the X-ray states of neutron star X-ray transients. ApJ 667, 1073–1086. doi:10.1086/521181

CrossRef Full Text | Google Scholar

Lin, D., Remillard, R. A., and Homan, J. (2010). Suzaku and BeppoSAX X-ray spectra of the persistently accreting neutron-star binary 4U 1705−44. ApJ 719, 1350–1361. doi:10.1088/0004-637X/719/2/1350

CrossRef Full Text | Google Scholar

Liu, B.-S., Tao, L., Zhang, S.-N., Li, X.-D., Ge, M.-Y., Qu, J.-L., et al. (2020). A peculiar cyclotron line near 16 keV detected in the 2015 outburst of 4U 0115+63? ApJ 900, 41. doi:10.3847/1538-4357/aba4a5

CrossRef Full Text | Google Scholar

Liu, Q., Wang, W., Chen, X., Ding, Y. Z., Lu, F. J., Song, L. M., et al. (2022). Variations of cyclotron resonant scattering features in Vela X-1 revealed with Insight-HXMT. MNRAS 514, 2805–2814. doi:10.1093/mnras/stac1520

CrossRef Full Text | Google Scholar

Longair, M. S. (2011). High energy astrophysics. Cambridge: Cambridge Univ. Press.

Google Scholar

Ludlam, R. M., Cackett, E. M., García, J. A., Miller, J. M., Bult, P. M., Strohmayer, T. E., et al. (2020). NICER-NuSTAR observations of the neutron star low-mass X-ray binary 4U 1735−44. ApJ 895, 45. doi:10.3847/1538-4357/ab89a6

CrossRef Full Text | Google Scholar

Ludlam, R. M., Cackett, E. M., García, J. A., Miller, J. M., Stevens, A. L., Fabian, A. C., et al. (2022). Radius constraints from reflection modeling of Cygnus X-2 with NuSTAR and NICER. ApJ 927, 112. doi:10.3847/1538-4357/ac5028

CrossRef Full Text | Google Scholar

Ludlam, R. M., Jaodand, A. D., García, J. A., Degenaar, N., Tomsick, J. A., Cackett, E. M., et al. (2021). Simultaneous NICER and NuSTAR observations of the ultracompact X-ray binary 4U 1543-624. ApJ 911, 123. doi:10.3847/1538-4357/abedb0

CrossRef Full Text | Google Scholar

Ludlam, R. M., Miller, J. M., Arzoumanian, Z., Bult, P. M., Cackett, E. M., Chakrabarty, D., et al. (2018). Detection of reflection features in the neutron star low-mass X-ray binary serpens X-1 with NICER. ApJ 858, L5. doi:10.3847/2041-8213/aabee6

CrossRef Full Text | Google Scholar

Ludlam, R. M., Miller, J. M., Bachetti, M., Barret, D., Bostrom, A. C., Cackett, E. M., et al. (2017a). A hard look at the neutron stars and accretion disks in 4U 1636−53, GX 17+2, and 4U 1705−44 with NuStar. ApJ 836, 140. doi:10.3847/1538-4357/836/1/140

CrossRef Full Text | Google Scholar

Ludlam, R. M., Miller, J. M., Cackett, E. M., Fabian, A. C., Bachetti, M., Parker, M. L., et al. (2016). NuSTAR and XMM-Newton observations of the neutron star X-ray binary 1RXS j180408.9-34205. ApJ 824, 37. doi:10.3847/0004-637X/824/1/37

CrossRef Full Text | Google Scholar

Ludlam, R. M., Miller, J. M., Degenaar, N., Sanna, A., Cackett, E. M., Altamirano, D., et al. (2017b). Truncation of the accretion disk at one-third of the Eddington limit in the neutron star low-mass X-ray binary aquila X-1. ApJ 847, 135. doi:10.3847/1538-4357/aa8b1b

CrossRef Full Text | Google Scholar

Lutovinov, A., Tsygankov, S., Molkov, S., Doroshenko, V., Mushtukov, A., Arefiev, V., et al. (2021). SRG/ART-XC and NuSTAR observations of the X-ray pulsar GRO J1008−57 in the lowest luminosity state. ApJ 912, 17. doi:10.3847/1538-4357/abec43

CrossRef Full Text | Google Scholar

Madej, O. K., García, J., Jonker, P. G., Parker, M. L., Ross, R., Fabian, A. C., et al. (2014). X-ray reflection in oxygen-rich accretion discs of ultracompact X-ray binaries. MNRAS 442, 1157–1165. doi:10.1093/mnras/stu884

CrossRef Full Text | Google Scholar

Madsen, K. K., García, J. A., Stern, D., Armini, R., Basso, S., Coutinho, D., et al. (2023). The High Energy X-ray Probe (HEX-P): Instrument and Mission Profile. arXiv. doi:10.48550/arXiv.2312.04678

CrossRef Full Text | Google Scholar

Maitra, C., and Paul, B. (2013). Pulse-phase-resolved spectroscopy of Vela X-1 with Suzaku. ApJ 763, 79. doi:10.1088/0004-637X/763/2/79

CrossRef Full Text | Google Scholar

Maitra, C., Paul, B., Haberl, F., and Vasilopoulos, G. (2018). Detection of a cyclotron line in SXP 15.3 during its 2017 outburst. MNRAS 480, L136–L140. doi:10.1093/mnrasl/sly141

CrossRef Full Text | Google Scholar

Makishima, K., Mihara, T., Nagase, F., and Tanaka, Y. (1999). Cyclotron resonance effects in two binary X-ray pulsars and the evolution of neutron star magnetic fields. ApJ 525, 978–994. doi:10.1086/307912

CrossRef Full Text | Google Scholar

Malacaria, C., Bhargava, Y., Coley, J. B., Ducci, L., Pradhan, P., Ballhausen, R., et al. (2022). Accreting on the edge: a luminosity-dependent cyclotron line in the Be/X-Ray binary 2S 1553-542 accompanied by accretion regimes transition. ApJ 927, 194. doi:10.3847/1538-4357/ac524f

CrossRef Full Text | Google Scholar

Malacaria, C., Ducci, L., Falanga, M., Altamirano, D., Bozzo, E., Guillot, S., et al. (2023a). The unaltered pulsar: GRO J1750−27, a supercritical X-ray neutron star that does not blink an eye. A&A 669, A38. doi:10.1051/0004-6361/202245123

CrossRef Full Text | Google Scholar

Malacaria, C., Heyl, J., Doroshenko, V., Tsygankov, S. S., Poutanen, J., Forsblom, S. V., et al. (2023b). A polarimetrically oriented X-ray stare at the accreting pulsar EXO 2030+375. A&A 675, A29. doi:10.1051/0004-6361/202346581

CrossRef Full Text | Google Scholar

Malacaria, C., Klochkov, D., Santangelo, A., and Staubert, R. (2015). Luminosity-dependent spectral and timing properties of the accreting pulsar GX 304−1 measured with INTEGRAL. A&A 581, A121. doi:10.1051/0004-6361/201526417

CrossRef Full Text | Google Scholar

Marino, A., Russell, T. D., Del Santo, M., Beri, A., Sanna, A., Coti Zelati, F., et al. (2023). The accretion/ejection link in the neutron star X-ray binary 4U 1820-30 I: a boundary layer-jet coupling? arXiv e-prints. arXiv:2307.16566. doi:10.48550/arXiv.2307.16566

CrossRef Full Text | Google Scholar

Meidinger, N., Albrecht, S., Beitler, C., Bonholzer, M., Emberger, V., Frank, J., et al. (2020). “Development status of the wide field imager instrument for Athena,” in Space telescopes and instrumentation 2020: ultraviolet to gamma ray. Editors J.-W. A. den Herder, S. Nikzad, and K. Nakazawa (of Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series), 11444, 114440T. doi:10.1117/12.2560507

CrossRef Full Text | Google Scholar

Meszaros, P. (1992). High-energy radiation from magnetized neutron stars. Chicago: Univ. Chicago Press.

Google Scholar

Meszaros, P., Novick, R., Szentgyorgyi, A., Chanan, G. A., and Weisskopf, M. C. (1988). Astrophysical implications and observational prospects of X-ray polarimetry. ApJ 324, 1056. doi:10.1086/165962

CrossRef Full Text | Google Scholar

Mihara, T. (1995). Observational study of X-ray spectra of binary pulsars with Ginga. Ph.D. thesis. Dept. of Physics, Univ. of Tokyo (M95).

Google Scholar

Mihara, T., Yamamoto, T., Sugizaki, M., and Yamaoka, K. (2010). Discovery of the cyclotron line at 51 keV from GX 304−1. ATEL, 2796.

Google Scholar

Miller, J. M., Maitra, D., Cackett, E. M., Bhattacharyya, S., and Strohmayer, T. E. (2011). A fast X-ray disk wind in the transient pulsar IGR J17480−2446 in terzan 5. ApJ 731, L7. doi:10.1088/2041-8205/731/1/L7

CrossRef Full Text | Google Scholar

Miller, M. C., Lamb, F. K., Dittmann, A. J., Bogdanov, S., Arzoumanian, Z., Gendreau, K. C., et al. (2019). PSR J0030+0451 mass and radius from NICER data and implications for the properties of neutron star matter. ApJ 887, L24. doi:10.3847/2041-8213/ab50c5

CrossRef Full Text | Google Scholar

Miller, M. C., Lamb, F. K., Dittmann, A. J., Bogdanov, S., Arzoumanian, Z., Gendreau, K. C., et al. (2021). The radius of PSR J0740+6620 from NICER and XMM-Newton data. ApJ 918, L28. doi:10.3847/2041-8213/ac089b

CrossRef Full Text | Google Scholar

Mitsuda, K., Inoue, H., Nakamura, N., and Tanaka, Y. (1989). Luminosity-related changes of the energy spectrum of X 1608−522. PASJ 41, 97–111.

Google Scholar

Mondal, A. S., Dewangan, G. C., Pahari, M., and Raychaudhuri, B. (2018). NuSTAR view of the Z-type neutron star low-mass X-ray binary Cygnus X-2. MNRAS 474, 2064–2072. doi:10.1093/mnras/stx2931

CrossRef Full Text | Google Scholar

Müller, S., Ferrigno, C., Kühnel, M., Schönherr, G., Becker, P. A., Wolff, M. T., et al. (2013). No anticorrelation between cyclotron line energy and X-ray flux in 4U 0115+634. A&A 551, A6. doi:10.1051/0004-6361/201220359

CrossRef Full Text | Google Scholar

Mushtukov, A., and Tsygankov, S. (2022). Accreting strongly magnetised neutron stars: X-ray Pulsars. arXiv e-prints. arXiv:2204.14185. doi:10.48550/arXiv.2204.14185

CrossRef Full Text | Google Scholar

Mushtukov, A. A., Suleimanov, V. F., Tsygankov, S. S., and Portegies Zwart, S. (2021). Spectrum formation in X-ray pulsars at very low mass accretion rate: Monte Carlo approach. MNRAS 503, 5193–5203. doi:10.1093/mnras/stab811

CrossRef Full Text | Google Scholar

Mushtukov, A. A., Suleimanov, V. F., Tsygankov, S. S., and Poutanen, J. (2015). The critical accretion luminosity for magnetized neutron stars. MNRAS 447, 1847–1856. doi:10.1093/mnras/stu2484

CrossRef Full Text | Google Scholar

Naik, S., and Paul, B. (2012). Investigation of variability of iron emission lines in Centaurus X-3. Bull. Astronomical Soc. India 40, 503.

Google Scholar

Nandra, K., Barret, D., Barcons, X., Fabian, A., den Herder, J.-W., Piro, L., et al. (2013). The Hot and Energetic Universe: a White Paper presenting the science theme motivating the Athena+ mission. arXiv e-prints. arXiv:1306.2307. doi:10.48550/arXiv.1306.2307

CrossRef Full Text | Google Scholar

Nishimura, O. (2003). The influence of a dipole magnetic field on the structures of cyclotron lines, 55. Publications of the Astronomical Society of Japan, 849–857. doi:10.1093/pasj/55.4.849

CrossRef Full Text | Google Scholar

Nishimura, O. (2011). Superposition of cyclotron lines in accreting X-ray pulsars. I. Long spin period. ApJ 730, 106. doi:10.1088/0004-637X/730/2/106

CrossRef Full Text | Google Scholar

Nishimura, O. (2014). Variations of cyclotron line energy with luminosity in accreting X-ray pulsars. ApJ 781, 30. doi:10.1088/0004-637X/781/1/30

CrossRef Full Text | Google Scholar

Oppenheimer, J. R., and Volkoff, G. M. (1939). On massive neutron cores. Phys. Rev. 55, 374–381. doi:10.1103/PhysRev.55.374

CrossRef Full Text | Google Scholar

Orlandini, M., Frontera, F., Masetti, N., Sguera, V., and Sidoli, L. (2012). BeppoSAX observations of the X-ray pulsar MAXI J1409−619 in low state: discovery of cyclotron resonance features. ApJ 748, 86. doi:10.1088/0004-637X/748/2/86

CrossRef Full Text | Google Scholar

Orosz, J. A., and Kuulkers, E. (1999). The optical light curves of Cygnus X-2 (V1341 Cyg) and the mass of its neutron star. MNRAS 305, 132–142. doi:10.1046/j.1365-8711.1999.t01-1-02420.x

CrossRef Full Text | Google Scholar

Parikh, A. S., Wijnands, R., Degenaar, N., Altamirano, D., Patruno, A., Gusinskaia, N. V., et al. (2017). Very hard states in neutron star low-mass X-ray binaries. MNRAS 468, 3979–3984. doi:10.1093/mnras/stx747

CrossRef Full Text | Google Scholar

Popham, R., and Sunyaev, R. (2001). Accretion disk boundary layers around neutron stars: X-ray production in low-mass X-ray binaries. ApJ 547, 355–383. doi:10.1086/318336

CrossRef Full Text | Google Scholar

Pottschmidt, K., Kreykenbohm, I., Wilms, J., Coburn, W., Rothschild, R. E., Kretschmar, P., et al. (2005). RXTE discovery of multiple cyclotron lines during the 2004 december outburst of V0332+53. ApJ 634, L97–L100. doi:10.1086/498689

CrossRef Full Text | Google Scholar

Poutanen, J., Mushtukov, A. A., Suleimanov, V. F., Tsygankov, S. S., Nagirner, D. I., Doroshenko, V., et al. (2013). A reflection model for the cyclotron lines in the spectra of X-ray pulsars. ApJ 777, 115. doi:10.1088/0004-637X/777/2/115

CrossRef Full Text | Google Scholar

Pradhan, P., Paul, B., Bozzo, E., Maitra, C., and Paul, B. C. (2021). Comprehensive broad-band study of accreting neutron stars with Suzaku: is there a bi-modality in the X-ray spectrum? Mon. Notices R. Astronomical Soc. 502, 1163–1190. doi:10.1093/mnras/stab024

CrossRef Full Text | Google Scholar

Raaijmakers, G., Greif, S. K., Hebeler, K., Hinderer, T., Nissanke, S., Schwenk, A., et al. (2021). Constraints on the dense matter equation of state and neutron star properties from NICER’s mass-radius estimate of PSR J0740+6620 and multimessenger observations. ApJ 918, L29. doi:10.3847/2041-8213/ac089a

CrossRef Full Text | Google Scholar

Riley, T. E., Watts, A. L., Bogdanov, S., Ray, P. S., Ludlam, R. M., Guillot, S., et al. (2019). A NICER view of PSR J0030+0451: millisecond pulsar parameter estimation. ApJ 887, L21. doi:10.3847/2041-8213/ab481c

CrossRef Full Text | Google Scholar

Riley, T. E., Watts, A. L., Ray, P. S., Bogdanov, S., Guillot, S., Morsink, S. M., et al. (2021). A NICER view of the massive pulsar PSR J0740+6620 informed by radio timing and XMM-Newton spectroscopy. ApJ 918, L27. doi:10.3847/2041-8213/ac0a81

CrossRef Full Text | Google Scholar

Rodes-Roca, J. J., Torrejón, J. M., Kreykenbohm, I., Martínez Núñez, S., Camero-Arranz, A., and Bernabéu, G. (2009). The first cyclotron harmonic of 4U 1538−52. A&A 508, 395–400. doi:10.1051/0004-6361/200912815

CrossRef Full Text | Google Scholar

Ross, R. R., and Fabian, A. C. (2005). A comprehensive range of X-ray ionized-reflection models. MNRAS 358, 211–216. doi:10.1111/j.1365-2966.2005.08797.x

CrossRef Full Text | Google Scholar

Rothschild, R. E., Kühnel, M., Pottschmidt, K., Hemphill, P., Postnov, K., Gornostaev, M., et al. (2017). Discovery and modelling of a flattening of the positive cyclotron line/luminosity relation in GX 304−1 with RXTE. MNRAS 466, 2752–2779. doi:10.1093/mnras/stw3222

CrossRef Full Text | Google Scholar

Rouco Escorial, A., van den Eijnden, J., and Wijnands, R. (2018). Discovery of accretion-driven pulsations in the prolonged low X-ray luminosity state of the Be/X-ray transient GX 304−1. A&A 620, L13. doi:10.1051/0004-6361/201834572

CrossRef Full Text | Google Scholar

Sanjurjo-Ferrín, G., Torrejón, J. M., Postnov, K., Oskinova, L., Rodes-Roca, J. J., and Bernabeu, G. (2021). X-ray variability of the HMXB Cen X-3: evidence for inhomogeneous accretion flows. MNRAS 501, 5892–5909. doi:10.1093/mnras/staa3953

CrossRef Full Text | Google Scholar

Schönherr, G., Wilms, J., Kretschmar, P., Kreykenbohm, I., Santangelo, A., Rothschild, R. E., et al. (2007). A model for cyclotron resonance scattering features. A&A 472, 353–365. doi:10.1051/0004-6361:20077218

CrossRef Full Text | Google Scholar

Schreier, E., Levinson, R., Gursky, H., Kellogg, E., Tananbaum, H., and Giacconi, R. (1972). Evidence for the binary nature of centaurus X-3 from UHURU X-ray observations. ApJ 172, L79. doi:10.1086/180896

CrossRef Full Text | Google Scholar

Schwarm, F. W., Ballhausen, R., Falkner, S., Schönherr, G., Pottschmidt, K., Wolff, M. T., et al. (2017). Cyclotron resonant scattering feature simulations. II. Description of the CRSF simulation process. A&A 601, A99. doi:10.1051/0004-6361/201630250

CrossRef Full Text | Google Scholar

Sibgatullin, N. R., and Sunyaev, R. A. (1998). Disk accretion in the gravitational field of a rapidly rotating neutron star with a rotationally induced quadrupole mass distribution. Astron. Lett. 24, 774–787. doi:10.48550/arXiv.astro-ph/9811028

CrossRef Full Text | Google Scholar

Sokolova-Lapa, E., Gornostaev, M., Wilms, J., Ballhausen, R., Falkner, S., Postnov, K., et al. (2021). X-ray emission from magnetized neutron star atmospheres at low mass-accretion rates. I. Phase-averaged spectrum. A&A 651, A12. doi:10.1051/0004-6361/202040228

CrossRef Full Text | Google Scholar

Sokolova-Lapa, E., Stierhof, J., Dauser, T., and Wilms, J. (2023). Vacuum polarization alters the spectra of accreting X-ray pulsars. A&A 674, L2. doi:10.1051/0004-6361/202346265

CrossRef Full Text | Google Scholar

Staubert, R., Ducci, L., Ji, L., Fürst, F., Wilms, J., Rothschild, R. E., et al. (2020). Cyclotron line energy in Hercules X-1: stable after the decay. A&A 642, A196. doi:10.1051/0004-6361/202038855

CrossRef Full Text | Google Scholar

Staubert, R., Klochkov, D., Wilms, J., Postnov, K., Shakura, N. I., Rothschild, R. E., et al. (2014). Long-term change in the cyclotron line energy in Hercules X-1. A&A 572, A119. doi:10.1051/0004-6361/201424203

CrossRef Full Text | Google Scholar

Staubert, R., Trümper, J., Kendziorra, E., Klochkov, D., Postnov, K., Kretschmar, P., et al. (2019). Cyclotron lines in highly magnetized neutron stars. A&A 622, A61. doi:10.1051/0004-6361/201834479

CrossRef Full Text | Google Scholar

Sunyaev, R. A., Arefev, V. A., Borozdin, K. N., Gilfanov, M. R., Efremov, V. V., Kaniovskii, A. S., et al. (1991). Broadband X-ray spectra of black-hole candidates X-ray pulsars and low-mass binary X-ray systems - KVANT module results. Sov. Astron. Lett. 17, 409.

Google Scholar

Tanaka, Y. (1986). “Observations of compact X-ray sources,”. IAU colloq. 89: radiation hydrodynamics in stars and compact objects. Editors D. Mihalas, and K.-H. A. Winkler (Berlin, Heidelberg: Springer), 255, 198. doi:10.1007/3-540-16764-1_12

CrossRef Full Text | Google Scholar

The LIGO Scientific Collaboration The Virgo Collaboration, B. P., Abbott, R., Abbott, T. D., Abraham, S., Acernese, F., et al. (2020). GW190425: observation of a compact binary coalescence with total mass ∼ 3.4 M_⊙. ApJ 892, L3. doi:10.3847/2041-8213/ab75f5

CrossRef Full Text | Google Scholar

Titarchuk, L. (1994). Generalized comptonization models and application to the recent high-energy observations. ApJ 434, 570. doi:10.1086/174760

CrossRef Full Text | Google Scholar

Tolman, R. C. (1934). Relativity, thermodynamics, and cosmology. Oxford: Clarendon Press.

Google Scholar

Tolman, R. C. (1939). Static solutions of einstein’s field equations for spheres of fluid. Phys. Rev. 55, 364–373. doi:10.1103/PhysRev.55.364

CrossRef Full Text | Google Scholar

Tomar, G., Pradhan, P., and Paul, B. (2021). New measurements of the cyclotron line energy in Cen X-3. MNRAS 500, 3454–3461. doi:10.1093/mnras/staa3477

CrossRef Full Text | Google Scholar

Tsygankov, S. S., Doroshenko, V., Mushtukov, A. A., Suleimanov, V. F., Lutovinov, A. A., and Poutanen, J. (2019a). Cyclotron emission, absorption, and the two faces of X-ray pulsar A 0535+262. MNRAS 487, L30–L34. doi:10.1093/mnrasl/slz079

CrossRef Full Text | Google Scholar

Tsygankov, S. S., Doroshenko, V., Poutanen, J., Heyl, J., Mushtukov, A. A., Caiazzo, I., et al. (2022). The X-ray polarimetry view of the accreting pulsar cen X-3. ApJ 941, L14. doi:10.3847/2041-8213/aca486

CrossRef Full Text | Google Scholar

Tsygankov, S. S., Rouco Escorial, A., Suleimanov, V. F., Mushtukov, A. A., Doroshenko, V., Lutovinov, A. A., et al. (2019b). Dramatic spectral transition of X-ray pulsar GX 304−1 in low luminous state. MNRAS 483, L144–L148. doi:10.1093/mnrasl/sly236

CrossRef Full Text | Google Scholar

Tugay, A. V., and Vasylenko, A. A. (2009). “XMM-Newton observations of X-ray pulsar cen X-3,”. Young scientists 16th proceedings. Editors V. Y. Choliy, and G. Ivashchenko, 58–61.

Google Scholar

Ursini, F., Farinelli, R., Gnarini, A., Poutanen, J., Bianchi, S., Capitanio, F., et al. (2023). X-ray polarimetry and spectroscopy of the neutron star low-mass X-ray binary GX 9+9: an in-depth study with IXPE and NuSTAR. A&A 676, A20. doi:10.1051/0004-6361/202346541

CrossRef Full Text | Google Scholar

van der Klis, M. (2005). Timing neutron stars. Electromagn. Spectr. Neutron Stars 210, 283. of NATO Advanced Study Institute (ASI) Series B.

CrossRef Full Text | Google Scholar

Vasilopoulos, G., Haberl, F., Sturm, R., Maggi, P., and Udalski, A. (2014). Spectral and temporal properties of RX J0520.5-6932 (LXP 8.04) during a type-I outburst. A&A 567, A129. doi:10.1051/0004-6361/201423934

CrossRef Full Text | Google Scholar

Vasilopoulos, G., Ray, P. S., Gendreau, K. C., Jenke, P. A., Jaisawal, G. K., Wilson-Hodge, C. A., et al. (2020). The 2019 super-Eddington outburst of RX J0209.6-7427: detection of pulsations and constraints on the magnetic field strength. MNRAS 494, 5350–5359. doi:10.1093/mnras/staa991

CrossRef Full Text | Google Scholar

Vybornov, V., Doroshenko, V., Staubert, R., and Santangelo, A. (2018). Changes in the cyclotron line energy on short and long timescales in V 0332+53. A&A 610, A88. doi:10.1051/0004-6361/201731750

CrossRef Full Text | Google Scholar

Vybornov, V., Klochkov, D., Gornostaev, M., Postnov, K., Sokolova-Lapa, E., Staubert, R., et al. (2017). Luminosity-dependent changes of the cyclotron line energy and spectral hardness in Cepheus X-4. A&A 601, A126. doi:10.1051/0004-6361/201630275

CrossRef Full Text | Google Scholar

White, N. E., Stella, L., and Parmar, A. N. (1988). The X-ray spectral properties of accretion discs in X-ray binaries. ApJ 324, 363. doi:10.1086/165901

CrossRef Full Text | Google Scholar

Wilms, J., Allen, A., and McCray, R. (2000). On the absorption of X-rays in the interstellar medium. ApJ 542, 914–924. doi:10.1086/317016

CrossRef Full Text | Google Scholar

Wolff, M., Becker, P. A., Coley, J., Fürst, F., Guillot, S., Harding, A. K., et al. (2019). The physics of accretion onto highly magnetized neutron stars. Bull. AAS 51, 386. doi:10.48550/arXiv.1904.00108

CrossRef Full Text | Google Scholar

Yang, W., Wang, W., Liu, Q., Chen, X., Wu, H. J., Tian, P. F., et al. (2023). Discovery of two cyclotron resonance scattering features in X-ray pulsar Cen X-3 by Insight-HXMT. MNRAS 519, 5402–5409. doi:10.1093/mnras/stad048

CrossRef Full Text | Google Scholar