- 1Scottish Universities Physics Alliance, Institute for Astronomy, University of Edinburgh, Edinburgh, United Kingdom
- 2Centre for Exoplanet Science, University of Edinburgh, Edinburgh, United Kingdom
The theory of how low mass stars form from the collapse of a dense molecular cloud core has been well-established for decades. Thanks to significant progress in computing and numerical modelling, more physical models have been developed and a wider parameter space explored to understand the early stages of star formation more fully. In this review, I describe the expected physical properties of the first and second core stages and how the inclusion of different physics affects those predicted characteristics. I provide an overview of chemical models and synthetic observations, looking towards the positive identification of the first core in nature, which remains elusive. However, there are a few likely candidate first cores, which are listed, and I briefly discuss the recent progress in characterising the youngest protostellar sources. Chemistry will be instrumental in the firm identification of the first core so we require robust theoretical predictions of the chemical evolution of protostellar cores, especially of the first and second core outflows. Looking ahead, simulations can shed light on how the protostellar collapse phase shapes the evolution of the protostellar disc. Simulations of dust evolution during protostellar core collapse show there is significant enhancement in grain size and abundance towards the centre of the core. Chemical models show that the warm, dense conditions of the first core drive chemical evolution. There is a wide scope for further study of the role that the first and second core stages play in determining the structure and composition of the protostellar disc and envelope and, of course, the eventual influence on the formation of planets.
1 Introduction
Stars form in collapsing dense cores within giant molecular clouds, a process involving contraction and density increases of several orders of magnitude. The concept of a temporary stable phase at the centre of a collapsing protostellar core was introduced in the seminal work of Richard Larson (Larson, 1969). The results of those first numerical solutions to the equations governing the collapse of a molecular cloud showed that the collapse is extremely non-homologous. Our understanding of the process remains essentially unchanged since it was first described over 50 years ago. Nonetheless, the technological progress of the last few decades, as well as new computational methods, has enabled sophisticated simulations to be performed in 2- and 3-dimensions and with additional physics. The purpose of this review is firstly to summarise the developments that have taken place since the protostellar collapse process was first described; and secondly to demonstrate that there is some variation in the predicted characteristics of the first and second hydrostatic cores1. In Section 6, I will also discuss what models are hinting at as to the role of the protostellar collapse stages in shaping the properties of protostellar discs and envelopes. Finally, we look to the future at the outlook for comparisons with observations and future directions for numerical simulations of protostellar core collapse.
1.1 Overview
Giant molecular clouds are thought to fragment to form protostellar cloud cores, which may then become unstable to gravitational collapse if there is insufficient thermal support. The now familiar process of an isolated spherical gas cloud collapsing under self-gravity has the following main stages:
1) Isothermal collapse2. At first the density and opacity are low so thermal energy can be freely radiated away. The gas is approximately in free-fall.
2) Formation of the first core. The density rises in the centre of the protostellar core and this region becomes opaque to infrared radiation. The collapse continues adiabatically in the central region and the pressure and temperature rise rapidly. The collapse pauses once hydrostatic equilibrium is reached and a pressure supported body, the first core, is formed. The central density of the protostellar core is roughly 10–12 g cm−3 when this occurs.
3) Growth of the first core. The envelope material falls onto the first core, increasing its mass and temperature.
4) Formation of the second core. At temperatures of
5) The second core accretes the remnants of the first core and the envelope continues to fall in. The second core continues to contract and heat as a pre-main sequence star.
2 Developments since 1969
A number of assumptions go into modelling protostellar collapse and these have been revisited over the years as new methods have been developed. Here, I will outline the most important developments that have been made since Larson’s first description of the gravitational collapse of a protostellar core. In Section 2.1 we look at the difference in outcome of employing grey radiative transfer rather than a barotropic equation of state and also the results of testing frequency dependent radiative transfer and an equation of state updated from live chemistry calculations. In Section 2.2 and Section 2.3 I summarise the progress enabled by 2- and 3-dimensional models and by the inclusion of magnetic fields in the calculations respectively.
2.1 Radiative transfer
The evolution through collapse to stellar core formation is driven by changes in opacity and the equation of state. Larson (1969) evolved the energy equation and a radiative diffusion equation in his original 1-D calculations, using pre-calculated values of the Rosseland mean opacity over the relevant temperature range. This approach, as he acknowledged, is valid only for optically thick gas and resulted in optically thin gas being set to the boundary temperature (10 K). For that reason, those calculations missed the heating of the inner envelope.
Rather than calculating radiative energy transport, earlier models with 2 and 3 dimensions made the simplifying assumption of a barotropic equation of state (e.g., Bate, 1998; Tomisaka, 2002) whereby the gas pressure is given by:
Here the exponent γ is the ratio of specific heats and K is a constant specific to each value of γ. To parameterize the effects of the changing opacity and hydrogen dissociation, γ is prescribed. For the isothermal phase, γ = 1; for the adiabatic phase γ = 7/5; to mimic the dissociation of H2, γ ≈ 1.1; and for the monatomic gas in the second core γ = 5/3. The application of a barotropic equation of state captures the qualitative behaviour of the collapse well but radiative transfer is required to reproduce the thermal evolution more accurately (Tomida et al., 2010b; Tomida et al., 2010a; Commerçon et al., 2010; Bate, 2011). The kinetic energy of the infalling material is radiated away at the first core accretion shock and barotropic treatments cannot reproduce this cooling mechanism (Commerçon et al., 2011).
The problem of handling radiative transport in both optically thin and optically thick regions is usually addressed by implementing the flux-limited diffusion (FLD) approximation (Levermore and Pomraning, 1981). An early application of FLD to 2-D models showed that the temperature structure was more spherical than the flattened density structure but was unable to follow the evolution to the formation of the first core due to computational limitations (Bodenheimer et al., 1990). Implementing radiative transfer via FLD in 3-D simulations led to higher temperatures than with a barotropic equation of state (Whitehouse and Bate, 2006; Tomida et al., 2010b; Bate, 2011). The higher temperatures provide increased thermal support which increases the lifetime of the first core. A striking difference was seen using the two-temperature (gas + radiation) model of Whitehouse and Bate (2006) whereby the lifetime of the first core increased from a maximum of 1,500 years with the barotropic equation of state to a maximum of 3,000 years (Bate, 2011). Regarding the second core phase, the inclusion of shock heating increases the second core radius and allows a transient expansion phase (Tomida et al., 2013). With radiative transfer, the energy released by second core formation transfers rapidly to the surrounding remnants of the first core, launching a bipolar outflow (Bate, 2011). The shock may expel the first core out to 500 au and this may be a cyclic process (Bate, 2010; Schönke and Tscharnuter, 2011).
The grey Rosseland mean opacity is normally used but more complex methods have been tested in radiation hydrodynamics models. 1-D simulations have compared the results of modelling the first collapse with frequency–dependent radiative transfer by binning wavelengths into 5 and 10 groups (Vaytet et al., 2012). This showed that the radius, mass and temperature of the first core are slightly underestimated with grey radiative transfer but there are no major differences in the outcomes, in agreement with prior results of (Masunaga et al., 1998). Continuing to the formation of the second core, the evolution of the first core was similar with frequency-dependent models to the grey models (Vaytet et al., 2013).
Chemical models can be combined with radiation hydrodynamical models to calculate the time-dependent mean molecular mass fractions for the changing density and temperature. The inclusion of basic chemical reactions of the most abundant species in hydrodynamical models showed that the dust evaporation phase can change the structure of the first core (Tscharnuter and Gail, 2007; Schönke and Tscharnuter, 2011). Dust free optically thin regions provide a pathway for cooling, but an optically thicker region at the edge of the first core can cause it to swell rapidly. Another approach to handling radiation in the optically thick envelope is to implement a radiative cooling approximation. The optical depth to a parcel of gas is approximated by assuming that it is located within a stable Bonnor-Ebert sphere with a known density profile (Stamatellos et al., 2007; Lombardi et al., 2015). This approach achieves similar results for protostellar collapse to 1-D radiative transfer models at a reduced computational expense.
In summary, radiative transfer does not change the qualitative picture of protostellar collapse. It does, however, slightly change the thermal evolution and increases the first core lifetime, which makes the first core more likely to be observed.
2.2 2- and 3- dimensions
The extension of models of cloud collapse to 2- and 3- dimensions allows for non-spherical structures to be studied which has arguably had the largest impact on study of the first and second cores. The first two-dimensional calculations were able to follow the collapse to the formation of the second core (Tscharnuter, 1987). The application of a nested grid in axisymmetric calculations allowed disc formation to be resolved in the same calculation as the whole cloud collapse (Yorke et al., 1993). These showed that rotation gave rise to a flattened first core. Three-dimensional calculations showed rotational instabilities developed in the first core (Boss, 1989). The bar-mode instability can lead to the formation of a disc which may then fragment (Bate, 1998; Bate, 2011, and see Section 3.1.2). In three dimensions, discs, fragments, outflows and jets can form and will be discussed in detail later.
2.3 Magnetic fields
The inclusion of magnetic fields allowed for the formation of outflows and a magnetically-supported pseudo-disc (e.g., Galli and Shu, 1993; Tomisaka, 2002; Matsumoto and Tomisaka, 2004; Banerjee and Pudritz, 2006; Hennebelle and Fromang, 2008). However, under ideal magnetohydrodynamics (MHD) angular momentum is extracted very efficiently from the central regions of the core, suppressing the formation of a rotationally-supported disc in what is known as the ‘magnetic braking catastrophe’ (Allen et al., 2003; Hennebelle and Fromang, 2008; Mellon and Li, 2008). This effect is reduced once non-ideal MHD processes are considered but the resulting discs are still smaller than those produced by purely radiation hydrodynamics simulations (e.g., Tomida et al., 2013). For further discussion of recent results regarding the influence of magnetic fields on protostellar collapse, disc formation and outflow structures see Maury et al. (2022).
3 Predicted properties from models
3.1 Features of first and second core stages
We saw above that the improvements and extensions to modelling protostellar collapse do not change the main results. The first core forms at the centre of the collapsing cloud core so is embedded within a dense envelope, the properties of which affect its evolution. The boundary of the first core is continuous in density with the infalling envelope, which means that the extent of the first core is not always well defined. Masunaga et al. (1998), for example, suggest the best definition of first core radius is where the gas pressure balances the ram pressure of the infalling envelope. This is where the shock will form at the boundary. Indeed, simulations that resolve that shock use the shock location to define the boundary (e.g., Bhandare et al., 2018).
Rotation gives rise to discs and MHD models show that an outflow may be launched from both the first and second core. The second core outflow is sometimes referred to as a jet but it is considerably slower than protostellar jets, so we will stick to the term “outflow.” These features are shown in the schematic in Figure 1. In this section, I will summarise the predicted properties of the cores, discs and outflows, and which effects are responsible for any variation. A summary of the properties is given for the first core in Table 1.
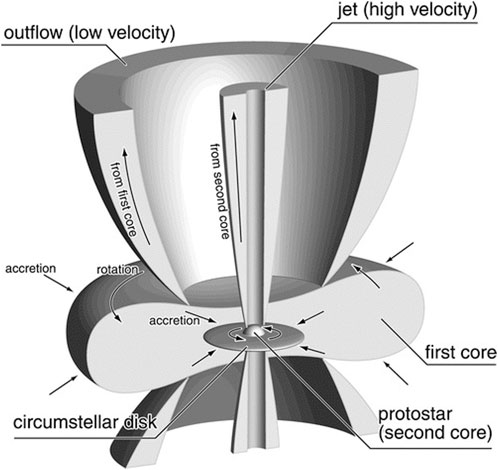
FIGURE 1. Schematic of the main structures associated with the first and second cores. The first core is flattened in a rotating protostellar core and launches a slow, broad outflow. The second core forms at the centre of the former first core and an accretion disc forms around it. The second core launches a faster, collimated outflow. From Machida et al. (2008), Fig 15. © AAS. Reproduced with permission.
3.1.1 Masses
The initial mass of the first and second core when formed are the values typically quoted. Of course, their masses increase substantially with ongoing accretion and the mass a first core reaches before undergoing second collapse may vary considerably depending on rotation, infall and the optical depth of the envelope.
The first estimate of the initial first core mass was 0.01 M⊙, considering a spherically symmetric, non-rotating protostellar core (Larson, 1969). Since then the masses, radii (in 1-D) and temperatures of first cores have been shown to be largely universal and unaffected by the initial mass or radius of the collapsing protostellar core (Masunaga et al., 1998; Vaytet et al., 2012; Vaytet et al., 2013). For the initial protostellar core mass range 0.2 ≤ Mcc ≤ 8 M⊙, 1-D models with frequency–dependent radiative transfer gave rise to first cores with Mfc ≈ 0.04 M⊙ and rfc ≈ 7 au (Vaytet and Haugbølle, 2017). The thermal evolution of the collapse phase changes slightly when the initial cloud properties are changed. This is due to the corresponding differences in opacity, which determines the rate of cooling and therefore the speed of collapse. In a very cold, and therefore especially unstable, model protostellar core, no first core may form; the collapse proceeds straight to the formation of the second core (Vaytet and Haugbølle, 2017; and see also Stamer and Inutsuka, 2018). Additionally, the radius of the first core is smaller for protostellar cores that are initially more unstable.
Extending the initial mass range to 0.1 < Mcc < 100 M⊙, Bhandare et al. (2018) demonstrated with 1-D models that there is a dependence of first and second core properties on the initial cloud core mass. Higher mass cores gave rise to larger and more massive first cores up to ≈10 M⊙. For progressively more massive protostellar cores, the first core became smaller and less massive because the ram pressure of infalling material is significant and leads to a high accretion rate. Since the ram pressure is always greater than the thermal pressure for M ≥ 40 M⊙, there is no real first core phase. The central temperature rises rapidly such that hydrogen dissociation occurs and collapse only stops in the centre when the second core forms.
Rotation provides additional support against gravitational collapse, alongside the thermal pressure, which allows the first core to reach a higher mass before the onset of second collapse. Rotation is described by the quantity β = Erot/Egrav, the ratio of rotational energy to gravitational potential energy. With a barotropic equation of state, the first core mass increased from 0.01 M⊙ to a maximum of 0.1 M⊙ with rotation (Saigo et al., 2008). In RHD simulations, the first core mass increased from
The initial mass of the second core is
Bhandare et al. (2020) followed the evolution of the second core for over 100 years after its formation for initial protostellar cores with the same range of initial masses as Bhandare et al. (2018) discussed above (0.1 < Mcc < 100 M⊙). By the end of the simulations the second core mass was 0.03 M⊙ for the 0.5 M⊙ cloud core and
Quoting masses for the second core is not particularly informative since the growth is so rapid. What we can say is that it is considerably more compact than the first core and, as such, can launch faster outflows as will be discussed later.
3.1.2 Discs, pseudo-discs and fragmentation
A rotating core gives rise to an oblate first core with a radius larger than that of a spherical core (10–20 au as opposed to
Magnetic fields act to reduce rotation (Banerjee and Pudritz, 2006; Hennebelle and Fromang, 2008; Hennebelle and Teyssier, 2008). Under ideal MHD with a strong magnetic field, the protostellar collapse occurs primarily along the field lines. The magnetic field lines threaded throughout the protostellar core couple the high density gas near the centre to low density gas further out. Since the gas closer to the centre of the core rotates faster, the field lines become twisted. The twisted field lines generate a torque that slows the rotation of the higher density gas and transfers angular momentum outwards to the lower density gas. This process of magnetic braking prevents the formation of a rotationally-supported disc but a magnetically-supported pseudo-disc develops (Matsumoto and Tomisaka, 2004; Hennebelle and Fromang, 2008). The pseudo-disc is thicker when the magnetic field is inclined with respect to the rotation axis and a mutual inclination of just 10°–20° allows a rotationally-supported disc to form even with a strong magnetic field (Machida et al., 2006b; Hennebelle and Ciardi, 2009).
Non-ideal MHD processes allow the gas to drift relative to the magnetic field such that discs can form and are able to fragment (e.g., Krasnopolsky et al., 2011; Tomida et al., 2013; Tomida et al., 2015; Masson et al., 2016). Discs are however prevented from forming when the magnetic field and rotation axis are aligned due to braking from the Hall effect (Tsukamoto et al., 2015; Wurster et al., 2018). Wurster et al. (2021) report the development of a counter-rotating envelope as well as a disc in some models. However, this model implements only the Hall effect, neglecting the other ideal MHD effects and begins with somewhat unrealistic conditions. Counter-rotating envelopes are therefore probably not formed in nature.
In summary, rotationally-supported discs are expected to form in the first and second core phases, and to have similar structures predicted by purely hydrodynamical models albeit with a smaller outer radius.
3.1.3 Outflows
Outflows have long been proposed as a feature to distinguish sources containing a first core from starless cores. Unfortunately this has produced a few “false alarms” among candidate first cores. In this section I will summarise the predictions for the properties of the first and second core outflows and evaluate the velocities that are most likely.
Simulations predict that the first core outflow is wide and could extend ∼ 600 au (Tomisaka, 1998; Tomisaka, 2002; Allen et al., 2003; Banerjee and Pudritz, 2006), though other models predict an extent of at most a few 10s au (e.g., Machida et al., 2005b; Bate et al., 2014). The outflow velocity is consistently predicted to be no more than a few km s−1 and the highest values are ∼ 5 km s−1 (Machida et al., 2008). The first core outflow may be slower than the infall velocity (
In contrast to most other works, the simulations of Price et al. (2012) produce highly collimated “jets” with velocities of up to 7 km s−1 driven from the first core. However, they note that the ideal MHD method employed is unrealistic for these conditions and therefore these jets are unlikely to form in reality. Lewis and Bate (2017) also reported similarly fast outflow velocities but point out that they implement a sink particle to represent the first core when the density exceeds 10–10 g cm−3 and this has an accretion radius of 1 au. Infalling material will therefore have a higher rotation velocity when it reaches the outflow launch radius, boosting the outflow velocity beyond what is realistic (Price et al., 2003). With this in mind, the conclusion from the simulations should be that first core outflows have maximum velocities of a few (most likely
The depth of the second core’s potential well is much greater hence it drives a faster outflow than the first core. The radiation hydrodynamical simulations of Bate (2010, 2011) showed that the high initial accretion rate onto the newly formed second core leads to rapid heating of the remnants of the first core, launching a slow outflow. This mechanism probably assists the launching of the magnetically-driven outflow. MHD simulations typically find that the second core drives a two-component outflow. The broader outflow is magneto-centrifugally-driven and contains a fast, narrow outflow, often referred to as a jet, launched by the magnetic pressure from the twisted magnetic field in the disc (e.g., Tomisaka, 2002; Banerjee and Pudritz, 2006; Tomida et al., 2010b; Machida and Basu, 2019). Velocities of the second core outflow obtained in simulations range from 1.5 km s−1 (Hennebelle and Fromang, 2008) to 30–40 km s−1 (Machida et al., 2006a; Machida et al., 2008) and as high as 100 km s−1 within the first 2000 years (Machida and Basu, 2019). The second core outflow velocity depends on the rotation of the protostellar core: in resistive MHD models, Tomida et al. (2013) find 6 km s−1 vs. 15 km s−1 respectively for slow and fast rotating cores. The outflow velocity is much greater than the maximum rotation velocity at the launch radius, indicating that there is some additional acceleration at work from the magnetic pressure (Wurster et al., 2021).
It is important to note that outflows do not always form. Firstly, a high accretion rate in the envelope can block the outflow, and this is not always considered in isolated disc models (Machida and Hosokawa, 2020; Wurster et al., 2021). Secondly, the outflow is always parallel to the magnetic field (Matsumoto and Tomisaka, 2004), which means that misalignments between the magnetic field and the rotation axis can disrupt the outflow. If the misalignment between rotation and magnetic field is small, a collimated outflow forms but with a 20°–45° misalignment the magnetic field winds up and disrupts the outflow (Lewis et al., 2015). For larger misalignments, the outflow is spherical. Thirdly, a fast outflow is not always produced in non-ideal MHD models (Machida et al., 2006a). The Hall effect suppresses the outflow when the magnetic field is anti-aligned to the rotation axis (Wurster et al., 2021). Finally, we must remember when comparing to observations that we measure the projected velocity of the outflow, which will be significantly slower than the maximum outflow speed.
3.1.4 First core lifetime
The lifetime of the first core is affected by the strength of the support against gravitational collapse and the rate at which it can cool to keep the temperature below that required to dissociate molecular hydrogen as it is heated by infalling material. Hence rotation, protostellar core mass, magnetic field strength and orientation, and opacity all come into play.
In purely hydrodynamical models, fast rotation leads to a disc-like first core with a lifetime of up to a few thousand years (Bate, 1998; Saigo et al., 2008; Bate, 2011). In non-ideal MHD models the lifetime is significantly shorter, at ∼200–600 years (Tomida et al., 2013; Tomida et al., 2015; Wurster et al., 2021). Bhandare et al. (2018) find that the first core lifetime scales as tfc ∝ M−0.5 for protostellar core mass Mcc < 10 M⊙ but steepens to tfc ∝ M−2.5 for Mcc > 10 M⊙, due to the additional ram pressure discussed above. Protostellar cores with M < 10 M⊙ give rise to first cores with lifetimes of a few hundred years. Beyond this, the first core lifetime is 10–100× shorter and the resulting first core is therefore essentially unobservable.
First cores that form in very low mass cloud cores (0.1 M⊙) are likely to have far longer lifetimes because they rely on radiative cooling and contraction rather than accretion to reach the central density and temperature required for the second core to form. Most of the envelope is accreted leaving the first core exposed. The increased lifetime, which could be
4 Predicted observational characteristics
In Larson (1969), it was pointed out that the stellar core remains obscured by dust for some time. Since then, simulated observations indicate that there may nevertheless be identifiable features. Estimates of the luminosity of the protostellar core during first and second core stages are a first step to identifying candidate sources. The spectral energy distribution has proved useful for classifying protostars and is another likely diagnostic of early star formation. I first discuss the predictions for the SEDs obtained from numerical simulations before giving an overview of the theoretical work to model molecular line emission and chemical evolution during protostellar collapse.
4.1 Luminosity and spectral energy distribution
Models agree that the protostellar core remains very dim throughout the first collapse stage with a luminosity in the range 0.003 ≲ Lfc ≲ 0.1 L⊙ (e.g., Yorke et al., 1993; Boss and Yorke, 1995; Masunaga et al., 1998; Saigo and Tomisaka, 2006; Commerçon et al., 2012a; Vaytet et al., 2013). However, the earlier estimates of the luminosity that are derived from barotropic models are likely underestimates because they do not consider the significant heating of the former first core region when the second core forms (Tomida et al., 2010b). The first core luminosity is therefore more likely to be Lfc ≳ 0.01 L⊙.
After second core formation the luminosity increases rapidly, due to the accretion luminosity rather than the intrinsic radiative luminosity of the second core. The emergent luminosity is predicted to be a few tens L⊙, increasing quickly as the accretion rate increases after second core formation (Masunaga and Inutsuka, 2000; Jones and Bate, 2018).
The spectral energy distribution (SED) of the first core peaks between 100 and 200 µm (e.g., Boss and Yorke, 1995; Saigo and Tomisaka, 2006; Omukai, 2007; Commerçon et al., 2012b). Radiative transfer models of the collapsing protostellar core show there is a gradual shift in the peak of the SED to shorter wavelengths (Figure 2) (Yorke et al., 1993; Masunaga and Inutsuka, 2000; Saigo and Tomisaka, 2011; Commerçon et al., 2012a; Young et al., 2018). Commerçon et al. (2012a) found that there is no clear change after the formation of the first core. Though the change in the SED is gradual, Young et al. (2018) showed that the first core is distinguishable from a protostellar core undergoing the first collapse phase because the 160 µm flux rises quickly after first core formation.
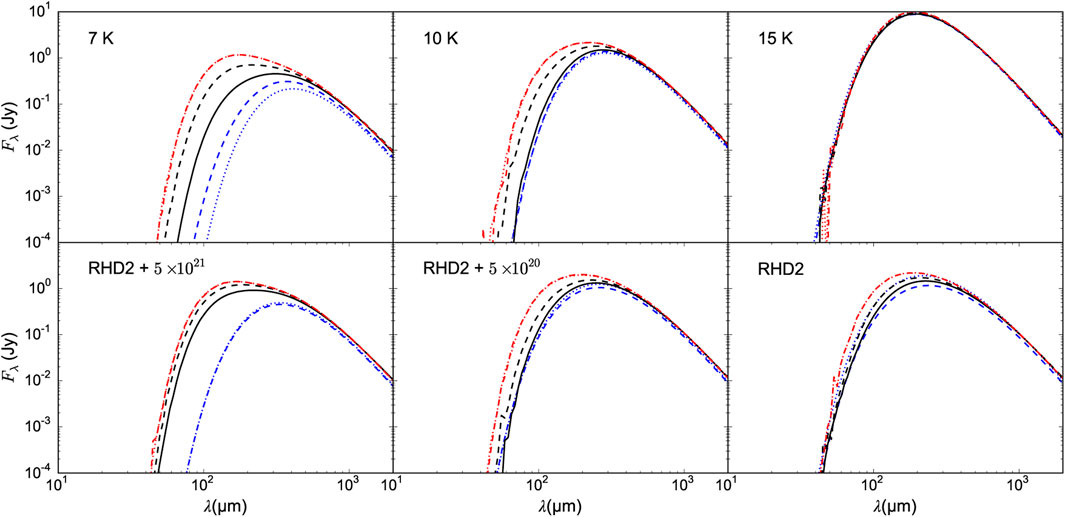
FIGURE 2. Examples of the simulated spectral energy distribution for key stages during protostellar collapse. The central density was 1.4×10−18 g cm−3 (blue dotted), 10–12 g cm−3 (first core formed, blue dashed), 5×10−11 (solid black), 10–9 g cm−3 (dashed black), 10−4 g cm−3 (second collapse, red dotted), and 10–2 g cm−3 (second core formed, red dashed). The three models in the top panel start from Bonnor-Ebert spheres at the uniform temperatures indicated in the top left corner of each panel. For models in the bottom panel the temperature was initialised from exposure to interstellar radiation, with added attenuation equivalent to an additional column density of H2 nH2=5×1021 and 5×1020 and without attenuation. From Young et al. (2018), Fig. 7.
We cannot probe the first core directly at wavelengths λ < 850 µm because the envelope is optically thick and flux emitted by the first core at these wavelengths is completely reprocessed by the time it emerges from the collapsing protostellar core. The shape of the infalling envelope affects the attenuation of the first core flux such that the flattened structure of a rotating core leads to significant emergent flux between 20 and 100 µm when viewed face-on (e.g., Bodenheimer et al., 1990; Boss and Yorke, 1995; Masunaga et al., 1998; Commerçon et al., 2012b; Young et al., 2018). This is because the optical depth is much lower in the polar direction than perpendicular to the rotation axis. Flux at wavelengths
There are unlikely to be any changes in the SED of an evolving first core either if it is observed pole-on and it has a dense outflow, or if it is observed edge on (Commerçon et al., 2012b). Furthermore, there is also no evolution of the SED if the edge of the protostellar core is exposed to the unattenuated interstellar radiation field and therefore heated to T > 10 K (Young et al., 2018) and see Fig. 2. This leaves us with something of a catch-22: first cores that are most likely to be detectable because they are less embedded are also unlikely to have a distinctive SED because they are exposed to more heating.
There is no immediate change in the SED after the formation of the second core despite the rapid increase in the central temperature. This is because the second collapse occurs within the former first core so the temperature in the region probed by the SED (the inner envelope) has changed little in this time (Young et al., 2018).
4.2 Continuum imaging
Since the collapsing envelope is largely optically thick, images of slowly rotating protostellar cores containing a first or second core will be similar to that of starless cores. However, first and second cores formed in moderately rotating and in magnetized protostellar cores have features that could be detected. The fragments and spiral features associated with fast rotating first and second cores should be detectable at distances of 150 pc with ALMA (Saigo and Tomisaka, 2011; Commerçon et al., 2012a). Synthetic continuum emission maps at different wavelengths are shown in Figure 3. In the mid-infrared the structure is unclear. At submillimetre wavelengths (850 µm) the envelope is optically thin and the spiral structure is clear. Simulated emission maps also indicate that the identification of an outflow, pseudo-disc or disc should be possible in ALMA bands 3 and 4, which means that magnetised and non-magnetised cases are distinguishable (Commerçon et al., 2012b).

FIGURE 3. Synthetic observations of a rotating first core developing spiral arms viewed face-on (top row) and edge-on (bottom row), at four different wavelengths. From Young et al. (2018) Fig. 6.
4.3 Molecular line emission and chemistry
Chemical abundances and gas kinematics are some important properties that can be derived from observations of molecular lines. First and second cores are deeply embedded so optically thin lines are required to probe them and their immediate surroundings. Hydrodynamical models are often used as a starting point for producing synthetic observations of line emission. Sometimes uniform molecular abundance fractions are assumed for post-processing snapshots of the hydrodynamical model with frequency–dependent radiative transfer and sometimes molecular depletion due to, e.g., freeze–out is parameterized with a dependence on temperature and/or density. These kinds of models are useful for predicting the line profiles and maps of common molecules.
Measuring the kinematics provides another approach to determining if a source contains a first or second core. Simulated CS emission using a uniform CS abundance show the signatures of infall, a rotating outflow and an increase in line width compared to during the first collapse (Tomisaka and Tomida, 2011). The line profiles of collapsing protostellar cores are sensitive to differences in depletion which means that chemistry should be considered (Rawlings and Yates, 2001). Accounting for chemical evolution would lead to stronger differences in the CS emission as the core evolves. While discs and pseudo-discs look like identical elongated structures in continuum images, kinematic measurements may tease apart the rotational motions. CO isotopologues can reveal the velocity gradients across the observed structure. The velocity gradient is parallel with the disc structure for models of a rotationally supported disc but is perpendicular for models of a pseudo–disc, in which the velocity gradient traces the infalling gas (Harsono et al., 2015).
Chemical modelling of a collapsing protostellar core adds an additional stage to modelling observations and a great deal more complexity. The temperature difference between the first core and more evolved sources drives changes in the abundances of many chemical species. Predicting changes in molecular abundances during the collapse of a protostellar core gives an idea of molecules that could be used to distinguish starless cores, first cores, second cores, and more evolved protostars.
During the isothermal collapse phase, the density increases, which accelerates the freeze-out of most species (Aikawa et al., 2008; van Weeren et al., 2009; Furuya et al., 2012). As the centre warms up, CO sublimates and complex organic molecules that formed on the grain surface at low temperatures are released into the gas phase (Aikawa et al., 2008). The chemical evolution speeds up within the first core and the abundances of many species increase by several orders of magnitude. CO and OCS, for example, saturate at maximum values very quickly after the formation of the first core. Others such as CS, CN and NH3, increase in abundance throughout the first core stage (Young et al., 2019). HCN,HCN, H2O, HNCO, H2CO, HC3N, C3H2 and CH3OH are also likely tracers of the first core (Hincelin et al., 2016). During the first core stage, the inner envelope surrounding the first core also heats up. In this region, ices frozen onto dust grains are sublimated and gas phase abundances increase. The relative abundance of HCO+ decreases in dense cold gas compared to the standard interstellar medium but, after the formation of the first core, the abundance peaks in a shell at the edge of the first core (Young et al., 2019). The increase in the abundance of CO (and other species) in the inner envelope means the first core may be observed in absorption against the cooler, optically thick gas (Young et al., 2019) as is observed in some young protostellar sources (e.g., Ohashi et al., 2014). The absorption feature is at redshifted velocities 0.5 ≲ v ≲ 1.5 km s−1, because the obscuring gas is infalling onto the first core (see Figure 4).
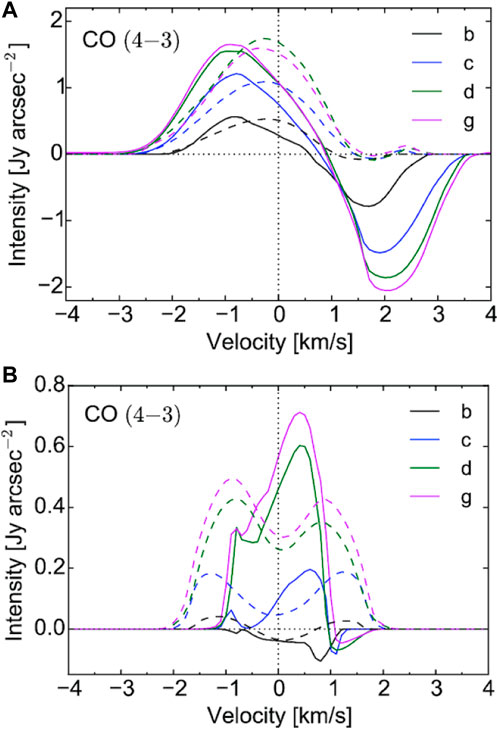
FIGURE 4. Simulated CO spectra averaged over a central 0.67 arcsec diameter aperture for an evolving first/second core at a distance of 150 pc. The chemical evolution was calculated as a post-process for an RHD model (A) and an ideal MHD model (B) of protostellar collapse. Solid lines: viewing inclination i =0° and dashed lines: i =90°. Early, mid and late first core stage are designated b,c and d, and g is just after the formation of the second core. From Young et al. (2019).
The velocity of the first core outflow is so low that rotation of the outflow may be easier to observe (Yamada et al., 2009; Young et al., 2019). It should be noted that although the first core outflow may extend to a few hundred au, the outflow is cold and probably only the inner few tens of au are warm enough during the first core lifetime for CO to be in the gas phase (Hincelin et al., 2016; Young et al., 2019). This means that it is only likely to be possible to detect the first core outflow close to the first core itself. Hincelin et al. (2016) suggest that an alternative signature of the first core outflow is the depletion of CS, CN, N2H+, C2H, and H2CN relative to the envelope. They additionally note that the molecular abundances of the outflow depend on the magnetic field strength.
After the second core forms the temperature rises quickly in the centre. If an outflow forms, it will sweep up hot gas from the former first core and inner envelope and send this outwards. By around 200 years after second core formation the CO sublimation radius shifts outward from
Models of chemical evolution are affected by the speed of collapse because of the change in the lifetime of the protostellar core compared to the chemical and freeze-out timescales. Magnetic support increases the lifetime of a protostellar core, allowing more time for freeze-out and therefore changing the chemical evolution (Priestley et al., 2018; 2019). However, despite extremely large differences in molecular abundances at the centre of protostellar cores with varying levels of magnetic support, the integrated molecular column density is similar, rendering the difference undetectable (Priestley et al., 2021). A related finding is that hydrodynamical simulations may overestimate abundances of HCO+, NH3, N2H+, CN and HCN because of the different collapse timescales (Tassis et al., 2012; Yin et al., 2021; Tritsis et al., 2022).
5 Observations of first cores and the youngest protostars
Millimeter interferometers such as ALMA probe the youngest embedded objects, unearthing compact sources that are challenging to interpret. These tend to be categorised as either ‘starless cores’ (dense prestellar cores without a compact central object), first core candidates or Class 0 protostars. After second collapse, the second core evolves very quickly into what would be categorised as a Class 0 source so is not an observable object in its own right.
5.1 Candidate first cores
Table 2 lists the 13 candidate first cores and their main characteristics. Although some of these have already been refuted, they are included because there are recent mentions in the literature that still consider them candidates.
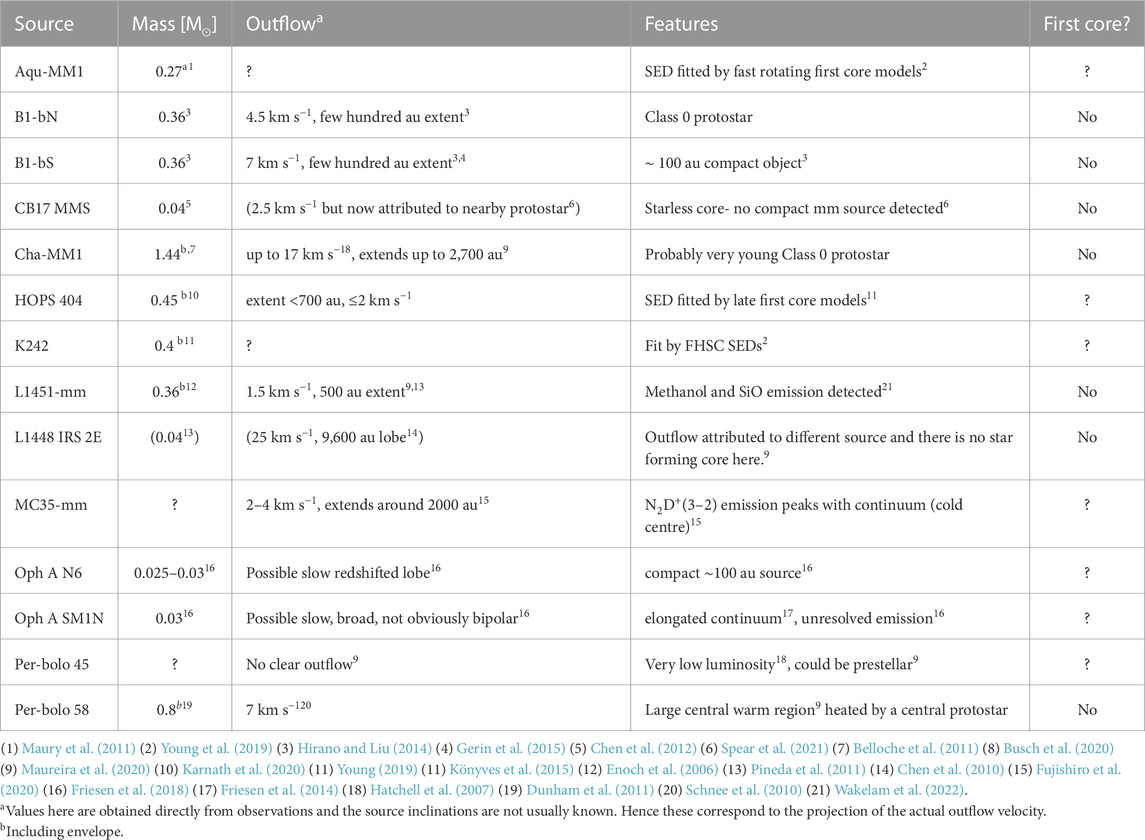
TABLE 2. Features of observed candidate first cores from the literature. References are given in the notes below.
A couple of former candidates (CB17 MMS and L1448 IRS 2E) were identified due to the presence of outflows and weak continuum detections at 1.3 mm. However, no compact continuum emission was detected in which means there is no compact object, first core or protostar, at that location and they are ‘starless cores’ (Maureira et al. 2020; Spear et al. 2021). As first cores are fully optically thick objects, with adequate sensitivity and resolution we would always expect to detect a compact source at millimeter wavelengths. The complex density structures of star forming regions can deflect outflows such that their origin is not always obvious. For these candidates, the outflows were later found to be driven by nearby protostars. Conversely, other former candidates were identified due to the lack of outflow associated with a faint continuum source. These, such as Cha-MM1, were subsequently rejected when an extended outflow was detected (Busch et al. 2020).
Among the observations of first core candidates, Fujishiro et al. (2020) and Maureira et al. (2020) demonstrate the application of molecular line observations with ALMA to characterising pre-and protostellar sources. Candidate Per-bolo 58 is rejected because the bright H13CO+(1–0) emission extends around 1,000 au across the centre of the source, indicating a large warm region within the core heated by a central protostar (Maureira et al., 2020). If the source contained a first core, the warm region where carbon-bearing molecules can be released into the gas phase after being frozen out would be far smaller. In contrast, in Per-bolo 45 the H13CO+(1–0) emission is much fainter in a region within 1,000 au of the central source which indicates that the central region is cold enough for carbon-bearing molecules such as CO to freeze out onto dust grains (Maureira et al., 2020). Hence, Per-bolo 45 is very unlikely to have evolved beyond the first core stage.
We are now left with eight candidate first cores. Two of these (Aqu-MM1 and K242) require high resolution interferometric observations to search for outflows and to verify that there is a compact object within the source. The remainder have all been observed with ALMA and have a variety of features. We now require observations on sub-100 au scales to probe the density, temperature and composition of very centre of the sources. The outlook for positively identifying the first core in observations is discussed further in Section 6.2.
5.2 Early evolution: beyond second core formation
While observing and firmly identifying a first core remains elusive, progress has been made in characterising very young protostars. Some of these sources are puzzling, having a very low luminosity yet driving an outflow. For example, 10 years ago a census of protostars in Orion with Herschel discovered a number of very young protostars, classified as “PACS Bright Red Sources” or “extreme class 0” objects (Stutz et al., 2013). Further observations with ALMA led to the identification of a first core candidate, HOPS 404, among these (Karnath et al., 2020). The other extremely young objects are all deeply embedded young protostars, providing a sample with which to study early outflows. More recently, the dynamics of several very young protostars that do not appear to have evolved far beyond the formation of the second core have been studied. The results include the characterisation of a disc in a system thought to be only around 35,000 years old (HH211, Lee et al., 2023a) and some perplexing sources. G208Walma, for example, is a cool, faint object with a significant envelope, similar to how first cores are expected to appear, but it also drives an outflow and a dense jet (Dutta et al., 2022). On the other hand, RCrA IRS5N is a Class 0 object that is thought to be too luminous to contain a first core but has no sign of an outflow (Sharma et al., 2023).
The chemical structures within pre- and protostellar cores can be explored thanks to ALMA observations of molecular line emission (e.g., Fujishiro et al., 2020; Maureira et al., 2020; Caselli et al., 2022) and the chemical evolution of star-forming cores is also becoming clearer. Many complex organic molecules have been detected, and “hot corinos,” compact warm regions surrounding some of the youngest protostars, are found to be especially rich in these species. This is thought to occur because complex organic molecules form on the surface of dust grains and are released into the gas phase when ices evaporate from the grain surface. Trends in the abundances of complex organic molecules have been found that correlate with the evolutionary stage. For example, the deuteration of methanol increases between the starless core phase and the formation of the protostar, before decreasing again within the hot corino region (Aikawa et al., 2012). ALMA observations of methanol lines illustrate an application by showing that the fraction of deuterated methanol in an “extreme Class 0” source (Stutz et al., 2013; and see Section 5.2) appears to mark a transition between that of a prestellar core to an embedded protostar (Figure 5; Lee et al., 2023b). Given the youth of the source, the authors propose that the recently-evaporated complex molecular species represent the species formed during the cold phase of the core, that is before the formation of the second core, or protostar. Hence, it may be possible to determine the chemical evolution that occurs during the first core phase through measuring abundances of complex organic molecules in the youngest Class 0 protostars.
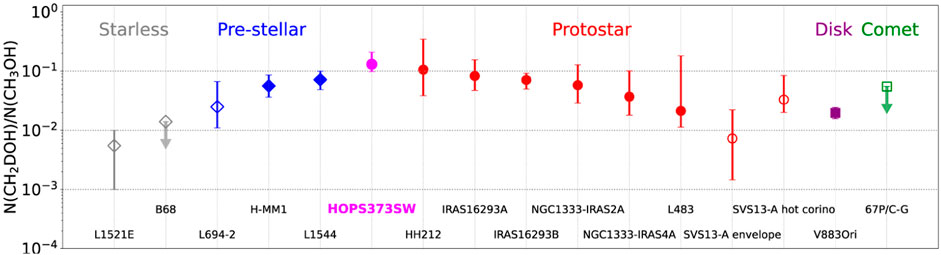
FIGURE 5. The trend in the fraction of deuterated methanol from starless core to comet as shown by the column density ratio of CH2DOH/CH3OH. Filled and open symbols indicate single-dish and interferometric observations, respectively. The ‘extreme Class 0’ source HOPS373SW represents a transition between the chemistry of a cold core and of a core in which the central region is warmed by the protostar. Figure adapted from Lee et al. (2023b), Fig. 9 (CC BY) reproduced with permission.
It is clearly an exciting time for studying young protostellar systems given the quantity of new data probing their inner regions. These kinds of observations provide useful tests of the dynamical and chemical states of young protostellar systems which will enable us to discriminate between models.
6 Discussion
6.1 What next for modelling?
6.1.1 Dust
With observations showing significant differences in the dust grain size distribution between the interstellar medium and protoplanetary discs, models are being developed to explore how and when grain growth occurs. We are beginning to explore grain growth during the first core stage and, by extension, the role that this stage plays in planet formation. Even before the first core forms, during the first stage of protostellar collapse, dust grains larger than 100 µm drift inwards and concentrate at the centre such that the dust content near the centre can be enhanced by a factor of
6.1.2 Chemistry
Measurements of molecular abundances and the distribution of molecular species within protostellar cores are providing a new insight into the evolutionary stage of young sources (see Section 5). The detection of molecular lines that trace warm cores has been used to discount first core candidates and so it is important that models of first core chemistry, and the simulated line maps, are sound. The finding that molecular line emission of young hot corinos may indirectly reveal the chemistry associated with the earlier, first core stage has useful implications. This strongly motivates new chemical models of the first and second core stages that include complex organic molecules, now that we have an observational test. This may reveal whether the first core and/or the formation of the second core play a role in enriching protostellar cores with complex organic molecules.
Chemical evolution is generally only modelled for isolated protostellar cores but there are predicted to be differences in the chemistry between embedded and isolated prestellar cores (Priestley et al., 2023). This needs to be considered because these differences could propagate through to change the later chemical evolution within the protostellar core and also because the chemistry in the outer envelope evolves very slowly along with the physical properties. Observations that probe the envelope with therefore be sensitive to the initial differences in abundance that are due to the environment. Synthetic observations of key molecular lines for evolving protostellar cores in both isolated and embedded environments would allow a more robust interpretation of the ages of these sources.
The significant grain growth and increase in dust to gas ratio in the dense regions described in Section 6.1.1 also has implications for the chemistry. A higher abundance of dust grains will increase freezeout but could also enhance the formation of complex organic molecules, which are thought to form on the icy surfaces of dust grains. Current models of the chemical evolution during protostellar collapse do not include grain sizes ≳ 100 µm. Chemical models incorporating the changing dust abundance and grain sizes in a collapsing protostellar are required to fully understand the gas composition. Furthermore, the initial composition of the protoplanetary disc is set by the first core and inner envelope so a better understanding of their chemistry would greatly benefit disc models.
6.2 Outlook for comparison to observations
Larson realised that the excess infra-red emission detected from T Tauri stars was consistent with them being young stars, still accompanied by infalling dust. He also compared infall velocities with the redshifted absorption lines and found them consistent. Unresolved observations cannot usually distinguish between features like discs and envelopes and give scant information as to the inclination and morphology of a source. Boss and Yorke (1995) asserted that a first core should be detectable at a distance of 100 pc with ISO (launched in 1995) and Spitzer. Furthermore, with the advent of ALMA, detection of the first core seemed within reach. Ten years on, many former “candidate first cores” have been eliminated and few new potential sources have been identified (See Table 2). Spitzer observations have however proved useful in excluding the more evolved sources as it has become clearer that first cores will be very faint at wavelengths
A reason why there were previously more candidate first cores was because of the generous interpretation of outflow velocities predicted by simulations. A low luminosity source is typically designated a “candidate first core” if its luminosity is L < 0.1 L⊙, it is faint or undetected at λ < 70 µm and no outflow faster than 10 km s−1 is observed. Given the results described in Section 3.1.3, the latter constraint must be tightened significantly and it seems sensible to exclude sources for which clear outflows are observed. Simulated observations show that there should still be other characteristics that can distinguish first cores from starless cores. For example, chemical evolution may be evident and the visibility amplitude of interferometric observations also shows differences (Tomida et al., 2010a).
There have now been several deep surveys of young stellar objects in all of the nearby star forming regions so why has a first core not yet been detected? Estimates of the expected population of first cores have been made by comparing their lifetimes to the estimated lifetimes of Class 0 and Class I objects. The lifetime of Class 0 protostars is estimated to be somewhere between a few × 104 years (Andre et al., 2000; Maury et al., 2011) and 1–3 × 105 years (Evans et al., 2009; Dunham et al., 2015). With lifetimes of a few hundred years, we can expect the fraction of first cores compared to Class 0 objects to be 0.002–0.02. The young stellar object catalogue of Dunham et al. (2015) includes around 103 Class 0 protostars. Based on this we would expect to find at most 1 or 2 first cores in total in the nearby star forming regions. If the Class 0 lifetime is at the upper end of the range of estimates, we would be unlikely to find any. (See Maureira et al. (2020) for similar discussion).
The now-cancelled Space Infrared Telescope for Cosmology and Astrophysics (SPICA) would have had the sensitivity to detect the first core in far-infrared continuum and H2O emission out to 1 kpc (Omukai, 2007). The MIRI instrument onboard the James Webb Space Telescope operates at 5–28 µm and could potentially detect flux from face-on oblate first cores, but a dense outflow may however obscure the flux at such short wavelengths. Though it may not be practically possible to observe objects in the first core stage due to the short lifetimes and lack of current far-infrared instruments, we may be able to infer its existence and properties nonetheless. The role that the first core appears to have in growing dust grains and forming a wide range of molecules may mean that we can make some estimates of its properties by comparing the dust grain and molecule distributions in Class 0 discs and outflows with model predictions. It could be worthwhile modelling the chemistry and dust evolution beyond second core formation to explore the variation in dust and molecular abundances and distribution with the properties of the protostellar core.
Nevertheless, we are left with 6 candidate first cores that have been observed with ALMA. What observations do we need to positively identify any of these as a first core? A low luminosity alone is insufficient because deeply embedded protostars and protostars with edge-on discs have also been found to be exceptionally faint. A slow outflow can be indicative, however this is not a necessary criterion which means that Per-bolo 45 should not be discounted. If the magnetic field and rotation axis are misaligned the first core, or indeed protostar, may not drive a typical outflow. Also, as we saw in the case of CB17 MMS, the uneven density structure of star forming regions can stem or redirect outflows in an unexpected direction. The detection of a source in millimetre continuum that shows no compact source smaller than a few au from analysis of the visibility amplitudes would strongly support identification as a first core. Signs of chemical evolution in a dense core that indicate a compact warm central region that is also too cool to be heated by a protostar are another strong indicator.
What, then, is required from theory to find the first core? In the ALMA era, simulated observations should now focus on visibility amplitudes and molecular lines at high angular resolution. Chemistry has become another way of assessing the evolutionary state of a source and the molecular structure probably changes very quickly following second core formation (Young, 2019). Consequently, more work is needed to clarify the chemical changes that occur during and after the formation of the second core and to predict the corresponding observables. We need to clarify the expected observational characteristics of first core outflows. In particular, simulations need to determine the observable extent of first core outflows: if the outflow does extend
6.3 Conclusion and outlook
The evolution of a collapsing protostellar core has been studied thoroughly over the last few decades. Given how little the theory has qualitatively changed with the consideration of additional physics in simulations, we can be confident of the central predictions of first and second core properties. A caveat is perhaps that our understanding is based on numerical models that all follow the collapse of isolated protostellar cores. Observations show that cores form in filaments and there may be ongoing accretion onto collapsing protostellar cores which could affect, for example, the first core lifetime.
An important development has been to show that discs can form early, during the first core stage, even in MHD simulations once nonideal process are taken into account. For first core outflows, the consensus from MHD simulations and chemical models is that they are probably very difficult to detect. However, these outflows could play a significant role in redistributing dust grains and molecular species from the first core to the envelope and disc. It could be, however, that the material forming the disc when the second core forms is all accreted very quickly. Further modelling of the evolution of the protostellar core beyond second core formation is needed to follow the development of the disc.
Now that protostellar collapse is well understood we can turn to studying how this phase shapes the resulting protostar system. We are beginning to see that the dust grain size distribution evolves significantly during protostellar collapse, particularly within the first core, and outflows redistribute large grains out into the disc and envelope. This has a number of implications that warrant further study. How does the changing dust composition affect the thermal properties of the first core, for example? Do the large dust grains survive the second core formation and do they seed grain growth in the young protostellar disc? Do we expect variations in the protostellar collapse process to lead to differences in the dust grain distribution in protostellar discs? Similarly, the warm first core seems to be an effective chemical factory. Further open questions are therefore: do these molecules survive beyond second core formation and how does this influence the composition of Class 0 discs and envelopes?
Finally, a positive observational identification of the first core remains difficult but is potentially within reach with the exceptional sensitivity and resolving power of ALMA. I have listed the remaining candidate first cores and there remains some tension between the predicted extent of the first core outflow and the outflow properties of first core candidates. We now require more detailed predictions of the chemical evolution of the envelope and outflow in order to firmly identify the first core for the first time.
Author contributions
AY: Writing–original draft, Writing–review and editing.
Funding
The authors declare financial support was received for the research, authorship, and/or publication of this article. AY is grateful for support from the UK STFC via grant ST/V000594/1.
Acknowledgments
I thank Matthew Bate, Ken Rice and the reviewers for helpful comments on the manuscript. I am very grateful to María José Maureira for suggestions and comments regarding observations of first core candidates.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1A note on definitions. The first hydrostatic core is also known in other works as the ”first core,” “first protostellar core,” “first Larson core,” “pre-stellar disc,” and even as a “Class −1 object” in Boss and Yorke (1995). The stable object that forms within the first hydrostatic core after the second collapse is known as the “stellar core,” “second hydrostatic core,” “second Larson core,” or just “protostellar core.” Boss (1989) further suggested that the two objects be known as the inner and outer cores, in acknowledgement that the first core persists while the second core forms at its centre. Here we refer to the first and second hydrostatic cores (first and second core for short) and suggest that these descriptive terms are clearest and most informative. In this review, I will use the term “protostellar core” to refer to the molecular cloud core for which collapse is modelled.
2The progression of the isothermal collapse phase depends on the initial structure of the cloud core. Whether the contraction of the core is best described by the Larson-Penston flow (Larson, 1969; Penston, 1969), ‘inside-out’ collapse of a singular isothermal sphere (Shu, 1977), quasi-static collapse of a Bonnor-Ebert sphere (e.g., Keto and Rybicki, 2010) or something else continues to be debated, though observations indicate that prestellar cores are supported by thermal rather than magnetic pressure which simplifies the problem somewhat. See, e.g., Whitworth et al. (1996); di Francesco et al. (2007); Keto et al. (2015) for further details and discussion.
3In 1995 Spitzer was known as SIRTF and subsequently launched in 2003.
References
Aikawa, Y., Wakelam, V., Garrod, R. T., and Herbst, E. (2008). Molecular evolution and star formation: from prestellar cores to protostellar cores. ApJ 674, 984–996. doi:10.1086/524096
Aikawa, Y., Wakelam, V., Hersant, F., Garrod, R. T., and Herbst, E. (2012). From prestellar to protostellar cores. II. Time dependence and deuterium fractionation. ApJ 760, 40. doi:10.1088/0004-637X/760/1/40
Allen, A., Li, Z.-Y., and Shu, F. H. (2003). Collapse of magnetized singular isothermal toroids. II. Rotation and magnetic braking. ApJ 599, 363–379. doi:10.1086/379243
Andre, P., Ward-Thompson, D., and Barsony, M. (2000). “From prestellar cores to protostars: the initial conditions of star formation,” in Protostars and planets IV. Editors V. Mannings, A. P. Boss, and S. S. Russell, 59. doi:10.48550/arXiv.astro-ph/9903284
Banerjee, R., and Pudritz, R. E. (2006). Outflows and jets from collapsing magnetized cloud cores. ApJ 641, 949–960. doi:10.1086/500496
Bate, M. R. (1998). Collapse of a molecular cloud core to stellar densities: the first three-dimensional calculations. ApJ 508, L95–L98. doi:10.1086/311719
Bate, M. R. (2010). Collapse of a molecular cloud core to stellar densities: the radiative impact of stellar core formation on the circumstellar disc. MNRAS 404, L79–L83. doi:10.1111/j.1745-3933.2010.00839.x
Bate, M. R. (2011). Collapse of a molecular cloud core to stellar densities: the formation and evolution of pre-stellar discs. MNRAS 417, 2036–2056. doi:10.1111/j.1365-2966.2011.19386.x
Bate, M. R. (2022). Dust coagulation during the early stages of star formation: molecular cloud collapse and first hydrostatic core evolution. MNRAS 514, 2145–2161. doi:10.1093/mnras/stac1391
Bate, M. R., and Lorén-Aguilar, P. (2017). On the dynamics of dust during protostellar collapse. MNRAS 465, 1089–1094. doi:10.1093/mnras/stw2853
Bate, M. R., Tricco, T. S., and Price, D. J. (2014). Collapse of a molecular cloud core to stellar densities: stellar-core and outflow formation in radiation magnetohydrodynamic simulations. MNRAS 437, 77–95. doi:10.1093/mnras/stt1865
Belloche, A., Schuller, F., Parise, B., André, P., Hatchell, J., Jørgensen, J. K., et al. (2011). The end of star formation in Chamaeleon I? A LABOCA census of starless and protostellar cores. A&A 527, A145. doi:10.1051/0004-6361/201015733
Bhandare, A., Kuiper, R., Henning, T., Fendt, C., Flock, M., and Marleau, G.-D. (2020). Birth of convective low-mass to high-mass second Larson cores. A&A 638, A86. doi:10.1051/0004-6361/201937029
Bhandare, A., Kuiper, R., Henning, T., Fendt, C., Marleau, G.-D., and Kölligan, A. (2018). First core properties: from low-to high-mass star formation. A&A 618, A95. doi:10.1051/0004-6361/201832635
Bodenheimer, P., Yorke, H. W., Rozyczka, M., and Tohline, J. E. (1990). The Formation phase of the solar nebula. ApJ 355, 651. doi:10.1086/168798
Boss, A. P. (1989). Protostellar Formation in rotating interstellar clouds. VIII. Inner core formation. ApJ 346, 336. doi:10.1086/168014
Boss, A. P., and Yorke, H. W. (1995). Spectral energy of first protostellar cores: detecting ’class -I’ protostars with ISO and SIRTF. ApJ 439, L55. –L58. doi:10.1086/187743
Busch, L. A., Belloche, A., Cabrit, S., Hennebelle, P., and Commerçon, B. (2020). The dynamically young outflow of the Class 0 protostar Cha-MMS1. A&A 633, A126. doi:10.1051/0004-6361/201936432
Caselli, P., Pineda, J. E., Sipilä, O., Zhao, B., Redaelli, E., Spezzano, S., et al. (2022). The Central 1000 au of a Prestellar Core Revealed with ALMA. II. Almost Complete Freeze-out. ApJ 929, 13. doi:10.3847/1538-4357/ac5913
Chen, X., Arce, H. G., Dunham, M. M., Zhang, Q., Bourke, T. L., Launhardt, R., et al. (2012). Submillimeter array and spitzer observations of bok globule CB 17: a candidate first hydrostatic core? ApJ 751, 89. doi:10.1088/0004-637X/751/2/89
Chen, X., Arce, H. G., Zhang, Q., Bourke, T. L., Launhardt, R., Schmalzl, M., et al. (2010). L1448 IRS2E: a candidate first hydrostatic core. ApJ 715, 1344–1351. doi:10.1088/0004-637X/715/2/1344
Commerçon, B., Audit, E., Chabrier, G., and Chièze, J. P. (2011). Physical and radiative properties of the first-core accretion shock. A&A 530, A13. doi:10.1051/0004-6361/201016213
Commerçon, B., Hennebelle, P., Audit, E., Chabrier, G., and Teyssier, R. (2010). Protostellar collapse: radiative and magnetic feedbacks on small-scale fragmentation. A&A 510, L3. doi:10.1051/0004-6361/200913597
Commerçon, B., Launhardt, R., Dullemond, C., and Henning, T. (2012a). Synthetic observations of first hydrostatic cores in collapsing low-mass dense cores. I. Spectral energy distributions and evolutionary sequence. A&A 545, A98. doi:10.1051/0004-6361/201118706
Commerçon, B., Levrier, F., Maury, A. J., Henning, T., and Launhardt, R. (2012b). Synthetic observations of first hydrostatic cores in collapsing low-mass dense cores. ii. simulated alma dust emission maps. A&A 548, A39. doi:10.1051/0004-6361/201220067
di Francesco, J., Evans, N. J., II, Caselli, P., Myers, P. C., Shirley, Y., Aikawa, Y., et al. (2007). Protostars and planets V, 17–32. China: University of Arizona Press.
Dunham, M. M., Allen, L. E., Evans, N. J., II, Broekhoven-Fiene, H., Cieza, L. A., Di Francesco, J., et al. (2015). Young stellar objects in the gould belt. ApJS 220, 11. doi:10.1088/0067-0049/220/1/11
Dunham, M. M., Chen, X., Arce, H. G., Bourke, T. L., Schnee, S., and Enoch, M. L. (2011). Detection of a bipolar molecular outflow driven by a candidate first hydrostatic core. ApJ 742, 1. doi:10.1088/0004-637X/742/1/1
Dutta, S., Lee, C.-F., Hirano, N., Liu, T., Johnstone, D., Liu, S.-Y., et al. (2022). ALMA survey of orion planck galactic cold clumps (ALMASOP): evidence for a molecular jet launched at an unprecedented early phase of protostellar evolution. ApJ 931, 130. doi:10.3847/1538-4357/ac67a1
Enoch, M. L., Young, K. E., Glenn, J., Evans, N. J., II, Golwala, S., Sargent, A. I., et al. (2006). Bolocam survey for 1.1 mm dust continuum emission in the c2d legacy clouds. I. Perseus. ApJ 638, 293–313. doi:10.1086/498678
Evans, I., Neal, J., Dunham, M. M., Jørgensen, J. K., Enoch, M. L., Merín, B., et al. (2009). The spitzer c2d legacy results: star-formation rates and efficiencies; evolution and lifetimes. ApJS 181, 321–350. doi:10.1088/0067-0049/181/2/321
Friesen, R. K., Di Francesco, J., Bourke, T. L., Caselli, P., Jørgensen, J. K., Pineda, J. E., et al. (2014). Revealing H2D+ depletion and compact structure in starless and protostellar cores with ALMA. ApJ 797, 27. doi:10.1088/0004-637X/797/1/27
Friesen, R. K., Pon, A., Bourke, T. L., Caselli, P., Di Francesco, J., Jørgensen, J. K., et al. (2018). ALMA detections of the youngest protostars in Ophiuchus. ApJ 869, 158. doi:10.3847/1538-4357/aaeff5
Fujishiro, K., Tokuda, K., Tachihara, K., Takashima, T., Fukui, Y., Zahorecz, S., et al. (2020). A low-velocity bipolar outflow from a deeply embedded object in taurus revealed by the atacama compact array. ApJ 899, L10. doi:10.3847/2041-8213/ab9ca8
Furuya, K., Aikawa, Y., Tomida, K., Matsumoto, T., Saigo, K., Tomisaka, K., et al. (2012). Chemistry in the first hydrostatic core stage by adopting three-dimensional radiation hydrodynamic simulations. ApJ 758, 86. doi:10.1088/0004-637X/758/2/86
Galli, D., and Shu, F. H. (1993). Collapse of magnetized molecular cloud cores. I. Semianalytical solution. ApJ 417, 220. doi:10.1086/173305
Gerin, M., Pety, J., Fuente, A., Cernicharo, J., Commerçon, B., and Marcelino, N. (2015). Nascent bipolar outflows associated with the first hydrostatic core candidates Barnard 1b-N and 1b-S. A&A 577, L2. doi:10.1051/0004-6361/201525777
Harsono, D., van Dishoeck, E. F., Bruderer, S., Li, Z. Y., and Jørgensen, J. K. (2015). Testing protostellar disk formation models with ALMA observations. A&A 577, A22. doi:10.1051/0004-6361/201424550
Hatchell, J., Fuller, G. A., Richer, J. S., Harries, T. J., and Ladd, E. F. (2007). Star formation in Perseus. II. SEDs, classification, and lifetimes. A&A 468, 1009–1024. doi:10.1051/0004-6361:20066466
Hennebelle, P., and Ciardi, A. (2009). Disk formation during collapse of magnetized protostellar cores. A&A 506, L29–L32. doi:10.1051/0004-6361/200913008
Hennebelle, P., and Fromang, S. (2008). Magnetic processes in a collapsing dense core. I. Accretion and ejection. A&A 477, 9–24. doi:10.1051/0004-6361:20078309
Hennebelle, P., and Teyssier, R. (2008). Magnetic processes in a collapsing dense core. II. Fragmentation. Is there a fragmentation crisis? A&A 477, 25–34. doi:10.1051/0004-6361:20078310
Hincelin, U., Commerçon, B., Wakelam, V., Hersant, F., Guilloteau, S., and Herbst, E. (2016). Chemical and physical characterization of collapsing low-mass prestellar dense cores. ApJ 822, 12. doi:10.3847/0004-637X/822/1/12
Hirano, N., and Liu, F.-c. (2014). Two extreme young objects in barnard 1-b. ApJ 789, 50. doi:10.1088/0004-637X/789/1/50
Jones, M. O., and Bate, M. R. (2018). Sink particle radiative feedback in smoothed particle hydrodynamics models of star formation. MNRAS 480, 2562–2577. doi:10.1093/mnras/sty1969
Karnath, N., Megeath, S. T., Tobin, J. J., Stutz, A., Li, Z. Y., Sheehan, P., et al. (2020). Detection of irregular, submillimeter opaque structures in the orion molecular clouds: protostars within 10,000 yr of formation? ApJ 890, 129. doi:10.3847/1538-4357/ab659e
Keto, E., Caselli, P., and Rawlings, J. (2015). The dynamics of collapsing cores and star formation. MNRAS 446, 3731–3740. doi:10.1093/mnras/stu2247
Keto, E., and Rybicki, G. (2010). Modeling molecular hyperfine line emission. ApJ 716, 1315–1322. doi:10.1088/0004-637X/716/2/1315
Koga, S., Kawasaki, Y., and Machida, M. N. (2022). Implementation of dust particles in three-dimensional magnetohydrodynamics simulation: dust dynamics in a collapsing cloud core. MNRAS 515, 6073–6092. doi:10.1093/mnras/stac2115
Könyves, V., André, P., Men’shchikov, A., Palmeirim, P., Arzoumanian, D., Schneider, N., et al. (2015). A census of dense cores in the Aquila cloud complex: SPIRE/PACS observations from the Herschel Gould Belt survey. A&A 584, A91. doi:10.1051/0004-6361/201525861
Krasnopolsky, R., Li, Z.-Y., and Shang, H. (2011). Disk Formation in magnetized clouds enabled by the Hall effect. ApJ 733, 54. doi:10.1088/0004-637X/733/1/54
Larson, R. B. (1969). Numerical calculations of the dynamics of a collapsing proto-star*. MNRAS 145, 271–295. doi:10.1093/mnras/145.3.271
Lebreuilly, U., Commerçon, B., and Laibe, G. (2019). Small dust grain dynamics on adaptive mesh refinement grids. I. Methods. A&A 626, A96. doi:10.1051/0004-6361/201834147
Lebreuilly, U., Commerçon, B., and Laibe, G. (2020). Protostellar collapse: the conditions to form dust-rich protoplanetary disks. A&A 641, A112. doi:10.1051/0004-6361/202038174
Lebreuilly, U., Vallucci-Goy, V., Guillet, V., Lombart, M., and Marchand, P. (2023). Protostellar collapse simulations in spherical geometry with dust coagulation and fragmentation. MNRAS 518, 3326–3343. doi:10.1093/mnras/stac3220
Lee, C.-F., Jhan, K.-S., and Moraghan, A. (2023a). First detection of a linear structure in the midplane of the young HH 211 protostellar disk: a spiral arm? ApJ 951, L2. doi:10.3847/2041-8213/acdbca
Lee, J.-E., Baek, G., Lee, S., Jeong, J.-H., Kim, C.-H., Aikawa, Y., et al. (2023b). Complex organic molecules in a very young hot corino, HOPS 373SW. ApJ 956, 43. doi:10.3847/1538-4357/ace34b
Lee, J.-E., Bergin, E. A., Evans, I., and Neal, J. (2004). Evolution of chemistry and molecular line profiles during protostellar collapse. ApJ 617, 360–383. doi:10.1086/425153
Levermore, C. D., and Pomraning, G. C. (1981). A flux-limited diffusion theory. ApJ 248, 321–334. doi:10.1086/159157
Lewis, B. T., and Bate, M. R. (2017). The dependence of protostar formation on the geometry and strength of the initial magnetic field. MNRAS 467, 3324–3337. doi:10.1093/mnras/stx271
Lewis, B. T., Bate, M. R., and Price, D. J. (2015). Smoothed particle magnetohydrodynamic simulations of protostellar outflows with misaligned magnetic field and rotation axes. MNRAS 451, 288–299. doi:10.1093/mnras/stv957
Lombardi, J. C., McInally, W. G., and Faber, J. A. (2015). An efficient radiative cooling approximation for use in hydrodynamic simulations. MNRAS 447, 25–35. doi:10.1093/mnras/stu2432
Machida, M. N., and Basu, S. (2019). The first two thousand years of star formation. ApJ 876, 149. doi:10.3847/1538-4357/ab18a7
Machida, M. N., and Hosokawa, T. (2020). Failed and delayed protostellar outflows with high-mass accretion rates. MNRAS 499, 4490–4514. doi:10.1093/mnras/staa3139
Machida, M. N., Inutsuka, S.-i., and Matsumoto, T. (2006a). Second core formation and high-speed jets: resistive magnetohydrodynamic nested grid simulations. ApJ 647, L151–L154. doi:10.1086/507179
Machida, M. N., Inutsuka, S.-i., and Matsumoto, T. (2008). High- and low-velocity magnetized outflows in the star formation process in a gravitationally collapsing cloud. ApJ 676, 1088–1108. doi:10.1086/528364
Machida, M. N., Inutsuka, S.-i., and Matsumoto, T. (2010). Formation process of the circumstellar disk: long-term simulations in the main accretion phase of star Formation. ApJ 724, 1006–1020. doi:10.1088/0004-637X/724/2/1006
Machida, M. N., and Matsumoto, T. (2011). The origin and formation of the circumstellar disc. MNRAS 413, 2767–2784. doi:10.1111/j.1365-2966.2011.18349.x
Machida, M. N., Matsumoto, T., Hanawa, T., and Tomisaka, K. (2005a). Collapse and fragmentation of rotating magnetized clouds - II. Binary formation and fragmentation of first cores. MNRAS 362, 382–402. doi:10.1111/j.1365-2966.2005.09327.x
Machida, M. N., Matsumoto, T., Hanawa, T., and Tomisaka, K. (2006b). Evolution of rotating molecular cloud core with oblique magnetic field. ApJ 645, 1227–1245. doi:10.1086/504423
Machida, M. N., Matsumoto, T., Tomisaka, K., and Hanawa, T. (2005b). Collapse and fragmentation of rotating magnetized clouds - I. Magnetic flux-spin relation. MNRAS 362, 369–381. doi:10.1111/j.1365-2966.2005.09297.x
Masson, J., Chabrier, G., Hennebelle, P., Vaytet, N., and Commerçon, B. (2016). Ambipolar diffusion in low-mass star formation. I. General comparison with the ideal magnetohydrodynamic case. A&A 587, A32. doi:10.1051/0004-6361/201526371
Masunaga, H., and Inutsuka, S.-i. (2000). A radiation hydrodynamic model for protostellar collapse. II. The second collapse and the birth of a protostar. ApJ 531, 350–365. doi:10.1086/308439
Masunaga, H., Miyama, S. M., and Inutsuka, S.-i. (1998). A radiation hydrodynamic model for protostellar collapse. I. The first collapse. ApJ 495, 346–369. doi:10.1086/305281
Matsumoto, T., and Tomisaka, K. (2004). Directions of outflows, disks, magnetic fields, and rotation of young stellar objects in collapsing molecular cloud cores. ApJ 616, 266–282. doi:10.1086/424897
Maureira, M. J., Arce, H. G., Dunham, M. M., Mardones, D., Guzmán, A. E., Pineda, J. E., et al. (2020). ALMA observations of envelopes around first hydrostatic core candidates. MNRAS 499, 4394–4417. doi:10.1093/mnras/staa2894
Maury, A., Hennebelle, P., and Girart, J. M. (2022). Recent progress with observations and models to characterize the magnetic fields from star-forming cores to protostellar disks. Front. Astronomy Space Sci. 9, 949223. doi:10.3389/fspas.2022.949223
Maury, A. J., André, P., Men’shchikov, A., Könyves, V., and Bontemps, S. (2011). The formation of active protoclusters in the Aquila rift: a millimeter continuum view. A&A 535, A77. doi:10.1051/0004-6361/201117132
Mellon, R. R., and Li, Z.-Y. (2008). Magnetic braking and protostellar disk formation: the ideal MHD limit. ApJ 681, 1356–1376. doi:10.1086/587542
Ohashi, N., Saigo, K., Aso, Y., Aikawa, Y., Koyamatsu, S., Machida, M. N., et al. (2014). Formation of a keplerian disk in the infalling envelope around L1527 IRS: transformation from infalling motions to kepler motions. ApJ 796, 131. doi:10.1088/0004-637X/796/2/131
Omukai, K. (2007). Observational characteristics of the first protostellar cores. PASJ 59, 589–606. doi:10.1093/pasj/59.3.589
Penston, M. V. (1969). Dynamics of self-gravitating gaseous spheres-III. Analytical results in the free-fall of isothermal cases. MNRAS 144, 425–448. doi:10.1093/mnras/144.4.425
Pineda, J. E., Arce, H. G., Schnee, S., Goodman, A. A., Bourke, T., Foster, J. B., et al. (2011). The enigmatic core l1451-mm: a first hydrostatic core? Or a hidden VeLLO? ApJ 743, 201. doi:10.1088/0004-637X/743/2/201
Price, D. J., Pringle, J. E., and King, A. R. (2003). A comparison of the acceleration mechanisms in young stellar objects and active galactic nuclei jets. MNRAS 339, 1223–1236. doi:10.1046/j.1365-8711.2003.06278.x
Price, D. J., Tricco, T. S., and Bate, M. R. (2012). Collimated jets from the first core. MNRAS 423, L45–L49. doi:10.1111/j.1745-3933.2012.01254.x
Priestley, F. D., Viti, S., and Williams, D. A. (2018). An efficient method for determining the chemical evolution of gravitationally collapsing prestellar cores. AJ 156, 51. doi:10.3847/1538-3881/aac957
Priestley, F. D., Whitworth, A. P., and Fogerty, E. (2023). Differences in chemical evolution between isolated and embedded prestellar cores. MNRAS 518, 4839–4844. doi:10.1093/mnras/stac3444
Priestley, F. D., Wurster, J., and Viti, S. (2019). Ambipolar diffusion and the molecular abundances in pre-stellar cores. MNRAS 488, 2357–2364. doi:10.1093/mnras/stz1869
Priestley, F. D., Wurster, J., and Viti, S. (2021). Erratum: ambipolar diffusion and the molecular abundances in pre-stellar cores. MNRAS 503, 2899–2901. doi:10.1093/mnras/stab702
Rawlings, J. M. C., and Yates, J. A. (2001). Modelling line profiles in infalling cores. MNRAS 326, 1423–1430. doi:10.1111/j.1365-2966.2001.04674.x
Saigo, K., and Tomisaka, K. (2006). Evolution of first cores in rotating molecular cores. ApJ 645, 381–394. doi:10.1086/504028
Saigo, K., and Tomisaka, K. (2011). Spectrum energy distribution and submillimeter image of a rotating first core. ApJ 728, 78. doi:10.1088/0004-637X/728/2/78
Saigo, K., Tomisaka, K., and Matsumoto, T. (2008). Evolution of first cores and formation of stellar cores in rotating molecular cloud cores. ApJ 674, 997–1014. doi:10.1086/523888
Schnee, S., Enoch, M., Johnstone, D., Culverhouse, T., Leitch, E., Marrone, D. P., et al. (2010). An observed lack of substructure in starless cores. ApJ 718, 306–313. doi:10.1088/0004-637X/718/1/306
Schönke, J., and Tscharnuter, W. M. (2011). Protostellar collapse of rotating cloud cores. Covering the complete first accretion period of the stellar core. A&A 526, A139. doi:10.1051/0004-6361/201015734
Sharma, R., Jørgensen, J. K., Gavino, S., Ohashi, N., Tobin, J. J., Lin, Z.-Y. D., et al. (2023). Early planet formation in embedded disks (eDisk). IX. High-Resolution ALMA observations of the class 0 protostar R CrA IRS5N and its surroundings. ApJ 954, 69. doi:10.3847/1538-4357/ace35c
Shu, F. H. (1977). Self-similar collapse of isothermal spheres and star formation. ApJ 214, 488–497. doi:10.1086/155274
Spear, S., Maureira, M. J., Arce, H. G., Pineda, J. E., Dunham, M., Caselli, P., et al. (2021). VLA and NOEMA views of bok globule CB 17: the starless nature of a proposed first hydrostatic core candidate. ApJ 923, 231. doi:10.3847/1538-4357/ac3083
Stamatellos, D., Whitworth, A. P., Bisbas, T., and Goodwin, S. (2007). Radiative transfer and the energy equation in SPH simulations of star formation. A&A 475, 37–49. doi:10.1051/0004-6361:20077373
Stamer, T., and Inutsuka, S.-i. (2018). Radiation-hydrodynamic simulations of spherical protostellar collapse for very low-mass objects. ApJ 869, 179. doi:10.3847/1538-4357/aaee81
Stutz, A. M., Tobin, J. J., Stanke, T., Megeath, S. T., Fischer, W. J., Robitaille, T., et al. (2013). A Herschel and APEX census of the reddest sources in orion: searching for the youngest protostars. ApJ 767, 36. doi:10.1088/0004-637X/767/1/36
Tan, J. C., Beltrán, M. T., Caselli, P., Fontani, F., Fuente, A., Krumholz, M. R., et al. (2014). “Massive star formation,” in Protostars and planets VI. Editors H. Beuther, R. S. Klessen, and C. P. Dullemond 149–172. doi:10.2458/azu_uapress_9780816531240-ch007
Tassis, K., Willacy, K., Yorke, H. W., and Turner, N. J. (2012). Non-equilibrium chemistry of dynamically evolving prestellar cores. I. Basic magnetic and non-magnetic models and parameter studies. ApJ 753, 29. doi:10.1088/0004-637X/753/1/29
Tomida, K., Machida, M. N., Saigo, K., Tomisaka, K., and Matsumoto, T. (2010a). Exposed long-lifetime first core: a new model of first cores based on radiation hydrodynamics. Astrophysical J. 725, L239–L244. doi:10.1088/2041-8205/725/2/L239
Tomida, K., Okuzumi, S., and Machida, M. N. (2015). Radiation magnetohydrodynamic simulations of protostellar collapse: nonideal magnetohydrodynamic effects and early formation of circumstellar disks. ApJ 801, 117. doi:10.1088/0004-637X/801/2/117
Tomida, K., Tomisaka, K., Matsumoto, T., Hori, Y., Okuzumi, S., Machida, M. N., et al. (2013). Radiation magnetohydrodynamic simulations of protostellar collapse: protostellar core formation. ApJ 763, 6. doi:10.1088/0004-637X/763/1/6
Tomida, K., Tomisaka, K., Matsumoto, T., Ohsuga, K., Machida, M. N., and Saigo, K. (2010b). Radiation magnetohydrodynamics simulation of proto-stellar collapse: two-component molecular outflow. ApJ 714, L58–L63. –L63. doi:10.1088/2041-8205/714/1/L58
Tomisaka, K. (1998). Collapse-driven outflow in star-forming molecular cores. ApJ 502, L163–L167. doi:10.1086/311504
Tomisaka, K. (2002). Collapse of rotating magnetized molecular cloud cores and mass outflows. ApJ 575, 306–326. doi:10.1086/341133
Tomisaka, K., and Tomida, K. (2011). Observational identification of first cores: non-LTE radiative transfer simulation. PASJ 63, 1151–1164. doi:10.1093/pasj/63.5.1151
Tritsis, A., Federrath, C., Willacy, K., and Tassis, K. (2022). Non-ideal magnetohydrodynamic simulations of subcritical pre-stellar cores with non-equilibrium chemistry. MNRAS 510, 4420–4435. doi:10.1093/mnras/stab3740
Tscharnuter, W. M., and Gail, H. P. (2007). 2-D preplanetary accretion disks. I. Hydrodynamics, chemistry, and mixing processes. A&A 463, 369–392. doi:10.1051/0004-6361:20065794
Tsukamoto, Y., Iwasaki, K., Okuzumi, S., Machida, M. N., and Inutsuka, S. (2015). Effects of Ohmic and ambipolar diffusion on formation and evolution of first cores, protostars, and circumstellar discs. MNRAS 452, 278–288. doi:10.1093/mnras/stv1290
van Weeren, R. J., Brinch, C., and Hogerheijde, M. R. (2009). Modeling the chemical evolution of a collapsing prestellar core in two spatial dimensions. A&A 497, 773–787. doi:10.1051/0004-6361/200811471
Vaytet, N., Audit, E., Chabrier, G., Commerçon, B., and Masson, J. (2012). Simulations of protostellar collapse using multigroup radiation hydrodynamics. I. The first collapse. A&A 543, A60. doi:10.1051/0004-6361/201219427
Vaytet, N., Chabrier, G., Audit, E., Commerçon, B., Masson, J., Ferguson, J., et al. (2013). Simulations of protostellar collapse using multigroup radiation hydrodynamics. II. The second collapse. A&A 557, A90. doi:10.1051/0004-6361/201321423
Vaytet, N., and Haugbølle, T. (2017). A grid of one-dimensional low-mass star formation collapse models. A&A 598, A116. doi:10.1051/0004-6361/201628194
Wakelam, V., Coutens, A., Gratier, P., Vidal, T. H. G., and Vaytet, N. (2022). Confirmation of the outflow in L1451-mm: SiO line and CH3OH maser detections. A&A 666, A191. doi:10.1051/0004-6361/202243459
Whitehouse, S. C., and Bate, M. R. (2006). The thermodynamics of collapsing molecular cloud cores using smoothed particle hydrodynamics with radiative transfer. MNRAS 367, 32–38. doi:10.1111/j.1365-2966.2005.09950.x
Whitworth, A. P., Bhattal, A. S., Francis, N., and Watkins, S. J. (1996). Star formation and the singular isothermal sphere. MNRAS 283, 1061–1070. doi:10.1093/mnras/283.3.1061
Wurster, J., Bate, M. R., and Bonnell, I. A. (2021). The impact of non-ideal magnetohydrodynamic processes on discs, outflows, counter-rotation, and magnetic walls during the early stages of star formation. MNRAS 507, 2354–2372. doi:10.1093/mnras/stab2296
Wurster, J., Bate, M. R., and Price, D. J. (2018). Hall effect-driven formation of gravitationally unstable discs in magnetized molecular cloud cores. MNRAS 480, 4434–4442. doi:10.1093/mnras/sty2212
Yamada, M., Machida, M. N., Inutsuka, S.-i., and Tomisaka, K. (2009). Emission from a young protostellar object. I. Signatures of young embedded outflows. ApJ 703, 1141–1158. doi:10.1088/0004-637X/703/1/1141
Yin, C., Priestley, F. D., and Wurster, J. (2021). Investigating the role of magnetic fields in star formation using molecular line profiles. MNRAS 504, 2381–2389. doi:10.1093/mnras/stab1039
Yorke, H. W., Bodenheimer, P., and Laughlin, G. (1993). The formation of protostellar disks. I - 1 M(solar). ApJ 411, 274. doi:10.1086/172827
Young, A. K. (2019). Observational characteristics of early star formation Phd thesis. Exeter, U.K: University of Exeter. http://hdl.handle.net/10871/39420.
Young, A. K., Bate, M. R., Harries, T. J., and Acreman, D. M. (2019). Synthetic molecular line observations of the first hydrostatic core from chemical calculations. MNRAS 487, 2853–2873. doi:10.1093/mnras/stz1485
Keywords: star formation, hydrodynamics, radiative transfer, magnetohydrodynamics
Citation: Young AK (2023) Insights into the first and second hydrostatic core stages from numerical simulations. Front. Astron. Space Sci. 10:1288730. doi: 10.3389/fspas.2023.1288730
Received: 04 September 2023; Accepted: 17 November 2023;
Published: 07 December 2023.
Edited by:
James Wurster, University of St Andrews, United KingdomReviewed by:
Vladimir Airapetian, National Aeronautics and Space Administration, United StatesDipen Sahu, Physical Research Laboratory, India
Copyright © 2023 Young. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Alison K. Young, YWxpc29uLnlvdW5nQGVkLmFjLnVr
 Alison K. Young
Alison K. Young