- 1Center for Space Physics, Boston University, Boston, MA, United States
- 2Johns Hopkins University Applied Physics Lab, Laurel, MD, United States
- 3German Aerospace Center (DLR), Institute for Solar-Terrestrial Physics, Neustrelitz, Germany
- 4Computer Science Department, University of Alabama in Huntsville, Huntsville, AL, United States
- 5Heliophysics Science Division, NASA/GSFC, Greenbelt, MD, United States
Introduction: For the last several decades, continuous monitoring of the solar wind has been carried out by spacecraft at the first Earth-Sun Lagrange point (L1). Due to computational expense or model limitations, those data often must be propagated to some point closer to the Earth in order to be usable by those studying the interaction between Earth’s magnetosphere and the solar wind. The current most widely used tool to propagate measurements from L1 (roughly 235 RE upstream) to Earth is the planar propagation method, which includes a number of known limitations. Motivated by these limitations, this study introduces a new algorithm called the Probabilistic Regressor for Input to the Magnetosphere Estimation (PRIME).
Methods: PRIME is based on a novel probabilistic recurrent neural network architecture, and is capable of incorporating solar wind time history from L1 monitors to generate predictions of near-Earth solar wind as well as estimate uncertainties for those predictions.
Results: A statistical validation shows PRIME’s predictions better match MMS magnetic field and plasma measurements just upstream of the bow shock than measurements from Wind propagated to MMS with a minimum variance analysis-based planar propagation technique. PRIME’s continuous rank probability score (CRPS) is 0.214σ on average across all parameters, compared to the minimum variance algorithm’s CRPS of 0.350σ. PRIME’s performance improvement over minimum variance is dramatic in plasma parameters, with an improvement in CRPS from 2.155 cm−3 to 0.850 cm−3 in number density and 16.15 km/s to 9.226 km/s in flow velocity VX GSE.
Discussion: Case studies of particularly difficult to predict or extreme conditions are presented to illustrate the benefits and limitations of PRIME. PRIME’s uncertainties are shown to provide reasonably reliable predictions of the probability of particular solar wind conditions occurring.
Conclusion: PRIME offers a simple solution to common limitations of solar wind propagation algorithms by generating accurate predictions of the solar wind at Earth with physically meaningful uncertainties attached.
1 Introduction
Earth’s geospace system is a dynamic ecosystem in which the majority of the energy input is extracted from the flowing solar wind (Dungey, 1961; Axford, 1964). In order to connect physical processes in the magnetosphere to their energy sources in the solar wind it is necessary to obtain a continuous historical record of what solar wind has impacted the Earth’s magnetosphere. Since orbital dynamics preclude placing a continuous monitor just upstream of the bow shock, the solar wind is primarily monitored by spacecraft at the L1 position roughly 235RE (1,500,000 km) ahead of the Earth. These measurements then need to be propagated to the Earth to account for the travel time of the solar wind plasma and interplanetary magnetic field (IMF), generally on the order 30–60 min.
The problem of how to propagate these measurements has many possible solutions. Calculating the delay time from dividing the distance from the solar wind monitor to the earth by the solar wind velocity, also known as ballistic propagation, has been shown to be insufficient. Studies correlating measurements between ISEE 3 at L1 and ISEE 1 and IMP 8 at the Earth showed that ballistic propagation between the spacecraft results in good correlations (Pearson’s r > 0.8) only 25% of the time and can produce delay time errors of an hour or more 30% of the time (Crooker et al., 1982; Richardson et al., 1998). A more accurate method is to assume that the solar wind advances in a series of large “phase fronts”, or planes in which the plasma and IMF conditions are constant (Collier et al., 1998), the orientation of which can be determined with minimum variance analysis (MVA) (Weimer, 2003; Bargatze, 2005; King, 2005; Weimer and King, 2008). This propagation technique is often called MVA planar propagation, distinct from ballistic planar propagation that assumes that phase fronts are normal to the Earth-Sun line. For some cases, MVA planar propagation produces more accurate delay times than ballistic propagation (Mailyan et al. 2008; Case and Wild 2012). However, the method still has some shortcomings. If an L1 monitor measures one apparent phase front, then measures a faster or more strongly inclined phase front some time later, it is possible that the MVA planar propagation algorithm would predict the later plane would arrive at the Earth first, essentially passing through the first plane unmodified. This is unphysical, as such a situation in the supersonic flow of the solar wind would result in a shock (Gosling et al., 1993). Complicating the central assumption of any flavor of planar propagation is evidence that the solar wind is made up of bundles of flux tubes on the order of 50–70RE in diameter (Borovsky, 2008; Neugebauer and Giacalone, 2015). Since the orbit of L1 monitors can often be 100RE or more away from the streamline from the Sun to the Earth, it could be often the case that a given L1 monitor is measuring a different flux tube (and therefore different plasma) than the one that will impact the Earth (Borovsky, 2018), violating planar propagation’s assumption that the solar wind is an infinite plane. Indeed, spacecraft in the solar wind often observe very different magnetic fields and plasma, whether they are located near to the Earth or at the L1 point (Chang and Nishida 1973; Paularena et al. (1997); Paularena et al. (1998); Zastenker et al., 2000; Walsh et al., 2019). It is also well observed that correlations between MVA planar propagation shifted data decrease as transverse distance between the monitors increases (Crooker et al., 1982; Milan et al., 2022), with sharp decreases in accuracy around the scale size of a typical solar wind flux tube.
One solution to these issues is the use of a physical model to propagate solar wind conditions from one monitor to the other. Hydrodynamic (Kömle et al., 1986) and magnetohydrodynamic (Cameron and Jackel, 2019) solvers have been used to conduct physics-based simulations of solar wind flow over large distances. This approach has been shown to far more accurately propagate shocks and other discontinuities than planar propagation does. However, it does have the disadvantage of being computationally expensive and difficult to implement which motivates the continued use of simpler MVA planar propagation approaches. Additionally, since these methods are typically implemented in 1 or 1.5 dimensions transverse separation of the points being propagated between can still affect the accuracy of the propagation. Another solution is to use a flexible machine learning algorithm rather than the MVA technique’s physical assumptions to calculate time delays for data from L1 monitors (Baumann and McCloskey, 2021). This method has been shown to be computationally lightweight and more accurate than the MVA planar propagation algorithm.
Uncertainty estimation is another crucial aspect of solar wind prediction and propagation that current algorithms do not address. It is recognized that there are uncertainties attached to propagated solar wind measurements that are often used as inputs to simulations or physical models that are greater than instrument errors, and that those uncertainties limit physical understanding that can be derived from solar wind inputs (Borovsky, 2021). There is evidence that correlation studies of the cross polar cap potential (Sivadas et al., 2022), development of solar wind-magnetosphere coupling functions (Lockwood et al., 2019), and global MHD simulation outputs (Al Shidi et al., 2023) are affected by these uncertainties, but the development of some method to systematically estimate physically motivated uncertainties for solar wind inputs has not been developed. A standard technique for terrestrial weather prediction is ensemble modeling, where a single model generates many predictions of a single event by taking many samples from predicted probability distributions of its input parameters (Slingo and Palmer, 2011). In order to do the same for space weather models, modelers must find some estimate of their input uncertainties on their own (Morley et al., 2018).
The aim of this study is to develop a new algorithm to determine the solar wind plasma and IMF conditions at the Earth from upstream measurements by L1 monitors, as well as to assign physically meaningful uncertainties to those conditions. This algorithm, called Probabilistic Regressor for Input to the Magnetosphere Estimation (PRIME), requires solar wind plasma and IMF data from a spacecraft close to the Earth for training and solar wind plasma and IMF data at the L1 point for prediction (Section 2) and a sufficiently representative probabilistic propagation algorithm (Section 3) in order to be developed. Predictions from the algorithm must be compared to an MVA planar propagation algorithm (Section 4), after which the results can be discussed in the context of the problems mentioned in the preceding paragraphs (Section 5).
2 Data
2.1 MMS target dataset
Plasma and magnetic field data from the Magnetospheric Multi Scale 1 (MMS-1) spacecraft’s (Burch et al., 2016) Fast Plasma Investigation (FPI) (Pollock et al., 2016) and Fluxgate Magnetometer (FGM) (Russell et al., 2016) instruments are utilized as targets for the algorithm to be optimized against. MMS is a constellation of four spacecraft designed to study magnetic reconnection at Earth’s magnetopause and neutral sheet, but has had numerous campaigns in its extended mission that have brought it outside of the magnetosheath into the solar wind in order to study physics such as solar wind turbulence and collisionless shocks. This means that its apogee has been raised twice, first from 12RE to 25RE in 2017 and then to 29RE in 2019, allowing it to regularly measure the solar wind1. Additionally, since a large volume of data is brought down from MMS, a number of automated tools have been developed to partition and cluster MMS data. These factors combine to make MMS data a good choice for assembling large target databases of solar wind data despite the fact that MMS is not specifically designed to measure the solar wind.
To assemble a solar wind dataset using MMS, an automatic tool developed by Olshevsky et al. (2021) is used to classify all MMS-1 FPI 3D ion distributions from 2 September 2015 to 1 January 2023. The classifier is capable of discriminating between magnetospheric, magnetosheath, (non-foreshock) solar wind, and ion foreshock plasma through the shape of the ion distribution function, and outputs a normalized probability that a given distribution belongs to each class. Periods of time where MMS-1 is in the solar wind with probability p > 0.7 are found using the classifier, all other time periods are removed (thereby removing the magnetosphere, magnetosheath, and foreshock from the dataset), then remaining FGM magnetic field and FPI ion and electron moments are averaged in 100 s bins. The foreshock is removed from the dataset since including it could complicate the use of PRIME’s outputs as inputs to models of magnetospheric response to solar wind driving (for instance, a simulation looking to produce foreshock structures given some solar wind conditions should not have foreshock structures included in its inputs). Since the classifier is trained only on data from the dayside orbits, any data on the nightside (GSE X < 0) are removed. The full spatial distribution of the solar wind data as well as similarly binned magnetosheath data are shown in Figure 1.
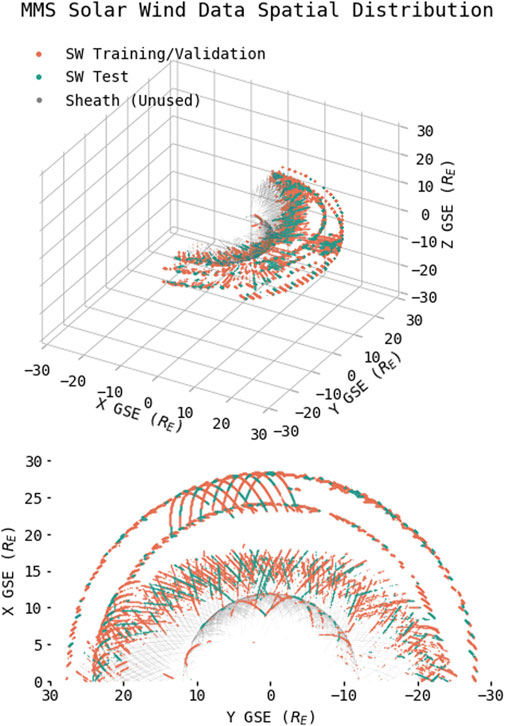
FIGURE 1. 3D spatial distribution of the 78,109 solar wind MMS-1 data points split into 80% training/validation (orange) and 20% test (green) subsets. Magnetosheath data (grey) also shown to highlight the ability of the classification algorithm to discern the two regions. The ion foreshock and magnetosphere data have been omitted for clarity. Data consists of
As previously mentioned, MMS is not specifically designed to measure the solar wind. This introduces some features to its FPI data that must be taken into account. Since solar wind ions are typically concentrated in a narrow beam, they tend to be measured in only a few pixels on the detector, saturating them. This saturation primarily affects calculation of the zeroth and second moments of the plasma distribution function (density and temperature). The first moment (velocity) has been shown to not be as affected by saturation through comparison to moments from the Wind spacecraft, but constant offsets arising from the coarseness of the FPI energy-azimuth table have been observed (Roberts et al., 2021). The ion density and temperature are therefore excluded from the target dataset. The FPI electron density has been shown to be more accurate than the ion density (Roberts et al., 2021), and may be used as a proxy for ion density by assuming quasineutrality. For timescales such as the ones considered here (100 s) quasineutrality is a fair assumption, and any overcounting due to heavy solar wind ions is smaller than other uncertainties affecting the density. As for the bulk velocities, the offsets are removed according to which energy-azimuth table was used to obtain each measurement. This leaves seven parameters as part of the target dataset: IMF
2.2 Wind input dataset
The input solar wind data at L1 comes from the Magnetic Field Investigation (MFI) (Lepping et al., 1995) and Solar Wind Experiment (SWE) (Ogilvie et al., 1995) aboard the Wind spacecraft. Wind was launched in 1994 and inserted into orbit around the L1 point in 2004, and is one of three currently operating in-situ solar wind monitors at L1. Wind was selected for this study because it had the best coverage over the time period of the MMS-1 dataset. Specifically the Wind key parameter (KP) moments data are utilized, resulting in time series of plasma flow velocity
3 Algorithm methodology
The overall class of algorithm selected for PRIME is a neural network. Neural networks are an extensible set of algorithms under the large umbrella of machine learning capable of approximating complex data representation with arbitrary accuracy (Leshno et al., 1993; Nielsen, 2015), which makes them suitable for the task of solar wind propagation where the underlying data representation is still not fully determined. Furthermore, the task of solar wind propagation is a regression task, for which neural networks are well suited. Neural networks have also been used in prior studies to make probabilistic estimates and predictions of geospace quantities with good results (Camporeale et al. (2019); Huang et al. (2022); Hu et al. (2022), e.g.).
One potential pitfall of neural networks is also their representational power: special care must be taken to ensure that they do not “overfit” and simply store the data used to optimize them as information in their tuning parameters. This study seeks to be transparent about the efforts taken with data preparation and network optimization to ensure this does not occur (Lugaz et al., 2021). For more information on the concepts in this section, see Pankaj Mehta’s excellent review of machine learning for physicists (Mehta et al., 2019).
3.1 Network architecture
Two main considerations guided the selection of PRIME’s network architecture: the fact that information about the time history of solar wind at L1 is important to predicting it at the Earth, and that it is desirable to quantify the uncertainty of the algorithm’s output in a physically meaningful way (Camporeale, 2019). The first consideration is addressed through a sequence of Gated Recurrent Units (GRU) that step through the input timeseries of Wind data to identify important features. GRUs (See Cho et al. (2014)) are a simple class of recurrent neural network (RNN) that show good performance relative to other recurrent network architectures (Chung et al., 2014). The vector size of the measurements at each timestep is 14: three units for ion flow velocity, one unit for ion number density, one unit for ion temperature, three units for magnetic field, three units for the Wind spacecraft positon, and three units for the MMS spacecraft postion. The amount of timesteps used to make a single prediction is a tunable parameter, the optimal value of which is determined in Section 3.2. The output of the GRU sequence is then fed into three layers of fully-connected neurons (Bebis and Georgiopoulos, 1994) in order to reduce the dimensionality of the features identified by the GRU sequence. In order to address the second consideration (uncertainty quantification), the last layer of neurons are taken to be the mean and variance of a Gaussian probability distribution for each parameter rather than single scalar values (Nix and Weigend, 1994; Lakshminarayanan et al., 2017). The outputs are enforced to be the mean and variance of a Gaussian probability distribution by the selection of a suitable loss function. In order to mitigate overfitting, layer normalization (Ba et al., 2016) and train-time dropout (Srivastava et al., 2014) are added at locations in the network that can be varied during hyperparameter optimization. The size of each layer, the locations of layer normalization and dropout, and the optimization routine and its learning rate are all determined via hyperparameter tuning (see Section 3.2). The general architecture of PRIME is shown in Figure 2. The algorithm is implemented in the Keras high-level API for tensorflow (https://keras.io/api/).
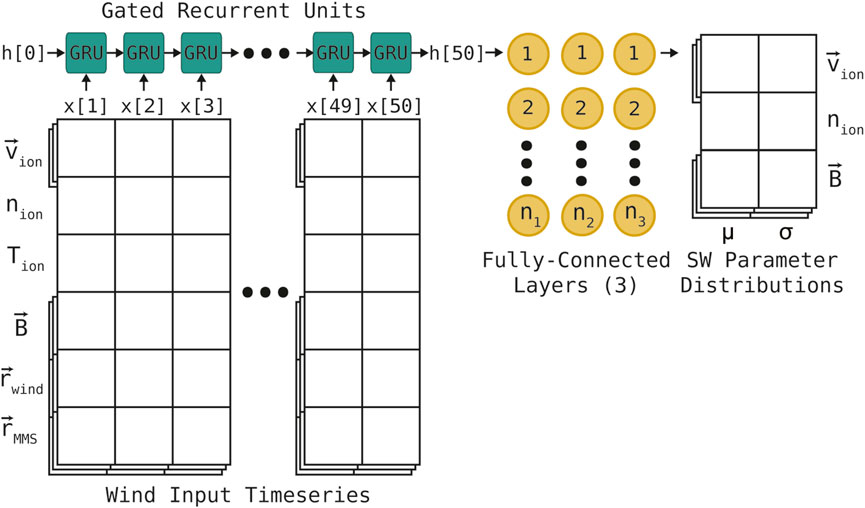
FIGURE 2. Schematic of PRIME’s neural network architecture. Note that the Gated Recurrent Unit (GRU) sequence feeds into a Fully Connected Neural Network (FCNN) in order to output a mean and variance for each desired parameter instead of a single value. Vector quantities such as magnetic field, flow velocity, and spacecraft position are stacked to show that they consitute three units in the input/output but describe one physical vector quantity. Exact layer size and additional regularization features (see Table 1) chosen via hyperparameter search.
The loss criterion used to optimize the algorithm during training is chosen to be the continuous rank probability score (CRPS) (Matheson and Winkler, 1976; Hersbach, 2000). While not yet a common tool in space weather applications, the CRPS is a common scoring metric used to compare probabilistic forecasts for weather prediction (Zamo and Naveau, 2018). The continuous rank probability score is given by
where F(y) is the cumulative distribution function of a probabilistic prediction for some true measurement yobs and H(y) is the Heaviside step function (Wilks, 2011). The continuous rank probability score is desirable as a loss function for several reasons. Firstly, it more symmetrically punishes over and under confident predictions than the negative log probability density (the most commonly used score for probabilistic predictions) (Camporeale and Carè, 2021). Secondly, for deterministic predictions the cumulative distribution function of the prediction ypred is given by F(y) = H(y − ypred) which yields
That is to say, the CRPS reduces to the mean absolute error (MAE) for deterministic predictions (Hersbach, 2000). For this reason, the CRPS can be used to fairly compare deterministic and probabilistic forecasts (Gneiting and Raftery, 2007). Lastly, the CRPS has the same unit as the variable of interest, making it more intuitively human-readable. For Gaussian predictions with mean μ and variance σ2 the CRPS is given by
(Gneiting et al. 2005) This is the functional form for CRPS used as a loss function during training, as it is negatively oriented. The 14 output units in PRIME’s last layer are taken to be the μ and σ defining a Gaussian probability distribution for each parameter. The CRPS over all seven parameters in the target dataset is averaged with equal weight assigned to all parameters. The derivatives of the CRPS with respect to μ and σ for Gaussian predictions are given by
One limitation of the CRPS for training probabilistic forecast algorithms is the fact that it does not explicitly enforce reliability of the algorithm’s output uncertainties (Camporeale et al., 2019). Reliability is a property of non-deterministic forecasts that measures how well its predictions are statistically consistent with observations (Anderson, 1996); an algorithm’s degree of reliability may also be referred to as how well calibrated it is. It has been shown that for probabilistic predictions with fixed mean values (i.e., constant error yobs − μ), uncertainties σ that maximize the reliability of the prediction do not minimize the CRPS (Camporeale and Carè, 2021). That is to say, accuracy and reliability are competing metrics that must be balanced. While the fact that both μ and σ vary simultaneously slightly complicates the picture outlined by Camporeale and Carè (2021), it is nonetheless still the case that simply minimizing the CRPS does not necessarily mean that the resulting model is well-calibrated. Since reliability is not explicitly enforced, the reliability of PRIME’s uncertainties must be verified after training (See Section 4.4) (Tasistro-Hart et al., 2021).
3.2 Algorithm optimization
Optimizing the algorithm proceeds in three phases. First, the optimal length, lead time, and composition of the input timeseries dataset is determined. Then, the algorithm hyperparameters are varied in order to find the optimal algorithm. Finally, an algorithm with the optimal input shape and hyperparameters is instantiated and fully trained, becoming the canonical version of PRIME.
PRIME’s architecture can technically accept any length of timeseries from any time period in the input dataset as input for any given target. It is therefore necessary to determine the optimal length of input time period (window), lead time ahead of the target PRIME is attempting to predict (stride), and the maximum data gap size that can be interpolated over. It is worth noting that unlike some other propagation approaches, once the optimal stride (lead time) is selected it cannot vary, thus PRIME’s lead time for operational contexts is fixed. To do so, a test version of PRIME (see Table 1) is instantiated and trained on datasets produced with various values of these three parameters. Whichever set produces a model that can achieve the best results on the validation dataset before overfitting is taken as optimal. For each of these datasets and the eventual optimal dataset, the input/target datasets are split into 60% training, 20% validation, and 20% test subsets. Since temporally adjacent entries in the input dataset are overlapping, randomly assigning points to each subset would result in significant data leakage. To mitigate this, the full dataset is split into independent blocks twice the length of the timeseries window used as input (i.e., for a window size of 50 measurements/∼1 h 20 min, the dataset is split into chunks of length 100 measurements/∼2 h 40 min) and those blocks are then assigned to each subset in order to achieve a 60%-20%-20% train-validation-test split. To ensure that no parameter dominates others due to their absolute relative values, each subset is rescaled to the interquartile range of the training set in order to account for outliers without leaking information about the validation/test sets during training. Results on the validation dataset from the search are shown in Figure 3. The optimal window size is 50 measurements (∼ 5,000 s, ∼1 h 20 min), the optimal stride/lead time is 18 measurements (∼1,800 s, ∼30 min). That is to say, for an MMS measurement at time t, the input timeseries from Wind runs from time t − 5, 000s − 1, 800s ≈ t − 83min to time t − 1, 800s = t − 30min. The largest data gap that can be interpolated over is 12.5 min (
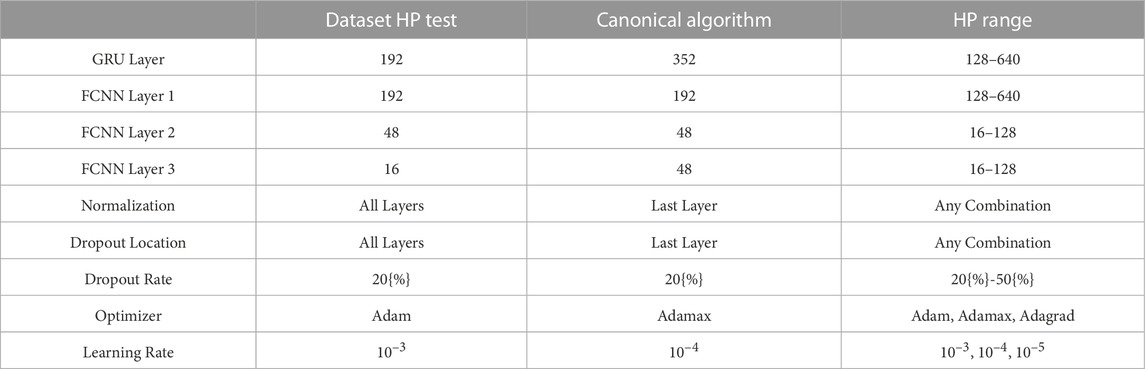
TABLE 1. Detailed layer sizes and architecture parameters for the version of PRIME used to optimize the dataset parameters (left column), the canonical version of PRIME determined by hyperparameter search (middle column), and the range of each parameter the hyperparameter search was conducted over (right column).

FIGURE 3. Results from dataset optimization trials over timeseries window (length), stride (lead time), and permitted fraction of interpolated data. Units for window and stride are Wind key parameter (KP) data cadence of roughly 100 s. The optimal set (window 50, stride 18, largest interp. Fraction
After finding the optimal way to construct the dataset, the optimal algorithm hyperparameters can be determined. There are nine hyperparameters that are searched over as part of the optimization routine. The first four are the node sizes of the GRU layer and the following three fully-connected layers, varied from 128 to 640 for the first two layers and from 16 to 128 for the last two layers. The fifth is where, if at all, in the sequence to perform a layer normalization step. Layer normalization is a process designed to stabilize neural networks during optimization to reduce the time it takes to optimize them (Ba et al., 2016). Layer normalization normalizes the hidden vector output by one layer before it is passed to the next, thereby reducing the extent to which the gradients with respect to the weights in one layer covary with the outputs of the previous layer and allowing the gradient descent optimization algorithm used to optimize the algorithm to more quickly converge on an optimal solution. The sixth and seventh hyperparameters are the dropout locations and rate used during training. Dropout is a technique to mitigate overfitting when training neural networks that involves randomly removing some percentage of the units from the network every training epoch, thereby disallowing the units to co-adapt and overfit (Srivastava et al., 2014). The range of dropout rates searched over during the hyperparameter search from 20% to 50%. The eighth and ninth hyperparameters are the optimization algorithm used to update the weights and biases in the network and that algorithm’s learning rate. The algorithms included in the search are Adam, Adamax, and Adagrad, which are all adaptive gradient descent algorithms. These algorithms are adaptive in the sense that they change the step size they use to update parameter weights during optimization to avoid getting stuck in local minima or skipping over minima. Adam updates parameters according to estimates of first order and second moments and has been shown to be suitable for optimizing large algorithms (Kingma and Ba, 2017), Adamax updates parameters according to first order moments and the infinity norm and has been shown to be suitable for recurrent networks (Kingma and Ba, 2017), and Adagrad updates its gradient descent step size per parameter based on the number of updates the parameter receives during training making it suitable for sparse gradients (Duchi et al., 2011). To save computational resources, the hyperparameter search is conducted using the efficient Hyperband tournament bracket style algorithm (Li et al., 2018) implemented in the KerasTuner API (O’Malley et al., 2019). The optimal hyperparameters as well as the bounds of the hyperparameter search are presented in Table 1. Those parameters define the canonical PRIME algorithm, the weights and biases of which are then optimized so that predictions can be made for the test dataset in order to evaluate PRIME’s predictive performance. The canonical version of PRIME is trained for 50 epochs (maximum before overfitting) and has a CRPS on the validation dataset of 0.175 (dimensionless units of parameter interquartile range to ensure comparability between all parameters).
4 Results
4.1 Model performance
PRIME’s performance is evaluated on the test dataset (not seen by the algorithm at any point during training) by calculating the CRPS between its predictions and the test dataset. It is also desirable to compare PRIME with the current state of the art algorithm used to propagate solar wind conditions from L1 to the Earth. The OMNI database is currently the most widely used database of solar wind conditions propagated to the bow shock nose, and relies on planar propagation and MVA for its propagation algorithm (in addition to extensive spacecraft intercalibration). In addition to the multispacecraft databases assembled from all L1 monitors, spacecraft-specific datasets with the phase front directions used for propagation still included are also publicly available. This allows the Wind-specific 1-min cadence data from the OMNI database to be shifted to MMS’s position using the same MVA/planar propagation algorithm used to shift it from L1 to the bow shock nose in order to make a fair comparison here (King and Papitashvili, 2020). Specifically, the timestamps of the Wind-specific OMNI data at the bow shock nose are shifted based on the MVA-calculated propagation delay time between the bow shock nose and MMS-1’s position. The shifted Wind data with the closest timestamp within 100s of each MMS-1 observation is taken as the MVA algorithm’s prediction. This is similar to the approach taken to construct the OMNI database, with the only difference being that the resulting timeseries is not resampled/interpolated to a new time cadence. Also like the OMNI database, out-of-sequence arrivals are left as they are. The CRPS between the shifted Wind-specific OMNI data (hereafter referred to as MVA shifted Wind data) and the MMS test dataset is calculated with Eq. 2 (CRPS in the case of deterministic predictions). Pearson’s r correlation coefficient is calculated between the MVA shifted Wind data and the MMS test set, as well as between the means of PRIME’s predicted probability distributions and the MMS test set (thereby ignoring the uncertainty information). Joint distributions of the MMS test dataset with PRIME’s predictions and the MVA shifted Wind data are shown in Figure 4, and the performance of each algorithm is compiled in Table 2.
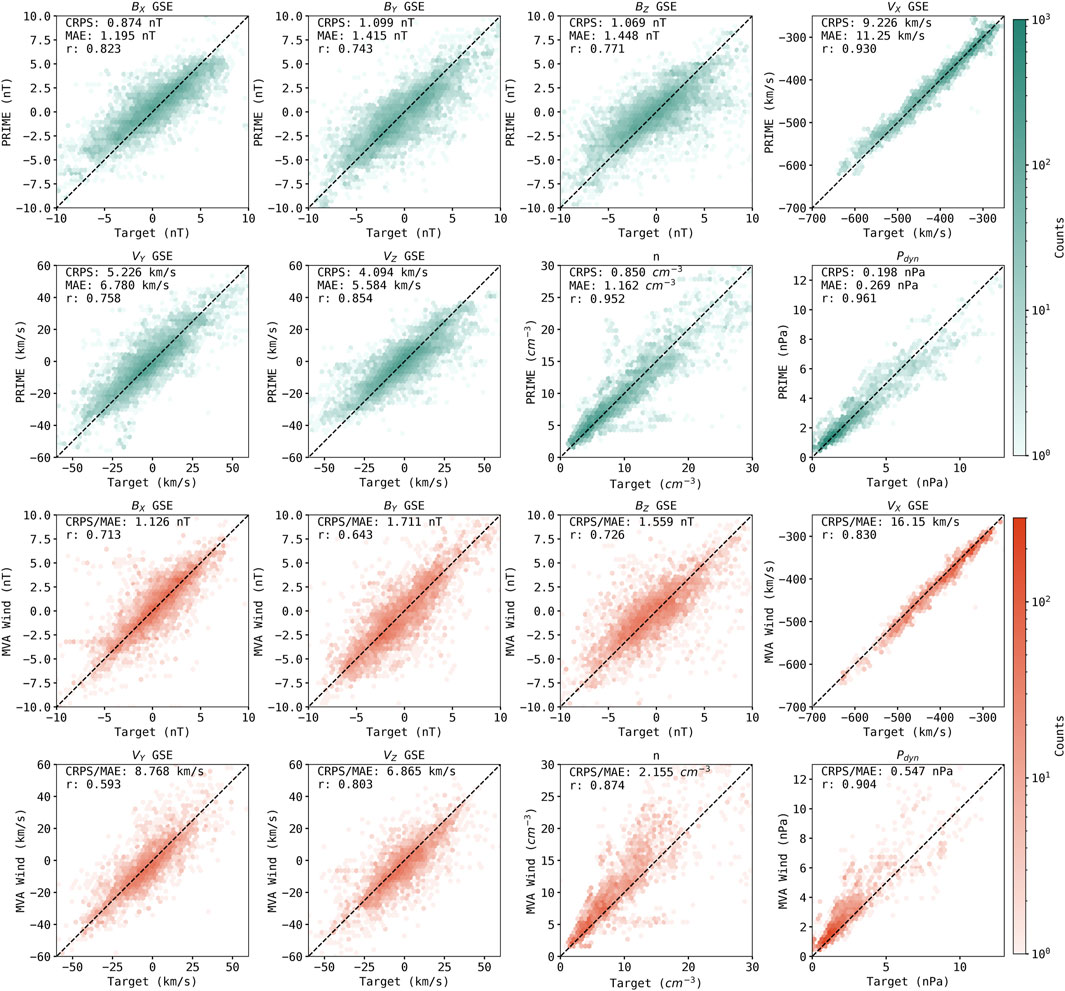
FIGURE 4. Joint distributions of MMS-1 data (x-axis) with predicted parameters from PRIME (top, green) and the MVA shifted Wind data (bottom, orange). CRPS, the mean absolute error (MAE), and Pearson’s r correlation coefficient for each parameter shown in the top left of each distribution. For PRIME, the MAE is calculated between the peaks of its predicted distributions and each MMS observation (thereby throwing away uncertainty information). For the MVA shifted Wind data, the CRPS and MAE are equivalent. A perfect prediction corresponds to the line y = x, plotted overtop of each distribution for convenience.
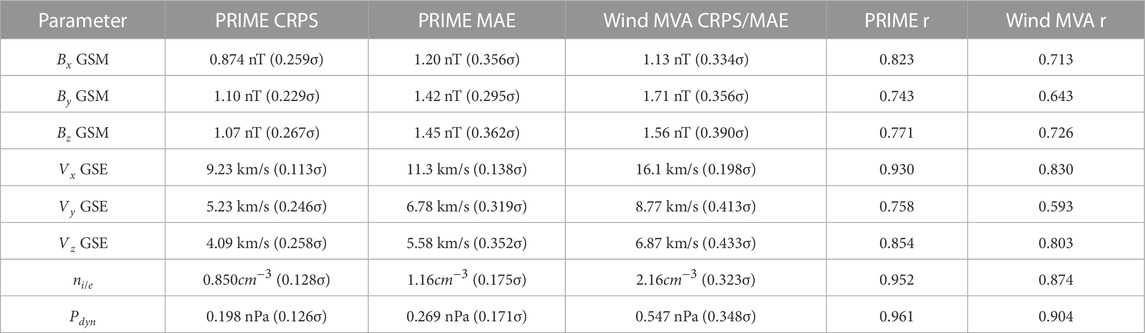
TABLE 2. Performance of PRIME and the MVA shifted Wind data on the MMS test dataset across continuous rank probability score (CRPS, Eq. 1), mean absolute error (MAE), and Pearson’s r correlation coefficient (also shown in Figure 4). CRPS is given in the units of each parameter as well as dimensionless units of standard deviations of each parameter in the MMS training dataset to facilitate comparison between each parameter.
For all parameters predicted, PRIME has a lower CRPS than the MVA shifted Wind data. This is most pronounced for plasma parameters
The calculated correlation coefficients show how the means of PRIME’s predicted distributions vary with the target data. Besides vy discussed above, the output means that correlate the poorest with MMS data are the predicted IMF components. This is likely due to the fact that the IMF varies more quickly than the solar wind plasma does, making it more difficult for an algorithm to accurately predict the timing of the fluctuations as neural network regression algorithms frequently have difficulty reproducing sharp/fast variation (Huang et al., 2022). However, the fact that PRIME’s outputs are probabilistic allows it to account for this difficulty by assigning higher uncertainty when the fluctuations in the IMF make propagation more difficult (see Section 4.4). This results in PRIME being able to predict the IMF more accurately than the MVA shifted Wind data despite the fact that its means and the MVA shifted Wind data correlate with the MMS data to roughly the same degree.
Examples of what PRIME’s outputs look like are shown in Figure 5. Only one parameter (number density) at two separate timesteps of MMS data are shown for clarity. The orange prediction-target pair are from a period where MMS was in fast solar wind (v = 633 km/s) and the green prediction-target pair are from a period where MMS was in slow solar wind (v = 362 km/s). As expected, the fast solar wind density is lower than the slow solar wind density. Additionally, the predicted uncertainty (Gaussian width) of the fast solar wind prediction is smaller than that of the slow solar wind, which is consistent with the understanding that the slow solar wind is more variable in density than the fast solar wind (Kallenrode, 2010). This also serves to highlight the difference between the uncertainty PRIME assigns to its prediction, its predicted mean value, and the accuracy metric used to optimize the model (CRPS). Despite the fact that the mean of the predicted slow solar wind distribution is closer to its associated observation than the mean of the fast solar wind distribution is to its associated observation (differences of 0.21cm−3 and 0.35cm−3 respectively), the fact that the slow solar wind prediction has a larger uncertainty than the fast solar wind prediction (1.35cm−3 vs. 0.65cm−3) means that in this case it is considered less accurate according to the CRPS metric (0.327cm−3 vs. 0.225cm−3). The CRPS is intended to balance the accuracy of the mean with the size of the confidence interval, so a larger σ does not always result in a larger or smaller CRPS.
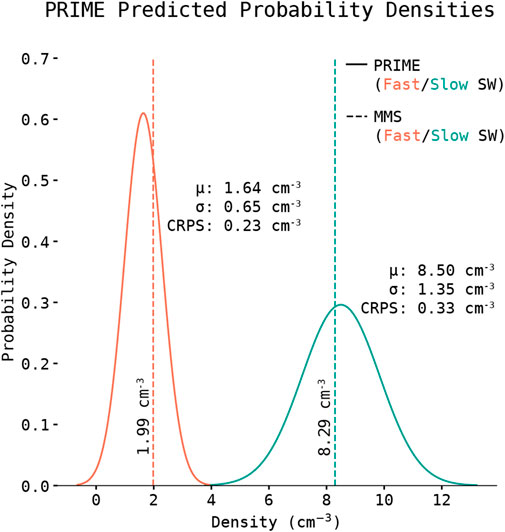
FIGURE 5. Probability densities predicted by PRIME (solid lines) for nominal plasma density in the fast (orange, measured 12 December 2017, 15:14:49 UTC) and slow (green, measured 2 April 2021, 15:13:35 UTC) solar wind. Values for corresponding MMS measurements in the solar wind are provided for reference. Means and standard deviations output by PRIME along with the CRPS between them and their associated MMS observation are annotated alongside the Gaussian curves they define. This display emphasizes that PRIME outputs a distribution function for possible predicted values rather than a single scalar value or a single scalar value with fixed error bars or confidence intervals.
Since PRIME can output predictions at any point in space, it is important to know where in space its predictions are most accurate. The CRPS between PRIME and the test dataset are shown as a function of MMS’s position in Figure 6. The scalar value for CRPS at each point is computed by scaling the CRPS for each of the seven solar wind parameters PRIME outputs to the standard deviation of each parameter, and then averaging all seven into a single scalar value. As can be seen, PRIME generally becomes less accurate the closer to the Earth radially it is attempting to predict, with its poorest performance on a set of measurements on the dawnside flank (visible roughly 5RE to 10RE X GSE and −5RE to −10RE Y GSE) that have the smallest radial distance to the Earth. These measurements were manually confirmed to be solar wind and were made months apart, indicating that this inaccuracy is not due to mislabeled data but rather is a feature of PRIME’s performance. Care should be taken when using PRIME outside of regions with good accuracy in Figure 6.
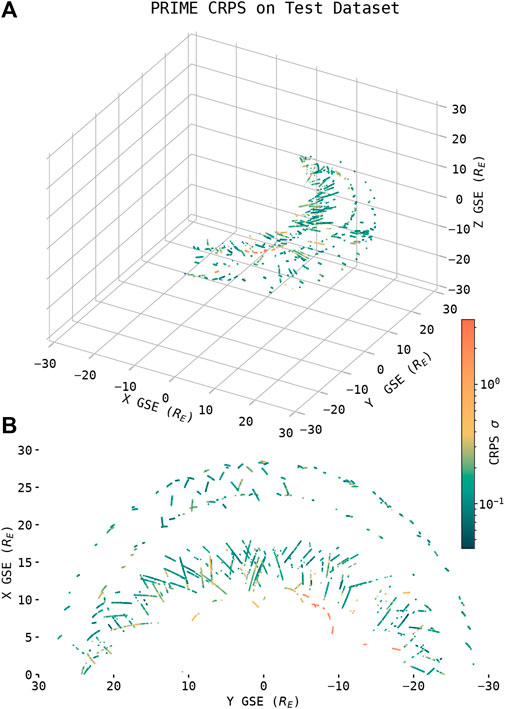
FIGURE 6. PRIME’s performance on the test dataset arranged in GSE coordinates in 3D (A) and in a projection on the GSE X-Y plane (B). The CRPS between PRIME’s predictions and the MMS measurments at each point are scaled to the standard deviation of the seven parameters and then averaged to obtain the scalar CRPS value at each point in the figure.
4.2 Timing
Metrics such as the CRPS capture the ability of each algorithm to instantaneously predict the magnitude of each solar wind parameter, but another important function of solar wind propagation algorithms is their ability to predict the arrival times of solar wind structures at the Earth. Timing uncertainty has been identified as a problem for correlation analysis between ground-based monitors and solar wind inputs, as well as understanding energy transfer between the solar wind and magnetosphere broadly (Lockwood, 2022). Delay times between L1 and the Earth calculated by traditional algorithms on two consecutive minutes of solar wind measurements can have differences on the order of the total delay time itself, so quantifying the timing accuracy of solar wind propagation algorithms has been the subject of extensive study (Collier et al., 1998; Mailyan et al., 2008; Case and Wild, 2012) and has been the focus of other propagation algorithms (Baumann and McCloskey, 2021). To quantify PRIME and the MVA shifted Wind data’s ability to predict the arrival time of structures in the solar wind, the correlation coefficient between the IMF clock angle measured by MMS and the IMF clock angle calculated from each algorithm’s output is calculated in a 10 minute sliding window over the test subset of the MMS solar wind dataset used in this study (10 min was selected following the method used by Case and Wild (2012)). Since PRIME’s outputs are probability distributions, the mean of the distribution is what is used to calculate the correlation coefficient for PRIME (thereby throwing away the uncertainty information). The correlation coefficients for all the windows are binned and shown in Figure 7 along with the length of data from PRIME and the MVA shifted Wind data in each 10-min chunk. Only time windows with no missing data are included in the figure.
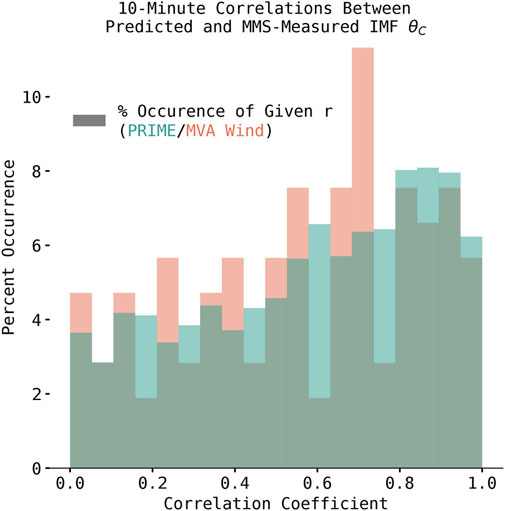
FIGURE 7. Correlation coefficients calculated between PRIME/the MVA shifted Wind data’s output IMF clock angle and MMS measured IMF clock angle over a 10 minute sliding window and then binned (bars). PRIME is shown in green and the MVA shifted Wind data is shown in orange. Only intervals that are more than half full (i.e., 4 or more entries) are included.
From Figure 7, it can be seen PRIME is more likely than the MVA shifted Wind data to produce good correlations in IMF clock angle, as 41.2% of the time intervals it produced had correlation r > 0.7 (as opposed to only 37.7% of the MVA shifted Wind data’s intervals). Additionally, PRIME produces poor correlations (r < 0.4) only 28.1% of the time as opposed to the MVA shifted Wind data doing so 30.2% of the time. This means that PRIME more accurately predicts the arrival of IMF rotations than the leading planar propagation algorithm. In an absolute sense, neither the MVA shifted Wind data nor PRIME’s mean value are perfect predictors of solar wind temporal variation. A quantity X that correlates with another quantity Y with Pearson’s r = 0.7 accounts roughly 50% of the variance in Y. PRIME’s means meet this level 41.2% of the time, and the MVA shifted Wind data meet this level only 37.7% of the time. However, PRIME does not seek to account for all of the variance in solar wind parameters with its predicted mean values alone, as the uncertainty of its output distributions also encodes information about the solar wind variation as can be seen in Section 4.3.
4.3 Case studies
Two events from outside the training and validation datasets are highlighted to examine PRIME’s performance for events that are difficult for traditional planar propagation algorithms to predict. The Wind-specific OMNI data compared against here is propagated to MMS-1 from the bow shock nose using the same phase fronts used to propagate the data from L1 to the bow shock to ensure a fair comparison and will be referred to as the MVA shifted Wind data for clarity.
4.3.1 Corotating interaction region (CIR)
The first is a Corotating Interaction Region (CIR) shock that passed over MMS-1 on 8 January 2018 (Starkey et al., 2020), shown in Figure 8. CIRs are formed when fast solar wind from coronal holes overtakes slow SW from coronal streamers forming a shock (Gosling et al., 1993). Planar propagation algorithms are prone to out of sequence arrivals during CIRs, as they allow fast streams to pass through slow streams without modifying the plasma in either flow. Implementations of planar propagation algorithms sometimes favor the earlier (Weimer, 2003) or the later (Weimer and King, 2008) plane, but there is no good physical reasoning for either. The approach taken by the OMNI team in assembling the spacecraft-specific datasets is to shift the data and accept the new time tags the order they come, then average to a 1-min cadence. This can result in plasmas from both early and late planes mixing, depending on their orientation (meaning one cannot say out of sequence arrivals in the OMNI dataset are always late or early, see https://omniweb.gsfc.nasa.gov/html/omni_min_data.html). Therefore, this event is one that could potentially be better predicted by PRIME, which is theoretically capable of accounting for the physics of the interacting flows.
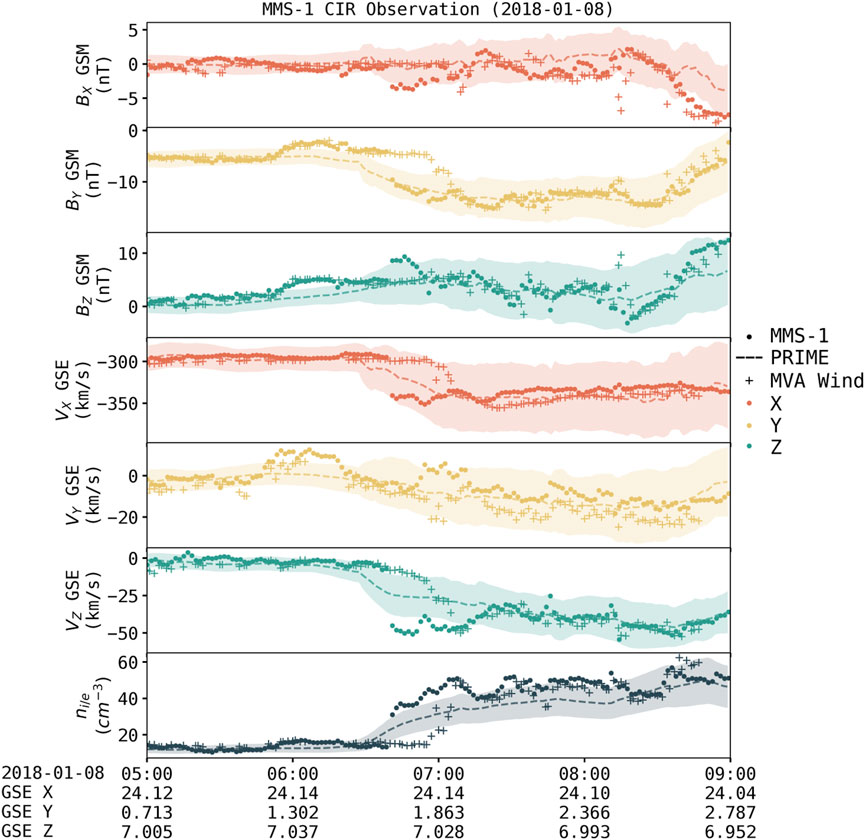
FIGURE 8. Case study comparing propagated solar wind with ground truth. Ground truth from MMS-1 upstream of the bow shock measuring Corotating Interaction Region (CIR) shock event. Solid lines are the MMS-1 ground truth, dashed lines are predictions from PRIME with 1σ uncertainty (shaded region), and crosses are Wind data propagated to MMS-1’s position with the OMNI database’s MVA technique.
As can be seen in Figure 8, PRIME accurately predicts the arrival time of the CIR at MMS-1, whereas the MVA shifted Wind data are almost 30 min late. Both algorithms capture the magnitude of each parameter before and after roughly as well as the other, but PRIME has the added benefit of capturing the uncertainty due to the turbulence downstream of the shock, as its predicted uncertainty increases for all parameters downstream of the shock. PRIME’s predicted uncertainty is largest for VX GSE, which is a result of the fact that its output probability distributions are Gaussian (and therefore symmetric). The large negative jump in VX increases the uncertainty a great deal in the negative direction, which is necessarily reflected in the positive direction. Despite the fact that it predicts the arrival time of the structure more accurately, PRIME transitions more slowly than the MVA shifted Wind data. Neural network outputs tend to have difficulties with sharp transitions, as it is often the case that they overfit during training before being able to reproduce such structure (Huang et al., 2022). Depending on the application, this behavior may not be desirable and should be noted by the user.
4.3.2 Coronal mass ejection (CME)
The second event is a Coronal Mass Ejection (CME) observed by MMS-1 on 1 February 2022. This CME was the first of a set of Earth-directed CMEs that caused the failure of 38 starlink satellites and is thought to have provided the necessary preconditioning for the unexpectedly strong geomagnetic activity over the following days (Dang et al., 2022). MMS-1 observed the leading edge of the CME starting around 22:15 UT on February 2nd, shown in Figure 9, alongside PRIME’s predictions and OMNI data propagated to MMS’s position.
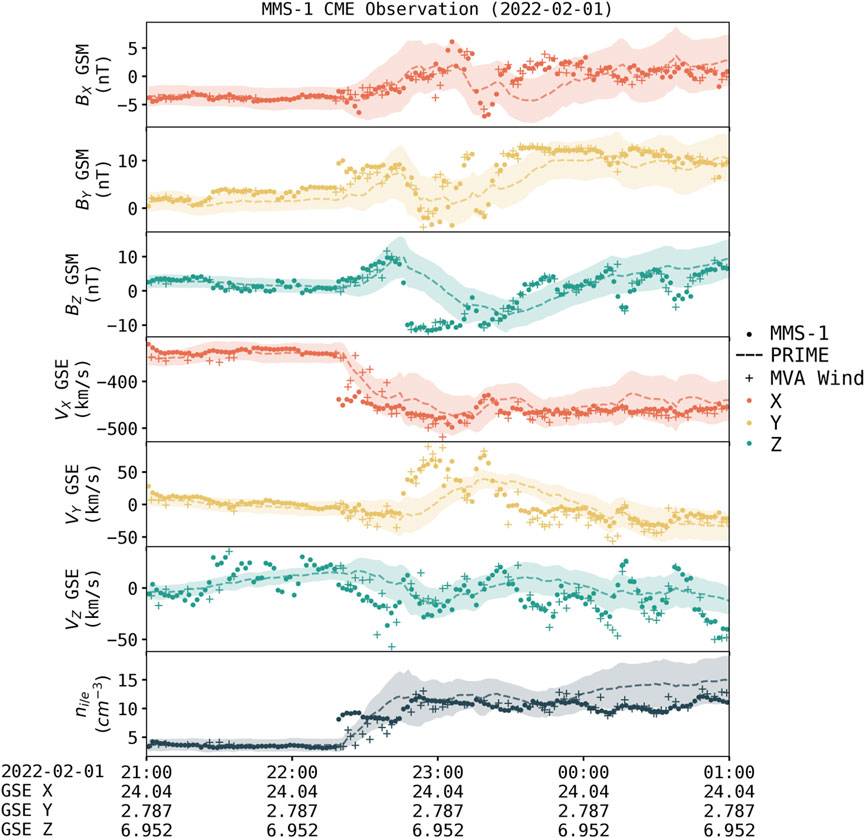
FIGURE 9. Case study comparing propagated solar wind with ground truth. Ground truth from MMS-1 upstream of the bow shock measuring Coronal Mass Ejection (CME). Solid lines are the MMS-1 ground truth, dashed lines are predictions from PRIME with 1σ uncertainty (shaded region), and crosses are Wind data propagated to MMS-1’s position with the OMNI database’s MVA technique.
For this event, both algorithms predict the arrival time of the event fairly accurately. It can be seen that PRIME has some difficulty capturing the exact variation in velocity, especially in the GSE Y and Z directions. This is possibly due to the fact that PRIME is trained on solar wind data that has had plasma resembling the magnetosheath and ion foreshock removed, both of which resemble parts of the CME. Indeed, the Olshevsky et al. (2021) classifier labels the CME sheath from 22:15–23:30 as the Earth’s magnetosheath rather than the solar wind; if this event were in the time range of the target dataset that section would be removed. In short, the fact that portions of shocked (i.e., magnetosheath-like) plasma are removed from the target dataset limits the representational power of PRIME for some situations. Additionally, PRIME misses the sharpness of the transition in Bz, much like the slow transition exhibited in the CIR event in Figure 8. One benefit PRIME has over the MVA shifted Wind data during this event is coverage, as the MVA/planar propagation routine from the bow shock to MMS fails over several intervals before and after the CME.
4.4 Uncertainty validation
As noted in Section 3.1, the statistical reliability of PRIME’s outputs is not explicitly enforced during training. The extent to which PRIME’s output distributions are statistically valid/meaningful must therefore be evaluated after training. PRIME’s output uncertainties can be validated quantitatively through the use of a reliability diagram (Hamill (1997); Hamill (2001)). Following the procedure outlined in Camporeale et al. (2019) and Camporeale and Carè (2021), define the standardized errors associated with prediction μi, σi with i = 1, … , N as
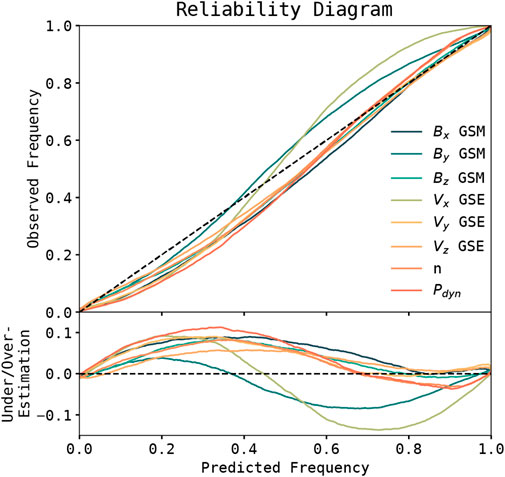
FIGURE 10. Reliability diagram constructed from PRIME’s outputs on the test dataset for each parameter. Shown versus the predicted frequency of the observation from PRIME are the absolute value of the observed frequency (top) and the deviation from perfect reliability (bottom). For the bottom plot, a given parameter being over (under) the line by an amount corresponds to PRIME over (under) predicting the frequency by that amount.
From Figure 10, it is clear that PRIME’s outputs are not perfectly reliable/calibrated as they do not correspond exactly to the dotted line. In general, PRIME tends to overestimate the likelihood of unlikely events, and underestimate the likelihood of likely events. This is a similar effect in uncertainty that is observed in the peak value of the distribution, where PRIME’s outputs are “smoother” than may be desirable for some uses. The largest departures from perfect calibration are observed in Ppdyn (predicts events that occur with p = 0.227 as occurring with p = 0.340), VX GSE (predicts events that occur with p = 0.588 as occurring with p = 0.725), and BY GSM (predicts events that occur with p = 0.585 as occurring with p = 0.670). With the exception of VX GSE and BY GSM PRIME tends to be conservative, as it overestimates the likelihood of rare events. Some departures from perfect calibration are expected, since even models perfectly calibrated on training data can suffer calibration loss on the test dataset (Kull and Flach, 2015). Across all parameters and predicted probabilities, PRIME is reliable to within 2.2% with a maximum difference 14% (calculated pobs − ppred). This is still fairly reliable relative to other probabilistic prediction algorithms for other space weather tasks (e.g., Tasistro-Hart et al., 2021), but less reliable those that use loss functions that enforce reliability explicitly (e.g., Hu et al., 2022).
It is a well known result that propagating solar wind and IMF conditions from L1 to the Earth becomes more difficult and uncertain as the monitor spacecraft at L1 strays further from the Earth-Sun line (Crooker et al., 1982; Paularena et al., 1998; Richardson et al., 1998; Milan et al., 2022). This is generally thought to be due to the fact that the L1 spacecraft becomes more likely to be in a solar wind flux tube or “parcel” that will not impact the Earth’s magnetosphere (Borovsky, 2018). Thus an important validation metric for PRIME is whether its output uncertainties get larger when Wind is further from the Earth-Sun line. In Figure 11 PRIME’s output uncertainties (σs) from the test dataset are binned with respect to Wind’s tangential distance from the Earth-Sun line in 20RE bins. The median value as well as the 10th-25th and 75th-90th percentiles in each bin are displayed in a box-and-whisker style. The median values show a somewhat upward trend as Wind gets further from the Earth-Sun line, with a dramatic increase in both median value and the 75th-90th percentile for the furthest bin (100RE to 120RE). Therefore, PRIME predicts that its predicted mean values are more uncertain when the input monitor is further from the Earth-Sun line. This is consistent with the result from Crooker et al. (1982) that showed that timing uncertainty for solar wind conditions propagated from L1 gets dramatically larger when the monitor is
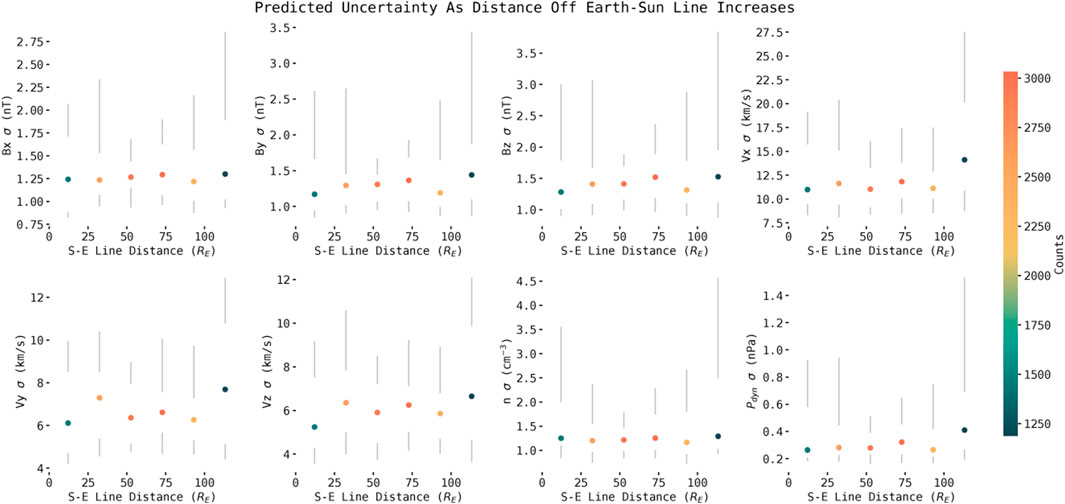
FIGURE 11. Box-and-whisker plot of PRIME uncertainties as the distance from the Earth-Sun line of the Wind spacecraft increases. Dots are the median uncertainty in each bin, and the lines are between the 10th-25th and 75th-90th percentiles. Note the uncertainties here are the variances of the distributions output by PRIME, not performance metrics for PRIME.
Another verification that the uncertainties output by PRIME are physical is whether its predicted uncertainties increase during times of high variation, particularly for the magnetic field. The IMF can exhibit a great deal of small scale variation that can be difficult for models to capture (See Figures 8, 9), and thus for periods of rapid or large variation one would expect the uncertainty PRIME assigns to its magnetic field output to increase. To investigate this, the standard deviation of each magnetic field component over the input timeseries (5000s, 1.4 h) for each output in the test set is calculated to be used as a measure of the magnitude of magnetic field variation. Then, the output uncertainties are binned with respect to these variations and presented in Figure 12. As can be seen, as the magnitude of magnetic field variation increases, so too does the uncertainty PRIME assigns its magnetic field predictions. This effect is strongest for variations in Bz, as the uncertainty is roughly 1.5× greater during times of maximum Bz variation than it is for maximum By or Bx variation. This could be due to the fact that Bz is much more variable than the other IMF components, with a maximum standard deviation of 14.0 nT (as opposed to 7.42 nT and 5.2 nT for By and Bx).

FIGURE 12. Box-and-whisker plot of PRIME uncertainties as the standard deviation of each magnetic field component over the input timeseries (5000s, 1.4 h) increases. Dots are the median uncertainty in each bin, and the lines are between the 10th-25th and 75th-90th percentiles. Note the uncertainties here are the variances of the distributions output by PRIME, not performance metrics for PRIME.
5 Conclusion
In this study, a probabilistic gated recurrent neural network is trained to predict observations of the solar wind near the Earth measured by MMS-1 given timeseries input measured by the Wind spacecraft at L1. The algorithm’s last layer is taken to be the means and variances of Gaussian distributions for each solar wind parameter (rather than single scalar values), and the algorithm is then optimized to minimize the continuous rank probability score (CRPS) between its outputs and the MMS dataset. In this way, the algorithm is able to simultaneously predict the solar wind conditions and assign uncertainties to its predictions. This algorithm, PRIME (Probabilistic Regressor for Input to the Magnetosphere Estimation), is a first-of-its kind method for solar wind propagation with uncertainty estimation.
PRIME’s performance is compared to the most widely used algorithm used to propagate solar wind conditions from L1 to the Earth (minimum variance analysis (MVA) and planar propagation, as used to construct the OMNI database). PRIME’s outputs are shown to be more accurate than Wind data propagated to MMS-1’s position using the MVA algorithm across the test dataset, with PRIME achieving a CRPS of 0.214σ on average across all parameters compared to the MVA algorithm’s CRPS of 0.350σ. This improvement in accuracy is due to both the improved accuracy of the mean values of PRIME’s predicted probability distributions as well as the uncertainty it is able to assign to its predictions. Through case studies of a corotating interaction region (Figure 8) and a coronal mass ejection (Figure 9), some of PRIME’s key benefits and drawbacks are shown. The magnitude of the solar wind parameters PRIME predicts before and after the events are in general more accurate than the MVA technique’s predictions. PRIME also predicts the arrival time of each structure more accurately than the MVA technique. PRIME’s outputs are in general “smoother” than the ground truth and the MVA shifted data, which is a known drawback of neural network algorithms. While it does predict the arrival time of each structure more accurately, it does not fully capture the sharpness of the discontinuities. Additionally, during the CME event PRIME has difficulty predicting the shocked plasma in the CME sheath since shocked plasma is removed from the training dataset. The probabilistic nature of PRIME’s predictions is also one of its key benefits. In order to verify that they are physically meaningful, the reliability of PRIME’s predicted uncertainties is also assessed. It is found that PRIME is not perfectly reliable, with maximum deviation from perfect reliability (pobs − ppred) of 14% and an average deviation of 2.2%. This is within the range of reliability demonstrated by other space weather prediction algorithms (Tasistro-Hart et al., 2021; Hu et al., 2022).
Uncertainty in solar wind conditions at Earth has been identified as a key problem for studies of solar wind/magnetosphere coupling (Lockwood et al., 2019; Borovsky, 2021). PRIME offers a simple solution by generating accurate predictions of the solar wind at Earth with physically meaningful uncertainties attached. These outputs can be used to correct for regression biases due to uncertainties associated with input data (Sivadas et al., 2022), and generally quantify the confidence associated with results that rely on solar wind input data. Furthermore, PRIME’s architecture can be readily adapted to other regression tasks in geophysics where assigning uncertainties to predictions is desirable, predicting magnetosheath conditions from L1 inputs or ionospheric currents from geomagnetic indices.
Data availability statement
Magnetospheric Multiscale, Wind, and OMNI data are available through the Coordinated Data Analysis Web (CDAWeb) online portal at https://cdaweb.gsfc.nasa.gov/istp_public/. Codes for dataset preparation, algorithm development, and analysis presented in this paper are available at https://github.com/connor-obrien888/prime, along with the latest version of PRIME and ISTP compliant CDF files with PRIME’s output at the bow shock nose (O’Brien 2023).
Author contributions
CO’B compiled the datasets, implemented the algorithm, developed algorithm comparisons and visualizations, and wrote the text. BW contributed to the dataset compilation methodology and algorithm evaluations. YZ contributed to the development of the propagation methodology. ST contributed comparisons to other propagation methodologies. HZ contributed the probabilistic aspects of the algorithm architecture. DS contributed interpretations of the case studies and output distributions. All authors contributed to the article and approved the submitted version.
Acknowledgments
The authors acknowledge the instrument teams for FPI, FGM, SWE, and MFI, as well as the other MMS and Wind instrument teams whose labor made this study possible. The authors acknowledge Barbara Giles and Steve Kreisler for their advice on working with FPI data products. The authors acknowledge use of NASA/GSFC’s Space Physics Data Facility’s OMNIWeb service, and OMNI data. The authors acknowledge discussions with Sheng Huang and Sam Evans about machine learning best practices. Authors CO’B, BW, and YZ would like to acknowledge support from NASA grants 80NSSC21K0026 and 80NSSC20K1710. Author ST acknowledges support from the German Aerospace Center (DLR). DS was supported by NASA’s MMS Theory and Modeling program.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1For more information on past, present, and future MMS mission phases and campaigns see the MMS FPI Data Users and Products Guide https://lasp.colorado.edu/galaxy/display/MFDPG/1.3+Mission+Phases+and+Science+Regions+of+Interest
References
Al Shidi, Q., Pulkkinen, T. I., Welling, D. T., and Tóth, G. (2023). Accuracy of Global Geospace Simulations: How much of the error arises from solar wind input uncertainties? Preprints. doi:10.22541/essoar.168565415.57893357/v1
Anderson, J. L. (1996). A method for producing and evaluating probabilistic forecasts from ensemble model integrations. J. Clim. 9, 1518–1530. doi:10.1175/1520-0442(1996)009⟨1518:AMFPAE⟩2.0.CO;2
Axford, W. (1964). Viscous interaction between the solar wind and the earth’s magnetosphere. Planet. Space Sci. 12, 45–53. doi:10.1016/0032-0633(64)90067-4
Ba, J. L., Kiros, J. R., and Hinton, G. E. (2016). Layer normalization. ArXiv:1607.06450 [cs, stat].
Bargatze, L. F. (2005). A new interpretation of Weimer et al.’s solar wind propagation delay technique. J. Geophys. Res. 110, A07105. doi:10.1029/2004JA010902
Baumann, C., and McCloskey, A. E. (2021). Timing of the solar wind propagation delay between L1 and Earth based on machine learning. J. Space Weather Space Clim. 11, 41. doi:10.1051/swsc/2021026
Bebis, G., and Georgiopoulos, M. (1994). Feed-forward neural networks. IEEE Potentials 13, 27–31. doi:10.1109/45.329294
Borovsky, J. E. (2008). Flux tube texture of the solar wind: strands of the magnetic carpet at 1 au? Flux tube texture of solar wind. J. Geophys. Res. Space Phys. 113. n/a–n/a. doi:10.1029/2007JA012684
Borovsky, J. E. (2021). Is our understanding of solar-wind/magnetosphere coupling satisfactory? Front. Astronomy Space Sci. 8, 634073. doi:10.3389/fspas.2021.634073
Borovsky, J. E. (2018). The spatial structure of the oncoming solar wind at Earth and the shortcomings of a solar-wind monitor at L1. J. Atmos. Solar-Terrestrial Phys. 177, 2–11. doi:10.1016/j.jastp.2017.03.014
Bröcker, J., and Smith, L. A. (2007). Increasing the reliability of reliability diagrams. Weather Forecast. 22, 651–661. doi:10.1175/WAF993.1
Burch, J. L., Moore, T. E., Torbert, R. B., and Giles, B. L. (2016). Magnetospheric Multiscale overview and science objectives. Space Sci. Rev. 199, 5–21. doi:10.1007/s11214-015-0164-9
Cameron, T. G., and Jackel, B. (2019). Using a numerical MHD model to improve solar wind time shifting. Space weather. 17, 662–671. doi:10.1029/2019SW002175
Camporeale, E., and Carè, A. (2021). Accrue: accurate and reliable uncertainty estimate in deterministic models. Int. J. Uncertain. Quantification 11, 81–94. doi:10.1615/Int.J.UncertaintyQuantification.2021034623
Camporeale, E., Chu, X., Agapitov, O. V., and Bortnik, J. (2019). On the generation of probabilistic forecasts from deterministic models. Space weather. 17, 455–475. doi:10.1029/2018SW002026
Camporeale, E. (2019). The challenge of machine learning in space weather: nowcasting and forecasting. Space Weather 17, 1166-1207. doi:10.1029/2018SW-002061
Case, N. A., and Wild, J. A. (2012). A statistical comparison of solar wind propagation delays derived from multispacecraft techniques: solar wind propagation. J. Geophys. Res. Space Phys. 117. n/a–n/a. doi:10.1029/2011JA016946
Chang, S. C., and Nishida, A. (1973). Spatial structure of transverse oscillations in the interplanetary magnetic field. Astrophysics Space Sci. 23, 301–314. doi:10.1007/BF00645159
Cho, K., van Merrienboer, B., Bahdanau, D., and Bengio, Y. (2014). On the properties of neural machine translation: Encoder-decoder approaches. ArXiv:1409.1259 [cs, stat].
Chung, J., Gulcehre, C., Cho, K., and Bengio, Y. (2014). Empirical evaluation of gated recurrent neural networks on sequence modeling. ArXiv:1412.3555 [cs].
Collier, M. R., Slavin, J. A., Lepping, R. P., Szabo, A., and Ogilvie, K. (1998). Timing accuracy for the simple planar propagation of magnetic field structures in the solar wind. Geophys. Res. Lett. 25, 2509–2512. doi:10.1029/98GL00735
Crooker, N. U., Siscoe, G. L., Russell, C. T., and Smith, E. J. (1982). Factors controlling degree of correlation between ISEE 1 and ISEE 3 interplanetary magnetic field measurements. J. Geophys. Res. 87, 2224. doi:10.1029/JA087iA04-p02224
Dang, T., Li, X., Luo, B., Li, R., Zhang, B., Pham, K., et al. (2022). Unveiling the space weather during the starlink satellites destruction event on 4 february 2022. Space Weather 20, e2022SW003152. doi:10.1029/2022SW003152
Duchi, J., Hazan, E., and Singer, Y. (2011). Adaptive subgradient methods for online learning and stochastic optimization.
Dungey, J. W. (1961). Interplanetary magnetic field and the auroral zones. Phys. Rev. Lett. 6, 47–48. doi:10.1103/PhysRevLett.6.47
Gneiting, T., and Raftery, A. E. (2007). Strictly proper scoring rules, prediction, and estimation. J. Am. Stat. Assoc. 102, 359–378. doi:10.1198/0162145060000-01437
Gneiting, T., Raftery, A. E., Westveld, A. H., and Goldman, T. (2005). Calibrated probabilistic forecasting using ensemble model output statistics and minimum CRPS estimation. Mon. Weather Rev. 133, 1098–1118. doi:10.1175/MWR2904.1
Gosling, J. T., Bame, S. J., McComas, D. J., Phillips, J. L., Pizzo, V. J., Goldstein, B. E., et al. (1993). Latitudinal variation of solar wind corotating stream interaction regions: ulysses. Geophys. Res. Lett. 20, 2789–2792. doi:10.1029/93GL03116
Hamill, T. M. (2001). Interpretation of rank histograms for verifying ensemble forecasts. Mon. Weather Rev. 129, 550–560. doi:10.1175/1520-0493(2001)129⟨0550:IORHFV⟩2.0.CO;2
Hamill, T. M. (1997). Reliability diagrams for multicategory probabilistic forecasts. Weather Forecast. 12, 736–741. doi:10.1175/1520-0434(1997)012⟨0736:RDFMPF⟩2.0.CO;2
Hersbach, H. (2000). Decomposition of the continuous ranked probability score for ensemble prediction systems. Weather Forecast. 15, 559–570. doi:10.1175/1520-0434(2000)015⟨0559:DOTCRP⟩2.0.CO;2
Hu, A., Camporeale, E., and Swiger, B. (2022). Multi-hour ahead dst index prediction using multi-fidelity boosted neural networks. ArXiv:2209.12571 [physics].
Huang, S., Li, W., Shen, X., Ma, Q., Chu, X., Ma, D., et al. (2022). Application of recurrent neural network to modeling earth’s global electron density. J. Geophys. Res. Space Phys. 127. doi:10.1029/2022JA030695
Kallenrode, M.-B. (2010). “Space physics: an introduction to plasmas and particles in the heliosphere and magnetospheres; with 12 tables,” in Numerous excercises and problems (Berlin Heidelberg: Springer), 3. ed., paperback ed edn.
King, J. H. (2005). Solar wind spatial scales in and comparisons of hourly Wind and ACE plasma and magnetic field data. J. Geophys. Res. 110, A02104. doi:10.1029/2004JA010649
Kömle, N. I., Lichtenegger, H. I. M., and Rucker, H. O. (1986). “Propagation of solar wind features: A model comparison using voyager data,” in The Sun and the heliosphere in three dimensions. Editor R. G. Marsden (Dordrecht: Springer Netherlands), 123, 205–210. Series Title: Astrophysics and Space Science Library. doi:10.1007/978-94-009-4612-5_26
Kull, M., and Flach, P. (2015). “Novel decompositions of proper scoring rules for classification: score adjustment as precursor to calibration,” in Machine learning and knowledge discovery in databases. Editors A. Appice, P. P. Rodrigues, V. Santos Costa, C. Soares, J. Gama, and A. Jorge (Cham: Springer International Publishing), 9284, 68–85. Series Title: Lecture Notes in Computer Science. doi:10.1007/978-3-319-23528-8_5
Lakshminarayanan, B., Pritzel, A., and Blundell, C. (2017). Simple and scalable predictive uncertainty estimation using deep ensembles. ArXiv:1612.01474 [cs, stat].
Lepping, R. P., Acũna, M. H., Burlaga, L. F., Farrell, W. M., Slavin, J. A., Schatten, K. H., et al. (1995). The WIND magnetic field investigation. Space Sci. Rev. 71, 207–229. doi:10.1007/BF00751330
Leshno, M., Lin, V. Y., Pinkus, A., and Schocken, S. (1993). Multilayer feedforward networks with a nonpolynomial activation function can approximate any function. Neural Netw. 6, 861–867. doi:10.1016/S0893-6080(05)80131-5
Li, L., Jamieson, K., DeSalvo, G., Rostamizadeh, A., and Talwalkar, A. (2018). Hyperband: A novel bandit-based approach to hyperparameter optimization. J. Mach. Learn. Res. 18, 1–52.
Lockwood, M., Bentley, S. N., Owens, M. J., Barnard, L. A., Scott, C. J., Watt, C. E., et al. (2019). The development of a space climatology: 1. Solar wind magnetosphere coupling as a function of timescale and the effect of data gaps. Space weather. 17, 133–156. doi:10.1029/2018SW001856
Lockwood, M. (2022). Solar wind—magnetosphere coupling functions: pitfalls, limitations, and applications. Space weather. 20. doi:10.1029/2021SW002989
Lugaz, N., Liu, H., Hapgood, M., and Morley, S. (2021). Machine-learning research in the space weather journal: prospects, scope and limitations. Atmos. Sci. preprint. doi:10.1002/essoar.10509033.1
Mailyan, B., Munteanu, C., and Haaland, S. (2008). What is the best method to calculate the solar wind propagation delay? Ann. Geophys. 26, 2383–2394. doi:10.5194/angeo-26-2383-2008
Matheson, J. E., and Winkler, R. L. (1976). Scoring rules for continuous probability distributions. Manag. Sci. 22, 1087–1096. doi:10.1287/mnsc.22.10.1087
Mehta, P., Bukov, M., Wang, C.-H., Day, A. G., Richardson, C., Fisher, C. K., et al. (2019). A high-bias, low-variance introduction to Machine Learning for physicists. Phys. Rep. 810, 1–124. doi:10.1016/j.physrep.2019.03.001
Milan, S. E., Carter, J. A., Bower, G. E., Fleetham, A. L., and Anderson, B. J. (2022). Influence of off-sun-earth line distance on the accuracy of L1 solar wind monitoring. J. Geophys. Res. Space Phys. 127. doi:10.1029/2021JA030212
Morley, S. K., Welling, D. T., and Woodroffe, J. R. (2018). Perturbed input ensemble modeling with the space weather modeling framework. Space weather. 16, 1330–1347. doi:10.1029/2018SW002000
Neugebauer, M., and Giacalone, J. (2015). Energetic particles, tangential discontinuities, and solar flux tubes. J. Geophys. Res. Space Phys. 120, 8281–8287. doi:10.1002/2015JA021632
Nielsen, M. A. (2015). Neural networks and deep learning, 25. San Francisco, CA: Determination press.
Nix, D., and Weigend, A. (1994). “Estimating the mean and variance of the target probability distribution,” in Proceedings of 1994 IEEE international conference on neural networks (ICNN’94) (Orlando, FL, USA: IEEE), 1, 55–60. doi:10.1109/ICNN.1994.374138
Ogilvie, K. W., Chornay, D. J., Fritzenreiter, R. J., Hunsaker, F., Keller, J., Lobell, J., et al. (1995). SWE, a comprehensive plasma instrument for the WIND spacecraft. Space Sci. Rev. 71, 55–77. doi:10.1007/BF00751326
Olshevsky, V., Khotyaintsev, Y. V., Lalti, A., Divin, A., Delzanno, G. L., Anderzen, S., et al. (2021). Automated classification of plasma regions using 3D particle energy distributions. J. Geophys. Res. Space Phys. 126. ArXiv: 1908.05715. doi:10.1029/2021JA029620
O’Malley, T., Bursztein, E., Long, J., Chollet, F., Jin, H., Invernizzi, L., et al. (2019). Kerastuner.
Paularena, K. I., Zastenker, G. N., Lazarus, A. J., and Dalin, P. A. (1998). Solar wind plasma correlations between IMP 8, INTERBALL-1, and WIND. J. Geophys. Res. Space Phys. 103, 14601–14617. doi:10.1029/98JA00660
Paularena, K., Richardson, J., Lazarus, A., Zastenker, G., and Dalin, P. (1997). IMP 8, WIND and INTERBALL observations of the solar wind. Phys. Chem. Earth 22, 629–637. doi:10.1016/S0079-1946(97)00188-2
Pollock, C., Moore, T., Jacques, A., Burch, J., Gliese, U., Saito, Y., et al. (2016). Fast plasma investigation for magnetospheric Multiscale. Space Sci. Rev. 199, 331–406. doi:10.1007/s11214-016-0245-4
Richardson, J. D., Dashevskiy, F., and Paularena, K. I. (1998). Solar wind plasma correlations between L1 and Earth. J. Geophys. Res. Space Phys. 103, 14619–14629. doi:10.1029/98JA00675
Roberts, O. W., Nakamura, R., Coffey, V. N., Gershman, D. J., Volwerk, M., Varsani, A., et al. (2021). A study of the solar wind ion and electron measurements from the magnetospheric Multiscale mission’s fast plasma investigation. J. Geophys. Res. Space Phys. 126. doi:10.1029/2021JA029784
Russell, C. T., Anderson, B. J., Baumjohann, W., Bromund, K. R., Dearborn, D., Fischer, D., et al. (2016). The magnetospheric Multiscale magnetometers. Space Sci. Rev. 199, 189–256. doi:10.1007/s11214-014-0057-3
Sivadas, N., Sibeck, D., Subramanyan, V., Walach, M.-T., Murphy, K., and Halford, A. (2022). Uncertainty in solar wind forcing explains polar cap potential saturation. Number: arXiv:2201.02137 arXiv:2201.02137 [astro-ph, physics:physics].
Slingo, J., and Palmer, T. (2011). Uncertainty in weather and climate prediction. Philosophical Trans. R. Soc. A Math. Phys. Eng. Sci. 369, 4751–4767. doi:10.1098/rsta.2011.0161
Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I., and Salakhutdinov, R. (2014). Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 15, 1929–1958.
Starkey, M., Fuselier, S. A., Desai, M. I., Schwartz, S. J., Gomez, R. G., Mukherjee, J., et al. (2020). MMS observations of accelerated interstellar pickup He + ions at an interplanetary shock. Astrophysical J. 897, 6. doi:10.3847/1538-4357/ab960c
Tasistro-Hart, A., Grayver, A., and Kuvshinov, A. (2021). Probabilistic geomagnetic storm forecasting via deep learning. J. Geophys. Res. Space Phys. 126, e2020JA028228. doi:10.1029/2020JA028228
Walsh, B. M., Bhakyapaibul, T., and Zou, Y. (2019). Quantifying the uncertainty of using solar wind measurements for geospace inputs. J. Geophys. Res. Space Phys. 124, 3291–3302. doi:10.1029/2019JA026507
Weimer, D. R. (2003). Predicting interplanetary magnetic field (IMF) propagation delay times using the minimum variance technique. J. Geophys. Res. 108, 1026. doi:10.1029/2002JA009405
Weimer, D. R., and King, J. H. (2008). Improved calculations of interplanetary magnetic field phase front angles and propagation time delays: calculations of IMF phase front angles. J. Geophys. Res. Space Phys. 113. n/a–n/a. doi:10.1029/2007JA012452
Wilks, D. S. (2011). “Statistical methods in the atmospheric sciences. No. v. 100,” in International geophysics series. 3rd (Amsterdam ; Boston: Elsevier/Academic Press). ed edn.
Zamo, M., and Naveau, P. (2018). Estimation of the continuous ranked probability score with limited information and applications to ensemble weather forecasts. Math. Geosci. 50, 209–234. doi:10.1007/s11004-017-9709-7
Zastenker, G., Dalin, P., Petrukovich, A., Nozdrachev, M., Romanov, S., Paularena, K., et al. (2000). Solar wind structure dynamics by multipoint observations. Phys. Chem. Earth, Part C Sol. Terr. Planet. Sci. 25, 137–140. doi:10.1016/S1464-1917(99)00055-0
Zhang, D., Liu, W., and Zhang, Z. (2022). Validation of the use of THEMIS-B and THEMIS-C as a near-Earth solar wind monitor. Earth Planet. Phys. 6, 546–554. School of Space and Environment, Beihang University, Beijing 100191, China, and Key Laboratory of Space Environment Monitoring and Information Processing, Ministry of Industry and Information Technology, Beijing 100191, China. doi:10.26464/epp2023003
Keywords: solar wind-magnetosphere interaction, solar wind, uncertainty, magnetosphere, machine learning, neural network, Bayesian, magnetospheric multiscale (MMS)
Citation: O’Brien C, Walsh BM, Zou Y, Tasnim S, Zhang H and Sibeck DG (2023) PRIME: a probabilistic neural network approach to solar wind propagation from L1. Front. Astron. Space Sci. 10:1250779. doi: 10.3389/fspas.2023.1250779
Received: 30 June 2023; Accepted: 22 August 2023;
Published: 19 September 2023.
Edited by:
Nishtha Sachdeva, University of Michigan, United StatesReviewed by:
Steven Morley, Los Alamos National Laboratory (DOE), United StatesEnrico Camporeale, University of Colorado Boulder, United States
Copyright © 2023 O’Brien, Walsh, Zou, Tasnim, Zhang and Sibeck. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: C. O’Brien, b2JyaWVuY29AYnUuZWR1
 Connor O’Brien
Connor O’Brien Brian M. Walsh
Brian M. Walsh Ying Zou
Ying Zou Samira Tasnim
Samira Tasnim Huaming Zhang
Huaming Zhang David Gary Sibeck
David Gary Sibeck