Simulation study of asteroid mass determination using CSST asteroid observations

The objective of this study is to explore the potential of the Chinese Space Station Telescope (CSST) in asteroid mass determination with asteroid-asteroid close encounters. The CSST is expected to observe some asteroids with an accuracy of several milliarcseconds and has a limiting magnitude of 26 (AB mag) or higher in the g and r bands. By combining CSST observations with existing ground-based observations, significant improvements in asteroid mass precision can be achieved. To quantify the CSST’s capability in asteroid mass determination, three types of simulations are conducted. In Type A simulation, 58 close encounters with available Gaia DR2 observations were considered, assuming CSST observes asteroids at a frequency similar to Gaia’s. After using the simulated CSST observations, asteroid mass precision is improved substantially. In seven events, the determined precision are better than 5%. Type B simulation is performed based on a tentative optical survey plan of CSST, but the limited opportunities to observe asteroids involved in a close encounter with strong perturbation from to-be-determined masses. As a result, the precision of mass determination is low, though the improvement brought by CSST data is obvious. This implies that the dedicated observations are necessary for CSST to contribute masses with high precision. Type C simulation is performed with a small amount of CSST observing time, to be specific for a strong encounter, 144 observations spanning 3 years centered at the encounter time, totaling about 7.2 observation hours. In this case, CSST can determine a number of asteroid masses, of which 10 asteroid’s precision are expected to be better than 10%.

1 Introduction

Density is a fundamental physical parameter of asteroids, and it plays a crucial role in understanding the composition and evolution of asteroids (Britt et al., 2002; Carry, 2012). However, the number of asteroids with known densities is only about 400 so far (Carry, 2012; Kretlow, 2020). This is mainly due to the small number of asteroids with precisely determined masses, which are essential for the density determination. Precisely determined masses of asteroids can improve the modeling precision of the gravitational field of the solar system, leading to an improved precision of the perturbations on the objects in the field (Standish, 2000). Furthermore, the precision of the present Mars ephemeris is mainly affected by the modeling precision of the main belt asteroids, and the continuous improvement of asteroid mass determination can help improving the precision of the Mars ephemeris (Standish, 2000; Fienga et al., 2009). At present, over 900 independent mass determinationshave been performed for more than 158 asteroids using the dynamical method of analyzing close encounters between asteroids (Carry, 2012; Goffin, 2014; Kretlow, 2020). This approach involves inferring the mass of a massive asteroid, usually referred to as a perturber, by analyzing the perturbations it causes on a massless asteroid, which is referred to as a test particle. One of the key scientific objectives of the Gaia mission is to determine the masses of about 100 asteroids (Mouret et al., 2008).

The Chinese Space Station Telescope (CSST), a major scientific project of the Space Utilization System within the China Manned Space Program, is scheduled to launch and fly with the Tiangong Space Station in 2024 (Zhan, 2021). It is a 2 m reflecting telescope that has a 1 deg² filed of view and 0.15 arcsec spatial resolution. It has the potential to advance our understanding from solar system to cosmology (Zhan, 2011; Gong et al., 2019; Cao et al., 2022; Gai et al., 2022). CSST Optical Survey (CSST-OS) aims to conduct a wide-field survey of over 17,500 square degrees and a deep-field survey of more than 400 square degrees over the course of 10 years (Cao et al., 2018; Zhan, 2018; Zhan, 2021). The typical exposure times for the wide-field and deep-field surveys are 150 and 250 s, respectively. Due to its large field of view and the capability to detect objects with a magnitude limit of 26 in g-band, CSST-OS is expected to capture numerous asteroids during its survey.

In this paper, we propose to evaluate the potential of the CSST in asteroid mass determination. On one hand, the high-precision observations provided by CSST-OS at the milliarcsecond level can extend the time span for observations. On the other hand, CSST-OS can also detect numerous faint asteroids, thereby increasing the sample of close encounters. Furthermore, CSST can improve the asteroid mass at a small cost by observing some specific asteroids.

The paper is organized as follows: Section 2 presents the algorithm used to determine asteroid masses with close encounters; Section 3 describes observable close encounter events with the CSST; Section 4 details the simulation experiments; and Section 5 presents the results and discussion; Section 6 is conclusion.

2 The mass determination method

Asteroid mass determination with close encounters involves three steps (Li et al., 2019). Firstly, selecting suitable close encounters (see Section 3). Secondly, obtaining observational data, including simulated and actual data used in this study (see Section 4). Lastly, fitting a properly determined dynamical model to the observational data.

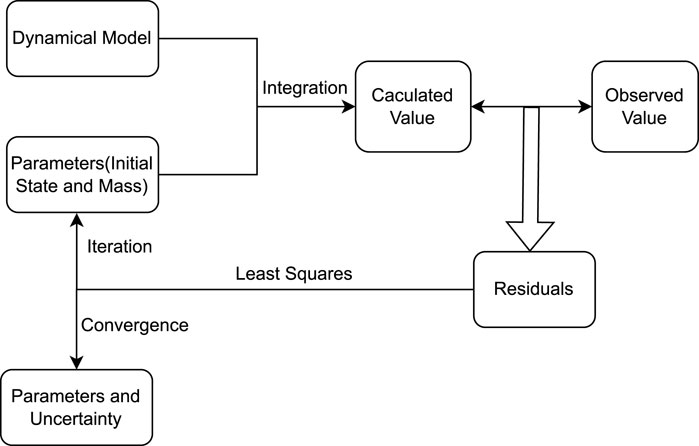
In the context of asteroid mass determination, the free parameters to be determined are the initial state s₀ = s(t₀) of the test particle at the epoch t₀ and the mass M of the perturber (Li et al., 2019). Figure 1 illustrates the main process flow of the algorithm for asteroid mass determination.

FIGURE 1

FIGURE 1. Asteroid mass determination algorithm flow.

In the simulations, the dynamical model for the test particles accounts for the point-mass gravitational effects of the Sun, the eight planets, Pluto, the three biggest asteroids in main belt (Ceres, Pallas, Vesta), and the perturber. Parameterized post-Newtonian general relativity corrections of the Sun, the eight planets, and Pluto are also considered. DE440 provides the positions and masses of the Sun and the eight planets as well as Pluto and the masses of three asteroids (Park et al., 2021). The Horizons system provides the positions of the asteroids. Least squares method is used to determine s₀ and M. The objective function is given by

${\chi }^2={\xi }^{T}W\xi ,(1)$

where ξ represents the residual (i.e., the difference between the observed and calculated values), W = Γ⁻¹ is the weight matrix, and Γ is the error matrix.

2.1 Selecting appropriate model parameters

Carpino et al. (2003) noted the issue of selecting model parameters in the process described above. Varying initial epoch t₀ leads to different model parameters, and changes the relationship between observables and parameters. Li et al. (2019) addressed this issue, selecting three specific epochs and studying the trend of Δ²(M) as a function of mass M. Here, Δ²(M) represents the average angular distance between the calculated and nominal orbits of the test particle at different values of M. Notably, this approach was developed without the consideration of differences in precision for the case that only ground-based observations were available.

However, after introducing observations from Gaia and CSST, the precision can vary significantly, ranging from milliarcseconds to arcseconds. To address this issue, we propose the utilization of Fisher information I(M), which captures the information that the observations contain about the mass parameter. The aim is to employ this information to select the appropriate model parameters. In this context, I(M) can be formally expressed as the expectation of the second-order derivative of the objective function χ², i.e., (Ly et al., 2017),

$\begin{array}{cc}\hfill I\left(M_0,t_0\right)& ={\left.\frac{1}{2}\mathbf{E}\left[\frac{{\partial }^2{\chi }^2}{\partial M^2}\right]\right|}_{M=M_0}\hfill \\ \hfill & =\frac{1}{2}\frac{{\partial }^2{\left({\mathit{C}}_{M_0}-{\mathit{C}}_M\right)}^T\left({\mathit{C}}_{M_0}-{\mathit{C}}_M\right)}{\partial M^2}\hfill \\ \hfill & =\frac{1}{2}\frac{{\partial }^2{\chi }_{M_0}^2}{\partial M^2},\hfill \end{array}(2)$

where C_M represents the calculated value of the observables, i.e., the right ascension and declination of the test particles, for a given mass M. The problem of selecting appropriate model parameters is transformed into an optimization problem that find the optimal value of t₀:

$\underset{t\in \left[t_{\text{min}},t_{\text{max}}\right]}{\arg \max }I\left(t;M\right).(3)$

In this paper, a second-order central difference approximation is used to compute $\frac{{\partial }^2{\chi }_{M_0}^2}{\partial M^2}$, and a grid method is employed to find the maximum for Eq. 3.

2.2 Real case study with (532) Herculina

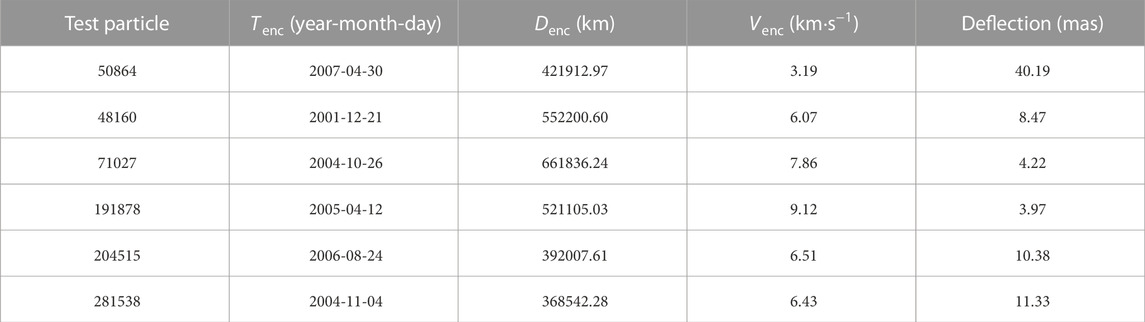
(532) Herculina is an S-type main-belt asteroid (Bus and Binzel, 2002; Carry, 2012). In Tang et al. (2017), a total of six close encounters listed in Table 1 are useful to determine the mass of (532) Herculina, and one of the encountering test particles, (50,864) 2000 GM2, has Gaia observations.

TABLE 1

TABLE 1. Close encounters used to determine the mass of (532) Herculina.

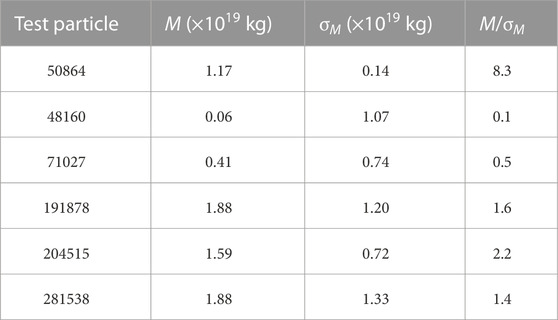
Table 2 gives the determined masses using Gaia and ground-based observations, as well as the root mean square of the residuals of the ground-based observations in the right ascension σ_{Δα cos  δ} and declination σ_Δδ, and Gaia observations in the AC σ_ΔAC and AL σ_ΔAL directions, respectively. The results using only ground-based observations are given in Table 3.

TABLE 2

TABLE 2. Determination of (532) Herculina mass using Gaia observations with (50,864) 2000 GM2.

TABLE 3

TABLE 3. Determination of (532) Herculina mass using only ground-based observations.

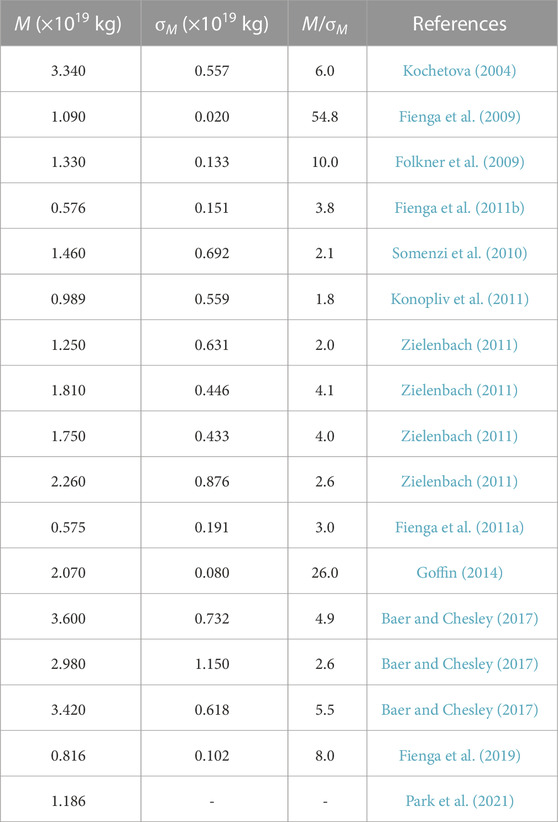
Table 4 gives the previously determined masses of (532) Herculina, and Figure 2 compares the masses determined in the present paper and the masses given by the previous authors.

TABLE 4

TABLE 4. (532) Herculina masses given by previous authors.

FIGURE 2

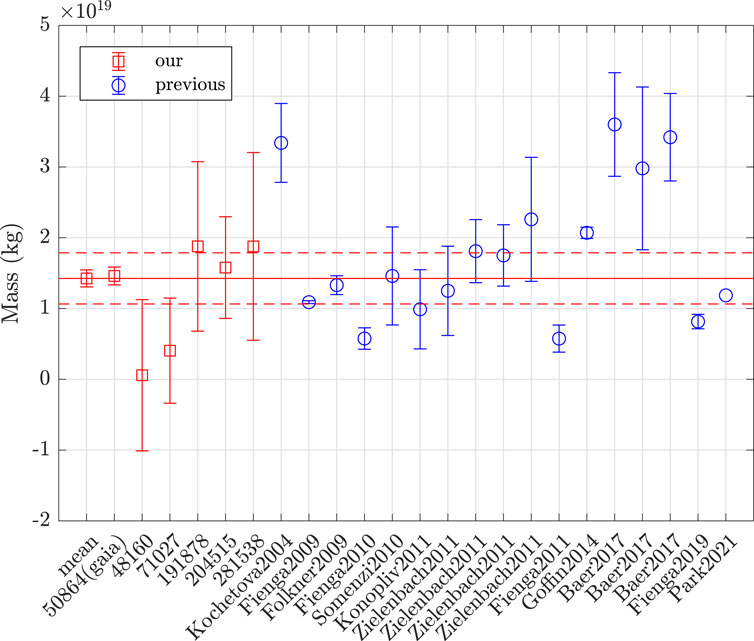
FIGURE 2. Comparison of the masses given in the present paper for (532) Herculina with those given by previous authors. The red boxes with 1σ error bars denote our results, the blue circles with 1σ error bars denote the previous results, the red solid line is the average value given in the present paper, and the dotted dashed line gives the 3σ boundaries.

As can be seen from Figure 2, the weighted average value of 1.43 ± 0.12 × 10¹⁹ kg given in the present paper is within 3σ boundaries of the masses determined for each independent close encounter, and four of them are within 1σ boundaries. Our determined masses are in good agreement with most of the previous results, and the precision is the highest among those determined with the similar method.

Based on the mass we determined and a diameter of 204 ± 3 km given by Hanuš et al. (2017), the density of (532) Herculina is 3.91 ± 0.41 g⋅cm⁻³, which is much higher than the density of S-type asteroids [2 to 3 g⋅cm⁻³ from Carry (2012)]. According to Gehrels and Drummond (1986), (532) Herculina may have undergone a process of differentiated melting. As a consequence, low-density, high-reflectivity silicate material cooled and covered its surface, which is responsible for observed characteristics of S-type. On the other hand, the presence of dark areas on its surface is due to collisions that broke the inner high-density material through to the surface. The high density we obtained support this point of view.

3 The selection of close encounters

This study uses Tang’s 2017 database (Tang et al., 2017) of close encounters that occurred between 2000 and 2030. To focus on the potential of the upcoming CSST, we selected encounters after 1 January 2010.

From the screened 1,667 events, involving 237 perturbers and 968 test particles, there are 148 events with predicted precisions better than 10%, 310 events better than 20%, and 720 events better than 50%. There are three events with minimum distances less than 0.0001 AU and 175 events less than 0.001 AU. Among those events, 160 occur between 2024 and 2030, which can be observed by CSST for 3 years before and after the encounters and may improve the asteroid mass precision significantly.

4 Simulations

The theoretical orbits of the test particles are obtained by numerical integration, with initial conditions sourced from JPL’s orbital elements database¹. We use the real observation moments for the ground-based MPC² and sapced-based Gaia observations as the reference for the simulated observations. To minimize the precision difference between the simulated and real observations, we use the real observation errors for ground-based and Gaia observations. For CSST observations, by referring to Fu et al. (2023), we estimate the error to be four times that of Gaia’s (Mouret et al., 2007), as shown in the following equation:

$\sigma =\left\{\begin{array}{cc}\hfill 1.2& \text{\hspace{0.17em}mas}\text{for\hspace{0.17em}}V\le 15\hfill \\ \hfill 4\times 10^{0.147V-2.71}& \text{\hspace{0.17em}mas}\text{for\hspace{0.17em}}V>15.\hfill \end{array}\right.(4)$

In order to investigate the ability of CSST in asteroid mass determination more specifically, we design simulations with three types of simulations, denoted as A, B, C, respectively. Type A simulation is designed for exploring the limiting capability of CSST in asteroid mass determination in the case of combing with Gaia observations. Type B and C simulations are designed to investigate the effects that could be achieved by using CSST in the current situation. Type B uses only observations from the tentative survey plan, while Type C will request a small amount of observation time.

We conduct Type A simulation with test particles that have Gaia observations available. We conducted a cross-matching between the close encounter database and asteroid observation data from Gaia DR2, resulting in a total of 58 events. The impact of adding CSST observations to the current ground-based and Gaia DR2 data was assessed. Specifically, the simulated CSST observations are obtained 3 years after the Gaia DR2 observations. Type B simulation focus on those test particles that could be observed by the CSST tentative survey plan. We searched for test particles in the database based on the tentative CSST survey plan and obtained 18 events with more than 10 observations. We evaluate the impact of incorporating CSST with the existing ground-based observations. In Type C simulation, the main focus is to identify specific events where the combination of CSST observations is expected to yield significant improvements. We selected 73 test events with predicted precision better than 20% and encountering after 2023. We assess the effect of combining CSST observations with existing ground-based observations. The simulation assumed a 3-year observation period before and after the close encounter, with a frequency of one observation every half month and four or two observations each time, denoting as C1 and C2, resulting in a total of 288 or 144 observations. Please refer to Table 5 for the relevant descriptions of all three simulation types. For each type, we utilized the mass determination algorithm described in Section 2. The algorithm initially calculate the Fisher information of the observations to determine the appropriate model parameters, followed by a least squares fit to obtain the mass and its corresponding uncertainty.

TABLE 5

TABLE 5. Simulation types.

5 Results and discussion

This section presents the results of the three types of simulations, including statistical analyses of the relative precision, σ_M/M, and comparison analysis. Here, σ_M represents the 1-sigma uncertainty in the mass, while M denotes the reference mass of the perturber.

5.1 Type A simulation

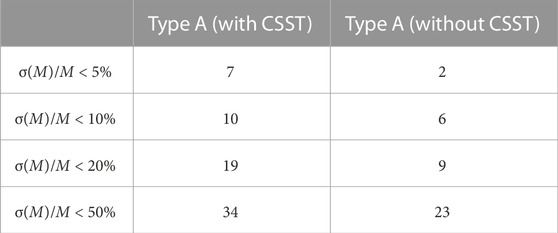
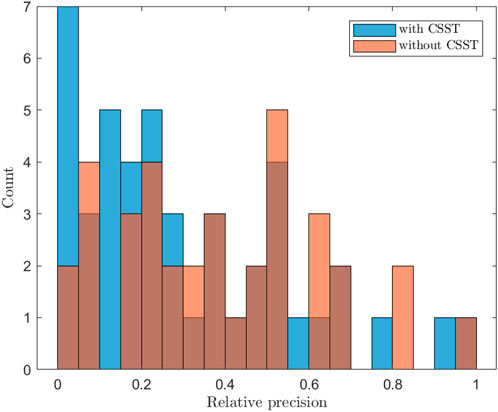
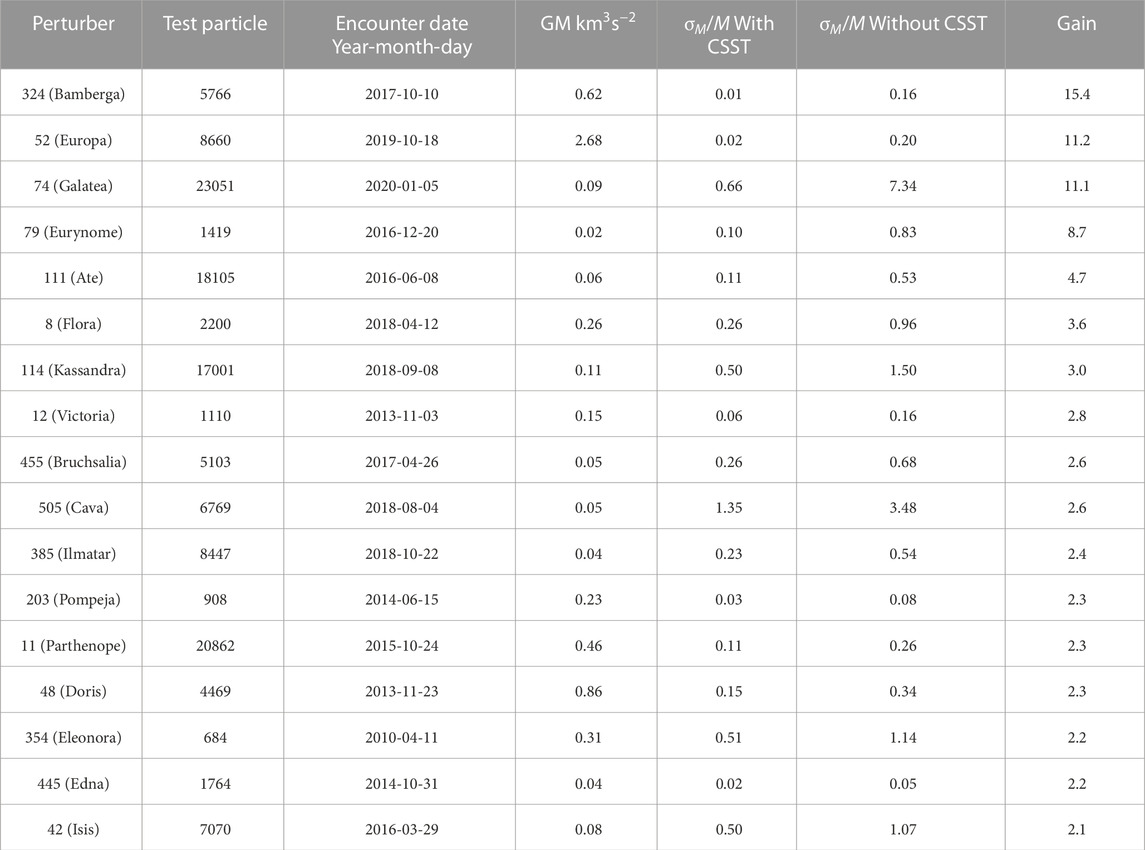
Table 6 presents the cumulative numbers within several precision ranges for both cases: using CSST data and not using it. Meanwhile, Figure 3 illustrates the precision distributions. As depicted in Figure 3 and summarized in Table 6, the inclusion of CSST observations significantly improve the precision of asteroid mass determinations. Notably, the number of determinations with precision better than 5% increases from 2 to 7. We quantitatively measure this improvement using a metric called “gain,” which represents the ratio of precision achieved with CSST observations to that achieved without them. Our results reveal an average gain of 2.4 across 57 events, with 17 events exhibiting a gain greater than 2. Further analysis of the relationship between the encounter moment and the gain for these 57 events indicates that the addition of CSST observations yields a more significant improvement for events occurring near the CSST survey period. For a concise summary of events with a gain exceeding 2, please refer to Table 7.

TABLE 6

TABLE 6. Precision statistics of Type A simulation.

FIGURE 3

FIGURE 3. Precision statistics of Type A simulation.

TABLE 7

TABLE 7. Events with gain greater than 2 in Type A simulation.

It is crucial to note that our Type A simulation assumes an equivalent frequency of asteroid observations for CSST and Gaia. However, this assumption does not align with the current tentative survey plan, which excludes the ecliptic, resulting in a significant reduction in the frequency of asteroid observations. Nevertheless, it is worth emphasizing that future adjustments to the survey plan could potentially align CSST’s observation frequency with that of Gaia. Combining these observations could greatly improve the precision of asteroid mass determination.

5.2 Type B simulation

Type B simulation comprise 18 events. Although the test particles involved in this simulation are expected to be observed an average of 20.7 times during the tentative CSST survey, the perturbation caused by their respective perturbers is relatively weak. Consequently, the expected precision of mass determination is not high. Even with the incorporation of CSST observations, only two events yield mass determinations with precision better than 50%.

Conversely, the addition of CSST observations does make a significant contribution to improving the precision of these events. On average, there is a gain of 4.2 across all 18 events, with 7 events displaying a gain of more than 2. Generally, these results suggest that the CSST tentative survey plan would not contribute much to asteroid mass determination.

5.3 Type C simulation

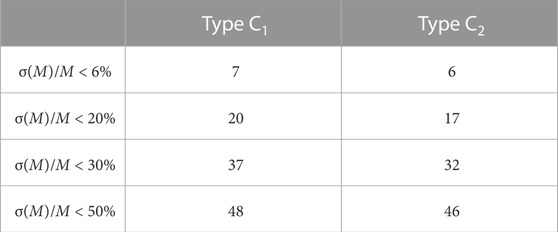
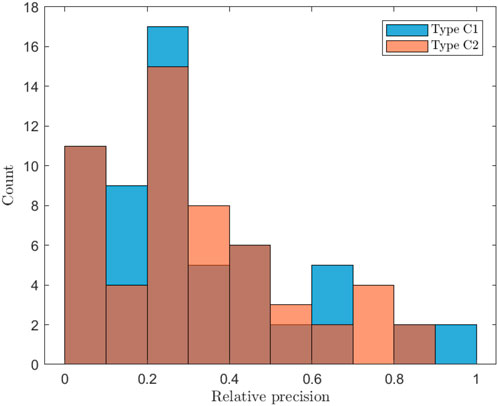
Type C simulation explores the option of requesting a small fraction of CSST observation time for selected test particles. This strategy has the potential to significantly enhance asteroid mass determination with minimal expenditure. In Table 8, we present the cumulative number of events for which the determined mass falls within specific precision ranges, and Figure 4 visualizes the precision distribution. C1 and C2 denote different observation strategies, and overall, C1 takes double the time of C2, and the specific strategies will be described below. The figure demonstrates the high effectiveness of adding CSST observations in asteroid mass determination. There are 6 events achieving precision better than 6%, and 17 events better than 20%. However, it’s important to note that doubling the number of observations (from C2 to C1) doesn’t result in a proportionate increase in gain. On average, the gain is only 1.25, with a maximum gain of 1.8 across the 65 events.

TABLE 8

TABLE 8. Precision statistics of Type C simulation.

FIGURE 4

FIGURE 4. Precision statistics of Type C simulation.

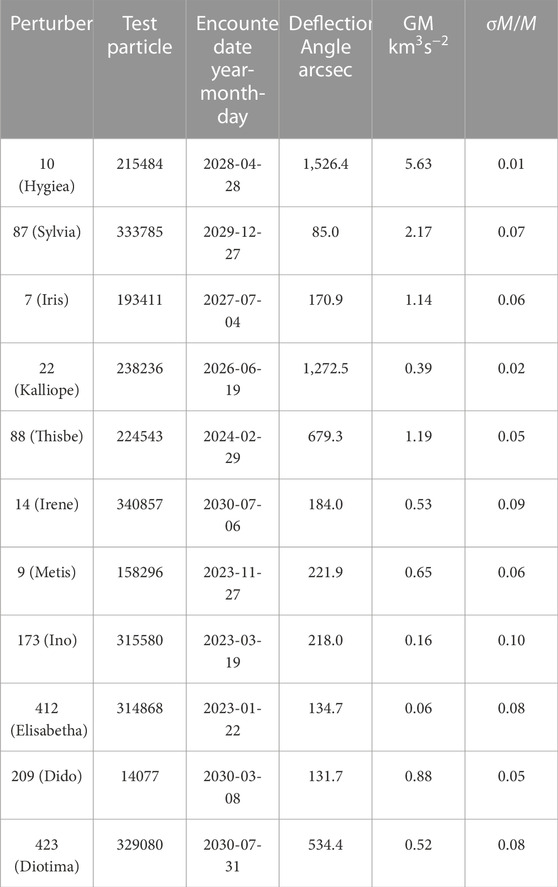
These findings suggest the potential for a specific observation strategy involving semi-monthly observations, each consisting of two 3-min exposures, over a total of 144 observations during the 3-year period before and after each encounter. This strategy would require approximately 7.2 h of CSST observation time. As a result, CSST could determine the masses of several asteroids, with 10 of them expected to achieve precision better than 10%, as detailed in Table 9. A proposal will be given for utilizing CSST observation time and coordinating with ground-based observations in the future.

TABLE 9

TABLE 9. Events with precision better than 10% in Type C simulation.

6 Conclusion

This paper assess the ability of CSST for asteroid mass determination. Based on the assumption that the frequency of CSST and Gaia observations of asteroids is equivalent, simulation results demonstrate that integrating CSST observations can considerably improve the precision of asteroid mass determination. The average precision gain reaches 2.4, and this effect is particularly notable for those encounter events that happen at times inside or close to the CSST observation time span. Due to the limited opportunities to observe asteroids with CSST tentative survey plan, the survey data are not as efficient as one would hope in increasing the number of asteroids with high precision mass. On the other hand, however, a small amount of dedicated observations would be efficient enough. Indeed, for each 10 close encounters, 144 observations (requiring only 7.2 observing hours) distributed over a period of 3 years centered at the encounter time would be enough to determine the mass with precision better than 10%.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

FL had the idea for the study and wrote the main part of code and manuscript. YF, YY, and JC helped develop and test the code and write the manuscript. YF made a critical review of the idea and supported the work throughout the process. All authors contributed to the article and approved the submitted version.

Funding

This work is financially supported by National Natural Science Foundation of China (Grants Nos 12103091, 11273066, and 12203105). We acknowledge the science research grants from the China Manned Space Project with Nos CMS-CSST⋅478 2021-A12 and CMS-CSST2021-B10.

Acknowledgments

We are grateful for the very fruitful criticism by the referee. This research has made use of data provided by the International Astronomical Union’s Minor Planet Center. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹See here https://ssd.jpl.nasa.gov/sb/elem_tables.html

²See here https://minorplanetcenter.net/

References

Baer, J., and Chesley, S. R. (2017). Simultaneous mass determination for gravitationally coupled asteroids. Astronomical J. 154, 76. doi:10.3847/1538-3881/aa7de8

CrossRef Full Text | Google Scholar

Britt, D. T., Yeomans, D., Housen, K., and Consolmagno, G. (2002). Asteroid density, porosity, and structure. 485–500.

Google Scholar

Bus, S. J., and Binzel, R. P. (2002). Phase II of the small main-belt asteroid spectroscopic survey. A feature-based taxonomy. Icarus 158, 146–177. doi:10.1006/icar.2002.6856

CrossRef Full Text | Google Scholar

Cao, Y., Gong, Y., Liu, D., Cooray, A., Feng, C., and Chen, X. (2022). Anisotropies of cosmic optical and near-IR background from the China space station telescope (CSST). Mon. Notices R. Astronomical Soc. 511, 1830–1840. doi:10.1093/mnras/stac151

CrossRef Full Text | Google Scholar

Cao, Y., Gong, Y., Meng, X.-M., Xu, C. K., Chen, X., Guo, Q., et al. (2018). Testing photometric redshift measurements with filter definition of the Chinese Space Station Optical Survey (CSS-OS). Mon. Notices R. Astronomical Soc. 480, 2178–2190. doi:10.1093/mnras/sty1980

CrossRef Full Text | Google Scholar

Carpino, M., Milani, A., and Chesley, S. R. (2003). Error statistics of asteroid optical astrometric observations. Icarus 166, 248–270. doi:10.1016/S0019-1035(03)00051-4

CrossRef Full Text | Google Scholar

Carry, B. (2012). Density of asteroids. Planet. Space Sci. 73, 98–118. doi:10.1016/j.pss.2012.03.009

CrossRef Full Text | Google Scholar

Fienga, A., Deram, P., Viswanathan, V., Di Ruscio, A., Bernus, L., Durante, D., et al. (2019). INPOP19a planetary ephemerides. Notes Scientifiques et Techniques de l’Institut de Mecanique Celeste 109.

Google Scholar

Fienga, A., Kuchynka, P., Laskar, J., Manche, H., and Gastineau, M. (2011a). Asteroid mass determinations with INPOP planetary ephemerides. EPSC-DPS Jt. Meet. 2011 2011, 1879.

Google Scholar

Fienga, A., Laskar, J., Kuchynka, P., Manche, H., Desvignes, G., Gastineau, M., et al. (2011b). The INPOP10a planetary ephemeris and its applications in fundamental physics. Celest. Mech. Dyn. Astronomy 111, 363–385. doi:10.1007/s10569-011-9377-8

CrossRef Full Text | Google Scholar

Fienga, A., Laskar, J., Morley, T., Manche, H., Kuchynka, P., Le Poncin-Lafitte, C., et al. (2009). INPOP08, a 4-D planetary ephemeris: from asteroid and time-scale computations to ESA Mars Express and Venus Express contributions. Astronomy Astrophysics 507, 1675–1686. doi:10.1051/0004-6361/200911755

CrossRef Full Text | Google Scholar

Folkner, W. M., Williams, J. G., and Boggs, D. H. (2009). The planetary and lunar ephemeris DE 421. Interplanet. Netw. Prog. Rep. 178, 1–34.

Google Scholar

Fu, Z.-S., Qi, Z.-X., Liao, S.-L., Peng, X.-Y., Yu, Y., Wu, Q.-Q., et al. (2023). Simulation of csst’s astrometric capability. Front. Astronomy Space Sci. 10. doi:10.3389/fspas.2023.1146603

CrossRef Full Text | Google Scholar

Gai, M., Vecchiato, A., Busonero, D., Riva, A., Cancelliere, R., Lattanzi, M., et al. (2022). Consolidation of the Gaia catalogue with Chinese space station telescope astrometry. Front. Astronomy Space Sci. 9, 1002876. doi:10.3389/fspas.2022.1002876

CrossRef Full Text | Google Scholar

Gehrels, T., and Drummond, J. (1986). 532 Herculina, A differentiated asteroid with two maria. Bull. Am. Astronomical Soc. 18, 798.

Google Scholar

Goffin, E. (2014). Astrometric asteroid masses: a simultaneous determination. Astronomy Astrophysics 565, A56. doi:10.1051/0004-6361/201322766

CrossRef Full Text | Google Scholar

Gong, Y., Liu, X., Cao, Y., Chen, X., Fan, Z., Li, R., et al. (2019). Cosmology from the Chinese space station optical survey (CSS-OS). Astrophysical J. 883, 203. doi:10.3847/1538-4357/ab391e

CrossRef Full Text | Google Scholar

Hanuš, J., Viikinkoski, M., Marchis, F., Ďurech, J., Kaasalainen, M., Delbo’, M., et al. (2017). Volumes and bulk densities of forty asteroids from ADAM shape modeling. Astronomy Astrophysics 601, A114. doi:10.1051/0004-6361/201629956

CrossRef Full Text | Google Scholar

Kochetova, O. M. (2004). Determination of large asteroid masses by the dynamical method. Sol. Syst. Res. 38, 66–75. doi:10.1023/B:SOLS.0000015157.65020.84

CrossRef Full Text | Google Scholar

Konopliv, A. S., Asmar, S. W., Folkner, W. M., Karatekin, Ö., Nunes, D. C., Smrekar, S. E., et al. (2011). Mars high resolution gravity fields from MRO, Mars seasonal gravity, and other dynamical parameters. Icarus 211, 401–428. doi:10.1016/j.icarus.2010.10.004

CrossRef Full Text | Google Scholar

Kretlow, M. (2020). “Size, mass and density of asteroids (SiMDA) - a web based archive and data service,” in European planetary science congress. EPSC2020–690. doi:10.5194/epsc2020-690

CrossRef Full Text | Google Scholar

Li, F., Fu, Y., and Yuan, Y. (2019). A new mass determination of (349) dembowska with close encounters. Astronomical J. 157, 210. doi:10.3847/1538-3881/ab1843

CrossRef Full Text | Google Scholar

Ly, A., Marsman, M., Verhagen, J., Grasman, R., and Wagenmakers, E.-J. (2017). A tutorial on Fisher information. arXiv e-prints, arXiv:1705.01064.

Google Scholar

Mouret, S., Hestroffer, D., and Mignard, F. (2007). Asteroid masses and improvement with Gaia. Astronomy Astrophysics 472, 1017–1027. doi:10.1051/0004-6361:20077479

CrossRef Full Text | Google Scholar

Mouret, S., Hestroffer, D., and Mignard, F. (2008). Asteroid mass determination with the Gaia mission. Planet. Space Sci. 56, 1819–1822. doi:10.1016/j.pss.2008.02.026

CrossRef Full Text | Google Scholar

Park, R. S., Folkner, W. M., Williams, J. G., and Boggs, D. H. (2021). The JPL planetary and lunar ephemerides DE440 and DE441. Astronomical J. 161, 105. doi:10.3847/1538-3881/abd414

CrossRef Full Text | Google Scholar

Somenzi, L., Fienga, A., Laskar, J., and Kuchynka, P. (2010). Determination of asteroid masses from their close encounters with Mars. Planet. Space Sci. 58, 858–863. doi:10.1016/j.pss.2010.01.010

CrossRef Full Text | Google Scholar

Standish, M. (2000). “Dynamical reference frame - current relevance and future prospects,” in IAU colloq. 180: towards models and constants for sub-microarcsecond astrometry. Editors K. J. Johnston, D. D. McCarthy, B. J. Luzum, and G. H. Kaplan (USA: IEEE), 120.

CrossRef Full Text | Google Scholar

Tang, H. J., Li, F., and Fu, Y. N. (2017). Application of close encounters in determining the masses of asteroids. Acta Astron. Sin. 58, 59. doi:10.15940/j.cnki.0001-5245.2017.06.008

CrossRef Full Text | Google Scholar

Zhan, H. (2011). Consideration for a large-scale multi-color imaging and slitless spectroscopy survey on the Chinese space station and its application in dark energy research. Sci. Sinica Phys. Mech. Astronomica 41, 1441–1447. doi:10.1360/132011-961

CrossRef Full Text | Google Scholar

Zhan, H. (2018). “An overview of the Chinese space station optical survey,” in 42nd COSPAR scientific assembly (USA: IEEE), 42.

Google Scholar

Zhan, H. (2021). The wide-field multiband imaging and slitless spectroscopy survey to be carried out by the survey space telescope of China manned space program. Chin. Sci. Bull. 66, 1290–1298. doi:10.1360/TB-2021-0016

CrossRef Full Text | Google Scholar

Zielenbach, W. (2011). Mass determination studies of 104 large asteroids. Astronomical J. 142, 120. doi:10.1088/0004-6256/142/4/120

CrossRef Full Text | Google Scholar