- 1Center for Astrostatistics, Department of Astronomy and Astrophysics, Penn State University, University Park, PA, United States
- 2Department of Physics and Astronomy, University of Alabama, Huntsville, AL, United States
We review the iid2022 workshop on statistical methods for X-ray and γ-ray astronomy and high–energy astrophysics event data in astronomy, held in Guntersville, AL, on Nov. 15–18 2022. New methods for faint source detection, spatial point processes, variability and spectral analysis, and machine learning are discussed. Ideas for future developments of advanced methodology are shared.
1 Statistical challenges arising in high–energy astrophysics
The science analysis of data in high–energy astrophysics differs from most fields of astronomy in important ways. The data, typically from space-based observatories, consist of energetic photons counted individually as they arrive in a detector. These datasets often can be viewed in tabular form as a sequence of events with four characteristics: arrival time, location in two-dimensions, and energy. The analysis commonly proceeds in stages: sources are identified in the 2-dimensional image, photons are extracted for individual sources or emitting regions, and 1-dimensional analysis proceeds for the energy distribution and arrival times. These univariate distributions are often complicated: multi-component spectral emission processes are convolved with instrumental sensitivity, and temporal processes can depend on unpredictable variations in accretion onto compact objects. Common analysis procedures include:
1) Individual photons are examined, often smoothed with knowledge of the telescope point spread function, in the image plane;
2) Sparse samples of individual events from faint sources are modeled along one-dimensional energy (spectra) or temporal axis (light curves);
3) Richer samples of events are grouped into bins along the spectral or temporal axis and then subject to statistical or astrophysical modeling.
Table 1 summarizes important statistical procedures developed in the high–energy astrophysical community over the past half century. The accomplishments are impressive, but the impact on the research community is mixed. Some methods, such as the Lomb-Scargle periodogram, are widely used, although there may be insufficient appreciation of the challenges of estimating reliable False Alarm Probabilities (VanderPlas, 2018). But other valuable statistical procedures − such as different limits for source existence and flux (Kashyap et al., 2010) and Bayesian estimates of faint-source hardness ratios (Park et al.,2006) − are not commonly used. Many have listened the warning that likelihood ratio tests should not be used near the boundary of parameter values (Protassov et al., 2002), but there is inadequate recognition that likelihood ratios should be penalized by model complexity as with the Bayesian Information Criterion.
There is also a general unawareness within the astronomical community of basic methods that are common in other fields. For example, multiple linear regression for count data (Cameron and Trivedi, 2013) is used extensively in econometrics and other areas, but astronomers often compare a response variable to single covariates in a sequential fashion. Aperiodic stochastic temporal behaviors (that might arise from accretion processes or magnetic activity) are analyzed using Fourier methods designed for periodic time series rather than autoregressive modeling (Box et al., 2015).
2 The iid2022 workshop
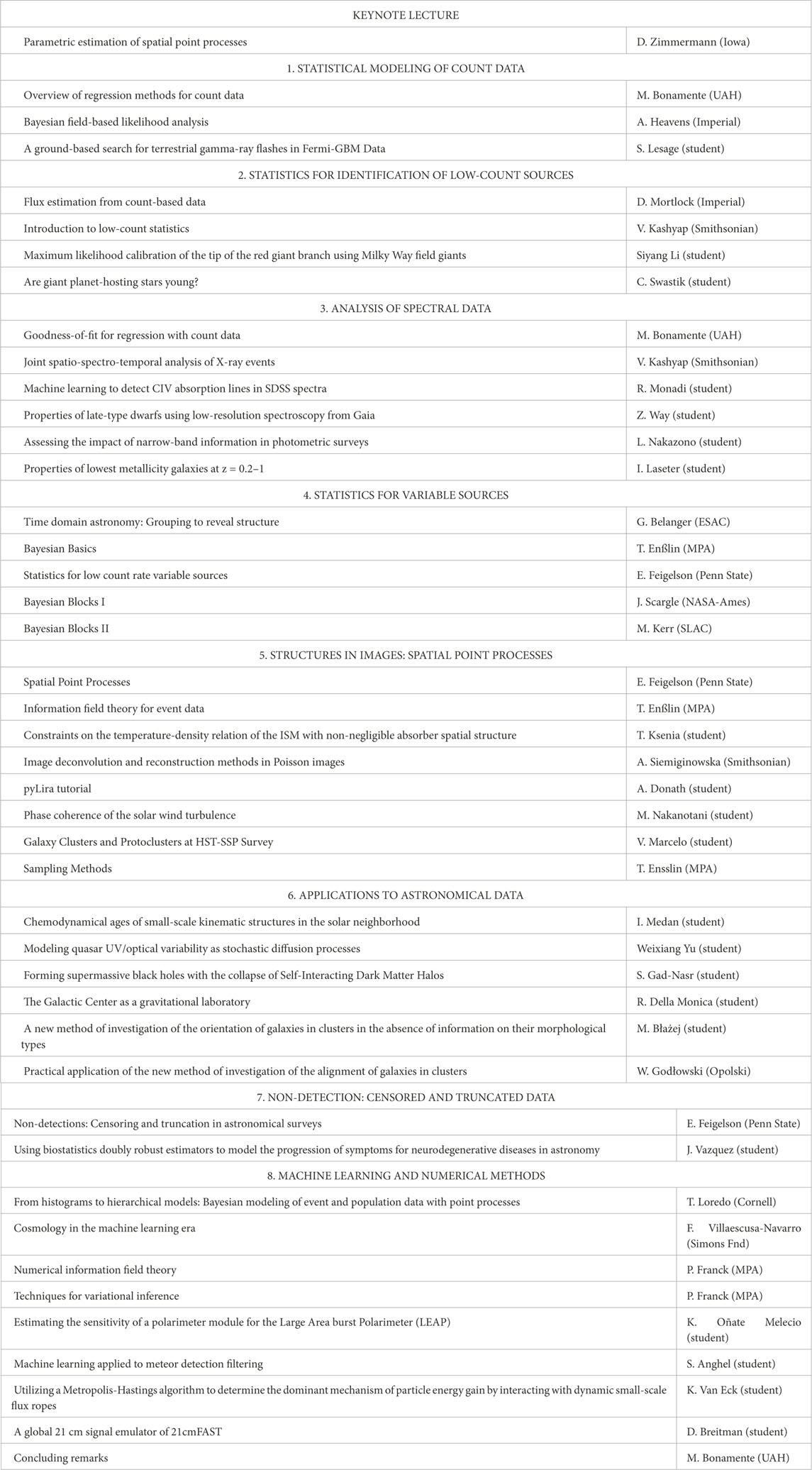
These issues motivated the workshop iid2022: Statistical Methods for Event Data-Illuminating the Dynamic Universe workshop, held in Huntsville Alabama on November 15–18, 2022. The spirit of the workshop was to give the participant an opportunity to review and learn about certain statistical methods, and also make presentations based on their own research. Accordingly, the eight sessions had introductory talks by more senior scientists, followed by oral presentations by students and early–career scientists. The National Science Foundation provided support for twenty students and early–career scientists to attend the workshop, via a grant issued to the University of Alabama in Huntsville. Such support was essential to attract students who would not otherwise have had the opportunity to attend.
Table 1 lists presentations made at the workshop. The vast majority of attendees were astronomers, with a few notable exceptions such as Prof. Dale Zimmermann of the University of Iowa, who gave the keynote lecture, and biostatistics graduate student Jesus Vasquez from the University of North Carolina at Chapel Hill.
3 Past accomplishments in methodology
High–energy astronomy has its roots in the study of cosmic rays on mountaintops during the 1930s and the discovery of X-rays from the solar corona during the 1950s (Rossi 1948; Tousey et al., 1951). The first detection of X-rays outside the Solar System involved a few thousand counts from the Galactic Plane obtained during a brief rocket flight (Giacconi et al., 1962). Early analyses involved simple statistical procedures such as the running mean (Bowyer et al., 1964) or (mathematically incorrect) least squares procedures applied to Poisson distributed data. The first use of the Poisson distribution to derive a cosmic source flux upper limit appears to be by Hearn (1968).
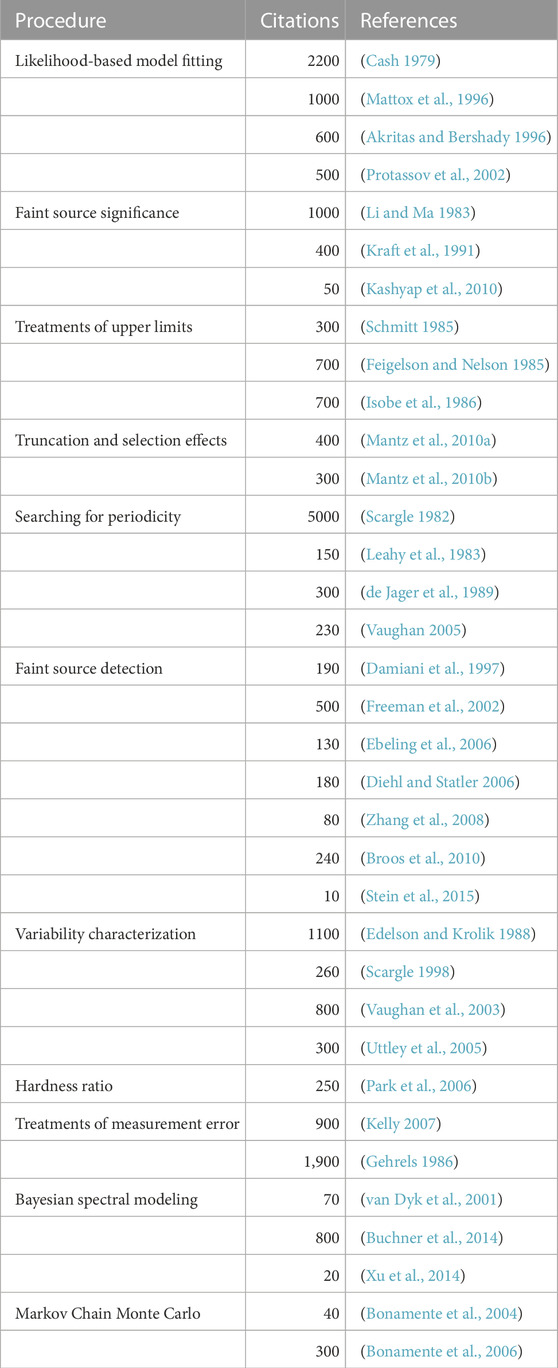
As satellite observatories replaced sounding rockets, more specialized statistical procedures began to emerge and accelerated in the early 21st century. Table 2 lists some of the important milestones classified by the scientific problem addressed. Some methods have had very broad impact with over a thousand citations by later studies. Altogether, the development and promulgation of analysis methods has been substantial and often quite successful.
In addition to procedures developed by practitioners within the field, methods for astronomy have been adopted from the wider arena of statistics. In early years, the textbook Data Reduction and Error Analysis for the Physical Sciences (Bevington, 1969) promoting least squares procedures had the greatest impact, not least because it included convenient Fortran codes that could be typed into IBM cards and used on main frame computers. It was largely supplanted by Numerical Recipes: The Art of Scientific Computing (Press et al., 1992) with editions providing code in Fortran, Pascal, C and C++. Numerical Recipes garnered
Other useful textbooks include Statistical Methods in Experimental Physics (Eadie et al., 1971), Practical Statistics for Astronomers (Wall and Jenkins, 2012), Modern Statistical Methods for Astronomy with R Applications (Feigelson and Babu, 2012), Statistics, Data Mining, and Machine Learning in Astronomy (Ivezić et al., 2019), and Statistics and Analysis of Scientific Data (Bonamente, 2022). Bayesian inference has become an important tool for modeling astronomical data as treated in texts like (Hilbe et al., 2017) and (Bailer-Jones, 2017). However, neither the classic works nor the newer volumes emphasize low-count rate problems as encountered in high–energy astronomy. Some require a basic knowledge of probability and statistics, and this can limit their diffusion among astronomers who are often missing such courses in their undergraduate education.
Table 3 lists a few of the methods discussed in the iid2022 workshop that are directly relevant to high–energy data and science analysis. Software implementation are combined with methodologies to allow quick implementation. In some cases, such as Baddeley’s book for analyzing Poisson images and variability detection procedures discussed by Feigelson, the codes are already available in the general purpose R statistical software environment. In other cases, such as Scargle’s Bayesian Blocks and Xu’s multidimensional change-point analysis, codes are written specifically for use in X-ray and γ-ray astronomy.
4 Looking towards the future
Presentations at the iid2022 workshop demonstrate that the development of innovative procedures for analyzing high–energy astronomical data is proceeding in a vibrant fashion. But there are considerable difficulties in promulgation of new methodology in the research communities. We outline here challenges that can be readily identified and suggest directions for improvements for the coming years.
4.1 Statistics education
One of the main needs in high–energy astronomy is a more rounded background in statistics for its practitioners. Most graduate degrees leading to an advanced degree in astronomy or astrophysics have no requirement of statistics courses, and are often limited to a course on ‘data analysis methods’ that lacks a foundation on statistical principles. Astronomers should be familiar with differences between nonparametric hypothesis testing and parametric modeling, Poisson and Gaussian distributions, least squares and likelihood based modeling, and stationary and nonstationary processes. Wavelet transforms, local regression, autoregressive models, and Fourier approaches to time series analysis should also be taught.
As both authors and teachers, it is our opinion that the typical high–energy data analyst should have a background that includes at least one undergraduate course using a statistics textbook such as Probability and Statistical Inference (Hogg et al., 2023). Such background would be beneficial to understand in detail the main statistical methods available, while giving the basic tools to undertake more complex tasks such as developing new statistical methods. At the graduate level, a course in methodology using textbooks like Statistics, Data Mining, and Machine Learning in Astronomy: A Practical Python Guide for the Analysis of Survey Data (Ivezić et al., 2019) and Modern Statistical Methods for Astronomy with R Applications (Feigelson and Babu, 2012) should be widely available in astronomy departments.
4.2 Integrate statistics into high–energy mission projects
High–energy astrophysics missions have traditionally included costs for ‘software development’ to write pipelines for processing telemetry data through Level 1 and Level 2 data products. But it is also important to fund, at the early stages, study of methods to be implemented in the pipeline and off-line science analysis by individual scientists. Methods as simple as maximum–likelihood analysis of count data (Cash, 1979) and as complex as information theory for gamma-ray astronomy (Enßlin, 2019) and 4-dimensional change-point analysis (Xu et al., 2021) should be considered.
Centralized facilities like NASA’s High Energy Astrophysics Science Archive Center and ESA’s European Space Astronomy Centre should institute organized procedures to evaluate newer methodologies and bring them into their code libraries for use by the research communities. Some methods can be incorporated into important existing software tools such as XSPEC (Arnaud, 1996) and SPEX (Kaastra et al., 1996), while other methods would be stand-alone codes added to libraries such as HEASoft. Documentation and tutorials for training community scientists in methodology should accompany software releases.
4.3 Funding for methodology
For two decades starting in 1990, NASA’s Science Mission Directorate had an Applied Information Systems Research program that included development of statistical tools, machine learning procedures, computational methods and algorithms for astronomical missions. But this program has changed focus and there is now no avenue for the research community to obtain funds for the development of new methodology for high–energy astrophysics. A program is needed similar to NASA’s Earth Science Division’s Advanced Information Systems Technology Program that includes development of advanced tools for data and science analysis. Several White Papers were submitted to the National Academy of Science Astro2020 Decadal Survey arguing for improved funding in astrostatistics and astroinformatics for all branches of the field.
4.4 Attitudes towards advances in methodology
A major reason for the slow advancement in usage of advanced − or even statistically acceptable − statistical methods in high–energy astrophysics is absence of penalty for inaccurate or misleading analysis methods. This includes review during mission planning, individual observing proposals, and the final published astrophysical literature. Sometimes forces lean towards mundane analysis procedures: authors who present advanced statistical methods in an astrophysics paper might encounter a reviewer poorly prepared in statistics. The journals of the American Astronomical Society now have a Statistics Editor, and reviewers expert in statistical analysis can be sought in addition to a reviewer expert in the scientific topic. A two-reviewer process is common for journals like Annals of Applied Statistics and Journal of Applied Statistics. The high–energy research community that widely encourages improvements in telescope and detector capabilities should also encourage improvements in data analysis capabilities that can improve the scientific return from any instrument or observing project.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
The iid2022 workshop was supported by NSF grant 2223560 “Conference: iid2022: Statistical Methods for Event Data—Illuminating the Dynamic Universe” awarded to the University of Alabama in Huntsville.
Acknowledgments
MB gratefully acknowledges University of Alabama in Huntsville students Stephen Lesage, Juan Alonso Guzmán and Samuel Johnson, whose dedication and support was essential for the success of the workshop.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Akritas, M. G., and Bershady, M. A. (1996). Linear regression for astronomical data with measurement errors and intrinsic scatter. Astrophysical J. 470, 706. doi:10.1086/177901
Arnaud, K. (1996). “Xspec: The first ten years,” in Astr. Data analysis software and Systems V. Editors G. H. Jacoby, and J. Barnes, 101, 17.
Baddeley, A., Rubak, E., and Turner, R. (2015). Spatial point patterns: Methodology and Applications with R. Chapman and Hall. 987-1-4822-1021-7.
Bailer-Jones, C. (2017). Practical bayesian inference: A primer for physical scientists. Cambridge University Park.
Bonamente, M., and Spence, D. (2022). A semi-analytical solution to the maximum-likelihood fit of Poisson data to a linear model using the Cash statistic. J. Appl. Statistics 49, 522–552. doi:10.1080/02664763.2020.1820960
Bonamente, M., Joy, M. K., Carlstrom, J. E., Reese, E. D., and LaRoque, S. J. (2004). Markov chain Monte Carlo joint analysis of chandra X-ray imaging spectroscopy and sunyaev-zel’dovich effect data. Astrophysical J. 614, 56–63. doi:10.1086/423420
Bonamente, M., Joy, M. K., LaRoque, S. J., Carlstrom, J. E., Reese, E. D., and Dawson, K. S. (2006). Determination of the cosmic distance scale from sunyaev-zel’dovich effect and chandra X-ray measurements of high-redshift galaxy clusters. Astrophysical J. 647, 25–54. doi:10.1086/505291
Bowyer, S., Byram, E., Chubb, T., and Friedman, H. (1964). Lunar occultation of X-ray emission from the crab nebula. Science 146, 912–917. doi:10.1126/science.146.3646.912
Box, G., Jenkins, G., Reinsel, G., and Ljung, G. (2015). Time series analysis: Forecasting and control, 5th ed. Wiley. (63K citations).
Broos, P. S., Townsley, L. K., Feigelson, E. D., Getman, K. V., Bauer, F. E., and Garmire, G. P. (2010). Innovations in the analysis of chandra-ACIS observations. Astrophysical J. 714, 1582–1605. doi:10.1088/0004-637X/714/2/1582
Buchner, J., Nandra, K., Hsu, L., Rangel, C., Brightman, M., Merloni, A., et al. (2014). X-ray spectral modelling of the AGN obscuring region in the CDFS: Bayesian model selection and catalogue. Astronomy Astrophysics 564, A125. doi:10.1051/0004-6361/201322971
Cameron, A. C., and Trivedi, P. K. (2013). Regression analysis of count data. United States: Cambridge University Press. (11K citations).
Cash, W. (1976). Generation of confidence intervals for model parameters in X-ray astronomy. Astronomy Astrophysics 52, 307.
Cash, W. (1979). Parameter estimation in astronomy through application of the likelihood ratio. Astrophysical J. 228, 939–947. doi:10.1086/156922
Connors, A., Stein, N. M., van Dyk, D., Kashyap, V., and Siemiginowska, A. (2011). Lira — the low-counts image restoration and analysis package: A teaching version via R. Astronomical Data Analysis Softw. Syst. XX 442, 463.
Damiani, F., Maggio, A., Micela, G., and Sciortino, S. (1997). A method based on wavelet transforms for source detection in photon-counting detector images. I theory and general properties. Astrophysical J. 483, 350–369. doi:10.1086/304217
de Jager, O. C., Raubenheimer, B. C., and Swanepoel, J. W. H. (1989). A powerful test for weak periodic signals with unknown light curve shape in sparse data. Astronomy Astrophysics 221, 180–190.
Diehl, S., and Statler, T. S. (2006). Adaptive binning of X-ray data with weighted Voronoi tessellations. Mon. Notices R. Astronomical Soc. 368, 497–510. doi:10.1111/j.1365-2966.2006.10125.x
Eadie, W. T., Drijiard, D., James, M., Roos, M., and Sadoulet, B. (1971). Statistical methods in experimental Physics. North Holland.
Ebeling, H., White, D. A., and Rangarajan, F. V. N. (2006). Asmooth: A simple and efficient algorithm for adaptive kernel smoothing of two-dimensional imaging data. Mon. Notices R. Astronomical Soc. 368, 65–73. doi:10.1111/j.1365-2966.2006.10135.x
Edelson, R. A., and Krolik, J. H. (1988). The discrete correlation function: A new method for analyzing unevenly sampled variability data. Astrophysical J. 333, 646. doi:10.1086/166773
Enßlin, T. A. (2019). Information theory for fields. Ann. Phys. 531, 1800127. doi:10.1002/andp.201800127
Feigelson, E., and Babu, G. J. (2012). Modern statistical methods for astronomy with R Applications. Cambridge University Press.
Feigelson, E. D., and Nelson, P. I. (1985). Statistical methods for astronomical data with upper limits. I Univariate distributions. Astrophysical J. 293, 192–206. doi:10.1086/163225
Feigelson, E. D., Kashyap, V. L., and Siemiginowska, A. (2022). “Time domain methods for X-ray and gamma-ray astronomy,” in Handbook for X-ray and gamma-ray astrophysics, volume 4: Analysis techniques, section XVIII: Timing analysis. Editor B. Bhattacharya (Springer).
Freeman, P. E., Kashyap, V., Rosner, R., and Lamb, D. Q. (2002). A wavelet-based algorithm for the spatial analysis of Poisson data. Astrophysical J. Suppl. Ser. 138, 185–218. doi:10.1086/324017
Gehrels, N. (1986). Confidence limits for small numbers of events in astrophysical data. Astrophysical J. 303, 336. doi:10.1086/164079
Giacconi, R., Gursky, H., Paolini, F., and Rossi, B. (1962). Evidence for X-rays from sources outside the solar System. Phys. Rev. Lett. 9, 439–443. doi:10.1103/PhysRevLett.9.439
Hearn, D. (1968). A search for celestial sources of gamma rays of energy greater than 100 MeV. Smithsonian astrophysical observatory special report 277.
Hilbe, J., de Souza, R., and Ishida, E. (2017). Bayesian models for astrophysical data: Using R, JAGS, Python, and stan. Cambridge University Press.
Hogg, R., Tanis, E., and Zimmerman, D. (2023). Probability and statistical inference, tenth edition. Pearson.
Isobe, T., Feigelson, E. D., and Nelson, P. I. (1986). Statistical methods for astronomical data with upper limits. II. Correlation and regression. Astrophysical J. 306, 490. doi:10.1086/164359
Ivezić, Z., Connolly, A., VanderPlas, J., and Gray, A. (2019). Statistics, data mining, and machine learning in astronomy: A practical Python Guide for the analysis of Survey data. Princeton University Press.
Kaastra, J. S., Mewe, R., and Nieuwenhuijzen, H. (1996). “Spex: A new code for spectral analysis of X and UV spectra,” in UV and X-ray spectroscopy of astrophysical and laboratory plasmas. Editors K. Yamashita, and T. Watanabe, 411–414.
Kashyap, V. L., Connors, A., Freeman, P. E., Siemiginowska, A., Xu, J., Zezas, A., et al. (2010). On computing upper limits to source intensities. Astrophysical J. 719, 900–914. doi:10.1088/0004-637X/719/1/900
Kelly, B. C. (2007). Some aspects of measurement error in linear regression of astronomical data. Astrophysical J. 665, 1489–1506. doi:10.1086/519947
Kraft, R. P., Burrows, D. N., and Nousek, J. A. (1991). Determination of confidence limits for experiments with low numbers of counts. Astrophysical J. 374, 344. doi:10.1086/170124
Leahy, D. A., Elsner, R. F., and Weisskopf, M. C. (1983). On searches for periodic pulsed emission - the Rayleigh test compared to epoch folding. Astrophysical J. 272, 256–258. doi:10.1086/161288
Li, T.-P., and Ma, Y.-Q. (1983). Analysis methods for results in gamma-ray astronomy. Astrophysical J. 272, 317–324. doi:10.1086/161295
Mantz, A., Allen, S. W., Rapetti, D., and Ebeling, H. (2010a). The observed growth of massive galaxy clusters - I Statistical methods and cosmological constraints. Mon. Notices R. Astronomical Soc. 406, 1759–1772. doi:10.1111/j.1365-2966.2010.16992.x
Mantz, A., Allen, S. W., Ebeling, H., Rapetti, D., and Drlica-Wagner, A. (2010b). The observed growth of massive galaxy clusters - II. X-ray scaling relations. Mon. Notices R. Astronomical Soc. 406, 1773–1795. doi:10.1111/j.1365-2966.2010.16993.x
Mattox, J. R., Bertsch, D., Chiang, J., Dingus, B. L., Digel, S. W., Eposito, J. A., et al. (1996). The likelihood analysis of EGRET data. Astrophysical J. 461, 396. doi:10.1086/177068
Mukherjee, S., Feigelson, E. D., Jogesh Babu, G., Murtagh, F., Fraley, C., and Raftery, A. (1998). Three types of gamma-ray bursts. Astrophysical J. 508, 314–327. doi:10.1086/306386
Park, T., Siemiginowska, A., van Dyk, D. A., Zezas, A., Heinke, C., Wargelin, B., et al. (2006). Bayesian estimation of hardness ratios: Modeling and computations. Astrophysical J. 652, 610–628. doi:10.1086/507406
Percival, W. J., Friedrich, O., Sellentin, E., and Heavens, A. (2022). Matching Bayesian and frequentist coverage probabilities when using an approximate data covariance matrix. Mon. Notices R. Astronomical Soc. 510, 3207–3221. doi:10.1093/mnras/stab3540
Protassov, R., van Dyk, D. A., Connors, A., Kashyap, V. L., and Siemiginowska, A. (2002). Statistics, handle with care: Detecting multiple model components with the likelihood ratio test. Astrophysical J. 571, 545–559. doi:10.1086/339856
Rossi, B. (1948). Interpretation of cosmic-ray phenomena. Rev. Mod. Phys. 20, 537–583. doi:10.1103/RevModPhys.20.537
Scargle, J. D., Norris, J. P., Jackson, B., and Chiang, J. (2013). Studies in astronomical time series analysis. VI. Bayesian block representations. Astrophysical J. 764, 167. doi:10.1088/0004-637X/764/2/167
Scargle, J. D. (1982). Studies in astronomical time series analysis. II. Statistical aspects of spectral analysis of unevenly spaced data. Astrophysical J. 263, 835–853. doi:10.1086/160554
Scargle, J. D. (1998). Studies in astronomical time series analysis. V bayesian Blocks, a new method to analyze structure in photon counting data. Astrophysical J. 504, 405–418. doi:10.1086/306064
Schmitt, J. H. M. M. (1985). Statistical analysis of astronomical data containing upper bounds: General methods and examples drawn from X-ray astronomy. Astrophysical J. 293, 178–191. doi:10.1086/163224
Selig, M., Vacca, V., Oppermann, N., and Enßlin, T. A. (2015). The denoised, deconvolved, and decomposed Fermi γ-ray sky. An application of the D3PO algorithm. Astronomy Astrophysics 581, A126. doi:10.1051/0004-6361/201425172
Stein, N. M., van Dyk, D. A., Kashyap, V. L., and Siemiginowska, A. (2015). Detecting unspecified structure in low-count images. Astrophysical J. 813, 66. doi:10.1088/0004-637X/813/1/66
Tousey, R., Watanabe, K., and Purcell, J. D. (1951). Measurements of solar extreme ultraviolet and X-rays from rockets by means of a CoSO4:Mn phosphor. Phys. Rev. 83, 792–797. doi:10.1103/PhysRev.83.792
Uttley, P., McHardy, I. M., and Vaughan, S. (2005). Non-linear X-ray variability in X-ray binaries and active galaxies. Mon. Notices R. Astronomical Soc. 359, 345–362. doi:10.1111/j.1365-2966.2005.08886.x
van Dyk, D. A., Connors, A., Kashyap, V. L., and Siemiginowska, A. (2001). Analysis of energy spectra with low photon counts via bayesian posterior simulation. Astrophysical J. 548, 224–243. doi:10.1086/318656
VanderPlas, J. T. (2018). Understanding the lomb-scargle periodogram. Astrophysical J. Suppl. Ser. 236, 16. doi:10.3847/1538-4365/aab766
Vaughan, S., Edelson, R., Warwick, R. S., and Uttley, P. (2003). On characterizing the variability properties of X-ray light curves from active galaxies. Mon. Notices R. Astronomical Soc. 345, 1271–1284. doi:10.1046/j.1365-2966.2003.07042.x
Vaughan, S. (2005). A simple test for periodic signals in red noise. Astronomy Astrophysics 431, 391–403. doi:10.1051/0004-6361:20041453
Wall, J. V., and Jenkins, C. R. (2012). Practical statistics for astronomers, second edition. Cambridge.
Xu, J., Kashyap, V. L., Siemiginowska, A., Connors, A., Drake, J., Meng, X., et al. (2014). A fully bayesian method for jointly fitting instrumental calibration and X-ray spectral models. Astrophysical J. 794, 97. doi:10.1088/0004-637X/794/2/97
Xu, C., Günther, H. M., Kashyap, V. L., Lee, T. C. M., and Zezas, A. (2021). Change-point detection and image segmentation for time series of astrophysical images. Astronomical J. 161, 184. doi:10.3847/1538-3881/abe0b6
Keywords: event data, count data, poisson statistics, regression, bayesian statistic analysis, astrostatistics
Citation: Feigelson ED and Bonamente M (2023) iid2022: a workshop on statistical methods for event data in astronomy. Front. Astron. Space Sci. 10:1228508. doi: 10.3389/fspas.2023.1228508
Received: 24 May 2023; Accepted: 22 June 2023;
Published: 24 July 2023.
Edited by:
Ewan Cameron, Curtin University, AustraliaReviewed by:
Reinaldo Roberto Rosa, National Institute of Astrophysics (INAF), ItalyCopyright © 2023 Feigelson and Bonamente. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Eric D. Feigelson, ZWRmQGFzdHJvLnBzdS5lZHU=; Massimiliano Bonamente, bWF4LmJvbmFtZW50ZUB1YWguZWR1
 Eric D. Feigelson
Eric D. Feigelson Massimiliano Bonamente
Massimiliano Bonamente