- 1ROT&Comp Lab, Department of Chemistry “Giacomo Ciamician”, University of Bologna, Bologna, Italy
- 2Centro de Astrobiología (CAB, CSIC-INTA), Madrid, Spain
The chemistry of the interstellar medium occurs under extreme conditions and can lead to the formation of exotic molecules. These are species that on Earth are unstable and/or highly reactive. Their discovery in space is usually based on the astronomical observation of their rotational fingerprints, which requires an accurate laboratory investigation. This is based on a strategy that starts from the interplay of experiment and theory. State-of-the-art quantum-chemical calculations are used to predict the relevant spectroscopic information required to guide the spectral recording, analysis and assignment. Rotational spectra measurements are then performed in the centimeter-/millimeter-/submillimeter-wave region, thereby exploiting efficient on-the-fly production protocols for exotic molecules. Subsequently, the spectral analysis leads to accurate spectroscopic parameters, which are then used for setting up accurate line catalogs for astronomical searches and detections. This review is based on the strategy developed and the results obtained at the ROT&Comp Lab of the University of Bologna.
1 Introduction
The chemical composition of the interstellar medium (ISM) systematically changes while the physical evolution proceeds from diffuse clouds toward star-forming regions (Yamamoto, 2017). Regardless of the environment, the chemistry of the interstellar space occurs under extreme conditions, with temperatures ranging between 10 and hundreds of K (with a few exceptions such as shocked regions where the gas kinetic temperature temporarily increases up to a few thousands of K), very low densities varying from 1 to 108 cm−3, and ionizing radiation (Yamamoto, 2017; Tielens, 2021). Because of such extreme conditions, the chemical reactions that involve either ions or radicals as one of the reactants are effective and efficient. These reactions are unusual or even unfeasible under terrestrial conditions. The ISM is also characterized by turbulence and shocked regions (Yamamoto, 2017; Tielens, 2021). Shock-wave-driven chemistry contributes to widen the unusual chemical reactivity and leads to the onset of both transient and stable molecular species, with different shock-wave velocities triggering different chemical processes (Cassone et al., 2018; García de la Concepción et al., 2021). In short, the ISM is characterized by a chemistry that can lead to the formation of unstable and/or highly reactive molecules, here broadly denoted as “exotic” (Negron-Mendoza and Ramos-Bernal, 2001; Yamamoto, 2017; Puzzarini, 2020; Herbst, 2021). These are radicals and ions, but also closed-shell unsaturated systems such as imines and carbon chains. Owing to the very low density of the ISM, these reactive species survive long enough to be detected (Müller et al., 2005; McGuire, 2018; Rivilla et al., 2018; Tennyson, 2019; Bizzocchi et al., 2020; McGuire, 2022; Alberton et al., 2023a). For the sake of completeness, we extend the classification of exotic molecules to unusual species, such as deuterated systems and functionalized building-blocks of polycyclic atomatic hydrocarbons (PAHs).
Molecules can be observed through their electronic, vibrational or rotational transitions at optical/ultraviolet, infrared or centi-/milli-/submillimeter wavelengths, respectively. However, more than 90% of the gas-phase molecules discovered in space so far have been detected owing to their rotational fingerprints. For this reason, in this review, laboratory spectroscopy refers to rotational spectroscopy and astronomical observations are those carried out with radiotelescopes in the microwave region, from centimeter to submillimeter wavelengths. In this respect, in the last decade, the improved sensitivity of ground-based facilities such as ALMA (Wootten and Thompson, 2009), GBT (Prestage et al., 2009), and Yebes (Tercero et al., 2021) have led to unexpected results in terms of number and complexity of molecules detected. While astronomical line surveys of a given astrophysical object should lead to a complete census of its molecular content, unknown features are still present and this is mainly due to the lack of the corresponding spectroscopic information. There is, therefore, a great need of investigating new potential interstellar molecules. The interest is mainly on short-living systems that have not been studied yet or have been poorly characterized in the lab.
In this review, the journey from the laboratory to space is addressed. To describe this journey, the strategy developed at the ROT&Comp Lab of the Department of Chemistry “Giacomo Ciamician”, University of Bologna, and the results there obtained are considered by way of example. The target is limited to gas-phase molecular systems, and emphasis is put on the methodology to be exploited, with particular focus on unstable species, for obtaining very accurate line catalogs, which are then employed in astronomical searches. Illustrative systems range from potential prebiotic species such as (Z)-1,2-ethenediol (Melosso et al., 2022; Rivilla et al., 2022) and allylimine (Alberton et al., 2023a) to radical species, passing through deuterated ammonia, a long carbon chain, and substituted benzene. The first two systems are typical examples of exotic molecules: closed-shell species that are, however, too reactive to be isolated and stored, thus requiring to be produced on-the-fly while performing spectroscopic measurements. The same applies to the radical here considered: a sulfur-bearing species, sulfeno (HSO; Cazzoli et al., 2016; Marcelino, N. et al., 2023), which provides a piece of the “missing sulfur” puzzle. For a stable and abundant molecule such as ammonia, the mono-deturated isotopologue (NH2D) has been considered (Melosso et al., 2020b; Melosso et al., 2021), which had to be prepared ad hoc inside the cell and allows for pointing out the importance of accounting for hyperfine effects in the rotational spectrum for the correct interpretation of astronomical spectra. Finally, a long carbon chain (DC7N; Puzzarini et al., 2023) and isomers of cyanoethynylbenzene (Spaniol et al., 2023) have been taken as examples of larger systems.
This review paper is organized as follows. In the next section, the methodology is presented in detail, with a subsection dedicated to each step of the strategy as outlined in Figure 1. Then, the results section addresses the case studies mentioned above. It has to be noted that, while at the ROT&Comp Lab (in collaboration with V.M. Rivilla) a great effort has been taken to rationalize the strategy here presented, this is not at all unique and several research groups employ methodologies that rely on the interplay of experiment and theory for the spectroscopic characterization which is then exploited for astronomical searches. Examples in this direction (the list being not at all exhaustive) are provided by Belloche et al. (2017); Bermúdez et al. (2018); Bizzocchi et al. (2020); McCarthy et al. (2021); Lee et al. (2021); Cabezas et al. (2022a); Changala et al. (2022); Koelemay et al. (2022); Alberton et al. (2023b); Cernicharo et al. (2023); Silva et al. (2023).

FIGURE 1. From the laboratory to space: Main steps of the strategy leading to the detection of gas-phase exotic species in the ISM.
2 Methodology
The main steps of the strategy pursued for the detection of new molecules in the ISM are introduced in Figure 1, with “new” denoting a molecular species for which the rotational spectroscopic information is entirely missing or not sufficient for astronomical purposes. As explained in the Introduction, these are often exotic molecules. The protocol starts from an accurate characterization of the spectroscopic parameters of interest by means of quantum-chemical calculations. These are used to simulate the rotational spectrum, the simulation allowing to guide, support and complement the next step: the experiment. This latter starts with the set up of the conditions for the efficient production of the target molecular species. Based on the simulated spectrum, the best frequency ranges are then chosen. The analysis of the experimental measurements is carried out by relying on the comparison between computed and recorded spectra. Such an analysis then leads to the accurate determination of the spectroscopic parameters required for setting up a line catalog to be used for guiding astronomical searches. The assignment of a sufficient number of unblended features in the astronomical survey to the rotational transitions belonging to the molecule under consideration leads to its detection and allows the derivation of its column density. These steps are detailed in the following sections.
2.1 Spectroscopic characterization: theory
The spectroscopic parameters required for predicting the rotational spectrum of a given molecule are its rotational and centrifugal distortion constants (Gordy and Cook, 1984; Puzzarini et al., 2010; Barone et al., 2021). In some cases, magnetic and/or electric interactions can occur and lead to the so-called hyperfine structure of the rotational spectrum (Gordy and Cook, 1984; Puzzarini et al., 2010; Barone et al., 2021). Even if, in most of the cases, these effects are not observable in astronomical spectra (i.e., they do not affect the transition frequencies in astronomical surveys), there are cases where hyperfine interactions play a role (Puzzarini et al., 2010; Guzmán et al., 2012; Barone et al., 2021; Melosso et al., 2021).
According to vibrational perturbation theory to second order (VPT2; Mills, 1972), rotational constants of a given vibrational state
In the equation above, the equilibrium term contributes to about 99% of the vibrational ground-state rotational constant,
To reach high accuracy in equilibrium structure determinations, basis-set and electron-correlation effects should be taken into account. This can be accomplished by exploiting quantum-chemical composite schemes, which account for the different contributions separately in order to improve their evaluation. Indeed, they are computed at the highest possible level and then combined to obtain the best theoretical estimate, thereby exploiting the additivity approximation. In the literature, several composite schemes have been proposed to find the best compromise between accuracy and computational cost (Császár et al., 1998; Tajti et al., 2004; Heckert et al., 2005; Heckert et al., 2006; Karton et al., 2006; Huang and Lee, 2009; Puzzarini et al., 2010; Puzzarini et al., 2019; Puzzarini and Barone, 2011; Karton and Martin, 2012; Peterson et al., 2012; Cheng et al., 2017; Morgan et al., 2018; Lupi et al., 2021).
For this specific review, we mention the so-called CBS+CV “gradient scheme”, which is entirely based on coupled-cluster (CC) theory (Heckert et al., 2005; Heckert et al., 2006), and is implemented in the CFOUR quantum-chemistry package in a black-box manner (Matthews et al., 2020). In this approach, the additivity approximation is exploited at the energy-gradient level, which has to be minimized for obtaining the equilibrium structure. This scheme employs the CCSD(T) method, the acronym standing for the CC singles and doubles approximation augmented by a perturbative treatment of triple excitations (Raghavachari et al., 1989). In the CBS+CV approach, CBS means that the extrapolation to the complete basis set (CBS) limit is accomplished, while CV refers to the incorporation of the core-valence correlation contribution. In more details, the energy gradient contains three terms. The first two contributions are the gradients for the extrapolation of the HF-SCF and CCSD(T) correlation energies to the CBS limit, which are performed separately. For the former, the exponential extrapolation formula by Feller (1993) is employed, while the n−3 (n being the basis-set cardinal number) extrapolation scheme by Helgaker et al. (1997) is used for the CCSD(T) correlation energy. Since the latter extrapolation is performed within the frozen-core (fc) approximation, the third term incorporates the missing CV correlation effects, the corresponding corrective term being obtained as difference between all-electron (ae) and fc CCSD(T) calculations in the same core-valence basis set. This latter is the cc-p(w)CVnZ set (Woon and Dunning Jr, 1995; Peterson and Dunning Jr, 2002). For the extrapolations to the CBS limit, the correlation-consistent valence cc-pVnZ bases are instead used (Dunning Jr, 1989; Wilson et al., 1996). To further improve the equilibrium structure, it is requires to go beyond the CCSD(T) model, and thus to incorporate corrections due to a full treatment of triples (fT) and quadruple excitations (fQ). This leads to the composite scheme usually denoted as CCSD(T)/CBS+CV+fT+fQ. As demonstrated in Puzzarini et al. (2008) and Alessandrini et al. (2018), CBS+CV and CCSD(T)/CBS+CV+fT+fQ equilibrium rotational constants have a relative accuracy better than 0.1% and 0.05%, respectively. If the dimension of the molecule is increased and the CBS+CV model is not affordable (such as in the case of substituted benzene or small building blocks of biomolecules), accurate equilibrium structures can be obtained by resorting to the so-called “cheap-composite” scheme (Puzzarini and Barone, 2011; Lupi et al., 2021), which is denoted by the acronyms ChS or junChS depending on the type of basis sets employed (junChS employs the partially augmented jun-cc-pVnZ basis sets by Papajak et al., 2011). This starts from fc-CCSD(T)/(jun-)cc-pVTZ calculations and incorporates the extrapolation to the CBS limit and the CV correlation effects at a lower level of theory (i.e., using second-order Møller-Plesset perturbation theory, MP2; Møller and Plesset, 1934). For larger systems for which even the (jun)ChS approach is not affordable (such as small PAHs), accurate equilibrium geometries can be obtained by means of the so-called “Lego brick” approach (Melli et al., 2021; Ye et al., 2022). Within it, the system is seen as formed by smaller fragments (i.e., the “Lego bricks”) whose accurate equilibrium geometries are available. The template molecule (TM) approach (Piccardo et al., 2015) is then used to account for the modifications occurring when moving from the isolated fragment to the same fragment within the molecular system under consideration. For the TM approach, we resort to the double-hybrid rev-DSDPBEP86 (revDSD) density functional (Santra et al., 2019), also incorporating dispersion corrections (D3BJ; Grimme et al., 2010; Grimme et al., 2011), in conjunction with the jun-cc-pVTZ triple-zeta basis set. For the accurate determination of the equilibrium structure of the fragments, we employ the so-called semi-experimental (SE) structures (Pulay et al., 1978; Piccardo et al., 2015; Demaison et al., 2016), which are determined by a linear least-squares fit of the SE equilibrium rotational constants of different isotopologues (these are obtained by correcting the experimental
For the vibrational corrections to rotational constants, as mentioned above, this contribution requires anharmonic force field calculations. Since ΔBvib accounts for less than 1% of B0, for its evaluation, exploitation of CC-based composite scheme is not required all. Indeed, the fc-CCSD(T)/cc-pVTZ level of theory is more than suitable. Actually, lower levels of theory involving the MP2 method or double-hybrid functionals (Grimme, 2006; Santra et al., 2019) perform very well in this respect (Puzzarini et al., 2019; Ye et al., 2022). As far as centrifugal-distortion constants are concerned, their evaluation involves force field computations as well and, thus, they can be obtained as byproducts of the calculations leading to the evaluation of ΔBvib (Puzzarini et al., 2010; Puzzarini et al., 2019). In detail, for the quartic terms, the knowledge of the harmonic force field is required, while the sextic terms need the anharmonic one (up to cubic force constants).
The approaches described above are able to provide predictions for rotational constants with a relative accuracy of 0.1%, while centrifugal distortion constants usually show deviations from experiment ranging from 5% to 10%. Overall, rotational transitions are predicted with uncertainties that mainly reflect the accuracy of the computed rotational constants. As pointed out in Puzzarini et al. (2008), Puzzarini et al. (2010) and Alessandrini et al. (2018), pushing theory to the limit allows one to reduce the relative errors on transition frequencies to less than 0.05%. However, this means that for a line at 100 GHz, the uncertainty is 50 MHz. While such an accuracy is suitable for guiding experiment in the lab, it is not at all sufficient for supporting astronomical searches. Furthermore, unlike vibrational spectroscopy, rotational spectroscopy does not show systematic effects that can be recovered by, e.g., ad hoc scaling factors.
For closed-shell species, electric and/or magnetic interactions occur whenever they contain one or more atoms with non-zero nuclear spin I. These split rotational energy levels and, consequently, rotational transitions giving rise to the hyperfine structure of the rotational spectrum. The interaction of major interest is the nuclear quadrupole coupling that takes place whenever I ≥ 1: the quadrupole moment of the quadrupolar nucleus interacts with the electric field gradient at the nucleus itself. From a computational point of view, the prediction of nuclear quadrupole coupling constants requires the calculation of the electric field gradient at the quadrupolar nucleus:
where i and j refer to the inertial axes. eQ is the nuclear quadrupole moment and qij represents the ij-th element of the electric-field gradient tensor (Puzzarini et al., 2010). Based on the literature on this topic (Puzzarini et al., 2009; Puzzarini et al., 2010; Puzzarini et al., 2019), ae-CCSD(T) computations in combination with core-valence basis sets and incorporating vibrational corrections provide quantitative predictions. In the case of open-shell species, the situation is more involved because the coupling of the rotational angular momentum with the electronic spin momentum should be incorporated in the treatment (Gordy and Cook, 1984; Cazzoli et al., 2016). If more than one unpaired electrons are present, the coupling between the electronic spins should also been considered (Gordy and Cook, 1984; Cazzoli et al., 2016; Bizzocchi et al., 2022).
2.2 Spectroscopic characterization: experiment
As it follows from the discussion above, theory is not able to provide line catalogs with the accuracy required by radioastronomy. For this reason, a mandatory step of our strategy is the experimental spectroscopic characterization of the molecular species to be searched in the ISM.
On general grounds, rotational spectroscopy is performed from the centimeter-wave to the submillimeter-wave region. The rotational spectrometers at the ROT&Comp lab1 are frequency-modulation millimeter/sub-millimeter-wave (mm/sub-mm) spec-trometers, which work in the 75–1.6 THz and 70–990 GHz frequency ranges. For interested readers, the former is described in detail in Cazzoli et al. (2012, 2016), Melosso et al. (2019a) and Melosso et al. (2019b), while for the latter the production phase has just started. To produce unstable molecules, such as ions and radicals, but also species that are highly reactive under terrestrial conditions, such as imines and carbon chains, the mm/sub-mm spectrometer is combined with either a flash vacuum pyrolysis (FVP) system (Melosso et al., 2018; Jiang et al., 2021; Melli et al., 2022) or a DC discharge apparatus (Cazzoli et al., 2012; Cazzoli et al., 2016). The FVP technique is mainly used for the production of closed-shell species, while DC discharge is mostly employed for the generation of radicals and ions (Puzzarini et al., 2023).
Concerning the FVP technique, two different apparatuses can be used, which are schematized in Figure 2. The first system is external to the spectrometer, it consists of a 30 cm long tubular oven surrounding a quartz tube directly connected to the inlet of the spectrometer cell (see Figure 2A). The maximum temperature reached by this oven is 1,200°C. The second apparatus is defined as an in situ system (see Figure 2B) because a 1.5 m long quartz tube is employed as absorption cell and is surrounded by a 90 cm tubular furnace (Jiang et al., 2021). In analogy to the first system, a maximum temperature of 1,200°C can be reached. For both apparatuses, in view of instability or reactivity of the target molecules, measurements are performed in dynamical conditions, which means that a tenuous flow of fresh pyrolysis products is continuously assured by the vacuum system.
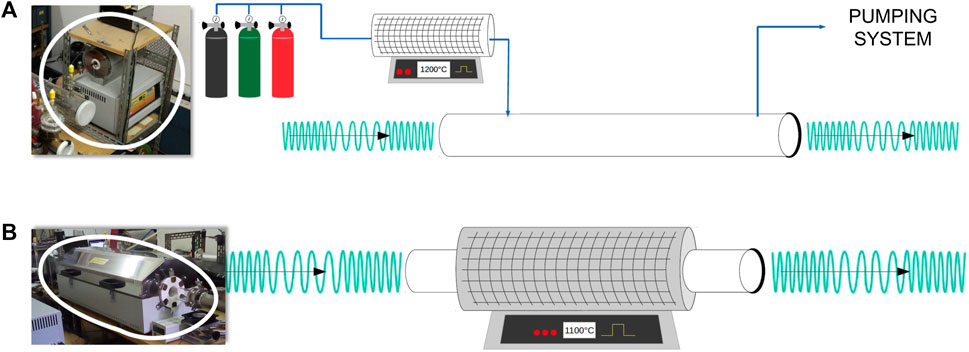
FIGURE 2. The two FVP systems available at the ROT&Comp Lab (the millimeter-/submillimeter-wave radiation is represented by green waves). (A) external FVP apparatus. (B) in situ FVP system. In both panels, pictures of the FVP oven are given on the left side.
For the production of ionic and radical species, the mm/sub-mm spectrometer is equipped with a negative glow-discharge cell (Cazzoli et al., 2012; Cazzoli et al., 2016), with measurements being performed at low temperatures to improve the signal-to-noise ratio. The experimental apparatus is schematized in Figure 3. Together with a suitable mixture of precursors, a buffer gas (usually, He or Ar) is often employed and a DC discharge ranging from a few mA to some tens of mA is applied. Analogously to FVP, measurements are carried out in dynamical conditions. During measurements, a longitudinal magnetic field can be applied: for ions, it is used for extending the negative glow discharge (thus improving ions production); for radicals, Zeeman effect disentangles their signal from those of the closed-shell species (such as precursors or undesired products).
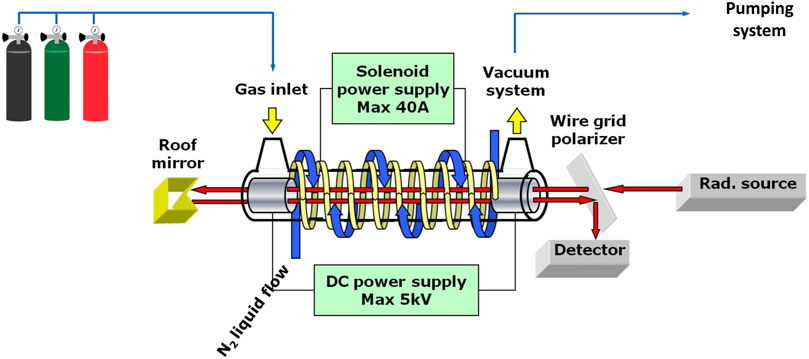
FIGURE 3. Scheme of the DC discharge system of the frequency-modulated mm-/submm spectrometer at the ROT&Comp Lab.
The resolution of rotational spectra is mainly limited by two effects, collisions and Doppler effect, which determine a broadening of lines. The collisional broadening, also denoted as pressure broadening, can be reduced by working at a sufficiently low pressure. The Lamb-dip technique allows for getting rid of the Doppler broadening, thus leading to a resolution of a few tens of kHz (see right panel of Figure 4) and a measurement accuracy of 0.5–5 kHz (Cazzoli et al., 2004; Cazzoli et al., 2009; Cazzoli et al., 2015; Puzzarini et al., 2009). Lamb-dip technique requires three conditions to be fulfilled.
• measurements are carried out at very low pressures in order to have rotational lines only broadened by the Doppler effect;
• measurements are performed using radiation power sufficiently intense to lead to partial saturation;
• the radiation should go back and forward inside the cell (double-pass arrangement) in order to have a pump-and-probe effect.
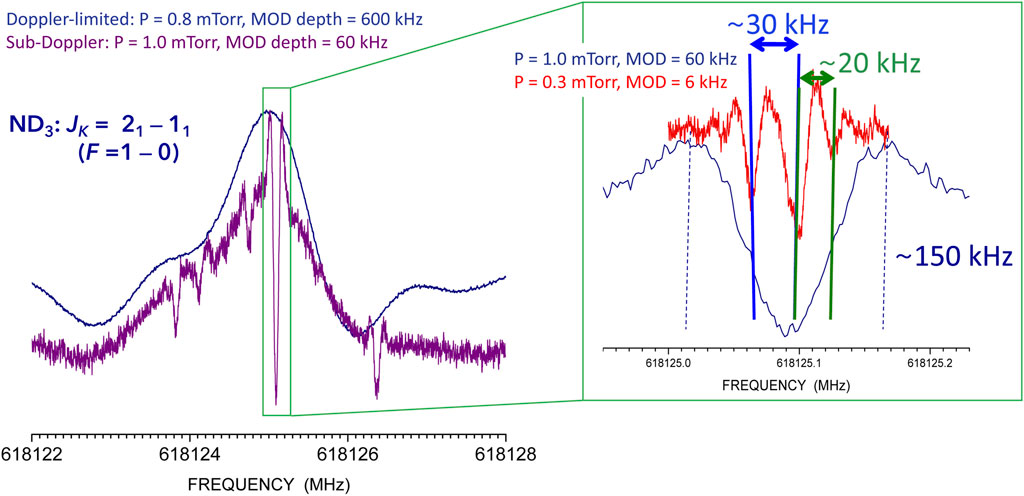
FIGURE 4. Lamb-dip recording of the F = 1 ←0 hyperfine component of the JK = 21 ← 11 transition of ND3. Left panel: Comparison between the Doppler-limited (dark blue line) and Lamb-dip (violet line) recordings. Right panel: zoom of the central hyperfine component (dark blue line) showing improved resolution (red line).
To exploit the double-pass configuration in the mm/sub-mm spectrometer, a roof-top mirror is located at the end of the cell to reflect the radiation back and rotate its polarization by 90°, while a wire-grid polarizer is placed at the other end. The overall result is that the radiation enters the cell passing through the polarizer, whereas the radiation back from the roof-top mirror with its polarization rotated by 90° is reflected at right angle onto the detector.
While hyperfine structures arising from strong interactions are evident in Doppler-limited rotational spectra (see left panel of Figure 4), weaker effects might be concealed by the Doppler profile and need sub-Doppler resolution to be disclosed (see Figure 4). Furthermore, when several interactions take place, the Doppler-limited profiles are distorted and preclude accurate frequency determinations. Figure 4 showing part of the hyperfine structure of the JK = 21 ← 11 transition of ND3 (J, K being the rotational quantum numbers for symmetric rotors), provides a significant example. In the case of ND3, both N and D are quadrupolar nuclei; however, nitrogen gives rise to a stronger quadrupole coupling than deuterium and the corresponding hyperfine components are well resolved, In the left panel, the F = 1 ← 0 hyperfine component is depicted, F being the quantum number associated to the hyperfine interaction due to N. The Doppler-limited (dark blue) and sub-Doppler (violet) profiles are compared: it is evident that a complex hyperfine structure due to the three D nuclei is hidden in the former. The right panel shows that the hyperfine structure of the left panel is even more complicated (red profile): the resolution of the Lamb-dip technique can be further pushed by adjusting the pressure inside the cell and the modulation amplitude (MOD). As evident in the right panel, features separated by ∼20 kHz are well resolved. The overall consequence is that, whenever the Lamb-dip technique is exploited (even in absence of hyperfine structure), the transition frequency is retrieved with great accuracy. It has to be noted that the spectral analysis needs to account for all interactions occurring. In the present case, these include (in addition to nitrogen and deuterium quadrupole couplings) nuclear spin-rotation interactions for all nuclei and all possible dipolar spin-spin couplings (Puzzarini et al., 2009; Puzzarini et al., 2015; Melosso et al., 2020b; Melosso et al., 2021).
2.3 Spectroscopic characterization: line catalog
Application of the contact transformation perturbation procedure to the Watson Hamiltonian leads to a block-diagonal effective Hamiltonian, whose pure rotational and centrifugal-distortion contributions are here considered (Aliev and Watson, 1985):
where H04 and H06 are the quartic and sextic centrifugal-distortion terms, respectively, and H02 is the rigid-rotor Hamiltonian:
where
Even if the rigid-rotor Hamiltonian H02 is the most important term, a realistic and accurate description of the rotational problem requires to go beyond the rigid-rotor approximation, thus including in the treatment at least the H04 Hamiltonian, which is expressed in terms of the quartic centrifugal distortion parameters (this requires some contact transformations; interested readers are referred–for example–to Aliev and Watson, 1985). Moving to higher terms, a simple general formula for H06 was obtained by Aliev and Watson (1976). Different results are then obtained depending on the Hamiltonian reduction chosen (Watson, 1968; Watson, 1977; Aliev and Watson, 1985). Moreover, the effect of molecular vibrations should be taken into account. Therefore,
If hyperfine interactions are present, the Hamiltonian incorporates their contribution:
where Hrot is the rotational part of the Hamiltonian operator introduced above, also including centrifugal distortion. Hhfs accounts for all possible hyperfine interactions, with the nuclear quadrupole coupling being the one of interest in this context. This latter is described by making use of the traceless tensor χ of Eq. 3. Other possible hyperfine interactions are the nuclear spin-rotation (SR) interaction (described in terms of the C tensor) and, if more than one nuclei with nonzero I are present, the dipolar spin-spin coupling. Hyperfine interactions lead to the definition of one or more additional quantum numbers (usually denoted with F or, if more than one, Fx with x denoting a coupling order or a coupling atom).
Moving to radical species, the effective Hamiltonian operator contains at least two contributions:
where Hrot is the usual rotational Hamiltonian term as above. Hfs is the fine structure Hamiltonian, which is—at least—due to electron spin-rotation interaction (described through the electron spin-rotation tensor ϵ). In all cases, the rotational angular momentum N and the electronic spin momentum S couple to lead to J (therefore, for radicals, the rotational quantum number is N and not J). If more than one electron is present, then Hfs also incorporates the electron spin-spin interaction (through the electron spin–spin coupling tensor λ which is symmetric and traceless). If nonzero nuclear spins are present in the molecule, in addition to the hyperfine interactions mentioned above, a hyperfine-structure term describing the interaction between the electron spin and the nuclear spins should be incorporated in the Hamiltonian above (Gordy and Cook, 1984; Bizzocchi et al., 2022).
The spectral analysis, guided by the simulated spectrum, leads to the assignment of the rotational transitions in terms of quantum numbers. These rotational transitions are then fitted using the effective Hamiltonian mentioned above. In the fitting procedure, the computed spectroscopic parameters provide the starting point, while the outcome is their experimental counterpart. In turn, the experimental spectroscopic parameters are employed to accurately predict all possible rotational transitions up to a given frequency limit which depends on quantum numbers sampled in the actual measurements. This collection of transitions together with their spectroscopic information is the line catalog to be used in astronomical searches. Such an application requires that the uncertainties affecting the transition frequencies are smaller than or, in the worst case, equal to 100–200 kHz, because astronomical line surveys are dense and only accurate rest frequency values allow for discriminating the features belonging to different molecules.
2.4 Radioastronomical observations: search and detection
To search for the transitions of the molecule under consideration, first of all, spectral surveys of the target molecular cloud are obtained. Then, the rotational spectroscopy information from the laboratory work needs to be incorporated into a suitable program that generates synthetic spectra under the assumption of local thermodynamic equilibrium (LTE) conditions. To properly evaluate possible line contamination by other molecules, the emissions from the molecules already identified toward that cloud are considered in the simulation. A tool able to provide the best nonlinear least-squares LTE fit to these data is then exploited, with the parameters of the LTE model being the molecular column density (N), the excitation temperature (Tex), the observed radial velocity of the astronomical object (vLSR), and full width at half maximum (FWHM) of the Gaussian line profiles (see, e.g., Martín et al., 2019).
A complementary analysis to retrieve N and Tex is offered by the “rotational diagram method” (Goldsmith and Langer, 1999) which, for multiple transitions, plots their log(Nu/gu) value (where Nu/gu is calculated from the integrated intensity) against the corresponding upper-state energy, Eu. The linear regression slope, 1/kBTex (kB being the Boltzmann constant), provides the excitation temperature, whereas the intercept, N/Q(T), gives the column density once the molecular partition function at the derived temperature (Q(T)) is computed. It is thus crucial to have accurate values of Q(T) to accurately determine N. In addition to the rotational and hyperfine contributions to Q(T) that can be easily obtained from the spectroscopic characterization (carried out to obtained the line catalog), the vibrational term should also be taken into account because its contribution can be greater than 1 already at low temperature (above 20–30 K). This requires the accurate knowledge of all fundamental vibrational frequencies of the molecule under consideration. This requirement can be fulfilled by means of experimental studies or state-of-the-art quantum-chemical computations (thereby exploiting composite schemes analogous to those introduced in the theory section). More details on the method can be found, in Goldsmith and Langer (1999).
Since at the very low density of the ISM the molecular energy level populations are rarely at the LTE, collisions compete with radiative processes (Kłos and Lique, 2017). Therefore, the interpretation of observed interstellar spectra in terms of molecular abundances requires the knowledge of collisional rate coefficients of the molecule under consideration, with the most abundant perturbing species (namely, molecular hydrogen) being considered. While a few experimental studies allow the determination of such parameters (see, e.g., Orr, 1995; James et al., 1998; Roueff and Lique, 2013; Hays et al., 2022), quantum inelastic scattering calculations offer an accurate and more accessible alternative (Roueff and Lique, 2013; Kłos and Lique, 2017). The first step of this approach is the determination of the corresponding collisional potential energy surface (Roueff and Lique, 2013; Tonolo et al., 2021; Tonolo et al., 2022). The collisional calculations provide a set of inelastic cross sections as a function of the collision energy and, starting from these quantities, the corresponding excitation and de-excitation rate coefficients are obtained for the desired temperature range (Roueff and Lique, 2013; Kłos and Lique, 2017; Tonolo et al., 2021; Tonolo et al., 2022).
3 Results
To present the strategy described in the Methodology section at work, illustrative examples have been chosen. The first two studies addressed are those that led to the detection of (Z)-1,2-ethenediol (Melosso et al., 2022; Rivilla et al., 2022) and the tentative detection of allylimine (Alberton et al., 2023a) toward the G+0.693-0.027 molecular cloud, located at the Galactic Center. The discussion then moves to touch the HSO radical species. This latter has been recently detected towards several cold dark clouds (Marcelino, N. et al., 2023). The subsequent example is NH2D, which is employed to point out the importance of accounting for hyperfine effects in astronomical spectra. Finally, as examples of larger systems, DC7N and isomers of cyanoethynylbenzene are considered.
3.1 (Z)-1,2-ethenediol: a precursor of the RNA world in space
Ethenediol exists in the E and Z stereoisomeric forms, with the latter being more stable by about 20 kJ/mol (Karton and Talbi, 2014). In turn, as shown in Figure 5A, the Z isomer has two possible configurations, the preferred one being the syn, anti form (the anti, anti conformer lies higher in energy; see Figure 5A). (Z)-1,2-ethenediol belongs to the C2H4O2 family, whose most stable isomer is acetic acid, followed by methyl formate, 1,1-ethenediol and glycolaldehyde (Karton and Talbi, 2014). Among these, prior to Melosso et al. (2022); Rivilla et al. (2022), 1,2- and 1,1-ethenediol were the only species still escaping detection in space, the reason being the lack of any rotational spectroscopy characterization. While we here present the strategy introduced above to 1,2-ethenediol, we mention that work is still in progress on the 1,1 isomer.
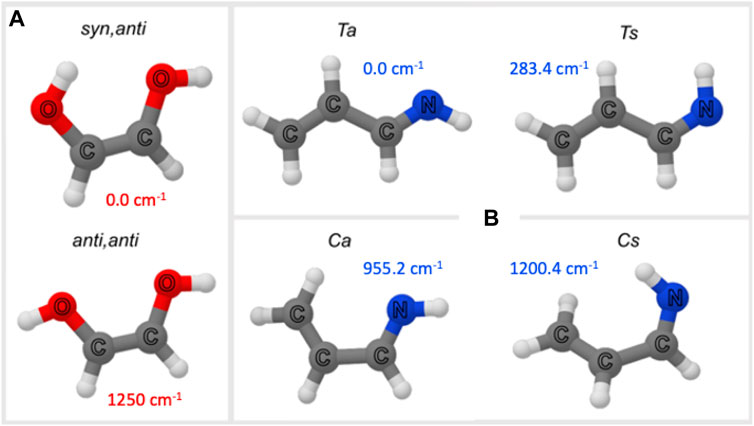
FIGURE 5. Molecular structure of (Z)-1,2-ethenediol (A) and allylimine isomers (B). Relative energies are also provided (for (Z)-1,2-ethenediol: B2PLYP/aug-cc-pVTZ level of theory from Melosso et al., 2022; for allylimine: CBS+CV level of theory from Alberton et al., 2023a).
Prior to the investigation by Melosso et al. (2022), no information was available for the rotational parameters of 1,2-ethenediol. Therefore, in Melosso et al. (2022), after a preliminary scan of the potential energy surface, the equilibrium structure (and thus the equilibrium rotational constants) of the syn, anti form of (Z)-1,2-ethenediol has been evaluated at the CBS+CV level. Vibrational corrections to rotational constants as well as centrifugal distortion constants have been computed at the fc-MP2/cc-pVTZ level. Such calculations allowed the prediction of the rotational spectrum to be used for guiding the recording and the analysis of the experimental counterpart.
(Z)-1,2-ethenediol is a highly reactive species that requires to be produced on-the-fly while performing spectroscopic measurements. For its production, the external FVP system was employed. For this purpose, bis-exo-5-norbornene-2,3-diol was considered as suitable precursor and purposely synthesized (for details, see Melosso et al., 2022). (Z)-1,2-ethenediol was produced by flowing the vapours of the precursor through the quartz tube heated at 750°C. The pressure inside the absorption cell was kept at ∼4 μbar. These conditions were obtained by monitoring the intensity of the (Z)-1,2-ethenediol transitions and adjusted to obtain the best signal-to-noise ratio (S/N). As shown in Figure 6, the oven temperature of 750 °C provides the best S/N. The temperature of the precursor also affects the production of (Z)-1,2-ethenediol, as evident in the right panel of Figure 6. While the best S/N is obtained by heating the sample at 80°C, the working temperature was maintained at 50°C because a mild heating decreases the intensity of the interfering lines produced by glycolaldehyde (Melosso et al., 2022). Indeed, even in the best conditions, signals belonging to glycolaldehyde and cyclopentadiene are observed. The former is produced by isomerization of (Z)-1,2-ethenediol, while the latter is a pyrolysis co-product (Melosso et al., 2022).
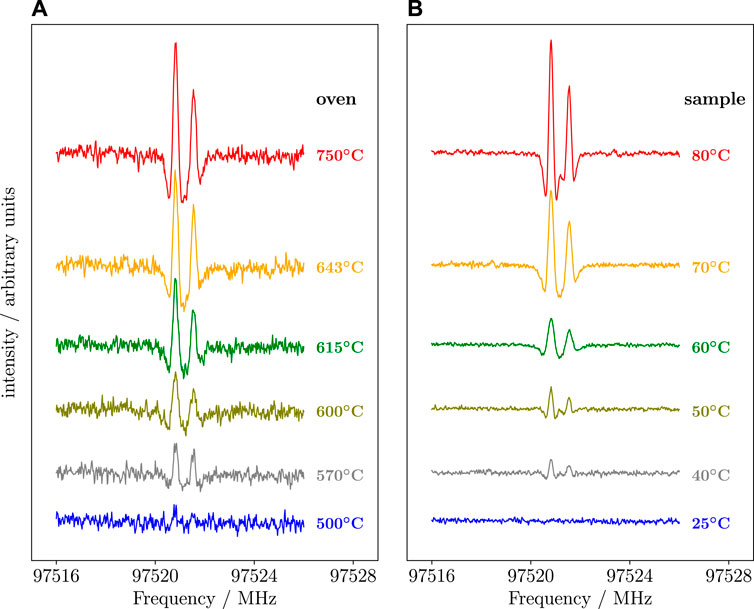
FIGURE 6. Recordings of the 92,8 ← 82,7 transition of the (Z)-1,2-ethenediol obtained at different pyrolysis conditions. (A) recording at different oven temperatures with that of precursor fixed at 55°C. (B) recording at different sample temperatures with the oven kept at 750°C.
Figure 1 of Melosso et al. (2022) provides an example of comparison between the simulated (based on computed spectroscopic parameters) and recorded spectra in the 255–260 GHz frequency range. That figure demonstrates that the computational strategy is very effective: it allows for obtaining a very good prediction of the rotational spectrum, thus enormously facilitating the spectral assignment. A further confirmation of the correct identification of (Z)-1,2-ethenediol was offered by the presence of a tiny splitting in most of the absorption features, which is a clear evidence of a tunneling motion. This was somewhat expected in view of the similarity with ethylene glycol (Christen et al., 1995). In detail, the –OH moieties undergo a concerted large amplitude tunneling motion between two equivalent positions of the syn, anti form of (Z)-1,2-ethenediol, which splits each rotational energy level into two.
The analysis of the recorded features was performed using a rotational-torsional Watson S-reduced Hamiltonian (Watson, 1977), with terms up to 8th power of the rotational angular momentum being incorporated in the Hamiltonian. This analysis led to the accurate determination of several spectroscopic parameters. For example, the rotational constants were obtained with an average error of 0.0016%, the uncertainty of the quartic centrifugal distortion parameters was found around 0.018%, and the energy difference between the two inversion states was determined at kHz accuracy (for all details the reader is referred to Melosso et al., 2022). From these spectroscopic constants, a line catalog was generated using the SPCAT routine of the CALPGM suite (Pickett, 1991) in the format of the CDMS and JPL catalogues (Pickett et al., 1998), and was ready to be used in astronomical line-analysis tools. In detail, the fit of the recorded lines between 80 and 125 GHz (115 distinct frequency values) allowed the accurate determination of the rotational constants and few centrifugal distortion terms. These combined with the computed values for the remaining centrifugal distortion parameters predicted the transitions in the 240–375 GHz range with an average error of 600 kHz. The fit of the recorded lines up to 260 GHz (263 distinct frequency values) reduced the average error to 77 kHz for the transitions lying in the 260–375 GHz interval. The incorporation of the recorded lines up to 375 GHz led to the final fit (578 distinct lines). The corresponding parameters were used to set up the line catalog, whose predictions are expected to be very accurate up to 500 GHz and to meet the requirements for guiding astronomical observations (see section 2.3) up to 750 GHz for transitions involving low Ka values.
(Z)-1,2-ethenediol has been searched toward the G+0.693-0.027 molecular cloud located in the Galactic Center by exploiting high-sensitivity unbiased spectral surveys obtained with the Yebes 40 m (Guadalajara, Spain) and the IRAM 30 m (Granada, Spain) telescopes (Rivilla et al., 2022). This led to the assignment of 18 unblended or slightly blended transitions (arising from nine pairs of unresolved transitions). To correctly evaluate possible line contaminations by other molecules, the emission from the more than 120 molecules already identified toward the G+0.693-0.027 molecular cloud were considered. To derive the physical parameters of the (Z)-1,2-ethenediol emission, a nonlinear least-squares LTE fit to the data was performed using MADCUBA2. This led to an excitation temperature of 8.5 ± 0.6 K (in line with the typical values found in G+0.693-0.027) and a column density of (1.8 ± 0.1)× 1013 cm−2 (Rivilla et al., 2022), with N(H2) being 1.35 × 1023 cm−2 (Martín et al., 2008).
3.2 Allylimine: a prebiotic molecule
Allylimine can be seen as a sort of substituted butadiene where a terminal =CH2 group is substituted by the =NH moiety. Therefore, in analogy to butadiene, it exists in two isomers: the cis (C) and trans (T) species (see Figure 5B). Additionally, for each of them, the position of the iminic H with respect to the closest H of the -CH=CH2 group leads to the syn (s) and anti (a) forms (see Figure 5B). Consequently, allylimine has four geometric isomers, which are denoted as Ta, Ts, Ca, and Cs (see Figure 5B). All these forms except the latter (Cs) have a planar structure. At the CBS+CV level, the Ta form is the most stable followed by Ts lying 282.4 cm−1 above Ta (Alberton et al., 2023a). Contrary, the cis species are highly unstable (Ca and Cs lie at 955.3 and 1,200.4 cm−1 with respect to Ta, respectively) and were not experimentally observed in the spectroscopic investigation reported in Alberton et al. (2023a). Therefore, in the following, only Ta and Ts are considered.
In Alberton et al. (2023a), the CBS+CV level of theory was employed for the evaluation of their equilibrium rotational and quartic centrifugal distortion constants. While a reliable estimate of rotational constants was already available owing to the experimental studies by Penn (1978) and Brown et al. (1981) in the centimeter-wave region (8–26 GHz), these calculations were crucial to provide accurate predictions of the centrifugal terms. The impact of these latter parameters is demonstrated in Figure 7, which shows how the transition frequencies of Ts at 261 GHz predicted using the rotational constants by Penn (1978) (red line) do not reproduce the experimental observations (black line). The simulated spectrum noticeably improves by incorporating the computed centrifugal distortion constants (yellow spectrum), while it agrees perfectly with the recorded spectrum once the distortion terms have been determined experimentally (green spectrum). Noted is that in Figure 7 some experimental features do not have the predicted counterparts because they do not belong to Ts. Among the spectroscopic parameters that are relevant for predicting/analyzing the rotational spectrum of allylimine, one has to consider the nuclear quadrupole coupling constants. In fact, nitrogen is a quadrupolar nucleus (I = 1) and a hyperfine structure is originated (see Section 2.3). The nuclear quadrupole coupling constants were experimentally determined by Brown et al. (1981) and, in Alberton et al. (2023a), computed at the ae-CCSD(T)/cc-pCVQZ level, also including ae-MP2/cc-pCVTZ vibrational corrections.
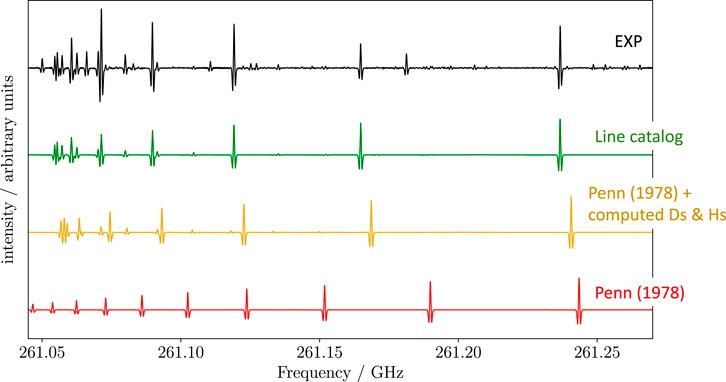
FIGURE 7. Excerpt of the rotational spectrum of Ts-allylimine (in black) and comparison with various simulations. The colored traces have been obtained by using: the rotational constants from Penn (1978) (red trace); the rotational constants from Penn (1978) augmented by the computed quartic and sextic centrifugal distortion constants from Alberton et al. (2023a) (yellow trace); line catalog derived in Alberton et al. (2023a) (green trace).
From the experimental side, in Alberton et al. (2023a), the rotational spectrum of allylimine was recorded in selected frequency regions from 84 to 307 GHz. As most of imines, allylimine is a reactive species that cannot be synthesized and stored for measurements. Instead, in analogy to (Z)-1,2-ethenediol, it required to be produced on-the-fly. At the ROT&Comp Lab, measurements were performed using the in situ FVP system, with the optical elements of the spectrometer arranged in a double-pass configuration in order to increase the absorption path-length. Allylimine was thus produced directly inside the absorption cell by using diallylamine as precursor and a temperature of 500°C.
The computed parameters together with the available experimental information were used to simulate the rotational spectrum in the millimeter-/submillimeter-wave region, as shown in Figure 7 (yellow trace). This figure provides a flavor of how the interplay experiment-theory enormously facilitated the spectral analysis. This was carried out using the CALPGM suite of programs (Pickett, 1991) and a S-reduced Watson-type rotational Hamiltonian combined with a hyperfine-structure Hamiltonian describing the nitrogen quadrupole coupling. From the comparison of the latest results with those previously reported in Brown et al. (1981), it is noted that all spectroscopic parameters were greatly improved. Concerning the rotational constants, for Ta, the uncertainties were reduced by more than two orders of magnitude, with differences between the two sets of constants exceeding the associated errors. For Ts, an analogous improvement has to be noted, with discrepancies even more accentuated. A similar situation is observed for the nuclear quadrupole coupling constants. However, for Ts, the differences are as large as a few hundreds of kHz and, consequently, the computed parameters turned out to be more accurate than the old experimental determination. Quartic and sextic centrifugal distortion constants were instead determined for the first time and, as mentioned above, the calculated values turned out extremely useful for predicting the line positions in the millimeter-wave region (Figure 7). From the improved spectroscopic parameters, a line catalog for guiding astronomical observations has been generated.
In analogy to (Z)-1,2-ethenediol, the Ta and Ts allylimine isomers have been searched toward the G+0.693-0.027 molecular cloud. The spectroscopic parameters above have been incorporated into the MADCUBA package (Martín et al., 2019) in order to generate, under the LTE assumption, the synthetic spectra for Ta and Ts to be compared with the observed spectra. For each isomer, such a comparison led to the tentative assignment of eight transitions that were found unblended or slightly blended with emissions from other species already identified in this source. This analysis allowed the derivation of a column density N = (1.5 ± 0.6) × 1013 cm−2 for Ta and N ∼ 0.5 × 1013 cm−2 for Ts, thus resulting in a [Ta]/[Ts] isomer ratio of about 3. Interestingly, this is much lower than the estimated value of 15 based on thermodynamic considerations. Thus, the [E]/[Z] isomeric ratio of imines in the ISM is still a topic of great interest which deserves further investigations.
3.3 Sulfeno: a piece of the “missing sulfur” puzzle
The HSO radical has been the subject of a few rotational studies. Endo et al. (1981) provided the first spectral characterization of this radical together with that of its deuterated isotopologue. In Cazzoli et al. (2016), the investigation of the rotational spectrum of HSO was extended up to the THz region, thus improving and enlarging the original dataset of spectroscopic parameters. The work of Cazzoli et al. (2016) was also supported by state-of-the-art quantum-chemical calculations, with particular focus on sextic centrifugal distortion constants as well as fine and hyperfine parameters (Cazzoli et al., 2016).
In Cazzoli et al. (2016), HSO was prepared by DC discharging (∼10–40 mA) a 1:2 mixture of H2S and O2, with starting pressures of about 3–10 mTorr of H2S, but without any buffer gas. In addition, sulfur adsorbed on cell walls because of the use of sulfur-bearing chemicals in previous unrelated experiments allowed the production of HSO by DC discharging (50–60 mA) a flow of ∼35–50 mTorr of H2O. In both cases, measurements were performed in a continuous flow of gas, in order to constantly provide fresh precursors, and using the apparatus shown in Figure 3. Zeeman effect (due to application of a magnetic field of several Gauss) allowed to confirm that the recorded features belonged to a radical species. The line catalog (at 1, 2, and 3 mm) obtained in Cazzoli et al. (2016) was also employed to carry out a search for HSO in two high-mass star-forming regions, namely, Orion KL and Sagittarius (Sgr) B2, and in the cold dark cloud Barnard 1 (B1-b). However, no HSO lines were found above the confusion limit of the surveys. In case of the dense core B1-b, in Cazzoli et al. (2016), the search did not involve the most favorable transitions, which—at very low temperatures—lie at lower frequencies than those considered.
Very recently, the spectral line surveys performed at the Yebes 40 m telescope at 7 mm allowed the discovery of HSO towards several cold dark clouds, namely, B1-b, TMC-1, L183, L483, L1495B, L1527, and Lupus-1A (Marcelino, N. et al., 2023), thus demonstrating that HSO is widespread in cold dense cores. The detection was mainly confirmed by the observation of one or more fine/hyperfine components of the fundamental transition lying at 39 GHz, which were not accurately predicted by the line catalog from Cazzoli et al. (2016), the average uncertainty on the fine/hyperfine components being ∼200 kHz. Therefore, the measured frequencies (from astronomical spectra) were used to improve the spectroscopic parameters and thus the line list. Observations performed at 3 mm using the IRAM 30 m telescope (improved with respect to those reported in Cazzoli et al., 2016) were used to complement the Yebes data (Marcelino, N. et al., 2023). In all cases, the HSO column densities were derived using LTE models able to reproduce the observed spectra. The retrieved N values range between 7.0 × 1010 cm−2 and 2.9 × 1011 cm−2, which result in abundances in the (1.4–7.0) × 10–12 range relative to H2.
3.4 Deuterated ammonia: the role of hyperfine interactions
Accurate determination of molecular abundances of astrochemical species is a crucial step towards the understanding of the chemistry occurring in the ISM. Even when LTE approximation holds (or provides reasonable results), this process requires a detailed and accurate knowledge of the molecular energy levels. If electric and/or magnetic interactions take place, then this knowledge should be extended to the hyperfine splittings of the rotational energy levels. As mentioned above, the main interaction to account for is the nuclear quadrupole coupling. In this respect, it has to be noted that, even if the effect on the radioastronomical spectrum is not evident, a hyperfine structure may cause a distortion of the line profile that, if not taken into account, can lead to biased results in terms of physical parameters and molecular abundance. A significant example is provided by incorporating or not the effect of the deuterium quadrupole coupling in the analysis of astrophysical emissions of NH2D at millimeter wavelengths in the recent observations of the starless core L1544, a low-mass star-forming core in a very early stage of evolution (Melosso et al., 2021).
The rotational spectrum of NH2D presents a hyperfine structure which is mainly due to the nitrogen quadrupole coupling, which splits the rotational transitions in hyperfine components that are resolved also at Doppler-limited resolution (see Figure 8). However, deuterium is a quadrupolar nucleus as well, thus contributing to the overall hyperfine structure. Being the interaction due to D weaker than that due to N, the overall result is that the hyperfine components further split because of this additional coupling, as evident in Figure 8 (top panel). Though, the deuterium hyperfine structure can be resolved only by exploiting sub-Doppler resolution (see Figure 8; Melosso et al., 2020b).
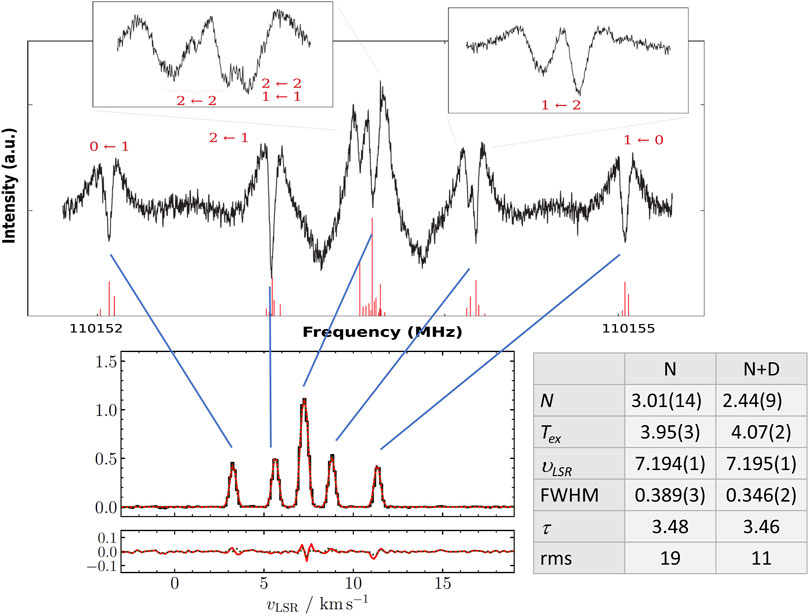
FIGURE 8. Top panel: Lamb-dip spectrum of the
In Melosso et al. (2021), the importance of including the deuterium hyperfine structure in the analysis of astrophysical emissions of NH2D at millimeter wavelengths has been pointed out for the recent observations of the starless core L1544. This source is a prototypical cold, quiescent core on the verge of the gravitational collapse exhibiting very narrow line emissions (Tafalla et al., 2002; Keto and Caselli, 2010). The rotational features considered were the ortho-NH2D
In Melosso et al. (2020b) and Melosso et al. (2021), the rotational spectrum of the singly-deuterated ammonia was recorded in the 265–1,565 GHz range, and the Lamb-dip technique exploited in the entire frequency region considered. NH2D was produced in situ by flowing a small amount of NH3 (less than 0.5 mTorr) into the absorption cell where deuterium (D2) was previously discharged for some minutes. A frequency modulation of 1 kHz was used and the modulation-depth varied between 8 and 24 kHz according to the frequency region. To analyze the recorded spectra, the hyperfine structure was predicted using the computed hyperfine constants together with the other spectroscopic parameters (rotational and centrifugal distortion constants) from Cohen and Pickett (1982) and Fusina et al. (1988). In Melosso et al. (2020b), the hyperfine parameters were calculated at the CCSD(T) level correlating all electrons, extrapolating to the CBS limit, and incorporating the fT and fQ corrections as well as those due to vibrational effects. Such a level of theory led to parameters in quantitative agreement with experiment, thus allowing an easy assignment of the complicated hyperfine structure to the correct hyperfine components.
3.5 Toward molecular complexity
3.5.1 DC7N: a long carbon chain
From the point of view of the terrestrial chemistry, carbon chains are definitely exotic species. In the ISM, instead, after the discovery of the first carbon-chain molecules in the 1970s (Avery et al., 1976; Broten et al., 1978; Guelin et al., 1978; Kroto et al., 1978), this type of systems has been largely detected (McGuire, 2022). In fact, they represent about 40% of all detected species (Burkhardt et al., 2017) and have been proposed as precursors of PAHs (Guzman-Ramirez et al., 2011). In Burkhardt et al. (2017), the first interstellar detection towards the dark cloud TMC-1 of DC7N, together with six 13C-bearing isotopologues of HC7N, was reported. In that study, for DC7N, a column density of 2.5(9) × 1011 cm−2 was derived.
In McCarthy et al. (2000), the rotational spectra of all single-substituted isotopologues of three long linear cyanopolyynes, namely, HC7N, HC9N, and HC11N, have been investigated at low frequency (6–18 GHz). While, in that work, the isotopic species of HC7N (as well as HC9N and HC11N) were produced by high-voltage low-current discharge, in Puzzarini et al. (2023), DC7N was produced by FVP, co-pyrolizing fully-deuterated toluene (toluene-d8) and trichloroacetonitrile (Cl3CCN) in a 1:20 ratio at 1,200 °C, and measurements were extended in the millimeter-wave region (80–90 GHz). The ground-state rotational constant retrieved in McCarthy et al. (2000) and that derived in Puzzarini et al. (2023) from a global fit are collected in Figure 9, while the comparison of the full set of spectroscopic parameters can be found in Puzzarini et al. (2023). Here, we limit ourselves to note that, as pointed out in Puzzarini et al. (2023), incorporation of millimeter-wave measurements in the fit led to a relevant improvement in the accuracy of the line catalog, with uncertainties reducing from 0.9 to 1 MHz to about 10–20 kHz. Furthermore, above 50 GHz, transition frequencies were found to vary up to ∼500 kHz.
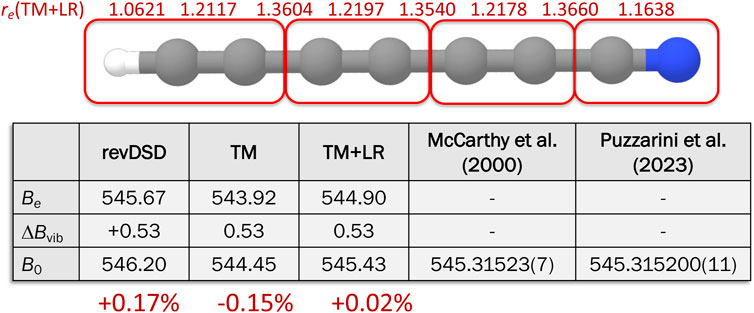
FIGURE 9. Molecular structure of HC7N: the TM+LR equilibrium parameters are reported. In the table, the equilibrium rotational constants at different level of theory are collected, and the corresponding ground-state rotational constants are compared with experiment (McCarthy et al., 2000; Puzzarini et al., 2023).
As shown in Figure 9, DC7N is an illustrative example to demonstrate the accuracy that can be obtained with the TM+LR approach and that increasing the number of “Lego bricks” does not affect the effectiveness of the TM+LR approach. The corresponding equilibrium structure is reported in Figure 9 together with the associated equilibrium rotational constant. To compare with the experiment, the vibrational correction (evaluated at the fc-MP2/cc-pVDZ level) has been incorporated, thus providing the theoretical estimate of the ground-state rotational constant. The comparison of Figure 9 points out that the relative deviation from experiment is +0.17% at the revDSD-D3BJ/jun-cc-pVTZ level and −0.15% for the TM structure. When resorting to the TM+LR approach, the discrepancy reduces by one order of magnitude, i.e., to +0.02%. Such an accuracy can be obtained only by exploiting high-level CC composite schemes. Therefore, TM+LR is a very powerful tool for accurately predicting rotational constants for systems of increasing complexity, as indeed demonstrated in Ye et al. (2022).
3.5.2 Toward PAHs and N-bearing derivatives
PAHs and their N-bearing derivatives are a prominent class of aromatics. Their elemental unit is benzene, which is however transparent to microwave radiation because of the lack of any permanent dipole moment. Consequently, its substituted species can be considered good proxies to trace its presence and abundance. The same applies to fused benzene rings such as naftalene and antracene. Among the possible substituents, the cyano (–CN) and ethynyl (–CCH) groups introduce good dipole moment and have led to the detection of benzonitrile (McGuire et al., 2018), cyanonaphtalenes (McGuire et al., 2021), ethynyl cyclopropenylidene (Cernicharo et al., 2021a), ethynyl cyclopentadienes (Cernicharo et al., 2021b), and cyanoindenes (Sita et al., 2022). The limiting factor to further interstellar identifications is the availability of accurate line lists obtained from high-resolution laboratory investigations. Even when production of the molecular species is not a challenge, the recorded rotational spectra are often characterized by a high density of the spectral lines. In such cases, their analysis becomes the limiting step to derive accurate catalogs. In this respect, accurate predictions is a key into simplifying and speeding up the spectral assignments. However, accuracy becomes an issue when dealing with large systems, with the TM+LR approach offering an excellent way-out.
In Ye et al. (2022), a set of small PAHs and polycyclic aromatic nitrogen heterocycles (PANHs) were considered to test the accuracy obtainable with the TM/TM+LR approach. The species considered ranged from one to four fused aromatic rings, with nitrogen being either a member of the ring or part of the substituents. A few molecules containing oxygen in the functional groups were also part of the set. The benchmark study of Ye et al. (2022) demonstrated that the TM+LR approach is able to provide, at a very limited computational cost, accurate rotational constants, with deviations from experiment as small as 0.01%–0.03% and in all cases well within 0.1%. A selection of results is shown in Figure 10: in order to compare theoretical and experimental data, the equilibrium rotational constants were augmented by vibrational corrections computed at the B3LYP-D3BJ/jun-cc-pVDZ level. In Ye et al. (2022), after the benchmark study, the TM/TM+LR approach was then applied to a set of 13 small PA(N)Hs not yet experimentally investigated (such as ethynylphenanthrene and pyrenecarbonitrile), thus providing accurate predictions for their rotational constants.
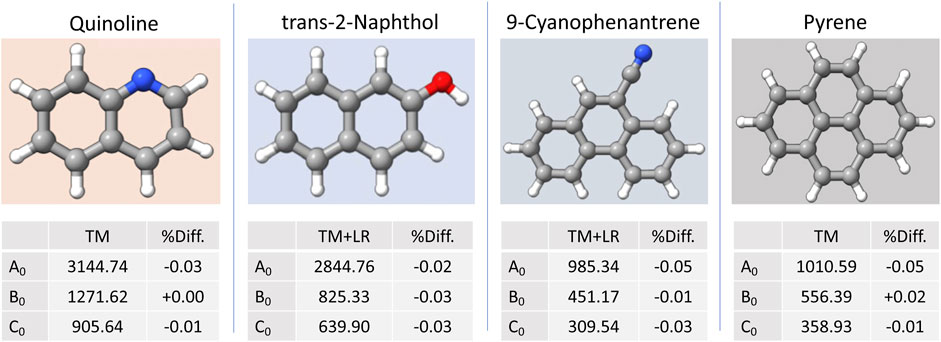
FIGURE 10. Selected examples from the benchmark set employed in Ye et al. (2022): for each system, the computed ground-state rotational constants and the relative deviation from experiment are reported. The “Lego bricks” used are: benzene and pyridine for quinoline, benzene and water for trans-2-naphthol, benzene and HCN for 9-cyanophenantrene, benzene for pyrene.
A first application of the TM+LR model to systems of astrophysical interest in order to support their experimental characterization has been reported in Spaniol et al. (2023), where the isomers of cyanoethynylbenzene (ortho −, meta − and para − HCC–C6H4–CN) have been considered. All of them are strong candidates for interstellar identification in view of the fact that benzonitrile (McGuire et al., 2018) and phenylacetylene (tentative; Cernicharo et al., 2021b) have already been detected, and both –CN and –CCH are polar and common functional groups. Indeed, the CN and CCH radicals are abundant and the gas-phase reaction of the CN and CCH radicals with benzene is the most accepted formation route for benzonitrile and phenylacetylene, respectively. For ortho −, meta − and para − HCC–C6H4–CN, the same methodology mentioned above (TM+LR approach for Be and the ΔBvib correction at the B3LYP-D3BJ/jun-cc-pVDZ level) was used not only for predicting the ground-state rotational constants, but also for the rotational constants of vibrational excited states. Another crucial information provided by theory was the prediction of the quartic centrifugal distortion constants (at the fc-MP2/cc-pVTZ level). In line with Ye et al. (2022), the computed B0 values were found to deviate from experiment, on average, by 0.026%. The discrepancy increased to 2.5% for quartic centrifugal terms (Spaniol et al., 2023). The experimental spectroscopic data obtained by Spaniol et al. (2023) will enable astronomical searches for these molecules.
Another recent example where the TM+LR predictions from Ye et al. (2022) were employed to guide the laboratory measurements, is provided by ethynylnaphthalene (Cabezas et al., 2022b). In Cabezas et al. (2022b), both 1- and 2-ethynylnaphthalene were considered, and the average deviation of TM+LR predictions was found to be 0.04%, thus in line with the outcomes of Ye et al. (2022).
4 Conclusion
In this review, a methodology to be exploited for the discovery of new molecules in the ISM has been presented. The steps (summarized in Figure 1) required to move from the laboratory spectroscopic characterization to the detection in space, are detailed. Different illustrative applications, ranging from small prebiotic molecules to radicals, to deuterated species and to larger systems such as long carbon chains and small PAHs, have been discussed.
In hunting for new interstellar molecules, the choice of the species to be investigated is driven by different reasons such as reaction mechanisms that suggest its formation in the ISM or astrochemical networks/theories that assume its presence in space. Rare isotopologues are also interesting targets because they can provide information on different physical properties such as isotopic ratios and fractionation. Then, the spectroscopic characterization (in the field of rotational spectroscopy) relies on a strong interplay of experiment and theory, which is crucial because exotic molecules are often not or poorly studied and produced using techniques, such as FVP and DC discharge, that lead to the concomitant formation of several other species, thus making the spectra crowded and difficult to be analyzed. An extensive spectral investigation combined with an accurate analysis then allows for obtaining a precise spectroscopic line catalog, which is used for astronomical searches. The detection in space of these exotic molecules, which have usually low abundances (especially when increasing molecular complexity) and hence low line intensities, requires unbiased (covering large bandwidths, to maximize the number of targeted transitions of interest) and ultra-sensitive spectral surveys (to increase sensitivity), like the ones obtained towards G+0.693−0.027 using Yebes 40 m and IRAM 30 m. As a part of the detection, the abundance of the new species is retrieved. This is usually based on assuming that the LTE approximation holds. However, a more accurate estimate is obtained by accounting for collisions competing with radiative processes. This however requires a major effort from the computational and/or experimental point of view, with the so-called COMs (complex organic molecules; Herbst and van Dishoeck, 2009) being an additional challenge for theoreticians and experimentalists because of the huge number of closely spaced rotational energy levels and the large number of internal coordinates.
While our strategy has been rationalized, it should be noted that each step is not at all straightforward but is instead hampered by challenges. The computational characterization suffers for the system dimension because of the unfavourable scaling of quantum-chemical models with the molecular size (even if an effective methodology has been proposed), but also for the possible presence of large amplitude motions, not to mention the theoretical difficulties when dealing with open-shell species. From the experimental point of view, envisioning suitable precursors and/or their synthesis are major difficulties together with finding efficient working conditions. The spectral analysis is also not devoid of difficulties because standard Hamiltonians might be not appropriate for the spectroscopic description of the system under investigation because of, for example, unexpected interactions. The detection of a new molecule is hampered not only by low line intensities (as stressed above), but also by the ‘forest’ of lines due to other species that makes it difficult to find unblended emissions. Furthermore, molecules with small dipole moments (and thus weak emissions) are hardly observable even if abundant, while the apolar ones require suitable proxies (Alessandrini et al., 2023). Finally, the derivation of accurate molecular abundances can be hampered by relevant deviation from the LTE model.
The last note concerns interstellar molecules adsorbed on or locked inside dust grains. While about 300 gas-phase molecules have been detected in the interstellar medium or circumstellar shells (Woon, 2004; Müller et al., 2005; McGuire, 2022), far more limited is the knowledge about the chemical composition of the ice covering dust grains. However, it is expected that, in the near future, the JWST will significantly improve our current knowledge (McClure et al., 2023).
Author contributions
CP contributed on conceptualization, project administration, methodology, data curation, validation, writing–original draft, writing–review and editing. CP and VR contributed on funding acquisition. SA, LB, MM, and VR contributed on methodology, investigation, data curation, formal analysis, validation, and writing–review and editing. All authors contributed to the article and approved the submitted version.
Funding
This work has been supported by MUR (PRIN Grant Number 202082CE3T) and by the University of Bologna (RFO funds). VR has received support from the project RYC2020-029387-I funded by MCIN/AEI/10.13039/501100011033.
Acknowledgments
The COST Action CA21101 “COSY–Confined molecular systems: from a new generation of materials to the stars” is acknowledged.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1https://site.unibo.it/rotational-computational-spectroscopy/en
2Madrid Data Cube Analysis on ImageJ is a software developed at the Center of Astrobiology (CAB) in Madrid: https://cab.inta-csic.es/madcuba/
References
Alberton, D., Bizzocchi, L., Jiang, N., Melosso, M., Rivilla, V. M., Charmet, A. P., et al. (2023a). Laboratory spectroscopy of allylimine and tentative detection towards the G+0.693-0.027 molecular cloud. Astron. Astrophys. 669, A93. doi:10.1051/0004-6361/202244618
Alberton, D., Lattanzi, V., Endres, C., Rivilla, V. M., Guillemin, J. C., Caselli, P., et al. (2023b). A high-resolution spectroscopic analysis of aminoacrylonitrile and an interstellar search toward G+0.693. Astrophys. J. 951, 108. doi:10.3847/1538-4357/acd8bd
Alessandrini, S., Bizzocchi, L., Melosso, M., and Puzzarini, C. (2023). Protonation of apolar species: from Cl2H+ to (E)-NCCHCHCNH+ through computational investigations. Front. Astron. Space Sci. 10, 1128896. doi:10.3389/fspas.2023.1128896
Alessandrini, S., Gauss, J., and Puzzarini, C. (2018). Accuracy of rotational parameters predicted by high-level quantum-chemical calculations: case study of sulfur-containing molecules of astrochemical interest. J. Chem. Theory Comput. 14, 5360–5371. doi:10.1021/acs.jctc.8b00695
Aliev, M. R., and Watson, J. K. (1976). Calculated sextic centrifugal distortion constants of polyatomic molecules. J. Mol. Spectrosc. 61, 29–52. doi:10.1016/0022-2852(76)90379-9
Aliev, M. R., and Watson, J. K. G. (1985). “Chapter 1 - higher-order effects in the vibration–rotation spectra of semirigid molecules,” in Molecular spectroscopy: Modern research. Editor K. N. Rao (New York: Academic Press), 1–67. doi:10.1016/B978-0-12-580643-5.50006-3
Avery, L. W., Broten, N. W., MacLeod, J. M., Oka, T., and Kroto, H. W. (1976). Detection of the heavy interstellar molecule cyanodiacetylene. Astrophys. J. Lett. 205, L173–L175. doi:10.1086/182117
Barone, V., Alessandrini, S., Biczysko, M., Cheeseman, J. R., Clary, D. C., McCoy, A. B., et al. (2021). Computational molecular spectroscopy. Nat. Rev. Methods Prim. 1, 38. doi:10.1038/s43586-021-00034-1
Belloche, A., Meshcheryakov, A. A., Garrod, R. T., Ilyushin, V. V., Alekseev, E. A., Motiyenko, R. A., et al. (2017). Rotational spectroscopy, tentative interstellar detection, and chemical modeling of N-methylformamide. Astron. Astrophys. 601, A49. doi:10.1051/0004-6361/201629724
Bermúdez, C., Tercero, B., Motiyenko, R. A., Margulès, L., Cernicharo, J., Ellinger, Y., et al. (2018). The millimeter-wave spectrum of methyl ketene and the astronomical search for it. Astron. Astrophys. 619, A92. doi:10.1051/0004-6361/201833267
Bizzocchi, L., Alessandrini, S., Melosso, M., Rivilla, V. M., and Puzzarini, C. (2022). Ab initio study of fine and hyperfine interactions in triplet POH. Molecules 27, 302. doi:10.3390/molecules27010302
Bizzocchi, L., Prudenzano, D., Rivilla, V. M., Pietropolli-Charmet, A., Giuliano, B. M., Caselli, P., et al. (2020). Propargylimine in the laboratory and in space: millimetre-wave spectroscopy and its first detection in the ism. Astron. Astrophys. 640, A98. doi:10.1051/0004-6361/202038083
Broten, N. W., Oka, T., Avery, L. W., MacLeod, J. M., and Kroto, H. W. (1978). The detection of HC9N in interstellar space. Astrophys. J. Lett. 223, L105–L107. doi:10.1086/182739
Brown, R. D., Godfrey, P. D., and Winkler, D. A. (1981). Hyperfine interactions in the microwave spectrum of 2-propen-1-Imine (vinylimine). Chem. Phys. 59, 243–247. doi:10.1016/0301-0104(81)85167-1
Burkhardt, A. M., Herbst, E., Kalenskii, S. V., McCarthy, M. C., Remijan, A. J., and McGuire, B. A. (2017). Detection of HC5N and HC7N isotopologues in TMC-1 with the green bank telescope. Mon. Not. R. Astron. Soc. 474, 5068–5075. doi:10.1093/mnras/stx2972
Cabezas, C., Agúndez, M., Marcelino, N., Tercero, B., Endo, Y., Fuentetaja, R., et al. (2022a). Discovery of the elusive thioketenylium, HCCS+, in TMC-1. Astron. Astrophys. 657, L4. doi:10.1051/0004-6361/202142815
Cabezas, C., Peña, I., and Cernicharo, J. (2022b). Laboratory rotational spectroscopy and astronomical search of ethynyl substituted naphthalene. Mon. Not. R. Astron. Soc. 519, 2590–2597. doi:10.1093/mnras/stac3698
Cassone, G., Saija, F., Sponer, J., Sponer, J. E., Ferus, M., Krus, M., et al. (2018). Dust motions in magnetized turbulence: source of chemical complexity. Astrophys. J. Lett. 866, L23. doi:10.3847/2041-8213/aae529
Cazzoli, G., Cludi, L., Buffa, G., and Puzzarini, C. (2012). Precise thz measurements of HCO+, N2H+, and CF+ for astrophysical observations. Astrophys. J. Suppl. Ser. 203, 11. doi:10.1088/0067-0049/203/1/11
Cazzoli, G., Lattanzi, V., Alonso, J. L., Gauss, J., and Puzzarini, C. (2015). The hyperfine structure of the rotational spectrum of HDO and its extension to the THz region: accurate rest frequencies and spectroscopic parameters for astrophysical observations. Astrophys. J. 806, 100. doi:10.1088/0004-637X/806/1/100
Cazzoli, G., Lattanzi, V., Kirsch, T., Gauss, J., Tercero, B., Cernicharo, J., et al. (2016). Laboratory measurements and astronomical search for the HSO radical. Astron. Astrophys. 591, A126. doi:10.1051/0004-6361/201628745
Cazzoli, G., Puzzarini, C., Harding, M. E., and Gauss, J. (2009). The hyperfine structure in the rotational spectrum of water: lamb-dip technique and quantum-chemical calculations. Chem. Phys. Lett. 473, 21–25. doi:10.1016/j.cplett.2009.03.045
Cazzoli, G., Puzzarini, C., and Lapinov, A. V. (2004). Precise laboratory frequencies for the J ← J − 1 (J=1, 2, 3, 4) rotational transitions of 13CO. Astrophys. J. 611, 615–620. doi:10.1086/421992
Cernicharo, J., Agúndez, M., Cabezas, C., Tercero, B., Marcelino, N., Pardo, J. R., et al. (2021a). Pure hydrocarbon cycles in TMC-1: discovery of ethynyl cyclopropenylidene, cyclopentadiene, and indene. Astron. Astrophys. 649, L15. doi:10.1051/0004-6361/202141156
Cernicharo, J., Agúndez, M., Kaiser, R. I., Cabezas, C., Tercero, B., Marcelino, N., et al. (2021b). Discovery of two isomers of ethynyl cyclopentadiene in TMC-1: abundances of CCH and CN derivatives of hydrocarbon cycles. Astron. Astrophys. 655, L1. doi:10.1051/0004-6361/202142226
Cernicharo, J., Cabezas, C., Pardo, J. R., Agúndez, M., Roncero, O., Tercero, B., et al. (2023). The magnesium paradigm in IRC+10216: discovery of MgC4H+, MgC3N+, MgC6H+, and MgC5N+. Astron. Astrophys. 672, L13. doi:10.1051/0004-6361/202346467
Ceselin, G., Barone, V., and Tasinato, N. (2021). Accurate biomolecular structures by the nano-LEGO approach: pick the bricks and build your geometry. J. Chem. Theory Comput. 17, 7290–7311. doi:10.1021/acs.jctc.1c00788
Changala, P. B., Gupta, H., Cernicharo, J., Pardo, J. R., Agúndez, M., Cabezas, C., et al. (2022). Laboratory and astronomical discovery of magnesium dicarbide, MgC2. Astrophys. J. Lett. 940, L42. doi:10.3847/2041-8213/aca144
Cheng, Q., Fortenberry, R. C., and DeYonker, N. J. (2017). Towards a quantum chemical protocol for the prediction of rovibrational spectroscopic data for transition metal molecules: exploration of CuCN, CuOH, and CuCCH. J. Chem. Phys. 147, 234303. doi:10.1063/1.5006931
Christen, D., Coudert, L., Suenram, R., and Lovas, F. (1995). The rotational/concerted torsional spectrum of the g′Ga conformer of ethylene glycol. J. Mol. Spectrosc. 172, 57–77. doi:10.1006/jmsp.1995.1155
Cohen, E., and Pickett, H. (1982). The rotation-inversion spectra and vibration-rotation interaction in NH2D. J. Mol. Spectrosc. 93, 83–100. doi:10.1016/0022-2852(82)90276-4
Császár, A. G., Allen, W. D., and Schaefer, H. F. (1998). In pursuit of the ab initio limit for conformational energy prototypes. J. Chem. Phys. 108, 9751–9764. doi:10.1063/1.476449
Demaison, J., Boggs, J. E., and Császár, A. G. (2016). Equilibrium molecular structures: From spectroscopy to quantum chemistry. Boca Raton: CRC Press. doi:10.1201/b10374
Dunning, T. H. (1989). Gaussian basis sets for use in correlated molecular calculations. I. the atoms boron through neon and hydrogen. J. Chem. Phys. 90, 1007–1023. doi:10.1063/1.456153
Endo, Y., Saito, S., and Hirota, E. (1981). Microwave spectra of the HSO and DSO radicals. J. Chem. Phys. 75, 4379–4384. doi:10.1063/1.442600
Feller, D. (1993). The use of systematic sequences of wave functions for estimating the complete basis set, full configuration interaction limit in water. J. Chem. Phys. 98, 7059–7071. doi:10.1063/1.464749
Fusina, L., Di Lonardo, G., Johns, J., and Halonen, L. (1988). Far-infrared spectra and spectroscopic parameters of NH2D and ND2H in the ground state. J. Mol. Spectrosc. 127, 240–254. doi:10.1016/0022-2852(88)90023-9
García de la Concepción, J., Puzzarini, C., Barone, V., Jiménez-Serra, I., and Roncero, O. (2021). Formation of phosphorus monoxide (PO) in the interstellar medium: insights from quantum-chemical and kinetic calculations. Astrophys. J. 922, 169. doi:10.3847/1538-4357/ac1e94
Goldsmith, P. F., and Langer, W. D. (1999). Population diagram analysis of molecular line emission. Astrophys. J. 517, 209–225. doi:10.1086/307195
Grimme, S., Antony, J., Ehrlich, S., and Krieg, H. (2010). A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 132, 154104. doi:10.1063/1.3382344
Grimme, S., Ehrlich, S., and Goerigk, L. (2011). Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 32, 1456–1465. doi:10.1002/jcc.21759
Grimme, S. (2006). Semiempirical hybrid density functional with perturbative second-order correlation. J. Chem. Phys. 124, 034108. doi:10.1063/1.2148954
Guelin, M., Green, S., and Thaddeus, P. (1978). Detection of the C4H radical toward IRC +10216. Astrophys. J. Lett. 224, L27–L30. doi:10.1086/182751
Guzmán, V., Roueff, E., Gauss, J., Pety, J., Gratier, P., Goicoechea, J. R., et al. (2012). The hyperfine structure in the rotational spectrum of CF+. Astron. Astrophys. 548, A94. doi:10.1051/0004-6361/201220174
Guzman-Ramirez, L., Zijlstra, A. A., NíChuimín, R., Gesicki, K., Lagadec, E., Millar, T. J., et al. (2011). Carbon chemistry in Galactic bulge planetary nebulae. Mon. Not. R. Astron. Soc. 414, 1667–1678. doi:10.1111/j.1365-2966.2011.18502.x
Hays, B. M., Gupta, D., Guillaume, T., Abdelkader Khedaoui, O., Cooke, I. R., Thibault, F., et al. (2022). Collisional excitation of HNC by He found to be stronger than for structural isomer HCN in experiments at the low temperatures of interstellar space. Nat. Chem. 14, 811–815. doi:10.1038/s41557-022-00936-x
Heckert, M., Kállay, M., and Gauss, J. (2005). Molecular equilibrium geometries based on coupled-cluster calculations including quadruple excitations. Mol. Phys. 103, 2109–2115. doi:10.1080/00268970500083416
Heckert, M., Kállay, M., Tew, D. P., Klopper, W., and Gauss, J. (2006). Basis-set extrapolation techniques for the accurate calculation of molecular equilibrium geometries using coupled-cluster theory. J. Chem. Phys. 125, 044108. doi:10.1063/1.2217732
Helgaker, T., Klopper, W., Koch, H., and Noga, J. (1997). Basis-set convergence of correlated calculations on water. J. Chem. Phys. 106, 9639–9646. doi:10.1063/1.473863
Herbst, E. (2021). Unusual chemical processes in interstellar chemistry: past and present. Front. Astron. Space Sci. 8, 776942. doi:10.3389/fspas.2021.776942
Herbst, E., and van Dishoeck, E. F. (2009). Complex organic interstellar molecules. Annu. Rev. Astron. Astrophys. 47, 427–480. doi:10.1146/annurev-astro-082708-101654
Huang, X., and Lee, T. J. (2009). Accurate ab initio quartic force fields for and CCH− and rovibrational spectroscopic constants for their isotopologs. J. Chem. Phys. 131, 104301. doi:10.1063/1.3212560
James, P. L., Sims, I. R., Smith, I. W. M., Alexander, M. H., and Yang, M. (1998). A combined experimental and theoretical study of rotational energy transfer in collisions between NO (X2Π1/2, v=3,J) and He, Ar and N2 at temperatures down to 7 K. J. Chem. Phys. 109, 3882–3897. doi:10.1063/1.476517
Jiang, N., Melosso, M., Tamassia, F., Bizzocchi, L., Dore, L., Canè, E., et al. (2021). High-resolution infrared spectroscopy of DC3N in the stretching region. Front. Astron. Space Sci. 8, 29. doi:10.3389/fspas.2021.656295
Karton, A., and Martin, J. M. L. (2012). Explicitly correlated wn theory: W1-F12 and W2-F12. J. Chem. Phys. 136, 124114. doi:10.1063/1.3697678
Karton, A., Rabinovich, E., Martin, J. M. L., and Ruscic, B. (2006). W4 theory for computational thermochemistry: in pursuit of confident sub-kJ/mol predictions. J. Chem. Phys. 125, 144108. doi:10.1063/1.2348881
Karton, A., and Talbi, D. (2014). Pinning the most stable HxCyOz isomers in space by means of high-level theoretical procedures. Chem. Phys. 436-437, 22–28. doi:10.1016/j.chemphys.2014.03.010
Keto, E., and Caselli, P. (2010). Dynamics and depletion in thermally supercritical starless cores. Mon. Not. R. Astron. Soc. 402, 1625–1634. doi:10.1111/j.1365-2966.2009.16033.x
Kłos, J., and Lique, F. (2017). “Cold molecular collisions: quantum scattering calculations and their relevance in astrophysical applications,” in Cold chemistry: Molecular scattering and reactivity near absolute zero (RSC Theoretical and Computational Chemistry Series). doi:10.1039/9781782626800-00046
Koelemay, L. A., Burton, M. A., Singh, A. P., Sheridan, P. M., Bernal, J. J., and Ziurys, L. M. (2022). Laboratory and astronomical detection of the SiP radical (X2Πi): more circumstellar phosphorus. Astrophys. J. Lett. 940, L11. doi:10.3847/2041-8213/ac9d9b
Kroto, H. W., Kirby, C., Walton, D. R. M., Avery, L. W., Broten, N. W., MacLeod, J. M., et al. (1978). The detection of cyanohexatriyne, H(C≡C)3CN, in Heile’s Cloud 2. Astrophys. J. Lett. 219, L133–L137. doi:10.1086/182623
Lee, K. L. K., Loomis, R. A., Burkhardt, A. M., Cooke, I. R., Xue, C., Siebert, M. A., et al. (2021). Discovery of interstellar trans-cyanovinylacetylene (HC ≡ CCH = CHC ≡ N) and vinylcyanoacetylene (H2C = CHC3N) in GOTHAM observations of TMC-1. Astrophys. J. Lett. 908, L11. doi:10.3847/2041-8213/abdbb9
Lupi, J., Alessandrini, S., Barone, V., and Puzzarini, C. (2021). junChS and junChS-F12 models: parameter-free efficient yet accurate composite schemes for energies and structures of noncovalent complexes. J. Chem. Theory Comput. 17, 6974–6992. doi:10.1021/acs.jctc.1c00869
Marcelino, N., Puzzarini, C., Agúndez, M., Fuentetaja, R., Tercero, B., de Vicente, P., et al. (2023). First detection of the HSO radical in space. Astron. Astrophys. 674, L13. doi:10.1051/0004-6361/202346935
Martín, S., Martín-Pintado, J., Blanco-Sánchez, C., Rivilla, V. M., Rodríguez-Franco, A., and Rico-Villas, F. (2019). Spectral line identification and modelling (SLIM) in the MAdrid data CUBe analysis (MADCUBA) package. Interactive software for data cube analysis. Astron. Astrophys. 631, A159. doi:10.1051/0004-6361/201936144
Martín, S., Requena-Torres, M. A., Martín-Pintado, J., and Mauersberger, R. (2008). Tracing shocks and photodissociation in the galactic center region. Astrophys. J. 678, 245–254. doi:10.1086/533409
Matthews, D. A., Cheng, L., Harding, M. E., Lipparini, F., Stopkowicz, S., Jagau, T. C., et al. (2020). Coupled-cluster techniques for computational chemistry: the CFOUR program package. J. Chem. Phys. 152, 214108. doi:10.1063/5.0004837
McCarthy, M. C., Lee, K. L. K., Loomis, R. A., Burkhardt, A. M., Shingledecker, C. N., Charnley, S. B., et al. (2021). Interstellar detection of the highly polar five-membered ring cyanocyclopentadiene. Nat. Astron 5, 176–180. doi:10.1038/s41550-020-01213-y
McCarthy, M. C., Levine, E. S., Apponi, A. J., and Thaddeus, P. (2000). Experimental structures of the carbon chains HC7N, HC9N, and HC11N by isotopic substitution. J. Mol. Spectrosc. 203, 75–81. doi:10.1006/jmsp.2000.8149
McClure, M. K., Rocha, W. R. M., Pontoppidan, K. M., Crouzet, N., Chu, L. E. U., Dartois, E., et al. (2023). An Ice Age JWST inventory of dense molecular cloud ices. Nat. Astron. 7, 431–443. doi:10.1038/s41550-022-01875-w
McGuire, B. A. (2018). 2018 census of interstellar, circumstellar, extragalactic, protoplanetary disk, and exoplanetary molecules. Astrophys. J. Suppl. Ser. 239, 17. doi:10.3847/1538-4365/aae5d2
McGuire, B. A. (2022). 2021 census of interstellar, circumstellar, extragalactic, protoplanetary disk, and exoplanetary molecules. Astrophys. J. Suppl. Ser. 259, 30. doi:10.3847/1538-4365/ac2a48
McGuire, B. A., Burkhardt, A. M., Kalenskii, S., Shingledecker, C. N., Remijan, A. J., Herbst, E., et al. (2018). Detection of the aromatic molecule benzonitrile (C6H5CN) in the interstellar medium. Science 359, 202–205. doi:10.1126/science.aao4890
McGuire, B. A., Loomis, R. A., Burkhardt, A. M., Lee, K. L. K., Shingledecker, C. N., Charnley, S. B., et al. (2021). Detection of two interstellar polycyclic aromatic hydrocarbons via spectral matched filtering. Science 371, 1265–1269. doi:10.1126/science.abb7535
Melli, A., Melosso, M., Bizzocchi, L., Alessandrini, S., Jiang, N., Tonolo, F., et al. (2022). Rotational spectra of unsaturated carbon chains produced by pyrolysis: the case of propadienone, cyanovinylacetylene, and allenylacetylene. J. Phys. Chem. A 126, 6210–6220. doi:10.1021/acs.jpca.2c05018
Melli, A., Tonolo, F., Barone, V., and Puzzarini, C. (2021). Extending the applicability of the semi-experimental approach by means of “Template Molecule” and “Linear Regression” models on top of DFT computations. J. Phys. Chem. A 125, 9904–9916. doi:10.1021/acs.jpca.1c07828
Melosso, M., Belloche, A., Martin-Drumel, M. A., Pirali, O., Tamassia, F., Bizzocchi, L., et al. (2020a). Far-infrared laboratory spectroscopy of aminoacetonitrile and first interstellar detection of its vibrationally excited transitions. Astron. Astrophys. 641, A160. doi:10.1051/0004-6361/202038466
Melosso, M., Bizzocchi, L., Dore, L., Kisiel, Z., Jiang, N., Spezzano, S., et al. (2021). Improved centrifugal and hyperfine analysis of ND2H and NH2D and its application to the spectral line survey of L1544. J. Mol. Spectrosc. 377, 111431. doi:10.1016/j.jms.2021.111431
Melosso, M., Bizzocchi, L., Gazzeh, H., Tonolo, F., Guillemin, J. C., Alessandrini, S., et al. (2022). Gas-phase identification of (Z)-1,2-ethenediol, a key prebiotic intermediate in the formose reaction. Chem. Commun. 58, 2750–2753. doi:10.1039/D1CC06919E
Melosso, M., Bizzocchi, L., Tamassia, F., Degli Esposti, C., Canè, E., and Dore, L. (2019a). The rotational spectrum of 15ND. Isotopic-independent Dunham-type analysis of the imidogen radical. Phys. Chem. Chem. Phys. 21, 3564–3573. doi:10.1039/c8cp04498h
Melosso, M., Conversazioni, B., Degli Esposti, C., Dore, L., Cané, E., Tamassia, F., et al. (2019b). The pure rotational spectrum of 15ND2 observed by millimetre and submillimetre-wave spectroscopy. J. Quant. Spectrosc. Radiat. Transf. 222, 186–189. doi:10.1016/j.jqsrt.2018.10.028
Melosso, M., Dore, L., Gauss, J., and Puzzarini, C. (2020b). Deuterium hyperfine splittings in the rotational spectrum of NH2D as revealed by lamb-dip spectroscopy. J. Mol. Spectrosc. 370, 111291. doi:10.1016/j.jms.2020.111291
Melosso, M., Melli, A., Puzzarini, C., Codella, C., Spada, L., Dore, L., et al. (2018). Laboratory measurements and astronomical search for cyanomethanimine. Astron. Astrophys. 609, A121. doi:10.1051/0004-6361/201731972
Mills, I. M. (1972). “Vibration-rotation structure in asymmetric- and symmetric-top molecules,” in Molecular spectroscopy: Modern research. Editors K. N. Rao, and C. W. Matthews (New York: Academic Press), 115–140.
Møller, C., and Plesset, M. S. (1934). Note on an approximation treatment for many-electron systems. Phys. Rev. 46, 618–622. doi:10.1103/physrev.46.618
Morgan, W. J., Matthews, D. A., Ringholm, M., Agarwal, J., Gong, J. Z., Ruud, K., et al. (2018). Geometric energy derivatives at the complete basis set limit: application to the equilibrium structure and molecular force field of formaldehyde. J. Chem. Theory Comput. 14, 1333–1350. doi:10.1021/acs.jctc.7b01138
Müller, H. S. P., Schlöder, F., Stutzki, J., and Winnewisser, G. (2005). The cologne database for molecular spectroscopy, CDMS: A useful tool for astronomers and spectroscopists. J. Mol. Struct. 742, 215–227. doi:10.1016/j.molstruc.2005.01.027
Negron-Mendoza, A., and Ramos-Bernal, S. (2001). “Interstellar molecules: an exotic chemistry,” in First steps in the origin of life in the universe. Editors J. Chela-Flores, T. Owen, and F. Raulin (Dordrecht: Springer Netherlands), 145–150.
Orr, B. J. (1995). Collision-induced state-to-state energy transfer in perturbed rovibrational manifolds of small polyatomic molecules: mechanistic insights and observations. Chem. Phys. 190, 261–278. doi:10.1016/0301-0104(94)00279-J
Papajak, E., Zheng, J., Xu, X., Leverentz, H. R., and Truhlar, D. G. (2011). Perspectives on basis sets beautiful: seasonal plantings of diffuse basis functions. J. Chem. Theory Comput. 7, 3027–3034. doi:10.1021/ct200106a
Penn, R. E. (1978). Microwave spectrum of 2-propene-1-imine, CH2=CHCH=NH. J. Mol. Spectrosc. 69, 373–382. doi:10.1016/0022-2852(78)90230-8
Penocchio, E., Piccardo, M., and Barone, V. (2015). Semiexperimental equilibrium structures for building blocks of organic and biological molecules: the B2PLYP route. J. Chem. Theory Comput. 11, 4689–4707. doi:10.1021/acs.jctc.5b00622
Peterson, K. A., and Dunning, T. H. (2002). Accurate correlation consistent basis sets for molecular core-valence correlation effects: the second row atoms Al-Ar, and the first row atoms B-Ne revisited. J. Chem. Phys. 117, 10548–10560. doi:10.1063/1.1520138
Peterson, K. A., Feller, D., and Dixon, D. (2012). Chemical accuracy in ab initio thermochemistry and spectroscopy: current strategies and future challenges. Theor. Chem. Acc. 113, 1079. doi:10.1007/s00214-011-1079-5
Piccardo, M., Penocchio, E., Puzzarini, C., Biczysko, M., and Barone, V. (2015). Semi-experimental equilibrium structure determinations by employing B3LYP/SNSD anharmonic force fields: validation and application to semirigid organic molecules. J. Phys. Chem. A 119, 2058–2082. doi:10.1021/jp511432m
Pickett, H. M., Poynter, R. L., Cohen, E. A., Delitsky, M. L., Pearson, J. C., and Müller, H. S. P. (1998). Submillimeter, millimeter and microwave spectral line catalog. J. Quant. Spectrosc. Radiat. Transf. 60, 883–890. doi:10.1016/S0022-4073(98)00091-0
Pickett, H. M. (1991). The fitting and prediction of vibration-rotation spectra with spin interactions. J. Mol. Spectrosc. 148, 371–377. doi:10.1016/0022-2852(91)90393-o
Prestage, R. M., Constantikes, K. T., Hunter, T. R., King, L. J., Lacasse, R. J., Lockman, F. J., et al. (2009). The green bank telescope. Proc. IEEE 97, 1382–1390. doi:10.1109/jproc.2009.2015467
Pulay, P., Meyer, W., and Boggs, J. E. (1978). Cubic force constants and equilibrium geometry of methane from Hartree–Fock and correlated wavefunctions. J. Chem. Phys. 68, 5077–5085. doi:10.1063/1.435626
Puzzarini, C., Alessandrini, S., Bizzocchi, L., and Melosso, M. (2023). Hunting for interstellar molecules: rotational spectra of reactive species. Faraday Discuss. doi:10.1039/D3FD00052D
Puzzarini, C., and Barone, V. (2011). Extending the molecular size in accurate quantum-chemical calculations: the equilibrium structure and spectroscopic properties of uracil. Phys. Chem. Chem. Phys. 13, 7189–7197. doi:10.1039/C0CP02636K
Puzzarini, C., Bloino, J., Tasinato, N., and Barone, V. (2019). Accuracy and interpretability: the devil and the holy grail. new routes across old boundaries in computational spectroscopy. Chem. Rev. 119, 8131–8191. doi:10.1021/acs.chemrev.9b00007
Puzzarini, C., Cazzoli, G., Harding, M. E., Vázquez, J., and Gauss, J. (2009). A new experimental absolute nuclear magnetic shielding scale for oxygen based on the rotational hyperfine structure of
Puzzarini, C., Cazzoli, G., Harding, M. E., Vázquez, J., and Gauss, J. (2015). The hyperfine structure in the rotational spectra of
Puzzarini, C. (2020). Grand challenges in astrochemistry. Front. Astron. Space Sci. 7, 19. doi:10.3389/fspas.2020.00019
Puzzarini, C., Heckert, M., and Gauss, J. (2008). The accuracy of rotational constants predicted by high-level quantum-chemical calculations. I. molecules containing first-row atoms. J. Chem. Phys. 128, 194108. doi:10.1063/1.2912941
Puzzarini, C., and Stanton, J. F. (2023). Connections between the accuracy of rotational constants and equilibrium molecular structures. Phys. Chem. Chem. Phys. 25, 1421–1429. doi:10.1039/D2CP04706C
Puzzarini, C., Stanton, J. F., and Gauss, J. (2010). Quantum-chemical calculation of spectroscopic parameters for rotational spectroscopy. Int. Rev. Phys. Chem. 29, 273–367. doi:10.1080/01442351003643401
Raghavachari, K., Trucks, G. W., Pople, J. A., and Head-Gordon, M. (1989). A fifth-order perturbation comparison of electron correlation theories. Chem. Phys. Lett. 157, 479–483. doi:10.1016/s0009-2614(89)87395-6
Rivilla, V. M., Colzi, L., Jiménez-Serra, I., Martín-Pintado, J., Megías, A., Melosso, M., et al. (2022). Precursors of the rna world in space: detection of (Z)-1,2-ethenediol in the interstellar medium, a key intermediate in sugar formation. Astrophys. J. Lett. 929, L11. doi:10.3847/2041-8213/ac6186
Rivilla, V. M., Martín-Pintado, J., Jiménez-Serra, I., Zeng, S., Martín, S., Armijos-Abendaño, J., et al. (2018). Abundant Z-cyanomethanimine in the interstellar medium: paving the way to the synthesis of adenine. Mon. Not. R. Astron. Soc. 483, L114–L119. doi:10.1093/mnrasl/sly228
Roueff, E., and Lique, F. (2013). Molecular excitation in the interstellar medium: recent advances in collisional, radiative, and chemical processes. Chem. Rev. 113, 8906–8938. doi:10.1021/cr400145a
Santra, G., Sylvetsky, N., and Martin, J. M. L. (2019). Minimally empirical double-hybrid functionals trained against the GMTKN55 database: revDSD-PBEP86-D4, revDOD-PBE-D4, and DOD-SCAN-D4. J. Phys. Chem. A 123, 5129–5143. doi:10.1021/acs.jpca.9b03157
Silva, W. G. D. P., Cernicharo, J., Schlemmer, S., Marcelino, N., Loison, J. C., Agúndez, M., et al. (2023). Discovery of H2CCCH+ in TMC-1. Astron. Astrophys. 676, L1. doi:10.1051/0004-6361/202347174
Sita, M. L., Changala, P. B., Xue, C., Burkhardt, A. M., Shingledecker, C. N., Lee, K. L. K., et al. (2022). Discovery of interstellar 2-cyanoindene (2-C9H7CN) in GOTHAM observations of TMC-1. Astrophys. J. Lett. 938, L12. doi:10.3847/2041-8213/ac92f4
Spaniol, J. T., Lee, K. L. K., Pirali, O., Puzzarini, C., and Martin-Drumel, M. A. (2023). A rotational investigation of the three isomeric forms of cyanoethynylbenzene (HCC–C6H4–CN): benchmarking experiments and calculations using the “lego brick” approach. Phys. Chem. Chem. Phys. 25, 6397–6405. doi:10.1039/d2cp04825f
Tafalla, M., Myers, P., Caselli, P., Walmsley, C., and Comito, C. (2002). Systematic molecular differentiation in starless cores. Astrophys. J. 569, 815–835. doi:10.1086/339321
Tajti, A., Szalay, P. G., Császár, A. G., Kállay, M., Gauss, J., Valeev, E. F., et al. (2004). Heat: high accuracy extrapolated ab initio thermochemistry. J. Chem. Phys. 121, 11599–11613. doi:10.1063/1.1811608
Tennyson, J. (2019). Astronomical spectroscopy. An introduction to the atomic and molecular physics of astronomical spectroscopy (WSPC). Europe: World Scientific. doi:10.1142/q0207
Tercero, F., López-Pérez, J. A., Gallego, J. D., Beltrán, F., García, O., Patino-Esteban, M., et al. (2021). Yebes 40 m radio telescope and the broad band Nanocosmos receivers at 7 mm and 3 mm for line surveys. Astron. Astrophys. 645, A37. doi:10.1051/0004-6361/202038701
Tielens, A. (2021). Molecular astrophysics. Cambrindge: Cambrindge Unversity Press. doi:10.1017/9781316718490
Tonolo, F., Bizzocchi, L., Melosso, M., Lique, F., Dore, L., Barone, V., et al. (2021). An improved study of HCO+ and He system: interaction potential, collisional relaxation, and pressure broadening. J. Chem. Phys. 155, 234306. doi:10.1063/5.0075929
Tonolo, F., Lique, F., Melosso, M., Puzzarini, C., and Bizzocchi, L. (2022). Hyperfine resolved rate coefficients of H
Watson, J. K. G. (1977). “Aspects of quartic and sextic centrifugal effects on rotational energy levels,” in Vibrational spectra and structure. Editor J. Durig (Amsterdam: Elsevier), 1–89.
Watson, J. K. G. (1968). Determination of centrifugal distortion coefficients of asymmetric-top molecules. III. sextic coefficients. J. Chem. Phys. 48, 4517–4524. doi:10.1063/1.1668020
Wilson, A. K., van Mourik, T., and Dunning, T. H. (1996). Gaussian basis sets for use in correlated molecular calculations. VI. sextuple zeta correlation consistent basis sets for boron through neon. J. Mol. Struct. THEOCHEM 388, 339–349. doi:10.1016/S0166-1280(96)80048-0
Woon, D. E. (2004). The astrochymist: an internet resource for astrochemists and interested bystanders. Avaliable At: https://www.astrochymist.org/.
Woon, D. E., and Dunning, T. H. (1995). Gaussian basis sets for use in correlated molecular calculations. V. Core-valence basis sets for boron through neon. J. Chem. Phys. 103, 4572–4585. doi:10.1063/1.470645
Wootten, A., and Thompson, A. R. (2009). The atacama large millimeter/submillimeter array. IEEE Proc. 97, 1463–1471. doi:10.1109/jproc.2009.2020572
Yamamoto, S. (2017). Introduction to astrochemistry: Chemical evolution from interstellar clouds to star and planet formation. Tokyo: Springer Tokyo. doi:10.1007/978-4-431-54171-4
Keywords: astrochemistry, interstellar medium, unstable/reactive species, quantum chemistry, rotational spectroscopy, astronomical observations
Citation: Puzzarini C, Alessandrini S, Bizzocchi L, Melosso M and Rivilla VM (2023) From the laboratory to the interstellar medium: a strategy to search for exotic molecules in space. Front. Astron. Space Sci. 10:1211784. doi: 10.3389/fspas.2023.1211784
Received: 25 April 2023; Accepted: 31 July 2023;
Published: 17 August 2023.
Edited by:
Ryan C. Fortenberry, University of Mississippi, United StatesReviewed by:
Marcin Gronowski, Institute of Physical Chemistry, PolandGiuseppe Cassone, National Research Council (CNR), Italy
Copyright © 2023 Puzzarini, Alessandrini, Bizzocchi, Melosso and Rivilla. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Cristina Puzzarini, Y3Jpc3RpbmEucHV6emFyaW5pQHVuaWJvLml0
 Cristina Puzzarini
Cristina Puzzarini Silvia Alessandrini
Silvia Alessandrini Luca Bizzocchi
Luca Bizzocchi Mattia Melosso
Mattia Melosso Víctor M. Rivilla2
Víctor M. Rivilla2