- 1Graduate School of Engineering and Science, Istanbul University, Istanbul, Türkiye
- 2School of Mathematical Sciences, Zhejiang Normal University, Jinhua, Zhejiang, China
- 3Department of Physics, Istanbul University, Istanbul, Türkiye
- 4Department of Mathematics, University of Management and Technology, Lahore, Pakistan
- 5Section of Mathematics, International Telematic University Uninettuno, Roma, Italy
- 6Department of Computer Science and Mathematics, Lebanese American University, Beirut, Lebanon
- 7Operational Research Center in Healthcare, Near East University, Nicosia, Cyprus
- 8Department of Statistics and Operations Research, College of Science, King Saud University, Riyadh, Saudi Arabia
This paper explores new neutron star models based on spherically symmetric space–time. We take into account the gravitational effects of
1 Introduction
The expansion of the Universe first came into discussion in 1998 (Riess et al., 1998). This knowledge was genuinely adverse to the expectations of observers. Observers became curious about the causes of this expansion at an accelerating rate. Eventually, the cosmological constant “Λ” is held responsible for the aforementioned expansion. “Λ” represents the existence of dark energy. This constant “Λ” is a negative pressure fluid that provides the accelerating forces and opposes the NECs (null energy condition). Some amendments in GR (general relativity) were suggested to elaborate the late-time cosmic-accelerated behavior of the Universe by reducing the effects of DE (dark energy). GR is based on the symmetric and torsion-free Levi-Civita connection (Aldrovandi and Pereira, 2012) (
TEGR (teleparallel equivalent to general relativity) is a curvature-free torsion-based theory. A generalized version of TEGR is f(T) gravity, which has close correspondence with the f(R) theory. In the f(T) theory, torsion T defines its gravitational field action rather than the Lagrangian function. This theory depends upon the Weitzenbock connection, so it is a curvature-less theory and has non-zero torsion (Aldrovandi and Pereira, 2012). Einstein defined torsion-based gravity depending on space–time (Einstein and Preuss, 1925). In setting up TEGR field equations, a tetrad plays a key role instead of the metric function. Different tetrads give rise to different field equations. Good tetrad and bad tetrad are two types of tetrads known as off-diagonal and diagonal tetrads, respectively. The application of a diagonal tetrad generates some solar system limitations in f(T) gravity (Iorio and Saridakis, 2012a; Xie and Deng, 2013a). Hence, the choice of a correct (good) tetrad frees the function “f” from the imposition of the aforesaid constraints. The use of a diagonal (bad) tetrad produces a theory that is only well settled with the Birkhoff theorem, but the Schwarzschild metric is not the solution to that particular theory. However, an off-diagonal (good) tetrad does not impose any constraint on the value of “f” or “T.” In this work, we use an off-diagonal tetrad.
Being TEGR and GR equivalent theories, every solution of TEGR is also the solution of GR. So, the problems which remain unaddressed in GR also carry with TEGR. One of the problems faced by researchers is of cosmological constant Λ, which serves as the negative pressure fluid pΛ = −ρΛ. When exploring the present behavior of accelerating the Universe, GR can only deal with it by adding a scalar field as an extra term. The observed value of Λ drastically varies from the expected value, and researchers term that issue as a “fine-tuning problem.” According to the collective view of researchers, this problem can only be dealt with by modifying GR, including an extra scalar field, or by altering the standard model of physics. Some theories suggest that GR modification can describe the late-time cosmic expansion behavior without the involvement of Λ. Regarding the early Universe, the rapid expansion in observations is called the inflationary era. This rapid expansion cannot be handled by the cosmological constant. This situation can be elaborated in the best way by including a scalar field. GR also does not provide any knowledge about the beginning and nature of inflation. Modified gravity (Nojiri and Odintsov, 2007; Sotiriou and Faraoni, 2010; Capozziello and De Laurentis, 2011) collectively explains the inflationary era called early-time expansion and the present DE era. The problem of coincidence suggests that matter’s energy density and end DE of the present day are the same. Some theorists also think that it is not an issue but merely a coincidence. However, some GR modifications may address this issue (Nojiri and Odintsov, 2007). Famaey and McGaugh (2012) and Clifton et al. (2012) have pointed out many more issues which cannot be addressed in detail by GR. However, when one generalizes TEGR to the f(T) gravity theory, this similarity is scattered as we consider Lagrangian as a function of the torsion scalar (Ferraro and Fiorini, 2008; Fiorini and Ferraro, 2009). Due to this reason, f(T) gravity is chosen as a strong applicant to elaborate the acceleration aspect of Universe expansion by eliminating the existence of DE (Li et al., 2011; Cardone et al., 2012).
When we consider modeling stellar structures, we have to deal with field equations. Like GR, f(T) gravity field equations have second-order derivatives, while f(R) gravity equations contain fourth-order derivatives (Nojiri and Odintsov, 2007), where Palatini’s version of f(R) gravity consists of second-order equations. So, EFEs in f(T) gravity, being of the second order, are easier to solve than the equations of f(R) gravity. Contrary to GR, f(T) gravity equations of motion are non-variant under the Lorentz transformation (Li et al., 2011), so they display an extra degree of freedom. Therefore, the f(T) theory tremendously explains the whole scenario of cosmic acceleration on a wider scale of observations, like the clustering of galaxies (Camera et al., 2014). However, the solar system and pulsar observations show good agreement with the GR theory (Will, 2006). Iorio and Saridakis (2012a) and Xie and Deng (2013a) attract attention toward constraints in the solar system dealing with f(T) gravity. However, in this paper, as mentioned previously, we choose an off-diagonal tetrad to eliminate constraints to construct structures of compact objects of anisotropic nature in
Compact stars are formed during the evolutionary stage of ordinary stars. At this stage, radiating pressure due to nuclear fission taking place inside the star does not resist the gravitational forces, and stars collapse under their own weight. This collapsing of the ordinary star is famously called stellar death, which results in the formation of a new star called a compact star. At this stage, all the reservoirs of helium are burnt up, which stops the fusion process, so the temperature inside the star decreases with the increase in internal pressure. Due to this increase in inner pressure, all matter of the star combine to a very high density. Compact stars have a very high density and smaller radii as compared to ordinary stars. High-density compact objects like a pulsar and many other spinning stars having strong magnetic fields are among the main discoveries of astrophysics. One belief about compact objects is that their matter composition is of subatomic particles like baryons, leptons, mesons, and strange quark matter. However, exact observational data about the composition of these high-density objects are not available. Therefore, the native problem in the construction of their configurations faced by astrophysicists is the determination of geometry used and interior surface matter distribution. Some valuable works are present in the literature on the study of compact stars (Mustafa et al., 2020; Mustafa et al., 2021; Maurya et al., 2022). In the background of other modified theories of gravity, interesting aspects related to astrophysical compact objects have been extensively explored (Mustafa et al., 2022a; Mustafa et al., 2022b; Mustafa et al., 2023).
Initial studies write that matter distribution on spherical symmetry is based on isotropic (perfect) fluid. Due to this isotropic condition, (pr = pt) on EFEs is applied as tangential and radial components of pressure coincide with each other. However, Jeans (1922) predicted the unusual conditions, which are dominant inside the interior of stellar objects, due to which involvement of the anisotropic factor was suggested for a good understanding of the distribution of matter inside heavenly objects. Anisotropy (Δ = pt − pr) is simply a measurement of deviation from isotropy. In Herrera and Santos (1997) and Mak and Harko (2002), a huge amount of detailed material is available to study the effects of anisotropy in stellar structures under spherical symmetry. In a relativistic stellar system, anisotropy is due to the existence of a variety of fluids, like a superfluid, magnetic or external field, phase transition, rotational motion, and other fluids. This work is under a static and spherically symmetric system of stellar objects, so anisotropy may arise due to the existence of superfluid or the elastic nature of superfluid or anisotropic fluid (Sawyer, 1972; Sokolov, 1980; Herrera and Santos, 1997). Ruderman’s (1972) prediction in his pioneer study of anisotropy in astrophysics is that it is an inherent property in high-density nuclear matter distribution. Bowers and Liang (1974) predicted that anisotropy is the result of strong interactions superconductivity and superfluidity inside heavily dense matter. It is of note that in a diverse situation when the radial component pr is not equal to the tangential component pt of pressure (pt ≠ pr), anisotropy rises. This form of pressure is called anisotropic pressure. When the spatial gradient of the scalar field is non-zero, then the physical system generates anisotropic pressure. Herrera and Santos (1997) first discussed the detailed effects of local-level anisotropy on the self-gravitating system. After that, the effects of local anisotropy were discussed by Ivanov (2002) and Maurya et al. (2016) on static bodies having spherical symmetry.
The schematic study of this paper is as follows: in the IInd section of this paper, we discuss the basics of
2 Basic concepts of
Since TEGR is a very close modification of GR gravity, factually, f(T) gravity is far different from TEGR as it is based on the function of torsion T. So, the description of f(T) gravity is considerably different from the curvature-dependent f(R) gravity. In particular, the action elaborates on the Lagrangian function of gravity. The action (Harko et al., 2014) describing
where
Here,
Like TEGR, the Lagrangian density, depending upon the torsion T, is written, in general, as follows (Harko et al., 2014):
Since spherical symmetry is a convenient way to start with the study of compact objects, which is written as
where ν(r) and λ(r) the gauge ingredients describing the gravity are the radial r functions.
Importantly, in TEGR, the prescription of the tetrad field harmonizes both the gravitational field and the reference frame. In the calculation of field equations, the tetrad field plays a defining role. Tamanini and Boehmer (2012) nominated two types of tetrads: off-diagonal and diagonal. They suggested that the use of a diagonal tetrad imposes few solar system limitations, as expressed in Iorio and Saridakis (2012a) and Xie and Deng (2013a). Here, in the current study, we incorporate an off-diagonal tetrad to reduce the impact of limitations that were discussed in Iorio and Saridakis (2012a) and Xie and Deng (2013a). The off-diagonal tetrad is given as follows:
where the notation e is used for
where
The expression of torsion T(r) calculated from equation (6) and its derivative T′(r) relative to “r” are written as
The generalized field expressions of ρ, pr, and pt in
where T represents the torsion and
3 Generalized solutions
Solutions of the field equations mainly depend upon the functions of gravitation-responsible components of the metric space. We take the function λ(r) given by Solanki and Jackson Levi Said (2022)
Here, c, R are constants with c, R > 0, and R is the radius at the boundary of the star. The potential metric (16) is a valid physical concept since it remains non-singular when c > 0 within the interior of a star, where 0 ≤ r ≤ R. This metric potential (16) is highly beneficial for describing various astrophysical phenomena. It has been used in simplified forms, such as in (16), to describe compact stars under general relativity (Sarma and Ratanpal, 2013). Conversely, its inverse has been utilized to depict wormholes in f (T) gravity (Jamil et al., 2013). Hence, the parameter c plays a crucial role in characterizing neutron stars that exhibit realistic masses. As discussed in the section, it is evident that the model parameter c holds significant physical importance, given its considerable influence on modeling stellar systems. Now, we select another metric potential eν(r) such that ν′(r) has the following form (Solanki and Jackson Levi Said, 2022):
where x, y, z, and R are constant parameters, where R represents the radius of a star and r is the radial coordinate. It is important to note that the constants x, y, and z have no relation to the space coordinates. Rather, they represent the model parameters and should not be confused with spatial coordinates. Integration of Eq. 17 results in the following form:
The function f defines the modified form of
where α β are arbitrary constants and ϕ is a cosmological constant. If we set n = 2 and ϕ = 0, this model reduces to the model used by Harko et al. (2014). This model 19 can be reduced to some generic torsion-based theories like f(T) gravity and TEGER depending upon the choice of parameters α, β and n. Taking β = 0 for different choices of n, we retrieve the f(T) gravity, and by choosing α = 1, n = 1, ϕ = 0, and β = 0, we retrieve the basic TEGER. In this study, we use the value n = 2 by taking the non-linear model of
4 Matching of the interior metric with the exterior metric to evaluate unknowns
At the boundary surface, r = R and the matching of the interior and exterior metrics is essential to make the unknowns known. In this study, we match the interior space–time (Eq. 7) with the exterior Schwarzschild space–time (Eq. 23) to evaluate k. We evaluate α from pr(r = R) = 0. The exterior Schwarzschild metric is given as
Matching Eqs 7, 23 we obtain the following system of equations.
The solution of the aforementioned Eqs. 25, 26 gives the value of k
where
For other constants, i.e., c, x, y, z, ϕ, β, we choose suitable values, as given in Table 1.

TABLE 1. Values of constants of strange stars for n = 2, y = −0.04, z = −0.0009, ϕ = 2.036 × 10−35, and β = −30 by choosing different values of c and β in the case of the off-diagonal tetrad.
5 Physical analysis and discussion of the calculated results
In this section, we analyze the results of our study by discussing the physical behavior of some properties of neutron stars (4U1538–52, J0437–4715, J0030 + 0451, and 4U1820–30) under the parameters of
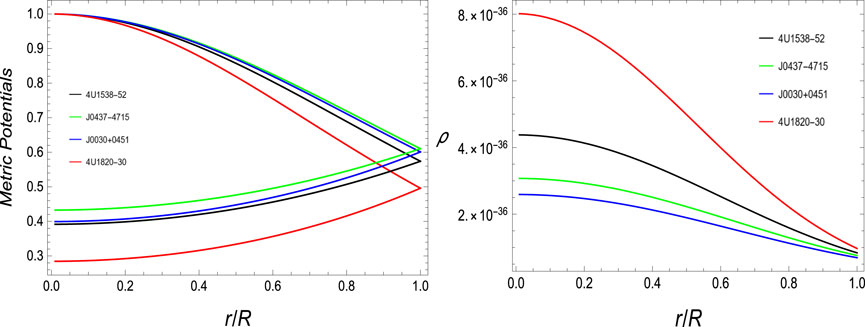
5.1 Metric potentials and energy density
As the responsibility of gravitational effects is mainly dependent upon the metric function, for the study of compact objects, these metric functions must be positive and smooth. As can be easily verified from their graphical results (graphed in the left panel of Figure 1), eλ(r) = 1 (at the center) and eν(r) > 0 (at the center) show positive and regular monotonic responses throughout the interior of the stellar system.
The importance of verifying the physical validity of stellar configurations in compact star research cannot be overstated. Any study lacking physical acceptability would render any effort invested in it meaningless. Density serves as a crucial parameter for ensuring the validity of such studies. The validity of the distribution of matter can be determined from the behavior of the energy density ρ, as shown graphically. For the physical presence of a compact star, the energy must be positive, maximal at the center, and have a decreasing trend with a minimal value at the boundary. The right graph in Figure 1 depicts the visualization of the behavior of energy density for our neutron star candidates, which falls completely within the required criteria.
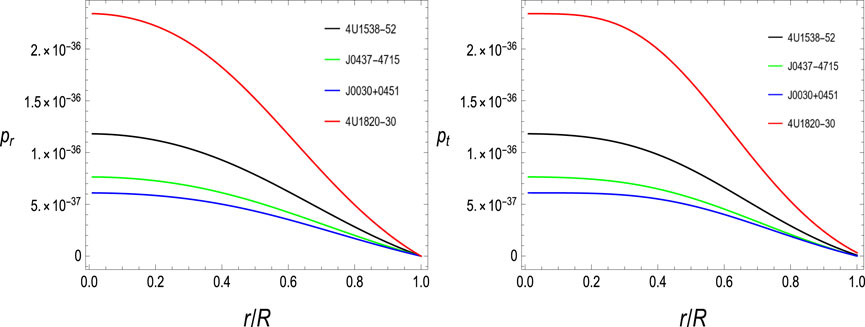
5.2 Pressure profiles
It is important to consider pressure components as another crucial parameter when assessing the validity of a stellar model. By following a similar trend as the density profile, the realistic distribution of stellar pressure profiles should also contain the positive and maximum values at the center and then decreasing propagation throughout the stellar system with a minimum value at the boundary; in addition, pr|r=R = 0; otherwise, pt & pr remain positive and pt > pr. Figure 2 shows the graphical representation of the pressure profiles. It should be noted that the behavior of pressure profiles is a genuine indicator of the physical existence of a stellar system in our case.
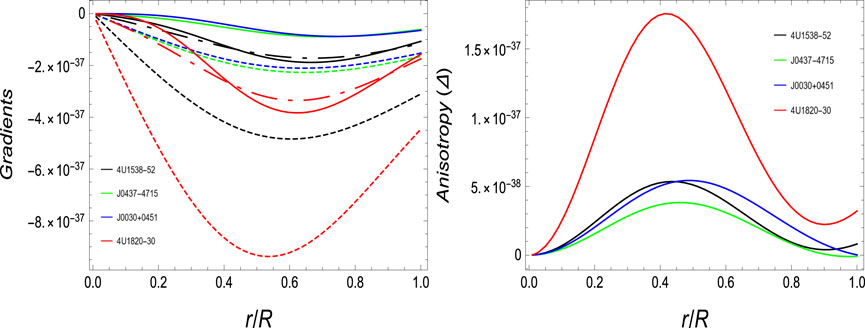
5.3 Gradients and anisotropy profiles
The graph of gradients is plotted in the right of Figure 3. It is required that for the compact formation of stellar configuration, the gradients should attain the negatively increasing trend starting from zero at the center to the boundary of the stellar configuration. In our study, it can easily be seen that
Anisotropy is another important property of the stellar system that justifies the stability system. The existence of positive anisotropy (Δ > 0) is basically a repulsive force against the inward gravitational force and keeps the system stable. Basically, the distribution of matter all over the stellar may not be uniform, which may cause the existence of anisotropy. The pressure profiles at the center of the star are identical, due to which Δ∣r=0 = pt − pr = 0, but it attains the peak value at the boundary r = R. The graphical conduct of the anisotropic profile is given in the right graph of Figure 3. It can easily be verified that it starts its propagation from zero at the center and attains the maximum value, and afterward, it again starts to decline and approaches zero for some candidates of neutron stars and subsequently shows an uplift in the value at the boundary. However, the overall trend is positive (Δ > 0) within the stellar system to justify the stability.
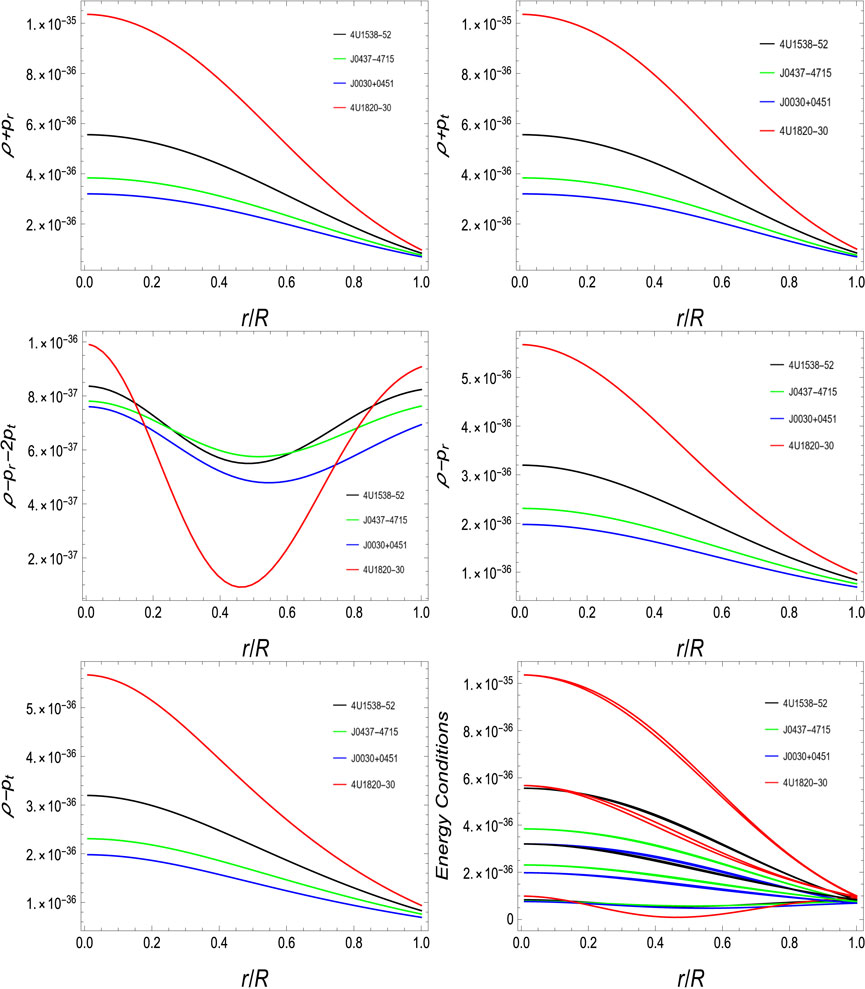
5.4 Energy conditions
The real essence of the matter in the stellar system is studied by energy constraints. The positive behavior of energy constraints in the complete spread of the stellar body justifies and ensures the real and physically acceptable distribution of matter of anisotropic form. Energy limits named SEC, WEC, NEC, and DEC should justify the given following conditions (29–32) during propagation in the compact formation of stellar bodies.
where γ = r, t. The graphical representation of energy conditions in Figure 4 indicates the real formation of compact matter in our neutron star candidates in the gravitational effects of
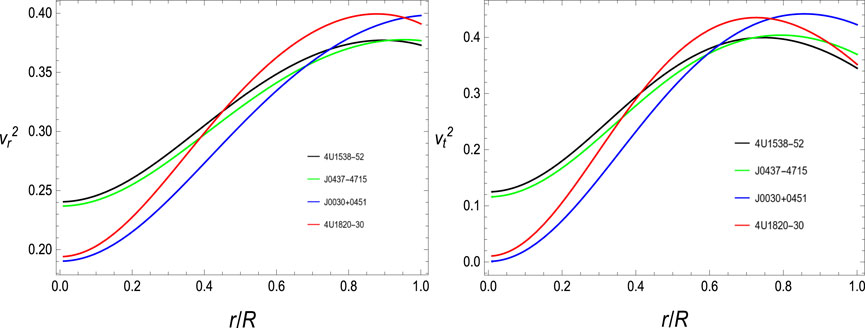
5.5 Sound speeds
Sound speeds
According to the stability region defined in Abreu et al. (2007), the region is stable, in which
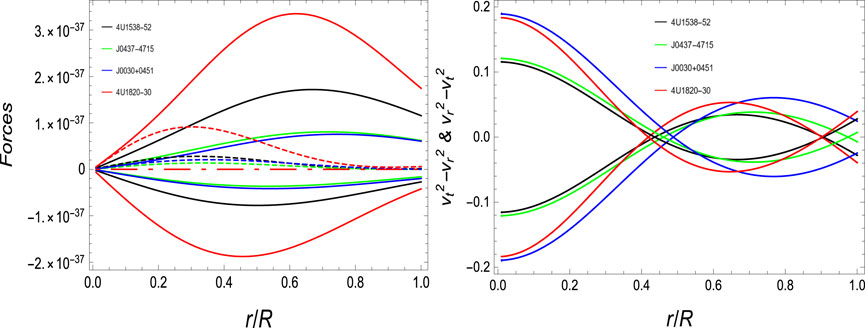
FIGURE 6. Forces (left) {Fh(solid–positive), Fg(solid–negative), Fa(dotted), Fe(dot-dashed)} and casuality conditions (right) versus the radial coordinate.
5.6 TOV forces
Stability and equilibrium of the stellar system are also discussed and recommended with the help of well-famed criteria suggested in the Tolman–Oppenheimer–Volkoff (TOV) equation (Oppenheimer and Volkoff, 1939; Tolman, 1939). The TOV equation in its most common version of GR is defined as
where Mg(r) is the gravitational mass present inside the radius of stellar radius r and can be evaluated by using the Tolman–Whittaker formula and FEs, which is given by
Eq. 35 can mold its form given by the following expression:
By substituting the value of Mg(r) from Eq. 36 into Eq. 34, we obtain
Equation 37 is the generic GR version of the TOV equation, but in the case of
where
TOV forces define the stability of the system by escaping it to collapse to a singular point during the gravitational forces as these forces cancel each other’s effect by giving the net impact equal to zero. The balancing behavior of TOV forces in our study is shown in the right graph of Figure 6.
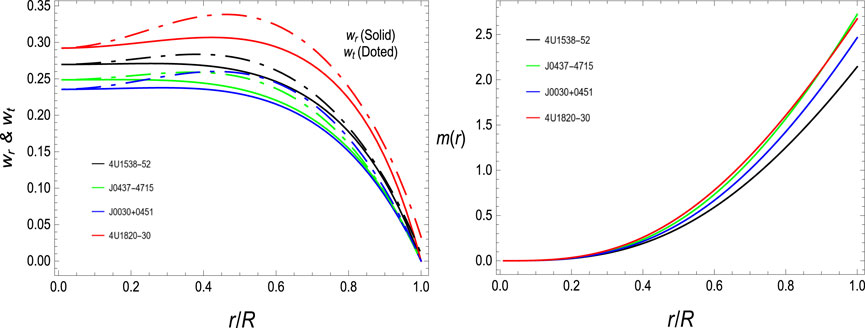
5.7 Equation of state profiles wr & wt
The matter composition of the stellar body may be real or dark matter. It is very important to discuss the essence of matter composition. Limits on the components of EoS 0 ≤ wr < 1, & 0 < wt < 1 guarantee the real nature of matter composition. If the compact star is composed of realistic anisotropic matter, the obtained results will satisfy this stability criterion. Violation of the limits defined for EOS could potentially indicate the presence of exotic matter or dark matter. The expression for EoS is given as
One can easily be satisfied by the behavior of EoS parameter graphs, which are shown on the graph on the left of Figure 7, that our stellar system under study shows the realistic composition of matter.
5.8 Mass function redshift and compactness profiles
The ratio
Using (42), one can evaluate the compactness u(r), which is given in Eq. 43, which is further used in the evaluation of the redshift function zs in Eq. 44. u(r) & zs are in the following equations:
Bowers and Liang (1974) defined the peak limit for the compactness parameter as
6 Conclusion
It is important to mention that the potential component of interior geometry is crucial in the study of stellar objects. In this study, we used the function
This study comprises the study of the anisotropic nature of neutron star candidates 4U1538–52, J0437–4,715, J0030 + 0451, and 4U1820–30. In this study, we elaborate the properties of compact objects under the formalism of
• Metric components eμ(r) & eλ(r) show regular positive behavior, as shown in the left graph of Figure 1.
• Energy density ρ, plotted in right of Figure 1, has the physically acceptable positive conduct by showing a maximum value at the center and a minimum value at the boundary.
• Behavior of pressure profiles, as shown in Figure 2, is also up to the mark according to the study of compact objects of anisotropic nature with a maximum value at the center and a minimum value at the boundary.
• Gradients profiles justify the condition
The positive anisotropic repulsive force Δ ≥ 0 ensures the stability of the system by acting against the inward gravitational force. The left graph of Figure 3 shows the positive behavior of anisotropy Δ.
• Matter distribution of the stellar system is real, which is ensured by the positive energy limits, which are graphed in Figure 4. It can easily be verified that all the energy limits are positive all over the stellar structure, which means that the matter is real in nature without any existence of dark matter.
• Speeds of sound also ensure the stability of the system by obeying the cracking limits
• The system is stable without any point singularity, which is ensured by the balance of TOV forces which are graphed in the left graph of Figure 6. All the four forces, Fa, Fg, Fh and Fe, are in balance.
• EoS components wr and wt are plotted in the right graph of Figure 7. A graphical representation of these components denies the existence of dark matter by fulfilling the real matter distribution criteria 0 < wr and wt < 1.
• Regular and acceptable behaviors of the mass function, redshift, and compactification are plotted in the left of Figures 7, 8. It can be confirmed from the graphs that these parameters fulfill all the stability limits discussed in Subsection 8 of section V.
DittaAshraf et al. (2021), Zubair et al. (2021), Gudekli et al. (2022), and Zubair et al. (2022) studied the stellar models in
Based on the detailed discussion regarding the results, the overall conclusion can be strengthened that our discussed models of neutron stars are stable and show the overall reliability of compact object studies. In this article, we present the results of a study on the quadratic model of
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Acknowledgments
This research was supported by the Researchers Supporting Project (RSP 2023R167), King Saud University, Riyadh, Saudi Arabia.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abbas, G., and Nazar, H. (2018). Complexity factor for anisotropic source in non-minimal coupling metric f(R) gravity. Eur. Phys. J. C 78, 957. doi:10.1140/epjc/s10052-018-6430-8
Abreu, H., Hernandez, H., and Nunez, L. A. (2007). Sound speeds, cracking and the stability of self-gravitating anisotropic compact objects. Calss. Quantum. Grav. 24, 4631–4645. doi:10.1088/0264-9381/24/18/005
Aldrovandi, R., and Pereira, J. G. (2012). Teleparallel gravity: An introduction. Dordrecht: Springer.
Bamba, K., Capozziello, S., Nojiri, S., and Odintsov, S. D. (2012a). Dark energy cosmology: the equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 345, 155–228. doi:10.1007/s10509-012-1181-8
Behar, S., and Carmeli, M. (2000). Intern. J. Theor. Phys. 39, 1375–1396. doi:10.1023/a:1003651222960
Bowers, R. L., and Liang, E. P. T. (1974). Anisotropic spheres in general relativity. Cl. Astrophys. J. 188, 657. doi:10.1086/152760
Buchdahl, H. A. (1959). General relativistic fluid spheres. Phys. Rev. D. 116, 1027–1034. doi:10.1103/physrev.116.1027
Camera, S., Cardone, V. F., and Radicella, N. (2014). Detectability of torsion gravity via galaxy clustering and cosmic shear measurements. Phys. Rev. D. 89, 083520. doi:10.1103/physrevd.89.083520
Capozziello, S., and De Laurentis, M. (2011). Extended theories of gravity. Phys. Rept. 509, 167–321. doi:10.1016/j.physrep.2011.09.003
Cardone, V. F., Radicella, N., and Camera, S. (2012). Acceleratingf(T)gravity models constrained by recent cosmological data. Phys. Rev. D. 85, 124007. doi:10.1103/physrevd.85.124007
Carmeli, M., and Kuzmenko, T. (2001), Value of the Cosmological Constant: Theory versus Experiment, arXiv: astro-ph/0102033.
Clifton, T., Ferreira, P. G., Padilla, A., and Skordis, C. (2012). Modified gravity and cosmology. Phys. Rept. 513, 1–189. doi:10.1016/j.physrep.2012.01.001
Dent, J. B., Duuta, S., and Saridakis, E. N. (2011). f(T) gravity mimicking dynamical dark energy. Background and perturbation analysis. J. Cosmol. Astropart. Phys. 1101, 009. doi:10.1088/1475-7516/2011/01/009
Ditta, A., Hussain, I., Mustafa, G., Errehymy, A., and Daoud, M. (2021). A study of traversable wormhole solutions in extended teleparallel theory of gravity with matter coupling. Eur. Phys. J. C 81, 880. doi:10.1140/epjc/s10052-021-09668-7
DittaAshraf, A. A., Zhang, Z., and Mustafa, G. (2021). Modeling of anisotropic spheres in extended teleparallel theory with matter coupling. Chin. J. Phys. 69, 240–252. doi:10.1016/j.cjph.2020.11.025
Famaey, B., and McGaugh, S. (2012). Modified Newtonian dynamics (MOND): observational phenomenology and relativistic extensions. Living Rev. rel. 15, 10. doi:10.12942/lrr-2012-10
Ferraro, R., and Fiorini, F. (2008). Born-Infeld gravity in Weitzenböck spacetime. Phys. Rev. D. 78, 124019. doi:10.1103/physrevd.78.124019
Fiorini, F., and Ferraro, R. (2009). Int. J. Mod. Phys. A 24, 1686–1689. doi:10.1142/s0217751x09045236
Gudekli, E., KamranZubair, M. J. M., and Ahmed, I. (2022). Study of anisotropic strange stars in Krori Barua metric under f(T,T) gravity. Chin. J. Phys. 77, 592–604. doi:10.1016/j.cjph.2021.08.006
Herrera, L. (1992). Cracking of self-gravitating compact objects. Phys. Lett. A 165, 206–210. doi:10.1016/0375-9601(92)90036-l
Herrera, L., and Santos, N. O. (1997). Local anisotropy in self-gravitating systems. Phys. Rep. 286, 53–130. doi:10.1016/s0370-1573(96)00042-7
Iorio, L., and Saridakis, E. N. (2012a). Solar system constraints onf(T) gravity: solar system constraints onf(T) gravity. Mon. Not. R. Astron. Soc. 427, 1555–1561. doi:10.1111/j.1365-2966.2012.21995.x
Ivanov, B. V. (2002). Maximum bounds on the surface redshift of anisotropic stars. Phys. Rev. D. 65, 104011. doi:10.1103/physrevd.65.104011
Jamil, M., Momeni, D., and Myrzakulov, R. (2013). Wormholes in a viable f(T) gravity. Eur. Phys. J. C 73 (1), 2267. doi:10.1140/epjc/s10052-012-2267-8
Jeans, J. (1922). The motions of stars in a kapteyn-universe. Mon. Not. R. Astron. Soc. 82, 122–132. doi:10.1093/mnras/82.3.122
Li, B., Sotiriou, T. P., and Barrow, J. D. (2011). f(T)gravity and local Lorentz invariance. Phys. Rev. D. 83, 064035. doi:10.1103/physrevd.83.064035
Mak, M. K., and Harko, T. (2002). An exact anisotropic quark star model. Chin. J. Astron. Astrophys. 2, 248–259. doi:10.1088/1009-9271/2/3/248
Maurya, S. K., Gupta, Y. K., Ray, S., and Deb, D. (2016). Generalised model for anisotropic compact stars. Eur. Phys. J. C 76, 693. doi:10.1140/epjc/s10052-016-4527-5
Maurya, S. K., Errehymy, A., Deb, D., Tello-Ortiz, F., and Daoud, M. (2019). Study of anisotropic strange stars in f (R, T) gravity: An embedding approach under the simplest linear functional of the matter-geometry coupling. Phys. Rev. D. 100 (4), 044014. doi:10.1103/physrevd.100.044014
Maurya, S. K., Mustafa, G., Govender, M., and Singh, K. N. (2022). Exploring physical properties of minimally deformed strange star model and constraints on maximum mass limit in f (𝒬) gravity. J. Cosmol. Astropart. Phys. 2022 (10), 003. doi:10.1088/1475-7516/2022/10/003
Mustafa, G., Shamir, M. F., and Tie-Cheng, X. (2020). Physically viable solutions of anisotropic spheres in f (R, G) gravity satisfying the Karmarkar condition. Phys. Rev. D. 101 (10), 104013. doi:10.1103/physrevd.101.104013
Mustafa, G., Ahmad, M., Ali, Ö., Shamir, M. F., and Hussain., I. (2021). Traversable wormholes in the extended teleparallel theory of gravity with matter coupling. Fortschritte Phys. 69, 8–9.
Mustafa, G., Gao, X., and Javed, F. (2022a). Twin peak quasi-periodic oscillations and stability via thin-shell formalism of traversable wormholes in symmetric teleparallel gravity. Fortschritte Phys. 70 (9-10), 2200053. doi:10.1002/prop.202200053
Mustafa, G., Maurya, S. K., and Ray, S. (2022b). On the possibility of generalized wormhole formation in the galactic halo due to dark matter using the observational data within the matter coupling gravity formalism. Astrophysical J. 941 (2), 170. doi:10.3847/1538-4357/ac9b00
Mustafa, G., Maurya, S. K., and Hussain, I. (2023). Relativistic wormholes in extended teleparallel gravity with minimal matter coupling. Fortschritte Phys. 71 (4-5), 2200119. doi:10.1002/prop.202200119
Nojiri, S., and Odintsov, S. D. (2007). Int. J. Geom. Meth.Mod. Phys. 4, 115–145. doi:10.1142/s0219887807001928
Oppenheimer, J. R., and Volkoff, G. M. (1939). On massive neutron cores. Phys. Rev. 55, 374–381. doi:10.1103/physrev.55.374
Pace, M., and Said, J. L (2017). Quark stars in
Rahaman, M., Singh, Ksh. N., Errehymy, A., Rahaman, F., and Daoud, M. (2020). Anisotropic Karmarkar stars in f(R, T)-gravity. Eur. Phys. J. C 80, 272. doi:10.1140/epjc/s10052-020-7842-9
Ruderman, R. (1972). Pulsars: structure and dynamics. Rev. Astron. Astrophys. 10, 427–476. doi:10.1146/annurev.aa.10.090172.002235
Salako, I. G., Khlopov, M., Ray, S., and Arouko, M. Z. (2020). Pameli saha. China: Ujjal Debnath. arXiv:2004.07959 [gr-qc].
Sarma, R., and Ratanpal, B. S. (2013). Int. J. Mod. Phys. D. 22, 1350074. doi:10.1142/s0218271813500740
Sawyer, R. F. (1972). Condensedπ−Phase in neutron-star matter. Phys. Rev. Lett. 29, 382–385. doi:10.1103/physrevlett.29.382
Singh, K. N., Maurya, S., Errehymy, A., Rahaman, F., and Daoud, M. (2020). Physical properties of class I compact star model for linear and Starobinsky−f(R,T) functions. Phys. Dark Universe 30, 100620. doi:10.1016/j.dark.2020.100620
Solanki, JayJackson Levi Said (2022). Anisotropic stellar model of neutron stars in f(T) gravity with off-diagonal tetrad. Eur. Phys. J. C 82, 35. doi:10.1140/epjc/s10052-022-09995-3
Sotiriou, T. P., and Faraoni, R. (2010). f(R)theories of gravity. Rev. Mod. Phys. 82, 451–497. doi:10.1103/revmodphys.82.451
Tamanini, N., and Boehmer, G. C. (2012). Good and bad tetrads inf(T)gravity. Phys. Rev. D. 86, 044009. doi:10.1103/physrevd.86.044009
Tolman, R. C. (1939). Static solutions of einstein's field equations for spheres of fluid. Phys. Rev. 55, 364–373. doi:10.1103/physrev.55.364
Waheed, S., Mustafa, G., Zubair, M., and Ashraf, A. (2020). Physically acceptable embedded class-I compact stars in modified gravity with karmarkar condition. Symmetry 12, 962. doi:10.3390/sym12060962
Will, C. F. (2006). The confrontation between general relativity and experiment. Living Rev. Relativ. 9, 3. doi:10.12942/lrr-2006-3
Xie, Y., and Deng, X. M. (2013a). f (T) gravity: effects on astronomical observations and Solar system experiments and upper bounds. Mon. Not. R. Astron. Soc. 433, 3584–3589. doi:10.1093/mnras/stt991
Zubair, M., and Abbas, G. (2016). Analytic models of anisotropic strange stars in f (T) $f(T)$ gravity with off-diagonal tetrad. Astrophys. Space Sci. 361, 27. doi:10.1007/s10509-015-2610-2
Zubair, M., Abbas, G., and Noureen, I. (2016). Possible formation of compact stars in f (R, T) $f(R,T)$ gravity. Astrophys. Space Sci. 361, 8. doi:10.1007/s10509-015-2596-9
Zubair, M., Ditta, A., Waheed, S., and Tello-Ortiz, F. (2022). Class I stars in the background of f(T,τ) cosmological model. Chin. J. Phys. 77, 1827–1842. doi:10.1016/j.cjph.2021.12.029
Appendix A
Keywords: gravitation, cosmology, modified gravity, f(T) gravity, f(T, T) gravity, f(R) gravity
Citation: Caliskan A, Zulqarnain RM, Güdekli E, Siddique I, Ahmad H and Askar S (2023) Structural properties of a new class of stellar structures in modified teleparallel gravity. Front. Astron. Space Sci. 10:1203777. doi: 10.3389/fspas.2023.1203777
Received: 11 April 2023; Accepted: 21 August 2023;
Published: 27 September 2023.
Edited by:
Ghulam Abbas, Department of Mathematics, PakistanReviewed by:
Hammad Nazar, Islamia University of Bahawalpur, PakistanMahmood Jasim, University of Nizwa, Oman
Izzet Sakalli, Eastern Mediterranean University, Türkiye
Abdul Jawad, COMSATS University Islamabad, Pakistan
Copyright © 2023 Caliskan, Zulqarnain, Güdekli, Siddique, Ahmad and Askar. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Rana Muhammad Zulqarnain, cmFuYXp1bHFhcm5haW43Nzc3QGdtYWlsLmNvbQ==
 Aylin Caliskan
Aylin Caliskan Rana Muhammad Zulqarnain
Rana Muhammad Zulqarnain Ertan Güdekli
Ertan Güdekli Imran Siddique4
Imran Siddique4 Hijaz Ahmad
Hijaz Ahmad