- 1Goddard Planetary Heliophysics Institute, University of Maryland, Baltimore County, Baltimore, MD, United States
- 2Geospace Physics Laboratory, NASA Goddard Space Flight Center, Greenbelt, MD, United States
Interplanetary shocks are disturbances commonly observed in the solar wind. IP shock impacts can cause a myriad of space weather effects in the Earth’s magnetopause, inner magnetosphere, ionosphere, thermosphere, and ground magnetic field. The shock impact angle, measured as the angle the shock normal vector performs with the Sun-Earth line, has been shown to be a very important parameter that controls shock geoeffectivess. An extensive review provided by Oliveira and Samsonov (2018) summarized all the work known at the time with respect to shock impact angles and geomagnetic activity; however, this topic has had some progress since Oliveira and Samsonov (2018) and the main goal of this mini review is to summarize all achievements to date in the topic to the knowledge of the author. Finally, this mini review also brings a few suggestions and ideas for future research in the area of IP shock impact angle geoeffectiveness.
1 Introduction
Interplanetary (IP) shocks are solar wind perturbations that directly trigger geomagnetic activity in the magnetosphere-ionosphere-thermosphere (MIT) system. IP shocks rapidly trigger magnetic sudden impulses in geosynchronous orbit (Wang et al., 2009), magnetotail (Huttunen et al., 2005), and on the ground (Smith et al., 1986; Echer et al., 2005; Hajra et al., 2020; Smith et al., 2020); enhance field-aligned currents (Belakhovsky et al., 2017; Kasran et al., 2019), trigger auroral substorms (Kokubun et al., 1977; Zhou and Tsurutani, 2001; Yue et al., 2010), cause dayside auroras (Zhou and Tsurutani, 1999; Tsurutani et al., 2001; Zhou et al., 2003), affect radiation belts (Schiller et al., 2016; Bhaskar et al., 2021), excite magnetospheric ultra-low frequency (ULF) waves (Kangas et al., 2001; Hartinger et al., 2022); cause geomagnetically induced currents (GICs) (Carter et al., 2015; Belakhovsky et al., 2017; Tsurutani and Hajra, 2021), ionospheric total electron content (Chen et al., 2023), and thermospheric neutral mass density enhancements that intensify satellite orbital drag (Oliveira et al., 2017; Shi et al., 2017; Oliveira and Zesta, 2019). Therefore, space weather-related effects can be observed in many regions of the MIT system.
IP fast forward shocks form when the driver gas has a speed relative to the upstream solar wind that is larger than the local magnetosonic wave speed (Landau and Lifshitz, 1960; Priest, 1981; Kennel et al., 1985). The most common and geoeffective type of shocks is named fast forward shock, which propagates away from the Sun (Tsurutani et al., 2011; Oliveira, 2017). Among several other shock properties, the shock impact angle,
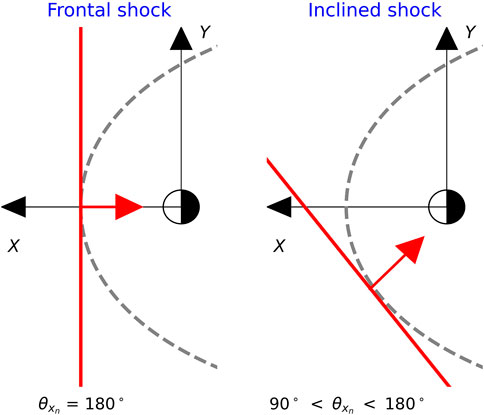
FIGURE 1. Two schematic representations of shock normal orientations: left, a purely frontal shock (
Since the review provided by Oliveira and Samsonov (2018) on geomagnetic activity triggered by IP shocks with different orientations, some progress has been made in the understanding of this research topic. The main goal of this mini review is to summarize all achievements in the field, including new research, as well as to show that more work is still needed in the area.
2 Magnetic sudden impulses on the ground
Perhaps the first clear connection between shock impact angles and the subsequent geomagnetic activity was reported by Takeuchi et al. (2002). The authors clearly showed that a very inclined IP shock observed by Wind took an unusually long time to sweep by the magnetosphere while slowly compressing it. The slow and gradual increase in total pressure (thermal plus magnetic pressures) observed by Geotail in the magnetosphere and the slow and gradual magnetic field increase observed by magnetometers on the ground were associated with the large shock inclination of the IP shock. Takeuchi et al. (2002) argued that these effects were caused by the asymmetric compression of the magnetosphere which led currents in the magnetosphere-ionosphere system to respond asymmetrically and slowly. Additionally; Takeuchi et al. (2002) introduced the concept of a geoeffective magnetosphere distance, which is the distance swept by the shock along its normal while the magnetosphere is being compressed. These results were later confirmed with numerical magnetohydrodynamic simulations by Guo et al. (2005), who simulated two similarly strong shocks with different inclinations, one being frontal, and the other inclined. The authors showed that magnetospheric magnetic field and ionospheric cross polar cap potential reached similar final values after the compression by the shocks, but the effects caused by the inclined shock took longer to take place; Wang et al. (2005) conducted numerical simulations of shocks with similar normal orientations and noted similar response (slow for the inclined shock, and rapid for the frontal shock) of the magnetic field at geosynchronous orbit.
These previous observation and numerical simulation studies were later confirmed by Wang et al. (2006), who performed a statistical analysis of ground magnetometer response to shocks with different inclinations. Their main conclusion was that the faster and the more frontal the shock, the shorter the sudden impulse rise time. Selvakumaran et al. (2017) performed a statistical analysis study of the same topic and reported on similar conclusions. Samsonov et al. (2015) noted dawn-dusk asymmetries in a numerical simulation of an inclined shock impact on the magnetosphere. The authors noted an overshoot in the field calculated by an artificial ground magnetometer located in the dusk sector where the shock first contacted the magnetopause, but an overshoot in another station in the dawn sector did not clearly occur. The lack of dawnside overshoots in the simulation and observations was then explained by the fact that the dawnside compression was preceded and followed by magnetopause expansions. These results were also confirmed with magnetic field observations by real ground magnetometers located in the same sectors as the artificial stations. Samsonov et al. (2015) explained this dawn-dusk asymmetry with the inclined shock having a very strong solar wind velocity vy component. As theoretically noted by Samsonov (2011), a very strong solar wind vy component greatly increases the solar wind ram pressure in the y direction, leading to the strong dawn-dusk asymmetry noted in ground magnetic field observed and simulated by Samsonov et al. (2015). Historical observations of very intense sudden impulses on the ground suggest that such response was caused by impacts of very fast and nearly frontal shocks on the Earth’s magnetosphere (Araki, 2014; Oliveira and Ngwira, 2017; Love et al., 2019a; Love et al., 2019b; Hayakawa et al., 2020a; Hayakawa et al., 2020b; Hayakawa et al., 2021a; Hayakawa et al., 2021b).
The geoeffective magnetosphere distance concept was investigated by Rudd et al. (2019), who performed a statistical study with more than 500 IP shocks with different inclinations. The authors reported that shorter sudden impulse rise times were associated with faster and more frontal shocks, confirming the experimental and simulation results abovementioned (Wang et al., 2005; Wang et al., 2006). Rudd et al. (2019) used each respective shock speed and the subsequent sudden impulse rise time to find that faster nearly frontal shocks traveled relatively smaller distances while compressing the magnetosphere in comparison to slower highly inclined shocks. These results confirmed the prediction of Takeuchi et al. (2002).
3 Substorm occurrence and intensities
Oliveira and Raeder (2014) conducted global numerical simulations of the impact of three IP shocks with different inclinations and strengths on the Earth’s magnetosphere. Two shocks were inclined (
Later on, Oliveira and Raeder (2015) performed a statistical study of ground magnetometer response to more than 400 shocks with different inclinations observed by the Wind and Advanced Composition Explorer satellites at L1. The authors looked particularly at the SuperMAG westward auroral electrojet index SML for each event. Oliveira and Raeder (2015) found that the faster and the more frontal the shock, the more intense the SML response, which indicates that the shock impact angle controls the subsequent substorm activity. Similar results for nightside auroral power intensity were reported by Oliveira et al. (2016). Therefore, these experimental results confirmed the predictions reported by Oliveira and Raeder (2014) with respect to effects of IP shock inclinations on the subsequent substorm activity.
It is important to note that effects of magnetospheric preconditioning caused by southward IMF Bz are an important factor for substorm triggering (Kokubun et al., 1977; Zhou and Tsurutani, 2001; Yue et al., 2010; Hajra and Tsurutani, 2018a; Sitnov et al., 2019). As shown by Oliveira and Raeder (2014) with simulations and Oliveira et al. (2021) with observations, nearly head-on shocks enhance the upstream IMF Bz component causing the downstream IMF Bz component to become even more negative which in turn intensifies the energetics of substorms, as first shown by Tsurutani et al. (1988). This sudden and explosive tail energy release can explain why supersubstorms are way more intense and last longer than intense substorms (Tsurutani and Hajra, 2023). Therefore, the possible role of shock impact angles in supersubstorm triggering is a topic that is yet to be investigated.
4 Ultra-low frequency waves
In their numerical simulations, Oliveira and Raeder (2014) also reported on the effects of IP shock impact angles on the occurrence of ULF waves. They noted a clear ULF wave perturbation with period ∼5 min triggered by the frontal shock, but such response was not clearly seen in either of the inclined shocks, even in the case of the strong inclined shock impact. Oliveira and Raeder (2014) attributed this effect to an effective excitation of cavity modes (Samson et al., 1992; Hughes, 1994; Lakhina and Tsurutani, 2020) in the magnetosphere-ionosphere system by the symmetric compression caused by the frontal shock. The inclined shocks, on the other hand, were not able to excite these cavity modes due to the asymmetric magnetospheric compressions. These simulation results were used by Belakhovsky et al. (2017) to explain the lack of ULF wave activity after the impact of a highly inclined shock on the magnetosphere. Takahashi et al. (2018) also noted intense ULF wave activity following the impact of an almost head-on shock on the magnetosphere. Baker (2019) reported that nearly frontal shocks triggered Pc5 waves with more intense wave power spectra in comparison to highly inclined shocks.
A comparative study of ULF activity triggered by two IP shocks with similar strengths, but with very distinct inclinations, was performed by Oliveira et al. (2020). The authors looked at ULF waves in the geospace and on the ground and observed stronger wave response in the case of the nearly head-on shock impact. Such response was characterized by wave amplitude and power spectra. In addition, Oliveira et al. (2020) suggested that a frontal shock can only excite odd-mode waves in the magnetosphere, whereas an inclined shock can excite both odd- and even-mode waves in the magnetosphere. This is supported by peaks in power spectral density that occurred periodically and “out of phase” when the results of the two shocks are compared. These results confirmed the predictions of Oliveira and Raeder (2014), but a comprehensive statistical study of ULF wave response to IP shocks with different orientations in the geospace and on the ground is yet to be conducted to confirm the statistical properties of such wave response.
5 Ground dB/dt variations
Ground dB/dt variations are the space weather drivers of GICs that can be detrimental to power infrastructure and transmission lines (Pirjola, 2002; Oliveira and Ngwira, 2017; Ngwira and Pulkkinen, 2019). The first connection between shock impact angles and the subsequent ground dB/dt variations was established by Oliveira et al. (2018). The authors found that the faster and the more frontal the shock, the more intense the resulting ground dB/dt variation within 20 min after shock impact, particularly in high latitude regions. With respect to low-latitude response, Oliveira et al. (2018) reported that high dB/dt variations surpassing the threshold of 100 nT/min at the equator was associated with nearly head-on shocks that struck the magnetosphere around noon local time. Such dB/dt intensifications resulted from enhancements of the dayside ionospheric equatorial electrojet current, as previously suggested by Carter et al. (2015).
The dB/dt response during two very intense substorms triggered by two IP shocks with different inclinations was investigated in a comparative case study by Oliveira et al. (2021). Hajra and Tsurutani (2018a) defined a supersubstorm as an event with minimum SML
Inter-hemispheric asymmetries in the ground dB/dt response triggered by shocks with different inclinations were reported by Xu et al. (2020). IP shock impact angles were expressed in solar magnetic coordinates to highlight north-south magnetic field response (Laundal and Richmond, 2017). Xu et al. (2020) used conjugated magnetic field data provided by ground magnetometers in Antarctica and Greenland to find that, in general, the hemisphere that is first struck by the shock shows the first and more intense dB/dt response.
6 Bow shock, field-aligned currents, and cross-tail currents
The Earth’s bow shock response to the impact of an inclined IP shock was theoretically investigated by Grib and Pushkar (2006). They considered the impact of a shock with
In their numerical simulations, Oliveira and Raeder (2014) found faster and more intense field-aligned current (FAC) response in the case of the frontal shock in comparison to the other two inclined shocks. The authors noted intense FAC activity around the magnetic midnight in response to the frontal shock. Oliveira and Raeder (2014) associated this FAC response to the substorm activity noted by the authors in the simulations, and such effects did not occur in response to the inclined shocks. Selvakumaran et al. (2017) found similar results in their numerical simulations of shocks with different orientations.
Shi et al. (2019) used FAC data provided by the Active Magnetosphere and Planetary Electrodynamics Response Experiment program to investigate how the shock impact angle affects the subsequent current dynamics. The authors found that FACs showed rapid intensifications after the shock impact, and FACs developed faster and stronger for the more frontal shocks. Shi et al. (2019) also found that nearly frontal shocks caused stronger currents particularly in the dayside sector near local noon, dawnside Region I currents, and duskside Region II currents in comparison to highly inclined shocks.
In the numerical simulation conducted by Samsonov et al. (2015), it was found that the cross-tail current was highly deformed after the impact of an inclined IP shock on the magnetosphere. This effect was caused by the high vy component of the solar wind downstream region that led to an elevated dynamic pressure enhancement in the east-west direction (Samsonov, 2011). Grygorov et al. (2014) used multi-satellite data to observe the effects caused by an IP shock on the magnetotail (X = ∼ − 240RE). The authors found that the tail was highly deflected
7 Conclusion and future work
In this mini review, with some updates to the review provided by Oliveira and Samsonov (2018), I have summarized many experimental and modeling studies concerning geomagnetic activity triggered by IP shocks with different impact angles. To the author’s knowledge, this review is the most up-to-date report on this topic. As expected, most studies reported here concluded that the faster and the more frontal the shock, the more intense the subsequent geomagnetic activity. Moreover, the solar wind flow angle also plays a significant role in the subsequent geoeffectiveness even during periods of non-shocked solar wind. For example, Rout et al. (2017) found that periodic equatorial ionospheric response to CIRs are higher when the solar wind azimuth flow angle is smaller than
1. Radiation belt response. How do IP shock impact angles control particle acceleration in the inner magnetosphere? And particle population flows in the inner magnetosphere? How does the shock impact angle control enhancements and dropouts of, e.g., electron densities in the inner magnetosphere? How does the shock impact angle control losses of magnetospheric relativistic electron fluxes (e.g., Tsurutani et al., 2016; Hajra and Tsurutani, 2018b)?
2. ULF wave activity. Do shock impact angles control ULF wave (Pc4-5, ∼2–22 mHz) amplitude/power spectra at different locations, and how does Pc4-5 wave energy spread throughout the magnetosphere as a function of local time for different impact angles? Do shock impact angles control the field-aligned mode structure of ULF waves, as suggested by Oliveira et al. (2020)?
3. Statistical properties of ground dB/dt variations. A logical step following the comparative study of Oliveira et al. (2021) is to perform statistical analyses of ground dB/dt variations during substorms induced by shocks with different inclinations. What are the conditions in geospace that trigger substorms under asymmetric magnetospheric compressions? What is the latitudinal extent and intensity of dB/dt variations as a function of shock impact angles?
4. Thermospheric neutral mass density response. How does the shock impact angle affect the high-latitude thermospheric neutral mass density response in low-Earth orbit? How does this density impact the subsequent satellite orbital drag? How does the impact angles of CIR-driven shocks impact the immediate density response and the subsequent azimuth solar wind flow and the resulting satellite orbital drag effects?
Finally, I would like to suggest modelers to consider IP shock inclinations in their numerical simulations. As argued by Welling et al. (2021), ground dB/dt variations were intensified and reached very low magnetic latitudes after the impact of a very fast and head-on CME on the magnetosphere. Moreover, this is also supported by previous observations showing that most shocks observed in the solar wind are moderately inclined shocks, with shock normal deviations of
Author contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
This work was possible thanks to the financial support provided by the NASA HGIO program through grant 80NSSC22K0756.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Akasofu, S.-I. (1964). The development of the auroral substorm. Planet. Space Sci. 12, 273–282. doi:10.1016/0032-0633(64)90151-5
Araki, T. (2014). Historically largest geomagnetic sudden commencement (SC) since 1868. Earth, Planets Space 66, 164. doi:10.1186/s40623-014-0164-0
Baker, A. B. (2019). Effect of interplanetary shock impact angle on the occurrence rate and properties of Pc5 waves observed by high-latitude ground magnetometers. Master’s thesis. Virginia Tech, Blacksburg, Virginia.
Belakhovsky, V. B., Pilipenko, V., Sakharov, Y. A., Lorentsen, D. L., and Samsonov, S. N. (2017). Geomagnetic and ionospheric response to the interplanetary shock on January 24, 2012. Earth, Planets Space 69, 105–125. doi:10.1186/s40623-017-0696-1
Berdichevsky, D. B., Szabo, A., Lepping, R. P., Viñas, A. F., and Mariani, F. (2000). Interplanetary fast shocks and associated drivers observed through the 23rd solar minimum by Wind over its first 2.5 years. J. Geophys. Res. 105, 27289–27314. doi:10.1029/1999JA000367
Bhaskar, A., Sibeck, D., Kanekal, S. G., Singer, H. J., Reeves, G., Oliveira, D. M., et al. (2021). Radiation belt response to fast reverse shock at geosynchronous orbit. Astrophys. J. 910, 154. doi:10.3847/1538-4357/abd702
Cameron, T. G., Jackel, B. J., and Oliveira, D. M. (2019). Using mutual information to determine geoeffectiveness of solar wind phase fronts with different front orientations. J. Geophys. Res. Space Phys. 124, 1582–1592. doi:10.1029/2018JA026080
Carter, B. A., Yizengaw, E., Pradipta, R., Halford, A. J., Norman, R., and Zhang, K. (2015). Interplanetary shocks and the resulting geomagnetically induced currents at the equator. Geophys. Res. Lett. 42, 6554–6559. doi:10.1002/2015GL065060
Chen, X., Zong, Q., Hao, Y., Li, Q., Zhang, D., and Zhang, H. (2023). Propagation of the interplanetary shock induced pulse: New observations by the global navigation satellite system. J. Geophys. Res. Space Phys. 128, e2022JA030975. doi:10.1029/2022JA030975
Echer, E., Gonzalez, W. D., Dal Lago, A., Vieira, L. E. A., Guarnieri, F. L., Gonzalez, A. L. C., et al. (2005). Interplanetary shocks and sudden impulses during solar maximum (2000) and solar minimum (1995-1996). Adv. Space Res. 36, 2313–2317. doi:10.1016/j.asr.2005.04.030
Grib, S. A., and Pushkar, E. A. (2006). Asymmetry of nonlinear interactions of solar MHD discontinuities with the bow shock. Geomagn. Aeron. 46, 417–423. doi:10.1134/S0016793206040025
Grib, S. A., Pushkar, E. A., and Leora, S. N. (2016). Some sources of plasma inhomogeneities in the solar wind in front of the Earth’s magnetosphere. Geomagn. Aeron. 56, 892–896. doi:10.1134/S0016793216070070
Grygorov, K., Pr̆ech, L., S̆afránková, J., Nĕmec̆ek, Z., and Goncharov, O. (2014). The far magnetotail response to an interplanetary shock arrival. Planet. Space Sci. 103, 228–237. doi:10.1016/j.pss.2014.07.016
Guo, X.-C., Hu, Y.-Q., and Wang, C. (2005). Earth’s magnetosphere impinged by interplanetary shocks of different orientations. Chin. Phys. Lett. 22, 3221–3224. doi:10.1088/0256-307X/22/12/067
Hajra, R., and Tsurutani, B. T. (2018a). Interplanetary shocks inducing magnetospheric supersubstorms (SML < −2500 nT): Unusual auroral morphologies and energy flow. Astrophys. J. 858, 123. doi:10.3847/1538-4357/aabaed
Hajra, R., and Tsurutani, B. T. (2018b). “Magnetospheric “killer” relativistic electron dropouts (REDs) and repopulation: A cyclical process,” in Extreme events in geospace: Origins, predictability and consequences. Editor N. Buzulukova (Cambridge, MA: Elsevier), 373–400. doi:10.1016/B978-0-12-812700-1.00014-5
Hajra, R., Tsurutani, B. T., and Lakhina, G. S. (2020). The complex space weather events of 2017 september. Astrophys. J. 899, 3. doi:10.3847/1538-4357/aba2c5
Hartinger, M. D., Takahashi, K., Drozdov, A. Y., Shi, X., Usanova, M. E., and Kress, B. (2022). ULF wave modeling, effects, and applications: Accomplishments, recent advances, and future. Front. Astron. Space Sci. 9. doi:10.3389/fspas.2022.867394
Hayakawa, H., Ebihara, Y., Pevtsov, A., Bhaskar, A., Karachik, N., and Oliveira, D. M. (2020a). Intensity and time series of extreme solar-terrestrial storm in 1946 March. Mon. Notices R. Astron. Soc. 497, 5507–5517. doi:10.1093/mnras/staa1508
Hayakawa, H., Ribeiro, P., Vaquero, J. M., Gallego, M. C., Knipp, D. J., Mekhaldi, F., et al. (2020b). The extreme space weather event in 1903 october/november: An outburst from the quiet Sun. Astrophys. J. Lett. 897, L10. doi:10.3847/2041-8213/ab6a18,
Hayakawa, H., Blake, S. P., Bhaskar, A., Hattori, K., Oliveira, D. M., and Ebihara, Y. (2021a). The extreme space weather event in 1941 february/march. Astrophys. J. 908, 209. doi:10.3847/1538-4357/abb772
Hayakawa, H., Oliveira, D. M., Shea, M. A., Smart, D. F., Blake, S. P., Hattori, K., et al. (2021b). The extreme solar and geomagnetic storms on 21-27 march 1940. Mon. Notices R. Astron. Soc. doi:10.1093/mnras/stab3615
Hughes, W. J. (1994). “Magnetospheric ULF waves: A tutorial with a historical perspective,” in Solar wind sources of magnetospheric ultra-low-frequency waves. Geophysical monograph series. Editors M. J. Engebretson, K. Takahashi, and M. Scholer (Washington, D.C.: American Geophysical Union), 81, 1–11. doi:10.1029/GM081p0001
Huttunen, K. E. J., Slavin, J., Collier, M., Koskinen, H. E. J., Szabo, A., Tanskanen, E., et al. (2005). Cluster observations of sudden impulses in the magnetotail caused by interplanetary shocks and pressure increases. Ann. Geophys. 23, 609–624. doi:10.5194/angeo-23-609-2005
Kangas, J., Kultima, J., Guglielmi, A., Potapov, A., and Hayashi, K. (2001). Impact of interplanetary shock on the ULF wave activity: A case study of the storm sudden commencement on september 22, 1999. Earth, Planets Space 53, 1177–1182. doi:10.1186/BF03352413
Kasran, F. A. M., Jusoh, M. H., Adhikari, B., and Rahim, S. A. E. A. (2019). Field-aligned currents (FACs) behaviour during the arrival of interplanetary magnetic shock. J. Phys. Conf. Ser. 1152, 012027. doi:10.1088/1742-6596/1152/1/012027
Kennel, C. F., Edmiston, J. P., and Hada, T. (1985). “A quarter century of collisionless shock research,” in Collisionless shocks in the heliosphere: A tutorial review. Geophysical monograph series. Editors R. G. Stone, and B. Tsurutani (Washington, D.C.: American Geophysical Union), 34, 1–36. doi:10.1029/GM034p0001
Kilpua, E. K. J., Lumme, K., Andréeová, E., Isavnin, A., and Koskinen, H. E. J. (2015). Properties and drivers of fast interplanetary shocks near the orbit of the Earth (1995-2013). J. Geophys. Res. Space Phys. 120, 4112–4125. doi:10.1002/2015JA021138
Klein, L. W., and Burlaga, L. F. (1982). Interplanetary magnetic clouds at 1 AU. J. Geophys. Res. 87, 613–624. doi:10.1029/JA087iA02p00613
Kokubun, S., McPherron, R. L., and Russell, C. T. (1977). Triggering of substorms by solar wind discontinuities. J. Geophys. Res. 82, 74–86. doi:10.1029/JA082i001p00074
Lakhina, G. S., and Tsurutani, B. T. (2020). “Electromagnetic pulsations and magnetic storms,” in Encyclopedia of solid Earth geophysics. Encyclopedia of Earth Sciences series. Editor H. Gupta (Dordrecht, The Netherlands,Cham: Springer), 1–5. doi:10.1007/978-3-030-10475-7_156-1
Landau, L. D., and Lifshitz, E. M. (1960). Electrodynamics of continuous media. Oxford, England: Pergamon Press.
Laundal, K. M., and Richmond, A. D. (2017). Magnetic coordinate systems. Space Sci. Rev. 206, 27–59. doi:10.1007/s11214-016-0275-y
Love, J. J., Hayakawa, H., and Cliver, E. W. (2019a). Intensity and impact of the New York railroad superstorm of may 1921. Space Weather 17, 1281–1292. doi:10.1029/2019SW002250
Love, J. J., Hayakawa, H., and Cliver, E. W. (2019b). On the intensity of the magnetic superstorm of september 1909. Space Weather 17, 37–45. doi:10.1029/2018SW002079
Molinski, T. S., Feero, W. E., and Damsky, B. L. (2000). Shielding grids from solar storms [power system protection]. IEEE Spectr. 37, 55–60. doi:10.1109/6.880955
Ngwira, C. M., and Pulkkinen, A. (2019). “An introduction to geomagnetically induced currents,” in Geomagnetically induced currents from the Sun to the power grid. Editors J. L. Gannon, A. Swidinsky, and Z. Xu (Washington, D.C.: American Geophysical Union), 3–13. doi:10.1002/9781119434412.ch1
Oh, S. Y., Yi, Y., and Kim, Y. H. (2007). Solar cycle variation of the interplanetary forward shock drivers observed at 1 AU. Sol. Phys. 245, 391–410. doi:10.1007/s11207-007-9042-2
Oliveira, D. M., and Ngwira, C. M. (2017). Geomagnetically induced currents: Principles. Braz. J. Phys. 47, 552–560. doi:10.1007/s13538-017-0523-y
Oliveira, D. M., and Raeder, J. (2014). Impact angle control of interplanetary shock geoeffectiveness. J. Geophys. Res. Space Phys. 119, 8188–8201. doi:10.1002/2014JA020275
Oliveira, D. M., and Raeder, J. (2015). Impact angle control of interplanetary shock geoeffectiveness: A statistical study. J. Geophys. Res. Space Phys. 120, 4313–4323. doi:10.1002/2015JA021147
Oliveira, D. M., and Samsonov, A. A. (2018). Geoeffectiveness of interplanetary shocks controlled by impact angles: A review. Adv. Space Res. 61, 1–44. doi:10.1016/j.asr.2017.10.006
Oliveira, D. M., and Zesta, E. (2019). Satellite orbital drag during magnetic storms. Space Weather 17, 1510–1533. doi:10.1029/2019SW002287
Oliveira, D. M., Raeder, J., Tsurutani, B. T., and Gjerloev, J. W. (2016). Effects of interplanetary shock inclinations on nightside auroral power intensity. Braz. J. Phys. 46, 97–104. doi:10.1007/s13538-015-0389-9
Oliveira, D. M., Zesta, E., Schuck, P. W., and Sutton, E. K. (2017). Thermosphere global time response to geomagnetic storms caused by coronal mass ejections. J. Geophys. Res. Space Phys. 122, 10,762–10,782. doi:10.1002/2017JA024006
Oliveira, D. M., Arel, D., Raeder, J., Zesta, E., Ngwira, C. M., Carter, B. A., et al. (2018). Geomagnetically induced currents caused by interplanetary shocks with different impact angles and speeds. Space Weather 16, 636–647. doi:10.1029/2018SW001880
Oliveira, D. M., Hartinger, M. D., Xu, Z., Zesta, E., Pilipenko, V. A., Giles, B. L., et al. (2020). Interplanetary shock impact angles control magnetospheric ULF wave activity: Wave amplitude, frequency, and power spectra. Geophys. Res. Lett. 47, e2020GL090857. doi:10.1029/2020GL090857
Oliveira, D. M., Weygand, J. M., Zesta, E., Ngwira, C. M., Hartinger, M. D., Xu, Z., et al. (2021). Impact angle control of local intense dB/dt variations during shock-induced substorms. Space Weather 19, e2021SW002933. doi:10.1029/2021SW002933
Oliveira, D. M. (2017). Magnetohydrodynamic shocks in the interplanetary space: A theoretical review. Braz. J. Phys. 47, 81–95. doi:10.1007/s13538-016-0472-x
Pirjola, R. (2002). Review on the calculation of surface electric and magnetic fields and of geomagnetically induced currents in ground-based technological systems. Surv. Geophys. 23, 71–90. doi:10.1023/A:1014816009303
Pulkkinen, A., Rastatter, L., Kuznetsova, M., Singer, H., Balch, C., Weimer, D., et al. (2013). Community-wide validation of geospace model ground magnetic field perturbation predictions to support model transition to operations. Space Weather 11, 369–385. doi:10.1002/swe.20056
Rout, D., Chakrabarty, D., Janardhan, P., Sekar, R., Maniya, V., and Pandey, K. (2017). Solar wind flow angle and geo-effectiveness of corotating interaction regions: First results. Geophys. Res. Lett. 44, 4532–4539. doi:10.1002/2017GL073038
Rudd, J. T., Oliveira, D. M., Bhaskar, A., and Halford, A. J. (2019). How do interplanetary shock impact angles control the size of the geoeffective magnetosphere? Adv. Space Res. 63, 317–326. doi:10.1016/j.asr.2018.09.013
Samson, J. C., Wallis, D. D., Hughes, T. J., Creutzberg, F., Ruohoniemi, J. M., and Greenwald, R. A. (1992). Substorm intensifications and field line resonances in the nightside magnetosphere. J. Geophys. Res. 97, 8495–8518. doi:10.1029/91JA03156
Samsonov, A. A., Sergeev, V. A., Kuznetsova, M. M., and Sibeck, D. G. (2015). Asymmetric magnetospheric compressions and expansions in response to impact of inclined interplanetary shock. Geophys. Res. Lett. 42, 4716–4722. doi:10.1002/2015GL064294
Samsonov, A. A. (2011). Propagation of inclined interplanetary shock through the magnetosheath. J. Atmos. Solar-Terrest. Phys. 73, 30–39. doi:10.1016/j.jastp.2009.10.014
Schiller, Q., Kanekal, S. G., Jian, L. K., Li, X., Jones, A., Baker, D. N., et al. (2016). Prompt injections of highly relativistic electrons induced by interplanetary shocks: A statistical study of van allen probes observations. Geophys. Res. Lett. 43, 12,317–12,324. doi:10.1002/2016GL071628
Schwartz, S. J. (1998). “Shock and discontinuity normals, Mach numbers, and related parameters,”. no. SR-001 in ISSI Scientific Report in Analysis methods for multi-spacecraft data. Editors G. Paschmann, and P. W. Daly (Noordwijk, The Netherlands: ESA Publications Division), 249–270.
Selvakumaran, R., Veenadhari, B., Ebihara, Y., Kumar, S., and Prasad, D. S. V. V. D. (2017). The role of interplanetary shock orientation on SC/SI rise time and geoeffectiveness. Adv. Space Res. 59, 1425–1434. doi:10.1016/j.asr.2016.12.010
Shi, Y., Zesta, E., Connor, H. K., Su, Y.-J., Sutton, E. K., Huang, C. Y., et al. (2017). High-latitude thermosphere neutral density response to solar wind dynamic pressure enhancement. J. Geophys. Res. Space Phys. 122, 11,559–11,578. doi:10.1002/2017JA023889
Shi, Y., Oliveira, D. M., Knipp, D. J., Zesta, E., Matsuo, T., and Anderson, B. (2019). Effects of nearly frontal and highly inclined interplanetary shocks on high-latitude field-aligned currents (FACs). Space Weather 17, 1659–1673. doi:10.1029/2019SW002367
Shue, J.-H., Song, P., Russell, C. T., Steinberg, J. T., Chao, J. K., Zastenker, G., et al. (1998). Magnetopause location under extreme solar wind conditions. J. Geophys. Res. 103 (17), 17691–17700. doi:10.1029/98JA01103
Sitnov, M., Birn, J., Ferdousi, B., Gordeev, E., Khotyaintsev, Y., Merkin, V., et al. (2019). Explosive magnetotail activity. Space Sci. Rev. 215, 31. doi:10.1007/s11214-019-0599-5
Smith, E. J., Slavin, J. A., Zwickl, R. D., and Bame, S. J. (1986). “Shocks and storm sudden commencements,” in Solar wind and magnetosphere coupling. Editors Y. Kamide, and J. A. Slavin (Tokyo, Japan: Terra Scientific), 345.
Smith, A. W., Rae, J., Forsyth, C., Oliveira, D. M., Freeman, P. M., and Jackson, D. (2020). Probabilistic forecasts of storm sudden commencements from interplanetary shocks using machine learning. Space Weather 18, e2020SW002603. doi:10.1029/2020SW002603
Takahashi, K., Lysak, R., Vellante, M., Kletzing, C. A., Hartinger, M. D., and Smith, C. W. (2018). Observation and numerical simulation of cavity mode oscillations excited by an interplanetary shock. J. Geophys. Res. Space Phys. 123, 1969–1988. doi:10.1002/2017JA024639
Takeuchi, T., Russell, C. T., and Araki, T. (2002). Effect of the orientation of interplanetary shock on the geomagnetic sudden commencement. J. Geophys. Res. 107, SMP 6-1–SMP 6-10. doi:10.1029/2002JA009597
Tsurutani, B. T., and Hajra, R. (2021). The interplanetary and magnetospheric causes of geomagnetically induced currents (GICs) > 10 A in the mäntsälä Finland pipeline: 1999 through 2019. J. Space Weather Space Clim. 11, 23. doi:10.1051/swsc/2021001
Tsurutani, B. T., and Hajra, R. (2023). Energetics of shock-triggered supersubstorms (SML < −2500 nT). Astrophys. J. 946, 17. doi:10.3847/1538-4357/acb143
Tsurutani, B. T., and Lin, R. P. (1985). Acceleration of >47 keV Ions and >2 keV electrons by interplanetary shocks at 1 AU. J. Geophys. Res. 90, 1–11. doi:10.1029/JA090iA01p00001
Tsurutani, B. T., Gonzalez, W. D., Tang, F., Akasofu, S.-I., and Smith, E. J. (1988). Origin of interplanetary southward magnetic fields responsible for major magnetic storms near solar maximum (1978-1979). J. Geophys. Res. 93, 8519–8531. doi:10.1029/JA093iA08p08519
Tsurutani, B. T., Zhou, X.-Y., Vasyliunas, V. M., Haerendel, G., Arballo, J. K., and Lakhina, G. S. (2001). Interplanetary shocks, magnetopause boundary layers and dayside auroras: The importance of a very small magnetospheric region. Surv. Geophys. 22, 101–130. doi:10.1023/A:1012952414384
Tsurutani, B. T., Gonzalez, W. D., Gonzalez, A. L. C., Guarnieri, F. L., Gopalswamy, N., Grande, M., et al. (2006). Corotating solar wind streams and recurrent geomagnetic activity: A review. J. Geophys. Res. 111, A07S01–25. doi:10.1029/2005JA011273
Tsurutani, B. T., Lakhina, G. S., Verkhoglyadova, O. P., Gonzalez, W. D., Echer, E., and Guarnieri, F. L. (2011). A review of interplanetary discontinuities and their geomagnetic effects. J. Atmos. Solar-Terrest. Phys. 73, 5–19. doi:10.1016/j.jastp.2010.04.001
Tsurutani, B. T., Hajra, R., Tanimori, T., Takada, A., Remya, B., Mannucci, A. J., et al. (2016). Heliospheric plasma sheet (HPS) impingement onto the magnetosphere as a cause of relativistic electron dropouts (REDs) via coherent EMIC wave scattering with possible consequences for climate change mechanisms. J. Geophys. Res. Space Phys. 121, 10,130–10,156. doi:10.1002/2016JA022499
Wang, C., Huang, Z. H., Hu, Y. Q., and Guo, X. C. (2005). “3D global simulation of the interaction of interplanetary shocks with the magnetosphere,” in 4th annual IGPP international astrophysics conference on the Physics of collisionless shocks. AIP conference proceedings. Editors G. Li, G. Zank, and C. T. Russell (Washington, D.C.: American Institute of Physics), 781, 320–324. doi:10.1063/1.2032716
Wang, C., Li, C. X., Huang, Z. H., and Richardson, J. D. (2006). Effect of interplanetary shock strengths and orientations on storm sudden commencement rise times. Geophys. Res. Lett. 33, 141044–L14113. doi:10.1029/2006GL025966
Wang, C., Liu, J. B., Li, H., Huang, Z. H., Richardson, J. D., and Kan, J. R. (2009). Geospace magnetic field responses to interplanetary shocks. J. Geophys. Res. 114. doi:10.1029/2008JA013794
Welling, D. T., Love, J. J., Joshua Rigler, E., Oliveira, D. M., Komar, C. M., and Morley, S. K. (2021). Numerical simulations of the geospace response to a perfect interplanetary coronal mass ejection. Space Weather 19, e2020SW002489. doi:10.1029/2020SW002489
Xu, Z., Hartinger, M. D., Oliveira, D. M., Coyle, S., Clauer, C. R., Weimer, D., et al. (2020). Inter-hemispheric asymmetries in the ground magnetic response to interplanetary shocks: The role of shock impact angle. Space Weather 18, e2019SW002427. doi:10.1029/2019SW002427
Yue, C., Zong, Q. G., Zhang, H., Wang, Y. F., Yuan, C. J., Pu, Z. Y., et al. (2010). Geomagnetic activity triggered by interplanetary shocks. J. Geophys. Res. 115, 1–13. doi:10.1029/2010JA015356
Zhou, X.-Y., and Tsurutani, B. T. (1999). Rapid intensification and propagation of the dayside aurora: Large scale interplanetary pressure pulses (fast shocks). Geophys. Res. Lett. 26, 1097–1100. doi:10.1029/1999GL900173
Zhou, X., and Tsurutani, B. T. (2001). Interplanetary shock triggering of nightside geomagnetic activity: Substorms, pseudobreakups, and quiescent events. J. Geophys. Res. 106, 18957–18967. doi:10.1029/2000JA003028
Keywords: interplanetary shocks, shock geometry, geomagnetic activity, geospace response, ionospheric response, ground response
Citation: Oliveira DM (2023) Geoeffectiveness of interplanetary shocks controlled by impact angles: past research, recent advancements, and future work. Front. Astron. Space Sci. 10:1179279. doi: 10.3389/fspas.2023.1179279
Received: 03 March 2023; Accepted: 17 April 2023;
Published: 26 April 2023.
Edited by:
Xu-Zhi Zhou, Peking University, ChinaReviewed by:
Chao Yue, Peking University, ChinaBruce Tsurutani, NASA Jet Propulsion Laboratory (JPL), United States
Copyright © 2023 Oliveira. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Denny M. Oliveira, ZGVubnlAdW1iYy5lZHU=
 Denny M. Oliveira
Denny M. Oliveira