- 1Center for Space Physics, Boston University, Boston, MA, United States
- 2Department of Space Physics, Institute of Atmospheric Physics of the Czech Academy of Sciences, Prague, Czechia
- 3Department of Atmospheric and Oceanic Sciences, University of California, Los Angeles, Los Angeles, CA, United States
This study analyzes the effects of electromagnetic ion cyclotron (EMIC) waves on relativistic electron scattering and losses in the Earth’s outer radiation belt. EMIC emissions are commonly observed in the inner magnetosphere and are known to reach high amplitudes, causing significant pitch angle changes in primarily
1 Introduction
Electromagnetic ion cyclotron (EMIC) waves are naturally occurring electromagnetic emissions in the Earth’s magnetosphere generated by unstable anisotropic hot ion populations (Kennel and Petschek, 1966; Anderson et al., 1996). Each ion component of the space plasma has a corresponding EMIC frequency band located below the gyrofrequency of the ion, with the hydrogen band (H+) and helium band (He+) being the most commonly observed (Min et al., 2012; Meredith et al., 2014; Saikin et al., 2015; Wang X. Y. et al., 2017; Jun et al., 2021). In the outer radiation belt, the wave frequencies in the near-equatorial source (Loto’aniu et al., 2005; Allen et al., 2015) fall mainly into the Pc1 range 0.2–5 Hz (Saito, 1969; Usanova et al., 2012). Initially generated in the left-handed mode, the waves may convert to the right-handed mode at higher latitudes (Rauch and Roux, 1982; Perraut et al., 1984; Kim and Johnson, 2016). These polarized waves can scatter relativistic electrons (kinetic energies Ek around 1 MeV and larger) in pitch angle α through cyclotron resonance interactions (Horne and Thorne, 1998; Summers et al., 1998), which leads to significant losses of radiation belt electrons to the atmosphere (Thorne and Kennel, 1971; Usanova et al., 2014; Clilverd et al., 2015; Kurita et al., 2018; Li and Hudson, 2019).
During geomagnetically active times, EMIC waves at lower L-shells (L < 6) can reach peak magnetic field amplitudes Bw higher than 1% of the background magnetic field strength B0 (Meredith et al., 2003; Engebretson et al., 2015). Trajectories of particles resonating with strong waves experience large perturbations, and a variety of associated non-linear effects appear (Karpman, 1974; Artemyev et al., 2018; Grach et al., 2022). Phase trapping of ions in the wave potential leads to non-local transport to higher pitch angles and the formation of phase space density (PSD) holes in the gyrophase space (Omura et al., 2010; Shoji et al., 2021), while phase-trapped electrons experience a decrease in pitch angle (Omura and Zhao, 2012; Zheng et al., 2019). At α ≈ 0°, the force-bunched electrons are transported predominantly to higher pitch angles; Bortnik et al. (2022) proposed that this non-linear effect may result in precipitation blocking due to the removal of electrons from the loss cone. Below the fundamental cyclotron resonance energy, non-resonant scattering by amplitude-modulated waves takes place and may extend the energy range of precipitating electrons down to hundreds of keV (Chen et al., 2016; An et al., 2022).
When the wave normal angle θk (WNA) of EMIC waves increases and the propagation becomes oblique, finite Larmor radius effects enable interaction with higher cyclotron harmonics. Approximate quasilinear formulas for pitch angle diffusion coefficients of waves with a given wave normal distribution can be found in the study by Albert (2008). Wang G. et al. (2017) studied the interaction of electrons with moderately oblique monochromatic EMIC waves through non-linear test-particle simulations and quasilinear diffusive modeling. They have shown that with increasing θk, harmonic resonances at ultrarelativistic energies can lead to significant scattering loss, while the fundamental resonance becomes weaker for oblique waves. Lee et al. (2018) analyzed the WNA and ellipticity of a set of EMIC waves detected by Van Allen Probe A, ran test-particle simulations of electron interaction with very powerful and oblique EMIC waves, and highlighted the complexity of pitch angle evolution due to higher-order resonance with the elliptically polarized wave. They also emphasized the advective aspects of non-linear scattering and noted the importance of ellipticity and WNA distributions in modeling the radiation belt electron transport.
In this paper, we perform test-particle simulations of non-linear electron interactions with quasiparallel and very oblique monochromatic EMIC waves, with the overall goal of describing the dependence of advection, diffusion, and subsequent particle losses on the wave amplitude and wave normal angle—special attention is given to the PSD evolution at low pitch angles. After describing the simulation setup in Section 2, we analyze the average and standard deviation of equatorial pitch angle changes for very oblique waves and discuss the influence of higher harmonics on advection and diffusion in Section 3.1. In Section 3.2, we demonstrate through Liouville mapping of phase space density in backward-in-time simulations that the force-bunching effects at low pitch angles are balanced out by transport from higher pitch angles and that there is no apparent precipitation blocking in the sense of decreasing precipitating electron PSD below the trapped PSD. Section 3.3 describes fractional resonances, a type of resonance acting below the fundamental resonance energy, and considers their effects on subrelativistic electrons. A summary of the most salient results and a discussion of the impacts of our findings on radiation belt electron modeling can be found in Section 4.
2 Methods and simulation setup
Before choosing representative wave and plasma parameters for our particle simulation, we must first consider which quantities can influence the behavior of resonant electrons. Wave amplitude Bw controls the transition from quasilinear to non-linear interaction, and wave normal angle θk is related to the perpendicular component of the wave vector and associated harmonic resonances. Varying the values of Bw or θk leads to major qualitative changes in the resonant behavior; therefore, they are the essential parameters in our simulation. We choose four values of wave normal angle {5°, 45°, 70°, 80°} to cover quasiparallel, moderately oblique, and very oblique wave propagation. The WNA values are combined with three values of amplitude Bw0 = {100 pT, 400 pT, 1.6 nT}, which approximately correspond to Bw0/B0eq ratios of {0.04%, 0.16%, 0.64%} for equatorial field strength B0eq = 248 nT at L = 5. This choice of L-shell is consistent with regions of enhanced EMIC wave activity identified by Meredith et al. (2014) and Jun et al. (2021) in spacecraft measurements during active geomagnetic conditions.
There are also several parameters that influence the value of the minimum resonance energy, which is given by the formula
where m is the electron mass, c is the speed of light, k‖ is the component of the wave vector parallel to B0, ω is the wave frequency, Ωe is the local electron gyrofrequency, and n is an integer determining the resonance harmonic (positive/negative for electrons streaming against/along the wave). The first approximation assumes ω ≪Ωe and
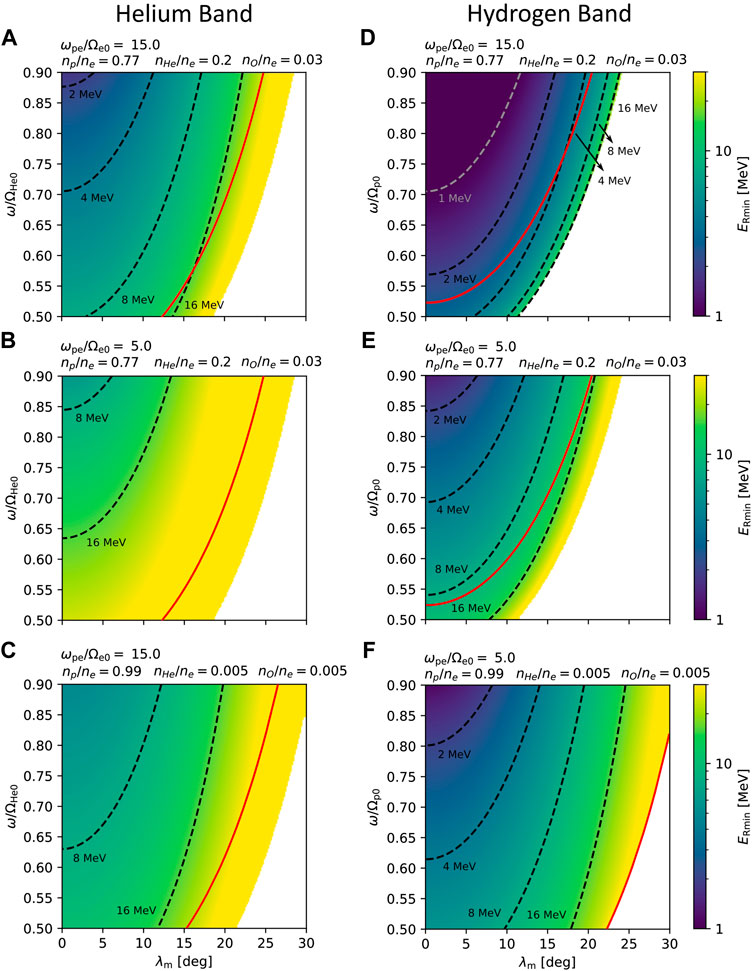
FIGURE 1. Minimum resonance energies ERmin of electrons interacting with a left-hand polarized parallel-propagating EMIC wave. Each panel shows a map of energies as a function of wave frequency and magnetic latitude. (A) Minimum resonance energies for interaction with a helium band wave in a high-density plasma with a high relative concentration of heavier ions—these conditions are used in our simulations. (B) Same as panel A, but in a low-density plasma. (C) Same as panel A, but with a low concentration of heavier ions. (D–F) ERmin for a hydrogen band wave under the same plasma conditions as in (A–C), except for panel F, where both the electron density and heavier ion concentrations are kept low. In all panels, dashed lines represent energy contours, and the solid red line signifies the crossover frequency. Note that for oblique waves, the left-handed dispersion branch is coupled to the right-handed branch, so the energies right of the red curve would have to be calculated for right-hand polarized waves.
Apart from the strong interaction near resonance energies, electrons can also experience non-resonant scattering due to wave amplitude gradients (Chen et al., 2016) or, equivalently, due to the spectral broadening of amplitude-modulated waves (An et al., 2022). To simplify our analysis, we suppress the non-resonant scattering by introducing a slow and smooth amplitude change at the edges of the wave packet. This is performed by multiplying the wave envelope by a half-period of the cos2 function, with a field-aligned distance from the minimum to the maximum of the function set to Δh = 2,200 km. Symbolically,
This amplitude profile is similar to the tanh model in the study by Bortnik et al. (2022). The envelope shape is plotted in Figure 2A. The packet ends at a field-aligned distance hmax, where the normalized frequency reaches ω/ΩO = 1.25. At this frequency, the helium wave is already right-handed, and the resonance energy of very oblique waves rapidly increases (Stix, 1992).
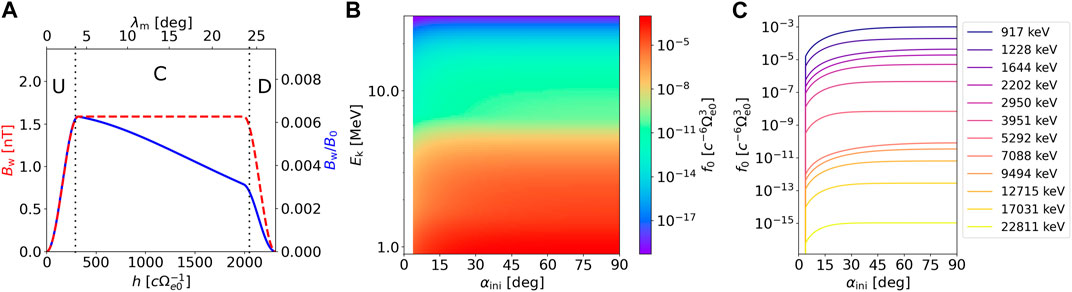
FIGURE 2. (A) Distribution of wave amplitudes along the field line. The wave experiences smooth growth in region U, stays constant in region C (1.6 nT in this example), and decreases back to zero in region D, as shown by the dashed red line. The solid blue line shows the relative wave amplitude with respect to the background field B0. (B) Phase space density distribution at the equator plotted in the energy–pitch angle space. The empty loss cone corresponds to the white region at αini < αloss = 3.7°. Normalized PSD is used in the simulation code. (C) Line plots of pitch angle profiles from the previous panel for representative energies. Note that the sin α term from Jacobian is not included; therefore, the decrease in PSD near the loss cone indicates a positive pitch angle anisotropy.
The test-particle simulation method is based on the solution of the Lorentz force law by a relativistic Boris algorithm with a phase angle correction, as described by Zenitani and Umeda (2018). The components of the electromagnetic wave field are defined according to the analysis of elliptically polarized waves presented by Omura et al. (2019); see also Eqs 8–11, Eqs 15–19 in Section 5. Wave packet motion can be neglected on short timescales since the group velocity of EMIC waves is much smaller than the velocity of relativistic electrons. In forward-in-time simulations, the particles start either at the equator and propagate until they reach the end of the wave packet (or their mirror point) or at the end of the wave packet and propagate back to the equator. Mirroring particles are not allowed to return to the equator so that we can separate the resonant effects experienced by co-streaming and counter-streaming electrons. In both cases, the initial particle energy is spaced logarithmically from 900 keV to 30 MeV with 96 bins, initial pitch angles go from 0° to 90° (or 180°–90° for counter-streaming electrons) with 90 linear steps, and the initial gyrophases φ uniformly cover the full 360° angle with 72 steps. It is of note that the grid boundaries in the (Ek, α, φ) space represent bin edges. In backward-in-time simulations, the pitch angle range is limited to 0°–20° (or 180°–160° for counter-streaming electrons) with 90 linear steps, providing increased resolution of the loss cone (αloss = 3.6° at the equator and 6.1° at the end of the packet). The time step of the Boris solver is adaptive and always stays at 128 steps per local electron gyroperiod.
The backward-in-time simulations are used to map the phase space density of an initial, unperturbed distribution to the final state and assess the PSD evolution due to resonant interactions (Nunn and Omura, 2015; Hanzelka et al., 2021). We assume that the initial hot (relativistic) distribution is in the form of a sum of subtracted bi-Maxwellian distributions that preserves phase space density along adiabatic trajectories (Summers et al., 2012; Omura, 2021). At a distance h, this distribution can be written for relativistic momenta u‖ = γv‖ and u⊥ = γv⊥ as
with
We set N = 5 and choose the following values of distribution parameters: loss cone width βi = 0.5 ∀i, loss cone height ρi = 1.0 ∀i, parallel and perpendicular thermal momenta Ut‖i/c = Ut⊥i/c = {0.2, 0.5, 1.0, 2.5, 9.0}, and hot electron density nhe0i = {2.2, 0.22, 0.022, 0.0022, 2.2 × 10−7} cm−3. PSD inside the loss cone is set to zero for all values of h. The equatorial distribution is plotted in Figure 2B in the (Ek, αini) space. The energy profile up to 10 MeV is constructed to loosely follow the Van Allen Probes measurements analyzed by Zhao et al. (2019); however, the energy distribution is of little importance for EMIC-electron resonance since the acceleration caused by this interaction is negligible (Summers et al., 1998). Line plots of pitch angle distributions for several initial energies are presented in Figure 2C. Although each component of the initial distribution has a zero temperature anisotropy
3 Results
3.1 Advection and diffusion
When studying the non-linear interactions between plasma waves and charged particles, it is illustrative to start by inspecting individual trajectories. In Figure 3, we plot the spatial evolution of the equatorial pitch angle for electrons propagating through a high-amplitude (Bw0/B0eq = 0.0064) moderately oblique (θk = 45°) EMIC wave. The equatorial minimum resonance energy for this wave is ERmin ≈ 3.3 MeV for n = ±1 and ERmin ≈ 7.1 MeV for n = ±2. Particles starting at the equator with initial pitch angle α = 0.5° and energy Ek = 3.95 MeV experience a significant increase in equatorial pitch angle Δαeq ≈ 11° due to the n = −1 resonance, with almost no dependence on the initial gyrophase (Figure 3A). This is the advective behavior caused by force bunching, as previously described by Grach and Demekhov (2020), Grach et al. (2022), and Albert et al. (2022). This type of scattering has also been called “anomalous phase trapping” in the whistler-mode wave case studied by Kitahara and Katoh (2019).
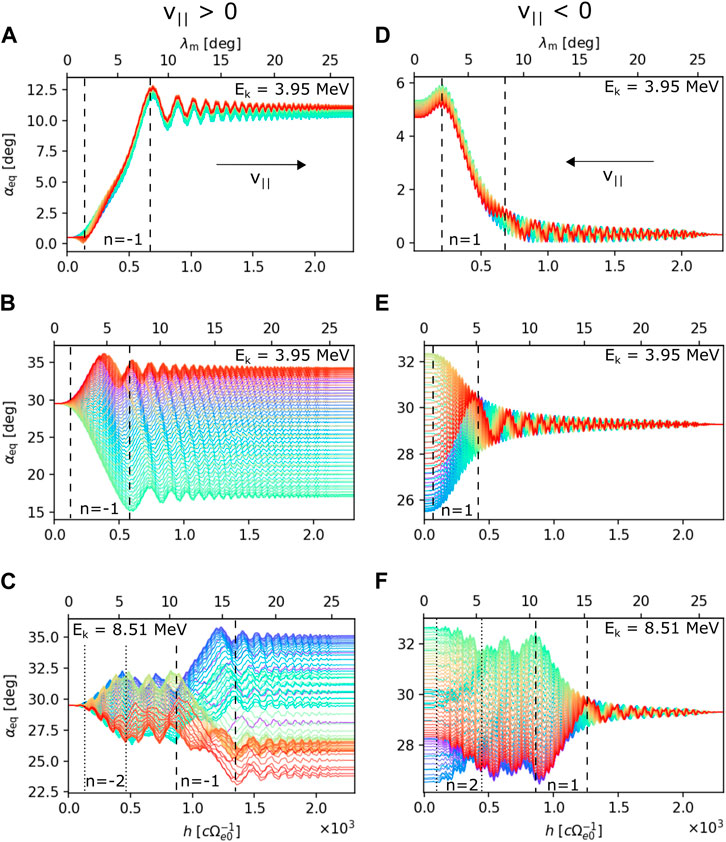
FIGURE 3. Trajectory examples showing the change in equatorial pitch angle over latitude due to interaction with a high-amplitude, moderately oblique wave (Bw0/B0eq =0.0064 and θk =45°). (A–C) Electrons propagating along the wave (from the equator), and (D–F) propagation against the wave (toward the equator). In each panel, electrons have the same initial energy, pitch angle, and latitude, and the line colors represent the initial uniform sampling in gyrophase. Pairs of dashed lines represent the approximate spatial interval on which the fundamental cyclotron resonance produces strong scattering; for the harmonic resonances n = ±2, the interval is marked by dotted lines.
Particles starting at larger pitch angles (αeq = 29.5°, Figure 3B) experience a large spread in αeq across the gyrophases, exhibiting a predominantly diffusive behavior. The asymmetry in Δαeq toward lower values is caused by phase locking of φ to the wave phase ψ, but the particles never become fully phase-trapped in this particular case. In Figure 3C, we increase the initial energy to Ek = 8.51 MeV and observe that particles first undergo scattering due to the n = −2 harmonic resonance and then encounter the n = −1 resonance at latitudes from 11° to 16°, resulting in pitch angle diffusion.
Figures 3D–F show particle trajectories of electrons starting at the end of the wave packet and streaming against the wave. Here, resonant interaction is enabled by the right-handed component of the elliptically polarized wave. Keeping the initial energies and initial equatorial pitch angles similar to the co-streaming case, we observe that the advective and diffusive effects of the n = 1 resonance are comparable to the n = −1 resonance. However, the maximum change in pitch angle is smaller, and the phase-locking effect does not appear. In the case with Ek = 8.51 MeV, the counter-streaming particles first encounter the stronger n = 1 resonance, and the weaker n = 2 resonance then has only a small effect on the spread in Δαeq.
To evaluate the pitch angle evolution of relativistic electrons across all initial pitch angles and energies, we introduce two statistical measures: the average
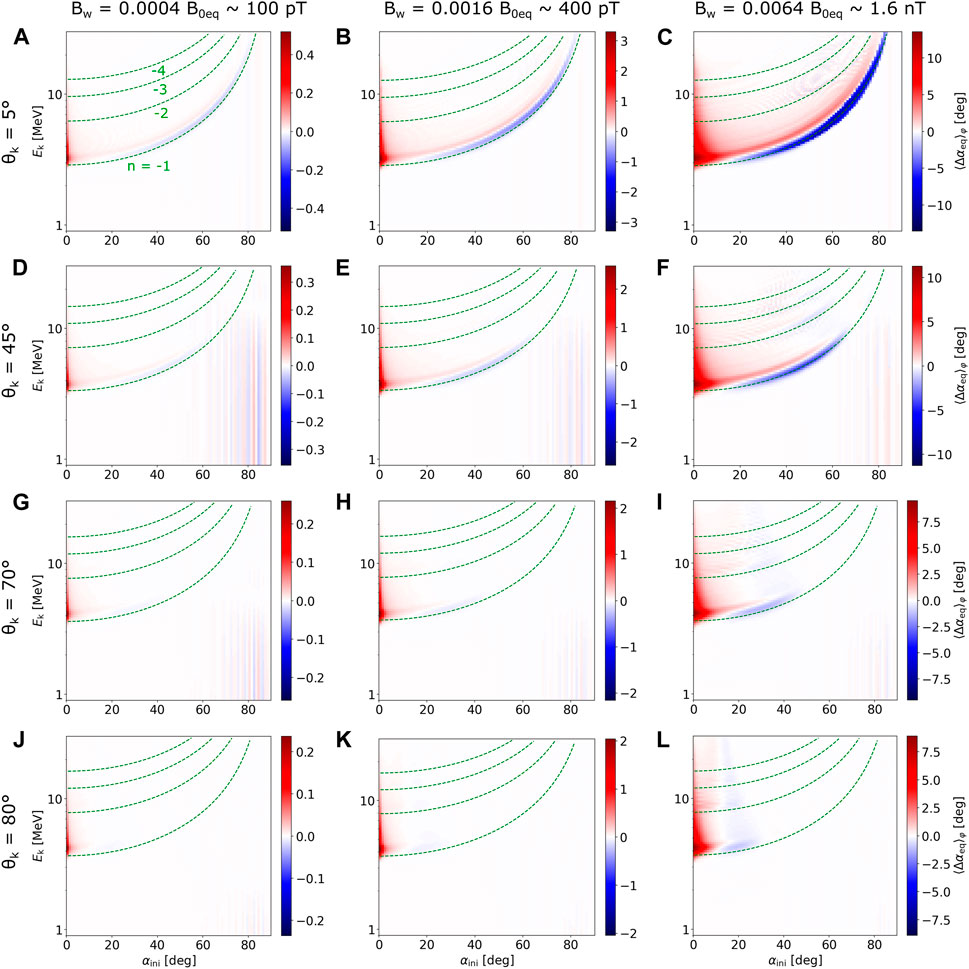
FIGURE 4. Average change
The appearance of strong negative advection associated with phase trapping can be explained through the behavior of the inhomogeneity parameter S. This parameter is proportional to the magnetic field gradient and inversely proportional to the wave amplitude and has a complicated dependence on wave dispersion properties (see Omura and Zhao (2012) and Omura (2021) for a detailed analysis and overview). When |S| drops below 1, a resonance island forms in the phase space, and non-linear phase trapping becomes possible. For parallel wave propagation, the absolute value of the parameter decreases with the equatorial pitch angle. In the case of fundamental resonance n = −1, |S| increases with the wave normal angle, while a decrease is seen in the case of harmonic resonances (Wang G. et al., 2017). However, scattering by very oblique waves becomes inefficient at high WNA. Therefore, the most favorable case for phase trapping is the fundamental resonance with high-amplitude quasiparallel waves at moderate-to-high pitch angles, as seen in Figure 4C. However, the inhomogeneity parameter is derived from the pendulum approximation of electron motion and cannot describe the behavior at low pitch angles. An extension of the electron motion analysis to small α based on the two-valley Hamiltonian was presented by Albert et al. (2021), where they concluded that as the initial pitch angle goes to zero, all particles are expected to experience force bunching, which can be understood as a special case of phase trapping.
The interaction with oblique waves (Figures 4D–L) introduces some new effects. First, we may notice the alternating blue and red vertical lines at high pitch angles, with almost no dependence on energy. These are the result of non-resonant oscillations at mirror points and would completely disappear if the particles were allowed to bounce back to the equator—the lines are not relevant to our analysis of the cyclotron resonance and will be omitted in the following sections. Harmonic resonances become visible at higher amplitudes, adding new pairs of positive and negative advective stripes along the corresponding resonance energy curves. However, as the wave normal angle increases, advective effects disappear at higher pitch angles; for θk = 80°, the average change in pitch angle becomes negligible for particles with αini > 30°. Moreover, a fine stripe structure traversing the resonance energy curves appears in the high-amplitude plots. These new effects will be explained when discussing diffusive behavior, where their origin becomes more apparent.
The standard deviation in the equatorial pitch angle of co-streaming particles is plotted in Figure 5, following the panel format of Figure 4. The color bars of each individual panel go from zero to
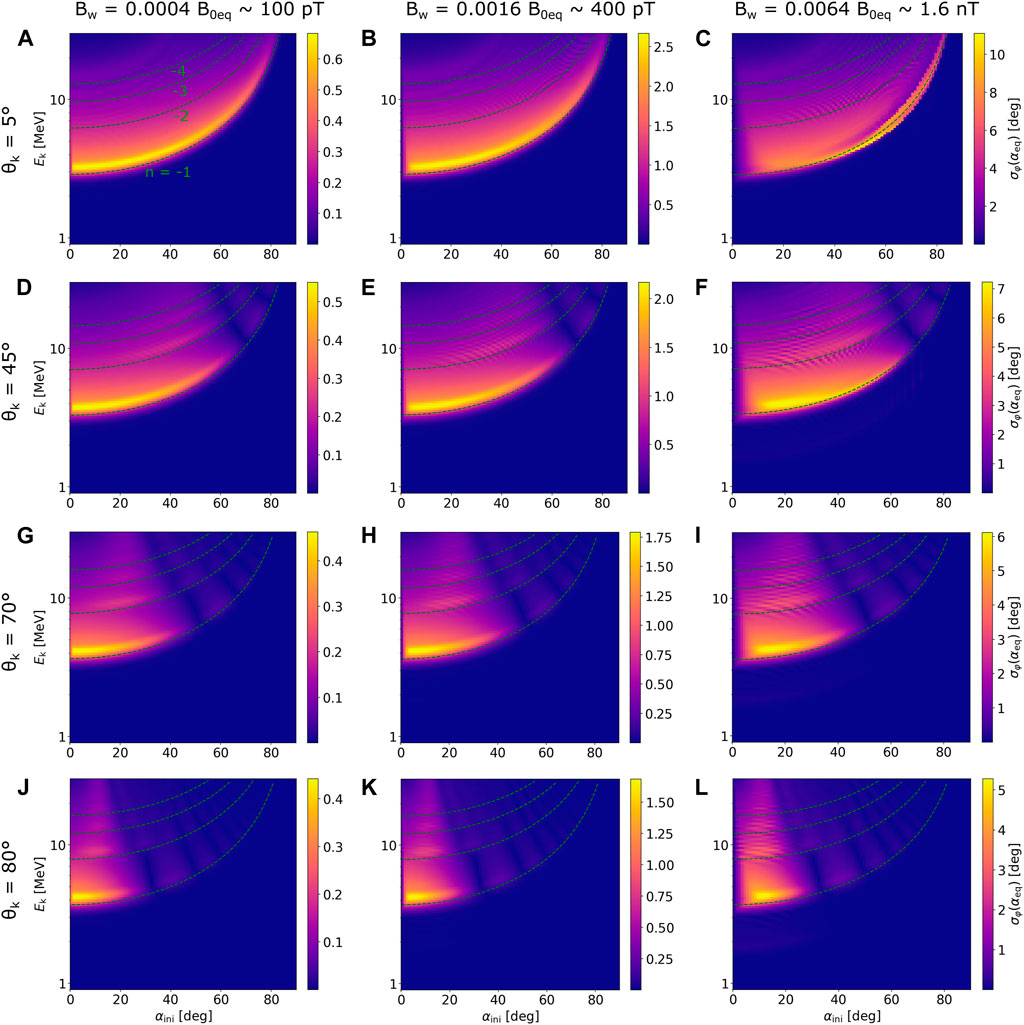
FIGURE 5. Standard deviation σφ(αeq) in electron equatorial pitch angle for propagation along the EMIC wave packet. (A–L) correspond to the same combinations of wave parameters as the respective panels in Figure 4, but the color bars in each panel now go from 0 to
Concerning the strength of diffusion at lower pitch angles, the test-particle simulations show a decreasing trend in σφ(αeq) with increasing WNA at energies close to the n = −1 resonance. Harmonic resonances get stronger compared to fundamental resonances, but the overall diffusion at higher energies does not change much because the increased strength of near-equatorial harmonic interaction is compensated by the weaker fundamental resonance encountered at higher latitudes. An exception is the extreme ultrarelativistic energies (Ek ≳ 15 MeV), where the interaction with very oblique waves causes slightly stronger diffusion (Figures 5I, L). This behavior will impact the transport of electrons into the loss cone, as discussed in the next section.
3.2 Phase space density near the loss cone
The scattering effects analyzed in Section 3.1 transport particles into the loss cone and, thus, contribute to the atmospheric precipitation of relativistic electrons. As described in Section 2, we trace particles back in time from the end of the wave packet to the equator and map the PSD values of a known equatorial distribution along particle trajectories to the starting point. The resulting PSD distributions at the end of the packet are plotted in Figure 6 in the (αend, Ek) space, where αend is the initial pitch angle value in the sense of backward-in-time propagation. Since the number density of relativistic electrons in our model is not scaled to any specific spacecraft observation, we keep the normalized phase space density units
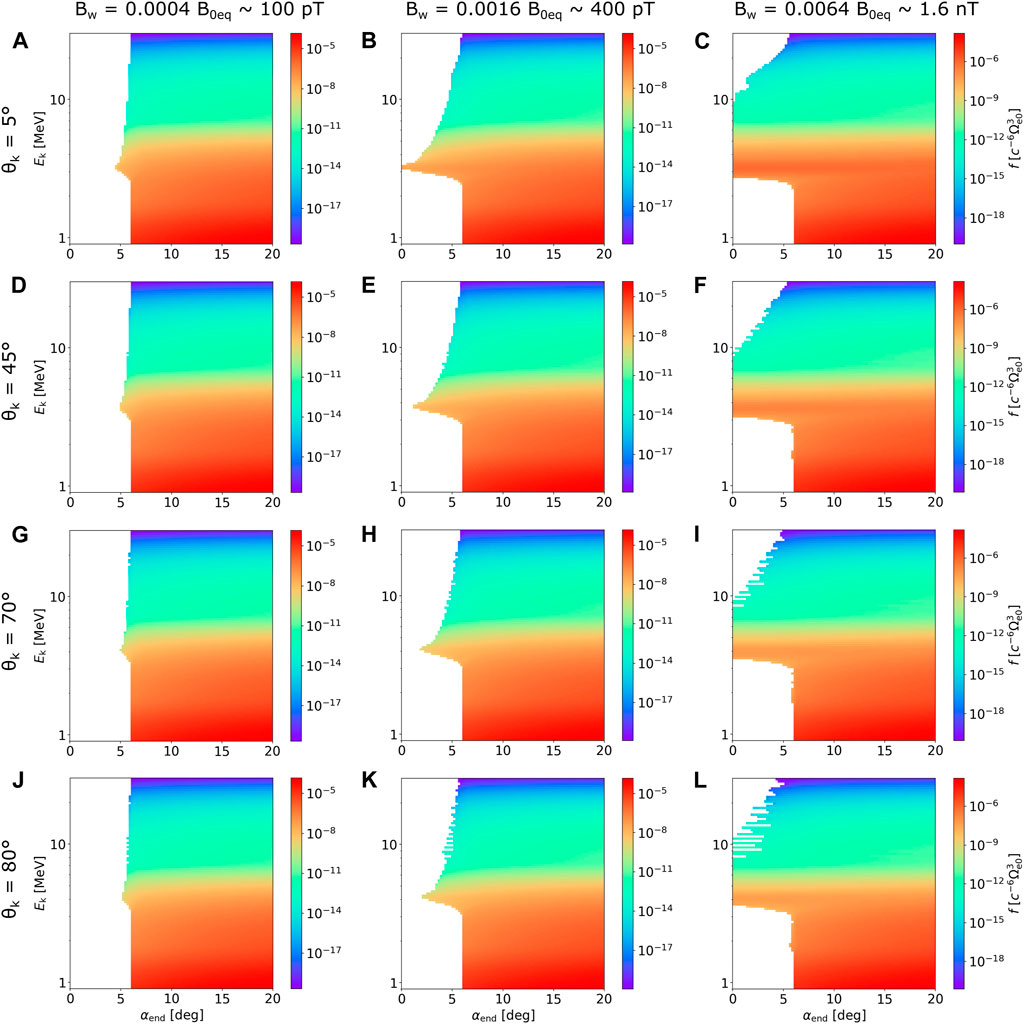
FIGURE 6. Electron phase space density distribution after resonant interaction with the EMIC wave captured at the end of the wave packet. Range in pitch angles is limited to 0°–20° to focus on the loss cone. (A–L) correspond to the same combinations of wave parameters as the respective panels in Figures 4, 5, but because the co-streaming particles were traced back in time, the pitch angle αend on the abscissa now represents the initial value at the end of the subpacket. The curious small bumps on the boundary between zero and finite PSD values near 2 MeV in (F, I, L) arise due to fractional resonances—see Section 3.3; Figure 8.
The quasiparallel EMIC wave manages to completely fill the loss cone near fundamental resonance energy when its amplitude is set to Bw0 = 400 pT (Figure 6B). Increasing the amplitude to Bw0 = 1.6 nT extends the range of energies, with the complete loss cone filling up to 10 MeV (Figure 6C). There are several noteworthy features to this strongly perturbed PSD distribution. First, we observe that particles near Ek = 13 MeV reach deeper into the loss cone, a feature not seen in the low-amplitude wave precipitation profile. This irregularity arises from the fast polarization reversal experienced by quasiparallel waves, which abruptly stops the resonant interaction—mild oscillations in σφ(αeq) across energy are seen in the top left corners of Figures 5A–C, but the effect on precipitation becomes clear only for strong waves. Second, the energy profile of trapped particles immediately above αloss has a local maximum near the fundamental resonance—this peak appears due to pitch angle anisotropy when particles from high PSD regions at higher pitch angles undergo scattering toward lower pitch angles. Third, the pitch angle distribution at energies from 3 MeV to 10 MeV is flattened, signifying a marked decrease in pitch angle anisotropy. Fourth, as a consequence of the third point, there is no apparent precipitation blocking, so phase space density inside the loss cone reaches the value of trapped particle PSD.
The lack of precipitation blocking contradicts the predictions of Bortnik et al. (2022) and may seem counterintuitive, especially after seeing the strong upward advection at low pitch angles in Figure 4C. To explain this observation, we consider the consequences of Liouville’s theorem (i.e., constancy of PSD along phase space trajectories), which is known to hold in the Hamiltonian system of charged particles and electromagnetic waves constituting a collisionless plasma (Ichimaru, 2004). Let us first assume that a state has been reached where the PSD of precipitating and trapped electrons are equal at a certain energy. Because EMIC waves cannot efficiently accelerate electrons and change their energy, the PSD along trajectories will always be the same. Therefore, no amount of force bunching or other non-linear effects can disturb the uniform pitch angle distribution. If the PSD in the loss cone were initially higher than outside, the EMIC-induced scattering would mix the distribution, thus decreasing the precipitating PSD, but it would not push it below the value of the trapped PSD. Non-uniformity along the field line could complicate the argument if a broader range of v‖ were considered, but the spread in v‖ at low pitch angles at a fixed energy level is negligible. The apparent discrepancy between backward-in-time PSD mapping and the transport coefficients from Section 3.1 can be resolved by considering the initial distributions of particles in the forward simulation. A uniform distribution in (α, Ek, φ) is not uniform in (vx, vy, vz); consequently, the number of particles per unit velocity space volume in the forward simulation is much higher at lower pitch angles than at higher pitch angles. Symbolically, we can write the unit volume as (working in a non-relativistic setting for simplicity)
The sin α term in the Jacobian expresses the smallness of velocity space volume near α = 0. Therefore, the few test particles scattered into the loss cone can have the same weight as all the force-bunched particles escaping from the loss cone.
The effect of increasing obliquity on the PSD evolution displayed in Figure 6D–L agrees with the analysis of diffusion from Section 3.1. The loss cone is only partially filled near the fundamental resonance energy for waves with Bw0 = 400 pT, and the range of complete loss cone filling with Bw0 = 1.6 nT becomes narrower with increasing θk. The penetration of non-zero PSD into the loss cone at higher energies turns out to be mostly independent of wave normal angle, except for ultrarelativistic energies, where the very oblique waves show larger increases in precipitating PSD. The jagged boundary between finite and zero values of PSD in the case of strong, oblique waves (mainly Figures 6I, L) comes from the fine multi-resonance structure observed in corresponding diffusion plots in Figures 5I, L. The weak losses near half of the fundamental resonance energy are related to non-linear fractional resonances, which will be analyzed in depth in Section 3.3. Finally, we note that the rapid decrease of σφ(αeq) with rising WNA at higher pitch angles is not reflected in the PSD perturbations after a single quarter-bounce but might become important after multiple bounces due to the weak transport of particles from high-density regions of the initial anisotropic distribution.
So far, we have investigated electron scattering and related losses for propagation along the wave. However, as indicated by Figures 3D–F, counter-streaming particles are also efficiently scattered by oblique EMIC waves, and significant particle losses are to be expected. In Figure 7, we plot the quantities
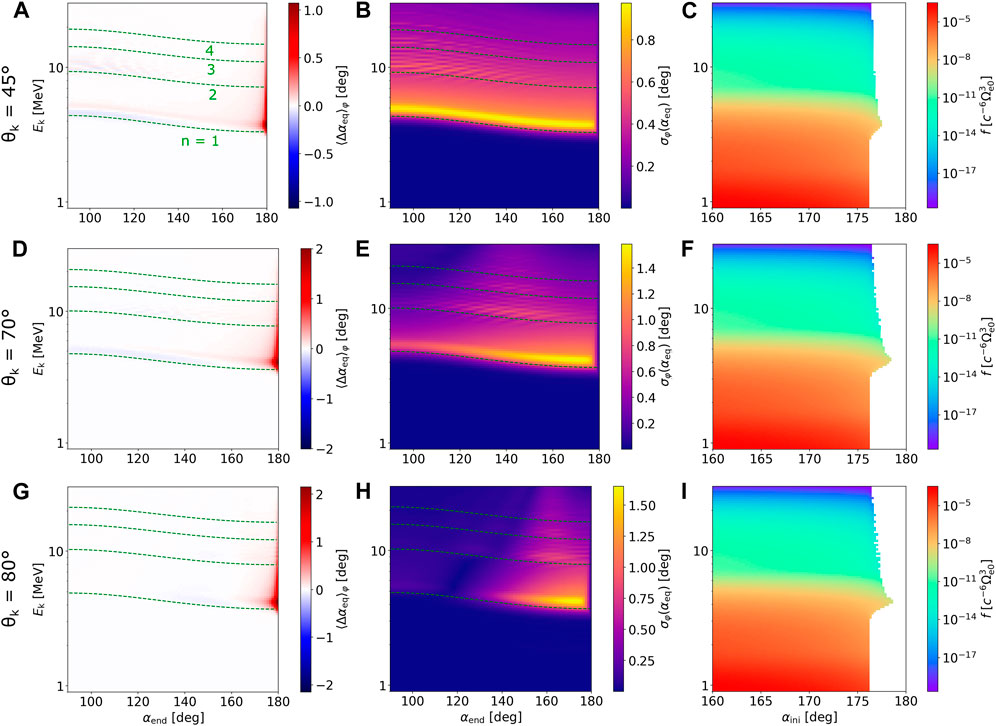
FIGURE 7. Effect of resonant interactions on electrons propagating against the EMIC wave packet. Physical quantities plotted in the first (A, D, G), second (B, E, H), and third (C, F, I) columns correspond to Figures 4–6, respectively. Only a single amplitude value is used, Bw0=400 pT, and the wave normal parametrization over rows of panels skips the quasiparallel case θk =5°, where the resonance effects would be negligible except for extremely ultrarelativistic energies (Ek ≳15 MeV). Note that because the electrons are now counter-streaming, the pitch angles on the abscissas αini and αend were swapped, and particles with initial equatorial pitch angles
3.3 Non-linear fractional resonances
In the discussion of Figures 6I, L, we mentioned the surprising detection of electron scattering into loss cone at energies Ek ≈ 2 MeV, far below the fundamental resonance energy. These losses cannot have origin in non-resonant scattering because we use a slowly varying amplitude profile along h, and also because the non-resonant scattering would show as a broadening of the fundamental resonance and not as a separate peak in energy profile (An et al., 2022). Trajectories of particles with energies Ek = 1.83 MeV and Ek = 2.12 MeV propagating along the high-amplitude wave with θk = 70° (Figures 8A, B) reveal a spread in αeq that does not disappear even after the particles leave the wave field. This spread is somewhat weaker than the oscillations caused by the fundamental cyclotron resonance. The oscillations can be understood as the maximum possible non-resonant scattering in a wave with a rectangular amplitude distribution along the field line.
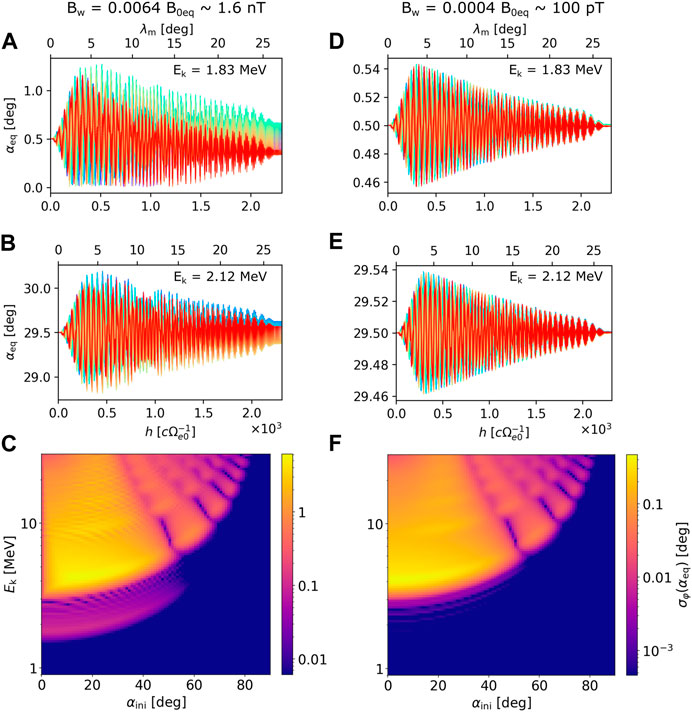
FIGURE 8. Behavior of fractional resonances explained by particle trajectories and standard deviations in equatorial pitch angle for an EMIC wave with wave normal angle θk =70°. (A–B) Changes in pitch angle along the field line at energies well below the equatorial fundamental resonance energy ERmin ≈4 MeV. The wave amplitude is Bw0=1.6 nT. (C) Standard deviation in equatorial pitch angle plotted in logarithmic scale that spans three orders of magnitude. Weak resonant effects near 2 MeV become apparent. (D–F) Same as (A–C), but for a 16 times smaller wave amplitude. The resonant effects near ERmin/2 are now insubstantial compared to the fundamental resonance.
Since the spread in αeq is too small to be clearly visible in the σφ(αeq) plot from Figure 5I, we re-plot the diffusion with a logarithmic color bar and show the results in Figure 8C. It becomes apparent that we are observing a new type of resonance with a minimum resonance energy near ERmin/2. This new resonance causes much weaker scattering than the fundamental resonance but is roughly comparable to non-resonant oscillations. However, when we look at the particle trajectories and diffusion from the simulation with a small-amplitude wave (Bw0 = 100 pT), the new resonance becomes much weaker than the non-resonant oscillations, and the corresponding σφ(αeq) values are more than three orders of magnitude below the fundamental resonance effect (Figures 8D–F).
Based on the numerical observations presented in Figure 8, we identify the new behavior as the non-linear fractional resonance of order n = −1/2. A simplified analytical derivation is provided in Section 5, where we also identify fractional resonances of order n = {±1/3, ±1/2, ±2/3, ±3/2} and suggest that the non-linear resonance energy spectrum is dense in the sense of rational numbers. These resonances seem to be analogous to the sub-cyclotron resonance of electrons with whistler waves described within the Hamiltonian framework by Fu et al. (2015). The concept of fractional resonances does not appear in quasilinear theory because it arises from integration along perturbed trajectories (compare with the integration along unperturbed trajectories employed in quasilinear theory, as mentioned in the theoretical works of Kennel and Engelmann (1966) and Allanson et al. (2022)). In the non-linear treatment of whistler-electron scattering presented by Omura et al. (2019), an integer resonance is chosen first, and the non-linear scattering effects are obtained from perturbations of near-resonant electrons. Suppose we instead implement a model of large perturbations without specifying a resonance velocity/energy, as in the example given in Eqs 27, 28, and proceed to analyze power transfer between waves and particles (which is directly related to pitch angle scattering through resonance diffusion curves, as explained by Summers et al. (1998)). In that case, fractional resonances will arise from the Bessel function expansion of gyrophase evolution. An important property of the n = −1/2 is the scaling of scattering strength with the square of wave amplitude—theoretically proven in Eqs 45, 46—which differs from the known linear dependence for integer resonances. The non-linear fractional resonances are, thus, expected to play a role only in precipitation induced by very strong oblique waves.
4 Summary and discussion
We have numerically analyzed the dependence of relativistic electron scattering on the wave normal angle and magnetic field amplitude of helium band EMIC waves. Unlike in the previous studies by Wang G. et al. (2017); Lee et al. (2018), we allow for very oblique wave normal angles, θk = 70° and θk = 80°, and keep the amplitudes more moderate (Bw0/B0eq < 1%). The presented analysis of advective and diffusive behavior is comparable to the analysis by Bortnik et al. (2022), where, however, much lower energy and pitch angle resolution was adopted for parallel waves only. On the other hand, the results of Bortnik et al. (2022) include a simulation of scattering induced by hydrogen band waves. We opted not to show figures from our hydrogen band simulations, as the only major difference from the helium band case is the shift in resonance energies. The input parameters for hydrogen band simulations differed in the following: wave frequency ω = 0.6Ωp0 = 2.3 Hz, plasma frequency ωpe0/Ωe0 = 5, and density model coefficient a = 1.0, and hmax is at the point where ω = 1.25ΩHe. The evaluation of diffusive and advective properties and PSD perturbations similar to Figures 4–7 is available in the Supplementary Material.
Our overall results can be summarized in three blocks:
1) Confirmation of previous results:
a) Harmonic resonances n < − 1 substantially affect the scattering of relativistic electrons at low pitch angles for waves with wave normal angles as small as θk = 5° (Wang G. et al., 2017). The contribution from n > 0 resonances requires at least moderate obliquity to become significant.
b) Positive advection of resonant particles at very low pitch angles was detected and shown to dominate over diffusion as wave amplitude increases. This is the effect described as boundary reflection by Zhu et al. (2020) and non-linear force bunching by Grach and Demekhov (2020) and Bortnik et al. (2022).
c) The advective behavior of resonant particles can be positive or negative, depending on their initial pitch angle and energy (Lee et al., 2018). Particles that start at energies lower than the resonance energy for a given pitch angle will, on average (over gyrophases), experience a decrease in pitch angle, while particles starting at higher energies will encounter the resonance curve at higher latitudes and experience an average increase in pitch angle. This is visualized by the blue–red stripe pairs in Figure 4.
d) Increasing obliquity weakens the effects of n = −1 resonance but enhances the resonant interaction for |n| > 1 and n = 1 (Wang G. et al., 2017).
e) Crossings of multiple resonance energies during one passage through the waves result in a more stochastic pitch angle evolution, described by Lee et al. (2018) as “complicated and time-dependent phase trapping and bunching effects.” Under our simplified wave model, these multi-resonance effects appear after one quarter-bounce as a fine structure in the plots of advection and diffusion when the EMIC wave is strong and oblique (Figures 4I, L, 5I, L).
2) Disagreement with previous results:
a) Oblique waves seem to weaken the advection effects at low pitch angles, contrary to the observations by Lee et al. (2018).
b) We do not observe any effects of precipitation blocking in the PSD analysis (Figure 6), which is in disagreement with the suggestion presented by Bortnik et al. (2022) that force bunching caused by strong EMIC waves will decrease the electron fluxes/PSD at low pitch angles.
3) New discoveries:
a) Losses of relativistic electrons by quasiparallel waves are comparable to losses induced by oblique waves (Figure 6). This behavior changes for ultrarelativistic electrons (Ek ≳ 15 MeV, depending on wave parameters), where the very oblique waves cause stronger precipitation.
b) Very oblique waves cannot efficiently scatter electrons at higher pitch angles (α > 30° for θk = 80°, see Figure 5J–L). Transport from high PSD regions at large pitch angles toward the loss cone is facilitated only by quasiparallel waves.
c) Very oblique waves scatter co-streaming and counter-streaming electrons with similar efficiency due to the high ellipticity, or in other words, due to comparable magnitude of right-handed and left-handed amplitude components (compare Figure 6K with Figure 7I).
d) High-amplitude oblique waves can scatter electrons below minimum resonance energy through non-linear fractional resonances. The pitch angle changes caused by n = −1/2 scale with the square of wave amplitude are faster than the linear scaling for n = −1 resonance.
When comparing our results to previous literature, a few points must be made to avoid confusion: under our sign convention, the interaction of right-handed waves with electrons happens at resonances of order n ≥ 1, and the interaction with left-handed waves corresponds with n ≤ 1, opposite to the convention used by Wang G. et al. (2017). Furthermore, the strongest wave we use has a relative amplitude Bw0/B0 = 0.64%, while that by Lee et al. (2018) goes up to 10% (above the amplitude of the extremely intense EMIC wave observations presented by Engebretson et al. (2015)); as a consequence, phase trapping has minimal impact on our PSD mapping results, especially for oblique waves.
The disagreement in the dependence of advection on obliquity between our results and those of Lee et al. (2018) comes from the different approaches to wave modeling. Lee et al. (2018) implement one wave field that is elliptically polarized but remains parallel, and another wave field where the wave normal angle is non-zero, but the polarization remains circular. According to the cold plasma dispersion relation, which is strictly followed in our study, oblique waves always have elliptical polarization (linear being considered as a special case of elliptical), and parallel waves are always circularly polarized, except for the singularity at the crossover frequency. Deviations from circular polarization decrease the advection effects, reconciling our results with those of Lee et al. (2018).
The lack of precipitation blocking is demonstrated in Section 3.2 through numerical PSD mapping and supported by arguments based on Liouville’s theorem. The concept of EMIC precipitation blocking was likely first introduced by Grach and Demekhov (2020), who concluded that due to competition between phase trapping and force bunching, the precipitating fluxes would reach the strong diffusion limit, with no apparent decrease near α = 0°. Our observations corroborate this conclusion, except that the transport of particles to low pitch angles is due to the symmetric (“diffusive”) scattering, as observed in Figure 3B, where the particles stay in the phase-trapping region only for a short time and do not become phase-locked. Bortnik et al. (2022) suggested that Van Allen Probes (RBSP) observations of dips in precipitating flux by Zhu et al. (2020) could be explained by force bunching. However, the EMIC-induced precipitating electron flux shown by Zhu et al. (2020) has a local maximum at α = 0°, while the force-bunching effects should be most effective at removing particles from this region. The spacecraft observations are consistent with the simulation results of Grach and Demekhov (2020), where the PSD distribution sometimes peaked inside the loss cone. This effect is not clearly visible in the perturbed distribution from Figure 6C because it requires strong phase trapping. Such trapping may be possible with Bw/B0 > 1% rising-tone EMIC emissions reported by Zhu et al. (2020) but not with the monochromatic waves at moderate amplitudes implemented in our simulations. We recall that transport caused by phase trapping is non-local, allowing the mixing of phase space density from distant points along the field line and violating the assumption of localized scattering processes that were used in our simplified argument against precipitation blocking (Section 3.2). Finally, we must emphasize that the force bunching indeed removes particles from the loss cone, but the important quantity for precipitation is the net effect of upward and downward pitch angle motion.
Most of our new and original results are related to very oblique propagation, which was omitted in previous literature on EMIC-induced precipitation. We have shown that the precipitation of relativistic electrons by very oblique waves is comparable to quasiparallel waves, except for electron energies corresponding to high-order resonances (n < − 4). Note that we are not making a comparison to the routinely investigated purely parallel waves with θk = 0° because in situ spacecraft measurements (Allen et al., 2015) always show at least a small amount of obliquity. Nevertheless, when we consider the increased scattering effects of very oblique waves on counter-streaming electrons, bounce-averaged diffusion might be significantly increased compared to quasiparallel waves. Unfortunately, we do not know how strong the oblique EMIC waves can be, as we are not aware of any study that shows the distribution of wave power over WNA and frequencies. Van Allen Probes observations presented by Saikin et al. (2015) suggest that strong helium band waves (average wave power
To our knowledge, the non-linear fractional resonances were never described before in the context of EMIC–electron interaction. They are, however, conceptually identical to the sub-cyclotron resonance of electrons with whistler waves, which was studied by Fu et al. (2015). Kramer et al. (2012) detected fractional resonances in fusion devices in the context of ion drift-orbit resonance with magnetohydrodynamic waves. Given the different physical settings, the theoretical approach taken by Kramer et al. (2012) is not the same as ours, but they arrive at a formula consisting of a multi-index sum over a product of Bessel functions, not unlike our Eqs 38–40. Non-linear interactions at fractions of the plasma frequency were theoretically described by Lewak and Chen (1969) and used to explain the observations made by the Alouette II spacecraft. The EMIC-electron fractional resonances, especially the resonance of order n = −1/2, might provide a possible explanation for the precipitation of subrelativistic electrons (Hendry et al., 2017; 2019; Capannolo et al., 2019) if we consider a high-density plasma where the fundamental resonance energy can drop to 1 MeV (compare with the ωpe dependence plotted in Figure 1). However, to evaluate how competitive this mechanism is in comparison to the non-resonant scattering (Chen et al., 2016; An et al., 2022), we need to obtain a realistic distribution of wave power/amplitude over wave normal angles, as mentioned earlier. Endeavors in this direction are left for future study.
5 Derivation of fractional resonances
The existence of fractional resonances from Section 3.3 can be derived from the equations of motion for an electron interacting with an elliptically polarized wave. We start by defining the wave fields.
where
and it includes the effects of finite Larmor radius (FLR) ρL through the quantity
while ψB represents the wave phase at the gyrocenter. The constant initial phase will be dropped in the following analysis.
The equations of motion for an electron with the gyrocenter at x = y = 0 propagating through the wave field on a homogeneous background field
Here, we decomposed the wave field into left-hand and right-hand circularly polarized components (Omura et al., 2019)
and defined the ratios
which are related to phase velocities (they reduce exactly to phase velocities in the case of circularly polarized parallel-propagating waves). In further calculations, we will also use the normalized amplitude components
The average change in electron kinetic energy per one wave period T can be expressed as
where we used the decompositions from Eqs 15–18. Let us denote the integrand I and restate it in the form
We may now apply the Jacobi–Anger expansion (Abramowitz and Stegun, 1965) and express the trigonometric functions in terms of Bessel functions of the first kind.
where
is the relative phase angle for the nth resonance. Note that while the changes in kinetic energy of electrons interacting with EMIC waves are typically negligible, these small energy changes are directly related to large changes in pitch angle through the particle motion along resonant diffusion curves (Summers et al., 1998).
The non-linear effect of individual resonances is usually studied by performing an expansion in vz about the nth resonance velocity.
Here, we instead expand the gyrophase to the first order of perturbations due to wave—particle interactions and plug them into the Jacobi—Anger expansions from Eqs 22–24. We write φ ≈ φ0 + φ1 with
where we have used the inequalities |UL|≪|vz| and |UR|≪|vz| for EMIC waves and relativistic electrons, and we also removed the
To cut off the perturbation expansion, we replace ψ with ψB in Eqs 27, 28. Then, by integrating φ1 over time, we can obtain the gyrophase perturbation,
Here, we introduced the substitutions
where
is a quantity expressing the deviation from the fundamental resonances n = ±1.
Going back to the Bessel function expansion from Eqs 22–24, we can now write
Using the second form of the expansions, we can expand each of the trigonometric functions from Eq. 35 into
Since R1 and L1 are proportional to the relative wave magnetic field Bw/B0, we can limit the summations to |r| ≤ 1 and |l| ≤ 1. As a further simplification, we will limit the resonance number n to −1, 0, 1, which is a reasonable approximation when β2 ≪ 1; i.e., when pitch angles are low and θk is not too close to the resonance cone. We then insert Eqs 34–37 into Eqs 33, 22 and finally obtain
Comparing the prefactors of φ0 and ψB results in resonant fractions.
Apart from the integer values (which represent fundamental and harmonic resonances), the fractions can also evaluate to ±1/3, ±1/2, ±2/3, and ±3/2; other fractional values would appear if we extended the summation range in n and removed the approximation β2 ≪ 1.
We now focus on the resonance −1/2, which contributes to electron diffusion near Ek = 2 MeV in Figure 8C. The related relative phase angle φ0 + 2ψB corresponds to resonance velocity
Going back to the average change in energy defined in Eq. 21, we can perform the Taylor expansion of Bessel function to the first order and show that the term with
where we have used Eqs 30, 11. The
Due to the terms
The derivation provided in this section works for whistler-mode waves as well, except for the approximations UR ≪ vz, UL ≪ vz.
Data availability statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found at: https://doi.org/10.6084/m9.figshare.22061159.v1.
Author contributions
MH wrote and ran the simulation code, analyzed the resulting data, derived the equations for fractional resonances, and prepared the original draft. WL initiated the study and provided frequent consultations. QM helped in validating the code. WL and QM provided advice during the pre-submission review and editing of the manuscript.
Funding
The research at Boston University was supported by NASA grants 80NSSC20K0698, 80NSSC20K1270, and 80NSSC21K1312, as well as the NSF grant AGS-2019950. QM would like to acknowledge the NASA grant 80NSSC20K0196 and the NSF grant AGS-2225445.
Acknowledgments
The authors gratefully acknowledge the discussion with Jacob Bortnik and Xin An on the topic of precipitation blocking.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2023.1163515/full#supplementary-material
References
Abramowitz, M., and Stegun, I. A. (1965). Handbook of mathematical functions: With formulas, graphs, and mathematical tables. New York: Dover Books on Advanced Mathematics (Dover Publications.
Albert, J. M., Artemyev, A., Li, W., Gan, L., and Ma, Q. (2022). Analytical results for phase bunching in the pendulum model of wave-particle interactions. Front. Astron. Space Sci. 9, 971358. doi:10.3389/fspas.2022.971358
Albert, J. M., Artemyev, A. V., Li, W., Gan, L., and Ma, Q. (2021). Models of resonant wave-particle interactions. J. Geophys. Res. Space Phys. 126, e29216. doi:10.1029/2021JA029216
Albert, J. M. (2008). Efficient approximations of quasi-linear diffusion coefficients in the radiation belts. J. Geophys. Res. Space Phys. 113, A06208. doi:10.1029/2007JA012936
Allanson, O., Elsden, T., Watt, C., and Neukirch, T. (2022). Weak turbulence and quasilinear diffusion for relativistic wave-particle interactions via a Markov approach. Front. Astron. Space Sci. 8, 232. doi:10.3389/fspas.2021.805699
Allen, R. C., Zhang, J. C., Kistler, L. M., Spence, H. E., Lin, R. L., Klecker, B., et al. (2015). A statistical study of EMIC waves observed by cluster: 1. Wave properties. J. Geophys. Res. Space Phys. 120, 5574–5592. doi:10.1002/2015JA021333
An, X., Artemyev, A., Angelopoulos, V., Zhang, X., Mourenas, D., and Bortnik, J. (2022). Nonresonant scattering of relativistic electrons by electromagnetic ion cyclotron waves in Earth’s radiation belts. Phys. Rev. Lett. 129, 135101. doi:10.1103/PhysRevLett.129.135101
Anderson, B. J., Denton, R. E., Ho, G., Hamilton, D. C., Fuselier, S. A., and Strangeway, R. J. (1996). Observational test of local proton cyclotron instability in the Earth’s magnetosphere. J. Geophys. Res. 101, 21527–21543. doi:10.1029/96JA01251
Artemyev, A. V., Neishtadt, A. I., Vainchtein, D. L., Vasiliev, A. A., Vasko, I. Y., and Zelenyi, L. M. (2018). Trapping (capture) into resonance and scattering on resonance: Summary of results for space plasma systems. Commun. Nonlinear Sci. Numer. Simulat. 65, 111–160. doi:10.1016/j.cnsns.2018.05.004
Bortnik, J., Albert, J. M., Artemyev, A., Li, W., Jun, C.-W., Grach, V. S., et al. (2022). Amplitude dependence of nonlinear precipitation blocking of relativistic electrons by large amplitude EMIC waves. Geophys. Res. Lett. 49, e2022GL098365. doi:10.1029/2022GL098365
Capannolo, L., Li, W., Ma, Q., Chen, L., Shen, X. C., Spence, H. E., et al. (2019). Direct observation of subrelativistic electron precipitation potentially driven by EMIC waves. Geophys. Res. Lett. 46 (12), 12711–12721. 711–12. doi:10.1029/2019GL084202
Chen, L., Thorne, R. M., Bortnik, J., and Zhang, X.-J. (2016). Nonresonant interactions of electromagnetic ion cyclotron waves with relativistic electrons. J. Geophys. Res. Space Phys. 121, 9913–9925. doi:10.1002/2016JA022813
Chen, M. W., Roeder, J. L., Fennell, J. F., Lyons, L. R., Lambour, R. L., and Schulz, M. (1999). Proton ring current pitch angle distributions: Comparison of simulations with CRRES observations. J. Geophys. Res. 104, 17379–17389. doi:10.1029/1999JA900142
Clilverd, M. A., Duthie, R., Hardman, R., Hendry, A. T., Rodger, C. J., Raita, T., et al. (2015). Electron precipitation from EMIC waves: A case study from 31 may 2013. J. Geophys. Res. Space Phys. 120, 3618–3631. doi:10.1002/2015JA021090
Denton, R. E., Goldstein, J., Menietti, J. D., and Young, S. L. (2002). Magnetospheric electron density model inferred from Polar plasma wave data. J. Geophys. Res. Space Phys. 107, 1386. doi:10.1029/2001JA009136
Engebretson, M. J., Posch, J. L., Wygant, J. R., Kletzing, C. A., Lessard, M. R., Huang, C. L., et al. (2015). Van Allen probes, NOAA, GOES, and ground observations of an intense EMIC wave event extending over 12 h in magnetic local time. J. Geophys. Res. Space Phys. 120, 5465–5488. doi:10.1002/2015JA021227
Fu, X., Guo, Z., Dong, C., and Gary, S. P. (2015). Nonlinear subcyclotron resonance as a formation mechanism for gaps in banded chorus. Geophys. Res. Lett. 42, 3150–3159. doi:10.1002/2015GL064182
Grach, V. S., Artemyev, A. V., Demekhov, A. G., Zhang, X.-J., Bortnik, J., Angelopoulos, V., et al. (2022). Relativistic electron precipitation by EMIC waves: Importance of nonlinear resonant effects. Geophys. Res. Lett. 49, e99994. doi:10.1029/2022GL099994
Grach, V. S., and Demekhov, A. G. (2020). Precipitation of relativistic electrons under resonant interaction with electromagnetic ion cyclotron wave packets. J. Geophys. Res. Space Phys. 125, e27358. doi:10.1029/2019JA027358
Hanzelka, M., Santolík, O., Omura, Y., and Kolmašová, I. (2021). Measurability of the nonlinear response of electron distribution function to chorus emissions in the Earth’s radiation belt. J. Geophys. Res. Space Phys. 126, e29624. doi:10.1029/2021JA029624
Hendry, A. T., Rodger, C. J., and Clilverd, M. A. (2017). Evidence of sub-MeV EMIC-driven electron precipitation. Geophys. Res. Lett. 44, 1210–1218. doi:10.1002/2016GL071807
Hendry, A. T., Santolik, O., Kletzing, C. A., Rodger, C. J., Shiokawa, K., and Baishev, D. (2019). Multi-instrument observation of nonlinear EMIC-driven electron precipitation at sub-MeV energies. Geophys. Res. Lett. 46, 7248–7257. doi:10.1029/2019GL082401
Horne, R. B., and Thorne, R. M. (1998). Potential waves for relativistic electron scattering and stochastic acceleration during magnetic storms. Geophys. Res. Lett. 25, 3011–3014. doi:10.1029/98GL01002
Horwitz, J. L., Baugher, C. R., Chappell, C. R., Shelley, E. G., Young, D. T., and Anderson, R. R. (1981). ISEE 1 observations of thermal plasma in the vicinity of the plasmasphere during periods of quieting magnetic activity. J. Geophys. Res. 86, 9989–10001. doi:10.1029/JA086iA12p09989
Jordanova, V. K., Albert, J., and Miyoshi, Y. (2008). Relativistic electron precipitation by EMIC waves from self-consistent global simulations. J. Geophys. Res. Space Phys. 113, A00A10. doi:10.1029/2008JA013239
Jun, C.-W., Miyoshi, Y., Kurita, S., Yue, C., Bortnik, J., Lyons, L., et al. (2021). The characteristics of EMIC waves in the magnetosphere based on the van allen probes and arase observations. J. Geophys. Res. Space Phys. 126, e29001. doi:10.1029/2020JA029001
Karpman, V. I. (1974). Nonlinear effects in the ELF waves propagating along the magnetic field in the magnetosphere. Space Sci. Rev. 16, 361–388. doi:10.1007/BF00171564
Kennel, C. F., and Engelmann, F. (1966). Velocity space diffusion from weak plasma turbulence in a magnetic field. Phys. Fluids 9, 2377–2388. doi:10.1063/1.1761629
Kennel, C. F., and Petschek, H. E. (1966). Limit on stably trapped particle fluxes. J. Geophys. Res. 71, 1–28. doi:10.1029/JZ071i001p00001
Kim, E.-H., and Johnson, J. R. (2016). Full-wave modeling of EMIC waves near the He+ gyrofrequency. Geophys. Res. Lett. 43, 13–21. doi:10.1002/2015GL066978
Kitahara, M., and Katoh, Y. (2019). Anomalous trapping of low pitch angle electrons by coherent whistler mode waves. J. Geophys. Res. Space Phys. 124, 5568–5583. doi:10.1029/2019JA026493
Kramer, G. J., Chen, L., Fisher, R. K., Heidbrink, W. W., Nazikian, R., Pace, D. C., et al. (2012). Fractional resonances between waves and energetic particles in tokamak plasmas. Phys. Rev. Lett. 109, 035003. doi:10.1103/PhysRevLett.109.035003
Kurita, S., Miyoshi, Y., Shiokawa, K., Higashio, N., Mitani, T., Takashima, T., et al. (2018). Rapid loss of relativistic electrons by EMIC waves in the outer radiation belt observed by arase, van allen probes, and the PWING ground stations. Geophys. Res. Lett. 45, 12,720–12,729. doi:10.1029/2018GL080262
Lee, D.-Y., Shin, D.-K., and Choi, C.-R. (2018). Effects of oblique wave normal angle and noncircular polarization of electromagnetic ion cyclotron waves on the pitch angle scattering of relativistic electrons. J. Geophys. Res. Space Phys. 123, 4556–4573. doi:10.1029/2018JA025342
Lewak, G. J., and Chen, C. S. (1969). Higher order resonances in a plasma. J. Plasma Phys. 3, 481–497. doi:10.1017/S0022377800004554
Li, W., and Hudson, M. K. (2019). Earth’s van allen radiation belts: From discovery to the van allen probes era. J. Geophys. Res. Space Phys. 124, 8319–8351. doi:10.1029/2018JA025940
Loto’aniu, T. M., Fraser, B. J., and Waters, C. L. (2005). Propagation of electromagnetic ion cyclotron wave energy in the magnetosphere. J. Geophys. Res. Space Phys. 110, A07214. doi:10.1029/2004JA010816
Meredith, N. P., Horne, R. B., Kersten, T., Fraser, B. J., and Grew, R. S. (2014). Global morphology and spectral properties of EMIC waves derived from CRRES observations. J. Geophys. Res. Space Phys. 119, 5328–5342. doi:10.1002/2014JA020064
Meredith, N. P., Thorne, R. M., Horne, R. B., Summers, D., Fraser, B. J., and Anderson, R. R. (2003). Statistical analysis of relativistic electron energies for cyclotron resonance with EMIC waves observed on CRRES. J. Geophys. Res. Space Phys. 108, 1250. doi:10.1029/2002JA009700
Min, K., Lee, J., Keika, K., and Li, W. (2012). Global distribution of EMIC waves derived from THEMIS observations. J. Geophys. Res. Space Phys. 117, A05219. doi:10.1029/2012JA017515
Nunn, D., and Omura, Y. (2015). A computational and theoretical investigation of nonlinear wave-particle interactions in oblique whistlers. J. Geophys. Res. Space Phys. 120, 2890–2911. doi:10.1002/2014JA020898
Omura, Y., Hsieh, Y.-K., Foster, J. C., Erickson, P. J., Kletzing, C. A., and Baker, D. N. (2019). Cyclotron acceleration of relativistic electrons through landau resonance with obliquely propagating whistler-mode chorus emissions. J. Geophys. Res. Space Phys. 124, 2018JA026374–2810. doi:10.1029/2018JA026374
Omura, Y. (2021). Nonlinear wave growth theory of whistler-mode chorus and hiss emissions in the magnetosphere. Earth Planets Space 73, 95. doi:10.1186/s40623-021-01380-w
Omura, Y., Pickett, J., Grison, B., Santolik, O., Dandouras, I., Engebretson, M., et al. (2010). Theory and observation of electromagnetic ion cyclotron triggered emissions in the magnetosphere. J. Geophys. Res. Space Phys. 115, A07234. doi:10.1029/2010JA015300
Omura, Y., and Zhao, Q. (2012). Nonlinear pitch angle scattering of relativistic electrons by EMIC waves in the inner magnetosphere. J. Geophys. Res. Space Phys. 117, A08227. doi:10.1029/2012JA017943
Perraut, S., Gendrin, R., Roux, A., and de Villedary, C. (1984). Ion cyclotron waves: Direct comparison between ground-based measurements and observations in the source region. J. Geophys. Res. 89, 195–202. doi:10.1029/JA089iA01p00195
Rauch, J. L., and Roux, A. (1982). Ray tracing of ULF waves in a multicomponent magnetospheric plasma: Consequences for the generation mechanism of ion cyclotron waves. J. Geophys. Res. 87, 8191–8198. doi:10.1029/JA087iA10p08191
Saikin, A. A., Zhang, J. C., Allen, R. C., Smith, C. W., Kistler, L. M., Spence, H. E., et al. (2015). The occurrence and wave properties of H+-He+-and O+-band EMIC waves observed by the Van Allen Probes. J. Geophys. Res. Space Phys. 120, 7477–7492. doi:10.1002/2015JA021358
Shoji, M., Miyoshi, Y., Kistler, L. M., Asamura, K., Matsuoka, A., Kasaba, Y., et al. (2021). Discovery of proton hill in the phase space during interactions between ions and electromagnetic ion cyclotron waves. Sci. Rep. 11, 13480. doi:10.1038/s41598-021-92541-0
Summers, D., Omura, Y., Miyashita, Y., and Lee, D.-H. (2012). Nonlinear spatiotemporal evolution of whistler mode chorus waves in Earth’s inner magnetosphere. J. Geophys. Res. Space Phys. 117, A09206. doi:10.1029/2012JA017842
Summers, D., Thorne, R. M., and Xiao, F. (1998). Relativistic theory of wave-particle resonant diffusion with application to electron acceleration in the magnetosphere. J. Geophys. Res. 103, 20487–20500. doi:10.1029/98JA01740
Thorne, R. M., and Kennel, C. F. (1971). Relativistic electron precipitation during magnetic storm main phase. J. Geophys. Res. 76, 4446–4453. doi:10.1029/JA076i019p04446
Usanova, M. E., Drozdov, A., Orlova, K., Mann, I. R., Shprits, Y., Robertson, M. T., et al. (2014). Effect of EMIC waves on relativistic and ultrarelativistic electron populations: Ground-based and Van Allen Probes observations. Geophys. Res. Lett. 41, 1375–1381. doi:10.1002/2013GL059024
Usanova, M. E., Mann, I. R., Bortnik, J., Shao, L., and Angelopoulos, V. (2012). THEMIS observations of electromagnetic ion cyclotron wave occurrence: Dependence on AE, SYMH, and solar wind dynamic pressure. J. Geophys. Res. Space Phys. 117, A10218. doi:10.1029/2012JA018049
Wang, G., Su, Z., Zheng, H., Wang, Y., Zhang, M., and Wang, S. (2017a). Nonlinear fundamental and harmonic cyclotron resonant scattering of radiation belt ultrarelativistic electrons by oblique monochromatic EMIC waves. J. Geophys. Res. Space Phys. 122, 1928–1945. doi:10.1002/2016JA023451
Wang, X. Y., Huang, S. Y., Allen, R. C., Fu, H. S., Deng, X. H., Zhou, M., et al. (2017b). The occurrence and wave properties of EMIC waves observed by the Magnetospheric Multiscale (MMS) mission. J. Geophys. Res. Space Phys. 122, 8228–8240. doi:10.1002/2017JA024237
Zenitani, S., and Umeda, T. (2018). On the Boris solver in particle-in-cell simulation. Phys. Plasmas 25, 112110. doi:10.1063/1.5051077
Zhao, H., Johnston, W. R., Baker, D. N., Li, X., Ni, B., Jaynes, A. N., et al. (2019). Characterization and evolution of radiation belt electron energy spectra based on the van allen probes measurements. J. Geophys. Res. Space Phys. 124, 4217–4232. doi:10.1029/2019JA026697
Zheng, L., Chen, L., and Zhu, H. (2019). Modeling energetic electron nonlinear wave-particle interactions with electromagnetic ion cyclotron waves. J. Geophys. Res. Space Phys. 124, 3436–3453. doi:10.1029/2018JA026156
Keywords: electron scattering, EMIC waves, non-linear wave–particle interactions, test-particle simulation, radiation belts, fractional resonance, loss cone, electron precipitation
Citation: Hanzelka M, Li W and Ma Q (2023) Parametric analysis of pitch angle scattering and losses of relativistic electrons by oblique EMIC waves. Front. Astron. Space Sci. 10:1163515. doi: 10.3389/fspas.2023.1163515
Received: 10 February 2023; Accepted: 27 March 2023;
Published: 19 April 2023.
Edited by:
Xiao-Jia Zhang, The University of Texas at Dallas, United StatesReviewed by:
Jay M. Albert, Air Force Research Lab, United StatesXin An, University of California, Los Angeles, United States
Copyright © 2023 Hanzelka, Li and Ma. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Miroslav Hanzelka, bWlyZWtoYW56ZWxrYUBnbWFpbC5jb20=
 Miroslav Hanzelka
Miroslav Hanzelka Wen Li
Wen Li Qianli Ma
Qianli Ma