Phase coherence of solar wind turbulence from the Sun to Earth

The transport of energetic particles in response to solar wind turbulence is important for space weather. To understand charged particle transport, it is usually assumed that the phase of the turbulence is randomly distributed (the random phase approximation) in quasi-linear theory and simulations. In this paper, we calculate the coherence index, C_ϕ, of solar wind turbulence observed by the Helios 2 and Parker Solar Probe spacecraft using the surrogate data technique to check if the assumption is valid. Here, values of C_ϕ = 0 and 1 indicate that the phase coherence is random and correlated, respectively. We estimate that the coherence index at the resonant scale of energetic ions (10 MeV protons) is 0.1 at 0.87 and 0.65 au, 0.18 at 0.29 au, and 0.3 (0.35) at 0.09 au for super (sub)-Alfvénic intervals, respectively. Since the random phase approximation corresponds to C_ϕ = 0, this may indicate that the random phase approximation is not valid for the transport of energetic particles in the inner heliosphere, especially very close to the Sun ($\sim 0.09$ au).

1 Introduction

The propagation of solar energetic particles (SEPs) is important in the context of space weather (Malandraki and Crosby, 2018). The Sun can be a frequent source of energetic particles ($>$ Mev) due to solar flares, shock waves associated with a coronal mass ejection, or the combination of both (Ryan et al., 2000; Li and Zank, 2005). Since SEPs are a high radiation risk for astronauts working in space and for future human-exploration missions in the solar system, mitigation of SEPs is necessary to protect human health (Chancellor et al., 2014). Therefore, it is valuable to understand how energetic particles travel from the Sun to Earth and especially how long it takes for them to arrive so that mitigating actions can be taken, whether to evacuate astronauts or prevent damage to instruments on spacecraft.

The trajectory followed by energetic particles is a random walk thanks to scattering by solar wind turbulence (van den Berg et al., 2020). According to Zank et al. (1998); Zhao et al. (2018), the parallel mean free path of an energetic particle diffusing in response to the solar wind turbulence can be approximated as,

${\lambda }_{\Vert }\approx 6.2742\frac{B_0^{5/3}}{<\delta b^2>}{\left(\frac{P}{c}\right)}^{1/3}{\lambda }_{\mathit{slab}}^{2/3},(1)$

where B₀ is the magnitude of the background magnetic field, $<\delta b^2>$ the turbulence magnetic energy, P ≡ pc/Ze (p momentum, c the speed of light, and Ze particle charge) the particle rigidity, and λ_slab the correlation length of slab (or Alvénic) turbulence. Considering 10 MeV protons as energetic particles, the rigidity becomes p = 137 MV. Typical solar wind turbulence parameters are $<\delta b^2>\sim 100$ nT² and λ_slab ∼ 0.5 × 10⁶ km at 0.5 au (1 au is the distance from the Sun to Earth) (Adhikari et al., 2020). Using these parameters and B₀ ∼ 10 nT, we obtain λ_‖ ∼ 0.01 au. Since this is much smaller than 1 au, the diffusion and transport processes of energetic particles are greatly affected by solar wind turbulence. Furthermore, a perpendicular diffusion of energetic particles is also an important process (Zank et al., 2004; Shalchi et al., 2010). The combination of parallel and perpendicular diffusion processes due to the turbulence makes estimates of the energetic particle arrival times complicated.

Although there are several studies of modeling and simulations to understand the diffusion and transport of solar energetic particles in turbulent magnetic fields, they usually assume that the phase of the turbulence is randomly correlated. The quasi-linear diffusion theory is built on the assumption of the random phase approximation (Sagdeev and Galeev, 1969). Giacalone and Jokipii (1994); Otsuka and Hada (2009); Tautz and Shalchi (2010); Guo and Giacalone (2014); Moradi and Giacalone (2022) investigate particle diffusion using test particle simulations combined with synthetic turbulence, which is described as a superposition of sine waves with random phases. The random phase approximation is useful and easily implemented in models and simulations. However, the phase coherence of turbulence in the solar wind has not been addressed well from the perspective of observational data, especially close to the Sun. While the intermittency of solar wind turbulence can be related to phase coherence (Matthaeus et al., 2015, and reference therein), which has been discussed frequently, in this paper, we directly measure the phase coherence of turbulence and focus on the link to particle diffusion and transport instead of intermittency.

Since it is possible that the phase coherence of turbulence modifies the motion of charged particles, it is valuable to consider whether the random phase approximation is reasonable in solar wind turbulence. A good example of coherent turbulence (or structures) is short large amplitude magnetic structures (SLAMS) (Schwartz and Burgess, 1991; Schwartz et al., 1992; Scholer, 1993), which commonly form upstream of parallel shock waves due to the non-linear evolution of ultra-low frequency waves excited by reflected ions. These structures are quite coherent, and the amplitude is comparable to the background magnetic field (Koga and Hada, 2003). Some studies show that particle diffusion in coherent structures differs from the quasi-linear theory (Kirk et al., 1996; Kuramitsu and Hada, 2000; Hada et al., 2003b; Laitinen et al., 2012). Note that Kis et al. (2013) observed efficient ion acceleration in SLAMS at Earth’s bow shock. If solar wind turbulence is coherent, this can modify the diffusion and transport processes of energetic particles and the estimates of energetic particle arrival time at Earth can be different from estimates based on quasi-linear theory. This motivates us to investigate the phase coherence of solar wind turbulence in the inner heliosphere.

In this paper, we investigate the phase coherence of solar wind turbulence from 0.09 to 0.87 au using Parker Solar Probe and Helios 2 observations. These observations provide us with a unique opportunity to investigate solar wind turbulence in the inner heliosphere. We use the surrogate data method to calculate the phase coherence in this study, which is explained in detail below. Using the calculated phase coherence, we estimate phase coherence at a scale that is resonant with energetic particles and evaluate whether the phase random approximation is appropriate in the inner heliosphere.

2 Method: Surrogate data technique

The surrogate data technique (Hada et al., 2003a; Koga and Hada, 2003) was developed originally to investigate the phase coherence of waves excited in the foreshock region of Earth’s bow shock. Suppose that B_O(t) is an original time series obtained by a spacecraft. We can describe the method as follows: I) decompose B_O into the spectral amplitude $|{\widehat{B}}_O(\omega )|$ and phase distribution $\varphi (\omega )={\tan }^{-1}\left[\mathrm{I}\mathrm{m}({\widehat{B}}_O(\omega ))/\mathrm{R}\mathrm{e}({\widehat{B}}_O(\omega ))\right]$, where ${\widehat{B}}_O(\omega )$ is the Fourier transformation of B_O(t). Here, we use a cosine cube-tapered rectangle function so that 2% of the data time interval is tapered off at each end to minimize the effects of the boundary (Sahraoui, 2008). II) We randomly shuffle the original phase distribution and perform an inverse Fourier transformation of the original spectral amplitude with the shuffled phase distribution. We call this derived time series, B_R(t), which is a phase-random surrogate. III) We repeat the same process as the previous one, but now use a correlated phase distribution (ϕ(ω) = 0). We call this, B_C(t), a phase-correlated surrogate. IV) Once we obtain B_O(t), B_R(t), and B_C(t), we calculate the first order structure function,

$L_j\left(\tau \right)=\sum _t|B_j\left(t+\tau \right)-B_j\left(t\right)|,(2)$

where j ∈ [O, R, C] and τ is the lag time. V) Finally, we evaluate the degree of phase coherence using the following equation (Sahraoui, 2008),

$C_{\varphi }\left(\tau \right)=\frac{|L_O\left(\tau \right)-L_R\left(\tau \right)|}{|L_O\left(\tau \right)-L_R\left(\tau \right)|+|L_O\left(\tau \right)-L_C\left(\tau \right)|}.(3)$

The phase coherence index, C_ϕ, is an indication that when C_ϕ is close to 0 1), the phase coherence of the original data is random (correlated). Note that Eq. 3 and the definition of C_ϕ in Hada et al. (2003a) are equivalent when L_R > L_O > L_C. It is useful to mention that it is not easy to determine whether the coherence is spatial or temporal since we use single-spacecraft data in this paper, and this can only be clarified using multi-point measurements, which are not manageable at this time in the inner heliosphere.

The original data B_O(t) is calculated from the observed magnetic fields B(t) = (B_x, B_y, B_z) so that B_O(t) corresponds to the largest relative fluctuation amplitude (Dudok de Wit and Krasnosel’Skikh, 1996). We first compute $\tilde{B}(t,\phi ,\theta )=\mathbf{B}(t)\cdot \mathbf{p}(\phi ,\theta )$ where p (φ, θ) = (cos φ cos θ, sin φ cos θ, sin θ) is a unit vector in spherical coordinates. Here, the azimuthal angle φ and elevation angle θ have a range of −π ≤ φ ≤ π and −π/2 ≤ θ ≤ π/2, respectively. When $\tilde{B}(t,\phi ,\theta )$ is projected onto the φ − θ plane by taking the time average, $<\tilde{B}(\phi ,\theta )>$, this gives us the distribution of the mean magnetic field. The average $<\tilde{B}(\phi ,\theta )>=0$ corresponds to the direction p (φ, θ) perpendicular to the mean magnetic field. The projection of the normalized standard deviation can be calculated as,

$\sigma =\frac{{⟨{\left(\tilde{B}-<\tilde{B}>\right)}^2⟩}^{1/2}}{<|\mathbf{B}|>}.(4)$

Then, we find a direction (φ_m, θ_m) that corresponds to the maximum value of σ in the projection. We use this direction to set B_O(t) = B(t) ⋅p (φ_m, θ_m) for the following analysis unless otherwise stated, and this means that we calculate the coherence index for fluctuations corresponding to the largest fluctuation amplitude. Note that since the choice of B_O is arbitrary, for instance, it is also possible to set B_O(t) as |B| − <|B| >.

In this paper, we choose well-studied turbulence cases in the inner heliosphere from Helios 2 and Parker Solar Probe observations. Table 1 shows three Helios 2 observations at 0.87, 0.65, and 0.29 au, respectively (Marsch and Tu, 1990). Magnetic field data were obtained by a flux-gate magnetometer (The Institute for Geophysics and Meteorology of the Technical University of Braunschweig magnetometer) (Musmann et al., 1977). The cadence of the magnetic field observations is 6 s. Each case is in the fast solar wind (U > 450 km⁻¹). Observations shown in Table 2 were made by the Parker Solar Probe (PSP) spacecraft on 28 April 2021 during Encounter 8 (Zhao et al., 2022). The distance was at 0.09 au. Magnetic field data were obtained by the FIELDS Fluxgate Magnetometer instrument (Bale et al., 2016). Here, we picked two cases of super- (U > v_A) and sub- (U < v_A) Alfvénic solar wind since the properties of solar wind turbulence are expected to be different across the Alfvén critical surface (U = v_A) (Kasper et al., 2021; Zank et al., 2022). During this period, PSP observed several sub-Alfvénic flows (Kasper et al., 2021). We resampled the data down to a 1 s resolution. Note that we linearly interpolate missing data.

TABLE 1

TABLE 1. Helios 2 observations (Marsch and Tu, 1990).

TABLE 2

TABLE 2. Parker Solar Probe observations (Zhao et al., 2022).

3 Result

Figure 1 shows an example of a (φ, θ) projection at 0.87 au. The top panel is the mean magnetic field $<\widehat{B}(\phi ,\theta )>$, and the dashed line corresponds to directions perpendicular to the mean magnetic field. The bottom panel displays the normalized standard deviation σ. A large value of σ means that the amplitude of fluctuations is large. The star symbol in the bottom panel denotes the direction where the fluctuation amplitude is the maximum. We can see that the maximum direction coincidently corresponds to a direction perpendicular to the mean magnetic field. For other cases, not shown here, the maximum direction is also nearly perpendicular to the mean magnetic field. Note that we also calculated the coherence index for other directions perpendicular to the mean magnetic field and found that the maximum direction tends to give the largest coherence index among other perpendicular directions (not shown here).

FIGURE 1

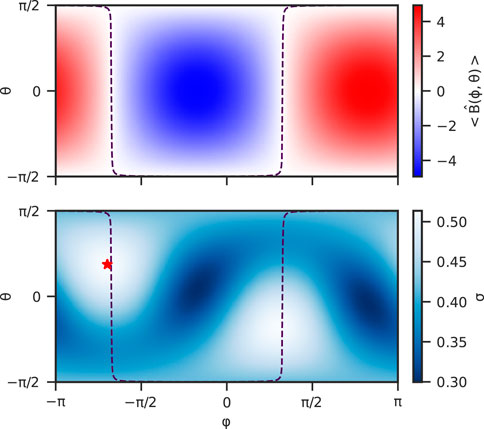
FIGURE 1. Top panel: projection of the time average of $\widehat{B}(t,\phi ,\theta )$ onto the φ-θ plane, and bottom panel: projection of the normalized standard deviation, σ (see the text for the definition of σ). The dashed line indicates the direction perpendicular to the mean magnetic field. The star symbol corresponds to the maximum σ value.

The coherence index C_ϕ at 0.87 au is shown as the black line in Figure 2. The index C_ϕ is moderately correlated (C_ϕ ∼ 0.45) when the timescale of fluctuations is comparable to the local proton gyro period (τ ∼ τ₀), and it gradually decreases as the fluctuation timescale increases and becomes randomly correlated (C_ϕ ∼ 0.05) after τ/τ₀ = 2 × 10². Here, the local proton gyro period τ₀ is defined as τ₀ = 2π/Ω_cp where Ω_cp is the proton cyclotron frequency. Note that the decrease of C_ϕ in the range of 0.6 < τ/τ₀ < 40 can be fitted by $\log {(\tau /{\tau }_0)}^{-0.1}$.

FIGURE 2

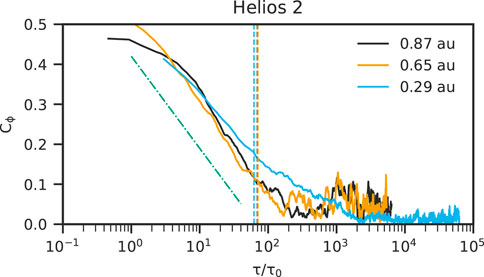
FIGURE 2. Coherence index, C_ϕ, calculated from Helios 2 observations (solid line). The dashed line corresponds to the resonant timescale of 10 MeV protons. Black, orange, and blue colors correspond to distances at 0.87, 0.65, and 0.29 au, respectively. The green dashed-dotted line is proportional to $\log \left[{(\tau /{\tau }_0)}^{0.1}\right]$. Here, τ₀ is the local proton gyro period calculated at each distance.

The profile of the coherence index is similar at smaller distances. The orange and blue lines in Figure 2 show the coherence index at 0.65 and 0.29 au, respectively, and the black and orange lines in Figure 3 correspond to super- and sub-Alfvénic solar wind at 0.09 au. At 0.65 au, the coherence index is 0.5 when τ/τ₀ ∼ 1, then gradually decreases until τ/τ₀ ∼ 2 × 10². On the other hand, the coherence indices at 0.29 and 0.09 au converge after τ/τ₀ ∼ 10³. The convergent value of C_ϕ at 0.29 au is almost 0, and that of C_ϕ at 0.09 au is around 0.05 and 0.1 for super- and sub-Alfvénic solar wind, respectively. Overall, the coherence index of the solar wind turbulence is moderately correlated when τ is comparable to τ₀ and becomes random for large-scale magnetic fluctuations in the inner heliosphere.

FIGURE 3

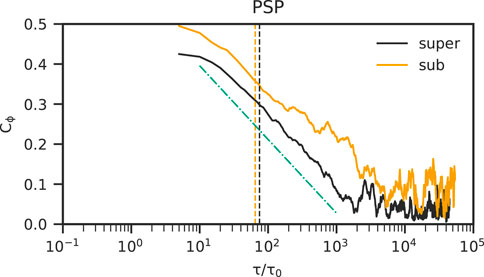
FIGURE 3. Coherence index, C_ϕ, calculated from PSP observations (solid line). The dashed line corresponds to the resonant timescale of 10 MeV protons. Black and orange colors correspond to the super- and sub-Alfvénic intervals, respectively. The green dashed-dotted line is proportional to $\log \left[{(\tau /{\tau }_0)}^{0.08}\right]$.Here, τ₀ is the local proton gyro period calculated at 0.09 au.

It seems that the coherence index for small-scale fluctuations becomes larger when closer to the Sun. From Figure 2, the coherence index at 0.29 au decreases more gradually than that at 0.87 and 0.65 au over the range of 1 < τ/τ₀ < 10³. The coherence index at 0.09 au for the super-Alfvénic case is 0.4 and 0.28 at τ/τ₀ = 10 and 100, respectively. These values are larger than those found in Helios 2 observations. This may indicate that fluctuations are more correlated closer to the Sun and turn more random as they propagate further in the solar wind.

The coherence indices at 0.09 au for the super- and sub-Alfvénic intervals are noticeably different. The black and orange lines in Figure 3 correspond to the super- and sub-Alfvénic intervals, respectively. Although the overall profile is similar, we can see that the sub-Alfvénic C_ϕ is larger than the super-Alfvénic C_ϕ over all the fluctuation timescale. This means that magnetic fluctuations are more correlated in the sub-Alfvénic region than the super-Alfvénic region. Note that the decrease of C_ϕ in the range of 5 < τ/τ₀ < 10³ for both cases can be fitted by $\log {(\tau /{\tau }_0)}^{-0.08}$.

The timescale for Alfvén waves resonant with energetic particles, τ_res, can be approximated as τ_res/τ₀ = (c_p/U)(Ω_cp/Ω_ci) and (c_p/|U cos Ψ + v_A|)(Ω_cp/Ω_ci) for the Helios 2 and PSP observations, respectively. Here, we assume that the observed fluctuations in the solar wind turbulence are dominated by Alfvén waves (Zank et al., 2022). We use Taylor’s hypothesis for the Helios 2 observations, ω_s/c ∼ kU, since the solar wind speed is much higher than the Alfvén speed, U ≫ v_A. Here, ω_s/c is the observed frequency in the spacecraft frame, and k the wavenumber. The resonant scale of energetic particles with Alfvén waves can be approximated as λ_res ∼ 2πc_p/Ω_ci (Isenberg, 2005) where c_p is the characteristic speed of energetic particles and Ω_ci the ion cyclotron frequency, and then the corresponding wavenumber is k_res = 2π/λ_res. Since the resonant frequency can be calculated as ω_res ∼ k_resU, the normalized resonant timescale is τ_res/τ₀ = (c_p/U)(Ω_cp/Ω_ci). For the PSP observations, we use a modified Taylor’s hypothesis (Zank et al., 2022; Zhao et al., 2022), which describes ω_s/c ∼|U cos Ψ ± v_A|k where Ψ is the angle between the mean magnetic field and the solar wind speed, since the solar wind speed is comparable to the Alfvén speed. Here, ± corresponds to forward- and backward-propagating waves. Using the same argument for k_res, we can write the resonant timescale as τ_res/τ₀ = (c_p/|U cos Ψ + v_A|)(Ω_cp/Ω_ci). Here, we only consider forward-propagating waves since the forward waves are more abundant than the backward waves (Zank et al., 2022; Zhao et al., 2022).

The coherence index corresponding to the resonant timescale of 10 MeV protons is at most 0.35 in the inner heliosphere. In the case of 10 MeV protons, Ω_ci = Ω_cp and c_p ∼ 4.4 × 10⁴ km/s. The dashed lines in Figures 2, 3 correspond to the resonant timescale at each distance. At the distance R = 0.87 and 0.65 au, the resonant timescales are almost the same, τ_res/τ₀ ∼ 70, and the corresponding coherence index is C_ϕ ∼ 0.1. The observation of Helios 2 at R = 0.29 au shows the resonant timescale, τ_res/τ₀ ∼ 62, and the resonant coherence index is larger, C_ϕ = 0.18. For the super- and sub-Alfvénic cases at 0.09 au (black and orange dashed line), τ_res/τ₀ ∼ 75 and 65, respectively. The corresponding C_ϕ are 0.3 and 0.35 for the super- and sub-Alfvénic intervals. The smallest coherence index for 10 MeV protons is C_ϕ ∼ 0.1 at 0.87 and 0.65 au, and the largest coherence index is C_ϕ ∼ 0.35 from the sub-Alfvénic case. This means that energetic particles interact with more correlated waves closer to the Sun.

Phase coherence of fluctuations parallel to the mean magnetic field is found to be strong in the inner heliosphere. While the above results are based on fluctuations perpendicular to the mean magnetic field, as suggested by the referee, we plot the coherence index of parallel fluctuations at each distance in Figure 4. At 0.09 au, the parallel coherence index in the sub-Alfvénic region is higher than 0.7 over the entire range except for τ/τ₀ > 2 × 10⁴, indicating that the flucutuations are highly correlated, whereas in the super-Alfvénic region, that is decreased, but still shows a strong coherence (0.4 < C_ϕ < 0.7 for 10 < τ/τ₀ < 5 × 10⁴). The parallel coherence indices at 0.87, 0.65, and 0.29 au are similar to the perpendicular coherence indices shown above, but slightly higher than them, and converge to around 0.2. It is also noticeable that the parallel coherence index increases with reduced distance to the Sun. It is not clear the reason of the strong coherence for parallel fluctuations in the inner heliosphere, this needs a further investigation.

FIGURE 4

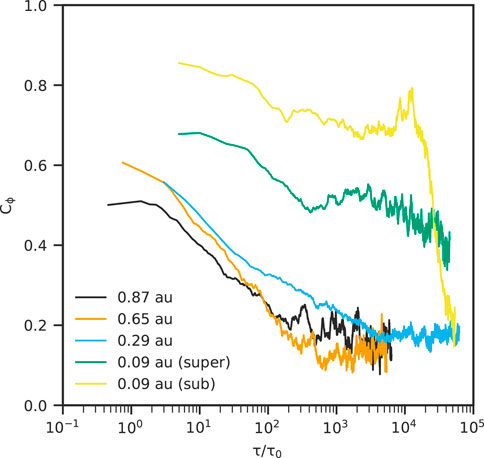
FIGURE 4. Coherence index, C_ϕ, calculated for fluctuations parallel to the mean magnetic field at each distance using Helios 2 and PSP observations. Here, τ₀ is the local proton gyro period calculated at each distance.

4 Summary and discussion

We have calculated the coherence of the solar wind turbulence in the inner heliosphere using the surrogate data technique. Well-known turbulence studies of Helios 2 and PSP observations (Marsch and Tu, 1990; Zhao et al., 2022) are used in this paper. The coherence index C_ϕ calculated by the surrogate data technique shows that C_ϕ is $\sim 0.45$ when the timescale of fluctuations, τ, is comparable to the local gyro period and converges to less than 0.1 as τ increases at 0.87 au. We found that the coherence index tends to be larger as the distance to the Sun decreases. There is an evident difference in the coherence index between the super- and sub-Alfvén intervals, showing that the sub-Alfvénic C_ϕ value is larger than the super-Alfvénic C_ϕ value over the entire range of τ.

Compared to the coherence index at the resonant timescale of energetic ions ($>10$ MeV), the random phase approximation can be regarded as valid in the inner heliosphere. We have assumed that the observed fluctuations are dominated by Alfvén waves, and computed the resonant scale of 10 MeV protons at each distance and the corresponding coherence index. We found that the coherence index is 0.1 at 0.87 and 0.65 au, 0.18 at 0.29 au, 0.3 and 0.35 at 0.09 au for the super- and sub-Alfvénic intervals, respectively. Overall, the coherence index for 10 MeV protons is still finite in the inner heliosphere. This is consistent with previous observations at Earth’s bow shock (Koga et al., 2007; Koga et al., 2008). Since the random phase approximation used in the quasi-linear theory and simulations corresponds to C_ϕ = 0, this may suggest that the random phase approximation is violated for the transport of energetic particles in the inner heliosphere, especially very close to the Sun ($\sim 0.09$ au). Note that more energetic particles ($>10$ MeV) interact with fluctuations less correlated since the resonant timescale becomes larger and the coherence index tends to be smaller for large τ. Since the coherence index at the resonant timescale is finite, it may require us to include the effects of phase coherence of turbulence in theories and simulations to fully understand the transport of energetic particles in finitely-correlated fluctuations. Furthermore, since the coherence of parallel fluctuations is also finite and seemingly strong, we may need to consider finite coherence for the transport of energetic particles due to parallel fluctuations. However, we have to keep in mind that the amplitude of parallel fluctuations is generally small compared to that of perpendicular fluctuations (see Figure 1 for instance).

Although we have assumed that the observed fluctuations are Alfvénic, we may need to consider the contribution of 2D modes to the transport of energetic particles. It has been pointed out that solar wind turbulence contains 2D modes as well as Alfvén waves. For 2D modes, the resonant scale for energetic particles can be considered as the Larmor radius, λ_res ∼ c_p/Ω_ci, and this yields a larger resonant timescale. Therefore, this corresponds to a smaller coherence index. Since the surrogate data technique used here cannot distinguish Alfvén waves and 2D modes, this needs further investigations.

Future work will examine more intervals of solar wind turbulence for better statistics and to strengthen our conclusion. Since we focus only on fast solar wind in this paper, it would be interesting to investigate the case of slow solar wind. Furthermore, it would be interest to investigate the coherence index in the outer heliosphere using Voyager spacecraft data.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

MN performed the analysis of the observational data and prepared the first draft. GZ and LZ contributed to the discussion of the method, results, and the preparation of the article.

Funding

We acknowledge the partial support of an NSF EPSCoR RII Track-1 Cooperative Agreement OIA-2148653, partial support from a NASA Parker Solar Probe contract SV4-84017, partial support from NASA awards 80NSSC20K1783 and 80NSSC23K0415, and partial support from a NASA IMAP sub-award under NASA contract 80GSFC19C0027. The SWEAP Investigation and this study are supported by the PSP mission under NASA contract NNN06AA01C.

Acknowledgments

The Parker Solar Probe was designed, built, and is now operated by the Johns Hopkins Applied Physics Laboratory as part of NASA’s Living with a Star (LWS) program (contract NNN06AA01C). Support from the LWS management and technical team has played a critical role in the success of the Parker Solar Probe mission. We thank the NASA Parker Solar Probe FIELDS team led by S. D. Bale for use of data. We are grateful to the referees for their thoughtful reports and valuable comments.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adhikari, L., Zank, G. P., and Zhao, L. L. (2020). A solar coronal hole and fast solar wind turbulence model and first-orbit parker solar Probe (PSP) observations. Astrophysical J. 901, 102. doi:10.3847/1538-4357/abb132

CrossRef Full Text | Google Scholar

Bale, S. D., Goetz, K., Harvey, P. R., Turin, P., Bonnell, J. W., Dudok de Wit, T., et al. (2016). The FIELDS instrument suite for solar Probe plus. Measuring the coronal pla and magnetic field, plasma waves and turbulence, and radio signatures of solar transients. Space Sci. Rev. 204, 49–82. doi:10.1007/s11214-016-0244-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Chancellor, J. C., Scott, G. B. I., and Sutton, J. P. (2014). Space radiation: The number one risk to astronaut health beyond low Earth orbit. Life (Basel) 4, 491–510. doi:10.3390/life4030491

PubMed Abstract | CrossRef Full Text | Google Scholar

Dudok de Wit, T., and Krasnosel’Skikh, V. V. (1996). Non-Gaussian statistics in space plasma turbulence: Fractal properties and pitfalls. Nonlinear Process. Geophys. 3, 262–273. doi:10.5194/npg-3-262-1996

CrossRef Full Text | Google Scholar

Giacalone, J., and Jokipii, J. R. (1994). Charged-particle motion in multidimensional magnetic field turbulence. ApJL 430, L137. doi:10.1086/187457

CrossRef Full Text | Google Scholar

Guo, F., and Giacalone, J. (2014). Small-scale gradients of charged particles in the heliospheric magnetic field. Astrophysical J. 780, 16. doi:10.1088/0004-637X/780/1/16

CrossRef Full Text | Google Scholar

Hada, T., Koga, D., and Yamamoto, E. (2003a). Phase coherence of MHD waves in the solar wind. Space Sci. Rev. 107, 463–466. doi:10.1023/A:1025506124402

CrossRef Full Text | Google Scholar

Hada, T., Otsuka, F., Kuramitsu, Y., and Tsurutani, B. T. (2003b). “Pitch angle diffusion of energetic particles by large amplitude MHD waves,” in International Cosmic Ray Conference, Tsukuba, Japan, July 31-August 7, 2003, 3709.

Google Scholar

Isenberg, P. A. (2005). Turbulence-driven solar wind heating and energization of pickup protons in the outer heliosphere. Astrophysical J. 623, 502–510. doi:10.1086/428609

CrossRef Full Text | Google Scholar

Kasper, J. C., Klein, K. G., Lichko, E., Huang, J., Chen, C. H. K., Badman, S. T., et al. (2021). Parker solar Probe enters the magnetically dominated solar corona. Phys. Rev. Lett. 127, 255101. doi:10.1103/PhysRevLett.127.255101

PubMed Abstract | CrossRef Full Text | Google Scholar

Kirk, J. G., Duffy, P., and Gallant, Y. A. (1996). Stochastic particle acceleration at shocks in the presence of braided magnetic fields. A&A 314, 1010–1016.

Google Scholar

Kis, A., Agapitov, O., Krasnoselskikh, V., Khotyaintsev, Y. V., Dandouras, I., Lemperger, I., et al. (2013). Gyrosurfing acceleration of ions in front of Earth’s quasi-parallel bow shock. Astrophysical J. 771, 4. doi:10.1088/0004-637X/771/1/4

CrossRef Full Text | Google Scholar

Koga, D., Chian, A. C. L., Hada, T., and Rempel, E. L. (2008). Experimental evidence of phase coherence of magnetohydrodynamic turbulence in the solar wind: GEOTAIL satellite data. Philosophical Trans. R. Soc. Lond. Ser. A 366, 447–457. doi:10.1098/rsta.2007.2102

PubMed Abstract | CrossRef Full Text | Google Scholar

Koga, D., Chian, A. C. L., Miranda, R. A., and Rempel, E. L. (2007). Intermittent nature of solar wind turbulence near the Earth’s bow shock: Phase coherence and non-Gaussianity. Phys. Rev. E 75, 046401. doi:10.1103/PhysRevE.75.046401

PubMed Abstract | CrossRef Full Text | Google Scholar

Koga, D., and Hada, T. (2003). Phase coherence of foreshock MHD waves: Wavelet analysis. Space Sci. Rev. 107, 495–498. doi:10.1023/A:1025510225311

CrossRef Full Text | Google Scholar

Kuramitsu, Y., and Hada, T. (2000). Acceleration of charged particles by large amplitude MHD waves: Effect of wave spatial correlation. Geophys. Res. Lett. 27, 629–632. doi:10.1029/1999GL010726

CrossRef Full Text | Google Scholar

Laitinen, T., Dalla, S., and Kelly, J. (2012). Energetic particle diffusion in structured turbulence. Astrophysical J. 749, 103. doi:10.1088/0004-637X/749/2/103

CrossRef Full Text | Google Scholar

Li, G., and Zank, G. P. (2005). Mixed particle acceleration at CME-driven shocks and flares. Geophys. Res. Lett. 32, L02101. doi:10.1029/2004GL021250

CrossRef Full Text | Google Scholar

Malandraki, O. E., and Crosby, N. B. (2018). “Solar energetic particles and space weather: Science and applications,” in Solar particle radiation storms forecasting and analysis. Editors O. E. Malandraki, and N. B. Crosby (Berlin, Germany: Springer), 1–26. doi:10.1007/978-3-319-60051-2_1

CrossRef Full Text | Google Scholar

Marsch, E., and Tu, C. Y. (1990). On the radial evolution of MHD turbulence in the Inner heliosphere. J. Geophys. Res. 95, 8211–8229. doi:10.1029/JA095iA06p08211

CrossRef Full Text | Google Scholar

Matthaeus, W. H., Wan, M., Servidio, S., Greco, A., Osman, K. T., Oughton, S., et al. (2015). Intermittency, nonlinear dynamics and dissipation in the solar wind and astrophysical plasmas. Philosophical Trans. R. Soc. Lond. Ser. A 373, 20140154. doi:10.1098/rsta.2014.0154

PubMed Abstract | CrossRef Full Text | Google Scholar

Moradi, A., and Giacalone, J. (2022). The effect of the fluctuating interplanetary magnetic field on the cosmic ray intensity profile of the ground-level enhancement (GLE) events. Astrophysical J. 932, 73. doi:10.3847/1538-4357/ac66e0

CrossRef Full Text | Google Scholar

Musmann, G., Neubauer, F. M., and Lammers, E. (1977). Radial variation of the interplanetary magnetic field between 0.3 AU and 1.0 AU. Observations by the Helios-1 spacecraft. J. Geophys. Zeitschrift Geophys. 42, 591–598.

Google Scholar

Otsuka, F., and Hada, T. (2009). Cross-field diffusion of cosmic rays in two-dimensional magnetic field turbulence models. ApJ 697, 886–899. doi:10.1088/0004-637X/697/1/886

CrossRef Full Text | Google Scholar

Ryan, J. M., Lockwood, J. A., and Debrunner, H. (2000). Solar energetic particles. Space Sci. Rev. 93, 35–53. doi:10.1023/A:1026580008909

CrossRef Full Text | Google Scholar

Sagdeev, R. Z., and Galeev, A. A. (1969). Nonlinear plasma theory. United Kingdom: University of oxford.

Google Scholar

Sahraoui, F. (2008). Diagnosis of magnetic structures and intermittency in space-plasma turbulence using the technique of surrogate data. Phys. Rev. E 78, 026402. doi:10.1103/PhysRevE.78.026402

PubMed Abstract | CrossRef Full Text | Google Scholar

Scholer, M. (1993). Upstream waves, shocklets, short large-amplitude magnetic structures and the cyclic behavior of oblique quasi-parallel collisionless shocks. J. Geophys. Res. 98, 47–57. doi:10.1029/92JA01875

CrossRef Full Text | Google Scholar

Schwartz, S. J., and Burgess, D. (1991). Quasi-parallel shocks: A patchwork of three-dimensional structures. Geophys. Res. Lett. 18, 373–376. doi:10.1029/91GL00138

CrossRef Full Text | Google Scholar

Schwartz, S. J., Burgess, D., Wilkinson, W. P., Kessel, R. L., Dunlop, M., and Luehr, H. (1992). Observations of short large-amplitude magnetic structures at a quasi-parallel shock. J. Geophys. Res. 97, 4209–4227. doi:10.1029/91JA02581

CrossRef Full Text | Google Scholar

Shalchi, A., Büsching, I., Lazarian, A., and Schlickeiser, R. (2010). Perpendicular diffusion of cosmic rays for a goldreich-sridhar spectrum. Astrophysical J. 725, 2117–2127. doi:10.1088/0004-637X/725/2/2117

CrossRef Full Text | Google Scholar

Tautz, R. C., and Shalchi, A. (2010). On the diffusivity of cosmic ray transport. J. Geophys. Res. (Space Phys. 115, A03104. doi:10.1029/2009JA014944

CrossRef Full Text | Google Scholar

van den Berg, J., Strauss, D. T., and Effenberger, F. (2020). A primer on focused solar energetic particle transport. Space Sci. Rev. 216, 146. doi:10.1007/s11214-020-00771-x

CrossRef Full Text | Google Scholar

Zank, G. P., Li, G., Florinski, V., Matthaeus, W. H., Webb, G. M., and Le Roux, J. A. (2004). Perpendicular diffusion coefficient for charged particles of arbitrary energy. J. Geophys. Res. (Space Phys. 109, A04107. doi:10.1029/2003JA010301

CrossRef Full Text | Google Scholar

Zank, G. P., Matthaeus, W. H., Bieber, J. W., and Moraal, H. (1998). The radial and latitudinal dependence of the cosmic ray diffusion tensor in the heliosphere. J. Geophys. Res. 103, 2085–2097. doi:10.1029/97JA03013

CrossRef Full Text | Google Scholar

Zank, G. P., Zhao, L. L., Adhikari, L., Telloni, D., Kasper, J. C., Stevens, M., et al. (2022). Turbulence in the sub-alfvénic solar wind. Astrophysical J. 926, L16. doi:10.3847/2041-8213/ac51da

CrossRef Full Text | Google Scholar

Zhao, L. L., Adhikari, L., Zank, G. P., Hu, Q., and Feng, X. S. (2018). Influence of the solar cycle on turbulence properties and cosmic-ray diffusion. Astrophysical J. 856, 94. doi:10.3847/1538-4357/aab362

CrossRef Full Text | Google Scholar

Zhao, L. L., Zank, G. P., Telloni, D., Stevens, M., Kasper, J. C., and Bale, S. D. (2022). The turbulent properties of the sub-alfvénic solar wind measured by the parker solar Probe. ApJL 928, L15. doi:10.3847/2041-8213/ac5fb0

CrossRef Full Text | Google Scholar