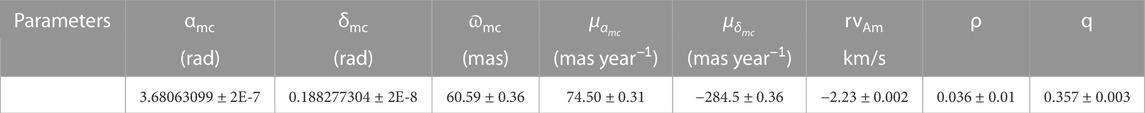- 1Purple Mountain Observatory, Chinese Academy of Sciences, Nanjing, China
- 2College of Physics and Electronic Engineering, Qilu Normal University, Jinan, China
- 3School of Astronomy and Space Science, University of Science and Technology of China, Hefei, China
The nearby astrometric-spectroscopic binary star Hip 68682 has an orbital period of ∼ 9.88 yr. The dynamical state (component masses and kinematic parameters) of this system is redetermined by fitting all the observational data available to us, including the radial velocity data (RVD), the relative position data (RPD), and the Hipparcos Intermediate Astrometric Data (HIAD). The precision-weighted sum of squared residuals calculated from our results is significantly smaller than the previous ones. With the simulated data based on Chinese Space Station Telescope (CSST), the relative orbit could be improved further.
Based on the known apparent magnitude information and the fitted parallax 60.59 ± 0.36 mas, we derive the absolute V magnitudes of the two components as 5.21 mag and 8.91 mag, respectively. The component masses are determined to be 0.946 ± 0.024M⊙ and 0.526 ± 0.014M⊙. These improved dynamical masses are helpful to constrain the stellar empirical mass–luminosity relation (MLR) for low mass stars. However, significant improvement of mass–luminosity relation for this mass region still needs more data.
1 Introduction
Hip 68682 (A and B, with barycenter Am and photocenter Ap) [other common name is WDS J14035 + 1047, Mason et al. (2001)] is a nearby metal-poor low mass binary star. The spectral classifications of this system is G6V. The unseen companion has a very low mass, thus it provides the possibility to better constrain the lower end of empirical mass–luminosity relation (MLR) for main-sequence stars. If more metal-poor binaries are resolved, and individual luminosities can be obtained, these new data could be used to reduce the current scatter in the metal-poor main sequence MLR, allowing for more stringent constraints on stellar models. It is thus very important to derive sufficiently precise dynamical masses and luminosities.
Hip 68682 is an astrometric binary that is also a single-spectrum spectroscopic binary [major semi-axis of photocentric orbit ∼ 0.105″, ESA (1997)]. Comparing to double-lined spectroscopic binaries, the physical properties, in particular, the masses of two components for single lined-spectroscopic binaries (SB1s) have large differences. Therefore, SB1s can provide much more stringent constraint on stellar models.
Based on the radial velocity data (RVD) and astromotric data with low precision, Kamper (2012) offered a preliminary relative orbit. But this orbit has large dispersion with the latest observations (Horch et al., 2015; Roberts & Mason, 2018; Hirsch et al., 2021). The time span of relative astrometric measurements is larger than the orbital period. However, it doesn’t have a good coverage of phase, thus the orbit solution has not been well constrained. The photocentric orbit from Hipparcos catalogue (ESA, 1997) is collected in the Sixth Catalog of Orbits of Visual Binary Stars [http://ad.usno.navy.mil/wds/orb6.html; Hartkopf et al. (2001)]. Jancart et al. (2005) tried to use the Hipparcos Intermediate Astrometric Data (HIAD) and RVD to give improved astrometric orbital elements. But according to specific statistical tests, this result is not accepted.
In this article, improved kinematic parameters of Hip 68682 are determined by fitting to all the collected RVD, relative position data (RPD), and HIAD. Meanwhile, we give the component dynamical masses and parallax for the system. Then, the lower end of the stellar empirical MLR is discussed. As this system is in the sky survey of CSST (Chinese Space Station Telescope), 22 observational points in average could be given to further improve the orbit. To test the ability of CSST to improve binary orbits, as called for by the CSST consortium, we simulate the effect of adding CSST data on this particular system. Also discussed are the possible contributions of CSST to binary orbit determination in general, and to stellar mass-luminosity relation improvement, especially for low mass main-sequence stars.
This paper is organized as follows. In Section 2, observational data are described. In Section 3, an improved dynamical state is presented and assessed. In Section 4, simulated CSST data are added to improve the fitted parameters and in the next section we discuss the empirical MLR. The last section summarizes our main results and makes concluding remarks.
2 Observational data
In our orbital redetermination, 8 RPD points spanning from 2003.3 to 2018.3 are collected from Horch et al. (2015), Roberts & Mason (2018) and Hirsch et al. (2021). Hirsch et al. (2021) used ShaneAO to get 4 data points and PHARO to get another 1 point with error
The preliminary spectroscopic orbit solution was given by Kamper (2012) and Duquennoy & Mayor (1991). We collected 17 historic RVD points from these two papers with error ∼ 0.3 km/s and 68 more points from Fischer et al. (2014) and Hirsch et al. (2021). Fischer et al. (2014) made measurements with the Lick/Hamilton spectrograph and Hirsch et al. (2021) got RV observations from the APF spectrometer. The errors of these two observations are
There are 155 HIAD with error
where t is measured in years since 1991.25, the modified right ascension α⋆ = α cos δ, the declination δ, the associated proper motions
where
Apart from the 15 model parameters mentioned above, more parameters are needed as there are systematic RV differences between measurements from various instruments. We have three data sets and the observation from Fischer et al. (2014) is the most accurate. To account for differences in the zero-points of the other two RV data sets relative to the measurements of Fischer et al. (2014), V1 and V2 are used as the velocity offsets (Torres et al, 2015). Therefore, there are totally 17 model parameters.
With the above-mentioned three kinds of observational data, the maximum likelihood estimate of model parameters is usually obtained by minimizing the following objective function.
where yi is the observed value with standard error σi, and y(xi; a1⋯aM) is the calculated value depending on the model parameters a1⋯aM,M=17.
3 Fitting and results
For Hip 68682, HIAD set has 155 data points with high precision and account for more than 60% of all the collected data. Because the fitting parameters have different dependency on the three kinds of data, tests show that simultaneous fitting could bring unphysical result. In fact, efficient two-step fitting procedure has been used in binary orbit fitting, especially for systems with high-accuracy spectral data (Pourbaix & Boffin, 2003; Jancart et al, 2005). In our work, as the RVD and RPD are two complementary types of observations, they could be used to determine the complete relative orbit solution. Therefore, we will firstly give DS, the 2 zero offset parameters in the RVD data sets (V1, V2) and the intermediate parameter KA. KA is the amplitude of the radial velocity curve of component A and writes.
When the relative orbit has been determined, the motion state parameters of Am, and ρ could be fitted using all the data while q is given based on K.
Here, as well as in the following, the Bounded Variable Least Squares algorithm (Lawson & Hanson, 1995) is used to give the least-square solution. And as Eq. 3 shows, each measurement is weighted by the inverse square of its own error. The uncertainty σ of each fitted parameter is given based on the method of constant delta δχ2 boundary, as the method used to estimate these parameters is chi-square minimization (Press et al., 1992). The total mass of the system M is derived according to the Kepler’s third law, the combination of the uncertainty of P, a, ϖ is propagated in the uncertainty of the total mass as (Martin & Mignard, 1998),
The uncertainties of the individual masses are given by the following expressions:
It is obvious that by minimizing Eq. 3 with a randomly chosen initial point, it is possible for us to obtain a local minimum. We find the global minimum by starting the minimization from different initial values. One thousand sets of initial values of the model parameters are randomly chosen from Kamper (2012) and van Leeuwen (2007), assuming maximum 10% relative errors for all parameters. For each starting set, an iterative process is used to discard outliers. At each step, the data outside the 3-σ confidence interval centered at their respective calculated value are considered to be outliers, and the process is terminated when there remains no such data.
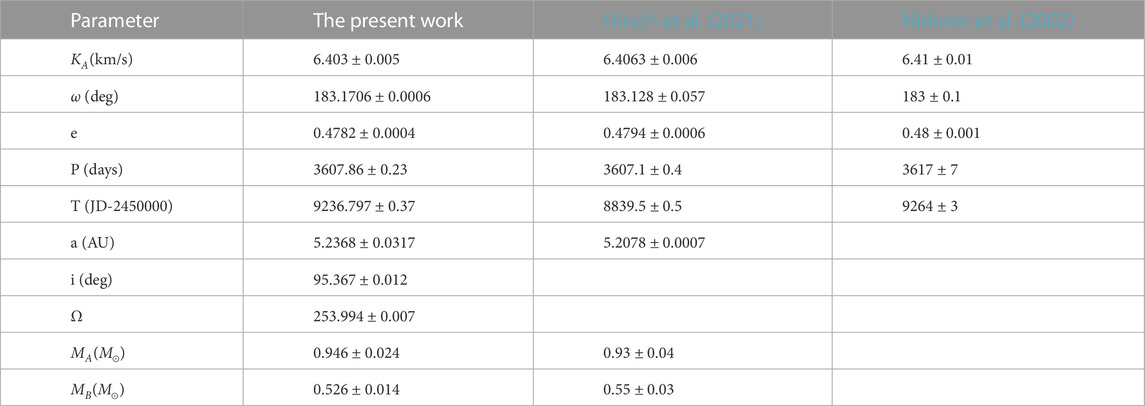
Via a simultaneous fitting to both RPD and RVD, we give a complete and improved orbit sultion with high precision. The derived parameter values including those of KA, DS and dynamical masses are shown in Table 1. The results of Hirsch et al. (2021) and Nidever et al. (2002) are also listed in Table 1. In comparison with Hirsch et al. (2021), all the listed parameters are consistent and most parameters given in our work are more accurate. The corresponding improved apparent orbit is plotted in Figure 1 as solid curve, the RPD used in fitting are also shown in Figure 1 as filled circles. The fitted radial velocity curve, the observed radial velocity measurements [the red square points are historic RVD, the triangle and circle points are corresponding to observations from Hirsch et al. (2021) and Fischer et al. (2014), respectively] are plotted in Figure 2. The 6 motion state parameters of Am and ρ, q are given in Table 2.
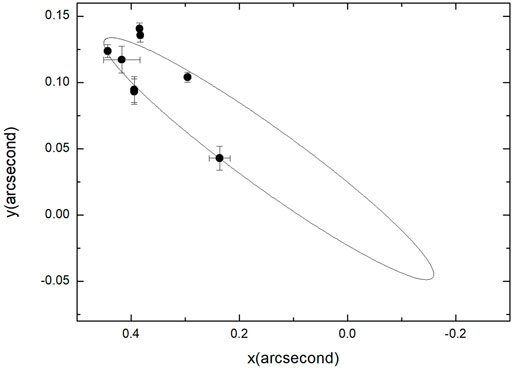
FIGURE 1. The apparent orbital motions of Hip 68682. The filled circles are the RPD used in our fitting. The solid curve is our improved two-body orbit.
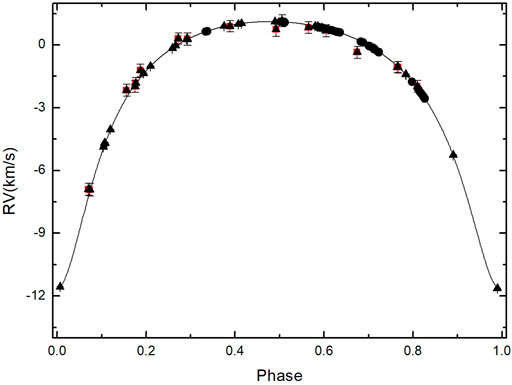
FIGURE 2. Fitted radial velocity curve and the observed radial velocity measurements. The red square points are historic RVD. The triangle and circle points are corresponding to observations from Hirsch et al. (2021) and Fischer et al. (2014), respectively.
The parallax of Hip 68682 given by Hipparcos mission and Gaia DR2, DR3 is 58.87 ± 0.62 mas, 60.84 ± 0.12 mas and 66.15 ± 0.27 mas, respectively (van Leeuwen, 2007; Luri et al., 2018; Brandt, 2021). The parallax in this paper is determined to be 60.59 ± 0.36 mas, which is in consistent with Gaia DR2. Based on the uncertain orbit given by Kamper (2012), Martin et al. (1998) gave the dynamical masses of 1.109 ± 0.057 M⊙ and 0.548 ± 0.033 M⊙ while in this paper component masses are determined to be 0.946 ± 0.024M⊙ and 0.526 ± 0.014M⊙. Martin et al. (1998) pointed that their mass estimates are slightly larger due to the Hipparcos parallax.
Our result is much better than the previous ones. The χ2 of our result is greatly reduced as the previous relative orbit was significantly deviated from the new RPD. The goodness-of-fit could be quantitatively measured by Q = gammq((N − 2)/2, χ2/2) which represents the probability that the χ2 should exceed a particular value χ2 by chance (Press et al., 1992; Xia et al., 2019). If Q is larger than 0.1 then the model is believable, while Q < 0.001 means that the model is not acceptable. The value Q of simultaneous fitting with all data is smaller than 0.001 while the final two-step simultaneous fitting has Q = 0.201, larger than the key value 0.1. This should imply that the error of HIAD could be over-estimated.
4 Results with CSST simulated data
CSST has 1.1 square degree field of view, it is expected to obtain position and photometry data for billions of stars. The position precision of point source can achieve better than 1 mas level for 18–20 mag stars in g band. The sky surveys of CSST cover a large sky area (17,500 deg2) (Zhan, 2011; Zhan & Tyson, 2018). Hip 68682 is in this area (see Figure 3, the triangle point is Hip 68682, the blue regions are for galactic latitude |b|⩾20°, the red regions are deep-field surveys of CSST). However, this system is too bright to be observed by CSST.
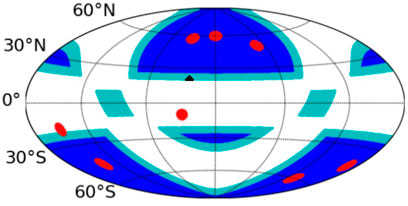
FIGURE 3. The covered region of CSST sky surveys. The blue regions are for galactic latitude |b|⩾20°, the red regions are deep-field surveys of CSST. The triangle point is Hip 68682.
It is believed that CSST will find new faint binaries with high-precision astrometric data spanning more than 10-years. It is then interesting to know how these data could contribute to the orbit determination of these new binaries. And it is also tempting to illustrate how the long time-span high-precision data could be used to improve an existing orbital solution. This is because the price to pay is low for a specific system and CSST encourages such studies. We use Hip 68682 as an example to show the ability of CSST data to improve binary orbital solutions.
According to the best-fit parameters given in the last section, the simulated 22 position data points of Ap are randomly distributed in 10 years with 1 mas uncertainty. Then we refit the orbit with simulated and other collected data. We could find that the relative error of some of the determined orbital parameter is reduced, although the effect is not significant. Tests also show that if the simulated data points lie in the phase of lacking data, most of the orbital parameters are better confined. In Wang et al. (2023), the ability of long time-span high-precision data of CSST to improve the orbital solutions of SB1s is quantitatively discussed in the view of statistics.
Moreover, CSST could have important role in identifying wide binaries. In Makarov (2020), based on Double and Multiple System Annex (DMSA) of Hipparcos catalogue and Gaia DR2, the author cross-matched 2590 components of 1295 doubles. But as Hipparcos could confidently measure only stars brighter than magnitude
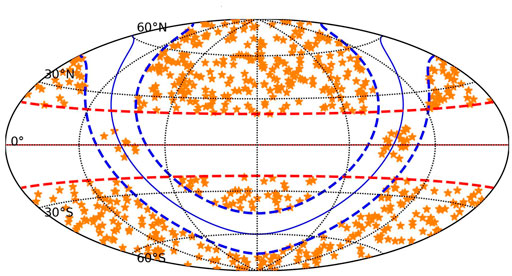
FIGURE 4. The 624 binaries from cross-matching DMSA and Gaia DR2 which are in the covered region of CSST sky surveys.
5 MLR (mass-luminosity relation)
With the exception of the HR diagram, the MLR is the single most important map in stellar astronomy (Henry et al., 1999). The empirical MLR remains poorly determined for low mass stars, mainly due to the scarcity of accurately determined masses (Xia et al., 2019).
Eker et al. (2018) pointed that the MLR function is better if expressed by a six-piece classical linear relation rather than a fifth or higher polynomial within the mass range from 0.179 M⊙ to 31 M⊙. The break point
As the improved component masses belong to the low mass and very low mass regions, we discuss these two mass regions. Based on our work (Xia & Fu, 2010), new (improved) 48 data points of mass and V magnitude are collected from Anguita-Aguero et al., 2022; Brogaard et al. (2021); Dieterich et al. (2021); Eker et al. (2018); Hussein et al. (2022); Mann et al. (2019); Milone et al. (2019); Torres (2019); Torres et al. (2019); Docobo et al. (2019) (see Figure 5 as green points with error bars). The other collected data points are shown as black circles with error bars. From this figure, we find that, though the MLR for stars with mass smaller than 0.6 M⊙ could be better confined, more data are still needed.
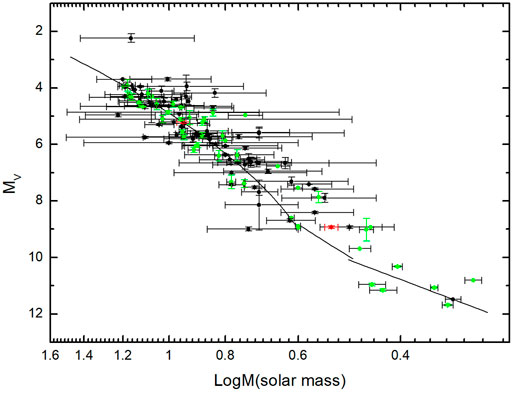
FIGURE 5. The empirical MLR. The red points are the components masses of Hip 68682. The collected data points are shown as black circles with error bars while new (improved) collected data are shown as green points. The MLRs given in Xia et al. (2008); Xia & Fu (2010) are ploted as solid lines.
As CSST has comparable precision with Gaia in observing faint stars, we collected 67 low mass systems which have incompatible dynamical and physical masses. Hip 68682 is one of these systems, and half of them are in the sky surveys of CSST. If more data are given, confident dynamical masses could be given, thus MLR could be further improved. CSST could have great contribution in this filed.
6 Summary and concluding remarks
The main results are summarized as follows.
The dynamical state (component masses and kinematic parameters) of this system is redetermined. Based on the improved dynamical masses and the other collected mass and V magnitude data, we discuss the empirical MLR for low mass and very low mass stars.
The Gaia DR3 was released on 13 June 2022, and all epoch and transit data in DR4 will be released in about the end of 2025. With these data and the high pricision data from CSST, further improvements of the relative orbits of more systems could be given, especially for systems with dark components. Moreover, based on the all kinds of data, the identified wide binaries could also be enlarged.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
YC is dedicated in identifying wide binaries and has contribution in cross-matching DMSA, Gaia DR2 with CSST deeper filed of surveys. XW has contribution in simultaneous fitting of RVD and RPD. YF give many useful suggestions to imporve the manuscript. FX collect the observational data and complete the fitting, the data simulation and all the other works. All authors contributed to the article and approved the submitted version.
Funding
This research is supported by the National Natural Science Foundation of China under Grant Nos. 11673071 and 12073008, the science research grants from the China Manned Space Project with No. CMS-CSST-2021-A12, CMS-CSST-2021-B10.
Acknowledgments
We thank the referee for his helpful comments. This research has made use of the SIMBAD database (http://cdsweb.u-strasbg.fr/).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The handling editor SL declared a shared affiliation with authors FX, YF at the time of the review.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Anguita-Aguero, J., Mendez, R. A., Clavería, R. M., and Costa, E. (2022). Orbital elements and individual component masses from joint spectroscopic and astrometric data of double-line spectroscopic binaries. AJ 163, 118. doi:10.3847/1538-3881/ac478c
Brandt, T. D. (2021). The hipparcos-gaia catalog of accelerations: Gaia EDR3 edition. ApJS 254 (2), 42. doi:10.3847/1538-4365/abf93c
Brogaard, K., Pakštienė, E., Grundahl, F., Mikolaitis, Š., Tautvaišienė, G., Slumstrup, D., et al. (2021). Properties of the Hyades, the eclipsing binary HD 27130, and the oscillating red giant ϵ Tauri. A&A 645, 25. doi:10.1051/0004-6361/202039250
Dieterich, S. B., Simler, A., Henry, T. J., and Jao, W. C. (2021). The solar neighborhood. XLVII. Comparing M-dwarf models with hubble space telescope dynamical masses and spectroscopy. AJ 161, 172. doi:10.3847/1538-3881/abd2c2
Docobo, J. A., Gomez, J., Campo, P. P., Andrade, M., Horch, E. P., Costa, E., et al. (2019). Orbits of 14 binaries based on 2018 SOAR speckle observations. MNRAS 482, 4096–4110. doi:10.1093/mnras/sty2704
Duquennoy, A., and Mayor, M. (1991). Multiplicity among solar-type stars in the solar neighbourhood. II - distribution of the orbital elements in an unbiased sample. A&A 248, 485.
Eker, Z., Bakış, V., Bilir, S., Soydugan, F., Steer, I., Soydugan, E., et al. (2018). Interrelated main-sequence mass–luminosity, mass–radius, and mass–effective temperature relations. mass-effective Temp. Relat. 479, 5491–5511. doi:10.1093/mnras/sty1834
ESA (1997). The Hipparcos and tycho catalogues, SP-1200. Noordwijk, Netherlands: ESA Publications Division.
Fischer, D. A., Marcy, G. W., and Spronck, J. F. P. (2014). The twenty-five year Lick planet search. ApJS 210 (1), 5. doi:10.1088/0067-0049/210/1/5
Hartkopf, W. I., McAlister, H. A., and Mason, B. D. (2001). The 2001 US naval observatory double star CD-ROM. III. The third catalog of interferometric measurements of binary stars. AJ 122, 3480–3481. doi:10.1086/323923
Henry, T. J., Franz, O. G., Wasserman, L. H., Benedict, G. F., Shelus, P. J., Ianna, P. A., et al. (1999). The optical mass-luminosity relation at the end of the main sequence (0.08–0.20m⊙). ApJ 512, 864–873. doi:10.1086/306793
Hirsch, L. A., Rosenthal, L., Fulton, B. J., Howard, A. W., Ciardi, D. R., Marcy, G. W., et al. (2021). Understanding the impacts of stellar companions on planet formation and evolution: A survey of stellar and planetary companions within 25 pc. AJ 161 (3), 134. doi:10.3847/1538-3881/abd639
Horch, E. P., van Altena, W. F., Demarque, P., Howell, S. B., Everett, M. E., Ciardi, D. R., et al. (2015). Observations of binary stars with the differential speckle survey instrument. V. Toward an empirical metal-poor mass-luminosity relation. AJ 149, 151. doi:10.1088/0004-6256/149/5/151
Hussein, A. M., Al-Wardat, M. A., Abushattal, A., Widyan, H. S., Abu-Alrob, E. M., Malkov, O., et al. (2022). Atmospheric and fundamental parameters of eight nearby Multiple stars. AJ 163, 182. doi:10.3847/1538-3881/ac4fc7
Jancart, S., Jorissen, A., Babusiaux, C., and Pourbaix, D. (2005). Astrometric orbits of SB9 stars. A&A 442 (1), 365–380. doi:10.1051/0004-6361:20053003
Kamper, K. W. (2012). “Astrometric - spectroscopic binary star oobits. I. HR 5273, 1987, AJ, 93, 683 K,” in Fundamentals of astrometry (Cambridge, UK: Cambridge University Press).
C. Lawson, and R. Hanson (Editors) (1995). Solving least squares problems (Philadelphia: SIAM), 279.
Luri, X., Brown, A. G. A., Sarro, L. M., Arenou, F., Bailer-Jones, C. A. L., Castro-Ginard, A., et al. (2018). GaiaData release 2: UsingGaiaparallaxes. A&A 616, A9. doi:10.1051/0004-6361/201832964
Makarov, V. V. (2020). Two-epoch orbit estimation for wide binaries resolved in Hipparcos and Gaia. AJ 160, 284. doi:10.3847/1538-3881/abbe1c
Mann, A. W., Dupuy, T., Kraus, A. L., Gaidos, E., Ansdell, M., Ireland, M., et al. (2019). How to constrain your M dwarf. II. The mass-luminosity-metallicity relation from 0.075 to 0.70 solar masses. ApJ 871, 63. doi:10.3847/1538-4357/aaf3bc
Martin, C., Mignard, F., Hartkopf, W. I., and McAlister, H. A. (1998). Mass determination of astrometric binaries with Hipparcos III. New results for 28 systems. A&AS 133, 149–162. doi:10.1051/aas:1998459
Martin, C., and Mignard, F. (1998). Mass determination of astrometric binaries with Hipparcos. II. Selection of candidates and results. A&A 330, 585.
Mason, B. D., Wycoff, G. L., Hartkopf, W. I., Douglass, G. G., and Worley, C. E. (2001). The 2001 US naval observatory double star CD-ROM. I. The Washington double star catalog. AJ 122, 3466–3471. doi:10.1086/323920
Milone, E. F., Schiller, S. J., Mellergaard, A., and Ds Andromedae, Th. (2019). DS andromedae: A detached eclipsing double-lined spectroscopic binary in the galactic cluster ngc 752. AJ 158, 82. doi:10.3847/1538-3881/ab22ba
Nidever, D. L., Marcy, G. W., Butler, R. P., Fischer, D. A., and Vogt, S. S. (2002). Radial velocities for 889 late-type stars. ApJS 141, 503–522. doi:10.1086/340570
Pourbaix, D., and Boffin, H. M. J. (2003). Reprocessing the Hipparcos intermediate astrometric data of spectroscopic binaries. II. Systems with a giant component. A&A 398, 1163–1177. doi:10.1051/0004-6361:20021736
Press, W. H., Teukolsky, S. A., and Vetterling, W. T. (1992). Numerical recipes in fortran. Second Edition. Cambridge: Cambridge University Press.
Roberts, L. C., and Mason, B. D. (2018). Astrometric and photometric measurements of binary stars with adaptive optics: Observations from 2001 to 2006. MNRAS 473 (4), 4497–4504. doi:10.1093/mnras/stx2559
Torres, G., Claret, A., Pavlovski, K., and Dotter, A. (2015). Capella (α aurigae) revisited: New binary orbit, physical properties, and evolutionary state. ApJ 807, 26.
Torres, G. (2019). Dynamical masses for the hyades binary 80 tauri. ApJ 883, 105. doi:10.3847/1538-4357/ab3a30
Torres, G., Stefanik, R. P., and Latham, D. W. (2019). Dynamical masses for the triple system HD 28363 in the hyades cluster. ApJ 885, 9. doi:10.3847/1538-4357/ab43e2
F. van Leeuwen (Editor) (2007). Hipparcos, the new reduction of the raw data. Berlin: Springer: (Astrophysics and Space Science Library). Vol 350.
Wang, X.-L., Xia, F., and Fu, Y.-N. (2023). The ability of CSST to improve the orbital solutions of nearby SB1s. submitted to Frontiers.
Xia, F., Fu, Y.-N., and Wang, X.-L. (2019). The nearby very low mass triple star LHS 1070. ApJ 882, 147. doi:10.3847/1538-4357/ab32de
Xia, F., Ren, S.-L., and Fu, Y.-N. (2008). The empirical mass-luminosity relation for low mass stars. APSS 314, 51–58. doi:10.1007/s10509-007-9729-8
Zhan, H. (2011). Consideration for a large-scale multi-color imaging and slitless spectroscopy survey on the Chinese space station and its application in dark energy research. Sci. Sinica Phys. 179 Mech. Astronomica 41, 1441–1447. doi:10.1360/132011-961
Keywords: stars: binaries, stars: fundamental parameters, stars: individual (HIP 68682), stars: kinematics and dynamics, methods: data analysis
Citation: Xia F, Wang X, Fu Y and Chen Y (2023) The nearby astrometric-spectroscopic binary star Hip 68682. Front. Astron. Space Sci. 10:1153912. doi: 10.3389/fspas.2023.1153912
Received: 30 January 2023; Accepted: 27 April 2023;
Published: 09 May 2023.
Edited by:
Shilong Liao, Chinese Academy of Sciences (CAS), ChinaReviewed by:
Giovanni Catanzaro, Osservatorio Astrofisico di Catania (INAF), ItalyFabo Feng, Shanghai Jiao Tong University, China
Copyright © 2023 Xia, Wang, Fu and Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fang Xia, eGZAcG1vLmFjLmNu
 Fang Xia
Fang Xia Xiaoli Wang
Xiaoli Wang Yanning Fu1
Yanning Fu1