- 1Department of Chemistry and Molecular Biology, University of Gothenburg, Gothenburg, Sweden
- 2Department of Physics, University of Latvia, Riga, Latvia
The degradation of indene is investigated using molecular dynamics (MD) with the ReaxFF force field and RRKM theory. Microcanonical rate constants are obtained over a broad energy range (8–25 eV). There is agreement between the results of the molecular dynamics and RRKM calculations at the lower energies, while the molecular dynamics rate constants are larger at the higher energies. At the lower energies there is also agreement with values obtained by using expressions for photodegradation of polyaromatic hydrocarbons from the literature. Values from those expressions however increase even faster with energy than our molecular dynamics rate constants do. At the same time those values are lower than an experimental result at 6.4 eV. This suggests that astrochemical models employing those values may result in unreliable polycyclic aromatic hydrocarbons abundances.
1 Introduction
Polycyclic aromatic hydrocarbons (PAHs) are believed to make up approximately 20% of the galactic carbon (Tielens and Allamandola, 2010). The existence of this class of organic compounds has however only been confirmed quite recently (McGuire et al., 2018; Cernicharo et al., 2021; Cernicharo et al., 2022a; Cernicharo et al., 2022b). Indene, C9H8 and cyanonaphthalene isomers were recently the first PAHs to be detected in Taurus Molecular Cloud 1 (TMC-1) (Burkhardt et al., 2021; McGuire et al., 2021). Indene consists of a five-membered hydrocarbon ring fused to a benzene moiety. It has a permanent dipole moment, which makes it detectable in radio observations. It has also been shown that it can be formed through a barrierless addition reaction between methylidyne and styrene in gas-phase (Doddipatla et al., 2021). This implies that the formation of indene is possible at low temperature interstellar environments such as in dark molecular clouds.
Interstellar PAHs are likely to be fragmented by collisions with electrons and ions, by photolysis and by galactic cosmic rays (Micelotta et al., 2010a; Micelotta et al., 2010b). PAH molecules are exposed to continuous broadband UV radiation in the ISM (Zhen et al., 2015). HI regions of the interstellar medium (ISM) are characterized by the presence of photons with energies up to about the hydrogen atom ionization energy, 13.6 eV. It is still expected that under these conditions hydrocarbon photodissociation rates are below 109 s−1 (Allain et al., 1996a; Allain et al., 1996b). Allain et al. (1996a) and Allain et al. (1996b) used a statistical model to estimate the rate of photodestruction of PAHs in the interstellar media. They concluded that PAHs having at least 50 carbon atoms may survive the UV field in environments like reflection nebulae, planetary nebulae and HII regions. This is in line with the study by Zhen et al. (2015) showing that photoionization competes with fragmentation and completely dominates for PAHs with at least 50 carbon atoms.
Allain et al. (1996a) used Rice-Ramsberger-Kassel (RRK) theory (Forst, 2012; Léger and d’Hendecourt, 1985) to predict energy-dependent rate constants for dissociation of a molecule:
Here, N is the number of atoms in the molecule and E is the internal energy. E0 and k0 are used as parameters whose values were set within the RRK model to fit experimental results for a set of PAHs ranging from benzene to coronene in size (Jochims et al., 1994). The E0 and k0 values were individually set (Allain et al., 1996a) for the possible elimination of three chosen moities from the PAHs, viz.: H, H2 and C2H2. This RRK model can give rate coefficients over a broad range of energy and has been employed in astrochemical modelling (Murga et al., 2019). The model gives rate constants for H elimination (E0 = 2.8eV, k0 = 1016s−1) that are larger than the corresponding values for C2H2 elimination (E0 = 2.9eV, k0 = 1015s−1) for all energies. The reaction channels in a chemical process may compete with each other, depending on the internal energy of the system (Ling and Lifshitz, 1998). Also, depending on the PAH of interest, it is possible that the carbon loss channels may be more significant than hydrogen atom loss processes (Le Page et al., 2001).
In this work we employ RRK-Marcus (RRKM) theory and molecular dynamics to determine the fate of indene after absorption of high energy UV photons. RRKM theory is a statistical approach where we find the required input data from electronic structure calculations. The absorbed photon energy is probably initially deposited locally in a large molecule. RRKM theory is then only applicable if the rate for energy redistribution among all the vibrational modes is faster than the dissociation rate, as otherwise there may be non-statistical effects in the dissociation process.
As an alternative to RRKM theory, molecular dynamics (MD) can be used to study the fragmentation of large molecules, thereby not relying on statistical assumptions. We note that it is still unfeasible in general to study chemical reactions involving large molecules with quantum dynamical approaches. In the present study, we employ molecular dynamics calculations using the Reax force field [ReaxFF MD (van Duin et al., 2001)] and RRKM theory as just mentioned, to investigate the fragmentation process of indene. First, the theoretical methods are presented. Then results are presented and discussed before conclusions are drawn.
2 Theoretical methods
In this section we briefly describe our molecular dynamics simulations, electronic structure calculations and finally the RRKM calculations.
2.1 ReaxFF molecular dynamic simulations
Reactive Force Field (ReaxFF) interatomic potentials can be used in MD simulations to describe bond breaking (van Duin et al., 2001). As illustrated by Eq. 2, ReaxFF includes several contributions to the potential energy, such as two-body energy terms which depend on interatomic distance and electrostatic, torsional and bond order dependent contributions.
Bond order dependent potentials allow description of different spn (n = 1, 2, 3) orbital hybridizations of carbon atoms. The bond order is found by analysing the chemical environment and interatomic distances around an atom. For a thorough description of the different energy terms in Eq. 2 we refer to the main paper written by van Duin et al. (2001). Tapered ReaxFF (Furman and Wales, 2020) eliminates discontinuities in the energy, which is inherent to ReaxFF potentials that use bond order terms and torsion angles in the potential energy expressions. The tapered ReaxFF approach is implemented in the Amsterdam Modeling Suite program (Franchini et al., 2021), which is used for the present study. Several ReaxFF potentials are available in this environment for hydrocarbon MD simulations. In our study we use the 2008-C/H/O parametrisation, which is capable of describing C-H bonds and their dissociation (Chenoweth et al., 2008).
Before the MD calculations are started, the indene geometry is optimized. We then wish to simulate the dynamics after absorption of a photon. The relaxation from high lying electronic states to low lying electronic states is typically fast (Allain et al., 1996a; Allain et al., 1996b). In this work we investigate the case where the vibrational relaxation occurs to the ground electronic state before interesting dynamics happens. It is thus assumed that after the absorption of a photon, the photon energy is quickly transferred to the nuclear motions and evolution proceeds on the lowest adiabatic PES, which is described by the ReaxFF potential that we use.
The assumption of fast energy transfer to the nuclei is expected to work better as the size of a system increases. A study of Ghanta et al. (2001) shows rates for non-radiative decay of low lying states of naphthalene and anthracene cations to occur within a few 10th of femtoseconds. In our calculations the energy is initially distributed among the vibrational modes of the molecule in two different ways, either according to a thermal Boltzmann distribution or alternatively the energy is put into a single C-C bond. The simulations are always started from the equilibrium geometry for a non-rotating spatially immobile indene molecule. Thermal initialization of velocities leads to slight overall rotation and translation of the molecule. These two types of motion are subtracted, so initially the total energy is completely in the form of vibrational kinetic energy, and measured from the bottom of the potential well. We report results from the molecular dynamics simulations for various total energies. For the single C-C bond excitation, equal oppositely directed momenta are assigned to the two atoms in the bond while all other atoms are left at rest, thus leaving the center momentum and rotational momentum equal to zero. Since the photo-excitation energy that we wish to simulate overwhelmingly exceeds the experimental thermal energy, neglecting the initial rotational motion is justified (and center of mass motion is as usual not relevant). The MD simulations continue in time until the molecule dissociates. There are however also cases where the dissociation is so slow that we could not follow the time evolution until dissociation occurs.
The MD calculations are performed for up to 10 ns, with a 0.01 fs time-step. Calculations longer than 1 ns may lead to non-physical heat up, thus increasing the total energy of the system by several percent or more. Such trajectories are discarded in the final analysis of the decay rate. In our calculations this problem typically appears if the molecule has considerable amount of kinetic energy thereby allowing angular parameters in the ReaxFF to often correspond to near linear configurations. Decreasing the energy cutoffs for the torsional angles seem to result in smoother changes of the potential energy landscape. We therefore suggest that reparameterising the ReaxFF potentials with lower energy cutoff values might increase the numerical stability and improve the conservation of energy in the MD calculations. Such reparametrization is however outside the scope of this work.
2.2 Electronic structure calculations
In order to employ RRKM theory to calculate microcanonical reaction rate constants, information about the energetics and rovibrational properties of the reactants and the transition states are required. Second-order Møller–Plesset (MP2) Perturbation Theory (Møller and Plesset, 1934) along with the 6-311+G(d,p) basis set is used to optimize the stationary points on the potential energy surface, i.e., reactants, intermediates, transition states and products. Rotational constants and vibrational frequencies are also obtained at the same level of theory. To compute more reliable relative energies with respect to the reactants, the composite quantum method CBS-QB3 is utilized (Montgomery Jr et al., 2000). Note that the reported energies include harmonic zero-point energies calculated at MP2/6-311+G (d,p) level of theory. Gaussian 16 (Frisch et al., 2016) is employed for all electronic structure calculations.
The obtained optimized geometries (Z-Matrices), vibrational frequencies and rotational constants are presented in the Supplementary Material.
2.3 RRKM theory
RRKM theory assumes that the molecular system behaves ergodically and that vibrational energy redistribution is faster than reaction (Nordholm and Bäck, 2001; Leitner et al., 2003). These conditions are not always fulfilled, but are typically good approximations. RRKM theory requires sums and densities of states. To find these, we make the separable harmonic oscillator—rigid rotor assumption. It should be noted that at high energies the separable harmonic oscillator approximation might not be good (Nguyen and Barker, 2010).
In RRKM theory, the energy-dependent rate constant, k(E), for a unimolecular reaction can be written (Holbrook et al., 1996; Steinfeld et al., 1999)
in which h is the Planck constant. N‡(E) and ρ(E) are the sum of states for the transition state and the density of states for the reactant, respectively. The precision of the rate constants predicted by RRKM theory relates to how accurately the sums and densities of states are evaluated. In the present study N‡(E) and ρ(E) are calculated using a direct count of vibrational quantum states but also using a classical expression to justify comparison to the classical MD simulations. Considering a molecular system which includes s vibrational degrees of freedom with non-degenerate vibrational frequencies (νi), which applies to indene, we may use the following expression to find the sum of states classically (Steinfeld et al., 1999):
We point out that in this classical expression we choose the bottom of the potential energy well as the reference level, which we also do in the MD simulations. For the quantal RRKM results we choose the zero point level as the reference level for the energy.
In this study, the code Densum in the MultiWell software suite (Barker et al., 2022) was used to perform the direct counts in order to obtain the sums and densities of states for separable harmonic vibrational degrees of freedom. Energy step sizes of 100 cm−1 were used and the densities of states were determined from the number of states in these energy bins. The classical density of states is simply evaluated as the derivative of Eq. 4.
Besides the vibrational motions, external rotations are also considered active in the present work. The rotational states for an asymmetric top like indene cannot be calculated using a simple mathematical expression. Here, we therefore approximate the indene molecule as a prolate symmetric top, for which the rotational constants A, B and C are related as A ≠ B = C. Here we set a rotational constant D = (BC)1/2 and use it in the rotational energy expression for a prolate symmetric top which becomes (Holbrook et al., 1996; Steinfeld et al., 1999):
where J is the total angular momentum quantum number (the ”J-rotor”) and K is the quantum number for the projection of J on the molecular symmetry axis. The vibrational sums and densities of states are combined with the contribution from the rotational states in the rate constant calculations.
3 Results
In this section we first describe aspects of the potential energy landscape for photodissiciation of indene. Thereafter we present our RRKM results and then finally the ReaxFF MD results. We will here focus on three types of fragmentation that occur when the molecule indene decomposes, viz. C2H2 loss, c-C3H4 loss and H-atom loss from the CH2 group, since it has the weakest C-H bonds. We restrict our RRKM study by keeping the six-membered ring in indene intact since its aromaticy makes its C-C bonds relatively strong and thus hard to break in comparison to breaking those in the five-membered ring.
3.1 Potential energy profile
There are three chemically different C-H bonds which can be broken in the five-membered ring of indene. These H elimination reactions have loose transition states. The energies relative to indene for these reaction channels are illustrated in Figure 1. The most favorable hydrogen loss channel, i.e., the one with lowest dissociation energy (D0), breaks one of the C-H bonds in the CH2 group. The dissociation energy for this is 3.60 eV at CBS-QB3 level. This value is at least 1.6 eV lower than the energy required for loss of any other H atom in indene. The dissociation energy for the elimination of hydrogen atoms in benzene, where all carbon atoms are sp2 hybridized, has been reported to be close to 5 eV (Kislov et al., 2004).
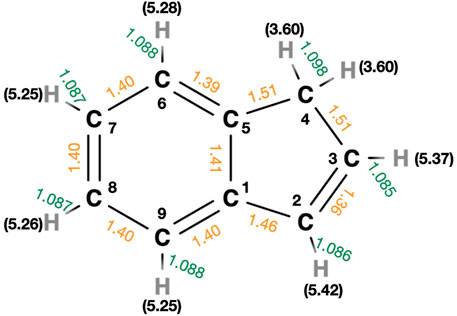
FIGURE 1. The geometry of indene optimized at MP2/6-311+G (d,p) level of theory. The bond lengths for C-H (in green) and C-C (in orange) bonds and hydrogen atom dissociation energies (in black), D0 are presented. The units are Å and eV.
If there is a concerted H2 loss channel, it would be expected to occur via a transition state centered on the CH2 group, similar to the H2 loss channel in the dissociation of benzene (Kislov et al., 2004). Despite our searches, such an H2 loss channel was not detected at MP2 level. Several possible pathways for dissociation of indene are shown in Figure 2, with relative energies at CBS-QB3//MP2/6-311+G(d,p) level of theory.
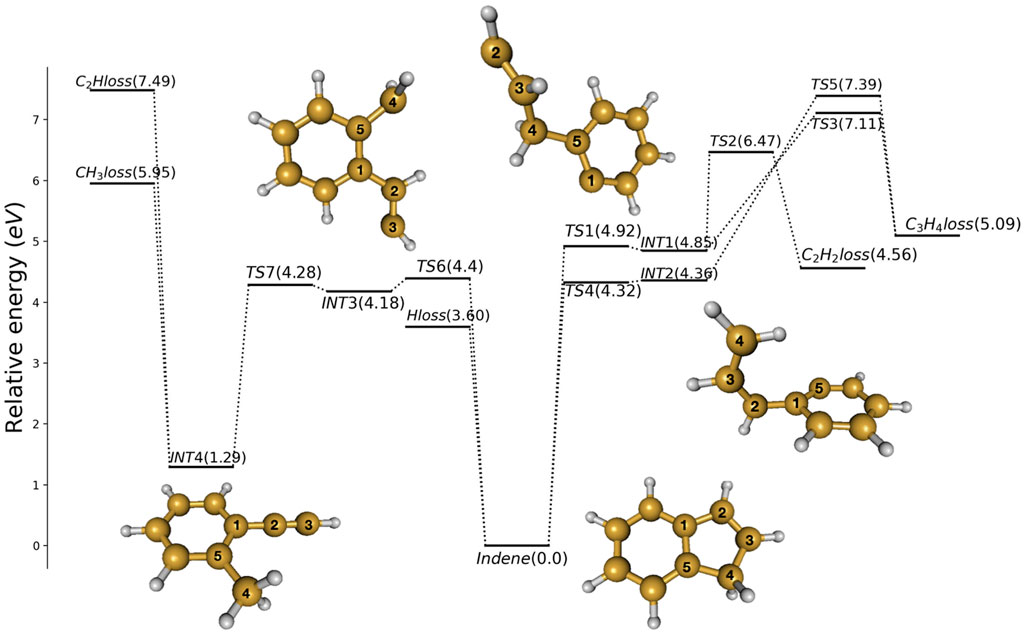
FIGURE 2. Potential energy profile obtained for indene decomposition at CBS-QB3 level of theory. Zero-point energy is included. The structures of indene and the intermediates are shown with the carbon atoms numbered as in Figure 1.
Breaking the C1-C2 bond leads to INT1 via TS1 (at 4.92 eV), see Figure 2. INT1 is 4.85 eV less stable than indene and can react to eliminate ethene (C2H2) and cyclopropene (c-C3H4). INT1 must surmount TS2 (at 6.47 eV) to form C2H2 and bicyclo[4.1.0]hepta-1,3,5-triene. It can alternatively pass through TS3 (at 7.11 eV), breaking the C4-C5 bond, to form C3H4 and benzyne.
The fission of the C4-C5 bond in indene produces INT2, with an energy 4.36 eV above indene. At MP2 level, a saddle-point is found in between indene and INT2, but at the CBS-QB3 level the energy estimated for this saddle-point is nearly 0.04 eV lower than INT2. The nature of this transition state is loose and its motion along the reaction coordinate corresponds to the very low vibrational frequency 98 cm−1. INT2 can react to form c-C3H4 and benzyne by passing TS5 (at 7.39 eV).
It is possible to form a quite stable isomer of indene, viz. 2-methylphenylacetylene which is 1.29 eV less stable than indene itself. Starting from indene this can happen through cleavage of the C3-C4 bond by passing the loose transition state TS6 4.4 eV above indene, to first form the bi-radical INT3. INT3 (at 4.18 eV) is only weakly bound and can via TS7 (at 4.28 eV) easily proceed to form 2-methylphenylacetylene (at 1.29 eV). The newly formed molecule can react to eliminate C2H (at 7.49 eV) or CH3 (at 5.95 eV).
3.2 RRKM results
The harmonic vibrational frequencies, rotational constants and energy barrier heights found above are used to obtain sums and densities of states and then finally energy-dependent (microcanonical) rate constants, k(E)′s, from Eq. 3.
Figure 3 shows k(E)′s that we have obtained by RRKM using direct count for indene fragmentation. The hydrogen elimination reaction channels are barrierless, i.e., there is no intrinsic saddle point along the reaction coordinate. For such reactions, the transition state can be found by a variational approach that finds the minimum flux (sum of states) along the reaction coordinate. The details of these calculations are discussed in the Supplementary Material.
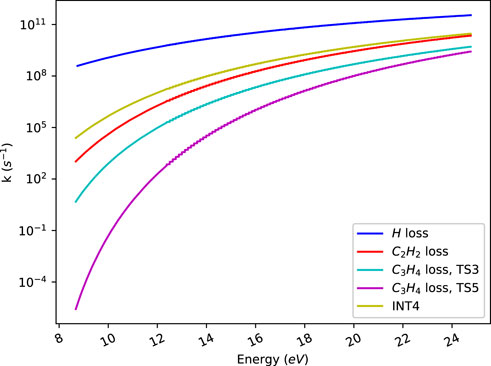
FIGURE 3. Microcanonical rate constants obtained from RRKM calculations. The labels refer to H atom loss from the CH2 group (H loss), C2H2 loss (initiated by C1-C2 bond breaking followed by cleavage of the bond C3-C4), C3H4 loss through transition states 3 (initiated by C1-C2 bond breaking followed by cleavage of the bond C4-C5) and 5 (initiated by C4-C5 bond breaking followed by cleavage of the bond C1-C2) respectively and formation of the isomer 2-methylphenylacetylene (initiated by C3-C4 bond breaking followed by hydrogen shift from C2 to C4). See the text for more details.
A hydrogen atom is most easily lost from the CH2 group due to the low dissociation energy for this process. Thus, in indene such hydrogen atoms require less energy for elimination than hydrogen atoms bonded to sp2 hybridized carbon atoms. Similarly loss of a hydrogen atom from the CH2 group requires less energy than loss of C2H2 or C3H4. The observation in Figure 3 that hydrogen atom loss has the largest rate constant is thus expected. An experimental study on the photo dissociation of hydrogen atoms from the CH2 group in indene obtained a rate constant of 7.4 × 106 s−1 at 193 nm (Yi et al., 1991) corresponding to a photon energy of 6.4 eV. This rate value is close to 1.7 × 107 s−1 predicted by our RRKM calculations.
As seen in Figure 3, C2H2 loss is faster than C3H4 loss. This is in accordance with the 6.47 eV barrier for C2H2 loss, being lower than the barriers for C3H4 loss. C3H4 loss occurs through two pathways with the barrier heights 7.11 and 7.39 eV respectively. The rate for formation of the molecule 2-methylphenylacetylene (INT4) due to isomerization of indene is also plotted in Figure 3. This molecule can further dissociate to for instance eliminate C2H and CH3, but with we have not further investigated these channels.
3.3 ReaxFF MD results
Figure 4 illustrates energy resolved rate constants obtained by our MD simulations using the reactive force field ReaxFF (2008-C/H/O parametrization). Two different sets of simulations were run in which either the initial energy was randomly distributed among all the vibrational modes or deposited into one specific bond of the indene molecule, viz. the C1-C2 bond in Figure 1.
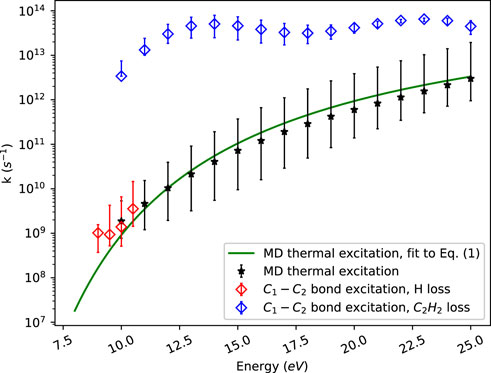
FIGURE 4. ReaxFF MD microcanonical rate constants for thermally excited indene and for excitation of a single carbon-carbon bond in the molecule.
Thermally excited indene fragments through several competing channels involving C-H bond breaking, C-C bond opening and rearrangement of chains of carbon atoms. At the lower energies studied, the dissociation is dominated by the loss of one of the two hydrogen atoms in the CH2 group. At higher energies, product molecules/radicals like C2H2 or C2H3 are also observed. Overall, around 500 simulations at random energies between 8 eV and 25 eV were performed. The obtained total rate constants are fitted to Eq. 1. This gives E0 = 2.54 eV and k0 = 3.73 × 1014 s−1. The error bars in Figure 4 include 67% of the data points and are calculated using a quantile regression (Koenker et al., 2005).
About 500 simulations were performed in which the energy was deposited into the C1-C2 bond. At high energies this leads to ring opening followed by C2H2 or C2H3 elimination. This rate of dissociation is much larger than the corresponding one for thermally excited indene. The fast dissociation of the molecule occurs before energy is redistributed among the vibrational modes. This is a manifestation of apparent non-RRKM behaviour not described by the statistical approach. At lower energies, the opened ring closes again right away and energy is redistributed within the molecule leading to subsequent dissociation of a hydrogen atom, primarily from the CH2 group.
Our electronic structure calculations show that it requires 10.2 eV energy to pass the barrier for C2H2 elimination. This agrees with the sudden drop in C2H2 loss seen in Figure 4 as the energy goes below about 10 eV. Further, the single bond excitation rate constants at energies below 10 eV are in accord with the average dissociation rate constants obtained with thermal excitation. This shows that both direct bond excitation and thermal excitation produce similar results for the lower energies where hydrogen elimination dominates.
Our study does not consider ionization of the molecule. It is expected that for larger molecules the importance of inclusion of ionization diminishes (Zettergren et al., 2021). PAH ions have been studied with on the fly dynamics, see Simon et al. (2017). To include charged species in our MD calculations, reparameterization of ReaxFF for potential terms involving C and H might be necessary in order to achieve quantitative predictions.
4 Discussion
Figure 5 compares our rate constants for indene fragmentation obtained by direct count RRKM based on ab initio calculations with our ReaxFF MD results for thermal excitation of indene. It also includes rate constants for indene fragmentation produced by Eq. 1 using the parameters for E0 and k0 from the study of Allain et al. (1996b). At low energies, where H elimination dominates in both the MD and RRKM calculations, the rate constants obtained by MD and RRKM agree. As energy increases they come to differ by an order of magnitude, the MD rate constants being larger. H loss remains dominant over the whole energy range in the RRKM study. In the MD study however, C2H2 loss becomes roughly as important as H loss at higher energies.
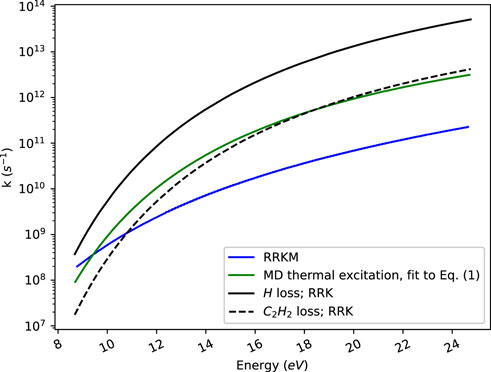
FIGURE 5. Illustration of RRKM, ReaxFF MD with thermal excitation, and RRK modelled microcanonical rate constants.
There can be several reasons for the difference in rate constants between RRKM and ReaxFF MD. Firstly, the ReaxFF potential that we use for the MD simulations may not exactly correspond to the electronic structure calculations on which we have based the RRKM calculations. Further, anharmonicity is not included in the RRKM study, but in the MD study. We surmise however that anharmonicity if anything would lower the RRKM rate constant. We argue that anharmonicity is typically more important at high energies than at low, and the densities of states of the reactants are evaluated at an energy that is higher, by the barrier height, than the energy at which the sum of states at the transition state is evaluated.
It is of course a general problem how to compare classical with quantal calculations. We have performed the MD simulations completely classically and thus fully ignored quantization of energy and thus set the reference energy at the bottom of the potential energy surface for the equilibrium geometry of indene. The RRKM calculations are reported with the energy reference level instead at the zero point level of the reactant, as is customary. If we had placed the reference level at the bottom of the well in the RRKM calculations, those rate constants would have become smaller. This is illustrated for C2H2 loss in Figure 6.
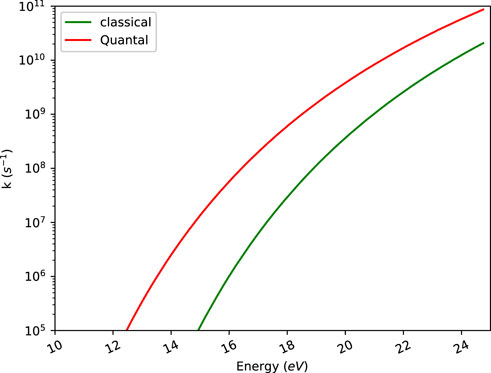
FIGURE 6. RRKM microcanonical rate constants calculated using the classical expression and direct count (Quantal) method for C2H2 loss.
Another reason for the difference between our RRKM and MD rate constants at higher energies may be that internal vibrational relaxation no longer is fast compared to the reaction rate whereby one of the tenets of RRKM theory is not fulfilled. Further, at high energy maybe all of phase space is not explored as dissociation is fast.
In Figure 5 we also show RRK results that are obtained by in Eq. 1 using the parameters for E0 and k0 found in the study on PAHs of Allain et al. (2016b). We find that the RRK modelled rate constants are generally larger than our MD and RRKM results. We note that the parameters that Allain et al. (2016b) used were obtained to fit the RRK model to experimental results for PAHs that only contain sp2 hybridized carbon atoms, i.e., all H atoms on those PAHs have clearly larger dissociation energies than those sitting on the CH2 group in indene. Thus, the RRK rate constants for H atom loss would have been expected to be smaller than ours, rather than larger. It thus appears that the RRK rate constants should not be used for indene, at least not over the whole energy range that we have studied.
It may be noted that at the energy of the experiments by Yi et al. (1991) the RRK rate constant would be 1.0 × 105 s−1, thus clearly below the experimental value of 7.4 × 106 s−1. Our RRKM rate constant is 1.7 × 107 s−1 at this energy, thus only about a factor of two larger than the experimental value. We could not perform MD calculations at this energy as dissociation is too slow to follow by the trajectories.
5 Conclusion
We have presented theoretically obtained, energy resolved, rate constants for photodissiciation of indene using RRKM theory based on electronic structure data and MD simulations using ReaxFF. At lower energies the RRKM and MD results agree. At higher energies the MD simulations give larger rate constants than the RRKM calculations. Several reasons for this were discussed including use of different potentials and non-statistical effects.
We compare our RRKM and MD rate constants with results that we obtain by applying a previous RRK expression (Allain et al., 1996b) to indene. Allain et al. (1996b) used two RRK parameters, set to fit experimental photodissiciation rates for several PAHs. The only remaining variable is determined by the number of atoms in the molecule, i.e., 17 in the case of indene. Our RRKM and MD rate constants are lower than those obtain from the RRK model in the studied energy range 8–25 eV. This is in contrast to what we expected as the RRK model is based on PAHs that only involve hydrogen atoms attached to sp2 hybridized carbon atoms, which have higher dissociation energies than the hydrogens in the CH2 group of indene. We however also note that at the lower energy, 6.4 eV, the RRK expression underestimates an experimentally available rate of Yi et al. (1991) by almost two orders of magnitude, while our RRKM value is about a factor of two larger than the experimental value. Our main conclusion from this is that the photodissiciation rate of PAHs that the RRK expression by Allain et al. (1996b) suggests is quite uncertain and varies too quickly with energy. This implies that astrochemical modelling employing the RRK model may give unreliable PAH abundances.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
SRH, GB, and GN contributed to the conception and design of the study. SRH performed the RRKM calculations. GB performed the MD simulations. All authors contributed to writing the manuscript, and read, and approved the submitted version.
Funding
Financial support from the Knut and Alice Wallenberg foundation is gratefully acknowledged. The computations involved the Swedish National Infrastructure for Computing (SNIC) at Chalmers Centre for Computational Science and Engineering (C3SE) partially funded by the Swedish Research Council through grant no. 2018-05973.
Acknowledgments
The authors thank Thiebaut-Antoine Schirmer for pointing to the importance of photodissociation of PAHs and Stefan Andersson for suggesting indene as an interesting molecule to investigate.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2023.1134729/full#supplementary-material
References
Allain, T., Leach, S., and Sedlmayr, E. (1996b). Photodestruction of pahs in the interstellar medium. ii. influence of the states of ionization and hydrogenation. Astronomy Astrophysics 305, 616.
Allain, T., Leach, S., and Sedlmayr, E. (1996a). Photodestruction of pahs in the interstellar medium. i. photodissociation rates for the loss of an acetylenic group. Astronomy Astrophysics 305, 602.
Barker, J., Nguyen, T., Stanton, J., Aieta, C., Ceotto, M., Gabas, F., et al. (2022). Multiwell-2022 software suite. jr barker. Ann Arbor, Michigan, USA: university of michigan.
Burkhardt, A. M., Lee, K. L. K., Changala, P. B., Shingledecker, C. N., Cooke, I. R., Loomis, R. A., et al. (2021). Discovery of the pure polycyclic aromatic hydrocarbon indene (c-c9h8) with gotham observations of tmc-1. Astrophysical J. Lett. 913, L18. doi:10.3847/2041-8213/abfd3a
Cernicharo, J., Agúndez, M., Cabezas, C., Fuentetaja, R., Tercero, B., Marcelino, N., et al. (2022a). Discovery of c5h+ and detection of c3h+ in tmc-1 with the quijote line survey. Astronomy Astrophysics 657, L16. doi:10.1051/0004-6361/202142992
Cernicharo, J., Agúndez, M., Cabezas, C., Tercero, B., Marcelino, N., Pardo, J. R., et al. (2021). Pure hydrocarbon cycles in tmc-1: Discovery of ethynyl cyclopropenylidene, cyclopentadiene and indene. Astronomy astrophysics 649, L15. doi:10.1051/0004-6361/202141156
Cernicharo, J., Fuentetaja, R., Agúndez, M., Kaiser, R. I., Cabezas, C., Marcelino, N., et al. (2022b). Discovery of fulvenallene in tmc-1 with the quijote line survey. Astronomy Astrophysics 663, L9. doi:10.1051/0004-6361/202244399
Chenoweth, K., van Duin, A. C. T., and Goddard, W. A. (2008). Reaxff reactive force field for molecular dynamics simulations of hydrocarbon oxidation. J. Phys. Chem. A 112, 1040–1053. doi:10.1021/jp709896w
Doddipatla, S., Galimova, G. R., Wei, H., Thomas, A. M., He, C., Yang, Z., et al. (2021). Low-temperature gas-phase formation of indene in the interstellar medium. Sci. Adv. 7, eabd4044. doi:10.1126/sciadv.abd4044
Franchini, M., Trnka, T., Yakovlev, A., van Lenthe, E., Philipsen, P., van Vuren, T., et al. (2021). Ams, scm, theoretical chemistry. amsterdam, the netherlands: vrije universiteit.
Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (2016). Gaussian∼16 revision C.01. Wallingford CT: Gaussian Inc.
Furman, D., and Wales, D. J. (2020). A well-behaved theoretical framework for reaxff reactive force fields. J. Chem. Phys. 153, 021102. doi:10.1063/5.0013906
Holbrook, K., Pilling, M., and Robertson, S. (1996). Unimolecular reactions 1996. Germany: Springer.
Jochims, H., Ruhl, E., Baumgartel, H., Tobita, S., and Leach, S. (1994). Size effects on dissociation rates of polycyclic aromatic hydrocarbon cations: Laboratory studies and astophysical implications. Astrophysical J. 420, 307–317. doi:10.1086/173560
Kislov, V., Nguyen, T., Mebel, A., Lin, S., and Smith, S. (2004). Photodissociation of benzene under collision-free conditions: An ab initio/rice–ramsperger–kassel–marcus study. J. Chem. Phys. 120, 7008–7017. doi:10.1063/1.1676275
Koenker, R., Chesher, A., and Jackson, M. (2005). Quantile regression. Cambridge: Econometric Society Monographs Cambridge University Press.
Le Page, V., Snow, T. P., and Bierbaum, V. M. (2001). Hydrogenation and charge states of PAHsPAHs in diffuse clouds. I. Development of a model. Astrophysical J. Suppl. Ser. 132, 233–251. doi:10.1086/318952
Léger, A., and d’Hendecourt, L. (1985). Are polycyclic aromatic hydrocarbons the carriers of the diffuse interstellar bands in the visible? Astronomy Astrophysics 146, 81–85.
Leitner, D. M., Levine, B., Quenneville, J., Martínez, T. J., and Wolynes, P. G. (2003). Quantum energy flow and trans-stilbene photoisomerization: An example of a non-rrkm reaction. J. Phys. Chem. A 107, 10706–10716. doi:10.1021/jp0305180
Ling, Y., and Lifshitz, C. (1998). Time-dependent mass spectra and breakdown graphs. 21. c14h10 isomers. J. Phys. Chem. A 102, 708–716. doi:10.1021/jp973167w
Micelotta, E., Jones, A., and Tielens, A. (2010a). Polycyclic aromatic hydrocarbon processing in a hot gas. Astronomy Astrophysics 510, A37. doi:10.1051/0004-6361/200911683
McGuire, B. A., Burkhardt, A. M., Kalenskii, S., Shingledecker, C. N., Remijan, A. J., Herbst, E., et al. (2018). Detection of the aromatic molecule benzonitrile (c-c6h5cn) in the interstellar medium. Science 359, 202–205. doi:10.1126/science.aao4890
McGuire, B. A., Loomis, R. A., Burkhardt, A. M., Lee, K. L. K., Shingledecker, C. N., Charnley, S. B., et al. (2021). Detection of two interstellar polycyclic aromatic hydrocarbons via spectral matched filtering. Science 371, 1265–1269. doi:10.1126/science.abb7535
Micelotta, E., Jones, A., and Tielens, A. (2010b). Polycyclic aromatic hydrocarbon processing in interstellar shocks. Astronomy Astrophysics 510, A36. doi:10.1051/0004-6361/200911682
Møller, C., and Plesset, M. S. (1934). Note on an approximation treatment for many-electron systems. Phys. Rev. 46, 618–622. doi:10.1103/physrev.46.618
Montgomery, J. A., Frisch, M. J., Ochterski, J. W., and Petersson, G. A. (2000). A complete basis set model chemistry. vii. use of the minimum population localization method. J. Chem. Phys. 112, 6532–6542. doi:10.1063/1.481224
Murga, M., Wiebe, D., Sivkova, E., and Akimkin, V. (2019). Shiva: A dust destruction model. Mon. Notices R. Astronomical Soc. 488, 965–977. doi:10.1093/mnras/stz1724
Nguyen, T. L., and Barker, J. R. (2010). Sums and densities of fully coupled anharmonic vibrational states: A comparison of three practical methods. J. Phys. Chem. A 114, 3718–3730. doi:10.1021/jp100132s
Nordholm, S., and Bäck, A. (2001). On the role of nonergodicity and slow ivr in unimolecular reaction rate theory—A review and a view. Phys. Chem. Chem. Phys. 3, 2289–2295. doi:10.1039/b009963p
Steinfeld, J. I., Francisco, J. S., and Hase, W. L. (1999). Chemical kinetics and dynamics. Upper Saddle River, NJ: Prentice-Hall.
Tielens, A. G. G. M., and Allamandola, L. J. (2010). Physics and chemistry at low temperatures. Patent country: Pan Stanford Publishing.
van Duin, A. C. T., Dasgupta, S., Lorant, F., and Goddard, W. A. (2001). Reaxff: A reactive force field for hydrocarbons. J. Phys. Chem. A 105, 9396–9409. doi:10.1021/jp004368u
Yi, W., Chattopadhyay, A., and Bersohn, R. (1991). Unimolecular dissociation of cyclopentadiene and indene. J. Chem. Phys. 94, 5994–5998. doi:10.1063/1.460433
Zettergren, H., Domaracka, A., Schlathölter, T., Bolognesi, P., Díaz-Tendero, S., Łabuda, M., et al. (2021). Roadmap on dynamics of molecules and clusters in the gas phase. Eur. Phys. J. D 75, 152–153. doi:10.1140/epjd/s10053-021-00155-y
Keywords: indene, ReaxFF MD, RRKM, PAH, photodegradation
Citation: Hashemi SR, Barinovs G and Nyman G (2023) A ReaxFF molecular dynamics and RRKM ab initio based study on degradation of indene. Front. Astron. Space Sci. 10:1134729. doi: 10.3389/fspas.2023.1134729
Received: 30 December 2022; Accepted: 23 February 2023;
Published: 07 March 2023.
Edited by:
Ankan Das, Institute of Astronomy Space and Earth Science, IndiaReviewed by:
Shubhadip Chakraborty, GITAM University, IndiaAndrea Maranzana, University of Turin, Italy
Copyright © 2023 Hashemi, Barinovs and Nyman. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Gunnar Nyman, bnltYW5AY2hlbS5ndS5zZQ==
 S. Rasoul Hashemi
S. Rasoul Hashemi Girts Barinovs2
Girts Barinovs2 Gunnar Nyman
Gunnar Nyman