- 1Bogolyubov Institute for Theoretical Physics, Kyiv, Ukraine
- 2Khmelnytskyi National University, Khmelnytskyi, Ukraine
Recently, the μ-deformation-based approach to modeling dark matter, which exploits μ-deformed thermodynamics, was extended to the study of galaxy halo density profile and of the rotation curves of a number of (dwarf or low brightness) galaxies. For that goal, μ-deformed analogs of the Lane–Emden equation (LEE) have been proposed, and their solutions describing density profiles obtained. There are two seemingly different versions of μ-deformed LEE which possess the same solution, and so we deal with their equivalence. From the latter property we derive new, rather unusual, μ-deformed Heisenberg algebra (HA) for the position and momentum operators, and present the μ-HA in few possible forms (each one at μ → 0 recovers usual HA). The generalized uncertainty relation linked with the new μ-HA is studied, along with its interesting implications including the appearance of the quadruple of both maximal and minimal lengths and momenta.
1 Introduction
The suggestion of the existence of minimal nonzero (uncertainty of) length linked with generalized uncertainty principle (GUP) or relation (GUR) has been advanced in the context of string theory and quantum gravity (Gross and Mende, 1988; Amati et al., 1989; Adler and Santiago, 1999; Scardigli, 1999; Maziashvili, 2006), see also (Chang et al., 2011) and the reviews (Garay, 1995; Hossenfelder, 2013). It was shown to follow from modified or deformed
Extension (Kempf et al., 1995) of the Heisenberg algebra (HA). It is worth to mention that the concept of maximum observable momenta can play as well important role, see, e.g., (Ali et al., 2009). Such a quantity was predicted, in particular, within the doubly special relativity theory suggesting rather simple (with terms linear and quadratic in momentum) modification of the right hand side of commutators (Magueijo and Smolin, 2002; Magueijo and Smolin, 2005). Further it became clear that besides such a minimal extension of the original HA, a lot of generalizations are possible, suggesting diverse ways to generalize (or deform) the HA. As a tools to classify diverse forms of deformed HA, the concept of deformation function(s) is of importance, see, e.g., (Saavedra and Utreras, 1981; Jannussis, 1993; Gavrilik et al., 2010; Dorsch and Nogueira, 2012; Maslowski et al., 2012; Gavrilik and Kachurik, 2016a). Clearly, the choice of such function must determine the corresponding GUR. As usual, most of the authors deal with position-momentum commutation relations of deformed HA that involve particular function of X, p and deformation parameter(s) in its right hand side (Jannussis, 1993; Dorsch and Nogueira, 2012; Maslowski et al., 2012). It is also possible that both the right and left hand sides of defining commutation relation are appropriately deformed (Gavrilik and Kachurik, 2012), although such approach may be overlapping with the case of standard commutator and the terms containing XP and PX in its right-hand side as it was considered in (Quesne and Tkachuk, 2007).
In the present paper, a special form of deformed HA will be derived in the context of the so-called μ-deformation based approach aimed to model (Gavrilik et al., 2018; Gavrilik et al., 2019) basic properties of dark matter that surrounds dwarf galaxies, and its consequences analyzed.
The case of GUR related with the minimal (ΔX)min is the best known and well studied one. In relation with this, due to the conjugated roles of position and momentum, the concept of (ΔP)min has appeared. As it was demonstrated in (Kempf, 1997), a single theory—single extended or generalized HA (GHA) and the corresponding GUR do exist which can jointly accommodate the both special quantities, (ΔX)min and (ΔP)min.
Then, an interesting question arises whether it is possible that the opposite concept of maximal uncertainties for the momentum and/or the position does exist. Quite recently, it was shown in some papers that such a possibility indeed can be realized (Pedram, 2012; Perivolaropoulos, 2017; Bensalem and Bouaziz, 2019; Skara and Perivolaropoulos, 2019; Hamil and Lutfuoglu, 2021; Bensalem and Bouaziz, 2022; Pramanik, 2022). Moreover, as a generalization of the already mentioned unified treatment of A. Kempf, in the work (Perivolaropoulos, 2017) of L. Perivolaropoulos, it was explicitly shown that one can provide a theory (based on appropriate generalization of HA) which incorporates the whole quadruple of (ΔX)min, (ΔP)min, (ΔP)max, and (ΔX)max.
Usual treatments in the most of papers are in a sense model-independent, implying a kind of universality. That means, physical meaning of (ΔX)min, (ΔP)min, (ΔP)max, and (ΔX)max is rather universal and depends on Planck length or its inverse, i.e., Planck energy scale (Planck mass).
On the contrary, our treatment is based on (related with) special deformed HA deduced in the framework of particular model of dark matter. It is remarkable that all the four quantities: (ΔX)min, (ΔP)min, (ΔP)max, and (ΔX)max do appear. So it is clear and natural that the physical meaning of this quadruple is tightly linked with physics of the model, i.e., with properties of the halo of DM hosted by dwarf galaxies.
For our case (connection with DM) some motivation was due to the work (Perivolaropoulos, 2017), since therein the cosmology-related uncertainty relation was explored, along with clear meaning of maximal length: as suggested in (Perivolaropoulos, 2017), this quantity can be naturally interpreted as cosmological horizon.
The uncertainty relation in its initial form due to Heisenberg is linked with the standard commutation relation and is shared by different states. Unlike, for all the deformed versions of HA, explicit dependence of GUR on particular state does appear—for deformed oscillators this was noticed in the pioneer papers (Biedenharn, 1989; Macfarlane, 1989). In our present paper, just this fact/property is in the focus and exploited to full extent.
Unlike the approach perceived in (Harko, 2011) and some other papers also exploring galaxy rotation curves with the use of the well-known Lane–Emden equation (LEE), in our line of research we deal with the (μ-)Bose-condensate model of dark matter (Gavrilik et al., 2018), and with such tool as μ-deformed analogs (Gavrilik et al., 2019) of LEE. In general, as it is well-known, deformation of an object under study is not unique, and in (Gavrilik et al., 2019) we encountered two different possible forms of μ-deformed LEE, with the corresponding different sets of solutions, one of which being the deformed function sinμ(kr)/(kr). In the present work, the third form of LEE will be introduced that nevertheless possesses the indicated solution as well. Just from the requirement of equivalence of two seemingly different deformed versions of LEE, the new μ-deformed HA can be deduced and its basic properties and consequences explored.
The paper is structured as follows. In Section 2, some basics of μ-deformation and μ-deformed calculus are presented. In Section 3.1 we describe relevant deformed analogs of LEE and, from the condition of their equivalence, obtain the μ-analog of HA which is the central object of this work. The corresponding GUR which involves the parameter μ is derived, and its main properties are explored in Section 3.2, including the appearance of minimal and maximal uncertainties of both position and momentum. Section 3.3 is devoted to discussion of implications of these quantities for dark matter. The paper is ended with concluding remarks.
2 Deformed functions and calculus
2.1 Basis functions
The so-called μ-bracket of a number or operator X,
and the related μ-deformed oscillator have been introduced 3 decades ago in (Jannussis, 1993). More recently, there appeared some papers (Gavrilik et al., 2010; Gavrilik and Mishchenko, 2012; Gavrilik et al., 2013) in which the μ-deformation based approach was initiated and developed.
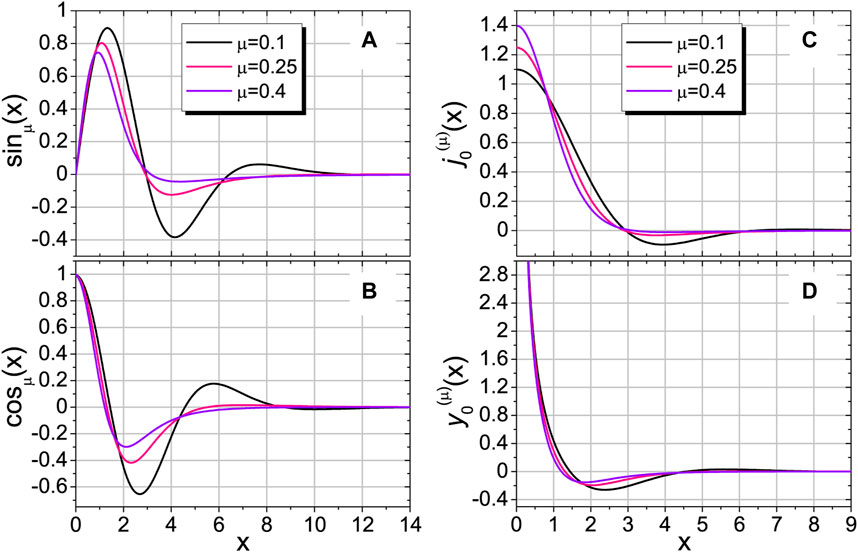
For our purposes we define the μ-deformed trigonometric function (see (Gavrilik et al., 2013; Gavrilik et al., 2019) and references therein) as
where [n]μ! = [1]μ [2]μ … [n]μ. Clearly, at μ → 0 one recovers customary sine and cosine.
For our purposes, we introduce the μ-deformed analogs of spherical Bessel functions, namely,
At μ = 0 these reduce to the familiar Bessel functions.
The physical motivation for introducing these functions is two-fold: the first one in Eq. (3) describes the density profile of the dark matter halo and also leads to the rotation curves within the μ-deformed extension (Gavrilik et al., 2019) of the Bose-condensate model, while both functions, taken jointly, are of importance for constructing the representation space of the position and momentum operators, see Sections 3.1–3.2 below.
Since the applied deformation concerns mainly the basic trigonometric functions, let us study sinμx and cosμx in detail. Contracting the corresponding series to the Gaussian hypergeometric function, we can then represent them in the analytic form
where
Therefore, in the case of μ-deformation, the main trigonometric identity is written as follows:
The behavior of the μ-deformed trigonometric and spherical functions is shown in Figure 1.
In principle, it is possible to express the deformed trigonometric functions in terms of the μ-deformed exponential function. The μ-analogs of exponential and logarithmic functions are
which give us the known functions at μ → 0− due to the asymptotic formulas:
Note that the μ-deformed functions exhibit a non-trivial property at μ > 0:
Focusing on the problems with spherical symmetry, we need to define an inner product ⟨f|g⟩ in terms of which the real functions
where the asterisk means complex conjugation; the Latin indexes i, j run from 1 to 2.
For the orthogonality of sin φ and cos φ on the interval φ ∈ [0; π], we constitute ad hoc
and obtain
where R(μ) coincides with the first zero of sinμx.
Expanding these as.
We see that the known quantities are restored at μ = 0.
2.2 Deformed differential calculus
We would like to define the μ-deformed derivative
The actions of
Were the prime means ordinary differentiation.
We see that ϕ(x) = f′(x) at μ → 0 due to vanishing (s/x)1/μ for s < x. By definition, the derivative
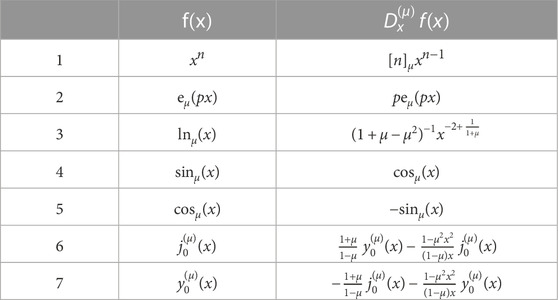
The μ-deformed derivatives of some functions are collected in Table 1. To derive expressions 4–7, we have used the known auxiliary integrals:
On the base of relations 4–5 (not 6–7) in Table 1, we define the Hermitian momentum operator
so that
To demonstrate the action of
In addition, we consider the radial part
It is easy to verify for positive n that
We also verify that
by the use of the integrals
3 Deformed Heisenberg algebra and uncertainty principle
3.1 Deformed equations and Heisenberg algebra
Here we are going to present the equations of some models using deformed differential calculus. The main model for us, from which the deformed Heisenberg algebra will follow, is described by the deformation of the Lane–Emden equation (LEE) for finite density function ρ(r) in the two possible formulations.
Where
Note that the version Eq. 26 of μ-deformed LEE was already dealt with earlier in (Gavrilik et al., 2019), whereas the version in Eq. 27 is completely new, unpublished one. As seen, gμ(r) → 1 and hμ(r) → 1 at μ → 0.
It is important that, due to the special form of gμ(r) and hμ(r), these two μ-deformed versions of LEE have the same physical solution
As result, we have come to the new (μ-deformed) generalization of Heisenberg algebra.
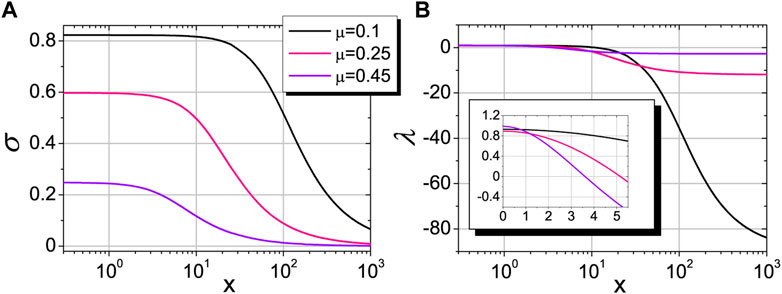
The functions λ(x) and σ(x) are real for 0 < μ < 0.5, tend to 1 at μ → 0, and are shown in Figure 2. We have 0 ≤ σ(x) ≤ 1, while the maximum of λ(x) is determined by λ(0) and is equal to
Although the function λ(x) has a tail in negative values for
as shown in Figure 2, consideration of the problem over finite interval of x ∈ [0; R(μ)] with R(μ) ≤ xmax(μ) for
It seems to be of interest to consider, elsewhere, the quantum-mechanical problem of the propagation of a particle, viewed as a spherical wave Ψ(r) in a space curved due to μ-deformation. Without specifying the boundary condition, it can be formulated as follows:
where the momentum operator Eq. 19 for x = r is used. Let us remark again that the operator
In view of the definition Eq. 19 of the momentum operator, we formulate our μ-deformed Heisenberg algebra:
In what follows, we will focus on the study of the uncertainty principle (relation) which follows from the algebra Eq. 34.
3.2 Generalized uncertainty principle
Denoting the standard deviations as
we proceed to the analysis of the generalized uncertainty relation (GUP)
where the commutator is taken from Eq. 34.
To gain insight into the general properties of Eq. 36 for the μ-deformed Heisenberg algebra Eq. 34, let us combine Eq. 34 with its Hermitian conjugate to obtain
Applying Eq. 36 to this commutation relation, we get
Taking into account that 1 ≥ σ(x) > 0 for μ < 0.5 in the left hand side, we come to the GUP
To evaluate the averages, we specify the states similarly to quantum ones. So, let us consider a normalized mixed state |ξ⟩ for
Here
In fact, the mixed state |ξ⟩ represents a general solution to the μ-deformed LEE, given by Eq. 26 and Eq. 27. Since the μ-deformed LEE is formulated for the local density of matter and, therefore, basically differs from the complex-valued Schrödinger equation, it is natural to describe its solution from Eq. 40 in terms of real-valued functions. Although the state |0⟩ for ξ = 0, such that
Thus, we define the mean:
for fixed ξ ∈ [0; 2π] and 0 < μ < 0.5.
In contrast to quantum mechanics, Eq. 41 suggests to evaluate a mean of some operator (…) in the basis generated by the μ-deformed LEE. There is no mathematical incorrectness in choosing basis functions coinciding with physical distributions. Only in turning to an interpretation, does one face the averaging (of powers) of the distribution function itself (this also happens in multifractal analysis).
The necessary matrix elements are given by.
It is immediately seen that
Therefore, the standard deviation ΔP = 1 is fixed for the set of states {|ξ⟩}.
On the other hand, let us introduce the functions
which represent the averages Δx and ⟨λ(x)⟩, respectively.
Thus, in the basis of the μ-deformed spherical waves, one has ΔP = 1, and it is required that
This relation can be analyzed with the help of Figure 3A.
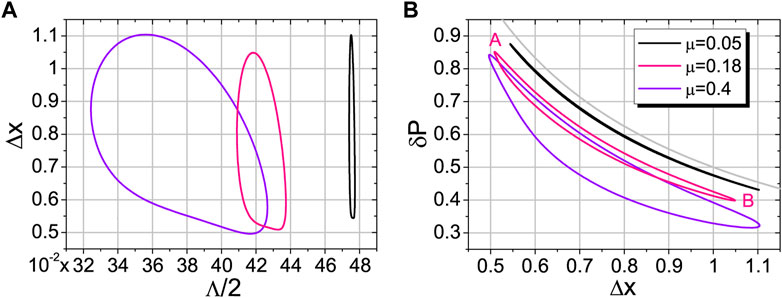
FIGURE 3. (A): Position deviation Δx (ξ, μ) versus mean ⟨λ(x)⟩= Λ(ξ, μ), which are computed in the state |ξ⟩ at fixed μ (B): Limiting momentum deviation δP (ξ, μ)= Λ/(2Δx) versus Δx (ξ, μ). Turning points of the pink banana-like curve are A (0.51;0.85), B (1.05;0.4). Grey line corresponds to δP =1/(2Δx).
Let us introduce the auxiliary momentum variance, accounting for Eq. 47:
We see that δP (ξ, μ) ≤ ΔP = 1 and δP (ξ, μ) Δx (ξ, μ) = Λ(ξ, μ)/2 by definition. The behavior of δP (ξ, μ) is shown in Figure 3B.
The admissible domain of variety of the running values of Δx and ΔP is shown in Figure 4. We see that the black and pink curves are in antiphase regime, as it should be. For comparison, the violet curve describes the change in the deviation Δx according to the hyperbolic law in accordance with the standard Heisenberg algebra.
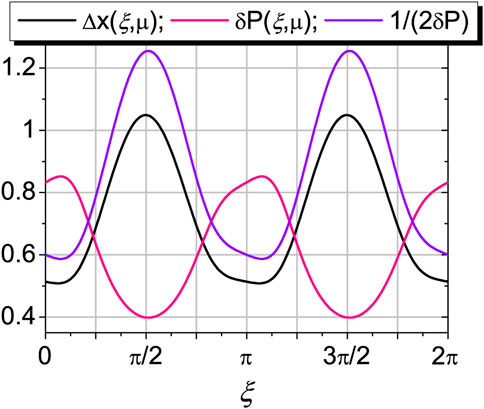
FIGURE 4. Dependence of the lower limit deviations Δx (ξ, μ) and δP (ξ, μ) on the state labeled by ξ at μ =0.18. The running deviations Δx and ΔP satisfy the GUP Δx ΔP ≥Λ/2 and vary in the ranges Δx (ξ, μ)≤ Δx ≤ R (μ =0.18)≃2.89 and δP (ξ, μ)≤ ΔP ≤1.
3.2.1 Alternative approach
To confirm the validity of Eq. 39 for the algebra Eq. 34 non-linear in x, it is worth to develop an alternative calculation scheme applicable to various ways of writing the commutator for x and
where
To analyze the GUP given by Eq. 36 for this commutation relation, we assume that the brackets ⟨(…)⟩ mean the quantum average over the state defined by the real wave function in the coordinate representation. Then, the action of the operator
when the positive first term on the right hand side dominates the second one.
In view of the inequality
At this stage, we obtain
To evaluate
Due to the Cauchy–Schwartz inequality
Since the dark matter flux is assumed to be absent in the halo, one can put
Substituting it into Eq. 36 and accounting for ⟨1⟩ = 1, we arrive at.
Where the new mean ⟨(…)⟩W with additional convex weighting function W(x) arises.
For a given function W(x) we get
where ⟨δW(x)δλ(x)⟩ is a covariance between the convex function W(x) and concave λ(x), and it determined by deviations like δf(x) = f(x) − ⟨f(x)⟩.
Since the function σ(x) (and W(x)) changes only slightly over the interval x ∈ [0; R(μ)] in Figure 2A, it can be approximated by a constant close to σ(0) when calculating integrals. This provides δW(x) → 0 and numerically leads to expressions:
when we use ⟨(…)⟩ = ⟨ξ|(…)|ξ⟩ in the range 0 < μ < 0.5.
This circumstance leads again to Eq. 39 for the states |ξ⟩, that is just Eq. 47.
Note that the appearance of the mean Eq. 57 is associated with the initial Eq. 49 for the commutation relation. In other cases, we may only encounter means of type Eq. 59, where it would be justified to use the estimate 1 ≥⟨σ(x)⟩.
3.3 Application to dark matter
Let us remind the connection between the operators in terms of the dimensionless variable x = kr and the operators of the physical radial coordinate r and the momentum
where k is the parameter of Eqs 26 and 27 and has the dimension of inverse length; the operator
The most successful results of paper (Gavrilik et al., 2019) for describing the dark matter halo of dwarf galaxies based on the μ-deformed Lane–Emden equation were obtained in the following range of parameters:
Using the turning points A ((Δx)min; (δP)max) and B ((Δx)max; (δP)min) for fixed μ as in Figure 3B, we relate extreme physical values Δr and ΔPr with dimensionless ones Δx and δP as.
The calculation results are collected in Table 2. Therein, we present the obtained data for five dwarf galaxies (from the eight ones given in Table 1 of (Gavrilik et al., 2019)), because just for these galaxies the μ-deformation based description of the rotation curves is most successful with respect to earlier approaches, as it provides the best agreement with observational data (certainly better then if one uses the profile from the usual Bose-condensate model of DM being the solution of non-deformed Lane–Emden equation as in (Harko, 2011), or uses the famous Navarro–Frenk–White profile (Navarro et al., 1997)).
Of course, the remaining three galaxies can also be considered, but the choice of five ones is both sufficient, trustful, and best suited for our treatment and conclusions.
Note that both the Lane–Emden equation and its μ-deformed extensions determine the distribution function ρ(r) of the matter, not the wave function of single particle. Therefore, the mean Eq. 41 is a quadratic form in the distribution, related here with |0⟩ which differs by a multiplicative constant defining ρ(0) (Gavrilik et al., 2019). Generally speaking, the state |0⟩ may not determine the turning points of a banana-like curve in the (Δx, δP) plane in Figure 3B, along with the extreme values of the deviations Δr and ΔPr. Nevertheless, the mathematically correct mean Eq. 41 can be used to obtain new additional information about dark matter, even by means of considering the moments ⟨ρn⟩ of the distribution similarly to multifractal analysis. Besides, the extreme deviations set the limits for the fluctuations of physical quantities at ξ = 0.
Without a deep study of the structure of averages here, let us analyze the physical consequences of the data in Table 2. We see that in the non-relativistic theory the momentum deviation ΔPr = m Δυr, where m is the particle mass, Δυr is the deviation of particle radial velocity υr. Since the original work (Gavrilik et al., 2019) was using bosons with m ∼ 10–22 eV/c2, we obtain from Table 2 that Δυr ∼ 10−5c in units of the speed of light c. Moreover, deviation of the kinetic energy
Due to the GUP given by Eq. 39, we relate the temperature Teff of the spherical layer in the vicinity of ⟨r⟩ to its width 2Δr:
This formula holds for a macroscopic system of finite volume when Δr does not exceed the radius of the system, and it shows that a smaller domain may have a higher temperature, and vice verse.
It is worth to note that the mean ⟨λ⟩ in Eq. 64 takes values in the limited interval ⟨λ⟩ = Λ(ξ, μ) ∈ [Λmin, Λmax], where the positive Λmin and Λmax depend on μ (see Eq. 46; Figure 3A). For μ = 0.18, we have Λmin ≃ 0.818 and Λmax ≃ 0.875.
4 Concluding remarks
In this work we have studied unusual consequences of the new (μ-deformed) generalization of the Heisenberg algebra Eqs 29 and 34 which is special as it was derived within the extension of Bose-condensate dark matter model based on μ-deformation. From the generalized algebra we obtained non-trivial GUR that generates minimal and maximal uncertainties of both positions (minimal/maximal lengths) and momenta. The obtained GUR is strictly dependent on the states (labeled by ξ) of the system, and such dependence was exploited to full extent.
In Table 2, the galaxies M81dwB and IC 2574 look as the two “extreme” cases. Namely, for the latter we have the largest (Δr)max and (Δr)min, while for the former these quantities show smallest values. Clearly, the situation concerning
For the considered galaxies (each labeled by its specific value of μ) we conclude: since the particle mass is same (namely, 10–22 eV/c2), we have differing scattering lengths in halos of different galaxies (vice versa, would we assume same scattering length for all the five galaxies we would have somewhat differing masses of DM particle in different galaxies, though this second option seems to be less realistic). As already shown in (Harko, 2011), where the BEC DM model is also based on the LEE, there is no universality of model parameters when describing all admissible objects. In fact, this issue remains in our model, which improves the previously fitted rotation curves by including an additional parameter μ. Physically, we can only control the applicability conditions of our model: consider DM-dominated dwarf galaxies leaving aside their rigid rotation, which contributes to the distribution function (Zhang et al., 2018; Nazarenko, 2020). Therefore, giving clear physical meaning to differing scattering lengths in halos of different galaxies remains an interesting task for future study.
Note that the parameter k is related to the observed radius rgal of the galactic halo by krgal = R(μ), where the right-hand side is determined by the parameter R(μ) from Eq. 12, replacing π = R (0) in the non-deformed case. We can easily find a small difference (of several percent) between the values of rgal in the deformed and non-deformed cases, by comparing these with the galaxy radii from (Harko, 2011). However, the simulation of rotation curves is more successful in the deformed case, as shown in (Gavrilik et al., 2019).
It is worth to remark that the values of (Δr)max and (Δr)min for the two galaxies M81dwB and IC 2574, and the others in Table 2, reside well within the observed sizes of DM halos as it should. Accordingly, the values of
It is of interest to analyze possible special meaning of our results on the existence of finite (Δr)max and (Δr)min in the context of treatment in (Lee and Lim, 2010; Lee, 2016) of minimum length scale of galaxies (note that for the candidate length scales one can take into consideration such concepts as coherence length, Compton wavelength, quantum Jeans length scale, gravitational Bohr radius, and de Broglie wavelength, see (Lee and Lim, 2010) and references therein). Time dependence of some of these quantities, e.g., characteristic length scale
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
AG and AN acknowledge support from the National Academy of Sciences of Ukraine by its Project No. 0122U000888.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2023.1133976/full#supplementary-material
References
Adler, R. J., and Santiago, D. I. (1999). On gravity and the uncertainty principle. Mod. Phys. Lett. A 14, 1371–1381. arXiv:gr-qc/9904026. doi:10.1142/s0217732399001462
Ali, A. F., Das, S., and Vagenas, E. C. (2009). Discreteness of space from the generalized uncertainty principle. Phys. Lett. B 678, 497–499. doi:10.1016/j.physletb.2009.06.061
Amati, D., Ciafaloni, M., and Veneziano, G. (1989). Can spacetime be probed below the string size? Phys. Lett. B 216, 41–47. doi:10.1016/0370-2693(89)91366-X
Bagchi, B., and Fring, A. (2009). Minimal length in quantum mechanics and non-Hermitian Hamiltonian systems. Phys. Lett. A 373, 4307–4310. doi:10.1016/j.physleta.2009.09.054
Bensalem, S., and Bouaziz, D. (2019). Statistical description of an ideal gas in maximum length quantum mechanics. Phys. A Stat. Mech. its Applic. 523, 583–592. doi:10.1016/j.physa.2019.02.033
Bensalem, S., and Bouaziz, D. (2022). Thermostatistics in deformed space with maximal length. Phys. A Stat. Mech. its Applic. 585, 126419. arXiv:2010.02203 [cond-mat.stat-mech]. doi:10.1016/j.physa.2021.126419
Biedenharn, L. C. (1989). The quantum group SUq(2) and a q-analogue of the boson operators. J. Phys. A Math. Gen. 22, L873–L878. doi:10.1088/0305-4470/22/18/004
Chang, L. N., Lewis, Z., Minic, D., and Takeuchi, T. (2011). On the minimal length uncertainty relation and the foundations of string theory. Adv. High Energy Phys. 2011, 1–30. arXiv:1106.0068. doi:10.1155/2011/493514
Chung, W. S., Gavrilik, A. M., and Nazarenko, A. V. (2019). Photon gas at the Planck scale within the doubly special relativity. Phys. A Stat. Mech. its Applic. 533, 121928. arXiv:1808.01243. doi:10.1016/j.physa.2019.121928
Dorsch, G. C., and Nogueira, J. A. (2012). Maximally localized states in quantum mechanics with a modified commutation relation to all orders. Int. J. Mod. Phys. A 27, 1250113. arXiv:1106.2737v3. doi:10.1142/S0217751X12501138
Garay, L. J. (1995). Quantum gravity and minimum length. Int. J. Mod. Phys. A 10, 145–165. arXiv:gr-qc/9403008. doi:10.1142/s0217751x95000085
Gavrilik, A., Kachurik, I. I., and Khelashvili, M. (2019). Galaxy rotation curves in the μ-deformation-based approach to dark matter. Ukr. J. Phys. 64, 1042. doi:10.15407/ujpe64.11.1042
Gavrilik, A., and Kachurik, I. (2016). Nonstandard deformed oscillators from q- and p, q-deformations of Heisenberg algebra. SIGMA 12, 047. doi:10.3842/SIGMA.2016.047
Gavrilik, A., and Kachurik, I. (2019). Pseudo-Hermitian position and momentum operators, Hermitian Hamiltonian, and deformed oscillators. Mod. Phys. Lett. A 34, 1950007. doi:10.1142/S021773231950007X
Gavrilik, A., and Kachurik, I. (2012). Three-parameter (two-sided) deformation of Heisenberg algebra. Mod. Phys. Lett. A 27, 1250114. arXiv:1204.2817v2 [math-ph]. doi:10.1142/S0217732312501143
Gavrilik, A. M., Kachurik, I. I., Khelashvili, M. V., and Nazarenko, A. V. (2018). Condensate of μ-Bose gas as a model of dark matter. Phys. A Stat. Mech. its Applic. 506, 835–843. arXiv:1805.02504 [gr-qc]. doi:10.1016/j.physa.2018.05.001
Gavrilik, A. M., and Kachurik, I. I. (2016). New version of pseudo-hermiticity in the two-sided deformation of Heisenberg algebra. Mod. Phys. Lett. A 31, 1650024. doi:10.1142/S0217732316500243
Gavrilik, A. M., Kachurik, I. I., and Rebesh, A. P. (2013). Elements of μ-calculus and thermodynamics of μ-bose gas model. Ukr. J. Phys. 58, 1182–1191. arXiv:1309.1363. doi:10.15407/ujpe58.12.1182
Gavrilik, A. M., Kachurik, I. I., and Rebesh, A. P. (2010). Quasi-Fibonacci oscillators. J. Phys. A Math. Theor. 43, 245204. arXiv:1002.0601. doi:10.1088/1751-8113/43/24/245204
Gavrilik, A. M., and Mishchenko, Y. A. (2012). Exact expressions for the intercepts of r-particle momentum correlation functions in μ-Bose gas model. Phys. Lett. A 376, 2484–2489. arXiv:1204.3067. doi:10.1016/j.physleta.2012.06.032
Gross, D., and Mende, P. (1988). String theory beyond the Planck scale. Nucl. Phys. B 303, 407–454. doi:10.1016/0550-3213(88)90390-2
Hamil, B., and Lutfuoglu, B. C. (2021). Black hole thermodynamics in the presence of a maximal length and minimum measurable in momentum. Europhys. Lett. 135, 59001. doi:10.1209/0295-5075/135/59001
Harko, T. (2011). Bose-Einstein condensation of dark matter solves the core/cusp problem. JCAP 11, 022. arXiv:1105.2996 [astro-ph.CO]. doi:10.1088/1475-7516/2011/05/022
Hossenfelder, S. (2013). Minimal length scale scenarios for quantum gravity. Living Rev. Relativ. 16, 2. doi:10.12942/lrr-2013-2
Jannussis, A. (1993). New deformed Heisenberg oscillator. J. Phys. A 26, L233–L237. doi:10.1088/0305-4470/26/5/011
Kempf, A., Mangano, G., and Mann, R. B. (1995). Hilbert space representation of the minimal length uncertainty relation. Phys. Rev. D. 52, 1108–1118. doi:10.1103/PhysRevD.52.1108
Kempf, A. (1997). Non-pointlike particles in harmonic oscillators. J. Phys. A 30, 2093–2101. arXiv:hep-th/9604045. doi:10.1088/0305-4470/30/6/030
Lee, J. W. (2016). Characteristic size and mass of galaxies in the Bose-Einstein condensate dark matter model. Phys. Lett. B 756, 166–169. doi:10.1016/j.physletb.2016.03.016
Lee, J. W., and Lim, S. (2010). Minimum mass of galaxies from BEC or scalar field dark matter. JCAP 01, 007. doi:10.1088/1475-7516/2010/01/007
Macfarlane, A. J. (1989). On q-analogues of the quantum harmonic oscillator and the quantum group SUq(2). J. Phys. A Math. Gen. 22, 4581–4588. doi:10.1088/0305-4470/22/21/020
Magueijo, J., and Smolin, L. (2002). Lorentz invariance with an invariant energy scale. Phys. Rev. Lett. 88, 190403. doi:10.1103/PhysRevLett.88.190403
Magueijo, J., and Smolin, L. (2005). String theories with deformed energy-momentum relations, and a possible nontachyonic bosonic string. Phys. Rev. D. 71, 026010. doi:10.1103/PhysRevD.71.026010
Maslowski, T., Nowicki, A., and Tkachuk, V. M. (2012). Deformed Heisenberg algebra and minimal length. J. Phys. A Math. Theor. 45, 075309. arXiv:1201.5545. doi:10.1088/1751-8113/45/7/075309
Maziashvili, M. (2006). Black hole remnants due to GUP or quantum gravity? Phys. Lett. B 635, 232–234. arXiv:gr-qc/0511054. doi:10.1016/j.physletb.2006.03.009
Mostafazadeh, A. (2002). Pseudo-Hermiticity versus PT symmetry: The necessary condition for the reality of the spectrum of a non-Hermitian Hamiltonian. J. Math. Phys. 43, 205–214. doi:10.1063/1.1418246
Navarro, J. F., Frenk, C. S., and White, S. D. M. (1997). A universal density profile from hierarchical clustering. Astrophys. J. 490, 493–508. doi:10.1086/304888
Nazarenko, A. V. (2020). Partition function of the Bose–Einstein condensate dark matter and the modified Gross–Pitaevskii equation. Int. J. Mod. Phys. D. 29, 2050018. doi:10.1142/S0218271820500182
Pedram, P. (2012). A higher order GUP with minimal length uncertainty and maximal momentum. Phys. Lett. B 714, 317–323. doi:10.1016/j.physletb.2012.07.005
Perivolaropoulos, L. (2017). Cosmological horizons, uncertainty principle, and maximum length quantum mechanics. Phys. Rev. D. 95, 103523. arXiv:1704.05681v1 [gr-qc]. doi:10.1103/PhysRevD.95.103523
Pramanik, S. (2022). A consistent approach to the path integral formalism of quantum mechanics based on the maximum length uncertainty. Cl. Quant. Grav. 39, 195018. doi:10.1088/1361-6382/ac8cc9
Quesne, C., and Tkachuk, V. M. (2007). Generalized deformed commutation relations with nonzero minimal uncertainties in position and/or momentum and applications to quantum mechanics. SIGMA 3, 016. doi:10.3842/SIGMA.2007.016
Saavedra, I., and Utreras, C. (1981). A generalization of quantum mechanics for high energies and quark physics. Phys. Lett. B 98, 74–76. doi:10.1016/0370-2693(81)90371-3
Scardigli, F. (1999). Generalized uncertainty principle in quantum gravity from micro-black hole gedanken experiment. Phys. Lett. B 452, 39–44. doi:10.1016/S0370-2693(99)00167-7
Skara, F., and Perivolaropoulos, L. (2019). Primordial power spectra of cosmological fluctuations with generalized uncertainty principle and maximum length quantum mechanics. Phys. Rev. D. 100, 123527. doi:10.1103/PhysRevD.100.123527
Keywords: deformed BEC model of dark matter, deformed lane-emden equation, deformed heisenberg algebra, generalized uncertainty relation, maximal/minimal length uncertainty
Citation: Gavrilik AM, Kachurik II and Nazarenko AV (2023) New deformed Heisenberg algebra from the μ-deformed model of dark matter. Front. Astron. Space Sci. 10:1133976. doi: 10.3389/fspas.2023.1133976
Received: 29 December 2022; Accepted: 31 March 2023;
Published: 17 April 2023.
Edited by:
Matthew J. Lake, National Astronomical Research Institute of Thailand, ThailandReviewed by:
Djamil Bouaziz, University of Jijel, AlgeriaDimitris M. Christodoulou, UMass Lowell, United States
Copyright © 2023 Gavrilik, Kachurik and Nazarenko. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: A.M. Gavrilik, b21nYXZyQGJpdHAua2lldi51YQ==
 A. M. Gavrilik
A. M. Gavrilik I. I. Kachurik2
I. I. Kachurik2 A. V. Nazarenko
A. V. Nazarenko