
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Astron. Space Sci. , 23 May 2023
Sec. Cosmology
Volume 10 - 2023 | https://doi.org/10.3389/fspas.2023.1121920
Bose-Einstein-condensed dark matter (BEC-DM), also called scalar field dark matter (SFDM), has become a popular alternative to the standard, collisionless cold dark matter (CDM) model, due to its long-held potential to resolve the small-scale crisis of CDM. Halos made of BEC-DM have been modelled using the Gross-Pitaevskii (GP) equation coupled to the Poisson equation; the so-called GPP equations of motion. These equations are based on fundamental microphysical conditions that need to be fulfilled in order for the equations to be valid in the first place, related to the diluteness of the DM gas and the nature of the particle scattering model. We use these conditions in order to derive the implications for the BEC-DM parameters, the 2-particle self-interaction coupling strength g and the particle mass m. We compare the derived bounds with the constraint that results from the assumption of virial equilibrium of the central cores of halos, deriving a relationship that connects g and m. We find that the GPP conditions are greatly fulfilled, for BEC-DM particle masses of interest, if such models also obey the virial condition that turns out to be the strongest constraint. We also derive the implications for the elastic scattering cross section (per particle mass) in BEC-DM halos, based on the scattering model of GPP, and find a huge range of possible values, depending on the self-interaction regime. We put our results into context to recent literature which predicts sub-kpc core size in BEC-DM halos.
In recent years, alternative models to the cold dark matter (CDM) paradigm have been studied for multiple reasons: 1) the hitherto non-detection of CDM candidates such as “weakly interacting, massive particles (WIMPs)”, or the quantum-chromodynamical (QCD) axion; 2) the small-scale crisis of CDM structure formation, such as “cusp-core problem”, “missing-satellite problem” or “too-big-to-fail problem”, established by astronomical observations, which could be interpreted to point to a minimum structure formation scale which is larger than that predicted by CDM (for reviews see, e.g., (Bullock and Boylan-Kolchin, 2017; Salucci, 2019)); and finally 3) the emergence of a plethora of dark matter (DM) candidates in new theories beyond the standard model of particle physics.
The models that we will consider in this paper belong to a large family of such alternative candidates, so-called Bose-Einstein-condensed dark matter (BEC-DM), introduced around the 2000s by several authors, see, e.g., (Sin, 1994; Goodman, 2000; Hu et al., 2000; Matos et al., 2000; Peebles, 2000; Lesgourgues et al., 2002; Mielke et al., 2006). Ultralight bosonic DM with particle masses of m ∼ (10–23—10–18) eV/c2 belongs to this category, which have been studied under various names: “scalar field dark matter (SFDM)”, “fuzzy dark matter (FDM)”, “wave dark matter”, “ultralight axion DM”. Reviews on SFDM can be found, e.g., in (Magaña and Matos, 2012; Ureña-López, 2019), on axions, e.g., in (Marsh, 2016). BEC-DM has become popular with astrophysicists, because its dynamics can be distinctive to CDM on galactic scales, possibly overcoming the CDM small-scale crisis. However, this feature depends upon the number of available particle parameters of the model and the respective values they can take. Thus, these parameters are subject to observational constraints, and many have been derived over the years, using different astronomical scales and probes, see, e.g., (Lora et al., 2012; Hlozek et al., 2015; Calabrese and Spergel, 2016; Armengaud et al., 2017; Iršič et al., 2017; Marsh and Niemeyer, 2019; Safarzadeh and Spergel, 2020; Nadler et al., 2021) for models which have only the particle mass as a free parameter. Recent constraints on models which include a strongly repulsive 2-particle self-interaction (SI), also called “SFDM-TF” where “TF” stands for “Thomas–Fermi” regime, can be found, e.g., in (Li et al., 2014; Fan, 2016; Dev et al., 2017; Li et al., 2017; Hartman et al., 2022a; Foidl and Rindler-Daller, 2022; Shapiro et al., 2022).
In this paper, we investigate the 2-particle SI in BEC-DM from the quantum scattering perspective that underlies the commonly adopted Gross-Pitaevskii framework, and consider the implications that arise for the BEC-DM particle parameter space.
For simplicity, we make the usual assumption in that we consider a single species of spin-0 bosons of mass m that forms a Bose-Einstein condensate (BEC), and makes up all of the cosmological DM abundance. We note that mixed-DM models have been also considered, albeit more rarely, where the energy density of DM is shared between BEC-DM and, say, a CDM component, see, e.g., (Hlozek et al., 2015). The particles of BEC-DM are considered fundamental without internal structure, and we adopt this premise here, as well. In the context of this paper, that means we disregard the possibility of inelastic collisions or bound states between these particles. Also, we assume that there is no coupling to the particles of the standard model (though there may have been some coupling in the very early Universe, upon the emergence of BEC-DM).
All these assumptions are encoded in the so-called nonrelativistic Gross-Pitaevskii-Poisson (GPP) system of equations for the complex-valued BEC-DM wavefunction ψ(r, t), whose application is widely accepted in the community (see references above). The GPP framework is appropriate as a description of galactic halos made of BEC-DM, where both gravitational and velocity fields are small enough that they can be treated in the Newtonian regime.
The GPP equations of motion are as follows:
Since we assume that all of the DM is in BEC-DM, the mass density of DM particles is given by ρ(r, t) = mn(r, t), where the number (probability) density is assigned to the wavefunction squared, n(r, t) = |ψ|2(r, t), according to the Born rule.
Φ(r, t) is the gravitational potential of the system under consideration, which couples to the mass density via the Poisson Equation 2. The last term in (1) describes the low-energy elastic scattering of the DM particles in this model, parametrized by the coupling constant
with the 2-particle s-wave scattering length as, whose sign determines whether the self-interaction (SI) is repulsive, g > 0, or attractive, g < 0. If SI is neglected, g = 0, the above system of equations is also known as Schrödinger-Poisson (SP) system1. The significance of the above scattering model, its implications for BEC-DM parameters and comparison with other constraints will be the subject of this paper.
By applying the GPP framework in (1, 2), we appreciate that the wave nature of the DM bosons cannot be neglected on astronomical or galactic scales anymore, i.e., their quantum properties can affect observational phenomenology, depending upon the parameters of the model. The GPP framework can be used for any DM bosons which form a BEC, whether they be ultralight m ∼ 10–22 eV/c2 appropriate for FDM, or whether they be QCD axions with m ∼ (10–6 − 10–5) eV/c2. However, the GP Equation 1 has been applied to BEC-DM in previous literature without consideration of the actual assumptions that underlie the equation in the first place. We will close this gap by determining the DM parameter space of m and g for which we can apply the GP description, the implications for the scattering cross section, and how these fit into dynamical constraints.
Some comments are in order before we proceed. First, different cosmological production mechanisms for BEC-DM in the very early Universe have been envisaged. However, the question as to whether the effective low-temperature and nonrelativistic description of equ. (1, 2) represents a proper mathematical limit for BEC-DM, which originates via different cosmological scenarios, has not been studied in detail and is also beyond the scope of this paper. Here, we merely start with the premise that GPP can be used as a phenomenological framework to study BEC-DM on galactic halo scales, along the lines of previous investigations in the literature. Second, many popular particle models for BEC-DM involve ultralight axions (ULAs), which are usually pseudo-scalar fundamental particles described via real fields. As such, ULAs can self-annihilate. However, the rate of this self-annihilation is very low; hence it is usually neglected and a complex wavefunction ψ is adopted, as well. (If the particle number is conserved -either exactly or approximately-system equ. (1-2 obeys a normalization condition, such that, e.g., N = ∫|ψ|2d3r for the wavefunction ψ of a given galactic halo with total number of bosons N.) More generally, we stress that specific particle models of BEC-DM may impose further relationships between the underlying particle parameters. In the above GPP framework, m and g are independent parameters (see more below), while, e.g., ULAs obey a relationship between mass m and their so-called decay constant f. The latter can be related to a coupling parameter akin to g. So, the GPP “mean-field” framework is meant to encompass a broad family of models, whose members behave very closely dynamically, and yet differ with respect to the individual particle model. To determine whether the differences in the latter play a role on astronomical scales, or not, requires a case-by-case analysis which is not subject of this work. We will focus on the generic SI-term in Equation 1, without consideration of how it arises from given particle Lagrangians2. Third, in the Newtonian regime, the self-consistent coupling of gravity to the mass density is established via the Poisson equation in Eq. 2). Yet, the smooth global gravitational potential Φ in the gravitational term mΦψ of the GP Equation 1 acts nevertheless akin to an “external potential”, similarly to magneto-optical trap potentials in typcial laboratory atomic BECs. In other words, Φ does not “feel” the particle SI, described via the SI-term g|ψ|2ψ, because Φ is basically uniform over the interaction range of the 2-particle SI-potential which is essentially contact-like. In fact, the equation for the SI coupling strength in (3) arises as a result of assuming a δ-distribution for the SI-potential; see textbook presentations, e.g., (Pitaevskii and Stringari, 2003; Pethick and Smith, 2008). This situation is very different from the case of, say, a laboratory molecular BEC with dipolar forces, where the 2-boson SI itself is a long-range 1/r-interaction. Here, we exclude such a case and assume throughout that the bosons of BEC-DM have short-range SI. Finally, it will become clear in due course why we will mostly focus on the cores of galactic halos. It is these (smaller) halo cores which serve as minimum-size equilibrium objects in BEC-DM.
This paper is organized as follows. In Section 2, we derive the microphysical conditions on the bosons of BEC-DM which are implied by the GPP framework. Section 3 includes a derivation of the relation that connects the BEC-DM parameters m and g from the condition of virial equilibrium of halo cores, and comparison with the results of Sec.2. In Section 4, we discuss the implications for the 2-particle elastic scattering cross sections in different collision regimes, including the question of velocity-dependence. Finally, Section 5 contains our conclusions and discussion.
Before we investigate the microphysical constraints on DM particle parameters, which are based upon the GP equation, we need to introduce an important characteristic length scale, namely, the de Broglie wavelength
Here, m is the mass of the DM boson and v is their “collective” velocity, which depends on the environment. If the bosons make up a galactic DM halo in gravitational equilibrium, v is close to its virial velocity (which can be associated with a “virial temperature”). If the bosons are part of uncollapsed “background matter”, the velocity will be correspondigly lower3. As also discussed below, it is the velocity dispersion pressure of random wave motion which gives rise to the collective velocity v in galactic halos (see (Dawoodbhoy et al., 2021; Hui, 2021)). As such, this velocity should be used in equ. (4). However, we will make the simplifying assumption that v in (4) as a proxy for the virial velocity can be approximated by the circular velocity, vcirc = (GM/R)1/2, with the mass M and radius R of the virialized object in question (typically a halo core in what follows).
A system is Bose-Einstein-condensed, if the matter waves of individual particles of size λdeB overlap, forming a giant matter wave, within which particles have become indistinguishable. This picture finds a more precise notion in the condition that the phase-space density be a number at least of order one (i.e., high),
where n is again the number density of particles. This is a fundamental condition, if DM bosons are to be described by a macroscopic wavefunction ψ that obeys the GPP equations. Rewriting (5) in terms of fiducial galactic units of interest to us, we have the following condition on the boson mass
where the bar indicates a mean mass density, obtained from n. Let us consider two illustrative cases. If we assume homogeneous halo cores of radius ∼ (0.1–1) kpc, which inclose a (core) mass of, say, 108 M⊙, we get m ≲ (200–700) eV/c2. On the other hand, for Milky Way parameters at the solar circle, using vcirc = 220 km/s and
Now, we move to the specific microscopic assumptions that underlie the GP equation, hence are binding for BEC-DM. It is well known from the theory of interacting quantum gases5 that two essential conditions are placed in the derivation of the GP equation, which can be expressed in terms of the number density of the gas n = |ψ|2, the range of the particle interaction6 r0, and the de Broglie wavelength of the bosons λdeB, as follows.
The first condition on BEC-DM as a quantum gas is the smallness of the “gas parameter”
describes the fact that a dilute system is considered. It is assumed that the interaction range of the 2-particle SI potential is much smaller than the mean interparticle distance. (In fact, the contact-SI alluded to in Section 1 has this property.) This assumption also guarantees that the probability of simultaneous
The second condition requires that
holds. As in (Stoof et al., 1996), we call r0/λdeB the “quantum parameter”. Then, the contribution due to the relative angular momentum of two interacting particles in the scattering process can be neglected. Consequently, it can be shown that for low energy and for a 2-particle potential W(r) decreasing faster than r−3 at infinity, the scattering amplitude f(k, n, n′), with k the wavenumber and n, n′ the direction of incoming and scattered particle, respectively, becomes isotropic. Furthermore, if the limit k → 0 (or E → 0, respectively) exists, it thereby defines the s-wave scattering length according to limk→0f(k, n, n′) = −as. The elastic scattering cross section of indistinguishable bosons in the limit k → 0 is then energy-independent and given8 by
Expanding the scattering length in terms of the potential, and truncating after the first term (the so-called “first Born approximation”), results9 in the following expression
where μ = m1m2/(m1 + m2) denotes the reduced particle mass (for more details on low-energy scattering, see textbook presentations e.g., (Joachain, 1975; Landau and Lifshitz, 1992; Pitaevskii and Stringari, 2003)). Thus, as is proportional to m for particles of the same species, m1 = m2 = m. As a result, the coupling strength g in (3) does not depend on the particle mass m and is an independent parameter of BEC-DM within the first Born approximation, apart from m. Therefore, with all these conditions in place, the particle interactions in a fully condensed (or almost completely condensed) BEC-DM quantum gas can be accurately described by considering only all the possible 2-particle s-wave scattering processes. This allows us to identify r0 in (7) and (8) in the forthcoming with the scattering length |as| (where the sign of as can be positive or negative), since |as|≲ r0 for the Born approximation to be valid.
Of course, in contrast to laboratory examples, the values for the parameters m and g for BEC-DM are unknown. The boson mass m is a free parameter in many particle models of BEC-DM (such as ULAs), with the common implication that its value is undetermined over many orders of magnitude. The same is mostly true for the SI coupling parameter g (or related couplings), although SI is often even neglected from the outset for mere simplicity. Therefore, experimental and observational constraints need to be placed on both, m and g, in order to scan the (dis-)allowed BEC-DM parameter spaces exhaustively. Here we ask what the implications are for these parameters from the fundamental conditions just described. First, it will be useful to write as and λdeB in fiducial units. Using (3) and (4), we can write
where |g| has units of eV cm3, and
where vcirc stands again for the circular velocity as a characteristic velocity. Now, the diluteness condition (7), expressed as |as|3n ≪ 1, demands that
which we write as a condition on the SI coupling strength, for given m and mean mass density
The second condition, which is the smallness of the quantum parameter (8), expressed as |as|/λdeB ≪ 1, results in
or, for given m and vcirc, a condition on the coupling strength, as follows
We stress again that these conditions on |g| need not be fulfilled in the early Universe when the density or kinetic energy (resp. velocity) of BEC-DM or its precursor was very high, such that the GPP formalism breaks down. However, the above conditions are applicable to galactic halos for which each
and likewise for the assumed constant core density,
In Figure 1, we plot the upper bounds on g for different halo core radii Rc but a fixed choice of core mass of Mc = 108 M⊙, where the right-hand side of (13) is labeled as ‘D’ (“diluteness”), while the right-hand side of (14) is labeled as ‘S’ (“scattering”). Before we comment on the results, we introduce a further condition here, as follows. The built-in requirement in the GPP formalism that the bosons be nonrelativistic also implies that any pressure contributions Pi of BEC-DM must be much smaller than its energy density,
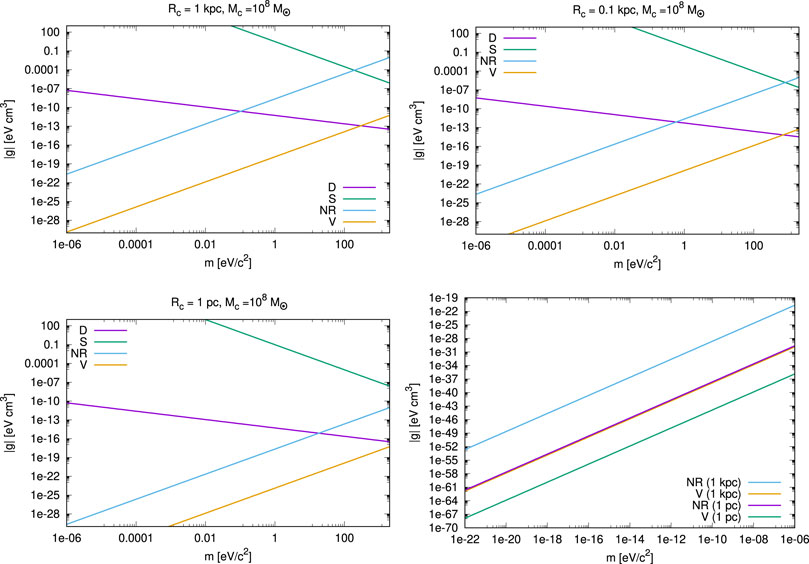
FIGURE 1. BEC-DM particle parameter space (m, g) for halos with core mass Mc =108M⊙, but different core radius: Rc =1 kpc (upper-left panel), Rc =0.1 kpc (upper-right panel) and Rc =1 pc (lower-left panel). Plotted are the respective strong upper bounds on the coupling strength |g| (in eV cm3), for a range of particle masses m ≥10–6 eV/c2, from the conditions of diluteness ‘D’ (equ.13), s-wave scattering ‘S’ (equ.14) and nonrelativistic pressure ‘NR’ (equ.17). The virial relation ‘V’ (equ (27)) is derived in Section 3. In each panel, the parameter space below the lowest-lying line fulfills all the bounds shown in turn. A change in Rc shifts the bounds, albeit not strongly. Lower-right panel: BEC-DM particle parameter space for a range of boson mass that includes the ultralight regime. As the tightest bounds, only the ‘NR’ and ‘V’ lines are shown. We plot them for two cases of core radii, Rc = 1 kpc and Rc = 1 pc, respectively. By coincidence, the curves for ‘V’ (1 kpc) and ‘NR’ (1 pc) lie visually almost on top of each other.
Moreover, for BEC-DM models with SI-term in the Lagrangian, as is the focus of this paper, another pressure arises. If SI is weak, this pressure may be simply negligible compared to the quantum pressure. If there is a strongly attractive SI, instead, the corresponding pressure is negative and acts in favour of gravity, and the system is prone to gravitational collapse (see footnote). However, if the pressure is due to a strongly repulsive SI, it acts against gravity and provides a stabilizing effect. For this pressure, the equation of state has the form of an (n = 1)-polytrope, PSI = Kρ1+1/n, where K = g/2m2 is a fixed constant for given BEC-DM model parameters m and g (Goodman, 2000; Peebles, 2000). The requirement on this pressure that
Of course, any other weaker SI-pressure must obey this bound, as well. In Figure 1, the label ‘NR’ refers to the right-hand side of (17). Finally, the plots in Figure 1 also include the bound–denoted ‘V’—that follows from the assumption of virial equilibrium of halo cores. Its derivation will be the subject of the next section. Now, let us comment on the results of Figure 1. The upper two panels, as well as the lower-left panel, display a range of boson mass at the high end, chosen as (10−6—2000) eV/c2; the panels include all bounds mentioned and show results for three different values of the core radius Rc, for the same core mass, as indicated in the panel’s title. We immediately see that the GPP microphysical conditions can be easily fulfilled, even for this higher boson mass range, because the bounds on |g| are generous. Indeed, we can see that the ‘NR’ condition, as well as the virial condition ‘V’, provide tighter constraints in general. Only around m ∼ (0.1–10) eV/c2, the ‘NR’ and ‘D’ bounds switch their roles, and this barely depends on the core size: above a boson mass of roughly that scale, the diluteness condition ‘D’ becomes the most demanding one of all micro-conditions, i.e., particles with higher m must have a corresponding |g|, which is quite smaller than what would be allowed by the ‘NR’ condition by itself. The condition from ‘S’ equ. (14) becomes comparable to the ‘NR’ condition equ. (17) at masses ≳ (30–80) eV/c2, quite at the limit of the phase-space bound (see equ. (6) and text below). Nevertheless, we note that condition ‘S’ provides us with an a posteriori justification for the validity of the SI regimes that we consider, which we will be able to appreciate in Section 4. Furthermore, we see that ultralight particles m ⋘ 1 eV/c2 demand a much stricter bound on g in order to fulfil the ‘NR’ condition, than do particles of higher mass, which makes sense. In fact, we can see that the ‘NR’ bound (and ‘V’) are much stronger for ultralight particles than any of the GPP conditions. Therefore, we exclusively plot the ultralight boson mass regime, between (10–22—10–6) eV/c2, in the lower-right panel of Figure 1 and focus entirely on the ‘NR’ and ‘V’ bounds (for the other ones lie outside this plot range in |g| and are automatically fulfilled once ‘NR’ and/or ‘V’ are fulfilled). However, we plot the bounds for two cases of halo core radii, Rc = 1 kpc and Rc = 1pc. The smaller the core, the smaller the remaining allowed parameter space for |g|, i.e., the curves shift correspondingly downwards. It so happens that the curves for ‘V’ (1 kpc) and ‘NR’ (1 pc) lie visually almost on top of each other which is a coincidence.
Before we move to the next section, let us make a final comment on the ‘NR’ condition. The argument concerning pressure versus energy density presumes that we can describe BEC-DM as a fluid, associated with a re-formulation of the GPP equations into fluid equations. In this sense, the ‘NR’ condition is of a different kind than the micro-conditions from the GP wave equation. In other words, it is assumed that the two pictures are equivalent. While not rigorously proven, there is plenty of evidence in the literature that this assumption is justified.
In this section, we put the results of Section 2 into perspective by comparing them to the conditions on BEC-DM parameters implied by the assumption of virial equilibrium. In general, once we demand that DM is able to form self-gravitating, bound galactic structures, we can use dynamical arguments involving the equilibrium state of such galactic halos. By the same token, however, we must remember that the constraints thereby derived on the DM parameters do depend on the assumption of equilibrium, which is approximately true at best. However, for certain halos or halo parts, such as their central cores, the equilibrium assumption may well be justified.
We stress that the previous conditions (7) and (8), or equivalently (13) and (14), remain valid as long as the gravitational potential induced by the BEC-DM mass density does not vary much over the scales of the particle interaction range, which is the case here of the contact-SI. On the other hand, equilibrium conditions of balancing forces on the scale of a given halo do impose constraints on the particle parameters, here m and g. Especially the virial theorem has been widely applied to infer constraints on DM parameters, in general.
In the past, the equilibrium size of hydrostatic BEC-DM halo cores has been analysed in two limit regimes, where gravity is opposed predominantly either by quantum pressure, or by the polytropic pressure due to the strongly repulsive SI. Ref. (Rindler-Daller and Shapiro, 2012) includes an early comparison; these two regimes were studied there under the header “BEC-CDM” of type I and type II, respectively. FDM without SI, i.e., g = 0, or with very weakly interacting bosons fall into type I. At the other end is BEC-DM with strongly repulsive SI (type II), more recently referred to as SFDM-TF in Refs. (Dawoodbhoy et al., 2021; Shapiro et al., 2022) or SIBEC-DM in Ref. (Hartman et al., 2022a; Hartman et al., 2022b). We discussed the conditions on pressure of BEC-DM to be nonrelativistic already in Section 2. Still, BEC-DM pressure can be non-negligible on galactic halo scales, and this feature motivates BEC-DM as a potential remedy to resolve the small-scale crisis of CDM, as mentioned in Section 1, because it provides a minimum scale, below which structure formation is suppressed, which can be much larger than for CDM. This statement, however, relies heavily on the parameters of the model, which are subject to observational constraints. From theory, we can only generally state that quantum pressure stabilizes halo cores against gravitational collapse, while for SFDM-TF it is the polytropic pressure. By the same token, either quantum or SI pressure will prevent formation of structure below a corresponding Jeans scale. For SFDM-TF, the SI-pressure determines that minimum scale (Shapiro et al., 2022), as opposed to the de Broglie length for FDM. Again, observations constrain the size of these length scales.
Now, the smallest self-bound equilibrium object in BEC-DM serves also as a model for halo cores, whose radius and mass we denote again with Rc and Mc. The general properties of this equilibrium object, especially its Mc − Rc-relationship and how it depends on BEC-DM particle parameters, have been known for a while, see, e.g., (Chavanis, 2011) (and references therein) which also includes some historic exposition. We present some of these fundamental results, before we derive the virial relationship that connects m with g.
In general, the GPP system of equations does not admit closed-form equilibrium solutions, except for some limit cases concerning SI. However, variational estimates have been found and the corresponding analytic expressions often constitute good approximations of the true equilibria solutions. For example, a Gaussian for the spherical BEC-DM core density distribution
has been widely applied to the GPP system of equations, or the corresponding stationary energy functional, as an ansatz or test function, respectively, and it has been shown that it yields the same particle and halo parameter dependencies in the Mc − Rc-relationship than the exact solution, with numerical prefactors deviating only by numbers of order ≲ 1–10, see e.g., (Guzmán and Avilez, 2018; Chavanis, 2019a; Padilla et al., 2021). Using that Gaussian ansatz, the mass-radius relationship of a spherical equilibrium halo core is
which is a re-written version of equation13 28 in (Padilla et al., 2021). Since the Gaussian has no compact support, the core radius is connected via the width of the Gaussian to the radius R99, which includes 99% of the core mass Mc, according to R99 = 2.38167Rc. The relationship (19) is valid for positive and negative14 SI-couplings g. For FDM without SI, g = 0, the mass-radius relationship of the so-called “solitonic core” (or “soliton”) is
where the prefactor
using (20) (or (23) below). This rough argument shows how the lower end of desired boson masses comes about: it is driven by the observational necessity for BEC-DM to account for the smallest galaxies that are known. Of course, the smallest galaxies may have yet to be found, let alone the smallest DM halos - by definition hard to accomplish and only possible indirectly for the latter. Therefore, bounds are provided by observations of ever smaller galaxies; favoured are now ultra-faint dwarf galaxies, which contain only hundreds to a few thousand stars. Recent works have used observations of such ultra-faint dwarfs in the Local Group in order to constrain the boson mass, and these yield lower bounds around m ∼ 10–21 eV/c2 (see (Marsh and Niemeyer, 2019; Nadler et al., 2021)) which are 1–2 orders of magnitude higher than the mass in (21), explored in the early FDM literature. Such boson masses imply sub-kpc core size of ≲ 0.5 kpc.
At the opposite end, we have the strongly repulsive TF regime. For this SFDM-TF, the second term under the square root in (19) is much larger than one, so we can approximate
(adding now a subscript “TF”). Different from the prefactor
The above relationships are based on the assumption that the considered halo cores with radius Rc and mass Mc are in virial (even hydrostatic) equilibrium. As such, the corresponding equilibrium solutions are asymptotic states of the dynamical evolution for t → ∞. Given that galactic halos are subject to mass infall from the ambient environment, including interactions and mergers with neighboring halos, we can use these cores as approximative models for the central parts of halos. The halo envelopes that enshroud those cores may be subject to perturbations and ongoing relaxation processes. Yet, a sufficiently isolated halo (core plus envelope) could still be in approximate virial equilibrium (if not in hydrostatic equilibrium), and this assumption is commonly made in order to estimate the dynamical mass of halos of galactic or galaxy-cluster size. Whatever the detailed dynamical state of a given halo, we will focus on their central cores and assume they are in virial equilibrium, an assumption that is justified from simulations (Dawoodbhoy et al., 2021; Hartman et al., 2022b; Shapiro et al., 2022). With this assumption on the cores, relationships between m and g are implied, that are independent of the dynamical halo state at large and more generally valid as a result, because there is no freedom left to pick different values for m or g in the halo envelopes.
Before we derive the virial condition, let us introduce characteristic units for the particle mass and SI coupling strength, defined in (Rindler-Daller and Shapiro, 2012) and (Rindler-Daller and Shapiro, 2014a), as follows
and
We described the physical meaning and significance of these parameters at length in (Rindler-Daller and Shapiro, 2012). We only re-iterate here that mH is the characteristic mass of a non-interacting particle whose de Broglie length λdeB, equ. (12), is comparable to the radius Rc of a given BEC-DM halo core of mass Mc. It is thus the smallest particle mass possible in order for quantum pressure to be solely responsible for holding that core up against gravitational collapse; in essence this provides the lower-bound estimate on mass m in the FDM regime, see again equ. (21). On the other hand, if there are density variations in the BEC-DM on the scale of the core radius Rc, then gH is the coupling strength for which the quantum and SI pressure force terms are equal, for BEC-DM models with SI.
In the TF regime, it has been shown already in (Rindler-Daller and Shapiro, 2012) that virial equilibrium of halo cores demand relationships of the form
where the constant prefactor of order one depends again on the details of the core geometry (in (Rindler-Daller and Shapiro, 2012) a relation such as (22), but for an (n = 1)-polytrope has been used). Also, an expression for the halo core radius has been derived in (Rindler-Daller and Shapiro, 2012) in the form of equation 46 there, which is
Using (25), g ≫ gH implies m ≫ mH in the TF regime. Notice, though, that the conditions ‘D’, ‘S’ and ‘NR’ described in the previous section are blind to virial equilibrium and to these inequalities.
In light of the mass-radius relationship of the core in (19), we can finally derive here the corresponding general virial condition. Inserting (23) and (24) into (19) yields an implicit function of m/mH, unlike the explicit function obtained in (Rindler-Daller and Shapiro, 2012). However, in terms of g/gH, we can derive an explicit equation which reads
If m/mH ≫ 1, equ. (26) reduces to
valid in the TF regime16, see (25). We plot both relationships, (26) and (27), in Figure 2 for comparison. The curves lie on top of each other in the validity range of the TF regime when m/mH ≫ 1, g/gH ≫ 1, as expected. In fact, the parameter space of SFDM-TF overlaps to such a great extent with the general parameter space of BEC-DM with repulsive SI, that we use relationship (27), denoted as ‘V’, in Figure 1 altogether. The virial relation is a function g = g(m), in contrast to the strong inequalities from GPP microphysics. It yields tighter constraints on g than the microphysical conditions, for m ≲ 100 eV/c2 which is just the range of interest given the phase-space condition in (6). Thus, BEC-DM models, for which (halo) cores fulfil virial equilibrium, will automatically fulfil the micro-conditions from GPP.
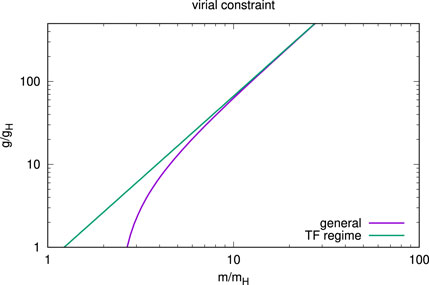
FIGURE 2. Virial relationships, equ.(26) (“general”) and equ.(27) (“TF regime”). The curves lie on top of each other for m/mH ≫ 1, g/gH ≫ 1.
Before we leave this section, we discuss some implications from recent literature, concerning the expected core size in SFDM-TF models. While the resolution of the CDM small-scale crisis demands core radii of order ≳ 1 kpc as shown in (Dawoodbhoy et al., 2021; Pils and Rindler-Daller, 2022), the recent studies of linear structure formation by (Hartman et al., 2022a; Foidl and Rindler-Daller, 2022; Shapiro et al., 2022) find that the core radius is more tightly constrained than previously believed: not only are kpc-size cores disfavoured, it strongly appears that their radii should be below ≲ 100 pc, if not even of order ∼ (1–10) pc. We refer the reader to these papers for details. For comparison and in light of these findings, we added a constraint plot in the case of a very small halo core of Rc = 1 pc into Figure 1 (lower-left panel). There are no substantial differences to the other cases shown in Figure 1, i.e., the GP microphysical conditions do not limit our choice of core size. How small a core can we eventually choose? Ref. (Padilla et al., 2021) analyzed the question for which BEC-DM particle parameters halo cores could become unstable with respect to general-relativistic gravitational collapse, forming central galactic black holes as a result, and thereby possibly explaining the presence of supermassive black holes in the centers of galaxies at high and low redshift. We can use their17 condition of non-formation of such a central black hole from a core for SFDM-TF models. In our notation, it reads as g/(m2c4) ≥ 1.23 × 10−29 eV−1 cm3. Translating this into a bound on the core radius, we get that the halo core will not be subject to collapse as long as Rc ≥ 2.76 × 10−3 pc
While lower-bound estimates on particle mass m of BEC-DM often invoke equilibrium/virial conditions applied to halos or their cores (see (21)), it has been argued that an upper bound on m arises by using the scattering cross section in the TF regime. For this purpose, it is useful to find an upper bound on the 2-particle scattering cross section per particle mass, σs/m with σs in (9). Independent of the SI regime, it has been pointed out by (Slepian and Goodman, 2012) and (Rindler-Daller and Shapiro, 2012) that σs/m may be re-expressed, using (3) and (9), according to
or in “fiducial units”, using (23) and (24),
It has become customary in the literature on self-interacting DM to choose cgs-units for σs/m (note: “g” stands for gram and shall not be confused with the coupling strength g), though we will see shortly that these units are not appropriate for BEC-DM. The canonical example of self-interacting DM, termed “SIDM”, encompasses a family of different particle models. In a dynamical context, the most minimal difference of SIDM to CDM is the addition of a finite scattering cross section, modifying the usual N-body gravitational dynamics to include the physics of non-gravitational particle (elastic) collisions. While we are also concerned here with an elastic scattering cross section between BEC-DM bosons, the implications on σs/m are different than in SIDM, as we show in this section. For this purpose, we will also need to make reference to some results pertaining to SIDM.
First, we introduce the well-known Knudsen number “Kn” as a measure that distinguishes the fluid regime of strong SI (many particle collisions) versus the kinetic regime of few collisions (if any during the relevant time scale of the problem). Now, we use the inverse of the elastic scattering cross section σs in equ. (9) to define the “mean-free path”, i.e., the average distance travelled by a particle between two scattering events,
where n denotes again the particle number density. We stress that this relationship assumes that the system is sufficiently dilute, such that Eq. 7 or (13) hold. So, the particles are supposed to interact only upon a scattering/collision event, when the separation between two particles is not much larger than the interaction range |as|. This picture is justified for short-range SI potentials, such as the contact-SI upon which the GP formalism in Equations 1–3 is based. Now, the Knudsen number is the ratio of λmf over the characteristic size of the system, which could be the halo virial radius, or more appropriately in our context, the halo core radius. So, we write Kn = λmf/Rc. The regime of Kn ≫ 1 describes a system with few collisions (“Knudsen gas limit”), i.e., long mean-free path, while Kn ≪ 1 indicates a system with short mean-free path. Depending on the DM and halo parameters, either regime may be at work, in principle. In fact, for SIDM one encounters both regimes as shown in (Ahn and Shapiro, 2005), where a “sweet spot” of maximum (core-)flattening of the halo central density has been identified, corresponding to a certain Knudsen number, or equivalently to a “Q-parameter” introduced by the authors and which goes proportional to Rvir/λmf. They find that SIDM in the low-Q regime, equivalent to a long mean-free path Kn ≫ 1, behaves kinetic, and flattening of halo density cores becomes stronger as Q increases. This regime can be studied by modified N-body dynamics, with typical values of σs/m ≃ (0.1–10) cm2/g. On the other hand, the high-Q regime corresponds to short mean-free path Kn ≪ 1, and central density flattening becomes weaker as Q increases. This fully collisional regime of SIDM behaves like ordinary gas dynamics, with typical numbers18 of σs/m ≈ (100–200) cm2/g. Which regimes do we encounter for BEC-DM ?
Let us look at equ.(29) and consider first BEC-DM models with weak SI where m/mH ≳ 1, |g/gH|≳ 1. We can readily see that in these cases σs/m is a tiny number close to zero, for any reasonable choice of Rc and Mc. Such models behave de facto collisionless and by the same token the scattering cross section per particle mass is useless as a means to constrain the particle parameters. The smallness of σs/m in this case comes with no surprise as soon as we realize that BEC-DM with weak SI is equivalent to Kn ≫ 1, i.e., the Knudsen gas limit, where
At the other extreme, we have the strongly interacting TF regime of BEC-DM–i.e., SFDM-TF-, which resembles the usual Boltzmann gas limit with
as first pointed out by (Slepian and Goodman, 2012) (but notice again the different prefactor that arises, if an (n = 1)-polytrope is considered versus the Gaussian ansatz that we use here). This re-expression of the cross section is very helpful, given that neither the scattering length as, nor the coupling strength g are direct observables, in contrast to the core radius Rc,TF that can be constrained by galactic data. Again, using “fiducial units”, equ. (31) becomes
In Figure 3, we plot this quantity as a function of mass m for three fixed values of the TF core radius Rc,TF. We notice that
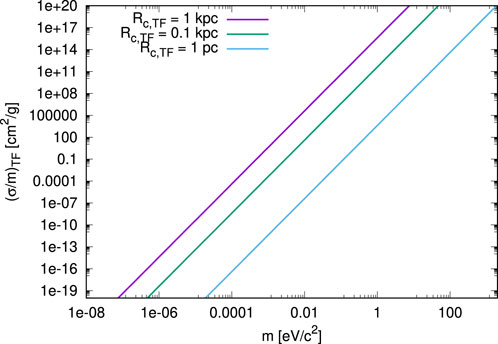
FIGURE 3. Specific scattering cross section in the TF regime as a function of boson mass m for three different TF core radii Rc,TF.
What shall we make with the result in Figure 3 ? Or phrased differently: What value or (upper) bound for σs/m is expected from astronomical observations, such that we can exclude parameter space regions in that figure ? In fact, there is no simple answer, because the inferred bounds from observations depend upon fitting the data to the underlying theoretical model of DM. The latter requires realistic simulations that are mostly still lacking for BEC-DM. Therefore, bounds from SIDM have been usually applied as a mere guess. For instance, it has been argued in (Slepian and Goodman, 2012), and earlier in (Matos and Ureña-López, 2002), that upper bounds on σs/m for SIDM, based upon comparing that model to observations, should apply to BEC-DM as well. This is a non-trivial assumption, though it may seem reasonable at first sight. Notably, the interpretation of the Bullet cluster observations as a nearly collisionless merger of two cluster-sized halos has been found to limit σs/m for SIDM halos to
There is another point on which we shall comment. Ref. (Slepian and Goodman, 2012) constructed a halo model, where a TF core of condensed BEC-DM described by an (n = 1)-polytrope, is enshrouded by an envelope as an isothermal sphere made of thermal non-condensed bosons. (The isothermal sphere provides rotation curves with constant velocity at large galactocentric radii.) By calculating the exact equation of state, that interpolates between core and envelope, the authors find that the transition region exemplifies a discontinuous feature that translates into a marked feature in the halo density profile. This feature is subject to observational constraints (via galactic rotation curves), concluding that, in order to avoid these constraints, the boson mass must fulfil contradicting lower and upper bounds, whereby the upper bound comes from the SIDM argument of forcing σs/m ≲ 1 cm2/g for the condensed core. As we have seen, there is no fundamental reason to apply this bound to BEC-DM. However, the adopted requirement of the non-condensed bosons in the envelope to be in local thermal equilibrium demands that these bosons (as a thermal gas) be in the small mean-free path regime, i.e., λmf ≪ R, with R a characteristic radius, equivalent to σs/m ≫ 1/ρR, or
where σs stands merely for an elastic cross section, not related to equ. (9), and
Let us finally make a last comment to add another illustration of why using bounds on scattering cross section from SIDM to BEC-DM is misleading. Remember that σs/m ≈ 1 cm2/g = 1.8 b/(GeV/c2), or
If we would like to have a typical SIDM (nuclear) cross section of σs,TF ≈ 10–24 cm2, we would need a BEC-DM boson mass of m ≈ 0.1 eV/c2 if Rc,TF = 1 kpc, or m ≈ 10 eV/c2 if Rc,TF = 1 pc. On the other hand, fixing the same choice of core radii and considering ultralight boson masses, m ≈ 10–21 eV/c2, implies a tiny number for σs,TF close to zero, i.e., negligible. Concerning the ratio σs/m, however, we have seen that it is always very small, if m ⋘ 1 eV/c2, due to the dependence on m5 in (32) which drives it to tiny numbers. Only the “extreme” TF regime, where m > 10–4 eV/c2, provides high σs/m.
Finally, we show that our conclusions in this paper do not change, if we include the dependence of the scattering cross section on “temperature”, which effectively here is equivalent to virial velocity, or another characteristic velocity of that order, such as vcirc. Taking into account the effects of finite temperature (k ≠ 0) in the calculation of the 2-particle interactions means to go beyond the first Born approximation in (3) and (9), which, again, is a well-established result in the literature on s-wave scattering at low energies. Including the first order term in kinetic energy E (or k2, respectively) in the expansion of the scattering amplitude for indistinguishable bosons, results in the following modified equation for the scattering cross section
see e.g., (Joachain, 1975) and references therein. This formula is valid so long as the 2-particle interaction potential W(r) under the integral in (10) is less singular than 1/r2 around the origin, and vanishes faster than 1/r3 at infinity21. The ‘effective range’ re, which appears in (36), is defined in terms of the free wavefunction and the scattering wavefunction at large radii, respectively. In the zero-temperature limit, k → 0; formula (36) goes over into (9). Using now k−1 = ℏ/(mv) = λdeB(vcirc)/(2π) (by setting v = vcirc), we rewrite equ. (36) as
which reduces to equ. (9) in the limit of small quantum parameter, see (8) or (14). The scattering length |as| is now no longer related to g in the form of equ. (3), and instead has become the first, albeit leading order term of the coupling strength; see also (Landau and Lifshitz, 1992). Also, we have |as|≳ re in general, as long as the SI is sufficiently short-range, which we assume, hence we can estimate that
using (9) and (12). The velocity-dependent cross section σ(vcirc)/m decreases with increasing velocity, however, the additional terms due to vcirc are negligible compared to the leading-order term
Bose-Einstein-condensed dark matter (BEC-DM), also called scalar field dark matter (SFDM) has become a popular alternative to the standard, collisionless cold dark matter (CDM) model. If the boson masses of BEC-DM are ultralight, m ≳ 10–22 eV/c2, the dynamics between BEC-DM and CDM differs on kpc scale, providing new signature effects and a possible resolution of the small-scale structure problems of CDM. However, in recent years, a collection of new constraints in the literature have been determined on “fuzzy dark matter (FDM)” models of BEC-DM, where the mass m is the only free parameter. These bounds concern the structural length scales equ. (20), pointing to the requirement of m > 10–21 eV/c2 which makes the distinction to CDM smaller than previously thought. On the other hand, BEC-DM with a self-interaction (SI) introduces a further parameter, the SI-coupling strength g, implying different constraints. For models in the Thomas-Fermi (TF) regime of strongly repulsive SI, also called SFDM-TF or SIBEC-DM, the characteristic structural length scale is again described by a single parameter combination, ∼ g/m2 see (22), which is subject to constraints. Regardless of regime, these length scales are also related to the typical core size of BEC-DM halos.
In this paper, we derived the conditions on the BEC-DM particle parameters which result from the fundamental microphysical assumptions, which underlie the equation of motion of BEC-DM used in the literature, the Gross-Pitaevskii (GP) equation coupled to the Poisson equation; the GPP framework. To our knowledge, it has never been checked before what these assumptions entail for the DM parameters. More precisely, we have derived upper bounds on g which follow from the requirements that the system is sufficiently dilute (smallness of “gas parameter” (7), aka condition ‘D’ of (13)), and that only s-wave scattering is important (smallness of “quantum parameter” (8), aka condition ‘S’ of (14)). BEC-DM models without SI, g = 0, or very weak SI are also covered thereby. Also, a bound on g follows from the condition that BEC-DM pressure be negligible, compared to its energy density (i.e., behaving like nonrelativistic “cold dust”, condition ‘NR’ of (17) on cosmological scales). We expressed our conditions on g as a dependence on boson mass m, as well as on (mean) density and (circular) velocity of the system, which are considered free parameters. Here, we probed the conditions using various halo core parameters. The ‘NR’ condition provides the best constraint for most of the parameter space in m, although the condition ‘D’ becomes more important for m ≳ (0.1–10) eV/c2. Condition ‘S’ has barely any constraining power, but by the same token it implies (the a posteriori justification) that s-wave scattering is the only relevant scattering process in BEC-DM for boson parameters of interest.
Apart from the microphysical conditions, we also derived a relationship that connects m and g under the premise that virial equilibrium can be assumed for BEC-DM halo cores. We thereby extended a previous result of (Rindler-Daller and Shapiro, 2012) that was limited to the TF regime. It turns out that this virial constraint is the most stringent condition on the BEC-DM parameters, for all m ≲ 100 eV/c2. So, this is an example where dynamical constraints are stronger than those from microphysics, if the assumption of virial equilibrium is correct.
We also revisited and derived the implications for the elastic scattering cross section per particle mass, σs/m, of BEC-DM, with and without the inclusion of velocity-dependence. In either case, σs/m is a very small number, close to zero, for BEC-DM models with weak SI, but also for many models of interest in the TF regime. Only in the extreme TF regime where m ≳ 10–4 eV/c2, can σs/m attain high values, also dependent on the assumed halo core size. In the process, we could show that the mere adoption of the “self-interacting dark matter (SIDM)”-inspired bound of σs/m ≲ 1 cm2/g on BEC-DM models is not correct. In fact, depending on boson parameters, σs/m can take on values that are many orders of magnitude below or above the typical numbers of SIDM, and a proper comparison of theoretically allowed values to observational galactic data would require realistic simulations of BEC-DM, e.g., Bullet cluster-type halo collision simulations in the GPP framework.
We also put our results into context to previous literature, as follows. By assuming the virial constraint, we have implicitly made use of the fact that BEC-DM halos generically form a core, surrounded by an envelope. The cores constitute basically the equilibrium states of BEC-DM (i.e., close to virialization), while the envelopes have been shown to be very dynamical, see, e.g., (Schive et al., 2014a; Schive et al., 2014b; Schwabe et al., 2016; Mocz et al., 2017) for FDM. One-dimensional halo formation simulations of SFDM-TF have been performed in (Dawoodbhoy et al., 2021), where it has been established that a core-envelope structure also arises; in this case a TF core–very close to an (n = 1)-polytropic core-was found, enshrouded by an envelope which is CDM-like. The basic results were subsequently confirmed by 3D simulations in (Hartman et al., 2022b), who also find a dynamical envelope structure.
The halo envelopes found in both FDM and SFDM-TF simulations are similar to isothermal spheres. Previously, it has been shown in (Slepian and Goodman, 2012) that, if a TF core of condensed BEC-DM is enshrouded by an isothermal envelope of non-condensed bosons in local thermodynamical equilibrium, the transition between the different equation of states between core and envelope would result in a very sharp feature in the halo density profiles. Since such a sharp feature would be in conflict with observed galactic velocity profiles, it was argued by (Slepian and Goodman, 2012) that either such a core-envelope model would be ruled out, or that it would require a boson mass in conflict with other bounds22. However, contrary to the findings in (Slepian and Goodman, 2012), the analysis of SFDM-TF in (Dawoodbhoy et al., 2021; Hartman et al., 2022b; Shapiro et al., 2022) has revealed that a fatal sharp feature between core and envelope need not arise. The important difference is that there is only condensed BEC-DM throughout the halos in (Dawoodbhoy et al., 2021; Hartman et al., 2022b; Shapiro et al., 2022) (core plus envelope), and the apparent “isothermality” of the envelope there results from a purely effective description of the complicated wave dynamics of BEC-DM. A proper coarse-graining of the quantum pressure of BEC-DM gives rise to a “velocity dispersion pressure”, similarly to CDM.
Finally, recent works by Refs. (Hartman et al., 2022a; Foidl and Rindler-Daller, 2022; Shapiro et al., 2022) have found that theoretical constraints from linear structure formation highly suggest that halo cores in SFDM-TF should be smaller than kpc size, even preferring core radii with ≲ (1–100) pc. Therefore, we have also probed very small halo cores in this paper, finding that the GPP microphysical conditions are no obstacle to that choice; we are safe to pick such small radii. Like in the case of large cores, the virial condition provides the most powerful constraint on g here as well. From an observational perspective, small halo cores are very hard to infer and may be indistinguishable from core-free CDM models altogether. However, we stress that the question of the smallest-allowed core size in BEC-DM is not yet settled, given the computational difficulties of cosmological halo formation simulations. The latter are the subject of ongoing research in the community.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
The author confirms being the sole contributor of this work and has approved it for publication.
This work was supported by the Austrian Science Fund FWF through an Elise Richter fellowship to the author, Projektnummer V656-N28.
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1The GP equation in (1) is formally a nonlinear Schrödinger equation, given the nonlinear SI-term. In addition, nonlinearity comes in via the coupling of GP to the Poisson equation 2, to describe self-gravitating systems. While the GP equation resembles formally the linear Schrödinger equation if g = 0, the overall Schrödinger-Poisson system is nonlinear in any case. Moreover, the wavefunction ψ of GP is interpreted as the “c-number” of a highly occupied many-body quantum state, in the limit of large particle number, thus it is not the wavefunction of a single particle, but rather that of the macroscopic condensate itself. The GP model is effectively a mean-field description.
2There are two prominent possibilities why a |ψ|4-term in the Lagrangian, that gives rise to the |ψ|2ψ-term in the equation of motion, arises. On the one hand, ψ could serve as a Landau “order parameter” that describes the BEC state after a phase transition. In that case, it obeys translational symmetry and in the expansion of the (free) energy (functional) only even powers of ψ occur, with the usual truncation after the quartic term. On the other hand, if ψ serves as some relic scalar field that acquires its mass through some vacuum misalignment mechanism, like the QCD axion, the resulting Lagrangian has a cosine potential, which can be expanded and is also usually truncated after the quartic term. As another comment, we add that a quadratic potential can always be absorbed in the definition of the chemical potential of the system.
3For comparison, in the formation of BECs in the laboratory it is customary to speak of the thermal de Broglie wavelength,
4This value stems from (Bovy and Tremaine, 2012). Newer studies using GAIA data find very similar estimates of
5A short and clear presentation can be found for instance in (Stoof et al., 1996).
6We follow the cited papers for the notation of the particle interaction range “r0”. It shall not be confused with a radial quantity related to the halo, such as a core radius. We avoid this confusion by designating the subscript “c” to halo core properties in the forthcoming.
7In fact, the GP description for the wavefunction of the condensate can be derived from the more general Heisenberg equation for the field operator by truncating terms higher than first order in this gas parameter; see, e.g., (Huang and Tommasini, 1996) and references therein.
8As opposed to the result
9In general, the Born approximation assumes a sufficiently weak scattering process, where the scattered wave is a small perturbation on the incident plane wave. Nevertheless, one may truncate the potential at higher-order terms, as we will discuss in Sec.4. Furthermore, we stress that the scattering process referred to here is a quantum-mechanical treatment in the nonrelativistic limit, where one considers scattering of a particle in a potential, justified as long as the relative velocities are much smaller than the speed of light. This assumption is applied in many calculations of scattering cross sections in self-interacting dark matter in general, see, e.g., (Girmohanta and Shrock, 2022). Going beyond this treatment requires a fully-fledged quantum-field theoretical calculation.
10The homogeneous sphere is not too bad an approximation for the central nearly constant DM density cores of dwarf spheroidal galaxies, with numbers as high as
11Sufficiently small pressures also guarantee the similarity to CDM on scales demanded by cosmological observables, e.g., the expansion history during structure formation, or the subsequent development of the latter. Still, differences between BEC-DM and CDM have been identified concerning the very early Universe, or the amount of small-scale structure. We do not discuss these here, but see, e.g., (Sikivie and Yang, 2009; Li et al., 2014; Rindler-Daller, 2021).
12In fact, in analogy to the derivation of Jeans equations from a collisionless Boltzmann equation, one can show that a fluid picture is also possible for collisionless CDM or stellar systems, respectively, see (Ahn and Shapiro, 2005; Mitchell et al., 2013). The corresponding Euler momentum fluid equation in that case has a pressure term due to the velocity dispersion of the underlying particles (CDM or stars, respectively).
13Note that there is a typo in that equation; there should be no square in the last factor under the root.
14There exists a maximum mass Mc, max in the attractive case g < 0, above which the system will undergo collapse. This has been known for laboratory BECs experimentally and theoretically, see, e.g., (Zhang, 2000), but has been also established in astrophysical contexts, see, e.g., (Guth et al., 2015; Eby et al., 2016; Chavanis, 2019b). Also, in order for Rc to be real, we require the condition
15A homogeneous-sphere approximation would give the prefactor as
16We note that the prefactor differs slightly from the polytrope-based result in (Rindler-Daller and Shapiro, 2012), because our expression here is based upon the Gaussian ansatz (18).
17We effectively use the results of (Padilla et al., 2021) in their Sec.V B, including their equation 94. Note that there is a typo in that equation: the factor in front should read 1025, instead of 1037. However, this typo does not affect the bounds and conclusions derived in (Padilla et al., 2021).
18A complication arises in that SIDM model fits to observational data actually seem to favour different σs/m, depending on astronomical scale, where they should decrease as a function of relative velocities vrel of the DM particles. Taking vrel as a proxy for the virial velocity, fits of SIDM to galactic data on scales of ∼ (1–10) kpc with vrel ∼ (50–200) km/s yield σs/m ∼ 1 cm2/g, while fits to data of galaxy clusters on scales of several Mpc and relative velocities of order
19Relations (31) and (32) implicitly assume that m/mH ≫ 1—in order to be in the TF regime in the first place-, in which case we noted already in (Rindler-Daller and Shapiro, 2012) (see equation 142 there), that (31) can be rewritten, using the virial relation that connects m with g. We can recover that formula here simply from (29) by inserting (27) for g/gH, which yields
In any case, the derivation of equ.(32) does not presume the virial condition g = g(m), but the results are not very different if we had used (33) instead, in Figure 3.
20As an illustration of some numbers, consider a laboratory atomic BEC gas. Take, e.g., typical values from (Egorov et al., 2013) for 87Rb atoms. They have a mass of m = 87 u = 1.44 × 10−25 kg = 8.1 × 1010 eV/c2, and a scattering length of as ≈ 98 a0 with the Bohr radius a0 = 5.3 × 10−11 m, i.e., as ≃ 5.2 × 10−7 cm. Therefore,
21These conditions guarantee the analyticity of the scattering amplitude as a function of k2 (or E), and, hence, its expansion into a power series in k2.
22In fact, any DM species whose equation of state changes sharply enough between inner halo region (“core”) and outer region (“envelope”) to produce observational features in the density and velocity profiles, could be constrained that way. Again, the statement in (Slepian and Goodman, 2012) applies only to bosons in thermal equilibrium; see also the discussion in (Chavanis, 2019a), particularly footnote 20.
Ahn, K., and Shapiro, P. R. (2005). Formation and evolution of self-interacting dark matter haloes. MNRAS 363, 1092–1110. doi:10.1111/j.1365-2966.2005.09492.x
Armengaud, E., Palanque-Delabrouille, N., Yèche, C., Marsh, D. J., and Baur, J. (2017). Constraining the mass of light bosonic dark matter using sdss lyman-α forest. MNRAS 471, 4606–4614. doi:10.1093/mnras/stx1870
Bovy, J., and Tremaine, S. (2012). On the local dark matter density. ApJ 756, 89. doi:10.1088/0004-637X/756/1/89
Bullock, J. S., and Boylan-Kolchin, M. (2017). Small-scale challenges to the ΛCDM paradigm. ARA&A 55, 343–387. doi:10.1146/annurev-astro-091916-055313
Burkert, A. (2015). The structure and dark halo core properties of dwarf spheroidal galaxies. Astrophysical J. 808, 158. doi:10.1088/0004-637X/808/2/158
Calabrese, E., and Spergel, D. N. (2016). Ultra-light dark matter in ultra-faint dwarf galaxies. MNRAS 460, 4397–4402. doi:10.1093/mnras/stw1256
Chavanis, P. H. (2019). Derivation of the core mass-halo mass relation of fermionic and bosonic dark matter halos from an effective thermodynamical model. Phys. Rev. D. 100, 123506. doi:10.1103/PhysRevD.100.123506
Chavanis, P. H. (2011). Mass-radius relation of Newtonian self-gravitating Bose-Einstein condensates with short-range interactions. I. Analytical results. Phys. Rev. D. 84, 043531. doi:10.1103/PhysRevD.84.043531
Chavanis, P. H. (2019). Predictive model of BEC dark matter halos with a solitonic core and an isothermal atmosphere. Phys. Rev. D. 100, 083022. doi:10.1103/PhysRevD.100.083022
Dawoodbhoy, T., Shapiro, P. R., and Rindler-Daller, T. (2021). Core-envelope haloes in scalar field dark matter with repulsive self-interaction: Fluid dynamics beyond the de Broglie wavelength. MNRAS 506, 2418–2444. doi:10.1093/mnras/stab1859
de Salas, P., Malhan, K., Freese, K., Hattori, K., and Valluri, M. (2019) On the estimation of the local dark matter density using the rotation curve of the milky way. J. Cosmol. Astropart. Phys. 2019, 037. doi:10.1088/1475-7516/2019/10/037
Dev, P. S. B., Lindner, M., and Ohmer, S. (2017). Gravitational waves as a new probe of Bose-Einstein condensate Dark Matter. Phys. Lett. B 773, 219–224. doi:10.1016/j.physletb.2017.08.043
Eby, J., Kouvaris, C., Nielsen, N. G., and Wijewardhana, L. C. R. (2016) Boson stars from self-interacting dark matter. J. High Energy Phys. 2016, 28. doi:10.1007/jhep02(2016)028(2016)028
Egorov, M., Opanchuk, B., Drummond, P., Hall, B. V., Hannaford, P., and Sidorov, A. I. (2013). Measurement of s-wave scattering lengths in a two-component bose-einstein condensate. Phys. Rev. A 87, 053614. doi:10.1103/PhysRevA.87.053614
Eilers, A. C., Hogg, D. W., Rix, H. W., and Ness, M. K. (2019). The circular velocity curve of the Milky Way from 5 to 25 kpc. Astrophysical J. 871, 120. doi:10.3847/1538-4357/aaf648
Fan, J. (2016). Ultralight repulsive dark matter and BEC. Phys. Dark Universe 14, 84–94. doi:10.1016/j.dark.2016.10.005
Foidl, H., and Rindler-Daller, T. (2022). Cosmological structure formation in complex scalar field dark matter versus real ultralight axions: A comparative study using CLASS. Phys. Rev. D. 105, 123534. doi:10.1103/PhysRevD.105.123534
Girmohanta, S., and Shrock, R. (2022). Cross section calculations in theories of self-interacting dark matter. Phys. Rev. D. 106, 063013. doi:10.1103/PhysRevD.106.063013
Guth, A. H., Hertzberg, M. P., and Prescod-Weinstein, C. (2015). Do dark matter axions form a condensate with long-range correlation? Phys. Rev. D. 92, 103513. doi:10.1103/PhysRevD.92.103513
Guzmán, F. S., and Avilez, A. A. (2018). Head-on collision of multistate ultralight BEC dark matter configurations. Phys. Rev. D. 97, 116003. doi:10.1103/PhysRevD.97.116003
Hartman, S. T. H., Winther, H. A., and Mota, D. F. (2022). Constraints on self-interacting Bose-Einstein condensate dark matter using large-scale observables. J. Cosmol. Astropart. Phys. 2022, 005. doi:10.1088/1475-7516/2022/02/005) 005.
Hartman, S. T. H., Winther, H. A., and Mota, D. F. (2022). Cosmological simulations of self-interacting Bose-Einstein condensate dark matter. A&A 666, A95. doi:10.1051/0004-6361/202243496
Hlozek, R., Grin, D., Marsh, D. J. E., and Ferreira, P. G. (2015). A search for ultralight axions using precision cosmological data. Phys. Rev. D. 91, 103512. doi:10.1103/PhysRevD.91.103512
Hu, W., Barkana, R., and Gruzinov, A. (2000). Fuzzy cold dark matter: The wave properties of ultralight particles. Phys. Rev. Lett. 85, 1158–1161. doi:10.1103/PhysRevLett.85.1158
Huang, K., and Tommasini, P. (1996). Methods for a nonuniform Bose gas. J. Res. Natl. Inst. Stand. Technol. 101, 435. doi:10.6028/jres.101.046
Iršič, V., Viel, M., Haehnelt, M. G., Bolton, J. S., and Becker, G. D. (2017). First constraints on fuzzy dark matter from Lyman-α forest data and hydrodynamical simulations. Phys. Rev. Lett. 119, 031302. doi:10.1103/physrevlett.119.031302
Landau, L., and Lifshitz, E. (1992). Lehrbuch der theoretischen Physik: Statistische Physik. Band IX. Berlin: Akademie Verlag.
Lesgourgues, J., Arbey, A., and Salati, P. (2002). A light scalar field at the origin of galaxy rotation curves. New Astron. Rev. 46, 791–799. doi:10.1016/s1387-6473(02)00247-6
Li, B., Rindler-Daller, T., and Shapiro, P. R. (2014). Cosmological constraints on Bose-Einstein-condensed scalar field dark matter. Phys. Rev. D. 89, 083536. doi:10.1103/PhysRevD.89.083536
Li, B., Shapiro, P. R., and Rindler-Daller, T. (2017). Bose-Einstein-condensed scalar field dark matter and the gravitational wave background from inflation: New cosmological constraints and its detectability by LIGO. Phys. Rev. D. 96, 063505. doi:10.1103/PhysRevD.96.063505
Lora, V., Magana, J., Bernal, A., Sánchez-Salcedo, F., and Grebel, E. (2012) On the mass of ultra-light bosonic dark matter from galactic dynamics. J. Cosmol. Astropart. Phys., (2012) 011, doi:10.1088/1475-7516/2012/02/011
Magaña, J., and Matos, T. (2012). A brief review of the scalar field dark matter model. J.Phys.: Conf.Ser. 378, 012012.
Marsh, D. J. E., and Niemeyer, J. C. (2019). Strong constraints on fuzzy dark matter from ultrafaint dwarf galaxy Eridanus II. Phys. Rev. Lett. 123, 051103. doi:10.1103/PhysRevLett.123.051103
Matos, T., Guzmán, F. S., and Ureña López, L. A. (2000). Scalar field as dark matter in the universe. Class. Quantum Gravity 17, 1707–1712. doi:10.1088/0264-9381/17/7/309
Matos, T., and Ureña-López, L. A. (2002). Scalar field dark matter, cross section and Planck-scale physics. Phys. Lett. B 538, 246–250. doi:10.1016/S0370-2693(02)02002-6
Membrado, M., Pacheco, A. F., and Sañudo, J. (1989). Hartree solutions for the self-Yukawian boson sphere. Phys. Rev. A 39, 4207–4211. doi:10.1103/PhysRevA.39.4207
Mielke, E. W., Fuchs, B., and Schunck, F. E. Dark matter halos as Bose-Einstein condensates. The Tenth Marcel Grossmann Meeting. On recent developments in theoretical and experimental general relativity, gravitation and relativistic field theories (2006), 39. doi:10.1142/9789812704030_0005
Mitchell, N. L., Vorobyov, E. I., and Hensler, G. (2013). Collisionless stellar hydrodynamics as an efficient alternative to N-body methods. MNRAS 428, 2674–2687. doi:10.1093/mnras/sts228
Mocz, P., Vogelsberger, M., Robles, V. H., Zavala, J., Boylan-Kolchin, M., Fialkov, A., et al. (2017). Galaxy formation with BECDM - I. Turbulence and relaxation of idealized haloes. MNRAS 471, 4559–4570. doi:10.1093/mnras/stx1887
Nadler, E. O., Drlica-Wagner, A., Bechtol, K., Mau, S., Wechsler, R. H., Gluscevic, V., et al. (2021). Constraints on dark matter properties from observations of Milky Way satellite galaxies. Phys. Rev. Lett. 126, 091101. doi:10.1103/PhysRevLett.126.091101
Padilla, L. E., Rindler-Daller, T., Shapiro, P. R., Matos, T., and Vázquez, J. A. (2021). Core-halo mass relation in scalar field dark matter models and its consequences for the formation of supermassive black holes. Phys. Rev. D. 103, 063012. doi:10.1103/PhysRevD.103.063012
Pethick, C. J., and Smith, H. (2008). Bose-einstein condensation in dilute gases. 2 edn. Cambridge, United Kingdom: Cambridge University Press. doi:10.1017/CBO9780511802850
Pils, K., and Rindler-Daller, T. (2022). Orbits and adiabatic contraction in scalar-field dark matter halos: Revisiting the cusp-core problem in dwarf galaxies. MNRAS 514, 1990–2009. doi:10.1093/mnras/stac1471
Pitaevskii, L., and Stringari, S. (2003). Bose-Einstein condensation. Oxford: Oxford University Press.
Randall, S. W., Markevitch, M., Clowe, D., Gonzalez, A. H., and Bradač, M. (2008). Constraints on the self-interaction cross section of dark matter from numerical simulations of the merging galaxy cluster 1E 0657-56. ApJ 679, 1173–1180. doi:10.1086/587859
Rindler-Daller, T., and Shapiro, P. (2014). Finding new signature effects on galactic dynamics to constrain Bose-Einstein-condensed cold dark matter. Astrophysics Space Sci. Proc. 38, 163–182. doi:10.1007/978-3-319-02063-1_12
Rindler-Daller, T., and Shapiro, P. R. (2012). Angular momentum and vortex formation in Bose-Einstein-condensed cold dark matter haloes. MNRAS 422, 135–161. doi:10.1111/j.1365-2966.2012.20588.x
Rindler-Daller, T., and Shapiro, P. R. (2014). Complex scalar field dark matter on galactic scales. Mod. Phys. Lett. A 29, 1430002. doi:10.1142/S021773231430002X
Rindler-Daller, T. (2021). To observe, or not to observe, quantum-coherent dark matter in the Milky Way, that is a question. Front. Astronomy Space Sci. 8, 114. doi:10.3389/fspas.2021.697140
Safarzadeh, M., and Spergel, D. N. (2020). Ultra-light dark matter is incompatible with the Milky Way’s dwarf satellites. ApJ 893, 21. doi:10.3847/1538-4357/ab7db2
Salucci, P. (2019). The distribution of dark matter in galaxies. A&ARv 27, 2. doi:10.1007/s00159-018-0113-1
Schive, H. Y., Chiueh, T., and Broadhurst, T. (2014). Cosmic structure as the quantum interference of a coherent dark wave. Nat. Phys. 10, 496–499. doi:10.1038/nphys2996
Schive, H. Y., Liao, M. H., Woo, T. P., Wong, S. K., Chiueh, T., Broadhurst, T., et al. (2014). Understanding the core-halo relation of quantum wave dark matter from 3D simulations. Phys. Rev. Lett. 113, 261302. doi:10.1103/PhysRevLett.113.261302
Schwabe, B., Niemeyer, J. C., and Engels, J. F. (2016). Simulations of solitonic core mergers in ultralight axion dark matter cosmologies. Phys. Rev. D. 94, 043513. doi:10.1103/PhysRevD.94.043513
Shapiro, P. R., Dawoodbhoy, T., and Rindler-Daller, T. (2022). Cosmological structure formation in scalar field dark matter with repulsive self-interaction: The incredible shrinking Jeans mass. MNRAS 509, 145–173. doi:10.1093/mnras/stab2884
Sikivie, P., and Yang, Q. (2009). Bose-Einstein condensation of dark matter axions. Phys. Rev. Lett. 103, 111301. doi:10.1103/PhysRevLett.103.111301
Sin, S. J. (1994). Late-time phase transition and the galactic halo as a bose liquid. Phys. Rev. D. 50, 3650–3654. doi:10.1103/PhysRevD.50.3650
Slepian, Z., and Goodman, J. (2012). Ruling out bosonic repulsive dark matter in thermal equilibrium. MNRAS 427, 839–849. doi:10.1111/j.1365-2966.2012.21901.x
Stoof, H., Bijlsma, M., and Houbiers, M. (1996). Theory of interacting quantum cases. J. Res. Natl. Inst. Stand. Technol. 101, 443. doi:10.6028/jres.101.047
Ureña-López, L. A. (2019). Brief review on scalar field dark matter models. Front. Astronomy Space Sci. 6, 47. doi:10.3389/fspas.2019.00047
Keywords: cosmology, Bose-Einstein-condensed dark matter, galactic halos, Gross-Pitaevskii theory, Particle scattering
Citation: Rindler-Daller T (2023) On particle scattering in Gross-Pitaevskii theory and implications for dark matter halos. Front. Astron. Space Sci. 10:1121920. doi: 10.3389/fspas.2023.1121920
Received: 12 December 2022; Accepted: 04 May 2023;
Published: 23 May 2023.
Edited by:
Antonino Marciano, Fudan University, ChinaReviewed by:
Paolo Salucci, International School for Advanced Studies (SISSA), ItalyCopyright © 2023 Rindler-Daller. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tanja Rindler-Daller, dGFuamEucmluZGxlci1kYWxsZXJAdW5pdmllLmFjLmF0
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.