
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Astron. Space Sci. , 29 September 2022
Sec. Space Physics
Volume 9 - 2022 | https://doi.org/10.3389/fspas.2022.989369
This article is part of the Research Topic Sources and Propagation of Ultra-Low Frequency Waves in Planetary Magnetospheres View all 9 articles
 Lucile Turc1*
Lucile Turc1* Hongyang Zhou1
Hongyang Zhou1 Vertti Tarvus1
Vertti Tarvus1 Matti Ala-Lahti1,2
Matti Ala-Lahti1,2 Markus Battarbee1
Markus Battarbee1 Yann Pfau-Kempf1
Yann Pfau-Kempf1 Andreas Johlander3
Andreas Johlander3 Urs Ganse1
Urs Ganse1 Maxime Dubart1
Maxime Dubart1 Harriet George1
Harriet George1 Maxime Grandin1
Maxime Grandin1 Konstantinos Horaites1
Konstantinos Horaites1 Fasil Tesema1
Fasil Tesema1 Jonas Suni1
Jonas Suni1 Markku Alho1
Markku Alho1 Konstantinos Papadakis1
Konstantinos Papadakis1 Minna Palmroth1,4
Minna Palmroth1,4Ultra-low frequency (ULF) waves in the Pc3 range, with periods between 10–45 s, are routinely observed in Earth’s dayside magnetosphere. They are thought to originate in the foreshock, which extends upstream of the quasi-parallel bow shock and is populated with shock-reflected particles. The foreshock is permeated with ULF waves generated by ion beam instabilities, most notably the “30-s” waves whose periods match those of the Pc3 waves and which are carried earthward by the solar wind flow. However, the global picture of Pc3 wave activity from the foreshock to the magnetosphere and its response to changing solar wind conditions is still poorly understood. In this study, we investigate the global distribution and properties of Pc3 waves across near-Earth space using global simulations performed with the hybrid-Vlasov model Vlasiator. The simulations enable us to study the waves in their global context, and compare their properties in the foreshock, magnetosheath and dayside magnetosphere, for different sets of upstream solar wind conditions. We find that in all three regions the Pc3 wave power peaks at higher frequencies when the interplanetary magnetic field (IMF) strength is larger, consistent with previous studies. The Pc3 wave power is significantly enhanced in all three regions for higher solar wind Alfvén Mach number. As this parameter is known to affect the shock properties but has little impact inside the magnetosphere, this brings further support to the magnetospheric waves originating in the foreshock. Other parameters that are found to influence the foreshock wave power are the solar wind density and the IMF cone angle. Inside the magnetosphere, the wave power distribution depends strongly on the IMF orientation, which controls the foreshock position upstream of the bow shock. The wave power is largest when the angle between the IMF and the Sun-Earth line is smallest, suggesting that wave generation and transmission are most efficient in these conditions.
Ultra-low frequency (ULF) waves permeate the near-Earth plasma environment and play an important role in its dynamics, for example in transferring energy from the solar wind to the magnetosphere or accelerating electrons in the Earth’s radiation belts (Zong et al., 2017). ULF waves in the Pc3 range, with periods between 10–45 s according to the classification proposed by Jacobs et al. (1964), are a common feature of the dayside magnetosphere, where they are frequently observed both by spacecraft and ground-based observatories (Troitskaya and Gul’Elmi, 1967; Takahashi et al., 1984; Yumoto et al., 1985; Engebretson et al., 1987; Clausen et al., 2009; Heilig et al., 2007; Heilig et al., 2010; Bier et al., 2014; Takahashi et al., 2016). They are thought to originate from the ion foreshock, extending upstream of the Earth’s quasi-parallel bow shock, that is, where the interplanetary magnetic field (IMF) and the normal to the shock surface make an angle θBn ≤ 45°. There, ULF waves in the Pc3 frequency range are produced by ion beam instabilities, due to the interaction of shock-reflected suprathermal ions with the incoming solar wind (Eastwood et al., 2005a; Wilson, 2016).
The dominant wave mode in the foreshock is produced by the ion-ion beam right-hand instability and has a typical period around 30 s in Earth’s foreshock (Eastwood et al., 2005a; Wilson, 2016). These waves are thus often designated as “30-s” waves. Their exact period however varies significantly depending on the solar wind conditions, in particular the IMF strength, between 10 and 80 s (Le and Russell, 1996; Eastwood et al., 2005b; Hsieh and Shue, 2013). Their wavelength is of the order of 1 Earth radius (RE = 6,371 km) and they are left-hand polarised in the spacecraft frame. Their intrinsic polarisation is however right-handed, indicative of a fast mode (Hoppe and Russell, 1983; Eastwood et al., 2005b). The polarisation reversal is due to the waves attempting to propagate sunward, while they are effectively carried earthward by the faster solar wind flow.
The fate of foreshock 30-s waves at Earth’s bow shock and in the downstream magnetosheath is a long-standing open question. There is compelling observational evidence indicating that the waves survive the shock crossing in some form, or at least that a signal retaining the same frequency travels all the way to the magnetopause. Multiple studies have reported simultaneous observations in the foreshock and inside the magnetosphere exhibiting waves at the same frequencies (Clausen et al., 2009; Regi et al., 2014). Furthermore, the occurrence of magnetospheric Pc3 waves is closely related to the foreshock position, which is controlled by the IMF direction, in particular its cone angle θBx, between the IMF and the Sun-Earth line. Small cone angles, for which the foreshock extends upstream of the subsolar magnetosphere, are most conducive to intense Pc3 wave activity, whereas these pulsations essentially disappear for θBx ∼ 90° (Wolfe et al., 1985; Yumoto et al., 1985; Odera, 1986; Chi et al., 1994; Heilig et al., 2007).
Another piece of evidence linking magnetospheric Pc3 waves with foreshock 30-s waves is that both show the same relationship with the IMF strength, with the wave frequency increasing with increasing IMF strength (Takahashi et al., 1984; Le and Russell, 1996). In the foreshock, this dependency is due to the waves being generated via cyclotron resonance (Eastwood et al., 2005b). Many studies have been dedicated to finding an empirical formula for the foreshock wave frequency, first as function of the IMF strength BIMF alone, for example f [mHz] = 5.81 ± 0.14BIMF [nT] (Russell and Hoppe, 1981), then including the contribution of the IMF cone angle (Le and Russell, 1996)
Based on theoretical considerations, Takahashi et al. (1984) derived the following equation:
More recently, Heilig et al. (2007) used Pc3 waves observations from the SWARM satellite constellation in the topside ionosphere to obtain a new expression:
including this time a dependency on the solar wind Alfvén Mach number MA rather than on the IMF cone angle. These expressions are widely used when studying magnetospheric Pc3 waves, especially when no direct observations of the foreshock waves are available (Bier et al., 2014; Takahashi et al., 2016).
While it remains unclear how foreshock waves reach the magnetopause, the next steps in their earthward journey are better known: they enter the dayside magnetopause and travel antisunward into the magnetosphere as compressional Pc3 fluctuations, transporting the wave energy towards the nightside (Odera et al., 1991; Chi et al., 1994). In the inner magnetosphere, they couple to Alfvénic field line resonances, where their frequency matches the eigenmodes of the Earth’s magnetic field lines (Southwood and Hughes, 1983). The amplitude of the compressional mode decays when moving further into the magnetosphere, yet they can sometimes be observed all the way to the midnight sector (Ponomarenko et al., 2010; Takahashi et al., 2016). Compressional Pc3 wave power associated with transmitted foreshock waves is confined near the equator (Takahashi and Anderson, 1992; Heilig et al., 2007).
As concerns the longitudinal distribution of Pc3 wave activity, there is a general consensus that the equatorial Pc3 wave power is stronger in the prenoon or noon sector, consistent with the foreshock extending upstream of the dawn flank bow shock for a Parker-spiral IMF orientation (Takahashi and Anderson, 1992; Cao et al., 1994; Howard and Menk, 2005; Heilig et al., 2007; Murphy et al., 2020). The statistical Pc3 wave survey by Howard and Menk (2005) shows that the occurrence of Pc3 field line resonances has a broad maximum between 07-13 MLT (magnetic local time). On the other hand, the wave survey carried out by Lessard et al. (1999), based on the data of the AMPTE spacecraft, provides apparently contradicting results, showing that compressional Pc3 waves occur predominantly in the afternoon sector. This discrepancy can be explained by other sources of compressional waves in the Pc3 range inside the magnetosphere, which are unrelated to foreshock waves (Takahashi, 1996). These statistical surveys include various levels of geomagnetic activity. However, contrary to Pc5 pulsations (150–600 s) (Simms et al., 2010), Pc3 wave activity does not show a clear correlation with the level of geomagnetic disturbances, although some studies suggest that Pc3 wave power may increase with geomagnetic activity (Takahashi and Anderson, 1992).
Numerical studies of Pc3 pulsations pose a significant challenge because these waves are generated by an ion kinetic instability, while their coupling with field line resonances in the inner magnetosphere requires a three-dimensional (3D) setup. Modelling the wave generation and transmission into the magnetosphere thus calls for a global simulation including ion-scale kinetics. Most numerical investigations of magnetospheric ULF waves concentrate on other wave sources which can be modelled in a magnetohydrodynamic (MHD) framework, allowing for 3D global simulations (Claudepierre et al., 2010; Ellington et al., 2016; Archer et al., 2022). On the other hand, studies based on hybrid models (ions treated kinetically, electrons modelled as a fluid) have mostly focused on foreshock wave generation and their interaction with the bow shock (Krauss-Varban and Omidi, 1991; Krauss-Varban, 1995; Lin and Wang, 2005; Blanco-Cano et al., 2006; Palmroth et al., 2015; Turc et al., 2018; Hao et al., 2021). In a recent study, Takahashi et al. (2021) used a 2D global hybrid-Vlasov simulation to interpret spacecraft observations of Pc3 wave activity during an interval of strong solar wind driving. The model showed that the waves had a shorter spatial scale length during this event, which could explain their rapid attenuation inside the magnetosphere. 3D global hybrid-Particle-in-Cell (PiC) simulations have also been employed to investigate mode conversion of fast-mode foreshock disturbances at the magnetopause and the resulting magnetospheric wave activity (Shi et al., 2013; Shi et al., 2017; Shi et al., 2021). Shi et al. (2021) found that ULF waves and field line resonances can be generated inside the magnetosphere by broadband foreshock perturbations, and that their power decreases at lower Mach number.
The present study pursues these numerical endeavours in analysing a set of 2D global simulations performed with the hybrid-Vlasov model Vlasiator (Palmroth et al., 2018), as used in the Takahashi et al. (2021) study. We examine six runs with different upstream parameters in order to determine how these affect the wave properties throughout near-Earth space. Foreshock wave properties have already been studied in detail in previous publications for three of these runs (Palmroth et al., 2015; Turc et al., 2018; Takahashi et al., 2021), showing their good agreement with spacecraft measurements in Earth’s foreshock. Here, we expand significantly upon these previous works in investigating the wave properties in a global manner, throughout the simulation domain, instead of focusing on selected virtual spacecraft positions. This allows us to obtain a global view of Pc3 wave activity for different sets of solar wind conditions. As already discussed in Takahashi et al. (2021), the 2D global simulations allow us to study the waves from their generation in the foreshock to their entry into the magnetosphere as compressional waves, but not their coupling with field line resonances. We focus in particular on the transverse Pc3 wave power in the foreshock, representative of 30-s waves, and on the compressional Pc3 wave power in the outer magnetosphere, and we discuss the links between Pc3 wave activity in the different geophysical regions.
In this work, we analyse numerical simulations performed with the Vlasiator model (von Alfthan et al., 2014; Palmroth et al., 2018). Vlasiator provides global simulations of near-Earth space which include ion kinetic processes. This allows us to simulate self-consistently the processes giving rise to foreshock ULF waves and their impact on the magnetosheath and the outer magnetosphere. This model is based on a hybrid-Vlasov description of the plasma, meaning that ions (here protons) are described as distribution functions, while electrons are a cold, massless, charge-neutralising fluid. The evolution of the ion distribution functions is governed by Vlasov’s equation, coupled with Maxwell’s equations. Closure of the system is provided by Ohm’s law, including the Hall term.
The runs analysed in this paper are two-dimensional (2D) in ordinary space and simulate the equatorial plane of near-Earth space, corresponding to the xy − plane in the Geocentric Solar Ecliptic (GSE) coordinate system. In this Earth-centred frame, the x-axis is oriented sunward along the Sun-Earth line, z points northward, perpendicular to the Earth’s orbital plane. y completes the right-handed three-axis set. The solar wind is injected at the + x boundary of the simulation domain, and Neumann copy-conditions are applied at the other in-plane boundaries. In the out-of-plane direction, the simulation domain has a finite, one grid cell wide, thickness and periodic boundary conditions are employed. Each grid cell in ordinary space is associated with a 3D velocity space in which the ion distribution functions evolve. In all runs, the velocity space resolution is 30 km s−1. The Earth’s magnetic dipole moment is implemented at its actual value of 8.0 × 1022 A m2. The inner boundary of the simulation is a perfectly-conducting circle at about 4.7 RE from the Earth’s centre in all runs but one, Run MC_B14, where it is located at 3.9 RE due to the high solar wind dynamic pressure which pushes the magnetopause inward. The velocity distribution functions are set as Maxwellian distributions with a density of 1 cm−3 at the inner boundary. The simulation time step is adjusted dynamically throughout the run to ensure that the proton gyroperiod is well resolved even in regions with high magnetic field strength. Its value is typically around dt ∼ 0.02 s, while simulation outputs are written every 0.5 s.
The six runs used in this study are performed with steady upstream solar wind conditions, and their main parameters are given in Table 1. In each run, the IMF vector lies in the simulation (xy GSE) plane. The fast solar wind velocities were chosen in order to speed up the initialisation of the runs and thus save on computational resources. IMF strengths of 3–5 nT correspond to typical values at Earth (Ma et al., 2020), while higher IMF strengths are typically encountered during large-scale solar wind structures such as magnetic clouds (Turc et al., 2016). The spatial resolution, although not resolving the solar wind ion inertial length in some of the runs (see Table 1), is sufficient to describe accurately the processes of interest here, as foreshock ULF waves have wavelengths of the order of 1 RE. As shown in Pfau-Kempf et al. (2018), ion kinetic effects arise in the simulation even when the ion inertial length is underresolved because of the hybrid-Vlasov formalism. Previous studies have confirmed that foreshock wave properties in those runs are consistent with observational results (Palmroth et al., 2015; Turc et al., 2018; Turc et al., 2019; Takahashi et al., 2021).
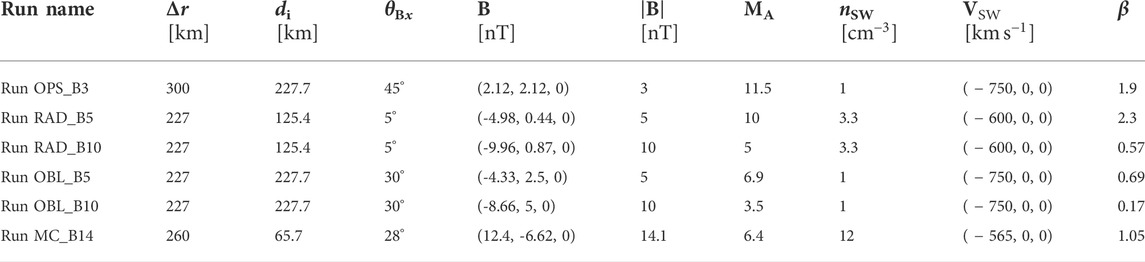
TABLE 1. Summary of the run parameters. Δr is the cell size, di the ion inertial length, θBx the IMF cone angle, B the IMF vector in GSE coordinates, ∣B∣ the IMF strength, MA the solar wind Alfvén Mach number, nSW the solar wind proton density, VSW the solar wind bulk speed and
We use the following naming convention for the runs under study: the first group of letters indicates the IMF orientation, OPS for ortho-Parker spiral, OBL for oblique (θBx = 30°), RAD for radial IMF (θBx = 5°), while MC stands for Magnetic Cloud to indicate the strong solar wind driving in this run. The second group of letter and numbers denotes the IMF strength in the simulation.
In Run OPS_B3, the IMF makes a 45° cone angle with the Sun-Earth line and points sunward and duskward, thus corresponding to an ortho-Parker spiral orientation. This orientation is equivalent to a Parker spiral orientation for the processes of interest here, albeit with the foreshock lying on the dusk flank rather than the dawn flank. Cone angles near 45° are most typical at Earth, observed about 41% of the time (45° ± 20°) (Génot and Lavraud, 2021). Runs RAD_B5 and RAD_B10 on the one hand, and Runs OBL_B5 and OBL_B10 on the other hand, form two sets of runs within which the only difference between one run and the other is the IMF strength, thus allowing us to investigate the influence of this parameter on the Pc3 wave properties in different regions of near-Earth space. The different cone angles, at 5° and 30° from the Sun-Earth line, are all conducive to the efficient transmission of foreshock waves into the dayside magnetosphere (Takahashi et al., 1984). Finally, Run MC_B14 corresponds to more extreme driving conditions, corresponding to the solar wind parameters during the magnetic cloud event on 2016-07-20 (Takahashi et al., 2021).
Figure 1 provides an overview of the six runs under study, showing the Bz, out-of-plane, magnetic field component in a portion of the simulation domain covering the regions of interest: dayside magnetosphere and magnetosheath, and part of the foreshock and upstream solar wind. Panel A shows slightly different x and y ranges than the other panels in order to better include the foreshock. A similar figure covering the entire simulation domain is included as Supplementary Material. It shows that the actual simulation domain extends at least 10 RE further in each direction, ensuring that no edge effects such as wave reflection at the outer boundaries impact the wave activity in the areas under study. The Bz oscillations upstream of the shock are mostly due to the 30-s waves, showing organised phase fronts with their normal roughly aligned with the IMF. The wavelength appears relatively constant across the foreshock in a given run, but varies significantly between runs. Inside the magnetosheath, a superposition of wave modes with different wavelengths can be observed. For oblique IMF orientations (panels a and d-f) the waves at shorter wavelengths in the quasi-perpendicular magnetosheath correspond to electromagnetic ion cyclotron (EMIC) waves (as shown in Dubart et al. (2020) for another Vlasiator run). Mirror modes are not visible in the Bz fluctuations but develop downstream of the quasi-perpendicular shock (Hoilijoki et al., 2016; Dubart et al., 2020).
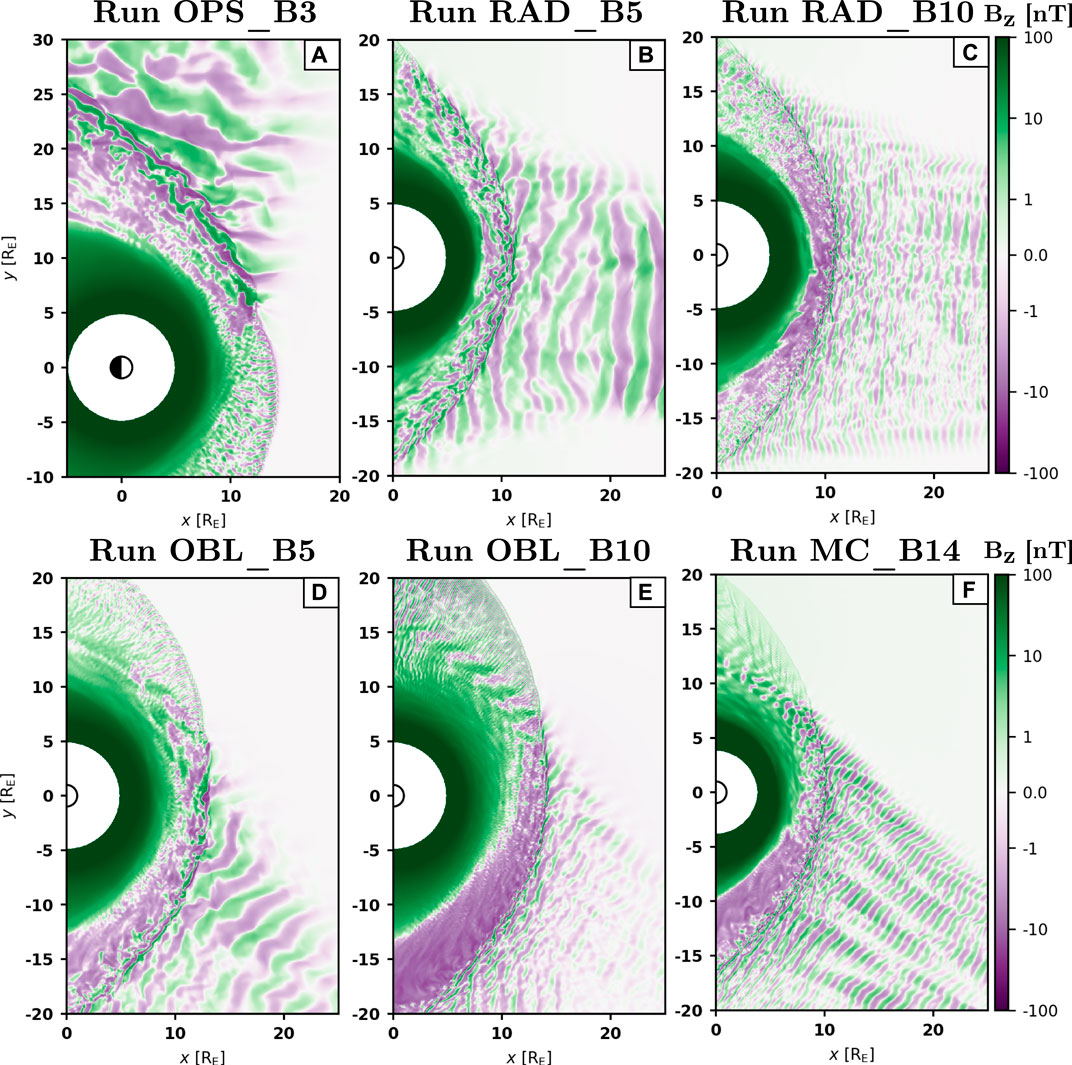
FIGURE 1. Bz magnetic field component in the runs under study at t = 500 s from the beginning of the simulation, in a portion of the simulation domain covering the dayside magnetosphere, magnetosheath and part of the foreshock and upstream solar wind. All panels have the same x and y axis extent, but panel (A) has different x and y ranges to better show the foreshock.
The power and the dominant periods of the magnetic field fluctuations at a given position in the simulation domain are obtained from a wavelet transform of the magnetic field time series extracted at the selected location, using a Morlet wavelet function (Torrence and Compo, 1998). This analysis can be repeated in each cell of the simulation domain, thus providing information about wave activity throughout near-Earth space. We concentrate here on the fluctuations of the magnetic field strength, indicative of compressional wave activity, and of the magnetic field Bz component, which is the out-of-plane component in our 2D simulations and thus provides information about the transverse waves outside of the magnetosphere, as the IMF lies in the xy − plane in all runs. Inside the magnetosphere, the dipolar field lines are essentially along z and the variations of Bz and |B| both correspond to compressive waves.
To facilitate the analysis of the wave properties from a global perspective, we calculate the mean, median and total wave power in the 10–60 s period band, which corresponds to the Pc3 range (10–45 s) and part of the Pc4 range (45–150 s). This is done by computing the mean, median, and sum of the wavelet power spectra integrated between 10 and 60 s and over 150 s of the simulation time, from 350 to 500 s from the beginning of the run. The upper limit of the period range is chosen in order to include the peak in wave power due to foreshock waves in Run OPS_B3, which, because of the low IMF strength in this run, is near 45 s. This is also consistent with spacecraft observations showing that foreshock 30-s wave periods can extend beyond the Pc3 range (Le and Russell, 1996; Eastwood et al., 2005b; Hsieh and Shue, 2013). For simplicity, the period range will still be referred to as the “Pc3 range” in the remainder of the paper, as it only slightly extends into the Pc4 range. The 150 s interval was chosen as it includes multiple wave periods even for the higher end of the Pc3 range while being short enough to limit the influence of the outward motion of the bow shock, due to the 2D setup of our simulations. The lack of a third dimension causes the IMF to pile up in front of the magnetosphere, resulting in a slight continual expansion of the bow shock [see for example Turc et al. (2020)].
We found that the mean, median and total Pc3 wave power showed comparable distributions in the simulation domain, although their actual values differ (not shown). Because we are interested in the wave power distribution and in the relative variations between the different runs, our results are not affected by the choice of one or the other of these quantities. In the remainder of this paper, only the mean wave power will be discussed, but identical conclusions were reached based on the median and total wave power.
Inside each simulation cell, we also calculated the power spectral density (PSD) of the fluctuations, again over the same 150-s interval. We then identified the peaks of the PSD in the Pc3 range, and retrieved the wave period associated with the highest PSD peak, which we consider as representative of the dominant wave mode.
The accurate determination of the magnetopause position is challenging in 2D global simulations covering the Earth’s equatorial plane, as we cannot trace the field lines to identify the boundary between closed and open field lines. Furthermore, because of the piling-up of the field lines around the magnetosphere, there is no sharp transition between the northward magnetospheric field and the in-plane IMF, as can be seen in Figure 1 where Bz increases progressively when moving earthwards. Another method to identify the magnetopause in global simulations, based on the magnetosheath flow pattern, was proposed by Palmroth et al. (2003). The magnetopause is then defined as the surface in which the magnetosheath flowlines do not enter. However, this method has some limitations in the subsolar region, as the flowlines diverge around the subsolar point.
More recently, Brenner et al. (2021) suggested a new identification method employing the β∗ parameter, a modified plasma β including the contribution of the dynamic pressure Pdyn, defined as:
where Pth is the thermal pressure and Pmag the magnetic pressure. The magnetopause is then defined as an isocontour of β*, as this parameter displays a clear gradient at the transition between magnetosphere and magnetosheath. Brenner et al. (2021) use β* = 0.7 and indicate that values within the range 0.1–1.5 yield similar results in their global MHD run. This method also has the advantage of being computationally inexpensive, compared to methods based on field line or streamline tracing.
For our Vlasiator runs, we calculated the average β* over the 150 s interval under study,
Figure 2 shows the period of the dominant transverse fluctuations in the Pc3 range upstream of the bow shock in the six runs, corresponding to the 30-s foreshock waves. The bow shock is identified as the position where the proton density increases to twice its solar wind value (Battarbee et al., 2020; Tarvus et al., 2021), and all the data points downstream of this are excluded from the analysis. Furthermore, if no peak could be identified from the PSD or when the PSD value associated with this peak was below 0.01 nT2/Hz, the cells are shown in white. The latter ensures that the identified periods are related to well-developed wave activity. We find a substantial spatial variation of the dominant wave period across the foreshock, especially in those runs with more oblique IMF orientations.
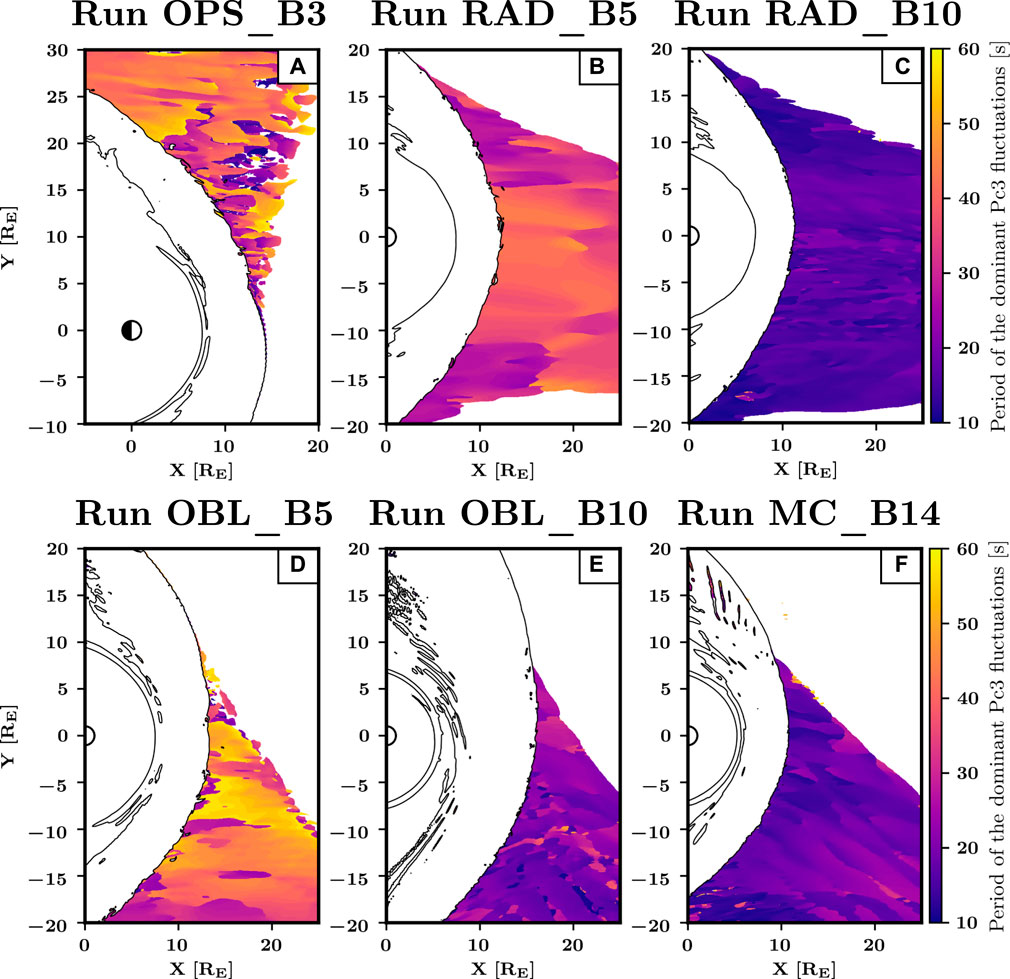
FIGURE 2. Period of the dominant Bz fluctuations upstream of the bow shock in the different runs. The black contours are plotted where n = 2nSW. The sunwardmost black contour in each panel corresponds to the bow shock position.
We then calculated the mean value of the foreshock wave period and its standard deviation for each of the maps shown in Figure 2. The results of this analysis are shown in Figure 3, where the error bars correspond to one standard deviation of the wave period. Also shown are the predicted foreshock wave periods obtained from the formulae by Takahashi et al. (1984) (Eq. 2), Le and Russell (1996) (Eq. 1) and Heilig et al. (2007) (Eq. 3). In the top panel, the different runs are arranged as a function of the IMF strength. We find that our simulations reproduce well the established trend that the wave period decreases when the IMF strength increases. The obtained wave periods are overall in good agreement with the predictions from these formulae, although the Takahashi et al. (1984) and Le and Russell (1996) predictions largely overestimate the wave period for the lowest IMF strength, yielding values above 80 s (not included in Figure 3 for clarity) compared to 30-50 s in our simulation. With the exception of this run, the best agreement is obtained with the Le and Russell (1996) formula (Eq. 1). The periods predicted by the Takahashi et al. (1984) formula (Eq. 2) tend to be lower than those computed in the simulation, whereas we found no consistent trend for the discrepancies with the Heilig et al. (2007) formula (Eq. 3). These different behaviours are likely due to the different methods used to build these formulae.
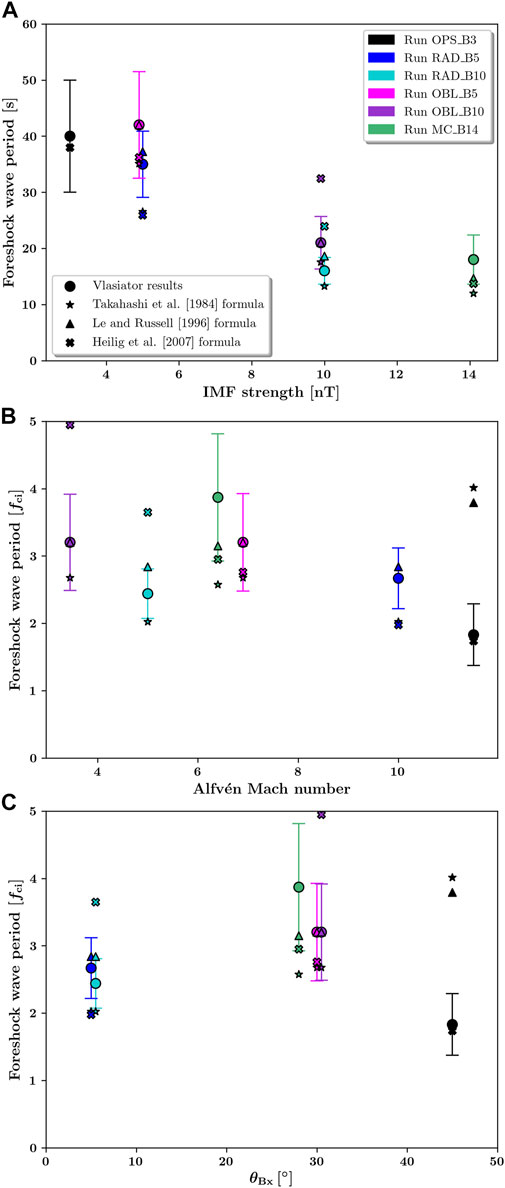
FIGURE 3. Mean foreshock wave period in the different runs and predictions from the Takahashi et al. (1984) (Eq. 2), Le and Russell (1996) (Eq. 1) and Heilig et al. (2007) (Eq. 3) formulae, as a function of (A) the IMF strength, (B) the Alfvén Mach number and (C) the cone angle θBx. The error bars for the simulation results correspond to one standard deviation of the wave period. The wave periods are given in seconds in panel (A) and are normalised with the proton gyrofrequency fci = qB/(2πmp) (with q the proton charge and mp the proton mass) in panels (B) and (C) in order to remove the dependency on the IMF strength. In panel (A), two outliers for B = 3 nT are beyond the y-axis range of the figure: 88 s for the Takahashi et al. (1984) formula and 83 s for the Le and Russell (1996) formula. To improve the legibility of the figure, the results for the two oblique runs (in pink and purple) have been shifted by −0.1 nT in panel (A) and the results of Runs RAD_B10 and OBL_B10 have been shifted by 0.1° in panel (C).
Figures 3B,C show the wave period normalised with the proton gyrofrequency (in order to remove the dependency on the IMF strength) as a function of the Alfvén Mach number and the cone angle. For MA > 5, we obtain the same trend as in the Heilig et al. (2007) formula, that is, a decreasing wave period with increasing Alfvén Mach number. For MA ≤ 5, however, we observe lower values than predicted by the Heilig et al. (2007) formula. We note that the vast majority of the events in the Heilig et al. (2007) dataset are associated with Alfvén Mach numbers between 5 and 11, which likely explains the deviations for low MA values. As concerns the IMF cone angle, no clear trend can be observed in our runs. The two oblique runs OBL_B5 and OBL_B10 have larger wave periods than the two radial runs, RAD_B5 and RAD_B10, as expected from both the Takahashi et al. (1984) and the Le and Russell (1996) formulae, but Run MC_B14 shows values higher than expected, possibly because of the extreme driving conditions characterising this run. As for Run OPS_B3, the normalised wave periods depart significantly from the predictions of both formulae including a cone angle dependency, suggesting that inaccuracies may arise at large cone angle values.
Figure 4 shows the mean power of the Bz fluctuations in the Pc3 range in the different runs, corresponding to the mean transverse wave power outside of the magnetosphere. In the foreshock, the Pc3 wave power is significantly higher in Runs RAD_B5 and OBL_B5 (Figures 4B,D) than in their counterparts with lower Alfvén Mach numbers (Figures 4C,E). It also decays more rapidly when moving away from the shock at lower Mach numbers (Runs RAD_B10 and OBL_B10).
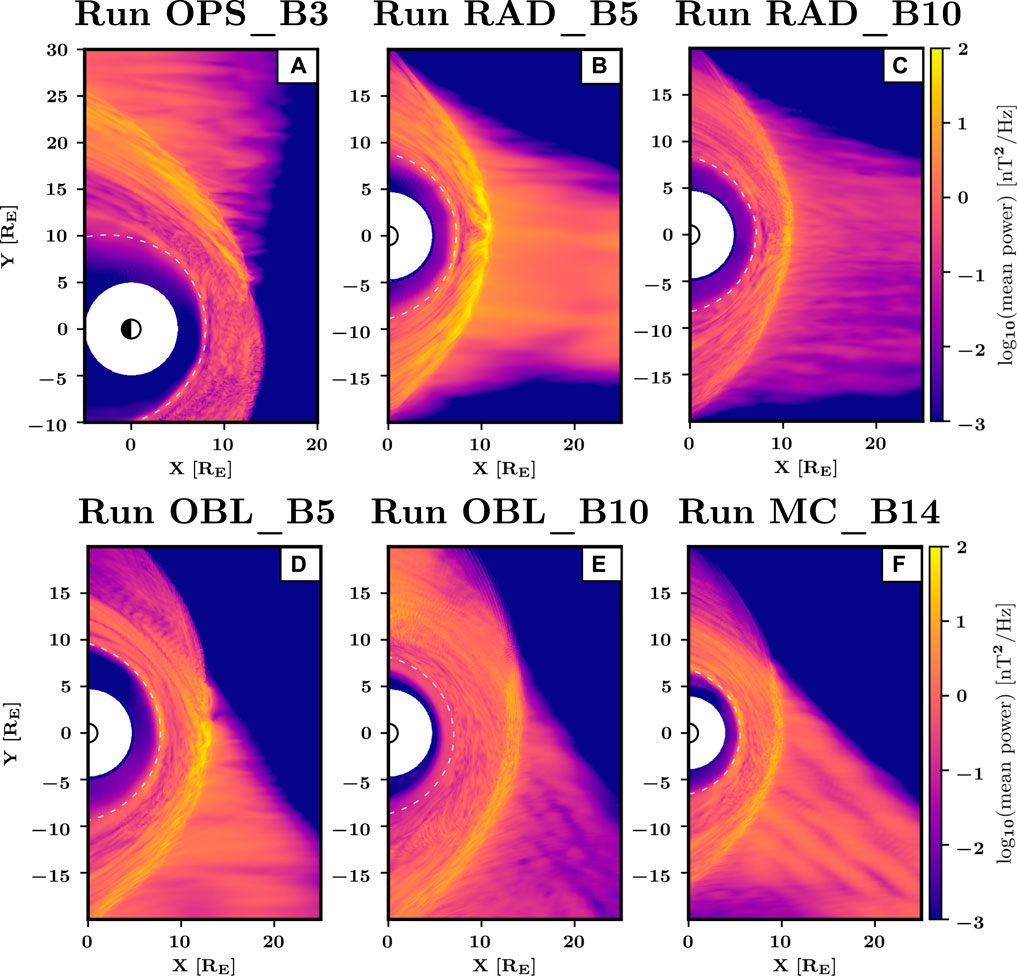
FIGURE 4. Mean wave power of the Bz fluctuations in the Pc3 range in the six runs under study. The white dashed line corresponds to
The Alfvén Mach number is not the only parameter that appears to control the Pc3 wave power in the foreshock. For example, the mean wave power is somewhat larger in Run MC_B14 than in Run OBL_B5 despite its slightly smaller MA (MA = 6.4, compared with MA = 6.9). The enhanced wave power in Run MC_B14 is likely due to the large solar wind ion density, which results in a higher suprathermal ion density at similar MA (not shown). Furthermore, while MA is largest in Run OPS_B3 (MA = 11.5), the foreshock wave power is significantly lower than for example in Run RAD_B5, and comparable to that in Run OBL_B5, where MA = 6.9. One of the major differences between Runs OPS_B3 and RAD_B5 is the IMF cone angle values, θBx = 45° and θBx = 30°, respectively. This suggests that the cone angle can also affect significantly the foreshock wave power.
Inside the magnetosheath, the transverse wave power is highest in the immediate downstream of the quasi-parallel bow shock. For a given IMF orientation, the thickness of the region of strongest wave power is larger at higher Mach number. This enhanced wave power could be due to fluctuations either transmitted from the foreshock or generated at the quasi-parallel shock. Note that localised or global bow shock motions can cause an increase in wave power in this region as a given simulation cell can sometimes sample upstream as well as magnetosheath plasma. For IMF cone angles around 30° (Figures 4D–F), there is also significant wave power in the quasi-perpendicular magnetosheath (y > 0). This enhanced wave power is located on flowlines and on magnetic field lines that are connected with the foreshock, as its edge extends duskward of the subsolar bow shock, suggesting a source in the foreshock or at the quasi-parallel shock. These fluctuations can be seen in Figures 1D–F as the large-scale Bz oscillations in the middle of the quasi-perpendicular magnetosheath. Interestingly, although the EMIC wave period is below the Pc3 range (typically a few seconds), we observe a spatial modulation of the magnetosheath Pc3 wave power at scales corresponding to that of the EMIC waves. This is particularly visible in Figure 4E, near x ∼ 0–5 RE and y ∼ 10–15 RE.
The mean Bz wave power inside the magnetosphere (earthwards of the white dashed line) shows much less small-scale spatial variability than in the magnetosheath. The magnetospheric wave power maximises at the magnetopause and decays when moving further inward, consistent with compressional Pc3 fluctuations entering the magnetosphere (Engebretson et al., 1987). In the two radial runs, the distribution of magnetospheric wave power appears relatively constant at all dayside local times, whereas there is a clear dawn-dusk asymmetry in the other runs, with a stronger wave power on the flank where the foreshock is located. Surprisingly, the Bz wave power is particularly large inside the magnetosphere in Run OBL_B10 compared to the other runs. We find that this is due to the magnetic field making a rather large angle with the z axis in the outer magnetosphere, possibly because of the large magnetic field pile-up in this run. As a result, the Bz wave power also includes transverse waves, which are not accounted for in the panels corresponding to the other runs. In the following section, we will focus instead on the wave power of the magnetic field strength, which accurately reflects the compressional wave power.
To quantify the variation of the wave power in the different regions as a function of the upstream MA, we calculate the ratio of the mean wave power in Runs RAD_B5 and RAD_B10, dividing the values in Figure 4B with those in Figure 4C. This is made possible because the bow shock and magnetopause positions are nearly identical in these two runs (Turc et al., 2018), whereas the bow shock positions in Runs OBL_B5 and OBL_B10 differ too much to plot a similar figure. Figure 5 shows that the transverse wave power is significantly larger in the higher Mach number run, in the foreshock but also in the magnetosheath and near the dayside magnetopause, suggesting a direct link between the Pc3 wave power in the foreshock and in the downstream regions. This difference is largest in the foreshock, where the wave power is more than ten times larger in the higher Mach number run. The regions in purple at both edges of the foreshock are due to the foreshock being broader in the lower Mach number run [as discussed in Turc et al. (2018)]. There are also areas just upstream of the magnetopause and inside the magnetosphere in the afternoon sector where the wave power from Run RAD_B10 dominates. We find that the dominant wave period differs strongly from that of the foreshock waves in those grid cells. This suggests that Pc3 wave activity in these areas is dominated by another wave mode which does not show the same dependency on the upstream Mach number.
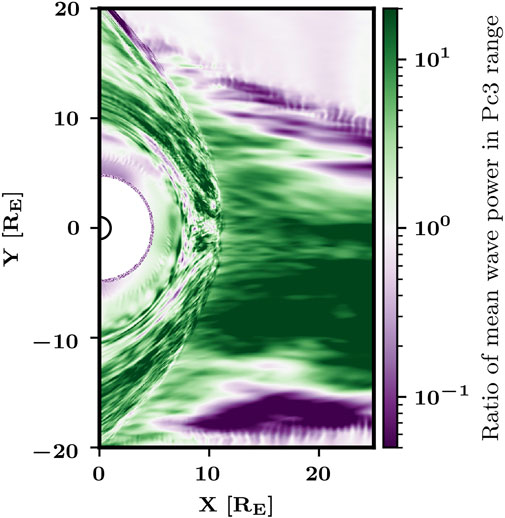
FIGURE 5. Ratio of the mean wave power of the Bz fluctuations in the Pc3 range in Runs RAD_B5 and RAD_B10.
The top panels of Figure 6 show the mean compressional Pc3 wave power as a function of magnetic local time, from the dawn terminator to the dusk terminator, at constant radial distances from Earth, r = 7 RE and r = 5.3 RE. To facilitate comparison with the other runs, the dawn and dusk sectors have been reversed for Run OPS_B3, so that the foreshock is located in the dawn flank as in the other runs. The positions of the data points at which the wave power was extracted are shown in Figure 7. In these plots, the magnetosphere can be identified as the region where Bz is the dominant magnetic field component (in purple). Note that the results for Runs OBL_B10 and MC_B14 are not displayed in Figure 6A because the subsolar magnetopause is located inwards of r = 7 RE in these simulations, and their wave power would thus correspond to magnetosheath wave activity rather than magnetospheric waves. The innermost radial distance has been chosen so that it lies inside the magnetosphere in Run MC_B14 while still being outside of the inner boundary in the other runs.
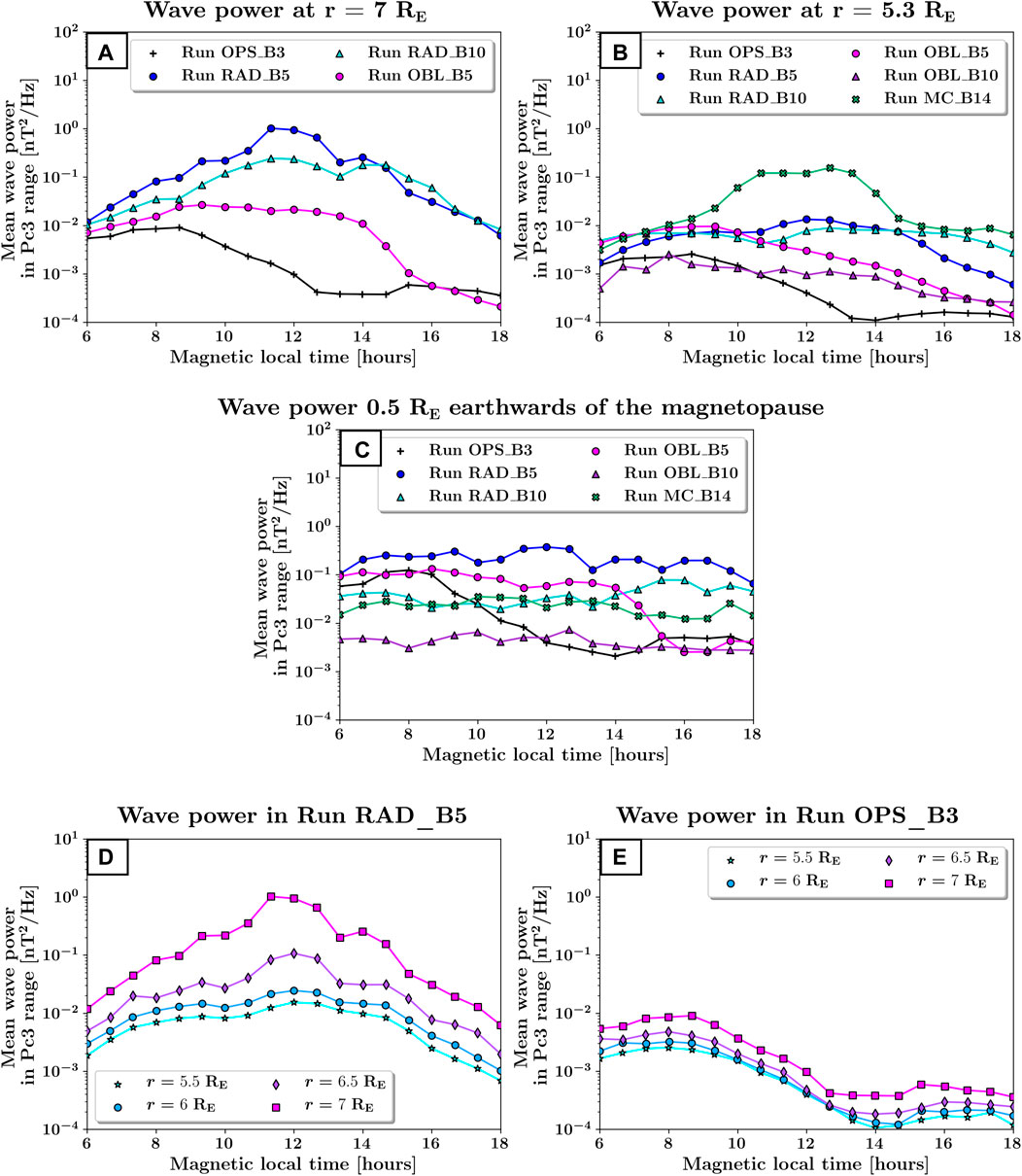
FIGURE 6. Top panels: Compressional wave power in the dayside magnetosphere at r = 7 RE and r = 5.3 RE. Middle panel: Compressional wave power 0.5 RE earthwards of the magnetopause, determined as an isocontour at β* = 0.28. Bottom panels: Compressional wave power in the dayside magnetosphere at different radial distances in Runs RAD_B5 (left) and OPS_B3 (right). Note that the dawn and dusk sectors have been reversed for Run OPS_B3 to facilitate comparison with the other runs, so that the foreshock is located in the dawn flank in all runs with non-radial IMF orientations.
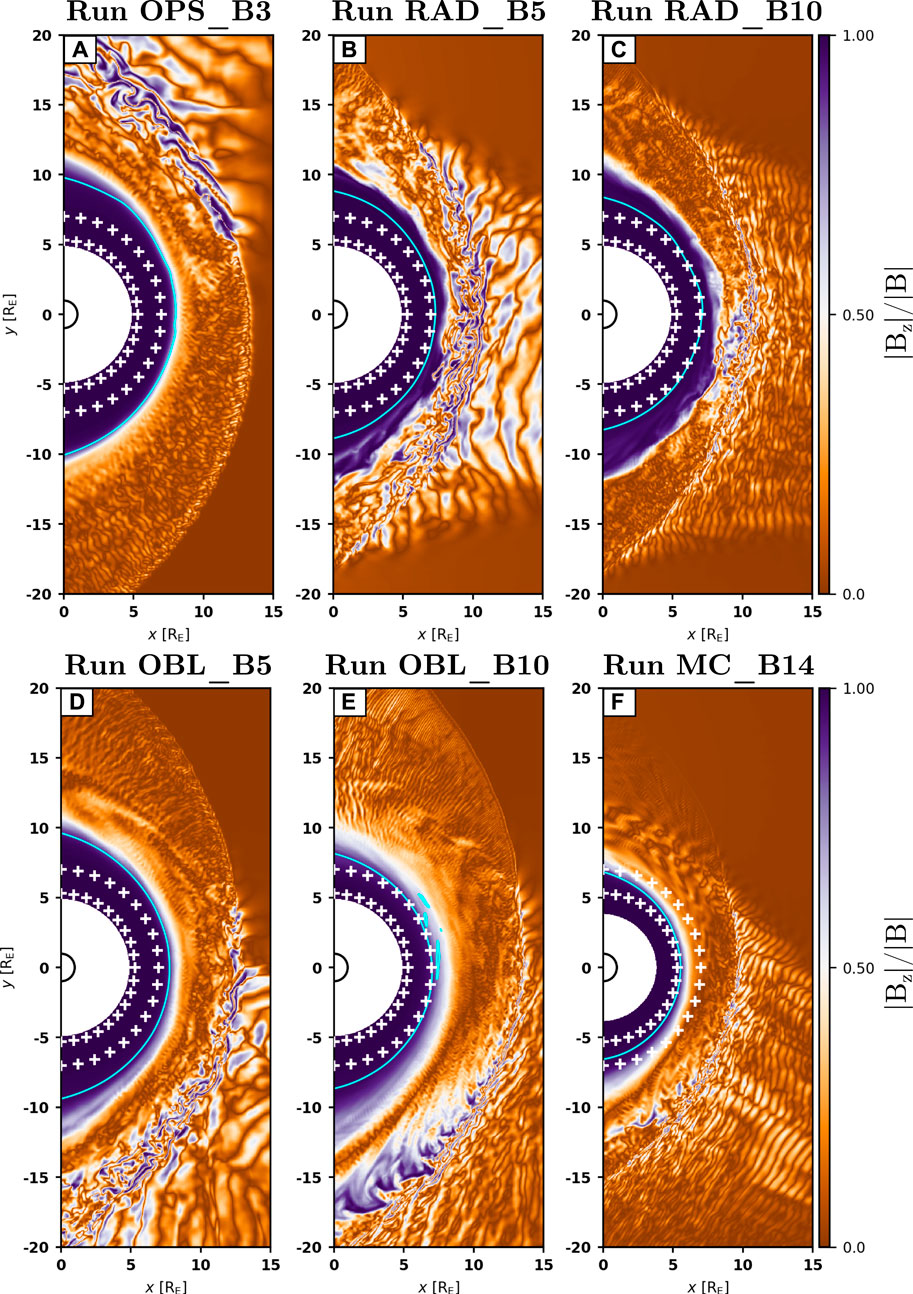
FIGURE 7. The colour scheme shows the fraction of Bz relative to the total magnetic field strength |Bz|/|B| at t = 425 s. Inside the magnetosphere, this ratio is close to 1 as the mean magnetic field is predominantly along Bz. Outside the magnetosphere, |Bz|/|B| highlights strong deviations from the IMF direction, which lies in the xy − plane. The white plus signs show the positions at which the mean compressional wave power was extracted for the top panels of Figure 6. The cyan contour corresponds to
We find that the compressional wave power at a fixed radial distance inside the magnetosphere varies by more than three orders of magnitude between the different runs. It is largest in Run MC_B14, most likely because the magnetopause is located much closer to Earth in this run, due to the high solar wind dynamic pressure. Consequently, the compressional wave power at r = 5.3 RE in Run MC_B14 is measured nearer the magnetopause than in the other runs and has not experienced as much decay. The foreshock wave power is also relatively high for these solar wind conditions, as discussed in Takahashi et al. (2021), which could contribute to the higher magnetospheric wave power.
As expected, radial IMF orientations appear to be most conducive to enhanced compressional Pc3 wave power in the dayside magnetosphere. Run RAD_B10 for example displays a mean wave power about an order of magnitude larger than Run OBL_B5 at r = 7 RE, although the Mach number is higher in the latter simulation. In the same way, the compressional wave power is significantly lower in Run OPS_B3, despite its large Mach number, likely due to the 45° IMF cone angle which limits wave transmission from the foreshock to the dayside magnetosphere. Deeper into the magnetosphere (Figure 6B), the differences between the runs are less pronounced (except for Run MC_B14, discussed above) but their ordering in terms of wave power remains comparable. The compressional wave power in Run OBL_B10 is among the lowest, likely due to the particularly low Mach number in this simulation.
As concerns the compressional wave power distribution as a function of magnetic local time (MLT), we find that for a 45° cone angle (in black), the mean compressional wave power is about an order of magnitude larger downstream of the foreshock than on the quasi-perpendicular flank. The maximum wave power is a few hours away from local noon, around 9 MLT. In Run OBL_B5 (in magenta), the cone angle is reduced to 30°, causing the transition between regions of higher and lower wave power to shift towards the quasi-perpendicular flank (Run OBL_B5, in magenta). This is likely due to the foreshock now extending upstream of the subsolar bow shock (see Figure 1D), which could facilitate wave transmission towards the afternoon sector, reshaping the typical dawn-dusk asymmetry because of the different geometry. This trend is further supported by the runs with radial IMF, in which the compressional wave power peaks near local noon and decreases towards both flanks, displaying little asymmetry. In Runs OBL_B10 and MC_B14, the lack of dawn-dusk asymmetry despite the cone angle values comparable with Run OBL_B5 probably stems from the foreshock edge lying even further on the dusk flank of the bow shock. This suggests that even with a significant cone angle (here near 30°), a nearly symmetric wave power distribution about the Sun-Earth line can be observed inside the magnetosphere, provided that the geometry of the foreshock-magnetosphere interaction is such that it enables wave transmission into the quasi-perpendicular flank.
We now compare the mean compressional Pc3 wave power in the different runs at a constant distance from the dayside magnetopause (Figure 6C). As described in Section 2.3, we use the isocontour of
Runs OBL_B5 and OPS_B3 again show a clear asymmetry in the compressional wave power entering the magnetosphere on the quasi-perpendicular and quasi-parallel flanks. In contrast, for those runs where the edge of the ULF foreshock lies beyond y = 5 RE, or approximately 14 MLT (Runs RAD_B5, RAD_B10, MC_B14 and OBL_B10), the compressional wave power is nearly constant across all dayside local times at a fixed distance from the magnetopause. The largest wave power is obtained for Run RAD_B5, further suggesting that the wave transmission from the foreshock to the dayside magnetosphere is most efficient when the IMF is radial. The wave power associated with Run MC_B14 lies now within the same range as that in the other runs, confirming that the discrepancies at r = 5.3 RE were due to different distances from the magnetopause. Its values are slightly lower than in the quasi-parallel flank in Run OBL_B5, possibly because of the small difference in Mach numbers between the two runs. The compressional wave power decreases very rapidly when moving closer to Earth in Run MC_B14 (compare Figures 6B,C), consistent with the rapid attenuation noted in Takahashi et al. (2021).
The bottom panels of Figure 6 show the compressional wave power at different radial distances, from r = 5.5 RE to r = 7 RE in Runs RAD_B5 and OPS_B3. These plots clearly evidence the decay in compressional wave power when moving closer to Earth, consistent with the entry of the waves through the dayside magnetopause and their subsequent earthward propagation (Howard and Menk, 2005). In Run RAD_B5, the mean compressional wave power decreases by about two orders of magnitude over a distance of 1.5 RE in the subsolar magnetosphere. In Run OPS_B3, the decrease is more modest, less than an order of magnitude, and is roughly constant at all local times across the dayside. Despite the rapid decay in Run RAD_B5, the compressional wave power remains significantly higher than in Run OPS_B3.
The foreshock wave periods obtained in our simulations range between 10 and 50 s, in excellent agreement with spacecraft observations in Earth’s foreshock (Le and Russell, 1996; Eastwood et al., 2005b). Furthermore, our results show that even for completely steady solar wind conditions, there is a significant variation of the dominant wave period within the foreshock. This is likely due to the wave period being partly controlled by the beam velocity (e.g., Eastwood et al., 2005b), which depends on the position inside the foreshock (for example, Kempf et al. (2015) show beam velocities ranging from 1 to 4 times the solar wind speed), as suggested by Takahashi et al. (1984). The variations of the dominant wave period become even more pronounced as the IMF becomes more oblique, likely due to the larger angle between the wavevector and the solar wind speed in these conditions. The wave fronts undergo refraction as they propagate through regions with varying suprathermal ion properties (Palmroth et al., 2015) and their wavelength projected along the solar wind speed varies, leading to a different Doppler shift of their frequency in different parts of the foreshock. These effects certainly contribute to the large scatter of foreshock wave periods in spacecraft measurements, even after normalisation with the ion gyrofrequency (Le and Russell, 1996; Eastwood et al., 2005b).
We found a good agreement between the mean foreshock wave period in our simulations and the predictions of three widely-used formulae (Takahashi et al., 1984; Le and Russell, 1996; Heilig et al., 2007), except for Run OPS_B3 (with a 45° cone angle), for which only the Heilig et al. (2007) formula yielded a comparable value. For the Le and Russell (1996) formula, the discrepancy might be due to the relatively high Mach number in Run OPS_B3 (MA = 11.5), whereas the majority of the 278 wave events from which the Le and Russell (1996) expression was derived corresponded to Mach numbers below 10. The Takahashi et al. (1984) formula on the other hand is based on a simplified model of wave generation, assuming in particular that particle reflection occurs at the bow shock nose to calculate the wave period. This assumption breaks down for this simulation where the foreshock extends further down on the flank (see Figure 1A), which may explain the differing results. As for the large discrepancy between the Heilig et al. (2007) prediction and the obtained wave period in Run OBL_B10, this could be due to the particularly low Mach number in this simulation.
From the comparison of the different runs, we identified three factors that can control the foreshock wave power: the solar wind Alfvén Mach number, the solar wind density and the IMF cone angle. The higher foreshock wave power observed at higher Mach numbers can be explained by the enhanced suprathermal ion density in the foreshock. For a given solar wind density, an increase in the Alfvén Mach number leads to an enhanced beam density because a larger fraction of the incident solar wind population is reflected at the shock to dissipate the additional energy. This was shown for Runs RAD_B5 and RAD_B10 in Turc et al. (2018). A denser beam provides a larger amount of free energy for the wave growth, which can explain why the wave power is larger in Runs RAD_B5 and OBL_B5 compared to their lower MA counterparts. The solar wind density likely impacts the foreshock wave power in a similar manner, as a larger solar wind density results in a larger suprathermal ion density at constant MA. As for the cone angle control of the wave power, the change in the foreshock position along the bow shock can affect the shock Mach number at the location where the backstreaming ions are generated: a large angle between the solar wind velocity and the shock normal effectively reduces the shock Mach number, as it depends on the component of the solar wind velocity along the shock normal. The relative velocity between the suprathermal ion beams and the solar wind is also reduced when the cone angle is larger, as the beams propagate approximately along the IMF direction. This could contribute to the lower wave amplitude at large cone angle.
A similar MA control of the wave power is also observed downstream of the shock, in the magnetosheath and the dayside magnetosphere. For the magnetosheath, these findings are consistent with the work of Krauss-Varban and Omidi (1991), in which the downstream wave power was ascribed to the upstream wave energy being transmitted through the shock and mode-converted from the fast-magnetosonic to the Alfvén mode. Part of the downstream wave power may also be generated at the shock, either from a local instability at the shock front, or because the shock surface becomes less coherent at larger MA, as processes such as large-scale shock rippling and reformation are enhanced (Scholer et al., 1993; Kajdič et al., 2021), which in turn causes downstream perturbations (Krauss-Varban, 1994). The fact that this change in wave power is also reflected in the dayside magnetosphere brings further support to foreshock waves being a source of Pc3 magnetospheric waves. The amplitude of the wave power variation for different MA values is however smaller than in the foreshock (only a factor of two to three instead of 10). This could either be due to the wave transmission being less efficient, or to other sources of compressional Pc3 waves acting inside the magnetosphere, that are independent of the upstream Mach number.
The distribution of Pc3 wave power inside the magnetosphere in our simulations is in good agreement with statistical surveys in the Earth’s magnetosphere (Takahashi and Anderson, 1992; Cao et al., 1994; Howard and Menk, 2005; Heilig et al., 2007): for a 45° cone angle IMF, we find that the wave power is stronger on the flank where the foreshock is located, with a peak a few hours away from local noon. We note that most of the wave power distributions in these previous works are obtained from data collected over long time intervals, associated with a broad range of upstream conditions. They are thus representative of the average IMF orientation and magnetopause shape for these data sets. In contrast, each of our simulations provides the wave power distribution for a single set of upstream conditions, and thus a given geometry of the foreshock-magnetosphere interaction. They reveal that the wave power distribution can differ widely depending on the upstream cone angle, and that Pc3 wave activity can extend far into the afternoon sector, with barely any dawn-dusk asymmetry, for radial IMF orientations.
In their statistical study of Pc3 wave power observed on the ground, Heilig et al. (2010) noted that Pc3 wave power is particularly low when the solar wind density drops below 2 cm−3. Low solar wind densities were used in three of the six runs studied here (Runs OPS_B3, OBL_B5 and OBL_B10 with nSW = 1 cm−3, see Table 1), but the Pc3 wave power was comparable with that in other runs with larger densities. We believe that the apparent discrepancy between our results and the conclusions from Heilig et al. (2010) is due to the rather typical values of the Alfvén Mach number in our runs (except for Run OBL_B10, which also has one of the lowest wave powers). In contrast, low solar wind densities are generally associated with low Alfvén Mach numbers in solar wind measurements at Earth, which result in lower suprathermal ion densities and thus weaker foreshock wave activity (Heilig et al., 2010).
The spatial resolution in our simulation is comparable to or coarser than the proton inertial length in the solar wind (see Table 1). This should not however affect the processes of interest here, as the wavelength of the 30-s foreshock waves is much larger than the grid resolution and the cyclotron resonance giving rise to the waves is well resolved thanks to the hybrid-Vlasov description used in the model. The simulation time step is chosen such that the ion gyration is properly resolved everywhere in the simulation domain as the evolution of the distribution functions is computed. The velocity space resolution used in our runs was shown to be sufficient to describe well the complex ion distributions observed in the foreshock (Pfau-Kempf et al., 2018), but leads to numerical heating in the solar wind, due to the limited resolution of the solar wind core population. Foreshock wave activity is dominated by ion beam instabilities, which depend on the beam properties (Gary, 1993). Therefore, the heating of the solar wind population due to numerical diffusion is not expected to impact significantly the foreshock wave activity. The wave properties in Run MC_B14 can be directly compared to spacecraft observations in the foreshock during the magnetic cloud event analysed in Takahashi et al. (2021), showing an excellent agreement for both the wave period and the wave power.
The main limitations of our study stem from the lack of a third spatial dimension in our global simulations. Inside the magnetosphere, we focused on the compressional component of Pc3 wave activity, as the coupling with field-line resonances cannot take place in a 2D geometry. The 2D setup also leads to an enhanced IMF pileup in front of the dayside magnetosphere, which causes a continuous outward bow shock motion and pushes the magnetopause closer to Earth. As a result, the magnetosheath thickness is overestimated in our runs. This may hinder wave transmission from the foreshock to the magnetosphere, especially in those runs where the magnetosheath is broadest, such as Run OBL_B10. However, we find that the compressional wave power in the Pc3 range does not noticeably decrease from the bow shock to the magnetopause in Run OBL_B10, nor in the other runs (not shown). This wave power includes those fluctuations which likely enable the transmission of the foreshock waves to the magnetosphere (Turc et al., 2022). This suggests that the magnetosheath thickness may not influence the wave transmission, and that the low Pc3 wave power in the magnetosphere in Run OBL_B10 is simply due to the low foreshock wave power.
The equatorial 2D setup also renders the identification of the magnetopause position challenging. Here we used a contour of the β* parameter (Brenner et al., 2021) which provided an identification method that could be applied in an identical manner to all runs to facilitate their comparison. We find however that the magnetopause stand-off distances identified with the selected β* value are much lower than typically observed at Earth. This could either be due to the field line pile-up pushing the magnetopause earthward, or to an underestimation of the magnetopause location with the β* parameter, or a combination of both. In any case, we can view the β* contour as a conservative estimate of the magnetopause location, which ensures that the wave power distributions in Figure 6C are all taken inside the magnetosphere and do not include magnetosheath wave activity.
In this paper, we have analysed Pc3 wave activity in six global hybrid-Vlasov simulation runs with different upstream conditions, to investigate the impact of parameters such as the Alfvén Mach number and the IMF cone angle on the wave properties and their spatial distribution. To our knowledge, this is the first comparative study of these waves in global numerical simulations, from their source in the foreshock to their transmitted counterparts in the outer magnetosphere, in a setup that is directly comparable to near-Earth space in terms of spatial and temporal scales. We have found that the wave period in the foreshock is in good agreement with the predictions of empirical and theoretical formulae established in previous works (Takahashi et al., 1984; Le and Russell, 1996; Heilig et al., 2007). The global view provided by our simulations further revealed the large spatial variability of the wave period inside the foreshock, even for completely steady upstream conditions. These spatial variations likely contribute to the large scatter of the measured wave periods even after normalisation with relevant solar wind parameters.
We have shown that the upstream Alfvén Mach number influences strongly the Pc3 wave power in all regions, the foreshock, the magnetosheath and the dayside magnetosphere, with a larger Mach number resulting in a higher wave power, all other parameters being equal. In the foreshock, we found a tenfold increase in the mean transverse wave power when the Mach number increased from 5 to 10. The Mach number control of the foreshock wave power is likely due to the changes in suprathermal beam density, as a higher suprathermal ion density provides more free energy for the instability to grow. The consistent variation with upstream MA both in the magnetosheath and the magnetosphere brings support to foreshock waves being a dominant source of Pc3 fluctuations in these regions. Other parameters that can influence the Pc3 wave power in the foreshock are the solar wind density and the IMF cone angle. A more detailed analysis with a larger set of runs is needed to accurately quantify the relative importance of these different parameters in controlling the foreshock wave power.
Inside the magnetosheath, we found significant spatial variations in the transverse Pc3 wave power. This is due to our analysis technique capturing not only those waves that originate from the foreshock or the quasi-parallel shock, but also other wave modes whose period falls within the range under study, such as mirror modes which typically populate the magnetosheath downstream of the quasi-perpendicular shock. It is noteworthy that fluctuations originating from the quasi-parallel shock can permeate a large fraction of the quasi-perpendicular magnetosheath as soon as the IMF orientation is such that the foreshock extends upstream of the subsolar point. This enables plasma flowlines threading through the subsolar bow shock to carry significant wave power into the quasi-perpendicular magnetosheath. Alternatively, these fluctuations may have propagated along the magnetic field lines which also connect this portion of the magnetosheath to the quasi-parallel shock.
In the dayside magnetosphere, we found that the compressional Pc3 wave power peaks a few hours away from local noon in our run with Parker spiral-like IMF orientation. This is consistent with previous studies showing that Pc3 wave power tends to be larger in the morning quadrant. In addition to this typical IMF orientation, our simulations also provide us with the wave power distribution for other IMF orientations, revealing that the dawn-dusk asymmetry reduces as the IMF becomes more radial.
Our study was limited by the 2D setup of our simulations: the coupling of compressional Pc3 waves entering the magnetosphere with field line resonances could not be investigated because of the lack of a third dimension. Field line resonances also strongly depend on the density profile inside the magnetosphere. Recent developments to the Vlasiator model are now making it possible to run 3D simulations, albeit with a coarser resolution. Efforts are also being made to improve the inner boundary of the model to include a more realistic ionospheric boundary, leading to a better description of the inner magnetosphere. Future investigations could include the study of field line resonances driven by compressional Pc3 waves, and how their properties depend on those of foreshock waves.
Our findings provide new insights into the global distribution of Pc3 wave activity in near-Earth space and its dependence on solar wind conditions. ULF waves are ubiquitous in planetary magnetospheres in our Solar System (Glassmeier and Espley, 2006; Liljeblad and Karlsson, 2017), and play an important role in transferring energy across different plasma regions (Zong et al., 2017). Therefore, elucidating how their properties vary as a function of the solar wind driving is key to understanding solar wind-magnetosphere coupling.
Vlasiator (Pfau-Kempf et al., 2021) is distributed under the GPL-2 open-source licence at GitHub. The Vlasiator global runs described here take several terabytes of disk space and are kept in storage maintained within the CSC–IT Centre for Science and at the University of Helsinki. Data presented in this paper can be accessed by following the data policy on the Vlasiator website (https://www.helsinki.fi/en/researchgroups/vlasiator/rules-of-the-road). Vlasiator uses a data structure developed in-house (https://github.com/fmihpc/vlsv/, Sandroos, 2021), which can be read using the Analysator software (https://github.com/fmihpc/analysator/, Battarbee et al., 2021; Hannuksela et al., 2021).
LT carried out the analysis of the numerical simulations and wrote the draft of the manuscript. The numerical simulations were performed by HZ, MB, YPK, and UG. HZ and VT participated in regular discussions about the study and provided valuable inputs throughout its progress. MA-L contributed to the determination of the magnetopause position. MP is the PI of the Vlasiator model. All co-authors helped in interpreting the results and proofread and commented on the manuscript.
This project was carried out with the support from the Academy of Finland (grant number 322544) and the University of Helsinki (three-year research grant 2020-2022 for the RESSAC project). We acknowledge the European Research Council for Starting grant 200141-QuESpace, with which Vlasiator was developed, and Consolidator grant 682068-PRESTISSIMO awarded to further develop Vlasiator and use it for scientific investigations. The work leading to these results has been carried out in the Finnish Centre of Excellence in Research of Sustainable Space (Academy of Finland grant number 312351). The work of VT is supported by the Academy of Finland (grant number 328893). MA-L acknowledges the Emil Aaltonen Foundation for financial support. UG is supported by the Academy of Finland through the PROFI4 grant (grant number 3189131). YPK is supported by the Academy of Finland (grant number 339756). MG is supported by the Academy of Finland (grant number 338629).
The CSC—IT Center for Science in Finland is acknowledged for providing computing time leading to the results shown here. We thank the Finnish Grid and Cloud Infrastructure (FGCI) and specifically the University of Helsinki computing services for supporting this project with computational and data storage resources.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2022.989369/full#supplementary-material
Archer, M. O., Southwood, D. J., Hartinger, M. D., Rastaetter, L., and Wright, A. N. (2022). How a realistic magnetosphere alters the polarizations of surface, fast magnetosonic, and Alfvén waves. J. Geophys. Res. Space Phys. 127, e2021JA030032. doi:10.1029/2021JA030032
Battarbee, M., Ganse, U., Pfau-Kempf, Y., Turc, L., Brito, T., Grandin, M., et al. (2020). Non-locality of Earth’s quasi-parallel bow shock: Injection of thermal protons in a hybrid-vlasov simulation. Ann. Geophys. 38, 625–643. doi:10.5194/angeo-38-625-2020
Battarbee, M. (2021). The Vlasiator team. Analysator: python analysis toolkit. doi:10.5281/zenodo.4462515
Bier, E. A., Owusu, N., Engebretson, M. J., Posch, J. L., Lessard, M. R., and Pilipenko, V. A. (2014). Investigating the IMF cone angle control of Pc3-4 pulsations observed on the ground. J. Geophys. Res. Space Phys. 119, 1797–1813. doi:10.1002/2013JA019637
Blanco-Cano, X., Omidi, N., and Russell, C. T. (2006). Macrostructure of collisionless bow shocks: 2. ULF waves in the foreshock and magnetosheath. J. Geophys. Res. 111, A10205. doi:10.1029/2005JA011421
Brenner, A., Pulkkinen, T. I., Al Shidi, Q., and Toth, G. (2021). Stormtime energetics: Energy transport across the magnetopause in a global MHD simulation. Front. Astron. Space Sci. 8, 180. doi:10.3389/fspas.2021.756732
Cao, M., McPherron, R. L., and Russell, C. T. (1994). Statistical study of ULF wave occurrence in the dayside magnetosphere. J. Geophys. Res. 99, 8731–8754. doi:10.1029/93JA02905
Chi, P. J., Russell, C. T., and Le, G. (1994). Pc 3 and Pc 4 activity during a long period of low interplanetary magnetic field cone angle as detected across the Institute of Geological Sciences array. J. Geophys. Res. 99, 11127–11140. doi:10.1029/94JA00517
Claudepierre, S. G., Hudson, M. K., Lotko, W., Lyon, J. G., and Denton, R. E. (2010). Solar wind driving of magnetospheric ULF waves: Field line resonances driven by dynamic pressure fluctuations. J. Geophys. Res. 115, A11202. doi:10.1029/2010JA015399
Clausen, L. B. N., Yeoman, T. K., Fear, R. C., Behlke, R., Lucek, E. A., and Engebretson, M. J. (2009). First simultaneous measurements of waves generated at the bow shock in the solar wind, the magnetosphere and on the ground. Ann. Geophys. 27, 357–371. doi:10.5194/angeo-27-357-2009
Dubart, M., Ganse, U., Osmane, A., Johlander, A., Battarbee, M., Grandin, M., et al. (2020). Resolution dependence of magnetosheath waves in global hybrid-Vlasov simulations. Ann. Geophys. 38, 1283–1298. doi:10.5194/angeo-38-1283-2020
Eastwood, J. P., Balogh, A., Lucek, E. A., Mazelle, C., and Dandouras, I. (2005b). Quasi-monochromatic ULF foreshock waves as observed by the four-spacecraft cluster mission: 1. Statistical properties. J. Geophys. Res. 110, A11219. doi:10.1029/2004ja010617
Eastwood, J. P., Lucek, E. A., Mazelle, C., Meziane, K., Narita, Y., Pickett, J., et al. (2005a). The foreshock. Space Sci. Rev. 118, 41–94. doi:10.1007/s11214-005-3824-3
Ellington, S. M., Moldwin, M. B., and Liemohn, M. W. (2016). Local time asymmetries and toroidal field line resonances: Global magnetospheric modeling in SWMF. JGR. Space Phys. 121, 2033–2045. doi:10.1002/2015JA021920
Engebretson, M. J., Zanetti, L. J., Potemra, T. A., Baumjohann, W., Luehr, H., and Acuna, M. H. (1987). Simultaneous observation of Pc 3-4 pulsations in the solar wind and in the Earth’s magnetosphere. J. Geophys. Res. 92, 10053–10062. doi:10.1029/JA092iA09p10053
Génot, V., and Lavraud, B. (2021). Solar wind plasma properties during ortho-Parker IMF conditions and associated magnetosheath mirror instability response. Front. Astron. Space Sci. 8, 153. doi:10.3389/fspas.2021.710851
Glassmeier, K. H., and Espley, J. (2006). ULF waves in planetary magnetospheres. Magnetos. ULF Waves Synthesis New Dir. 169, 341–359. doi:10.1029/169GM22
Hao, Y., Lu, Q., Wu, D., Lu, S., Xiang, L., and Ke, Y. (2021). Low-frequency waves upstream of quasi-parallel shocks: Two-dimensional hybrid simulations. Astrophys. J. 915, 64. doi:10.3847/1538-4357/ac02ce
Heilig, B., Lotz, S., Verō, J., Sutcliffe, P., Reda, J., Pajunpää, K., et al. (2010). Empirically modelled Pc3 activity based on solar wind parameters. Ann. Geophys. 28, 1703–1722. doi:10.5194/angeo-28-1703-2010
Heilig, B., Lühr, H., and Rother, M. (2007). Comprehensive study of ULF upstream waves observed in the topside ionosphere by CHAMP and on the ground. Ann. Geophys. 25, 737–754. doi:10.5194/angeo-25-737-2007
Hoilijoki, S., Palmroth, M., Walsh, B. M., Pfau-Kempf, Y., von Alfthan, S., Ganse, U., et al. (2016). Mirror modes in the Earth’s magnetosheath: Results from a global hybrid-Vlasov simulation. JGR. Space Phys. 121, 4191–4204. doi:10.1002/2015JA022026
Hoppe, M. M., and Russell, C. T. (1983). Plasma rest frame frequencies and polarizations of the low-frequency upstream waves: ISEE 1 and 2 observations. J. Geophys. Res. 88, 2021–2028. doi:10.1029/JA088iA03p02021
Howard, T. A., and Menk, F. W. (2005). Ground observations of high-latitude Pc3-4 ULF waves. J. Geophys. Res. 110, A04205. doi:10.1029/2004JA010417
Hsieh, W. C., and Shue, J. H. (2013). Dependence of the oblique propagation of ULF foreshock waves on solar wind parameters. J. Geophys. Res. Space Phys. 118, 4151–4160. doi:10.1002/jgra.50225
Jacobs, J. A., Kato, Y., Matsushita, S., and Troitskaya, V. A. (1964). Classification of geomagnetic micropulsations. J. Geophys. Res. 69, 180–181. doi:10.1029/JZ069i001p00180
Kajdič, P., Pfau-Kempf, Y., Turc, L., Dimmock, A. P., Palmroth, M., Takahashi, K., et al. (2021). ULF wave transmission across collisionless shocks: 2.5D local hybrid simulations. JGR. Space Phys. 126, e29283. doi:10.1029/2021JA029283
Kempf, Y., Pokhotelov, D., Gutynska, O., Wilson, L. B., Walsh, B. M., von Alfthan, S., et al. (2015). Ion distributions in the Earth’s foreshock: Hybrid-Vlasov simulation and THEMIS observations. J. Geophys. Res. Space Phys. 120, 3684–3701. doi:10.1002/2014JA020519
Krauss-Varban, D. (1994). “Bow shock and magnetosheath simulations: Wave transport and kinetic properties,” in Washington DC American geophysical union geophysical monograph series, 81, 121–134. doi:10.1029/GM081p0121
Krauss-Varban, D., and Omidi, N. (1991). Structure of medium mach number quasi-parallel shocks: Upstream and downstream waves. J. Geophys. Res. 96, 17715–17731. doi:10.1029/91JA01545
Krauss-Varban, D. (1995). Waves associated with quasi-parallel shocks: Generation, mode conversion and implications. Adv. Space Res. 15, 271–284. doi:10.1016/0273-1177(94)00107-C
Le, G., and Russell, C. T. (1996). Solar wind control of upstream wave frequency. J. Geophys. Res. 101, 2571–2575. doi:10.1029/95JA03151
Lessard, M. R., Hudson, M. K., and Lühr, H. (1999). A statistical study of Pc3-Pc5 magnetic pulsations observed by the AMPTE/Ion Release Module satellite. J. Geophys. Res. 104, 4523–4538. doi:10.1029/1998JA900116
Liljeblad, E., and Karlsson, T. (2017). Investigation of ∼ 20-40 mHz ULF waves and their driving mechanisms in Mercury’s dayside magnetosphere. Ann. Geophys. 35, 879–884. doi:10.5194/angeo-35-879-2017
Lin, Y., and Wang, X. Y. (2005). Three-dimensional global hybrid simulation of dayside dynamics associated with the quasi-parallel bow shock. J. Geophys. Res. 110, A12216. doi:10.1029/2005JA011243
Ma, X., Nykyri, K., Dimmock, A., and Chu, C. (2020). Statistical study of solar wind, magnetosheath, and magnetotail plasma and field properties: 12+ years of THEMIS observations and MHD simulations. JGR. Space Phys. 125, e28209. doi:10.1029/2020JA028209
Murphy, K. R., Inglis, A. R., Sibeck, D. G., Watt, C. E. J., and Rae, I. J. (2020). Inner magnetospheric ULF waves: The occurrence and distribution of broadband and discrete wave activity. JGR. Space Phys. 125, e27887. doi:10.1029/2020JA027887
Odera, T. J. (1986). Solar wind controlled pulsations: A review. Rev. Geophys. 24, 55–74. doi:10.1029/RG024i001p00055
Odera, T. J., van Swol, D., Russell, C. T., and Green, C. A. (1991). PC 3, 4 magnetic pulsations observed simultaneously in the magnetosphere and at multiple ground stations. Geophys. Res. Lett. 18, 1671–1674. doi:10.1029/91GL01297
Palmroth, M., Archer, M., Vainio, R., Hietala, H., Pfau-Kempf, Y., Hoilijoki, S., et al. (2015). ULF foreshock under radial IMF: THEMIS observations and global kinetic simulation vlasiator results compared. J. Geophys. Res. Space Phys. 120, 8782–8798. doi:10.1002/2015JA021526
Palmroth, M., Ganse, U., Pfau-Kempf, Y., Battarbee, M., Turc, L., Brito, T., et al. (2018). Vlasov methods in space physics and astrophysics. Living Rev. comput. Astrophys. 4, 1. doi:10.1007/s41115-018-0003-2
Palmroth, M., Pulkkinen, T. I., Janhunen, P., and Wu, C. C. (2003). Stormtime energy transfer in global MHD simulation. J. Geophys. Res. 108, 1048. doi:10.1029/2002JA009446
Pfau-Kempf, Y., Battarbee, M., Ganse, U., Hoilijoki, S., Turc, L., von Alfthan, S., et al. (2018). On the importance of spatial and velocity resolution in the hybrid-Vlasov modeling of collisionless shocks. Front. Phys. 6. doi:10.3389/fphy.2018.00044
Pfau-Kempf, Y., von Alfthan, S., Sandroos, A., Ganse, U., Koskela, T., Battarbee, M., et al. (2021). fmihpc/vlasiator Vlasiator 5, 1. doi:10.5281/zenodo.4719554
Ponomarenko, P. V., Walters, C. L., and St-Maurice, J. P. (2010). Upstream Pc3-4 waves: Experimental evidence of propagation to the nightside plasmapause/plasmatrough. Geophys. Res. Lett. 37, L22102. doi:10.1029/2010GL045416
Regi, M., De Lauretis, M., Francia, P., and Villante, U. (2014). The propagation of ULF waves from the Earth’s foreshock region to ground: The case study of 15 february 2009. Earth Planets Space 66, 43. doi:10.1186/1880-5981-66-43
Russell, C. T., and Hoppe, M. M. (1981). The dependence of upstream wave periods on the interplanetary magnetic field strength. Geophys. Res. Lett. 8, 615–617. doi:10.1029/GL008i006p00615
Scholer, M., Fujimoto, M., and Kucharek, H. (1993). Two-dimensional simulations of supercritical quasi-parallel shocks: Upstream waves, downstream waves, and shock re-formation. J. Geophys. Res. 98, 18971–18984. doi:10.1029/93JA01647
Shi, F., Cheng, L., Lin, Y., and Wang, X. (2017). Foreshock wave interaction with the magnetopause: Signatures of mode conversion. J. Geophys. Res. Space Phys. 122, 7057–7076. doi:10.1002/2016JA023114
Shi, F., Lin, Y., and Wang, X. (2013). Global hybrid simulation of mode conversion at the dayside magnetopause. J. Geophys. Res. Space Phys. 118, 6176–6187. doi:10.1002/jgra.50587
Shi, F., Lin, Y., Wang, X., Wang, B., and Nishimura, Y. (2021). 3-D global hybrid simulations of magnetospheric response to foreshock processes. Earth Planets Space 73, 138. doi:10.1186/s40623-021-01469-2
Simms, L. E., Pilipenko, V. A., and Engebretson, M. J. (2010). Determining the key drivers of magnetospheric Pc5 wave power. J. Geophys. Res. 115, A10241. doi:10.1029/2009JA015025
Southwood, D. J., and Hughes, W. J. (1983). Theory of hydromagnetic waves in the magnetosphere. Space Sci. Rev. 35, 301–366. doi:10.1007/BF00169231
Takahashi, K., and Anderson, B. J. (1992). Distribution of ULF energy (ƒ < 80 mHz) in the inner magnetosphere: A statistical analysis of AMPTE cce magnetic field data. J. Geophys. Res. 97, 10751–10773. doi:10.1029/92JA00328
Takahashi, K., Hartinger, M. D., Malaspina, D. M., Smith, C. W., Koga, K., Singer, H. J., et al. (2016). Propagation of ULF waves from the upstream region to the midnight sector of the inner magnetosphere. JGR. Space Phys. 121, 8428–8447. doi:10.1002/2016JA022958
Takahashi, K., McPherron, R. L., and Terasawa, T. (1984). Dependence of the spectrum of Pc 3-4 pulsations on the interplanetary magnetic field. J. Geophys. Res. 89, 2770–2780. doi:10.1029/JA089iA05p02770
Takahashi, K. (1996). New observations, new theoretical results and controversies regarding PC 3-5 waves. Adv. Space Res. 17, 63–71. doi:10.1016/0273-1177(95)00696-C
Takahashi, K., Turc, L., Kilpua, E., Takahashi, N., Dimmock, A., Kajdic, P., et al. (2021). Propagation of ultralow-frequency waves from the ion foreshock into the magnetosphere during the passage of a magnetic cloud. J. Geophys. Res. Space Phys. 126, e2020JA028474. doi:10.1029/2020ja028474
Tarvus, V., Turc, L., Battarbee, M., Suni, J., Blanco-Cano, X., Ganse, U., et al. (2021). Foreshock cavitons and spontaneous hot flow anomalies: A statistical study with a global hybrid-vlasov simulation. Ann. Geophys. 39, 911–928. doi:10.5194/angeo-39-911-2021
Torrence, C., and Compo, G. P. (1998). A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 79, 61–78. doi:10.1175/1520-0477(1998)079<0061
Troitskaya, V. A., and Gul’Elmi, A. V. (1967). Geomagnetic micropulsations and diagnostics of the magnetosphere. Space Sci. Rev. 7, 689–768. doi:10.1007/BF00542894
Turc, L., Escoubet, C. P., Fontaine, D., Kilpua, E. K. J., and Enestam, S. (2016). Cone angle control of the interaction of magnetic clouds with the Earth’s bow shock. Geophys. Res. Lett. 43, 4781–4789. doi:10.1002/2016GL068818
Turc, L., Ganse, U., Pfau-Kempf, Y., Hoilijoki, S., Battarbee, M., Juusola, L., et al. (2018). Foreshock properties at typical and enhanced interplanetary magnetic field strengths: Results from hybrid-vlasov simulations. J. Geophys. Res. Space Phys. 123, 5476–5493. doi:10.1029/2018JA025466
Turc, L., Roberts, O., Verscharen, D., Dimmock, A. P., and Kajdic, P. (2022). Transmission of foreshock waves through Earth’s bow shock. under review.
Turc, L., Roberts, O. W., Archer, M. O., Palmroth, M., Battarbee, M., Brito, T., et al. (2019). First observations of the disruption of the Earth’s foreshock wave field during magnetic clouds. Geophys. Res. Lett. 46 (12), 12644–12653. doi:10.1029/2019GL084437
Turc, L., Tarvus, V., Dimmock, A. P., Battarbee, M., Ganse, U., Johlander, A., et al. (2020). Asymmetries in the Earth’s dayside magnetosheath: Results from global hybrid-vlasov simulations. Ann. Geophys. 38, 1045–1062. doi:10.5194/angeo-38-1045-2020
von Alfthan, S., Pokhotelov, D., Kempf, Y., Hoilijoki, S., Honkonen, I., Sandroos, A., et al. (2014). Vlasiator: First global hybrid-Vlasov simulations of Earth’s foreshock and magnetosheath. J. Atmos. Solar-Terrestrial Phys. 120, 24–35. doi:10.1016/j.jastp.2014.08.012
Wilson, L. B. (2016). Low frequency waves at and upstream of collisionless shocks, 216. Washington DC American: Geophysical Union Geophysical Monograph Series, 269–291. doi:10.1002/9781119055006.ch16
Wolfe, A., Meloni, A., Lanzerotti, L. J., Maclennan, C. G., Bamber, J., and Venkatesan, D. (1985). Dependence of hydromagnetic energy spectra near L=2 and L=3 on upstream solar wind parameters. J. Geophys. Res. 90, 5117–5132. doi:10.1029/JA090iA06p05117
Yumoto, K., Saito, T., Akasofu, S. I., Tsurutani, B. T., and Smith, E. J. (1985). Propagation mechanism of daytime Pc 3–4 pulsations observed at synchronous orbit and multiple ground-based stations. J. Geophys. Res. 90, 6439. doi:10.1029/JA090iA07p06439
Keywords: ultra-low frequency waves, foreshock, dayside magnetosphere, plasma waves, hybrid simulations, Pc3 waves, vlasiator
Citation: Turc L, Zhou H, Tarvus V, Ala-Lahti M, Battarbee M, Pfau-Kempf Y, Johlander A, Ganse U, Dubart M, George H, Grandin M, Horaites K, Tesema F, Suni J, Alho M, Papadakis K and Palmroth M (2022) A global view of Pc3 wave activity in near-Earth space: Results from hybrid-Vlasov simulations. Front. Astron. Space Sci. 9:989369. doi: 10.3389/fspas.2022.989369
Received: 08 July 2022; Accepted: 11 August 2022;
Published: 29 September 2022.
Edited by:
John C. Dorelli, National Aeronautics and Space Administration, United StatesReviewed by:
Ari Le, Los Alamos National Laboratory (DOE), United StatesCopyright © 2022 Turc, Zhou, Tarvus, Ala-Lahti, Battarbee, Pfau-Kempf, Johlander, Ganse, Dubart, George, Grandin, Horaites, Tesema, Suni, Alho, Papadakis and Palmroth. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lucile Turc, bHVjaWxlLnR1cmNAaGVsc2lua2kuZmk=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.