Off-equatorial effects of the nonlinear interaction of VLF chorus waves with radiation belt electrons

Nonlinear processes are involved in both the growth of VLF chorus waves and the energization of radiation belt electrons trapped in the wave potential. Nonlinear theory has led to analytic formulae describing both these processes. To investigate these processes, observations from the Van Allen Probes twin spacecraft provide simultaneous in situ information on VLF chorus waves, radiation belt and injected electrons, and local plasma parameters. We combine the theoretical treatment summarized by Omura (2021) with these in situ observations to investigate the characteristics and effects of nonlinear radiation belt processes at the off-equatorial location of the spacecraft observations. We show the smooth phase transition between initial subpackets of chorus wave elements, conducive to extended trapping and enhancement of resonant electrons. The structure of the chorus wave element changes as it propagates away from the equator. Frequency dispersion due to the variation of parallel wave group velocity with frequency contributes to the chorus waveform frequency sweep rate observed at an off-equatorial location. Nonlinear damping at the local value of ½ f_ce progressively erodes wave amplitude at frequencies above ½ f_ceEQ. We examine the important dependencies of the nonlinear inhomogeneity factor on the time rate of change of the wave frequency and the field-aligned gradient of the magnetic field and discuss their implication for the energization of trapped non-relativistic and MeV electrons. The 0.5–2% energy gain we find for 3–6 MeV seed electrons indicates that prompt local acceleration of highly relativistic and ultra-relativistic radiation belt electrons can take place directly through their nonlinear interaction with an individual VLF chorus wave element.

1 Introduction

Baker et al., 2014 show that both slow diffusive and rapid energization are important physical mechanisms for radiation belt recovery following large geomagnetic storms, as exemplified by dynamic conditions during March 2013. In particular, the time scale of energization for relativistic particles can be greatly shortened by nonlinear processes. The energization of radiation belt electrons is a multi-step process involving VLF chorus waves and a population of seed particles (Jaynes et al., 2015). Using in situ Van Allen Probes observations, Foster et al., 2014 focused on conditions surrounding a prompt relativistic electron recovery following the major geomagnetic storm on 17 March 2013. They concluded that nonlinear processes must be involved to account for the 30–60 min 10x increase in multi-MeV fluxes observed at L ∼ 4.

The growth of rising-frequency chorus elements involves nonlinear cyclotron resonance (n = 1) with 10–100 s keV electrons that are injected into the inner magnetosphere during substorm dipolarization events (e.g. Foster et al., 1976). The chorus waves in turn can energize 100 s keV seed electrons to MeV energies through further nonlinear processes (Kubota and Omura, 2018). The electrons giving energy to the wave are untrapped resonant electrons that form a hole in velocity phase space and are decelerated by the wave electric field, transferring energy to the wave. By contrast, those electrons accelerated by the wave are trapped by the wave potential with a number density much less than that of the untrapped resonant electrons. Demekhov et al., 2006’s theoretical investigation shows that generating resonant particles are untrapped, but relativistic/higher energy electrons satisfy the trapping condition. Important in both these nonlinear processes is the inhomogeneity factor, S (Omura et al., 2008; 2019). S is a function of local parameters, the time rate of change of the wave frequency, df/dt, and the gradient of the Earth’s magnetic field along the direction of wave propagation, dB/dx (x is distance along the wave propagation direction away from the wave generation region). The generation of a wave subpacket with fixed frequencies occurs in a critical region near the equator where the df/dt term in the S-factor equations dominates the dB/dx gradient term. For the Van Allen Probes data we present, the gradient term is dominant and our point of observation is off-equatorial in the sense that it is outside the critical region of wave development where the df/dt terms are dominant. Omura (2021) has provided an extensive review of the nonlinear theory of the generation of chorus wave elements and their effect in the nonlinear acceleration of radiation belt electrons, and notes that the acceleration of electrons >100 keV and the wave generation by electrons <100 keV can be treated independently.

Combining nonlinear theory with Van Allen Probes observations, Foster et al., 2017 quantitatively investigated the energization potential of observed chorus waves, finding good overall agreement with characteristics of local acceleration of 1–3 MeV radiation belt electron population seen during the 17 March 2013 event. Later, Hsieh and Omura (2018) and Omura et al. (2019) further extended the theoretical analysis of the nonlinear energization potential of VLF chorus rising tones to the case of obliquely propagating waves [e.g. Santolik et al. (2009)], including both cyclotron (n = 1) and Landau (n = 0) interactions. They found that nonlinear trapping of relativistic electrons by the Lorentz force of the perpendicular wave magnetic field resulted in effective electron acceleration (Omura et al., 2019). The analysis of Demekhov et al., 2006 concluded that energy gain is independent of wave amplitude for trapped particles. Artemyev et al. (2012) found that Landau-resonant acceleration, including low-latitude effects from magnetic field inhomogeneity driving phase velocity variation, is most effective for 10–100 keV particles.

In the following sections, we illustrate further aspects of nonlinear acceleration processes, using a merger of in situ observations with nonlinear theoretical analyses that focus on the specific off-equatorial location of the Van Allen Probes observations. We show the smooth phase transition between initial subpackets of chorus wave elements, conducive to extended trapping and enhancement of resonant electrons. Foster et al., 2021 pointed out the steepening of the observed chorus waveform frequency sweep rate, df/dt, near the local value of 1/4 f_ce for several cases and noted that it was generally seen in their observations of strong chorus elements. Here we address the effects of frequency dispersion on df/dt with a simple model based on the off-equatorial observations of df/dt and the frequency dependences of the wave group velocity, V_g, and wave normal angle, WNA. Invoking the theory/simulation studies of Hsieh and Omura (2018) of chorus wave damping around 1/2 f_ce, half the local electron cyclotron frequency, we use the observed characteristics of lower-band chorus emissions to determine both the magnetic field strength (f_ce) and starting frequency for the chorus emission in the equatorial wave generation region.

We employ the theoretical treatment developed in Omura et al., 2019 to investigate the dependency of the nonlinear inhomogeneity factors S0 and S1, for Landau and cyclotron resonant interactions, on df/dt and dB/dx using directly observed wave and plasma parameters. We examine the separate contributions of df/dt and dB/dx terms to the nonlinear energization of sub-relativistic through ultra-relativistic seed electrons. We find that prompt local acceleration of highly relativistic and ultra-relativistic (>3 MeV) radiation belt electrons can take place directly through their nonlinear interaction with an individual VLF chorus wave element.

2 17 March 2013 event

During the 17 March 2013 storm, the Van Allen Probes A and B spacecraft (Mauk et al., 2012) crossed the inner portions of the outer electron radiation belt at the time of a substorm injection with ∼1 h time separation along the same spatial orbital trajectory. They were well situated to observe the characteristics and effects of local acceleration through quantification of conditions before and after energization took place. As RBSP-A traveled inbound from L ∼ 5.5 to L ∼ 3, its observations form a time history of the lower energy (50–several 100 keV) electron population [MagEIS (Blake et al., 2013)], resultant VLF chorus intensification [EMFISIS (Kletzing et al., 2012)], and MeV electron recovery [REPT (Baker et al., 2012)]. RBSP-A data for this period are presented in Figure 1, showing intensification of 2.6 MeV electron flux reaching > 10⁴ cm⁻² s⁻¹ sr⁻¹ MeV⁻¹ following the onset of intense rising tone chorus and the earthward injection of 50–100 s keV electrons. RBSP-B preceded RBSP-A across the same region of the outer radiation belt by ∼1 h and those data are presented in Figure 2. Temporal change is seen by comparing RBSP-A observations (disturbance) with those of RBSP-B (background) over the same spatial region. Both RBSP-A at L ∼ 6.0 and RBSP-B at L ∼ 4.9 observed a sharp increase of 50–200 keV electron flux at ∼15:50 UT, indicative of the earthward injection of low energy electrons accompanied by VLF chorus intensification. RBSP-A 2.6 MeV electron flux began increasing immediately after 15:50, exceeding the background RBSP-B observations by 10x over the range of L from ∼5.7 to 4.9. During the event 100 keV electron injection was accompanied by chorus wave growth at 1–3 kHz frequencies and an order of magnitude increase in MeV electron flux in ∼1 h.

FIGURE 1

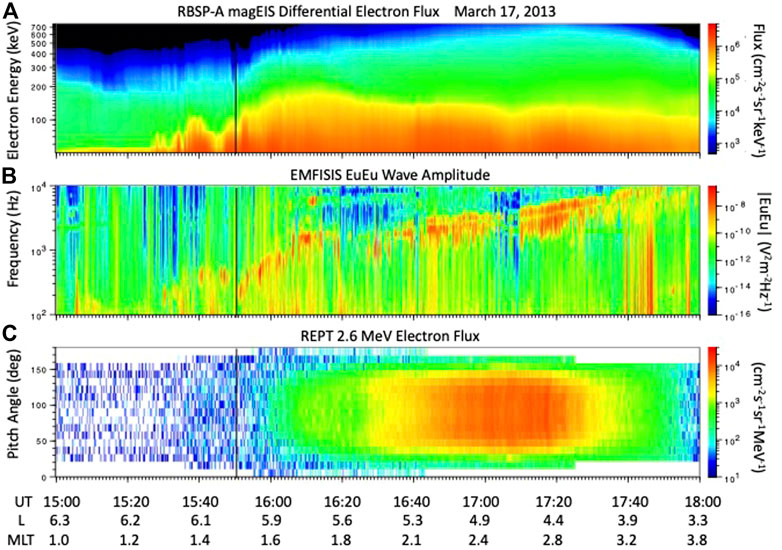
FIGURE 1. RBSP-A in situ observations of the rapid recovery of MeV radiation belt electron fluxes on 17 March 2013. The black line marks the spacecraft location (L ∼ 6; 1.5 MLT) at 15:50 UT.(A) MagEIS spectogram of lower energy electron fluxes associated with chorus wave growth.(B) EMFISIS WFR electric field spectorgram showing the onset of strong VLF chorus waves. (C) Pitch angle dependence of REPT 2.6 MeV electron flux.

FIGURE 2

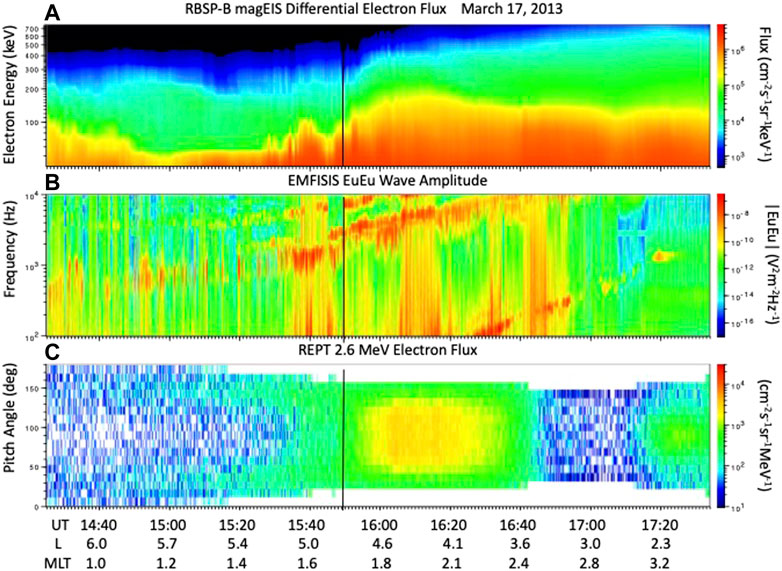
FIGURE 2. RBSP-B in situ observations following the format of Figure 1. The black line marks the spacecraft location (L ∼ 4.8; 1.7 MLT) at 15:50 UT. RBSP-B observed pre-recovery background conditions across L 6 to 4.8 as it preceded RBSP-A by ∼ 1 h. (A) MagEIS spectogram of lower energy electron flux. (B) EMFISIS WFR electric field spectorgram. (C) Pitch angle dependence of REPT 2.6 MeV electron flux.

Figure 3 presents the variation of REPT relativistic phase space density (PSD) observed as RBSP-B preceded RBSP-A along successive outbound (curves 1 and 2, before the injection/recovery event) and inbound (curves 3 and 4, during recovery) orbits. PSD is labeled by the three phase space momentum coordinates: the first adiabatic invariant M, the second adiabatic invariant K, and the drift shell L* associated with the third adiabatic invariant (Chen et al., 2006). In Figure 3 PSD for M = 2,500 MeV/G, K = 0.25 is plotted vs. L*. At the ∼15:50 UT time of the 100 s keV injection, both RBSP-A at L* = 4.45 and RBSP-B at L* = 3.95 began to see increasing 2,500 MeV/G PSD as the multi-MeV electron flux began to increase. For the subsequent 1-h interval, RBSP-A observed a post-injection PSD that amounted to a 10x increase at L* = 4 with respect to the RBSP-B observations at that position 1 hour earlier. Figure 3 gives clear evidence of the rapid local acceleration (Reeves et al., 2013) of MeV radiation belt electrons that occurred during this recovery event.

FIGURE 3

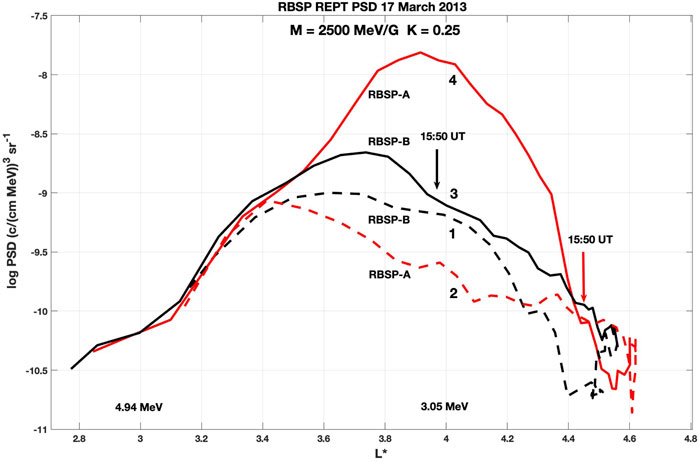
FIGURE 3. Van Allen Probes A and B power spectral density (PSD) vs. L plots showing the onset of the rapid recovery at 15:50 UT seen in Figure 1A. Curve numbers indicate the order in which the spacecraft crossed L* = 4 as RBSP-B preceded RBSP-A by ∼ 1 h along successive outbound (dashed curves 1 and 2) and inbound (solid curves 3 and 4) orbits. A 10x increase in 2,500 MeV/G PSD observed by RBSP-A was associated with the injections and development of strong VLF risers.

3 Chorus wave observations

Three-axis burst mode EMFISIS (Kletzing et al., 2012) observations of wave electric and magnetic fields (28.6 μs time resolution; ∼12 kHz maximum observable frequency) are used to investigate electron interactions with individual chorus rising tones on a sub-millisecond time scale. We analyze individual chorus wave elements following the method described by Foster et al., 2017, determining wave magnetic and electric field components, wave frequency, wave vector, and wave normal angle on a wave cycle by cycle basis. An example of this analysis is shown in Figure 4 for a 65 msec segment of the chorus element highlighted in the theoretical study of Omura et al., 2019. E_R, the right hand circularly polarized wave electric field, is the dominant wave component throughout the chorus element [panel (a)].

FIGURE 4

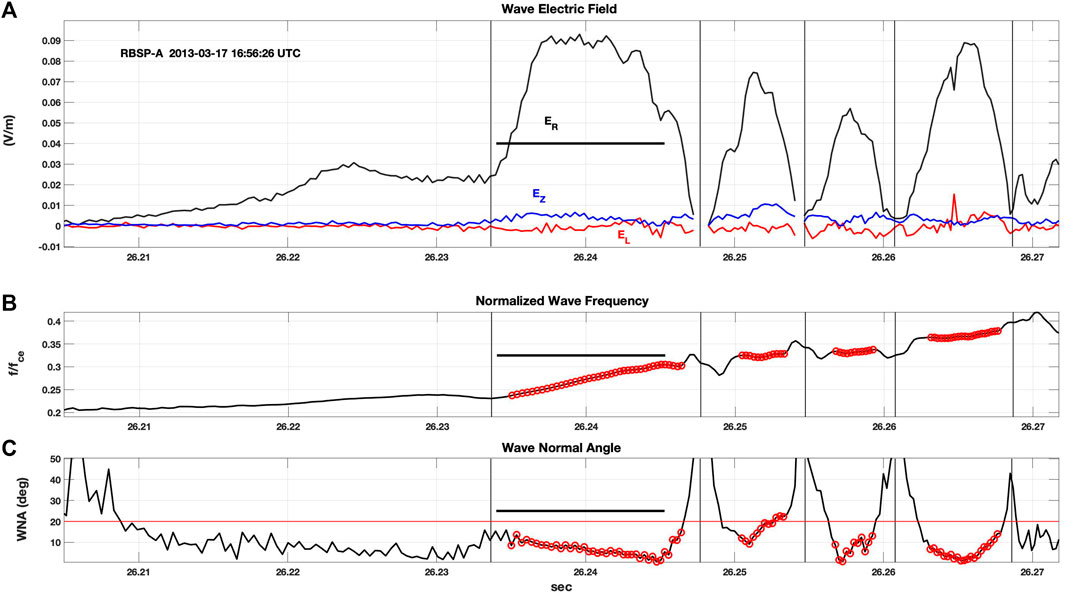
FIGURE 4. Five well-defined subpackets are seen during a strong chorus element at 16:56:26 UT. A black horizontal line in each panel highlights the 11 ms interval further analyzed and described in Figures 5, 6, 9–11. (A) Magnetic field aligned (E_Z) and right (E_R) and left (E_L) circularly polarized components of the wave electric field reveal an initial slowly growing subpacket followed by a second strong subpacket with E_R reaching 80 mV/m. (B) Normalized wave frequency (f/f _ce local) rises steeply during the strong second subpacket. Time intervals with E_R > 40 mV/v are highlighted in red in all panels.(C) Subpacket development is characterized by wave normal angle (WNA) < 20 deg (red line). During the second subpacket WNA decreases steadily from 16 deg to 2 deg.

The chorus element shown in Figure 4 displays five clear subpackets (Santolik et al., 2014). Foster et al., 2021 give a detailed description of the characteristics of the strong subpacket structure observed during the 17 March 2013 event. At the point of observation (L ∼ 5.0, magnetic latitude −3.8 deg), f_pe/f_ce = 3.2. An initial long (>20 ms) coherent subpacket (times <26.233 s) exhibits slowly rising frequency [panel (b)], and wave normal angle (WNA) < 20 deg [panel (c)]. A second stronger subpacket centered near 1/4 f_ce at the point of observation (∼26.24 s) exhibits rapidly rising frequency (df/dt) and small WNA <10 deg. Figure 5 presents wave magnetic field, Bw, and phase (Δt measured across 5 half wave cycles). Wave frequency and phase vary smoothly both within these first and second subpackets and across the transition between them, providing appropriate conditions for continuous resonant electron phase trapping and leading to good potential for MeV electron acceleration. Pronounced phase discontinuities are seen between higher order subpackets. As described by Zhang et al., 2020, such jumps in phase would cause de-trapping of electrons, and reduce energization caused by phase trapping. The noticeable frequency dip between first and second subpackets has been reported previously in Van Allen Probes observations (Santolik et al., 2014; Foster et al., 2021) and is in keeping with numerical simulations of chorus elements (Hanzelka et al., 2020). Foster et al., 2021 has shown the relative contributions of first and second subpackets to electron energization. In the following we address nonlinear effects associated with a single subpacket and limit our discussion to the strong second subpacket, shown by the black horizontal lines in Figure 4.

FIGURE 5

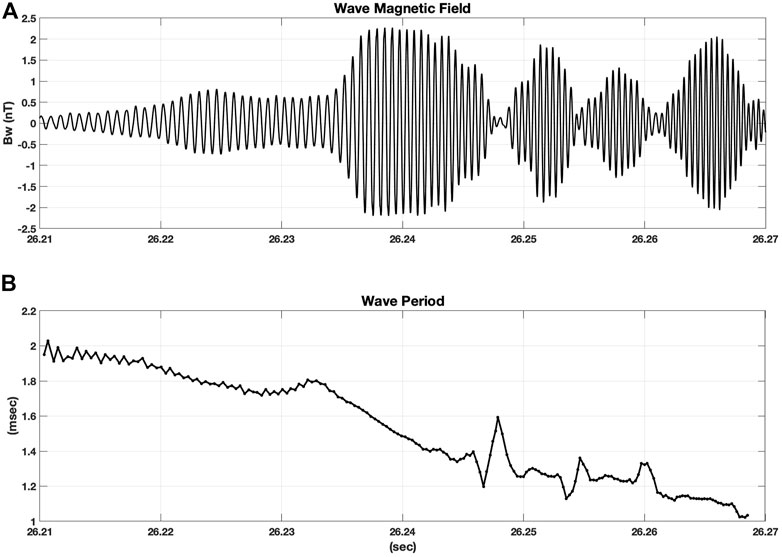
FIGURE 5. (A) Wave magnetic field (Bw)for the chorus element shown in Figure 4 exhibits a smooth transition between the first and second subpackets at ∼ 26.233 s |Bw| exceeds 2.2 nT during the strong second subpacket.(B) A smooth phase transition occurred between the first and second subpackets with sharp discontinuities across higher order subpacket transitions. Wave period is determined across 2.5 wave cycles at 1/2 wave cycle intervals for Bw shown in panel (A).

4 Pitch angle effects

The simulation studies of Hiraga and Omura (2020) examined electron trapping and acceleration for seed electrons with a wide range of pitch angles. They find that the interrelationship between the chorus wave propagation velocity and the electron velocity parallel to Earth’s magnetic field is an important condition for ultra-relativistic acceleration (URA; Summers and Omura (2007); Omura et al., 2007). When wave propagation and parallel electron velocities are nearly the same, chorus waves cannot interact with electrons traveling in the same direction as the wave propagation. Electrons with higher or lower initial equatorial pitch angles, however, interact with a chorus wave by being either overtaken or catching up with the chorus wave.

The formulae used in our study determine the resonant velocity and pitch angle for electrons of a given energy that are separately in cyclotron or Landau resonance with waves at frequency ω. Eq. 1 gives the relativistic formula for the nth-order electron resonance velocity V_R⁽ⁿ⁾ where Ω_e is the local electron cyclotron frequency, γ is the relativistic Lorentz factor for an electron of given energy, and k_|| is the magnetic field-aligned component of the wave vector.

$V_R^{\left(n\right)}=\frac{\mathrm{1}}{k_{\parallel }}\left(\omega -\frac{n{\mathrm{\Omega }}_e}{\gamma }\right)(1)$

For the chorus element indicated in Figure 4, the pitch angles for 500 keV–5 MeV cyclotron resonant electrons were <10 deg from perpendicularity as shown in Figure 6A. At lower energies (<∼1 MeV) resonant electron velocities are oppositely directed to the wave propagation and the pitch angles are >90 deg. For Landau resonance, n = 0 and V_R = ω/k_||, the field-aligned wave phase velocity is important. As seen in Figure 6B, pitch angles for relativistic Landau resonant electrons lie in the narrow range of 80–83 deg at the off-equatorial point of observation.

FIGURE 6

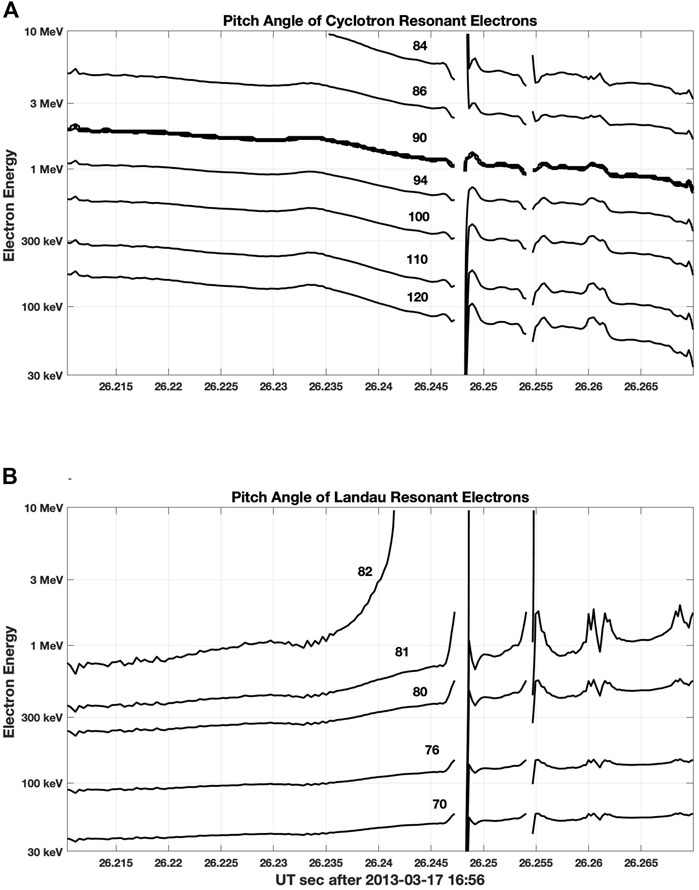
FIGURE 6. Pitch angles for seed electrons resonant with the strong chorus subpacket shown in Figure 4 are shown for (A) cyclotron resonant electrons, and (B) Landau resonant electrons. For pitch angles >90 deg, the resonance velocity V_R is negative.

Our calculations of energy increase for a given initial electron energy in Section 6 consider only those electrons with a resonant pitch angle (i.e. a fraction of the overall population). We note that for electrons of given energy the pitch angles for Landau and cyclotron resonance differ.

5 Off-equatorial effects on subpacket structure

Van Allen Probes measurements of the chorus waveform are made at a fixed location along the magnetic field line, some distance from the chorus subpacket source region near the equator. Wave frequencies within the rising tone chorus element are fixed in the near-equatorial critical region of wave generation where wave growth is dominated by the df/dt term in S. However, several subsequent processes alter the strength and appearance of the waveform as the subpacket propagates to the observation point off the equatorial plane.

Van Allen Probes observations (Santolik et al., 2014) indicate that chorus generation within the critical region near the equator is characterized by continuous rising frequency (positive df/dt) arising from optimum nonlinear wave growth conditions. Theory shows that beyond the critical distance away from the equator, convective wave growth saturates when the flux of resonant electrons decreases as the absolute resonance velocity value increases (Omura, 2021). Katoh and Omura (2013; 2016) confirm through simulation that beyond the critical distance, nonlinear wave growth cannot occur as the optimum amplitude of growth becomes less than the threshold amplitude for triggered growth. Our observations in this study are outside the critical distance.

5.1 Frequency dispersion

From magnetoionic propagation considerations, frequency dispersion of VLF waves in the magnetosphere can lead to pronounced distortions of the frequency sweep rate observed at distances away from the source, as observed in whistlers (Storey, 1953). Prominent in our off-equator observations of strong chorus elements is a large-amplitude second subpacket with steep frequency sweep rate, df/dt, near the local value of 1/4 f_ce (cf. Figure 4). When frequency dispersion is active, as constant-frequency wave elements propagate away from the equator, frequencies with greater field-aligned wave velocities catch up with slower wave elements. This leads to a distortion of the observed frequency sweep rate, and such distortion will increase with distance, x, away from the wave generation region. Foster et al. (2021) suggested two potential dispersive processes that could alter the chorus element waveform observed at an off-equatorial location. First, the wave group velocity (V_g) has a maximum at frequencies near the local value of 1/4 f_ce. Second, the observed decrease in wave normal angle (WNA) as the wave amplitude increases provides a further increase in parallel propagation velocity. Both such effects could be significant for the strong subpackets observed near 1/4 f_ce at the Van Allen Probes location.

For each subpacket, observations, theory, and simulations all indicate a continuous rising frequency generated in the region of chorus development near the equator. To examine the effect of subsequent trajectory-dependent variations of the parallel group velocity (V_{g para}) on the observed chorus element waveform, we have constructed a simple model using as input the values of df/dt, V_g, and WNA for a chorus wave element observed during the 17 March 2013 event at 16:39:07 UT (L = 5.2; MLT = 2.1; maglat = −4.4). By first combining Vg and WNA to produce an effective V_{g para}, we then back-project each observed frequency element toward the equator in 1/4 msec steps to estimate the frequency sweep profile at a given distance, −x, upstream from the point of observation. For simplicity and to reflect the qualitative nature of this model, in the calculation, V_{g para} is held constant for each frequency and no variation of f_ce along the field line has been included. Figure 7 presents the observed variation of wave electric field amplitude, group velocity, wave normal angle, and frequency in panels (a), (b), (c), and (d) respectively. All parameters are calculated at each 1/2 wave cycle following the method of Foster et al., 2017. The resulting back-projected frequency sweep rate at x = −3,000 km (the approximate distance to the equator) is shown as red circles overplotted on the off-equatorial observation in (d). These model results show that variations in V_{g para} can, by themselves, produce a noticeable, but small, sweep rate distortion associated most closely with the decrease and increase of WNA during the strong second subpacket (720–730 msec).

FIGURE 7

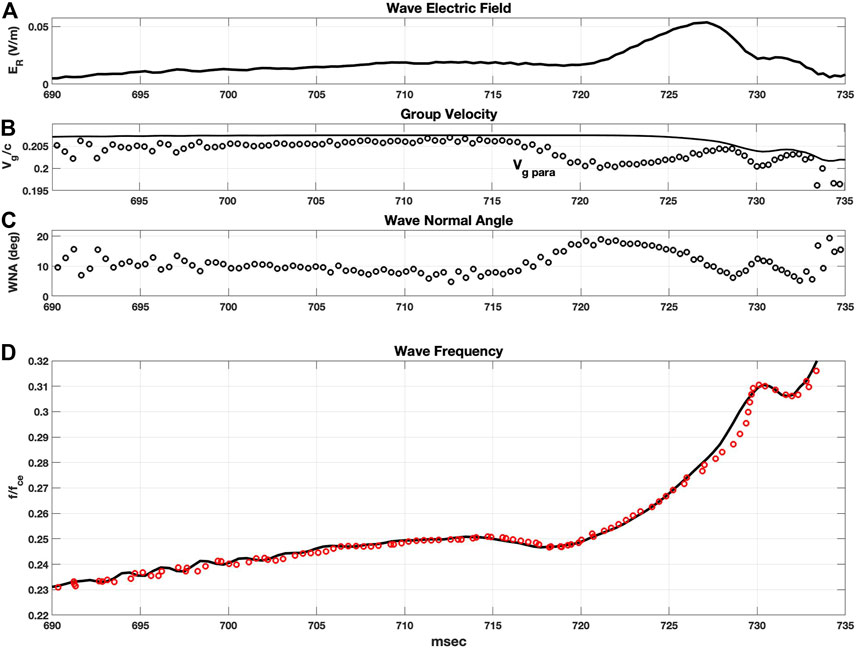
FIGURE 7. Wave parameters evaluated at each 1/2 wave cycle for a chorus wave element observed during the 17 March 2013 event at 16:39:07 UT are shown in black. (A) Wave electric field (E _R) shows an initial weak subpacket (690–720 msec) ans a strong (50 mV/m) second subpacket (720–730 msec). (B) Wave group velocity is shown by the solid curve while the parallel group velocity, including the effects of varying wave normal angle, is shown as circles. (C) Low wave normal angle (<20 deg) is observed through both subpackets with significant variation across the second subpacket. (D) The frequency sweep rate observed at the off-equatorial location is shown as the solid black curve. Back projection 3,000 km toward the equator using the observed values of V _{g para} estimates the chorus sweep rate profile at the equator (red circles, shifted forward in time 50 msec for comparison with the observed profile).

The dominant sweep rate characteristics, such as the steeply rising frequency observed in the strong second subpackets described in Foster et al., 2021, most likely are formed within the critical region of wave generation near the equator as described by e.g. Omura (2021). Beyond this region, however, the propagation effects just described generally depend on the variation of V_g and WNA with frequency. We note that the level of variation of V_{g para} for the case shown in Figure 7 is typical of that seen in our off-equatorial chorus observations. However, this match is not universally the case. For example, modeling of observations with nearly constant V_g and WNA across the observed waveform would result in no frequency distortion and no distortion of df/dt. (Ultimately, the actual variation of V_g and WNA along the wave trajectory is not known from measurements at a single location.) In addition, the variations of plasma density and magnetic field along the particle trajectory would change the frequency dependence of V_g and the normalized frequency (f/f_ce) for each wave element, producing a different waveform distortion. However, despite its simplicity, the model results shown in Figure 7, and their general agreement with aspects of the observed frequency variation in subpackets, suggest that frequency dispersion effects can make a noticeable contribution to the characteristics of the chorus element waveform observed at an off-equatorial location.

5.2 Damping at ½ f_ce

The structure of the chorus wave element also changes as it propagates away from the equator into regions of increasing magnetic field. Both Tsurutani and Smith (1974) and Omura et al. (2019) predict a gap in chorus at 0.5 f_ce due to nonlinear damping. Damping at the local value of ½ f_ce progressively erodes wave amplitude at frequencies above ½ f_ceEQ. As a result, away from the equator, chorus elements are divided into lower and upper band emissions by a pronounced amplitude minimum below the local value ½ f_ce [e.g. Tsurutani and Smith (1974)]. Figure 8 presents an example of this effect, plotting magnetic field spectral power as a function of time and focusing on the gap between the lower and upper band emissions. Integrated signal power across the ∼400 ms of observations shown in panel (A) is plotted in panel (B), and clearly identifies ½ f_ceEQ as the point of onset of the ∼1,000x decrease in the lower band chorus element integrated wave power. Thus determined, the value of f_ceEQ also indicates that the frequency of initial chorus element wave growth occurred near 0.25 f_ceEQ. The wave power damping seen between ½ f_ce and ½ f_ceEQ is in keeping with the nonlinear damping mechanism described by Hsieh and Omura (2018). We cannot prove that the gap between the lower and upper chorus bands is due to nonlinear damping, but its observation is consistent with that mechanism.

FIGURE 8

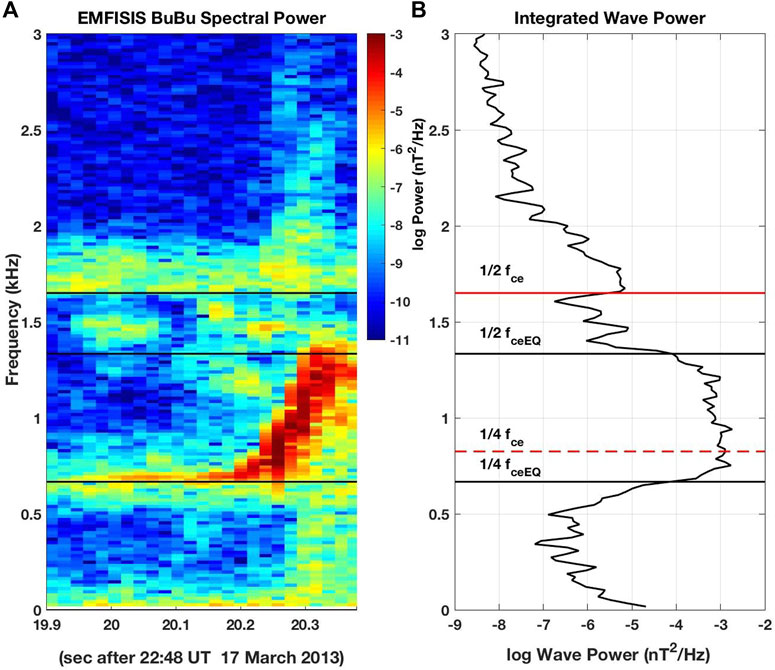
FIGURE 8. (A) The magnetic field spectrogram observed near L = 6.5 by Van Allen Probe B at 22:48:20 UT on 17 March 2013 exhibited clear damping at frequencies below 1/2 the local electron cyclotron frequency (1/2 f_ce). (B) Integrated signal power at each frequency is shown for the ∼400 ms of observations shown in (A). The local value of f_ce is observed at the spacecraft and the equatorial value of f_ceEQ is determined from the characteristics of the damping of the chorus element (from Foster et al. (2021)).

Beside nonlinear damping around 1/2 f_ce, several other plausible models exist for the observed lower-upper band gap. Li et al. (2010) states that very isotropic distributions at a few keV produced by Landau resonance are commonly observed in dayside THEMIS data and would contribute to chorus gap formation. Li et al. (2019) use simulations to state that initially excited single-band chorus waves alter the electron distribution immediately via Landau resonance (and suppress it at medium energies), naturally dividing electron anisotropy into low and high energy components exciting upper-band and lower-band chorus waves, respectively. Gao et al. (2016; 2019) posit a natural chorus gap emerging from upper band chorus excitation through lower band cascade and second harmonic generation. Simulations by Fu et al. (2014) predict that warm and hot chorus components separately drive quasi-electrostatic upper band and electromagnetic lower band emissions, resulting in a gap. Fu et al. (2015) predict power gaps at several frequencies (including 0.5 fce) due to sub-cyclotron resonances between oblique chorus and thermal electrons.

6 Relativistic electron acceleration—Effect of the inhomogeneity factor

For acceleration of energetic electrons, both a smooth frequency increase and a gradient of the magnetic field are needed at appropriate magnitudes. Zhang et al., 2018 have investigated the properties of intense chorus waves, i.e. those capable of nonlinearly resonating with electrons. They find that 10–15% of chorus wave packets have sufficient effective wave amplitude (B_w > 2–3 nT) for nonlinear interaction to occur and that longer wave packets (>10 wave cycles) are needed to produce a significant energy increase for trapped electrons.

The formula for the nonlinear inhomogeneity factor S has two terms (Eq. 2). The first depends on the frequency sweep rate, df/dt, and the second on the gradient of the magnetic field along the field line, dB/dx. Coefficients A and B are derived in Omura et al., 2019 for each nonlinear resonance. Near the magnetic equator where dB/dx is ∼0 or very small, S is determined by the frequency sweep rate df/dt, which is nearly constant through propagation of the wave packet away from the equator. The critical distance away from the equator identifies the location marked by a change of the dominant term of the inhomogeneity factor. Within the critical region, triggering of nonlinear wave growth due to frequency variation is possible and this can be regarded as the generation region of the subpackets forming chorus emissions. Whether inside or outside the critical region, we can make the simplified form of S as

$\mathbf{S}=\mathbf{A}\frac{\mathbf{d}\mathbf{f}}{\mathbf{d}\mathbf{t}}\mathbf{+}\mathbf{B}\frac{\mathbf{d}\mathbf{B}}{\mathbf{d}\mathbf{x}}(2)$

The Van Allen Probes observations during the 17 March 2013 event were taken at magnetic latitude = −3.8 deg, outside the critical distance. To examine the relative importance of the individual terms in the inhomogeneity factor at this off-equatorial location, we use a maximum effect approach and artificially set either df/dt or dB/dx to 0 for S0 and S1 in the equations for cyclotron (S1) and Landau (S0) electron energization in Omura et al., 2019).

6.1 Off-equatorials S factor

In Figure 9, we present cycle by cycle calculations of cyclotron and Landau inhomogeneity factors as functions of initial electron energy and time across the single strong second subpacket indicated by the horizontal black line in Figure 4. For that 11 ms (19 wave cycles) subpacket, |E_R| = 84 mV/m, |B_R| = 2 nT. Local conditions for RBSP-A at 16:56 UT were L = 4.9, MLT = 2.3, magnetic latitude = −3.8 deg, local f_ce = 6,050 Hz, f_pe = 19,440 Hz, f_pe/f_ce = 3.2. For the gradient terms, dω/dt = 2.5e5 radians/sec and dω_ce/dx = 9.0e-4 radians s⁻¹ m⁻¹. White regions on each panel indicate that |S| > 1, at which point trapping does not take place. The number of trapped particles decreases to 0 as |S| increases from 0 to 1 as the size of the trapping potential in velocity phase space, F(|S|) is given by equation 71 of Omura et al., 2019, shrinks to zero. The values of S0 and S1, plotted in Figure 9 and used in the subsequent sections to determine electron energy gain, have been multiplied by F(|S0|) or F(|S1|) respectively. The fraction of trapped electrons is a decreasing function of |S|, in a manner such that S *F(|S|) for maximal nonlinear acceleration occurs when |S| ∼ 0.4.

FIGURE 9

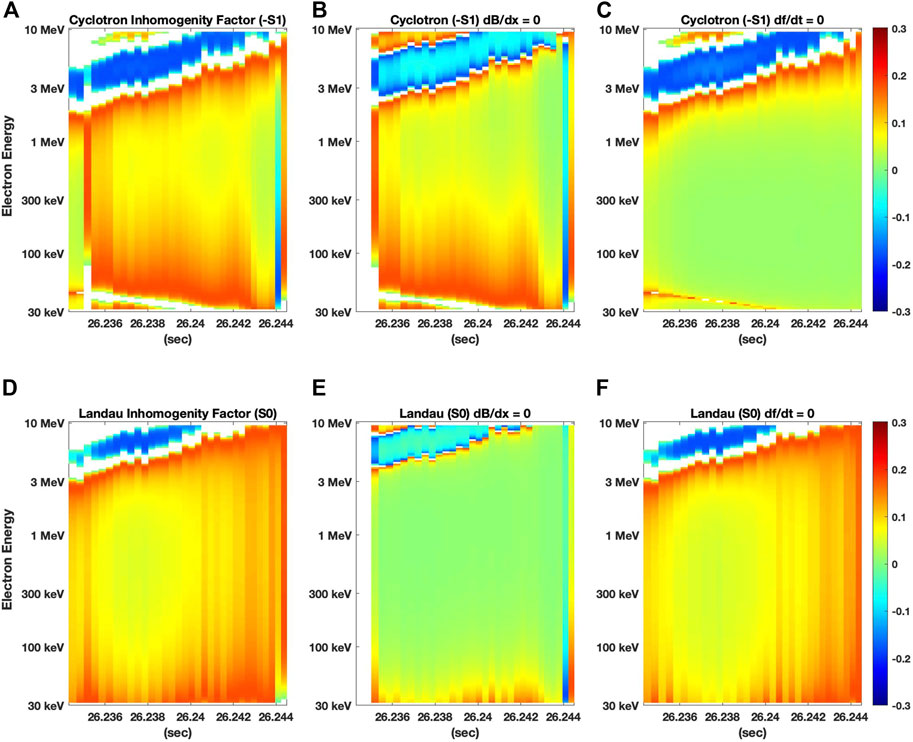
FIGURE 9. The nonlinear inhomogeneity factors for cyclotron (−S1) and Landau (S0) resonance are shown in the upper and lower panels respectively. S factors have been calculated wave cycle by cycle for a range of resonant electron energies for the subpacket indicated in Figure 4. Each value of S1 and S0 has been multiplied by the trapping potential in velocity phase space, F (|S|). White regions on each panel indicate that |S| > 1 where F (|S|) = 0 and trapping does not take place (see text). (A,D) present the full calculations for S1 and S0 including both df/dt and dB/dx terms. For panels (B,E), dB/dx has been set to zero. In (C,F), df/dt = 0.

Panels (A) and (D) of Figure 9 present the full calculations for S1 and S0 including both df/dt and dB/dx terms. For panels (B) and (E), the magnetic field gradient has been set to zero, leaving only the contribution from the df/dt terms to contribute. Conversely, in panels (C) and (F), df/dt = 0. Panel (B) indicates that cyclotron acceleration at MeV energies is significantly reduced when the dB/dx term is cancelled, while cyclotron acceleration is nearly unchanged at sub-relativistic seed energies. Panel (E) indicates that the Landau S0 factor is significantly at all relativistic electron energies when the magnetic field gradient is zero or very small. Cyclotron acceleration at MeV energies is significant, although reduced somewhat, while nearly eliminated completely at non-relativistic energies when frequency sweep rate (df/dt) is near zero [cf. Panel (C)].

For the majority of the Van Allen Probes cases we’ve examined, the dB/dx term dominates the df/dt term in determining the S factor in keeping with the location of our observing points outside the critical region. It is to be noted, however, that the critical region relates to nonlinear chorus generation, not to the acceleration of seed electrons.

6.2 S factor dependance of electron energy gain

Having derived full and modified S factors, we can proceed with energy gain calculations for seed electrons for each of the cases shown in Figure 9. As discussed in Section 4, pitch angles differ for electrons in cyclotron or Landau resonance at a given energy so that these different populations are treated separately. In Figure 10, panels 1) and 2) break down the total cyclotron and total Landau contributions to the energization for 30 keV–10 MeV initial electron energies, making the assumption that electrons remain trapped across the entire 11 ms segment of the subpacket indicated in Figure 4. In panels 1) and 2) the solid black curve shows the percent energy gain calculated from equations 69 or 62 in Omura et al., 2019 respectively with both df/dt and dB/dx terms in S1 and S0 unaltered. For the black dashed curves in each panel the contribution to the electron energization from only the dB/dx gradient term is shown (df/dt has been set to zero). Conversely, for the red curves, the dB/dx terms have been set to zero in the inhomogeneity factors and only the contribution from the frequency variation is shown. Again, it is important to remember that our calculations of seed electron energy gain relate to the specific conditions at the point of the observations.

FIGURE 10

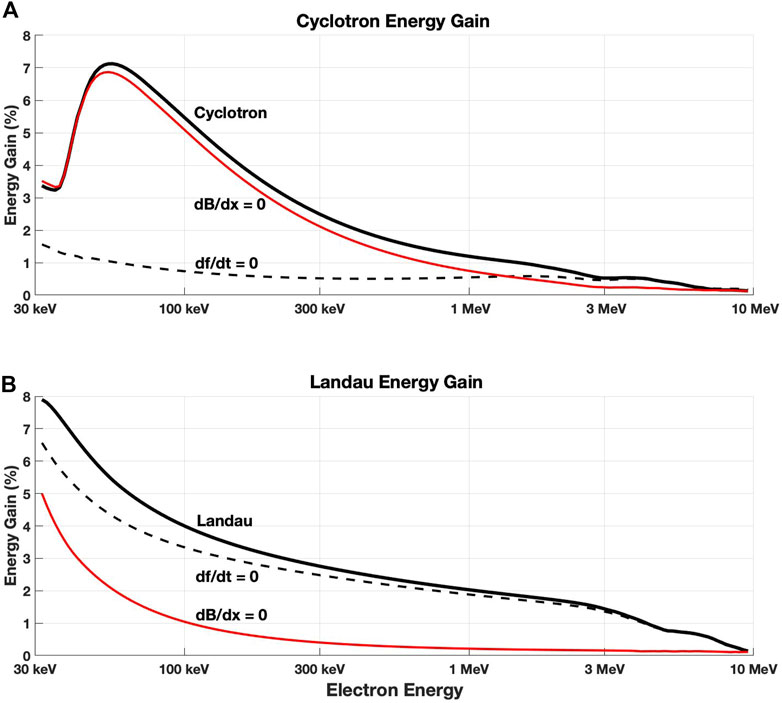
FIGURE 10. Percent energy gain (solid black curves) for electrons with for 30 keV–10 MeV initial energy in cyclotron (A) or Landau (B) resonance is shown assuming the electrons remain trapped across the 11 ms subpacket indicated in Figure 4. Panels (A) and (B) respectively show the S-factor dependencies of the cyclotron and Landau energization. For the black dashed curves in both panels the contribution to the electron energization from only the dB/dx gradient term is shown (df/dt has been set to zero). For the red curves the dB/dx terms have been set to zero in the inhomogeneity factors such that the only the contribution to the electron energization is from the frequency variation.

Comparing the solid black curves in Figure 10, it is apparent that cyclotron acceleration is dominant for this individual subpacket at this off-equatorial location for the energization of sub-relativistic seed electrons with energies <250 keV and negative pitch angles of −20 to −30 deg. However, at relativistic energies >500 keV, Landau acceleration is dominant for electrons with ∼80 deg pitch angle. Setting the df/dt term to zero reduces the cyclotron energization by up to 60% for non-relativistic seed electrons [panel (a)], while the Landau energization is little changed when df/dt = 0 [panel (b)]. Setting dB/dx to zero results in a minor decrease in cyclotron energization but decreases the Landau energization at all seed energies, reducing the dominant Landau energization by 90⁺ % for relativistic electrons.

The presentation of our analysis of S-function effects and radiation belt electron energization has focused on a single strong chorus wave subpacket observed during the onset of the MeV radiation belt electron recovery event on 17 March 2013. We have performed similar analyses for multiple chorus elements observed at different times and L-space locations during different storms, with similar results and conclusions (Foster et al., 2021 discusses aspects of several further examples). Many of the features presented here are repeatable in nearly every observation (strong second subpacket, steeply rising df/dt near the local value of 1/4 f_ce, dominance of cyclotron energization at sub-relativistic seed electron energies). However, there is significant variability among the different cases examined and this is important to remember for future studies aimed at generalizing these results. Figure 11 presents examples of chorus wave elements observed during separate injection/acceleration events on 17 March 2013 by RBSP-A (left panels) and RPSP-B (right panels). These cases differ significantly from the more usual observations shown in Figures 4, 7. RBSP-A (16:39 UT, L = 5.3) observed the smooth growth of an initial 50 msec subpacket to apparent saturation amplitude (E_R 30 mV/m; |B_perp| 0.5 nT). For this case, cyclotron energization was dominant at electron energies <300 keV. During the later injection event described by Foster et al., 2014, RBSP-B (22:48 UT; L 6.5) observed weak cyclotron energization such that Landau resonance energization was dominant at all energies.

FIGURE 11

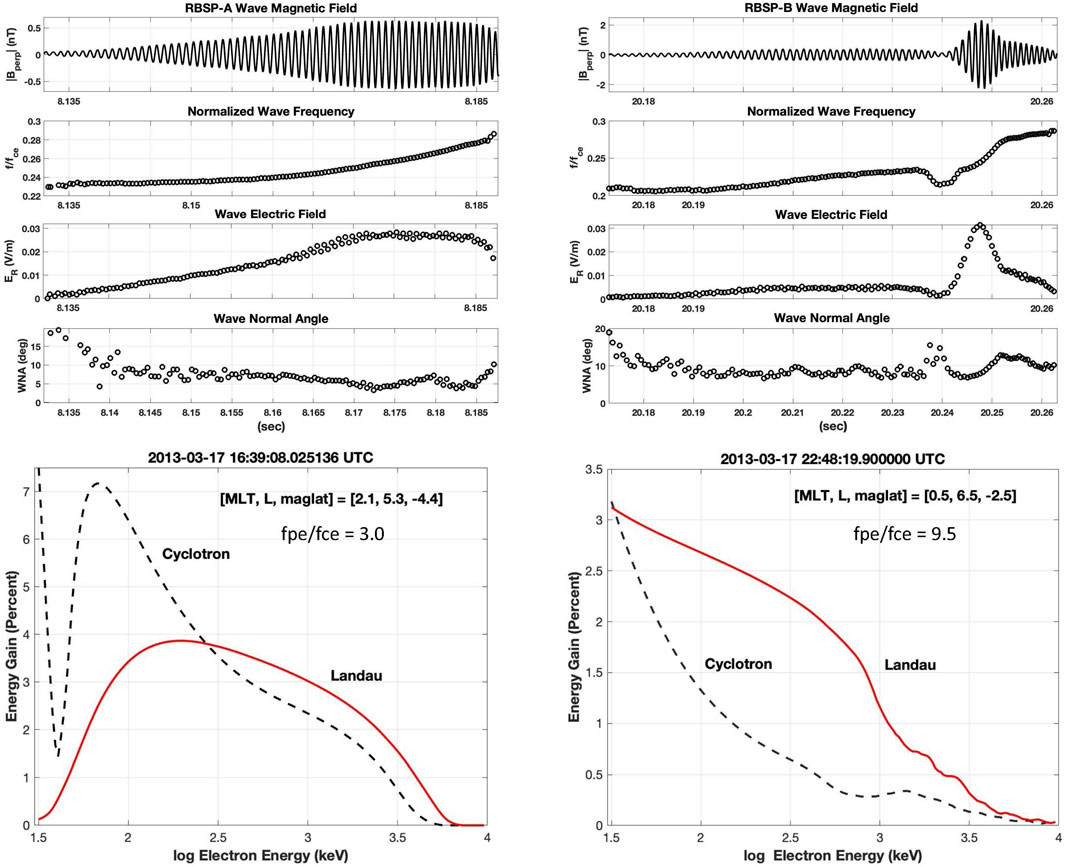
FIGURE 11. Examples of chorus wave elements observed during different injection/acceleration events on 17 March 2013 are shown for RBSP-A at 5.3 R_E (left panels) and RPSP-B at L = 6.5 R_E (right panels). (top panels) Wave magnetic field, normalized wave frequency, wave electric field, and wave normal angle. (bottom panels) Percent energy for seed electrons with for 30 keV–10 MeV initial energy in cyclotron (dashed curve) or Landau (red curve) resonance.

7 Summary and conclusion

We have examined characteristics and nonlinear effects of strong VLF chorus elements observed at the off-equatorial location of their Van Allen Probes observation. The strong chorus elements we have investigated have maximum wave amplitudes in the range |E_w| ∼ 20–100 mV/m. Large wave amplitude depends on a strong source (injection) of resonant electrons combined with proper conditions for the growth of long coherent wave subpackets. For the 16:56 UT subpacket analyzed in this study, frequency varied from 1,400–1900 Hz (0.23–0.31 f_ce) and wave growth was associated with the injection of 50–100 s keV resonant electrons as seen in Foster et al., 2021. We have shown the smooth frequency and phase transition between the initial and strong second subpackets, and have found that frequency dispersion can contribute to the chorus frequency sweep rate observed at an off-equatorial location. The frequency gap below 1/2 f_ce at the point of observation is consistent with the effects of the progressive erosion of wave amplitude at frequencies above ½ f_ceEQ by nonlinear damping near the local value of ½ f_ce.

The inhomogeneity factor S that controls the effectiveness of the nonlinear process for electron energization has important dependence on both the time rate of change of the wave frequency and the field-aligned gradient of the magnetic field. Cyclotron acceleration at < MeV energies is significantly reduced when df/dt is very small, and is little changed at all energies when dB/dx is reduced. Landau acceleration is greatly reduced at all relativistic energies when the magnetic field gradient very small and is slightly reduced at sub-relativistic energies when df/dt is very small.

Nonlinear acceleration by strong chorus waves applies both to seed electrons with sub-relativistic and relativistic initial energies. In Figure 12 we emphasize the considerable energy gain experienced by trapped seed electrons with relativistic (>500 keV) and ultra-relativistic (>3 MeV) initial energies. Trapped through with a single coherent subpacket, a 3 MeV electron can experience a 1.5% Landau energy gain in ∼11 ms. Nonlinear Landau energy gain for a 6 MeV ultra-relativistic seed electron is 0.75% (45 keV). Significantly, these findings indicate that prompt local acceleration of highly relativistic and ultra-relativistic radiation belt electrons can take place directly through their nonlinear interaction with an individual VLF chorus element.

FIGURE 12

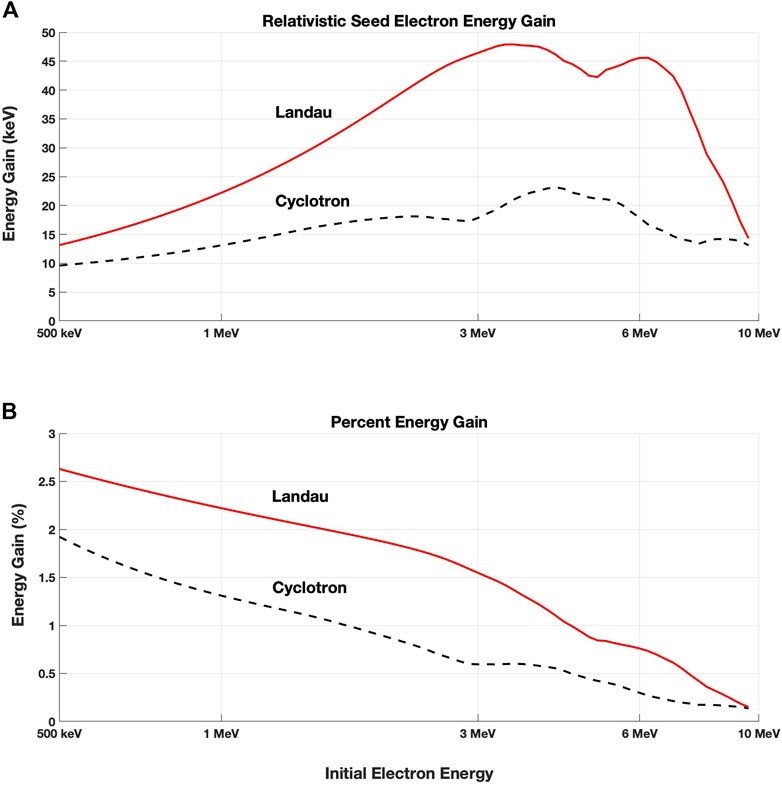
FIGURE 12. Nonlinear energy gain is shown for relativistic and ultra-relativistic seed electrons.(A) Energy gains for cyclotron and Landau resonant electrons are shown separately. Landau resonant energization exceeds cyclotron energization at all energies. (B) 0.5%–2% energy gain is determined for highly-relativistic and ultra-relativistic seed electrons in their ∼11 ms nonlinear interaction with the single strong subpacket denoted in Figure 4.

In general, the multiple in situ parameters available in the Van Allen Probes observations permit detailed examination of the features of the nonlinear theory of VLF chorus wave development and the acceleration of radiation belt electrons to MeV energy. In particular, the spacecraft observations provide important information on the chorus wave element at an off-equatorial nearly fixed position. This study analyzed a well sampled and strong subpacket to investigate the characteristics of the nonlinear inhomogeneity factors and their effect on sub-relativistic to relativistic electron acceleration. It is found in this particular case that cyclotron energization provides the dominant contribution at sub-relativistic electron energies while at energies >500 keV Landau acceleration provides the larger contribution. Future similar studies using a large sample of Van Allen Probes observed events can help generalize and advance understanding of this important acceleration pathway for radiation belt dynamics.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: Van Allen Probes observations used in this study can be obtained through instrument websites (EMFISIS wave data: http://emfisis.physics.uiowa.edu; MagEIS and REPT particle data: https://rbsp-ect.lanl.gov/rbsp_ect.php. PSD data presented in Figure 3 can be obtained through the Van Allen Probes Science Gateway (https://rbspgway.jhuapl.edu/psd). The S Functions and electron energy gain shown in Figures 9, 10, and 11 are calculated from the nonlinear formalism presented in Omura et al., 2019.

Author contributions

JF and PE shared in the conception and design of the study. JF performed the analysis of the observations, drafted the discussion and conclusions, and prepared the manuscript. All authors have reviewed the final manuscript and approve it for publication.

Funding

Research at the MIT Haystack Observatory was supported by the NASA Van Allen Probes (RBSP) funding provided under NASA prime contract NAS5-01072, including the EFW investigation (PI: J.R. Wygant, University of Minnesota), and the ECT investigation (PI: H. Spence, University of New Hampshire).

Acknowledgments

The authors thank Y. Omura for guidance and many discussions on nonlinear wave-particle interaction theory, and C. Kletzing and W. Kurth for assistance in obtaining the high-resolution EMFISIS wave observations, and the Reviewers for helpful comments. We acknowledge in particular the architects and contributors to the ‘Autoplot’ data browser (NASA Grant 05-S3CVO05-11) for its capabilities, which were important for this Van Allen Probes detailed analysis.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Artemyev, A. V., Krasnoselskikh, V. V., Agapitov, O. V., Mourenas, D., and Rolland, G. (2012). Non-diffusive resonant acceleration of electrons in the radiation belts. Phys. Plasmas 19 (12), 122901. doi:10.1063/1.4769726

CrossRef Full Text | Google Scholar

Baker, D. N., Foster, J. C., Erickson, P. J., Henderson, M. G., Kanekal, S. G., Reeves, G. D., et al. (2014). Gradual diffusion and punctuated phase space density enhancements of highly relativistic electrons: Van allen Probes observations. Geophys. Res. Lett. 41, 1351–1358. doi:10.1002/2013GL058942

CrossRef Full Text | Google Scholar

Baker, D. N., Kanekal, S. G., Hoxie, V. C., Batiste, S., Bolton, M., Li, X., et al. (2012). The Relativistic electron-Proton Telescope (REPT) instrument on board the Radiation Belt Storm Probes (RBSP) spacecraft: Characterization of Earth’s radiation belt high-energy particle populations. Space Sci. Rev. 179, 337–381. doi:10.1007/s11214-012-9950-9

CrossRef Full Text | Google Scholar

Blake, J. B., Carranza, P. A., Claudepierre, S. G., Clemmons, J. H., Crain, W. R., Dotan, Y., et al. (2013). The magnetic electron ion spectrometer (MagEIS) instruments aboard the radiation belt storm Probes (RBSP) spacecraft. Space Sci. Rev. 179, 383–421. doi:10.1007/s11214-013-9991-8

CrossRef Full Text | Google Scholar

Chen, Y., Friedel, R. H. W., and Reeves, G. D. (2006). Phase space density distributions of energetic electrons in the outer radiation belt during two geospace environment modeling inner magnetosphere/Storms selected storms. J. Geophys. Res. 111, A11S04. doi:10.1029/2006JA011703

CrossRef Full Text | Google Scholar

Demekhov, A. G., Trakhtengerts, V. Y., Rycroft, M. J., and Nunn, D. (2006). Electron acceleration in the magnetosphere by whistler-mode waves of varying frequency. Geomagn. Aeron. 46 (6), 711–716. doi:10.1134/s0016793206060053

CrossRef Full Text | Google Scholar

Foster, J. C., Erickson, P. J., Baker, D. N., Claudepierre, S. G., Kletzing, C. A., Kurth, W., et al. (2014). Prompt energization of relativistic and highly relativistic electrons during a substorm interval: Van Allen Probes observations. Geophys. Res. Lett. 41, 20–25. doi:10.1002/2013GL058438

CrossRef Full Text | Google Scholar

Foster, J. C., Erickson, P. J., Omura, Y., Baker, D. N., Kletzing, C. A., and Claudepierre, S. G. (2017). Van Allen Probes observations of prompt MeV radiation belt electron acceleration in nonlinear interactions with VLF chorus. J. Geophys. Res. Space Phys. 122, 324–339. doi:10.1002/2016JA023429

CrossRef Full Text | Google Scholar

Foster, J. C., Rosenberg, T. J., and Lanzerotti, L. J. (1976). Magnetospheric conditions at the time of enhanced wave-particle interactions near the plasmapause. J. Geophys. Res. 81 (13), 2175–2182. doi:10.1029/JA081i013p02175

CrossRef Full Text | Google Scholar

Foster, J. C., Erickson, P. J., and Omura, Y. (2021). Subpacket structure in strong VLF chorus rising tones: Characteristics and consequences for relativistic electron acceleration. Earth Planets Space 73, 140. doi:10.1186/s40623-021-01467-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Fu, X., Cowee, M. M., Friedel, R. H., Funsten, H. O., Gary, S. P., Hospodarsky, G. B., et al. (2014). Whistler anisotropy instabilities as the source of banded chorus: Van Allen Probes observations and particle-in-cell simulations. J. Geophys. Res. Space Phys. 119, 8288–8298. doi:10.1002/2014JA020364

PubMed Abstract | CrossRef Full Text | Google Scholar

Fu, X., Guo, Z., Dong, C., and Gary, S. P. (2015). Nonlinear subcyclotron resonance as a formation mechanism for gaps in banded chorus. Geophys. Res. Lett. 42, 3150–3159. doi:10.1002/2015GL064182

CrossRef Full Text | Google Scholar

Gao, X., Chen, L., Li, W., Lu, Q., and Wang, S. (2019). Statistical results of the power gap between lower-band and upper-band chorus waves. Geophys. Res. Lett. 46, 4098–4105. doi:10.1029/2019GL082140

CrossRef Full Text | Google Scholar

Gao, X., Lu, Q., Bortnik, J., Li, W., Chen, L., and Wang, S. (2016). Generation of multiband chorus by lower band cascade in the Earth's magnetosphere. Geophys. Res. Lett. 43, 2343–2350. doi:10.1002/2016GL068313

CrossRef Full Text | Google Scholar

Hanzelka, M., Santolík, O., Omura, Y., Kolmašová, I., and Kletzing, C. A. (2020). A model of the subpacket structure of rising tone chorus emissions. J. Geophys. Res. Space Phys. 125, e2020JA028094. doi:10.1029/2020JA028094

CrossRef Full Text | Google Scholar

Hiraga, R., and Omura, Y. (2020). Acceleration mechanism of radiation belt electrons through interaction with multi-subpacket chorus waves. Earth Planets Space 72, 21. doi:10.1186/s40623-020-1134-3

CrossRef Full Text | Google Scholar

Hsieh, Y. K., and Omura, Y. (2018). Nonlinear damping of oblique whistler mode waves via Landau resonance. J. Geophys. Res. Space Phys. 123, 7462–7472. doi:10.1029/2018JA025848

CrossRef Full Text | Google Scholar

Jaynes, A. N., Baker, D. N., Singer, H. J., Rodriguez, J. V., Loto'aniu, T. M., Ali, A. F., et al. (2015). Source and seed populations for relativistic electrons: Their roles in radiation belt changes. JGR. Space Phys. 120, 7240–7254. doi:10.1002/2015JA021234

CrossRef Full Text | Google Scholar

Katoh, Y., and Omura, Y. (2013). Effect of the background magnetic field inhomogeneity on generation processes of whistler-mode chorus and broadband hiss-like emissions. J. Geophys. Res. Space Phys. 118, 4189–4198. doi:10.1002/jgra.50395

CrossRef Full Text | Google Scholar

Katoh, Y., and Omura, Y. (2016). Electron hybrid code simulation of whistler-mode chorus generation with real parameters in the Earth’s inner magnetosphere. Earth Planets Space 68, 192. doi:10.1186/s40623-016-0568-0

CrossRef Full Text | Google Scholar

Kletzing, C. A., Kurth, W. S., Acuna, M., MacDowell, R. J., Torbert, R. B., Averkamp, T., et al. (2012). The electric and magnetic field instrument and integrated science (EMFISIS) on RBSP. Space Sci. Rev. 179, 127. doi:10.1007/s11214-013-9993-6

CrossRef Full Text | Google Scholar

Kubota, Y., and Omura, Y. (2018). Nonlinear dynamics of radiation belt electrons inter- acting with chorus emissions localized in longitude. J. Geophys. Res. Space Phys. 123, 4835–4857. doi:10.1029/2017JA025050

CrossRef Full Text | Google Scholar

Li, J., Bortnik, J., An, X., Li, W., Angelopoulos, V., Thorne, R. M., et al. (2019). Origin of two-band chorus in the radiation belt of Earth. Nat. Commun. 10, 4672. doi:10.1038/s41467-019-12561-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, W., Thorne, R. M., Nishimura, Y., Bortnik, J., Angelopoulos, V., McFadden, J. P., et al. (2010). THEMIS analysis of observed equatorial electron distributions responsible for the chorus excitation. J. Geophys. Res. 115, A00F11. doi:10.1029/2009JA014845

CrossRef Full Text | Google Scholar

Mauk, B. H., Fox, N. J., Kanekal, S. G., Kessel, R. L., Sibeck, D. G., and Ukhorskiy, A. (2012). Science objectives and rationale for the radiation belt storm Probes mission. Space Sci. Rev. 179, 3–27. doi:10.1007/s11214-012-9908-y

CrossRef Full Text | Google Scholar

Omura, Y., Hsieh, Y. K., Foster, J. C., Erickson, P. J., Kletzing, C. A., and Baker, D. N. (2019). Cyclotron acceleration of relativistic electrons through landau resonance with obliquely propagating whistler mode chorus emissions. J. Geophys. Res. Space Phys. 124, 2018JA026374–2810. doi:10.1029/2018JA026374

CrossRef Full Text | Google Scholar

Omura, Y., Katoh, Y., and Summers, D. (2008). Theory and simulation of the generation of whistler-mode chorus. J. Geophys. Res. 113, A04223. doi:10.1029/2007JA012622

CrossRef Full Text | Google Scholar

Omura, Y. (2021). Nonlinear wave growth theory of whistler-mode chorus and hiss emissions in the magnetosphere. Earth Planets Space 73, 95. doi:10.1186/s40623-021-01380-w

CrossRef Full Text | Google Scholar

Omura, Y., Furuya, N., and Summers, D. (2007). Relativistic turning acceleration of resonant electrons by coherent whistler mode waves in a dipole magnetic field. J. Geophys. Res. 112, A06236. doi:10.1029/2006JA012243

CrossRef Full Text | Google Scholar

Reeves, G. D., Spence, H. E., Henderson, M. G., Morley, S. K., Friedel, R. H. W., Funsten, H. O., et al. (2013). Electron acceleration in the heart of the Van Allen radiation belts. Science 341 (6149), 991–994. doi:10.1126/science.1237743

PubMed Abstract | CrossRef Full Text | Google Scholar

Santolik, O., Gurnett, D. A., Picket, J. S., Chum, J., and Cornilleau-Wehrlin, N. (2009). Oblique propagation of whistler mode waves in the chorus source region. J. Geophys. Res. 114, A04586. doi:10.1029/2009JA014586

CrossRef Full Text | Google Scholar

Santolík, O., Kletzing, C. A., Kurth, W. S., Hospodarsky, G. B., and Bounds, S. R. (2014). Fine structure of large-amplitude chorus wave packets. Geophys. Res. Lett. 41, 293–299. doi:10.1002/2013GL058889

CrossRef Full Text | Google Scholar

Storey, L. R. O. (1953). An investigation of whistling atmospherics. Philosophical Trans. R. Soc. Lond. Ser. A, Math. Phys. Sci. 246, 113–141. doi:10.1098/rsta.1953.0011

CrossRef Full Text | Google Scholar

Summers, D., and Omura, Y. (2007). Ultra-relativistic acceleration of electrons in planetary magnetospheres. Geophys. Res. Lett. 34, L24205. doi:10.1029/2007GL032226

CrossRef Full Text | Google Scholar

Tsurutani, B. T., and Smith, E. J. (1974). Postmidnight chorus: A substorm phenomenon. J. Geophys. Res. 79, 118–127. doi:10.1029/JA079i001p00118

CrossRef Full Text | Google Scholar

Zhang, X.-J., Agapitov, O., Artemyev, A. V., Mourenas, D., Angelopoulos, V., Kurth, W. S., et al. (2020). Phase decoherence within intense chorus wave packets constrains the efficiency of nonlinear resonant electron acceleration. Geophys. Res. Lett. 47, e2020GL089807. doi:10.1029/2020GL089807

CrossRef Full Text | Google Scholar

Zhang, X. J., Thorne, R., Artemyev, A., Mourenas, D., Angelopoulos, V., Bortnik, J., et al. (2018). Properties of intense field-aligned lower-band chorus waves: Implications for nonlinear wave-particle interactions. JGR. Space Phys. 123 (7), 5379–5393. doi:10.1029/2018JA025390

CrossRef Full Text | Google Scholar