2D modelling of pulsating stars with rapid rotation

Rapid stellar rotation is an important phenomenon in stellar physics, particularly for massive and intermediate mass main-sequence stars. This affects all aspects of the star’s physics including its structure, evolution, and pulsations, and makes it necessary to use 2D numerical approaches rather than the 1D approaches typically used. In this contribution, we will review 2D numerical methods for modelling and interpreting pulsation modes in rapidly rotating stars. We will start by deriving the pulsation equations, both in an adiabatic and non-adiabatic setting, then provide a description of the 2D numerical implementation. We will then explain approximate implementations of the effects of rotation, namely first, second, and third order perturbative approaches, as well as the traditional approximation. This will then be followed by a description on how to calculate disk-integrated mode visibilities in various photometric bands, and how to apply this to mode identification in rapid rotators. Finally, we will review some of the recent works that interpret the pulsation spectra of various stars as viewed in either a single photometric band or in multiple bands, and including supplementary constraints from interferometry and spectroscopy.

1 Introduction

Much progress has been made in our understanding of stellar physics thanks to the advent of elaborate 1D numerical simulations of stars. The basic hydrostatic structure, energy transport, and essential stages of stellar evolution are understood. Nonetheless, the shortcomings of 1D spherically symmetric models are becoming increasingly apparent, particularly on a macroscopic scale. Indeed, rotation, convection, and transport processes remain poorly understood and require the use of higher dimensional simulations to be modelled correctly. In particular, rapid stellar rotation causes significant departures from spherical symmetry thanks to centrifugal distortion and gravity darkening, as confirmed by increasingly sophisticated observations such as those coming from interferometry (e.g., Domiciano de Souza et al., 2003; Monnier et al., 2007). Furthermore, it affects the evolution, lifetimes, and chemical yields of such stars (Meynet and Maeder, 2000) through transport processes caused by rotation-related instabilities. As can be seen in Figure 1, based on Royer, (2009), the majority of intermediate and high mass main sequence stars rotate rapidly. Accordingly, in order to describe such stars, it is necessary to use a 2D approach when modelling the structure, evolution, and pulsations of these stars.

FIGURE 1

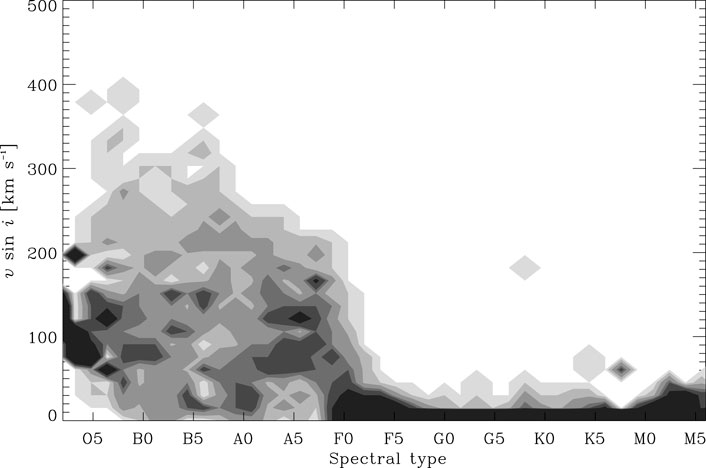
FIGURE 1. Distribution of projected equatorial velocities, v sin i, as a function of stellar spectral type. As can be seen, there is a clear distinction between stars earlier than F0, and later type (solar-like) stars (Credit: F. Royer, based on Royer, 2009).

In the present contribution, we will focus on the 2D modelling and interpretation of stellar pulsations in rapidly rotating stars. Understanding such pulsations is one of the keys to understanding such stars and the effects of rotation, as it is currently the only way to probe their internal structure. However, rotation greatly complicates the pulsation spectra of these stars thus making them more difficult to decipher. In particular, correctly identifying modes, i.e., finding the match between observed and theoretically calculated pulsations, is a long-standing obstacle but also a prerequisite to detailed seismic investigations of such stars. Therefore, various strategies have been devised in order to overcome this obstacle as described below.

This contribution is organised as follows: Section 2 describes how to calculate stellar pulsations in rotating stellar models. More specifically, it briefly addresses rotating stellar models before explaining how to carry out 2D pulsation calculations, both in the adiabatic and non-adiabatic cases. It also describes approximate methods for including the effects of rotation, namely the perturbative approach and the use of the traditional approximation. Section 3 briefly describes some of the impacts of rapid rotation on stellar pulsations and introduces acoustic island modes. Section 4 describes some of the mode observables that may be used to help identify the observed modes, namely mode visibilities, amplitude ratios, and phase differences. Section 5 then provides a few recent examples of mode identification and seismic interpretation of rapidly rotating stars. Finally, Section 6 briefly concludes this paper.

2 Calculating stellar pulsations

2.1 Rotating models

The equations describing stellar pulsations are obtained by perturbing the fluid dynamic equations around an equilibrium model of the star. Accordingly, in order to fully account for the effects of rotation, it is essential to have at one’s disposal an equilibrium model that fully takes into account the effects of rotation. In particular the effects of centrifugal acceleration on the hydrostatic equilibrium of the model are crucial for calculating pulsations, even when the adiabatic approximation is being made, i.e., where energy exchanges are neglected during the pulsations. This is expressed via the following relation:

${\vec{v}}_0\cdot \vec{\nabla }{\vec{v}}_0=-\frac{\vec{\nabla }{P}_0}{{\rho }_0}-\vec{\nabla }{\mathrm{\Psi }}_0(1)$

where $\vec{v}$ is the fluid velocity field, ρ the density, P the pressure, Ψ the gravitational potential, and where we have neglected viscosity. The subscript “0” signifies that these are equilibrium quantities as opposed to perturbations resulting from oscillations (see following section). The velocity field is mainly caused by rotation and therefore takes on the expression ${\vec{v}}_0=\mathrm{\Omega }(s,z)s{\vec{e}}_{\varphi }$, where Ω(s, z) is the rotation profile. Accordingly, the left-hand side of the above equation takes on the following expression:

${\vec{v}}_0\cdot \vec{\nabla }{\vec{v}}_0=-{\mathrm{\Omega }}^2\left(s,z\right)s{\vec{e}}_s(2)$

where we have used cylindrical coordinates (s, ϕ, z) and their associated unit vectors for convenience. This expression is easily recognised as the centrifugal acceleration.

Various models fully take into account centrifugal deformation such as ROTORC models (Deupree, 1990; Deupree, 1995), Self-Consistent Field (SCF) models (Jackson et al., 2005; MacGregor et al., 2007), or Evolution STEllaire en Rotation (ESTER) models (Espinosa Lara and Rieutord, 2013; Rieutord et al., 2016). Another approach is to deform 1D (i.e., spherically symmetric) models by subsequently introducing the effects of the centrifugal acceleration. This approach was first proposed by Roxburgh, (2006) for arbitrary 2D rotation profiles. More recently, Manchon, (2021) applied a similar strategy for CESTAM models (Marques et al., 2013). The advantage of such an approach is the possibility of using highly sophisticated 1D stellar evolution models which take into account in a 1D formalism the horizontally-averaged effects of rotation (Meynet and Maeder, 2000; Palacios et al., 2003; Maeder, 2009; Marques et al., 2013).

If one wishes to take into account energy exchanges during the pulsations, i.e., carry out fully non-adiabatic pulsation calculations, it is necessary to deal with the energy conservation equation in a self-consistent way in the model itself. Taking these effects into account leads to baroclinic models, i.e., models where lines of constant pressure, density, and temperature do not coincide. Indeed, lines of constant pressure are determined by the hydrostatic equilibrium whereas lines of constant temperature depend on the propagation of energy inside the star, and typically tend to be more spherical. As a result, this leads to baroclinic flows, namely a non-conservative (i.e., non-cylindrical) rotation profile and meridional circulation. To show the link between non-cylindrical rotation and baroclinicity, one can take the curl of Eq. 1:

$-s\frac{\partial {\mathrm{\Omega }}^2}{\partial z}{\vec{e}}_{\varphi }=\frac{\vec{\nabla }{\rho }_0\times \vec{\nabla }{P}_0}{{\rho }_0^2}(3)$

The right hand side of this equation differs from zero because lines of constant pressure and density do not coincide, and thus leads to a vertical gradient of the rotation profile. Figure 2 illustrates a differential rotation profile and meridional circulation resulting from baroclinic effects¹, obtained in an ESTER model. This in turn causes various instabilities, turbulence, and transport processes. Currently, the only models where the energy equation and baroclinic effects are taken into account in a fully 2D setting are ESTER models. In 1D models such as those from the Geneva code, STAREVOL, or CESTAM, this is achieved in a horizontally-averaged rather than local way based on the assumption of anisotropic turbulence and mixing (Zahn, 1992).

FIGURE 2

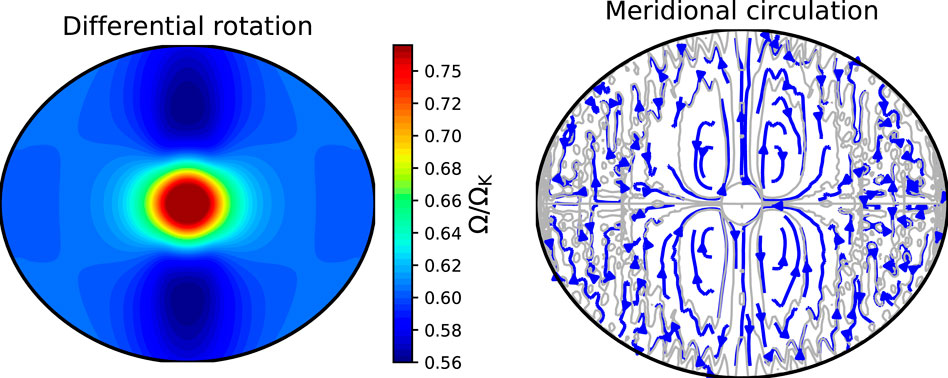
FIGURE 2. Differential rotation (A) and meridional circulation (B) as a result of baroclinic effects in a 2 M ESTER model rotating at 0.6 Ωk (see also Espinosa and Rieutord 2013, and Rieutord et al., 2016 for similar plots).

Having briefly described the rotating models at our disposal, we now turn our attention to the pulsation calculations themselves.

2.2 Adiabatic analysis

As a first step, it is simpler to calculate stellar pulsations using the adiabatic approximation, i.e., to neglect energy exchanges (primarily in the form of heat) during the pulsations. When rotation is present, various effects must be taken into account. Firstly, the centrifugal deformation must be taken into account, typically through the use of surface-fitting spheroidal coordinates in the pulsation equations. Indeed, using such coordinates are necessary in order to maintain accuracy when imposing boundary conditions. Figure 3 illustrates a multi-domain surface-fitting coordinate system in an ESTER model. Secondly, the Coriolis acceleration intervenes in the oscillatory motions. In some cases such as inertial modes, it is the restoring force and thus the reason for their existence. Putting this together leads to the following set of equations in an inertial frame:

$\frac{\delta \rho }{{\rho }_0}+\vec{\nabla }\cdot \vec{\xi }=0(4)$

$\frac{D_0^2\vec{\xi }}{D{t}^2}-\vec{\xi }\cdot \vec{\nabla }\left({\vec{v}}_0\vec{\nabla }\cdot {\vec{v}}_0\right)=-\frac{\vec{\nabla }{P}^{\prime }}{{\rho }_0}+\frac{{\rho }^{\prime }{\vec{g}}_{\mathrm{e}\mathrm{ff}}}{{\rho }_0}-\vec{\nabla }{\mathrm{\Psi }}^{\prime }(5)$

$\frac{\delta p}{P_0}={\mathrm{\Gamma }}_1\frac{\delta \rho }{{\rho }_0}(6)$

$\mathrm{\Delta }{\mathrm{\Psi }}^{\prime }=4\pi G{\rho }^{\prime }(7)$

where Eq. 4 corresponds to the continuity equation, Eq. 5 to Euler’s momentum equation, Eq. 6 to the adiabatic relation, and Eq. 7 to Poisson’s equation. Quantities preceded by δ correspond to Lagrangian perturbations, and quantities with a prime to Eulerian perturbations. The operator $\frac{D_0}{Dt}=\frac{\partial }{\partial t}+{\vec{v}}_0\cdot \vec{\nabla }$ denotes the Lagrangian time derivative, $\vec{\xi }$ the Lagrangian displacement, ${\vec{g}}_{\mathrm{e}\mathrm{ff}}=\vec{\nabla }{P}_0/{\rho }_0$ the effective gravity (i.e., including both gravity and the centrifugal acceleration), Γ₁ the first adiabatic exponent, and G the gravitational constant. We note that Eq. 5 is obtained by taking the Lagrangian perturbation of Euler’s momentum equation (e.g., Lynden-Bell and Ostriker, 1967), and rearranging some of the terms thanks to the hydrostatic equilibrium (Eq. 1).

FIGURE 3

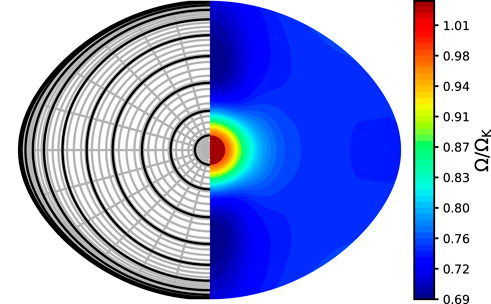
FIGURE 3. Multi-domain coordinate system (A) and rotation profile (B) in the best fitting model for Altair from Bouchaud et al. (2020) (see also Rieutord et al., 2016 for a similar plot involving a 3 M⊙ rotating model).

When studying pulsation modes, one assumes a harmonic time dependence of the form exp(iωt), where ω corresponds to the pulsation frequency. Furthermore, although the star is no longer spherically symmetric because of centrifugal deformation, it is still symmetric around the rotation axis. As a result, pulsation modes have an azimuthal dependence of the form exp(imϕ), where m is the azimuthal order. This can be used to rewrite the left-hand side of Eq. 5:

$\begin{array}{ll}\hfill \frac{D_0^2\vec{\xi }}{D{t}^2}-\vec{\xi }\cdot \vec{\nabla }\left({\vec{v}}_0\vec{\nabla }\cdot {\vec{v}}_0\right)& =-{\left(\omega +m\mathrm{\Omega }\right)}^2\vec{\xi }+2i\left(\omega +m\mathrm{\Omega }\right)\vec{\mathrm{\Omega }}\times \vec{\xi }\hfill \\ \hfill & +\vec{\mathrm{\Omega }}\times \left(\vec{\mathrm{\Omega }}\times \vec{\xi }\right)+\vec{\xi }\cdot \vec{\nabla }\left(s{\mathrm{\Omega }}^2{\vec{e}}_s\right)\hfill \end{array}(8)$

where $\vec{\mathrm{\Omega }}=\mathrm{\Omega }{\vec{e}}_z$ is the rotation vector. The above dependencies on t and ϕ lead prograde modes (i.e., modes that travel in the same direction as stellar rotation) to having negative m values and retrograde modes to having positive m values. This could be described as the “retrograde convention”. Some authors, notably in helioseismology, prefer the opposite convention (i.e., prograde modes have positive m values—we will call the “prograde convention”) and therefore introduce a time dependence of the form exp(−iωt) (while maintaining an azimuthal dependence of the form exp(imϕ)). With such a convention, the occurrences of $\left(\omega +m\mathrm{\Omega }\right)$ would need to be replaced by (−ω + mΩ) in the above expression.

The right-hand side of Eq. 5 can also be re-expressed in terms of the Lagrangian perturbations to pressure and density, thus leading to:

$\begin{array}{ll}\hfill -\frac{\vec{\nabla }{P}^{\prime }}{{\rho }_0}+\frac{{\rho }^{\prime }{\vec{g}}_{\mathrm{e}\mathrm{ff}}}{{\rho }_0}-\vec{\nabla }{\mathrm{\Psi }}^{\prime }& =-\frac{P_0}{{\rho }_0}\vec{\nabla }\left(\frac{\delta p}{P_0}\right)+\frac{\vec{\nabla }{P}_0}{{\rho }_0}\left(\frac{\delta \rho }{{\rho }_0}-\frac{\delta p}{P_0}\right)\hfill \\ \hfill & -\vec{\nabla }\mathrm{\Psi }+\vec{\nabla }\left(\frac{\vec{\xi }\cdot \vec{\nabla }{P}_0}{{\rho }_0}\right)\hfill \\ \hfill & +\frac{\left(\vec{\xi }\cdot \vec{\nabla }{P}_0\right)\vec{\nabla }{\rho }_0-\left(\vec{\xi }\cdot \vec{\nabla }{\rho }_0\right)\vec{\nabla }{P}_0}{{\rho }_0^2}\hfill \end{array}(9)$

The last term in the alternate formulation is particularly interesting as it only appears in baroclinic models. In barotropic models, $\vec{\nabla }{P}_0$ and $\vec{\nabla }{\rho }_0$ are parallel thus causing the term to vanish.

Various boundary conditions must be added to the above equations to ensure the solutions are regular in the centre, the Lagrangian pressure perturbations vanish at the surface, and the perturbations to the gravitational potential vanish at infinity. This leads to a generalised eigenvalue problem where the pulsation frequency is the eigenvalue, and the pulsation mode the eigenfunction. This problem must then be solved numerically as described in the next section.

2.2.1 Numerical implementation

Various steps must be carried out before implementing the above equations numerically. The first step is to express them explicitly in a suitable coordinate system, typically surface-fitting spheroidal coordinates as described above. For instance, the continuity equation expressed in the coordinate system used in Reese et al. (2006) is:

$\frac{\delta \rho }{{\rho }_o}+\frac{{\zeta }^2}{r^2{r}_{\zeta }}\left[\frac{{\partial }_{\zeta }\left({\zeta }^2{\xi }^{\zeta }\right)}{{\zeta }^2}+\frac{{\partial }_{\theta }\left(\sin \theta {\xi }^{\theta }\right)}{\zeta \sin \theta }+\frac{{\partial }_{\varphi }{\xi }^{\varphi }}{\zeta \sin \theta }\right]=0(10)$

where (ζ, θ, ϕ) designates the spheroidal coordinate system, r the distance from the centre, and $r_{\zeta }=\frac{\partial r}{\partial \zeta }$. Usually, such a coordinate system is non-dimensionalised so that ζ = 1 corresponds to the stellar surface.

The next step is to discretise the equations. This can be subdivided into two parts. The first is the horizontal discretisation. Two options exist: using finite-differences or projecting onto the spherical harmonic basis. Various authors have used finite differences² (e.g., Clement, 1998; Espinosa et al., 2004; Lovekin and Deupree, 2008). However, many authors nowadays prefer to project the equations onto the spherical harmonic basis in order to improve the accuracy (this amounts to applying a spectral method based on spherical harmonics). This projection takes place in two steps. First the unknowns are expressed as a sum of spherical harmonics, e.g.:

$\left(\frac{\delta \rho }{\rho }\right)=\sum _{{\ell }^{\prime }=|m|}^{\infty }{\left(\frac{\delta \rho }{{\rho }_o}\right)}_m^{{\ell }^{\prime }}\left(\zeta \right)Y_{{\ell }^{\prime }}^m\left(\theta ,\varphi \right)(11)$

$\begin{array}{ll}\hfill \vec{\xi }& =\sum _{{\ell }^{\prime }=|m|}^{\infty }\left({{\xi }_{\zeta }}_m^{{\ell }^{\prime }}\left(\zeta \right){\vec{R}}_{{\ell }^{\prime }}^m\left(\theta ,\varphi \right)+{{\xi }_{\theta }}_m^{{\ell }^{\prime }}\left(\zeta \right){\vec{S}}_{{\ell }^{\prime }}^m\left(\theta ,\varphi \right)\right.\hfill \\ \hfill & +\left.{{\xi }_{\varphi }}_m^{{\ell }^{\prime }}\left(\zeta \right){\vec{T}}_{{\ell }^{\prime }}^m\left(\theta ,\varphi \right)\right)\hfill \end{array}(12)$

where ${\left(\frac{\delta \rho }{{\rho }_o}\right)}_m^{{\ell }^{\prime }}(\zeta )$, ${{\xi }_{\zeta }}_m^{{\ell }^{\prime }}(\zeta )$, ${{\xi }_{\theta }}_m^{{\ell }^{\prime }}(\zeta )$, and ${{\xi }_{\varphi }}_m^{{\ell }^{\prime }}(\zeta )$ are unknown radial functions, $Y_{{\ell }^{\prime }}^m(\theta ,\varphi )$ the spherical harmonic of harmonic degree ℓ′ and azimuthal order m, and $({\vec{R}}_{{\ell }^{\prime }}^m,{\vec{S}}_{{\ell }^{\prime }}^m,{\vec{T}}_{{\ell }^{\prime }}^m)$ vectorial spherical harmonics³ given by the following expressions:

${\vec{R}}_{{\ell }^{\prime }}^m=Y_{{\ell }^{\prime }}^m{\vec{a}}_{\zeta },(13)$

${\vec{S}}_{{\ell }^{\prime }}^m=\frac{\partial Y_{{\ell }^{\prime }}^m}{\partial \theta }{\vec{a}}_{\theta }+\frac{1}{\sin \theta }\frac{\partial Y_{{\ell }^{\prime }}^m}{\partial \varphi }{\vec{a}}_{\varphi },(14)$

${\vec{T}}_{{\ell }^{\prime }}^m=\frac{1}{\sin \theta }\frac{\partial Y_{{\ell }^{\prime }}^m}{\partial \varphi }{\vec{a}}_{\theta }-\frac{\partial Y_{{\ell }^{\prime }}^m}{\partial \theta }{\vec{a}}_{\varphi }(15)$

$({\vec{a}}_{\zeta },{\vec{a}}_{\theta },{\vec{a}}_{\varphi })$ being a vector basis suitable for the spheroidal coordinate system. As can be seen, the sums in Eqs 11, 12 are only carried out over the harmonic degree ℓ′ and not over m, since the different azimuthal orders are decoupled as a result of the symmetry around the rotation axis (hence the reason why modes are proportional to exp(imϕ)). Furthermore, in practice, the sums are truncated at a maximal harmonic degree, ℓ_max. Then the equations are projected onto the spherical harmonic basis by calculating the dot product between the equation and the complex conjugate of successive spherical harmonics (or vectorial spherical harmonics in the case Euler’s momentum equation), and integrating the result over 4π steradians. For the continuity equation, this would yield:

$\begin{array}{ll}\hfill 0& ={\left(\frac{\delta \rho }{{\rho }_o}\right)}_m^{\ell }+\sum _{{\ell }^{\prime }=|m|}^{{\ell }_{\max }}\left[I_{\ell {\ell }^{\prime }}^m\left(\frac{{\zeta }^2}{r^2{r}_{\zeta }}\right){\partial }_{\zeta }{{\xi }_{\zeta }}_m^{{\ell }^{\prime }}+I_{\ell {\ell }^{\prime }}^m\left(\frac{2\zeta }{r^2{r}_{\zeta }}\right){{\xi }_{\zeta }}_m^{{\ell }^{\prime }}\right.\hfill \\ \hfill & -\left.I_{\ell {\ell }^{\prime }}^m\left(\frac{{\ell }^{\prime }\left({\ell }^{\prime }+1\right)\zeta }{r^2{r}_{\zeta }}\right){{\xi }_{\theta }}_m^{{\ell }^{\prime }}\right]\hfill \end{array}(16)$

where the coupling integral operator, $I_{\ell {\ell }^{\prime }}^m\left(\cdot \right)$, is defined as follows for a generic function G(ζ, θ):

$I_{\ell {\ell }^{\prime }}^m\left(G\right)\left(\zeta \right)=\int {\int }_{4\pi }G\left(\zeta ,\theta \right)Y_{{\ell }^{\prime }}^m\left(\theta ,\varphi \right){\left\{Y_{\ell }^m\left(\theta ,\varphi \right)\right\}}^{\ast }\mathrm{d}\mathrm{\Omega },(17)$

in which dΩ is a solid angle element, and where we have made use of the following spherical harmonic identity:

$-{\ell }^{\prime }\left({\ell }^{\prime }+1\right)Y_{{\ell }^{\prime }}^m=\frac{1}{\sin \theta }\frac{\partial }{\partial \theta }\left(\sin \theta \frac{\partial Y_{{\ell }^{\prime }}^m}{\partial \theta }\right)+\frac{1}{{\sin }^2\theta }\frac{{\partial }^2{Y}_{{\ell }^{\prime }}^m}{\partial {\varphi }^2},(18)$

By varying ℓ from |m| to ℓ_max, i.e., by projecting the continuity equation onto spherical harmonics of successive degrees, and applying the above methodology to the entire system, Eqs 4–7, we end up with a large system of 1D differential equations which depends on the pseudo-radial variable ζ, the solution of which yields the unknown radial functions introduced above. Due to the symmetry with respect to the equatorial plane, only even or odd harmonics intervene in this system (apart from the ${{\xi }_{\varphi }}_m^{{\ell }^{\prime }}$ functions which typically have the opposite parity).

The second part is the radial discretisation, i.e., according to radial variable ζ. Once more, different options exist and are typically chosen to suit the equilibrium model. A number of authors use finite differences (e.g., Clement, 1998; Lovekin and Deupree, 2008; Ouazzani et al., 2012; Reese et al., 2013). We note that the finite difference scheme used in Ouazzani et al. (2012), first introduced by Scuflaire et al. (2008), is very stable and achieves a 4^th order accuracy using only two consecutive grid points at a time, thanks to the use of equilibrium quantities and their radial derivatives. Reese et al. (2013) used a different 4^th order scheme which is stable to mesh drift, makes use of superconvergence, and does not require the radial derivatives of equilibrium quantities (see Reese, 2013, for a derivation of the scheme). The main advantage of using finite differences is their high flexibility in the choice of the underlying grid which can be essentially arbitrary. Accordingly, grids that are dense near the surface can be used to resolve acoustic modes in that region as well as rapid variations in the Γ₁ profile. Grids with a higher density of points in the central regions of the star will be more suitable for gravity modes.

The second option for the radial discretisation is using spectral methods, i.e., where the solutions are decomposed over a function basis for which the analytical derivatives are known. Various authors use spectral methods based on Chebyshev polynomials (e.g., Rieutord and Valdettaro, 1997; Lignières et al., 2006). The main advantage of spectral methods is their high accuracy (provided the calculations have converged). However, unlike for finite differences, the choice of grid is imposed by the spectral method. Hence, there is little freedom to increase the grid density in a specific region of the star. To overcome this limitation, one may apply a multi-domain approach. For instance, ESTER models are cut up into a number of concentric spheroidal domains in which a Chebyshev spectral method is applied (e.g., Rieutord et al., 2016). Interface conditions are applied between the domains in order to ensure the continuity of various quantities such as the pressure. Likewise, pulsation calculations using these models also apply a multi-domain spectral approach (Reese et al., 2021). With such an approach, one can set up a thin domain near the surface with a high resolution that captures rapid variations in the model and in the pulsation modes.

Once the problem has been discretised, it takes on the form of an algebraic generalised eigenvalue problem:

$\mathcal{A}\vec{v}=\omega \mathcal{B}\vec{v}(19)$

where $\mathcal{A}$ and $\mathcal{B}$ are matrices, $\vec{v}$ the eigenvector (containing all of the variables relevant to the pulsation mode), and ω the associated frequency. Such problems can be solved either using a QR decomposition⁴ which searches for all of the eigensolutions (but typically this would be too costly numerically for even a moderate resolution), or an iterative method that searches for a limited number of solutions around target frequencies. Iterative methods include the simple power method or more sophisticated approaches such as the Arnoldi-Chebyshev method which applies a QR decomposition on a reduced matrix representative of the original matrix. However, given that these methods find the eigenvalues with the largest absolute value, a shift-invert strategy must first be applied in order to transform the above eigenvalue problem into an equivalent problem where the largest eigenvalues in the new formulation correspond to those closest to a given target, σ, in the original problem:

${\left(\mathcal{A}-\sigma \mathcal{B}\right)}^{-1}\mathcal{B}\vec{v}=\mu \vec{v}(20)$

The original eigenvalues are then deduced from the eigenvalues μ via the relation $\omega =\sigma +\frac{1}{\mu }$.

A number of authors have carried out adiabatic oscillation calculations using a 2D approach to fully account for the effects of rapid rotation. Clement studied acoustic and gravity modes in N = 1, 2, and 3 polytropic uniformly rotating models, as well as 15 M_⊙ uniformly rotating models, appropriate for β Cep pulsators, using a full 2D finite-difference method (Clement, 1981; Clement, 1998) as well as a method based on the variational principle and involving approximate eigenfunctions (Clement, 1984; Clement, 1986; Clement, 1989). Later on, Espinosa et al. (2004) developed a finite-difference code⁵ called OMASS2d in which the system of pulsation equations is reduced to a single equation thanks to a number of approximations (Cowling approximation, neglect of Coriolis force, neglect of Brunt-Väisälä frequency). He used this code to study acoustic pulsation modes in uniform density models and realistic models. Lovekin and Deupree, (2008) used Clement’s pulsation code (called NRO for “Nonradial Oscillation code”) to study pulsation modes in 10 M_⊙ uniformly rotating ZAMS models based on the 2D stellar evolution code ROTORC (Deupree, 1990; Deupree, 1995). They went on to extend this work to 10 M_⊙ models with a nonuniform cylindrical rotation profile (Lovekin et al., 2009). Meanwhile, a new 2D approach based on spectral methods was being developed starting with Lignières et al. (2001). This led to the development of the TOP (Two-dimensional Oscillation Program) pulsation code as well as accurate calculations of acoustic pulsation modes in uniformly rotating N = 3 polytropic models, first without (Lignières et al., 2006) then with the Coriolis force (Reese et al., 2006). This allowed Reese et al. (2006) to establish validity domains for third-order perturbative methods. TOP was subsequently extended to models based on the SCF method which have cylindrical differential rotation (Reese et al., 2009) then to models based on the ESTER code with full 2D rotation profiles (Reese et al., 2021). Ballot et al. (2010) used TOP to study gravity modes in polytropic models and to establish the corresponding validity domains. Later on, Ouazzani et al. (2012) developed the ACOR pulsation code and compared its results with those from TOP. In Ouazzani et al. (2015), they then went on to study acoustic and gravity pulsation modes in a 2 M_⊙ model with a radial (or shellular) differential rotation, obtained using the centrifugal deformation code from Roxburgh, (2006).

In addition to these works, there are a number of studies focusing on oscillations of rapidly rotating neutron stars. These have made use of polytropic models (e.g., Ipser and Lindblom, 1991; Yoshida and Eriguchi, 1995; Stergioulas et al., 2004) as well as realistic neutron star models (e.g., Yoshida and Eriguchi, 1999; Ferrari, 2005). A key difference when calculating pulsations in polytropic neutron star models is the fact that the polytropic and adiabatic exponents are kept the same, whereas they typically differ for classical stars. Some of the important goals in studying such oscillations include determining the stability of neutron stars with respect to gravitational-wave radiation which may help to limit their rotation rate (e.g., Ipser and Lindblom, 1991; Yoshida and Eriguchi, 1995), and testing the equation of state (e.g., Ferrari, 2005). Some authors have also inspected mode damping due to mass-shedding at near-critical rotation rates, thus requiring the use of time evolution simulations of pulsating neutron stars (e.g., Stergioulas et al., 2004). Such simulations typically yield less accurate pulsation frequencies since these depend on the time span covered by the simulation, but are able to take into account in a straightforward way non-linear effects including amplitude saturation, mode coupling, and pulsation-induced mass-shedding.

2.2.2 Variational principle

Given the complexity of the pulsation calculations in the presence of rapid rotation, it is important to check the accuracy of the calculations. One way of achieving this is by recalculating the frequencies thanks to a variational formula. Such a formula may be obtained by calculating the dot product of Euler’s momentum equation and the complex conjugate of the Lagrangian displacement field, ${\vec{\xi }}^{*}$, integrating over the star’s volume, and rearranging the various terms thanks to integration by parts and other manipulations (see, e.g., Appendix B of Reese et al., 2021, for a full derivation). This leads to a second order equation in ω of the form:

$-{\omega }^2⟨\vec{\xi },\vec{\xi }⟩+\omega ⟨\vec{\xi },\mathcal{C}\vec{\xi }⟩+⟨\vec{\xi },\mathcal{L}\vec{\xi }⟩=0,(21)$

where $\mathcal{C}$ is an operator associated with the Coriolis force, $\mathcal{L}$ an operator representing a combination of other fluid dynamic terms, and where we have introduced the following dot product:

$⟨\vec{\xi },\vec{\eta }⟩={\iiint }_V{\vec{\xi }}^{\ast }\cdot \vec{\eta }{\rho }_{0}dV,(22)$

$\vec{\xi }$ and $\vec{\eta }$ being two displacement fields, and {.}* denoting the complex conjugate of a quantity. Solving Eq. 21 then leads to an independent estimate of the pulsation frequency which furthermore benefits from the variational principle. Indeed, as was shown in Lynden-Bell and Ostriker, 1967 in a very general case, the fluid dynamic operators are symmetric with respect to the above dot product. One of the consequences of this is that a small variation or error on the displacement field, $\delta \vec{\xi }$, leads to a second order error on the variational frequency thus obtained:

${\omega }_{\text{var}}=\omega +\mathcal{O}\left(\Vert \delta \vec{\xi }{\Vert }^2\right)(23)$

As a result, this property has been used to check the accuracy with which pulsation modes have been calculated or to increase their accuracy, both in the 1D non-rotating case (e.g., Christensen-Dalsgaard, 1982; Christensen-Dalsgaard and Mullan, 1994), and 2D rapidly rotating case (e.g., Reese et al., 2006; Reese et al., 2021). Some authors have used this as a means of calculating pulsation frequencies by assuming an approximate analytical form for the eigenfunctions (e.g., Clement, 1984; Clement, 1986; Clement, 1989).

2.3 Non-adiabatic calculations

Although adiabatic pulsation calculations have the advantage of being simpler yet sufficiently realistic to provide accurate pulsation frequencies, they also have various disadvantages compared to non-adiabatic calculations. Indeed, it is only possible to calculate damping or growth rates and to predict which modes are unstable with non-adiabatic calculations. Furthermore, accurate perturbations of the effective temperature, which are essential for correctly calculating mode visibilities and associated amplitude ratios, may only be obtained in a non-adiabatic context.

In order to carry out non-adiabatic calculations, one must replace the adiabatic relation by a perturbed version of the energy equation:

$\begin{array}{ll}\hfill i\left(\omega +m\mathrm{\Omega }\right){\rho }_0{T}_0\delta S& ={ϵ}_0{\rho }_0\left(\frac{\delta ϵ}{{ϵ}_0}+\frac{\delta \rho }{{\rho }_0}\right)-\vec{\nabla }\cdot \delta \vec{F}+\vec{\xi }\cdot \vec{\nabla }\left(\vec{\nabla }\cdot {\vec{F}}_0\right)\hfill \\ \hfill & -\vec{\nabla }\cdot \left[\left(\vec{\xi }\cdot \vec{\nabla }\right){\vec{F}}_0\right]\hfill \end{array}(24)$

where T corresponds to temperature, S to entropy, ϵ to energy generated via nuclear reactions, and $\vec{F}$ the energy flux. The energy flux may be decomposed into a radiative, ${\vec{F}}^{\mathrm{R}}$, and convective flux, ${\vec{F}}^{\mathrm{C}}$. The perturbed radiative energy flux may be obtained by perturbing the radiative transfer equation:

$\begin{array}{ll}\hfill \delta {\vec{F}}^{\mathrm{R}}& =\left[4\frac{\delta T}{T_0}-\frac{\delta \kappa }{{\kappa }_0}-\frac{\delta \rho }{{\rho }_0}\right]{\vec{F}}_0^{\mathrm{R}}\hfill \\ \hfill & -\frac{4ac{T}_0^3}{3{\kappa }_0{\rho }_0}\left[T_0\vec{\nabla }\left(\frac{\delta T}{T_0}\right)+\vec{\xi }\cdot \vec{\nabla }\left(\vec{\nabla }{T}_0\right)-\vec{\nabla }\left(\vec{\xi }\cdot \vec{\nabla }{T}_0\right)\right]\hfill \end{array}$

where κ is the opacity and $a=\frac{4\sigma }{c_l}$ the radiation constant, σ being the Stefan-Boltzmann constant and c_l the speed of light. The perturbed convective flux is usually neglected in what is generally known as the frozen convection approximation. To these equations must be added perturbed equations of state and of opacity.

There are relatively few works on non-adiabatic pulsation calculations in rapidly rotating stars using a fully 2D approach. Lee and Baraffe, (1995) devised a first approach involving a perturbative modelling of the centrifugal distortion and a two-term expansion of the pulsation modes over the spherical harmonic basis. This has been followed by various works using a larger number of spherical harmonics when calculating the pulsation modes (e.g., Lee, 2001). In a particularly interesting study, Lee, (2008) compares this approach with an approach based on the traditional approximation (Section 2.5) and finds that in full 2D calculations low frequency retrograde modes tend be damped, in contrast with what is obtained using the traditional approximation. More recently, Savonije, (2007) studied the non-adiabatic tidal response of a 20 M_⊙ stellar model using a 2D finite difference scheme. The effects of the Coriolis force were included whereas those of the centrifugal force were neglected. Finally, Reese et al. (2017a) devised a non-adiabatic version of the TOP code, applicable to 2D models from the ESTER code. This approach has the advantage of using models in which the energy equation is satisfied in a 2D context. It also takes into account the baroclinic structure of the model and differential rotation.

2.3.1 Work integral

As was done above in the adiabatic case, one can once more calculate the dot product of Euler’s momentum equation with ${\vec{\xi }}^{*}$, integrate over the volume, and rearrange the various terms. This leads to an equation that is analogous to Eq. 21, except that the terms involved are now complex. This equation can be separated into a real and imaginary part. The real part once more provides an independent formula for the frequency. However, it does not benefit from the variational principle since the non-adiabatic terms in the fluid operators are not symmetric with respect to the dot product defined in Eq. 22. The imaginary part provides an integral expression for the damping/excitation rate and corresponds to what is commonly known as the work integral:

$\tau =\frac{W}{2\left(A\omega +C\right)}(25)$

where τ is the excitation rate, and where

$A={\iiint }_V{\rho }_0{\xi }^2\mathrm{d}\mathrm{V},(26)$

$C={\iiint }_V{\rho }_0\left[m\mathrm{\Omega }{\xi }^2-i\vec{\mathrm{\Omega }}\cdot \left(\vec{\xi }\times {\vec{\xi }}^{\ast }\right)\right]\mathrm{d}\mathrm{V},(27)$

$W=-{\iiint }_V\mathfrak{I}\left\{\frac{\delta P\delta {\rho }^{\ast }}{{\rho }_0}\right\}\mathrm{d}\mathrm{V}(28)$

where $\mathfrak{I}(\cdot )$ corresponds to the imaginary part of a given complex quantity. As can be seen from the above expression, excitation or damping occurs when there is a phase shift between the Lagrangian pressure and density perturbations, as can be expected from the thermodynamic identity δW = −PdV.

The work integral is useful for pinpointing what parts contribute to mode excitation or damping. In particular, by looking at what temperatures excitation occurs, it is possible to narrow down which chemical elements are responsible for the underlying κ-mechanism. Figure 4 shows various work integrals for a multiplet of modes in a 9 M_⊙ ESTER model rotating at 0.3 Ω_K. As can be seen in this plot, only the most retrograde mode (m = 3) is damped and the other modes are excited. As the rotation rate increases in the model, all of the modes in this multiplet are progressively damped starting with the retrograde modes first. Inasmuch as this multiplet is representative of pulsation modes in β Cep stars, one can expect to see more prograde modes excited than retrograde modes, as seems to be confirmed by observations (e.g., Balona, 2000).

FIGURE 4

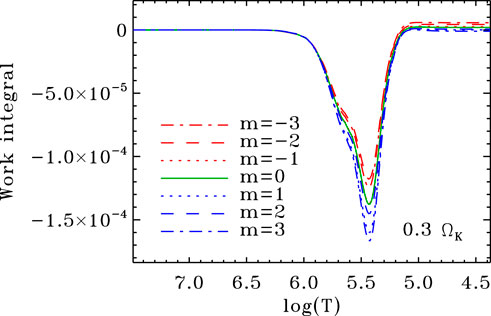
FIGURE 4. Work integrals for a set of modes from the same multiplet, in a 9 M_⊙ ESTER model rotating at 0.3 Ω_K. Integration has already been carried out along the horizontal directions, only leaving the radial direction as shown in this plot. The left of the plot corresponds to the centre of the star, whereas the right corresponds to its surface. Only the most retrograde mode (m = 3) is damped, i.e., its work integral is negative at the surface (taken from Reese et al., 2017a).

2.4 Perturbative analysis and its limits

An alternate approach for calculating the effects of rotation on stellar pulsations is to apply a perturbative approach. In this approach, the rotation rate, or more specifically the ratio of the rotation rate to the Keplerian break-up velocity ϵ = Ω/Ω_K where ${\mathrm{\Omega }}_{\mathrm{K}}=\sqrt{GM/R_{\mathrm{e}\mathrm{q}}^3}$ and R_eq is the equatorial radius, is treated as a small parameter and the pulsation modes and frequencies are expanded into a series expression in terms of this parameter. The advantage of this approach is that the successive terms at each order are solutions to 1D problems thus reducing the numerical cost. Furthermore, it establishes a clear link between the solutions in the non-rotating case, which are thus the zeroth order solutions, and the solutions in the rotating case, thereby naturally extending the mode labelling, i.e., quantum numbers, from the former to the latter. As described in Mirouh (this volume—see also Mirouh et al., 2019), mode labelling is far from trivial when considering pulsations modes calculated using a 2D approach.

Historically, perturbative methods have been applied to first, second, and third order. Frequencies thus take on the following expression:

$\begin{array}{ll}\hfill \omega & ={\omega }_0-m\left(1-C\right)\mathrm{\Omega }+\left(D_1+m^2{D}_2\right){\mathrm{\Omega }}^2+m\left(T_1+m^2{T}_2\right){\mathrm{\Omega }}^3\hfill \\ \hfill & +\mathcal{O}\left({\mathrm{\Omega }}^4\right)\hfill \end{array}(29)$

where the various coefficients C, D₁, D₂, T₁ and T₂ come from the different order methods, and ω₀ corresponds to the pulsation frequency in the non-rotating case. In general, due to the symmetry of the pulsation equations with respect to the ϕ = 0 meridional plane, the coefficients of even powers of Ω are even functions of m, and those of odd powers are odd functions (Reese et al., 2006).

Ledoux (1951) came up with a first order integral expression of the effects of rotation which takes into account both mode advection by rotation and the effects of the Coriolis force. The latter is typically represented by a mode-dependent coefficient, C, known as the Ledoux constant. This expression, initially derived for a uniform rotation profile, was subsequently generalised to profiles that depend on the radial coordinate alone (e.g., Gough, 1981; Christensen-Dalsgaard et al., 1990), and on the radial coordinate and colatitude (e.g., Schou et al., 1994). It has been used to probe rotation profiles of slowly rotating stars starting with the Sun (e.g., Schou et al., 1998; Thompson et al., 2003; Hatta et al., 2019).

To go to higher rotation rates, second order methods have been derived (e.g., Saio, 1981; Gough and Thompson, 1990; Goode and Thompson, 1992). Compared to first order methods, this approach has the added difficulty of including first order effects of the centrifugal deformation of the model (which scales as ${(\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{K}})}^2$) as well as first order perturbed eigenfunctions (as opposed to just the perturbed frequency, see e.g., Saio, 1981). Such an approach leads to departures from uniform rotational splittings, even for uniform rotation profiles. Another phenomenon which intervenes is the effects of avoided crossings, also known as near-degeneracies. As shown in Suárez et al. (2010), such effects start to play an important role on the pulsation frequencies.

Only few authors have ventured to third order methods (Soufi et al., 1998; Karami, 2008). To achieve such high orders, these methods include the first order rotation effects into the zeroth order solution, and third order effects into the second order solution. This avoids having to calculate eigenfunction perturbations for successive powers of ϵ. Furthermore, it was necessary to introduce a second small parameter, namely $\mu =\frac{2\mathrm{\Omega }}{\omega }$ the ratio of the Coriolis to the pulsation frequency. This parameter is indicative of the impact of Coriolis force on pulsations and is particularly relevant to low frequency modes such as gravity and inertial modes. In contrast, the former parameter, ϵ = Ω/Ω_K, is characteristic of the amount of centrifugal deformation of the star and is thus relevant to acoustic modes. Figure 5 (adapted from Goupil and Talon, 2002) shows the μ-ϵ domains associated with various classes of pulsating stars. As can be seen, large values⁶ of ϵ and μ are reached by these classes of stars, thus raising the question as to the validity of perturbative methods for these stars.

FIGURE 5

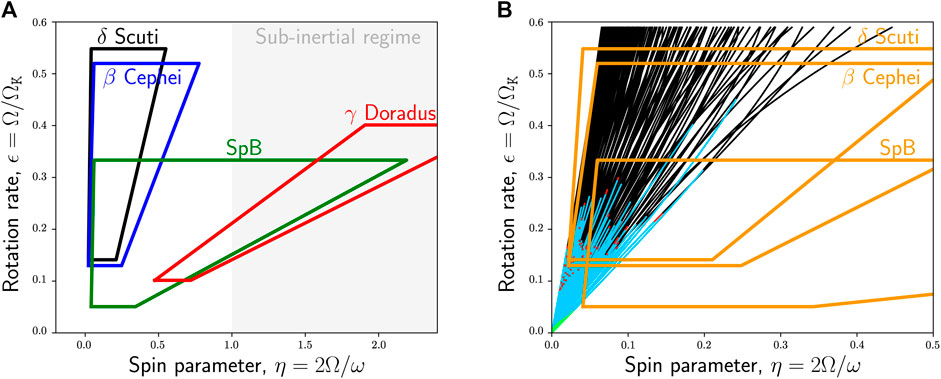
FIGURE 5. (A, B) Domains covered by various classes of pulsating stars in a μ-ε diagram. Panel (A) also shows the region corresponding to the sub-inertial regime (see Section 3.1). Panel (B) is a zoom of panel (A) and shows validity domains of perturbative methods of various orders using error bars of 0.1 μHz for acoustic pulsation modes superimposed on the domains of the different classes of pulsating stars. The various curves correspond to individual pulsation modes for a range of rotation rates: the green, cyan, and red sections correspond to the portions where first, second, and third order perturbative methods are valid. The black sections show where full 2D calculations are needed. (adapted from Goupil and Talon, 2002 and Reese, 2006).

In order to answer this question, Reese et al. (2006) carried out full 2D calculations of acoustic pulsation modes in rapidly rotating polytropic models. They then fitted polynomial functions to the frequencies thus obtained in order to mimic perturbative calculations. This enabled them to come up with validity domains for perturbative methods of various orders. A similar analysis was carried out by Burke et al. (2011) using realistic models from the ASTEC code (Christensen-Dalsgaard, 2008) and including a perturbative description of their centrifugal deformation. Ballot et al. (2010) subsequently applied a similar method to gravity modes in polytropic models, thus extending the validity domains to low frequencies. Figure 6 shows such validity domains for a polytropic model of a typical A-type star. The error bars used to define these domains are 0.1 μHz (which corresponds to 116 days of observation, as based on the Rayleigh criterion).

FIGURE 6

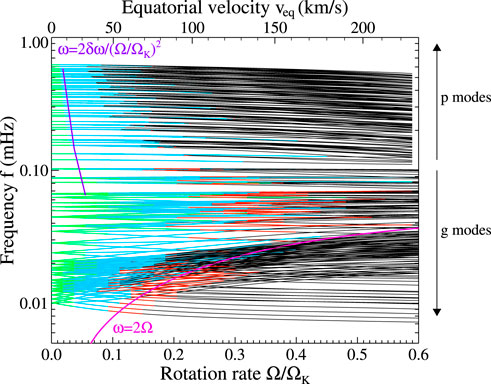
FIGURE 6. Validity domains for perturbative methods of various orders. Green, cyan, and red curves correspond to the domain where first, second, and third order methods reproduce full 2D calculations to within an error bar of δω = 0.1 μHz. The purple line labelled ω = 2Ω delimits sub-inertial gravito-inertial modes (below) from the super-inertial modes (above). The blue line shows the expected frequency threshold that comes from neglecting centrifugal deformation (see text for details). (Material from: Ballot et al., 2013).

It is interesting to note that at high frequencies, the validity domains of perturbative methods shrink. This is because the wavelength of acoustic pulsation modes is smaller at these frequencies, and thus these modes are more sensitive to the centrifugal deformation. In first order perturbative methods, the centrifugal deformation is neglected entirely, thus leading to a relative error on the pulsation frequency, δω/ω, that scales as the flattening of the star, $(R_{\mathrm{e}\mathrm{q}}-R_{\mathrm{p}\mathrm{o}\mathrm{l}})/R_{\mathrm{e}\mathrm{q}}\simeq \frac{1}{2}\mathrm{\Omega }/{\mathrm{\Omega }}_{\mathrm{K}}$, where R_eq and R_pol are the equatorial and polar radii, respectively. If we use an error bar of δω = 0.1 μHz, this leads to the blue curve shown in Figure 6.

Likewise, at low frequencies, the validity domains of perturbative methods become smaller. This is due to the increasing influence of the Coriolis force on the pulsations, as can be seen by the ratio between the pulsation and rotation periods. Also shown in this plot is the curve ω = 2Ω, which marks the separation between sub- and super-inertial modes. As can be seen, it correlates nicely with the validity domains for gravito-inertial modes.

2.5 Traditional approximation

Another approximate approach to calculating stellar pulsations in the presence of rapid rotation is to apply what is known as the traditional approximation. In this approach, the horizontal component of the rotation vector, $-\mathrm{\Omega }\sin \theta {\vec{e}}_{\theta }$, is neglected. If furthermore, the centrifugal distortion is neglected, and the Cowling⁷ and adiabatic approximations are made, then the pulsation equations become separable in r and θ. Specifically, the horizontal parts of the pulsation modes are no longer described by spherical harmonics but by Hough functions, which are the solutions to the eigenvalue problem known as Laplace’s tidal equation. The associated eigenvalues correspond to the horizontal wavenumber.

The traditional approximation was first introduced in the context of stellar pulsations by Berthomieu et al. (1978), thus enabling them to obtain asymptotic expressions for the frequencies of gravity modes in rotating stars. Since then, other authors have also applied the traditional approximation (e.g., Lee and Saio, 1987; Savonije et al., 1995; Bildsten et al., 1996; Townsend, 1997; Bouabid et al., 2013). Townsend, (2003b) carried out an extensive asymptotic analysis of the behaviour of Hough functions and provided a classification of gravito-inertial modes. Ballot et al. (2012) showed that the period spacings of gravito-inertial modes predicted by the traditional approximation are a close match to those from full 2D calculations, apart from some cases where the centrifugal deformation causes a slight mismatch.

Savonije et al. (1995) showed how to generalise the traditional approximation to non-adiabatic calculations. This approach was subsequently used by Townsend, (2003a) when calculating the disk-integrated visibilities of pulsation modes and by Townsend, (2005) and Bouabid et al. (2013) when studying the instability domains of slowly pulsating B stars and γ Doradus stars. Lee, (2008) compared non-adiabatic calculations based on the traditional approximation with those based on full 2D calculations. He showed that retrograde g-modes are unstable when applying the traditional approximation, but stable when applying a 2D approach. Mode coupling and centrifugal deformation play a role in stabilising these modes.

3 Impact of rapid rotation on stellar pulsations

Having described how to calculate pulsation modes in the presence of rapid rotation, we now briefly look at some of its effects on stellar pulsations. For a more complete review of these effects, in particular on mode frequencies, geometry, and classification, we refer to the review by Mirouh (this volume).

3.1 General effects

One of the first impacts of rotation on pulsation frequencies is to lift the degeneracy between modes with the same radial order, n, and harmonic degree, ℓ, but different azimuthal orders, m. Hence, a frequency multiplet composed of 2ℓ + 1 frequencies appears where there was only a single frequency. This is a simple consequence of first order perturbative effects (Eq. 29). For rotation profiles that do not depend on θ, the frequencies in a multiplet are evenly spaced (to first order). Such a spacing is known as the rotational splitting. As the rotation rate increases, the multiplets become uneven as was already pointed out in Section 2.4. They also start to overlap thus leading to a complex spectrum. Progressively, a new frequency organisation emerges.

At this point, it is useful to distinguish between acoustic modes, which typically have high frequencies, and gravity modes at low frequencies. At rapid rotation rates, acoustic modes subdivide into several classes of pulsation modes each with its own frequency organisation and characteristic mode geometry, as was shown by Lignières and Georgeot, 2008 and Lignières and Georgeot, 2009 using ray dynamics. These include acoustic island modes, chaotic modes, and whispering gallery modes. Probably, the most important of these different classes when it comes to interpreting observed pulsations are acoustic island modes, as described below.

In the rotating case, gravity modes subdivide between modes in the super-inertial regime (ω > 2Ω) and those in the sub-inertial regime (ω < 2Ω). Those in the super-inertial regime keep a mode geometry which is similar to that of their non-rotating counterparts. A notable exception are the “rosette” modes discovered by Ballot et al. (2012). These have a non-separable geometric structure and cannot be described correctly using the traditional approximation (see Figure 7). Modes in the sub-inertial regime are affected by forbidden regions which appear around the poles. Indeed, above and below the critical latitudes⁸ ±Θ_c, where Θ_c = arcsin[ω/(2Ω)], gravito-inertial waves are evanescent and are thus confined to the equatorial region (e.g., Dintrans and Rieutord, 2000; Townsend, 2003b). If centrifugal deformation is taken into account, this boundary takes on a more complex shape (Ballot et al., 2010). Furthermore, the period spacings of gravity modes go from being uniform in the non-rotating case to following well-defined functions which depend on the pulsation period, harmonic degree, ℓ, and azimuthal order, m. This result was first predicted thanks to the traditional approximation before being confirmed by 2D pulsation calculations (Ballot et al., 2012; Ouazzani et al., 2017).

FIGURE 7

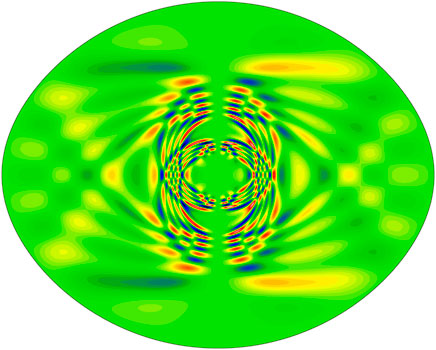
FIGURE 7. Meridional cross-section of a rosette mode in an SCF model rotating at 70 % of the critical rotation rate (Credit: Resse (2013), reproduced with permission © ESO).

Finally, we note the emergence of inertial modes at low frequencies, for which the Coriolis acceleration acts as the restoring force. These can be subdivided into modes with a singular structure in the ideal inviscid limit as they focus around wave attractors (e.g., Rieutord and Valdettaro, 1997; Dintrans et al., 1999; Baruteau and Rieutord, 2013; Mirouh et al., 2016), thus potentially playing an important role in tidal dissipation (e.g., Ogilvie, 2009; Rieutord and Valdettaro, 2010), and modes with a more regular structure such as r-modes (e.g., Papaloizou and Pringle, 1978; Saio, 1982; Rieutord, 2001; Lee, 2006). Recently, Ouazzani et al. (2020) studied mixed modes which take on an inertial characteristic in the convective core and a gravito-inertial behaviour above. These lead to kinks in the period separation relation described above and have been observed in some stars (Saio et al., 2021).

3.2 Acoustic island modes

Among the different types of acoustic modes, island modes are particularly important. Indeed, these are the rotating counterparts to low degree modes and are thus typically the most visible of the acoustic modes. Accordingly, they are likely candidates to explain some of the pulsations observed in rapidly rotating stars. As shown in Figure 8, these modes focus around periodic ray orbits that start at mid-latitudes and go around the equator.

FIGURE 8

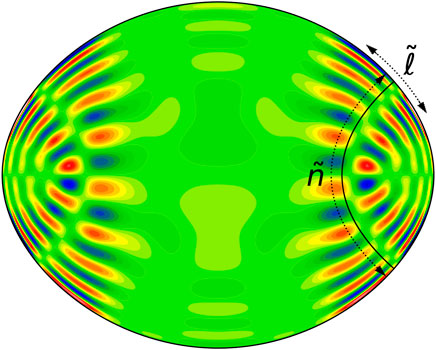
FIGURE 8. Meridional cross-section of an acoustic island pulsation mode in a 2 M_⊙ ESTER model rotating at 0.7 Ω_K. The underlying periodic orbit is indicated by the solid black line. The quantum numbers $\tilde{n}$ and $\tilde{\ell }$ correspond to the number of nodes in the directions that are indicated on the plot.

Various authors have studied their pulsation spectra starting with Lignières et al. (2006). In Reese et al. (2009), the following empirical formula was obtained (after taking into account into account the fact that the frequencies depend on $m/\sqrt{\tilde{n}}$ rather than m):

${\omega }_{\tilde{n},\tilde{\ell },m}=\tilde{n}{\mathrm{\Delta }}_{\tilde{n}}+D_{\tilde{m}}\left(\tilde{\ell }\right)\sqrt{\frac{m^2}{\tilde{n}}+\mu {\left(\tilde{\ell }\right)}^2}-m\mathrm{\Omega }+\tilde{\alpha }\left(\tilde{\ell }\right).(30)$

where $\tilde{n}$, and $\tilde{\ell }$ are quantum numbers specific to island modes (Figure 8). Reese et al. (2008) and Mirouh et al. (2019) showed that the pseudo-large separation⁹, ${\mathrm{\Delta }}_{\tilde{n}}$, that intervenes in this formula roughly scales with the mean density of the star (Figure 9). This theoretical prediction was subsequently confirmed thanks to δ Scuti stars in binary systems (García Hernández et al., 2015). Lignières and Georgeot, (2008) and Lignières and Georgeot, (2009) showed that the large separation (or twice the pseudo-large separation) is the inverse of the time it takes for an acoustic wave to travel along the underlying ray orbit from one end to the other (Figure 8).

FIGURE 9

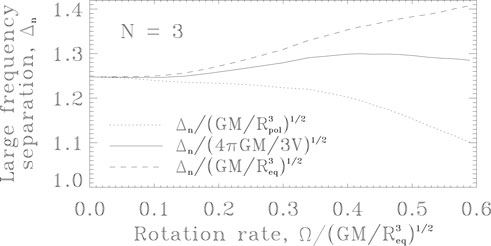
FIGURE 9. Large frequency separation, Δ_n, as a function of rotation rate in rotating polytropic models. As can be seen, Δ_n scales with volume rather than the cube of the equatorial or polar radii (Credit: Reese et al. (2008), reproduced with permission © ESO).

4 Mode observables

Before reviewing some of the recent works on interpreting pulsations of rapidly rotating stars, it is important to describe various mode observables, namely mode visibilities, amplitude ratios, phase differences, and line profile variations. Indeed, one of the long-standing obstacles to detailed seismic investigations of rapidly rotating stars is mode identification, i.e., finding the correspondence between observed pulsations and theoretical modes, as is particularly well illustrated, for instance, in Figure 5 of Deupree (2011). Finding observational constraints, such as those based on the above observables, become particularly crucial in narrowing down plausible mode identifications.

4.1 Mode visibilities

Mode visibilities correspond to disk-integrated luminosity variations for some given normalisation of the mode amplitude. If multiplied by the intrinsic mode amplitudes, these provide the observed pulsation amplitudes. However, predicting the intrinsic mode amplitudes is a formidable and unsolved problem as the pulsations of such stars are typically excited by the κ mechanism and are thus subject to non-linear saturation effects as well as mode coupling, all of this, in a centrifugally deformed stellar structure. Some of these effects have been explored in various theoretical works (e.g., Dziembowski, 1982; Dziembowski and Krolikowska, 1985; Dziembowski et al., 1988; Gastine and Dintrans, 2008) but a full comprehensive theory is currently out of reach. Hence, mode visibilities only give an idea of what modes are most visible and the least affected by disk cancellation effects, but should by no means be used in a quantitative comparison with observed mode amplitudes.

In order to calculate mode visibilities, we first need to express the disk-integrated energy radiated by a star in some given direction:

$E=\frac{1}{d^2}{\iint }_{\mathit{Vis.\hspace{0.17em}Surf.}}I\left(\mu ,g_{\mathrm{e}\mathrm{ff}},T_{\mathrm{e}\mathrm{ff}}\right){\vec{e}}_{\mathrm{o}\mathrm{b}\mathrm{s}.}\cdot \overrightarrow{\mathrm{d}S}(31)$

where d is the distance to the observer, I the specific radiation intensity, $\mu ={\vec{e}}_{\mathrm{o}\mathrm{b}\mathrm{s}.}\cdot \vec{n}$ where ${\vec{e}}_{\mathrm{o}\mathrm{b}\mathrm{s}.}$ is the unit vector in the direction of the observer and $\vec{n}$ the outward normal to the surface, g_eff the effective gravity (including the centrifugal acceleration), T_eff the effective temperature, and “Vis. Surf.” the part of the stellar surface that is visible to the observer. We note that the shape of the boundary between the visible and hidden side of the star is not trivial when the star is deformed by the centrifugal force. It can only be determined by calculating whether the orientation of each surface element is towards or away from the observer. This expression then needs to be perturbed to account for the variations caused by a pulsation.

$\begin{array}{ll}\hfill \mathrm{\Delta }E\left(t\right)& =\frac{1}{d^2}\mathfrak{R}\left\{{\iint }_{\mathit{Vis.\hspace{0.17em}Surf.}}\delta I\left(\mu ,g_{\mathrm{e}\mathrm{ff}},T_{\mathrm{e}\mathrm{ff}},t\right){\vec{e}}_{\mathrm{o}\mathrm{b}\mathrm{s}.}\cdot \overrightarrow{\mathrm{d}S}\right.\hfill \\ \hfill & +\left.{\iint }_{\mathit{Vis.\hspace{0.17em}Surf.}}I\left(\mu ,g_{\mathrm{e}\mathrm{ff}},T_{\mathrm{e}\mathrm{ff}}\right){\vec{e}}_{\mathrm{o}\mathrm{b}\mathrm{s}.}\cdot \delta \left(\overrightarrow{\mathrm{d}S}\right)\right\}\hfill \end{array}(32)$

where we have neglected the perturbation to the visible surface since it turns out to be of second order compared to the other terms. The variations of the specific radiation intensity can be expanded as follows:

$\delta I=I\left(\frac{\partial \ln I}{\partial \ln T_{\mathrm{e}\mathrm{ff}}}\frac{\delta T_{\mathrm{e}\mathrm{ff}}}{T_{\mathrm{e}\mathrm{ff}}}+\frac{\partial \ln I}{\partial \ln g_{\mathrm{e}\mathrm{ff}}}\frac{\delta g_{\mathrm{e}\mathrm{ff}}}{g_{\mathrm{e}\mathrm{ff}}}\right)+\frac{\partial I}{\partial \mu }\delta \mu (33)$

These expressions show that pulsations cause light variations in multiple ways. They cause local variations of effective temperature and gravity which in turn affect I. They also cause geometric variations of the surface which affect the size and orientation of surface elements, as well as I via limb darkening effects.

The various terms related to pulsation modes are calculated as follows. The Lagrangian variations of effective temperature, δT_eff/T_eff, are deduced from full non-adiabatic calculations. If the pulsation modes have been calculated using the adiabatic approximation, δT_eff/T_eff may be approximated by the local temperature variations, δT/T (a rather drastic approximation according to Dupret et al., 2003), which in turn are deduced from the Lagrangian pressure perturbations. Some authors (e.g., Watson, 1988; Garrido et al., 1990; Heynderickx et al., 1994) include an ad-hoc parameter to account for non-adiabatic effects. The Lagrangian variations in effective gravity are fairly complex to derive as they include the variations in the gravitational field caused by perturbations to the distribution of matter as well as variations related to the fact that the surface is displaced in this field, and finally the acceleration of the surface itself. This leads to the following expression (Reese et al., 2013):

$\begin{array}{ll}\hfill \delta {\vec{g}}_{\mathrm{e}\mathrm{ff}}& =-\vec{\nabla }\mathrm{\Psi }-\vec{\xi }\cdot \vec{\nabla }\left(\vec{\nabla }{\mathrm{\Psi }}_0\right)+{\left(\omega +m\mathrm{\Omega }\right)}^2\vec{\xi }\hfill \\ \hfill & -2i\left(\omega +m\mathrm{\Omega }\right)\vec{\mathrm{\Omega }}\times \vec{\xi }-\vec{\mathrm{\Omega }}\times \left(\vec{\mathrm{\Omega }}\times \vec{\xi }\right).\hfill \end{array}(34)$

Finally, the geometric terms may be deduced from the Lagrangian displacement. The perturbations to the surface elements is given by:

$\delta \left(\overrightarrow{\mathrm{d}S}\right)=\left({\partial }_{\theta }\vec{\xi }\times {\partial }_{\varphi }\vec{r}+{\partial }_{\theta }\vec{r}\times {\partial }_{\varphi }\vec{\xi }\right)\mathrm{d}\theta \mathrm{d}\varphi (35)$

and those of μ by:

$\delta \mu ={\vec{e}}_{\mathrm{o}\mathrm{b}\mathrm{s}.}\cdot \left\{\frac{\delta \overrightarrow{\mathrm{d}S}}{\Vert \overrightarrow{\mathrm{d}S}\Vert }-\left(\vec{n}\cdot \frac{\delta \overrightarrow{\mathrm{d}S}}{\Vert \overrightarrow{\mathrm{d}S}\Vert }\right)\vec{n}\right\}(36)$

Figure 10 illustrates the different terms that intervene in mode visibility calculations for a particular pulsation mode.

FIGURE 10

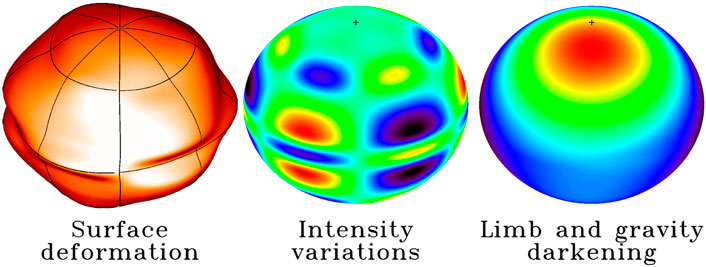
FIGURE 10. Plots showing the different terms that intervene in mode visibility calculations. The surface deformation is greatly exaggerated to make it easier to see.

4.2 Amplitude ratios and phase differences

Besides calculating mode visibilities, one can also calculate amplitude ratios and phase differences using essentially the same set of equations as above. The main difference is that the intensity I should be multiplied by the instrument’s and filter’s transmission curves, prior to calculating the integrals. Repeating this procedure for different filters provides pulsation amplitudes and phases in different photometric bands. One can then calculate the amplitude ratios and phase differences between these bands. Unlike mode visibilities, these do not depend on the intrinsic mode amplitudes since these factor out. Furthermore, in the non-rotating stars, amplitude ratios and phase differences do not depend on the azimuthal order, m, or the inclination of the star. Hence, amplitude ratios and phase differences only depend on the geometric properties of the modes, and as such, may be used to constrain mode identification, and more particularly the harmonic degree, ℓ, in non-rotating stars.

Historically, Dziembowski, (1977) is among the first to have obtained an expression for pulsation-induced light variations in non-rotating stars. Subsequent expressions were derived by including further effects such as perturbations to limb darkening and the surface normal, culminating in the work by Heynderickx et al. (1994). At this point, non-adiabatic effects were only approximated via an ad-hoc parameter and the effects of rotation were not included. Later on, fully non-adiabatic calculations were included thus improving mode identification in non-rotating or slowly rotating stars (Dupret et al., 2002; Dupret et al., 2003).

Then, Daszyńska-Daszkiewicz et al. (2002); Daszynska-Daszkiewicz et al. (2007) and Townsend (2003a) included the effects of rotation when calculating mode visibilities. They showed that in contrast to the non-rotating case, amplitude ratios and phase differences depend both on the azimuthal order and the inclination. This complicates mode identification as there are more cases to investigate, but may also help to place tighter constraints on mode identification. However, the effects of rotation on the pulsation modes in the above works where approximated using either a perturbative approach or the traditional approximation. In contrast, Lignières et al. (2006); Lignières and Georgeot, (2009) fully included the effects of rotation in the pulsation calculations thanks to a 2D numerical approach but approximated the mode visibility calculations by only including the terms related to the temperature variations. They showed that chaotic acoustic modes have visibilities which are higher than that of their non-rotating counterparts, i.e., modes with intermediate ℓ − |m| values. Accordingly, they may be visible alongside acoustic island modes thus complicating the interpretation of pulsation spectra. Finally, Reese et al. (2013) calculated mode visibilities including all of the terms for full 2D mode calculations. However, these calculations were done with the adiabatic approximation. Later on, Reese et al. (2017b) approximated non-adiabatic effects by deriving the effective temperature variations from the radial displacement using an ad-hoc function calibrated on 1D non-adiabatic pulsation calculations by the MAD code (Dupret, 2001). They also tested a mode identification strategy which consists in grouping together modes with similar amplitude ratios. This allowed them to group island modes with similar quantum numbers together but required having a large number of observed pulsation modes.

4.3 Line profile variations

Another observable associated with pulsation modes is line profile variations (LPVs). LPVs typically take on the form of bumps that move over time within a spectroscopic line profile and are mainly caused by the Doppler shifts induced by the oscillatory motions from the pulsations. Accordingly, they can also be used to constrain mode geometry and hence identification. A more detailed description of LPVs in the case of rapid rotation is provided in the review by Mirouh (this volume).

5 Interpreting pulsation spectra of rapid rotators

The various attempts that have been made to interpret pulsation spectra in rapidly rotating stars fit into two broad categories: ensemble seismology and seismology “a la carte”. The first category applies to whole groups of stars whereas the second concerns detailed seismic investigations of individual targets. In what follows, we will especially focus on the second type of approach by providing a non-exhaustive list of examples. As pointed out above, one of the main obstacles to carrying out a detailed seismic interpretation is the lack of a reliable mode identification. Hence, all of the examples below include some sort of strategy for identifying modes, either based on frequency patterns or on amplitude ratios and phase differences. Finally, apart from μ Eridani, the examples below focus on acoustic modes. An extensive literature also exists on interpreting gravity modes in rapidly rotating stars such as γ Dor and SPB stars (e.g., Van Reeth et al., 2016; Ouazzani et al., 2019). Mirouh (this volume) provides a detailed review of these works.

5.1 Frequency patterns in δ Scuti stars

Recently, Bedding et al. (2020) worked on the seismic interpretation of 60 young δ Scuti stars, most of which were observed by TESS (Ricker et al., 2015). Assmuing the dominant observed modes are axisymmetric, they matched ℓ = 0 and 1 frequencies from non-rotating models to the observed pulsation spectra with the help of echelle diagrams. Figure 11 shows echelle diagrams for two of the more rapidly rotating stras in the sample along with the expected positions of the ℓ = 0 and 1 ridges or theoretical frequencies from non-rotating models. They justified this approach by noting that these modes, once normalised by the large separation, remain relatively invariant, even in models rotating at roughly 50% of the critical rotation rate, as shown by full 2D calculations using models based on the SCF method. Although the methodology may differ, this work follows a number of previous efforts using both seismology “a la carte” and ensemble seismology (e.g., García Hernández et al., 2009; Paparó et al., 2016; Michel et al., 2017; Bowman and Kurtz, 2018) to identify frequency patterns and large separations in δ Scuti stars.

FIGURE 11

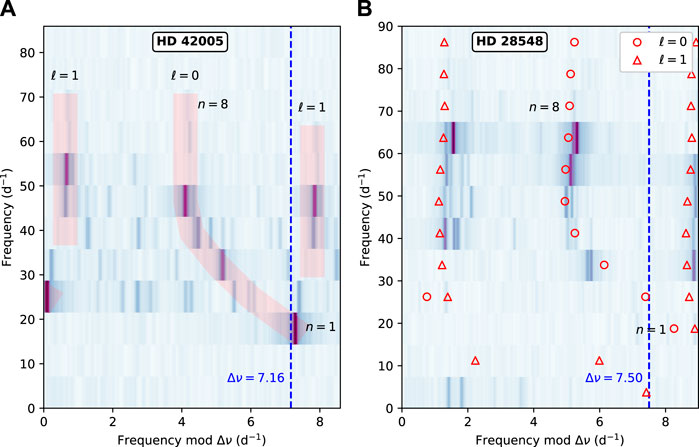
FIGURE 11. Echelle diagrams for HD 42005 (A) and HD 28548 (B), with projected equatorial velocities of 130 ± 30 km s⁻¹ and 200 ± 50 km s⁻¹, respectively. The stripes in the left correspond to what may be ℓ = 0 and 1 sequences. The symbols in the right panel are frequencies from non-rotating models that roughly match the observations (Material from: Bedding et al., Nature 581, 7807, 147‐151 (2020), Springer Nature Limited).

5.2 μ Eridani

μ Eridani is an SPB star of spectral type B5 IV. With a projected equatorial velocity v sin i = 130 km s⁻¹, it is rotating at least at 30% of the critical rotation velocity. This star was observed using the Strömgren uvy filters in 2012–2013 thus leading to a number of modes detected in all three photometric bands. Daszyńska-Daszkiewicz et al. (2015) therefore devised and applied a multicolour mode identification technique which consisted in carrying out a χ² minimisation of the differences between observed amplitude ratios and phase differences, and the corresponding theoretical predictions. This required the use of non-adiabatic pulsation calculations in the presence of rapid rotation, which they carried out using the traditional approximation (thus neglecting the centrifugal deformation). They only included excited modes in their comparisons. Although several possible sets of mode identifications were found, their results point to an equatorial velocity v between 135 and 140 km s⁻¹ and hence an inclination not too far from equator-on (i ≳ 70°). They also concluded that modes with ℓ ≤ 2 were not sufficient to carry out the identification and went up to ℓ = 6.

5.3 β Pictoris

The star β Pictoris has attracted considerable interest since the direct imaging of an exoplanet orbiting around it thanks to adaptive optics (Lagrange et al., 2009; Lagrange et al., 2010). Furthermore, it is a bright star of spectral type A6 V, located at 19.76 pc from us (as based on Gaia DR2 parallax, Gaia Collaboration et al., 2018). It has a disk orbiting around it and rotates with a projected equatorial velocity of v sin i = 124 ± 3 km s⁻¹, thus making it a moderately fast rotator (Koen et al., 2003). Various instruments observed β Pictoris in 2017–2018 in an attempt to detect the transit of the planet’s Hill sphere in front of the star. In addition, β Pic was observed by the BRITE-Constellation (Weiss et al., 2014). This resulted in multiple light curves in separate photometric bands that could be used for the purposes of asteroseismology.

Zwintz et al. (2019) carried out a seismic analysis of this star using rapidly rotating models based on the SCF method. Given that it was observed in multiple photometric bands, it was an ideal target to carry out mode identification based on amplitude ratios. Furthermore, the constraints provided by the orbital dynamics of the exoplanet as well as interferometric observations lead to fairly accurate estimates of the mass and radius, thus narrowing down the set of possible solutions. An MCMC search was carried out to find best matching solutions and corresponding stellar parameters. Figure 12 compares the frequencies and amplitude ratios from two of the solutions with the observational constraints. As can be seen, it turned out to be difficult to find models that simultaneously reproduce the observed amplitude ratios and frequencies. In particular, some of the amplitude ratios were reproduced by none of the theoretical modes, regardless of inclination and rotation rate. The causes behind these discrepancies may be shortcomings in the models thus leading to inaccuracies in the frequencies, approximations in the mode visibility calculations such as an ad-hoc modelling of non-adiabatic effects, and/or the fact that not all of the light curves were obtained at the same epoch, which could lead to erroneous amplitude ratios if the mode amplitudes vary over time. As was shown in Bowman et al. (2016), amplitude modulation is common in δ Scuti stars. Nonetheless, among the best solutions obtained by the MCMC procedure were near equator-on solutions with an inclination around 89° and a rotation rate of 27% of the Keplerian break-up velocity. This would agree with the inclination of the planet’s orbit as well as that of the disk.

FIGURE 12

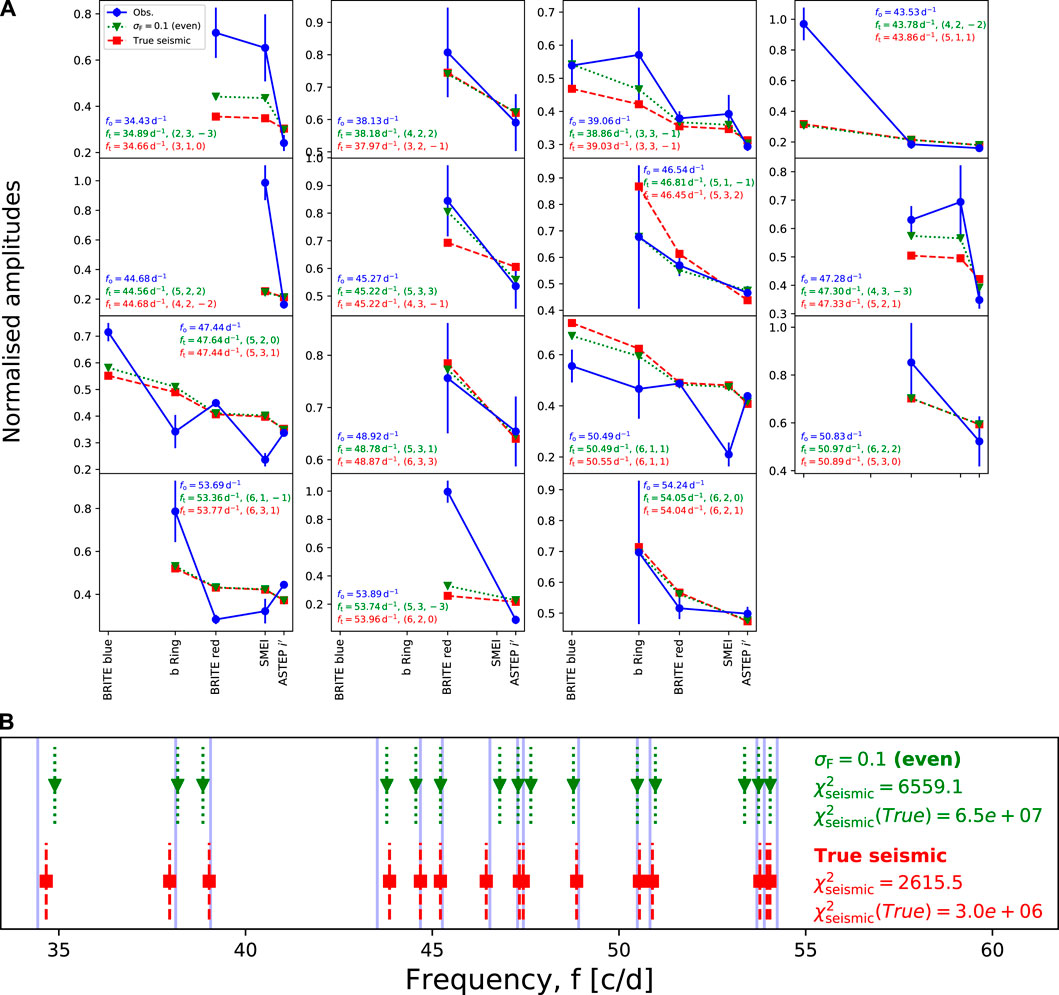
FIGURE 12. Amplitude ratios (A) and corresponding pulsation spectra (B) coming from best-fitting solutions for β Pictoris. The dark and light blue lines in both panels correspond to the observed amplitude ratios and frequencies. The green and red lines and symbols correspond to two solutions obtained with different error bars on the frequencies (Credit: Zwintz et al. (2019), reproduced with permission © ESO).

5.4 Altair

Altair, also known as α Aquilae, is one of the three stars in the summer triangle. It has been a prime target for interferometry due to its proximity (5.13 pc from the Sun) and its rapid rotation. Indeed, both its centrifugal deformation and gravity darkening may be observed (van Belle et al., 2001; Ohishi et al., 2004; Domiciano de Souza et al., 2005; Peterson et al., 2006; Monnier et al., 2007). Various spectroscopic studies have found v sin i values ranging from 190 km s⁻¹ (Carpenter et al., 1984) to 250 km s⁻¹ (Stoeckley, 1968). Furthermore, as shown in Buzasi et al. (2005), it is a δ Scuti pulsator, with low-frequency acoustic modes, and possibly some gravito-inertial modes.

Suárez et al. (2005) therefore carried out a seismic study of Altair. They used models produced by the 1D stellar evolution code CESAM (Morel, 1997; Morel and Lebreton, 2008) and calculated pulsation modes using the Filou pulsation code, which applies a second order perturbative method to model the effects of rotation (Tran Minh and Léon, 1995; Suárez et al., 2002). Their study favoured models in a 1.70–1.76 M_⊙ mass range with an age between 225 and 775 Myrs. However, given the rapid rotation rate, it proved to be necessary to use full 2D calculations to interpret the pulsations in this star (Reese et al., 2006).

Accordingly, Bouchaud et al. (2020) carried out an extensive study using interferometric, spectroscopic, and seismic data. Given the diversity of observational constraints, a multi-step optimisation procedure was carried out. Using an MCMC approach, models were first selected based on interferometric and spectroscopic constraints before being fine-tuned using the seismic constraints. The four higher frequency modes (starting from 20.785 c/d) were assumed to be l = 0 and 1, m = 0 modes (i.e., $\tilde{\ell }=0$ island modes), thus leading to alternating high and low mode visibilities in qualitative agreement with the observed amplitudes. Interestingly, this is the same type of mode identification as that used in Bedding et al. (2020). By adjusting the model to reproduce the frequencies, it was possible to obtain a model which roughly reproduces all of the constraints. Figure 13 shows a comparison between the observed and theoretical pulsation spectra for Altair along with the meridional cross-section of one of the modes selected to match the observed pulsations. The mass of this model is 1.863 M_⊙, its rotation rate 0.744 Ω_K thus leading to v sin i = 243 km s⁻¹, and its central hydrogen content X_c = 0.71 (to be compared with a surface composition of X_s = 0.739). This leads to a rough estimate of 100 Myrs for the star’s age when compared with 1D stellar evolution models from CESAM. Such an age is lower than the estimate by Suárez et al. (2005) and considerably lower than some of the estimates based on isochrone fitting which exceed 1 Gyr (e.g., Lachaume et al., 1999; Domiciano de Souza et al., 2005). It may thus provide a natural explanation for why the rotation rate is still high.

FIGURE 13

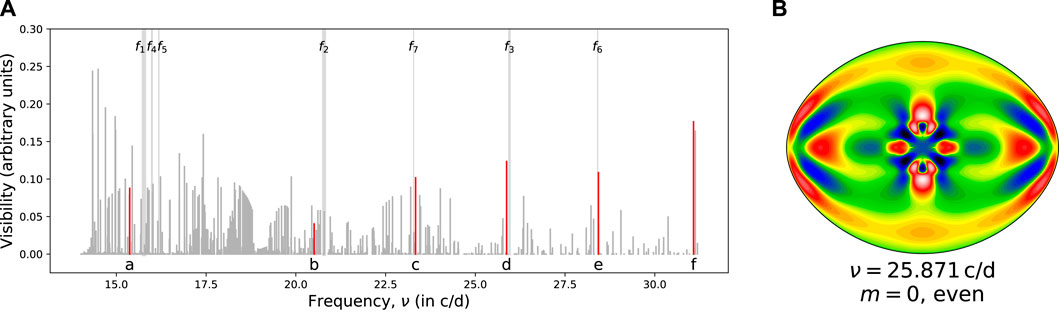
FIGURE 13. (A) Observed and theoretical pulsation spectra for Altair. The observed frequencies are shown by the vertical light grey lines that span the plot and are indicated by the labels f₁ to f₇. The thickness of the lines correspond to the observed amplitudes. The darker grey lines correspond to theoretical pulsation modes. Their height corresponds to mode visibilities. The red lines with the labels “a” to “f” correspond to island modes or mixed gravito-island modes selected to match the observed pulsations. (B) Meridional cross-section of mode “d”. The colours indicate Lagrangian pressure perturbations on a pseudo-logarithmic scale (Credit: Bouchaud et al. (2020), reproduced with permission © ESO).

6 Conclusion

In this review, we have described 2D modelling of pulsations in rapidly rotating stars. Compared to the 1D spherically symmetric case, calculating pulsation modes in rapidly rotating stars is a formidable problem. As a result, various approximate methods, namely perturbative approaches of various orders and methods based on the traditional approximation, have been devised. These have lead to a number of results and insights in the effects of rotation on stellar pulsations, such as rotational multiplets or a modified period spacing pattern for gravity modes. Then, with the advent of more powerful computers, efficient full 2D numerical approaches were implemented. This has lead to a wealth of theoretical results, thus considerably extending our understanding of pulsations in rapidly rotating stars as well as their structure, and has helped to show some of the limitations of previous methods. As is briefly addressed here, new mode geometries and pulsation frequency patterns emerge at rapid rotation, thus leading to pulsation spectra that are considerably more complicated than that of non-rotating stars.

Given the increased complexity of pulsation spectra in such stars, it is much more difficult to correctly match observed pulsations with those that are calculated in stellar models. Accordingly, it is necessary to extend mode identification techniques to these stars, namely those based on multicolour photometry and line profile variations. However, as described in this review, this first requires generalising all of the relevant formulae to a centrifugally distorted stellar geometry thus increasing their complexity. This then allows us to theoretically predict amplitude ratios and phase differences between different photometric bands, which unlike in the non-rotating case, depend both on the azimuthal order of the mode and the inclination of the star. Comparing such predictions with observations can then be used to constrain the geometry of the observed pulsation modes and hence their identification.

Armed with these new theoretical developments, several authors have looked into interpreting the pulsation spectra of various rapidly rotating stars. They have been able to make headway into identifying the observed pulsations and have started to characterise these stars, including the rotation rate, inclination, mass, and age. Some of these results have brought out some of the limitations in our understanding of the physical phenomena that take place in these stars, and are in sharp contrast with previous results based on 1D numerical approaches, thus highlighting the importance of using full 2D approaches. Much effort is still needed to generalise the use of such methods to large numbers of stars and to interpret the wealth of pulsation data currently available, particularly those coming from recent space missions.

In the future, 3D pulsation calculations may become important for certain types of stars that are not symmetric around the rotation axis due to supplementary physical phenomena. For instance, rapidly oscillating Ap (roAp) stars have a strong magnetic field which is inclined with respect to the rotation axis, and close binaries undergo tidal deformation that can only be described in a 3D context. Pulsation calculations in such stars would probably use a similar approach as the one described here except that summations over multiple azimuthal orders rather than a single m value would intervene in the pulsation modes and equations, and the ϕ component of coupling integrals (Eq. 17) would not separate out. Accordingly, this would require heavy computational resources, particularly to store the discretised system in memory and to speed up calculations through parallelisation. However, it may provide further insights into the pulsation physics and underlying stellar structure as did 2D calculations for rotating stars, and provide answers to long-standing questions such as the orientation of the pulsation modes with respect to the rotation and magnetic axes in roAp stars (e.g., Kurtz, 1990; Bigot and Dziembowski, 2002). From an observational point of view, one might expect highly complicated pulsation spectra with frequency multiplets being further subdivided, thus leading to (2ℓ + 1)² rather than (2ℓ + 1) components per multiplet (e.g., Gough and Thompson, 1990).

Author contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

Funds for this publication came from the Agence Nationale de la Recherche (ANR) via the MASSIF project under grant ANR-21-CE31-0018-01, which is gratefully acknowledged.

Acknowledgments

DRR thanks the various researchers with whom he has had the privilege to work with on this fascinating topic: François Lignières, Michel Rieutord, Jérôme Ballot, Kévin Bouchaud, Giovanni Mirouh, Rhita-Maria Ouazzani, Marc-Antoine Dupret, Keith MacGregor, MarieJo Goupil, Armando Domiciano de Souza, Antonio García Hernández, Juan-Carlos Suárez, Frédéric Royer, Tim Bedding, Simon Murphy, Konstanze Zwintz, and many others. DR thanks both referees, Catherine Lovekin and Dominic Bowman, for helpful comments that have improved the manuscript.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹We note that viscosity must also be taken into account in order to fully determine Ω (Espinosa Lara and Rieutord, 2013).

²Even in these cases, the solutions are typically projected onto the spherical basis to facilitate comparison with the non-rotating case.

³We note that these are slightly different than the usual vectorial spherical harmonics due to the use of spheroidal basis vectors in the definition.

⁴A QR decomposition consists in decomposing a matrix A into a product QR where Q is an orthogonal matrix and R an upper triangle matrix. It serves as the basis for an algorithm which searches for all of the eigenvalues of A.

⁵The discretised problem is subsequently projected onto the spherical harmonic basis.

⁶We note that Soufi et al., 1998; Karami, 2008 actually used the small parameter Ω/ω. However, we prefer keeping the extra 2 factor in the numerator as it leads to a more straightforward physical interpretation and corresponds to the spin parameter commonly used when applying the traditional approximation.We note that ϵ = 0.4 leads to equatorial radius 8% larger than the polar radius in a Roche model, that ϵ = 1 roughly corresponds to the critical break-up rotation rate beyond which the star decretes matter at the equator, and that modes with μ ≥ 0.5 are in the sub-inertial regime thus leading to forbidden regions (Section 3).

⁷In the Cowling approximation, the perturbations to the gravitational potential are neglected (Cowling, 1941).

⁸We use the notation Θ to distinguish the latitude (the angle from the equator) from the colatitude θ (the angle from the north pole).

⁹The pseudo-large separation, ${\mathrm{\Delta }}_{\tilde{n}}$, corresponds to half the large separation, Δ_n, from the non-rotating case due to the relationship between the pseudo-radial order, $\tilde{n}$, and the radial order,n, of pulsation modes in non-rotating stars.

References

Ballot, J., Lignières, F., Prat, V., Reese, D. R., and Rieutord, M. (2012). “2D computations of g-modes in fast rotating stars,”Progress in solar/stellar physics with helio- and asteroseismology. Editors H. Shibahashi, M. Takata, and A. E. Lynas-Gray (Astronomical Society of the Pacific Conference Series), 389.

Google Scholar

Ballot, J., Lignières, F., and Reese, D. R. (2013). Numerical exploration of oscillation modes in rapidly rotating stars. Lect. Notes Phys. 865, 91. doi:10.1007/978-3-642-33380-4_5

CrossRef Full Text | Google Scholar

Ballot, J., Lignières, F., Reese, D. R., and Rieutord, M. (2010). Gravity modes in rapidly rotating stars. Limits of perturbative methods. Astron. Astrophys. 518, A30. doi:10.1051/0004-6361/201014426

CrossRef Full Text | Google Scholar

Balona, L. A. (2000). “Understanding pulsations in OB stars,” in ASP conf. Ser. 203: IAU colloq. 176: The impact of large-scale surveys on pulsating star research. Editors L. Szabados, and D. Kurtz, 401–407.

CrossRef Full Text | Google Scholar

Baruteau, C., and Rieutord, M. (2013). Inertial waves in a differentially rotating spherical shell. J. Fluid Mech. 719, 47–81. doi:10.1017/jfm.2012.605

CrossRef Full Text | Google Scholar

Bedding, T. R., Murphy, S. J., Hey, D. R., Huber, D., Li, T., Smalley, B., et al. (2020). Very regular high-frequency pulsation modes in young intermediate-mass stars. Nature 581, 147–151. doi:10.1038/s41586-020-2226-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Berthomieu, G., Gonczi, G., Graff, P., Provost, J., and Rocca, A. (1978). Low-frequency gravity modes of a rotating star. A&A 70, 597–606.

Google Scholar

Bigot, L., and Dziembowski, W. A. (2002). The oblique pulsator model revisited. Astron. Astrophys. 391, 235–245. doi:10.1051/0004-6361:20020824

CrossRef Full Text | Google Scholar

Bildsten, L., Ushomirsky, G., and Cutler, C. (1996). Ocean g-modes on rotating neutron stars. Astrophys. J. 460, 827. doi:10.1086/177012

CrossRef Full Text | Google Scholar

Bouabid, M.-P., Dupret, M.-A., Salmon, S., Montalbán, J., Miglio, A., Noels, A., et al. (2013). Effects of the Coriolis force on high-order g modes in γ Doradus stars. Mon. Not. R. Astron. Soc. 429, 2500–2514. doi:10.1093/mnras/sts517

CrossRef Full Text | Google Scholar

Bouchaud, K., Domiciano de Souza, A., Rieutord, M., Reese, D. R., and Kervella, P. (2020). A realistic two-dimensional model of Altair. Astron. Astrophys. 633, A78. doi:10.1051/0004-6361/201936830

CrossRef Full Text | Google Scholar

Bowman, D. M., Kurtz, D. W., Breger, M., Murphy, S. J., and Holdsworth, D. L. (2016). Amplitude modulation in δ sct stars: Statistics from an ensemble study of kepler targets. Mon. Not. R. Astron. Soc. 460, 1970–1989. doi:10.1093/mnras/stw1153

CrossRef Full Text | Google Scholar

Bowman, D. M., and Kurtz, D. W. (2018). Characterizing the observational properties of δ Sct stars in the era of space photometry from the Kepler mission. Mon. Notices R. Astronomical Soc. 476, 3169–3184. doi:10.1093/mnras/sty449

CrossRef Full Text | Google Scholar

Gaia Collaboration Brown, A. G. A., Vallenari, A., Prusti, T., de Bruijne, J. H. J., and Babusiaux, C. (2018). Gaia Data Release 2. Summary of the contents and survey properties. Astron. Astrophys. 616, A1. doi:10.1051/0004-6361/201833051

CrossRef Full Text | Google Scholar

Burke, K. D., Reese, D. R., and Thompson, M. J. (2011). On the effects of rotation on acoustic stellar pulsations: Validity domains of perturbative methods and close frequency pairs. Mon. Not. R. Astron. Soc. 414, 1119–1126. doi:10.1111/j.1365-2966.2011.18453.x

CrossRef Full Text | Google Scholar

Buzasi, D. L., Bruntt, H., Bedding, T. R., Retter, A., Kjeldsen, H., Preston, H. L., et al. (2005). Altair: The brightest δ Scuti star. Astrophys. J. 619, 1072–1076. doi:10.1086/426704

CrossRef Full Text | Google Scholar

Carpenter, K. G., Slettebak, A., and Sonneborn, G. (1984). Rotational velocities of later B type and A type stars as determined from ultraviolet versus visual line profiles. Astrophys. J. 286, 741. doi:10.1086/162650

CrossRef Full Text | Google Scholar

Christensen-Dalsgaard, J. (2008). ASTEC—The aarhus STellar evolution code. Astrophys. Space Sci. 316, 13–24. doi:10.1007/s10509-007-9675-5

CrossRef Full Text | Google Scholar

Christensen-Dalsgaard, J., and Mullan, D. J. (1994). Accurate frequencies of polytropic models. Mon. Not. R. Astron. Soc. 270, 921–935. doi:10.1093/mnras/270.4.921

CrossRef Full Text | Google Scholar

Christensen-Dalsgaard, J. (1982). On solar models and their periods of oscillation. Mon. Not. R. Astron. Soc. 199, 735–761. doi:10.1093/mnras/199.3.735

CrossRef Full Text | Google Scholar

Christensen-Dalsgaard, J., Schou, J., and Thompson, M. J. (1990). A comparison of methods for inverting helioseismic data. Mon. Not. R. Astron. Soc. 242, 353–369. doi:10.1093/mnras/242.3.353

CrossRef Full Text | Google Scholar

Clement, M. J. (1981). Normal modes of oscillation for rotating stars. I - the effect of rigid rotation on four low-order pulsations. Astrophys. J. 249, 746. doi:10.1086/159335

CrossRef Full Text | Google Scholar

Clement, M. J. (1984). Normal modes of oscillation for rotating stars. II Variational solutions. Astrophys. J. 276, 724. doi:10.1086/161658

CrossRef Full Text | Google Scholar

Clement, M. J. (1986). Normal modes of oscillation for rotating stars. III - variational calculations with an improved set of basis vectors. Astrophys. J. 301, 185. doi:10.1086/163886

CrossRef Full Text | Google Scholar

Clement, M. J. (1989). Normal modes of oscillation for rotating stars. IV. Nonaxisymmetricvariational solutions for 15 M_odot models. Astrophys. J. 339, 1022. doi:10.1086/167356

CrossRef Full Text | Google Scholar

Clement, M. J. (1998). Normal modes of oscillation for rotating stars. V. A new numerical method for computing nonradial eigenfunctions. Astrophys. J. Suppl. Ser. 116, 57–74. doi:10.1086/313097

CrossRef Full Text | Google Scholar

Cowling, T. G. (1941). The non-radial oscillations of polytropic stars. Mon. Not. R. Astron. Soc. 101, 367–375. doi:10.1093/mnras/101.8.367

CrossRef Full Text | Google Scholar

Daszyńska-Daszkiewicz, J., Dziembowski, W. A., Jerzykiewicz, M., and Handler, G. (2015). Oscillation modes in the rapidly rotating slowly pulsating B-type star μ Eridani. Mon. Not. R. Astron. Soc. 446, 1438–1448. doi:10.1093/mnras/stu2216

CrossRef Full Text | Google Scholar

Daszyńska-Daszkiewicz, J., Dziembowski, W. A., Pamyatnykh, A. A., and Goupil, M.-J. (2002). Photometric amplitudes and phases of nonradial oscillation in rotating stars. Astron. Astrophys. 392, 151–159. doi:10.1051/0004-6361:20020911

CrossRef Full Text | Google Scholar

Daszynska-Daszkiewicz, J., Dziembowski, W. A., and Pamyatnykh, A. A. (2007). On the prospects for detection and identification of low-frequency oscillation modes in rotating B type stars. Acta Astron. 57, 11–32.

Google Scholar

Deupree, R. G. (1995). Stella evolution with arbitrary rotation laws. 2: Massive star evolution to core hydrogen exhaustion. Astrophys. J. 439, 357. doi:10.1086/175179

CrossRef Full Text | Google Scholar

Deupree, R. G. (1990). Stellar evolution with arbitrary rotation laws. I - mathematical techniques and test cases. Astrophys. J. 357, 175. doi:10.1086/168903

CrossRef Full Text | Google Scholar

Deupree, R. G. (2011). Theoretical p-mode oscillation frequencies for the rapidly rotating δ Scuti star α ophiuchi. Astrophys. J. 742, 9. doi:10.1088/0004-637x/742/1/9

CrossRef Full Text | Google Scholar

Dintrans, B., and Rieutord, M. (2000). Oscillations of a rotating star: A non-perturbative theory. A&A 354, 86–98.

Google Scholar

Dintrans, B., Rieutord, M., and Valdettaro, L. (1999). Gravito-inertial waves in a rotating stratified sphere or spherical shell. J. Fluid Mech. 398, 271–297. doi:10.1017/s0022112099006308

CrossRef Full Text | Google Scholar

Domiciano de Souza, A., Kervella, P., Jankov, S., Abe, L., Vakili, F., di Folco, E., et al. (2003). The spinning-top Be star Achernar from VLTI-VINCI. Astron. Astrophys. 407, L47–L50. doi:10.1051/0004-6361:20030786

CrossRef Full Text | Google Scholar

Domiciano de Souza, A., Kervella, P., Jankov, S., Vakili, F., Ohishi, N., Nordgren, T. E., et al. (2005). Gravitational-darkening of Altair from interferometry. A&A. 442, 567–578. doi:10.1051/0004-6361:20042476

CrossRef Full Text | Google Scholar

Dupret, M.-A., De Ridder, J., De Cat, P., Aerts, C., Scuflaire, R., Noels, A., et al. (2003). A photometric mode identification method, including an improved non-adiabatic treatment of the atmosphere. Astron. Astrophys. 398, 677–685. doi:10.1051/0004-6361:20021679

CrossRef Full Text | Google Scholar

Dupret, M. A. (2001). Nonradial nonadiabatic stellar pulsations: A numerical method and its application to a beta cephei model. Astron. Astrophys. 366, 166–173. doi:10.1051/0004-6361:20000219

CrossRef Full Text | Google Scholar

Dupret, M., De Ridder, J., Neuforge, C., Aerts, C., and Scuflaire, R. (2002). Influence of non-adiabatic temperature variations on line profile variations of slowly rotating beta Cep stars and SPBs. I. Non-adiabatic eigenfunctions in the atmosphere of a pulsating star. Astron. Astrophys. 385, 563–571. doi:10.1051/0004-6361:20020193

CrossRef Full Text | Google Scholar

Dziembowski, W., Krolikowska, M., and Kosovichev, A. (1988). Nonlinear mode coupling in oscillating stars. III. Amplitude limiting effect of the rotation in the Delta Scuti stars. Acta Astron 38, 61–75.

Google Scholar

Dziembowski, W., and Krolikowska, M. (1985). Nonlinear mode coupling in oscillating stars. II - limiting amplitude effect of the parametric resonance in main sequence stars. Acta Astron 35, 5–28.

Google Scholar

Dziembowski, W. (1977). Light and radial velocity variations in a nonradially oscillating star. Acta Astron. 27, 203–211.

Google Scholar

Dziembowski, W. (1982). Nonlinear mode coupling in oscillating stars. I - second order theory of the coherent mode coupling. Acta Astron 32, 147–171.

Google Scholar

Espinosa, F., Pérez Hernández, F., and Roca Cortés, T. (2004). Oscillation modes in axially symmetric stars. ESA SP-559 SOHO 14 Helio- Asteroseismol. Towards a Gold. Future 559, 424–427.

Google Scholar

Espinosa Lara, F., and Rieutord, M. (2013). Self-consistent 2D models of fast-rotating early-type stars. Astron. Astrophys. 552, A35. doi:10.1051/0004-6361/201220844

CrossRef Full Text | Google Scholar

Ferrari, V. (2005). Imprint of the equation of state of dense matter on gravitational waves emitted by oscillating neutron stars. J. Phys. Conf. Ser. 8, 58–70. doi:10.1088/1742-6596/8/1/008

CrossRef Full Text | Google Scholar

García Hernández, A., Martín-Ruiz, S., Monteiro, M. J. P. F. G., Suárez, J. C., Reese, D. R., Pascual-Granado, J., et al. (2015). Observational dν-ρ relation for δ sct stars using eclipsing. Bin. Space Photometry 811, L29.

Google Scholar

García Hernández, A., Moya, A., Michel, E., Garrido, R., Suárez, J. C., Rodríguez, E., et al. (2009). Asteroseismic analysis of the CoRoT δ Scuti star HD 174936. Astron. Astrophys. 506, 79–83. doi:10.1051/0004-6361/200911932

CrossRef Full Text | Google Scholar

Garrido, R., Garcia-Lobo, E., and Rodriguez, E. (1990). Modal distribution of pulsating stars by using Stroemgren photometry. A&A 234, 262.

Google Scholar

Gastine, T., and Dintrans, B. (2008). Direct numerical simulations of the κ-mechanism. II. Nonlinear saturation and the Hertzsprung progression. Astron. Astrophys. 490, 743–752. doi:10.1051/0004-6361:200809891

CrossRef Full Text | Google Scholar

Goode, P. R., and Thompson, M. J. (1992). The effect of an inclined magnetic field on solar oscillation frequencies. Astrophys. J. 395, 307. doi:10.1086/171653

CrossRef Full Text | Google Scholar

Gough, D. O. (1981). A new measure of the solar rotation. Mon. Not. R. Astron. Soc. 196, 731–745. doi:10.1093/mnras/196.3.731

CrossRef Full Text | Google Scholar

Gough, D. O., and Thompson, M. J. (1990). The effect of rotation and a buried magnetic field on stellar oscillations. Mon. Not. R. Astron. Soc. 242, 25–55. doi:10.1093/mnras/242.1.25

CrossRef Full Text | Google Scholar

Goupil, M. J., and Talon, S. (2002). “Seismology of δ Scuti stars: Problems and prospects (invited paper),” in ASP conf. Ser. 259: IAU colloq. 185: Radial and nonradial pulsationsn as probes of stellar physics. Editors C. Aerts, T. R. Bedding, and J. Christensen-Dalsgaard, 306.

CrossRef Full Text | Google Scholar

Hatta, Y., Sekii, T., Takata, M., and Kurtz, D. W. (2019). The two-dimensional internal rotation of KIC 11145123. Astrophys. J. 871, 135. doi:10.3847/1538-4357/aaf881

CrossRef Full Text | Google Scholar

Heynderickx, D., Waelkens, C., and Smeyers, P. (1994). A photometric study of β Cephei stars. II. Determination of the degrees L of pulsation modes. A&A Supp. 105, 447–480.

Google Scholar

Ipser, J. R., and Lindblom, L. (1991). The oscillations of rapidly rotating Newtonian stellar models. II - dissipative effects. Astrophys. J. 373, 213. doi:10.1086/170039

CrossRef Full Text | Google Scholar

Jackson, S., MacGregor, K. B., and Skumanich, A. (2005). On the use of the self-consistent-field method in the construction of models for rapidly rotating main-sequence stars. Astrophys. J. Suppl. Ser. 156, 245–264. doi:10.1086/426587

CrossRef Full Text | Google Scholar

Karami, K. (2008). Third order effect of rotation on stellar oscillations of a B star. Chin. J. Astron. Astrophys. 8, 285–308. doi:10.1088/1009-9271/8/3/06

CrossRef Full Text | Google Scholar

Koen, C., Balona, L. A., Khadaroo, K., Lane, I., Prinsloo, A., Smith, B., et al. (2003). Pulsations in β Pictoris. Mon. Not. R. Astron. Soc. 344, 1250–1256. doi:10.1046/j.1365-8711.2003.06912.x

CrossRef Full Text | Google Scholar

Kurtz, D. W. (1990). Rapidly oscillating AP stars. Annu. Rev. Astron. Astrophys. 28, 607–655. doi:10.1146/annurev.aa.28.090190.003135

CrossRef Full Text | Google Scholar

Lachaume, R., Dominik, C., Lanz, T., and Habing, H. J. (1999). Age determinations of main-sequence stars: Combining different methods. A&A 348, 897–909.

Google Scholar

Lagrange, A. M., Bonnefoy, M., Chauvin, G., Apai, D., Ehrenreich, D., Boccaletti, A., et al. (2010). A giant planet imaged in the disk of the young star β Pictoris. Science 329, 57–59. doi:10.1126/science.1187187

PubMed Abstract | CrossRef Full Text | Google Scholar

Lagrange, A. M., Gratadour, D., Chauvin, G., Fusco, T., Ehrenreich, D., Mouillet, D., et al. (2009). A probable giant planet imaged in the β Pictoris disk. VLT/NaCo deep L’-band imaging. Astron. Astrophys. 493, L21–L25. doi:10.1051/0004-6361:200811325

CrossRef Full Text | Google Scholar

Ledoux, P. (1951). The nonradial oscillations of gaseous stars and the problem of beta Canis majoris. Astrophys. J. 114, 373. doi:10.1086/145477

CrossRef Full Text | Google Scholar

Lee, U., and Baraffe, I. (1995). Pulsational stability of rotating main sequence stars: The second order effects of rotation on the nonadiabatic oscillations. A and A 301, 419.

Google Scholar

Lee, U. (2006). r modes of slowly pulsating B stars. Mon. Not. R. Astron. Soc. 365, 677–687. doi:10.1111/j.1365-2966.2005.09751.x

CrossRef Full Text | Google Scholar

Lee, U. (2008). Pulsation in rapidly rotating stars. Commun. Asteroseismol. 157, 203–208.

Google Scholar

Lee, U. (2001). Pulsational stability of g-modes in slowly pulsating B stars. Astrophys. J. 557, 311–319. doi:10.1086/321554

CrossRef Full Text | Google Scholar

Lee, U., and Saio, H. (1987). Low-frequency oscillations of uniformly rotating stars. Mon. Not. R. Astron. Soc. 224, 513–526. doi:10.1093/mnras/224.3.513

CrossRef Full Text | Google Scholar

Lignières, F., and Georgeot, B. (2009). Asymptotic analysis of high-frequency acoustic modes in rapidly rotating stars. Astron. Astrophys. 500, 1173–1192. doi:10.1051/0004-6361/200811165

CrossRef Full Text | Google Scholar

Lignières, F., and Georgeot, B. (2008). Wave chaos in rapidly rotating stars. Phys. Rev. E 78, 016215. doi:10.1103/physreve.78.016215

CrossRef Full Text | Google Scholar

Lignières, F., Rieutord, M., and Reese, D. (2006). Acoustic oscillations of rapidly rotating polytropic stars. Astron. Astrophys. 455, 607–620. doi:10.1051/0004-6361:20065015

CrossRef Full Text | Google Scholar

Lignières, F., Rieutord, M., and Valdettaro, L. (2001). “Acoustic modes in spheroidal cavities,” in SF2A-2001: Semaine de l’Astrophysique Francaise. Editors F. Combes, D. Barret, and F. Thévenin, 127.

Google Scholar

Lovekin, C. C., Deupree, R. G., and Clement, M. J. (2009). Effects of uniform and differential rotation on stellar pulsations. Astrophys. J. 693, 677–690. doi:10.1088/0004-637x/693/1/677

CrossRef Full Text | Google Scholar

Lovekin, C. C., and Deupree, R. G. (2008). Radial and nonradial oscillation modes in rapidly rotating stars. Astrophys. J. 679, 1499–1508. doi:10.1086/587615

CrossRef Full Text | Google Scholar

Lynden-Bell, D., and Ostriker, J. P. (1967). On the stability of differentially rotating bodies. Mon. Not. R. Astron. Soc. 136, 293–310. doi:10.1093/mnras/136.3.293

CrossRef Full Text | Google Scholar

MacGregor, K. B., Jackson, S., Skumanich, A., and Metcalfe, T. S. (2007). On the structure and properties of differentially rotating, main-sequence stars in the 1-2 m_solar range. Astrophys. J. 663, 560–572. doi:10.1086/518303

CrossRef Full Text | Google Scholar

Maeder, A. (2009). Physics, Formation and Evolution of rotating stars. Astronomy and astrophysics library. Berlin, Heidelberg: Springer-Verlag.

Google Scholar

Manchon, L. (2021). On the transport of angular momentum in stellar radiative zones in 2D. Ph.D. thesis. Saclay: Université de Paris.

Google Scholar

Marques, J. P., Goupil, M. J., Lebreton, Y., Talon, S., Palacios, A., Belkacem, K., et al. (2013). Seismic diagnostics for transport of angular momentum in stars. I. Rotational splittings from the pre-main sequence to the red-giant branch. Astron. Astrophys. 549, A74. doi:10.1051/0004-6361/201220211

CrossRef Full Text | Google Scholar

Meynet, G., and Maeder, A. (2000). Stellar evolution with rotation. V. Changes in all the outputs of massive star models. A&A 361, 101–120.

Google Scholar

Michel, E., Dupret, M.-A., Reese, D., Ouazzani, R.-M., Debosscher, J., Hernández, A. G., et al. (2017). What CoRoT tells us about δ Scuti stars. Existence of a regular pattern and seismic indices to characterize stars. Eur. Phys. J. Web Conf. 160, 03001.

CrossRef Full Text | Google Scholar

Mirouh, G. M., Angelou, G. C., Reese, D. R., and Costa, G. (2019). Mode classification in fast-rotating stars using a convolutional neural network: Model-based regular patterns in δ Scuti stars. Mon. Notices R. Astronomical Soc. Lett. 483, L28–L32. doi:10.1093/mnrasl/sly212

CrossRef Full Text | Google Scholar

Mirouh, G. M., Baruteau, C., Rieutord, M., and Ballot, J. (2016). Gravito-inertial waves in a differentially rotating spherical shell. J. Fluid Mech. 800, 213–247. doi:10.1017/jfm.2016.382

CrossRef Full Text | Google Scholar

Monnier, J. D., Zhao, M., Pedretti, E., Thureau, N., Ireland, M., Muirhead, P., et al. (2007). Imaging the surface of Altair. Science 317, 342–345. doi:10.1126/science.1143205

PubMed Abstract | CrossRef Full Text | Google Scholar

Morel, P. (1997). Cesam: A code for stellar evolution calculations. Astron. Astrophys. Suppl. Ser. 124, 597–614. doi:10.1051/aas:1997209

CrossRef Full Text | Google Scholar

Morel, P., and Lebreton, Y. (2008). Cesam: A free code for stellar evolution calculations. Astrophys. Space Sci. 316, 61–73. doi:10.1007/s10509-007-9663-9

CrossRef Full Text | Google Scholar

Ogilvie, G. I. (2009). Tidal dissipation in rotating fluid bodies: A simplified model. Mon. Not. R. Astron. Soc. 396, 794–806. doi:10.1111/j.1365-2966.2009.14814.x

CrossRef Full Text | Google Scholar

Ohishi, N., Nordgren, T. E., and Hutter, D. J. (2004). Asymmetric surface brightness distribution of Altair observed with the navy prototype optical interferometer. Astrophys. J. 612, 463–471. doi:10.1086/422422

CrossRef Full Text | Google Scholar

Ouazzani, R.-M., Roxburgh, I. W., and Dupret, M.-A. (2015). Pulsations of rapidly rotating stars. II. Realistic modelling for intermediate-mass stars. Astron. Astrophys. 579, A116. doi:10.1051/0004-6361/201525734

CrossRef Full Text | Google Scholar

Ouazzani, R.-M., Salmon, S. J. A. J., Antoci, V., Bedding, T. R., Murphy, S. J., Roxburgh, I. W., et al. (2017). A new asteroseismic diagnostic for internal rotation in γ Doradus stars. Mon. Not. R. Astron. Soc. 465, 2294–2309. doi:10.1093/mnras/stw2717

CrossRef Full Text | Google Scholar

Ouazzani, R. M., Dupret, M. A., and Reese, D. R. (2012). Pulsations of rapidly rotating stars. I. The ACOR numerical code. Astron. Astrophys. 547, A75. doi:10.1051/0004-6361/201219548

CrossRef Full Text | Google Scholar

Ouazzani, R. M., Lignières, F., Dupret, M. A., Salmon, S. J. A. J., Ballot, J., Christophe, S., et al. (2020). First evidence of inertial modes in γ Doradus stars: The core rotation revealed. Astron. Astrophys. 640, A49. doi:10.1051/0004-6361/201936653

CrossRef Full Text | Google Scholar

Ouazzani, R. M., Marques, J. P., Goupil, M. J., Christophe, S., Antoci, V., Salmon, S. J. A. J., et al. (2019). γ Doradus stars as a test of angular momentum transport models. Astron. Astrophys. 626, A121. doi:10.1051/0004-6361/201832607

CrossRef Full Text | Google Scholar

Palacios, A., Talon, S., Charbonnel, C., and Forestini, M. (2003). Rotational mixing in low-mass stars. Astron. Astrophys. 399, 603–616. doi:10.1051/0004-6361:20021759

CrossRef Full Text | Google Scholar

Papaloizou, J., and Pringle, J. E. (1978). Non-radial oscillations of rotating stars and their relevance to the short-period oscillations of cataclysmic variables. Mon. Not. R. Astron. Soc. 182, 423–442. doi:10.1093/mnras/182.3.423

CrossRef Full Text | Google Scholar

Paparó, M., Benkő, J. M., Hareter, M., and Guzik, J. A. (2016). Unexpected series of regular frequency spacing of δ Scuti stars in the non-asymptotic regime. II. Sample-echelle diagrams and rotation. Astrophys. J. Suppl. Ser. 224, 41. doi:10.3847/0067-0049/224/2/41

CrossRef Full Text | Google Scholar

Peterson, D. M., Hummel, C. A., Pauls, T. A., Armstrong, J. T., Benson, J. A., Gilbreath, G. C., et al. (2006). Resolving the effects of rotation in Altair with long-baseline interferometry. Astrophys. J. 636, 1087–1097. doi:10.1086/497981

CrossRef Full Text | Google Scholar

Reese, D. (2006). La modélisation des oscillations d’étoiles en rotation rapide. Ph.D. thesis. Paul Sabatier: Université Toulouse III -.

Google Scholar

Reese, D., Lignières, F., and Rieutord, M. (2006). Acoustic oscillations of rapidly rotating polytropic stars. II. Effects of the Coriolis and centrifugal accelerations. Astron. Astrophys. 455, 621–637. doi:10.1051/0004-6361:20065269

CrossRef Full Text | Google Scholar

Reese, D., Lignières, F., and Rieutord, M. (2008). Regular patterns in the acoustic spectrum of rapidly rotating stars. Astron. Astrophys. 481, 449–452. doi:10.1051/0004-6361:20078075

CrossRef Full Text | Google Scholar

Reese, D. R., Dupret, M.-A., and Rieutord, M. (2017a). Non-adiabatic pulsations in ESTER models. Eur. Phys. J. Web Conf. 160, 02007. doi:10.1051/epjconf/201716002007

CrossRef Full Text | Google Scholar

Reese, D. R., Lignières, F., Ballot, J., Dupret, M.-A., Barban, C., van’t Veer-Menneret, C., et al. (2017b). Frequency regularities of acoustic modes and multi-colour mode identification in rapidly rotating stars. Astron. Astrophys. 601, A130. doi:10.1051/0004-6361/201321264

CrossRef Full Text | Google Scholar

Reese, D. R., MacGregor, K. B., Jackson, S., Skumanich, A., and Metcalfe, T. S. (2009). Pulsation modes in rapidly rotating stellar models based on the self-consistent field method. Astron. Astrophys. 506, 189–201. doi:10.1051/0004-6361/200811510

CrossRef Full Text | Google Scholar

Reese, D. R., Mirouh, G. M., Espinosa Lara, F., Rieutord, M., and Putigny, B. (2021). Oscillations of 2D ESTER models. I. The adiabatic case. Astron. Astrophys. 645, A46. doi:10.1051/0004-6361/201935538

CrossRef Full Text | Google Scholar

Reese, D. R., Prat, V., Barban, C., van ’t Veer-Menneret, C., and MacGregor, K. B. (2013). Mode visibilities in rapidly rotating stars. Astron. Astrophys. 550, A77. doi:10.1051/0004-6361/201220506

CrossRef Full Text | Google Scholar

Reese, D. R. (2013). Stable higher order finite-difference schemes for stellar pulsation calculations. Astron. Astrophys. 555, A148. doi:10.1051/0004-6361/201321725

CrossRef Full Text | Google Scholar

Ricker, G. R., Winn, J. N., Vanderspek, R., Latham, D. W., Bakos, G. Á., Bean, J. L., et al. (2015). Transiting exoplanet survey satellite (TESS). J. Astronomical Telesc. Instrum. Syst. 1, 014003.

Google Scholar

Rieutord, M. (2001). Ekman layers and the damping of inertial R-modes in a spherical shell: Application to neutron stars. Astrophys. J. 550, 493. doi:10.1086/321676

CrossRef Full Text | Google Scholar

Rieutord, M., Espinosa Lara, F., and Putigny, B. (2016). An algorithm for computing the 2D structure of fast rotating stars. J. Comput. Phys. 318, 277–304. doi:10.1016/j.jcp.2016.05.011

CrossRef Full Text | Google Scholar

Rieutord, M., and Valdettaro, L. (1997). Inertial waves in a rotating spherical shell. J. Fluid Mech. 341, 77–99. doi:10.1017/s0022112097005491

CrossRef Full Text | Google Scholar

Rieutord, M., and Valdettaro, L. (2010). Viscous dissipation by tidally forced inertial modes in a rotating spherical shell. J. Fluid Mech. 643, 363–394. doi:10.1017/S002211200999214X

CrossRef Full Text | Google Scholar

Roxburgh, I. W. (2006). 2-dimensional models of rapidly rotating stars. II. Hydrostatic and acoustic models with Ω = Ω(r, θ). Astron. Astrophys. 454, 883–888. doi:10.1051/0004-6361:20065109

CrossRef Full Text | Google Scholar

Royer, F. (2009). “On the rotation of A-type stars,” in The rotation of Sun and stars (Berlin Springer Verlag), 207–230.

CrossRef Full Text | Google Scholar

Saio, H. (1982). R-mode oscillations in uniformly rotating stars. Astrophys. J. 256, 717. doi:10.1086/159945

CrossRef Full Text | Google Scholar

Saio, H. (1981). Rotational and tidal perturbations of nonradial oscillations in a polytropic star. Astrophys. J. 244, 299. doi:10.1086/158708

CrossRef Full Text | Google Scholar

Saio, H., Takata, M., Lee, U., Li, G., and Van Reeth, T. (2021). Rotation of the convective core in γ Dor stars measured by dips in period spacings of g modes coupled with inertial modes. Mon. Not. R. Astron. Soc. 502, 5856–5874. doi:10.1093/mnras/stab482

CrossRef Full Text | Google Scholar

Savonije, G. J. (2007). Non-radial oscillations of the rapidly rotating Be star HD 163868. Astron. Astrophys. 469, 1057–1062. doi:10.1051/0004-6361:20077377

CrossRef Full Text | Google Scholar

Savonije, G. J., Papaloizou, J. C. B., and Alberts, F. (1995). Nonadiabatic tidal forcing of a massive uniformly rotating star. Mon. Not. R. Astron. Soc. 277, 471–496. doi:10.1093/mnras/277.2.471

CrossRef Full Text | Google Scholar

Schou, J., Antia, H. M., Basu, S., Bogart, R. S., Bush, R. I., Chitre, S. M., et al. (1998). Helioseismic studies of differential rotation in the solar envelope by the solar oscillations investigation using the michelson Doppler imager. Astrophys. J. 505, 390–417. doi:10.1086/306146

CrossRef Full Text | Google Scholar

Schou, J., Christensen-Dalsgaard, J., and Thompson, M. J. (1994). On comparing helioseismic two-dimensional inversion methods. Astrophys. J. 433, 389. doi:10.1086/174653

CrossRef Full Text | Google Scholar

Scuflaire, R., Montalbán, J., Théado, S., Bourge, P. O., Miglio, A., Godart, M., et al. (2008). The liège oscillation code. Astrophys. Space Sci. 316, 149–154. doi:10.1007/s10509-007-9577-6

CrossRef Full Text | Google Scholar

Soufi, F., Goupil, M.-J., and Dziembowski, W. A. (1998). Effects of moderate rotation on stellar pulsation. I. Third order perturbation formalism. A&A 334, 911–924.

Google Scholar

Stergioulas, N., Apostolatos, T. A., and Font, J. A. (2004). Non-linear pulsations in differentially rotating neutron stars: Mass-shedding-induced damping and splitting of the fundamental mode. Mon. Not. R. Astron. Soc. 352, 1089–1101. doi:10.1111/j.1365-2966.2004.07973.x

CrossRef Full Text | Google Scholar

Stoeckley, T. R. (1968). Determination of aspect and degree of differential rotation, from line profiles in rapidly rotating stars. Mon. Not. R. Astron. Soc. 140, 121–139. doi:10.1093/mnras/140.2.121

CrossRef Full Text | Google Scholar

Suárez, J.-C., Michel, E., Pérez Hernández, F., Lebreton, Y., Li, Z. P., Fox Machado, L., et al. (2002). A study of correlation between the oscillation amplitude and stellar parameters of δ Scuti stars in open clusters. Astron. Astrophys. 390, 523–531. doi:10.1051/0004-6361:20020565

CrossRef Full Text | Google Scholar

Suárez, J. C., Bruntt, H., and Buzasi, D. (2005). Modelling of the fast rotating δ Scuti star Altair. Astron. Astrophys. 438, 633–641. doi:10.1051/0004-6361:20042410

CrossRef Full Text | Google Scholar

Suárez, J. C., Goupil, M. J., Reese, D. R., Samadi, R., Lignières, F., Rieutord, M., et al. (2010). On the interpretation of echelle diagrams for solar-like oscillations effect of centrifugal distortion. Astrophys. J. 721, 537–546. doi:10.1088/0004-637X/721/1/537

CrossRef Full Text | Google Scholar

Thompson, M. J., Christensen-Dalsgaard, J., Miesch, M. S., and Toomre, J. (2003). The internal rotation of the Sun. Annu. Rev. Astron. Astrophys. 41, 599–643. doi:10.1146/annurev.astro.41.011802.094848

CrossRef Full Text | Google Scholar

Townsend, R. H. D. (2003a). A semi-analytical formula for the light variations due to low-frequency g modes in rotating stars. Mon. Not. R. Astron. Soc. 343, 125–136. doi:10.1046/j.1365-8711.2003.06640.x

CrossRef Full Text | Google Scholar

Townsend, R. H. D. (2003b). Asymptotic expressions for the angular dependence of low-frequency pulsation modes in rotating stars. Mon. Not. R. Astron. Soc. 340, 1020–1030. doi:10.1046/j.1365-8711.2003.06379.x

CrossRef Full Text | Google Scholar

Townsend, R. H. D. (2005). Influence of the Coriolis force on the instability of slowly pulsating B stars. Mon. Not. R. Astron. Soc. 360, 465–476. doi:10.1111/j.1365-2966.2005.09002.x

CrossRef Full Text | Google Scholar

Townsend, R. H. D. (1997). Spectroscopic modelling of non-radial pulsation in rotating early-type stars. Mon. Not. R. Astron. Soc. 284, 839–858. doi:10.1093/mnras/284.4.839

CrossRef Full Text | Google Scholar

Tran Minh, F., and Léon, L. (1995). Numerical solution of stellar nonradial oscillations: The galerkin and B-splines method. Part. Phys. Astrophysics 458, 219. doi:10.1007/BFb0118720

CrossRef Full Text | Google Scholar

van Belle, G. T., Ciardi, D. R., Thompson, R. R., Akeson, R. L., and Lada, E. A. (2001). Altair’s oblateness and rotation velocity from long-baseline interferometry. Astrophys. J. 559, 1155–1164. doi:10.1086/322340

CrossRef Full Text | Google Scholar

Van Reeth, T., Tkachenko, A., and Aerts, C. (2016). Interior rotation of a sample of γ Doradus stars from ensemble modelling of their gravity-mode period spacings. Astron. Astrophys. 593, A120. doi:10.1051/0004-6361/201628616

CrossRef Full Text | Google Scholar

Watson, R. D. (1988). Contributing factors to flux changes in nonradial stellar pulsations. Astrophys. Space Sci. 140, 255–290. doi:10.1007/BF00638984

CrossRef Full Text | Google Scholar

Weiss, W. W., Rucinski, S. M., Moffat, A. F. J., Schwarzenberg-Czerny, A., Koudelka, O. F., Grant, C. C., et al. (2014). BRITE-Constellation: Nanosatellites for precision photometry of bright stars. Publ. Astron. Soc. Pac. 126, 573–585. doi:10.1086/677236

CrossRef Full Text | Google Scholar

Yoshida, S., and Eriguchi, Y. (1999). A numerical study of normal modes of rotating neutron star models by the cowling approximation. Astrophys. J. 515, 414–422. doi:10.1086/307012

CrossRef Full Text | Google Scholar

Yoshida, S., and Eriguchi, Y. (1995). Gravitational radiation driven secular instability of rotating polytropes. Astrophys. J. 438, 830. doi:10.1086/175126

CrossRef Full Text | Google Scholar

Zahn, J.-P. (1992). Circulation and turbulence in rotating stars. A&A 265, 115–132.

Google Scholar

Zwintz, K., Reese, D. R., Neiner, C., Pigulski, A., Kuschnig, R., Müllner, M., et al. (2019). Revisiting the pulsational characteristics of the exoplanet host star β Pictoris. Astron. Astrophys. 627, A28. doi:10.1051/0004-6361/201834744

CrossRef Full Text | Google Scholar