Importance of lower atmospheric forcing and magnetosphere-ionosphere coupling in simulating neutral density during the February 2016 geomagnetic storm

During geomagnetic storms a large amount of energy is transferred into the ionosphere-thermosphere (IT) system, leading to local and global changes in e.g., the dynamics, composition, and neutral density. The more steady energy from the lower atmosphere into the IT system is in general much smaller than the energy input from the magnetosphere, especially during geomagnetic storms, and therefore details of the lower atmosphere forcing are often neglected in storm time simulations. In this study we compare the neutral density observed by Swarm-C during the moderate geomagnetic storm of 31 January to 3 February 2016 with the Thermosphere-Ionosphere-Electrodynamics-GCM (TIEGCM) finding that the model can capture the observed large scale neutral density variations better in the southern than northern hemisphere. The importance of more realistic lower atmospheric (LB) variations as specified by the Whole Atmosphere Community Climate Model eXtended (WACCM-X) with specified dynamics (SD) is demonstrated by improving especially the northern hemisphere neutral density by up to 15% compared to using climatological LB forcing. Further analysis highlights the importance of the background atmospheric condition in facilitating hemispheric different neutral density changes in response to the LB perturbations. In comparison, employing observationally based field-aligned current (FAC) versus using an empirical model to describe magnetosphere-ionosphere (MI) coupling leads to an 7–20% improved northern hemisphere neutral density. The results highlight the importance of the lower atmospheric variations and high latitude forcing in simulating the absolute large scale neutral density especially the hemispheric differences. However, focusing on the storm time variation with respect to the quiescent time, the lower atmospheric influence is reduced to 1–1.5% improvement with respect to the total observed neutral density. The results provide some guidance on the importance of more realistic upper boundary forcing and lower atmospheric variations when modeling large scale, absolute and relative neutral density variations.

1 Introduction

Geomagnetic storms are characterized by immense high latitude energy input from the magnetosphere into the upper atmosphere. Joule heating, which is the dominant energy source during large geomagnetic storms, describes the conversion of electromagnetic energy into heat through ohmic current (e.g., Richmond, 2021). The top 5% of geomagnetic storms between 1975–2004 produced on average approximately 331 GW in Joule heating and 73 GW in kinetic energy via particle precipitation (Knipp et al., 2004). During very strong storms Joule heating increases significantly to over 1000 GW and dominates over auroral particle precipitation (Lu et al., 2016). This high latitude energy input is approximately 10 times larger than the more continuous wave energy input from the lower atmosphere (around 100–150 GW) (Liu, 2016). The neutral density is affected by all of these energy sources e.g., Joule heating (e.g., Fedrizzi et al., 2012), auroral particle precipitation (e.g., Deng et al., 2013), lower atmosphere (e.g., Liu et al., 2017), direct solar radiation (e.g., Emmert, 2015), and varies spatially and temporally depending on these energy source.

Neutral density is sensitive to changes in geomagnetic activity with its associated energy input into the upper atmosphere (e.g., Müller et al., 2009). There are efforts to quantify the correlation between Joule heating and the neutral density change (e.g., Fedrizzi et al., 2012; Kalafatoglu Eyiguler et al., 2019a). The effect of Joule heating on the neutral density depends on the heating magnitude and on the altitude distribution of the energy deposition. While only 18–34% of the Joule heating is dissipated above 150 km, the energy at these higher altitude is more effective in changing the neutral density on shorter time scales (hours) (e.g., Deng et al., 2011; Huang et al., 2012). For a comprehensive review of neutral density variation during geomagnetic storms we refer to e.g., Prölss (2011).

The neutral density variations are affected by the interplay between heating, atmospheric expansion, neutral wind, and compositional changes. An excellent review about neutral density variations is provided by e.g., Emmert (2015). Thermospheric composition as measured by the ratio of atomic oxygen to molecular nitrogen, O/N₂, plays an important role in understand neutral density variations (e.g., Zhang and Paxton, 2021). In general, heating in the polar region leads to upwelling and a decrease of the O/N₂ ratio by transporting molecular nitrogen from N₂ rich regions into regions with lower N₂ (e.g., Zhang et al., 2004). The modification of the large scale wind system leads to equatorward and downward winds at lower latitudes transporting oxygen rich air from higher to lower altitudes and increases the O/N₂ ratio there (e.g., Forbes, 2007).

The neutral density response to geomagnetic disturbances is spatially and temporally varying. During geomagnetic storms large scale traveling atmospheric disturbances (TADs) are launched with associated neutral density variation propagating away from region of sudden large energy deposition (e.g., Bruinsma and Forbes, 2009; Ritter et al., 2010). Therefore, the equatorial neutral density response lags by approximately 3–5 h with a shorter response time on the dayside than on the nightside e.g., as suggested by Müller et al. (2009); Bruinsma and Forbes (2009); Sutton et al. (2009). In this study we focus on a moderate geomagnetic disturbed period and its large-scale neutral density response, and TADs with their associated neutral density variations are not the focus of this study.

The background atmospheric condition modulates the geomagnetic storm responses in neutral composition and neutral density. For geomagnetic storms during solar minimum compared to solar maximum conditions the magnitude and extend of compositional changes are found to be larger, which is explained by more efficient transport and smaller scale heights during solar minimum conditions (e.g., Emmert, 2015).

The seasonal mean circulation can enhance or reduce the effect of high latitude heating on the composition. During average geomagnetic storm conditions the compositional changes extends more equatorward in the summer hemisphere than in the winter hemisphere (e.g., Zuzic et al., 1997). However, Zhang and Paxton (2021) pointed out that GUVI observed larger O/N₂ depletion extending more equatorward in the northern winter than southern summer hemisphere during the 20–21 November 2003 geomagnetic storm. The authors suggested that this hemispheric asymmetry is associated with interhemispheric differences in the auroral hemispheric power.

Comprehensive overview of solar-cycle, seasonal and diurnal neutral density variation can be found in e.g., Qian and Solomon (2012); Emmert (2015); Liu et al. (2017). The neutral density scales approximately linearly with solar radiation but more strongly during day-time than night-time (e.g., Müller et al., 2009). The neutral density is larger in the summer than in the winter and the latitudinal variation is reduced around the equinox transition. The equinoctial neutral density is larger than the solstice neutral density and larger in March than September (e.g., Müller et al., 2009; Qian and Solomon, 2012) due to lower atmospheric forcing and the associated large scale “turbulent eddy” suppressing the maximum density at solstices (e.g., Fuller-Rowell, 1998).

Qian et al. (2009) modified the eddy diffusion in a numerical model to mimic the effect of wave dissipation and improved the agreement with the observed daily averaged neutral density variations, highlighting the importance of lower atmospheric forcing for capturing seasonal variations in daily averaged neutral density. The magnitude of the eddy diffusion coefficient in numerical models depends on the resolved waves as demonstrated by Siskind et al. (2014) who reduced the eddy diffusivity by a factor of five from Qian et al. (2009) when using realistic planetary wave and tidal perturbations. The present study will focus on the influence of the lower atmospheric forcing on the neutral density without changing the default eddy diffusivity in the numerical model, TIEGCM. So far, it is not understood how to adjust eddy diffusivity in the model to account for the changing complexity in the prescribed wave spectra.

In the upper mesosphere and lower thermosphere (MLT) region the atmosphere transitions from a well-mixed fluid to being dominated by molecular diffusion. Increasing the eddy mixing will move this transition to higher altitude and therefore lead to a reduction of atomic oxygen. Another effect of eddy diffusion is an increase in heat conduction from the hotter atmosphere above to the cooler atmosphere below in the MLT region (Roble, 1995). Jones et al. (2014b,a) found an approximate 10% decrease in the low latitude upper thermospheric atomic oxygen at equinox due to including lower atmospheric tides in their simulations. They attributed these depletion to tidal-induced net transport of atomic oxygen. Yamazaki and Richmond (2013) carefully examined the role of migrating tides finding that a major contributor to the atomic oxygen reduction is the modified mean circulation through tidal dissipation. In addition residual circulation in the lower thermosphere was suggested to influence the neutral density by locally modifying the composition which is then transferred to the atmosphere above (Qian and Yue, 2017).

Depending on the focus of a modeling study special attention is often given either to realistic high latitude forcing when examining geomagnetic storm or lower atmospheric forcing when focusing on vertical coupling. Several studies pointed out that neutral density variations of quiescent and storm times can be evaluated separately, assuming linear behavior (e.g., Müller et al., 2009; Kalafatoglu Eyiguler et al., 2019b). The interplay of both forcing on neutral density variations is not well understood and neither is their importance for capturing the absolute and relative neutral density variations.

In this study we focus on a moderate geomagnetic storm and quantify the relative effect of the lower atmosphere forcing and the high latitude forcing on the large scale neutral density variations in different latitudinal regions. As we will show below, there are strong interhemispheric differences in the neutral density variation that cannot be solely explained by the interhemispheric differences in the forcings.

In section 2 we first describe the geophysical conditions associated with the storm, the Swarm neutral density data, and the TIEGCM with its boundary condition. In section 3 the influence of the lower atmosphere on the neutral density is studied. In section 4 we examine the importance of realistic high latitude forcing on the neutral density variation. In section 5 we conclude by comparing the two effects.

2 Data and model

In this study we examine the effect of the lower atmospheric and high-latitude forcing on the neutral density during the moderate geomagnetically disturbed period of 31 January to 3 February 2016. We would like to point out that according to Gonzalez et al. (1994) the period is characterized as a moderate geomagnetic storm while using the NOAA Space Weather scale it is a minor geomagnetic storm (G1). This period was a focused study in the project “Next Generation Advances in Ionosphere-Thermosphere Coupling at Multiple Scales for Environmental Specifications and Predictions” mainly due to interesting meso-scale magnetosphere-ionosphere coupling phenomena. Among others, a preliminary data-model comparison revealed significant hemispheric differences in the simulation results for capturing the Swarm neutral mass density measurements, which prompted the current study to further examine the role of the lower atmospheric forcing in addition to the high-latitude forcing from the magnetosphere. In this study we use the Swarm-C neutral density observations and TIEGCM simulations, which are described in the following.

The geophysical conditions for 30 January to 3 February 2016 are summarized in Figure 1. The geomagnetic activity starts late on 30 January (day of year doy 30) with IMF B_y becoming positive (approximately 5nT), followed by IMF B_z turning southward a few hours later and staying southward throughout 31 January (doy 31) till approximately 1 February (doy 32) six UT. While IMF B_y and B_z oscillate frequently on 2 February (doy 33) a more sustained southward IMF B_z period starts late on 2 February lasting a few hours before becoming northward around four UT on 3 February. The Sym-H index, a measure of the symmetric ring current strength, becomes negative on 31 January lasting till 1 February (minima around -50nT), recovers on 2 February, and then is disturbed again on 3 February with a minimum of roughly -60nT. The observed solar radio flux F_10.7 varies only slightly between 100 and 112 solar flux unit (1 sfu is $10^{-22}\frac{W}{m^{2}Hz}$).

FIGURE 1

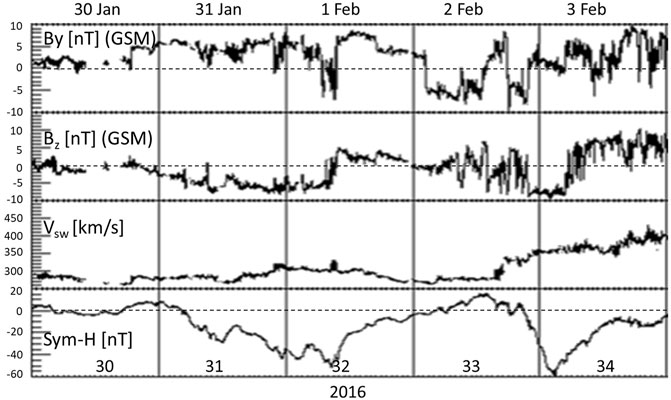
FIGURE 1. Geophysical conditions for 30 January—3 February 2016: IMF B_y (top), B_z [nT] (second from top), solar wind velocity V_sw [km/s] (second from bottom), and Sym-H index [nT] (bottom) based on NASA SPDF-OMNIweb data [https://omniweb.gsfc.nasa.gov].

2.1 Swarm neutral density

The neutral density are from the Swarm data product (DNSxACC version 0201) derived in a four-stage process as described by Siemes et al. (2016). During this time period Swarm-C orbit altitude is between 450 km and 478 km (see Figure 2). The orbit altitude is approximately 20 km higher in the southern than northern high latitude region. Only considering the altitude difference, the neutral density is roughly a factor of 1.4–1.5 larger at lower than higher altitudes based on NRLMSIS2.0 (Emmert et al., 2021). The night-time part of the orbit is around 2.5–3 h solar local time (SLT) at middle and low latitudes and the day-time orbit is around 14–15 h SLT. The average solar zenith angle is given in Figure 2 indicating that the night-time orbits are sunlit in the southern polar region and in darkness in the northern hemisphere.

FIGURE 2

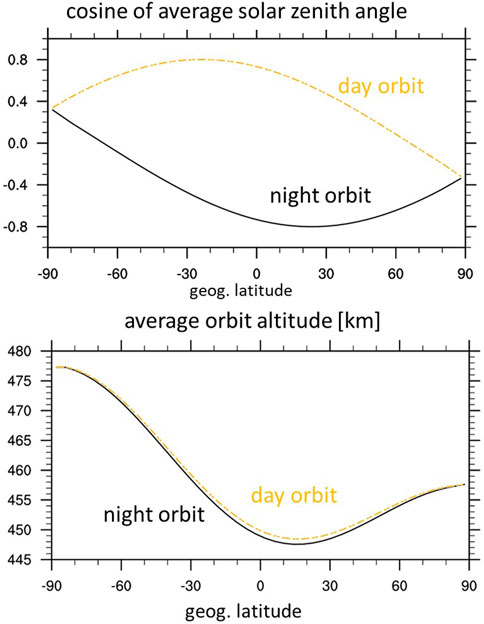
FIGURE 2. Cosine of average solar zenith angle (top) and average orbit altitude (bottom) (averaged between doy 30.0–35.0)

There are different ways to quantify and compare neutral densities, highlighting specific aspects of the variation. Neutral density can be measured as a global mean (e.g., Solomon et al., 2011), orbit averaged (e.g., Fedrizzi et al., 2012), along orbit tracks (e.g., Shim et al., 2012), absolute (e.g., Yamazaki and Kosch, 2015) and relative, or scaled to a particular altitude (e.g., Kalafatoglu Eyiguler et al., 2019b). In the following we will use the neutral density along the orbit track to avoid any potential biasing due to scaling to a common altitude.

To better compare to the simulated neutral density, the observed neutral density is averaged in 2 h and 4^o geographic latitude bins (each bin includes values from no more than two orbits). The geographic latitude and time variation of the binned neutral density is shown in Figures 3A,B for the night- and day-time orbit, respectively. The enhanced neutral density due to the moderate geomagnetic activity is clearly visible around doy 32 and doy 34. In general the observed neutral density is larger in the southern (SH) than northern (NH) hemisphere, however during the daytime at middle and low latitudes this is not the case.

FIGURE 3

FIGURE 3. Neutral density [kg/m³] at Swarm-C orbit binned in latitude and time: (A). For the night-time orbit, (B). For day-time orbit.

To better quantify the temporal variations of the neutral density we focus on average densities in latitudinal ranges shown in Figure 4. Note that similar to orbit averaged calculation we do not weight by the decreasing area toward the pole. The top and bottom two panels are for the night- and day-time orbit, respectively, for the polar region with 60^o < |λ_g| ≤ 90⁰ on the left, and middle latitude region 20^o < |λ_g| ≤ 60⁰ on the right (λ_g is the geographic latitude). In the polar region during the night-time orbit the SH neutral density is on average approximately 30% larger than in the NH, while during the day-time orbit the SH neutral density is on average 18% larger than in the NH with respect to the average density in both hemispheres. During the night-time orbits there is an approximate 22% difference in the middle latitude neutral density between the two hemispheres but during the day-time both hemispheres have similar average neutral density variations.

FIGURE 4

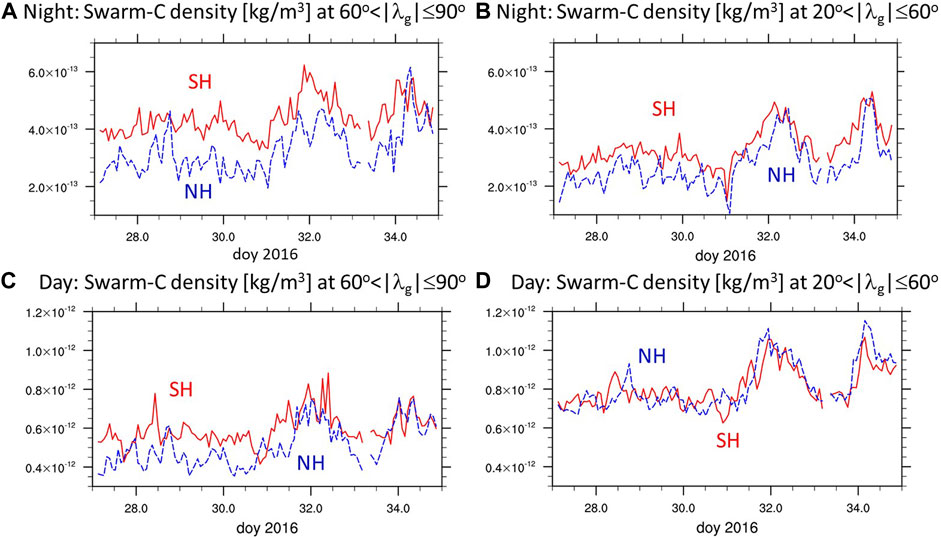
FIGURE 4. Average neutral density [kg/m³] at Swarm-C orbit in different geographic latitude λ_g bins for the SH (red lines) and NH (blue lines): (A). For night-time orbit at 60^o < |λ_g| < 90^o, (B). For night-time orbit at 20^o < |λ_g| < 60^o, (C). For day-time orbit at 60^o < |λ_g| < 90^o, (D). For day-time orbit at 20^o < |λ_g| < 60^o.

Several factors can contribute to the interhemispheric differences in the neutral density. The seasonal solar zenith angle change leads to hemispheric differences in neutral dynamics and composition. Counteracting the seasonally higher neutral density in the SH summer than NH winter is the difference in Swarm orbit altitude. In addition, the lower atmospheric forcing, which itself has an inherent seasonal variation, can modify the thermospheric and ionospheric state, including the neutral density. During geomagnetic storms the enhanced high latitude energy input into the IT system can contribute to hemispheric differences. In the following we will focus on the importance of lower atmospheric and high latitude forcing in simulating the neutral density variations with TIEGCM.

2.2 TIEGCM

The TIEGCM is a self-consistent model which includes atmospheric dynamics, chemistry and energetics of the thermosphere and ionosphere. The ionospheric electrodynamics in the TIEGCM is driven by the wind dynamo, gravity and plasma pressure gradient driven current, and effects due to magnetosphere-ionosphere coupling (Richmond and Maute, 2013). Detailed information about the model can be found in Qian et al. (2014); Maute (2017).

The model spans from approximately 97 km to 450–600 km depending on the solar cycle conditions. We use a horizontal resolution of 2.5^o × 2.5^o in geographic latitude and longitude. At high latitude the magnetosphere-ionosphere coupling is simulated by either prescribing empirical high latitude electric fields based on Weimer (2005) or observed field-aligned current (FAC) based on AMPERE data (Anderson et al., 2000, 2014). The auroral particle precipitation in both simulations is defined via an analytical auroral model (Roble and Ridley, 1987; Emery et al., 2012). Modifications of the default TIEGCM auroral parametrization in the Weimer and FAC driven simulations are described in Supporting Information 1. Hereafter, we label the Weimer driven simulation with “Weimer” and the field-aligned current driven simulation with “FAC”.

The high latitude FAC patterns are derived in the two hemispheres by processing the AMPERE magnetic field observations from the Iridium satellites using principal component analysis as described by Shi et al. (2020). The limited number of used principal components (PC) results in a smoother FAC distribution compared to the original AMPERE field-aligned current. Therefore, the magnitude of the hemispheric integrated upward and downward FAC is reduced using PC based FAC compared to the original AMPERE FAC. To get hemispheric integrated FAC strength comparable to the original AMPERE data, we increase the FAC magnitude in the simulations by 45% in both hemispheres.

Maute et al. (2021) describe the method of prescribing high latitude FAC in the TIEGCM and the key points are summarized in the following. The electric potential is determined in a three step process. In the first step, the electric potential is calculated due to the global wind dynamo and the hemispherically symmetric, with respect to the geomagnetic field, component of the prescribed FAC. In the second step, the FAC at the top of the ionosphere in each magnetic hemisphere due to the symmetric potential solution from step 1 and the local wind dynamo is calculated. The difference between the original prescribed FAC and the calculated FAC from step 2 in a given hemisphere is used in step 3. In step 3 the FAC determined in step 2 in a given hemisphere is prescribed at the upper boundary at high latitudes with a zero potential constraint at the equatorward edge of the region (here at |40^o| magnetic latitude). The potential from step 1 is hemispherically symmetric and from step 3 is hemispherically asymmetric on a magnetic grid. The total electric potential is the sum of the solutions from step 1 and step 3. In each step we have to ensure that the current into and out of the ionosphere are balanced by adjusting the FAC. We distribute any non-balanced FAC according to the local Pedersen conductance as described in Marsal et al. (2012).

At the TIEGCM lower boundary (LB) (approximately at 97 km) we can specify the background variations as well as perturbations in the horizontal wind, neutral temperature, and geopotential height. To evaluate the importance of the lower atmospheric forcing on the neutral density variation we conduct two simulations. In one simulation we use a climatological LB background and perturbations. We employ the tidal climatology from Global Scale Wave Model (GSWM) (Zhang et al., 2010) and specify the LB background using the mass spectrometer and incoherent scatter radar (MSIS00) model and the horizonal wind model (HWM07) (see Jones et al., 2014b; Maute, 2017). GSWM includes the effect of migrating and nonmigrating, diurnal and semidiurnal tidal components. In the TIEGCM GSWM perturbations are specified hourly for the day in the middle of each month and interpolated temporally. We label this simulation with “Climate”.

For comparison we conduct a TIEGCM simulation with the LB specified by output from the Whole Atmosphere Community Climate Model- eXtended with Specified Dynamics (WACCMX-SD) (WACCMX-SD, 2019; Gasperini et al., 2020; Pedatella et al., 2021). WACCM-X is a whole atmosphere climate model spanning from the Earth surface to the thermosphere (Liu et al., 2018). To simulate specific time periods the WACCM-X dynamics are nudged up to approximately 50 km towards reanalysis data, here Modern-Era Retrospective analysis for Research and Applications, Version 2 (MERRA-2) (Gelaro et al., 2017). Using the WACCMX-SD results at the TIEGCM LB allows us to prescribe the specific background “B” and perturbations “P”, including planetary waves and tides, for this time period. We use WACCMX-SD output at the pressure level closest to the TIEGCM LB pressure level. In this study we also examine the effects of a more realistic background atmosphere versus perturbation at the TIEGCM lower boundary on the simulated neutral density. Therefore, the background is represented by the daily zonal and diurnal mean of the horizontal winds, neutral temperature, and geopotential height. The perturbation fields are the difference between the total fields and the background. We label the simulation with WACCMX-SD at the LB as “WacXBP” (B for background and P for perturbation from WACCMX-SD simulation). In a control case we use only the WACCMX-SD perturbations (WacXP) with the climatological background (CB) from the “Climate” simulation and we will refer to this simulation as “WacXP-CB”. We provide an overview of all simulations in Table 1. All simulations are using the TIEGCM but differ by either the lower boundary forcing and/or the high latitude forcing.

TABLE 1

TABLE 1. Overview of simulation set up: all simulations are done with the TIEGCM; the simulations WacXBP and TIEGCM(FAC) are the same and the former abbreviation is used in section 3 highlighting the lower boundary forcing and the latter in section 4 focused on the high latitude forcing; simulations WacXBP, Climate, WacXP-CB, WacXB-symP are described in section 3 while simulations TIEGCM(FAC) and TIEGCM(Weimer) are described in section 4. We abbreviated in the table WACCMX-SD with WACX-SD and climatology with ‟Climat”

We start all simulations at doy 10, 2016 with the respective lower boundary forcing and the high latitude electric potential defined by Heelis et al. (1982) driven by 3-hourly Kp index (Emery et al., 2012). At doy 30 we continued the simulations with the respective high latitude forcing. For comparing with the neutral density from Swarm-C, we determine the TIEGCM simulated neutral density along the Swarm-C orbit and apply the same binning as for Swarm-C data to the synthetic TIEGCM data. Note that for this time period the TIEGCM upper boundary is always above the Swarm-C orbit altitude. To measure the difference between the simulated and observed neutral density we use the sum of the absolute differences (L-1 norm) of the binned data which does not include any weighting by the error magnitude like the root mean square error does. Relative errors are calculated with respect to the sum of the observed Swarm-C neutral density variations if not stated otherwise.

3 Effects of lower atmospheric forcing

We first examine the effect of lower atmospheric forcing on the neutral density at Swarm-C altitude by comparing the simulation with climatological forcing at the lower boundary (Climate) to the simulation with WACCMX-SD at the lower boundary (WacXBP). Both simulations use the same high latitude FAC forcing. Figure 5 illustrates the error in the Climate and WacXBP simulations with respect to Swarm-C neutral density for the night-time orbit in the top row and day-time orbit in the bottom row. The absolute simulated neutral density variation is included in the Supplementary Figure S1.

FIGURE 5

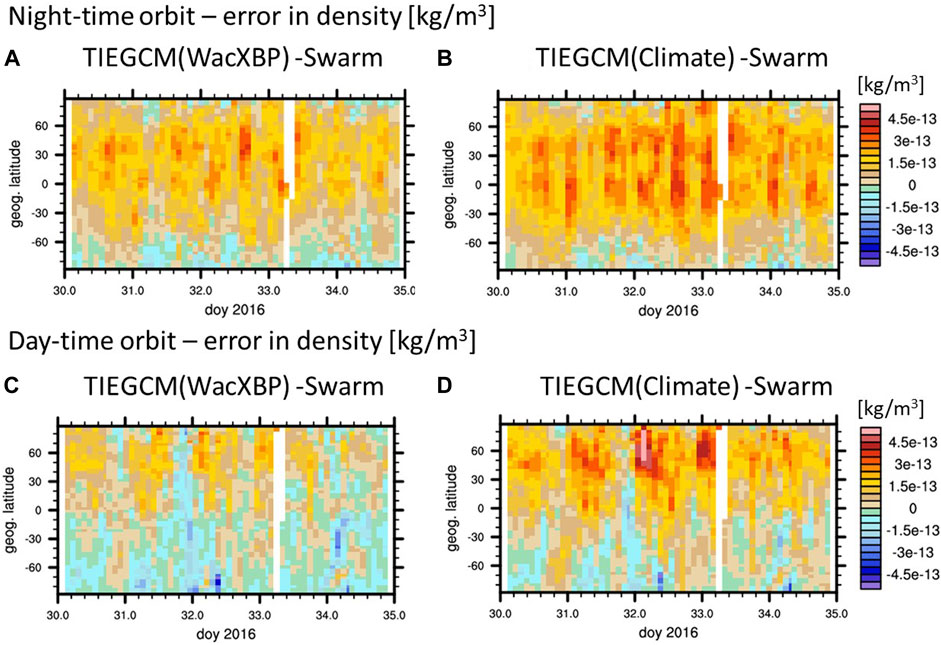
FIGURE 5. Variations for night-time orbit [panel (A–B)] and day-time orbit [panel (C–D)] of neutral density difference between TIEGCM(WacXBP) and Swarm-C [(A). and (C).] and between TIEGCM(Climate) and Swarm-C [(B). and (D).].

In general, the error in the simulated neutral density is larger during the night-time than day-time orbit. During the day-time the simulated neutral density tends to be larger than the observed one in the northern hemisphere while the simulated neutral density tends to be smaller or equal to the observed one in the southern hemisphere. At night-time the simulated neutral density is overestimated almost everywhere except poleward of 60^oS. There is no significant increase in the neutral density error during the disturbed period around doy 32 and 34.

Comparing the error of the Climate simulation (right panels) with the WacXBP simulation (left panels) in Figure 5 illustrates that including more realistic LB variations reduced the error especially in the northern hemisphere. The error is also reduced in the mid- and low-latitude region in the southern hemisphere at night-time but not much at day-time. In the southern polar region there is no large difference between the simulation’s ability to capture the neutral density variations.

In Figure 6 we simplify the results by focusing on the average neutral density variation in specific latitudinal ranges. In general, the error is larger during the night-time. In the illustrated northern hemisphere cases the error is reduced in the WacXBP simulation compared to the Climate one, however the reduction tends to be less during the night-time. We summarize in Table 2 the relative error in the different latitudinal regions. The error is reduced by approximately 15% in the northern hemisphere in the WacXBP simulation compared to the Climate one. While the WacXBP simulation with the wave spectrum from the February 2016 period performs better in capturing the neutral density than using the climatology, we cannot rule out that using lower boundary conditions from other years with similar variability would lead to similar results. Examining this is beyond the scope of the current study which focuses on the general importance of the lower atmosphere and the high latitude forcing.

FIGURE 6

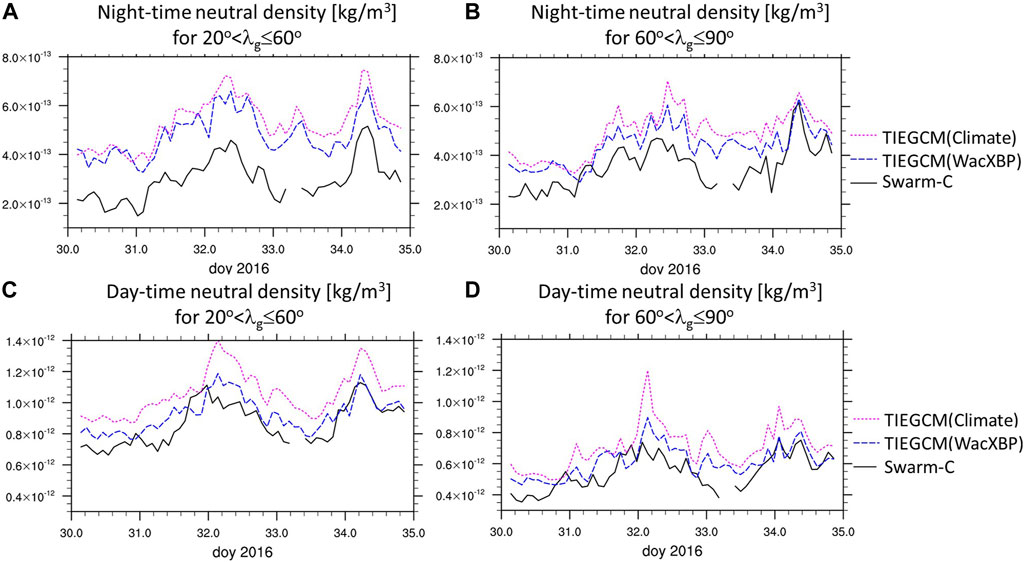
FIGURE 6. Northern hemisphere latitudinal average neutral density variations of Swarm-C (black solid lines), TIEGCM(WacXBP) (dark blue dashed lines), and TIEGCM(Climate) (magenta dotted lines) for night-time orbit (A–B) and day-time orbit (C–D) for 20⁰ < λ_g ≤ 60⁰ (A) and (C) and for 60⁰ < λ_g ≤ 90⁰ (B) and (D).

TABLE 2

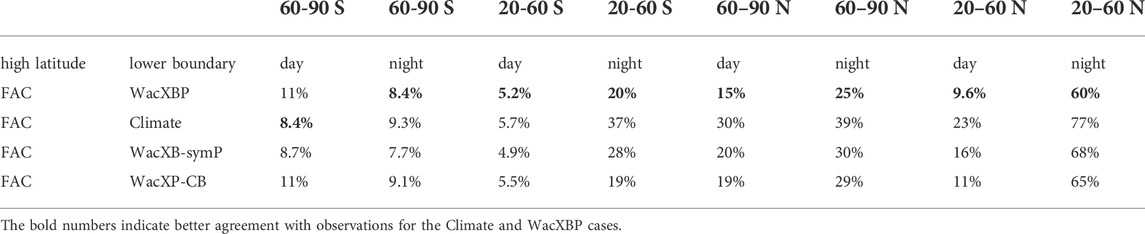
TABLE 2. Relative error with respect to the absolute observed neutral density |ρ_model − ρ_data|₁/|ρ_data|₁ for the different lower atmospheric forcing over the 5 day period (doy 30–34).

In the following we analyze the simulations to better understand the larger improvement in neutral density in the NH compared to the SH. In the lower thermosphere, approximately below 120 km, the zonal mean wind pattern averaged over 5 days (doy 30–34) is different between the Climate and WacXBP simulations (Figure 7A SI Supplementary Figure S2). In Supplementary Figure S5 we provide a simplified schematic to support the main points of the following discussion. The Climate simulation tends to have a summer to winter circulation throughout the thermosphere with upward velocity in the southern hemisphere (poleward of 20 S), a northward turning, and then downward in the northern hemisphere (equatorward of 70 N). In the WacXBP simulation the mean velocity tends to be weakly poleward and downward in the southern hemisphere equatorward of 70 S below approximately 120 km (see SI Supplementary Figure S2).

FIGURE 7

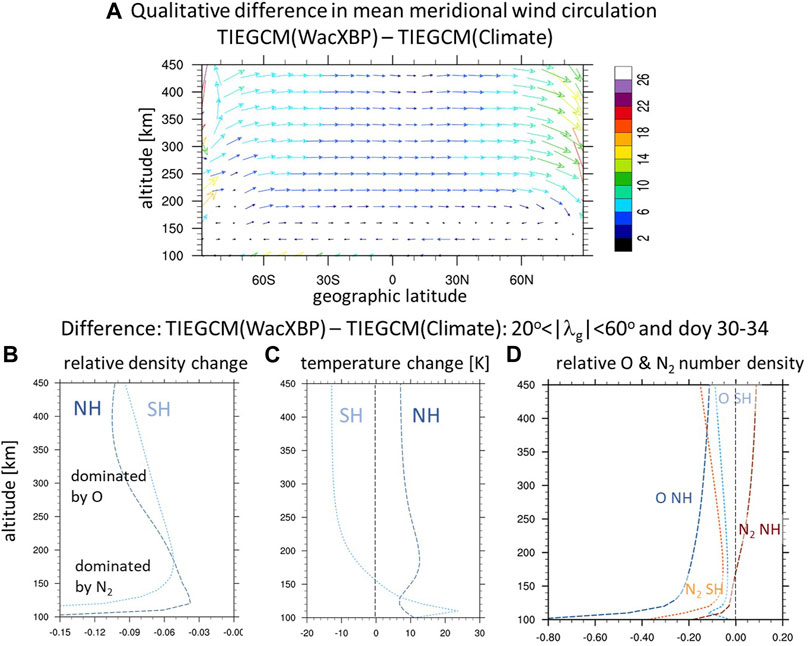
FIGURE 7. (A). Difference between TIEGCM(WacXBP) and TIEGCM(Climate) of doy 30–34 in (A). the diurnal and zonal mean circulation (qualitative, the vertical velocity is increased by a factor of 30 for better illustration); (B–D). average changes over 20^o < |λ_g| ≤ 60^o and doy 30–34 between TIEGCM(WacXBP) and TIEGCM(Climate) with altitude of (B). neutral density with respect to TIEGCM(WacXBP); (C). temperature [K], (D). O and N₂ number density with respect to TIEGCM(WacXBP).

Above approximately 140 km the two simulations have a similar summer to winter circulation. But the WacXBP simulation has a stronger circulation than the Climate simulation, which modifies the temperature and composition (see Figure 7). Figure 7C illustrates the zonal mean neutral temperature changes averaged over 5 days (doy 30–34) between 20⁰ < |λ_g| ≤ 60^o. Above approximately 150 km the WacXBP simulation is colder than the Climate simulation in the SH associated with increased upwelling and adiabatic cooling in the WacXBP case. In the NH there is increased downwelling in the WacXBP simulation leading to a warmer thermosphere compared to the Climate simulation.

Below approximately 140km the WacXBP simulation is warmer in the southern hemisphere than the Climate simulation probably associated with the tendency of more downward or less upward circulation in the WacXBP simulation compared to the Climate simulation. The mean circulation and the temperature influence the composition and neutral density. Below approximately 180 km the N₂ number density is larger than the O₁ number density and therefore a larger contributor to the neutral density. In the southern hemisphere below approximately 140 km, the N₂ number density is decreased in the WacXBP versus the Climate simulation (Figure 7D) since the Climate simulation’s upward velocity transports N₂ from regions of larger number densities to higher altitudes, while the WacXBP simulation has downward or less upward velocity in this region. This decrease in N₂ in the lower thermosphere leads to the reduced neutral density in the southern hemisphere in the WacXBP compared to the Climate case at these altitudes (Figure 7B).

In the northern hemisphere the circulation at the lower altitudes is not significantly different between the simulations. The results suggest that increased tidal variability and associated mixing of the atmosphere leads to smaller N₂ number density in the WacXBP case compared to the Climate simulation which is then reflected in the smaller neutral density at these altitudes in WacXBP compared to the Climate simulation.

At Swarm altitudes around 450km atomic oxygen is expected to be the dominant species. In general, the scale height is larger in the summer than in the winter hemisphere, leading to smaller vertical gradients in the O₁ number density in the southern summer than northern winter hemisphere. Due to larger vertical gradients in the NH the changes in the vertical velocity due to the LB boundary will have increased effects on the number density in the northern winter hemisphere than southern summer hemisphere (Qian and Yue, 2017). In the northern hemisphere an increased downwelling in the WacXBP simulation compared to the Climate one (see SI Supplementary Figure S2) transports more efficiently O₁ into regions of higher recombination rates leading to a larger reduction of O₁. Since the scale height in the northern hemisphere tends to be larger in the WacXBP than in the Climate simulation, the absolute difference in O₁ number density between the simulations decreases with altitude (Figure 7D).

In the SH the absolute change in O₁ number density between the simulations are much smaller than in the NH but as in the NH the O₁ number density in the WacXBP simulation is smaller than in the Climate simulation. This might be associated with the competing effects of more atmospheric mixing due to increased tidal variability and vertical winds in the WacXBP simulation. The absolute difference in O₁ number density between the Climate and WacXBP simulations grows slowly with altitude most likely associated with the larger mean temperature and scale height in the Climate than WacXBP simulation in the southern hemisphere. Therefore, the southern hemisphere absolute neutral density changes between Climate and WacXBP simulation increase almost linearly with altitude but are smaller than the absolute difference in the NH between approximately 200–470 km. The simulations suggest that eventually at higher altitudes (above 450 km) the average changes in O₁ number density due to different lower boundary forcings will be similar in both hemispheres (Figure 7D).

The simulations suggest that the magnitude of the interhemispheric difference in the neutral density response to the lower atmospheric forcing depends on altitude and that in the upper thermosphere the maximum interhemispheric difference is around 350 km. Swarm-C is above the maximum differences but still in the altitude region where the NH response to LB changes is stronger than the SH response.

To delineate the effect of LB perturbations and LB background (zonal and diurnal mean) on the IT system, we conduct an additional simulation with WACCMX-SD perturbations (WacXP) by replacing the WacXB background with the climatological LB background from the Climate simulation (CB). The differences between this WacXP-CB simulation and the previously described WacXBP simulation can be attributed to the difference in the LB background forcing. The result is summarize in Table 2 labeled by WacXP-CB. The error is only slightly increased using WacXP-CB compared to WacXBP. This finding aligns with previous studies (e.g., Jones et al., 2014b; Maute, 2017) pointing out that details of the LB background forcing are less important than the LB perturbations.

While the presented numerical experiments indicate that the LB perturbations are important to capture the large scale neutral density variations in simulations, it is less understood if hemispherically asymmetric component in the WACCMX-SD perturbations contribute especially to the hemispheric difference in the response. We conduct a simplified numerical experiment by including only symmetric LB perturbations based on WACCMX-SD output labeled “WacXB-symP” and the results are summarized in Table 2. For this simulation we include at the LB symmetric zonal wind, temperature and geopotential height, and antisymmetric meridional winds (meridional winds are positive northward) with respect to the geographic equator. Omitting any asymmetric perturbations in the LB leads to an increase in the error difference between southern and northern hemisphere in most latitude regions. Compared to the WacXBP simulation there are systematic changes with up to 2% reduced error in the SH and up to 8% larger error in the NH. More detailed studies are needed to understand the different effect in the two hemispheres. Overall, the simulation results suggest that the asymmetric LB perturbations contributes to the hemispheric differences in the neutral density but it is not the sole driver of such differences.

4 Effects of high latitude forcing

Details of the magnetospheric energy input into the IT system are important especially when examining regional and local effects in the thermosphere and ionosphere, such as the cusp neutral density enhancements (e.g., Lühr et al., 2004; Lu et al., 2016). It is less clear if a more realistic description of high-latitude forcing is also important for the large scale response at middle and low latitudes. Therefore, in the following, we compare the simulation using the empirical Weimer electric field model (labeled Weimer) to the simulation using field-aligned current based on AMPERE observations (labeled FAC). Both simulations use WACCMX-SD forcing at the TIEGCM lower boundary.

Figure 8 illustrates the latitude-time variation of the neutral density error between the simulations and Swarm-C observations. In general TIEGCM(FAC) outperforms the TIEGCM(Weimer) with a smaller neutral density error of up to 7%–20% in the northern hemisphere especially during the night-time. However, the neutral density error of TIEGCM(FAC) and TIEGCM(Weimer) is similar during the day-time at northern middle latitudes. In the southern middle latitude region the night-time orbit neutral density agreement with Swarm-C is improved using TIEGCM(FAC) but otherwise the TIEGCM(Weimer) simulation has slightly smaller errors by 1–3% in the southern hemisphere compared to TIEGCM(FAC).

FIGURE 8

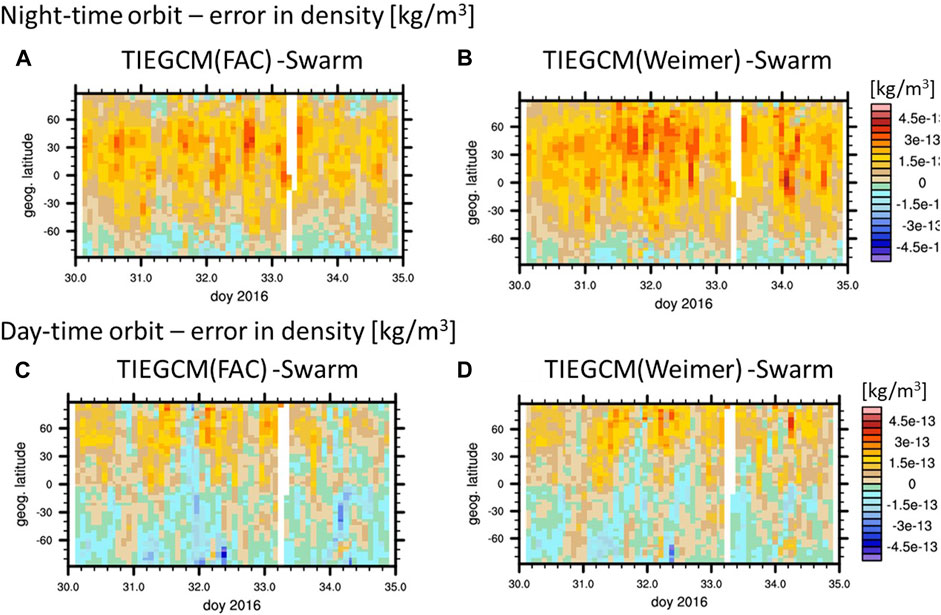
FIGURE 8. Neutral density difference between TIEGCM(FAC) and Swarm-C (A) and (C) and between TIEGCM(Weimer) and Swarm-C (B) and (D) for night-time orbit (A) and (B) and day-time orbit (C) and (D).

The neutral density error is in general larger in the northern than southern hemisphere especially for the night-time orbit as illustrated in Figure 9B by the neutral density variation poleward of |60^o| geographic latitude. The average errors are summarized in Table 3. Using FAC forcing instead of Weimer leads to larger neutral density changes and improvement at Swarm-C orbit at northern high latitudes, especially during the night-time (Figure 9B blue line), than in southern hemisphere (Figure 9A). This hemispheric difference in the response to the different high latitude forcing cannot be solely explained by the hemispheric difference in Joule heating between the simulations. In Figure 10B we illustrate the difference in hemispheric integrated Joule heating (poleward of 50^o geographic latitude) between the TIEGCM(FAC) and TIEGCM(Weimer) simulations. In general, the northern and southern polar region have similar differences in Joule heating input into the IT system between the two simulations.

FIGURE 9

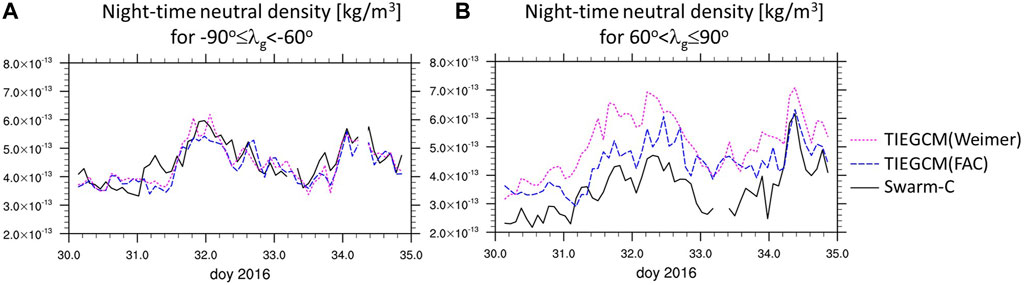
FIGURE 9. Night-orbit high latitudinal average neutral density variations of Swarm-C (black solid lines), TIEGCM(Weimer) (magenta dotted lines), and TIEGCM(FAC) (blue dashed lines) for night-time orbit for − 90⁰ ≤ λ_g < − 60⁰ (A) and for 60⁰ < λ_g ≤ 90⁰ (B).

TABLE 3

TABLE 3. Relative error with respect to the absolute observed neutral density |ρ_model − ρ_data|₁/|ρ_data|₁ averaged over doy 30–34 for different high latitude forcing.

FIGURE 10

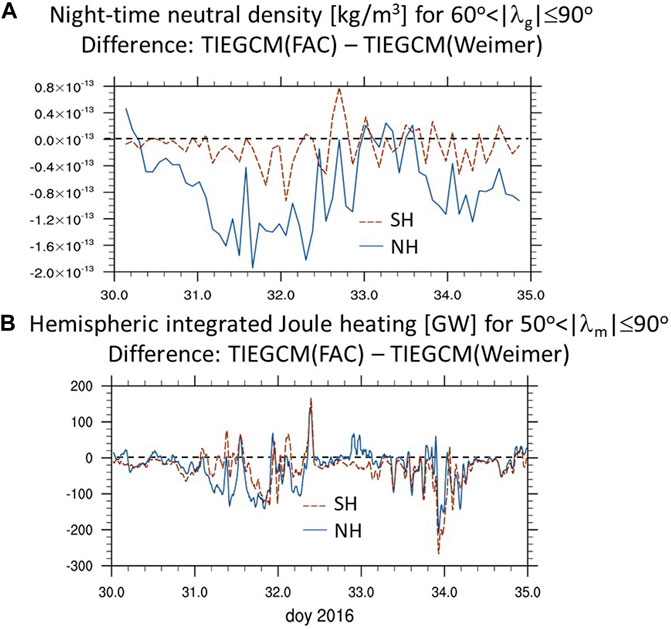
FIGURE 10. Difference of (A). night-orbit high latitudinal averaged (60⁰ < |λ_g| ≤ 90⁰) neutral density [kg/m³] between TIEGCM(FAC) and TIEGCM(Weimer) and (B). of height and high latitudinal integrated (50⁰ < |λ_m| ≤ 90⁰) Joule heating rate [GW] between TIEGCM(FAC) and TIEGCM(Weimer) for northern hemisphere (blue solid line) and southern hemisphere (orange dashed line).

There is no simple connection between the neutral density difference of the two simulations in the two hemispheres (Figure 10A) and the Joule heating difference of the two simulations in the two hemispheres (Figure 10B). A simple correlation between the difference in neutral density and hemispheric integrated Joule heating of the two simulations in each hemisphere is very low, even when considering a time lag (northern hemisphere correlation coefficient r = 0.45 and southern hemisphere r = 0.3). Note that a difference of approximately 100 GW in Figure 10B around doy 31.5 to 32.0 represents around 40–50% of the total hemispheric integrated Joule heating from the TIEGCM(Weimer) and almost 100% of the TIEGCM(FAC) (see SI Supplementary Figure S4 for the absolute Joule heating variation).

To better understand why similar amount of Joule heating differences leads to larger neutral density difference in the northern than southern high latitude region we focus on average quantities poleward of 60^o geographic latitude at 3 h SLT for doy 31.5 to 32.0. During this time period there is a similar hemispheric integrated Joule heating difference between the simulations in the two hemispheres (Figure 10B) but the neutral density difference is smaller in the SH than in the NH (Figure 10A).

Figure 11A reiterates that in the upper thermosphere the neutral density difference is much larger in the NH than SH. The effect of Joule heating becomes more pronounce in the dark winter hemisphere, since the same amount of Joule heating difference between the two simulations yields a much larger neutral temperature change in the NH than in the SH (Figure 11C). In addition, Figure 11B shows that the TIEGCM(Weimer) simulation compared to the TIEGCM(FAC) simulation has a slightly larger integrated Joule heating value in the NH than SH and that the energy tends to be dissipated at higher altitudes (above 120 km) in the NH than SH where it can change more efficiently the atmosphere and the neutral density (Deng et al., 2011; Huang et al., 2012). The results are illustrated for 3 h SLT but are similar for 2–4 h SLT.

FIGURE 11

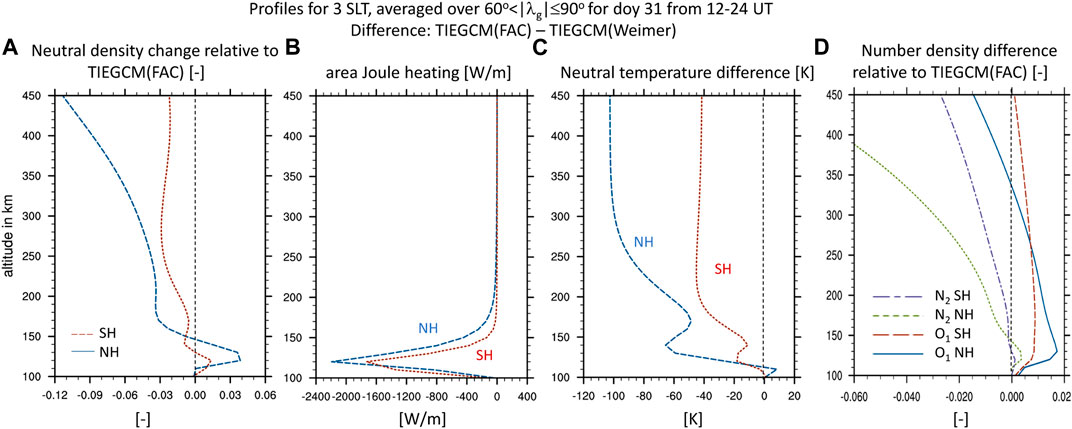
FIGURE 11. Profiles of differences between TIEGCM(FAC) and TIEGCM(Weimer) for northern hemisphere (dark blue dashed lines) and southern hemisphere (dark orange dotted lines)at 3 h SLT averaged between 60⁰ < |λ_g| ≤ 90⁰ and doy 31.5 to 32. (A). relative neutral density change with respect to TIEGCM(FAC), (B). integrated Joule heating difference [W/m], (C). neutral temperature difference [K], and (D). number density difference with respect to TIEGCM(FAC) for N₂ (green short dashed for north, purple long-short dashed for south) and O₁ (blue solid for north and orange long dashed for south).

The relative difference in the composition between these two simulations is shown in Figure 11D. Below approximately 150 km the N₂ number density in TIEGCM(FAC) is larger than in TIEGCM(Weimer) in the NH and this difference is slightly larger than in the SH leading to an associated positive neutral mass density difference (Figure 11A). The difference in atomic oxygen is positive in both hemispheres below approximately 340 km. In the northern hemisphere the smaller scale height in TIEGCM(FAC) compared to TIEGCM(Weimer) eventually leads to negative differences in atomic oxygen above approximately 340 km with values from TIEGCM(FAC) being smaller than from TIEGCM(Weimer). Above approximately 150 km the northern hemisphere N₂ number density in TIEGCM(FAC) becomes smaller with increasing altitude compared to values from TIEGCM(Weimer). Between 180km and 230km the NH neutral density difference is more-or-less constant in altitude which might indicate that the positive atomic oxygen difference tends to compensate for the faster decrease in N₂ number density in the TIEGCM(FAC) compared to TIEGCM(Weimer). However, above 300 km the NH neutral density difference between the two simulations becomes more negative with increasing altitude associated with the temperature and compositional changes.

Compared to the northern hemisphere, the southern hemisphere differences in N₂ and O₁ between the TIEGCM(FAC) and TIEGCM(Weimer) simulations are much smaller, mostly negative for N₂ and positive for O₁, and less changing with altitude than in the northern hemisphere. The smaller SH than NH neutral density difference between the TIEGCM(FAC) and TIEGCM(Weimer) simulations at almost all altitudes might be associated with the increase in O₁ number density at all altitudes and the smaller reduction in N₂ number density together with a smaller temperature change in the SH than NH below 450 km. The southern neutral density difference between the simulations is almost constant between 250 km and 450 km but should become increasingly negative above 450 km.

Even during this moderate geomagnetically disturbed period the dynamical and compositional changes are complex. The TIEGCM(Weimer) simulation has stronger equatorward thermospheric winds in the NH compared to the TIEGCM(FAC) simulation and the TIEGCM(FAC) exhibits even some poleward winds at subauroral regions in the NH. These neutral wind differences might contribute to the more equatorward movement of the zonal mean atomic oxygen peak in the TIEGCM(Weimer) simulation from 60 N at quiescent time to approximately 35 N while the zonal mean atomic oxygen peak for the TIEGCM(FAC) simulation moves only to 45 N (not depicted). In the TIEGCM(FAC) simulation the atomic oxygen below 350km is larger in the polar region compared to the TIEGCM(Weimer) simulation. Comparing the TIEGCM(Weimer) to TIEGCM(FAC) simulation suggests it might be associated with the increased and steady meridional transport of atomic oxygen away from the polar region.

Many studies focus on the effect of the geomagnetic activity by subtracting a quiescent time variation from the neutral density. In the following we evaluate if the details of the lower atmospheric forcing also influences the neutral density result when removing the average quiescent time variation. For that purpose we will use the Climate and WacXBP simulations and remove an average quiescent time latitudinal variation leading to the “disturbed” neutral density.

Figures 12A,D illustrate the Swarm-C “disturbed” neutral density with the average quiescent time latitudinal variation between doy 30, 0–22 UT removed. As expected, the moderate geomagnetically disturbed period is emphasized around doy 32 and doy 34. The same procedure of removing the quiescent time latitudinal variation is applied to the simulations. The simulation error is determined by subtracting the “disturbed” Swarm-C neutral density. Comparing the error of the TIEGCM(WacXBP) simulation (Figure 12B,E) with the error of the TIEGCM(Climate) simulation (Figure 12C,F) indicates that the error tends to be smaller using WacXBP at the lower boundary.

FIGURE 12

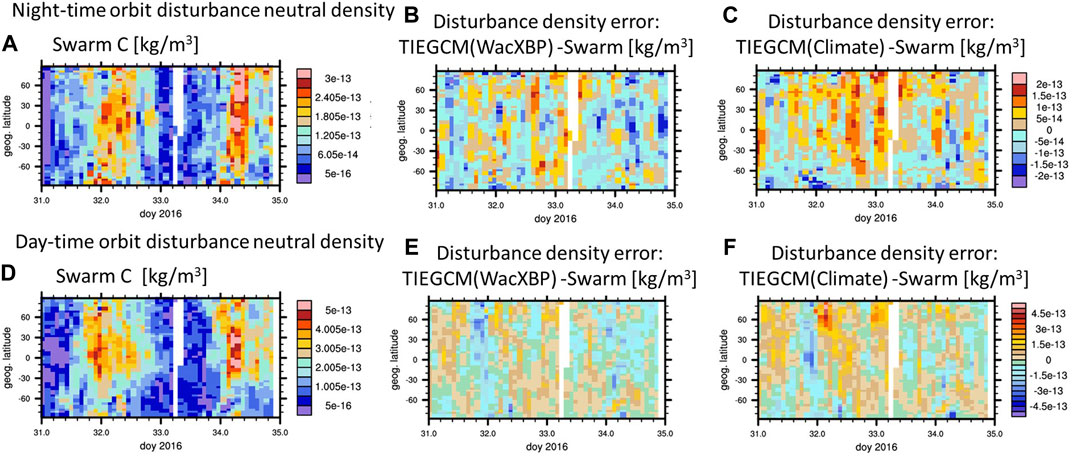
FIGURE 12. Disturbance neutral density variation by removing average of doy 30 UT 0–21 for night-time orbit [panel (A–C)] and day-time orbit (D) and (F) of Swarm C disturbance neutral density (A) and (D) and difference of disturbance variations between TIEGCM(WacXBP) and Swarm-C (B) and (E) and between TIEGCM(Climate) and Swarm-C (C) and (F).

To provide a more objective measure we determine the relative error which is summarized in Table 4. As before we calculate the relative error with respect to the total Swarm-C neutral density over the whole time period but with the difference that the numerator represents the “disturbed” contribution. Therefore the relative error tends to be lower compared to the previously presented errors but the percentage difference can be better compared to the previous results since the denominator is the same. There is a slight, approximately 1–1.5% average improvement, in the”‘disturbance”’ neutral density in the northern hemisphere with WacXBP at the lower boundary as compared with the simulation with climatology at the lower boundary, but locally the improvement can be larger (see Figure 12).

TABLE 4

TABLE 4. Relative error of the disturbance neutral density variation (by removing the average quiescent time variation of doy 30 UT 0–22) for using WacXBP and climatology at the lower boundary with respect to the absolute observed neutral density |Δρ_model − Δρ_data|₁/|ρ_data|₁ for doy 30.0 to 35.0.

5 Conclusion

In this study we focus on large scale neutral density variations between Swarm-C observations and TIEGCM simulations during the moderate geomagnetically disturbed period of 31 January to 3 February 2016. The larger neutral density error between the simulated and observed neutral density in the northern than southern hemisphere motivated us to examine the influence of the lower atmospheric forcing as well as the high latitude forcing on the simulated neutral density variations.

We found that using lower atmospheric forcing based on WACCM-X with specified dynamics compared to using climatological lower atmospheric forcing improves the agreement of the simulation with the observed neutral density, even during the disturbed condition. The improvements are larger in northern (up to 15%) than southern hemisphere during this February period and emphasize the importance of the background atmospheric conditions in facilitating the neutral density change. In general, the winter northern hemisphere is more sensitive to changes associated with LB forcing, leading to larger temperature and compositional changes compared to the southern sunlit hemisphere. While we have seen a larger response at Swarm altitudes to the lower atmospheric forcing in the northern than southern hemisphere, we want to emphasize that the simulation suggest that the magnitude and direction of the change are altitude dependent. The presented simulations suggest that above approximately 470 km (at middle latitudes) the southern hemisphere is more susceptible to the changes in the lower atmospheric forcing. Hemispheric differences in the employed LB forcing contribute to the interhemispheric difference in the neutral density at Swarm-C altitude but do not dominate them. Our study does not address the question of the importance of an accurate wave spectrum versus the importance of generally increased tidal activity at the lower boundary for capturing observed neutral density variation. Future studies should examine the details of the lower atmospheric forcing and their importance for capturing the large scale neutral density and its variability.

While more realistic LB variations compared to climatological LB forcing leads to a neutral density improvement of approximately 15% in the NH, more realistic high latitude forcing improves the neutral density by 7%–15% compared to using empirical high latitude forcing, and again a larger improvement is seen in the northern than southern hemisphere. Further examination indicates that the larger improvement in the northern compared to southern neutral density cannot be solely attributed to the difference in Joule heating input between the simulations. Closer examination of a specific time period indicates that there is a slight difference in Joule heating magnitude in the two hemispheres between the simulations but more importantly more Joule heating is dissipated at higher altitudes in the northern hemisphere in the TIEGCM(Weimer) compared to the TIEGCM(FAC) simulation, where it can more effective change the neutral density aloft (Deng et al., 2011; Huang et al., 2012). In addition, there is a seasonal effect that energy deposited in the winter hemisphere leads in general to larger changes in temperature and composition (Qian and Yue, 2017) compared to the sunlit hemisphere and therefore contributing to the larger neutral density change in the NH than SH. The simulations indicate that the difference in neutral dynamics due to the different high latitude forcing contribute to the neutral density changes by modifying the transport of constituents.

When focusing on the disturbance neutral density variations by removing the quiescent time variation, more realistic lower atmospheric forcing via WacXBP in a simulation still leads to better agreement with the observed disturbances by 1–1.5% on average compared to using tidal climatology at the simulation lower boundary. This average improvement in the “disturbance” density is much smaller than the improvement considering the total neutral density, but the local improvement along the orbit can be larger. We want to note that the presented results depend on how the quiescent variations is defined.

The study highlights the importance of realistic forcing specification at both lower and upper boundary of the IT system even during moderate geomagnetically disturbed period. The background atmospheric conditions are very important to determine the response of the atmosphere to lower atmospheric forcing and to high latitude forcing. Methods correlating Joule heating to neutral density changes (e.g., Kalafatoglu Eyiguler et al., 2019a) need to consider the atmospheric background conditions. The simulations indicate larger night-time than day-time errors in neutral density which can be partially attributed to a bias in ion and viscous drag forces influencing the neutral wind and day-night temperature difference (Hsu et al., 2016). More systematic studies are needed to evaluate the efficiency of realistic concurrent lower atmospheric variations and high latitude forcing on the middle and low latitude thermosphere during different seasons and geophysical conditions.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: The TIEGCM results associated with this publication are available at the UCAR/NCAR Geoscience Data Exchange (GDEX) https://doi.org/10.5065/22v8-b441. The Iridium derived data products are available at the AMPERE Science Center at http://ampere.jhuapl.edu/dataget/index.html. The Swarm neutral density is available from the European Space Agency at https://swarm-diss.eo.esa.int/\#swarm\%2FLevel2daily\%2FLatest\_baselines\%2FDNS\%2FACC\%2FSat\_C. The solar wind parameters are available from the NASA/GSFC's Space Physics Data Facility's OMNIWeb service at https://omniweb.gsfc.nasa.gov/form/omni\_min.html.

Author contributions

AM conducted the analysis, drafted the manuscript and worked on the interpretation of the analysis. GL contributed to the interpretation of the data and simulations. DK provided the optimal interpolation maps for the field-aligned current used in the TIEGCM. BA and SV provided the magnetic perturbations used in the optimal interpolation maps for the FAC. AM, GL, DK, BA, and SV contributed to the interpretation of data analysis.

Funding

AM, GL, DK, BA and SV are in part supported by NASA Living with a Star grant 80NSSC20K1784. AM and GL are partly funded by AFOSR through award FA9559-17-1–0248. GL is supported in part by the Living With a Star program under NASA grant 80NSSC17K0719 and by the Heliophysics Supporting Research program under NASA grant 80NSSC21K1673. We would like to acknowledge high-performance computing support from Cheyenne (doi:10.5065/D6RX99HX) provided by NCAR’s Computational and Information Systems Laboratory, sponsored by the National Science Foundation. This material is based upon work supported by the National Center for Atmospheric Research, which is a major facility sponsored by the National Science Foundation under Cooperative Agreement No. 1852977.

Acknowledgments

AM would like to thank Christian Siemes for helping with the Swarm-C neutral density data and Art Richmond for helpful comments on an earlier draft.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2022.932748/full#supplementary-material

References

Anderson, B., Korth, H., Waters, C., Green, D., Merkin, V., Barnes, R., et al. (2014). Development of large-scale birkeland currents determined from the active magnetosphere and planetary electrodynamics response experiment. Geophys. Res. Lett. 41, 3017–3025. doi:10.1002/2014GL059941

CrossRef Full Text | Google Scholar

Anderson, B., Takahashi, K., and Toth, B. A. (2000). Sensing global Birkeland currents with Iridium engineering magnetometer data. Geophys. Res. Lett. 27, 4045–4048. doi:10.1029/2000GL000094

CrossRef Full Text | Google Scholar

Bruinsma, S. L., and Forbes, J. M. (2009). Properties of traveling atmospheric disturbances (TADs) inferred from CHAMP accelerometer observations. Adv. Space Res. 43, 369–376. doi:10.1016/j.asr.2008.10.031

CrossRef Full Text | Google Scholar

[Dataset] WACCMX-SD (2019). Dataset: SD WACCM-X V2.1. Climate Data Gateway at NCAR. doi:10.26024/5b58-nc53

CrossRef Full Text | Google Scholar

Deng, Y., Fuller-Rowell, T. J., Akmaev, R. A., and Ridley, A. J. (2011). Impact of the altitudinal Joule heating distribution on the thermosphere. J. Geophys. Res. 116. doi:10.1029/2010ja016019

CrossRef Full Text | Google Scholar

Deng, Y., Fuller-Rowell, T. J., Ridley, A. J., Knipp, D., and Lopez, R. E. (2013). Theoretical study: Influence of different energy sources on the cusp neutral density enhancement. JGR. Space Phys. 118, 2340–2349. doi:10.1002/jgra.50197

CrossRef Full Text | Google Scholar

Emery, B., Roble, R., Ridley, E., Richmond, A., Knipp, D., Crowley, G., et al. (2012). Parameterization of the ion convection and the auroral oval in the NCAR thermospheric general circulation models. Boulder CO, USA: Tech. rep., National Center for Atmospheric Research. doi:10.5065/D6N29TXZ

CrossRef Full Text | Google Scholar

Emmert, J. T., Drob, D. P., Picone, J. M., Siskind, D. E., Jones, M., Mlynczak, M. G., et al. (2021). Nrlmsis 2.0: A whole-atmosphere empirical model of temperature and neutral species densities. Earth Space Sci. 8, 1. doi:10.1029/2020EA001321

CrossRef Full Text | Google Scholar

Emmert, J. (2015). Thermospheric mass density: A review. Adv. Space Res. 56, 773–824. doi:10.1016/j.asr.2015.05.038

CrossRef Full Text | Google Scholar

Fedrizzi, M., Fuller-Rowell, T. J., and Codrescu, M. V. (2012). Global Joule heating index derived from thermospheric density physics-based modeling and observations. Space Weather 10. doi:10.1029/2011SW000724

CrossRef Full Text | Google Scholar

Forbes, J. M. (2007). Dynamics of the thermosphere. J. Meteorological Soc. Jpn. 85, 193–213. doi:10.2151/jmsj.85b.193

CrossRef Full Text | Google Scholar

Fuller-Rowell, T. J. (1998). The “thermospheric spoon”: A mechanism for the semiannual density variation. J. Geophys. Res. 103, 3951–3956. doi:10.1029/97JA03335

CrossRef Full Text | Google Scholar

Gasperini, F., Liu, H., and McInerney, J. (2020). Preliminary evidence of Madden-Julian oscillation effects on ultrafast tropical waves in the thermosphere. JGR. Space Phys. 125, e2019JA027649. doi:10.1029/2019JA027649

CrossRef Full Text | Google Scholar

Gelaro, R., McCarty, W., Suárez, M. J., Todling, R., Molod, A., Takacs, L., et al. (2017). The modern-era retrospective analysis for research and applications, version 2 (MERRA-2). J. Clim. 30, 5419–5454. doi:10.1175/JCLI-D-16-0758.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Gonzalez, W. D., Joselyn, J. A., Kamide, Y., Kroehl, H. W., Rostoker, G., Tsurutani, B. T., et al. (1994). What is a geomagnetic storm? J. Geophys. Res. 99, 5771–5792. doi:10.1029/93JA02867

CrossRef Full Text | Google Scholar

Heelis, R. A., Lowell, J. K., and Spiro, R. W. (1982). A model of the high-latitude ionospheric convection pattern. J. Geophys. Res. 87, 6339–6345. doi:10.1029/JA087iA08p06339

CrossRef Full Text | Google Scholar

Hsu, V. W., Thayer, J. P., Wang, W., and Burns, A. (2016). New insights into the complex interplay between drag forces and its thermospheric consequences. JGR. Space Phys. 121, 10–417. doi:10.1002/2016ja023058

CrossRef Full Text | Google Scholar

Huang, Y., Richmond, A. D., Deng, Y., and Roble, R. (2012). Height distribution of Joule heating and its influence on the thermosphere. J. Geophys. Res. 117. doi:10.1029/2012JA017885

CrossRef Full Text | Google Scholar

Jones, M., Forbes, J. M., Hagan, M. E., and Maute, A. (2014b). Impacts of vertically propagating tides on the mean state of the ionosphere-thermosphere system. J. Geophys. Res. Space Phys. 119, 2197–2213. doi:10.1002/2013JA019744

CrossRef Full Text | Google Scholar

Jones, M., Forbes, J. M., and Hagan, M. E. (2014a). Tidal-induced net transport effects on the oxygen distribution in the thermosphere. Geophys. Res. Lett. 41, 5272–5279. doi:10.1002/2014gl060698

CrossRef Full Text | Google Scholar

Kalafatoglu Eyiguler, E. C., Kaymaz, Z., Kuznetsova, M. M., Soon Shim, J., and Rastätter, L. (2019a). “Relation between Joule heating and thermospheric neutral density during geomagnetic storms,” in 2019 9th international conference on recent Advances in Space technologies (RAST) (IEEE), 663–666. doi:10.1109/RAST.2019.8767867

CrossRef Full Text | Google Scholar

Kalafatoglu Eyiguler, E. C., Shim, J. S., Kuznetsova, M. M., Kaymaz, Z., Bowman, B. R., Codrescu, M. V., et al. (2019b). Quantifying the storm time thermospheric neutral density variations using model and observations. Space Weather 17, 269–284. doi:10.1029/2018SW002033

CrossRef Full Text | Google Scholar

Knipp, D., Tobiska, W. K., and Emery, B. (2004). Direct and indirect thermospheric heating sources for solar cycles 21–23. Sol. Phys. 224, 495–505. doi:10.1007/s11207-005-6393-4

CrossRef Full Text | Google Scholar

Liu, H.-L., Bardeen, C. G., Foster, B. T., Lauritzen, P., Liu, J., Lu, G., et al. (2018). Development and validation of the whole atmosphere community climate model with thermosphere and ionosphere eXtension (WACCM-X 2.0). J. Adv. Model. Earth Syst. 10, 381–402. doi:10.1002/2017ms001232

CrossRef Full Text | Google Scholar

Liu, H.-L. (2016). Variability and predictability of the space environment as related to lower atmosphere forcing. Space Weather 14, 634–658. doi:10.1002/2016sw001450

CrossRef Full Text | Google Scholar

Liu, H., Thayer, J., Zhang, Y., and Lee, W. K. (2017). The non–storm time corrugated upper thermosphere: What is beyond MSIS? Space Weather 15, 746–760. doi:10.1002/2017SW001618

CrossRef Full Text | Google Scholar

Lu, G., Richmond, A. D., Lühr, H., and Paxton, L. (2016). High-latitude energy input and its impact on the thermosphere. JGR. Space Phys. 121, 7108–7124. doi:10.1002/2015JA022294

CrossRef Full Text | Google Scholar

Lühr, H., Rother, M., Köhler, W., Ritter, P., and Grunwaldt, L. (2004). Thermospheric up-welling in the cusp region: Evidence from CHAMP observations. Geophys. Res. Lett. 31. doi:10.1029/2003gl019314

CrossRef Full Text | Google Scholar

Marsal, S., Richmond, A., Maute, A., and Anderson, B. (2012). Forcing the TIEGCM model with birkeland currents from the active magnetosphere and planetary electrodynamics response experiment. J. Geophys. Res. 117. doi:10.1029/2011JA017416

CrossRef Full Text | Google Scholar

Maute, A., Richmond, A. D., Lu, G., Knipp, D. J., Shi, Y., and Anderson, B. (2021). Magnetosphere-ionosphere coupling via prescribed field-aligned current simulated by the tiegcm. JGR. Space Phys. 126. doi:10.1029/2020JA028665

CrossRef Full Text | Google Scholar

Maute, A. (2017). Thermosphere-ionosphere-electrodynamics general circulation model for the ionospheric connection explorer: TIEGCM-ICON. Space Sci. Rev. 212, 523–551. doi:10.1007/s11214-017-0330-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Müller, S., Lühr, H., and Rentz, S. (2009). Solar and magnetospheric forcing of the low latitude thermospheric mass density as observed by champ. Ann. Geophys. 27, 2087–2099. doi:10.5194/angeo-27-2087-2009

CrossRef Full Text | Google Scholar

Pedatella, N. M., Liu, H.-L., Conte, J. F., Chau, J. L., Hall, C., Jacobi, C., et al. (2021). Migrating semidiurnal tide during the september equinox transition in the northern hemisphere. Geophys. Res. Atmos. 126. doi:10.1029/2020JD033822

CrossRef Full Text | Google Scholar

Prölss, G. W. (2011). Density perturbations in the upper atmosphere caused by the dissipation of solar wind energy. Surv. Geophys. 32, 101–195. doi:10.1007/s10712-010-9104-0

CrossRef Full Text | Google Scholar

Qian, L., Burns, A. G., Emery, B. A., Foster, B., Lu, G., Maute, A., et al. (2014). The NCAR TIE-GCM: A community model of the coupled thermosphere/ionosphere system. Model. Ionosphere-Thermosphere Syst. Geophys. Monogr. Ser 201, 73–83.

CrossRef Full Text | Google Scholar

Qian, L., Solomon, S. C., and Kane, T. J. (2009). Seasonal variation of thermospheric density and composition. J. Geophys. Res. 114. doi:10.1029/2008JA013643

CrossRef Full Text | Google Scholar

Qian, L., and Solomon, S. C. (2012). Thermospheric density: An overview of temporal and spatial variations. Space Sci. Rev. 168, 147–173. doi:10.1007/s11214-011-9810-z

CrossRef Full Text | Google Scholar

Qian, L., and Yue, J. (2017). Impact of the lower thermospheric winter-to-summer residual circulation on thermospheric composition. Geophys. Res. Lett. 44, 3971–3979. doi:10.1002/2017GL073361

CrossRef Full Text | Google Scholar

Richmond, A. D. (2021). “Joule heating in the thermosphere,” in Upper atmosphere dynamics and energetics. Editors L. P. W. Wang, and Y. Zhang (USA: American Geophysical Union), 1–18. doi:10.1002/9781119815631.ch1

CrossRef Full Text | Google Scholar

Richmond, A., and Maute, A. (2013). Ionospheric electrodynamics modeling (AGU geophysical monograph series.), vol. 201. Chichester, UK: John Wiley & Sons. also published online in 2014 by. doi:10.1029/2012GM001331

CrossRef Full Text | Google Scholar

Ritter, P., Lühr, H., and Doornbos, E. (2010). Substorm-related thermospheric density and wind disturbances derived from champ observations. Ann. Geophys. 28, 1207–1220. doi:10.5194/angeo-28-1207-2010

CrossRef Full Text | Google Scholar

Roble, R. G. (1995). Energetics of the mesosphere and thermosphere. Up. Mesos. Low. Thermosphere A Rev. Exp. Theory, Geophys. Monogr. Ser 87, 1–21.

Google Scholar

Roble, R., and Ridley, E. (1987). An auroral model for the NCAR thermospheric general circulation model (TGCM). Annales Geophysicae 5A, 369–382.

Google Scholar

Shi, Y., Knipp, D., Matsuo, T., Kilcommons, L., and Anderson, B. (2020). Modes of (FACs) variability and their hemispheric asymmetry revealed by inverse and assimilative analysis of Iridium magnetometer data. J. Geophys. Res. Space Phys. 125, 1. doi:10.1029/2019JA027265

CrossRef Full Text | Google Scholar

Shim, J. S., Kuznetsova, M., Rastätter, L., Bilitza, D., Butala, M., Codrescu, M., et al. (2012). Cedar electrodynamics thermosphere ionosphere (eti) challenge for systematic assessment of ionosphere/thermosphere models: Electron density, neutral density, NmF2, and hmF2 using space based observations. Space Weather 10. doi:10.1029/2012SW000851

CrossRef Full Text | Google Scholar

Siemes, C., de Teixeira da Encarnação, J., Doornbos, E., van den IJssel, J., Kraus, J., Pereštỳ, R., et al. (2016). Swarm accelerometer data processing from raw accelerations to thermospheric neutral densities. Earth Planets Space 68, 92–1186. doi:10.1186/s40623-016-0474-5

CrossRef Full Text | Google Scholar

Siskind, D. E., Drob, D. P., Dymond, K. F., and McCormack, J. P. (2014). Simulations of the effects of vertical transport on the thermosphere and ionosphere using two coupled models. J. Geophys. Res. Space Phys. 119, 1172–1185. doi:10.1002/2013JA019116

CrossRef Full Text | Google Scholar

Solomon, S. C., Qian, L., Didkovsky, L. V., Viereck, R. A., and Woods, T. N. (2011). Causes of low thermospheric density during the 2007–2009 solar minimum. J. Geophys. Res. 116. doi:10.1029/2011JA016508

CrossRef Full Text | Google Scholar

Sutton, E. K., Forbes, J. M., and Knipp, D. J. (2009). Rapid response of the thermosphere to variations in joule heating. J. Geophys. Res. 114. doi:10.1029/2008JA013667

CrossRef Full Text | Google Scholar

Weimer, D. R. (2005). Improved ionospheric electrodynamic models and application to calculating Joule heating rates. J. Geophys. Res. 110, A05306. doi:10.1029/2004JA010884

CrossRef Full Text | Google Scholar

Yamazaki, Y., and Kosch, M. J. (2015). The equatorial electrojet during geomagnetic storms and substorms. J. Geophys. Res. Space Phys. 120, 2276–2287. doi:10.1002/2014JA020773

CrossRef Full Text | Google Scholar

Yamazaki, Y., and Richmond, A. D. (2013). A theory of ionospheric response to upward-propagating tides: Electrodynamic effects and tidal mixing effects. J. Geophys. Res. Space Phys. 118, 5891–5905. doi:10.1002/jgra.50487

CrossRef Full Text | Google Scholar

Zhang, X., Forbes, J. M., and Hagan, M. E. (2010). Longitudinal variation of tides in the MLT region: 1. Tides driven by tropospheric net radiative heating. J. Geophys. Res. 115, 1. doi:10.1029/2009JA014897

CrossRef Full Text | Google Scholar

Zhang, Y., and Paxton, L. J. (2021). Storm-time neutral composition changes in the upper atmosphere. American Geophysical Union, 115–133. chap. 7. doi:10.1002/9781119815631.ch7

CrossRef Full Text | Google Scholar

Zhang, Y., Paxton, L., Morrison, D., Wolven, B., Kil, H., Meng, C.-I., et al. (2004). O/N2 changes during 1–4 october 2002 storms: IMAGE SI–13 and TIMED/GUVI observations. J. Geophys. Res. 109, A10308. doi:10.1029/2004ja010441

CrossRef Full Text | Google Scholar

Zuzic, M., Scherliess, L., and Prölss, G. (1997). Latitudinal structure of thermospheric composition perturbations. J. Atmos. Sol. Terr. Phys. 59, 711–724. doi:10.1016/S1364-6826(96)00098-3

CrossRef Full Text | Google Scholar