Ultraviolet and magnetic perspectives at Reiner Gamma and the implications for solar wind weathering

With the wealth of missions selected to visit the lunar surface in the decade ahead, preparatory investigations into surface conditions are underway to explore potential challenges and science returns during these missions. One such mission, Lunar Vertex, is slated to explore a much-anticipated region–the lunar swirl and magnetic anomaly known as Reiner Gamma. Lunar swirls are unique natural laboratories for exploring solar wind interactions with partially magnetized rocky bodies, and possess characteristics that have not yet been observed on any other body in the Solar System. This work aims to combine current magnetic mapping of Reiner Gamma with ultraviolet wavelength datasets, towards further understanding the sensitivities of ultraviolet measurements in regions that may be partially magnetically shielded from solar wind weathering and magnetospheric plasma populations. Observations and models herein are collected and derived from orbital sources and will be used for comparison to future orbital and surface observations of Reiner Gamma by Lunar Vertex.

1 Introduction

While the Moon presently lacks a global, internally-generated magnetic field, the lunar crust contains many regions of localized magnetization known as magnetic anomalies (MAs) (Dyal et al., 1974). These MAs are frequently co-located with anomalous features known as lunar swirls, which are currently thought to be unique to the Moon (Blewett et al., 2011; Denevi et al., 2016). Lunar swirls are a type of surface feature characterized by sinuous patterns of atypical reflectance relative to their surroundings which show spatial similarities to the associated MAs. Several hypotheses have been proposed to explain the formation of swirls. One concept suggests that swirls result from electromagnetic shielding via their associated MAs, leading to reduced solar-wind exposure effects on the rocks and soils in the shielded areas (Hood & Schubert, 1980).

To investigate the archetypal lunar swirl Reiner Gamma (RG) and its associated MA, NASA selected Lunar Vertex (LVx) as a joint lander and rover mission to visit the lunar surface locality and characterize its electromagnetic and regolith properties (Blewett et al., 2021c). The lander will be outfitted with an array of fluxgate magnetometers, an ion-electron plasma spectrometer, and camera array, and the rover will carry an array of fluxgate magnetometers and a multispectral microscope (Blewett et al., 2021c). Over the primary mission duration of approximately 13 Earth days, LVx will monitor solar wind, magnetosheath, and magnetotail plasma interactions with the magnetic anomaly and regolith, detailing surface conditions for future exploration and habitation.

We have simulated solar wind interactions with RG to explore potential observations by the lander and rover at the swirl. In this context, the charged particles constituting solar wind are deflected by the MA as a function of lunar phase, possibly leading to decreased weathering. Figure 1 illustrates the relative location of RG throughout a lunar orbit of the Earth. Before local lunar dawn, RG would be located just outside of the Earth’s bow shock before transiting across the magnetosheath and magnetotail until entering back into the solar wind near lunar noon (e.g., Halekas et al., 2005; Li et al., 2018). Thus, particle flux at the surface will vary spatially and temporally over the course of the LVx mission as the swirl-associated MA responds to dynamic solar wind conditions in different stages of the lunar orbit (Figure 1).

FIGURE 1

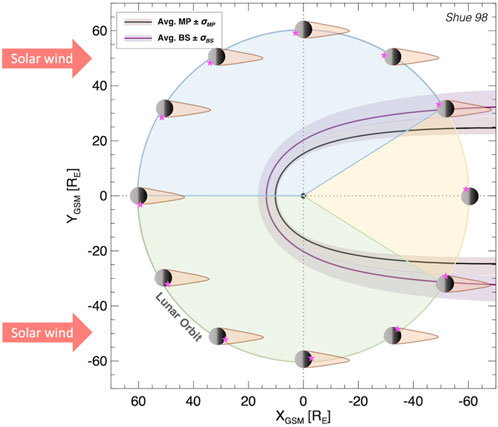
FIGURE 1. Depiction of the RG swirl (pink star) over one lunar orbit, rotating in and out of the lunar wake (orange tail) and Earth magnetopause (black line with salmon shaded variance) and bow shock (purple line with lilac shaded variance) in an aberration-corrected frame of reference (Shue et al. 1998; Jelinek et al., 2012). The average magnetopause and bow shock location are based on 10 years (2010–2020) of solar wind and IMF observations from the OMNI dataset (Papitashvili and King 2020). Moon and wake scaled 200 × to visualize illumination at RG/LVx landing site. The blue slice of the orbit is when RG is outside of Earth’s magnetosphere (unabated solar wind), the green slice is when RG is within the lunar wake (attenuated solar wind), and the yellow slice is when RG is within Earth’s magnetosphere (no/minimal solar wind).

It is thought that MAs may establish a protective boundary based on a dynamic balance of above-surface magnetic field intensity and directionality with incident solar wind velocity and density, similar to a planetary magnetosphere (e.g., Hood & Schubert, 1980; Lin et al., 1998; Hemingway & Garrick-Bethell, 2012). In this study, we explore the effect of varying solar wind conditions on theoretical boundary layers above the swirl to model potential surface conditions during different stages of the LVx lunar daytime mission. Then we examine the boundary morphology at the surface relative to surface magnetic and spectral variations, utilizing cross-anomaly spatial profiles of a Lunar Prospector-derived surface magnetic field model co-registered to ultraviolet (UV) image datasets from the Lunar Reconnaissance Orbiter (LRO) Lyman Alpha Mapping Project (LAMP) and LRO Camera (LROC) Wide Angle Camera (WAC) (Lin et al., 1998; Ravat et al., 2020; Gladstone et al., 2010; Robinson et al., 2010). These model results and observations are explored in the context of solar-wind standoff and discussed with regard to future surface measurements from the LVx mission.

Section 1 of this paper includes a review of lunar magnetism and weathering with framework for interpretation of solar wind standoff at lunar swirls. Section 2 describes the model developed for exploring potential boundary layers above RG and how solar wind dynamic pressure may influence weathering patterns. Section 3 presents the preliminary model results and observations of potential variable weathering effects across the swirl in ultraviolet wavelengths. Section 4 discusses these results and observations with respect to future surface measurements from LVx and implications for solar wind weathering at RG.

1.1 Lunar crustal magnetics

Initial data from magnetometers carried by the Apollo missions revealed weak, patchy surface magnetism on the Moon (e.g., Coleman et al., 1972; Dyal et al., 1974), and recent missions such as NASA’s Lunar Prospector (LP) and JAXA’s Kaguya confirmed that magnetic anomalies are distributed across both maria and highlands, with the highest concentration of anomalies occurring on the far side of the Moon on the outskirts of and within the South-Pole Aitken basin (Lin et al., 1998; Tsunakawa et al., 2010). While the origin of these MAs is currently unknown, several studies have suggested that the global distribution (Figure 2), indicates that MAs are a form of natural remanent magnetization within crustal sources (e.g., Sonett & Mihalov, 1972; Halekas et al., 2001; Hood et al., 2001; Gong & Wieczorek, 2020).

FIGURE 2

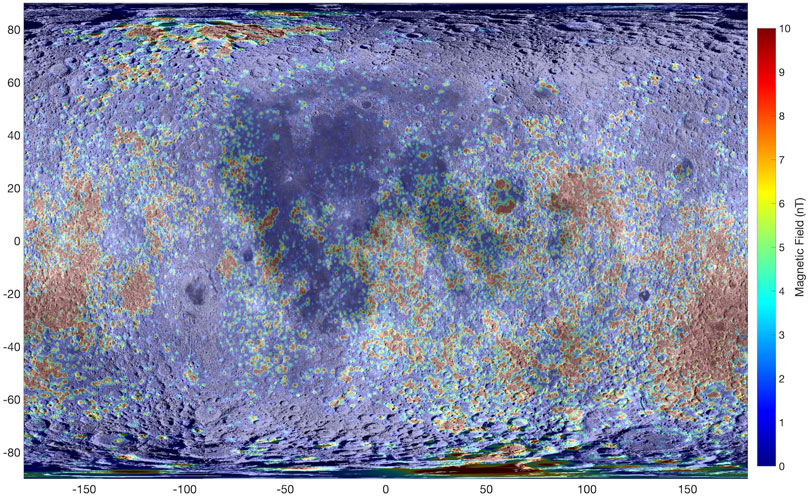
FIGURE 2. Lunar Prospector-derived surface model magnetic field intensity (Ravat et al., 2020) overlaid on an LROC WAC 100 m/pixel Global Morphologic basemap (I/F stretch: 0–0.07) in Mercator projection. Magnetic anomalies are distributed broadly across the surface with little apparent topographic dependence.

Despite the current lack of a global magnetic field, recent work indicates the Moon may have previously sustained an internally generated magnetic field during a period of active dynamo (e.g., Tikoo et al., 2017; Laneuville et al., 2014; Dwyer et al., 2011). This global magnetic field is estimated to have had a peak mean surface intensity of ∼77 μT between 3.85 billion and 3.56 billion years ago (Ga) and declined to ∼4 μT by 3.19 Ga, weakening further until around 2.5 Ga and completely ceasing to exist between ∼0.80–1.92 Ga (Strauss et al., 2021; Mighani et al., 2020). Potential paleopoles have been calculated from MAs in many recent studies to establish a relative timeline of dynamo precession and lunar magnetism (e.g., Takahashi et al., 2014; Arkani-Hamed & Boutin, 2014; Oliveira & Wieczorek, 2017; Nayak et al., 2017; Ravat et al., 2020; Maxwell & Garrick-Bethell, 2020; Nichols et al., 2021). However, uncertainty remains due to disagreement on longevity of dynamo activity (e.g., Tarduno et al., 2021) and adding a further temporal complication, it has been noted that impact events that occur after the decline of a dynamo may demagnetize the surrounding crust (e.g., Halekas et al., 2002; Wieczorek, 2018).

Multiple studies have aimed to determine the age of individual MAs by constraining the geologic context and potential source geometry, towards understanding when the MA may have been emplaced in the crust and the method of magnetization (e.g., Nicholas et al., 2007; Weiss & Tikoo, 2014; Wieczorek, 2018; Lee et al., 2019; Baek et al., 2019; Kelley & Garrick-Bethell, 2020). Two primary magnetization mechanisms have been proposed: 1) thermoremanent magnetization (TRM) during geologic processes (e.g., impacts and crystallization) within a period of active dynamo (e.g., Purucker et al., 2012; Wieczorek et al., 2012; Arkani-Hamed & Boutin, 2014; Hood & Spudis, 2016; Hemingway & Tikoo, 2018; Wakita et al., 2021), and 2) shock remanent magnetization (SRM) or pressure remanent magnetization (PRM) during impact or collision events that generated transient fields or amplified external fields in the immediate locality of the impact (e.g., Schultz and Srnka, 1980; Crawford & Schultz, 1999; Gattacceca et al., 2010; Bruck Syal and Schultz, 2015). Absent a dynamo, sources of magnetizing external fields have been proposed such as compressed fields associated with a cometary collision (Schultz and Srnka, 1980). Impacts may also be capable of TRM in the absence of a dynamo, as electrostatic charge separation in the vaporized material may generate transient, localized electric and magnetic fields which last long enough for the impact melt or cracks to heat and subsequently cool back down through the Curie temperature and create a magnetic anomaly (e.g., Crawford & Schultz, 1999; Crawford 2020).

An extension of hypothesis 2) proposes that some (but not all) MAs are the result of remanent magnetization from basin-forming impact events, where impact-generated transient fields or enhanced external fields traveled around the surface of the Moon via ejecta-related plasma and/or diffusion through the crust, resulting in magnetization at the antipode of the impact (e.g., Hood, 1987; Richmond et al., 2005; Hood & Artemieva, 2008). The methods described in 2) are influenced by both impactor and target composition, as well as impactor size, velocity, and angle of incidence, which could explain why not all MAs are antipodal or otherwise spatially correlated with craters or basins (Crawford, 2020; Wakita et al., 2021). However, recent work suggests that fields temporarily generated or amplified by antipodal impacts may be too weak and crustal circulation/diffusion too inefficient to singularly create the existing magnetic characteristics of impact-antipodal MAs (Tikoo et al., 2015; Oran et al., 2020). This is notable for the associated magnetic anomaly at Reiner Gamma, which is not antipodal to an impact basin. Thus, the formation of many crustal sources remains up for debate.

The ongoing work around the timeline and processes that gave rise to lunar magnetism as observed today (Figure 2) is critical to understanding a number of lunar surface processes. Current crustal magnetism appears to extend its influence well above the surface to interact with other complex phenomena that shape the lunar environment. These include but are not limited to impact magnetization, and/or demagnetization, and formation of volatile phases on the lunar surface. A well-constrained history of lunar dynamo intensity and longevity is necessary to analyze its potential interaction with other geologic surface processes and volatile cycles on the Moon, and to fully understand the evolution of the lunar environment (e.g., Garrick-Bethell et al., 2019; Green et al., 2020). However, localized MAs may be used to reconstruct the current effects of these processes, such as modification of regolith spectral reflectance properties related to ongoing volatile cycle disruption and solar-wind deflection.

1.2 Lunar spectroscopy and photometry

One of the most unique aspects of lunar MAs is their frequent co-location with regions of atypical reflectance relative to their surroundings that have been termed “lunar swirls” (e.g., Schultz and Srnka, 1980; Blewett et al., 2011; Denevi et al., 2014). Lunar swirls are effectively photometric anomalies (e.g., Shkuratov et al., 2010; Kinczyk et al., 2016; Korokhin et al., 2016; Cahill et al., 2019), however, they are considered a unique class of feature based upon distinguishing characteristics that separate them from other atypical reflectance regions. First, the label “swirl” is attributed to the sinuous appearance of the high-reflectance features, with “dark lanes” often found within these atypical reflectance regions (Figure 3) (El Baz, 1972; Schultz, 1972). However, dark lanes are not observed at all photometric anomalies (Cahill et al., 2019). Second, while not all MAs are coincident with a photometric anomaly, all lunar swirls are coincident with an MA (Blewett et al., 2011; Denevi et al., 2016; Cahill et al., 2019). Finally, lunar swirls do not have measurable thickness and were generally thought to be unrelated to any topographic features, as they are found to drape over regions of varying topography. However, recent work by Domingue et al., (2022) suggest that the Mare Ingenii swirl cluster may exhibit meter-scale topographic dependence.

FIGURE 3

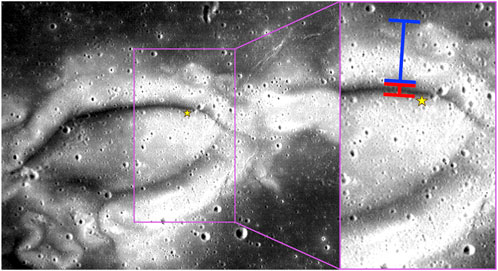
FIGURE 3. The heart of the lunar swirl named, Reiner Gamma, from the LROC WAC 100 m/pixel Global Morphologic basemap (I/F stretch: 0.017–0.037). The “bright lanes” are the regions of unusually high reflectance such as the region demarcated by the blue bracket, and the “dark lanes” are the regions of low reflectance similar to the mare background such as the region demarcated by the red bracket. The targeted LVx landing site (7.585°N, 58.725°W) is denoted by a yellow star, just below the highlighted dark lane.

Like MAs, the process by which the atypical reflectance of lunar swirls originated has been debated for several decades during which multiple mechanisms have been proposed. These include: 1) the associated MA shielding the surface from weathering via solar wind standoff (Hood & Schubert, 1980; Hood & Williams, 1989), 2) comet collisions exposing or depositing fresh material on the surface via coma gas and dust scouring (Schultz and Srnka, 1980; Bruck Syal and Schultz, 2015; Pinet et al., 2000) or meteoroid swarms plowing (i.e., roughening) the regolith (Starukhina & Shkuratov, 2004), or 3) electromagnetic surface fields associated with the MA preferentially sorting charged fine dust particles, causing accumulation and/or disturbance of high-reflectance particles along field lines when such particles are lofted at the lunar terminator (Garrick-Bethell et al., 2011; Pieters et al., 2014).

The latter two of these hypotheses suggest fleeting or punctuated events by which the atypical reflectance of a swirl might form in a short period of time. Generally, these types of events should add or expose new compositional or unweathered materials and roughen the surface. However, S-band (12.6 cm) radar observations suggest that swirl deposits may be extremely shallow, extending less than a few decimeters below the surface, and possess radar-wavelength scale roughness characteristics indistinguishable from their surroundings (Neish et al., 2011). Similarly, at thermal-infrared sensitivity scales, swirls are thermophysically indistinguishable from the surrounding regolith, further indicating that swirls do not possess roughness or compaction differences relative to their surroundings (Glotch et al., 2015). Thus, solar wind deflection will be considered here as the primary formation mechanism as it would not introduce roughness differences at such scales described above.

Under typical space weathering conditions of the lunar surface (i.e., non-swirl regions), solar wind particles and micrometeoroids incident upon the surface cause regolith maturation that manifests as brightening at Lyman-alpha wavelengths (∼121.6 nm; Cahill et al., 2019) and blueing of far-ultraviolet spectral slopes (150–200 nm; Hendrix et al., 2012; Vilas & Hendrix, 2015), whilst reddening of spectral slopes and darkening in near-ultraviolet to near-infrared wavelengths (e.g., Pieters et al., 2000; Hapke, 2001; Noble et al., 2007). In these regions, assessment of a regolith’s optical maturity (OMAT) is based upon the detection of the byproduct sub-microscopic iron (SMFe) particles created in part by sputtering and implantation of solar wind ions, and in part by micrometeoroid bombardment (e.g., Hapke, 2001, Hapke, 2012; Lucey & Riner, 2011; Pieters & Noble, 2016). The term “SMFe” encompasses smaller (<∼40 nm) particles known as nanosize iron (nsFe) particles and larger (>∼40 nm) particles known as microsize iron (msFe) particles, which are also referred to as Britt-Pieters particles (e.g., Keller & Clemett, 2001; Britt & Pieters, 1994; Blewett et al., 2021a).

It has been suggested that impact processes control the rate of lunar weathering by producing the majority of both nsFe and msFe particles, by examining thicknesses of vapor-deposited rims and solar wind amorphized rims and estimating exposure times derived from solar flare track densities (e.g., Zhang & Keller, 2011; Keller & Zhang, 2015). However, these exposure times contradict results from laboratory experiments designed to simulate weathering by micrometeoroid impact (laser pulses) and ion bombardment, which estimated that the spectral effects of solar-wind weathering should saturate ∼2 orders of magnitude faster than the effects of micrometeoroids at 1 AU (Loeffler et al., 2009). Recent work has used the potential attenuation of solar-wind weathering at swirls as a proxy to explore the formation of nsFe and msFe particles, based on radiative transfer modeling and comparison of near-ultraviolet and near-infrared swirl characteristics to lab spectra and nsFe-bearing silica gel analogs (Trang & Lucey, 2019; Blewett et al., 2021a).

The high-reflectance portion of lunar swirls closely resemble immature material in some ways, with similar bulk SMFe abundances, but differ in the abundance of the smallest scale particles (<15 nm), or nsFe abundances (Trang & Lucey, 2019; Chrbolková et al., 2019; Blewett et al., 2021a). This is interpreted to be the result of decreased solar wind weathering due to charged-particle deflection by swirl-associated MAs. Note that the magnetic fields are not expected to deflect micrometeoroids and inhibit the production of larger (>15 nm) nsFe and msFe (Richmond et al., 2003). Thus, in swirls only the nsFe abundances would differ from other immature material. Although this indicates solar wind weathering may be attenuated at swirls, swirl surfaces are not completely identical to immature, fresh craters, which implies that swirls may be the result of lessened (but not zero) solar wind exposure as a function of the age of their associated MAs (Kramer et al., 2011a; Hemingway et al., 2015; Denevi et al., 2016). Differences have also been observed between swirls in mare and swirls in highlands, as the local mineralogy determines the typical expression of space weathering within these regions (e.g., Denevi et al., 2016; Chrbolková et al., 2019; Blewett et al., 2021a).

Typical space weathering on the Moon results in optical maturation in the visible to near-infrared range on time scales of hundreds of millions of years (Grier et al., 2001), but swirls may violate the assumptions of OMAT-based age estimation schemes, which were developed for areas of normal space weathering. The lessened weathering of swirls and the fact that swirls overprint both steep and flat topography make it very difficult to constrain swirl formation to any epoch in the lunar geologic time scale, as swirl-associated MAs may be interrupting, or even convoluting, typical weathering timelines and furthermore, the anomaly source may have been magnetized at a different time than the formation of the geologic unit where the swirl exists (Neish et al., 2011; Garrick-Bethell et al., 2016).

Conclusion drawn from any swirl formation hypothesis require assumptions about the influence of the mysterious MAs coincident with each swirl. As described above, the precise age and subsurface geometry of MAs are currently indeterminate due to insufficient information about the timeline of lunar magnetism and the lack of surface measurements at swirls. The variability in width, depth, and direction of magnetization of these sources may present a broad diversity of magnetic field morphologies, each of which may interact with the surface in a different manner (e.g., Hemingway & Garrick-Bethell, 2012; Hemingway & Tikoo, 2018). Thus, it is critical to consider both the influence of the magnetic anomaly on the solar wind particle flux that reaches the surface and the local mineralogy and geologic context that could influence weathering expression in the surrounding region when analyzing weathering at swirls.

1.3 Framework for interpreting solar wind standoff

The solar wind component of space weathering consists of charged particles which are influenced by electromagnetic forces, as seen in magnetospheres such as those created by internally generated magnetic fields on Earth and Mercury (for example, see Russell, 1993). It is theorized that lunar MAs create small-scale “mini-magnetosphere” counterparts to these global magnetospheres, as some MAs are capable of reducing the flux of solar-wind particles to the coincident surface (e.g., Halekas et al., 2008; Lue et al., 2011). These mini-magnetospheres act as magnetic mirrors that deflect particles as a function of the magnitude of the magnetic field, creating a pressure balance that reduces solar-wind ion flux above and at the surface as observed by THEMIS-ARTEMIS, Chandrayaan-1, and Chang’e-4 (Halekas et al., 2014; Vorburger et al., 2012; Bhardwaj et al., 2015; Xie et al., 2021).

The solar-wind shielding swirl formation model suggests that the reflectance patterns of swirls are a result of charged solar wind particles being deflected due to the Lorentz force when incident upon the associated magnetic field above the surface, which leads to a local decrease in nsFe abundances as well as attenuated OH/H₂O abundances (e.g., Kramer et al., 2011a, 2011b; Li & Milliken, 2017; Li & Garrick-Bethell, 2019; Hess et al., 2020). However, the spatial scales of swirl-associated MAs do not permit total standoff of the solar wind, as the initial gyroradius of solar wind protons (on the order of hundreds to ∼1,000 km) is larger than the pressure balance altitude established by most MAs; thus, mini-magnetospheres do not have a typical bow shock or magnetopause (e.g., Halekas et al., 2011; Kallio et al., 2012). Despite this, the solar-wind electron population is largely magnetized, thus electron dynamics and the presence of ambipolar electric fields above some MAs allows for the formation of mini-magnetospheres that are capable of deflecting a significant fraction of solar wind ions at low altitudes (Deca et al., 2020, 2021). Studies and simulations based upon orbital measurements have estimated that some swirl-associated MAs reflect on average ∼10%, but up to 50%, of incident protons, compared to the surrounding less-magnetized lunar surface which only reflects an average of ∼0.1%–1% of incident protons (Saito et al., 2008; Lue et al., 2011; Poppe et al., 2017).

This deflection mechanism is twofold: the magnitude as well as the directionality of particular components of the field influence the proportion of particles deflected and the degree to which flux is reduced to the surface. Following the Lorentz force law, the magnetic deflection force is maximized when the bulk solar wind particle trajectory is perpendicular to the direction of the magnetic field, and the deflection force is zero when the trajectory is parallel (Hemingway & Garrick-Bethell, 2012). There is an energy dependence in particle deflection at these regions, such that the bulk thermal population (i.e., 1 keV protons) may be deflected but higher energy protons are still capable of reaching the surface. Here we only consider the bulk thermal population and do not account for potential current sheet systems, strictly studying the relationship between magnetic structure and intensity and swirl morphology. The shielding efficiency of MAs decreases with increasing solar wind dynamic pressure, as the standoff distance above the surface is reduced, ions that penetrate the mini-magnetosphere can access the surface more readily to continue weathering the regolith (e.g., Vorburger et al., 2012).

To explore the maximum particle flux at the surface and thus the potential highest weathering, the location of the swirl must be considered relative to the angle of incident particles upon the surface. Reiner Gamma is located at ∼7.5°N, 59°W, in the Western part of the near side of the Moon, near the lunar equator in Oceanus Procellarum. This positions the swirl and associated MA uniquely to observe the variability of solar wind flux at the surface near the equator, which is latitudinally the most weathered region on the Moon (Hendrix et al., 2012; Hemingway et al., 2015; Sim et al., 2017). However, the near side of the Moon may be less weathered than the far side because the near side is tidally locked to face Earth and spends most of its sun-facing orientation within Earth’s magnetotail and magnetosheath, where dynamic plasma pressure is greatly reduced by Earth’s magnetosphere (Hurley & Farrell, 2013; Li et al., 2018). Thus, the location of the RG swirl suggests it will experience peak weathering near local solar noon just outside of Earth’s bow shock, when the solar zenith angle is approximately normal to the surface locality (Deca et al., 2020).

For a swirl like RG located near the lunar equator, the surface-normal or radial magnetic field component $\left(B_r\right)$ is the most influential component of the total magnetic field in deflection, as determined by the direction of incident solar wind particles. Total magnetic field $\left(B_{total}\right)$ is the scalar magnitude of a vector quantity $B\left(\varphi ,\theta ,r\right)$ where the three components ($B_{\varphi },B_{\theta },B_r)$ describe the direction of the field and determine its geometry. $B_r$ is the local surface-normal field component, $B_{\theta }$ is the local southward field component, and $B_{\varphi }$ is the local eastward field component and form $B_{total}$ as the magnitude of the vector quantity:

$B_{total}=\left|B\left(\varphi ,\theta ,r\right)\right|=\sqrt{B_{\varphi }^2+B_{\theta }^2+B_r^2}$

To determine the contribution of the radial vector component to the total field intensity, we compute a ratio of $B_r$ intensity in $B\left(\varphi ,\theta ,r\right)$ relative to the field magnitude $B_{total}$:

$B_{total}=\sqrt{B_{\varphi }^2+B_{\theta }^2+B_r^2}$

$\frac{B_r}{B_{total}}=\pm 1\Rightarrow B_{total}=\sqrt{B_r^2}=\left|B_r\right|$

$\frac{B_r}{B_{total}}=0\Rightarrow B_{total}=\sqrt{B_{\varphi }^2+B_{\theta }^2}$

When ${\mathrm{B}}_{\mathrm{r}}/{\mathrm{B}}_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}=\pm 1$ then $B_r$ is the dominant or driving component of the field $B\left(\varphi ,\theta ,r\right)$ at that location, and when ${\mathrm{B}}_{\mathrm{r}}/{\mathrm{B}}_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}=0$ then $B_{\varphi }$ and $B_{\theta }$ are the dominant or driving field components.

Adhering to the Lorentz force law, if the formation of an equatorial photometric anomaly is due to decreased soil weathering via solar wind deflection, we expect a B_r/B_total ratio near zero over the least-weathered region of the anomaly (Figure 4). Additionally, in regions of the photometric anomaly that begin to experience ever increasing weathering exposure, due to decreased deflection ability of the MA, the B_r/B_total ratio will approach $\pm 1$. These regions include the lateral surface borders of the photometric anomaly and internal dark lanes as described in (Figure 3).

FIGURE 4

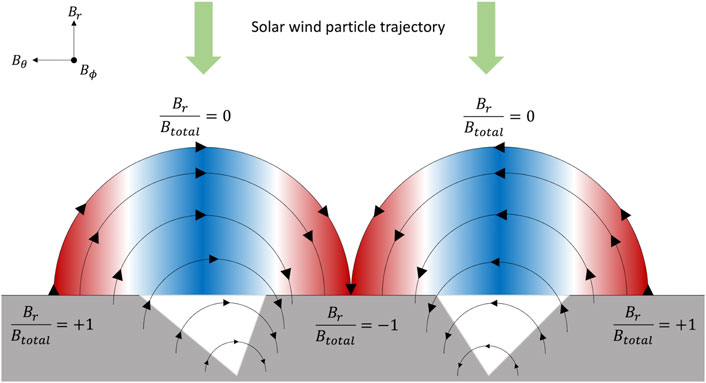
FIGURE 4. Maximum solar wind particle deflection via the Lorentz force would occur at a mini-magnetosphere where the incident solar wind trajectory is perpendicular to the magnetic field lines; for an equatorial MA, maximum particle deflection occurs where B_r/B_total is near zero between two regions of B_r/B_total near ± 1. This diagram represents the reduced weathering effect of particle deflection observed in albedo, where the bright areas suffer less weathering than the surrounding regolith due to deflection by the above-surface magnetic structure. As in Figure 3, the bright portions of the swirl correspond to the highlighted blue region in the figure and the dark lanes correspond to the highlighted red region.

Due to the inherent behavior of potential fields, magnetic field strength decreases rapidly with distance from the source (a factor of 1/r³ for a dipole source in free space), and this attenuation is difficult to overcome in analysis of orbital data to obtain an accurate view of magnetic intensities and vector component strength at the surface (e.g., Richmond & Hood, 2008; Mitchell et al., 2008; Purucker & Nicholas, 2010; Tsunakawa et al., 2015; Ravat et al., 2020; Hood et al., 2021). What is seen in orbit is effectively a fraction of the crustal field intensity, so in this paper we model magnetic intensity and structure in a three-dimensional perspective from a normalized spacecraft orbital altitude to the surface, to capture detail not possible in the use of orbital data alone.

We point out that inversion models of magnetic fields at the lunar surface do have caveats and necessary assumptions that need to be acknowledged. Surface models of magnetic fields derived from orbital data may not present a complete picture when applied to swirl-associated magnetic fields and optical surface morphology. This is because downward continuation of orbital data cannot recover attenuated information or determine superposition or coalescing of potentially overlapping magnetic sources. In reality, vector fields follow smooth functions away from the source which make inversion problems challenging to constrain (for examples, see Hinze et al., 2013). As noted by Hemingway & Tikoo (2018), current inversion techniques can underestimate crustal field intensity by more than an order of magnitude, and the spatial resolution of apparent magnetic structure is limited by the spacecraft altitude. The LVx mission will provide surface measurements from both the lander and the rover that may greatly improve orbital estimations of magnetic field intensity and resolvable field geometry at RG.

Despite an inherent sensitivity to distance from the surface, surface models derived from orbital data are still useful for quantifying the potential influence of swirl-associated MAs on spatial reflectance variations, and are certainly an improvement upon orbital data sets that assume values many kilometers above the surface (Figure 5).

FIGURE 5

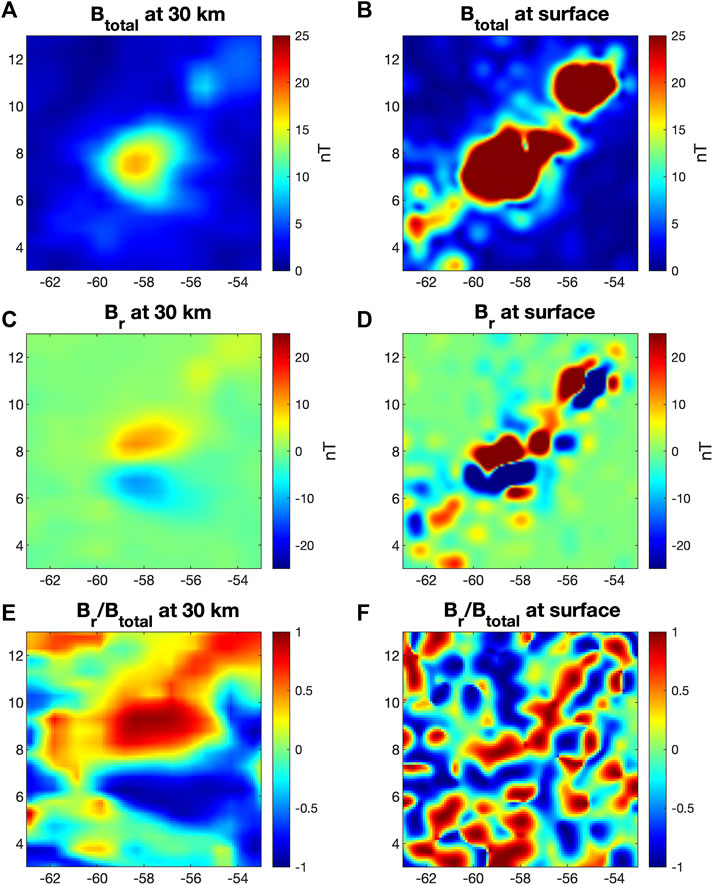
FIGURE 5. Comparison of RG-associated magnetic fields modeled at LP average orbital height of 30 km (left column) and at the lunar surface (right column). The top row (A,B) visualizes the total field magnitude, B_total, which contains no directional information. The middle row (C,D) visualizes the radial component, B_r, which indicates field direction and intensity into or out of the page. The bottom row (E,F) visualizes B_r/B_total which contains only directional information ( + 1 out of the page and −1 into the page), to elucidate field structure visible in surface models compared to 30 km models.

In this paper we examine multiple spatial perspectives, at the surface and at varying altitudes, as well as two temporal perspectives before entering and after exiting the Earth’s magnetosheath. During the LVx mission, surface magnetic information will be collected upon the exit crossing of Earth’s bow shock, which will refine the local models in this paper. In the future, data from LVx and other magnetometer-equipped surface missions like Astrobotic’s Peregrine Mission One, Firefly’s Blue Ghost lander, and the Southwest Research Institute PRISM LITMS payload may be used to validate and refine global models of lunar crustal fields (Figure 2). Until then, Lunar Prospector-derived surface models are used here to most closely resemble the conditions that may be observed by LVx during operations within the heart of RG. The LVx lander and rover magnetometers will reveal much more detail about the surface fields and geometry of the MA associated with RG, and may provide enough information to describe the crustal source of the anomaly and determine the method of magnetization (Wieczorek, 2018; Hemingway & Tikoo, 2018; Blewett et al., 2021b).

2 Materials and methods

The possible underestimation of crustal fields from surface models is used here to establish theoretical minimum field intensities for boundary layers at swirl-associated MAs, and thus explore the lower bounds of mini-magnetosphere formation and relative surface weathering. Using a surface model of magnetic fields derived from Lunar Prospector magnetometer data and interpolating to the average orbital altitude (30 km above surface), here we created an altitude-varying (Figure 6) magnetic field model in the lunar wake (i.e., a minimally compressed perspective at the time of least exposure to solar wind) (Ravat et al., 2020).

FIGURE 6

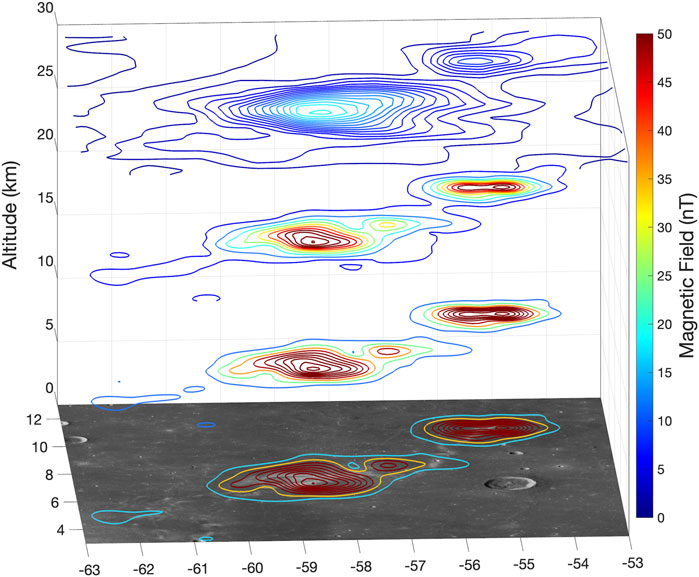
FIGURE 6. The Reiner Gamma magnetic anomaly total field in the lunar wake is represented by contour slices at 1 m, 10, and 30 km altitude, where the last slice is at LP average orbital height.

The day side of the Moon is directly exposed to a stream of solar wind particles at nominal speeds of 400 km/s and density around 5 ions/cm³, while plasma concentrations on the night side of the Moon are 1/500 of nominal solar wind density (Farrell et al., 2014). Magnetic anomalies experience compression on the day side due to the increased solar wind dynamic pressure, which modifies the intensity and height above the surface (standoff distance) of the potential mini-magnetosphere (Fatemi et al., 2015; Giacalone & Hood, 2015; Halekas et al., 2017; Cruz et al., 2017). Here we model two cases (Figure 7): 1) t_{wake}, where the swirl is in the lunar orbital wake and the mini-magnetosphere is experiencing the minimum amount of compression (teal box), and 2) t_{noon}, where the swirl is near local solar noon and outside of Earth’s magnetosphere (purple box), thus the mini-magnetosphere is experiencing the maximum amount of compression.

FIGURE 7

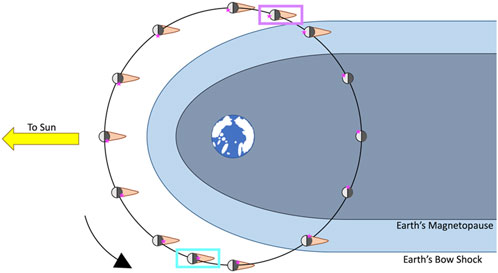
FIGURE 7. The orbital locations of the two cases modeled in this study, twake is the phase in the teal box in the lower left quadrant and tnoon is the phase in the purple box in the upper right quadrant. Both phases are outside of Earth’s magnetosphere so solar wind density and velocity are assumed to be nominal and are modulated by a constant that represents the local lunar solar wind conditions.

For MAs that cannot sustain a mini-magnetosphere above the surface under increased solar wind dynamic pressure (i.e., compression of the standoff distance into the regolith), weathering of the regolith may occur as a function of phase over a lunation. Since MAs may not be spatially large enough to create a typical bow shock, the surface of maximum particle deflection at the standoff distance referred to as the “boundary layer” here is modeled under the same constraints as a planetary magnetopause. The mini-magnetosphere boundary layer will be located where the dynamic pressure of the incident solar wind balances that of the magnetic pressure from the MA, from which a minimum field intensity at the boundary layer can be defined as a dynamic function of solar wind velocity $u$ and density $\rho$:

$\rho u^2\approx \frac{B^2}{2{\mu }_0}=\frac{{\left[B_{surf}{\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$r$}\right.\right)}^3\right]}^2}{2{\mu }_0}$

Where B is the field strength in the boundary layer, which is a function of distance from the crustal source, $B=B_{surf}{\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$r$}\right.\right)}^3$. The standoff distance, or height of the boundary layer above the surface, is defined by the Chapman-Ferraro equation to be:

$\frac{r_t}{r_{source}}={\left[\frac{B_{surf}^2}{2{\mu }_0\rho u^2}\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.}$

The wake side $\left(t=t_{wake}\right)$ anomaly was assumed to be the mini-magnetosphere established under minimal plasma incidence in the lunar wake, and a factor of 500 was applied to the solar wind wake dynamic pressure term to model the compression of the anomaly at solar noon $\left(t=t_{noon}\right)$ plasma conditions. Assuming the anomaly source is dipolar with constant $r_{source}$, the standoff distance becomes:

$r_{t_{wake}}={\left[\frac{B_{surf}^2}{2{\mu }_0\left(\rho u^2\right)}\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.}$

$r_{t_{noon}}={\left[\frac{B_{surf}^2}{2{\mu }_0\left(500\rho u^2\right)}\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.}={\left[\frac{1}{500}\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.}{\left[\frac{B_{surf}^2}{2{\mu }_0\left(\rho u^2\right)}\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.}=\frac{r_{t_{wake}}}{{\left[500\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.}}$

$\Rightarrow r_{t_{noon}}=\frac{r_{t_{wake}}}{2.817}$

Then the boundary layer height at solar noon was found by compressing the wake side boundary layer height by up to a factor of 2.817, so the standoff distance at solar noon is compressed downwards towards the surface as the increased solar wind dynamic pressure requires an increased magnetic intensity to maintain the mini-magnetosphere. In some locations, the standoff distance may be compressed beneath the surface if the above-surface magnetic field intensity cannot balance the increased dynamic pressure. Thus, the radial field component $B_r$ will determine the maximum Lorentz force deflection as previously described, where $B_{total}$ is capable of balancing incident solar wind dynamic pressure (Figure 8).

FIGURE 8

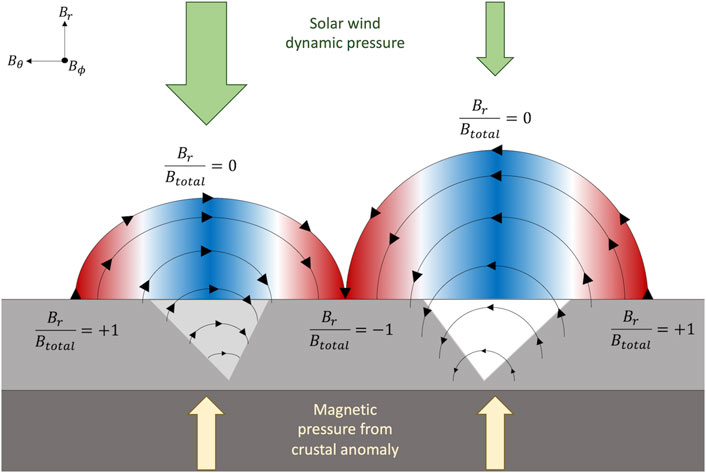
FIGURE 8. When the magnetic pressure from the source is less than the solar wind dynamic pressure, the anomaly is maximally compressed (left) and the regolith below experiences more weathering, similar to that at a non-magnetic background area, thus the bright portion of the swirl could become less apparent over time. When the magnetic pressure is equal to or greater than the solar wind dynamic pressure, the anomaly is minimally compressed (right) and the regolith below experiences less weathering, thus the bright region could become more apparent over time because of a greater contrast in weathering compared with the background. In both cases, the field geometry is preserved at normal incidence angles to sustain maximum deflection of solar wind particles.

From previous observations and simulations, the minimum crustal magnetic field intensity necessary to deflect ≥10% of solar wind particles ranges from 50 to 90 + nT at the boundary layer (Fatemi et al., 2015; Poppe et al., 2016; Jarvinen et al., 2014; Zimmerman et al., 2015), although recent work on surface water abundances and distribution shows ∼10–30 ppm water suppression relative to background values at even lower magnetic intensity thresholds of ∼15–50 nT (Li & Garrick-Bethell, 2019). The model presented in this paper follows the compression of six potential mini-magnetospheres established at six respective boundary layers of average magnetic intensity across the previously described ranges, at 15, 35, 55, 75, and 95 nT above the surface.

Contributions from the interplanetary magnetic field (IMF) are ignored since the pressure in the solar wind is dominated by the plasma pressure (i.e., plasma beta is greater than 1) and the average IMF intensity (5 nT) is at least one order of magnitude smaller than the crustal magnetic anomaly intensity, and has been shown to have a relatively small effect on weathering patterns (Deca et al., 2015). All mini-magnetosphere boundary layers are computed in two cases at local noon and midnight, outside of Earth’s magnetotail and magnetosheath (Figure 7), excluding mini-magnetosphere interactions with Earth’s magnetic field and considering any weathering within Earth’s magnetosphere negligible compared to weathering outside of the magnetosphere.

3 Results

3.1 Compression model

The boundary layers in the lunar wake are significantly compressed towards the lunar surface under high solar wind dynamic pressure at solar noon (Figure 9), but maintain a steady-state balance with solar wind such that the boundary layer connections with the surface are extremely well spatially correlated with the photometric anomaly of Reiner Gamma. This supports the solar wind deflection hypothesis that the magnetic anomaly is influencing the development of the associated swirl photometric anomaly.

FIGURE 9

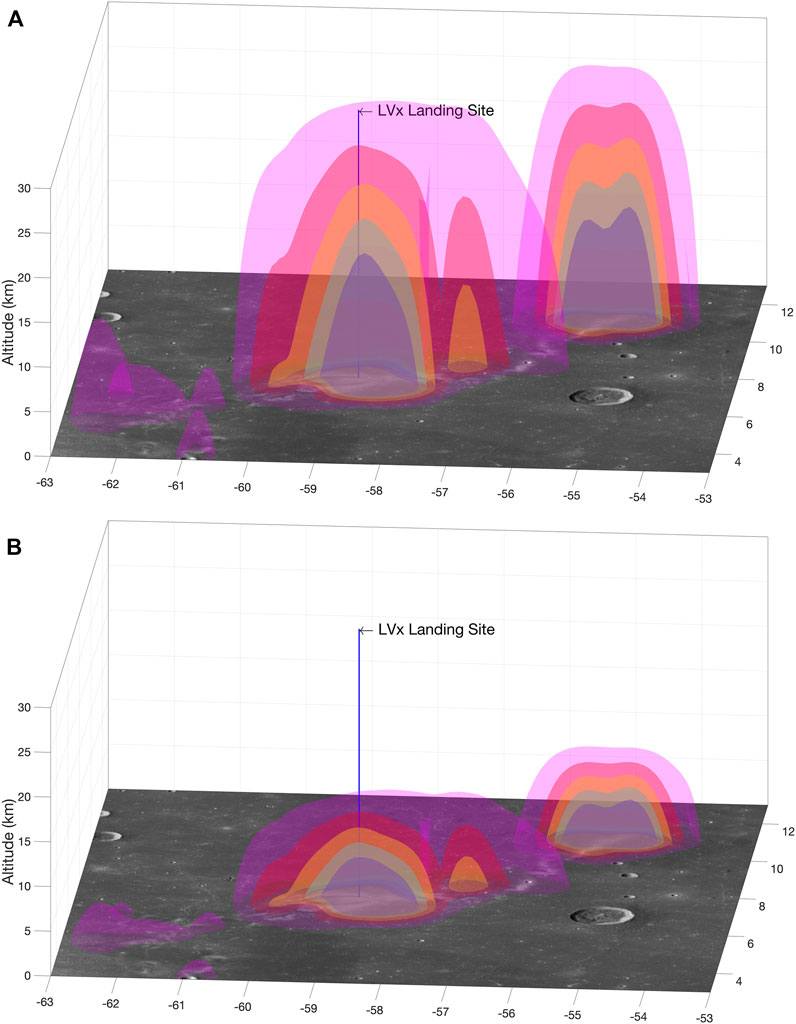
FIGURE 9. The top plot (A) visualizes minimally compressed mini-magnetospheres (I = t_wake). The bottom plot (B) visualizes maximally compressed mini-magnetospheres (t = t_noon). The mini-magnetosphere boundaries were defined at 5 layers of intensity as 15 nT (purple), 35 nT (pink), 55 nT (orange), 75 nT (green), and 95 nT (light blue) then projected onto a base map of 415 nm wavelength data from LROC WAC. Lunar Vertex landing site indicated by the vertical dark blue arrow at 7.585°N, 58.725°W.

Comparison of these two cases suggest that weathering may not be occurring evenly across Reiner Gamma due to the extreme compression of magnetic anomalies in the face of solar wind, and that there may be measurable spectral evidence of this unevenness. The compression of the magnetic field may also generate secondary electromagnetic interactions within the uppermost layer of the regolith, and contribute currently unquantified expressions in regolith via electrostatic discharging (e.g., Jordan et al., 2019). Surface measurements from the magnetometers and ion-electron spectrometer of LVx may resolve the temporal and spatial scales of near-surface electromagnetic fields and induced fields from external sources such as the IMF and solar energetic particles.

As the standoff distance is reduced, the magnetic field at the boundary layer intensifies, which serves to reinforce the standoff distance at a lower altitude. This establishes an equilibrium with the increased incident solar wind dynamic pressure, thus the mini-magnetospheres do not completely compress into the surface for most regions of RG. However, the reduced standoff distance allows more particles to access the surface therefore solar wind weathering may continue at a lower rate at the surface below, producing predominantly small (<15 nm) nsFe particles. In addition, micrometeoroids will continue to weather the regolith, producing predominantly large (>15 nm) nsFe and msFe particles, as these mini-magnetospheres will have no influence on micrometeoroid bombardment rates.

Based on this model, it is expected that there are variations in small nsFe abundances across the swirl, as particle deflection is not temporally constant and will depend on the intensity and geometry of the local magnetic fields. This was explored using spatial profiles that sampled the ultraviolet and magnetic datasets across the mini-magnetospheres defined by these boundary layers (Figure 9), and comparing profiles to explore potential small nsFe abundance variation.

3.2 Spectral and magnetic profiles

Cross-sectional spatial profiles (Figure 10) were collected across regions of the anomaly that are predicted to experience varying amounts of weathering based on the magnetic field intensity at each boundary layer. Each profile was used to take measurements in LROC WAC 415 nm reflectance and 321/415 nm ratio at 32 pixels per degree resolution, LAMP daytime Off-band (155–190 nm)/On-band (130–155 nm) (simply referred to from here on as FUV Off/On band) ratio at 32 pixels per degree, LAMP nighttime Lyman-ɑ (integrated 119–125 nm) albedo at 32 pixels per degree, and LP-derived surface model total magnetic field intensity and radial component intensity (20 km source spacing at 20 km depth) at 2 pixels per degree (Boyd et al., 2012; Gladstone et al., 2012; Ravat et al., 2020; Byron et al., 2021). Measurements were sampled at 500 m along 112–184-km profiles that cross the anomaly approximately NNW to SSE (Figure 10).

FIGURE 10

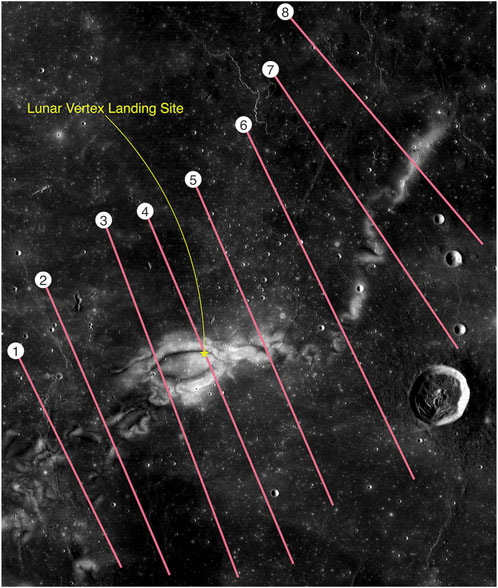
FIGURE 10. Reiner Gamma from LROC WAC 100 m/pixel global morphologic basemap (I/F stretch: 0.017 to 0.037) with cross-anomaly pink profiles at 8 locations that exhibit different weathering signatures, from which samples were extracted in multiple wavelengths and ratios. The LVx landing site (7.585°N, 58.725°W) is indicated by a yellow star on profile #3.

Some of these weathering differences within the swirl may be seen through inspection of multiple spectral datasets, five of which are focused on in this study (Figure 11). Some regions of the upper tail visible in (Figures 11C,F) are less apparent or not discernible in (Figures 11A,B). This may be interpreted as regions of Reiner Gamma that are a product of temporally uneven weathering as solar wind dynamic pressure compresses the magnetic anomaly, allowing increased particle flux to the regolith and influencing SMFe abundances, or perhaps secondary electromagnetic interactions as the field is compressed to the surface by high solar wind dynamic pressure.

FIGURE 11

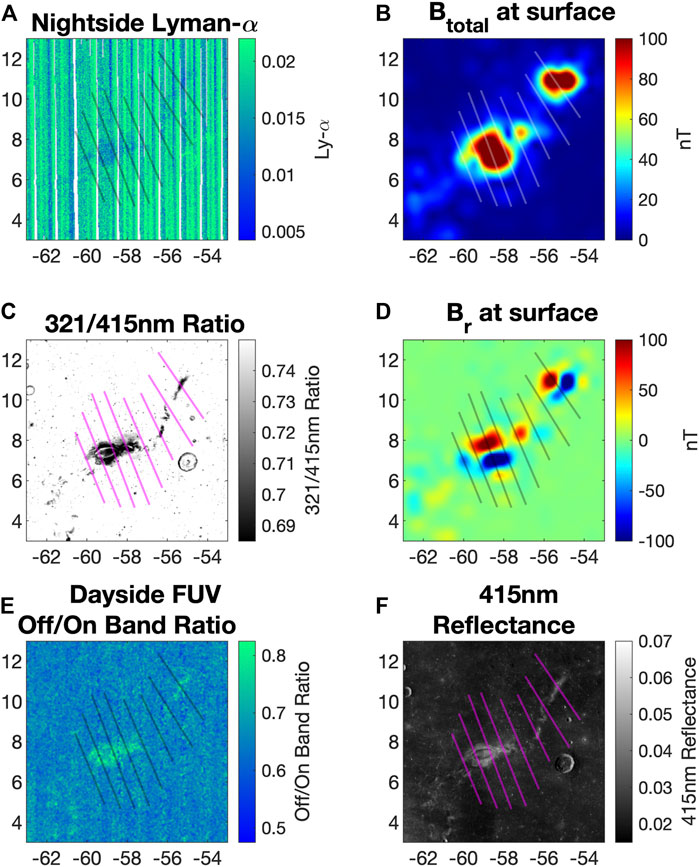
FIGURE 11. For the region of Reiner Gamma, (A) shows LAMP nightside Lyman-ɑ albedo, (B) displays the Lunar Prospector derived total (B_total) field intensity at the surface, (C) visualizes the LROC WAC NUV 321/415 nm ratio, (D) visualizes the Lunar Prospector derived radial (B_r) field component intensity, (E) visualizes the LAMP dayside FUV Off/On Band ratio, and (F) visualizes the LROC WAC 415 nm reflectance. Spatial profiles are contrasted in either pink or black to show the variety of morphology sampled.

From Figure 12, Profile 1 meets the 55 nT theoretical minimum intensity threshold and samples across the fringes of the boundary layers established at 15 nT and 35 nT minimum magnetic field intensities (Figure 9). There is one strong ( >2σ) peak and a region of weak (∼1σ) signatures in the FUV Off/On band ratio and 321/415 nm ratio measurements that may be the result of reduced SMFe at bright lanes. There is no apparent signature in Lyman-ɑ data, which may be because FUV radiation is less penetrating than NUV radiation, as surface scattering dominates the reflected light, rather than volume scattering. Short wavelengths such as Lyman-ɑ are more sensitive to thin coatings on grains that may be the result of weathering processes, thus the FUV region may be saturated by lower SMFe abundances than the NUV region. This may indicate enough solar wind particles penetrate the relatively weak boundary layers in this region to produce small amounts of SMFe, which may be reduced enough to present as bright areas in the NUV, but present enough to saturate the FUV. The bright areas in this region are weakly spatially correlated with the peak magnetic field intensity, however, the small (<10 km) spatial scale of these bright regions may indicate similarly small-scale magnetic field structure that is below the resolvable scale of this surface model.

FIGURE 12

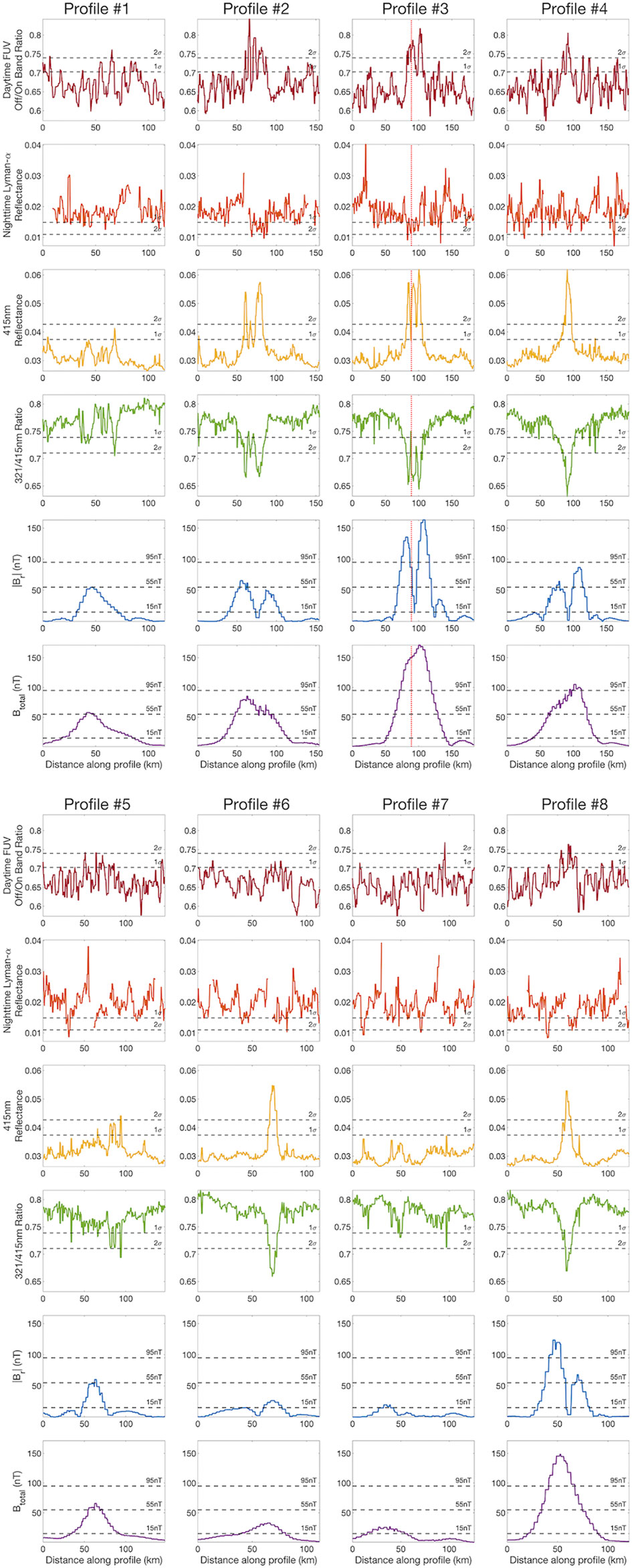
FIGURE 12. (Continued). Comparison of magnetic and ultraviolet parameter cross-sectional spatial profiles across Reiner Gamma. Horizontal dashed lines on the first four rows of plots indicate 1σ or 2σ deviations from the regional spectral mean in the respective directions of reduced weathering expression. Horizontal dashed lines on the last two rows of plots indicate 15, 55, and 95 nT thresholds of the magnetic field. The targeted Lunar Vertex landing site is denoted by a vertical red dotted line on plots of Profile 3. A side-by-side comparison of all profiles may be found in the Supplementary Materials S1 of this text.

From Figure 12, Profile 2 surpasses the 55 nT theoretical minimum intensity threshold and samples the fringe of the boundary layer established at 55 nT minimum magnetic field intensity. The presence of a strong ( >2σ) FUV signature associated with the bright lanes in this location may indicate that SMFe abundances in Profile 2 are significantly less than Profile 1, implying that particle deflection increases proportionally to magnetic field intensity. The radial magnetic field peaks are spatially correlated to strong ( >2σ) NUV and FUV spectral signatures that correspond to the bright portions of the swirls, however, there are small inflections associated with internal dark lanes of the swirl that are present within NUV and FUV measurements which do not spatially correlate with the expected radial field component structure described in Figure 8. This may indicate previously described unresolved near-surface magnetic structure due to the attenuation limitation of the surface field model.

From Figure 12, Profile 5 just meets the 55 nT theoretical minimum field intensity assumed to create a boundary layer in this paper, and the NUV wavelength profiles have moderately strong (∼2σ) peaks which indicate decreased SMFe abundances. However, there appears to be fine scale structure within the bright and dark lanes that could indicate the existence of near-surface magnetic structure not resolved by the LP-derived model, most likely as a result of the previously mentioned attenuation weakness of inversion techniques and limited spatial resolution. In addition, at oblique incidence angles (i.e., in the lunar afternoon), the stronger mini-magnetosphere peak to the west of this profile (Figure 9) may create a local wake that extends to the East as described in Xie et al. (2021) providing additional particle deflection that may reduce SMFe abundances within the wake. There are also unusual ∼2σ FUV signatures in this profile that appear to be spatially correlated with the 55 nT intensity magnetic peak, although a gore in the Lyman-ɑ data makes it difficult to draw firm conclusions. This profile, like Profile 1, samples across the fringes of the boundary layers established at 15 and 35 nT minimum magnetic field intensity, where secondary processes may contribute to atypical reflectance development under moderate solar wind influence.

From Figure 12, Profile 6 exceeds the 15 nT theoretical minimum intensity boundary layer threshold defined in this paper, and the mini-magnetosphere standoff distance is predicted to be very close to the surface, allowing attenuated but continued weathering. However, this profile has very strong ( >2σ) NUV signatures associated with the bright lane of the swirl, implying SMFe abundances are reduced to similar levels as higher magnetic intensity regions. Similar to Profile 5, to the west of Profile 6 lies a relatively stronger mini-magnetosphere peak, which may create a local wake in the solar wind at oblique incidence angles. Thus, Profile 6 may deflect some proportion of particles under its own magnetic intensity and geometry and is further shielded from weathering by nearby regions of stronger intensity at oblique angles of solar wind incidence, leading to locally decreased SMFe abundances. However, particle penetration of the weak boundary layer may result in low levels of SMFe production and surface hydration, such that the signal saturates the sensitive FUV wavelengths and the bright lane is only apparent in the NUV, which is less sensitive to subtle variations in reduced SMFe abundances.

From Figure 12, Profile 7 has a magnetic peak that meets the 15 nT theoretical minimum intensity boundary layer threshold defined in this paper, where the theoretical standoff distance is predicted to be compressed near or into the surface under high solar wind dynamic pressure. The FUV measurements do not indicate any significant weathering differences along the bright lane relative to the background, but slightly reduced SMFe abundances as a result of weak deflection may present as weak (∼1σ) NUV signatures. This may be because this region is not receiving any additional shielding similar to Profile 6, as from Figure 9 there exists no nearby higher intensity region which may create a local wake in solar wind at oblique incidence angles. Thus, the field along Profile 7 may be capable of deflecting enough particles to maintain the visible bright swirl by decreased ion weathering, but the amount of SMFe produced by particles penetrating the mini-magnetosphere lessens the bright-area signal in the NUV compared to stronger intensity regions and is enough to saturate the signal at FUV wavelengths such that the weathering appears similar to the background.

From Figure 12, Profiles 3, 4, and 8 all meet or surpass the 95 nT theoretical minimum total field intensity predicted here to create a mini-magnetosphere boundary layer above the surface, and the strongest peaks of the radial field component correspond spatially to the steepest changes in slope in all spectral measurements (i.e., the edges of the swirl reflectance patterns closely mimic the shape of the boundary layer reconnection with the surface). The spectral signatures associated with the bright lanes of the swirls are >2σ above the regional mean, corresponding to a steep decline of SMFe abundances across the bright lanes. However, as in Profile 2, there are small inflections associated with internal dark lanes of the swirl that are present within NUV and FUV measurements of Profiles 3 and 4 which do not spatially correlate with the expected radial field component structure described in Figure 8. This again suggests unresolved near-surface magnetic structure, and Profile 3 was selected to sample the targeted landing site of LVx (Figure 10) for future comparison of these orbital-derived measurements with surface measurements, at the red dotted line within Profile 3 (Figure 12).

In all profiles, the bright portions of the Reiner Gamma swirl have a lower NUV ratio than the mature background, and are spatially correlated with boundary layers which may be capable of deflecting solar wind. Assuming that the small NUV and FUV variations associated with internal dark lanes (Figure 3) along Profiles 2, 3, and 4 are the result of weathering along unresolved surface-connected field lines, then the profile measurements may indicate mini-magnetosphere structure not reflected in this model (Figure 9). The profiles indicate the bright portions of the swirl have significantly ( >2σ) higher reflectance and lower NUV ratios than the surrounding region, which agree with the high reflectance and steep NUV slopes typical of mare swirls as noted in Blewett et al., 2021a. Furthermore, the dark lanes inside the swirl do not appear to be “over matured” relative to the background as previously predicted to be the result of ion bombardment along surface-connected field lines, which could be a result of maturity saturation due to the high availability of ferrous iron in this mare location [Coman et al., 2011; McFadden et al., 2019]. Overall, the strongest slope changes in the NUV and FUV profiles align spatially with regions where the lowest intensity theoretical boundary layer reconnects with the surface. This agrees with previous work that lower NUV ratio values correspond to a lessened degree of space weathering as magnetic shielding lowers the flux of incident solar wind ions and limits the formation and abundance of nsFe particles coating lunar soil grains. The weak NUV ratio signatures associated with bright swirl areas that occur at the lowest minimum intensity boundary layer threshold indicate that deflection occurs proportionally to magnetic field intensity, and the minimum magnetic field intensity threshold for swirl detection in spectral profiles is lower than the values assumed herein. Additionally, within some regions there may be secondary processes such as dielectric breakdown (e.g., Jordan et al., 2019) and charged dust lofting or compaction (e.g., Garrick-Bethell et al., 2011; Hess et al., 2020) occurring as a result of compression-induced currents and field line connection with the regolith, which may contribute to the unusual reflectance patterns in currently unquantifiable ways.

When the incident solar wind dynamic pressure is sufficiently large, the standoff distance at weaker regions of the anomaly may be completely compressed into the surface and magnetic fields could be converted to induced current that may be dissipated (poorly) away into the regolith. These currents may be generating both secondary near-surface electric and magnetic fields, and may also induce temperature fluctuations. The Wiedemann-Franz law states that thermal conductivity and electrical conductivity are proportional under temperature and the Lorenz constant. On the day side of the Moon, temperatures can reach up to ∼120°C (∼400 K) which would minimally increase the crustal conductivity, allowing for induced currents to travel further horizontally through the uppermost regolith. Dielectric breakdown has been suggested as a space weathering mechanism, and electrostatic discharging may be possible around swirls if induced currents are generated within the regolith as a function of mini-magnetosphere compression. Additional in situ studies on the conductivity and resistivity of regolith could explore this mechanism and possible effects on weathering patterns (e.g., Jordan et al., 2019; Jordan, 2021; Jordan, 2022; Hapke, 2022].

4 Discussion

As mini-magnetospheres are compressed under increasing solar wind dynamic pressure, more particles may penetrate the boundary layer and solar wind weathering may occur as a temporally and spatially reduced process at magnetic anomalies. The spectral end members of the Reiner Gamma swirl occur near the strongest region of magnetic intensity, which is the most stable region capable of long-term particle deflection. However, as our modeling shows, there are regions of the swirl that do not exist beneath temporally stable mini-magnetospheres, yet still exhibit spectral signatures that correspond to attenuated weathering. This suggests that mini-magnetospheres need not be completely plasma-free or have absolute temporal stability to deflect enough solar wind particles to form a photometric anomaly, although there does seem to be a strong relationship between magnetic geometry and spectral variation across the portions of RG that are bright in visible wavelengths. As mini-magnetospheres cannot deflect micrometeoroids, which also produce SMFe through impact processes, the measurements in this paper support the hypothesis that swirls such as RG may be the long-term product of a steady state balance of micrometeoroids weathering and decreased, or cyclically varying, solar wind weathering. Further work is necessary to quantify with greater precision the minimum magnetic field intensity at which swirls may form relative to their magnetic field geometry and varying angles of incident solar wind. This line of inquiry will be greatly advanced by the LVx mission and other missions such as Firefly’s Blue Ghost lander and Astrobotic’s Peregrine Mission One lander, which are slated to carry surface magnetometer suites (Grimm et al., 2020; Purucker, 2019).

In this study only the maximally and minimally compressed mini-magnetospheres are considered under normally incident solar wind. In reality, this compression is a function of varying angles of incidence of solar wind particles, which ultimately change the deflection angle and may create a “trailing” plasma wake feature behind the mini-magnetosphere structure at oblique solar wind incidence angles (e.g., Halekas et al., 2017; Deca et al., 2021; Xie et al., 2021). Magnetic compression is a function of the periodic variation of solar wind dynamic pressure over the lunar day (Earth month), and is also subject to events like coronal mass ejections and geomagnetic storms. These events may transiently enhance plasma conditions around the Moon and increase the dynamic pressure. Because of these greater periods of solar wind pressure, some bright regions of RG with relatively weak magnetic intensity ( <55 nT) may as a result be more heavily weathered compared to RG proper, and after some threshold of exposure, may not be detected in FUV. A non-detectable FUV signal in a swirl relative to its surroundings, as we observe in some Southwestern and Northeastern portions of RG, may be due to the higher levels of short-term, but cyclically repeated, weathering exposure reaching the surface in those regions as opposed to the regions traditionally referred to as the RG bright swirl and that are associated with strong magnetic intensity ( >55 nT). In summary, variable compression of the weak magnetic regions ( <∼15 nT) exposes the regolith to increased solar wind ion flux during high solar wind dynamic pressure events.

The reason for the absence of an FUV signature in these particular weak magnetic regions of RG may be due signal saturation. That is, the FUV wavelengths (150–200 nm) may darken and develop a bluer spectral slope earlier due to heightened sensitivity to SMFe as compared to NUV, VIS, and NIR wavelengths, as previously suggested by Hendrix et al. (2012), and Hendrix et al.,(2016). It is also noted that FUV datasets used in this study are averaged separately over lunar daytime and nighttime, and include data taken when the Moon is both in and out of the Earth’s magnetotail, which may be averaging out some deflection effects as incident solar wind conditions vary within these time frames over the lunar orbit (Figure 2). Future work is needed to examine FUV datasets under a similar wake and solar noon criteria (Figure 7) to that used for magnetic field modeling in this paper.

In April 2024, LVx will land in central Reiner Gamma near the highest-intensity region of the entire anomaly, just south of one of the dark lanes that define the heart of the swirl (Figure 3) (Blewett et al., 2021c). The current targeted landing site of the LVx mission places the lander within any mini-magnetosphere as defined in this paper, so the mission will observe the change in magnetic shielding as the Moon moves out of Earth’s magnetosphere and into unabated solar wind (Figure 13). The evolution of the mini-magnetosphere and weathering conditions observed by LVx will be heavily influenced by the solar wind conditions over the mission duration as well as LVx’s locality within the mini-magnetosphere.

FIGURE 13

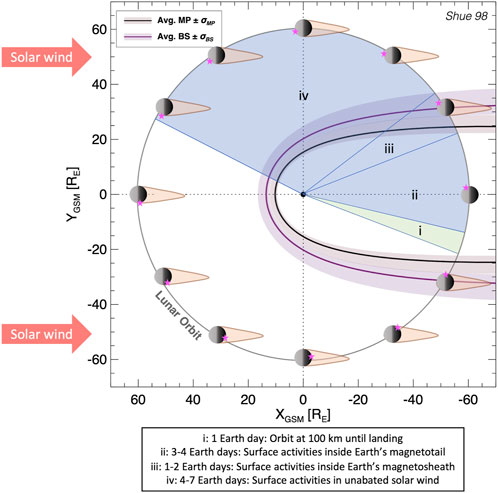
FIGURE 13. Timeline of orbit, landing, and surface activities of LVx with respect to Earth’s magnetosphere (Shue et al., 1998; Jelinek et al., 2012). The average magnetopause and bow shock location are based on 10 years (2010–2020) of solar wind and IMF observations from the OMNI dataset (Papitashvili and King 2020). Moon and lunar wake scaled 200 × to visualize illumination conditions at RG/LVx landing site (pink star). Earth’s average magnetopause location is indicated by a black line with salmon shaded variance and the average bow shock location is indicated by a purple line with lilac shaded variance. The lunar wake is indicated by an orange tail behind the Moon. Timeline based on solar wind conditions observed by the Apollo Solar Wind Spectrometer experiment (Snyder et al., 1970; Clay et al., 1972).

Based on typical solar wind conditions, LVx will likely arrive at the Moon when it is near the Earth’s bow shock or within the Earth’s magnetosheath (Figure 13 stage i.) before descending to the surface. This will provide more insight into lunar magnetic anomaly interactions with Earth’s magnetotail (Figure 13 stage ii.), and the plasma conditions in the magnetosheath (Figure 13 stage iii.) may shed insight into lunar mini-magnetosphere formation and compression. After exiting Earth’s magnetosphere on the dawn flank and passing again through the bow shock in the last stage of the mission (Figure 13 stage iv.), LVx will observe the mini-magnetosphere under maximum solar wind dynamic pressure, recording the surface response during maximum anomaly compression at local noon and the subsequent effects of solar wind angle of incidence as the Sun sets on RG. Should the LVx instrument suite survive a very short time into the lunar night, it could provide a more detailed view of mini-magnetosphere decompression as solar wind dynamic pressure decreases in the lunar plasma wake. The ion-electron plasma spectrometer may also observe the effects of dust lofting at the terminator and the influence of surface fields on charged dust particles that could contribute to atypical reflectance patterns of the swirl.

Magnetic data returned from the LVx lander and rover will also facilitate the development of higher-resolution surface field models. The lander magnetometer will be turned on prior to the landing phase of the mission (Figure 13 stage i.) to record the magnetic field above the anomaly through descent to the surface. Measurements acquired by the lander during descent may be used for optimization and normalization of orbital datasets for magnetic field inversion modeling. This may improve surface model structure and resolution, and once on the surface, the combined lander and rover magnetometer suites will provide a wealth of information about near-surface magnetic structure that is currently not resolvable from spacecraft observations, even at 30 km altitude (Figure 5). The resulting time series surface measurements may also be used to improve orbital datasets by identifying periodic effects from external field contributions such as the IMF and Earth’s magnetotail, and measurements from the rover over its traverse of the anomaly will provide inflection points for refinement of this mini-magnetosphere model. These high-resolution crustal field measurements and resulting improved models will have profound impact towards modeling and simulation of the lunar plasma environment and volatile distributions (e.g., Liuzzo et al., 2021; Tucker et al., 2021).

The temporal and spatial variations of mini-magnetospheres at swirls may be observable as described above in spectral profiles of Reiner Gamma, as the modification of solar wind weathering produces remarkable signatures in many wavelengths. However, over-maturation may not be resolvable in some mare regions, as the local mineralogy may limit the spectral expression of increased weathering effects from ion bombardment along the cusps of the boundary layer and along unrecovered internal magnetic field structure (e.g., McFadden et al., 2019; Blewett et al., 2021a). Radiation dosimetry may be inferred by the ion-electron plasma spectrometer on the LVx lander over the duration of the mission, as well as the local sputtering flux as a function of anomaly compression during the portion of the mission outside of Earth’s magnetosphere. This may resolve some effects of bombardment currently not seen in orbital remote sensing datasets, including foreshock plasma bombardment which may transiently enhance solar-wind weathering as accelerated ions from Earth’s bow shock impact the lunar surface (e.g., Nishino et al., 2017). These measurements will further inform this model and the role that magnetic anomaly compression may play in temporally varying weathering at the lunar surface.

As Hood et al. (2022) points out, there are also magnetic anomalies at the lunar poles (Figure 2) where Artemis activities will be focused. These regions may contain both benefits and hazards, as of yet unexplored. If some MAs are capable of continuously shielding 10%–50% of solar wind ions from reaching the surface beneath a mini-magnetosphere, this may provide a basis for “reduced radiation zones” at swirls (or MAs in general) for limited astronaut and equipment shielding during solar storms such as coronal mass ejections (CMEs), or shielding from downstream effects of geomagnetic storms when the Moon is within Earth’s magnetosphere. Alternatively, if mini-magnetospheres create “bombardment zones” when charged solar wind particles are focused and accelerated along surface-connected field lines, then dark lanes within swirls and similar structures within other MAs may be hazardous regions for human exploration.

The characterization of the role that surface electromagnetic forces play in the lunar volatile cycle may also inform future exploration and long-term human habitation of the Moon. Potential compression-induced fields in regions around magnetic anomalies may interact with local fields generated during human or robotic activity (e.g., Wang et al., 2013; Jackson et al., 2011; Zimmerman et al., 2012; Stubbs et al., 2014; Jackson et al., 2015), leading to ionization and/or electrostatic discharging that may inhibit exploration and resource extraction, particularly during periods of increased solar-wind dynamic pressure. If swirls are dehydrated compared to the surrounding regolith (e.g., Kramer et al., 2011a; Kramer et al., 2011b; Li & Milliken, 2017; Li & Garrick-Bethell, 2019], this may discourage human habitation on swirls as resource extraction may not prove fruitful. The apparent dehydration of swirls may be a result of the deflection of solar wind protons and thus decreased hydrogen flux at the surface, which could interrupt the implantation and transportation of volatiles such as OH/H₂O (e.g., Nakauchi et al., 2021). In addition, ion deenergization and deflection above strong magnetic anomalies may locally reduce some proportion of sputtered neutrals and affect regional exosphere composition (e.g., Poppe et al., 2014; Halekas et al., 2015).

The effects of mini-magnetosphere compression on the Moon could be analogous to magnetospheric compression at Mercury, which has a weak but global magnetic field generated by an active dynamo (Anderson et al., 2011; Johnson et al., 2015). At times of high solar wind dynamic pressure, the mercurian magnetosphere is compressed into the surface and the regolith is exposed to unabated solar wind bombardment, which may measurably affect sputtering rates and exosphere composition (Winslow et al., 2020). This may indicate similar processes occurring on a smaller scale during Lunar External Magnetic Enhancements caused by high dynamic pressure when the Moon is outside of Earth’s magnetic field, which may also include possible effects from the polarity of the IMF (e.g., Halekas et al., 2006; Nishino et al., 2012). Although LVx will encounter varying solar wind conditions during the mission as described in Figure 13, future surface missions capable of surviving multiple lunar days could provide a more detailed perspective on exosphere evolution as a function of solar wind exposure and the influence of near-surface magnetic fields on local sputtering rates. As solar wind fluence to the lunar surface is a function of longitude and latitude, future work on this model will take into account the solar zenith angle with respect to anomaly location to explore mini-magnetosphere compression at other lunar swirls and MAs.

Our results suggest that solar wind weathering is reduced but not coherent, or uniform, across the entirety of Reiner Gamma based on varying expressions of regolith immaturity in FUV and NUV wavelengths. Thus, the unusual reflectance patterns may be the result of a combination of attenuated solar wind weathering and other near-surface processes. There may be secondary electromagnetic processes occurring near or within the surface related to the compression of the associated MA during periods of high solar wind dynamic pressure, the effects of which are currently unquantified. In addition, despite the apparent lack of “over-matured” regions around swirls, there may still be regions of increased radiation via ion bombardment within dark lanes and around the outer fringes of the photometric anomaly, as the apparent maturity may be limited by the local mineralogy. Future surface measurements from LVx may be used to refine this mini-magnetosphere model to study magnetic compression effects at Reiner Gamma. More surface measurements of both plasma conditions and magnetic field conditions will be necessary to properly address the potential exploration hazards and benefits of lunar swirls and MAs in general.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

CW. wrote the original manuscript draft and the compression model code, extracted profiles and made initial interpretation of results, and created 3D visualizations and figures. JC. advised on the model development and profile extraction, refined the initial interpretations, and edited the manuscript. KR. and AH. contributed to the final interpretations and edited the manuscript. RA. contributed to model validation and edited the manuscript. SV. contributed Shue model code and data and edited the manuscript. HM. contributed text on the Lunar Vertex mission and interpretation of results for Vertex observations and edited the manuscript. AW-S. contributed to formulation of the model.

Funding

Work was supported by NASA LDAP program, Grant #80NSSC17K0342, and the LRO LAMP Science Team, contract #NNG05EC87C, both to JC.

Acknowledgments

The authors are grateful to David T. Blewett for providing feedback that improved this manuscript, as well as Huapei Wang and two anonymous reviewers for their constructive feedback and comments. The surface magnetic field model was coregistered to spectral base maps of Reiner Gamma and measurements were extracted through spatial profiles across the extent of the swirl using Quantum Geographic Information System (QGIS). QGIS is open-source geographic information system software available at https://qgis.org/. and the Geospatial Data Abstraction Library (GDAL) toolbox was used to create profiles and extract samples (http://gdal.osgeo.org).

Conflict of interest

RA is a Topic Editor of this Research Topic and will not participate in the review process of this paper.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2022.926018/full#supplementary-material

Supplementary Figure S1 | A side-by-side comparison of all profiles in ultraviolet and magnetic perspectives. The current planned LVx landing site is indicated by a red dotted line on Profile 3.

References

Anderson, B. J., Johnson, C. L., Korth, H., Purucker, M. E., Winslow, R. M., Slavin, J. A., et al. (2011). The global magnetic field of Mercury from MESSENGER orbital observations. Science 333, 1859–1862. doi:10.1126/science.1211001

PubMed Abstract | CrossRef Full Text | Google Scholar

Arkani-Hamed, J., and Boutin, D. (2014). Analysis of isolated magnetic anomalies and magnetic signatures of impact craters: Evidence for a core dynamo in the early history of the Moon. Icarus 237, 262–277. doi:10.1016/j.icarus.2014.04.046

CrossRef Full Text | Google Scholar

Baek, S.-M., Kim, K.-H., Garrick-Bethell, I., and Jin, H. (2019). Magnetic anomalies within the crisium basin: Magnetization directions, source depths, and ages. J. Geophys. Res. Planets 124, 223–242. doi:10.1029/2018JE005678

CrossRef Full Text | Google Scholar

Bhardwaj, A., Dhanya, M. B., Alok, A., Barabash, S., Wieser, M., Futaana, Y., et al. (2015). A new view on the solar wind interaction with the Moon. Geosci. Lett. 2, 10. doi:10.1186/s40562-015-0027-y

CrossRef Full Text | Google Scholar

Blewett, D. T., Coman, E. I., Hawke, B. R., Gillis-Davis, J. J., Purucker, M. E., Hughes, C. G., et al. (2011). Lunar swirls: Examining crustal magnetic anomalies and space weathering trends. J. Geophys. Res. 116, E02002. doi:10.1029/2010JE003656

CrossRef Full Text | Google Scholar

Blewett, D. T., Chabot, N. L., Denevi, B. W., Ernst, C. M., Head, J. W., Izenberg, N. R., et al. (2011). Hollows on Mercury: MESSENGER evidence for geologically recent volatile-related activity. Science 333, 1856–1859. doi:10.1126/science.1211681

PubMed Abstract | CrossRef Full Text | Google Scholar

Blewett, D., Halekas, J., Ho, G., Greenhagen, B., Anderson, B., Vines, S., et al. (2021c). Exploring a lunar magnetic anomaly: The lunar Vertex PRISM mission. doi:10.1002/essoar.10509480.1

CrossRef Full Text | Google Scholar

Blewett, D. T., Denevi, B. W., Cahill, J. T. S., and Klima, R. L. (2021a). Near-UV and near-IR reflectance studies of lunar swirls: Implications for nanosize iron content and the nature of anomalous space weathering. Icarus 364, 114472. doi:10.1016/j.icarus.2021.114472

CrossRef Full Text | Google Scholar

Blewett, D. T., Halekas, J. S., Waller, D., Cahill, J. T. S., Deutsch, A., Glotch, T. D., et al. (2021b). Science case for a lander or rover mission to a lunar magnetic anomaly and swirl. Bull. AAS 53. doi:10.3847/25c2cfeb.9295af86

CrossRef Full Text | Google Scholar

Britt, D. T., and Pieters, C. M. (1994). Darkening in black and gas-rich ordinary chondrites: The spectral effects of opaque morphology and distribution. Geochimica Cosmochimica Acta 58, 3905–3919. doi:10.1016/0016-7037(94)90370-0

CrossRef Full Text | Google Scholar

Bruck Syal, M., and Schultz, P. H. (2015). Cometary impact effects at the Moon: Implications for lunar swirl formation. Icarus 257, 194–206. doi:10.1016/j.icarus.2015.05.005

CrossRef Full Text | Google Scholar

Byron, B. D., Retherford, K. D., Czajka, E., Cahill, J. T. S., Hendrix, A. R., Greathouse, T. K., et al. (2021). Lunar surface composition constraints from maturity-corrected far-ultraviolet reflectance maps. Planet. Sci. J. 2, 189. doi:10.3847/PSJ/ac1d53

CrossRef Full Text | Google Scholar

Cahill, J. T., Wirth, A. A., Hendrix, A. R., Retherford, K. D., Greathouse, T. K., Mandt, K. E., et al. (2019). An examination of several discrete lunar nearside photometric anomalies observed in lyman-alpha maps. J. Geophys. Res. Planets 124, 294–315. doi:10.1029/2018JE005754

CrossRef Full Text | Google Scholar

Chrbolková, K., Kohout, T., and Durech, J. (2019). Reflectance spectra of seven lunar swirls examined by statistical methods: A space weathering study. Icarus 333, 516–527. doi:10.1016/j.icarus.2019.05.024

CrossRef Full Text | Google Scholar

Clay, D. R., Goldstein, B. E., Neugebauer, M., and Snyder, C. W. (1972). Solar-wind spectrometer experiment (No. NASA SP-289), Apollo 15 preliminary science report. Washington, D.C: National Aeronautics and Space Administration.

Google Scholar

Coleman, P. J., Schubert, G., Russell, C. T., and Sharp, L. R. (1972). The particles and fields subsatellite magnetometer experiment (No. NASA SP-289), Apollo 15 preliminary science report. Washington, D.C: National Aeronautics and Space Administration.

Google Scholar

Crawford, D. A., and Schultz, P. H. (1999). Electromagnetic properties of impact-generated plasma, vapor and debris. Int. J. Impact Eng. 23, 169–180. doi:10.1016/S0734-743X(99)00070-6

CrossRef Full Text | Google Scholar

Crawford, D. A. (2020). Simulations of magnetic fields produced by asteroid impact: Possible implications for planetary paleomagnetism. Int. J. Impact Eng. 137, 103464. doi:10.1016/j.ijimpeng.2019.103464

CrossRef Full Text | Google Scholar

Cruz, F., Alves, E., Bamford, R., Bingham, R., Fonseca, R. A., and Silva, L. O. (2017). Formation of collisionless shocks in magnetized plasma interaction with kinetic- scale obstacles. Phys. Plasmas 24, 022901. doi:10.1063/1.4975310

CrossRef Full Text | Google Scholar

Deca, J., Divin, A., Lembège, B., Horányi, M., Markidis, S., Lapenta, G., et al. (2015). General mechanism and dynamics of the solar wind interaction with lunar magnetic anomalies from 3-D particle-in-cell simulations. J. Geophys. Res. Space Phys. 120, 6443–6463. doi:10.1002/2015JA021070

CrossRef Full Text | Google Scholar

Deca, J., Hemingway, D., Divin, A., Lue, C., Poppe, A. R., Garrick-Bethell, I., et al. (2020). Simulating the reiner Gamma swirl: The long-term effect of solar wind standoff. J. Geophys. Res. Planets 125. doi:10.1029/2019JE006219

CrossRef Full Text | Google Scholar

Deca, J., Poppe, A. R., Divin, A., and Lembège, B. (2021). The plasma environment surrounding the Reiner Gamma magnetic anomaly. JGR. Space Phys. 126. doi:10.1029/2021JA029180

CrossRef Full Text | Google Scholar

Denevi, B. W., Robinson, M. S., Boyd, A. K., Blewett, D. T., and Klima, R. L. (2016). The distribution and extent of lunar swirls. Icarus 273, 53–67. doi:10.1016/j.icarus.2016.01.017

CrossRef Full Text | Google Scholar

Denevi, B. W., Robinson, M. S., Boyd, A. K., Sato, H., Hapke, B. W., Hawke, B. R., et al. (2014). Characterization of space weathering from lunar reconnaissance orbiter camera ultraviolet observations of the moon. J. Geophys. Res. Planets 119, 976–997. doi:10.1002/2013JE004527

CrossRef Full Text | Google Scholar

Domingue, D., Weirich, J., Chuang, F., Sickafoose, A., and Palmer, E. (2022). Topographic correlations within lunar swirls in mare Ingenii. Geophys. Res. Lett. 49. doi:10.1029/2021GL095285

CrossRef Full Text | Google Scholar

Dwyer, C. A., Stevenson, D. J., and Nimmo, F. (2011). A long-lived lunar dynamo driven by continuous mechanical stirring. Nature 479, 212–214. doi:10.1038/nature10564

PubMed Abstract | CrossRef Full Text | Google Scholar

Dyal, P., Parkin, C. W., and Daily, W. D. (1974). Magnetism and the interior of the moon. Rev. Geophys. 12, 568. doi:10.1029/rg012i004p00568

CrossRef Full Text | Google Scholar

El-Baz, F. (1972). The alhazen to abul wafa swirl belt: An extensive field of light-colored sinuous markings (No. NASA SP-315), Apollo 16 preliminary science report. Washington, D.C: National Aeronautics and Space Administration.

Google Scholar

Farrell, W. M., Hurley, D. M., and Zimmerman, M. I. (2014). Solar wind implantation into lunar regolith: Hydrogen retention in a surface with defects. Icarus 255, 116–126. doi:10.1016/j.icarus.2014.09.014

CrossRef Full Text | Google Scholar

Fatemi, S., Lue, C., Holmström, M., Poppe, A. R., Wieser, M., Barabash, S., et al. (2015). Solar wind plasma interaction with Gerasimovich lunar magnetic anomaly. J. Geophys. Res. Space Phys. 120, 4719–4735. doi:10.1002/2015JA021027

CrossRef Full Text | Google Scholar

Garrick-Bethell, I., Head, J. W., and Pieters, C. M. (2011). Spectral properties, magnetic fields, and dust transport at lunar swirls. Icarus 212, 480–492. doi:10.1016/j.icarus.2010.11.036

CrossRef Full Text | Google Scholar

Garrick-Bethell, I., Poppe, A. R., and Fatemi, S. (2019). The lunar paleo-magnetosphere: Implications for the accumulation of polar volatile deposits. Geophys. Res. Lett. 46, 5778–5787. doi:10.1029/2019GL082548

CrossRef Full Text | Google Scholar

Garrick-Bethell, I., Weiss, B. P., Shuster, D. L., Tikoo, S. M., and Tremblay, M. M. (2016). Further evidence for early lunar magnetism from troctolite 76535. J. Geophys. Res. Planets 121, 76–93. doi:10.1002/2016JE005154

CrossRef Full Text | Google Scholar

Gattacceca, J., Boustie, M., Hood, L. L., Cuq-Lelandais, J. P., Füller, M. D., Bezaeva, N. S., et al. (2010). Can the lunar crust be magnetized by shock: Experimental groundtruth. Earth Planet. Sci. Lett. 299, 42–53. doi:10.1016/j.epsl.2010.08.011

CrossRef Full Text | Google Scholar

Giacalone, J., and Hood, L. L. (2015). Hybrid simulation of the interaction of solar wind protons with a concentrated lunar magnetic anomaly. J. Geophys. Res. Space Phys. 120, 4081–4094. doi:10.1002/2014JA020938

CrossRef Full Text | Google Scholar

Gladstone, G. R., Retherford, K. D., Egan, A. F., Kaufmann, D. E., Miles, P. F., Parker, J. W., et al. (2012). Far-ultraviolet reflectance properties of the Moon’s permanently shadowed regions. J. Geophys. Res. 117. doi:10.1029/2011JE003913

CrossRef Full Text | Google Scholar

Gladstone, G. R., Stern, S. A., Retherford, K. D., Black, R. K., Slater, D. C., Davis, M. W., et al. (2010). Lamp: The lyman alpha mapping Project on NASA’s lunar reconnaissance orbiter mission. Space Sci. Rev. 150, 161–181. doi:10.1007/s11214-009-9578-6

CrossRef Full Text | Google Scholar

Glotch, T. D., Bandfield, J. L., Lucey, P. G., Hayne, P. O., Greenhagen, B. T., Arnold, J. A., et al. (2015). Formation of lunar swirls by magnetic field standoff of the solar wind. Nat. Commun. 6, 6189. doi:10.1038/ncomms7189

PubMed Abstract | CrossRef Full Text | Google Scholar

Gong, S., and Wieczorek, M. A. (2020). Is the lunar magnetic field correlated with gravity or topography? J. Geophys. Res. Planets 125. doi:10.1029/2019JE006274

CrossRef Full Text | Google Scholar

Green, J., Draper, D., Boardsen, S., and Dong, C. (2020). When the Moon had a magnetosphere. Sci. Adv. 6, eabc0865. doi:10.1126/sciadv.abc0865

PubMed Abstract | CrossRef Full Text | Google Scholar

Grier, J., McEwen, A. S., Lucey, P. G., Milazzo, M., and Strom, R. G. (2001). Optical maturity of ejecta from large rayed lunar craters. J. Geophys. Res. 106 (32), 32847–32862. doi:10.1029/1999JE001160

CrossRef Full Text | Google Scholar

Grimm, R. E., Delory, G. T., Espley, J. R., and Stillman, D. E. (2020). Presented at the lunar and planetary science conference. Houston, TX Lunar and Planetary Institute, 1568.A magnetotelluric sounder to probe terrestrial planet and satellite interiors.

Google Scholar

Halekas, J. S., Bale, S. D., Mitchell, D. L., and Lin, R. P. (2005). Electrons and magnetic fields in the lunar plasma wake. J. Geophys. Res. 110, 27841–27852. doi:10.1029/2004JA010991

CrossRef Full Text | Google Scholar

Halekas, J. S., Benna, M., Mahaffy, P. R., Elphic, R. C., Poppe, A. R., Delory, G. T., et al. (2015). Detections of lunar exospheric ions by the LADEE neutral mass spectrometer. Geophys. Res. Lett. 42, 5162–5169. doi:10.1002/2015GL064746

CrossRef Full Text | Google Scholar

Halekas, J. S., Brain, D. A., Mitchell, D. L., Lin, R. P., and Harrison, L. (2006). On the occurrence of magnetic enhancements caused by solar wind interaction with lunar crustal fields. Geophys. Res. Lett. 33, L08106. doi:10.1029/2006GL025931

CrossRef Full Text | Google Scholar

Halekas, J. S., Delory, G. T., Brain, D. A., Lin, R. P., and Mitchell, D. L. (2008). Density cavity observed over a strong lunar crustal magnetic anomaly in the solar wind: A mini-magnetosphere? Planet. Planet. Space Sci. 56, 941–946. doi:10.1016/j.pss.2008.01.008

CrossRef Full Text | Google Scholar

Halekas, J. S., Mitchell, D. L., Lin, R. P., Frey, S., Hood, L. L., Acuña, M. H., et al. (2001). Mapping of crustal magnetic anomalies on the lunar near side by the Lunar Prospector electron reflectometer. J. Geophys. Res. 106 (27), 27841–27852. doi:10.1029/2000JE001380

CrossRef Full Text | Google Scholar

Halekas, J. S., Mitchell, D. L., Lin, R. P., Hood, L. L., Acuña, M. H., and Binder, A. B. (2002). Demagnetization signatures of lunar impact craters. Geophys. Res. Lett. 29, 1645. doi:10.1029/2001GL013924

CrossRef Full Text | Google Scholar

Halekas, J. S., Poppe, A. R., Lue, C., Farrell, W. M., and McFadden, J. P. (2017). Distribution and solar wind control of compressional solar wind-magnetic anomaly interactions observed at the Moon by ARTEMIS. J. Geophys. Res. Space Phys. 122, 6240–6254. doi:10.1002/2017JA023931

PubMed Abstract | CrossRef Full Text | Google Scholar

Halekas, J. S., Poppe, A. R., McFadden, J. P., Angelopoulos, V., Glassmeier, K.-H., Brain, D. A., et al. (2014). Evidence for small-scale collisionless shocks at the Moon from ARTEMIS. Geophys. Res. Lett. 41, 7436–7443. doi:10.1002/2014GL061973

CrossRef Full Text | Google Scholar

Halekas, J. S., Saito, Y., Delory, G. T., and Farrell, W. M. (2011). New views of the lunar plasma environment. Planet. Space Sci. 59, 1681–1694. doi:10.1016/j.pss.2010.08.011

CrossRef Full Text | Google Scholar

Hapke, B. W. (2022). Do deep electrical discharges initiated by solar energetic particle events occur in the lunar regolith? Icarus 372, 114758. doi:10.1016/j.icarus.2021.114758

CrossRef Full Text | Google Scholar

Hapke, B. W. (2001). Space weathering from Mercury to the asteroid belt. J. Geophys. Res. 106 (10), 10039–10073. doi:10.1029/2000JE001338

CrossRef Full Text | Google Scholar

Hapke, B. W. (2012). Theory of reflectance and emittance spectroscopy. 2nd ed. Cambridge: Cambridge University Press.

Google Scholar

Hemingway, D. J., Garrick-Bethell, I., and Kreslavsky, M. A. (2015). Latitudinal variation in spectral properties of the lunar maria and implications for space weathering. Icarus 261, 66–79. doi:10.1016/j.icarus.2015.08.004

CrossRef Full Text | Google Scholar

Hemingway, D. J., and Garrick-Bethell, I. (2012). Magnetic field direction and lunar swirl morphology: Insights from Airy and Reiner Gamma. J. Geophys. Res. 117. doi:10.1029/2012JE004165

CrossRef Full Text | Google Scholar

Hemingway, D. J., and Tikoo, S. M. (2018). Lunar swirl morphology constrains the geometry, magnetization, and origins of lunar magnetic anomalies. J. Geophys. Res. Planets 123, 2223–2241. doi:10.1029/2018JE005604

CrossRef Full Text | Google Scholar

Hendrix, A. R., Greathouse, T. K., Retherford, K. D., Mandt, K. E., Gladstone, G. R., Kaufmann, D. E., et al. (2016). Lunar swirls: Far-UV characteristics. Icarus 273, 68–74. doi:10.1016/j.icarus.2016.01.003

CrossRef Full Text | Google Scholar

Hendrix, A. R., Hurley, D. M., Farrell, W. M., Greenhagen, B. T., Hayne, P. O., Retherford, K. D., et al. (2019). Diurnally migrating lunar water: Evidence from ultraviolet data. Geophys. Res. Lett. 46, 2417–2424. doi:10.1029/2018GL081821

CrossRef Full Text | Google Scholar

Hendrix, A. R., Retherford, K. D., Gladstone, G. R., Hurley, D. M., Feldman, P. D., Egan, A. F., et al. (2012). The lunar far-UV albedo: Indicator of hydration and weathering. J. Geophys. Res. 117. doi:10.1029/2012JE004252

CrossRef Full Text | Google Scholar

Hess, M., Wöhler, C., Bhatt, M., Berezhnoy, A. A., Grumpe, A., Wohlfarth, K., et al. (2020). Processes governing the VIS/NIR spectral reflectance behavior of lunar swirls. Astron. Astrophys. 639, A12. doi:10.1051/0004-6361/201937299

CrossRef Full Text | Google Scholar

Hinze, W. J., Frese, R. R. B. von, and Saad, A. H. (2013). Gravity and magnetic exploration: Principles, practices, and applications. 1st ed. Cambridge: Cambridge University Press.

Google Scholar

Hood, L. L., and Artemieva, N. A. (2008). Antipodal effects of lunar basin-forming impacts: Initial 3D simulations and comparisons with observations. Icarus 193, 485–502. doi:10.1016/j.icarus.2007.08.023

CrossRef Full Text | Google Scholar

Hood, L. L., Bryant, I., and van der Leeuw, J. (2022). Presented at the lunar and planetary science conference. The Woodlands, TX: Lunar and Planetary Institute, 2102.Magnetic anomalies over permanently shadowed craters near the lunar south Pole: Mapping and implications.

Google Scholar

Hood, L. L. (1987). Magnetic field and remanent magnetization effects of basin-forming impacts on the Moon. Geophys. Res. Lett. 14, 844–847. doi:10.1029/GL014i008p00844

CrossRef Full Text | Google Scholar

Hood, L. L., and Schubert, G. (1980). Lunar magnetic anomalies and surface optical properties. Science 4, 49–51. doi:10.1126/science.208.4439.49

CrossRef Full Text | Google Scholar

Hood, L. L., and Spudis, P. D. (2016). Magnetic anomalies in the Imbrium and Schrödinger impact basins: Orbital evidence for persistence of the lunar core dynamo into the Imbrian epoch. J. Geophys. Res. Planets 121, 2268–2281. doi:10.1002/2016JE005166

CrossRef Full Text | Google Scholar

Hood, L. L., Torres, C. B., Oliveira, J. S., Wieczorek, M. A., and Stewart, S. T. (2021). A new large-scale map of the lunar crustal magnetic field and its interpretation. J. Geophys. Res. Planets 126, e2020JE006667. doi:10.1029/2020JE006667

CrossRef Full Text | Google Scholar

Hood, L. L., and Williams, C. (1989). Presented at the lunar and planetary science conference. Houston, TX: Lunar and Planetary Institute, 99–113.The lunar swirls: Distribution and possible origins.

Google Scholar

Hood, L. L., Zakharian, A., Halekas, J. S., Mitchell, D. L., Lin, R. P., Acuña, M. H., et al. (2001). Initial mapping and interpretation of lunar crustal magnetic anomalies using Lunar Prospector magnetometer data. J. Geophys. Res. 106, 27825–27839. doi:10.1029/2000JE001366

CrossRef Full Text | Google Scholar

Hurley, D. M., and Farrell, W. M. (2013). Presented at the lunar and planetary science conference. The Woodlands, TX: Lunar and Planetary Institute.Solar wind fluence to the lunar surface.

Google Scholar

Jackson, T. L., Farrell, W. M., Killen, R. M., Delory, G. T., Halekas, J. S., Stubbs, T. J., et al. (2011). Discharging of roving objects in the lunar polar regions. J. Spacecr. Rockets 48, 700–704. doi:10.2514/1.51897

CrossRef Full Text | Google Scholar

Jackson, T. L., Farrell, W. M., and Zimmerman, M. I. (2015). Rover wheel charging on the lunar surface. Adv. Space Res. 55, 1710–1720. doi:10.1016/j.asr.2014.12.027

CrossRef Full Text | Google Scholar

Jarvinen, R., Alho, M., Kallio, E., Wurz, P., Barabash, S., Futaana, Y., et al. (2014). On vertical electric fields at lunar magnetic anomalies. Geophys. Res. Lett. 41, 2243–2249. doi:10.1002/2014GL059788

CrossRef Full Text | Google Scholar

Jelínek, K., Němeček, Z., and Šafránková, J. (2012). A new approach to magnetopause and bow shock modeling based on automated region identification. J. Geophys. Res. 117, A05208. doi:10.1029/2011JA017252

CrossRef Full Text | Google Scholar

Jordan, A. P. (2021). Evidence for dielectric breakdown weathering on the Moon. Icarus 358, 114199. doi:10.1016/j.icarus.2020.114199

PubMed Abstract | CrossRef Full Text | Google Scholar

Jordan, A. P. (2022). Reevaluating how charged particles cause space weathering on airless bodies. Icarus 376, 114878. doi:10.1016/j.icarus.2021.114878

CrossRef Full Text | Google Scholar

Jordan, A. P., Stubbs, T. J., Shusterman, M. L., Izenberg, N. R., Wilson, J. K., Hayne, P. O., et al. (2019). How dielectric breakdown may contribute to the global weathering of regolith on the moon. Icarus 319, 785–794. doi:10.1016/j.icarus.2018.10.025

CrossRef Full Text | Google Scholar

Kallio, E., Jarvinen, R., Dyadechkin, S., Wurz, P., Barabash, S., Alvarez, F., et al. (2012). Kinetic simulations of finite gyroradius effects in the lunar plasma environment on global, meso, and microscales. Planet. Space Sci. 74, 146–155. doi:10.1016/j.pss.2012.09.012

CrossRef Full Text | Google Scholar

Keller, L. P., and Clemett, S. J. (2001). Presented at the lunar and planetary science conference. The Woodlands, TX: Lunar and Planetary Institute, 2097.Formation of nanophase iron in the lunar regolith.

Google Scholar

Keller, L. P., and Zhang, S. (2015). Presented at the space weathering of airless bodies: An integration of remote sensing data. Houston, TX: Laboratory Experiments and Sample Analysis Workshop, Lunar and Planetary Institute.Rates of space weathering in lunar soils.

Google Scholar

Kelley, M. R., and Garrick-Bethell, I. (2020). Gravity constraints on the age and formation of the Moon’s Reiner Gamma magnetic anomaly. Icarus 338, 113465. doi:10.1016/j.icarus.2019.113465

CrossRef Full Text | Google Scholar

Kinczyk, M. J., Denevi, B. W., Boyd, A. K., Clegg-Watkins, R. N., Hapke, B. W., Henriksen, M. R., et al. (2016). Presented at the lunar and planetary science conference. The Woodlands, TX: Lunar and Planetary Institute, 2343.Controls on the photometric properties of lunar swirls in comparison to fresh crater ejecta.

Google Scholar

Korokhin, V., Shkuratov, Y., Kaydash, V., Basilevsky, A., Rohachova, L., Velikodsky, Y., et al. (2016). Characterization of a photometric anomaly in lunar Mare Nubium. Planet. Space Sci. 122, 70–87. doi:10.1016/j.pss.2016.01.011

CrossRef Full Text | Google Scholar

Kramer, G. Y., Besse, S., Dhingra, D., Nettles, J., Klima, R., Garrick-Bethell, I., et al. (2011a). M3 spectral analysis of lunar swirls and the link between optical maturation and surface hydroxyl formation at magnetic anomalies. J. Geophys. Res. 116, E00G18. doi:10.1029/2010JE003729

CrossRef Full Text | Google Scholar

Kramer, G. Y., Combe, J.-P., Harnett, E. M., Hawke, B. R., Noble, S. K., Blewett, D. T., et al. (2011b). Characterization of lunar swirls at mare Ingenii: A model for space weathering at magnetic anomalies. J. Geophys. Res. 116, E04008. doi:10.1029/2010JE003669

CrossRef Full Text | Google Scholar

Laneuville, M., Wieczorek, M. A., Breuer, D., Aubert, J., Morard, G., Rückriemen, T., et al. (2014). A long-lived lunar dynamo powered by core crystallization. Earth Planet. Sci. Lett. 401, 251–260. doi:10.1016/j.epsl.2014.05.057

CrossRef Full Text | Google Scholar

Lee, J.-K., Maxwell, R., Jin, H., Baek, S.-M., Ghassemi, O., Kelley, M., et al. (2019). A small lunar swirl and its implications for the formation of the Reiner Gamma magnetic anomaly. Icarus 319, 869–884. doi:10.1016/j.icarus.2018.09.015

CrossRef Full Text | Google Scholar

Li, S., and Garrick-Bethell, I. (2019). Surface water at lunar magnetic anomalies. Geophys. Res. Lett. 46, 14318–14327. doi:10.1029/2019GL084890

CrossRef Full Text | Google Scholar

Li, S., Lucey, P. G., Milliken, R. E., Hayne, P. O., Fisher, E., Williams, J.-P., et al. (2018). Direct evidence of surface exposed water ice in the lunar polar regions. Proc. Natl. Acad. Sci. U. S. A. 115, 8907–8912. doi:10.1073/pnas.1802345115

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, S., and Milliken, R. E. (2017). Water on the surface of the moon as seen by the moon mineralogy mapper: Distribution, abundance, and origins. Sci. Adv. 3, e1701471. doi:10.1126/sciadv.1701471

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, R., Mitchell, D., Curtis, D., Anderson, K., Carlson, C., McFadden, J., et al. (1998). Lunar surface magnetic fields and their interaction with the solar wind: Results from lunar prospector. Science 281, 1480–1484. doi:10.1126/science.281.5382.1480

PubMed Abstract | CrossRef Full Text | Google Scholar

Liuzzo, L., Poppe, A. R., Halekas, J. S., Simon, S., and Cao, X. (2021). Investigating the moon’s interaction with the terrestrial magnetotail lobe plasma. Geophys. Res. Lett. 48, e2021GL093566. doi:10.1029/2021GL093566

CrossRef Full Text | Google Scholar

Loeffler, M. J., Dukes, C. A., and Baragiola, R. A. (2009). Irradiation of olivine by 4 keV He+: Simulation of space weathering by the solar wind. J. Geophys. Res. 114, E03003. doi:10.1029/2008JE003249

CrossRef Full Text | Google Scholar

Lucey, P. G., and Riner, M. A. (2011). The optical effects of small iron particles that darken but do not redden: Evidence of intense space weathering on Mercury. Icarus 212, 451–462. doi:10.1016/j.icarus.2011.01.022

CrossRef Full Text | Google Scholar

Lue, C., Futaana, Y., Barabash, S., Wieser, M., Holmström, M., Bhardwaj, A., et al. (2011). Strong influence of lunar crustal fields on the solar wind flow. Geophys. Res. Lett. 38. doi:10.1029/2010GL046215

CrossRef Full Text | Google Scholar

Maxwell, R., and Garrick-Bethell, I. (2020). Evidence for an ancient near-equatorial lunar dipole from higher precision inversions of crustal magnetization. J. Geophys. Res. Planets 125. doi:10.1029/2020JE006567

CrossRef Full Text | Google Scholar

Mighani, S., Wang, H., Shuster, D. L., Borlina, C. S., Nichols, C. I. O., Weiss, B. P., et al. (2020). The end of the lunar dynamo. Sci. Adv. 6, eaax0883. doi:10.1126/sciadv.aax0883

PubMed Abstract | CrossRef Full Text | Google Scholar

Mitchell, D. L., Halekas, J. S., Lin, R. P., Frey, S., Hood, L. L., Acuña, M. H., et al. (2008). Global mapping of lunar crustal magnetic fields by Lunar Prospector. Icarus 194, 401–409. doi:10.1016/j.icarus.2007.10.027

CrossRef Full Text | Google Scholar

Nakauchi, Y., Abe, M., Ohtake, M., Matsumoto, T., Tsuchiyama, A., Kitazato, K., et al. (2021). The formation of H2O and Si-OH by H2+ irradiation in major minerals of carbonaceous chondrites. Icarus 355, 114140. doi:10.1016/j.icarus.2020.114140

CrossRef Full Text | Google Scholar

Nayak, M., Hemingway, D., and Garrick-Bethell, I. (2017). Magnetization in the South Pole-Aitken basin: Implications for the lunar dynamo and true polar wander. Icarus 286, 153–192. doi:10.1016/j.icarus.2016.09.038

CrossRef Full Text | Google Scholar

Neish, C. D., Blewett, D. T., Bussey, D. B. J., Lawrence, S. J., Mechtley, M., Thomson, B. J., et al. (2011). The surficial nature of lunar swirls as revealed by the Mini-RF instrument. Icarus 215, 186–196. doi:10.1016/j.icarus.2011.06.037

CrossRef Full Text | Google Scholar

Nicholas, J. B., Purucker, M. E., and Sabaka, T. J. (2007). Age spot or youthful marking: Origin of reiner Gamma. Geophys. Res. Lett. 34, L02205. doi:10.1029/2006GL027794

CrossRef Full Text | Google Scholar

Nichols, C. I. O., Weiss, B. P., Getzin, B. L., Schmitt, H. H., Béguin, A., Rae, A. S. P., et al. (2021). The palaeoinclination of the ancient lunar magnetic field from an Apollo 17 basalt. Nat. Astron. 5, 1216–1223. doi:10.1038/s41550-021-01469-y

CrossRef Full Text | Google Scholar

Nishino, M. N., Fujimoto, M., Tsunakawa, H., Matsushima, M., Shibuya, H., Shimizu, H., et al. (2012). Control of lunar external magnetic enhancements by IMF polarity: A case study. Planet. Space Sci. 73, 161–167. doi:10.1016/j.pss.2012.09.011

CrossRef Full Text | Google Scholar

Nishino, M. N., Harada, Y., Saito, Y., Tsunakawa, H., Takahashi, F., Yokota, S., et al. (2017). Kaguya observations of the lunar wake in the terrestrial foreshock: Surface potential change by bow-shock reflected ions. Icarus 293, 45–51. doi:10.1016/j.icarus.2017.04.005

CrossRef Full Text | Google Scholar

Noble, S. K., Pieters, C. M., and Keller, L. P. (2007). An experimental approach to understanding the optical effects of space weathering. Icarus 192, 629–642. doi:10.1016/j.icarus.2007.07.021

CrossRef Full Text | Google Scholar

Oliveira, J. S., and Wieczorek, M. A. (2017). Testing the axial dipole hypothesis for the Moon by modeling the direction of crustal magnetization. J. Geophys. Res. Planets 122, 383–399. doi:10.1002/2016JE005199

CrossRef Full Text | Google Scholar

Oran, R., Weiss, B. P., Shprits, Y., Miljković, K., and Tóth, G. (2020). Was the moon magnetized by impact plasmas? Sci. Adv. 6, eabb1475. doi:10.1126/sciadv.abb1475

PubMed Abstract | CrossRef Full Text | Google Scholar

Papitashvili, Natalia E., and King, Joseph H. (2020). OMNI 1-min data. Greenbelt, MD NASA Space Physics Data Facility. doi:10.48322/45bb-8792

CrossRef Full Text | Google Scholar

Pieters, C. M., Moriarty, D. P., and Garrick-Bethell, I. (2014). Presented at the lunar and planetary science conference. The Woodlands, TX: Lunar and Planetary Institute.Atypical regolith processes hold the key to enigmatic lunar swirls.

Google Scholar

Pieters, C. M., and Noble, S. K. (2016). Space weathering on airless bodies. J. Geophys. Res. Planets 121, 1865–1884. doi:10.1002/2016JE005128

PubMed Abstract | CrossRef Full Text | Google Scholar

Pieters, C. M., Taylor, L. A., Noble, S. K., Keller, L. P., Hapke, B. W., Morris, R. V., et al. (2000). Space weathering on airless bodies: Resolving a mystery with lunar samples. Meteorit. Planet. Sci. 35, 1101–1107. doi:10.1111/j.1945-5100.2000.tb01496.x

CrossRef Full Text | Google Scholar

Pinet, P. C., Shevchenko, V. V., Chevre, S. D., Daydou, Y., and Rosemberg, C. (2000). Local and regional lunar regolith characteristics at Reiner Gamma Formation: Optical and spectroscopic properties from Clementine and Earth-based data. J. Geophys. Res. 105, 9457–9475. doi:10.1029/1999JE001086

CrossRef Full Text | Google Scholar

Poppe, A. R., Fatemi, S., Garrick-Bethell, I., Hemingway, D., and Holmström, M. (2016). Solar wind interaction with the Reiner Gamma crustal magnetic anomaly: Connecting source magnetization to surface weathering. Icarus 266, 261–266. doi:10.1016/j.icarus.2015.11.005

CrossRef Full Text | Google Scholar

Poppe, A. R., Fatemi, S., Halekas, J. S., Holmström, M., and Delory, G. T. (2014). ARTEMIS observations of extreme diamagnetic fields in the lunar wake. Geophys. Res. Lett. 41, 3766–3773. doi:10.1002/2014GL060280

CrossRef Full Text | Google Scholar

Poppe, A. R., Halekas, J. S., Lue, C., and Fatemi, S. (2017). ARTEMIS observations of the solar wind proton scattering function from lunar crustal magnetic anomalies. J. Geophys. Res. Planets 122, 771–783. doi:10.1002/2017JE005313

PubMed Abstract | CrossRef Full Text | Google Scholar

Purucker, M. E. (2019). A vector fluxgate magnetometer to Lacus Mortis on the Moon. San Francisco, CA: Presented at the American Geophysical Union Fall Meeting.

Google Scholar

Purucker, M. E., Head, J. W., and Wilson, L. (2012). Magnetic signature of the lunar South Pole-Aitken basin: Character, origin, and age. J. Geophys. Res. 117. doi:10.1029/2011JE003922

CrossRef Full Text | Google Scholar

Purucker, M. E., and Nicholas, J. B. (2010). Global spherical harmonic models of the internal magnetic field of the Moon based on sequential and coestimation approaches. J. Geophys. Res. 115, E12007. doi:10.1029/2010JE003650

CrossRef Full Text | Google Scholar

Ravat, D., Purucker, M. E., and Olsen, N. (2020). Lunar magnetic field models from lunar prospector and SELENE/Kaguya along-track magnetic field gradients. J. Geophys. Res. Planets 125, e2019JE006187. doi:10.1029/2019JE006187

CrossRef Full Text | Google Scholar

Richmond, N. C., and Hood, L. L. (2008). A preliminary global map of the vector lunar crustal magnetic field based on Lunar Prospector magnetometer data. J. Geophys. Res. 113, E02010. doi:10.1029/2007JE002933

CrossRef Full Text | Google Scholar

Richmond, N. C., Hood, L. L., Halekas, J. S., Mitchell, D. L., Lin, R. P., Acuña, M. H., et al. (2003). Correlation of a strong lunar magnetic anomaly with a high-albedo region of the Descartes mountains. Geophys. Res. Lett. 30. doi:10.1029/2003GL016938

CrossRef Full Text | Google Scholar

Richmond, N. C., Hood, L. L., Mitchell, D. L., Lin, R. P., Acuña, M. H., and Binder, A. B. (2005). Correlations between magnetic anomalies and surface geology antipodal to lunar impact basins. J. Geophys. Res. 110, E05011. doi:10.1029/2005JE002405

CrossRef Full Text | Google Scholar

Robinson, M. S., Brylow, S. M., Tschimmel, M., Humm, D., Lawrence, S. J., Thomas, P. C., et al. (2010). Lunar reconnaissance orbiter camera (LROC) instrument overview. Space Sci. Rev. 150, 81–124. doi:10.1007/s11214-010-9634-2

CrossRef Full Text | Google Scholar

Russell, C. T. (1993). Planetary magnetospheres. Rep. Prog. Phys. 56, 687–732. doi:10.1088/0034-4885/56/6/001

CrossRef Full Text | Google Scholar

Saito, Y., Yokota, S., Tanaka, T., Asamura, K., Nishino, M. N., Fujimoto, M., et al. (2008). Solar wind proton reflection at the lunar surface: Low energy ion measurement by MAP-PACE onboard SELENE (KAGUYA). Geophys. Res. Lett. 35, L24205. doi:10.1029/2008GL036077

CrossRef Full Text | Google Scholar

Schultz, P. H. (1972). A preliminary morphologic study of the lunar surface. Austin, TX: Ph.D. Thesis). University of Texas at Austin.

Google Scholar

Schultz, P. H., and Snrka, L. J. (1980). Cometary collisions on the moon and Mercury. Nature 284, 22–26. doi:10.1038/284022a0

CrossRef Full Text | Google Scholar

Shkuratov, Yu., Kaydash, V., Gerasimenko, S., Opanasenko, N., Velikodsky, Yu., Korokhin, V., et al. (2010). Probable swirls detected as photometric anomalies in Oceanus Procellarum. Icarus 208, 20–30. doi:10.1016/j.icarus.2010.01.028

CrossRef Full Text | Google Scholar

Shue, J.-H., Song, P., Russell, C. T., Steinberg, J. T., Chao, J. K., Zastenker, G., et al. (1998). Magnetopause location under extreme solar wind conditions. J. Geophys. Res. 103 (17), 17691–17700. doi:10.1029/98JA01103

CrossRef Full Text | Google Scholar

Sim, C. K., Kim, S. S., Lucey, P. G., Garrick-Bethell, I., and Choi, Y.-J. (2017). Asymmetric space weathering on lunar crater walls. Geophys. Res. Lett. 44 (11), 11273–11281. doi:10.1002/2017GL075338

CrossRef Full Text | Google Scholar

Snyder, C. W., Clay, D. R., and Neugebauer, M. (1970). Solar-wind spectrometer experiment (No. NASA SP-235), Apollo 12 preliminary science report. Washington, D.C: National Aeronautics and Space Administration.

Google Scholar

Sonett, C. P., and Mihalov, J. D. (1972). Lunar fossil magnetism and perturbations of the solar wind. J. Geophys. Res. 77, 588–603. doi:10.1029/JA077i004p00588

CrossRef Full Text | Google Scholar

Starukhina, L., and Shkuratov, Y. (2004). Swirls on the Moon and Mercury: Meteoroid swarm encounters as a formation mechanism. Icarus 167, 136–147. doi:10.1016/j.icarus.2003.08.022

CrossRef Full Text | Google Scholar

Strauss, B. E., Tikoo, S. M., Gross, J., Setera, J. B., and Turrin, B. (2021). Constraining the decline of the lunar dynamo field at ≈3.1 Ga through paleomagnetic analyses of Apollo 12 mare basalts. J. Geophys. Res. Planets 126, e2020JE006715. doi:10.1029/2020JE006715

CrossRef Full Text | Google Scholar

Stubbs, T. J., Farrell, W. M., Halekas, J. S., Burchill, J. K., Collier, M. R., Zimmerman, M. I., et al. (2014). Dependence of lunar surface charging on solar wind plasma conditions and solar irradiation. Planet. Space Sci. 90, 10–27. doi:10.1016/j.pss.2013.07.008

CrossRef Full Text | Google Scholar

Takahashi, F., Tsunakawa, H., Shimizu, H., Shibuya, H., and Matsushima, M. (2014). Reorientation of the early lunar pole. Nat. Geosci. 7, 409–412. doi:10.1038/NGEO2150

CrossRef Full Text | Google Scholar

Tarduno, J. A., Cottrell, R. D., Lawrence, K., Bono, R. K., Huang, W., Johnson, C. L., et al. (2021). Absence of a long-lived lunar paleomagnetosphere. Sci. Adv. 7, eabi7647. doi:10.1126/sciadv.abi7647

PubMed Abstract | CrossRef Full Text | Google Scholar

Tikoo, S. M., Gattacceca, J., Swanson-Hysell, N. L., Weiss, B. P., Suavet, C., Cournède, C., et al. (2015). Preservation and detectability of shock-induced magnetization. J. Geophys. Res. Planets 120, 1461–1475. doi:10.1002/2015JE004840

CrossRef Full Text | Google Scholar

Tikoo, S. M., Weiss, B. P., Shuster, D. L., Suavet, C., Wang, H., Grove, T. L., et al. (2017). A two-billion-year history for the lunar dynamo. Sci. Adv. 3, e1700207. doi:10.1126/sciadv.1700207

PubMed Abstract | CrossRef Full Text | Google Scholar

Trang, D., and Lucey, P. G. (2019). Improved space weathering maps of the lunar surface through radiative transfer modeling of Kaguya multiband imager data. Icarus 321, 307–323. doi:10.1016/j.icarus.2018.11.014

CrossRef Full Text | Google Scholar

Tsunakawa, H., Shibuya, H., Takahashi, F., Shimizu, H., Matsushima, M., Matsuoka, A., et al. (2010). Lunar magnetic field observation and initial global mapping of lunar magnetic anomalies by MAP-LMAG onboard SELENE (Kaguya). Space Sci. Rev. 154, 219–251. doi:10.1007/s11214-010-9652-0

CrossRef Full Text | Google Scholar

Tsunakawa, H., Takahashi, F., Shimizu, H., Shibuya, H., and Matsushima, M. (2015). Surface vector mapping of magnetic anomalies over the Moon using Kaguya and Lunar Prospector observations. J. Geophys. Res. Planets 120, 1160–1185. doi:10.1002/2014JE004785

CrossRef Full Text | Google Scholar

Tucker, O. J., Farrell, W. M., and Poppe, A. R. (2021). On the effect of magnetospheric shielding on the lunar hydrogen cycle. J. Geophys. Res. Planets 126, e2020JE006552. doi:10.1029/2020JE006552

CrossRef Full Text | Google Scholar

Vilas, F., and Hendrix, A. R. (2015). The UV/blue effects of space weathering manifested in S-complex asteroids. I. Quantifying change with asteroid age. Astron. J. 150, 64. doi:10.1088/0004-6256/150/2/64

CrossRef Full Text | Google Scholar

Vorburger, A., Wurz, P., Barabash, S., Wieser, M., Futaana, Y., Holmström, M., et al. (2012). Energetic neutral atom observations of magnetic anomalies on the lunar surface. J. Geophys. Res. 117. doi:10.1029/2012JA017553

CrossRef Full Text | Google Scholar

Wakita, S., Johnson, B. C., Garrick-Bethell, I., Kelley, M. R., Maxwell, R. E., Davison, T. M., et al. (2021). Impactor material records the ancient lunar magnetic field in antipodal anomalies. Nat. Commun. 12, 6543. doi:10.1038/s41467-021-26860-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, X., Howes, C. T., Horányi, M., and Robertson, S. (2013). Electric potentials in magnetic dipole fields normal and oblique to a surface in plasma: Understanding the solar wind interaction with lunar magnetic anomalies. Geophys. Res. Lett. 40, 1686–1690. doi:10.1002/grl.50367

CrossRef Full Text | Google Scholar

Weiss, B. P., and Tikoo, S. M. (2014). The lunar dynamo. Science 346, 1246753. doi:10.1126/science.1246753

PubMed Abstract | CrossRef Full Text | Google Scholar

Wieczorek, M. A. (2018). Strength, depth, and geometry of magnetic sources in the crust of the moon from localized power spectrum analysis. JGR. Planets 123, 291–316. doi:10.1002/2017JE005418

CrossRef Full Text | Google Scholar

Wieczorek, M. A., Weiss, B. P., and Stewart, S. T. (2012). An impactor origin for lunar magnetic anomalies. Science 335, 1212–1215. doi:10.1126/science.1214773

PubMed Abstract | CrossRef Full Text | Google Scholar

Xie, L., Li, L., Zhang, A., Zhang, Y., Cao, J., Wieser, M., et al. (2021). Inside a lunar mini-magnetosphere: First energetic neutral atom measurements on the lunar surface. Geophys. Res. Lett. 48, e2021GL093943. doi:10.1029/2021GL093943

CrossRef Full Text | Google Scholar

Zhang, S., and Keller, L. P. (2011). Space weathering effects in lunar soils: The roles of surface exposure time and bulk chemical composition. In Presented at the lunar and planetary science conference. The Woodlands, TX: Lunar and Planetary Institute.

Google Scholar

Zimmerman, M. I., Farrell, W. M., and Poppe, A. R. (2015). Kinetic simulations of kilometer-scale mini-magnetosphere formation on the Moon. J. Geophys. Res. Planets 120, 1893–1903. doi:10.1002/2015JE004865

CrossRef Full Text | Google Scholar

Zimmerman, M. I., Jackson, T. L., Farrell, W. M., and Stubbs, T. J. (2012). Plasma wake simulations and object charging in a shadowed lunar crater during a solar storm. J. Geophys. Res. 117. doi:10.1029/2012JE004094

CrossRef Full Text | Google Scholar