Frequency Transition From Weak to Strong Turbulence in the Solar Wind

During a specific time window while approaching the Sun, the longitudinal speed of Parker Solar Probe matches that of the Sun’s rotation. The spacecraft therefore co-rotates with the Sun, and as long as it does so, it is immersed in the solar-wind plasma of the same flow tube. This unique feature of the Parker Solar Probe’s orbital configuration is exploited in this work for the first time, to investigate the spectral properties of the turbulence of the same plasma stream, from large to small scales, very close to the Sun. Standard diagnostics for spectral power, compressibility, and intermittency are applied to the magnetic field data acquired by Parker Solar Probe during its seventh encounter with the Sun. The results clearly show the presence of a frequency transition (at about 5 × 10^–3 Hz in the spacecraft frame) within the inertial range, where the spectrum steepens from an Iroshnikov-Kraichnan-like 3/2 to a Kolmogorov-like 5/3 scaling, the Alfvénic content decreases, whereas intermittency grows. This observational evidence is interpreted as the transition from scales dominated by Alfvénic fluctuations (and thus poorly intermittent and turbulent) to scales dominated by nonlinear interactions (and thus more intermittent and turbulent). To the author’s knowledge, this is the first time that such a transition from weak to strong turbulence in the inertial range has been observed, and it certainly deserves further investigation, both from an observational and theoretical perspective.

1 Introduction

The interplanetary space is permeated by the solar wind, a supersonic and super-Alfvénic plasma flow coming from the outermost layer of the Sun’s atmosphere, the solar corona (Hundhausen, 1972). Early in the space exploration era (in the 1960s), it became immediately apparent that the solar wind is in a state of fully developed turbulence. Indeed, the first observations of the spectral properties of magnetic fluctuations in the solar wind by Mariner two indicated the existence of a Kolmogorov-like − 5/3 energy spectrum spanning almost 4 decades of scales (Coleman and Paul, 1968), a universally known distinctive feature of turbulence. Since then, the solar wind has been regarded as a natural wind tunnel laboratory, where turbulence in space plasmas can be uniquely studied over a wide range of scales, through in-situ spacecraft measurements of fluctuations in all fields describing the plasma state (Bruno and Carbone, 2013). Beginning with the groundbreaking multiple versions of the Mariner and Pioneer space missions, a plethora of spacecraft have been thus launched to explore the Sun and its environment, throughout the Solar System, from the inner heliosphere (such as Helios 1 and 2) to its final Frontier and beyond (Voyager). It is thus now widely recognized that, despite some theoretical complications (inhomogeneities, compressibility, anisotropy), low-frequency fluctuations in the solar wind can be described by magnetohydrodynamic (MHD) equations in the framework of classical turbulence (Kraichnan, 1965; Tu and Marsch, 1995; Biskamp, 2003).

Actually, the solar wind fluctuations exhibit three different spectral regimes, corresponding to the injection, inertial, and dissipative ranges, which are governed by the characteristic scales of the flow system (Verscharen et al., 2019). Energy is injected into the system at the largest scales by any external force (such as shear flow). Within this range of spatial scales magnetic fluctuations are uncorrelated and often display a −1 power-law scaling, whose origin is not well understood (different theories exist trying to explain the nature of fluctuations within the injection range, see Verscharen et al., 2019). The largest separation distance over which eddies begin to be correlated with each other, known as the correlation length λ_C, marks the transition from the injection to the inertial range. This is where energy begins to be transferred by inertia (through nonlinear interactions) from larger to smaller eddies in the turbulent cascade à la Richardson, and the magnetic fluctuations scale as k^−5/3 (where k is the wavenumber). The energy cascade continues down to the Taylor scale λ_T, where the size of the eddies is so small that viscous effects become prominent: energy hence stops being efficiently transferred at the smaller scales, but rather begins to be dissipated thus heating the plasma. At scales below λ_T, solar wind fluctuations exhibit a kinetic nature and can no longer be described within the MHD framework: small scales fall in the realm of kinetic physics (Marsch, 2006). The transition from fluid to kinetic domain is associated with a steepening of the magnetic-field spectrum, which drops off with a power-law index larger than two and generally close to 2.8 (e.g., Verscharen et al., 2019).

It should be noted that fast and slow wind show important differences in terms of spectral properties, which highlight the different nature of the turbulence fluctuations. Specifically, the slow wind spectra do not always display a transition from energy-containing scales to inertial scales (Bruno et al., 2019). Even when a low-frequency break is observed, this is located at much lower frequencies with respect to fast wind. The origin of the k⁻¹ scaling could be explained in terms of magnetic amplitude saturation (Matteini et al., 2018; Bruno et al., 2019). It follows that fast-wind magnetic fluctuations reach a saturation level at higher frequencies (and, in turn, the low-frequency break shifts to higher frequencies) with respect to slow wind, since they are Alfvénic in nature and, as such, much larger than the typical non-Alfvénic slow-wind magnetic field fluctuations (Bruno and Carbone, 2013). In addition, if the relative amplitude of the slow-wind fluctuations with respect to the local magnetic field were extremely small, the low-frequency break could be located at lower frequencies than observed due to not long enough slow-wind intervals.

The low- and high-frequency breaks observed in the ecliptic fast wind, associated with the correlation length λ_C and the Taylor scale λ_T, respectively, both shift to lower and lower frequencies as the wind expands, albeit with a different scaling law. Specifically, while the high-frequency break decreases with distance r from the Sun as r^−1.1 (Bruno and Trenchi, 2014), that separating the injection from the inertial range has a faster radial evolution, dropping off as r^−1.5 (Bruno et al., 2009). It follows that the inertial range becomes wider moving away from the Sun (Telloni et al., 2015). Incidentally, since the effective magnetic Reynolds number can be estimated as $R_m^{eff}={({\lambda }_C/{\lambda }_T)}^2$ (Matthaeus et al., 2005), it turns out that $R_m^{eff}$ increases with distance from the Sun: hence, the fast wind plasma evolves toward a more turbulent state as it expands into interplanetary space (Telloni et al., 2015). Finally, a similar, though shallower (r^−1.1), radial dependence of the breakpoint between the injection and the inertial range is also observed in the polar fast wind (Horbury et al., 1996), indicating a slower evolution of fast wind turbulence at high latitudes than on the ecliptic, due to the lack of forcing large-scale stream shears.

Studying the whole range of turbulent fluctuation scales relies on the possibility of sampling the plasma coming from the same solar source, i.e., the same solar wind stream, with high-temporal resolution instrumentations (to investigate dissipative scales) for a time interval considerably (at least 10 times) longer than the correlation length λ_C (to explore energy-containing scales). Since, as discussed above, the location of λ_C strongly depends on the amplitude of magnetic fluctuations (and, therefore, whether fast or slow wind is being probed) and the distance from the Sun, this last request could imply that for detecting the injection range of fluctuations it might be necessary to sample the same stream for a time interval ranging from a few hours to a few days. While at distances probed by Helios 1 and 2 in the early 70s and beyond both high and low-speed streams last for days (e.g., Bavassano et al., 1982a,b), in the very inner heliosphere where Parker Solar Probe (PSP, Fox et al., 2016) orbits the picture can be much more challenging. Indeed, the very high PSP orbital speed in combination with a smaller longitudinal extension of the Parker spiral-related streams closer to the Sun means that PSP crosses, along its trajectory, adjacent streams very quickly and, in turn, do not sample the same solar wind plasma for more than a few hours (at best), especially at perihelion. Thankfully, the PSP’s unique orbital characteristic of going into co-rotation with the Sun allows the sampling of the same plasma flux for a relatively long time (more than a day) and, thereby, the investigation of solar wind turbulence in the very inner heliosphere from (tentatively) injection scales to the kinetic domain. Indeed, as PSP approaches the Sun it has a longitudinal speed much higher than the Sun’s rotational velocity, thus moving forth in longitude relative to the Sun. As PSP then exits the perihelion passage, its orbital speed decreases, becoming lower than that of the solar rotation, and PSP will therefore move back in longitude with respect to the Sun. At some instant, therefore, PSP will be co-rotating with the Sun. That is, in the reference frame co-rotating with the Sun, the longitude of PSP will only weakly change. This means that as long as PSP is in quasi co-rotation with the Sun, the spacecraft will be immersed in the same solar wind stream, providing an interesting opportunity to study the spectral properties of the same plasma flow over the whole range of spatial scales, very close to the Sun. This is the approach followed, for the first time, in the present work, whose layout is as follows: §2 deals with the identification of the PSP quasi co-rotation period during encounter 7 with the Sun, §3 presents the results of the PSP data analysis, while concluding remarks are given in § 4.

2 Parker Solar Probe Co-Rotation With the Sun

In order to identify when PSP and the Sun co-rotate during encounter 7, the longitude of PSP’s position λ was conveniently displayed in the reference frame co-rotating with the Sun (Figure 1A). In doing so, λ increases (decreases) as the spacecraft moves forth (back) in longitude with respect to the Sun (in red and blue, respectively). λ = 0 (full dot) corresponds to PSP—Sun co-rotation. By applying a tolerance of 1° in longitude (horizontal dashed line), a quasi co-rotation interval (in thick black, delimited between vertical dotted lines) can be identified ¹. The selected period lasts 1.17 days, from 20 January 2021 at 03 : 52 UT to 21 January 2021 at 07 : 57 UT. The periods along the PSP trajectory when the spacecraft is faster or slower than the Sun’s rotation, or is in quasi co-rotation are shown (color-coded), in the top view of the equatorial plane (in the HelioCentric Inertial (HCI) coordinate frame ²), in Figure 1B. It is worth noting that it has been further verified that the solar wind plasma sampled by PSP in this interval originates from the same source region at the Sun, by back-mapping the spacecraft position onto the source surface according to Panasenco et al. (2020) (not shown).

FIGURE 1

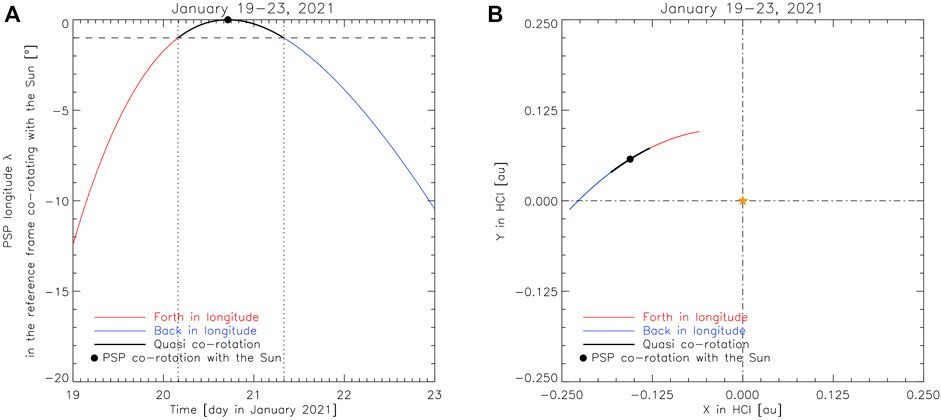
FIGURE 1. PSP longitude λ in the reference frame co-rotating with the Sun (A) and PSP trajectory around the Sun (yellow star) on the HCI equatorial plane (B), during PSP encounter 7 with the Sun, from January 19−23, 2021. Periods when PSP moves back and forth relative to the Sun or is in quasi co-rotation are indicated in blue, red, and thick black, respectively; the full dot marks the instant when PSP is co-rotating with the Sun. The horizontal dashed line at 1° in (A) displays the longitude tolerance applied to identify the PSP—Sun quasi co-rotation period (delimited by vertical dotted lines).

Some relevant solar wind parameters observed in this PSP—Sun quasi co-rotation interval are shown, between vertical dotted lines, in Figure 2, which overall spans a 4-day period from January 19, 23, 2021. PSP magnetic field and plasma data (merged at 1-min resolution) come from the MAG fluxgate magnetometer and the SPAN-Ai top-hat electrostatic analyzer of the FIELDS (Bale et al., 2016) and Solar Wind Electrons Alphas & Protons (SWEAP, Kasper et al., 2016) instrument suites, respectively. From top to bottom, the panels display 1) the plasma V and Alfvén V_A ($\equiv B/\sqrt{{\mu }_0\rho }$, being B, μ₀, and ρ the magnetic field magnitude, vacuum magnetic permeability, and mass density, respectively) speed, 2) the magnetic field vector intensity and components (B_R, B_T, B_N) in the Radial Tangential Normal (RTN) coordinate system, 3) the θ_RB and θ_VB angles between the magnetic field and either radial or flow direction, 4) the proton density n_p, 5) temperature T_p, 6) temperature anisotropy T_⊥,p/T_∥,p, and 7) plasma beta β_p (≡ P/(B²/2μ₀), where P = n_pk_BT_p is the plasma pressure, being k_B the Boltzmann constant, and B²/2μ₀ is the magnetic pressure), and (8) the PSP altitude r above the Sun.

FIGURE 2

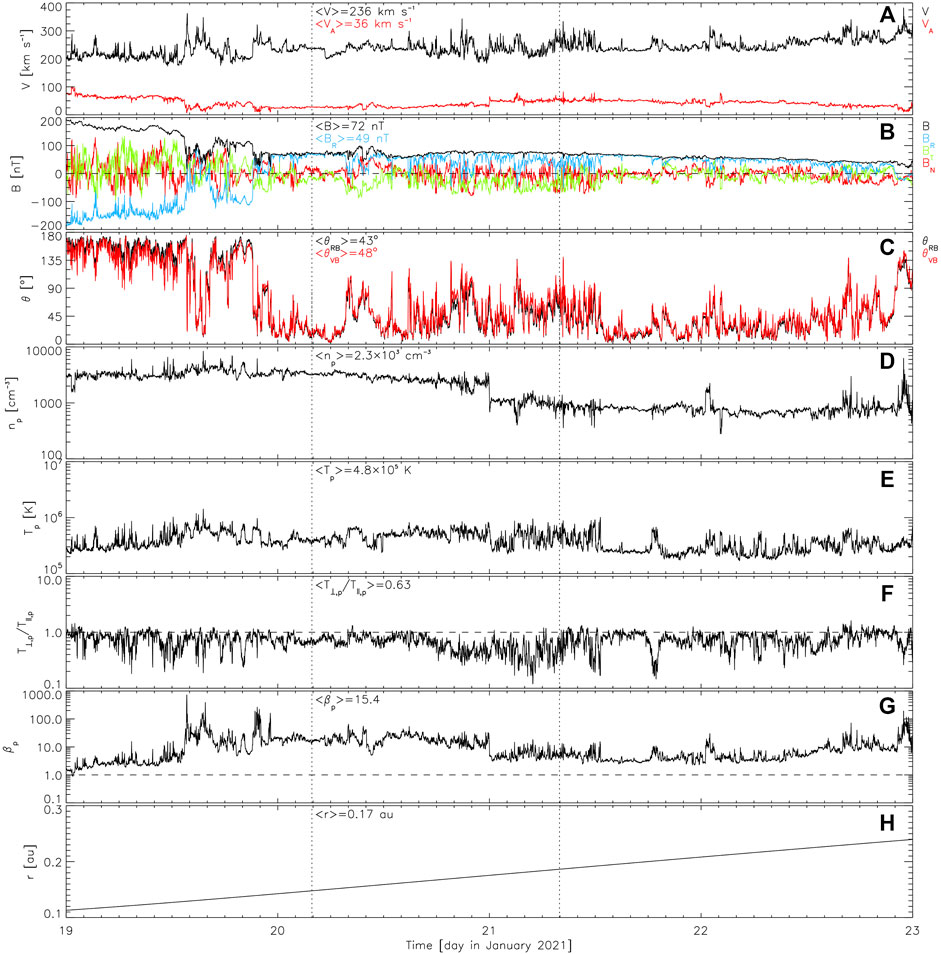
FIGURE 2. Overview of the PSP—Sun quasi co-rotation interval (between vertical dotted lines) identified during encounter 7, showing (A) the solar wind V and Alfvén V_A speed, (B) the magnetic field vector components (B_R, B_T, B_N) and intensity B, (C) the angles θ_RB and θ_VB of the magnetic field vector with the radial direction and the plasma flow velocity vector, (D) the proton density n_p, (E) temperature T_p, (F) temperature anisotropy T_⊥,p/T_∥,p, and (G) plasma beta β_p, and (H) the distance r of PSP from the Sun. Average values during quasi co-rotation are reported within each panel.

The PSP—Sun quasi co-rotation interval lies just downstream of the heliospheric current sheet (HCS) crossing occurred in late 20 January 2021, as clearly evidenced by the sudden and full rotation of the magnetic field (Figure 2B). During quasi co-rotation with the Sun, the magnetic field was thus outwardly oriented and PSP was immersed in a slow flow of super-Alfvénic plasma, characterized by several bursts of accelerated wind (especially in the second part of the interval), as indicated by the spikes in the V profile (Figure 2A). These wind accelerations coincide with sharp rotations of the magnetic field (see B_R in Figure 2B), the largest ones reversing the field direction and causing major excursions from alignment with the flow (Figure 2C). These are attributed to switchbacks (Bale et al., 2019). Nevertheless, the magnetic field intensity B is rather smooth (Figure 2B), suggesting a high incompressibility of the large-scale magnetic fluctuations embedded in the wind. The plasma parameters n_p, T_p, T_⊥,p/T_∥,p, and β_p are all relatively smoother during the first part of quasi co-rotation than in the second half, which is instead dominated by larger fluctuations (Figures 2D–G). Interestingly, the temperature anisotropy is on average 0.63, thus significantly below isotropy, as expected in case of switchbacks generated by interchange magnetic reconnection (Zank et al., 2020a).

3 Solar Wind Turbulence From Large to Small Scales

This section deals with the spectral analysis of magnetic field fluctuations (acquired by FIELDS/MAG at 4 Hz), in order to asses the turbulence properties of the slow-wind stream observed by PSP while nearly co-rotating with the Sun, over the whole range of scales involved. The results are reported in Figure 3.

FIGURE 3

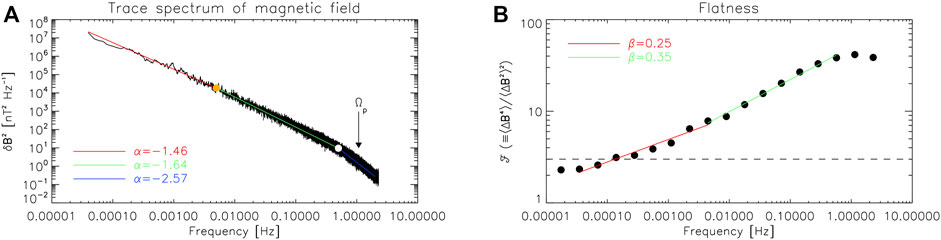
FIGURE 3. Magnetic field trace power spectrum δB² (A) and flatness $\mathcal{F}$ as a function of spacecraft frequency (B) for the slow-wind plasma flow sampled by PSP during quasi co-rotation with the Sun. Color-coded power-law fits at three different ranges of scales are displayed: the relative scaling exponents are given in the legend. The arrow indicates the proton gyro-frequency Ω_p. The horizontal dashed line in (B) refers to fluctuations with Gaussian distributions at all scales.

The power spectral density (PSD) of the magnetic field fluctuations δB² (Figure 3A) exhibits a triple-power-law scaling, as evidenced by the power-law fits reported, along with the corresponding spectral exponents, in the figure. At the lowest frequencies in the spacecraft frame, the magnetic fluctuations scale as k^−3/2 (red fit), thus resembling the Iroshnikov-Kraichnan (IK, Iroshnikov, 1963; Kraichnan, 1965) spectrum ³. This range of scales is separated by a low-frequency break located at approximately 5 × 10^–3 Hz (orange full dot) from an intermediate range, which follows the standard −5/3 Kolmogorov-like (Kolmogorov, 1941) power law (green fit). At the highest spacecraft frequencies, above the breakpoint at $\sim 5\times 10^{-1}$ Hz (white full dot), the PSD steepens dropping off with a scaling index close to −2.8 (blue fit), as generally observed at ion scales in the kinetic domain (Verscharen et al., 2019). The high-frequency break is somewhat below the proton gyro-frequency Ω_p = qB/(2πm_p) = 1.1 Hz (where q and m_p are the proton electric charge and rest mass, respectively), which is characteristic of ion cyclotron waves (e.g., Telloni et al., 2019). It is worth pointing out that in spite of large deviations from the radial, on average PSP sampled a solar wind flow rather aligned with the background magnetic field (⟨θ_RB⟩ = 43°, Figure 2C). It follows that slab fluctuations are mostly observed in the selected interval and, in the context of nearly incompressible magnetohydrodynamics (NI MHD, Zank et al., 2017), a − 3/2 spectrum thus corresponds to weak turbulence (Zank et al., 2020b). Hence, evidence for an IK-like spectrum below the low-frequency break suggests weak turbulence, dominated by Alfvénic fluctuations. Conversely, the Kolmogorov-like spectrum at intermediate scales is indicative of a stronger, more developed and less Alfvénic turbulence, controlled by nonlinear interactions.

The above insights are confirmed by the magnetic compressibility C values found in the different three frequency ranges. C is defined as the ratio between the magnetic field magnitude variance and the total magnetic fluctuations variance, i.e., C = δB²/δB² (Bavassano et al., 1982a). It is thus a measure of the contribution of the magnetic intensity fluctuations to the total magnetic fluctuations (due to changes in the magnetic field vector, either in magnitude or orientation), and is therefore always less than 1. Since Alfvénic fluctuations are not compressive, they yield low values of C: in this respect, C can be considered as a proxy for Alfvénicity. In the interval of interest, C is extremely low (2.3%) at the lowest spacecraft frequencies (below $\sim 5\times 10^{-3}$ Hz), increasing to 3.6% at intermediate scales to reach a maximum value of 8.6% in the dissipative range (above $\sim 5\times 10^{-1}$ Hz). It thus turns out that Alfvénic fluctuations dominate the scales where an IK-like spectrum is found, as expected, since Alfvénic fluctuations are known to damp nonlinear interactions and thus slow down the turbulent cascade and prevent the system from reaching a fully developed turbulent state (Dobrowolny et al., 1980). On the other hand, at the scales corresponding to the Kolmogorov fully developed turbulence, the magnetic fluctuations are less Alfvénic, as indicated by the larger value of C.

The analysis of intermittency also corroborates the scenario outlined above. Intermittency is a common feature of turbulence and implies a departure from self-similarity, i.e., a scale-independent Gaussian distribution of magnetic fluctuations. Flatness $\mathcal{F}$ is a widely used descriptor of intermittency (e.g., Bruno et al., 2003; Dudok de Wit et al., 2013). It is defined as the ratio between the fourth and the squared second-order structure functions, i.e., $\mathcal{F}=⟨\mathrm{\Delta }{\mathbf{B}}^4⟩/{⟨\mathrm{\Delta }{\mathbf{B}}^2⟩}^2$, where ΔB are the increments of the magnetic field vector over a given scale. It is displayed, for the PSP sample under study, in Figure 3B, where the $\mathcal{F}=3$ value, typical of self-similar, mono-fractal fluctuations, is also shown for reference. Interestingly, as indicated by the red and green power-law fits, the flatness exhibits a double-power-law spectrum: the transition from a shallower β = 0.25 scaling to a steeper β = 0.35 spectrum occurs at the same $\sim 5\times 10^{-3}$ Hz low-frequency break also observed in the magnetic-fluctuation PSD. As a result, intermittency is lower (higher) in the range heavily (poorly) populated by Alfvénic fluctuations. This is in agreement with expectations. In fact, Alfvénic fluctuations tend to decrease intermittency because of their stochastic nature. It follows that at the scales where the Alfvénic content is lower, intermittent structures may emerge more clearly. Their origin might be attributed to switchbacks (largely present in the analyzed interval as discussed in the previous section). Indeed, it is well known that localized, highly energetic burst of magnetic field orientation (such as switchbacks) represent the main ingredient for intermittency (Bruno and Carbone, 2013) (a more thorough analysis based on the Local Intermittency Measure (LIM), Farge, 1992, would be useful to identify intermittent structures and thus possibly couple them to switchbacks, but this is beyond the scope of the present paper). In addition, the compressible (at least theoretical) nature of switchbacks could also explain why more intermittent scales are also more compressive. Alternatively, intermittent structures might be generated spontaneously within the fully developed turbulence by nonlinear interactions as, e.g., current sheets.

While the high-frequency break certainly marks the transition from the fluid to the kinetic domain, the low-frequency break at $\sim 5\times 10^{-3}$ Hz should not be confused with the Taylor scale-related breakpoint separating the energy-containing from the inertial scales. That is, the low-frequency magnetic fluctuations in Figure 3A do not belong to the injection regime, which in fact is not observed (as discussed above, it might be shifted to lower frequencies, implying longer intervals to be detected, because of the observed small-amplitude magnetic fluctuations), but rather to the inertial regime. The physical interpretation of the $\sim 5\times 10^{-3}$ Hz break within the inertial range is in fact different. The observed transition from a flatter IK-like spectrum to a steeper Kolmogorov-like spectrum can indeed be regarded as a transition from a regime governed primarily by Alfvénic fluctuations to a regime controlled by nonlinear interactions. To the author’s knowledge, this is the first time that such a transition within the inertial range is observed in PSP data. It can be viewed as a snapshot of the ongoing process of turbulence evolution from a less developed, weakly intermittent and Alfvénic fluctuation-dominated state (leading to an IK spectrum, widely observed at PSP distances, e.g., Chen et al., 2020; Telloni et al., 2021; Zhao et al., 2022) to a fully developed intermittent turbulent flow, generally observed at larger heliocentric distances (Telloni et al., 2021), where nonlinear interactions have had sufficient time to form the Kolmogorov spectrum and build small-scale intermittent structures. It is finally worth noting that a similar wavenumber transition (albeit from a steep to a flatter spectrum) is expected within the inertial range for slab fluctuations in the low plasma beta regime, within the framework of the 2D + slab superposition model of solar wind turbulence (Zank et al., 2020b).

4 Concluding Remarks

In this paper the property of PSP to go into quasi co-rotation with the Sun has been exploited to sample for long time periods (more than 1 day) the same plasma flow from the Sun in order to study its turbulence properties on more than 5 decades of scales, from precisely 1 day down to fractions of seconds. The spectral analysis showed a typical break at ion scales separating the fluid and kinetic regimes. Because of the small amplitude of the magnetic fluctuations relative to the mean background field, the injection range is below the sampled frequencies (that is, a longer period would be required to observe it, though at the expense of the quasi co-rotation condition between PSP and the Sun). Surprisingly, however, a break was observed within the inertial range marking the transition between two regimes governed by different physics. Specifically, the transition is from scales dominated by Alfvénic fluctuations (and thus weakly turbulent and intermittent, described by IK phenomenology) to scales governed by nonlinear interactions (and thus more strongly turbulent and intermittent, in agreement with Kolmogorov turbulence). This is the first time that such a wavenumber transition is evidenced at distances so close to the Sun. Having analyzed data strictly from the same flow tube (a condition that, at PSP distances, is fulfilled only in co-rotation with the Sun) may have allowed this spectral feature to emerge clearly. Analyzing longer datasets of solar wind plasmas with similar characteristics and possibly also from the same source region, though during periods of non PSP—Sun co-rotation (e.g., D’Amicis et al., 2021; Zhao et al., 2021), could result in mixing of plasmas from different adjacent streams (recall that the PSP longitudinal speed is so high that different flow tubes can, in principle, be crossed even in a few hours when PSP is not co-rotating with the Sun), thus preventing this spectral characteristics of solar wind turbulence from being exposed. Clearly, further investigations are needed to draw more definitive conclusions, for example by analyzing all periods of quasi co-rotation of PSP during its so far 11 encounters with the Sun. This is, however, devoted to a future work.

Data Availability Statement

The Parker Solar Probe data analyzed in this paper are publicly available at NASA's Space Physics Data Facility (https://cdaweb.gsfc.nasa.gov/index.html/).

Author Contributions

The author confirms being the sole contributor to this paper, having conceived and written it, and approved it for publication.

Funding

The author was partially supported by the Italian Space Agency (ASI) under contract 2018-30-HH.0.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹A lower tolerance would shorten the data sample duration, whilst a higher tolerance would result in losing quasi co-rotation with the Sun.

²In the HCI coordinate system the X-axis points toward the solar ascending node on ecliptic, the Z-axis is aligned with the Sun’s north pole, and the Y-axis completes the right-handed orthogonal triad.

³In order to validate the IK-like slope at the lowest frequencies, the PSD fitting was also performed in a sliding window of one frequency decade over the range from 4 × 10^–5 to 5 × 10^–3 Hz.

References

Bale, S. D., Badman, S. T., Bonnell, J. W., Bowen, T. A., Burgess, D., and Case, A. W. (2019). Highly Structured Slow Solar Wind Emerging from an Equatorial Coronal Hole. Nature 576, 237–242. doi:10.1038/s41586-019-1818-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Bale, S. D., Goetz, K., Harvey, P. R., Turin, P., Bonnell, J. W., Dudok de Wit, T., et al. (2016). The FIELDS Instrument Suite for Solar Probe Plus. Measuring the Coronal Plasma and Magnetic Field, Plasma Waves and Turbulence, and Radio Signatures of Solar Transients. Space Sci. Rev. 204, 49–82. doi:10.1007/s11214-016-0244-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Bavassano, B., Dobrowolny, M., Fanfoni, G., Mariani, F., and Ness, N. F. (1982a). Statistical Properties of Magnetohydrodynamic Fluctuations Associated with High Speed Streams from HELIOS-2 Observations. Sol. Phys. 78, 373–384. doi:10.1007/BF00151617

CrossRef Full Text | Google Scholar

Bavassano, B., Dobrowolny, M., Mariani, F., and Ness, N. F. (1982b). Radial Evolution of Power Spectra of Interplanetary Alfvénic Turbulence. J. Geophys. Res. Space Phys. 87, 3617–3622. doi:10.1029/JA087iA05p03617

CrossRef Full Text | Google Scholar

Biskamp, D. (2003). Magnetohydrodynamic Turbulence. Cambridge, UK: Cambridge University Press.

Google Scholar

Bruno, R., Carbone, V., Sorriso-Valvo, L., and Bavassano, B. (2003). Radial Evolution of Solar Wind Intermittency in the Inner Heliosphere. J. Geophys. Res. Space Phys. 108, 1130. doi:10.1029/2002JA009615

CrossRef Full Text | Google Scholar

Bruno, R., and Carbone, V. (2013). The Solar Wind as a Turbulence Laboratory. Living Rev. Sol. Phys. 10, 2. doi:10.12942/lrsp-2013-2

CrossRef Full Text | Google Scholar

Bruno, R., Carbone, V., Vörös, Z., D’Amicis, R., Bavassano, B., Cattaneo, M. B., et al. (2009). Coordinated Study on Solar Wind Turbulence during the Venus-Express, ACE and Ulysses Alignment of August 2007. Earth, Moon, Planets 104, 101–104. doi:10.1007/s11038-008-9272-9

CrossRef Full Text | Google Scholar

Bruno, R., Telloni, D., Sorriso-Valvo, L., Marino, R., De Marco, R., and D’Amicis, R. (2019). The Low-Frequency Break Observed in the Slow Solar Wind Magnetic Spectra. Astron. Astrophys. 627, A96. doi:10.1051/0004-6361/201935841

CrossRef Full Text | Google Scholar

Bruno, R., and Trenchi, L. (2014). Radial Dependence of the Frequency Break between Fluid and Kinetic Scales in the Solar Wind Fluctuations. Astrophys. J. Lett. 787, L24. doi:10.1088/2041-8205/787/2/L24

CrossRef Full Text | Google Scholar

Chen, C. H. K., Bale, S. D., Bonnell, J. W., Borovikov, D., Bowen, T. A., Burgess, D., et al. (2020). The Evolution and Role of Solar Wind Turbulence in the Inner Heliosphere. Astrophys. J. Suppl. Ser. 246, 53. doi:10.3847/1538-4365/ab60a3

CrossRef Full Text | Google Scholar

Coleman, J., and Paul, J. (1968). Turbulence, Viscosity, and Dissipation in the Solar-Wind Plasma. Astrophys. J. 153, 371. doi:10.1086/149674

CrossRef Full Text | Google Scholar

D’Amicis, R., Perrone, D., Bruno, R., and Velli, M. (2021). On Alfvénic Slow Wind: A Journey from the Earth Back to the Sun. J. Geophys. Res. Space Phys. 126, e28996. doi:10.1029/2020JA028996

CrossRef Full Text | Google Scholar

Dobrowolny, M., Mangeney, A., and Veltri, P. (1980). Fully Developed Anisotropic Hydromagnetic Turbulence in Interplanetary Space. Phys. Rev. Lett. 45, 144–147. doi:10.1103/PhysRevLett.45.144

CrossRef Full Text | Google Scholar

Dudok de Wit, T., Alexandrova, O., Furno, I., Sorriso-Valvo, L., and Zimbardo, G. (2013). Methods for Characterising Microphysical Processes in Plasmas. Space Sci. Rev. 178, 665–693. doi:10.1007/s11214-013-9974-9

CrossRef Full Text | Google Scholar

Farge, M. (1992). Wavelet Transforms and Their Applications to Turbulence. Annu. Rev. Fluid Mech. 24, 395–457. doi:10.1146/annurev.fl.24.010192.002143

CrossRef Full Text | Google Scholar

Fox, N. J., Velli, M. C., Bale, S. D., Decker, R., Driesman, A., Howard, R. A., et al. (2016). The Solar Probe Plus Mission: Humanity’s First Visit to Our Star. Space Sci. Rev. 204, 7–48. doi:10.1007/s11214-015-0211-6

CrossRef Full Text | Google Scholar

Horbury, T. S., Balogh, A., Forsyth, R. J., and Smith, E. J. (1996). The Rate of Turbulent Evolution over the Sun’s Poles. Astron. Astrophys. 316, 333–341.

Google Scholar

Hundhausen, A. J. (1972). Coronal Expansion and Solar Wind. Berlin Heidelberg New York: Springer-Verlag 5, 101.

Google Scholar

Iroshnikov, P. S. (1963). Turbulence of a Conducting Fluid in a Strong Magnetic Field. Astron. Zh. 40, 742.

Google Scholar

Kasper, J. C., Abiad, R., Austin, G., Balat-Pichelin, M., Bale, S. D., Belcher, J. W., et al. (2016). Solar Wind Electrons Alphas and Protons (SWEAP) Investigation: Design of the Solar Wind and Coronal Plasma Instrument Suite for Solar Probe Plus. Space Sci. Rev. 204, 131–186. doi:10.1007/s11214-015-0206-3

CrossRef Full Text | Google Scholar

Kolmogorov, A. (1941). The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds’ Numbers. Dokl. Akad. Nauk. SSSR 30, 301–305.

Google Scholar

Kraichnan, R. H. (1965). Inertial-Range Spectrum of Hydromagnetic Turbulence. Phys. Fluids 8, 1385–1387. doi:10.1063/1.1761412

CrossRef Full Text | Google Scholar

Marsch, E. (2006). Kinetic Physics of the Solar Corona and Solar Wind. Living Rev. Sol. Phys. 3, 1. doi:10.12942/lrsp-2006-1

CrossRef Full Text | Google Scholar

Matteini, L., Stansby, D., Horbury, T. S., and Chen, C. H. K. (2018). On the 1/f Spectrum in the Solar Wind and its Connection with Magnetic Compressibility. Astrophys. J. Lett. 869, L32. doi:10.3847/2041-8213/aaf573

CrossRef Full Text | Google Scholar

Matthaeus, W. H., Dasso, S., Weygand, J. M., Milano, L. J., Smith, C. W., and Kivelson, M. G. (2005). Spatial Correlation of Solar-Wind Turbulence from Two-Point Measurements. Phys. Rev. Lett. 95, 231101. doi:10.1103/PhysRevLett.95.231101

PubMed Abstract | CrossRef Full Text | Google Scholar

Panasenco, O., Velli, M., D’Amicis, R., Shi, C., Réville, V., Bale, S. D., et al. (2020). Exploring Solar Wind Origins and Connecting Plasma Flows from the Parker Solar Probe to 1 au: Nonspherical Source Surface and Alfvénic Fluctuations. Astrophys. J. Suppl. Ser. 246, 54. doi:10.3847/1538-4365/ab61f4

CrossRef Full Text | Google Scholar

Telloni, D., Bruno, R., and Trenchi, L. (2015). Radial Evolution of Spectral Characteristics of Magnetic Field Fluctuations at Proton Scales. Astrophys. J. 805, 46. doi:10.1088/0004-637X/805/1/46

CrossRef Full Text | Google Scholar

Telloni, D., Carbone, F., Bruno, R., Zank, G. P., Sorriso-Valvo, L., and Mancuso, S. (2019). Ion Cyclotron Waves in Field-Aligned Solar Wind Turbulence. Astrophys. J. Lett. 885, L5. doi:10.3847/2041-8213/ab4c442

CrossRef Full Text | Google Scholar

Telloni, D., Sorriso-Valvo, L., Woodham, L. D., Panasenco, O., Velli, M., Carbone, F., et al. (2021). Evolution of Solar Wind Turbulence from 0.1 to 1 au during the First Parker Solar Probe-Solar Orbiter Radial Alignment. Astrophys. J. Lett. 912, L21. doi:10.3847/2041-8213/abf7d1

CrossRef Full Text | Google Scholar

Tu, C. Y., and Marsch, E. (1995). Magnetohydrodynamic Structures Waves and Turbulence in the Solar Wind - Observations and Theories. Space Sci. Rev. 73, 1–210. doi:10.1007/BF00748891

CrossRef Full Text | Google Scholar

Verscharen, D., Klein, K. G., and Maruca, B. A. (2019). The Multi-Scale Nature of the Solar Wind. Living Rev. Sol. Phys. 16, 5. doi:10.1007/s41116-019-0021-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Zank, G. P., Adhikari, L., Hunana, P., Shiota, D., Bruno, R., and Telloni, D. (2017). Theory and Transport of Nearly Incompressible Magnetohydrodynamic Turbulence. Astrophys. J. 835, 147. doi:10.3847/1538-4357/835/2/147

CrossRef Full Text | Google Scholar

Zank, G. P., Nakanotani, M., Zhao, L. L., Adhikari, L., and Kasper, J. (2020a). The Origin of Switchbacks in the Solar Corona: Linear Theory. Astrophys. J. 903, 1. doi:10.3847/1538-4357/abb828

CrossRef Full Text | Google Scholar

Zank, G. P., Nakanotani, M., Zhao, L. L., Adhikari, L., and Telloni, D. (2020b). Spectral Anisotropy in 2D Plus Slab Magnetohydrodynamic Turbulence in the Solar Wind and Upper Corona. Astrophys. J. 900, 115. doi:10.3847/1538-4357/abad30

CrossRef Full Text | Google Scholar

Zhao, L. L., Zank, G. P., Adhikari, L., and Nakanotani, M. (2022). Inertial-range Magnetic-Fluctuation Anisotropy Observed from Parker Solar Probe’s First Seven Orbits. Astrophys. J. Lett. 924, L5. doi:10.3847/2041-8213/ac4415

CrossRef Full Text | Google Scholar

Zhao, L. L., Zank, G. P., He, J. S., Telloni, D., Adhikari, L., Nakanotani, M., et al. (2021). MHD and Ion Kinetic Waves in Field-Aligned Flows Observed by Parker Solar Probe. Astrophys. J. 922, 188. doi:10.3847/1538-4357/ac28fb

CrossRef Full Text | Google Scholar