- Space Science Institute, Boulder, CO, United States
In this Brief Report it is pointed out that there are three dusk-dawn aberrations of the solar-wind plasma and magnetic structure approaching Earth and the magnitudes of these aberrations are estimated for various solar-wind types monitored from L1. Solar-wind monitors closer to the Earth than L1 would have superior performances.
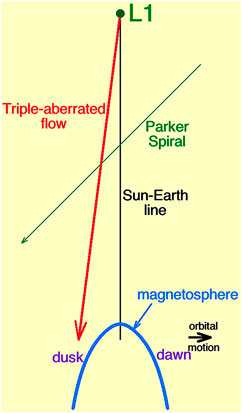
The solar-wind plasma and its magnetic structure that hit an L1 monitor on the Sun-Earth line will on average pass duskward of the Earth’s magnetosphere. This is depicted in Figure 1 with L1 at the top of the sketch and with the shape of the magnetosphere drawn in blue using the Lin et al. (2010) magnetopause model (eq. (3) of Lin et al. (2010) with ro = 10.8 RE, m = 0.1, and β = −1.1).
The solar-wind velocity vector at 1 AU varies with time by about ±5° in both the dawn-dusk and north-south directions (cf. Borovsky 2012; Borovsky, 2018). With L1 being 235 RE upstream from the Earth (cf. Figure 1), the ±5° time variation of the flow vector corresponds to a ±20.5 RE time variation in the location at Earth of a flow streamline passing through an L1 monitor. The timescales of these velocity-vector changes can be slow (e.g., the days-long variations about stream interfaces discussed below) or fast [e.g., the 98 km/s change in the solar-wind velocity vector over 3 s shown in Fig. 6b of Borovsky (2020a)].
In addition to this variation in the streamline location at Earth, there is a systematic triple aberration (shift) in the dawn-dusk direction. The plasma flow of the solar wind experiences the first two aberrations and the magnetic structure of the solar wind experiences all three aberrations. The origins of the triple aberration are as follows.
(1) The motion of the Earth around the Sun. The 29.8 km/s dawnward motion of the Earth in its orbit (black arrow in Figure 1) means that for a perfectly radial solar-wind flow with a speed vsw hitting L1 at the Sun-Earth line will have a streamline that passes the Earth on the dusk side by a distance of (235 RE) (29.8/vsw) (e.g., Fairfield, 1993). For vsw = 350 km/s this distance is 20 RE and for vsw = 650 km/s this distance is 10.8 RE (cf. Table 1). In Borovsky (2018) the variability of this first aberration owing to the variability of the solar-wind flow vector is examined in comparison with the typical structure sizes of the solar wind magnetic field (10’s of RE to 100 RE): cf. Fig. 5 of Borovsky (2018).
(2) The non-radial average flow vector of the solar wind. Using multiple spacecraft at 1 AU, Nemecek et al., (2020a) found a systematic nonradial component to the proton-solar-wind flow that tends to be in the direction of the solar rotation [see also Pizzo et al., (1983) and Finlay et al., (2019)]. As noted in Table 1, this systematic flow is ∼10 km/s dawnward for slow solar wind and is ∼5 km/s duskward for mid-range solar-wind speed. Note that there are also very large ∼40 km/s dawn-dusk flows at Earth associated with stream interfaces (Gosling et al., 1978): for slow-to-fast (leading-edge) stream interfaces the solar-wind flow is strongly dawnward on the day before the interface passes the Earth and the flow is strongly duskward on the day after the passage of the interface [cf. Fig. 4b of Borovsky and Denton (2010)] and for fast-to-slow (trailing-edge) stream interfaces the solar-wind flow is systematically duskward for about 3 days prior to the interface passage and the flow is systematically dawnward for about 3 days after the interface passage [cf. Fig. 14b of Borovsky and Denton (2016)]. As noted in Table 1, the Nemecek et al., (2020a) 10 km/s dawnward velocity in a 350 km/s wind yields an offset of 6.7 RE for the streamline at Earth.
(3) The magnetic structure of the heliosphere moves out from the Sun along the Parker spiral faster than the proton flow. In the Alfvenic fast wind and in the Alfvenic slow wind, the magnetic structure of the heliosphere moves outward from the Sun at a speed of about 0.7 vA along the Parker-spiral direction relative to the proton flow (Borovsky, 2020b; Nemecek et al., 2020b). [Alfvénic wind has strong temporal correlations between the flow vector v(t) and the magnetic-field vector B(t).] A nominal 45° Parker-spiral orientation is sketched as the green arrow in Figure 1. For vsw in the range 500–650 km/s, the mean Alfven speed in the OMNI2 data set (King and Papitashvili, 2005) is vA = 73 km/s. Accounting for the angle of the Parker spiral from the Sun-Earth line (39° for 500 km/s and 32° for 650 km/s) the aberration of the magnetic structure is estimated to be 31.7 km/s duskward for 500 km/s Alfvenic solar wind and 27.1 km/s for 650 km/s Alfvenic solar wind (cf. Table 1). These aberrations yield “streamline” duskward displacements of 14.9 RE and 9.8 RE. Note that the alpha particles of the solar wind are approximately at rest in the reference frame moving with the magnetic structure (Nemecek et al., 2020b), so the alpha-particle flow has the same aberration as the magnetic structure. Also note that at 1 AU the instantaneous magnetic-field direction varies by about ±45° with respect to the calculated Parker-spiral direction [cf. Table 1 of Borovsky (2010)], but the magnetic structure moves in the mean-field direction which is the calculated Parker-spiral direction.
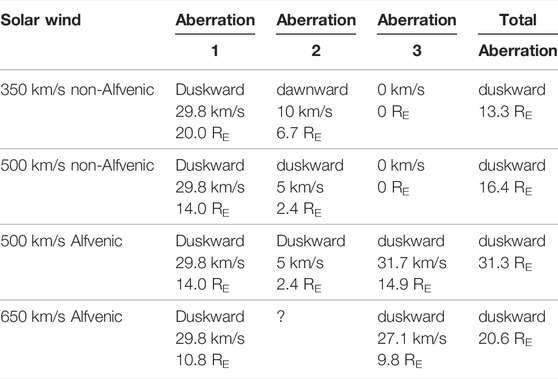
TABLE 1. Estimates of the dusk-dawn aberrations of the proton plasma and the magnetic structure for typical solar wind types.
These aberrations are on the order of the 10s-of-RE magnetic structure sizes in the background Parker-spiral solar wind at 1 AU (Borovsky, 2008; 2018).
Assuming a radial proton flow, the magnitude of the first aberration is straightforward to calculate with the formula (29.8/vsw): if the flow is not radial the correction to the first aberration is very small. The second aberration (caused by the non-radial flow) is very variable with time: with a ±5° variation in the flow vector this is a ∼ ±20-RE variation at Earth. The variability of the third aberration has yet to be explored: the Parker-spiral direction varies according to the known formula (405/vsw) however the statistics of the magnetic-structure velocity vector with respect to the Parker-spiral direction have not been studied.
The aberration problem from L1 gets better or worse depending on the location of the solar-wind monitor about the L1 point. And during the systematic large deflections of the solar wind in the days around the passages of stream interfaces, the aberration problem gets worse.
There have been a number of recent criticisms of using L1 monitoring for solar-wind/magnetosphere coupling studies (Sandahl et al., 1996; Ashour-Abdalla et al., 2008; Borovsky, 2018, 2020a; Walsh et al., 2019; Burkholder et al., 2020) and several estimates of the solar-wind errors between L1 and Earth (Crooker et al., 1982; Ridley, 2000; Weimer et al., 2002; Mailyan et al., 2008; Case and Wild, 2012). These criticisms and error calculations were based on the temporal flow deviations of the solar wind, the magnetic-structure scalesizes in the solar wind, and cross correlations between L1 measurements and near-Earth measurements.
In studying the driving of the Earth by the solar wind, recent work indicates that errors in the solar-wind values make it difficult to uncover or confirm the physics of the driving. In particular in data-analysis studies the “best fit” formulas obtained by optimizing correlations change depend on the amount of noise in the solar wind measurements (Borovsky, 2022; Sivadas et al., 2022).
To make needed progress in understanding solar-wind/magnetosphere interaction, a call is made for solar-wind monitors much closer to the Earth than L1. A study to optimize the monitor mission is needed. One suggestion would be multiple spacecraft in IMP-type circular orbits (r ∼ 30 RE) wherein one of the spacecraft would always be in the upstream solar wind.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
JEB was supported by the NSF GEM Program via grant AGS-2027569 and by the NASA HERMES Interdisciplinary Science Program via grant 80NSSC21K1406.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The author thanks Bob McPherron, Zdenek Nemecek, and Nithin Sivadas for helpful conversations.
References
Ashour-Abdalla, M., Walker, R. J., Peroomian, V., and El-Alaoui, M. (2008). On the Importance of Accurate Solar Wind Measurements for Studying Magnetospheric Dynamics. J. Geophys. Res. 113, A08204. doi:10.1029/2007ja012785
Borovsky, J. E., and Denton, M. H. (2010). Solar-wind Turbulence and Shear: A Superposed-Epoch Analysis of Corotating Interaction Regions at 1 AU. J. Geophys. Res. 115, A10101. doi:10.1029/2009ja014966
Borovsky, J. E., and Denton, M. H. (2016). The Trailing Edges of High-Speed Streams at 1 AU. J. Geophys. Res. Space Phys. 121, 6107–6140. doi:10.1002/2016ja022863
Borovsky, J. E. (2022). Noise, Regression Dilution Bias, and Solar-Wind/magnetosphere Coupling Studies. Front. Astron. Space Sci. 9, 867282. doi:10.3389/fspas.2022.867282
Borovsky, J. E. (2020b). On the Motion of the Heliospheric Magnetic Structure through the Solar Wind Plasma. J. Geophys. Res. Space Phys. 125, e2019JA027377. doi:10.1029/2019JA027377
Borovsky, J. E. (2010). On the Variations of the Solar Wind Magnetic Field about the Parker Spiral Direction. J. Geophys. Res. 115, A09101. doi:10.1029/2009ja015040
Borovsky, J. E. (2012). The Effect of Sudden Wind Shear on the Earth’s Magnetosphere: Statistics of Wind-Shear Events and CCMC Simulations of Magnetotail Disconnections. J. Geophys. Res. 117, A06224. doi:10.1029/2012ja017623
Borovsky, J. E. (2008). The Flux-Tube Texture of the Solar Wind: Strands of the Magnetic Carpet at 1 AU? J. Geophys. Res. 113, A08110. doi:10.1029/2007ja012684
Borovsky, J. E. (2018). The Spatial Structure of the Oncoming Solar Wind at Earth and the Shortcomings of a Solar-Wind Monitor at L1. J. Atmos. Solar-Terrestrial Phys. 177, 2–11. doi:10.1016/j.jastp.2017.03.014
Borovsky, J. E. (2020a). What Magnetospheric and Ionospheric Researchers Should Know about the Solar Wind. J. Atmos. Solar-Terrestrial Phys. 204, 105271. doi:10.1016/j.jastp.2020.105271
Burkholder, B. L., Nykyri, K., and Ma, X. (2020). A Multispacecraft Solar Wind Monitor. J. Geophys. Res. 125, e2020JA027978. doi:10.1029/2020ja027978
Case, N. A., and Wild, J. A. (2012). A Statistical Comparison of Solar Wind Propagation Delays Derived from Multispacecraft Techniques. J. Geophys. Res. 117, A02101. doi:10.1029/2011ja016946
Crooker, N. U., Siscoe, G. L., Russell, C. T., and Smith, E. J. (1982). Factors Controlling Degree of Correlation between ISEE 1 and ISEE 3 Interplanetary Magnetic Field Measurements. J. Geophys. Res. 87, 2224–2230. doi:10.1029/ja087ia04p02224
Fairfield, D. H. (1993). Solar Wind Control of the Distant Magnetotail: ISEE 3. J. Geophys. Res. 21265, 21276.
Finlay, A. J., Hewitt, A. L., Matt, S. P., Owens, M., Pinto, R. F., and Reville, V. (2019). Direct Detection of Solar Angular Momentum Loss with the Wind Spacecraft. Astrophys. J. Lett. 885, L30.
Gosling, J. T., Asbridge, J. R., Bame, S. J., and Feldman, W. C. (1978). Solar Wind Stream Interfaces. J. Geophys. Res. 83, 1401. doi:10.1029/ja083ia04p01401
King, J. H., and Papitashvili, N. E. (2005). Solar Wind Spatial Scales in and Comparisons of Hourly Wind and ACE Plasma and Magnetic Field Data. J. Geophys. Res. 110, 2104. doi:10.1029/2004ja010649
Lin, R. L., Zhang, X. X., Liu, S. Q., Wang, Y. L., and Gong, J. C. (2010). A Three-Dimensional Asymmetric Magnetopause Model. J. Geophys. Res. 115, A04207. doi:10.1029/2009ja014235
Mailyan, B., Munteanu, C., and Haaland, S. (2008). What Is the Best Method to Calculate the Solar Wind Propagation Delay? Ann. Geophys. 26, 2383–2394. doi:10.5194/angeo-26-2383-2008
Nemecek, Z., Durovcova, T., Safrankova, J., Nemec, F., Matteini, L., StansbyJantizek, D. N., et al. (2020b). What Is the Solar Wind Frame of Reference? Astrophys. J. 889, 163.
Nemecek, Z., Durovcova, T., Safrankova, J., Richardson, J. D., Simunek, J., and Stevens, M. L. (2020a). (Non)radial Solar Wind Propagation through the Heliosphere. Astrophys. J. Lett. 897, L39.
Pizzo, V., Schwenn, R., Marsch, E., RosenbauerMuhlhauser, H., Muehlhaeuser, K.-H., and Neubauer, F. M. (1983). Determination of the Solar Wind Angular Momentum Flux from the HELIOS Data - an Observational Test of the Weber and Davis Theory. ApJ 271, 335–354. doi:10.1086/161200
Ridley, A. J. (2000). Estimations of the Uncertainty in Timing the Relationship between Magnetospheric and Solar Wind Processes. J. Atmos. Solar-Terrestrial Phys. 62, 757–771. doi:10.1016/s1364-6826(00)00057-2
Sandahl, I., Lundstedt, H., Koskinen, H., and Glassmeir, K.-H. (1996). On the Need for Slar Wind Monitoring Close to the Magnetosphere. Asp. Conf. Ser. 95, 300.
Sivadas, N., Sibeck, D., Subramanyan, V., Wlach, M.-T., Murphy, K., and Halford, A. (2022). Uncertainty in Solar Wind Forcing Explains Polar Cap Potential Saturation. Cornell University, Ithaca New York, United States: arXiv:2201.0217v1. doi:10.48550/arXiv.2201.02137
Walsh, B. M., Bhakyapaibul, T., and Zou, Y. (2019). Quantifying the Uncertainty of Using Solar Wind Measurements for Geospace Inputs. J. Geophys. Res. Space Phys. 124, 3291–3302. doi:10.1029/2019ja026507
Keywords: solar wind, magnetosphere, solar wind monitor, solar wind magnetosphere coupling, space weather
Citation: Borovsky JE (2022) The Triple Dusk-Dawn Aberration of the Solar Wind at Earth. Front. Astron. Space Sci. 9:917163. doi: 10.3389/fspas.2022.917163
Received: 10 April 2022; Accepted: 20 May 2022;
Published: 06 June 2022.
Edited by:
Xochitl Blanco-Cano, National Autonomous University of Mexico, MexicoReviewed by:
Steven Petrinec, Lockheed Martin Solar and Astrophysics Laboratory (LMSAL), United StatesRyan McGranaghan, Atmospheric and Space Technology Research Associates, United States
Copyright © 2022 Borovsky. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Joseph E. Borovsky, amJvcm92c2t5QHNwYWNlc2NpZW5jZS5vcmc=
 Joseph E. Borovsky
Joseph E. Borovsky