Which Parameter Controls Ring Current Electron Dynamics

Predicting the electron population of Earth’s ring current during geomagnetic storms still remains a challenging task. In this work, we investigate the sensitivity of 10 keV ring current electrons to different driving processes, parameterised by the Kp index, during several moderate and intense storms. Results are validated against measurements from the Van Allen Probes satellites. Perturbing the Kp index allows us to identify the most dominant processes for moderate and intense storms respectively. We find that during moderate storms (Kp $<$ 6) the drift velocities mostly control the behaviour of low energy electrons, while loss from wave-particle interactions is the most critical parameter for quantifying the evolution of intense storms (Kp $>$ 6). Perturbations of the Kp index used to drive the boundary conditions at GEO and set the plasmapause location only show a minimal effect on simulation results over a limited L range. It is further shown that the flux at L ∼ 3 is more sensitive to changes in the Kp index compared to higher L shells, making it a good proxy for validating the source-loss balance of a ring current model.

1 Introduction

The Earth’s ring current is a dynamic region and the enhancement of its electron and ion populations is one of the main characteristics during geomagnetic storms. While ions contribute most of the energy to the ring current (Williams, 1981; Zhao et al., 2016), low energy electrons (∼ 1–100 keV) are also an important field of research, as the main source of spacecraft charging (Baker, 2000; Choi et al., 2011; Ganushkina et al., 2017). The focus of this study is the 10 keV electron flux, which constitutes a major portion of the population responsible for surface charging, and can additionally excite whistler-mode chorus waves (Hwang et al., 2007), which have a profound impact on radiation belt dynamics (see reviews by Millan and Thorne, 2007; Shprits et al., 2008a,b; Thorne, 2010, and references therein). Although there have been major advances in ring current modeling in recent years, accurately reproducing electron flux during storm times still remains a challenge.

The main source of ring current electrons is the plasma sheet population which gets transported towards Earth due to the convection electric field and substorm-associated impulsive electric fields (e.g. Zhao et al., 2016). Electrons are transported from the nightside to the dayside, due to the gradient-curvature (GC) drifts and the E ×B-drift (Roederer, 1970), and can complete drifts around Earth. Depending on the energy of the particles, either the GC drift or E ×B drift dominates. For the electrons at approximately 10 keV considered in this study, the E ×B drift dominates. During active periods, the strong convection electric field is capable of transporting these electrons down to L shells of 3 (Zhao et al., 2016), and they typically need about 8 h to complete a full drift around the Earth (Schulz and Lanzerotti, 1974). This means that at the beginning of a geomagnetic storm, strong flux enhancements are apparent at low L shells first on the nightside and the ring current shows a great magnetic local time (MLT) asymmetry, until electrons have completed their first drift around the Earth.

The ring current source mechanisms are counteracted by different loss processes. First of all, electrons inside the bounce or drift loss-cone are lost to the Earth’s atmosphere. Electrons are scattered into the loss-cone by wave-particle interactions leading to a diminution of electron flux. It has been shown that whistler-mode chorus waves are very effective in scattering low energy electrons (e.g. Millan and Thorne, 2007). Whistler mode chorus waves are observed in the low density plasmatrough and therefore the plasmapause location is an important parameter for the dynamics of the ring current. Inside the plasmasphere, hiss waves can lead to pitch-angle scattering of electrons, but several previous studies speculated, that these waves resonate more effectively with $>$100 keV electrons and do not significantly scatter 10 keV electrons (e.g. Orlova et al., 2016). Electrons can also be lost, during their drift, when they encounter the magnetopause, which moves closer to Earth when the geomagnetic activity increases. Owing to the slow drift period of ring current electrons, encounters with the dayside magnetopause can introduce asymmetries in the distributions of the electron populations around Earth (Allison et al., 2017).

In the last decades, several ring current models have been developed, incorporating the processes mentioned above (e.g. Jordanova et al., 2006; Ganushkina et al., 2012; Fok et al., 2014; Aseev et al., 2019). The influence of different electric and magnetic field models on the ring current has been studied in detail (Jordanova et al., 2010; Yu et al., 2017; Aseev et al., 2019) and electron lifetime models due to whistler waves have been validated (Chen et al., 2015; Ferradas et al., 2019). Aseev et al. (2019) investigated the influence of the coupling of source and loss processes on the electron phase space density during the St. Patrick’s Day 2013 geomagnetic storm. It was found that the electric field and electron lifetimes are likely to be the main cause of discrepancies between model results and observations at L $<$ 4.5. However, it is difficult to determine the contribution of each process on the overall dynamics of the ring current as magnetospheric models are often driven by different input parameters. Hence, it is challenging to directly compare the sensitivity of different model parameters. This work circumvents this issue by using the Kp index as the only input to the model. Kp is a geomagnetic index with a 3 h cadence and monitors the subauroral geomagnetic disturbance globally in a semi-logarithmic manner. Despite the rather large time cadence, Kp has been shown to be a good proxy for various processes in the magnetosphere including the strength of the convection electric field (Thomsen, 2004), wave power of whistler-mode waves (e.g. Wang et al., 2019), and plasmapause location (Carpenter and Anderson, 1992), making it a widely used activity metric in radiation belt and ring current modelling.

In this work, we investigate which input parameters are most critical for the dynamics of the electron ring current under different levels of geomagnetic activity. To this end, we perform a sensitivity analysis of ring current processes in terms of Kp, for several intense storms and moderately disturbed periods. The results of one intense storm and one moderate event, both of which occurred in March 2013, are presented here, while four more events are displayed in the Supplementary Material.

2 Methodology

2.1 Geomagnetic Storms in March, 2013 and Electron Flux Observations

Two geomagnetic storms occurred in March 2013, both of which are analysed in this work. The first event is the St. Patrick’s Day storm, with a Dst minimum of −132 nT (see Figure 1A). This intense storm has a Kp maximum of 7- by convenction and has been well studied previously (e.g. Boyd et al., 2014; Yu et al., 2015; Zhao et al., 2015; Ferradas et al., 2019). The second event is a moderately disturbed time with a Kp maximum of 5+ and a Dst minimum of −59 nT (see Figure 1E), which occurred at the end of March 2013 and has been also considered in several studies (e.g. Zhao et al., 2016; Ripoll et al., 2017; Reidy et al., 2021). Following Reeves et al. (2003), we characterize this event as a moderate storm. These two events are selected, since the Van Allen Probes twin satellites (RBSP-A and RBSP-B), providing us with in situ electron flux measurements for validation, have their apogee at ∼ 00–01 MLT during March 2013 and therefore directly measure the incoming electrons from the plasmasheet, enabling us to better validate the source-loss balance on the nightside.

FIGURE 1

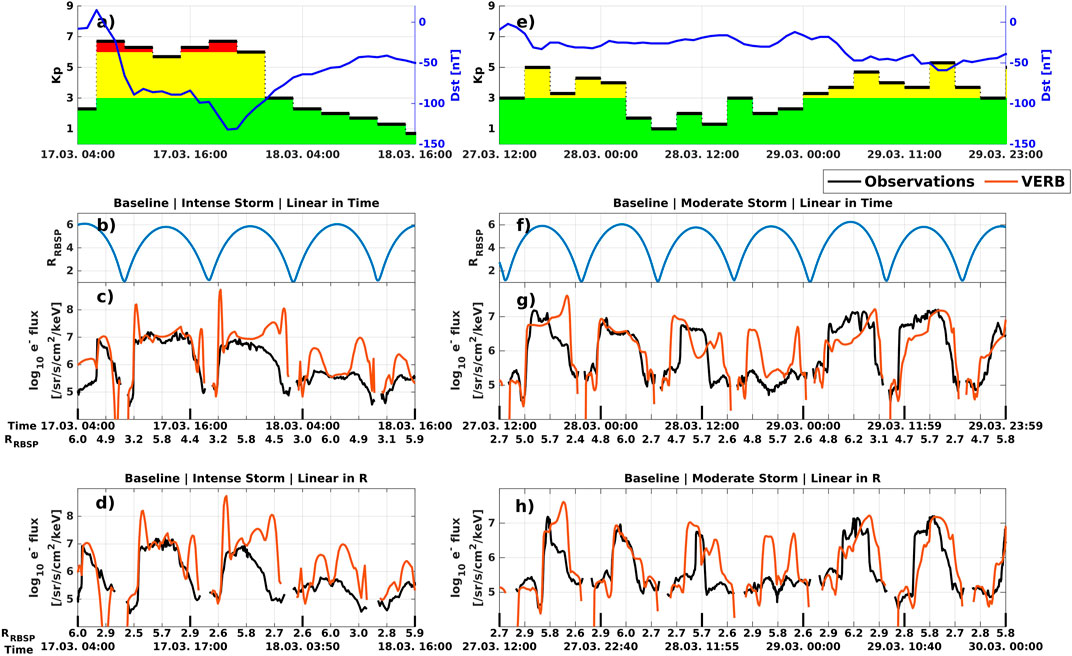
FIGURE 1. Kp and Dst time series and results of the simulations in March 2013. (A) Kp (bars) and Dst (blue line) time series of the intense storm. (B) Radial distance of RBSP-B orbit mapped to the equatorial plane during the intense storm. (C) Comparison of RBSP-B (black) and baseline VERB-CS result (red) for 10 keV electron flux at 54°local pitch-angle at the spacecraft’s location. (D) Same data as in (C) but linearized in radial distance. Panels (E–H) have the same format as (A–D) but for the moderate storm.

We use data from the Helium, Oxygen, Proton, and Electron (HOPE) instrument (Funsten et al., 2013), which is capable of measuring unidirectional electron flux from 1 eV to 50 keV. In this work, we compare against observations at 10 keV and local 54°pitch-angle. We are choosing this pitch-angle channel because missing data is rare for this channel and a pitch-angle in the middle of the distribution should reflect better the whole distribution compared to a pitch-angle at one of the edges. For each point in time, the local pitch-angle channel is mapped to the equatorial plane using the T89 magnetic field model (Tsyganenko, 1989), and we interpolate the simulation results in time, radial distance, MLT, energy and equatorial pitch-angle to those of the observations.

2.2 Quantification of Comparison

We quantify this validation by calculating three different metrics following the suggestions in Liemohn et al. (2021). The accuracy of the simulation is described by the root-mean-square error (RMSE), bias by the mean error (ME) and association by the Pearson correlation coefficient (CC). Additionally, we use the mean absolute error (MAE) to quantify the spread of simulation results in the sensitivity analysis. Since the electron flux can span over several magnitudes, these metrics are calculated on logarithmic flux. Hence, values lie within one order of magnitude, allowing us to use these simple metrics instead of more complicated ones, which are more difficult to interpret (Liemohn et al., 2021). Because of the nature of the satellite’s orbit, it spends most of his time at large radial distances from Earth (L $>$ 4.5). These would result in a strong bias in the calculated metrics towards errors at those distances. Therefore, additionally to the uncorrected metrics, we provide bias-corrected metrics by weighting them inversely to the number of data points at a given radial distance:

$\begin{array}{ll}\text{wRMSE}\hfill & =\frac{\sqrt{\sum _i{w}_i{\left(x_i-y_i\right)}^2}}{\sqrt{\sum _i{w}_i}},\text{wMAE}=\frac{\sum _i{w}_i|x_i-y_i|}{\sum _i{w}_i},\hfill \\ \text{wME}\hfill & ={\bar{x}}_w-{\bar{y}}_w=\frac{\sum _i{w}_i{x}_i-\sum _i{w}_i{y}_i}{\sum _i{w}_i}\text{and}\hfill \\ \text{wCC}\hfill & =\frac{\text{cov}\left(x,y,w\right)}{\sqrt{\text{cov}\left(x,x,w\right)\text{cov}\left(y,y,w\right)}},\text{with}\hfill \\ \hfill \text{cov}\left(x,y,w\right)& =\frac{\sum _i{w}_i\left(x_i-{\bar{x}}_w\right)\left(y_i-{\bar{y}}_w\right)}{\sum _i{w}_i}.\hfill \end{array}(1)$

The weights w_i are calculated by counting the number of observations in the corresponding 0.25 L bin and reciprocate the result. Measurements below L = 2 are stripped since simulation results very close to Earth do not change much during the simulation and are only effected by the initial condition.

2.3 Reduced VERB-4D Model: VERB-CS

The four-dimensional Versatile Electron Radiation Belt code (VERB-4D) Shprits et al. (2015); Aseev et al. (2019) solves the modified Fokker-Planck equation in MLT, radial distance R and the two modified adiabatic invariants V and K Subbotin and Shprits (2012):

$K=\frac{J}{\sqrt{8m_0\mu }}\text{and}V=\mu {\left(K+0.5\right)}^2,(2)$

where μ and J are the first and second adiabatic invariants (Schulz and Lanzerotti, 1974) and m₀ is the electron rest mass. In this work, we are dealing with $<$ 10 keV ring current electrons, which are dominated by convection rather than diffusion. Under weak pitch-angle diffusion, and for relatively monotonic diffusion coefficients in the pitch-angle dimension (Albert and Shprits, 2009), the pitch-angle distribution is expected to reach the lowest normal mode and decay with the same rate at all pitch-angles. This allows us to treat pitch-angle diffusion as an exponential loss process with electron lifetimes estimated as an inverse of the diffusion coefficient right at the edge of the loss cone (Shprits et al., 2006). Additionally, in this setup the loss in the loss cone does not need to be explicitly modeled, allowing us to simulate only a limited range of pitch-angles. Radial diffusion is also very weak at low energies (Lyons and Schulz, 1989) and for energies $<$ 300 keV chorus waves lead to a competition between acceleration and loss (Horne et al., 2005). Finally, we are only looking at events, where the magnetopause stays outside GEO for almost the full simulation duration, and is therefore unlikely to affect our results. We end up with the reduced modified Fokker-Planck equation solved in this work:

$\frac{\partial f}{\partial t}=\langle v_{\phi }\rangle \frac{\partial f}{\partial \phi }+\langle v_R\rangle \frac{\partial f}{\partial R}-\frac{f}{{\tau }_{\mathit{wave}}}(3)$

that describes the time evolution of phase space density (PSD) f. The equation contains advection terms $\frac{\partial f}{\partial \phi }$ and $\frac{\partial f}{\partial R}$ with respect to MLT, φ, and equatorial radial distance, R, and a loss term due to wave-particle interactions. This model has been previously used for data assimilative predictions of Earth’s ring current (Aseev and Shprits, 2019) and is hereinafter referred to as VERB-CS (Convection Simplified).

The coefficients of these terms are bounce averaged drift velocities ⟨v_φ⟩ and ⟨v_R⟩, consisting of the E ×B drift and the gradient and curvature drift. These drifts are calculated using the Kp-dependent T89 magnetic field model (Tsyganenko, 1989) and in the case of the E ×B drift, the Volland-Stern (Volland, 1973; Stern, 1975) electric field model with the Maynard-Chen (Maynard and Chen, 1975) Kp-dependent parameterization is used.

The 4D numerical grid used in this work consists of 49 points in MLT and 29 points in R starting at 1 R_E and ending at 6.6 R_E. The logarithmic V and linear K grids consist of 31 and 11 points respectively and are set up in such a way that ensures that the desired energy of 10 keV for the equatorial pitch-angle range, which is defined by the equatorially mapped 54° local pitch-angle channel of RBSP-B, is covered over the whole spatial grid.

The initial condition for PSD is extracted from the last full trajectory of the RBSP-B satellite before the start of the simulation, assuming that the initial flux is symmetric in MLT. Periodic boundary conditions are used for MLT and the lower radial boundary condition at R = 1 is set to 0, while the upper boundary condition at geostationary orbit (R = 6.6) is provided by the Kp-dependent Denton model (Denton et al., 2015).

Electron lifetimes, τ_wave, due to wave-particle interactions correspond to either hiss or chorus associated lifetimes depending on whether a particle is inside the plasmasphere or outside. The plasmapause location is determined by the Kp-dependent C&A model (Carpenter and Anderson, 1992). Orlova and Shprits (2014) calculated and parameterised electron lifetimes associated with interactions with chorus waves, using wave properties derived from CRRES data (Spasojevic and Shprits, 2013). Similarly, Spasojevic et al. (2015) calculated wave properties of hiss waves from RBSP data, which was later translated into electron lifetimes (Orlova et al., 2016). Both the hiss and chorus lifetime models depend on radial distance, MLT, electron energy and Kp.

2.4 Setup of the Sensitivity Analysis

To find the dominant process or processes controlling the dynamics of the ring current electrons, we perform several sensitivity runs of VERB-CS with various perturbations of the Kp time series. In this work, the sensitivity analysis focuses on describing how uncertainty in the input variables affects the final output. Since all variability of the inputs of the VERB-CS model are driven by the Kp index, we can introduce variability by perturbing Kp and quantify the resulting uncertainty in flux. By doing a one-factor-at-a-time (OAT) analysis, we can see the effects of different processes in the model and quantify the effect of the variability of each input on the ring current simulation. To this end, the Kp input of a single part of the model is perturbed, while all other parts of the model are driven by the original Kp history. We perform two different experiments: one adding Gaussian noise with a variance of one to the original Kp time series; and another adding a uniform offset of ±1 to the original Kp history. Examples of such perturbed Kp time histories can be seen in Figures 2A, 3A.

FIGURE 2

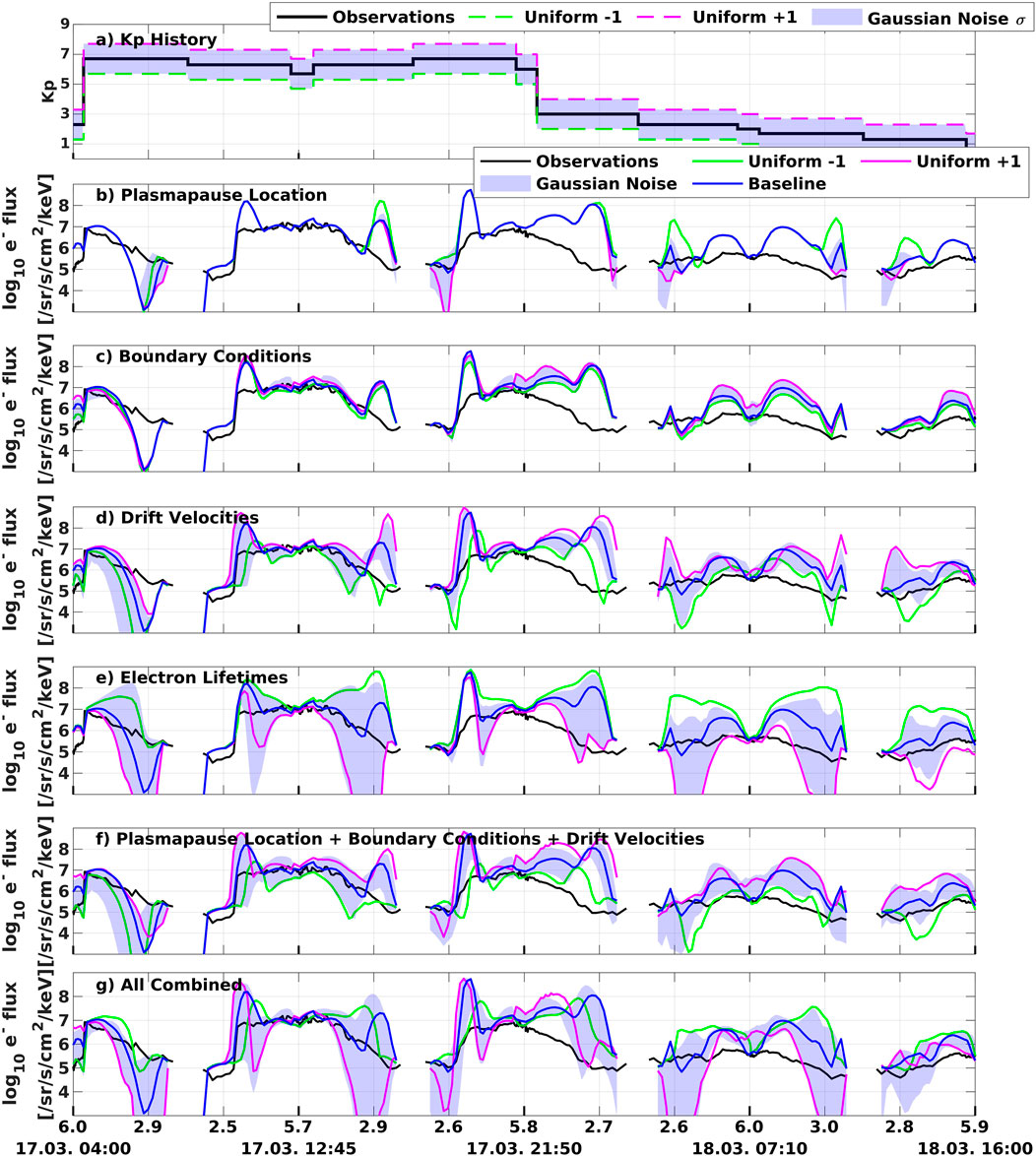
FIGURE 2. Perturbation results of 10 keV electron flux and 54°local pitch-angle at the spacecraft’s location for the intense event along the RBSP-B orbit. The blue areas show the range of simulation results, when Kp is perturbed using Gaussian noise. The black line in panels b–g shows the RBSP-B flux data. (A) Original Kp history and perturbed ones. (B) Perturbing plasmapause location model. (C) Perturbing boundary condition model. (D) Perturbing drift velocities. (E) Perturbing electron lifetime models. (F) Perturbing plasmapause location, boundary conditions and drift velocities combined. (G) Perturbing all processes combined.

FIGURE 3

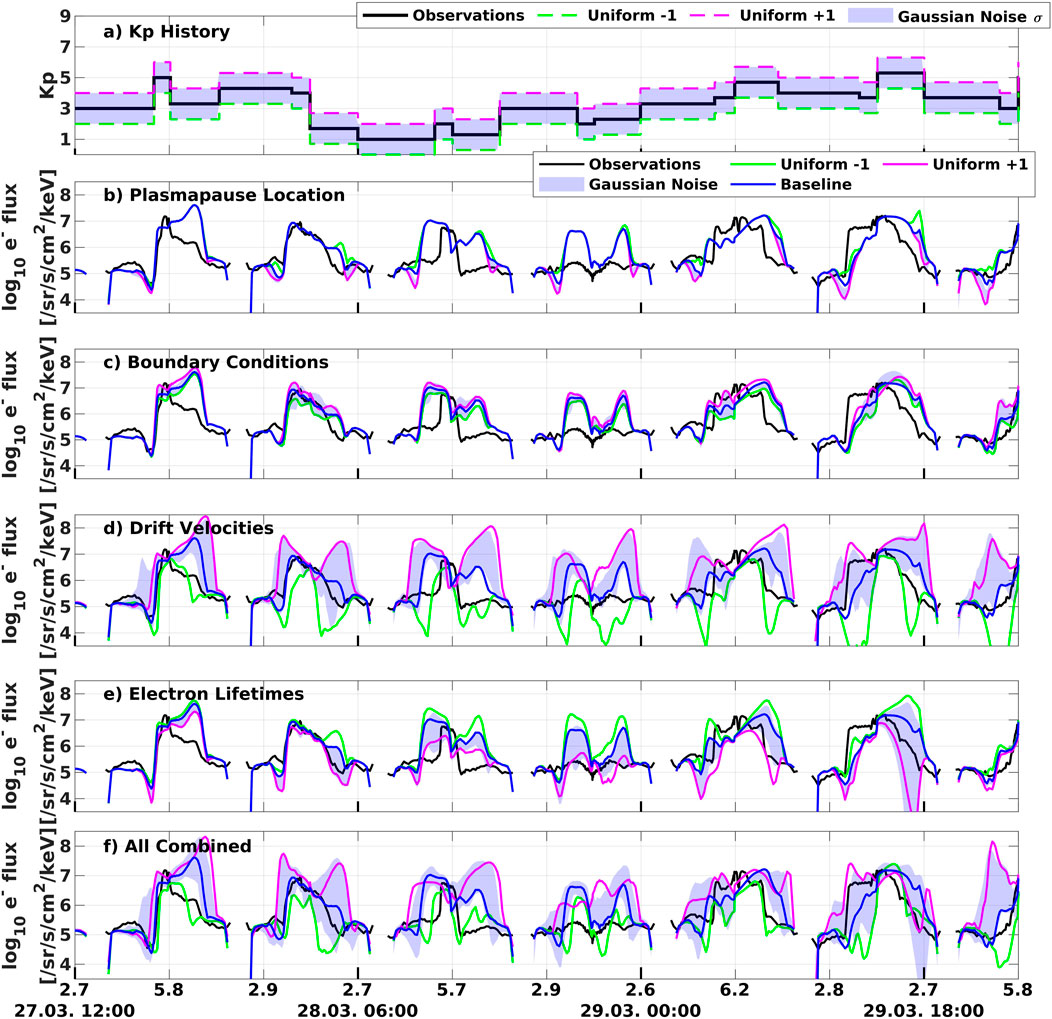
FIGURE 3. Perturbation results of 10 keV electron flux and 54° local pitch-angle at the spacecraft’s location for the moderate event along the RBSP-B orbit. The blue areas show the range of simulation results, when Kp is perturbed using Gaussian noise. The black line in panels b–g shows the RBSP-B flux data. (A) Original Kp history and perturbed ones. (B) Perturbing plasmapause location model. (C) Perturbing boundary condition model. (D) Perturbing drift velocities. (E) Perturbing electron lifetime models. (F) Perturbing all processes combined.

In the case of the Gaussian noise experiments, we are interested in the range of simulation results, defined as the 10th and 90th percentiles of electron flux along the RBSP-B trajectory for each point in time. We make this choice so that the impact of statistical outliers is reduced. We have tested how many simulations are necessary for convergence and found that 16 simulations are enough to see no significant change when adding additional simulations (see Supplementary Figure S2).

In the OAT sensitivity analysis we investigate the influence of changes in the plasmapause location; boundary conditions at GEO; drift velocities calculated from the electric and magnetic field; and electron lifetimes due to chorus and hiss scattering. We also present simulation results when the Kp input is perturbed for all processes combined.

3 Baseline Simulation Results

In Figure 1 the VERB-CS results are displayed alongside RBSP-B observations and geomagnetic indices (Panel a and e) for the two considered events: a storm that occurred on 17 March 2013 and a period of disturbed activity from 27 until 29 March 2013. Panels b and f show the radial distance of the satellite mapped to the equatorial plane during the events. Panels c and g show observations and results along the satellite’s orbit presented linearly in time, while the x-axis of Panels d and h is modified in a way such that the radial distance and not the time is presented linearly, ensuring that there is no bias towards certain radial distances in our plots. The exact setup is displayed in Supplementary Figure S1. For this study, plotting with equidistant radial distance on the x-axis is preferred, since it is later shown that at middle radial distances (L ∼ 3), we see the highest variance of model results.

Looking at VERB-CS results for the St. Patrick Day storm (left column), we can see that the VERB-CS model predicts an enhancement with the rise of Kp and agrees well for L $>$ 5, although there is an overestimation at radial distances of three to four Earth radii. This issue is discussed further in Section 5 where the contributions of each parameter are investigated. The simulation results for the moderate geomagnetic activity (right column) show good agreement with observations and the enhancement of the 10 keV electron flux is correctly reproduced during this geomagnetically disturbed time.

Table 1 displays metrics quantifying the comparison between measurements and simulation results. It is apparent that the weighted metrics show worse performance of the model compared to the uncorrected metrics, which indicates that the model performs better at high L shells near GEO. All three weighted metrics indicate as well that the model gives worse results for the intense storm than the moderate storm. The model shows a positive bias in both events, although it is much higher for the intense storm as indicated by ME and wME. The correlation coefficient is comparable between both events, which is surprising because of the relatively good agreement for the second event. Small scale fluctuations in the flux measurements could be the cause for this, which are not resolved by our model. The simulation results shown in Figure 1 are our baseline simulations for the following sensitivity analysis.

TABLE 1

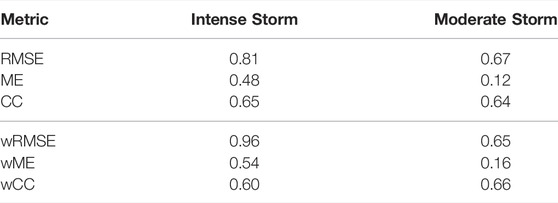
TABLE 1. Metrics computed for the comparison of log10 (flux) of VERB results and RBSP-B observations for both events. For details, see Section 2.2.

4 Sensitivity Analysis Results

The simulated electron flux when perturbing the processes in an OAT manner can be seen in Figures 2B–E. Comparing the range of simulated 10 keV electron flux when adding Gaussian noise (blue shaded regions) shows that perturbing the plasmapause location and boundary conditions does not have as large of an effect as compared to perturbing electron lifetimes, or drift velocities, through perturbations in the electric and magnetic field. The impact of the variance of the plasmapause location and boundary conditions is confined in a limited L range: plasmapause location only effecting low L shells; and boundary conditions effecting high L shells close to the boundary. Conversely, perturbing drift velocities and electron lifetimes results in a large variance across all L shells, with a maximum variability around L ∼ 3. This is especially the case for electron lifetimes, where the perturbations show a substantial effect on the electron flux in this region.

Adding uniform offsets to the model’s processes (green and magenta lines), leads to a larger change in the resulting electron flux in almost all cases as compared to using the Kp with added Gaussian noise.

As a final step, Figure 2F shows the variance, when perturbing plasmapause location, boundary conditions and drift velocities simultaneously, but leaving the lifetime as in the baseline simulation. It should be noted that this variance is not as large as when perturbing electron lifetimes alone. Interestingly enough, when we perturb all processes combined including electron lifetimes (Panel g), the uncertainty is again smaller compared to perturbing electron lifetimes alone (Panel e). Adding a positive uniform offset to all processes results in the simulated electron flux becoming smaller, as electron loss dominates over other processes, which is a very interesting and somewhat counter-intuitive result.

Table 2 reinforces these statements quantitatively, by displaying the wMAE and wME calculated by comparing the positive offset against the negative offset simulations, and the 10th and 90th percentiles of the Gaussian-noise-simulations. The metrics in this case do not describe the errors of simulations but rather the range of them. Looking at the uniform offset results, the wMAE describes the span between the simulation while the sign of the wME shows whether the positive (positive sign) or negative (negative sign) offset simulation leads to higher flux results. For the Gaussian-noise-experiments, the wMAE equals the wME, since the difference between the 90th to the 10th percentile is always positive by definition.

TABLE 2

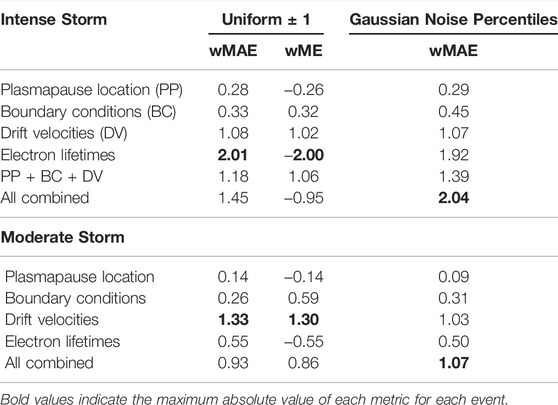
TABLE 2. Metrics computed for the comparison between the simulation results using uniform offsets, and the results of the 10th and 90th percentile when adding Gaussian noise. For details, see Section 2.2.

Figure 3 has the same format as Figure 2, showing the results for the moderate storm. As it has been seen for the intense storm, the perturbations of plasmapause location and boundary conditions result only in small variances over a limited L range. Panel e shows that electron lifetimes have less of an effect on the simulation results compared to the intense storm, while the most impactful parameter on the electron flux for the moderate storm are the drift velocities (Panel d). Perturbing drift velocities, through perturbations in electric and magnetic field, using the Gaussian noise method leads to a clear positive bias, due to the non-linearity of the electric and magnetic field models and the semi-logarithmic nature of the Kp index itself. The largest range of simulation results when perturbing electron lifetimes or drift velocities is apparent at L ∼ 3, as it has been already observed for the intense storm. This region is very sensitive to perturbations of the source-loss balance of the model.

Adding a uniform offset of ±1 to the Kp input that drives various processes leads to large variability of simulation results, especially when perturbing drift velocities. This substantial effect is also apparent, when all processes combined are perturbed (Panel f), where adding a positive offset to Kp leads to higher electron flux, while adding a negative offset leads to smaller flux values.

Comparing the calculated metrics for both events (Table 2), we can see that the maximum wMAE, observed for drift velocities for the moderate storm, is substantially lower than the maximum value observed for electron lifetimes in the case of the intense event. Generally speaking, the moderate storm shows a smaller range of perturbed simulation results. It is also interesting that the sign of the wME is different for both events, when the full simulation is perturbed. Contrary to the intense storm, it is not the loss processes controlling the dynamics of the ring current, but for moderate events, the drift velocities due to the changes of electric and magnetic field.

5 Discussion

We have presented the results of a sensitivity analysis in terms of Kp for a moderate and an intense storm. Perturbing the Kp input for the calculation of the plasmapause location and the boundary condition model does not have a very significant influence on the resulting electron flux in the case of either a strong or a moderate storm. The Denton et al. (2015) model provides the mean values of electron flux at GEO, which are used in this work, as well as statistical percentiles for each value of Kp. Aseev et al. (2019) investigated how this statistical variance influences the ring current and comparing with their results, the influence on electron flux due to this statistical spread is larger than the influence of a perturbation of the model’s Kp input. It is well known that the plasmapause location influences magnetosphere dynamics (e.g. Wang et al., 2020), and it is therefore surprising, that perturbing this plasma boundary has only a small impact on simulation results. This effect may not be most accurately estimated due to uncertainties of the C&A model, which describes the plasmapause location in a very simple MLT-independent manner and therefore, does not represent the full dynamics of the plasmasphere during a geomagnetic storm.

The parameters with the largest impact, when perturbed through their Kp input, are drift velocities and electron lifetimes (see Figures 2, 3). Drift velocities are strongly influenced through the change of the convection electric field during geomagnetically disturbed times. For intense storms, it has been shown that the convection electric field can saturate Liemohn et al. (2002); Califf et al. (2014), hence reducing the effect of the electric field during those times. This can also be seen in our results: for the moderate storm, the sensitivity due to the electric field still dominates over loss processes, while loss dominates over convection for the considered intense storm.

Whether loss or source processes dominate shows the largest effect at L ∼ 3, which is consistent with the results presented in Aseev et al. (2019). While the electron flux at higher L near the GEO boundary responds quickly to changes in the convection field and boundary conditions, deeper L shells show slower dynamics. We conclude that the flux at L ∼ 3 is a good proxy for validating the balance of source and loss processes during geomagnetic storms. For moderate storms (Kp $<$ 6), this balance seems to be correctly modelled by VERB-CS for 10 keV electrons, while we see overestimation in the simulated flux blow L = 4 during intense storms. Figures 3D,F show that decreasing the Kp uniformly by one does not resolve the overestimation completely (third pass of the satellite). This shows that modeling errors of the electron flux supplied by the outer radial boundary are unlikely to be responsible for this source-loss imbalance alone.

To understand how our model behaves with a more complex electric field model, we run the same events using the model by Weimer (2005) and see almost the same overestimation of flux for the intense storm (see Supplementary Figure S8) and similar behaviour for the moderate event. It is concluded that VS. captures the general dynamics of the global convection field correctly compared to more complex models. Statistical studies have shown that strong large-scale electric fields are present at low L shells during intense storms. (Rowland and Wygant, 1998; Califf et al., 2014), which are not described by the simple Volland-Stern model. Fine electric field structures like these could alter the drift trajectories of electrons, and therefore also our simulation results, significantly. However, since we observe overestimation of flux for different events and MLT sectors (see Supplementary Figures S3, S6, S7), it seems unlikely that such a local phenomenon is the main issue of a global source-loss imbalance.

Another potential parameterization error is the magnetic field used for calculating drift velocities. The T89 model predicts compression and stretching of the magnetosphere during geomagnatically active times, but not to the same extend as newer models (e.g. Tsyganenko and Sitnov, 2005) explicitly designed for handling storm times (McCollough et al., 2008). On the dayside, compression of the magnetic field leads to more loss of particles to the magnetopause (Keika et al., 2005), while on the nightside the stretching results in a weaker magnetic fields. Since the strength of the E ×B-drift scales inversely with |B| and electrons at 10 keV are not affected much by the gradient-curvature-drift, this results in stronger convection and higher flux enhancements on the nightside during storms (Ganushkina et al., 2012). We conclude that newer magnetic field models would not help to reduce overestimation observed on the nightside, but should still be considered in future studies to represent a more accurate picture of the Earth’s magnetic field.

These points make the investigation of the loss of electrons very important to better reproduce electron flux during intense storm events. Recent statistical wave studies have shown that chorus waves can be effective in scattering low energy electrons in the pre-midnight sector (Wang et al., 2019) and an event specific study has also shown stronger chorus wave activity in the pre-midnight sector as expected (Yu et al., 2022). This scattering process is currently not properly accounted for in the lifetimes used in our model and therefore this lack of loss may be responsible for the overestimation at L ∼ 3.

For the moderate geomagnetically disturbed time, with a Kp maximum of 5+, electron flux observations are well reproduced by our model (see Figure 1) and all input models used in VERB-CS have been validated to at least Kp 6. The T89 models uses six bins between Kp = 0 and Kp = 5- for its parameterization, which could cause inaccuracies in the sensitivy analysis when combined with other models which use different parameterization boundaries. With the exception of T89, all the parameterized models used here are smooth functions of Kp, which reduces the effect of boundaries in the Kp parameterizations to a minimum. Therefore, we can conclude that for these Kp levels, our model is a realistic representation of Earth’s ring current and the sensitivity analysis represents the sensitivity of the ring current itself. Regarding intense storm events, most of the empirical input models are not valid for such high Kp levels, hence it is difficult to estimate how well they will perform when extrapolated to very high activity levels. Despite these limitations, magnetospheric models often achieve convincing results using these parameterizations (e.g. Ganushkina et al., 2012; Aseev and Shprits, 2019; Ferradas et al., 2019) and also VERB-CS is capable of reproducing electron flux observations at a range of L shells for the St. Patrick’s Day storm. Our results reveal the state as well as the limits of our current understanding of the electron dynamics of the ring current and allow prioritizing future efforts of improving predictive capabilities.

6 Conclusion

In this work we have investigated the sensitivity of the major driving processes on electron ring current dynamics. Although only two events were presented here, the same controlling processes were identified for comparable storm events (see Supplementary Figures S4–S7). We showed that for moderate and intense storms, different processes dominate the behavior of the 10 keV electron population. Our conclusions are as following:

1. During intense storm events, perturbing electron lifetimes has the strongest effect on the evolution of the ring current electron flux within geosynchronous orbit. This result indicates the dominant role of wave-particle interactions and potentially other loss processes, that are currently not accounted for in VERB-CS, for the dynamics at these energies.

2. For moderate storms, the ring current is most strongly affected by changes of the drift velocities caused by the changes in the electric and magnetic fields.

3. High L shells near GEO are not strongly affected by perturbations of Kp, while the electron flux at L ∼ 3 is very sensitive to the assumed parameters and shows under- and overestimation. The validation of the ring current codes at tens of keV should include the low L-shell region at L ∼ 3 where the simulations are most sensitive to the assumptions about loss and transport mechanisms.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: https://omniweb.gsfc.nasa.gov/form/dx1.html http://rbsp.space.umn.edu/data/rbsp/ect/rbspa/hope/level3/PA/.

Author Contributions

BH and YS conceived the idea of the study. BH performed the analysis with input from YS, HA, MW, and DW. BH wrote the first draft of the manuscript; YS, HA, MW, and, DW contributed to structuring and editing the manuscript, and approved of the submitted version.

Funding

This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 870452 (PAGER). HA was supported by the Alexander von Humboldt foundation.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor RH is currently organizing a Research Topic with the author(s) YS.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors acknowledge the NASA OMNI database (https://omniweb.gsfc.nasa.gov/form/dx1.html) and thank the developers of the IRBEM library (https://github.com/PRBEM/IRBEM), which was used for magnetic field calculations. The authors are grateful to the RBSP-ECT team for the provision of Van Allen Probes observations. All RBSP-ECT data are publicly available at the web site http://rbsp.space.umn.edu/data/rbsp/ect/rbspa/hope/level3/PA/.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2022.911002/full#supplementary-material

References

Albert, J. M., and Shprits, Y. Y. (2009). Estimates of Lifetimes against Pitch Angle Diffusion. J. Atmos. Solar-Terrestrial Phys. 71, 1647–1652. doi:10.1016/J.JASTP.2008.07.004

CrossRef Full Text | Google Scholar

Allison, H. J., Horne, R. B., Glauert, S. A., and Zanna, G. D. (2017). The Magnetic Local Time Distribution of Energetic Electrons in the Radiation Belt Region. J. Geophys. Res. Space Phys. 122, 8108–8123. doi:10.1002/2017JA024084

CrossRef Full Text | Google Scholar

Aseev, N. A., and Shprits, Y. Y. (2019). Reanalysis of Ring Current Electron Phase Space Densities Using Van Allen Probe Observations, Convection Model, and Log‐Normal Kalman Filter. Space weather. 17, 619–638. doi:10.1029/2018SW002110

CrossRef Full Text | Google Scholar

Aseev, N. A., Shprits, Y. Y., Wang, D., Wygant, J., Drozdov, A. Y., Kellerman, A. C., et al. (2019). Transport and Loss of Ring Current Electrons inside Geosynchronous Orbit during the 17 March 2013 Storm. JGR Space Phys. 124, 915–933. doi:10.1029/2018JA026031

PubMed Abstract | CrossRef Full Text | Google Scholar

Baker, D. N. (2000). The Occurrence of Operational Anomalies in Spacecraft and Their Relationship to Space Weather. IEEE Trans. Plasma Sci. 28, 2007–2016. doi:10.1109/27.902228

CrossRef Full Text | Google Scholar

Boyd, A. J., Spence, H. E., Claudepierre, S. G., Fennell, J. F., Blake, J. B., Baker, D. N., et al. (2014). Quantifying the Radiation Belt Seed Population in the 17 March 2013 Electron Acceleration Event. Geophys. Res. Lett. 41, 2275–2281. doi:10.1002/2014GL059626

CrossRef Full Text | Google Scholar

Califf, S., Li, X., Blum, L., Jaynes, A., Schiller, Q., Zhao, H., et al. (2014). THEMIS Measurements of Quasi‐static Electric Fields in the Inner Magnetosphere. J. Geophys. Res. Space Phys. 119, 9939–9951. doi:10.1002/2014JA020360

CrossRef Full Text | Google Scholar

Carpenter, D. L., and Anderson, R. R. (1992). An Isee/whistler Model of Equatorial Electron Density in the Magnetosphere. J. Geophys. Res. 97, 1097. doi:10.1029/91JA01548

CrossRef Full Text | Google Scholar

Chen, M. W., Lemon, C. L., Orlova, K., Shprits, Y., Hecht, J., and Walterscheid, R. L. (2015). Comparison of Simulated and Observed Trapped and Precipitating Electron Fluxes during a Magnetic Storm. Geophys. Res. Lett. 42, 8302–8311. doi:10.1002/2015GL065737

CrossRef Full Text | Google Scholar

Choi, H.-S., Lee, J., Cho, K.-S., Kwak, Y.-S., Cho, I.-H., Park, Y.-D., et al. (2011). Analysis of GEO Spacecraft Anomalies: Space Weather Relationships. Space weather. 9, a–n. doi:10.1029/2010SW000597

CrossRef Full Text | Google Scholar

Denton, M. H., Thomsen, M. F., Jordanova, V. K., Henderson, M. G., Borovsky, J. E., Denton, J. S., et al. (2015). An Empirical Model of Electron and Ion Fluxes Derived from Observations at Geosynchronous Orbit. Space weather. 13, 233–249. doi:10.1002/2015SW001168

CrossRef Full Text | Google Scholar

Ferradas, C. P., Jordanova, V. K., Reeves, G. D., and Larsen, B. A. (2019). Comparison of Electron Loss Models in the Inner Magnetosphere during the 2013 St. Patrick's Day Geomagnetic Storm. J. Geophys. Res. Space Phys. 124, 7872–7888. doi:10.1029/2019JA026649

CrossRef Full Text | Google Scholar

Fok, M.-C., Buzulukova, N. Y., Chen, S.-H., Glocer, A., Nagai, T., Valek, P., et al. (2014). The Comprehensive Inner Magnetosphere-Ionosphere Model. J. Geophys. Res. Space Phys. 119, 7522–7540. doi:10.1002/2014JA020239

CrossRef Full Text | Google Scholar

Funsten, H. O., Skoug, R. M., Guthrie, A. A., Macdonald, E. A., Baldonado, J. R., Harper, R. W., et al. (2013). Helium, Oxygen, Proton, and Electron (Hope) Mass Spectrometer for the Radiation Belt Storm Probes Mission. Space Sci. Rev. 179, 423–484. doi:10.1007/s11214-013-9968-7

CrossRef Full Text | Google Scholar

Ganushkina, N., Jaynes, A., and Liemohn, M. (2017). Space Weather Effects Produced by the Ring Current Particles. Space Sci. Rev. 212, 1315–1344. doi:10.1007/s11214-017-0412-2

CrossRef Full Text | Google Scholar

Ganushkina, N. Y., Liemohn, M. W., and Pulkkinen, T. I. (2012). Storm-time Ring Current: Model-dependent Results. Ann. Geophys. 30, 177–202. doi:10.5194/ANGEO-30-177-2012

CrossRef Full Text | Google Scholar

Horne, R. B., Thorne, R. M., Glauert, S. A., Albert, J. M., Meredith, N. P., and Anderson, R. R. (2005). Timescale for Radiation Belt Electron Acceleration by Whistler Mode Chorus Waves. J. Geophys. Res. 110. doi:10.1029/2004JA010811

CrossRef Full Text | Google Scholar

Hwang, J. A., Lee, D.-Y., Lyons, L. R., Smith, A. J., Zou, S., Min, K. W., et al. (2007). Statistical Significance of Association between Whistler-Mode Chorus Enhancements and Enhanced Convection Periods during High-Speed Streams. J. Geophys. Res. 112, a–n. doi:10.1029/2007JA012388

CrossRef Full Text | Google Scholar

Jordanova, V. K., Miyoshi, Y. S., Zaharia, S., Thomsen, M. F., Reeves, G. D., Evans, D. S., et al. (2006). Kinetic Simulations of Ring Current Evolution during the Geospace Environment Modeling Challenge Events. J. Geophys. Res. 111, 1–16. doi:10.1029/2006JA011644

PubMed Abstract | CrossRef Full Text | Google Scholar

Jordanova, V. K., Zaharia, S., and Welling, D. T. (2010). Comparative Study of Ring Current Development Using Empirical, Dipolar, and Self-Consistent Magnetic Field Simulations. J. Geophys. Res. 115, a–n. doi:10.1029/2010JA015671

CrossRef Full Text | Google Scholar

Keika, K., Nosé, M., Ohtani, S., Takahashi, K., Christon, S. P., and McEntire, R. W. (2005). Outflow of Energetic Ions from the Magnetosphere and its Contribution to the Decay of the Storm Time Ring Current. J. Geophys. Res. 110. doi:10.1029/2004JA010970

CrossRef Full Text | Google Scholar

Liemohn, M. W., Kozyra, J. U., Hairston, M. R., Weimer, D. R., Lu, G., Ridley, A. J., et al. (2002). Consequences of a Saturated Convection Electric Field on the Ring Current. Geophys. Res. Lett. 29, 62-1–62-4. doi:10.1029/2001gl014270

CrossRef Full Text | Google Scholar

Liemohn, M. W., Shane, A. D., Azari, A. R., Petersen, A. K., Swiger, B. M., and Mukhopadhyay, A. (2021). RMSE Is Not Enough: Guidelines to Robust Data-Model Comparisons for Magnetospheric Physics. J. Atmos. Solar-Terrestrial Phys. 218. doi:10.1016/j.jastp.2021.105624

CrossRef Full Text | Google Scholar

Lyons, L. R., and Schulz, M. (1989). Access of Energetic Particles to Storm Time Ring Current through Enhanced Radial “Diffusion”. J. Geophys. Res. 94, 5491. doi:10.1029/ja094ia05p05491

CrossRef Full Text | Google Scholar

Maynard, N. C., and Chen, A. J. (1975). Isolated Cold Plasma Regions: Observations and Their Relation to Possible Production Mechanisms. J. Geophys. Res. 80, 1009–1013. doi:10.1029/JA080I007P01009

CrossRef Full Text | Google Scholar

McCollough, J. P., Gannon, J. L., Baker, D. N., and Gehmeyr, M. (2008). A Statistical Comparison of Commonly Used External Magnetic Field Models. Space weather. 6, a–n. doi:10.1029/2008SW000391

CrossRef Full Text | Google Scholar

Millan, R. M., and Thorne, R. M. (2007). Review of Radiation Belt Relativistic Electron Losses. J. Atmos. Solar-Terrestrial Phys. 69, 362–377. doi:10.1016/J.JASTP.2006.06.019

CrossRef Full Text | Google Scholar

Orlova, K., and Shprits, Y. (2014). Model of Lifetimes of the Outer Radiation Belt Electrons in a Realistic Magnetic Field Using Realistic Chorus Wave Parameters. J. Geophys. Res. Space Phys. 119, 770–780. doi:10.1002/2013JA019596

CrossRef Full Text | Google Scholar

Orlova, K., Shprits, Y., and Spasojevic, M. (2016). New Global Loss Model of Energetic and Relativistic Electrons Based on Van Allen Probes Measurements. J. Geophys. Res. Space Phys. 121, 1308–1314. doi:10.1002/2015JA021878

CrossRef Full Text | Google Scholar

Reeves, G. D., McAdams, K. L., Friedel, R. H. W., and O'Brien, T. P. (2003). Acceleration and Loss of Relativistic Electrons during Geomagnetic Storms. Geophys. Res. Lett. 30, a–n. doi:10.1029/2002GL016513

CrossRef Full Text | Google Scholar

Reidy, J. A., Horne, R. B., Glauert, S. A., Clilverd, M. A., Meredith, N. P., Woodfield, E. E., et al. (2021). Comparing Electron Precipitation Fluxes Calculated from Pitch Angle Diffusion Coefficients to LEO Satellite Observations. JGR Space Phys. 126, e2020JA028410. doi:10.1029/2020JA028410

CrossRef Full Text | Google Scholar

Ripoll, J. F., Santolík, O., Reeves, G. D., Kurth, W. S., Denton, M. H., Loridan, V., et al. (2017). Effects of Whistler Mode Hiss Waves in March 2013. J. Geophys. Res. Space Phys. 122, 7433–7462. doi:10.1002/2017JA024139

CrossRef Full Text | Google Scholar

Roederer, J. G. (1970). Dynamics of Geomagnetically Trapped Radiation. Springer-Verlag Berlin.

Google Scholar

Rowland, D. E., and Wygant, J. R. (1998). Dependence of the Large-Scale, Inner Magnetospheric Electric Field on Geomagnetic Activity. J. Geophys. Res. 103, 14959–14964. doi:10.1029/97JA03524

CrossRef Full Text | Google Scholar

Schulz, M., and Lanzerotti, L. J. (1974). Particle Diffusion in the Radiation Belts, Vol. 7. Springer Science & Business Media.

Google Scholar

Shprits, Y. Y., Elkington, S. R., Meredith, N. P., and Subbotin, D. A. (2008a). Review of Modeling of Losses and Sources of Relativistic Electrons in the Outer Radiation Belt I: Radial Transport. J. Atmos. Solar-Terrestrial Phys. 70, 1679–1693. doi:10.1016/J.JASTP.2008.06.008

CrossRef Full Text | Google Scholar

Shprits, Y. Y., Kellerman, A. C., Drozdov, A. Y., Spence, H. E., Reeves, G. D., and Baker, D. N. (2015). Combined Convective and Diffusive Simulations: Verb-4d Comparison with 17 March 2013 Van Allen Probes Observations. Geophys. Res. Lett. 42, 9600–9608. doi:10.1002/2015GL065230

CrossRef Full Text | Google Scholar

Shprits, Y. Y., Li, W., and Thorne, R. M. (2006). Controlling Effect of the Pitch Angle Scattering Rates Near the Edge of the Loss Cone on Electron Lifetimes. J. Geophys. Res. 111, 12206. doi:10.1029/2006JA011758

CrossRef Full Text | Google Scholar

Shprits, Y. Y., Subbotin, D. A., Meredith, N. P., and Elkington, S. R. (2008b). Review of Modeling of Losses and Sources of Relativistic Electrons in the Outer Radiation Belt Ii: Local Acceleration and Loss. J. Atmos. Solar-Terrestrial Phys. 70, 1694–1713. doi:10.1016/J.JASTP.2008.06.014

CrossRef Full Text | Google Scholar

Spasojevic, M., and Shprits, Y. Y. (2013). Chorus Functional Dependencies Derived from Crres Data. Geophys. Res. Lett. 40, 3793–3797. doi:10.1002/GRL.50755

CrossRef Full Text | Google Scholar

Spasojevic, M., Shprits, Y. Y., and Orlova, K. (2015). Global Empirical Models of Plasmaspheric Hiss Using Van Allen Probes. J. Geophys. Res. Space Phys. 120, 10370–10383. doi:10.1002/2015JA021803/FORMAT/PDF

CrossRef Full Text | Google Scholar

Stern, D. P. (1975). The Motion of a Proton in the Equatorial Magnetosphere. J. Geophys. Res. 80, 595–599. doi:10.1029/JA080I004P00595

CrossRef Full Text | Google Scholar

Subbotin, D. A., and Shprits, Y. Y. (2012). Three-dimensional Radiation Belt Simulations in Terms of Adiabatic Invariants Using a Single Numerical Grid. J. Geophys. Res. Space Phys. 117. doi:10.1029/2011JA017467/FORMAT/PDF

CrossRef Full Text | Google Scholar

Thomsen, M. F. (2004). WhyKpis Such a Good Measure of Magnetospheric Convection. Space weather. 2, a–n. doi:10.1029/2004SW000089

CrossRef Full Text | Google Scholar

Thorne, R. M. (2010). Radiation Belt Dynamics: The Importance of Wave-Particle Interactions. Geophys. Res. Lett. 37. doi:10.1029/2010GL044990

CrossRef Full Text | Google Scholar

Tsyganenko, N. A. (1989). A Magnetospheric Magnetic Field Model with a Warped Tail Current Sheet. Planet. Space Sci. 37, 5–20. doi:10.1016/0032-0633(89)90066-4

CrossRef Full Text | Google Scholar

Tsyganenko, N. A., and Sitnov, M. I. (2005). Modeling the Dynamics of the Inner Magnetosphere during Strong Geomagnetic Storms. J. Geophys. Res. 110. doi:10.1029/2004JA010798

CrossRef Full Text | Google Scholar

Volland, H. (1973). A Semiempirical Model of Large-Scale Magnetospheric Electric Fields. J. Geophys. Res. 78, 171–180. doi:10.1029/JA078I001P00171

CrossRef Full Text | Google Scholar

Wang, D., Shprits, Y. Y., Zhelavskaya, I. S., Agapitov, O. V., Drozdov, A. Y., and Aseev, N. A. (2019). Analytical Chorus Wave Model Derived from Van Allen Probe Observations. JGR Space Phys. 124, 1063–1084. doi:10.1029/2018JA026183

CrossRef Full Text | Google Scholar

Wang, D., Shprits, Y. Y., Zhelavskaya, I. S., Effenberger, F., Castillo, A. M., Drozdov, A. Y., et al. (2020). The Effect of Plasma Boundaries on the Dynamic Evolution of Relativistic Radiation Belt Electrons. J. Geophys. Res. Space Phys. 125. doi:10.1029/2019JA027422

CrossRef Full Text | Google Scholar

Weimer, D. R. (2005). Improved Ionospheric Electrodynamic Models and Application to Calculating Joule Heating Rates. J. Geophys. Res. 110, 1–21. doi:10.1029/2004JA010884

CrossRef Full Text | Google Scholar

Williams, D. J. (1981). Ring Current Composition and Sources: An Update. Planet. Space Sci. 29, 1195–1203. doi:10.1016/0032-0633(81)90124-0

CrossRef Full Text | Google Scholar

Yu, Y., Hosokawa, K., Ni, B., Jordanova, V. K., Miyoshi, Y., Cao, J., et al. (2022). On the Importance of Using Event‐Specific Wave Diffusion Rates in Modeling Diffuse Electron Precipitation. JGR Space Phys. 127. doi:10.1029/2021JA029918

CrossRef Full Text | Google Scholar

Yu, Y., Jordanova, V. K., Ridley, A. J., Toth, G., and Heelis, R. (2017). Effects of Electric Field Methods on Modeling the Midlatitude Ionospheric Electrodynamics and Inner Magnetosphere Dynamics. J. Geophys. Res. Space Phys. 122, 5321–5338. doi:10.1002/2016JA023850

CrossRef Full Text | Google Scholar

Yu, Y., Jordanova, V., Zou, S., Heelis, R., Ruohoniemi, M., and Wygant, J. (2015). Modeling Subauroral Polarization Streams during the 17 March 2013 Storm. J. Geophys. Res. Space Phys. 120, 1738–1750. doi:10.1002/2014JA020371

CrossRef Full Text | Google Scholar

Zhao, H., Li, X., Baker, D. N., Claudepierre, S. G., Fennell, J. F., Blake, J. B., et al. (2016). Ring Current Electron Dynamics during Geomagnetic Storms Based on the Van Allen Probes Measurements. J. Geophys. Res. Space Phys. 121, 3333–3346. doi:10.1002/2016JA022358

CrossRef Full Text | Google Scholar

Zhao, L., Yu, Y., Delzanno, G. L., and Jordanova, V. K. (2015). Bounce‐ and MLT‐averaged Diffusion Coefficients in a Physics‐based Magnetic Field Geometry Obtained from RAM‐SCB for the 17 March 2013 Storm. J. Geophys. Res. Space Phys. 120, 2616–2630. doi:10.1002/2014JA020858/FORMAT/PDF

CrossRef Full Text | Google Scholar