Magnetosphere-Ionosphere Coupling: Implications of Non-Equilibrium Conditions

The response times of the coupled magnetosphere-ionosphere-thermosphere system are, on average, greater than the autocorrelation timescales of solar wind forcing. This means that the system is rarely, if ever, in equilibrium. Departures from equilibrium are a key component of the Expanding-Contracting Polar Cap (ECPC) model of convection excitation in both the magnetosphere and ionosphere, driven by the Dungey reconnection cycle of opening and re-closing magnetospheric field lines. Averaging over sufficiently long timescales reduces data to the equivalent of steady-state conditions, which hides the physical mechanisms involved and allows us to map electric fields from interplanetary space to the ionosphere–but this is not valid, either physically or generally, because of magnetic induction effects. Only for transient phenomena on sufficiently short timescales do the mechanisms associated with non-equilibrium fully manifest themselves. Nevertheless, because of both ever-changing solar wind conditions and Earth’s dipole tilt, eccentricity and rotation, the magnetosphere is always tending towards a perpetually-evolving equilibrium configuration and there are important implications of transient events for understanding the general behavior of the coupled magnetosphere-ionosphere-thermosphere system and its response to solar wind forcing. We here discuss one example: as a consequence of the importance of departures from equilibrium inherent in the ECPC model, the solar wind dynamic pressure P_SW influences the magnetosphere-ionosphere convection response to the generation of open field lines by reconnection in the dayside subsolar magnetopause. We here demonstrate this effect in a statistical survey of observations and show that it is as predicted by the ECPC model and that, through it, P_SW has an influence on flux transport in the magnetosphere-ionosphere system.

Introduction

The Development of Solar Wind-Magnetosphere Coupling Science

The concept of what we now call Earth’s magnetosphere was first introduced by Chapman and Ferraro (1931), who envisaged geomagnetic storms as being caused by plasma clouds ejected by the Sun impacting upon Earth’s magnetic field and confining it in space. This accords with modern understanding of the effect of Coronal Mass Ejections (CMEs). However, because Chapman and Ferraro considered the solar wind to be absent during the intervals between the events, this meant that they envisaged the confined geomagnetic field as a transient, storm-time condition and not the persistent feature that we now know the magnetosphere to be. Paradoxically, they applied equilibrium concepts to these transient compressions, with the magnetic pressure of the geomagnetic field envisaged as balancing the dynamic pressure of the plasma cloud in a series of evolving equilibria. Later, multi-spacecraft observations showed the locations and motions of the magnetospheric boundary (the magnetopause), caused by changing solar wind dynamic pressure, did agree to first order with Chapman and Ferraro’s concept of evolving equilibria (e.g., Farrugia et al., 1989).

Chapman and Ferraro knew nothing of the existence of the interplanetary magnetic field (IMF), the discovery of which was not made until the space age, when it was detected by the Pioneer-5 spacecraft (Coleman et al., 1960). There had been indications of its existence in the early 1950s from Forbush decreases in Galactic Cosmic Rays and from the propagation time of Solar Cosmic Rays (now called Solar Energetic Particles) seen following solar flares by neutron monitors (see Parker, 2001). However, even before this, several scientists had been certain enough of the existence of an IMF to be thinking about its terrestrial implications, including Fred Hoyle, his PhD student Jim Dungey (see Cowley, 2016), and Hannes Alfvén (1950a). How near-Earth IMF could be generated by the Sun and solar wind was understood from Alfvén’s formulation of magnetohydrodynamics (MHD) (Alfvén, 1950b) which in the “ideal MHD” limit shows that the solar wind drags the “frozen-in” solar coronal magnetic field with it to give, on average, the Parker spiral configuration of the IMF (Parker, 1958). It became recognized that the solar wind, and hence the frozen-in IMF, was an ever-present feature because of the continuous nature of its action on comet tails (Hoffmeister, 1943; Ahnert, 1943; Biermann, 1951). The role of the north-south IMF component in the coupling of energy and momentum into the magnetosphere from the solar wind, was postulated by Dungey (1950, 1961). He introduced the concept of magnetic reconnection which, through a breakdown in ideal MHD at thin current sheets, generates open field lines that thread the magnetopause, and then closes them again in the cross-tail current sheet. A snapshot of the Dungey cycle during southward IMF, showing open and closed field lines and the reconnection sites in the noon-midnight meridian plane is shown schematically in Part A of Figure 1. Dungey still applied inherently steady, equilibrium concepts to this “Dungey cycle” as he saw antisunward transport of frozen-in flux in the polar ionosphere on open field lines as being due to interplanetary electric field (the electric field in the Earth’s frame due to the motion of the solar wind with its frozen-in magnetic field) mapped down to the ionosphere. This concept of mapped interplanetary electric field (e.g., Volland, 1973; Stern, 1975a) has been widely used in the interpretation of results from both observations and numerical MHD models and even in the derivation and use of some indices, such as the polar cap index (Stauning, 2022). This would be valid for fully steady-state conditions when the rate of change in the magnetic field is everywhere zero: by Faraday’s law, steady state means that the electric field is curl-free and would, in this special case only, map from interplanetary space, through the magnetosheath and magnetosphere, to the ionosphere.

FIGURE 1

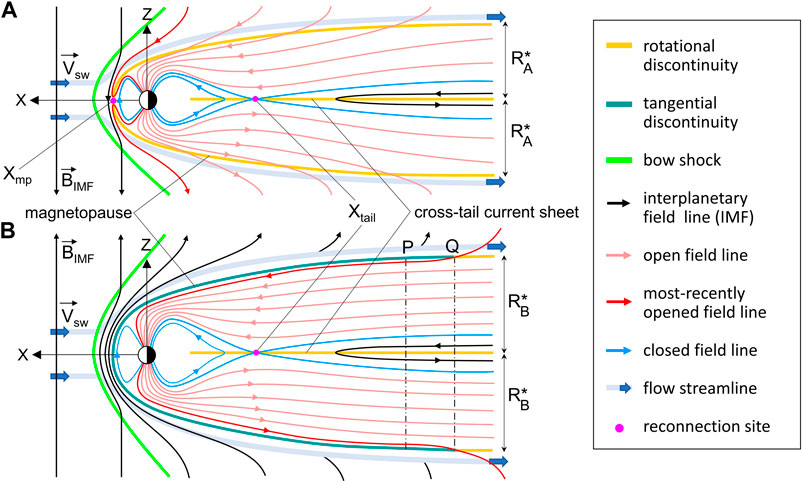
FIGURE 1. Noon-midnight meridian cuts of the magnetosphere, viewed from the from the dusk flank: the X (sunward) and Z (northward) axes in the Geocentric Solar Magnetospheric frame (GSM, in which the X axis points towards the Sun and the Z axis is the projection of Earth’s magnetic axis onto the YZ plane) are shown. Parts (A) and (B) are for times t_A and t_B when the IMF was southward and northward respectively where t_B > t_A, and the IMF has been northward for all the interval t_A < t ≤ t_B. In A the southward-directed interplanetary magnetic field (IMF) gives magnetic shear across the dayside magnetosphere, and this drives magnetic reconnection at X_mp between closed geomagnetic field lines (in blue) and (shocked) interplanetary field lines (in black), and thereby generating open field lines that thread the magnetopause current sheet (in red/pink: most open field lines are shown in pink but the most recently opened one is shown in darker red). Open field lines threading the magnetopause current sheet make it a rotational discontinuity, shown in orange. Open-field lines are re-closed by reconnection at X_tail in the cross-tail current sheet (also a rotational discontinuity and so also shown in orange). In part (B), the northward pointing IMF means that reconnection in the subsolar magnetopause has ceased and the because the northward IMF has persisted for a long interval (t_B − t_A), the last field line to be opened (in red) has been swept a large distance in the −X direction by the solar wind flow (a typical solar wind speed of 400 kms⁻¹ corresponds to 150R_E per hour (where 1R_E is a mean Earth radius = 6370 km). In comparison, the dayside magnetopause is typically at X of between 10R_E and 15R_E and so, given we here consider intervals (t_B − t_A) of several hours, the X axis in the tail is necessarily greatly compressed in these schematics. In part (B), most of the magnetopause is now a tangential discontinuity (shown in dark green) and is only threaded by open flux at the most negative X values shown. Note that three of the northward-pointing IMF/magnetosheath field lines are shown as remaining in the non-midnight meridian, being draped over the nose of the magnetosphere, but two others are moving round the dawn or dusk flank, out of the plane of the diagram. The appending of open field lines to the tail by the solar wind flow between the times t_B and t_A has flared the tail, increasing its asymptotic radius from R^*_A to R^*_B. The point where the last field lines to be opened thread the magnetopause have, by the time t_B, reached the tail cross-section shown by the vertical black dot-dash line labelled Q (at X = X_Q) and all open field lines are parallel to the solar wind flow by the tail cross section labelled P (at X = X_P). Earthward of the X = X_P, the solar wind flow is no longer generating field-perpendicular convection.

Dungey’s seminal schematic (the origin of Figure 1A) showing how reconnection between the IMF and the geomagnetic field would drive the magnetospheric and ionospheric circulation of plasma and frozen-in magnetic field (flow that we call convection), was included in his 1950 PhD thesis (Dungey, 1950), but was not published in the open literature until 1961. In that year, Axford and Hines (1961) proposed a second, unspecified, mechanism could also cause the solar wind flow to excite magnetospheric and ionospheric convection. The key difference was that Axford and Hines proposed the forcing acted on closed field lines and this is now referred to as a “viscous-like interaction” and, being unspecified in nature, this name effectively means “anything but reconnection.” Kelvin-Helmholtz wave-breaking on the magnetopause is one proposed mechanism. The key and observable difference between reconnection-driven and non-reconnection-driven convection is that reconnection transfers magnetic flux and frozen-in plasma antisunward over the poles and out of the magnetospheric equatorial plane and hence, in that plane only the sunward return motion of re-closed field lines and frozen-in plasma is seen. On the other hand, for any viscous-like interaction both the antisunward and sunward transport must be seen in the equatorial plane. This difference was used to show that the contribution of the viscous-like interaction was relatively minor (Cowley, 1982). The same conclusion was reached from studies of the dependence of the observed convection voltage in the polar cap (the transpolar voltage Φ_PC, a.k.a. the cross-cap potential difference) on the north-south IMF component, B_Z, in the Geocentric Solar Magnetospheric frame of reference (GSM, in which the X axis points towards the Sun and the Z axis is the projection of Earth’s magnetic axis onto the YZ plane): larger values of Φ_PC were only found when the IMF pointed southward (B_Z < 0), the orientation that gives greatest rate of opening of field lines. During intervals of B_Z > 0 (northward IMF) observed antisunward transport voltages were considerably smaller (see review by Cowley, 1984). However, the assumption that all antisunward convection in the polar cap during northward IMF must be caused by a viscous-like mechanism is far from correct. Studies using data from satellites (Wygant et al., 1983) and radar networks (Lockwood and McWilliams, 2021a) have shown a large range of transpolar voltages can exist during northward IMF intervals but the largest values are at times of enhanced auroral electrojet activity and these largest values decay with time since the IMF turned northward, revealing a residual effect of the prior interval of southward IMF. This is explained by the Expanding-Contracting Polar Cap (ECPC) model of convection excitation discussed below (Cowley and Lockwood, 1992) which shows how and why effects of continuing nightside reconnection, closing residual open field lines generated during a prior period of southward IMF, are often wrongly attributed to a viscous-like mechanism, which consequently explains only about 10 kV of antisunward flux transport, and very probably less, compared to the larger reconnection-driven antisunward transfer rates of up to about 150 kV.

In most early papers, the concept of a steady equilibrium, or at least an evolving series of equilibria, was applied. Only with a growing understanding of the substorm cycle did it become clear that the magnetospheric response to the solar wind forcing was not, in general, a steady-state one (McPherron, 1979). In these studies, non-steady conditions are applied to the Dungey cycle, with the rate at which open flux is generated during the substorm growth phases (i.e., the voltage Φ_D along the reconnection X-line in the dayside magnetopause, labelled X_mp where it crosses the noon-midnight plane in Figure 1A) exceeding the rate at which the open flux is lost (the voltage Φ_N along the nightside reconnection X-line in the cross-tail current sheet at which open field lines are re-closed, labelled X_tail in Figure 1A). The converse applies during the expansion and recovery phases when Φ_N > Φ_D. In general, imbalance between Φ_D and Φ_N makes the open flux F_o change at a rate

$\text{d}{F}_{\mathrm{o}}/\text{dt}=\left({\Phi }_{\mathrm{D}}-{\Phi }_{\mathrm{N}}\right)(1)$

This equation can be seen as a statement of continuity of open flux or, alternatively, of Faraday’s law (in integral form) applied to any closed loop that surrounds the open flux region.

Because the ionosphere is incompressible, in the sense that the magnetic field there is approximately constant, this means that the region of open flux there (that we here term the “polar cap”) expands and contracts in area (Holzer et al., 1986). Open flux is rapidly swept into the tail by the solar wind flow during the substorm growth phase, making the magnetic flux in the tail lobes increase until the onset of the expansion phase, after which it decreases again (Caan et al., 1973, 1978; McPherron et al., 1993): as a result, steady-state, curl-free electric field does not apply. Siscoe and Huang (1985) introduced an important concept for understanding and interpreting the pattern of convection flows driven in the ionosphere, namely the effect of the movement of non-reconnecting (“adiaroic”) segments of the open polar cap boundary associated with this expansion and contraction of the polar cap. This understanding is also based on the fact that the ionosphere is incompressible and so there are negligible sources or sinks of flow. This time-dependent behavior reveals that mapping electric field from interplanetary space is not the mechanism by which solar wind energy and momentum is coupled into the magnetosphere and polar ionosphere and only when we average on timescales long enough that the dayside and nightside reconnection voltages become the same does the concept of electric field mapping give a valid answer.

Our paper from 30 years ago this year (Cowley and Lockwood, 1992) provided an alternative to the idea of mapping electric fields by discussing a mechanism that applied on shorter timescales as well as on longer timescales. This paper introduced what we called the “Expanding Contracting Polar Cap” model (ECPC–or “easy-peasy”) of how reconnection drives flow in the magnetosphere-ionosphere system and the ionosphere in particular (Lockwood, 1993). The model was developed by taking the above concepts of non-steady flux transport driven by differing time-dependent reconnection voltages Φ_D and Φ_N, ionospheric incompressibility, moving adiaroic boundaries and solar wind dynamic pressure compression of the magnetosphere: it was applied to explain observations made using the EISCAT incoherent scatter radars of the ionospheric flow response to sudden southward turnings of the IMF.

The Dungey cycle is well observed in ionospheric convection (e.g., Zhang et al., 2015 and references therein). The ECPC model is a conceptual model of how reconnection drives this ionospheric convection. Momentum is transferred from the outer magnetosphere down to the F-region ionosphere by matched pairs of oppositely-directed field-aligned currents connected by Pedersen currents (Southwood, 1987), but this does not answer the question of what determines the intensity of those currents and where they occur, and hence the speed and pattern of ionospheric convection. In steady-state there are no inductive effects and so that question is answered by mapping the interplanetary electric field into the polar cap ionosphere down open magnetic field lines. However, induction effects mean that this cannot be applied to non-steady conditions and the ECPC model provides the required understanding by considering the magnetosphere-ionosphere response to changes in the tangential and normal stresses applied to the magnetosphere by changing the total open flux in the system. Hence ECPC is a conceptual model of the how electric fields and voltages of interplanetary space (in the Earth’s frame of reference) are transferred into the magnetosphere and ionosphere: it generalizes the commonly-used (often tacitly used) assumption of mapped electric fields to which it reduces in the special case of steady state. Details of the ECPC concept are reprised in Section 3 of this paper. Note that because it deals only with reconnection-driven flow, the ECPC model does not consider viscous-like mechanisms acting on closed field lines and that can operate simultaneously with the reconnection-driven flow. Having said that, as mentioned above, ECPC does have implications for our understanding of viscous-like mechanisms because it shows that much or even all of the ionospheric voltage often ascribed to them can be due to continuing tail reconnection after the IMF has turned northward. Note also that the concepts of non-steady electric field mapping inherent in ECPC would also apply to any electric fields generated on closed field lines near the magnetopause by a viscous-like mechanism. In this paper, we explore a point that has not been considered before, namely the implications of the ECPC model for how the dynamic pressure of the solar wind influences the convection response to changes in the rate of production of open flux by magnetic reconnection in the dayside magnetopause induced by IMF orientation changes.

Figure 1B helps us define some terms and principles. It is a parallel schematic to Figure 1A, but is for northward IMF and considerable time (tB−tA) after the IMF last pointed southward. Antisunward motion of open flux in the interval (tB−tA), in the absence of any magnetopause reconnection, would turn the dayside magnetopause and near-Earth tail magnetopause from a Rotational Discontinuity (i.e., it is threaded by the open flux) into a Tangential Discontinuity (which is not threaded by open flux). In both parts of Figure 1, we can see the “tail flaring”–meaning the increase in the cross-section tail radius, R with increasingly negative X coordinates, until a maximum “asymptotic” limit is reached (R = R*). Comparison of Figure 1A and Figure 1B also highlights a second meaning of the term “tail flaring” that has been used in the literature, namely the increase in R with time at a given X due to open flux being appended to the tail. To distinguish these spatial and temporal uses of the word flaring, we here refer to the spatial effect as the “tail flaring” and the temporal effect as the “an increase in the tail flaring.” The asymptotic limit is a somewhat simplified concept as the pressure of draped interplanetary field lines means that the tail tends to be flattened and the effect of the IMF BY component twists the cross-tail current sheet out of the XY plane (Sibeck and Lin, 2014). In addition, there is the slight tail aberration due Earth’s motion in the −Y direction and the solar wind flow close to the −X direction. Nevertheless, to first order, R = R* is reached when the tail magnetopause becomes aligned with the solar wind flow so that, in equilibrium, the lobe magnetic pressure equals the static pressure of interplanetary space and the dynamic pressure is no longer constraining the magnetopause. Hence beyond the asymptotic limit, the equilibrium lobe field is set by the interplanetary static pressure and adding more open flux only causes the tail flaring to increase (i.e., R at a given X rises) and does not cause field perpendicular motion in the magnetosphere (the lobe field remains constant). Conversely, removing open flux (by tail reconnection and its exhaust in the −X direction along the current sheet) reduces R and the tail flaring and does cause field-perpendicular convection throughout the lobes and towards the current sheet, even though the lobe field strength remains constant and set by the static pressure of interplanetary space.

Mapping Electric Fields From Interplanetary Space to the Ionosphere

The previous section makes the point that a key component of the ECPC model is the fact that electric field does not map down open field lines from interplanetary space into the ionosphere for anything other than steady-state conditions. To define specifically what we mean by “steady-state mapping” consider two points on open field lines a distance L_SW apart in interplanetary space, between which there is an electric field E_SW applied in a geocentric frame. These points map magnetically down the open magnetic field lines into the ionosphere, to two points that are L_i apart, between which the electric field is E_i in the same frame of reference. Steady-state mapping of a (curl-free) electric field would mean that E_i = E_SW(L_SW/L_i) in the ionosphere: in other words, the voltage difference between the two field lines in the ionosphere, E_i L_i, is equal to that in interplanetary space, E_SW L_SW. In this section, we outline some observations that specifically discriminate between the ECPC model and this steady-state electric-field mapping concept. Because steady-state applies for data that is averaged over sufficient timescales, many scientists do not see the need to allow for the effects of a breakdown of steady-state mapping: we here stress how and why it is inadequate, being a consequence of averaging rather than a physical mechanism.

The reason why electric field does not, in general, map down open field lines can be seen from application of Faraday’s induction law to the tail lobes. Figure 2 is based on similar schematics in Lockwood and Cowley (1992) and Lockwood and Morley (2004) and part A shows the magnetosphere and part B the polar ionosphere, with closed field lines occupying the pale blue areas and open field lines in the pink areas. During strong substorms, the near-Earth lobe field can increase during the growth phase from about 30 to 40 nT in about Δt = 25 min (e.g., McPherron et al., 1993). Assuming that the lobes are semi-circular in cross section with a (constant) radius 15 R_E (a mean Earth radius, 1R_E = 6370 km), this means that the magnetic flux in one lobe, F_L, increases from about 0.4 GWb to about 0.6 GWb and, by Faraday’s law, such a rise of ΔF_L = 0.2 GWb corresponds to an e.m.f. around any closed loop surrounding the lobe of ΔF_L/Δt = 133 kV. This gives an order of magnitude estimate of the possible voltage decoupling between interplanetary space and the ionosphere caused by induction. Because some of the open polar cap flux F_o threads the dayside magnetopause, in general F_L will be smaller than F_o; however, F_L will still be a significant fraction of F_o because open flux is swept into the tail on short timescales compared to the time lag between opening and closure of a given field line. Surveys by Milan et al. (2007) and Boakes et al. (2009) found a distribution of F_o between 0.2 and 0.9 GWb with a mode value near 0.4 GWb and a mean of 0.46 GWb. The smallest estimated F_o that we know of is for the “nearly closed” magnetosphere observed by Wang et al. (2022) for which F_o was estimated to have fallen to about 0.08 GWb. Substorm onsets are typically initiated when F_o reaches about 0.7 GWb (Milan et al., 2008) but larger values, up to about 1.1 GWb, have been deduced in sawtooth events and steady convection events (DeJong et al., 2007; Lockwood et al., 2009; Brambles et al., 2013). It has been estimated that in large superstorms, F_o saturates near 1.2 GWb (Mishin and Karavaev, 2017). For all these F_o estimates, the inferred changes in tail lobe flux ΔF_L during substorms, sawtooth events, and steady convection events are significant fractions of the increases in the total open polar cap flux, ΔF_o.

FIGURE 2

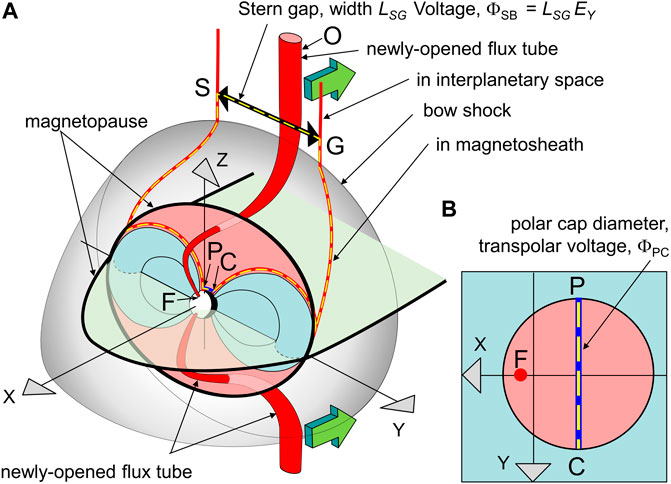
FIGURE 2. Schematic illustrating how interplanetary voltages and electric fields are decoupled from those in the ionosphere by the inductive effects of growth or decay of magnetic fluxes threading parts of the magnetosphere: in this case the lobe flux is growing during a substorm growth phase as newly-opened field lines like OF are appended to the tail lobe by the solar wind flow (green arrows) and so thread the loop PSGC, shown by the yellow dashed line, that is fixed in the XYZ GSM frame shown. Part (A) is a view of the magnetosphere from the northern hemisphere, mid-afternoon sector and pink and light blue areas show, respectively, open and closed field line areas in the GSE YZ plane. Part (B) is looking down on the northern hemisphere polar cap and, again, pink and light blue areas show, respectively, open and closed field line areas. Red lines are selected open flux tubes.

Open field lines, by definition, thread the magnetopause. They then thread the magnetosheath and the bow shock and define a region called the “Stern Gap” in interplanetary space (the name originated from a NASA Technical report (Stern, 1975b) in which this region was actually called a “window”). The red lines PS and CG in Figure 2 are the open field lines closest to, respectively, the dawn and dusk flanks of the magnetosphere and so define the full extent (in the Y dimension) of both the Stern Gap, SG, and the polar cap, PC, in the ionosphere. The yellow dashed line is a closed loop PSGC round the lobe, which is fixed in the GSM frame of reference. Faraday’s law (in integral form) applied to this loop gives

${\displaystyle \underset{PSGC}{\oint }\overrightarrow{E}.\overrightarrow{dl}}={\Phi }_{PS}+{\Phi }_{SG}+{\Phi }_{GC}+{\Phi }_{CP}=d{\displaystyle \underset{PSGC}{\oint }\overrightarrow{B}.\overrightarrow{dA}/dt}=d{F}_T/dt(2)$

Where F_T is the total magnetic flux threading the loop and Φ_AB is the voltage between generic points A and B. If there are no changes in the magnetosheath, the flux of sheath field threading the loop remains constant and so dF_T/dt = dF_L/dt, where F_L is the flux in the lobe. The segments of the loop PS and GC are everywhere aligned with the magnetic field. In ideal MHD, the field-aligned potential drops Φ_PS and Φ_GC are zero and so, although field lines at these segments of the loop are convecting, the electric field associated with that motion is field-perpendicular and so also perpendicular to the loop segments (i.e., E. dl = 0 along the PS and GC segments of the loop). One cannot explain the magnitude of the decoupling of the voltages across SG and PC by invoking a static situation and field-aligned potential differences. Information of field-parallel electric fields comes from energies of field-aligned beams of accelerated ions and electrons (upgoing or downgoing) seen both above and below the acceleration region (see review by Marklund and Lindqvist, 2021). To be effective in generating these beams, the potential drops need to be present for at least the flight time of the particles across them and are referred to as “quasi-static.” Hence there is debate between the relative influence of electric fields in Alfvén wave phenomena (e.g., Watt et al., 2005) and longer-lived structures giving field-parallel potential drops (such as proposed double layers) and so it is not clear how persistent they are on timescales of convection and hence to what extent they are averaged out on such timescales. However, the largest values are typically 1–3 kV in the auroral oval (Marklund and Lindqvist, 2021) and about a 10th of this inside the polar cap (Hosokaw et al., 2020). These values are considerably smaller than both the typical field-perpendicular voltages Φ_PC (= −Φ_CP) of 50–150 kV (e.g., Lockwood and McWilliams, 2021a) and the typical scale of the electromotive force around the loop PSGC inferred above (dF_L/dt = 1.33 × 10⁵ Wb s⁻¹ = 133 kV). Hence, to first order, even without the averaging effect of their quasi-static nature, we can discount quasi-static field parallel potential drops. This gives

${\Phi }_{SG}-{\Phi }_{PC}=d{F}_L/dt(3)$

Hence only in steady state, when dF_L/dt = 0, does Φ_PC = Φ_SG and the interplanetary voltage maps into the ionosphere. Numerical MHD models of the magnetosphere provide evidence for the magnitude of decoupling of the Stern gap voltage Φ_SG and the transpolar voltage Φ_PC indicated by Eq. 3. For example, Gordeev et al. (2017) compare the predictions of three different models following a southward turning of the IMF, after which B_Z is held steady at −5 nT with a solar wind speed V_SW = −V_X = 600 km s⁻¹. From E = −V × B, the dawn-to-dusk interplanetary electric field is E_Y = V_X B_Z = +3 mVm⁻¹ after the southward turning (where V_X is the solar wind velocity in the +X direction so V_X < 0 and E_Y > 0 for B_Z < 0). Note that even if the E_Y arriving at Earth changes with time, all field lines opened at a given E_Y keep that value for their entire transit over the polar cap because neither V_X nor B_Z change significantly for each field line in the relevant extent of interplanetary space. We here just use the results from the BATSRUS model to illustrate the point about how E_Y maps to the ionosphere. The model predicts that the tail flux rises almost linearly in the resulting substorm growth phase from 0.4 to 0.6 GWb over an interval 25 min long giving dF_L/dt = 133 kV (as estimated above for a typical substorm from magnetic field observations in the tail lobe). The rise is caused by newly-opened field lines, such as OF in Figure 2, being transferred antisunward along the Stern Gap from the dayside to the nightside, the rate of flux transfer being Φ_SG, while their ionospheric footpoints are not moved across the polar cap diameter PC. In fact, Φ_SG will exceed this value of dF_L/dt as some tail lobe flux is lost by reconnection in the cross tail current sheet and convected sunward out of the tail as closed flux. The tail reconnection site is not immediately influenced by the increase in magnetopause reconnection as it takes time for any information about the southward turning to reach it; hence we can assume this loss of lobe flux carries on at the rate of 21 kV which was the modelled quasi-steady value before the southward IMF turning. This means that Φ_SG is approximately 133 + 21 = 154 kV, giving a Stern gap width of L_SG = Φ_SG/E_Y = 8.1 R_E, which is a realistic value. Substorm onset in the model occurs about 30 min after the southward turning and during that interval, the model predicts that the ionospheric transpolar voltage rises from 21 to 93 kV. Hence at no time in the growth phase does the interplanetary electric field or voltage map from interplanetary space to the ionosphere in these simulations. The other models tested by Gordeev et al. (2017) show the same general behavior.

Possibly the most straightforward evidence for the need for something like the ECPC model is that transpolar voltage Φ_PC depends both on the prevailing IMF B_Z component (and hence the dawn-dusk interplanetary electric field, E_Y = −V_SW B_Z) and on the AL auroral electrojet index. This is demonstrated in the contour plot from 25 years of SuperDARN Φ_PC data shown in Figure 3 (this is a version of the −AL versus B_Z contour plot for the same dataset presented in Figure 8 of Lockwood and McWilliams (2021a) but uses E_Y along the x-axis instead of B_Z). The diagonal orientation of the contours shows that, in general, Φ_PC increases both with E_Y at a fixed AL and with −AL at a fixed E_Y. For northward IMF (E_Y < 0), the contours become almost horizontal showing a dominant dependence on −AL: for southward IMF (E_Y > 0) both have an influence but at the largest E_Y the contours become almost vertical, indicating E_Y is the dominant influence. Hence the plot shows Φ_PC increases with auroral electrojet strength, quantified by −AL, at all but the largest E_Y and that for northward IMF (E_Y < 0), Φ_PC depends almost entirely on AL. If the interplanetary electric field always mapped to the ionosphere, as predicted by steady-state, then Φ_PC would be equal to the voltage across the Stern gap Φ_SG = E_Y L_SG where L_SG is the width (in the Y dimension) of the Stern gap. This value would then persist on those field lines until they were closed again. Hence the only way that mapped electric fields could explain the observed dependence on both −AL and E_Y in Figure 3 is if L_SG increased monotonically with −AL. Given that L_SG is set by the length of the magnetopause reconnection X-line and the field line draping in the magnetosheath and AL is determined by processes in the near-Earth tail and that information takes time to travel between the two regions, there can be no mechanism that could give such a relationship. Strictly speaking, this argument shows that application of steady-state mapping of the electric field cannot explain Figure 3. However, we also note that the ECPC model is the only proposed alternative to steady-state mapping in the literature. In addition, substorm theories and observations show there is a monotonic average relationship between −AL and Φ_N and the polar cap contraction that Φ_N causes (Milan et al., 2009a; Lockwood et al., 2009; Mooney et al., 2020; Milan et al., 2021) and simultaneous lobe field decreases at well-separated locations (Caan et al., 1978; McPherron et al., 1993). The −AL index can therefore be considered to be a proxy indicator of Φ_N. Hence Figure 3 shows that Φ_N and Φ_D are separate contributors to Φ_PC which is a central prediction of the ECPC model.

FIGURE 3

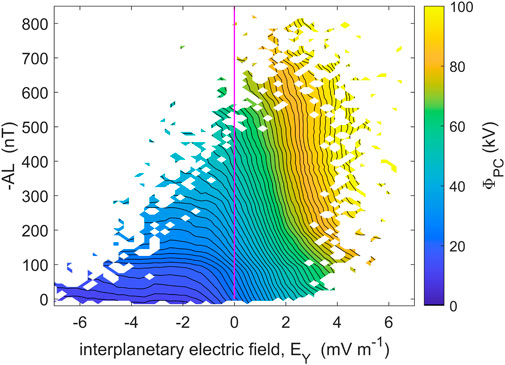
FIGURE 3. Contours of average transpolar voltage, Φ_PC, observed over 25 years by the northern hemisphere SuperDARN radar network (Lockwood and McWilliams, 2021a) as a function of the dawn-dusk interplanetary electric field, E_Y, and the auroral electrojet index, −AL.

Another key piece of evidence is the behavior of transpolar voltage Φ_PC after the IMF returns northward following a period of southward IMF. A northward turning of the IMF ceases the production of new opened field lines, or at least reduces their rate of production, but does not remove pre-existing ones. The open field lines generated during the prior southward IMF interval remain open until they are closed by reconnection in the cross tail current sheet and their interplanetary E_Y, L_SG and Φ_SG values all stay constant all that time. Hence if steady-state mapping applied, Φ_PC would also remain constant and then drop rapidly as the last-to-be-opened field lines are re-closed. This is not what is observed (Wygant et al., 1983; Lockwood et al., 2006; Lockwood and McWilliams, 2021a): rather, a range of Φ_PC values are observed between almost zero and largest values that decay exponentially with time after the northward turning and that depend on the −AL value. This is a prediction of the ECPC model because one substorm expansion does not remove all the extra lobe magnetic flux that is built up during the prior growth phase and so one isolated growth phase can generate a string of subsequent substorm expansions of declining amplitude, each giving a peak in Φ_PC due to an associated rise in the reconnection voltage in the cross-tail current sheet, Φ_N. Northward-IMF intervals are often thought of as giving an equilibrium to which the magnetosphere returns because they give geomagnetically quiet conditions. This is not the case. During these intervals the interplanetary electric field points from dusk to dawn (E_Y < 0) and reconnection taking place poleward of the magnetic cusps, near the sunward edges of the tail lobe magnetopause boundary, gives penetration of that negative E_Y into the magnetosphere (e.g., Lockwood and Moen, 1999). The tail never decays away completely and so, at the same time as the lobe reconnection, magnetic shear remains across the cross-tail current sheet and reconnection there can only give either E_Y > 0 or, if it ceases, E_Y = 0. In both scenarios, there is a curl in electric field and so this is a slow decline of the lobe field and not steady state (Lockwood, 2019). That decline can be understood because any ongoing reconnection in the cross-tail current sheet causes a loss of open flux and reconnection taking place at the sunward edge of both lobes can also cause a loss of dayside open flux, giving a “horse-collar” auroral form, with a teardrop-shaped open polar cap with most remaining open flux confined to the nightside (Lockwood and Moen, 1999; Imber et al., 2006; Milan et al., 2020). The most extreme example of this was observed by Wang et al. (2022), but even in this case a residual open flux of about 0.08 GWb remained. Hence, as far as we can tell, the magnetosphere is never subject to a long enough period of strongly northward IMF that it becomes completely closed and so northward IMF conditions, although geomagnetically quiet, give a slow decline of the lobe fields rather than an equilibrium steady state.

A more complex test of the ECPC model was provided by Soterelis et al. (2017). These authors showed that when the polar cap is expanding the observed transpolar voltage correlates best (correlation coefficient r = 0.86) with the solar wind/IMF driving, integrated over the previous 10 min (compared to r = 0.57 for when the polar cap is contracting). On the other hand, when the polar cap is contracting the transpolar voltage correlates best (r = 0.87) with averages of solar wind/IMF driving over the previous 90 min (compared with 0.51 for when the polar cap is expanding). This is consistent with the ECPC model and also specifically inconsistent with the idea that electric field maps from the solar wind and magnetosheath to the ionosphere for which correlations would not depend on whether the polar cap was expanding or contracting.

Note that polar cap expansion (when Φ_D > Φ_N) and contraction (when Φ_N > Φ_D) are both observed and the transpolar voltage is raised during both, by the increased Φ_D and by increased Φ_N, respectively (Lockwood, 1993; Milan, 2004; Hubert et al., 2006a; Hubert et al., 2006b; Lockwood et al., 2009; Milan et al., 2009b; 2021), consistent with the ECPC model. For electric field mapping transpolar voltage would be set by Φ_SG only.

Applications of the ECPC model have been predominantly in describing transient effects. In particular, it has been widely used to investigate the ionospheric signatures of Flux Transfer Events (FTEs: burst of enhanced reconnection voltage in the dayside magnetopause) (Cowley et al., 1991; Smith and Lockwood, 1996; Milan et al., 2016) and convection during the substorm cycle (Milan et al., 2021). It has also been applied to the magnetospheres of other planets (e.g., Cowley et al., 2005). Here we are making a somewhat different point. Because the magnetosphere is rarely, if ever, in a steady-state equilibrium, some part or all of it is always responding to prior variations in the solar wind (Lockwood, 2022b) which means the ECPC concept will always have some relevance. We here investigate this idea in relation to the observed effects of solar wind dynamic pressure on transpolar voltage and geomagnetic activity.

Effects of Solar Wind Dynamic Pressure

Equilibrium concepts balance the dominant magnetic pressure in the magnetosphere with the dominant pressure in interplanetary space, which, for the near-Earth magnetopause, is the dynamic pressure of the solar wind flow (P_SW = m_SWN_SWV_SW² = ρ_SWV_SW², where m_SW is the mean ion mass, N_SW the number density, ρ_SW is the solar wind mass density and V_SW the solar wind speed).

A number of papers have indicated that solar wind dynamic pressure has an influence in flux transport through the magnetosphere and on geomagnetic activity (e.g., Lukianova, 2003; Lee et al., 2004; Boudouridis et al., 2005; Stauning & Troshichev, 2008; Lockwood et al., 2020b; Lockwood et al., 2020c): this is beyond, and separate from, the known generation of transient filamentary field aligned currents and travelling convection vortices (e.g., Glassmeier and Heppner, 1992; Lühr et al., 1996). These “TCV” events are caused by filamentary pairs of field aligned currents generated by the magnetopause deformation but they move laterally (along the line between the two currents) which means that although flow is generated, there is no net effect as they pass through and do not add to the convection cycle. There are physical reasons to expect both the dayside and the nightside reconnection voltages (respectively, Φ_D and Φ_N) to be enhanced by increased solar wind dynamic pressure P_SW. In both cases, the compression brought about by greater P_SW should increase the magnetic shear across the current sheet and so would be expected to enhance the reconnection rate: an effect that has been identified in global MHD model simulations (e.g., Palmroth et al., 2004). However, in observational studies it is not clear how much of the response is a TCV.

One caveat to this idea is that the nightside reconnection must be taking place at a GSM X-coordinate at which the tail is still flaring (i.e., dR/dX < 0), which enables the dynamic pressure to squeeze the tail lobe and so increase the field there (Caan et al., 1973) and hence the cross-tail current (Lockwood, 2013). Scurry and Russell (1991) inferred statistically that dayside reconnection voltage Φ_D was enhanced by increased P_SW using the am geomagnetic activity index as a proxy for the reconnection rate (we will discuss the validity of this below). Transient responses to individual events in which P_SW increases suddenly include a rise in Φ_D (e.g., Boudouridis et al., 2007), a rise in Φ_N (Boudouridis et al., 2008a) and hence a rise in Φ_PC (Boudouridis et al., 2008b). Karlsson et al. (2000) reported events in which the energy content of the near-Earth tail was reduced following decreases in P_SW at the end of a substorm growth phase, inferring that they even caused quenching of any substorm expansion that had recently begun. These authors deduced that reducing P_SW can also reduce Φ_N. Conversely, increases in P_SW have been seen to trigger onsets of full substorm expansion phases (Schieldge and Siscoe, 1970; Kokubun et al., 1977; Yue et al., 2010) consistent with the idea that increased P_SW can increase Φ_N. In some cases, a rise in Φ_N due to increases in P_SW has been inferred from a loss of open flux as aurora on closed field lines expands into what appears to have been open flux (Hubert et al., 2006a; b). Various observational studies suggest that increases in P_SW cause an enhancement in general magnetospheric convection and in field-aligned current systems as well as enhanced geomagnetic activity (e.g., Lukianova, 2003; Lee et al., 2004; Hubert et al., 2006b; Boudouridis et al., 2008a; Stauning and Troshichev, 2008). This phenomenon has also been modelled using global MHD models of the magnetosphere as being caused by rises in both Φ_D and Φ_N induced by rises in P_SW (Palmroth et al., 2004; Ober et al., 2006; Connor et al., 2014; Lockwood et al., 2020b).

Many of these studies relate to the effects of sudden rises or falls in P_SW and from the transient responses it is not clear what influence different constant levels of P_SW have on the overall average reconnection voltages, flux circulation through the magnetosphere and on the overall level of geomagnetic activity. The observed “McIntosh” (a.k.a. “equinoctial”) pattern of the average am geomagnetic index with time-of-day and time-of-year, associated with the dipole tilt, has been shown to have an amplitude that is proportional to the value of P_SW (Lockwood et al., 2020a). This geomagnetic effect has been reproduced using global MHD modelling by Lockwood et al. (2020c) and explained by the effectiveness with which P_SW can squeeze the tail and how that varies with the dipole tilt. This shows a strong influence of P_SW on geomagnetic activity. Lockwood et al. (2020b) show that P_SW has a distinct influence on geomagnetic activity from that of the estimated power input on the magnetosphere, P_α (see Lockwood, 2019), despite the fact that they share common dependencies on N_SW, m_SW and V_SW. We here use the estimate of the power input P_α = B^2αV_SW ^(7/3−2α)ρ_SW ^(2/3-α) sin⁴(θ_GSM/2), where B is the IMF magnitude, and θ_GSM the IMF clock angle in the GSM frame of reference (Vasyliunas et al., 1982). Hence although P_SW = ρ_SW V_SW², the best-fit coupling exponent of α = 0.44 found by Lockwood et al. (2020b) means that P_α is proportional to ρ_SW^0.227V_SW^1.453 and it has an additional dependence on the IMF strength and orientation. Specifically, Lockwood et al. (2020b) show that the geomagnetic activity level generated per unit P_α depends on P_SW (and on Earth’s dipole tilt and hence time of year and Universal Time). What was unclear from this study was to what extent this is caused by enhanced flux transport through the magnetosphere (and hence transpolar voltage) or by enhanced energy storage in a compressed geomagnetic tail.

Lockwood and McWilliams (2021b) and Lockwood (2022a) studied best-fit coupling functions for simultaneous Φ_PC, SML and am data for 1996–2020 and found optimum exponents b for a mass density term (ρ_SW^b) of 0.02, 0.06, and 0.36 for Φ_PC, SML and am, respectively. We mention the am index here for two reasons. Firstly, Scurry and Russell (1991) used am as a proxy to infer that dayside reconnection voltage Φ_D was enhanced by increased P_SW. Secondly am has the most uniform response in terms of time-of-day and and time-of-year of all geomagnetic indices (Lockwood et al., 2019a) and is genuinely planetary: however, it has the disadvantage that it is has only a 3-hourly cadence. The best-fit exponent b for the SML and AL indices was found to be essentially identical by Lockwood and McWilliams (2021b) and Lockwood (2022a). These values for b are very similar to those found in other studies using AL (e.g., McPherron et al., 2015). The low value of b for Φ_PC accords with the highly successful coupling function for transpolar voltage of Boyle et al. (1997), which makes no allowance for ρ_SW (i.e., b = 0) whereas other coupling functions designed to predict geomagnetic activity have non-zero exponents b (see Lockwood and McWilliams, 2021b and references therein). Hence these statistical studies suggest that P_SW has a significant effect on geomagnetic activity indices such as AL, SML and am but a smaller effect (if any) on flux transport and transpolar voltage, Φ_PC.

Some clarification of the effects of higher constant solar wind dynamic pressure P_SW (as opposed to transient increases in P_SW) is brought by Figure 4, which is from the survey of 25 years of data by Lockwood and McWilliams (2021a) and shows contour plots of average values (normalized by the parameter standard deviation) as a function of IMF B_Z along the x axis and P_SW (normalized to the overall mean value <P_SW>) along the y axis. The values of B_Z and P_SW are 15-min boxcar means for the same intervals as the terrestrial indices, using the derived optimum propagation lag. Parts A, B and C are for am, AL and Φ_PC, respectively. In general, the contours for all three slope diagonally, showing mean values increase with increasingly negative B_Z at a fixed P_SW and with increasing P_SW at a fixed B_Z. However, the plots are not identical in form. For am the contours are the most inclined to the vertical and are inclined at all B_Z; for AL and Φ_PC the contours are less inclined to the vertical and, indeed, for strongly southward IMF become vertical. Hence Φ_PC and AL have a weaker dependence on P_SW than am and one that is mainly significant for northward IMF or weakly southward IMF. Note that, whereas Figure 11 of Lockwood and McWilliams (2021a) the colour scale used was absolute values of the parameter means, in Figure 4 they have been normalized to the standard deviation, SD, of the parameter. It can be seen that the amplitude of the pattern is a smaller fraction of the overall variability for AL and a larger fraction for Φ_PC. However, it is not possible to draw a physical conclusion from these pattern amplitude differences because of the different construction of the three indices used: all values are 15-min boxcar means of 1 min values but there the similarities end. For AL we have used raw 1-min values which gives a high SD σ_AL; for the am index we are using interpolated values from maximum range values (over 3-h intervals) of 3-hourly cadence and for Φ_PC we are using interpolated values from hourly integrations of 2-min data. What is significant in Figure 4 is the similarities and differences in the form of the pattern and the evidence for an effect of P_SW at all but the largest negative B_Z. In this paper, we use the ECPC model of flow excitation of Cowley and Lockwood (1992) to look at the implications of the effect of P_SW on these magnetospheric state indicators.

FIGURE 4

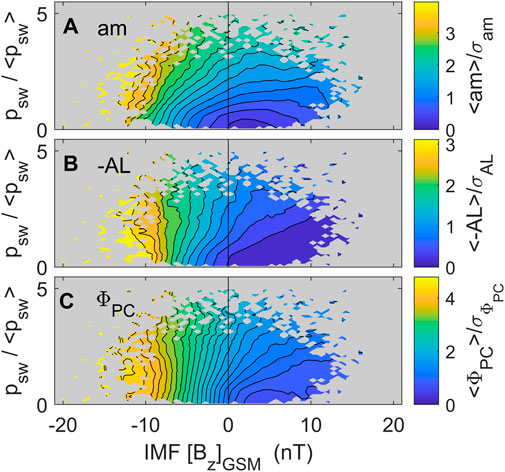
FIGURE 4. Variations with IMF B_Z in the GSM frame and solar wind dynamic pressure, P_SW, of: (A) the am planetary geomagnetic index; (B) the −AL auroral electrojet index; and (C) the transpolar voltage, Φ_PC. All data are simultaneous with the valid Φ_PC samples from 1996 to 2020. The x axis is north-south IMF component (B_Z, defined as positive northward) in the GSM frame of reference and the y axis is the normalized solar wind dynamic pressure, P_SW/< P_SW > where P_SW = m_SWN_SWV_SW², m_SW is the mean ion mass, N_SW is the number density and V_SW is the speed of the solar wind. The normalizing factor < P_SW > is the mean for all data. The −AL, Φ_PC and P_SW data are all 15-min boxcar running means of 1-min data whereas the $am$ data are linearly interpolated to the time of the hourly Φ_PC sample and the mean value in each B_Z - normalized P_SW bin, divided by the parameter SD is plotted: the absolute values were presented in Figure 11 of Lockwood and McWilliams (2021a). Grey areas are where data are too sparse for contours to be fitted.

Data Employed

We here use 1-min interplanetary data from the Omni2-dataset (King, and Papitashvili, 2005) from 1996 onwards when data gaps are both rarer and shorter (Lockwood et al., 2019b). To estimate the dynamic pressure P_SW and the power input into the magnetosphere P_α, we need the solar wind mass density ρ_SW which we estimate by neglecting ions heavier than Helium and using observations of the Helium abundance at the highest resolution available (either 5 min, 15 min or 1 h) and linearly interpolating to minute values.

These data are compared to a number of magnetospheric state indicators. We use 1-min data on the auroral electrojet from the SuperMAG SML index (Newell and Gjerloev, 2011) which is constructed the same way as the AL auroral electrojet index (Davis and Sugiura 1966). Specifically, for both of these two indices, magnetograms of the horizontal components from the stations used are superimposed and the lower envelope defines the index. Like AL, SML is a measure of the strength of the nightside westward auroral electrojet. The difference between SML and AL is that all available stations in the northern hemisphere at middle and high latitudes are used (typically 100 in number) instead of the ring of 12 auroral stations used to construct AL. This means is has a more unform response with Universal Time than AL because it does not have the large longitudinal gaps (on average 30° in width) that cause such problems for AL. In addition, by having stations at lower latitudes, SML avoids the problem that AL suffers from that at large activities the auroral oval expands to lower latitudes than the stations, reducing the response. Both SML and AL are from observations in the northern hemisphere only which means they have a strong annual variation due to the axial tilt of the Earth and the effect that has on ionospheric conductivities. A comparison of the performance of SML and AL has been presented by Bergin et al. (2020). Results for SML and AL were here found to be similar in all important respects and we here show only the results for SML. For a monitor of (mainly) the ring current, we here use the SuperMAG SMR index (Newell and Gjerloev, 2012) that is based on the SYM-H index and compiled from the baseline-subtracted northward component of the geomagnetic field from all available ground magnetometer stations at geomagnetic latitudes between −50 and +50° (again typically 100 in number). An inverse cosine correction for magnetic latitude is then applied and it is averaged globally. Bergin et al. (2020) compare the performance of SMR and the frequently-employed Dst index. Both SMR and SML are available at 1-miute integrations which enables us to process them in the same way as we do the interplanetary data.

We also make some use of the planetary am geomagnetic index (Mayaud, 1980). This index is a range index (between maximum and minimum values of the horizontal field component) taken over 3-h intervals; a time resolution that makes unsuitable for, for example, superposed epoch studies on timescales of a day and less. However, the use of uniform rings of mid-latitude stations in both hemispheres, and the adoption of weighting functions to allow for necessary longitudinal gaps because of oceans, makes the response of the am index truly planetary in nature and exceptionally uniform in time-of-year and time-of-day response (Lockwood et al., 2019a): we employ am when these characteristics are most important.

In addition to these geomagnetic indices, we use the transpolar voltage Φ_PC derived from the SuperDARN radar network. A dataset of hourly averages of 2-min integrations over the past 25 years has been generated by Lockwood and McWilliams (2021a). However, unlike the above geomagnetic indices, it cannot be used as a continuous data series. The reason is that the “map-potential” method used to derive Φ_PC is a data assimilation technique employing a model of the ionospheric convection pattern, driven by the IMF orientation in the upstream solar wind (Ruohoniemi and Baker, 1998; Provan et al., 2002). Lockwood and McWilliams (2021a) tested these SuperDARN Φ_PC estimates against values from satellite over-passes and found that an average number of radar echoes for the thirty 2-min pre-integrations in each hour must exceed 255 for the influence of the model in the Φ_PC data to be reduced to an undetectable level. This condition left 65,133 usable hourly mean Φ_PC values, about one third of the total obtained over 25 years. Despite not being a continuous record and despite the fact that it is only of hourly time resolution, these data are included in the present study because magnetic flux transport (i.e., voltage) is known to be a key and fundamental part of the coupling of solar wind mass, momentum and energy into the magnetosphere and Lockwood and McWilliams (2021b) and Lockwood (2022b) have shown it has a significantly different behavior to geomagnetic indices.

The Non-equilibrium Nature of the Magnetosphere

Milan et al. (2021) make the point that if interplanetary conditions vary slowly enough, the magnetosphere-ionosphere system can evolve through a series of quasi-steady-state equilibria. We can quantify roughly what “slowly” means in this context from their Figure 8: for small polar caps (initial open flux F_o ≈ 0.4 GWb) it means rises in dayside reconnection voltages Φ_D of <25% in 2 h; for mid-sized polar caps (F_o ≈ 0.5 GWb) it means Φ_D rises of <30% in 2 h; and for large polar caps (F_o ≈ 0.6 GWb) it means Φ_D rises of <35% in 2 h. To investigate how likely this is to occur, Figure 5 studies the normalized autocovariance functions (a.c.f.s) of various parameters. To ensure that we compare like-with-like we use parameters that have only one polarity because the a.c.f. of, for example, the IMF B_Z component would be different from that of, for example, the am index because it has both positive and negative whereas am is only positive. Hence instead of B_Z, we use the IMF orientation factor B_⊥sin⁴(θ/2) (where B_⊥ is the transverse component of the IMF perpendicular to the Sun-Earth line, B_⊥ = (B_Y²+B_Z²)^1/2, and θ is the IMF clock angle defined as θ = arctan(|B_Y|/B_Z), B_Y and B_Z being the Y and Z components of the IMF in the GSM frame). We also use the half-wave rectified dawn-dusk electric field E_Y′ (where E_Y′ = E_Y for E_Y > 0 and E_Y′ = 0 for E_Y ≤ 0). In addition, we use a pressure-corrected SuperMAG SMR index that only has negative values: the pressure correction uses the form that Burton et al. (1975) proposed for the Dst index, namely SMR* = SMR − γP_SW^1/2 −β with derived coefficients γ = 31.45 nT nPa^−1/2 and β = 11.51 nT that give the peak linear correlation coefficient of 0.9 between hourly values of SMR* and the pressure-corrected Dst index, Dst*. (Note that we also used the raw SMR index and the a.c.f.s for SMR* and SMR were very similar indeed because positive excursions of SMR are short and small compared to negative ones). In addition, we try to use the same integration and averaging timescales for the data as far as is possible. For the solar wind and IMF parameters, the SMR* index and the SML index we use 1-min integrations of data that are smoothed into hourly means using 60-point running (boxcar) means, before taking the autocovariance. The Φ_PC data are slightly different being initially 2-min integrations and the am data are necessarily radically different being originally range values in 3-h windows.

FIGURE 5

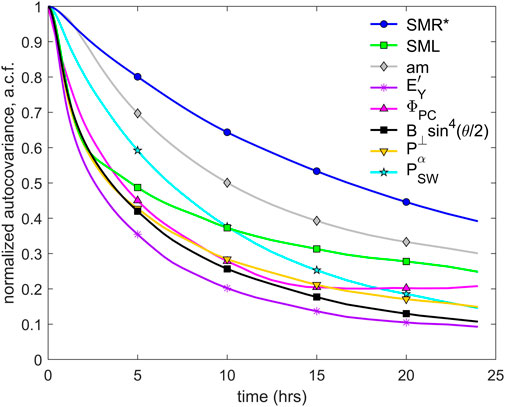
FIGURE 5. Normalized autocovariance functions of 60-point (hourly) 1-min values of: (black line with filled square symbols) an estimate of the geoeffective IMF component of the interplanetary magnetic field, B_⊥sin⁴(θ/2); (purple with asterisk symbols) the half-wave rectified dawn-dusk component of the interplanetary magnetic field, E_Y′ (where E_Y′ = E_Y when E_Y′ > 0 and E_Y′ = 0 when E_Y < 0); (cyan with star symbols) the solar wind dynamic pressure, P_SW; (mauve with upward-pointing triangle symbols) the transpolar voltage measured by the SuperDARN radar array, Φ_PC (1 min values, obtained from linear interpolation between hourly values are used); (gray with diamond symbols) the am geomagnetic index (1 min values, obtained from linear interpolation between 3-hourly values are used); (green with open squares) the SuperMAG SML auroral electrojet index; (blue with circle symbols) the pressure-corrected SuperMAG geomagnetic index SMR* (dominated by the effect of the ring current). All curves are for all available data for 1996–2019, inclusive. Note that the symbols have been added at intervals of 5 h to help distinguish between the different color lines. but a.c.f.s were computed for lags 1 min apart.

The most variable (lowest persistence and shortest autocorrelation timescale) is the interplanetary electric field E_Y′. The a.c.f. for the IMF orientation factor B_⊥sin⁴(θ/2) and the estimated power input to the magnetosphere P_α are similar but show slightly greater persistence than E_Y′. The least variable (highest persistence and longest autocorrelation timescale) of those shown is the SMR* geomagnetic index, which is dominated by the ring current. Of the terrestrial indices shown, the order of increasing variability is SMR*, am, Φ_PC and SML. Note that persistence, as quantified by autocovariance and autocorrelation is a measure of average behavior and individual cases can differ considerably from the average. All of these terrestrial indices are less variable on average than the key driving solar wind parameters, namely: the IMF orientation factor, the half-wave rectified dawn-dusk interplanetary electric field E_Y′ and the estimated power input to the magnetosphere, P_α. The solar wind dynamic pressure has greater persistence because of its dependence on higher-persistence parameters, the solar wind flow speed, mean ion mass and number density (Lockwood, 2022).

Figure 5 demonstrates that the key driving solar wind parameters tend to change faster than the terrestrial state indicators can respond and so the magnetosphere will, in general, not have time to reach equilibrium with the solar wind.

However, there is a caveat we must place on this analysis. The interplanetary parameters are point values from a single spacecraft whereas the magnetosphere will respond to solar wind impacting over an extended area (in the YZ plane) of unknown size. Spatial structure within that area would make the point interplanetary values more variable in time than is the area-averaged values that the magnetosphere responds to. There is very little data pertaining to such an effect and much of it of only quite distant relevance. Walsh et al. (2019) and Lockwood (2022a) have studied the correlations (at optimum propagation lags) between L1 values of interplanetary parameters and coupling functions and those evaluated from near-Earth observations by spacecraft in the magnetosheath and undisturbed solar wind. There are distributions of correlations because the solar wind that passes over the L1 spacecraft may miss the near-Earth craft and/or because conditions can change during the transit between the two and/or there are variations in the propagation delay. Walsh et al. (2019) show that the difference in magnetic field clock-angle θ measured at the two locations, Δθ, increases with the distance of the L1 craft from the Sun-Earth line, R_XY showing an effect of spatial structure in the YZ plane. The effect is modest, the SD of Δθ increasing by about 1% per 1R_E increase in R_XY, but nevertheless present. On the other hand, Lockwood (2022b) shows that the distributions of correlations (for 1-min, 10-min and 1-h averages) between an L1 coupling functions and auroral activity indices were only degraded at R_XY exceeding about 80R_E. Together, these results indicate that there is very likely to be an effect of spatial averaging in the correlations between L1 craft and terrestrial space weather activity. However, directly-relevant evidence that the spatial averaging effect is relatively minor comes from Figure 5 itself. Such an effect would necessarily influence all internal magnetospheric responses at all lags. The autocovariance function of the SML index is therefore interesting because at lags below about 2 h it falls essentially as rapidly with lag as the interplanetary factors that are strongly influenced by IMF orientation (B_⊥sin⁴(θ/2), E_Y′ and estimated power input into the magnetosphere, P_α). At lags above 2 h, the a.c.f. for SML does become larger than for these interplanetary factors, but because the difference is very small at low lags, this must be predominantly because of delayed magnetospheric responses (for example, due to energy stored in the geomagnetic tail or the particle and energy content of the ring current) and not due to the averaging effect of spatial structure in near-Earth interplanetary space inherent in solar wind-magnetosphere coupling that would have an effect at all lags.

Figure 5 does not say anything explicitly about the response lags and evolution times of the magnetosphere. To study their influence, Figure 6 presents a superposed-epoch study of the response to southward turnings of the IMF. These are here defined as when the 30-min means of IMF B_Z, < B_Z >_30min, change from positive to negative with a decrease in successive < B_Z >_30min values of exceeding 0.75 nT. This definition of a southward turning was chosen as a compromise between selecting large amplitude events and having a large number of events. Various values of this threshold and averaging timescale were adopted in a sensitivity study and the character of the responses in superposed epoch plots was always the same and only differed in amplitude: response lags only differed by 5 min at most, which can be used as a general uncertainty estimate. The above definition yielded 160 distinct usable events (at times t_o) of near-continuous data for all parameters from the years 1996–2019, inclusive. One-minute values at epoch times (t−t_o) are then averaged together. In the case of Φ_PC, these 1-min values were linearly interpolated from the hourly data. Values are excluded for which (t_o−t) ≥ (t_o − t_o′) or (t− t_o) ≥ (t_o″− t_o), where t_o′ and t_o″ are the times of the events, respectively, preceding or after the one at time t_o. This means that sample numbers n are lower at larger |t− t_o|. Figure 6I shows the variation of n with (t− t_o): by (t− t_o) = 16 h n falls from 160 to 120, much of that fall occurring at small (t− t_o) because of a tendency for large southward-turning events to cluster. Note there is also some noise in the variation of n caused by short data gaps.

FIGURE 6

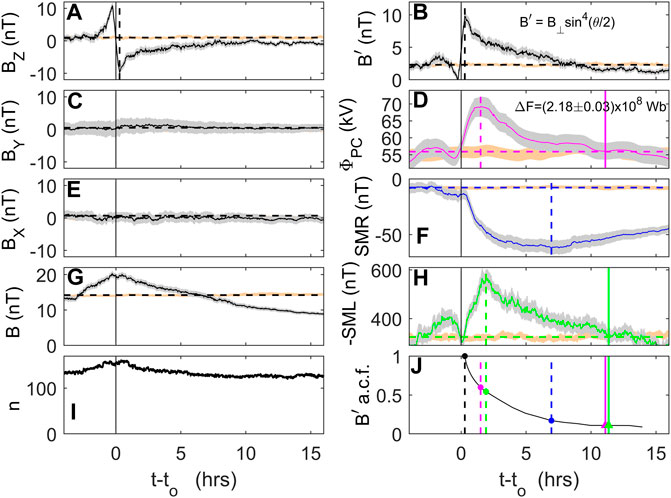
FIGURE 6. Superposed epoch study of responses to southward turnings in the IMF. A total of 160 southward turning events (at time t_o) were identified in the data for 1996–2019 (inclusive) from times when 30-min running means of 1-min values of the northward IMF component, B_Z, turned from positive to negative with a decrease in successive values exceeding 0.75 nT. The line in each panel gives the mean of 1-min values at epoch time (t − t_o) and the gray area around it is plus and minus one standard error in the mean. The left hand panels are for the IMF and parts (D–J) of the right hand panels are about the magnetospheric response. From top to bottom the left hand panels are for: (A) the IMF B_Z component; (C) the IMF B_Y component; (E) the IMF B_X component and (G) the IMF magnitude, B. Panel (I) shows the number of samples n at each (t − t_o). The top right-hand panel, (B), is for the IMF factor B′ = B_⊥sin⁴(θ/2) where (where B_⊥ = (B_Y²+B_Z²)^1/2, and θ is the IMF clock angle defined as θ = arctan(|B_Y|/B_Z). Panel (D) is for the transpolar voltage Φ_PC; (F) the SMR geomagnetic index; and (H) the SML geomagnetic index. The bottom panel, (J), shows the a.c.f of B′ = B_⊥sin⁴(θ/2) for the subset of data contributing to the superposed epoch events, starting from the time of peak B′ to illustrate the probability that the IMF factor has changed from its peak value after the southward turning. Vertical dashed lines mark the epoch times at which the mean disturbance peaks and vertical solid colored lines mark the times the parameter returns to its pre-event level (only shown for Φ_PC and SML because this is greater than 1 day for SMR and so off scale). These vertical lines are repeated in part (J). For all superposed epoch panels, the mean observed over a pre-event calibration period of −4 ≤ (t − t_o) < −2 h is shown by the horizontal line. The orange bands is the same as the grey ones, but from a random event time selection procedure repeated 500 times and then averaged using the same number of event epoch times. This has been normalized by multiplying by the ratio of the calibration period means for the observed and the randomly-selected events so that the magnitude of the observed event response can be evaluated.

The top left panel, A, of Figure 6 shows the average variation of B_Z (in GSM) around the events and shows that, on average, B_Z reaches is maximum southward value about 15 min after the southward turning and then returns towards zero with an approximately (1-e^−t/τ) variation and an e-folding timeconstant τ ≈ 2 h. This plot also reminds us that strong southward turnings tend to be preceded by strong northward IMF. Panels C and E show there is almost no net signature of these events in the other two IMF components and Panel G shows the IMF magnitude B peaks at the time of the southward turnings, an effect of selecting large swings in B_Z. Panel B also presents IMF data and shows the factor B′ = B_⊥sin⁴(θ/2) that is designed to be a monotonic, unipolar indicator of solar wind coupling (Lockwood and McWilliams, 2021b; Lockwood, 2022b) that peaks when the southward component is strongest.

Panels D, F and H show the lagged response of magnetospheric state indicators Φ_PC, SMR and SML for which the peak in average disturbance associated with the southward turning is at (t−t_o) of 1.5, 6.9 and 2.0 h, respectively. Pre-event conditions are taken to be the mean over the interval −4 h < (t−t_o) ≤ −2 h, shown by the horizontal dashed lines. The return to these pre-event conditions takes, respectively, 11.0 h, several days (off scale) and 11.3 h, for Φ_PC, SMR and SML. The bottom right panel, J, shows the a.c.f. of the IMF B′ = B_⊥sin⁴(θ/2) factor with lag zero at the time of peak negative B_Z, which gives us an indicator of the probable change of the IMF coupling factor component from the peak southward values in the event by the time that the terrestrial state indicators are reaching their peak disturbance level or have returned to pre-event values. Note that this a.c.f is derived for only the data that contributed to the superposed epoch plots and it falls somewhat more rapidly with lag than that shown in Figure 5 for the same parameter but for the whole dataset. This means the IMF coupling function factor B′ varies somewhat more rapidly around times of large southward turnings. Figure 6 shows that the solar wind forcing is always likely to have changed by the time peak disturbance is reached and almost certain to have by the time the system takes to return to pre-disturbance levels. For these reasons we should regard the magnetosphere-ionosphere-thermosphere system as usually a non-equilibrium system.

If we integrate the excess Φ_PC above the pre-event level between (t−t_o) = 0 and (t−t_o) = 11.0 h (the epoch time at which the average Φ_PC returns to its pre-event level) we get the average open flux generated and transported over the polar cap following the southward turning is about ΔF = 0.218 GWb. As discussed earlier, this is typical of the antisunward transport seen in substorm growth phases in both observations and models.

The Expanding-Contracting Polar Cap (ECPC) Model and Departures From Equilibrium

Because electric fields do not, in general, map from interplanetary space to the ionosphere, we need to re-consider why magnetopause and tail reconnection drive ionospheric convection. This was why, 30 years ago this year, we introduced the Expanding-Contracting Polar Cap (ECPC) model (Cowley and Lockwood, 1992). To do this, we introduced the concept of a zero-flow equilibrium magnetospheric configuration for a given amount of open flux, F_o. If such an equilibrium is ever attained is unlikely: there have been times when something close to it appears to have been reached (e.g., Farrugia et al., 2007); however, it is not necessary to know if equilibrium is ever attained. Note this is separate to the question of whether or not the magnetosphere ever loses all open flux and becomes fully closed: that would be the special case of a no-flow equilibrium for open flux F_o = 0.

In a “gedanken experiment,” consider what would happen in the hypothetical case that reconnection ceased completely, in both the dayside magnetopause and the cross tail current sheet, at a time when the open magnetospheric flux was F_o. Without any reconnection, that open flux value remains constant thereafter. All open flux would be soon removed from the dayside and appended to the tail by the solar wind flow. Pressure equilibrium would become possible between the eroded dayside magnetic flux and the dayside magnetosheath which would depend on the solar wind dynamic pressure and on how much open flux had been removed and appended to the tail (i.e., on the value of the open flux F_o). Because the open field lines are embedded in the solar wind flow they would be extended antisunward and so in the near-Earth and middle tail they would eventually become aligned with the solar wind velocity. Consider the last field line to be opened before the reconnection ceased and let Q be the point where it passes through the magnetopause and P be the point where it becomes parallel to the solar wind flow in the tail lobe–the X coordinates of these points are marked in Figure 1B. The field line passing through the point Q is moving antisunward and in interplanetary space it experiences the same dawn-dusk electric field E_Y that it did when it was opened. To first order, the point P is where the tail reaches is asymptotic radius R* (Nakamura et al., 1997; Tsyganenko, 2013; Liu, et al., 2015), and also where the lobe field strength falls to an almost constant value (Fairfield and Jones, 1996; Slavin et al., 1983). Both of these typically occur at X = X_P between about −60R_E and −120R_E. Using a typical solar wind speed of 400 km s⁻¹, MHD simulations show it takes open field lines of order an hour after opening to reach these distances down the tail. Hence for there to be no open field lines threading the magnetopause sunward of Q (as in Figure 1B) requires the IMF be northward (and potentially quite strongly northward to shut off all reconnection that opens closed field lines) for at least about 1 h. At P the antisunward motion of open field lines threading the magnetopause at Q (or further down the tail) is not causing any field-perpendicular motion and so the electric field there is zero. This means that there are changes in the field in the furthest tail (between P and Q) that inductively decouple the electric fields and the solar wind flow is driving no flow sunward of P. As Q moves away from the Earth so does P and both attain velocities in the −X direction that are super-Alfvénic and so information about the tail beyond P cannot propagate back to the near-Earth and middle tail. Hence equilibrium is established sunward of P even though tailward of P is not in equilibrium. Because pressure equilibrium sunward of P is established between the magnetosheath and the tail magnetosphere, all flow in the magnetosphere sunward of P ceases. Again, the details of this equilibrium will depend on the solar wind pressure and on the open flux F_o (e.g., Lin et al., 2010; Liu et al., 2015). Hence we arrive at the concept of a zero-flow equilibrium in the magnetosphere-ionosphere system, for a given value of open flux, F_o.

Note that this “no-flow equilibrium” in the complete absence of both magnetopause and tail reconnection will be rarely be achieved, and may never be so fully. The reason is that even after the most prolonged periods of northward IMF, the tail never goes away and so locations in the cross tail current sheet where there is magnetic shear between oppositely-directed open flux are probable, which means that tail reconnection that closes open flux is probable, even if at a very low voltage.

The key point is not if such a zero-flow equilibrium is ever achieved or not: it is that perturbations by reconnection in either the dayside magnetopause or in the cross tail current sheet will, respectively increase or decrease F_o and, in general, will take the magnetosphere away from that equilibrium. Hence both will excite convection as the magnetosphere-ionosphere system tends towards the equilibrium condition for the prevailing F_o. The observation that convection appears to never completely die away is an indicator that these no-flow equilibria are almost never achieved.

Figures 7, 8 show the sequence of events following, respectively, an isolated burst of reconnection in the dayside magnetopause current sheet and in the cross-tail current sheet. Figure 7 therefore looks at the flow induced by the open flux being increased by an amount ΔF_o and Figure 8 at the flow induced by the open flux being decreased by ΔF_o. For simplicity we consider the IMF B_Y component to be zero.

FIGURE 7

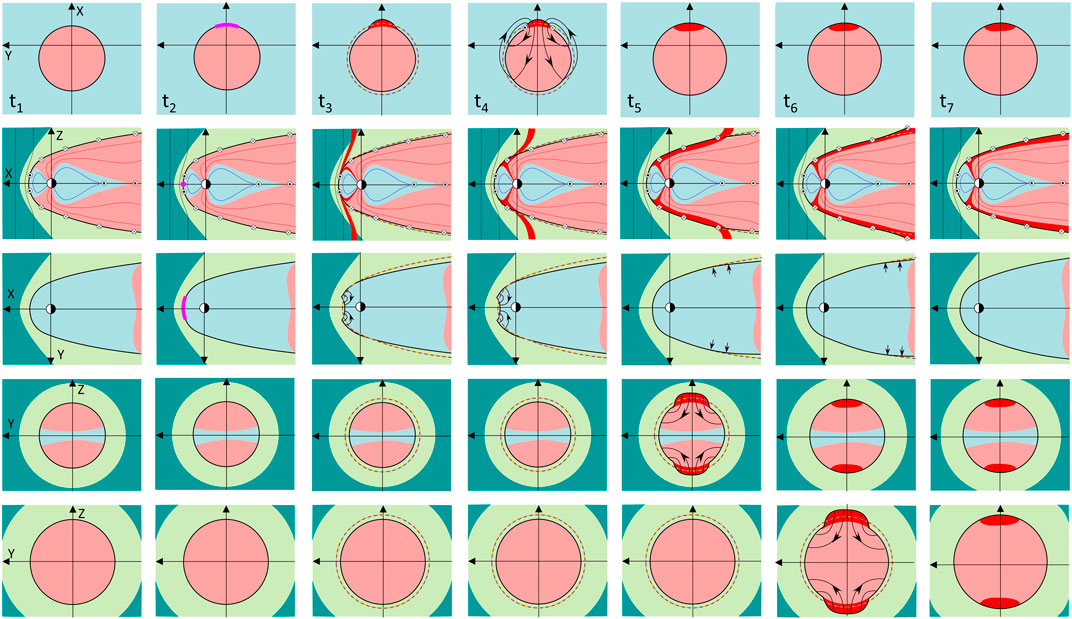
FIGURE 7. Schematics of the expanding-contracting polar cap (ECPC) model predictions of the evolution of the magnetosphere-ionosphere system in response to an isolated pulse of magnetopause reconnection, generating newly-opened flux, shown in red. The colored regions and lines are defined in the legend to Figure 8. The seven columns are for increasing times from t₁ to t₇. Axes in the GSM frame are defined in the left-hand plot for each row. From top to bottom rows show: the ionospheric polar cap looking down from above, the pink area being open field lines and the pale blue being closed; the magnetosphere viewed from the dusk flank with dark green showing the undisturbed solar wind and light green showing the magnetosheath; the equatorial magnetosphere viewed from the north; the cross-section of the near-Earth tail viewed from downstream from the Earth; and the cross-section of the middle tail viewed from downstream from the Earth. Black lines with arrows show flows, mauve lines and dots an active reconnection site or its ionospheric footpoint; mauve and orange dashed lines show the equilibrium location of the open-closed and magnetopause boundaries for the amount of open flux. In some cases, this is not seen because the boundary in question is at its equilibrium location, in which case it is covered by the black line that shows the current location of the boundary. In the second row, the magnetopause and cross-tail current directions are shown. Note that at times t₅ and t₆ in the equatorial plane (row 3) only short arrows are used to denote the flows associated with the tail flaring increase in, respectively, the mid tail and (at the later time) the further tail. That is because, as shown for the mid-tail cross section at time t₅ (row 4. column 5) and for the further tail cross section at time at time t₆ (row 5, column 6), these flows originate at higher latitudes in both lobes and only descend into the equatorial plane close to the magnetopause.

FIGURE 8

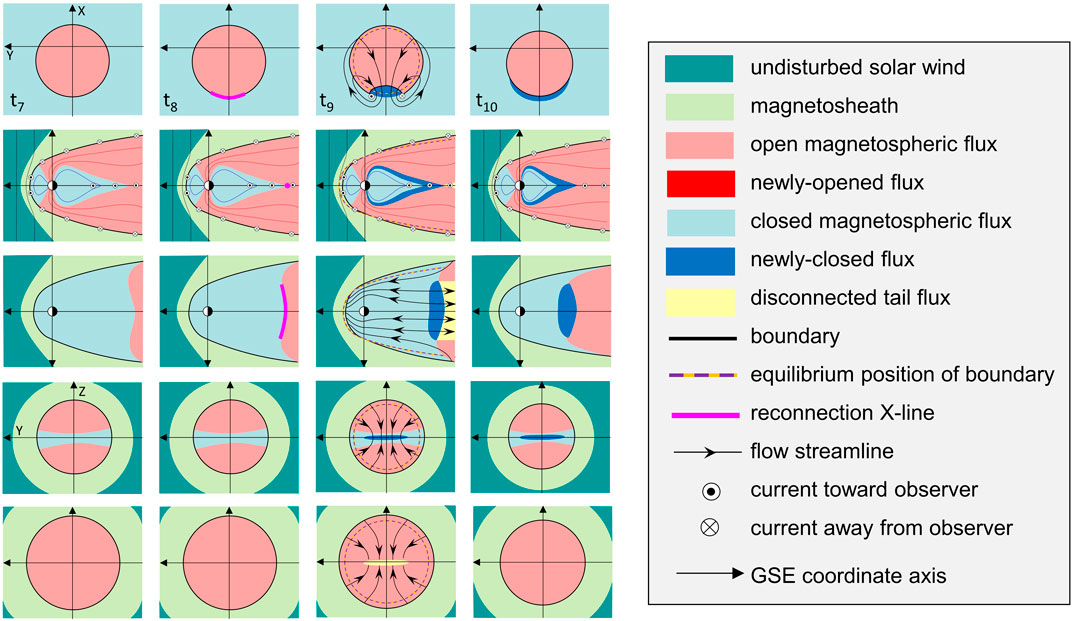
FIGURE 8. Same a Figure 7 but showing the response (at times t₇ - t₁₀) to the closure of open flux by a burst of reconnection in the cross-tail current sheet. The newly-closed flux is shown in dark blue.

At time t₁, the first column in Figure 7, we consider the magnetosphere-ionosphere system in an equilibrium state for an open flux F_o. As explained above, this may never actually occur. The rows in Figure 7, from top to bottom, show: the polar caps looking down from above; the ZX plane of the magnetosphere (i.e., a noon-midnight meridian cross section), viewed from the dusk side; the XY plane of the magnetosphere (the equatorial cross section), viewed from the north; a ZY plane at X = X₁ (a cross-section cut of the near-Earth tail) viewed from the far tail; and a ZY plane at X = X₂ where | X₂ | > | X₁ | (a cross-section cut of the middle tail) viewed from the far tail. Pre-existing closed flux is colored light blue and pre-existing open flux is shaded pink. The undisturbed solar wind, outside the bow shock, is shaded dark green and the magnetosheath is in pale green.

At time t₁ there is no magnetospheric flow, by definition, because the magnetosphere system is at its zero-flow equilibrium state. At time t₂ a subsolar reconnection X-line forms, shown by the mauve line (this appears as a mauve dot in the XZ plane and in the view of the ionosphere the mauve line is the magnetic footprint of the X-line). Reconnection at this X-line starts just after t₂ and persists until time t₃ when it ceases, by which time it has generated an open flux ΔF_o (and hence the average reconnection voltage is ΔF_o/{t₃ − t₂}). The newly-opened flux generated by this reconnection burst is colored red.

Initially no flow that contributes to convection circulation and the Dungey cycle commences in the ionosphere. (However, there are likely to be oscillatory flows associated with transient filamentary field aligned currents and phenomena such as Alfvén waves). While the newly-opened flux tube threads the dayside magnetopause, the magnetopause current J is from dawn-to-dusk and the point where it threads the magnetopause moves poleward under the so-called magnetic “tension” force in the reconnection outflow jet. This tension force acts normal to the newly-opened field lines only where they are curved and in such a way as to straighten them. (The name tension is somewhat misleading because, unlike a taught wire or elastic band, the force must necessarily disappear once the field line has straightened). In addition, it causes flow only where there is insufficient magnetic or plasma pressure to oppose the straightening of the field lines: this must necessarily be the case in the dayside magnetopause when the field line curvature has suddenly been created by the reconnection process. In summary, while the field line is only shortening there is no new poleward force on the ionospheric footpoint of the newly-open field lines (in the cusp region). Hence new open flux has been generated but poleward flow does not commence until the field line has straightened (after which the newly opened flux is moving poleward because of the magnetosheath flow). Consequently, the dayside ionospheric open-closed field line boundary must migrate equatorward. We expect the delay before ionospheric flow starts to be shorter if the reconnection site is at higher latitudes as the field lines have less distance to travel before they straighten. We also expect the delay to be greater/shorter in the summer/winter hemisphere, respectively, because the dipole tilt favors reconnection sites that are shifted from the subsolar point to higher latitudes in the winter hemisphere (see Lockwood et al., 2020c and references therein). This means that not only do newly-opened field lines in the summer/winter hemisphere have to travel longer/shorter distances around the magnetopause before they straighten, but initially the tension force is antiparallel/parallel to a component of the magnetosheath flow.

This delay and the consequent erosion of the dayside ionospheric open-closed boundary must occur to some degree. The reason is that it takes at least an Alfvén wave travel time down the dayside field lines (t_f, typically a minute) before there can be any response in the ionosphere and in that time the topological open-closed boundary must erode equatorward. The magnetic flux in this erosion is t_f ΔΦ_D and so it covers an area in the ionosphere of {t_f ΔΦ_D}/B_i where B_i is the ionospheric magnetic field strength and ΔΦ_D is the increase in magnetopause reconnection voltage. The fact that the stress balance in the ionosphere does not change initially adds an additional delay δt before ionospheric flow commences and the eroded area is {(t_f +δt)ΔΦ_D}/B_i. Lu et al. (2002) used flows inferred from magnetometer network data in response to a sudden southward turning and estimate that (t_f+δt) is 9 min. Throp et al. (2005) and Lockwood et al. (2006) studied the response to a more gradual southward turning (a rotation in clock angle) using global images of the proton aurora and observations of flows from the SuperDARN radar network. The eroded area after the IMF turned southward could be monitored directly in the proton aurora due to solar wind protons precipitating down the newly-opened field lines and was clearly and directly observed. Even for this gradual southward turning event, Lockwood et al. (2006) find (t_f+δt) = 9.7 min with an uncertainty range (at the 80% confidence level) of between 8.4 and 10.9 min. The ionospheric flows seen in both events, with new flow cells initially centered on the dayside, were consistent with those predicted by the ECPC model (Figure 7 at time t₄) and were modelled by Lockwood et al. (2006) using the quantitative implementation of ECPC by Lockwood and Morley (2004). This delay and patterns of flow were first reported by Lockwood and Cowley (1992) using data from the CDAW-6 interval, an example for which (t_f+δt) was 12.5 min.

In contrast to the lagged response in the ionosphere, flows commence in the equatorial dayside magnetosphere immediately the reconnection starts. Sunward flows in the magnetosphere are inflows to the reconnection site and continue to allow the dayside magnetopause to relax back sunward where it has been eroded Earthward by the poleward removal of the opened flux along the magnetopause.

After time t₃ the magnetopause reconnection ceases and so the open flux remains constant at (F_o +ΔF_o) and the equilibrium location of the magnetopause has changed, now having reduced flux on the dayside but more flux in the tail. Because the ionosphere is incompressible the equilibrium polar cap is larger and drawn here as remaining circular, which we can consider to be the minimum energy configuration with the surrounding closed field line region. The new equilibrium locations of the magnetopause and the OCB in the ionosphere are shown by mauve and orange dashed lines. The reconnection burst leaves the ionospheric open-closed boundary around noon equatorward of its new equilibrium position but everywhere else poleward of it. At the time t₄ ionospheric flows have begun which are poleward around noon and equatorward at all other local times–these are flows that bring the OCB back towards its new equilibrium location. Note at this time, the equilibrium location of the tail magnetopause has flared outward but no flow has commenced because the newly open flux has not yet reached X = X₁. This happens at time t₅ by when almost all ionospheric flow has ceased because the OCB is now close to its new equilibrium position. As soon as the newly open flux arrives at X = X₁ it forms bulges on the magnetopause that the pressure of the magnetosheath flattens giving the flows shown which bring the magnetopause back towards its new equilibrium location. Some time later (at time t₆) this sequence is repeated at X = X₂ when the newly-open flux has reached that far down the tail. By the time t₇ all flow has ceased because both the OCB and the magnetopause have reached their new equilibrium locations, at least for the range of the X coordinate covered by the schematics.

Figure 8 shows the corresponding sequence for a burst of tail reconnection. If we continue from t₇ in Figure 7, we start from an equilibrium magnetosphere for an open flux (F_o +ΔF_o). At time t₈ a reconnection X-line forms in the cross tail current sheet (mauve line): this time will usually be close to onset of the expansion phase of a substorm cycle. Between t₇ and t₈ this reconnection line closes a flux of ΔF_o (an average reconnection voltage of ΔF_o/{t₈ − t₇}), returning the open flux to F_o. Equilibrium for this open flux has less magnetic flux in the tail and more on the dayside. The dark blue patch is the newly closed field flux. Flows in the ionosphere and magnetosphere are to bring the existing locations of boundaries from their present position toward the equilibrium positions for the new open flux F_o.

Note that at no time in this gedanken experiment has steady-state mapping of electric field been invoked, and so inductive changes in the magnetospheric magnetic field configuration have been allowed, whereas they are not allowed if electric fields are mapped. And yet flows and changes in the ionosphere have been generated by the reconnection processes occurring in the magnetosphere.

Effects of Solar Wind Dynamic Pressure

We have reprised our description of the ECPC model in the previous section to make an important point. If one adopts a non-physical mechanism by mapping electric fields in non-steady situations one will make incorrect deductions if the assumed steady state does not fully apply. From the response times and lags, we can infer that the magnetosphere will almost always be recovering from a prior change in solar wind driving and so, rather being in steady state, it is almost permanently recovering from a prior change in either solar wind driving or in the configuration of both the dayside and near-Earth tail from the ever-changing geomagnetic axis tilt (and, in general, its offset from the origin in a geocentric frame) as Earth rotates (Lockwood et al., 2020c, 2021).

The ECPC scenario discussed in the previous section makes an interesting prediction. If we generate a given amount of newly-opened flux, it is the pressure in the magnetosheath at the magnetopause that determines how quickly the system would return towards the new equilibrium location as it is ultimately this pressure that drives the magnetospheric motions that act towards restoring the no-flow equilibrium for the new amount of open flux. The resulting changes in the magnetospheric configuration are communicated to the ionosphere through the field-perpendicular pressure balance between closed field lines and open field lines and it is this that determines where the field-aligned currents form and what magnitude they have. The pressure on the magnetopause depends on the dynamic pressure of the upstream solar wind: this applies throughout the dayside and in the near-Earth and middle tail where the tail is still flaring (i.e., where the tail radius increases with increasingly negative X). Hence the ECPC concept predicts that the response time of the magnetosphere-ionosphere system will be shorter if the wind dynamic pressure is greater because the restoring force per unit area is greater for a larger P_SW for a given F_o and ΔF_o.

Sorting by Solar Wind Dynamic Pressure, P_SW

To look for such an effect, we here divide the 160 examples of southward turnings used to compile Figure 6 into two subsets of 80 samples each. To do that, we used the dynamic pressure P_SW, averaged over the 3 h after the southward turning, <P_SW>_(0–3h). An interval of 3 h was chosen because it is enough to cover most of the length of the tail where it is increasing in radius with -X and so P_SW has an influence on pressure balance at the magnetopause. It was found a threshold value of <P_SW>_(0–3h) of 6.5 nPa divided the southward turning events into two equal-sized datasets of 80 events each. The superposed epoch study shown in Figure 6 was then repeated for the <P_SW>_(0–3h) ≥ 6.5 nPa and <P_SW>_(0–3h) < 6.5 nPa subsets: the results are shown by, respectively, the left and right columns in Figure 9. The top four rows shows parameters presented in Figure 6, but the bottom row is for P_SW. Panels A–E are for the high-pressure cases, panels F–J for the low-pressure cases.

FIGURE 9

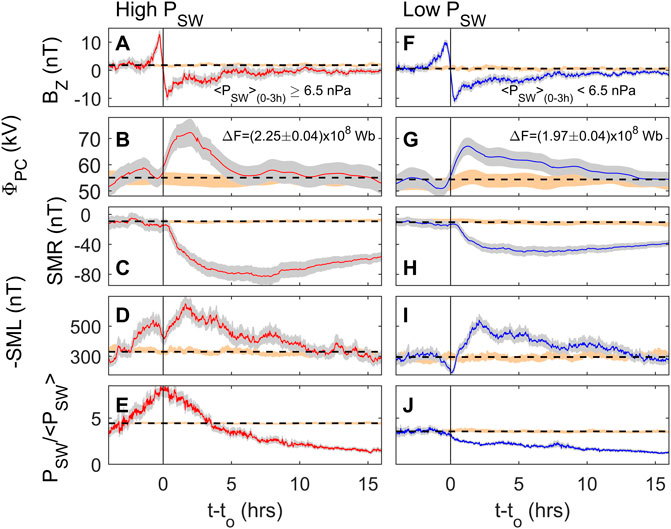
FIGURE 9. Superposed epoch study illustrating the effect of solar wind dynamic pressure, P_SW, on the events discussed in Figure 5. The southward turning are divided into two sets with P_SW, averaged over the 3 h after the southward turning, < P_SW >_(0–3h), exceeding or less than 6.5 nPa, that being the threshold that divides the data into two equal sets of 80 events. The format is as in Figure 5 with left hand panels (and red lines) for < P_SW >_(0–3h) ≥ 6.5 nPa and right-hand columns (and blue lines) for < P_SW >_(0–3h) < 6.5 nPa. The bottom panels are the superposed epoch plots of the solar wind dynamic pressure, P_SW.

Panels E and J show the effect of the high-P_SW versus low-P_SW sort on the average variation of P_SW during these events: the high-pressure events show a pronounced peak in average P_SW at the time of the southward turning (panel E) that is almost completely absent in the averages for the low pressure events (panel J): indeed, for the low-pressure events, P_SW falls below the average value seen before the southward turning for all positive (t−t_o), whereas for the high-pressure events this only happens at (t−t_o) > 4 h. Panels A and F show that the average behavior of the IMF B_Z component is very similar for these two event subsets. However, the other panels show a markedly different responses in the magnetospheric state indicators. To enable us to contrast high and low pressure cases, the responses in the terrestrial indices are re-plotted in Figure 10. These variations are the same data as shown in parts C - H of Figure 9 but in each case, the changes relative to the pre-event mean, ΔΦ_PC, ΔSMR and ΔSML, are plotted.

FIGURE 10

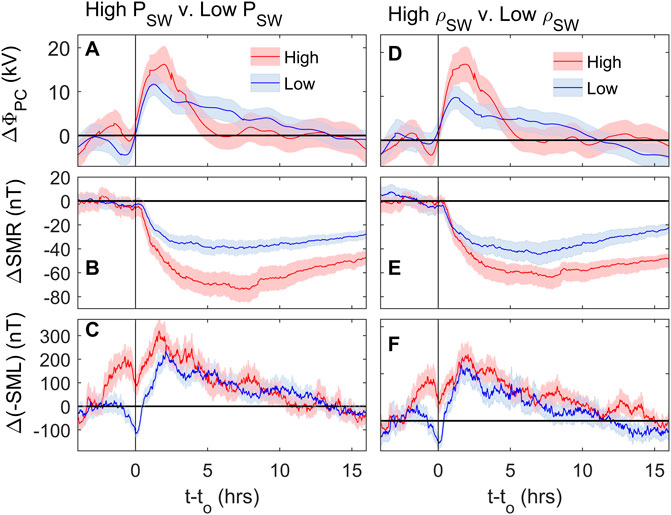
FIGURE 10. Comparison of the terrestrial responses to the southward turning events of the IMF for (left column, parts A, B and C) high- and low-solar wind dynamic pressure P_SW and (right column, parts D, E and F) high- and low-solar wind mass density ρ_SW. In both cases red lines with pink uncertainty bands are for the “high” event subset and blue lines with pale blue uncertainty bands are for the “low” cases. Rows from top to bottom are for (A and D) transpolar voltage Φ_PC, (B and E) the SMR index, (C and F) the SML index. Note that these plots are similar to those in (left column) Figure 9 and (right column) Figure 12 and are plotted here with high and low cases on a single panel to allow comparison. However, they are not quite the same as, to allow comparison, the pre-event means have here been subtracted from the values at general elapsed time (t-t_o) to show the response and so the plots show the changes in Φ_PC, SMR and SML, denoted by ΔΦ_PC, ΔSMR and ΔSML, respectively.

Comparing panels B and G of Figure 9 (and panel A of Figure 10) we see that the amplitude of the transpolar voltage Φ_PC response is greater for the case of high-P_SW data subset. However, the response for the low-P_SW data subset lasts longer: it takes 13.8 h before the average Φ_PC is returned to pre-event levels, whereas this takes just 6.3 h for the high-P_SW dataset. If we integrate the mean additional Φ_PC (over the pre-event levels) after the events, we obtain an estimate of the average extra flux transported over the polar cap caused by the southward turning: for the high-P_SW cases it is ΔF = 0.225 ± 0.004 GWb and for the low-P_SW case it is 0.197 ± 0.004 GWb. A large contribution to these uncertainties comes from the uncertainty in the average pre-event voltage. These two values are very similar, but there is a difference of 0.028 ± 0.008 GWb. The origins of this difference are discussed in Section 6. However, the main point we want to stress in this section is that there is a marked difference in how this integrated flux transport is manifest in the ionosphere with larger-amplitude but shorter-duration burst of voltage for the high-P_SW data subset. This effect of P_SW is well predicted by the ECPC model, as discussed above.

There is a greater difference in the effects on the SMR geomagnetic activity index between the high-P_SW and low-P_SW cases: the average response to the southward turning event in the SMR index data (panels C and H of Figure 9 and panel B of Figure 10) is considerably weaker for the low-P_SW cases. The same effect is seen, but much less marked, in SML from comparison of panels D and H of Figure 9 (and panel C of Figure 10) that shows the response in the SMR index is consistently weaker for the low-P_SW cases.

Before discussing these results in greater detail, we should also look at the average variations in other interplanetary variables during these events. These are shown in Figure 11. Panels B and G show the solar wind number density, N_SW, which has very similar variations to those for P_SW (shown in the bottom panels of Figure 9). However, there are also variations in the mean ion mass of the solar wind, m_SW (panels C and H) and the solar wind speed, V_SW (panels D and I) that contribute. These variations are consistent with the large IMF southward turning events being caused mainly by impacts of coronal mass ejections or the compressions in interaction regions ahead of fast flow streams.

FIGURE 11

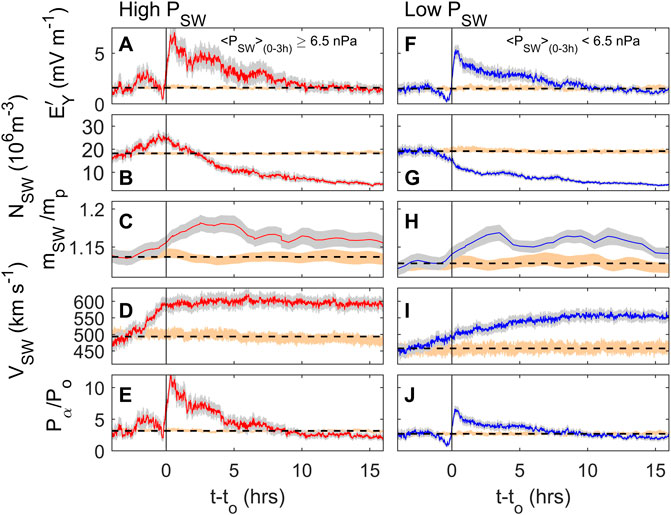
FIGURE 11. Superposed epoch study of the interplanetary conditions for the events studied in Figure 9. The left hand column are for the 80 high-P_SW southward turnings of the IMF and the right hand panels for the low-P_SW set. From top to bottom panels are for: (A and F) the half-wave rectified dawn-to-dusk electric field, E_Y′; (B and G) the solar wind number density, N_SW; (C and H) the solar wind mean ion mass in amu m_SW/m_p; (D and I) the solar wind speed, V_SW; and (E and J) the estimated power input into the magnetosphere, P_α, as a ratio of its overall mean value, P_o, as computed by the procedure and formulae of Vasyliunas et al. (1982).

The difference in the variations of average V_SW for the two sets of cases (seen in the comparison of panels D and I of Figure 11) is significant for three reasons. Firstly, it has an influence on the interplanetary electric fields, E_Y = − V_X B_Z. Panels A and F of Figure 11 contrast the variations of the half-wave rectified dawn-to-dusk electric field, E_Y′ (the rationale for using half-wave rectification is that subsolar reconnection is greatly reduced in rate when the IMF points northward). The higher average V_SW for the high-P_SW cases has a marked effect and although the average E_Y′ variation is very similar in form for the two cases, it is of smaller amplitude for the low-P_SW cases. The second effect of V_SW is on variations of the estimated power input to the magnetosphere, P_α. Because power in the solar wind is delivered predominantly in the form of kinetic energy of the particles (Lockwood, 2019), the solar wind speed also influences the power input to the magnetosphere. Panels E and J show P_α, P_α/P_o, as a ratio of its overall mean value P_o = <P_α>_all. The third effect of V_SW is on the time taken for newly-opened field lines to be appended to the tail: for the average speeds shown in Figure 11, the open field lines in the Stern Gap have, on average, moved 283 R_E antisunward after 1 h for the low-P_SW cases but 334R_E for the high-P_SW cases. Hence there are a number of effects of varying P_SW that are actually caused by solar wind speed V_SW rather than being specifically caused by pressure effects.

Sorting by Solar Wind Mass Density, ρ_SW

To eliminate the potential additional effects of solar wind speed V_SW on the sorting criterion we here repeat Figures 9 and 11, but divide the data into two equal size datasets by the mass density of the solar wind ρ_SW = m_SW.N_SW. This influences the dynamic pressure P_SW = ρ_SWV_SW² and the power input to the magnetosphere P_α = B^2αV_SW ^(7/3-2α)ρ_SW ^(2/3-α) sin⁴(θ_GSM/2). The results are shown in Figures 12 and 13. The high ρ_SW and low ρ_SW terrestrial responses are compared in the right-hand panels of Figure 10. Comparing parts D and I in Figure 13 we can see this gives more similar (but not identical) variations in V_SW and hence the E_Y′ variations (Panels A and F) and the P_α variations (Panels E and J) are also much more similar than they are for the P_SW sort shown in Figure 11. In fact, for this sort, the low-ρ_SW cases give very slightly higher average V_SW, E_Y′ and P_α after the event. Note that differences in the V_SW variations have not been eliminated by moving from a P_SW sort to a ρ_SW sort, however they have been reduced and we know V_SW did not enter into the event selection and that remaining effects are caused by inter-relations between the parameters of interplanetary space. Comparison of parts C and H of Figure 12 (panel E of Figure 10) and of parts D and I of Figure 12 (panel F of Figure 10) show that the geomagnetic responses are more similar for the data sorted by ρ_SW than they were for P_SW, but that the response to the southward turning is still larger for the high-ρ_SW cases than for the low-ρ_SW cases. Panels B and G of Figure 11 (panel D of Figure 10) show that the extra magnetic flux transport following the southward turning is again similar in the high-ρ_SW and low-ρ_SW cases, being 0.199 ± 0.004 GWb per event, on average, for the high-ρ_SW cases and 0.186 ± 0.004 GWb per event for the low-ρ_SW cases. As for the high- and low-P_SW cases the difference between the two sets of events, in terms of total flux transport, is still very small, but it does appear to be larger than uncertainties. This is discussed further in section 6. The same behavior for Φ_PC is seen as in Figure 9, with the high-ρ_SW cases giving a larger-amplitude but shorter-duration response than the low-ρ_SW cases, but the total flux transport being only marginally greater for the high-ρ_SW cases.

FIGURE 12

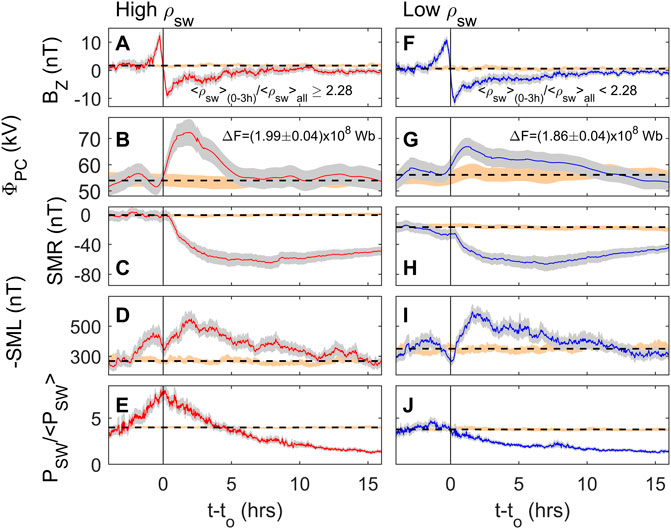
FIGURE 12. The same as Figure 9 but with the 160 southward turning events sorted by the solar wind mass density, ρ_SW. The left hand panel are for the events with normalized ρ_SW over the subsequent 3 h <ρ_SW >_0–3h/<ρ_SW >_all (where <ρ_SW >_all is the mean value for all data) greater than or equal to the median value for the events of 2.58; the right-hand panel are for the events with <ρ_SW >_0–3h/<ρ_SW >_all < 2.58.

FIGURE 13

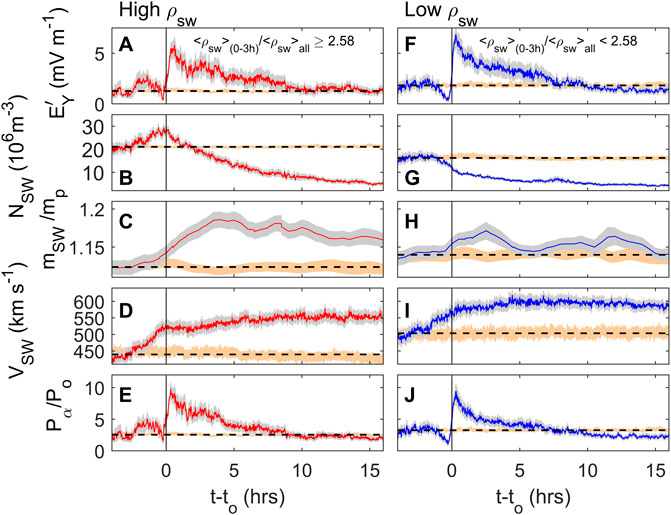
FIGURE 13. The same as Figure 11 but with the 160 southward turning events sorted by the solar wind mass density, ρ_SW as in Figure 12.

Discussion and Conclusion

Induction effects associated with magnetic field changes in the magnetosphere mean that mapping electric fields from interplanetary space to the ionosphere is only valid for steady-state conditions. Steady state can be achieved in data series if we average over long enough timescales. From the statistical analyses of Milan et al. (2021) this implies averaging over about 4 h in the cases of substorms but over of order 12 h for steady convection events or sawtooth events. In addition, as discussed below, the rotation of the Earth means that equilibrium concepts are only really valid when averaging over a whole number of days.

Effects of Solar Wind Dynamic Pressure on Convection Response

We have used superposed epoch studies of 160 clear southward turnings of the IMF that give near-continuous data in all parameters. The transpolar voltage data for all subsets of these events show that they cause an average of close to 0.2 GWb of additional magnetic flux transfer from the dayside to the nightside. As discussed in the introduction, this value is consistent with the total rise in tail lobe field seen in substorm growth phases (e.g., McPherron et al., 1993), as well as with numerical global MHD model simulations of the effects of strong southward turnings of the IMF (Gordeev et al., 2017), with inferences from polar cap expansion and contraction seen in global auroral images (Milan et al., 2003; 2012) and with the latitudinal variations of the locations of the Region 1 field-aligned current sheets (Clausen et al., 2012; Milan et al., 2021).

Subdividing the southward turnings into two datasets of 80 cases each using the solar wind dynamic pressureP_SW, averaged over the 3 h after the southward turning, has allowed us to look for an effect of dynamic pressure on these strongly southward IMF events. We note that Figure 4C shows dynamic pressure increases transpolar voltage for northward-IMF conditions but as the IMF becomes more southward the effect diminishes and is not present for the most southward IMF. Also, note that by taking averages over 3 h we are looking at the effect of the average dynamic pressure and not the transient effects of pressure increases that are complicated by transient phenomena such as travelling convection vortices. We find that the integrated flux transport over the polar cap is only slightly greater in the high-P_SW cases, being 0.225 ± 0.004 GWb compared with 0.197 ± 0.004 GWb for the low-P_SW cases. The difference is therefore small but significant. To check that this is not associated with the solar wind speed influence on the interplanetary electric field, we repeated the analysis using the mass density of the solar wind, ρ_SW, again averaged over the 3 h after the southward turning and again dividing the data into two subsets of 80 cases. The integrated flux transport over the polar cap was only marginally higher for the high-ρ_SW cases, being 0.199 ± 0.004 GWb compared to 0.186 ± 0.004 GWb for the low-ρ_SW cases. Hence sorting using high- and low-ρ_SW, the same sense of difference is seen as for the P_SW sort. The difference in total flux transport caused was 0.013 ± 0.006 GWb (a 7% increase for the high-ρ_SW cases relative to the low-ρ_SW cases). Lockwood and McWilliams (2021b) found that the optimum coupling function for transpolar voltage Φ_PC depended only very weakly on ρ_SW, finding a ρ_SW^b dependence with the best-fit exponent of b = 0.018. The high ρ_SW dataset gives [ρ_SW]_hi/<ρ_SW > _all = 3.72 whereas [ρ_SW]_lo/<ρ_SW > _all = 1.48 which predicts a factor ([ρ_SW]_hi/[ρ_SW]_lo)^b = 1.02 (a 2% increase). Hence the increase in total flux transport found here for the high ρ_SW cases is somewhat larger that we would expect from the optimum coupling function of Lockwood and McWilliams (2021b). An explanation of this discrepancy is provided by Figure 13 that shows that, due to correlations between interplanetary parameters, the solar wind velocity V_SW is also higher after for the high ρ_SW cases with a ratio of average values after the event of about [V_SW]_hi/[V_SW]_lo ≈ 580/520 and using the V_SW^a (with exponent a = 0.55) dependence found by Lockwood and McWilliams (2021b), this gives a factor ([V_SW]_hi/[V_SW]_lo) ^a = 1.05 (a 5% increase). Hence a larger part of the increase in total flux transport after the event (about 5% of the 7%) can be attributed to the fact that V_SW is somewhat higher after the high ρ_SW cases. However, there is an additional 2% that does appear to be associated with the increased ρ_SW and that is consistent with the coupling function prediction of Lockwood and McWilliams (2021b). We conclude increased solar wind mass density does (very slightly) increase the magnetopause reconnection voltage through increased reconnection rate and/or increased length of the reconnection X-line, as proposed by Scurry and Russell (1991). The effect of increased mass density would be to reduce the cross-section radius of the dayside magnetosphere which we might expect to also reduce the length of the reconnection X-line. Therefore, is seems likely that any effect on Φ_D would be through increased magnetic shear across the dayside magnetopause elevating the reconnection rate along the X-line or via the same effect of increased lobe field on the tail reconnection Φ_N.

However, the dominant effect of increased P_SW (one that is almost identical in the high/low ρ_SW analysis) in that there is a marked effect on the time profile of the flux transfer. For the high-P_SW cases, the transpolar voltage is enhanced to larger values soon after the southward turning, but elevated values persist for a shorter time. This effect is predicted by the ECPC model because it is the dynamic pressure that generates the pressure on the newly opened flux that drives the flow acting to return the magnetosphere towards the new equilibrium for the new open flux. The effect defined here is predicted by the ECPC model and cannot arise if electric fields are mapped from interplanetary space to the ionosphere: we know of no other model that can explain it.

The ECPC Model and Effects of Earth Rotation With a Tilted and Eccentric Dipole Axis

We note that, although this effect has been defined using the transient response to southward IMF turnings, the ECPC model has still important implications for understanding solar-wind magnetosphere coupling under even constant interplanetary solar wind conditions. Lockwood et al. (2021) have recently used the ECPC model to closely match all features of the observed fraction-of-year (f) - Universal Time (UT) pattern of geomagnetic activity (called the “McIntosh” or “equinoctial” pattern). This is seen in the am index (and there are corresponding patterns in its two hemispheric sub-indices an and as). As mentioned earlier, Lockwood et al. (2019a) show that am is the most suitable index to use in this context as it is genuinely global and has the most uniform f-UT response. Lockwood et al. (2021) show that there are four effects at work in generating this f-UT pattern: 1) the Russell and McPherron (1973) effect of the dipole tilt on the magnetic shear, and hence reconnection rate, at the dayside magnetopause; 2) the dipole tilt effect on polar ionospheric conductivities; 3) the dipole tilt effect on the tail geometry; and 4) the diurnal motions of the geomagnetic poles in a geocentric frame as the Earth rotates. Effects (2) and (3) are dominated by the effect of the dipole tilt on the ability of the solar wind dynamic pressure to squeeze the tail and together they give the basic McIntosh form that varies in amplitude with P_SW (Lockwood et al., 2020b, 2021). This is complicated by effect (1), but combining effects (1), (2) and (3) gives does not give the total UT variation (averaged over all times of year, f) that is seen in geomagnetic activity (Russell, 1989). This is because adding the Russell-McPherron effect to the other two causes UT variations in both the March and September equinox peaks in geomagnetic activity, but these UT variations are in antiphase and so cancel each other when averages over all times of year (all f) are taken.

Lockwood et al. (2021) show that the observed UT variation is consistent with an effect of the diurnal pattern of sunward and antisunward motion of the geomagnetic poles caused by Earth’s rotation and the offset of the geomagnetic poles from the rotational axis. This rotation is different in the two poles because of the eccentricity of Earth’s dipole axis which does not pass through the center of the Earth. As described by Lockwood et al. (2021), the effect is caused by a motion of the ionospheric polar caps, as a whole, toward and away from the Sun in a geocentric frame (the frames in which the interplanetary electric field is quantified). When a given polar cap (including its diameter, PC) is moving toward/away from the Sun, the transpolar voltage Φ_PC is increased/decreased in the geocentric frame (the same frame in which the interplanetary electric field and Stern Gap voltage Φ_SG are measured): by Eq. 1, this increases/decreases the rate of increase in the tail lobe flux in that hemisphere, dF_L/dt. In this context, it should be noted that the open flux F_o must always be identical in the two hemispheres but, at any X coordinate, the open flux divides into the flux F_d that threads the magnetopause sunward of X and the lobe flux that threads the tail cross-section at that X, F_L. Transfer from the dayside into the lobe (i.e., conversion of F_d into F_L for a given X) is faster for the polar cap that is tipped away from the Sun than the one that is tipped toward the Sun. Hence although F_o is the same in the two hemispheres F_L and dF_L/dt are both generally different in the two hemispheres. This effect of dipole tilt has been demonstrated using an MHD model of the magnetosphere (Lockwood et al., 2020c). The Earth’s rotation and the offset geomagnetic poles from the rotational axis therefore cause a diurnal cycle with 12 h in which dF_L/dt was lower in one hemisphere followed by 12 h in which it was lower in the other. The alternate faster loading of the tail in one hemisphere then the other would average out if the offset of the geomagnetic pole from the rotational axis were the same in the two hemispheres; however, it is much larger in the southern hemisphere which leaves a net effect of the Earth’s eccentric tilted dipole and causes the marked UT variation in global geomagnetic activity that is superposed on the dipole tilt pattern to give the total McIntosh pattern. Adding this effect to effects (1), (2) and (3), Lockwood et al. (2021) obtained a very close match to the observed f-UT patterns for am index and its hemispheric sub-indices, an and as. This effect would not happen if electric field just mapped from the solar wind to the ionosphere and the explanation of the UT variation of geomagnetic activity depends upon the application of the ECPC model.

Hence the equilibrium that the magnetosphere-ionosphere system is constantly in the process of returning toward is not just a function of the amount of open flux in the system, it also depends on both time-of-year, f, and the Universal Time, UT, through the dipole tilt effects and the (different and antiphase) motions of the geomagnetic poles in a geocentric frame. Hence, even if the solar wind driving is completely constant with time, the response of the magnetosphere-ionosphere-thermosphere system will not be and the ECPC model of that response is still required.

Applications and Limitations of ECPC

Looking at the potential future applications of the conceptual ECPC model we have to also think about its limitations. It is obviously not a full model of the magnetosphere and so there is a wide variety of phenomena that it does not predict. It is a conceptual model and therefore, its major use in quantitative predictions will be in conjunction with other models. Before the present paper looking at pressure effects on convection responses, ECPC has had four main applications. The first has been quantitative in the application of Faraday’s law to the open-closed field line boundary in the ionospheric polar cap and its use in understanding and exploiting observations of changes in the area of the polar cap (e.g., Milan et al., 2021 and references therein), particularly during substorm cycles, steady convection events and sawtooth events. A second specific application has been in the interpretation of ionospheric signatures of flux transfer events (transient increases in the magnetopause reconnection voltage, Φ_D) which has grown from the initial papers by Southwood (1987) and Cowley et al. (1991) (see reviews by Smith and Lockwood, 1996 and Milan et al., 2016). More recently, ECPC has been applied to understanding UT and time-of year variations in geomagnetic activity and transpolar voltage, as discussed in section 6.2. The fourth application is less specific and has been more qualitative in aiding the avoidance of incorrect assumptions about how electric fields map down field lines in interpretations of observations or model simulations of time-dependent events (e.g., Lockwood et al., 2020c).

Because it is an application of the principles of MHD and of Maxwell’s equations, all behavior predicted by ECPC should, in principle, also be predicted by numerical MHD models of the magnetosphere. However, there are highly complex issues in ensuring that the lower ionospheric boundary in these models is fully self-consistent with the simulated magnetosphere: the lower boundary of most MHD models has to be at considerably greater altitudes (typically 2R_E) than the real ionosphere for numerical reasons. A commonly used method to determine the spatial distribution of potential in this ionospheric boundary is to solve a Poisson equation using current continuity in the ionosphere (e.g., Raeder et al., 2001; Ridley et al., 2002; Lyon et al., 2004; Wiltberger et al., 2004). However, Lockwood (1993) pointed out that it is not adequate to just impose a pattern of convection on the ionosphere. The reason is that expanding and contracting an ionospheric convection pattern (without consideration of what are open and what are closed field lines or some other equivalent safeguard) will result in, respectively, closed field lines incorrectly migrating antisunward and open field lines incorrectly moving sunward in the ionosphere. The ECPC does not allow this and so provides a method that could ensure this does not occur; however, this has yet to be exploited in this context.

Author Contributions

ML and SC co-wrote the text. ML developed the schematics from SC’s originals and also generated the autocorrelations and superposed epoch analysis.

Funding

The work of ML at Reading University is supported by the UK Science and Technology Facilities Council (STFC) consolidated grant number ST/R000921/1 and the work of SWHC at Leicester University by STFC Grant number ST/N000749/1.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The work on ML at Reading University was supported by STFC consolidated grant number ST/M000885/1 and by the SWIGS NERC Directed Highlight Topic Grant number NE/P016928/1/. The work of SWHC at Leicester University by STFC Grant number ST/N000749/1. The authors thank Steve Milan and Joe Borovsky for many helpful conversations. The authors acknowledge the use of data from the SuperDARN project and particularly thank Kathryn McWilliams of University of Saskatchewan for processing the data. SuperDARN is a collection of radars funded by national scientific funding agencies of Australia, Canada, China, France, Italy, Japan, Norway, South Africa, United Kingdom and the United States of America. In addition, we are grateful to the staff of the Space Physics Data Facility, NASA/Goddard Space Flight Center, who prepared and made available the OMNI2 dataset used and of L'École et Observatoire des Sciences de la Terre (EOST), a joint of the University of Strasbourg and the French National Center for Scientific Research (CNRS), and the International Service of Geomagnetic Indices (ISGI) for making the am index data available. They are also grateful to the many groups who built and operated the instruments that have monitored near-Earth interplanetary space, particularly on the spacecraft ACE and Wind, and to the SuperMAG project for the SML and SMR indices and acknowledge the following projects and PIs: Intermagnet; USGS, Jeffrey J. Love; CARISMA, PI Ian Mann; CANMOS; The S-RAMP Database, PI K. Yumoto and K. Shiokawa; The SPIDR database; AARI, PI Oleg Troshichev; The MACCS program, PI M. Engebretson, Geomagnetism Unit of the Geological Survey of Canada; GIMA; MEASURE, UCLA IGPP and Florida Institute of Technology; SAMBA, PI Eftyhia Zesta; Chain, PI K. Yumoto; SAMNET, PI Farideh Honary; The institutes who maintain the IMAGE magnetometer array, PI Eija Tanskanen; PENGUIN; AUTUMN, PI Martin Connors; DTU Space, PI Rico Behlke; South Pole and McMurdo Magnetometer, PI’s Louis J. Lanzarotti and Alan T. Weatherwax; ICESTAR; RAPIDMAG; PENGUIn; British Antarctic Survey; McMac, PI Peter Chi; BGS, PI Susan Macmillan; Pushkov Institute of Terrestrial Magnetism, Ionosphere and Radio Wave Propagation (IZMIRAN); GFZ, PI Juergen Matzka; MFGI, PI B. Heilig; IGFPAS, PI J. Reda; University of L’Aquila, PI M. Vellante; BCMT, V. Lesur and A. Chambodut; Data obtained in cooperation with Geoscience Australia, PI Marina Costelloe; and the SuperMAG, PI Jesper W. Gjerloev.

References

Ahnert, P. (1943). Der Komet 1942 G (Whipple-Fedtke). Z. Astrophys. 22, 288.

Google Scholar

Alfvén, H. (1950b). Cosmical Electrodynamics. Oxford: Clarendon Press.

Google Scholar

Alfvén, H. (1950a). Discussion of the Origin of the Terrestrial and Solar Magnetic Fields. Tellus 2, 74–82. doi:10.3402/tellusa.v2i2.8540

CrossRef Full Text | Google Scholar

Axford, W. I., and Hines, C. O. (1961). A Unifying Theory of High-Latitude Geophysical Phenomena and Geomagnetic Storms. Can. J. Phys. 39 (10), 1433–1464. doi:10.1139/p61-172

CrossRef Full Text | Google Scholar

Bergin, A., Chapman, S. C., and Gjerloev, J. W. (2020). A E, D S T, and Their SuperMAG Counterparts: The Effect of Improved Spatial Resolution in Geomagnetic Indices. J. Geophys. Res. Space Phys. 125, e2020JA027828. doi:10.1029/2020JA027828

CrossRef Full Text | Google Scholar

Biermann, L. (1951). Kometschweife und solare Korpuskularstrahlung. Z. Astrophys. 29, 274.

Google Scholar

Boakes, P. D., Milan, S. E., Abel, G. A., Freeman, M. P., Chisham, G., and Hubert, B. (2009). A Statistical Study of the Open Magnetic Flux Content of the Magnetosphere at the Time of Substorm Onset. Geophys. Res. Lett. 36, L04105. doi:10.1029/2008gl037059

CrossRef Full Text | Google Scholar

Boudouridis, A., Lyons, L. R., Zesta, E., and Ruohoniemi, J. M. (2007). Dayside Reconnection Enhancement Resulting from a Solar Wind Dynamic Pressure Increase. J. Geophys. Res. 112, a–n. doi:10.1029/2006JA012141

CrossRef Full Text | Google Scholar

Boudouridis, A., Lyons, L. R., Zesta, E., Ruohoniemi, J. M., and Lummerzheim, D. (2008a). Nightside Flow Enhancement Associated with Solar Wind Dynamic Pressure Driven Reconnection. J. Geophys. Res. 113, a–n. doi:10.1029/2008JA013489

CrossRef Full Text | Google Scholar

Boudouridis, A., Zesta, E., Lyons, L. R., Anderson, P. C., and Ridley, A. J. (2008b). Temporal Evolution of the Transpolar Potential after a Sharp Enhancement in Solar Wind Dynamic Pressure. Geophys. Res. Lett. 35, L02101. doi:10.1029/2007GL031766

CrossRef Full Text | Google Scholar

Boyle, C. B., Reiff, P. H., and Hairston, M. R. (1997). Empirical Polar Cap Potentials. J. Geophys. Res. 102 (A1), 111–125. doi:10.1029/96JA01742

CrossRef Full Text | Google Scholar

Brambles, O. J., Lotko, W., Zhang, B., Ouellette, J., Lyon, J., and Wiltberger, M. (2013). The Effects of Ionospheric Outflow on ICME and SIR Driven Sawtooth Events. J. Geophys. Res. Space Phys. 118, 6026–6041. doi:10.1002/jgra.50522

CrossRef Full Text | Google Scholar

Burton, R. K., McPherron, R. L., and Russell, C. T. (1975). An Empirical Relationship between Interplanetary Conditions and Dst. J. Geophys. Res. 80 (31), 4204–4214. doi:10.1029/ja080i031p04204

CrossRef Full Text | Google Scholar

Caan, M. N., McPherron, R. L., and Russell, C. T. (1973). Solar Wind and Substorm-Related Changes in the Lobes of the Geomagnetic Tail. J. Geophys. Res. 78 (34), 8087–8096. doi:10.1029/ja078i034p08087

CrossRef Full Text | Google Scholar

Caan, M. N., McPherron, R. L., and Russell, C. T. (1978). The Statistical Magnetic Signature of Magnetospheric Substorms. Planet. Space Sci. 26 (3), 269–279. doi:10.1016/0032-0633(78)90092-2

CrossRef Full Text | Google Scholar

Chapman, S., and Ferraro, V. C. A. (1931). A New Theory of Magnetic Storms. J. Geophys. Res. 36 (3), 171–186. doi:10.1029/TE036i003p00171

CrossRef Full Text | Google Scholar

Clausen, L. B. N., Baker, J. B. H., Ruohoniemi, J. M., Milan, S. E., and Anderson, B. J. (2012). Dynamics of the Region 1 Birkeland Current Oval Derived from the Active Magnetosphere and Planetary Electrodynamics Response Experiment (AMPERE). J. Geophys. Res. 117, a–n. doi:10.1029/2012JA017666

CrossRef Full Text | Google Scholar

Coleman, P. J., Davis, L., and Sonett, C. P. (1960). Steady Component of the Interplanetary Magnetic Field: Pioneer V. Phys. Rev. Lett. 5 (2), 43–46. doi:10.1103/physrevlett.5.43

CrossRef Full Text | Google Scholar

Connor, H. K., Zesta, E., Ober, D. M., and Raeder, J. (2014). The Relation between Transpolar Potential and Reconnection Rates during Sudden Enhancement of Solar Wind Dynamic Pressure: OpenGGCM-CTIM Results. J. Geophys. Res. Space Phys. 119, 3411–3429. doi:10.1002/2013JA019728

CrossRef Full Text | Google Scholar

Cowley, S. W. H. (1991). Acceleration and Heating of Space Plasmas—Basic Concepts. Ann. Geophys. 9, 176–187.

Google Scholar

Cowley, S. W. H., Badman, S. V., Bunce, E. J., Clarke, J. T., Gérard, J.-C., Grodent, D., et al. (2005). Reconnection in a Rotation-Dominated Magnetosphere and its Relation to Saturn's Auroral Dynamics. J. Geophys. Res. 110, A02201. doi:10.1029/2004JA010796

CrossRef Full Text | Google Scholar

Cowley, S. W. H., Freeman, M. P., Lockwood, M., and Smith, M. F. (1991). “The Ionospheric Signature of Flux Transfer Events,” in CLUSTER ‐ Dayside Polar Cusp. ESA SP‐330. Editor C. I. Barron (Nordvijk, Netherlands: European Space Agency Publications), 105–112.

Google Scholar

Cowley, S. W. H. (2016). Hoyle and the Magnetosphere. A&G 57 (1), 1.12. doi:10.1093/astrogeo/atw033

CrossRef Full Text | Google Scholar

Cowley, S. W. H., and Lockwood, M. (1992). Excitation and Decay of Solar‐wind Driven Flows in the Magnetosphere‐ionosphere System. Ann. Geophys 10, 103–115. Available at: http://www.personal.reading.ac.uk/∼ym901336/pdfs/92_CowleyandLockwood_1992.pdf.

Google Scholar

Cowley, S. W. H. (1984). “Solar Wind Control of Magnetospheric Convection,” in Achievements of the International Magnetospheric Study (IMS), Proceedings of an International Symposium, Graz, Austria, 26-28 June 1984, ESA-SP-217. Editors B. Battrick, and E. J. Rolfe (Paris, France: European Space Agency), 483. ISSN 0379-6566.

Google Scholar

Cowley, S. W. H. (1982). The Causes of Convection in the Earth's Magnetosphere: A Review of Developments during the IMS. Rev. Geophys. 20 (3), 531–565. doi:10.1029/RG020i003p00531

CrossRef Full Text | Google Scholar

Davis, T. N., and Sugiura, M. (1966). Auroral Electrojet Activity Index AE and its Universal Time Variations. J. Geophys. Res. 71 (3), 785–801. doi:10.1029/JZ071i003p00785

CrossRef Full Text | Google Scholar

DeJong, A. D., Cai, X., Clauer, R. C., and Spann, J. F. (2007). Aurora and Open Magnetic Flux during Isolated Substorms, Sawteeth, and SMC Events. Ann. Geophys. 25, 1865–1876. doi:10.5194/angeo-25-1865-2007

CrossRef Full Text | Google Scholar

Dungey, J. W. (1961). Interplanetary Magnetic Field and the Auroral Zones. Phys. Rev. Lett. 6, 47–48. doi:10.1103/physrevlett.6.47

CrossRef Full Text | Google Scholar

Dungey, J. W. (1950). Some Researches in Cosmic Magnetism. PhD thesis (Cambridge: Cambridge University).

Fairfield, D. H., and Jones, J. (1996). Variability of the Tail Lobe Field Strength. J. Geophys. Res. 101 (A4), 7785–7791. doi:10.1029/95JA03713

CrossRef Full Text | Google Scholar

Farrugia, C. J., Freeman, M. P., Cowley, S. W. H., Southwood, D. J., Lockwood, M., and Etemadi, A. (1989). Pressure‐driven Magnetopause Motions and Attendant Response on the Ground, Planet. Space Sci. 37, 589‐608. doi:10.1016/0032-0633(89)90099-8

CrossRef Full Text | Google Scholar

Farrugia, C. J., Grocott, A., Sandholt, P. E., Cowley, S. W. H., Miyoshi, Y., Rich, F. J., et al. (2007). The Magnetosphere under Weak Solar Wind Forcing. Ann. Geophys. 25 (1), 191–205. doi:10.5194/angeo-25-191-2007

CrossRef Full Text | Google Scholar

Glassmeier, K.-H., and Heppner, C. (1992). Traveling Magnetospheric Convection Twin Vortices: Another Case Study, Global Characteristics, and a Model. J. Geophys. Res. 97 (A4), 3977–3992. doi:10.1029/91JA02464

CrossRef Full Text | Google Scholar

Gordeev, E., Sergeev, V., Tsyganenko, N., Kuznetsova, M., Rastäetter, L., Raeder, J., et al. (2017). The Substorm Cycle as Reproduced by Global MHD Models. Space Weather. 15, 131–149. doi:10.1002/2016SW001495

CrossRef Full Text | Google Scholar

Hoffmeister, C. (1943). Physikalische Untersuchungen an Kometen. I. Die Beziehungen des primären Schweifstrahls zum Radiusvektor. Z Astrophys. 22, 265.

Google Scholar

Holzer, R. E., McPherron, R. L., and Hardy, D. A. (1986). A Quantitative Empirical Model of the Magnetospheric Flux Transfer Process. J. Geophys. Res. 91 (A3), 3287–3293. doi:10.1029/ja091ia03p03287

CrossRef Full Text | Google Scholar

Hosokawa, K., Kullen, A., Milan, S., Reidy, J., Zou, Y., Frey, H. U., et al. (2020). Aurora in the Polar Cap: A Review. Space Sci. Rev. 216, 15. doi:10.1007/s11214-020-0637-3

CrossRef Full Text | Google Scholar

Hubert, B., Milan, S. E., Grocott, A., Blockx, C., Cowley, S. W. H., and Gérard, J.-C. (2006b). Dayside and Nightside Reconnection Rates Inferred from IMAGE FUV and Super Dual Auroral Radar Network Data. J. Geophys. Res. 111, A03217. doi:10.1029/2005JA011140

CrossRef Full Text | Google Scholar

Hubert, B., Palmroth, M., Laitinen, T. V., Janhunen, P., Milan, S. E., Grocott, A., et al. (2006a). Compression of the Earth's Magnetotail by Interplanetary Shocks Directly Drives Transient Magnetic Flux Closure. Geophys. Res. Lett. 33, a–n. doi:10.1029/2006GL026008

CrossRef Full Text | Google Scholar

Imber, S. M., Milan, S. E., and Hubert, B. (2006). The Auroral and Ionospheric Flow Signatures of Dual Lobe Reconnection. Ann. Geophys. 24 (11), 3115–3129. doi:10.5194/angeo-24-3115-2006

CrossRef Full Text | Google Scholar

Karlsson, S. B. P., Opgenoorth, H. J., Eglitis, P., Kauristie, K., Syrjäsuo, M., Pulkkinen, T., et al. (2000). Solar Wind Control of Magnetospheric Energy Content: Substorm Quenching and Multiple Onsets. J. Geophys. Res. 105, 5335–5356. doi:10.1029/1999JA900297

CrossRef Full Text | Google Scholar

King, J. H., and Papitashvili, N. E. (2005). Solar Wind Spatial Scales in and Comparisons of Hourly Wind and ACE Plasma and Magnetic Field Data. J. Geophys. Res. 110, A02104. doi:10.1029/2004JA010649

CrossRef Full Text | Google Scholar

Kokubun, S., McPherron, R. L., and Russell, C. T. (1977). Triggering of Substorms by Solar Wind Discontinuities. J. Geophys. Res. 82 (1), 74–86. doi:10.1029/ja082i001p00074

CrossRef Full Text | Google Scholar

Lee, D.-Y., Lyons, L. R., and Yumoto, K. (2004). Sawtooth Oscillations Directly Driven by Solar Wind Dynamic Pressure Enhancements. J. Geophys. Res. 109, A04202. doi:10.1029/2003JA010246

CrossRef Full Text | Google Scholar

Lin, R. L., Zhang, X. X., Liu, S. Q., Wang, Y. L., and Gong, J. C. (2010). A Three-Dimensional Asymmetric Magnetopause Model. J. Geophys. Res. 115, a–n. doi:10.1029/2009JA014235

CrossRef Full Text | Google Scholar

Liu, Z. Q., Lu, J. Y., Wang, C., Kabin, K., Zhao, J. S., Wang, M., et al. (2015). A Three‐dimensional High Mach Number Asymmetric Magnetopause Model from Global MHD Simulation. J. Geophys. Res. Space Phys. 120, 5645–5666. doi:10.1002/2014JA020961

CrossRef Full Text | Google Scholar

Lockwood, M., Bentley, S. N., Owens, M. J., Barnard, L. A., Scott, C. J., Watt, C. E., et al. (2019b). The Development of a Space Climatology: 1. Solar Wind Magnetosphere Coupling as a Function of Timescale and the Effect of Data Gaps. Space Weather. 17, 133–156. doi:10.1029/2018SW001856

CrossRef Full Text | Google Scholar

Lockwood, M., Chambodut, A., Finch, I. D., Barnard, L. A., Owens, M. J., and Haines, C. (2019a). Time-of-day/time-of-year Response Functions of Planetary Geomagnetic Indices. J. Space Weather Space Clim. 9, A20. doi:10.1051/swsc/2019017

CrossRef Full Text | Google Scholar

Lockwood, M., and Cowley, S. W. H. (1992). “Ionospheric Convection and the Substorm Cycle in “Substorms 1,” in Proceedings of the First International Conference on Substorms, ICS‐1. ESA‐SP‐335. Editor C. Mattock (Nordvijk, Netherlands: European Space Agency Publications), 99–109. Available at: http://www.personal.reading.ac.uk/∼ym901336/pdfs/95_lockwood_ICS1.pdf.

Google Scholar

Lockwood, M. (2019). Does Adding Solar Wind Poynting Flux Improve the Optimum Solar Wind‐Magnetosphere Coupling Function? JGR Space Phys. 124 (7), 5498–5515. doi:10.1029/2019JA026639

CrossRef Full Text | Google Scholar

Lockwood, M., Haines, C., Barnard, L. A., Owens, M. J., Scott, C. J., Chambodut, A., et al. (2021). Semi-annual, Annual and Universal Time Variations in the Magnetosphere and in Geomagnetic Activity: 4. Polar Cap Motions and Origins of the Universal Time Effect. J. Space Weather Space Clim. 11, 15. doi:10.1051/swsc/2020077

CrossRef Full Text | Google Scholar

Lockwood, M., Hairston, M., Finch, I., and Rouillard, A. (2009). Transpolar Voltage and Polar Cap Flux during the Substorm Cycle and Steady Convection Events. J. Geophys. Res. 114, a–n. doi:10.1029/2008JA013697

CrossRef Full Text | Google Scholar

Lockwood, M., LanchesterLanchester, B. S. B. S., Morley, S. K., Throp, K., Milan, S. E., Lester, M., et al. (2006). Modeling the Observed Proton Aurora and Ionospheric Convection Responses to Changes in the IMF Clock Angle: 2. Persistence of Ionospheric Convection. J. Geophys. Res. 111, A02306. doi:10.1029/2003JA010307

CrossRef Full Text | Google Scholar

Lockwood, M., and McWilliams, K. A. (2021a). A Survey of 25 years' Transpolar Voltage Data from the SuperDARN Radar Network and the Expanding‐Contracting Polar Cap Model. JGR Space Phys. 126, e2021JA029554. doi:10.1029/2021JA029554

CrossRef Full Text | Google Scholar

Lockwood, M., and McWilliams, K. A. (2021b). On Optimum Solar Wind‐Magnetosphere Coupling Functions for Transpolar Voltage and Planetary Geomagnetic Activity. JGR Space Phys. 126, e2021JA029946. doi:10.1029/2021JA029946

CrossRef Full Text | Google Scholar

Lockwood, M., McWilliams, K. A., Owens, M. J., Barnard, L. A., Watt, C. E., Scott, C. J., et al. (2020b). Semi-annual, Annual and Universal Time Variations in the Magnetosphere and in Geomagnetic Activity: 2. Response to Solar Wind Power Input and Relationships with Solar Wind Dynamic Pressure and Magnetospheric Flux Transport. J. Space Weather Space Clim. 10, 30. doi:10.1051/swsc/2020033

CrossRef Full Text | Google Scholar

Lockwood, M. (1993). Modelling High-Latitude Ionosphere for Time-Varying Plasma Convection. IEE Proc. H. Microw. Antennas Propag. U. K. 140, 91. doi:10.1049/ip-h-2.1993.0015

CrossRef Full Text | Google Scholar

Lockwood, M., and Moen, J. (1999). Reconfiguration and Closure of Lobe Flux by Reconnection during Northward IMF: Possible Evidence for Signatures in Cusp/cleft Auroral Emissions. Ann. Geophys. 17, 996–1011. doi:10.1007/s00585-999-0996-2

CrossRef Full Text | Google Scholar

Lockwood, M., and Morley, S. K. (2004). A Numerical Model of the Ionospheric Signatures of Time-Varying Magneticreconnection: I. Ionospheric Convection. Ann. Geophys. 22, 73–91. doi:10.5194/angeo-22-73-2004

CrossRef Full Text | Google Scholar

Lockwood, M., Owens, M. J., Barnard, L. A., Haines, C., Scott, C. J., McWilliams, K. A., et al. (2020a). Semi-annual, Annual and Universal Time Variations in the Magnetosphere and in Geomagnetic Activity: 1. Geomagnetic Data. J. Space Weather Space Clim. 10, 23. doi:10.1051/swsc/2020023

CrossRef Full Text | Google Scholar

Lockwood, M., Owens, M. J., Barnard, L. A., Watt, C. E., Scott, C. J., Coxon, J. C., et al. (2020c). Semi-annual, Annual and Universal Time Variations in the Magnetosphere and in Geomagnetic Activity: 3. Modelling. J. Space Weather Space Clim. 10, 61. doi:10.1051/swsc/2020062

CrossRef Full Text | Google Scholar

Lockwood, M. (20132013). Reconstruction and Prediction of Variations in the Open Solar Magnetic Flux and Interplanetary Conditions. Living Rev. Sol. Phys. 10 (4). doi:10.12942/lrsp-2013-4

CrossRef Full Text | Google Scholar

Lockwood, M. (2022a). Solar Wind-Magnetosphere Coupling Functions: Pitfalls, Limitations, and Applications. Space Weather. 20 (2), e2021SW002989. doi:10.1029/2021SW002989

CrossRef Full Text | Google Scholar

Lockwood, M. (2022b). The Joined-Up Magnetosphere. Front. Astron. Space Sci. 9, 856188. doi:10.3389/fspas.2022.856188

CrossRef Full Text | Google Scholar

Lu, G., Holzer, T. E., Lummerzheim, D., Ruohoniemi, J. M., Stauning, P., Troshichev, O., et al. (2002). Ionospheric Response to the Interplanetary Magnetic Field Southward Turning: Fast Onset and Slow Reconfiguration. J. Geophys. Res. 107 (A8), 2–1. doi:10.1029/2001JA000324

CrossRef Full Text | Google Scholar

Lühr, H., Sandholt, M. P. E., and Moretto, T. L. T. (1996). Multi-instrument Ground-Based Observations of a Travelling Convection Vortices Event. Ann. Geophys. 14, 162–181. doi:10.1007/s00585-996-0162-z

CrossRef Full Text | Google Scholar

Lukianova, R. (2003). Magnetospheric Response to Sudden Changes in Solar Wind Dynamic Pressure Inferred from Polar Cap Index. J. Geophys. Res. 108 (A12), 1428. doi:10.1029/2002JA009790

CrossRef Full Text | Google Scholar

Lyon, J. G., Fedder, J. A., and Mobarry, C. M. (2004). The Lyon-Fedder-Mobarry (LFM) Global MHD Magnetospheric Simulation Code. J. Atmos. Solar-Terrestrial Phys. 66, 1333–1350. doi:10.1016/j.jastp.2004.03.020

CrossRef Full Text | Google Scholar

Marklund, G., and Lindqvist, P. A. (2021). Cluster Multi‐Probing of the Aurora during Two Decades. JGR Space Phys. 126, e2021JA029497. doi:10.1029/2021JA029497

CrossRef Full Text | Google Scholar

Mayaud, P. N. (1980). Derivation, Meaning, and Use of Geomagnetic Indices. Geophys. Monogr. Ser. 22, 154. doi:10.1029/GM022

CrossRef Full Text | Google Scholar

McPherron, R. L., Angelopoulos, V., Baker, D. N., and Hones, E. W. (1993). Is There a Near-Earth Neutral Line? Adv. Space Res. 13 (4), 173–186. doi:10.1016/0273-1177(93)90331-5

CrossRef Full Text | Google Scholar

McPherron, R. L., Hsu, T.-S., and Chu, X. (2015). An Optimum Solar Wind Coupling Function for the AL Index. J. Geophys. Res. Space Phys. 120, 2494–2515. doi:10.1002/2014JA020619

CrossRef Full Text | Google Scholar

McPherron, R. L. (1979). Magnetospheric Substorms. Rev. Geophys. 17 (4), 657–681. doi:10.1029/RG017i004p00657

CrossRef Full Text | Google Scholar

Milan, S. E., Boakes, P. D., and Hubert, B. (2008). Response of the Expanding/contracting Polar Cap to Weak and Strong Solar Wind Driving: Implications for Substorm Onset. J. Geophys. Res. 113, a–n. doi:10.1029/2008JA013340

CrossRef Full Text | Google Scholar

Milan, S. E., Carter, J. A., Bower, G. E., Imber, S. M., Paxton, L. J., Anderson, B. J., et al. (2020). Dual‐Lobe Reconnection and Horse‐Collar Auroras. J. Geophys. Res. Space Phys. 125, e2020JA028567. doi:10.1029/2020JA028567

CrossRef Full Text | Google Scholar

Milan, S. E., Carter, J. A., Sangha, H., Bower, G. E., and Anderson, B. J. (2021). Magnetospheric Flux Throughput in the Dungey Cycle: Identification of Convection State during 2010. J. Geophys. Res. Space Phys. 126, e2020JA028437. doi:10.1029/2020JA028437

CrossRef Full Text | Google Scholar

Milan, S. E. (2004). Dayside and Nightside Contributions to the Cross Polar Cap Potential: Placing an Upper Limit on a Viscous-like Interaction. Ann. Geophys. 22, 3771–3777. doi:10.5194/angeo-22-3771-2004

CrossRef Full Text | Google Scholar

Milan, S. E., Gosling, J. S., and Hubert, B. (2012). Relationship between Interplanetary Parameters and the Magnetopause Reconnection Rate Quantified from Observations of the Expanding Polar Cap. J. Geophys. Res. 117, a–n. doi:10.1029/2011JA017082

CrossRef Full Text | Google Scholar

Milan, S. E., Grocott, A., Forsyth, C., Imber, S. M., Boakes, P. D., and Hubert, B. (2009b). A Superposed Epoch Analysis of Auroral Evolution during Substorm Growth, Onset and Recovery: Open Magnetic Flux Control of Substorm Intensity. Ann. Geophys. 27 (2), 659–668. doi:10.5194/angeo-27-659-2009

CrossRef Full Text | Google Scholar

Milan, S. E., Imber, S. M., Carter, J. A., Walach, M. T., and Hubert, B. (2016). What Controls the Local Time Extent of Flux Transfer Events? J. Geophys. Res. Space Phys. 121, 1391–1401. doi:10.1002/2015JA022012

CrossRef Full Text | Google Scholar

Milan, S. E., Lester, M., Cowley, S. W. H., Oksavik, K., Brittnacher, M., Greenwald, R. A., et al. (2003). Variations in the Polar Cap Area during Two Substorm Cycles. Ann. Geophys. 21, 1121–1140. doi:10.5194/angeo-21-1121-2003

CrossRef Full Text | Google Scholar

Milan, S. E., Lester, M., Cowley, S. W. H., Oksavik, K., Brittnacher, M., Greenwald, R. A., et al. (2009a). Variations in the Polar Cap Area during Two Substorm Cycles. Ann. Geophys. 21 (5), 1121–1140. doi:10.5194/angeo-21-1121-2003

CrossRef Full Text | Google Scholar

Milan, S. E., Provan, G., and Hubert, B. (2007). Magnetic Flux Transport in the Dungey Cycle: A Survey of Dayside and Nightside Reconnection Rates. J. Geophys. Res. 112, a–n. doi:10.1029/2006JA011642

CrossRef Full Text | Google Scholar

Mooney, M. K., Forsyth, C., Rae, I. J., Chisham, G., Coxon, J. C., Marsh, M. S., et al. (2020). Examining Local Time Variations in the Gains and Losses of Open Magnetic Flux during Substorms. J. Geophys. Res. Space Phys. 125, e2019JA027369. doi:10.1029/2019JA027369

CrossRef Full Text | Google Scholar

Мишин, В., Mishin, V., Караваев, Ю., and Karavaev, Y. (2017). Saturation of the Magnetosphere during Superstorms: New Results from the Magnetogram Inversion Technique. Solar-Terrestrial Phys. 3 (3), 28–36. doi:10.12737/stp-33201704

CrossRef Full Text | Google Scholar

Nakamura, R., Kokubun, S., Mukai, T., and Yamamoto, T. (1997). Changes in the Distant Tail Configuration during Geomagnetic Storms. J. Geophys. Res. 102 (A5), 9587–9601. doi:10.1029/97JA00095

CrossRef Full Text | Google Scholar

Newell, P. T., and Gjerloev, J. W. (2011). Evaluation of SuperMAG Auroral Electrojet Indices as Indicators of Substorms and Auroral Power. J. Geophys. Res. 116, a–n. doi:10.1029/2011JA016779

CrossRef Full Text | Google Scholar

Newell, P. T., and Gjerloev, J. W. (2012). SuperMAG-based Partial Ring Current Indices. J. Geophys. Res. 117, a–n. doi:10.1029/2012JA017586

CrossRef Full Text | Google Scholar

Ober, D. M., Wilson, G. R., Maynard, N. C., Burke, W. J., and Siebert, K. D. (2006). MHD Simulation of the Transpolar Potential after a Solar-Wind Density Pulse. Geophys. Res. Lett. 33 (33), L04106. doi:10.1029/2005GL024655

CrossRef Full Text | Google Scholar

Palmroth, M., Pulkkinen, T. I., Janhunen, P., McComas, D. J., Smith, C. W., and Koskinen, H. E. J. (2004). Role of Solar Wind Dynamic Pressure in Driving Ionospheric Joule Heating. J. Geophys. Res. 109, A11302. doi:10.1029/2004JA010529

CrossRef Full Text | Google Scholar

Parker, E. N. (2001). A History of Early Work on the Heliospheric Magnetic Field. J. Geophys. Res. 106 (A8), 15797–15801. doi:10.1029/2000ja000100

CrossRef Full Text | Google Scholar

Parker, E. N. (1958). Dynamics of the Interplanetary Gas and Magnetic Fields. ApJ 128, 664. doi:10.1086/146579

CrossRef Full Text | Google Scholar

Provan, G., Yeoman, T. K., Milan, S. E., Ruohoniemi, J. M., and Barnes, R. (2002). An Assessment of the “Map-Potential” and “Beam-Swinging” Techniques for Measuring the Ionospheric Convection Pattern Using Data from the SuperDARN Radars. Ann. Geophys. 20, 191–202. doi:10.5194/angeo-20-191-2002

CrossRef Full Text | Google Scholar

Raeder, J., McPherron, R. L., Frank, L. A., Kokubun, S., Lu, G., Mukai, T., et al. (2001). Global Simulation of the Geospace Environment Modeling Substorm Challenge Event. J. Geophys. Res. 106 (A1), 381–395. doi:10.1029/2000JA000605

CrossRef Full Text | Google Scholar

Ridley, A. J., Hansen, K. C., Tóth, G., De Zeeuw, D. L., Gombosi, T. I., and Powell, K. G. (2002). University of Michigan MHD Results of the Geospace Global Circulation Model Metrics Challenge. J. Geophys. Res. 107 (A10), 1290. doi:10.1029/2001JA000253

CrossRef Full Text | Google Scholar

Ruohoniemi, J. M., and Baker, K. B. (1998). Large-scale Imaging of High-Latitude Convection with Super Dual Auroral Radar Network HF Radar Observations. J. Geophys. Res. 103, 20797–20811. doi:10.1029/98ja01288

CrossRef Full Text | Google Scholar

Russell, C. T., and McPherron, R. L. (1973). Semiannual Variation of Geomagnetic Activity. J. Geophys. Res. 78, 92–108. doi:10.1029/JA078i001p00092

CrossRef Full Text | Google Scholar

Russell, C. T. (1989). The Universal Time Variation of Geomagnetic Activity. Geophys. Res. Lett. 16 (6), 555–558. doi:10.1029/GL016i006p00555

CrossRef Full Text | Google Scholar

Schieldge, J. P., and Siscoe, G. L. (1970). A Correlation of the Occurrence of Simultaneous Sudden Magnetospheric Compressions and Geomagnetic Bay Onsets with Selected Geophysical Indices. J. Atmos. Terr. Phys. 32 (11), 1819–1830. doi:10.1016/0021-9169(70)90139-x

CrossRef Full Text | Google Scholar

Scurry, L., and Russell, C. T. (1991). Proxy Studies of Energy Transfer to the Magnetosphere. J. Geophys. Res. 96 (A6), 9541–9548. doi:10.1029/91JA00569

CrossRef Full Text | Google Scholar

Sibeck, D. G., and Lin, R.-Q. (2014). Size and Shape of the Distant Magnetotail. J. Geophys. Res. Space Phys. 119, 1028–1043. doi:10.1002/2013JA019471

CrossRef Full Text | Google Scholar

Siscoe, G. L., and Huang, T. S. (1985). Polar Cap Inflation and Deflation. J. Geophys. Res. 90 (A1), 543–547. doi:10.1029/ja090ia01p00543

CrossRef Full Text | Google Scholar

Slavin, J. A., Tsurutani, B. T., Smith, E. J., Jones, D. E., and Sibeck, D. G. (1983). Average Configuration of the Distant (<220 Re) Magnetotail: Initial ISEE-3 Magnetic Field Results. Geophys. Res. Lett. 10, 973–976. doi:10.1029/GL010i010p00973

CrossRef Full Text | Google Scholar

Smith, M. F., and Lockwood, M. (1996). Earth's Magnetospheric Cusps. Rev. Geophys. 34 (2), 233–260. doi:10.1029/96RG00893

CrossRef Full Text | Google Scholar

Sotirelis, T., Keller, M. R., Liou, K., Smith, D., Barnes, R. J., Talaat, E., et al. (2017). Testing the Expanding‐contracting Polar Cap Paradigm. J. Geophys. Res. Space Phys. 122, 7077–7086. doi:10.1002/2017JA024238

CrossRef Full Text | Google Scholar

Southwood, D. J. (1987). The Ionospheric Signature of Flux Transfer Events. J. Geophys. Res. 92 (A4), 3207–3213. doi:10.1029/JA092iA04p03207

CrossRef Full Text | Google Scholar

Stauning, P. (2022). The Polar Cap (PC) Index: PCS Version Based on Dome‐C Data. Space Weather. 20, e2021SW002941. doi:10.1029/2021SW002941

CrossRef Full Text | Google Scholar

Stauning, P., and Troshichev, O. A. (2008). Polar Cap Convection and PC Index during Sudden Changes in Solar Wind Dynamic Pressure. J. Geophys. Res. 113, a–n. doi:10.1029/2007JA012783

CrossRef Full Text | Google Scholar

Stern, D. P. (1975a). The Motion of a Proton in the Equatorial Magnetosphere. J. Geophys. Res. 80 (4), 595–599. doi:10.1029/JA080i004p00595

CrossRef Full Text | Google Scholar

Stern, D. P. (1975b). The Source of the Electric Field in the Nightside Magnetosphere. Greenbelt, MD: NASA Goddard Space Flight Center. Technical report, N-75-28596; NASA-TM-X-70837; X-602-75-17, OSTI Identifier: 7338032.

Google Scholar

Throp, K., Lockwood, M., Lanchester, B. S., Morley, S. K., and Frey, H. U. (2005). Modeling the Observed Proton Aurora and Ionospheric Convection Responses to Changes in the IMF Clock Angle: 1. Persistence of Cusp Proton Aurora. J. Geophys. Res. 110, A12311. doi:10.1029/2003JA010306

CrossRef Full Text | Google Scholar

Tsyganenko, N. A. (2013). Data-based Modelling of the Earth's Dynamic Magnetosphere: a Review. Ann. Geophys. 31 (10), 1745–1772. doi:10.5194/angeo-31-1745-2013

CrossRef Full Text | Google Scholar

Vasyliunas, V. M., Kan, J. R., Siscoe, G. L., and Akasofu, S.-I. (1982). Scaling Relations Governing Magnetospheric Energy Transfer. Planet. Space Sci. 30 (4), 359–365. doi:10.1016/0032-0633(82)90041-1

CrossRef Full Text | Google Scholar

Volland, H. (1973). A Semiempirical Model of Large-Scale Magnetospheric Electric Fields. J. Geophys. Res. 78 (1), 171–180. doi:10.1029/JA078i001p00171

CrossRef Full Text | Google Scholar

Walsh, B. M., Bhakyapaibul, T., and Zou, Y. (2019). Quantifying the Uncertainty of Using Solar Wind Measurements for Geospace Inputs. J. Geophys. Res. Space Phys. 124, 3291–3302. doi:10.1029/2019JA026507

CrossRef Full Text | Google Scholar

Wang, X.–Y., Zhang, Q.–H., Wang, C., Zhang, Y.–L., Tang, B.–B., Xing, Z.–Y., et al. (2022). A Small and Nearly Fully Closed Earth’s Magnetosphere for Strongly Northward Interplanetary Magnetic Field. Geophys. Res. Lett. submitted.

Google Scholar

Watt, C. E. J., Rankin, R., Rae, I. J., and Wright, D. M. (2005). Self-consistent Electron Acceleration Due to Inertial Alfvén Wave Pulses. J. Geophys. Res. 110, A10S07. doi:10.1029/2004JA010877

CrossRef Full Text | Google Scholar

Wiltberger, M., Wang, W., Burns, A. G., Solomon, S. C., Lyon, J. G., and Goodrich, C. C. (2004). Initial Results from the Coupled Magnetosphere Ionosphere Thermosphere Model: Magnetospheric and Ionospheric Responses. J. Atmos. Solar-Terrestrial Phys. 66, 1411–1423. doi:10.1016/j.jastp.2004.03.026

CrossRef Full Text | Google Scholar

Wygant, J. R., Torbert, R. B., and Mozer, F. S. (1983). Comparison of S3-3 Polar Cap Potential Drops with the Interplanetary Magnetic Field and Models of Magnetopause Reconnection. J. Geophys. Res. 88 (A7), 5727–5735. doi:10.1029/JA088iA07p05727

CrossRef Full Text | Google Scholar

Yue, C., Zong, Q. G., Zhang, H., Wang, Y. F., Yuan, C. J., Pu, Z. Y., et al. (2010). Geomagnetic Activity Triggered by Interplanetary Shocks. J. Geophys. Res. 115, a–n. doi:10.1029/2010JA015356

CrossRef Full Text | Google Scholar

Zhang, Q. H., Lockwood, M., Foster, J. C., Zhang, S. R., Zhang, B. C., McCrea, I. W., et al. (2015). Direct Observations of the Full Dungey Convection Cycle in the Polar Ionosphere for Southward Interplanetary Magnetic Field Conditions. J. Geophys. Res. Space Phys. 120, 4519–4530. doi:10.1002/2015JA021172

CrossRef Full Text | Google Scholar