Analysis of Reconstructed Modified Symmetric Teleparallel f(Q) Gravity

The existing analysis reports a reconstruction scheme of the newly proposed gravity say f(Q) gravity through the scale factor of the form $a(t)=a_0{t}^n=\frac{1}{1+z}$ by describing the power-law cosmology. The reconstructed f(Q) gravity models disclosed how this modified gravity model is capable to replicate dissimilar epochs of the cosmological history. Also, the reconstructed f(Q) gravity models are castoff to develop the expressions for density and pressure and the equation of state parameter. We reconstruct two cases of interacting fluid scenario ghost and pilgrim dark energy with pressureless dark matter. The physical behavior of the models is talked over the evolution of the Universe is accelerated. Moreover, the well-known cosmological planes i.e., $({\omega }_D-{\omega }_D^{\prime })$ and (r − s) constructed for our models, also include a comparison of our findings of these dynamical parameters with observational constraints. It is also quite interesting to mention here that the results of the equation of state parameter, $({\omega }_D-{\omega }_D^{\prime })$ and (r − s)-planes coincide with the modern observational data.

1 Introduction

Currently the modern theoretical observational data like type-Ia supernovae (Riess, 1998; Perlmutter, 1999), Cosmic Microwave Background Radiation (CMBR)(Spergel, 2003; Komatsu, 2011), Baryon Acoustic Oscillations (BAO) and Weak Lensing (WL) (Jain and Taylor, 2003; Eisenstein, 2005) Large Scale Structure (LSS) (Tegmark, 2004; Seljak, 2005), have been accounted for an accelerating expansion of the Universe. Fundamentally there are two apparent access for this kind of accelerating expansion of the Universe. First is the modified theories of gravity can also explain such an accelerating expansion of the Universe. In the foregoing epoch, a lot of investigation has been primed in the modified theories of gravitation such as $f(R),f(R,\mathcal{T}),f(G),f(R,G)$, and f(T, B) gravity, where R, G, $\mathcal{T}$ and T denotes the Ricci scalar, Gauss-Bonnet invariant, trace of energy-momentum tensor and torsion scalar of the Universe respectively. Innumeral works have been established in the framework of this modified theories of gravity and interesting results have been found in (Capozziello et al., 2007; Nojiri and Odintsov 2007; Azadi et al., 2008; Capozziello et al., 2008; Nojiri and Odintsov 2008; Harko et al., 2011; Daouda et al., 2012; Wei et al., 2012; Sharif and Yousaf 2013; Sahoo et al., 2014; Abbas et al., 2015; Chirde and Shekh 2015; Chirde and Shekh, 2016a; Chirde and Shekh, 2016b; Sharif and Fatima 2016; Bhatti et al., 2017; Bhoyar et al., 2017; Chirde and Shekh, 2018a, Chirde and Shekh, 2018b; Chirde and Shekh, 2019; Pawar et al., 2018; Shekh and Chirde, 2019; Shekh and Chirde, 2020; Shekh et al., 2020b; Dagwal and Pawar 2020; Sahoo and Bhattacharjee 2020; Shekh et al., 2020a; Shekh and Chirde 2020; Shekh et al., 2021; Shekh, 2021a; Shekh 2021b). Among the all determinations, one model which is based on the so-called f(Q) gravity theory or symmetric teleparallel gravity, where the nonmetricity scalar Q is works as gravitational interaction. The theory of f(Q) gravity was first introduced by Jimenez et al. (2018) later on Lazkoz, (2019) investigated an interesting restrictions on f(Q) gravity theory by involving the polynomial functions of the redshift in Lagrangian and successfully derived using data from the expansion rate, type-Ia Supernovae, Quasars, Gamma-Ray Bursts, BAO data, and CMBR distance. An examination on f(Q) theory of gravity have been speedily progressed as well as astrophysical data observational constraints to provoke it in contrast to the formulation of standard Einsteinian General Relativity. Mandal et al. (2020a) analyzed the cosmography in f(Q) gravity while the same author in Mandal et al. (2020b) gave a full of energy conditions constraints like weak, strong, dominant and null energy conditions for two models of f(Q) gravity theory. Frusciante, (2021) focused on a specific model of f(Q) gravity theory which at the background level is indistinguishable from ΛCDM model, while demonstrating measurable and peculiar signatures at linier perturbation level.

Second is dark energy which can be represented by using the equation of state parameter (ω_D) and characterized as ${\omega }_D=\frac{p_D}{{\rho }_D}$. More about the ω_D parameter is that, if ω_D ≈ − 1: it behaves like a standard cosmology, if ω_D > − 1: the dark energy quintessence model behavior or ω_D < − 1: dark energy phantom model behavior and the probability ω_D ≪ − 1 is governed out by existing cosmological data as well as K-essence, Chaplygin gas and several supplementary limits of ω_D are acquired from observation data results which come from the combination of data SNe-Ia and CMBA as well as Statistics of Galaxy Clustering which are −1.66 < ω_D < − 0.62 and −1.33 < ω_D < − 0.79 respectively. − 1.44 < ω_D < − 0.92 from luminosity, CMB anisotropy, galaxy clustering statistics and distances of high red-shift SNe-Ia. Notwithstanding the fact that it is preferred by the observational data, the ΛCDM model tests cosmological constant problems. To overwhelm the theoretical observations mentioned above, various models of dark energy have been proposed in literature. A dynamical dark energy model one, known as ghost dark energy which has a remarkable some non-trivial properties for the expanding Universe having non-trivial topological formation which resolve U(1) problem (Witten, 1979; Kawarabayashi and Ohta, 1980; Nath and Arnowitt, 1981). Sheykhi and Movahed, (2012) observed expansion of the Universe using model parameter constraints in general relativity for an interacting ghost dark energy model. Sadeghi et al. (2013) computed dynamical parameters such as deceleration and equation of state parameters numerically to examine the behavior of the Universe in an interacting ghost dark energy models by varying Λ as well as G. Next is the pilgrim dark energy which devours a phantom-like Universe to prevent the formation of black hole (2012). Sharif and Jawad, (2013) observed the cosmic evolutionary actions of pilgrim dark energy with event horizons and apparent using non-flat Universe while considering the different IR-cutoffs as particle horizon, event horizon and conformal age of the Universe. Sharif and Zubair, (2014) noted cosmological evolution of pilgrim dark energy whereas Jawad et al. (2016a) investigated cosmic behavior of pilgrim dark energy in loop quantum cosmology using Hubble horizon in forms IR-cutoff for interacting scenario. By assuming the interacting scenario of unified pilgrim ghost dark energy and cold dark matter in the flat FRW Universe framework. Jawad et al. (2017) have constructed the equation of state parameter which exhibits the transition from region of quintessence and then approaches to region of phantom at z = −0.9 whereas Jawad et al. (2016b) illustrated the cosmic acceleration of the Universe under two interacting dark energy models say pilgrim dark energy with Granda-Oliveros cut-off and its generalized ghost version in the DGP braneworld framework and observed that the equation of state parameter behaves like the phantom era of the Universe while the deceleration parameter shows the accelerated expansion of the Universe. Keep in mind an interaction between pilgrim dark energy as a future event and apparent horizons with cold dark matter. Rani et al. (2016) studied the cosmic acceleration in dynamical modified Chern-Simons gravity in the framework of non-flat FRW Universe.

Nevertheless, for the certain geometrical models ascending from the modifications of Einstein’s gravitational field equations, the equation of state (ω_D) is no longer playing a vital role and its influence becomes unclear. Consequently, a new diagnosis is required to discriminate all classes of cosmological models. In order to accomplish these classes Sahni et al. (2003) introduced the pair of parameters (r, s) which has no dimension or so-called statefinder parameter of the form:

$r=\frac{\stackrel{...}{a}}{a{H}^3},s=\frac{r-1}{3\left(q-1/2\right)}(1)$

As, the Universe involving with two component fluid matter Ω_m and exotic form of energy Ω_D. In this situation the statefinder parameters attains the form (Sahni et al., 2003)

$r=1+\frac{9{\omega }_D}{2}{\mathrm{\Omega }}_D\left(1+{\omega }_D\right)-\frac{3{\dot{\omega }}_D}{3H}{\mathrm{\Omega }}_D(2)$

$s=1+{\omega }_D-\frac{{\dot{\omega }}_D}{3{\omega }_{D}H}(3)$

where ω_D is the equation of state parameter of dark energy.

In the past works so many authors have effectively validated the statefinder diagnostic that it can distinguish a series of cosmological models. In case of ΛCDM and CDM models, the statefinder parameters respectively are fixed as (r, s) = (1, 0) and (r, s) = (1, 1). Also, for quintessence field the trajectories of (r − s) plane lie in the range (s > 0, r < 1) whereas for chaplygin gas which look a lot like to (s < 0, r > 1). In addition to the geometrical diagnostic say statefinder diagnosis, there is another one dynamical diagnostic which was firstly intended by Caldwell and Linder, (2005) and verified the deeds of quintessence scalar field dark energy model through this plane called $({\omega }_D-{\omega }_D^{\prime })$-plane analysis and also used extensively in the literatures. In the $({\omega }_D-{\omega }_D^{\prime })$-plane, ${\omega }_D^{\prime }$ signifies the advancement of ω_D. Over and done with this plane, the models can be considered as in two different classes as thawing and freezing. The thawing region is described as ${\omega }_D^{\prime }>0,{\omega }_D<0$ while freezing region as ${\omega }_D^{\prime }<0,{\omega }_D<0$ on $({\omega }_D-{\omega }_D^{\prime })$-plane.In this paper, we study the correspondence scheme with ghost dark energy and pilgrim dark energy model using reconstruction technique in f(Q) gravity. The paper is prearranged in the following format. Section 2, contains FRW Universe with the source of fluid as an interaction between matter and dark energy from which the equation of state parameter is derived in Section 3 while Section 4, 5 enclose the brief discussion of cosmographic observations through cosmic diagnostic parameters and phase planes by reconstructing f(Q) gravity model with the help of ghost and pilgrim dark energy respectively. Finally, we conclude our results in Section 6.

2 FRW Universe With Interacting Sourse

Consider the spatially homogeneous and isotropic Friedman-Robertson-Walker (FRW) line element of the form:

$d{s}^2=-d{t}^2+a^2\left(t\right)\left[\frac{d{r}^2}{1-k{r}^2}+r^{2}d{\theta }^2+r^2{\sin }^2\theta d{\varphi }^2\right],(4)$

where a be the scale factor of the Universe.The angle θ and ϕ are the usual azimuthal and polar angles of spherical coordinates. Also, k is a constant which represent the curvature of the Universe. If k = 1, 0, −1, then this corresponds to closed, flat, open Universe.The energy momentum tensor for dark matter and dark energy are defined as

$\widehat{\mathcal{T}}={\mathcal{T}}_{\mu \nu }+{\bar{\mathcal{T}}}_{\mu \nu }(5)$

where ${\mathcal{T}}_{\mu \nu }$ and ${\bar{\mathcal{T}}}_{\mu \nu }$ are the energy momentum tensors for pressureless dark matter and dark energy, defined as ${\mathcal{T}}_{\mu \nu }={\rho }_m{u}_{\mu }{u}_{\nu }\text{and}{\bar{\mathcal{T}}}_{\mu \nu }=\left({\rho }_d+p_d\right)u_{\mu }{u}_{\nu }+p_d{g}_{\mu \nu }$ in which ρ_m, ρ_d are the energy densities of dark matter and dark energy respectively and p_d is the pressure of dark energy, u_i is the four velocity of the fluid. Also, $u_i={\delta }_4^i$ is a four-velocity vector which satisfies

$g_{\mu \nu }=u^{\mu }{u}_{\nu }=-x^{\mu }{x}_{\nu }=-1\text{and}{u}^{\mu }{x}_{\nu }=0(6)$

For a Universe where dark energy and dark matter are interacting to each other the total energy density satisfies the continuity equation as following:

${\dot{\rho }}_D+3H\left({\rho }_D+p_D\right)=0(7)$

where ρ_D be the combine energy density of two fluids of the form ρ_D = ρ_m + ρ_d.The curvature energy density ρ_k and the critical energy density ρ_cr as usual defined by (Yang, 2020):

${\rho }_k=\frac{3k}{8\pi G{a}^2}\text{and}{\rho }_{cr}=3H^2(8)$

Now, the three fractional form of energy densities Ω_D, Ω_m and Ω_k as (Yang, 2020):

${\mathrm{\Omega }}_D=\frac{{\rho }_D}{{\rho }_{cr}}=\frac{{\rho }_D}{3H^2},(9)$

${\mathrm{\Omega }}_m=\frac{{\rho }_m}{{\rho }_{cr}}=\frac{{\rho }_m}{3H^2}(10)$

${\mathrm{\Omega }}_k=\frac{{\rho }_k}{{\rho }_{cr}}=\frac{k}{H^2{a}^2}(11)$

Then from the above Eqs 9–11, the Friedmann equation can then be written as:

$1+{\mathrm{\Omega }}_k={\mathrm{\Omega }}_D+{\mathrm{\Omega }}_m.(12)$

Consider the interaction between two fluids. So, the energy densities of two fluids do not conserve separately, the continuity of matter of two fluids yields (Yang, 2020)

${\dot{\rho }}_D+3H\left({\rho }_D+p_D\right)=-\mathrm{\Gamma }(13)$

where Γ represents the interaction between dark matter and dark energy. In general Γ should be a function with units of inverse of time. For the convenience, choose the following form of interaction term:

$\mathrm{\Gamma }=3\eta H\left({\rho }_m+{\rho }_D\right)=3\eta H{\rho }_D\left(1+u\right)(14)$

where η be the coupling parameter. Considering η = 0, the equation of continuity reduces to the non-interacting case. Here u is defined as:

$u=\frac{{\rho }_m}{{\rho }_D}=\frac{{\mathrm{\Omega }}_m}{{\mathrm{\Omega }}_D}=\frac{1-{\mathrm{\Omega }}_D}{{\mathrm{\Omega }}_D}(15)$

Under the above defined parameters, the equation of state parameter for dark energy can be derived as (Yang, 2020):

${\omega }_D=-\frac{1}{2-{\mathrm{\Omega }}_D}\left(1-\frac{{\mathrm{\Omega }}_k}{3}+\frac{2\eta }{{\mathrm{\Omega }}_D}\left(1+{\mathrm{\Omega }}_k\right)\right)(16)$

For flat Universe after taking k = 0, the equation of state parameter for dark energy from Eq. (16) can be rewritten as (Yang, 2020):

${\omega }_D=-\frac{1}{2-{\mathrm{\Omega }}_D}\left(1+\frac{2\eta }{{\mathrm{\Omega }}_D}\right)(17)$

There exist several dynamical dark energy models, in literature, presented by various authors both in general relativity and in modified theories of gravitation. The most of the authors who have analyzed some cosmological models with dark energy both in general relativity and modified theories of gravitation, some of them are mentioned in Ref. (Chirde and Shekh, 2015, Chirde and Shekh, 2018a; Bhoyar et al., 2017; Shekh and Chirde 2020); Naidu et al., 2012; Sarkar and Mahanta 2013; Kiran et al., 2015; Santhi et al., 2017; Aditya and Reddy, 2018). The reconstruction phenomenon of a well-known PDE model with f(G) gravity in the presence of power law scale factor Jawad and Rani, (2015) have reconstructed f(G) models with respect to two values of PDE parameter; that is, u = 2, −2 and checked the significant cosmological aspects of these reconstructed models while Jawad et al. (2016a); Jawad et al. (2017) studied the cosmological consequences of pilgrim dark energy model in the framework of generalized teleparallel gravity by considering the reconstruction scheme for f(T) models with power law scale factor taking Hubble horizon and Nojiri-Odintsov length as infrared cut-offs also observed that the Hubble parameter lies within observational suggested ranges while deceleration parameter represents the accelerated expansion behaviour of the Universe and the model corresponds to the quintessence region and phantom region for different cases of pilgrim dark energy parameter u under pilgrim dark energy models in fractal Universe while very recently Shekh, (2021a) analyzed the dynamical investigation of different models of holographic dark energy using Friedman-Lemâitre-Robertson-Walker cosmological model in the context of same f(Q) gravity by governing the features of the model in view of the relation between cosmic time and redshift which yields a purely accelerating evolving Universe.In order to obtain the analytic solution, consider the following form of dimensionless scale factor as of the form:

$a\left(t\right)=a_0{t}^n(18)$

where the subscript 0 denote the value of a quantity at present, a₀ is a constant represents the present day value of the scale factor and moreover set a₀ to 1.The deceleration parameter (q) of the Universe, reads ast

$q=-\frac{a\ddot{a}}{{\dot{a}}^2}=-1+\frac{1}{n}(19)$

The cosmic scale factor in terms of the deceleration parameter may be written as

$a\left(t\right)=t^{1/\left(1+q\right)}(20)$

From the above Eq. (20), it is observed that q > − 1 is the condition for expanding Universe in the power-law expansion cosmological model.

The expansion history of the Universe and the present expansion rate of the Universe are respectively described by the Hubble parameter as:

$H=\left(\frac{1}{1+q}\right)t^{-1}\text{and}{H}_0=\left(\frac{1}{1+q}\right)t_0^{-1}(21)$

The above Eq. (21), shows that the expansion history of the Universe in power-law cosmology depends on the two parameters say H₀ and q.

Considering the connection between a and z, the time derivatives of H using Eq. (21) are obtained as:

$H=H_0{\left(1+z\right)}^{1+q},\dot{H}=-H_0{\left(1+z\right)}^{2\left(1+q\right)},\ddot{H}=2H_0{\left(1+z\right)}^{3\left(1+q\right)}\text{and}\stackrel{...}{H}=-6H_0{\left(1+z\right)}^{4\left(1+q\right)}.(22)$

3 Some Basics and Field Equations of f(Q) Gravity

Let us consider the action for f(Q) gravity of the form (Shekh, 2021b)

$S=\left(\frac{1}{2{\kappa }^2}\int f\left(Q\right)+\int {\mathit{\pounds }}_m\right)\sqrt{-g}{d}^{4}x,(23)$

where f(Q) is a general function of Q, ${\mathcal{L}}_m$ is the matter Lagrangian density and g is the determinant of metric g_μν.

The non-metricity tensor and its traces are such that

$Q_{\gamma \mu \nu }={\nabla }_{\gamma }{g}_{\mu \nu },(24)$

$Q_{\gamma }={{Q_{\gamma }}^{\mu }}_{\mu },{\tilde{Q}}_{\gamma }={Q^{\mu }}_{\gamma \mu }.(25)$

Moreover, the superpotential as a function of non-metricity tensor is given by

$4{P^{\gamma }}_{\mu \nu }=-{Q^{\gamma }}_{\mu \nu }+2Q_{\left({\mu }^{\gamma }\nu \right)}-Q^{\gamma }{g}_{\mu \nu }-{\tilde{Q}}^{\gamma }{g}_{\mu \nu }-{\delta }_{\left({\gamma }^Q\nu \right)}^{\gamma },(26)$

where the trace of non-metricity tensor Eq. (20) has the form

$Q=-Q_{\gamma \mu \nu }{P}^{\gamma \mu \nu }.(27)$

Expression for energy-momentum tensor for the matter, whose definition is

$T_{\mu \nu }=-\frac{2}{\sqrt{-g}}\frac{\delta \left(\sqrt{-g}{\mathcal{L}}_m\right)}{\delta g^{\mu \nu }}.(28)$

Variation of action Eq. (18) with respect to metric tensor, one can obtain gravitational equation

$\frac{2}{\sqrt{-g}}{\nabla }_{\gamma }\left(\sqrt{-g}{f}_Q{P^{\gamma }}_{\mu \nu }\right)+\frac{1}{2}{g}_{\mu \nu }f+f_Q\left(P_{\mu \gamma i}{Q_{\nu }}^{\gamma i}-2Q_{\gamma i\mu }{P^{\gamma i}}_{\nu }\right)=-{\kappa }^2{\widehat{\mathcal{T}}}_{\mu \nu },(29)$

where $f_Q=\frac{df}{dQ}$. The variation of Eq. (24) with respect to the connection term, obtain

${\nabla }_{\mu }{\nabla }_{\gamma }\left(\sqrt{-g}{f}_Q{P^{\gamma }}_{\mu \nu }\right)=0.(30)$

For isotropic, homogeneous and spatially FRW space-time provided in Eq. (4), one can find the modified Friedmann equations for f(Q) gravity as

$\dot{H}+3H^2+\frac{\dot{f_Q}}{f_Q}H=\frac{1}{2f_Q}\left({\kappa }^2{p}_D+\frac{f}{2}\right)(31)$

$3H^2=\frac{1}{2f_Q}\left(-{\kappa }^2{\rho }_D+\frac{f}{2}\right)(32)$

The overhead dot represents the differentiation with respect to cosmic time t.

Also, the modified Friedmann equations enable us to write the pressure and the density for the Universe as

${\kappa }^2{\rho }_D=\frac{f}{2}-6H^2{f}_Q(33)$

${\kappa }^2{p}_D=\left(\dot{H}+3H^2+\frac{\dot{f_Q}}{f_Q}H\right)\left(2f_Q\right)-\frac{f}{2}(34)$

which are the pressure and the density for the f(Q) gravity.For the spatially homogeneous and isotropic FRW Universe, the non-metricity Q term is defined as Q = 6H². With the use of Eq. (22), the term Q is observed as

$Q=6H_0^2{\left(1+z\right)}^{\left(2+2q\right)}(35)$

4 Reconstruction of Ghost Dark Energy f(Q) Gravity

As, we know the ghost dark energy model is one of the dynamical dark energy model whose energy density is defined as (Pawar et al., 2018)

${\rho }_{\mathit{GDE}}=\alpha H(36)$

where α is an arbitrary model constant parameter having square dimension. We establish the correspondence between ghost dark energy and f(Q) gravity model by equating the corresponding densities. Using Eqs 33, 36, it follows that

$\frac{1}{2}f-6H^2{f}_Q=\alpha H(37)$

The re-arrangement of the above Eq. (37) provide

$f_Q-\left(\frac{1}{12H^2}\right)f=-\frac{\alpha }{6H}(38)$

which is the first order linear differential equation in Q whose solution is of the form as

$f\left(Q\right)=\left(clnQ+c_1\right)Q^{1/2}(39)$

where c and c₁ both are the positive constants of integration.Eq. (39), represents the reconstructed ghost dark energy f(Q) gravity model. The plot which shows the behavior of reconstructed ghost dark energy f(Q) gravity model versus redshift and the non-metricity parameter are respectively presented in Figures 1, 2 which described that the reconstructed ghost dark energy f(Q) gravity model is always positive and increases exponentially with respect to both z and Q. Also, it is noted that the values of positive constants of integration not affect on the behavior of f.

FIGURE 1

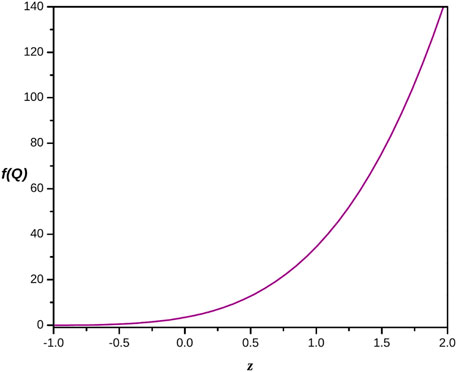
FIGURE 1. Plot of reconstructed ghost dark energy f(Q) gravity model versus redshift for the appropriate choice of constants c = 0.1 and c₁ = 3.0.

FIGURE 2

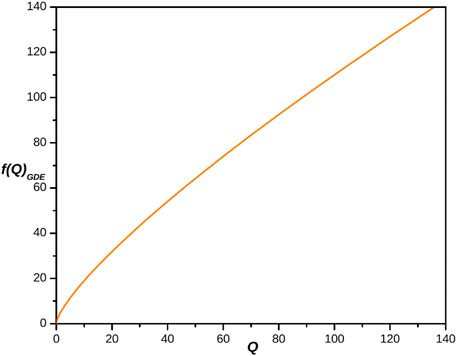
FIGURE 2. Plot of reconstructed ghost dark energy f(Q) gravity model versus non-metricity parameter for the appropriate choice of constants c = 0.1 and c₁ = 3.0.

4.1 Cosmographic Observations in Reconstructed Ghost Dark Energy f(Q) Gravity Model

Using Eq. (39) in Eqs 33 and 34, the expression for energy density and pressure are obtained as:

${\kappa }^2\rho =\left(c+c_1+clnQ\right)Q^{1/2}(40)$

${\kappa }^{2}p=2\left(\dot{H}+6H^2\right)\left(c+\frac{c_1}{2}+\frac{c}{2}lnQ\right)Q^{-1/2}+2H\left(\frac{-c_1}{4}-\frac{c}{4}lnQ\right)\dot{Q}{Q}^{-3/2}-\left(\frac{c_1}{2}+\frac{c}{2}lnQ\right)Q^{1/2}(41)$

The behavior of both pressure and energy density versus redshift of reconstructed ghost dark energy f(Q) gravity model is clearly shown in Figures 3, 4 respectively. Figure 4 depicted that the energy density of reconstructed ghost dark energy f(Q) gravity model is always positive and exponentially increases (see Figure 4) while pressure is always negative and shows negatively decreasing behaviour (see Figure 3) for all z = −1 to z > 0. Hence, such a behavior of pressure is the evidence of existance of dark energy.

FIGURE 3

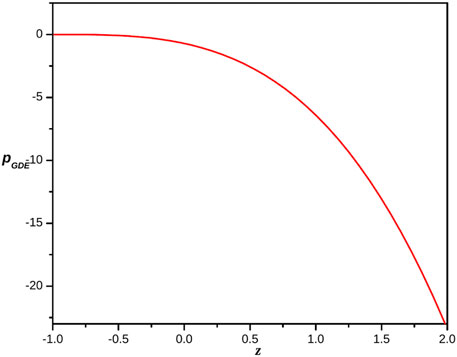
FIGURE 3. Plot of the pressure of the reconstructed ghost dark energy f(Q) gravity model versus redshift for the appropriate choice of constants.

FIGURE 4

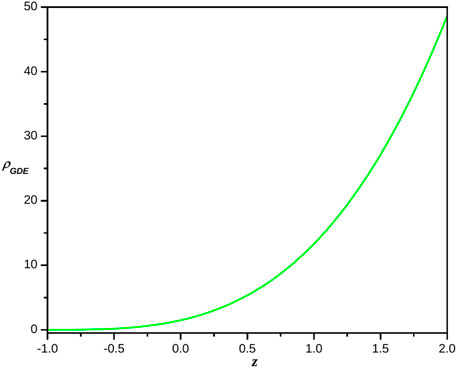
FIGURE 4. Plot of the energy density of the reconstructed ghost dark energy f(Q) gravity model versus redshift for the appropriate choice of constants.

4.1.1 Equation of State Parameter

${\omega }_D=\frac{-1}{2-\left(c+c_1+clnQ\right)Q^{-1/2}}\left(\frac{\left(c+c_1+clnQ\right)Q^{-1/2}-2\eta }{\left(c+c_1+clnQ\right)Q^{-1/2}}\right)(42)$

Eq. (42) represents the expression for equation of state parameter of ghost dark energy f(Q) gravity model. Figure 5 represents the dynamical evolution of the equation of state parameter of ghost dark energy f(Q) gravity model for three consecutive values of η. One can see in Figure 5 that at late Universe (z < − 1) towords η = 0.10, 0.15 and 0.20 the value of equation of state parameter of ghost dark energy f(Q) gravity model is less than −1 i.e. ${({\omega }_D)}_{\mathit{GDE}}<-1$ which represents the model involve phantom field dark energy whereas for present Universe (z = 0), it is a little bit upper than −1 i.e. ${({\omega }_D)}_{\mathit{GDE}}>-1$ and early Universe (z > 0) it has the value ${({\omega }_D)}_{\mathit{GDE}}>0$. Hence the present Universe consist of a quintessence field dark energy and early Universe involve barotropic fluid. Also, notice that by increasing the value of interaction parameter η, equation of state parameter takes more negative values, below the -1. It is observed that the equation of state in our framework can cross the phantom divide line as supported by recent astrophysical observations as well as the analysis of holographic dark energy inflation with Hubble’s cut-off analyzed by Shekh, (2021a) and also with Jawad and Rani, (2015), Jawad, (2015).

FIGURE 5

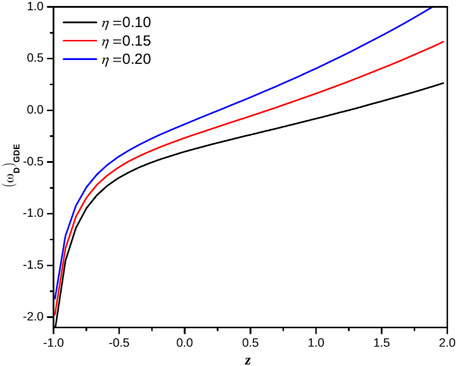
FIGURE 5. Plot of equation of state parameter of ghost dark energy f(Q) gravity model versus redshift for the appropriate choice of constants.

4.1.2 $({\mathit{\omega }}_{\mathit{D}}-{\mathit{\omega }}_{{\mathit{D}}^{\prime }})$-plane

The derivative of Eq. (42) with respect to ℓn(a), gives

${\omega }_D^{\prime }=\frac{\left(c/2+c_1/2+\left(c/2\right)lnQ\right)\dot{Q}{Q}^{-3/2}}{2-\left(c+c_1+clnQ\right)Q^{-1/2}}\left\{2\eta -\frac{2\eta -\left(c+c_1+clnQ\right)Q^{-1/2}}{\left(c+c_1+clnQ\right)Q^{-1/2}\left(2-\left(c+c_1+clnQ\right)Q^{-1/2}\right)}\right\}(43)$

The plot of ${\omega }_D^{\prime }$ with respect to ω_D for the ghost dark energy f(Q) gravity model is shown in Figure 6. Figures 5, 6, indicates that when ω_D < 0 then also ${\omega }_D^{\prime }<0$ which represents freezing region.

FIGURE 6

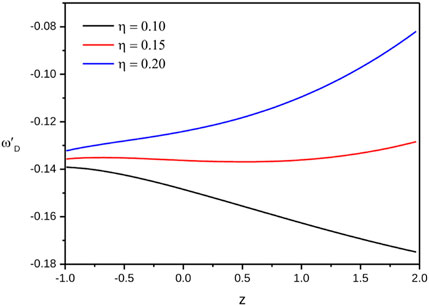
FIGURE 6. Plot of ${\omega }_D^{\prime }$ of ghost dark energy f(Q) gravity model versus redshift for the appropriate choice of constants.

4.1.3 (r−s)-plane

$r=\left\{\begin{array}{c}\hfill 1-\frac{9}{2}\frac{1}{2-\left(c+c_1+clnQ\right)Q^{-1/2}}\left(\frac{\left(c+c_1+clnQ\right)Q^{-1/2}-2\eta }{\left(c+c_1+clnQ\right)Q^{-1/2}}\right)\left(1+\frac{-1}{2-\left(c+c_1+clnQ\right)Q^{-1/2}}\left(\frac{\left(c+c_1+clnQ\right)Q^{-1/2}-2\eta }{\left(c+c_1+clnQ\right)Q^{-1/2}}\right)\right)\times \hfill \\ \hfill \left(c+c_1+clnQ\right)Q^{-1/2}-\frac{3}{2}\left(\frac{2\eta \dot{Q}}{\left(2-\left(c+c_1+clnQ\right)Q^{1/2}\right.}+\frac{\left(c+c_1+clnQ\right)\dot{Q}-2\eta \dot{Q}{Q}^{-1/2}}{2{\left[2-\left(c+c_1+clnQ\right)Q^{-1/2}\right]}^2{Q}^{3/2}}\right)\times \left(c+c_1+clnQ\right)Q^{-1/2}\hfill \end{array}\right\}(44)$

$s=1+\frac{-1}{2-\left(c+c_1+clnQ\right)Q^{-1/2}}\left(\frac{\left(c+c_1+clnQ\right)Q^{-1/2}-2\eta }{\left(c+c_1+clnQ\right)Q^{-1/2}}\right)+\frac{\left(\frac{2\eta \dot{Q}}{\left(2-\left(c+c_1+clnQ\right)\right.Q}+\frac{\left(c+c_1+clnQ\right)\dot{Q}-2\eta \dot{Q}{Q}^{-1/2}}{2{\left[2-\left(c+c_1+clnQ\right)Q^{-1/2}\right]}^2{Q}^{5/2}}\right)}{3\left(\frac{\left(c+c_1+clnQ\right)Q^{-1/2}-2\eta }{\left(c+c_1+clnQ\right)Q^{-1/2}}\right)}(45)$

Figure 7, shows the evolution trajectory for ghost dark energy f(Q) gravity model in (r − s)- plane towards different value of η. From Figure 7, the evolution trajectories of (r − s)- plane favors the chaplygin gas model with s < 0 and r > 1. Hence, our results are consistent with the analysis of Wu and Yu, (2006) and the authors who have achieved the state finder diagnostic for the phantom and quintom dark energy model (Sharif and Zubair, 2014; Sharif, 2018).

FIGURE 7

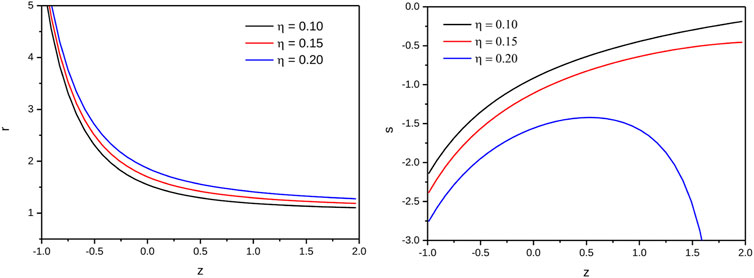
FIGURE 7. Plot of r and s of ghost dark energy f(Q) gravity model versus redshift for the appropriate choice of constants.

5 Reconstruction of Pilgrim Dark Energy f(Q) Gravity

Proceeding the same as it is in section 3. In this section, we reconstructed the pilgrim dark energy f(Q) gravity model.For this consider an interesting model for the description of dark energy is pilgrim dark energy in which the total energy in a box of size L could exceed the mass of a black hole of the same size i.e., ${\rho }_p{L}^3\ge m_{pl}^{2}L$, where m_pl be the Plank reduced mass. Therefore, the first property of pilgrim dark energy is (Jawad et al., 2016b)

${\rho }_p\ge m_{pl}^2{L}^{-2}(46)$

the simplest way to set the above equation is:

${\rho }_p=3n^2{m}_{pl}^{4-s}{L}^{-s}(47)$

where n and s are the conventional constant and pilgrim dark energy parameter respectively. Thus, from Eqs 46, 47, $L^{2-s}\ge m_{pl}^{s-2}={\ell }_{pl}^{2-s}$, where $m_{pl}=1/\sqrt{8\pi G}$ is the reduced Planck length, which is extremely short length. Obviously, since L > ℓ_pl in general, it is required that

$s\le 2(48)$

Keeping the box of size L = 1/H towards Hubble’s cutoff, the dynamical pilgrim dark energy model whose energy density from Eq. (47) is obtained as

${\rho }_{\mathit{PDE}}=3n^2{m}_{pl}^{4-s}{H}^s(49)$

We establish the correspondence between pilgrim dark energy and f(Q) gravity model by equating the conforming densities. Using Eqs 33, 49, it follows that

$\frac{1}{2}f-6H^2{f}_Q=3n^2{H}^u(50)$

The re-arrangement of above Eq. (50) provide

$f_Q-\left(\frac{1}{12H^2}\right)f=-\frac{3n^2{H}^u}{6H^2}(51)$

which is the first order linear differential equation in Q whose solution is of the form as

$f\left(Q\right)=-c_2{Q}^{\frac{u}{2}}+c_3{Q}^{1/2}(52)$

where $c_2=\frac{n^2}{(u-1)6^{u/2-1}}$ and c₃ be the constant of integration.Eq. (52) represents the reconstructed pilgrim dark energy f(Q) gravity model. The plot which shows the behavior of reconstructed pilgrim dark energy f(Q) gravity model versus redshift and the non-metricity parameter are respectively presented in Figures 8, 9 which described that the reconstructed pilgrim dark energy f(Q) gravity model is always negative and decreases negatively with respect to both z and Q.

FIGURE 8

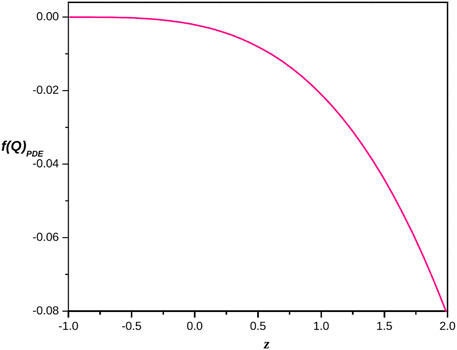
FIGURE 8. Plot of reconstructed pilgrim dark energy f(Q) gravity model versus redshift for the appropriate choice of constants c₂ = 0.0018 and c₃ = 0.1.

FIGURE 9

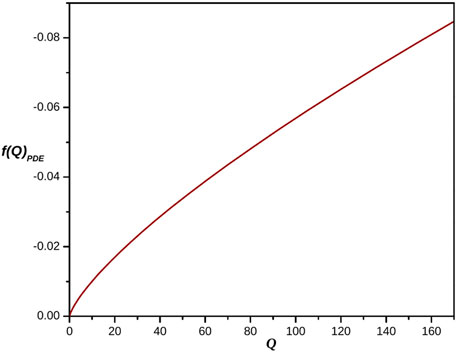
FIGURE 9. Plot of reconstructed pilgrim dark energy f(Q) gravity model versus non-metricity parameter for the appropriate choice of constants c₂ = 0.0018 and c₃ = 0.1.

5.1 Cosmographic Observations in Reconstructed Pilgrim Dark Energy f(Q) Gravity Model

Using Eq. (52) in Eqs 33 and 34, the expression for energy density and pressure are obtained as:

$\rho =\frac{c_2\left(1-u\right)}{2}{Q}^{u/2}(53)$

$p=\left(\dot{H}+3H^2\right)\left(c_{2}u{Q}^{\frac{u}{2}-1}+c_3{Q}^{-1/2}\right)+\frac{H}{2}\left(c_{2}u\left(u-2\right)Q^{\frac{u}{2}-1}-c_3{Q}^{-1/2}\right)\frac{\dot{Q}}{Q}-\frac{c_2}{2}{Q}^{u/2}-\frac{c_3}{2}{Q}^{1/2}(54)$

The behavior of both pressure and energy density versus redshift of reconstructed pilgrim dark energy f(Q) gravity model is clearly seen in Figures 10, 11 respectively. The energy density of reconstructed ghost dark energy f(Q) gravity model is always positive and exponentially increases (see Figure 11) whereas pressure is always negative and shows negatively decreasing behevior (see Figure 10) for all z = −1 to z > 0 which is the evidance of existance of dark energy.

FIGURE 10

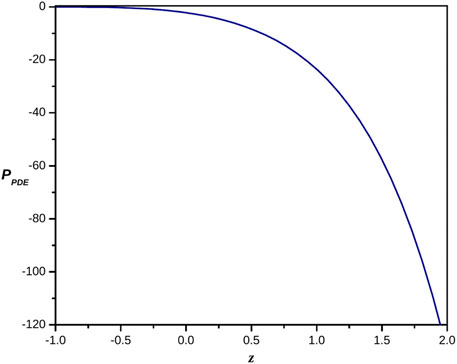
FIGURE 10. Plot of the pressure of the reconstructed pilgrim dark energy f(Q) gravity model versus redshift for the appropriate choice of constants.

FIGURE 11

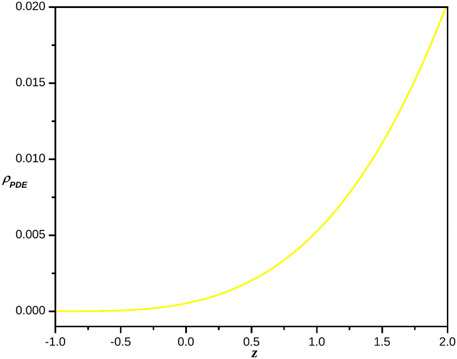
FIGURE 11. Plot of the energy density of the reconstructed pilgrim dark energy f(Q) gravity model versus redshift for the appropriate choice of constants.

5.1.1 Equation of State Parameter

${\omega }_D=-\frac{1}{2-c_2\left(1-u\right)Q^{\frac{u}{2}-1}}\left(1+\frac{2\eta }{c_2\left(1-u\right)Q^{\frac{u}{2}-1}}\right)(55)$

Eq. (55) represents the expression for equation of state parameter of pilgrim dark energy f(Q) gravity model. Figure 12 represents the dynamical evolution of the equation of state parameter of pilgrim dark energy f(Q) gravity model for three consecutive values of η. One can see in Figure 12 that at late Universe (z < − 1) towords η = 0.10, 0.15 and 0.20 the value of equation of state parameter of pilgrim dark energy f(Q) gravity model is less than −1 i.e., ${({\omega }_D)}_{\mathit{PDE}}<-1$ which represents the model involving phantom field dark energy which is the same as that of ghost dark energy f(Q) gravity model whereas for present (z = 0) and early Universe (z > 0), the equation of state parameter of pilgrim dark energy f(Q) gravity model is a little bit upper than -1 i.e. ${({\omega }_D)}_{\mathit{PDE}}>-1$. Hence the present and early Universe consist quintessence field dark energy. Also, in the pilgrim dark energy f(Q) gravity model it is noticed that by increasing the value of interaction parameter η, equation of state takes more negative values, below the −1. It is observed that the equation of state in our framework can cross the phantom divide line as supported by recent astrophysical observations along with the work holographic dark energy inflation with Granda-Oliveros cut-off and Renyi holographic dark energy in both Hubble’s as well as Granda-Oliveros cut-off investigated by Shekh, (2021b) also with the work of Jawad and Rani, (2015), Jawad et al. (2015).

FIGURE 12

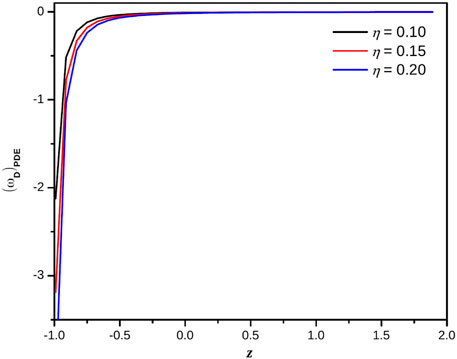
FIGURE 12. Plot of equation of state parameter of pilgrim dark energy f(Q) gravity model versus redshift for the appropriate choice of constants.

5.1.2 $({\omega }_D-{\mathit{\omega }}_{{\mathit{D}}^{\prime }})$ plane

${\omega }_D^{\prime }=\frac{2\eta c_2\left(1-u\right)\left(u/2-1\right)Q^{\frac{u}{2}-2}\dot{Q}}{\left(2-c_2\left(1-u\right)Q^{\frac{u}{2}-1}\right)}-\frac{c_2\left(1-u\right)\left(u/2-1\right)Q^{\frac{u}{2}-2}\dot{Q}}{{\left(2-c_2\left(1-u\right)Q^{\frac{u}{2}-1}\right)}^2}+\frac{2\eta \left(u/2-1\right)}{{\left(2-c_2\left(1-u\right)Q^{\frac{u}{2}-1}\right)}^2}\frac{\dot{Q}}{Q}(56)$

The plot of ${\omega }_T^{\prime }$ with respect to ω_T for the pilgrim dark energy f(Q) gravity modelis shown in Figure 13. Figures 12, 13, indicates that when ω_T < 0, ${\omega }_T^{\prime }>0$ it represents thawing region.

FIGURE 13

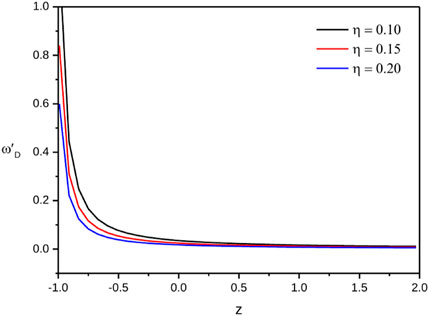
FIGURE 13. Plot of ${\omega }_D^{\prime }$ of Pilgrim dark energy f(Q) gravity model versus redshift for the appropriate choice of constants.

5.1.3 (r−s)-plane

$r=\left\{\begin{array}{c}\hfill 1-\frac{9}{2}\frac{c_2\left(1-u\right)Q^{u/2-1}}{2-c_2\left(1-u\right)Q^{\frac{u}{2}-1}}\left(1+\frac{2\eta }{c_2\left(1-u\right)Q^{\frac{u}{2}-1}}\right)\left(1-\frac{1}{2-c_2\left(1-u\right)Q^{\frac{u}{2}-1}}\left[1+\frac{2\eta }{c_2\left(1-u\right)Q^{\frac{u}{2}-1}}\right]\right)\hfill \\ \hfill -\frac{3c_2\left(1-u\right)}{2H}\left(\frac{2\eta c_2\left(1-u\right)\left(u/2-1\right)Q^{\frac{u}{2}-2}\dot{Q}}{\left(2-c_2\left(1-u\right)Q^{\frac{u}{2}-1}\right)}-\frac{c_2\left(1-u\right)\left(u/2-1\right)Q^{\frac{u}{2}-2}\dot{Q}}{{\left(2-c_2\left(1-u\right)Q^{\frac{u}{2}-1}\right)}^2}+\frac{2\eta \left(u/2-1\right)}{{\left(2-c_2\left(1-u\right)Q^{\frac{u}{2}-1}\right)}^2}\frac{\dot{Q}}{Q}\right)Q^{u/2-1}\hfill \end{array}\right\}(57)$

$s=\left\{\begin{array}{c}\hfill 1-\frac{1}{2-c_2\left(1-u\right)Q^{\frac{u}{2}-1}}\left(1+\frac{2\eta }{c_2\left(1-u\right)Q^{\frac{u}{2}-1}}\right)-\frac{1}{3H}\left(\frac{2\eta c_2^2{\left(1-u\right)}^2{Q}^{u-3}\dot{Q}}{2\eta +c_2\left(1-u\right)Q^{u/2-1}}\right)+\hfill \\ \hfill \frac{1}{3H}\left(\frac{c_2^2{\left(1-u\right)}^2\left(u/2-1\right)Q^{u-3}\dot{Q}}{2-c_2\left(1-u\right)Q^{u/2-1}}-\frac{2\eta c_2\left(1-u\right)\left(u/2-1\right)Q^{u/2-1}}{2-c_2\left(1-u\right)Q^{u/2-1}}\right)\frac{\dot{Q}}{Q}\hfill \end{array}\right\}(58)$

Figure 14, shows the evolution trajectory for pilgrim dark energy f(Q) gravity model in (r − s)- plane towards different value of η. From Figure 14, the evolution trajectories of (r − s)- plane favor the quintessence field dark energy model with s > 0 and r < 1. Hence, our results are consistent with the analysis of (Sharif and Zubair, 2014; Sharif, 2018).

FIGURE 14

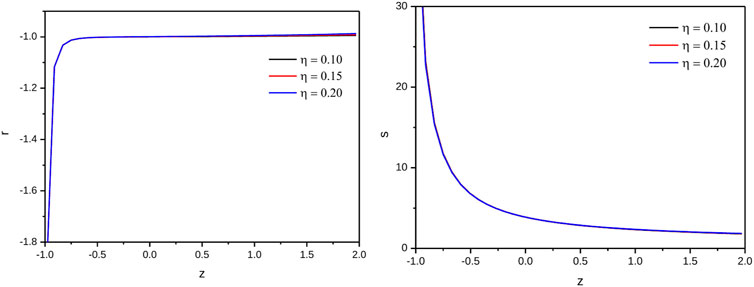
FIGURE 14. Plot of r and s of pilgrim dark energy f(Q) gravity model versus redshift for the appropriate choice of constants.

6 Conclusion

In the present analysis, to talk over the evolution of the Universe We have considered the interacting f(Q) gravity with pressureless matter in an FRW Universe via the reconstruction scheme with power-law form of the scale factor. For this purpose, we have used a newly proposed ghost and pilgrim dark energy model which has a strong repulsive force without a formation of black holes also these are the remarkable models that solves the recent cosmic acceleration problem. The Hubble horizon is taken as the IR cutoff, which provides reliable results with interaction. To establish the correspondence between ghost, pilgrim dark energy and f(Q) gravity model, the corresponding densities have been considered equal. The physical motivation and the consequence of considering this equality show whether the reconstructed model is a realistic one or not. Such methods i.e. equating two densities have been extensively studied in the literature on ghost and pilgrim dark energy in the framework of different modified gravities.To discuss the ghost and pilgrim dark energy f(Q) gravity models, We have explored the evolution trajectories of the equation of state parameter, the $({\omega }_D-{\omega }_D^{\prime })$-phase plane, and the state finder (r − s)- plane.The final results in both ghost and pilgrim dark energy models are respectively concise as follows.

6.1 Ghost Dark Energy f(Q) Gravity Model

(1) The reconstructed ghost dark energy f(Q) gravity model represents increasing behavior forever with respect to both z and Q which shows that the reconstructed model is a realistic one.

(2) The equation of state parameter represents the late Universe it involves phantom field dark energy while the present Universe consist of a quintessence field dark energy and early Universe involve barotropic fluid. Also, we should notice that with the different increasing value of interaction parameter η, equation of state parameter takes more negative values below the -1. Hence, our results are consistent with the current accelerated cosmic behavior and hence I conclude that the ghost dark energy f(Q) gravity model favors the dark energy phenomenon. The equation of state in our framework can crosses the phantom divide line as supported by recent astrophysical observations.

(3) The evolutionary behavior of the $({\omega }_D-{\omega }_D^{\prime })$-phase plane towards all η represents freezing region which confirmed the cosmological expansion is more accelerating in interacting Ghost dark energy f(Q) gravity model.

(4) The corresponding trajectories of (r − s)-plane indicate Chaplygin gas model for all η. Furthermore, it attains CDM limit but cannot achieve ΛCDM limit.

6.2 Pilgrim Dark Energy f(Q) Gravity Model

(1) The reconstructed ghost dark energy f(Q) gravity model is always negative and decreases negatively with respect to both z and Q.

(2) The equation of state parameter at late Universe is less than -1 which represents the model involved phantom field dark energy which is the same as that of Ghost dark energy f(Q) gravity model whereas for present and early Universe it is a little bit upper than -1. Hence the present and early Universe consists of a quintessence field dark energy. Also, in the Pilgrim dark energy f(Q) gravity model, it is noticed that by increasing the value of interaction parameter η, equation of state takes more negative values, below the -1. It is observed that the equation of state in our framework can cross the phantom divide line as supported by recent astrophysical observations.

(3) The evolutionary behavior of the $({\omega }_D-{\omega }_D^{\prime })$-phase plane towards all η represents thawing region in an interacting Ghost dark energy f(Q) gravity model.

(4) The corresponding trajectories of (r − s)- plane favor the quintessence field dark energy model for all η. Furthermore, it crosses ΛCDM limit.

Hence, the results obtained in both the reconstruction scheme under ghost and pilgrim dark energy are rusumbles with the recent modern theoretical observational data as well as the work analyzed by (sharf and Zuber, 2014; Jawad and Rani, 2015; Jawad et al., 2016a; Wu and Yu, 2006; Shafiz and Saba, 2019).

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

All of the authors listed have contributed a significant, direct, and intellectual contribution to the work and have given their permission for it to be published.

Funding

This research was funded by the Science Committee of the Ministry of Education and Science of the Republic of Kazakhstan (Grant No. AP09058240).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The content of this manuscript has been presented in part at the “Two day International Virtual Conference on Recent Trends in Mathematical Sciences (IVCRTMS-2021)”, https://www.ijirmf.com/ivcrtms-oct-2021/. The authors are very much grateful to the honorary referee and the editor for the illuminating suggestions that have significantly improved our work in terms of research quality and presentation.

References

Abbas, G., Momeni, D., Aamir Ali, M., Myrzakulov, R., and Qaisar, S. (2015). Anisotropic Compact Stars in F(G) Gravity. Astrophys. Space Sci. 357, 158. doi:10.1007/s10509-015-2392-6

CrossRef Full Text | Google Scholar

Aditya, Y., and Reddy, D. R. K. (2018). FRW Type Kaluza-Klein Modified Holographic Ricci Dark Energy Models in Brans-Dicke Theory of Gravitation. Eur. Phys. J. C 78, 619. doi:10.1140/epjc/s10052-018-6074-8

CrossRef Full Text | Google Scholar

Azadi, A., Momeni, D., and Nouri-zonoz, M. (2008). Cylindrical Solutions in Metric F (R) Gravity. Phys. Lett. B 670, 210. doi:10.1016/j.physletb.2008.10.054

CrossRef Full Text | Google Scholar

Bhatti, M. Z.-u. -H., Yousaf, Z., and Hanif, S. (2017). Role off(T)gravity on the Evolution of Collapsing Stellar Model. Phys. Dark Universe 16, 34–40. doi:10.1016/j.dark.2017.04.003

CrossRef Full Text | Google Scholar

Bhoyar, S. R., Chirde, V. R., and Shekh, S. H. (2017). Stability of Accelerating Universe with Linear Equation of State in F (T) Gravity Using Hybrid Expansion Law. Astrophysics 60, 259–272. doi:10.1007/s10511-017-9480-y

CrossRef Full Text | Google Scholar

Caldwell, R. R., and Linder, E. V. (2005). Limits of Quintessence. Phys. Rev. Lett. 95, 141301. doi:10.1103/physrevlett.95.141301

PubMed Abstract | CrossRef Full Text | Google Scholar

Capozziello, S., Stabile, A., and Troisi, A. (2007). Spherically Symmetric Solutions in F ( R ) Gravity via the Noether Symmetry Approach. Cl. Quantum Grav. 24, 2153–2166. doi:10.1088/0264-9381/24/8/013

CrossRef Full Text | Google Scholar

Capozziello, S., Martin-Moruno, P., and Rubano, C. (2008). Dark Energy and Dust Matter Phases from an Exact F(R)-cosmology Model. Phys. Lett. Sect. B 664, 12. doi:10.1016/j.physletb.2008.04.061

CrossRef Full Text | Google Scholar

Chirde, V. R., and Shekh, S. H. (2015). Dark Energy Cosmological Model in a Modified Theory of Gravity. Astrophysics 58, 106–119. doi:10.1007/s10511-015-9369-6

CrossRef Full Text | Google Scholar

Chirde, V. R., and Shekh, S. H. (2016a). Isotropic Background for Interacting Two Fluid Scenario Coupled with Zero Mass Scalar Field in Modified Gravity. Bul. J. Phys. 43, 156.

Google Scholar

Chirde, V. R., and Shekh, S. H. (2016b). Plane Symmetric Dark Energy Models in the Form of Wet Dark Fluid in F (R,T) Gravity. J. Astrophys. Astron. 37, 1–16. doi:10.1007/s12036-016-9391-z

CrossRef Full Text | Google Scholar

Chirde, V. R., and Shekh, S. H. (2018a). Dynamic Minimally Interacting Holographic Dark Energy Cosmological Model in F(T) Gravity. Indian J. Phys. 92, 1485–1494. doi:10.1007/s12648-018-1236-y

CrossRef Full Text | Google Scholar

Chirde, V. R., and Shekh, S. H. (2018b). Transition between General Relativity and Quantum Gravity Using Quark and Strange Quark Matter with Some Kinematical Test. J. Astrophys. Astron 39, 56. doi:10.1007/s12036-018-9555-0

CrossRef Full Text | Google Scholar

Chirde, V. R., and Shekh, S. H. (2019). Dynamics of Magnetized Anisotropic Dark Energy in f(R, T) Gravity with Both Deceleration and Acceleration. Bulg. J. Phys. 46, 94.

Google Scholar

Dagwal, V. J., and Pawar, D. D. (2020). Two-fluid Sources in F (T ) Theory of Gravity. Mod. Phys. Lett. A 35, 1950357. doi:10.1142/s0217732319503577

CrossRef Full Text | Google Scholar

Daouda, M. H., Rodrigues, M. E., and Houndjo, M. J. S. (2012). Static Anisotropic Solutions in F(T) Theory. Eur. Phys. J. C 72, 1890. doi:10.1140/epjc/s10052-012-1890-8

CrossRef Full Text | Google Scholar

Eisenstein, D. J. (2005). Detection of the Baryon Acoustic Peak in the Large-Scale Correlation Function of SDSS Luminous Red Galaxies. Astrophys. J. 633, 560. doi:10.1086/466512

CrossRef Full Text | Google Scholar

Frusciante, N. (2021). Signatures of f(Q)-Gravity in Cosmology. Phys. Rev. D 103 (4), 044021. doi:10.1103/PhysRevD.103.044021

CrossRef Full Text | Google Scholar

Harko, T., Lobo, F. S. N., Nojiri, S., and Odintsov, S. D. (2011). f(R,T) Gravity. Phys. Rev. D. 84, 1. doi:10.1103/physrevd.84.024020

CrossRef Full Text | Google Scholar

Jain, B., and Taylor, A. (2003). Cross-Correlation Tomography: Measuring Dark Energy Evolution with Weak Lensing. Phys. Rev. Lett. 91, 141302. doi:10.1103/physrevlett.91.141302

PubMed Abstract | CrossRef Full Text | Google Scholar

Jawad, A., and Rani, S. (2015). Cosmological Evolution of Pilgrim Dark Energy in F(G) Gravity. Adv. High Energy Phys. 2015, 952156. doi:10.1155/2015/952156

CrossRef Full Text | Google Scholar

Jawad, A., Debnath, U., and Batool, F. (2015). Generalized Ghost Pilgrim Scalar Field Models of Dark Energy. Commun. Theor. Phys. 64, 590–596. doi:10.1088/0253-6102/64/5/590

CrossRef Full Text | Google Scholar

Jawad, A., Chattopadhyay, S., and Rani, S. (2016a). Viscous Pilgrim F ( T ) $F(T)$ Gravity Models. Astrophys. Space Sci. 361, 231. doi:10.1007/s10509-016-2814-0

CrossRef Full Text | Google Scholar

Jawad, A., Rani, S., Salako, I. G., Gulshan, F., and Gulshan, F. (2016b). Aspects of Some New Versions of Pilgrim Dark Energy in DGP Braneworld. Eur. Phys. J. Plus 131, 236. doi:10.1140/epjp/i2016-16236-x

CrossRef Full Text | Google Scholar

Jawad, A., Rani, S., Salako, I. G., and Gulshan, F. (2017). Pilgrim Dark Energy Models in Fractal Universe. Int. J. Mod. Phys. D. 26, 1750049. doi:10.1142/s0218271817500493

CrossRef Full Text | Google Scholar

Jawad, A. (2015). Cosmological Analysis of Pilgrim Dark Energy in Loop Quantum Cosmology. Eur. Phys. J. C 75, 206. doi:10.1140/epjc/s10052-015-3430-9

CrossRef Full Text | Google Scholar

Jimenez, J. B., Heisenberg, L., and Koivisto, T. (2018). Coincident General Relativity. Phys. Rev. D. 98, 044048. doi:10.1103/physrevd.98.044048

CrossRef Full Text | Google Scholar

Kawarabayashi, K., and Ohta, N. (1980). The η Problem in the Large-N Limit: Effective Lagrangian Approach. Nucl. Phys. B 175, 477–492. doi:10.1016/0550-3213(80)90024-3

CrossRef Full Text | Google Scholar

Kiran, M., Reddy, D. R. K., and Rao, V. U. M. (2015). Minimally Interacting Holographic Dark Energy Model in Brans-Dicke Theory. Astrophys. Space Sci. 356, 407–411. doi:10.1007/s10509-014-2213-3

CrossRef Full Text | Google Scholar

Komatsu, E. (2011). Seven-year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Interpretation. Astrophys. J. Suppl. 192, 18. doi:10.1088/0067-0049/192/2/18

CrossRef Full Text | Google Scholar

Lazkoz, R. (2019). Observational Constraints of F(Q) Gravity. Phys. Rev. D. 100, 104027. doi:10.1103/PhysRevD.100.104027

CrossRef Full Text | Google Scholar

Mandal, S., Sahoo, P. K., and Santos, J. R. L. (2020a). Energy Conditions in F (Q ) Gravity. Phys. Rev. D. 102, 024057. doi:10.1103/physrevd.102.024057

CrossRef Full Text | Google Scholar

Mandal, S., Wang, D., and Sahoo, P. K. (2020b). Cosmography in F(Q) Gravity. Phys. Rev. D. 102, 124029. doi:10.1103/physrevd.102.124029

CrossRef Full Text | Google Scholar

Naidu, R. L., Satyanarayana, B., and Reddy, D. R. K. (2012). LRS Bianchi Type-II Dark Energy Model in a Scalar-Tensor Theory of Gravitation. Astrophys. Space Sci. 338, 333–336. doi:10.1007/s10509-011-0935-z

CrossRef Full Text | Google Scholar

Nath, P., and Arnowitt, R. (1981). U(1) Problem: Current Algebra and Theθvacuum. Phys. Rev. D. 23, 473–476. doi:10.1103/physrevd.23.473

CrossRef Full Text | Google Scholar

Nojiri, S. i., and Odintsov, S. D. (2007). Modified Gravity and its Reconstruction from the Universe Expansion History. J. Phys. Conf. Ser. 66, 012005. doi:10.1088/1742-6596/66/1/012005

CrossRef Full Text | Google Scholar

Nojiri, S., and Odintsov, S. (2008). Future Evolution and Finite-Time Singularities in F(R) Gravity Unifying Inflation and Cosmic Acceleration. Phys. Rev. D. 78, 046006. doi:10.1103/PhysRevD.78.046006

CrossRef Full Text | Google Scholar

Pawar, D. D., Bhuttampalle, G. G., and Agrawal, P. K. (2018). Kaluza-Klein String Cosmological Model in f(R, T) Theory of Gravity. New Astron. 65, 1–6. doi:10.1016/j.newast.2018.05.002

CrossRef Full Text | Google Scholar

Perlmutter, S. (1999). Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys. J. 517, 565. doi:10.1086/307221

CrossRef Full Text | Google Scholar

Rani, S., Jawad, A., Ines, G., and SalakoAzhar, N. (2016). Non-Flat Pilgrim Dark Energy Frw Models in Modified Gravity. Astrophys. Space Sci. 361, 386. doi:10.1007/s10509-016-2868-z

CrossRef Full Text | Google Scholar

Riess, A. G. (1998). Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 116, 1009. doi:10.1086/300499

CrossRef Full Text | Google Scholar

Sadeghi, J., Khurshudyan, M., Movsisyan, A., and Farahani, H. (2013). Interacting Ghost Dark Energy Models with variableGand Λ. J. Cosmol. Astropart. Phys. 2013, 031. doi:10.1088/1475-7516/2013/12/031

CrossRef Full Text | Google Scholar

Sahni, V., Saini, T. D., Starobinsky, A. A., and Alam, U. (2003). Statefinder-A New Geometrical Diagnostic of Dark Energy. Jetp Lett. 77, 201–206. doi:10.1134/1.1574831

CrossRef Full Text | Google Scholar

Sahoo, P. K., and Bhattacharjee, S. (2020). Revisiting the Coincidence Problem in F(R) Gravitation. New Astron. 77, 101351. doi:10.1016/j.newast.2019.101351

CrossRef Full Text | Google Scholar

Sahoo, P. K., Mishra, B., and Chakradhar, R. (2014). Axially Symmetric Cosmological Model in f(R, T) Gravity. Eur. Phys. J. Plus. 129, 1. doi:10.1140/epjp/i2014-14049-7

CrossRef Full Text | Google Scholar

Santhi, M. V., Rao, V. U. M., and Aditya, Y. (2017). Bianchi type-VI0 Modified Holographic Ricci Dark Energy Model in a Scalar-Tensor Theory. Can. J. Phys. 95, 179–183. doi:10.1139/cjp-2016-0628

CrossRef Full Text | Google Scholar

Sarkar, S., and Mahanta, C. R. (2013). Holographic Dark Energy Model with Quintessence in Bianchi Type-I Space-Time. Int. J. Theor. Phys. 52, 1482–1489. doi:10.1007/s10773-012-1468-0

CrossRef Full Text | Google Scholar

Seljak, U. (2005). Cosmological Parameter Analysis Including SDSS Ly α Forest and Galaxy Bias: Constraints on the Primordial Spectrum of Fluctuations, Neutrino Mass, and Dark Energy. Phys. Rev. D. 71, 103515. doi:10.1103/PhysRevD.71.103515

CrossRef Full Text | Google Scholar

Sharif, M., and Fatima, H. I. (2016). Built-in Inflation in F(G) Gravity. Int. J. Mod. Phys. D. 25, 1650011. doi:10.1142/s0218271816500115

CrossRef Full Text | Google Scholar

Sharif, M., and Jawad, A. (2013). Pilgrim Dark Energy with Apparent and Event Horizons in Non-flat Universe. Eur. Phys. J. C 73, 2600. doi:10.1140/epjc/s10052-013-2600-x

CrossRef Full Text | Google Scholar

Sharif, M., and Yousaf, Z. (2013). Dynamical Instability of the Charged Expansion-free Spherical Collapse in F(R) Gravity. Phys. Rev. D. 88, 024020. doi:10.1103/physrevd.88.024020

CrossRef Full Text | Google Scholar

Sharif, M., and Zubair, M. (2014). Cosmological Evolution of Pilgrim Dark Energy. Astrophys. Space Sci. 352, 263–272. doi:10.1007/s10509-014-1889-8

CrossRef Full Text | Google Scholar

Sharif, M., and Saba, S. (2018). Pilgrim Dark Energy in f(G, T) Gravity. Mod. Phys. Lett. A 33, 1850182. doi:10.1142/s0217732318501821

CrossRef Full Text | Google Scholar

Sharif, M., and Saba, S. (2019). Ghost Dark Energy Model in f(G) Gravity. Chin. J. Phys. 58, 202–211. doi:10.1016/j.cjph.2018.12.023

CrossRef Full Text | Google Scholar

Shekh, S. H., and Chirde, V. R. (2019). Analysis of General Relativistic Hydrodynamic Cosmological Models with Stability Factor in Theories of Gravitation. Gen. Relativ. Gravit. 51, 87. doi:10.1007/s10714-019-2565-7

CrossRef Full Text | Google Scholar

Shekh, S. H., and Chirde, V. R. (2020). Accelerating Bianchi Type Dark Energy Cosmological Model with Cosmic String in $F(T)$ Gravity. Astrophys. Space Sci. 365, 60. doi:10.1007/s10509-020-03772-y

CrossRef Full Text | Google Scholar

Shekh, S. H., Arora, S., Chirde, V. R., and Sahoo, P. K. (2020a). Thermodynamical Aspects of Relativistic Hydrodynamics in f(R,G) Gravity. Int. J. Geom. Methods Mod. Phys. 17, 2050048. doi:10.1142/s0219887820500486

CrossRef Full Text | Google Scholar

Shekh, S. H., Chirde, V. R., and Sahoo, P. K. (2020b). Energy Conditions of the f(T, B) Gravity Dark Energy Model with the Validity of Thermodynamics. Commun. Theor. Phys. 72, 085402. doi:10.1088/1572-9494/ab95fd

CrossRef Full Text | Google Scholar

Shekh, S. H., Katore, S. D., Chirde, V. R., and Raut, S. V. (2021). Signature Flipping of Isotropic Homogeneous Space-Time with Holographic Dark Energy in f(G)gravity. New Astron. 84, 101535. doi:10.1016/j.newast.2020.101535

CrossRef Full Text | Google Scholar

Shekh, S. H. (2021a). Models of Holographic Dark Energy in F(Q) Gravity. Phys. Dark Universe 33, 100850. doi:10.1016/j.dark.2021.100850

CrossRef Full Text | Google Scholar

Shekh, S. H. (2021b). Dynamical Analysis with Thermodynamic Aspects of Anisotropic Dark Energy Bounce Cosmological Model in f(R, G) Gravity. New Astron. 83, 101464. doi:10.1016/j.newast.2020.101464

CrossRef Full Text | Google Scholar

Sheykhi, A., and Movahed, M. S. (2012). Interacting Ghost Dark Energy in Non-flat Universe. Gen. Relativ. Gravit. 44, 449–465. doi:10.1007/s10714-011-1286-3

CrossRef Full Text | Google Scholar

Spergel, D. N. (2003). First-Year Wilkinson Microwave Anisotropy Probe (WMAP)* Observations: Determination of Cosmological Parameters. Astrophys. J. Suppl. 148, 175. doi:10.1086/377226

CrossRef Full Text | Google Scholar

Tegmark, M. (2004). Cosmological Parameters from SDSS and WMAP. Phys. Rev. D. 69, 103501. doi:10.1103/PhysRevD.69.103501

CrossRef Full Text | Google Scholar

Wei, H., Qi, H.-Y., and Ma, X.-P. (2012). Constraining F(T) Theories with the Varying Gravitational Constant. Eur. Phys. J. C 72, 2117. doi:10.1140/epjc/s10052-012-2117-8

CrossRef Full Text | Google Scholar

Witten, E. (1979). Current Algebra Theorems for the U(1) "Goldstone Boson". Nucl. Phys. B 156, 269–283. doi:10.1016/0550-3213(79)90031-2

CrossRef Full Text | Google Scholar

Wu, P., and Yu, H. (2006). Statefinder Parameters for Phantom Dark Energy. Mod. Phys. Lett. A 21, 1305–1311. doi:10.1142/s0217732306019293

CrossRef Full Text | Google Scholar

Yang, L. (2020). Universal Bounds on the Size of a Black Hole. Eur. Phys. J. C 80, 1204. doi:10.1140/epjc/s10052-020-08521-7

CrossRef Full Text | Google Scholar